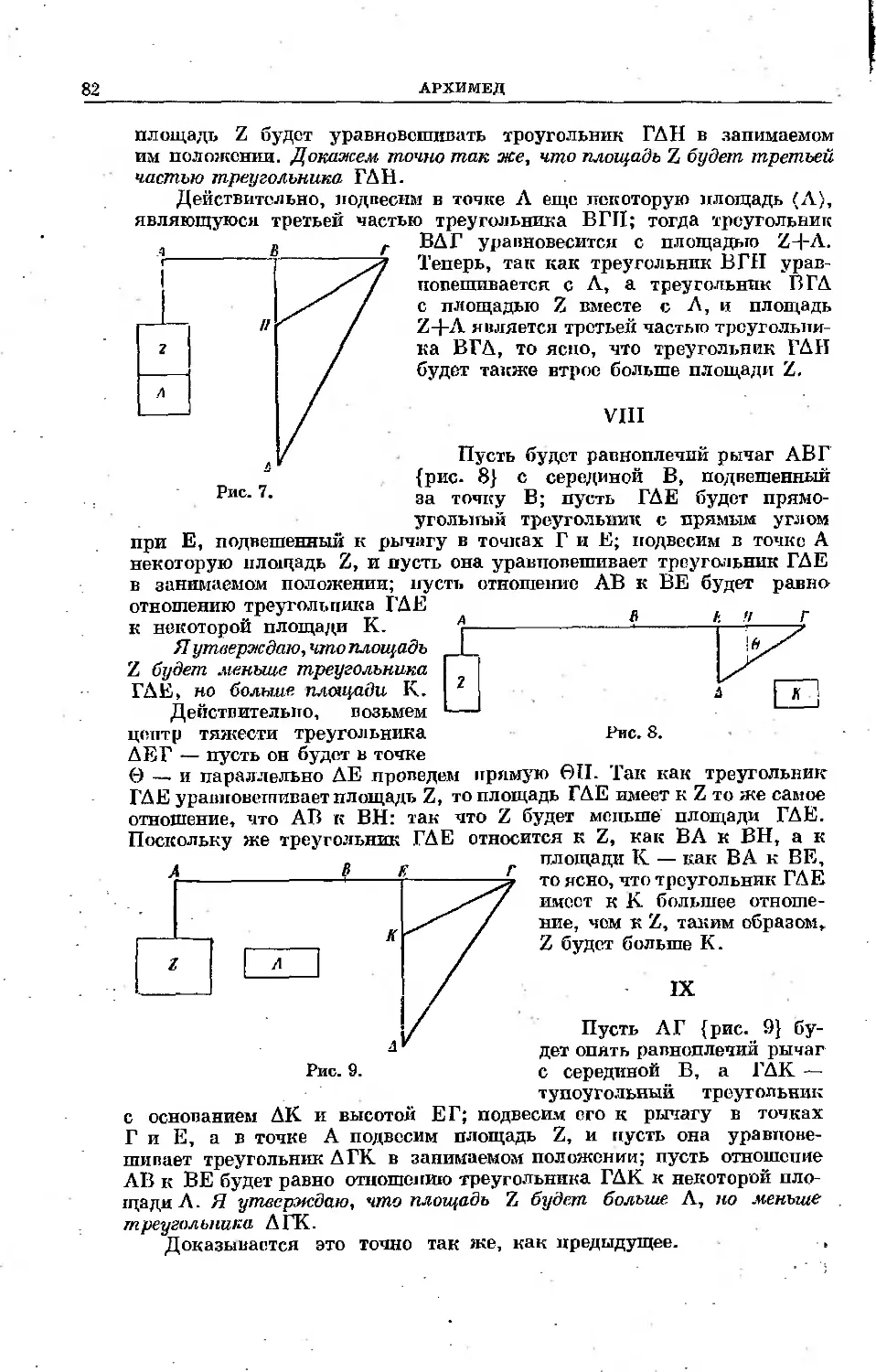
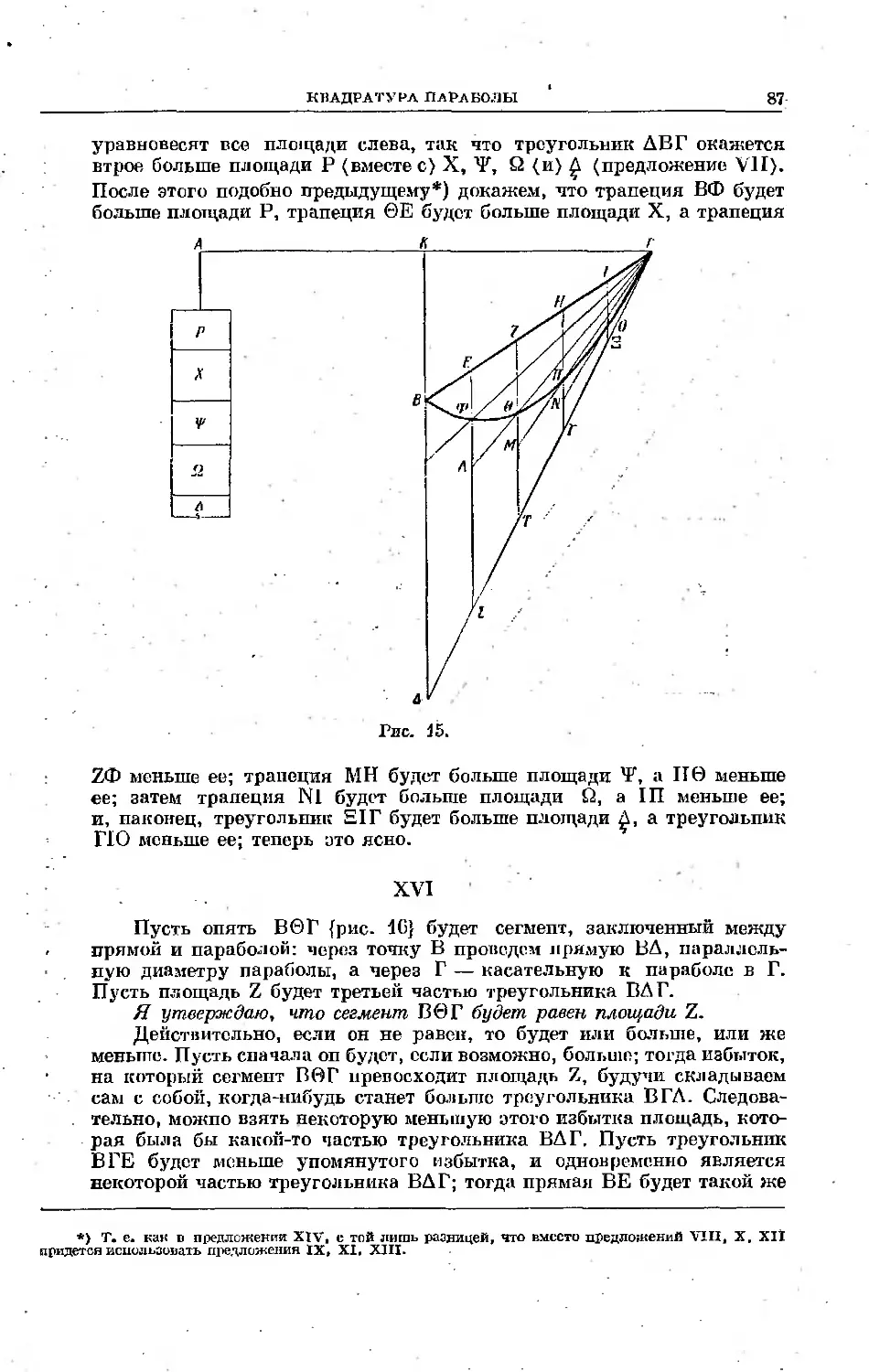
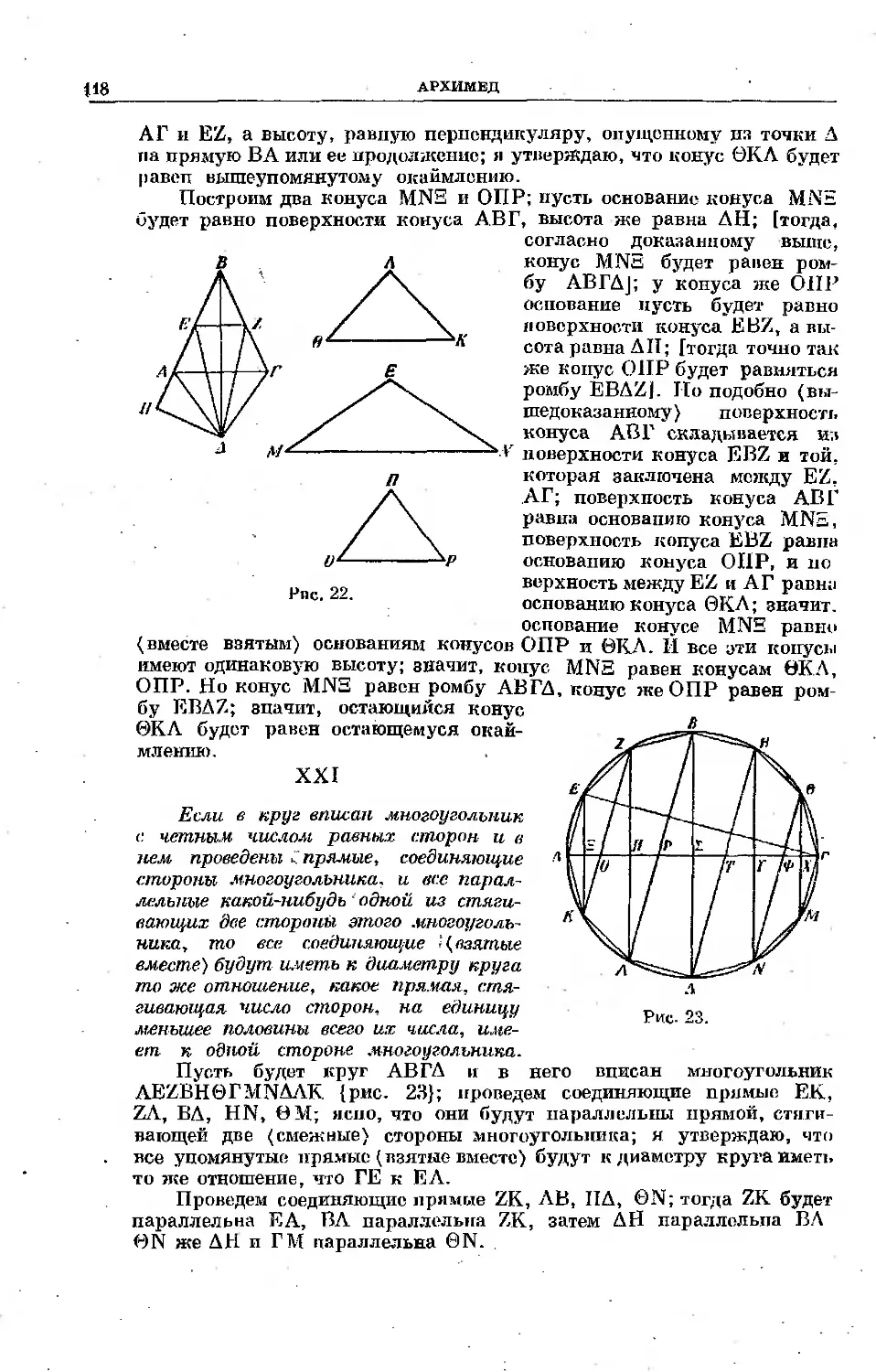
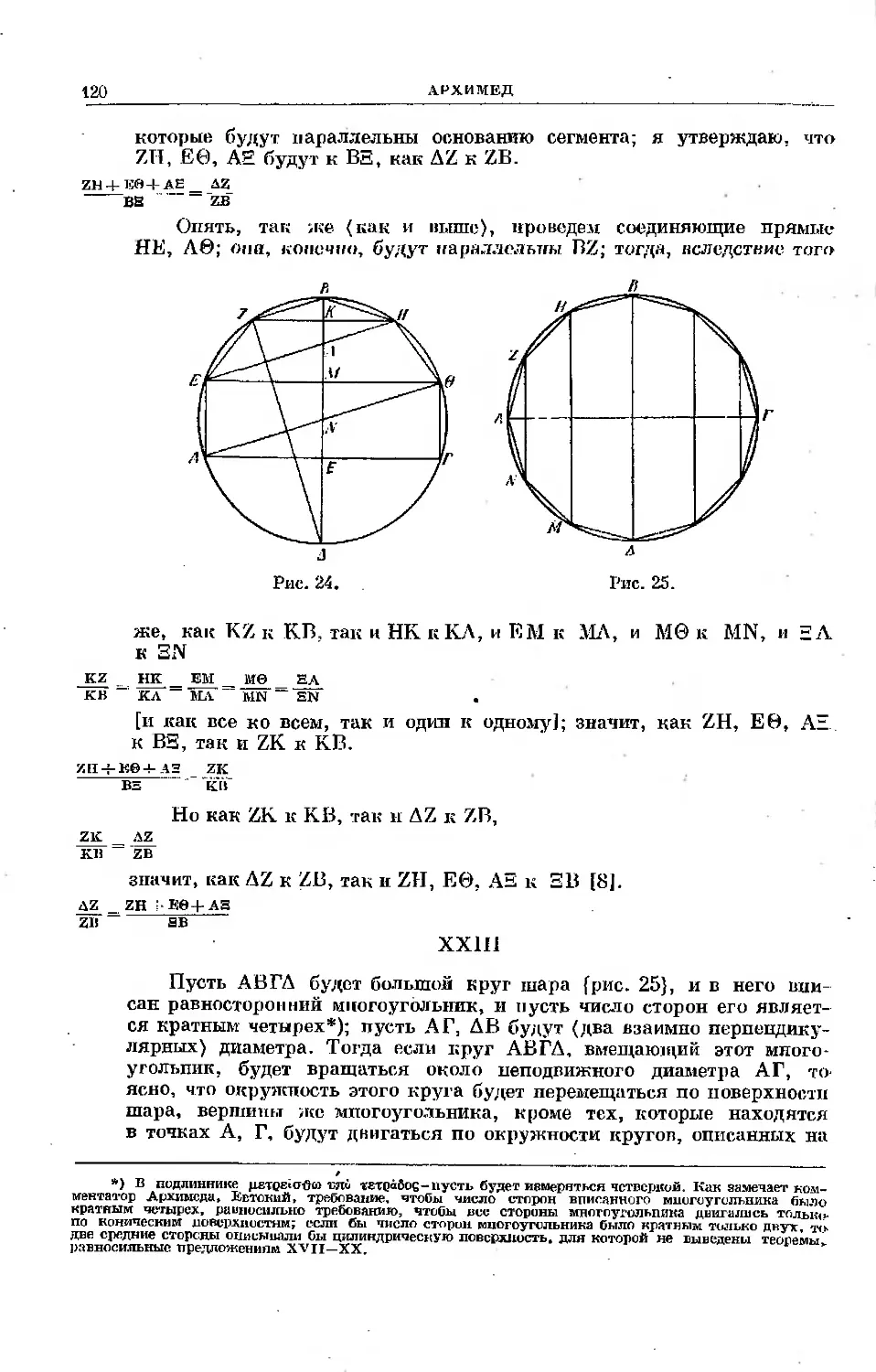
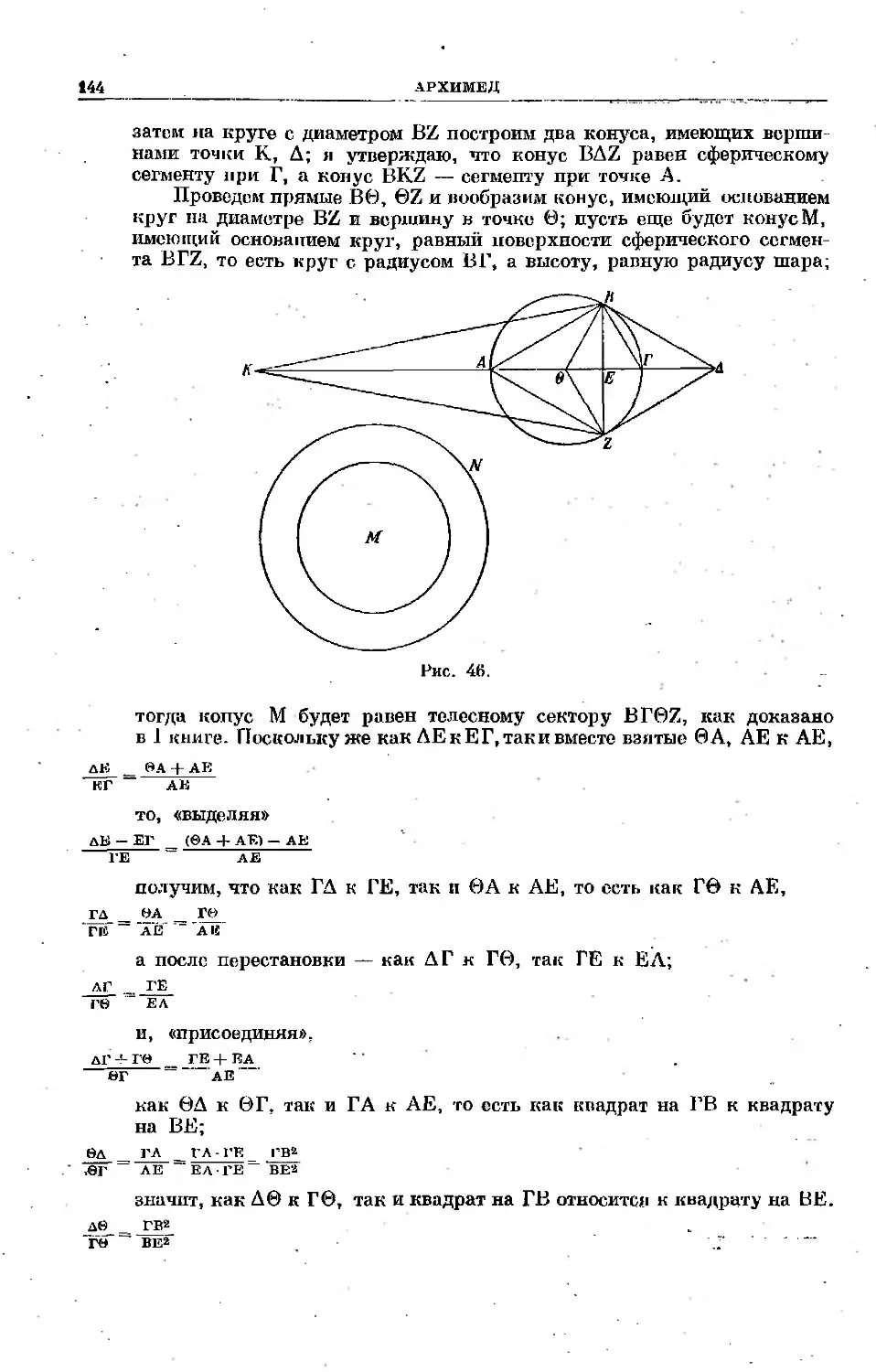
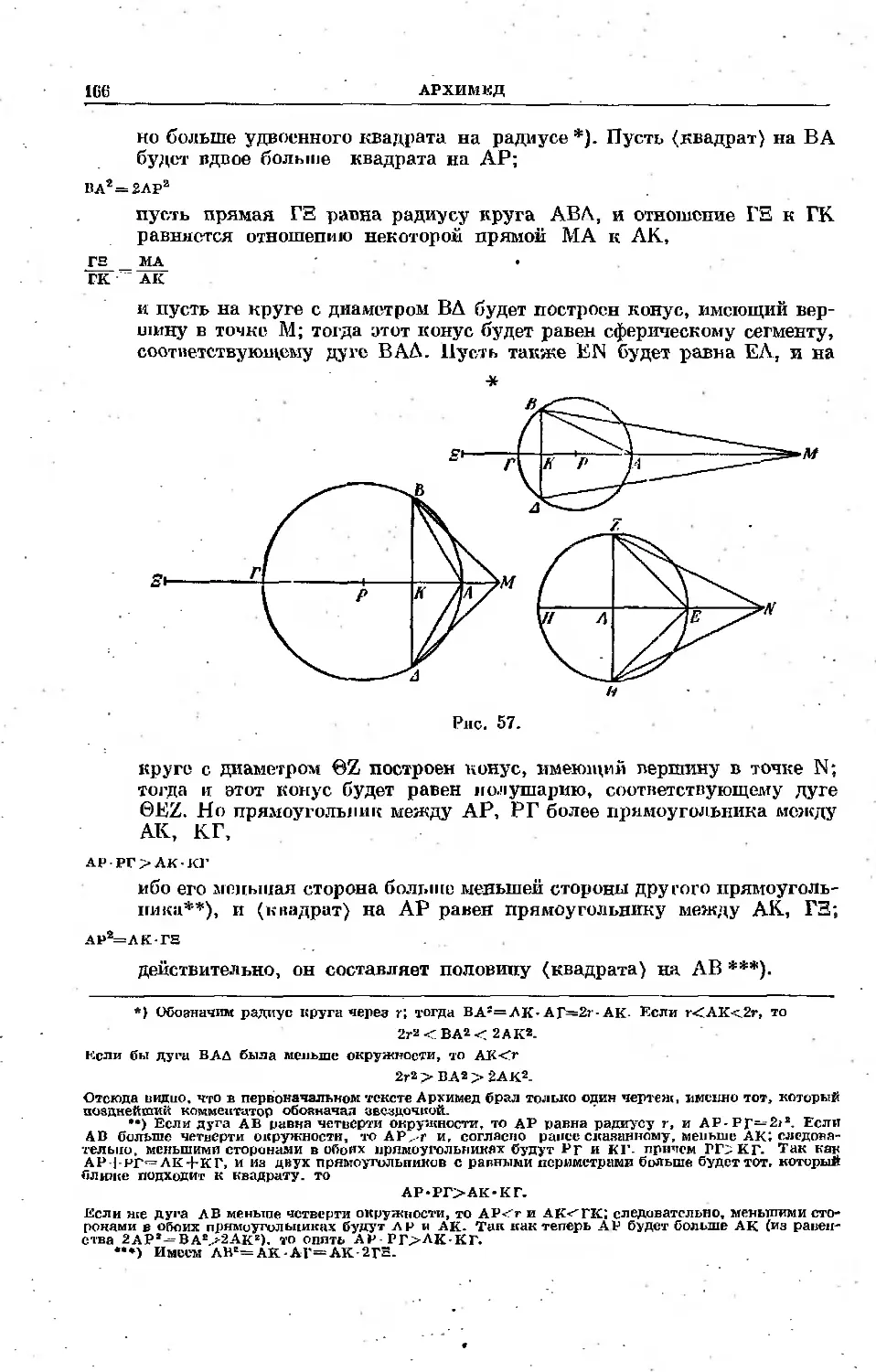
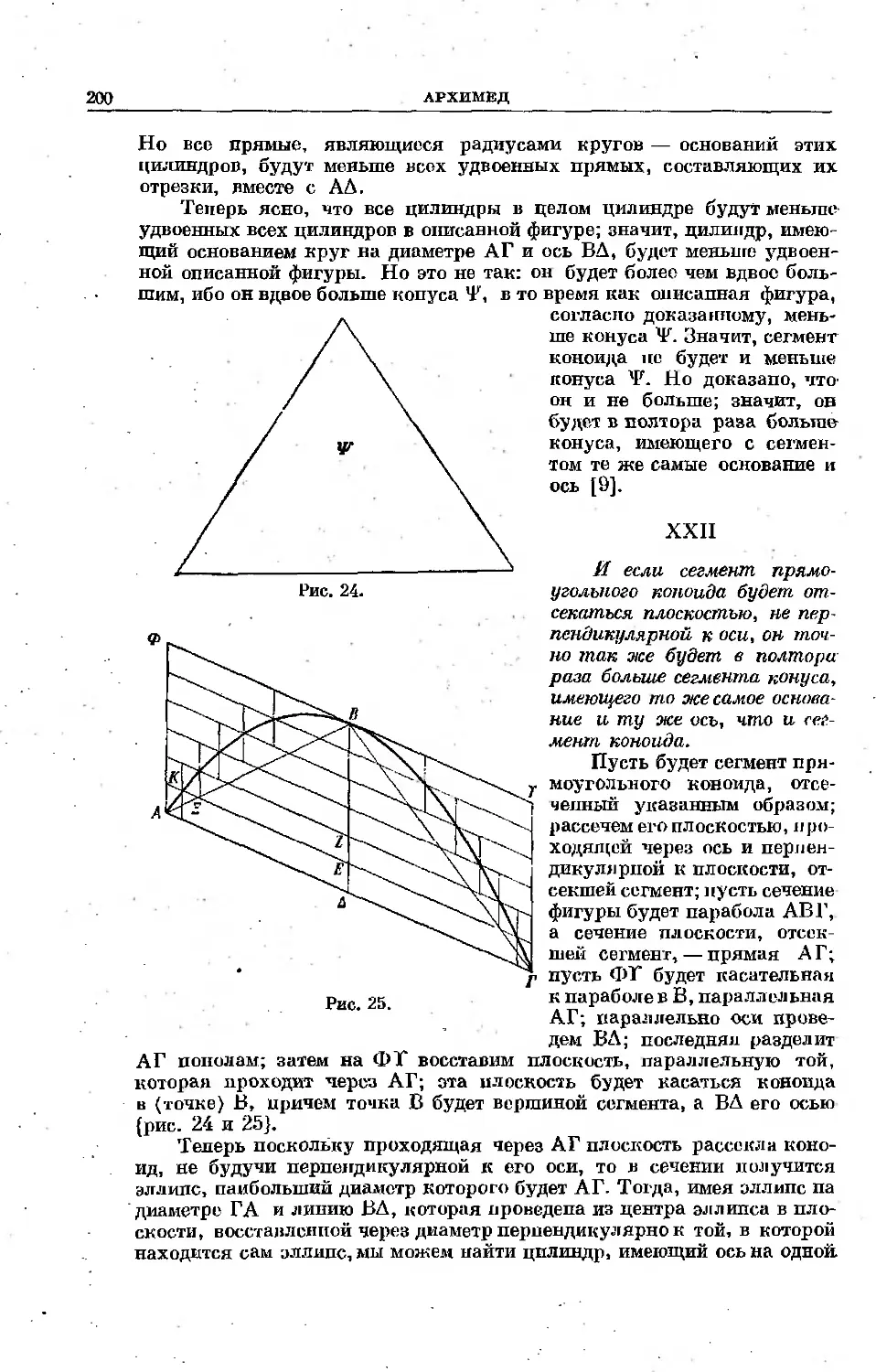
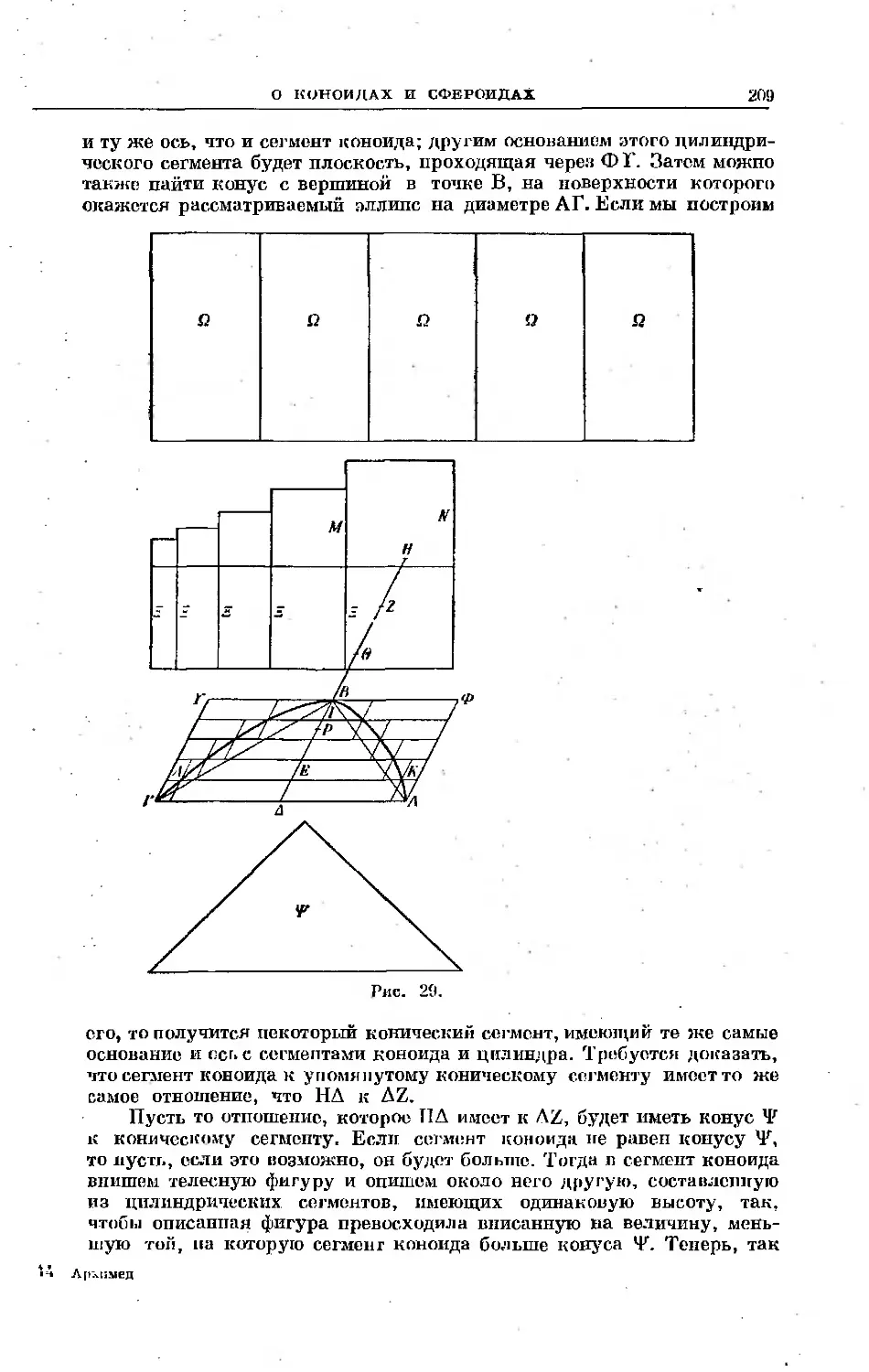
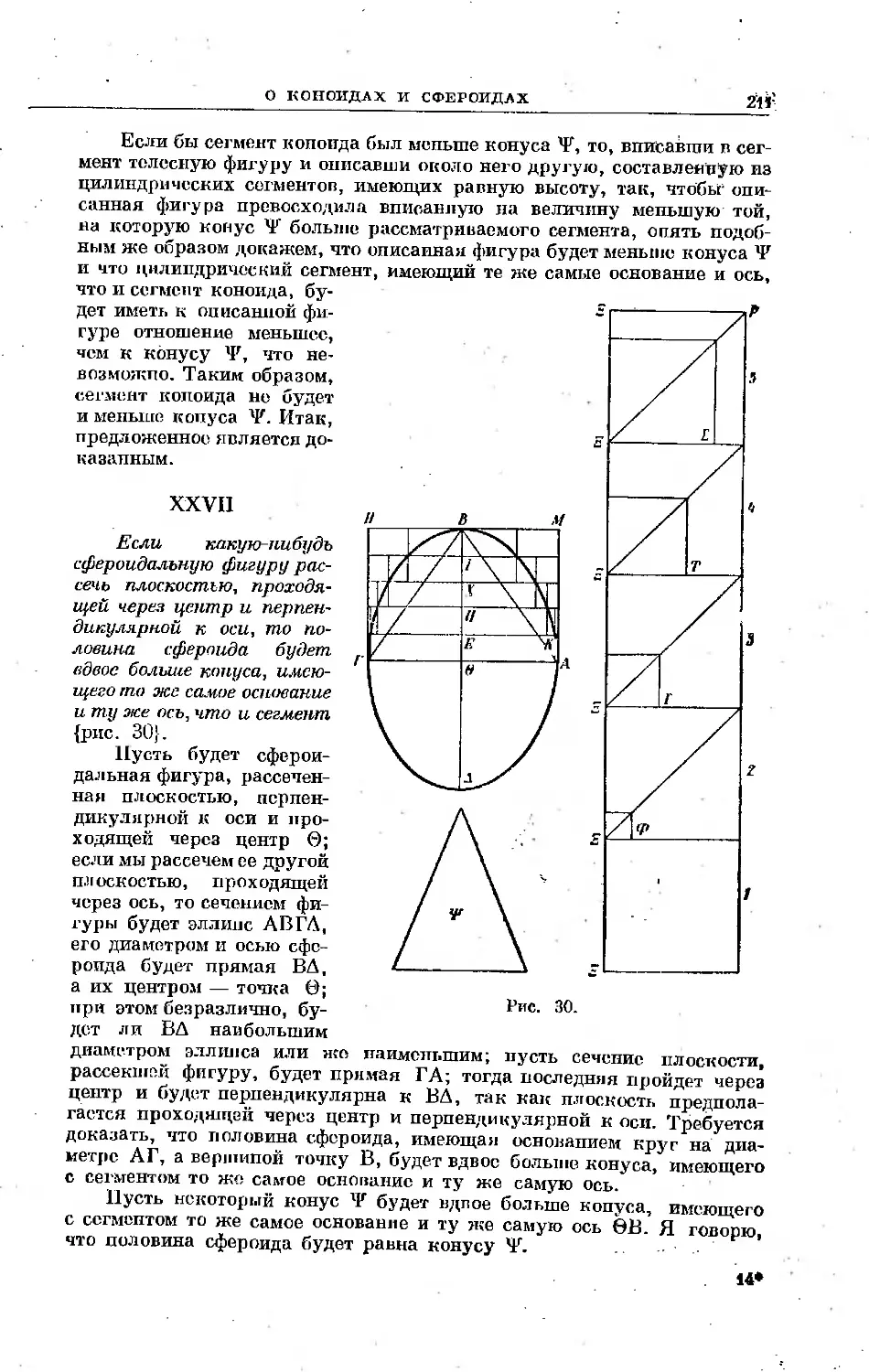
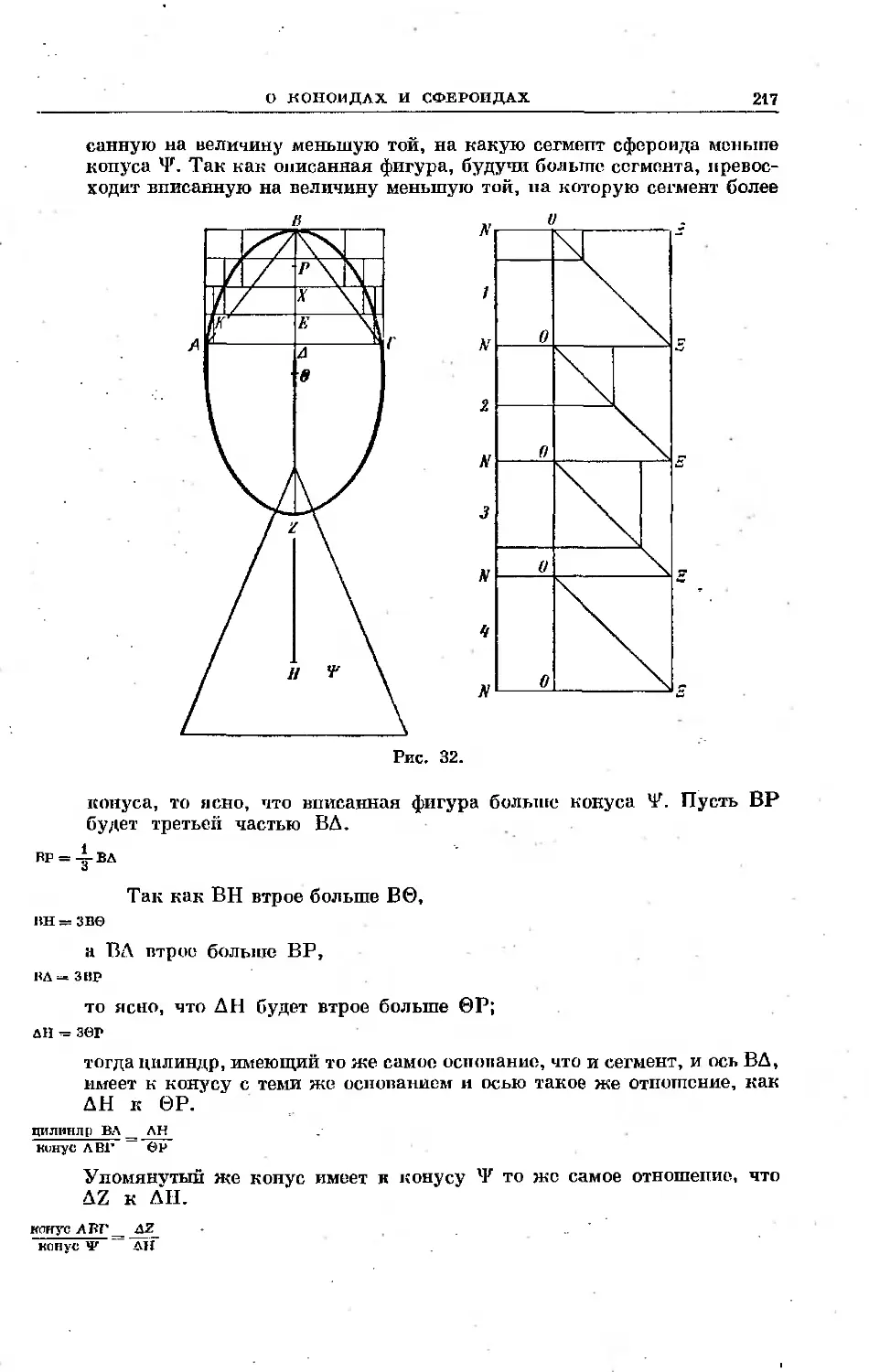
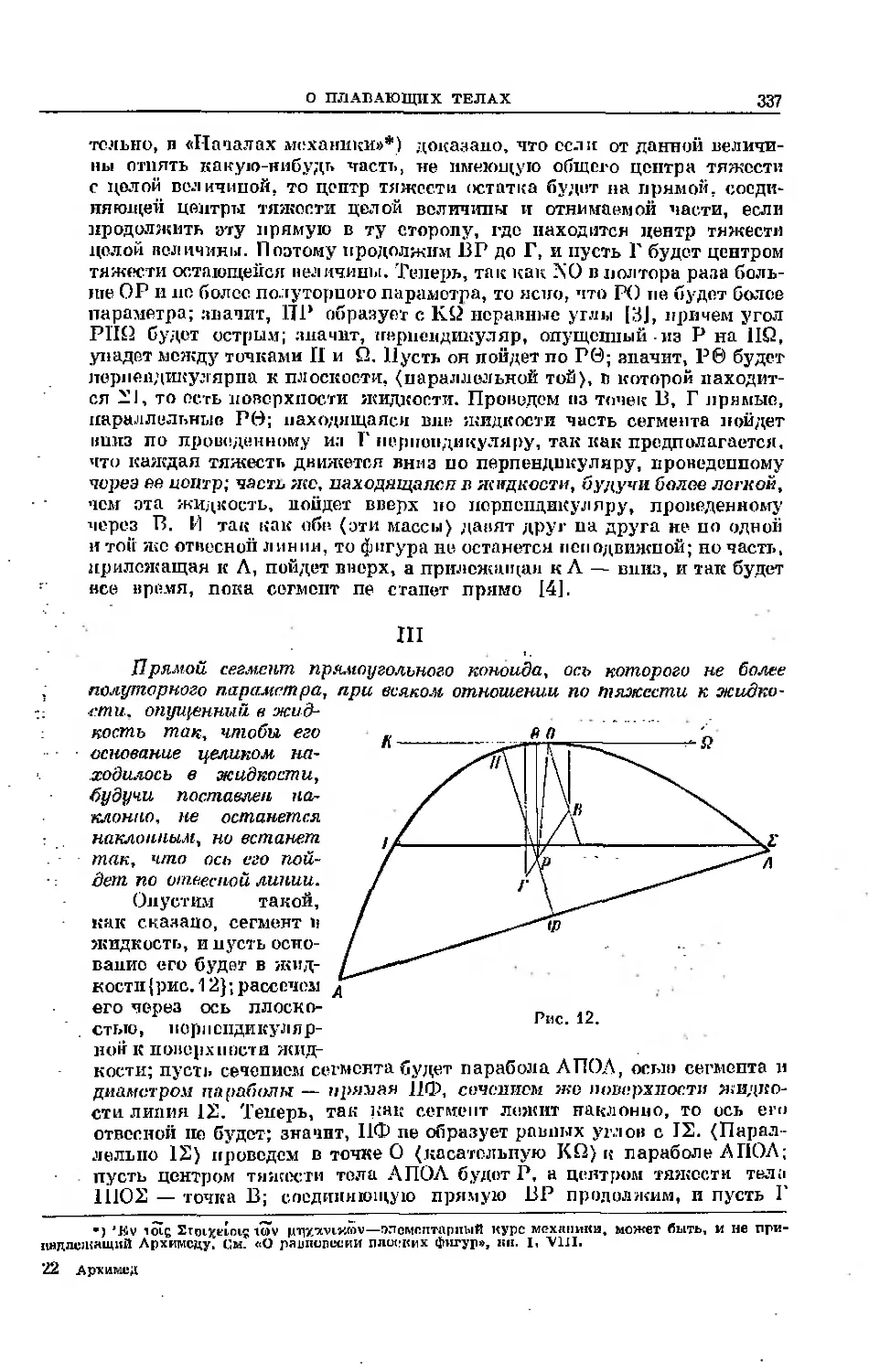
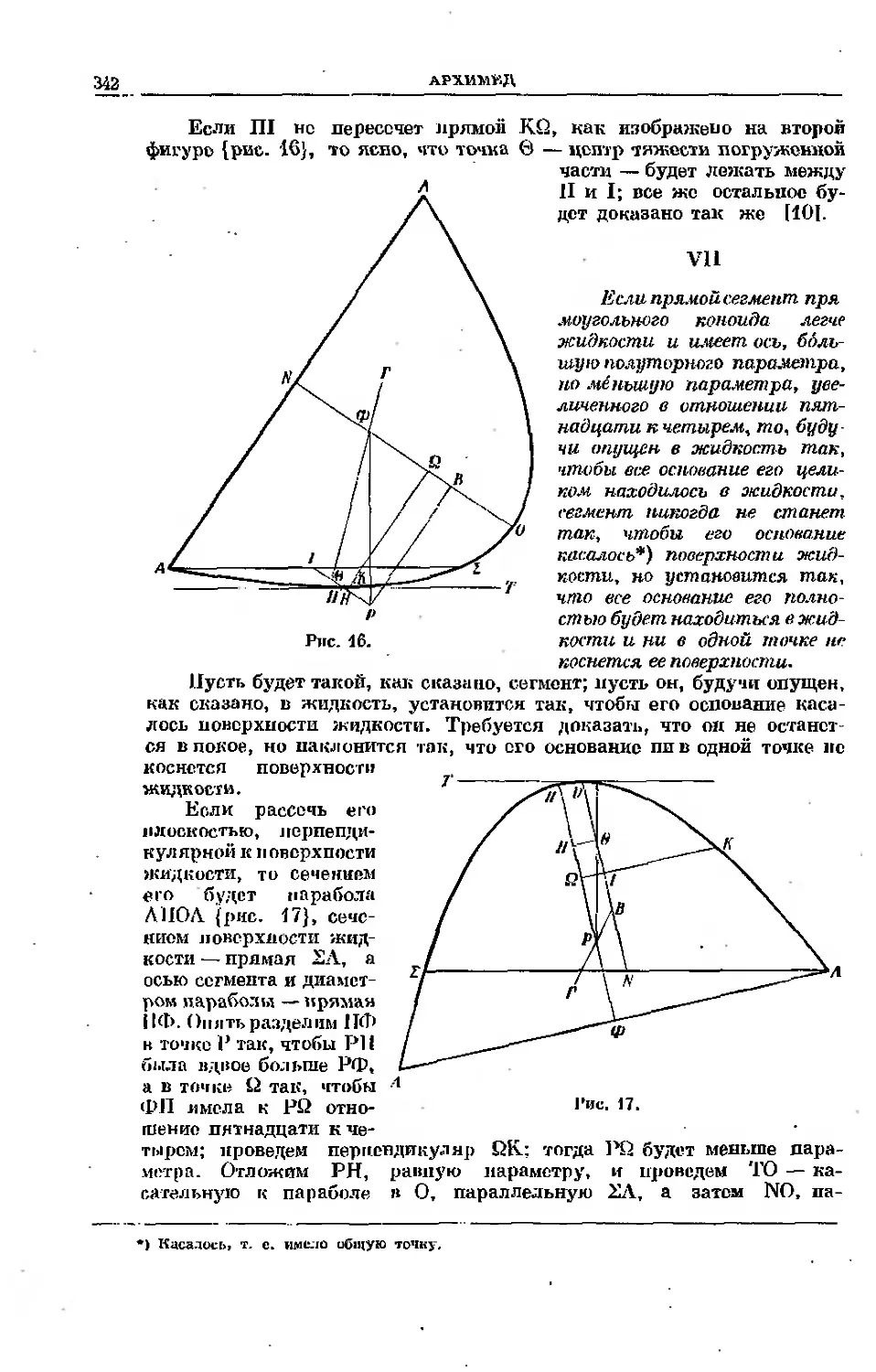
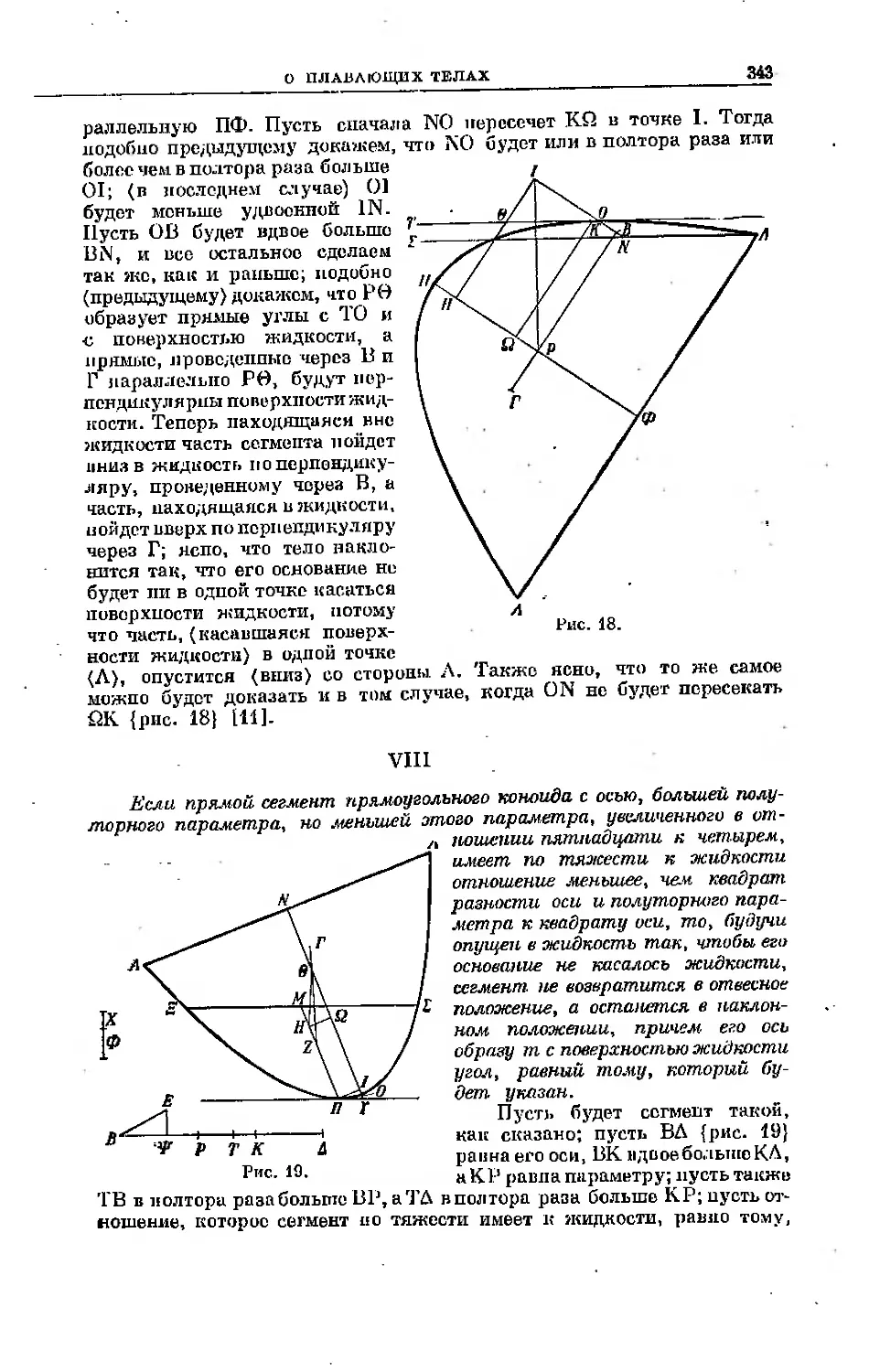
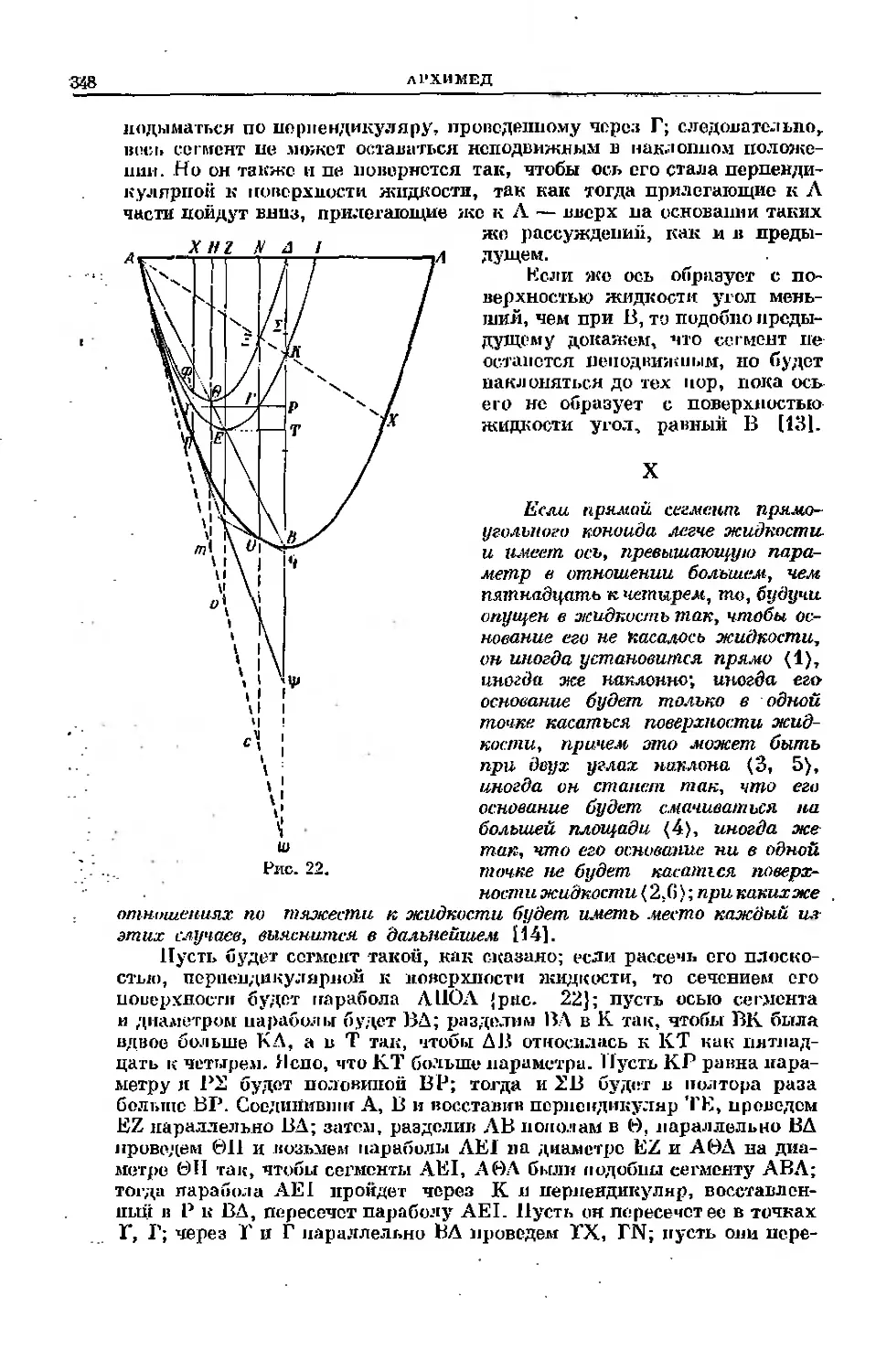
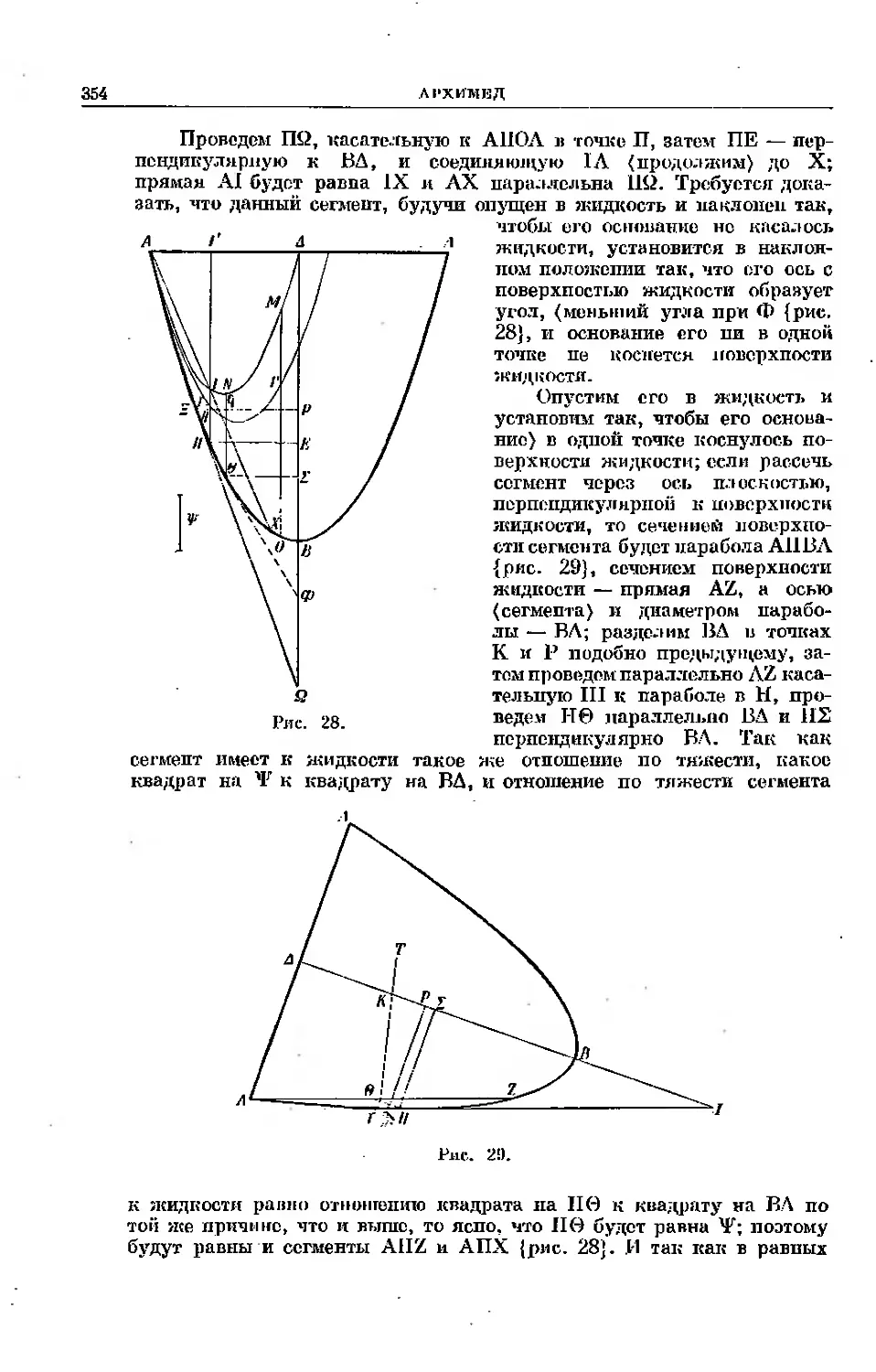
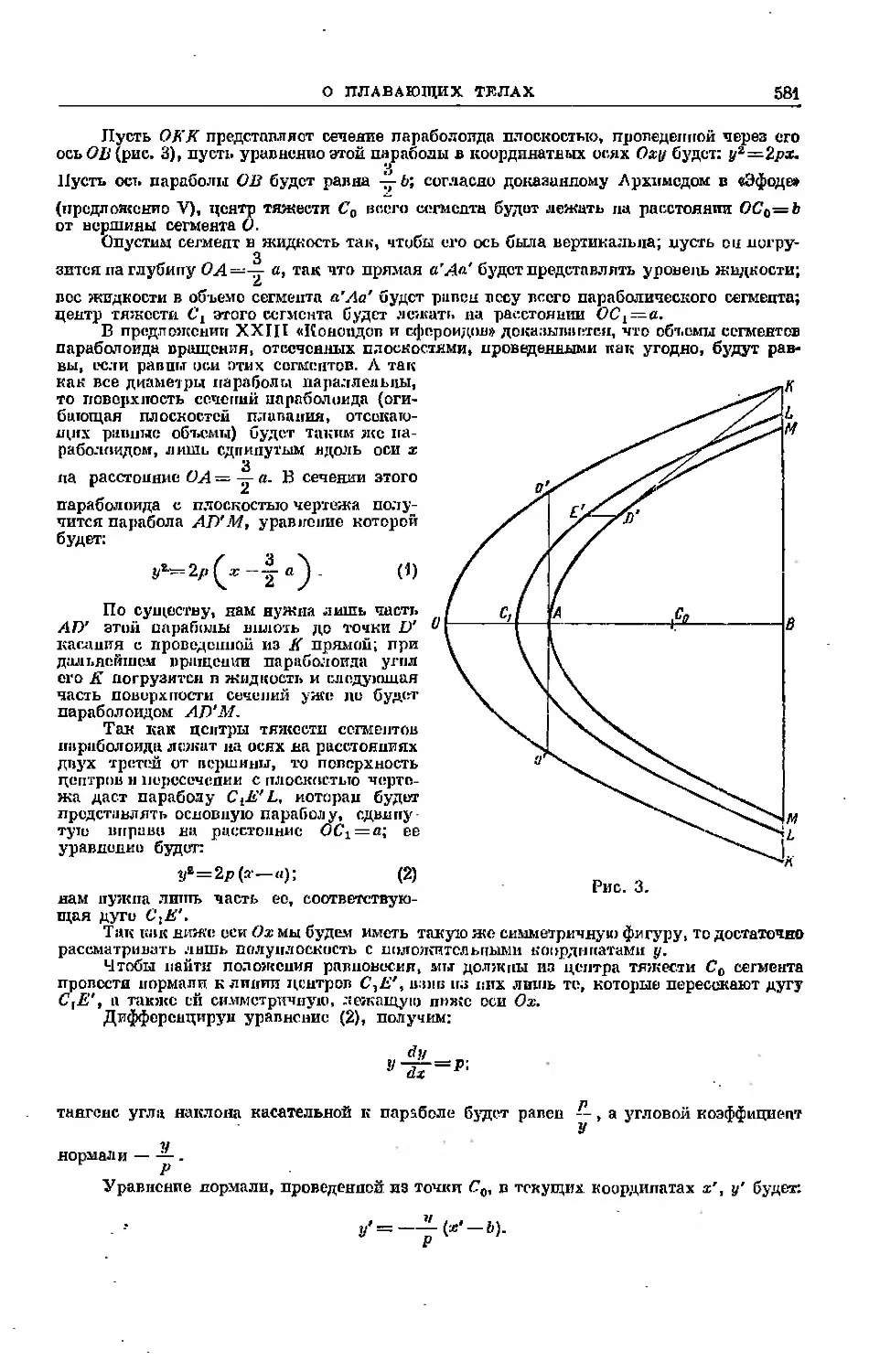
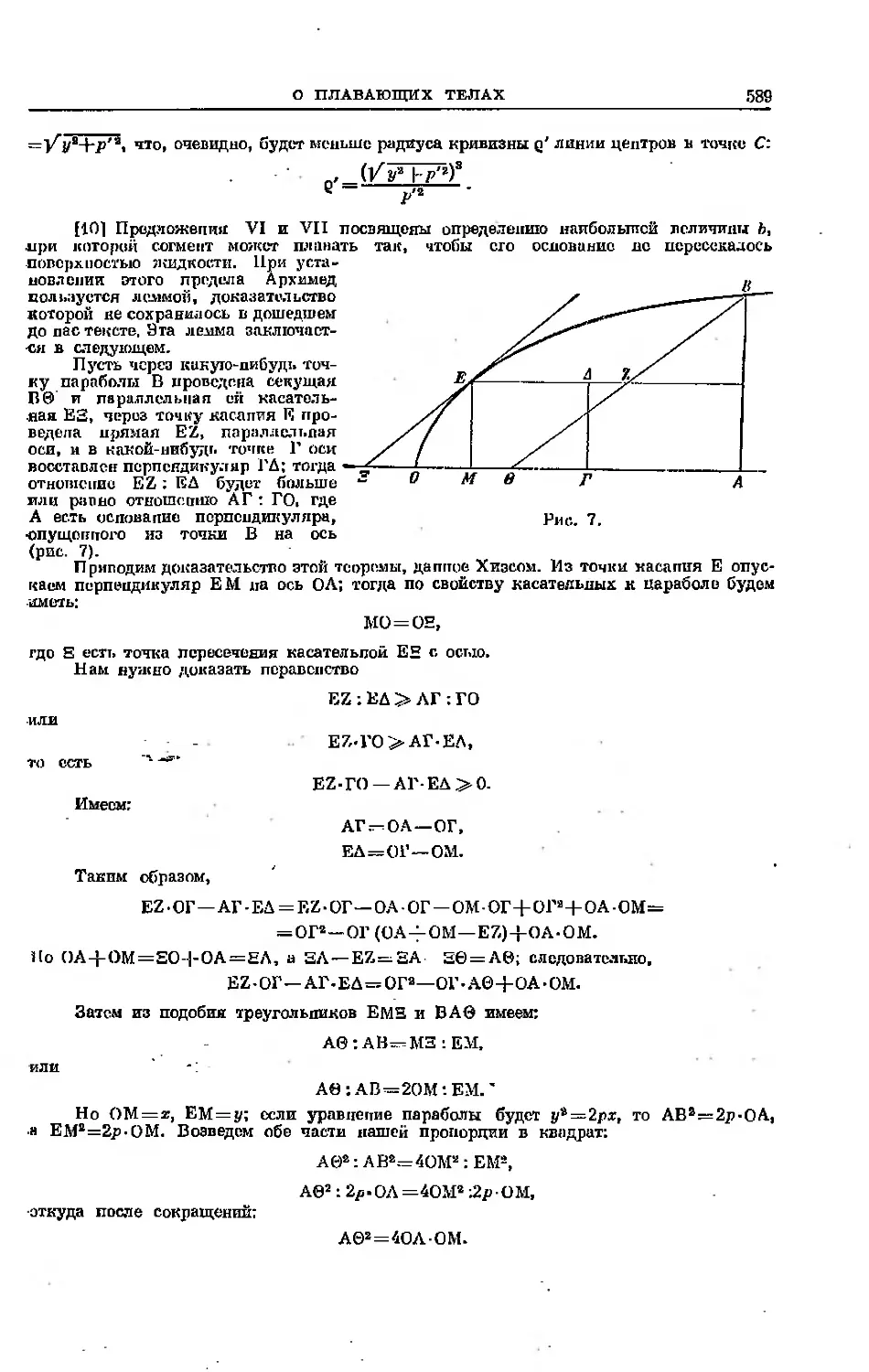
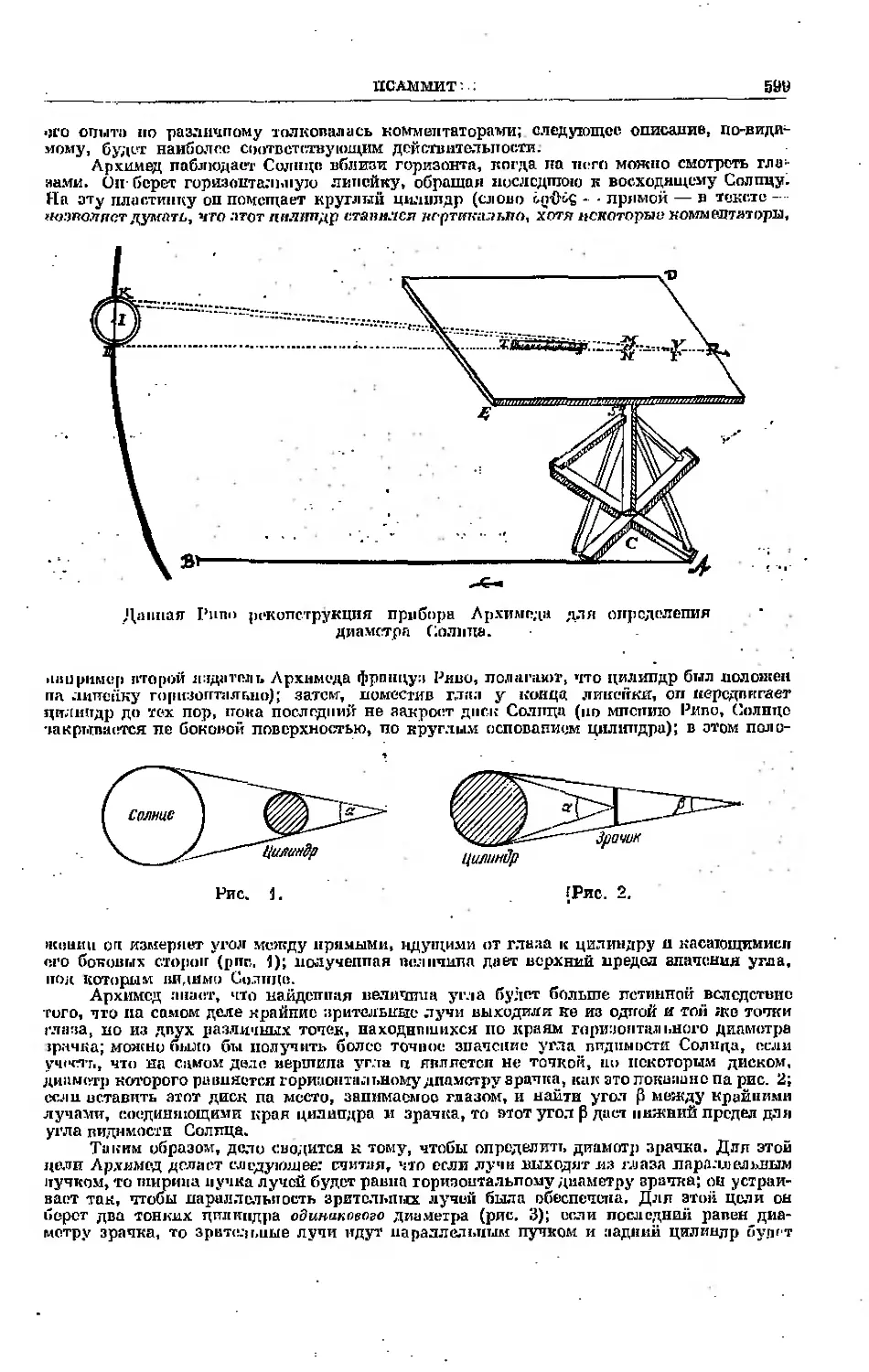
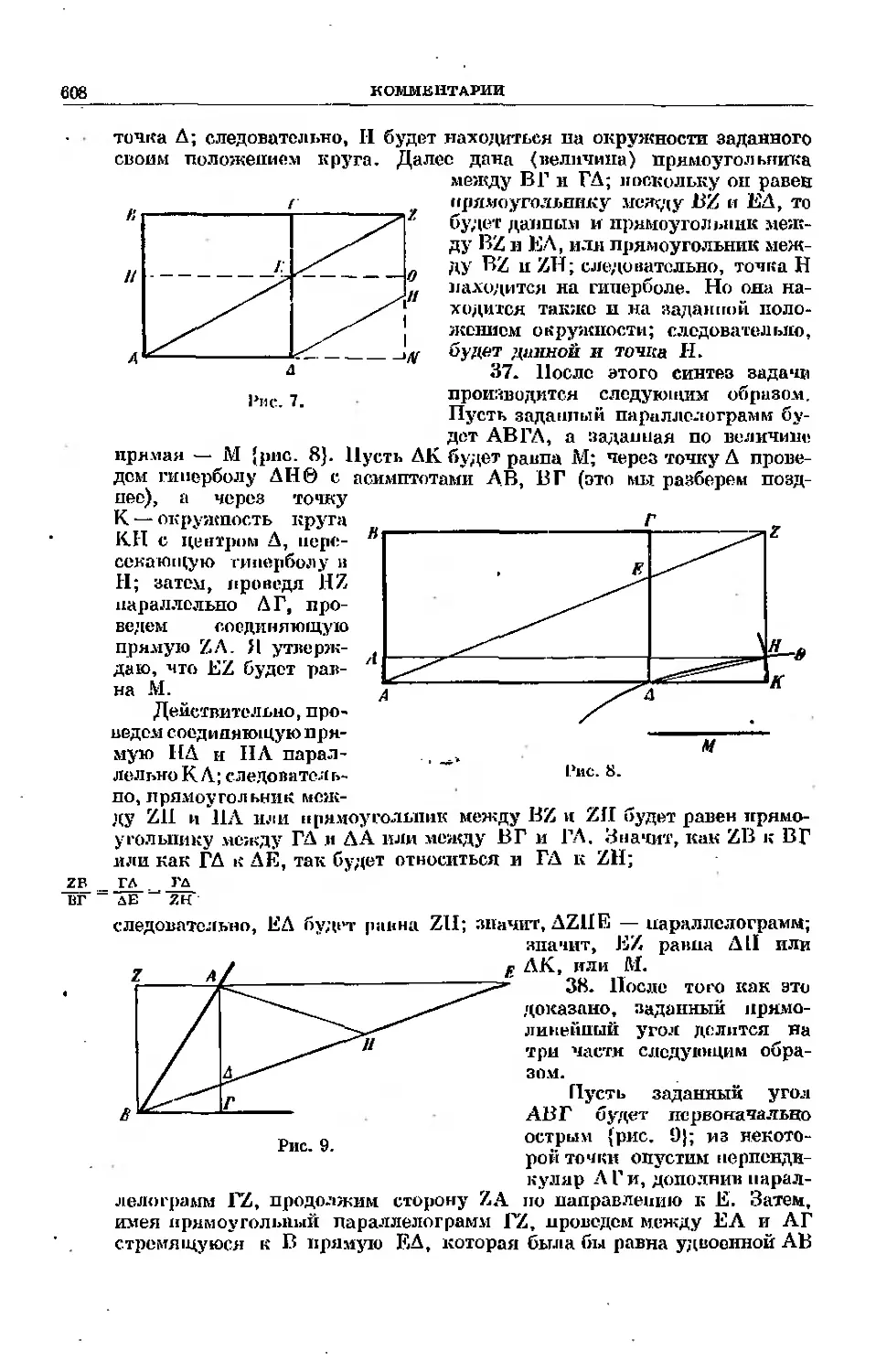
Текст
ЙМИ IB
С О Ч И Н Е НИЯ
ПЕРЕВОД АРАБСКИХ ТЕКСТОВ
Б. А. РОЗЕНФЕЛЬДА
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1 9 6.2
ПРЕДИСЛОВИЕ ПЕРЕВОДЧИКА
В настоящей книге переводчик попытался собрать все. что уцелело
от произведений Архимеда. Перевод был сделан по тексту сочинений Архи-
меда, изданному Гсйбергом (2-е издание). Кроме этого, переводчик добавил
в комментариях вес относящиеся к Архимеду тексты, имеющиеся у Паппа
и Геропа. Наконец, в предлагаемую книгу вошли арабские тексты Архи-
меда, в частности сделанный с любезно предоставленной каирскими уче-
ными рукописи перевод «Книги о семиугольнике», появляющиеся в печати
впервые. Перевод с арабского выполнен Б. А. Розенфельдом.
Есть дна способа переводить древних классиков математики: можно
строго держаться характера изложения подлинника, как в случае Архи-
меда сделал бельгийский норсводчик Ver Eecke, или же дать его в современ-
ном изложении, как поступил Th. TTealh. Подготовляя настоящее издание,
переводчик избрал средний путь: сохранив изложение Архимеда постольку,
поскольку его чтение не затруднит’ читателя, он добавил современные алге-
браические формулировки; правильно ли он поступил, об этом пусть судят
читатели.
В отдельных местах помещены переводы греческих текстов, не при-
* надлежащих Архимеду (позднейшие интерполяции); такие тексты заключены
в квадратные [ ] скобки. В угловых < > скобках стоят добавления
переводчика. Числа в квадратных скобках (например, [2]) представляют
ссылки па комментарий или па список литературы.
В заключение переводчик должен выразить благодарность Издатель-
ству за заботы об улучшении издания книги, Б. А. Розенфельду — за пере-
вод арабских текстов Архимеда и хлопоты по их разысканию, М. Я. Вы-
годскому и В. II. Зубову — за рецензии, оказавшие помощь переводчику в
его работе над текстом, А. А. Коноплянкину — за подбор иллюстраций
греческих рукописей и Л. Ю. Чернышевой — за ее работу по редакти-
рованию перевода.
И. Веселовский
Архимед. Один из античных бюстов.
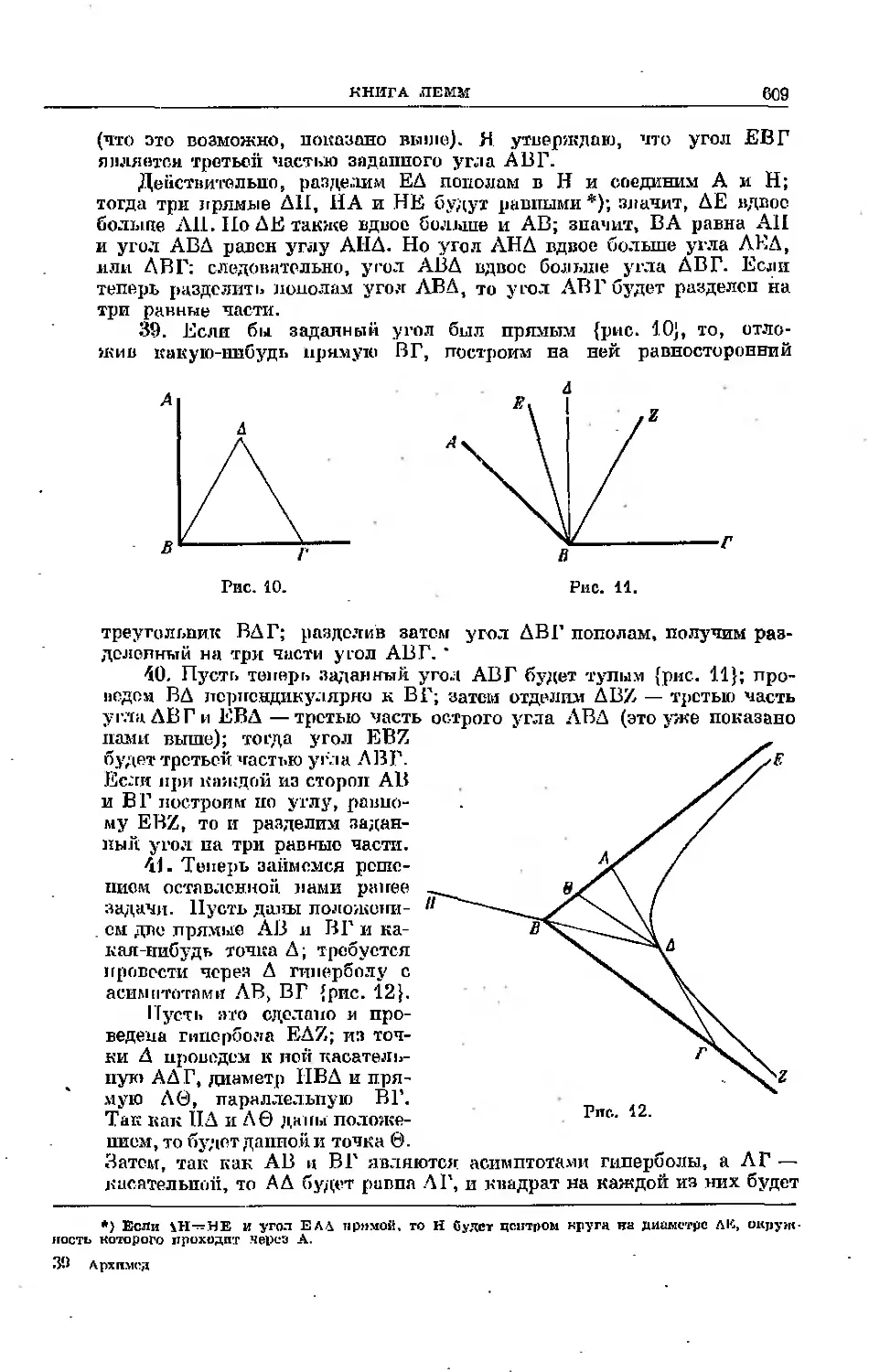
I
Жизнь Архимеда была описана неким Гераклидом, вероятно, его уче-
ником (это имя упоминается в сочинениях Архимеда). Биография эта, суще-
ствовавшая еще в шестом веке и. э. (ее читал комментатор Архимеда Евтокий
Аскалонский), до нас не дошла, так что теперь обстоятельства жизни и дея-
тельности Архимеда приходится восстанавливать по крайне скудным и отры-
вочным упоминаниям у различных авторов.
Если начинать с абсолютно достоверных дат, то мы располагаем лишь
датой смерти Архимеда: он был убит в 212 году до н. э. при взятии Сиракуз
римлянами во время второй Пунической войны Рима с Карфагеном. Визан-
тийский писатель конца XII века н. э. Цеци, автор «Хилиад (тысяч) исто-
рий», сообщает, что Архимеду в момент смерти было около 75 лет; тем самым
определяется приблизительная дата его рождения — 287 год до н. а. Отцом
Архимеда был астроном Фидий (упоминаемый им в «Псаммите»).
Архимед жил в эпоху, когда греческая культура и язык получили миро-
вое значение в связи с завоеваниями Александра Македонского и с образо-
ванием эллинистических государств. Эпоха эллинизма занимает три века
мировой истории: ее началом принято считать основание Александрии (332 г.
до и. э.) и концом — завоевание Римом Египта, последнего остававшегося
свободным эллинистического государства (30 г. до н. э.). Литература и искус-
ство этого времени, конечно, не могли сравниться с классическими образ-
цами эпохи демократической Греции V—IV веков до н. э., но в области точ-
ных наук эллинистические ученые добились очень многого: III век до в. э.
был, пожалуй, апогеем научного творчества Древней Греции в ряде спе-
циальных областей. В математике в течение этого времени от Евклида, автора
«Начал», до Аполлония Пергского, автора «Конических сечений», были
созданы настоящие шедевры, остающиеся до нашего времени классическими
образцами математического творчества.
Главным центром научной деятельности в рассматриваемый период
была Александрия с ее громадной библиотекой и музеем. В области точных
наук (математики и естествознания) в III веке до н. э., а также в области
филологии во II веке до н. э. александрийские ученые сделали очень много,
и с александрийскими математиками Архимед ноддсрживал тесные связи. Из
них в первую очередь надо назвать астронома Конона Самосского, известно-
го главным образом по анекдоту с волосами Вереники *). Этот «галантный
*) Когда в 24 6 году до и. э. египетский властитель Птолемей IfI Эвергет отправился в далекий
поход на Антиохию и начал третью Сирийскую войну, его супруга Вероника, молись аа благо-
получное окончание похода, принесла в жертву богам свои волосы. Через некоторое время после
окончания похода оказалось, что се волос в храме кет; тогда галантный придворный астроном
Нонои заявил, что эти волосы были помещены богами на небе в качестве нового созвездии «Волос
Всрснини»,
6
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. Н. ВЕСЕЛОВСКОГО
астроном» был в действительности очень крупным ученым, оказавшим
большое влияние па научное развитие Архимеда. Архимед мог познакомиться
с Коионом или непосредственно в Сицилии, где Коион одно время произво-
дил астрономические наблюдения, или в Александрии во время своего пре-
бывания там. Конон давал Архимеду темы для научных работ, как, напри-
мер, задачу о спиралях, о чем говорит в «Математическом собрании» Папп
Александрийский (книга IV, 21); «эту теорему предложил (npouteiva) Ко-
нон, самосский геометр, а доказал ее Архимед». Как мы зпаем из собствен-
ных слов Архимеда, последний посылал Коиону для критики свои мате-
матические работы, а с учеником его Досифеем поддерживал отношения
и после смерти Коиона, которую относят к тридцатым годам III века
до н. а.
Другим александрийцем, с которым Архимед поддерживал связи, был
Эратосфен Кирепский (285—205 гг. до н. э.). В 245 г. до н. э. Эратосфен был
приглашен в Александрию упомянутым уже Птолемеем III Эвергетом в каче-
стве воспитателя наследника престола Птоломея IV Филопатора. Эратосфен
был весьма разносторонним ученым: он занимался арифметикой («решето
Эратосфена» для нахождения простых чисел известно каждому школьнику),
геометрией (об его решении делийской задачи мы еще будем говорить) и астро-
номией (он составил описание звездного неба — «Катастеризмы»); он про-
извел первое измерение дуги земного меридиана, положив тем начало мате-
матической географии, занимался хронологией и заведовал Александрий-
ской библиотекой. За разносторонность враги называли его о p-qra (бета —
вторая буква греческой азбуки) — «во всем второй». К Эратосфену Архимед
обратился со своим замечательным «Эфодом», излагающим те методы, при
помощи которых Архимеду удалось сделать свои выдающиеся открытия;
наконец, Эратосфену же была послана «Задача о быках».
Родина Архимеда, Сиракузы, в течение всего Ш века до п. э. находи-
лась между двумя, и даже тремя, враждующими пародами, боровшимися
за обладание богатой и плодородной Сицилией, а именно греками, карфаге-
нянами и римлянами. Когда Архимеду было около десяти лет, в Сицилии
знаменитый эпирский царь Пирр, стремившийся основать новую монархию
на западе греческого мира в Италии и Сицилии, вел войну с римлянами и кар-
фагенянами. Война Пирра оказалась безрезультатной; в борьбе с ним выдви-
нулся Гиерон (возможно, бывший родственником Архимеда), в 270 г. до н. э.
сделавшийся правителем Сиракуз. Первая половина его царствования не
была мирной: ему сначала пришлось отбиваться от мамертинцев -италийских
наемников,— захвативших Мессину; затем в эту борьбу вмешались, с одной
стороны, римляне, с другой — карфагеняне, и разразилась первая Пуниче-
ская война (264—241 гг. до н. э.), в результате которой вся Сицилия, за
исключением области Сиракуз, стала римской «провинцией». Во время этой
войны Гиерон первоначально действовал в союзе с карфагенянами, по во-
время вышел из войны, так что Сиракузы остались «свободными». С 241 г.
до н. э. начинается мирный период царствования Гиерона, старавшегося
поддерживать хорошие отпошения со всеми сторонами; тем не менее он дея-
тельно готовился к отражению возможных покушений на свободу Сиракуз
и усиливал обороноспособность родного города, привлекши к этой работе,
как говорит Плутарх, и Архимеда. В 227 г. до и. э. Гиерон вместе с сопра-
вителем Гелоном (своим сыном) оказали помощь Родосу после постигшего
его землетрясения; интересно отметить, что в числе подарков были «пять-
десят трехлоктевых катапульт» (Полибий, История, книга V, 88).
Невольно приходит’ в голову, что эти катапульты представляли особую цен-
ность потому, что были созданиями Архимеда.
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И, Н. ВЕСЕЛОВСКОГО
7
Вероятно, в течение этого мирного промежутка Архимеду удалось побы-
вать в Александрии и познакомиться там с Кононом и Эратосфеном. Во время
своего пребывания в Египте, как говорит историк Диодор (вторая половила
I века до и. э.), Архимед изобретает к ох лею, или архимедов винт, служа-
щий для поднятия наверх воды. Знакомство с Копоном, вероятно, послу-
жило толчком к развитию огромных математических способностей Архимеда.
Архимед. Доминико Фстя (XVII в.). Картинная
галерея. Дрезден.
Первые его произведения были посвящены механике; после же смерти Коно-
па Архимед пишет ряд выдающихся математических произведений. Инте-
ресно отметить, что в 240 г. до н. э. Архимеду было уже около сорока семи
лет, так что дошедшие до пас его математические произведения написаны
им уже по меныпеп мере » пнтидесятилетпем возрасте. Первое из дошедших
до нас сочинений Архимеда «Квадратура параболы» можно предположи-
тельно отнести к 235 г. до н. э.; Архимед умер в 212 г. до и. э. Таким обра-
зом, расцвет математической деятельности Архимеда обнимает какие-нибудь
20—25 лет. Этот период был прерван начавшейся в 218 г. до н. э. второй
Пунической войной между Римом и Карфагеном. Сиракузы были вовлечены
в эту войну, и в 212 г. до н. э. Архимед, руководивший обороной Сиракуз,
погиб от меча римского солдата.
Каким рисовался образ Архимеда следующим поколениям? Полибий,
описывавший осаду Сиракуз всего через какие-нибудь 50—60 лет поел©
8
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. Н. ВЕСЕЛОВСКОГО
смерти Архимеда, в дошедшем до нас и приведенном ниже (см. стр. 44)
тексте говорит только об инженерной деятельности Архимеда, по соответ-
ствующая часть истории Полибия дошла до нас только в извлечениях.
Римский историк Тит Ливий, использовавший Полибия в своей истории
Рима, называет Архимеда unions spectator coeli siderumqiie — «не имею-
щий себе равных наблюдатель неба и звезд».
Главным образом как об астрономе пишет об Архимеде и Цицерон;
однако последний знал Архимеда и как математика, так как сумел найти
могилу Архимеда по помещенному на ней изображению шара и цилиндра —
в память одного из математических достижений Архимеда, которое послед-
ний считал самым большим своим открытием.
Диодор, историк середины I века до н. э., говоря об изобретении архи-
медова винта пишет: «По не только поэтому нужно удивляться таланту Архи-
меда. Мы обязаны ему еще многими другими более замечательными произ-
ведениями, известными всему миру. Мы опишем их с тщательностью и в под-
робностях, когда дойдем до описания эпохи Архимеда» (Историческая библио-
тека, книга V, 37). К сожалению, часть истории Диодора, описывавшая
эпоху Архимеда, до пас не дошла.
В конце того же века знаменитый архитектор Витрувий говорит об Архи-
меде как о разностороннем ученом. Во введении к первой книге «Архитек-
туры» он пишет об идеальном архитекторе: «Но такие гении очень редки;
мало людей, вроде Аристарха Самосского, Филолая, Архита Тарентского,
Аполлония Пергского, Эратосфена Киренского, Архимеда и Скопина
Сиракузского, которые сумели с помощью расчетов и знания тайн природы
сделать большие открытия в механике и гномонике и оставили потомству
об этом ученые труды». Интересны лица, с которыми Витрувий сопоставляет
Архимеда: это Аристарх Самосский — математик, физик и астроном, созда-
тель первой гелиоцентрической системы мира; затем пифагореец Филолай —
философ, математик и тоже автор системы мира, согласно которой в сере-
дине мира находился центральный огонь; Архит Тарентский — друг Плато-
па, известен как математик, механик и замечательный полководец; Аполло-
ний Пергский — автор ряда замечательных математических произведений
ио арифметике и геометрии («Конические сечения»), и, по-видимому, творец
астрономической теории эпициклов; об Эратосфене мы уже говорили; все
зто люди больших и, главное, разносторонних интересов и способностей.
Во второй половине первого века пашей эры Силий Италик — ученый
поэт эпохи Флавиев, автор исторического зпоса о второй Пунической войне-
ценит Архимеда как человека «поднявшегося своим гением далеко за пре-
делы человеческого», «знавшего все тайны природы», которому известпог
«является ли Земля неподвижной, или прикрепленной к оси вращения;
по какой причине разлитое ио земному шару море остается прикованным
к поверхности Земли; в чем заключается причина волнения его вод и различ-
ных фаз Луны; какому закону следуют явления прилива и отлива». «Можно*
верить, продолжает поэт, что Архимед исчислил все земные песчинки» и что-
оп мог «руками одном слабой женщины спустить па воду корабль и поднять-
вверх по наклону нагроможденные па нем скалы» (De ЬсПо punico secundo,
книга XfV).
Все эти отзывы рисуют Архимеда как всестороннего ученого — астро-
пома, естествоиспытателя, механика, они мало говорят об Архимеде как-
о математике, но это вполне попятно: математика нс была предметом, зна-
комство с которым было распространенным среди широкой публики. Мы при-
вели зти отзывы в противовес очень распространенной характеристике Архи-
меда, данной Плутархом, который в противоположность этим авторам
Афипская школа, Рафаэль (XVI в.). Фреска. Ватикан. Рим. Архимед в правом ппжром углу склонился
с циркулем над абаком,
40
ВСТУПИТЕЛЬНАЯ СТАТЬЯ и. И. ВЕСЕЛОВСКОГО
рисует Архимеда преимущественно как математика. Причина этого заклю-
чается совсем не в том, что Плутарх был математиком, или по крайней мере
любил математику. Причина этого заключается в том, что все вы шеприведеп-
ные авторы писали еще под очень сильным влиянием эллинистического образа
мышления, в то время как деятельность Плутарха относится уже к совер-
шенно другой эпохе. Плутарх жил в начале II века пашей эры в эпоху,
когда консервативные настроения, зародившиеся еще во времена Августа,
достигли своего полного развития. В эту эпоху классической реставрации
забывается и реализм эллинистической литературы, и разносторонность
научной деятельности эллинистических ученых. В качестве идеалов выста-
вляются поэты, ораторы и философы классической эпохи Афинского госу-
дарства, начинается возрождение философии Аристотеля и Платона. В обла-
•сти науки развиваются лишь медицина и математика, прячем последняя
не как самостоятельная наука, а скорее как служанка астрономии, или,
верное, астрологии; при этом, конечно, много значил и культ математики,
имевший место у Платона и пифагорейцев, возрождение философии которых
как раз приходится па первые два пека нашей эры. Истинный ученый
рисуется как человек не от мира сего, погруженный в созерцание идей выш-
него мира, к которому принадлежат и математические образы. Все это сле-
,дует иметь в виду, читая характеристику Архимеда, данную Плутархом
в биографии римского полководца Марцелла.
«Архимед имел возвышенную душу и глубокий ум, и, обладая громад-
ными богатствами геометрических теорий, он не хотел оставить пи одного
сочинения относительно построения тех машин, которые доставили ему
славу знания, не только доступного человеку, но почти божественного...
Во всей геометрии нельзя найти более трудных и глубокомысленных задач,
которые были бы решены так просто и ясно, как те, которыми занимался
Архимед. Одни приписывают эту ясность его высоким дарованиям, другие
же — тому напряженному труду, при помощи которого ему удавалось дать
своим открытиям такое выражение, что они становятся доступными без
труда. Если читатель сам не находит доказательства, то при изучении архи-
медовых сочинений у него создается впечатление, что он и сам смог бы без
труда найти решение,— таким легким и быстрым путем Архимед приводит
к тому, что он хотел доказать. Поэтому не кажется невероятным, что он, Kai?
рассказывают, будучи околдован геометрией, забывал о пище и пренебре-
гал заботами о своем теле. Часто его насильно заставляли принимать ванну
и натираться мазями, а он чертил на золе геометрические фигуры и на своем
намазанном маслом теле проводил пальцем линии,— настолько он был
охвачен этики занятиями и действительно одухотворен музами. И хотя
у него было много прекрасных открытий, он, говорят, просил своих род-
ственников и друзей начертить на его могиле только цилиндр и содержащийся
в нем шар и указать соотношение между объемами этих тел. Таков был
Архимед, который благодаря своим глубоким познаниям в механике смог,
насколько это от него зависело, сохранить от поражения и себя самого
и свой город».
Отношение Архимеда к механике Плутарх рисует следующим образом:
«Архимед не придавал большого значения всем этим (римским) маши-
нам, которые, по слчцеству, не могли идти в сравнение с его собственными,
и нс потому, что он как-нибудь особенно ценил свои изобретения; он сам
рассматривал их лишь как простые геометрические игрушки, которыми
он занимался в свободное время и то большей частью но настоянию царя
Гиероиа, который постоянно старался направить его занятия от чисто интел-
лектуальных предметов к материальным вещам и сделать ого рассуждения
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. Н. ВЕСЕЛОВСКОГО
11
в некоторой степени доступными чувствам и ощутимыми для среднего чело-
века при помощи применения их к общежитейским занятиям».
Стоит отметить наконец, также следующее свидетельство Паппа (Биб-
лиотека, книга VIII, 3).
«Причину же и количественные характеристики (т^тАоуот) всего этого
(то есть механических и р и б о р о в) познал сиракузянип
Архимед, как утверждают некоторые. Вплоть до наших времен только он
один пользовался для всяких целей разнообразием и своих природных
дарований и замысла, как говорит Гемин в книге «О порядке математических
наук». Антиохиец Карп говорит где-то, что сиракузяпин Архимед сочинил
только одну книгу по механике, а именно касающуюся построения небес-
ного глобуса, считая все остальное недостойным описания».
Опираясь па мнение Плутарха, иногда рисуют Архимеда как чистого
математика, взявшегося за презираемую им технику только в тот момент,
когда его родному городу стала грозить смертельная опасность. Такого рода
оценка основана на однобокой характеристике Архимеда; если придержи-
ваться фактов, то Архимед и начал свою научную деятельность как меха-
ник, и закончил ее как механик же, и в математических его произведениях
механика является могучим средством для получения математических
результатов, да и сами эти результаты не являются бесплодно висящими
в воздухе, а применяются для обоснования механических теорий.
II
Так как первые работы Архимеда были посвящены механике, то необхо-
димо коротко остановиться на истории развития античной механики, тем
более, что в настоящее время нет еще специальных работ, посвященных
этому вопросу механики.
Название «механика» произошло от греческого «pT)x<xvizT) (подразуме-
вается Ti'/vT])» — механическое искусство. Самое слово ртдоахт; — машина —
1первоначально обозначало подъемную машину, употреблявшуюся в театрах;
отсюда произошло известное выражение Deus ex machine — бог, спускаю-
щийся на театральной машине для разрешения запутанного хода действия
трагедии. Таким образом, «механическое искусство» родилось на сцене, но
это не должно нас удивлять: в обществе, основанном на рабском труде, не
•было и не могло быть никаких экономических стимулов для развития маши-
ностроения. Что же касается специально театра, то нужно отметить, что
в то же самое время, о котором идет речь (V век до и. э.), театр дал толчок
к развитию еще одной математической науки, а именно геометрической опти-
ки, или лучше сказать — перспективы, появление которой было вызвано
нуждами сценических декораторов.
Греки различали два вида движений — естественные и искусственные.
Первые совершались сами собой без всякого постороннего вмешательства;
к ним греки относили падение тяжелых и поднятие легких тел, а ташке
круговые движения небесных светил. Что касается вторых, то они для своего
осуществления непременно требовали некоторого двигателя. То, что мы
теперь понимаем под термином «сила», в обоих этих видах движений носило
различные имена. В естественных движениях пашей силе соответствовала
ролц (от pEiraiv — тот же корень и смысл, что в нашем «ринуться», или
лучше, «рыпаться»), что мы в дальнейшем, следуя Галилею, переводим тер-
мином «момент» (этот смысл понятие momentum до известной степени сохра-
нило в английской математической терминологии и в настоящее время).
Эта рблт], вероятно, считалась присущим телам стремлением, неотделимым
12
ВСТУПИТЕЛЬНАЯ СТА ТЕЯ И. П. ВЕСЕЛОВСКОГО
от материи, хотя Аристотель сделал попытку и в случае естественного дви-
жения искать причину его вне тела, в так называемом свойственном каждому
роду тел «месте», к которому эти тела должны стремиться; так «местом»
тяжелых тел была Земля, а «местом» легких тел — огня — находящаяся
над воздухом огненная сфера. Что же касается искусственного или насиль-
ственного движения, то причину его древние греки искали уже определенно
вне движущегося тела: причина эта называлась dAvap-ig. Количественное
определение fiwapig мы находим у Аристотеля: он определяет ее как вели-
чину, пропорциональную весу движущегося тела и скорости его движения
(вернее — пройденному пути, разделенному па время). Понимаемая в таком
смысле 66vap.ig в точности соответствует нашему понятию «мощности»,
и действительно, па латинском языке термин fi’j'vap.ig передавался как potentia,
откуда произоп1ло французское puissance — мощность. Было бы неправиль-
ным толковать формулу Аристотеля в том смысле, как это делает Мах, кото-
рый в ньютоновском определении силы как произведения массы па ускоре-
ние, смело заменяет слово «ускорение» словом «скорость» и утверждает, что,
по Аристотелю, сила равнялась произведению массы на скорость. Прежде
всего, у Аристотеля отсутствует термин «равнялась»; затем наше понятие
«массы» оставалось грекам неизвестным (его в механике заменяла чисто
геометрическая piyeQog величина); что же касается веса, то все указывает
на то, что греки не считали его постоянным; вес тела, по представлению
даже средневековых механиков, мог увеличиваться при помещении тела
на более длинное плечо рычага, затем при увеличении скорости движения
(знаменитое vires acquirit eundo — приобретает силу от движения — вполне
естественный вывод из наблюдения, что удержать падающее тело гораздо труд-
нее, чем поддерживать покоящееся) и т. д. Это определение силы вполне
отвечало уровню технического развития общества, в котором в качестве
двигателей употреблялись животные и люди: если хочешь свезти вдвое бо-
лее тяжелый груз, то запряги вдвое больше лошадей, если хочешь втрое
увеличить скорость движения, возьми втрое больше живых двигателей.
Такое понятие о «силе» еще до сих пор живет в нашем термине «лошади-
пая сила».
Очень трудпо ответить на вопрос, знал ли Аристотель принцип возмож-
ных перемещений. Некоторые исследователи, в частности академик
А. П. Крылов, решают зтот вопрос утвердительно; лично я нс мог найти
ничего похожего ни в произведениях самого Аристотеля, ни в вышедших
из его школы «Механических задачах» — первом дошедшем до нас произве-
дении, посвященном механике. Следует, однако, заметить, что этот принцип
совершенно естественно получается из аристотелевского определения fiovapig,
если только считать коэффициент пропорциональности одинаковым у срав-
ниваемых мощностей; равенство «сил» будет требовать и равенства произве-
дении грузов на скорости. В этом убеждает нас сама формулировка так назы-
ваемого «золотого правила» механики: «что выигрывается в силе, то теряется
в скорости». Правда, эту формулировку мы в первый раз встречаем только
в «Механике» Геропа (I век н. э.), но Герои, несомненно, воспроизводит более
раннюю литературу. Во всяком случае нужно отметить, что греки приме-
няли принцип возможных перемещений лишь к машинам, которые можно
свести к рычагу; закона равновесия сил на наклонной плоскости они так
и по смогли открыть, и он был впервые установлен только в Х1П веке н. э.
Аристотелево определение «силы» как мощности страдало очень боль-
шим недостатком: из него вытекало, что если сила равна нулю, то и ско-
рость должна обратиться в нуль, если устранить двигатель, то прекратится
и движение, а если движение существует, то всегда должна существовать
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. Н. ВЕСЕЛОВСКОГО
13
и вызывающая это движение сила. Такое воззрение годилось для объясне-
ния движения повозок, везомых лошадьми, ни никак пе могло удержаться
с развитием греческой артиллерии. Когда в 409 г. до п. э. карфагеняне начали
завоевательные походы в Сицилии, то наемный характер их армий требовал
быстрых военных действий и развития осадной техники. В борьбе с карфа-
генянами в Сиракузах, родине Архимеда, возникла военная тирания Дио-
нисия Старшего (IV век до и. э.), который произвел «мобилизацию промыш-
ленности» для военных целей. Результатом этой мобилизации было изобрете-
ние метательных орудий (катапульт и др.), усовершенствование осадных
магнии и кораблестроения. Из западной Греции новые открытия перекину-
лись и в восточную, которая в IV веке до н. э. тоже от гражданских ополче-
ний перешла к наемным армиям; Филипп и Александр Македонские имели
в своих «штабах» большое количество «военных инженеров», и поенная тех-
ника играла уже большую роль в последующих войнах эллинистических
государств; чтобы убедиться в этом, достаточно прочитать относящиеся к рас-
сматриваемому периоду части истории Диодора Сицилийского. Быстрота тем-
пов развития военной техники в течение IV века до н. э. характеризуется сле-
дующим фактом: еще в V веке до п. э. вплоть до самого его конца господ-
ствующим типом греческого судна была так называемая триера, имеющая
три ряда весел, но уже около .300 г. до н. э. в морских флотах эллинисти-
ческих государств употребляются декеры-корабли с десятью рядами весел
и появляются еще более крупные суда. Возможно, что именно развитие
воеппой техники вызвало в области математики интерес к делийской задаче
и способствовало развитию теории конических сечений, в области же меха-
ники оно привело к возникновению теории механического подобия, к по-
явлению большого количества литературы по воеппой механике и, наконец,
к крушению аристотелевой теории силы, которая, по существу, была уста-
ревшей уже в самый момент своего возникновения; если полет стрелы еще
можно было объяснять тем, что ее движет возмущенный спуском тетивы воз-
дух (так называемая теория антиперистазнса), то искать в воздухе причину
движения тяжелого камня, выброшенного из катапульты, было уже совер-
шенно невозможно.
Каково же было новое определение силы? Ввиду почти полного исчез-
новения эллинистической литературы приходится отыскивать это новое
определение в сочинениях более поздних авторов, главным образом коммен-
таторов Аристотеля. Как упомянуто Галилеем, один из таких комментато-
ров, Александр Афродизский (около 200 г. н. э.) сообщает, что знаменитый
астроном древности Гиппарх (писавший и в области механики) объяснял дви-
жение брошенного тела тем, что двигатель сообщает брошенному телу неко-
торую «силу», которая поддерживает движение, постепенно расходуясь; ког-
да эта сила полностью иссякнет, движение прекращается. Вряд ли можно
считать, что Гиппарх действительно является автором такого определения
силы; по всей вероятности, он, для которого механика пе была основ-
ной специальностью, просто воспроизводит обычное в его эпоху опреде-
ление силы (Галилей приводит это определение в своем юношеском неза-
конченном произведении «De motu»). Это эллинистическое определение си-
лы встречается ташке и в комментариях Симпликия и Иоанна Филонова к
Аристотелю (VI век н. э.); через посредство этих комментаторов (Симпликий
был переведен во второй половине XIII века Вильгельмом из Мербеке —
переводчиком Архимеда) эллинистическое определенно силы становится
известным и западноевропейским механикам позднего средневековья; под
именем impetus это определение силы встречается у Альберта Саксонского,
Николая Кузапского и Леонардо да Винчи. Понимаемая в таком смысле
14 ВСТУПИТЕЛЬНАЯ СТАТЬЯ И- Н. ВЕСЕЛОВСКОГО
«сила» полностью отвечает современному понятию о живой силе; еще Декарт
измерял силу (если пользоваться современной терминологией) тон работой,,
которую надо сообщить движимому телу, чтобы поднять его па определен-
ную высоту. Можно думать, что укреплению этого определения па европей-
ской почве способствовало развитие артиллерии, также как создание гречес-
кой артиллерии было причиной его появления.
Весьма вероятно, что Архимед пользовался общепринятым в его время
определением силы при построении своих военных машин; однако в чисто
теоретических его произведениях это определение силы не встречается. Ио-
видимому, это объясняется тем, что вопросы динамики в то время математи-
ческой трактовке еще не поддавались, я Архимед вполне правильно сосредо-
точил свое внимание на вопросах, касающихся статического равновесия.
Одним из ранних произведений Архимеда было какое-то (нс дошедшее
до нас) сочинение по механике, точное название которого неизвестно, то ли
это nept (о равноплечих рычагах), то ли просто pi]ywuvixa. Этим сочи-
нением пе мог быть дошедший до нас трактат «О равновесии плоских фигур»,
так как он не соответствует тем ссылкам, которые содержатся в трудах
Геропа, Паппа и самого Архимеда, и не содержит самого главного — опре-
деления центра тяжести, которое Архимед, очевидно, считал в то время ужи
вполне известным. Составить себе представление об этом раннем сочинении
Архимеда позволяют фрагменты, сохранившиеся у Паппа, в «Механике»
Геропа, а также у самого Архимеда.
Стержневым понятием всей статики Архимеда является понятие о цен-
тре тяжести, которое по всем данным самим Архимедом и было установлено.
Действительно, пи Аристотель, ни «Механические проблемы», которые при-
писываются третьему преемнику Аристотеля в управлении Лицеем Стратону
Лампсакскому, ничего о центре тяжести по зпают, в то время как уже около
250 г. до н. э. если не раньше, Архимед свободно оперирует этим понятием*).
Доархпмедовское происхождение понятия о центре тяжести отстаивает
С. Я. Лурье в своем сочинении «Архимед» (стр. 71), опираясь па следую-
щий отрывок из «Механики» Герона.
«Стоик Посидоний дал центру тяжести, или момента, физическое объяс-
нение, сказавши, что центр тяжести, или момента, есть такая точка, что если
за последнюю подвесить даппый груз, то ок будет в пей разделен па две рав-
ные части. Поэтому Архимед и его последователи в механике более подробно
рассмотрели это положение и установили разницу между точкой подвеса
и центром тяжести».
Так как Архимед упоминается здесь после Посидония, то получается
впечатление, что он и жил после Посидония, и исправил введенное Посидо-
нием неправильное определение центра тяжести. Но следует, однако, иметь
в виду, что «Механика» Геропа дотла до нас в арабском переводе сирийца
Косты ибн-Лука из Баалбека и что у пас ист никакой гарантии, что в под-
линнике действительно стояло tea (равные), а но iaopponou'vta (уравновеши-
вающиеся). За последнее говорит упоминаемое в тексте «подвешивание за
точку»; термин «равновесие относительно точки» мы у Архимеда встречаем,
но «деление точкой тела па две равные части», да еще при «подвешивании»
несколько нас удивляет; приходится помогать делу тем, что центр тяжести
рассматривать как точку пересечения линий или плоскостей, делящих на
две равные части данную плоскую фигуру или тело.
’) В связи с этим стоит отметить, что в своих ранних механических произведениях («Книга
опор») Архимед понятия о центре тяжести еще не имел, чем и (.(л-нсинютсн некоторые его олтпйни
и расчетах.
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. Н. ВЕСЕЛОВСКОГО
15
С. Я. Лурье замечает, что указанное понимание центра тяжести повто-
ряется и в других местах «Механики» Герона; так, на основании упомянутого
неправильного определения находится центр тяжести треугольника (кни-
га II, 35), затем деление тела па две уравновешивающиеся части плоскостью,
проведенной через точку опоры, встречается при изучении подъема цилиндра
по наклонной плоскости (книга I, 23) и при определении действия рычага
на тело, опирающееся на землю (книга II, 9). Основываясь ла этих местах,
а также на том, что Посидоний в тексте Герона упоминается раньше Архи-
меда, С. Я, Лурье, следуя английскому историку математики Хису, пред-
положи.;!, что автором вышеупомянутой теории является нс хорошо всем
известный сирийский стоик 1 века до н. э. Посидоний Родосский, учитель
Цицерона, а совсем почти неизвестный стоик Посидоний Александрийский,
живший несколько ранее Архимеда; этому самому Посидонию и нужно при-
писать честь введения в науку понятия о центре тяжести, причем сначала
это понятие было получено из неправильного предположения, что линия,
пли плоскость, делящая тело на две равные части, должна обязательно
пройти через центр тяжести.
При более тщательном изучении дела выясняются следующие обстоя-
тельства. Второй и третий тексты, упомянутые С. Я. Лурье, а именно, тек-
сты, относящиеся к рычагу и наклонной плоскости, должны быть просто
устранены из рассмотрения на том основании, что они пе содержат никакого
упоминания о центре тяжести (н примере с подъемом цилиндра по наклонной
плоскости говорится только о «центре круга», в случае же с рычагом вообще
никакой центр нс упоминается). Что же касается первого текста, приводи-
мого С. Я. Лурье, а именно относящегося к центру тяжести треугольника,
то детальное рассмотрение его является для теории С. Я. Лурье роковым.
Этот текст представляет собой часть довольно большого отрывка, касаю-
щегося определения центров тяжести некоторых плоских фигур*). В самом
пачале автор действительно говорит, что треугольник АВС, положенный на
медиану АГ), «не будет иметь момента пи в какую сторону, так как
треугольники ABD и ЛГ)С равны» (подчеркнуто мной, И. В.), но все даль-
нейшее изложение, касающееся определения центров тяжести четырех-
угольника и пятиугольника, совершенно пе основывается на упомянутом
ложном принципе; там, наоборот, везде подразумевается равенство не пло-
щадей, а моментов. Все изложение может быть сделано совершенно правиль-
ным, если в подчеркнутой фразе опять вместо слов «равны» читать «равпо-
весягци». Можно, конечно, думать, что слона «равны» в рассматриваемом
тексте являются подливными, по что Посидоний Родосский, который вряд ли
шел далее определения центров тяжести самых простых фигур (параллело-
граммов, треугольников, кругов), предпочел дать, если не совсем правиль-
ное, то во всяком случае более короткое и наглядное объяснение; для
периода упадка механики в конце эллинистической эпохи это но всяком
случае вполне подходит. Правда, в рассматриваемой книге Посидоний
упоминается раньше Архимеда, по порядок упоминания авторов в тексте
сочинения не всегда совпадает с хронологическим порядком их опублико-
вания: Герои мог начать с популярного произведения Посидония, а потом
перейти уже к более серьезному и трудному тексту Архимеда. Таким обра-
зом, предшественника Архимеда, стоика Посидония Александрийского,
как автора понятия о центре тяжести можно целиком вычеркнуть из исто-
рии механики.
«) Этот отрывок помещен в нашем издании среди «Механических фрагментов» Архимеда (см...
стр. 73—75),
16
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. И. ВЕСЕЛОВСКОГО
Безусловно верным в тексте Герона является то, что понятие о центре
тяжести как о точке подвеса он считает предшествующим всякому иному
пониманию центра тяжести, но и определение центра тяжести как точки
подвеса тоже принадлежит Архимеду. У Паппа (книга VL1I, 5) архимедово
определение центра тяжести читается так:
«Центром тяжести каждого тела является некоторая расположенная
внутри него точка — такая, что если за нее мысленно подвесить груз, то
•оп остается в покос и сохраняет первоначальное положение».
Приблизительно такое же определение центра тяжести как точки под-
веса мы встречаем у Евтокия и Симпликия (см. «Механические фрагменты»,
стр. 68, 72): варианты заключаются лишь в том, что подвешивание иногда
заменяется подпиранием, как можно видеть из упомянутого текста Паппа
и параллельного ему текста из «Механики» Герона (книга Т, 24), определенно
восходящих к одному источнику. Что касается этого источника, то Папп
называет два имени — Герона и Архимеда; поскольку в тексте Герона
имеются некоторые неясности, а у Паппа все изложено правильно, то с ве-
роятностью, близкой к достоверности, можно утверждать, что этим основным
источником как для Паппа, так и для Герона является Архимед.
Понятие о центре тяжести сложилось у Архимеда па основании чисто
практических исследований распределения давления груза между поддер-
живающими его опорами. Это можно видеть, с одной стороны, из выше-
упомянутого текста Паппа — Герона, с другой — из того обстоятельства,
что, как мы знаем из арабских источников, Архимед папнеал «Кингу опор»,
отрывки из которой содержатся в вышеприведенной «Механике» Герона.
Правда, если судить по этим отрывкам, он пе оказался особенно счастливым
в полученных результатах; его теория расчета многооиорпой балки («Меха-
ника», Герона, книга I, 26) совершенно неверна, так как из приведенных
там рассуждений вытекает, что в случае балки, лежащей на трех опорах,
средняя опора будет всегда нести половину веса всей балки, независимо от
своего положения; точно так же нельзя согласиться с архимедовским расче-
том консольной балки (там же, 27—28). Удивляться этому7 не приходится;
в распоряжении Архимеда пе было никаких приборов для измерения давле-
ний на опоры. В связи с этим можно отметить, что Леонардо да Винчи тоже
ошибался при определении давлений на опоры и подставки, хотя натяжения
веревок определялись им совершенно правильно (конечно, в статически опре-
делимых случаях).
Работы Архимеда в области строительной механики не были единствен-
ными плодами его технических занятий; Архимеду приписывается целый ряд
механических изобретений. Правда, подробный список их, составленный
его соотечественником историком Диодором Сицилийским, к сожалению,
до нас не дошел, так что нам приходится собирать у античных писателей
сохранившиеся отрывки этого списка.
На первом месте среди этих изобретений следует поставить архимедов
винт или кохлею (улитку). Вот тексты, касающиеся этого прибора.
Об употреблении'его в Египте говорит историк Диодор (книга I, 34):
«Нил после разливов наносит на поля новые количества ила, и обитатели
легко могут орошать все поле при помощи изобретенной Архимедом Сира-
кузским машины, которая по причине своей формы, носит название улитки».
Об употреблении его в Испании тот же Диодор сообщает (книга V, 37):
«Горнорабочие встречаются иногда с подземными реками, быстрое тече-
ние которых они уменьшают, отводя их в наклонные рвы, и неутолимая
жажда золота заставляет их доводить до конца свои предприятия. Самое
удивительное заключается в том, что они могут целиком вывести всю воду
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. Н. ВЕСЕЛОВСКОГО
17
при помощи египетских винтов, которые изобрел Архимед Сиракузский во
время своего пребывания в Египте. Они таким образом постепенно подымают
воду вплоть до отверстия рудника и после осушения подземных галерей
спокойно в них работают. Эта машина так искусно устроена, что с ее помощью
можно поднять громадные массы воды и даже легко вывести целую реку из
земных глубин на поверхность».
Об этом же говорит писатель TI века пашей эры Атепей в своих «Демм-
пософистах» (книга V):
«Хотя бы отстойная вода (в трюме корабля) была бы л очень
глубокой, ее отсасывал один человек при помощи изобретенного Архиме-
дом бесконечного винта».
Некоторые авторы оспаривают авторство Архимеда в этом изобретении
на том основании, что пи географ Страбон, упоминающий об этой машине
в своем описании Египта, ни Витрувий, ни механик Филон не называют
при ее описании имени Архимеда; однако в этом случае можно поверить
Диодору, по-видимому, специально занимавшемуся изобретениями своего
великого земляка.
Иначе обстоит дело с изобретением Архимедом винта. Его изобретение
приписывает Архимеду тот же Атсней («ДеЙппософнсты», книга X), который,
рассказывая известный анекдот о том, как Архимед либо вытащил на сушу
корабль, либо наоборот спустил его на воду, говорит:
«Кыда люди много трудились над тем, чтобы спустить этот корабль
на воду, знаменитый механик Архимед сделал это один с помощью неболь-
шого числа людей. Действительно, он добился успеха при помощи выдуман-
ного им винта, так как именно ему мы обязаны этим изобретением».
О том же говорит византийский автор XII века, известный комментатор
Гомера, Евстафий, епископ Фессалоникийский:
«Архимед считается первым изобретателем винта (eZig), причем эта
машина доставила ему большую славу» (Комментарии к Илиаде, III).
Приведенные свидетельства не могут считаться доказательными по сле-
дующим причинам:
1°. Рассказ Атенея является второй версией известного рассказа Плу-
тарха, с той только разницей, что у Плутарха в качестве машины упоми-
нается полиспаст, что более вероятно. Мы имеем еще и третью версию у Сим-
плиния (VI век и. э.) в комментарии к «Физике» Аристотеля, где знаменитое
«дай точку опоры, и я приведу в движение Землю» связывается с изобрете-
нием «харистиона» (нечто вроде десятичного рычага или весов) — прибора,
который под названием «карастуна» был предметом исследований арабских
и средневековых механиков, а у французского историка науки Дюэма изо-
бретение «харистиона» приписывается сыну известного астронома Птолемея.
По видимому, и Атеной, и Симпликий называли прибор Архимеда послед-
ним словом механической пауки их времени.
2е. Свидетельство Евстафия сомнительно и в том отношении, что гре-
ческое слово употреблялось для обозначения и винтовой линии, и спи-
рали (о которой Архимед действительно писал), так что смешение в этом
случае вполне вероятно.
III
Греческая геометрия в то время, когда к ее изучению приступил Архи-
мед, была уже вполне сложившемся дисциплиной. Она уже имела свою кано-
ническую книгу — дошедшие до пас «Начала» Евклида, завершившие собой
целую эпоху, в течение которой вырабатывалась стройная система греческой
2 Архимед
18
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. Н. ВЕСЕЛОВСКОГО
геометрии. Можно отметить следующие три характерные черты грече-
ской геометрии: это, во-первых, геометрические построения при помощи
циркуля, во-вторых, воззрение на геометрические фигуры и тела как на
некоторые величины и, наконец, в-третьих, строгие логические доказатель-
ства в изложении геометрии.
Геометрические построения при помощи циркуля, по всей видимости,
были введены в ионийской геометрической школе, из представителей кото-
рой нам известны Фалес и Эноннд Хиосский. Ионийская школа была тесно
связана с вавилонской наукой, откуда были заимствованы и космологи-
ческие представления милетцев, и астрономические предсказания затмений,
и знаменитая теорема Фалеса о вписанном в круг угле, опирающемся на диа-
метр, и, по-видимому, даже само употребление циркуля для геометрических
построений. Результаты работ этой школы сохранились в первой половине
книги I «Начал» Евклида и в большей части теорем книги III; характер-
ными для нее являются исследование вписанных в круг прямолинейных
фигур*), понимание равенства фигур в нашем современном смысле как сов-
падающих при наложении и, наконец, отсутствие метрических элементов
(одно и то же слово aspi^epeia употреблялось щл« обозначения и всей окруж-
ности, и какой-нибудь ее части — дуги).
Метрические понятия разрабатывались во второй греческой школе,
которая восходит к Пифагору. Основным понятием пифагорейской мате
матики было число, которое мыслилось материально как собрание единиц—
монад. Из этих монад те, которые обладали положением, представляли маши
точки, те же монады, которые были лишены положения, представляли наши
арифметические единицы. Геометрия пифагорейцев была своего рода отде-
лом арифметики, учением о специальных группировках единиц в виде квад-
ратов, прямоугольников, линий, многоугольников, кубов, параллелепипе-
дов и т. д. Понятие равенства фигур и тел в этой школе совпадало с нашим,
понятием о равновеликости. Наиболее характерными чертами пифагорей-
ской геометрии являются преобразования равновеликих фигур (квадратура,
«приложение (ларароЛг) площадей», то есть построение на данной прямой
прямоугольника, равновеликого заданной площади, и т. п.) и своеобразный
математический атомизм, тесно связанный с идеей целочисленности отноше-
ний между геометрическими величинами. Первоисточник пифагорейской
математики мы можем искать в Египте с его модулярной теорией архитек-
туры, где размеры всех деталей здания определялись через отношения
к некоторой длине, взятой за единицу,— модулю. Если египетские жрецы
могли сказать историку Геродоту (Г век до п. з.), что площадь грани Хеопсо-
вой пирамиды равняется квадрату, построенному на высоте пирамиды, то
они могли сказать то же самое и Пифагору во время пребывания последнего
в Египте**), а это уже представляет первый пример употребления средней
пропорциональной.
Если первые две характерные черты греческой геометрии имеют негре-
ческое происхождение, то третья — введение логических доказательств —
является специфически греческой; по существу, именно оно сделало геометрию
настоящей наукой, а не только собранием практических правил. Если вави-
лонские и индусские математики дали очень точные приближенные значе-
ния для квадратного корня из двух, то только греки могли доказать, что
отношение длины диагонали квадрата к стороне последнего не может быть.
*) Характерно, что диагональ квадрата или прямоугольника Евклид называет диаметром.
.**) У нас нет серьезных оснований для сомнений в пребывании Пифагора в .Египте (см. ком-
ментарии к третьему тому русского издания «Начал» Евклида, М.. 1050, стр. 297—-299).
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. II. ВЕСЕЛОВСКОГО
19
выражено точно при помощи отношения двух целых чисел; таким образом,
родилось понятие о несоизмеримых отношениях.
Открытие иррациональности квадратного корня из двух имело очень
важное значение в истории греческой математики. Оно нанесло такой удар
пифагорейской философии, от которого последняя уже нс могла оправиться.
Оказалась неверной ее исходная идея — математический атомизм,— и пифа-
горейская школа со второй половины V века начинает быстро вырождаться,
обращаясь в ту математическую мистику, которая характерна для пифа-
горейцев эпохи Платона, много воспринявшего от идеалистической фило-
софии пифагореизма. После крушения пифагореизма греческая математика
получает определенный уклон в сторону геометрии, ибо если нельзя совер-
шенно точно вычислить у 2, то можно всегда построить и его, и все другие
квадратные иррациональности; таким образом, ионийские методы снова
выступают на первый план; во второй книге «Начал» Евклида обыкновен-
ные алгебраические преобразования трактуются чисто геометрически,
создается столь характерная для греков и хорошо заметная также и у Архи-
меда геометрическая алгебра.
Объединителем ионийской и пифагорейской геометрии выступил в конце
V века до и. э. Гиппократ Хиосский, автор первого учебника геометрии типа
«Начал» Евклида. Символом такого объединения является впервые поста-
вленная Гиппократом задача о квадратуре круга — построении квадрата,
равновеликого данному кругу: чисто пифагорейское представление о квад-
ратуре соединяется с употребительной у ионийцев фигурой круга (следы
употребления круга в пифагорейской геометрии нам совершенно неизвестны).
Поставленная Гиппократом задача о квадратуре круга была одним из пред-
метов геометрических исследований Архимеда; последний в сочинении
«О спиралях» дал способ построения прямой, длина которой равна длине
окружности некоторого круга, а в «Измерении круга» вычислил (конечно,
приближенно) отношение между длинами окружности круга и его диаметра.
После крушения идеи целочисленности отношении между элементами
геометрических фигур греческая геометрия конца V и начала IV веков до
н. э. занялась исследованием квадратичных иррациснальностей, правильных
многоугольников (в частности, пятиугольника и связанного с ним понятия
о золотом сечении) и, наконец, пяти правильных многогранников. Этот
этап развития греческой математики тоже, отразился в творчестве Архимеда,
который занимался обобщением теории правильных многогранников (три-
надцать архимедовых полуправильных многогранников); сюда же можно
отнести материал «Стомахия», в котором идет речь о слежении фигур из раз-
личных заданных элементов и о разделении площади на части, находящиеся
с пой в рациональных отношениях. Нужно, однако, иметь в виду, что то, что
для пифагорейцев представляло предмет серьезных исследований, у Архимеда
разрабатывалось п связи с математической игрой типа наших головоломок.
Математический атомизм Пифагора был также отправной точкой иссле-
дований великого материалиста древности Демокрита, который высоко ста-
вил самого Пифагора. Однако материалистическая философия Демокрита
была. диаметрально противоположной пифагорейскому идеализму. Если
у Пифагора основой было «число», применение которого к физическим явле-
ниям приводило к математическому атомизму, то отправной течкой всей
философии Демокрита были реальные физические атомы — «неделимые»,
из которых составляются все тела природы, в том числе и математические,
тела и фигуры. Даже в математике Демокрит пошел дальше Пифагора; он
рискнул определить объем нирамиды и конуса при помощи разбиения на
весьма малые элементы — «неделимые». Архимед хорошо знал великого
20
ВСТУПИТЕ,! |,ПАЯ СТАТЬЯ И. II. ВЕСЕЛОВСКОГО
атомиста и с похвалой упоминает его в «Эфоде»; однако атомистические ме-
тоды он считал пригодными лишь для предварительных исследований, после
чего полученные геометрические предложения должны были доказываться
при помощи строго логических методов; в математике учителем Архимеда
был пе Демокрит, а Евдокс-
Евдокс Книдский (около 410—356 гг. до п. э.) является одним из вели-
чайших математиков всех времен и народов. Трудно переоценить заслуги
этого математика, результаты работ которого мы имеем в V, VI, второй
половило XI и в ХП книгах «Начал» Евклида. В книге V «Начал» излагается
евдоксова теория отношений для несоизмеримых величии, полное значение
которой было попито в широких математических кругах лишь в XIX веке
мосле создания Дедекиндом теории иррациональных чисел. Евдокс построил
первую кинематическую модель планетных движений (гомоцентрические сфе-
ры Евдокса), положил начало сферической геометрии. Он же, по-видимому,
дал тс методы определения сравнительных величин и расстояний Солнца,
Лупы и Земли, которыми впоследствии воспользовался «Коперник антично-
го мира» Аристарх Самосский (III век до и. э.). В геометрии Евдокс создал
метод исчерпывания, который для Архимеда был единственным строго науч-
ным методом определения площадей и объемов криволинейных фигур и тел.
Поскольку евдоксов метод исчерпывания по всегда правильно пони-
мается, не будет лишним более детально рассмотреть его сущность. Теория
Евдокса дошла до пас в книгах XI (вторая половина) и XII «Начал», где
методом Евдокса доказываются следующие теоремы:
1) Площади двух кругов относятся, как квадраты диаметров.
2) Объемы двух треугольных пирамид с равными высотами относятся,
как площади оснований.
3) Конус равен третьей части цилиндра с теми же основанием и высотой.
4) Объемы двух равновысоких конусов или цилиндров относятся, как
площади их оснований.
Г>) Объемы подобных конусов или цилиндров относятся, как кубы их
диаметров.
Для нашей цели достаточно будет проанализировать доказательство
одной из этих теорем, хотя бы первой из вышеупомянутых, поскольку метод
доказательства всех их является, по существу, одним п тем же. Этот анализ
полезно будет провести, сопоставляя рассуждения Евдокса с современным
доказательством.
Мы сначала определяем площадь круга как предел площадей вписанных
и описанных многоугольников при неограниченном удвоении их сторон;
Евдокс ограничивается лишь вписанными многоугольниками и опирается
при доказательстве на следующие два предложения: 1у. Если от некоторой
величины отнять больше половины, от остатка тоже отнять больше поло-
вины и так делать постоянно, то можно получить остаток, меньший любой
заданной величины. 2Э. Площадь треугольника, вписанного в сегмент, больше
половины площади этого сегмента. Евдокс доказывает, что разность между
площадью круга и площадью вписанного в этот круг многоугольника при
неограниченном удвоении числа стороп последнего может быть сделана мень-
ше любой заданной величины.
Мы доказываем, что площади подобных вписанных многоугольников
относятся, как квадраты диаметров; Евдокс делает то же самое.
После этого мы говорим, что если две переменные величины находятся
все время в одинаковых отношениях, то в тех же самых отношениях будут
находиться и их пределы, так что, поскольку площади двух подобных
вписанных многоугольников относятся, как квадраты диаметров описанных
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. Н. ВЕСЕЛОВСКОГО
21
около них кругов, то, следовательно, площади этих кругов толю будут отно-
ситься, как квадраты их диаметров. При этом паше исходное положение
о переменных и их пределах долгое время принималось почти за аксиому.
Евдокс же доказывает положение, равносильное нашему.
Доказательство Евдокса может быть изложено следующим образом.
Пусть мы имеем две последовательности величии
«1, «з......
Ь.,, &3, .... bIL, ...,
соответственные члены которых связаны соотношением а^—кЪ^ где к —
некоторое постоянное пиело.
При увеличении и члены первой последовательности неограниченно
приближаются к некоторой величине Л’„, а члены второй последователь-
ности точно так же приближаются к величине Sb, оставаясь все время меньше
своих соответственных пределов. Требуется доказать, что эти пределы
Sa и Sb будут тоже связаны соотношением
sa-k.sb.
Допустим, что это неверно, по одна из этих величин, например 3',.,
будет меньше, чем k-,Sb, и равна Т:
[Sa—T<k-Sb.
Увеличивая п, мы всегда можем добиться, чтобы разность Sb—bn сде-
в
лилась меньше любого заданного числа —:
К
Sb
Отсюда
kbn > kSb — е.
Так как число е может быть выбрано сколь угодно малым, то мы всегда
можем сделать, чтобы
кЪп>Т.
Но ап—кЪп-, следовательно,
<in>T = Sa,
что невозможно, ибо величина ап приближается к своему пределу, оставаясь
всегда меньше его. Таким образом, мы показали, что
Л а kSb.
Представив основное равенство
«П =
в виде
' - Ьп=-^-ап^к'ап,
мы можем аналогично показать, что
Sb>k’Sa,
22
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. Н. ВЕСЕЛОВСКОГО
ИЛИ . .
kSb>Sa.
Оба эти неравенства показывают то, что требовалось доказать:
kSb = Sa.
Рис, 1.
У Архимеда мы можем проследить дальнейшую эволюцию метода
Евдокса.
Во второй (чисто математической) части «Квадратуры параболы» Архи-
мед, совершенно так же как и Евдокс, пользуется последовательностью вели-
чин, приближающихся к предельной величине снизу — площадь параболы
постепенно «исчерпывается» вписываемыми в рассматриваемый сегмент тре-
угольниками. Но уже в механической части доказательства (первой) Архи-
мед заключает исследуемую площадь между двумя суммами трапеций,
из которых одна больше, а другая меньше ее. В трактате «О inapo и цилиндре»
Архимед показывает, что отношение ука-
занных двух сумм может быть сделано
сколь угодно близким к единице. В сле-
дующих за этим произведениях «О спира-
лях» и «О коноидах и сфероидах» доказа-
тельство приобретает другой вид: Архимед
показывает, что разность рассматриваемых
двух сумм может быть сделана сколь
угодно малой. Так как имеппо эта форма
метода исчерпывания применяется н в
«Измерении круга», то мы получаем осно-
вание думать, что «Измерение круга» напи-
сано не лозжо двух последних упомяну-
тых произведений (в трактате «О спиралях» Архимед дает геометриче-
ское построение прямой, длина которой равняется длине окружности),
и во всяком случае пе раньше двух книг «О шаре и цилипдре».
К Евдоксу же, или во всяком случае к его школе, следует отнести и соз-
дание совершенно новой отрасли геометрии, а именно теории кривых вто-
рого порядка, пли, если пользоваться термином греческой математики,
конических сечений.
Причины, вызвавшие к жизни этот новый отдел математики, можно
видеть в следующем.
Одним из наиболее важных вопросов геометрии V века было определе-
ние, или, лучше сказать, сравнение между собой различных площадей. Вся-
кий многоугольник можно разбить на треугольники, площадь каждого тре-
угольника равна площади прямоугольника со сторонами, равными основа-
нию и половине высоты. Чтобы представить площадь многоугольника в виде
одной фигуры, надо уметь складывать друг с другом площади различных
прямоугольников, а для этого нужно уметь строить их па одном основании,
после чего суммирование площадей приводится к простому суммированию
высот. Операция «приведения площадей к одному основанию» называлась
у греков «приложением (лараРоА./;)» и производилась так:
Пусть OABG — заданный прямоугольник (рис. 1), ОТ) — то осно-
вание, к которому нужно «приложить» этот прямоугольник. Продолжаем НО
и откладываем на ее продолжении OD, затем дополняем прямоугольник
ОПТА и проводим в нем диагональ ТО до пересечения в точке Н с продол-
жением другой стороны GB заданного прямоугольника. Получив точку .11,
дополняем прямоугольник DJTZB — продолжения сторон АО и ВО выделят
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. П. ВЕСЕЛОВСКОГО
23
в нем прямоугольник 0DE7Jy который и будет искомым; он построен па осно-
вании OD и имеет площадь, равную площади заданного прямоугольника
OABG. Алгебраически, нахождение второй стороны ОЕ, как нетрудно видеть,
сводится к нахождению четвертой пропорциональной для линий О А, ОВ и 01):
др _ О А ОБ
ОВ ’
При помощи «nagapoZr» любой многоугольник может быть преобразован
в прямоугольник. Дальнейший шаг на этом пути заключался в преобразова-
нии полученного многоугольника в квадрат. Эта операция выполнялась при
помощи нахождения третьей, или, как мы теперь гово-
рим, средней пропорциональной, равносильной реше-
нию уравнения
. ж2 — ab,
где а и b — стороны заданного прямоугольника, а
х — сторона равного ему квадрата. При помощи
упомянутых пропорциональных можно было построить
квадрат, площадь которого равна площади любого
многоугольника, так что оставалось лишь сравнивать
между собой различные квадраты. Для этого строился
ряд квадратов, площади которых относились бы как
числа натурального ряда. Если некоторый квадрат мы
принимаем за единицу (рис. 2), то квадрат, равный двум,
получался на диагонали |/ 2 этого квадрата. Чтобы Рис- 2-
построить квадрат, равный трем, нужно найти гипотенузу
прямоугольного треугольника, катеты которого равняются стороне =1 и диа-
гонали - у 2 первого квадрата. Продолжая таким образом, можно получить
сколько угодно квадратов, образующих натуральный ряд чисел. Существо-
вание такой операции доказано для древних египтян, употреблявших два
локтя в 20 и в 28 дюймов (чтобы удвоить данный квадрат, или вообще данную
площадь, надо размеры его, измеренные в двадцатидюймовых локтях, пере-
строить в двадцативосьмидюймовые: отношение 28: 20=14 : 10—1,4 = р 2);
ее знали вавилоняне, помещавшие в своих строительных справочниках
довольно точное значение у 2; ее применяли индусы первого тысячелетия
до н. э., которым приходилось, сохраняя форму жертвенника, увеличивать
его площадь от 2 до 7 раз.
Когда эта теория была построена, встал вопрос о распространении ее
на многогранники и в первую очередь на параллелепипеды. Первым шагом
на этом пути было построение натурального ряда кубов и в первую очередь
построение куба, равного удвоенному данному кубу. Необходимость реше-
ния этой задачи вызывалась еще тем, что в самом конце V века возникла
метательная артиллерия и для увеличения дальности полота выбрасываемых
стрел и камней требовалось пропорциональное увеличение объема упругих
тяжей, приводивших в движение катапульту.
Уже Гиппократ Хиосский показал, что задача удвоения (или вообще
увеличения в произвольное число раз) куба может быть выполнена при
номо1ци нахождения двух средних пропорциональных ж, у между задан-
, а
ными величинами а и о, отношение -р которых представляло то, в котором
следовало увеличить объем заданного куба:
а: х~ х: у == у : Ь.
24
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И- Н. ВЕСЕЛОВСКОГО
Эта задача могла быть решена при помощи пересечения каких-нибудь
двух из трех следующих кривых:
ж2 = ау, у2 — Ьх; ху — аЬ.
Первые две представляют параболы с взаимно перпендикулярными
осями, а третья --- равностороннюю гиперболу. Такова, конечно, точка
зрения современного нам математика, владеющего в полной мере алгебраи-
ческим знакоположением; для нас уравнение является гораздо более удоб-
ным к употреблению, чем изображаемая им кривая: для греков же, пе имев-
ших такого символического аппарата, любивших конкретность и нагляд-
ность, наоборот, кривая линия
была более удобным орудием для
математических и сел едований.
Греки пользовались двумя
способами получения новы х кри-
вых. Во-первых, кривая могла
быть образована движением
некоторой точки; первым при-
мером таких «геликоидальных»,
как их называли греки, кривых
была квадратриса софиста Гип-
пия Элидского (V век до и. э.),
придуманная им, по всей види-
мости, для деления угла на про
пзвольпое число частей. Во-вто-
рых, кривую можно было полу-
чить, рассекая какую-нибудь из-
вестную кривую поверхность: это были так называемые «выгнутые» (хпрлблш)
кривые. Мы знаем, что Евдокс решил задачу об удвоении куба именно при поме
щи таких xctpnuAai ypappat. Решение его до нас по дошло, но его брат и ученик
Мепехм решал задачу при помощи пересечения двух парабол или гиперболы
с параболой, и в «Конических сечеппях» Аполлония (книга I, определение 4
и сл.) под именем харлоХш урацаей понимаются именно конические сечения.
Таким образом, именно Евдокс указал один из способов, которым могли
быть получены соответствующие кривые; они получались при помощи сече-
ния различных конусов, образующие которых яри вершине составляли пря-
мой, тупой или острый угол.
Известный историк математики Цейтсн очень убедительно рисует кар-
тину получения параболы у2—2рх как «сечения прямоугольного конуса»;
под этим именем знает параболу Архимед; оно употреблялось вплоть до
Аполлония, который первый ввел современное привычное нам название.
Возьмем конус OEF (рис. 3) с прямым углом при вершине О, пересе-
чем его плоскостью, проходящей через точку А и перпендикулярной к обра-
зующей ()Е\ эта плоскость в сечении с поверхностью конуса дает параболу
NAP, ось симметрии которой будет прямая AKL — сечение проведенной
плоскости с другой, проведенной через ось конуса перпендикулярно к пер-
вой секущей плоскости. Следуя современной терминологии, будем назы-
вать абсциссами х расстояния А К, AL, измеряемые по этой оси,
а перпендикулярные к ней прямые, вроде LM'— ордината м и у *).
♦) Последнее слово представляет переделку латинского ordinatim applicatac, что в свою очередь
является переводом греческого иаюхуцёуал, проведенные правильным, упорядоченным
образом; так назывались прямые, перпендикулярные к оси параболы, проведенные до пересечении
с кривой, или вообще половины корд, соответствующих какому-нибудь диаметру.
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. Н. ВЕСЕЛОВСКОГО
25
Через какую-нибудь точку Л оси параболы проводим плоскость, пер-
пендикулярную к оси конуса; она в пересечении с конической поверхно-
стью даст окружность CMD, и мы по известному свойству окружности можем
написать:
у* = ЕМ* = СЕЕП_]
Но для гипотенузы CL равнобедренного прямоугольного треугольника ACL
имеем
CL = ЛЕ\/ 2;’
точно так же, если через вершину А перпендикулярно к оси конуса про-
вести АВ, то
LD -_-AB -=AKV 2.
где точка А' представляет пересечение оси AKL параболы с осью ОК конуса.
Таким образом, если положить ЛК- ~р, то получим
г/2 - Я Л |Л2 ЛК\/ 2 =- 2рх,
где x=AL — абсцисса точки М параболы.
Правильность этой реконструкции Цейтена подтверждается древней
терминологией: у Архимеда параметр р=ЛК параболы называется ps/Qi
той a£ovog — прямой, проведенной до оси, т. е. до оси того конуса, сечение
которого образует нашу параболу.
Самоназвание «парабола»связано с операцией «приложения» (ларароЛт|'):
площадь квадрата у2, будучи «приложена» к прямой 2р как к основанию,
дает высотой абсциссу х. Остальные две кривые связаны с так называемыми
«приложениями с недостатком или с избытком»; возможно, одпако, что сна-
чала были исследованы геометрические свойства тех кривых, которые полу-
чаются в сечениях тупоугольного и остроугольного конуса, а потом уже
сопоставлены с указанными типами «приложений».
Пусть OEF (рис. 4) будет осевое сечение конуса с тупым углом при вер-
шине О, а прямая ОК — его ось. Через какую-нибудь точку А проведем
плоскость, перпендикулярную к образующей ОЕ; эта плоскость в сечении
с поверхностью конуса образует кривую AAJK.
Продолжим другую образующую OF конуса до пересечения в точке А'
с прямой AQ — линией пересечения проведенной секущей плоскости с осе-
вым сечением OEF конуса; прямая AQ, очевидно, будет осью симметрии
нашей кривой. Возьмем на этой оси какую-нибудь точку L на расстоянии
х от вершины и попытаемся найти связь между абсциссой х и соответ-
ствующей ей ординатой y~~LM нашей кривой. Через точку L перпендику-
лярно к оси конуса проведем плоскость, которая в сечении с поверхностью
конуса образует круг с диаметром CD. Тогда
\y2^LM^CLLD.\
Так как СА перпендикулярна к AQ, a CD перпендикулярна к DQ, про-
веденной параллельно оси конуса, то все четыре точки С, A, D, Q будут
лежать на окружности, построенной па CQ как па диаметре; тогда по свой-
ству секущих в круге, проведенных через одну точку, будем иметь
. CL LD — AL-LQ.
Если К — точка пересечения. AQ с осью конуса, прямая АВ парал-
лельна CD, а ВР параллельна оси конуса, то из подобия треугольников
26
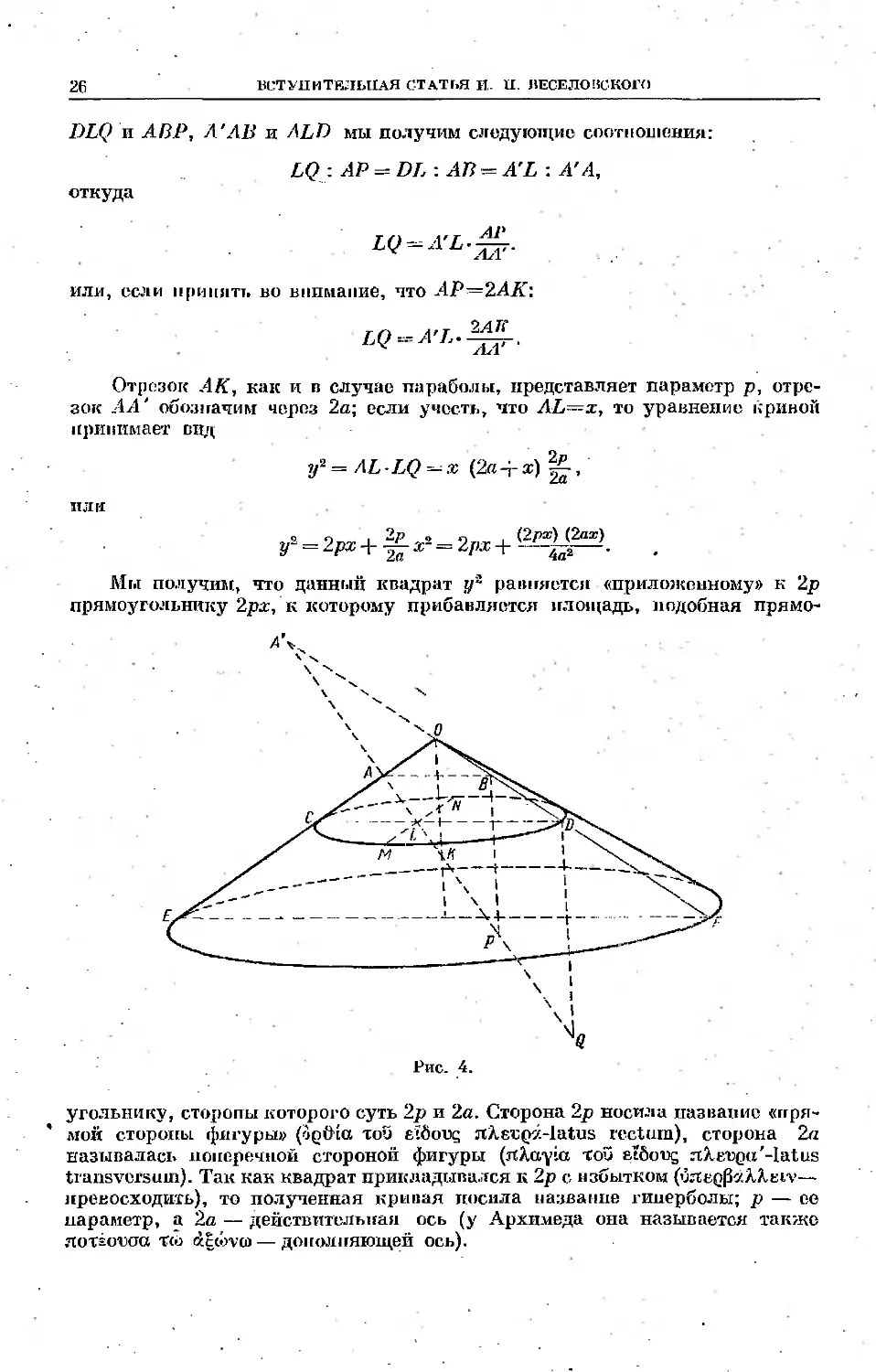
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. II. ВЕСЕЛОВСКОГО
DLQ и АВР, Л'АВ и ALT) мы получим следующие соотношения:
LQ : АР -= DL : АВ = A'L : А'А,
откуда
LQ^A’L—.
х АЛ
или, если принять во внимание, что АР—2АК’.
Отрезок АК, как и в случае параболы, представляет параметр р, отре-
зок АА' обозначим через 2а; если учесть, что AL=x, то уравнение кривой
принимает вид
y*=AL LQ -x (2a-i-z)g-,
пли
,,2 9 nr 4- 2р т* 2 nr -I- (2рт> (2лж)
Мы получим, что данный квадрат уй равняется «приложенному» к 2р
прямоугольнику 2рх, к которому прибавляется площадь, подобная прямо-
угольнику, стороны которого суть 2р и 2а. Сторона 2р носила название «пря-
' мой стороны, фигуры» (opftia too etSoug лЛесра-latus rectum), сторона 2a
называлась поперечной стороной фигуры (rtXayia той etfioug rtlerpu'-latus
transversum). Так как квадрат прикладывался к 2р с избытком (илерраХХегу—
превосходить), то полученная кривая иосила название гиперболы; р — ее
параметр, а 2а — действительная ось (у Архимеда она называется также
яотаогоа T(o decovo — дополняющей ось).
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. II. ВЕСЕЛОВСКОГО
27
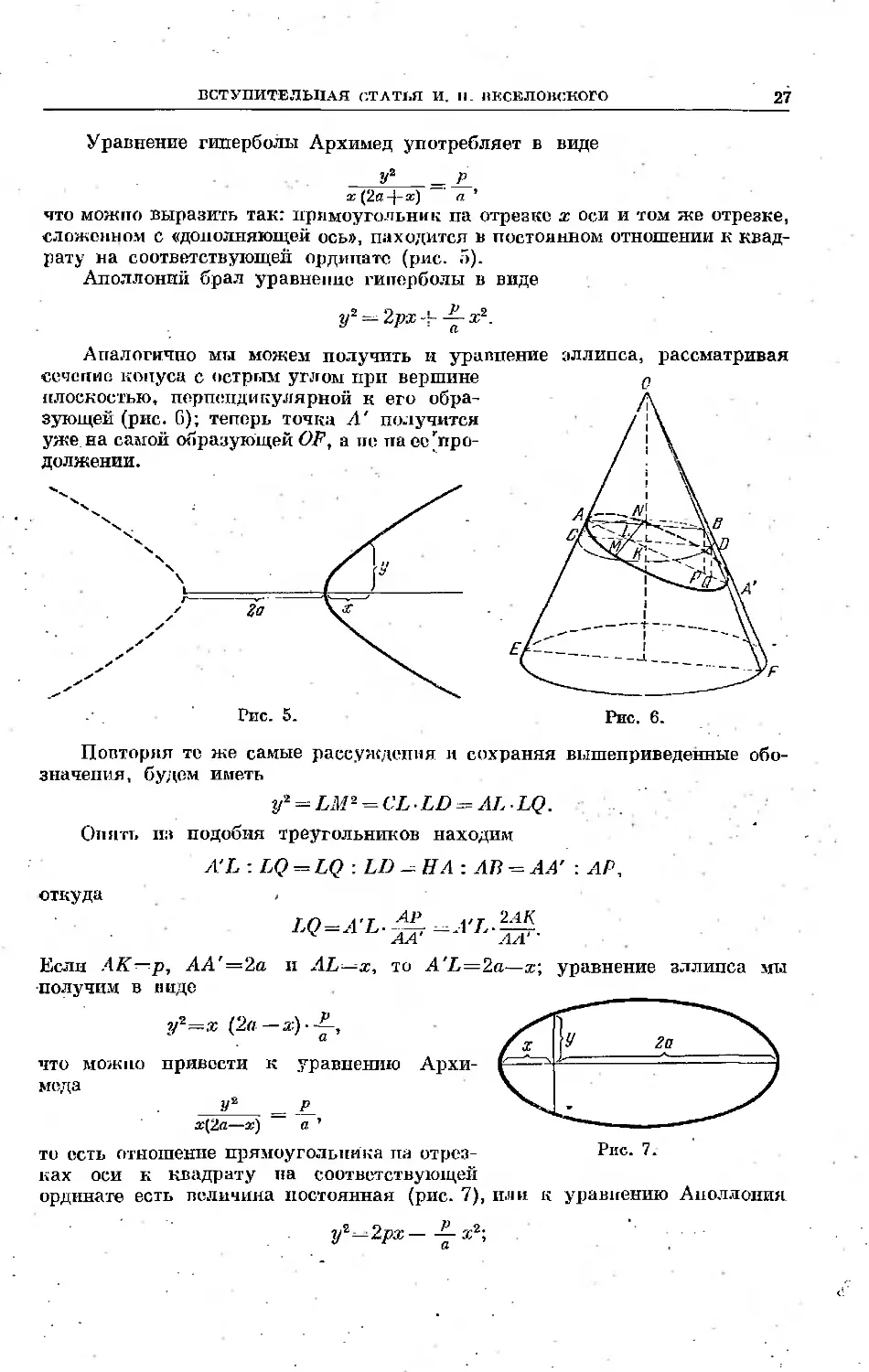
Уравнение гиперболы Архимед употребляет в виде
У2 _ Р
х (2а-}- х) а ’
что можно выразить так: прямоугольник па отрезке х оси и том же отрезке,
сложенном с «дополняющей ось», находится в постоянном отношении к квад-
рату на соответствующей ординате (рис. 5).
Аполлоний брал уравнение гиперболы в виде
у~ — 2рх X2.
Аналогично мы можем получить и уравнение эллипса, рассматривая
сечение конуса с острым углом при вершине
плоскостью, перпендикулярной к его обра-
зующей (рис. б); теперь точка Л' получится
уже на самой образующей OF, а не па ее'про-
должении.
Повторяя тс же самые рассуждения и сохраняя вышеприведенные обо-
значения, будем иметь
у2 = LM2 = CL • LD = AL LQ.
Опять из подобия треугольников находим
A'L : LQ = LQ : LD HA : АВ ~= АА' : АР,
откуда
LQ=A'L-
4 АА
Если /1А'—р, АА'=2а и AL^x, то
получим в виде
у2==х (2а—
что можно привести к уравнению
меда
у2 _ р_
х(2а—х) а ’
то есть отношение прямоугольника па
ках оси к квадрату па соответств
ординате есть величина постоянная (
. 7), или к уравнению Аполлония
у2—2рх---х2;
28
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. И. ВЕСЕЛОВСКОГО
так как теперь при «приложении» у2 к прямой 2р «недостает» (^aAsihei) пло-
щади, подобной прямоугольнику со сторонами 2а, 2р, то полученная кривая
носит название «эллипса». Прямая 2а является большой осью этого эллипса.
Если положить х—а, то получится выражение для малой оси эллипса. Если
через b обозначить ее половину, то дни будем иметь
Ь2=2ра— ра=ра,
откуда получается известное выражение для параметра эллипса:
Классическими книгами ио теории конических сечений во времена
Архимеда были «Начала теории конических сечений», составленные Евкли-
дом, а также друган книга, принадлежащая геометру Аристою. Па ту или
другую из этих книг ссылается Архимед везде, где оп без доказательства
приводит теоремы, полученные своими предшественниками. Обе эти книги
до нас, не дошли, но о содержавшемся в них материале мы можем составить
себе представление, читая первые четыре книги «Конических сечений Апол-
лония», в которых он резюмирует труды предшествующих ему авторов.
Во всяком случае Архимеду были известны следующие свойства кони-
ческих сечении:
1°. Середины хорд, параллельных какому-нибудь направлению, лежат
на одной прямой — диаметре, сопряженном этому направлению. Диаметр
в общем случае не будет перпендикулярным к сопряженным с ним хордам,
но в косоугольных координатах с началом в точке пересечения диаметра
с кривой и осями, направленными соответственно по диаметру и касатель-
ной к кривой в точке — начале координат, уравнение кривой будет иметь,
тот же вид, только соответствующий этому направлению параметр р будет
иметь другую величину.
Если учесть, что Архимед знал, что касательная к коническому сече-
нию, проведенная в конце диаметра, будет параллельна хордам, сопряжен-
ным с этим диаметром, то можно сказать, что Архимеду были известны урав-
нения всех трех кривых второго порядка, отнесенных к косоугольным осям
координат, а именно диаметру и касательной в его вершине.
2°. Бее диаметры параболы параллельны. Но Архимед рассматривает
гиперболу как состоящую только из одной ветви; центр гиперболы и свой-
ства сопряженных диаметров были открыты только Аполлонием.
3°. Свойства касательных к коническим сечениям, а именно, что каса-
тельная к параболе пересекает ось в точке, расстояние которой от вершины
параболы равно абсциссе точки касания и что для эллипса это расстояние
будет больше, а для гиперболы — меньше соответствующей абсциссы. Затем
он знал, что поднормаль к параболе имеет постоянную величину.
4°. Если из какой-нибудь точки провести касательные к любому кони-
ческому сечению, а из другой точки внутри или вне кривой провести парал-
лельные зтим касательным две секущие, то произведения отрезков этих секу-
щих относятся, как квадраты параллельных им касательных.
5°. Существование асимптот у гиперболы, а также, что площадь прямо-
угольника па прямых, проведенных из какой-нибудь точки гиперболы парал-
лельно ее асимптотам до пересечения с последними, является величиной
постоянной (наше уравнение ату—const). Точно так же Архимед знал, что
отрезки касательной к гиперболе между точкой касания и асимптотами равны,
как можно видеть из найденного Евтокием доказательства Архимеда одной
леммы из второй книги «О шаре и цилиндре».
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. Н. ВЕСЕЛОВСКОГО 29
IV
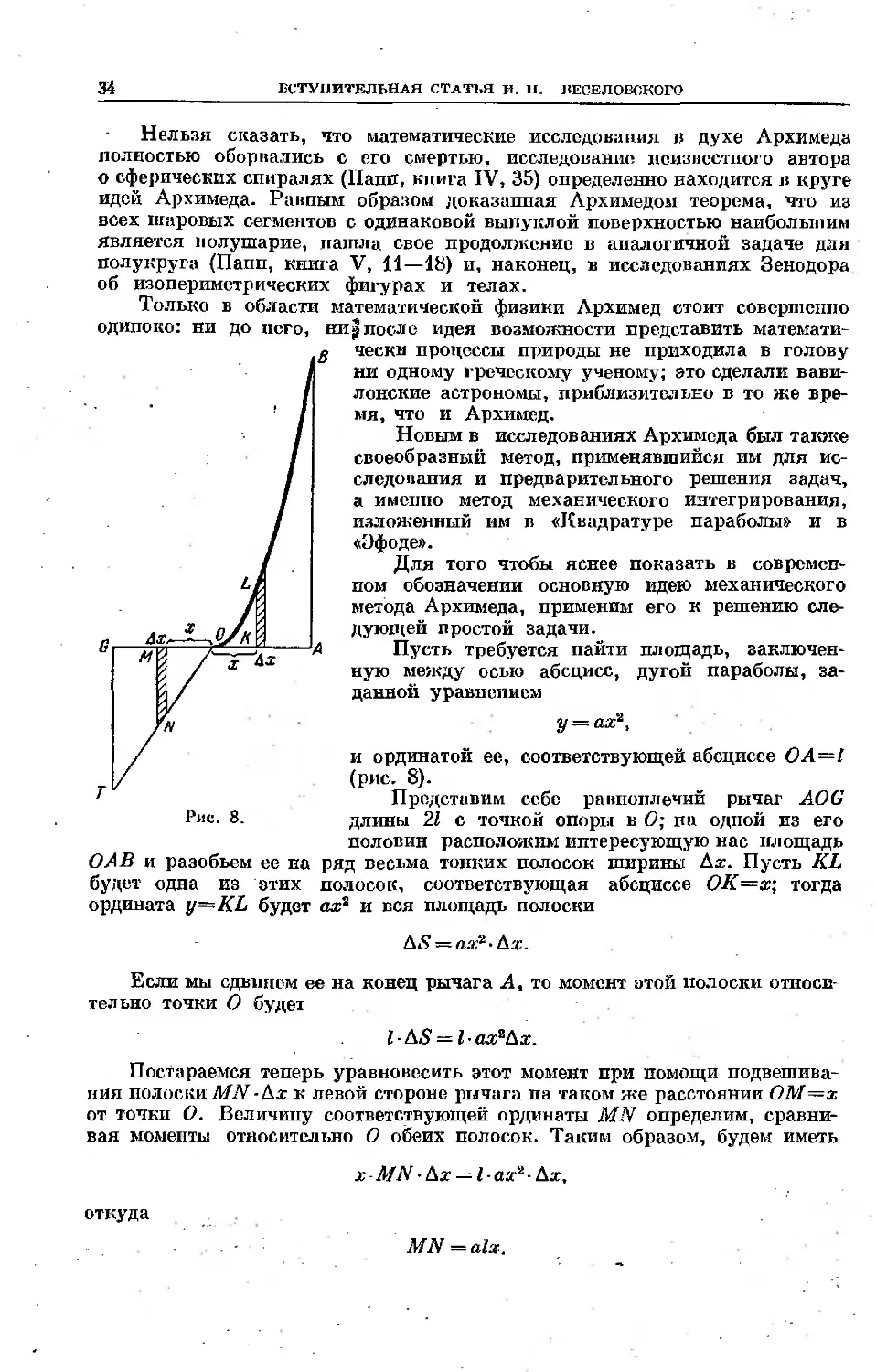
Новый период деятельности Архимеда начался, вероятно, после 240 г.
до и. э., когда с наступлением мира Архимед получил возможность побывать
в Александрин и завязать дружеские отношения с Эратосфеном и Колопом
(Архимеду в это время было уже около пятидесяти лет). За это время (при-
близительно тридцатые годы III века до н. э.) Архимед создал ряд произве-
дений, доставивших ему бессмертную славу. Первым из этих произведении
является «Квадратура параболы», написанная вскоре после смерти Конона
и открывающая ряд «посланий» Архимеда к ученику и другу Конона мате-
матику Досифсю, с которым Архимед, как видно из вступлений к посланиям,
поддерживал переписку. Эта «досифееиская» группа сочинений Архимеда
состоит из «Квадратуры параболы», первой и второй книг сочинения «О шаре
и цилиндре», составлявших первоначально два совершенно самостоятельных
произведения *), затем книги «О спиралях» и, наконец, сочинения «О конои-
дах и сфероидах». Порядок появления этих произведений легко устанавли-
вается на основе тех сведений, которые дают нам введения к этим посланиям.
Самым ранним произведением в этой группе является «Квадратура пара-
болы», представляющая, как можно видеть из вступления, первое послание
к Досифею, написанное после получения известия о смерти Конона. В этом
послании Архимед использует открытый им механический метод определе-
ния площадей и объемов геометрических фигур и тел, разнообразные при-
ложения которого он описывает позднее в своем «Эфоде». Из вступления
к «Эфоду» видно, что нахождение площади параболического сегмента было
первой задачей, решенной Архимедом при помощи механического метода.
За «Квадратурой параболы» идет первая книга сочинения «О шаре и цилин-
дре»; во вступлении к этой книге Архимед упоминает о посланном уже ранее
сочинении «Квадратура параболы». Задачи, исследуемые во второй книге
сочинения «О шаре и цилиндре», как видно из предисловия, были поста-
влены Архимедом еще до смерти Конона, равно как и те, которые были разо-
браны в первой книге; в этом сочинении «О шаре и цилиндре» Архимед обе-
щает «как можно скорее» прислать предложения, касающиеся спиралей
и коноидов. Как мы знаем из «Эфода», теоремы, касающиеся объема шара
и его частей, а также коноидов и сфероидов, были первоначально найдены
.механическим методом; однако в отличие от того, что было сделано в «Квад-
ратуре параболы», Архимед теперь дает только окончательный строго мате-
.матический вывод установленных теорем. После сочинения «О шаре и цилин-
дре» была написана работа «О спиралях», тема которой была дана Архимеду
еще Коионом. Во вступлении Архимед говорит, что после смерти Конона
уже «прошло много лет», однако тот факт, что Архимед работал над темой,
начатой им еще до смерти Конона, не позволяет понимать это «много» иначе
как 5—10 лет. В том же самом предисловии Архимед говорит о «Коноидах
и сфероидах» как о еще не посланной книге. Содержащиеся в этой работе
предложения доставили Архимеду при доказательстве много труда, так что
эта книга, которая по первоначальному плану должна была идти перед кни-
гой «О спиралях», оказалась самым последним произведением рассматривае-
мой группы: математические доказательства теорем, содержащихся в сочи
нении «О коноидах и сфероидах» Архимед нашел только после того, как им
ужо была решена поставленная задача относительно спиралей.
•) Предложения нерпой книги Папп цитирует просто как «О шаре и цилиндре», ив называя
книгу «первой».
30
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. И. ВЕСЕЛОВСКОГО
Все предложения, доказываемые в посланиях к Досифею, представляют
собой целостную группу. Как таковую их рассматривал и сам Архимед (см.
вступление к книге «О спиралях»), причем объединяющим звеном для Архи-
меда было то, что соответствующие задачи были поставлены им еще до смерти
Конопа и, по всей вероятности, обсуждались в переписке с последним,
а может быть, в той или другой мере и были поставлены Коионом Архимеду.
Вот это единство всей группы и не позволяет растягивать на слишком боль-
шой промежуток времени работу, произведенную Архимедом при решении
этих задач.
В отношении следующих произведений Архимеда мы находимся в не-
сколько более трудном положении, так как далеко не все из них дают доста-
точно материала, позволяющего нам совершенно точно определить их хро-
нологическую последовательность. Среди этих произведений можно выде-
лить «механическую» группу, состоящую из трех произведений: двух книг
«О равновесии плоских фигур», послания к Эратосфену о механических тео-
ремах (так называемый «Эфод») и, наконец, двух книг «О плавающих телах».
Что касается произведения «Равновесие плоских фигур», то, следуя за
Гейбергом, большинство исследователей (Хис, у нас С. Я. Лурье) считают
его самым ранним из дошедших до пас сочинений Архимеда и разбивают его
на два самостоятельных произведения: первую книгу, содержащую общие
теоремы о нахождении центра тяжести, и вторую книгу, касающуюся нахо-
ждения центра тяжести сегмента параболы, причем эта последняя поме-
щается после «Квадратуры параболы». Вряд ли молото согласиться с таким
разделением на две части рассматриасмого произведения. Во-первых, «Рав-
новесие плоских фигур» по структуре очень похоже на сочинение «О плаваю-
щих телах», которое тоже разбито па две книги, первая из них посвящена
общим теоремам, а вторая — одному частному вопросу, а именно условиям
равновесия плавающего сегмента параболоида. Во-вторых, первую книгу
«Равновесия» трудно рассматривать как самостоятельное произведение, спе-
циально посвященное вопросу о нахождении центра тяжести: в ней нет далее
определения понятия о центре тяжести, не рассматривается положение центра
тяжести круга, неправильного четырехугольника и вообще многоугольника;
по существу, даются лишь положения центров тяжести тех фигур (прямо-
угольник, треугольник, трапеция), которые нужны для доказательства теорем
второй книги; затем основную теорему — о равновесии рычага — Архимед
доказывает три раза: для соизмеримых и несоизмеримых прямоугольников
в первой книге и для криволинейных площадей, могущих быть приведен-
ными к прямоугольникам (квадрируемых) в предложении I второй книги.
Наконец, формально-математический характер самого произведения
не позволяет считать его первым наброском теории центра тяжести; есте-
ственнее всего считать основной целью этого произведения определение
пептра тяжести сегмента параболы, а первую книгу рассматривать как
своего рода введение. Само собой разумеется, что если рассматривать обе
книги как единое произведение, то они должны быть написаны после «Квад-
ратуры параболы». По .можно думать, что они паписаны и после «Коноидов
и сфероидов»: действительно, в последнем сочинении Архимед сформулировал
• новые определения подобия кривых второго порядка и как раз этими опре-
делениями он пользуется при доказательстве теорем второй книги (подроб-
ности см. в комментарии к рассматриваемому сочинению); кроме того, при
доказательстве предложения V второй книги «Равновесия плоских фигур»
Архимед пользуется предггожением XXXI «Коноидов».
Точно так же после «Коноидов» написан и «Эфод». Это вытекает из сле-
дующих соображений:
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. II.' ВЕСЕЛОВСКОГО
31
1°. Во вступлении к «Эфоду» Архимед, говоря о посылаемых в этом
сочинении новых теоремах, указывает, что они отличаются от найденных
им ранее теорем, в которых объемы коноидов, сфероидов и их частей срав-
нивались с объемами конусов и цилиндров.
2е. Последней леммой 11 «Эфода» является предложение, доказанное
в сочинении «О коноидах».
3°. В первом предложении «Эфода» содержится ссылка на сочинение
«О равновесии» и ряд лемм текстуально повторяют предложения первой
книги «Равновесия плоских фигур»; таким образом, получается, что «Эфод»
написан после «Равновесия плоских фигур».
Трактат «О плавающих телах» написан после «Коноидов», в тексте
которых находятся предложения XX HI и XXIV, являющиеся основными
при выводе условий равновесия плавающего сегмента параболоида. Далее,
во втором книге «О плавающих телах» цитируется сочинение «О равнове-
сии», в связи с определением центра тяжести сегмента параболоида; это.
позволяет думать, что «О равновесии плоских фигур» — первая часть более
общего сочинения «О равновесии» — была уже написана. Затем механи-
ческий способ определения центра тяжести сегмента параболоида дается
в предложении V «Эфода»; таким образом, вполне естественно предполо-
жить, что трактат «О плавающих телах» написан после «Эфода». То обстоя-
тельство, что вторая книга трактата «О плавающих телах» имеет вид незакон-
ченного сочинения, позволяет думать, что мы имеем дело с самым послед-
ним произведением Архимеда.
Два оставшихся произведения Архимеда «Измерение круга» и «Псам-
мит» своим характером резко выделяются из ряда остальных произведений
Архимеда; в пих па первое место выступает вычислительная сторона мате-
матики. Достоверно лишь то, что «Псаммит» написан после «Измерения
круга», поскольку в последнем сочинении имеется ссылка на первое. Что
касается «Измерения круга», то нужно отметить следующее:
1°. Одна из основных тем «Измерения круга» — определение длины
окружности — тесно связана с предложением XVIII книги «О спиралях»;
мы уже говорили выше, что форма, в которой применяют метод Евдокса,
является одинаковой в обеих рассматриваемых книгах.
2е. Во втором предложении «Эфода» упоминается о том, что площадь
круга равна площади треугольника, основание которого равно окружности,
а высота — радиусу (первое предложение «Измерения круга»); отсюда видно,
что Архимед во время написания «Эфода» во всяком случае уже работал над
этим вопросом.
3°. При доказательстве предложения ХП1 «Эфода» Архимед стоял на
пороге открытии центра тяжести полукруга, который ои обязательно полу-
чил бы, если бы знал числовую величину площади полукруга. То обстоя-
тельство, что в предложении XIV он избрал обходный путь для доказатель-
ства теоремы об отношении площади полукруга к квадрату на диаметре при
помощи введения вспомогательной параболы, позволяет думать, что число-
вая величина отношения окружности к диаметру была еще ему неизвестна,,
и это свидетельствует о том, что «Эфод» был написан до «Измерения круга».
Так как «Псаммит» посвящен умершему в 216 г. Гелону, сыну и сопра-
вителю царя Гисрона, то он должен был быть написанным до этого года.
Общий хронологический порядок сочинений примерно таков:
Г'. Квадратура параболы.
2°. О шаре и цилиндре.
3°. О спиралях.
4°. О коноидах и сфероидах.
32
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. Н. ВЕСЕЛОВСКОГО
5°. О равновесии плоских фигур.
6°. Эфод.
7°. О плавающих телах.
8'. Измерение круга.
ГГ. Псаммит *).
Первые четыре произведения относятся к периоду, когда Архимед
переходил от механики к математике, стараясь добиться наибольшей воз-
можной строгости доказательств, даже задерживая ради этой цели опубли-
кование уже полученных результатов, как это вмело место с «Коноидами».
Следующие три произведения относятся к новому периоду деятельности
Архимеда, когда он выступил в роли создателя математической физики,
прилагая строгие математические теории к объяснению физических явле-
ний. Эту сторону деятельности Архимеда тем более важно отметить, что,
по мнению Плутарха, Архимед был ученым, готовым забыть ради матема
тики и практическую деятельность, и материальный мир, и прозу окру-
жающей жизни. На самом деле вышедший из технической среды Архимед
снова в нее вернулся, причем он сделал это не только под влиянием грозив-
шей родному городу опасности.
Таким образом, в научной деятельности Архимеда мы можем различить
следующие периоды:
1°. Период инженерной деятельности — введение понятия о центре
тяжести и его определение в случае простейших фигур и тел.
2е. Период посланий к Досифею — разработка методов определения
площадей и объемов математических фигур и тел.
3°1 Период запцтий математической физикой — установление матема-
тической теории рычага, центров тяжести и равновесия плавающих тел.
4е’. К последнему периоду относятся арифметико-астрономические
работы, которыми в дальнейшем нам еще придется заняться более детально;
пока же перейдем к описанию других сочинений Архимеда, дошедших до
пас а отрывках или в отдельных цитатах позднейших писателей.
Па первом месте мы должны поставить опубликованную в 1773 г. изве-
стным немецким писателем .Лессингом «Задачу о быках», принадлежность
которой Архимеду некоторыми исследователями оспаривается. Если она
действительно принадлежит Архимеду (таково мнение и автора этих строк),
то ее можно отнести к четвертому периоду деятельности Архимеда.
Затем по упоминаниям в «Математическом собрании» Паппа нам изве-
стно сочинение «О полуправильных многогранниках». Вероятно, в некото-
рой связи с этим произведением находится «Стомахий», от которого до пас
дошло дна отрывка: один в арабском переводе, а другой, открытый Гейбер-
гом в Константинопольском палимпсесте вместо с «Эфодом».
* Наконец, в «Метрике» Герона сохранилось несколько отрывков сочи-
нений Архимеда, посвященных измерению площадей и объемов правильных
и неправильных тел, которые тоже можно отнести к последнему периоду
деятельности Архимеда. К их числу принадлежат сочинения «О призмах
и цилиндрах» и «О неправильных поверхностях и телах».
К разряду астрономических работ Архимеда относятся «Катоптрика»,
«О величине года» и, наконец, «Об изготовлении небесной сферы».
Кроме того, в том же «Псаммите» Архимед упоминает еще об арифме-
тическом сочинении «Послании к Зевксиппу»nepi'agxti/v—«О началах», в кото-
ром излагались основы придуманной Архимедом системы суислепия.
*) Два последних произведения могли быть написаны и ранее (после 3° и 4°).
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. Н. ВЕСЕЛОВСКОГО
33
Арабские источники относят к Архимеду еще следующие произведения:
1) 6 круге, 2) О семиугольнике в круге, 3) О взаимно касающихся кругах,
4) О параллельных прямых, 5) О треугольниках, 6) О свойствах прямоуголь-
ных треугольников, 7) Данные.
Из этих книг нам в какой-то степени известно содержание «Книги о семи-
угольнике» по публикации немецкого исследователя Карла Шоя в 1927 г.
[22J. Рассмотрение этой книги показывает, что она в целом не принадлежит
Архимеду, но содержит ряд извлечений из сочинений Архимеда в перера-
ботанном виде. Оригинал этой книги был наиисап большим знатоком Архи-
меда, харрапским астрономом и математиком Сабитом ибн Курра (он же
написал «Книгу лемм», впервые изданную в 1(559 г. Фостером в латинском
переводе); возможно, что материал последней в какой-то мерс заимствован
из сочинения «О круге», доказательства из которого приводятся аль-Бируни
в «Книге нахождения хорд в круге»*).
Нам остается теперь дать общую характеристику математических дости-
жений Архимеда. Говорят, что Архимед был гений, далеко опередивший свое
время. Конечно, гениальность Архимеда оспаривать не приходится, но
нужно еще подчеркнуть, что вся математическая деятельность Архимеда
представляет непосредственное продолжение и развитие тех идей, которые
были заложены его предшественниками. Основная идея всей математической
деятельности Архимеда второго периода заключалась в определении пло-
щадей и объемов различных тел и фигур. Определение площадей много-
угольников удалось свести к определению площадей квадратов: оставалась
лишь площадь круга, которую сквадрировать не сумели. В области стерео-
метрии еще пифагорейцами была поставлена задача об объемах параллеле-
пипедов и призм; сведение их к кубам повлекло за собой постановку делий-
ской задачи. Исследования Евдокса показали, что определение объемов
пирамид, а следовательно и многогранников вообще, может быть сведено
к кубатурам, а нахождение объема конуса — к объему цилиндра, во времена
Евклида еще ничего не было известно ни об объеме, пи о поверхности шара.
Архимед показал, что определение поверхностей конуса, цилиндра **) и шара
может быть сведено к нахождению площади круга, что определение объе-
мов шара и его частей, а также объемов эллипсоида, гиперболоида и пара-
болоида вращения, тоже сводится к определению объема конуса, а следо-
вательно в конечном счете к определению объема цилиндра. Таким образом,
элементарными фигурами для Архимеда оказались квадрат и круг и куб
и цилипдр. Дальнейшей задачей исследования стало выражение площади
круга в виде некоторого прямоугольника, для чего понадобилось опреде-
лить длину окружности круга. Соответствующая задача была поставлена
и решена Архимедом в трактате «О спиралях» (предложение XV1II, дающее
построение прямой, равной длине данной окружности) и в «Изме-
рении круга», где та же задача решалась вычисление м. Для цилин-
дров соответствующая задача, по всей вероятности, была разрешена Архи-
медом в по дошедшем до нас сочинении «О призмах и цилиндрах». Таким
образом, были заложены основы измерения поверхностей и объемов; в не
дошедшем до нас сочинении «О неправильных поверхностях и телах» (упо-
мпниомом в «Метрике» Герона) Архимед дял практические способы и для
самого общего случая.
*) Перевод отрывка ив Бируни, а также «Книги о кругах», выполненный Б. А. Розенфельдом
помещен в этом издании.
•*) Обратите внимание на своеобразную формулировку в первой книге «О шаре и цилиндре»
предложений, в которых Архимед дает боковые поверхности цилиндра и конуса.
3 Архимед
34
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. II. ВЕСЕЛОВСКОГО
Нельзя сказать, что математические исследования в духе Архимеда
полностью оборвались с его смертью, исследование неизвестного автора
о сферических спиралях (Папп, книга IV, 35) определенно находится и круге
идей Архимеда. Равным образом доказанная Архимедом теорема, что из
всех шаровых сегментов с одинаковой выпуклой поверхностью наибольшим
является полушарие, нашла свое продолжение в аналогичной задаче для
полукруга (Папп, книга V, 11—18) и, наконец, в исследованиях Зенодора
об изоперимстрических фигурах и телах.
Только в области математической физики Архимед стоит совершенно
одиноко: ни до пего, ни^ после идея возможности представить математи-
чески процессы природы не приходила в голову
ни одному греческому ученому; это сделали вави-
лонские астрономы, приблизительно в то же вре-
мя, что и Архимед.
Новым в исследованиях Архимеда был также
своеобразный метод, применявшийся им для ис-
следонапия и предварительного решения задач,
а именно метод механического интегрирования,
изложенный им в «Квадратуре параболы» и в
«Эфоде».
Для того чтобы яснее показать в современ-
ном обозначении основную идею механического
метода Архимеда, применим его к решению сле-
дующей простой задачи.
Пусть требуется найти площадь, заключен-
ную между осью абсцисс, дугой параболы, за-
данной уравнением
у = ах2,
и ординатой ее, соответствующей абсциссе ОА—1
(рис. 8).
Представим себе равноплечий рычаг AOG
длины 21 с точкой опоры в О; па одной из его
половин расположим интересующую нас площадь
ОАВ и разобьем ее на ряд весьма тонких полосок ширины Ах. Пусть KL
будет одна из этих полосок, соответствующая абсциссе ОК=х‘, тогда
ордината y~KL будет ах2 и вся площадь полоски
Д5 = ах2 • Ах.
Если мы сдвинем ее на конец рычага А, то момент этой полоски относи-
тельно точки О будет
I AS = I ах2Ах.
Постараемся теперь уравновесить этот момент при помощи подвешива-
ния полоски MN Ах к левой стороне рычага па таком же расстоянии ОМ=х
от точки О. Величину соответствующей ординаты MN определим, сравни-
вая моменты относительно О обеих полосок. Таким образом, будем иметь
х - A/N • Ах = l-ах2- Ах,
откуда
MN = alx.
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. Н. ВЕСЕЛОВСКОГО
35
Поступая так с каждой полоской, мы получим на левом плече рычага
ряд полосок, непрерывно распределенных по длине GO. Так как ординаты
полосок па левом плече рычага будут пропорциональны расстояниям х,
то концы их расположатся по прямой линии ONT', величина последней
ординаты GT будет aZ2.
После того как распределение полосок по левому плечу OG рычага будет
закончено, мы получим, что вся интересующая нас площадь ОАВ, сосре-
доточенная на конце А, будет уравновешена треугольником OGT, прикреп-
ленным к стороне OG. Площадь этого треугольника равна
-^-aZM,
расстояние от вершины О его центра тяжести будет
Следовательно, сравнивая момент этого треугольника с моментом от во
сительпо О искомой площади S, сосредоточенной в А, мы будем иметь
О Z
откуда находим величину 5:
О
Но соответствующая абсциссе ОА=1 ордината будет al2=AB; таким
образом:
S = ±OA-AB,
О
то есть искомая площадь равна одной трети площади прямоугольника,
построенного на абсциссе ОА и конечной ординате АВ.
Мы видим, что успех вывода получается в результате понижения сте-
пени рассматриваемой кривой — нахождение площади, ограниченной
кривой 2-й степени и двумя прямолинейными отрезками, сводится к опре-
делению ц е п т р а тяжести площади, ограниченной кривой первой
степени, то есть прямом.
Этот механический метод, конечно, являлся индивидуальным достоя-
нием Архимеда, несомненно пришедшего к нему в результате своих предше-
ствующих занятий в области механики.
В этой связи уместно остановиться на вопросе об отношении Архимеда
к двум своим великим предшественникам Демокриту и Евдоксу. Их обоих
Архимед упоминает в своих сочинениях; во введении к «Эфоду» Архимед
говорит о Демокрите как о первом авторе, нашедшем теорему об объеме
пирамиды и конуса, а в первой книге «О шаре и цилиндре» оп, говоря о той
Mie самой теореме, упоминает только Евдокса. На основании этих фактов
проф. С. Я. Лурье выставил гипотезу о том, что после сочинения первой
книги «О шаре и цилиндре» Архимед «впервые познакомился с работами
Демокрита», на которые он «несомненно с жадностью набросился», оказав-
шись «у истоков того атомистического интегрирования, которое ему с тру-
дом и по частям приходилось реставрировать из отдельных намеков и прие-
мов в трудах по механике, написанных его предшественниками», и в кото-
рых он нашел «как раз то, что он искал и чего пе хватало ему в математике».
(С. Я. Лурье, «Архимед», стр. 138—139).
3*
36
ВСТУЛИТЕЛЫНЛП СТАТЬЯ И. II. ВЕСЕЛОВСКОГО
С- Я. Лурье можно сделать следующие два возражения:
Во-первых, он забывает, что своеобразный механический способ инте-
грирования был в полной мере использован Архимедом уже при написании
«Квадратуры параболы» и при доказательстве предложений первой книги
сочинения «О шаре и цилиндре», когда, как признает сам С. Я. Лурье,
Архимед «не знал еще трудов Демокрита».
Во-вторых, можно заключить, что Архимед был знаком с атомистиче-
ской математикой даже при написании первой книги «О шаре и цилиндре».
Во втором предложении первой книги «О шаре и цилиндре» Архимед
доказывает, что для двух данных неравных величии можно всегда найти две
такие неравные прямые, чтобы отношение большей прямой к меньшей было
меньше отношения большей величины к меньшей. Даваемое Архимедом
доказательство носит очень искусственный характер: если две заданные
величины суть А и В (А>В), то искомое отношение мы просто получили
бы, взяв отношение
(' Л—В\ г. . / .. . >4—
А-----—j '-В ,1ЛИ ----------— j .
Однако доказательство Архимеда, избегающее деления разности А~В
становится вполне целесообразным, если он учитывал возможность, что две
бесконечно близкие друг к другу величины А и В разнятся па одно неде-
лимое.
При доказательстве предложения IX этой книги Архимеду нужно пока-
зать, что выпуклая поверхность конуса между двумя образующими будет
больше площади треугольника, заключенного между теми же образующими.
Для этого он опирается на положение, что в трехграпной пирамиде одна
боковая грань всегда будет меньше суммы двух других граней. Соответ-
ствующее положение может быть очень легко усмотрено из следующего
рассуждения: так как одна сторона треугольника всегда меньше суммы двух
других, то же самое будет иметь место для каждого из тех треугольников,
на которые можно будет разбить пирамиду плоскостями, параллельными
основанию. Таким образом, или Архимед совершенно не думал о доказатель-
стве вспомогательной теоремы, считая ее очевидной, или же он употребил
изложенное доказательство по той простой причине, что другого доказатель-
ства пет и не может быть, так как указанная вспомогательная теорема
в общем случае является неверной (см. комментарий к этому
месту, стр. 451 —453); изложенного же доказательства Архимед не хотел поме-
щать, не считая его (и совершенно правильно) вполне строгим ввиду его
атомистичности *).
Таким образом, то, что Архимед умолчал о Демокрите в книге «О шаре
и цилиндре» и упомянул о нем в «Эфоде», проще всего объясняется тем, что,
давая описание предварительного метода получения решения,
Архимед счел возможным упомянуть и о Демокрите; что же касается стро-
гих математических доказательств, то для Архимеда образцом был нс Демо-
крит, по Евдокс.
Но и по отношению к Евдоксу Архимед сохранил свою индивидуальт
ность. В то время как в чистом методе Евдокса к предельному значению
приближались только с одной стороны, «исчерпывая» определяемую вели-
чину, Архимед при доказательстве большинства теорем, связанных с опре-
делением площади фигуры, подлежащую определению величину заключает
♦) Нужно, впрочем, отмстить, что в разобранном Архимедом частном, случае теорема будет впол-
не правильной.
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. Н. ВЕСЕЛОВСКОГО
:®7
между двумя фигурами — вписаппой и описанной,— разность площадей
которых может быть сделана меньше любой наперед заданной величины;
затем он определяет величину, которая заключается между площадями
вписанной и описанной фигур, и доказывает, что эта величина и предста-
вляет определяемую площадь. По существу, он делает то же, что и мы при
введении понятия об интеграле. Таким образом, Архимедом были вычислены
интегралы, равносильные нашим . sin ж dx при определении поверхности
шара и ж2йжи (axa~t~bx)dx при определении поверхности, описанной спи-
ральной линией, и объема сегментов параболоида, гиперболоида и эллипсоида
вращения.
Можно, кроме «предвосхищения» интегрального исчисления, как выра-
жается Хис, найти у Архимеда известное предвосхищение и основных поня-
тий дифференциального исчисления,— того, что мы назвали бы теперь опре-
делением отношения беско-
нечно малых величин. С с----
этой точки зрения инте-
респо предложение XVIII
книги «О спиралях», в г 'ч.
котором длина окружпо- / f \
сти сравнивается с дли- I \ .
ной подкасательной к спи- \______о ________]
ради. Пусть точка О пред- “ I V । 1.
ставляет полюс спирали, \ \ J / '
радиус-вектор которой за \ /
время первого оборота \ / .
сделался равным г=ОЛ, а '
прямая АО является каса-
тельной в точке А к спира- 1’ис- 9-
ли. Пусть CD и АС пред-
ставляют перемещения описывающей спираль точки по радиусу и 'перпен-
дикулярно к нему (рис. 9). Проводим ОВ перпендикулярно к О А ипродол1
жаем касательную АО до пересечения в В с этой прямой; тогда длина ОБ
будет представлять дл ину окружности радиуса г. Доказательство сводится к
установлению пропорции
ОЛ-.ОВ^ AC-.CD.
Треугольник АСО по существу представляет не что иное, как диффе7
репциальный треугольник Барроу — Ньютона, и не исключена возможу
ность, что идея этого треугольника появилась у Исаака Барроу именно
в результате изучения сочинений Архимеда, которые были изданы Барроу
в 1675 г. с переделанными доказательствами. Во всяком случае изучение
Архимеда математиками XVII века было необходимой подготовительной
работой к появлению классического анализа бесконечно малых.
Еще с большим правом мы можем видеть в Архимеде основателя мате-
матической физики: как творения его колоссального инженерного таланта
в сочетании с математической подготовкой появляются работы третьего
«механического» периода деятельности Архимеда, когда он определил поло1
жение центров тяжести сегмента параболы («О равновесии плоских фигур»),
а также конуса и сегментов параболоида, гиперболоида и эллипсоида вращения
(«Эфод»); знание положения центра тяжести сегмента параболоида позво-
лило ему математически определить положения равновесия плавающего
38
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. 11. ВЕСЕЛОВСКОГО!
в жидкости сегмента параболоида («О плавающих телах»). Инженерная
интуиция Архимеда была настолько велика, что, как показывает детальный
разбор его выводов (см. комментарий к предложениям II—X второй киши
«О плавающих телах»), в основе его исследований, по существу, лежат те
самые теоремы, которые были установлены только во второй половине
XIX века проф. Московского университета А. Ю. Давыдовым и француз-
ским математиком Дюпеном. Основным отличием метода Архимеда от сов-
ременного является то, что Архимед определяет устойчивые положения
равновесия не при помощи формального критерия метацентра, а непосред-
ственно исследуя поведение плавающего тела при его отклонениях от поло-
жения рановесия. При таком чисто физическом методе исследования у Архи-
меда, естественно, получаются только положения, соответствующие устой-
чивому равновесию.
Эта «физичность» мышления совершенно исключает представление об
Архимеде как о гениальном математике-формалисте. В «Псаммите», есть
одно место, па которое комментаторы-математики не всегда обращают вни-
мание. Архимед пытается определить видимый диаметр Солнца. Он хорошо
знает, что «получить точное значение этого угла — дело нелегкое, потому
что ни глаз, ни руки, ни приборы, с помощью которых производится
отсчет, не являются достаточно надежными для точности результата».
Искомую величину он находит не из умозрительных соображений, а чисто
экспериментальным способом, вводя даже поправку на ширину зрачка.
Найденная им величина углового диаметра Солнца оставалась непревзой-
денной вплоть до XVII века (результат Архимеда 32’55',5 — верхняя гра-
ница и 32°27' — нижняя граница; Коперник считал 31° 48'; истинные зна-
чения 31°28' в апогее и 32°37' в перигее. Таким образом, верхняя граница,
полученная Архимедом, пе хуже величины, найденной Коперником).
V
К последнему периоду творчества Архимеда мы отнесли «Измерение
круга» и «Псаммит». Специфически новым моментом в этом периоде является
то, что Архимед от геометрических построений определяемых величин пере-
ходит к вычислению их; это подводит нас к рассмотрению еще недостаточно
изученного вопроса о греческой арифметике, или, лучше сказать, логис-
тике — искусству вычислений *), так как под арифметикой у греков пони-
малось то, что мы теперь назвали теорией чисел.
Однако Архимед не только использовал достижения современной ему
науки относительно способов вычисления; он был и в этой области актив-
ным создателем повых научных ценностей. Так как греческая система счис-
ления не позволяла удобно изображать большие числа, Архимед в не дошед-
шем до нас сочинении nepi 'zpyoiv — «О началах» — заложил основание
новой системы счисления, усовершенствованной им в дошедшем до нас
«Псаммите», где он дал систему счисления, пригодную для изображения дей-
ствительно астрономических чисел, могущих выразить количество песчи-
нок, содержащееся в объеме вселенной. «Астрономическая направленность»
«Псаммита» позволяет нам дать ответ па вопрос о том, какие причины заста-
вили Архимеда под конец его жизни, примерно в двадцатых годах 111 века
до н. э., заинтересоваться вычислительной математикой и создать системы
счисления, приспособленные к обозначениям очень больших чисел. О том,
’) О способах вычислений у греков см. Приложение I.
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. Н. ВЕСЕЛОВСКОГО
39
что эти причины заключались не только в индивидуальных интересах Архи-
меда как ученого, говорит тот факт, что Архимед пе был единственным мате-
матиком той эпохи, интересовавшимся способом записи очень больших чисел.
В дошедшем до нас отрывке второй книги «Математической библиотеки»
Паппа имеется пересказ одного из арифметических сочинений младшего
современника Архимеда и, вероятно, его соперника Аполлония Пергского,
автора известных «Конических сечений». Это сочинение, называвшееся,
вероятно, Qzurixiov (средство для ускорения родов), говорило о способах
умножения больших чисел и о новой системе счисления, позволявшей запи-
сывать эти большие числа. Как мы знаем из комментария Евтокия к «Изме-
рению круга», Аполлонии дал более точное значение отношения окруж-
ности к диаметру, чем то, которое приводится в «Измерении круга»; воз-
можно, что полемика между Архимедом и Аполлонием повела к появлению
«Задачи о быках».
Эти «вычислительные» тенденции в греческой математике еще более
усиливаются в последующем ее развитии. Творения Архимеда и Аполлония
являются своего рода венцом гречеркой геометрии, но вместе с тем они озна-
меновали и ее завершение; после Аполлония развитие греческой геометрии
как-то сразу обрывается: «род» великих математиков по иссякает, по они
начинают заниматься совершенно другими вопросами. Эратосфен является
творцом математической географии, Гиппарх кладет начало сферической
тригонометрии и вычислительной астрономии. После Гиппарха математику
приблизительно на две тысячи лет «берет под опеку» астрономия, причем
это имеет место не только у греков, но и у индусов, и у арабов, и у средне-
вековых математиков, вплоть до времен Коперника, Кеплера и Ньютона.
Создается впечатление, что греческая математика испытала какие-то мощ-
ные влияния нового фактора, который коренным образом изменил весь
дальнейший процесс ее развития. Таким фактором, как показали исследо-
вания первой половины двадцатого века, была вавилонская планетная
астрономия, которая начала развиваться примерно с VI века до н. э. Этот
век в истории науки явился такой же переломной эпохой, какой в дальней-
шем ее развитии был, например, XVII век. Именно в этом веке произошла
ликвидация старого религиозного миропонимания. В Греции он был озна-
менован рождением светской науки — материалистической и рационали-
стической философии ионийской школы и основанной на строгих логических
доказательствах математики. На востоке тот же самый процесс шел иначе.
Точно так же были сданы в архив все старые легенды о божественном сотво-
рении мира. Религия сосредоточилась всецело в области морали и ушла
из области естествознания. Боги перестали быть творцами и деспотическими
правителями мира; переселившись на небо и разместившись по различным
планетам, они стали лишь подчиненными и толкователями какой-то высшей
силы — фатума, предначертания которой можно открыть по движениям
планет; их движения стали рисоваться настолько закономерными, что их
уже можно заранее предсказать и нрсдвычислить. Начиная с VI века до н. э.,
вавилоняне предвычисляют небесные явления и к 111—II векам до н. э.
достигают таких успехов, что оказываются в состоянии предсказывать нас-
тупление затмений, противостояний и соединений планет. Вавилонские
астрономы Набурианпу и Кидинну определяют длину года, продолжитель-
ность различных видов месяца и периоды планетных обращений. Восточная
философия в лицо стоицизма с его пестрой смесью материалистических пред-
ставлений с фатализмом и астрологией начинает господствовать в греческом
мире; обоснованием зтой философии считалась не знающая никаких богов
вавилонская вычислительная астрономия. Крушение эллинистических
40 ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. II. ВЕСЕЛОВСКОГО
государств под железной пятой римских завоевателей еще более усиливает
и тяжелое настроение среди порабощенных народов, и надежды на лучшее
будущее, время наступления которого можно будет определить, если суметь
надлежащим образом прочесть веления фатума, выраженные в закономер-
ных движениях планет не только в течение настоящего, но — самое важ-
ное — в течение будущего времени.
Но для того чтобы предсказывать' движения планет, нужно уметь их
предвычислять, а для этого уже недостаточно было «домашней логистики»,
дававшей правила счета в пределах только первой тысячи; необходимо было
познакомиться с той математикой, которой пользовались вавилонские
астрономы, а эта математика оперировала с числами, гораздо большими тех,
которые могло представить себе воображение среднего грека. Перед наукой
поэтому встала задача разработки новых методов вычислений. Работы Архи-
меда и Аполлония являются первыми шагами в этом направлении, когда
из вавилонской системы счисления берется лишь основной принцип пози-
ционности. В дальнейшем следование вавилонским способам вычислений
становится все более и более рабским и закапчивается принятием целиком
вавилонских способов вычислений для всех астрономических расчетов.
Вскоре после смерти Архимеда, в самом пачале II века, автор так называе-
мой XIV книги «Начал» Евклида алексапдриец Гипсикл в своем «Анафо-
рике» пользуется введенным вавилонским астрономом Кидипну способом
представления постепенного изменения скорости движения планет при
помощи арифметической прогрессии — нечто аналогичное введенному Гали-
леем равноускоренному и равнозамедленному движениям. Немного позже
великий греческий астроном Гиппарх пользуется вавилонскими данными
относительно продолжительности года и месяца. От греков вавилонская
астрономия и математика переходят и к римлянам. Как широко было рас-
пространено у ппх знание астрономии, показывают, например, следующие
факты. Накануне решительного сражения при Пидне во время Персеевой
войны Сульпиций Галл предсказал наступление лунного затмения. В I веке
до и. э. друг Цицерона Нигидцй Фигул, астролог и математик, уже вполне
усвоил методы вавилонской вычислительной астрономии; немного позже
появление вавилонской астрологии в Риме отличено у Горация:
Tu пе quaesieris, scire netas, quern mihi quern tibi
Fincm di dedcrint, Lenconoe, nec Babylonios:
Temptaris nurneros...*)
В эпоху Птолемея вавилонские шестидесятсричные дроби являются
уже основным средством астрономических вычислений. Как показывают
схолии к Евклиду, византийским математикам XI—ХП веков п. э. эти
дроби были очень хорошо известны, а в Западной Европе гаестидесятерич-
пые дроби под названием minutiae physicales, в противоположность обык-.
повенным дробям (minutiae vulgares), были в употреблении вплоть до XVII ве-
ка, и в настоящее время еще живут в наших минутах и секундах.
VI
Когда Тит Ливий называл Архимеда «единственным в своем роде наб-
людателем неба и звезд», то он, возможно, повторял высказывания об Архи-
меде ближайших к пому поколений, в первую очередь, вероятно, Полибия,
изложению которого Ливий следует, рассказывая события второй Пуни-
•) Не спрашивай ты> ведать грешно, какой мне и тебе Левконоп» пошлют боги конец, и вавилоя-
М.сла не пытай. (Сды, книга I, И).
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. Н. ВЕСЕЛОВСКОГО
41
ческой войны. Для Полибия, бывшего прежде всего государственным дея-
телем, тонко понимавшим взаимную связь политических событий, а не уче-
ным, Архимед, конечно, был важен в первую очередь как защитник Сира-
куз; общую характеристику Архимеда Полибий дал, вероятно, в соответ-
ствии с теми представлениями о нем, которые сложились в кругах широкой
публики, помнившей только последние работы Архимеда пород самой осадой
Сиракуз. Если ото верно, то Архимед занялся астрономией уже на склоне
лет; чтобы правильно оценить значимость полученных им результатов в обла-
сти астрономии лучше всего сравнить их с результатами измерения расстоя-
ния Солнца и Луны от Земли, которые были получены его непосредственным
предшественником, а именно упоминаемым им в «Псаммите» Аристархом
Самосским.
Согласно исследованиям Аристарха, диаметрСолпца - 7 диаметрам
Земли.
1 7
Диаметр Лупы — диаметра Солнца = диаметра Земли.
Расстояние Лупы от 3омли=30 диаметрам Луны^Ю-^- диаметрам
Земли.
Расстояние Солнца от Земли—210 диаметрам Земли.
Интересно сравнить результаты исследований Аристарха с работой
Архимеда. Пршкде всего, Аристарх считал Землю за точку, иными словами,
считал, что наблюдатель находится в центре Земли, а Архимед учитывал,
что наблюдатель находится па поверхности Земли, и поэтому приводил
наблюдения к центру. Затем Аристарх давал только относительные размеры
мира, Архимед ввел величину земного радиуса и, таким образом, получил
и абсолютные размеры мира. С другой стороны, Аристарх искал верхнюю
И нижнюю границы измеряемых величин (у него, например, отношение диа-
1 1
метра Солнца к диаметру Земли заключается между пределами бу в 7у),
в то время как Архимед брал одну только верхнюю границу. Расстояние
от центра Земли до центра Солнца у него составляет 5000 диаметров Земли
и диаметр Солнца в 30 раз больше диаметра Земли; что касается Луны, то
он просто принимает ее диаметр равным диаметру Земли; так как угол, под
которым виден диаметр Луны с поверхности Земли равен 30', то расстояние
от Земли до Луны будет равно диаметру Лупы, деленному на sin 30', то
есть 120 диаметрам Луны (в четыре раза больше, чем у Аристарха), или,
так как Архимед считает диаметры Земли и Луны равными — 120 диамет-
рам Земли.
Астрономические сочинения Архимеда не ограничиваются «Псаммитом»,
им было написано сочинение, посвященное построению небесной сферы;
инженерные устремления были настолько сильны в Архимеде, что они про-
явились даже в области чистой астрономии. Историю этой сферы лучше всего
рассказать, цитируя известные нам источники.
На первом месте надо поставить диалог Цицерона «О государстве»;
описываемые в нем события происходят во второй половине П века до н. э.
Упоминаемый в нем Сульпиций Галл был очень образованным римлянином.
В первой книге «О государстве» мы читаем (книга I, 14):
«Я вспоминаю, как К. Сульпиций Галл, как вы хорошо знаете, один
из самых ученых людей пашей страны, находился однажды в гостях у М. Мар-
целла, бывшего недавно консулом вместе с пим, и разговор зашел о чудесном
явлении, в точности похожем на случившееся недавно. Галл заставил при-
нести ту знаменитую сферу, единственную добычу, которой предок
42
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. Н. ВЕСЕЛОВСКОГО
Марцелла захотел украсить свой дом после взятия Сиракуз, города полного
всяких сокровищ и диковинок. Я часто слышал разговоры об этой сфере,
считавшейся шедевром Архимеда, и признаюсь, что с первого взгляда опа
мне пе показалась чем-то особенно выдающимся. Марцелл пожертвовал
в храм Доблести другую архимедову сферу, которая была гораздо более
известна и имела более представительный вид. Но когда Галл начал с не-
обыкновенным знанием дела объяснять устройство этого прекрасного про-
изведения, я не мог не подумать, что в этом сицилийце был гений, равняться
с которым человеческая природа не казалась способной. Галл рассказывал
нам, что изобретения таких сплошных сфер относятся к глубокой древности,
что первый образец такой сферы был построен Фалесом Милетским, что
в дальнейшем учепик Платона Евдокс Книдский изобразил на ее поверх-
ности различные созвездия, прикрепленные к небесному своду, и что много
лет спустя не бывший астрономом, но имевший известный поэтический
талант Арат описал в стихах все небо по Евдоксу. Он прибавил, что для
возможности представления движений Солнца, Луны и пяти звезд, которые
мы называем блуждающими, пришлось отказаться от употребления сплош-
ной сферы, па которой было бы невозможно их воспроизвести, и придумать
другую совершенно отличного вида; и что в изобретении Архимеда чудес-
ным было искусство, с которым оп мог объединить в одной системе и вос-
произвести при помощи одного вращения все очень отличающиеся друг от
друга движения и различные периоды обращения различных светил. Когда
Галл приводил сферу в движение, то при каждом обороте можно было видеть,
как Луна появлялась вслед за Солнцем на земном горизонте, подобно тому
как опа появляется каждый день на небе; далее можно было видеть, как
Солнце исчезает так же, как и па пебе, и затем понемногу Луна погружается
в земную тень в тот самый момент, когда Солнце с противоположной
стороны...».
На этом интересном месте к сожалению обрывается дошедший до нас
текст Цицерона.
Сфера Архимеда, пожертвованная Марцеллом в храм Доблести, по-види-
мому, для многих римлян была основным пособием для изучения астроно-
мии. Следы знакомства с этой сферой можно установить в течение долгого
времени после эпохи Цицерона.
Во второй половине II века н. э. мы встречаемся с несколько загадоч-
ным свидетельством неистового карфагенского пресвитера Тертуллиана:
«Обрати внимание на изумительное чудо Архимеда; я говорю об этой
гидравлической машине, где столько колес, столько различных деталей,
столько сочленений, столько выходов для голоса, и целые армии флейт соста-
вляют одну неразличимую массу».
Обыкновенно это понимают в смысле изобретенного Архимедом гидра-
влического органа. Однако такому толкованию препятствуют следующие
соображения:
1°. Архимед нс является изобретателем гидравлического органа; все
историки древности признают в этом вопросе приоритет александрийца
Ктесибия.
2°. Вряд ли можно допустить, чтобы гидравлические органы III века
до н. э. могли уцелеть в конце II века п. э.
3°. Собрание «колес» не подходит к гидравлическому органу.
С другой стороны, мы знаем, что сфера Архимеда приводилась в движе-
ние «скрытым внутри воздухом» (spiritus inclusus), согласно описанию нозта
Клавдиана (V век п. э.). Так как от такого врага науки, каким был Тертул-
лиан, нельзя ожидать очень большой точности, то можно думать, что «изу-
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. Н. ВЕСЕЛОВСКОГО
43 .
митсльпым чудом» Архимеда была именно сохранявшаяся в храме Доблести
астромомичсская сфе ра.
Через каких-нибудь сто лет в эпоху Диоклетиана об архимедовой сфере
говорит Лактанций (De niortibus persecutoruin, книга 111, 5):
«Я вас спрашиваю, ведь мог же сицилиец Архимед воспроизвести образ
и подобие мира в выпуклой округлости меди, где он так разместил и поста-
вил Солнце и Луну, что они как-будто совершали каждодневно неравные
движения и воспроизводили небесные вращения; он мог нс только показать
восход и заход Солнца, рост и убывание Лупы, по сделать так, чтобы при
вращении этой сферической поверхности можно было видеть различные тече-
ния планет; так неужели же Вог пе мог воспроизвести и сотворить натураль-
ные вещи, подобие которых мог сделать человек своим искусством и хит-
ростью».
В конце IV века, когда при Грациане и Феодосии I христианство одер-
жало окончательную победу над язычеством, о сфере Архимеда вспоминает
один из последних языческих писателей Макробий в комментарии ко «Сну
Сципиона», книга И, 3):
«Так же и Архимед считал, что он определил число стадий, на которое
от поверхности Земли удалена Луна, а от Луны — Меркурий, от Мерку-
рия — Вейера, от Венеры — Солнце, от Солнца — Марс, от Марса —
Юпитер и от Юпитера — Сатурн; все же расстояние от Сатурна до самого
звездоносного неба он думал измерить только рассуждением».
Для определения расстояния Солнца от Земли Архимед, как мы знаем,
прибег к измерению при помощи опыта. Задача действительного определе-
ния расстояний между различными планетами была в его время совершенно
непосильной; их можно было определить только предположительно, исходя
из периодов их обращений. Для «звездоносного неба» у него не было даже
и этих числовых даппых, поэтому ему, конечно, пришлось ограничиться
лишь рассуждением. Единственной целью, для достижения которой
такие вычисления были необходимы, является только построение небес-
ной сферы.
Еще раз мы встречаемся с этой сферой в произведениях последнего
талантливого римского поэта Клавдиапа (начало V века п. э.), который
посвятил ей одну из своих эпиграмм:
«Неба устав, законы богов, гармонию мира —
Все Сиракузский старик мудро па Землю принес.
Воздух, скрытый внутри, различные движет светила
Точно но данным путям, сделав творенье живым.
Ложный бежит зодиак, назначенный ход выполняя,
Лик поддельный Лупы вновь каждый месяц идет.
Смелым искусством гордясь, свой мир приводя во вращенье,
Звездами вышних псбсс правит умом человек».
Вскоре после написания этого гордого стихотворения в 410 г. готы
захватили Рим; в последовавшем грабеже языческих храмов, вероятно,
погибла и небесная сфера Архимеда.
VII
В самом конце своей жизни Архимеду снова пришлось вернуться
к тому, чем он занимался в начале своей творческой деятельности: ему
пришлось применить свои инженерные и механические познания для обо-
роны родного города. Во время второй Пунической войны Сиракузы
.44
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. II. ВЕСЕЛОВСКОГО
оказались вовлеченными в борьбу Карфагена с Римом и римский пол-
ководец Марцелл осадил Сиракузы, душой обороны которых стал семи-
десятипятилетнпй Архимед. Дальнейшее течение событий лучше всего из-
ложить языком подлинных источников, каковыми в данном случае явля-
ются Полибий, Тит Ливий и Плутарх.
Наиболее ранний источник — «История» Полибия, написанная при-
мерно через 50—60 лет после разрушения Сиракуз. В книге VTII его «Исто-
рии», дошедшей до нас во фрагментах, мы читаем следующее:
«Когда Епикид и Гиппократ *) завладели Сиракузами, то сами прервали
дружбу с римлянами и прочих граждан принудили к тому же. Римляне,
раньше еще уведомленные о насильственной смерти сиракузского тирана
Гисропима **), выбрали в проконсулы Аппия Клавдия, дали в его распоря-
жение сухопутное войско, а начальство над флотом возложили на Марка
Клавдия ***). Начальники расположились станом невдалеке от города и реши-
ли, что сухопутное войско поведет приступ против города со стороны Гек-
сапил, а флот—против Ахрадины ****) у портика, именуемого Скитским,
где стена тянется вдоль моря. Приготовивши шалаши *****), метательные
орудия и все прочее, нужное для осады, римляне надеялись при многочис-
ленности рабочих рук покончить с приготовлениями в течение пяти дней
и не дать неприятелю подготовиться. По при этом они не приняли в расчет
искусства Архимеда, не догадались, что иногда дарование одного человека
способно сделать больше, чем огромное множество рук. Теперь они убеди-
лись в этом по опыту. Город был достаточно крепок уже тем, что окружаю-
щая его стена покоилась на высотах и поднимающемся перед городом
утесе; к ним трудно было подойти, за исключением немногих определенных
пунктов, даже и тогда, если бы осаждаемые не оказывали никакого со-
противления.
Кроме того, упомянутый Архимед заготовил внутри города, а равно
и против нападающих с моря такие средства обороны, что защитникам не
было необходимости утруждать себя непредусмотренными работами на
случай неожиданных способов нападения; у них заранее готово было все
к отражению врага в любом случае.
Итак, А1ШИЙ сделал попытку приблизиться с шалашами и лестницами
к той части стеньг, которая с востока упирается в Гексапилы, г1 Марк сшестью-
десятью пятипалубными судами направился против Ахрадипы. Находив-
шиеся на каждом судне люди вооружены были луками, пращами и легкими
дротиками, чтобы прогонять врага, нападающего с зубцов стен. Вместе
с тем римляпе сняли у восьми пятипал убпых судов весла, у одних с правой
стороны, у других с левой, открытыми стенками связали суда попарно
и, действуя веслами только с наружных боков, стали подвозить к городской
степе так называемые самбуки. Устройство этого осадного орудия следую-
щее: делается лестница в четыре фута ширины и такой длины, чтобы опа
при установке достигала верхнего края стены, с обеих сторон ее ограждают
и закрывают высокими перилами, йотом кладут ее наискось вдоль сопри-
касающихся стенок связанных между собою судов, так что лестница высту-
пает далеко за корабельные носы. На вершинах мачт укрепляют блоки
с канатами. Когда нужно действовать, канат привязывают к верхнему
•) Вожди демократической антирммской партии в Сиракузах.
♦*) Пятна дцатилетпего внука Гиерона, последнего отпрыска его династии.
•••) Марцелла.
•*♦*) Часть города Сиракуз.
•♦*•*) так назывались подвижные крытые галереи, подвозимые или подносимые к стенам для
прикрытия осаждавших.
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. Н. ВЕСЕЛОВСКОГО
45
краю лестницы, и люди, стоящие иа корме, тянут его на блоке, а другие,
находящиеся на передней части корабля, следят за правильным подъемом
лестницы и подпирают со шестами. Наконец, при помощи гребцов, разме-
щенных по обоим наружным бортам, римляне подходят с кораблями к суше
и стараются только что описанное сооружение приладить к стене. Иа вер-
шине лестницы находится доска, с трех сторон огороженная плетнем; на ной
стоят четыре человека, которые и ведут борьбу с неприятелем, находя-
щимся на зубцах степы и противодействующим установке самбуки. Как
только лестница установлена так, что эти четыре воина возвышаются над
стелой, боковые стенки плетня снимаются, и воины тотчас с двух сторон
взбираются на зубцы или башни: прочие товарищи их следуют за
ними но самбуке, надежно прикрепленной канатами к обоим кораблям.
Сооружение зто не без основания получило такое название: когда ма-
шина поднята, то корабль в соединении с лестницей напоминает по виду
самбуку *).
Итак, по изготовлении самбуки римляне решились подойти к башням.
Однако Архимед соорудил машины, приспособив их к метанию снарядов
на любое расстояние. Так, если неприятель подплывал издали, то Архимед
поражал его из дальнобойных кампеметальниц тяжелыми снарядами или
стрелами и повергал в трудное и беспомощное положение. Когда же снаряды
начинали летать поверх неприятеля, то Архимед употреблял в дело мень-
шие машины, каждый раз сообразуясь с расстоянием, и наводил на римляп
такой ужас, что они никак пе решались идти иа приступ или приблизиться
к городу па судах. Наконец, Марк, раздосадованный неудачами, вынужден
был сделать попытку тайком ночью подойти к городу па кораблях. Когда
римляне подошли к берегу на расстояние выстрела, Архимед употребил
другое средство, направленное против воипов, сражавшихся с судов, именно:
он велел сделать в степе приблизительно на высоте человеческого роста
множество отверстий, с наружной стороны имевших в ширину пальца четы-
ре; у отверстий изнутри стены он поставил стрелков и маленькие скорпи-
оны**), через отверстия обстреливал корабельных воипов и тем отнимал
у них всякую возможность сделать что-нибудь. Таким образом, далеко
или близко находился неприятель, Архимед не только разрушал все его
планы, по и производил в его рядах большие опустошения. Как только
римляне покушались поднять самбуки, Архимед приводил машины в бое-
вое состояние по всей степе. Все время они оставались невидимы, но лишь
только требовалось употребление их в дело, машипы изнутри выдвигались
за зубчатые укрепления. Некоторые машины метали камни весом не менее
десяти талантов***), другие выбрасывали груды свинца. Каждый раз, как
только самбуки приближались, жерла архимедовых машин отклонялись
вместе с подставкой вправо или влево, смотря ио надобности, и при помощи
освобождаемого блока сбрасывали камни на неприятельское сооружение.
Вследствие этого не только ломалась машина римлян, но и корабль, и нахо-
дившиеся на нем солдаты подвергались большой опасности.
Некоторые машины отражали нападение неприятеля, защищенного
и прикрытого плетнем от стрел, выпускаемых через отверстия в стене;
в таком случае бросаемые камни соответствующей тяжести прогоняли напа-
дающих римлян с передних частей корабля. Кроме того, с машины спуска-
лась прикрои лепная к цепи железная лапа; управлявший жерлом машины
•) Самбукой назывался музыкальный инструмент.
Стреломсты небольшого калибра!.
•••) Около 2Ъ0 кг.
46
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. 11. ВЕСЕЛОВСКОГО
захватывал в каком-нибудь месте этой лапой нос корабля и потом опускал
вниз находящийся внутри города конец машины. Когда нос судна был таким,
образом поднят и судно поставлено отвесно на корму, то плечо рычага за-
креплялось неподвижно, а лапа вместе с цепью отделялись от машины осво-
бождающего приспособления. Вследствие этого некоторые суда ложились,
на бок, другие совсем опрокидывались, большинство же от падения носом
с значительной высоты в море погружались и наполнялись водой, внося
большой беспорядок и ужас среди экипажа. Изобретательность Архимеда
приводила Марка в отчаяние; с прискорбием он видел, как осажденные глу-
мятся над его усилиями и какие они причиняют ему потери. Однако, под-
шучивая пад своим положением, Марцелл говорил, что Архимед уго-
щает его корабли морской водой, а его самбуки как бы с позором про-
гоняются с попойки палочными ударами. Так окончилась осада Сира-
куз с моря.
Аппий с сухопутным войском очутился в столь же трудном положении,
и потому совсем отказался от приступа. Действительно, находясь еще на
далеком расстоянии от города, римляне сильно терпели от камнеметальниц
и катапульт, из которых были обстреливаемы; ибо сиракузяне имели в за-
пасе множество превосходных и метких метательных орудий. Оно и понятно,
так как Гиероп дал па них средства, а Архимед изобрел и мастерски построил
машины.
Итак, когда римляне приближались к городу, то одни были
непрерывно обстреливаемы через отверстия в стене, о которых было сказано
выше, терпели урон и не могли продолжать наступление, другие же, рас-
считывавшие пробиться вперед силой и огражденные плетенками, гибли
под ударами камней и бревен, падавших сверху. Много бед римлянам
сиракузяне причиняли и теми лапами у машин, о которых я говорил раньше;
лапы поднимали воинов в полном вооружении и кидали их оземь. Наконец,
Аппий с товарищами возвратился па стоянку, устроил совещание с трибу-
нами, на котором и было принято единогласное решение испытать всевоз-
можные другие средства, но только отказаться от надежды взять Сиракузы
приступом; согласно принятому решению, они так и действовали. Римляне
оставались под степами города в течение восьми месяцев, и пе было такой
уловки или отважного дела, перед которым они остановились бы, по па при-
ступ идти они уже ни разу не осмеливались.
Такова чудесная сила одного человека, одного дарования, умело напра-
вленного на какое-либо дело. Вот и теперь: располагая столь значительными
силами сухопутными и морскими, римляне могли бы быстро овладеть горо-
дом, если бы кто-либо изъял из среды сиракузян одного старца. Ио так как
этот один был среди сиракузяп, то римляне не дерзали нападать на город
или по крайней мере употреблять те способы нападения, отразить кото-
рые Архимед был в силах».
Приведенный текст Полибия интересен в следующем отношении. Иногда
приходится слышать, что Архимеда, бывшего, по супщству, замечательным
математиком и склонным, по свидетельству Плутарха, лишь к теоретиче-
ским паукам, только опасность, грозящая родному городу, заставил а взяться
за практическую деятельность по его обороне. Внимательное чтение приве-
денного отрывка Полибия показывает, что оборона Сиракуз Архимедом
не была и не могла быть импровизацией; наоборот, Архимед готовился
к пей очень давно и по заданию и па средства царя Гиерона построил ряд
военных машин. В связи с этим очень интересно то, что Архимед имел ряд
метательных орудий, действовавших на различные расстояния; это уже пред-
полагает известный математический расчет. Какого рода этот расчет был,.
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. Н. ВЕСЕЛОВСКОГО
47
мы можем составить себе представление на основании сохранившейся воен-
ной литературы. Считалось, что длина полета выброшенного ядра прямо
пропорциональна объему того упругого тяжа, который приводил в движение
детали машины, сообщающие скорость ядру. Между прочим, этот расчет
совершенно правилен, так как можно очень просто показать, что при посто-
янстве угла возвышения орудия дальность полета ядра будет прямо про-
порциональна его начальной живой силе, последняя же получается из
потенциальной энергии закрученного тяжа, которая при одинаковой сте-
пени напряженного состояния прямо пропорциональна объему тяжа. Таким
образом, на основе некоторого числа опытов вполне возможно конструиро-
вать камнеметы и стреломсты, действующие на заданном расстоянии; Архи-
мед, очевидно, это хорошо знал. То обстоятельство, что зта теория была
известна около 240 года до н. э., доказывается упоминанием о ней в письме
Эратосфена к царю Птоломею Эвергету, касающемся задачи об удвое-
нии куба.
То, что Архимед не был кабинетным ученым, убедительно доказы-
вается той необычайной его изобретательностью в организации оборонных
мероприятий, которая так ярко изображена в приведенном ниже рассказе
Полибия.
Полибий был одним из источников для описания истории второй Пуни-
ческой войны у Тита Ливия (1 век до н. э.). Мы находим в книге XXIV его
римской истории:
«После этого началась осада Сиракуз и с суши — от Гсксапил —
и с моря — от Ахрадиньт, степы которой омываются морем. При этом рим-
ляне, взявшие Леонтины с первого же натиска под действием только ужаса,
были вполпе уверены, что в каком-нибудь месте они прорвутся в обширный
и разбросанный по большому пространству город, и придвинули к стенам
всю наличность осадпых машин. И начатое с такой силой предприятие
увенчалось бы успехом, если бы в то время пе было одного человека.
Этим человеком был Архимед, единственный в своем роде созерцатель неба
и светил, но еще более удивительный изобретатель и конструктор военных
машин и сооружений, при помощи которых он с очень небольшим усилием*)
мог делать тщетными все попытки врагов, даже если эти попытки стоили
колоссальных усилий. Стена города проходила по неровной и холмистой
местности; многие части ее были очень высокими и трудно доступными, но
в некоторых местах она была ниакой и пологие стены делали возможным
восхождение. Поэтому Архимед поставил па стене в качестве защиты раз-
личного рода метательные оружия, сообразуя их с природой местности.
На стену же Ахрадины, которая, как сказано было выше, омывалась морем,
Марцелл вел наступление с шестнадцатью пентерами **). Находившиеся же
па других судах лучники, пращники и легковооруженные велиты***), мета-
тельные орудия которых очень трудно отражать для неопытных воинов,
не позволяли никому безнаказанно оставаться на степах. Так как для мета-
тельных орудий требуется некоторое расстояние, то эти корабли стояли
вдали от стен. Другие пентеры были соединены попарно бок к боку, причем
внутренние весла были сняты и оба корабля как один приводились в движе-
ние лишь внешними веслами; на них стояли многоэтажные башни и другие
приспособления для разрушения стен. Против всего зтого морского воору-
жения Архимед расположил по стенам метательные орудия различной
*) Parvo momento — выражение, ваимствованное ив механики.
••) Пантера — судно с пятью рядами весел.
•••) Велиты — род войска у римлян.
48
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. II. ВЕСЕЛОВСКОГО
величины. В далекие корабли он метал громадного веса камни, а близкие
осыпал более легкими, а вследствие этого и в большем количестве, метатель-
ными снарядами. Наконец, для того чтобы сиракузские воины безнаказанно
могли обстреливать неприятеля, он проделал в стене снизу до верху отвер-
стия шириной почти в фут, из которых они, оставаясь скрытыми, могли
поражать врага стрелами и среднего калибра скорпионами *). Пате же кораб-
ли, которые подходили ближе, чтобы выйти из пора7каемой орудиями обла-
сти, он при помощи выступающего за стену рычага, набрасывал прикреплен-
ную крепкой цепью железную лапу: когда последняя захватывала пос
корабля, то при помощи опускающегося до земли тяжелого свинцового
противовеса нос корабля подымался и последний становился па корму;
затем после внезапного освобождения корабль, как бы сброшенный со стены,
к громадному ужасу матросов так ударялся о морскую поверхность, что
набирал воды даже в том случае, когда падал в прямом положении. Таким
образом, был отражен приступ с моря и всю надежду римляне возлагали
на нападение всеми силами с суши. По и эта часть стен была вооружена раз-
личного рода метательными орудиями, которые в течение долгого времени
изготовлялись за счет Гиерона единственным в своем роде искусством
Архимеда. Последнему помогала также п природа местности, так как скала,
на которой находились фундаменты степ, большей частью была настолько
крутой, что врагу тяжелый урон причиняли снаряды не только выбро-
шенные из орудия, по даже двигавшиеся только под действием собствен-
ного веса.
По той же самой причине подъем был очень труден вследствие крутизны
и движение было очень опасным. Таким образом, после обсуждения, видя
тщетность всякого рода попыток, римляне постановили прекратить штурм
и только при помощи блокады с суши и с моря отрезать осажденных от
подвоза провианта».
Наконец, третью версию истории Сиракузской осады мы читаем у Плу-
тарха, автора начала II века н. в его жизнеописании Марцолла.
«Марцелл производил нападения и с суши, и с моря. Аппий водил в сра-
жение сухопутные войска, Марцелл командовал шестьюдесятью пентерахми,
наполненными всякого рода оружием и стрелами. Он приказал связать между
собой восемь больших кораблей, поставил на них осадную машину и под-
плывал с нею к стенам, надеясь на успех ввиду обширности и тщательности
своих приготовлений и славы своего имени. Но все это было пустяками для
Архимеда и архимедовых машин. Последний до сих пор еще не создал ничего,
заслуживающего внимания. Большая часть того, что он сделал, было сде-
лано мимоходом,— оп занимался математикой как бы для забавы. Первым
польстил самолюбию царь Гиерон. Он убедил Архимеда, вместо занятий
отвлеченными предметами, заняться хотя бы отчасти предметами реальными
и, соединив свои теоретические построения с практикой, сделать их понят-
нее и яснее для обыкновенных люден. Механике — науке, любимой многими
и пользующейся широким распространением,— положили начало Евдокс
и Архит. Они желали сделать геометрию интереснее, менее сухой, и нагляд-
ными примерами, с помощью механики, решали задачи, которые не легко
получались путем логических доказательств и чертежей. Так, например,
они решили посредством механики задачу о двух средних пропорциональ-
ных линиях, задачу, на которую необходимо ссылаться в математике во
многих случаях, и решили ее при помощи «месографа» **), проводя кривые ** *)
*) См. примечание на стр. 45.
Прибор для черчения средних пропорциональных (от цЛоц — срсдиян).
•♦*) В подлиннике к разряду которых относились конические ссчспин.
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. Н. ВЕСЕЛОВСКОГО
49
и делая сечения тел. Платон был недоволен. Он укорял их в том, что они
уничтожают математику и .'пинают ее достоинств, переходя от предметов
умопостигаемых, отвлеченных, к реальным, и снова сводят ее к занятию
реальными предметами, требующему продолжительной и трудной работы
ремесленника *). Тогда механика отделилась от чистой математики. Фило-
софы долгое время не интересовались ею, пока она ле сделалась одной из
наук, находящих себе применение на войне. Архимед, между прочим, писал
однажды своему родственнику и другу, царю Гиерону, что данной силой
(fim’apei) можно поднять данную тяжесть (Papog). В юношески смелом
доверии к силе своего доказательства он сказал, говорят, что, если бы у него
была другая земля, он перешел бы на пее и сдвинул с места нашу. Удивлен-
ный Гиерон стал просить его доказать свои слова и привести в движение
какое-либо большое тело малой силой. Архимед приказал посадить на цар-
скую грузовую триеру, с громадным трудом с помощью многих рук выта-
щенную па берег, большой экипаж, положить на нее обыкновенный груз,
и, усевшись на некотором расстоянии, без всяких усилий, спокойно двигая
рукой конец полиспаста, стал тянуть к себе триеру так тихо и ровно, как
будто она плыла по морю. Пораженный этим, царь оценил важность меха-
ники и упросил Архимеда построить для него машины, которые служили
бы и для наступления и для обороны от какой угодно осады. Царю но приш-
лось употреблять их — почти вся его жизнь протекла в мире и спокой-
ствии; по теперь машины эти пригодились сиракузцам, а вместе с машинами
и их изобретатель. Когда римляне осадили город с двух сторон, сиракузцы
испугались. От страха каждый молчал, потому что не надеялся оказать
сопротивление такой грозной силе. Но когда Архимед привел в действие свои
машины, то в неприятельскую пехоту понеслись пуще иные им различного
рода стрелы и камни невероятной величины, которые летели с таким шумом
и силой, что ничто не могло выдержать их удара; опрокидывая всех задетых
ими, они приводили в смятение ряды воинов. Со стороны моря он разместил
на стенах другие машины, которые опускали сразу па корабли громадные
бревна в виде лапы, захватывали их, подымали силой противовеса, затем
выпускали их и погружали в волны. Другие корабли он зацеплял за нос
железными лапами или носами наподобие журавлиных и, поставив на корму,
топил. /Некоторые корабли он притягивал к земле при помощи тянувших
в разные стороны веревок; там, повертевшись немного, они разбивались
о скалы, находившиеся под городской стопой, и большая часть экипажа
погибала. Часто .можно было видеть поднятый в воздух корабль, который
к ужасу окружающих вертелся с большой быстротой; когда его экипаж был
разбросан в разные стороны, как камни из пращи, то корабль разбивался
о стену, или, мосле освобождения от крюка, падал в море. Машина, кото-
рую Марцслл поставил на восьми кораблях, связанных вместе, называлась
самбукой, по сходству ее с музыкальным инструментом того же имени.
Она находилась на довольно далеком расстоянии от стен, когда Архимед
бросил на псе камень в десять талантов, а за ним другой и третий, которые
ударив машину со страшным шумом и силон, разбили се связи и так расша-
тали корабли, что они отделились друг от друга. Марцслл, не знак что
делать, поспешно отступил с флотом и приказал также отойти и пехоте.
*1 Знаменитое место, повторяющееся и л других сочинениях Плутарха, из которого в середине
XIX лека возникла легенда, что греческие математики, в частности Платон, запрещали пользоваться
каким бы то ни было инструментами, кроме циркуля и линейки. В этом отношении верно лишь то,
чггв в «Началах» Евклида нет других построении. Как мл увидим ииже. Архимед совершеянч
спокойно пользовался так называемыми vt-icreu; (вставками) для решения задач, приводившихся
к кубическим уравнениям.
4 Архимед
50
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. И. ВЕСЕЛОВСКОГО
Ла военном совете было решено па следующий день до наступления
утра, если удастся подойти поближе it стенам, чтобы дальнобойные машины
Архимеда бросали стрелы поверх их голов, а те, которые он мог бы употре-
бить на близком расстоянии оказались бы бесполезными, так как удар на
таком малом расстоянии не мог бы получить большой силы. Но Архимед
уже заранее приготовил для этой цели машины, которые могли действовать
на всех расстояниях, и короткие стрелы, вылетавшие-друг за другом почти
непрерывно*). Он проделал в стенах отверстия па небольшом расстоянии
друг от друга и поставил в пих среднего калибра скорпионы, которых враги
не могли заметить и которые часто поражали всех приближающихся. Когда
римляне подошли вплотную к стенам и уже думали, что находятся в безо-
пасности, то на них посыпался дождь стрел и па их головы полетели отвесно
падающие камни, так что не было ни одного места в стене, откуда бы в них
не стреляли. Они решили отступить, но едва они удалились на некоторое
расстояние, как Архимед обрушил на отступающих такое количество стрел,
что истребил большое количество воипов и разбил много кораблей, в то время
как сами они не могли причинить врагу никакого уропа, так как Архимед
большую часть своих машин расставил в укрытии за стенами;- поражаемые
отовсюду римляне, не видя, откуда наносятся удары, казалось, сражались
с богами. Между тем Марцелл, избавясь от опасности, шутил над своими
техниками, говоря, что они дерутся с математиком Бриареем **), который,
как бы играя, погружает их корабли п море и с позором прогоняет их, а, бро-
сая разом столько стрел, оставляет далеко позади мифических сторуких
великанов. Все остальные сиракузяпс были только телом для архимедовых
машин — один оп был душой, которая все двигала и всех направляла.
Все другие средства защиты были оставлены; город и для защиты, и для
нападения пользовался только машинами Архимеда. Наконец, видя, что
римляне так напуганы, что при одном виде спускавшейся со стены веревки
или бревна обращались в бегство, крича, что это какая-нибудь новая маши-
на, которую Архимед хочет па них направить, Марцелл прекратил всякие
нападения и превратил осаду в блокаду».
После этого следует та характеристика Архимеда, которая была при-
ведена нами в самом начале статьи. Нетрудно видеть, что рассказ Плутарха,
восходящий в конечном счете к Полибию, представляет не совсем грамотную
амплификацию простого рассказа Полибия. Восемь попарно связанных судов
Полибия с четырьмя самбуками превратились в одну колоссальную самбуку,
носимую всеми восемью судами, связанными имеете. В рассказе появились
поднятые в воздух корабли, приводимые во вращение и разбрасывающие
экипаж в стороны, как будто из пращи; ничего подобного у Полибия пет
и сам по себе этот факт невероятен. Еще; хуже та ретушировка, которой
Плутарх подвергает Архимеда. В его рассказе есть определенное противо-
речие. В начале оп говорит, что «последний до сих пор еще не создал ничего,
заслуживающего внимания»; можно подумать, что только опасность, грозив-
шая родному городу, заставила Архимеда запяться механикой. В дальней-
шем же, говоря о первой встрече Архимеда с Гиероном, он употребляет вы-
ражение: «в юношески смелом доверии (veuviE-u^dpevog ***)) к силе своего
доказательства»; иными словами, можпо думать, что Архимед занимался
механикой с самого юношества. Мы видели, что Архимед действительно
•) Такие прототипы пулемета, или, лучше сказать, стрел омета, действительно были
в эллинистической военной технике (полнболы).
*•) -Мифический сторукяй гигаит.
***) От veavueuogrzi поступать или говорить, как юноша.
известны
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. Н. ВЕСЕЛОВСКОГО
51
обратился к чистой математике сравнительно поздно; первой его специаль-
ностью была именно механика. Для всякого беспристрастного читателя,
познакомившегося с рассказами Полибия и Тита Ливия, совершенно ясно,
что Архимед был тем, что мы сейчас назвали бы главным военным инжене-
ром царя Гиерона, и его работа по подготовке военных машин была выпол-
нена во всяком случае до 216 года до н. — года смерти Гиерона, т. е. ио
крайней мерс за четыре года до осады Сиракуз Марцеллом.
При установлении порядка, в котором были написаны сочинения Архи-
меда, мы видели, что после «Досифеевских» сочинений Архимед снова воз-
вращается к механике, пишет трактат «О равновесии», определяет положение
Смерть Архимеда. Мозаика, вероятно, из школы Рафаэля.
Городская галерея во Фрапкфурте-па-Майпе.
центров тяжести различных тел и, наконец, закладывает основы гидро-
статики. Внимательное чтение рассказа Полибия позволяет сделать, как
кажется, довольно вероятное предположение о причинах такого возвращения
Архимеда к механике. Полибий говорит о машине, которая, захватывая нос
корабля, ставила его на корму и приподымала. Для того чтобы рассчитать
такую машину, нужно, кроме знания законов рычага, иметь совершенно
ясное представление о потере веса, которую испытывает погруженное в воду
тело, иными словами, знать известный закон Архимеда, изложенный в пер-
вой книге его трактата «О плавании». В связи с этим позволительно сделать
предположение, что причиной, заставившей Архимеда вернуться к механике,
были именно военные заказы царя Гиерона. Если этот царь, как мы знаем
из истории Полибия (книга V, 88) и Диодора (книга XXVI, 8), помог Родосу
после землетрясения 227 г. до л. э. также и военными машинами *), то в это
время Архимед уже должен был работать у Гиерона; таким образом,
*) «Гаеров и Гелон . . . даровали им свободу от пошлин дли идущих к ним судов родии и пять-
десят трех локтевых катя пульт» (Полибий, V, 88),
4*
52
ВСТУПИТЕЛЬНАЯ СТАТЬЯ II. И. ВЕСЕЛОВСКОГО
двадцатые годы II века до п. э. будут наиболее вероятным временем,
к которому мы должны отнести механические произведения Архимеда второ-
го периода.
У Плутарха же мы находим и наиболее полное описание обстоятельств
смерти Архимеда, погибшего во время грабежа римлянами взятых Сиракуз.
«Всего более жалел Марцелл о смерти Архимеда. Последний находился
дома, рассматривая какую-то геометрическую фигуру; так как он погрузился
в это исследование всем своим умом и всеми чувствами, то не заметил шума,
производимого бегавшими туда и сюда римлянами, и не знал, что город
уже был в их власти. Вдруг перед ним явился солдат с приказом следовать
за ним к Марцеллу. Архимед отказался идти, пока не найдет доказатель-
ства своей задачи. Раздраженный римлянин вытаскивает меч и убивает его.
Другие говорят, что какой-то солдат пошел на него с мечом чтобы убить,
а Архимед настоятельно стал просить его подождать немного, пока он
закончит задачу, но солдат, которому было мало дела до его доказательства,
пронзил ого мечом. Третьи говорят, что Архимед сам пошел к Марцеллу,
неси в ящике математические инструменты — солнечные квадранты, небес-
ные глобусы и угломеры для измерения видимой величины Солнца, но попав-
шиеся ему по дороге солдаты подумали, что он несет в ящике золото, и убили
его, чтобы овладеть этим золотом. Во всяком случае, все историки признают,
что Марцелл был очень опечален смертью Архимеда, сторонился убийцы,
как святотатца и, приказавши отыскать родственников Архимеда, милостиво
с ними обошелся».
У Тита Ливия (книга XXV7, 31) говорится только, что Архимед был убит
не знавшим его солдатом, в то время, как он занимался геометрическими
исследованиями, от которых его не мог отвлечь шум, происходивши во взя-
том городе.
VIII
Так погиб Архимед, один из величайших математиков всех времен
и народов. Нам остается проследить за дальнейшей судьбой его математи-
ческого наследства.
Мы уже говорили, что эпоха Архимеда и его младшего современника
Аполлония была временем наивысшего расцвета классической греческой
геометрической школы; со II века до н. э. характер греческой математики
резко изменяется, па первый план выдвигаются вычислительные методы,
и греческая математика становится, если можно так выразиться, «служан-
кой астрономии». Мы видели, что это течение проявилось уже в конце науч-
ной деятельности Архимеда, который отдал ему дань в «Псаммите»; после
него эта сторона математического развития настолько усиливается, что
Архимеда как математика просто забывают. Цицерон, открывший заново
могилу Архимеда во время свой службы в Сицилии, знает Архимеда как
инженера и «открывателя числовых соотношений»; Тит Ливий, как мы
видели, считает Архимеда только астрономом и конструктором военных
машип. Однако сочинения Архимеда продолжали жить; в I веко н. э. их
знает Герои Александрийский, в конце III века Архимедом много занимается
Лапп Александрийский; но уже в VI веке строитель Св. Софии Исидор
Милетский и его ученик и комментатор Архимеда Евтокий Аскалонский
знают только трактаты «О равновесии плоских фигур», «О шаре и цилин-
дре» и в очень фрагментарном виде «Измерение крута». В IX. веке в эпоху
расцвета при Македонской династии Константинопольского университета
Архимеда начинают зпать гораздо больше; к этому времени относятся две
Страница из найденного Райбергом в иерусалимском монастыре Константи-
нопольского палимпсеста (X в.).
54
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. И. ВЕСЕЛОВСКОГО
основные рукописи сочинений Архимеда; утраченная рукопись, принадле-
жавшая в XV веке Георгию Валле, и недавно (1907 г.) найденный констан-
тинопольский палимпсест, которые являются основой всех современных
изданий текстов Архимеда.
Несколько более посчастливилось Архимеду у арабов. Здесь на первом
месте следует поставить харранца Сабита ибп Курра (836—901 гг.), пере-
водчика сочинения Архимеда «О шаре и цилиндре» и «Геометрии» Евклида.
По-видимому, он был единственным арабским математиком, от которого оста-
лись специально механические произведения; ого особенно интересовал
вопрос об определении условий равновесия неравноплечего рычага с учетом
веса последнего, необходимый для правильной конструкции десятичных
весов. От Сабита до нас дошли две архимедовские антологии; одна из них
«Книга лемм» в средневековом латинском переводе (Liber assumptorum)
была известна очень давно (впервые издана Фостером в Miscellanea — Лон-
дон, 1659), другая же «О семиугольнике» найдена очень недавно и в составе
собрания сочинений Архимеда публикуется нами впервые. Кроме того,
Сабит самостоятельно занимался и другими темами из работ Архимеда:
ему принадлежит «Книга о правильном четырнадцатиграниике», предста-
вляющем одно из полуправильных архимедовых тел.
Около 1000 г. н. э. знаменитый каирский астроном ибп аль-Хаптам,
«Оптика» которого была настольной книгой всех западноевропейских астро-
номов вплоть до Кеплера, тоже занимался архимедовскими темами, вполне
владея интеграционными методами Архимеда. Он определяет объем сегмента
параболоида вращения, причем делает это другим способом, чем Архимед,
и независимо от него, так как «Коноиды и сфероиды» оставались неизвест-
ными арабским математикам. Он также решает задачу об определении объема
параболического веретена — так называлось тело, полученное от вращения
параболы вокруг хорды, перпендикулярной к се оси — и правильно опре-
- я гг
деляет его объем как объема цилиндра, описанного около веретена.
Кроме того, он занимался теорией правильного семиугольника, давши его
построение при помощи конических сечений, отличное от того, которое мы
находим в трактате ибн Курры.
В Западную Европу сочинения Архимеда попали только после кон-
стантинопольского погрома 1204 г., когда, вероятно, и был перевезен в Евро-
пу манускрипт, находившийся позже у Георгия Валлы. Первый перевод
сочинений Архимеда на латинский язык был сделан францисканцем Виль-
гельмом из Мербеке, другом Фомы Аквинского. Этот перевод, законченный
в 1269 г., был найден Розе в Ватикане только в 1884 г. Этот перевод настолько
буквален, что передаются даже греческие члены (6, т,, тс), так что может
служить независимым источником для установления текста Архимеда, но
в существе дела ученый францисканец вряд ли разбирался. Для пас пере-
вод этот важен тем, что до самого недавнего времени мы лишь ни него знали
трактат «О плавающих телах» Архимеда; только открытие константинополь-
ского палимпсеста Гейбергом познакомило нас примерно более чем с двумя
третями греческого текста. Часть перевода Мербеке была напечатана Лукой
Гауриком в Венеции в 1503 г. (первое печатное издание сочинений Архи-
меда); однако это издание осталось настолько незамеченным, что знаменитый
Тарталья смело присвоил его себе и опубликовал в 1543 и 1565 гг. как «пере-
вод с греческого».
Около 1450 г. был выполнен второй латинский перевод Архимеда Яко-
вом Кремонским. В 1468 г. его переписал зпамепитый Региомонтан и привез
в Нюренберг для опубликования. Однако ранняя смерть Региомоптапа по
к Ъ ^Й.^ЙНЙ*’’ _^;
к *₽•»</•
Rl-GIS
п f м ы,- М I lvm, via 1ас&Ь«а,
^vb-4»-**
Титульный лист сочинений Архимеда издания Рино (Париж, 1<> •))
56
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. Н. ВЕСЕЛОВСКОГО
позволила ему выполнить свое намерение, так что первое издание греческого
текста Архимеда было выпущено только в 1544 гг. в Базеле на основе
рукописей, происходящих от текста Георгия Валлы). После итого рабо-
ты Архимеда входят в обиход ученого мира. В 1558 г. выходит в Вене-
ции перевод Комманднно (второе издание с добавлением трактата «О пла-
вающих телах» вып гл о в Болонье в 1565 г.), который уже вполне понимал
Архимеда.
К 1548 г. относится переработка сочинений Архимеда фра Мавролико
из Мессины. Последний не только вполне понимал Архимеда, но даже
использовал его методы для получения новых результатов. К трактату
«О равнонесии» Мавролико добавил книгу о равновесии пространственных
тел, в которой были определены центры тяжести шара и его частей, паралле-
лепипеда, призмы, октаэдра с параллельными гранями, пирамиды и сег-
мента параболоида. Это первое самостоятельное применение метода инте-
грации Архимеда, к сожалению, было напечатано только в 1685 г. Поэтому
первым появивлтмся в печати самостоятельным исследованием при помощи
методов Архимеда было De Centro gravitatis solidorum («Книга о центре
тяжести тел» Комманднно (Болонья, 1565)), в котором даются положения
центров тяжести призмы, цилиндра, конуса, шарового сегмента (иным
способом, чем у Мавролико), усеченной пирамиды п конуса (вместо с их
объемами), правильных многогранников и сегмента параболоида вращения.
Начиная с этого времени, появляется целый ряд сочинений, посвященный
вопросу о нахождении центра тяжести. В числе их нужно назвать одно из
первых научных произведений Галилея, опубликованное им только в виде
приложения к Discorsi е dimosttazioni matcmatiche, посвященное определе-
нию центра тяжести пирамиды (в дошедших до нас сочинениях Архимеда
этот центр нс определен). Затем идет не представляющее ничего нового по
сравнению с Комманднно «Beghinselcn der Weeghkonst« («Основания
статики») Стевипа (Лейден, 1586), «In duos Archimedi aequiponderantiurn
libros paraphrasis» («Переложение двух архимедовых книг о равновесии»
Гвидо Убальди (Пезаро, 1588), De centre gravitatis li'bri tres» («Три книги
о центре тяжести») Луки Валерио (1604), «Theoremata de Centro Gravitatis
solidorum» («Теоремы о центре тяжести тел») Жана Шарля делля Файль
(Антверпен, 1632) и, наконец, венчающие весь ряд таких произведений
четыре тома «Do Centro Gravitatis» («О центре тяжести») венского иезуита
Гульдена (Вена, 1635—1641). Из этих произведений наибольший интерес
представляет сочинение Луки Валерио. В нем даются положения центров
тяжестей тетраэдра, октаэдра, трапеции, усеченной трехгранной пирамиды,
причем определение производится при помощи алгебраических формул, так
что Валерио является своего рода предшественником предельного перехода;
данный им способ определения объема шара перешел в наши школьные
учебники геометрии. После определения объемов сферических сегментов
и усеченных пирамид даются положения центра тяжести полушара и сфе-
рического сегмента (как мы теперь знаем, они были найдены Архимедом,
но решения его стали нам известными только после открытия «Эфода»).
Затем рассматриваются параболоид и гиперболоид вращения (так же и усе-
ченные), сферические пояса и, наконец, центры, тяжести сегментов сфероида
и гиперболического коноида. Небольшая книжка делля Фаиля интересна
тем, что в ней впервые определяются центры тяжести круговых сектора
и сегмента.
В XVII веке на первое место выступают общие интеграционные методы
Архимеда, а также его гидростатические работы; в этом смысле Архи-
меда можно было бы назвать ведущим математиком XVI! века. Галилей,
Фронтиспис к оксфордским изданиям классических математических
произведений (Евклид, Архимед и др.). Перевод надписи: «Аристипп,
сократический философ, будучи выброшен после .кораблекрушения па
берег Родоса и увидев начерченные геометрические фигуры, как пере-
дают, сказал громко своим спутникам; «Будем надеяться на лучшее,
ибо я вижу следы людей». Витрувий, Об архитектуре, предисловие
к fi-ii книге».
58 ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. Н. ВЕСЕЛОВСКОГО
довольно пренебрежительно относившийся к Аристотелю, не называет Архи-
меда иначе как «divinissimo Archimcdc». Занятия Галилея бесконечно малы-
ми величинами, о которых мы узнаем из его писем и упоминаний в первом
диалоге «Бесед и доказательств...», были продолжены его учениками: Тор-
ричелли, первым определившим длину дуги параболы, и Кавальери в его
«Геометрии неделимых» (Болонья, 1635). Крупным архимедистом был уже
упомянутый выше Стевии. Отдал дань Архимеду и молодой Гюйгенс, про-
долживший работы Архимеда по исследованию равновесия плавающих тел
(этой теме была посвящена одна из оставшихся не напечатанными юноше-
ских работ Гюйгенса) и определению длины окружности. Мы встречаемся
с бесконечно малыми у Кеплера, не стремившегося к строгости опубликован-
ных произведений Архимеда, в его «Stereomelria doliorum». В этом отно-
шении интересно отметить, что хотя «Эфод» был найден только в 1906 г.,
но описанный в нем метод квадратур Архимеда был, по существу, угадан
и Гюйгенсом, и другими архнмсдистами. Архимедова строгость, например,
характерное заключение определяемой криволинейной площади или тела
между двумя прямолинейными фигурами — вписанной и описанной —
была оценена значительно позже, чуть ли не Эйлером, или даже только
с начала XIX века, когда встал вопрос о строгом обосновании основных
теорем интегрального исчисления.
В связи с этим встает интересный вопрос, почему греческая математика,
так далеко продвинувшаяся вперед в лице Архимеда, не дошла до открытия
анализа бесконечно малых. Иногда зто объясняют статичностью, уравнове-
шенностью классического идеала, исключающей всякую возможность изме-
нения, которая является характерной особенностью современного исчисле-
ния бесконечно малых. Дело, однако, объясняется не особенностями грече-
ского национального характера, но особенностями греческой математической
мысли эпохи Архимеда и ему предшествующего времени.
Как мы видели выше, основной идеей ионийской школы была идея гео-
метрического построения, исключающая всякие метрические элементы.
С другой стороны, основной идеей пифагорейской математики была идея
ч и с л а; с точки зрения пифагорейской школы геометрия была учением
о фигурах — об известных формах распределения единиц в пространстве.
Понятие о psysOog — геометрической величине, представляющей часть
континуума,— носило тоже вполне определенный количественный характер
и исключало идею об изменении: числа и фигуры могли быть больше или
меньше одна другой, по нс могли увеличиваться или уменьшаться. Идея
изменения у греков была связана с совершенно другой категорией — кате-
горией качества: два человека не могли быть более д в у м я, чем два яблока,
но л гобой предмет мог быть более или менее красным, теплым, тяжелым
и т. д. Таким образом, идея изменения лежала вне области математики
и попала в последнюю очень отдаленным обходным путем. В эпоху позднего
европейского средневековья в XIV веке у англичанина Суиссета в его «Cal-
culator» и несколько позднее у француза Николая Орема появилась идея
графического изображения изменения качеств — появились произведения,
носившие заглавия «De latitudinibus formarum, De intensiono et remissione
formarum» («Об увеличении и уменьшении качеств»), в которых равномер-
ное движение изображалось прямоугольником — ширина (latitude) формы
оставалась неизменной (uniformis), откуда, между прочим, и произошло
позднейшее латинское название равномерного движения — motus unifor-
mis; равномерно-переменное изменение изображалось в виде треугольника
или трапеции и называлось uniformitcr — difformis и т. д. Конечно, из такой
чисто словесной классификации различных типов изменения, которую мы
•„.АРХИ ME ДА ; '•
ДВЬ КНИГИ :
6 ШАР'Ь и. ЦИЛИНДР%^
ИЗМЕРЕН IE кругл
и л Е м м ы М"...
ПВ?Е 8 ОДЪ СЪ Г РЕЧЗВСК а
(Леммы t* л*твисклго) ’
«'л в. п Е Т Р у шЕ В С К А Г О.
: Съ прим4чаи1ямн и доаолр.с-иямв. ' V х;
Титульный лист первого перевода сочинений Архимеда
на русский язык (СПб., 1823L
АО
ВСТУПИТЕЛЬНАЯ СТАТЬЯ И. Н. ВЕСЕЛОВСКОГО
находим в сочинениях Орема (из них не нее еще опубликованы или даже
описаны), вряд ли могло получиться что-нибудь серьезное, но самый шаг —
объединение качественного изменения с геометрической интерпретацией —
был очень важным: идея изменения выражалась в геометрической интерпре-
тации*). Конечно, в настоящий момент мы не можем показать, каким образом
из идей Суиссета и Орема возникли (или даже могли возникнуть) современ-
ные нам понятия переменной величины, но дальнейшее развитие математики
второй половины XVII века пошло именно по линии развития понятия
о переменной величине; если Архимеда можно считать родоначальником
интегрального исчисления, то открытие дифференциального исчисления
Лейбницем и Ньютоном дало такие простые и сильные методы, что способы
прямого интегрирования Архимеда оказались выброшенными за борт,
и Архимед оказался в ряду почитаемых, по не читаемых классиков мате-
матической науки, которыми занимаются лишь филологи, но не математики.
Вслед за базельским изданием последовало издание учителя Людовика XIII
француза Риво (Rivaltus), дающее лишь греческим текст предложений, за
которым следует латинский перевод доказательств с произвольными изме-
нениями (Париж, 1615). Третьим по счету было оксфордское издание Торел-
ли (1792), за которым последовало издание датского филолога Гейберга
в трех томах (1880—1881); второе издание гейберговского текста вместе
с повопапденным «Эфодом» и другими сочинениями Архимеда появилось
в 1910—1913 гг.; с этого последнего издания и сделан предлагаемый перевод.
*) Основная идея предшествующего наложения заимствована мной из доклада В. П. Зубово
на семинаре по истории математики прн МГУ, которому л приношу свою благодарность.
СОЧИНЕНИЯ
МЕХАНИЧЕСКИЕ ФРАГМЕТ1 ТЫ
Наиболее ранние произведения Архимеда были посвящены механике. Они по дошли
до лас, но некоторое представление о них (правда, далеко не полное) можно составить
но цитатам из сочинений Архимеда у более поздних авторов. '
К числу таких авторов относятся:
1°. Герои Александрийский, эпоху жизни которого в настоящее время относят
к I веку нашей эры. От него мы имеем «Механику», которая дошла до нас в арабском пере-
воде Косты ибн ..Гуки ал-Ба’лбакки (т. е. из Баальбека); опа была пайдспа в конце
XIX века и впервые опубликована в тейбнеровском издании Герона (т. I, Лейпциг,
1900 г.) в арабском подлиннике и немецком переводе. Не все места в этом тексте понятны
и верны, и мы не всегда можем точно установить авторов имеющихся ошибок. Может
быть, некоторые из этих ошибок сделаны самим Архимедом, ио еще более вероятно, что
они принадлежат Герону млн Косте ибн Луке.
2е. Лапп Александрийский (III век и. э.), автор «Математической библиотеки»,
последняя (восьмая) книга которой посвящена механике.
R этим двум авторам нужно добавить Симпликия, византийского комментатора
Аристотеля (VI век н. э.) и его близкого современника Евтокия Аскалолского, оставив-
шего важные комментарии к сочинениям Архимеда; эти комментарии принято помещать
в полных изданиях сочинений Архимеда.
Сам Архимед в трактате «О плавании» упоминает свое механическое сочинение
«О равновесии (iaoQQonixa). Это, очевидно, трактат «О равновесии плоских фигур», но
ряд ссылок (касающихся центров тяжести круга, цилиндра, призмы, конуса, параболоида
вращения) не может относиться к этому сочинению. Возможно, что оно дошло до лас
в неполном виде и, что, кроме книг о равновесии плоских фигур, были и книги, посвя-
щенные равновесию телесных фигур; однако можно утверждать, что дошедшее до пас
сочинение «О равновесии плоских фигур» не могло быть первым сочинением Архимеда
по механике. Вторая книга этого сочинения совершенно определенно должна быть напи-
сана после «Квадратуры параболы». Поэтому некоторые авторы считают, что первая книга
«О равновесии плоских фигур» представляла самостоятельное сочинение, предшествовав-
шее «Квадратуре параболы». Но даже и в этом случае оно не могло быть первым сочи-
нением Архимеда по механике. Действительно, в нем нет определения центра тяжести,
которое, очевидно, предполагается известным; затем, самые доказательства часто (центр
тяжести прямоугольника и треугольника) ведутся искусственным способом от против-
ного, так что они скорее обращены к любящим строгость математикам, чем к механикам-
практикам; первоначальный способ нахождения центров тяжести прямоугольника и тре-
угольника, конечно, был совершенно отличным и может быть заключался в разложении
площади на ряд «неделимых» прямых (см. отрывок из «Механики» Герона, II, 35—41).
На существование более раннего сочинения но механике Архимеда указывают
и ссылки, имеющиеся в «Квадратуре параболы». Этим сочинением, посвященным опре-
делению центра тяжести простейших фигур, могло быть упоминаемое Паппом сочинение
«О рычагах» (Пед! £vy«>v • собственно «О равноплечих рычагах»). Возможно, что в нем
п давилось то определение центра тяжести, которое мы находим у Паппа (VIII, 5) и Геро-
на («Механика», 1, 24): оба последних текста настолько близки друг к другу, что в выс-
шей степени вероятно, что они восходят к одному и тому же источнику, которым и явля-
лось упомянутое сочинение Архимеда. Вероятно, к нему же относится и упоминание
<64
АРХИМЕД
nevTQopaQizi («О центрах тяжести») у Симпликия, так что нет надобности принимать
гипотезу об особом сочинении под указанным заглавием.
Наконец, в арабской «Механике» Геропа имеются ссылки па «Книгу опор» Архи-
меда («Механика», I, 25, 26—28, 30—31). В указанном тексте имеется довольно значи-
тельное количество ошибок и несообразностей, и если уж приписывать их в какой-то
доле Архимеду, то мы должны признать «Книгу опор» самым ранним его сочинением.
Сопоставив все сказанное, можно высказать следующее предположение.
Самым ранним произведением Архимеда была вышеупомянутая «Книга опор».
Изучение вопросов распределения давлений и устойчивости равновесия привело Архи-
меда к введению понятия о центре тяжости, причем соответствующая теория (вероятно,
с точки зрения практической механики) была развита в книге «О рычагах». Наконец,
математическое изложение теории центра тяжести было дало им в сочинении «О равно-
весии», которое было значительно больше дошедших до нас двух книг «О равновесии
плоских фигур».
Распределение механических фрагментов в настоящем издании произведено сле-
дующим образом.
Па первом месте помещен большой отрывок из «Механики» Геропа, соответствую-
щий архимедовой «Книге опор». Изложение в нем еще детское. Вес мпогоопорной балки
для каждого пролета считается распределенным поровну между ограничивающими этот
пролет опорами. В случае копсольпой балки считается, что опора под консолью выдер-
живает нагрузку, соответствующую удвоенной длине выступающей части плюс половина
длины оставшейся части; вес этой части, таким образом, считается распределенным по-
ровну между опорой под консолью и оставшейся опорой как и в случае простой мпого-
опорпой балки. Только в случае сосредоточенных нагрузок давления на опоры нахо-
дятся правильно. Это показывает, что во время написания «Книги опор» Архимед (если
вышеупомянутые ошибки принадлежат ему, а не Городу) еще ле знал, что нес тела можно
считать сосредоточенным в его центре тяжести.
Рассмотрение давлений па опоры естественно привело Архимеда к одпоопорпой
балке или рычагу; следующие фрагменты относятся к предполагаемой книге «О равно-
плечих рычагах». Здесь на нервом месте стоят две цитаты из Паппа, касающиеся архи-
медова доказательства закона рычага; доказательство, имеющееся у Геропа, отнести
к Архимеду можно только условно. Далее помещен отрывок из комментария Ентокия,
важный для уяснения понятия о мамонте (рол»]). Затем идут два текста из Геропа и Паппа,
касающиеся определения цоптра тяжести, относительно которых можно сказать с уверен-
ностью, что их источник восходит к Архимеду; места в них, восходящие к Архимеду,
отмечены курсивом. Оба последних текста важны в том отношении, что они раскрывают
самый процесс возникновения понятия о центре тяжести из рассмотрения давлений па
опоры. После них дап небольшой фрагмент из Симпликия.
Затем идут две цитаты из «Квадратуры параболы» и большой отрывок из Г крона,
касающийся определения центра тяжести треугольника и многоугольников и показы-
вающий начальные стадии развития способов его нахождения; какая-то часть его может
восходить к Архимеду.
Наконец, последними идут цитаты из «Эфода» и «О плавающих телах», проливаю-
щие некоторый свет па то, что содержалось в не дошедших до пас книгах сочинения
«О равновесии».
КНИГА ОПОР
I. ГЕРОИ, МЕХАНИКА, КН. 1, 25—28, 30—31*)
(25) Лам совершенно необходимо разъяснить кое-что о давлении,
передаче и переносе с количественной стороны в той мерс, как это нужно
для введения. Архимед применял в этой части (механики) искус-
ство, доведенное им до совершенства в книге, озаглавленной «Книга
опор». Мы разъясним то из нее, в чем мы нуждаемся для других вопро-
сов; воспользуемся из нее тем, что относится к количественной стороне
В той мерс, в которой это нужно для изучающих.
Постановка (задачи) здесь такова: если имеется несколько
колони, па которых находятся поперечные балки или стена, причем
положения на краях одинаковы или различны, то есть балка или стена
*) См. [31J, стр. 71—85.
МЕХАНИЧЕСКИЕ ФРАГМЕНТЫ
65
могут выступать за один из концов или за оба конца, а расстояния
между колоннами могут быть равны или пе равны, то мы хотим узнать,
сколько веса приходится на каждую колонну.
Пример этого: люди несут длинное бревно, равномерное по весу,
(встав) па равных расстояниях по длине бревна, причем выступает
один из концов или оба конца; мы хотим узнать, сколько веса прихо-
дится на каждого человека; это требуется (узнать) и при обоих
(выступающих концах) и при одном.
(26) Пусть на колоннах находится груз АВ равномерный по тол-
щине и однородный {рис. 1}. Если он находится на двух колон-
нах АС и BD, то на каждую из них приходится половина веса АВ.
Пусть имеется еще одна колонна EF, делящая расстояние АВ
как угодно, и мы хотим узнать, сколько
веса приходится на каждую из колонн АС,
EF и BD. Представим себе, что груз АВ
разделен в точке Е вертикальной линией
но колонне {EF), тогда нам ясно, что
со стороны АЕ на каждую из колонн АС
и EF приходится половина ее веса, а со
стороны ЕВ на каждую из колонн EF и
BD приходится половина ее веса, так как
лет никакой разницы в том, как распреде-
ляется (вес) на колоппы, находится ли
на них целая или разделенная (тя-
жесть), поскольку как целая, так и разде-
ленная все равно находится на колоннах. Следовательно, па колон-
ну EF приходится половина веса ЕВ, и половина веса АЕ, то есть поло-
вина всего веса АВ, па колонну АС приходится половина веса АЕ, а па
колонну BD половина веса ЕВ. Поэтому если мы разделим половину
АВ в отношении расстояния АЕ к расстоянию ЕВ, то вес части,
пропорциональной (расстоянию) АЕ, придется па АС, а вес (части),
пропорциональной расстоянию ЕВ, — на BD.
Если мы поставим еще одну колонну HG, то нам ясно, что на АС
придется половина (веса) АЕ, на BD — половина (веса) ИВ,
на EF — половина АН, а па ПС — половина BE. Половина АЕ, поло-
вина НВ, половина АН и половина ЕВ вместе (равны) АВ, то есть
тому, что находится на всех колоннах.
Если колони еще больше, мы узнаем, сколько веса получает каждая
из лих, с помощью того же способа.
(27) Если так, то предположим, (что имеются) две одинаково
расположенные опоры АВ и CD {рис. 2} и пусть на них находится
тело АС, равномерное по размерам и весу. Мы уже говорили, что на
каждую из опор АВ и CD приходится половипа веса АС. Перенесем
теперь опору CD, приблизив ее к АВ, пусть ее положение — EF.
Мы хотим узнать, сколько веса теперь приходится на долю АВ и EF.
Заметим, что расстояние АЕ или равно расстоянию ЕС, или меньше
его, или больше его. Пусть сначала {АЕ) равно {ЕС). Тогда нам
ясно, что вес АЕ уравновешивается весом ЕС. Поэтому, если мы
уберем опору АВ, груз АС останется в том же состоянии (равнове-
сия), поэтому нам ясно, что на опору АВ не придется никакого веса
и весь вес АС придется (только) на одну (опору) EF.
Если расстояние СЕ больше расстояния ЕА, груз АС опустится
со стороны С.
Архимед
66
АРХИМЕД
Если же расстояние СЕ меньше ЕА, пусть СЕ равна ЕН {рис. 3}.
Тогда СН находится в равновесии на одной (колонне) ЕЕ. Поме-
стим (в точке Н} колонну HG и представим себе, что груз разделен
в точке Н. Тогда (вес) СН придется (только) па одну EF, а на
каждую из опор АВ м HG— по половине (веса) А И. Поэтому, если
мы уберем опору HG, к точке Н будет приложена вся сила, (которая
приходилась) на эту опору, если тело (груза) соединено. Поэтому
на (опору) АВ i придется половина веса НА, а на (опору) EF —
все остальное, то есть С И и половина АН. Если мн представим себе,
что (груз) АС разделен пополам в точке К, то КЕ — половина АН.
Поэтому если опора, которая сначала была под Е, теперь будет под
точкой К, на пес придется весь вес АС, и чем больше удалится опора
от точки, делящей груз пополам, тем
большая часть веса придется па (опору)
АВ, остальной же вес (придется) на
другую опору.
(28) Если так, то предположим, что
две опоры АВ и EF расположены, как
указано в предыдущем случае, и пусть
груз ЕС избыточный. Разделим груз АС
пополам в точке К. Мы доказали, что
на опору АВ (приходится) вес КЕ, а на
опору EF — остальная часть веса АС.
Предположим теперь, что под точкой С
(помещена) опора CD {рис. 4). Уже
Рис. 4.
доказано, что (в этом случае) на опору АВ придется половина
веса АЕ, на опору DC — половина веса ЕС, а на опору EF — половина
(всего) веса АС. Перед тем, как мы поставили опору CD, мы
показали, сколько веса приходится па каждую из (опор) АВ и EF.
Поэтому пам ясно, что после того, как под грузом помещена опора {CD},
на опору АВ придется веса больше, чем раньше, на половину ЕН,
то есть на половину ЕС, а (опора) EF получит веса меньше, чем
опа получала сначала, на величину ЕС. В силу сказанного иа (опо-
ру) DC придется вес половины ЕС, так как после того, как под груз
была помещена добавочная опора, па опору EF приходится меньше
(веса) па величину, равную ЕС, а на опору АВ приходится больше
веса на половину ЕС. Поэтому на (опору) CD придется остальная
половина веса ЕС. Та же величина получится и по другому способу.
Поэтому нам ясно, что если груз находится па опорах, которые
• поддерживают его, и к этим опорам добавлена еще одна опора, то на
одни из первоначальных опор будет приходиться больше веса, чем
MEХАНИЧКСКИЕ ФРАГМЕНТЫ
67
до добавления (опоры), а на другие опоры — меньше веса, чем до
добавления. Так, если были опоры АВ, EF и CD и на АВ приходилась
половина веса АЕ, то как мы видели, после того как (опора) CD убра-
па, па АВ приходится половина веса АК. Нам яспо, что (часть гру-
за) ЕС повиснет и станет действовать, как рычаг. Поэтому опа снимет
часть тяжести, (приходящейся) на АВ, а на ЕЕ
придется (тяжести) больше, чем на ней было /-1 А р
сначала, и груз АВ останется на своем месте. п ГТ“ J
(30) Предположим, что на опорах АВ и
CD {рис. 5} находится тело EF, однородное
по весу и равномерное по толщине, и пусть
оно выступает со стороны обеих опор. Мы я В
хотим узпать, сколько веса приходится на , _
каждую из опор. Так как мы доказали, что
если груз AF находится на (опорах) CD и АВ,
то CD получает больше веса, чем АВ, на удвоенную величину CF, а
если (груз) СЕ находится на (опорах) CD и АВ, то АВ получает
больше веса, чем CD, на удвоенную величину АЕ, нам ясно, что
на CD приходится настолько больше веса, чем на АВ, па сколько
удвоенная величина CF превышает удвоенную величину АЕ. Если CF
и АЕ равны, то па каждую из (опор) CD и АВ приходится одина-
ковый вес; чем больше одно расстояние по сравнению с другим, тем
больше веса придется на соответствующую опору.
Из сказанного нами следует, что если на колоннах или опорах
находятся поперечные балки или степа, равномерные по толщине
и однородные по весу, и расстояния между опорами различны, мы
можем узнать, па какую из опор приходится больший вес и каков избы-
ток веса. Если на опорах находятся поперечные балки или нечто подоб-
ное, это уяснится для нас благодаря тому же самому способу. Точно
так же если люди песут дерево или камень на руках или на веревках.
причем некоторые из них находятся посередине, а некоторые — на
концах, и груз выступает с одной сто-
роны или с обеих сторон, для нас ясно,
сколько веса приходится на каждого.
(31) Пусть другой груз АВ, также
равномерный (по толщине) и однород
пый но весу, находится на одинаковых
опорах АС и BD {рис. 6}. Тогда нам
ясно, что каждая из опор получит
половину веса АВ. Подвесим к АВ в
точке Е груз. Если точка Е делит АВ
Гис. 6. пополам, нам ясно, что па каждую из
опор приходится половина веса АВ и
половина веса груза, подвешенного или положенного в точке Е.
Если же точка Е пе делит (АВ) пополам, то разделим вес груза
в отношении BE к АЕ, тогда часть веса, пропорциональная ЕВ, при-
ходится на (опору) АС, а часть веса, пропорциональная ЕА, на
(опору) BD^ii, кроме того, каждая из опор получает половину
(веса) $ AS. Если мы подвесим другой груз в точке F и разделим
его вес в отношении AF к FB, то на (опору) DB придется часть
веса, пропорциональная AF, а на (опору) АС — часть веса, пропор-
циональная FB и, кроме того, на каждую из опор придется поло-
вина (веса)' АВ. О том, (чему равно) отношение FB к АС, уже
68
АРХИМЕД
сказано, сказано и о том, какие веса приходятся на опоры до подве-
шивания грузов в Е и F, следовательно, сказано о полной нагрузке,
которая приходится па опоры АС и BD. Тем же способом мы узнаем,
сколько веса приходится на каждую из них и при подвешивании дру
гих грузов.
О РЫЧАГАХ
И. ПА1Ш, МАТЕМАТИЧЕСКАЯ БИБЛИОТЕКА, КН. V1U, 24*)
«В книге «О рычагах» Архимеда, а также в «Механике» Фило-
на* **) и Геропа доказано, что большие круги пересиливают меньшие,
если вращение происходит около одного и того же центра».
III. ГЕРОИ, МЕХАНИКА, КН. II, П. 7***)
Представим себе два круга с одним и тем же центром Л {рис. 7),
пусть линии ВС и DE — их диаметры. Пусть оба круга могут вра-
щаться около точки А, являющейся их центром, и
установлены перпендикулярно горизонту. Если мы
подвесим в точках В и С равные грузы F и И, то пам
ясно, что круги не наклонятся пи в одну сторону,
так как веса F и II равны, расстояния ВА и АС
также равны, так что ВС — коромысло весов,
которое может вращаться около точки подвеса Л
Если же перепости груз, находящийся в С, и
подвесить его в Е, то груз F опустится вниз и
наклонит оба круга. Если мы добавим [в точку/?]
груз G, то он уравновесит груз F, если груз G
относится к грузу F как расстояние ВА к рас-
стоянию АЕ. Поэтому мы можем рассматривать
линию BE как весы, которые могут вращаться
около точки подвеса Л. Это доказал Архимед в своей книге о равновесии
(книга первая, предложения VI и VI1). Отсюда ясно, что можно сдвинуть
большую величину малой силой.
IV. ПАПП, МАТЕМАТИЧЕСКАЯ БИБЛИОТЕКА, КН. VIII, 11****)
«Т? той же самой теории*****) относится задача: как двинуть данный
груз заданной силой******); это механическое изобретение Архимеда,
о котором он, как передают, сказал «дай мне где стать, и я сдвину Землю».
V. ЕВТОКИЙ, КОММЕНТАРИЙ К ТРАКТАТУ
«О РАВНОВЕСИИ ПЛОСКИХ ФИГУР»*******)
«Момент (рстг»|)... является общеродовым понятием для тяжести
и легкости, как говорит Аристотель и, следуя ему,— Птолемей. Тимей
же у Платона утверждает, что всякий момент рождается лишь от тяже-
•> См [32]. стр. 1OGB. 19 и сл.
**) Филон Византийский (II век до н. э.), автор большого курса «Механики» (из которого до
нас дошли фрагменты двух книг).
**») См. [31]. стр. 111— '13
**•*) См. [32]. стр. 1080.
»••**) Подразумевается теория поднятия тяжелых тел.
♦ »»***) ,В подлиннике бНарк. что соответствует нашей «мощности» (см. вступительную статью).
>•»•**•) см. [15], 1-е издание, т. HI, стр. ЗОВ.
МЕХАНИЧЕСКИЕ ФРАГМЕНТЫ
69
сти, а легкость он считает лишением*). Любители паук могут
прочитать об этих мнениях в составленной Птолемеем книге о момен-
тах, в физических сочинениях Аристотеля, в Платоновой «Тимее»
и в комментариях к ним. В рассматриваемой книге Архимед называет
центром момента (zevxpov -tv); pwvj;) плоской
фигуры точку, при подвешивании за которую
фигура остается параллельной горизонту; цен- / X.
тром момента или тяжести двух или более пло- / X.
ских фигур он называет точку подвеса рычага, / л X.
остающегося параллельным горизонту, если -------------------Хе
прикрепить к его концам упомянутые фигуры.
Пусть, например, дан треугольник АВС {рис. 8} _ с —
и в середине его точка D, обладающая тем -----------•"-----
свойством, что при подвешивании за нее тре-
угольник остается параллельным горизонту. Гис-
В таком случае ясно, что части его А, В и С
уравновешивают друг друга и ни одна из них не будет иметь боль-
шего момента (р-z..lov penei) к горизонту. Точно так же, если дан
рычаг АВ и к нему подвешены такие величины А и В, что при подве-
шивании за С части А и В рычага уравновешивают друг друга, то он
останется параллельным горизонту и точка С будет центром подвеса
для величия А и В».
VI. ГЕРОИ, МЕХАНИКА, КН. I, I, 24**) '
Никто не отрицает, что о наклонении и отклонении в действитель-
ности говорят только о телах. Если же мы говорим о плоских или телес-
ных геометрических фигурах, что некоторая точка является их цен-
тром поворота и центром тяжести, то это достаточно разъяснено Архи-
медом. Это будет понятно после того, что мы сооб|цим. Посидоний***)
из школы стоиков дал физическое определение центра наклона и тяже-
сти: он сказал, что центр тяжести или наклона это такая точка, что
если подвесить в пей груз, он разделится на две равные части. Архимед
и его последователи в искусстве механики уточнили эти слова и уста-
новили разницу между точкой подвеса и центром наклона. Точка под-
веса — это такая точка тела или другого предмета, что если подвесить
его в этой точке, все его части будут находиться в равновесии, а не
будут качаться и наклоняться; равновесие же наступает тогда, когда
один предмет уравновешивает другой, как это имеет место в случае
весов, колеблющихся в плоскости горизонта или в параллельной ей
плоскости. Архимед сказал, что грузы не наклоняются {если они под-
вешены} на некоторой линии или в некоторой точке. Это бывает па
линии, когда груз (подвешен) в двух точках этой линии, причем эта
линия не наклонена и плоскость, проведенная через эту линию перпен-
дикулярно горизонту, остается перпендикулярной (горизонту), как
бы ни перемещалась линия; тогда груз, (подвешенный) па линии,
не наклоняется. Когда мы говорим, что груз наклоняется, мы имеем
в виду его падение вниз, т. е. движение к земле. Равновесие в точке
бывает, когда груз подвешен в нем и при всяком движении части тела
*) (пвстртс — технический термин аристотелевской физики; в данном случае подразуме-
вается лишение тяжести.
•*) См. [31], стр. 63—71.
*•*) См. вступительную статью, главу II. . . .:
70 АРХИМЕД
движутся одинаково по отношению друг к другу. Груз уравновешивает
другой груз, если они подвешены в двух точках линии, разделенной
(точкой опоры) пополам, или в точке, делящей ее (в другом отно-
шении), причем линия становится параллельной горизонту, если
величины грузов относятся друг к другу обратно расстояниям точек,
в которых они подвешены, (от точки опоры). То, что подвешенные
таким образом грузы будут находиться в равновесии по отношению
к наклону, доказал Архимед в своих книгах о равновесии фигур, поль-
зуясь при этом рычагами.
Точка подвеса и опоры — одно и то же, так как и точка подвеса
и опоры оказывают одно и то же силовое действие: опора, к которой
подвешен груз, несет его; только опор может быть много и даже беско-
нечно много.
Что же касается центра наклона, то это единственная точка
в каждом теле, в которой сходятся перпендикуляры (к горизонту),
проведенные из точек подвеса*). У некоторых тел центры наклона
бывают впе их самих, как это имеет место в случае сводов и запястий.
То, что линии подвеса сходятся в одной общей точке, нам будет ясно,
если мы представим себе плоскость, перпендикулярную горизонту,
рассекающую тело на уравновешивающие друг друга части**). Тогда нам
ясно, что эта плоскость делит тело пополам, поэтому она проходит
через тело. Если мы представим себе другую плоскость, делящую тело
так же, как эта плоскость, она также пройдет через тело. Эти две
плоскости пересекутся по линии и если бы эта линия пересечения не
прошла через точку подвеса, оказалось бы, что тела и уравновешивают
и не уравновешивают друг друга.
Применим эти выводы к опорам. Представим себе тело, опираю-
щееся на линию в плоскости***). Пусть части тела находятся в равно-
весии (относительно) этой линии. Если продолжить эту линию, она
пройдет внутри тела. Если бы она находилась вне тела, то впе тела
находилась бы и плоскость, но мы видели, что это невозможно. Следо-
вательно, линия пройдет внутри тела и разделит его на части, уравно-
вешивающие друг друга. Если мы представим себе в качестве точки
равновесия другую точку, отличную от этой, окажется, как в первом
случае, что линия, проходящая через эту точку, пройдет внутри тела,
поэтому эти две линии различны. Если провести через них две пло-
скости, они не {обязательно) пересекутся, так как через две линии
можно провести две пепересекающиеся плоскости****). Получится то же
самое, что в первом случае, поэтому это невозможно. Таким образом,
мы узнаем, что эти плоскости пересекаются и линии встречаются',
поэтому эти линии находятся в одной плоскости. Если продолжить
эту плоскость до поверхности тела, то точки пересечения образуют
линию. Тогда имеется третья точка, попадающая вне этой липни.
Представим себе, что эта точка — также точка равновесия, то есть
*) Имеется в виду обычный спос< б определения центра тяжести путем подвешивания тела в
различных точках и нахождения точки пересечения вертикалей, проходящих через точки подвеса.
•*) Дальнейший текст Герона следует читать вместе с приведенным ниже текстом Паппа.
Курсивом отмечены места совпадающие в обоих текстах, ати места с наибольшей вероятностью
можно считать текстом самого Архимеда. Отметим, что текст Паппа лучше текста Герона, у кото-
рого встречаются несообразности и неясности.
***) Необходимость вставки итого слова видпа из текста Паппа (п. 7).
*•••) По-вицимому. мысль автора такопа: если имеются две точки равновесия, ие находящиеся
на одной вертикали, через них можно провести дпе вертикали, а через них — дпе непсресекакщие
друг друга плоскости. Так как каждая такая плоскость должна делить тело на две уравновешиваю
щие друг друга части; в таком случае получилось бы. что одна и та же часть тела находилась бы
одновременно в равновесии с двумя частями тела, одна из которых превосходит другую на часть
тела, находящуюся между двумя параллельными плоскостями.
МЕХАНИЧЕСКИЕ ФРАГМЕНТЫ
71
что тело (подвешенное) в этой точке, находится в равновесии*).
Проведем через эту точку линию (равновесия) внутрь тела. В силу
сказанного нами если провести эту линию., она встретит две линии
(подвеса), через которые проведена плоскость, и притом только
в точке их пересечения, так как если линия встречает две пересекающиеся
линии, а сама находится в другой плоскости, она встречает их в их
точке пересечения, ибо если бы опа встречала их пе в их точке пере-
сечения, то необходимо часть этой линии находилась бы в одной пло-
скости, а остальная часть — в другой плоскости. Следовательно, все
линии подвеса встречаются в одной точке' эта точка и называется
центром наклона и тяжести.
VH. ПАПП, МАТЕМАТИЧЕСКАЯ БИБЛИОТЕКА, КН. VITI, 5-8**)
(5)... Мы говорим, что центром тяжести некоторого тела является
некоторая расположенная внутри него точка, обладающая тем свой-
ством, что если за нее мысленно подвесить тяжелое тело, то оно остает-
ся в покое и сохраняет первоначальное поло-
жение. Эта точка, существующая пе только в УН----------------\в
геометрически правильных телах, но и в телах
неправильной формы, может быть найдена при
помощи следующих рассуждений.
Вообразим некоторую вертикальную пло-
скость ABCD {рис. 9], направленную к центру с*---------------щ
мира, куда, по-видимому, имеют стремление
(обхту) все тела, обладающие весом; пусть пря- Рис' 9‘
мая АВ параллельна той плоскости, на кото-
рой мы находимся***). Если какое-нибудь обладающее весом тело поло-
жить па прямую АВ так, чтобы оно полностью рассекалось продолже-
нием упомянутой плоскости, то оно может иногда занять такое положе-
ние, что будет оставаться в покое, не вращаясь и пе падая вниз.
Если это случилось и мы мысленно продолжим плоскость A BCD, то
она рассечет лежащее тело на две части, обладающие одинаковыми
моментами и взаимно уравновешивающиеся, если тело как бы под-
переть этой плоскостью****). Если затем переставить груз так, чтобы
он касался прямой АВ другой своей частью, то можно при поворачива-
нии дать ему такое положение, что он, будучи отпущен, останется
в покое и не упадет. Если снова вообразить плоскость ABCD продолжен-
ной, то она разделит груз на две взаимно уравновешивающиеся
части и пересечется с первой плоскостью, делившей тот же груз
на две взаимно уравновешивающиеся части; если бы эти плоскости не
пересеклись, то те же самые части были бы и уравновешивающимися
и не уравновешивающимися, что нелепо.
(7) После этих предпосылок вообразим прямую АВ, перпендику-
лярную к горизонтальной плоскости {рис. 10} и, следовательно,
направленную к центру мира; затем аналогичным образом положим
груз на точку А так, чтобы он, пользуясь прямой АВ в качестве
*) Ымскь автора такова: он нашел две точки подвеса, провел через них две линии подвеса,
которые отказались в некоторой плоскости, образующей в сечении с поверхностью тела кривую,
на которой находятся обе первые точки подвеса. Он берет третью точку подвеса, не находящуюся на
этой кривой, и доказывает, что линия подвеса, проходящая через эту точку, проходит через точку
пересечения мерных двух линий подвеса.
♦•) См. [32 J, стр. 1030 и ел,
** *) То есть горизонтальной.
•* **) То есть плоскостью ABCD ' •
72
АРХИМЕД
подставки, когда-нибудь остался в покое па точке А, как он оставался
неподвижным на проведенной через нее плоскости. Если теперь, сохра-
няя тело неподвижным, продолжить прямую АВ, то некоторая ее
часть будет находиться внутри рассматриваемого тела. Вообразим,
что последнее стало в некотором положении неподвижным; тогда
снова наложим его на указанную прямую другой частью так, чтобы
оно опять стало неподвижным', я утверждаю, что тогда продолженная
прямая АВ встретится с первоначально заключавшимся внутри тела
отрезком. Действительно, если бы она tie встретилась, то
оказалось бы возможным, что некоторые плоскости, проведен-
ные через каждую из этих прямых, не пересекаются друг с
другом внутри тела, причем каждая из них разделяет груз на
части, которые одновременно являются и уравновешивающими-
ся и не уравновешивающимися, что нелепо', следовательно,
упомянутые прямые встретятся внутри тела. Точно так же
д если в других положениях помещать груз на точку А так,
чтобы он оставался в покое, то снова продолженная АВ обя-
ис' ‘ зательно встретится с заключающимися внутри тела отрез-
ками первоначальных прямых. Из этого ясно, что такие вооб-
ражаемые прямые будут пересекать друг друга в одной и той же
точке-, эта точка и называется центром тяжести. Яспо, что если
груз мысленно подвесить за центр тяжести, то он не перевернется,
но будет сохранять любое приданное ему в начале положение, так
как все плоскости, проведенные через эту точку, будут разделять
груз на взаимно уравновешивающиеся части, у которых не будет
никакой причины для переворачивания.
(8) Вот в этом и заключается сущность теории центра тяжести;
доказываемые ею элементарные свойства последнего ты можешь узнать,
познакомившись с книгами Архимеда «О равновесии» и с «Механи-
кой» Герона; в дальнейшем же мы изложим лишь то, что не является
известным большинству.
VIII. СИМПЛИКИЙ. КОМЕПТАРИИ К КНИГЕ АРИСТОТЕЛЯ «О НЕБЕ»
«Теория центра тяжести, относительно которой много и хорошо
написали Архимед и многие другие, имеот своей целью определить
центр данной тяжести, то есть некоторую точку на теле, при подве-
шивании за которую веревкой тело остается в том же положении без
изменения наклона».
IX. АРХИМЕД, КВАДРАТУРА ПАРАБОЛЫ, 6*)
«Действительно, каждое из подвешенных тел, укрепленное в ка-
кой-нибудь точке, остается неподвижным в таком положении, когда
точка подвеса и центр тяжести подвешенного тела находятся на одном
перпендикуляре; это тоже доказано».
X. ГЕРОИ, МЕХАНИКА, КН. П, 35—41**)
(35) Нам необходимо доказать кое-что... о более важных вещах,
которые разъясняли Архимед и другие.
*) См. стр. 81 этого издания.
•*) См. [32J, стр. 189—19».
МЕХАНИЧЕСКИЕ ФРАГМЕНТЫ
73
Рис. 11.
В
• * С
Рис. 12.
Прежде всего сообщим, как определяем центр тяжести треуголь-
ника, равномерного по толщине и однородного по весу. Пусть данный
треугольник — треугольник АВС {рис. 11}. Разделим линию ВС
пополам в точке D и соединим точки А и D. Если опереть треугольник
на линию AD, он не наклонится ни в ту, ни в другую сторону, так как
треугольники ABD и ADC равны*). Точно так же, если мы разделим
линию АС в точке Е и соединим точки В и Е и если опереть треуголь-
ник на линию BE, он также не наклонится ни в ту, ни в другую сто-
рону. Так как треугольник, будучи оперт на каждую из линий AD
и BE, находится в равновесии
своих частей и не наклоняется ни
в ту, ни в другую сторону, общая
точка, в которой эти две линии
пересекаются, является центром
тяжести, это — точка F. Необхо-
димо представлять себе точку F в
середине толщины треугольни-
ка АВС. Поэтому нам ясно, что
если мы соединим точки А и D,
разделим линию AD в точке F
на такие две части, (одна) из которых AF — удвоенная (другой)/7),
то точка F будет центром тяжести. Действительно, если мы соеди-
ним точки D и Е, линия АВ будет параллельна линии DE, так как
линии АС и ВС разделены в точках D и Е (пополам); таким обра-
зом, отношение АС к СЕ равно отношению АВ к ED, но линия
АС — удвоенная линия СЕ, откуда следует,
что линия А В — удвоенная ED. Но линия АВ
X относится к ED как линия AF к DF, сле-
довательно, AF — удвоенная FD, в силу
того, что фигуры ABF и DFE обладают
равными углами.
(36) Мы хотим определить то же самое
для четырехугольника. Пусть данный че-
тырехугольник — четырехугольник ABCD
В {рис. 12}. Соединим точки В и D и разде-
лим BD пополам в точке Е, соединим также
(точки) А и Е, Е и С и разделим линии АЕ
и ЕС в точках F и Н таким образом, что-
бы AF была удвоенной/7?, а СИ — удвоенной НЕ. Тогда центр (тя-
жести) треугольника ABD — точка F, а центр треугольника ВВС —
— точка /I. Мы получим то же самое, если будем представлять себе
весь вес треугольника ABD (сосредоточенным) в точке F, а весь
вес треугольника BCD — в точке II. Тогда линия FH становится веса-
ми, па концах которых находятся зти величины. Поэтому если мы
разделим линию FH в точке G таким образом, что GB относится к FG
как вес F, то есть вес треугольника ABD, к весу И, т. е. весу треуголь-
ника BDC, то точка G, в которой оба веса уравновешиваются, являет-
ся центром (тяжести) этого четырехугольника.
(37) Мы хотим определить то же самое для пятиугольника ABCDE
{рис. 13}. Соединим BE и определим центр тяжести треугольника
*) Под равными треугольниками здесь имеются в виду равновеликие треугольник-? (кон-
груэнтные треугольники назывались «равными и подобными треугольниками»). В подлиннике могло
также стоить «равиовссящис».
74
АРХИМЕД
АВЕ, пусть это будет точка F-, пусть центр тяжести четырехугольника
BCDE будет в точке Н. Соединим точки F и И и разделим линию FII
па две части таким образом, чтобы часть HG относилась к GF, как
вес треугольника АВЕ к весу четырехугольника BCDE. Поэтому
точка G — центр тяжести фигуры ABCDE.
Такой же способ мы будем применять и для всех многоугольников.
(38) . Если дан треугольник АВС, равномерный по толщине и весу,
и под точками А, В и С находятся одинаково расположенные опоры
{рис. 14}, то мы хотим определить, ка-
кую величину веса треугольника АВС
Разделим линию ВС пополам в точке D,
несет каждая из этих опор.
соединим точки А и D и разделим линию AD на дне части в точ-
ке Е таким образом, что часть АЕ — удвоенная ED. Тогда точ-
ка Е — центр тяжести всего треугольника. Нам нужно распределить
этот вес по опорам. Если мы пред-
ставим себе линию AD в равно-
весии подвешенной в точке Е, то
вес в D будет удвоенным весом
в А, так как линия ЛЕ — удвоен-
ная линия ED. Если мы предста-
вим себе, что вес в D распреде-
лен
л образом, чтобы линия ВС находи-
лась в равновесии, то на каждую
из точек В и С придется половина
веса в D, так как линии BD и DC
был удвоенным весом в А. Следовательно, веса во
А, В и С равны и, значит, опоры будут нести
по точкам В и С таким
равны. Но вес в D
всех трех точках
равные нагрузки.
(39) Пусть дан
и толщине и находящийся на одинаково расположенных опорах
{рис. 15}, и пусть в точке Е, расположенной где угодно, положен
или подвешен груз. Мы хотим определить, какую долю веса, (поме-
щенного) в Е, несет каждая из опор. Соединим (точки) А и Е и про-
должим АЕ до D. Разделим вес в Е на две части таким образом, чтобы
треугольник находился в равновесии, будучи оперт па линии AD.
Тогда отношение веса в D к весу в А равно отношению линии АЕ к ли-
• пии ED. Далее разделим вес в D так, чтобы (линия) ВС находилась
в равновесии, будучи подвешена (в Z>). Тогда отношение веса в С
треугольник АВС, также равномерный по весу
МЕХАНИЧЕСКИЕ ФРАГМЕНТЫ
75
к весу в В равно отношению линии ВВ к линии СВ. Вес в В найден,
следовательно, найдены и веса в В и С; вес в А также найден. Следо-
вательно, найдены веса во (всех трех) опорах.
(40) Если дан треугольник АВС и подвешены известные грузы
в точках А, В и С {рис. 16}, то мы хотим определить внутри тре-
угольника такую точку, что если подвесить треугольник в этой точке,
оп будет находиться в равнове-
сии. Разделим линию АВ в точ-
ке В таким образом, что линия ВВ
относится к АВ как вес в Л к ве-
су в В. Тогда точка В будет
общим центром тяжести обоих
грузов. Соединим точки D иС ли-
нией ВС и разделим ее в точке Е
таким образом, что отношение ли- 8
нии СЕ к линии ЕВ равпо отно-
шению веса в В к весу в С. Тогда
точка Е будет общим центром
тяжести всех трех грузов. Следовательно, опа и будет точкой подвеса.
(41) Мы хотим определить то же самое и для многоугольников.
Пусть фигура АВСВЕ — многоугольник {рис. 17}. Подвесим в точ-
ках А, В, С, В и Е известные грузы. Разделим линию АВ в точке F
таким образом, что отношение линии BF к FА равно отношению веса
в Л к весу в В. Тогда точка F — (об-
щий) центр (тяжести) двух грузов, нахо-
дящихся на АВ. Разделим также ли-
нию BE в точке Н таким образом, что
отношение линии ВН к линии НЕ равпо
отношению веса в Е к весу в В. Тогда
точка Н — общий центр тяжести точек Е
и В. Соединим FH и разделим FH в точ-
ке G таким образом, что отношение об-
щего (веса) в Л и В к общему (весу)
в В и Е равно отношению HG к GF.
Тогда точка G — общий центр тяжести
точек Л, В, В и Е. Соединим точки С и
Рис. 17.
сится к KG как (общий)
G линией CG и разделим ее в точке К
таким образом, что липия СК отно-
вес в Л, В, В и Е к весу в С. Тогда,
следовательно, точка К будет общим центром тяжести всех грузов.
XI. АРХИМЕД, КВАДРАТУРА ПАРАБОЛЫ, 6 /
Разделим липию ВС в Е так, что- г-
бы СЕ была вдвое больше ЕВ, прове- 1
дем КЕ параллельно ВВ, и разделим
ее в G пополам {рис. 18}; тогда точ-
ка G будет центром тяжести треуголь-
ника ВВС\ зто действительно доказа-
но в «Механике»*).
F
Рис. 18.
*) Архимед не говорит: «доказано в книге «О равновесии»: следовательно, в момент
написания трактата «Квадратура параболы» книга «О равновесии» еще не существовала.
76
АРХИМЕД
XII- АРХИМЕД, О ПЛАВАНИИ, КП. II, 2*)
«Действительно в «Началах механики» доказано, что если отпять
какую-нибудь величину, пе имеющую одного и того же центра тяжести
с целой величиной, то центр тяжести остатка будет находиться на
прямой, соединяющей центр» тяжести целой и отнимаемой величин,
если продолжить ее в ту сторону, в которой находится центр тяжести
целой величины»**).
О РАВНОВЕСИИ
XIII- АРХИМЕД, ЭФОД, ЛЕММЫ***)
7. Центром тяжести круга является точка, которая одновременно
является и геометрическим центром круга.
8. Центр тяжести всякого цилиндра находится на середине его оси.
9. Центр тяжести всякой призмы находится на середине ее оси.
10. Центр тяжести всякого конуса находится па ого оси в точке,
делящей последнюю так, чтобы отрезок, прилегающий к вершине, был
втрое больше остатка.
XIV. АРХИМЕД, ЭФОД, 1***»)
«Разделим прямую ГК (медиану треугольника AVZ) в точке X
так, чтобы ГА была втрое больше АХ; тогда точка X будет центром
тяжести треугольника AZT; это действительно доказано в книге
«О равновесии» taoppoKizon;)».
XV. АРХИМЕД, О ПЛАВАНИИ, КН. II, 2»****)
* ш
«Действительно, в книге «О равновесии» доказано, что у вся-
кого сегмента прямоугольного коноида (-параболоида вращения)
центр тяжести будет находиться на оси в точке, разделяющей послед-
нюю так, чтобы отрезок, прилегающий к вершине, был вдвое
больше остатка».
•) См. стр. 336 этого издания.
** ) См. предложение VIII первой книги «О равновесии плоских фигур». Однако употреблен-
ный в рассматриваемой книге способ Доказательства от противного, а также употребленные Архи-
медом при цитировании выражения позволяют думать, что в данном случае Архимед имел в виду
более раине?, сочинение, тем более, что он несколькими строками выше, говори о центре тяжести
сегмента параболоида вращения. цитирует трактат «О равновесии» (см. ниже, фрагм. XV).
*“) См. стр. 299 этого издании.
•♦♦*) См. стр. 301 этого издания.
•••**) см. стр. 336 этого издания.
КВАДРАТУРА ПАРАБОЛЫ
Архимед Досифею желает благоденствия!
Узпавши о смерти Коиона, делавшего все для пас из дружбы,
и о том, что ты был близок к Конону и сведущ в геометрии, мы очень
опечалились о покойном и как о друге и как о выдающемся матема-
тике. Поэтому мы решили написать тебе, подобно тому как обычно
писали Конону, и послать некоторые геометрические теоремы, оставав-
шиеся ранее неизвестными, а теперь полученные нами; они были
сначала обнаружены нами при помощи механических методов, а затем
доказаны также и геометрически.
Некоторые из занимавшихся ранее геометрией пытались доказать,
что возможно найти площадь, ограниченную прямыми линиями и рав-
ную заданному кругу или его сегменту; затем они пробовали пре-
вратить в квадрат площадь, заключающуюся между прямой и сече-
нием целого конуса*), пользуясь нри этом не вполне дозволенными
предположениями, вследствие чего большинство математиков и не
признало за ними решения этой задачи. Что же касается сегмента,
ограниченного прямой и параболой, то, насколько пам известно,
никто из предшествующих математиков не пытался его квадрировать,
нами же эта квадратура в настоящее время найдена. Действительно,
можно доказать, что всякий сегмент, заключенный между прямой
и параболой, составляет четыре трети треугольника, имеющего с сег-
ментом одно и то же основание и равные высоты. При этом доказатель-
стве принимается следующее предположение.
Если имеются две неравные площади, то, постоянно прибавляя
к самому себе избыток, на который большая площадь превосходит
менишую, можно получить площадь, которая была бы больше любой
заданной ограниченной площади. Этой леммой пользовались также
и жившие рапсе геометры.
При помощи именно этой леммы они доказали, что круги находят-
ся друг к другу в двойном отношении их диаметров, шары — друг
к Другу в тромпом отношении их диаметров, и также что всякая пира-
мида составляет третью часть призмы, имеющей с пирамидой одно
*) 1Год несколько струйным выражением «сечение целого конуса» (следовало бы сказать
«остроугольного конуса*), по леей видимости, подразумевается эллипс.
78
АРХИМЕД
и то же основание и одинаковую высоту. Доказательство того, что
всякий конус составляет третью часть цилиндра, имеющего с конусом
одно и то же основание и одинаковую высоту, они изложили, приняв
некоторое предположение, подобное упомянутой лемме. При этом
каждая из упомянутых теорем считается ничуть нс менее правильной,
чем другие, доказываемые без помощи упомянутой леммы; поэтому
совершенно достаточно, чтобы такую же степень достоверности имели
и теоремы, излагаемые нами теперь. При доказательстве мы сначала
показываем, как эта теорема была обнаружена нами при помощи меха-
й ники, а затем уже, как она доказывается
геометрически. Предварительно излагаются
основные свойства конических сечений, не-
обходимые для доказательства. Будь здоров!
Рис. 1.
I
Если А13Г {рис. 1) — парабола, прямая
ВД параллельна диаметру или сама, является
диаметром*), а прямая АГ параллельна каса-
тельной к параболе в точке В, то АД будет равна ДГ; и если АД рав-
на ДГ, то прямая АГ и касательная к параболе в В будут параллельны*
II
Если АВГ {рис. 2} — парабола, прямая ВД параллельна диаметру
или сама является диаметром, прямая АДГ параллельна касательной
к параболе в точке В и ЕГ — касатель-
ная к параболе в точке
ВД и BE будут равны.
Г, то прямые
III
Если АВГ {рис.
прямая ВЛ параллельна
3} — парабола,
диаметру или
и параллельно касательной
то
сама является диаметром,
ле в точке В проведены какие-нибудь прямые АД и EZ,
линий ВД и BZ будет равно отношению квадратов на АД
Все эти теоремы доказаны в «Началах теории конических сече-
;ний» [1].
к парабо-
отногаение
и EZ.
“) Под диаметром здесь и ниже подразумевается ось параболы
КВАДРАТУРА ПАРАБОЛЫ
79
IV
Пусть АВГ {рис. 4.} будет сегмент, заключающийся между прямой
и параболой, пусть прямая ВА проведена из середины АГ параллель-
но диаметру или сама является диаметром, и соединя/ощая прямая ВГ
продолжена. Если параллельно ВД провести в
какую-нибудь другую прямую Z0 так, что-
бы она пересекала прямую, проходящую через / \
Рис. 4.
точки В и Г, то Z© будет иметь к ©Н то же самое отношение, что
ДА к &Z-
Действительно, через точку II проведем прямую КП параллельно
АГ; тогда отношение линий ВД и ВК будет таким же, как отношение
квадратов на ДГ и КН;
вА = ага
ВК кн2
это доказано (в предложении III). Следовательно, отношение линий
ВГ и В1 будет равно отношению квадратов па ВГ и па В8,
вг вга
Bi ве2
так как AZ равна КН; значит, линии ВГ, В© и BI будут составлять
пропорцию*). Таким образом, ВГ к В© имеет то же самое отноше-
ние, что Г© к ©I;
вг _ Г0 *»)
ве - ei
значит, как ГД относится к AZ, так и ©Z будет относиться к 0Н***).
гд ez
AZ OH
Но ДГ равна ДА; тогда ясно, что ДА будет иметь к AZ то же самое
отношение, что Z0 к 0Н.
ЛА _ ZO
az ~ ен
V
Пусть АВГ {рис. 5} будет сегмент, заключающийся между пря-
мой и параболой, из точки А параллельно диаметру проведена пря-
мая ZА, а из точки Г — касательная 1'Z к параболе в точке Г. Если
в треугольнике ZAT параллельно AZ провести какую-нибудь прямую,
•) Так как ВГ ; BI-- ВД : ВК = ДГ2 : КП2 = (ДГ : AZ)2 — (ВГ : В©)2, т<.. значит,
вг-ве2-вг2-вх, т. е. ве2=вг-вг и вг:ве=ве:В1.
**) Имеем ВГ ; ВО — Вв : BI; отсюда
ВГ : ве =~ (ВГ i ВО) : (ВО ± BI) = ГО : HI.
«♦•) В самом деле,
ГЛ : AZ ВГ : ВО — ГО : ei = ez : ОН.
80
АРХИМЕД
то эта прямая разделится параболой в том же самом отношении,
в каком АГ разделится проведенной прямой, причем отрезок прямой
АГ, прилежащий к А, будет соот-
ветствовать ближайшему к А отрез-
ку проведенной прямой.
Проведем параллельно AZ ка-
кую-нибудь прямую ДЕ, и пусть
сначала ДЕ разделит АГ пополам.
Тогда, так как АВ Г есть парабола,
прямая БД проведена параллельно
диаметру, а прямые АЛ и ДГ рав-
ны, то АГ будет параллельна каса-
тельной к параболе в точке В (пред-
ложение 1).
Далее, так как АЕ параллельна
диаметру и из точки Г проведена
касательная ГЕ к параболе в точке
Г, а прямая ДГ параллельна каса-
тельной к параболе в точке В, то ЕВ
будет равна ВД (предложение II);
таким образом, АД к ДГ имеет то
же самое отношение, что ДВ к BE.
АД _ АВ
ВГ ~ BE
Рис. 5.
Теперь, если проведенная пря-
мая сечет АГ пополам, то теорема
уже доказана; в противном случае проведем параллельно AZ какую-
нибудь другую прямую КА; следует доказать, что АК будет иметь к КГ
то же самое отношение, что К© к ©Л.
ак _ ко
кг " ел
Действительно, так как BE равна ВД, то и 1Лбудст равна KI; значит,
ЛК относится к КТ, как АГ к ЛА.
лк _ дг
КГ ДА
Но KI так же относится к К©, как ДА к ЛК.
кг _ да
к© ак
что доказано в предыдущем*); таким образом, К® к ©А и АК к КГ име-
ют одно и то же отношение**)
кв АК
ел кг
Итак, предложение доказано [2].
») Согласно предложению IV. имеем:
KI: 1© = ЛА : КД
Отсюда, «переворачивая»,
(KI - 16) : KI = (А А - KD) : АА, т. с. Кб : KI - АК . Л А.
• *) Действительно, ин предыдущисй пропорции, имеем:
КА: Кб-АГ: АК.
-Отсюда
(КА - Кб) : КЙ-- (АГ - АК) : ЛК, т. е. Лб : К0= КГ : ЛК.
КВАДРАТУРА ПАРАБОЛЫ
81
VI
Вообразим, [как это делается в теоретических исследованиях]*),
что лежащая перед нами [видимая] плоскость перпендикулярна
к горизонту, [затем] представим, что та ее часть, которая от линии
АВ {рис. 6} простирается в сторону А, будет нижней, простирающая-
ся же в противоположную сторону — верхней; пусть ВАГ будет
прямоугольный треугольник с пря- р, р
мым углом при В, сторона ВГ кото-
рого равна половине равноплечего
рычага; [предполагается, конечно,
что АВ равна В Г]; подвесим рас-
сматриваемый треугольник в точках
В и Г, а с другой стороны рычага, в
точке А, подвесим некоторую пло- j
щадь Z, и пусть площадь, подве- Рис. 6.
шейная в точке А, уравновешивает
треугольник ВАГ в том положении, какое оп теперь имеет. Я утверж-
даю, что площадь Z будет третьей частью треугольника ВАГ.
Действительно, так как рычаг предполагается уравновешенным,
то мы можем считать, что линия АГ параллельна горизонту, а прямые
в плоскости, перпендикулярной к горизонту, проведенные под прямым
углом к АВ, будут тоже перпендикулярны к горизонту. Разделим
линию ВГ в точно Е так, чтобы ГЕ была вдвое больше ЕВ: параллельно
АВ проведем прямую КЕ и разделим ее пополам в точке 0; тогда, как
доказано в «Механике»**), точка 0 будет центром тяжести треуголь-
ника ВАГ. Если теперь у треугольника ВАГ уничтожить подвесы в В
и Г и подвесить его в точке Е, то треугольник останется в том же самом
положении, какое оп имел перед этим; действительно, доказано так-
же и то, что каждое тело, подвешенное в какой угодно точке, будет
оставаться неподвижным в таком положении, когда точка подвеса
и центр тяжести подвешенного тела находятся на одном перпендикуля-
ре. Так как положение треугольника В ГД относительно рычага остает-
ся тем же самым, то оп будет продолжать уравновешивать площадь Z.
Если же подвешенная в точке А площадь Z и подвешенный в точке Е
треугольник ВАГ находятся в равновесии, то ясно, что они будут
обратно пропорциональны длинам (соответствующих плеч), и получится,
что, как АВ относится к BE, так и треугольник ВАГ будет относиться
к площади Z: но АВ втрое больше BE; значит, и треугольник ВАГ
будет втрое больше площади Z.
Очевидно также, что и обратно, если треугольник ВАГ будет
втрое больше площади Z, то равновесие сохранится.
VII
Пусть будет опять равноплечий рычаг АГ {рис. 7} с серединой
в точке В; подвесим его за точку В. Пусть ГАП — тупоугольный тре-
угольник с основанием АН и высотой, равной половине рычага; под-
весим треугольник А ГН в точках В и Г, и пусть подвешенная в точке А
•) ё'тг eCTiv то 4v та йЕГйр’а—неясное место, которое Гейберг считает позднейшей вставкой
и поятому ставит в квадратных скобках.
*•) Это может быть вообще каким-нибудь сочинением по механике; но более вероятно, что это
одно иг ранних сочинений самого Архимеда, например, Hepi
6 Архимед
82
АРХИМЕД
площадь Z будет уравновешивать треугольник ГАН в занимаемом
им положении. Докажем точно так же, что площадь Z будет третьей
частью треугольника ГАН.
Действительно, подвесим в точке Л еще некоторую площадь (Л),
являющуюся третьей частью треугольника ВГП; тогда треугольник
ВАГ уравновесится с площадью Z-J-A.
Теперь, так как треугольник ВГН урав-
новешивается с Л, а треугольник В ГА
с площадью Z вместе с Л, и площадь
Z-J-A является третьей частью треугольни-
ка ВГА, то ясно, что треугольник ГАН
будет также втрое больше площади Z,
VIII
Рис. 8.
Пусть будет равноплечий рычаг АВГ
{рис. 8} с серединой В, подвешенный
за точку В; пусть ГАЕ будет прямо-
угольный треугольник с прямым углом
при Е, подвешенный к рычагу в точках Г и Е; подвесим в точке А
некоторую площадь Z, и пусть она уравновешивает треугольник ГАЕ
в занимаемом положении; пусть отношение АВ к BE будет равно
отношению треугольника ГАЕ
к некоторой площади К.
Я утверждаю, что площадь
Z будет меньше треугольника
ГДЕ, но больше площади К.
Действительно, возьмем
цептр тяжести треугольника
АЕГ — пусть он будет в точке
О — и параллельно ДЕ проведем прямую
ГДЕ уравновешивает площадь Z, то площадь ГАЕ имеет к Z то же самое
отношение, что АВ к ВН: так что Z будет меньше площади ГАЕ.
Поскольку же треугольник ГАЕ относится к Z, как ВА к ВН, а к
площади К — как ВА к BE,
то ясно, что треугольник ГАЕ
имеет к К большее отноше-
ние, чем к Z, таким образом,
Z будет больше К.
6П. Так как треугольник
IX
Пусть АГ {рис. 9} бу-
дет опять равноплечий рычаг
с серединой В, а ГАК —
тупоугольный треугольник
с основанием АК и высотой ЕГ; подвесим его к рычагу в точках
Г и Е, а в точке А подвесим площадь Z, и пусть она уравнове-
шивает треугольник АГК в занимаемом положении; пусть отношение
АВ к BE будет равно отношению треугольника ГАК к некоторой пло-
щади Л. Я утверждаю, что площадь Z будет больше Л, но меньше .
треугольника АГК.
Доказывается это точно так же, как предыдущее. •
КВАДРАТУРА ПАРАБОЛЫ
83
Пусть АВ Г {рис. 10} будет опять равноплечий рычаг с середи-
ной В, а ВДНК — трапеция с прямыми углами при В и Н и со сторо-
ной КД, стремящейся к точ-
ке Г*), пусть отношение АВ
к ВН будет равно отношению
трапеции ВДКН к некоторой
площади А.
В точках В и Н подвесим к
рычагу трапецию ВДНК, а в
то’же А — площадь Z, и пусть
она уравновешивает трапецию
ВДКН в занимаемом ею поло-
жении. Я утверждаю, что
площадь Z будет меньше. А.
Разделим прямую АГ в точке Е так, чтобы ЕН имела к BE такое
же отношение, как удвоенная ДВ и КП к удвоенной КН и ВД.
ЕН _ 2ДВ+КП
BE ~2KH-i-BA
Затем проведенную через Е параллельно ВД прямую EN разделим
в точке ©.пополам; тогда, как доказано в Механике**), точка © будет
центром тяжести трапеции ВДКН. Если теперь подвесить трапецию
в Е, а в точках В и Н освободить, то на основании того же, что и в пре-
дыдущем, она будет оставаться н покое в том же самом положении
и уравновесит площадь Z. Так как теперь подвешенная в Е трапеция
ВДНК уравновешивает подвешенную в А площадь Z, то отношение
АВ к BE будет равно отношению трапеции ВДНК к площади Z; так
как АВ имеет к BE большее отношение, чем к ВН, то значит и трапеция
ВД1ТК будет иметь к Z большее отношение, чем к А; таким образом Z
будет мепыпе А.
XI
Рис. 11.
Пусть АГ {рис. 11} будет равноплечий рычаг с серединой В,
а КДТР — трапеция, у которой стороны КД, ТР стремятся к точке Г,
а ДР и КТ перпендикулярны к В Г, причем
сторона ДР попадает в точку В. Пусть отно-
шение АВ к ВП будет равно отношению
трапеции ДКТР к некоторой площади А.
Подвесим к рычагу трапецию ДКТР в
точках В, Н, а площадь Z — в точке А, и
пусть Z уравновешивает трапецию ДКРТ в
занимаемом ею положении. Тогда подобно
предыдущему докажем, что площадь Z будет
меньше Л.
«) В тексте употребляется техническое выражение греческой математики—veiowa— стремя-
щаяся, склоняющаяся; так называлась прямая, продолжение которой проходило через заданную-
точку. [См. комментарии к работе «О спиралях», стр. 51 9.]
»•) В сохрэнивтпихсн сочинениях Архимеда соответствующее доказательство имеется в XV пред-
ложении первой книги трактата «О равновесии плоских фигур». • -
6*
84
АРХИМЕД
Рис. 12.
XII
Пусть АГ {рис. 12} будет опять равноплечий рычаг с серединой В,
а ДЕКН — трапеция с прямыми углами при точках Е, II и со сторо-
нами КД и ЕН, стремящимися к точке Г. Пусть отношение АВ к ВП
будет равно отношению трапеции АКЕН к некоторой площади М;
пусть также отношение АВ к BE будет равно отношению трапеции
ДКЕН к некоторой площади Л. Под-
весим к рычагу трапецию ДКЕП в
точках Е, Н, а площадь Z — в точ-
ке А, и пусть Z уравновешивает
трапецию в занимаемом ею положе-
нии. <7 утверждаю, что площадь Z
будет больше Л, но меньше М.
Действительно, я взял центр тя-
жести трапеции АКЕН, и пусть он
будет © (оп находится подобно пре-
дыдущему); затем я провожу пря-
мую ©I параллельно ЛЕ. Теперь если подвесить трапецию к рычагу
в точке I, а в точках Е и Н освободить, то она останется в покое в том
же самом положении, и на основании того же, что и выше, будет по-
прежнему уравновешиваться площадью Z. Но так как трапеция, под-
вешенная в точке I, уравновешивает площадь Z, подвешенную в точ-
ке А, то трапеция будет иметь к площади Z то же самое-отношение, что
АВ к BI. Теперь ясно, что
трапеция АКЕН имеет к Л
большее отношение, чем к Е,
а к М меньшее, чем к Z; та-
ким образом, площадь Z бу-
дет больше Л, но меньше М.
а в точке А
XIII
Пусть АГ {рис. 13} бу-
дет опять равноплечий рычаг
с серединой В, а КДТР —
трапеция, у которой стороны
КД, ТВ стремятся к точке Г,
а стороны ДТ, КР перпенди-
кулярны к В Г. Подвесим ее к рычагу в точках Е и П,
подвесим площадь Z, и пусть она уравновешивает трапецию ДКТР
в занимаемом ею положении. Пусть отношение АВ к BE будет равно
отношению трапеции ДКТР к некоторой площади Л, и пусть отно-
шение АВ к ВП будет равпо отношению этом же самой трапеции
к некоторой площади М. Тогда подобно предыдущему докажем,
что площадь Z будет больше Л, но меньше М.
XIV
Пусть ©à {рис. 14} будет сегмент, заключенный между прямой
и параболой. Пусть сначала прямая В Г будет перпендикулярна
к диаметру параболы; иа точки В параллельно диаметру проведем пря-
мую ВД, а из точки Г проведем касательную ГД к параболе в Г; тогда
КВАДРАТУРА ПАРАБОЛЫ
85
треугольник В ГД будет прямоугольным. Разделим прямую В Г на
какое-нибудь количество равных отрезков BE, EZ, ZH, HI, 1Г и из
точек деления параллельно диаметру параболы проведем прямые
EZ, ZT, НГ, 13, затем из точек пересечения этих прямых с парабо-
лой проведем к Г соединительные прямые и продолжим их. Я утвер-
ждаю, что треугольник ВДГ будет меньше утроенных трапеций КЕ,
AZ, МП, NI вместе, с треуголь-
ником 31Г, но больше утроенных
трапеций Z<I>, 110, Ill с тре-
угольником ЮГ.
Действительно, проведем
прямую АВГ, отложим АВ,
равную В Г и вообразим равно-
плечий рычаг АГ с серединою В;
подвесим ею за В; подвесим
также к рычагу треугольник
ВДГ в точках В и Г, а с другой
стороны рычага, и точке А под-
весим площади Р, X, V, Q,
и пусть площадь Р уравнове-
шивает трапецию ДЕ в занимае-
мом сю положении, площадь X
уравновешивает трапецию Z2,
площадь Y — трапецию TH,
площадь Q — трапецию П и,
наконец, площадь £ — треуголь-
ник ЕТГ; тогда и все площади справа уравновесят все площади слева,
так что треугольник ВДГ окажется втрое больше площади P+X+T-j-
-f- Q+£ (предложение VI). Так как ВГ0 есть сегмент, заключенный
между прямой и параболой, из точки В параллельно диаметру прове-
дена прямая ВД, а из точки Г — касательная ГД к параболе в Г,
и также проведена некоторая прямая ХЕ, параллельная диаметру, то
ВГ будет иметь к BE то же самое отношение, что ХЕ к ЕФ {предло-
жепие V); также и прямая ВА будет иметь к BE то же отношение,
что трапеция ДЕ к КЕ*). Подобным же образом докажем, что прямая
АВ относится к BZ, как трапеция XZ к AZ, что она же относится к ВН,
как трапеция TH к МН и, наконец, к В1 — как трапеция П к N1.
Теперь, так как имеется трапеция ДЕ с прямыми углами при точках В,
Е и со стремящимися к точке Г сторонами, уравновешенная в занима-
емом сю положении площадью Р, подвешенной к рычагу в точке А,
и так как отношение ВА к BE равно отношению трапеции ДЕ к трапе-
ции КЕ, то значит, как было доказано (предложение X), площадь КЕ
будет больше площади I’.
Далее, имеется трапеция ZS с прямыми углами при точках Z, Е
и со стремящейся к Г стороной 2Т, уравновешенная в занимаемом ею
положении площадью X, подвешенном к рычагу в точке А, и отношение
АВ к BE равно отношению трапеции ZE к Z®**), а отношение АВ к BZ
«) В самом деле, ВА = ВГ; кроме того:
ЕФ: EZ — ВК : Вд = (ЕФ + ВК): (ЕХ + ВД) — трап. КЕ : трап. ДЕ.
*•) Действительно,
АВ : BE = Е2: Еф = трап. Z2 : трап. ЕФ.
86
АРХИМЕД
равно отношению трапеции ZE к AZ*); тогда, как тоже было доказа-
но (предложение XII), площадь X будет меньше трапеции AZ, но
больше ZO.
На том же основании и площадь V будет меньше трапеции МН,
но больше ©Н, площадь £2 будет меньше трапеции NOITI, но больше
Ш, и так же площадь £ будет меньше треугольника Е1Г, но больше
треугольника ПО (предложение VIII). Теперь, так как трапеция КЕ
больше площади Р, трапеция AZ больше X, трапеция ММ больше Т,
трапеция N1 больше Q и треугольник 01Г больше то ясно, что все
первые упомянутые площади будут больше площади Р (вместе с) X,
Чг, 0(н) Но площадь Р (вместе с) X, 4f, Q (и) £ составляет третью
часть треугольника ВДГ; значит, ясно, что треугольник В ГА будет
меньше взятых вместе утроенных трапеции KE, AZ, МН, NI и тре-
угольника Е1Г. Далее, так как трапеция 2Ф меньше площади X, тра-
пеция ©П меньше Чг, трапеция 1П мспыпе О и треугольник ЮГ
меньше то ясно, что все упомянутые выше площади (вместе взятые)
будут меньше площади £ (вместе с) Q, Чг (и) X; теперь ясно, что
треугольник ВАГ будет больше взятых вместе утроенных трапеций
ZO, ©II, 1П и треугольника 1Г0**), но меньше взятых вместе утроен-
ных (площадей) поименованных ранее.
XV
Пусть опять ©à {рис. 15} будет сегмент, заключенный между
прямой и параболой, но только теперь прямая В Г уже нс будет пер-
пендикулярна к диаметру параболы. Тогда ВГ необходимо образует
тупой угол или с параллельной диаметру прямой, проведенной в сто-
рону сегмента из точки В, или с прямой, проведенной таким же обра-
зом из точки Г. Пусть тупой угол образуется с прямой, проведенной
из В. Из точки В проведем прямую ВД, параллельную диаметру, а из
точки Г — касательную ГЛ к параболе в Г, прямую В Г разделим на
какое-нибудь количество равных отрезков BE, EZ, ZH, III, I Г, из
точек Е, Z, Н, I параллельно диаметру проведем прямые EX, ZT, II Г,
1Е и из точек пересечения этих прямых с параболой проведем к Г сое-
динительные прямые и продолжим их.
Я утверчедаю, что треугольник ВАГ будет меньше утроенных тра-
пеций ВФ, AZ, МН, NI вместе с треугольником. Г1Е, но больше утро-
енных трапеций Z<$, II©, 1П вместе с треугольником Г01.
Продолжим ВД в обратную сторону. Проведя перпендикуляр
ГК, я откладываю АК., равную ГК. Теперь опять вообразим равно-
плечий рычаг АГ с серединой К и подвесим его за К; к одной половине
рычага подвесим треугольник ГКА в точках ГК в том положении,
какое он теперь занимает, а с другой стороны рычага в точке А подве-
сим площади Р, X, У, Q, и пусть площадь Р уравновешивает тра-
пецию АЕ в занимаемом положении,площадь X уравновешивает тра-
пецию Z2, площадь Т — трапецию ТП, площадь £2 — трапецию П и,
наконец, площадь £ — треугольник Г13; тогда все площади справа
*) Аналогично
AB: BZ = ZT: Z© = EX: EA~(ZT + EX); (ZO + ЕД> = трап. ZX : трап. ZA.
** ) Действительно, треугольник ВГД, равный утроенной сумме площадей Р+Х+'Ч'Ч £2 | ^, будет
более чем втрое больше суммы этих площадей, без первой Р, а значит, и подавно более чем втрое
больше суммы трапеций Z®, 6Н, 1Г1 и треугольника 1Г0-
КВАДРАТУРА ПАРАБОЛЫ
87-
уравновесят все площади слева, так что треугольник ДВГ окажется
втрое больше площади Р (вместе с) X, Ч*-, Q (и) £ (предложение VII).
После этого подобно предыдущему*) докажем, что трапеция ВФ будет
больше площади Р, трапеция 0Е будет больше площади X, а трапеция
ZO меньше ее; трапеция МН будет больше площади Ч*1, a IT0 меньше
ее; затем трапеция N1 будет больше площади Q, а 1П меньше ее;
и, наконец, треугольник Е1Г будет больше площади 0, а треугольник
ГЮ меньше ее; теперь это ясно.
XVI
Пусть опять ВОГ {рис. 46} будет сегмент, заключенный между
прямой и параболой: через точку В проведем прямую ВД, параллель-
ную диаметру параболы, а через Г — касательную к параболе в Г.
Пусть площадь Z будет третьей частью треугольника ВДГ.
Я утверждаю, что сегмент В0Г будет равен площади Z.
Действительно, если он не равен, то будет или больше, или же
менытте. Пусть сначала оп будет, если возможно, больше; тогда избыток,
на который сегмент В0Г превосходит площадь Z, будучи складываем
сам с собой, когда-нибудь станет больше треугольника ВГА. Следова-
тельно, можно взять некоторую меньшую этого избытка площадь, кото-
рая была бы какой-то частью треугольника ВДГ. Пусть треугольник
ВГЕ будет меньше упомянутого избытка, и одновременно является
некоторой частью треугольника ВДГ; тогда прямая BE будет такой же
*) Т. е. как в предлежении XIV, е той лишь разницей, что вместо предложений VIII, X, XII
придется использовать предложения XX, XI, XIII.
88
АРХИМЕД
частью от ВД. Разделим ВЛ на части, равные BE и пусть точки делений
будут Н, I, К; из точек Н, I, К проведем к Г соединительные прямые;
они, конечно, пересекут параболу, так как прямая ГЛ является касатель-
ной к ней в точке Г. Через точки пересечения этих прямых с параболой
проведем параллельно диаметру прямые МФ, NP, Е©, ПО; они будут
параллельны и прямой ВЛ. Теперь, так как треугольник 13ГЕ меньше
избытка, на который сегмент В0Г превосходит площадь Z, то ясно,
что площадь 2 и треугольник ВГЕ, вместе взятые, будут меньше сег-
мента. Но треугольник ВГЕ равен
трапециям ME, ФЛ, ©Р, 00, через
которые проходит парабола, взя-
тым вместе с треугольником ГОХ,
действительно, трапеция ME яв-
ляется общей, трапеция МЛ равна
трапеции ФЛ, трапеция ЛЗ равна
0Р, трапеция ХЕ равна 00 и тре-
угольник ГХП равен треугольнику
ГОХ; следовательно, площадь Z
будет меньше вместе взятых тра-
пеций МЛ, ЕР, П© и треугольни-
ка НОГ ♦).
Но треугольник ВДГ втрое
больше площади Z; тогда треуголь-
ник ВДГ будет меньше утроенных
трапеций МЛ, ЕР, 0П и треуголь-
ника ПОГ, а это невозможно,
так как доказано (предложения XIV
и ХШ), что оп будет более чем
втрое больше. Итак, сегмент В0Г
пе будет больше площади Z.
Теперь я утверждаю, что он
не будет и меньше. Действительно,
пусть он будет, если возможно, меньше. Значит, и в данном случае
избыток, па который площадь Z превосходит сегмент В0Г, будучи
прибавляем сам к себе, когда-пибудь превзойдет и треугольник ВДГ.
Но можно взять некоторую меньшую этого избытка площадь, которая
была бы какой-то частью треугольника ВДГ. Пусть треугольник ВГЕ
будет меньше этого избытка и одновременно некоторой частью тре-
угольника ВДГ, все остальное сделаем так же, как раньше. Теперь,
так как треугольник ВГЕ меньше избытка, на который площадь Z
превосходит сегмент В0Г, то вместе взятые треугольник ВЕГ и сег-
мент В0Г будут меньше площади Z. Но площадь Z меньше вместе
взятых четырехугольников ЕМ, ФР1?, ТЕ, ПТ и треугольника ГПХ,
так как треугольник ВДГ, втрое больший площади Z, одновременно
меньше утроенных упомянутых площадей, вместе взятых, как это
доказано в предыдущем (предложения XIV, XV); значит, треуголь-
ник ВГЕ вместе с сегментом ©à будут меньше четырехугольников
ЕМ, ФХ, ЕЧГ, ПТ и треугольника ГПХ. Таким образом, по отнятии
*) ME -f- NO -f- З'Г -|- ПТ ПГГ > сегм. ВОГ,
ме+фл+ев+ео+гох=вге,
откуда, вычитая,
мл + ер + пе 4- пог > вег - ВГЕ> Z-
КВАДРАТУРА ПАРАБОЛЫ
89
общего сегмента треугольник ВЕГ оказался бы меньше оставшихся
площадей; зто же невозможно, так как доказано, что треугольник ВЕГ
равен вместе взятым трапециям ЕМ, ФА, ©Р, 60 и треугольнику
ГО2, которые больше оставшихся площадей. Значит, сегмент ВОГ не
будет меньше площади Z [3]. Но также доказано, что он не будет
и больше; значит, этот сегмент равен площади Z [4|.
XVII
После того как это доказано, ясно,
что всякий сегмент, заключенный между прямой и параболой,
составляет четыре трети треугольника, имеющего с сегментом то же
самое основание и равную высоту.
Действительно, пусть будет сегмент, заключенный между прямой
и параболой, пусть его вершина*) будет в точке 0 {рис. 17}. Впишем
в него треугольник ВОГ, имеющий с
сегментом то же основание и равную
высоту. Так как точка О есть вер-
шина сегмента, то прямая, проведен-
ная из О параллельно диаметру,
разделит ВГ пополам и ВГ будет
параллельна касательной к пара-
боле в точке О (предложение I).
Проведем Е0 параллельно диаметру;
затем из В также параллельно диа-
метру проведем прямую ВА, а из
Г — касательную ГД к параболе в
Г. Так как КО параллельна диамет-
ру, ГД — касательная к параболе в
Г, а ЕГ параллельна касательной к
параболе в 0, то треугольник ВДГ
будет в четыре раза больше треу-
гольника ВОГ**). Но так как тре-
угольник ВДГ втрое больше сегмен-
та В0Г (предложение XVI) и вчет-
веро больше треугольника ВОГ, то
ясно, что сегмент ВОГ будет состав-
лять четыре трети треугольника ВОГ.
Рис. 17.
Для сегментов заключенных между прямой и какой-нибудь кри-
вой линией***), я называю основанием эту прямую, высотой — наи-
больший перпендикуляр, который можно опустить из точки кривой на
основание сегмента, а вершиной — ту точку, из которой проводится
па ибол ы п ий перпендикуля р.
*) Интересно 'отметить, что Архимед уже п атом месте пользуется термином «вершина пара-
болического сегмента», определение которого будет дано ниже (перед предложением XV1I1). Это
вначит. что остальная часть трактата (предложения XAI11—XXIV) первоначально составляла осо-
бое сочинение.
** ) Действительно, Кб —®К «предложение 11>,и значит, Вд — 4 Ев. так как ВЕ = ЕГ.
** *) яарэтй'Ход yoapixac. В трактате «О шаре и цилиндре» (кв. I аксиома 1) Архимед употре-
бляет итог термин для обозначения кривой линии. Стоит отметить, что в некоторых местах «Кони-
ческих сечений» Аполлония, а также, вероятно, и в тексте Евдокса (см. вступительную статью,
гл. 111) под етим термином понимались маши кривые второго порядка.
90
АРХИМЕД
Рис. 18.
XVIII о
Если в сегменте, заключенном между прямой и параболой, провести
из середины основания прямую, параллельную диаметру, то вершиной
сегмента будет та точка, в которой
прямая, проведенная параллельно диа-
метру, пересекает параболу.
Пусть АВГ {рис. 18} будет сег-
мент, заключенный между прямой и
параболой; из середины АГ проведем
прямую ЛВ параллельно диаметру. Так
как в параболе прямая ВЛ проведена
параллельно диаметру, а прямые АД
и А Г равны, то ясно, что прямая АГ
и касательная к параболе в точке В будут параллельны (предложе-
. ние 1). После этого ясно, что из перпендикуляров, опущенных на АГ
с параболы, наибольшим будет проведенный из 13; таким образом,
точка В будет вершиной сегмента.
XIX
В сегменте, заключенном между прямой и параболой, линия, про-
веденная из середины основания {параллельно диаметру), будет
составлять четыре трети прямой, про-
веденной {таким же образом) из середины
половины основания.
Пусть АВГ {рис. 19} будет сегмент,
заключенный между прямой и параболой;
из середины прямой АГ параллельно
диаметру проведем прямую ВД, а из
середины АД — прямую EZ, а также
проведем прямую Z0 параллельно АГ.
Теперь, так как в параболе прямая ВЛ
проведена параллельно диаметру, а прямые АД, Z0 параллельны
касательной к параболе в В, то отношение линий ВД и ВО будет
равно отношению квадратов на
АЛ и Z0 (предложение 111); зна-
чит, линия ВД будет в четыре раза
больше ВО*). Теперь ясно, что ли-
ния ВЛ будет составлять четыре тре-
ти от EZ**).
л
Рис. 20.
XX
Если в сегмент, заключенный ме-
жду прямой и параболой, вписать
треугольник, имеющий с сегментом
одно и то же основание и равную высоту, то вписанный треугольник
будет больше половины сегмента.
Пусть АВГ {рис. 20} будет упомянутый сегмент; впишем в него
треугольник АВГ, имеющий с сегментом то же самое основание и рав-
ную высоту. Так как этот треугольник имеет с сегментом то же самое
*) Так как ZO является половиной АД.
**) Так как ОД -=ЗВ6 и 6& = EZ.
КВАДРАТУРА ПАРАБОЛЫ
91
основание и ту же высоту, то точка В необходимо будет вершиной
сегмента; значит, АГ будет параллельна касательной к параболе
в точке В. Через В параллельно АГ проведем прямую АЕ, а из точек
А и Г параллельно диаметру проведем прямые АА и ГЕ; они по-
падут: вис сегмента. Теперь, так как треугольник АВГ составляет
половину параллелограмма ААЕГ, то ясно, что он будет больше
половины сегмента.
Следствие
После доказанного ясно, что в данный сегмент можно вписать
такой многоугольник, чтобы остающиеся (по краям) сегменты были
меньше всякой наперед заданной площади; действительно, если отни-
мать все время больше половины, то на основании доказанного ясно,
что, постоянно уменьшая остающиеся но краям сегменты, мы можем
сделать их меньше всякой наперед заданной площади*).
XXI
Если в сегмент, заключенный между прямой и параболой, вписать
треугольник, имеющий с сегментом то же самое основание и ту же
высоту, а в оставшиеся сегменты вписать другие треугольники, имею-
щие те же самые основания и высоты, что и у этих сегментов, то
треугольник, вписанный в весь сегмент, будет в восемь раз больше
каждого из треугольников, вписанных в сегменты, оставшиеся (по
краям).
Пусть АВГ {рис- 21], будет сегмент такой, как сказано выше; пря-
мую АГ разделим пополам в точке А и параллельно диаметру проведем
прямую ВД; тогда точка В будет вер-
шиной сегмента (предложение XVII1).
Значит, треугольник АВГ имеет с сег-
ментом то же самое основание и ту же \/|
высоту. Затем разделим прямую АД попо- / /\ 1
лам в точке Е и проведем прямую EZ, 4г/ ' / / \ I
параллельную диаметру параболы и пере- г / / ч?
секающую АВ в точке 0; тогда точка Z Ева
будет вершиной сегмента AZB. Таким
образом, треугольник AZB имеет то же ис‘
самое основание и ту же высоту, что и
сегмент [AZBJ. Требуется доказать, что треугольник АВГ будет в
восемь раз больше треугольника AZB.
Прямая ВД составляет четыре трети от EZ (предложение XIX)
и вдвое больше Е0; значит, Е0 будет вдвое больше 0Z**). Таким
образом, треугольник АЕВ вдвое больше треугольника ZBA, так как
треугольник AE0 вдвое больше A0Z***), а треугольник 0BE вдвое
*) На основании леммы Евдокса («Начала» Евклида, X, I).
12
** ) Действительно; Е0 =—Бд = —-EZ; значит, ...-— -------- ---
2 &
ez = -1- ez и ке = 20Z.
***) Треугольники AE0 и AZ© имеют одну и ту же вершину А и лежащие на одной прямой
основания Z0 и ЕО = 2ZO. Точно также треугольники ZB0 и 0BE имеют общую вершину В и ле-
жащие на одной прямой основания Е0 и ZO, ,
92
АРХИМЕД
больше ZOB. Таким образом, треугольник АВГ будет в восемь раз
больше треугольника AZB*). Подобным же образом проведем доказа-
тельство и относительно треугольника, вписанного в сегмент ВНГ.
XXII
Если имеется сегмент, заключенный
взято любое количество площадей,
между прямей и параболой,
составляющих непрерывную
{пропорцию) в отношении четырех к одному, причем наибольшая из
этих площадей равна треугольнику, имеющему с сегментом то же
самое основание и ту же высоту, то все эти площади, вместе взятые.
будут меньше сегмента.
Пусть АЛВЕ Г {рис. 22} будет сегмент, заключенный между пря-
мой и параболой, и взято несколько площадей Z, Н, ©, I, составляю-
щих непрерывную пропорцию, в которой
каждая предыдущая площадь в четыре
раза больше последующей; пусть наиболь-
шая из них Z равна треугольнику, имею-
щему с сегментом одно и то же основание
и равную высоту.
Я утверждаю, что сегмент будет
больше площадей Z, Н, ©, I (вместе
Рис. 22.
взятых).
Пусть В будет вершина всего сегмен-
та, а А и Е — вершины сегментов, остаю-
щихся (по краям). Так как треуголь-
ник АВГ в восемь раз больше каждого
из треугольников АД В и ВЕГ, то ясно,
что он будет в четыре раза больше их
обоих вместе. И если треугольник АВГ
равен площади Z, то вследствие этого
треугольники АД В и ВЕГ вместе будут
равны площади II. Точно так же дока-
и
жем, что треугольники, вписываемые в остающиеся во краям сегменты,
имеющие с ними те же самые основания и высоты, будут все вместе
равны площади ©, а треугольники, вписываемые в сегменты, получаю-
щиеся после этого, будут равны площади I; значит, все эти взятые
площади будут вместе равны некоторому многоугольнику, вписанному
в сегмент. После этого ясно, что они будут меньше этого сегмента.
ХХШ
Если взять несколько величин, образующих непрерывную пропор-
цию в отношении четырех к одному, то все эти величины вместе, сло-
женные с третьей частью наименьшей, составят четыре трети наи-
большей {рис. 23}**).
*) Если треугольник AZB есть половина А ЕВ, а ДЕВ—половина АБД и> наконец, А ВД—по-
ловина АВГ, то следовательно;
AAZB= ААВГ.
О
•*) В рукописях ати величины изображены отревками прямых.
КВАДРАТУРА ПАРАБОЛЫ
93
Пусть будет взято в непрерывной пропорции несколько величин
А, В, Г, Д, Е, из которых каждая в четыре раза больше последующей,
и пусть Л будет наибольшей; затем пусть Z будет третью от В, Н —
третью от Г, © — третью от Л и I — третью от Е. Tai? как Z — треть В,
а В — четвертая часть А,
то обе величины В и Z
вместе составят третью
часть А. На том же ос-
новании Н и Г вместе
составят треть В, за-
тем, © и А вместе соста-
вят треть Г и, наконец.
I и Е вместе составят
треть Д; тогда вместе
взятые В, Г, Д, Е, Z,
Н, 0, I составят третью
часть от вместе взятых
г
Рис. 23.
А, В, Г, Д. Но величи-
ны Z, Н, 0 составляют третью часть от В, Г, Д; значит, оставшиеся
величины В, Г, Д, Е, I будут третьей частью остатка Л. После этого
ясно, что величины А, В, Г, Д, Е, взятые вместе с I — третьей частью
от Е,— составят четыре трети от А.
XX Г V
Всякий сегмент, заключенный между прямой и параболой, состав-
ляет четыре трети треугольника, имеющего с ним одно и то же осно-
вание и равную высоту.
Пусть АД BE Г {рис. 24} будет сегмент, заключенный между пря-
мой и параболой, а АВГ — треугольник, имеющий с сегментом одно
и то же основание и равную
высоту; пусть площадь К со-
ставляет четыре трети тре-
угольника АВГ. Требуется
доказать, что эта площадь
равна сегменту ААВЕ Г.
Действительно, если она
не равна, то будет или боль-
ше, или меньше. Пусть сна-
чала сегмент АД BE Г будет,
если возможно, больше пло-
щади К.
Итак, я вписал треуголь-
ники АД В, ВЕГ, как было
сказано выше, в оставшиеся
по краям сегменты вписал
другие треугольники, имею-
щие с этими сегментами те же
самые основания и высоты, и
затем в получающиеся после этого сегменты постоянно вписываю по
два треугольника, имеющие с этими сегментами те же самые основа-
ния и высоты; тогда остакицисся сегменты сделаются когда-нибудь
меньше того избытка, на который сегмент А ДВЕ Г превосходит
94
АРХИМЕД
площадь К, так что вписанный многоугольник будет больше площади К,
а это невозможно. Действительно, имеются площади, образующие
непрерывную пропорцию в отношении четырех к одному, а именно
первая — треугольник АВГ, в четыре раза больший обоих треуголь-
ников АДВ и ВЕГ вместе взятых, затем эти самые треугольники,
которые в четыре раза больше треугольников, вписываемых в следую-
щие сегменты, и так все время далее; яспо, что все эти площади вместе
будут меньше, чем четыре трети от наибольшей площади (АВГ), тогда
как К составляет четыре трети от наибольшей площади.
Значит, сегмент АД BE Г ис будет больше площади К.
Пусть теперь, если возможно, он будет меньше.
Возьмем площадь Z, равную треугольнику АВГ, затем пло-
щадь Н, равную четверти Z, далее — 0, равную четверти И, и будем
так брать постоянно в непрерывной пропорции до тех пор, пока по-
следняя площадь не окажется меньше того избытка, на который пло-
щадь К превосходит сегмент; пусть эта меньшая площадь будет I;
тогда площади Z, Н, 0, 1 вместе с третью от I составят четыре трети
от Z (предложение ХХ1П).
Но и К также составляет четыре трети от Z; значит, К будет равна
площадям Z, Н, 0, I, взятым вместе с третьей частью от I. Так как
площадь К превосходит площади Z, II, 0, 1 на величину, меньшую 1,
а сегмент (АДВЕГ) — на величину, большую I, то ясно, что пло-
щади Z, П, ©, I будут больше сегмента. Это же невозможно, так как
доказано, что если взято любое количество площадей, образующих
непрерывную пропорцию в отношении четырех к одному, причем
наибольшая равна вписанному в сегмент треугольнику, то все эти
площади . вместе будут меньше сегмента (предложение XXII); зна-
чит, сегмент АДВЕГ ис меньше площади К. По доказано также, что
он не будет и больше; значит, он будет равен площади К. Но площадь К
составляет четыре трети треугольника АВГ; значит, сегмент АДВЕГ
равен четырем третям треугольника АВГ [5].
О ШАРЕ И ЦИЛИНДРЕ [1]
КНИГА I
Архимед Досифею желает радоваться!
Я уже послал тебе запись наших открытий вместе с доказатель-
ством, что всякий сегмент, заключенный между прямой и параболой,
составляет четыре трети треугольника, имеющего с сегментом одно и то
же основание и одинаковую высоту; позднее, когда нам пришли на
ум другие стоящие внимания теоремы, мы потрудились над их доказа-
тельствами. Теоремы эти таковы:
во-первых, поверхность всякого шара в четыре раза больше его
большого круга-,
затем, поверхность всякого шарового сегмента равна кругу, радиус
которого равен прямой, проведенной из вершины сегмента к окружности
круга, ссставляюгцего основание сегмента-,
кроме того, для всякого шара цилиндр, имеющий основанием боль-
шой круг этого шара, а высотой — прямую, равную диаметру шара,
и сам,*) будет в полтора раза больше этого шара, и поверхность его
тоже в полтора рала больше поверхности этого шара.
Конечно, эти свойства были и раньше по самой природе присущи
упомянутым фигурам, но они все же оставались неизвестными тем,
кто до нас занимался геометрией, и никому из них не пришло на ум,
что все эти фигуры являются соизмеримыми друг с другом; поэтому
я не поколебался бы сравнить эти теоремы с теми, которые были откры-
ты другими геометрами, и в частности с наиболее выдающимися теоре-
мами, которые были установлены для тол Евдоксом, а именно, что вся-
кая пирамида составляет третью часть призмы, имеющей с пирамидой
одно и то же основание и одинаковую высоту, и что всякий конус со-
ставляет третью часть цилиндра, имеющего с конусом одно и то же осно-
вание и одинаковую высоту; действительно, хотя эти свойства по самой
природе всегда были присущими указанным телам, новее же оказалось,
что они остались неизвестными многим жившим до Евдокса знамени-
тым геометрам и ни одному из них не пришли на ум. Теперь же их
могут усмотреть все, имеющие к тому силы. Было бы очень хорошо,
* То есть объем его.
96
АРХИМЕД
если бы они были обпародовапы еще при жизни Конона; он был, как
мы считаем, наиболее способным продумать их и дать о них подходя-
щий отзыв. Полагая, что было бы очень хорошо передать их сведущим
в математике людям, мы посылаем тебе запись их доказательств;
теперь их могут рассмотреть все занимающиеся математикой. Будь
здоров!
Прежде всего излагаются аксиомы и необходимые для доказатель-
ства их допущения.
Аксиомы [2]
1. На плоскости существуют некоторые ограниченные кривые*)
линии, которые или целиком находятся, по одну сторону от прямых,
соединяющих их концы, или ничего не имеют по другую их сторону.
2. Тогда выпуклой в одну и ту же сторону я называю такую
линию, для которой прямые, соединяющие две произвольные ее точки,
будут или все находиться по одну сторону этой линии, или же неко-
торые по одну ее сторону, другие же на самой линии, но никакая такая
прямая не. будет находиться по другую ее сторону.
3. Подобным же образом существуют некоторые ограниченные
поверхности, которые не лежат сами на плоскости, ио имеют на
плоскости свои границы, причем эти поверхности будут или целиком,
находиться по одну сторону от плсскссти, содержащей их границы,
или ничего не будут, иметь по другую сторону от нее.
4. Выпуклыми в одну и ту же сторону я называю такие поверх-
ности, для которых прямые, соединяющие две произвольные их точки,
будут или все находиться по одну сторону этой поверхности, или же
некоторые по одну сторону, другие же на самой поверхности, но ника-
кая из них не будет находиться с другой ее стороны.
5. Телесным сектором я называю фигуру, ограниченную поверхно-
стью конуса, отсеченного шаром с центром в вершине конуса, и той
частью поверхности шара, которая лежит, внутри конуса.
б. Телесным ромбом я называю фигуру, состоящую из двух конусов,
имеющих одно основание, вершины, расположенные по разные стороны
от плоскости основания, а оси — на одной прямой.
Допу щ опия
Я принимаю следующее:
1. Из всех линий, имеющих одни и те же концы, прямая будет
наименьшей.
2. Две другие линии, расположенные на плоскости и имеющие те
же самые концы, будут всегда неравными, если обе они выпуклы в одну
и ту же сторону, и одна из них или целиком, обьемлется другой линией
и соединяющей их концы прямой, или же часть ее объемлется другой,
часть же является общей обеим линиям; при этом меньшей будет объем-
лемая линия.
3. Подобным же образом из поверхностей, имеющих общую грани-
цу, расположенную на плоскости, наименьшей будет плоскость.
*) Как видно из далытейшего текста, пол словом кривые (харлфХаО Архимед попинает здесь
вообще любые лилии, отличающиеся от прямой.
О ШАРЕ И ЦИЛИНДРЕ
97
4. Две другие поверхности, имеющие общую границу, расположен-
ную на плоскости, будут всегда неравными, если обе они выпуклы в одну
и ту же сторону и одна из них или целиком объемлется другой поверх-
ностью и плоскостью, содержащей их общую границу, или же часть ее
объемлется другой, часть же является общей обеим поверхностям',
при этом меньшей будет объемлемая поверхность.
5. Далее, большая из двух неравных линий, поверхностей или тел
превосходит меньшую на такую величину, которая, будучи складываема
сама с собой, может превзойти любую заданную величину из тех, кото-
рые могут друг с другом находиться в определенном отношении [3J.
При наличии этих допущений ясно, что если мн впишем в круг
многоугольник, то периметр вписанного многоугольника будет меньше
окружности круга, так как каждая из сторон д
этого многоугольника будет меньше отсекав-
мой ею дуги окружности. Вх^
Если около круга описать многоугольник,
то периметр описанного многоугольника будет
больше периметра круга.
Опишем около круга многоугольник, как ух.
предполагается {рис. 1}. Я утверждаю, что \
периметр описанного многоугольника будет
больше периметра круга. *
Действительно, прямые В А, ДА, вместе Рис-
взятые, будут больше дуги ВА вследствие того,
что они объемлют эту дугу, имеющую с ними те же самые концы; по-
добным же образом вместе взятые прямые ДГ и ГВ будут больше дуги
ДВ, а вместе взятые АК и КО больше дуги АО, вместе взятые ZH,
ПО больше Z0 и, наконец, вместе взятые ДЕ, EZ больше AZ; следо-
вательно, весь периметр рассматриваемого многоугольника будет
больше окружности круга.
Если даны две неравные величины, то можно найти две неравные
прямые таким образом, чтобы большая прямая имела к меньшей отно-
шение меньшее, чем отношение большей величины к меньшей.
Пусть будут две неравные величины АВ и Д, и пусть большей бу-
дет АВ {рис. 2}. Я утверждаю, что можно найти две неравные прямые,
которые удовлетворяли бы высказанному требованию.
Пользуясь построением второго предложения первой книги
Евклида, отложим ВГ, равную Д, и возьмем некоторую прямую ZH;
тогда, складывая ГА с самой собой, мы когда-нибудь превзойдем Д.
Возьмем се нужное число раз кратпой; пусть полученная линия бу-
дет АО. Определим теперь НЕ так, чтобы ZH была больше НЕ во столь-
ко же раз, во сколько АО больше АГ; значит, как ©А к АГ, так
и ZH к НЕ,
6А _ ZH
АГ ^НК
и обратно — как ЕП (относится) к HZ, так и АГ к АН.
ЕН АГ
hz ле
7 Архимед
98
АРХИМЕД
Поскольку же Л0 больше Д, или, что то же, больше ГВ, то, значит,
ГА имеет к Л© отношение меньшое, чем ГЛ к ГВ.
ГА ГА
АО <ГВ
По как ГА (относится) к А0, так и ЕП к IIZ; значит, ЕН к HZ
имеет
Е
А
Н -
Г -
отношение меньшее, чем ГА к ГВ; тогда, «присоединяя»*), най-
дем, что EZ к ZT.I будет иметь отношение меньшее, чем АВ
к В Г. Пр В Г равна Д; значит, EZ имеет к ZIT отношение
меньшее, чем АВ к Д.
Итак, найдены две неравные прямые, удовлетворяющие
поставленному условию, [т. с., что большая имеет к мень-
шей отношение, меньшее того, которое большая величина
имеет к меньшей] [4].
III
Если даны две неравные величины и, круг, то можно впи-
сать в круг многоугольник и описать около него другой та-
ким образом, чтобы сторона описанного многоугольника
имела к стороне вписанного многоугольника отношение
меньшее, чем отношение большей величины к меньшей.
Пусть обе заданные величины будут Л, В (рис. 3}, за-
данный же круг расположен выше. Я утверждаю, что
можно выполнить задание.
В
г в
Рис. 2. Найдем две прямые 6 и КА, из которых большей пусть
будет 0, таким образом, чтобы 0 находилась к КА в отно-
шении меньшем, чем большая величина (Л) к меньшей (В); из
точки Л под прямым углом к ЛК
проведем ЛМ, а из К проведем КМ
так, чтобы КМ равнялась 0; [это ведь
возможно].
Затем в круге проведем под пря-
мым углом два диаметра ГЕ и AZ. Те-
перь, разделив угол ДНГ пополам,
половину его еще раз пополам и про-
должая такое деление все время, мы
придем к некоторому углу, мспыпему,
чем удвоенный угол ЛК. М. Пусть таким
углом будет NHT.
Соединим точки N, Г; тогда NT
будет стороной равностороннего мно-
гоугольника с четным числом сторон
[действительно, поскольку угол Nil Г
целое число раз измеряет прямой угол
ДНГ, то н дуга NT целое число раз
измеряет четверть окружности ГД, а
значит целое число раз измеряет и всю
окружность. Таким образом, NT, оче-
видно, является стороной равностороннего многоугольника]. Разделим
*) Это яяаяят составляв производную пропорцию со сложением:
КН + HZ _ АГ I- ГВ
HZ 'С ГВ
О ШЛИК И ЦИЛИНДРЕ
99
угол THN пополам прямой НН, проводом из точки S касательную ОНП
к кругу и продолжим линии HJN11 и НГО; тогда ПО будет стороной
описанного около круга равностороннего многоугольника; [очевидно,
что этот многоугольник будет подобен вписанному многоугольнику со
стороной NT]. Теперь, поскольку угол NHT меньше удвоенного угла
ЛКМ и равен удвоенному углу ТПГ, то угол ТНГ будет меньше угла
ЛКМ. Углы же при Л и Т прямые; значит, МК будет иметь к ЛК отно-
шение, большее, чем ГН к НТ.
МК ГН *)
лк > нт
Но ГН равна HS; значит, отношение HS к НТ, а также ПО
к НГ, будет меньше, чем отношение МК к ЛК.
нв = по МК
НТ NF ' КЛ
Далее, МК находится к КЛ в отношении меньшем, чем А к В,
мк л
кл в
и ПО есть сторона описанного многоугольника, a NT — вписанного,
что и требовалось найти.
IV .
Далее, если, имеются две неродные величины и сектор, то можно
описать вокруг сектора многоугольник и вписать в него другой так,
чтобы сторона описанного многоугольника находилась к стороне вписан-
ного в отношении, меньшем того, кото-
рое большая величина имеет к меньшей.
Пусть будут опять две неравные
величины Е и Z {рис. 4}, и пусть боль-
шая из них Е; пусть будет некоторый
круг АВГ, имеющий центр в А, и при
точке А построен сектор АДВ; требует-
ся около сектора АВА описать и в пего
вписать многоугольник, имеющий рав-
ными все стороны, за исключением сто-
рон ВД, ДА* **), так, чтобы выполнить
задание.
Пайдем две неравные прямые Н и
ОК (пусть большая будет Н) такие,
чтобы Н имела к 0К отношение мень-
шее, чем большая величина к меньшей
H Е
ОК ' Z
[это ведь возможно]; и точно так же, проведя из © под прямым углом
к К© прямую ©Л, построим КЛ, равную II [это возможно, поскольку
Н больше ОК]. Разделяя угол ЛДВ пополам, половину его опять попо-
лам и продолжая так все время, мы придем к некоторому углу,
♦) С нашей точки зрения, это равносильно утверждению» что если ос < р, то вес ос > see р.
**) Предполагается, что боковые радиусы сектора входят в периметр обоих многоугольников
как вписанного, так и описанного.
7*
100
АРХИМЕД
I который будет меньше удвоенного угла КЛ®. Пусть таким углом будет
АДМ: тогда ЛМ будет стороной многоугольника, вписанного в круг.
Если рассечем угол АДМ прямой AN пополам и из N проведем каса-
с , тельную к кругу прямую N3O, то ата прямая будет стороной описап-
г . ного около того же круга многоугольника, подобного вышеупомянутому;
: тогда совершенно так же, как и раньше, покажем, что SO будет нахо-
диться к AM в отношении меньшем, чем отношение величины Е к Z.
ЕО Е
AM Z
V
1 ' Дан круг и две неравные величины', описать около круга многоуголь-
ник и вписать в него другой так, чтобы описанный имел к вписанному*)
отношение меньшее того, которое большая величина имеет к меньшей.
Пусть будут круг А {рис. 5} и две неравные величины Е, Z, из
которых большая Е; требуется вписать в круг многоугольник и описать
Около него другой так, чтобы выполнялось поставленное задание.
Я беру две неравные прямые Г, А, из которых большей пусть бу-
дет Г, таким образом, чтобы Г имела к А отношение меньшее, чем
'• Е к Z;
Д Z
если взять для Г и А среднюю пропорциональную Н,
н д
, то Г будет больше Н.
Опишем около круга многоугольник и впишем в него другой так,
чтобы сторона описанного многоугольника имела к стороне вписанного
; отношение меньшее, чем Г к Н, [как мы уже выучились]; тогда ква-
!драт**) первого отношения будет меньше квадрата второго. Но квад-
рат отношения сторон равен отношению
(площадей) многоугольников, [так как по-
следние подобны], квадрат же отношения Г
к П равен отношению Г к А.
Таким образом, описанный многоуголь-
ник имеет к вписанному отношение мень-
шее, чем Г к А; значит, и подавно, описан-
ный многоугольник имеет к вписанному
отношение меньшее, чем Е к Z.
Рис. 5.
первому, так, чтобы
VI
Подобным же образом докажем, что,
если даны две неравные величины и сек-
тор, то можно описать около сектора мно-
гоугольник и вписать в него другой, подобный
отношение описанного многоугольника ко вписан-
ному было меньше того, которое большая величина имеет к меньшей.
Точно так же ясно, что если даны круг, сектор и некоторая пло-
щадь, то можно, вписывая в круг или в сектор равносторонние много-
*) Мы сказали бы: «чтобы площадь описанного имела к площади вписанного».
= **) В подлиннике diTtftaaioS : W^og—двойное отношение:: у греков сложение отношений было
фаидосильно их умножению.
' 1
О ШАРЕ И ЦИЛИНДРЕ
101
угольники и продолжая делать то же самое с получающимися по
краям сегментами, дойти до такого сегмента круга или сектора, кото-
рый был бы меньше заданной площади: это доказано в «Началах»*).
Требуется доказать, что если даны круг, сектор и некоторая пло-
щадь, то можно около круга или сектора описать многоугольник та-
ким образом, чтобы оставшиеся по краям части**) описанной фигуры
были меньше заданной площади; достаточно будет доказать это для
круга и провести то же рассуждение и для сектора.
Пусть будут даны круг А {рис. 6} и некоторая площадь В. Около
этого круга можно описать многоугольник так, чтобы его части, оста-
ющиеся между многоугольником и окружностью,
взятые вместе, были меньше площади В; ибо если
имеются две неравные величины, из которых боль-
шая равна вместе взятым кругу и заданной пло-
щади, а меньшая одному только кругу, то опи-
шем около круга многоугольник и впишем в него
другой так, чтобы описанный имел но вписанному
отношение меньшее, чем упомянутая большая
величина к меньшей. Тогда этот описанный мно-
гоугольник и будет тем, остающиеся части кото-
рого будут меньше заданной площади В.
Действительно, если описанный многоуголь-
ник имеет ко вписанному отношение меньшее того,
в котором вместе взятые круг и площадь В на-
ходятся к этому же кругу, и круг больше впи- Рис. 6.
санного многоугольника, то описанный много-
угольник и подавно будет иметь к кругу отношение меньшее, чем
вместе взятые круг и площадь В имеют к этому же кругу; тогда
после «выделения»***) части описанного многоугольника будут иметь
к кругу отношение меньшее, чем площадь В к кругу; значит, части
описанного многоугольника будут меньше площади В.
Или таким образом, поскольку описанный многоугольник имеет
к кругу отношение меньшее, чем вместо взятые круг и площадь В
к кругу, то вследствие этого описанный многоугольник будет меньше
указанных величин, вместе взятых; таким образом, и все его части
(лежащие вне круга) будут меньше площади В.
То же самое и относительно сектора.
VII
Если в равнобедренный конус****} вписать пирамиду, имеющую
основанием равносторонний многоугольник, то поверхность этой пира-
миды за вычетом основания равна треугольнику, имеющему основание
равным периметру основания пирамиды, а высотой — перпендикуляр,
опущенный из вершины пирамиды на одну из сторон основания.
*) Евклид, ХИ, 2.
**) Буквально: отрезки. •, .
***) Это значит—составления производной пропорции с вычитанием:
*4-)
Опис. мн-к—А (А Ч- В) - А
А ' А
****) То есть конус, имеющий в осевом сечении равнобедренный треугольник, иными словами,
обыкновенный прямой круговой конус.
.102
АРХИМЕД
Пусть будет равнобедренный конус, основание которого есть
круг АВГ {рис. 7} и в него вписана пирамида, имеющая основанием
равносторонний многоугольник АВГ: я утверждаю, что поверхность
се за вычетом основания равна вышеназванному треугольнику.
Так ьак конус является равнобедренным и в <с овании пирамиды
лежит равносторонний многоугольник, то высоты ограничив ю.ьих
пирамиду треугольников будут равны меж-
ду собой. Основаниями этих треугольников
являются АВ, ВГ, ГА, (общая) высота же
упомянутая; таким образом, эти треуголь-
ники вместе, [то есть поверхность пирамиды
за вычетом треугольника АВГ{, будут рав-
ны треугольнику, имеющему основание, рав-
ное вместе взятым АВ, В Г, ГА, высотой
же — упомянутую прямую.
[Более ясно другое доказательство*).
Пусть будет равнобедренный конус,
основанием которого является круг АВГ
{рис. 8}, вершиной же точка А: пусть в этот
конус вписана пирамида, имеющая основа-
нием равносторонний треугольник АВГ,
и проведены линии АА, АГ, АВ; я утверждаю, что треугольники АДВ,
АДГ, ВДГ равны треугольнику, основание
которого равно периметру треугольника
АВ Г, а опущенный нз верппшы на это осно-
вание перпендикуляр равен перпендикуляру,
опущенному из А на сторону В Г.
Проведем перпендикуляры ДК, АЛ, ДМ;
они, конечно, равны между собой. Возьмем
треугольник EZH, имеющий основание EZ
равным периметру треугольника АВГ и
высоту Н(н) равной /кА. Так как прямоуголь-
ник на ВГ, АЛ вдвое больше треугольни-
ка АВГ, прямоугольник между /кВ, ДК
вдвое больше треугольника АВА и прямо-
угольник между АГ, ДМ вдвое больше тре-
угольника АДГ, то, зпачит, прямоугольник
между периметром треугольника АВГ, то
есть между EZ, и ДА, или НО, будет вдвое
больше треугольников АДВ, ВАГ, /ХАГ,
вместе взятых. Также и прямоугольник
между EZ,H0 вдвое больше треугольника
EZII; значит, треугольник EZH будет равен треугольникам /ХАВ, ВДГ
и АДГ, вместе взятымJ.
VIII
Если около равнобедренного конуса описана пирамида, то поверх-
ность пирамиды за вычетом основания равна треугольнику, имеющему
основанием прямую, равную периметру основания {пирамиды}, а высо-
той — сторону конуса.
'»)' Из' этих слов индии, что шпкепомещенное доказательство ие принадлежит Архимеду.
О ШАРЕ И ЦИЛИНДРЕ
ЮЗ
Пусть будет конус, основание которого есть круг АВГ, и около
конуса описана пирамида {рис. 9], так что ее основание, то есть много-
угольник AEZ, будет описано около круга АВГ.
Я утверждаю, что поверхность этой пирамиды за
вычетом основания равна вышеупомянутому тре-
угольнику-
Действительно, так как [ось конуса перпен-
дикулярна к основанию, т. е. к кругу АВГ, и[
прямые, соединяющие центр этого круга с точ-
ками касания, перпендикулярны к касатель-
ным, то прямые, соединяющие вершину конуса
с точками касания, будут перпендикулярны к АЕ,
EZ.ZA. Таким образом, вышеупомянутые перпен-
дикуляры ПА, ПВ, ИГ равны между собой, ибо
они являются сторонами конуса. Возьмем тре-
угольник (Н)КА, имеющий сторону ©К равной
периметру треугольника AEZ, а перпендику-
ляр AM равным НА. Так как прямоугольник
между АЕ, АН вдвое больше треугольника ЕАИ,
прямоугольник между AZ, НВ вдвое больше
треугольника AZH и прямоугольник между EZ,
ГП вдвое больше треугольника EHZ, то, значит,
прямоугольник между ©К и АП, или МА, вдвое
больше треугольников ЕАН, ZAH, EHZ вместе
взятых. Также и прямоугольник между ©К,
AM вдвое больше треугольника AK0; вследст-
вие этого поверхность пирамиды за вычетом основания будет равна
треугольнику, имеющему основанием прямую,
равную периметру AEZ, а высотой сторону
конуса.
IX
Если прямая линия пересекает круг, явля-
ющийся основанием некоторого равнобедренного
конуса, и от ее концов проведены прямые линии
к вершине конуса, то треугольник, заключенный
между, этой секущей и прямыми, соединяющими
ее концы с вершиной, будет меньше поверхности
конуса между этими соединяющими с вершиной
прямыми.
Пусть круг АВГ {рис. 10} будет основа-
нием равнобедренного конуса, а точка А — его
вершиной; проведем в круге какую-нибудь пря-
мую АГ и соединим точки А, Г с вершиной
прямыми АА, А Г. Я утверждаю, что треуголь-
ник АДГ будет меньше конической поверхности, заключенной между
АД, АГ.
Разделим дугу АВГ пополам в точке В и проведем соединяющие
прямые АВ, ГВ, ДВ; тогда треугольники АВА, ВГД вместе будут
больше треугольника АДГ. Пусть 0 будет величина, на которую выше-
упомянутые треугольники превышают треугольник АДГ; тогда © будет
или меньше (суммы) сегментов АВ, ВГ, или же пет.
Рис. 10.
104 АРХИМЕД
Пусть сначала © будет не меньше их (суммы).
e^sAEB+SBzr
Так как имеются две поверхности — коническая между АД, АВ
вместе с сегментом ЛЕВ и треугольник АДВ — и обе они имеют одну
и ту же границу — периметр треугольника АДВ, то объемлющая
поверхность будет больше объемлемой: значит, коническая поверхность
между АД, ДВ вместе с сегментом АЕВ будет больше треугольника
АВД. Точно так же (коническая поверхность) между ВД, ДГ вместе
с сегментом TZB больше треугольника ВДГ; тогда вся коническая
поверхность вместе с площадью © будет больше обоих упомянутых
треугольников. Но упомянутые треугольники равны треугольнику
АДГ вместе с площадью 0. Отнимем общую площадь ©; тогда остав-
шаяся коническая поверхность между АД, ДГ будет больше треуголь-
ника АДГ.
Пусть теперь © будет меньше (суммы) сегментов АВ, ВГ.
Разделяя пополам дуги АВ, ВГ, а затем пополам их половинки,
. мы придем к сегментам (в сумме), меньшим площади ©*). Пусть это
будут сегменты (£де +Seb +£bz+<$zr < ограниченные прямыми
АЕ, ЕВ, BZ, 7>Г.
Проведем ДЕ и AZ. Тогда по той же причине поверхность конуса
между7 АД, ДЕ вместе с сегментом па АЕ будет больше треугольника
АДЕ, а поверхность между ЕД, ДВ вместе с сегментом па ЕВ больше
треугольника ЕД В; значит, поверхность (конуса) между АД, АВ
вместе с сегментами на АЕ, ЕВ будет больше треугольников АДЕ,
ЕВА. Поскольку же, согласно доказанному, треугольники АЕД, ДЕВ
больше треугольника АВД, то значит, и подавно поверхность конуса
между АД, ДВ вместе с сегментами на АЕ, ЕВ будет больше треуголь-
ника АДВ. На том же основании и поверхность конуса между ВД, ДГ
вместе с сегментами на BZ, ZT больше треугольника ВДГ; значит,
вся поверхность между АД, А Г вместе с упомянутыми сегментами будет
больше треугольников АВА и АВГ. Но эти треугольники равны тре-
угольнику АД Г и площади ©, причем упомянутые сегменты (в сумме)
меньше площади ©; значит, остающаяся поверхность конуса между
АД, ДГ будет больше треугольника АДГ 15, 6].
X
Если к кругу, являющемуся, основанием конуса, мы проведем каса-
тельные, лежащие в одной плоскости с кругом и пересекающиеся между
собой, а затем полученные точки касания и пересечения касательных
соединим прямыми с вершиной конуса, то треугольники, заключаю-
щиеся между касательными и прямыми, соединяющими с вершиной
конуса, будут больше отсекаемой ими части конической поверхности.
Пусть будет конус, основанием которого является круг АВГ
{рис. 11}, а вершиной — точка Е; к кругу АВГ проведем касатель-
ные АД и ГД, расположенные в той же самой плоскости, и вершину
конуса Е соединим с точками А, А, Г прямыми ЕА, ЕА, ЕГ. Я утвер-
ждаю, что треугольники ААЕ, АЕГ**) будут больше конической поверх-
ности, находящейся между прямыми АЕ, ГЕ и дугой АВГ.
• На основании предложения Vf.
•* То есть сумма этих треугольников.
О ШАРЕ И ЦИЛИНДРЕ
105
Разделим дугу ЛВГ в точке В пополам и проведем к кругу
касательную HBZ, параллельную АГ; точки Н, Z соединим с Е пря-
мыми НЕ, ZE. И так как прямые ДН, AZ, взятые вместе, боль-
. ше HZ, то добавим к обеим НА, ZF, тогда АД и ДГ вместе будут боль-
ше АН, HZ, ZE
АД + ДГ > АН 4- HZ + 2Г
Так как АЕ, ЕВ, ЕГ суть образующие*) конуса, то они равны между
собой, поскольку конус равнобедренный; точно так же они перпенди-
кулярны**); [прямоугольники ?ке между вы-
сотами и основаниями вдвое больше соответствую-
щих треугольников;] следовательно, треугольни-
ки АЕА, ДЕГ будут больше треугольников
АНЕ, IIEZ, ZEF, [ибо АП, НГ, ZF меньше ГА,
ДА, высоты же у тех и других равны.] [Ясно,
что прямая, соединяющая вершину прямого ко-
нуса с точкой касания иа основании, будет перпен-
дикулярна к касательной.!***)
Пусть треугольники АЕА и ДЕГ превышают
треугольники АЕП, HEZ, ZET на площадь в.
Тогда площадь 0 будет ил и меньше отрезков АП ВК
й BZTA (между касательными и окружностью
круга), или же не меныпе их.
Пусть сначала опа будет пе меныпе. Так как
имеются две составленные поверхности, а именно
поверхность пирамиды с основанием — трапецией
HAFZ и вершиной Е и коническая поверхность
междуАЕ, ЕГ вместе с сегментом АВГ, и обе они
Рис. 11.
имеют одну и ту же границу — периметр треугольника ЛЕГ, то ясно,
что поверхность пирамиды за вычетом треугольника /ХЕГ будет больше
конической поверхности вместе с сегментом АВГ. Отнимем общий сег-
мент ЛВГ; тогда оставшиеся треугольники АЫЕ, HEZ, ZET вместе с
отрезками по краям ЛПВК, BZTA будут больше конической поверх-
ности между прямыми АЕ, ЕГ. Но площадь 0 не менее отрезков
АПВК, BZTA; значит, и подавно треугольники АНЕ, HEZ, ZET
вместе с 6 будут больше конической поверхности между ЛЕ, ЕГ.
Но треугольники АНЕ, HEZ, FEZ вместе с 0 равны треугольни-
кам АЕД, ДЕГ; значит, треугольники АЕА, ДЕГ больше упомянутой
конической поверхности.
Пусть теперь 0 будет меньше этих отрезков по краям.
Тогда, точно так же описывая все время около сегментов много-
угольники, разделяя пополам остающиеся по краям дуги и проводя
касательные, мы придем к некоторым отрезкам, которые будут меньше
площади 0. Пусть полученные такие отрезки будут АМК, KNB,
ВЕЛ, ЛОГ, которые вместе меньше площади 0.
Соединим полученные точки с Е. Тогда опять ясно, что треуголь-
ники АНЕ, HEZ, ZET, взятые вместе, больше треугольников АЕМ,
MEN, NEE, ЕЕО, ОЕГ, [ибо основания у первых больше, а высоты оди-
наковы]. Кроме того, пирамида, имеющая основанием многоугольник
•) Буквально: стороны (лХЕясаО.
**) К карательным AH, HZ. Zr.
•**) Отмеченная Гейбергом двойная интерполяция.
106 АРХИМЕД
AMNHOr, а вершиной Е, точно так же будет, если вычесть тре-
угольник АЕГ, иметь поверхность большую, чем коническая поверх
пость между /ХЕ, ЕГ, взятая вместе с сегментом АВГ. Отнимем общий
сегмент АВГ; тогда оставшиеся треугольники АЕМ, MEN, NEH,
ЕЕО, ОЕГ вместе с отрезками по краям АМК, KNB, ВЕЛ, ЛОГ будут
больше конической поверхности между АЕ, ЕГ. Но площадь 0 больше
упомянутых отрезков по краям; треугольники ясе АЕН, HEZ, ZET,
как показано, больше треугольников АЕМ, MEN, NE3, ЕЕО, ОЕГ;
значит, и подавно треугольники /ХЕН, HEZ, ZET вместе с площадью 0,
то есть треугольники АДЕ, АЕГ, будут больше конической поверхно-
сти между прямыми АЕ, ЕГ [6].
XI
Рис. 12,
Если на поверхности прямого цилиндра имеются две прямые, то
поверхность цилиндра между этими прямыми больше параллелограмма,
заключающегося между находящимися на поверхности цилиндра пря-
мыми и другими, соединяющими их концы.
Пусть будет прямой цилипдр, основание которого круг АВ,
а противоположное — круг ГА*) {рис. 12}; проведем соединяющие
прямые АГ и ВЛ; я утверждаю, что цилиндриче-
ская поверхность, отсеченная прямыми АГ, ВД,
больше параллелограмма АГВА.
Разделим каждую из дуг АВ, ГА пополам в
точках Е, Z и проведем соединяющие прямые АЕ,
ЕВ, PZ, ZA. Так как АЕ и ЕВ вместе больше АВ,
и построенные па них параллелограммы равновы-
соки, то параллелограммы, основания которых АЕ
и ЕВ, а высота та же, что и у цилиндра, вместе
взятые, будут больше параллелограмма АВГА. На
сколько же они будут больше? Пусть опи больше
на площадь Н. Тогда площадь Н будет или мень-
ше плоских сегментов АЕ, ЕВ, TZ, ZA, или же
не меньше.
Пусть сначала она будет не меньше. Так как
отсеченная прямыми АГ, ВД цилиндрическая по-
верхность вместе с (сегментами **)) AEB, TZA
имеет границей плоскость параллелограмма
поверхность, составленная из параллелограммов
АГВА, и так как
с основаниями АЕ, ЕВ и высотой той же, что у цилиндра, и [плоских
фигур] ЛЕВ, BZA, имеет границей (ту же самую) плоскость парал-
лелограмма АВА Г, и первая поверхность объемлет вторую, причем
обе они выпуклые в одну сторону, то отсеченная прямыми АГ, ВЛ
цилиндрическая поверхность вместе с плоскими сегментами AEB, TZA
будет больше поверхности, составленной из параллелограммов с осно-
ваниями ЛЕ, ЕВ и с той же высотой, что у цилиндра, и из треуголь-
ников AEB, TZA.
Отнимем общие треугольники АЕВ, TZA; тогда оставшаяся цилин-
дрическая поверхность, отсеченная прямыми АГ, ВА, вместе с плоскими
сегментами АЕ, ЕВ, TZ, ZA будет больше поверхности, составленной
*) dvP'Joig |isv б ЛВ ибхХок. «tnEvavTiov йе ГД-терминология «Начал» Квклица. Мы сказали
бы просто- с основаниями ЛВ и ГД-
•• ) Сегмент ЛЕВ—сегмент, опирающийся на хорду АВ и содержащий точку К.
О ШАРЕ И ЦИЛИНДРЕ
1.07
из параллелограммов с основаниями АЕ, ЕВ и с той же высотой, что
у цилиндра.
Но параллелограммы с основаниями АЕ, ЕВ и с высотой той же,
что у цилиндра, равны параллелограмму АГВА вместе с площадью II;
значит, оставшаяся цилиндрическая поверхность, отсеченная прямыми
АГ, ВД, будет больше параллелограмма АГВА.
Пусть теперь площадь Н будет меньше плоских сегментов АЕ, ЕВ,
TZ, ZA.
Разделим пополам каждую из дуг АЕ, ЕВ, TZ, ZA в точках 0, К,
А, Ми проведем соединяющие прямые А0, GE, ЕК, КВ, ГА, AZ, ZM,
МА; [таким образом, от плоских сегментов АЕ, ЕВ, TZ, ZA отнимутся
треугольники AGE, EKB, TAZ, ZMA, не меньшие их половин!- Если
мы будем действовать так все время, то получатся некоторые сегменты,
которые будут меньше площади И. Пусть они получены и будут А0,
GE, ЕК, КВ, ГА, AZ, ZM, МА- Тогда подобным же образом докажем,
что параллелограммы, основания которых суть AG, GE, ЕК, КВ,
а высота —та же, что и у цилиндра, будут больше параллелограммов,
основания которых суть АЕ, ЕВ, а высота — та же, что и у цилиндра.
И так как цилиндрическая поверхность, отсекаемая прямыми АГ, ВА,
вместе с плоскими сегментами AEB, TZA, имеет границей плоскость
параллелограмма АГВА, а поверхность, составленная из параллело-
граммов, основания которых суть AG, GE, ЕК, КВ, а высота — та же,
что и у цилиндра, и из прямолинейных фигур А0ЕКВ, 1AZMA (тоже
имеет границей плоскость параллелограмма АГВА, то отсекаемая пря-
мыми АГ, ВА цилиндрическая поверхность вместе с плоскими сегмен-
тами AEB, I'ZA будет больше поверхности, составленной из параллело-
граммов, основания которых суть AG, 0Е, ЕК, КВ, а высота — та же,
что и у цилиндра, и из прямолинейных фигур AGEKB, TAZMA)*).
Отнимем общие прямолинейные фигуры A0EKB, EAZMA; тогда оста-
ток — отсекаемая прямыми АГ, ВА цилиндрическая поверхность вместе
с плоскими сегментами АО, 0Е, ЕК, КВ, ГА, AZ, ZM, МА будет боль-
ше поверхности, составленной из параллелограммов, основания кото-
рых суть AG, GE, ЕК, КВ, ГА, AZ, ZM, МА, а высота — та же, что
и у цилиндра.
Параллелограммы же, основания которых суть AG, 0Е, ЕК, КВ,
а высота — та же, что и у цилиндра, больше параллелограммов, осно-
вания которых суть АЕ, ЁВ, а высота та же, что и у цилиндра; значит,
и цилиндрическая поверхность, отсекаемая прямыми АГ, ВА, вместе
с плоскими сегментами АВ, ОЕ, ЕК, КВ, ГА, AZ, ZM, МА, будет боль-
ше параллелограммов, основания которых суть АЕ, ЕВ, а высота —
та же, что и у цилиндра.
Но параллелограммы, основания которых суть АЕ, ЕВ, а высо-
та — та же, что и у цилиндра, равны параллелограмму АГАВ и пло-
щади Н; значит, и цилиндрическая поверхность, отсекаемая прямы-
ми АГ, ВА, вместе с плоскими сегментами AG, GE, ЕК, КВ, ГА,
AZ, ZM, МА будет больше параллелограмма АГВА и площади Н
вместе взятых.
После же отнятия сегментов AG, GE, ЕК, КВ, ГА, AZ, ZM, МД,
меньших площади Н, оставшаяся цилиндрическая поверхность, отсе-
каемая прямыми АГ, ВД, будет больше параллелограмма АГВА.
*) Оборванный конец фразы восстанавливается Гейбергом_согласмо сделанному в XIII веке
латинскому переводу Вильгельма из Мербеке.
408
АРХИМЕД
хп
Если на поверхности какого-нибудь прямого цилиндра имеются две
прямые и от конца этих прямых к кругам, являющимся основаниями
цилиндра, проведены некоторые касательные, находящиеся в плоскости
оснований и (попарно) пересекающиеся, то параллелограммы, заклю-
ченные между касательными и сторонами цилиндра, будут больше
поверхности цилиндра между обеими прямыми, находящимися на
поверхности цилиндра.
Пусть круг АВГ {рис. 13} является основанием некоторого
прямого цилиндра, и
пусть на поверхности последнего имеются две
прямые, концы которых суть А и Г; из то-
чек А и Г проведем касательные к кругу,
лежащие в его плоскости, и пусть они
пересекутся в Н. Вообразим также, что и
на другом основании цилиндра из концов
тех же самых прямых па его поверхности
проведены прямые, касательные к соответ-
ствующему кругу. Требуется доказать, что
параллелограммы, заключающиеся между
касательными и сторонами цилиндра,
будут больше поверхности цилиндра, со-
ответствующей дуге АВГ.
Проведем касательную EZ и из точек
Е, Z параллельно оси цилиндра проведем
прямые до [поверхности] другого основа-
ния; тогда параллелограммы, заключаю-
щиеся между АН, ПГ и сторонами ци-
линдра, будут больше параллелограм-
мов, заключающихся между АЕ, EZ, ZT и боками цилиндра, [ибо ЕН, HZ
более EZ, и после прибавления ЛЕ, ZT общих, НА, ИГ взятые вме-
сте будут больше АЕ, EZ, ZT вместе взятых]. Тогда пусть площадь
К будет то, на сколько первые параллелограммы больше вторых. Поло-
вина площади К будет или больше вместе взятых фигур, заключенных
между прямыми АЕ, EZ, ZT и дугами АА, АВ, В®, ®Г, или нет.
Йусть сначала опа будет больше. Поверхность, составленная из
параллелограммов на ЛЕ, EZ, ZT, трапеции AEZT и (трапеции),
противолежащей ей на другом основании цилиндра, имеет границей
периметр параллелограмма на АГ. Но тот же самый периметр будет
границей и поверхности, составленной из поверхности цилиндра,
соответствующей дуге АВГ, сегмента АВГ и (сегмента), противо-
лежащего ему; таким образом, обе упомянутые поверхности оказывают-
ся имеющими одну и ту же границу, которая расположена на плоско-
сти, обе они являются выпуклыми в одну сторону и одна из них объем-
лет другую и имеет с ней некоторую общую часть; значит, объемлемая
поверхность будет меньше. Тогда после отнятия общих сегмента АВГ
и противолежащего ему поверхность цилиндра, соответствующая дуге
АВГ, будет меныпе поверхности, составленной из параллелограммов
на АЕ, EZ, ZT, фигур AEB, BZI' и им противолежащих. Но поверхно-
сти упомянутых параллелограммов вместе с упомянутыми фигурами
меньше поверхности, составленной из параллелограммов на АН, НГ,
(ибо они были бы равны только после прибавления площади К, боль-
шей упомянутых фигур]; после этого ясно, что параллелограммы,
О ШАРЕ И ЦИЛИНДРЕ
109
заключающиеся между ATI, ГН и боками цилиндра, будут больше
поверхности цилиндра, соответствующей дуге АВГ.
Если же половина площади К ле больше упомянутых фигур, то
к сегменту проводятся касательные до тех пор, пока остающиеся по
краям фигуры не сделаются меньше половины К, и все остальное
докажется совершенно так же, как и раньше.
После доказанного ясно, что если в равнобедренный конус вписать
пирамиду, то поверхность пирамиды за вычетом основания будет
меньше конической поверхности, [так как каждый из треугольников,
ограничивающих пирамиду, будет меньше конической поверхности,
заключенной между сторонами треугольника; значит, и вся поверх-
ность пирамиды за вычетом основания будет меньше поверхности
конуса, тоже за вычетом основания], и что если около равнобедренного
конуса описать пирамиду, то поверхность пирамиды за вычетом осно-
вания будет больше поверхности конуса за вычетом основания.
Из доказанного также ясно, что если в прямой цилиндр вписать
призму, то поверхность призмы, составленная из параллелограммов,
меньше поверхности цилиндра за вычетом обоих оснований, [так как
каждый параллелограмм призмы меньше соответствующей ему части
цилиндрической поверхности], и что если около прямого цилиндра
описать призму, то составленная из параллелограммов поверхность
призмы больше поверхности цилиндра за вычетом обоих оснований.
XIII
Поверхность всякого прямого цилиндра аа вычетом оснований равна
кругу, радиус которого является средней пропорциональной между сто-
роной цилиндра и диаметром его основания.
Пусть круг А {рис. 14} будет осно-
ванием некоторого прямого цилиндра; пусть
прямая ГД равна диаметру круга A, a EZ рав-
на стороне цилиндра; пусть Н будет средней
пропорциональной между ГД, EZ, и круг
В имеет радиус, равный Н; требуется дока-
зать, что круг В равен поверхности цилин-
дра за вычетом оснований.
Действительно, если он не равен, то будет
или больше, пли меньше. Пусть сначала он
будет, если возможно, меньше. Тогда име-
ются две неравные величины, а именно
поверхность цилиндра и круг В, и мы
можем в круг В вписать равносторонний
многоугольник и около пего описать другой
Рис. 14.
так, чтобы описанный имел ко вписанному
отношение, меныпее того, которое поверх-
ность цилиндра имеет к кругу В. Нред-
ставим себе, что первый многоугольник вписап, а
второй описан; около
круга А опишем прямолинейную фигуру, подобную той, которая опи-
сана около В, и на этой прямолинейной фигуре построим призму; опа,
конечно, тоже будет описанной около цилиндра. Пусть периметр пря-
молинейной фигуры, описанной около круга А, будет равен КД, пусть
прямая AZ равна КД, а ГТ составляет половину ГД; тогда треугольник
КДТ будет равен прямолинейной фигуре, описанной около круга А.
ЙО
АРХИМЕД
[таи как он имеет основание, равное ее периметру, а высоту, равную
радиус^7 круга А], параллелограмм жо ИЛ равен (боковой) поверх-
ности призмы, описанной около цилиндра, [так как он заключается
между стороной цилиндра и прямой, равной периметру основания
призмы]. Отложим прямую ЕР, равную EZ; тогда треугольник ZPA
будет равен параллелограмму ЕЛ, а, следовательно и (боковой)
поверхности призмы. И так как описанные около кругов А и 13 прямо-
линейные фигуры подобны, то [эти фигуры] будут иметь то же самое
отношение, что и квадраты на радиусах; значит, треугольникКТД будет
относиться к прямолинейной фигуре, описанной около круга В, как
квадрат на ТА к квадрату на 11, [ибо ТД и Н равны радиусам соответ-
ствующих кругов]. Но отношение квадрата на ТД к квадрату на Н
равно отношению линий ТД и PZ.
тдз тд
Н2 “ PZ
[ибо Н, будучи средней пропорциональной для ГД и EZ, будет также
средней пропорциональной и для ТА и PZ. Это по следующей причине:
так как ДТ равна ТГ, а РЕ равна EZ, то ГД вдвое больше ТД, a PZ
вдвое больше РЕ; значит, как ДГ (относится) к ДТ, так будет и PZ
к ZE. Следовательно, произведение ГД и EZ равно произведению ТД
и PZ. Но произведение ГД и EZ равно квадрату 11; значит, и произве-
дение TA, PZ равно квадрату Н. Следовательно, как ТД к Н, так будет
и Н к PZ; значит, как ТД к PZ, так и квадрат ТД к квадрату И, ибо
если имеются три прямые в непрерывной пропорции, то первая будет
относиться к третьей, как фигура, построенная па первой, относится
к фигуре, подобной и подобно построенной на второй прямой*)]; отно-
шение же липин ТД и PZ равно отношению (площадей) треугольни-
ков КТД и PAZ, [ибо КД и AZ равны]; следовательно, треугольник
КТД будет относиться к прямолинейной фигуре, описанной около кру-
га В, как треугольник ТКД к треугольнику PZA. Значит, треугольник
ZAP будет равен прямолинейной фигуре, описанной около круга В;
таким образом, (боковая) поверхность призмы, описанной около цилин-
дра Л, будет равна прямолинейной фигуре, описанной около круга В.
И поскольку прямолинейная фигура, описанная около круга В, к фигу-
ре, вписанной в этот же круг, имеет отношение, меньшее того, которое
поверхность цилиндра А имеет к кругу В, то и (боковая) поверх-
ность призмы, описанной около цилипдра, к прямолинейной фигуре,
вписанной в круг В, будет иметь отношение меньшее, чем (боковая)
поверхность цилипдра к кругу В; и после перестановки (боковая
поверхность призмы к боковой поверхности цилиндра будет иметь отно-
шение мепыпее, чем вписанная в круг В фигура к кругу В), а это
невозможно, [ибо доказано, что поверхность призмы, описанной около
цилиндра, больше поверхности цилиндра, а вписанная в круг В фигура
меньше круга В]. Таким образом, круг В не будет меньше (боковой)
поверхности цилипдра.
Пусть теперь, если возможно, он будет больше. Тогда опять вообра-
зим прямолинейную фигуру, вписанную в круг В, и другую, описан-
ную около пего таким образом, чтобы описанная имела ко вписанной
отношение меньшее, чем круг В к поверхности цилиндра; в круг А
впишем многоугольник, подобный вписанному в круг В, и на много-
*) Из пропорции а : Ъ=Ъ : с следует а : с — ай : б2.
О ШАРЕ И ЦИЛИНДРЕ
111
угольнике, вписанном в этот круг (А), построим призму. Пусть опять
прямая КД будет равна периметру прямолинейной фигуры, вписанной
в круг А, и ZA равна КД. Тогда треугольник КТД будет больше прямо
липсйпой фигуры, вписанной в круг А, [так как основанием он имеет
ее периметр, а высота его больше перпендикуляра, опущенного из
центра на одну из сторон многоугольника], а параллелограмм ЕД равен
составленной из параллелограммов поверхности призмы, [так как он
заключается между стороной цилиндра и прямой, равной периметру
прямолинейной фигуры, являющейся основанием призмы]; таким обра-
зом, и треугольник PAZ будет ранен поверхности призмы. Но так как
прямолинейные фигуры, вписанные в круги А и В, подобны, то они
относятся друг к другу, как квадраты радиусов соответствующих кру-
гов. Но и треугольники КТД, ZPA находятся друг с другом в двойном
отношении*) радиусов этих кругов; следовательно, прямолинейная
фигура, вписанная в круг А, будет иметь к прямолинейной фигуре,
вписанной в В, то же самое отношение, что треугольник КТД к тре-
угольнику AZP.
По прямолинейная фигура, вписанная в круг А, меньше треуголь-
ника КТД; следовательно, и фигура, вписанная в круг В, будет меньше
треугольника ZPA, а следовательно, меньше и (боковой) поверхности
призмы, вписанной в цилиндр, а это невозможно, [так как прямолиней-
ная фигура, описанная около круга. В, имеет ко вписанной фигуре
меньшее отношение, чем круг В к (боковой) поверхности цилиндра,
и после перестановки (описанная около круга В фигура имеет к кру-
гу В меньшее отношение, чем вписанная фигура к боковой поверхно-
сти цилиндра). По фигура, описаппая около круга В, больше круга В;
значит, вписанная в круг В-фигура больше (боковой) поверхности
цилиндра, а следовательно, и (боковой) поверхности призмы].
Итак, круг В будет не больше поверхности цилиндра. Доказано же, что
оп и по меньше; значит, он будет ей равен [7].
XIV
Поверхность всякого равнобедренного конуса за вычетом основания
равна кругу, радиус которого есть средняя пропорциональная между
стороной конуса и радиусом круга, являющегося
основанием конуса.
Пусть будет равнобедренный конус, основа-
ние которого круг А {рис. 45}; пусть радиус
этого круга будет Г, а сторона конуса Д; пусть
Е будет средней пропорциональной между Г и Д,
и круг В имеет радиус, равный Е; я утверждаю,
что круг В равен поверхности конуса за вычетом
основания.
Действительно, если оп по равен ей, то бу-
дет или больше, или мэньше.
Пусть сначала он будет меньше. Тогда имеются
две неравные величины — поверхность конуса и круг В, причем большей
является поверхность конуса; значит, можно вписать в круг В равносто-
ронний многоугольник и описать около него другой, подобный вписанно-
му, так, чтобы описанный имел ко вписанному отношение меньшее того,
*) То есть как квадраты радиусов.
112
АРХИМЕД
которое поверхность конуса имеет к кругу В. Теперь вообразим, что
около круга Л описан многоугольник, подобный описанному около
круга В, и па многоугольнике, описанном около круга А, построена
пирамида, имеющая ту же вершину, что и конус. Так как многоуголь-
ники, описанные около кругов Л и В, подобны, то они имеют друг
к другу отношение, равное двойному отношению их радиусов, то есть
двойному отношению Г и Е, или (отношению) линий Г и А. Но
отношение линий Г и А равно отношению многоугольника, описанного
около круга Л, к (боковой) поверхности пирамиды, описанной око-
ло конуса, [ибо Г равна перпендикуляру, опущенному из центра на
одну из сторон многоугольника, а А равна стороне конуса; периметр же
упомянутого многоугольника будет общей высотой двух прямоуголь-
ников, половины которых соответственно равны многоугольнику, опи-
санному около круга А и боковой поверхности пирамиды, описанной
около конуса}*). Значит, прямолинейная фигура, описанная около
круга А, к прямолинейной фигуре около круга В имеет то же самое
отношение, что и к (боковой) поверхности пирамиды, описанной
около конуса; таким образом, (боковая) поверхность пирамиды рав-
на многоугольнику, описанному около круга В. Теперь так как много-
угольник, описанный около круга В, ко вписанному многоугольнику
имеет меньшее отношение, чем поверхность конуса к кругу В, то и
(боковая) поверхность описанной около конуса пирамиды будет
к многоугольнику, вписанному в круг В, иметь меньшее отношение,
чем (боковая) поверхность конуса к кругу В, а это невозможно,
[ибо доказано, что поверхность пирамиды больше поверхности конуса,
тогда как многоугольник, вписанный в круг В, меньше круга BJ. Итак,
круг В не будет меньше (боковой) поверхности конуса.
Теперь я утверждаю, что он нс будет и больше. Действительно,
пусть, если возможно, он будет больше. Тогда опять вообразим много-
угольник, вписанный в круг В, и другой, описанный около пего, так,
чтобы описанный имел ко вписанному отношение менынее того, которое
круг В имеет к (боковой) поверхности конуса, вообразим много-
угольник, вписанный в круг А и подобный вписанному в круг В, и по-
строим на нем пирамиду, имеющую ту же вершину, что и копус. Теперь
так как вписанные в круги А и В многоугольники подобны, то они
будут находиться друг к другу в двойном отношении их радиусов;
значит, отношение одного многоугольника к другому будет равняться
отношению линий Г и А. Но Г имеет к А большее отношение, чем то,
которое многоугольник, вписанный вокруг Л, имеет к (боковой) поверх-
ности пирамиды, вписанной в конус, [ибо радиус крута Л к стороне
конуса имеет большее отношение;, чем перпендикуляр, опущенный из
центра на одну из сторон многоугольника, имеет к перпендикуляру,
опущенному на эту сторону из вершины конуса]; значит, многоуголь-
ник, вписанный в круг А, к многоугольнику, вписанному в В, будет
иметь большее отношение, чем к (боковой) поверхности пирамиды;
так что (боковая) поверхность пирамиды будет больше многоуголь-
ника, вписанного в круг В. Но многоугольник, описанный около кру-
га В, имеет ко вписанному мепыцее отношение, чем круг В к (боковой)
поверхности конуса; значит и подавно описанный около круга В много
*)'В тексте просто xol-voV М -i^oG -fj то» vroXry*ovou та тщлот) T<uv ennprxvei&v. -TaK
как 0то темное место наверняка нс принадлежит Архимеду, то я счел себя в праве дать более рас-
пространенный и имеющий смысл перевод. ‘ '
о ШЛРИ И ЦИЛИНДРЕ
113
угольник будет к (боковой) поверхности пирамиды, вписанной в конус,
иметь меньшее отношение, чем круг В к (боковой) поверхности
конуса, а это невозможно, [так как описанный многоугольник больше
круга В, (боковая) же поверхность пирамиды в конусе меньше (боко-
вой) поверхности копуса]. Значит, круг В не будет больше поверх-
ности конуса.
Но уже доказано, что он по будет и меньше; значит, он ей равен.
XV
Поверхность*) всякого равнобедренного конуса имеет к основанию
такое же отношение, как сторона конуса к радиусу его основания.
Пусть будет равнобедренный конус, основание
которого — круг А {рис. 16}; пусть прямая В
равна радиусу круга А, а Г равна стороне конуса;
требуется доказать, что поверхность конуса имеет
к кругу А такое же отношение, как Г к В.
Возьмем В — среднюю пропорциональную
между В и Г — и построим круг Д, имеющий
радиус, равный Е;значит, круг Д будетравен( боко-
вой) поверхности конуса; [это доказало п преды-
дущем].
Доказано также, что круг Д имеет к кругу
А отношение, равное отношению линии Г и В,
[ибо каждое из этих отношений равно двойному
отношению Е и В, так как круги будут относиться
друг к другу, как квадраты на диаметрах или на радиусах, а диаметры
относятся, каких половины, или радиусы; последние же равны В и Е].
Теперь ясно, что (боковая) поверхность конуса имеет к кругу А
отношение, равное отношению линий Г и В.
XVI
Если рассечь равнобедренный конус плоскостью, параллельной
основанию, то поверхность конуса между обеими параллельными плос-
костями будет равна кругу, радиус которого является средней пропор-
циональной для стороны конуса между параллельными плоскостями и
прямой, равной вместе взятым радиусам обоих кругов, лежащих
в параллельных плоскостях.
Пусть будет конус, у которого треугольник осевого сечения есть
АВГ {рис. 17}; рассечем его параллельной основанию плоскостью:
пусть она образует сечение ЛЕ; осью конуса пусть будет ВЦ; построим
круг, радиус которого является средней пропорциональной между АЛ
и вместе взятыми AZ и ПА; пусть это будет круг 0; я утверждаю, что
круг 0 будет равен поверхности конуса, заключенной между ЛЕ и АГ.
Действительно, построим круги Л и К так, что радиус круга К
квадрирует прямоугольник между ВД, AZ, а радиус круга А квадрирует
прямоугольник между ВА, АП; тогда круг Л будет равен (боковой)
поверхности конуса АВГ, а круг К — (боковой) поверхности кону-
са ЛЕВ. Так как (прямоугольник) между ВЛ, АН равен (прямо-
угольнику) между ВЛ, AZ (вместе с прямоугольником) между АД
*) Подразумевается боновая поверхность.
S Архимед
114
АРХИМЕД
и вместе взятыми AZ и АН,
ВА- А Н — ВЛ - AZ 4- АД (AZ + ЛИ)
вследствие параллельности AZ и АН*), а прямоугольник между АВ, АН
квадрируется радиусом круга Л, прямоугольник
Рис, 17.
между ВД, AZ квадрируется радиусом круга К и
(прямоугольник) между ДА и вместе взятыми AZ,
АЙ квадрируется радиусом круга ©, то, значит,
квадрат на радиусе круга А равен вместе взятым
квадратам на радиусах кругов К и 0; таким обра-
зом, и круг Л будет равен вместе взятым кругам К,
©. Но кругЛ равен (боковой) поверхности конуса
ВАГ, а круг К — (боковой) поверхности конуса
ДВЕ; значит, остаток—поверхность конуса между
параллельными плоскостями ДЕ, АГ — будет
равен кругу 0.
[Пусть имеется параллелограмм ВАН
[рис. 18}, и пусть ВН будет его диаметр. Рассе-
чем сторону ВА в какой-нибудь точке Д и че-
рез Д проведем Л© параллельно АП, а через Z
проведем КЛ параллельно ВА; я утверждаю, что
(прямоугольник) между ВА, АН равен вместе
взятым (прямоугольнику) между ВД, AZ (и прямоугольнику) .между
АД и вместе взятым AZ, АН.
Действительно, так как (прямоугольник) между В А, АН пред-
ставляет весь параллелограмм ВИ, (прямоугольник) между ВЛ,
AZ—параллелограмм BZ и прямоугольник
между ДА и вместе взятыми AZ,AH — гно-
мон (ибо (прямоугольник) между
ДА, АН представляет параллелограмм КН
вследствие равенства «дополнений»**) К© и
ДЛ,: а (прямоугольник) между ЛА, AZ —
параллелограмм ДА), то, следовательно,
весь параллелограмм ВН, то есть (прямо-
угольник) между- ВА, АН, равен прямо- рИС1 is.
угольнику между ВД, AZ вместе с гномо-
ном MNS, который в свою очередь равен прямоугольнику между ДА
н вместе взятыми AH, AZ]***).
Л е м м ы
1. Конусы, имеющие равные высоты, относятся друг к другу, как
основания; имеющие же равные основания относятся, как высоты
(Начала, XII, 11, 14).
2. Если цилиндр рассечен плоскостью, параллельной основаниям,
то один из получившихся цилиндров относится к другому, как одна из
соответствующих осей к другой (Начала, XII, 13).
*) Имеем ВЛ АН = Вл-АН -1- ДА-АН и АН : AZ — АВ : Вд, откуда АН-ВД —AB-AZ, т. о.
ВЛ•АН — AB-AZ -Г АД-АН = ВД-AZ | АД (AZ !- АН).
** ) — термин «Начал» Евклида (1,43).
** *) Эта теорема, вспомогательная к предложению XVI, является поздпейтей вставкой. Бего-
ний имел рукопись Архимеда бея этой теоремы, так как оп дает специальное пояснение к предложе-
цю XVI.
О ШАРЕ И ЦИЛИНДРЕ
115
3. Конусы, имеющие с цилиндрами одни и те же основания {и рав-
ные высоты), имеют друг к другу то же самое отношение, что и цилин-
дры (Следует из предложения 10 книги XII «Начал»}.
4. У равных конусов основания обратно пропорциональны высотам-,
и конусы, у которых основания обратно пропорциональны высотам,
будут равны (Начала, XII, 15).
5. И конусы, диаметры оснований которых относятся, как оси,
[то есть как высоты], будут друг к другу в тройном*) отношении
диаметров (Начала, XII, 12).
Все это доказано предшествующими писателями.
XVII
верхности
к одному
ние], то,
пию AEZ, так будет и поверхность AEZ к
Если даны два равнобедренных конуса и поверхность одного конуса
равна основанию другого, а перпендикуляр, опущенный из центра основа-
ния первого конуса на сторону, равен высоте {второго конуса), то оба
конуса будут равны.
Пусть будут дпа равнобедренных конуса АВГ, AEZ {рис. 19},
и пусть основание копуса АВГ равно поверхности конуса AEZ, высо-
та же АН равна перпендикуляру К0, опущенному из центра 6 основа-
ния на одну из сторон конуса, например ДЕ;
я утверждаю, что оба конуса будут равны.
Так как основание (конуса) АВГ равно по-
(конуса) AEZ, [равные же величины
и тому же имеют одно и то же отноше-
значит, как основание ВАГ к осиова-
ос нова-
цию AEZ. Но поверхность конуса относится к
своему основанию, как А© к ©К, [ибо доказано, что
поверхность всякого равнобедренного конуса иднмгг
к основанию то же самое отношение, как сторона
конуса к радиусу основания, то | есть как ДЕ к
Е©. Но как ЕД к ©А, так будет и Е© к ©К,
ЕД Е0 , .
од = ек
Рис. 19.
ибо соответствующие треугольники] имеют] равные
углы!.
Затем ©К равна АН; значит, основание ВАГ бу-
дет к основанию AEZ, как высота AEZ к высоте АВГ.
Таким образом, у конусов АВГ, AEZ основания
иорциональпы высотам; значит, конус ВАГ равен конусу AEZ.
XVIII
обратно и [!0-
Всякий ромб, составленный из двух равнобедренных конусов, равен
конусу, имеющему основание, равное {боковой) поверхности одного из
конусов, составляющих ромб, а высоту, равную перпендикуляру, опущен-
ному из вершины второго конуса на сторону первого конуса.
Пусть будет составленный из двух равнобедренных конусов
[рис. 20] ромб АВ ГД, основание которого есть описанный на диаметре ВГ
*) То есть в возведенном в третью степень.
116
АРХИМЕД
круг, высота же АЛ; возьмем также некоторый другой (конус) ТЮК,
имеющий основание, равное (боковой) поверхности конуса АВГ,
высоту же, равную перпендикуляру, опущенному из точки А на АВ
или на ее продолжение; пусть этот перпендикуляр будет AZ, высота же
конуса ©НК будет 0А; тогда ©А равна AZ; я утверждаю, что этот конус
будет равен вышеназванному ромбу.
Построим другой конус MNE, имеющий основание, равное осно-
ванию конуса АВГ, а высоту, равную АА; пусть эта высота будет NO.
Так как NO равна АД, то значит — как NO к ДЕ, так и АД к ДЕ.
NO АД
де” лк
Но как АД к ДЕ, так и ромб АВГД к конусу ВГД,
АД ромб АВГЛ
ЛК “ конус ВГД
а как NO к ДЕ, так и конус MNB к конусу ВГД,
NO _ конус MNS
ЛЕ ~ конус ВГД
[ибо основания их равны]; значит, как конус MN3 к конусу ВГД, так
и ромб АВГД к конусу ВГД;
конус MNE ромб АВГД
леону с ВГД — конус ВГД
следовательно, конус равен ромбу АВГД. Но так как поверх-
ность конуса АВГ равна основанию конуса H0K, то, значит, как
поверхность конуса АВГ к его основанию, так и основание конуса H0K
к основанию конуса MNE, [ибо основание конуса АВГ равно осно-
Рис. 20.
ванию конуса MNSJ. Но как поверхность ко-
нуса АВГ к его основанию, так будет и АВ к
BE, или АД к ZA [вследствие подобия треуголь-
ников]; значит, как основание И ©К. к основа-
нию MNS, так и АД к AZ.
Но АД равна NO [по предположению], а
AZ равна ©Л; значит, как основание конуса
H0K к основанию конуса MNE, так и вы-
сота NO к ©Л. Значит, у конусов Н©К, MN-
основания обратно пропорциональны высотам;
следовательно, эти конусы равны. Но дока-
зано, что конус MNE равняется ромбу АВГД;
значит, и конус НОК равен ромбу АВГД.
XIX
Если равнобедренный конус рассечен пло-
скостью, параллельной основанию, затем на
полученном круге построен конус, имеющий
вершиной центр основания, и образовавшийся
ромб отнят от всего конуса, то Окаймление
будет равно конусу, имеющему основание, равное поверхности конуса,
заключенной между параллельными плоскостями, а высоту, равную
перпендикуляру, опущенному из центра основания на одну из сторон
конуса.
Пусть будет равнобедренный конус АВГ {рис. 21}; рассечем
его плоскостью, параллельной основанию; пусть полученное сечение
О ШАРЕ И ЦИЛИНДРЕ
117
будет ДЕ, а центр основания Z; на круге к диаметром ДЕ построим
конус, имеющий вершину Z, тогда ромб BAZE будет составлен из двух
равнобедренных конусов. Возьмем еще некоторый конус К0А, осно
ванис которого равно поверхности (конуса ЛВГ, заключенной)
между ДЕ, АГ, а высота равна перпендикуляру ZH, опущенному из
точки Z на АВ. Я утверждаю, что если
ромб BAEZ вообразить отнятым от кону-
са АВГ, то окаймление будет равно ко-
нусу ©КЛ.
Построим два конуса ММВ, ОПР та-
кие, чтобы основание конуса М№ было
равпо поверхности конуса ЛВГ, а высота
равнялась ZH, [тогда вследствие этого
конус MNS будет равен конусу АВГ;
действительно, если имеются два равнобед-
ренных конуса, у которых поверхность
одного конуса равна основанию другого
и перпендикуляр, опущенный из центра
основания первого конуса на сторону
его, равен высоте второго, то оба конуса
будут равны], и чтобы основание конуса
ОПР было равно поверхности конуса
ДВЕ, а высота равнялась ZH; [тогда ко-
нус ОПР будет равен ромбу BAEZ, как
уже было доказано выше]. Так как по-
верхность конуса АВГ складывается из
поверхности конуса ДВЕ и той, которая
заключается между ДЕ и АГ, и поверх-
й
ность конуса АВГ равна основанию ко-
нуса MNB, поверхность конуса АВЕ равна основанию копуса ОПР, а по-
верхность между ДЕ, АГ равна основанию конуса ОКА, то. значит,
основание конуса MNS равно (вместе взятым) основаниям конусов
ОКА и ОПР. И все конусы имеют одинаковую высоту; значит, ко-
нус MN3 равен конусам ОКА и ОПР. По конус MNS равен кону-
су ЛВГ, конус же ОПР — ромбу BAEZ; значит, остающийся конус
ОКА будет равен окаймлению.
XX
Если в составленном из равнобедренных конусов ромбе рассечь один
конус плоскостью, параллельной основанию, и на полученном круге
построить конус, имеющий ту же вершину, что и другой конус, затем
полученный таким образом ромб отнять от всего ромба, то окаймление
будет равно конусу, имеющему основание, равное поверхности, заключен-
ной между параллельными плоскостями, а высоту, равную перпенди-
куляру, опущенному из вершины второго конуса на сторону первого
конуса.
Пусть будет ромб АВ ГД, составленный из равнобедренных конусов
{рис. 22}; один из этих конусов рассечем плоскостью, параллельной
основанию, и пусть полученное! сечение будет EZ; на круге, описанном
на диаметре EZ, построим конус, имеющий вершину в Д; пусть полу
ченный ромб будет EBAZ. Вообразим, что он отнят от целого ромба,
и построим конус ОКА, имеющий основание, равное поверхности между
118
АРХИМЕД
Рис. 22.
АГ и EZ, а высоту, равную перпендикуляру, опущенному пл точки Д
па прямую ВА или ее продолжение; я утверждаю, что конус 0КЛ будет
равеп вышеупомянутому окаймлению.
Построим два конуса М.№ и ОПР; пусть основание конуса MNE
будет равно поверхности конуса АВГ, высота же равна АН; [тогда,
согласно доказанному выше,
конус MNE будет равен ром-
бу АВГД]; у конуса же 0111’
основание пусть будет равно
поверхности конуса EBZ, а вы-
сота равна ДП; [тогда точно так
же конус ОПР будет равняться
ромбу EBAZj. Но подобно (вы-
ше доказанному) поверхность
конуса АВГ складывается из
•Г поверхности конуса EBZ и той,
которая заключена мопеду EZ,
АГ; поверхность конуса АВГ
равна основанию конуса MNE,
поверхность копуса EBZ равна
основанию конуса ОПР, и но
верхность между EZ и АГ равна
основанию конуса ОКА; значит,
основание конусе MNE равно
(вместе взятым) основаниям конусов ОПР и ОКА. Й все эти конусы
имеют одинаковую высоту; значит, конус MNS равен конусам 0КЛ,
ОПР. Но конус МНЕ равен ромбу АВГД, конус же ОПР равен ром-
бу EBAZ; значит, остающийся конус
ОКА будет
млению.
Рис- 23.
равен остающемуся окай-
XXI
круг вписан многоугольник
Если в
с четным числом равных сторон и в
нем проведены б прямые, соединяющие
стороны многоугольника, и все парал-
лельные какой-нибудь ‘одной из стяги-
вающих две стороны этого многоуголь-
ника, то все соединяющие {взятые
вместе) будут иметь к диаметру круга
то же отношение, какое прямая, стя-
гивающая число сторон, на единицу
меньшее половины всего их числа, име-
ет к одной стороне многоугольника.
Пусть будет круг АВГД и в него
AEZBHOrMNAAK {рис. 23}; проведем соединяющие прямые ЕК,
ZA, ВА, HN, ОМ; ясно, что они будут параллельны прямой, стяги-
вающей две (смежные) стороны многоугольника; я утверждаю, что
все упомянутые прямые (взятые вместе) будут к диаметру круга иметь
то ясе отношение, что ГЕ к ЕЛ.
Проведем соединяющие прямые ZK, ЛВ, ПА, 0N; тогда ZK будет
параллельна ЕЛ, ВЛ параллельна ZK, затем АН параллельна ВЛ
ON же АН и ГМ параллельна 0N. .
вписан многоугольник
О ШАРЕ И ЦИЛИНДРЕ
119
[Поскольку имеются две параллели ЕА, KZ и проведены две пере-
секающие ЕК, АО, то], значит, как ЕЕ к ЕА, так и КЕ к ЕО.
ЕВ КЕ ' '
ВА SO’
Но как КЕ к ЕО, так и Z1I к ПО,
КВ ZH
so “° ио
как же Z1I к ПО, так и АП к ПР,
211 лп
по _ ПР
и как АП к ПР, так и BS к SP,
АП ВТ
ПР' ‘ ХР
и далее, как BS к SP, так и AS к ST,
НТ = ДГ
ХР ~ ST
как же AS к ST, так и НГ к ГТ,
AS ПГ
ST ' ГТ
затем как НГ к ГТ, так и NT к ГФ,
ПГ _ NT
ГТ ГФ
как яге NT к ГФ, так и ©X к ХФ,
кг _ ех_
ГФ ' ХФ
и наконец, как ©X л ХФ, так и MX к ХГ.
ох мх
ХФ ХГ
[И как все (предыдущие) ко всем (последующим), так и один
(из предыдущих) к одному (своему последующему)]; значит, как
ЕЕ к ЕА, так и ЕК, ZA, ВА, HN, ОМ (вместе взятые) к диаметру АГ
ЕВ EE + BK + Zn-l-nA + BS + SA-f-HT + rN + eX-l-XM ЕК 4- ZA ВД -J-HN 4-ОМ
ВА АЕ + НО + ОП + ПР + РГ + ХТ+ТГ + ГФ + ФХЧ-ХГ ' АГ"
Но как ЕЕ к ЕА, так и ГЕ к ЕА; значит, как ГЕ к ЕА, так и все
ЕК, ZA, ВД, HN, ОМ к диаметру АГ [8].
ГЕ ЕК I- ZA 4- ВД 4- HN4- ОМ
ЕЛ ~ АГ ’
XXII
Если в круговой сегмент вписан многоугольник, имеющий кроме
основания четное число равных сторон, и проведены прямые, параллель-
ные основанию сегмента, соединяющие стороны многоугольника, то все
проведенные прямые и половина основания будут иметь к высоте сегмен-
та то же отношение, какое прямая, соединяющая (конец) диаметр(а)
круга со стороной многоугольника, имеет к этой стороне много-
угольника.
В круге ЛИГА {рис. 24} проведем какую-нибудь прямую АГ
и па АГ построим вписанный л сегмент АВГ многоугольник, имеющий
кроме основания АГ четное число равных сторон; проведем ZH, ЕО,
120
АРХИМЕД
который будут параллельны основанию сегмента; я утверждаю, что
ZTI, Е0, АЕ будут к ВВ, как AZ к ZB.
ZH + ЕЙ-!- АЕ _ AZ
ВВ ZB
Опять, так же (как и выше), проведем соединяющие прямые
НЕ, Л.&; они, конечно, будут параллельны BZ; тогда, вследствие того
же, как KZ к КВ, так и НК кКЛ, и ЕМ к МЛ, и МО к MN, и ВЛ
к SN
kz нк _ ем _ ме ал
КВ ’ кл МЛ "" MN ~ SN
[и как все ко всем, так и один к одному); значит, как ZH, Е0, АВ
к ВВ, так и ZK к КВ.
ZH-bKH+AS ZK
bs "кв-
Но как ZK к КВ, так и AZ к ZB,
zk az
кн _ ZB
значит, как AZ к ZB, так и ZH, Е0, АЕ к ВВ [8).
AZ _ ZH ЬВв+АВ
ZB SB
ХХШ
Пусть АВ ГА будет большой круг шара {рис. 25}, и в него впи-
сан равносторонний многоугольник, и пусть число сторон его являет-
ся кратным четырех*); пусть АГ, АВ будут (два взаимно перпендику-
лярных) диаметра. Тогда если круг АВГА, вмещающий этот много-
угольник, будет вращаться около неподвижного диаметра АГ, то-
ясно, что окружность этого круга будет перемещаться по поверхности
шара, вершины же многоугольника, кроме тех, которые находятся
в точках А, Г, будут двигаться по окружности кругов, описанных на
*) В подлиннике д.втре<<Юв> олй те-грабое-пусть будет измеряться четверкой. Как замечает ком-
ментатор Архимеда, Евтокий, требование, чтобы число сторон вписанного многоугольника было
кратным четырех, равносильно требованию, чтобы вес стороны многоугольника двигались только
по коническим повсрхиостнм; если бы число сторон многоугольника было кратным только двух, то
две средние стороны описывали бы цилиндрическую поверхность, для которой не выведены теоремы,
равносильные предложениям XVII—XX.
О 1ПАРВ И ЛИЛИЦДРЕ 121
поверхности сферы и перпендикулярных к кругу АВГД; диаметрами
этих кругов будут служить параллельные ВД прямые, соединяющие
вершины многоугольника. Стороны многоугольника будут двигаться
по некоторым конусам, а именно AZ и AN по поверхности конуса,
основанием которого является круг на диаметре ZN, а вершина нахо-
дится в точке А; затем ZII, MN будут двигаться ло некоторой кони-
ческой поверхности, имеющей основанием круг ла диаметре МП, а вер-
шиной — точку пересечения продолжений ZTT и MN друг с другом
и с АГ; стороны ВН, МД будут двигаться но конической поверхности,
основанием которой является круг на диаметре ВД, перпендикулярный
к кругу АВГД, а вершиной — точка, в которой продолжения ВН и ДМ
пересекаются между собой и с ГА. Точно так же и в другом полукруге
стороны будут двигаться по коническим поверхностям, тоже подобным
вышеуказанным. Таким образом, получится некоторая вписанная
в шар и ограниченная упомянутыми коническими поверхностями фигу-
ра, поверхность которой будет меньше поверхности шара.
Если рассечь шар проходящей через ВД и перпендикулярной
кругу АВГД плоскостью, то поверхность каждого полушария и поверх-
ность вписанной в пего фигуры будут иметь общую границу, лежащую
на одной плоскости; действительно, границей обеих поверхностен
является окружность круга, построенного па диаметре 13Д и перпенди-
кулярного к кругу АВГД; обе эти поверхности будут выпуклыми
в одну сторону, причем одна из них объемлется другой поверхностью
и плоскостью, заключающей их общую границу. Подобным же обра-
зом, и поверхность заключенной во втором полулхарии фигуры будет
меньше поверхности полушария. Таким образом, вся поверхность
фигуры, заключенной в шаре, будет меньше поверхности шара [9].
XXIV
Поверхность фигуры*), вписанной в шар, равняется кругу, радиус
которого квадрирует прямоугольник между стороной фигуры и прямой,
Рис. 2К.
равной всем вместе взятым линиям, соединяющим вершины много-
угольника и параллельным прямой, стягивающей две его стороны
{рис. 26}.
Пусть АВГД будет большой круг шара, и пусть в пего вписан
равносторонний многоугольник, число сторон которого есть крат-
ное четырех; на этом вписанном многоугольнике; вообразим фигуру,
') О которой шла речь в XXIII.
122
АРХИМЕД
вписанную в шар, и проведем соединяющие прямые EZ, II©, ГД,
КЛ, MN, параллельные прямой, стягивающей две стороны много-
угольника; построим круг Е, радиус которого квадрировал бы прямо-
угольник между АЕ и прямой, равной вместе взятым EZ, Н0, ГД,
КЛ, MN; я утверждаю, что этот круг будет равен поверхности фигуры,
вписанной в шар.
Построим круги О, П, Р, 2, Т, Е; пусть радиус- О квадрирует
прямоугольник между ЕА и половиной EZ, радиус П квадрирует
прямоугольник между ЕА и половиной вместе взятых EZ, II©, радиус Р
квадрирует прямоугольник между ЕА и половиной вместе взятых
Н© и ГД, радиус 2 квадрирует прямоугольник между ЕА и полови-
ной вместе взятых ГД, КЛ, радиус Т квадрирует прямоугольник между
АЕ и половиной вместе взятых КА, MN, радиус Е квадрирует прямо-
угольник между АЕ й половиной MN.
Тогда вследствие этого круг О будет равняться поверхности конуса
AEZ, круг II — поверхности конуса, заключающейся между EZ, II©.
круг Р — между II©, ГД, круг 2 — между ДГ, КЛ, затем круг Т
будет равен конической поверхности между КЛ, MN, и круг Г равен
поверхности конуса MBN; значит, все эти круги вместе взятые будут
равны поверхности вписанной фигуры. Затем ясно, что радиусы кру-
гов О, И, Р, 2, Т, Е квадрируют прямоугольник между АЕидваж
ды взятыми половинами EZ, Н©, ГД, КЛ, MN, или просто на EZ, II©.
ГД, КЛ, MN; значит, вместе взятые квадраты на радиусах кругов
О, II, Р, 2, Т, Е будут равняться прямоугольнику между ЛЕ и все-
ми EZ, Н©, ГД, КЛ, MN.
По также и радиус круга Е квадрирует прямоугольник между ЛЕ
' и составленной из всех EZ, Н©, ГД, КЛ, MN прямой; значит, радиус
круга S квадрирует все вместе взятые квадраты на радиусах кругов
С. II, Р, 2, Т, Е, следовательно, круг Е будет равен всем кругам
С, II, Р, 2, Т, Е.
Но, как показано, круги О, 11, Р, 2, Т, Е взятые вместо равны
поверхности вышеупомянутой фигуры; таким образом, круг Е будет
равен поверхности рассматриваемой фигуры [9].
XXV
Поверхность вписанной в шар фигуры, ограниченной коническими
поверхностями, меньше учетверенного большого круга шара {рис. 27}.
Пусть АВ ГД будет большим кругом шара, и пусть в него будет
вписан равносторонний [и равноугольный]*) многоугольник, число
сторон которого есть кратное четырех; вообразим (построенную) на
нем фигуру, ограниченную коническими поверхностями; я утверждаю,
что поверхность вписанной фигуры будет меньше учетверенного боль-
шого круга шара.
Проведем El, ©М, стягивающие две стороны многоугольника,
и параллельные им ZK, ДВ, НА; построим круг Р так, чтобы его ради-
ус квадрировал прямоугольник на ЕА и на прямой, равной всем вместе
взятым El, KZ, ВЛ, НА, ©М.
ряд. Г)2---еа (Ei+kz+вд+нл ’ ем}
Тогда, согласно доказанному выше, этот кру!' будет равен поверхности
*) В подлиннике 'ccQTioytoviv—четноугольный.
II ШАРЕ И ЦИЛИНДРЕ
123
упомянутой фигуры. Но поскольку доказано, что прямая, рапная всем
El, KZ, ВД, HA, 0М, относится к диаметру АГ круга, как ГЕ к ЕА,
ля + zk -i- ва + ил+ем __ ГЕ
АГ ЕА
то, значит, прямоугольник па прямой, равной всем упомянутым
вместе взятым, и на ЕА, или квадрат па радиусе круга Р, будет равен
прямоугольнику между АГ и ГЕ.
Но прямоугольник между АГ, ГЕ меньше квадрата на АГ, зна-
чит, и квадрат на радиусе Г’ меньше квадрата на АГ; [значит, радиус
круга Р будет меньше АГ; таким образом, диаметр круга Р меньше
удвоенного диаметра круга АВГД; следовательно, два диаметра круга
АВГД больше диаметра круга Р, и учетверенный квадрат на дна
метре круга АВГД, то есть АГ, больше квадрата па диаметре
круга Р. Но как учетверенный квад-
рат АГ к квадрату на диаметре круга
Р, так будут и четыре круга АВГД к
кругу Р; значит, четыре, круга АВГД
•больше круга PJ; значит, круг Р мень-
ше учетверенного большого круга. Но
круг Р, по доказанному, равен по-
верхности вышеупомянутой фигуры;
значит, поверхность этой фигуры бу-
дет меньше учетверенного большого
круга шара [9[.
XXVI
Вписанная в шар фигура, ограничен-
ная коническими поверхностями, равна
конусу, имеющему основанием круг, рав-
ный поверхности фигуры, вписанной в
шар, а высотой прямую, равную перпен-
дикуляру, опущенному из центра шара
на одну из сторон многоугольника.
Пусть будет шар, в нем большой
круг АВГД {рис. 28} и все остальное,
как выше; пусть будет прямой конус Р,
имеющий основанием поверхность вписанной в шар фигуры, а высоту.
равную перпендикуляру, опущенному из центра шара на одну из сторон
многоугольника; требуется доказать, что конус Р равен вписанной
в шар фигуре.
На кругах, диаметры которых ZN, НМ, 0А, ГК, построим конусы,
имеющие вершину в центре шара; получится телесный ромб, состав-
ленный из копуса, основание которого есть построенный на диаметре
ZN круг, вершина же — точка А, и из конуса, основанием которого
является тот же самый круг, вершиной же точка X; он будет равен
конусу, имеющему основанием поверхность конуса NAZ, высоту же,
равную опущенному из X на AZ перпендикуляру. Далее, окаймление
ромба, ограничепносповерхностыо конуса, заключающейся между парал-
лельными плоскостями, проведенными через ZN, НМ, и двумя кони-
ческими поверхностями ZNX, IIMX, будет равно конусу, имеющему
основание, равное поверхности конуса между параллельными плоско-
стями через МП, ZN, а высоту, равную перпендикуляру, опущенному
124
АРХИМЕД
из X на ZH, как это уже было доказано. Затем окаймление конуса.,
ограниченное конической поверхностью между параллельными пло-
скостями через НМ, ВЛ, поверхностью конуса МИХ и кругом
па диаметре .ВД, будет равно конусу, имеющему основание, равное
поверхности конуса между плоскостями через НМ, ВД, а высоту,
равную опущенному из X на ВН перпендикуляру. Подобным же обра-
зом и в другом полушарии ромб ХКГ1 и окай-
мления конусов будут равны таким же и в та-
ком же числе конусам, как и те, которые были
рассмотрены выше. Теперь ясно, что и вся впи-
санная в шар фигура будет равна всем упомяну-
тым конусам. Но конусы эти равны конусу Р,
так как конус Р имеет высоту, равную высок;
каждого из упомянутых конусов, основание
же, равное всем их основаниям. Итак, ясно, что
вписанная в шар фигура будет равна построен-
ному конусу [9].
XXVII
Вписанная в шар фигура, ограниченная
коническими поверхностями, будет меньше
учетверенного конуса, имеющего основанием
большой круг шара, а высоту, равную радиусу
шара.
Пусть будет конус I* {рис. 29}, равный
вписанной в шар фигуре, имеющий основа-
ние, равное поверхности вписанной фигуры, а высоту, равную пер-
пендикуляру, опущенному из центра шара на одну из сторон впи-
санного мн огоугольника;
пусть еще будет копус Е,
имеющий основание, рав-
ное кругу АВГД, а высо-
ту. равную радиусу круга
АВГД.
Теперь,
пус Р имеет основание,
равное поверхности вп н-
саипой в шар фигуры, а
высоту, равную перпенди-
куляру, опущен гному из X
на AZ, и, по доказанному,
поверхность вписанной
фигуры меньше учетверен-
ного большого круга в
шаре, то, значит, основа-
ние конуса Р будет
меньше учетверенного
основания конуса Е. Также
нуса Е; поскольку же конус Р имеет основание, меныпое учетверен
ного основания конуса Е, и высоту, меньшую высоты последнего, то
ясно, что и сам копус Р будет меньше учетверенного конуса Е. Но
конус Р равен вписанной фигуре; значит, вписанная фигура меньше
учетверенного конуса Е [9J.
и высота конуса Р меньше высоты ко
•гак как ко-
О ШАРЕ И ЦИЛИНДРЕ
125
XXVIII
Пусть АВГД {рис. 30] будет большим кругом шара; опишем
около круга АВГД равносторонний и равноугольный многоугольник,
и пусть число сторон его будет кратным четырех; затем вокруг много-
угольника, описанного около круга, опишем еще один охватывающий
его круг с тем же центром, что и у круга АВГД. Затем плоскость EZlI(->,
в которой находятся многоугольник и круг, будем вращать около
неподвижной (оси) ЕН; тогда ясно, что окружность круга АВ ГЛ
будет перемещаться по поверхности шара, а окружность круга EZHC-)
пойдет но поверхности другого шара, имеющего тот же центр, что
и меньший шар, точки касания сторон многоугольника опишут па
поверхности мепьшего шара кручи,
(плоскости которых) перпендикулярны
(плоскости) круга АВГД, углы яге
многоугольника, кроме тех, которые
при точках Е, Н, пойдут по окружпо
стям кругов, начерченных на поверхно-
сти большого шара и перпендикуляр-
ных кругу' EZHO, а стороны много-
угольника будут двигаться ио кониче-
ским поверхностям совершенно так же,
как и в предшествующем; таким обра
зом, фигура, ограниченная копиче
-сними поверхностями, будет описана
около меньшего шара и вписана в боль-
ший. А что поверхность описанной фи-
гуры больше поверхности шара, дока-
жется так. Пусть КД будет диамет-
ром некоторого крута на меньшем шаре, причем К и Д суть точки.
в которых (две) стороны описанного многоугольника касаются кру
га АВГД. Рассечем шар плоскостью, проходящей через КД (и) пер-
пендикулярной к плоскости круга АВГД; тогда топ же плоскостью рас-
•сечется и поверхность описанной около шара фигуры. Ясно также, что
(обе поверхности отсеченных частей — и шара, и фигуры —) будут
иметь одни и те же границы, лежавшие на плоскости, так как границей
обеих поверхностей будет окружность круга, построенного на диаметре
КД и перпендикулярного к кругу АВГД; затем обе поверхности будут
выпуклыми в одну и ту же сторону, и одна из них объемлется другой
поверхностью и плоскостью, имекмцеп те же границы; объомлемая
поверхность сегмента шара будет меньше поверхности описанной около
него фигуры. Подобным же образом и поверхность другого сегмента
шара будет меньше поверхности описанной около пего фигуры; следо-
вательно, ясно, что и вся поверхность шара будет меньше поверхности
описанной около него фигуры [10].
XXIX
Поверхность фигуры, описанной около шара, равна кругу, радиус
которого квадрирует прямоугольник между одной стороной много-
угольника и прямой, равной всем вместе взятым прямым, соединяющим
углы многоугольника и параллельным какой-нибудь прямой, стягиваю-
щей две стороны многоугольника.
126
АГХНМКД
Действительно, фигура, описанная около меньшего шара, будет
одновременно вписанной в больший; но доказано, что поверхность
вписанной в шар фигуры, ограниченной коническими поверхностями,
равна кругу, радиус которого квадрирует прямоугольник между
одной стороной многоугольника и прямой, равной всем соединяющим
углы многоугольника прямым, параллельным какой-нибудь стягиваю-
щей две стороны многоугольника прямой; так что ясно и высказанное
выше.
XXX
Поверхность описанной около шара фигуры больше учетверенного-
большого круга в шаре.
Пусть будут шар, круг и все остальное так же, как и рапыпе,
и пусть круг Л будет равен поверхности заданной фигуры, описанной
около меньшего шара [рис. 31}.
Так как в круг EZH0 вписан равносторонний многоугольник
с четным числом углов, |.то все (вместе взятые) прямые, соединяющие-
стороны многоугольника, являясь параллельными Z0, будут иметь,
к Z0 то же отношение, как 0К к KZ; значит, прямоугольник между
одной стороной многоугольника и прямой, равной всем (прямым),
соединяющим стороны многоугольника, будет равен прямоугольнику
между Z© и 0К; поэтому радиус круга Л будет квадрировать прямо-
угольник между Z© и ©К; значит, радиус круга Л будет больше ОК.
Но ©К равна диаметру^круга АВГД, [ибо она в два раза больше ХМ —
радиуса круга АВ ГД].^Теперь ясно, что кругЛ, или поверхность фигу-
ры, описанной около меньшего шара, будет больше учетверенного-
большого круга в этом шаре [101.
XXXI
Фигура, описанная около меньшего шара, равна конусу, имеющему
основанием круг, равный поверхности (фигуры, а высоту, равную радиусу
шара.
Действительно, описанная около меньшего шара фигура будет
одновременно вписанной в больший шар; вписанная же фигура, огра-
О ШАРЕ И ЦИЛИНДРЕ
127
ниченная коническими поверхностями, будет, согласно доказанному,
равна конусу, имеющему основанием круг, равный поверхности фигуры,
а высоту, равную перпендикуляру, опущенному из центра шара на
одну из сторон многоугольника; этот же перпендикуляр равен радиусу
меньшего шара; теперь предложенное ясно.
С л е д с т в и е
Из этого ясно, что описанная около меньшего шара фигура
более учетверенного конуса, имеющего основанием большой
круг (меньшего} шара, а высоту, равную радиусу (того же} шара.
Действительно, так как этой фигуре равен конус, имеющий осно-
вание, равное ее поверхности, высоту же, равную [перпендикуляру,
опущенному из центра шара на одну из сторон многоугольника, то
есть] радиусу меньшего шара, и так как поверхность фигуры, описанной
около того же шара, больше учетверенного большого круга в шаре, то,
значит, описанная около шара фигура будет более учетверенного кону-
са, имеющего основанием большой круг, а высотой радиус шара, так
как конус, равный фигуре, будет более учетверенного упомянутого
конуса, [так как при равных высотах он имеет более чем в четыре раза
большее основание].
XXXII .
Если в шар вписана фигура и около него описана другая такая же,,
построенная, как и раньше, на подобных многоугольниках, то поверх-
ность описанной фигуры к поверхности вписанной будет иметь {отноше-
шение, равное} двойному отношению стороны многоугольника, опи-
санного около большого круга, к стороне вписанного в тот же круг
многоугольника, сама же {описанная) фигура будет иметь ко вписанной
тройное отношение*) тех же прямых.
Пусть АВГД будет (большим} кругом шара {рис. 32}; в пишем в не-
го ранносторопггий многоугольник с числом сторон, кратным четырех.
Рис. 32.
и опишем другой, подобный вписанному,, так, чтобы стороны'1 опи-
санного многоугольника касались круга в серединах дуг, отсекаемых
сторонами вписанного многоугольника; пусть в круге, охватывающем
описаппый многоугольник, ЕН, Z0 будут взаимно перпендикулярные
диаметры, одинаково расположенные с диаметрами АГ, ВД; вообразим
*) ТсГесть возведенное в третью степень.
128
АРХИМЕД
прямые, соединяющие противоположные углы многоугольника и парал-
лельные друг другу и прямой ZBA0. При вращении периметров много-
угольников но дугам окружностей около неподвижного диаметра ЕН
получатся две фигуры — одна вписанная в шар и другая— около него
описанная. Требуется доказать, что поверхность описанной фигуры
имеет к поверхности вписанной отношение, равное двойному отноше-
нию ЕЛ к АК, сама же описанная фигура имеет ко вписанной отноше-
ние, равное тройному тому же самому.
Пусть круг М будет равен поверхности фигуры, описанной около
шара, а круг N равен поверхности вписанной; тогда радиус круга М
будет квадрировать прямоугольник между ЕЛ и прямой, равной всем
(прямым), соединяющим углы описанного многоугольника, радиус
же круга N будет квадрировать прямоугольник между АК и прямой,
равной всем (прямым), соединяющим углы вписанного многоугольни-
ка. И так как упомянутые многоугольники подобны, то будут подобны
и прямоугольники, построенные на упомянутых линиях, [то есть со-
единяющих углы или стороны многоугольников, так что они будут
иметь друг к другу то же отношение, как квадраты сторон многоуголь-
ников. Но отношение прямоугольников между упомянутыми линиями
будет одинаково с двойным отношением радиусов кругов М, Ь1; таким
образом, диаметры кругов М, N будут находиться в том же отношении,
что и стороны .многоугольников, круги же имеют друг к другу отно-
шение, равное двойному отношению диаметров, сами же круги равны
поверхностям описанной и вписанной фигур]; отсюда ясно, что поверх-
ность фигуры, описанной около шара, к поверхности фигуры, вписан-
ной в шар, имеет отношение, равное двойному отношению ЕЛ к АК.
Возьмем еще два конуса О, Е; пусть конус Е имеет /юнованием
круг Е. равный кругу М, а конус О — круг О, равный кругу N;
пусть высота конуса Е будет равна радиусу шара, а высота О равна
перпендикуляру, опущенному из центра шара па АК; тогда, [как уже
было доказано,] конус Е будет равен фигуре, описанной около шара,
а конус О — вписанной. Но так как оба многоугольника подобны, то
ЕЛ имеет к ЛК такое же отношение, как радиус шара к опущенному
из центра шара на АК перпендикуляру; значит, высота конуса Е имеет
к высоте конуса О такое ясс отношение, как ЕЛ к АК. Также и диаметр
круга М относится к диаметру круга N, как ЕЛ к АК; значит, диаме-
тры оснований конусов Е и О имеют с высотами одинаковое отношение;
[значит, конусы этн подобны]; поэтому конус Е к конусу О будет
иметь отношение, равное тройному отношению диаметра круга А[
к диаметру круга X. Теперь ясно, что описанная фигура ко вписанной
имеет отношение, равное тройному отношению ЕЛ к АК.
XXXIII
11 оверхностъ всякого шара равна его учетверенному большому кругу.
Пусть будет какой-нибудь шар, и пусть Л — его учетверенный боль-
шой круг; я утверждаю, что круг А равен поверхности шара {рис. 331.
Действительно, если он не равен, то будет или больше, или меньше.
Пусть сначала поверхность шара будет больше круга А. Тогда имеются
две неравные величины — поверхность шара и крут А; значит, можно
взять две неравные прямые так, чтобы отношение большей к меттыпей
было меньше того, в каком поверхность шара находится к кругу (А).
Возьмем такие прямые В и Г, и пусть А будет средней пропорциональ-
О ШАРЕ И ЦИЛИНДРЕ
129
Рис. 33.
пой между В и Г. Вообразим, что шар рассечен по кругу EZIIO пло-
скостью, проходящей через центр; вообразим также вписанный в этот
круг и описанный около него многоугольники такие, чтобы описанный
был подобен вписанному и чтобы сторона описанного имела к стороне
вписанного отношение, меньшее того, которое В имеет к Д; [значит,
двойное отношение сторон будет меньше двойного отношения прямых.
Но двойное отношение В к Д будет равно отношению В к Г, и двойное
отношение стороны описанного многоугольника к стороне вписанного
будет отношением поверхности описан- в
ной фигуры к поверхности вписанной!;
значит, поверхность фигуры, описанной
около шара, к поверхности вписанной
фигуры имеет меньшее отношение, чем
поверхность шара к кругу А, а это не-
возможно; действительно, поверхность
описанной фигуры больше поверхности
шара, поверхность же вписанной фигу-
ры меньше круга А, [так как доказа-
но, что поверхность вписанной фигуры
меныпе учетверенного большого круга
в шаре, круг же А равен учетверен-
ному большому кругу]. Значит, поверх-
ность шара не будет больше круга А.
Теперь я утверждаю, что опа не
будет и меньше. Действительно, пусть
опа будет меньше, если это возможно;
таким же образом найдем прямые В и
Г так, чтобы В имела к Г отношение,
меньшее того, в котором круг А нахо-
дится к поверхности шара, и среднюю
пропорциональную между В и Г пря-
мую Д; затем снова впишем и опишем
два многоугольника таких, чтобы сто-
рона описанного имела (к стороне впи-
санного) отношение, меньшее В к Д,
[что будет и после удвоения*) обоих
отношений]; таким образом, поверхность
верхности вписанной будет иметь отношение меньшее, [чем В к Г.
Но В имеет к Г отношение меньшее], чем круг А к поверхности шара,
а это невозможно; действительно, поверхность описаппой фигуры боль-
ше круга А, а поверхность вписанной меньше поверхности шара.
Таким образом, поверхность шара нс будет и меньше круга А.
Доказано же, что она и не больше; значит, поверхность шара равна
кругу А, то есть учетверенному большому кругу.
описанной фигуры к по-
XXXIV
Всякий шар в четыре раза больше конуса, имеющего основание,
равное большому кругу шара, а высоту, равную радиусу шара.
Пусть будет некоторый шар и в нем большой круг ДВГД {рис. 34}.
Теперь если шар не будет {ровно) в четыре раза больше упомянутого
*) То есть возведения в квадрат.
9 Архимед
130
АРХИМЕД
конуса, то пусть, если возможно, он будет более чем в четыре раза
больше. Пусть будет конус S, имеющий основание, в четыре раза боль-
шее круга АВГД, высоту же, ранную радиусу шара; тогда шар будет
больше конуса Е. Итак, имеются две неравные величины — шар
и конус; значит, можно взять две неравные прямые так, чтобы большая
имела к меньшей отношение, меньпгес того, в каком шар находится
к конусу S. Пусть это будут К и Ц. Возьмем I и 0 так, чтобы К от I,
I от О и 0 от II разнились бы на одно и то же;
к - - н
вообразим также, что, как и раньше, в круг АВГД вписан многоуголь-
ник с числом сторон, кратным четырем, и около него описан другой,
подобный вписанному, и пусть сто-
К ^•^-'^'"''''^55', рона описанного многоугольника
7 имеет к стороне вписанного отноше-
й I \л ние, меньшее того, в котором К бу-
Н л/д______________Г\к дет к I. Пусть АГ, ВД будут взаим-
\К” Ту по перпендикулярные диаметры.
V. /I Если теперь около неподвижного
диаметра АГ будем вращать лло-
.11* скость, в которой находятся оба мно-
гоугольнлка, то лол учатся две фи-
гуры, из которых одна будет описа-
на, другая же вписана в шар, при-
чем отношение описанной фигуры к
вписанной будет равняться тройному
Рис. 3-4. отношению стороны многоугольника,
описанного около круга АВГД к сто-
роне вписанного в него. По сторона к стороне имеет отношение, мень-
шее чем К к I; значит, описанная фигура имеет к вписанной отноше-
ние, меньшее тройного отношения К к I. Но отношение К к Н
больше тройного отношения К к I;
к . к3
Н J»
[это ясно из сделанных предположений] £11]. Значит, и подавно опи-
санная фигура имеет к вписал нон отношение, меньшее того, которое К
имеет к Я.
Но К имеет к Н отношение меныпее, чем шар к конусу Е: (зна-
чит, описанная фигура имеет к вписанной отношение меньшее, чем
шар к конусу S), и после перестановки (описанная фигура к шару
. имеет отношение меныпее, чем вписанная к конусу Е); это же невоз-
можно, так как описанная фигура больше шара, вписанная же меньше
конуса Е [вследствие того, что конус Е в четыре раза больше конуса,
имеющего основание, равное кругу АВГД, а высоту, равную радиусу
шара, вписанная же фигура меньше четырежды взятого упомянутого
конуса]. Таким образом, шар не будет более чем в четыре раза больше
упомянутого конуса.
Пусть теперь, если возможно, он будет менее четырежды взятого
упомянутого конуса: иными словами, шар будет меньше конуса Е.
Возьмем прямые К и Н так, чтобы К была больше II и имела к пей отно-
шение меныпее того, в каком копус Е находится к шару, затем постро-
им такие же прямые 0 и I, как и раньше. Вообразим многоугольник,
О ШАРЕ И ЦИЛИНДРЕ 131
вписанный в круг АВГД, и другой, описанный около него, такие, что-
бы сторона описанного многоугольника имела к стороне вписанного
отношение меньшее, чем К к I, и все остальное устроим так же, как и
раныпэ. Таким образом, отношение описанной телесной фигуры ко впи-
санной будет равняться тройному отношению стороны многоугольника,
описанного около круга АВГД, к стороне вписанного. Но сторона
к стороне имеет отношение меныпее, чем К к I; значит, описанная
фигура к вписанной будет иметь отношение, меньшее тройного отно-
шения К к I,
Но К к Н имеет отношение, большее» тройного отношения К к I;
к . кя
н гя
значит, описанная фигура будет иметь к вписанной отношение мень-
шее, чем К к Н. Но К к Н имеет отношение меньшее, чем конус Е
к шару: (значит, описанная фигура имеет к вписанной отношение
меныпее, чем конус Е к шару); это же невозможно, ибо вписанная
фигура меньше шара, описанная же больше конуса Е. Значит, шар не
будет меньше четырежды взятого конуса, имеющего основание, равное
кругу АВГД, а высоту, равную радиусу сферы. Но доказано, что оп
не будет и больше; значит, шар будет равняться упомянутому конусу,
четырежды взятому.
[С л е д с т в и е]. Из доказанного ясно, что всякий цилиндр,
имеющий основанием большой круг шара, а. высоту, равную его диаметру,
будет в полтора раза больше шара, и что поверхность его вместе с осно-
ваниями будет в полтора, раза больше поверхности шара.
Действительно, вышеупомянутый цилиндр в шесть раз больше
конуса, имеющего то же самое основание и высоту, равную радиусу
шара, а шар, по доказанному, будет в четыре раза больше того же
конуса; отсюда ясно, что цилиндр будет в полтора раза больше шара.
Затем поверхность цилиндра за вычетом основания, по доказанному,
равна кругу, радиус которого является средней пропорциональной
между стороной цилипдра. и диаметром его основания, сторона же
упомянутого обнимающего сферу цилиндра равна диаметру основания
[так что, очевидно, их средняя пропорциональная будет тоже равна
диаметру основания]. Далее, круг, имеющий радиусом диаметр осно-
вания, будет в четыре раза больше этого основания, то есть боль-
шого круга шара. Таким образом, поверхность цилиндра за вычетом
оснований будет в четыре раза больше упомянутого круга, а значит,
вся поверхность цилиндра вместе с основаниями — в шесть раз больше
большого круга. Поверхность же шара в четыре раза больше большого
круга; значит, вся поверхность цилиндра в полтора раза больше поверх-
ности шара.
XXXV
Поверхность фигуры, вписанной в сферический сегмент, равна
кругу, радиус которого квадрирует прямоугольник, построенный на
одной стороне многоугольника, вписанного в соответствующий сегмент
большого круга, и прямой, равной всем прямым, параллельным основанию
сегмента, вместе с половиной этого основания.
Пусть будет шар и в пем сегмент, основанием которого является
построенный на АН круг {рис. 35}. [Впишем в шар, как было
сказано раньше, фигуру, ограниченную коническими поверхностями);
9*-
132
АРХИМЕД
пусть также будут большой круг АП0 и многоугольник АГЕбХАП
с четным числом (равных) сторон за исключением стороны АИ;
возьмем круг Л, радиус которого квадрирует прямоугольник между
стороной АГ и прямой, равной всем EZ, ГД, взятым вместе с половиной
основания, то есть АК;
(рад. Л)* = ЛГ(Е2 | ГД+АЮ
требуется доказать, что
этот круг равняется по-
верхности вписанной фи-
гуры.
Возьмем круг М, ра-
диус которого квадрирует
” прямоугольник между сто-
' - роной Е0 и половиной EZ;
:(’рад.- М)2-=Ев-| EZ
; круг М будет тогда равен поверхности конуса, основанием которого
г является круг, построенный на EZ, а вершиной точка 0. Возьмем и дру-
гой круг N, радиус которого квадрирует прямоугольник между ЕГ
и половиной вместе взятых EZ, ГА;
(рад. N)2=Er-|(HZ + rA) •” ‘
он будет равен поверхности конуса между проведенными через EZ, ГД
параллельными плоскостями. Так же возьмем еще круг Е, радиус кото-
рого квадрирует прямоугольник между АГ и половиной вместе взя-
; тых ГА, АН;
(рад. Е)г = ЛГ-^(ГД+АП)
он будет равен конической поверхности между параллельными плоско-
стями через АН, ГА.
Теперь все круги вместе будут равны полной поверхности фигуры
и квадраты на их радиусах равны прямоугольнику между одной сторо-
ной АГ и прямой, равной EZ, ГД, взятым вместе с ЛК — половиной
основания.
(рад. М)®+(рад. Юг + (рад. Е)*=АГ (еИЧ-ГЛ + |лн)
Но также и радиус круга Л квадрирует ту же самую площадь;
значит, круг А будет равен всем кругам М, N, Е (вместе взятым),
а следовательно, и поверхности вписанной фигуры.
XXXVI
Рассечем шар плоскостью, не проходящей через центр; пусть AEZ
{рис. 30} будет его большой круг, пересекающий под прямым углом
секущую плоскость; в сегмент АВГ впишем равносторонний много-
угольник с четным числом сторон за исключением основания АВ.
Если, подобно предыдущему, будем вращать фигуру около неподвиж-
ной (оси) TZ, то углы А, Е, Л, В будут двигаться по кругам с диамет-
рами АЕ и АВ, стороны же многоугольника — по коническим; поверх-
О ШАРЕ И ЦИЛИНДРЕ
ГЗЗ
ностям; таким образом, получится ограниченная коническими поверх-
ностями телесная фигура, имеющая основанием круг на диаметре АВ
и вершину в Г. Подобно предыдущему, эта фигура будет иметь по-
верхность, меньшую поверхности охватывающего
сегмента; действительно, и фигура, и сегмент име-
ют одну и ту же лежащую в плоскости границу,
а именно окружность круга, построенного па диа-
метре АВ; кроме того, обе поверхности являются
выпуклыми в одну и ту же сторону и одна из них
объемлстся другой.
XXXVII
Поверхность вписанной в сферический сегмент. 1ис‘ А '
фигуры -меньше круга, радиус которого равен пря-
мой, проведенной из вершины сегмента до окружности круга,
являющегося основанием сегмента.
Пусть будет шар и в нем большой круг ABEZ (рис. 37]; возьмем
сферический сегмент, основанием которого служит описанный на
диаметре АВ круг; [впишем затем в шар
упомянутую фигуру, а в сегмент круга—
многоугольник], и также все остальное,
причем ©А будет диаметром шара; затем по-
сле проведения АЕ и ©А построим круг М,
радиус которого будет равен А0. Требует-
ся доказать, что круг М будет больше по-
верхности {вписанной) фигуры.
Действительно, было доказано, что
поверхность фигуры равна кругу, радиус
которого квадрирует прямоугольник меж-
ду Е 0 и вместе взятыми EZ, ГД, КА, и так-
же было доказано, что прямоугольник меж-
ду Е0 и вместо взятыми EZ. ГД, КА
равен прямоугольнику между ЕД и К©*);
Е6 (EZ + Г А + КА) -ЕЛ К©
(прямоугольник) же между EzV и К© меныпе (квадрата) па. АО,
вл-ке< л«а
[то есть (прямоугольника) между Л0 и К©]**). , 1
Теперь видно, что радиус круга, равного поверхности (вписан-
ной) фигуры, будет меньше радиуса круга М; следовательно, ясно, что
круг М больше поверхности (вписанной) фигуры.
XXXVIII
Вписанная в сегмент {меньший полушария} фигура, ограничен-
ная коническими поверхностями, взятая вместе с конусом, имеющим
основание одно и то же с фигурой, а вершину в центре шара, будет равна
конусу, имеющему основание, равное поверхности фигуры, а высоту,
*) Согласно предложению XXII.
* * ) J (ейст нительно,
де®~ке-ле > ко- ел.
1А4
АРХИМЕД
равную перпендикуляру, опущенному из центра шара на одну из сто-
рон многоугольника {образующего вращением фигуру}.
Пусть будет шар и в нем большой круг с центром Е и сегмент АВГ,
меньший полукруга {рис- 38.}. Подобно предыдущему, в сегмент
АВГ впишем многоугольник с четным числом (равных) сторон за
исключением АГ; пусть при вращении
шара около неподвижной (прямой) ВЛ
получится ограниченная коническими
поверхностями фигура; па круге с диамет-
ром АГ построим конус, имеющий верши-
ну в центре (шара), и возьмем конус К,
имеющий основание, равное поверхности
фигуры, а высотой перпендикуляр, опущен -
ный из центра Е па одну из сторон много-
угольника. Требуется доказать, что конус
К будет равен ограниченной (кониче-
скими поверхностями) фигуре, взятой
вместе с конусом АЕГ.
На кругах с диаметрами ®Н, AZ по-
строим конусы, имеющие вершину в точ-
ке Е; тогда телесный ромб 1IB0E будет
Рис. 38. равен конусу, основание которого равно
поверхности конуса HB0, а высота равна
перпендикуляру, опущенному изЕ па НВ, окаймление же, ограниченное
(конической) поверхностью между параллельными плоскостями, (про-
веденными) через П0, ZA и конусами ZEA, НЕ®, будет равно конусу,
основание которого равно (конической) поверхности между парал-
лельными плоскостями через 110, ZA, а высота равна перпендикуляру,
опущенному из Е на ZH. Далее, окаймление, ограниченное (кониче-
ской) поверхностью между параллельными плоскостями через ZA,
АГ и конусами АЕГ, ZEA, будет равно конусу, основание кото-
рого равно (конической) поверхности между параллельными плоско-
стями через ZA, АГ, а высота - - перпендикуляру, опущенному
из Е на ZA.
Теперь (все) вышеназванные конусы будут1 равны рассматривае-
мой (вписанной телесной) фигуре вместе с конусом ЛЕГ. Действи-
тельно, они имеют высоту, равную перпендикуляру, опущенному из Е
на одну- из сторон многоугольника, а основания, равные (вместе)
поверхности фигуры AZHB0AT; также и конус К имеет ту же высо-
ту и основание, равное поверхности тон же фигуры; значит, этот конус
будет равен всем упомянутым конусам. Ио было доказано, что упомя-
нутые копусы равны рассматриваемой фигуре вместе с конусом АЕГ;
и значит, конус К равен рассматриваемой фигуре вместе с кону-
сом АЕГ.
С л о д с т в и е
Из этого ясно, что конус, имеющий основанием круг, ради-
ус которого равен прямой, проведенной из вершины сегмента
к окружности круга, являющегося основанием сегмента, а высоту,
равную радиусу шара, будет больше упомянутой вписанной фигуры,
взятой вместе с конусом (АЕГ). Действительно, упомянутый конус
больше конуса, равного рассматриваемой фигуре, взятой вместе
с конусом, имеющим то же основание, что и сегмент, а вершину в цент-
О ШАРЕ и ЦИЛИНДРЕ
135
ре шара, иными словами, больше конуса, имеющего основание равным
поверхности фигуры, а высоту, равную перпендикуляру, опущенному
из центра па одну из сторон многоугольника; в самом деле [как уже
было доказано!, основание, первого конуса больше основания второго,
и его высота больше высоты второго.
XXXIX
Пусть будет шар и в нем большой круг АВГ {рис. 39}; пусть
прямая АВ отсечет сегмент, меньший полукруга; пусть центр будет в Д;
из центра Д до А, В проведем соеди-
няющие прямые АД, ДВ и около полу-
чившегося сектора опишем многоуголь-
ник (с четным числом равных сторон),
а около пего круг; тогда последний
будет иметь тот же центр, что и круг
АВГ. Если вращающийся около непо-
движной прямой ЕК многоугольник
вернется в исходное положение, то опи-
санный круг будет перемещаться по
поверхности шара, углы многоуголь-
ника опишут окружности с параллель-
ными АВ диаметрами, соединяющими
углы многоугольника, а точки каса-
ния сторон многоугольника с меныпим
кругом опишут окружности на меньшем
шаре, диаметрами которых будут пря-
мые, параллельные АВ, соединяющие
эти точки касания и, наконец, стороны многоугольника будут пере-
мещаться по коническим поверхностям. Так будет образована огра-
ниченная коническими поверхностями описанная фигура, основанием
которой будет построенный на Z11 круг. Поверхность упомянутой фигуры
будет больше поверхности меньшего сегмента, основанием которого
является построенный на АВ круг.
Действительно, проведем касательные AM и BN; они будут дви-
гаться по конической поверхности, и фигура, образованная много-
угольником AM0EANB, будет иметь поверхность большую, чем сфе-
рический сегмент, основанием которого является построенный па
диаметре АВ круг; [действительно, они имеют одну и ту нее лежащую
в одной плоскости границу, а именно круг па диаметре АВ, и сегмент
объемлется фигурой]. Но коническая поверхность, образованная ZM,
HN, будет больше поверхности, образованной МА, NB; действитель-
но, ZM будет больше МА [ибо она стягивает прямой угол], и NH
больше NB, а если так, первая поверхность будет больше второй,
[как это принято в постулатах]. После этого ясно, что поверхность
описанной фигуры будет больше поверхности сегмента в меньшем
шаре.
Следствие
Кроме того, ясно, что поверхность фигуры, описанной около
сектора, равна кругу, радиус которого квадрирует прямоугольник
между одной стороной многоугольника и всеми прямыми, соеди-
няющими углы многоугольника, взятыми вместе с половиной
136
АРХИМЕД
основания упомянутого многоугольника, [так как описанная около
сегмента фигура является одновременно вписанной в сегмент большо-
го шара]; [все это ясно из вышеизложенного].
XL
Поверхность описанной около сектора фигуры, больше круга, радиус
которого равен прямой, проведенной из вершины, сегмента к окружно-
сти круга, являющегося его основанием.
Пусть будет шар с большим кругом АВГД и центром Е; опишем
около сектора многоугольник AKZ и около последнего круг; пусть будет
образована фигура, как и раньше {рис. 40]. Пусть N будет круг,
радиус которого квадрирует прямоуголь-
ник между одной стороной мпогоуголь-
. ника и всеми соединяющими прямыми,
взятыми вместе с половиной КА. Но упо-
мянутая площадь равняется прямоуголь-
нику между MQiiZII; [последняя является
высотой сегмента большего шара]; зна-
чит, радиус круга N квадрирует прямо-
угольник между М0 и IIZ.
рад. N)3=Me-HZ
По HZ больше, чем Д 3, [которая
является высотой меньшего сегмента. Дей-
ствительно, если мы проведем соединяю-
щую KZ, то она будет параллельной ДА.
И АВ параллельна KA, a ZE общая; зна-
чит, треугольник ZKH подобен треуголь-
нику ДДЕ. Далее, ZK более АД; значит,
и ZH больше Да], М8 же равна диаметру
ГД; [действительно, проведем соединяю-
щую прямую ЕО; поскольку МО равна OZ, а ©Е равна EZ, то, зна-
чит, ЕО будет параллельна М©п, следовательно, М© в два раза боль-
ше ЕО. Но и ГД в два раза больше ЕО; значит, М0 равна ГД], и
прямоугольник между ГД и ДЕ равен квадрату на АД.
ГД.ДВ = АД2
Таким образом, поверхность фигуры KZA будет больше круга,
радиус которого равняется прямой (АД), проведенной из вершины сег
мента к окружности круга, являющегося его основанием, а именно,
построенного на диаметре АВ; действительно, круг N равняется поверх-
ности фигуры, описанной около сектора.
Следствие!
Описанная около сектора фигура, взятая вместе с конусом,
основанием которого служит круг, построенный на диаметре
КА, а вершиной — центр шара, оказывается равной конусу, основа-
ние которого равно поверхности фигуры, а высота — перпенди-
куляру, опущенному из центра на сторону многоугольника, [которым,
конечно, равен радиусу шара, так как описанная около сектора фигура
будет и вписанной в сегмент большего шара, имеющего тот же самый
центр; сказанное ясно из предыдущего].
о ШАРЕ И ЦИЛИНДРЕ
137
Следствие 2
Из этого же ясно, что описанная фигура, взятая вместе
с конусом, будет больше конуса, имскяцего основанием круг,
радиус которого равен прямой, проведенной от вершины сегмента
меньшего шара к окружности круга, являющегося его основанием,
а высота равна радиусу (меньшего шара), так как конус, равный
фигуре, взятой вместе с конусом, будет иметь основание, большее выше-
сказанного круга, высоту же, равную радиусу меньшего шара.
XLI
Пусть будут опять шар и в нем большой круг, сегмент АВГ, мень-
ший полукруга, и центр Д {рис. 41}
угольник с четным числом (равных)
другой, ему подобный, так, чтобы
стороны одного были параллельны
сторонам другого, затем около опи-
санного многоугольника опишем
круг, и пусть подобно предыдущему
при вращении обоих кругов (вместе
с многоугольниками) около непо-
движной прямой НВ образуются
фигуры, ограниченные коническими
поверхностями. Требуется доказать,
что поверхность описанной фигуры
имеет к поверхности вписанной
отношение, равное двойному отно-
шению стороны описанного мно-
гоугольника к стороне вписанного,
отношение же самих фигур, взятых
вместе' с соответствующими конуса-
ми, будет равпо тройному тому же
отношению.
Действительно, пусть будет круг
М, радиус которого квадрирует
прямоугольник между одной сто-
роной описанного многоугольника
и всеми прямыми, соединяющими
его углы, вместе с половиной EZ;
круг М будет равен поверхности
описанной фигуры. Затем возьмем
другой круг IN, радиус которого
квадрирует прямоугольник между од
; впишем в сектор АВГ много-
сторон и опишем около него
Рис. 41.
стороной вписанного многоу-
гольника и всеми прямыми, соединяющими его углы, вместе с половиной
АГ; и он будет равен поверхности вписанной фигуры. Но упомянутые
площади относятся между собой, как (квадраты) на сторонах ЕК и АА
[и, следовательно, как многоугольник к многоугольнику, так будет
и круг М к кругу N]; теперь ясно, что поверхность описанной фигуры
к поверхности вписанной имеет отношение, равное двойному отноше-
нию ЕК к АА, [тому же самому, что и у многоугольников].
Пусть будет еще конус Е, имеющий основание, равное кругу М,
а высоту, равную радиусу меньшего шара; этот конус равен описанной
i3H
АРХИМЕД
фигуре вместе с конусом, основанием которого является круг на EZ,
а вершина в Д. Пусть будет другой конус О, имеющий основание, равное
N, а высоту, равную перпендикуляру, опущенному из Д па АЛ; он
равен вписанной фигуре вместо с конусом, основанием которого являет-
ся круг на диаметре АГ, вершиной ?ке центр Д; обо всем этом было напи-
сано раньше,. Теперь (поскольку!*) ЕК относится к радиусу меньшего
шара, как АЛ к перпендикуляру, опущенному из центра [Л] на АЛ;
доказано же, что как ЕК к АЛ, так будет и радиус круга М к радиусу
круга N [и один диаметр к другому]; тогда получится, что как диаметр
круга, являющегося основанием конуса 3, к диаметру круга, являю-
щегося основанием конуса О, так и высота конуса 2 к высоте конуса О;
[следовательно, конусы подобны]. Значит конус 2 к конусу О имеет
отношение, равное тройному отношению одного диаметра к другому.
Теперь ясно, что описанная фигура вместе с конусом ко вписанной
фигуре с конусом же имеет отношение, равное тройному отношению
ЕК к АЛ.
XLII
Поверхность всякого сферического сегмента., меньшего полушария,
равна кругу, радиус которого равен прямой, проведенной из вершины
сегмента до окружности круга, являющегося основанием сегмента.
Пусть будет шар, в нем большом круг АВГ {рис. 42} и сегмент,
меньший полушария, основанием которого является построенный на
АГ круг, перпендикулярный к кругу АВГ; возьмем круг Z, радиус
которого равен АВ; требуется доказать, что поверхность сегмента
АВГ равна кругу Z-
Действительно, если они не равны, то пусть эта поверхность будет
больше круга Z.
Возьмем центр Л и продолжим прямые, соединяющие Д с А и Г.
Затем, имея две неравные величины — поверхность сегмента и круг Z —
впишем в сектор АВГ равносторонний многоугольник с четным числом
сторон и опишем другой, ему подобный, так, чтобы описанный
многоугольник имел ко вписанному отношение меньшее, чем отношение
поверхности сферического сегмента к кругу Z. После вращения круга,
как и раньше, получатся две ограниченные коническими поверхностя-
ми фигуры, из которых одпа будет описанной, а другая вписанной,
*) Как видно из комментария Евгения, слова «поскгшг.ку» (cnei) в тексте Архимеда, которым
ов располагал, не было.
О ШАРЕ И ЦИЛИНДРЕ
139
и поверхность описанной фигуры будет относиться к поверхности
вписанной, как описанный многоугольник ко вписанному, так как
каждое из этих отношений равняется двойному отношению стороны
описанного многоугольника к стороне вписанного. Но, (согласно
предположению), описанный многоугольник имеет ко вписанному
отношение меныпее, чем поверхность упомянутого сегмента к кругу Z,
и поверхность описанной фигуры больше поверхности сегмента; сле-
довательно, поверхность вписанной фигуры больше круга Z, а это
невозможно, так как доказано, что упомянутая поверхность фигуры
меньше круга такой величины.
Пусть теперь круг (Z) будет больше поверхности (сегмента);
тогда опишем и впишем подобные многоугольники, и пусть описанный
будет ко вписанному иметь отношение меньшее того, которое круг (Z)
имеет к поверхности сегмента*). (Так как многоугольники отно-
сятся, как поверхности соответствующих фигур, то поверхность опи-
санной фигуры к поверхности вписанной будет иметь отношение, мень-
шее отношения круга Z к поверхности сегмента, и следовательно,
после перестановки — отношение поверхности описанной фигуры к кру-
гу Z будет меньше отношения поверхности вписанной фигуры к поверх-
ности сегмента; но так как поверхность вписанной фигуры меньше
поверхности сегмента, то и поверхность описанной фигуры должна
быть меньше круга Z, а это невозможно). Итак, поверхность сег-
мента не будет меньше* **) круга Z. Доказано же, что и не больше***),
значит, обе эти поверхности равны.
XU11
Далее, если сферический сегмент больше полушария, то его поверх-
ность точно так же будет равна кругу, радиус которого равен прямой,
проведенной из вершины сегмента к. окружности круга, являющегося
его основанием,.
Пусть будет шар и в нем большой круг (АВГ) {рис. 43};
вообразим шар рассеченным плоскостью, перпендикулярной к той,
Рис. 43.
которая проходит через АТ?; пусть сегмент АВА будет меньше полуша-
рия и диаметр В Г перпендикулярен к АА; точки В и Г соединим с А
♦) II атам месте текст представляет лакуну» которая заполняется примерно так» как показано
в угловатых скобках.
**) В тексте ошибочно «больше».
***) В тексте ошибочно «меныпе».
140
АРХИМЕД
прямыми ВА и АГ. Пусть Е будет круг, радиус которого равен АВ,
a Z — круг, радиус которого ранен АГ, и Н — круг, радиус которого
равен В Г; следовательно, круг П будет равен кругам Е, Z*). Но круг
II равен всей поверхности тара, [так как он в четыре раза боль-
ше круга, построенного на диаметре ВГ], а круг Е равен поверхности
сегмента АВД, [это ведь доказано для сегмента, меньшего полушария];
значит, остающийся круг Z будет равен поверхности сегмента А ГД,
который уже больше полушария. ,>, •
XLIV
Всякий сферический сектор равен конусу, имеющему основание,
равное поверхности сферического сегмента, соответствующего &тому
сектору, а высоту, равную радиусу шара.
Пусть будет шар и в нем большой круг АВД {рис. 44} с центром Г:
пусть еще будет конус, имеющий основанием круг, равный поверх-
• ности (сегмента), соответствующей
дуге АВД, и высоту, равную ВГ;
требуется доказать, что сектор АВГД
будет равен упомянутому конусу.
Если это не так, то пусть сектор
будет больше конуса; пусть упомя-
нутый конус будет 0; тогда, имея
две неравные величины — сектор и
конус,— найдем две линии Д, Е, и
пусть Д будет больше Е и имеет к
Е отношение меньшее, чем сектор к
конусу.
Возьмем еще две. прямые Z, Н та-
кие, чтобы Д от Z, Z от Н и Н от Е
отличались на равные (отрезки);
д-Z=Z-H=H-Е
затем около плоского сектора кру-
га опишем равносторонний много-
угольник с четным числом сторон и
впишем в него ему подобный так,
чтобы сторона описанного имела к
меныпее того, которое Д имеет к Z; затем, подобно предыдущему, вра-
щая круг, образуем две фигуры, ограниченные коническими поверх-
ностями; тогда описанная фигура, взятая вместе с конусом, имеющим
вершину в Г, будет иметь ко вписанной фигуре’с соответствующим кону-
сом отношение, равное тройному отношению стороны описанного мно-
гоугольника к стороне вписанного. Но сторона описанного много-
угольника (к сторопе вписанного) имеет отношение меньшее, чем
Д к Z; значит, упомянутые телесные фигуры (описанная ко вписан-
ной с их конусами) будут иметь отношение меньшее, чем тройное
д отношение Д к Z. Но Д к Е имеет отношение, большее тройного отно-
шения Д к Z**); значит, телесная фигура, описаштая около сектора,
будет иметь ко вписанной отношение меньшее того, какое прямая Л
* ) Действительно, Н = rt • ВГ2 - я (А В2 I • А Г2) — Е -|- Z.
*•) См. комментарий [11] к аналогичному месту в предложении XXXIV.
О ШАРЕ If ЦИЛИНДРЕ
141
имеет к Е. А (согласно предположению) Д к Е имеет отношение
. . меньшее, чем телесный сектор (АВГД) к конусу 0; значит, телесный
сектор (АВГД) к конусу 0 будет иметь отношение большее, чем
описанная около сектора фигура ко вписанной. И после перестановки:
. (сектор АВГД к описанной фигуре вместе с конусом будет иметь отно-
шение большее, чем отношение конуса 0 ко вписанной фигуре вместе
с ее конусом); но описанная телесная фигура (вместе с ее конусом)
. больше сектора (АВГД)*), и, значит, вписанная в сектор фигура (с ее
конусом) будет больше конуса О, а это невозможно; действительно,
выше было доказано, что она меньше такого конуса, [имепно имеющего
основанием круг, радиус которого равен прямой, соединяющей верши-
ну сегмента с (какой-нибудь точкой) окружности круга, являюще-
гося основанием сегмента, а высотой — радиус шара; таким же кону-
сом будет упомянутый конус 0, ибо основанием он имеет круг, равный
. поверхности сегмента, то есть упомянутому кругу, а высота его равна
радиусу шара]. Итак, телесный сектор не будет больше конуса 0.
Тогда пусть конус 0 будет больше телесного сектора (АВГД).
Опять точно так же пусть Д, будучи более Е, имеет к ней отношение,
меньшее того, которое конус (0) имеет к сектору (АВГД); затем
точно та!£ же возьмем прямые Z и Н так. чтобы их разности были оди-
наковы,
д z=.z —н=п-в f
и пусть сторона многоугольника с четным числом (равных) сторон,
описанного около плоского сектора, имеет к стороне такого же вписан-
ного отношение, меньшее того, которое Д имеет к Е, [и образуем вокруг
телесного сектора соответствующие телесные фигуры]. Теперь точно
так же докажем, что описанная около сектора телеспая фигура имеет ко
вписанной отношение, меньшее того, которое прямая Д имеет к Е
и конус 0 имеет к сектору (АВГД); [таким образом, этот сектор
имеет к конусу (0) меньшее отношение, чем вписанная в сектор**)
телесная (фигура) к описанной]. Но- сектор больше вписаппой
в него фигуры; значит, и конус 0 больше описанной фигуры, а это
невозможно; [действительно, доказано, что такой конус меньше этой
фигуры, описанной около сектора]; значит, рассматриваемый сектор
будет равен конусу 0.
. . КНИГА II
Архимед желает радости Досифею
Ты уже просил меня написать доказательства для тех проблем,
формулировки которых я посылал к Конону; при изложении большей
части их приходится пользоваться теоремами, доказательства которых
я уже послал тебе, а именно;
(1) что поверхность всякого шара в четыре раза больше его боль-
шого круга,
(2) что поверхность всякого сферического сегмента равняется
кругу, радиус которого равен прямой, проведенной из вершины сегмента
к окружности основания,
*) В тексте написано ошибочно «тцтдостос;» (сегмента).
•*) В тексте опять ошибочно написано «в сегмент».
142
АРХИМЕД
(3) что для, всякого шара цилиндр, имеющий основанием большой
круг шара и высоту, равную диаметру шара, и сам будет по величине
в полтора рала больше шара, и его поверхность в полтора, раза больше
поверхности шара, и
(4) что всякий телесный сектор равен конусу, имеющему основа-
нием, круг, равный поверхности сферического сегмента, находящегося
в этом, секторе*), а высоту, равную радиусу соответствующего шара.
В этой, книге я посылаю тебе запись доказательств тех теорем
и задач, которые получаются из вышеупомянутых теорем; что же касает-
ся тех, решение которых находится при помощи других исследований,
а именно относительно спиралей и коноидов, то я постараюсь послать
их тебе возможно скорее.
Первая из вышеупомянутых проблем была такая. Для заданного
шара найти плоскую фигуру, равную поверхности этого шара. Ее
решение непосредственно получается из вышеупомянутых теорем:
действительно, учетверенный большой круг шара будет плоской фигу-
рой и равен поверхности шара.
I
Вторая задача была такова: для заданного конуса или цилиндра
найти шар, разный этому конусу или цилиндру.
Пусть Л будет данный конус или цилиндр, а В — шар, равный
этому А {рис. 45.}. Возьмем цилиндр TZA, в полтора раза больший
ГДЗ
НО2
конуса, или цилиндра А, и другой
цилиндр, в полтора раза больший ша-
ра В; основанием этого цилиндра будет
круг па диаметре 110, а ось КЛ равна
диаметру шара В; тогда цилиндр Е будет
равен цилиндру К. [У равных цилинд-
ров основания обратно пропорциональны
высотам]; значит, круг Е относится к
кругу К, или (квадрат) на ГД к (квад-
рату) на Н0, как прямая КЛ к EZ.
КА
EZ
Но КЛ равна П0, [ибо у цилиндра, в
полтора раза большего шара, ось равна
диаметру шара, а круг К является
большим кругом шара]; значит, как
(квадрат) на ГД к (квадрату) па Н0.
так будет и Н0 к EZ.
Рис. 45.
газ __ по
не» ez
Пусть квадрат на II© будет равен прямоугольнику между ГД и МД’;
не» = гд ihn
тогда как ГД к МЛ7, так и квадрат на ГД к квадрату на Н0, или 110
*) Речь идет, конечно, о сегменте шарм, опирающемся на ту же часть поверхности шара, что
сектор.
О ШАРЕ И ЦИЛИНДРЕ
143
к EZ, после же перестановки — как ГД к НС), так и НС) к MN,
и MN к EZ,
гд не мк
не ' MN ~ EZ
Но обе прямые ГД и EZ даны; значит, Н8 и MN будут двумя средними
пропорциональными для двух данных прямых; значит, будут данными
и обе Н8, 'MIS.
Синтез же задачи производится так: пусть данный копус или
цилиндр будет А; требуется найти шар, который был бы равен конусу
или цилиндру А.
Для конуса или цилиндра Л построим в полтора раза больший ци-
линдр, основанием которого будет круг на диаметре ГД, а осью — пря-
мая EZ, и возьмем между ГД и EZ две средние пропорциональные П8,
MN, так чтобы было — как ГД к НО, так и Н8 к MN и MN к EZ,
ГА HO MN
не " MN~— EZ
и вообразим цилиндр, основанием которого был бы круг на диаметре
НО, а ось КЛ равнялась диаметру НС); тогда я утверждаю, что
цилиндр Е будет равен цилиндру К.
Действительно, поскольку ГД будет к НО, как MN к EZ,
ГА МЛ
НО ” EZ
и после перестановки, ГД к MN, как НС) к EZ,
гл = по
MN EZ
а ПО равна КЛ, [следовательно, как ГД к MN, то есть как квадрат
па ГЛ к квадрату на НО, так будет и круг Е к кругу K.J, то, значит,
как круг Е к кругу К, так будет и КЛ к EZ, [следовательно, у цилин-
дров Е и К основания обратно пропорциональны высотам]; значит,
цилиндр Е равен цилиндру К. Но цилиндр К в полтора раза больше
шара, диаметр которого 110; значит, и шар, диаметр которого равен
ПО, то есть шар В, будет равен данному конусу или цилиндру А [1].
11
Всякий сферический сегмент равен конусу, имеющему то же осно-
вание, что и сегмент., а высотой прямую, которая к высоте сегмента
имеет такое же отношение, как вместе взятые радиус шара и высота
дополнительного сегмента к высоте дополнительного сегмента.
Пусть будет шар и в нем большой круг, диаметр которого АГ
(рис. 46); рассечем шар плоскостью, проходящей через BZ и перпенди-
кулярной к АГ; пусть центр шара будет 8. Сделаем, чтобы отношение
вместе взятых 8А, ЛЕ к ЛЕ равнялось отношению некоторой прямой
ДЕ к ТЕ;
ел + а к ли
АЕ ~ ГЕ
кроме того, сделаем, чтобы отношение вместе взятых 8Г, ГЕ к ГЕ
равнялось отношению некоторой прямой КЕ к ЕА;
Ы'4-ГЕ КЕ
ГЕ ЕА'
«44
АРХИМЕД
затем на круге с диаметром BZ построим два конуса, имеющих верши
нами точки К, Д; и утверждаю, что конус BAZ равен сферическому
сегменту при Г, а конус BKZ — сегменту при точке А.
Проведем прямые В©, ©Z и вообразим конус, имеющий основанием
круг па диаметре BZ и вершину в точке В; пусть еще будет конусМ,
имеющий основанием круг, равный поверхности сферического сегмен-
та BTZ, то есть круг с радиусом ВГ, а высоту, равную радиусу шара;
тогда конус М будет равен телесному сектору BT0Z, как доказано
в 1 книге. Поскольку же как ЛЕ к Е Г, так и вместе взятые 0А, АЕ к АЕ,
ДЕ НА + АЕ
КГ “ АЕ
то, «выделяя»
дБ - ЕГ (0А + АЕ) — АЕ
ГЕ ~ АЕ
получим, что как ГД к ГЕ, так и ©А к АЕ, то есть как Г© к АЕ,
ГД _ оа _ ге
ГЕ ~ "а'Ё А15
а после перестановки — как ДГ к Г©, так ГЕ к ЕЛ;
АГ ГЕ
ге ел
и, «присоединяя»,
ДГ 4- ГН ГЕ + ЕА
ег = ~ АЕ
как ©А к ©Г, так и ГА к АЕ, то есть как квадрат на ГВ к квадрату
на BE;
ед _ га гл-ге гвз
,®Г — ЛЕ ’ЕЛ-ГЕ- BE2
значит, как Д© к Г©, так и квадрат на ГВ относится к квадрату на BE.
де гв2
ге" ве» ' ’ ' "
JA /к/
» . ,' । ’.*
сЛ%£ *&$* f£$ ом # А'*,л*?**’
^*«6**^ ’SiT**»?**
» A* t#» <^4м)( i А ntur-fi
t* Adf члнмг ~*
„.-•fj-it Ji » f»*i*
irfff 9Tf> j-sft-x,: X-. »'iS^AC fKMfft • • SJW
(угл у,*,, e^/*»Ar
«Z'-. ! /ч. ‘ f- ’*♦ M f ♦’ »’« 1»-
»*»/ •аЦм»,^ v**Z* 5^ t4* <ry><*' ^>v% иЙ> »jr*
<::' .7-л> «t«*-# «W *><w"«’5r»»g?4 #*•
4*:W •&*$ •*/’?. I: -xД fc ’7* <
<'*.< 7^» »?^,-'^<» r Sk^ar^A^tr ЛЯ*
у 4.. * j а Л.Ч5^й* »<« !« .t *«••
if (''/••.j‘. .• »«,?>•• ?*-,-'S’ 1^4! Jfytik &7 /4Г#
\ • • -z i "” ** ♦ - v • * j
<?\ » л/ /V <£• /^’ /?» > «*’*'<•'«>-, «»f «*<^« <r
:: Х^у6>/ '//Kt f >* f-
Фотокопия страницы греческой р^укописи, содержащей отрывок сочипепня
Архимеда «О шаре и цилиндре».
10 Архимед
146
АРХИМЕД
Но ГБ равна радиусу круга М, а БЕ — радиусу круга на диаметре
BZ; значит, как А© к 0Г, так будет и круг М к кругу на диаметре
BZ. И ©Г равна оси копуса М; значит, как А© к оси конуса М, так
и круг М к кругу на диаметре BZ; следовательно, конус, имеющий осно-
ванием круг М, а высотой радиус шара, равен телесному ромбу BAZ©,
[как доказывается в леммах 1 книги. Или же таким образом: поскольку
как А© к высоте конуса М, так и круг М к кругу на диаметре BZ,
то, значит, конус М равен коттусу, основанием которого является круг
на диаметре BZ, а высотой Д0, ибо у них основания обратно пропор-
циональны высотам. Ио конус, имеющий основанием круг па диаметре
BZ, а высотой А©, будет равен телесному ромбу BAZ©J. По конус М
равен телесному сектору BBZ©; значит, телесный сектор BTZ0 будет
равен телесному ромбу BAZ©. Если отнять общий им конус, основанием
которого является круг на диаметре BZ, а высотой Е0, то оставшийся
конус BAZ будет равен сферическому сегменту BZT.
Точно так же докажем, что копус BKZ равен сферическому сег-
менту BAZ. Действительно, так как вместе взятые ©Г, ГЕ относятся
к ГЕ, как КЕ к ЕА,
ОГ + ГЕ _ КЕ
ГВ ЕЛ
то, значит, после «выделения»
«Г КЕ - ЕА
ГЕ ЕЛ
как КЛ к АЕ, так и ©Г к ГЕ.
кд _ ег
ЛЕ ” ГЕ
Но ©Г равна ©А; значит, после перестановки как КА к А©, так
и АЕ к ЕГ;
КА лв
ле ~ ег
отсюда же, «присоединяя»,
К Л + АО АЕ + ЕГ
А.6 ЕГ
как К© к ©А, так и АГ к ГЕ, то есть как (квадрат) на ВА к (квад-
рату) на БЕ.
ке _ лг _ ва*_
«Л — ГЕ — В В®
Построим еще круг N, имеющий радиус, равный АВ; он будет,
следовательно, равен поверхности сегмента BAZ. Затем вообразим
копус N, имеющий высоту, равную радиусу шара; он будет равен
телесному сектору B©ZA, как это доказано в первой книге. Поскольку
же доказано, что как К© к ©А, так и (квадрат) на ЛВ к (квадрату)
на БЕ, то есть как (квадрат) на радиусе круга N к квадрату на радиусе
круга с диаметром BZ, или же как круг N к кругу на диаметре BZ,
и так как А© равна высоте конуса N, то, значит, как К© к высоте
копуса N, так и круг N к кругу на диаметре BZ; значит, конус N,
или же сектор B©ZA, будет равен телу B©ZK. Добавим общий конус,
основанием которого является круг на диаметре BZ, а высота Е©; тог-
да весь сферический сегмент ABZ будет равен конусу BZK, что и тре-
бовалось доказать.
о ШАРЕ И ЦИЛИНДРЕ
147
Следствие
Отсюда ясно, что и вообще сферический сегмент к конусу, имею-
щему то же самое основание, что и сегмент, и равную высоту, отно-
сится, как вместе взятые радиус шара и высота дополнительного'
сегмента относятся к высоте дополнительного сегмента; таким образом,,
как ДЕ к ЕГ, так и конус AZB, или сегмент BTZ, к конусу BFZ.
При тех же самых предположениях докажем, что конус KBZ рав-
няется сферическому сегменту BAZ. Пусть будет конус JN, имеющий
основание, равное поверхности шара, а высотой — радиус шара; этот
конус равен шару, [ибо как доказано, шар в четыре раза больше кону-
са, имеющего основанием большой круг шара, а высотой его радиус.
Но и конус N будет в четыре раза больше этого конуса, так как и его
основание, и поверхность шара в четыре раза больше соответственно
основания второго конуса, и большого круга в шаре]. Поскольку же
вместе взятые. О А, АЕ будут к АЕ, как АЕ к ЕГ,
0А + АЕ _ АЕ
АЕ ЕГ
то, «выделяя»
0А АЕ - ЕГ
АЕ — ЕГ
и переставляя, получим, что как ©Г к ГД, так и АЕ к ЕГ.
ег _ ае
Та""" ег
Затем, так как КЕ кЕА относится, как вместе взятые 0Г, ГЕ к ГЕ,
ке ег + гЕ
НА ' ГЕ
то, «выделяя»
КЕ - ЕЛ = -ОГ-
ЛЕ ЕГ
и переставляя, получим, что КА к ©Г, то есть к ©А, будет, как АК
к ЕГ,
КА _ АЕ
ел ег
то есть как ©Г к ГД.
ка ег
ел ' гл
. После этого, «присоединяя», получим,
KA-J-A0 ег + ГА
ел лг
10*
148
АРХИМЕД
поскольку же А0 равна ©Г, то как К© к ©Г, так и 0Д к ДГ,
ке __ед_
ег " дг
и вся КД будет к Д©, как Д© к ДГ,
кд _ де
до ~ дг
то есть как К© к ©А;
кд ке
де ед
значит, прямоугольник между ДК и ©А равен прямоугольнику менаду
Д© к ©К.
дк-ед = доек
Далее, так как К© относится к ©Г, как ©Д к ГД,
ке = ед
ег дг
или после перестановки: (К© к ©Д, кап ©Г к ГД), и доказано, что
как ©Г к ГД, так и АЕ к ЕГ,
ег _ АЕ
ГД “ ЕГ .
то, значит, как К© к ©Д, так и ЛЕ к ЕГ.
_ке_ _ АЕ
ед ег
Следовательно, как (квадрат), на КД к (прямоугольнику) между
К© и ©Л, так и квадрат на АГ к прямоугольнику между АЕ, ЕГ*).
КД2 ЛГ2
кд-ле” ае ег
Но (прямоугольник) между К© и ©Д, согласно доказанному,
равен прямоугольнику менаду КД и А©; значит, как квадрат на КД
к прямоугольнику между КД, А©, то есть как КД к А©, так и квадрат
на АГ к прямоугольнику между АЕ, ЕГ, то есть к квадрату па ЕВ8.
КД АГ®
де‘ ев2
Но АГ равна радиусу круга JN; значит, как (квадрат) па радиусе
круга N к (квадрату) на BE, то есть как круг N к кругу па диаметре
BZ, так и КД к А©, то есть КД к высоте конуса N: значит, конус N,
то есть шар, будет ранен телесному ромбу BAZK. [Или же так: посколь-
ку круг N относится к кругу на диаметре BZ, как ДК к высоте конуса N,
то, значит, конус N будет равняться конусу, основанием которого
является круг на диаметре BZ, а высота ДК, так как у обоих основания
обратно пропорциональны высотам. Но последний конус равен телес-
*) Ото равенство может быть получено так. Из иропорцнп ке: ОД-- АН: ЕГ получаем сна-
чала «присоединением»
(Кб 4- ОД) : ед = (АТС 4 КГ): ГЕ
Возводим оба члена к квадрат;
КД2 : Д02 = АГ2 : ГЕ2. (I )
Первоначальную пропорцию КеЧИЛ—ЛЕгЕГ мы можем предотаппть в виде
(ке-ел) : еД« = (АЕ-ЕГ) : ЕГ®. (2)
Теперь на сравнения обеих пропорций (I) и (2) получаем
КД® : (ке ед) «= АГ2 : (АЕ- ЕГ) .
О ЩЛРЕ И ЦИЛИНДРЕ
149
ному ромбу BKZA; следовательно, конус N, то есть шар, будет равен
телесному ромбу BZKA]. Из конусов, составляющих последний, конус
BAZ будет, согласно доказанному, равняться сферическому сегменту
BBZ; значит, остающийся конус BKZ будет равен сферическому сег-
менту BAZ.
III
Третья задача была такова: данный шар рассечь плоскостью так,
чтобы поверхности, получившихся сегментов находились бы друг к другу
в отношении, равном заданному.
Пусть это уже сделано; пусть большой круг шара будет АЛВЕ, а
его диаметр АВ. Проведем плоскость, перпендикулярную к АВ, и пусть
Рис. 48.
гл
ГВ
эта плоскость образует в круге АЛВЕ сечение ДЕ; проведем соединяю-
щие прямые АД и ВД.
Так как отношение поверхности сегмента ДАЕ к поверхности сег-
мента ДВЕ (является данным), и круг, радиус которого равен АЛ, равен
поверхности сегмента ДАЕ, а круг, радиус которого равен ДВ, равен
поверхности сегмента ДВЕ и упомянутые круги будут друг к другу, как
квадрат па А/Х к квадрату па ЛВ, то есть как АГ к ГВ, то, значит,
будет данным и отношение АГ к ГВ; следовательно, будет данной
и точка Г. Далее, АВ перпендикулярна к ДЕ; значит, будет дана поло-
жением и проходящая через ДЕ плоскость.
Синтез задачи производится так. Пусть будет шар, у которого
большой круг ЛВДЕ и диаметр АВ; и пусть заданное отношение будет
тем, которое прямая Z имеет к Н. Разделим АВ в точке Г так, чтобы
отношение АГ к ГВ равнялось отношению Z кН;
z
н
через полученную точку Г рассечем шар плоскостью, перпендикуляр-
ной прямой АВ; пусть общее сечение будет ДЕ; проведем соединяющие
прямые АД и ДВ и построим два круга К, 0 такие, чтобы круг 0 имел
радиус, равный ЛА, а круг К — радиус, равный ДВ; тогда круг 0 будет
равен поиерхпости сегмента ДАЕ, а круг К — поверхности сегмента
ДВЕ, как уже доказано в первой книге. И так как угол АДВ — прямой
и ГД — перпендикуляр, то будет, что как АГ к ГВ, то есть как Z к Н,
150
АРХИМЕД
так и квадрат па АД к квадрату на ДВ, то есть квадрат на радиусе
круга 0 к квадрату на радиусе круга К, то есть как круг 0 к кругу К,
и, наконец, как поверхность сферического сегмента ДАЕ к поверхно-
сти сегмента ДВЕ.
IV
Разделить данный шар так, чтобы его сегменты имели друг к дру-
гу отношение, равное заданному.
Пусть данный шар будет АВГД (рис. 49}; требуется рассечь его
плоскостью так, чтобы сферические сегменты имели друг к другу отно-
шение, равное заданному.
Рассечем его плоскостью через АГ; тогда отношение сферического
сегмента АДГ к сферическому сегменту АВГ будет заданным. Рассечем
также шар через центр (плоскостью, перпендикулярной к АГ);
пусть сечепием будет большой круг АВГД с центром К и диаметром ДВ;
затем сделаем так, чтобы вместе взятые КД, ДХ имели к ДХ такое же
отношение, как некоторая прямая РХ к ХВ,
кд+дх_ рх
дх — хв
а вместе взятые КВ, ВХ имели к ВХ такое же отношение, как некоторая
другая прямая АХ к ХД,
кв+вх _ дх
””ВХ ХД*
и проведем соединяющее прямые АЛ, АГ, АР, РГ; тогда копус АЛГ
будет равен сферическому сегменту АДГ, а копус АРГ — сегменту
АВГ; значит, будет заданным и отношение конуса АЛГ к конусу АРГ
[2]. Но как один конус относится к другому, так будет относиться
и АХ к ХР, [поскольку конусы имеют одно и то же основание — круг
на диаметре АГ]; следовательно, отношение АХ к ХР является даппым.
(1) . Па основании предыдущего, согласно построению, имеем,
что ЛД будет к КД, как КВ к ВР и ДХ к ХВ.
АД КВ ДХ
КД ВР хв
(2) . И так как РВ будет к ВК, как КД к АД, то после «присо-
единения» РК будет к КВ, или к КД, как КЛ к ЛД;
рв+вк _ кд+лл _ рк кл
КВ АЛ КД ЛД \
значит, вся РЛ будет ко всей КЛ, как КЛ к ЛД,
РК+КЛ _ РЛ = кл
КДт-ДЛ ~ кл ЛД '
О ШАРИ И ЦИЛИНДРЕ
151
и, следовательно, (прямоугольник) между РА, АД равен квадрату
на ЛК. Значит, как РЛ к ЛА, так будет и (квадрат) на КА к (квад-
рату) на ЛД.
гл кла
ЛД — ЛА*
(3) . И поскольку АЛ будет к ДК, как ДХ к ХВ,
лл _ ДХ
дк ЙГ
то после «обращения» и'«присоединения» будет, как КЛ к ЛД, так
и ВД к ДХ,
КД4-ЛЛ = вх+хд кл _ вд
ЛД ДХ ЛД ДХ
[и, значит, как квадрат на КЛ к квадрату на ЛД, так будет и квадрат
на ВД к квадрату на ДХ.
(4) . Далее, поскольку ЛХ будет к ДХ, гсак вместе взятые КВ,
ВХ к ВХ, то после «выделения» — как ЛД к ДХ, так и КВ к ВХ].
лх—хд лд _ кв
ДХ " ДХ ВХ
(5) . Теперь отложил» прямую BZ, равную КВ; ясно, что (ее
конец Z) упадет далее Р, [и получится, что как ЛД к ДХ, так будет
и ZB к ВХ; таким образом, как ДЛ к ЛХ, так и BZ к ZX].
(6) . Поскольку же отношение ДЛ к ЛХ является данным, то,
значит, будет данным и отношение РЛ к ЛХ. Теперь, так как отношение
РЛ к ЛХ составлено из отношений РЛ к ЛД и ДЛ к ЛХ,
РА ГА АД
ЛХ ' АД ’ ЛХ
и РЛ будет к ЛД, как квадрат на ДВ к квадрату па ДХ,
ГЛ АВД
ЛД - дкд
а ДЛ к ЛХ, как BZ к ZX,
АЛ _ FZ
ЛХ” ZX
то, значит, отношение РЛ к ЛХ составится из отношения квадрата на
ДВ к квадрату на ДХ и отношения BZ к ZX.
гл _ ВД2 BZ
лх — ДХ2 их
(7) . Сделаем теперь, чтобы отношение РЛ к ЛХ равнялось отно-
шению BZ к некоторой прямой Z0.
1’Л
ЛХ = ~Й»
Но отношение РЛ к ЛХ дано; значит, будет дано и отношение ZB к Z0.
Дана также и прямая BZ, ибо опа равна радиусу; значит, будет дан-
ной и Z0. Следовательно, отношение BZ к Z0 составляется из отноше-
ния квадрата на ВД к квадрату на ДХ и отношения BZ к ZX.
BZ ВД2 BZ
ZW — ДХ2 ZX
Но отношение BZ к Z& сложится из отношений BZ к ZX и ZX к Z0;
HZ В7. 7V
152
АРХИМЕД
[отбрасываем общее отношение BZ к ZXJ; тогда останется, что (квад-
рат) па ВЛ, то есть заданная величина, так относится к квадрату
(на) АХ, как XZ к Z0, то есть тоже к заданной величине.
ВД2 JCZ
ЛХ2 —
По прямая ZA дана; следовательно, заданную прямую AZ требуется
разделить в точке X так, чтобы отношение XZ к заданной прямой
[Z0J равнялось отношению заданной площади [квадрата на BAJ
к (квадрату) на АХ. Выраженная в таком общем виде задача требу-
ет диоризма*), но при наличии условий, присущих рассматриваемой
задаче, [а именно, когда АВ вдвое больше BZ и Z0 меньше ZB, как
следует из произведенного анализа], диоризм пе требуется. Итак, дело
сводится к такой задаче:
Даны, две прямые ВД, BZ, причем ВД вдвое больше BZ, и на прямой
BZ дана точка 0; требуется рассечь АВ в некоторой точке X так,
чтобы (квадрат) на ВД относился бы к (квадрату) на ДХ., как
отрезок XZ к Z0; анализ и синтез этой задачи будут даны в конце.
Синтез же основной задачи производится так:
Пусть заданное отношение представляется отношением большей
прямой П к меньшей S; пусть дан некоторый шар, рассеченный через
центр плоскостью, причем в сечении получается круг .АВГД с диаметром
ВД и центром К. {рис. 50}. Отложим равную К.В прямую BZ и рас-
сечем BZ в точке 0 так, чтобы 0Z относилась к 0В, как П к S, затем
рассечем ВД в точке X так, чтобы XZ относилась к 0Z, как (квадрат)
на ВД к (квадрату) на ДХ,
хи вд»
WZ. ДХ2
и проведем через X перпендикулярную к ВД плоскость. Я утверждаю,
что эта плоскость так рассечет шар, что больший сегмент будет отно-
ситься к меньшему, как прямая II к S.
Действительно, сделаем, чтобы вместе взятые прямые КВ, ВХ от-
носились к ВХ так же, как ЛХ к ДХ,
квт-вх лх
вх ~ дх
а вместе взятые прямые КД, ДХ относились к ХД, как РХ к ХВ,
кд+дх рх
хд ” хв
') См. комментарий £2], стр. 483 и сл.
о шаре и ЦИЛИНДРЕ
153
и проведем соединяющие прямые АЛ, Л Г, АР, РГ; тогда, как мы дока-
зали в анализе, согласно построению, (прямоугольник) между
РЛ, ЛД будет равен (квадрату) на ЛК,
рл-лд=лк2
и как КЛ к ЛЛ, так будет п ВА к АХ;
КЛ _ вд
ЛД ДХ
таким образом, 'как (квадрат) на КЛ к (квадрату) на ЛД, так будет
и (квадрат), на ВД к (квадрату') на ДХ.
кл2 вда
ЛД2“ ДХ2"
Но так как (прямоугольник) между РЛ и ЛА равен (квадрату) на
ЛК [и отношение РЛ к ЛД равно отношению (квадрата) на ЛК к
(квадрату) наЛЛ], то получится, что РЛ относится кЛА,как (квадрат)
на ВА к (квадрату) на АХ или как XZ к Z0.
вл _ ИД2 XZ
лд
Далее, поскольку вместе взятые КВ, ВХ относятся к ВХ, как ЛХ к ХА,
л КВ равна BZ, то, значит, ZX будет к ХВ, как ЛХ к ХА*).
ки+ву _ 7Х _ ЛХ
ВХ ХВ — хд
После «переворачивания»**), как XZ к ZB, так и ХЛ к ЛЛ;
хи _ хл
ив — ЛД
таким образом, как ЛА к ЛХ, так и BZ к ZX. Затем, поскольку РЛ
к ЛА, как XZ к Z©,
вл хи
лд ~ и«'
И АЛ к ЛХ, как BZ к ZX,
л л _ их
ДА Хд.
то по равенству в «перемешанной» пропорции***) будет, что как РЛ
кЛХ, так и BZ к Z0;
гл ни
лх ' и<->
и, следовательно, как ЛХ к ХР, так и Z0 к 0В.
лх ze лх ze>
РЛ-ЛХ“ВХ Z6 ' ХР “ НВ
Но как Z0 к ©В, так и П к X;
ИН _ II
"мВ X
и значит, как ЛХ к ХР, то есть как копус АГЛ к конусу АР Г или сфе-
рический сегмепт АДГ к сферическому сегменту АВГ, так и прямая
П к S.
*) ZX=Zm-BX, лх=лд-ьдх.
<2 С
**) Операция «переворачивания (avcarrcei|’Ctvti)» состоит в том, что ив пропорции —=j-
„ а с XZ ХЛ
оОразуется Здесь ~ .
•**) Си. «Начала», V. 21.
154
АРХИМЕД
V
Построить сферический сегмент, подобный одному и равный дру-
гому, из заданных сферических сегментов.
Пусть АВГ и EZII будут два заданных сферических сегмента;
пусть у сегмента АВГ основанием будет круг па диаметре АВ, а верши-
ной точка Г, и у сегмента EZH основанием будет круг на диаметре EZ,
а вершиной точка II. Требуется найти сферический сегмент, который был
бы равен сегменту АВГ и подобен сегменту EZH {рис. 51}.
Пусть он найден и будет 0КЛ; пусть его основанием будет круг
на диаметре ОК, а вершиной точка Л. В соответствующих шарах возь-
мем (большие) круги ANBT, ©±КЛ, EOZH; пусть их диаметры
TN, ЛЕ, НО будут перпендикулярны к основаниям соответствующих
сегментов, а центры находятся в точках П, Р, 2. Сделаем, чтобы
отношение вместе взятых прямых nN, NT к NT равнялось отношению
некоторой прямой XT к ТГ;
пи+хт XT
КТ~ —ТГ
отношение же вместе взятых РЗ, ЕГ к ЕГ равнялось отношению
некоторой прямой ТГ к ГЛ
РЕД ВГ _ ЧТ
в Г — ГД
и отношение вместе взятых 20, ОФ к ОФ равнялось отношению некото-
рой прямой НФ к ФН,
2О+ОФ П !
оф чТн
и вообразим конусы, основаниями которых будут круги на диаметрах
ЛВ, OK, EZ, а вершинами точки X, У, Й; тогда кснус АВХ будет равен
сферическому сегменту АВГ, конус W0K равен сегменту ОКА и конус
EQZ — сегменту EIIZ; все это уже было доказано.
Так как сферический согмепт ЛВГ равен сегменту ОКА, то, значит,
и копус ЛХВ будет равен конусу Т ОК; |у равных же конусов основа-
ния обратно пропорциональны высотам!; значит, круг на диаметре АВ
О JIIAPE И ЦИЛИНДРЕ
155
будет к кругу на диаметре ©К, как прямая ЧЕ к XT. Но первый круг
относится ко второму, как (квадрат) на АВ к (квадрату) на ©К.;
значит, как (квадрат) на АВ к (квадрату) па ©К, так будет и ЧЕ
к XT.
два
йка ~ "хт"
И так как сегмент EZH подобен сегменту ©КЛ, то, значит, и конус
EZQ будет подобен конусу Ч©К [это еще будет доказано]*); следова-
тельно, как ЙФ к EZ, так будет и ЧЕ к ©К.
<гт
EZ “«IT
Но отношение ЙФ к EZ дано; следовательно, будет дано и отношение ЧЕ
к ©К. Пусть это отношение будет таким же, как отношение XT к не-
которой прямой А;
Ч’Г _ хт
нк д’
так как ХТ дана, то, значит, будет дала и А. И поскольку ЧТ к ХТ,
или (квадрат) на АВ к (квадрату) на ©К, относятся, как прямые
©К и А,
ч’г ав2 _ ек
хт — ька ~ Ь
то положим (квадрат) на ©К равным (прямоугольнику) между ЛВ
и некоторой прямой 1;
ОК2=АВ-1
тогда получится, что как (квадрат) на АВ к (квадрату) на ©К,
так будет и АВ к I.
AB2 АВ
ока "" 1
Но доказало, что отношение (квадратов) на АВ и на ©К равно отно-
шению ©К и А, и после перестановки отношение АВ к ©К будет равно
отношению I к А.
АВ I
ек ’ а
Но как АВ к ©К, так будет ©К к I
ав «к
ек ’ I
[вследствие равенства (квадрата) па ©К (прямоугольнику) между
АВ и I]; значит, как АВ к ©К, так и ©К к I и I к А.
ав д ек I
ек I ' д
Следовательно, ©К и I будут двумя средними пропорциональными
в непрерывной пропорции между двумя заданными прямыми АВ и А.
Л синтез этой задачи производится так. Пусть АВГ будет тот
сегмент, которому искомый должен быть равеп, a EZH — тот, кото-
рому он должен быть подобен; пусть большие круги соответствующих
шаров будут ABTN, EHZO, их диаметры TN, НО и центры П, Z.
*) Для нас и, вероятно, длп Архимеда это является очевидным, но Евтокий дает этому поло-
жению подробное доказательство. Это объясняется тем, что греки ле имели общего понятия о подобии
фигур и определяли его для каждого типа фигур самостоятельно; так, условием подобия сегментов
было равенство соответствующих им нейтральных углов, а условием подобия конусов — равенство
отношений высот к диаметрам оснований.
156
АРХИМЕД
Сделаем, чтобы отношение вместе взятых прямых ITN, NT к NT равня-
лось отношению некоторой прямой XT к ТГ,
HN-INT XT
NT ТГ
а отношение вместе взятых SO, Оф к ОФ равнялось отношению неко-
торой прямой С2Ф к ФН;
хо+оф по»
ОЧ> ФН
тогда конус ХАВ будет равен сферическому сегменту АГВ, а (конус)
ZQE — (сегменту) EHZ. Сделаем, чтобы отношение ЙФ к EZ равня-
лось отношению XT к некоторой прямой Л,
йф хт
EZ л
и между двумя заданными прямыми АВ, Д возьмем две средние пропор-
циональные 0К, I так, чтобы как АВ к ©К, так и К® к I и I к А;
ав _ кн, I
ек I а
на ®К построим круговой сегмент ©КЛ, подобный круговому сег-
менту EZH, затем дополним круг; пусть его диаметр будет AS. После
этого вообразим шар с большим кругом Л0ЕК. и центром Р, и через 0К
проведем перпендикулярную ЛЕ плоскость; тогда сферический сег-
мент, расположенный со стороны Л, будет подобен сферическому
сегменту EHZ вследствие того, что подобны и соответствующие кру-
говые сегменты.
Теперь я утверждаю, что этот сегмент будет также равен сфери-
ческому сегменту АВГ. Сделаем, чтобы отношение вместе взятых
РЕ, ЕГ к ЕГ равнялось отношению некоторой прямой гГГ к ГЛ;
РЕ+5Г _ _ЧТ
ЕГ — ГЛ
тогда конус Чг0К будет равеп сферическому сегменту ®КЛ. И так
как конус ЧГОК подобен конусу ZQE, то значит, как РФ к EZ, то есть
как ХТ к А, так и ТТ к 0К;
яф _хт _чт
EZ “ Д “ ВК
а после перестановки и «обращения» получится, что как *РГ к ХТ,
так и 0К кА.
чт ек
хт ~ д’
И так как АВ, К®, I, А составляют (непрерывную) пропорцию, то
отношение (квадратов) на АВ и ®К равно отношению ©К к А.
лв* ек
ек* д
Но как ©К к Л, так и "ЕГ к ХТ;
ек _ чт
д ~ хт
и, значит, как (квадрат) на ДВ к (квадрату) на К®, то есть как
круг на диаметре АВ к кругу на диаметре ©К, так будет и прямая VY
к ХТ;
АВ* ЧТ
КО* XT ....
О ШАРЕ И ЦИЛИНДРЕ
157
следовательно, конус ХАВ будет равен конусу V0K, так что и сфери-
ческий сегмент АВГ будет равен сферическому сегменту 0КЛ. Итак,
построен сегмент OKA, равный данному сегменту АГВ и подобный
другому данному сегменту EZH.
VI
Для двух данных сегментов, принадлежащих одному или различ-
ным шарам, построить сферический сегмент, подобный одному из дан- '
ных и имеющий поверхность, равную поверхности другого сегмента.
Пусть на дугах АВГ и AEZ будут даны два сферических сегмента
{рис. 52j, пусть дуге АВГ соответствует тот, которому должен быть
в
Рис. 52.
подобен искомый, а дуге AEZ — тот, поверхности которого должна
равняться поверхность искомого.
Пусть требуемое будет выполнено и сферический сегмент КАМ
подобен сегменту АВГ и имеет поверхность, равную поверхности сег-
мента AEZ. Представим себе центры этих шаров и проведем через них
плоскости, перпендикулярные к основаниям сегментов, и пусть в сече-
ниях с шарами получатся большие круги KAMN, ВАГ0, EZHA, а в се-
чениях с основаниями сегментов — прямые КМ, АГ, AZ; пусть AN,
В0, ЕН будут диаметры шаров, перпендикулярные к КМ, АГ, AZ,
и проведены прямые ЛМ, ВГ, EZ.
Так как поверхность сферического сегмента КАМ равна поверх-
ности сегмента AEZ, то, значит, круге радиусомЛМ будет равен кругу
с радиусом EZ, [ибо поверхности упомянутых сегментов, как было
доказано, равны кругам, радиусы которых представляют прямые, про-
веденные от вершин сегментов к окружностям оснований], так что
прямая МЛ будет равна EZ. Поскольку же сегмент КАМ подобен сег-
менту АВГ, то АР будет к PN, как ВП к П0,
ар вп
pn ~ не
тогда после «обращения»
NP 6П
РА ПВ . . L
и «присоединения»
NP+PA _ вп+ПВ
АР - ВП - '
158
АРХИМЕД
NA будет к ЛР, как ©В к ВП.
кл ев
лр ~ ви
Но как РА к ЛМ, так будет и ВП к ГВ,
рл вп
лм гв
[ибо соответствующие треугольники подобны]; значит, как NA кЛМ,
или к EZ, так и 0В к В Г.
NA NA OB
ЛМ KZ ’" ВГ
После перестановки {NA к В©, как EZ к ВГ};
_NA __EZ
ве _ вг
отношение ?ке EZ к ВГ дано, ибо даны обе прямые, следовательпо,
будет дано и отношение AN к В©. И прямая В© дана; значит, дана
и AN; таким образом, будет дан и соответствующий шар.
А синтез производится так. Пусть данные два сферических
сегмента будут АВГ, AEZ, причем искомый должен быть подобен сег-
менту АВГ и иметь поверхность, равную поверхности сегмента AEZ.
Выполним те же самые построения, что и при апализе, и сделаем, чтобы
отношение ВГ к EZ равнялось отношению В© к некоторой прямой AN;
вг ве
EZ - AN
на диаметре AN построим круг и вообразим шар с большим кругом
AKNM; прямую NA разделим в точке Р так, чтобы NP была к РА,
как 0П к ПВ,
NP «П
РА ПВ
поверхность шара рассечем плоскостью, проведенной через Р
и перпендикулярной к AN, и проведем соединяющую прямую AM; тог-
да круговые сегменты, построенные ла прямых КМ, АГ, будут подобны,
так что будут подобны и соответствующие сферические сегменты.
И поскольку ©В будет к ВП, как NA к АР
©В _ NA
ВП АР'
(ибо так получается после «выделения»*)), и как ИВ к ВГ, так и РА
к ЛМ,
пв РЛ
вг — лм
то, значит, ©В будет к NA, как ВГ к ЛМ.
©в вг
NA — ЛМ
Но также было, что как ©В к AN, так и ВГ к EZ;
ев вг
AN EZ
значит, EZ равна ЛМ, так что и круг с радиусом EZ будет равен кругу,
радиус которого равен ЛМ. Но круг, имеющий радиусом EZ, равен
*) В действительности после «присоединения»
(0П4.ПВ) : В11=(МГ+РЛ): ЛР.
О ШАРЕ И ЦИЛИНДРЕ
159
поверхности сегмента AEZ, а круг, радиус которого равен ЛМ, равен
поверхности сегмента КЛМ (это было доказано в первой книге); зна-
чит, и поверхность сегмента КЛМ будет равна поверхности сфериче-
ского сегмента AEZ, и сегмент КЛМ подобен сегменту ЛВГ.
VI
От данного шара отсечь плоскостью сегмент так, чтобы этот сег-
мент имел заданное отношение к конусу, имеющему с сегментом одно
и то же основание и равную высоту.
Пусть дан шар с большим кругом АВГД {рис. 53}; пусть ВД будет
его диаметр. Плоскостью, проходящей через ЛГ, требуется рассечь
этот шар так, чтобы сферический
сегмент ЛВГ имел заданное отно-
шение к конусу АВГ.
Пусть все это сделано; пусть
центр шара будет в точке Е, и пусть
отношение вместе взятых ЕД, AZ
к AZ будет равно отношению неко-
торой прямой HZ к ZB;
EA-|-AZ_ HZ
Д2 “ ZB
тогда конус АГН будет равен сегмен-
ту АВГ. Значит, дапо и отношение
конуса АН Г к конусу АВГ, а следо-
вательно, и отношение прямой HZ к ZB. Но HZ относится к ZB, как
вместе взятые ЕД. AZ к AZ; значит, будет данным и отношение вместе
взятых ЕД, AZ к AZ, [а также и отношение ЕД к AZ; следовательно,
будет дана и AZ,], а также и АГ. И так как вместе взятые ЕД, AZ имеют
к AZ отношение большее, чем вместе
взятые ЕД, ДВ к ДВ,
ЕД+Д2 _ ЕД ] ДВ
'' ЛВ
и вместе взятые ЕД, ДВ равны утро-
енной ЕД, а ВД равна удвоенной ЕД,
то, значит, вместе взятые ЕД, AZ
имеют к AZ отношение большее, чем
три к двум. И отношение вместе взя-
тых ЕД, AZ к AZ равно заданному;
значит,
заданное
больше, чем три к двум.
Синтез проблемы произво-
дится так. Пусть будет дан шар
с большим кругом АВГД, диаметром
ВД и центром Е {рис. 54], и пусть заданное отношение, равное
отношению прямых 0К к КЛ, будет больше, чем три к двум. Но-
отношение трех к двул! представляет отношение вместе взятых пря-
мых ЕД, ДВ к ДВ;
ЕА+ДВ _ 3
ДВ ’ 2
Рис. 54.
Л7.
при выполнении синтеза
отношение должно быть
160
АРХИМЕД
значит, ©К будет иметь к КЛ отношение, большее того, которое вместе
взятые ЕД, АВ имеют к АВ;
ек ЕА+ЛВ
кл дв
значит, после «выделения»*) ©Л будет иметь к ЛК большее отношение,
чем ЕА к АВ.
ел Ед
лк > дв
Сделаем, чтобы отношение ©Л к ЛК равнялось отношению ЕА к неко-
торой прямой AZ;
ед _ ед
лк ~ AZ
через полученную точку Z перпендикулярно к. ВД проведем прямую
AZB, и через эту прямую ЛГ перпендикулярно к ВЛ проведем плос-
кость. Я утверждаю, что сферический сегмент АВГ имеет к конусу
АВГ то же отношение, что ©К к КЛ.
Действительно, сделаем, чтобы отношение вместе взятых ЕД, AZ
к AZ равнялось отношению некоторой прямой HZ к ZB;
EA+AZ__HZ
AZ~" ZB
тогда конус ГАН будет равен сферическому сегменту АВГ. И так как
©К относится к КЛ, как вместе взятые ЕА, AZ к AZ, или как HZkZB,
то есть как конус АН Г к конусу АВГ, и конус АН Г равен сферическо-
му сегменту АВГ, то, значит, как сегмент ЛВГ к конусу ЛВГ, так
будет и ©К к КЛ.
VIII
Если шар рассечен плоскостью, не проходящей через центр, то боль-
ший сегмент имеет к меньшему отношение, которое будет меньше
двойного, но больше полуторного отношения поверхности большего
сегмента к поверхности меньшего [3].
Пусть будет шар и в пем большой круг АВГА с диаметром ВД
{рис. 55); рассечем его плоскостью, проходящей через АГ и перпен-
дикулярной к кругу АВГА; пусть больший сегмент шара будет АВГ.
Я утверждаю, что сегмент АВГ имеет к АД Г отношение, меньшее двой-
ного, но большее полуторного отношения поверхности большего сег-
мента к поверхности метшего сегмента.
> (ОК—КЛ) : ЛК > ЕЛ : ДВ.
О ШАРЕ И ЦИЛИНДРЕ
161
Действительно, проведем соединяющие прямые ВА и АА; пусть
центр шара будет Е; сделаем, чтобы отношение вместе взятых ЕА, AZ
к AZ равнялось отношению некоторой прямой ©Z к ZB,
Ea+az ez
az “ zb
а отношение вместе взятых ЕВ, BZ к BZ равнялось отношению некото-
рой прямой HZ к ZA,
KB+BZ HZ
bz — za
и вообразим конусы, имеющие основанием круг на диаметре АГ, а вер-
шины в точках би Н; тогда конус А© Г будет равен сферическому сег-
менту АВГ, а конус АГН — сегменту АДГ, и поверхность сегмента
АВГ к поверхности сегмента ЛАГ будет относиться, как (квадрат) на
В А к (квадрату) па АД; ото уже было написано выше. [Требуется
доказать, что больший сферический сегмент имеет к меньшему отно-
шение, меньшее двойного отношения поверхности большего сегмента
к поверхности меньшего сегмента.] Я утверждаю, что отношение кону-
са АВГ к конусу АН Г, или прямой Z© к прямой ZH, будет меньше
двойного отношения (квадрата) на В А к (квадрату) на АД, то
есть отношения прямой BZ к прямой ZA.
Так как отношение вместе взятых ЕЛ, AZ к AZ равно отношению
©Z к ZB,
ед+az ez
AZ — ZB
[и отношение вместе взятых ЕВ, BZ к BZ равно отношению ZH к ZA],
то BZ будет к ZA, как ©В к BE,
bz _ oz _ ez—bz _ ев
ZA E A - j- Л X ЕЛ BE
ибо BE равна ДЕ; [все это уже было доказано раньше].
Далее, поскольку отношение вместе взятых ЕВ, BZ к BZ равно
отношению IIZ к ZA,
KB+BZ HZ
bz za
то пусть прямая ВК будет равна BE (ясно, что ©В будет больше BE,
так как BZ больше ZA); тогда получится, что как KZ к ZB, так и
IIZ к ZA.
KZ 'HZ
“zb _“za“
Но как ZB к ZA, так, согласно доказанному, будет и ©В к BE,
zb _ ев
za be
и BE равна КВ; значит, как ©В к ВК, так и KZ к ZH.
0В^ _ KZ_
ВК ZII
И так как ©Z имеет к ZK отношение меньшее, чем ©В к ВК,
<->z _ ев
zk- ВК
а как 0В к ВК, так по доказанному и KZ к ZH, то, значит, ©Z имеет
к ZK отношение меньшее, чем KZ к Z1I;
ez _к?_
zk < zh
11 Архимед
162
АРХИМЕД
значит (прямоугольник) между ©Z, ZH меньше (квадрата) на ZK.
az-zh<- zk®
Следовательно, (прямоугольник) между ©Z, ZII к (квадрату) па
ZH, [то есть Z© к ZII], имеет отношение меньшее того, какое (квадрат)
на KZ имеет к (квадрату) на ZII.
HZ-ZH KZ*
ZH® ZIP
[Но (квадрат) на KZ к (квадрату) на ZH имеет (отношение,
равное) двойному отношению KZ к ZH]; значит, 0Z имеет к ZIT отно-
шение, меньшее двойного отношения K.Z к ZH.
AZ , ( KZ
“zh \ ZH )
[По K.Z к ZII (будет, как BZ к ZA; значит, ©Z к ZT[) имеет отноше-
ние, меныпее двойного отношения BZ к ZA], а это мы и искали.
И так как BE равна ЕД, то (прямоугольник) между HZ, ZA
меньше (прямоугольника) между BE, ЕД*),
BZ-ZA < BE-ЕД
значит, ZB имеет к BE отношение меньшее, чем ЕД к AZ, или ©В к BZ;
zb вд ев
be < az ~ bz
значит, (квадрат) на ZB будет меньше (прямоугольника) между
0В, BE или (прямоугольника) между 0В, ВК.
ZB2 <ев-вк
Пусть (прямоугольник) между 0В, ВК будет равен (квадрату)
на некоторой прямой BN;
ев - вк В№
тогда как ©В к ВК, так будет и (квадрат) па 0N к (квадрату)
на NK**)'.
ев ек®
Вк"~ NK®
Но (квадрат) на ©Z к (квадрату) на ZK имеет большее отношение,
чем (квадрат) на ©N к (квадрату) на NK,
HZ2 . AN®
7. ><2 '' NK®
[и, значит, (квадрат) па ©Z к (квадрату) на ZK имеет отношение
большее, чем ©В к ВК, или 6) В к BE, или же KZ к ZH]; значит, ©Z
имеет к ZH отношение, большее полуторного отношения KZ к ZII;
з
AZ ( KZ \2
ZH ' ( ZH /
[это (будет доказано) под конец] [4]. Но отношение 0Z к ZH равно
отношению конуса АВГ к конусу АНГ, или сегмента АВГ к сегменту
АДГ, отношение же KZ к ZII равно отношению BZ к ZA, или (квад-
рата) на ВА к (квадрату) па ЛД, или поверхности сегмента АВГ
к поверхности сегмента АДГ. Итак, больший сегмент имеет к меньшему
отношение, меныпее двойного, но большее полуторного отношения
поверхности большего сегмента к поверхности меныпего.
*) Геометрически йго равносильно тому, что при равных периметрах площадь киадрата'Судет
дольше площади соответствующего прямоугольника.
'*) BN : ВК—АВ : BN^(OB+BN) : (BN+ BK)=AN : NK-
О ШАРЕ И ЦИЛИНДРЕ
ieb
Иным способом
Пусть будет шар с большим кругом АВГД, диаметром АГ и цент-
ром Е; рассечем его проходящей через ВД плоскостью, перпендикуляр-
ной к АГ {рис- 56}. Я утверждаю, что больший сегмент ДАВ к мень-
шему ВГД имеет отноше-
ние, меньшее двойного, но
большее полуторного от-
ношения поверхности сег-
мента АВД к поверхно-
сти сегмента ВГД.
Проведем соединяю-
щие прямые /\В и В Г;
тогда отношение одной
поверхности к другой бу-
дет таким же, как отноше-
ние круга с радиусом АВ
к кругу с радиусом В Г, или отношение прямой АО к ОГ. Положим,
что каждая из прямых AZ и ГН будет равна радиусу круга. Тогда отно-
шение сегмента ВАД к сегмепту ВГД составляется из того отношения,
которое сегмент ВАД имеет к конусу с основанием, равным кругу на
диаметре ВД и с вершиной в точке А, затем из того, которое этот копус
имеет к конусу с тем же основанием и с вершиной и точке Г и, наконец,
из того, которое только что упомянутый конус имеет к сегменту ВГД.
сегмент ВАД сегмент ВАЛ кпнус ВЛД кпнус ВГД
сегмент ВГД конус ВАЛ конус ВГД сегмент ВГД
Но отношение сегмента ВАЛ к конусу ВАЛ есть отношение НО к ОГ,
сегмент ВАД Н6
конус ВАЛ “ «Г
отношение конуса ВАД к конусу ВГД есть отношение АО к О Г,
конус ВАД _ А0
кон ус ВГД —’ 0Г
и отношение конуса ВГД к сегмепту ВГД есть отношение АВ к OZ,
КОцус ВГА _ АО
сегмент ВГА — OZ
отношение же, составленное из (отношений) НО к ОГ и АО к ОГ,
будет отношением (прямоугольника) между НО, НА к (квадратур
на О Г,
не ай не-ел
ег ег"' era
отношение же (прямоугольника) между ПО, ОА к (квадрату) на
©Г, составленное с отношением АН к 0Z, будет отношением (прямо-
угольника) между НО, ©А, (умноженного) на ОА, к (квадрату)
на О Г, (умноженному) на 0Z,
не-ел ле _ (не ель ле
ег2 ' ez ’ er«ez
а (прямоугольник) между ПО, ©А, (умноженный) на ОА, пред-
ставляет (квадрат) па ОА, (умноженный) на ОП. Таким образом,
(нужно доказать, что) квадрат на ОА, (умноженный) па ОН, имеет
И*
164
АРХИМЕД
к (квадрату) на ©Г, (умноженному) па ©Z, отношение, меньшее
, двойного отношения А® к ©Г,
йа2-йн _ де»
era-oz • era
[ибо двойное отношение А® к ®Г есть отношение (квадрата) на А®
к (квадрату) на ®Г]. Следовательно, (квадрат) на А®, (умножен-
ный) на ©Н, к (квадрату) на ®Г, (умноженному) на ®Z, (дол-
жен) иметь отношение, меньшее, чем (квадрат) на А®, (умно-
женный) на ®П, к (квадрату) на ®Г, (умноженному) на ©Н.
АОа.ен ' ЛЙ2-ЙН
era-ez - геа-ен
Итак, (нужно доказать), что (квадрат) на ®Г, (умноженный)
на Z©, больше (квадрата) на ®Г, (умноженного) на ©И,
er2-z&> ег2-ен
или что ©Z больше 0Н; (последнее же очевидно).
Теперь я утверждаю, что больший сегмент имеет к меньшему отно-
шение, большее полуторного отношения поверхностей.
Ио доказанному, отношение сегментов равно отношению (квад-
рата) на Л®, (умноженного) на ©Н, к (квадрату) на Г0,
(умноженному) на 0Z, а полуторное отношение поверхностей равпо
отношению куба на АВ к кубу на ВГ; итак, я утверждаю, что (квад-
рат) па А®, (умноженный) па ©И, к (квадрату) на Г®, (умно-
женному) на ©Z, имеет отношение большее, чем [куб па АВ к кубу
на ВГ, или чем! куб па А® к кубу на ©В *), или чем отношение,
составленное из отношения (квадрата) на /X® к (квадрату) на В©,
и отношения А® к ©В.
По отношение (квадратов) па А© к ®В, взятое с отношением
Л® к ©В, равно отношению (квадрата) на А® к (прямоугольнику)
между Г® и ©В **);
Ай2 АЙ __ АЙ2
ев2' ев” ге-ев
отношение же (квадрата) на Л© к (прямоугольнику) между В®,
®Г равпо отношению (квадрата) па А®, умноженного на 0Н,
к (прямоугольнику) между 150, ©Г, (умноженному) па ©Н;
АЙ2 Ай2-НН’
ве ег _ вй-йг йн
я утверждаю, следовательно, что (квадрат) па А®, (умноженный)
па ©Н, имеет к (квадрату) на Г®, (умноженному) на ©Z, отно-
шение большее, чем [(квадрат) па А® к (прямоугольнику) между
В0, ©Г или! чем (квадрат) па А©, (умноженный) на ©Н, к (пря-
моугольнику) между В©, ©Г, (умноженному) на ©Н.
АЙ2-ЙН АйЗ-ЙП
гй2- ez > ве- ег- ен
Значит, нужно доказать, что (квадрат) на ©Г, умноженный па
©Z, будет меньше (прямоугольника) между В®, ©Г, (умножен-
ного) на П©,
re2-ez < ве-ег-не
а это то же самое, что доказать, что (квадрат) на Г0 имеет к (прямо-
*) Это следует иа подобия треугольников АВГ и АВЙ.
**) Так как ев'=АЙ.ЙГ.
О ШАРЕ И ЦИЛИНДРЕ
165
угольнику} между В0, ©Г отношение меньшее, чем Н0 к ©Z
во-ег «z
[иными словами, нужно доказать, что П0 имеет к ©Z отношение
большее, чем Г© к ©В].
Из Е перпендикулярно к ЕГ проведем прямую ЕК и из точки
В опустим на нее перпендикуляр ВЛ. Нам остается доказать, что II©
имеет к 0Z отношение большее, чем Г© к ©В.
не г<->
6Z > «В *
Но 0Z равна вместе взятым Л© и КЕ; значит, нужно доказать, что Н0
к вместе взятым ©А и КЕ имеет отношение, большее, чем Г© к ©В;
не ги
АН+КЕ еВ
если из 0Н отнять Г0, а из КЕ прямую ЕЛ, равную В©, то остается
доказать, что полученные остатки ГИ и вместе взятые А© и КЛ имеют
друг к другу отношение большее, чем Г© к 0В, или 0В к ©А, или же
ЛЕ к ©А,
гн _ ги _ нВ _ ЛЕ '
ле+кл^ йв ~ па ~ «а
или после перестановки, что (ГН, или) КЕ имеет к ЕЛ отношение
большее, чем вместе взятые КЛ, 0А к ©А,
J<I!^ КЛ+иА
ЕЛ > оЛ
или же, после выделения, что КЛ имеет к ЛЕ отношение большее, чем
КЛ к ©А. (Следовательно, остается доказать, что) ЛЕ меньше 0А;
(это же очевидно) [4].
IX
Из всех сферических сегментов, ограниченных равными поверхностя-
ми, наибольшим, будет полушарие.
Пусть будет шар с большим кругом АВГД и диаметром АГ, и дру-
гой шар с большим кругом EZH0 и диаметром ЕП. Рассечем один шар
плоскостью через центр, а другой — не через центр; пусть секущие пло-
скости будут перпендикулярны к диаметрам АГ, ЕН и дадут сечения
по линиям ДВ и Z0; тогда соответствующий духе ZE0 сферический сег-
мент будет полушарием, [из сегментов же, соответствующих дуге
ВАД (рассматриваемый может быть) па одном чертеже меньше полу-
шария, а на другом, обозначенном звездочкой, больше полушария],
пусть поверхности упомянутых сегментов будут равны. Я утверждаю,
что полушарие, соответствующее дуге ZE0, будет больше сегмента,
соответствующего дуге ВАД {рис. 57;.
Так как поверхности упомянутых сегментов равны, то ясно, что ВА
равна прямой EZ, [ибо доказано, что поверхность всякого сегмента равна
кругу, радиус которого равняется прямой, проведенной из вершины
сегмента к окружности круга, составляющего основание сегмента.
Поскольку на чертеже со звездочкой дуга ВАД болыпеполуокружности],
то ясно, что квадрат на ВА будет меньше удвоенного квадрата на АК,
166
АРХИМЕД
но больше удвоенного квадрата на радиусе *). Пусть (квадрат) на ВА
будет вдвое больше квадрата на АР;
ВАг = 2ЛР2
пусть прямая ГЗ равна радиусу круга АВА, и отношение ГН к ГК
равняется отношению некоторой прямой МА к АК,
ГВ МА
ГК АК
и пусть на круге с диаметром ВА будет построен конус, имеющий вер-
шину в точке М; тогда этот конус будет равен сферическому сегменту,
соответствующему дуге ВАА. Пусть также EN будет равна ЕЛ, и на
круге с диаметром 6Z построен конус, имеющий вершину в точке N;
тогда и этот конус будет равен полушарию, соответствующему дуге
0EZ. Но прямоугольник между АР, РГ более прямоугольника между
АК, КГ,
АР РГТ'АК-КГ
ибо его меньшая сторона больше меньшей стороны другого прямоуголь-
ника**), и (квадрат) на АР равен прямоугольнику между АК, ГЗ;
ар2=лкге
действительно, он составляет половину (квадрата) на УКВ ***).
*) Обозначим радиус круга через г; тогда BAS=AK-АГ=2г-АК- Если г<АК<.2г, то
2г2<ВА2< 2 А К®.
Если бы дуга ВАД была меньше окружности, то АК<г
2r®> BA2> 2АК2.
Отсюда видно. что в первоначальном тексте Архимед брал только один чертеж, именно тот, который
позднейший комментатор обозначал звездочкой.
••) Если дуга АВ равна четверти окружности, то АР равна радиусу г, и АР-РГ—2/2. Если
АВ больше четверти окружности, то АР..-r и, согласно ранее сказанному, меньше АК; следова-
тельно. меньшими сторонами в обоих прямоугольниках будут Рг и КГ- причем ГТ;. КГ- Так как
АР рРГ^ЛК+КГ, и из двух прямоугольников с равными периметрами больше будет тот, который
ближе подходит к квадрату, то
АР-РГ>АК-КГ.
Если же дуга ЛВ меньше четверти окружности, то АР<т и АК<"ГК; следовательно, меныпими сто-
ронами в обоих прямоугольниках будут лр и АК. Так как теперь АР будет больше АК (из равен-
ства 2ДР2^=ВА2..>2Акг). то опять АР-РГ_>Л1£.КГ.
*•*) Имеем ЛН2=АК-АГ=-АК-2Г2-
О ШАРЕ И ЦИЛИНДРЕ
167
Теперь вместе взятые (левые части) будут больше вместе взятых
(правых);
АР-РГ -Ь АРг> АК-КГ -!-АК ГЗ
[значит, (прямоугольник) между ГА, АР больше (прямоугольника)
между ЕК, КА]. По (прямоугольник) между ЕК, КА равняется
(прямоугольнику) между МК, КГ *),
ЗК-КА = МК-КГ
[так что (прямоугольник) между ГА, АР будет больше (прямоуголь-
ника) между МК, КГ]; таким образом, ГА будет иметь it КГ отноше-
ние большее, чем МК к АР.
га . мк
кг ар
Но отношение АГ к ГК равно отношению (квадрата) на АВ к (квад-
рату) на ВК**);
АГ а в2
ГК ‘ вк2
теперь ясно, что половина (квадрата) на АВ, равная квадрату на АР,
будет иметь к (квадрату) на ВК отношение большее, чем МК к уд-
военной АР, которая равна AN***);
ЛР2 . мк_
вк^йар
значит, круг па диаметре Z0 к кругу на диаметре ВА будет иметь отно-
шение большее, чем МК к AN. Таким образом, конус, имеющий основа-
нием круг на диаметре Z0, а вершиной точку N, будет больше конуса,
имеющего основанием круг на диаметре ВА, а вершиной точку М;
теперь ясно, что полушарие, соответствующее дуге EZ0, будет больше
сегмента, соответствующего дуге ВАЛ.
„ ГН МА ЕГ4-ГК МЛ+ЛК
*) Из пропорции получаем «присоединением» —----в---• » откуда
ГК АК ГК ЛК
2К-АК=МК-КГ.
**) Так как АВ’=ЛК ЛГ и ВК*=ЛК-КГ.
** ) Из ртизкетв 2ЛР*=ВА2 и ВЛ —EZ (условие равенства поверхностей сегментов) имеем:
2AP4=BA8=EZS—2ЛЕЯ, отсюда ЛГ=ЛЕ и AN—2 АР, так Как EN равна ЕЛ—радиусу круга
EZ6H.
О КОНОИДАХ И СФЕРОИДАХ
Архимед Досифею желает благоденствия!
В этой книге я посылаю тебе запись доказательств остальных пред-
ложений, еще не имеющихся у тебя в посланном ранее, а также некото-
рых других, найденных мною позднее, к рассмотрению которых я уже
часто приступал, но должен был отступить, так как видел некоторые
трудности в их исследовании; ио этой причине я не издал в свет эти
предложения одновременно с другими. Потом уже, занявшись ими более
тщательно, я разрешил те трудности, которые задерживали меня ранее.
Это были оставшиеся от прежних теоремы, касавшиеся прямоугольного
коноида *); к ним я добавил теперь найденные позже теоремы относи-
тельно тупоугольного коноида **) и сфероидальных фигур, из которых
одни я называю удлиненными, другие же сплющенными***).
Предложения, касавшиеся прямоугольного коноида, были таковы:
Если какое-нибудь сечение прямоугольного конуса ****), вращаясь
около неподвижного своего диаметра *****), иерпстся в исходное поло-
жение, то фигуру, описанную при этом сечением прямоугольного ко-
нуса, мы будем называть прямоугольным коноидом, диаметр, оста-
вавшийся неподвижным—его осью, а точку, в которой ось коноида
доходит до его поверхности,—вергпипой коноида.
Если какая-нибудь плоскость касается прямоугольного коноида,
то всякая другая плоскость, проведенная параллельно касательной,
отсечет от коноида некоторый сегмент; основанием отсеченного сегмента
мы будем называть часть секущей плоскости, ограниченную линией пере-
сечения с коноидом, вершиной — ту точку, в которой первая плоскость
касается коноида, а осью — заключенную в сегменте часть прямой,
проведенной через вершину этого сегмента параллельно оси коноида.
Для рассмотрения было предложено доказать следующее.
Если от прямоугольного коноида отсечь сегмент плоскостью, пер-
пендикулярной к его оси, то отсеченный сегмент будет в полтора раза
больше конуса, имеющего с этим сегментом те же самые основание и ось.
*) То есть параболоида вращения.
**) Гиперболоид вращения (двуполый). вернее, одна его полость.
***) Эллипсоиды вращения вокруг большой и малой осей.
****) Параболи.
*****) Ось параболы.
О КОНОИДАХ И СФЕРОИДАХ
169
Также если от прямоугольного коноида отсечь два сегмента прове-
денными произвольно плоскостями, то отсеченные сегменты будут иметь
ДРУГ к другу отношение, равное двойному *) отношению их осей.
Относительно же тупоугольного коноида мы предлагаем следующее.
Если в плоскости имеются сечение тупоугольного конуса**),
его диаметр***) и ближайшие к сечению тупоугольного конуса пря-
мые****), и если около удерживаемого неподвижным диаметра вращать
ту плоскость, в которой .находятся упомянутые линии, то после ее воз-
вращения в исходное положение ближайшие к сечению тупоугольного
конуса прямые, очевидно, опишут равнобедренный конус, вершиной
. которого будет точка пересечения ближайших прямых, а осью — оста-
вавшийся неподвижным диаметр. Фигуру, описанную сечением тупо-
угольного конуса, будем называть тупоугольным коноидом, неподвиж-
ный диаметр — его осью, а точку, в которой эта ось доходит до поверх-
ности коноида,— его вершиной. Конус, описанный ближайшими к
сечению тупоугольного конуса прямыми, мы назовем объемлющим
коноид *****), а прямую, заключенную между вершинами коноида и
объемлющего коноид конуса, назовем дополняющей ось******).
Если какая-нибудь плоскость касается тупоугольного коноида
и другая плоскость, проведенная параллельно касательной, отсечет
некоторый сегмент коноида, то основанием, отсеченного сегмента мы
будем называть часть секущей плоскости, ограниченную линией пере-
сечения с коноидом, вершиной — ту точку, в которой касательная
плоскость касается кспоида, а осью — заключенную в сегменте часть
прямой, проведенной через вершины сегмента и конуса, объемлющего
коноид, часть же этой прямой между упомянутыми вершинами будем
называть дополняющей ось.
Все прямоугольные коноиды будут подобными друг дру-
гу а******). из тупоугольных же коноидов будем называть подобными
тс, у которых подобны конусы, объемлющие коноид ********).
Для рассмотрения и доказательства предлагается следующее:
Если от тупоугольного ксноида отсечь сегмент плоскостью, перпен-
дикулярной к его оси, то отсеченный сегмент к кспусу с теми же осно-
ванием и осью, что и у сегмента, будет находиться в том же отношении,
какое вместе взятые ось этого сегмента и утроенная прямая, дополняю-
щая ось, имеют к оси сегмента и удвоенной прямой, дополняющей ось.
Также если от тупоугольного коноида отсечь сегмент плоскостью
не перпендикулярной к оси, то отсеченный сегмент к фигуре, имеющей
с сегментом то же основание и ту же ось (эта фигура будет коническим
сегментом), будет находиться в том же отношении, какое вместе взятые
ось этого сегмента и утроенная прямая, дополняющая ось, имеют ко вме-
сте взятым оси сегмента и удвоенной прямой, дополняющей ось.
Относительно же сфероидальных фигур мы предлагаем следующее.
Если сечение остроугольного конуса (эллипс), вращаясь около
удерживаемого неподвижным наибольшего диаметра, вернется в исход-
ное положение, то описанную фигуру назовем удлиненным сфероидом.
*) То есть возведенному во вторую степень.
*♦) Гипербола; вернее, одна ее ветвь,
***) Ось гиперболы.
****) Асимптоты гиперболы. Этот термин (буквально: несовпадающие) бил введен уже
после Архимеда Аполлонием Пергским.
****•) Асимптотический конус.
••*♦**) Это будет дейстпительнап полуось гиперболы.
••*••*♦) Все параболы подобны. См. Аполлоний. Конические сечения, книга 'VT, 11.
*•*•**••) Согласно Евклиду («Начала». книга XI, определение 24), подобными конусами
навиваются те. у которых пропорциональны оси и диаметры оснований.
170
АРХИМЕД
Если же эллипс вращается около удерживаемого неподвижным
наименьшего диаметра (малой оси}, то фигуру, описанную после
возвращения в исходное положение, назовем сплющенным сфероидом.
Осью каждого из сфероидов назовем удерживаемый неподвижным диа-
метр (ось эллипса}, вершиной — точку, в которой ось доходит до
поверхности сфероида, центром — середину оси и диаметром — про-
веденную через центр перпендикулярно к оси прямую.
Если параллельные плоскости касаются какого-нибудь из сферои-
дов, не пересекая его, и параллельно касательным плоскостям проведена
другая плоскость, рассекающая сфероид, то основанием обоих образован-
ных таким образом сегментов назовем часть секущей плоскости, содер-
жащуюся внутри кривой сечения со сфероидом, их вершинами — точки,
в которых параллельные плоскости касаются сфероида, и осями — за-
ключенные внутри сегментов части прямой, соединяющей их вершины.
Л что касательные плоскости имеют с поверхностью сфероида л ишь одну
общую точку, и что соединяющая точки касания прямая проходит через
центр сфероида, это мы еще докажем.
Подобными мы назовем такие сфероиды, оси которых находятся
в том же отношении, что и диаметры. Сегменты же сфероидов и коноидов
мы назовем подобными, если они отсекаются от подобных фигур, имеют
подобные основании, а оси их, которые или перпендикулярны к пло-
скостям оснований, или образуют равные углы с соответствующими диа-
метрами оснований, находятся в том же отношении, что и соответствую-
щие оси диаметры оснований.
Относительно сфероидов предлагается рассмотреть и доказать сле-
дующее. Если рассечь какой-нибудь сфероид плоскостью, проходящей
через центр и перпендикулярной к его оси, то каждый из получающихся
сегментов будет в два раза больше конуса с теми же основанием и осью,
что и у сегмента. Если же секущая плоскость перпендикулярна к оси,
но не проходит через цептр, то наибольший из полученных сегментов
будет относиться к конусу с теми же основанием и осью, как вместе взя-
ты!! половина оси сфероида п ось меньшего сегмента относятся к оси мень-
шего сегмента, а меньший сегмент будет относиться к конусу с теми же
основанием и осью, что и у сегмента, как вместе взятые половина оси
сфероида и ось большего сегмента относятся к оси большего сегмента.
Если какой-нибудь из сфероидов рассечен плоскостью, проходящей
через центр, но не перпендикулярной к оси, то каждый из получившихся
сегментов будет в два раза больше фигуры с теми же основанием и осью,
что и у сегмента (это будет конический сегмент).
Если же сфероид рассечен плоскостью, не проходящей через цептр
и не перпендикулярной к оси, то наибольший из полученных сегментов
будет относиться к фигуре с теми же основанием и осью, что и сегмент,
как вместе взятые половина прямой, соединяющей вершины сегментов,
и ось меньшего сегмента относятся к оси меньшего сегмента, а меньший
сегмент к фигуре с теми же основанием и осью будет относиться, как
вместе взятые половина соединяющей вершины обоих сегментов пря-
мой и ось большего сегмента относятся к оси большего сегмента. (Полу-
чаемая фигура и в этик случаях будет коническим сегментом.)
Если упомянутые предложения доказаны, то при их помощи можно
найти и много других теорем и задач, как, например:
подобные сфероиды и сегменты сфероидов и коноидов находятся
друг с другом в тройном *) отношении их осей;
J То есть вовведенном в третью степень.
О КОНОИДАХ И СФЕРОИДАХ
171
у равных сфероидов квадраты диаметров обратно пропорциональ-
ны осям, и если у двух сфероидов квадраты диаметров обратно пропор-
циональны осям, то эти сфероиды равны;
а также задачи, как, иапример:
от данного сфероида или коноида отсечь сегмент плоскостью, прове-
денной параллельно заданной, так, чтобы отсеченный сегмент был равен
данному конусу, цилиндру или тару*).
Предварительно я напишу все необходимые для доказательства
теоремы и указания, а затем перейду и к объяснению предложений.
Будь счастлив!
Определения
Если рассечь копус плоскостью, встречающейся со всеми его сто-
ронами (образующими), то сечение будет или кругом, или эллипсом.
Если сечение — круг, то ясно, что часть, отнятая с той стороны, где
находится вершина конуса, будет и сама конусом. Если же в сечении
получается эллипс, то часть, отнятую от конуса с той стороны, где на-
ходится вершина конуса, будем называть коническим сегментом.
Основанием сегмента будем называть часть плоскости, ограниченную
эллипсом, вершиной — ту точку, которая будет и вершиной конуса,
а осью — прямую, соединяющую вершину конуса с центром эллипса.
И если цилиндр рассечь двумя параллельными плоскостями, встре-
чакицими все стороны (образующие) цилиндра, то сечения будут или
кругами, или же равными и подобными эллипсами. Если сечения будут
кругами, то ясно, что отсеченная параллельными плоскостями часть
цилиндра тоже будет цилиндром. Если же сечения будут эллипсами, то
часть цилиндра между параллельными плоскостями назовем цилиндри-
ческим сегментом. Основаниями сегмента назовем части плоскостей,
ограниченные эллипсами, а осью — прямую, соединяющую центры
эллипсов-, эта ось будет находиться па одной прямой с осью цилиндра.
(Л е м м а.) Лели имеется любое число величин, одинаково превы-
шающих одна другую {составляющих арифметическую прогрессию),
причем разность равна наименьшей из этих величин {первому члену},
а также одинаковое количество других величин, каждая из которых
равна наибольшей из первых величин, то все величины, равные наиболь-
шей, взятые вместе, будут меньше удвоенных всех величин, одинаково пре-
вышающих одна другую, но больше удвоенных этих величин, оставшихся
после исключения наибольшей.
Доказательство этого очевидно**).
I
Если имеется любое количество некоторых величин и равное количе-
ство других величин, причем одинаково расположенные {величины обоих
- рядов} имеют, попарно одно и то же отношение, и если первые величины
все, или только некоторые из них, находятся в каких-нибудь отношениях
*) Архимедовы доказательства этих теорем и задач или нс сохранились, или, может быть, даже
не были опубликованы.
•*) В нашем обозначении
2{а+2а-Р . . . + (п—1)а}<п-гш<2 . 4-па} ,
или
п(п-1)а<п!а<п(п-| 1 )а.
172
АРХИМЕД
с третьими величинами, а соответствующие величины второго ряда
находятся в тех же самых отношениях с величинами четвертого ряда,
то все первые величины ко всем соответствующим им величинам (треть-
его ряда} будут иметь то же самое отношение, как все величины второго
ряда ко всем соответствующим им величинам (четвертого ряда} [1].
Пусть имеются некоторые величины А, В, Г, А, Е, Z и равное коли-
чество других величин Н, 0, I, К, Л, М, имеющих с ними попарно одно
и то же отношение, и пусть Л имеет к В то же самое отношение, как Н к 0,
А П1
В ' О
а В к Г (то же самое), как © к I
в
г — 1
и точно так же и все остальные;
г _ _1
д 1 к
д к
Е ~ Л
Е Л
Z ~~ М
пусть также величины А, В, Г, Д, Е, Z находятся в каких-нибудь отно-
шениях с (третьими) величинами N, Е, О, П, Р, S, а величины П, 0,
I, К, Л, М находятся в тех же самых отношениях с соответствующими
величинами (четвертого ряда) Т, Г, Ф, X, V, Й, и пусть то отношение,
которое А имеет к N, будет тем же самым, которое Н имеет к Т,
_а_ п
N ~ Т
а отношение, которое В имеет к Е, будет тем же самым, которое 0
имеет к Г;
в е
Е Г
и точно так же и все остальные {рис. 1}. Требуется доказать, что все
А, В, Г, А, Е, Z вместе взятые ко всем N, Е, О, П, Р, S будут иметь то же
самое отношение, как все вместе взятые Н, 0, I, К, Л, М ко всем Т,
Г, Ф, X, Й.
Поскольку N имеет к Л то же самое отношение, как Т к Н,
n т
А Н
а А к В то же отношение, как Н к 0,
а _ н -
в ~ е
О КОНОИДАХ И СФЕРОИДАХ
173
и В к Е то же, как в к Г,
в _ е
в — г
то N будет иметь к Е то же самое отношение, как Т к Г;
n__ т
S — г
вследствие того же, как Е к О, так будет и I* к Ф
Л_ X.
о Ф
и точно так же и все остальные.
о Ф
п — х
п_= 2L
р w
р _
S'- £2
Тогда все А, В, Г, Д, Е, Z имеют к А то же самое отношение, как все
Н, 0, I, К, А, М к И,
а + в+гч-д + е+2_ н + е i-i-i k+a+m
А ~ И
а А имеет к N то же отношение, как Н к Т,
А Н
N - Т
и N ко всем N, Е, О, II. Р. S имеет то же самое отношение, как Т ко
всем Т, Г, Ф, X, Т, Й;
N Т
N -h S + O т II-г Г -г— Т + Г-|-Ф+ X -j- Т + £2
теперь ясно, что все А, В, Г, A, Е, Z ко всем N, Е, О, П, Р, S будут иметь
то же самое отношение, как все П, 0,1, К, А, М ко всем Т, Т, Ф, X,
¥, Я.
А+- B + r + A+E-[-Z_ H + 0+H-K + A + M-
N + Ё |-b + fl+P-i-X Т+Г4-Ф-КХ +V+B
Так же ясно, что если из величин А, В, Г, Д, Е, Z выбрать А, В, Г,
*Д, Е, имеющие отношения к N, Е, О, II, Р, причем Z не будет иметь отно-
шения ни к одной величине, а из величии II, 0, 1, К, А, М, выбрать
Н, 0, I, К, А, имеющие соответственно те же самые отношения к Т,
Г, Ф, X, Т, причем М не будет иметь отношения пи к одной величине,
то точно так же все А, В, Г, Д, Е, Z ко всем N, 3, О, П, Р будут
иметь то же самое отношение, как все II, 0, I, К, А, М ко всем Т, Е,
Ф, X, V.
а + вч-г4-лч-вz _ н+е-м+к + л + м
N + EtO + 11 + Р “ Т + Г + Ф —X + W
II
Если имеется некоторое количество равных друг другу линий и к каж-
дой из них с избытком в виде квадрата прикладывается, некоторая пло-
щадь, причем стороны этих избыточных {квадратов} будут одинаково
превышать одна другую и разность {двух последовательных сторон}
174
АРХИМЕД
будет равняться, наименьшей из них*), и если имеются другие пло-
щади, количество которых равняется количеству первых, а величина
каждой равняется наибольшей из первых, то эти площади его есем {взя-
тым вместе первым.) будут иметь отношение, меньшее того, которое
{прямая), равная вместе взятым стороне наибольшего избыточного
{квадрата) и одной из {первоначально данных) равных друг другу
прямых, имеет к {прямой), равной вместе взятым, третьей части сто-
роны наибольшего избыточного {квадрата) и половине одной из рав-
ных друг другу прямых, а если {из первых площадей) исключить наи-
большую, то к оставшимся эти {вторые) площади будут иметь отно-
шение, большее упомянутого**).
Пусть имеется некоторое количество равных друг другу прямых,
на которых стоит А {рис. 2}, п к каждой из них с избытком в виде
.4
л Л Л л
я л к я к
/ / ! / 1
0 н f) в е
Рис. 2.
квадрата прикладывается площадь, пусть стороны В, Г, Д, Е, Z, Н
этих избытков одинаково превышают одна другую, и пусть разность их
равна наименьшей; пусть наибольшая будет В, а наименьшая — Н;
пусть также имеются и другие площади, на каждой из которых стоят
6, Т, К, Л, причем количество этих площадей равняется количеству
первых, а величина каждой равняется наибольшей, (а именно) той,
которая приложена к линии А + В; пусть прямая 0 вместе с I будет рав-
на А, а К вместе с Л равна В, и каждая из линий 0 вместе с I будет вдвое
больше I, а каждая из К вместе с Л втрое больше К. Требуется доказать,
что все площади, которые обозначены (буквами) 0, I, К, А, ко всем
*) Архимед пользуется терминологией так называемого «приложения площадей». «Приложить
заданную площадь S к некоторой прямой а», значит на отрезке а построить ирнмоугольпик, пло-
щадь которого раина S; другая сторона итого прямоугольника х определится из уракиспин
ах — S.
«Приложение с избытком в виде квадрата», с нашей точки зрения, равносильно решению квадрат-
ного уравнения
«л- ; ав_к.
**) Архимед строит площади
0x4 №. я- 2х ; (2л)2, .... н-пд-;(пх)3
и утверждает, что
« п {а-ях-;-(пх)Д!________ ,. nx-'j a
(оа-: л-2).;-(«• 2х ! 4№)-j-. - .-| (0-п.х 1-п2.№) ' пх_ «
.'. . "3 '2
п {а-7гх)-Цпз:)2> пх | а
(ох; .№)’! (л.2х-|-4хХ) । . . ,4{« (n-i)x-(n- -|)S№} их , а
3 "*”2
О КОНОИДАХ И СФЕРОИДАХ
175
другим площадям АВ, ЛГ, ЛД, АЕ, AZ, АН будут иметь отношение,
меньшее того, которое прямая 0-|-1-]-К+Л имеет к прямой Ц-К, а
к площадям, оставшимся после исключения наибольшей АВ, будут
иметь отношение, большое упомянутого.
Пусть имеются некоторые площади, обозначенные (буквой) А,
одинаково превышающие одна другую, причем разность равняется наи-
меньшей (из этих площадей), [ибо и прикладываемые площади и их
ширины одинаково превышают одна другую]*), а ташке другие пло-
щади, обозначенные 6, 1, количество которых равняется количеству
первых, а величина каждой равняется наибольшей; тогда все площади
0,1, взятые вместе, будут меньше удвоенных всех площадей А, но боль-
ше удвоенных всех таких площадей, оставшихся после исключения наи-
большей **). Эти площади, обозначенные 1, меньше всех площадей А,
но больше всех их за исключенном наибольшей***). Далее, имеются
некоторые линии В, Г, А, Е, Z, Н, одинаково превышающие одна дру-
гую, причем разность равна наименьшей (из пих), и другие линии,
обозначенные К, Л, по количеству равные этим, а по величине равные
каждая наибольшей (из пих); тогда квадраты па всех прямых, рав-
ных друг другу и наибольшей, будут менее утроенных квадратен на
прямых, одинаково превышающих одна другую, но более утроенных
квадратов па этих прямых, если исключить квадрат на наибольшей; это
доказано в уже изданной книге о спиралях****). Таким образом, все
площади, обозначенные К, будут меньше всех площадей В, Г, А, Е,
Z, Н, но больше площадей Г, А, Е, Z, И*****); так что псе площади,
обозначенные 1, К, будут меньше всех площадей, обозначенных АВ,
АГ, АЛ, АЕ, AZ, АН, но больше площадей ЛГ, АД, АЕ, AZ, АН******).
Теперь ясно, что все площади 0, I, К, Л ко всем площадям АВ, АГ,
АА, АЕ, AZ, АН имеют отношение, мспьптее того, которое прямая НА
имеет к ТК, ко всем же таким площадям, кроме АВ, имеют отношение,
большее упомянутого [1].
*) Гейбсрг устраняет фразу, поставленную в скобках, на основании языковых данных. Под
«прикладываемой площадью» (ларарХтща) следует подразумевать приложенную н прямой А площадь
прямоугольника, обозначенного буквой А.
** ) На основании леммы, стоящей перед первым предложением, мы можем написать:
2 { Ах + А,2х+ ... + Апх} ~>п (А-пх) > 2 { А^+А«2,т.-+ . . . гА (те—1)л} ,
где -г, как и выше, обозначает сторону наименьшего из избыточных квадратов, а Л=е-)-1 или а,
как выше.
***) Мы имеем 1+2 +.. .и 1-,2+...+(п—1)—-. Архимед хочет ска-
те (те+1) те те (ti— I)
зать, что ——->п->—.
*'*’) В предложении X. В наших обозначениях ото равносильно неравенствам
3 <х, + (2.т)2+. . .+(«»:)=} >те(тех)2> 3{х2 + (2х)2+. . .+(те—1)2а:а}.
**»“) R наших обозначениях
№+(2х)2+, . . -Гх2+(2х)2 Г . . . +(тех)2,
_, (ПЛ’)2
так кгш площадь К——~ .
•**♦**) Так как прямая I равна половине прямой А, то площадь 1~Л . Полученные неравен-
ства в наших обозначениях запишутся таи:
(Ях+х2)-(а-2х+4з:2)+. . . i {а(те-1)х j (те-1)2x2^ (^^'+’-^) ,
(«ьх+х2)+(а-2л'+4л2)+. . ,-| (а тех+п2зс2)>те (—~ + дт^) .
176
АРХИМЕД
III
<1>. Если прямые, проведенные из одной и той же точки, каса-
ются какого-нибудь конического сечения, и внутри конического сечения
проведены другие прямые, параллельные карательным и пересекающие
друг друга, то прямоугольники между их *) отрезками находятся между
собой в том же отношении, как и квадраты на касательных, причем
прямоугольник между отрезками каждой прямой соответствует квадра-
ту на, касательной, параллельной этой прямой.
Это доказано в «Началах теории конических сечений» [2].
< 2>. Если от одной и тойже.параболы каким-либо образом отсечь
два сегмента, имеющих одинаковые диаметры, то будут равны и сами
эти сегменты, и вписанные в них треугольники, имеющие те же основа-
параболы. Возьмем прямую, на
болы, вдвое большую (расстояния от вершины параболы)
ния и высоты, что и соответствующие
сегменты: диаметром же сегмента я
называю прямую, делящую пополам
все прямые, проведенные параллель-
но основанию этого сегмента.
Пусть будет парабола АВГ и
от псе отсечены два сегмента ААЕ
и 0ВГ; пусть AZ будет диаметр
сегмента АДЕ, а ВН — диаметр сег-
мента @ВГ, и пусть AZ и ВП будут
равны. Требуется доказать, что бу-
дут равны и сегменты АДЕ, 0ВГ и
вписанные в них упомянутым обра-
зом треугольники {рис. 3}.
Пусть сначала прямая (Н)Г, от-
секающая один из сегментов, будет
перпендикулярна к диаметру (о с и)
которой квадрируются абсциссы пара-
до оси
(производящего копуса); пусть эта прямая будет N. Из точки А
опустим перпендикуляр АК на AZ. Так как AZ является диаметром
сегмента, то прямая АЕ делится в точке Z пополам, и AZ будет парал-
лельна диаметру параболы; значит, опа разделит пополам нее прямые,
проведенные параллельно АЕ. Пусть отношение квадрата на AZ к
квадрату на АК будет равно отношению некоторой прямой М к N.
А 7? М
АК2 N
Тогда прямые, проведенные параллельно АЕ от кривой до AZ**),
квадрируются, если на прямой, равной М, построить прямоугольник,
ширина которого будет равна прилежащему к точке А отрезку, отсекае-
мому ими от прямой AZ (это доказывается в теории конических сече-
ний) ***), поэтому AZ, квадрируясь, будет равняться прямоугольнику
между М и AZ.
az2 m az
Но и 0Н, квадрируясь, равняется прямоугольнику между N и ВН,
ей2 -N BH
*) Прямых, проведенных внутри конического сечения.
**) Ото будут ординаты точек параболы в системе координат, обраяуемой диаметром пара-
болы и касательной п се начале.
♦**) Речь идет об уравнении параболы в косоугольных координатах: у2~ 2р'х, где параметр 2р'
и есть наша прямая N.
О КОНОИДАХ И СФЕРОИДАХ
177
так как 0Н перпендикулярна к диаметру; значит, поскольку мы пред-
положили AZ и ВН равными, квадрат на AZ к квадрату на ©IT будет
иметь отношение, как у М к N.
AZ2 м
он* ы '
Но квадрат на AZ имеет к квадрату па АК то же отношение, что М к N;
значит, ©Н и АК равны.
ен = ак
> Также равны и ВП с AZ; значит, прямоугольник между ©Н и ВП будет
равен прямоугольнику между АК и AZ.
енвн=лк.лг
Таким образом, треугольник ©НВ будет равен треугольнику AAZ;
значит, будут равны и удвоенные треугольники (é и АЕА). Но
сегмент АДЕ составляет четыре трети треугольника АДЕ, а сегмент
©ВГ — четыре трети треугольника ©ВГ. Таким образом, ясно, что будут
равны и сегменты и вписанные в них треугольники*).
Если ни одна из прямых, отсекающих сегменты, не будет перпен-
дикулярна диаметру параболы, то отложим на диаметре параболы пря-
мую, равную диаметру одного сегмента, и через конец - -----
прямой проведем перпендикуляр к
диаметру; таким образом, получится
сегмент, который будет равен каж-
дому из данных сегментов. Теперь
предложенное становится очевид-
ным.
отложенной
Рис. 4.
IV
Всякая площадь, ограниченная
эллипсом, имеет к кругу с диаметром,
равным большему диаметру эллипса,
то же самое отношение, что мень-
ший диаметр эллипса к большему
или к диаметру круга.
Пусть будет [рис. 4} эллипс
АВ ГА с наибольшим диаметром АГ
и наименьшим ВД; пусть еще будет
круг с диаметром АГ. Требуется
доказать, что ограниченная эллипсом
площадь имеет к кругу то же самое
отношение, что ВА к ГА или к EZ.
Пусть отношение ВД к EZ равняется
отношению некоторого круга, обо-
значенного 'F, к кругу AEFZ. Я ут-
• верждаю, что круг Y будет равен
эллипсу.
Если круг УИ не равен площади,
ограниченной эллипсом, то пусть
сначала он, если возможно, будет больше. Тогда можно вписать в круг
Y многоугольник с четным числом сторон, который был бы больше пло-
щади АВГД. Представим, что он вписан; впишем также и в круг AETZ
*) См. «Квадратура параболы», предложения XVII и XXIV..
12 Архимед
178
АРХИМЕД
прямолинейную фигуру, подобную вписанной в круг Y; через ее вер-
шины проведем прямые, перпендикулярные к диаметру АГ и соединим
прямыми точки пересечения этих перпендикуляров с эллипсом; полу-
чится некоторая вписанная в эллипс прямолинейная фигура, которая
будет относиться к прямолинейной фигуре, вписанной в круг AETZ,
как ВА к EZ.
Действительно, так как перпендикуляры ©Е и КЛ разделяются
в точках Ми В в одном и том же отношении, то ясно, что трапеция ЛЕ
будет иметь к трапеции ©М то же отношение, что ©Е к €)В. По той же
причине и каждая из остальных трапеций в круге к соответствующей
трапеции в эллипсе будет иметь то же отношение, что Е© к В©. Точно
так же и прилежащие к точкам А и Г треугольники в круге будут иметь
то же отношение к таким же треугольникам в эллипсе; но тогда и вся
прямолинейная фигура, вписанная в круг AETZ, ко всех! прямолиней-
ной фигуре, вписанной в эллипс, будет иметь то же отношение, что EZ
к ВА. Эта фигура будет находиться в том же самом отношении и к впи-
санной в круг Т, так как и оба круга находятся в том же самом отноше-
нии; значит, прямолинейная фигура, вписанная в круг 'F, будет равна
прямолинейной фигуре, вписанной в эллипс; а это невозможно, так как
эта фигура больше всей площади, ограниченной эллипсом.
Тогда пусть, если это возможно, круг У будет меньше эллипса.
Опять можно вписать в эллипс многоугольник с четным числом сторон,
который был бы больше круга ЧЕ Впишем его, проведем через его вер-
шины прямые, перпендикулярные к АГ, и продолжим их до окружности
круга; опять получится вписанная в круг АЕ прямолинейна^ фигура,
которая будет ко вписанной в эллипс, иметь отношение, как EZ к ВА.
Вписавши подобную ей фигуру в круг V,
мы докажем, что эта вписанная в круг Чг
фигура будет равна вписанной в эллипс,
а это невозможно*); значит, круг V не
будет и меньше площади, ограниченной
эллипсом. Таким образом, ясно, что
упомянутая площадь эллипса имеет к кру-
гу AETZ то же отношение, что ВД к EZ.
V
Всякая площадь, ограниченная эллип-
сом, ко всякому кругу имеет, такое же
отношение, как прямоугольник между
главными диаметрами эллипса к квадрату
на диаметре круга {рис. 5}.
Пусть будет некоторая площадь X,
ограничен пая эллипсом, диаметры которо-
го суть АГ и ВА, причем большим диа-
метром будет АГ; пусть, кроме того, будет
круг Чг с диаметром EZ. Требуется доказать,
что площадь X к кругу Ч*" имеет то же отношение, что прямоугольник
между АГ и ВА к квадрату на EZ.
На диаметре АГ опишем круг. Тогда площадь X к кругу на диамет-
ре АГ имеет то же отношение, как прямоугольник между АГ и ВА к ква-
*) Тан как тогда вписанная в круг W фигура оказалась бы больше круга
О КОНОИДАХ и СФЕРОИДАХ
179
драту па АГ, так как уже доказано, что они относятся, как ВА к АГ.
Далее, круге диаметром АГ к кругу с диаметром EZ имеет то же отно-
шение, что квадрат на АГ к квадрату
на EZ. Отсюда ясно, что площадь X от-
носится к кругу Y, так же, как прямо-
угольник между АГ и В А к квадрату
на EZ.
VI
Площади, ограниченные эллипсами, на-
ходятся друг к другу в таком же отноше-
нии, как прямоугольники между диамет-
рами эллипсов [рис- 6}.
Пусть А и В будут площади, огра-
ниченные двумя эллипсами, пусть ГА
будет прямоугольник, построенный на
диаметрах эллипса, ограничивающего пло-
щадь Л, a EZ — прямоугольник на диа-
метрах другого эллипса. Требуется дока-
зать, что площадь А так относится к В,
как ГА к EZ.
Возьмем какой-нибудь круг 'Г; пусть
КЛ будет квадрат на его диаметре. Пло-
щадь Л относится к кругу Чг, как ГА кКЛ,
круг же 'Г к площади В относится, как КЛ it EZ; таким образом,
ясно,что площадь Л имеет к В то же самое отношение, что ГА к EZ.
Следствие
Отсюда обнаруживается, что площади, ограниченные подобными
эллипсами, имеют друг к другу то же отношение, что и квадраты на
соответственных диаметрах эллипсов.
VII
Если дан эллипс с прямой, восставленной из его центра перпендику-
лярно к плоскости, в которой этот эллипс находится, то можно найти
конус, имеющий вершиной конец восстановленной прямой, причем задан-
ный эллипс будет находиться на поверхности этого конуса {рис. 7].
Пусть дан некоторый эллипс и из его центра восстановлена прямая,
перпендикулярная к плоскости, в которой этот эллипс находится.
Через восставленную прямую и наименьший диаметр эллипса про-
ведем плоскость; пусть в этой плоскости АВ будет наименьший диа-
метр, а А — центр эллипса, далее, ГА будет восставленная из центра
перпендикулярная прямая и Г — ее конец; заданный же эллипс пред-
ставим описанным на диаметре АВ в плоскости, перпендикулярной
к ГА. Требуется найти конус, имеющий вершиной точку Г, на поверх-
ности которого будет находиться заданный эллипс.
Продолжим прямые, проведенные из Г к А, В и из А проведем AZ
так, чтобы прямоугольник между ЛЕ и EZ относился к квадрату на ЕГ,
как квадрат половины наибольшего диаметра относится к квадрату на
АГ; это возможно потому, что рассматриваемое отношение будет больше
12*
180
АРХИМЕД
отношения прямоугольника между АД и ДВ к квадрату на ДГ.
AE.EZ АД-ДВ
ЕГ2 ДГ2
Через AZ проведем плоскость, перпендикулярную к той, в которой
находятся АГ и AZ; в этой плоскости опишем круг на диаметре AZ и пос-
троим на этом круге конус, имеющий
вершиной точку Г. Докажем, что за-
данный эллипс будет находиться па
поверхности этого копуса.
Если оп нс будет находиться на
поверхности этого конуса, то необхо-
димо, чтобы на эллипсе существовала
некоторая точка, которая не была бы
на поверхности рассматриваемого ко-
нуса. Представим, что на эллипсе
взята некоторая точка 8, которая нс
находится на поверхности этого ко-
нуса. Через точку 0 проведем 0К
перпендикулярно к АВ; проведенная
прямая будет перпендикулярна и
к плоскости, в которой находятся АГ
и TZ. Продолжим проведенную из Г к К прямую; пусть она встретит AZ
в точке Л. Через Л перпендикулярно к Z А в круге, описанном на AZ,
проведем прямую Л М; точку М, находящуюся на окружности круга AZ,
вообразим приподнятой (над плоскостью чертежа). Кроме того, через Л
и Е параллельно АВ проведем ЕО и ПР. Так как прямоугольник
между ЕА и EZ к квадрату на ЕГ имеет то же самое отношение, что
квадрат на Половине наибольшего диаметра (нА) к квадрату на А Г,
EA-EZ аАа
ЕГ2 ДГ2
а квадрат па ЕГ к прямоугольнику между ЕП и ЕР имеет то же отно-
шение, что квадрат на АГ к прямоугольнику между АД и АВ,
ег2 _ дг2
ЕП-ЕР-АД АВ
то прямоугольник между ЛЕ и EZ будет иметь к прямоугольнику между
ПЕ, ЕР то же отношение, что квадрат па половине наибольшего диа-
метра (аД) к прямоугольнику между АД и ДВ.
AE-EZ «А2
ПЕ-ЕР АД-АВ
Ио как прямоугольник между АЕ и EZ к (прямоугольнику) между
ПЕ и ЕР, так и прямоугольник между АЛ и AZ относится к (прямоуголь-
нику) между ЕЛ, АО,
АЕ • EZ_ АЛ * AZ
ПЕ-ЕР ~ 5Л-Л0
а как квадрат на половине наибольшего диаметра к (прямоугольнику)
между АД и ДВ, так и квадрат на 0К относится к (прямоугольнику)
между АК и КВ,
ад2 ек®
АД-ДВ АК-КВ .... ,
к*
7.
tAty* ?«V /** ЛМЛГ** »#- im-
<9Г»^1н Лл-.Л»л vryw^o
«»»*»** -
Лке*4* /4 мСм'мГ Лг^»
U <<ziftyw •***’
д^*4**аДиМ**.^ »^л'^
•pt A tef»*1» & f <A*%* ч^^м>- »f
чНй 1Л«4*^**'^**<,*>|*
ж*й*г Л>***
Фотокопия страницы греческой рукописи, содержащей отрывок сочинения.
Архимеда *0 коноидах и сфероидах».
182
АРХИМЕД
значит, прямоугольник между АЛ и AZ к прямоугольнику между ЕЛ
и ЛО имеет то же отношение, что и квадрат па 0К к (прямоугольнику)
между АК. и КВ.
ал-ля ек®
SA-ЛО АК-КВ
Но (прямоугольник) между ЕЛ и ЛО имеет к квадрату на ГЛ то же
отношение, что прямоугольник между АК и КВ к квадрату па КГ,
вл-ло_ лк-кв
гл® кг®
значит, (прямоугольник) между АЛ и AZ будет относиться к квад-
рату на ГЛ как квадрат на ©К к квадрату на КГ.
АЛ • Л2» _ 01^2
Но прямоугольник между АЛ, AZ равен квадрату на ЛМ,
лл-лг=лм®
так какЛМ проведена перпендикулярно к диаметру в полукруге на AZ;
значит, квадратна ЛМ имеет к квадрату на ЛГ то же отношение, что
квадрат па ОК к квадрату на КГ;
лм® ек®
лг® кг®
таким образом, точки Г, О, М будут находиться на одной прямой. Но
ГМ лежит на поверхности конуса; значит, яспо, что и точка 0 будет
находиться на поверхности конуса. Но было предположено, что она пе
находится; значит, на эллипсе не будет ни одной точки, которая не нахо-
дилась бы на поверхности вышеупомянутого конуса. Таким образом,
и весь эллипс будет находиться на поверхности .этого конуса [3].
VIII
Если дан эллипс и прямая, восставленная из его центра, не перпен-
дикулярная к плоскости эллипса, но лежащая в плоскости, проведенной
через другой диаметр эллипса перпендикулярно к той плоскости, в ко-
торой находится эллипс, то можно найти конус, имеющий вершиной
конец восставленной прямой, причем заданный эллипс будет находиться
на его поверхности {рис. 8j [4J.
Пусть ВА будет диаметр эллипса, Л — его центр, а ДГ — восстав-
леппая, как сказано, из центра прямая; сам эллипс вообразим себе
расположенным па диаметре АВ в плоскости, перпендикулярной к той,
в которой находятся ЛВ и ГЛ. Требуется найти конус, с вершиной
в точке Г, на поверхности которого будет находиться заданный эллипс.
Так как ГД не перпендикулярна к плоскости эллипса, то прямые АГ
и ВГ пе будут равными. Пусть прямая ЕГ будет равна ГВ, a N равпа
половине второго диаметра, сопряженного с АВ. Через А параллельно ЕВ
проведем прямую ZH; на ЕВ восставим плоскость, перпендикулярную
к топ, в которой находятся АГ и ГВ, и в этой плоскости на диаметре ЕВ
опишем круг, если квадрат на N будет равняться прямоугольнику между
ZA и ЛП, или же, если он нс будет равняться, то эллипс — так чтобы
квадрат на другом диаметре относился к квадрату на ЕВ, так же как
квадрат на N к прямоугольнику между ZA и АН. Затем возьмем
конус, имеющий вершину в точке Г, на поверхности которого будут
О КОНОИДАХ И СФЕРОИДАХ
183
находиться описанные на диаметре ЕВ круг или эллипс; это возможно,
так как прямая, проведенная из Г к середине ЕВ, перпендикулярна
к плоскости, проведенной через ЕВ;
па этой же поверхности будет нахо- /к
диться и эллипс, описанный на дна- //\ \\
метре АВ. / \ \\я
Действительно, если бы он там / I \ /\\
не находился, то на эллипсе име- / I У \ \^
лась бы точка, которая по будет па д/ //Л \Z
поверхности конуса. Вообразим, что /л?С \ /\
взята некоторая точка 8, не находя- / \
щаяся па поверхности конуса; из 8 у 7 \
на ЛВ опустим перпендикуляр ©К и \
соединяющую ГК продолжим; пусть ,/
опа встретится с ЕВ в Л, а через Л ' \
в плоскости, перпендикулярной*) \
к проходящей через ЕВ, проведем \
некоторую прямую ЛМ, перпепди- \
кулярпую к ЕВ; точку М на поверх- \
ности конуса представим себе припод- \
пятой (над плоскостью чертежа). •--------
Через Л проведем также параллель- т Р
ную ЛВ прямую ПР; тогда как квад- Рис. 8.
рат на N к прямоугольнику между
ZA и ЛТТ, так и квадрат на Л М относится к прямоугольнику между
ЕЛ и ЛВ,
.N2 .ЛМа
гд.дн. ел-лв
и как (прямоугольник) между ZA и АН к (прямоугольнику) между
ЛА и ЛВ, так и прямоугольник между ЕЛ, ЛВ к (прямоугольнику)
между ПЛ, ЛР;
хд-дн вл-лв
АД ДВ ПД.ЛР
тогда получится, что квадрат на N относится к (прямоугольнику)
между АЛ и ЛВ, как квадратна ЛМ к (прямоугольнику) между ПЛ
и ЛР.
К» ЛМ2
ЛА-ЛВ ПЛ-ЛР .
Но мы имеем также, что квадрат па N к прямоугольнику между АД
иЛВ относится, как квадратна 8К к прямоугольнику между ЛК и КВ,
№ ек2
АА-АВ” А К-КВ
так как в одном и том же эллипсе проведены два перпендикуляра (N
и 0К) к диаметру АВ; значит, отношение квадрата наЛМ к прямоуголь-
нику между ПЛ, ЛР будет таким же, как отношение квадрата на 8К
к прямоугольнику между АК и КВ.
лм2 = нка
ПЛ АР АК КВ
Но прямоугольник между ПЛ и ЛР относится к квадрату на ГЛ, как
) К прямым Л Г и ГВ.
184
• АРХИМЕД
прямоугольник между АК и КВ к квадрату на КГ;
ПЛ-ЛР ЛК-КВ
гл3 ’ ’ кг2
значит, квадрат на ЛМ имеет к квадрату на Л Г то же отношение, что
и квадрат на 0К к квадрату на КГ;
дм2 ек3
лг3 кг3 . . . \ .
отсюда следует, что точки Г, 0, М расположены на одной прямой. Но
ГМ находится на поверхности конуса; отсюда ясно, что и точка 0 будет
находиться на поверхности конуса; мы же предположили, что она там
нс находится; таким образом, обнаруживается правильность утверж-
дения, подлежащего доказательству.
IX
Если дал эллипс и прямая, восставленная из его центра, не перпен-
дикулярная (к плоскости эллипса}, но лежащая в плоскости, проведен-
ной через некоторый диаметр эллипса перпендикулярно к той плоскости,
в которой находится эллипс, то
можно найти цилиндр, имеющий
ось на продолжении восставленной
линии, причем заданный эллипс
будет находиться на поверхности
этого цилиндра (рис. 9}.
Пусть ВА будет некоторым
диаметром эллипса, Д — его цент-
ром, а ГД — восставленной, как
сказано, из центра прямой; сам
эллипс вообразим себе расположен-
ным на диаметре АВ в плоскости,
перпендикулярной к той, в которой
находятся АВ и ГД. Требуется пайти цилиндр, имеющий ось на пря-
мой ГД, на поверхности которого будет находиться заданный эллипс.
Из точек А и В параллельно ГД проведем прямые AZ и ВН; взятый
диаметр эллипса будет или равен расстоянию между прямыми AZ, ВП,
или больше его, или же меньше.
Пусть он, во-первых, будет равен ZH, a ZH перпендикулярна 1£ ГД.
Восставим па ZH плоскость, перпендикулярную к ГД; в этой плоскости
пусть будет круг на диаметре ZH и пусть на этом круге будет цилиндр,
имеющий осью ГД; на поверхности этого цилипдра и будет находиться
заданный эллипс.
Действительно, если бы он там не находился, то на эллипсе будет
некоторая точка, которая не была бы на поверхности цилиндра. Пред-
ставим себе, что взята такая не находящаяся на поверхности цилиндра
точка эллипса 0; опустим из 0 на прямую АВ перпендикуляр ©К;
он будет перпендикулярен и к плоскости, в которой находятся АБ
и ГД. Через К параллельно ГД проведем КЛ и из Л восставим к ZH пер-
пендикуляр ЛМ в описанном на ZH круге; точку М представим себе
приподнятой (над плоскостью чертежа) па окружности полукруга
на диаметре ZH; тогда одно и то же отношение будут иметь квадрат на
перпендикуляре ©К к прямоугольнику между АК и КВ и (квадрат)
О КОНОИДАХ И СФЕРОИДАХ
185
на 2Г к прямоугольнику между АД и ДВ, .
WK® zr2
АК-К8” АД-ДВ
так как ZH равна другому диаметру (эллипса согласно предположе-
нию) *). Но прямоугольник между ZA и АН относится к прямоуголь-
нику между АК и КВ, как квадрат на ZT к квадрату на АД**);
ZA-AH Zr2 "
АК-КВ ' АДа
значит, прямоугольник между ZA, АН будет равен квадрату на ©К.
гл.лн=ек2
Но он также равен и квадрату па ЛМ***); значит, перпендикуляры
©К и МЛ равны. Далее, прямые ЛК и М© параллельны****), так что
будут параллельны и ДГ и М©- Следовательно, прямая ©М будет нахо-
диться на поверхности цилиндра, так как она проведена параллельно
оси цилиндра из точки, лежащей па его поверхности; после этого ясно,
что и точка © будет находиться на поверхности цилиндра. Было же
предположено, что опа там не находится; таким образом, обнаруживает-
ся истинность предложения, которое требовалось доказать.
Если другой диаметр эллипса равен расстоянию между прямыми,
проведенными через концы первого диаметра параллельно прямой, вос-
ставленной (из центра эллипса), то ясно, что цилиндр, объемлющий
этот эллипс, будет прямым (круговым).
Пусть теперь второй диаметр эллипса будет больше ZH (расстоя-
ния между параллельными ГД прямыми, проведенными через концы
диаметра эллипса Л и В); пусть прямая IIZ будет равна этому второму
диаметру {рис. 10]. Восставим на IIZ плоскость, перпендикулярную
к той, в KOTOpoii находятся прямые АВ и ГЛ; возьмем в этой плоскости
круг с диаметром ITZ, и пусть на этом круге будет цилиндр с осью ДР.
Тогда при помощи тех же самых рассуждений докажем, что заданный
эллипс будет находиться на поверхности этого цилиндра.
Пусть, наконец, второй диаметр будет меньше ZIT ’рис. 11). Пусть
квадрат на Г5 представляет избыток квадрата на ZT (половине ZII)
*) Точка А является центром эллипса, a Zr—^ZH перпендикулярным к АВ диаметром
„ ZA AH Zr
‘*)Иа пропорции—= — = • г
***) По известному свойству круга.
****) Это следует из равенства перпендикуляров МЛ. ©К. восставленных к плоскости чертежа..
486
АРХИМЕД
над квадратом на половине второго диаметра. Восставим из точки
Е перпендикулярно к плоскости, в которой находятся АВ и ГА, пря-
мую, равную половине этого диаметра; пусть это будет прямая EN;
точку N представим приподнятой (над плоскостью чертежа); пря-
мая ГМ будет равна TZ*). В плоскости, в которой находятся прямые
. ZH и TN, опишем круг на диаметре ZH; он пройдет через точку N.
На этом круге пусть будет цилиндр с осью ГА; на поверхности этого
цилипдра и будет находиться заданный эллипс.
Действительно, если бы он там не находился, то на нем была бы
некоторая точка, не лежащая на поверхности цизгиндра. Возьмем на
эллипсе такую точку в; перпендикулярно к прямой АВ проведем 0К;
затем пусть из К параллельно ГД пройдет КЛ, а из Л в полукруге с диа-
метром'ХН проведем прямую ЛМ перпендикулярно к ZH. Представим, что
точка М находится па окружности полукруга, описанного на ZII; из точки
М на продолжение прямой КЛ опустим перпендикуляр МО; оп будет
перпендикулярен и к плоскости, в которой находятся АВ и ГД, так как
КЛ перпендикулярна к ZII. Тогда (квадрат) па МО относится к (ква-
драту) на МЛ, как квадрат EN к квадрату на NT**)
мо2 _
мл2 кг2
Но квадрат на МЛ так относится к прямоугольнику между АК и КВ,
как квадрат на L'N к квадрату на АД,
мл8 г№
АК КВ~ АД2
так как квадрат на МЛ равен прямоугольнику между ZA и АН, а квад-
рат на ГМ равен квадрату на rZ***); значит, квадрат на МО будет отно-
ситься к прямоугольнику между АК и КВ, как квадратна EN к ква-
драту на АД.
МО2 _ SIM2
АК • КВ АД2
Но квадрат на К0 относится к прямоугольнику между АК и КВ, как
квадрат на EN к квадрату на АД,
Кб'* _ BN2
АК-КВ^ АД2
так как EN равна половине другого диаметра эллипса; отсюда ясно, что
перпендикуляры МО и КО равны; следовательно, КО и ОМ будут
параллельны. Так как МО параллельна оси цилиндра и точка М нахо-
дится на поверхности последнего, то и МО необходимо будет находиться
па поверхности цилипдра; отсюда ясно, что на поверхности последнего
будет находиться и точка О. Этого же, (согласно предположению),
не было; отсюда ясно, что эллипс необходимо должен лежать на поверх-
ности цилиндра [3].
*) Так как NS будет половина второго диаметра и
ГЕ«=ЯГг—№=.
•*) Из подобия треугольников TEN и ЛОМ с параллельными сторонами.
***) Кроме того, А. *— — ГА
’ лрите ю АК кв Ад
О КОНОИДАХ И СФЕРОИДАХ
187
X
Более ранними математиками*) было доказано, что всякий конус
имеет к другому конусу отношение, равное составленному из отноше-
ний оснований и высот; таким же образом можно доказать, что всякий
конический сегмент к другому коническому сегменту имеет отношение,
равное составленному из отношений оснований и высот.
Далее, что всякий цилиндрический сегмент в три раза больше кони-
ческого сегмента с теми же основанием и высотой, может быть доказано
тем же способом, как и то, что всякий цилиндр в три раза больше конуса
•с теми же основанием и высотой, что и у цилиндра.
XI
(1) Если прямоугольный коноид рассечь плоскостью, проходящей
через ось, или параллельной оси, то сечение будет параболой, и притом
тождественной с той, которая охватывает упомянутое тело', ее диа-
метр будет общей линией пересечения двух плоскостей, из которых одна
является секущей фигуру, а другая проводится через ссь перпендикуляр-
но к секущей плоскости.
Если же рассечь его плоскостью, перпендикулярной к оси, то сече-
ние будет кругом, имеющим центр на. сси.
(2) Если тупоугольный коноид рассечь плоскостью, проходящей
через ссь, или параллельно оси, или через вершину конуса, объемлющего
коноид, то сечение будет гиперболой', при этом если секущая плоскость
проходит через ось, то эта гипербола будет тождественна с той, кото-
рая охватывает фигуру, если же сечение происходит параллельно оси,
то только ей подобна, если же плоскость сечения проходит через вершину
копуса, объемлющего коноид, то сечение не будет даже ей {то есть упо-
мянутой гиперболе) подобно; диаметром гиперболы будет общая линия
пересечения плоскости, секущей фигуру, с плоскостью, проведенной через
ссь перпендикулярно к секущей.
Если же рассечь его плоскостью, перпендикулярной к оси, то сечение
будет кругом, имеющим центр на оси.
(3) Если какой-нибудь из сфероидов рассечь плоскостью, прохо-
ходящей через ось или параллельной оси, то сечение будет эллипсом,
причем если плоскость сечения проходит через ось, то тождественным
с охватывающим фигуру, если же она параллельна оси, то только ему
подобным; диаметром эллипса будет общая линия пересечения плоско-
сти, секущей фигуру, с плоскостью, проведенной через ось перпендикуляр-
но к езкущей.
Если же рассечь его плоскостью, перпендикулярной к оси; то сече-
ние будет кругом, имеющим центр на оси.
(4) Если какое-нибудь из упомянутых тел рассечь плоскостью,
проходящей через ссь, то перпендикуляры, опущенные на секущую пло-
ксстъ из точек, лежащих на поверхности тела, но не на линии сечения,
упадут внутри сучения тела.
Доказательства всех этих предложений очевидны [5].
*) Под этими «более ранними математиками» подразумевается Евдокс, труды которого дошли
до нас и книге XII евклидовых «Начал».
188
АРХИМЕД
XII
Если прямоугольный коноид рассечь плоскостью, не проходящей через
ось, а также не параллельной и не перпендикулярной к оси, то в сечении
получится эллипс, большим диаметром которого будет заключенный
внутри коноида отрезок линии пересечения плоскости, секущей фигуру,
с плоскостью, проходящей через ось и перпендикулярной к ней, а меньший
диаметр будет равен расстоянию между двумя проведенными через концы
большого диаметра прямыми, параллельными оси.
Пусть прямоугольный коноид будет расссчсп плоскостью, как
указано {рис. 12}; пусть АВГ будет сечение коноида другой плоскостью,
перпендикулярной к секущей и проходящей
через ось, а прямая ГЛ — пересечением этой
же плоскости с плоскостью, секущей фигуру;
пусть прямая ВД будет осью коноида и диа-
метром параболы. Требуется доказать, что
сечение коноида плоскостью, проходящей
через АГ, будет эллипсом, больший диаметр
которого равен АГ, а меньший равен ЛА,
если прямая ГЛ проведена параллельно ВД, а
АЛ перпендикулярна к ГЛ.
Рис. 12.
Вообразим, что взята какая-нибудь точ-
ка К сечения и из К опустим на ГА перпен-
дикуляр К0; тогда К© будет также перпен-
дикуляром к плоскости, в которой находится
парабола ЛГВ, так каки секущая плоскость
будет перпендикулярна к той же самой пло-
скости. Через 0 под прямым углом к ВД проведем EZ, и через прямые
EZ и К© проведем плоскость; последняя будет перпендикулярна к ВД;
тогда коноид будет рассечен плоскостью, перпендикулярной к оси; так
что полученное сечение будет кругом с центром в Д; значит, К© будет
квадрировать прямоугольник на Z© и ©Е,
ке’=2в.ев
[ибо на EZ построен полукруг и перпендикуляр К© будет средней про-
порциональной для отрезков Е0, 0Z]. Параллельно АГ проведем ка-
сательную MN к параболе (пусть точкой касания будет N), а параллель-
но EZ проведем прямую ВТ. Прямоугольник на А© и ©Г будет отно-
ситься к прямоугольнику между Е©, ©Z, как квадрат на NT к квадрату
на ВТ,
ле-ег nt2
Ee-ez цт2
как уже было доказано (предложение III, 1). Но NT равна ТМ, так-
как ВР равна ВМ; значит, и прямоугольник между Л© и ©Г имеет
к квадрату на К© то же отношение, что квадрат на Т М к квадрату па ТВ;
де.er _ тмя
ке2
значит, квадрат на перпендикуляре ©К к прямоугольнику между А0,
©Г будет иметь то же отношение, что квадрат на ВТ к квадрату на ТМ.
, ек2
ВТ2
Ав-©Г ТМ2
О КОНОИДАХ И СФЕРОИДАХ
189
Так как треугольники ГАЛ и Т МВ подобии, то квадрат на перпенди-
куляре (ЭК к прямоугольнику между АО и ОГ будет иметь то же отно-
шение, что квадрат на АЛ к квадрату па АГ.
(Ж2 АЛ2
Ав-ег- АГ2
Подобным же образом докажем, что квадраты на других перпендику-
лярах, опущенных па прямую АГ с (линии) сечения, будут к пря-
моугольникам между (соответствующими) отрезками АГ иметь то же
отношение, что квадрат АЛ к квадрату АГ; таким образом, ясно, что
сечение будет эллипсом, наибольшим диаметром которого будет АГ,
а наименьший будет равен АЛ.
. XIII
Если тупоугольный коноид рассечь плоскостью, которая встречала
бы все стороны конуса, объемлющего коноид, и не была бы перпендикуляр-
на к сси, то сечение будет эллипсом, наибольшим диаметром которого
является заключенный виу-
три коноида отрезок ли- Л_Г''\т
нии пересечения плоскости,
секущей коноид, с плоско- s'
стою, к ней перпендикуляр-
ной, проведенной через ось. / Т'чхЧ
Рассечем тупоуголь-
ПЬШ КОНОИД плоскостью,
как указано {рис. 13}.
Пусть гипербола АВГ пред-
ставляет сечение коноида ₽ис- 13-
другой плоскостью, про-
ходящей через ось, и перпендикулярной к первой секущей плоско-
сти; пусть прямая АГ будет сечением плоскости, секущей фигуру,
а ВД — осью коноида и диаметром гиперболы. Вообразим какую-ни-
будь точку К, взятую на линии сечения и опустим из К па АГ перпенди-
куляр КО; последний будет также перпендикуляром к плоскости, в ко-
торой лежит гипербола АВГ. Через О перпендикулярно к ВД проведем
EZ, а через прямые EZ и КО проведем плоскость, пересекающую
коноид; таким образом, последний будет рассечен плоскостью, перпен-
дикулярной к оси, так, что в сечении получится круг с центром в Д;
следовательно, перпендикуляр па КО будет квадрировать прямоуголь-
ник между ЕО, 0Z;
кег-Ев-oz
теперь проведем параллельно АГ касательную MN к гиперболе в точ-
ке N и прямую ВТ, параллельную EZ; тогда прямоугольник между ВО
и ®Z будет относиться к прямоугольнику между АО, ОГ, как квадрат на
ВТ к квадрату на TN;
ES-OZ^ ВТ2
Ав-’ёг “ та»
таким образом, квадрат на перпендикуляре К® относится к прямоуголь-
нику между АО и ОГ, как (квадрат) на ВТ к квадрату на TN.
КО2 ВТ2
АО0Г~ TN2
Подобным же образом докажем, что квадраты других перпендикуляров,
190
АРХИМЕД
опущенных с липни сечения на АГ, к прямоугольникам между отрез-
ками, образуемыми этими перпендикулярами на АГ, будут относиться,
как квадраты на ВТ и па TN. При этом ВТ будет меньше TN, так как
и МТ меньше TN, (а МТ больше ВТ), поскольку МВ меньше, чем
ВР; последнее же является характерным свойством гиперболы. Таким
образом, ясно, что сечение будет представлять эллипс с наибольшим
диаметром АГ [6].
XIV
Если удлиненный сфероид рассечь плоскостью, не перпендикулярной
к оси, то в сечении получится эллипс, наибольшим диаметром которого
будет заключенный внутри сфероида отрезок общей линии пересечения,
плоскости секущей фигуры с плоскостью, перпендикулярной к ней и про-
ходящей через ось.
Если сечение производится плоскостью, проходящей через ось
или параллельной оси, то предложенное очевидно. Рассечем сфероид
какой-нибудь другой плоскостью;
скостыо, проходящей через ось и
Рис. 14.
Подобно предыдущему докажем,
ели, кроме того, рассечь его пло-
перпондикулярной к секущей, то
в сечении со сфероидом получится
эллипс АВГД, а в сечении с секу-
щей плоскостью — прямая ГА.
Пусть ВД будет осью сфероида и
диаметром эллипса, точка X —цен-
тром и ПР — наименьшим диамет-
ром {рис. 14}. Проведем ВТ, пер-
пендикулярную к ВД, и касатель-
ную HN к эллипсу в точке N,
параллельную АГ; через X парал-
лельно АГ проведем также МА.
то квадраты на перпендикулярах,
опущенных из точек кривой сечения на АГ, находятся с прямоуголь-
никами между отрезками АГ в том же самом отношении что квадрат на
ВТ к квадрату па TN.
BT2
Ав ОТ — Т№
Что полученное сечение будет эллипсом и АГ его диаметром, очевидно,
а что АГ будет наибольшим диаметром, требуется доказать.
Прямоугольник между ПХ, ХР имеет к (прямоугольнику) меяеду
MX, ХА то же отношение, что (квадрат) на ВТ к (квадрату) на NT,
пх хр _ нт®
МХ-ХЛ ~ NT’»
так как ПР и МЛ проведены параллельно касательным. Но прямоуголь-
ник между ПХ, ХР будет меньше (прямоугольника) между MX, ХЛ,
так как ХП меньше ХЛ; значит, и квадрат на ВТ будет меньше квадрата
на TN; таким образом, и квадраты на перпендикулярах, опущенных на
АГ из (точек) кривой сечения, будут меньше прямоугольников между
отрезками ЛГ.
ек»< леев
Теперь ясно, что диаметр ЛГ будет наибольшим*).
*) Действительно, если точка 0 будет совпадать с серединой Л Г, то мы имеем: ©К1 <
/ АГ Л Г
, то есть—---полудиаметр, соответствующий АГ, — будет больше дерпепдшеуллрного-
ему полудиамстра ©К.
О КОНОИДАХ И СФЕРОИДАХ
191
Если сплющенный эллипсоид рассечь плоскостью, то все получится
так же, но отрезок внутри сфероида будет наименьшим диаметром.
Из этого ясно, что во всех этих телах сечения параллельными друг
другу плоскостями будут подобными, так как квадраты перпендикуля-
ров {опущенных из точек линии сечопия) будут иметь одинаковые
отношения к прямоугольникам между (соответствующими) отрезками.
XV
(1) В прямоугольном коноиде прямые, проведенные параллельно оси
из любой точки на поверхности коноида, будучи продолжены в сторону
выпуклости коноида, пройдут вне последнего, продолженные же в про-
тивоположную сторону— попадут внутрь последнего.
Действительно, если провести плоскость через ось и ту точку, через
которую проводится прямая, параллельная оси, то в сечении получится
парабола, диаметр которой будет и осью коноида; для параболы же пря-
мая, проведенная параллельно диаметру через всякую точку кривой,
со стороны выпуклости попадает вне параболы, с противоположной же
стороны—внутри последней; таким образом, предложенное очевидно.
(2) В тупоугольном коноиде прямые, проведенные из любой точки
на его поверхности параллельно какой-нибудь линии, проведенной в ко-
ноиде через вершину объемлющего коноид конуса, будучи продолжены
в сторону выпуклости коноида, пройдут вне последнего, продолженные
же в противоположную сторону попадут внутрь его.
Действительно, осли провести плоскость через прямую, проведен-
ную в коноиде через вершину объемлющего коноид конуса, и через ту
точку, мз которой проводится рассматриваемая прямая, то в сечении
получится гипербола, диаметром которой будет прямая, проведенная
в коноиде через вершину объемлющего конуса*). Для гиперболы же
прямая, проведенная через всякую точку кривой, идущая параллельно
с прямой, проведенном указанным способом, и продолженная в сторону
выпуклости кривой, пройдет вне ее, продолженная же в противополож-
ную сторону попадет внутрь.
(3) Если плоскость касается коноида, не пересекая его, то она
касается только в одной точке, причем плоскость, проведенная через
ось и точку касания, перпендикулярна, к касательной плсскести.
Действительно, пусть, если возможно, она будет касаться конопда
в нескольких точках. Если мы возьмем какие-нибудь две точки, в кото-
рых эта плоскость касается коноида, и через каждую из них проведем
прямую, параллельную оси, то плоскость, проведенная через эти пря-
мые, будучи продолжена, или пройдет через ось, или же будет ей парал-
лельна; таким образом, в сечении получится какое-нибудь коническое
сечение, и взятые точки окажутся на некотором коническом сечении,
так как они лежат и на поверхности коноида и на секущей плоскости.
Тогда прямая, соединяющая взятые две точки, будет внутри конического
сечения, а следовательно, окажется и внутри поверхности коноида. Но
эта прямая находится па касательной плоскости, так как па последней
лежат обе выбранные точки; значит, некоторая часть касательной пло-
скости окажется внутри коноида; это же невозможно, так как предполо-
жено, что эта плоскость пе пересекает коноида. Таким образом, рассмат-
риваемая плоскость будет касаться коноида только в одной точке.
') См. комментарий 17].
192
АРХИМЕД
А что плоскость, проведенная через точку касания и ось, будет
перпендикулярна к касательной плоскости, то это очевидно, если каса-
ние происходит в вершине коноида. Действительно, если через ось
коноида провести две плоскости, то в сечениях получатся конические
сечения, имеющие своим диаметром ось, и лежащие на касательной пло-
скости прямые будут касаться этих конических сечений в конце диа-
метра. Прямые же, касающиеся конических сечений в конце диа-
метра, образуют с последним прямые углы; таким образом, в касатель-
ной плоскости будут две прямые, перпендикулярные к оси. Значит,
касательная плоскость будет перпенди-
кулярна к оси, а поэтому и к всякой
проходящей через ось плоскости.
Пусть теперь плоскость будет ка-
саться коноида не в вершине послед-
него. Проведем плоскость через точку
касания и ось; в сечении с коноидом
получится коническое сечение АВГ
{рис. 15). Пусть ВД будет осью (ко-
ноида) и диаметром (сечения), сече-
нием касательной плоскости будет пря-
мая же E©Z, касающаяся конического
сечения в точке ©.Из 0 опустим на ВД
перпендикуляр ©К и проведем через К
плоскость, перпендикулярную к оси; она
образует в сечении круг с центром К,
Сечение этой (последней пл оскости) и ка-
касательпой к кругу прямой; значит,
сатсльной плоскости будет
последняя образует с ©К прямые углы; отсюда же следует, что она
будет перпендикулярна и к плоскости, в которой находится К© и ВД.
Таким образом, ясно, что к этой же самой плоскости будет перпенди-
кулярна и касательная плоскость, так как расположенная в пей пря-
мая*) будет перпендикулярна к этой же самой плоскости.
XVI
(1) Если какой-нибудь из сфероидальных фигур касается плоскость,
не пересекающая этой фигуры, то она будет касаться только в одной
точке, и плоскость, проведенная через точку касания и ось, будет пер-
пендикулярна к касательной плоскости.
Действительно, пусть она будет касаться в нескольких точках.
Тогда, если мы возьмем точки, в которых эта плоскость касается сферо-
ида, и через каждую из иих проведем параллельную оси прямую, и через
эти прямые проведем плоскость, то ее сечение с коноидом будет эллип-
сом, и эти точки окажутся па коническом сечении. Теперь прямая,
соединяющая эти точки, будет внутри конического сечения, а следова-
тельно, окажется внутри и поверхности сфероида. Но эта прямая нахо-
дится па касательной плоскости, Tait как на ней же лежат и взятые точки;
значит, какая-то часть касательной плоскости будет внутри сфероида.
Но это не имеет места, ибо, согласно предположенному, опа не пересе-
кает сфероида. Таким образом, ясно, что опа будет касаться только
в одной точке. А что проведенная через точку касания и через ось пло-
*) Речь идет о проведенной через 6 касательной к кругу.
О КОНОИДАХ И СФЕРОИДАХ
193
скость будет перпендикулярна к касательной плоскости, мы докажем
подобно тому, как и для коноидов.
(2) Если, какую-нибудь из коноидалъных или сфероидальных фигур
рассечь проходящей через ось плоскостью и провести прямую, касаю-
щуюся полученного сечения, и на касательной восставить плоскость,
перпендикулярную к секущей, то она будет касаться фигуры в той же
самой точке, в которой проведенная прямая касается конического сечения.
Действительно, она пе коснется поверхности этой фигуры в какой-
нибудь другой точке; иначе перпендикуляр, опущенный из этой точки
на секущую плоскость, попал бы вне конического сечения, так как он
попадет на касательную плоскость, поскольку упомянутые плоскости
будут перпендикулярны друг к другу; это же невозможно, ибо дока-
зано, что он упадет внутрь сечения *).
(3) Если какой-нибудь из сфероидальных фигур касаются две парал-
лельные плоскости, то прямая, соединяющая точки касания, пройдет,
через центр сфероида.
Действительно, это очевидно, если обе плоскости перпендикулярны
к оси; пусть же они не будут перпендикулярны. Тогда плоскость, про-
веденная через ось и точку касания одной пло-
скости, будет перпендикулярна к касательной
плоскости, а следовательно, и к плоскости, ей .s’"
параллельной. Значит, необходимо, чтобы пло- [ /
скость, проходящая через ось и каждую точку I-----у/- ----Д
касания, была одной и той же. В противном слу- / J
чае будут две плоскости, перпендикулярные к
одной и той же плоскости, и проведенные через
одну и ту же прямую, не являющуюся пер-
нендикулярной к этой плоскости, ибо мы пред- ис*
положили, что ось не будет перпендикулярной
к параллельным плоскостям; значит, ось и обо точки касания будут
находиться в одной и той же плоскости, и сфероид будет рассечен пло-
скостью, проходящей через ось {рис. 16}. В таком случае сечение будет
эллипсом, сечения же касательных плоскостей будут параллельными
прямыми, касающимися эллипса в точках касания плоскостей; если же
две параллельные прямые касаются эллипса, то центр эллипса и точки
касания будут находиться на одной прямой.
XVII
Если к какой-нибудь из сфероидальных фигур провести две парал-
лельные касательные плоскости и. кроме того, через центр сфероида про-
вести плоскость, параллельную касательным, то прямые, проведенные
через точки полученной линии сечения параллельно прямой, соединяющей,
точки касания, попадут впе сфероида {рис. 17}.
Предположим все сказанное уже существующим и возьмем на полу-
ченной линии сечения какую-нибудь точку, затем через взятую точку
и прямую, соединяющую точки касания, проведем плоскость; тогда
последняя рассечет как сфероид, так и обо параллельные плоскости.
•) Так как втот перпендикуляр лежит в касательной плоскости, то он должен обязательно
попасть иа прямую, касательную к коническому сечению; все же точки касательной, кроме точки
касания, будут находиться вне конического сечения. Доказательство, что указанный перпендикуляр
попадет внутрь конического сечения, дано (или, вернее, подразумевается) в последней части пред-
ложения XI.
13 Архимед
194
АРХИМЕД
Пусть сечение сфероида будет [эллине] АВГД, сечения касательных пло-
скостей — прямые EZ, (ЭН, взятая точка Л, прямая, соединяющая точки
касания, пусть будет ВД (последняя, конечно, пройдет через центр),
сечение же плоскости, параллельной касательным плоскостям, бу-
дет ГЛ; эта прямая также пройдет через
центр, поскольку через центр проходит и
соответствующая плоскость. Теперь так
как АВГД будет или кругом или эллипсом,
и ее касаются две прямые EZ, П<Э, а через
центр проведена параллельная им АГ, то
ясно, что проведенные через АГ, парал-
лельно ВД прямые будут касательными к
сечению и попадут вне сфероида [8].
Если же параллельная касательным
рис. и. плоскость пе будет проведена через центр,
как, например, КЛ, то ясно, что из проводи-
мых через точки сочепия(параллельно ВД)
прямых те, которые будут со стороны меныпего сегмента, попадут вне
сфероида, те же, которые с противоположной стороны — внутрь его.
XVI11
Всякая сфероидальная фигура, рассекаемая плоскостью через
центр, и сама рассекается этой плоскостью пополам, и ее поверхность.
Действительно, рассечем сфероид через центр плоскостью; тогда
он будет рассечен или через ось, или же перпендикулярно к ней, или же
не перпендикулярно к оси. Если сфероид сечется через ось, или
же перпендикулярно к оси, то ясно, что и сам
разделятся пополам, так как одна
совпадать с другой, а также и по-
верхность одной его части с поверх-
ностью другой.
Так пусть теперь сфероид будет
рассечен плоскостью, не проходящей
через ось и не перпендикулярной
к осп. Если мы рассечем сфероид
плоскостью, перпендикулярной к
секущей и проходящей через ось, то
сечением самой фигуры пусть будет
эллипс АВГД, его диаметр и ось
сфероида — прямая ВД и центр — 0,
сечением же плоскости, рассекшей
сфероид через центр, пусть будет
прямая АГ {рис. 18]. Возьмём еще
оп и его поверхность
его часть будет, очевидно,
какой-нибудь другой сфероид.
равный этому и подобный; пусть при сечении его плоскостью через ось
получится эллипс EZITN, его диаметр и ось сфероида пусть будет ЕВ,
а центр К {рис. 19); проведем через К прямую ZN, образующую угол К ,
равный углу 0, и пусть на ZN будет восставлена плоскость, перпен-
дикулярная к той, в которой находится сечение EZHN; тогда полу-
чатся два равных и подобных друг другу эллипса АВГА и EZIIN;
они совпадут друг с другом, если совместить EII с ВД, a ZN с А Г. Тогда
и плоскость, проходящая через NZ, совпадет с плоскостью через АГ,
так как обе они проходят через одну и ту же прямую и перпендмку-
О КОНОИДАХ И СФЕРОИДАХ
195
лярвы к одной и той лее плоскости. Тогда и сегмент, отсеченный по
-NZ от сфероида и находящийся с той стороны, где Е, совпадет с другим
сегментом, отсеченным по АГ от другого сфероида и находящимся с той
стороны, где В; совпадут также и оставшиеся сегменты и поверхности
одних сегментов с поверхностями других. Затем если мы поместим ЕН на
ВА так, чтобы точка Е легла на Д, а Н — на В, прямая же между точ-
ками N, Z—на прямую между точками А, Г, то ясно, что друг с дру-
гом совпадут и оба эллипса и что Z попадет в Г, a N в А. Точно так же
и проходящая через NZ плоскость совпадет с плоскостью, проходящей
через АГ, и из отсеченных плоскостью по АГ сегментов тот, который
находится со стороны Н, совпадет с тем из отсеченных плоскостью по
АГ сегментов, который будет со стороны В, а тот, который находится
со стороны Е, совпадет с тем, что со стороны А. Но так как один и тот
же сегмент совпадает с каждым из двух сегментов, то ясно, что оба
эти сегмента будут равны; поэтому же будут равны и поверхности
(сегментов).
XIX
Если дан сегмент какого-нибудь ия коноидов, отсеченный перпендику-
лярной к оси плоскостью, или же сегмент какого-нибудь из сфероидов,
не больший половины этого сфероида и точно так же отсеченный, то
можно вписать в него телесную
фигуру и описать около него дру-
гую, состоящую из имеющих рав-
ную высоту цилиндров, и притом
так, чтобы, описанная, (фигура была
больше вписанной на величину,
меньшую любой наперед заданной
телесной величины.
Пусть дан сегмент, как, на-
пример, АВГ, сечение его прове-
денной через ось плоскостью бу-
дет АВГД, сечение же отсекшей
его плоскости пусть будет прямая
АГ, а ось сегмента и диаметр сече-
ния ВД {рис. 20}. Поскольку секу-
щая плоскость предполагается
перпендикулярной к оси, то сече-
ние будет кругом с диаметром ГА.
Пусть на этом круге будет ци-
линдр, имеющий осью ВД; тогда
его поверхность пройдет вне сег-
мента, поскольку последний является сегментом коноида или сфероида,
не большим половины сфероида. Если этот цилиндр мы будем постоян-
но делить пополам перпендикулярной к оси плоскостью, то когда-нибудь
получится остаток, меныпий заданной телесной величины; пусть таким
его остатком будет цилиндр, имеющий основанием круг на диаметре АГ,
а осью ЕД, и меньший заданной телесной величины. Разделим ВД в Р,
О, 1.1, В на равные ЕД части, через точки деления параллельно АГ
проведем к коническому сечению прямые, и на этих проведенных пря-
мых восставим перпендикулярные к ВД плоскости; в сечениях получат-
ся круги, имеющие центры па ВД. На каждом из этих кругов построим
13*
J96
АРХИМЕД
два цилиндра, оба с осью, равной ЕД, один в ту сторону от круга, где
находится Д, другой же в ту, где находится В; таким образом в сегменте
получится некоторая вписанная телесная фигура, составленная из
цилиндров, построенных в ту сторону, где находится Д, и другая опи-
санная, составленная из цилиндров, построенных в ту сторону, где
находится В. Остается лишь доказать, что описанная фигура превосхо-
дит вписанную на величину, мепьшую любой заданной телесной вели-
чины. Каждый из цилиндров во вписанной фигуре будет равен цилиндру,
построенному на том же круге в ту сторону, где находится В, как,
например, цилиндр &Н равен 01, цилиндр КЛ равен КМ и точно так
же и остальные, причем все вместе взятые такие цилиндры одной фигуры
будут равны всем цилиндрам другой. Теперь ясно, что описанная фигу-
ра будет больше вписанной па цилиндр, имеющий основанием круг па
диаметре АГ и ось ЕД; этот же цилипдр меньше заданной телесной вели-
чины.
XX
Если дан сегмент какого-нибудь из коноидов, отсеченный плоскостью,
не перпендикулярной к оси, или же сегмент какого-нибудь из сфероидов,
не больший половины этого сфероида и точно так же отсеченный, то
можно вписать в него телесную фигуру и описать около него другую,
составленную из цилиндриче-
ских сегментов, имеющих рав-
ную высоту, и притом так,
чтобы описанная фигура была
больше вписанной на величину,
меньшую любой наперед задан-
ной телесной величины.
Пусть будет дан такой сег-
мент, как сказано; рассечем его
другой плоскостью через ось,
перпендикулярной к отсекшей
заданный сегмент плоскости;
пусть сечение данной фигуры
будет коническое сечение АВГ
{рис. 21}, сечение же отсекшей
сегмент плоскости пусть будет
прямая ГА. Теперь, поскольку
отсекшая сегмент плоскость
предполагается не перпендику-
лярной к оси, то сечение будет
эллипсом с диаметром ЛГ. Пусть
будет параллельная ЛГ касательная ФГ к коническому сечению, и
пусть она касается в В; восставим наФГ плоскость, параллельную той,
которая проходит через АГ; и эта плоскость будет в В касаться нашей
^фигуры. И если сегмент принадлежит прямоугольному коноиду, то из
В параллельно оси проведем ВЛ, если же тупоугольному,то прямую,
проведенную к В от вершины объемлющего коноид конуса, продолжим
в виде ВД, если же сегмент принадлежит сфероиду, то пусть ВА будет
отсеченной частью прямой, проведенной (из цептра) до В; ясно, что ВД
разделит АГ пополам, так что В будет вершиной сегмента, прямая же
ВД — его осью. Получится некоторый эллипс на диаметре АГ и линия
ВД, восставленная из центра в плоскости, перпендикулярной к той,
О КОНОИДАХ И СФЕРОИДАХ
1S7
в которой находится эллипс, и проходящей через другой диаметр (эл-
липтической грани). Теперь можно найти цилиндр, имеющий ось ВЛ,
на поверхности которого будет находиться эллипс, построенный на диа-
метре АГ (предложение IX); поверхность этого цилиндра окажется вне
сегмента, поскольку последний принадлежит коноиду или сфероиду
и (в последнем случае) не больше половины сфероида. Получится неко-
торый цилиндрический сегмент, имеющий основаниями эллипсы на
диаметре АГ и осью прямую ВД; если этот сегмент мы будем делить
пополам плоскостями, параллельными той, что проходит через АГ.
то (в конце концов) получится остаток, меньший наперед заданной
телесной величины. Пусть сегмент, имеющий основанием эллипс на
диаметре АГ, а осью ЕД, будет меньше наперед заданной телесной
величины. Разделим ДВ на части, равные ДЕ, через точки деления па-
раллельно АГ проведем до конического сечения прямые и на этих
проведенных прямых восставим плоскости, параллельные той, которая
проходит через АГ; эти плоскости рассекут поверхность сегмента и об-
разуют эллипсы, подобные тому, который ла диаметре АГ, вследствие
параллельности соответствующих плоскостей. На каждом таком эллип-
се построим два цилиндрических сегмента, имеющих ось, равную ДЕ,
один в ту сторону от эллипса, где находится Д, другой же — в ту, где
находится В; тогда получатся две некоторые телесные фигуры, одна впи-
санная в сегмент, другая же описанная около него, составленные из
цилиндрических сегментов, имеющих равную высоту. Остается дока-
зать, что описанная фигура превосходит вписанную на величину, мень-
шую наперед заданной телесной величины. Подобно предыдущему дока-
жем, что описанная фигура превышает вписанную па сегмент, имеющий
основанием эллипс на диаметре АГ и ось ЕД; последний же меньше па-
перед заданной телесной величины. . .
XXI
Изложив все это, перейдем к доказательству теорем, предложен-
ных относительно рассматриваемых фигур.
Всякий сегмент прямоугольного коноида, отсеченный плоскостью,
перпендикулярной к оси, будет в полтора раза больше конуса, имеющего
те же самые основания и ось, что и сегмент.
Пусть будет сегмент прямоугольного коноида, отсеченный пло-
скостью, перпендикулярной к оси; рассечем его через ось другой пло-
скостью, и пусть в сечении с поверхностью получится парабола АВГ,
в сечении же с плоскостью, отсекшей сегмент, прямая ГА, ось сегмента
будет ВД; пусть также будет конус, имеющий с сегментом тс же
самые основание и ось, вершина которого В. Требуется доказать, что
сегмент коноида будет в полтора раза больше этого конуса.
Построим конус Т {рис. 22], который был бы в полтора раза боль-
ше конуса, основанием которого является круг на диаметре АГ,
а осью—прямая ВД; пусть также будет цилиндр, имеющий основанием
круг на диаметре АГ и ось ВД; тогда копус Y будет половиной цилиндра,
{поскольку конус Y в полтора раза больше упомянутого выше копуса].
Я утверждаю, что сегмент коноида будет равен конусу Y.
Действительно, если он ему не равен, то будет или больше или
меньше. Пусть сначала, если возможно, он будет больше. Впишем
в сегмент телесную фигуру {рис. 23] и опишем около него другую^
198
АРХИМЕД
составленную из цилиндров, имеющих одинаковую высоту, таким обра-
зом, чтобы описанная фигура превосходила вписанную на величину,
мепьшую той, на которую сегмент копоида больше конуса Уг, и пусть
из цилиндров, составляющих описанную фигуру, наибольший
будет иметь основанием круг
на диаметре АГ и ось ЕД,
наименьший ясе будет иметь
основанием круг на диамет-
ре ST и ось 131, а из ци-
линдров, которые составляют
вписанную фигуру, наиболь-
шим будет имеющий основа-
нием круг на диаметре КЛ, а
осью ДЕ, наименьшим ясе —
имеющий основанием круг
на диаметре ST и осью 61;
плоскости всех этих цилинд-
ров продолжим до поверхно-
сти цилиндра, имеющего ос-
нованием круг на диаметре
ЛГ и осью ВД; тогда весь
цилипдр будет разделен на
цилиндры, количество кото-
рых равпо их количеству в
описанной фигуре, и которые
по величине равны наиболь-
шему из этих цилиндров. И
так как описанная около сег-
мента фигура превосходит
вписанную на величину,
меньшую той, на которую
сегмент больше конуса, то
ясно, что и вписанная в сег-
мент фигура будет больше ко-
нуса У/1. Первый цилиндр из
содержащихся в целом ци-
линдре, а именно, имеющий
осью ДЕ, с первым цилиндром во вписанной фигуре, имеющим осью ДЕ,
находится в том же самом отношении, какое квадрат на ДА имеет к
квадрату на КЕ; это яге отношение равно тому, которое ВД имеет к BE *),
дла = ВА
КЕа BE
и тому, которое ДА имеет к ЕЕ.
ВД ДА
BE ' ЕЕ
Точно так же докажем, что второй цилиндр из содержащихся в целом
цилиндре, а именно имеющий ось EZ, со вторым цилиндром во вписан-
ной фигуре с той же осью EZ будет находиться в том же отношении,
что ПЕ, или АД. к ZO, и что каждый из остальных цилиндров, содср-
*) На основании, основного свойства параболы, выражаемого па современном математичс-
^буду' *ЕГ УРапнСи11-см р“—'2jpx, абсциссами ж будут ВЕГ Вд} а соответствующими ординатами
О КОНОИДАХ И СФЕРОИДАХ
199
жащихся в целом цилиндре и имеющих оси, равные ДЕ, с соответствую-
щим цилиндром во вписанной фигуре с той же самой осью будет находить-
ся в таком же отношении, как половина диаметра его основания к отрез-
ку итого самого диаметра между прямыми А13 и ВД. Таким образом,
все цилиндры, находящиеся в цилиндре, основание которого есть круг
иа диаметре ЛГ, а ось — прямая Д1, со всеми цилиндрами во вписан-
ной фигуре будут находиться в том же самом отношении, которое все
взятые вместе прямые — радиусы кругов, являющихся основаниями
упомянутых цилиндров, имеют ко вместе взятым всем прямым —
отрезкам этих радиусов, содержащихся между ЛВ и ВЛ.
Но все первые упомянутые прямые будут более чем вдвое больше
вторых упомянутых прямых без АД*); таким образом, и все цилиндры,
заключающиеся в цилиндре с осью AI, будут более чем вдвое больше
вписанной фигуры; значит, и подавно целый цилиндр, ось которого ДВ,
будет более чем вдвое больше вписапной фигуры.
Но этот цилиндр был вдвое больше конуса 1Р ; значит, вписанная
фигура меньше конуса *Е, а это невозможно, ибо доказано, что она боль-
ше. Таким образом, коноид ле будет больше конуса Т,
Точно так же он не будет и меньше. Действительно, снова впишем
и опишем рассматриваемые две фигуры так, чтобы они различались
между собой на величину, меньшую той, па которую конус Т больше
коноида, и устроим все остальное совершенно так же, как и прежде.
Теперь, поскольку вписанная фигура будет меньше сегмента и вписанная
отличается от описанной па величину, меньшую той, па которую сег-
мент меньше конуса Чг, то ясно, что описанная фигура будет меньше кону-
са Т. Тогда точно так же первый из цилиндров в целом цилиндре, именно
имеющий ось ДЕ, к первому из цилиндров в описанной фигуре с той же
самой осью ЕД, будет иметь то же самое отношение, что квадрат на АД
к себе самому; второй же из цилиндров целого цилиндра, имеющий ось
EZ, ко второму цилиндру в описанной фигуре с осью EZ будет иметь
то же самое отношение, что квадрат на ДА к квадрату на КЕ.
Это же отношение будет тождественно с тем, которое имеют ВД
к BE и ЛЛ к ЕЕ,
Ада _ ВД ДА
КЕ2‘ ~ BE “ КЗ
и каждый из остальных цилиндров в целом цилиндре, имеющих оси
равными ДЕ, к соответствующему цилиндру и описанной фигуре с той
же самой осью будет иметь такое же отношение, как половина диаметра
его основания к своему отрезку между прямыми АВ и ВД; таким обра-
зом, все цилиндры в целом цилиндре, ось которого есть прямая ВД,
ко всем цилиндрам в описанной фигуре будут иметь то же самое отно-
шение, что все первые прямые ко всем вторым прямым.
тлиндр АВГД_ п-АД
-оп. фигГАВГД “ АД-?-ЕЕ i OZ ...
г», раз
*) Следует отметить небольшой недосмотр Архимеда. Если считать, что прямая ВЛ разделена
на л частей, равных ЕА, то в написанную пропорцию входит всего и—1 цилиндров и соответственно
прямых АД, а также ЕЕ, ZO и т. д. Пусть прямая АД будет равна пх, тогда п—1 прямых ЕЕ, ZO
и т, Д. дадут в сумме:
:t“4-2х-г ... -г (n— 1 )*х—- пх(п— 1),
что будет ровно вдвое меньше (гг—1)АЛ 1)пх, Таким образом, вое цилиндры, заключающиеся
в цилиндре с осью Д1, ровно вдвое больше вписанной фигуры; более чем вдвое больше будет только
свесь цилиндр АВГ, состоящий из п цилиндрических сегментов.
200
АРХИМЕД
Но все прямые, являющиеся радиусами кругов — оснований этих
цилиндров, будут меньше всех удвоенных прямых, составляющих их
отрезки, вместе с АА.
Теперь ясно, что все цилиндры в целом цилиндре будут меныпе-
удвоенных всех цилиндров в описанной фигуре; значит, цилиндр, имею-
щий основанием круг на диаметре АГ и ось ВД, будет меньше удвоен-
ной описанной фигуры. Но это не так: он будет более чем вдвое боль-
шим, ибо он вдвое больше копуса Т, в то время как описанная фигура,
согласно доказанному, мень-
ше конуса V. Значит, сегмент
коноида пе будет и меньше
конуса Чг. Но доказано, что-
он и не больше; значит, он
будет в полтора раза больгао
конуса, имеющего с сегмен-
том те же самые основание и
ось [9].
XXII
И если- сегмент прямо-
угольного коноида будет от-
секаться плоскостью, не пер-
пендикулярной к оси, он точ-
но так же будет в полтора
раза больше сегмента конуса,
имеющего то же самое основа-
ние и ту же ось, что и сег-
мент коноида.
Пусть будет сегмент пря-
моугольного коноида, отсе-
ченный указанным образом;
рассечем его плоскостью, про-
ходящей через ось и перпен-
дикулярной к плоскости, от-
секшей сегмент; пусть сечение
фигуры будет парабола АВГ,
а сечение плоскости, отсек-
шей сегмент, — прямая А Г;
пусть ФГ будет касательная
к параболе в В, параллельная
АГ; параллельно оси прове-
дем ВА; последняя разделит
АГ пополам; затем на ФТ восставим плоскость, параллельную той,
которая проходит через АГ; эта плоскость будет касаться коноида
в (точке) Б, причем точка В будет вершиной сегмента, а ВА его осью
{рис. 24 и 25].
Теперь поскольку проходящая через АГ плоскость рассекла коно-
ид, не будучи перпендикулярной к его оси, то в сечении получится
эллипс, наибольший диаметр которого будет АГ. Тогда, имея эллипс па
диаметре ГА и линию ВА, которая проведепа из центра эллипса в пло-
скости, восставленной через диаметр перпендикулярно к той, в которой
находится сам эллипс, мы можем найти цилиндр, имеющий ось на одной.
О КОНОИДАХ И СФЕРОИДАХ
201;
прямой с ВД, на поверхности которого будет находиться этот эллипс
(предложение IX); также можно найти и конус, имеющий вершиной
точку В, на поверхности которого будет находиться рассматриваемый
эллипс (предложение VIII); таким образом, получится некоторый
цилиндрический сегмент, имеющий основанием эллипс на диаметре ЛГ
и осью—прямую ВД, и вместе с ним конический сегмент, имеющий те же
самые ось и основание, что и сегменты цилиндра и коноида. Требуется
доказать, что сегмент коноида будет в полтора раза больше этого кони-
ческого сегмента.
Пусть будет конус Т, в полтора раза больший этого конического
сегмента; тогда цилиндрический сегмент, имеющий те же основание
и ось, что и рассматриваемый сегмспт, будет в два раза больше конуса Т,
ибо последний в полтора раза больше конического сегмента, имеющего
те же основание и ось, что и рассматриваемый сегмент, упомянутый же
конический сегмент будет третьей частью цилиндрического сегмента,
имеющего то же основание и ту же ось, что и конический сегмент. Необ-
ходимо, чтобы сегмент коноида равнялся конусу Т".
Действительно, если он не равен, то будет или больше, или меньше.
Пусть сначала он, если возможно, будет больше. Тогда впишем в сег-
мент телесную фигуру и опишем около него другую, составленную из
цилиндрических сегментов, имеющих равные высоты, так, чтобы
описанная фигура превосходила вписанную на вел ичину меньшую той,
на которую сегмент коноида больше конуса Ч*-; и плоскости сечений
продолжим до поверхности цилиндрического сегмента, имеющего те
же основание и ось, что и сегмент коноида. Опять первый сегмент
в целом цилиндрическом сегмспте, имеющий ось ДЕ, будет к первому
сегменту вписанной фигуры с осью ДЕ иметь то же самое отношение,
что квадрат па АД к квадрату на КЕ; ибо сегменты с одинаковой высотой
имеют друг к другу то же самое отношение, что и основания, осно-
вания же их, являясь подобными эллипсами, имеют то же самое отно-
шение, что соответственные их диаметры в квадратах, и АД, КЕ будут
половинами соответственных диаметров. Но какое отношение имеют АД
к КЕ в квадратах, такое же отношение будет иметь и ВЛ к БЕ линейно,
АЛ° ВД
КЕД BE
так как ВД параллельна диаметру, а АД и КЕ параллельны касатель-
ной в В; какое же отношение ВД имеет к BE, то же самое имеет и АД
к ЕЕ.
ВД _ АД
BE ЕЕ
Таким образом, первый сегмент в целом цилиндрическом сегменте
к первому ссгмспту вписаппой фигуры будет иметь то же самое отноше-
ние, что АД к ЕЕ; и каждый из остальных сегментов в целом цилинд-
рическом сегменте с высотой, равной ДЕ, к соответствующему сегменту
во вписанной фигуре с той же осью будет иметь такое же отношение,
как половина диаметра его основания к заключающемуся между АВ
и ВД ее отрезку. Таким образом, подобно предыдущему докажем, что
вписанная фигура больше конуса Т", а цилиндрический сегмент с теми
же основанием и осью, что и у сегмента коноида, более чем в два раза
больше вписанной фигуры; таким образом, он будет более чем в два
раза больше и конуса Это же не так, но он только в два раза больше
его. Значит, сегмент коноида не будет больше конуса У. При помощи
202
АРХИМЕД
таких же рассуждений докажем, что он и не меньше; таким образом,
ясно, что он будет ему равен. Итак, сегмент коноида в полтора раза боль-
ше конического сегмента, имеющего то же самое основание и ту же ось,
что и рассматриваемый сегмент.
XX Ш
Если от прямоугольного коноида отсечь два сегмента — один пло-
скостью, перпендикулярной к оси, другой же — не перпендикулярной,
так, чтобы оси обоих сегментов были равны, то будут- равны и сами
сегменты.
Отсечем от прямоугольного коноида два сегмента, как было ска-
зано; рассечем также коноид плоскостью через ось [и другой плоско-
стью, перпендикулярной к оси]; пусть сечение коноида будет пара-
бола ЛВГ с диаметром
ВД, сечеттия же обоих
упомянутых плоско-
стей —прямые AZ, ЕГ,
причем ЕГ будет сече-
нием плоскости, перпен-
дикулярной к оси, а
ZA — не перпендику-
лярной; пусть равные
друг другу оси этих
сегментов будут ВО,
КЛ, а вершины В, Л.
Требуется доказать, что
сегмент коноида с вер-
шиной В будет равеп
сегменту коноида с вер-
шиной Л {рис. 2(5}.
Действительно, так
как от одной и той же
параболы отсечены два
сегмента AAZ и ЕВ Г, и
их диаметры КЛ и В© равны, то и треугольник ЛАК будет равен Е©В;
ибо уже доказано (предложение ТГТ), что треугольник AAZ ранен
треугольнику ЕВГ. Опустим перпендикуляр АХ на продолжение КЛ.
Поскольку В© и КЛ равны, то будут равпы и Е©, АХ*).
Пусть в сегмент с вершиной В будет вписан конус, имеющий с этим
сегментом то же самое основание и ту же ось, в сегмент же с вершиной Л
пусть будет вписан конический сегмент, имеющий то же самое основа-
ние, что сегмент коноида, и ту же ось; изЛ опустим па AZ перпендикуляр
AN; он будет высотой конического сегмента с вершиной Л. Конический
сегмент с вершиной Л и конус с вершиной В имеют друг к другу отно-
шение, составленное из отношений оснований и высот; значит, опи будут
иметь отношение, составленное из того, которое площадь, ограни-
ченная эллипсом с диаметром AZ, имеет к кругу на диаметре ЕГ,
и из того, которое NA имеет к В©.
шг. с.егм. AZA_____эллипс AZ NA
конус 1ПВК круг ЕГ В6
Из равенства площадей треугольников B0E и АКЛ следует Вв«Ев=КЛ»ЛХ.
О КОНОИДАХ И СФЕРОИДАХ
203
Площадь ясс, ограниченная эллипсом, к рассматриваемому кругу
имеет то же самое отношение, что прямоугольник между обоими диа-
метрами к квадрату на ЕГ,
эллипс AZ AZ nz
'круг ЕГ — ЕГ2
[и конический сегмент с вершиной Л имеет к конусу с вершиной
В отношение, составленное из того, которое КА имеет к Е©, и того,
которое NA имеет к В©,
е;он. сегм. AZA _ КЛ ХА
•конус ГВЕ ~~ Е© " ВО
ибо КА является половиной диаметра основания конического сегмента
с вершиной А, а Е0 — полови пой диаметра основания конуса, в то
время как AN, В© являются их высотами. Но AN имеет к В© то же
самое отношение, что и к КЛ, так как В© равна КЛ; также и AN имеет
к КА отношение, как ХА к AKJ*).
AN _ ХА
КА ~ АК
Теперь конический сегмент имеет к конусу отношение, составленное
из того, которое АК имеет к АХ (ибо АХ равно Е©), и из того, кото-
рое AN имеет к В©**).
леи. сегм. AZA АК AN
конус ГВЕ . АХ ' В©
Но одно из упомянутых отношений, а именно АК к АХ, будет тем же
самым, что и отношение АК к AN,
АК АК
ЛХ AN
значит, конический сегмент имеет к конусу отношение, как ЛК к AN
и AN к В0.
нои. ссгм. AZA_ЛК AN
конус ГВЕ “AN" ВО
Но В© равна КА; ясно, что конический сегмент с вершиной А будет
равен конусу с вершиной В. Теперь очевидно, что рассматриваемые сег-
менты будут равпы, ибо один из них будет в полтора раза больше кону-
са, а другой — конического сегмента, равного упомянутому конусу.
XX IVj
Если от прямоугольного коноида отсечь два сегмента произвольно
проведенными плоскостями, то сегменты будут иметь друг к другу
такое же отношение, как и квадраты на их осях.
Отсечем от прямоугольного коноида как-нибудь два сегмента,
и пусть ось одного из них равна будет К, а другого — Л; требуется
доказать, что эти сегменты будут иметь друг к другу то же самое отно-
шение, что квадраты на К и Л {рис. 27].
Рассечем коноид плоскостью через ось сегмента, и пусть сечение бу-
дет парабола ЛВГ с осью ВЛ; отложим ВД равной К и проводом через Д
*) Гсйберг не считает стоящее в квадратных скобках место подлинным, так как оно не вяжется
с общим ходом доказательства.
** ) Согласно предложению XII, диаметры оллипса AZ будут AZ и 2511, половинами которых
будут АК и АХ. Радиус круга в основании конуса будет EG= АХ; таким образом, отношение пло-
лцалей эллипса и круга будет:
:ДК-АХ _ АК
Е02 ах ’
204
АРХИМЕД
плоскость, перпендикулярную к оси; тогда сегмент коноида, имеющим
основанием круг на диаметре АГ и осью ВА, будет равен сегменту, имею-
Рис. 27.
щему ось, равную К. Теперь если
К равна А, то очевидно, что и эти
сегменты будут равны друг другу,
ибо каждый из них равен одному
и тому же; равны также и квадра-
ты на К, А, так что сегменты бу-
дут иметь такое же отношение, как
квадраты на их осях. Если же А
не равна К, то пусть А будет раи-
на В©; проведем через 0 пло-
скость, перпендикулярную к оси;
тогда сегмент, имеющий основа-
нием круг на диаметре EZ, а
осью В©, будет равен сегменту,
имеющему ось, равную А. Теперь
впишем в них конусы, имеющие
основаниями круги на диамет-
рах АГ, EZ и вершиной точку В;
тогда конус, имеющий ось ВД, к
конусу, имеющему ось В©, будет
иметь отношение, составленное из
того, которое квадрат на АА имеет к квадрату на ©Е, и того, которое
АВ имеет к ВО линейно.
конус ВД _ АД2 ДВ
конус ВО '" 6Е2 В0
Какое же отношение ДА имеет к ©Е в квадратах, такое же отношение
будет иметь ВА к В© линейно,
ДА2 __ вд
6Е2 ~ве
значит, конус, имеющий ось ВД,к конусу с осью В© имеет отношение,
составленное из того, которое АВ имеет к ©В, и вз того, которое ДВ
имеет к В©; а это будет тождественно с тем, которое квадрат на АВ
имеет к квадрату на ©В. Но отношение конуса, имеющего ось ВА,
к копусу, имеющему ось ©В, будет тем же самым, какое сегмепт коно-
ида с осью ДВ имеет к сегменту с осью 0В [ибо каждый в полтора раза
больше соответствующего конуса]. И сегменту с осью ВД будет равен
сегмент коноида, имеющий ось, равную К, сегменту же с осью ©В равен
сегмент коноида, имеющий ось, равную А, и ВД равна К, а ©В равна А;
после этого ясно, что сегмент коноида, имеющий ось, равную К, будет
с сегментом коноида, имеющим ось, равную А, находиться в том же самом
отношении, что квадрат на К к квадрату на А.
XXV
Всякий сегмент тупоугольного коноида, отсеченный плоскостью,
перпендикулярной к его оси, к конусу, имеющему с сегментом одно и то>
лее основание и равную высоту, имеет такое же отношение, какое прямая,
равная вместе взятым оси сегмента и утроенной дополняющей ось*},
) Действительной полуоси гиперболы.
О КОНОИДАХ И СФЕРОИДАХ
205
имеет к прямой, равной вместе взятым оси сегмента и удвоенной допол-
няющей ось {рис. 28}.
Пусть будет некоторый сегмент тупоугольного коноида, отсеченный
плоскостью, перпендикулярной к оси; рассечем его другой плоскостью,
проходящей через ось;
пусть сечение самого
коноида будет гипербо-
ла АВГ, а отсекшей сег-
мент плоскости — пря-
мая АГ; пусть ось сег-
мента будет ВА, а до-
полняющая ось В©, и
пусть прямой В© будут
равны Z0 и ZII- Тре-
буется доказать, что
этот сегмент к конусу,
имеющему с сегментом
те же самые основание
и высоту, будет иметь
отношение, как НА к ZA.
Пусть будет ци-
линдр, имеющий с сег-
ментом то же самое
основание и ту же ось;
пусть его стороны бу-
дут ФА, Г Г; пусть так-
же будет некоторый ко-
нус Т, который к ко-
нусу, имеющему с сег-
ментом то же основание
и ось ВД, имеет то же
отношение, что НА к
AZ; я говорю, что этот
сегмент копоида будет
равен конусу Чг.
Действительно, если
он не равен, то будет
или больше, или мень-
Рис. 28.
ше. Пусть сначала оп,
если возможно, будет больше. Впишем в этот сегмент телесную фигуру
и опишем около пего другую, составленную из цилиндров равной высо-
ты, так, чтобы описанная фигура превосход ила вписанную на вели-
чину, меньшую той, на которую сегмент коноида больше конуса V;
затем плоскости всех этих цилиндров доведем до боковой поверхности
цилиндра, имеющего основанием круг на диаметре АГ и осью ВА;
тогда целый цилиндр будет разделен на цилиндры, по количеству
равные цилиндрам в описанной фигуре, а по величине равные наиболь-
шему из этих цилиндров. И так как описанная фигура превышает впи-
санную па величину, меньшую того, чем сегмент коноида превышает
конус V, и описаппая фигура больше сегмента, то ясно, что и впи-
санная фигура больше конуса V. Пусть ВР будет третьей частью ВА;
ВР=
ВА
206
АРХИМЕД
тогда НД будит утроенной @Р *).
НА—ЗОР
И так как цилиндр, имеющий основанием круг на диаметре АГ и ось.
ВД, к копусу с тем же самым основанием и той же осью имеет то же
отношение, что НД к ©Р * **),
цшшЯДР ВА__ НА
«ойус ВА вр
и упомянутый конус к конусу Чг относится, как ZA к НД,
испуг ВА ZA
конус Ч' НЛ
то в переставленной пропорции трех величин ***) упомянутый цилиндр
к конусу Т будет иметь такое же отношение, как ZA к 0Р.
цилиндр BA 2Л_
конус Чг — НГ
Отложим линии, обозначенные 3, количество которых равнялось бьь
количеству отрезков прямой ВЛ, а величина каждой была бы равна ZB;
к каждой из них приложим площадь с избытком в виде квадрата,
и пусть наибольшая площадь будет равна прямоугольнику между ZA,
ДВ, а наименьшая — прямоугольнику между ZI, IB, причем стороны,
избытков одинаково превышают одна другую, [ибо равные им отрезки,
находящиеся на прямой, тоже одинаково превышают один другого];
пусть сторона наибольшего избытка N равна прямой ВД, а наименьшего-
равна BI****), пусть также будут и другие площади, обозначенные Q,
количество которых равно количеству первых, а величина каждой равна,
наибольшей из них — прямоугольнику между ZA и ЛВ. Тогда цилиндр,
имеющий основанием круг на диаметре АГ и ось ЛЕ, с цилппдром,.
имеющим основанием круг на диаметре КЛ и ось ДЕ, будет находиться
в том же отношении, какое имеют квадраты на ДА и КЕ,
цилиндр АГЕ _ ДА2
цилиндр КАД ~ КМ2
но это отношение будет тем же самым, которое прямоугольник между Z&
и ВД имеет к прямоугольнику между ZE и BE,
ДА2 ZA-ДВ
КЕ2 'ZE-BE
так как это имеет место для всякой гиперболы *****), [ибо удвоенная,
«дополняющей», то есть прямой, проведенной из центра, является по-
«) Так как НВ=ЗОВ и ВД--ЗВР.
*•) То есть 3. так как НА—36)Г.
»»*) См. «Начала» Евклида, книга V, предложение t8.
»***) Таким образом, крайняя правая площадь будет равна
EN-I № =-ZB.BA + BA2=ZA»AB,
следующая за ней плево
Я М -1- М2- ZB. ВЕ4-ВЕ‘=ZE-EB,
и крайняя левая
E-BH-BI’—ZB.BI+BI®=ZI-IB.
Если череа х и у будем обозначать абсциссу и ординату гиперболы, отиесешюйс
к действительной оси и касательной в вершине, а черев 2а обозначим длину действительной оси»
то архимедова «уравнение» гиперболы мы записали бы так:
____________= У1
Д1(2о ' х,)_х,(2а-|-хв)
В патом случае у(—АД, ;/3=КЕ. а1=ВЛ, лу-ВЕ, 2a=ZB, откуда и следует написанная}
Архимедом пропорция:
ЛА2 BA(ZB-PBA)
КК2 = ВИ(ХВЧ-ВЕ) ‘
О КОНОИДАХ И СФЕРОИДАХ
207’
перечной стороной фигуры]*). Теперь прямоугольник между ZA и ВД
равен площади EN**), прямоугольник между ZE и BE равен площа-
ди ЕМ, ибо Е равна ZB, М равна BE и N равна ВД; значит, цилиндр,
имеющий основанием круг на диаметре ЛГ и ось ДЕ, с цилиндром,
имеющим основанием круг па диаметре КЛ и ось ДЕ, будет находиться
в таком же отношении, как площадь О с площадью ЕМ.
Подобным же образом докажем, что и каждый из остальных цилинд-
ров в целом цилиндре, имеющий ось, равную ДЕ, с цилиндром во впи-
санной фигуре с той же самой осью будет находиться в таком же отно-
шении, какое площадь Q имеет к соответствующей из площадей, при-
ложенных к Е с избытком в виде квадрата. Таким образом, имеются
некоторые величины, а именно цилиндры в целом цилиндре, каждый из
которых имеет ось, равную ДЕ, и другие величины—площади О- в рав-
ном с ними количестве, которые попарно имеют одно и то же с Q отноше-
ние, так как и цилиндры равны друг другу, и площади тоже равны
друг другу, и некоторые из этих цилиндров находятся в определенных
отношениях с другими цилиндрами, а именно с теми, что во вписан-
ной фигуре, последний же цилиндр не имеет отношения пи к чему***),
а также и некоторые из площадей находятся в тех же самых отноше-
ниях с другими соответствующими им площадями, приложенными
к Е с избытком в виде квадрата, последняя же площадь не имеет отно-
шения ни к чему; после этого ясно, что все цилиндры в целом цилиндре
ко всем цилиндрам во вписанной фигуре будут иметь то же самое отно-
шение, что все площади Q ко всем приложенным площадям за исклю-
чением наибольшей. По доказано (предложение И), что все площади
Q ко всем приложенным плолщдям за исключением наибольшей будут
иметь отношение большее того, которое имеет (прямая) N вместе
с Е к {прямой), равной вместе взятым половине Е и третьей части N;
таким образом, и весь цилиндр ко вписанной фигуре будет иметь боль-
шее отношение, чем ZA к 6Р****); но, согласно доказанному, последнее
отношение имеет целый цилиндр к конусу Ч1'; значит, целый цилиндр
ко вписанной фигуре имеет отношение большее, чем к копусу ЧЛ Таким
образом, конус 4f будет больше вписанной фигуры; это же невозможно,
так как доказано, что вписанная фигура больше конуса Ч?. Значит,
сегмент коноида не будет больше конуса ЧЛ
Но он также не будет и меньше. Действительно, пусть он, если воз-
можно, будет меньше. Спова впишем в сегмент телесную фигуру и опи-
шем около него другую, составленную из цилиндров, имеющих равную
высоту, таким образом, чтобы описанная фигура превосходила вписан-
ную на величину меньшую той, на которую конус больше сегмента;
и все остальное сделаем таким же. Теперь поскольку вписанная фигура
меньше сегмента, а описанная превосходит’ вписанную на величину,
*) '« YctQ Ciaftaoux Tag лотеоуоас. tohtsoti, Tag, ex той xsvtqov, яХауса ёат? той £’6oi?g jtAerQa—
дополнение интерполятора с терминологией эпохи Аполлония- Если мы перепишем уравнение
гиперболы в виде
где к- некоторая постоянная, то 2а будет горизонтальной, то есть поперечной» стороной прямо*
J-голышка 2а4-хя к котор< й «прикладывается с избытком в виде квадрата» площадь ку%.
** ) То есть сумме пллгцадей с буквами N н Е.
** *) Тан как число цилиндров во вписанной фигуре па один меньше числа цилиндров в целом
пил индре.
** **) мы имеем N—-Вл, E--ZB, N-|-S—ZA.
Е N Е К
V = -г = ВР’ т г-у’-ег.
208
АРХИМЕД
меньшую той, на которую конус Т меньше сегмента, то ясно, что и опи-
санная фигура будет меньше конуса Ч?. Тогда опять первый цилиндр
в целом цилиндре, имеющий ось ДЕ, с первым цилиндром в описанной
фигуре, тоже имеющим ось ДЕ, будет находиться в том же отношении,
как площадь £2 с EN, [ибо они равны друг другу], и каждый из осталь-
ных цилиндров в целом цилиндре, имеющих оси, равные ДЕ, с соответ-
ствующим цилиндром в описанной фигуре, имеющим ту же самую ось,
будет находиться в таком же самом отношении, как площадь £2 с соот-
ветствующей ей площадью, приложенной к Е вместе с избытком, вслед-
ствие того, что каждый из описанных цилиндров, кроме наибольшего,
будет равен каждому соответствующему из вписанных, считая и наи-
больший. После этого и целый цилиндр к описанной фигуре будет иметь
то же самое отношение, что и все площади £2 к соответствующим им пло-
щадям, приложенным вместе с избытками. И опять уже было доказано,
что все площади Q ко всем другим имеют меньшее отношение, чем то,
в котором прямая Е (вместе) с N находится к прямой, равной вместе
взятым половине S и третьей части N; таким образом, и весь цилиндр
к описанной фигуре будет иметь отношение меньшее, чем ZA к 0Р.
Но как ZA к 0Р, так будет и весь цилиндр к конусу У; значит, тот же
•самый цилиндр к описанной фигуре имеет отношение меныпее, чем
к 'F. Таким образом, описанная фигура будет больше конуса Т, а это
невозможно, так как доказано, что описанная фигура меньше конуса Т.
Значит, сегмент коноида не будет и меньше конуса ЧА Поскольку же
он не будет ни больше, ни меньше, то предложенное доказано [10].
XXVI
И также, если сегмент тупоугольного коноида отсекается плоско-
стью, не перпендикулярной к оси, то он к коническому сегменту с теми
же самыми основанием и осью, что и у сегмента коноида, будет иметь
такое же отношение, какое прямая, равная вместе взятым оси сегмента
и утроенной дополняющей ось, имеет к прямой, равной вместе взятым
оси сегмента и удвоенной дополняющей ось {рис. 29}.
Действительно, пусть будет отсеченный, как сказано, сегмент
тупоугольного коноида; рассечем эту фигуру другой плоскостью,
проходящей через ось и перпендикулярной к плоскости, отсекшей сег-
мент; пусть сечение фигуры будет гипербола АВГ, сечение же отсекшей
сегмент плоскости — прямая ГЛ, вершина же конуса, объемлющего
коноид, пусть будет точка 0; проведем через В параллельно АГ касатель-
ную ФЕ к коническому сечению, и пусть она будет касаться его в точке
В, затем продолжим прямую, соединяющую © с В; тогда последняя раз-
делит АГ пополам, и вершиной сегмента будет точка В, осью его ВД
и дополняющей ось — В0; пусть прямой В0 будут равны ©Z и ZH.
Восставим на ФГ некоторую плоскость, параллельную той, которая
проходит через АГ; она будет касаться коноида в В. И так как коноид
рассекла плоскость через АГ, появляющаяся перпендикулярной коси,
то сечение будет эллипсом с наибольшим диаметром ГА. Итак, имеется
эллипс па диаметре АГ и линия ВД, проведенная из центра к плоскости,
которая восставлена через диаметр перпендикулярно к той, в которой
находится этот эллипс; тогда можно найти цилиндр, имеющий ось
на одной прямой с ВД, на поверхности которого окажется рассматри-
ваемый эллипс на диаметре АГ. Если мы построим его, то получится
некоторый цилиндрический сегмент, имеющий то же самое основание
О КОНОИДАХ И СФЕРОИДАХ
209
и ту же ось, что и сегмент коноида; другим основанием итого цилиндри-
ческого сегмента будет плоскость, проходящая через ФГ. Затем можно
также пайти конус с вершиной в точке В, на поверхности которого
окажется рассматриваемый эллипс на диаметре АГ. Если мы построим
Я я я Q
его, то получится некоторый конический сегмент, имеющий те же самые
основание и ось с сегментами коноида и цилиндра. Требуется доказать,
что сегмент коноида к упомянутому коническому сегменту имеет то же
самое отношение, что НД к AZ.
Пусть то отношение, которое ПД имеет к AZ, будет иметь конус Ч;
к коническому сегменту. Если сегмент коноида не равен конусу У,
то пусть, если это возможно, он будет больше. Тогда в сегмент коноида
впишем телесную фигуру и опишем около него другую, составленную
из цилиндрических сегментов, имеющих одинаковую высоту, так,
чтобы описанная фигура превосходила вписанную на величину, мень-
шую той, на которую сегмент коноида больше конуса У. Теперь, так
210
АРХИМЕД
как описанная фигура, будучи больше сегмента, превышает вписан-
ную фигуру иа величину меньшую той, на которую сегмент коноида
превышает конус 4е, то ясно, что вписанная фигура будет больше конуса
V. Продолжим плоскости всех вписанных в сегмент цилиндрических
сегментов до поверхности цилиндрического сегмента, имеющего те же
самые основание и ось, что и сегмент- коноида, и пусть ВР будет третьей
частью ВД; и все остальное устроим точно так же, как и раньше. Тогда
опять первый цилиндрический сегмент в целом сегменте цилиндра,
а именно имеющий ось ДЕ, к первому цилиндрическому сегменту во
вписанной фигуре, тоже имеющему ось ДЕ, будет иметь такое же отно-
шение, как квадрат на АД к квадрату КЕ, так как сегменты цилиндра,
имеющие равные высоты, относятся друг к другу, как основания, осно-
вания же их вследствие подобия эллипсов будут иметь друг к другу то
же самое отношение, что квадраты на соответствующих диаметрах их.
Но отношение квадрата на АД к квадрату на КЕ будет тем же самым,
какое прямоугольник между ZA, ДВ имеет к прямоугольнику между
ZE, ЕВ,
ад* гд-дв
KI^ ZE-ЕВ
так как ZA проведена через 0 — точку пересечения асимптот, а ЛД
и КЕ параллельны касательной в В. Но прямоугольник между ZA,
ДВ равен площади Q, а прямоугольник между ZE, ЕВ — площади 3
(вместе с) М; тогда первый сегмент в целом цилиндрическом сегменте,
имеющий осью ДЕ, к первому сегменту во вписанной фигуре с той же
осью ДЕ будет иметь то же самое отношение, что площадь Q к пло-
щади Е (вместе с) М. И каждый из других сегментов в целом цилиндри-
ческом сегменте, имеющих ось, равную ДЕ, к соответствующему ему
сегменту во вписанной фигуре с осью, равной ДЕ, будет иметь то же •
самое отношение, что площадь Q к соответственной площади, прило-
женной к Е с избытком в виде квадрата. Таким образом, снова имеются
некоторые величины, а именно сегменты в целом цилиндрическом сег-
менте, и другие величины — площади U в равном с цилиндрическими
сегментами количестве, которые попарно имеют одинаковое отношение
с первыми, и сегменты цилиндра находятся в определенных отношениях
с другими сегментами во вписанной фигуре за исключением последнего,
который не имеет себе соответствующего, а также площади Q, находя-
щиеся в таких же отношениях соответственно с другими площадями,
приложенными к Е с избытком в виде квадрата, причем последняя пло-
щадь не имеет себе соответствующей; таким образом, ясно, что все пер-
вые цилиндрические сегменты ко всем вторым цилиндрическим сег-
ментам будут иметь то же самое отношение, что все площади Q ко всем
. приложенным площадям за исключением наибольшей. Но все площади
£> ко всем приложенным площадям за исключением наибольшей имеют
. большее отношение, чем прямая Е (вместе с) N к прямой, равной вме-
сте взятым половине Е и третьей части N. Таким образом, весь цилинд-
рический сегмент ко вписанной фигуре имеет большее отношение,
чем Е (вместе с; N к прямой, равной вместе взятым половине Е и
третьей части N, а следовательно, большее и того отношения, какое
ZA имеет к ©Р. Значит, весь цилиндрический сегмент ко вписанной фи-
гуре имеет большее отношение, чем к конусу Чр, что невозможно, так
как доказано, что вписанная фигура больше конуса V. Итак, сегмент
коноида не будет больше конуса Т.
О КОНОИДАХ И СФЕРОИДАХ
211'
Если бы сегмент копоида был мспыпе конуса V, то, вписавши в сег-
мент телесную фигуру и описавши около него другую, составленную из
цилиндрических сегментов, имеющих равную высоту, так, чтобы1 опи-
санная фигура превосходила вписанную на величину меньшую той,
на которую конус У больше рассматриваемого сегмента, опять подоб-
ным же образом докажем, что описанная фигура будет меньше конуса 'Г
и что цилиндрический сегмент, имеющий те же самые основание и ось,
что и сегмент коноида, бу-
дет иметь к описанной фи-
гуре отношение меньшее,
чем к конусу Чг, что не-
возможно. Таким образом,
сегмент копоида не будет
и меньше конуса Т. Итак,
предложенное является до-
казанным.
XXVII
Если какую-нибудь
сфероидальную фигуру рас-
сечь плоскостью, проходя-
щей через центр и перпен-
дикулярной к оси, то по-
ловина сфероида будет
вдвое больше конуса, имею-
щего то же самое основание
и ту же ось, что и сегмент
{рис. 30}.
Пусть будет сферои-
дальная фигура, рассечен-
ная плоскостью, перпен-
дикулярной к оси и про-
ходящей через центр 0;
если мы рассечем ее другой
плоскостью, проходящей
через ось, то сечением фи-
гуры будет эллипс АВГД,
его диаметром и осью сфе-
роида будет прямая ВД,
а их центром — точка 0;
при этом безразлично, бу-
дет ли ВД наибольшим
диаметром эллипса или же наименьшим; пусть сечение плоскости,
рассекшей фигуру, будет прямая ГА; тогда последняя пройдет через
центр и будет перпендикулярна к ВД, так как плоскость предпола-
гается проходящей через центр и перпендикулярной к оси. Требуется
доказать, что половина сфероида, имеющая основанием круг на диа-
метре АГ, а вершиной точку В, будет вдвое больше конуса, имеющего
с сегментом то же самое основание и ту же самую ось.
Пусть некоторый конус Т будет вдвое больше конуса, имеющего
с сегментом то же самое основание и ту же самую ось 0В. Я говорю,
что половина сфероида будет равна конусу Y.
14*
212
АРХИМЕД
Действительно, если половина сфероида не равна конусу Т, то
пусть она, во-первых, будет, если возможно, больше. Тогда и сегмент,
равный половине сфероида, впишем телесную фигуру и опишем около
пего другую, состоящую из цилиндров, имеющих равную высоту, так.
Фотокопия страницы греческой рукописи, содержащей отрывок сочи-
нения Архимеда «О коноидах и сфероидах».
чтобы описанная фигура превышала вписанную на величину, меньшую
той, на которую половина сфероида превосходит конус У. Теперь,
поскольку описанная фигура, будучи больше половины сфероида, пре-
восходит вписанную фигуру на величину, меньшую той, на которую
половина сфероида больше конуса ¥, то ясно, что и фигура, вписанная
в этот сегмент, равный половине сфероида, будет больше конуса Чг
Пусть будет цилипдр, имеющий основанием круг на диаметре АГ
О КОНОИДАХ И СФЕРОИДАХ
213
и ось В0. Поскольку этот цилиндр втрое больше конуса с теми же осно-
ванием и осью, что и у сегмента, а конус Т вдвое больше того же
конуса, то ясно, что цилиндр будет в полтора раза больше конуса Т.
Плоскости всех цилиндров, из которых складывается вписанная фигура,
продолжим до поверхности цилиндра, имеющего то же самое основание,
что и сегмент, и ту же самую ось; тогда весь цилиндр окажется разде-
ленным па цилиндры, количество которых будет равно количеству
цилиндров в описанной фигуре, а величина равна наибольшему из
этих цилиндров. Отложим теперь линии, обозначенные Е, количество
которых равно количеству отрезков прямой ВО, а величина каждой
равна В0; на каждой из этих линий построим квадрат. От последнего из
этих квадратов отнимем гномон *), имеющий сторону, равную В1; этот
гномон будет равен прямоугольнику между BI и1Д**). От пред-
шествующего квадрата отнимем гномон, ширина которого равняется
удвоенной ВТ; он будет равен прямоугольнику между БХ и ХД. Затем
от каждого следующего квадрата будем отнимать гномон, ширина
которого па одни отрезок (ВТ) будет больше ширины предшествующего
отнятого гпомопа; каждый из этих гномонов будет равен прямоуголь-
нику, построенному на двух отрезках прямой ВД, один из которых
равен ширине соответствующего гномона. Таким образом, остаток от
второго квадрата будет квадрат, имеющий сторону, равную 0Е. Теперь
первый цилиндр из составляющих целый цилиндр, а именно имеющий
ось 0Е, с первым цилиндром во вписаппой фигуре с той же самой осью
GE будет находиться в таком же отношении, какое квадрат па А0 имеет
к квадрату на КЕ или какое прямоугольник между В0 и 0Д имеет
к прямоугольнику между BE и ЕД ***);
ар2 во-ед
КЕ2 ВЕ-ЕА
таким образом, первый цилиндр к соответствующему ему другому
цилиндру имеет то же отношение, как первый квадрат к гномону, отни-
маемому от второго квадрата. Точно так же и каждый из остальных
цилиндров, имеющих ось, равную 0Е, с соответствующим цилиндром
во вписанной фигуре с той же самой осью находится в таком же отно-
шении, какое квадрат, стоящий на месте, соответствующем рассматри-
ваемому цилиндру, имеет к гномону, отнятому от следующего за ним
квадрата. Таким образом, имеются некоторые величины, а именно
цилиндры, составляющие целый цилиндр, и другие, а именно пост
роенные на прямых Е, Е-квадраты, количество которых равпо
количеству цилиндров и которые находятся попарно в тех же самых
отношениях, и эти цилиндры имеют отношение к другим величинам,
а именно к цилиндрам во вписанной фигуре, причем последний цилиндр
ни к чему не имеет отношения, и квадраты находятся в таких же отно-
шениях к соответствующим другим величинам, а именно отнимаемым
от квадратов гномонам, причем последний квадрат ни к чему не имеет
отношения: таким образом, все цилиндры в целом цилиндре ко всем
*) Так называется остаток в виде буквы Г, получившийся после отнятии из данного квадрата
другого квадрата. Стороной гномона называется разность сторон обоих квадратов — уменьшаемого
и вычитаемого.
** ) Действительно, этот гномон ранен разности квадратов
ве»—(ве—bi)2—2Вв- BI-B12-- bi (2вн - bi) вх хд.
** *) По известному свойству отрезков диаметра эллипса, частным случаем которого является
теорема элементарной геометрии о произведении отрезков диаметра круга или гипотенузы прямо-
угольного треугольника.
-214
АРХИМЕД
другим рассматриваемым цилиндрам будут иметь такое же самое отно-
шение, как все квадраты ко всем отнимаемым от них гномонам; значит,
цилиндр, имеющий с сегментом то же самое основание и ту же ось, будет
к вписанной фигуре иметь такое же отношение, как все квадраты ко
всем отнимаемым от них гномонам. Но все эти квадраты будут более
чем н полтора раза больше всех отнимаемых от них гномонов; действи-
тельно, имеются некоторые отложенные линии ЕР, EZ, ЕТ, ЕГ, ЕФ,
одинаково превышающие одна другую, причем наименьшая из них равна
их разности; имеются также и другие линии, а именно обозначенные
двумя буквами ЕЕ, количество которых равно количеству первых,
а величина каждой из которых равна наибольшей из первых; тогда
квадраты всех величин, каждая из которых равна наибольшей, будут
менее чем в три раза больше всех квадратов величин, одинаково пре-
вышающих одна другую, по более чем в три раза больше всех этих квад-
ратов за исключением наибольшего *); это доказано в уже изданной
книге «О спиралях», (предложение X, следствие). Поскольку же все
первые квадраты будут меньше утроеппых отнимаемых от них вторых
квадратов, то ясно, что они будут более чем в полтора разаболыио остат-
ков; значит, они будут более чем в полтора раза больше гномонов. Таким
образом, и цилиндр, имеющий с сегментом то же самое основание
и ту же ось, будет более чем в полтора раза больше вписанной фигуры,
что невозможно, так как он в полтора раза больше конуса V, а вписан-
ная фигура, как доказано, больше копуса Т. Значит, половина сфероида
не будет больше конуса Чг.
, Но опа также и не меньше. Действительно, пусть она, если воз-
можно, будет меньше. Тогда снова впишем в половину сфероида телес-
ную фигуру и опишем около нее другую, составленную из цилиндров,
имеющих одинаковую высоту, так, чтобы описанная фигура превосхо-
дила вписанную на величину, меньшую той, на которую конус Чг более
половины сфероида, и все остальное сделаем совершенно так же, как
и прежде. Теперь, поскольку вписанная фигура меньше сегмента, то
ясно, что описанная фигура будет меньше конуса У. Тогда опять пер-
вый цилиндр в целом цилиндре, имеющий ось 6Е, к первому цилиндру
в описанной фигуре с той же осью 0Е, будет находиться н том же отно-
шении, какое первый квадрат имеет к себе самому, второй же цилиндр
в целом цилиндре, имеющий ось ЕП, со вторым цилиндром в описанной
фигуре с той же осью ЕП будет находиться в том же самом отношении,
какое второй квадрат имеет к отнимаемому от пего гномону; и каждый
из остальных цилиндров в целом цилиндре, имеющих ось, равную 0Е,
с соответствующим цилиндром в описанной фигуре с той же самой
осью будет находиться в том же самом отношении, какое занимающий то
же место квадрат имеет к отнимаемому от него гномону; значит, и все
цилиндры в целом цилиндре ко всем цилиндрам в описанной фигуре
будут иметь то же самое отношение, как все квадраты к (величине),
равной вместо взятым первому квадрату и отнимаемым от всех осталь-
ных гномонам. И все квадраты будут менее полтора раза взятой (ве-
личины), равной первому квадрату вместе со всеми отнимаемыми от
остальных гномонами, так как они будут более чем втрое больше квад-
ратов па одинаково превышающих одна другую (прямых) за исключе-
*> Иными словами,
1’4-12-1- . . .+(П- 1)2< — < 12-4-224-- - . -1-м-1.
О КОНОИДАХ И СФЕРОИДАХ
.215
нием квадрата па наибольшей; значит, цилиндр, имеющий то же осно-
вание, что сегмент, и ту же ось, будет менее чем в полтора раза больше
описанной фигуры, что невозможно, так как он в полтора раза больше
конуса W. Значит, половина сфероида не будет меньше конуса V.
Поскольку же она не будет ни больше, ни меньше, то значит, она будет
ей равна [И].
XXVIII
И если сфероид будет рассечен проходящей через центр плоскостью,
не перпендикулярной к оси, то точно так же половина сфероида будет
вдвое больше конического сегмента, имеющего те же самые основание
и ось, что и сегмент коноида {рис. 31}.
Действительно, рассечем (так) сфероидальную фигуру; если, кро-
ме того, рассечь ее другой плоскостью, проходящей через ось и пер-
пендикулярной к (первой) секущей плоскости, то сечением фигуры
будет эллипс АВГД с центром 0, а сечением плоскости, рассекшей фигу
ру, будет прямая АГ; последняя будет проходить через 0, поскольку
рассматриваемая плоскость предполагается проведенной через центр.
Таким образом, получится некоторый эллине на диаметре АГ, ибо отсе-
кающая плоскость предполагается проведенной не под прямым углом
к оси. Проведем параллельно АГ прямые КЛ, MX, касающиеся эллипса
• в В и Л, затем на КЛ и MN восставим плоскости, параллельные той,
которая на АГ; эти плоскости будут касаться сфероида в точках В и А,
соединяющая ВА пройдет через 0, и точки В, А будут вершинами полу
лившихся сегментов, а В0, 0А — их осями. Теперь можно найти ци-
' линдр, имеющий ось В0, па поверхности которого будет находиться
рассматриваемый эллипс па диаметре АГ; после же его построения полу-
чится некоторый цилиндрический сегмент, имеющий одни и те.же осно-
вание и ось с полусфероидом; далее можно также найти и конус с вер-
шиной в точке В, па поверхности которого, будет находиться рассмат-
риваемый эллипс на диаметре ЛГ. После его построения получится
некоторый конический сегмент, имеющий те же основание и ось, что
и сегмент сфероида. Я утверждаю, что половина сфероида будет вдвое
больше этого конуса. . .. . . о i.
216
АРХИМЕД
Пусть будет конус Т" в два раза больший упомянутого конического
сегмента. Если половила сфероида не равна конусу Чг, то пусть сначала
она, если возможно, будет больше; тогда я вписываю в половину сфе-
роида некоторую телесную фигуру и описываю другую, составленную
из цилиндрических сегментов равной высоты, так, чтобы описанная
фигура была больше вписанной на величину меньшую той, на которую
половила сфероида больше конуса Т. Теперь подобно предыдущему
докажем, что вписанная вполовину сфероида фигура будет больше кону-
са Чг и что цилиндрический сегмент, имеющий те же основание и ось,
что и сегмент сфероида, будет в полтора раза больше конуса Чг, но
более чем в полтора раза больше фигуры, вписанной в половину сфе-
роида, что невозможно. Значит, половина сфероида пе будет больше
копуса Т.
Если бы половина сфероида была меньше конуса Т, то впишем
в половину сфероида некоторую телесную фигуру и опишем около нее
другую, составленную из цилиндрических сегментов одинаковой высоты,
так, чтобы описанная фигура была больше вписанной на величину,
меньшую той, на которую конус 4е больше половины сфероида. Затем
опять подобно предыдущему докажем, что описанная фигура будет
меныпе копуса Ф и что цилиндрический сегмент, имеющий те же самые
основание и ось, что и сегмент сфероида, будет в полтора раза больше
описанной фигуры, что невозможно. Таким образом, половина сфероида
пе будет и меньше конуса V. Поскольку же она нс больше и не меньше,
то должна быть равна. Теперь становится явным то, что требовалось
доказать [11].
XXIX
Если любую сфероидальную фигуру рассечь плоскостью, перпенди-
кулярной к оси, но не проходящей через центр, то меньший сегмент к ко-
нусу с теми же основанием и осью, что и у сегмента, будет иметь то же
самое отношение, что вместе взятые половина оси сфероида и ось боль-
шего сегмента к оси большего сегмента {рис. 32].
Пусть будет какой-нибудь сегмент сфероидальной фигуры, отсе
полный плоскостью, перпендикулярной к оси, но нс проходящей через
центр; если рассечь его другой плоскостью, проходящей через ось,
то сечение фигуры будет эллипс АВГ, диаметр сечения и ось сфероида
BZ, центр 0, сечепие же плоскости, отсекающей сегмент, будет прямая
АГ; последняя образует с BZ прямые углы, так как рассматриваемая
плоскость предположена перпендикулярной к оси; пусть отсеченный
сегмент, вершина которого в точке В, будет меньше половины сфероида
и пусть ZII равна В0. Требуется доказать, что сегмент с вершиной
в точке В к конусу, имеющему с сегментом то же самое основание и ту
же ось, будет иметь то же самое отношение, что АН к AZ.
Пусть будет цилиндр, имеющий то нее самое основание и ту же ось,
что и меньший сегмент; пусть также будет конус Т, который к конусу,
имеющему то же основание (и ту же ось, что и сегмент), имеет то же
отношение, что ЛН к AZ; я говорю, что конус Т будет равен сегменту,
имеющему вершиной точку В.
Действительно, если он не равен, то пусть сначала, если возможно,
будет меныпе. Тогда я вписываю в сегмент телесную фигуру и описы-
ваю около пего другую, составленную из имеющих равную высоту
цилиндров, таким образом, чтобы описанная фигура превосходила впи-
О КОНОИДАХ И СФЕРОИДАХ
217
санную на величину меньшую той, на какую сегмепт сфероида меньше
копуса Чг. Так как описанная фигура, будучи болыпс сегмента, превос-
ходит вписанную на величину меньшую той, па которую сегмент более
конуса, то ясно, что вписанная фигура больше конуса ЧЛ Пусть ВР
будет третьей частью ВД.
вр = -|-вд
Так как ВН втрое больше В0,
вн = зво
а ВЛ втрое больше ВР,
нд™ знр
то ясно, что ДН будет втрое больше 0Р;
дн = зер
тогда цилиндр, имеющий то же самое основание, что и сегмент, и ось ВД,
имеет к конусу с теми же основанием и осью такое же отношение, как
ДН к 0Р.‘
цилннлр ВА _ АН
конус ЛВГ 6Р
Упомянутый же конус имеет к конусу 'К то же самое отношение, что
AZ к ДН.
клггус ARP__ AZ
конус W ~ ДН
218
АРХИМЕД
Теперь, в переставленной пропорции цилиндр, имеющий с сегментом
те же самые основание и ось, к конусу Т будет иметь то же отношение,
что AZ к (ЭР. -
Пилиндр ВД _ AZ
кин ус ОГ
Теперь отложим линии, обозначенные EN, количество которых равно
количеству отрезков па прямой ВД, а величина каждой равна ZA;
пусть также каждая из линий ЕО равна будет ВД; тогда каждая из NO
будет вдвое больше 0Д. Приложим к каждой из них некоторую пло-
щадь, имеющую шириной ВД, так, чтобы каждая из фигур с диаметром
была квадратом. Затем от первого квадрата отнимем гномон, имеющий
ширину, равную BE, от второго — гномон с шириной, равной ВХ,
и таким же образом от каждой следующей площади будем отнимать гно-
мон, имеющий ширину, на единицу меньше ширины предшествующего
ему отнимаемого гномона; тогда гномон, отнимаемый от первой площади,
будет ранен прямоугольнику между BE, EZ *), и остающаяся площадь,
приложенная к NO с избытком в виде квадрата, будет иметь сторону
избытка равной ДЕ; отнимаемый от второй площади гномон равен пря-
моугольнику между ZX, ХВ, и остающаяся площадь, приложенная к NO
с избытком в виде квадрата, (будет иметь сторону избытка равной 2ДЕ)
и все остальные будут иметь подобно этим. Плоские грани всех цилин-
дров, из которых составляется вписанная в сегмент фигура, продол-
жим до поверхности цилиндра, имеющего те же самые основание и ось,
что и сегмент; тогда весь цилиндр окажется разделенным па цилиндры,
количество которых будет равпо количеству цилиндров в описанной
фигуре, а величина равна наибольшему из них. Теперь первый цилипдр
в целом цилиндре, имеющий ось ДЕ, к первому цилиндру во вписанной
фигуре с той же осью ДЕ будет иметь то же самое отношение, что квад-
рат па ДГ к квадрату на КЕ.
пилипдр АВД = ДГ2
цилиндр КВД ~ КЕа
Это отношение будет таким же, которое прямоугольник между ВД
и AZ имеет к прямоугольнику между BE и EZ. ;
ДГ2 ВД-AZ
КЕ2 ВВ • EZ
Итак, один цилипдр имеет к другому то же самое отношение, что первая
площадь к отнимаемому от псе гномону. Точно так же и каждый из
остальных цилиндров в целом цилиндре, имеющих ось, равную ДЕ,
к соответствующему ему цилиндру во вписанной фигуре с той же самой
осью будет иметь то же отношение, что занимающая одинаковое с ним
место площадь к отнимаемому от нее гномону. Теперь имеются некото-
рые величины, а именно цилиндры во всем цилиндре, и другие величи-
ны, приложенные к SN площади, имеющие ширину, равную ВД,
в одинаковом количестве с упомянутыми цилиндрами и находящиеся
попарно в том же самом отношении, и первые цилиндры находятся в от-
ношениях с другими цилиндрами, а именно теми, которые во вписан-
ной фигуре, причем последний цилиндр первого ряда нс имеет себе
соответствующего, а также площади, (относящиеся) к другим шгоща-
*) Действительно, если учесть, что ЯД—ВДт-2Дв, то рассматриваемый гномон будет равен
(В\4-2аЧ)ВА — (210 4-ЕА)ЕЛ = В \’+2Дв-ВД—2Д0. ЕД—ЕД’ = Вд!—ЕД’+2Д0.ВЕ=ВЕГЕД->-ВДЗ+
+2ле1Ш = ВЕ(ВА+2ДО + ЕД)=ВЕ-ЕХ. ...
О КОНОИДАХ И СФЕРОИДАХ
219
дям, а именно к отнимаемым от них (гномонам), причем соответствую-
щие будут в тех же самых отношениях, последняя же площадь не имеет
себе соответствующей; теперь ясно, что все первые цилиндры ко всем
вторым будут иметь то же самое отношение, что все упомянутые пло-
щади ко всем гномонам; значит, цилиндр, имеющий с сегментом то же
самое основание и ту же ось, ко вписанной в сегмент фигуре будет иметь
то же самое отношение, что все площади ко всем гномонам. И так как
имеются некоторые отложенные равные линии NO, и к каждой при-
ложена некоторая площадь с избытком в виде квадрата, причем стороны
избытков одинаково превышают одна другую, причем разность равна
наименьшей стороне, а также имеются и другие площади, приложенные
к EN, имеющие ширину, равную ВД, в количестве, одинаковом с первы-
ми, а по величине равные каждая наибольшей из них, то ясно, что все
площади, каждая из которых равна наибольшей, ко всем другим пло-
щадям будут иметь отношение меньше того, которое EN имеет к прямой,
равной вместе взятым половине NO и третьей части ЕО (предложение
III). Таким образом, ясно, что эти же самые площади ко всем гномонам
будут иметь отношение больше того, которое имеет EN к прямой, рав-
ной вместе взятым половине NO и двум третям ЕО; значит, цилиндр,
имеющий с сегментом то же самое основание и ту же ось, ко вписанной
в сегмент1 фигуре имеет большее отношение, чем NE к прямой, равной
вместе взятым половине NO и двум третям ЕО. Но EN равна AZ,
половина NO равна АО, а две трети ЕО равны ДР; значит, весь цилиндр
ко вписанной в сегмент фигуре имеет большее отношение, чем AZ
к 0Р. Но отношение AZk 0Р, как доказано, равно тому, которое тот же
самый цилиндр имеет к конусу V; значит, цилиндр имеет ко вписанной
фигуре большее отношение, чем к конусу Чг, что невозможно, ибо дока-
зано, что вписанная фигура будет больше конуса V. Таким образом,
сегмент сфероида не будет больше конуса Ч\
Но пусть, если возможно, ои будет меньше его. Тогда опять впи-
шем в сегмент некоторую телесную фигуру и опишем около него
другую, составленную из цилиндров равной высоты, так, чтобы опи-
санная фигура превосходила вписанную на величину меньшую той, на
которую конус Ч? будет больше сегмента, и все остальное мы устроим
совершенно так же, как и раньше. Теперь, поскольку вписанная фигура
меньше сегмента, а описанная превышает се на величину меньшую той,
на какую конус V больше сегмента, то ясно, что и описанная фигура
будет меньше конуса Чг. Затем опять первый цилиндр в целом цилиндре,
имеющий ось ДЕ, к первому цилиндру в описанной фигуре с той же
самой осью будет иметь то же самое отношение, что последняя площадь
из приложенных к EN и имеющих ширину, равную ВА, к себе самой,
так как оба рассматриваемых цилиндра равны; второй же цилиндр в де-
лом цилиндре, имеющий ось, равную АЕ, к соответствующему ему
цилиндру в описанной фигуре имеет то же самое отношение, что первая
из приложенных к EN площадей с шириной, равной ВЛ, к отнимаемому
от нее гномону, и каждый из остальных цилиндров в целом цилиндре,
имеющих ось, равную АЕ, к соответствующему ему цилиндру в описан-
ной фигуре имеет то же самое отношение, что занимающая то же место
площадь среди приложенных к EN к отнимаемому от нее гномону, при-
1 чем первым считается последний *). Теперь все цилиндры в целом ци-
линдре ко всем цилиндрам в описанной фигуре будут иметь то же самое
*) Именно тот, от которого ничего не отнимается, все же остальные следуют ва ним в своем
порядке, который на нашем чертеже будет 4, 1, 2, 3.
220
АРХИМЕД
отношение, что все. площади, приложенные к EN, к площади, равной
вместе взятым занимающей последнее место площади и всем гномонам,
отнимаемым от других, на основании тех же соображений, что и выше.
Поскольку доказано, что все площади, приложенные к EN, ко всем
площадям, приложенным к NO с избытком в виде квадрата за исключе-
нием наибольшей, имеют отношение большое того, которое EN имеет
к прямой, равной вместе взятым половине NO и третьей части ЕО *),
то ясно, что эти же самые площади к остаткам, которые вместе равны
площади, занимающей последнее место, и всем гномонам, отнимаемым
от остальных, будут иметь отношение меньшее того, которое EN имеет
к прямой, равной вместе взятым половипе NO и двум третям ЕО. Теперь
ясно, что цилиндр, имеющий то же основание, что и сегмент, и ту же
ось, будет к описанной фигуре иметь отношение меньшее того, какое
ZA имеет к ОР. Отношение же AZ к ОР равно отношению упомянутого
цилиндра к конусу Чг; значит, этот цилиндр к описанной фигуре имеет
отношение меньшее, чем к конусу Т', что невозможно, так как, согласно
доказанному, описанная фигура меньше конуса Т. Значит, сегмент
сфероида пе будет меньше этого конуса. Поскольку же оп нс будет
ни больше пи меньше, то, значит, оп будет равен последнему.
XXX
И также если сфероид рассечь плоскостью, не перпендикулярной к оси
и не проходящей через центр, то меньший его сегмент к коническому сег-
менту с тем же основанием и той же осью будет иметь то же самое
отношение, что прямая, равная
вместе взятым половине прямой,
соединяющей вершины получивших-
ся сегментов, и оси большего сег
мента, имеет к оси большего
сегмента (рис. 33}.
Рассечем какую-нибудь сфе-
роидальную фигуру, как сказано;
если рассечь се другой плоскостью,
проходящей через ось и перпенди-
кулярной к секущей плоскости, то
сечение фигуры будет эллипс АВГ,
а плоскости, секущей фигуру, пря-
мая ГА; параллельно АГ проведем
ИР и ST, касающиеся конического
сечения в В и Z, и восставим на них
плоскости, параллельные той, ко-
торая н рох одит через А Г; они будут
также касаться сфероида в В и Z,
и вершинами получившихся сег-
ментов будут точки В, Z. Теперь
проведем прямую, соединяющую
вершины сегментов; пусть она
будет BZ; она пройдет через центр;
пусть центром сфероида и эллипса будет 0. Так как фигура предпола-
гается рассеченной плоскостью, пе перпендикулярной к оси, то сечепие
*) Предложение II.
О КОНОИДАХ И СФЕРОИДАХ
221
будет эллипсом с диаметром ГА. Возьмем теперь цилиндр, имеющий
ось па одной прямой с ВА, на поверхности которого будет находиться
эллипс, что на диаметре АГ, а также конус, имеющий вершину в точке
В, на поверхности которого будет тот же эллипс с диаметром АГ; тогда
получится некоторый цилиндрический сегмент, имеющий то же самое
основание и ту же ось, что и сегмент сфероида, а также конический сег-
мент с теми же основанием и осью. Требуется доказать, что сегмент
сфероида с вершиной В к коническому сегменту с теми же основанием
и осью имеет то же отношение, что АП к AZ; пусть ZH равна 0Z.
Возьмем некоторый конус Т, имеющий к коническому сегменту
с теми же основанием и осью, что и у сегмента сфероида, то же самое
отношение, что АН к AZ. Если теперь сегмент сфероида пе равен кону-
су V, то пусть сначала, если возможно, он будет больше. Тогда я вписываю
в сегмент сфероида телесную фигуру и описываю около него другую,
составленную из цилиндрических сегментов одинаковой высоты, так,
чтобы описанная фигура превышала вписанную на величину меньшую
той, на какую сегмент сфероида больше конуса Т. Тогда подобно преды-
дущему докажем, что вписанная фигура больше конуса Чг, а цилинд-
рический сегмент, имеющий те же основание и ось, что и сегмент
сфероида, ко вписанной фигуре имеет отношение большее, чем к кону-
су 4f, что невозможно. Итак, сегмент сфероида по больше конуса Т.
Ио пусть он, если возможно, будет меньше. Тогда опять впишем
в сегмент телесную фигуру и опишем около него другую, составленную
из цилиндрических сегментов равной величины, так, чтобы описанная
фигура превышала вписанную на величину меньшую той, на какую
конус Ч*1 больше сегмента.
Опять на основании таких же рассуждений докажем, что описанная
фигура меньше конуса 4J и что цилиндрический сегмепт с теми же осно-
ванием и осью, что и у сегмента сфероида, будет к описанной фигуре
иметь меньшее отношение, чем к конусу 4f, что невозможно. Значит,
сегмент сфероида пе будет также и меньше конуса. Теперь становится
явным то, что требовалось доказать.
XXXI
Если любую сфероидальную фигуру рассечь плоскостью, перпендику-
лярной к оси и не проходящей через центр, то больший сегмент к кону-
су, имеющему с ним то же самое основание и ту же ось, имеет такое
же отношение, как прямая, равная вместе взятым половине оси сферо-
ида и целой оси меньшего сегмента, к оси меньшего сегмента (рис. 34}.
Рассечем какой-нибудь сфероид, как сказано; если рассечь его дру-
гой плоскостью, проходящей через ось и перпендикулярной к секущей
плоскости, то сечением фигуры будет эллипс АВГ, диаметр которого
и ось фигуры будет ВД, а сечением секущей плоскости будет прямая ГА;
она, конечно, перпендикулярна к ВЛ. Пусть большим из сегментов будет
тот, у которого вершина В, а центр сфероида — точка 0. Приложим пря-
мую АП, равную Л@, и BZ, равную ей же; требуется доказать, что сег-
мент сфероида с вершиной В к конусу с тем же самым основанием, что
и у сегмента, и тойже осью будет иметь такое же отношение, как ЕП к ЕА.
Рассечем сфероид пл ост,остью, проходящей через центр и перпен-
дикулярной к оси, и пусть на полученном круге будет конус, имеющий
вершиной точку А; тогда весь сфероид будет вдвое больше сегмента,
имеющего основанием круг на диаметре КЛ, а вершиной __точку А,
222
АРХИМЕД
упомянутый же сегмент в два раза больше конуса, имеющего то же
основание, что и сегмент, и ту же ось (это доказано) *); значит, целый
сфероид будет в четыре раза больше упомянутого конуса. Этот же копус
с конусом, имеющим основанием круг на диаметре АГ, а вершину
Рис. М.
в точке А, находится в отношении, составленном из того, которое прямая
(ЭД имеет к ЕД, и того, которое квадрат на К.О имеет к квадрату на ЕА;
ио отношение, которое квадрат на Кв имеет к квадрату па ЕА,
будет тем же самым, которое прямоугольник между ВО и ОД имеет
к прямоугольнику между BE и ЕД.
ке2 ве- ва
ЕА2
Пусть теперь отношение ОД к ЕД будет равно отношению некото-
рой прямой ЕД к ОД;
в а _ гд
ЕД ~ 0Л
тогда прямоугольник между ЕД и ВО к прямоугольнику между ВО
и ОД будет иметь такое же отношение, как ДО к ДЕ.
еа-во де
во-ёд “ ЛЕ
Отношение же, составленное из того, которое прямоугольник между ЕД,
0В имеет к прямоугольнику между ВО, ОД, и из того, которое прямо-
угольник между ВО, ОД имеет к (прямоугольнику) между ВЕ, ЕД,
будет тем же самым, которое прямоугольник между ЕД, ВО имеет
к прямоугольнику между ВЕ, ЕД;
ед-ев ве-ел ел- во
ве-елВЕ-Ел’ вк.ед
тогда конус, имеющий основанием круг на диаметре КЛ, а вершиной
точку Д, с конусом, имеющим основанием круг на диаметре АГ, а вер-
шиной точку Д, будет находиться в таком же отношении, как прямо-
угольник между ЕД, ВО с прямоугольником между ВЕ, ЕД.
ХГНУС КАЛ_ЕЛ В0
Ki ll ус АГД Ыь ЁД
*) В предложении XXVII.
О КОНОИДАХ И СФЕРОИДАХ
22а
> Конус же, имеющий основанием кругла диаметре АГ, а вершиной точку
, . Д, к сегменту сфероида с теми же основанием и осью имеет такое же
отношение, как прямоугольник между BE, КД к прямоугольнику между
ZE, ЕД.
конус АГД__НЕ ЕД
сегмент АГД ~ 2ЁЁД
[то есть как БЕ к EZ, ибо сегмент, меньший половины сфероида, к ко-
нусу с теми же основанием и осью, что и у сегмента, имеет, согласно
доказанному, такое же отношение, как прямая, равная вместе взятым
половине оси сфероида и оси большего сегмента, к оси большего сег-
мента; зго же отношение будет то, какое ZE имеет к BE], значит, конус,
содержащийся в половине сфероида, к сегменту сфероида, меньшему его
половины, имеет то же самое отношение, что прямоугольник между ЕД,
В0 к прямоугольнику между ZE, ЕД.
конус КАД _ sд ВН
сегмент А ГЛ — ZE • Ед
Поскольку целый сфероид к конусу, содержащемуся в половине сфе-
роида, имеет такое же отношение, как прямоугольник между ZH, ЕД
к прямоугольнику между В0, ЕД,
сфероид ZH -ЕЛ .
конус КЛД — Вы £д
[ибо первый прямоугольник вчетверо больше второго], конус же, что
в половине сфероида, к сегменту, меньшему половины сфероида, имеет
то же самое отношение что прямоугольник между ЕД, В<Э к (прямоуголь-
нику) между ZE, ЕД,
Гкснуе. КАЛ _ ЕЛ ве
сегмент Л ГЛ ~ ZE- ЁД
то и целый сфероид к своему меньшему сегменту имеет то же отноше-
ние, что прямоугольник между ZH, ЕЛ к прямоугольнику между ZE, ЕД;
сфероид ZH Ед
сегмент А1 Д “ ZE- ЕЛ
итак, больший сегмент сфероида имеет к меньшему то же отношение,
что избыток, на какой прямоугольник между ZII, ЕД превышает
прямоугольник между ZE, ЕЛ, имеет к прямоугольнику между ZE, ЕД.
сегмент АГВ_ Z FT - ед — ZE ЕД
Сегмент АГД • ЕД
Но прямоугольник между ZH, ЕЛ превосходит прямоугольник между
ZE, ЕД на вместе взятые прямоугольники между ЕД, ЕН и ZE, ЕЕ*),
ZH-ЕД - ZE-ЕД — ЕД-ЕП-1- ZE-EE
значит, больший сегмент сфероида имеет к меньшему то же самое отно-
шение, которое (величина), равная обоим прямоугольникам между
ЕД, ЕН, и ZE, ЕЕ, имеет к прямоугольнику между ZE, ЕД. Но мень-
ший сегмепт сфероида к конусу, имеющему с ним те же основание
и ось, относится, как прямоугольник между ZE, ЕЛ к прямоугольнику
между ВЕ, ЕД,
сегмент АГД _ ZIC - ЕД
к<.нус АГД “ ВЕ ЁД
[ибо последнее отношение то же, что и у ZE к BEJ, конус же, что
*) Действительно, ZH-ЕД-ZE-ЕД-ZE ЕЛ+ЕН ЕЛ- ZE-EA+ZE ЕЕ=ЕН ЕД I ZE ЕЕ.
224
АРХИМЕД
в меньшем сегменте, к конусу, что в большем сегменте, имеет то же
самое отношение, что прямоугольник между BE, ЕА к квадрату на BE,
конус АГА BE-ЕЛ
конус АГВ — зв2
ибо эти конусы находятся в отношении их высот, так как они имеют одно
и то же основание; таким образом, больший сегмент сфероида ко впи-
санному в него конусу относится, как (величина), равная вместе взя-
тым прямоугольникам между НД, ЕН, и ZE, ЕЕ к квадрату на БЕ.
сегмент Л ГВ _ ЕД•ЕН + ZE - ЕЕ
конус Л ГВ вЕ2
Это лее отношение будет тем, которое прямая ЕН имеет к ЕД,
сегмент АГВ ЕН
конус АГ В ЕД
ибо прямоугольник между ЕЛ, ЕН к прямоугольнику между ЕД, ЕЛ
имеет такое же отношение, как ЕН к ЕД, а прямоугольник на ЕЕ,
ZE к прямоугольнику между ZE, 0Е имеет такое ясс отношение, как
ЕН к ЕД;
SE-ZE ЕН
ZE-0E ЕД
действительно, ЕЕ имеет к 0Е то же самое отношение, что ЕП к ЕЛ
SE -ЕН
НЕ ~ ЕД
вследствие того, что ЕД, ©Д, ЛЕ составляют пропорцию, и ©Д рав-
на НД *). Теперь (величина), равная вместе взятым ттрямоуголь-
никам между ЕД, ЕН и ZE, ЕЕ к (величине), равной вместе взятым
прямоугольникам между ЕД, ЕД, и ZE, ©Е, будет иметь то же отноше-
ние, что ЕН к ЕЛ. Затем квадрат на ЕВ равен обоим прямоугольникам
между ЕД, ЕД и ZE, ©Е,
EBS = SA ЕД-|. ZE-0E
так как квадрат на В© равен прямоугольнику между ЕД, ЕЛ **),
во1 = ЕДЕЛ
а избыток, на который квадрат на BE превышает квадрат на В0, равен
прямоугольнику между ZE, ©Е, так как В0 и BZ равны ***).
BE® - B02 = ZE-OE
Теперь ясно, что больший сегмент сфероида с конусом, имеющим
те же основанием ось, находится в том же отношении, как ЕП с ЕД.
, XXXII
И так нее, если сфероид рассекается плоскостью, не перпендикулярной
к оси и не проходящей через центр, то больший его сегмент к коническому
сегменту с теми же основанием и осью будет иметь такое же отношение,
какое прямая, равная вместе взятым половине {прямой), соединяющей
„ зд ел зд—де ол Зв ;ел
*) Мы имеем —я- — —, или г,-—ггт — ттг, т- « — -ттг . «ли, вследствие равенства
гтж ИЛ Л _ SGI GE НЛ4-ЛЕ НЕ ПЕ
©Л и ПЛ: . Отсюда «присоединением» —— -——— или ♦
**) Так как и вл8=ВЛ’ЕД, согласно пропорции, определяющей точку Н.
*♦*> Действительна, ВЕХ-—(BE-V ВН)(НЕ- —BG)—EZ - ЁЬ,
О КОНОИДАХ И СФЕРОИДАХ
.'2е
вершины полученных сегментов, и оси меньшего сегмента, имеет к оси
меньшего сегмента, {рис. 35}.
Рассечем сфероид плоскостью, как сказано выше; если рассечь его
плоскостью, проходящей
другой
кущей плоскости, то сечение
фигуры будет эллипс АВГД,
а плоскости, секущей фигуру,
— прямая ГА; параллельно
АГ проведем ПР и ST — ка-
сательные к эллипсу в В, А—
и восставим на них плоскости,
параллельные той, которая
проходит через ЛГ; эти пло-
скости будут касаться сферо-
ида в В, Д, и точки В, Д бу-
дут вершинами получивших-
ся сегментов. Проведем ВД,
соединяющую вершины полу-
чившихся сегментов; послед-
няя пройдет через центр.
Пусть центр будет О, сегмент
через ось и перпендикулярной к се-
же, больший пол овины сфе-
роида, — тот, вершина которого В; приложим прямую ЛИ, равную ДО,
и BZ, равную ей же. Требуется доказать, что больший сегмент сфероида
к коническому сегменту с теми же основанием и осью имеет то же самое
отношение, что ЕН к ЕД.
Рассечем сфероид через центр плоскостью, параллельной той, кото-
рая проходит через АГ, и впишем в половину сфероида конический
сегмент, имеющий вершиной точку Д; пусть отношение ДО к ЕД будет
равно тому, которое некоторая прямая БД имеет к ОД.
де вд
ЕД ~ ед ‘ •
Тогда подобно предыдущему докажем, что конический сегмент, впи-
санный в половину сфероида, к коническому сегменту, вписанному
в меньший сегмент сфероида, будет иметь то же самое отношение, что
прямоугольник между ЕД, ВО к (прямоугольнику) между ВЕ, ЕД,
кон, сегм. КАД _ ЕД • ВН
кон. сегм. АГД- ВЕ-ЕД
и конический сегмент, вписаппый в меньший сегмент сфероида, к тому
сегменту, в который он вписан, будет иметь то же самое отношение,
что прямоугольник между ВЕ, ЕД к прямоугольнику между ZE, ЕД;
НОм. спгм. АГА ЕЕ-ЕД .... ... '
сегм. сфер. АГД 2Е-ЕЛ
теперь конический сегмент, вписанный в половину сфероида, будет
относиться к меньшему сегмепту сфероида, как прямоугольник между
ЕД, ВО к прямоугольнику между ZE, ЕД.
кон, сегм. КАД __ На- ВО
сегм. еф.р. Л ГД ~ ZE- ЕЛ
Теперь целый сфероид к коническому сегменту, вписанному в по-
ловину сфероида, будет иметь то же самое отношение, что нрямоуголь-
t5 Архимед
226
АРХИМЕД
ник между ZH, ЕД к прямоугольнику между В0, ЕА,
сфероид АВГД _ ZH ЕД
кон. сегм. клд — В0. ед
ибо каждый предыдущий в четыре раза больше своего последующего;
упомянутый же конический сегмент к меныпему сегменту сфероида
будет иметь то же самое отношение, что прямоугольник между ЕД,
ВО к прямоугольнику между ZE, ЕЛ;
кон. сегм. КЛД ЕД • ВО
сегм. сфер. АГД —ZE-ЕД
тогда целый сфероид к своему меньшему сегменту будет иметь то же са-
мое отношение, что прямоугольник между ZH, ЕД к прямоугольнику
между ZE. ЕД,
сфероид ZH-EA
сегм. сфер. АГД ZE-ЕД
а больший сегмент будет иметь к меньшему то же самое отношение, что
избыток, па который прямоугольник между ZH, ЕД превышает прямо-
угольник между ZE, ДЕ, имеет к ZE, ЕД.
сегмент А ВГ _ |ZH- ЕА — ZE - ЕА
сегмент АЛГ ZE* ЕД
Меньший же сегмент ко вписанному в него коническому сегменту имеет
то же самое отношение, что прямоугольник между ZE, ЕД к прямоуголь-
нику между ВЕ, ЕД,
сегмент АДГ __ ZE. ЕД
кои. сегм. АДГ-ВЕ.ЕД
[ибо доказано, что он будет иметь то же отношение, что ZE к ВЕ]; кони-
ческий же сегмент, вписаппый в меньший сегмент сфероида, к кониче-
скому сегменту, вписанному в больший сегмент сфероида, будет иметь
такое же отношение, как прямоугольник между ВЕ, ЕД к квадрату
па ВЕ;
КОн. сегм. АГД _ ВЕ-ЕД
кон. сегм. А ГВ — ве2
действительно, упомянутые конические сегменты имеют отношение
своих высот, так как основание у них одно и то же, а их высоты имеют
то же отношение, что ДЕ к ЕВ; теперь больший сегмент сфероида ко
вписанному иного коническому сегменту будет иметь то же отношение,
что избыток, на который прямоугольник между HZ, ЕЛ превышает
прямоугольник между ZE, ЕД, имеет к квадрату па ВЕ.
сегмент Л ГВ _ HZ - ЕД — ZE- ВД
йен. сегм. АГВ — ве2
Это же отношение, как мы докажем подобно предыдущему, будет тем
же самым, которое ЕН имеет к ЕЛ.
О СПИРАЛЯХ
Архимед приветствует Досифея
В тех книгах, которые были посланы через Гераклида, ты имеешь
запись большей части тех ранее посланных Конону теорем, доказатель-
ства которых ты все время просил меня дать; в этой же книге я посы-
лаю тебе запись некоторой части из оставшихся. Нс удивляйся, что
я публикую их доказательства только после долговременной задержки;
это произошло вследствие того, что я хотел сначала показать их людям,
занимающимся математикой и пожелавшим в них разобраться; ведь
сколько геометрических теорем, которые в начале казались плохо обос-
нованными, с течением времени получили окончательную разработку;
Коион скончался, так и не имев достаточно времени для того, чтобы
в них разобраться; а он мог бы сделать их совершенно ясными, нашел бы
доказательства и всех этих теорем, прибавил бы к ним и многие другие
и далеко продвинул бы вперед геометрию; мы ведь хорошо знаем
присущую ему незаурядную способность понимания математики и не-
обычайное трудолюбие. Теперь же, хотя много лет уже прошло после
смерти Конопа, мы еще не слышали, чтобы кто-нибудь продвинул вперед
решение хотя бы одной из поставленных задач.
Все эти задачи я хочу представить тебе одну за другой, поскольку
вышло так, что после тех задач, которые не были мною решены,
я прибавил еще две задачи для того, чтобы тех, которые утверждают,
что они все открыли, и не приводят никаких доказательств открытого,
можно было бы уличить и заставить согласиться с тем, что они открыли
невозможное. Поэтому мы сочли необходимым сообщить тебе и пере-
числить все эти задачи, упомянувши и те, доказательства которых уже
отосланы тебе, и те, которые отправляются в этой книге.
Первая из этих задач была такова: для заданного шара найти пло-
скую фигуру, равную поверхности этого шара. Она первая и была
решена в изданной книге о шаре; действительно, после того как было
доказано, что поверхность всякого шара в четыре раза больше боль-
шого круга этого шара, стало ясно, что можно найти плоскую фигуру, рав-
ную поверхности этого шара. («О шаре и цилиндре», книга 1, XXXIII.)
Вторая задача: для данного конуса или цилипдра найти шар, равный
этому конусу или цилиндру. (Там же, кп. 11,1.) Третья: данный шар рас-
сечь плоскостью так, чтобы его сегменты имели друг к другу заданное
15*
228
АРХИМЕД
отношение. (Там же, кн. II, IV.) Четвертая: данный , шар рассечь
плоскостью так, чтобы его сегменты имели поверхности, находящиеся
в заданном отношении друг к другу. (Там же, кн. 11, III.) Пятая:
заданный сегмент шара сделать подобным другому данному сфериче-
скому сегменту. (Там же, кп. II, V.) Шестая: для двух заданных сег-
ментов одного и того же или же разных шаров пайти некоторый сфери-
ческий сегмент, который был бы подобен одному из этих сегментов
и имел бы поверхность, равную поверхности другого сегмента. (Там же,
кн. 11, VI.) Седьмая: от заданного шара отсечь плоскостью такой сег-
мент, чтобы к конусу с тем же основанием, что у этого сегмента, и с рав-
ной высотой он имел заданное отношение, большее чем три к двум.
(Там же, кн. Il, VII.)
Решения всех вышеупомянутых задач доставил тебе Гераклид,
а то, что было помещено после, было неверным. Ото были следующие
предложения: если какой-нибудь шар рассечен плоскостью на
неравные части, то больший сегмент будет иметь к меньшему двойное
отношение большей поверхности к меньшей. Что это неверно, вполне
ясно из того, что уже послано к тебе, ибо там находится следующее:
если какой-нибудь шар рассечь плоскостью, перпендикулярной к ка-
кому-нибудь диаметру этого шара, то. поверхность большего сегмента
к поверхности меньшего будет иметь то же самое отношение, что боль-
ший отрезок диаметра к меньшему, и что больший сегмент шара имеет
к маныпэму отношение, которое меньше двойного, но больше полутор-
ного отношения большей поверхности к меньшей. (Там же, кн. II,
V111.) Неверной была и помещенная последней задача, а именно, что
если рассечь диаметр какого-нибудь шара так, чтобы квадрат па боль-
шем отрезке был равен утроенному квадрату на меньшем отрезке,
и через получеппую точку перпендикулярно к диаметру провести рассе-
кающую шар плоскость, то фигура такого же вида, какой является
большой сегмент этого шара, будет наибольшей из всех других шаровых
сегментов, имеющих одинаковую поверхность. Что это неверно, ясно
из уже отосланных теорем, так как доказано, что полушарие является
наибольшим из всех сферических сегментов, ограниченных равными
поверхностями. (Там же, кн. Il, IX.)
После этого были следующие предложения, касающиеся конуса.
Если парабола при неподвижном диаметре сделает полный оборот
вокруг диаметра как оси, то фигуру, описанную параболой, назовем
коноидом; если какая-пибудь плоскость касается коноидальной фигуры
и другая плоскость, проведенная параллельно касающейся, отсекает
некоторый сегмент коноида, то отсекающую плоскость назовем осно-
ванием отсеченного сегмента, а его вершиной — ту точку, в которой
другая плоскость касается коноида. Тогда, если упомянутую фигуру
рассечь плоскостью, перпендикулярном к оси, то ясно, что сечение будет
кругом, и надлежит доказать, что отсеченный сегмент будет в полтора
раза больше копуса, имеющего то же самое основание, что и сегмент,
и одинаковую высоту. («О коноидах и сфероидах», XXI.) Затем, если
от коноида отсечь два сегмента проведенными как-нибудь плоскостями,
то ясно, что полученные сечения будут эллипсами, если только секу-
щие плоскости не перпендикулярны к оси вращения, и надлежит дока-
зать, что эти сегменты имеют друг к другу то же самое отношение, какое
в квадратах имеют друг к другу прямые, проведенные параллельно оси
из вершин сегментов до секущих плоскостей. («Оконоидах и сфероидах»,
XXIV.) Доказательств этих предложений я пока тебе не посылаю.
О СПИРАЛЯХ
229.
После пих были следующие предложения относительно спирали
(они в некотором роде представляют совершенно отличный класс задач,
не имеющий ничего общего с перечисленными выше), доказательства
их мы для тебя и написали в этой книге. Эти предложения таковы:
Если какая-нибудь прямая в плоскости, равномерно вращаясь
вокруг одного своего конца, удерживаемого неподвижным, вернется
опять в исходное положение, и одновременно по вращающейся пря-
мой равномерно движется некоторая точка, выходя из неподвижного
конца, то эта точка на упомянутой плоскости опишет спираль. Я утвер-
ждаю, что площадь, заключенная между этой спиралью и прямой,
вернувшейся в исходное положение, будет третьей частью круга, опи-
санного из неподвижной точки, как из центра, радиусом, равным
части прямой, пройденной движущейся точкой в течение одного оборота
этой прямой. (Предложение XXIV.)
И если какая-нибудь прямая касается спирали в самой крайней ее
точке, а другая прямая, перпендикулярная к вращающейся и вернув-
шейся в исходное положение прямой, проведена из неподвижного ее
конца до пересечения с касательной, то я утверждаю, что эта проведен-
ная (до касательной) прямая будет равна окружности упомянутого
круга. (Предложение XVIII.)
И если вращающаяся прямая с движущейся по ней точкой сделает
несколько оборотов и вернется опять в исходное положение, то я ут-
верждаю, что по отношению к площади, прибавившейся при описыва-
нии второго оборота спирали, площадь, прибавившаяся при третьем
обороте, будет вдвое больше, прибавившаяся при четвертом — втрое,
при пятом — вчетверо больше, и во всех последующих оборотах при-
бавившиеся площади будут всегда больше площади, прибавившейся
при втором обороте, в число раз соответственно ряду последовательных
чисел, а площадь, описанная при первом обороте, будет шестой
частью площади, прибавившейся при втором обороте. (Предложение
XXVII.)
И если па части спирали, описанной в течение одного оборота,
взять две точки, соединить их прямыми с неподвижным концом вращаю-
щейся прямой линии, из неподвижной точки, как из центра, описать
два круга радиусами, равными этим соединяющим с неподвижным кон-
цом прямым, и меньшую из этих соединяющих продолжить, то я утвер-
ждаю, что площадь, ограниченная дугой большего круга, находящейся
между упомянутыми прямыми с той же стороны, что и спираль, затем
самой спиралью и продолжением соединяющей прямой, будет иметь
такое же отношение к площади, ограниченной дугой менынсго круга,
той же самой частью спирали и соединяющей их концы прямой, какое
радиус меньшего круга вместе с двумя третями разности радиусов
большего и меньшего кругов имеют к радиусу меньшего круга вместе
с одной третью упомянутой разности. (Предложение XXV111.)
В этой книге я даю доказательства этих и некоторых других пред-
ложений относительно спирали; при этом, как делается и в других гео-
- метрических сочинениях, предварительно излагаются нужные для их
доказательства предложения. При этом из лемм, находящихся в ранее-
изданных книгах, я и здесь пользуюсь следующей:
Если имеются две неравные прямые или площади, то, прибавляя
к себе самой разность, на которую большая превосходит меньшую, М0Ж7
по превзойти всякую наперед заданную величину из тех, которые могут
иметь друг к другу отношение. '
£30
АРХИМЕД
Если некоторая точка равномерно *) движется по какой-нибудь
линии и на последней берутся две линии, то взятые линии будут иметь
друг к другу то же самое отношение, что и времена, в течение которых
точка прошла эти линии.
Пусть некоторая точка равномерно движется по линии Л13 {рис. 1},
и на ней взяты две липии ГД, ДЕ; пусть ZII будет время, в течение
которого она прошла ГД, а Н0 — время, в течение которого она про-
шла ДЕ. Требуется доказать, что ли-
А гаёв ния ГА имеет к ДЕ то же самое отно-
.........1---'----1—*—1—' шение, что и время ZII к Н0.
1 7, П В К Действительно, составим линии АД,
‘—'—'— ДВ из линий ГД, ДЕ, складывая каж-
рис j дую из них произвольное число раз
саму с собой, лишь бы АД оказалась
больше ДВ; затем пусть время ZH
уложится в некотором времени АН столько же раз, сколько линия ГД
укладывается в АД, а время 0Н уложится во времени КН столько же
раз, сколько линия ДЕ укладывается в ДБ. Так как предполагается,
что точка равномерно движется по линии АВ, то ясно, что каждую
линию, равную ГД, она проходит в то же самое время, что и самое ГД;
отсюда следует, что и составленную линию АД она пройдет в такое же
время, каким будет составленное время АН, поскольку линия ГД в
липии АД и время ZII во времени АН содержатся одинаковое число
раз. Вследствие того же самого и линию БД точка пройдет в такое
же время, каким будет и время КН. Так как линия АД более ВД, то
ясно, что линию ДА точка пройдет в большее время, чем линию ВД, так
что и время АН будет больше, чем время КП- Точно так же докажется,
что если составить какие-нибудь времена из времен ZH, Н©, складывая
каждое из них произвольное число раз само с собой, так, чтобы одно
из полученных времен было больше другого, то и из линий, получен-
ных сложением такое же число раз ГД и ДЕ, будет больше та, которая
соответствует большему времени. Теперь ясно, что линия ГД будет
иметь к ДЕ то же самое отношение, что и время ZH к времени 110 [1].
II
Если каждая из двух точек, равномерно движется по некоторой линии
не одной и той же {для обеих точек) и на каждой из этих линий берутся
по две линии, из которых первые проходятся обеими точками в одинако-
вое время, и точно так же и вторые, то взятые линии будут иметь друг
к другу одно и то же отношение.
Пусть некоторая точка равномерно движется по линии АВ, а дру-
гая — но КА {рис. 2}; возьмем на АВ две линии ГД, ДЕ, а па КА —
линии ZH, 110; пусть точка, движущаяся по линии АВ, проходит
линию ГД во время, равное тому, в какое другая точка, движущаяся по
КА, проходит ZH, и точно так ясс пусть первая точка проходит линию
*) В подлиннике 'Оотяхчоб <Х'>т6 —буквально «равиоскоро сама с собой». У греков «ско-
рости» как самостоятельного понятия еще не было; скорость по существу была только качеством.
Различались более или менее скорые движения; термин «равноскорый» употреблялся при срав-
нения скоростей двух тел; вот почему Архимед снецнально добавляет «равноскоро сема
е- о о б о й».
О СПИРАЛЯХ
231
АЕ во время, равное тому, в какое вторая точка проходит II0. Требуется
доказать, что ГД будет иметь к АЕ то же самое отношение, что ZH
к не.
Пусть MN будет время, в течение которого первая точка проходит
линию ГА; тогда вторая точка в то же самое время пройдет ZH.
Далее, пусть NS будет время, в течение которого первая точка про-
ходит линию АЕ; тогда вторая точка в то же время пройдет НО;
и одно и то же отношение будут иметь линия ГА к АЕ и время MN
к NS, а также линия ZH к НО и время MN
к NH. Теперь ясно, что ГА будет иметь к ДЕ то д г__д_____// в
же самое отношение, что ZII к НО. 1 1 1 1 1
л z И 6 К
Ш
м к з
Для любого количества заданных кругов
можно найти прямую, которая была бы больше Рис. 2.
вместе взятых окружностей этих кругов.
Действительно, если около каждого круга описать многоугольник,
то ясно, что прямая, составленная из всех этих периметров, будет боль-
ше всех (вместе взятых) окружностей кругов.
IV
Если даны две неравные линии, а именно прямая и окружность круга,
то можно найти прямую, которая была бы меньше большей из задан-
ных линий, но больше меньшей.
Действительно, если разность, на которую большая линия превос-
ходит меньшую, повторить слагаемой такое число раз, чтобы результат
оказался больше данной прямой, и последнюю разделить на такое же
число равных частей, то одна такая часть будет меньше этой разности.
Теперь, если окружность будет больше прямой, то ясно, что после добав-
ления одной такой части к прямой последняя будет больше, чем мень-
шая из заданных линий, но меньше, чем большая; если же окружность
будет меньше, то после добавления одной та-
кой части к окружности последняя будет
больше, чем мсныпая из заданных линий, но
меньше, чем большая; действительно, прибав-
ляемая часть будет меньше разности.
Е
Д
Рис. 3.
V
Если дан круг и касающаяся круга пря-
мая, то можно из центра круга провести к
касательной прямую так, чтобы (отрезок)
прямой между касательной и окружностью
круга имел к радиусу меньшее отношение,
чем дуга круга между точкой касания и проведенной прямой к любой
заданной окружности *).
Пусть будет дан круг АВГ {рис. 3} и цептр его К, и пусть AZ ка-
сается круга в В; пусть также будет дапа и какая-нибудь окружность
*’) Греческий язык не знает разницы между всей окружностью и какой-нибудь ее часть
(дугой) i и та и другая обозначаются одним словом HEQKpeQELU.
232
АРХЙМКД
круга; можно взять некоторую прямую, которая была бы больше задан-
ной окружности, и пусть прямая Е будет больше этой заданной окруж-
ности. Из центра К параллельно AZ проведем ЛИ и отложим прямую
II0, равную Е, так, чтобы она «стремилась» к В. Прямую, соединяющую
центр К с 0, продолжим; тогда 0Z будет иметь к ©К то же самое отпо
шение, что ВО к ©II.
62 _ ве
ек ен
Значит, Z8 к ©К имеет меньшее отношение, чем дуга В© к заданной
окружности, потому что прямая В© меньше дуги В0, а ©И больше
заданной окружности. Итак Z© имеет к радиусу меньшее отношение,
чем дуга В© к заданной окружности [2].
VI
Если дан круг и в круге линия, меньшая диаметра, то между цент-
ром круга и его окружностью можно вставить прямую, которая так
пересекла бы заданную в круге линию, чтобы часть вставленной прямой
между окружностью и прямой, данной в круге,
имела заданное отношение к {линии}, соеди-
няющей находящиеся на окружности концы
обеих прямых — вставленной и данной в круге,
если только заданное отношение будет меньше
того, которое половина прямой, данной в
•А; круге, имеет к перпендикуляру, опущенному на
нее из центра.
Рис. 4.
Пусть будет дан круг АВГ с центром К
{рис. 4); пусть в нем дана линия ГА, меньшая
диаметра, и задано отношение Z к II, меньшее
того, которое Г0 имеет к К©, где К© — пер-
пендикуляр, (опущенный па АГ). Проведем
параллельно АГ из центра прямую KN и перпендикулярно к КГ
прямую ГЛ; тогда треугольники Г8К и ГКЛ будут подобны.
Теперь как Г© к ©К, так будет и КГ к ГЛ;
ге _ кг
ек — гл
значит, Z будет иметь к И отношение меньшее, чем КГ к ГЛ.
z . кг
н < гл
Тогда отношение Z к Н равняется тому, которое КГ имеет к некоторой
прямой, большой, чем ГЛ. Пусть эта прямая будет BN;
z = кт
н BN
поместим BN между окружностью и прямой (KN) так, чтобы (она про-
ходила) через Г (действительно, так провести секущую можно).
Поскольку она больше ГЛ, то попадет вне ее. Так как КВ имеет к BN
то же самое отношение, что Z к И,
кв 7.
BN п
то, значит, и ЕВ будет иметь к ВГ то же самое отношение, что Z к II [3].
О СПИРАЛЯХ
233.
VII
Если при тех же самых данных продолжить прямую в круге, то
между центром, и продолженной прямой можно так вставить прямую,
> ..„„л.. ..........— - -о.. а х -----х имела
концы
’ чтобы ее часть между окр1жностью и продолженной прямой
заданное отношение к соединяющей {находящиеся на окружности}
вставленной и продолженной прямых, если
только заданное отношение будет, больше
того, которое половина прямой, заданной в
круге, имеет к перпендикуляру, опущенному
на нее из центра.
Пусть при тех же самых данных ли-
ния (АГ) в круге будет продолжена {рис. 5};
пусть заданное отношение Z к Н будет боль-
ше того, которое Г© имеет к ©К, оно будет
больше и того, которое КГ имеет к ГЛ*).
Тогда отношение Z к II равняется тому,
которое КГ имеет к некоторой прямой, мень-
шой, чем ГЛ. Пусть эта прямая будет «стремящаяся» к Г прямая IN
(действительно, так провести секущую можно);
z кг
Н ~ IN
поскольку она меньше ГЛ, то попадет внутрь ГЛ. Так как КГ (или KI)
имеет к IN то же самое отношение, что Z к И, то и EI будет иметь
к IГ то же самое отношение, что Z к II [4].
EI и
ir п
н
VIII
Если дан круг и в круге линия, меньшая диаметра, а также другая,
которая касается круга в конце прямой, заданной в круге, то между
центром круга и данной (в круге} прямой можно вставить некоторую
прямую так, чтобы ее часть между окружностью круга и прямой, дан-
ной в круге, имела заданное отношение к
отсеченной ею части касательной, если
только заданное отношение будет меньше
того, которое половина прямой, заданной
в круге, имеет к перпендикуляру, опущен-
ному на нее из центра круга.
Пусть данный круг будет АВГД
{рис. 6) и в круге дана прямая ГА, мень-
шая диаметра; пусть прямая ЕА касается
этого круга в точке Г; и (заданное) отно-
шение Z к II будет меньше того, которое
ГО имеет к ©К; тогда оно будет меньше
и того, которое ГК имеет к ГЛ,
z г« _ гк
н «к...гл
если провести КЛпараллельно ©Г. Пусть
шснис, что Z к II;
кг у.
ГЗ ' II
') Как и в предыдущем предложении, ГЛ предполагается перпендикулярной к КГ.
234
АРХИМЕД
тогда ЕГ будет больше ГЛ. Проводом окружность круга через точки К,
Л, Е. Так как ЕГ более ГЛ и прямые КГ, ЕЛ взаимно перпендикуляр-
ны, то можно вставить еще одную прямую IN, «стремящуюся» к К
и равную МГ. Тогда прямоугольник между EJ и ТЛ имеет к прямоуголь-
нику между КЕ и 1Л то же отношение, что EI к КЕ;
BI-ГЛ EI
KE-JA КЕ
а прямоугольник между KI, IN к прямоугольнику между К1, ГЛ— то
же отношение, что IN к ГЛ,
КТ-IN TN
KI-ГЛ - ГЛ
так что IN будет к ГЛ, как ,Е1 к КЕ *);
1N ЕГ
ГЛ ~ КЕ"
и-, значит, Г М будет к ГЛ, как Е Г к ГК,
ГМ ЕГ
ГЛ “ кг
или ЕГ к КВ, как EI к КЕ**);
ег _ ат
кв ’ ’ КЕ
и остатки 1Г и^ВЕ будут иметь то же самое отношение, что ЕГк ГК***),
тг _ ЕГ
ВЕ ГК
или Н к Z. Итак, к касательной проведена прямая KN и часть ее ВЕ
между касательной и данной прямой (АГ)
Е/'"'__________________имеет к отрезку <1Г> касательной то же
j/_\ / \ самое отнош ние, что Z к И.
/ И /X / ix
г Если при тех же самых данных продол-
\ j жить прямую, данную в круге, то между
х. 7 , Z , центром круга и продолженной прямой мож-
Н , но вставить другую прямую так, чтобы ее
рис 7 часть между окружностью и продолженной
прямой имела заданное отношение к отсечен-
ной части касательной от точки касания,
если только заданное отношение будет больше того, которое половина
прямой, данной в круге, имеет к перпендикуляру, опущенному на нее из
центра.
Пусть дан круг АВГД {рис. 7} и в этом круге проведена прямая
ГА, меньшая диаметра; пусть Е Г касается круга в точке Г и (заданное)
отношение Z к Н будет больше того, которое ГО имеет к ©К;
rz re
н > ек
тогда оно будет больше и того, которое КГ имеет к ГЛ.
♦) Так как K1-IN=EI-IA как произведении отрезков секущих, проведенных через точку I,
и KI : КЕ=Л1 : Л г вследствие параллельности КЛ и ЕГ.
По построению ГМ—IN.
... _ ЕГ ЕТ ЕГ-SI 1Г ................................... -
) Имеем - КЕ - КВ_КЕ - ВЕ '
О СПИРАЛЯХ
235
Пусть КГ имеет к ГЗ то нее отношение, что Z к Н;
кг z
гв ' н
тогда (ГЕ) будет меньше ГА.
Опять проведем круг через точки 3, К, Л. Так как ЗГ меньше ГЛ
и прямые КМ, ЕГ взаимно перпендикулярны, то можно вставить пря-
мую IN, «стремящуюся» к К и равную ГМ. Так как прямоугольник
между El, 1Л имеет к прямоугольнику между Л1, КЕ то же отношение,
что EI к КЕ,
EI-IA зг
Л1. КЕ КЕ
и прямоугольник между 31, 1Л равен прямоугольнику менаду KI, LN,
EI-IA = КГ IN
а прямоугольник между AI, КЕ равен прямоугольнику менаду KI, ГЛ
ЛТ-КЕ — К1-ГЛ
вследствие того, чтоКЕ относится к IK, какЛГ кЛ1, то, значит, как 31
к КЕ, так будет и прямоугольник между KI и 1N к прямоугольнику
между КГ и ГЛ, то есть как NI к ГЛ или ГМ к ГЛ.
21 KI-1N NI ГМ
КЕ KI-ГЛ — ГЛ — ГЛ
Но и ГМ так относится к ГЛ, как ЕГ к КГ или к КВ;
ГМ ЕГ _ ЕГ
ГЛ кг кв
значит, как 31 к КЕ, так будет ЕГ к КВ;
EI _ ЕГ
КЕ КВ
и остаток 1Г будет к остатку ВЕ, как ЕГ к ГК.
гг ЕГ
ВЕ ГК
Но отношение ЕГ к ГК равпо тому, которое Нимеет к Z; значит, к про-
долженной прямой (АГ) приставлена прямая КЕ, и
ду продолженной прямой и окружностью имеет
к отсеченной части ГТ касательной то же самое ,
отношение, что Z к
II.
ее
часть ВЕ меж-
Л'
К
Л
м
X
о
любое количество последо-
одинаково возвышающихся
причем соответствующая
наименьшей {из этих ли-
количество других линий,
в
л
Z
н
Рис. 8.
Если отложено
вателъных линий,
одна над другой *),
разность равняется
ний), и такое же
равных каждая наибольшей (из первых), то
квадраты на прямых, равных наибольшей, взя-
тые вместе с квадратом на этой наибольшей
построенным на наименьшей {линий) и {линии),
ково возвышающимся одна над другой, вместе взятым, будут втрое
и
прямоугольником,
равной всем, одина-
больше всех вместе взятых квадратов на одинаково возвышающихся
одна над другой прямых.
Пусть отложено любое количество последовательных линий, одина-
ково возвышающихся одна над другой {рис. 8} А, В, Г, А, Е, Z, Н, ©,
*) Мы сказали бы просто «составляющих арифметическую прогрессию».
23(5
АРХИМЕД
и пусть & равна соответствующей разности; к В прибавим I, равную 0,
к Г же К, равную Н, к А же Л, равную Z, к Е же М, равную Е, к Z же N,
равную А, к Н же Е, равную Г, к 0 же О, равную В; тогда все полу-
ченные линии будут равны друг другу и наибольшей.
А=В+1=Г+К=А+Л=Е I H«Z+N«H I Е=О+О
Требуется доказать, что квадраты на всех :>тих прямых, то есть А
и вновь получившихся, взятые вместе с квадратом па Л и прямоуголь-
ником, построенным па 0 и на прямой, равной всем А, В, Г, A, Е, Z,
Н, 0, вместе взятым, будут втрое больше всех квадратов па А, В, Г, А,
Е, Z, Н, О, взятых вместе.
Д2 + (В-}- Q2 Г (Г+К)Н (A + a)B + (E + M)« + (Z4-K)8 4-(H-! Е)2 + (0+О)2 + Д2р
+ е(А + в+ г + дч-e + z [ Н4-е)~3(А8-|-в2+г9 + л1! + Е8 । zaч-нг + е2)
Действительно, квадрат на прямой ВХ равен вместе взятым квадратам
па I, В с двумя прямоугольниками между В, I;
(В+ 1)2 = 12 4-В'2 -| -2B-I
квадрат на К Г равен вместе взятым квадратам на К, Г и двум прямо-
угольникам между К, Г;
(Г + К)2 = к» + Г»+ 2Г-К -• - \
подобным же образом и квадраты на всех других линиях, равных А,
будут равны квадратам соответствующих отрезков вместе с двумя пря-
моугольниками между этими отрезками.
(А + Л)2 =. Л» + А» -|- 2Д-Л
(Е + М)2 = М2 + Е2-|-2Е-М
(Z + №) = № + Z2 + 2Z-N
(Н + 3)2 = Е2 + Н2 + 2П.Е .
(О + 0)2 == О2 + 02 -и2в-0
Теперь квадраты на А, В, Г, A, Z, Е, П, 0 вместе- с квадратами ва I,
К, Л, М, JN, Е, О и с добавленным квадратом па Л будут вдвое больше
взятых вместе квадратов на А, В, Г, А, Е, Z, Н, 0.
А2 ; 1)2 + Г» + Д2 + № + Z2 + 112 + е>2 + 12 + К2 + да + М2 + М2 + S2 -) о2 + А2 =
=2 (А2 I В2 +1'3 -!- да [- ЕЗ + Z2 + И2 + 02)
Пам остается доказать, что удвоенные прямоугольники между отрез-
ками каждой линии, равном А, с добавлением прямоугольника па ©
и прямой, равной всем А, В, Г, А, Е, Z, И, 0, вместо взятым, будут
равны квадратам на А, В, Г, А, Е, Z, Н, 0.
2 (В-1 + I-К Д.Д I E-M + Z-Nd H-E + 0-O) Ч «(А 1 В + Г + А I К I Z + Н + О) =
= А2 + В2 + 1’3 Ч- Л2 I- ЕЗ + Z2 | И 2 ! 02
Так как два прямоугольника между В, I равны двум прямоугольникам
между В, 0,
2B-I-- 2В-0
два же прямоугольника между К, Г равны прямоугольнику между 0
и учетверенной Г, ибо К вдвое более 0,
2Г-К-- 4Г-0
дна прямоугольника на А, Л равны прямоугольнику между 0 и уше-
стеренной А, ибо А втрое больше 0,
2д-Л = 6Д-0
и точно так же все остальные удвоенные прямоугольники на соответ-
О СПИРАЛЯХ 237
ствующих отрезках будут равны прямоугольникам между 0 и линиями
(Е, Z, Ы, 0), взятыми в кратности последовательных четных чисел,
2Е-М = 8Е-0 ....,
2Z-N=lOZ-0 Г. .. •..? ' : ;
2Н-3 = 12НО
20-0 = 140-0
то все они, взятые вместе с добавлением прямоугольника между 0 и пря-
мой, равной вместе взятым всем Л. В, Г, Д, Е, Z, Н, в, будут равны
прямоугольнику между 0 и прямой, равной вместе взятым А, утроен-
ной В, упятеренной Г и всем следующим линиям в кратностях после-
довательных нечетных чисел.
2 (B-I + Г-К + Д-Л -Г- Е-М + Z-N 4- П-Е -? 0.0)4 О (А -] В + Г Ч Д + Е-|- Z-Ь Н-j 0)_=
=е (А + ЗВ-f- 6Г-;- 7ДЧ-9Е н- 11Z+ 1311 + 150)
Но квадраты на А, В, Г, Д, Е, Z, Н, 0 будут тоже равны прямоуголь-
нику между теми же самыми линиями. Действительно, квадрат на А
равен прямоугольнику между <3 и прямой, равной вместе взятым А
и всем остальным линиям, каждая из которых равна А,
А« = в[А-КЙ + 1) + (Г+К) -1 (Д-1-Л) +(Е + М)-| (Z -; N) I (HЕ) и-(О + О)]
ибо (-) измеряет А такое же число раз, как сама Л измерит (вместе
взятые) все равные ей прямые вместо с А *); таким образом, квадрат на
А будет равен прямоугольнику между О и прямой, равной А вместе с
удвоенными В, Г, Д, Е, Z, Н, 0, 1
А2 - О [А +- 2 (В + Г -Ь А Е + Z П +- 6)]
ибо все равные Л прямые, за исключением лишь самой А, будут вдвое
больше всех вместе взятых В, Г, Д, Е, Z, Н, 0. Точно так же й квадрат
на В будет равен прямоугольнику между 0 и прямой, равной В вместе
с удвоенными Г, Д, Е, Z, II, 0;
на =_- е [В + 2 <г + а + е 4- z ч- п •; в)]
далее, квадрат на Г будет равен прямоугольнику между 0 и прямой,
равной Г вместе с удвоенными Д, Е, Z, Н, 0;
Г2= efr -l 2 (АЧ-ЕЧ-Z Ч-ПЧ-О)] ‘ '
и точно так же квадраты па других будут равны прямоугольникам
между 0 и прямыми, равными рассматриваемой прямой вместе с удвоен-
ными оставшимися. . <’
Д2 = 0[ЛЧ-2 (ЕЧ- Z4-II4-®)] г
Е2 = 0[Е + 2 (Z4- И Ч-®)] ‘ ' • ' '
Z2 = 0 [Z 4-2 (II Ч-0)]
JH2 = 0 [Н-Ь 2®]
02 = 0.0
Теперь ясно, что квадраты на всех этих прямых будут равны прямо-
угольнику между 0 и прямой, равной вместе взятым Л, утроенной В,
упятеренной Г и всем следующим в кратностях последовательных не-
четных чисел.
Следствие
Из этого ясно, что все квадраты на прямых, равных наибольшей,
взятые вместе, будут меныпе утроенных квадратов на всех одинаково
возвышающихся одна над другой прямых, поскольку они будут втрое
*) В нашем случае А=86 и имеется семь прямых, равных А, а именно В4-1 и т.'Л.’ ' 1 ’
238
АРХИМЕД
больше, (чем квадраты на всех одинаково возвышающихся прямых),
только после добавления некоторой величины, но они будут больше
вместе взятых утроенных квадратов на всех таких прямых, кроме наи-
большей, так как добавленная величина
А« + О(А [- В + Г -|- Д + Е -I- z+ НН- О)
меньше утроенного квадрата на наибольшей*). И, следовательно, если
построить подобные фигуры на всех таких прямых, как на одинаково
возвышающихся одна над другой, так и па прямых, равных наиболь-
шей, то построенные на прямых, равных наибольшей, вместе взятые,
будут меньше вместе взятых утроенных фигур на прямых, одинаково
возвышающихся одна над другой, по будут больше вместе взятых ут-
роенных всех таких фигур, за исключением лишь построенной на наи-
большей прямой, ибо подобные фигуры имеют те же отношения, что
и квадраты соответственных сторон [5].
XI
Если отложено любое количество последовательных линий, одина-
ково возвышающихся одна над другой, а затем будут отложены и другие
линии, количество которых на единицу меньше количества линий,
одинаково возвышающихся одна над другой, и величина каждой равна
наибольшей {из первых), то все вместе взятые квадраты на линиях,
равных наибольшей, к квадратам на одинаково возвышающихся одна над
другой линиях, кроме наименьшей, будут иметь отношение меньшее,
чем квадрат на наибольшей к (пло-
щади), равной вместе взятым прямо-
угольнику, (построенному) на наи-
большей и наименьшей линиях, и
третьей части квадрата на разно-
сти между наибольшей и наименьшей
линиями, а к квадратам на одина-
ково возвышающихся одна над другой,
линиях, кроме квадрата на наиболь-
шей, они будут иметь отношение,
большее указанного.
Пусть отложено любое количе-
ство последовательных линий, одина-
ково возвышающихся одна над дру-
гой, гдеЛВ брлыве ГД,ГД больше EZ,
, IK больше ЛМ и ЛМ больше NE
{рис. 9}; прибавим к ГД прямую ГО, равную взятой один раз разности
(между двумя последовательными прямыми), к EZ прямую ЕП, равную
удвоенной разности, к II0 прямую HP, равную утроенной разности,
и таким же образом ко всем остальным; тогда получатся линии, которые
будут равны между собой и каждая из пих равна наибольшей. Требует-
ся доказать, что вместе взятые квадраты па всех таких получившихся
линиях ко всем квадратам на одинаково возвышающихся одна над
другой линиях, кроме лишь квадрата на NE, будут иметь отношение
*) Результат, выраженный в следствии, в современной формулировке может быть записан тан:
3 (°? + “1 + ... + < чип < 3 (“1 + «14* • + «п), ....
EZ больше 110, И0 больше IK
где a. =iai.
О СПИРАЛЯХ
239
меныпес, чем квадрат па АВ к (площади), равной вместе взятым пря-
моугольнику между АВ, N3 и третьей части квадрата на NT,
ОА® + ZH® + 0Р® + КХ® -ь МТ® ЕГ® АВ®
А В® + ГД® + EZ® + не® 4- IK® [- AM® < АВ NT®
а к квадратам на тех же самых линиях, кроме квадрата на АВ, они будут
• иметь отношение, большее указанного.
од® + zn® + ер® + кг® + мт® + гв® ~
ГА® 4 EZ® 4- не® 4- IK® 4- AM® + NE®
АВ®
AB-NE 4- А. КГ®
От каждой из линий, одинаково возвышающихся одна над другой, отде-
лим часть, равную разности [6]; тогда отношение квадрата на АВ ко
вместе взятым прямоугольнику между АВ, ФВ и третьей части квадрата
па АФ будет равно тому, которое квадрат на ОА имеет к прямоуголь-
нику между ОА, АХ и третьей части квадрата па ХО, а также тому,
которое квадрат на IIZ имеет к прямоугольнику между I1Z, 4'Z и
третьей части квадрата на УП, а также том, которые квадраты на
других линиях имеют к подобно образованным площадям;
ав®_______ ОА® = nz®________________ре®
АВ-ФВ4-А- АФ® OA-XA 4- 4-ХО® HZ-WZ 4-А- ч<п® ре 6£2 4- ЙР®
— гк® ___________ ТМ® _______________ГВ®
ТМ-МЦ4--|-ЦТ2 ra-EN4--g- Nr®
тогда все квадраты на ОА, IIZ, Р0, 2К, ТМ, ГН ко всем прямоуголь-
никам между NH и прямой, равной всем упомянутым линиям, а также
третьим частям квадратов па ОХ, ПТ, PQ, TCj, TN будут иметь
то же самое отношение, что квадратна АВ ко вместе взятым прямоуголь-
нику между АВ, ФВ и третьей части квадрата на ФА *).
_______________ОА® HZ® 4- ре® + хк® 4- ТМ® 4- ГЕ®_________=_____АВ®
NE (ОД 4- nz 4- ре 4- ХК 4- ТМ 4- ГЕ) 4- 4-(0Х® 4- НТ® 4- PH® + 2^2 4- тЦ® -J- Г№) АВ • ФВ 4- 4- ФА®
Если теперь показать, что прямоугольник между NB и прямой, рав-
ной всем вместе взятым ОА, nZ, Р0, SK, ТМ, TH, и третьей части
квадратов на ОХ, ПТ, Р Й, 27^, ТЦ, TN будет меньше квадратов на
АВ, ГА, EZ, Н0, IK, AM, но больше квадратов па ГА, EZ, Н0, IK,
AM, NH, то предложение будет доказано.
Прямоугольник на NH и прямой, равной всем вместе взятым ОА,
HZ, PG, SK, ТМ, TH, и третьи части квадратов на ОХ, ПТ", Р Й,
SSfo, TQ, TN будут вместе равны квадратам на ХА, VZ, QK, ^К,
ЦМ, NH вместе с прямоугольником между NH и прямой, равной всем
вместе взятым ОХ, ПТ", PQ, ТЦ, TN, и с третьей частью квадра-
тов па ОХ, ПЧГ, Рй, 2^, Tq; TN; а квадраты иа АВ, ГД, EZ, II0,
IK, ДМ, (вместе взятые), равны (вместе взятым) квадратам на ВФ,
ХД, VFZ, Q0, $£К, ОМ, квадратам па АФ, ГХ, EV, HQ, 1^>, АЦ и пря-
моугольнику между ВФ и удвоенной прямой, равной вместе взятым АФ,
ГХ, EZ, HQ, Yfc, АЦ.
АВ® 4- ГД® 4- EZ® 4- не® 4- IK® 4- AM® = (ВФ® 4- ХД2 4- VZ® 4- Об2 4-/^К® 4- Цм®) 4-
4- (АФ® 4- ГХ2 4- W® 4- на® 4- l5fc® + лЦ2) 4- 2ВФ (АФ 4- ГХ 4- EZ 4- НИ 4-1 лЦ)
*) См. Комментарий. Предполагается, что ФВ=ХД=Ч’2=ae=)^K=C|M=NE.
2Z0
АРХИМЕД
Теперь для обоих этих (выражений) будут общими квадраты на пря-
мых, равных N3, а прямоугольник между № и прямой, равной ОХ,
ПЧГ, £2Р, 2&S, ЦТ. TN, меньше прямоугольника на ВФ и удвоенной пря-
мой, равной АФ, ГХ, EV, II£2, ЛЦ, так как только что упомяну-
тые липии равны ГО, ЕП, РИ, IS, AT, TN
АФ ГХ + ЕЧГ ч № + 1 %) ч лЦ = ГО + ЕП ч- PH 4- 12 4- АТ 4- TN
и больше остатков (после вычитаний ОХ—ГО, IlV—ЕП, £2Р—PH,
5^2—12, ЦТ—ЛТ),
АФ4-ГХ4-ЕЧ'4-П£2 ; iSJb 4 лЦ>гх Ч-еф-а-)1П4-1^4-лЦ .
.... а квадраты на ЛФ, ГХ, ЕЧГ, Н £2, ЛЦ, (вместе взятые), больше
третьей части квадратов на ОХ, 11V, PQ, ГГЦ, TN, (вместе взя-
тых),
аф2 4- гх2 4- Е’Р2 + на2 । i^b24- лц2 -^-(ох2 4- nv2 47 гп2 4- 2 -I- тЦ2 4-1'^5
как доказано выше (следствие к предложению X); значит, упомянутые
’ 1' (первыми) площади будут меньше (вместе взятых) квадратов на АВ,
ГД, EZ, НО, 1К, ЛМ.'
№ (ОД 4- П2 4- PO J ZK 4- ТМ 4- ГЕ) 4- 3 (ОХ2 4- I14r24-rQ2 4- Х)^2 + ТЦ2 + гь'2) <
< АВ2 |-ГД2 4-EZ2 4-НЕ2 4-IK2 4-ЛМ2
Остается доказать, что они будут больше квадратов па ГД, EZ, НН, IK,
AM, N3. Опять квадраты на ГЛ, EZ, НО, IK, ЛМ, NB равняются
(вместе взятым) квадратам на ХГ, EV, HQ, I$t>, ЛЦ, квадратам на ХД,
VZ, £20, /^К, Ц М, № и прямоугольнику между № и прямой,
равной удвоенным всем (вместе взятым) ГХ, ЕЧГ, Н£2, 1)^, ЛЦ.
ГД« 4- EZ2 4- не2 4- IK2 4- AM2 + NE2 = ГХ2 4- ЕЧ1"2 + Н£22 4- 1^524- лЦ2 4- X А2 + TZ2 + Н02 4-^ К2 +
4- Цы2 4- №2 4- 2N3 (ГХ+ EW 4- HQ 4- Ш 4 лЦ)
И квадраты па ХД, VZ, £26, МЦ, NE будут общими (для обоих
выражений), а прямоугольник между N3 и прямой, равной всем ОХ,
. ПТ, Р £2, ТЦ, TN, больше прямоугольника между NS и удвоен-
ной прямой, равной всем ГХ, EV, И £2, ЛЦ. И, наконец, квадраты
на ХО, ЧШ, £2Г, ЦТ, TN будут более чем втрое больше квадратов
на ГХ, ЕЧГ, И£2, ЛЦ; ибо было доказано и это. Итак, упомянутые
площади, взятые вместе, будут больше квадратов на ГД, EZ, II0, 1К,
; AM, №.
Следствие
И поэтому, если мы построим подобные фигуры па всех прямых,
, и на одинаково возвышающихся одна над другой, и на равных наиболь-
шей из них, то все фигуры, построенные на прямых, равных наиболь-
шей, ко всем фигурам на прямых, одинаково возвышающихся одна над
другой, кроме лишь фигуры па наименьшей, будут иметь отношение,
меньшее того, которое квадрат на наибольшей примой имеет к (площади),
, равной вместе взятым прямоугольнику между наибольшей и наимень-
шей линиями и третьей части квадрата на разности между наибольшей
и наименьшей; ко всем же (построенным) па них фигурам, за исклю-
чением фигуры, построенной на наибольшей, они будут иметь отноше-
ние, большее того же самого; действительно, подобные фигуры будут
иметь то же самое отношение, что и квадраты (па соответствующих
линиях).
О СПИРАЛЯХ
241
Определи и и я
1. Если на плоскости проведена прямая линия, которая, сохраняя
один свой конец неподвижным и вращаясь с одинаковой скоростью,
любое число раз вернется в исходное положение, и если одновременно
с вращением этой линии какая-нибудь точка будет с постоянной скоро-
стью перемещаться по этой прямой, начиная движение из неподвиж-
ного конца, то эта точка опишет на плоскости спираль.
2. Конец прямой, остающийсяпри ее вращении неподвижным, назо-
вем началом спирали.
3. Положение, линии, от которого рассматриваемая прямая начала
вращаться, назовем началом вращения.
4. Прямую * *), которую в течение первого оборота пройдет точка,
движущаяся по прямой, назовем первой прямой, а ту, которую та же
точка пройдет в течение второго оборота, назовем второй прямой;
подобным жо образом назовем и все. остальные одинаковыми именами
с соответствующими оборотами.
5. Площадь же, -заключенную между спиралью, описанной при
первом обороте, и той прямой, которая является первой, будем назы-
вать первой площадью, заключенную между спиралью, описанной при
втором обороте, п второй прямой, мы назовем второй, и все последую-
щие будем называть так же.
6. И если из точки, являющейся началом спирали, провести какую-
нибудь прямую линию, то все, что находится с той стороны прямой,
в которую происходит вращение, мы будем называть передним, что же
находится с другой стороны — задним**).
7. Круг, описанный из той точки, которая является началом спи-
рали, как из центра, радиусом, равным первой прямой, будем назы-
вать первым, описапиый из того же центра вдвое большим радиусом,
будем называть вторым, и таким же образом будем называть все за ним
следующие.
XII
Если к спирали, описанной в течение одного какого-нибудь оборота.
провест и из начала спирали несколько прямых, образующих друг с другом
равные углы, то эти прямые будут превы-
шать друг друга на равные величины.
Пусть будет некоторая спираль и про-
веденные к пей прямые АВ, АГ, АД, АЕ,
AZ {рис. 10}, образующие друг с другом
одинаковые углы. Требуется доказать, что
одинаково АГ превышает АВ, АД превыша-
ет АГ, и подобно этому все остальные.
Рис. 10.
Действительно, в то же самое, время, в
которое вращающаяся прямая из положения АВ доходит до положения
АГ, и движущаяся по прямой точка пройдет то расстояние, на кото-
рое ГА превышает АВ, в то же время, в которое прямая перейдет из
АГ в АД, точка пройдет расстояние, накоторое АД превышает АГ. По
вращающаяся прямая проходит в одинаковое время из АВ в АГ и из
АГ в АД, так как соответствующие углы равны; значит, в одинаковое
*) Собственно говоря, «отрсаок». Греки мыслили прямую лилию всегда ограниченной.
• *) В тексте лооатойцвуя (ведущие) и Or-ijieva (следующие).
Н> Архимед
242
АРХИМЕД
время и движущаяся по прямой точка пройдет как то расстояние,
на которое ГЛ превышает АВ, так и то, на которое АД превышает АГ.
Значит, одинаково прямая АГ превышает АВ и АД превышает ЛГ;
точно так же и все остальные.
ХШ
Если какая-нибудь прямая касается спирали, то она касается
ее только в одной точке.
Пусть будет спираль с точками А, В, Г, Д, {рис. 11}; пусть нача-
лом спирали будет точка А, началом же вращения — прямая АД,
и пусть какая-нибудь прямая ZE каса-
ется спирали. Я говорю, что она касает-
ся последней только в одной точке.
Пусть, если возможно, она будет
касаться спирали в двух точках Г, Н;
соединим Л с Г и А с И и угол, заклю-
чающийся между АГ, АП, разделим
пополам; пусть © будет точка, в кото-
рой прямая, делящая пополам данный
угол, встречается со спиралью. Тогда
прямая АН на такую же величину
будет превышать А©, как Л© — прямую ЛГ, поскольку рассматри-
ваемые прямые образуют друг с другом равные углы; таким образом,
АП и АГ, вместе взятые, будут вдвое больше А©.
Но в треугольнике обе стороны будут более чем вдвое больше пря-
мой [А©], делящей пополам угол между ними [7]; ясно, что та точна,
в которой Л© встречается с прямой ГН, будет находиться между А и
0; значит, EZ пересекает спираль, так как одна из точек на прямой ГбН
будет внутри спирали. Предположено же, что опа является касательной;
значит, RZ касается спирали только в одной точке.
XIV
Если к спирали, описанной в течение, первого оборота, провести две
прямые из точки, являющейся началом спирали, и продолжить их до
окружности первого круга, то проведенные к спирали прямые будут иметь
между собой то же самое отношение, что и дуги круга, заключающиеся
между концом спирали и концами продолженных
прямых на окружности, если брать дугу от
конца спирали до передней стороны {прямой}.
Пусть спираль, описанная в течение первого
оборота, будет АВГА© {рис. 12}, пусть точка А
будет началом спирали, а прямая ©Л —началом
вращения; пусть круг ©КП будет первым, пусть
из точки Л идут к спирали прямые АЕ и АЛ и
доходят до окружности первого круга в точках
Z, Н. Требуется доказать, что ЛЕ будет иметь
к АД то же самое отношение, что дуга ©KZ
к Дуге ©КН.
Действительно, если вращать линию А©,
то ясно, что точка © будет равномерно пере-
мещаться по окружности круга ©КН, и точка А при своем
движении пойдет по лилии Л©: когда точка ©, двигаясь по окруж-
О СПИРАЛЯХ
243
пости круга, пройдет дугу 0KZ, то А пройдет прямую АЕ, и также,
когда точка А пройдет прямую АА, то 0 пройдет дугу 0КП,
причем каждая будет двигаться равномерно; отсюда ясно, что АЕ
к АА будет иметь то же самое отношение, что дуга 0KZ к дуге ©КН,
[как было доказано выше в первых предложениях] (см. предложение II).
Подобным же образом докажем, что то же самое будет иметь место
и тогда, когда одна из проведенных прямых попадет в конец спирали.
XV
Если к спирали, -описанной в точение второго оборота,"провести пря-
мые из начала спирали, то эти прямые будут иметь друг к другу то же
самое отношение, что и вышеупомянутые дуги, если взять их вместе
с целой окружностью рассматриваемого круга.
Пусть будет спираль АВГА© {рис. 13}, причем дуга АВГА© опи-
сана в течение первого оборота, а дуга 0AEM
«пусть к ней идут прямые АЕ и АА. Требуется
доказать, что АА имеет к АЕ то же самое отноше-
ние, что дуга ©KZ вместе с целой окружностью
круга к дуге ©КН, (тоже взятой вместе) с целой
окружностью того же круга.
Действительно, в одно и то же время точ ка
А, двигаясь по прямой, пройдет линию АЛ, и
точка 0, двигаясь по окружности круга, пройдет
всю окружность этого круга и еще дугу ©KZ,
и точно так же точка А пройдет прямую АЕ,
в течение второго,
а точка 0 — всю окружность круга и еще дугу
©КН, причем каждая будет двигаться равномерно. Теперь ясно, что
линия АЛ к АЕ будет иметь то же самое отношение, что дуга 0KZ
вместе с целой окружностью круга к дуге ©КП тоже с целой окруж-
ностью круга.
Таким же образом докажем, что если к описанной в течение третьего
оборота спирали провести прямые, то они будут иметь друг к другу то
же самое отношение, что упомянутые дуги вместе с дважды взятой ок-
ружностью целого круга. Точно так же можно показать, что прямые,
проведенные к другим спиралям, будут иметь друг к другу то же самое
отношение, что вышеупомянутые дуги, если брать каждую с окружностью
целого круга, взятою столько раз, сколько раз без одного будет
совершено обращений, даже если одна из проведенных прямых попадет
в конечную точку спирали.
XV!
Если прямая линия касается спирали, описанной в течение первого
оборота, и точка касания соединена прямой линией с точкой, которая
является началом, спирали, то углы, образованные касательной с соеди-
няющей, будут не равны, причем угол с передней стороны будет тупым,
а с задней стороны — острым.
Пусть АВГД© {рис. 14} будет спираль, описанная в течение пер-
вого оборота, пусть точка Л будет началом спирали, прямая А© —
началом вращения, а ©КТТ —первым кругом, и пусть некоторая пря-
мая EAZ касается спирали в точке А; от А к Л проведем соединяющую
прямую АЛ. Требуется доказать, что AZ образует с АА тупой угол.
Hi*
244
АРХИМЕД
Рис. 14.
Из центра А радиусом АЛ опишем круг ATN; дуга этого круга
с передней стороны (прямой АД) необходимо попадет внутрь спирали,
а с задней стороны—вне ее, так как прямая, проведенная из А к спирали,
в передней стороне будет больше АЛ, а про-
веденная л задней — меньше. Что угол, за-
ключенный между прямыми АД и ДХ, нс будет
острым, очевидно, поскольку он больше угла
полукруга*), а что он не будет прямым,
следует доказать так.
Пусть, если возможно, он будет прямым;
тогда прямая EAZ будет касаться круга ATN.
В таком случае возможно пз точки А так под-
ставить прямую к касательной, чтобы пря-
мая, заключающаяся между касательной и
дугой круга, имела к радиусу этого круга
отношение меньшее того, которое дуга, заклю-
ченная между точкой касания и подставлен-
ной прямой, имеет к некоторой данной дуге
(предложение V). Пусть подставленная прямая будет AI: она пересечет
спираль в точке Л, а окружность круга ANT в Р; и пусть прямая Р1
имеет к АР отношение меньшее того, которое дуга ДР имеет к дуге Д NT;
PI АР
АР акт
значит, вся прямая IA будет иметь к ЛР отношение меньшее того, кото-
рое дуга PANT имеет к дуге ANT, или того, которое дуга ХНК© имеет
к дуге НК©.
IP РА , РД J- ANT ГНК
' др ----~ —------
ANT ЦК®
Но отношение дуги SITK0 к дуге НК© будет тем же самым, какое
прямая АЛ имеет к АЛ:
хнке_ал
нке Ад
(это доказано (в предложении XIV», значит, А1 будет иметь к АР
отношение меныпее, чем ЛА к АЛ,
AJ_ . ЛЛ
АР 4 АД
а это невозможно, ибо РА равна АД. Значит, угол, заключенный
мзжду АЛ, AZ, пе будет прямым. Доказано также, что он и не острый;
значит, он будет тупым, а остающийся (АДЕ) острым.
Подобным же образом докажем, что то же самое будет иметь место
и если касательная будет касаться спирали в ее конечной точке [8J.
XV ГТ
И то же самое, будет иметь место, если прямая касается спирали,
описанной в течение второго оборота.
Действительно, пусть прямая EZ {рис. 15} будет касаться в Л спи-
рали, описанной в течение второго оборота, и пусть все остальное, будет
*) На криволинейный угол АДР. Ср. Евклид, III, 16.
О СПИД"АЛЯХ
245
сделано так же, как и рапыпс. Тогда точно так же окружность круга
PNA с передней стороны попадет внутрь спирали, с задней же — вне ее;
угол AAZ не будет прямым, а обязательно тупым. Пусть он,
*"? Л' {’ -Г хе’ . &. '* % • &
/’iffy?
w жсяи^даЙ^Ди* JV >$* <**?£*.. />'
ж» * ~'~j 'nty/1 .. » •'
j** " *' '? *?СС:'4Г >'<**"<< К-/»» -»" -•-
yp */** ‘Л*Х*'Х ’** -*•<?#v
*&** <-,**•« A «pAw «’M/* ’.
ЧТ”*? .» -. * * ,t <*?«$
V g-‘ • v'A -...'»/ « «*Л -f .f л.хс.^,1?
Г « -.• /*«’ Л ¥' У'- #> *
** <a,-\ ~И& 'г/^-г^ »«:.’’• ^eZV*’’ ’’’»">.- ..Л***^
, i - ..•*> , ‘ z «> x
/ *У-«Р <ЙЛГ ! »»’•W1’ *< »А<и«-Л> -f(y g/i *#>** r*
**jT" -ЯаЯИЯ S Л-^* **?
Л/Др(Л«иг A f.J -Л - “ e../.i •,. «1-;
•» >- •:«-,/«. -•• ,'<•• /.Л s. izjijjtb л-^ -jrer'-изучит- '
Фотокопия страницы греческой рукописи, содержащей отрывок
сочинения Архимеда «О спиралях».
если возможно, будет прямым; тогда EZ будет касаться круга PNA
в точке А. Опять проведем к касательной прямую А1, и пусть опа пересе-
чет спираль в X, а окружность круга PNA — в Р, и пусть РТ имеет
к РА отношение меньшее того, которое дуга АР имеет ко всей окружно-
сти круга APN вместе с дугой ATNT (было доказано, что это возможно
246
АРХИМЕД
(предложение V)); и значит, вся 1А к АР будет иметь меньшее отноше-
ние, чем дуга PANT вместе со всей окружностью круга к дуге Л NT
тоже вместе со всей окружностью круга. Но отношение дуги PANT
вместе со всей окружностью круга ANTP к дуге ANT со всей окруж-
ностью круга ANTP будет тем же самым, какое дуга 2ПК0 со всей
окружностью круга ©ХНК имеет к дуге
НК© со всей окружностью круга ©2НК,
отношение же упомянутых последними
дуг будет тем же самым, какое прямая
ХА имеет к прямой АА (это доказано
(в предложении XII}); значит, IA к АР
будет иметь меньшее отношение, чем
АХ к АД, а это невозможно, [ибо РА
равна АА, a IA больше АХ]. Теперь
ясно, что угол, заключенный между AAZ,
будет тупым, а остающийся (ААЕ} —
острым.
То же самое будет иметь место и
(втом случае), когда касательная будет
касаться спирали в ее конечной точке.
Подобным же образом докажем,
что если какая нибудь прямая будет
касаться спирали, описанной в течение какого угодно оборота,
пусть даже в конечной ее точке, то эта касательная образует неравные
углы с прямой, соединяющей точку касания с началом спирали, при-
чем с передней стороны этот угол будет тупым, а с задней стороны —
острым.
XV Ш
Если прямая линия касается спирали, описанной в течение первого
оборота, в конечной ее точке и если из точки, являющейся началом спи-
рали, проведена некоторая прямая перпендикулярно к началу вращения,
то проведенная прямая встре-
тится с касательной и прямая,
заключенная между касатель-
ной и началом спирали, будет
равна окружности первого круга.
Пусть будет спираль АВГД©
{рис. 16}, пусть точка Л будет
началом спирали, линия ©А —
началом вращения, круг ©НК — Рис. 16.
первым кругом; пусть некоторая
прямая ©Z касается спирали в точке © и из А провсдспа прямая AZ
перпендикулярно к ©Л; тогда она обязательно встретится с 0Z, так
как Z©, ©Л заключают острый угол. Пусть она встретится с ней в
точке Z. Требуется, доказать, что прямая ZA будет равна окружности
круга ©КН.
Если нет, то опа будет или больше, или меньше. Пусть сначала она,
если возможно, будет больше. Тогда я беру некоторую прямую ЛА,
которая меньше прямой ZA, но больше окружности круга ©ПК. Теперь
имеются некоторый круг ©ИК, в этом круге линия ©Н, меньшая*) его
*) Архимед вабыл указать, что точка Н представляет пересечение с кругом ЙНК каса-
тсльний 0Z к спирали-
О СПИРАЛЯХ
247
диаметра, и отношение ©А к АЛ, которое будет больше того, которое
половина II0 имеет к перпендикуляру, опущенному на нее из А, так
как оно больше отношения ©А к AZ*). Тогда можно пз А так под-
ставить прямую AN к продолжению (Н0), чтобы ее часть NP между
окружностью и продолжением (Н8) имела к 0Р тоже самое отноше-
ние, что ©Л к АЛ (предложение VII);
NP ОА
ер = ал
тогда N Р будет иметь к РА такое же отношение, как прямая 0Р к АЛ.
КГ ег
РА " АЛ
Но 0Р имеет к АЛ меньшее отношение, чем дуга ©Р к окружности
круга ©НК,
ее ор
АЛ ' окр- ©ПК
так как прямая 0Р меньше дуги ©Р, а прямая АЛ больше окружности
круга ©НК; значит, и NP будет иметь к РЛ отношение меньшее, чем
У дуги 0Р с окружностью круга ©НК,
np ер
ра окр. енк
и вся NA будет иметь к АР отношение меньшее того, которое дуга 0Р
вместе со всей окружностью этого круга имеют к окружности круга
©НК.
хг । ра ... ер 1 г.кр. енк
ра окр. енк
Но отношение дуги 0Р вместе со всей окружностью круга ©НК к этой
окружности круга ©ПК будет тем же самым, какое ХА**) имеет к А©
(это доказано (в предло-
жении XV)); значит, NA v
имеет к АР меньшее отно-
шение, чем ХА к Л0,
NA _ ХА
др ле
а это невозможно, так как '
NA больше АХ, а АР рав-
на ©А. Итак ZA не будет
больше окружности круга
©НК.
Тогда пусть, если воз
можно, ZA будет меньше
Рис. 17.
окружности круга ©НК {рис. 17}. Я опять взял некоторую прямую
АЛ, которая теперь будет больше AZ, но меньше окружности круга
©НК, и провожу из точки © * параллельно AZ прямую ©М. Тогда
опять имеются круг ©НК, в нем линия ©II, меньшая диаметра, другая
(0М), касающаяся круга в точке ©, и отношение А© к АЛ меньшее
того, которое половина Н0 имеет к перпендикуляру, опущенному на
*) Отношение половины ПО к перпендикуляру, опущенному из А на НО, равняется тангенсу
угла AZ0, или отношению А0:ЛИ.
**) Архимед опять яабыл указать, что точка X представляет пересечение вставленной прямой AN
со спиралью.
248
АРХИМЕД
пес из А, поскольку оно меньше отношения ©А к AZ. Тогда можно
из А провести к касательной такую прямую АП, чтобы ее часть PN
между заданной в круге прямой (НН) и окружностью имела к отсечен-
ной части ©П касательной такое же отношение, как у ©А к АЛ (предло-
жение VUI);
PN 6А
0П “ АЛ
эта прямая АП пересекает круг в Р, а спираль в X. После перестановки
NP будет иметь к РА то же самое отношение, что ©И к АЛ.
np _ ел
РА АЛ
Но ©П имеет к АЛ большее отношение, чем дуга ©Р к окружности
круга ©НК,
оп . ер
АЛ икр. 0ПК
так как прямая ©П больше дуги ©Г* ), а АЛ меньше окружности круга
©ПК; значит, ©11 имеет к (АА, или NP к) АР большее отношение, чем
дуга 0Р к окружности круга ©НК,
еп np _ ёр
АЛ — АР '"> окр. енк
; так что и РА будет иметь к AN большее отношение, чем окружность
круга ©НК к дуге ©КР **).
ра .. окр. енк
Но отношение окружности круга ©НК к дуге ©КР будет тем же
самым, какое прямая ©А имеет к АХ; (это доказано (в предложении
XIX)); значит, РА имеет к AN большее отношение, чем ©Л к АХ,
РА _ QA
AN АХ
а это невозможно. Итак ZA не будет ни больше, ни меньше окружности
круга ©НК; следовательно, равна ей [9].
*) Это показывает, что Архимеду было известно предложение, равносильное нашему, что тан-
генс дуги больше этой дуги.
** ) Это неравенство получается из исходного
NP дуга ОР
РА окр. ОНК
при помощи «обращения»
АР ... окр. енк
PN дуга ер
и «переворачивания»
АР окр. енк
AP-PN окр. енк-дуга ег ‘
Мы получили бы его, вычти обе части основного неравенства из единицы
1 NP I ДУга 6Р
РА " окр. енк’ ’
откуда
NA дуга бКР
АР < окр. 6НК ’
О СПИРАЛЯХ
249
XIX
Если прямая, касается спирала, описанной в течение второго оборота.,
в конечной ее точке, и если из начала спирали проведена какая-нибудь
прямая перпендикулярно к началу вращения, то она встретится с ка-
сательной, и прямая между касательной и началом спирали будет, вдвое
больше окружности второго круга.
Пусть АВГ0 {рис. 18} будет спираль, описанная в течение пер-
вого оборота, а ВЕТ — в течение второго, пусть 6КН будет первый
круг, a TMN — второй; пусть также будет некоторая прямая TZ,
касающаяся спирали в Т, и ZA проведена под прямым углом к ТА;
она встретится с TZ, так как доказано, что угол ATZ острый. Требуется
доказать, что прямая ZA будет вдвое больше окружности круга TMN.
Действительно, если она не вдвое больше, то будет или более чем
вдвое больше, или же менее чем вдвое больше. Пусть сначала опа будет,
если возможно, более чем вдвое больше; возьмем некоторую прямую ЛА,
которая была бы менее, чем прямая ZA, и более чем вдвое больше окруж-
ности круга TMN.
ZA > ЛА > 2 окр. TMN
Теперь имеется некоторый круг TMN и в этом круге данная
линия TN, меньшая диаметра, и (отношение) ТА к АЛ большее того,
которое половина TN имеет к перпендикуляру, опущенному на нее из А;
тогда можно из А приставить к продолжению TN прямую AS так,
чтобы ее часть PS между окружностью и продолженной прямой имела
к ТР то же самое отношение, что ТА к АЛ (предложение VII);
РД ТА
ТР ~ АЛ
пусть AS пересекает круг в Р, а (второй оборот) спирали — в X;
и после перестановки PS будет иметь к ТА то же самое отношение,
что ТР к АЛ.
Р2 ТР
ТА — АЛ
Но ТР имеет к АЛ отношение меныпее, чем дуга ТР к удвоенной
окружности_круга TMN, , .
ТР ТР
АЛ 2<>ьр. TMN
:250
ЛРХИМИД
так как прямая ТР меньше дуги ТР, а прямая ЛА больше, чем удвоен-
ная окружность круга TMN; значит, Р21 имеет к АР меньшее отноше-
ние, чем дуга ТР к удвоенной окружности круга TMN;
РЕ ТР
АР 2 окр. TMN
тогда вся 2А к АР будет иметь меньшее отношение, чем дуга ТР вме-
сте с дважды взятой окружностью круга TMN к дважды взятой окруж-
ности круга TMN.
-ЕР + РА ТР + 2 Щф. TMN
АР ' 2 окр. TMN
По отношение обеих упомянутых дух' будет тем же самым, какое*
ХА имеет к АТ (это доказано (в предложении XV); значит, AS будет
иметь к АР отношение, меньшее чем ХА к ТА, что невозможно. Итак,
прямая ZA пе будет более, чем удвоенная окружность круга TMN.
Подобно же этому докажем, что опа пе будет и менее, чем удвоенная
(окружность). Таким образом, ясно, что опа будет ровно вдвое больше.
Тем же самым способом можно доказать, что если какая-нибудь
прямая касается спирали, описанной при каком-нибудь обороте в ко-
нечной ее точке, и прямая, проведенная из начала спирали перпен-
дикулярно к началу вращения, встречается с касательной, то (получен-
ная при пересечении прямая) будет равна окружности круга, взятой
в кратности, соответствующей (порядковому) числу оборотов.
XX
Если прямая линия касается спирали, описанной в течение первого
оборота, не в конечной ее точке, и точка касания соединена с началом спи-
рали, затем из начала спирали, как из центра, описан круг радиусом,
равным этой соединяющей прямой, и из начала спирали проведена неко-
торая прямая перпендикулярно к (прямой), соединяющей точку каса-
ния с началом спирали, то проведенная прямая встретится с касателъ
ной и прямая между местом встречи и началом, спирали будет равна
дуге описанного круга между точкой касания и сечением описанного круга
с началом вращения, если брать дуги от точки на начале вращения
к передней стороне.
Пусть АВГА {рис. 19} будет спираль, описанная в течение первого
оборота, и пусть некоторая прямая EZ касается ее в точке А; соединим А
прямой АЛ с началом спирали, и из центра А радиусом АД опишем круг
О СПИРАЛЯХ
251
A MN; пусть он пересечет начало вращения в К; проведем также ZA.
перпендикулярную к АД. То, что опа встретится (с AZ), очевидно; а то,
что прямая ZA равна дуге К М NA, требуется доказать.
Если она не равна, то будет или больше или меньше. Пусть сна-
чала она будет, если возможно, больше. Возьмем некоторую прямую
ДА, которая была бы меньше прямой ZA, но больше дуги KMNA.
ХА > ЛА > дуга KMNA _
Опять имеется круг KMN, в нем линия AN, мсныпая диаметра, и от-
ношение А А к АЛ большее того, которое половина AN имеет к перпен-
дикуляру, опущенному на пес из А; в таком случае можно из А приста-
вить к продолжению NA прямую АЕ так, чтобы ЕР имела к ДР то же
самое отношение, что ДА к АЛ;
ер _ АА
ЛР ~ АЛ
((в предложении VII) доказано, что это возможно). Тогда ЕР будет
иметь к АР то же самое отношение, что ДР к АЛ.
ер _ др
АР АЛ
Но ДР имеет к АЛ меньшее отношение, чем дуга ДР к дуге КМА,
ар дг
АЛ
к МЛ
так как прямая ДР меньше дуги АР, а АЛ больше дуги КМА; таким
образом, прямая ЕР имеет к РА отношение мепыттее, чем дуга АР
к дуге КМА,
ЕР ДР
РА КМД
так что и АЕ имеет к АР меньшее отношение, чем дуга КМР к дуге КМД.
ер + ра ' кмд + др
АР кмд
Но отношение дуги КМ Р к дуге КМА будет тем же самым, какое пря-
мая ХА имеет к АА;
КМР _ ХА
КМА ЛЛ
значит, ЕА имеет к АР отношение меньшее, чем АХ к ДА,
ЕА ах ’ ,
АР “'ЛА -•
что невозможно. Итак, ZA будет не больше дуги КМА. Подобно пре-
дыдущему покажем, что опа будет и не меньше; следовательно, она
равна (дуге КМА).
Тем же самым образом можно доказать, что, если прямая касается
спирали, описанной в течение второго оборота, не в конечной ее точке
и если все остальное будет сделано совершенно так же, то прямая меж-
ду местом встречи с касательной и началом спирали будет равна всей
уже вычерченной окружности круга и еще дуге между упомянутыми
точками, отсчитываемой совершенно так же. И если какая-нибудь пря-
мая касается спирали, описанной в течение какого-нибудь оборота не
252
АРХИМЕД
в конечной ее точке и все остальное будет сделано совершенно так же,
то прямая между упомянутыми точками будет равна окружности опи-
санного круга, взятой в кратности па единицу меньше сделанного
числа оборотов, и еще (дуге) между упомянутыми точками, взятой
тем же самым образом*).
XXI
Рис. 20.
Если взять площадь, заключенную между спиралью, описанной
при первом обороте, и первой прямой**) на начале вращения, то можно
описать около нее плоскую фигуру и вписать другую такую же, состоя-
щую из подобных секторов так, чтобы описанная фигура была больше
вписанной на величину, меньшую любой заданной площади.
Пусть АВГД {рис. 20} будет спираль, описанная ври первом обо-
роте, пусть точка © будет началом спирали, прямая ©А — началом вра-
щения, ZHIA — первым кругом, а АН и
ZI— его взаимно перпендикулярными диа-
метрами. Если мы будем все время делить
пополам прямой угол и заключающий его
сектор, то когда-нибудь оставшаяся часть сек-
тора будет меньше заданной; пусть получив-
шийся сектор A0K будет меньше наперед
заданной площади. Разделим все четыре пря-
мых угла па части, равные углу, заключен-
ному между А© и ©К, и прямые, образу-
ющие эти углы, продолжим до спирали. Пусть
точка пересечения прямой ©К со спиралью
будет А; из центра© оцйшемкруградиусомбА;
тогда части его окружности, находящаяся с передней стороны, попадет
внутрь спирали, ас задней стороны — вне ее. Теперь опишем дугу [ОМ]
до встречи с ©А [в точке О], а также до следующей за ©К прямой (©М).
доходящей до спирали. Пусть точка пересечения 0М со спиралью
будет Ы; из центра © радиусом ©N опишем круг так, чтобы дуга этого
круга встретилась с ©К и со следующей за ©М прямой (0Р), дохо-
дящей до спирали. Точно так же через все остальные точки, в которых
прямые, образующие равные углы, пересекают спираль, опишем из
центра 0 круги так, чтобы дуга каждого из них встретилась с предыду-
щей и с последующей прямыми; тогда около взятой площади будет
описала некоторая фигура, состоящая из подобных секторов, и другая
такая вписана. Докажем, что описанная фигура будет больше вписан-
ной па величину, меньшую наперед заданной площади.
Действительно, сектор ©АО равен ©МА, сектор <S*JNП равен ©NP,.
а ©Х£ равен ©ХТ, и каждый из остальных секторов вписанной фигуры
равен имеющему с ним общую сторону сектору описаппой фигуры.
Таким образом, ясно, что все секторы (описанной фигуры) равны
(соответствующим секторам вписанной); значит, фигура, вписанная
в эту площадь, равна описанной около нее, за исключением лишь
сектора ©АК, так как из всех секторов описанной фигуры не будет взят
только он один. Теперь ясно, что описанная фигура будет больше впи-
санной на сектор АК©, который меньше наперед заданной (площади).
*) То есть от начала вращения н передней стороне.
**) См. определение 4.
О СПИРАЛЯХ
253
С л е д с т в и е
Ив этого ясно, что около упомянутой площади можно описать, как
сказано, фигуру так, чтобы описанная фигура была больше этой пло-
щади на величину, меньшую всякой напсрод заданной площади, а затем
и вписать фигуру так, чтобы рассматриваемая площадь была больше
вписанной фигуры на величину, меньшую всякой паперед заданной
площади.
XXII
Если взять площадь, заключенную между спиралью, описанной при
втором обороте, и той прямой, которая является второй прямой на
начале вращения, то можно описать около нее плоскую фигуру, соста-
вленную из подобных секторов, и вписать другую так, чтобы описанная
фигура была больше вписанной на {величину),
меньшую всякой наперед заданной площади.
Пусть АВГДЕ {рис. 21} будет спираль,
описанная при втором обороте; пусть точка
® будет началом спирали, прямая А® — на-
чалом вращения, а ЕА — второй из прямых,
находящихся на начале вращения; пусть круг
AZTT будет вторым кругом, а АГИ, Z1 — его
взаимно перпендикулярными диаметрами.
Тогда опять, разделяя пополам прямой угол
и сектор, заключающий этот прямом угол, мы
когда-нибудь придем к остатку, меныпему па-
перед заданной (величины), и пусть пол учен-
ный сектор 0KA будет меньше наперед задан-
ной площади. Теперь если разделим прямые углы на части, равные углу
К6А, и все остальное сделаем точно так же, как и раныпе, то описан-
ная фигура будет больше вписанной на величину меньшую, чем сектор
A0K; действительно, она будет больше па тот избыток, которым сектор
©АК превосходит сектор ©ЕР.
С л е д с т в и е
Теперь ясно, что можно (сделать так), чтобы описанная фигура
была больше взятой площади на (величину), меньшую всякой наперед
заданной площади, а также чтобы взятая площадь была больше вписан
ной фигуры на (величину), меньшую всякой наперед заданной площади.
Тем же самым способом выясняется, что если взять площадь, заклю-
ченную между спиралью, описанной в течение какого угодно оборота,
и соответствующей ей по порядку прямой из тех, которые находятся па
начальном положении вращения, то можно описать около нее упомяну-
тую плоскую фигуру так, чтобы описанная фигура была больше взятой
• площади на (величину), меньшую всякой наперед заданной площади,
и затем вписать такую же фигуру так, чтобы взятая площадь была
больше вписанной фигуры на (величину), меньшую всякой наперед
заданной площади.
XXIII
Если взять площадь, заключенную между {дугой) спирали, мень-
шей описанной в течение одного оборота и не имеющей конца в начале
впирали, и прямыми, проведенными из обоих концов этой {дуги) спирали
254
АРХИМЕД
{к началу спирали}, то молено описать около этой площади плоскую фи-
гуру, состоящую из подобных секторов, и вписать в нее другую такую
же, так, чтобы описанная фигура превосходила вписанную на (величину),
меньшую всякой наперед заданной площади.
Пусть будет спираль ЛВГДЕ {рис. 22}, концы которой суть А, Е;
пусть начало спирали будет ©; проведем соединяющие прямые АО и
0Е. 3 атем из цеитра О опишем круг радиусом ©А;
пусть оп встретится с 0Е в точке Z. Постоянно
разделяя пополам угол при 0 и соответствующий
сектор 0AZ, мы когда-нибудь получим остаток,
меньший наперед заданной (площади). Пусть
сектор 0AK будет меньше наперед заданной
площади. Тогда подобно предыдущему опишем
круги, проходящие через те точки, в которых
спираль пересекают прямые, образующие при 0
равные углы, так, чтобы каждая дуга встречала
предшествующую и следующую за ней прямую;
тогда получится некоторая плоская фигура,
состоящая из подобных секторов, описанная
Рис.. 22.
около площади, заключенной между спиралью ЛВГДЕ и прямыми Л0,
0Е, и другая такая же вписанная, причем описанная фигура будет
превосходить вписанную на (величину), меныпую заданной площади,
так как сектор 0AK будет меньше этой последней *).
Следствие
Из этого ясно, что около упомянутой площади можно описать, как
указано, плоскую фигуру так, чтобы описанная фигура была больше этой
площади на (величину), меньшую всякой наперед заданной площади,
и затем вписать так, чтобы упомянутая площадь была больше вписан-
ной фигуры на величину, меньшую всякой наперед заданной площади.
XXIV
Площадь, заключенная между спиралью, описанной в течение пер-
вого оборота и первой из прямых, находящихся на начале вращения,
будет третьей частью первого круга.
Пусть будет спираль АВГАЕ0 {рис- 23}, описанная в течение пер-
вого оборота, пусть точка 0 будет началом спирали, а ©А — первая
прямая из тех, которые находятся на начале вращения; круг AKZHI
будет первым кругом, а круг q — его третьей частью. Требуется дока-
зать, что вышеупомянутая площадь равна кругу q.
Действительно, если это не так, то она будет или больше, или же
меньше. Пусть сначала она, если возможно, будет меньше. Тогда около
площади, заключенной между спиралью АВГДЕ0 и прямой ©Л, можно
описать плоскую фигуру, составленную из подобных секторов, так,
чтобы описанная фигура была больше этой площади на величину, мень-
шую того избытка, на который круг q превышает упомянутую пло-
щадь. Опишем ее, и пусть из секторов, составляющих упомянутую
фигуру, наибольшим будет ©АК, а наименьшим ©ЕО; ясно, что они-
*) Избыток площади оиисашюй фигуры вад вписанной равен избытку площади сектора в ЛК
над площадью сектора ДЕН, что меньше площади сектора 0Лк.
О СПИРАЛЯХ
255
Рис. 23.
Рис. 2-1
санная фигура будет меньше круга q. Теперь продолжим прямые, обра-
зующие при 0 равные углы, вплоть до встречи их с окружностью кру-
га; получатся некоторые линии, а именно проведенные из ® до спирали,
одинаково возвышающиеся одна над другой, из которых наибольшей
будет 0А, а наименьшей 0Е, и
наименьшая будет равна разно-
сти (между двумя последова-
тельными прямыми); кроме того,
имеются и некоторые другие
линии, а именно доходящие из 0
до окружности круга, причем
по количеству они будут равны
первым, по величине же каждая
из них будет равна наибольшей
из первых; далее, на всех этих
прямых, как на тех, которые
одинаково возвышаются одна
над другой, так и на тех, кото-
рые равны друг Другу и наибольшей из первых, построены подобные
секторы; значит, секторы, построенные на прямых, равных на-
ибольшей, будут менее взятых вместе утроенных секторов, построен-
ных на прямых, одинаково возвышающихся одна лад другой; зто
доказано (следствие предложения X). Но .
секторы на прямых, равных друг другу и
наибольшей, равны кругу AZHJ, секторы же
па прямых, одинаково возвышающихся одна
над другой, равны описанной фигуре; значит,
круг AZII1 будет менее утроенной описан-
ной фигуры. Но он в три раза больше круга
q; значит круг q будет меньше описанной
фигуры. Но он не меньше, а больше; значит,
площадь, ограниченная спиралью АВГДЕ®
и прямой А0, будет не меньше площади q.
Но она также будет и не больше. Дейст-
вительно, пусть она будет, если возможно,
больше. Тогда опять можно в площадь, за-
ключенную между спиралью АВГДЕ®
{рис. 24} и прямой Д0, вписать фигуру так,
чтобы упомянутая площадь была больше
вписанной фигуры на (величину), меньшую
той, на которую упомянутая площадь более
круга q. Впишем ее, и пусть из составляющих
вписанную фигуру секторов наибольшим
будет 0PE, наименьшим же О0Е; тогда ясно, что вписаппая
фигура будет больше круга q. Теперь продолжим прямые, образующие
при 0 равные углы, пока они не попадут на окружность круга. Тогда
опять получатся некоторые линии, одинаково возвышающиеся одна
над другой, именно доходящие из точки 0 до спирали, из которых наи-
большей будет 0А, наименьшей же 0Е, причем наименьшая равна раз
ности (двух последовательных линий), имеются также и другие линии,
имеппо доходящие из 0 до окружности круга AZHI, причем по количе-
ству они будут равны первым, по величине же каждая из них будет рав-
на наибольшей из первых; и на всех этих прямых, как на тех, которые
256
АРХИМЕД
равны друг другу и наибольшей, таи и па тех, которые одинаково воз-
вышаются одна над другой, построены подобные секторы; значит, сек-
торы, построенные па прямых, равных наибольшей, будут более чем
в три раза больше тех секторов, которые построены на прямых, одина-
ково возвышающихся одна над другой, если исключить сектор на наи-
большей; это доказано (следствие предложения X). Но секторы, пост-
роенные па прямых, равных наибольшей, равны кругу AZHI, секторы
же ла прямых, одинаково возвышающихся одна над другой, кроме наи-
большего, равны вписанной фигуре; значит, круг AZIII будет более
чем в три раза больше вписанной фигуры. Но он в три раза больше круга
q; значит, круг q будет больше вписанной фигуры. По он не больше,
а меньше; значит, площадь, ограниченная спиралью АВГДЕО и пря-
мой Л0, не будет и больше круга q. Итак, круг q будет равен [пло-
щади, заключенной между спиралью и прямой A0J [10].
XXV
Площадь, заключенная между спиралью, описанной в течение
второго оборота, и второй из прямых, находящихся на начале враще-
ния, имеет ко второму кругу то же отношение, что 7 к 12; это не что
относиться к AZII1,
иное, как отношение, которое вместе взя-
тые прямоугольники между радиусами пер-
вого и второго кругов и третья часть квад-
рата на разности {между радиусами} второго
и первого кругов имеют к квадрату на
радиусе второго круга.
Пусть будет спираль ЛВГАЕ {рис. 25],
описанная в течение второго оборота, пусть
точка 0 будет началом спирали, прямая
0Е — первой из прямых па начале враще-
ния, а АЕ — второй из прямых на начале,
вращения; пусть круг AZHI будет вторым
и АН, IZ будут его взаимно перпендикуляр-
ными диаметрами. Требуется доказать, что
площадь, ограниченная спиралью ЛВГАЕ
и прямой АЕ, имеет к кругу AZIII такое
же отношение, как 7 к 12.
Пусть будет некоторый круг q, и пусть
квадрат на радиусе круга q равен прямо-
угольнику между А0, ОЕ вместе с третьей
частью квадрата на ЛЕ: тогда круг q будет
так 7 к 12, так как взятое в квадрате отношение
его радиуса и радиусу круга AZHI будет именно таковым*).
Докажем теперь, что круг q будет равен площади, заключенной
между спиралью АВГДЕ и прямой АЕ.
В самом деле, если это не так, то он будет или больше, или мень-
ше. Пусть сначала он будет, если возможно, больше. Тогда можно
около рассматриваемой площади описать плоскую фигуру, составлен-
*) Действительно, так как Л0=20Е, то
A0-0K-r-i-ЛЕ2 20Е2 + А-0Е2 ?
__ — ___ __.
О СПИРАЛЯХ.
257
будут и другие линии,
ную из подобных секторов, так, чтобы описанная фигура была больше
рассматриваемой площади на (величину), меньшую той, на которую
круг q больше этой площади.
Опишем ее, и пусть из секторов, составляющих описанную фигу-
ру, наибольшим будет 0AK, наименьшим же ©ОД; ясно, что описан-
ная фигура будет меньше круга q. Продолжим прямые, образующие
при 0 равные углы, пока они нс попадут па окружность второго круга.
Теперь имеются некоторые линии, одинаково возвышающиеся одна
над другой, а именно проведенные из О к спирали, из которых наиболь-
шей будет НА, наименьшей же 0Е; также
а именно доходящие из 0 до окружности кру-
га AZHI, причем количество их па одну ли-
нию меньше количества первых, а по величине
они равны друг другу и наибольшей (из пер-
вых); затем и на тех, которые равны наиболь-
шей, и на тех, которые одинаковн возвы-
шаются одна над другой, построены подобные
секторы, только на наименьшей (0Е) сектор
не достроен; значит, секторы па прямых,
равных наибольшей, к секторам, построенным
на прямых, одинаково возвышающихся одна
над другой, кроме лишь наименьшей, будут
иметь меньшее отношение, чем квадрат на
наибольшей 0А ко вместе взятым прямо-
угольнику между А0, ©Е и третьей части
квадрата на ЕА; это доказано (в следствии
предложения XI). Но секторам, постро-
енным на прямых, равных друг другу и
наибольшей, равен круг AZHI, секторам же,
построенным на прямых, одинаково возвы-
шающихся одна над другой, кроме лишь
сектора на наименьшей, будет равна описанная фигура; значит, круг
(AZHI) к описанной фигуре будет пметь меньшее отношение, чем
квадрат на А© к вместе взятым прямоугольнику’ между А0, ©Е и
третьей части квадрата па АЕ.
Но отношение квадрата на А© ко вместе взятым прямоугольнику
между А0 и 0Е с третьей частью квадрата на АЕ будет тем же самым,
какое круг AZH1 имеет к кругу q; значит, круг AZHI к описанной
фигуре будет иметь меньшее отношение, чем к кругу q; значит, круг q
будет меныпе описанной фигуры. По он пе меныпе, а больше; значит,
круг q не будет больше площади, заключенной между спиралью
АВ ГАЕ и прямой АЕ.
Но он также и пе меньше. Действительно, пусть он будет, если
возможно, меньше. Тогда опять можно в площадь, заключенную меж-
ду спиралью и прямой АЕ, вписать плоскую фигуру, составленную
из подобных секторов, так, чтобы площадь заключенная между спи-
ралью АВГАЕ и прямой АЕ, была больше вписанной фигуры на (ве-
личину) меньшую той, на которую та же самая площадь больше
круга q.
Впишем ее, и пусть из составляющих вписанную фигуру секторов
наибольшим будет ©КР {рис. 26}, а наименьшим ©ЕО; ясно, что впи-
санная фигура будет больше круга q. Продолжим прямые, образующие
при О равные углы, пока они пе попадут па окружность круга. Опять
1> Архимед
258
АРХИМЕД
у нас имеются некоторые линии, одинаково возвышающиеся одна над
другой, а именно доходящие из 0 до спирали, наибольшей из которых
является ©А, наименьшей же 0Е; имеются также и другие линии,
а именно доходящие из 0 до окружности круга, причем количество их
будет на одну меньше количества первых, по величине же они будут
равны друг другу и наибольшей из первых; и на одинаково возвышаю-
щихся одна над другой и па равных наибольшей построены подобные
секторы; значит, секторы па прямых, равных наибольшей, к секторам,
построенным на одинаково возвышающихся одна на другой, кроме
лишь сектора ня наибольшей, будут иметь большее отношение, чем
квадрат на 0А ко вместе взятым прямоугольнику между А0 и 0Е
с третьей частью квадрата на ЕЛ- Но всем секторам, построенным на
прямых, одинаково возвышающихся одна над другой, кроме лишь
наибольшей, равна вписанная в рассматриваемую площадь фигура,
а другим (секторам) — круг (AZH1); значит, круг AZUL ко впи-
санной фигуре будет иметь отношение большее, чем квадрат па 0А
ко вместо взятым прямоугольнику между 0А и 0Е с третьей частью
квадрата на АЕ, то есть большее чем круг AZHI к кругу q.
Значит, круг q будет больше вписанной фигуры, что невозможно,
так как он был меньше ее. Значит, круг q не будет и меньше площади,
ограниченной спиралью ЛВГДЕ и прямой ЛЕ; таким образом, оп
будет ей равен.
Следствие
Таким же образом докажем, что площадь, заключенная между
(дугой) спирали, описанной в течение какого-нибудь оборота, и пря-
мой, порядок которой соответствует (порядковому) числу того же
оборота, к кругу, порядок которого соответствует (порядковому)
числу того же оборота, будет иметь такое же отношение, какое вместе
взятые прямоугольник между радиусом круга того же самого порядка
и радиусом круга, порядок которого на единицу меньше числа оборо-
тов, и третья часть квадрата на разпости между большим и меньшим
радиусами упомянутых кругов имеют к квадрату па радиусе большего
круга из упомянутых.
XXVI
Площадь, заключенная между дугой спирали, меньшей описанной
в течение одного оборота и не имеющей конца в начале спирали, и пря-
мыми, проведенными из обоих концов этой (дуги) к началу спирали,
имеет к сектору, радиус которого равен большей прямой, соединяющей
конец этой дуги с началом спирали, а дуга заключается между обеими
упомянутыми прямыми с той же стороны, где и спираль, такое же
отношение, какое вместе взятые прямоугольник между обеими пря-
мыми, проведенными из концов дуги к началу спирали, и третья часть
квадрата на разности между большей и меньшей из этих прямых имеют
к квадрату на большей прямой из соединяющих концы дуги с началом
спирали.
Пусть будет (дуга) спирали АВГДЕ {рис. 27} меньшая той,
которая описывается в течение одного оборота, пусть ее концами будут
А, Е, началом же спирали — точка 0; из точки 0, как из центра, опи-
шем круг радиусом 0А, и пусть ©Е встречается с его окружностью
О СПИРАЛЯХ
259
в Z. Требуется доказать, что площадь, заключенная между спиралью
АВГАЕ и прямыми Л©, ©Е, имеет такое же отношение к сектору A0Z,
какое вместе взятые прямоугольник между А0, ©Е и третья часть квад-
рата па EZ имеют к квадрату на ©А.
Пусть будет круг q, имеющий радиус, квадрирующий (вместе
взятые) прямоугольник между А© и ©Е и третью часть квадрата
ла EZ, и угол при центре, равный углу при ©; тогда сектор qX к сек-
тору ©AZ будет иметь такое же отношение, какое прямоугольник меж-
ду А©, ©Е и третья часть квадрата на EZ имеют к квадрату на ©А;
АЙ-ЙИ | Д- EZ2
сектор qx_________ 3
сектор 6AZ 0д2
ведь именно таково взятое в квадрате отношение их радиусов. Дока-
жем, что сектор Xq будет равен площади, заключенной между спи-
ралью АВГДЕ и прямыми А©,
0Е. Действительно, если не
так, то он будет или больше,
или меньше. Пусть сначала он //ч/у / /\\\ /•—""х
будет, если возможно, больше; //Г\\ // \\\ / \
тогда около упомянутой пл о- I р/Дс-щ//______। X Г --______1
щади можно описать плоскую I \ / / \ ** 7
фигуру, составленную из по- \ \
добных секторов так, чтобы \ х. / /
описанная фигура была больше --—
упомянутой площади па вели- "
чину, мепьшую тон, на которую 1>ик 27
сектор qX превосходит упомя-
нутую площадь. Опишем ее, и
пусть из секторов, составляющих описанную фигуру, наибольшим
будет ©АК, наименьшим же ©ОД; ясно, что описанная фигура будет
меньше сектора Xq. Продолжим прямые, образующие при © равные
углы, до тех пор, пока они не попадут на окружность сектора ©AZ.
Теперь имеются некоторые прямые, одинаково возвышающиеся одна
над другой, а именно доходящие из © до спирали, наибольшей из кото-
рых является ©А, а наименьшей ©Е; имеются также и другие прямые
по количеству на одну меньше количества первых, а по величине рав-
ные друг другу и наибольшей (0А), а именно прямые, доходящие
от © до дуги сектора A0Z, кроме прямой 0Z; на всех этих прямых,
как на равных друг другу и наибольшей, так и на одинаково возвы-
шающихся одна над другой, построены подобные секторы, только на
0Е сектор не построен; тогда секторы на прямых, равных друг другу
и наибольшей, к секторам на прямых, одинаково возвышающихся одна
над другой, кроме лишь сектора на наименьшей, будут иметь меныпее
отношение, чем квадрат па ©А ко вместе взятым прямоугольнику
между А©, ©Е и третьей части квадрата ла EZ. Но секторам, построен-
ным на прямых, равных друг другу и наибольшей, равен сектор 0AZ,
секторам же па прямых, одинаково возвышающихся одна над другой,
равна описанная фигура; таким образом, сектор 0AZ к описанной фигу-
ре имеет отношение меньшее, чем квадрат на ©А ко вместе взятым (пря-
моугольнику) между ©А, ©Е и третьей части квадрата на ZE. Но
отношение квадрата на 0А к упомянутым будет тем же самым, какое
сектор 0AZ имеет к сектору Xq; таким образом, сектор Xq будет
17*
260
АРХИМЕД
меньше описанном фигуры. Но он нс меньше, а больше; значит, сектор Xq
будет не больше площади, заключающейся между спиралью АВ ГДЕ
и прямыми Л©, 0Е.
Но он не будет также и меньше. Действительно, пусть он будет
меньше, и пусть все остальноо будет сделано совершенно так же. Тогда
опять можно вписать в эту площадь плоскую фигуру, состоящую из
подобных секторов, так, чтобы упомянутая площадь была больше впи-
санной фигуры на (величину) меныпую той, на которую эта же самая
Рис. 28.
площадь превосходит сектор Xq.
Впишем ее, и пусть из секто-
ров, составляющих вписанную
фигуру, наибольшим будет ©В Г
{рис. 28}, наименьшим же 0©Е;
ясно, что вписанная фигура
будет больше сектора Xq. Те-
перь опять имеются некоторые
линии, одинаково возвышаю-
щиеся одна над другой,— имен-
но, доходящие от © до спира-
ли, из которых наибольшей бу-
дет ©Л, а наименьшей ©Е;
имеются также и другие ли-
нии,— именно доходящие из 0 до окружности сектора 0AZ, кроме
лишь ©А, по количеству на одну меньше одинаково возвышающихся
одна над другой, по величине же равные друг другу и наибольшей
(из них); па каждой из них построены подобные секторы, лишь на
наибольшей из одинаково возвышающихся одна над другой сектор не
достроен; тогда секторы да прямых, равных друг другу и наиболь-
шей, к секторам на одинаково возвышающихся одна над другой, кроме
лишь сектора на наибольшей, будут иметь большее отношение, чем
квадрат на 0А к (прямоугольнику) между 0А, 0Е, и третьей части
•квадрата на части EZ, так что и сектор 0AZ имеет ко вписанной фи-
гуре большое отношение, чем к сектору Xq; таким образом, сек-
тор Xq будет больше вписанной фигуры. Но он не больше, а мень-
ше; значит, сектор Xq не будет и меньше площади, заключенной
между спиралью АВ ГАЕ и прямыми А0,
«0Е; значит, он будет ей равен.
XXVII
м
л
к
Из площадей, заключенных между спира-
лями и прямыми на начале вращения, третья
будет вдвое больше второй, четвертая втрое
больше ее, пятая вчетверо, и всегда каждая
следующая будет больше второй площади в
кратности, соответствующей последователь-
ным числам, а первая площадь будет ше-
стой частью второй.
Пусть предложенная спираль будет ",с- 2У-
описапа в течение первого оборота, второ-
го и взятых в любом числе следующих, пусть началом спирали
будет точка 0 {рис. 29}, началом же вращения прямая ©Е,
;а из площадей пусть К будет первая, А — вторая, М третья, N —
О СПИРАЛЯХ
2(4
четвертая, Е — пятая. Требуется доказать, что площадь К будет -у
частыо следующей, площадь М — вдвое больше Л, a N — втрое боль-
ше Л, и каждая следующая больше Л в кратности, соответствующей
последовательным числ ам.
Что К является -g- частью от Л, доказывается так. Поскольку дока-
зано, что площадь К (вместе с) Л имеет ко второму кругу такое же
отношение, как 7 к 12, а второй круг к первому — как 12 к 3 (зто ведь
очевидно), и первый круг относится к площади К, как 3 к 1, то, значит,
площадь К будет от Л *). Далее доказано, что площадь К (с) Л
и М относится к третьему кругу, как вместе ввятые прямоугольник
между ©Г, 0 В и третья часть квадрата на ГВ относятся к квадрату
на Г©.
К1-Л+М ге-ев+±гва
площ. 3-ги круга “
Но третий круг относится ко второму, как квадрат на Г© к квадрату
па ©В,
илощ. 3-г<> круга _ ГОа
пяти. 2-го круга
а второй круг к площади К (с) Л — как квадрат на В© ко вместе
взятым прямоугольнику между В0, ©Л и третьей части квадрата
на ЛВ;
площ. 2-го круга _ BOS
К'гЛ BO-OAl-^-AB2
значит, площадь К (с) Л (и) М относится к К (с) Л, как прямо-
угольник между Г0, 0В и третья часть квадрата на ГВ к прямоуголь-
нику между В© и ©А с третьей частью квадрата иа АВ.
геев-1-4- гва
к+л-км _______з
к-!"л ве.ел+-|-Ав2
Оба же последних относятся друг к другу, как 19 к 7 **), так что пло-
щадь К (с) Л (и) М относится к площади Л (с) К, как 19 к 7;
тогда одна М относится к К (с) А, как 12 к 7. А К (с) Л относится
к Л, как 7 к 6; теперь ясно, что М будет вдвое больше Л.
Докажем теперь, что следующие площади имеют (к Л) отноше-
ния соответственно последовательным числам.
*) Действительно, площадь К 4-Л, ограниченная спиралью и второй прямом, относится
ко второму кругу, как 7 к 12 (предложение XXV) второй круг вчетверо больше первого. Tait кам
вВ^2ЬА, и площадь К равна 1/3 первого круга (предложение XX1V), Таким образом, площадь К
lit .716
равна -5- - —- ~=второго круга, а площадь Л равна 77г — второго круга, и следовательно,
о ч 12 12 12 12
площадь К составляет одну шестую площади Л.
32Ц Ю
-•) Положим вА=ЛВ=ВГ=4; тогда отношение, стоящее «права, будет -=-=!
21+з
АРХИМЕД
262
Площадь К (с) Л, М, N (и) Е имеет к кругу с радиусом 0Е
такое же отношение, как вместе взятые прямоугольник между Е0,
0Д и третья часть квадрата на ДЕ к квадрату на 0Е.
K+A4-M+N+B _ EQ-Q-M -g- ЛЕ2
Круг 6Е —
Круг с радиусом 0Е относится к кругу с радиусом 0Д, как квад-
рат на 0Е к квадрату на 0Д,
круг 6)Е ев2
КРУГ ё)Д
круг же с радиусом Д0 относится к площади К (с) Л, М (и) N, как
квадрат на 0Д ко вместе взятым (прямоугольнику) между 0Д
и 0Г и третьей части квадрата на ДГ;
круг вД 6i2
к+л+м+Sr е^вг+^дг2
и, значит, площадь К (с) Л, М, N (и) 2 относится к К с Л, М
и N, как вместе взятые (прямоугольник) между €)Е, ©Д и третья
часть квадрата на ЛЕ относятся к (прямоугольнику) между Л0, ОГ
и третьей части квадрата на ДГ;
K+A|M!N+S_ »E-«A+4ak2
K-hAi-MHN д0.вг+^.дг2
и после «выделения» площадь Е относится к К (с) Л, М и N, как избы-
ток прямоугольника Е0, 0Д с третьей частью квадрата на ЕД
над прямоугольником между Д0, О Г, (взятым) с третьей частью
квадрата на ГД, относится к прямоугольнику между Д© и 0Г с третьей
частью квадрата на ДГ.
в (ое-<эл+-^де2) - (деег+-1-дг2)
о
Но избыток вместе взятых (первых) над вместо взятыми (вторыми)
будет таким же, как разность прямоугольников между Е©-0Д и меж-
ду Д® и 0Г, разность же ата будет прямоугольник между Д0, ГЕ;
(ек ед-| ле2) — (де-егн- -у лг2)—ен-ед -де-ег -деигЕ-еп-де.гв
значит, Е относится к площади К (с) Л, М и N, как (прямоуголь-
ник) между 0Д, ГЕ ко вместе взятым прямоугольнику между Д®,
©Г и третьей части квадрата на ГД.
s __ де-ге
К+Л+М ьл - де ет+ _1_ гдй
При помощи тех же самых (рассуждений) докажем, что N относит-
ся к площади К (с) Л (и) М, как (прямоугольник) между ®Г
и ВД ко вместе взятым (прямоугольнику) между Г®, ©В и третьей
части квадрата на ГВ;
__n__ ег- вд
K-J-A-f-M гв.ев_|__|.гв2
О СПИРАЛЯХ
263
значит, N относится к площади К (с) Л, М и N, как (прямоуголь-
ник) между ©Г, ВЛ ко вместе взятым прямоугольникам между 0Г,
ВД и ©Г, ©В вместе с третьей частью квадрата на ГВ,
N____________НГ- НА____
к-1-A+Mi-N ег вд+ь>г. ев г Д- гв2
[и обратно]; последние же равны прямоугольнику между ДО, ©Г
и третьей части квадрата на ГД.
«г - вд+ег • ев!- гв2=де • ег । А гд2
Теперь так как площадь S относится к К (с) А, М и N, как прямо-
угольник на 0Д, ГЕ ко имеете взятым (прямоугольнику) между Д©,
©Г и третьей части квадрата на ГД, а К (с) Л, М и N относятся к N,
как вместе взятые (прямоугольник) между Д0, ©Г и третья часть
квадрата на ГД относятся к прямоугольнику между ©Г, ДВ *), то,
значит, 3 будет относиться к N, как (прямоугольник) между ©Д,
ГЕ к (прямоугольнику) между ©Г, ДВ.
= . ел-ги
N “er-да
По (прямоугольник) между ©Д, ГЕ имеет к (прямоугольнику)
между ©Г, ДВ то же отношение, что ©Д к ©Г, так как ГЕ равна
ВД; теперь яспо, что и Е будет иметь к N то же отношение, что ©Д
к ©Г.
5__ед
к " ег
Подобным же образом докажем, что N относится к М, как ©Г
к ©В,
n _ с-щ
"м" “ев
а М относится к Л, как В© к Л©,
в _ ве
л "асГ
прямые же ГЕ©], Д0, Г©, В©, А© относятся как последовательные
(целые) числа.
XXVIII
Если на спирали, описанной а течение какого угодно оборота.,
взять две точки, не являющиеся ее концами, взятые точки соединить
прямым,и с началом спирали и из начала спирали, как из центра, описать
круги радиусами, равными расстояниям от взятых точек до начала
спирали, то площадь, ограниченная большей дугой окружности между
этими прямыми, (частью) спирали между теми же прямыми и про-
должением (меньшей) прямой, будет относиться к площади, ограни-
ченной меньшей дугой, той же самой (частью) спирали и прямой, сое-
диняющей их концы, как радиус меньшего круга с двумя третями раз-
нести между радиусами большего и меньшего кругов относится к радиу-
су меньшего круга с одной третью той же самой разности.
*) Сюда, ио существу, и должно относиться выражение «и обратно*, поставленное и квад,
гатпых скобках.
264
АРХИМЕД
Пусть будет спираль АВГД {рис. 30}, описанная в течение одного
оборота; возьмем на ней две точки Л и Г так, что точка 0 будет нача-
лом спирали *); соединим А и Г с © и из центра 0 опишем круги радиу-
сами ©А, ©Г. Требуется доказать, что площадь Е относится к II, как
А© с двумя третями НА относятся ко вместе взятым А© и одной тре-
ти ПА.
ле+ НА
АН 1-уНА
Согласно доказанному (в предложении XXVI), площадь-N (вместе
с) П относится к сектору НГ0, как (прямоугольник) между Н©,
А© с третьей частью квадрата на АН относятся к квадрату на Нй;
не-ле+-~- ап®
нго ' не®
значит, одна площадь Е относится к N + П, как (прямоугольник)
между ©А, АН с двумя третями квадрата на НА относится ко вместе
взятым (прямоугольнику) между А©, ©Н и
третьей части квадрата на НА**). ~
2
, ел-лп+— пд2
ле-ен+^-пл2 / s\/ / \ \
I___у V/ \ 1
И так как площадь N, II относится к секто- I// A I I
ру N,n, Е, как вместе взятые (прямоугольник) \ —s J /
между ©А, ©II и третья часть квадрата на НА \ ----' /
относятся к квадрату на ©Н, X. /
n+п ле-еп-ь-уАна
N-t-11-.-Е = ©Ц2 Рис. 30.
а сектор N,n, Е относится к сектору N как (квадрат) на ©Н к
(квадрату) на ©Л,
N4-H-+S _ 0I12
OA2
то площадь N,II относится к N так же, как вместе взятые (прямоуголь-
ник) между ©А и ©II и третья часть (квадрата) на НА относится
к (квадрату) на ©А;
ед-ен-’г 4-нл2
N- =" ёА2
значит, N, П относится к П, как вместе взятые (прямоугольник)
между II0, ©А и третья часть квадрата на НА относятся ко вместе
взятым (прямоугольнику) между ПА и ©А и третьей части квадра-
*) XeAatptfW еЯ’ a’VTagdaO <Ш|18Г<Х та А, Г, СО ОТЕ Ти 6 <Jap£?OV aQXaV eiyev rag fiAlxOg.
**) Имеем
не2_/iie-A0-;-jAH2)-=He AH- Уан? = на« +ah-ah - I ah2-ah-ah+Sah®.
\ O / i> О О
О СПИРАЛЯХ
265-
та на НА *).
wjn не-еА+4-нА*
НА-0А+ А- НА2
Так как площадь Е относится к N,H, как имеете взятые «пря-
моугольник» между ВА, АН и дне трети квадрата на НА относят-
ся ко вместе взятым (прямоугольнику) между Н0, В А и третьей части
квадрата на ПА, а площадь ?\,П относится к II так же, как вместе
взятые (прямоугольник) между НВ, ВА и третья часть квадрата на НА
относятся ко вместе взятым (прямоугольнику) между НА, АВ
и третьей части квадрата на НА, то Е будет относиться к II, как вме-
сте взятые (прямоугольник) между ВА, АН и две трети квадрата
па НА относятся ко вместе взятым (прямоугольнику) на ВА, АН
и одной трети (квадрата) на НА.
2
©А«АН+-у АН3
©А-АН |- АН2
Но вместе взятые (прямоугольник) между ВА, АН и две трети (квад-
рата) на. НА относятся ко вместе взятым (прямоугольнику) между
ВА, АН с одной третью (квадрата) на НА, как вместе взятые ВА
и две трети НА относятся ко вместе взятым ВА и одной трети НА;
теперь яспо, что площадь Е к площади П имеет то же самое отношение,
что вместе взятые ВА и две трети ПА ко вместе взятым ВА и одной,
трети ПА.
2
ОА-Н -д НА
©А+ -у ПА
Н 14 И В
*> Если
вА-еН + | АП2
©А2
то
ц
©А-©Н + |аН2 ©А-еН + ^АН2
©А • ©Н -Ц АН2 -А©2 ©А-НА-Ц АП2
ИЗМЕРЕНИЕ КРУГА
Всякий круг равен прямоугольному треугольнику, причем радиус
круга равен одной из прилегающих к прямому углу сторон, а периметр —
основанию треугольника.
Пусть круг АВГД {рис. 1} относится к треугольнику Е, как
высказано в предложении; я утверждаю, что он будет ему равен.
Рис. 1.
Действительно, пусть, если возможно, круг будет больше; впишем
в него квадрат АГ, будем (постоянно) делить дуги пополам, (и прово-
дить прямые BZ, ZA, AM, МЛ и т. д.), и пусть (когда-нибудь) полу-
чатся сегменты меньшие той разницы, на которую круг больше тре-
угольника; тогда полученная прямолинейная фигура будет также
больше треугольника. Возьмем центр (круга) N и (проведем) перпен-
дикуляр N3; тогда ЛН будет меньше соответствующей стороны тре-
угольника (Е). Также и периметр прямолинейной фигуры меньше
•оставшейся стороны, поскольку оп меньше периметра круга; значит,
подученная прямолинейная фигура будет меньше треугольника Е,
а это нелепо.
ИЗМЕРЕНИЕ КРУГЛ
267
Пусть теперь круг, если возможно, будет меньше треугольника Е;
опишем около него квадрат, разделим пополам его стороны и через
полученные точки (делений) проведем касательные; тогда угол ОАР
будет прямым. Следовательно, ОР будет больше Ml’, так как РМ рав-
на РА; и значит, треугольник РОП будет больше половины фигуры
OZAM. Возьмем такие сегменты, подобные 1IZA, чтобы они были (вместе)
меньше избытка, на который треугольник Е больше круга АВГД;
тогда и описанная прямоугольная фигура будет менее Е, а ото пелепо;
действительно, она больше, так как NA равна (вертикальному) кате
ту итого треугольника, а периметр ее больше основания треугольника.
Значит, круг будет равен треугольнику Е.
II
Круг к квадрату на диаметре относится *), как 11 к 14 {рис. 2}.
Пусть будет круг с диаметром АВ; опишем около него квадрат ПТ,
и пусть ДЕ равна удвоенной ГД, a EZ — седьмой части ГЛ. Теперь,
так как АГЕ имеет к А ГД
отношение как 21 к 7, и
АГД имеет к AEZ отноше-
ние, как 7 к 1, то ATZ будет
к АГД, как 22 к 7.
Но квадрат Г1Т в че-
тыре раза больше тре-
угольника АГД, треуголь-
ник же ATAZ равен кру-
гу АВ, [так как катет АГ
равен радиусу, а основание, как будет доказано, чуть-чуть больше трех
диаметров и одной седьмой!; значит, круг к квадрату на ГН относится
как 11 к 14 [1].
III
Периметр всякого круга равен утроенному диаметру с избытком,
который .меньше седьмой части диаметра, но больше десяти семьдесят
первых [2].
Пусть будет круг с диаметром АГ и центром Е (рис. 3], затем каса-
тельная TAZ и угол ZET — третья часть прямого угла; тогда EZ отно-
сится к ZT, как 306 к 153, а ЕГ к TZ относится, как 265 к 153.
Разделим угол ZET ионолам прямой ЕП; тогда как ZE к ЕГ,
так будет и ZII к НГ,
ZE ZII
ИГ пг
[будем также «переставлять» и «присоединять»];
ZE+rer _ zh+пг
ге пг
тогда как вместе взятые ZE, ЕГ к ZI', так и ЕГ к ГП;
ZE+КГ ЕГ
яг~ ~ ГН
таким образом, ГЕ и ГН имеет отношение большее, чем 571 к 153.
•) Такая формулировка (без указания на приближенный характер отношения) подтверждает,
что до пас дошел испорченный текст Архимеда.
268
АРХИМЕД
Значит, в квадратах ЕН имеет к НГ отношение, как 349450 к 23409,
ЕН2 349 4 ьо
НГ2 23 409"
следовательно, в первых степенях имеет отношение как 591 -g- к 153-
Рис. 3.
1
основании Е Г будет иметь к Г0 большее отношение, чем 1162-у- к 153;
ег .
ге > 15з"
значит, 0Е имеет к 0Г большее отношение, чем 1172 к 153.
О
RE... И724
ОГ 1эЗ
Делим пополам еще угол 0ЕГ прямой ЕК; тогда ЕГ имеет к ГК
большее отношение, чем 2334 -г к 153.
„„ 2384 4-
ЕГ 4
ГК '> 153
Значит ЕК имеет к ГК большее отношение, чем 2339 4- к 153.
’ 4
9S39 ~
ЕК k
ГК 153
Делим еще пополам угол КЕГ прямой ЛЕ; тогда ЕГ имеет к ЛГ
[в первой степени] отношение большее, чем 4673 у к 153.
ЕГ-., 46731
ЛГ ' 153
Теперь, так как угол ZET, будучи третьей частью прямого, раз-
делен пополам четыре раза, то угол ЛЕГ будет прямого. Отложим
от Е в другую сторону равный ему угол ГЕМ; тогда угол ЛЕМ равен i
прямого; и, значит, прямая ЛМ будет стороной описанного около круга
ИЗМЕРЕНИЕ КРУГА
269
. многоугольника, имеющего 96 сторон. Теперь, так как ЕГ, ло доказан-
ному, имеет к ГЛ отношение большее, чем 4673 у к 153, и АГ вдвое
больше ГЕ, аЛМ вдвое больше ГЛ, то значит, АГ к периметру 96-уголь-
ника имеет большее отношение, чем 4673-^- к 14688.
АГ .. 4673 4-
I’se i t «88
И (эти 14 688) будут втрое больше, (чем 4673 ~), причем остаются
667 4, которые несколько меньше седьмой части 4673-] , так что (пери-
метр) многоугольника, описанного около круга, будет более диаметра
в три раза с дробью, которая меньше седьмой его части; значит,
периметр круга будет и недавно меньше, чем (диаметр, взятый)
три раза с добавлением седьмой части.
Пусть будет круг с диаметром ЛГ {рис. 4} и угол ВАГ составляет
третью часть прямого; тогда ЛВ имеет
к ВГ отношение меньшее, чем 1351 к 780.
ав ।заt
ИГ ' 780 //
[а ЛГ к ГВ, как 1560 к 780].
Разделим пополам угол ВАГ прямой *
АП. Теперь так как угол ВА11 равен
НГВ , а также и НАГ, то и угол НГВ
ранен ПЛ Г. Далее прямой угол АН Г
является общим; значит, и третий угол
(IZr ранен третьему углу А ГН. Тогда треугольник ЛИГ будет равно-
угольным с треугольником T11Z; следовательно, отношение АП к НГ
равпо отношениям ГН к IJZ и Л Г к FZ.
ли _ гн _ АГ
нг nz~ rz
По как АГ к TZ, так и вместе взятые ГА, АВ к ВГ,
АГГЛ-j-AB
rz вг
и, значит, как вместо взятые ВА, АГ к В Г, так и АН к НГ.
ВА-гАГ _ АН
ВГ ’ НГ
Вследствие этого АП будет иметь к IIГ меныпее отношение, чем
2911 к 780, а АГ к ГН меньшее отношение, чем 3013 4 _ к 780.
Делим пополам угол ГАН прямой А0; тогда вследствие того же
А6> будет иметь к 6Г меныпее отношение, чем 5924 ^--1 ~т к 780, или
4
1823 к 240, так как каждый (последующий) составляет (предыдуще-
го); таким образом, АГ будет иметь к Г0 отношение меньшее, чем
1838^ к 240. (Делим) еще пополам угол ©ЛГ прямой КЛ; [тогда]
АК имеет к КГ меныпее отношение, чем 1007 к 66,
ЛК 1007
кн 88
270
АРХИМЕД
так как каждый (последующий) составляет (предыдущего); зна-
шт, АГ к КГ (имеет меньшее отношение), чем 1009 к 66. (Делим)
еще пополам угол КАГ прямой ЛА; тогда ЛА имеет к ЛГ меныиее отно-
» 1 1
шепие, чом 2016-77 к 66, а Л Г к ГЛ — меныпсе, чем 2017 к 66.
Ь 4
Г 1
Значит, обратно |отиолгепие ГЛ к ЛГ больше, чем 66 к 2017 7-.
Но ГЛ есть сторона многоугольника с 96 сторонами; поэтому!*) пери-
метр рассматриваемого многоугольника имеет к диаметру большее отно-
тонне, чем 6336 к 2017 , что больше 2017 более чем в три раза с де-
сятью 71-ми долями; следовательно, периметр 96-угольника, вписанного
в круг, более чем в три и раза больше диаметра, так что окружность
г 10
оудет и подавно оолыпе, чем в три и yj раза.
Итак, периметр круга будет более чем в три раза больше диаметра
с избытком мепыпим седьмой части, по большим 13]-
ФРАГМЕНТЫ, ОТНОСЯЩИЕСЯ К «ИЗМЕРЕНИЮ КРУГА»
1. Диофант |20] (изд. Таниери, П, стр. 22, 16).
«Архимед показал, что 30 равносторонних треугольников равны 13 квадратам».
Если через а обозначим сторону треугольника и соответственно квадрата, то их
площади будут соответственно равны с2-^Аи йа_ Из равенства 30-«2 -^^-—13-а~
2(5
находим уз=—.
2. Героя, Метрика, кп. 1, 37.
«Архимедом в «Измерении круга» доказано, что всякий сектор будет половиной
прямоугольника, заключенного между дутого сектора и радиусом того круга, к которому
принадлежит сектор».
3. Герои, Метрика, кп. I, 26.
«Тот же самый Архимед и книге «О призмах (лец) n.Z.iv Oittav) и цилиндрах» пока-
зывает, что периметр всякого круга имеет к диаметру большее отношение, чем 211875
ка ____ g ________________ 1.0 ______________________________ g ______________
(М.аюое) к 67 411 (M.^vjia), но меньшее, чем 197 888 (М, gconn) к 62351 (М, ptva)».
Гсйберг замечает, что приведенные числа, по-видимому, испорчены, так как
1211875 1737
67441 —), (йз51 ... ).
Таким образом, оба предложенных отношения будут больше, чем л=3,14159. Гейберг
£ ____ £ ____ 211375
предлагает вместо М, £vp.a читать М, —67 444; тогда =3,14149 .,
t«----- 10----- 195 888 ,, .„M
вместо же М, £;<о.тц читать М, е<ояц—195 888; тогда — 3,141 Ьи ...
ка ____
R. Таинери (см. Гсйберг [15,1], стр. 542) предлагает исправить так: вместо М, awoe
хсг. ____ lG ________________________ i6 ____________
читать М, а«оор=2П 872, а вместо М, gtojrq читать М, еюлр—195 882.
*) Текст в фигурных скобках вставлен ив «Математической библиотеки» Паппа, книга VII.
49, стр. 088.
•*» Точнее 3,14t03.:>...
••*> Точнее ЗЛ "3'74...
ИЗМЕРЕНИЕ КРУГЛ
27 f
О НЕПРАВИЛЬНЫХ ПОВЕРХНОСТЯХ И ТЕЛАХ
ГЕРОИ, МЕТРИКА, КН. I, 39:
«Теперь, как я полагаю, необходимо скапать и относительно неправильных поверх-
ностей, каким образом падо их измерять. Если поверхность является плоской, ограни-
чивающая же ее, нянин пепрапильпой, то нужно па -.пой. линии взять несколько смежных
точек так, чтобы последовательно соединяющие их прямые линии не слишком отклоня-
лись от линии, ограничивающей фигуру, и после итого измерить фигуру как многоуголь-
ник, подразделил па треугольники. Если же поверхность не будет плоской, кик, напри-
мер, у статуи или чего-нибудь подобного, то нужно взять возможно более топкий папирус
или полотно и обтянуть им но частям поверхность, пока ноглединя не будет им кругом
охвачена, а затем, расправив папирус или полотно на плоскости, измерять, как сказало
выше, ограниченную неправильней лилией площадь и тиким образом, найти величину
поверхности. Если будут какие-нибудь другие поверхности пли фигуры ва поверхностях,
то их нужно измерить согласно вышесказанному».
ТАМ ЖЕ, КН. П, ВВЕДЕНИЕ.
«После измерения прямолинейных и но прямолинейных поверхностей мы должны
в порядке очереди перейти к телам, поверхности которых мы уже измерили в предыдущей
книге, а именно к телам, ограниченным плоскостями, сферическим, затем коническим
и цилиндрическим и, наконец, неправильным; так как соответствующие методы предста-
и.тнкпт.я удивительными, то их ш’крытие некоторые, следуя уетаношпппсйся традиции,
относит к Архимеду. Принадлежат ли они Архимеду или кому-нибудь другому, все равно
необходимо будет описать и их».
ТАМ ЖЕ, КН. 11, 20.
«Поело того как мы измерили геометрически правильные тела, мы считаем не лиш-
ним при описании методов измерении сказать кое-что и относительно пеиранильвых тел,
вроде похожих па древесные корни пли камин; некоторые рассказывают, что необходимый
для итого способ был изобретен Архимедом. Если подлежащее измерению тело является
удобонсреиосимым, то нужно будет, сделан прямоугольный сосуд, могущий вместить
это тело, наполнить его водой и опустить в нее неправильное тело; тогда ясно, что неко-
торое; количество воды выльется, так что, какой был объем у опущенного в воду тела,
столько вода недостанет в этом вместилище после того, как тело будет пз «его вынуто.
Если мы измерим сделавшееся пустым прес.трапстно, то и найдем объем опущенного тела.
Можно таь-жс измерить его и иначе; если обленить неправильное тело воском пли глиной
так, чтобы оно после покрытия сделалось вполне прямоугольным; затем после его изме-
рении нужно спить глину, сделать из ясс прямоугольный параллелепипед, измерить его
и отнять от полученного в первом измерении; тогда остаток покажет объем тела. Мето-
дом пблеплтшапия должно пользоваться также и пии измерении тез, которые нельзя
Переносить».
МММ
О РАВНОВЕСИИ ПЛОСКИХ ФИГУР, ИЛИ О ЦЕНТРАХ
ТЯЖЕСТИ ПЛОСКИХ ФИГУР
КНИГА ПЕРВАЯ
Сделаем следующие допущения:
1. Равные тяжести на. равных длинах уравновешиваются, на нерав-
ных же длинах не уравновешиваются, но перевешивают тяжести на
большей длине.
2. Если при. равновесии тяжестей иа каких-нибудь длинах к одной
из тяжестей будет что-нибудь прибавлено, то они не будут уравнове-
шиваться, но перевесит та тяжесть, к которой было прибавлено.
3. Точно так же если от одной из тяжестей будет отнято что-
нибудь, то они не будут уравновешиваться, но перевесит та тяжесть,
от которой не было отнято.
к. При совмещении друг с другом равных и подобных *) плоских
фигур совместятся друг с другом и их центры тяжести.
5. У неравных же, но подобных фигур центры тяжести будут по-
добно же расположены.. Под подобным расположением точек в подобных
фигурах мы подразумеваем такое, в котором прямые, проведенные из
этих точек к вершинам равных углов, образуют равные углы с соот-
ветстиенными сторонами.
6. Если величины уравновешиваются на каких-нибудь длинах, то
на тех же самых длинах будут уравновешиваться и равные им.
7. Во всякой фигуре, периметр которой везде выпукл в одну и ту же
•сторону, центр тяжести должен находиться внутри фигуры.
При этих предположениях:
Т
Тяжести, уравновешивающиеся на равных длинах, будут тоже
равны.
Действительно, если бы они были неравными, то после отнятия
от большей избытка они не уравновесятся, поскольку что-то отнято
от одной из двух уравновешивающихся тяжестей. Таким образом, урав-
новешивающиеся па равных длинах тяжести будут тоже равны.
*) То есть конгруэнтных, так как геометрическое равенство греки понимали в смысле
•р а в и о в в л и к о с т и.
О РАВНОВЕСИИ ПЛОСКИХ ФИГУР
273
11
Неравные тяж/сти на равных длинах не уравновешиваются, но
перевешивает, большая.
Действительно, после отнятия избытка они будут уравновешивать-
ся, поскольку равные тяжести на равных длинах уравновешиваются.
Тогда после прибавления отнятого перевесит большая, поскольку
было что-то прибавлено к одной из уравновешивающихся тяжестей.
Ш
Неравные тяжести будут уравновешиваться на неравных длинах,
причем большая тяжесть на меньшей длине.
Пусть А, В будут неравные тяжести, и пусть А будет большая,
причем они уравновешиваются на длинах АГ, ГВ {рис. 1}. Требуется
доказать, что .АГ будет мень-
ше ГВ. 74 г /к
Действительно, пусть она а1 х ’
не будет меньше. Тогда после
отнятия избытка, па который А Р,1С- 1 •
превышает В, переносит В, по-
скольку что-то было отнято от одной нз уравновешивающихся тяжестей.
Но она не перевесит; действительно, если ГА равна ГВ, то опи уравно-
весятся (как равные тяжести на равных длинах], если же ГА больше
ГВ, то перевесит А, так как равные тяжести на неравных длинах пе
уравновешиваются, по перевешивает тяжесть па большей длине. На
основании этого АГ будет меньше ГВ.
Таи же ясно, что уравновешивающиеся па неравных длинах тяже-
сти по равны, причем большая тяжесть будет на меньшей длине.
IV
Если две равные величины не имеют одного и того же центра тяже-
сти, то для величины, составленной из обеих этих величин, центром
тяжести будет середина прямой, соединяющей центры тяжести этих
величин.
Пусть точка А будет центром тяжести для (величины) А, а точ-
ка В — для (величины) В, и пусть соединяющая ЛВ разделяется
пополам в Г {рис. 2}; я утверждаю,
что для величины, составленной из
обеих этих величин, центром тяже-
сти будет Г.
Действительно, если это не так,
то пусть центром тяжести {для ве-
личины, составленной нз .А, В], бу-
рИС- 2. Дет, если возможно, Л, [ибо раньше
было показано, что он находится
па АВ] *). Тогда если точка Д бу-
дет центром тяжести величины, составленной из А, В, то при за-
креплении Д получится равновесие; значит, величины А, В будут
’) Возможно, что комментатор, которому нрипадлежит выражение, заключенное о квадрат-
ные скобки. отсылает читателя к одному из предшествующих сочинений Архимеда, которое еще
было ему доступно.
18 Архимед
274
АРХИМЕД
уравновешиваться на длинах АД, ДВ; это же невозможно, [ибо рав-
ные тяжести па неравных длинах пе уравновешиваются]. После этого
ясно, что Г будет центром тяжести величины, составленной из А, В.
Если, центры тяжести трех величин, лежат на одной прямой, при-
чем эти величины имеют одинаковую тяжесть, и прямые, лежащие меж-
ду центрами, равны, то для величины, составленной из всех этих вели-
чин, центром тяжести будет точ-
ка, которая является центром тя-
жести для средней {величины}.
Пусть будут три величины А,
В, Г, а их центры тяжести — точ-
ки А, В, Г, лежащие на одном
прямой; пусть также {величины
Рис- 3- А, В, Г) равны, и АГ, ГВ — рав-
ные прямые {рис. 3}; я утверж-
даю, что для величины, составленной из всех этих величин, центром
тяжести будет точка Г.
Действительно, так как величины Л, В имеют одинаковую
тяжесть, то центром их тяжести будет точка Г, поскольку АГ, ГВ рав-
ны. Пои для величины Г центром тяжести будет точка Г; тогда ясно,
что и для величины, составленной из всех, центром тяжести будет точ-
ка, которая является центром тяжести для средней.
Следствие I
Из этого ясно, что если имеется любое нечетное количество вели-
чин, центры тяжести которых лежат на одной прямой, причем вели-
чины, одинаково отстоящие от середины, имеют равные тяжести, и
прямые, заключающиеся между их центрами, равны, то для величины,
составленной из всех этих величин, центром тяжести будет точка,
которая является центром тяжести ____ ___ ___
для средней из них.
С л е д с т в и е 2 ' 1 ' ' ’ ' '
Также если эти величины будут — — — — — —
в четном количестве, причем их рис
центры тяжести лежат на одной пря-
мой, и как средние величины, так и одинаково от них отстоящие
имеют равную тяжесть, а прямые между центрами равны, то для
величины, составленной из всех этих величин, центром тяжести
будет середина прямой, соединяющей центры тяжести этих величин,
как нарисовано ниже (рис. 4].
VI
Соизмеримые величины уравновешиваются на длинах, которые
будут, обратно пропорциональны тяжестям.
Пусть А, В будут соизмеримые величины, центры которых А, В;
возьмем некоторую длину ЕД, причем пусть как Л к В, так будет и
О РАВНОВЕСИИ ПЛОСКИХ ФИГУР
275
длина ДГ к длине ГЕ {рис. 5}; требуется доказать, что для величины,
составленной из обеих величин Л, В, центром тяжести будет Г.
Действительно, поскольку А относится к В, как ДГ к ГЕ,
А дг
В ~ ГЕ
и А соизмерима с В, то, значит, ГД соизмерима с ГЕ, то есть прямая
соизмерима с прямой, так что у ЕГ, ГД есть общая мера. Пусть опа
будет N; отложим ДН, ДК, равные каждая ЕГ, и ЕЛ, равную Л Г.
Тогда поскольку ДН равна ГЕ, то и __________
ДГ равна ЕН, так что и ЛЕ равна ЕН.
Значит, ЛИ вдвое больше ДГ, а НК
вдвое больнее ГЕ, так что Л измерит и s
каждую из АН, НК, поскольку она изме- --
ряет их половины. И поскольку как А к г
В, так и ДГ к ГЕ,
как же ДГ к ГЕ, так и ЛН к ПК it
дг лн Рис-5-
ге нк
(так как каждая из вторых вдвое больше соответствующей из первых
прямых), то, значит, как А к В, тал и ЛН к НК.
л _ ЛИ
в "'нк
Пусть А будет во столько раз больше Z, во сколько ЛН больше N;
тогда как ЛН к N, так и А к Z.
АП А
N =" Z
Но также будет, что как КП к ЛН, так и В к А;
кн в
ЛН В А
тогда «по равенству» как КП к N, так и В к Z;
кн____в_
n ~ z
значит, КН от N и В от Z будут равнократными, /(оказано же, что и А
есть кратное Z, так что Z будет общей мерой для А, В. Теперь если
мы разделим прямую ЛН на части, равные N, величину же А на части,
равные Z, то равновеликие N отрезки в ЛН будут в равном количе-
стве с частями в А, равными Z. Таким образом, если па каждый из
содержащихся в ЛН отрезков наложить величину, равную Z, так,
чтобы опа имела центр тяжести в середине отрезка, то все эти величи-
ны вместо будут равны Л и для составленной из всех их величины
центром тяжести будет Е, так как все они будут в четном числе и в
одинаковом количестве с каждой стороны от Е вследствие того, что ЛЕ
• равна ЕН,
Подобным же образом докажем, что если па каждый из содержа-
щихся в КН отрезков нал ожить величину, равную Z, так, чтобы опа
имела центр тяжести в середине отрезка, то все ати величины вместе
будут равны В, и для составленной из всех их величины центром тяже-
сти будет Д; тогда величина А будет наложена в Е, величина же В в А.
18*
276
АРХИМЕД
Таким образом, получатся рапные друг другу величины, расположен-
ные по прямой, центры тяжести которых равно удалены друг от друга,
причем в четном числе; следовательно, ясно, что для составленной из
всех их величины центром тяжести будет точка, делящая пополам пря-
мую, на которой находятся центры промежуточных величин. Посколь-
ку жоЛЕ равна ГД, а ЕГ равна ЛК, то, значит, и вся Л Г будет равна
ГК; так что для составленной из всех величины центром тяжести будет
точка Г. Итак, если А приложить в Е, а В в А, то они будут находиться
в равновесии по отношению к Г.
VII
И далее, если величины будут несоизмеримыми, то они точно так же
уравновесятся на длинах, которые обратно пропорциональны этим
величинам.
Пусть ЛВ, Г будут несоизмеримые величины, а ДЕ, EZ — длины,
и пусть АВ имеет к Г то же самое отношение, что длина ЕД к длине EZ
{рис. (>}; я утверждаю, что для
д Е z величины, составленной из обоих
АВГ, центром тяжести будет Е.
Действительно, если АВ, поме-
щенная в Z, пе уравновесится с Г,
помещенной в Д, то ЛВ или будет
больше, чем нужно для равно-
весия с Г, или нет.
Пусть опа будет больше; от-
нимем от ЛВ меньше того избыт-
ка, на который АВ является боль-
ше, чем нужно для равновесия
с Г, так, чтобы остаток А был
соизмерим с Г. Поскольку теперь величины А, Г соизмеримы и Л
имеет к Г отношение меныпее, чем ЛЕ к EZ, то А и Г не уравновесятся
на длинах ДЕ, EZ, если А поместить в Z, а Г в Д. Таким же образом
докажем и в том случае, когда Г будет больше того, что нужно для
равновесия с АВ *).
VIII
Если от какой-нибудь величины отнимем некоторую се часть,
не имеющую того же самого центра тяжести, что и целая, то для
остающейся величины центр тяжести получится, если линию, соеди-
няющую центры тяжести целой величины и отнимаемой, продолжим
в ту сторону. где находится центр целой величины, и на продолжении
соединяющей упомянутые центры отложим отрезок так, чтобы к рас-
стоянию между центрами он имел то же самое отношение, какое тя-
жесть отнимаемой величины имеет к тяжести остающейся.
♦) Доказательство должно быть дополнено так. Если мы от Л В отнимем В так. что А. являясь
о измерим ой с Г» все же будет перевешивать последнюю, то отношение Л к Г должно быть больше
•отношения ЕЛ к RZ в самом деле, при равновесии относительно точки Е мы имели бы равенство
А ЕЛ . А „ ЕЛ „ Л ЕД
если же А перевешивает, то - - > ; но в действительности — < =- , так как
Г KZ 1 EZ X -ЬЛ
ЕД
EZ
; полученное противоречие и доказывает теорему.
О РАВНОВЕСИИ ПЛОСКИХ ФИГУР
277
Пусть центр тяжести некоторой величины АВ будет Г; от АВ
отнимем (величину) АА, центр тяжести которой пусть будет Е; затем
на продолжении соединяющей ЕГ отложим EZ, имеющую к ГЕ то же
самое отношение, как величина АД
имеет к ДН {рис. 7); требуется до-
казать, что у величины ДН центром
тяжести будет точка Z.
Действительно, пусть это не так,
по, если возможно, пусть им будет
точна 0. Тогда, так как у величины
АД центром тяжести является Е,
Рис. 7.
у Д11 же — точка 0, то для величины, составленной из обеих, центр
тяжести будет на Е0, разделенной так, чтобы ее отрезки были обратно
пропорциональны этим величинам; тогда точка Г не будет сечением, соот-
ветствующим упомянутому. Значит, Г пе будет центром величины, со-
ставленной из АД, ДП, то есть А13. Но она им является, ибо так было
предположено; значит, 0 не будет центром тяжести величины ДН.
IX
У всякого параллелограмма центр тяжести находится на пря-
мой, соединяющей середины противоположных сторон параллелограмма.
Пусть будет параллелограмм АВГД и EZ — прямая, соединяющая
середины АВ, ГД {рис. 8}; я говорю, что у параллелограмма АВГД
центр тяжести будет на EZ.
Действительно, пусть это не так, по, если возможно, пусть он
будет и 0; проведем 01 параллельно АВ.
Будем все время делить ЕВ пополам до тех пор, пока не получит-
ся отрезок (ЕК), меньший 10; разделим каждую из АЕ, ЕВ на рав-
ные ЕК части и из точек деления
В проведем прямые, параллельные
EZ; т огда весь л а ра л л ел огра м м р аз-
делится на параллелограммы, рав-
ные и подобия е KZ. Теперь, если
а равные и подобные KZ параллело-
граммы наложить друг па друга, то
совпадут друг с другом и их центры
тяжести. Таким образом, получатся
некоторые величины, а именно равные К Z параллелограммы, и в четном
количестве, причем их центры тяжести расположены на прямой, и как
среднее величины, так и все находящиеся по обе стороны от сред-
них равны, и прямые между центрами равны; значит, у величины,
составленной пз всех этих, центр тяжести будет па прямой, соединя-
ющей центры тяжести двух средних площадей. Но он не будет там, ибо
0 находится вне средних параллелограммов. Теперь яспо, что центр
тяжести параллелограмма АВГД будет па прямой EZ.
X
У всякого параллелограмма центром тяжести будет точка, в ко-
торой встречаются диаметры, {то есть диагонали).
Пусть будет параллелограмм АВГД и в пем прямые—EZ, де-
лящая пополам АВ и ГД, и КА, делящая АГ и ВД {рис. 9}; тогда
Рис. 8.
АРХИМЕД
у параллелограмма АВГД центр тяжести будет па EZ, ибо это доказа-
но. Но по той же причине он будет и на КЛ; значит, точка 0 и есть
центр тяжести; но в 6 встречаются диаметры параллелограмма, так
что предложенное допазапо.
Иначе
То же самое можно доказать и иначе.
Пусть будет параллелограмм АВГД, и пусть его диаметр будет ДВ
{рис. 10}. Значит, треугольники АВД, ВДГ равны и подобны друг
Другу, так что при наложении треугольников друг на друга совпадут
и их центры тяжести. Пусть у треугольника АВД центром тяжести
Рис. 9. Рис. 10.
будет точка Е; разделим ДВ в 0 пополам, продолжим и отложим Z0,
равную 0Е. Тогда если наложить треугольник АВД на треугольник
ВДГ и поместить сторону АВ на ДГ, а ЛД на ВГ, то и прямая 0Е
ляжет на Z0 и точка Е попадет па Z. Но она также должна попасть
и па центр тяжести треугольника ВДГ. Теперь, так как у треугольника
АВА центром тяжести является точка Е, у ДВГ же — Z, то ясно, что
у величины, составленной из обоих этих треугольников, центром тяже-
сти будет середина прямой EZ, какой и является точка 0.
XI
АГ
AZ
Если, будут два подобных друг другу треугольника и в них взяты
точки, подобно расположенные по отношению к треугольникам, причем
одна точка будет центром тяжести того треугольника, в котором она
находится, то и другая точка будет центром тяжести того треуголь-
ника, в котором она находится. [Под подобным расположением точек
по отношению к подобным фигурам мы подразумеваем такое, в котором
прямые, проведенные из этих то-
чек к ранным углам, образуют рав-
ные углы с соответствующими
сторонами.]
Пусть будут два треугольника
АВГ, AEZ, и пусть как АГ к AZ,
так и АВ к ДЕ, и ВГ к EZ;
ав = вг
ДЕ EZ £
пусть в упомянутых треугольниках Гис. 11.
будут подобно расположенные
{по отношению к треугольникам АВГ, AEZ] точки 0, N, и пусть 0
будет центром тяжести треугольника АВГ {рис. 11}; я утверждаю, что
N будет центром тяжести треугольника AEZ.
О РАВНОВЕСИИ ПЛОСКИХ ФИГУР
279
Действительно, пусть зто по так, но, если возможно, пусть цент-
ром тяжести треугольника zXEZ будет 11; проведем соединяющие пря-
мые 0А, 0В, 0Г, AN, EN, ZN, АН, Ell, ZH. Теперь, поскольку тре-
угольник АВГ подобен треугольнику AEZ и центрами тяжести являют-
ся точки 0, Н, у подобных же фигур подобно расположены и центры
тяжести, [так что образуются равные углы с соответственными сторо-
нами каждой с каждыми], то, значит, угол ПАЕ будет равен углу ©АВ.
Но угол 0AB равен углу EAN [вследствие того, что точки 0, N подоб-
но расположены]; значит, и угол EAN будет равен углу ЕА11, больший
меныпему; ото же невозможно. Значит, точка N не может не быть цент-
ром тяжести треугольника AEZ; значит, она им является.
XII
Если, будут два подобных треугольника и у одного треугольника
центр тяжести находится на прямой, которая проведена от какого-
нибудь угла к середине основания, то и у другого треугольника центр
тяжести будет на подобно прове-
денной линии.
Пусть будут два треугольника
АВГ, AEZ, и пусть как АГ к AZ,
так и АВ к ДЕ, и ВГ к ZE;
аг _ АВ _ _В£
&Z “ АЕ ’ ZE
разделив АГ пополам н Н, про-
водом ВН, и пусть центр тяжести 0 j /' i ?
треугольника АВГ будет на ВП ' I/ V
{рис. 12}; я утверждаю, что и у р
треугольника AZ центр тяжести бу-
дет на и од об ио проведенной прямой.
Разделим AZ пополам в М, соединим Е с М и сделаем, чтобы как
ВН к В0, так и ME к EN,
вн _ ME
ве EN
и проведем соединяющие прямые А0, 0Г, AN, NZ. Поскольку поло-
вина ГЛ есть АН, половина жо AZ есть ДМ, то, значит, как В А к ЕД,
так и АП к ДМ;
ва _ ЛИ
ЕЛ Л.VI
и при равных углах стороны пропорциональны; значит, угол АН В
равен углу АМЕ, и как АН к ДМ, так и ВП к ЕМ;
АП _ ВН
дм “ем
но также как ВП к В0, так и ME к EN,
вн _ ME
ВО ЕМ
и значит, «по равенству» как АВ к ДЕ, так В0 к EN,
лв . ве
ДЕ EN
Но при равных углах стороны пропорциональны; если же так, то угол
BA0 будет равен углу EAN, так что и остающийся угол ©АГ будет
280
АРХИМЕД
равен углу NAZ. На том же основании и угол ВГ0 будет равен EZN,
и угол 0ГП равен NZM. Доказано же, что и угол АВО равен ДЕМ;
так что и остающийся угол ©ВГ будет равен NEZ. На основании всего
этого точки 0, N будут подобно расположенными, {образуя ранные
углы с соответственными сторонами]. Теперь, поскольку точки 0, N
подобно расположены и 0 является центром тяжести треугольника АВГ,
то, значит, и N будет центром тяжести AEZ.
XIII
У всякого треугольника центр тяжести будет иа прямой, которая
проведена из угла к середине основания.
Пусть будет треугольник АВГ и в нем прямая АД, проведенная
к середине основания В Г {рис. 13}; требуется доказать, что центр тя-
жести АВГ будет па АА.
Действительно, пусть это не так, но, если возможно, он будет в 0;
проведем через него 01 параллельно В Г. Постоянно деля ДГ пополам,
Ряс. 13.
придем когда-нибудь к отрезку»
который будет меньше 01; раз-
делим каждую из ВД, ДГ на
равные ому- части, проведем через
точки деления прямые, парал-
лельные АД, и соединим EZ, ПК,
ЛМ; они будут, конечно, парал-
лельны ВГ. Теперь у парал-
лелограмма MN центр тяже-
сти будет на ГХ, у КН же на ТГ,
у ZO же на ТД; значит, у величи-
ны, составленной из всех их,
центр тяжести будет на прямой
ХД. Пусть он будет в Р; соединим Р0 (прямой), продолжим ее и парал-
лельно АД проведем ГФ. [Треугольник] ЛДГко всем вместе треугольни-
кам, построенным па AM, МК, К Z, ZT и подобным АДГ, имеет такое же
отношение, какое ГА имеет к ЛЛ1, вследствие того, что прямые AM, МК,
ZI\ KZ равны. Поскольку же и треугольник АДВ ко всем вместе подоб-
ным треугольникам, построенным на АА, АН, НЕ, ЕВ, имеет то же
самое отношение, что ВЛ к АЛ, то, значит, треугольник АВГ ко всем
упомянутым треугольникам имеет то же отношение, какое ГА имеет
к AM. Но ГА имеет к AM большее отношение, чем ФР к Р0,
ГА ФР
AM > Р«
так как отношение ГА к AM будет том же самым, что у [всей] ФР к PII
[вследствие подобия соответствующих треугольников]; и, значит,
треугольник АВГ ко всем упомянутым имеет большее отношение, чем
ФР к Р0; и таким образом, «выделяя» *) — параллелограммы MN,
KS, ZO к треугольникам, оставшимся (в окаймлении), будут иметь
большее отношение, чем Ф0 к 0Р. Сделаем теперь так, чтобы прямые
Х0 и ©Р были между собой в отношении этих параллелограммов к
оставшимся треугольникам. Тогда, поскольку имеется некоторая вели-
*) Треугольник АВГ бе» окаймления будет иметь к треугольникам окаймления большее
отношение, чем ФР—Рб к в!\
О РАВНОВЕСИИ ПЛОСКИХ ФИГУР
281
чина АВГ, центром тяжести которой является 0, и от нее отнимается
величина, составленная из параллелограммов MN, КЕ, причем цент-
ром тяжести отнимаемой величины будет точка Г, то, значит, у остаю-
щейся величины, составленной из окаймляющих треугольников, центр
тяжести получится, если на продолжении прямой Р0 отложить отре-
зок, имеющий к 0Р то же отношение, какое имеет отнятая величина
к остатку. Значит, точка X будет центром тяжести величины, составлен-
ной из окаймления; ато же невозможно, так как если провести через X
прямую, параллельную АД, то все треугольники будут в плоскости
за ней, [то есть по одну сторону]. После этого предложенное становится
очевидным.
То же самое иначе
Пусть будет треугольник АВГ; проведем прямую АД к середине
ВГ {рис. 14}; я утверждаю, что на АД находится центр тяжести тре-
угольника АВГ.
Действительно, пусть это не так; если возможно, пусть он будет
в 0; соединим А и 0, 0 и В, 0 и Г, затем проведем ЕД, ZE к серединам
ВА, АГ, далее параллельно АО приведем ЕК,
ZA и соединим К и А, А и Д, Д и К, Д и
0, М и N.
Так как треугольник АВГ подобен тре-
угольнику Д/Г вследствие того, что ВА па-
раллельна ZA, и центром тяжести треуголь-
ника АВГ является точка 0, то, значит, у
треугольника ZAT центром тяжести будет
точка А, так как точки (-), А подобно распо-
ложены в каждом из этих треугольников,
[поскольку спи образуют равные углы с
соответственными сторонами; это ведь ясно].
Рис. 14.
На том же основании и у ЕВД центром
тяжести будет точка К; таким образом, у величины, составленной из
обоих этих треугольников ЕВД, /.АГ, центр тяжести будет на сере-
дине примой КА, [так как треугольники ЕВД, /ДГ равны]. И сере-
диной КА будет N; поскольку как ВЕ к ЕА, так и ВК к 0К,
вв _ вк
иа — ек
как же TZ к ZA, так и ГА к А0;
rz _ гл
za “ли
если же так, то ВГ будет параллельна КЛ. Мы соединили Д и 0; зна-
чит, как ВД it ДГ, так и KN к NA;
ВД _ KN
ДГ NA
таким образом, у величины, составленной из обоих упомянутых тре-
угольников (ЕВД и /ДГ), центром будет N. У параллелограмма же
ЛЕД/ центром тяжести будет точка М; таким образом, у величины,
составленной из всех их, центр тяжести будет на прямой МЛ:. Ноу АВГ
центром тяжести будет точка О; значит, MN, будучи продолжена, прой-
дет через точку 0, это же невозможно. Значит, центр тяжести треуголь-
ника АВГ пе может не быть на прямой АД; значит, он будет на пей.
282
АРХИМЕД
XIV
У всякого треугольника центром тяжести будет точка, в которой
встречаются прямые, проведенные из углов к серединам сторон.
Пусть будет треугольник АВГ {рис. 15}; проведем АД к середине
ВГ и ВЕ к середине АГ; тогда центр тяжести треугольника АВГ будет
па каждой из ЛД, ВЕ, ибо это доказано. Таким образом, точка 0 (их
пересечения) будет центром тяжести.
XV
У всякой трапеции, имеющей две стороны, параллельные друг дру-
гу, центр тяжести будет на прямой, соединяющей середины парал-
лельных, разделенной таким образом, чтобы отрезок ее, кончающийся
в середине меньшей из параллельных, имел бы к остающемуся отрезку
то отношение, которое имеет прямая, равная удвоенной большей сторо-
не, взятой вместе с меньшей, к прямой, равной удвоенной меньшей вме-
сте с большей из параллельных.
Пусть будет трапеция АВГД, имеющая параллельными АД, ВГ,
и пусть EZ соединяет середины ЛД, В Г {рис. 16}. Тогда очевидно, что
центр (тяжести) трапеции будет на EZ. Действительно, если продол-
жить ГД11, ZEH, ВАН, то ясно, что они придут в одну и ту же точку,
и цептр тяжести треугольника НВ Г будет па HZ, и точно так же центр
тяжести треугольника АИД будет на HZ; значит, и у остающейся тра-
пеции АВГД центр тяжести будет на EZ. Соединяющую ВА разделим
па три равные части в точках К, 0, через них параллельно ВГ проведем
ЛЭ И, NKT и соединим Л и Z, В и Е, О и 3; тогда у треугольника
ДВГ центр тяжести будет на 0М, так как 0В является третьей частью
от ВД [и М0 проведена через точку 0 параллельно основанию].
По центр тяжести треугольника ДВГ будет также и на AZ; таким обра-
зом, 3 будет центром тяжести упомянутого треугольника. На том же
основании и точка О будет центром тяжести треугольника ЛВД; значит,
у величины, составленной из обоих треугольников АВД, ВДГ, которой
и является трапеция, центр тяжести будет на прямой ОЕ. Но также
на EZ будет и центр тяжести упомянутой трапеции; таким образом,
центром тяжести трапеции АВГД будет точка II. Тогда треугольник
ВДГ должен относиться к АВД, как ОП к ИЗ.
тр-к ВАГ ОП
Тр-к АВД П3~
О РАВНОВЕСИИ ПЛОСКИХ ФИГУР
283
Но как треугольник ВДГ к треугольнику АВД, так будет и В Г к АД,
тр-и ВДГ вг
тр-и АВД АД
как же. ОП к ПЕ, так и РП к ПХ,
оп РП
ns в пх
и, значит, как ВГ к АД, так и РП к 112,
вг РП
ад ' не
так что и как дно ВГ вместе с АД к двум АД вместе с ВГ, так и две РП
вместе с ПХ к двум ПХ вместе с РП *).
2ВГ4-ДД __ 2РП | ПХ
2АД+ВГ^ 21IX4IIP
Но две РП вместе с ПХ будут вместе взятыми ХР, РП, то есть ПЕ,
две же ПХ имеете с PH будут вместе взятыми РХ, XII, то есть HZ;
значит, предложенное доказано.
КПИГА ВТОРАЯ
1
Если две площади, ограниченные {каждая} прямой и параболой
и могущие быть «приложенными» к заданной прямой, не имеют одного
и того же центра тяжести, то для величины, составленной из них
обеих, центр тяжести будет на прямой, соединяющей их центры тяже-
сти, причем вышеупомянутую прямую он разделит, таким образом,
что ее отрезки будут обратно пропорциональны этим площадям.
Пусть АВ, ГД |рис. 17; будут упомянутые площади, пусть их
центры тяжести будут в точках Е, Z, и пусть Z& имеет к ©Е такое же
отношение, как АВ к ГД.
ze гл. АВ
“ЙЕ иЛ .Г. А
Требуется доказать, что для величины, составленной из обеих площа-
дей АВ, ГД, цептр тяжести будет в точке 0.
Пусть каждая из Zll, ZK равна EG, ЕА же пусть будет равна Z8,
то есть НЕ; тогда А0 будет равна КО;
ле=[лЕ+Ее=024-2К]-ке
«) Рассматриваеман пропорция может быть установлена таким образом:
ВГ _ P1I ЙВГ 2PII
ЛД UX ’АД ИХ ’
отсюда, «присоединив», находим:
2ВГ 1-АД _ 2PII !-П2
АД ИХ
Аналогично
2АД-1 ВГ _ 2П2—РП
ВГ РП
Теперь ив пропорций
2ВГ г АД _ 2РИ-1 ПХ АЛ ПХ ВГ 1>П
АД — 112 ’ ВГ J‘’ 1'11 ’ 2АД+ВГ 21JX |-11Р
мы заключаем «во равенству», что
2ВГ+АД _ 2РП+ПХ
2АД+ВГ 2ПХ+РП ‘
284
АРХИМЕД
и далее, как ЛН к НК, так и АВ к ГД,
АН _ пл. АВ * Z&
НК ИЛ. ГД ВЕ
ибо члены первого отношения вдвое больше соответствующих членов
второго.
АН—2ЕП—2ZO
HK==2HZ=2EO
Приложим теперь к ЛН площадь ЛВ по обе стороны от ЛН так, чтобы
площадь MN равнялась ЛВ; тогда точка Е будет центром тяжести
(прямоугольника) MN. Теперь дополним (прямоугольник) КВ; тогда
ММ будет относиться к N3, как
лн к нк.
пл. ММ АН
пл. N3 —' НК
Но также и АВ находится с ГД в
отношении АП к НК,
пл. АВ __ ^ЛП
пл. ГД ПК~
и, значит, как АВ к ГД, так и MN
к NE, или
пл. Л В пл. MN
пл. ГЛ пл. NS
«перестановкой» (площади АВ и MN
относятся, как площади ГД и NB);
л. АВ _ ил. ГД
ал. MN * лл. XS
Рис. 17.
но АВ равна ММ; значит, ГД равна N3, и центром тяжести последней
будет точка Z. И так как Л© раина ©К, а вся ЛК делит пополам проти-
воположные стороны, то для всей площади ИМ центром тяжести будет
точка 0. Но площадь МП равна составленной из обеих MN, N3; зна-
чит, точка 0 будет центром тяжести площади, составленной из обеих
АВ, ГД [1].
II
Если в сегмент, ограниченный прямой и параболой, вписать тре-
угольник, имеющий с сегмептом то же самое основание и равную высо-
ту, затем в оставшиеся сегменты вписать треугольники, имеющие с эти-
ми сегментами те же самые основания п равные высоты, и постоянно
вписывать тем же самым образом треугольники в остающиеся сегменты,
то получится фигура, которую будем называть вписаппой в сегмент
«определенным образом». Тогда ясно, что во вписанной таким образом
фигуре прямые, соединяющие ближайшие к вершине углы и следующие
за ними, будут параллельны основанию сегмента, разделятся пополам
диаметром сегмента и сами разделят этот диаметр в отношениях
ряда последовательных нечетных чисел, если за единицу принять отрезок
у вершины сегмента. Все это должно быть доказано в надлежащем
месте J2].
Если в сегмент, ограниченный прямой и параболой, вписывается
«определенным образом» прямолинейная фигура, то центр тяжести
вписанной фигуры будет на диаметре сегмента.
О РАВНОВЕСИИ ПЛОСКИХ ФИГУР
285
Пусть АВГ {рис. 18} будет такой сегмент, как сказано; шпилем в него
«определенным образом» прямолинейную фигуру AEZHBOIKT; тре-
буется доказать, что центр тяжести этой прямолинейной фигуры будет
на ВД.
Действительно, так как у трапеции АЕКГ центр тяжести будет
па АД, у трапеции EZTK центр на МА, у трапеции ZIIGI центр на MN
и, наконец, у треугольника ИВ© центр тяжести на BN, то ясно, что
и у всей прямолинейной фигуры центр тяжести будет па ВД.
III
Если в каждый из двух подобных сегментов, ограниченных прямой
и параболой, вписать «определенным образом» прямолинейную фигуру,
так, чтобы вписанные прямолинейные фигуры имели равное количество
сторон, то центры тя-
жести этих прямоли-
нейных фигур одинаково
разделят диаметры
этих сегментов.
Пусть будут два
сегмента АВГ, ЕОП
{рис. 19}; впишем в пих
«определенным образом»
прям ол и иейпыс фигуры,
и пусть они имеют рав-
ное друг другу количе-
ство всех сторон. Пусть
диаметры этих сегмен-
тов будут ВД, ОР;
проведем соединяющие
прямые ЕК, ZT, II©
и ST, ГФ, Х’Р. Так
как ВД и РО пропедеп-
ным и । г а рал л ел ьными
разделятся в отношениях ряда последовательных нечетных чисел и ко-
личества их отрезков одинаковы, то ясно, что отрезки этих диаметров
будут в таких же отношениях и параллельные прямые будут иметь
такие же отношения. И у трапеций АЕКГ и ЕХ’ТП центры тяжести
будут подобно расположены на прямых АД, QP, поскольку АГ с ЕК
имеют то же самое отношение, что п ЕП с ST. Затем у трапеций EZ1K,
,2ГфТ центры тяжести подобно разделят AM, и У трапеций Z1I0I,
286
АРХИМЕД
ТХ¥Ф центры тяжести подобно разделят MN, q^b. Также и у треуголь-
ников 11130, ХОТ центры тяжести будут подобно расположены на BN,
Oq. Значит, трапеции и треугольники имеют (по площади) одно и то же
отношение. Теперь яспо, что у всей прямолинейной фигуры, вписанной
в сегмент А13Г, центр тяжести разделит ВД подобно тому, как центр
тяжести фигуры, вписанной в сегмент ЕО11, разделит ОР. Это и тре-
бовалось доказать [3}.
IV
Во всяком сегменте, ограниченном прямой и параболой, центр тя-
жести будет на диаметре сегмента.
Пусть АВГ {рис. 20} будет такой сегмент, как сказано, и пусть его
диаметром будет ВД. Требуется доказать, что у упомянутого сегмента
центр тяжести будет на ВЛ.
Действительно, если это не так, то пусть он будет (в точке) Е;
проведем через пего EZ параллельно ВД. Затем впишем в сегмент
треугольник АВГ, имеющий (с сег-
ментом) то же самое основание и
равную высоту; и пусть треуголь-
ник ЛВГ к площади К имеет то же
самое отношение, что TZ к AZ.
пл. авг. rz
1U1. К Д7.
Затем виишем в сегмент «опреде-
ленным образом» прямолинейную
фигуру так, чтобы остающиеся но
краям сегменты были меньше К.
Тогда у вписанпой прямолинейной
фигуры центр тяжести будет на ВД.
Пусть оп будет 0; проведем соеди-
няющую прямую вЕ, продолжим ее
и параллельно ВД проведем ГЛ. Яс-
Рае. 20.
но, что вписанная в сегмент прямо-
линейная фигура к остающимся сегментам имеет отношение большее, чем
треугольник АВГ к К *). Но как треугольник АВГ к К, так и TZ
к ZA. Значит, и вписанная прямолинейная фигура к остающимся по
краям сегментам имеет большее отношение, чем TZ к ZA, то есть как
ЛЕ к Е0. Пусть теперь ME к ЕО имеет то же самое отношение, что пря-
молинейная фигура к сегментам. Тогда, поскольку Е есть центр тяжести
всего сегмента, а 0 — вписанной в него прямолинейной фигуры, то
ясно, что центр тяжести остатка, то есть величины, составленной из
остающихся по краям сегментов, получится, если продолжить 6Е
и отложить некоторую прямую, которая имела бы к 0Е то же отноше-
ние, что вписанная прямолинейная фигура к остающимся по краям
сегментам. Таким образом, цептр тяжести величины, составленной из
остающихся по краям сегментов, был бы в точке М; это же нелепо.
Действительно, если провести через М прямую параллельно ВД, то
все остающиеся по краям сегменты будут лежать по одну ее сторону.
Теперь ясно, что центр тяжести (параболического сегмента) будет на ВД.
*) Действительно, эта фигура больше треугольника ЛВГ, а площадь К в свою олсредь больше
остающихся сегментов.
О РАВНОВЕСИИ ПЛОСКИХ ФИГУР
287
V
Если в сегмент, ограниченный прямой и параболой, вписать «опре-
деленным образом» прямолинейную фигуру, то цептр тяжести всего
сегмента будет ближе к вершине сегмента, чем центр вписанной пря-
молинейной фигуры.
Пусть АВ Г [рис. 21} будет сегмент такой, как сказано, а ЛВ —
его диаметр. Сперва впишем в пего «ов редел ен ным образом» треуголь-
ник ЛВГ и разделим ВД в Е так, чтобы ВЕ была в два раза больше ЕД.
Тогда точка Е будет центром тяже-
сти треугольника АВГ. Каждую из
АВ, В Г разделим в точках Z, Н по-
полам и через Z и Н параллельно ВД
проведем ZK, Л В. Тогда центр тя-
жести сегмента АКВ будет иа ZK,
центр же тяжести сегмента В ГЛ—
на ПЛ. Пусть эти центры тяжести
будут 6,1; проведем соединяющую
прямую 01. И так как 0ZH1 —
параллелограмм и ZN равна NH,
то, значит, и Х0 будет равпа XI.
Таким образом, цептр тяжести величины, составленной из обоих сег-
ментом АКВ, ВЛ Г, будет на середине 61, то есть в точке X, [ибо оба
сегмента равны] *). Поскольку же у треугольника АВГ цептр тяжести
есть точка Е, у величины же, составленной из обоих сегментов АКВ,
ВЛГ, цептр есть точка X, то ясно, что центр тяжести всего сегмента АВГ
будет на ХЕ, то есть между точками X, Е.
Таким образом, цептр тяжести всего сегмента будет ближе к вер-
шине, чем центр тяжести треугольника, вписанного в него «определен
ным образом».
После этого впишем в сегмент «определенным образом» пятиуголь-
ную прямолинейную фигуру ЛКВЛГ {рис. 22 j. И пусть для всего сег-
мента диаметром будет ВЛ, для
. каждого /Ко из (боковых) сегментов
диаметрами будут KZ, Л11. И так
как и сегмент ЛК.В вписывается
«определенным образом» прямоли-
нейная фигура, то центр тяжести
всего сегмента будет ближе к верши-
не, чем центр тяжести прям олиней-
Г пой фигуры. Пусть теперь центром
тяжести сегмента (АКВ) будет 0,
а центром тяжести треугольника—
I; далее, пусть центром тяжести
сегмента ВЛГ будет М, а центром тяжести треугольника — N. Тогда
у величину, составленной из обоих сегментов АКВ, ВЛГ, центром тяже
сти будет X, у величины же, составленной из обоих треугольников АКВ,
ВЛГ, центром тяжести будет Т. Далее, так как у треугольника АВГ
Н
Рис. 22.
♦J Сегмент ЛК» рацеи четырем третям треугольника АКВ пли восьми третям треугольника
BKZ; точно так ?ке сегмент ИЛ г ровен ъисьмп третим треугольника НЛН. Но треугольники BKZ
и ИЛ 11 равновелики, как имеющие равные, параллельные и одинаково отстоящие от вершины В
основания KZ и ATI»
288
АРХИМЕД
центром тяжести будет Е, у всдичиша же, составленной из обоих сег-
ментов АКВ, ВАГ, цс пт ром будет X, то ясно, что центр тяжести всего
сегмента АВГ будет па прямой ХЕ, если рассечь ее так, чтобы отноше-
ние треугольника АВГ к вместе взятым сегментам АКБ, ВАГ было
таким же, как отношение кончающегося в точке X отрезка этой прямой
к меньшему се отрезку. У пятиугольника же АКВЛГ центр тяжести
будет па прямой ЕТ, если рассечь ее так, чтобы отношение треугольни-
ка АВГ к вместе взятым треугольникам АКВ, ВАГ было таким же,
как отношение кончающегося в Т се отрезка к остатку. Теперь, так как
треугольник АВГ имеет к треугольникам КАВ, Л13Г отношение боль-
шее, чем к соответствующим сегментам, то ясно, что у сегмента АВГ
центр тяжести будет ближе к вершине, чем у упомянутой вписаппой
прямолинейной фигуры. И то же самое рассуждение будет и относитель-
но всех прямолинейных фигур, вписываемых в сегменты «определен-
ным образом».
VI
Если дан сегмент, ограниченный прямой и параболой, то возможно
«определенным образом» вписать в него прямолинейную фигуру так,
чтобы прямая между центрами тяжести сегмента и вписанной прямо-
линейной фигуры была меньше любой наперед заданной прямой.
Пусть будет дан сегмент АВГ {рис. 23} такой, как сказано, цент-
ром тяжести которого будет ©; впишем в пего «определенным образом»
треугольник АВГ. Пусть наперед задан-
ная прямая будет Z, и пусть отношение
треугольника АВГ к некоторой площади
X будет такое же, как у В© к Z.
пл. АВГ _ ВО
ил. X ' ’ 2
Впишем «определенным образом» в сегмент
АВГ прямолинейную фигуру АКВЛГ так,
чтобы остающиеся по краям сегменты
вместе были меньше X. Пусть у вписан-
ной прямолинейной фигуры центром тяже-
сти будет Е. Я говорю, что 0Е будет
меньше Z.
Действительно, если ис так, то она
будет или равна, или больше. Так как
прямолинейная фигура АКВЛГ имеет к
остающимся по краям сегментам отношение
большее, чем треугольник АВГк площади
X, то ость 0В к Z, а также и В© имеет к Z отношение не меньшее, чем к©Е,
вследствие того, что ©Е ле меньше Z, то, значит, и подавно прямоли-
нейная фигура АКВЛГ будет иметь к остающимся по краям сегментам
отношение большее, чем В© к 0Е. Таким образом, если мы сделаем,
чтобы прямолинейная фигура АКВЛГ к остающимся по краям сегмен-
там относилась, как некоторая прямая к ЙЕ, [так как центр тяжести
сегмента АВГ будет 0, то продолжим Е© и отложим некоторую пря-
мую, которая имела бы к Е0 то же отношение, что и прямолинейная
фигура АКВЛГ к остающимся по краям сегментам], то эта прямая будет
больше ©В. Пусть теперь 110 будет к ©Е, (как АКВЛГ к остающимся
сегментам). Тогда II будет центром тяжести величины, составленной
О РАВНОВЕСИИ ПЛОСКИХ ФИГУР
289
из остающихся по краям сегментов; это же невозможно. Действитель-
но, если через Н провести прямую параллельно ЛГ, то эти сегменты
будут по одну сторону от нее. Теперь ясно, что ®Е будет меньше Z.
Это и требовалось доказать.
VII
У двух подобных сегментов, ограниченных прямой и параболой,
центры тяжести делят, диаметры в том же самом, отношении.
Пусть ЛВГ, EZ11 {рис. 24} будут два сегмента такие, как сказано,
диаметры которых суть ВД, Z0, и пусть у сегмента АВГ центром тяже-
сти будет точка К, у EZH же—А.
Требуется доказать, что точки К, Л
делят диаметры в одном и том же
отношении.
Действительно, если это ко так,
то пусть как КВ к КД, так и ZM
к М@;
КВ ZM ~ W
КА ” М<3
впишем в сегмент EZH «определен-
ным образом» прямолинейную фигу-
ру так, чтобы расстояние между цент-
рами тяжести сегмента и вписанной
прямолинейной фигуры было мень-
ше ЛМ, и пусть у вписанной прямо-
линейной фигуры центром тяжести
будет точка Е; впишем также в
сегмент АВГ прямолинейную фигу-
ру, подобную вписанной в EZH;
[это
«определенным образом»]; у псе центр
чем у сегмента *); это же невозможно
что ВК имеет к КЛ то же самое отношение,
Рис. 24.
значит: подобную вписанной
тяжести будет ближе к вершине,
(предложение V}. Теперь ясно,
что ZA к Л®.
VIII
У всякого сегмента, ограниченного прямой и параболой, центр тя-
жести делит диаметр сегмента так, что прилежащий к вершине
сегмента отрезок в полтора раза
больше отрезка у основания.
Пусть ЛВГ [рис. 25} будет
сегмент такой, как сказано; пусть
его диаметр будет ВД, центр же
тяжести — точка ®. Требуется
доказать, что В® будет в полто-
ра раза больше ®Д.
Впишем «определенным обра-
рис 2- зом» в сегмент АВГ треугольник
‘ АВГ, центр тяжести которого
пусть будет Е; разделим пополам каждую из АВ, ВГ и проведем
*) Действительно, если S есть центр тяжести многоугольника EZH. лежащий выше М, то
центр тяжести подобного много угольника АВ г должен лежать выше точки К, делящей ВД н том же
самом отношении, в каком М делит ZB; точна же К является центром тяжести сегмента АВГ.
Архимед
290
АРХИМЕД
KZ, НЛ (параллельно 13Д); они будут диаметрами сегментов АКВ,
ВЛ Г. Теперь пусть у сегмента АКВ центром тяжести будет М, у ВАГ
же — N; проведем соединяющие прямые ZU, MN, КЛ; тогда у вели-
чины, составленной ив обоих сегментов, центром тяжести будет X.
И поскольку как В0 к 0Л, так и КМ к MZ,
ни км
НД “ MZ
то после присоединения и перестановки: как ВД к KZ, так и АО к MZ.
вд до
KZ MZ
Но ВД в четыре раза больше KZ; (это доказываете» в конце, где знак
NB [4]); значит, и Д0 в четыре раза больше MZ, так что и остаток ВН
в четыре раза больше остатка КМ, то ость XX; и, значит, вместе в.чя-
тые остатки BS, Х0 втрое больше XX.
ВХ+Х6~ЗХХ
Пусть В2 втрое больше 22; значит, и Х0 будет втрое больше
2Х. И поскольку ВД в четыре раза больше В2 (ибо и это доказывает-
ся), BS гке втрое больше ES, то, значит, ЕВ будет третьей частью
ВД *). По м КЛ будет третьей частью ЛВ, так как центр тяжести тре-
угольника АВГ будет л Е; значит, и остаток ВЕ будет третьей частью
ВД. И так как для всего сегмента центром тяжести является точка 0,
для величины же, составленной из обоих сегментов АКВ, ВЛ Г, центром
тяжести будет X, для треугольника же АВГ — точка Е, то получится,
что как треугольник АВГ к остающимся сегментам, так и Х0 к 0Е.
Но треугольник АВГ втрое больше обоих сегментов, [так как весь
сегмент составляет четыре трети треугольника АВГ]; значит, и X©
втрое больше НЕ. По было доказано, что Х0 втрое больше ХЕ; зна-
чит, ЕЕ будет в пять раз больше Е0,
= E=fSK-|-X0 | НЕ—НЕ ‘ ЗНЕ | 8Е]=5НЕ
то есть ДЕ в пять раз больше Е0 (ибо ДЕ и ВЕ равны).
Таким образом, А0 будет в шесть раз больше BE. t
ле-цдЕ |-Ев=5еЕ+ке]=беЕ
Но ВД втрое больше ДЕ; значит, В0 будет в полтора раза больше 0Д,
Нл-.:дЕ
В«=Вд~де=158В-6Е0—9ЕН
9 *
нет=-£-ел
что и требовалось доказать [5].
IX
Если четыре линии будут пропорциональны в непрерывной про-
порции и отношение наименьшей к разности между наибольшей, (то
есть первой), и наименьшей, (то есть четвертой), будет равно отно-
шению некоторой взятой линии к трем пятым разности между наи-
большей из пропорциональных и третьей, отношение же, в котором
1 4
*) Действительно. ВД—4ВЕ, В2 = НХ 4- ХЕ ~ BE 4- — ВЕ = ВЕ, откупа
Л, , В- : Вд BE : 4BZ =1.
О РАВНОВЕСИИ ПЛОСКИХ ФИГУР
291
вместе взятые удвоенная наибольшая из пропорциональных, учетверен-
пая вторая, ушестеренная третья и утроенная четвертая находятся
к вместе взятым упятеренной наибольшей, удесятеренной второй,
удесятеренной третьей и упятеренной четвертой, будет равно отно-
шению другой взятой линии к разности между наибольшей из про-
порциональных и третьей, то обе взятые линии вместе составят две
пятых от наибольшей (6J-
Пусть будут четыре пропорциональные линии АВ, ВГ, ВД, ВЕ
{рис. 20}, и пусть линия ZH имеет то же отношение к трем
пятым АД, что ВЕ к ЕА,
ZH BE
'3 д ” ЕА ... • .
ТАА
отношение же линии Н0 к АД пусть будет равно отноше-
нию удвоенной АВ, учетверенной В Г, ушестеренной ВД и
утроенной ВЕ, (вместе взятых), к упятеренной АВ, уде-
сятеренной ГВ, удесятеренной НА и упятеренной ВЕ.
не 2АК-Р4ВГ4-СВй+ЗВЕ
АЛ ' аАН+10ГВ+10ВЛ I-6BE
Требуется доказать, что Z0 составляет две пятых от АВ.
Так как АВ, ВГ, ВЛ, ВЕ пропорциональны,
л в вг вл
вг ~ пл " пн
то н том же самом отношении будут и АГ, ГД, ДЕ *).
АГ ГД АЕ
ВГ — вд " ик
И вместе взятые ЛВ, ВГ к ВД, а также удвоенная от вместе взятых ЛВ,
ВГ к удвоенной ВД имеет то же самое отношение, что АЛ к ЛЕ, а также
и вместе взятые ДВ, В Г к ЕВ, и все предыдущие ко всем последую-
щим **).
’ (ЛИ-1-ВГ) _ АД . АВ+ВГ _ ДВ-=-ВГ • ?. .
2ВЛ — ДЁ ВД ' ' ЕВ
Значит, АД к ДЕ имеет то же самое отношение, что удвоенная АВ с ут-
роенной ВГ и ВЛ к равной удвоенной ВЛ и ВЕ.
2ЛВ-1-ЗВГ1 вд ад • л.'
ZiBA-f'BE ДЕ ' .
И отношение, в каком удвоенная АВ с учетверенной ВГ, учетверенной
ВД п удвоенной ВЕ находится к удвоенной ДВ вместе с ЕВ, это отно-
шение ДЛ будет иметь к меньшей чем ДЕ (прямой); пусть она имеет
его к ДО. . ..
ЗАВ1-4ВГ+4ВД+2ВК АЛ ’ ' • ' .
----2ВД+ВЕ-------" АО ,Л° ЛК)
ВГ ВД АВ - ВГ ВГ - ВД ВД - ВЕ
ВГ ВД ВЕ ВГ ВД ВЕ
АГ _ ВГ _ ДВ
ГВ ВД “ ВЕ '
АГ __ АВ + ВГ АГ + ГД АВ ) ВГ АД „
= — следует иг - • - г& . или вг Поснольлу
АВ+ВГ. ВГ + ВД
ВД ВЕ
и
гг « АВ
•) Ии осноиной пропорции -|
АГ ГД ДЕ
но.пч.|ем иг - Бд — вк
... „ АВ
•*> Ив равенства - -^д- -------—— ,
ВГ АГ ГД АВ + ВГ . АД
вл ^Тд-=ле-- то *по РЯЕСНСТиУ’ нд- -Тк и дял™
2 (АВ + ВГ) + ВГ ВД
2ВД + ВЕ
нд
19*
292
АРХИМЕД
-а: - И то же отношение будут иметь попарно взятые члены этой пропорции
as:.:;' к первым.
АД+ДО (2ВД 1-ВЕ) )(2АВ+4ВГ4-4ВД+2ВЕ)
АД " “2АВ+4ВГ+4ВД+2ВЁ
Теперь ОА будет иметь к АД то же отношение, что удвоенная АВ с учет-
верейной ВГ, ушестеренной ВД и утроенной ВЕ к (линии), составлен-
ной из удвоенной от вместе взятых АВ, ВЕ и учетверенной от вместе
взятых ГВ, ВД.
ОА _ 2А И| 4ВГ-1-6ВДЧ-ЗВЕ
АД " 2(AB-i-BEH-4 (ВГ+ВД) . .
Но и АД имеет к НО то же отношение, что и упятеренная от вместе
взятых АВ, ВЕ с удесятеренной от вместе взятых ГВ, ВД к составлен-
ной из удвоенной АВ, учетверенной ГВ, утроенной ЕВ и ушестерен-
ной ВД.
АД 5(ЛИ|-РЕН 10(ГВ+ВД)
не 2АВ+4ГВ4-ЗЕВ-1-6ВД
Так как отношения поставлены несогласно, то есть в перемешанной
пропорции, то «по равенству» О А будет иметь к НО то же otmobjoiihc,
что упятеренная от вместе взятых АВ, ВЕ с удесятеренными ГВ, ВД
к составленной из удвоенной от вместо взятых ЛВ, ВЕ и учетверенной
от вместе взятых ГВ, ВД.
ОА 5 (АВЧ-ВК)-Ц О (ГВ | ВД)
нё 2 (ЛВ- НЮ4-4 (ГВ+ВД)
Но составленная из упятеренной от вместе взятых АВ, ВЕ с удесяте-
ренной от вместо взятых ГВ, ВД к составленной из удвоенной от вместе
взятых АВ, ВЕ и учетвсропвоя от вместо взятых ГВ, 13Л имеет то же
• отношение, как пять к двум. И, значит, АО относится к Нб, как пять
' к двум.
АО &
НО ~ 2
Далее, так как ОД имеет к ЛА то же отношение, что ЕВ с удвоен-
ной ВД к составленной из удвоенной от вместо взятых А13, ВЕ с учет-
’ воренной от вместе взятых ГВ, ВД,
ОД________ЕЩ-2ВД_______
ЛА ~ 2(А1Н ВК)+4(ГВ{-ВД>
и как АД к ДЕ, так и составленная из удвоенной АВ, утроенной ГВ
и ВД относится к ЕВ с удвоенной ВЛ,
АД _ 2ЛВ |-2ГВ-!-ВД
ДЕ - ЕВ г2ВД
то при несогласно поставленных отношениях, то есть в перемешанной
пропорции, будет «по равенству», что как ОД к ЛЕ, так и удвоенная ЛВ
с утроенной ВГ и с ВД к составленной из удвоенных от вместе взятых
АВ, ВЕ и учетверенных ГВ, ВД.
од ' 2ЛВ | звгч-па
лё “ 2 (ав-;-ве)-;-4 (гв+вд)
Таким образом, как ОЕ к ЕД, так будет и ГВ с утроенной ВД и удвоен-
ной ЕВ к удвоенной от вместе взятых АВ, ВЕ и учетверенной от вместе
взятых ГВ, ВД,
ОН 1 ДК ОД 2(АВ+ВЕ)+4(ГВ+ВД)-(2АВ+ЗГВ-|ВД)1_________ГН+ЗВД+2ЕВ
ЁЛ - I ЛР - ~2 (АВ+ВЕЫ-4 (ГВ+ВД) J’ 2 (АВ+ВЕН-4 (ГВ ЬВД) ......
О РАВНОВЕСИИ ПЛОСКИХ ФИГУР
293
Но как ДЕ к ЕВ, так поело «присоединения» будет и АГ к ГВ *),
ЛЕ АГ
ЕВ ~ ГВ
а также и утроенная ГД к утроенной ДВ и удвоенная ДЕ к удвоен-
ной ЕВ,
АГ ГД _ А ГС _ .4 ГД _ ИЛЕ -
ГВ ~ ВД ЕВ- ЗДН — ЗЕВ
а, следоватсльпо, и составленная из ЛГ, утроенной ГД и удвоенной ДЕ
к составленной из ГВ, утроенной ЛВ и удвоенной ЕВ. .......
АГ АГ+.ЧГД1-2ДЕ ЛЕ • • ’ ‘
ГВ ГВ-|-ЗдВ| 2КВ ЕВ
Теперь опять при йесогласно поставленных отношениях, то есть в пере-
мешанной пропорции, «по равенству» ЕО будет иметь к ЕВ то же отно-
шение!, что АГ с утроенной ГД и удвоенной ДЕ к удвоенной от вме-
сте взятых АВ, ВЕ с учетверенной от вместе взятых ГВ, ВД.
ЕО АГ|-ЗГД+2ДЕ
ЕВ ~ 2 (АВ| ВЕН-4 (ГВ+ВД) • . ' '
: Теперь вся ОВ к ВЕ имеет то же отношение, что утроенная АВ с ушесте-
ренной ГВ и утроенной ВД к удвоенной от вместе взятых АВ, ВЕ
с учетверенной от вместе взятых ГВ, ВД.
ОВ гОЕГ-ЕВ 2АВЧ-(АГ+ГВ)+ЗГВ+(ЛГА+ЗВД) 1-ВД-К2ДЕ-1-2ВЕ)! __ ЗАВ+ВгВ 1-ЗВД
BE L ВЕ “ 2 (АВ+ВЕ)Ч-4 (ГВ+ВД) J “ 2 (AB PB14)-f-4 (ГВ 1-ВД)
И поскольку ЕД, ДГ, ГА находятся в том же отношении,
ЕД ДГ ЕВ+ВД ДН+ВГ
ДГ — ГА ~ ДВ-гВГ 'Г.Н-J-BA
что и каждая (сумма двух вместе взятых) ЕВ и ВД,ДВ и В Г, ГВ и
ВА**), то получится, что как ЕД к ДА, так и вместе взятые ЕВ, ВД
относятся к вместе взятым ДВ, ВГ с вместе взятыми ГВ, ВА.
ЕЛ г ЛЕ 7 ВВ+-ВД
ДА _ ( ДГ4-ГЛ J “ (ДВ+ВГ)+(ГВ-|-БА)
И значит, после «присоединения» будет как АЕ к АД, так и вместе
взятые ЕВ, ВД с вместе взятыми АВ, В Г и вместе взятыми ГВ, ВД
(а ото будут вместе взятые ЕВ, ВА с удвоенной от вместе взятых ДВ,
В Г) ко вместе взятым ВД, В А с удвоенной В Г.
ЛЕ г АД+ДЕ . (ЕВЧ-ВД)+(АВ+ВГ)+(ГВ+ВД)| (ЕВ+ВАН-2 (ДВЧ-ВГ)
АЛ I ДА (АВ-:-ВГ)Ч-(ГВ-|-ВЛ) I ’ (ВД+ВД)-|-2ВГ
То же самое отношение будут иметь и удвоенные, то есть как ЕЛ к АД,
так и удвоенная от вместе взятых ЕВ, ВА с учствереппой от вместе взя-
тых ГВ, ВД к удвоенной от вместе взятых АВ, ВД с учствереппой ГВ.
ЕА 2(ЕВ-( ВА)+4 (ГВ—ВА)
ЛА 2 (АВ4-ВД)+4ГВ
*) Собственно говоря, после «выдолспип», так как из исходной пропорции = получаем
ВГ нь
АВ - ВГ _ ВД — ВЕ АГ _ ДЕ
ВГ — ВЕ ’ Т‘ ГВ "" ЕВ ’
*•) Мы имеем
АВ _ ГВ _ АВ АГ _ ГЛ
'ВГ Вд = ВЕ ГВ ЛВ
ДЕ „ ЛВ ( ВГ ГВ-f-BA ДВ/-ВЕ
Ёв Отсвда —гв— ~ -------вв-
и. наконец.
ЛВ -I- ВГ . ГД + ВД
ГА ДГ
ЛВ+ ВЕ
ЕД
294 ' АРХИМЕД
Таким образом, как ЕА к трем пятым АД, так и составленная из
удвоенной от вместе взятых АВ, ВЕ и учетверенной от вместе взятых
ГВ, ВЛ относится к трем пятым составленной из удвоенной от вме-
сте взятых АВ, ВД и учетверенной ГВ. г.
КА _ 2 (АВ ВЕ)+4 (ГВ ВД)
4- АД -4-{2(АВ |ВД)-НГВ>
Но как ЕЛ к трем пятым АД, так будет и ЕВ к ZH.
ЕА ЕВ ' ' ' . .
И, значит, как ЕВ к ZH, так и удвоенная от вместе взятых АВ, ВЕ
с учетверенной от вместе взятых АВ, 13Г относится к трем пятым состав-
ленной из удвоенной от вместе взятых АВ, ВД с учетверенной ГВ.
ЕВ __ 2 (АВ-)-ВЕ)-;-4 (ДВ I ВГ)
ZH 4-{2 (АВ+ВДН-4 ГВ}
Но также было доказано, что как ОВ к ЕВ, так и утроенная от вместе
взятых АВ, ВД с ушестеренной ГВ относится к удвоенной от вместо
взятых АВ, ВЕ с учетверенной от вместе взятых ГВ, ВД.
ОВ_____3 (АВ »-ВД)+КГВ
ЕВ 2 (АН-I"НЕ) г4 (ГВ-( ВД)
И, значит, «по равенству» как ОВ к ZH, так н составленная из утроен-
ной от вместе взятых АВ, ВД с ушестеренной ГВ относится к трем
пятым составленной из удвоенной от вместе взятых АВ, ВД с учетве- ‘
рениол ГВ.
ОВ 3 (ЛВ4-ВД)+6ГВ ' /
2н 4-{2 (АВ+ВД)4-4ГВ>
Но составленная из утроенной от вместе взятых АВ, ВД с ушестерен-
ной ГВ к составленной из удвоенной от вместе взятых АВ, ДВ с учет-
веренной ГВ имеет отношение, как три к двум,
3 (АВ + ВД)-|-6ГВ з
2 (AB-f-ВД) | 4ГВ 2
к трем пятым же ее имеет отношение, как пять к двум. Также доказано,
что и АО имеет к ПО отношение, как пять к двум. Значит, и вся ВА
ко всей ZO имеет отношение, как пять к двум.
Если ate так, то Z& составляет две пятых от АВ. Это я требова
лось доказать.
X
У всякого усеченного сегмента параболы- центр тяжести находится
на прямой, являющейся диаметром сегмента, и расположен следующим
образом: если разделить эту прямую на пять равных частей, то он
лежит на средней части так, что отрезок ее, ближайший к меньшему
основанию {сегмента'), имеет к оставшемуся отрезку такое же отно-
шение, как прямоугольный параллелепипед, имеющий основанием квадрат
на большем из оснований сегмента, а высотой прямую, равную вместе
взятым удвоенному меньшему из оснований и большему, к параллелепи-
педу, имеющему основанием квадрат на меньшем из оснований сегмента,
высотой же прямую, равную вместе взятым удвоенному большему из
оснований и меньшему.
О РАВНОНИСИИ плоских ФИГУР
295
Пусть в параболе будут две (параллельные} прямые АГ, ДЕ.
Пусть диаметром сегмента ЛВГ будет BZ {рис. 27}. Тогда ясно, что Z1I
будет также диаметром усеченного сегмента ЛДЕГ, [так как АГ, ДЕ
параллельны касательной в В к сечению]. Пусть при разделении
прямой HZ на пять равных частей средней частью будет 0К. Пусть
01 имеет к IK то же отноше-
ние, что и параллелепипед, м д ° Г ,д,
имеющий основанием квад-
ной ДН и AZ, к параллеле-
пипеду, имеющему основани-
ем квадрат на ДН, высоту
же, равную вместе взятым
удвоенной AZ и ДП.
Hl _ AZa(2AH+AZ) . - Рис 27.
гк AHS(2AZ|AH)
Требуется доказать, что у сегмента АДЕГ центр тяжести есть I.
Пусть MN будет равна ZB, и NO равна НВ; возьмем для MN, NO
среднюю пропорциональную NE и четвертую пропорциональную TN.
И пусть как ТМ к TN, так будет и Z0 к некоторой прямой, начинаю-
щейся от I, куда бы ни попала другая ее точка (ибо безразлично, будет ли
она между Z, Н или же между ИВ); пусть зто будет 1Р.
'ГМ _ ZH
TN ” “IP
И так как прямая ZB является диаметром сегмента параболы, то она
будет или главной осью параболы или параллельной этой оси, прямые
же AZ, Д11 будут проведенными к ней ординатами *), ибо они параллель-
ны касательной в В к параболе. Если же ото так, то будет: как квадрат
на AZ к квадрату на ДИ, так и ZB к ВН линейно, то есть, как MN
линейно к NO, так в квадраты на MN и №,
А2г ... ZB MN = мк*
ЛН2 Вн NO N32
и, значит, как квадраты на AZ и ДН, так и квадраты на MN к NE;
так что и линейно они будут в том ?нс самом отношении.
AZ . .. MN
ЛН N3
И, значит, как куб на AZ к кубу па ДП, так и куб на MN к кубу па NE.
AZ3 _ MN3 ' .-
ЛИ® КЗ*
Но как куб на AZ к кубу на ЛН, так будет и сегмент АВГ к сегмен-
ту ДВЕ;
AZ3 г AZS-AZ _ ZB-AZ т сегмент ВАГ .
.All3 "I ДН3-ДН — ВЦ-АН ] t-сгмспт ДВЕ
как же куб на MN к кубу па NE, так и MN к NT.
MN» г MN М№ MN М№ _ MN MN _ MN NS MN
№« гKS ’ №» “ № ' MN-NO “ NS~' NO NS TN ] ' TN
*) teray^ivinc xa-rxYlUvai. — «нровсдсчшме упорядоченным образом», откуда наш термин
^ордината».
296
А РХИМЕД
Таким образом, «выделяя», получим •/
сегмент ВЛ Г—сегмент ДВЕ MN-NT
сегмент ДВЕ " КТ
как сегмент АЛ ГЕ к сегменту ДВЕ, так и МТ к NT, то есть три пятых
HZ к IP *).
И так как параллелепипед, имеющий основанием квадрат на AZ,
высотой яге прямую, составленную из удвоенной ДН и AZ, относится
к кубу на AZ, как удвоенная ДН с AZ к ZA, и так же, как удвоенная
NS с NM к NM,
AZ* (3AII I-AZ) 2ДН+А2 ДН NS , NM । _ 2NS-5-NM
AZ» AZ — Г AZ + MN "Г NM J 1 NM
и как куб на AZ к кубу па ДН, так и MN к NT,
AZ» [-MN»1 MN
ди» Ins»]- nt
как яге куб на ДН к параллелепипеду, имеющему основанием квадрат
на ДП, высотой же прямую, составлгнную из удвоенной AZ с ДН, так
и ДН к составленной из удвоенной AZ и ДН, и как TN к составленной
из удвоенной ON и TN,
ДМ» ДП г 1 1
ДН2(2А2|-ДН) 2АЯ+ДН -| „ А7. “ .MN ,, ~
L2Arf'H j_ns‘+1
_ 1 I 1 i TN
„ MN _Np , . — o _NS_ NO - NO X1 - 2N0-TN
NO ' NS"1- “ TN ' NS +I’ " TN ' ’ J
то получились четыре величины, а именно: параллелепипед, имеющий
основанием квадрат на AZ, высотой же прямую, составленную из удво-
енной ДН и AZ, затем куб на AZ, куб па ДН и параллелепипед, имею-
щий основанием квадрат на ДН, высотой же прямую, составленную
из удвоенной AZ и АН. Ути величины, взятые попарно, образуют про-
порцию с четырьмя следующими величинами: с составленной из удвоен-
ной NS и N.M, затем с MN, затем еще с NT и, наконец, с составленной
из удвоенной NO и NT. Значит, «по равенству» получится, что паралле-
лепипед, имеющий основанием квадрат на AZ, высотой же — прямую,
составленную из удвоенной ДН и AZ, относится к параллелепипеду,
имеющему основанием квадрат на ДН, высотой же — прямую, состав-
ленную из удвоенной AZ и Д11, как прямая, составленная из удвоенной
N3 и MN, к прямой, составленной из удвоенной NO и NT.
AZ»(2AI1 | AZ) 2NS1-MN
ДН2 (2AZ | ЛИ) 2NO NT
Но как первое упомянутое тело ко второму, так и 01 к IK.
AZa (2ДН I AZ) _ OI
ДН2 (2AZ+AH) IK .’ '
И, значит, как ©I к IK, так и одна составленная прямая к другой.
в! = 2NH-I NM
IK 2KO+NT
Таким образом, «присоединяя»,
0I+IK (2NS+NM) М2КО I NT)
• IK ‘ ‘ 2N0 i.NT
и взявши пять раз предыдущие,
:>6К _ IONS I-5NM : I ОМС) • SNT
IK 2ND I NT
получим, что как ZII к IK, так и упятеренная от вместе взятых MN,
„ мт ze 5
> п° условию nt =-1F = "ip“
О РАВНОВЕСИИ ПЛОСКИХ ФИГУР
297
NT и удесятеренная от вместе взятых NE, NO к удвоенной ON и NT.
ZH = 5 (MN-t-NTH-IО (NB4-N0)
IK 2ON—NT
И как ZH к ZK, являющейся (по построению) двумя пятыми первой,
так будут упятеренная от вместе взятых MN, NT и удесятеренная от
вместо взятых EN, NO к удвоенной от вместе взятых MN, NT и учет-
веренной от вместе взятых EN, NO.
ZH 5 (MN ’ NT) • I О (NS I КО)
ZK 2 (MN--NT)+4 (NE : NO)
Следовательно, будет, что ZH к ZI, как и упятеренная от вместе взятых
MN, NT и удесятеренная от вместо взятых EN, NO к составленной из
удвоенной MN, учетверенной №, утостерспной ON и утроенной NT.
IZH ZII S (MN4-NT) I 10(NS | NO)
ZI ZK—KI ' 2MN4-4NE--6ON- 3NT’
Так как имеются в непрерывной пропорции 4 прямые MN, NE, ON, NT
MN _ _NS _ ON •
NS ON NT
и как NT к ТМ, так будет и некоторая взятая прямая PI к трем пятым
от ZH, то есть от МО;
NT । PI ] PI________PT
тм I ze J ZH _j_ 110
a v
как же составленная из удвоенной NM, учетверенпой NE, ушестерен-
ной NO и утроенной NT к составленной из упятеренной от вместо взя-
тых MN, NT и удесятеренной от вместо взятых EN, NO, так и некото-
рая другая прямая JZ к ZH, то есть к МО,
2MN4-4N8-I вко ! 3NT _ IZ _ IZ
& (MN-j-KT)-) -10 (SN ; NO) ZH МО
то, согласно предыдущему предложению, получится, что (PI+ IZ)
составляют две пятых от MN, то есть от ZB. Таким образом, у сегмента
АВГ центром тяжести будет точка Р (предложение VI11). Пусть у сег-
мента ДВЙ центром тяжести будет точка X. Значит, у сегмента АДЕГ
центр тяжести будет на продолжении прямой ХР, причем это продол-
жение будет так относиться к названной прямой, как верхний сегмент
к оставшемуся усеченному сегменту. Это же и будет точка 1. Действи-
тельно, так как 13Р составляет три пятых от ZB, а ВХ — три пятых от
НВ, то, значит, три пятых от остатка HZ будет ХР.
хв = [вр - вх = -|-<zb- hb)J =»-Л nz
Теперь, поскольку как усеченный сегмент АДЕГ к сегменту АВЕ, так
и МТ к NT, как же МТ к TN, так и три пятых 1JZ, то есть ХР, к PI,
то, значит, как усеченный сегмент АДЕГ к сегменту ДВЕ, так и ХР
к Р1. 11 у всего сегмента центром тяжести является точка Р, у сегмента
же ДВЕ центр тяжести X. Теперь ясно, что у усеченного сегмента АДЕГ
центром тяжести будет точка I [7].
ПОСЛАНИИ К ЭРАТОСФЕНУ.
О МЕХАНИЧЕСКИХ ТЕОРЕМАХ
Архимел) Эратосфену желает благоденствовать!
Я ужо послал тебе запись предложений найденных мной теорем,
предоставив тебе найти их доказательства, о которых я до сих пор ничего
еще не говорил. Предложении теорем были таковы.
Первой теоремы: если, в прямую призму с основаниями в виде парал-
лелограммов *) вписать цилиндр, имеющий основания на противолежа-
щих параллелограммах, а стороны на остальных плоских {гранях} приз-
мы, и провести плоскость через центр круга, лежащего в основании
цилипдра, и одну из сторон квадрата в противолежащем основании,
то проведенная плоскость отсечет от цилиндра сегмент, заключаю-
щийся между двумя плоскостями и поверхностью цилиндра (одной из
этих плоскостей является сама проведенная, другой — основание
цилиндра, а поверхность будет та, которая заключается между упомя-
нутыми плоскостями), то отсеченный от цилиндра сегмент будет ше-
стой частью целой призмы.
Предложение второй теоремы было таким: если в куб вписать ци-
линдр с основаниями на противолежащих параллелограммах и с поверх-
ностью, касающейся четырех остальных плоских {граней), и затем в тот
же самый куб вписать другой цилиндр с основаниями на других паралле-
лограммах и с поверхностью, касающейся четырех остальных плоских
{граней), то фигура, заключенная между поверхностями этих цилинд-
ров, то есть находящаяся внутри обоих цилиндров, составляет две
трети всего куба.
Так вот, эти теоремы получились отличными от найденных рапсе:
действительно, в прежних теоремах копоидальные и сфероидальные
тела, а также их сегменты мы сравнивали по величине с конусами
и цилиндрами, и ни одно из этих тел не оказалось равным телесной
фигуре, ограниченной плоскостями; из рассматриваемых же тел, огра-
ниченных двумя плоскостями и цилиндрическими поверхностями,
каждое оказывается равным одной из телесных фигур, ограниченных
плоскостями.
) Прямоугольников, в данноВг случае просто квадратов.
послание: к Эратосфену, о механических теоремах
299
В этой книге я посылаю тебе запись доказательства двух этих
теорем.
Зная, что ты являешься, как я говорю, ученым человеком и но
праву занимаешь выдающееся место в философии, а также при случае
можешь оценить и математическую теорию, я счел нужным написать
тебе и в этой же самой книге изложить некоторый особый метод, при
помощи которого ты получишь возможность при помощи механики
находить некоторые математические теоремы. JJ уверен, что этот метод
будет тебе ничуть не менее полезен и для доказательства самих теорем.
Действительно, кое-что из того, что ранее было мною усмотрено ври
помощи механики, позднее было также доказано и геометрически, так
как рассмотрение при помощи этого метода еще не является доказа-
тельством; однако получить при помощи этого метода некоторое пред-
варительное представление об исследуемом, а затем найти и само
доказательство, гораздо удобнее, чем производить изыскания ничего
нс зная. Поэтому и относительно тех теорем о конусе и пирамиде, для
которых Евдокс первый нашел доказательство, а именно, что всякий
конус составляет третью часть цилиндра, а пирамида — третью часть
призмы с тем же самым основанием и равной высотой, немалую долю
заслуги я уделю и Демокриту, который первый высказал это положение
относительно упомянутых фигур, хотя и без доказательства. И нам
довелось найти публикуемые теперь теоремы тем же самым методом,
как и предыдущие; поэтому я и решил написать об этом методе и обнаро-
довать его, с одной стороны, для того, чтобы нс оставались пустым зву-
ком прежние мои упоминания о нем, а с другой, поскольку я убежден,
что оп может принести математике немалую пользу; я предполагаю, что
некоторые современные нам или будущие .математики смогут при помо-
щи указанного метода найти и другие теоремы, которые нам еще пе
приходили в голову.
Первым мы опишем то, что первым и было нами обнаружено при
помощи механики, а имеппо, что всякий сегмент параболы составляет
четыре трети треугольника с тем же основанием и равной высотой, а за-
тем и каждую из теорем, нолучеппых нами при помощи этого метода;
в конце же книги мы напишем геометрические доказательства тех тео-
рем, предложения которых мы ранее послали тебе.
Леммы
1. Если от одной величины отнять другую, причем центром тяже-
сти и первоначальной величины и отнимаемой является одна и та же
точка, то эта же точка будет центром тяжести и остатка.
2. Если от одной величины отнять другую, причем центры тяжести
первоначальной величины и отнимаемой не находятся в одной и той же
точке, то центр тяжести величины, получающейся в остатке, будет
находиться на прямой, соединяющей центры тяжести первоначальной
и отнимаемой величин, если продолжить ее и нанести на ней отрезок,
имеющий к расстоянию между указанными центрами то же самое
отношение, какое вес отнимаемой величины имеет к весу остающейся.
(«О равновесии», кп. I, предложение V111.)
3. Если центры тяжести Любого количества величин находятся на
одной прямой, то иа этой же прямой будет находиться и центр тяже-
сти величины, составленной из всех этих величин.
4. Центром тяжести всякой прямой будет ее середина.
300
АРХИМЕД
5. Центром тяжести, всякого треугольника будет точка, в которой
пересекают друг друга прямые, проведенные из вершин треугольника
к серединам его сторон («О равновесии», ки. I, предложение XIV.)
6. Центром тяжести всякого параллелограмма будет точка, в ко-
торой сходятся его диаметры. («О равновесии», кн. ], предложение Х.>
7. Центром тяжести круга будет его центр.
8. Центром тяжести всякого цилиндра будет середина его оси.
9. Центром тяжести всякой призмы будет середина ее оси.
10. Центром тяжести всякого конуса будет точка, разделяющая
его ось так, что прилегающий к вершине отрезок будет втрое больше
остатка.
11. Также будем пользоваться и следующей теоремой. («О коноидах
и сфероидах», предложение J.)
Если имеется любое количество величин в равном числе с другими
величинами, причем одинаково расположенные величины, взятые попар-
но, находятся в одном и том же отношении, затем, если первые величины
все или частью будут находиться в каких-нибудь отношениях к треть-
им, а соответственные им вторые величины в таких же отношениях
к четвертым, то взятые вместе все первые величины, ко всем третьим
будут иметь то же самое отношение, что все вторые ко всем четвер-
тым [1].
I
Пусть АВГ будет сегмент, заключающийся между прямой АГ
и параболой ЛВГ; разделим АГ пополам в Л, параллельно диаметру
проведем ДВЕ я соединяющие прямые АВ и ВГ {рис. 1}.
Я утверждаю, что сегмент AjjJF составляет четыре трети тре-
угольника АВГ *).
*) См. номмонтаряй к «Квадратуре лярабалы», стр. 450.
ПОСЛАНИЕ К ЭРАТОСФЕНУ. О МЕХАНИЧЕСКИХ ТЕОРЕМАХ 301
Из точек А и Г проведем AZ, параллельную ДВЕ, и TZ, касатель-
ную л параболе; продолжим ГВ до К и отложим К (-), ранную ГК. Вообра-
зим равноплечий рычаг Г0 с серединой К и какую-нибудь прямую М3,
параллельную ЕД.
Так как ГВА — парабола, TZ — касательная к ней и ГД — ордина-
та, то ЕВ равна ВД (это доказывается в началах теории конических
сечений); вследствие этого, а также вследствие того, что ZA и М3
параллельны ЕД, прямая MIN будет равна ]\'3, a ZK равпа КА. И по-
скольку ГА относится к AS, как АГЕ к ЕО,
ГА MS
as so
[это доказывается в лемме) *), и ГА к АЗ, как ГК к KN,
Г/\ _ ГК
AS KN
и ГК равпа К0, то, значит, 0К будет к KN, как ME к ИО.
ек _ мв
кй ЕО
И так как точка N есть центр тяжести прямой ME, ибо MN раина NE,
то, следовательно, если взять прямую ТЛ, равную ЕО и имеющую
центр тяжести в 0, так, чтобы Т0 равнялась 011, то прямая T0I1
уравновесит ME, остающуюся в своем положении, вследствие того,
что отрезки 0N обратно пропорциональны весам TH и М3, то есть
ОК к KN будет, как МИ к НТ.
вк = мв •
KN _ пт
Таким образом, точка К будет центром тяжести величины, составленной
иэ обоих весов (TH и М3). Аналогично и все проведенные парал-
лельно ЕД прямые в треугольнике ZAI’ будут в своих положениях урав-
новешиваться со своими отрезками, отсеченными параболой, если пере-
нести последние в 0 так, чтобы К была центром тяжести величины,
составленной иэ каждой пары таких прямых. И так как треугольник
TZA составляется из всех таких прямых, находящихся в треугольни-
ке TZA, а сегмент АВГ составляется из всех подобных ЕО прямых,
взятых внутри параболы, то, значит, треугольник /АГ, оставаясь в сво-
ем положении, будет относительно точки К уравновешивать параболи-
ческий сегмент, помещенный центром тяжести в О так, чтобы К была
центром тяжести величины, составленной иэ пих обоих. Разделим теперь
ГК в точке X так, чтобы ГК была втрое больше КХ; тогда точка X
будет центром тяжести треугольника AZT (это доказано в сочинении
«О равновесии»). Тогда поскольку треугольник ZA1\ оставаясь в своем
положении, уравпоиешинает относительно К сегмент ВАГ, помещен-
ный центром тяжести в 0, и центр тяжести треугольника AZT будет в X,
то, значит, треугольник AZT к сегменту АВГ, помещенному центром
в 6, будет относиться, как 0К к ХК.
Но 0К втрое больше КХ: значит, и треугольник AZ1’ будет втрое
больше сегмента АВГ. Но треугольник ZAr в четыре раза больию тре-
угольника АВГ, так как ZK равна КА, а АД равпа ЛГ; значит, сег-
мент АВГ составляет четыре трети треугольника А13Г; [это теперь
ясно] **).
*) В действительности это доказано п предложении V «Квадратуры параболы».
»*) Последние слова Гсйберг удаляет, как по вяжущиссгГс начальными словами следующего
параграфа.
302
АРХИМЕД
II
Хотя это всем вышеприведенным рассуждением и ле доказано,
но все же оно производит впечатление, что окончательный вывод правн
лен; поэтому мы, видя недоказанность выведенного, но подозревая его
правильность, предложим найденное нами и опубликованное ранее
геометрическое доказательство *).
При помощи того же .метода можно найти, что всякий шар будет
в четыре раза больше конуса с основанием, равным большому кругу ша-
ра, и с высотой, равной радиусу шара, а также, что всякий цилиндр
с основанием, равный большому кругу шара, и высотой, равной диаметру
шара, будет в полтора раза
больше шара. Это усматривает-
ся так [рис. 2).
Пусть будет шар с большим
кругом Л В ГЛ и взаимно пер-
пендикулярными диаметрами
АГ, ВД; возьмем в шаре круг
на диаметре ВД, перпендику-
лярный к кругу АВГД; на этом
перпендикулярном круге по-
строим копус с вершиной в точ-
ке А; затем, продолжив (боко-
вую) поверхность этого конуса,
рассечем его проходящей че-
рез Г плоскостью, параллель-
ной основапию; в сечении полу-
чится перпендикулярный к АГ
круг с диаметром EZ. Jia этом
круге построим цилиндр, имею-
щий ось, равную АГ; пусть ЕЛ.
Z11 будут боковыми сторонами
цилиндра. Затем продолжим ГА,
отложим А©, равную ей, п вообразим равноплечий рычаг Г© с середи-
ной А. Параллельно ВД проводом какую-нибудь прямую MN; пусть
она пересечет круг АВГД в точках S, О, диаметр АГ в S, прямую
АЕ в II, a AZ в Р.
На прямой MN восставим перпендикулярную к АГ плоскость:
последняя в сечении с цилиндром образует круг с диаметром MN, в се
пенни с шаром АВГД круг с диаметром 30 и с конусом AEZ —
круг с диаметром ПР.
И так как (прямоугольник) между ГА. AS равен (прямоуголь
пику) между MS, Sil,
ГА AT=MX-SI|
(ибо ЛГ равна ХМ, a AS равна ПХ), а (прямоугольник) между ГА.
AS равен (квадрату) па АЗ, или вместе взятым (квадратам) на ВХ
и ХП;
ГА-АХ = АВ2 = ВЁа+И!4
♦) В сохранившемся тексте «Эфода* итого доказательства нет; вероятно, переписчик просто
ве счел нужным повторять доказательство, которое уже было им воспроизвел ев о при списывания
«Квадратуры параболы».
ПОСЛАНИЕ К ЭРАТОСФЕНУ. О МЕХАНИЧЕСКИХ ТЕОРЕМАХ
303
то, -значит, (прямоугольник) на MX, SIT будет равен квадратам на
32 и ЕП.
М2.2П =Е22 |- 2П* ’
Поскольку же ГЛ относится к ЛЕ, как ME к ЕП,
га мд
А£ ХП
и ГА равна Ав, то, значит, 0А будет к АЕ, как MS к ЕП или как
(квадрат) на MS к (прямоугольнику) между MS, ЕП.
ЭЛ MX MS*
AS “ 2П ~М2-2П
Согласно же доказанному, (прямоугольник) между MS, ЕП ра-
нен (квадратам) па ЕЕ и SII; значит, Л0 будет к АЕ, как (квадрат)
на MS к (квадратам) на ЕЕ и ЕП, (вместе взятым).
Но (квадрат) на MS к (квадратам) па ЕЕ и S11 будет, как
(квадрат) па MN к (квадратам) па ЕО и ПР.
_МХ^_______MN*
аг* тп2 а о2 + пр*
Как же (квадрат) на MN к (квадратам) па 30 и ПР, так и круг
в цилиндре с диаметром MN будет относиться ко вместе взятым обоим
кругам, и тому, что в конусе с диаметром Г1Р, и тому, что в шаре с диа-
метром ЕО;
MN* ________круг па MN__
SO* + ПР2 ~ КРУГ Fa nF '! ВРУГ иа 20
зпачит, как 0А к АЕ, так и круг н цилиндре будет относиться к кругам
в шаре и в конусе.
вл________круг на MN
АЕ ~ круг иа UP круг ка ВО
Теперь, поскольку (ЗА относится к AS, как (указанные круги, то)
круг в цилипдре, оставаясь в своем положении, будет относительно
точки А находиться в равновесии с обоими кругами на диаметрах ЕО.
ПР, если перенести их в О и расположить так. чтобы центр тяжести
каждого из них находился в точке О. Теперь, если в параллелограм-
ме AZ провести параллельно EZ какую-нибудь другую прямую и нв
проведенной прямой восстановить плоскость, перпендикулярную
к АГ, то мы подобным же образом докажем, что круг, полученный в.ци-
линдре, оставаясь в том же положении, будет относительно точки А
находиться в равновесии с обоими кругами, получившимися в шаре
и в конусе, если последние перенести на рычаг и поместить в 0 так,
чтобы центр тяжести каждого из них оказался в 6. Если теперь, беря
такие круги, заполнить ими как цилиндр, так и шар с, конусом, то
цилиндр, оставаясь в том же положении, будет относительно точки А
находиться в равновесии со вместе взятыми шаром и конусом, если
перенести их на рычаг в 0 и поместить так, чтобы центр тяжести каждо-
го из них оказался в 0. Теперь, так как упомянутые тела будут нахо-
диться в равновесии относительно точки А, причем цилиндр остается
расположенным вокруг центра тяжести К, а шар и конус, как сказано,
перенесены и расположены вокруг центра тяжести 0, то получится, что
6А к АК будет относиться так же, как цилиндр к шару с конусом.
НА____цилиндр \
ак шар конус х I '
304
АРХИМЕД
Но ®А вдвое больше АК; значит, и цилиндр будет вдвое больше вместе
взятых шара и копуса.
Цилиндр же втрое больше конуса; значит, три конуса будут равны
двум таким же конусам и двум шарам. Отнимем два общих конуса;
значит, одни конус, имеющий в осевом сечении треугольник ЛЕХ,, равен
двум упомянутым шарам.
Но конус, имеющий в осевом сечении треугольник AEZ, будет ра-
вен восьми конусам с осевым сечением — треугольником АВД, так как
EZ вдвое больше ВД. Значит, восемь упомянутых конусов будут равны
двум шарам; следовательно, шар с большим кругом АВГД будет в четы-
ре раза больше копуса, у которого вершина сеть точка А, а основание —
круг на диаметре ВД, перпендикулярный к АГ.
В параллелограмме AZ через точки В, Д параллельно АГ проведем
прямые ФВХ, ЧГД£3 и вообразим цилиндр, у которого основания будут
круги на диаметрах ФЧ7, Хй, а ось АГ. Теперь так как цилиндр с осе-
вым сечением — параллелограммом ФЙ вдвое больше цилиндра с осе-
вым сечением — параллелограммом ФА, последний же втрое больше
конуса с осевым сечением — треугольником АВД, как доказывается
в «Началах» [Евклид, кн. XII, предложение 10J, то, значит, цилиндр
с осевым сечением — параллелограммом ФЙ будет в шесть раз больше
конуса с осевым сечением — треугольником АВД. Но доказано, что
шар с большим кругом АВГД в четыре раза больше этого самого конуса;
значит, рассматриваемый цилиндр будет в полтора раза больше шара,
что и требовалось доказать.
Когда все это было установлено, то у меня появилась мысль, что
поверхность всякого шара будет в четыре раза больше большого круга
в этом шаре, так как всякий шар в четыре раза больна? копуса, имею-
щего основанием большой круг, а высоту, равную радиусу шара.
Я предположил это потому, что, с одной стороны, всякий круг равен
треугольнику, имеющему основанием окружность круга, а высоту, рав-
ную радиусу круга *), а с другой, всякий шар равен конусу, имеющему
основанием поверхность шара, а высоту, равную радиусу шара [2J.
III
При помощи того же метода обнаруживается, что цилиндр, имею-
щий основание, равное наибольшему кругу сфероида **), а высоту, равную
оси сфероида, будет в полтора раза больше этого сфероида', если ясе это
усмотрено, то ясно, что, если любой сфероид рассечь плоскостью, про-
ходящей через центр и перпендикулярной к оси, то полученная половина
сфероида будет вдвое больше конуса с теми же основанием и осью, что
и у отсеченной части.
Действительно, пусть будет некоторый сфероид [рис. 3}; рассечем
его проходящей через ось плоскостью; на поверхности сфероида полу-
чится эллипс АВГД, у которого диаметры пусть будут АГ, ВД, а центр К.
В сфероиде возьмем перпендикулярный к АГ круг на диаметре ВД
и вообразим конус, имеющий основанием упомянутый круг, а верши-
ной — точку А, затем, продолжив поверхность этого конуса, рассечем
его параллельной основанию плоскостью, проходящей через Г; тогда
в сечении получится перпендикулярный к Л Г круг па диаметре EZ.
*) Это — первое предложение в «Измерении круга» (стр. 26^).
*•) Так Архимед называет эллипсоид вращении. ;
ПОСЛАНИЕ К ЭРАТОСФЕНУ. О МЕХАНИЧЕСКИХ ТЕОРЕМАХ
305
Пусть также будет цилиндр, имеющий основанием тот же самый круг
на диаметре EZ, а осью — прямую АГ; продолжив ГА, отложим равную
ей прямую АО и вообразим равноплечий рычаг с серединой в А; в па-
раллелограмме AZ параллельно EZ проведем какую-нибудь прямую
MN и на этой прямой MN восставим плоскость, перпендикулярную
к АГ. Эта последняя образует в цилиндре сечепио-круг с диаметром
MN, в сфероиде сечение-круг с диаметром ЕО и и конусе сечение-круг
с диаметром ПР.
И поскольку ГА относится к AS, как ЕА к АП или как MSkSII,
ГА _ ЕД _ М2
"АХ " ЛИ — ХП ~
и ГА рАвпа А®, то, значит, как 6А к AS, так и MS к SIL
ел _м£
лх = ЁН
Но как MS к S11, так будет и (квадрат) на MS к (прямоугольнику)
мсяаду MS и SH,
MX _ MX2
ХП — МХ-ХП
а (прямоугольнику) между MS и SII будут равны (квадраты) на
nS2 и SEa 131.
МГ-ХП = ПХ3 + ХВ2
Действительно, как (прямоугольник) между AS, ST относится
к (квадрату) на SE, так будет и (прямоугольник) между АК, КГ,
то ость (квадрат) на АК, к (квадрату) па КВ, [так как оба отношения
будут равны отношению большой полуоси эллипса к параметру] *);
АХ ВГ = АККГ = А К8
XS3 ” КВ2 ” КВ2
*) sv Тй тт)8 nQog e--<nv—буквально «в отношении поперечной (гориеон-
талыюй) к прямой» -термины, заимствованные иа ^Конических сечений» Анопгюния (книга I. upc;i-
гпмвение 21). Если напишем уравнение эллипса в пиде
ia Ъ® «
ч'2 -- 2—к-з-х® или ——а’.
то рассматриваемое отношение будет равно отношению откладынасмий горизонтально большой
f,2
полуоси а к перпендикулярному ей параметру р =—эллипса. Поставленную в квадратных скоб-
ках фразу Гсйбсрг считает позднейшей вставкой вследствие у истребления принадлежащих Апол-
лонию терминов.
20 Архим ед
306
АРХИМЕД
как же (квадрат) иа ЛК к (квадрату) на КВ, так будет и (квадрат) иа
AS к (квадрату) на ЕП.
АКа _ АЕ2 Г AbST '!
КВ2 ЕП2 L= ЕЕ" J
Тогда после перестановки получится, что как (квадрат) на AS
к (прямоугольнику) между AS, ЕГ, так будет и (квадрат) на ITS
к (квадрату) на S3.
ле2 ПЕ2
АЕ-ЕГ~ 2Еа
Но как (квадрат) »на AS к (прямоугольнику) между AS, ЕГ, так
будет и (квадрат) па S1I к (прямоугольнику) между ЕП, ПМ;
ле2 ЕП2
ЛЕ ХГ~ XII-ПМ
значит, (прямоугольник) между МП, ПЕ будет равен (квадрату)
на BS,
мп ms=ss*
Прибавим общий (квадрат) иа FIS; значит, (прямоугольник) меж-
ду MS, S1I будет равен вместе взятым (квадратам) на ПЕ и
на ЕВ.
МП • ПЕ + ПЕ2 =» ЕЕ2 - ПЕ2
ME -ЕП = ПЕ2 ЕЕ2
След ока тел ь но, ©А будет относиться к АЕ, лак (квадрат) на .V1S
ко вместе взятым (квадратам) на НЕ и ЕВ. •
ел МЕИ
А2 ПЕ2 г ЯЕ2
’ Но как (квадрат) на MS ко вместе взятым квадратам па ЕП и SB,
так и круг в цилиндре с- диаметром MN будет относиться к обоим
кругам с диаметрами ПР и 03;
MS2 = круг MN
ПЕ2 ! ЕЕ2 круг IIP + круг OS
. таким образом, но отношению к точке А круг с диаметром MN, остава-
ясь в своем положении, будет уравновешиваться с обоими кругами на
диаметрах 30, ПР, если их перенести на рычаг в 0 так, чтобы центр
тяжести каждого круга был в точке 6.
(Но у круга с диаметром MN, остающегося в своем положении,
• центр тяжести будет в S), у обоих же кругов с диаметрами 30, ПР
после их перенесения центр тяжести будет в О; и, значит, как ©А
к AS, так будет и круг с диаметром MN к обоим кругам с диаметра-
ми ВО, ПР/
ВА круг MN
А.£ круг 20 -Ькруг п±*
Теперь, ее-тиУв^параляелограмме AZ параллельно EZ провести какую-
нибудь другую прямую и па проведенной прямой восставить плоскость,
перпендикулярную к АГ, то подобным же образом можно будет дока-
зать, что по отношению к точке А круг, получившийся в цилиндре.
ПОСЛАНИЕ К ЭРАТОСФЕНУ. О МЕХАНИЧЕСКИХ ТЕОРЕМАХ 307
оставаясь в своем положении, будет уравновешивать оба круга, полу-
чившиеся в сфероиде и в конусе, если перенести их на рычаг в © так,
чтобы центр тяжести каждого из них был в 0. Если такими кругами
заполнить как цилиндр, так и сфероид с конусом, то по отношению it точ-
ке А цилиндр, оставаясь в своем положении, будет находиться в равно-
весии со сфероидом и конусом, если перевести их на рычаг в (-) и поль-
стить так, чтобы центр тяжести каждого из них был в тонко (-). Но у ци-
линдра центролг тяжести будет точка К, у вместе взятых же сфероида
и конуса центром тяжести будет, как уже сказано, точка 0; тогда полу-
чится, что как 0А я АК, так и цилипдр будет ко вместе взятым сфероиду
и конусу. Но Л0 вдвое больше ЛК; значит, и цилиндр будет вдвое
больше, сфероида и конуса, вместе взятых: значит, один цилипдр будет
равен двум конусам и двум сфероидам. Но один цилипдр равен трем
таким конусам; значит, три конуса будут равны двум конусам и двум
сфероидам.
Отнимем общие два конуса; значит, остающийся конус с осевым
сечением — треугольником AEZ — будет равен двум сфероидам; но
тот же салгый единственный конус равен восьми конусам с осевым сече-
нием — треугольником АВ'Х; значит, воселгь упомянутых конусов
будут равны двум сфероидам и, следовательно, четыре конуса равны
одному сфероиду; значит, сфероид будет в четыре раза больше конуса,
у которого вершиной является точка А, а основанием — перпендикуляр-
ный к АГ круг на диаметре ВЛ, и половина сфероида будет вдвое боль-
ше упомянутого конуса.
Теперь в параллелограмме AZ через точки В, Д проведем прямые
ФХ, TQ, параллельные АГ, в вообразим цилиндр, у которого основа-
ниями будут круги па диаметре ФУ, Хй, а осью — прямая ЛГ. Этот
цилиндр с осевым сечением — параллелограммом Ф£2 — вдвое больше
цилиндра с осевым сечением — параллелограммом ФА, так как у них
основания равны и одна ось вдвое больше другой, сам же цилиндр
с осевым сечением — параллелограммом ФА — втрое больше конуса
с вершиной в точке А и с основанием — перпендикулярным к АГ кру-
гом на диаметре ВД; значит, цилипдр с осевым
сечением — параллелограммом Ф£2 — будет в
шесть раз больше упомянутого конуса. Но дока-
зано, что сфероид в четыре раза больше этого
самого конуса; значит, цилиндр будет в пол-
тора раза больше сфероида.
IV
его получится
Л что всякий сегмент прямоугольного ко-
ноида, отсеченный плоскостью, перпендикуляр-
ной к оси, будет в полтора раза больше ко-
нуса, имеющего с сегментом те же самые осно-
вания и высоту, при помощи тот'о же метода
можно обнаружить так:
Пусть будет прямоугольный коноид
{рис. 4}; рассечем его проходящей через ось
плоскостью, и пусть в сечении с поверхностью его получится
парабола АВГ; рассечем его также другой плоскостью, перпен-
дикулярной к оси, и пусть В Г будет общим сечением обеих этих пло-
скостей. Пусть ось сегмента будет ДА; продолжим ДА в сторону в.
20*
308_______' АРХИМЕД
• отложим ранную ей прямую А& и вообразим равноплечий рычаг Дв
•• ! с серединой А. Пусть основанием сегмента будет перпендикулярный
к АА круг на диаметре ВГ; вообразим конус, имеющий основанием круг
с диаметром ВГ, а вершиной точку А. Пусть будет также цилиндр,
имеющий основанием круг с диаметром ВГ, и ось АД; в полученом
параллелограмме проведем какую-нибудь параллельную ВГ прямую МН
и па этой прямой MX восставим перпендикулярную к АД плоскость;
она в сечепии с цилиндром образует круг, диаметр которого MN,
в сечении же с прямоугольным коноидом — круг, диаметр которого SO.
• • И так как ВЛГ — парабола, АД — ее диаметр и Е2, ВД будут
•’ч; проведенными ординатами, то как ДА к А2, так будут относиться
и (квадраты) на ВД и BS.
. АА —• ЕА* .
" АЕ E2s
Но ДА равна АО; значит, ОА относится к AS, как (квадрат) на М2
к (квадрату) па SB.
6А _М2®
ЛЕ"’ XS8
Но как (квадрат) на М2 к (квадрату) на 2Е, так и находящийся
в цилиндре круг с диаметром MN будет относиться к кругу с диамет-
ром ЕО в сегменте прямоугольного коноида,
MS2 круг MN
ЕВ® ’ «РУГ so
значит, ОД к AS будет, как круг с диаметром MN к кругу с диамет-
ром ЕО.
,9А .круг
АЕ — круг SO
Следовательно, находящийся в цилиндре круг с диаметром MN, оста-
ваясь в своем положении, будет относительно точки Л уравновешивать
круг с диаметром SO, перенесенный на рычаг О и помещенный так,
(чтобы его центром тяжести была точка) О. И (у круга с диаметром)
MN центром тяжести будет 2, у круга же с диаметром ЕО после его
перенесения центром тяжести будет О, и в обратной пропорционально-
сти ОД к AS имеет то же самое отношение, что круг с диаметром MN
к кругу с диаметром ЕО.
НА _ круг MN
аЗ: ’«руг =о
Теперь если в параллелограмме ЕГ параллельно ВГ провести какую-
нибудь другую прямую я иа этой проведенной прямой восставить пер-
левдикулярную к АО плоскость, то можно будет подобным же образом
доказать, что полученный в цилиндре круг, оставаясь в своем положе-
нии, будет относительно точки А уравновешивать полученный в сегмен-
те прямоугольного коноида круг, перенесенный на рычаг в 6 так, чтобы
его центром тяжести была точка О. Если таким образом заполнить
и цилиндр, и сегмент прямоугольного коноида, то остающийся в своем
: положении цилиндр букет относительно точки Л уравновешивать сег-
мент прямоугольного коноида, перенесенный в О па рычаг и помещен-
ный так, чтобы его центр тяжести был в О. Поскольку же упомянутые
ПОСЛАНИЕ К ЭРАТОСФЕНУ. О МЕХАНИЧЕСКИХ ТЕОРЕМАХ
309
величины уравновешиваются относительно точки А и если разделить
АД в точке К пополам, полученная точка К будет центром тяжести
цилиндра, а у перенесенного сегмента центром тяжести будет 0, то
в обратной пропорциональности 0А будет иметь к АК то же самое
отношение, что цилиндр к сегменту. Но 0Л вдвое больше АК; значит,
и цилиндр вдвое больше сегмента.
Но этот же самый цилиндр втрое больше конуса, имеющего основани-
ем круг с диаметром В Г, а вершиной точку А; теперь ясно, что сегмент
будет в полтора раза больше этого самого конуса.
V
А что у сегмента прямоугольного коноида, отсеченного плоскостью,
перпендикулярной к оси, центр тяжести будет на оси сегмента е точ-
ке, делящей ее таким образом, чтобы прилегающая к вершине ее часть
была вдвое более остающегося отрезка,
этим методом усматривается так:
Пусть будет сегмент прямоуголь-
ного коноида, отсеченный перпенди-
кулярной к оси плоскостью {рис. 5}.
Рассечем его другой плоскостью, про-
ходящей через ось, и пусть в сечении *
ее с поверхностью получится парабола
АВГ; пусть ВГ будет общим сечением
этой секущей плоскости с той, кото-
рая первоначально отсекла сегмент.
Пусть осью сегмента и диаметром па-
раболы АВГ будет прямая ЛА; (про-
должив ДА. отложим равную ей пря-
мую А0 и) вообразим равноплечий
рычаг Л6 с серединой А. Пусть также
в сегмент будет вписан конус с боковыми сторонами ВА и АГ. В па-
раболе проведем какую-нибудь прямую ЕО, параллельную ВГ, и пусть
опа пересечет параболу в точках 3, О. стороны же конуса в точ-
ках П, Р.
Гак как в параболе опущены на диаметр перпендикуляры ES, ВД,
то ДА будет к АХ, как (квадрат) па ВД к (квадрату) на ЕХ.
АА ВА*
as S2s
Но паи ЛА к АХ, так будет и ВД к П2;
аа вд
лх _ П2
а как ВД к ПХ, так будет и (квадрат) ВД к (прямоугольнику) между
ВД, ПХ;
ВД ВЛ4
ПЕ ВЛ- ПХ
следовательно, получится, что (квадрат) на ВД к (квадрату) на ЕХ
будет, нал (квадрат) на ВД к (прямоугольнику) на ВЛ, ПХ.
вд* вд*
su* 'вд-ns
310
АРХИМЕД
Значит, (квадрат) на SX будет равен (прямоугольнику) менаду
ВД-ПХ;
SEa- ВД-111!
поэтому ВД, ХЕ, ХП составляют (непрерывную) пропорцию,
вд _ ГЕ
ЕЕ ЕП
и вследствие этого ВД к ПХ будет, как (квадрат) па ВХ к (квадрату)
на ХП.
вд _ ее8
ПЕ ХП8
По как ВД к ПХ, так будет и ДА к АХ, то есть 0А к АХ,
вд да = ел
ПЕ АЕ - ЛЕ
и, значит, как ®А к АХ, так и (квадрат) на ВХ к (квадрату) па ХП-
ОА ЕЕ3
АЕ sn2
Теперь восставим на SO перпендикулярную к АД плоскость; она
в сегменте прямоугольного копоида образует круг с диаметром ВО,
в конусе же — круг с диаметром ПР. И поскольку 0А к АХ, как
(квадрат) па SX к (квадрату) па XIT, а как (квадрат) па ВХ к
(квадрату) на ХП, так будет и круг с диаметром ВО к кругу с диа-
метром ПР,
ЕЕ8 круг ВО
ЕП2 «РЬ’1* ПР
то, значит, 0А будет к АХ, как круг с диаметром ЕО к кругу с диа-
метром ПР.
вА __ круг ВО
ЛЕ — круг нр
Значит, круг с диаметром ЕО, оставаясь в своем положении, уравнове-
сит относительно точки А круг с диаметром ПР, перепосенный на ры-
чаг в 0 так, чтобы центром его тяжести была точка 0. Теперь так как
у остающегося в своем положении круга с диаметром ЕО центром тя-
жести является X. у перенесенного же круга с диаметром ПР центром
тяжести будет, как сказано, точка 0 и в обратной пропорциональности
6 А к АХ имеет то же отношение, что круг с диаметром SO к кругу с
диаметром ПР, то, значит, эти круги будут по отношению к точке А
уравновешиваться.
Теперь если в параболе параллельно ВГ провести какую-нибудь
другую прямую и на проведенной прямой восставить плоскость, пер-
пендикулярную к ЛД, то подобным же образом можно будет доказать,
что полученный в сегменте прямоугольного коноида круг, оставаясь
в своем положении, уравновесит относительно точки А полученный в ко-
нусе круг, перенесенный па рычаг в 0 и помещенный так, чтобы его
центром тяжести была точка 0. Если теперь такими кругами запол-
нить и сегмепт, и конус, то все круги в сегменте, оставаясь в своих поло-
жениях, будут относительно точки А уравновешиваться со всеми круга-
ми в конусе, перенесенными на рычаг в 0 и помещенными так, чтобы
ПОСЛАНИЕ К ЭРАТОСФЕНУ, О МЕХАНИЧЕСКИХ ТЕОРЕМАХ
311
их центром тяжести была точка 0; тогда и сегмент прямоугольного
коноида, оставаясь в своем положении, будет уравновешивать относи-
тельно точки Л копус, перенесенный па рычаг в © и помещенный тан,
чтобы: его центром тяжести была точка 0. Далее, так как у обеих вели-
чин *), рассматриваемых как одна, центром тяжести является А,
а у конуса после перенесения центром тяжести будет 0, то, значит, у ос-
тавшейся величины **) центр тяжести будет на прямой А0, если продол-
жить ее за А и отложить на пой такую прямую АК., чтобы А© имела
к пой то же отношение, что сегмент к конусу. Но сегмент в полтора
раза больше конуса; значит, и ©А будет в полтора раза больше ЛК,
и центром тяжести (сегмента) прямоугольного коноида будет точка К,
разделяющая прямую АЛ так, чтобы часть ее при вершине сегмента
была вдвое больше остающегося отрезка.
VI
Центр тяжести всякого полушария находится на прямой, являю-
щейся его осью, если рассечь ее так, чтобы прилегающий к поверхности
полушария отрезок ее имел.
. к остающемуся отрезку то
же отношение, что пять к у м
трем.
Пусть будет шар {рис. б};
рассечем его плоскостью,
проходящей через центр, и
пусть в сечении с поверхно-
стью получится круг АВГД.
Пусть АГ, ВЛ будут вза-
имно перпендикулярные диа-
метры круга; восставим на
ВД плоскость, перпендику-
лярную к АГ. Пусть, далее, будет конус, имеющий основанием круг на
диаметре ВД, а вершину в точке А, и пусть ВА, АД будут боновые
стороны конуса. Продолжим ГА, отложим А©, равную ГА, и вообра-
зим, что прямая ©Г будет равноплечим рычагом с серединой в Л.
В полукруге ВАД проведем какую-нибудь параллельную ВД прямую
ЕО, и пусть опа пересечет окружность полукруга в точках Н, О,
боковые стороны конуса в точках II, Р, а прямую АГ в Е. Восставим
на ЕО плоскость, перпендикулярную АЕ; пусть она в полушарии
образует круг с диаметром ЕС), а в конусе круг с диаметром ПР.
Поскольку мы имеем, что ЛГ к АЕ будет, как (квадрат) па ЕА
к (квадрату) на АЕ, • •• ••
АГ- ВА2
АЕ = А14В ’
я (квадрат) на ЗА равен вместе взятым (квадратам) на АЕ и ЕЕ,
ЁА2 — АЕ2 I- ЕЕ2
а АЕ равна ЕП, то, значит, АГ будет к АЕ, как вместе взятые (квадра-
ты) на ЗЕ и ЕП к (квадрату) на ЕП.
АГ _ ЕЕ2 ЕЦ2
ЛЕ — ЕЦ2..............'.............._____________________________________
*) То есть и сегмента, и конуса,
** ) То есть сегмента.
312
АРХИМЕД
Но как (квадрат) на ЕЕ вместе с (квадратом) на ЕП будут к (квадра-
ту) па ЕП, так и круг па диаметре ВО вместе с кругом па диаметре ПР
будут относиться к кругу па диаметре ПР. И ГА равна АО; значит,
как ©А к АЕ, так и круг на диаметре ВО вместе с кругом на диаметре
ПР будут к кругу на диаметре ПР.
gA _ круг £0 4- Круг ПР
АВ круг ПР
Значит, оба круга с диаметрами ЕО, ПР, оставаясь в своих положениях,
уравновесят относительно точки А круг с диаметром ПР, перенесен-
ный в 8 так, чтобы его центром тяжести была точка О. Теперь, так-
как у обоих остающихся в своих положениях кругов с диаметрами ВО,
IIP центром тяжести является Е, у перенесенного же круга с диа-
метром ПР центром тяжести будет 0, то как ЕА к А 8, так и круг
с диаметром ПР относится к кругам с диаметрами ЕО, ПР,
ВА _ круг ПР
АО круг SO -г круг ПР
Подобным же образом если мы в полуокружности *) проведем какую-
нибудь другую прямую, параллельную ВНД, и на проведенной прямой
восставим перпендикулярную к АГ плоскость, то оба круга, получен-
ные в полушарии и в копусе, оставаясь в своих положениях, будут
относительно точки Л уравновешивать получившийся в конусе круг,
перенесенный на рычаг и помещенный при 8. Теперь если такими кру-
гами заполнить и полушарие, и конус, то все круги в полушарии и в ко-
нусе, оставаясь в своих положениях, уравновесят относительно точки
А все круги в копусе, перенесенные на рычаг в 8 и помещенные так,
чтобы центром их тяжести была точка 8; таким образом, полушарие
и конус, оставаясь в своих положениях, уравновесят относительно'
точки Л копус, перенесенный на рычаг в 8 и помещенный так, чтобы
его центром тяжести была точка 0... **).
(Пусть цилиндр MN, подвешенный в 0, равен конусу АВД; рассечем его пло-
скостью, перпендикулярной к оси, так, чтобы цилиндр М уравновешивал относительно-
точки Л конус АВД; тогда остающаяся часть цилиндра N будет уравновешивать
полушарие.
Возьмем теперь да прямой АН такую точку Ф, чтобы АФ была втрое больше ФИ,
тогда Ф будет центром тяжести копуса А ВЛ. Затем возьмем такую точку X, чтобы АН
относилась к ЛХ, как 8 к 5. Так как цилиндр М уравновешивает копус АВД относи-
тельно точки А, то, значит, цилиндр М будет к конусу АВД, как ФА к 6А или как 3 к 8.
Но конус АВД равен всему цилиндру MN; значит, цилиндр ММ будет относиться к своей
части М, как 8 к 3; значит, остающаяся часть X будет относиться ко всему цилиндру,
как 5 к 8, или копус А ВЛ будет относиться к цилиндрической части N, как 8 к а или как
АН к АХ).
И так как шар в четыре раза больше конуса, основанием которого
является круг на диаметре ВД, а осью прямая АН, то...
{...полушарие будет относиться к конусу, как 2 к 1, то есть как Ав к АП. Значит, «не-
равенству» получится, что полушарие будет к цилиндру X, как А0 к АХ. Но цилиндр
N с центром тяжести О относительно точки А уравновешивает полушарие; значит, цен-
тром тяжести полушария будет точка X, рассекающая ось так, чтобы ее часть, прилегаю-
щая к поверхности нолушара, относилась к оставшемуся отрезку, как 5 к 3).
*) В подлиннике ошибочно «в Сечении прямоугольного конуса-». то есть в параболе.
‘Ч Остальная часть предложения, аа исключением одной фразы, утрачена. В .угловых скобках
дается реконструкция, помещенная в издании Гейберга.
ПОСЛАНИЕ К ЭРАТОСФЕНУ. О МЕХАНИЧЕСКИХ ТЕОРЕМАХ
313
VII
При помощи того Hie метода можно обнаружить, что всякий сфери-
ческий сегмент относится к конусу с теми же самыми основанием
и осью, что вместе взятые радиус шара и высота оставшегося сегмента
к высоте оставшегося сегмента * •*)).
(Пусть оудет шар с оольптим кругом АВГД и взаимно лериспдикулярвыми диа-
метрами АГ, ТТ {рис. 7J; рассечем его перпендикулярной к А)’ плоскостью, которая
образует сегмент, имеющий основанием круг на диаметре ВА, и пусть ВД пересекает
прямую АГ в точке Н: на полученном круге построим конус с вершиною А. Затем
па круге, описанном па диаметре ТУ, построим конус с той же вершиной А; по-
верхность этого копуса, будучи продолжена, пересечет плоскость, проведенную
через ВЛ, и образует в сечении
круг с. диаметром EZ; в этой же
самой плоскости из центра И ра-
диусом, равным прямой АГ, опи-
шем круг с диаметром КЛ и ла
этом круге построим цилипдр с
осью АН, прямоугольное осевое
сечение которого будет ФА. За-
тем, продолжив в обе стороны
прямую АГ, отложим ГС2, рав-
ную радиусу тара, и А0, равную
ЛГ; вообразим, что Г® будет
равноплечим рычагом с середи-
ной А.
Теперь в параллелограмме
ФА параллельно БД проведем
прямую MN, и на этой прямой)
1MN восставим пло-
скость, перпендикуляр-
ную к АГ; она в сечении
с цилиндром образует
круг с диаметром MN,
в сечении же со сфериче-
Рпс. 7.
ским сегментом—круг с диаметром ЕО, в конусе же, у которого основа-
ние—круг на диаметре EZ, а вершина в точке Л, она образует круг с
диаметром ПР. Затем подобно предыдущему докажем, что круг с диамет-
ром MN, оставаясь в споем положении, относительно точки А уравнове-
сит оба круга с диаметрами SO, ПР, если их перенести па рычаг в О так,
чтобы центром тяжести каждого из них была точка 0; то ate самое мож-
но будет доказать и по отношению ко всем таким кругам. Теперь, если
такими кругами заполнить и цилиндр, и конус, и сферический сегмент,
то цилиндр, оставаясь в споем положении, уравновесит (относительно
точки А) вместе взятые копус и сферический сегмент, перенесенные на
рычаг и помещенные в 0. Рассечем ЛН в точках Ф, X так, чтобы АХ
была равна XII, а НТ была третьей частью АП; тогда центром тяжести
цилиндра будет точка X, ибо она является серединой оси АН. Теперь,
так как упомянутые тела * *) относительно точки А находятся в равнове-
сии, то цилипдр будет относиться ко вместе взятым конусу с диаметром
основания EZ и сферическому сегменту ВАЛ, как 0А к АХ. И так как
ИА втрое больше НТГ, то (прямоугольник) между ГИ, IIЧ7 будет
*) Дальше в подлиннике испорченное место, восстанавливаемое по образцу предложении И.
•*) В подлиннике характерное выражение «jievtfHio-величины.
314
АРХИМЕД
третьей частью (прямоугольника) между АН, НГ.
гн-н1р = 4-ан-нг
Но (прямоугольник) между АН, НГ раней (квадрату) на НВ;
АН-НГ=НВв
тогда (прямоугольник) между ГН, HW будет третьей частью (квадрата)
па ВН *).
ГН •НФ’--4-ВЦ2
(Но квадрат ла ATI равен утроенному прямоугольнику между ЛН, НТ или утроен-
ному прямоугольнику между tAX, АТ.
ЛИ*—ЗАТЫ1Т—ЗЛХ-АТ,
так как АП к ЛХ будет, как ЛТ к TH, или как два к единице.
И так как ©Л равна К. II и ЛН равна НЕ, то квадрат на в А будет относиться
К третьей части квадрата на ЛИ, как цилиндр с основанием - - кругом па диаметре КЛ—
к конусу AEZ:
0А; ___цилиндр КА
1 д — конус AEZ
<>
Но квадрат па НА относится к третьей части квадрата ла АВ, как квадрат на ©А к прямо-
угольнику между АХ-АТ:
©А2 _ ©А2
1 ~ЛХ-АТ’
-у АН2
иоатому как квадрат па ©Л к прямоугольнику между АХ, ЛТ, таи будет и цилиндр
к конусу).
/Доказано же, что как 0А к ЛХ, так будет и цилиндр с основанием—
кругом на КЛ—к шаровому сегменту АВД и конусу.
НЛ цилиндр ФА_______
ЛХ сегмент АВД-|-конус AEZ
(И ©Л равна АГ, или ЛТ с ТГ):
значит, как квадрат на НА ко вместе
(взятым прямоугольникам между ЛТ, АХ и ТГ, АХ, так будет относиться и цилиндр
к сегмепту АВД вместе с конусом AEZ
НЛ ©А2 ©Л2 ©А2 цилиндр ФЛ
АХ “ ©лТлХ' “CAT ТГ )АХ ЛТ • АХ-|- ТГ • ЛХ “ сегмент ЛВД~ конус AEZ ’
Отсюда езгедует, что цилиндр будет относиться к сегменту, как квадрат па ©А к прямо-
угольнику между ТГ, ЛХ:
цилиндр ФЛ ©А2
сегмент АВД — ТГ • АХ "
Но цилиндр к конусу ЛВЛ относится, как квадрат па ©А к третьей части квадра-
та па ВН:
* цилиндр ФЛ _ ©А2
"копус'ЛВГ 1 п„2 ’
*) Дальше в подлиннике Испорченное место, которое может быть приблизительно яосстацов-
«тено на осноьакии достаточно большого количества сохранившихся отрывочных слои. ,
ПОСЛАНИЕ К ЭРАТОСФЕНУ. О МЕХАНИЧЕСКИХ ТЕОРЕМАХ
315
а» квадрат на 0А. к третьей части квадрата на ВН будет, как квадрат на НА к прямо
угольнику между ГЛ, I1Y *);
НА* НА*
1 „„.“ГН нт-
-Значит, сегмент АВД будет относиться к конусу АВЛ, как прямоугольник между ЧТ,
АХ к прямоугольнику между ГН, ЦЧЛ. Нискольку же АП вдвое больше АХ и 'равна
вместе взятым Л¥ и Ч'П, то есть трем ЧЧ1, а ЧТ равна ЧП? с IIГ, то есть трети АН и НГ,
то прямоугольник между ’ГГ, АХ будет равен имеете взятым прямоугольникам между
-АН, А УН и НГ, 4УН:
-О Z /5
УГ ЛХ =4 АН.4^11 : нг. 4 Ч'Н,
или прямоугольнику между УН н ~ 1’
УН и НЯ:
nr).
то есть
прямоугольнику между
УГ-АХ^УП^у АН i4-НГ | НГ^У11^4ЛГ г 1,1
УН НО.
Таким образом получается, что сегмент АВЛ будет относиться к конусу ЛВД, как HQ
к ПГ>* **).
VIII
Подобным же образом можно обнаружить, что всякий сегмент, сфе-
роида, отсеченный плоскостью, перпендикулярной {к оси), будет отно-
ситься к конусу, имеющему с сегментом те. же самые основания и ось,
как вместе взятые полуось сфероида и ось противолежащего сегмента
относятся к оси противолежащегося сегмента ***).
IX
У всякого сферического сегмента центр тяжести находится на
той же прямой, которая будет и осью сегмента, если разделить ее
так, чтобы часть ее при вершине сегмента имела к остатку то же
самое отношение, какое вместе взятые ось этого сегмента и учетверен-
пая ось противолежащего сегмента имеют ко вместе взятым оси это-
го сегмента и удвоенной оси противолежащего сегмента.
(Пусть будет шар {рис. 8}; отсечем от него некоторой плоскостью сегмент, пусть при
сечении шара другом плоскостью, проходящей через центр и перпендикулярной к
нерпой, получается в сечении с поверхностью шара круг АВГД),
в сечении же »***) с нлоскостыо, отсекшей сегмент,— прямая ВД;
пусть также прямая ГА будет диаметром, перпендикулярным к пря-
мой ВД, и пересечет ос в точке Н; таким образом, у того сегмента, вер-
шина которого находится в точке А, осью будет прямая АН, у противо-
лежащего же сегмента осью будет НГ. Разделим прямую АН в точке X
«) Так как ВН’=АН. ГН-З'ЕН. ГП.
**) Нужно иметь в виду, что прямая ГО по построению равна радиусу шара или - АГ. Далее
мы имеем:
сегмент АВЛ Wr-AX __ УП-НВ ПО
«опус АВЛ ГН-Н.Ч' ГП-llV -ГН
«**) Доказательство этого предложения ем. в Комментарии {41.
*«**) Начало утрач?но; формулировка предложения восстанавливается по типу предложении л-.
316
АРХИМЕД
так, чтобы АХ относилась к ХН, как ЛН вместе с учетверенной НГ
к АН вместе с удвоенной НГ.
АХ АП+4ПГ
ХН " АН -Г 2ПГ
Я утверждаю, что у того сегмента, вершина которого в точке А, цент-
ром тяжести будет X.
сте взятых . . . свгме .... вершина которого . - точка . . ..
НА. . . име...........точку Н. Отношение...........центр . . .X.
Если . . . рассечь .........игур . - . очк...........вот в . . .
сто взят . . .*) и продолжим АГ, отложим равную ей прямую АО и
ранную радиусу шара прямую ГЕ; затем вообразим равноплечий рычаг
ГО с серединою Л. В плоскости, отсекающей сегмент, опишем круг с-
центром Н и радиусом, равным АН, и па этом круге построим конус,
имеющий вершину в точке А; пусть боковые стороны копуса будут АЕ
и AZ. Параллельно EZ проведем какую-нибудь прямую КЛ; пусть она
встретится с окружностью сегмента в точках К, Л, с боковыми сторо-
нами конуса AEZ в точках Р, О, а с прямой ЛГ в точке П. Теперь,
поскольку ЛГ относится к ЛП, как (квадрат) па КА к (квадрату) на
АП,
АГ _ КА2
АГ* АН2
и (квадрат) на КА равен вместе взятым (квадратам) на АП и ПК,
кл2 = лп8 + пкя
(квадрат) же па АП равен (квадрату) на ПО,
ап4« по2
ибо (квадрат) на АН равен (квадрату) на ЕН, то, значит, как ГА
к АП, так будут вместе взятые (квадрат) на КП и (квадрат) на ПО
к (квадрату) на ОН.
га = кп2-|- по2
АП он2
*) Относительно этих пяти с половиной строк, которым соответствует 11 строк первоначаль-
ной рукописи, Гсйберг делает примечание: «Восполнить эти строки не могу, так как нс вижу, чегм
не хватает для подготовки доказательства».
ПОСЛАНИЕ К ЭРАТОСФЕНУ. О МЕХАНИЧЕСКИХ ТЕОРЕМАХ
317
Но кап вместе взятые (квадраты) па КН и на ПО к (квадрату) на ПО,
так будут и вместе взятые круги па диаметрах КЛ и ОР к кругу па
диаметре ОР.
И ГА равна АО; значит, как О Л к АП, так будут и круги па диа-
метрах КЛ и ОР к кругу на диаметре ОР.
8А круг КА + яруг ОР
АП “ кругОР
Теперь, так как вместе взятые крути на диаметрах КЛ, ОР относятся
к кругу па диаметре ОР, как АО к ПА, то переставим круг на диаметре
ОР и поместим его на рычаг в 0 так, чтобы его центром тяжести была
точка 0; значит, как ОЛ к АП, так и круги па диаметрах КЛ и ОР,
оставаясь в своих положениях, будут относиться к кругу па диаметре
ОР, перенесенному на рычаг в 0 и помещенному так, чтобы его центром
тяжести была то'нга 0; алавит, круги в сегменте ВАЛ и в конусе AEZ
будут уравновешивать относительно точки А круг в конусе AEZ.
Подобным же образом и все круги в сегменте ВАД и в конусе AEZ,
вместе взятые, оставаясь в своих лолоткешиях, будут уравновешивать
относительно точки А все круги в конусе AEZ, перенесенные на рычаг
в 0 и помещенные так, чтобы у них центром тяжести была точка 0;
таким образом, сферический сегмент АВД вместе с конусом AEZ,
оставаясь в своих положениях, будут уравновешивать относительно
точки Л конус EAZ, перенесенный на рычаг в 0 и помещенный так,
чтобы его центром тяжести была точка 0. Пусть теперь конусу, имею-
щему основанием круг па диаметре EZ и вершиной — точку А, будет
равен цилиндр MN. Рассечем АН в точке Ф так, чтобы АН была в че-
тыре раза больше ФИ; тогда точка Ф будет центром тяжести конуса EAZ
(ибо это уже было написано раньше), (лемма 10). Затем перпендикуляр-
ной (к оси А0) плоскостью рассечем цилиндр MN так, (чтобы цилиндр
М) уравновешивался с конусом EAZ. Теперь так как вместо взятые
конус EAZ и сегмент АВД, оставаясь в своих положениях, уравновеши-
ваются с конусом EAZ, перенесенным на рычаг в 0 и помещенным так,
чтобы его центром тяжести была точка 0, и так как цилиндр MN
равен конусу EAZ, каждый из цилиндров М и N расположен при 0
и цилипдр MN уравновешивается со вместе взятыми сегментом и копу-
сом, то цилипдр N будет относительно точки А уравновешивать сфери-
ческий сегмент. И [поскольку] сферический сегмент ВЛД относится
к конусу, основанием которого является круг на диаметре ВД, а вер-
шиной — точка А, как 8Н к НГ,
сегмент ВАД _ ЕН
гетпус ВАЛ ~ НГ
ибо это написано раньше (предложение VII). Но как конус ВАД к ко-
нусу EAZ, так и круг на диаметре ВД к кругу на диаметре EZ,
конус ВАД_круг ВЛ
конус EAZ круг 1CZ
а как один круг к другому, так и будет и (квадрат) па ВП к (квадрату)
на НЕ,
круг ВД _ ВНД
круг EZ " HES
и (квадрат) на ВН равен (прямоугольнику) между ГН, ПА;
вна = ГН-НА
318
АРХИМЕД
а квадрат на НЕ равви квадрату на ПА; и, наконец, (прямоугольник)'
между ГН и НА к (квадрату) на НА относится, как ГН к НА;
ГИЛА гн
НА2 НА
значит, как копус ВАД к конусу EAZ, так будет и ГП к НА. Но выше
было доказано, что конус ВАД к сегменту ВАД относится, как ГН к НЕ;
конус ВАД ГН
сегмент Вад ~ НЕ
значит, «по равенству» — как сегмент ВАД к конусу EAZ, так будет
и ЕП к ПА- И нескольку ЛХ относится к ХН, как НА вместе с учет-
веренной НГ к АН с удвоенной НГ,
ах _ ид-миг
ХН АН + 2НГ
то и «обратно» — как ПХ к ХА, так и удвоенная ГН вместе с НА будет
к учетверенной ГН вместе с НА.
НХ 2ГН + НА
ХА 4ГП НА
Отсюда «присоединением» получится, что НА будет к ЛХ, как ушесте-
ренная ГН вместе с удвоенной НА будут к НА вместе с учетверенной II Г.
НА 6ГН + 2НА
АХ ИА+4НГ
И четвертой частью ушестеренной ГП вместе с удвоенной ПА
будет НЕ;
бгнч-гнл
-i “
для учетверенной же НГ вместе с НА четвертой частью будет ГФ
(это действительно очевидно) *); значит, как НА к АХ, так будет
к ЕП к ГФ;
НА = ЕН_
ЛХ ' ГФ
таким образом, ЕН будет к ПА, как ГФ к ХА.
ЕН _ ГФ
НА ' ХА
Но было доказано, что как ЕП к ПА, так и сегмент с вершиной в точ-
ке Л и с основанием — кругом на диаметре ВД — относится к конусу
с вершиной в точке Л и основанием — кругом на диаметре EZ.
Значит, как сегмент ВАД к конусу EAZ, так будет и ГФ к ХЛ.
И так как цилиндр М по отношению к А уравновешивает конус EAZ,
и у цилиндра ( М) центром тяжести будет 0, у конуса же EAZ центром
тяжести будет Ф, то, значит, получится, что конус EAZ будет относить
ся к цилиндру М, как 0Л к АФ, то есть как ГА к АФ. И конус EAZ
•) В самом деле:
ГФ = ГН -) НФ -= ИГ 4- ИА,
НЕ ИГ -1- ГЕ - НГ 1-4- АГ ИГ -г Г—А
— £>
ПОСЛАНИЕ К ЭРАТОСФЕНУ. О МЕХАНИЧЕСКИХ ТЕОРЕМАХ
31‘)
равен цилиндру MN; значит, после «выделения» *) цилипдр MN будет-
к цилиндру -X', как АГ к ГФ.
цилиндр MN_. АГ
ЦП ЛИНД]! N 1*|>
Но цилиндр MIX район конусу EAZ; значит, конус EAZ будет к цилинд-
ру N, как ГА к ГФ, то есть как 0А к ГФ.
кину с EAZ ГА НА
цилипдр X — ГФ ГФ
Но было доказано, что сегмент ВАД относится к конусу EAZ, как ГФ
к ХА;
СГГМИНТ ВАД __ ГФ
конус EAZ ”' ХА
значит, «ио равенству» будет, что как сегмент АВД к цилиндру W, так
и 0А к /XX.
сегмент А ВД_ 6А
цилиндр N АХ
И было доказано, что сегмент ВАД ио отношению к Л уравновешивает
цилиндр N, а у цилиндра N центром тяжести является точка 0; значит,
у сегмента ВАД центром тяжести будет точка X.
X
Подобно этому можно обнаружить, что у всякого сегмента сферои-
да центр тяжести находится на той же прямой, которая будет и осью
сегмента, если разделить ее так, чтобы часть ее при вершине сегмента
имела к остатку то же самое отношение, какое вместе взятые ось это-
го сегмента и учетверенная ось противолежащего сегмента имеют ко
вместе взятым оси этого сегмента и удвоенной оси противолежащего
сегмента [5J.
XI
При помощи того же метода можно обнаружить, что всякий сег-
мент тупоугольного коноида **) имеет к конусу с теми же самыми осно-
ванием и высотой такое же отношение, как вместе взятая ось сегмента
и утроенная «добавленная к оси» ***) ко вместе,взятым оси сегмента коно-
ида и удвоенной «добавленной к оси», и что центр тяжести {сегмента}
тупоугольного коноида {получится}, если рассечь ось так, чтобы от-
резок при вершине имел к остатку то же самое отношение, какое утро-
енная ось вместе с увосьмеренной «добавленной к оси» имеют к оси того же
самого коноида вместе с учетверенной этой самой «добавленной к ней».
”) Правильнее было сиаеать «переворачивая» («vaarpeHiavri); деСстлитслыю, операции «выде-
ления» состоит в том, что на пропорции и : Ь = с : d получается пропорция («—») : »=(<:—Д) : <1,
операции же «переворачивания» приводит к пропорции (а—Ъ) : а—(с -d) : с. В нашем случае
цилиндр MN ГА цилипдр MN — цилиндр М _ АГ — АФ ГФ
цп.тцидр М - /\Ф ’ ’ цилиндр ММ АГ — АГ
откуда «обращением»
цилиндр MN _ АГ
цилиндр N ГФ
"*} Так Архимед называет то. что мы назвали бы одной полостью двуполого гиперболоида вра-
щении.
***) Так Архимед называет действительную полуось гиперболы.
320
АРХИМЕД
И из многих других . . . обнаруживаемых . . . мы опустим - . . ,
так как рассматриваемый метод достаточно разъяснен всем вышесказан-
ным*} [6|.
ХИ
При помощи того же самого метода можно обнаружить, что если
в прямую призму с квадратными основаниями вписать цилиндр, у ко-
торого основания расположены на противоположных квадратах, а по-
верхность касается остальных четырех [параллелограммов} граней,
и провести плоскость через центр круга,
являющегося основанием цилиндра, и одну
из сторон противолежащего квадрата, то
фигура, отсеченная проведенной плоско-
стью, составляет шестую часть всей приз-
мы. Показавши, (как это делается при
помощи механического метода), мы в даль-
нейшем дадим геометрическое доказатель-
ство.
Вообразим прямую призму с квадрат-
ными основаниями и в этой призме впи-
санный, как сказано, цилиндр; пусть
параллелограмм АВ будет сечением содер-
жащей цилиндр призмы плоскостью, пер-
пендикулярной к той, которая отсекла цилиндрический сегмент, а общим
сечением плоскости, отсекшей от цилиндра сегмент, и той плоскости,
которая была проведена через ось перпендикулярно отсекшей от цилин-
дра сегмент, пусть будет прямая ВГ{рис. 9}; пусть, далее, осью цилиндра
и призмы будет при-мая ГД, и пусть прямая EZ рассекает ее под пря-
мым углом и пополам; проведем через EZ плоскость, перпендикуляр-
ную к ГД; она в сечении с призмой образует
квадрат, в сечении же с цилиндром — круг
{рис. 10}. Пусть сечением призмы будет
квадрат MN, а сечением цилиндра — круг
ЕОП Р, и пусть этот круг касается сторон
указанного квадрата в точках 3, О, 11, Р;
пусть общим сечением плоскости, отсекшей
от цилиндра сегмент, и плоскости, проведен-
ной через EZ перпендикулярно к оси цилин-
дра, будет прямая КЛ; прямая ПОЗ пересечет
ее пополам **).
В полукруге ОПР под прямым углом к
ПХ проведем некоторую прямую 2JT и вос-
ставленную на £Т перпендикулярно к 311
Рис. 10.
плоскость продолжим в обе стороны от плоскости, в которой находится
кругЗОПР; в сечении с полуцилиндром, основанием которого является
*) Конечную фразу можно дополнить так: «и из многих других < теорем?, обнаруживаемы к
отпм же методом, остальные; мы опустим (<ои> np.oiXirtopev <ие> возьмем)...»-
После слова «опустим» в подлиннике идет непонятнее слово он . • • но; с сомнительными бук-
вами о и ш.
»•) Оба рис. 9 и 10 представляют своего рола вертикальную и горизонтальную проекции рас-
сматриваемой геометрической фигуры. Однако не нужно забывать, что по существу дела обе они
являются двумя взаимно перпендикулярными сечениями, проведенными через центр призмы.
ПОСЛАНИЕ К ЭРАТОСФЕНУ. О МИХАПИЧКСКПХ ТЕОРЕМАХ
321
полукруг ОПР, а высотой — ось призмы, она образует параллелограмм,
у которого одна сторона равна ST, а другая будет образующей цилинд-
ра; в сечении же с сегментом, отсеченным от цилиндра, опа образует
параллелограмм, у которого одна сторона раина ST, а другая NT;
таким образом, прямая NT должна быть так проведена в параллело-
грамме ДЕ {рис. 9}, чтобы опа, будучи параллельна ВЕ1, отсекла пря-
мую EI, равную 11Х. Так как ЕГ является параллелограммом, прямая
NI параллельна 0Г н через них проведены прямые Е0 и ГВ, то полу-
чится, что как Е0 к 01, так и £2Г к ГХ, то есть В£2 к T1N.
во _ тог _ _ш>_
«Г- гк = гк
По как BQ к Г.Х, так и получившийся в полуцилиндре параллелограмм
будет относиться к параллелограмму, получившемуся в отсеченном
от цилиндра сегменте, ибо у обоих параллелограммов будет одна и та же
сторона ST. Далее, Е0 равна 011, а 10 равна Х0 *); и так как П0
равна 0Н, то, значит, как 03 к 0Х, так и получившийся в полуцилинд-
ре параллелограмм относится к тому, который получился в отсеченном
от цилиндра сегменте.
Вообразим, что получившийся в сегменте параллелограмм перенесен
и помещен в Е так, чтобы его центром тяжести была точка 3; затем
вообразим рапноплечий рычаг ПЗ с серединой в 0; тогда параллело-
грамм в полуцилиндре, оставаясь в своем положении, будет по отноше-
нию к точке 0 уравновешиваться с параллелограммом, получившимся
в цилиндрическом сегменте, перенесенным па рычаг n Е и помещенным
так, чтобы его центром тяжести была точка Е. И так как у получивше-
гося в полуцилиндре параллелограмма центром тяжести является X,
а у получившегося в отсеченном сегменте и перенесенного параллело-
грамма центром тяжести ялястся Е, и 0Е будет к 0Х так же, как
параллелограмм, имеющим, как мы сказали, центром тяжести точку X,
будет относиться к параллелограмму, имеющему, как мы сказали,
центром тяжести точку Е, то, значит, по отношению к точке 0 паралле-
лограмм с центром тяжести X будет уравновешиваться с параллелограм-
мом, у которого центр тяжести в Е. Подобным же образом докажем, что
если в полукруге 0111’ лол прямым углом к 110 провести какую-нибудь
другую прямую, на проведенной прямой восставить перпендикулярную
к 1.10 плоскость и продолжить ее в обе стороны от той плоскости, в кото-
рой находится круг ЕОПР, то получившимся в полуцилиндре паралле-
лограмм, оставаясь в синем положении, будет относительно точки 0
уравновешивать параллелограмм, получившийся в отсеченном от цилин-
дра сегменте, перенесенный на рычаг в Е и помещенный так, чтобы его
центром тяжести была точка Е. Значит, и все получившиеся в полу-
цилиндре параллелограммы, оставаясь в своих положениях, будут
относительно точки 0 уравновешивать все параллелограммы, получив-
шиеся п отсеченном от цилиндра сегменте, перенесенные и помещенные
на рычаге в точке S; таким образом, и полуцилиндр, оставаясь в своем
положении, будет относительно точки 0 уравновешивать отсеченный
сегмент, перенесенный на рычаг в Е и помещенный так, чтобы его цент-
ром тяжести была точка 3.
*) Яти ралепстпа и следующие за ними нужны Архимеду, когда он переходит от рис. 9 х рис. 10.
на которым и будут вестись иве рассуждения как в атом, так и в следующем предложениях.
21 АрздумсА
322
АРХИМЕД
XIII
Пусть опять будет перпендикулярным к оси параллелограмм*)
MN и круг SO (ПР) {рис- 11}; проведем соединяющие прямые ОМ,
011, восставим на них плоскости, перпендикулярные к той, в которой
находится полукруг ОШ’, и упомянутые плоскости продолжим в обе
стороны; получится некоторая призма,
имеющая основание такое же, каким явля-
ется треугольинк©М11**), а касту, равную
оси цилиндра, и эта призма будет четвертой
частью всей призмы, содержащей цилипдр.
Теперь в полукруге ОПР и в квадрате M.N
проведем какие-нибудь прямые КЛ, ТГ,
одинаково отстоящие от прямой ПЕ; они
пересекут окружность полукруга ОПР в
точках К, Т, диаметр ОР — в точках 2,Z
и прямые ОН, ОМ — в точках Ф, X; затем
па прямых КЛ, ТУ восставим плоскости,
перпендикулярные к ОР, и продолжим их
в обе стороны от той плоскости, в которой
находится (круг SOUP; тогда каждая из
1»н«. и.
них в) полуцилиндре с основанием — полукругомOUP — и с той же са-
мой высотой, что и у цилиндра, образует сечением параллелограмм, одна
сторона которого равпа К25, а другая равна оси цилиндра; в призме
©ИМ они точно также образуют параллелограмм, одна сторопа которо-
го равна ЛХ, а другая равна оси; точно так же в том же самом полу-
цилиндре получится некоторый (другой) параллелограмм, у которого
одна сторона равна TZ, а другая равна оси цилиндра, а в призмо —
параллелограмм, у которого одна сторона равна прямой ТФ, а другая
равпа оси цилиндра... ***),
<Так как центры тяжести параллелограммов, расположенных ла прямых ЕК,
ZT, находятся в серединах прямых ЕК, ZT, то центром тяжести обоих этих параллело-
граммов, взятых вместе, будет точка А', в которой прямая, соединяющая центры тяжести
этих параллелограммов, пересечет 6П. На том же основании центром тяжести обоих
параллелограммов, расположен пых на прямых ХА, ТФ, будет точка В', в которой пря-
мая, соединяющая середины прямых ХЛ, ТФ, пересечет прямую Ев. По параллелограм-
мы на прямых ЕК, ZT так относятся к параллелограммам на ХЛ, ТФ, как прямая ЕК
к ЛХ, или как прямая ЕК к ЕР. По ЕК относится к ЕР, как квадрат на КЕ к прямо-
угольнику между ЕК и ЕР, и квадрат ла ЕК ранен прямоугольнику между ЕР-ЕО;
значит, КЕ будет к ЕР, как прямоугольник между ЕР, ЕО к примоуголышку между
ЕК, ЕР, то есть как ЕО к ЕК
ЕК _ ЕК2 ЕР ЕО_ЕО
ЕР — 21».ЕК “ ЕР-ЕК“ ЕК ’
Далее, ЕО равняется ЕР вместе в удвоенной Ев, или АХ вместе с удвоенной ХЕ
£О^ЕР+2Е0=ЛХ-|-2ХЕ;
значит, ЕО будет к ЕК, как вместе взятые АХ с удиоеппой XX относятся к ЕК, или,
взяв половины, как ХЕ с половиной ЛХ будет к половине ЕК.
ух ,ЛХ
SO AX-I-2XS _ А + 2
ЕК ЕК “ ЕК.
2
*) Следовало бы сказать «квадрат».
**) Нужно иметь л Лиду, что треугольник в.цн расположен б среднем сечении призмы, и сле-
доьательпо, не может быть ее основанием.
Конец предложения утрачен* и переводе дается рскошигрукипи 1’ейбсрга; в подлинных Чер-
тежах букв Л' и вг не имеется.
ПОСЛАНИЕ К ЭРАТОСФЕНУ. О МЕХАНИЧЕСКИХ ТЕОРЕМАХ
323
Но половина АХ имеете с ХЕ равна В'в, половина же ХК есть А'Н; значит, параллело-
граммы ла SK и ZT к параллелограммам ла ХА и ГФ будут относиться, как В'8 к А'8.
Таким образом, вышеупомянутые параллелограммы будут относительно точки 0 уравно-
вешивать друг друга. То же самое будет справедливо и относительно всех других построен-
ных таким же образом параллелограммов; значит, полуцилиндр ОПР и призма НОМ,
заполненные такими параллелограммами, будут уравновешивать друг друга относительно
точки 8. Но относительно точки 0 полуцилиндр ОПР, оставаясь в своем положении,
уран довешивает отсеченный ог цилиндра сегмент, помещенный на рычаге так, чтобы
его центр тяжести был в точке 3 (предложение ХП). Далее, 38 равна П8; значит,
отсеченный от цилиндра сегмент, помешенный в П, будет относительно точки 8 уравно-
вешивать призму Н8М. По Центр тяжести упомянутом призмы будет на прямой £8,
если рассечь ее так, чтобы ее часть при 8 была вдвое больше остающегося отрезка. Зна-
чит, отсеченным от цилиндра сегмент так относится к призме 118 М, как две трети Е0
к П0, млн как 2 к 3. Но призма Н©М составляет четвертую часть всей призмы; значит,
цилиндрический сегмент будет равен ее шестой части [7].
XIV
Пусть будет прямая призма с квадратными основаниями, и пусть
одно из ее оснований будет квадрат АВГД {рис. 12}. Впишем в эту приз-
му цилиндр, и пусть основанием цилиндра будет круг EZTK-), касаю-
щийся сторон квадрата АВГД в точках Е, Z, 11, В. Через центр этого
круга и ту нз сторон квадрата, которая
находится л противолежащей АВГД пло- [>
скости и соответствует ГД, проведем пло-
скость; эта плоскость от целой призмы
отсечет другую призму, которая будет чет-
вертой частью целой призмы; эта самая
(отсеченная) призма будет заключаться #
между тремя параллелограммами и двумя
противолежащими друг другу треуголь-
никами. В полукруге EZH опишем парабо-
лу, и пусть... (ес диаметром, заключен-
ным)... в сечении, будет ZK. В парал- а
лслограмме АТТ параллельно KZ проведем
некоторую прямую MN; опа пересечет
окружность полукруга в точке 3, а па-
раболу — в А. И (прямоугольник) между MN и NA ранен (квадрату)
на NZ
мккл = ш®
(это действительно очевидно *)). Вследствие этого получится, что MN
будет относиться к NA, как (квадрат) на КП к (квадрату) на AS**).
UN КП2
NA ' л22
Па прямой MN восставим плоскость, перпендикулярную к ЕН; эта
») Действительно, если взять Z » качестве. начала координат, направить ось х нс ZK. а ось v
по ЕГ, то уравнение параболы ZAH будет иметь вид
V2 — 2рм.
Тач пак парабола должна проходить через точку н, дли которой х~ ZK и у = НК будут соответ-
ственно равны радиусу круга Я, то уравнение параболы ZAII будет
р2 = Их,
Архимед пишет его и виде
NZ® = MN-KA.
**) Мы имеем:
MN __ MN2 MNa _ КНЯ
NA МЛ’-Ыд NZ2 АЕ2 ’
21*
324
АРХИМЕД
плоскость в сечении с призмой, отсеченной от целой призмы, образует
прямоугольный треугольник, у которого одна на сторон, прилегающих
к прямому углу, будет MN, а другая, лежащая в плоскости, проходящей
через ГЛ, и проведенная из N перпендикулярно к ГД, будет равна оси
цилиндра; гипотенуза же этого треугольника будет находиться в самой
секущей плоскости, (Восставленная иа MN перпендикулярная к ЕН
плоскость) в сечении с сегментом, отсечеппым от цилиндра плоскостью,
проведенною через ЕН и противолежащую ГД сторону квадрата (верх-
него основания призмы), образует прямоугольный треугольник, у ко-
торого одна из сторон, прилегающих к прямом у углу, будет ME, а дру-
гая — проведенная ла поверхности цилиндра из точки В, лериопди-
куляриая к плоскости KN прямая, гипотенуза же (в секущей пло-
скости). Теперь поскольку (прямоугольник) между MN и МД
равен (квадрату) на ME
м» ил = НЕ2
(это действительно очевидно *)), точно так же получается, что (MN)
будет к (МД, как квадрат па MN) к (квадрату па ME).
мк _ MN2
МЛ Ms®
Но как квадрат на ( MN к (квадрату) па ) ME, так будет и получивший-
ся в призме треугольник ла MN к получившемуся в отсеченном
поверхностью цилиндра сегменте треугольнику на ME; значит, как
MN к МЛ, так будет и один треугольник к другому.
MN _ MN2 Тр К па MX
МЛ м=® Тр-к па МЛ
Если в параллелограмме, описанном (около параболы, параллельно)
KZ провести какую-нибудь другую прямую и на проведенной прямой
(восставить перпендикулярную) к ЕН плоскость, то подобным же
образом докажем, что получившийся в призме треугольник будет отно-
ситься к (треугольнику) в сегменте... (отсеченном)... от цилиндра,
как прямая, проведенная в параллелограмме АН параллельно KZ,
будет относиться к своему отрезку между параболой E11Z и диаметром
ЕП. Теперь, если заполнить параллелограмм ДН прямыми, проведен-
ными параллельно KZ, а заключенный между параболой и диаметром
сегмент заполнить заключенными в этом сегменте отрезками...**),
(прямым)... проведенным в параллелограмме Д11 параллельно KZ,
и получится, что все треугольники в призме будут относиться ко всем
треугольникам, заключенным в отсеченном сегменте цилиндра, как
все прямые в параллелограмме ДП ко всем прямым, заключенным меж-
ду параболой и прямой ЕН. Но из треугольников в призме составляется
эта самая призма, из треугольников в (отсеченном от цилиндра) сег-
менте составляется (этот сегмент), из параллельных KZ прямых в па-
раллелограмме ДН составляется параллелограмм ДН, из... (отрезков)
... между параболой и прямой ЕН составляется (сегмент) [параболы].
Значит, призма будет относиться к сегменту цилиндра, как параллело-
грамм ДП к сегменту EZTI, заключенному между параболой и прямой ЕН.
*) Действительно:
ME® —- HM-ME=(MN—МК) ( MN-r ЛК)= М№-№<= М№—MN- Кл= MX- МЛ.
•*) В подлиннике лакуна в 17 строк.
ПОСЛАНИЕ К ЭРАТОСФЕНУ. О МЕХАНИЧЕСКИХ ТЕОРЕМАХ
325
Но параллелограмм ДН в полтора раза больше сегмента, заключен-
ного между параболой и прямой ЕН (это доказывается в ранее изданных
сочинениях *)); значит, и призма будет в полтора раза больше сегмента,
отсеченного от цилиндра; значит, каких частей будет две в сегменте
цилиндра, таких же будет в призме три. Каких же частой в этой призме
три, таких в целой призме, заключающей цилиндр, будет 12, нследстние
того, что первая призма составляет 1/4 второй. Значит, каких частей
в цилиндрическом сегменте две,, таких в целой призме будет 12; таким
образом, отсеченный от цилиндра сегмент составляет шестую часть
призмы [8].
XV
Пусть будет прямая призма с квадратными основаниями, одним
из которых является квадрат АВГД; впишем в эту призму цилиндр,
основанием которого пусть будет круг EZII; этот круг (касается) сто-
рон квадрата в точках Е, Z, И, 0. Пусть его центр (будет К; через)
диаметр ЕП (и одну из сторон)... (противолежа-
щего квадрата )...(провед ем плоскость), эта пло-
скость от целой призмы отсечет некоторую призму,
а от цилиндра — цилиндрический сегмент. (Я ут-
верждаю, что) этот сегмент, отсеченный от. цилин-
дра проведенной плоскостью, будет, как мы дока-
жем, шестой частью целой призмы..
Прежде всего докажем, что в отсеченный от
цилиндра сегмент можно вписать телесную фи-
гуру, составленную из призм, имеющих равные
высоты и подобные треугольные основания, и
другую такую же описать так, чтобы описанная
фигура была больше вписанной на величину, мень-
шую всякой заданной величины... **)
(В полукруге EZH {рис. 13} будем все время делить ионо-
лам диаметр ЕН и через точки деления параллельно Кйпрово-
Рлс. 13.
дить прямые, пересекающие окружность полукруга; через
точки же, в которых :>ти прямые пересекают окружность, будем проводить парал-
лельные КП прямые и продолжать их в обе стороны до встречи е двумя ближайшими
параллельными KZ прямыми; затем на них и других параллельных прямых будем вос-
ставлять плоскости, перпендикулярные к плоскости полукруга; тогда зти плоскости как
внутри цилиндрического сегмента, так и вис его образуют призмы с равными высотами
и с основаниями — прямоугольными треугольниками, расположенными на прямых,
параллельных KZ. Деление прямой ЕН ионолам будем продолжать до тех пор, пока две
прилегающие к К Z призмы пе окажутся меньше заданной величины; тогда составленная
из прпзм и описанная около пилипдричсекшт) сегмента телесная фигура будет такую же
вписанную превосходить лн величину, меныпую заданной. Действительно, описанная
фигура будет отличаться от вписанной на две призмы, прилегающие к KZ, так как всем
остальным призмам описанной фигуры будет соответствовать столько лес равных им призм
вписаппой фигуры.
Затем, сын в том лес полукруге описать параболу EZH {рис. 14} и через точки
пересечения с прямыми, параллельными ZK, провести прямые, параллельные ЕН, про-
должая их в обе стороны, как было сказано раньше, то получится составленная из парал-
лели гриммов фигура, описанная около параболического сегмента, и другая такая жп,
вписанная в пего, из которых первая будет превосходить иторую на два параллелограмма,
*) См. предлежание XXI у «Квадратуры параболы».
**) В подлиннике пропуск чстырвх столбцов или приблизительно 80 строк, от которых сохра-
нились лишь последние слова. Дальнейшая реконструкция дается Гейбергом применительно к пред-
ложением XIX, XXV трактата «О коноидах и сфероидах»; в текст Гейбсрга внесены некоторые
исправлении.
326
АРХИМЕД
прилегающие к ZK; при этом каждому из таких параллелограммов будет соответствовать
призма вышеупомянутых телесных фигур.
Теперь, если отсеченный от цилиндра сегмент пс будет равен шестой части целой
призмы, то оп будет или больше, паи меньше. Пусть сначала оп, если возможно, будет
6t.i.n мне; тогда отсеченная наклонной плоскостью призма будет менее чем в полтора раза
больше цилиндрического сегмента.
Впишем в последний телесную фигуру и опишем около пего другую тан, как это
было указано выше, и пусть оиисаппан фигура будет превосходить вписанную па вели-
чину, мнившую разности между
сегментом и двумя третями. призмы; тогда, поскольку
описанная около сегмента фигура будет больше этого
сегмента, вписанная фигура будет больше двух третей
призмы. Теперь мы уже доказали (предложение XIV),
что все прямые в параллелограмме АЛ (рис. 12) отно-
сятся по всем прямым в параболическом сегменте EZI1,
как все треугольники в призме, отсеченной наклонпой
плоскостью, ко всем треугольникам л сегменте, отсе-
ченном от цилиндра. Построим па этих треугольниках,
как па основаниях, призмы, высоты которых будут
равны отрезкам, па которые разделена прямая ЕП;
тогда каждой призме, из которых составляется отсе-
ченная наклонной плоскостью призма, за исключением
лишь двух прилегающих к ZK, будет соответствовать
призма, из которых составляется вписанная в цилин-
дрический сегмент телесная фигура. По как упомя-
нутые прямые в параллелограмме АН к прямым в
параболическом сегменте EZH, так будут и параллело-
граммы, па которые разделен параллелограмм АН,
относиться к параллелограммам, вписанным в кониче-
ское сечение; значит, каждому' параллелограмму, на
которые разделяется параллелограмм АН, за исключе-
нием лишь двух, прилежащих к ZK, будет соответ-
ствовать параллелограмм в фигуре, вписанной в
параболический сегмент. Таким образом (лемма 11), отсеченная наклонной плоско-
стью призма будет относиться к телесной фигуре, вписанной в цилиндрический сегмент,
как весь параллелограмм АН к фигуре, вписанном в параболический сегмент, И так как
отсеченная наклонной плоскостью призма меньше взятого полтора раза цилиндрического
сегмента, последний же превосходит вписанную в него телесную фигуру па величину,
меньшую заданной, то есть меньшую, чем разность между цилиндрическим сегментом
и двумя трстнми описанной наклонной призмы, >
то значит отсеченная наклонной плоскостью призма будет меньше
в полтора раза взятого тела, вписанного в цилиндрический сегмент-
Но уже доказано, что призма, отсеченная наклонпом плоскостью, от-
носится к телу, вписанному в цилиндрический сегмент, как параллело-
грамм АН ко всем параллелограммам, вписанным в сегмент, заключен-
ный между параболой и прямой ЕП; значит, параллелограмм АН
будет менее чем в полтора раза больше всех параллелограммов, впи-
санных в сегмент, заключенный между параболой и прямой ЕН; это же
невозможно, так как в другом месте *) доказано, что параллелограмм
АН будет в полтора раза больше сегмента, заключающегося между пара-
болой и прямой ЕН. Значит,
(цилиндрический сегмент не будет больше... шестой части целой призмы.
Пусть теперь он, если возможно, будет меньше; тогда отсеченная наклонной пло-
скостью призма будет более чем в полтора раза больше цилиндрического сегмента. Впи-
шем в сегмент и опишем около пего такие же телесные фигуры, как и выше, так, чтобы
описанная фигура превосходила вписанную на величину меньшую той, па которую две
трети призмы, отсеченной наклонной плоскостью, превосходят упомянутый цилиндри-
ческий сегмент; тогда, поскольку вписанная телесная фигура меньше цилиндрического
сегмента, то и «писанная телесная фигура будет меньше, чем две трети призмы, отсечен-
ной наклонной плоскостью.
) См. «Квадратура параболы», XX1V (стр. РЗ).
ПОСЛАНИИ К ЭРАТОСФЕНУ. О МЕХАНИЧЕСКИХ ТЕОРЕМАХ
327
Затем, вписав в сегмент, заключенный между параболой EZIT и. прямой ЕН, и опи-
сав около пего параллелограммы так же, как это делили и выше, мы подобно тому,
как и выше, докажем, что отдельные призмы в призме отсеченной иаь-лониой плоскостью,
будут относиться к отдельным призмам твлссяой фигуры, описанной около цилиндри-
ческого Сегмента, как отдельные параллелограммы, содержащиеся п параллелограмме
ДЛ, к отде.тьлыл параллелограммам в фтгтурс, описанной около сегмента, заключенного
между параболой EZH и)
прямой (ЕН), и что все. призмы в отсеченной наклонной плоскостью
призме, ко всем призмам в фигуре, описанной около цилиндрического
сегмента, будут иметь то же самое отношение, какое все параллелог-
раммы в параллелограмме АН имеют ко всем параллелограммам в
фигуре, описанной около сегмента, заключенного между параболой
и прямой ЕН; иными словами, призма, отсеченная наклонной плос-
костью, будет иметь такое же отпошеяяе к описанной около цилин-
дрического сегмента фигуре, какое параллелограмм АН имеет к фигу-
ре, описанной около сегмента, заключенного между параболой и
прямой ЕН; но отсеченная наклонной плоскостью призма более чем
в полтора раза больше телесной фигуры, описанной
{около цилиндрическою сегмента: значит, и параллелограмм ДН будет более чем в пол-
тора рапа больше фигуры, описанной около сегмента, заключенного между параболой
и призмой ЕН. Это же невозможно, так кик в другом месте докапало, что параллело-
грамм ДИ в полтора раза больше сегмента, заключеялого между шцшбгмюй EZH л пря-
мой ЕН. Следовательно, цилиндрический (пимент по будет меньше шестой части всей
призмы. Поскольку же доказано, что он ле будет и больше се, то значит, ок будет равен
шестой части этой призмы, что и требовалось доказать) [9].
*) Конец сочинения утрачен. Он должен был содержать механическое и геометрическое дока-
зательство второй предложенной Архимедом теоремы, н имение, что тело, заключенное между двумя
цилиндрами с взаимно перпендикулярными осями, вписанными в куб так, чтобы их основания
лежали на противоположных гранях, а боковые поверхности касались остальных четырех граней
куба, будет равняться двум третий отого куба. Попытка реконструкции обоих зтих доказательств
приведена в комментарии [10].
О ПЛАВАЮЩИХ ТЕЛАХ
КНИГА ПЕРВАЯ
Предположим, что жидкость имеет такую природу, что из ее ча-
стиц, расположенных па одинаковом уровне и прилежащих друг к дру-
гу, менее сдавленные выталкиваются более сдавленными, и что каж-
дая из ее частиц сдавливается жидкостью, находящейся пад ией по отве-
су, если только жидкость но заключена в каком-нибудь сосуде и не
сдавливается еще чем-нибудь другим.
Если поверхность, рассекаемая, любой плоскостью, проходящей через
одну и ту же точку, всегда дает в сечении окружность круга с центром
в той самой точке, через которую проводятся
секущие плоскости, то эта поверхность будет
шаровой.
Действительно, пусть будет некоторая поверх-
ность, которая при сечении плоскостью, проходя-
щей через точку К {рис. 1}, всегда образует окруж-
ность круга с центром в этой самой точке К. Если
эта поверхность не будет поверхностью шара, то но
будут равными все линии, которые идут от центра
к поверхности. Пусть Л, В, Г, Д будут точки на
поверхности, причем /пиши АК и ВК не раины;
проведем через КА, КВ плоскость, и пусть она образует в сечении с
поверхностью линию ЛАВГ; эта линия, будет, конечно, круговой с цент-
ром в точке К, так как рассматриваемая поверхность предполагалась
обладающей таким свойством *). Значит, линии КА, КВ не будут нерав-
ными; поэтому необходимо, чтобы эта поверхность была шаровой.
П
Поверхность всякой жидкости, установившейся неподвижно, будет
иметь форму шара, центр которого совпадает с центром Земли.
*) Именно, что все сечения ее плоскостями, приходящими через точку К, являются круговыми^
О ПЛАВАЮЩИХ ТКЛАХ
329'
этого круга пойдет так, что-
Вообразим некоторую жидкость, которая установилась неподвиж-
но; рассечем ое поверхность через центр Земли плоскостью; пусть центр
Земли будет К. {рис. 2}, а линия сечения поверхности АВГД. Я утвер-
ждаю, что линия АВГД будет окружностью круга с центром в К.
Действительно, если это не так, то прямые, выходящие из К. к линии.
АВГД, пе будут равны друг другу. В таком случае возьмем некоторую’
прямую, которая была бы больше одних и меныпе других из линий,
выходящих из К н липни АВГД, и из центра К опишем круг радиусом,
равным этой линии; тогда поверхность
часть ее расположится вне. липни
АВГД, часть же внутри, так как
радиус ее будет больше некото-
рых из линий, выходящих от К к
линии АВГД, и меньше других.
Пусть окружность описанного
круга будет ZB1I; проведем из В
в К прямую и построим прямые 7. Л Е К Л ft
ZK, КЕА, образующие равные
углы (АКВ и ВКА), затем из Рис’ 2‘
центра К опишем некоторую дугу
ЕОП, которая находилась бы на плоскости (чертежа) и в жидкости;,
тогда расположенные по дуге НОII частицы жидкости будут находиться
на одном уровне и прилегать друг к другу. Те из них, которые нахо-
дятся на дуге ЕО, будут сдавливаться жидкостью, расположенной до-
уровня ZB, а тс, которые находятся на дуге ОН,— жидкостью до уров-
ня ВЕ; следовательно, частицы жидкости, расположенные на дугах
ЕО и ОН, будут сдавливаться неодинаково; таким образом, менее сдав-
ливаемые будут вытеснены более сдавливаемыми; следовательно,
жидкость не останется неподвижной. Мы же предположили, что она.
установилась так, что остается неподвижной; значит, необходимо, чтобы
линия АВГД была окружностью круга с центром в К. Подобным же
образом докажем, что если как-нибудь иначе рассечь поверхность жидко-
сти плоскостью, проходящей через центр Земли. то сечение будет
окружностью круга и центр ее будет тот же, что и центр Земли. Теперь,
ясно, что поверхность установившейся неподвижно жидкости имеет
форму шара с тем же центром, что и у Земли, ибо она такова, что при
рассечении ее плоскостями, проходящими через одну в ту же точку,
в сечении получаются окружности с центрами в той самой точке, через
которую проходят секущие плоскости.
ТТТ
Тела*), равнотяжелые с жидкостью, будучи опущены, в эту
жидкость, погружаются так, что никакая, их часть не выступает
над поверхностью жидкости, и не будут двигаться вниз.
Опустим в жидкость какое-нибудь тело из равнотяжелтях с этой
жидкостью, и пусть, если возможно, некоторая часть его будет высту-
пать над поверхностью жидкости; пусть жидкость установится в таком.
*) У Архимеда интересное выражение: tojv птэдеш? га lOofkiQeovTa— буквально:
«те из объемных величии, которые равно тяжелы...» Архимед, ио существу» имел дело с геометриче-
скими телами, и его atepea представляют пространственную аналогию enureta jxeyeftea*
(плоских величии), о которых шла речь в книгах «О равновесии плоских фигур».
ЛТП
АРХИМЕД
положении, что будет оставаться неподвижной. Вообразим некоторую
плоскость, проведенную через центр Земли, через жидкость и через
это тело; пусть ее сечение с поверхностью жидкости будет дуга АВГД
{рис. 3}, а с рассматриваемым телом — фигура EZ011, центр же Земли
пусть будет К. Тогда часть ВГН0 тела будет в жидкости, часть же
ВЕХГ — вне ее. Вообразим, что тело охвачено пираммдообразной фигу-
рой, имеющем в основании на поверхности воды параллелограмм *),
а вершиной — цептр Земли. Пусть КЛ
и К Л1 будут сечения граней пирамиды
с той плоскостью, в которой находится
дуга АВГД. Около центра К опишем
еще одну шаровую поверхность так,
чтобы она проходила впутри жидкости
и ниже тела EZTTO, и рассечем ее пло-
скостью; затем возьмем другую пира-
миду, равную и подобную той, кото-
рая охватывает погруженное тело, и
смежную с ней; пусть КМ и KN будут
сечения се граней; в жидкости вообра-
зим некоторый объем Р2ТГ, охвачен-
ный жидкостью, равный и подобный части ВН0Г первого тела, по-
груженной в жидкость. Тогда частицы жидкости в первой пирамиде,
расположенные под той частью поверхности, где находится дуга 50,
а также соответствующие частицы в другой пирамиде, где находится
дуга ПО, будут лежать иа одном уровне и в непрерывной связи друг
с другом. Однакоопи не испытывают одинакового давления; действитель-
но, те частицы, которые расположены но 50, сдавливаются телом 0I1EZ
и той жидкостью, которая находится между поверхностями 50, ЛМ
и гранями первой пирамиды, те же, которые расположены по ПО,
сдавливаются жидкостью, находящейся между поверхностями ПО,
М.\ и гранями второй пирамиды. Тогда давление па жидкость, находя-
щуюся между MN, ОН, будет меныпе, так как (объем) .Р2ТГ будет
меныпе тела EZH0 (ибо этому (объему) раина только часть НВГ0, и
опа предполагается одинаковой по величине и равнотяжелой (с жидко-
стью)**), а остальные части в обеих пирамидах одинаковы). Теперь
ясно, что часть жидкости, соответствующая дуге ОП, будет вытолкну-
та той частью, которая соответствует дуге 05, и жидкость никак ие бу-
дет неподвижной. Было же предположено, что она неподвижна; значит,
никакая часть тела не будет выступать пад поверхностью жидкости.
Погрузившись же, тело не будет двигаться вниз, так как все части
жидкости, находящиеся па одном уровне, будут давить одинаково вслед-
ствие того, что тело является равпотяжслым с жидкостью 11].
TV
Тело, более легкое, чем жидкость, будучи опущено в эту жидкость,
не погружается целиком., но некоторая часть его остается над поверх-
ностью жидкости.
Пусть будет тело более легкое, чем жидкость, и пусть оно, будучи
опущено в жидкость, погрузится целиком, если возможно, так что
*) То есть прямоугольник.
»*) Фраза в скобках, по-видимому, представляет позднейшую вставку; во всяком случае слова
«одинаковой по величине» совершенно излишни.
О ПЛАВАЮЩИХ ТЕЛАХ
331
над поверхностью жидкости не будет никакой его части, и жидкость
установится неподвижно. Вообразим некоторую плоскость, прове-
денную через центр Земли, жидкость и погруженное тело; пусть по-
верхность жидкости рассечется этой плоскостью по дуге ДВГ {рис. 4},
погруженное тело даст » сечении фигуру, обозначенную через Z, а
центр Земли пусть будет К; вообразил!, как и выше, некоторую пирами-
ду, охватывающую тело Z, имеющую вершину в точке К; пусть прове-
денной через АВГ плоскостью ос грани будут пересекаться jjo линиям
ЛК, КВ; возьмем также другую пирамиду, равную и подобную этой,
31 пусть ее грани той же самой плоскостью
пересекаются по линиям КВ, КГ; затем в
•жидкости, ниже погружоппого тела опи-
шем другую шаровую поверхность с цент-
ром в К, и пусть она пересекается выше-
упомянутой плоскостью по дуге ЕОП;
вообразим еще во второй пирамиде выде-
ленный объем жидкости II, равный телу Z;
тогда частицы жидкости в первой пира-
К
миде, расположенные под поверхностью, Рис. 4.
соответствующей дуге SO, а также во
второй пирамиде под поверхностью, соответствующей дуге ОП, будут
находиться на одном уровне и прилегать друг к другу. Ио они нс
испытывают одинакового давления, так как в первой пирамиде опи
сдавливаются телом Z и окружающей его жидкостью, занимающей
в этой пирамиде место А, В, О, В, а во второй пирамиде они сдавливают-
ся окружающей жидкостью, занимающей в пирамиде место ТТ, О, В, Г;
нес же тела (Z будет меньше веса) II, поскольку тело Z, будучи ран-
иг, iM II по величине, предполагается более легким, чем жидкость;
веса же окружающей объемы Z, 11 жидкости будут в каждой из пирамид
одинаковыми; значит, частицы жидкости, расположенные по поверх-
ности, соответствующей дуге ОП, будут испытывать большое давление;
следовательно, менео сдавливаемые частицы вытсснятся и жидкость
не будет оставаться неподвижной. Но она предполагалась таковой;
значит, тело не погрузится целиком, но
некоторая его часть будет находиться
над поверхностью жидкости.
V
Тало, более легкое, чем жидкость,
будучи опущено в эту жидкость, погру-
жается настолько, чтобы объем жидко-
сти, соответствующий погруженной
{части тела}, имел вес, равный весу
рис. 5. всего тела.
Пусть будет сделапо то же, что и
раньше, и пусть жидкость будет не-
подвижной; пусть тело EZHO (рис. 5) будет более легким, чем
жидкость. Теперь, поскольку жидкость ог.отастся неподвижной, частицы
ее, расположенные па одном уровне, будут испытывать одинаковое
давление; следовательно, жидкость под поверхностями, сотлетствугощи-
ми дугам ВО и ПО, будет сдавливаться одинаково, так что одинакова
будет и тяжесть, которой они придавливаются. По вес жидкости
332
АРХИМВД
в первой пирамиде, за исключением объема В110Г, будет ранен весу
(жидкости во второй пирамиде), за исключением части жидкости
РЕТ Г; теперь ясно, что вес тела EZI10 будет равен весу жидкости
l’S'1'Г. После этого очевидно, что объем ?кидкости, соответствующий
погруженной части опущенного тела, имеет вес, равный весу всего тела..
VI
Тела более легкие, чем жидкость, опущенные в эту жидкость на-
сильственно, будут выталкиваться вверх с силой, равной тому весу,
на который жидкость, имеющая равный объем с телом, будет тяжелее-
этого тела.
Пусть будет некоторое тело А {рис. 6} более легкое, чем жидкость;,
пусть В будет вес тела А, а В + Г — вес жидкости в объеме, равном Л.
Требуется доказать, что насильно по-
груженное в жидкость тело Л будет
выталкиваться вверх с силой, равной
весу Г.
Возьмем какое-нибудь тело А,
имеющее пес, равный Г; тогда тело,,
составленное из объединенных вместе
обоях тел А, А, будет легче жидкости
(в том же объеме), так как вес тела, со-
ставленного из обоих, будет В 4- Г, вес
же жидкости в равном объеме будет
больше, чем В 4“ Г, так как В 4- Г
представляет вес (жидкости) в объеме,
равном Л. Теперь тело, составленное и»
обоих тол А, А, будучи оиущепо в жидкость, погрузится настолько,
чтобы жидкость в объеме, равном погруженной части, имела вес, рав-
ный весу всего тела, как это доказано шише. Пусть дуга АВГД пред-
ставляет поверхность некоторой жидкости. Теперь, поскольку коли-
чество жидкости в объеме, ранном телу Л, имеет вес одинаковый с
весами обоих тел Л, А, то ясно, что погруженная часть этого тела,
будет иметь объем, равный А, остальная же часть его, именно А, будет'
находиться над поверхностью жидкости; действительно, если бы это-
тело погрузилось иначе, то получилось бы (противоречие) с тем, что-
было доказано (раньше). Теперь ясно, что (с какой силой) тело А
выталкивается кверху, (с такой же силой оно будет придавливаться)
книзу находящимся над ним телом А, поскольку нн то, ни другое не-
пересиливают друг друга. Но А давит вниз с тяжестью, равной весу
Г, так как было предположено, что вес тела А равен Г; теперь то, что
требовалось доказать, будет очевидно.
VII
Тела, более тяжелые, чем жидкость, опущенные в эту жидкость,,
будут погружаться, пака не дойдут до самого низа, и в жидкости ста-
нут.*) легче на величину веса жидкости в объеме, равном объему погру-
женного тела.
*) Характерное выражение «станут легче (шяянтас. хоидотеоа)», показывающее, что греки
вес одного н того же тела не считали постоянным; они «вес» понимали как сдавление».
О ПЛАВАЮЩИХ ТЕЛАХ
333
Что тело будет погружаться, пока не дойдет до самого дна, очевид-
но, так как находящиеся под ним частицы жидкости будут испытывать
большее давление, чем другие, располо?кснные на одном с ним уровне,
так как тело предполагается более тяжелым, чем жидкость; а что оно,
как сказано, (в жидкости) станет легче, это следует доказать.
Пусть будет некоторое тело А {рис. 7} более тяжелое, чем жидкость;
пусть вес тела А будет В -|- Г, вес же жидкости в объеме, ранном А,
пусть вес тела А будет В -|- Г, вес же жидкости в
будет В. Требуется доказать, что тело А.
находясь в жидкости, будет иметь вес,
равный Г.
Возьмем некоторое тело А, (более
легкое, чем жидкость в его объеме: пусть)
вес тела А будет равен несу В, нос же
жидкости, имеющей одинаковый с А объем,
пусть будет равен весу В Г. Если мы
сложим оба наши тела А и А в одно, то
составленное тело будет равнотяжелым с
жидкостью; действительно, вес обоих этих
тел равен вместе взятым весам В -|- Г и В,
объем, равный обоим телам, равен тем же самым весам. Значит, если
эти тела опустить в жидкость, то они будут в равновесии с жидкостью
и не будут двигаться пи вверх, пн вниз; вследствие этого тело А пойдет
вниз с такой же силой, с какой тело А будет увлекаться вверх; тело
же А, поскольку оно легче жидкости, будет двигаться вверх с силой,
равной весу Г, так как доказано, что более легкие, чем жидкость, тела,
будучи насильно погружены в эту жидкость, движутся вверх с силой,
ранной тому весу, на который жидкость, имеющая объем, равный этому
телу, будет тяжелее последнего. Но жидкость, имеющая равный объем
с телом А, будет тяжелее тела А на вес Г;
теперь ясно, что тело А будет двигаться
вниз (с силой, равной весу Г).
Предположим, что все тела, движу-
щиеся*) (в жидкости вверх), будут поды-
маться по отвесной линии, проведенной
через их центр тяжести.
ранном А,
вес же жидкости, имеющей
Гис. 8.
VIII
Если какое-нибудь тело, более легкое,
чем жидкость, и имеющее форму сегмента
шара, будет опущено в жидкость таким
образом, чтобы основание сегмента не ка-
салось жидкости, то это тело установит-
ся е прямом положении, так что ось сег-
мента будет расположена по отвесу, и
если кто-нибудь принудит тело стать так, чтобы основание сегмента
касалось жидкости, то оно не останется в наклонном положении, но.
будучи отпущено, снова станет прямо.
Представим, что в жидкость опущено такое тело, как сказано;
вообразим плоскость, проведенную через ось сегмента и центр Земли,
и пусть АВГА {рис. 8} будет сечение этой продолженной плоскости
*> Нади помнить, чти в 1’реческой механике идея движения была исрпврышю сьяаана с идеей
силы; поэтому ближе к смыслу было бы сказать «выталкиваемые в жидкости вьерзг».
334
АРХИМЕД
с поверхностью жидкости, а дуга EZH0 — с опущенным в жидкость,
телом; пусть ось сегмента будет 0Z; тогда центр шара будет на 6Z.
(Предположим) сначала, что сегмент больше полушария; пусть
центр (его) будет К, и пусть тело, если возможно, будет наклонено
само по себе или под чьим-нибудь воздействием. Требуется доказать,
что оно не останется в покое, но вернется в прямое положение, так что
Z и б) будут находиться па отвесной линял.
Действительно, поскольку тело предполагается наклоненным, то
Z и 0 не будут находиться на отвесной линии. Через К и Л проведем
прямую КЛ (Л мы предполагаем цептром Земли); на прямой КА будет
лежать ось находящейся в жидкости части тела, отсекаемой поверх-
ностью жидкости, ибо если поверхности двух шаров пересекают друг
друга, тосечепис будет кругом, перпендикулярным к прямой, соединяю-
щей центры этих шаров. Центр тяжести фигуры, находящейся в воде
и отсеченной дугой BN Г, находится на КЛ; пусть это будет Р. Центр
же тяжести всего сегмента, соответствующего дуге 0HZE, находится
на Z&, пусть оп будет Е. Тогда центр тяжести (оставшейся фигуры,
находящейся вне) поверхности воды, найдется па продолжении РЕ,
если отложить некоторый отрезок ХЕ, который имеет к ЕР то жо
отношение, что вес части сегмента, соответствующей дуге 13ХГ, к весу
той его части, которая будет впе жидкости; это уже доказано («О равно-
весии плоских фигур», кн. I, предложение VIII). Пусть центр упомя-
нутой фигуры будет 2. Теперь, так как вес той части тела, которая на-
ходится вис жидкости, будет стремиться впиз по прямой Л2, вес же
той части, которая в жидкости (будет стремиться) вверх но прямой
РК, то ясно, что тело нс останется в покое, но что части его, прилежа-
щие к Е, пойдут впиз, прилежащие же к 11 — вверх и что так двигать-
ся они будут все время, пока Z0 нс станет отвесной. Когда же Z(-) ста-
нет отвесной, то центры тяжести обоих частей, как той, что в жидкости,
так и той, что вис се, будут па одной и той же отвесной линии (они будут
на ZC->); тогда веса будут взаимно давить друг на друга по одной и той
же отвесной линии, один вниз, а другой вверх. Таким образом, тело
будет оставаться неподвижным, ибо ни
один не сможет вытолкнуть другой.
То же самое получится, если фигура
будет полушарием или меньше полуша-
рия Г2|.
так, что его ось
IX
И так же если какое-нибудь телоТ
более легкое, чем жидкость, будет опу-
щено в эту жидкость так, чтобы все его
основание было целиком в жидкости, то
тело установится в прямом положении
расположится по отвесной линии.
Вообразим, что в жидкость опущено тело такое, как сказано;
вообразим также плоскость, пронедепную через ось сегмента и через
центр Земли; пусть сечение поверхности жидкости будет окружность
АВГЛ {рис. 9), а тела — дуга EZH и прямая EII; пусть ось сегмента
будет Z0, и пусть, если возможно, ZO нс будет отвесной; требуется
доказать, что тело не останется в покое, по вернется в прямое положение.
Центр шара будет па Z6) (предположим сначала опять, что тело
будет больше полушария); пусть он будет К. Через К н центр Земли Л
О ПЛАВАЮЩИХ ТЕЛАХ
335
проврдем прямую КА; тогда часть тела, находящаяся вне жидкости
и отсекаемая, поверхностью жидкости, будет иметь свою ось (на прямой,
проходящей) через К., и на основании того же, что и выше, со центр
тяжести будет на NK; пусть он будет в Р. Центр тяжести всего сегмента
будет на Z0 между К и Z; пусть он будет Т. Значит, центр тяжести
остальной части сегмента, находящейся в воде, найдется на продолже-
нии прямой ТР, если нанести на ней некоторый отрезок1, который имел
бы к ТР то же самое отношение, что нес части сегмента, паходшцейся
вне жидкости, к весу той части, которая в жидкости; пуст], центр упо-
мянутой фигуры будет О, а отвесная линия, проведенная через О,
будет ОА; теперь, вес части сегмента, которая вне жидкости, пойдет
вниз по прямой РЛ, а той части, что в жидкости,— вверх по прямой ОА.
Следовательно, талоне останется в покое, но те его части, которые при-
легают к II, пойдут вниз, тс же, что к Е — вверх, и так будет все время,
пока OZ пе сделается отвесной *).
КНИГА ВТОРАЯ
I
Если какое-нибудь тело, более легкое, чем жидкость, опустить в эту
жидкость, то оно по тяжести будет находиться в том. же отношении
с. жидкостью**), какое погруженный объем имеет,
ко всему объему. Л
Опустим в жидкость какое-нибудь тело ФА
{рис. 10}, являющееся более легким, чем эта 0
жидкость; пусть погруженная часть его будет Л,
находящаяся же вне жидкости—Ф. Требуется
доказать, что ФА по тяжести будет относиться р
к равному объему жидкости, как Л к ФА. 1
Возьмем какую-нибудь жидкую массу NI,
имеющую с ФА равный объем, и пусть объем Ф
будет равен N, а А равен I, и далее, пусть вес
массы ФА будет В, все массы XI будет РО, а вес I
будет I’; значит, ФА имеет к NT то же самое отно-
шение, что В к РО. Но так как тело ФА опу- Рис.
щепо в жидкость, будучи легче этой жидкости,
то ясно, что (жидкость) в объеме погруженной части имеет равный
вес с массой ФА, как это доказано (в предложении V книги I); значит,
*) Разбор случаев, когда сегмент paneir полушарию или меньше сто, отсутствует; и тексте
перевода Вильгельма из Мербеке в конце помещены, чертежи, иллюстрирующие оба вти случая:
Значение букв: 07< — ось сегмента (® — точка со пересечения с основанием), Т — центр
тяжести сегмента, О и Г . центры тяжести погруженной и находящейся вне жидкости его частей,.
ОА и РЛ — вертикали, соединяющие центр Л Земли с центрами тяжести О и Р обеих частей сегмента.
♦*) У греков термины «тяжелый» и «легкий» понимались также и п смысле большего и мень-
шего удельного веса.
33fi
АРХИМВЦ
вес В будет равен Р, так как В ость вое всего тела ФЛ, а Р — вес жидко-
сти объем которой был сделан равным объему погруженной части А;
значит, вес тела ФА будет относиться к весу NI, как Р к РО. Ио от-
ношение Р к РО будет равно отношениям Г к JN и А к ФЛ; значит,
предложенное доказано.
II
Прямой сегмент прямоугольного коноида *), ось которого не более
полуторной прямой «до оси»**), опущенный е жидкость так, чтобы его
основание не касалось жидкости, при всяком отношении по тяжести
к жидкости, будучи поставлен наклонно, не остается наклонным,
ио возвращается в прямое положение. Прямым же положением сегмента
я называю такое, когда отсекшая его плоскость оказывается параллель-
ной поверхности воды.
Пусть будет сегмент прямоугольного коноида такой, как сказано
выше; поставим его в наклонное положение. Требуется доказать, что
он не останется в по-
1 кое. но возвратится в
прямое положение.
Рассечем его пло-
скостью, проходящей
через ось и перпендику-
лярной к (плоскости,
совпадающей с поверх-
ностью) жидкости; пусть
сеченном сегмента бу-
дет парабола АПОЛ
(рис. 11), осью сегмента
и диаметром параболы
будет прямая NO, сече-
нием же поверхности
жидкости прямая J2.
Так как сегмент не
стоит прямо, то АЛ не
будет параллельна 12,
IX. Проведем теперь па-
так что NO не образует прямого угла с
раллельную (поверхности жидкости) касательную KQ к параболе
в точкв II, и из П нарал.тельно NO проведем ПФ; тогда НФ разделит
IX пополам, как это доказало в теории конических сечений. Раз-
делим ПФ так, чтобы ПН была вдвое больше ВФ, а NO разделим в Р
так, чтобы ОР была вдвое больше PN; тогда Р будет центром тяжести
большого телесного сегмента, а В — центром тяжести телесного сег-
мента 1ПОЕ; действительно, в (книгах) «О равновесии»***) доказано,
что центр тяжести ссгмепта прямоугольного коноида находится па оси,
разделенной так, чтобы прилегающий к вершине отрезок оси был вдвое
больше оставшейся части. Далее, если отпять телесный сегмент 1П02
от всего тела, то центр тяжести остатка будет па прямой ВГ; действи-
*) То ость Семента параболоида вращения, отсеченного плоскостью, перпендикулярной
к оси.
*•) Ого параметр р в уравнении р*=2рх в дальнейшем переводится словом «.параметр».
***> Вероятно, в продолжении трактата «О равновесии плоских фигур». J3 сохршгиютнхея сочи-
нениях Архимеда это доказательство имеется и «Эфоде» (предложение V).
О ПЛАВАЮЩИХ ТЕЛАХ
337
тольно, л «Началах механики»*) доказано, что если от данной величи-
ны отпять какую-нибудь часть, не имеющую общего центра тя?кссти
с целой величиной, то центр тяжести остатка будет па прямой, соеди-
няющей центры тяжести целой величины и отнимаемой части, если
продолжить эту прямую в ту сторону, где находится центр тяжести
целой величины. Поэтому продолжим ВР до Г, и пусть Г будет центром
тяжести остающейся величины. Теперь, так как 50 в полтора рала боль-
ше ОР и по более полуторного параметра, то ясно, что РО не будет более
параметра; значит, ПР образует с K.Q неравные углы [3], причем угол
РП£2 будет острым; значит, перпендикуляр, опущенный .из Р на 110,
упадет между точками П и О. Пусть он пойдет по РО; значит, Р0 будет
перпендикулярна к плоскости, (параллельной той), в которой находит-
ся S1, то ость поверхности жидкости. Проведем из точек В, Г прямые,
параллельные Р0; находящаяся вне жидкости часть сегмента пойдет
вниз по проведенному n:i Г перпендикуляру, так как предполагается,
что каждая тяжесть движется вниз по перпендикуляру, проведенному
через ее центр; часть же, находящаяся в жидкости, будучи более легкой,
чем эта жидкость, пойдет вверх по перпендикуляру, проведенному
через В. И так как обе. (эти массы) давят друг на друга не по одной
и той же отвесной линии, то фигура не останется неподвижной; но часть,
прилежащая к Л, пойдет вверх, а прилежащая к Л — впиз, и так будет
нее время, пока сегмент пе станет прямо 14].
III
Прямой сегмент прямоугольного коноида, ось которого не более
полуторного параметра, при всяком отношении по тяжести к жидко-
сти. опущенный в жид-
кость так, чтобы его
основание целиком на-
ходилось в жидкости,
будучи поставлен на-
клонно, не останется
наклонным, но встанет
так, что ось его пой-
дет по отвесной линии.
Опустим такой,
как сказано, сегмент в
жидкость, и пусть осно-
вание его будет в жид-
костн{рис. 12}; рассечем
его через ось плоско- „
... . _ Рис. 12.
стыо, перпендикуляр-
ной к поверхности жид-
кости; пусть сечением сегмента будет парабола А ПОЛ, осью сегмента и
диаметром параболы — прямая НФ, сеченном же ловорхпости жидко-
сти линия 12. Теперь, так как сегмент лежит наклонно, то ось его
отвесной не будет; значит, ПФ пе образует равных углов с IS. (Парал-
лельно 1S) проведем в точке О (касательную КП) к параболе А ПОЛ;
пусть центром тяжести тола АПОЛ будет Р, а центром тяжести тела
lilOS — точка В; соединяющую прямую ВР продолжим, и пусть Г
•) 'Hv ioi£ Srmxeieijwv jrnz’xviWBV—элементарный куре механики, может быть, и не при-
надлежащий Архимеду. См. «О раипокиеии плоских фигур», ни. I, VIII.
22 Архимед
338
АРХИМЕД
будет центром тяжести тела IXAA. Теперь совершенно так же дока-
жем, что угол между РО, ОК будет острым, так что перпендикуляр,
опущенный из Р на KQ, упадет между К и О; пусть он будет РО.
Если через Г и В проведем прямые, параллельные РО, то часть сег-
мента, заключенная в жидкости, пойдет вверх по прямой, проведенной
через Г, находящаяся же вне жидкости — вниз по прямой, прове-
денной через В, и тело Л ПОЛ нс останется в жидкости в приданном
ему положении, но прилежащая it А часть будет двигаться вверх, а
прилежащая к Л — вниз, пока линия ПФ не сделается отвесном f5J, [G1-
IV
Если прямой сегмент прямоугольного коноида будет легче жидкости
и ось его более полуторного параметра, а по весу к равному объему жид-
кости он имеет отношение не меньшее, чем квадрат (па отрезке),
равном разности между осью и полуторным параметром к квадрату
на оси, то, будучи опущен в жидкость так, чтобы его основание не каса-
лось жидкости, и поставлен наклонно, сегмент не остается наклонным,
но возвращается в прямое положение.
Пусть будет сегмент прямоугольного коноида такой, как сказано,
и пусть он, будучи опущен в жидкость, если возможно, станет по прямо,
по наклонно; если рассечь
его через ось плоскостью,
перпендикулярной к по-
верхности жидкости, то
сечсписм сегмента будет
парабола АНОЛ {рис. 13},
осью сегмента и диаметром
параболы —прямая NO и,
наконец, сечением поверх-
ности жидкости IX. Если
сегмент не стоит прямо, то
NO не образует е IX рав-
ных углов. Проведем
KQ — касательную к па-
раболе в точке 11, парал-
лельную IX; затем из П
параллельно ON проведем
ПФ и найдем центры тяжести; у тела АПОЛ центром пусть будет Р.
а у погруженном в воду части центром будет В; проведем соединяющую
прямую ВР и продолжим до Г, и пусть Г будет центром тяжести
части, находящейся над жидкостью. И так как NO в полтора раза
больше РО и более полуторного параметра, то ясно, что РО будет
больше параметра. Пусть РМ равпа параметру, и ОМ вдвое больше ИМ.
Так как NO в полтора раза больше РО, а 110 в полтора раза боль-
ше ОМ, то, значит, остаток NH будет в полтора раза больше остатка РА1,
значит, ось сегмента будет на отрезок НО больше полуторного парамет-
ра РМ.
И так как предполагалось, что по тяжести сегмент имеет к жидкости
отношение нс меныпсс того, которое квадрат на разпости между осью
и полуторным параметром имеет к квадрату на оси, то ясно, что пв
тяжести сегмент имеет к жидкости отношение но меньшое того, которое
квадрат на НО имеет к квадрату на NO. Отношение по тяжести сегмен-
О ПЛАВАЮЩИХ ТЕЛАХ
339
та к жидкости равно отношению погруженной части ко всему сегменту,
как уже доказано (в предложении /}, а отношение погруженной частя
ко всему сегменту равно тому, которое имеет квадрат па 11Ф к квадрату
па NO; действительно, в книге «О коноидах» доказано, что если от пря*
моуголыгого коноида отсечь два сегмента произвольно Проведенными
плоскостями, то эти сегменты будут иметь друг к другу то же самое
отношение, что и квадраты их осей («О коноидах», предложение XXIV).
Такилг образом, квадрат на 11Ф к квадрату на АО имеет отношение
не меньшее, чем квадрат на НО к квадрату на NO; поэтому ПФ пе менее
НО, и ВП не менее МО*); значит, если из М провести перпендикуляр
МО к NO, то он упадет между В и П. И так как ПФ параллельна
диаметру, М® перпендикулярна диаметру и РМ равна параметру, то
прямая, соединяющая Р с €), будучи продолжена, образует прямые углы
с .касательной в П**); значит, она образует прямые углы и с IX, и с с<ь
ответствующей IX поверхностью жидкости. Если через В и Г провести
прямые, параллельные Р0, то у поверхности жидкости получатся яря-
мыо углы и заключенная в жидкости часть сегмента коноида пойдет
вверх по прямой, проведенной через В параллельно РО, находящаяся же
вне жидкости часть пойдет вниз но проведенной через Г параллели
к Р®, и так будет все время, пока сегмент коноида не станет прямо {7J.
V
Исли прямой сегмент прямоугольного коноида легче жидкости и ось
его более полуторного параметра, а по весу он имеет к жидкости отно-
шение не большее, чем разность между квадратом оси и квадратом раз-
ности между осью и полуторным параметром имеет к квадрату оси,
то будучи опущен в жидкость так, чтобы его основание было целиком
погружено в воду, и поставлен наклонно, он не останется наклонным,
ио встанет так, что его ось будет направлена по отвесу.
Опустим такой, как сказано, сегмент в жидкость, и пусть его осно-
вание будет целиком в жидкости {рис. 14}; есл и рассечь его через ось пло-
скостью, перпендикулярной к поверхности жидкости, то в сечении по
лучится парабола АПОЛ, осью сегмента и диаметром параболы будет
прямая NO и сечением поверхности жидкости прямая IX. И так как ось
сегмента нс будет отвесной, то NO не образует с IX равных углов. Про-
ведем К£2 — касательную к параболе АНОЛ в точке П, параллельную IX,
а через II прямую ПФ, параллельную NO, и возьмем центры тяжести;
пусть у сегмента АНОЛ центром будет Р, а у части его, находящейся
вис жидкости,— В; соединяющую прямую ВР продолжим до Г; пусть Г
будет центром тяжести части, погруженной в жидкость. Возьмем РМ
равной параметру и сделаем так, чтобы ОМ была вдвое больше НМ,
и пусть все остальное будет сделано так же, как и выше. Теперь,
поскольку предполагается, что сегмент ио тяжести имеет к жидкости отно-
шение не большее, чем разность квадратов на NO и 011 имеет к квадрату
на NO, а отношение по тяжести сегмента к равному объему жидкости
равно отношению погруженной части тела ко всему этому телу (как
доказано в первой теореме), то, значит, погруженная часть сегмента
ко всему сегменту имеет отношение, не большее указанного; значит.
*) Действительно, для центра тяжести В сегмента 1П02 имеем ВГ1=— ФП и ыо = -| ОН.
*‘) Действительно, РМ есть субнормаль. а ем — ордината точки касания п.
2k*
•ИО
АРХИМЕД
весь сегмент к части, находящейся пне жидкости, имеет отношение не
большее, чем квадрат на NO к квадрату на ИО.
Ио весь сегмент к своей части, находящейся вне жидкости, отно-
сится как квадрат NO к квадрату ПФ; значит, квадрат на NO к квадра-
ту на ПФ имеет отношение не большее, чем квадрат на NO к квадрату
на НО.
КО2 NO2
по8 '* IJO2
Следовательно, НФ будет не менее ОН и НВ не менее МО. Значит, отвес-
ная линия, проведенная из М к РО, пересечет ВП между И и В; пусть
она пересечет ее в 0. И так как в параболе прямая ПФ параллельна РО,
а М© перпендикулярна к диаметру, и, наконец, РМ равна параметру,
то ясно, что проведенная прямая РО образует прямые углы с K1IQ,
а значит, и с 1Z. Следовательно, РО перпендикулярна к поверхности
жидкости, и прямые, проведенные через точки В и Г параллельно РО,
будут перпендикулярны к поверхности жидкости; значит, часть тела,
находящаяся вне жидкости, пойдет книзу в жидкость по перпендикуля-
ру, проведенному через В, находящаяся же в жидкости часть пойдет
вверх во перпендикуляру, проведенному через Г, и сегмент АНОЛ
не останется в покое, во будет двигаться в жидкости, пока NO по сде-
лается отвесной [8J.
VI
Если прямой сегмент прямоугольного коноида легче жидкости
и имеет ось, отношение которой к параметру более чем три к двум,
по менее чем пятнадцат ь к четырем,, то, будучи опущен. е жидкость так,
чтобы его основание касалось жидкости, сегмент не останется наклонен-
ным так, чтобы его основание имело одну общую точку с жидкостью [9].
Пусть будет сегмент такой, как сказано: пусть оп, будучи опущен
в жидкость, установится, как показано {рис. 15}, так, что его основа-
ние будет касаться жидкости в одной точке. Если рассечь его через ось
плоскостью, перпендикулярной к поверхности жидкости, то сечением
сегмента будет парабола АНОЛ, сечением поверхности жидкости —
О ПЛАВАЮЩИХ ТЕЛАХ
341
прямая AS, а осью сегмента и диаметром (параболы) — прямая NO.
Разделим последнюю в точке Ф так, чтобы ОФ была вдвое больше Ф1Ч,
а в точке £2 так, чтобы NO относилась кФ£2, как пятнадцать к четырем;
затем проведем £2 К перпендикулярно к NO. Тогда отношение NO
кфо будет больше отношения NO к параметру. ПустьФВ равпа пара-
метру; параллельно AS проведем прямую ПТ, касательную к параболе
АНОЛ в точке II, а также прямую 111, параллельную NO. Пусть снача-
ла прямая IJI пересечет прямую К£2. Так как в сегменте АПОЛ, за-
ключенном между прямой и параболой, прямая КН параллельна АЛ,
прямая III параллельна диаметру и пересекается с КУ и, наконец.
AS параллельна касательной в П, то необходимо, чтобы отношение 1JI
к ПП было равно или больше отношения N£2 к ЙО; ато уже было
доказано в леммах [10]. Прямая £2N в полтора раза больше £20, и
следовательно, 1П или ровно в полтора раза, или же более чем в пол-
тора раза больше НИ; поэтому 1111 или равна, или же меньше уд-
военной НТ*).
Пусть 110 в два раза больше Ш; тогда О будет центром тяжести
заключенной и жидкости части сегмента; проведем 6Ф и продолжим;
пусть Г будет центром тяжести части, выступающей из жидкости.
Из В перпендикулярно NO пронедем ВР. 'Гак как 111 параллельна диа-
метру NO, а ВР ему перпендикулярна, иФВ равна параметру, то ясно,
что продолженная ФР образует равные углы с касательной в точке П
к параболе АНОЛ, а следовательно, и с AS, и с поверхностью жидко-
сти. Если мы через 0 и Г. проведем прямые, параллельные ФР, то они
тоже будут перпендикулярны к поверхности жидкости; заключенная
внутри жидкости часть сегмента АПОЛ будет итти вверх по отвесной
прямой, проходящей через 0, а часть, находящаяся вне жидкости, будет
опускаться вниз по отвесной прямой, проходящей через Г. Таким обра-
зом, тело повернется и его основание нс будет касаться жидкости в одной
точке.
*) Действительно, Ш : ПН(ПН 1- III) : ПН—откуда MJ ; ПП .
3i2
АРХИМВД
Если П1 нс
фигуре {рис. 16},
пересечет прямой KQ, как изображено на второй
то ясно, что точка © — цептр тяжести погруженной
Рис. 16.
части — будет лежать между
II и I; все же остальное бу-
дет доказано так же [101.
VII
Если прямой сегмент пря
моуголъного коноида легче
жидкости и имеет ось, боль-
шую полуторного параметра,
но мёныиую параметра, уве-
личенного в отношении пят-
надцати к четырем, то, буду-
чи опущен в жидкость так,
чтобы все основание его цели-
ком находилось в жидкости,
сегмент никогда не станет
так, чтобы его основание
касалось*) поверхности жид-
кости, но установится так,
что все основание его полно-
стью будет находиться в жид-
кости и ни в одной точке не
коснется ее поверхности.
Пусть будет такой, как сказано, сегмент; пусть он, будучи опущен,
как сказано, в жидкость, установится так, чтобы его основание каса-
лось поверхности жидкости. Требуется доказать, что оя не останет-
ся в покое, но наклонится так, что его основание пив одной точке пе
коснется поверхности
жидкости.
Если рассечь его
плоскостью, перпенди-
кулярной к поверхности
жидкости, то сечением
его будет парабола
Л ИОЛ {рис. 17}, сече-
нием поверхности жид-
кости — прямая SA, а
осью сегмента и диамет-
ром параболы — прямая
i IФ. Опять раздел им 11Ф
в точке Р так, чтобы Pl I
была вдвое больше РФ,
а в точке Q так, чтобы
ФП имела к PQ отно-
1’ис. 17.
гпенио пятнадцати к че-
тырем; проведем перпендикуляр Qlv: тогда РЙ будет меньше пара-
метра. Отложим PH, равную параметру, и проведем ТО — ка-
сательную к параболе » О, параллельную ЕЛ, а затем NO, па-
) Касалось, т. е. имело общую точку.
О ПЛАВАЮЩИХ ТЕЛАХ
343
раллельную ПФ. Пусть сначала NO пересечет Kfl в точке I. Тогда
подобно предыдущему докажем, что NO будет или в полтора раза или
более чем в полтора раза больше
01; (в последнем случае) 01
будет меньше удвоенной 1N.
Пусть ОВ будет вдвое больше
LJN, и все остальное сделаем
так же, как и раньше; подобно
(предыдущему) докажем, что Р(-)
образует прямые углы с ТО и
•с поверхностью жидкости, а
прямые, проведенные через В и
Г параллельно РО, будут пер-
пендикулярны поверхности жид-
кости. Теперь находящаяся вне
жидкости часть сегмента пойдет
вниз в жидкость по перпендику-
ляру, проведенному через В, а
часть, находящаяся в жидкости,
пойдет вверх по перпендикуляру
через Г; яспо, что тело накло-
нится так, что его основание не
будет пи в одной точке касаться
поверхности жидкости, потому л
что часть, (касавшаяся поверх- Рис- 18-
нести жидкости) в одной точке
(Л), опустится (вниз) со стороны. Л, Также ясно, что то же самое
можно будет доказать и в том случае, когда ON не будет пересекать
{рис. 18} 111].
VIII
Если, прямой, сегмент прямоугольного коноида с осью, большей полу-
торного параметра, но меньшей
ТВ в полтора раза больше 13Р, аТД
ого параметра, увеличенного в от-
ношении пятнадцати к четырем,
имеет по тяжести к жидкости
отношение меньшее, чем квадрат
разности оси и полуторного пара-
метра к квадрату оси, то, будучи
опущен в жидкость так, чтобы его
основание не касалось жидкости,
сегмент не возвратится в отвесное
положение, а останется в наклон-
ном положении, причем его ось
образу т с поверхностью жидкости
угол, равный тому, который бу-
дет. указан.
Пусть будет сегмент такой,
как сказано; пусть ВД {рис. 19}
равна его оси, ВК вдвое больше КА,
аКР равпа параметру; пусть также
полтора раза больше КР; пусть от-
ношение, которое сегмент по тяжести имеет к жидкости, равно тому,
:J44
АРХИМЕД
которое квадрат на Ф+Х имеет к квадрату на АВ, и пусть Ф будет
вдвое больше, чем X. Ясно, что Ф-;-Х имеет к АВ отношение, мень-
агее того, которое ТВ имеет к 13Д, так как ТВ есть разность, па ко-
торую ось больше полуторного параметра * *); значит, Ф+Х меньше ВТ,
так что и Ф будет меньше ВР. Пусть Ф равна РЧ'; перпендикулярно
, БД проведем ТЕ, квадрат па которой равняется половине прямо-
. угольника между КР и BY, и проведем соединяющую прямую ВИ.
Требуется доказать, что упомянутый сегмент, опущенный, как сказано,
в жидкость, установится в наклонном положении так, что ого ось обра-
зует с поверхностью жидкости угол, равный ЕВУ**).
Опустим в жидкость .некоторый сегмент, и пусть его основание
нс будет касаться поверхности жидкости; при этом, если возможно, пусть
ось образует с поверхностью жидкости угол, пе равный В, по сначала
больший. Если рассечь сегмент через ось плоскостью, перпендикулярной
к поверхности жидкости, то его сечением будет парабола АПОЛ, сече-
нием поверхности жидкости — прямая ES, а осью [сегмента! и диа-
метром (параболы) — прямая NO. Параллельно ES проведем каса-
тельную ПГ к параболе АПОЛ в точке П, затем проведем ПМ парал-
лельно КО и Ш перпендикулярно NO, и пусть OQ равна В В, а РК
равна QO, и QII перпендикулярна к оси. Поскольку предполагается,
что осьсегментаобразует с поверхностью жидкости угол больший, чем В,
то ясно, что в треугольнике Ш Г угол при Y будет больше В; тогда
квадрат нй III к квадрату на ГТ будет иметь отношение большее, чем
квадрат на Е Y к квадрату па YB. Но квадрат на III к квадрату па IГ
имеет то же отношение, что КР к EI; отношение же квадрата па EY
к квадрату на ЧГВ равно отношению половины КР и ЧГВ; значит, КР
к TI будет иметь большее отношение, чем половина КР к YB;
КР , ~2~Kt>
Г1 «ГВ
значит, Г! будет меньше удвоенной ТВ. I Jo IT вдвое более 01; значит,
01 меньше YB,
OKW
и IQ будет больше ЧТ***).
V » V < » с и ~ ' — и
*) а уеt&i)v ?) цшпЛюк о a£cov Tag цеуп*- 'too agovo? — буквально» опа которую ось более чем
в з/й раза больше параметра (прямой до оси)».
**) В наших обозначениях: EA--ON—ВК- ь, КР—р, отношение d плотностей тела-
и жидкости будет:
(Ф Х>2 . (~2~)
(W
9 Q 1
Далее, ТВ= — ВР= — (Ь — р), Ф-|-Х < В'Г иФ < Ъ— р = ВР. Полагаем Ф = РЧГ и ЧРЕ*=— р- ВЧ'=г=
= где В'К—-ВР—Р’К=1)—р—Ф. Если обозначим угон ЕВЧГ через В, то
l£ Б V 2 ’ BV
Имеем ОО = Ь, OQ—р и. следовательно, ОЙ—Ь—р=ВР. Если угол ПГ1> В, то
щг . КЧГ£
ц-2 '>-^-В2 ’
Исли в II пронедем нормаль, то начинающаяся в I субнормаль будет равна параметру р —КР.
В тавом случае ПР-КР-П,
О ПЛАВАЮЩИХ ТЕЛАХ
345
Но ЧГР равна Ф; значит, IQ больше- Ф. И так как, согласно пред-
положению, сегмент но тяжести имеет к жидкости отношение, как квад-
рат на Ф-|-Х к квадрату на ВД, и отношение ио тяжести сегмента к жид-
кости равпо отношению погруженной части ко всему сегменту, а отно-
шение по груженной части ко всему сегменту будет тем же, что у (квадра-
та) на ПМ к (квадрату) па ON, то, значит, квадрат па Ф-| X. к квадрату
на ВЛ будет иметь то же самое отношение, что квадрат па МН к квадра-
ту па ON; значит, Ф+Х будет равняться ТТМ. Но ПН, согласно дока-
занному, больше Ф; значит, ясно, что ИМ будет меньше ПН, взятой
полтора раза, а 1111 более чем вдвое больше НМ*).
llycTii HZ вдвое больше ZM; тогда (-) будет центром тяжести всего
тела, a Z — центром тяжести его части, погруженной в жидкость;
цептр тяжести остающейся части будет на продолжении соединяющей
прямой ZH. Пусть ото про-
должение дойдет до Г;после
□того так же, как и раньше,
докажем, что (т)Н будет пер-
пендикуляром к поверх-
ности жидкости и находя-
щийся внутри жидкости
сегмент пойдет из жидкости
вверх по проведенному че-
рез Z перпендикуляру к по-
верхности жидкости, а на-
ходящаяся впе жидкости
часть пойдет вниз, в жид-
кость, по перпендикуля-
ру, проведенному через Г;
таким образом, при упо-.
минутом угле наклона сег-
мент нс останется в покос.
Но он также не .вернется
дующего; из проведенных через
проходит через Z, упадет с той стороны от TZ**), где находится А,
а проведенный через Г — с той стороны, где Л, поэтому ясно, что,
согласно вышесказанному, центр Z пойдет вверх, а Г вниз, так что
прилегающая к Л часть всего тела пойдет вниз.
Это было важно для доказательства.
Пусть теперь при тех же предположениях ось сегмента образует
с поверхностью жидкости угол меньший, чем В {рис. 20}; тогда
в
отвесное положение. Это ясно из сле-
Z и Г перпендикуляров тот, который
откуда
ПР _ КР
ГР П '
М ы имеем
КР _ Е'У2 1 КР ВЧ^_ 1 КР
“рр цгда — 2 ЧГВ2 — 2 ЧГВ
и, следовательно, Г1<2ЧГВ. Так ван вершина О параболы делит пополам еубтавгенс 1'1, то OI’i.VB
и, следовательно, ....
IS2 = OU - 01 = (Ъ - р) - 01 > BP - WB = ТР.
^Отношение d плотностей тела и жидкости будет
, (Ф | Х)2 ИМ2
ВД2 ~ ONS ’
Так как ПД ON, то И М = Ф -I- X. Так как IG = ПН > Ф п X =* Ф, то ИМ < 1Ш и ПН >2НМ.
Это покалывает, что 7. — центр тяжести погруженной части сегмента находится между II нН.
“) Так в подлиннике. Мы сказали бы «от вн».
346
АРХИМЕД
квадрат иа Ш к квадрату иа IT будет иметь меньшее отношение, чем
квадрат на EV к квадрату на VB, и, значит, К1‘ имеет к TI меньшее
отношение, чем половина КР к VB. Тогда 1Г будет более чем вдвое
больше ТВ, и, значит, £21 меньше, чем VP. Тогда и ПН будет мень-
ше Ф. Ио МП равна Ф-|-Х; ясно, что ПМ более полуторной 1111, а ПН
меньше удвоенной НМ. Пусть nZ будет вдвое больше ZM. Тогда цент-
ром тяжести всего сегмента будет 0, а части, находящейся в жидкости,
—Z; если провести соединяющую прямую Z& и продолжить, то центр
тяжести части, находящейся вне жидкости, будет на продолжении.
Пусть оп будет Г; проведем через Z и Г перпендикуляры к поверхности
жидкости, параллельные Н0; тогда ясно, что весь сегмент пе останется
неподвижным, ио наклонится так, что ось ого образует с поверхностью
жидкости угол, больший того, который опа образует теперь.
Поскольку сегмент пе установится пи при большем, ни при мень-
шем чем В угле наклона оси с жидкостью, то ясно, что он установится
только при угле, равном В; в таком случае 10 будет равна ТВ, £21
равна VP и Ф равна 1111; значит, МН будет в полтора раза больше ПН,
а ПН в два раза больше ПМ. Следовательно, II будет центром тяжести
части, находящейся в жидкости; таким образом, последняя пойдот
вверх по тому же самому перпендикуляру, по какому пойдет вниз
часть, находящаяся вне жидкости, значит, сегмент останется неподвиж-
ным, так как обе части будут толкать друг друга в противоположные
стороны [12J.
IX
Если прямой сегмент прямоугольного коноида с осью, большей полу-
торного параметра, но меньшей этого последнего, увеличенного в отно-
по тяжести к жидкости отноше-
ние большее, чем разность
квадрата оси и квадрата
излишка оси над полутор-
ным параметром к квадра-
ту оси, то он, будучи опу-
щен в жидкость так чтобы
его основание целиком нахо-
дилось в жидкости, и по-
ставлен наклонно, не вста-
нет отвесно, но останется
X в наклонном положении,
причем ось его с поверхно-
стью жидкости составит
----угол, равный тому же, что
и выше.
Рис. 21. Пусть будет сегмент та -
кой, как сказано; отложим
ДВ {рис. 21} равной оси сегмента, и пусть ВК будет вдвое больше КД, аКР
равна параметру, и ТВ в полтора раза больше ВР; пусть также отноше-
ние, которое по тяжести сегмепт имеет к жидкости, будет том, какое раз-
ность квадрата на ВД и квадрата па Ф-}-Х имеет к квадрату на ВД,
причем Ф вдвое больше X. Теперь ясно, что разность, на которую квад-
рат па ВД превышает квадрат па ВТ, имеет к квадрату па ВД меныпее
отношение, чем то, какое разность, на которую квадрат ВД превышает
О ПЛАВАЮЩИХ ТКЛАХ
347
квадрат па Ф+Х, имеет к квадрату на ВА, так’ как ВТ есть разность,
на которую ось больше полуторного параметра. Значит, квадрат на ВД
больше квадрата на Ф+Х на (величину), большую той, на кото-
рую квадрат па ВД больше квадрата на ВТ, так что Ф+Х будет мень-
ше ВТ и, следовательно, Ф. меньше ВР.
Пусть теперь РТ равна Ф; перпендикулярно ВА проведем ЧГЕ,
квадрирующую пол овину {прямоугольника] между КР и ЧГВ. Я гово-
рю, что сегмент, опущенный в жидкость так, чтобы его основание было
целиком в жидкости, установится так, что ось его с поверхностью жидко-
сти составит угол, равным В.
Опустим сегмент в жидкость, как сказано, и пусть ось его не состав-
ляет с поверхностью жидкости угол, равный В, по сначала составит
угол больший, чем В.
Если рассечь его плоскостью, перпендикулярной к поверхности
жидкости, то сечением сегмента будет парабола АПОЛ, сечением по-
верхности жидкости — прямая TI, а осью [сечения] и диаметром пара-
болы — прямая NO; разделим последнюю в Q, 6 так же, как и рань
пге; параллельно Т1 проведем ГГ1 касательную к параболе в 11, а так-
же НМ параллельно NO п 112 перпендикулярно к оси. Так как ось
сегмента составляет с. поверхностью жидкости угол, больший угла при
В, то и угол 2ГП будет больше угла В; значит, квадрат на П2 к квад-
рату па 2 Г будет иметь большое отношение, чем квадрат на Ч'Е к квад-
рату на ТВ.
Значит, КР будет иметь к 2 Г отношение большее, чем полови-
на КР к ТВ;
КР
КР _2_
ГГ Ч'В
значит, 2 Г меньше удвоенной ТВ, а 20 меньше ТВ, л, следовательно,
2Q будет больше РТ и НН больше Ф. И так как сегмент по тяжести
относится к жидкости, как излишек квадрата на ВД пад квадратом
на Ф+Х относится к квадрату на ВД, а отношение сегмента по тяжести
к жидкости равпо отношению погруженной части ко всему сегменту,
то ясно, что погруженная его часть ко всему сегменту будет иметь то же
отношение, какое излишек квадрата на ВД пад квадратом па Ф+Х
имеет к квадрату па ВД; тогда и весь сегмент к своей части, находящем-
ся вне жидкости, будет иметь то же отношение, какое квадрат на ВА
имеет к квадрату па Ф+Х. Отношение ясе всего сегмеггта к части,
находящейся вне жидкости, равпо отношению квадрата на NO к квадрат
ту на ПМ;
вд* _ ко8
4Ф1Х)8 им2
значит, МП равна Ф+Х. По доказано, что 1JH более Ф; значит, МП
будет менее X; следовательно, ПН будет больше удвоенной НМ.
Пусть IIZ будет вдвое более ZM; продолжим соединяющую Z0 до Г;
тогда центр тяжести всего сегмента будет 0, части, находящейся вне
жидкости —Z, а части, находящейся внутри ее, на О Г; пусть он будет
в Г. Подобно предыдущему докажем, что 0Н будет перпендикулярна
к (поверхности жидкости и что прямые, проведенные через Z и Г па-
раллельно 6Я), будут тоже перпендикулярны к поверхности жидко-
сти. Значит, находящаяся вне жидкости часть сегмента пойдет вниз
но перпендикуляру, проведенному через Z, а находящаяся внутри будет
348
АРХИМЕД
подыматься по перпендикуляру, проведенному через Г; следовательно,.
весь сегмент не может оставаться неподвижным в наклонном положе-
нии. по он также н пе повернется так, чтобы ось его стала перпенди-
кулярной к поверхности жидкости, так как тогда прилегающие к Л
части дойдут вниз, прилегающие же к Л — вверх на основании таких
жо рассуждении, как и в преды-
дущем.
Нели ate ось образует с по-
верхностью жидкости угол мень-
шим, чем при В, то подобно преды-
дущему докажем, что сегмент пе-
останется неподвижным, но будет
наклоняться до тех пор, пока ось
его но образует с поверхностью
жидкости угол, равный В [131.
X
Если прямой сегмент прямо-
угольного коноида легче жидкости
и имеет ось, превышающую пара-
метр в отношении большем, чем
пятнадцать к четырем, то, будучи
опущен е жидкость так, чтобы ос-
нование его не Касалось жидкости,
он иногда установится прямо (1),
иногда же наклонно1, иногда его
основание будет только в одной
точке касаться поверхности жид-
кости, причем это может быть
при двух углах наклона (3, 5),
иногда он станет так, что его
основание будет смачиваться на
большей площади (4), иногда же
так, что его основание ни в одной
точке не будет, касаться поверх-
ности и жидкости {2fi');npu каких же
ш
Рис. 22.
отношениях по тяжести к жидкости будет иметь место каждый ил
этих случаев, выяснится в дальнейшем [141.
Пусть будет сегмент такой, как сказано; если рассечь его плоско-
стью, перпендикулярной к поверхности жидкости, то сечением его
поверхности будет парабола АНОЛ jpuc. 22}; пусть осью сегмента
и диаметром параболы будет ВА; разделим ВЛ в К так, чтобы ВК была
вдвое больше КА, а в Т так, чтобы ДВ относилась к КТ как пятнад-
цать к четырем. Ясно, что КТ больше параметра. Пусть КР равна пара-
метру и РЕ будет половиной ВР; тогда и ЕВ будет в полтора раза
больше ВР. Соединивши А, В и восставив перпендикуляр ’ГЕ, проведем
EZ параллельно ВЛ; затем, разделив ЛВ пополам в О, параллельно ВЛ
проведем 011 и возьмем параболы ЛЕ1 на диаметре EZ и А0Д на диа-
метре 0П так, чтобы сегменты AEI, ЛОЛ были подобны сегменту АВЛ;
тогда парабола AEI пройдет через К и перпендикуляр, восставлен-
ный в Р к ВЛ, пересечет параболу AEI. Пусть он пересечет ее в точках
Г, Г; через Г и Г параллельно ВА проведем I’X, TN; пусть они пере-
О ПЛАВАЮЩИХ ТИЛАХ
349
секут параболу А (ЭД в точках Е, Ф; проведем также касательные ПТ
и ОЦ к параболе А ПОЛ в точках О, II. Таким образом, даны трп заклю-
ченных между прямом п параболами сегмента Л1ЮЛ, АЕ1, A0A,
прямые и подобные друг другу, но нс равные; их основания лежат
на одной и той же прямой, и из точки N проведены прямые NE, NT,
NO; значит, О Г имеет к ГЕ отношение, составленное из тех, которые
1Л имеет к ЛЛ, и ЛА к Д1*).
ОГ IA АД
ГЕ ЛА Д1
Но ЛТ относится к ЛА, как дна к пяти, ибо ТВ будет к ВД, как дна
к пяти; такжо и ЕВ к ВЛ п AZ к /ХЛ, а Л1 и ЛА являются удвоенными
прямыми AZ и ДА; затем ЛЛ относится к Д1, кт пять к одному, и от-
ношение, составленное из тех, которые- имеют два к пяти и пять к одно-
му, будет тем же, что отношение двух к одному; значит, О.I.’будет вдвое
больше ГЕ. На том же, основании ПТ будет вдвое, больше, ТФ. По-
скольку же, Д2 в полтора раза больше КР, то ясно, что BS представ-
ляет разпость оси и полуторного параметра [15J.
(1) Теперь, если сегмент по тяжести, имеет к жидкости то же отно-
шение, что квадрат па В2 к квадрату на ВЛ, или же большое этого
•отношения, то он, будучи опущен в жидкость так, чтобы его основание
нс касалось жидкости, станет прямо, ибо ранее (предложение IV) было
доказано, что если сегмент имеет ось, большую полуторного параметра,
и если ио тяжести он имеет к жидкости отношение нс меньшее того,
которое квадрат разности между осью и полуторным параметром имеет
к квадрату па оси, то он, будучи опущеп в жидкость так, как сказано,
установится в прямом положении.
(2) Если же сегмент по тяжести имеет к жидкости отношение мень-
шее того, которое квадрат па SB имеет к квадрату на ВЛ, но большее
того, которое квадрат па ()Е имеет к квадрату на ВД, то оп, будучи
опущен в жидкость и наклонен так, чтобы его основание, пе касалось
жидкости, установится наклонно так, что его основание пе будет ни
в одной точке касаться поверхности жидкости и его ось образует
с поверхностью жидкости угол, больший чем Cj (рис. 22).
•) Проведем гбщую касательную Лига всем трем параболам л тонне А; ето возможно, так
«ак если ЛВ- Hub то п ZE — Ей и IiO = O«i, где точки m, i>, с, ю представляют пересечения этой
касатсльн< й с прямыми ПО. ZK, КО и ДВ. Мы внаем («Квадратура параболы», V), что всякая
параллельна)! оси пряма и, приведенная между основанием параболического сегмента и касательной,
в конце пгиеплнил рассекается параболой на отреаки, кокфые пропорциональны отрезкам ос.иовааин:
иными словами,
со : ON —AN: NA,
сГ : TN = AN : NJ,
cc : EN — AN : NA.
Составлял производные пропорции co сложением, мы можем написать:
СО : (СО + ON) = AN : (AN + NA).
сГ : (сГ + TN) — AN : (AN |- NJ),
cE : (cE -J- EN) AN : (AN | NA).
•откуда
„ AN-eN „ AN-cN _ AN-cN
C0 = ^A~- ----АД- ;
теперь
ОГ = cl' - CO =- AN- <.N (-Л- - .
X Al АЛ /
ГЕ — cS- сГ = AN- cN {-Г---Д-\ ,
\ АЛ Л1 /
14 наконец.
ОГ __ АЛ — AT . AT — АД __ 1Л . ЛД ........... ' ....Л.
IS ЛД-Л1 ‘ AA’AI ЛЛ la . < s
350
ЛI» хим кд
(3) Если же сегмент по тяжести имеет к жидкости то же отношение,
что квадрат на ЕО к квадрату па ВД, то он, будучи опущен в жидкость
и наклонен так, чтобы его основание по касалось жидкости, установит-
ся наклонно так, что ого основание только в одной точке (А) коснется
поверхности жидкости, и его ось образует с поверхностью жидкости
угол, равный Q.
(4) Если же сегмент по тяжести имеет к жидкости отношение мень-
шее того, которое квадрат на ЕО имеет к квадрату на ВД, но большее
того, которое квадрат на ПФ имеет к квадрату па ВД, то он, будучи опу-
щен а жидкость и поставлен наклонно так, чтобы его основание не каса-
лось жидкости, установится наклонно так, что основание его рассе-
чется жидкостью иа большем протяжении.
(5) Если же сегмент но тяжести имеет к жидкости то же самое
отношение, что квадрат на ПФ к квадрату на ВД, то он, будучи опущен
в жидкость и поставлен наклонно так, чтобы его основание нс касалось
жидкости, установится наклонно так, что его основание только в одной
точке будет касаться поверхности жидкости и его ось образует с послед-
ней угол, равпый Т (рис. 22).
(6) Если же сегмент по тяжести имеет к жидкости отношение мевь-
шео того, которое квадрат иа ПФ имеет к квадрату па ВД, то он, будучи
опущен в жидкость и поставлен наклонно так, чтобы его основание
не касалось жидкости, установится наклонно так, что его ось образует
с поверхностью жидкости угол, мень-
д шнй V, а основание его ни в одной
точке не коснется поверхности жид-
кости.
Все это будет доказано после-
довательно.
(Случай 2)
Пусть сначала сегмент имеет но
тяжести к жидкости отношение боль-
шее того, которое квадрат на НО име-
ет к квадрату на ВД, по меныпее того,
которое квадрат разности между оськ>
и полуторным параметром имеет к
квадрату на ВД; предположим, что
вышеприведенная фигура построена
{рис. 23}, и пусть отношение сегмента
к жидкости по тяжести будет равно
отношению квадрата на некоторой
прямой *F к квадрату на ВД; тогда ¥
будет больше, чем ЕС) {рис. 22}, ио
меныпе разности между осью и полуторным параметром. Между парабо-
лами АПОА и ЛЕД вставим некоторую прямую NO, равную ¥, и пусть опа
оставшуюся параболу пересечет в а прямую Ра в точке В'; докажем,
что 62^ будет вдвое больше. совершенно так же, как было дока-
зано, что Ос*) вдвое больше аЕ; затем из точки О проведем касатель-
ную ВЦ к параболе АНОЛ и прямую ОТ, перпендикулярную к ВД,
и соединим А с X; тогда прямые AN и XN будут равны друг другу,
*> Чертеподл шишка для ясности несколько изменен; в подлиннике О стоит вместо нашего
Н и имеете е тем в дальнейшем изложении совпадает с М.
О ПЛАВАЮЩИХ ТЕЛАХ
351
так как проведенные н подобных сегментах АПОЛ и ЛЕД прямые AN
и АХ, образующие одинаковые, углы г основаниями, будут иметь-
то же отношение, что и ЛА к АЛ,
AN _ АД
АХ АЛ
и па основании второй из построенных фигур (рис- 23) AN будет
равна XN и параллельна (касательной) 0Ц * *).
Требуется доказать, что сегмент, опущенный в жидкость так, что
его основание пе будет ни в одной точке касаться жидкости, устано-
вится наклонно в этом положении, и его ось образует с поверхностью-
жидкости острый угол, больший угла Cj, Пусть сегмент будет опущен
и станет так, что его основание в одной точке коснется поверхности-.
жидкости; если рассечь его через ось
плоскостью, перяендикулярпои к по-
верхности жидкости, то сечением сег-
мента будет парабол а АПОЛ {рис. 24},
поверхности жидкости — прямая
ОЛ, а осью (сегмента) и диаметром
(параболы) будет ВЛ. Рассечем ВД в
точках К и В, как сказано выпи?'*),
затем параллельно АО пронедем пря-
мую ПГ, касающуюся параболы в
точке П, далее проведем П0 парал-
лельно ВА и IIS перпендикулярно
к ВЛ. Так как сегмент по тяжести
имеет к жидкости то яге отношение,
что квадрат па Чг к квадрату па ВЛ,
отношение жо по тяжести сегмепта
к жидкости равно отношению погру-
женной части ко всему сегменту, и
отношение погруженной части ко все-
му телу равно отношению квадрата
на 011 к квадрату на ДВ, то, значит, Ч7
будет равна 011. Значит, и NB (рис. 23) будет равна 0П; следовательно,
сегменты А ИХ [рис. 23} и Л11О {рис. 24} будут друг другу равны.
А так как в равных и подобных сегментах АПОЛ {рис. 24} и АМХЛ
{рис. 23} от концов оснований проведены прямые ОА, АХ, и отсечен-
ные части образуют с диаметрами равные углы (на основании третьей
из построенных фигур), то углы при Ц и Г будут равны. Значат, ЦВ
и ГВ тояге будут равны; следовательно, раины и SP с ТР, и nZ с ©В',
- и Z0 с B'N. Так как 0В' меньше удвоенной B'N***), то ясно, что 11Z
будет меньше удвоенной Z0. Пусть П£2 будет равна удвоенной £20;
проведя соединяющую прямую KQ, продолжим ее до Е; точка К будет
центром тяжести всего сегмента, Q — центром тяжести части, находя-
щейся в ягидкости; тогда центр тяжести части, которая вне жидкости,
найдется на линии КЕ; пусть он будет Е. Но K.Z перпендикулярна-
к поверхности жидкости, а значит, будут перпендикулярами и прямые,
проведенные через Е и £2 параллельно K.Z. Следовательно, сегмент
*) Если AN—NX, то прямая N6 Судет диаметром параболы АПОЛ, сопряженным хпрлс-
АХ и, значит, хорда АХ параллельна касательной eCj в иерптиие диаметра.
*) То есть чтобы К была центром тяжести сегмента, а КР — параметром.
•“) Действительно, ®)^b=2)^5N {рис. 23}.
352
ЛРХИМКД
не останется в покос, по станет так, что его основание ин в одной точке
не коснется жидкости, ибо в настоящем положении оно касается жидко-
сти только в одной точке. Ясно, что сегмент установится так, что ось
ого образует с поверхностью жидкости угол больший, чем Ц.
(Случай 3)
Пусть сегмент имеет но тяжести к жидкости такое отношение, как
квадрат па ВО к квадрату на ВД {рис. 25}, и опущен в жидкость в на-
клонном положении. Если рассечь ого через ось плоскостью, перпенди-
кулярной к поверхности жидкости, то сечением тела будет парабола
A1IOA {рис. 26}, сечением поверхности жидкости — прямая ОТ, а осью
сегмента и диаметром параболы — прямая ВЛ; разделим ВЛ так же,
как л раньше, параллельно ТО крове/цем касательную ИХ к параболе
в точке П, затем параллельно ВЛ проведем 110, а перпендикулярно
к ВЛ проведем U2. Требуется доказать, что сегмент не останется на-
клонным в таком положении, но будет наклоняться до тех пор, пока его
осионаиио ле коснется жидкости в одном точке.
Пусть будет перед памп (фигура) {рис. 25} и сделано то же, что
и на предшествующей фигуре; проведем ТО перпендикулярно к ВЛ
и соединяющую ЛН продолжим до X; тогда АН будет равпа ЕХ;
проведем также ОЦ, параллельную АХ. И так как предполагается, что
сегмент имеет но тяжести к жидкости то же отношение, что квадрат
па ЕО к квадрату на ВД, то такое отношение будет иметь и погружен-
ная часть ко всему телу, то есть квадрат на П0 к квадрату па ВД, а зна-
чит, 110 { рис. 26} будет равняться ЕО {рис. 25}. И так как у сегментов
IBO и ЛВХ диаметры равны, то будут равны и сегменты. Далее, так
как в равных н подобных сегментах АНОЛ и АОХЛ {рис. 25 и 26} про-
ведены прямые АХ и 10, отсекающие, равные сегменты, исходя одна
О ПЛАВАЮЩИХ ТЕЛАХ
353
из конца основания, друган же пе из конца, то ясно, что меньший
острый, угол с диаметром всего сегмента поста нит та прямая, которая
проведена из конца основания. И так как угол С] будет меньше угла N,
то значит, и ВТ {рис. 25} будет больше, чем В2 {рис. 26}, а ТР {рис. 25}
меньше, чем Р2 {рис. 26}; поэтому и Ост меньше, чем П^, (и оЕ)
больше, чем И так как Ост вдвое больше стЕ, то ясно, что и
будет больше удвоенной 5^<Э. Пусть ПН будет'вднос больше Н0; про-
ведем соединяющую ПК и продолжим до £2. Тогда центром тяжести
всего сегмента будет К, части, находящейся в жидкости — И, а внеш-
ней — некоторая точка на К£2; пусть она будет £2. После этого совер-
шенно так же докажем, что будет перпендикулярна к поверхности
жидкости так же, как и прямые, про-
веденные через Н и £2 параллельно
Ясно, что сегмент не останется
неподвижным, по будет наклоняться
до тех пор, пока его основание пе
коснется в одной точке, поверхности
жидкости, как это показано па треть-
ей фигуре (рис. 27), относящейся к
рассматриваемой третьей теореме; и
в таком положении сегмент устано-
вится неподвижным.
Действительно, в равных сегмен-
тах АНОЛ {рис. 27} и АОХЛ
{рис. 25} от концов оснований про-
ведены прямые АХ, АО, отсекающие
одинаковые части; совершенно так
же, как и раньше, докажем, что
сегмент ЛГТХ равен АПО; следова-
тельно, АО и АХ образуют равные
острые углы с диаметрами сегмсн-
1’ис. 27.
тов, так как углы при X и С} равны.
Пусть прямая будет вдвое больше. если провести соединяю-
щую прямую и продолжить до £2, то центром тяжести всего сегмен-
та будет К, той его части, которая в‘жидкости,—а цептр тяжести
внешней части (будет лежать) па линии К£2; пусть он будет £2. Далее,
перпендикулярна к поверхности жидкости. Теперь часть, находя-
щаяся в жидкости, будет подниматься, а находящаяся вне жидкости —
опускаться по одной и той же прямой; таким образом, сегмент остается
неподвижным и основание его касается жидкой поверхности в одной
точке, а ось сегмента с поверхностью жидкости образует угол, равный
вышеук аза иному.
(Случай 6) [16]
Далее, пусть сегмент но тяжести имеет к жидкости отношение
мепьшсс того, которое квадрат па 140 имеет к квадрату ла ВД {рис. 28};
пусть опо будет равно отношению квадрата на Т (к квадрату на ВД);
тогда Я' будет меньше 0N. Между сегментами Л МД и АПОЛ вставим
прямую Ш, параллельную ВД и равную Чг; пусть она пересечет про-
межуточную параболу в Г, а прямую ЕР — в Н. Тогда, так же как
было доказано, что ГО вдвое больше ГЕ {рис. 22}, докажем, что ПГ
вдвое больше TI.
23 Архимед
354
АРХИМЕД
Проведем ПЙ, касательную к АНОЛ в точке П, затем ПЕ — пер-
пендикулярную к ВД, и соединяющую 1Л (продолжим) до X;
прямая АХ будет равпа IX и АХ параллельна 1ХЙ. Требуется дока-
зать, что данный сегмент, будучи опущен в жидкость и наклонен так,
Рис. 28.
чтобы его основание нс касалось
жидкости, установится в наклон-
ном положении так, что его ось с
поверхностью жидкости образует
угол, (меньший угла при Ф {рис.
28}, и основание его пи в одной
точке пе коснется поверхности
жидкости.
Опустим его в жидкость и
установим так, чтобы его основа-
ние) в одной точке коснулось по-
верхности жидкости; если рассечь
сегмент через ось плоскостью,
перпендикулярной к поверхности
жидкости, то сеченной поверхно-
сти сегмента будет парабола АЙВА
{рис. 29), сечением поверхности
жидкости — прямая AZ, а осью
(сегмента) и диаметром парабо-
лы — ВЛ; разделим ВЛ в точках
К и 1’ подобно предыдущему, за-
тем проведем параллельно AZ каса-
тельную III к параболе в Н, про-
ведем ГТ© параллельно ВЛ и НИ
перпендикулярно ВЛ. Так как
сегмент имеет к жидкости такое же отношение по тяжести, какое
квадрат на Y к квадрату на ВД, и отношение по тяжести сегмента
к жидкости равно отношению квадрата па II© к квадрату на ВЛ по
той же причине, что и выше, то ясно, что II© будет равна W; поэтому
будут равны и сегменты A1IZ и АПХ {рис. 28}. И так как в равных
О ПЛАВАЮЩИХ ТЕЛАХ
355
и подобных сегментах АПОЛ, AHZA из концов оснований проведены
прямые ЛХ, AZ, отсекающие равные части, то ясно, что они образуют
равные углы с диаметрами сегментов. Поэтому в треугольниках HIS,
ПЙЕ углы при I н Й равны; следовательно, будут равны и прямые
SB и ЕВ, а значит, будут раины и XI’ с ЕР, а также и с ПИ
и ^Ь0 с НТ*). И так как И Г вдвое больше Г1, то ясно, что меньше
удвоенной $Ь0. Пусть IIГ будет вдвое больше Г0; продолжим соеди-
няющую ТКТ; центром тяжести всего сегмента будет К, части находя-
щейся в жидкости — Г, а той, что ине жидкости, (точка) па линии КТ;
пусть она будет Т. Тогда
совершенно так же, как в
предыдущей теореме, обна-
ружится, что сегмент не
останется неподвижным, по
наклонится так, что его
основание не будет ни н од-
ной точке касаться поверх-
ности жидкости.
Теперь докажем, что
оп установится так, что
его ось с поверхностью
жидкости образует угол,
меньший угла Ф. Дейст-
вительно, пусть, если воз-
можно, он установится так,
что будет составлять угол,
не меньший угла Ф; сде-
лаем все остальное {рис. 30}
так же, как и на тре-
тьей фигуре. Тогда совершенно так же докажем, что 011 будет рав-
на ¥, а, следовательно, и ТП {рис. 28}. Так как угол Л нс меньше Ф,
то, значит, ГВ пе будет более SB, а ГР пе менее SP, и Н 7^ не менее
0Ц**). Итак как IIIв полтора раза больше ПГ {рис. 28}, ИГ же мень-
ше ©q, и НО {рис. 30} равна ГП, а 11$й не меньше 0Q, то Н будет
больше II Г; значит, будет болыпе удвоенной ^>0. Пусть НГ
будет вдвое больше ГО; продолжим соединяющую ГК; тогда подобно
предыдущему обнаружится, что сегмент не останется неподвижным,
по наклонится так, что его ось с поверхностью (жидкости будет состав-
влять угол, меньший Ф),
(Случай 5)
Подобно этому докажем, что если сегмент имеет по тяжести к жидко-
сти то же самое отношение, что квадрат на N0 {рис. 28} к квадрату на
ВД, то оп, будучи опущен в жидкость так, чтобы его основание не каса-
лось поверхности жидкости, установится так, что его основание только
в одной точке коснется поверхности жидкости, и ось его с поверхностью
жидкости составит угол, равный углу при Ф.
*) Тр-к ШХ и лшиш ZB.ZP. П$Ь, берутся на рис. 29, а тр-к PZR и линии ЕВ, ЕР,
ПП и HI — на рис. 28.
Линии ГВ, ГР, П^1 берутся на рис. 30, a ZB. ZV ч вЦ на рис. 28.
23*
356
АРХИМЕД
(Случай 4) [17]
Пусть оудет опять сегмент, имеющий к жидкости отношение по
тяжести большее того, которое квадрат на ZIJ {рис. 31} имеет к (квад-
рату) па ВД, но меньшее того, которое квадрат на 30 имеет к (квадра-
Рис. 31.
ту) на ВД; пусть отношение но тя-
жести, которое сегмент имеет к жид-
кости, будет равно тому, которое
квадрат на Ч7 имеет к (квадрату)
на ВД; ясно, что Т будет больше
ZTI, но меньше ЕО. Вставим менаду
сегментами АБД, АНОЛ прямую,
равную У и параллельную ВЛ,
а имеппоФ1, пересекающую проме-
жуточную параболу в Г; опять дока-
жем, что ФГ будет вдвое больше
П, подобно тому как О Г вдвое боль-
ше ЕГ {рис. 22}. Через Ф прове-
дем Фй — касательную к парабо-
ле А ПОЛ в Ф; подобно преды-
дущему докажем, что А1 равна XI
и АХ параллельна ФЙ. Требуется
доказать, что рассматриваемый сег-
мент, опущенный в жидкость так,
чтобы основание его не касалось
наклонно,
во многих
наклонится так,
точках.
Рис. 32.
поверхности жидкости, и поставленный
что его основание рассечется жидкостью
Опустим его в жидкость, как
сказано. И пусть сначала оп
станет наклонясь, так, что его
основание пи в одной точке
пе коснется поверхности жид-
кости; если рассечь его через
ось плоскостью, перпендикуляр-
ной к поверхности жидкости,
то на поверхности сегмента по-
лучится сечение АВГ {рис. 32}, д
на поверхности жидкости EZ,
а осью [сечения] и диаметром
[сегмента] будет ВД; разделим
ВА в К и Р подобно тому, как
выше, и параллельно EZ прове-
дем ИЛ касательную к параболе
АВГ в II, затем проведем Н©
параллельно ВД и IIS перпен-
дикулярно к ВД. Так как сег-
мент относится нотяжести к жид-
кости, как квадрат на Ч7 к квадрату на ВД, то ясно, что Ч7 будет равна Н®
(это д окажется совершенно так же, как и раньше), так что 110 будет
равна ФТ {рис. 31} и, значит, сегменты ЛФХ, EBZ будут равны друг
другу. Поскольку же в равных и подобных сегментах АПОА, АВГ
проведены прямые АХ, EZ, отсекающие равные сегменты, и одна про-
ведена из конца основания, другая же не из конца, то прямая, прове-
О ПЛАВАЮЩИХ ТЕЛАХ
357
Рис. 33.
денная из конца основания, образует меныпий острый угол с диаметром
сегмента. И так как в треугольнике НАХ угол А больше угла Я в тре-
угольнике ФТР, то ясно, что ВХ будет меньше ВТ, a SP больше РТ,
л Н% больше ФН; значит, % О будет меньше, чем III; » так как ФТ
вдвое больше П, то ясно, что Н%
будет более чем вдвое больше %0.
Пусть НА' будет вдвое боль-
ше А'О; тогда из всего этого
ясно *), что сегмент вс останется в
покос, но будет наклониться до тех
пор, пока его основание нс кос-
нется в одной точке поверхности
жидкости.
Пусть оно коснулось сев одной
точке, как это изображено на треть-
ей фигуре {рис. 33}, и пусть все ос-
тальное будет устроено как и рань-
ше; тогда опят), докажем, что ОН
будет равпа Ф1, и что сегменты
АФХ и ABZ равны друг другу. И
поскольку в равных и подобных
сегментах А ПОЛ {рис. 31}, АВГ
проведены прямые ЛХ, AZ, отни-
мающие равные сегменты, то они образуют равные углы с диаметрами
сегментов; значит, у (треугольников) АНХ, ФТ£2 углы при Л и £2 равны,
и прямая BS равна ВТ, а ХР равна РТ, равна ФН и равна III;
поскольку же Ф Г вдвое больше П, то ясно, что 11% будет более чем вдвое
больше Пусть HP будет вдвое больше PH; из этого опять ясно,
что сегмент пе останется в покое, по будет наклоняться в сторону А.
II так как было предположено, что сегмент касается жидкости только
в одной точке, то ясно, что основание будет охвачено водой на большем
п р отяжении {181.
*) Точка А' — центр тяжести погруженной части — будет локагь правее вертикали
а центр тяжести Т выступающей части будет, наоборот, левее
ПСАММИТ
I
Некоторые люди полагают, государь Гелон, что число песка ио
величине бесконечно; я говорю не только о песке, который имеется
в окрестностях Сиракуз и остальной Сицилии, но и о том, который
имеется во всех странах, как населенных, так и не населенных. Есть,
однако, и такие, которые нс считают его бесконечным, но тем не менее
думают, что нс существует такого имеющего название числа, которое
было бы больше его количества.
Для держащихся такого мнения ясно, что если вообразить состав-
ленную из песка массу такой величины, какой стала бы масса Земли
после заполнения всех имеющихся на ней морей и впадин вплоть до
высоты, равной высочайшим горам, то и подавно нельзя определить
имеющее название число, которое было бы больше такого количества
песка. Что касается меня, то я постараюсь показать тебе при помощи
геометрических доказательств, которые ты можешь понять, что среди
чисел, которые получили от нас название и опубликованы в написанной
к Зевксиппу книге *), некоторые превосходят не только число песчинок
в объеме, равном заполненной, как мы сказали, Земле, но даже в объеме,
рапном миру. Как ты знаешь, большинство астрономов **) называют
миром шар, центр которого совпадает с центром Земли, а радиус равен
прямой, заключающейся между центрами Солнца и Земли; это ты узнал
из написанных астрономами доказательств. Но Аристарх Самосский [11
выпустил в спет книгу о некоторых гипотезах, из которых следует,
что мир гораздо больше, чем понимают обычно. Действительно, он
предполагает, что неподвижные звезды и Солнце находятся в покое,
а Земля обращается вокруг Солнца по окружности круга, расположен-
ной посредине между Солнцами неподвижными звездами***), а сфера
неподвижных звезд имеет тот же центр, что и у Солнца, и так велика,
что круг, по которому, как он предположил, обращается Земля, так же
относится к расстоянию неподвижных звезд, как центр сферы к ее
поверхности. Но хороню известно, что это невозможно; так как центр
*) Не дошедшее до нас сочинение Архимеда. Зевксипп — неизвестное лицо.
**) В подлиннике астрологов.
♦ **) У Архимеда сказано более картинно ev |дэтгр тф бсчп» — «посредине беговой доролши»
в круглом ипподроме или цирке, где происходили конские состязания.
ПСАММИТ
359
сферы не имеет пинакон ве«тичины, то нельзя предполагать, чтобы он
имел какое-нибудь отношение к поверхности сферы. Надо поэтому ду-
мать, что Аристарх подразумевал следующее: поскольку мы пред-
полагаем, что Земля является как бы центром мира, то Земля к тому,
что мы назвали миром, будет иметь то же отношение, какое сфера, по
которой, как думает Аристарх, обращается Земля, имеет к сфере
неподвижных звезд; из таких предпосылок он объясняет наблюдающиеся
явления и, по-видимому, считает, что величина сферы, по которой оп
заставляет двигаться Землю, и будет равна тому, что мы называем ми-
ром. Так вот мы утверждаем, что если бы нз песка был составлен
шар такой же величины, какую, по предположению Аристарха, имеет
сфера неподвижных звезд, то и в таком случае можно было бы указать
некоторые из чисел, получивших название и вышеупомянутом сочине-
нии, которые превзошли бы число песка, заполняющего объем, равный
названной сфере. Сделаем следующие предположения: во-первых,
окружность Земли составляет приблизительно 300 мириад стадий [2];
по пе больше, хотя, как ты знаешь, некоторые *) пытались доказать,
что она составляет- приблизительно 30 мириад стадий. Я же иду дальше
и, полагая, что величина Земли приблизительно в десять раз больше той,
которую принимали предшествовавшие, считаю, что ее окружность
составляет примерно 300 мириад стадий, но не больше; затем, что диа-
метр Земли больше диаметра .Пупы, а диаметр Солнца больше диаметра
Земли, принимая то же, что и большинство предшествующих астроно-
мов; далее, что диаметр Солнца приблизительно в тридцать раз больше
диаметра Луцы, но не больше, хотя из предшествующих астрономов
Евдокс считал его только в девять раз больше, Фидий же, мой отец,—
в двенадцать раз больше, а Аристарх пытался доказать, что диаметр
Солнца белес чем в восемнадцать раз, ио менее чем в двадцать раз боль-
ше диаметра Луны; я же иду дальше этого и, чтобы мое предложение
было бесспорно доказанным, принимаю, что диаметр Солнца приблизи-
тельно в тридцать раз больше диаметра Лупы, по не больше; [3] кроме
этого, я считаю, что диаметр Солнца больше стороны (правильного)
тысяче угольника, вписанного в большой круг сферы мира. Такое пред-
положение я делаю, ибо Аристарх нашел, что {диаметр) видимого
(диска) Солнца составляет приблизительно семьсот двадцатую часть
круга зодиака; в моих исследованиях я также пытался способом, изло-
женным ниже, при помощи инструментов найти угол, в который может
вместиться Солнце, если взять вершину в глазу [4]. Получить точное
значение этого угла — дело нелегкое, потому что ни глаз, ни руки,
пн приборы, при помощи которых производится отсчет, не обеспечивают
достаточной точности; однако теперь па этом долго задерживаться не
время, так как это разъяснялось и много раз в других местах; мне же
для доказательства предложенного достаточно найти угол, не больший
того, имеющего вершину в глазу угла, в который вмещается Солнце,
и затем другой угол, нс меньший имеющего вершину в глазу угла,
в который вмещается Солнце. Поместив длинную линейку на отвесную
подставку, расположенную в месте, откуда я предполагал наблюдать
восходящее Солнце, обточив па токарном станки небольшой цилиндр
и поставив его отвесно на линейку, я сейчас ясе после восхода направ-
лял линейку на Солнце, когда оно находится близ горизонта и на него
еще можно прямо смотреть, и помещал глаз у конца линейки; при этом
») Пи-видимому, Диисарх Месссиский, один иа учеников Аристотеля, нанимавшийся опре-
делением высоты гор и вообще величины поверхности Земли.
360
АРХИМЕД
помещенный между Солнцем и глазом цилиндр затопил Солнце. Отодви-
гая цилиндр от глаза, я устанавливал ого в положении, когда Солнце
начинало чуть-чуть появляться с обеих сторон цилиндра. Теперь, если
бы смотрящий глаз был как бы точкой, и из места на конце линейки,
где помещался глаз, были проведены касательные к цилиндру, то угол,
заключенный между проведенными прямыми, был бы меньше имеющего
вершину в глазу угла, в который может вместиться Солнце, так как кое-
что от Солнца усматривалось по обе стороны цилиндра; поскольку
же глаз нельзя считать смотрящим как бы из одной точки, но из
некоторой площади, то я взял круглую площадку, по величине не
мепьшую зрачка, и поместил ее на конец упомянутой линейки в то
место, где находился глаз: если провести прямые, касательные и к этой
ллощадко, и к цилиндру, то заключенный между ними угол будет
меньше имеющего вершину в глазу угла, в который может быть вмещено
Солнце. Площадочка же с величиной, не меньшей зрачка, отыскивается
следующим образом: берутся два тонких цилиндра одинаковой толщи-
ны, из которых один белый, а другой пет, н помещаются перед глазом
так, чтобы белый был на некотором расстоянии от него, не белый же
помещался возможно ближе к глазу, и даже касался бы лица. Если
взятые цилиндры уже зрачка, то ближайший цилиндр будет охватывать-
ся лучами зрения, и белый цилиндр будет за ним видеп целиком, если
оба они намного уже зрачка; если же они пе намного уже зрачка., то
с обеих сторон ближайшего к глазу цилиндра будут видны какие-то
части белого; если взять цилиндры подходящей толщины, чтобы один
из них заслонял другой, но не большую площадь, то площадочка, шири-
на которой равнялась бы толщине производящих такое действие
цилиндров, несомненно была бы но меньше зрачка. Угол, не меньший
имеющего вершину в глазу угла, в который вмещалось бы Солнце,
находился следующим образом: если на линейке отодвинуть от глаза
цилипдр настолько, чтобы он целиком заслонял Солнце, и от конца
линейки, где помещался глаз, провести прямые, касательные к цилин-
дру, то угол, заключенный между проведенными прямыми, будет пе
меньше имеющего вершину в глазу угла, в который могло бы вместиться
Солнце [5]. Если найденными таким способом углами измерить прямой
угол, то оказалось, что при делении прямого угла на 164 части угол с
вершиной в точке *) меныпе одной такой доли, при делении же прямого
угла на 200 частой меньший (из наблюденных углов) будет больше
одной такой доли; из этого ясно, что имеющий вершину в глазу угол,
в который молото было бы вместить Солнце, будет меньше одной 164-й
доли прямого угла, по больше одной 200-й его доли [61. Если верить
этому, то можно показать, что диаметр Солнца будет больше стороны
тысячеугольника, вписанного в большой круг мировой (сферы). Во-
образим плоскость, проведенную через центр Солнца, центр Земли
и глаз, когда Солнце стоит невысоко над горизонтом; пусть продолже-
ние этой плоскости пересечет мировую сферу по кругу АВГ (рис. 1),
Землю — по AEZ, а Солнце — по кругу 211; пусть центр Земли будет
в В, Солнца — в К, а глаз в Д; проводом из точки Д касающиеся круга
211 прямые ДА и ДЗ (пусть они касаются в точках N и Т), а из
центра 0 — касательные 0М и 00 (пусть они касаются в X и Р),
и пусть прямые 0М и 00 пересекают круг АВГ в точках А и В. Прямая
0К будет более АК, так как Солнце предполагается находящимся над
*> ev атхуф (or — делаю укол, точку); вдееь. возможно, текст испорчен. По-видимому,
б тот угол соответствовал полученному без поправки на величину зрачка.
ПСАММИТ
361
па величину, меньшую одной седьмой
.горизонтом; таким образом, угол, заключенный между АЛ и ДЕ,
будет больше угла, заключенного между ©М и ©О. Угол же, заключен-
ный между ДА и ДЕ, будет больше одной двухсотой доли прямого
угла, по меньше доли, которая получится при делении прямого угла
на 164 части, ибо оп ранен имеющему вершину в глазу углу, в который
вмещается Солнце; таким образом, угол, заключенный между 0М
и ©О, будет меньше одной
делении последнего на 164
части, а прямая АВ будет
меньше отрезка, стяги-
вающего дугу окружности
круга АВ Г, разделенной
на 656 частей *). Но пери-
метр упомянутого много-
угольника имеет к радиу-
су круга АВ Г отношение
меньшее чем 44 к 7, так
как у всякого многоуголь-
ника, вписанного в круг,
периметр имеет к радиусу
меньшее отношение, чем г
44 к 7; как ты зпаешь,
нами было доказано, что
окружность всякого круга
больше утроенного диаметра
части, а периметр вписанного многоугольника меньше окружности.
Тогда В А будет иметь к ©К отношение меныпее, чем 11 к 1148**);
таким образом ВА будет меньше сотой доли ©К. Но прямая ВА равна
диаметру круга 511, так как со половина ФА равна КР; действитель-
но, из концов равных прямых ©К и. ©А опускаются перпендикуляры
в одном и том же углу; ясно, что диаметр круга 511 будет меньше сотой
доли ©К. Далее диаметр Ей Г меньше диаметра круга SH, так как
круг AEZ меньше круга 511 17]; значит, оба (радиуса) ©Г и К5
вместе будут меньше сотой доли ©К; таким образом ©К имеет к Т5
меньшее отношение, чем 100 к 99. И так как ©К нс меньше 0Р, а 5Г
меньше ДТ, то, значит, ©Р будет иметь к ДТ отношение меньшее, чем
100 к 99. Так как у прямоугольных треугольников ©КР и ДКТ сторо-
ны КР и КТ равны, а 0Р и ДТ не равны, и ©Р больше, то угол, заклю-
ченный между ДТ, ДК к углу, заключенному между ©Р, ©К, имеет
большее отношение, чем ©К к ЛК, по меньшее чем 0Р к z\T; действи-
тельно, если у двух прямоугольных треугольников будутравныпо одной
из сторон, прилегающих к прямому углу, две же другие пе равны, то
больший из углов при неравных сторонах имеет к меньшему углу
отношение большое того, которое большая сторона из стягивающих пря-
мой угол имеет к меньшей, но меньшее того, которое большая пз при-
легающих к прямому углу линий имеет к меньшей [8]. Таким образом,
угол, заключенный между ДА и ДЕ, имеет к углу, заключенному между
00 и ©М, отношение меныпее, чем ©Г к ДТ, которое меньше, чем 100к 99;
так что угол, заключенный между ДА, Д 2, к углу, заключенному между
0М и 00, имеет меньшее отношение, чем 100 к 99. И так как угол,
*) Имеем 656=4' 164.
1 44 4 4 1 11
**) Отношение В А к 0К будет меньше ат •=- , тс есть мепсс — - а ,
656 7 7 Оэи 1 [4S
362
. АРХИМЕД
зак/почеппый между ДА и ДЕ, больше одной двухсотой доли прямого
угла, то и угол, заключенный между О М и 00, будет больше, чем 99 до-
лей прямого угла, разделенного на 20 000 частей; таким образом, он бу-
дет больше одной доли, получающейся при делении прямого угла на 203
части*). Значит, В А будет больше (хорды), стягивающей один отрезок
окружности круга ЛВГ, разделенной ла 812 частей **). Ио АВ равна
диаметру Солнца; значит ясно, что диаметр Солнца будет больше
стороны тысячеугольпика [9].
П
После этих предпосылок можно доказать, что диаметр мира будет
меньше диаметра Земли, увеличенного в десять тысяч раз, или что
диаметр мира будет меньше, чем мириад раз взятые сто мириад (100 х
X10 000-10 000 - 10U)) стадий. Действительно, поскольку пред-
полагается, что диаметр Солнца по более чем в тридцать раз больше
диаметра Луны, а диаметр Земли больше диаметра Луны, то ясно,
что диаметр Солнца будет меньше взятого тридцать раз диаметра Земли.
.Далее, так как было доказано, что диаметр Солнца больше стороны
тысячеугольннка, вписанного п большой круг мировой (сферы), то
ясно, что периметр упомянутого тысячеугольннка будет меньше взя-
того тысячу раз диаметра Солнца. Но диаметр Солнца меньше, чем
тридцать раз взятый диаметр Земли, так что периметр этого тысяче-
угольпика будет меньше, чем тридцать тысяч раз взятый диаметр Зем-
ли. Теперь, так как периметр тысячеугольннка меньше трех мириад
раз взятого диаметра Земли, ио более чем в три раза больше диаметра
мира (ибо доказано, что диаметр всякого круга меньше третьей части
периметра всякого многоугольника, вписанного в круг, если только
этот многоугольник равносторонний и имеет большее число углов,
чем у шестиугольника), то и диаметр мира будет меньше мириады раз
взятого диаметра Земли. Итак, доказано, что диаметр мира меньше
мириады раз взятого диаметра Земли. А что диаметр мира будет мень-
ше чем мириады раз взятые сто мириад стадий, ясно из следующего;
так как предположено, что периметр Земли не более трехсот мириад
стадий, и периметр Земли более чем в три раза больше ее диаметра
(так как у всякого круга окружность более чем в три раза больше диа-
метра), то ясно, что диаметр Земли будет меньше чем 100 мириад ста-
дий. Теперь, так как диаметр мира меньше мириады раз взятого диа-
метра Земли, то ясно, что диаметр мира будет меньше чем мириад раз
взятые 100 мириад стадий.
Такие предположения я сделал относительно величин и расстоя-
ний (в мире), относительно же песка предполагаю следующее: если
взять количество его (в объеме), не большем макового зернышка, то
в нем число песчинок будет пе больгпе десяти тысяч, а диаметр мако-
вого зернышка пе меньше сороковой части дюйма. Эти предположения
я делаю из следующего наблюдения: я положил па гладкой линейке
маковые зернышки но прямой так, чтобы они касались друг друга и
нашел, что 25 маковых зернышек занимают длину, большую дюйма.
Желая возможно бесспорнее доказать выставленное положение, я беру
диаметр макового зернышка еще меньше, а именно равным сороковой
части дюйма, но не меньше-
1
*) Дейстиитслыго, 9£>>20 000- 57-7.
•») 812=4-203.
ПСАММИТ
363
III
Вот каковы мои предположения; кроме того, я думаю, что было
бы полезным изложить здесь правила наименования чисел, чтобы
другие (читатели), которые нс имели в руках книги, написанной мной
Зсвксинлу *), не затруднились тем, что в настоящей книге об этих чис-
лах ничего не сказано **). Так вот для чисел до десятков тысяч (мириад)
остаются обычно употребляемые нами названия, после же десятков
тысяч, как мы полагаем, достаточно считать мириадами вплоть до
мириады мириад. Упомянутые до сих лор числа вплоть до мириады
мириад назовем первыми, а мириаду мириад первых чисел назовем
единицей вторых чисел, далее будем считать единицы вторых чисел
и из таких единиц составим десятки, сотни, тысячи и мириады вплоть
до мириады мириад. Затем мириаду мириад вторых чисел назовем еди-
ницей третьих чисел; после этого будем считать единицы третьих
чисел, а за единицами десятки, сотни, тысячи в мириады вплоть до
мириады мириад. Таким же образом, мириаду мириад третьих чисел
назовем единицей четвертых чисел, а мириаду мириад четвертых
чисел назовем единицей пятых чисел. Продолжая так постоянно, мы
дадим названия числам вплоть до мириады мириад мириадо-мириад-
ных чисел. Вполне достаточно знать числа только до этих пор, но мож-
но идти и далее. Действительно, пусть упомянутые до сих пор числа
называются числами первого периода, а последнее число первого перио-
да назовем единицей первых чисел второго периода. Далее мириаду
мириад первых чисел второго периода пазовом единицей вторых чисел
второго периода. Точно так же последнюю единицу этих чисел назовем
единицей третьих чисел второго периода; если постоянно продолжать
таким образом, то числа второго периода получат имена вплоть до ми-
риады мириад мириадо-мириадяых чисел. Далее, последнее число
второго периода назовем единицей первых чисел третьего периода
и будем так продолжать вплоть до мириады мириад мириадо-мириад-
ных чисел мириадо-мириадного периода. После установления
таких названий возьмем числа в непрерывной пропорции, начи-
ная от единицы, причем следующей за единицей будет десятка;
восемь первых таких чисел вместе с единицей будут принадлежать
к так называемым первым числам, другие следующие за ними восемь —
к так называемым вторым числам, и остальные будут называться ана-
логично упомянутым в соответствии с расстоянием октады рассматри-
ваемых чисел от первой октады. Таким образом, восьмое число первой
октады этих чисел будет тысячей мириад, а первое число второй октады,
поскольку оно в десять раз болыпе предшествующего, будет мириадой
мириад; оно является единицей вторых чисел. Восьмое число второй
октады будет тысяча мириад вторых чисел. Далее первое число третьей
октады, поскольку оно в десять раз больше предшествующего, будет
мириадой мириад вторых чисел; оно является единицей третьих чисел.
Ясно, что так можно получить октады любого порядка I10J.
Полезно также знать и нижеследующее. Если некоторые из чисел,
составляющих непрерывную пропорцию, начиная от единицы, пере-
множаются с другими из той же самой пропорции, то полученное число
будет принадлежать к той же самой пропорции, отстоя от большего
”> См. сноску на стр. 3D8.
*к) T&v иХХшу о!т'Ь pipfjra рч леостстктзубгге тш nori V®VQ« |Hwo рч aXavivrcti; neoirire-u
Xote; относится к «тем иа других <читатслей>», а не к числам, как иногда переводят.
364
АРХИМЕД
из перемножаемых чисел настолько, насколько меныпее из перемно-
жаемых чисел в пропорции отстоит от единицы, причем расстояние
произведения от единицы будет па единицу меньше числа, получаю-
щегося от сложения расстояний от единицы взаимно перемножаемых
чисел. Действительно, пусть будут некоторые числа в непрерывном
пропорции, пачппан от единицы: А, 13, Г, Д, Е, Z, Н, 0, I, К, Л, пусть
единицей будет А; помножим Д на 0, и пусть в результате получит-
ся Ф. Возьмем в непрерывной пропорции Л, которое отстоит от ©
настолько же, насколько Д отстоит от единицы; требуется доказать,
чтоФ будет равно А. Действительна, так как в непрерывной пропорции
чисел Д от А и .А от О отстоят одинаково, то Д будет иметь к А то же-
самое отношение, что Л к 0. Но Д будет Д раз кратным А; значит,
и Л будет Д ра-з кратным 0; таким образом, А будет равна Ф. Теперь
ясно, что полученный результат будет принадлежать к той же непре-
рывной пропорции и будет настолько же отстоять от большего из (чи-
сел), перемножаемых между собой, насколько меньшее отстоит от
единицы. Ясно также, что его расстояние от единицы будет на единицу
меньше числа, равного сумме расстояний чисел Д и 0 от единицы;
действительно, ряд А, В, Г, Д, Е, Z, II, 0 дает столько чисел, насколь-
ко О отстоит от единицы, а ряд I, К, Л содержит на одно число меньше-
тех чисел, на которые Д отстоит от единицы; их будет ровно столько,,
если присчитаем числа от А до ©*).
IV
Теперь, установив такие отчасти предположения, а отчасти доказа-
тельства, перейдем к доказательству основного предложения. Так как
предположено, что диаметр макового зернышка не меньше сороковой,
части дюйма, то ясно, что шар, имеющий диаметр в один дюйм,
может вместить пе больше шести мириад и четырех тысяч (то есть 64 000)
маковых зернышек, так как имеппо в упомянутое число раз этот шар
будет больше тара, имеющего диаметром одну сороковую часть дюй-
ма; ибо доказано, что шары находятся друг к другу в тройном отноше-
нии их диаметров. Поскольку предположено, что число песчинок в объе-
ме, соответствующем величине макового зернышка, не будет больше-
чем десять тысяч, то ясно, что если шар дюймового диаметра-
наполнить песком, то число последнего пе будет больше мириады раз
взятых шести мириад и четырех тысяч. Это число представляет шесть
единиц вторых чисел и четыре тысячи мириад первых чисел: значит,
оно будет меньше чем 10 единиц вторых чисел. Шар, имеющий диаметр
в 100 дюймов, будет больше шара дюймового диаметра в 100 мириад
раз, ибо шары имеют друг к другу тройное отношение своих диаметров.
Таким образом, если сделать из песка шар такой величины, чтобы
диаметр его равнялся 100 дюймам, то ясно, что число находящихся
в нем песчинок будет меньше того, которое получилось бы от умножения
десяти единиц вторых чисел на 100 мириад. Поскольку десять единиц
вторых чисел являются десятым числом от единицы в непрерывной
*) Надо иметь в виду, что. веди счет, греки всегда учитывали и то число, от которого счет
начинялся; например 2 по гречески било вторым числом от 1,4 — вторым числом от 3 и т. л. В про-
грессии
1, 10, 102, 10®, 10’, 10s. 10®, IO7, ID8, 10®, 10й’
число 10“ было шестым, а 10* — пятым числом от единицы; их произведение 10“*’ было десятым
числом от единицы (10 = 6 | 5—1).
ПСАММИТ
365
пропорции с десятикратным возрастанием членов, а сто мириад явля-
ются седьмым числом после единицы в той же самой пропорции, то
ясно, что полученное число в той же самой непрерывной пропорции
будет шестнадцатым членом, если считать от единицы (так как доказано,
что оно отстоит от единицы на число, которое будет на единицу меньше
вместе взятых расстояний от единицы взаимно перемножаемых чисел).
Из этих шестнадцати чисел восемь первых, считая и единицу, принад-
лежат к названным нами первым числам, следующие за ними восемь
относятся ко вторым, причем последнее число из них будет тысячей
мириад вторых чисел. Теперь ясно, что количество песчинок в (объеме),
равном по величине шару с диаметром в 100 дюймов, будет меньше,
чем тысяча мириад вторых чисел. Далее, шар, имеющий диаметр в
мириаду дюймов, будет в 100 мириад раз больше шара, имеющего
диаметр в 100 дюймов. Если теперь сделать из песка шар такой вели-
чины, чтобы его диаметр равнялся мириаде дюймов, то ясно, что число
песка будет меньше того, которое получается от умножения тысячи
мириад (единиц) вторых чисел па сто мириад. Поскольку же тысяча
мириад вторых чисел является шестнадцатым числом в пропорции от
единицы, а 100 мириад будут седьмым от единицы в той же самой про-
порции, то ясно, что получившееся число будет двадцать вторым в той
же самой пропорции, считая от единицы. Из этих двадцати двух (чисел)
восемь первых от единицы принадлежат к названным нами первым
числам, восемь следующих за ними будут так называемыми вторыми,
а остальные шесть — третьими, причем последнее из них будет десятью
мириадами единиц третьих чисел. Теперь ясно, что количество песчи-
нок в (объеме), равном по величине шару, имеющему диаметр в десять
тысяч дюймов, меньше чем 10 мириад (единиц) третьих чисел. И так
как шар, имеющий диаметр в одну стадию, меньше шара, имеющего
диаметр в десять тысяч дюймов*), то ясно, что количество песчинок
в шаре, имеющем диаметр в одну стадию, будет меньше чем 10 мириад
третьих чисел. Далее шар, имеющий диаметр в 100 стадий, будет в сто
мириад раз больше шара, имеющего диаметр в одну стадию. Следова-
тельно, если сделать из песка шар такой величины, чтобы его диаметр
равнялся 100 стадиям, то ясно, что число песчинок в нем будет меньше
того, которое получается от умножения десяти мириад (единиц) треть-
их чисел иа 100 мириад, И так как десять мириад (единиц) третьих
чисел будет двадцать вторым числом в пропорции от единицы, а 100
мириад — седьмым от единицы в той же самой пропорции, то ясно, что
получающееся число будет двадцать восьмым от единицы в той же самой
пропорции. Из этих двадцати восьми чисел восемь первых от единицы
будут так называемыми первыми, восемь следующих за ними будут
вторыми, еще восемь следующих третьими, остальные же четыре будут
принадлежать к так называемым четвертым, причем последнее из них
будет тысячей единиц четвертых чисел. Теперь ясно, что количество
песчинок в объеме, равном пе величине шару, имеющему диаметр
в 100 стадий, будет меньше чем тысяча единиц четвертых чисел. Далее,
шар, имеющий диаметр в десять тысяч стадий, будет в 100 мириад раз
больше шара, имеющего диаметр в 100 стадий. Поэтому, если сделать
из песка шар с диаметром и десять тысяч стадий, то ясно, что количе-
ство песчинок в нем будет меньше числа, получающегося при умножении
тысячи единиц четвертых чисел на 100 мириад. И так как тысяча единиц
*) По Героку (Def ini Hones, 131) стадия содержит 9Ь00 дюймов.
366
АРХИМЕД
четвертых чисел будет двадцать восьмым числом в пропорции от
единицы, а сто мириад — седьмым от единицы в той же пропорции, то
ясно, что получающееся число (1033) будет тридцать четвертым от еди-
ницы в той же пропорции. Из этих тридцати четырех чисел восемь пер-
вых, считая и единицу, будут так называемыми первыми, восемь сле-
дующих за ними — вторыми, восемь следующих за ними — третьими,
еще восемь следующих — четвертыми, а дна остальных будут принад-
лежать к Tait называемым пятым, причем последнее из них будет пред-
ставлять десять единиц пятых чисел. Теперь ясно, что количество пес-
чинок в объеме, равном по величине шару, имеющему диаметр в мириаду
стадий, будет меньше чем 10 единиц пятых чисел. Далее шар, имеющий
диаметр в 100 мириад стадий, будет в сто мириад раз больше шара,
имеющего диаметр в мириаду стадий. Таким образом, если сделать из
песка шар диаметром 100 мириад стадий, то ясно, что число песка в нем
будет меньше того, которое получается при умножении десяти единиц
пятых чисел на 100 мириад. И так как десять единиц пятых чисел будут
тридцать четвертым числом в пропорции от единицы, а 100 мириад —
седьмым от единицы в той же самой пропорции, то ясно, что получаю-
щееся число будет сороковым от единицы в той же пропорции. Из этих
сорока чисел восемь первых, считая и единицу, будут так называемыми
первыми, восемь следующих за ними — вторыми, восемь за этими —
третьими, восемь после третьих — четвертыми, а восемь мосле них —
так называемыми пятыми, причем последнее из них будет тысячей
мириад (единиц) пятых чисел. Теперь ясно, что количество песчинок
в объеме, равном по величине шару, имеющему диаметр в 100 мириад
стадий, будет меныпе чем тысяча мириад (единиц) пятых чисел. Шар же,
имеющий диаметром десять тысяч .мириад стадий, будет в 100 мириад раз
больше шара, имеющего диаметром 100 мириад стадий. Поэтому если
сделать из песка шар диаметром десять тысяч мириад стадий, то ясно,
что количество песка будет меньше числа, получающегося при умноже-
нии тысячи мириад (единиц) пятых чисел на 100 мириад. Но так как
тысяча мириад (единиц) пятых чисел будет в пропорции сороковым
от единицы, а 100 мириад — седьмым от единицы в той же самой про-
порции, то ясно, что получающееся число будет сорок шестым от едини-
цы. Из этих сорока шести чисел восемь первых, считая и единицу,
будут так называемыми первыми, восемь за ними — вторыми, восемь
за этими — третьими, восемь за третьими — четвертыми, восемь за
четвертыми — пятыми, остальные же шесть принадлежат к так назы-
ваемым шестым, причем последнее число из них будет 10 мириад единиц
шестых чисел. Поэтому ясно, что количество песчинок в (объеме),
равном по величине шару, имеющему диаметром десять тысяч мириад
стадий, будет меньше чем 10 мириад (единиц) шестых чисел. Шар же,
имеющий диаметром десять тысяч раз 100 мириад стадий, будет в 100 ми-
риад раз больше шара, имеющего диаметр в десять тысяч мириад
стадий. Теперь, если сделать из песка шар диаметром десять тысяч
раз 100 мириад стадий, то ясно, что количество песка в нем будет мень-
ше, чем число, получающееся при умножении 10 мириад единиц шестых
чисел на 100 мириад. Но так как десять мириад (единиц) шестых чисел
будут в пропорции сорок шестым числом от единицы, а 100 мириад —
в той же самой пропорции седьмым от единицы, то ясно, что получаю-
щееся число будет в той же пропорции пятьдесят вторым от единицы.
Из этих пятидесяти двух чисел сорок восемь, считан и единицу, будут
так называемыми первыми, вторыми, третьими, четвертыми, пятыми
ПСАММИТ
3(57.
и шестыми, остальные же четыре относятся к седьмым, причем последнее
из них будет тысячей единиц седьмых чисел. После ;хгого ясно, что коли-
чества песчинок в (объеме), по величине равном шару, имеющему диа-
метр в десять тысяч раз по 100 мириад стадий, будет меньше, чем тысяча
единиц седьмых чисел. Так как доказано, что диаметр мира меньше,,
чем десять тысяч раз но 100 мириад стадий, то ясно, что количество пес-
ка в (объеме), ранном но величине миру, будет меныпе, чем 1000единиц
седьмых чисел. Теперь доказано, что количество песка в (объеме),
равном по величине тому, что большинство астрономов называют миром,
меньше чем 1000 единиц седьмых чисел; а что количество песка и (объе-
ме), равном по величине такому шару, каким, по предположению Ари-
старха, является сфера неподвижных звезд, будет меньше 1000 мириад
(сдипиц) восьмых чисел, еще нужно доказать. Если предположить,
что Земля к тому, что мы называем, миром, имеет то же отношение, что.
этот мир к сфере неподвижных звезд, как полагает Аристарх, то то же
отношение будут иметь друг к другу и диаметры этих сфер. Но, как
доказано, диаметр мира меньше, чем взятый десять тысяч раз кратным-
диаметр Земли; следовательно, ясно, что диаметр сферы неподвгпкпых
звезд будет меньше чем десять тысяч раз взятый диаметр мира. Посколь-
ку же шары, имеют друг к другу тройное отношении диаметров, то ясно,
что сфера неподвижных звезд, согласно предположению Аристарха,
будет меньше, чем десять тысяч раз взятая мириада мириад наших
миров. Доказано же, что количество песчинок в (объеме), равном по-
вал ичипе миру, будет меньше 1000 единиц седьмых чисел; следовательно,
ясно, что, если сделать из песка шар такой величины, какой, но пред-
положению Аристархи, является сфера неподвижных звезд, то соответ-
ствующее число песчинок будет меньше того числа, которое полу-
чается при умножении тысячи единиц седьмых чисел на десять тысяч
раз взятую мириаду мириад. И так как 1000 единиц седьмых чисел,
будет в пропорции пятьдесят вторым числом от единицы, а десять тысяч,
раз мириада мириад — тринадцатым от единицы в той же пропорции,
то ясно, что получающееся число будет шестьдесят четвертым числом-
от единицы в той же самой пропорции; это число будет восьмым в ряду
восьмых чисел, то есть тысячей мириад (единиц) восьмых чисел. После-
этого ясно, что количество песчинок в (объеме), равном по величине
сфере неподвижных звезд, как се мыслит Аристарх, будет меньше, чем
тысяча мириад (единиц) восьмых чисел. Все это, государь Гелон,
я предполагаю, покажется не очень вероятным большинству людей
и всем не освоившимся с математикой; для тех же, которые восприняли
ее и усвоили касающееся расстояний и величин Земли, Солнца, Луны
и всего мира, это будет после данного мной доказательства вполне-
достоверным; поэтому я полагал, что и для тебя пе будет недостойным-
поразмыслить об этом 111].
КАТОПТРИКА
1. ТЕОН, КОММЕНТАРИЙ К «ПТОЛЕМЕЮ» 1, ст. 10
«И падающие из него (глаза) на воздух лучи подвергаются пре-
ломлению и делают угол зрения большим, как и доказывает Архимед
в «О катоптрике», говоря, что помещенные в воду пред-
меты кажутся большими и тем больше, чем
ниже они уходя т».
2. ОЛИМПИОДОР, КОММЕНТАРИЙ К МЕТЕОРОЛОГИИ АРИСТОТЕЛЯ
(ст. 211, 18 Busse (II, ст. 94 изд. fdcler)
«Иначе это же самое, а именно, что луч зрения преломляется,
доказывает Архимед на примере брошенного в сосуд перстня».
3. ПСЕВДО-ЕВКЛИД, КАТОПТРИКА, post 6 (ст. 28В, 17)
«Если поместить что-нибудь в сосуд и удалить глаз настолько,
чтобы этот предмет не был виден, то после вливания воды помещенный
предмет может быть снова увиден с того же самого расстояния».
СХОЛИЯ К КАТОПТРИКЕ ПСЕВДО-ЕВКЛИДА, № 7 (ст. 348, 17)
«Архимед же
2?- предмет
Рис. 1.
ставляются
говорит так {рис. 1): угол F или будет равен Е,
или же меньше, или больше. Пусть сначала F
будет больше А’; значит, Е будет меньше. Предпо-
ложим теперь, что глаз будет в Н и луч снова от
глаза отразится к наблюдаемому предмету D\ зна-
чит, угол Е будет больше, чем F. По он был и
меньше, что нелепо».
4. АПУЛЕЙ, Анология, 16
«Кроме того, что я сказал им (то есть филосо-
фам), необходимо и такое рассуждение, почему в
плоских зеркалах предметы и изображения пред-
одинаковыми, в выпуклых и сферических уменьшен-
ными, в вогнутых же, наоборот, увеличенными; но какой при-
чине правая меняется местом с ясной, когда в одном и том же зеркале
КАТОПТРИКА
369
изображение то уходит вглубь, то выходит наружу; почему вогнутые
зеркала, помещенные против Солнца зажигают подложенный трут;
отчего происходит то, что радуги в облаках являются различными,
а два солнца одинаково подобными, и многое другое в том же роде,
о чем в огромном томе рассуждает сиракузянин Архимед».
5. ПСЕВДО-ПСЕЛЛ, Synopsis mathematics, ст. 73, изд. Xylander’a
При отсутствии («нор(а) диоптры можно и иначе воспользоваться
тем методом, как когда-то Архимед. Когда некоторые спросили отно-
сительно высоты находящейся перед ними пирамиды, он искусно при-
крепил отвесный шест у солнечной тони от пирамиды, так чтобы обе
тени как шеста, так и пирамиды, были па одной плоскости; получив
таким образом два подобных треугольника, оп выпел отсюда следующее
заключение: отношение лежащей на плоскости тени шеста к самому
шесту будет том же самым, что тени пирамиды на той же плоскости
к самой пирамиде. После этого, измерив тень пирамиды, он объявил
вопрошающим высоту пирамиды.
24 Архимед
ОБ УСТРОЙСТВЕ НЕБЕСНОЙ СФЕРЫ
ПАПП, VHT, 3, ст. 1026, 9
«Карп Антиохийский где-то говорит, что сиракузянин Архимед
составил только одно механическое сочинение, а именно, об устройстве
небесного глобуса, пе найдя из других предметов ничего достойного
сочинения».
ПРОК Л,’ КОММЕНТАРИЙ К ЕВКЛИДУ, ст. 41. 16
«Устройство небесной сферы, воспроизводящей круговращения
небесных тел, книгу о котором сочинил также и Архимед».
МАКРОБИЙ, СОП СЦИПИОНА, Ц, 3
«Также и Архимед считал, что оп определил число стадий, па ко-
торое от поверхности Земли удалена Луна, а от Лупы — Меркурий,
от Меркурия — Венера, от Венеры — Солнце, от Солнца — Марс,
от Марса — Юпитер, от Юпитера — Сатурн; все же расстояние от Са
турна до самого звездоносного неба он, как думал, измерил только
рассуждением. Однако это архимедово измерение отвергнуто платони-
ками, как не сохраняющее двойных и тройных интервалов».
ИППОЛИТ, ОПРОВЕРЖЕНИЕ ВСЕХ ЕРЕСЕЙ, изд. Dnnckor, ст. 66. 52
«Расстояние от поверхности Земли до лунной орбиты сам... Ари-
старх оценивает в своем сочинении в... стадий, Архимед же в 554 мириа-
ды и 4130 единиц, от лунной до солнечной орбиты стадий 502G мириад
и 20(55 единиц, от нее до орбиты Венеры стадий 2027 мириад и 20G5 еди-
ниц, от пес до орбиты Меркурия стадий 5081 мириада и 7165 единиц,
от пее до орбиты Марса стадий 4054 мириады и 1108 единиц, от нее до
орбиты Юпитера стадий 2027 мириад 50G5 единиц, от лее до орбиты
Сатурна стадий 4037 мириад 20(55 единиц, от нее же до зодиака и самой
последней окружности стадий 2008 мириад 4005 единиц. Таковы пере-
данные Архимедом расстояния орбит друг от друга и глубины сфер;
периметр же зодиака оп принимает стадий: 4 вторых числа 4731 мириа-
да; таким образом, получается, что расстояние от центра Земли до
ОБ УСТРОЙСТВЕ НЕБЕСНОЙ СФЕРЫ
371
самой крайней поверхности будет шестой частью упомянутого числа*),
расстояние же от поверхности Земли, па которой мы живем, до зодиака
получится, если шестую часть упомянутого числа уменьшить на четыре
мириады стадий, которые представляют расстояние от центра «Земли
до ее поверхности. От орбиты Сатурна до Земли, как он говорит, будет
вторых чисел одна единица 2160 мириад 4454 единицы, от Меркурия
(Erriptov) до Земли 5268 мириад 8259 единиц, от 13оперы до Земли
5081 мириада 5160 единиц... так вот расстояния и глубины сфер Архимед
даст такими. Изложенные Архимедом числа п пронодимыо другими
отношения касательно расстояний, если они нс будут находиться
в созвучных отношениях, то есть в так называемых платоновских
двойных и тройных, то оказываясь вне созвучий, они по могут сох-
ранить гармоничного строения вселенной..., а что остальные данные
Архимедом числа относительно расстояний планет нс находятся в со-
звучных отношениях, легко установить, если подумать, как и в каких
отношениях они находятся друг к другу.
О ВЕЛИЧИНЕ ГОДА
ГИППАРХ У ПТОЛЕМЕЯ, АЛЬМАГЕСТ, III, 1
Из этих наблюдений ясно, что различия продолжительности
разных годов совершенно ничтожны; что же касается солнцестояний,
то я упорен, что или Архимед и п наблюдениях и в вычислениях сине-
лись но более чем на четвертую часть дня.
*) Числи л принимается равный 3.
ЗАДАЧА,
КОТОРУЮ АРХИМЕД НАШЕЛ В ЭПИГРАММАХ И ПОСЛАЛ
НА РАЗРЕШЕНИЕ ЗАНИМАЮЩИМСЯ ПОДОБНЫМИ ВОПРОСАМИ
АЛЕКСАНДРИЙСКИМ УЧЕНЫМ В ПОСЛАНИИ
К ЭРАТОСФЕНУ ВИРЕПСКОЛ1У
Сколько у Солпца быков, найди для меня, чужестранец.
(Ты их, подумав, считай, мудрости если пе чужд).
Как па полях Тринакрийской Сицилии острова тучных
Их в четырех стадах много когда-то паслось.
5 Цветом стада различались: блистало одно млечно-белым,
Темной морской волны стада другого был цвет.
Рыжим третие было, последнее пестрым. И в каждом
Стаде была самцов множеством тяжкая мощь,
Все же храня соразмерность такую: представь, чужестранец.
Белых число быков в точности было равно
10 Темных быков половине и трети и полностью рыжим;
Темных число быков четверти было равно
Пестрых с прибавленной пятой и также полностью рыжим;
Построй же шерсти быков так созерцай число:
15 Части шестой и седьмой от стада быков серебристых
Также и рыжим всем ты их число поравняй.
В тех же стадах коров было столько: число белошерстых
В точности было равно темного стада всего
Части четвертой и третьей, коль сложишь ты обе их вместе;
'20 Темных число же коров части четвертой опять
Пестрого стада равнялось, коль пятую долю добавишь
И туда же быков в общее стадо причтешь.
'Ге же, чья вострая шерсть, равночисленным множеством были
Рыжего стада частям пятой и с пою тестой.
25 Рыжих коров же считалось количество равным полтрети
Белого стада всего с частию взятой седьмой.
Сколько у Солпца быков, чужестранец, коль точно ты скажешь
Нам раздольно назвав тучных быков число,
Так же раздельно коров, сколько каждого цвета их было,
30 Нс назовет хоть никто в числах невеждой тебя,
Все ж к мудрецам причислен пе будешь. Учти же, пожалуй.
Свойства такие еще Солнца быков числа.
ЗАДАЧА, КОТОРУЮ АРХИМЕД НАШЕЛ В ЭПИГРАММАХ
373
Если быков среброшерстых ты с темными вместе смешаешь
Так, чтобы тесно они стали бы в ширь и в длину
35 Мерою равной, тогда на обширных полях Сицилийских
Плотным квадратом они площадь большую «займут.
Если же рыжих и пестрых в одно смешаешь ты стадо,
Лесенкой станут они, счет с единицы начав,
Так что фигуру опи треугольную нам образуют;
40 Цвета иного быков нам нот нужды добавлять.
Если ты зто найдешь, чужестранец, умом пораскинув,
И сможешь точно назвать каждого стада число,
То уходи, возгордившись победой, и будет считаться
Что в этой мудрости ты все до конца превзошел.
Текст задачи о быках был впервые опубликован Лессингом в Beitrago zur Geschiclile
and Litteratur (Braunschweig, 1773, стр. 421 и сл.). Нет никаких оснований сомне-
ваться в принадлежности этой эпиграммы Архимеду, так как и во стилю, и по содер-
жанию она подходит к арифметическим эпиграммам той эпохи и, кроме того, с именем
Архимеда упоминается в дрепкей схолии к платоновскому Хармиду. Из математиков
ей занимались Нессельманн (Algebra dcr Griechcn, стр. 481 и сл.), Поль Таняери (Мemoi-
res de la Societe de Sciences de Bordeaux, 1880, 111, стр. 369 и сл.) и Хизс (Heath, Dio-
phantus of Alexandria, стр. 142).
Пусть X, У, Z, T обозначают соответственно числа белых, черных, рыжих и пестрых
быков, а х, у, з, t — числа корон такого же цвета. Тогда между этими неизвестными
мы имеем следующую систему уравнений:
(стр. 10—11) Х=( (1)
(стр. 12—13) У = ( 'т-' £)т+г' (2)
(стр. 14— 16) м 1 -[с- W- [о ч J (3)
(стр 17 - 19) *=( л Ч У 0)
(стр. 20—-22) н 'т-l (о)
(стр. 23—24) г=( (6)
(стр. 25—26) *=( 1-1 7 >-!’> (7)
К этим уравнениям прибавляются еще такие условия:
(стр. 33—36) квадратному числу.
(стр. 37—39) Z--T= треугольному числу.
Мы имеем семь уравнений с восемью неизвестными, причем полученные решения
должны удовлетворят!, двум условиям: суммы двух полученных пар должны давать квад-
ратное (прямоугольно!') число и треугольное.
Начнем решение с первых трех уравнений, которые можно представить в следую-
щем виде:
6Z =57-1-62,
20У = 92'-)-20Z,
42Г= 13А-|-42Z.
Исключая из первых двух уравнений У, найдем:
24Х=97'-|-44Z.
374
Л РХИМЕ Д
Решая это уравнение вместе с третьим, находим:
т_1580_
891 Z’
Найди Т, последовательной подстановкой определяем Y и X:
Тан как 89) = 3*-11, а 297 = 3'-11 и 99=3®-11 и коэффициенты при Z являются
несократимыми дробями, а все неизвестные должны быть числами целыми, то наимень-
шими значениями А', У, Z, Т, удовлетворяющими этим уравнениям, будут:
Л'=2226, У=1602, 2=891, Г=1580
или, вообще:
А’=2226п=2.3-7.53а,
У = 1602п=2-3»-89п,
2=891й=34-11к,
Т= 1580л=22-5-79л.
Будем подставлять найденные значения в уравнения 4—7, которые можно пере-
писать так:
(4) » = ^(2.32.89л4-у),
(5) 2/=^(2®.5>79re-|-t),
11
(6) г==(3*.11»-|-з),
(7) 3=g (2-3.7.53»-Hr).
Последовательная подстановка у, I, 2 в уравнение (4) приведет нас к уравнению
4057а:=7 206 360«
и.пи, если разложить на множители, помня, что 4657 есть простое число:
4657®= 2» 3 • 5 7-23-373л.
Отсюда получаем, что длн целости х необходимо, чтобы
п=4657лх=7 206 ЗбОге',
где ге' — произвольное целое, число.
Подставляя найденные, значения в уравнения (1)—(7), находим:
X=2 • 3 • 7 • 53-4657«' = 10 366 482л',
У=2-32-89-4657п' = 7 460514ге',
Z = ЗМ1 • 4657л/ = 4149 387ге',
Т=22 • 5 79-4657м'=7 358 060ге',
г=2я • 3 • 5 • 7 23 • 373л'= 7 206 360п',
у = 2- 3«-17 - 15991ге' = 4 893 246п',
z=3®. 13- 46489ге' -= 5 439 213п',
£=2®.3.5-7.11.761п' = 3 515 820л'.
Если положить re’ --1, то мы получим наименьшие, числа, удовлетворяющие первым
семи уравнениям. Быть в состоянии найти эти числа, значит по Архимеду ве ааслумш-
вать названии «невежды в числах».
В гейберговском издании Архимеда после текста изложенной эпиграммы приве-
дена древняя схолия:
«При помощи этого стихотворения Архимед очень ясно выразил поставленную за-
дачу: его слова надо понимать так, что всего должно быть четыре стада быков, а именно.
ЗАДАЧА. КОТОРУЮ АРХИМЕД НАШЕЛ В ЭПИГРАММАХ
375
первое белошерстых быков и коров, общее количество которых составляет двойных,
мириад 14 простых 582 и единиц 7360 (т. е. 1 405 827 360), другое темных быков и коров,
общее количество которых будет 9 двойных мириад 8830 простых и 800 единиц
( = 988 300 800), еще одно пестрых быков и коров, общее количество которых будет
8 двойных мириад 6991 простых и 400 единиц (869 910 400); последнее яке стадо рыжих
имеет общее количество 7 двойных мириад, 6708 простых и 8000 единиц (т. е. 767 088 000);
таким образом, общее количество во всех четырех стадах составляет 40 двойных мириад
3112 простых и 6560 единиц (4 031 126 560). И стадо белошерстых имеет быков — 8 двой-
ных мириад 2931 простых и 8560 единиц (829 318 560), и коров 5 двойных мириад 7650
простых и 8800 единиц (576 508 800), темное стадо имеет быков 5 двойных мириад 9684
простых н 1120 единиц (596 841 120) и коров 3 двойных мириады 9145 простых и 9680
единиц (391 459 680), стадо пестрых имеет быков 5 двойных мириад 8864 простых в 4800
единиц (588 644 800) п коров 2 двойных мириады 8126 простых и 5600 едициц
(281 265 600), стадо же рыжих имеет быков 3 двойных мириады 3195 простых и 960 еди-
ниц (331 950 960) и коров 4 двойных мириады 3513 простых н 7040 единиц (435 137 040).
И количество белых быков равно половине и третьей части количества темных быков
и, кроме того, всему стаду рыжих, количество темных равно четвертой и пятой части
пестрых быков и всему количеству рыжих, количество пестрых быков равно шестой
и седьмой части белых и еще всему количеству рыжих; далее, количество белых коров
равно третьей и четвертой частям всего стада темных, количество темных коров равно чет-
вертой и пятой частям всего стада пестрых, количество же пестрых равно пятой и шестой
частям всего стада рыжих. Затем количество рыжих коров было равно шестой и седьмой
частям всего стада белых. И стадо белых и темных быков вместе образует квадратное
число, стадо же рыжих и пестрых быков вместе образует треугольник, как и следует для
каждого цвета из предположенных пропорций».
Относительно этой схолии следует сделать два замечания. Во-первых, употребляю-
щаяся в ней система нумерации принадлежит Аполлонию: она соответствует делению па
классы по четыре разряда (вместо наших трех): единицы, мириады (десятки тысяч), двой-
ные, тройные и т. д. мирипды. Во-вторых, найденные решения являются совершенно пра-
вильными, если ограничиться первыми семью уравненными: они получаютсы из наших
формул, если прпиятг, п' —80. Дело, одпако, обстоит совершенно плаче, если мы попро-
буем проверить остальные требования. Сумма белых и черных быков будет:
^ГУ = 2.3-7.53-4657-80 |- 2 • 3« 89 4657 80-
=2-3-4657-8() (7-53-J-3-89)=2-3-4657-80-2-11-29,
что никоим образом не равняется квадратному числу. Точно так яке и сумма стад рыжих
и пестрых быков
2~Г=34.11-4657-80 1-22-5-79-4657-80=
= 4657 -80 (3« -11 (- 2г - 5 • 79) = 4657 80 • 7 • 353 =24 • 5 • 7 • 353 4657
не может быть приведена к виду
треугольного числа.
2
Нужно добавить, что строки 33—36 в подлиннике читаются так:
/ fit f
aQYOTplXeS TtX’JQOl puv SJICI pi^aiQTO яХ^йчяу
xvaveuiS, -ornvT spnefiov iuupBTQOi
etg pa-&og sig e^og тс, ri б jiepijiiptea лаутц
t t
niiinkavTO nlivOov (вар. nV.Oovg) Gorvtrxnqg лебкх.
Слова IcopeTQoi 6-g JteOog eig e\»g можно понимать, что п глубину и в ширину
ч и с л и быков были одинаковыми, или яке, что д л и н ы были одинаковыми. Так
как вместо .iKivOoi! (-плиты, четыреугольднка) можно читать и гЩОо-ве (-множества, коли-
чества), то более вероятным будет толкование, что квадратным должно быть число
быков; однако это место мояппо понимать и в смысле квадратлости занимаемой и л о-
щ а д и; тогда число быков должно состоять из двух миоякитслей, лишь приблизительно
равных один другому.
Таким образом, мы можем различать задачи: во-первых, считать, что сумма Х-4-У
должна быть только прямоугольным числом: тогда получается так называемая задача
Вурма, решенная им в Zcitsclirift f. Maihemalik und Physik (llislorisch, Litteral. Ablei-
Lung), т. XXV (1880), стр. 156 и сл.; во-вторых, что указанная сумма должна быть дей-
ствительно полным квадратом. В дальнейшем изложении я следую тексту немецкого
перевода хисопского издании Архимеда.
376
АРХИМЕД
Потребуем, чтобы сумма 7.-\-Т равнялась треугольному числу вида ' ;
Л
(З4 -11 4- 22.5- 79) • 4657п.'=.
Сумма, стоящая в скобках, равпа 2471 = 7-353, таким образом:
"-у-~ == 7 ’353 ’4С57/г''
Так как q может быть или четным, или нечетным числом типа 2s, или 2s—1, то
наше уравнение принимает вид
s (2s ± 1)^ 7 -353-4657п'.
Представим п' в виде произведения двух множителей, из которых один и содержатся
без остатка в s, другой ясс v в 2s±l; тогда мы будем иметь следующие 1(5 пар совместных
уравнении:
S = K 2s ± 1=7-353-4657щ
(3)-(4) s — Ju, 2s ± 1 = 353-4657щ
(5)-(6) s=353t* 2s i l = 7-4657i>,
(7)-(8) s=4657и 2s i 1 — 7-353г>,
(9)-(10) s=7-353u 2s 1 =4657f.
(И) -(12) s=7-4657u 2s ± 1 — 353f,
(13)-(14) s= 353-4657м 2s± 1=7г>,
(15)-(16) s=7-353-4657« 2s± 1=F.
Если решить каждую из этих совместных пар и сравнить наименьшие полученные
результаты, то окажется, что самый маленький из этих результатов будет соответствовать
уравнениям
s=7и, 2.«— 1—353- 4657i>,
что дает нам
117 423, о=1, »' = не =117 423=3s-4349.
Соответствующие этому п' решения будут:
Х=1217 263 415 886,
У= 876035 935 422,
2= 487 233465)701,
Т= 864 005479380,
х= 846192 410280,
у— 574 579 625 058,
z= 638 688 708099,
t= 412838 131860.
Сумма чисел Х+У будет при этом:
X -!-У = 2- 3- (7 • 53 3 • 8!)) • 4657 • 117423=
=2® 3-11 • 29-4657 Зз 4349, =
= (2= - З4 - 4349) - (11 - 29 - 4657)=
= 1409 076-1485 583,
что представляет число, близкое к квадратному.
Если же мы потребуем, чтобы сумма X-f-У была бы точным квадратом, то нам при-
дется удовлетворить уравнению
X •Y=p*
или
2-3-(7-53 4-3-89) 4657л'=рг,
22-3-ll-29-4657rt'=p2,
ЗАДАЧА, КОТОРУЮ АРХИМЕД НАШЕЛ В ЭПИГРАММАХ
377
что удовлетворяется, если мы положим;
«' = 3 11 29 4657g2 4 456 749g2,
где g — любое целое, число.
Соответствующие решения будут:
X=2 З2 7 11 29 53 4657® • |2=46 200 808 287 018g2,
У = 2 • З3 11 • 29 89 - 4657® |2 33 249 638 308 986 £®,
Z=3s 11* 29 4657® |® -= 18 492 776 362 863g2,
Т = 2® - 3 5 -11 29 • 79 - 4б572 - £® 32 793 026 546 940g2,
23 З2 5 7 11 • 23 29 373• 4657 - £®= 32 116 937 723 640g2,
у = 2- З3 • 11 • 17 29 15991 . 4657 g®=21807 969 217 254g2,
z=33-1 l-13-29-46489-4657-g®= 24 241 207098 537g2,
t 2®- 32- 5 - 7 11® 29 761 4657 g2= 15 669 127 269 180g2.
Теперь величина g2 должна еще удовлетворить уравнению
z : у'7(7-1 1)
ИЛИ
<7 fr-f 3- 7 ц. 29-353 -46572g®. •
Если умножить обе части на 8 и положить:
2q |-1=7, 2-4657|=и,
то мы получаем уравнение Пелля
/®— 1=2-3-7-11-29-353в®
или
г3—4 729 494а2=1.
Если бы провести решение итого ура в пения дальше, то для числа X белых бы кои
получилось бы значение порядка
А' —1598-1021>'1541
для общего числа быков
7766-Ю2"6541.
Для того, чтобы записать нее восемь чисел, понадобился бы том в 660 страниц,
если считать, что на каждой странице умещается 2500 цифр. Вот, что значило для Архи-
меда «будет считаться, что в этой мудрости ты все до конца Превзошел». Архимед сделал
хладнокровный вызов своему противнику (Эратосфену или Аполлонию), поставил ему
задачу, которая, как он знал, физически не может быть разрешена.
СТОМАХИЙ
I
Рис. I.
1. Поскольку так называемый Стомахий может служить предметом
разнообразных теорий относительно перестановок составляющих его
фигур, то я стел необходимым сначала изложить ... (об отдельных
его частях) ..., на которые он разделяется, о том, чему каждая из них
может быть уподоблена, затем о том, какие углы, взятые но два...
(дают в сумме два прямых), причем это сказано для того, чтобы можно
было знать условия взаимного прикладывания получающихся из них
фигур, а именно, когда получающиеся в этих фигурах стороны будут
точно расположены по одной прямой, и когда они,
представляя незначительные отклонения, все же могут
обмануть зрение; все это имеет прямое отношение к
технике складывания, так как не должпо отбрасывать
составленные фигуры, если при самом небольшом
отклонении (от двух прямых углов, они) могут обма-
нуть зрение.
2. Может теперь случиться, что из них немалое
количество фигур ... (может быть сложсно(?)) ... вслед-
ствие того, что ... (возмо)жно переставить в другое
место равной и равноугольной фигуры... и взять
Дру( тую)...*). Иногда бывает, что две фигуры вместе рав-
ны и подобны одной фигуре, или же две фигуры вместе
равны и подобны вместе взятым двум (другим) фигурам, и при помощи
перестановки можно получить большее количество фигур. Предвари-
тельно мы изложим некоторую теорему, относящуюся сюда.
3. Пусть будет прямоугольный параллелограмм Z1” (рис. 1);
(разделим пополам) EZ в К и проведем из Г и В прямые ГК, BE. (Про-
ведем также) TZ, продолжим ГК, BZ, и пусть они встретятся в А)
...ГН. Поскольку ЕК равна KZ, то и ГЕ, то есть BZ, будет (равна) ZA.
Таким образом, TZ будет больше ZA и, следовательно, угол ZAT будет
больше угла Zl’A. Но углы НВЛ, ZTB равны, так как каждый из них
есть половина прямого; следовательно, и угол ГНВ будет больше
*) Приводим ото томное место в подлиннике:
Eotl |iiv oiv 65 airwv ойк 6Xiy<ov ox'npaTo»v.-.0-..6ia-TrJ...<At>>v<a>TOv eivai s:g frepovxenov too too»
xai ,ooT<oviov ex4...XanpivovraS-
СТ ОМ А ХИ Й
379
НГВ, поскольку угол ГПВ равен двум внутренним противолежащим
углам НВД и IIДВ *), так что ГВ будет больше ВН. Значит, если мы
разделим ГН пополам в X, то угол ГХВ будет тупым; дейст-
вительно, так как ГХ равна ХН, а ХВ — общая, то (в треу-
гольниках ГХВ и НХВ) по две стороны равны, .____________ .
а основание ГВ больше ВН, значит, и одип угол '
будет больше другого. Следовательно, угол ГХВ будет X/ /
тупым, а смежный— острым. Но угол ГВН есть по- /
ловина прямого (ибо это предположено относительно / jf/\
параллелограмма), угол же ВХН острый... К / 2
4 **) \>/
5. Разделим ГА {рис. 2} пополам в Е, и через Е л/ х.
проведем EZ параллельно ВГ; тогда ГЙ, ZA будут
квадратами. Проведем диаметры ГД, ВЕ, ЕД и раз- Д---
делим ГН, ЕД пополам в (-) и X, затем проведем сое- Гис 2
диняющис прямые В0, XZ и через К... параллель-
но ВД проведем К..., ...2. Следовательно, па основании предыду-
щей теоремы в треугольнике ВГв угол при в будет тупой, остающийся
же острый ...ясно же..
II
Книга Архимеда о делении ф и гуры
Ст см ах и я на четырнадцать связанных
с пей фигур, находящихся с ней
в (рациональных) отношениях
Нарисуем параллелограмм***), и пусть он будет ABGD {рис. 3);
разделим BG пополам, в Е, восставим EZ перпендикулярно к BG,
проведем диагонали AG, BZ и ZG, разделим также ВЕ пополам в И
и восставим НТ перпендикулярно к ВЕ; затем приложим к точке Н
линейку, направим ее на точку А и проведем ПК, разделим ЛЬ логюлам
в М и проведем НМ; тогда прямоугольник АЕ
будет разделен на семь частей. После этого
разделим GD пополам в /V, а также ZG в С,
проведем ЕС, приложим, линейку к точкам В
и С и проведем СО, проведем еще СП; тогда и
прямоугольник ZG будет разделен па семь ча-
стей, но иным способом, чем первый прямо-
угольник, а весь квадрат будет разделен на
четырнадцать частей.
Докажем теперь, что каждая из четыр-
надцати частей находится со всем квадратом
л рациональном отношении.
Так как ZG является диагональю прямо-
угольника ZG, то треугольник DZG будет
Рис. 3. .
половиной этого прямоугольника и, следова-
тельно, х/4 квадрата. Но треугольник GHC есть 1/#1 от треугольника
DZG, потому что если продолжить ЕС, то опа пройдет через точку D, и
тогда треугольник GDC будет половиной треугольника D'AC и равен
вместе взятым треугольникам G NC uDNC; следовательно, треуголь-
*) И Угол НГ7. меньше угла ПАВ, и пВД равен НГВ.
•*) Конец 3 и весь 4 прочесть невозможно.
••*) то есть квадрат.
380 АРХИМЕД
ник GNC будет 1/1В квадрата:
тр-к GNC = ABGD.
Если мы, кроме этого, учтем, что линия ОС направлена в точку В,
как она в действительности и начерчена, и линия Л'С будет параллель-
на стороне BG квадрата, а следовательно, и треугольника OBG,
то, таким образом, мы будем иметь пропорцию
BG : ЛО « GO : ЛО.
Но BG в четыре раза больше NC, значит, и GO будет в четыре раза
больше NO; поэтому GN будет в три раза больше NO, и треугольник
GNC равен трем треугольникам ONC. Но так как мы показали, что
треугольник GNC составляет 1/1в квадрата, то треугольник ONC
будет ~ квадрата:
тр-к ONG = ABCD.
Далее, так как треугольник GDZ есть-^- квадрата и коатому треуголь-
1 1
ник GNC будет его, а треугольник NCO ero^g , то для четырехуголь-
ника DOCZ остается площади квадрата
oocz^ -1 abgd.
Затем, согласно предположению, линия NC проходит через точку
F, и CF является параллельной к GE; поэтому мы имеем пропорцию
EG : Ci- =EQ: CQ~CQ: I<'Q.
И так как EQ равна 2CQ и GQ равпа 2 FQ*), то треугольник EQG
будет вдвое больше каждого из треугольников GCQ и EFQ. Но ясно,
что треугольник EGZ равен двум треугольникам EFG, так как ZE
4
равна двум FE. И так как треугольник EGZ составляет квадрата, то
треугольник EFG будет последнего. Но треугольник EFG втрое
О
больше каждого из треугольников EFQ и GCQ; значит, каждый из
этих треугольников будет квадрата AG.
тр-к EFQ=-^-ABCD; тр-к ОС» = AJ3GD.
И треугольник EGQ вдвое больше каждого из треугольников EFQ
и GCQ; значит, он будет квадрата -
тр-к EGQ = ABGD.
Далее, так как ZF равпа EF, то треугольник ZFG равен
треугольнику EFG; если мы теперь отнимем треугольник GCQ, рав-
ный треугольнику EFQ, то останется четырехугольник FQCZ, равный
треугольнику EGQ; следовательно, четырехугольник FQCZ будет
1
-ф квадрата AG:
eqcz=A-abgd.
’) Так как EG=2CF.
СТОМАХИЙ
381
Теперь мы разделили прямоугольник ZG на 7 частей и переходим
к делению другого прямоугольника.
Так как BZ и ЕС являются двумя параллельными диагоналями,
и ZF равна EF, то треугольник ZLF ранен EFQ-, поэтому треугольник
ZLF есть квадрата АС\
тр-в ZLF= ABGD.
Поскольку ВН равна НЕ, то треугольник BEZ будет в четыре раза
больше треугольника ВНТ, так как каждый из пих будет прямо-
угольным. Но так как BEZ есть у- квадрата ABGD, то треугольник
ВНТ будет ^7 последнего.
тр-к ВНТ = ~ ABGD
Далее, согласно нашему предположению, линия НК проходит через
точку А, следовательно, мы имеем пропорцию:
АВ : НТ=ВК : КТ.
Но АВ равна 2НТ\ значит, и ВК равна 2К.Т и, следовательно, ВТ
равна ЗК.Т-, таким образом, треугольник ВНТ будет втрое больше
л
треугольника КНТ. Но так как треугольник ВНТ есть всего квад-
I
рата, то треугольник КНТ будет последнего:
тр-к] KHT^-^ABGD.
Далее, треугольник ВКН вдвое больше треугольника КНТ и, следо-
1.
вательпо, равен квадрата.
тр-1Г IIKH “ ABGD
Затем, так как BL равна 2ZL и XL равна 2LF*), то треугольник
ABL будет вдвое больше треугольника ALZ и треугольник ALZ
вдвое больше треугольника ZLF. Но так как треугольник ZLF
1 1
составляет всего квадрата, то треугольник ALZбудет р последнего,
тр-к AbZ — ABGD
и значит, треугольник ABL будет его. По треугольник АВМ
равен треугольнику BML', значит, каждый из этих трсугольни-
- 1
нов будетр квадрата.
тр-к АВМ = Тр-К B.ML = ~ ABGD.
Еще остается пятиугольник LFEIIT, равный половине шестой части
) В подобных треугольниках ABL и ZI.F сторона AB—2ZF.
382
АРХИМЕД
вместе с половиной восьмом части всего квадрата *).
LFEH-l^. ±(-L + -L) ABGO.
Таким образом, мы разделили и (прямоугольник) АЕ на 7 частей;
тем самым и вся фигура ABGD разделена па 14 частей, находящихся
с ней в (рациональных) отношениях; а это и есть то. что мы хотели.
СТОМАХИЙ АРХИМЕДА
Рассматриваемое сочинение имеет своей цельте дать математическую теорию игры
вроде современных головоломок, в которой составлялись из данных кусочков геометри-
ческие фигуры заданного вида, прячем составление должно было быть или совершенно
точным, или же допускалось и некоторое приближение.
Предлагаемый текст состоит из двух отрывков. Начальный греческий текст нвй-
ден Гейбергом в знаменитом Константинопольском палимпсесте, открывшем нам «Эфод»
и греческий текст трактата «О плавающих телах»; он найден в достаточно испорченном
состоянии и в некоторой степени исправлен по консультации Гейбсрга с датским матема-
тиком И. Хегардом (1*. Deegan)). Вторая часть сохранилась в арабском переводе в руко-
писях берлинской библиотеки и бодлеянской библиотеки и Оксфорде. По берлинским
рукописям этот отрывок был издан Генрихом Зутером в 1.899 г. (Abhandlungen z. Ge-
schichte der Matlieniatik, IX, 491 и сл. (1899)); данный Зутером немецкий перевод и поме-
щен в издании Гейбсрга с небольшими изменениями.
О Стомахии Архимеда (латинский термин loculus) говорят латинские грамматики
поздней эпохи Марий Викторин и Атилий Фортунациан (Keil, Grammalici latini т. VI,
стр. 100 и сл. и 271 и сл.).
Первый пишет: «Как тот архимедовский loculus, составленный из четырнадцати
пластинок слоновой кости квадратных, или треугольных, и в том и в другом случае раз-
лично оформленных, подобных как бы строительным деталям; в нем при ограниченном
И определенном количестве пластинок вследствие многообразного их вида можно изобра-
зить то корабль, то меч, то деревцо или какие-нибудь другие фигуры».
Атилий Фортунациап пишет: «Архимедовский loculus, имеющий 14 пластивок из
слоновой кости с разнообразными углами, заключенных в квадратную форму, и, когда
мы перекладываем, изображающий то шлем, то кинжал, то колонну, то корабль, и про-
изводящий бесчисленные фигуры; в нашем детстве этот loculus принес, много пользы
для укрепления памяти».
Соответствующая игра была распространенной в Пояднюю эпоху римской импе-
рии (IV—VI века к. :>.).
у
*) Нетрудно показать» что этот пятиугольник составляет шеего квадрата, что Архимед
ааписыиает по египетскому образцу:
LF7iHr 1’4.^='(‘+ь.
2 24 2 24 g J
О МНОГОГРАННИКАХ
ПАПП, МАТЕМАТИЧЕСКАЯ БИБЛИОТЕКА V, 34 MttlLsch, т. Г, стр. 3.52
«Таковыми являются пе только указанные божественнейшим
Платоном пять тел. а именно — тетраэдр, гексаэдр, октаэдр и доде-
каэдр, пятое же икосаэдр, но и найденные Архимедом тринадцать
числом {рис. 1}, заключающиеся между равносторонними, равноуголь-
ными, но по подобными друг другу многоугольниками.
Первым из них является октаэдр, заключенный между 4 тре-
угольниками и 4 шестиугольниками.
За ним следуют три чстырнадцатиграппнка, из которых первый
заключается между 8 треугольниками и 6 квадратами, второй — мельчу
6 квадратами и 8 шестиугольниками, третий же между 8 треугольни-
ками и 6 восьмиугольниками.
После них идут д»а днадцатишестиграппика, из которых первый
заключается между 8 треугольниками и 18 квадратами, второй же-
между 12 квадратами, 8 шестиугольниками и 6 восьмиугольниками.
После них будут три тридцатидвухгранпика, из которых первый
заключается между 20 треугольниками и 12 пятиугольниками, второй —
между 12 пятиугольниками и 20 шестиугольниками, третий ate — меж-
ду 20 треугольниками и 12 десятиугольниками.
После них идет один трпдцативосьмиграниик, заключающийся
между 32 треугольниками и 6 квадратами.
За ним следуют два шестидесятидвуграппика, из которых первый
заключается между 20 треугольниками, 30 квадратами и 12 пятиуголь-
никами, второй же — 30 ииадратамп, 20 шестиугольниками и 12 деся-
тиугол ьннкамп.
После них идет последний довяностодвухгранник, заключающийся
между 80 треугольниками и 12 пятиугольниками.
Сколько же углов и ребер имеет каждая из этих 13 многогранных
фигур, можно усмотреть следующим образом: у тех многогранников,
у которых телесные углы заключаются только между тремя плоскими
углами, если пересчитать все плоские углы, которые содержат все
грани многогранника, то ясно, что число телесных углов будет равно
третьей части полученного числа, у тех же многогранников, у которых
телесные углы заключаются только между четырьмя плоскими, то,
если пересчитать все плоские углы, которые имеют все грани много-
.384
АРХИМЕД
грапника, то четвертая часть полученного числа будет числом телес-
ных углов многогранника; точно так же у тех многогранников, у кото-
рых телесный угол заключается между 5 плоскими углами, пятая часть
всего количества плоских углов будет числом телесных углов.
Количество же ребер каждого многогранника мы найдем таким
способом. Если пересчитать все стороны, которые имеют ограничи-
вающие многогранник плоские фигуры, то ясно, что их число будет
равпо количеству плоских углов. Но так как каждое из ребер много-
гранника, будет общим для двух граней, то ясно, что половина указан-
ного количества будет числом ребер многогранника.
Так вот первый из 13 неоднородных многогранников, поскольку
он содержится между 4 треугольниками и 4 птествусольниками, будет
иметь 12 телесных углов и 18 ребер. Действительно, у четырех тре-
угольников будет 12 углов и 12 сторон, у четырех же шестиуголь-
О МНОГОГРАННИКАХ
385
ников 24 угла и 24 стороны; так как общее число получается равным
36, то число телесных углов необходимо будет третьей частью выше-
упомянутого числа, поскольку каждый ив его телесных углов заклю-
чается между 3 плоскими углами, количество же ребер будет полови-
ной этого числа; то есть 36, так что ребер будет 18.
Из четырыадцатиграппиков первый заключается между 8 тре-
угольниками и 6 квадратами, так что он имеет 12 телесных углов, ибо
каждый его угол я а кл го чается между четырьмя плоскими углами; ребер
же он будет иметь 24. Второй из чстырпадцатигранпиков, поскольку он
заключается между 6 квадратами и 8 шестиугольниками, будет иметь
24 телесных угла, ибо каждый из его углов заключается между 3 плос-
кими углами; ребер же он имеет 36... (третий же из чстырпадцатигран-
пиков, заключающийся между 8 треугольниками и 6 восьмиугольни-
ками, будет иметь 24 угла и 36 ребер)...
Из двадцатипгсстигранипков первый, поскольку он содержится
между 8 треугольниками и 18 квадратами, будет иметь 24 т. л< спых угла
и 48 ребер. Второй же из двадцатишестигранников, поскольку он со-
держится между 12 квадратами, 8 шестиугольниками и 6 восьмиуголь-
никами, будет иметь 48 углов и 72 ребра.
Из тридцатидвуграппиков первый, поскольку он содержится
между 20 треугольниками и 12 пятиугольниками, будет иметь 30
телесных углов и 60 ребер. Второй же из тридцатидвугранников,
поскольку он содержится между 12 пятиугольниками и 20 шести-
угольниками, будет иметь 60 телесных углов и 90 ребер. Третий же из
тридцатидвугранников, поскольку он содержится между 20 тре-
угольниками и 12 десятиугольниками, будет иметь 60 телесных углов
и 90 ребер.
Тридцативосьмигранник, содержащийся между 32 треугольни-
ками и шестью квадратами, будет иметь 24 телесных угла и
60 ребер.
Из шестидесятидвуграпников первый, поскольку он заключается
между 20 треугольниками, 30 квадратами и 12 пятиугольниками, будет
иметь 60 телесных углов и 120 ребер. Остающийся шестидесятидну-
гранник, поскольку он заключается между 30 квадратами, 20 шести-
угольниками и 12 десятиугольниками, будет иметь 120 телесных углов
и 180 ребер.
Допяностодвугранник же, заключающийся между 80 треугольни-
ками и 12 пятиугольниками, будетиметьбО телесных углов и 150 ребер».
ВАТИКАНСКИЕ СХОЛИИ К ПАППУ (Hullsch, т. 111)
(1) «Октаэдр имеет 4 треугольника., 4 шестиугольника, 18 ребер,
12 телесных углов; каждый из телесных углов заключается между
3 плоскими углами, ни которых два шестиугольника н один треуголь
пик, так что до 4 прямых по хватает одного и двух третей прямого
угла. Он получается из первой пирамиды, если разделить со ребра па
три равные части и через точки деления провести плоскости и выбросить
углы.
(2) (Первый) четырнадцатиграипик заключается между 8 тре-
угольниками и 6 квадратами; он имеет 24 ребра и 12 телесных углов,
каждый из которых содержится можду 4 плоскими углами, из которых
два принадлежат квадрату, два же треугольнику, тан что до 4 прямых
не достает одного п двух третей прямого угла. Он получается из куба,
25 Архимед
38В
АРХИМЕД
• если разделить ребра его пополам и через точки деления провести
плоскости, отбросив все 8 углов.
(3) (Второй) четырпадцатнграиппк заключается между 6 квадра-
тами и 8 шестиугольниками, имеет 36 ребер и 24 телесных угла, каж-
дый из которых заключается между 3 плоскими углами, из которых два
принадлежат шестиугольнику и один квадрату. Он получается ив
октаэдра, если разделить па три части каждое из его ребер, провести
через точки деления плоскости и отбросить 6 углов.
(4) Третий (из четырнадцатоерашшков). поскольку оп заклю-
чается между 8 треугольниками и (5 восьмиугольниками, будет иметь
24 телесных угла, каждый из которых содержится между 3 плоскими
углами, из которых два принадлежат восьмиугольнику и один тре-
угольнику; ребер же он имеет 36. Он получается из куба, если каждое
из его ребер разделить так, чтобы получилось три отрезка, из которых
средний в квадрате будет вдвое больше каждого нз крайних (то ость
если а средний, а 1> крайний, то а — 6р'2).
(5) \Первый) двадцатшпестигранник получается из четырнадцатп-
граппика, заключающегося между 8 треугольниками и 6 квадратами,
если разделить каждое из его ребер пополам, через точки деления
провести плоскости и ...»
ГЕРОИ, Dcfinilioncs, 104 стр. 66 в сл.
«Архимед же говорит, что он всего нашел тринадцать тел, могущих
быть вписанными в шар, добавив к вышеупомянутым пяти (правильным
многогранникам) еще восемь. Из них четырмадцатпграшшк был из-
вестен и Платону; был же он двоякого рода — один составленный из
8 треугольников и 6 квадратов, то есть из земли и воздуха, какой знали
и некоторые из древних, другой же — из восьми квадратов и 6 тре-
угольников, что кажется более трудным».
В гороно неких словах содержатся дпе ошибки: Архимед открыл по 8, а 13 много-
гранников, которые все могут быть пппсанными в шар; затем относительно второго
четырнадиатигранпика он дает неправильные снедения, как можно видеть из приведен-
ного выше. Упоминание о земле и полдухе объясняется тем, что Платон считал атомы,
земли имеющими форму куба, атомы же воздуха—форму октаэдра, состоящего из
при пильных треу ГОЛ 1.11 и ков.
ТРАКТАТ АБУ-Л-Х АСАНА С А ВИТА ИБН КУРРЫ
О ПОСТРОЕНИИ ОПИСАННОЙ ОКОЛО ГПА РА ТЕЛЕСНОЙ ФИГУРЫ
С ЧЕТЫРНАДЦАТЬЮ (. )С 1.1 ()ВА И И ЯМ И
Мы хотим объяснить, как построить обнимающую данный шар
фигуру с четырнадцатью ратшогтороннимн п ра вн оу сольными осно-
ванными.
Эта фигура пс принадлежит к числу многогранников с подобными
гранями; наоборот, восемь из ее граней являются треугольниками и
шесть — четырехугольниками, прич<
рыми согласно одинаковому распо-
ложению, и сторона полученного
тела является половиной диаметра
шара.
Пусть {рис. Г] круг АВС будет
наибольшим кругом из всех кругов
данного шара, в котором мы хотим
построить многогранник; пусть I) бу-
дет его центром. Если мы желаем по-
строить в данном круге телесную фи-
гуру с четырнадцатью основаниями,
как мы описали выше, то строим
сначала в круге АВС равносторонний
и равноугольный шестиугольник
AEFBCG. Из центра!) к углам шести-
угольника проводим липни DA, DB.
DF, /)В, DC, DG. Тогда треугольник
линиями шестиугольная фигура, будут равносторонними треугол1>-
ииками. Па треугольниках ADE, FDB, CDG строим из равносторон-
них треугольников пирамиды, которые называются тетраэдрами *}.
Пусть их вершины будут в точках Н, J, А'; проведем соединительные
прямые HJ, JK, КН. Затем на треугольниках EDF, BDC, DGA
м первъи1 складываются со вто
И J
Гис. 1.
, на которые разделяется этими
*) Буквально «фигурами огня», так как в илатоловеной фмаоссфии агсмы огня считались
•иеющими ферму правильного тетраэдра; правильный октаадр. куВ п правильный икосаэдр по анало-
>-.1>П|ЫМ причинам назывались Ла средневековом Вмогокс «фигурой воздуха», «фигурой зсяилие и «фигу-'
jfi.i воды», а правильный додевоодр назывался «фигурой веба», так кап, согласно Платону, ату форму
имел весь иир в целом.
25*
388 АРХИМЕД
с другой стороны площади круга построим другие тетраэдры совершен-
но так же, как мы строили вышеупомянутые. Затем между точками на
их вершинах проведем соединительные прямые.
Теперь я утнерждаю: Мы построили в данном шаре фигуру с четыр-
надцатью равносторонними и равноугольными основаниями, из кото-
рых восемь являются равносторонними треугольниками, а шесть остаю-
щихся — равносторонними и прямоугольными четырехугольниками.
И каждая иа их сторон равпа каждой из сторон упомянутых треуголь-
ников, их взаимное соединение следует совершенно особому располо-
жению, причем ребро полученного тела является половиной диаметра
шара.
Доказательство этому таково: из точки ZZ, являющейся вершиной
тетраэдра ADE11, опускаем перпендикуляр на плоскость его основа
имя ADE\ пусть этот перпендикуляр будет HL. Из точки L проводим
к точкам A, E,F,D линии АЕ, ЕЕ, EF, LD. Так как линия HL перпен-
дикулярна к плоскости ADE, то она будет перпендикулярна ко всем
лилиям, которые можно через ее конец провести в упомянутой пло-
скости. Следовательно опа будет также перпендикулярна к обоим
линиям AL и LD. Тогда оба квадрата, построенные па обеих линиях
ПЕ и АЕ, будут вместе равны квадрату, построенному на АН,
Л Ь2 ЛЬа —-ЛН2
а оба квадрата, получающиеся ла обоих линиях IIL и LD, будут вместе
равны квадрату, построенному на DH.
.HI." f LD2^ DH2
Но квадрат линии ЛН равен квадрату линии DH, так как треугольник
AHD равносторояси, ибо он является одной из граней тетраэдра.
Следовательно, оба квадрата обеих линяй HL и AL будут вместе равны
обоим квадратам па обеих лилиях НЕ и LD.
VL2 | ,U? = H».2+LD2
Если мы вычтем общий квадрат линии HL, то останется, что квадрат
линии АЕ равен квадрату линии LD. В таком случае обе линии АЕ,
ED н обоих треугольниках ALE, LDE равны;
AI. - LD
точно так же в этих треугольниках будут равны обе линии ЛЕ и ED.
Mi = ED
так как сторона шестиугольника является половиной диаметра. Затем
сторона ЕЕ будет в обоих треугольниках общей. Следовательно, оба
эти треугольника будут равны; и каждый из углов этих треугольников
будет так же равен ему соответствующему. Таким образом, линия ЕЕ
делит угол AED пополам. Но угол ЛЕЕ равен двум третям прямого,
так как треугольник ЛЕЕ) равносторонний. В таком случае угол LED
будет третью прямого угла, а угол DEF — двумя третями прямого
угла, так как треугольник EDF равносторонний; следовательно, сово-
купность LEF этих углов составит прямой угол. Тогда квадраты,
• построенные на обеих линиях ЕЕ, ЕЕ, будут вместе равны квадрату.
построенному на LF.
zi-Л, /а-2-»-/-2
ТРАКТАТ АБУ-Л-ХАСАНА САБИТА ИБП КУРРЫ 389s
Прибавим общий квадрат, построенный на 11L. Тогда квадраты,
построенные на линиях ЕЕ, EF, HL, будут имеете равны квадратам
на линиях LF и LII.
1.Н1 | EF® + HL® - LFS -I- I.1F
Что касается обоих квадратов на линиях LE и HL, то они будут
равны квадрату, построенному на ЕН,
Z.b*-f Я/.а-ЕДг
так как HL перпендикулярна ко всея прямым, проведенным из точки Л
на плоскости АВЕ, которая совпадает с плоскостью круга АВС.
Г1 точно так же, если провести соединительную линию HF, то оба
квадрата, построенные на обеих линиях HL, LF, будут вместо равны
квадрату, построенному на линии HF.
111.1 I LF® = lit"
Следовательно, оба квадрата, построенные на обоих линиях ЕН,
EF, равны квадрату, построенному ва липни FII.
К11г + EF® FH3
Следовательно, угол FEII будет прямым. Подобным же способом
установим, что угол EFJ тоже будет прямым. Далее фигура IIEFJ
будет четырехсторонником, у которого две. стороны ЕН, FJ перпен-
дикулярны к стороне. EF. И эта фигура расположена н одной пло-
скости. И так как мы имеем три липни ЕН, FJ, ЕЕ, одна из которых
является стороной (правильного) шестиугольника в круге АВС,
а остальные две липин равны двум сторонам итого шестиугольника,
то три стороны плоской фигуры EIIJF равны, и два вышеупомянутых
угла являются прямыми. И таким образом выясняется, что эта фигура
представляет равносторонний прямоугольный четырехугольник.
И точно так же выяснено, что каждый из двух четырехугольников,
соответствующих упомянутому четырехугольнику, а именно оба четы-
рехугольника BJKC и GKHA, будут прямоугольными и равносторон-
ними, и что лежащие с другой стороны три четырехугольника, основа-
ниями которых являются линии АЕ, FB, CG, будут также прямо-
угольными и равносторонними. И стороны всех этих шести четырех-
угольников равны, так как они равны сторонам шестиугольника в круге
АВС. Точно так же стороны выходящих из этих чстырехуголыгикон-
шсстп треуголыгиков, которыми являются треугольники ЛЕН, FJB.
CKG и им соответствующие с другой стороны, имеющие основаниями:
липни EF, ВС и GA, оудут тоже равны друг другу и сторонам шести--
угольника в круге АВС. Следовательно, они будут равны сторонам
шести вышеупомянутых квадратов. Что же касается треугольника
HJK, то каждая из его сторон будет одновременно одной из сторон
четырехугольников EHJF, BJKC, GKHA, каждая из которых раня»
стороне шестиугольника. Следовательно, все они равпы друг другу.
Точно так же обстоит и с треугольником, лежащим с другой стороны
и соответствующим треугольнику HJК. Таким образом, оба эти тре
угольника ралносторолпи и оба равны остальным шести треугольни-
кам, о которых мы уже упоминали.
Теперь все эти фигуры заключают тело с четырнадцатью основа-
ниями, построенное нами согласно описанному. И его основания имеют
одинаковое расположение, так как каждый из треугольников окружен
по сторонам тремя четырехугольниками, а каждый из четырехуголь-
390
АРХИМЕД
пиков окружен пи сторонам четырьмя треугольниками. И каждый
из углов этого тела заключается между двумя углами четырехуголь-
ника и двумя углами заключенного между ними треугольника. И то же
самое одинаковым образом имеет место у всех его углов. Таким обра-
зом, все ого углы тоже будут равны.
Что касается того, что упомянутый нами заданный шар обпимает
построенную телесную фигуру, то это ясно потому, что круг АВС
проходит через принадлежащие углам телесной фигуры точки А, Е, F,
В, С, С. И линии, проведенные из центра этого шара к остальным
углам мри точках If, J, К, а именно линии D//, DJ, DK. и им соответ-
ствующие с другой стороны, будут равны друг другу и также равны
половине диаметра шара, так как они являются сторонами перво-
начально построенных нами тетраэдров. Таким образом, поверхность
шара проходит через все углы этой построенной нами телесной фигуры,
и сторона упомянутой телесной фигуры с четырнадцатью основаниями
равна половине диаметра шара.— Да будет хвала Гюгу, властителю
мира*).
*) Текст опубликован п Qut-llen и. Slud ten z. Gesehtclite d. Matheinatik. Abtti. B. Studies,
in. IL стр. 1BG--I9B.
КНИГА ЛЕММ АРХИМЕДА *}
В ПЕРЕВОДЕ ТЕБИТЛ БЕН КОРЫ fl] С РАЗЪЯСНЕНИЯМИ
УЧЕНОГО ЛЛЬМОХТДССО ЛБИЛЬГАСАНЛ ГАЛИ БЕП АХМАДА
11 АСУ ЭНСКОГО [2]
Ученый Альмохгассо увернет, что эта книга относится к Архиме-
ду; в ней находится ряд красивых предложений, хотя л малочислен-
ных, по и высшей степени полезных, касающихся начал геометрии,
великолепных и изящных; занимающиеся геометрией ученые причи-:
еляют эту книгу к тем промежуточным сочинениям, которые надлежит
читать между книгой Евклида и Альмагестом; действительно, некото-
рые места предложений последней книги нуждаются для своего разъяс-
пепия в других предложениях. И сам Архимед указал на такие пред-
ложения и ссылался на них в других своих произведениях, говоря,
например, «как мы показали в предложениях о прямоугольниках**)
и еще «как мы доказали л пашем изложении, рассуждая о треугольни-
ках», наконец, «как мы доказали в предложениях о четырехугольни-
ках»; в пятом предложении он приводит в высшей степени оригиналь-
ное доказательство.
Затем Абусахль Алыгухи [3] паписал книгу под заглавием «О по-
рядке предложений в книге лемм Архимеда», и дал более общее и луч-
шее доказательство этого предложения, а также разобрал все те «дока-
зательства», которые зависят от присоединения отношения [4]. Когда
я узнал вб этом, то к более темным местам этой книги я добавил объяс-
нения или примечания па полях, затем все им указанное подкрепил
предложениями, как мне показалось нужным, и взял из предложений
Абусахля дна, необходимых для объяснения пятого предложения [5J,
опустив остальные ряди краткости и вследствие того, что они не
являются необходимыми.
Если, два круга А ЕВ и CED взаимно касаются в точке Е {ряс. 1}
и их диаметры ЛВ, Ci) параллельны и если соединить две точки В, D
сточкой касания Е (прямыми) DE и ВЕ, то линия BDE будет прямой.
•) Книга переведена с латинского С сохранением латинизированных имен арабских пятеро jt.
*•) См. сноску к Гфодлпжетятю II.
3!)2
АРХИМЕД
Я
Рис. 1.
Пусть оба центра будут G, F; проведем соединяющую линию GF
и продолжим до Е; затем проведем DH параллельно GF. Так как ПР
равна CD и GD будет равной EG, то от рав-
ных прямых FB,FE останутся GF, или DB,
п НВ, которые будут друг другу равны, и так-
же будут равны углы HDB и HBD. И так как
углы EGD, EFB прямые, а углы EGD, DIIB
я равны, то останутся дна угла GED, GDE,
которые будут равны друг другу и двум
углам HDB, HBD; следовательно, угол EDG
будет равен углу DBF. И угол GDB возь-
мем общим; значит, оба угла GDB, FBI)
(которые равны двум прямым) равны двум
углам GDB, GDE. Следовательно, и эти
углы будут также равны двум прямым;
значит, линия ЕВ В будет прямой; а это и есть то, чего мы хотели f К].
П
Пусть СВ А {рис. 2} будет полукруг, которого касаются пря-
мые ВС, О В и {прямая} BE перпендикулярна АС; если соединить А
и В, то BF будет равна FE.
Доказательство. Соединим -1 с В, продолжим ее по пря-
мой и проведем CD до пересечения с ней в
G; затем соединим С с В. И так как угол
СВ А есть угол в полукруге, то оп будет пря-
мым; остающийся угол CBG тоже будет пря-
мым н DBEC будет прямоугольным паралле-
лограммом. Следовательно, в прямоугольном
треугол ьпике GBC из В проводится перпенди-
куляр BD к основанию и прямые BD н DC
равны, так как они являются касательными
к кругу; значит, CD будет равняться DG,
как мы это показали в составленных памп
предложениях о прямоугольных *). И так
как в треугольнике GAC линия BE прове-
дена параллельно основанию и из D — сере-
дины основания— проведена линия DA, пересекающая параллель
в F, то BF будет равна FE. А это и есть то, чего мьг хотели Г7}.
Ш
Пусть С А {рис. 3} будет сегмент круга и. В какая-нибудь на
нем точка; если BD перпендикулярна к АС и отрезок DE равен ВА,
а дуга BF равна дуге В А, то соединяющая CF будет равна СЕ.
Доказательство. Проведем соединяющие л ними АВ, BF,
ЕЕ, ЕВ. Так как дуга ВА равна дуге BF, то и прямая АВ будет равна
BF. И так как AD равна ED и оба угла при D прямые, a DB — общая,
то, значит, АВ равна BE, а вследствие того, что BF и BE равны, будут
равны и оба угла BFE, BEF. И так как четырехугольник СРВ А вписан
> Вероятно, пропущено слово «треугольниках».
КНИГА ЛЕММ АРХИМЕДА
393
к круг, то угол СРВ с, противолежащим ему углом СЛВ, или с углом
ВЕЛ, будут равны двум прямым. По угол СЕВ вместе с углом ВЕА
раины двум прямым; значит, оба угла СЕВ и СЕВ будут равны.
И (после вычитания BFE и BEF} оста-
ются равные углы CFE, CEF; значит,
СЕ будет равна CF. А это и есть то,
чего мы хотели [8],
IV
Пусть АВС {рис. 4} будет полу-
круг; построим на диаметре АС два
полукруга AD и DC и восставим пер-
пендикуляр DB; получающаяся фигура,
которую Архимед называет «арбело-
ном» *) (это будет площадь, ограниченная дугой большого полукруга
и двумя окружностями малых кругов) будет равна кругу, диаметром,
которого является перпендикуляр DB [f)J.
Доказател ь с т в о. Так как линия DB будет средней про-
порциональной между обеими линиями DA, DC, то прямоугольник
я ва AD н DC будет равен квадрату ня
—DB. Возьмем (дважды) прямоугольник
\ на AD и DC вместе с квадратами на AD
/1 \ \ и па DC; получится удвоенный прямо-
/ I У"'') угольник на AD,DC с- двумя квадратами
'Х / / на AD и иа DC, то есть квадрат на АС,
¥ \. у у 1 равный удвоенному квадрату на DB
I------------------------J вместо с двумя квадратами на DC.
Отношение кругон таково же, как отно-
J’nc. 'i. птенис квадратов (их диаметров); сле-
довательно, круг с диаметром АС будет
равен удвоенному кругу с диаметром DB вместе с двумя кругами на
диаметрах AD и DC и полукруг АС будет равен кругу с диаметром DB
и двум полукругам AD, DC. Отнимем два общих полукруга AD, DC;
останется фигура, заключенная между полукругами AC, AD, DC (это
и есть фигура, которую Архимед назвал «арбелон») и равная кругу,
диаметр которого DB. А это и есть то. чего мы хотели.
V
Если дан полукруг АВ {рис. 5.}, ни его диаметре где-нибудь взята
точка С, на диаметре построены два полукруга АС и СВ, из С восста-
влен перпендикуляр CD к АВ и с обеих сторон (от него) построены
два. круга, касающиеся как этого перпендикуляра, так и обоих полу-
кругов, то эти два круга будут равны.
Д о к а з а т о л ь с т н о. Пусть один из этих кругов касается DC
в Е, полукруга АВ в F и полукруга ЛС в С; проведем диаметр НЕ;
он будет параллелен диаметру АВ, вследствие того, что углы НЕС,
АСЕ прямые. Проведем соединяющие линииFII и II А; тогда линия AF
будет прямой, как сказано в предложении Т. Пусть AF и СЕ встретятся
в D так, как они выходят под углами /1, С, которые (в сумме) меньше
двух прямых. Проведем также соединяющие лилии FE и ЕВ; линия
') Se₽r^J.ov— скребок, coitiipit.'i.
394
АРХИМЕД
FEB тоще будет прямой, кап мы сказали (предложение 1), и перпен-
дикулярной к AD, так как угол AFB прямой, как угол в полукруге ИВ.
Проведем соединяющие прямые IIG и GC; тогда ПС будет тоже пря-
мой [10]. Проведем соединяющие прямые EG и G/1; тогда ЕА будет
прямой; продолжим ее до I и
соединим В с. I, прямая BI то-
же будет перпендикулярной к
.4/; проведем соединяющую
прямую Dl\ И так как AD и
АВ суть две прямые и из D про-
ведена DC. перпендикулярная
к АВ, я из В проведена BF.
перпендикулярная к DA, и атн
перпендикуляры пересекаются
друг с другом н Е, а АЕ, про-
долженная до I, перпендику-
лярна к BI, то BID будет пря-
Рис. 5.
мой, как мы показали в пред-
ложениях, написанных в комментарии к трактату о прямоугольных
треугольниках 141]. Л так как углы AGC, AIB прямые, то BD и CG
будут параллельными и отношение AD к DH. равное отношению АС
к НЕ*), будет равно отношению АВ к ВС-,
AD
DH
_ АС _ ЛВ_
НН ~ НС
прямоугольник между АС, СВ, следовательно, будет равен прямо-
угольнику между АВ, НЕ. И точно так же для круга LMN докажем,
что прямоугольник между АС, СВ будет равен прямоугольнику между
АВ и диаметром итого круга; отсюда докажем, что диаметры кругов
EFG, LMN равны; значит, эти два круга будут равны. А это и есть
то, что мы хотели.
VI
Если, дан полукруг. АВС {рис. 6} и на его диаметре вяята точка D,
причем AD в полтора раза больше DC, затем на AD и DC описаны,
два полукруга и между тремя
(указанными) полукругами по-
строен касающийся каждого из
них круг. EF, в котором проведен
диаметр EF, параллельный
диаметру АС, то требуется
найти, отношение диаметра АС
к диаметру EF.
Проведем две соединяющие
линии АЕ и ЕВ, а также две
линии CF и FB; тогда СВ и АВ Л О D р С
будут прямыми, как сказано в
J J о Рис. 0.
первом предложении. Затем на-
чертим две линии FGA, ЕНС —
можно показать, что они тоже будут прямыми; точно так же {будут
прямыми) и обе .линии DE и DF", проведем соединяющие прямыеD1,
*, Из подобия треугольников Л DC и Шш.
КНИГА ЛЕММ АРХИМЕДА
395
л»
lit:
CL>
J>A
DL, а также EM и FN и продолжим последние до О и /*. И так как в
треугольнике AED прямая AG перпендикулярна к ED, a. DJ перпенди-
кулярна к ЛЕ, и обе эти прямые взаимно пересекаются в М, то, значит,
ЕМО тоже будет перпендикуляром, как это мы показали и написанием
вами рассуждении о свойствах треугольника, с доказательстном чего
мы уже встретилисг. в предыдущем предложении; точно так же и FP
будет перпендикуляром к СЛ. И так как два угла у L и у В прямые,
то DL будет параллельна АВ, и также DI параллельна СВ\ значит,
отношение АГ) к DC будет таким же, как отношение AM к FM и
как отношение АС к СР,
AM АО
fM ~~ ОР
и отношение CD к DA будет таким же, как CN к ЕЕ, или как СР
к РО.
CN _ СР
NK ~ 14)
Но AD в полтора раза больше DC; значит, АО будет в полтора раза
больше ОР и ОР в полтора раза больше СР. Значит, три линии АО.
ОР и PC будут пропорциональны, и каких единиц будет в СР четыре,
таких в ОР будет шесть, в АО девять и в С А девятнадцать. И так как
РО равна EF, то отношение Л С к EF будет таким же, как отношение
девятнадцати к шести.
Таким образом, мы нашли требуемое отношение.. Точно так же,
если бы отношение AD к DC было каким угодно, например четырех
к трем, или пяти к четырем, или каким-нибудь другим, то рассужде-
ния были бы такими же. Это и есть то, чего мы хотели [12].
VII
Если около квадрата один круг описан, а другой вписан в него.
то описанный круг будет вдвое больше вписанного.
Действительно, пусть АВ {рис. 7}, будет круг, обнимающий
квадрат AB, a CD — вписанный в него; пусть диаметр квадрата
будет АВ, он же будет диаметром описанного круга; прове-
дем CD —диаметр вписанного круга — па-
раллельно (стороне) ЛЕ, которая будет
ему равна. И гак как квадрат ла АВ никое
больше квадрата на АЕ, или CD, и отно-
шение квадратов на диаметрах равно отно-
шен ию одного круга к другому, то, сле-
довательно, круг Л В будет вдвое больше
круга CD. Это и ость то, чего мы хо-
тели.
VIII
Если в круге как-нибудь проведена линия Рис. 7.
АВ {рис. 8}, продолжена по прямой, на ней
отложена ВС, равная гюлудиаметру круга, полученная точка С сое-
динена с центром D круга и соединяющая прямая продолжена до Е,
то дуга АЕ будет втрое больше дуги BF Г131-
Действнтелыю, проведем EG параллельно АВ и проведем сое-
диняющие прямые DB. DG. 'Гак как два угла DEC и DGE равны, то
396
АРХИМЕД
угол GDC будет вдвое больше угла DEG. И так как угол BDC равен
углу BCD, а угол CEG равен углу АСЕ, то угол GDC будет вдвое
больше угла CDB, и весь угол BDG
втрое больше угла BDC, и дуга BG, рав-
ная
ВЕ.
Рис. 8.
дуге АЕ, будет
Л ото и есть, то,
втрое больше дуги
чего мы хотели.
IX
прямые линии АН,
Если в круге две
{рис. 9} пересекают друг друга под
прямым углом (ио не в центре), то две
дуги AD, СВ
AC, DB.
11роведем
ЕЕ, который
CD
будут равны двум дугам
параллельно АВ диаметр
рассечет CD пополам в С;
тогда дуга ЕС будет равна ED. Таи как дуги ЕРЕ я. ЕСЕ являются одно-
временно полуокружностями, и дуга ED равна дуге ЕЛ вместе с дугой
AD, то дуга СЕ с двумя дугами ЕЛ, AD будет равна полуокружности.
Затем дуга ЕЛ равна дуге ВЕ; значит, дуга
СВ с дугой ЛР будет равна полуокружности.
И остаются две дуги ЕС. ЕЛ, то есть ду-
га ЛС вместе с дугой DB, тоже равные полу-
окружности. А
тели.
ОТО И ОСТЬ ТО, 401’0 МЫ хо-
X
круг АВС {рис. 10}, каса-
DA, секущая его DB и еще
Если будет
тельная к нему
касательная DC, то после того как будут,
проведены СЕ, параллельно DB, соединяющая
ЕА, пересекающая DB в Е, и опущен из Е
перпендикуляр EG на СЕ, последний рассечет
Соединим Л и С
к кругу, то угол D А С равен углу,
сегмепт ЛС, то есть углу ЛЕС.
Последний же равен углу AED
вследствие того, что СЕ и BD па-
раллельны; значит, и углы DAC,
AFD будут равны. И в двух тре-
угольниках DAF, AHD равны два
угла AFD, HAD и угол D общий;
вследствие этого *) прямоугольник
между FD, DH будет равен квад-
• рату иа DA, или квадрату на DC.
fd пн - пл2 = по2
СЕ пополам в точке G.
Так как DA — касательная, а АС — секущая
попадающему в противоположный
И так как отношение ED к DC то
fd ^_ср_
DC ’ ОН
же, что у CD к DH,
) Иа подобия треугольников ЛР’1> w имеем FD : AD-^=AD; DH.
КНИГА ЛЕММ АРХИМЕДА
397
и угол D общий, то треугольники DFC, DCH будут подобными и угол
DFC равным DCH, который в свою очередь равен углу DAH. А этот
последний равен углу AFD\ следовательно, два угла AFD, CFD равны
и угол DFC равен углу FCE. Но DFA равен углу АЕС\ следовательно,
в треугольнике FEC два угла при С и Е равны, два угла при G пря-
мые и сторона GF общая; вследствие этого CG будет равна GE. Зна-
чит, СЕ рассекается в G пополам. А это и есть, то, чего мы хотели.
XI
Если в круге две линии АЕ, CD {рис. 11} взаимно пересекаются
под прямыми углами в точке Е, которая не является центром, то все.
квадраты на АЕ, BE, ЕС, ED равны квадрату на диаметре.
Проведем диаметр AF и соединяющие прямые AC, AD, CF, DB.
Й так как угол AED прямой, то он ранен углу ACF. Угол ADC ра-
вен углу AFC, вследствие того, что они стоят
треугольниках ADE, AFC остальные углы CAF
и DAE равны; одновременно будут равны две
дуги CF, DB, а значит, равны и их хорды. Два
квадрата па DE, ЕВ равняются квадрату па
BD или CF,
KBS-’ODS=-CFS
два квадрата па АЕ, ЕС равняются квадрату на
СА,
1Яа |-ЯСВ-=СА»
и два квадрата на CF. СЛ равняются квадрату
па FA,
<.Т5 } CAa==FA4
или па диаметре. Значит, все квадраты на АЕ, ЕВ, СЕ, ED будут
равны квадрату па диаметре.
IE8 i ява + сн3 4- ЕО8 = лИ
Л это и есть то, чего мы хотели.
XII
Если к полукругу на диаметре Л В {рис. 12} из точки С проведены,
касательные в точках D, Е, также соединяющие прямые ЕА, DB, вза-
имно пересекающиеся в F, затем соединяющая прямая CF продолжена до
G, то CG будет перпендикулярна к ЛВ.
Проведем соединяющие прямые DA, ЕВ. Так как угол BDA пря-
мой, то в треугольнике остальные два угла DAB. DBA будут
равны одному прямому. Но так как угол ЛЕВ тоже прямой, то они
будут и ему раины. Возьмем общий угол FBE', оба угла DAB, АВЕ
будут равны вместе взятым FBE, FEB или углу DFE — внешнему
в (треугольнике) FBE. И так как CD касается круга, a DB его пере-
секает, то угол CD В равняется углу D А В и равным образом угол CEF
равняется углу ЕВА\ значит, два угла CEF, CDF вместо будут равны
углу DFE. Из нашего трактата о четырехугольных фигурах стано-
вится ясно, что если между двумя равными линиями, встречающимися
в некоторой точке (как обе наши линии CD и СЕ), провести две взаимно
398
АРХИМЕД
псрссокаюп|,иеся липни (как паши. DF и EF), так что содержащийся
между ними угол (наш угол /’’) будет равен двум имеете взятым углам,
которые получаются в точках взаимного пересечения обеих пар линий
(это будут дна угла при D
н
и Е), то линия, выходящая из точки встречи
в точку пересечения (наша лилия CF),
будет равна любой из встречающихся ли-
пни (то есть Ci) или СЕ) *); вследствие
этого СЕ будет раина CD; значит, угол CFD
равен углу CDF или углу DAG. Но угол
CFD вместе с углом DFG равен двум
прямым; значит, угол DAG с углом DFG
равен двум прямым, и в четырехугольнике
ЛDFG остаются два угла ADF, AGF, рав-
ные вместо двум прямым. Но угол ADR
прямой; значит, будет прямым и угол A.GC,
и GC будет перпендикулярной к АВ. Л
это и есть то, чего мы хотели.
XIII
Если в круге две линии АВ, CD
{рис. 13' взаимно пересекаются, причем АВ,
ио не CD будет диаметром круга, то по
проведении из обеих точек Л. В двух перпендикуляров АЕ, BF к пря-
мой CD, на. последней будут отсечены равные {отрезки) CF, DE.
Проведем соединяющую прямую ЕВ и из 7 —центра круга — пер-
пендикуляр 1G к CD и продолжим его до В на прямой ЕВ. Так как
IG есть перпендикуляр, опущенный из центра па линию CD, то он
разделит ее пополам в G, и так как IG, ЛЕ суть два перпендикуляра
к той же прямой CD, то они будут параллельны.
Поскол ьку же Bt равна 7 J, то и В11 будет равна
НЕ; и вследствие этого равенства, а также по-
тому, что BF параллельна HG, прямая/’С будет
равна GE, и из двух равных прямых GC, GD
(по вычитании равных), останутся равпые пря-
мые FC, ED. А эго и есть то, чего мы хотели.
XIV
Рис. 13.
Если будет полукруг АВ (рис. 14}, от его
диаметра. АВ отсечены равные прямые AC, BD
и. на линиях AC, CD, DB построены полукруги,
причем центром, двух полукругов на АВ и CD будет точка. Е, то по
проведении к АВ перпендикуляра EF, продолженного до точки G, круг
на диаметре. FG будет равен площади фигуры, заключающейся между
большим полукругом, находящимися внутри его двумя полукругами
и средним полукругом, который будет вне большого полукруга. Й это
есть фигура, которую Архимед называет «салинонъ [141.
») Борелли к споем издании доказывает ото следующим обраао.ч. Продолжим /к;, и пусть СП
будет о авиа сЕ. Так как угол СНЕ ранен углу СЕН и согласно предположению, угол DIE равен
сумме С1)Г и CEE. то DEE+COE—CUE-1,-liKF; следовательно, четырехугольник 01 Jill может
быть вписан и круг. Так как СН=Си--СЕ, то центром итога круга будет С; следовательно, (J7- — <1>.
КНИГА ЛКММ АРХИМЕДА
Рис. 14.
Так как АС разделена пополам в Е и к пей прибавлена СА, то два
квадрата на /9<1, <’.4 вдвое больше двух квадратов па DE, ЕЛ
ил--\-САй= 2 (ПЕ2 |-.Kzl3)
(Евклид «Начала», II, 10). HoAG равна DA;
FG = [EG + EF = ЕА + Ь1»| :г.. .1 О
значит
на DE, ЕЛ.
FG- i 2 (Ш52 ЕД2)
И так как АВ вдвое больше ИА, и CD
вдвое больше ED,
AU 2АЕ, СО — 2ED
то два квадрата на АВ, DC и четыре
раза больше двух квадратов па DE,EA
или вдвое больше двух квадратов на
GF, АС.
АП~ + DC2-- А (ЛЕ2 — ЕЛ2» 2 (О К8 г ЛС1)
Вследствие этого два круга с диамет-
рами Л В, DC вдвое больше тех, диа-
метры которых суть GF, АС, и половины кругов с диаметрами АВ
и CD равпы двум кругам с диаметрами GF и АС. По
тром АС равен двум полукругам AC, BD. Значит, если
два общих полукруга AC, BD, то останется фигура,
четырьмя полукругами АВ, CD, DB, АС (которая и
которую Архимед называет «салинон»), равная кругу,
рого FG. А это и есть то, чего мы хотели.
КА + Ы>1
два квадрата на FG, АС вдвое Польше двух квадратов
круг с диаме-
ОТНПТЬ от них
ограниченная
является той,
диаметр ПОТО-
XV
Если дан полукруг АВ {рис. 15} и в нем АС хорда пятиугольника,
причем половиной дуги АС будет AD, и проведены, соеЛипякшртя пря-
мая CD, продолженная вплоть до Е, затем соединяющая прямая DB,
пересекающая С Л в F и опущен из F
перпендикуляр FG иа АВ, то линия EG
будет равна, полудиаметру круга [15J.
Проведем соединяющую прямую
СВ-, пусть /7 будет центр круга, про-
ведем HD, DG, и AD. Так как угол
АВС, основанием которого является
сторона пятиугольника, равен двум
пятым прямого угла, то каждый из
двух углов CBD, DBA будет пятой
частью прямого. II угол DBA вдвое больше угла DBB-, значит, уго.т
DBA будет двумя пятыми прямого угла. Так как в двух треугольниках
CBF, GBF два угла при В равны, углы G и С прямые и сторона АЛ’
общая, то ВС равна BG. И так как в двух треугольниках CBD, GBD
две стороны СВ ц BG равпы и так же равны два угла при В, а сторона
BD общая, то два угла BCD и BCD равны. И каждый из них есть шесть
пятых прямого*) н равен внешнему углу DAE вписанного в круг четы-
’) Угол ВС А примой, а угол ACD = A HD= [/Ь части прямого.
400
АРХИМЕД
рехугольяикаВАОС *), значит, остается угол DAB, равный углу DGA,
и DA будет равна DG. Итак как угол. DHG равен двум пятым частям
прямого, а угол DGH — шести пятым, то в остатке получается угол
HDG — две пятых прямого, и DG будет равпа GII. Так как угол ADE,
являющийся 1IHC1IT1IIU1 для вписанного в круг четырехугольника ADCB,
будет равен углу СВ А, то он будет составлять две пятых прямого угла
и равен углу GDH. И так как в двух треугольниках EDA, HDG
будут дна равных угла EDA, IIDG, а также два угла DGH, DAE и две
стороны DA, DG, то ЕА будет равпа HG. Возьмем AG общей; тогда EG
будет равна АН. А это и есть то, чего мы хотели.
И отсюда ясно, что линия DE равпа полудиаметру круга; так
паи угол DAE равен углу DGII, то линия DH поэтому равна линии
DE. И я утверждаю, что ЕС разделяется в D в крайнем и среднем
отношении, причем большим отрезком является DE', н так как ED
есть хорда шестиугольника, a DC — десятиугольника, то это уже
доказано в книге «Начал» (Евклид, кн. XIII, предложение 9). А это
и есть то, чего мы хотели.
*) Действительно» угол ПЛ В образует 1К0° пан с углом BCD (по свойству вписанного четы-
рехугольника). так и с углом DAK (ио свойству смежных углов).
КНИГА АРХИМЕДА О ПОСТРОЕНИИ КРУГА,
РАЗДЕЛЕННОГО ПА СЕМЬ РАВНЫХ ЧАСТЕЙ
Перевод Абу-л-Хасана Сабита ибн- Курры ал-Харрани [1]
Исправление а редакция бедного Мустафы Сиддики [2],
да помилует его Аллах]
Wo м.«л Аллаха милостивого, милосердного]
Сочинение состоит из одной книги и восемнадцати предложений.
Я говорю поело хвалы Аллаху и молитвы за пророка-избранника, за его семей-
ство и за его друзей. Желая переписать эту книгу, я смог достать только дефектный
экземпляр, испорченный из-за невежества того, кто его персвисыиал, и недостаточного
понимания им (предмета). С большим трудом мне удалось исследовать и проанализи-
ровать задачи этой книги и привести предложения этой ппигм п порядок при помощи
легких и близких ио значению разъяснений. К ним я добавил некоторые доказатель-
ства позднейгпих (ученых) (3|. Да поможет Аллах этому своим содействием!
Предложения
I
Проведем {линию) АВ и отметим на ней две точки С и D {рис. 1}
таким образом, что квадрат CD равен квадратам АС и BD. Тогда
В П С л
---------1--.-------1------1
45 3
Рис. 1.
я утверждаю, что квадрат АВ равен удвоенной плоскости из AD на.
СВ [4].
*) Номера предложений написаны п рукописи ин полях.
2(> Архимед
402
ЛРХИМЯД
Так как квадраты АС и DB равны квадрату CD,
лс2 + впа = cd2
то, если мы прибавим к обоим сторонам квадрат CD и удвоенную пло-
скость из АС на CD, получится, что три квадрата AC, CD и DB
и удвоенная плоскость из АС па CD равны удвоенному квадрату CD
и удвоенной. плоскости из ЛС на CD.
ле2 | cd2 hd2 ] 2.4с. cd ... гео2 -|- 2ле-ап
Но удвоенным квадрат CD и удвоенная плоскость из АС па CD равны
удвоенной плоскости из AD па DC.
2(:D®4- 2АС-CD *- 2.4D- DC
Поэтому три квадрата AC, CD и DB и удвоенная плоскость из .4С
на CD равны удвоенной плоскости из /179 на DC. Так как квадрат AD
равен квадратам АС и CD и удвоенной плоскости из /1С на CD,
AD2~- AC.2 I- CD® 4- 2AC-CD
то квадраты AD и DB равны удвоенной плоскости из /177 па DC.
AD2 -| DHe= azD-DC
Прибавим к обеим сторонам удвоенную плоскость из DB на AD. Тогда
квадраты AD и DB и удвоенная плоскост»» из AD на DB, то есть квад-
рат Л7?, равны удвоенным плоскостям из AD на DC п из AD на DB,
то есть удвоенной плоскости из AD на СВ.
ли2 2.4D-CD
Это н есть то, чего мы хотели.
II
[Д Р У ’11 м 11 0 с о и о м {Р1|с. -Д- Так как квадрат АВ ранги
трем квадратам AC, CD и DB и трем удвоенным плоскостям из .-И’
на CD, из ЛС на DB и из CD на DB,
.4 fl2 = ЛС® -? CD2 Dll2 -I- 2(.4е. r’D ! ЛС* Dll ' CD. Dll)
и квадрат CD равен квадратам ЛС н DB,
CD2^AC2 ! Du2
то квадрат AB равен удвоенному квадрату CD и трем удшл...............
В В С А
I- 1----------—~Ч
Рас. 2.
плоскостям из АС на CD, из АС па DB и из CD па DB. Так как
удвоенная плоскость из АВ па CD равна удвоенному квадрату CD и
удвоенным плоскостям из АС на CD и из DB на CD,
2 А К • CD = 2-1 ’D® 4 2 (.4с - CD 4 DB- CD)
то квадрат АВ равен удвоенным плоскостям из АВ на CD и из ,4 Сна DB.
Л!:2 — 2 (Al:.CD | ЛС-ОВ)
КНИГА О ПОСТРОЕНИИ КРУГЛ, РЛЗДКЛЕННОГО НЛ СЕМЬ РАВНЫХ ЧАСТЕЙ 4j)g
Но удвоенная плоскость из ЛВ па CD равна удвоенным плоско-
стям из СВ на CD п из АС на CD, а удвоенные. плоскости иа ЛС па CD
и из АС па DB раппы. удвоенной плоскости из АС на СВ. Поэтому
квадрат ЛВ равен удвоенным плоскостям ни СВ мн CD и нз АС па СВ,
то есть удвоенной плоскости из AD па СВ.
1П® - 2 (СП-CD -I- АС-СИ) 2AD-CII
А это и есть то, чего мы хотелп. |
III
В каждом прямоугольном треугольнике удвоенная плоскость из
одного катета и гипотенузы как одной линии на другой катет и гипо-
тенузу как одну линию равна квадрату периметра как одной линии.
Пусть треугольник — АВС 8
{рис. 3}, а прямой угол — В.
Продолжим ЛС в се паправле- .S \
пни в обе стороны н отложим S \
AD, равную АВ, и СЕ, равную >--------------------------------------<
ВС. Тогда очевидно, что DC
равна АВ и ЛС, АЕ равна Рпс- 3-
Л С и СВ, a DE равна периме-
тру треугольника. Так как квадрат АС равен сумме квадратов ЛВ и
ВС, то есть AD и СЕ,
АС* — АН2 -! ВС* — СЕ*
то удвоенная плоскость из DC па ЛЕ равна квадрату DE (продл. I).
2/Х -Л/; - D1-*
А это и есть то, чего мы хотели.
Я г<пю|ш>: другим способом, принадлежащим Абу Дли ал-Хубуби (5J.
'1'ак как плоскость иа DC па АЕ р.нша квадрату АС п трем плоскостям из АС
на СЕ, иа АС па AD и из AD па СЕ,
Dv-AE= АС* + ЛС-СК + ЛС-АП -| -ЛОСК
а квадрат -16 panini квадратам 7J/I н СЕ,
ас2 ad*h- ск°-
тн удновнная плоскость нз DC на АЕ равна трем квадратам DA, zl6, СЕ и трем
удвоенным плоскостям из АС на СЕ, из АС па AD и из AD на СЕ, ' a nfte это
вместе равпо квадрату DE.
2D4-AE =- ПА2 4- АС’2 + СЕ2-|- 2ЛС-СК 4- 2AC-AD Ч- 2AD-CE =“ DE*
Поэтому удвоенная плоскость из DC на АЕ равна квадрату DE.
211С- ЛЕ = DE*
А это н есть то, чего мы хотели [GJ.
IV
В каждом прямоугольном- треугольнике, если опустить из ено пря-
мого угла высоту на его гипотенузу, то квадрат периметра {треуголь-
ника} как одной линии равен удвоенной п.тскости из гипотенузы на
периметр и эту высоту как иа одну линию. -- • • - .л.-..-
2fi*
404
АРХИМЕД
Пусть в треугольнике АВС {рис. 4}, прямой угол — В, а
опущенная высота — BD. Продолжим АС в ее направлении в обе
стороны. Отложим ЕА, равную АВ, СС, равную СВ, и GH, равную^/).
Тогда я утверждаю, что квадрат EG равен удвоенной плоскости из АС
на ЕН.
Действительно, так как HG или BD относится к CG или СВ, как
ЕА, или АВ, к АС,
НО ВА
CG ~ АС
то, «присоединяя», получим, что ПС относится к CG, как ЕС к АС,
НС ЕС
СО ‘ АС
переставляя, получим, что СП относится к ЕС, как CG к АС,
CH CG
"ЁС— АС
и, (скова) «присоединяя», получим, что ЕП относится к ЕС, как A Gv А С.
ЕН AG
ЕС “ АС
Поэтому плоскость из ЕП па АС равна плоскости из ЕС на AG и удвоен-
ная плоскость из ЕН па АС равна удвоенной плоскости из ЕС па АС.
Но удвоенная плоскость из ЕС на AG равна квадрату EG (предл. ITI).
ХЕН • АС = 2ЕС - AG b'G®
Поэтому квадрат EG раней удвоенной плоскости из АС на ЕН. Л это
и есть то, чего мы хотели [71.
V
Д р у г и м с п о с о б о м. Вернемся к тому же треугольнику
и его высоте и продолжим ВС в ее направлении в обе стороны {рис.5;.
Отложим CG, равную
z АС, ВЕ, равную АВ, и
\ ЕН, равную BD. Тогда я
\ утверждаю, что квадрат
EG ранен удвоенной лло-
скости из GC на СП.
л______£________й / \С______________6’ Действительно, так
!2 20 /5 25 ~~1 как плоскость из ВЕ, или
АВ, па ВС равна плоско-
Рлс‘ 5" сти из ЕН, или BD, на СС.
или АС, то удвоенная
плоскость из ЕВ на ВС равна удвоенной плоскости из ЕН па CG.
:UiB-I3C.^2EH‘CG ...
КНИГА О ПОСТРОЕНИИ КРУГЛ, РАЗДЕЛЕННОГО НА СЕМЬ РАВНЫХ ЧАСТЕЙ 4()5
Но квадраты ЕВ и ВС равны квадрату CG
НЕ2 I- НС2 = CG®
и квадрат ЕС равен удвоенной плоскости из ЕВ на ВС и квадратам ЕВ
и ВС.
ЕС2 = 2ЕН- НС + ЕВ3 ВС2
Поэтому квадрат ЕС равен удвоенной плоскости из ЕЕ па CG и квад-
рату CG.
КС* => 2ЕН CG CG2
Прибавим к обеим сторонам квадрат CG. Тогда квадраты ЕС и CG
равны удвоенной плоскости из ЕН па CG и удвоенному квадрату CG.
Поэтому квадрат EG равен удвоенной плоскости из GC па СЕ и квадра-
там GC и СЕ, то есть равен удвоенному квадрату GC и удвоенным
плоскостям из GC на ЕН и из GC па СЕ,
KG2 = 2GC СЕ + GC2 + СВ2 2 (GC3 + GC - ЕН + GG СЕ)
а это равно удвоенной плоскости из GC на СН и удвоенному квадрату
GC, то есть удвоенной плоскости GC па GH. Поэтому квадрат EG равен
удвоенной плоскости из GC на СИ.
EG* = 2GC.GH
А это и есть то, чего мы хотели.
[Я говорю: другим способом, принадлежащим Абу ал-Хубуби. Квад-
рат GA' равен трем квадратам ЕВ, ВС и GC вместе с удвоенными плоскостями
из GC на GE и из ВС на ВИ,
GEb=EB2+BC2+GC2+2(GC- CE+liC BE)
а удвоенная плоскость GC на GH равна удвоенному квадрату GC и удвоенной
плоскости на GC на СИ.
GC GH=2GC2+2GC- СН
Но квадрат GC раней квадратам BE и ВС, удвоеннан плоскость ия GC на СН
равна удвоенным плоскостям из GC на ЕН и из GC па СЕ, а удвоенная пло-
скость из GC на ИН равна удвоенной плоскости из ЕВ на ВС. Поэтому удвоенная
плоскость из GC па СН равна трем, квадратам ЕВ, ВС и GC и удвоенным пло-
скостям из GC на СЕ и иа ВС на BE.
2GC СН=ЕН* I- ВС2+GC2+ 2 (GC. СЕ+ВС BE)
Поэтому квадрат GE равен удвоенной плоскости из СС на GH.
GE2=2GC-GH
А это и есть то, чего мы хотели.
Другим способом, принадлежащим Абу Абдаллаху аш-Шаини [8].
Квадрат GE равен квадратам GC и СЕ и удвоенной плоскости из GC на СЕ.
GEB=GC2+СЕа+2GC • СЕ
Но квадрат СЕ равеп квадратам СВ и BE, то есть квадрату GC, и удвоенной
плоскости из СВ на BE.
CE2=CB“ + BE4=GC2+2CB . BE
Поэтому квадрат GE равен удвоенному квадрату GC и удвоенным плоскостям и»
GC на СЕ и из СЛ на BE.
GE2=2GC2+2(GC-CE+CB-BE)
По удвоенный квадрат GC и удвоенная плоскость из GC на СЕ равны удвоенной
плоскости из GC на GE,
2GC’t-2GC CK=2GC GE
406
АРХИМЕД
удвоенная плоскость из СВ на ВЕ равна удвоенной плоскости из СС на ЕН,
2CBBE=2GC-KU
. а удвоенные плоскости из GC на GE и из СС на ЕП — это удвоенная плоскость
ив СС на СП. Следовательно, квадрат СЕ равеп удвоенной плоскости из СС на СП.
СЕ'^гсс-сп
А ото и есть то, чего мы хотели.)
VI
В каждом прямоугольном треугольнике с разними катетами квад-
рат периметра как одной линии вместе с квадратом разности между
катетами равен квадрату гипотенузы и одно-
в :-о из катетов как одной линии вместе с квад-
рангом гипотенузы и. другого катета как од-
\ ш>& липии.
\ Пусть в треугольнике ЛВС {рис. 6} пря-
rZ/b____________\ л мои угол — В. Отложим на ВС линию BD,
25 равную ЛВ. Тогда я утверждаю, что квадрат
периметра как одной .пинии имеете с квадратом
ВС равен квадрату АВ и ЛС как одной липни
вместе с квадратом ЛС и ВС как одной линии.
Действительно, квадраты ВС и BD равны квадрату СВ и удвоен-
ной плоскости из ВС на BD.
КС* + HD3 — CD3 -r 2НС- BD
Но BD равна ЛВ и квадрат АС ранен квадрату CD п удвоенном пло-
скости из ЛВ па ВС.
АС3 = со3 •-2Л13 НС
Прибавим к обеим сторонам квадрат ЛН и удвоенную плоскость из АВ
па АС. Тогда квадраты АВ и ЛС и удвоенная плоскость из АВ па АС,
то есть квадрат АВ вместе с АС как одной липни, равны квадратам
АВ и CD и удвоенной плоскости из ЛВ на АС вместо с СВ как одном
лимин.
АВ2 -I- АС3 + 2AH-AG -= (АВ-1- AC)3--Air ; CD3 Ч- 2ЛВ (АС 4- СВ)
Прибавим еще раз к обеим сторонам квадрат ЛС и ВС как одной линии.
Тогда квадрат АС и ВС как одной линии вместе с квадратом АВ и АС
как одной линии равен квадратам ЛВ и CD, квадрату АС и ВС как
одной линии и удвоенном плоскости из АВ па ЛС и ВС как па одной
липин. Но квадрат АВ, квадрат ЛС и ВС как одной линии И удвоенная
плоскость из АВ на АС и ВС как па одной липни равны квадрату пери-
метра треугольника. Следовательно, квадрат АС н ВС как одной
липпи вместе с квадратом АВ и АС как одной липни равен квадрату
периметра треугольника как одной линии вместе с квадратом CD. А это
и есть то, чего мы хотели [9].
VII
Д р у г и м с н о с о б о м. Пусть в треугольнике АВС {рис. 7}
прямой угол — В. Продолжим ЛС в ее направлении в обе стороны.
Отложим ЛА’, равную АВ, СС, равную СВ, и GH, равную избытку ВС
над А В. Тогда ВС равна АВ и AC, AG равпа ЛС и ВС, а вся EG равна
КНИГА О ПОСТРОЕНИИ КРУГА. РАЗДЕЛЕННОГО НА СЕМЬ РАВНЫХ ЧАСТЕЙ 407
периметру треугольника и я утверждаю, что квадраты EG и GH равны
квадратам ЕС и АС.
Действительно, так как квадрат ЛС равен квадратам АВ и ВС,
то есть квадратам СП и CG, а квадраты СИ и CG равны квадрату СП
и удвоенной плоскости из СП на CG, то квадрат ЛС равен квадрату GH
и удвоенной плоскости из СН па CG.
ЛС2 = л В3 - • ВС2 СИ2 + СО2 = СН2 4- 2СН CG
Но СН равна АЕ, поэтому квадрат АС ранен квадрату GH и удвоенной
плоскости из АЕ на CG.
АС2 сп2 2ЛЕ CG
Прибавим к обеим сторонам удвоенную плоскость из ЕЛ ла АС. Тогда
квадрат АС и удвоенная плоскость из ЕА па АС равпы квадрату GH
и удвоенной плоскости из ЕЛ да ЛС.
4Св-!-2КА- ЛС^Ь’П3 | 2ЛЕ- AG
Прибавим еще раз к обеим сторонам квадрат ЕА. Тогда квадрат ЕС
равен квадратам ЕА и GH и удвоенной плоскости из ЕЛ на AG.
EC2~EA2+GH2-2EA. AG
Затем прибавим еще раз к обоим сторонам квадрат АС. Тогда квад-
раты ЕС и AG равпы трем квадратам ЕА, AG н СП и удвоенной пло-
скости из ЕЛ па AG.
ЕС2-]- Л «я=КЛв+ЛС®4-СП3—2ЕА . АС
Но квадрат EG равен квадратам ЕА и AG и удвоенной плоскости из
ЕЛ на ЛС.
ЙСг=ЛЛа-’-ЛС34-2Е-А AG
Поэтому квадраты EG и СН равны квадратам ЕС и AG.
EG2 + G IIs—JECS+AG2
Это и есть то, чего мы хотели.
|Я говорю: д р у г и м с и о с о б о ы, принадлежащим Лбу Али ал-Хубу-
би. Кпадрпты Л’С и A(i раины квадратам ЕА и СС, удвоенному квадрату АС
и удвоенным плоскостям из ЕЛ на АС и из СС на ЛС.
AC8 I -Н}2=ЕА2+СС2-]-2ЛС2-1-2 (ЕЛ ЛС-]-CG. ЛС)
Квадраты EG и СН равны четырем квадратам ЕА, AC, СС и GH и трем удвоен-
ным плоскостям из ЕА на СС, из ЕА па АС и па АС па CG.
KO2+Glfi—EA2+AC'!‘+cti2+GH2+2iEA-CC | ЕЛ-ЛС ;AC-CGj
Ио удвоенная плоскость из ЕЛ на СС, то есть из СН на СС, равна удвоенному
квадрату СН и удвоенной плоскости из СП па СН.
2ЕЛ (!G=2CH CG—2Cff2-\-2GU СН
408
АРХИМЕД
Поэтому, если мы прибавим к обеим сторонам квадрат б’Й, получитсн, что квад-
рат СП и удвоенная плоскость из ЕА на СС равны квадратам СН и CG, то есть
квадратам ЕА и CG, а квадраты ЕЛ и CG равны квадрату АС.
СН2-|-ЗЕА • CG=CHBH-CG®"- EAa-|-CG2=ACs
Поэтому квадраты EG и СП равны квадратам ЕА и СС, удвоенному квадрату
АС а удвоенным нлоскостям из ЕА на АС и из АС на CG.
KQi |-ОНв=ЕА*+СС2+2ЛС84ЦЕЛ- ЛС+АС. CG)
Следовательно, квадраты EG и GH равны квадратам ЕС и ЛС.
EG2+GH2"=EC2+AO2
А это и есть то, чего мы хотели.
Другим способом, принадлежащим Абу Абдаллаху аш-Шанни.
Квадрат ЕС равен квадратам ЕА и АС и удвоенной плоскости из ЕА на АС,
еся=ле* |.дс8-|-злв. ас
а квадрат AG равен квадратам АС и СС и удвоенной плоскости из АС на CG.
ag2=acb 1 cgz ?2ас .<;g
Но квадраты ЕЛ и CG равны квадрату АС, поэтому квадраты ЕС и AG равны
утроенному квадрату АС и удвоенным плоскостям из ЕА на АС и из CG на АС.
EC2-I-AG2=3ACS-|-2(AE АС 1-АС CG)
Так как удвоенный квадрат АС, удвоенные плоскости из ЕА на АС и из СС на АС
и удвоенная плоскость из ЕЛ на CG равны квадрату EG,
2 АС2 1 2(АЕ • AC-I-CG АС-) ЕЛ - CG)—EG2
то если мы произведем сложение и отбросим общее, останется: квадраты ЕС и /1G
и удвоенная плоскость из ЕА па CG равны квадратам EG и ЛС.
EC2-|-AGa4-2EA - CG^EG2-|-AC2
Прибавим к обеим сторонам квадрат СП. Представим себе, что липни ЕА и CG
составляют одну линию, разделенную пополам, и к чей присоединена HG. Тогда
квадрат всей (линии, состоящей из> ЕА и CG вместе с квадратом HG равен
удвоенным квадратам ЕА и CG.
(ЕЛ J-CG)a-|-HGs=2EA2+2CG2
Поэтому удвоенная плоскость из ЕА иа CG и квадрат СП равны квадратам ЕА
и СС, то есть квадрату АС.
2ЕЛ. CG+Gtf*^EA2+CG2=AGe
Если отбросить это, останется: квадраты EG и GH равны квадратам ЕС и AG.
egs+ge2=ec2+ag2
А это и есть то, чего мы хотели.]
VIII
Проведем (линию) АВ и отметим на ней две точки С и В {рис. 8}
таким образом, чтобы плоскость из CD на АВ была равна плоскости
• . В I) С А
I----------1—-—I-------------------)
«2 в
Рис. 8.
из АС на BD. Тогда я утверждаю, что удвоенная плоскость из АВ на
CD равна плоскости из AD на СВ.
Действительно, так как плоскость из АС на DB равна плоскости
из CD на АВ,
ac-db^cd-ab . *
КНИГА О ПОСТРОЕНИИ КРУГЛ, РАЗДЕЛЕННОГО НА СЕМЬ РАННЫХ ЧАСТЕЙ 409
то удвоенная плоскость из ЛС на DB равна трем плоскостям из ЛС
па CD, из ВС на CD и из АС на DB. Поэтому удвоенная плоскость
из АВ на CD равна трем указанным плоскостям.
20 D.4/1 = 2АС- DB-ЛС-CD -[-BC-CD + AC-DB
Но плоскости из АС на CD и из АС па DB равны плоскости из АС
на СВ,
АС-CD AC-DB — АС-СВ
поэтому удвоенная плоскость из ЛВ на CD равпа плоскостям из АС
па СВ и из ВС на CD. Но плоскости из АС на СВ и из ВС на CD равны
плоскости из AD на СВ,
2AB-CD^-AC'CB+ ВС CD=AD-CB
поэтому удвоенная плоскость из ЛВ на CD равпа плоскости из AD
на СВ. А это и есть то, чего мы хотели [10].
ГХ
Пусть АВС — треугольник с прямым углом В [рис. 9}. В него
вписан круг DEG. Проведем {линию} DE и продолжим ее и {линию) ВС
в их направлениях, пока они не встретятся в точке Н. Тогда я утвер-
ждаю, что ВП равна AD.
Доказательство этого. Соединим А и П. Тогда AD равна АЕ.
Продолжим DE до встречи с АП. Поэтому плоскость из HD на
НЕ вместе с квадратом АЕ равпа квадрату АН [И]. Но квадрат АН
Отнимем от обеих сторон квадрат ВП, останется: квадрат АВ равен
удвоенной плоскости из НВ на BG и квадратам BG и АЕ.
АВ2 = 2НВ. BG + BG® -|- АЕ2
Отнимем от обоих сторон квадрат AZ?, останется: удвоенная плоскость
пз АЕ на ЕВ и квадрат ЕВ равны удвоенной плоскости из НВ на BG
и квадрату BG.
2АЕ- ЕВ н кл®= 2HB.BG + BG2
Но ЕВ равна BG, поэтому удвоенная плоскость из АЕ на ЕВ равна
А Г.)
АРХИМЕД
удвоенной плоскости из НВ иа BG.
2AE-EIf = 2ftH HG
Так как ЕВ равна ВС, то ЛЕ, то есть ЛИ, равна ВН. А это и есть то,
чего мы хотели.
X
Сохраним morn же чертеж. Мы утверждаем, что СН относится
к НВ, как DC к ЕВ.
Доказательство этого. Восставим и точке С перпендикуляр СЕ
(к ВС), продолжим HD в ее
направлении и будем продол-
жать эти две линии, пока они
не встретятся в Е {рис. 10}.
Так как СЕ и ЛЕ параллельны,
треугольник ECD подобен тре-
угольнику ADE и АЕ отно-
сится к CF, как AD к CD.
АЕ АР
GF СО
Поэтому, переставляя, полу-
чим, что АЕ относится к AD, н
как СЕ к CD. Но АЕ раина AD,
поэтому СЕ' равна CD. Так как Уис- 10.
(треугольник ВЕН подобен
треугольнику FCH), то СН относится к ИВ, как СЕ, то есть CD,
к ЕВ.
CH CF CD
ИР ЕН Ь'В
Л это и есть то, чего мы хотели.
XI
пло-
что
к НВ, как СС к СВ,
из НС на BG равна
из НВ на CG.
Сохраним тот же чертеж {рис. 11}. Мы утверждаем,
скосгпь из AD на DC равна площади треугольника (АВС).
Доказательство этого. Так
как(в силу X предложения) ПС
относится
плоскость
плоскости
НС-КС- HU-CG
Тан как (в силу VIII предло-
жения) плоскость из HG па ВС
равна удвоенной плоскости из
AD иа DC
ЦС-вс «= < 2BG-CH = 2ВН . CG > = 2AD.DC
и НВ равна АЕ, a BG равна
ВЕ и вся АВ равна IIG. то
плоскость из АВ па ВС равна
удвоенной плоскости из AD на DC. Но (плоскость из) Л В па ВС
равна удвоенной площади треугольника. Поэтому плоскость из AD на
DC равна площади треугольника. Л это и есть то, чего мы хотели [12].
КНИГА О ПОСТРОЕНИИ КРУГЛ. РАЗДЕЛЕННОГО НА СЕМЬ РАИНЫХ ЧАСТЕЙ 4Ц
XII
Друг и м с и о с 11 б о м. Представим себе прямоугольный тре-
угольник АВС с прямым углом Л (рис. 12}. В него вписан круг DEG.
Тогда я утверждаю, что плоскость из AD на DC равна площади
треугольника.
Действительно, линия AD равна ЛЕ, a CD равна CG. Поэтому
квадрат АС равен квадратам АЕ и CG и
из AD на DC.
АС* = АЕ2 4- СО2 + ЗАО • DC
Но квадрат АС равен квадратам АВ и ВС,
дсл=* ав2+ вс2
поэтому квадраты АВ и ВС раины квадра-
там АЕ и CG и удвоенной плоскости из AD
на DC. Если мы отнимем от обеих сторон
квадрата ЛЕ и CG, останется: квадраты ЕВ
и BG и удвоенные плоскости из ЕВ на ЛЕ и
из CG па GB равны удвоенной плоскости из
AD на DC.
£BS-f- ВО2 4- 2 (ЕВ. АЕ + CG-CB) = 2AD. ПС
удвоенной плоскости
BG вместе с плоско-
По квадрат ЕВ равен квадрату BG и квадрат
стью из CG на GB равен плоскости из СВ на BG.
но* л- со -с в с в BG
Поэтому удвоенные плоскости из ЕВ па АЕ и из СВ па BG равны
удвоенной плоскости из AD па DC.
2КВ-ЛВ -? 2СВ. ВО = 2Л11. DC
Но ЕВ равна BG, поэтому удвоенные плоскости из GB на ЛЕ и из ЕВ
на СВ равны удвоенной плоскости из AD на DC.
2GB- ли -|- 2ЕВ СВ 2AD • DC
Так как удвоенная плоскость из АЕ па ВС равна удвоенным плоско-
. стям из GB па АЕ и из СС на ЛЕ, то есть (удвоенной плоскости из
GB на ЛЕ и) удвоенной плоскости из AD на DC,
ЗАК-ВС = 2 (GB-AE -- CG-AK) — 2 (GB-AK -I- AD-DC)
то, если мы сложим каждую сторону с соответствующей ей из двух
других сторон и отнимем общую удвоенную плоскость из GB па АЕ,
то останется: удвоенные плоскости из АЕ па СВ и из ЕВ на СВ равны
учетверенной плоскости из AD па DC.
2 (АЕ- ВСЧ- КВ- BC) = <2(AD DC : 2CG-AK» = 4 AD DC
Поэтому удвоенная плоскость из AD ua DC равна плоскостям из АЕ
на СВ и из ЕВ на ВС, то есть равна плоскости из АВ на ВС.
2AD-DC = AB-BC
Но плоскость из АВ па СВ равна двум плопщдям треугольника. Сле-
довательно, плоскость из AD па DC равна площади треугольника.
Л это и ость то, чего мы хотели.
412
АРХИМЕД
XIII
Другим способом. Построим лилии DH и EF, каждая
из которых равпа CD {рис. 13}. Тогда ВЕ равпа СВ. Так как квадрат
ЛС равен квадратам AD и DII и удвоенной плоскости из AD на
DH, а также квадратам АВ и BF, то квадраты AD и DII и удвоенная
плоскость из AD на DH равны квадратам АВ
и BF. Но квадраты AD и DII и удвоенная
плоскость из AD n&DH равны квадрату ЛН и
учетверенной плоскости из AD на DH. Поэто-
му квадраты АВ и BF равны квадрату АП и
учетверенной плоскости из AD па DH.
АС^-АЕ?-]- DHS J- 2AD-DII = АН®-}-440-DH = .IB2 | HF*
Но квадрат АП и учетверенная плоскость из
AD на DH равны квадрату AF и удвоенной
плоскости из АВ и BF.
АН 2 4- tAD. DH = < АВ2 + BF®>= AF2 4- 2ЛВ BF
Поэтому если мы отнимем равные квадраты АН
и AF, останется: учетверенная (плоскость из) AD па DH равна
удвоенной плоскости из АВ на BF.
IAD DH = 2AB-BF
Если мы возьмем половины этого, (получим, что удвоенная плоскость
из AD на DH равна плоскости из АВ па BF, то есть удвоенной пло-
щади треугольника. Поэтому если) мы еще раз поступим так же, (мы
получим площадь треугольника). А это и есть то, чего мы хотели.
XIV
Пусть треугольник АВС — прямоугольный треугольник с прямьйм
углом В, и пусть AD равна АВ, а ЕС равна ВС (рис. 14}. Тогда я утвер-
ждаю, что {удвоенная} плоскость из ED на периметр треугольника
равна учетверенной площади треугольника.
Продолжим АС в ее направлении в обе стороны и отложим AG,
равную АВ, СН, равную СВ, и HF, равную ED. Тогда вся GH равна
периметру треугольника, а линии GA и CF, вместе взятые, равны АС.
Так как удвоенная плоскость из АС иа GH вместе с плоскостью из HF
на GH равна квадрату GII, а квадрат GII равен трем квадратам GA,
АС а СН и трем удвоенным плоскостям иа GA на АС, из GA на СП
и из АС на СН, то удвоенная плоскость из АС на GH вместе с пло-
скостью из HF на GH равна трем квадратам GA, АС и СН и трем
КНИГА О ПОСТРОЕНИИ КРУГА, РАЗДЕЛЕННОГО НА СЕМЬ РАННЫХ ЧАСТЕЙ 413
удвоенным плоскостям из GA на ЛС, из GA па 67/ и из АС на СН.
2АС СП + HF-GH - CA®-|- AC®’- СН® J- 2 (GAAC + GA-СН + АС-СП)
Но плоскость из АС на GH равна квадрату АС и плоскостям из GA
на АС и из СН на АС,
AC-GH = AC® + GAAC + СНАС
а квадрат АС равен квадратам GA и СН.
АС® — GA® Л-СН®
Поэтому удвоенная плоскость из АС на GH равна трем квадратам СИ,
АС и СП и удвоенным плоскостям из GA на АС и из СП на АС.
2 АС. СП = GA2 + АС® + СН® -|- 2 (GA .ЛС СН. АС)
Если мы от обеих сторон (одного из предыдущих равенств) отнимем
общую удвоенную плоскость из Л С на GH, останется: плоскость из HF
на GH равна удвоенной плоскости из GA па СН, то есть удвоенной
плоскости из АВ па ВС.
Н F ан = 2СА-СП = 2ЛВ-ВС
Но плоскость из АВ на ВС равна двум площадям треугольника. Сле-
довательно, плоскость из HF на GH, то есть плоскость из ED па
периметр треугольника, раина учетверенной площади треугольника.
А это и есть то, чего мы хотели ИЗ].
XV
Пусть ACDB — полукруг с центром G, в нем хорда АС {рис. 15].
Разделим дугу ВС пополам в D. Соединим В и D и отложим АЕ, рав-
ную АС. Тогда я утверждаю, что плос-
кость ua GB на ВЕ равна квадрату DB. с_______
Соединим D и С, D и A. D и G, D \
и Е. Так как дуги CD и DB равны, /s 'к
углы CAD и DAB равны. Так как AC ^Х. \
равна АЕ, a AD— общая (сторона // x'X "—\
двух равных треугольников), то DE и \ X. " --ХХ \
равна CD, то есть DB, и угол DEB pa- \
вен углу DBE, то есть BDG. Поэтому £ ь
ЕВ относится к BD, как DB к BG. Рис. 15.
ев = DB
мп ~ BG
Поэтому плоскость из GB па ВЕ равна квадрату DB. А это и ость то,
чего мы хотели [14].
XVI
Сохраним предыдущий чертеж. Мы утверждаем, что плоскость
из полудиаметра на ЛС вместе с квадратом DB равна удвоенному
квадрату полудиаметра.
(Действительно), удвоенный квадрат GB, то есть плоскость ни
АВ па GB, ранен плоскости из GB на АЕ вместе с плоскостью из GB
на ВЕ,
?Gl:a = AB-GR — Gli. АК ч GB- Bft
то есть из GB па АС (или из полудиаметра на АС) вместе с плоскостью
из GB на ЕВ.
414
АРХИМЕД
Но в силу предыдущего (предложения) плоскость из GB па ВЕ
равна квадрату DB. Поэтому удвоенный квадрат GB равен плоскости
из полудиаметра па АС вместе с квадратом DB. Л это и есть то, чего
мы хотели.
XVII
Представим себе квадрат ABCD
АВ в ее направлении до Е и проведем
Рис. 16.
[рис. 16}. Продолжим сторону
диагональ ВС. Поместим один
конец линейки в точке D, а другой
ее конец — на линии ЕА так,
чтобы он рассек ЕА в та,кой точ-
ке G, а АС в такой точке П и ВС
в такой точке F, что треуголь-
ник С А Н равен треугольнику CFD.
Проведем через точку F линию
KFK, параллельную АС. Тогда я
утверждаю, что плоскость из АВ
на КВ равна квадрату б?Л, пло-
скость из GK на АК равна квад-
рату К В и каждая из линий ВК и
GA длиннее линии АК.
Дойствителыи», так как плоскость из CD на FL равпа плоскости
и» GA на АН,
CD-Fb — СЛ-Ли
то линия CD, или АВ, относится к GA, как АН к FL.
ср = лн
ал ~ кь
Так как каждый из треугольников GAH и GKF подобен треугольнику
FLD, то АН относится к FL, -как GA к /А) или КВ.
ан ал _ GA
Fl. LV ~ КН
Поэтому Л В относится к С/1, как GA к КВ.
ли ОА
ал = кн
Точно так же, FL, или .-I К, относится к KF, или КВ. как Л/>, или КВ,
к GK.
11. _рр
К К “ GK
Поэтому плоскость из Я7? на КВ равна квадрату С А, плоскость из
GK на ЛК равна квадрату КВ н каждая из линии G.4 и КВ длиннее
линии ЛК. Л это и есть то, чего мы хотели 115).
XVIII 1 -
Мы хотим построить круг, разделенный на семь равных частей.
Проведем линию ЛВ с известными концами {рис. 17} и при помощи пре-
дыдущего построения отметим иа пей такие две точки С и./.), что пло-
скость из AD па CD равпа квадрату DB, плоскость из СВ иа DB равна
квадрату АС,
ЛО-CD DB2 . ‘
CB-DB--AC^
- ' ." , /?*., w Jf*-e
, ',<Л>i~- 5»r~A« фИ/ДАЛ.-#
? •*>.'* i к* r £a- У» »’U'>e л Д <gj y_ V
.» •>'""Э“‘2* » 'V-* ‘ .,•**
J . V'«->W.C- -I»
«, «'A*'.'11** *- •*,>«**
'•• ’-- _•'', <X»- ъ , •
> a .• *-» ^ »• , „ < i,4 jv j ч>«Ъ
7 >i— ..’й1/***»->»'«"-_-»»>,’i^> 4U< .»»£,•
/. -,-»i
- • • « *<.
л"'*'•***“• •’•ft-i '/ ’'_*
|. •'••Д •; «* -*•«»»- Л / •
kw'**’ - “ * * '>: ' '• f ' “ ' ’ * *’• '
. •' > Z A
>’ *>Хл1£\й.»-л-'»'— ' *-'<j
f- >-*\'1V ' -/;
I ‘ • X « ' r
I •»“^-“«i*** . / /<
*->»»*4э! .•. ’-.
«Л.». .J.>x " >- ..^i
. »♦> »>4 . . ,', . ’ /
r -k'sJ ‘X.’ -мАа*»
Г л'*^",'»»к?>Д»*i
Фотокопия страницы арабской рукописи, содержащей
начало Книги о построении круга., разделенного ни
семь ранных частей
416
АРХИМЕД
и каждая из линий ЛС и DB цлипсе CD. Построим из трех линий АС,
CD и DB треугольник CED так, что сторона СЕ равна линии Л С, а сто-
рона DE равна линии DB, и соединим Л с Е, пЕсВ. Опишем около тре-
угольника ЛЕВ круг AEBHG и про-
должим линии ЕС и ED в их напра-
влениях до окружности; пусть они
пересекут ее в точках G и II. Сое-
диним В с G и проведем из С ли-
нию CF до пересечения (линий BG и
ЕН). Так как стороны ЛС и СЕ тре-
угольника АСЕ равны, то угол ЕАС
равен углу ЛЕС и дуга AG рав-
на дуге ЕВ. Так как плоскость из
AD па CD^ равна квадрату DB, то
есть DE,
AOCD—DIfl^DE1
то треугольник AED подобен тре-
угольнику CED и угол DAE равен
Рис. 17.
углу CED, а дуга GH равпа дуге
ЕВ. 'Гаким образом, три дуги ЕВ,
AG и GH равны друг другу. Поэтому GB параллельна АЕ и угол САЕ,
то есть CED, равен углу DBF. Поэтому угол CED равен углу DBF.
'Гак как угол CDE равен углу FDB и линия ED равна линии DB, то
CD раина DF, -л СЕ равна/7? и четыре точки В, Е, С nF лежат на одном
круге. Так как плоскость из СВ на DB равпа квадрату АС, или ЕС, и
линия СВ равна FE, a DB равна DE, то плоскость из FE на ED равна
квадрату ЕС
УК* КОЛЕСЯ
и треугольник FEC подобен треугольник у CED. Поэтому угол DCE
равен углу EFC. Но угол DCE равен двум углам САЕ, поэтому угол
CFE равен двум углам САЕ. Но угол CFD равен углу DBE. Поэтому
угол DBE равеи двум углам САЕ и дуга АЕ равна двум дугам ЕВ.
Так как угол DEB равен углу DBE, то дуга НВ также равна удвоенной
дуге ЕВ. Поэтому если разделит!» каждую из дуг АЕ и ВН пополам,
то половины будут равны дуге ЕВ. Следовательно, круг AEBIIC раз-
делен на семь равных частей. А это и есть то, чего мы хотели [16].
Хвала единому Аллаху и молитва за пророка, после которого ужо нс было про-
роков. Исправление и редактирование итого замечательного сочипепия закопчено испра-
вляющим пером бедного хаджи Мустафы Си.едики ибтт Салиха, Да благословит его все-
вышний Аллах и да помилуетего и всех муседьман, в воскресенье седьмого (числа месяца>
джумада ал-ула тысяча сто пятьдесят третьего года (хиджры) [17].
ТЕОРЕМЫ АРХИМЕДА, СОХРАНИВШИЕСЯ
В ПЕРЕДАЧЕ АЛ-БИРУНИ
1. ТЕОРЕМА О ЛОМАНОЙ ЛИНИИ, ВПИСАННОЙ В КРУГ
УТВЕРЖДЕНИЕ
Если вписанная в дугу круга прямая линия сломана на две неравные
части и я опущу на нее из середины этой дуги перпендикуляр, то она
разделится им пополам pl J.
Рис. 1.
При м с р. На ломаную линию АВС {рис. 1J на середины D дуги
АВС опущен перпендикуляр DE. Я утверждаю, что ломаная линия АВС
разделена ионолам, то есть АЕ раина
сумме ЕВ и ВС.
ДОКАЗАТЕЛЬСТВО ЭТОГО ИЗ «КНИГИ
КРУГОВ» АРХИМЕДА И КНИГИ «НАЧАЛА
ГЕОМЕТРИИ» СЕРЕНА ФИНСКОГО
Он говорил: отложим дугу ОН,
равную дуге DB {рис. 2{, соединим
DH и DB. построим EG, равную ЕВ.
и соединим DG и В А. Тогда в силу
того, что перпендикуляр ВЕ общий,
линии DG и DB равны. 'Гак как ду-
рапна дуге ОН. a acTuinnancH дуга НА равна дуге ВС, дна
га !.)В
угла НТ)Л и DAB равны углу DBA, то octi, углу DGB. По угол DGT1
27 Хрхпмед
418
АРХИМЕД
равен углам GAD и GDA, поэтому углы GDA и HD А равны. Так кап DG
равна DH, a DA—обща», основания AG и ЛН равны. Но AG равна ЛН.
поэтому AG равна ВС. Так как GE равна ЕВ, то GA вместо с EG
равна ЕВ вместе с СВ. [Л это и есть то, что мы хотели доказать}.
АРХИМЕД В «КНШ'Е КРУГОВ»
С другой стороны, достоверно, что Архимед в «Книге кругов» и
Серен в «Началах геометрии» доказывали это и пе так, как мы рас,ска
зывали.
Он продолжал АВ в ее направлении {рис. 3}, строил EG, раину и»
ЕЛ, и соединял DA, DC, DG и DB. Так как хорды AD и DC равны,
то DG и DC равны и боковые стороны (равнобедренного треугольника)
AD и DG равны. Коатому, так как DG и DC равны, углы DAB, DGB
и DC В равны, поскольку дуга DA
равна дуге DC. Добавим общую
дугу АНС‘, тогда дуга DAHC рав
на дуге DCHA. Но угол DBC опи-
рается иа дугу DAHC, а углы
DAB и ADB на дугу DC А.
Поэтому угол DBC равен углам
DAB и ADB и внешнему углу
DBG треугольника ADB, равному
углам!)АВ и A.DB, не смежным с
ним. Поэтому углы О ВС и DBG
равны. Но было доказано, что
углы DGB и DCB равны. Поэтому
Риг. 3.
СВ и BG равны. Поэтому линии
то есть ЕЛ. {А это я есть то, что
оставшиеся углы CD В и GDB так-
же равны. Но DG равна DC,.
DB....общая, поэтому основания
СВ и ВЕ (вместе) равны линии СЕ,
мы хотели доказать}.
АРХИМЕД И НЕКОТОРЫЕ ГРЕКИ
Архимеду в «Книге кругов» и Серону принадлежит и третье дока
зательство. Оно же находится и среди задач, принадлежащих грекам,
по-видимому, Аполлонию, которые перевел Юханна ибн Юсуф.
Он говорил: [продолжим АВ в ее направлении {рис. 3} и отложим
EG, рапную ЕА, и пропадем соединяющие DC, DB и DG. Так как/
корда круга ВС образует сегмент DBC, меньший полукруга, и не воз
можно, чтобы этот сегмент был больше полукруга, так как дуга AD рав
на дуге ОС, а от круга нельзя отделить две равные дуги, каждая из ко-
торых больше полукруга, если они но имеют общей части, то угол DBC,
вписанный в сегмент,— тупом. Так как AD — хорда в круто [равная
хорде DC), то сегмент DC А больше полукруга. Поэтому вписанный угол
DBA — острый, и оставшийся угол DBC — тупой. Поэтому углы DGB
и DCB равны, линии DC и DG равны и их отношение к общей линии DB
одно и то же. Поэтому треугольники DBG и DBC таковы, что угол С
одного из них равен углу G другого, а их стороны, примыкающие к дру
сим углам, пропорциональны. Так как каждый из углов DBC и DBG
больше прямого, то остальные углы (этих треугольников) равны и эти
треугольники подобны. Они также равны [и!?б? раина ВС. Поэтому ВС,
вместе с ВЕ равны ЕА. Л это и есть то, что мы хотели доказать].
ТЕОРЕМЫ АРХИМЕДА, СОХРАНИВШИЕСЯ В ПЕРЕДАЧЕ АЛ-БИРУНИ
41»
2. ТЕОРЕМЫ АРХИМЕДА О ТРЕУГОЛЬНИКЕ
ДОКАЗАТЕЛЬСТВО ДЕЙСТВИИ АРХИМЕДА ДЛЯ ОПРЕДЕЛЕНИЯ (МЕСТА
ПАДЕНИЯ) ВЫСОТЫ ТРЕУГОЛЬНИКА С ИЗВЕСТНЫМИ СТОРОНАМИ
Архимед сказал: отнимем квадрат одной из двух сторон (треуголь-
ника) от квадрата, другой, разделим остаток на основание и прибавим
частное к основанию и, возьмем половину суммы; получится более длин-
ный из двух отрезков основания, на которые оно делится высотой, то
есть «местом падения камня»; если, же мы вычтем частное из основа-
ния и возьмем половину остатка, получится более короткий из этих
отрезков [2].
(Доказательство.) Пусть (дан) треугольник ADB {рис. 4J и его
высота DE. Опишем около него круг и отложим иа нем (.цугу) DC, рав-
ную DA, проведем соединяющую ВС, построим на АЕ квадрат AG,
а на ВЕ — квадрат ЕЕ, отложим ЕМ, равную ЕВ, проведем МО парал-
лельно EG и FKL параллельно ЛВ и дополним плоскую фигуру АР.
Поэтому, так uaiiDB равна в квадрате DE и ВЕ. а 1>.\ равна в квадрате
1)Е и ЕА н квадрат DE общий в обоих
квадратах, то если мы вычтем квадрат
BD из квадрата DA, получится то же.
что и ири вычитании квадрата ВЕ из
квадрата ЕА. Этот остаток является
гномоном QZN. 'Гак как л ни пн FK, КХ
и ХМ равны и линии ЕР, КС и МА
также равны, то равны и плоские фи-
гуры FG, КО и MZ). Поэтому плоская
фигура ЕН равна гномону QZN, Но ЕР,
го есть .-IМ, равна ВС, так как линии
AM и ME равны линиям ЕВ и ВС*).
Следовательно, плоская фигура FH
есть произведение из АВ на ВС. Поэто-
му если мы разделим ее на основание,
в частном получится ВС. Если мы
прибавим к этому основание, то в сумме будет ломаная линия АВС, а
ее половина .4/1 есть более длинная часть основания: если же мы
вычтем се из основания,
то останется МВ, ее половила ВЕ
более
короткая часть основания до «места падения камня».
ДОКАЗАТЕЛЬСТВО ДЕЙСТВИЙ АРХИМЕДА ДЛЯ (ОПРЕДЕЛЕНИЯ)
ПЛОЩАДИ ТРЕУГОЛЬНИКА ПО ИЗБЫТКАМ
Архимед сказал: если умножить половину суммы трех сторон тре-
угольника на ее избыток над одной из них, (умножитъ) произведение
на ее избыток над второй и. (умножить) произведение на избыток
над третьей и извлечь корень из произведения, получится площадь
треугольника [3J.
А) Тан канг по теоремо .*юмац**й линии (стр. 416), — СВ 4-ВС, то AMАЬ’~Ь’К «==
-ЛК ЕВ = ИС.
V*
420
АРХИМЕД.
Доказательство. (Возьмем) треугольник ЛВС {рис. о},
ОШ1ЛГСЛ1 около него круг, опустим ’ из середины дуги АВС—точки
D — перпендикуляр DE на АВ, опишем из центра А расстоянием
AG дугу GHF, тогда АТ) равна в квадрате DG и GA, а квадрат DF,
. (удвоенное) произведение /)/’ иа FA и квадрат FA,. (вместе Взятые),
равны квадратам DG и GA, равной. FА. Поэтому если мы отнимем
равные квадраты AF и AG, останется: квадрат DF и (удвоенное) лро-
изнодоиие DF на FA равны квадрату J)G. Точно так же АТ) раина
я квадрате DE и ЕА, поэтому квадраты DF и FA и удвоенное про-
изведение 1)F па FA равны квадрату
' 11 j) DE, квадратам ЕН и IIА и удвоенному
' 5 ’ произведению ЕН на НА. По ПА равна
Л С, ||(,ЭТОМУ если мы отбросим оба
/7/ \ равных квацрата, останется.* кнацрат
/Т/ I и УД,,оеинов произведение DF на
pic_________4-----_FA равны квадратам DE и ЕН и
lj удвоенному произведению ЕН па НА;
рис 5 это равпо также квадрату DG. Тре-
угольник DGA подобен треугольнику
DEB, так как угол DCG, равный углу
DAG, равен углу Т)ВЕ, так как «ни опираются на одну дугу.
Поэтому DE относится к ЕВ, как DG к GA; но DC относится
к GA, как квадрат DG к произведению DG иа GA и как произведе-
ние />С па СЛ к квадрату GA, а также как квадрат DE к произ-
ведению DE на ЕВ и как произведение DE па ЕВ к квадрату ЕВ.
Челн отпять от пропорциональных величин пропорциональные вели-
чины, находящиеся в том же отношении, отношение остатков будет
тем же самым. Поэтому отнимем квадрат ВЕ от квадрата DG,
остаток равен квадрату ЕН и удвоенному произведению ЕП на НА,
то есть произведению ЕП на сумму ЕН и (удвоенной НА, то есть
произведению ЕП па сумму ЕА и) ИА, взятую один раз. Отнимем про-
изведение DE на ЕВ от iipOHuBCffpmui DG па GA; остаток есть площадь
треугольника АВС, что вытекает из равенства треугольника ADC
сумме треугольников ABCnBDM [4J. Пусть СК равпа ЕВ; если мы выч-
тем квадрат СК, то есть ЕВ, из квадрата GA, то остаток равен произве-
дению СК ла КЛ, по разность пропорциональных величин*), то есть
произведение ЕП на сумму ЕЛ и ЛС, относится к площади треуголь-
ника АВС, как эта площадь к произведению СК на КА. Но АЕ — по-
ловина (суммы) сторон ЛВ и ВС, a AG—половина стороны ЛС, поэ-
тому* ЕА и ЛС вместе дают половину суммы сторон треугольника {АВС),
и, следовательно, ЕН — избыток (суммы) ЕЛ и АС, или половины
суммы сторон (треугольника ЛВС), над суммой ПА и АС, или ЛС,—
это один избыток. В силу равенства GK и ЕВ сумма АЕ и СК равна
стороне Л В; следовательно, ЛК — избыток суммы ЕЛ я AG нац ЕВ
и ЕЛ, или Л В, это •— второй избыток. Так как ЕВ и ВС равны АЕ,
то ЕВ, ВС и ЛС равны половине суммы сторон (треугольника АВС),
поэтому избыток этого вад ВС — это ЕВ и АС. По КС равпа ЕВ и GC
равна AG, поэтому КС — избыток полусуммы сторон пад ВС, это —
третий избыток. Если умножим плоскую фигуру из ЕН па ЕА и АС,
то есть оцна из двух крайних членов (пропорции), на плоскую фигуру
из СК на КЛ, то есть па другой крайний член, получится квадрат сред-
♦) (OG2 ... DE2) : ЬЕ ЕН) — tl>(; ЧА ПНИЩ : (G/I2 ЬВ2) или (ЛАВС)г=
=(ЕА I АО).ИП АК.Кг:. .
ТЕОРЕМЫ АРХИМЕДА. СОХРАНИВШИЕСЯ В ПЕРЕДАЧЕ АЛ-БИРУНИ 421
него члена, или площади треугольника (АВС). Таким образом, если
мы умножим ЕН,'то есть первый избыток, па ЕЛ (вместе с) AG, то
есть па половину суммы сторон (треугольника ЛВС), умножим А К,
или второй избыток, на СК, то есть третий избыток, а затем умножим
одно из этих произведений на другое, или если мы умножим ЕА (име-
ете с) AG, или половину суммы сторон на КЛ, произведение — па ЕН,
а (полученное) произведение — на СК, получится квадрат площади
треугольника. Следовательно,если мы извлечем корень из этого, полу-
чится искомое
qMg) aiaw
КНИГА О КАСАЮЩИХСЯ КРУГАХ
АРХИМЕДА,
УБИТОГО В ДВЕСТИ ДВЕНАДЦАТОМ ГОДУ ДО РОЖДЕСТВА
Во имя Аллаха милостивого, милосердного!
Архимед сказал: если даны несколько кругов, последовательно
касающихся друг друга, причем, их центры находятся на одной (прямой)
линии и из точки, отмеченной на продолжении отпой линии, в ее напра-
влении проведена карательная к ;тим кругам, то круги •) **) находятся
в непрерывной пропорции, а если эти круги находятся в непрерывной
пропорции, то при продолжении касательной к двум последовательным
кругам из них она будет касаться остальных кругов.
Пример итого. Предположим, что круги, последовательно ка-
сающиеся друг друга, круги с центрами А, В и С. и пусть центры .4,
Рис. 1.
В и С находятся на прямой линии АС {рис. 1}. Предположим, что кру-
ги касаются друг Друга в точках D и Е. Отметим на линии АС точку G
и проведем из нее линию, касающуюся кругов в точках Н, F и К.
Тогда я утверждаю, что круг (.4) относится к кругу В, как круг В
к кругу С.
•) Номера предложений п хайдарабадском издании отсутствуют.
*•> То есть площади кругов.
КНИГА О КАСАЮЩИХСЯ КРУГАХ 423
Декада т е л ь с т к о этого. Из точек касания черен центры
проведем диаметры (это будут линии К ЛЬ, FBM и HCN) и соединим
(точки) L н D, D и F, М и К и Е и Н. Так как линии KL, FM и НН
проведспы из точек касания, через центры, то все они перпендикулярны
касательной. Следовательно, они параллельны. Поэтому угол LAD
равен углу DBF и равнобедренные треугольники LAD и DBF (подоб-
ны). Следовательно, угол ADL равен углуйДА. Поэтому, так как линия
АВ прямая, линия LF также прямая. Точно так же доказывается, что
линия MII прямая. В силу того, что о прямоугольных треугольниках
LKF и MFH углы ALF п ВМП раины, их остальные углы, то ость KFL
и FIIM также равны. Следовательно, линия LF параллельна линии
МН. В силу того, что треугольники KLF и MFH подобны, отношение
LK к KF равно отношению MF kFH, или, переставляя, отношение LK
и MF равно отношению KF к FH. Но отношение KL к ЕМ равно отно-
шению К/4 к ЕВ. то есть равно отношению KG к GF.
кь ко
FM = GF
Следовательно, отношение {KG} к GF равно отношению KF к КН.
KG _ КР
gf = кн
В силу того, что отношение всей KG ко всей GF равно отношению вычи-
таемой KF к вычитаемой ЕН. отношении остатка FG к остатку GH равно
отношению KG к GF.
FG КС
GH Gi-
llo отношение KGkFG равно отношению КА kFB, то есть равно отно-
шению KL к FM,
KG _ KI,
FG “ М
а отношение FG к GII равно отношению FB к НС, то есть равно отно-
шению FM к П N.
FG FAf
GH HN~
Следовательно, отношение АЛ к FM равно отношению FM к /УЛ.
К/. FM
FM “ НА
Поэтому отношение квадрата КL к квадрату ЕМ равно отношению квад-
рата FM к квадрату НН.
KL1 FM3
Fif* ЯЛ‘2
Но круги относятся друг к другу, как квадраты их диаметров, поэтому
круг Л относится к кругу В, как круг В к кругу С. А это и есть то,
что мы хотели доказать.
Пусть эти круги находятся и непрерывной пропорции и мы пред-
положим, что линия GH касается двух кругов С и В в точках II и F.
Тогда я утверждаю, что если мы продолжим линию GH в се напра-
влении, она будет касаться оставшегося круга.
Доказательство этого. Проведем через точку А линию
параллельно линии FM, это будет диаметр КЛЬ. Соединим (точки)
F и К и дополним оставшуюся часть чертежа так же, как в предыдущем
424
АРХИМЕД
предложении. Тогда нам ясно, что линия LD — в одном направлении
с линией DF, а линия ЕЕ параллельна линии МН. Поэтому треугольник
KEF подобен треугольнику FMH. Так как круги находятся в непрерыв
ной пропорции, отношение KL к FM равпо отношению FM к Н N.
KL FM
FM ' HN
Но отношение KL к/’М, то есть отношение ЛЬ к FE, равно отношению
LD к DF, то есть равно (отношению) LD к ME,
KL LD __ LD . .
F.M ' !>l< Mil!
а отношение FM к H N, то есть отношение BM к СП, равно отношению
ME к ЕН, то есть равпо отношению DF к ЕН.
FM _ В .И _ МК _ DF
/1Л' ~ СП ЕП ~~ ЁН
Ио отношение ED к ЕМ было равпо отношению КЕ к FM и, следо-
вательно, отношение КЬ к FM равпо отношению LD к ME и равно отно-
шению DF к ЕП, то есть равно отношению всей Lfi ко всей МН.
ILL 1.D _ DF = LF
FM ’ ME ~ КН МН
Так как отношение ЬК к FM равно отношению LF к МН, то заключен-
ные между ними углы равны и треугольники KLF и FMH подобны.
Поэтому угол LKF равен углу MFH и, так как угол MFH прямой, угол
LKF также прямой и линия КЬ параллельна линииFM. Следовательно,
угол KFM тоже прямой. Ио, так как угол BFH также был прямым, ли-
ния HF — в одном направлении с линией ЕК и, следовательно, касается
круга А.
Точно так ясе доказывается, что если кругов больше, эта линия
касается всех их.
II.
(Д о к а и а т с л ь с т в о этого предложения друг и м с и о-
с о б о м). Предположим, что круги такие же, как раньше. Соединим L
к К, К iaD,{D и F), F и Е, Е и Н, Н и Лг и проведем из точки О линию.
касающуюся обоих кругов А и В; это будет линия DM {рис. 2). Поэто-
му линия DM перпендикулярна к линии EG. В силу того, что обе линии
КМ н MD касаются круга А, л ипия/fJl равна липин MD. Точно так же
линия FM равна линии MD. Поэтому все три линии КМ, MD и FM
раины и круг, описанный из центра М расстоянием МК, является
кругом KDF, проходящим через точки К, D, F. Поэтому угол KDF
прямой. Но угол LKD также прямой и линии ЬК и FD параллельны.
КНИГА О КАСАЮЩИХСЯ КРУГАХ
425 .
Точно так же доказывается, что линии DF и ЕН тоже параллельны.
В силу того, что линия GHK касается круга J в точке К, а линия KD
образует с ней угол FK (D), равный углу KLD, треугольники EKD
и KDF — прямоугольные и оставшийся угол KDL равен оставшемуся
углу KFD. Понтону треугольники LKD и KDF подобны. Но треуголь-
ник LKD подобен треугольнику DFE, а треугольник KDF подобен
треугольнику FF.H Следовательно, треугольники LKD, KDF,{DFE),
FEH и EI1N подобны. Поэтому отношение LK kKD равно отношению
KD к FD, равно отношению DF к FЕ и равно отношению FE к ЕН.
LK _ ко _ PF _ ЕЕ
КО “ ЕР FE ЕН
Поэтому, если мы отбросим средние члены, получится: отношение LK
к DF равно отношению DF к ЕН. Но отношение LK к DF равно отно-
шению LD к DE,
L.K = Г.Р
DF РЕ
а отношение DF к ЕН ранне отношению DE к ЕЛ7.
DF РК
КН ” KN
Следовательно, отношение Ы) к DE равно отношению DE к Е /V.
LD РЕ
РЕ = ЬЛ
Следовательно, отношение квадрата LD к квадрату DE равно отноше-
нию квадрата DE к квадрату Е N.
сод РК*
DE4 EN'i
Поэтому круг А относится к кругу В, как круг В к кругу' С. А это и
есть то, что мы хотели доказать.
Пусть теперь эти круги находятся в непрерывной пропорции и пусть
линия GH касается кругов В и С в точках II и F. Тогда я утверждаю,
что если мы продолжим линию GHF в ее направлении, то опа будет
касаться круга А.
Док а зато л ь с т в о этого. Соединим (точки) Л7 и II, Н и
Е, Е и F, F и D и проводом через точку D линию параллельно линии
FE, это будет линия DК. Соединим (точки)/* и Л', Е и L. В силу того,
что линии КО параллельна линии FE, угол KDi> равен углу FED.
Угол EFD прямой, он ранен углу FDK, так как линии DK и FE парал-.
дельны. Угол DKL прямой, так как оп вписан в полукруг LKD. Сле-
довательно, угол FDK равен углу DKL. Следовательно, линия LK
параллельна линии DF. В силу того, что эти треугольники {FEII и
EHN) подобны, как было доказано раньше, отношение Л7Н к НЕ
равно отношению НЕ к EF и равно отношению EF к FD. Следовательно,
отношение Л7/ к EF равно двойному отношению NH к НЕ.
КН _ / АН у»
KF \ НЕ )
Но отпошелие NII к ЕЕ равно отношению EF к DK, a NH относится
к НЕ, как EF к FD. Следовательно, otuojuuuhc EF к DK равно двой-
ному отношению EF к FD.
ЕЕ t EF .
DK ~\ ЕР ) . . •
426
АРХИМЕД
Поэтому отношение EF к FD равно отношению FD к DK,
tsjf FD
FD ~ DK
Но между этими линиями заключены равные углы, поэтому треуголь-
ник KDF подобен треугольнику DFE и угол DKF равен углу FDE.
Но раньше (установлено, что) угол HFE равен углу FDE, поэтому угол
HFE равен углу FKD.R силу того, что угзпл KFD, FDK (и FKD} равны
двум прямым, а угол KDF равен углу DFE, углы KFD, DFE (и HFE}
также равпы двум прямым. П оэтому липни KF находится па продолжении
линии СН. Точно так же, если угол FKD равен углу DLK, то линия
GK касается круга А н силу того, что сказало в третьей книге сочинения
Евклида, озаглавленного «Начала» [1].
У пас получилось также доказательство того, что если дна круга
касаются друг друга внешним образом и между ними имеется общая
«касательная» линия, именно линия FK, то касательная является сред-
ней в непрерывной пропорции между диаметрами кругов, так как в силу
подобия треугольников LD относится к KF, как KF к Г)Е.
Ill
Если даны два касающихся круга, центры которых находятся на
некоторой прямой линии, и иг точки, взятой на продолжении этой линии,
проведена прямая, касающаяся обоих кругов, то круги относятся друг
к другу, как
11 р н м е
рами А и В,
квадраты касательных.
р этого. Предположим, что два круга — круги с цент-
и пусть центры А и В находятся на некоторой прямой
линии {рис. 3}. Продолжим ли-
нию АВ, отметим па круге. В точ-
ку Е и проводом линию, встречаю-
щую линию АВ н {D} и касаю-
щуюся круга В н Е и круга А в G.
Тогда я утверждаю, что отношение
круга А к кругу В равпо отноше-
нию квадрата касательной GD к
квадрату касательной ED.
Доказательство это-
го. Соединим (точки) Е и В. В силу
того, что оба угла AGD и BED прямые, линия GA параллельна линии
ЕВ. Поэтому отношение GA к ЕВ, то есть отношение диаметра круга А
к диаметру круга В, равно отношению касательной GD к касательной
ED. Поэтому отношение квадрата диаметра круга Л к квадрату диа-
метра круга В, то есть отношение круга А к кругу В, равно отношению
квадрата касательной GD к квадрату касательной DE. Л это и есть то.
что мы хотели доказать.
IV
Если даны круги, последовательно касающиеся друг друга, причем
их центры находятся на одной {прямой} линии, а сами они нахо-
дятся в непрерывной пропорции, и из их центров проведены касательные
к ним по порядку, то круги относятся друг к другу, как квадраты
касательных.
(11 р и мер этого.) Предположим, что касающиеся круги—круги
с центрами Л, В, С и D, и пусть центры Л, В, С и D находятся на од-
КНИГА О КАСАЮЩИХСЯ КРУГАХ
427
ной линии [рис. 4}; пусть круги находятся я непрерывной пропорции.
Проведем из (точек В, С и D) на линии Л (D) касательные к кругам
А, В и С по порядку; ото будут линии BF, СК и DL. Тогда я утверждаю,
что круг А относится к кругу В, как квадрат линии ВЕ к квадрату ли-
нии СК, а круг В относится к кругу С, как квадрат линии СК к квад-
рату линии J)f..
Д о к а з а т е л ь с т в о итого. В силу того, что круги находятся
в непрерывной пропорции, отношение диаметра МК к (диаметру) EG
равно отношению EG к GH. Если мы заменим (диаметры ЕС и GH их
половинами), то получится, что ME относится к ЕВ, как EG к GC.
Мк ку
ЕВ GG
или, присоединяя, МВ относится к ВЕ. как ЕС к CG.
МЬ КС
не “ СС
Но линия ВЕ — средняя в непрерывной пропорции между МВ и ВЕ,
BF*=“MB НЕ
а линия КС — средпня в непрерывной пропорции между ЕС и CG.
КС’--ЕС-СС
Следовательно, ВЕ относится к ВЕ, как КС к CG или, переставляя, ВЕ
относится к КС, как ЕВ к СС*).
UF КВ
КС ~ СУ
Но ЕВ относится к СС, как ME к EG. Следовательно, BF относится
к КС, как диаметр ME к (диаметру) EG.
HF ME
КС ~ EG
Поэтому отношение квадрата ME к квадрату EG, то есть отношение
круга Л к кругу В, равно отношению квадрата ВЕ к квадрату КС.
А это и есть то, что мы хотели доказать.
.мв _ МН HF (nF У
НЕ ВЕ НЕ ' ВК '
EG ЕС КС j ' КС XI
со КС LG ' ' CG >
BF КС RF ВЕ
НЕ CG КС CG
428
АРХИМЕД
У нас получилось отсюда доказательство того, что линииFB, К(’
и LD, находящиеся в непрерывной пропорции, параллельны. Доказать
это легко, мы приблизимся к этому, если соединим точки касания с цент-
рами, тогда у нас получатся прямоугольные треугольники, подобные
и по форме и по положению.
Я утверждаю, что то же самое будет, если провести касательные
не из центров, а из концов диаметров, как изображено на этом чертеже
{рис. «5}.
Д о к а з а т е л ь с т в о этого. В силу того, что диаметр ME отно-
сится к (диаметру) EG, кап ЕС к GH, «присоединяя», получим, что
отношение MG к СЕ рав-
но отношению ЕН к IIG.
Рис. 5.
MG = ЕН
GE ~ HG
Но линия GF — средняя в
непрерывной пропорции #
между линиями MG и СЕ,
GF^MG-GE
а линия КН— средняя
в непрерывной пропорции
между линиями ЕН и HG.
КНй=ЕП ПС
Поэтому отношение FG к КН равно отношению EG к СН.
FG EG
КН GH
то есть отношению ME к EG*). Поэтому отношение квадрата ME
к квадрату EG, то есть отношение круга А к кругу В, равно отношению
квадрата касательной FG к квадрату касательной КН.
MES._ FG?
EG* ~ К НО
Так же, как раньше, доказывается, что эти касательные, находя-
щиеся в непрерывной пропорции, параллельны, сколько бы их ни было.
VI
Если даны круги, касающиеся внутренним образом в одной точке
и находящиеся в непрерывной пропорции и из концов их диаметров про-
ведены, касательные к ним по порядку, то круги относятся друг к другу,
как квадраты касательных.
II р и м е р этого. Предположим, что эти круги — круги с диамет-
рами АВ, ЛС и AD, и пусть они находятся и непрерывной пропорции
и касаются друг друга в точке А {рис. 6}. Проведем из точек С и D
касательные к кругам (с диаметрами АВ и АС), это будут линии СЕ
•) / FG ,2 FG2 MGCE t GE \2 , ME ,2
( KIf ) № ~ EH-HG ~ I HG ' EG ) '
КНИГА О КАСАЮЩИХСЯ КРУГАХ
42Й
и DG. Тогда я утверждаю, что круг АКВ относится к кругу AGC, как
квадрат касательной ЕС к квадрату касательной GD.
Д о к а з а т е л ь ст в о итого. В силу того, что DA относится
к АС, как С А к ЛВ, «выделяя», переставляя (и рассуждая), как раньше,
получим, что GD относится к ЕС, как СЛ
к АВ. Следовательно, отношение квадрата GD
.к квадрату ЕС равпо отношению квадрата СЛ
к квадрату АВ, то есть отношению круга CGA
к кругу ВЕЛ. А нто и есть то, что мы хотели
доказать.
VII
Вообще, если, даны круги, касающиеся ли-
ний, образующих вместе с линиями, проведен-
ными через и:с центры, равные углы, то круги
относятся друг к другу, как {квадраты) каса-
тельных.
II р и м с р этого. Предположим, что два круга — круги с центра-
ми А и В, проведем через эти центры линии ЛС и BD, проведем каса-
тельную СЕ к кругу А и касательную DG к кругу В, и пусть угол АСЕ
равен углу BDG {рис. 7}. Тогда я утверждая), что круг .4 относится
к кругу В, как квадрат касательной СЕ к квадрату касательной DG.
Д о к а з а т е л ь с т в о этого. В силу того, что прямоугольные
треугольники ЛЕС и BGD подобны, отношение ЕС к GD равно отно-
шению ЕЛ н GB. Поэтому квадрат ЕС относится к квадрату GD, как
квадрат линии АЕ к квадрату линии GB, то есть как (квадрат) диа-
метра круга А к (квадрату) диаметра круга В, то есть как круг А
к кругу В. А это и есть то, что мы хотели доказать. . ...
V1H ; '.Л • ...
Если даны два касающихся круга й из концов линии, проходящей
через их центры и точку касания, проведены две линии, пересекающиеся
между собой и касающиеся кругов, то отношение кругов друг к другу равно
двойному отношению {квадратов) линий, пересекающихся между собой
и касающихся кругов [2]. . , .. ....
П ример этого. Предположим, что два круга — круги с цент-
рами А и В, касающиеся в точке С {рис. 8}. Проведем и линию,, про-
ходящую через их центры, это будет линия ВСЕ. Проведем из точек D
и Е две пересекающиеся линии, касающиеся кругов в точках G. и П.
430
ЛРХИМЕД
Тогда я утверждаю, что отношение круга .1 к кругу В равно двойном>
отношению (квадрата) касательной Г)Н к (квадрату) касательной EG.
Доказател ь с т к о этого. В силу того, что отношение круга
.4 к кругу В равно двойному отношению диаметра DC к диаметру СЕ.
а отношение диаметра DC к диаметру СЕ равно отношению плоскости
из ED на DC к плоскости из DE на ЕС [3J, отношение круга А к кругу В
равпо двойному отношению плоскости ня ED на DC к плоскости ня DE
на ЕС, то есть равно (двойному) от-
ношению квадрата касательной DH
к квадрату касательной EG. А это
и есть то, что мы хотели доказать.
[X
Если дан круг и из одного из кон-
цов его диаметра проведена касатель
ная к нему, а из другого конца
этого диаметра проведена секущая,
встречающаяся с касательной. то
плоскость из секущей но ее часть, находящуюся внутри круга, равна
квадрату диаметра.
(Л р и мер этого). Предположим, что этот круг — круг с диа-
метром АВ {рис. 9}. Проведем из точки А касательную к нему (это будет
лилия АС) и соединим BDC. Тогда
я утверждаю, что плоскость из СВ
на BD равна квадрату ЛВ.
Д о к а я а т с. л ь с. т в о этого.
Соединим (точки) А и D. В силу
того, что прямоугольный треуголь-
ник СВА подобен прямоугольному
треугольнику ADB, отношение СВ
к ВЛ равпо отношению ВЛ к В/).
Поэтому плоскость из СВ на BD
равна квадрату АВ. А это и есть
то, что мы хотели доказать.
Дока з а т е л ь с т в о этого
предложения д р у г и м снос о-
б ом. В силу того, что квадрат СВ, то есть плоскость из СВ на CD
вместе с плоскостью из СВ иа RD, pawn квадрату С А вместе с ква-
дратом АВ,
i Нг—С13 СD-i-Cи-В£>=СА~±Л332
а плоскость из ВС на CD равна квадрату СА, оставшаяся площадь из
СВ на BD равна оставшемуся квадрату АВ. А это и есть то, что мы хо
тел и доказать.
X
Доказател ь с т в о этого предложения еще одним способом -
В силу того, что плоскость из CD на BD равна квадрату AD, то если
мы прибавим общий квадрат DB, получится: квадраты AD и DB, то
есть квадрат АВ, равны плоскости из CD на DB вместо, с квадратом DB,
то есть плоскости из СВ на DB. А это и есть то, что мы хотели доказать.
КНИГА О КАСАЮЩИХСЯ КРУГАХ
431
Точно так же, если провести какую угодно линию, как EGB {рис. 10},
плоскость из всей линии па ео часть, находящуюся внутри круга, равна
квадрату ого диаметра,и плоскости,
заключенные между каждой линией
и ее частью, находящейся внутри
круга, равны.
XI
Если линия касается круга в кон-
це. его диаметра и из точки, взятой
на ней, проведена другая линия, каса-
ющаяся этого круга, то плоскость
аз одной ив частей касательной на
другую равна плоскости, из всей линии,
проходящей через центр, на ее часть от центра круга до его окружности,
а плоскость из всей касательной на ее часть между точкой встречи и точ-
кой касания равна плоскости из линии, проходящей через центр, на. ее
часть между точкой встречи- и центром круга.
Прим в р итого. Предположим, что зтот круг — круг с центром Л
и диаметром ВС {рис. 11}. Проведем из точки В касательную к ному.
это будет линия BD. Возьмем на линии BD произвольную точку (пусть
это будет точка D) и проведем из пес другую линию, касающуюся круга
в точке Е, зто будет линия BEG. Опа пересечет линию, проходящую
через центр, в точке G. Тогда я утверждаю, что плоскость DE на EG
равна плоскости из GB па ВА и что плоскость из BG на GE равна
плоскости из BG на GA.
Д о к а з а т е л ъ с т в <> этого. Соединим (точки) А и. Е. Тогда
в силу того, что в треугольниках DBG и GEA прямой угол DBG одного
из них равен прямому углу другого треугольника, а угол DGB общий,
эти треугольники подобны. Поэтому отношение GB к BD, то есть к DE.
равно отношению GE к ЕЛ, то есть к ВЛ. Поэтому плоскость из GB
па ВЛ равна плоскости из DE на EG.
Я утверждаю, что плоскость ил DG я» GE равна плоскости
из BG на GA.
Доказательство этого. В силу того, что треугольники
DBG и GAE подобны, отношение DG к GB равно отношению AG к GE
Поэтому плоскость из DG на GE равна плоскости из BG на GA. Л ато
и есть то, что мы хотели доказать.
432
АРХИМЕД
XII
Если касательная, проведенная из конца диаметра, касается не
в точке В, а в точке С, как линия CD {рис. 12}, то плоскость из DE на
EG равна плоскости из АС на CG, а плоскость из EG на CD равна пло-
скости из АС на CG.
Доказательство этого. В силу того, что треугольники
GEA й GCD подобны, отношение GE к ЕА, (то есть к АС}, равно
{отношению) GC к CD, то есть к ED. Поэтому плоскость из GE на ED
равна плоскости из АС иа CG.
Я утверждаю, что плоскость нз EG на CD равна плоскости
из AG па GC.
Д о к а з а т е л ь с т в о этого. В силу того, что треугольники
{GEA и GCD} подобны, отношение EG к GA равпо отношению CG
к GD . Поэтому плоскость из EG ва GD равна плоскости из GA па GC.
Это и ость то, что мы хотели доказать.
XIII
Д о к а з а т е л ь с т в о этого предложения д р у г и м с н о с о-
б о м. Опишем около прямоугольного треугольника АСЕ круг GF{A}
{рис. 13}. Тогда липни AG— его диаметр. Проведем линию FCH.
В силу того, что липин/'//разделена
ионолам в точке С и на две [различ-
ные части в точке D, плоскость из FD
па DH вместе с квадратом CD равны
квадрату СП.
> 1> DH '-CD2=CH-
Но плоскость vaFD на DH раина
... плоскости из GD на DE, а квадрат CD
равен квадрату ED. Поэтому пло-
скость из GD на DE вместе с квадра-
том ED, то есть плоскость из GE на
ED, равна квадрату СН.
UD DE---Dli2---GE • ОЕ=С.Н2
Но квадрат СН равен плоскости из ЯС па CG. Поэтому плоскость из
А С на CG равна плоскости из GE на ED. А это и есть то, что мы хотели
доказать.
Точно Tait же, в силу того, что плоскость из HD на DF, то есть пло-
скость нз ED на GD, меньше квадрата ПС, то есть плоскости из АС на
КНИГА О КАСАЮЩИХСЯ КРУГАХ
433
СС, на квадрат CD, а квадрат DG больше квадрата СС на квадрат CD,
плоскость из ED на DG вместе с квадратом CD, то есть плоскость из
EG на DG, равна плоскости из АС иа CG вместе с квадратом GC,
та есть плоскости из АС на GC, А это и есть то, что мы хотели доказать.
XIV
Если даны два круга, касающихся друг друга внутренним образом,
и проведена линия, касающаяся их обоих, образующая прямой угол
с линией, проходящей через точку касания и центры, а из точки,
взятой на линии, проходящей че-
рез центры, проведены две другие
касательные к этим кругам, пере-
секающие первую касательную, то
отношение большего круга к мень-
шему равно двойному отношению
плоскости, заключенной между
частями касательной к большему
кругу, к плоскости, заключенной
между частями касательной к мень-
шему кругу.
11 р и м с р этого. Предполо-
жим, что круг с центром А каса-
Рис. 14.
ется круга с центром!? внутренним
образом л точке С {рис. 14}. При-
ведем через точку касания и центры линию CDEG, так что диаметр кру-
га Л —линия CD, а диаметр круга В— линия СЕ. Проведем из точки G
линии GHF к GKL, касающиеся этих кругов в точках Я и К. Тогда
я утверждаю, что отношение круга Л к кругу В равно двойному
отношению плоскости лз G11 па 11F к плоскости из СК иа KL.
Доказательство этого. В силу того, что линии С А от-
носится к СВ, как плоскость из СС па С Л к плоскости из GC па СВ,
то, как доказано в предыдущем предложении (XI), плоскость из GC
на СЛ. равпа плоскости из GH на НЕ,
GC-t:A=GHHf
а плоскость из СС на СВ равна плоскости из СК па KL,
GC-Clf=GK-KI.
отношение СЛ к СВ равпо отношению плоскости из GH на HF к пло-
скости из СК на KL.
СА OHBF
СИ ~ C.K-KL
Но СЛ относится к СВ, как удвоенная СЛ к удвоенной СВ, то ость как
диаметр СГ) к диаметру СЕ.
са сп
си ~ СЕ
Поэтому диаметр CD относится к диаметру СЕ, как плоскость из GH
на IIF н плоскости СК па КГ.
ае> сп-нр
СЕ CIC-KL
Но отношение квадрата диаметра CD к квадрату диаметра СЕ равно
двойному отношению CD к СЕ, а квадраты диаметров кругов относятся
28 Архимед
434
АРХИМЕД
друг к другу, как сами кругл. Поэтому отношение круга Л к кругу В
равно двойному отношению диаметра CD к диаметру СЕ, то ость равно
двойному отношению плоскости из GII на ПЕ к плоскости GK на KL.
Л это и есть то, что мы хотели доказать.
XV
Если даны два непересекающихся круга с центрами на некоторой
{прямой} линии и ив их центров проведены пересекающиеся линии,
касающиеся этих кругов, то плоскость, заключенная между частями одной
из касательных, равна плоскости,,
заключенной между частями другой .
касательной.
II р м м с р этого. Предположим,
что дна непересекающихся круга-
круги с центрами в точках А и В
линии АВ {рис. 15}. Пронедем из
центров А и В линии АС и BD, каса-
ющиеся кругов в точках D и С и
пересекающиеся в точке Е. Тогда я
утверждаю, что плоскость из АЕ на
ЕС равна плоскости BE на ED.
Д о к а и а т е л ь с т в о этого. Соединим (точки) Г) и А, С и В.
В силу того, что прямоугольные треугольники ADE и ВСЕ подобны,
отношение АЕ к ED равно отношению ВЕ к ЕС. Поэтому плоскость из
ЛЕ на ЕС равна плоскости из BE на
ED. Л это и есть то, что мы хотели
доказать.
XVI
Доказательство этого
предложения другим с и о с о-
б о м. В силу того, что оба угла
ЛЕВ и АСЕ — прямые, а треуголь-
ники ADB и АСВ находятся на одной
линии АВ, треугольники ЛТ)В и АСВ
вписаньг в полукруг. Проведем через
них полукруг ADCB {рис. 1(5}. В силу того, что липни ЛЕС и BED
пересекаются в круге в точке £, плоскость из АЕ на ЕС равна плоско-
сти из BE на ED. А это и есть то, что мы хотели доказать.
XVII
Если даны две касательные к одному кругу и из точки, взятой на
продолжении линии, проходящей через точки касания, в ее направлении,
проведена касательная к кругу, пересекающая одну из касательных
и оканчивающаяся на другой, то отношение всей проведенной линии к ее
части, находящейся вне касательных, равно отношению большей из ча-
стей между касательными, на которые она делится точкой касания,
к меньшей.
(Пример этого.) Предположим, что две линии АВ*) и АС
касаются круга 2?C’[G] в точках В и С {рис. 17, 18, 19}. Соединим
*) На рис. 17 лилии ЦП.
КНИГА О КАСАЮЩИХСЯ КРУГАХ
435
(точки) /? и С и продолжим линию ВС в ее направлении. Возьмем да
ее продолжении точку I) и проведем из точки D еще одну касательную
к кругу; нто будет липин DEGH, пусть опа
ке G. Тогда я утверждаю, что IID относится
Доказательство этого. Ли-
нии НВ 11 АС должны быть обязательно
либо параллельны, либо не параллельны.
Предположим, что они параллельны
{рис. 17}. Тогда угол ВИГ) (треуголь-
ника BIID) равен углу СЕТ) треуголь-
ника СЕВ. Поэтому отношение III) к
Г)Е равно отношению НВ к ЕС. Но
линия HG равна липни НВ, так как
эти линии — касательные к кругу,
проведенные из одной точки II, и точно
так же линия ИС равна липни ЕС.
Поэтому HI) относится к Т)Е, как IIG
к GE.
Если же они по параллельны, то
они встречаются в точке {рис. 18 и 19}.
Проведем из точки Елинию, параллель-
ную линии ЛВ, это будет линия EF. В
силу того, что линии А В и Л С — каса-
тельные к кругу, они равпы. Поэтому
угол АС В равен углу АВС. Но угол
касается [круга] в точ-
к как НС к GE.
EEC равен углу ЛВС в силу параллельности линий. Поэтому угол EFC
равен углу ECF. Поэтому линия EF равна линии ЕС. Точно так же,
в силу того, что IID относится к 1)Е, как НВ к EF, то есть к ЕС, ли-
ния НВ равна линии НС и линия ЕС равна липин ЕС, то I1D отно-
сится к Г)Е, как НС к GE. А это тг есть то, что мы хотели доказать.
XV111
Если, дана касательная к кругу, проведенная, в конце диаметра,
и иа точки, взятой на продолжении диаметра в его направлении, про-
ведена другая касательная к кругу, встречающая перпендикуляр к диамет-
ру и перпендикуляр, опущенный на нее из точки касания,, являющейся-
концом диаметра, то отношение есей проведенной линии к ее части между:
28’
436
АРХИМЕД
взятой точкой (на продолжении диаметра} и точкой касания равно от-
ношению ее части между точкой касания и перпендикуляром к части
этой линии между точкой касания и точкой падения перпендикуляра,
опущенного на нее.
II р и м о р этого. Предположим, что этот круг - - круг с центром
Л н пусть его диаметр -- линия CF {рис. 20}. Восставим перпендикуляр
к диаметру, касающимся круга,
f-J/ это будет линия СЕ. Продолжим
линию СЕ л возьмем на се про-
у / долженни точку, это будет точка
г / \ __,__ D. Пронедем из точки 1) ли-
С-----------D мию, касающуюся круга в точке
\ / G, это будет линия DE. Опустим
\. ./ из точки С перпендикуляр па
линию DE, это будет линия СП.
Рис. 20. Тогда я утверждаю, что ED от-
носится к DC, как EG к СН.
Доказательство этого. Соединим (точки) И (и) G.
"Тогда в силу того, что угол AGD прямом и угол CI1D также пря-
мой, СН параллельна линии АС и прямоугольный треугольник DEC
подобен прямоугольному треугольнику DAG. Поэтому отношение DE
к ЕС, то есть отношение DE к ЕС, равно отношению DA к AG, то
есть к ЛС.
Die _ da
EG ~ АС
Но DA относится к ЛС, как DG к GH.
РА = DG
AC ~ GH
Поэтому DE относится к EG, как GD к GH,
РЕ DQ
KG GH
или, переставляя, ЕГ) относится к DG, как EG к GH.
ЕР EG
DG СП
Это и есть то, что мы хотели доказать.
Выделяя, мн докажем, что EG относится к GD, как ЕН к НС.
GD HG
XIX
При том же положении
я, утверждаю, что ЕС отно-
сится к GD как ЛЕ, проведен-
ная из центра*), kFD.
Д о к а з а т е л ь с т в о
этого. Соединим (точки) Е и
A, G и Л’{рис. 21}. Тогда в сил
.линия С Л равна линии Л С, и у tj
у того, что линия СЕ равна линии ЕС,
юуголышков {АСЕ и АСЕ) одно и то же
•) Греческое ’ex iov xevroov-таи греки обоакячяли радиус. Этот термин, а также е.расстоя-
иио» (греч. Лихотздкк) ля стр. 42Л и ссылка на то, что Архимед Аил убит в 212 г. «ди Рождества»
да ггр. 422 показывают, что оригинал книги Был написан по-гречески.
КНИГА О КАСАЮЩИХСЯ КРУГАХ
437
основание, угол С ЛЕ равен углу GAE. Поэтому угол СЛ G - - удвоенный
угол САЕ. Но угол CAG — удвоенный угол CFG, так кап один из них
центральный угол, а другой вписанный угол, и они опираются на одну
и ту же дугу. Поэтому угол САЕ равен углу CFG и линии ЕА
параллельна линии GF. Поэтому
EG относится к GT), как AF к
FD. А это и есть то, что мы хо-
тели доказать.
XX
Если дана касательная {к
кругу}, проведенная в конце диа-
метра, но не в точке С, а е дру-
гом конце диаметра, как на этом чертеже линия FK {рис. 22}, то я
утверждаю, что HG относится к НВ, как GK к КВ.
Д о к а з а т с л ъ с т в о этого. В силу того, что прямоугольный
треугольник CHD подобен прямоугольному треугольнику FKD, отно-
шение СН к HD равно отношению KF к КВ, то есть равно отношению
СК к КВ. А это и есть то, что мы хотели доказать.
XXI
Если диаметр круга продолжен в ено направлении и из точки, взятой
на его продолжении, проведена касательная к кругу, а из точки касания
опущен перпендикуляр на диаметр, то вся линия, проведенная через
центр, относится к ее части, находящейся вне круга, как большая из
частей, на которые диаметр де-
лится перпендикуляром, к мень-
шей части.
(Пример этого.) Пред-
положим, что этот круг—круг
с центром А, и пусть его диамет-
ром будет ВС {рис. 23}. Продол-
жим его н его направлении и
Рис- отметим на его продолжении
точку В. Проведем из нее ли-
нию, касающуюся круга и точке Е. Опустим из точки Е перпендику-
ляр на линию ВС, это будет EG. Тогда я утверждаю, что ВВ относится
к T)G, как BG к GC.
Доказатель с т в о этого. Соединим (точки) Е и В, Е и С.
Тогда в силу того, что треугольники ВВЕ и EDC подобны, ВТ) относит-
ся к ВЕ, как Т)Е к ВС, и ВВ относится к ВЕ, как ВЕ к ЕС.
HD = НЕ
DE - DC КС
Поэтому отношение ВВ к /)С равпо двойному отношению ВВ к ВЕ
и, следовательно, равпо двойному отношению ВЕ к ЕС.
Ill) , HD yg / ль? 4s
Dl. ( )>Ji ) ~( AC )
(В силу того, что треугольники BGE и EGC подобны, BG отно-
сится к GE, как GE к GC, a BE относится к ЕС, как GE к GC). Поэтому
отношен не ВС к GC равно (двойному отношению СЕ к СС, или) двойному
отношению BG к СЕ.
на = / на
GC \ GK )
438
АРХИМЕД
Следовательно, BD относится к DC, как BG к СС.
HD НС,
DC ~ СС
А это и есть то, что мы хотели доказать.
Д о к а з а т о л ь ство этого предложения Друг и м с и о-
с о 6 о м. (Продолжим линию DF до точки II.} Проведем от линии ВС
дне линии ВН и CF, образующие вместе с ней прямой угол и за-
капчивающиеся на линии HD {рис. 24} [4]. Тогда лилии ВН, $Е
и CF параллсльиы. В силу того,что BD относится к DC, как ВН
к С/’.или как Н/i к EF,
BD _ НЕ
DC ЬС
& НЕ относится к EF, как ВС к GC,
НЕ _ ЛС
ке ас
то BD относится к DC, как BG к GC.
ВР ВС
DC “ GC 1
Ято и есть то, что мы хотели доказать.
XXI1
Если в сегменте круга сломана {прямая} линия {на две части},
стягивающие две неравные дуги, и из точки, делящей сегмент пополам,
опущен перпендикуляр на большую из частей ломаной линии, то он раз-
делит ломаную линию пополам Ь>].
(Пр и м е р этого.) Предположим, что сегмент круга имеет
основание АВ {рис. 25}, и сломаем в нем линию АСВ в точке С. Пусть
линия АС больше линии СВ. Разделим дугу АВ сегмента пополам
в точке D и опустим из нее
перпендикуляр на линию АС,
это будет 1)Е. Тогда я утвер
ж даю, что линия Ж? {В} разде-
лится в точке Е пополам,то есть,
что линия АЕ равна линиям ЕС
и СВ (вместе.)
Рис 25 Дока з а т« л ь с т в о это-
го. Отложим на болынейдуге/М
Дугу, равную меньшей дуге DC, это будет дуга DII. Соединим, (точки)
А н II, II и D, А и D. Отложим на большей линии АЕ линию, рапную
(меньшей) лилии ЕС; это будет линия EG. Соединим (точки) D и G.
В силу того, что перпендикуляр DE является общей линией (треуголь-
ников CDE и GDE), DG равна DC, а также DII, поэтому эти три линии
равны. В силу того, что дуга АН относится к дуге AIID, как угол ADH
КНИГА О КАСАЮЩИХСЯ КРУГАХ
439
к углу ACD и. отношение дуги НТ) к дуге АПЛ равно отношению угла
HAD к углу ACD , то дуги АП и Н1) вместе относятся к дуге AHD,
как углы HAD и ADH к углу ACT). Но дуги AHnHD равны дуто A1ID;
поэтому углы НПА xiHAD равны углу ЛCD, то сеть углу DGR. 1.1о угол
DGH равен углам GAD и GDA. Следовательно, углы 111)Л и HAD
равны углам GAD и GDA. Но угол HAD равен углу GAD, поэтому
оставшийся угол/Л) А равен оставшемуся GDA. В силу того, что ли-
нии DG и ВН равны, линия DA общая (линия) треугольников ADG
и ADH, а два угла (HAD и GAD) равны, основание АС равно основа-
нию АН. Ио линия АП равпа линии СВ, а линия СЕ равна литии ЕС;
следовательно, вся линия АЕ равна линиям ЕС и СВ. А это и ость то,
что мы хотели доказать.
XX 11.1
Д о н а з а т е л ь с т в о этого предложения другим с п о-
с о б о м. Начертим тот же чертеж, что и раньше. Дополним круг
AGBD {рис. 26 и 27} и продолжим линию АС в се направлении. Пред-
положим, что линия ЕП равпа
линии ЕЛ и соединим (точки) С
и 1), D н //, В я В, А и D.
В сил у того, что дуга АТ) равна
дуге DCB, хорда АТ) раина хор-
де DB, а линии DH равна ли-
нии AD. Поэтом у линия ПН
равна линии DB. В силу того,
что угол ВАС равен углу DBC,
так как они опираются на одну
и ту же дугу, а угол DHE ра-
вен углу ПАЕ, то угол ВНЕ
равен углу ВВС. Точно так же,
в силу того, что дуга DAGB
равна всей дуге DCBGA, угол
DCВ опирается на дугу DAGB,
а углы D А С и АВС вместе опи-
раются на дугу DCBGA, так
какВЛС опирается на дугу DC,
а угол ADC — на дугу CBGA,
то мы получаем, что углы 1)ЛС >;
и ADC (вместе) равны углу
DCB. По угол DCH равен углам
ВАС и АВС (вместе). Поэтому
угол DCTI равен углу DCB.
По было доказано, что угол
DHC равен углу ВВС. Поэтому
оставшийся угол HDC (н тре-
угольнике HDC) равен остав-
шемуся углу В1)С{ в треуголь-
нике BDC) и, в силу того, что
линия D1I равна линии ВВ, ли-
ния DC — общая (линия треугольников ВВС и 1IDC) и два угла (этих
треугольников) рнвпы, то линия СП равпа СВ. Поэтому линия ЕС
« СВ (вместе) равны лилиям ЕС и ЕП (вместе), то естт. линии АЕ.
А это и есть то, что мы хотели доказать.
440
АРХИМЕД
XXIV
Д о к а з а т е л ь с т в о этого предложения е щ с о д л и м
с п осо б о м. Сохраним тот жо чертеж. Мы утверждаем, что в силу
того, что дуга DCВ меньше полукруга, угол, вписанный в нее, именно
угол DC В, ту ной. Точно так яге, в силу того, что дуга DBA. больше полу-
круга, угол, вписанный в псе, именно угол DCA. острый. Поэтому угол
DCH тупой. Таким образом, углы DC В и DCH тупые. Так как угол
DHC равен углу ВВС, линия DB равна линии DII, а линия DC —
общая (линия) треугольников DCU и DCB, то угол 11 одного из этих
трсугольшпсов равен углу В другого из них. Поэтому стороны, заклю-
чающие два других угла, пропорциональны, а оставшиеся два угла DCIJ
и DCB, каждый из которых больше прямого, раины. (По так как линия
DB равна линии Dlf, а линия DC — общая линия этих треугольников,
эти треугольники равны.) Поэтому линия СН равна линии СВ и вся
линия ЕН, то есть линия АЕ, равна линиям ЕС и СВ (вместе). Это
и есть то, что мы хотели доказать.
«Книга о касающихся кругах» Архимеда закончена-
Хвала Аллаху единому, и молитва за его пророка Мухаммеда и его
семейство!
КОММЕНТАРИИ
КВАДРАТУРА 1 (АРАБОЛЫ
Точное название рассматриваемого сочинения нам неизвестно: имеющееся н руко-
писях заглаиие «Гетраусогюрдё ,TaQafio?.i)g» не может принадлежит!. Архимеду, так
как последний называл параболу «сечением прямоугольного конуса».
Как видно аз введения Архимеда, это сочинение является самым псрпьтм его посла-
нием к Доспфею. паписаппым вскоре после получения известия о смерти Кнноиа, т. с.
но всяком случае 1кх:ле240 г. до и. э. Из ввод чтя к «Эфоду» следувт.что определение пло-
щади параболического сегмента было нерпой задачей, разрешенном Архимедом с по-
мощью его метода механического интегрирования.
Упоминаемая во введении лемма а настоящее время носит название аксиомы Архи-
меда, хотя сам Архимед указывает, что аналогичным предложением пользовались
п жившие до пего геометры. Таковыми являются Евдокс, данttiий доказательство теорем
о площади круга (Евклид, Начала, XII, 2) о относительно обьемов пирамиды (Евклид,
XII, 7) и конуса (Евклид, XII, 10), а за ним Евклид, которому при надлежит доказатель-
ство теоремы, касающейся объема тара (Евклид, XII, 18).
В архимедовских формулировках упомянутых предложений в «Квадратуре пара-
болы» следует отметить слова «двойное» и «тройное» отношение. Когда Архимед, сле-
дуя своим предшественникам, пишет, что круги находятся в двойном, а шары в тройном
отношении их диаметров, то это значит, что речь идет об этом отношении, возведенном
во вторую или соответственно третью степень.
[11 Архимед дает без всяких доказательств три основные теоремы теории параболы,
ссылаясь л-ч «Начала теории конических сечввий» Евклида или Ариетея. Оба эти сочи-
нения до пас недошли, по изложенный н них материал вошел в сохранившиеся до настоя-
Щ|;гн времени «Кинические сечения» Аполлония Пергского (265—170 гг. до п. а.), млад-
шего современника Архимеда. Чтобы познакомить читателя с тем, как доказывались
эти теоремы в эпоху Архимеда, приводим доказательства соответствующих теорем вместе
с некоторыми другими, к ням относящимися, из парной книги упомянутого сочинения
Аполлония.
XI. Если конус сечется плоскостью, проходящей через ось,
и также другой, плоскостью, пересекающей основание конуса по пря-
мой, перпендикулярной к основанию треугольника, получаемого в осевом
сечении, если, кроме того, диаметр конического сечения будет парал-
лелен одной из сторон треугольника в осевом сечении, то всякая пря-
мая, проведенная от конического сечения параллельно линии пересе-
чения секущей плоскости с основанием конуса вплоть до диаметра
конического сечения, будет квадрировать прямоугольник, заключенный
между отсекаемым ею отрезком диаметра, считая от вершины кони-
ческого сечения, и некоторой другой прямой, которая к отрезку
образующей конуса между его вершиной и вершиной конического
сечения имеет такое же отношение, как квадрат на основании треу-
гольника, получающегося в осевом сеченаа, к прямоугольнику между
двумя остальными сторанами треугольника. Такие коническое сечение
мы будем называть параболой.
Пусть будет конус (рис. 1), вершина которого точка А, а основание—
круг ВГ; рассечем его плоскостью, проходящей через ось, и пусть
и сечении получится треугольник АВГ; рассечем конус также и другой
444
КОММЕНТАРИИ
плоскостью, пересекающей это основание по прямой АЕ, перпендику-
лярной к ВГ, н пусть эта плоскость образует на поверхности конуса
сечение — кривую AEZ; пусть диаметр Z11 этого сечения будет парал-
лелен одной из сторон треугольника осевого сечспия, а именно АГ;.
из точки Z перпендикулярно к прямой ZII про-
ведем Z6 и сделаем, чтобы как квадрат на В Г
к прямоугольнику между ВА и ЛГ, так была
и ZH к ZA;
нг2 Zf>
вааг _[za"
возьмем на сечении какую-нибудь произволь-
ную точку К и через К пронедем КЛ парал-
лельно ДЕ. Я утверждаю, что квадрат на КЛ
будет ранен, прямоугольнику между 9Z и ZA.
Действительно, через Л проведем MN
параллельно ВГ; тогда и КЛ будет параллель-
на ДЕ; слсдоиательно, проходящая через КА,
MN плоскость будет параллельна плоскости
через В Г, ДЕ, то есть основанию конуса. Зна-
чит, плоскость, проведенная через КЛ, MN,
даст круг с диаметром MN. Но КЛ будет пер-
пендикулярна к MN, поскольку ДЕ перпендикулярна ВГ; следователь-
но, прямоугольник между МЛ и AN будет равен квадрату на КЛ.
МЛ-ЛИ=КЛ2
И поскольку как квадратна В Г (относится) к прямоугольнику между
В А, АГ, так и OZ к ZA,
В г2 F>z
вл-лг_“хл
и квадрат на ВГ к прямоугольнику между ВА, АГ имеет отношение,
составляющееся нз отношений В Г к ГА и В Г к ВЛ:
вг2 вг иг
BA-ЛГ- Га ’ вл
то, значит, отношение! HZ к ZA составляется из отношений ВГ к ГА
п ВГ к RA.
07. B£ НГ
ZA ' ГА НА
Ио как ВГ к ГА, так и MN к NA, то есть МА к AZ,
ВГ _ МК _ МЛ
ГА~— А’Д ~ лт.
как же В Г к ВЛ, так и MN к МА, то есть AM к MZ. и остаток NA.
к ZA.
НГ MN _ ЛМ_ __ _КЛ
ВА МЛ " MZ ” za"
Значит, отношение 6Z к ZA складывается нз отношений МЛ
к AZ и NA к ZA.
ez мл na
za" az ’ ZA
Но отношение, составленное из МЛ к AZ и NA к ZA, будет отноше-
нием прямоугольника между МЛ и AN к прямоугольнику между AZ
КВАДРАТУРА ПАРАБОЛЫ
445
hZA. Значит, как 0Z к ZA, так и прямоугольник между MA nAN к пря-
моугольнику между AZ и ZA. Но как 0Z к ZA, так будет н прямоуголь-
ник между 0Z и ZA к прямоугольнику между AZ и ZA, если взять
AZ н качестве, общей высоты.
ez oz-za
za AZ-ZA
Значит, как прямоугольник между МЛ и AN к прямоугольнику
между AZ и ZA, так и прямоугольник между 0Z и ZA к прямоугольнику
между AZ и ZA.
мл-an ez-ZA
Л2-2А — AZ-ZA
Следовательно, прямоугольник между МЛ и AN будет равен пря-
моугольнику между 0Z и ZA.
MA-ANt=®Z-ZA
Но прямоугольник между МЛ и AN равен квадрату па КЛ; значит,
и квадрат на КЛ будет равен прямоугольнику между 0Z и ZA.
KAS=«ZZA
Подобное сечение мы будем называть параболой, прямую же 0Z,
на которой квадрируются проведенные к диаметру
называть «прямой стороной» (ipfjia яХвгрх — latus
rectum)*).
XX. Если в параболе провести к диаметру от
кривой две ординаты, то отсеченные ими на диаметре
отрезки, считая от вершины, относятся, как квад-
раты на этих ординатах.
Пусть будет парабола с диаметром АВ; возьмем
па пен некоторые точки Г, А и из :>тих точек прове-
дем к АВ ординаты ГЕ, AZ. Я утверждаю, что кап
квадрат на AZ ft квадрату на ГЕ, так будет и ZA
к АЕ (рис. 2).
az8 ZA
ГЕ2 ~~ АЕ
Действительно, пусть прямая, па которой квадрируются ординаты
(параметр), будет ЛН; тогда квадрат па AZ будет равен прямоуголь-
нику между ZA и All,
az8=za- ли
а квадрат на ГЕ равен прямоугольнику между ЕА а АП.
ге2-.ка-ап
Следовательно, как квадрат па AZ к квадрату па ГЕ, так будет и пря-
моугольник между ZA и АП к прямоугольнику между ЕА и All.
az2 za-aii
ГЕ3 ' l-.A-AH
По как прямоугольник между 7, А и ЛИ к прямоугольнику между
ЕА и ЛН, так и ZA к АЕ; и, следовательно, как квадрат AZ к квад-
рату на ГЕ, так и ZA к АЕ.
г) -Это наш параметр 2р п уравнении параболы
у- — 2рх.
446
КОММЕНТАРИИ
XXX И Г. Если на параболе взять какую-нибудь точку и провести
через нее ординату к диаметру, и если затем отсекаемый ею на диаметре
отрезок, считая от вершины, приставить на
\ продолжении диаметра к вершине (в противо-
наложную сторону}, то прямая, соединяющая
/ полученную таким образом точку со взятой {на
1 / \ \ параболе}, будет касаться конического сечения.
if] Пусть будет парабола с диаметром АВ; про-
В Л JE А ведем ординату ГД, отложим АЕ равной ЕД и
/ соединим А и Г. Я утверждаю, что АГ при про-
У должении окажется вне конического сечения
(рис. 3).
Действительно, пусть она, если возможно.
Рис. 3. попадет внутрь как прямая TZ; проведем орди-
нату 11В. Квадрат на ВН имеет к квадрату на ГД
большем? отношение, чем квадрат на ZB к квадрату на ГД,
вп® zb*
ГА® ГД®
по как квадрат иа ZB к квадрату на ГД, так будет и квадрат на ВЛ
к квадрату па ЛД,
XB* ВА*
ГД* АЛ®
а как квадрат на НВ к квадрату па ГД, так и BE к ДЕ;
л в* ВЕ
га* ДЕ
значит, ВЕ имеет к ЕД большее отношение, чем квадрат на ВА к квадрату
на АД.
ВЕ .. ВА* ' ”
ЕЛ > АЛ*
Но как ВЕ к ЕД, так- будет и учетверенный прямоугольник между
ВЕ и ЕА к учетверенному прямоугольнику между АЕ и ЕД;
_ВЕ _4ВЕ- КА
Ка’ 4АЕГел~
и, значит, учетверенный прямоугольник между ВЕ и ЕЛ к учетверенному
прямоугольнику между ЛЕ и ЕЛ имеет большее отношение, чем квад-
рат на ВЛ к квадрату на АД.
4ВЕ-ЕА . ВА*
4ЛЁ-ЕД АД*
Следовательно, после перестановки, учетверенный прямоугольник
между В13 и ЕА к квадрату на АВ имеет большее отношение, чем учет-
веренный прямоугольник между АЕ и ЕД к квадрату па АД;
4ВЕ ЕЛ 4АЕ-ЕЛ
АВ* Л АЛ®
это же невозможно; действительно, вследствие равенства АЕ и ЕД
учетверенный прямоугольник между ЛЕ и ЕД, будет равен квадрату на
АД,
4 4И ЕД=АД*
КВАДРАТУРА ПАРАБОЛЫ
447
учетверенный ?ке прямоугольник между ВЕ и Е А будет меньше квадрата
на В А,
4ВК-ЕА HAS
так как точка Е нс будет делить АВ пополам*).
Следовательно, прямая АГ пе попадет внутрь конического сече-
ния; значит, опа будет его касаться.
XL11. ЛЪш прямая, касательная к параболе, встречается с диамет-
ром и из точки касания проведена к диаметру ордината, если затем из-
какой-нибудь точки, взятой па коническом, сечении, проведены к диаметру
две прямые, из которых одна парал-
лельна касательной, а другая — про-
веденной из точки касания ординате,
то образованный этими прямыми тре-
угольник будет равен параллелограмму, i---—I11
заключающемуся между ординатой, про- I I
веденной из точки касания, и отрезком д__________у] /
{диаметра} между параллельной ей ———ы л х х
прямой и вершиной конического сечения. I /
Пусть будет парабола с диаметром / /
АЕ; проведем к данному коническому I
сечению касательную АГ, опустим
ординату 0Г, затем из какой-нибудь
произвольной точки (А) проведем AZ, z
через А проведем прямую АЕ парал- м" 1
дельно АГ, а через Г прямую ГН
параллельно BZ, наконец, через В прямую ВН параллельно О Г.
Я утверждаю, что треугольник AEZ будет равен параллелограмму IIZ.
Действительно, так как АГ касается конического сечения и ГВ
проведена ординатой, то АВ будет равна ВО;
ав^вв
значит, АО вдвое больше ОВ. Следовательно, треугольник ДОГ будет
равен параллелограмму В Г. И поскольку, как квадрат на ГН к квад-
рату на AZ, так п ОВ к BZ,
г«2 _ а к
Д22 _ HZ
вследствие основного свойства данного конического сечения, а как
квадрат на Г0 к квадрату па AZ, так относится треугольник АГ0
к треугольнику EAZ, как же (-)В к BZ, так относится параллелограмм
110 к параллелограмму T1Z; следовательно, как треугольник АГЙ
к треугольнику EAZ, так и параллелограмм 011 к параллелограмму ZH.
Значит, после перестановки, как треугольник А0Г к параллело-
грамму ВГ, так и треугольник EAZ к параллелограмму IIZ.
Но треугольник АГО равен параллелограмму 110; значит, и тре-
угольник EAZ будет равен параллелограмму I1Z
XIЛ'Г. Исли прямая, касающаяся параболы, встречается с диамет-
ром, то прямая проведенная через тачку касания параллельно диаметру
в сторону этого конического сечения, разделит, пополам все прямые,
проведенные внутри параболы параллельно касательной.
*) Дспыяательство, очевидно, основано на том, что при « 4-b=const проиаведение ab будет иметь
максимум при
448
КОММЕНТАРИИ
Пусть будет парабола с диаметром АВА, и пусть АГ касается сече-
ния; через Г параллельно ЛЛ проведем (?)Г, возьмем па сечении какую-
нибудь произвольную точку Л
и проведем Л NZE параллельно
АГ. Я утверждаю, что AN бу-
дет равна NZ (рис. 5).
Проведем ординаты ВО,
KZH, ЛА. 'Гак как на основа-
нии доказанного в сорок вто-
рой теореме треугольник ЕЛД
будет равен параллелограмму
ВМ, а треугольник EZH —
параллелограмму ВК, то, зна-
чит, остающийся параллело-
грамм НМ будет равен остаю-
щемуся четырехугольнику
AZHA. Отнимем общий пятиугольник MAJ1ZN; тогда остаток — тре-
угольник KZ.N будет равен треугольнику АМХ. Но KZ параллельна
ЛМ; значит, ZN будет равна AN.
Интересно отмстить различие терминология у Архимеда и Аполлония. Послед-
кий j понимает диаметр в паитем смысле этого слова как геометрическое место се-
редин хорд, параллельных данному направлению; у Архи-
меда же диаметр соответствует нашей оси параболы —
.диаметру, перпендикулярному к разделяемым нм пополам
хордам.
# ]2) Хизс указывает, что доказываемое предложение
равносильно с современном точки зрения преобразованию
уравнения параболы к другим координатным осям (рис. 6).
Если первоначально ось абсцисс х шла по НД и начало
координат было в точке В, то уравнение параболы имело
вид
*у2 = 2/ле, ’
откуда
ЛЛ«--=2/>ВА.
Если положим АД = а и возьмем новые координатные оси х и у с началом в
точке А, как показано иа чертеже, то
а2
ЛК--•=», КО-у, ВА—-.
2/*
Доказанная п предложении V пропорция
Кв : 0Л==ЛК : КГ
представится так:
У : |(2«—х) —у} -х: (2а—х),
у (2л—х) — х {‘1а —х) —-ху.
и окончательно:
У
х (2а—г)
что и представляет уравнение параболы, отпесеннои к координатным осям Аху и про-
«-О-
ходящей через начало координат А и точку В с координатами
КВАДРАТУРА ПАРАБОЛЫ
44»
|31 Идея механического доказательства Архимеда заключается в следующем. Возь-
мем равноплечий рычаг ГА7, в точкой опоры в А и плечом АГ, равным основанию 2а
параболического сегмента. Пусть КЛ —р будет ордината, соответствующая абсциссе
АК = я. Если мы разобьем всю площадь параболического сегмента на бесконечно тон-
кие прямоугольники с основаниями А.х и высотами, равными ординатам параболы, то
площадь прямоугольной полоски, соответствую-
щей ординате КА—у, будет:
2/'
Перенесем эту полоску в точку Г; ее момент отно-
сительно Л будет:
у-Дя>2«=-2й-(2а—х)
&Р
Если мы хотим уравновесить этот момент
полоской, помещенной на левом плече рычага
на таком же. расстоянии АМ-л от точки опоры
А, то необходимая длина y'^MN полоски
будет:
2#
у' = у-(2а—ж).
Нетрудно видеть, что эта длина соответствует прямой КЛ предыдущего чертежа.
Если взять все такие полоски, то их концы расположатся по прямой ZE, а сами
2аа
они заполнят площадь треугольника AZE с основанием AZ = 2a и высотой АЕ= —.
Так как этот треугольник, расположенный по всей длипе левого илоча рычага уравнове-
шивает параболический сегмент, помещенный на конце правого плеча рычага, ти, обо-
значив 5тР=5’1 и «S'cei'M-*5’"» мы имеем:
или “*
1 Л. 2a2 \ 2a „ _
( 2a------ । ——- =:1Уа"2а,
2 \ Р J 3
откуда
о «2 2
6’а=-^ (2a) = ~ АГ-ВД,
о ' 2р 3
что и требовалось доказать.
[4] Очень важно отметить изменение, внесенное Архимедом в доказательство по
сравнению с первым предложением «Эфода», Подобно тому, как мы теперь при опреде-
лении площади крипол инейной трапеции заключаем ео между двумя суммами площадей
прямой инейных трапеций, нз которых одна больше, а другая меньше определяемой пло-
щади, так и Архимед строит два ряда трапеций, (рис. 15, стр. 87;., из которых трапеции
ВФ, AZ, МН, NI пмссто с треугольником Г1Е больше параболического сегмента В6Г, в
трапеции <I>Z, 0Н, Ш н треугольник Г1О меньше его. Отличие заключается лишь в том,
что мы определяем площадь при поли пей пой трапеции как общий предел, к которому
стремятся обе указанные суммы при неограниченном увеличении числа рапных отрезков,
па которые делится основание трапеции, а Архимед довольствуется интуитивным шнш-
тием площади параболического сегмента. В связи с этим нужно отметин, одно обстоя-
тельство: в предложениях XIV и XV на равные отрезки делится ослопапмс ВГ сегмента
а в предложении XVI — сторона ВА треугольника ВАГ. Можно, конечно, доказать,
что из равенства отрезков ВГ следует равенство отрепков ВА и наоборот, по видеть в этом
ошибку Архимеда нельзя, так как в предложении XVI равенство отрезков ВД играет
существенную роль в доказательстве, тогда как в предложениях XIV и XV равенство
отрезков В Г упоминается только при построении и лс имеет никакого значения для дока-
зательства теоремы.
29 Архимед
450
КОММЕНТАРИИ
1.51 Предложения XVIII—XXIV представляют собой, по существу, работу отдель-
ную, присоединенную к изложению механического метода определении площади пара-
болического сегмента. Часть, содержащая предложения XVIII—XXIV, написана в не-
сколько ином стиле, чем предшествузощая часть трактата: сначала даются определения,
и текст каждой теоремы содержит формулировку ирсдлогкспия, за которой следует дока-
зательство.
Данное Архимедом в этих предложениях доказателз.ство сводится, ио существу,
к суммированию геометрической прогрессами:
, п . а л , а 4
°" 4 ’j’‘4® ’"4^ ’ = “ Г " 3
1 _
Архимед, живший в зпоху, когда для бесконечных процессов математикой не было
еще выработано специального алгоритма, вынужден был каждый раз заново воспроизво-
дить то, что у пас охватывается общей теорией пределов. В предложении X X ] ] I он дока-
зывает, что сумма конечного числа такой бесконечно убывающей геометрическим. прогрес-
4
спи отличается от - а на величину, равную одпон трети последнего члена взятом суммы.
О ШАРЕ И ЦИЛИНДРЕ
ПЕРВАЯ КНИГА
[1 ] Рассматриваемое сочинение принадлежит к числу наиболее читавшихся произ-
ведений Архимеда; поэтому в сохранившихся до нашего времени списках совершенно
исчезли особенности дорийского диалекта Архимеда, нчпль заметные в его «Квадратуре
параболы». Кроме того, текст этого сочинения испещрен вставками позднейших ком-
ментаторов, которые мы помешаем в квадратных скобках.
Оно состоит из двух совершенно независимых друг от друга сочинений, из кото-
рых позднейшие издатели сделали «первую» и «вторую» книги; это видно из того, что
Ванн, цитируя первую книгу’ «Шара и цилиндра», ничего пе говорят о том, что цитируе-
мое место принадлежит первой книге. И даже в этой «нерпой книге», имеются две отдель-
ные части. Первая из них обнимает предложения I— XVI и посвишспа определению
боковой поверхности конуса я цилиндра, вторая же (предложении XVН—XLIV) имеет
целью определение поверхности и объема шара.
|2| Архимед начинает свое изложение с некоторых «аксиом». По существу, тако-
ными можно назвать лишь 1-е и 3-е положения, остальные же носят характер опреде-
лений; в латписком нсреподо Гейберга опП так и называются Defiiiilionus. Настающими
аксиомами, с нашей точки зрения, являются лишь тс, которые Архимед называет допу-
щениям и (ля nPuv6p.Bv а).
|3| Допущение 5 представляет известную аксиому Архимеда; аналогичное поло-
жение было уже сделано Евдоксом, но в формулировке Архимеда есть отличие. Он гово-
рит о разности двух величин, которая будучи складываема сама с собой может превзойти
любую заданную величину, а у Евдокса эту роль играет меньшая из сравниваемых вели-
чин. Изменение, формулировки у Архимеда Дсйкстсрхснс ибъпекяит тем, что Архимед
хотел исключить случай, когда разность величин прсдстнвляот неделимую (сточки зре-
ния математического атомизма).
[4] С нашей точки зрения, это предложен нс может показаться тривиальным,
а доказательство, которой даст Архимед, неоправданно сложным. Это докозательстно
можно было бы заменить примерно слсдуп.тим:
Пусть имеются Две неравные величины, которые мы, следуя примеру Архимеда,
изобразили бы Л1иА; пусть ЛВ'>А. Возьмем разность АН—D — &- Разделим А пополам
и образуем две величины D-- и D; тогда отношение Г D
A V „ г
у J: В будет меньше
заданного отношения А В ; Л, что и требовалось доказать.
Косточки зрении Архимеда., такое доказательство не нвлцется правомерным. Дока-
зываемая теорема нужна Архимеду для доказательства третьего предложения — воз-
можности построении двух многоугольников — одного описанного, а другого вписан-
ного в яруг,— так, чтобы отнншецис стороны описанного многоугольника н гоотпстствут-
тцей стороне вписанного (отношение .-тведомо большее единицы) было меньше любого
.чнданпого отношения большего единицы. Так как разность сторон описанного и вписан-
ного многоугпл[.ников является величиной бесконечно малой, it значит, и прямые АВ
и )i (отношении которых изображает заданное, большее единицы, отношение) могут отли-
чаться друг от друга гга очень малую величину, то с точки зрении античной математики
могло быть сделано глелукипое возражение: что будет, если обе прямые ЛВ и V втли-
чаются друг от друга па одну неделимую, математический атом, из которых состав'
ляюгпея прямые? При такой постановке вопроса приведенное выше доказательстпо,
основанное па возможности деления этого неделимого, отпадает ввмо собой.
Интересно, что Архимед построил свое доказательстпо так, что подобное возраже-
ние сделать ужо нельзя.
|5] В основе доказательства теоремы лежит следующее положение; «треугольники
АВА, В ГА будут больше треугольника АДГ».
2У*
452
КОММЕНТАРИИ
Доказательство этого положения доставило очень много затруднений комментато-
рам Архимеда, начиная от Евтокия. Упомянутое положение можно доказать таким
образом *).
Пусть круг с центром О представляет основание рассматриваемого конуса; перпен-
дикулярной плоскости чертежа из точки О восставлена высота ОД = h конуса. Пусть АГ
представляет какую-нибудь хорду, а В — середина дуги
АВ Г. Требуется доказать, что сумма площадей граней АВА
и В ГЛ больше грани АГА.
Рассмотрим сначала случай А Г>ЛВ (рис. 1). Тогда пер-
пендикуляр ОП, опущенный из центра круга на хорду АГ,
будет меньше перпендикуляра OZ, онущснпого ив О на АВ.
Точки Z и Н будут основаниями перпендикуляров, опущен-
ных из вершины А конуса на АВ и АГ. Мы имеем:
пл. АВА-=4-АВ y'OS^OZ2 ,
пл. ЛАГ—4 АГ /ОД84-ОН2 . :
Имеем
ил. АВА | пл. ВАГ =4 ’2ЛВ /бд2 “OZa
Так как
АГ < АВ->ВГ=2ЛВ,
/OA^f-OH2 < VОД2-г OZ2,
то
пл. АДГ < пл. АВА |-пл. ВАГ.
Пусть теперь АГ < АВ (рис. 2). Проведем диаметр
ВОЕ. Так как хорды АЕ = ЕГ будут каждая меньше АГ,
то, согласно предыдущему,
пл. АДГ < пл. АДЕ 4- пл. ЕДГ.
Для доказательства теоремы лам остается сравнить площади граней АВА и А ЕЛ. Так
как площадь треугольника ОАВ равна площади треугольника ОЛЕ, то
OZ-AB = OK-AE,
где ОК представляет перпендикуляр, опущенный из О на хорду АЕ, откуда
O2-.OK.4I.
Площадь грани АВА будет:
1 1 .________.
4 AB-AZ-y АВ /OA2+OZ2 ,
а грани АЕД:
4 ЛЕ /0Дг4-0К2 .
Квадраты удвоенных площадей ЛВД и ЛЕД будут:
(2пл. ABA)2=AB2-OA2-!-AB2 OZ2=AB2-OA2-| АЕ2-ОК2,
(2 пл. АЕД)2=АЕ2-ОД24-ЛЕ2 ОК2.
Так как ЛЕ<ЛГ<АВ, то и.ч. АЕД<пл. ЛВД, и, следовательно,
пл. АДГ < пл. ЛВД-• пл. ВГД.
*) Идея нижеприведенного доказательства сообщена мне проф. М. Я. Выгодским которому
н приношу яа это благодарность.
О ШАРЕ И ЦИЛИНДРЕ
453
Затруднения комментаторов объясняются тем, что лемма, принимаемая Архимедом
без доказательства, в общем случае не является справедливой. Действительно, предста-
вим себе трехгранпую пирамиду (рис. 3), вершина которой совпадает с вершиной прямого
угла равнобедренного прямоугольного треугольника с горизонтальной гипотенузой,
являющегося большей гранью боковой поверхности этой пирамиды (пусть катеты этого
треугольника равны с), а остальные две грани представляют лежащие в вертикальных
плоскостях прямоугольные треугольники, общий катет Ь которых является высотой пира-
миды, и два остальных представляют проекции а катетов с на горизонтальную плоскость
основания; в таком случае
с»=л2-|-й2.
Сумма площадей обеих вертикальных граней нашей пирамиды равна будет:
ab,
а площадь наклонной грани
•p=4(«s i **)
Если взять высоту b так, чтобы удовлетворялось неравенство
то
1
“ь<4 (“21 ^а)>
то есть площадь большей наклонной грани будет более суммы площадей двух остальных,
математики рассматриваемая
Интересно отмстить, что методами атомистической
лемма «доказывается» очень просто. Сечениями, парал-
лельными основанию, разбиваем боковую поверхность
нишей пирамиды па ряд бесконечно топких треугольни-
ков, в каждом пи которых одна сторона будет меньше
суммы двух других. Если мы составим все неравенства
подобного рода и просуммируем их, то получится, что 5
одна из боковых граней пирамиды будет меньше суммы
площадей двух остальных граней, что и требовалось
доказать.
[б] Основная идея доказательства Архимеда обоих
предложений проста до гениальности, но изящество ее
выступает лишь, если избавить доказательство от излиш-
них математических подробностей.
В девятом предложении Архимеду требуется до-
казать, что боковая поверхность копуса будет больше
боковой поверхности вписанной в него пирамиды. До-
статочно провести доказательство лишь для кониче-
ского сектора, соответствующего одной граня пирамиды, как Архимед это и делает.
Все доказательство основывается па том, что, вписывая в сегмент круга много-
угольники, можно сделать отрезочки между периметром этих многоугольников и дугой
окружности меньшими любой заданной величины. /А (предложение. VI). Пусть такой много-
угольник вписан, и пусть па нем построена пирамида, одной гранью которой служит тот
самый треугольник, площадь .Утр которого должна быи. меньше отрезка конической
поверхности между крайними сторонами этого треугольника. Каждая грань пирамиды
отделит от копуса некоторый конический сегмент. Пусть заданная величина А будет
меньше разности между боковой поверхностью <УГир пирамиды, винсавиой в конический
сегмент, за исключением, конечно, треугольной грани с. площадью 6'^,, и этой последней:
А >$гир—
Кроме того, мы можем написать, что отрезок конической поверхности ^иоп вместе
с суммой отрезочков между окружностью и периметром вписанного многоугольника будет
больше упомянутой боковой поверхности пирамиды; при этом вместо суммы площадей
отрезочков круга мы можем взять большую ее величину Л:
А коп 1* А > A’nup
пир — А'гр.
454
КОММЕНТАРИИ
Вычтем почленно из обоих членов верхнего неравенства соответствующие члены
нижнего; после очевидных сокращении получаем:
Л кои
что и требовалось доказать.
Доказательство десятого предложения основывается на том. что сумма площадей
отрезочков между окружностью и неримстром описанного около лее многоугольника
может быть сделана меньше любой заданной величины Л.
Требуется доказать, что площадь двух треугольников, образованных двумя обра--
нующими конуса и проведенными в концах этих образующих касательными, будет больше
соответствующего отрезка конуса. Описываем около основания конуса последовательные
многоугольники, строим па них пирамиды так, чтобы удовлетворялись неравенства
2Л,тр- ^иир > Л,
Л’нир- !"Д ^'Укон-
Складывая почленно полученные неравенства, получаем:
25’ > 5
-мтр “’iphp
что и требовалась доказать.
Совершенно аналогично доказываются и предложения XI и XII для цилиндра.
[71 Рассматриваемое предложение касается определения боковой поверхности
цилиндра — первый известный нам пример в истории греческой математики, когда пло-
щадь, расположенная па кривой поверхности, сралппваетсм с некоторой плоском фигу-
рой. Если данную Архимедом теорему вырв.шть и современной формулировке, то для
боковой поверхности цилиндра мы будем иметь формулу
.У=п(/2ЛЙ)\
что вполне соответствует современной
Л”=2л«Я,
если за Г, считать радиус основания цилиндра, а за II — его высоту.
Архимед знает, что лежащий в основании данного цилиндра круг радиуса II можно
заключить между дпумя описанным и вписанным многоугольниками, отношение площа-
дей которых может быть сделано меньше любого взятого отношения, большего единицы.
Площадь описанного многоугольника он определяет как произведение половины его
периметра L на радиус круга IV.
Г-Н-
С другой стороны, ясно, что боковая поверхность 5 описанной около цилиндра
призмы, построенной на этом же самом описанном многоугольнике, будет равна
*%пис—Ы1,
гц,о Н общая высота цилиндра н призмы. Отношение двух этих площадей будет равно
1
7'отшс : Лдпис —-.у Ч ' II ~It : HI.
Если мы хотим представить полученное; отношение в виде отношения площадей
двух подобных е)>игур, то рассматриваемое линей нею отношение Н : ‘111 мы должны будем
замешит]. отношением двух квадратов; таким образом, совершенно естественно появляется
подобный первому многоугольник, оппсанпын около круга, радиус g которого является
средней пропорциональной между 11 и ‘111, или, что то же, между 21i и //:
Q*=R-‘2H=2Iin.
Площадь многоугольника, описанного около этого круга, будет равна боковой
поверхности призмы, ошн-апион около цилиндра.
Если чс‘[)ез Д обозначим круг, составляющим основание рассматриваемого цилнпдра,
а через Н •• • круг, осшсансеый. радиусом то мы будем иметь следующие шесть величин*.
,$1'111IC—A,ja многоугольника и круге Д:
•Ь’сиис’ *'п|шс—"ва многоугольника в круге; В;
О ШАРЕ И ЦИЛИНДРЕ
455
S — боновая поверхность цилиндра,
£? — площадь круга В.
К этим величиной прибавляются cute две боковые поверх тюти »?опис я »S‘UI„1C двул
призм, опием иной и вписанной около цилиндра (^оши^^'впис)’ па аТ1,х величинах Архи-
мед и сгроит свое, основанное на методе нсчсрпнпия докизнтсльсггво.
Требуется доказать, что 5 = В.
Предположим сначала, что 6>В. Строим около круга В такие дли многоугольники —
вписанный и описанный, чтобы имело место неравенство
С другой стороны,
сА с*В с г,
° опии °спис ° опис «
"Та ~ н '
’untie 1 лоне ’’вине
так как 6’oinic>^, а-^Впис<н- Гнким образом, мы пришли к противоречию, заставляющему
нас отбросить сделанную гипотезу.
Предположим теперь, что 5</J. Тогда опять строим такие многоугольники, чтобы
имело место неравенство
•Ssibic - В
1ИТ11Г
Тик кик ‘УОщ1С'>^>. то для опровержении упомянутого неравенства нам остается лишь
доказать, что будет всегда меньше S'.
Вписываем и круг Л и описываем около него многоугольники, подобные построен-
ным для круга В; тогда
..л sh
° пике впке
сА 1’Н
"с лис онис
Пусть /. будот периметр многоугольника, вписанного в круг Л, а Н радиус
последнего; мы имеем:
$л <— RL.
-"игше ~ 2
боковая поверхность призмы, вписанной в цилиндр Л, будет:
А'пиис — BL.
Так как
отношение
Н равно отношению соответственных
м । югоугольников,
вписанных и описанных в круги Л и В-
ул <ГЛ !'
ц впис . _ °опис _*•
S11 ~ 5В "”’2Н И
1UIUC огню
•Уцпис В
Авпис 2Я
то
.Л оЛ
вшк: > ° впис
*"пис S 6 *’ЕП,1С ’
то есть Л'В^1С будот меньше Лши,.- — поверхности вписаппой в цилиндр призмы, а следо-
вательно, и подавно меньше .9 — боковой поверхности цилиндра. Полученное противо-
речие устраняет и :>ту гипотезу, так что у нас остается липп. одна возможность S=B.
Любопытно, что Архимед но определяет поверхность цилиндра как произведение
окружности основания па сторону цилиндра; по-видимому. «Измерение круга» еще не
было написано.
[8] Оба предложения XXI -XXIF, по существу, равносильны получению суммы
ряда тригонометрических функции.
450
КОММЕНТАРИИ
п
2
Пусть 2л будет число сторон правильного многоугольника, вписанного в круг или
в сегмент. Тогда предложение XXI будет равносильно следующему равенству:
. и , . 2л . , . (я—1)л 1 , л
Sin----j-Sin--b . . . - SIH ------ cig — ,
n 1 n n 2 2n
& предложение XXII — такому равенству:
. 6 . . 20 . . . (n- -1)0 \ , . „
2 ( sm —t-sin----k ... -4-sin —----— 1 sin 0 . „
\ n n n 1 0
1—cost) ' cts2« ’
если черен fl обозначить угол, соответствующий половине дуги того сегмента, в который
вписывается правильным, многоугольник с 2п сторонами.
19] Группа предложений XXIII—XXVII определяет
нижнюю границу дли величины поверхности и объема
шара — :>то будет поверхность и объем тола вращения,
образованного вписанным в большой круг шара правиль-
ным многоугольником с 4» сторонами.
Поверхность рассматриваемого теда вращении пред-
ставится как сумма поверхностей усеченных конусов,
осповапиями которых являются круги, описанные при
вращении вершинами правильного многоугольника.
Пусть КА представляет одну из сторон правильного
многоугольника (рис. 4), описавшую коническую повер-
хность КЛК1Л1, а ЛВ представляет такую же сторону пра-
вильного многоугольника, прилегающую к оси вращения
А АР Обозначим радиус шара через Q, угол А ОК через а
и угол КОЛ через Ан (этот угол мы, конечно, стали бы
считать бесконечно малым). Тогда боковая поверхность АЗ’ усеченного конуса KKtAAt
будет:
ДА’ = л (К М -j- ЛМХ) КЛ=л: {р sin а | р sin (a+Да) {рАа.
Искомая поверхность S будет равна сумме AS:
S= 2 AS—я 2q sin a-рДй.
Согласно предложению XXI, мы имеем:
2q sin a AtB _ рЛ(2р)а—(pAa)»
2q AB qAcc
откуда
2q sin a-QAa — (2q)s 1- -^=4q®(1—^5-).
Таким образом,
/ Act2 \
Л-4ЛН •
то есть
S < 4KQS,
причем, обе указанные величины'различаются на бесконечно малую величину -^-Да®.
В обозначениях интегрального исчисления процесс, применяемый Архимедом, может
быть совершенно точно выражен формулой
я я
А’ = л J 2р sin ag da=2лр2 J sin a da—4лр®.
6 о
Что касается объема рассматриваемого тела вращения, то он получится как сумма
объемов тел, происшедших от вращения треугольников типа ОКЛ; каждый из таких
объемов будет равниться одной трети произведения поверхности, описанной стороной
КЛ, на длину перпендикуляра ОН, опущенного из О на КЛ- Так как длина этого перпен-
дикуляра будет одной и той же для всех треугольников типа ОКЛ, то рассматриваемый
О ШАРЕ И ЦИЛИНДРЕ
457
об ьем будет равен
v=4s-oh==~w(i-^) Q
4 /' Да2 X /. Да* X 4 . ( Да2 X
= з«с\1—г) ~~i~)'
Он бгдот меньше объема конуса, имеющего основанием учетверенный большой круг
4
шара, а высотой — радиус последнего, по разница между ними, равная — л(гДа3, будет
величиной бесконечно малой.
[101 В предложениях XXVJTT—XXX] Архимед строит верхний предел для поверх-
ности и объема шара. Он рассматривает тело, полученное и результате вращения пра-
вильного многоугольника, описанного около большого круга заданного шара. Так как
этот многоугольник можно считать вписанным в некоторый другой круг радиуса К, то
к телу, полученному от его вращения, можно приложить те же самые выводы, что и ранее;
единственная разница будет заключиться в том, что длина перпендикуляра, опущенного
из центра шара па сторону описанного многоугольника, будет равняться радиусу г внут-
реннего шара, а длина хорды yi,77, соединяющей конечную точку At диаметра с другим
концом В прилегающей к последнему стороны АВ, будет равна диаметру’ 2г внутреннего
шара.
Если И — радиус внешнего шара, то сторона описанного многоугольника будет
7?Дн. Формула для S' - - поверхности описанной фигуры — примет вид
S’ —я 27? sin а-7?Да,
где
2 27? sin a-7?Да=2.7?-2г,
и окончательно
S'=n-4Rr > 4лга,
так как 7?>г.
Что касается объема V, то оп будет равен
11 4
V=— S'r=4-4nRia> — n>»,
Л 3 3
то есть больше объела конуса, имеющего в качество основания учетвороппый большой
круг внутренней сферы, а высотой — радиус г последней.
[111 В подробностях вывода имеется очень интересная деталь, на которой стоит
остановиться.
Архимед задастся двумя прямыми К и Н, отношение которых меньше отношения
пгара к конусу. Требуется построить два многоугольника, кубы сторон которых имели бы
отношение меньшее К : Н. Можно было бы получить стороны этих многоугольников,
иияпшн две средние пропорциональные между К и Н:
К :А = А:М=М:Н;
тогда
К А _М_ К
V A J А ' М ’ Н — Н ’
так что отношение прямых К и А можно было бы взять в качестве отношений сторон иско-
мых многоугольников. Две средние пропорциональные в геометрической пропорции Архи-
мед заменяет двумя средними пропорциональными в арифметической пропорции;
К—1 = 1 — 0 = 0 — И,
считая, очевидно, общеизвестным, что
К3 К
I3 < И ’
Для последнего-неравенства Евтокий в споем комментарии дает следующее доказа-
тельство: • - . .............
45Я
КОММЕНТАРИИ
«Пусть даны две неравные линии АВ и ГК (рис. 5). Отнявши от
АВ лцыию ВА, равную ГК, разделим остаток АЛ на три равные части
АВ
Ь
в точках Е и Z и затем положим ЕВ II и ZB---0,
тогда 8 и II удовлетворяют поставленному усло-
вию *).
Итак, я утверждаю, что отношение АВ -. ГК
будет больше куба отношения АВ : 11.
Пусть отношение АВ к И будет равно отно-
шению 11 к некоторой линии Л:
к
Л
Так как линия АВ превышает Н на ту же самую
свою часть, на которую II, в свою очередь, пре-
вышает Л,
Рис. 5.
АН—II _ II—Д
АВ 11
и всякая часть линии АВ будет больше той же части линии II, то,
следовательно, разность между ЛВ и 11 больше разности между Н и Л:
АВ-н > н-л
По разность между АВ и II равна разности между Н и 8;
лв-п-н- о
следовательно, Н превышает 0 на величину, большую разности 11—А;
н е> н-л
поэтому Л будет больше 0.
Затем сделаем так, чтобы отношение Н :Л равнялось отношению Л
к некоторой прямой М;
Н :Л—Л:М
тогда М и подавно будет больше ГК Теперь так как четыре длины АВ,
В, Л, М находятся в непрерывной пропорции,
ЛВ:Н = Ц :Л=Л :М
то отношение АВ ; М будет равно кубу отношения ЛВ : Ц. Следова-
тельно, отношение АВ : ГК больше куба отношения АВ : Н».
С пашей точки арспия, утверждение Архимеда равносильно следующему.
Даны две прямые К —и л Н—1>, причем а— Ь=—А и построены еще две прямые:
2 1 2 19
1-4й-|-4ь=н-тл.»=4« 1-4•>.
«> А А А А
Так как
1 ' V' Hh / 1,3 |-2Ь2Л+^Л2+г^Л3 Ь Ь2-!-9М-|-^Л2
4 1
поскольку вторая дробь < 1, ибо Z>2-- 2ЬЛ-1-; Д2=о2-и,тД2,
<5 о
то I3 > 1<2П или
4«-i 4ь>г^-
о о
*) У Еятотиш ЛВ соответствует арх яясдопой линии К. прямая ГК—архимедовой II, а ЕВ = Н
и ZB=O соответствуют архимедовым прямым 1 и О.
О ШАРЕ И ЦИЛИНДРЕ
459
-Это керппсоство аналогично неравенству для квадратного корня
1 1 Z-------
У « + -^ 5>У ab ,
то есть средняя ирифмстнческан двух чисел более их средней геометрической.
ВТОРАЯ КНИГА
Вторая книги «О шаре и цилиндре» знакомит нас с методами, при помощи которых
греки заменили пашу современную школьную алгебру. Решение задачи распадалось на
лае части -аналитическую и синтетическую. В аналитической части задача предпола-
гается решенной и отыскивается соотношение между заданными величинами и искомыми;
к современном обозначении это было бы равпосязгыю составлению уравнения, содержа-
щего неизвестную, и определению веизнес.тпон из этого уравнения. Мы считаем геомет-
рическую задачу рептеннои, если нам удалось ее свести к алгебраическому уравнению
тон или другой степени, решение которого производится ио известным формулам. У гре-
ков аналитическое исследование задачи считалось законченным, если ее удалось свести
к некоторой стандартной геометрической задаче, решение которой было общеизвестным.
Собранием таких стандартных задач были евклидовские «Data», указывающие, когда
ту или другую геометрическую ве-шчниу можно считать данной, то сеть можно опреде-
лить иа основании заданных условий. После того как аналитическая часть решения была
закончена, начинался синтез, равносильный в некотором смысле нашей проверке реше-
нии путем подстановки найденного корня и первоначальное уравнение пли построении;
цепь рассуждений прослеживалась обратным ходом — от найденных решений греческий
математик посходил к данным и таким образом доказывал правильность найденного реше-
ния. Пнпгему исследованию уравнения у греков соответствовал диоризм — определение
условий, при которых рассматриваемая задача могла иметь решение.
[1] В качестве иллюстрации вышесказанного разберем ход рассуждений Архимеда
ирп решении задачи, разобранной в первом предложении: требуется построить шар, объем
которого был бы равен заданному конусу или. цилиндру.
Так как объем цилиндра, описанного около шара, и полтора раза больше объема
этого пгпра, то решение задачи сводится к следующей: нужно построить цилиндр, объем
которого был бы в полтора раза больше заданного конуса или цилиндра (зто легко может
быть достигнуто при помощи соответствующего увеличения высоты конуса или цилиндра
при сохранении неизменным основания), а затем построить второй цилиндр с квадрат-
ным осевым сечением, ривионелнкпн первому цилиндру. Диаметр основания парного
цилиндра А и'высота И являются, таким образом, заданными; ищется равная диаметру
высота Z второго цилиндра, оннсапного около шара. С пашей точки зрения, решение
задачи сводится к кубическому уравнению
4-aZ:,^=4- лД°П,
4 4
пли
Z3— Д2Н.
Так как у греков геометрические задачи, связанные г извлечением квадратного
корпя из произведения двух прямых, решались при ноиощн нахождения средней пропор-
циональной между этими прямыми, а задачи, связанные с извлечением кубического корпя,
еще со времен Гиппократа Хиосского (2-и половина V века до н. з.) приводились к нахо-
ждению двух средних пропорциональных, то Архимед сводят решение рассматриваемой
задачи тоже к нахождению двух средних пропорциональных между заданными диамет-
ром А основания и высотой Н цилиндра, согласно соотношению
А® : А21( —Л2[( : ДП2 = АН2 : Н®,
плн после извлечения кубического корпя
Д : Гд2Н= ГА2Н : A(Is-: 1^Д112 : И.
Первая средняя пропорциональная ]?'Д2И п будет искомой прямой Z, равной диаметру
и e.ooTiieTCTiieoiio высоте искомого цилиндра, описанного около шара.
Евтокнй в своем комментарии к Архимеду приводит л высшей степени интересный
текст, касающийся ис.ториии так называемой Делийской проблемы (задачи об удвоении
куба), к которой Архимед сводит рассматриваемую задачу:
«Произведя анализ задачи и найдя, что ее решение сводится к определению двух
средних пропорциональных, образующих непрерывную пропорцию с двумя заданными
460
КОММЕНТАРИИ
прямыми, он (Архимед) говорит просто «пайдем», но описания самого способа построения
их мы у него не находим и должны обратиться к сочинениям многих знаменитых людей,
занимавшихся этой задачей. Из них мы оставляем в стороне решение Евдокса Книдского,
так как последний во введении говорит, что задача решена ям при помощи «кривых*
(хсщ.-tvXat) линий, а в доказательстве он этими «кривыми» линиями совсем не пользуется;
кроме того, найдя обыкновенную <6it]op,ueVT) — буквально: разделенная, то есть состоя
1цая иа четырех членов пропорция) пропорцию, он пользуется ею как непрерывной, а такая
выдумка недопустима ire только для Евдокса, по и для лиц, очень мало занимавшихся
геометрией. Итак, для выяснения хода мыслей известных мужей опишем в отдельности
предложенные каждым из иих способы решения этой задачи.
Рс ше н и с Илатона
Даны, две прямые; найти две средние пропорциональные, обра-
зующие с ними непрерывную пропорцию.
Пусть прямые АВ, В Г (рис. 6а), для которых требуется найти две
средние пропорциональные. будут перпендикулярны друг к другу.
Продолжим эти прямые до А и Е и построим прямой угол ZH6 (рис. 66),
пусть по одной его стороне ZH двигается линейка КЛ в некотором жело-
бе, врезанном в ZH так, чтобы линейка оставалась все время парал-
лельной 116. Этого можно добиться, если взять другую линейку ОМ,
составляющую одно целое с 116 и параллельную ZH. Если мы да перед-
них поверхностях линеек ZH, 6 М прорежем желоба секировидного
сечения *) и в эти желоба поместим шпеньки, составляющие с линей-
кой К Л одно цел оо, то мри движении КА будет все время оставаться
параллельной 116. Устроивши все это, поместим одну из сторон угла,
например НО, так, чтобы она проходила через точку Г, затем передви-
нем весь угол и линейку КЛ так, чтобы точка И попала на прямую ВЕ.
но сторона И© все время проходила бы через Г; после этого сделаем
так, чтобы линейка КЛ точкой К касалась прямой ВД, а остальной своем
частью проходила через А. Тогда все будет, как па левом чертеже;
прямой угол М6Н займет положение ГЕД, а линейка ZH расположится
по прямой ДА. Как только удастся этого добиться, задача будет решена;
действительно, так как мри точках Д и Е находятся прямые углы, то
мы будем иметь, что ГВ относится к ВЕ, как ВЕ к ВД и ДВ к ВА.
ГВ _ ВЕ _ д_в_
НЕ ~ ВД — ВА
*) Мы сказали бы: п гиде «ласточкина хвоста».
О ШАРЕ И ЦИЛИНДРЕ
<61
Р с ш о и и в Герина («М с с h a a i с а» к «Т1 el t> р о I с а»)
Пусть даны две прямые АВ, В Г, для которых требуется пайти
две средние пропорциональные. Расположим их так, чтобы они обра-
зовали при В прямой угол и дополним параллелограмм ВД; проведем
прямые АГ, БД; они, очевидно, рав-
ны между собой и пересекаются
пополам; построенный на одной из
пих круг пройдет и через концы дру-
гой, так как рассматриваемый парал-
лелограмм будет прямоугольным.
Продолжим ДГ, ДА и вообразим ли-
нейку ZBH, которая вращалась бы
окон о некотор ого неподвижного гвоз-
дя В. Будем двигать зту линейку
так, чтобы она пересекла ДН и AZ
в точках, находящихся на равных
расстояниях EZ и ЕН от точки Е. Представим, что ото уже сделано,
и линейка находится в положении ZBH, причем, как сказано, прямые
EZ и Eli сделались равными. Из точки Е опустим на ГД перпендикуляр
Е0, который, очевидно, разделит ГД пополам.
Так как ГД разделилась в точке 0 пополам и к ней добавился
отрезок TZ, то прямоугольник между AZ и ZT вместе с квадратом на
Г8 равен квадрату па 0Z.
az zr+r®2.-ez3
Прибавим к обоим членам квадрат на Е0, тогда прямоугольник
между AZ и ZT вместе с квадратам па Г0 и квадратом на 0Е равен
квадрату па Z0 вместе с квадратом на 0Е.
az z r+re>a+6E2-ze2 [- ев®
Но квадрат на Z0 вместо с квадратом na 0Е равен квадрату на ГЕ,
гвг I НЕа=ГЕа
квадрат на Z0 имеете с квадратом на 0Е равен квадрату на EZ.
ZfW 0E2^EZ«
Значит, прямоугольник между AZ и ZT вместе с квадратом на ГЕ
равен квадрату на EZ. Точно так же докажем, что прямоугольник
между АН и НА вместе с квадратом па АЕ равен квадрату па ЕН.
ДП • НА-;-АЕ’’=ЕНЗ
Затем АЕ равпа ЕГ и НЕ равпа EZ; значит, прямоугольник между AZ
и ZT равен прямоугольнику между All и НА.
Л/.ЙГ-^ДННА
Если жо прямоугольник между крайними равен прямоугольнику между
средними, то четыре прямых составляют пропорцию; значит, ZA так
относится к ДП, как All к ZT.
za = ан •
ан zr
Но ZA относится к АН, как ZT к ГВ и как ВА к АП,
Za zr = BA
ап гв "ан •
462
КОММЕНТАРИИ
так как в треугольнике ZAH проведены ГВ и ЛВ параллельно ЛИ
и AZ. Влачит, ВЛ. к АН, как АН к FZ, или ГХ к Г.В.
ВЛ _ Л1£ Г7.
ЛН "" ГВ'
Таким образом, АП. u I’Z будут средними пропорциональным и
для ЛВ и ВГ, что и требовалось найти.
Р е in е н и е Ф и л о и а В и а а и т и некого
(1 к и и га «В е I о р о i с а»)
Пусть липни, к которым требуется найти две средние пропорцио-
нальные, будут ЛВ и В Г (рис. 8).
зоваии при В прямой угол; затем,
EZ. Я утверждаю, что ЛЛ и
для АВ и В Г.
’асноложим их так, чтобы они обра-
проведя прямую ЛГ, опишем полу-
окружность Л ВЕГ и проведем АЛ
перпендикулярно к ВА и FZ пер-
пендикулярно к ВГ. К точке В при-
ложим движущуюся линейку, кото-
рая пересекла бы АД и TZ, и будем
вращать ее около В до тех пор, пока
расстояние ВД пе станет равным
расстоянию EZ, то есть расстоя-
нию между точками пересечения
линейки с окружностью круга и
прямой TZ. Представим, что ли-
нейка занимает положение ABEZ,
причем, как уже сказано, ЛВ раина
TZ будут средними пропорциональными
Действительно, представим себе ДА и Z1' продолженными до пере-
сечения в точке 0. Ясно, что вследствие параллельности ВА и Z0
угол при точке 0 будет прямым, и окружность ЛЕГ при своем продол-
жении пройдет и через точку 0. Теперь, поскольку ЛВ равпа EZ и,
следовательно, прямоугольник между ЕД и ДВ равен прямоугольнику
между BZ и ZE,
но прямоугольник между ЕЛ, ДВ равеп прямоугольнику между 0Л,
ДА,
ЕД-ДВ-НЛ-ДЛ
ибо каждый из этих прямоугольников равен кнадрату иа касательной
к окружности, проведенной из точки А. Точно так же. прямоугольник
между BZ и ZE равеп прямоугольнику между 0Z и ZT,
BZ-ZH^HZ-Zl’
так как каждый из этих прямоутолышков точно так же будет равен
квадрату на касательной из точки Z; отсюда следует, что прямоугольник
между 0Д н ЛЛ равен прямоугольнику между 0Z и ZF
®Д.ДА=О2-2Г
и, значит, Д0 относится к 0Z, как TZ к ДА
ЛО FZ
~ АЛ
и как 0Д относится к 0Z, так и ВГ к TZ и ДА к АВ,
ел вг да
ez rz ab
О ШАРЕ И ЦИЛИНДРЕ
4(>Л
В г
7-2
так как и треугольнике A8Z прямые В Г и ВА проведены параллельно
А© и (-JZ. Значит, ВГ относится к TZ, как PZ к АЛ и как ДА к АВ,
rz ДА
АЛ АВ
что и треиовалось доказать.
Должно наметить, что :>то построение почти сов ершен л о тождественно с: лостро!*-
писм Герока. Действительно, прямоугольник В0 будет тем же самым прямоугольником,
который берется и н построении Герона; то же можно сказать и о продолженных сторо-
нах 0А и НГ и дни гнущейся около В линейке. От героповского рассмат[>ипаемое построе-
ние отличается только тем, что а первом случае мы двигаем линейку около В, вока прове-
денные от середины Л Г (то есть точки К) прямые не дадут в пересечениях с 0Л и 07.
равных отрезков КД н KZ; в рассматриваемом жо построении — до тех пор, пока ДВ
не станет равным EZ. Таким образом, оба построения дают одни и тот жо результат,
но ф1Ь’101|01>ст;ое построение; является более удобным для практики; д<й!стпителы1О, гораздо-
проще добиться рапеиетва ЛВ и EZ (для чего достаточно разделить линейку А 7. па неко-
торое число ирилежапгнх друг к другу равных отрезков), чем устанавливать при помощи
циркуля*) равенгтно липин КЛ и KZ.
Р е hi с н и о А п о л л о н и я
Пусть прямые, для которых, требуется
циональпые, будут ВА и АГ, образующие
Из центра В радиусом АГ опишем дугу К ©А.
Затем и» центра 1’ радиусом АВ опишем дугу
M0N; пусть опа пересечет К ©А в точке 0;
проведем соединяющие прямые ©A, 8В и
©Г; тогда В Г будет прямоугольником и ©А
его диагональю. Разделим ©А пополам в точ-
ке Е и опишем из центра Е окружность,
пересекающую продолжения прямых АВ
и АГ в точках А, Е таким образом,, чтобы А
и Е были на одной прямой с 0; этого можно
добиться, если около точки 8 двигать линей-
ку, пересекающую АД и АЕ, до тех пор,
пока прямые, проведенные из точки Е до А
и Е, нс будут равны друг другу.
Добившись этого, мы получим искомое решение, так как
построение тождественно с данными Героном и Филином,
применить то же самое доказательство.
пое
и в
этом случае можно будет
найти две средние пропор-
при точке А прямой угол.-
описан-
так что
Р е г.п е л п с Д и о к л а в к и и г е «О к а у с т и к а х»
Проведем в круге два взаимно перпендикулярных диаметра
АВ и ГА, по обе стороны от точки В отложим две равные дуги ЕВ
и BZ, через точку Z проведем ZII параллельно АВ и соединим точки А
и Е прямой. Я утверждаю, что Z1I и 1IA будут двумя средними пропор-
циональными для ГII и II8.
Проведем через Е прямую ЕК, параллельную АВ; тогда ЕК
равна ZH и КГ равна НА; это будет очевидным, если соединить А
прямыми с Е и Z; в самом деле, углы ГАЕ, ZAA равны, и при точках К
и Н будут прямые углы; тогда вследствие равенства АЕ nAZ все стороны
•) Интересно отмстить греческий термин дли циркуля xaQxivog-paK. По-ьпдимому. первые
циркули были с изогнутыми ножками наподобие нашего кронциркуля.
464
КОММЕНТАРИИ
и углы одного треугольника будут равны соответствующим сторонам
и углам другого, а значит, будут равны и остатки ГК и НД. Теперь,
так как ЛК относится к КЕ, как ДН к Н0
ЛК
КВ
АК
КВ
и ЛК к КЕ, как ЕК к КГ
вк
пе _ кг
(ибо ЕК будет сродной пропорциональной
для ДК, КГ), то, значит, ДК откосится к
КЕ, как ЕК к КГ и как ДП к Кб.
КК ЛИ
кг _ МО
Далее, ДК равна ГН, КЕ равна ZH,
КГ равпа 11Д; значит, ГН относитсм к IIZ,
как ZH к ПД и как All' к Н0.
Рис. 10.
ГН
HZ
!ZH ДН
нд не
Если с каждой стороны В взять равные дуги MB, BN, через Nпровести
N S параллельно АВ и соединить Д и М прямом, то совершенно так
же NE и ЕД будут средними пропорциональными между ГЕ и ЕО.
Если мы подобным образом между В и Д проведем достаточно большое
число непрерывно расположенных параллельных прямых, затем отло-
жим от В к Г дуги, соответственно равные отсекаемым этими прямыми
от точки В дугам, и полученные концы соединим с Д прямыми вроде
ДЕ и Д М, то эти прямые пересекут соответствующие им между В и Д
параллели в некоторых точках (в нашем примере в 0 и О); если соеди-
нить эти точки по линейке прямыми, то мы получим некоторую начер-
ченную в круге линию, обладающую тем свойством, что если через любую
ее точку провести прямую, параллель-
ную ЛВ, до пересечения с окружностью,
то эта проведенная прямая и отсекае-
мый ею па диаметре ио направлению
к Д отрезок будут средними пропорцио-
нальными для другого отрезка диаметра
по направлению к Г и той части прове-
денной прямой, которая заключена меж-
ду диаметром ГД и построенной в круге
лйпией.
После этой предварительной под-
готовки возьмем две прямые, для ко-
торых требуется отыскать две средние
пропорциональные; пусть это будут А и
В. Возьмем круг с двумя взаимно перпен-
дикулярными диаметрами и начертим в
нем при помощи последовательных точек упомянутую кривую A0Z.
Сделаем, чтобы отношение ГИ к НК было равно отношению А к В.
затем продолжим соединяющую прямую ГК до пересечения с построен-
ной линией; пусть точка пересечения будет 0. Через 0 проведем ЛМ
параллельно EZ; тогда, согласно вышеизложенному, МЛ и ЛД будут
средними пропорциональными для ГЛ и Л0.
гл
лм
ЛМ ЛА
лд ’ л«
О ШАРЕ И ЦИЛИНДРЕ
465
Затем, поскольку ГА относится к А0, как ГН к ПК
iv._ _ г]!
де ок
и ГН к НК, как Л к В,
г и = _А
нк-- в"
то если мы между А и В вставим прямые N и5 так, чтобы все эти прямые
были соответственно пропорциональны ГЛ, z\M, АД, Л®,
А____N S ~ В
ГЛ “ ЛМ ЛЛ ЛР
то N, Е и будут средними пропорциональными для А и В, что и тре-
бовалось отыскать.
Решение Паппа но «Введении и механик у»
<к п и г а VIII, 26 >
Папп поставил задачу; определить куб, который находился бы
в данном отношении к другому кубу. Данный им способ доказатель-
ства применим и к рассматриваемой пами задаче, так как вполне
очевидно, что, решив его задачу, мы одновременно найдем решение
и предложенной нам; ибо если для двух данных прямых будет
найдена вторая пз нужных нам средних пропорциональных, то сей-
час же будет известна н третья. Сам он дословно говорит следую-
щее: опишем полукруг АВГ, из центра А опустим перпендикуляр ЛВ
и около точки А будем двигать линейку так, чтобы один ее конец лежал
неподвижно на закрепленном в точ-
ке А гвоздике, а другой переме-
щался между точками В и Г, дви-
гаясь вокруг гвоздя А как центра.
Сделавши это, поставим себе целью
отыскать два куба, находящиеся
между собой в заданном отношении.
Пусть это отношение будет равнять-
ся отношению прямых В А и ДЕ;
проведя соединяющую прямую ГЕ,
продолжим ее до точки Z. Судом за-
тем двигать между В и Г линейку, по-
ка часть ее между прямыми ZE, ЕВ
не сделается равной части, заклю-
ченной между прямой ВЕ и окруж-
ностью ВК Г. Если двигать соответст-
венно линейку, то этого мы легко до-
стигнем после нескольких попыток.
Пусть это будет сделано, и линейка займет положение ЛК, так что
отрезки 110 и (т)К будут равными. Я утверждаю, что куб па ВД будет
иметь к кубу на Д0 отношение, равное заданному, то есть отноше-
нию ВД к ДЕ.
Вообразим, что паша окружность описана полностью; соединяю-
щую линию КД продолжим до точки Л, после чего проведем ЛИ. Нос-
30 Архимед
466
КОММЕНТАРИИ
ледняя будет параллельна ВД, так как Кб равно Н®, и КД равно ДА.
Проведем ЛА и Л Г. Так как угол АДГ прямой (как вписанный в полу-
круге) и ЛМперпендикулярна к АГ, то квадрат на ЛМ к квадрату на
AM относится, как ГМк МЛ и как квадрат на AM к квадрату на МП.
ЛМ2 = ГМ АМ8
AM8 МА МН4
Прибавим *) к обеим частям последнего равенства отношение А М
к МП. Тогда отношение, составленное из ГМ к МЛ и AM к МП, то
есть отношение ГМ к МН, будет тем же самым, что и отношение, сос-
тавленное нз (отношений) квадрата на ЛМ к квадрату па МН и (отно-
шения) AM к МП. Но отношение, составленное из (отношения) квад-
рата па AM к квадрату на МН и (отношения) AM к МН, будет равно
отношению куба на AM к кубу на МН.
ГМ ЛМ8
мн М11»
Но ГМ относится к МН, как ГД к ДЕ,
гм _ га
МН ДЕ
и AM относится к МН, как ЛД к Д0;
АМ АД
мн де
следовательно, отношение ВД к ДЕ **), то есть заданное, будет равно
отношению куба на ВЛ к кубу на ДО.
Должно обратить внимание па то, что это построение совпадает
с предложенным Дноклом, отгтчаясь от него только тем, что Диокл
при помощи ряда последовательных точек описывает некоторую распо-
ложенную между А и В кривую линию, на которой в ее пересечении
с продолжением ГЕ берется точка II, а в рассматриваемом построении II
находится при помощи линейки ЛК, движущейся около Л. А что точка
II будет одной и той же, найдем ли мы ее при помощи линейки, как в
данном построении, или же но способу Днокла, в этом мы можем убе-
диться следующим образом. Продолжив МН до N, проводом прямую
К.\. Поскольку К® равна 0Н и UN параллельна ©В, то и К В будет
равна EN. Линия ЗВ будет общим перпендикуляром, так как KN
делится пополам прямой, проведенной через центр, и они встречаются
под прямым углом. Таким образом, в треугольниках К<УЕ и E0A
одно основание равно другому, а вследствие этого и дуга КВ равна
В.\. Отсюда вытекает, что точка Н находится на кривой Диокла, и рас-
суждения остаются теми же самыми. Действительно, Диокл сказал, что
ГМ относится к MN, как MN к МА и как АМ к МП.
гм МЛ АМ
мм" мл" мн
По NM равно МА, так как диаметр пересекает NA под прямым
углом; значит, ГМ относится к МА как АМ к МА и как АМ к Л1Н.
’ _£?[ ЛМ am
МЛ .ИА ‘ МН
*) Ну-,кп<> помнить, что на языке греческой математики прибавить отношение — значит
на пего помножить.
•*) вд— ал- га «эк радиусы.
О ШАРЕ И ЦИЛИНДРЕ
46'/
Таким образом, для ГМ и МН средними пропорциональными будут
ДМ и МЛ. Но ГМ к МП, кап ГД к ДЕ
ГМ ГА
мп ‘ лк
и ГМ относится к МЛ как ЛМ к МН и как Гг\ к ДО.
гм .. am _ ГА
мл ми ле
Следовательно, для двух прямых ГЛ и ДЕ второй пропорциональной
будет та самая ДО, которую нашел и Папп.
Р е иг е н и е Спора
Пусть даны две неравные прямые ЛВ, В Г; требуется найти, для
АВ, В Г две средние пропорциональные в непрерывной пропорции.
Проведем из В прямую ДВЕ под прямым углом к АВ, затем опишем
полукруг ДЛЕ с центром В и радиусом ВА; прямую, соединяющую
точки Е и Г, продолжим до Z и че-
кв
ВЦ
рез Д проведем некоторую прямую
так, чтобы НО равнялась ОК (это
действительно всегда можно сде-
лать). Затем из точек Н и К опу-
стим па ЛЕ перпендикуляры НЛ и
KNM. Итак, поскольку мы имеем,
что КО относится к ОН, как МВ
к ВЛ,
МВ
ВЛ
и КО равна ОН, то, значит, и МВ у 13
равна ВЛ, а следовательно, и оста-
ток ME равен ЛД, и вся ДМ рав-
на ЛЕ. Отсюда следует, что МД относится к АЛ, как ЛЕ к ЕМ.
МД ЛЕ
АЛ ЕМ
Но МД относится к АЛ, как КМ к НЛ, а ЛЕ относится к ЕМ, как КМ
к ПЛ;
МД КМ ЛЕ
ЛЛ ” НЛ им
затем, так как ДМ. относится к МК, как КМ к ME, то значит, ДМ
относится к ME, как квадрат иа ДМ к квадрату на МК, или как квад-
рат на ДВ к квадрату на ВО, или как квадрат на АВ к квадрату на ВО,
ДМ _ Л АГ- _ Л В? л в*
ME МК« ” ВН*" веа
так как ДВ равна ВА.
Затем, поскольку МД относится к АВ, как ЛЕ к ЕВ, МД к ДВ,
как КМ к ОВ, и ЛЕ к ЕВ, как НЛ к ГВ, то, значит, КМ относится
к ОВ, как НЛ к ГВ,
КМ НЛ
«В ' ГВ
и после перестановки КМ относится к НА, как ОВ к ГВ.
км ев .......
НА ' ГВ . < . .....
30*
4(58
КОММЕНТАРИИ
•i _ Но КМ относится к НА, как МД к ДА и как ДМ к ME,
км _ мх дм
НА — ЛЛ МЕ
затем, как мы видели выше, ДМ относится к МЕ, как квадрат на АВ
к квадрату на 0В,
ДМ _ два
МЕ “ 6В2
и, значит, квадрат на АВ к квадрату па 0В относится, как К М к НА.
AB8 _ г км ] _ во
овв _ I на J ~ вг
Возьмем среднюю пропорциональную 3 между 8В и ВГ; так как
,. . квадрат на АВ относится к квадрату на 0В, как 0В к ВГ, квадрат на
АВ к квадрату на В0 имеет отношение, равное двойному отношению
АВ к В0,
ABB / ЛВ , , АВ у
ВО» — (. ВО Д ВО )
и отношение ©В к ВГ равно двойному отношению 0 В к 3,
ев _ ев он
ВГ ' S в
то, значит, АВ относится к 0В, как В0 к 3.
« Но 8В относится к 3, как Е к ВГ,
ев в ’
s " вг
и, следовательно, ЛВ относится к В0, как 0В к 3 к как 3 к ВГ.
ав _ ев _ s
ве в _ вг ' ь1
Это построение будет, очевидно, ]
тем же самым, которое описали Папп ' 1
и Диокл. \
Решением спех и а \
Пусть будут две прямые А, Е и А|
требуется для Л, Е найти две средние / X.
пропорциональные. /
Пусть это сделано, и соответствую- /
щие прямые будут В, Г; Л относится j 1-------------i-----------7,
к В, как В к Г и как Г к Е.
После этого отложим где-пибудь *) Рис. 14.
прямую ЛН, ограниченную в точке Д,
затем к Л приложим линию AZ, равную Г, проведем под прямым
углом. 8Z и отложим Z0, равную В. Поскольку три прямые А, В, Г
составляют пропорцию, то прямоугольник между А и Г равен
квадрату па В.
Таким образом, прямоугольник между А и Г, то есть на AZ, будет
равен квадрату на В, или квадрату па Z0; следовательно, точка 0
•) Характерное иырадание: cxxetc&to отложим положением; то есть без ©того допол-
нении xetotfw милеет пониматься и и смысле нашего льо&ьмем» прямую, определенную только по вели-
чине. но ис Заданную нили-гкеннсм.
О ШАРЕ И ЦИЛИНДРЕ
469
•: .’ будет лежать на проходящей через Д параболе*). Проведем параллели
0К и ДК. Поскольку дан прямоугольник между В, Г (он равен пря-
моугольнику между А, Е **), то будет известен и прямоугольник между
К0, 0Z. Следовательно, точка 8 будет находиться па гиперболе, пос-
троенной на асимптотах КД и AZ***). Таким образом, точка 0 дана,
• а следовательно, будет дана и точка Z.
Построение производится так. Пусть данные прямые будут А
и Е; отложим ограниченную в точке Д прямую ДН и через точку Д про-
водом параболу с осью ДН и параметром А; пустьпр сведенные под пря-
мым угломкДН линии будут квадрировать****) площади, построенные
на А и имеющие своей шириной отсекаемые ими отрезки на оси ДН,
начиная от точки Д. Построим эту параболу; пусть опа будет Д0, а
ДК будет перпендикулярна к ДН. Затем па асимптотах КД и AZ пост-
роим гиперболу так, чтобы проведенные (иатауоргтаь) от нее параллельно
КД и &Z прямые образовали площадь, равную прямоугольнику между
А, Е*****). Эта гипербола пересечет параболу; пусть точка пересечения
будет 0. Проведем перпендикуляры 8К и 0Z. Так как квадрат па Z0
. равен прямоугольнику между А и AZ,
Z65 = A.AZ . ....
то А относится к Z0, как 0Z к ZA.
A 0Z . .
Z® ZA ‘ ......
Далее, поскольку прямоугольник между А и Е равен прямоугольнику
между 0Z, ZA,
A-B = ez-ZA
то получится, что как А относится к Z0, так и ZA к Е.
а _ ял -*' ’
zo к
По А относится к Z0, как Z0 к ZA, и как ZA к Е.
А _ Z0 __ za^ :
"да za “"is
) Если положим А7.=а, ВЯ—Ц И А—2р. то уравнение ЭТОЙ параболы будет:
уВ=2р.т.
*») Этот рсаультат мшкио легко получить следующим способом. Возьмем пропорцию
А ; IfeB : Г=Г : В.
Мы имеем:
В2—-А-Г. Г2=В-Е.
отсюда
ВЗ-1’а=А-Е-В-Г,
«
В-Г-А-Е.
••*) Если положим А®-—а. В=Ь, то уравнение этой гиперболы будет;
ту=аЬ-
•**•) бъгч/дтАсооал’. Ото значит, что линия GZ и квадрате должна равняться площади прямо-
угольника с шириной AZ=^ и длиной А=2р. Это выражение равносильно нашему уравнению пара-
болы ?/2— 2pJC. ™
••••♦) Мы сказали бы: проиавсдение ос координат AZ=x и Z6-=y равнялось бы А-Е или аЪ, что
равносильно уравнению гиперболы; -ту=аЬ. . .
470
КОММЕНТАРИИ
Положим В равным 0Z, Г равным AZ; тогда’’А относится к В, как
В к Г и как Г к Е.
А В Г
В Г К
Таким образом, А, В, Г, Е составляют непрерывную пропорцию, что
и требовалось сделать.
И ным способе м
Пусть две заданные прямые АВ, ВГ будут перпендикулярны друг
к другу. Пусть для пих средние пропорциональные будут АВ и ВЕ,
так что ГВ относится к ВД, как I3A к ВЕ и как ВЕ к ВА.
гв _ на в к
ВА ВЕ — НА
Проведем перпендикуляры AZ и EZ. Так как ГВ относится [к ВД,
как ДВ к ВЕ,
г в дв
В А ВЕ
то, значит, прямоугольник между ГВ и ВЕ, то сеть прямоугольник
между одной из заданных линий и ВЕ, будет равен квадрату на ВД,
или квадрату на EZ.
ГВ ВЕBA2-= EZa
Так как прямоугольник между заданной линией и ВЕ равен квад-
рату на EZ, то точка Z находится на параболе, построенной на оси
ВЕ. Затем, так как АВ относится к ВЕ,
как ВЕ к ВД,
ав _ ВЕ
BH - ВА
то прямоугольник между АВ и ВЛ. то
есть другой заданной линией и ВД. бу-
дет ранен квадрату па ЕВ юти на AZ;
ав- нд^ кв2 = AZ2
значит, Z находится на параболе с осью ВД.
Н о опа находится и па другой параболе с
осью ВЕ. значит, точка Z известна. Затем,
так как Z-Д и ZE перпендикулярны, то будут известны и точ-
ки Д с Е.
Построение производится так: пусть две заданные прямые АВ
и ВГ будут взаимно перпендикулярны; продолжим их из точки В до
бесконечности. На оси ВЕ построим параболу так, чтобы ее опущенные
на ВЕ ординаты квадрировались ла ВГ *). Затем на оси ДВ строим
параболу так, чтобы ее ординаты квадрировались па АВ **). Обе эти
параболы пересекут друг друга; пусть точка их пересечения будет Z.
Проведем из Z перпендикуляры ZA и ZE. Так как в одной параболе
*) Это выражение равносильно формуле ZE* —ВЕ-ВГ. или уравнению х'=ВГ-р.
**) Строим параболу ZA'-—АВ ВА п:гн у: = лВ-х.
О ШАРЕ И ЦИЛИНДРЕ
47J
проведена ордината ZE, то ость АВ, то, значит, прямоугольник между
ГВ и ВЕ равеп квадрату па 13Д
гв-ве = вд£
и поэтому ГВ относится к ВД как ДВ к ВЕ. Но ДВ относится к ВЕ,
как ГВ к ВД и, следовательно, ГВ относится к ВА, как ВД к ВЕ
и как ЕВ к ВА,
гв вд = ER
ВА ’’ ВЕ - ЛА
что и требовалось получить.
Строится же парабола при помощи «диабета» изобретенного
нашим учителем милетским мохаппком Исидором и описанного им
в составленном нм комментарии к работе Геропа «О построении
сводов».
Решение Л рх и т а в изложении Е вдеиа
Пусть (рис. 16) заданные две прямые будут АД и Г; требуется для
АЛ и Г найти две средние пропорциональные.
Иа большой из них АД опишем круг ABAZ и вставим в него пря-
мую ЛВ, ранную Г; пусть опа, будучи продолжена, пересечет в точке И
касательную к кругу, прове-
денную из точки Л. Проведем
BEZ, параллельную ИДО, и во-
образим на полукруге АВД
прямой полуцилиндр, а на АД
перпендикулярный к АВД по-
лукруг. расположенный на
прямоугольнике осевого сече-
ния полуцилиндра. Этот полу-
круг при своем вращении от А
к В около неподвижною кон-
ца Л диаметра будет пересе-
кать цилиндрическую поверх-
ность и, таким образом, вычер-
тит иа пой некоторую линию.
Треугольник АИД будем вра-
щать около неподвижной пря-
мой АЛ в сторону, противопо-
ложную движению полукруга;
тогда этот треугольник образу-
ет коническую поверхность с
образующей АП, которая при
вращении пересечет начерчен-
ную па цилиндре кривую в не-
которой точке; одновременно В опишет на конической поверхности
полукруг. Пусть в пересечении вышеупомянутых линий движущийся
полукруг занимает положение Д'КА, вращающийся треугольник
находится в положении ДАЛ, причем точкой упомянутого пересечения
будет К; далее, пусть В .VIZ будет описанной точкой В полукруг,
a BZ — общая линии его пересечения с кругом BAZA. Проведем через К
перпендикуляр к плоскости полукруга ВАД; конец этого перпендику-
ляра попадет на окружность круга АВД, так как цилиндр будет прямым.
472
КОММЕНТАРИИ
Пусть этот перпендикуляр будет KI, пусть далее соединяющая прямая
А1 пересечет BZ в точке 0, а образующая конуса АЛ пересечет полу-
круг BMZ в точке М. Проведем прямые КД', ML М0. Так как каж-
дый из полукругов Д'КАи BMZ перпендикулярен к расположенной под
ними плоскости, то значит, и общее сечепие М© будет перпендикулярно
к плоскости круга ВАД; следовательно, М© будет перпендикулярна
и к BZ.
Таким образом, прямоугольник между 0В и 0Z, или прямоуголь-
ник между ©А и 0L равен квадрату па М0;
ев-ez = ол-ш — и®2
следовательно, треугольник AMI будет подобен каждому из треуголь-
ников МТ© и MA0. Далее, угол 1МЛ прямой; прямым будет также
и угол А'КА; значит, КД' и Ml будут параллельны, и получится про-
порция: Д'А относится к АК, как КА к А1 н как 1Л к AMJ
Л'А _ К_А_ ТА
АК _ [AI °\лм
вследствие подобия треугольников. Таким образом, четыре прямые
Д'Л, АК, Al, АМ составляют непрерывную пропорцию. Затем АМ
равна Г, так как она равпа АВ; значит, для заданных прямых АД
и Г найдены дне средние пропорциональные АК и AL
Решение Эратосфена.
Царю Птоломею Эратосфен желает радости!
Рассказывают, что один из древних трагиков вывел на сцену Миноса,
заботящегося о построении могилы для Главка. Когда он узнал, что
эта могила будет иметь во всех направлениях по сто футов, то сказал:
И зил слишком малый объем ты гроба царского;
Двойной пусть будет он; так, красоты лс трогая,
Удвой скорее гроба каждое; членение.
Ясно, что он ошибся, так как после удвоения сторон, площадь уве-
личивается в четыре раза, а объем в восемь раз. Поэтому гсомстры
и разыскивали, каким образом, удвоить данный объем, сохраняя его
в той же самой форме. Эта задача и получила название удвоения куба,
так как ояи, предполагая некоторый куб данным, старались его удво-
ить. В течение долгого времени эта задача затрудняла всех математиков;
первым Гиппократ Хиосский нашел, что если для двух данных линий,
из которых большая равпа удвоенной меныпен, найти две средние
пропорциональные, составляющие с ними непрерывную пропорцию, то
тем самым будет достигнуто и удвоепие куба, так что его трудная зада-
ча превратилась в другую не лш’че.
Немного времени спустя некоторые делийцы, пытаясь, согласно обе-
ту, удвоить жертвенник, пришли, как рассказывают, к тем же самым
трудностям и в послании к геометрам, работавшим у Платонв в Акаде-
мии просили дать им решение. Те трудолюбиво принялись за это дело
и стали искать, каким образом для двух данных прямых найти две
средние пропорциональные: говорят, что Архит Таронтский получил
решение при помощи полуцилиндров, а Евдокс при помощи так
называемых выгнутых (xapnukov) линий*). Однако вышло, что
*) Под атим названием подразумевались кривые, получаемые сечением кривых поверхно-
стей, простейшими пз которых являются конические сечения.
О ШАРЕ И ЦИЛИНДРЕ
473
они доказали лишь возможность такого построения, выполнить же
его па самом деле и дать практический способ не смогли, если нс счи-
тать короткого способа Мспсхма, да и то затруднительного. Нами же
придуман легкий способ решения при помощи инструментов; пользу-
ясь им, дли двух данных прямых мы можем найти нс только две, но
и сколько угодно средних пропорциональных. После этого мы сможем
вообще любой заданный ограни-
ченный параллелограммами объем
превращать в куб. одну форму
преобразовывать в другую, делать
подобной и увеличивать, сохра-
няя подобие, и жертвенники и
храмы. Также меры жидкостей и
сыпучих тел (как, например, ме-
димп и метрет) мы сможем пре-
вращать в куб и по стороне послед-
Рис. 17а.
него измерять вместимость раз-
личных сосудов. Это .изобретение
будет полезно и для желающих
увеличить размеры катапульт и камнеметов, так как для увеличения
длины броска нужно пропорционально увеличить все — и ширину, и ве-
личину, и отверстия, и втулки, и вставляемые тяжи, а этого нельзя сде-
лать без нахождения средпих пропорциональных. Доказательство
способа, а' также устрой-
ство упомянутого инстру-
мента, я описал тебе ниже.
Пусть ЛЕ и ДО
(рис. 17а) будут дне за-
данные неравные прямые,
для которых требуется
пайти две средние пропор-
циональные в непрерыв-
ной пропорции. Восставим
перпендикуляр ЛЕ к не-
которой прямой ЕО, по-
строим на ЕО три после-
довательных одинаковых прямоугольника AZ, ZT, 10 и проведем их
диаметры AZ, ЛН, 10; последние будут параллельны.
Затем, сохраняя па месте средний прямоугольник Z1, надвинем па
него AZ и задвинем под него 10, как это изображено па рис. 176,
и будем передвигать их, пока точки А, В, Г, Д пе окажутся ла одной
прямой. Проведем через точки А, В, Г, Д прямую; пусть она пересечет-
ся в точке К с продолжением ЕЁ). Тогда АК относится к КВ, как
ЕК к KZ,
АК ЕК
КВ - KZ
вследствие параллелизма прямых ЛЕ к ZB и ЛК относится к КВ,
как ZK к КН,
АЕ АК _ ZK
ZB _ кв _ КП
вследствие параллелизма прямых AZ, ВП. Следовательно, АК отно-
КОММЕНТАРИИ
сится it КВ, или ЕК к KZ, как KZ к КП.
А К кк KZ
КВ — KZ кн
Затем, так как ВК. относится к КГ, как ZK к КН,
вк ZK
кг ~ кн
вследствие параллелизма BZ и ГН, и ВК относится к КГ, как НК к К Н,
вк нк
кг _ к«
вследствие параллелизма ВП и Г©, то, значит, ВК относится к КГ
как ZK к КИ и как* ЛК к КС).
нк _ ZK нк
кг кн “ ко
Но ZK относится к КП, как ЕК к KZ, л, значит, ЕК относится
к KZ, как ZK к КН или НК к КС-).
КК ZK _нк_
KZ КН К0
Но ЕК относится к KZ, как АЕ к BZ,
ЕК АЕ
KZ BZ
ZK к КП, как BZ к ГН, и НК к К© как ГН к А©
ZK = _BZ_ нк гп
КН — ГН ’ кё" АН
и, значит, АЕ относится к BZ, как BZ к ГП и как ГП к А©.
АВ BZ _ ГП
BZ ГН — до
Таким образом, для АЕ и А© найдены две средние пропорциональ-
ные BZ и ГП.
Теперь геометрически задача является решенной. Для нахождения
двух средних пропорциональных ла практике при помощи инструмен-
тов устроим из дерева или из слоновой кости, или же из меди, пластин-
ку, которая складывалась бы из трех тончайших одинаковых табличек;
средняя из этих табличек закреплена неподвижно, а две крайние могут
двигаться в желобках. Размеры и пропорции этих табличек могут быть
какими угодно, так как доказательство производится дли всех размеров
совершенно одинаково; для получения возможно большей точности
при нахождении линий нужно постараться устроить так, чтобы все
таблички при сближении оставались параллельными, не образовывали
между собой промежутков и равномерно налегали друг на друга.
Па даре, принесенном по обету, инструмент сделан из меди и укре-
плен свинцом мод самой канителью колонны, мод ним же помещены
краткое доказательство, фигура и надпись.
Я. сообщу тебе и это для того, чтобы у тебя было и то, что находится
на принесенном по обету даре. Из обеих фигур па колонне нарисована
только вторая.
«Для двух данных прямых найти две средние пропорциональные
в непрерывной пропорции. Пусть будут даны прямые АЕ и А©. Я свожу
вместе таблички на инструменте, пока точки А, В, Г, А пе окажутся
па одной прямой; вообразим, что они при этом расноложатси, как на
фигуре. В таком случаи как АК к КВ, так в параллелях АЕ, BZ будет
О ШАРЕ И ЦИЛИНДРЕ
475
и ЕК к KZ, а в параллелях AZ, ВП так будет и ZK к КН. Значит, как
ЕК к KZ, так и KZ к КП. Но как будут друг к другу последние, так
будут и АЕ к BZ и BZ к ГН. Подобным же образом докажем, что
как ZB к ГН, так и ГН к ДО; следовательно, АЕ, BZ, ГН, /Х0состав-
ляют пропорцию. Таким образом, для двух данных линий найдены две
средние пропорциональные. Если же данные линии пе будут равпы
АЕ и Д0, то, сделавши их пропорциональными АЕ и А0, найдем две
средние для последних и перенесем иа первые, выполнив таким обра-
зом задание. Если ?кс требуется найти большее число средних пропор-
циональных, то в приборе число табличек нужно взять на одну больше,
чем число отыскиваемых средних; доказательство останется тем же
самым».
Если из малого куба днепнюй замышляешь устроить,
Друг, или данный объем к форме другой припасти,
Чтоб хорошо удалось тебе это, надумал ли погреб
Ты измерять, или ров, или широкую пасть
Глуби колодца, возьми на смежных концами пластинках
Средние лилии дне, сжатые между таблиц.
Нс прибегай для того ты к тяжелым цилиндрам Лрхита,
Конуса ты но секи, корня Мспсхма триад;
Также по надо держать с богоравным Евдоксом совета,
Выгнутых .пиний его формы не надо чертить.
С этими' ж ты. табличками тысячи средних построишь,
Двигаясь смело вперед, с мшп.шей из данных начав.
Счастлив ты, Птолемей, ты с сыном отец вечно юный.
Всем, что приятно всогда и для царей, и для муз,
Сам ты его одарил, в конце же, о Зевс, царь пебссвый,
Пусть из твоей он руки скипетр высокий возьмет.
Пусть же свершится вес это, и каждый смотрящий пусть скажет:
«Это Кирены сын выдумал Эрат<к:фоп».
Р«шени« Никомеда в книге
«О к о п х о и д а л ь п ы. х линиях»
Затем устройство прибора, служащего для той же самой цели,
описывает Никомед в составленном им сочинении о конхоидах. Этим
он, по-видимому, необычайно гордится и
очень осмеивает изобретение Эратосфена ___
как и немеханическое. и вместе с тем
лишенное геометрического смысла. Мы
присоединяем к ужо написанному и его, \ ____________
чтобы по пропустить никого ни занимав- л j у,у,Ьд
шихся этой задачей, а также и для срав- Г)" ~
пения его изобретения с. Эратосфенов ым.
Сущность его теории такова. \\V\
Представим себе две взаимно пер-
лендикулнрные линейки. АВ и ГД, сое-
диненные между собой так, чтобы они со- '•'Z
стапляли одну поверхность; пусть на ли-
нейке АВ будет бороздка с секировидным
сечением, в которой может перемещаться /’
ползупша, а на линейке ГЛ на линии,
делящей пополам ее ширину, в приле- Рис‘ ,8‘
гающей к Д части будет цилиндр, состав-
ляющий одно целое с линейкой и лишь немного возвышающийся над
ее поверхностью; затем пусть будет друган линейка EZ, имеющая
476
КОММЕНТАРИИ
на небольшом расстоянии от конца Z прорез Нг), могущий охватить
цилиндр А; в точке Е этой линейки пусть будет круглое отверстие,
в котором может поместиться ось, составляющая одно целое с пол душ-
кой, движущейся в сокировидной бороздке, которая находится на
линейке АВ. Линейку EZ насаживают прорезом НВ па цилиндр Д,
а отверстием Е на соединенную с ползушкой ось. Если взять конец К
линейки и двигать его по направлению от А к В и обратно, то точка Е
будет ное время перемещаться но линейке АВ, а прорез 118 будет дви-
гаться около цилиндра Д; во время движения средняя линия линейки
I'.Z будет постоянно проходить через
Рис. 19.
ось цилиндра А, а отрезок ЕК
линейки — сохранять свою ве-
личину. Если в точке К поме-
стить что-нибудь пишущее, то
на поверхности пачертится не-
которая линия A MN, которую
Никомед называет первой кон-
хоидальной линией; длина от-
резка ЕК называется радиусом
конхоиды, а точка Д — ее по-
люсом.
Никомед доказывает, что. одним из свойств этой линии является
то, что опа до малости близко может подойти к линейке АВ, так что
если между этой линией и линейкой АВ провести какую-нибудь прямую,
то опа всегда будет пересекать конхоиду. Первое легче уяснить па
другом чертеже. Пусть АВ (рис. 19) будет линейка, Г — полюс, АЕ —
радиус конхоиды, и ZE11 — конхоидальная- линия; проведем из Г
две прямые ГО и Г2, отрезки КО
и ль которых оудут, конечно, рав-
ными. Я утверждаю, что перпенди-
куляр Z М будет меньше перпен-
дикуляра 0N.
Действительно, так как угол
МАГ больше угла NKT, то допол-
нение МАГ первого угла до двух
прямых будет меньше такого же
дополнения NK0 второго угла.
А так как углы при М и N пря-
мые, то угол при Z будет больше
угла при О. Если построить угол
MZ Н, равный углу при 0, то К0,
илв AZ, будет иметь к 0N то же
самое отношение, что SZ к ZM.
лн
нг
Значит, ZA будет иметь к ОД1 отно-
шение, меньшее чем к ZM, а поэтому ON будет больше ZM.
Второе свойство заключается в том, что всякая прямая, проведен-
ная между АВ и кривой, обязательно пересечет кривую. Это можно
выяснить так.
Проведенная прямая будет или параллельна АВ, или нет. Пусть
сначала опа будет параллельна, как, например, ZH0 (рис. 20). Пусть
отношение ДП к ПГ равняется отношению ДЕ к некоторой прямой К.
ДЕ
к“
Радиусом К опишем из центра Г окружность; пусть она пересечет
Z1I в точке Z: проведем соединяющую прямую TZ. Тогда ДН относится
О ШАРЕ И ЦИЛИНДРЕ
477
к НГ, как ZA к ZT.
ан 2л
нг zr
Но ДН относится к НГ, или ДЕ к К, как ДЕ к TZ.
ДН _ _ДЕ_ _ ДЕ
нг _ k rz
Следовательно, ДЕ равно AZ; значит, точка Z лежит на кривой.
Пусть теперь проведенная прямая не будет параллельна АВ, по
пойдет, например, как M11N. Через 11 проведем прямую ZH, парал-
лельную ЛВ; тогда ZH пересечется с кривой, a MN и подавно.
Все это вытекает как следствие из свойств прибора, а нужное для
дальнейшего мы докажем так.
Пусть заданы угол А и находящаяся вне его точка Г; требуется
провести прямую ГН так, чтобы отрезок ее КН равнялся данной прямой.
Из точки Г опустим на ЛВ перпендикуляр Г0 и продолжим его
прямой. Из полюса Г опишем
(рис. 21); пусть Д0 будет равна данной
на линейке Л13 первую конхоидаль-
ную линию EAZ с заданным радиу-
сом Д0; согласно доказанному, она
пересечет АН. Пусть точка пересе-
чения будет Н; проведем прямую ГН,
тогда КН и будет равна заданной
прямой ДН.
Доказавши это, возьмем две взаимно перпендикулярные прямые
ГЛ и ЛА (рис. 22), для которых требуется найти две средние пропорци-
ональные в непрерывной пропорции. Дополним прямоугольник АВГЛ
и разделим каждую из АВ и ВГ в точках Л и Е пополам; соединяющую
прямую ДА продолжим, и пусть она с продолжением ГВ пересечется
в точке II; затем перпендикулярно к В Г проведем EZ и сделаем TZ
равной ЛА, проведем соединяющую прямую ZH и параллельную ей
линию Г0. Получивши угол КГ0, проведем Z0K из заданной точки Z
так, чтобы 6К равнялась АД пли TZ (что это возможно, ясно из свойств
конхоиды). Тонер г» соединяющую прямую КЛ продолжим, и пусть она
в точке М пересечет продолжение АВ. Я утверждаю, что ГЛ к КГ, как
КГ к МА и как МА к АЛ.
гл = кг _мд_
КГ — МА ' "АЛ
Так как В Г разделена в Е пополам и к ней прибавлена КГ, то,
значит, прямоугольник между ВК и КГ вместе с квадратом па ГЕ
равен квадрату на ЕК.
ВК КГ ГК= = ЕКа
478
КОММЕНТАРИИ.
Прибавим к обеим частям квадрат на EZ; тогда прямоугольник
между ВК. н КГ вместе с квадратами на ГЕ и EZ, равными квадрату на
TZ, будет равен квадратам на КЕ и EZ, равным квадрату ла KZ.
ПК КГ ГЕ3 EZ3-= КЕ*-|- EZ3-= KZ3
Затем, поскольку МА относится к АВ, или МЛ к ЛК, как ВГ к ГК,
_МЛ мл вг_
АН ЛК Т’К
то, значит, МЛ относится к АВ, как В Г к ГК.
МА ВГ
АН “ ГК
Теперь АЛ будет половиной ЛВ, а ГН удвоенной ВГ (так как Л Г
в два раза больше ДВ); тогда МЛ относится к АД, как НГ к ГК.
МА _ НГ
АД ГК
Но НГ относится к ГК, как Z0 к 0К,
иг Z0
гк вк
вследствие параллельности HZ и Г0; поэтому, «присоединяя», (имеем)
МА и АЛ вместе относятся к ДА, как Z0 и 0К вместе к К0,
МЛ - АЛ ZO 1 «к
ДА Кв
то есть МД относится к ДА, как ZK к К0.
МЛ ZK
ДА' -К0
Но, но предположению, ЛД равна TZ, равпа 0К; значит, и МД
равна ZK, ы квадрат на МД равен квадрату на ZK. Теперь квадрат на
МЛ равен прямоугольнику между В М и МЛ вместе с квадратом па ДА
МЛ3 - ВМ-МА | АЛ*
и, по доказанному, квадрат на ZK равен прямоугольнику между ВК
и КГ вместе с квадратом па IZ.
Zi<3- Вк кг-j-rz2
Затем, согласно предположению, АД равна TZ; значит, и прямо-
угольник между ВМ и МА равен прямоугольнику между ВК и КГ.
вм-ма-вк кг
Таким образом, МВ относится к БК, как КГ к ЛМ,
мв кг
вк лм
по ВМ относится к ВК, пак ГЛ к ГК,
ВМ _ ГЛ
вк гк
и, значит, ГЛ к ГК относится, как ГК к АМ.
гл __ гк ’
ГК AM
И также ГЛ к ГК относится, как МА к АЛ,
ГЛ МА
ГК “ ЛА
О ШАРЕ 11 ЦИЛИНДРЕ
479
следопатслъно, АГ относится к ГК, как ГК к AM, как AM к ЛА.
ЛГ_ _ ГК = AM
ГК " лм АЛ
На этом кончается текст Евтокия, касающийся задачи о нахождении двух средних
пропорциональных, к которой сводится задача об удвоении куба. Остается сказать не-
сколько слон об истории этой задачи.
Уже древние египтяне знали, каким образом можно увеличить вдвое площадь
.'Побои фигуры, нс меняя ее формы. Дли этой цели они имели два локтя — один в 28 дюй-
мов, п другой в 20. 'Гак как отношение этих локтей 28:20 = 3,4 можно приблизительно
принять равным 1^2 = 1,414, то для двукратного увеличения площади какой-нибудь
фигуры нужно, измерив все длины ее в двадцатидюймовых локтях, построить ее, откла-
дывая подученные размеры в двадцативосьмидюймовых локтях, что сводится к увели-
чению линейных размеров в \'2 рва, Очень точные значения у 2 помещены и вавилон-
ских строитель[гых справочниках и в индийских книгах. На греческой почве это привело
к открытию иррациональности 1/2, что было сделано приблизительно около 500 г. до и. э.
Открытие иррациональностей повело в математике и ламеце вычислелий построениями.
В планиметрии все соответствующие операции легко могли быть выполнены при помощи
простейших Инструментов — циркуля я линейки, при переходе же к стереометрическим
задачам греческие математики сразу столкнулись с необходимостью иметь дело с кубами
и кубичными корнями. Задачи об удвоении куба, требующая решения простевшего урав-
нения третьей: степени, была, конечно, первой, которую им пришлось разрешать. Первым
математиком, имя которого связано <: этой задачей, был Гинвократ Хиосским (вторая
воловина V вока до к. о,), показавший, что эта задача может быть приведена к нахожде-
нию двух средних цргшорциояальлых. Толчком к этому открытию для Гиппократа, ве-
роятно, были музыкальные исследования пифагорейцев V века до и. э., занимавшихся
вопросом о делении основного музыкального интервала — октавы - на две и на три
равные части. При этих изысканиях было установлено, что музыкальный ицтервал может
быть разбит ца два или на три равных интервала, выражающихся целочисленными отно-
шениями, только в тех случаях, когда делимый интервал характеризуется отношением
двух квадратных или кубических чисел. С конца V пека до п. о. в связи с изобретением
артиллерии—стрелометов и камнеметов, основанных на применении упругих тяжей,
появился еще один стимул для попыток уеншниого решения делийской задачи — работы
но .................о метательных машин. Мы знаем, что для увеличения вдвое даль-
ности полета снаряда и параболическом движении нужно вдвое увеличит!, его начальную
кинетическую энергию, а так как потенциальная энергия упругого тела пропорциональна
его объему, то для указанной цели требовалось удвоение объема тяжа. По всей вероят-
ности, не случайно, что первый давший теоретическое решение этой задачи Лрхнт Тарант-
ский (первая половина IV века до н. о.) был выдающимся полководцем. Дальнейшие
решения были даны Евдоксом и Мснехмом (около 350 г. до л. ».), по всей вероятности,
оба па оснонании теории кинических сечений. Что касается приводимого Евтокпем реше-
нии Платона, то око вне всякого сомнения является подложным*). Эратосфен ни во вве-
дении к посланию к царю Птолемею, ни в посвитительной надписи (стихотворная ее
часть) пе упоминает имени Платона в числе решивших задачу, хотя говорит о послании
делнйпен к Платину. Следующим но времени решением делийской задачи было предло-
женное Эратосфеном, современником Архимеда. Все остальные упоминаемые Евге-
нием решения принадлежат уже к послеархимедовской анохе. Их можно разделить па
три группы; Аполлонии, Нпкомеда к Диокла. .К группе Аполлония (младшего современ-
ника Архимеда) относятся решения Филона Византийского (автора первого частично
дошедшего до пас. курса механики, жившего около 100 г. до я. э.) и Геропа Алексаид-
рийского, известного компилятора, время жизни которого определялось очень рашич-
по — между II веком до и после пашей эры**). Никомед и Днокл относятся, но всей
вероитности, к первой половине П века до и. (до Гиппарха), являясь во всяком случае
эпигонами классического периода греческой геометрии. Решение Пнкомеда основано ин
применении конхоиды, криной, развившейся на основе применения так называемых
«вставок* или «стремлений» (vckreig, incline Li ones); что касается Диокла, то его рвше-
*) Ван-дср-Бардси в «Пробуждающейся науке» (стр. 225 русского перевода) убедительно дока-
зал. что это решение, равпо как и истории о посольстве делийцев к Платону, взяты № диалога Эрато-
сфена «Платоник».
«») Нейгебауэр показал (см. «Пробуждающаяся наука», стр. 372), что описываемое Геропом
зптмвппе имело место в 62 году н. в. Текст Евгении дает еще опцп докааатсиьстио ионцией даты
знивии Герояи. 'гак ван рэслростраисшие в Риме сирийской архитектуры со сводами (нерсотрС1йг;а
Аиоллопором Пантеона) относится ко времени Траяна, то автор «О построении сводов* (Cainarica)
жил около 100 г. К. а.
480
КОММЕНТАРИИ
нис основано на применении так называемой циссоиды — кривой третьего порядка, урав-
нение которой легко может быть получено, если положим:
ОА = х, АС^у, 1Х) = а.
Действительно, согласно принципу построения
кривой:
некие которой легко может быть
Рис. 23.
АЕ
АН _ AI)
~AK~^AD~~AC ’
что после подстановки дает:
У ая — х£
х-}-а
а — х
а — х
j/ в1 2—а:2
или, после очевидных упрощений:
у у а2—а:2 = (а—г)2,
?/аЙя+х) ~ (й—г)й-
У
Кривая состоит из двух симметричных ветвей, которые в точках М и Л' выходит
эн пределы окружности п стремятся к асимптоте, проходящей через Е ис^яюпдикулярио
к оси Ох. Ми том же принципе основывается решение писателя конца 111 в. и. э. Паппа
Александрийского, автора «Математической библиотеки», и Спора, о котором мы ничего
не знаем.
|2J С современной точки зрения, решение этой задачи может быть выполнено сле-
дующим образом.
Пусть секугцая плоскость будет АГ: объем сегмента ЛДГ, согласно доказанному
в предложении 11, будет равен объему конуса, основание которого составляет круг ва диа-
метре ЛГ, а высота ЛХ так отно-
сится к высоте ДХ рассматривае-
мого сегмента, как сумма радиуса
КВ— 11 шара с высотой ВХ сег-
мента, дополнительного к сегменту
АВГ, относится к высоте ВХ этого
второго сегмента. Аналогично, д
объем сегмента АВГ будет равен
объему конуса АРГ с тем же осно-
ва пнем и с высотой РХ, отношение
которой к ВХ будет равпо (КД—
-|-ЛХ): ДХ. Положим ДХ—z,
ХВ—1/, ЛХ = н, ХР=г, радиус
шара обозначим через Я, и пусть
заданное отношение объемов сег-
ментов ЛДГ и АВГ будет А-; тогда к
летворяст уравнению
Ряс. 24.
х и неизвестное х удов-
С В—2К-ХЛ .
1 2Н -х
что после очевидных упрощений приведет нас к уравнению третьей степени относительно а::
ж2 (ЗА—х)
(2/1-а)2(А -ж)
Сущность метода, который применяет Архимед, заключается в следующем. Ом пред-
полагает задачу рстпепной, иными словами, найденной точку X диаметра ВД, через кото-
рую проводится искомая секущая плоскость; с нашей точки зрения, это равносильно
введению двух неизвестных х и у, связанных уравнением
х-\-у-—2Н.
Затем он вводит вспомогательные неизвестные ЛХ —и и ХГ
уравнениями
(0
определяемые
R-1-s __ у
х ~ у
KA-V и
(2)
У
(3)
О ПТ АРК и ЦИЛИНДРЕ
481
и связанные соотношением ’ •
i-*. W
Вместо папшх четырех пеизвестпых величин Архимед имеет три неизвестных
точки X, А, Р. Мы определили бы из уравнений (2) и (3) неизвестные иисн подста-
вили их и уравнение (4); Архимед при помоши соотношений (2) и (3) исключает точки А
и Р и старается выразить отношение и : v через величины, определяемые только положе-
нием точки X. Забегая несколько вперед, мы должны сказать, чти вместо отношения
и : <> — к Архимед берет отношение
и-|-о__ Лг-|-1
и к
причем это отношение он представляет в таком виде:
iz-| о _ РА_РА АЛ___ и-}- у и—х
и — АХ АД АХ и—х и ' '
После этого мы проследим по пунктам весь ход решения Архимедом задачи.
<1> Архимед преобразует уравнения (2) и (3) к более удобному лиду. В его обозна-
чениях уравнение (2) будет:
КДЧ АХ _ РХ ‘ :
АХ ‘ХВ ’
откуда «выделением»:
КД_РХ-ХВ РВ
АХ — ХВ ВХ
или, так как КД—КВ:
КВ АХ
ВР ~ ХВ ’
Аналогично из уравнения (3)
KB-I-BX _ АХ
ВХ ХА
получается
КВ __ АД
ВХ ~ АХ ’
— ДА ДХ
*ДК ” ХВ
Таким образом, соединяя обе полученные пропорции вместе, будем иметь:
ДА КВ ДХ
ДК " ВР “ ХВ ’
или в наших обозначениях:
и — х _ В ___ х
В ~ и—у ~ у
<2> После этого Архимед о предел нет РА : АД, стоящее первым множителем в равен-
стве (4'). Для этого пропорцию
ВР _ КА
ВК - АД
он последовательно преобразует присоединением:
РВ^-ВК КАЧ-АА
ВК -1 ДА ’
РК _ КА
КД — АД ’
РКЦ-КА _ КА
КДЦ-ЛЛ ЛД ’ . .
РА _ К А
КЛ ЛД '
31 Архимед
482
КОММЕНТАРИИ
и так как КЛ есть средняя пропорциональная между РЛ и АЛ, то
РЛ _ КЛ8
ЛД ЛД8 *
(3) Теперь Архимед определяет отношение КЛ : ЛД. Из основного равенства
пункта <1)
КД ВХ
ДЛ хд
он получает «обращением»
КД _ ВХ
АЛ "ХД
и «присоединением»
КЛ-1-ДЛ ВХ + ХД
ЛД ДХ
К Л ВД
ЛД — ДХ "
После этого отношение РЛ : ЛД выражено только через величины, зависящие от точки Хг
РА ВД8
ЛЛ “ ДХ8 ’
или в буквенных обозначениях:
u-^-v'__________________________________4R2
и—X X2
< 4> Этот пункт Гейберг считает позднейшей вставкой, основываясь па том, что
в комментарии Евтокия рассматриваемое место пе содержится. Он посаящен определе-
нию второго множителя ДЛ : ЛХ в соотношении (4')- Из основного соотношения, опре-
деляющего ЛХ
ЛХ КВЦ-ВХ
Хд “ ХВ
(а)
имеем «выделением»
ЛХ-ХЛ КВ
ДХ ВХ ’
ЛЛ кв
ДХ - ВХ
Отсюда при помощи следующего преобразования, не отмеченного в тексте Архи-
меда, мы можем последовательно получить из (а):
ДХ ВХ
ЛД-ДХ КВ-1 ВХ ’
ДХ ВХ
~ЛХ~ КВ—ВХ ’
что после привлечения исходном пропорции принимает пид
ЛЛ _ КВ
ЛХ — КВ f-BX *
или в буквенных обозначениях
и-х П
и Л -у
< 5> Откладываем XZ —/?+»/, или BZ — ВК. —/?; конец Я полученного отрезка ляжет
вправо от точки Р. Действительно, в конце пункта <1> мы имели равенство
РВ _ КД
ВК — ЛД ’
О ШАРЕ И ЦИЛИНДРЕ
483
откуда
BZ=BK=BP-^A- ;
КД
так как
лд лх z ГГГ)
кд-=хв >4’ то DZ>BP-
Основная пропорция
ЛД :ЛХ-КИ ; (КП-| ВХ)
теперь перепишется в виде
АЛ : ЛХ = BZ : ZX.
< 6> После этого мы читаем у Архимеда: «Поскольку же отношение ЛЛ к ЛХ является
данным, то, значит, будет данным и отношение РЛ к ЛХ». Так как отношение ДЛ к ЛХ
BZ Н
рнпнястея ,7v=7T~;— то, строго говоря, его нельзя считать «данным»; оно будет «дан-
Х.Л. 21 - jC
ным» только н том случае, когда положение точки X станет уже язпсстным, а это будет
1’Л
только после подстановки в наше уравнение (4'), где отношение действительно ока-
АЧ-1
зываетсн равным заданной величине —— . Результат этой подстановки Архпмед полу-
чает в виде
РЛ РЛ ЛЛ ВЛ» BZ
ЛХ - ЛЛ ' ЛХ - ДХ® ’ ZX :
(Ь)
п правой части этого «уравнения» точки В, A, Z, являются известными и единственным
«неизвестным» будет лишь положение точки X.
С нашим точки зрения, полученное равенство равносильно уравнению
4Л‘3 _ А-|-1
х2 (л/г—аг) — Л ’
или
4А
< 7) После этого Архимед приступает к «решению» полученного уравнения». Он
«понижает его степень», вводя вспомогательную точку 0, определяемую из пропорции
РЛ: ЛХ — BZ: Z0
и переписывает основную пропорцию (Ь) в виде
BZ ZX _ ВЛ» BZ
ZX ’ Z0 — ДХ» ZX ’
BZ
что после сокращения па приводится к виду
BA»:AX»=XZ: Z0.
Заданную прямую AZ требуется разделить в точке X так, чтобы заданная площадь (ВЛ®)
так оти<х:плась к квадрату первого отрезка ДХ. как агорой огрезэк XZ к заданной
длине Z6. Решение этой задачи Архимед обещал дать в конце сочинения, по пи в до-
шедшем до нас тексте Архимеда, пи в том, который читали ближайшие к Архимеду
комментаторы Диокл и Дпописодор, и конце книги никакого решения поставленной
задачи нс находится. Это решение было найдено более поздним комментатором
А р.х и меда Е вто к нс м.
В кнммеягарии Евтокин к этому ме:ту говорится следующее.
Архимед обещал дать решение этой задачи в конце, по обещанное
нельзя было пайти ни в одном из списков. Поэтому, как мы выяснили,
и Днонисодор пс мог отыскать обещанного; не будучи в состоянии
справиться с недостающей леммой, оп в решении этой задачи пошел
совершенно другим путем, который мы ниже и опишем. Точно так же
и Диокл в своей книге «О каустиках» высказал мнение, что Архимед.
31*
484
КОММЕНТАРИИ
лишь обещал решение, но своего обещания не сдержал; поэтому сам
Диски попытался восполнить недостающее; его решение мы тоже при-
ведем в дальнейшем. По он, так же как и Диописодор, решил задачу
при помощи способа, не имеющего ничего общего с потерянным дока-
зательством. Между тем я, не;боясь продолжительных поисков, в одной
старой книге нашел запись некоторых теорем; хотя эта запись пред-
ставляла большие неясности и ошибки, а также различного рода
неправильности в чертежах, однако она была очень похожа на искомое,
тем более, что опа сохраняла излюбленное Архимедом дорийское наре-
чие и, кроме того, была написана со свойственной древности термино-
логией (так, парабола называлась «сечением прямоугольного копуса»,
а гипербола — «сечением тупоугольного конуса»); поэтому у меня
возникло подозрение, что эти тео-
ремы как раз представляют то са-
мое, что Архимед обещался напи-
сать в конце.
Так вот мы старательно за-
нялись разбором записанного
текста, который нам показался
очень трудным вследствие .упомяну-
того множества ошибок, и понем-
ножку выясняя его смысл, записали
его более современным и ясным
языком. Сначала дадим полностью
Рис. 25.
запись первой теоремы, чтобы выяснить самым общим способом то, что
Архимед говорит о границах возможности решения задачи; отсюда
вытекут более специальные приложения, касающиеся условий, содер-
жащихся в сделаппом им анализе этой задачи.
Даны прямые АВ и АГ и площадь А; требуется найти на АВ такую
точку Е, чтобы отношение АЕ к АГ равнялось бы отношению площа-
ди А к ЕВг {ряс. 25}.
Анализ
Пусть это будет сделано; построим АГ перпендикулярно к АВ
и соединяющую прямую ГЕ продолжим до Z. Затем через Г проведем
прямую ГН, параллельную АВ, а через В прямую ZBH, параллельную
АГ и пересекающую обе линии ГЕ и ГН. Дополним прямоугольник
И ® и через Е проведем прямую КЕА, параллельную каждой из прямых
Г0, HZ; пусть затем площадь А будет раина прямоугольнику .между
ГН И им.
гн-им- д
Итак, поскольку ЕА относится к АГ, как А к квадрату на ЕВ,
ВА _ А
АГ ЕВ*
и как ЕА к АГ, так и ГН к HZ,
ЕА гп
АГ 117.
и ГН к I1Z, как квадрат па ГН к прямоугольнику между ГН, HZ,
гн гн* • ’ . . ‘
HZ. “ ГП-HZ
О ИГАРЕ И ЦИЛИНДРЕ 4g 5
то, значит, как квадрат на ГН к прямоугольнику между ГН, HZ, так
и площадь Д к квадрату на ЕВ, то есть к квадрату па KZ.
ГН* Д = А
ГЯЛ2 ЕВ3 KJJ2
Затем, после перестановки — как квадрат на ГП к площади Д,
• то ость к прямоугольнику между ГП, II М, так и прямоугольник между
ГИ, HZ к квадрату иа ZK.
гвг гннх
Гн-нм 2Ка
Но как квадрат на ГН к прямоугольнику между ГП, ПМ, так
и ПТ к И М; и значит, как ГП к 11 М, так и прямоугольник между ГН,
I1Z к квадрату на ZK.
гн _ ITI.I1Z
нм хх2
Но как ГН к НМ, так и прямоугольник между ГП, HZ к прямоуголь-
нику между МН, HZ,
гн гп-пя
НМ Mn-llZ
если взять HZ в качестве общей высоты.
Значит, как прямоугольник между ГП, 1IZ, к прямоугольнику
между МП, HZ, так и прямоугольник между ГП, 11Z к квадрату на ZK
гн-nz гн-wz
M1I-I1Z ~ ZK«
Таким образом, прямоугольник между МП, 1IZ ранен квадрату на ZK.
mhiiz = zk*
Итак, если мы на оси ZH построим проходящую через точку Н пара-
болу так, чтобы ее ординаты квадрировались па НМ,
2К3 = нм - IIZ
то она пройдет через К и будет вполне определена по своему положе-
нию, таи’ как ПМ является заданной по величине (она вместе с заданной
линией ГП заключает заданную площадь Д).
мп-нг — А
Таким образом, точка К лежит на заданной своим положением
параболе; пусть эта парабола построена, как сказано, и будет ПК.
Далее, так как площадь (ЭД равна ГВ, то есть прямоугольник
между ®К, КА равен прямоугольнику между АВ, 1311,
ек-кдав-вп
и если мы через точку В проведем гиперболу с асимптотами ®Г и ГН,
ОК-КА-яц = AB-BH
то она пройдет через точку К [иа основании теоремы, обратной 8-й тео-
реме*) книги ТТ «Конических сечений» Аполлония], и будет определена
по своему положению, так как каждая из прямых 0Г, ГП, а также
точка В будут заданы своим положением.
Пусть эта гипербола, согласно сказанному, построена и будет КВ.
Таким образом, точка К находится на заданной по своему положению
) в действительности втг> можно вывести из 12-й.теоремы той же книги.
486
КОММЕНТАРИИ
гиперболе. Но опа находится также и на заданной но своему положе-
нию параболе; значит, точка К будет заданной. Опустим из пес перпен-
дикуляр КЕ на заданную своим положением прямую АВ; значит, будет
дана и Е.
Исследование (fiiootopog)
Так как ЕЛ относится к заданной прямой АГ, как заданная пло-
щадь А к квадрату па ЕВ, 3 о
ЕА_ = А
АГ ЕВв
то, значит, в двух параллелепипедах с основаниями, соответственно квад-
ратом на ЕВ и площадью Д, и соответственно высотами ЕА и АГ,
основания обратно пропорциональны высотам: значит, оба параллеле-
пипеда будут равны; значит, квадрат па ЕВ, умноженный на ЕА, равен
заданной площади А, помноженной на АГ.
ЕВа-ВА = д.лг
Но квадрат па ВЕ, умноженный на ЕА, будет наибольшим из всех
построенных подобным образом на ВА произведений, если только, как
будет доказано впоследствии, ВЕ будет вдвое больше ЕА. Таким обра-
зом, произведение заданной площади и заданной линии не должно быть
больше квадрата на ВЕ, умноженного на ЕД.
Синтез задачи производится так.
Пусть заданная прямая будет АВ и некоторая другая данная АГ
и данная площадь А. Требуется разделить АВ так, чтобы отношение
одного ее отрезка к заданной прямой АГ равнялось отношению данной
площади i\ и квадрата на оставшемся отрезке {рис. 2G}.
Возьмем АЕ — третью часть АВ. Тогда параллелепипед на А и АГ
будет или больше параллелепипеда на квадрате ВЕ с высотой ЕА,
или равен этому параллелепипеду, или же меньше. Если он будет
больше, то, согласно доказанному' в анализе, построение будет невоз-
можным. Если он будет равен, то точка Е удовлетворяет условиям зада-
чи: действительно, при равенстве объемов параллелепипедов основания
будут обратно пропорциональны
высотам, так что как ЕА к АГ,
так и А к квадрату ня ВЕ.
Если же площадь А, умножен-
ная на АГ, будет меньше квадрата
на ВЕ, умноженного на ЕА, то
построение производится так.
Построим АГ перпендикуляр-
но к АВ и через Г проведем пря-
мую TZ, параллельную АВ, а через
Впрямую BZ, параллельную АГ,
и пусть она с продолжением ГЕ пересечется в точке Н. Дополним пря-
моугольник ZO и через Е проведем прямую КЕЛ, параллельную ZH.
Так как площадь А, умноженная на АГ, меньше квадрата па ВЕ,
умноженного на ЕА,
Д ЛГСВЕ3 ЕЛ
то как ЕЛ к Л Г, так будет и А к некоторой площади, меньшей квадрата
на ВЕ или квадрата на ПК.
О ШАРЕ И ЦИЛИНДРЕ
487
Тогда пусть отношение ЕА к ЛГ будет равно отношению площади Л
к квадрату на ИМ, и пусть площадь А равна прямоугольнику между
TZ, ZN.
rZ.ZN’ = Л
Теперь поскольку Е А к А Г относится, как площадь А, то есть пря-
моугольник между TZ и ZN, к квадрату па НМ
еа rz ZN
АГ " UM2
и как ЕА к ЛГ, так TZ относится к ZH,
' ЕА Г7.
аг — ziT
как же rZnZII.TaK и квадрат на TZ к прямоугольнику между TZ, ZH,
и как прямоугольник между rz, ZN к квадрату па НМ.
rz____rz^_= rz ZN
ZH _ fZ-ZH
Затем после перестановки — как квадрат па PZ к прямоугольнику между
TZ, ZN, так и прямоугольник между TZ, ZII к квадрату на ИМ.
Но как квадрат да TZ к прямоугольнику между TZ и ZN, так же
и TZ к ZN. Также будет, если взять ZU общей высотой, и прямоуголь-
ник между TZ и ZII к прямоугольнику между NZ и ZH,
_rz rz-zii
ZN"' NZ- ZII
и -значит, как прямоугольник между TZ п ZH к прямоугольнику между
NZ и ZH, так и прямоугольник между TZ и ZH к квадрату на ИМ;
tz-zh rz-zn
' wz zh им2
следовательно, квадрат на ИМ будет равен прямоугольнику между
HZ и ZN.
НМ2 = HZ-ZN
Таким образом, если па оси ZI1 построить проходящую через Z
параболу так, чтобы се ординаты квадрировались на ZN, то опа прой-
дет через точку М. Построим ее, и пусть Она будет MEZ.
Затем, поскольку площадь 6Л равна AZ, то есть прямоугольник
между (ЭК и КЛ равеп прямоугольнику между АВ и BZ,
«Ж.КЛ = А В- BZ
то сели через точку В провести гиперболу с асимптотами ОГ и 1’Z, опа
пройдет через К
ек.кл -яу ™ ab-bz
[па основании теоремы, обратной 8-й (12-й) теореме книги II «Кони-
ческих сечений» Аполлония|. Построим ее; пусть это будет кривая ВК,
пересекающая параболу в точке Е. Из S на АВ опустим перпендику-
ляр 30 П к проведем через S прямую Р 32, параллельную АВ.
Теперь, так как ВЕК есть гипербола, (ЭГ, TZ — ее асимптоты, и пря-
мые PS, ЕП проведены параллельно АВ и BZ, то прямоугольник
между РЕ и ЕП. будет ранен прямоугольнику между ЛВ и BZ,
РЕ.ЕП —АП-НЗ
и значит, прямоугольник РО будет равен OZ. Поэтому, если соединить
точку Г с 2 прямой, то последняя пройдет через О. Проведем ее; пусть
488
КОММЕНТАРИИ
она будет ГОХ. Теперь, поскольку О А относится к АГ, как ОВ к ВХ,
то есть как TZ к ZX,
ОА ОП rZ - •
АГ “ BE ZE
как же T’Z к ZX, так относится, если взять ZN общей высотой, и пря-
моугоиьиик между TZ, ZN к прямоугольнику между XZ, ZN,
rz rz ZN
ZE ” EZ-ZN
то значит, как О А к АГ, так и прямоугольник между TZ, ZN к прямо-
угольнику между XZ, ZN.
ОА rz ZN
АГ “ EZ-ZN
По прямоугольник между TZ, ZN равен площади А, а прямоуголь-
ник между XZ и Z1N равен квадрату па ХЕ или квадрату на ВО
EZ - ZN -- ssa = во® - . '
по свойствам параболы. Значит, как ОА к АГ, так будет и площадь Л
К квадрату на ВО.
ОА _ а
аг ио2
Таким образом, точка О, удовлетворяющая условиям задачи, найдена.
Доказательство ле ммы д и о р и з ма
Л что при ВЕ, вдвое большем ЕА, квадрат па ВЕ, умноженный на
ЕА, будет наибольшим из всех построенных подобным образом на ВА
произведений, до кажется так {рис. 27}:
Пусть опять, как »то было в анализе,
данная прямая АГ будет перпендикулярна к АВ;
продолжим соединяющую прямую ГЕ, и пусть
опа в точке Z пересечет прямую, проведенную
через В параллельно АГ. Через точки Г, Z па-
раллельно АВ проведем прямые 0Z и ГН, про-
должим ГЛ до (-) и через Е параллельно ей
проведем прямую КЕЛ. Пусть отношение ЕА
к Л Г будет равно отношению прямоугольника
между ГН, Н М к квадрату на ЕВ;
ЕА _ ГП-НМ
ЕВ2
тогда квадратна ВЕ, умноженный па Е А, будет
ранен прямоугольнику между ГИ, НМ, умно-
женному па Л Г,
ЕН». КА (ГП - НМ) ЛГ
так как у двух равных параллелепипедов оспопа-
ния обратно пропорциональны высотам. Я ут-
верждаю, что прямоугольник между ГН, П М,
умноженный па Л Г, будет наибольшим из всех
объемов, построенных подобным образом на АВ. Проведем через точку
II параболу с осью ZH так, чтобы се ординаты квадрировались на Н М-
1/®=мН -лс
О ШАРЕ И ЦИЛИНДРЕ
489
Она, согласно доказанному во время анализа, пройдет через К
и пересечется с параллельным диаметру параболы продолжением ©Г
[па основании 27-й *) теоремы книги 1 «Конических сечений» Аполлония].
Продолжим ее, и пусть она пересечется н точке 1N. Затем через точку В
проведем гиперболу с асимптотами КГ и ГП; она тоже пплйдет через
точку К, как зто было доказано во время анализа. Пусть эта гипербо-
ла будет ВК.
Продолжив ZH, отложим равную ей прямую II S, проведем соеди-
няющую прямую ЕК и продолжим до О. |Па основании 34-й (33-й)
теоремы книги I «Конических сечений» Аполлония] прямая ЕК будет
касательной к параболе. Так, кик согласно предположению, ВЕ в два
. ; раза больше ЕА, то есть ZK в два раза больше К0, и треугольник О ©К
подобен треугольнику EZK, то и ЕК будет в два раза больше КО.
гк = 2ко
Затем ЕК в два раза больше КП вследствие того, что EZ в два
раза больше ЕН и ПН параллельна K.Z];
ЕК = 2КП . -
значит, ОК равпаКII. Таким образом, прямая ОКИ, имеющая с гипер-
болой общую точку К и заключенная между асимптотами, делится в точ-
• кеК пополам; это значит, что она будет касаться гиперболы [па основа-
• \ пии теоремы, обратной 3-й теореме книги II «Конических сечений»
Аполлония]. Нов топ же точке К эта прямая касается и параболы; зна-
? чит, и парабола коснется гиперболы в точке К.
• . Представим теперь, что гипербола продолжена до Р; возьмем па АВ
' ; ‘какую-нибудь точку Е, затем через проведем прямую TST, нарал-
лсльную ГВ; пусть она пересечется с гиперболой в точке Т; через Т
параллельно ГН проведем ФТХ. Теперь, поскольку по свойству асим-
птот гиперболы площадь ФТ будет равна ГВ, то после отнятия об-
щей площади Г2 площадь Ф2 будет равпа 211, и поэтому прямая,
соединяющая.точки Г и X, пройдет и через S**): пусть это будет
прямая ГЕХ.
Если гР есть точка пересечения параболы с прямой ФТХ и по
. свойству параболы квадрат на ТХ равен прямоугольнику между ХН
и НМ,
WXS-HM-XH
то квадрат на ТХ будет меньше прямоугольника между ХН и НМ.
Пусть квадрат па ТХ равен прямоугольнику между ХН и П £2.
тхя = хп-по
Так как SA к АГ относится, как ГН к НХ,
2А гн .
аг нх
п как ГТТ к ИХ, так, если взять IIQ общей высотой, и прямоугольник
между ГП, 1IQ относится к прямоугольнику между ХН и Н£2, или
к равному ему квадрату на XT, то есть к квадрату па BS,
гн _ гн- пя ги-ия _ гп ня
НХ ХН ПЯ хти В2а
*} 2«-й.
**) Из равенства ФА-А2]=2Г-ВЕ следует ВХ : ВХ—УХ : ГГ, то сеть треугольники ГГХ
и XXR подобны; следовательно, г£Х Судет ирнмик. •• *
490
КОММЕНТАРИИ
то, значит, квадрат па 132, умпожеппый на 2А, будет равен прямо-
угольнику между ГН и Н R, умноженному на ГА.
BXB-SA (ГИВД-ГА
Но прямоугольник между ГП, II Й, умноженный па ГА, меньше
прямоугольника между ГН, НМ, умноженного на ГЛ.
(ГН* ПО) ГА < (ГН-НМ) ГА
Значит, квадрат на 132, умноженный на 2Л, будет меньше квадра-
та на 13Е, умноженного па ЕА.
ВЕ2-ЕЛ < ВЕ3- КА
Подобным же образом докажем это и для всех точек, взятых меж-
ду Е и В.
Теперь возьмем любую точку 2 между Е и А {рис. 28}. Я
утверждаю, что точно так же квадрат на ВЕ, умноженный на ЕА,
будет больше квадрата па В2, умноженного ла 2Л. Действитель-
но, произведи те же самые построения,
проведем через 2 параллельную КЛ пря-
мую Т2Д, и пусть опа пересечется с ги-
перболой в точке Т (опа с псп действительно
пересечется вследствие своей параллельности
асимптоте); затем проведенная через Т па-
раллельно Л13 прямая ФТХ пусть пересе-
чется с продолжением HZ в точке X. Далее,
так как по свойству гиперболы прямоугольник
фД равен ЛН, то прямая, соединяющая точ-
ки Г мХ, пройдет и через 2. Проведем ее,
и пусть она будет Г2Х. < Точка Т есть пересе-
чение прямой ФХ с параболой 1IKN. > Затем
поскольку по свойству параболы квадрат на
Y‘X равен прямоугольнику между XII и ИМ,
гх ™хюнм
то, значит, квадрат на ТХ будет меньше пря-
моугольника между ХН и НМ.
тх®<хн-нм
Пусть квадрат на ТХ равняется прямо-
угольнику между ХН и HZ.
TX2 = XH-HZ
Так как 2А относится к АГ, как ГП к ПХ, и так же, если взять
1IZ общей высотой, относится прямоугольник между ГН и IIZ к прямо-
угольнику между XII и HZ, то есть к квадрату на ТХ или к квадрату
на В2,
га гп _ гп-nz _ гн-hz rii-nz
aF =_ ИХ - ХН*MZ ” Тхг Bv2
то значит, квадрат па В2, умноженный па 2А, будет равен прямо-
угольнику между ГН, HZ, умноженному на ГА.
Но прямоугольник между 11 Г, НМ больше прямоугольника между
ГН и HZ; значит, квадрат па 13Е, умноженный на ЕА, будет больше
квадрата на Г32, умноженного па 2А.
ве2 еа >bs2-sa
О ШАРЕ И ЦИЛИНДРЕ
491
Подобным же образом докажем и для всех точек, взятых между Е
и А. Но то же самое доказано и для всех точек между Е и В; значит,
квадрат на ВЕ, умложондынна ЕЛ, будет больше всех подобных же пост-
роенных па ВАпараллслетшодои, если ВЕ будет в два раза больше ЕА.
Иа этом 7>опчаотся приводимый Евтокием текст. Есть очень серьезные соображе-
ния в пользу тою, что он действительно принадлежит .Архимеду. Что можно ска urn,
о времени его возникновении? Некоторая искусственность.постановки задачи — деление
пропорционально аадапным отрезку и площади — делает очень сомнительной возмож-
ность самостоятельного появления этом задачи, тогда как связь ее с делением шара в дан-
ном отпоптеиии у Архимеда вполне удовлетворительно объясняет причину не появления.
Если задача опреднлвпип объема тиара была впервые разрешена только Архимедом, то
рассматриваемый текст нс мог возникнуть ранее эпохи Архимеда. С другой стороны,
упоминаемая Евгением устарелость терминологии (определение параболы как сечение
прямоугольного конуса) показывает, что этот текст записан еще до .Аполлоциопон реформы
терминологии — введении современных названий: эллипса, гиперболы, параболы, так
что и много позже эпохи Архимеда этот текст
возникнуть пе. мог. Если принять вн внимание
еще упоминаемый Евгением дорийский диалект
и то обстоятельство, что после 212 г. до н. э.—
крушения Сиракуз — основного представителя
дорпзма в эллинистический период — трудно
ожидать каких-нибудь научных подвигов иа
почве Великой Греции и Сицилии, а также
и то, что этой задачей занимался Архимед, то
проще и естественнее всего действительно от-
нести этот текст к Архимеду. Единственное
пизражеине, которое можно было бы сделать,
заключающеесп в том, что пн в одном списке «О
шаре и цилиндре» рассматриваемое решение не
встречается, доказывает лишь то, что Архимед
по какой-то причине не поместил его в отосланное
Доеифшо послание, и больше ничего.
Затем нужно, конечно, принять во внима-
ние и необычайное изящество самого решения;
для этого представим задачу в современном
обозначении (рис. 29).
Требуется прямую >Ш = а разделить так,
чтобы отношение верного се отрезка AM к задан-
ной прямой ЛС = Ь равнялось отиоптспию ладнп.-
иой площади Д — ар к квадрату второго отрезка
лепное требование приведет к уравнению
МВ. Положим МВ—яг, тогда постав-
а —я _а-р
~Ь
или
(«—х) ха=лрЬ,
Нетрудно видеть, что получвппоо уравнение равносильно системе следующих двух
уравнений с двумя лемзвестпымп:
у (а—х) —ab
— уравнение гиперболы с асимптотами СО и CG — а
- - уравнение параболы с осью Оу. Мы имеем примерно то же самов, что было предложено
Молохмом для решения делийской задачи; том самым проливается некоторый свет па общий
ход рассуждений Архимеда при решении этой задачи. В особенности красиво получается
исследование возможности решения (диорпзм) (рис. 30).
Но меняя общности задачи, мы можем считать постоянными АВ а, АС — Ь
и менять лишь величину площади Д = ар; это значит, что при различных данных мы можем
пользоваться одной и той же гиперболой (u х}у—аЬ; что же. касается параболы, то по
мере увеличении Д будет увеличиваться и р, иными словами, наши парабола х3 — ру будет
нее более и более отходить плево ин иапраплсвито к прямой АС. Для возможности реше-
492
КОММЕНТАРИИ
Ш
К
Ш1Я задачи необходимо, чтобы рассматриваемые гипербола и парабола пересекались
Если р сравнительно невелико, то переегчепие будет иметь место, причем, как нетрудно-
видеть, мы будем получать д в с точки пересечении, пз которых одна N дана на пер*
теже, а другая получится там, где парабола подойдет
достаточно близко к асимптоте гиперболы. На чертеже
изображена гипербола ВА'КР на три параболы. Одла иа
них (/) дает две точки пересечения N и Р, вторая (III)
лежит целиком вне гиперболы, лс имея с последней
никаких общих точек, наконец, для третьей (II) две точки
пересечения сливаются в одну и гипербола с параболой
имеют общую касательную в точке К. Этот предельный слу-
чай и является наиболее важным дли исследования, так как
дает границу между областью возможных решении (параболы
типа У) и невозможных (параболы типа III). Архимед пока-
зывает, что это будет тогда, когда перпендикуляр КЕ
разделит прямую АВ в отношении 1 : 2. Он проводит общую
касательную ОКПЕ. Так как ОП являетси касательной к
гиперболе, то точка касания К. будет серединой заключенного
между асимптотами отрезка этой касательной. Далее, так
как прямая OS будет касательной к параболе, то расстоя-
ние ПЕ точки Е пересечения касательной с осью параболы
от ее вершины должно равняться абсциссе HZ точки каса-
ния. Отсюда легко получается:
ОК—КП=ПЕ
Рис. 30. что и дает пам пушное предельное условие возможности
решения.
Разобрав постановку задачи в самом общем виде, Рвтокий переходит к выяснению
особенностей ее постановки в том частном случае, который требуется при решении задачи
о делении шара. Он пишет:
АВ=4 ЕВ,
Чтобы ближе подойти к самому способу выражений Архимеда,
представим себе, как па чертеже в основном тексте {рис. 31}, диаметр
шара АВ, радиус BZ и заданную пря-
мую ZG. Мы дошли до того, гово-
рит он, что «данную прямую AZ нуж-
но разделить в точке X так, чтобы
отношение XZ к заданной прямой
(ZO) равнялось отношению задан-
ной (площади) к квадрату па ДХ.
Выраженная в таком общем виде
задача требует диоризма». Дей-
ствительно, если заданная площадь,
помноженная па заданную прямую,
будет больше квадрата па АВ,
(помноженного) на BZ, то задача, как доказано, невозможна; если
же опа равна, то условиям задачи удовлетворяет точка В и полученное
решение не имеет никакого значения для поставленной Архимедом
в самом начале цели, так как шар ни в каком отношении делиться
не будет.
Значит, понимаемая в общем виде задача требовала диоризма.
«Но при тех условиях, которые присущи рассматриваемой задаче», то
есть чтобы ДВ была в два раза больше ZB и BZ была больше Z8, «дио-
ризм не нужен». Действительно, заданные площадь — квадрат па ДВ
и прямая Z0 дают в произведении величину, меньшую квадрата на АВ,
(умноженного) иа BZ, так как BZ больше ©Z, а при этом условии,
О ШАРЕ И ЦИЛИНДРЕ
493
как мы доказали, возможно решение задачи и известен самый способ
се решения.
После этого Евтокий приводит решения основной задачи о делении шара, данное
Днонисодорои и Диоклом:
«Как мы уже сказали, Дипнисодор, по находя нигде обещанного
Архимедом окончания н не чувствуя себя в состоянии восстановить не-
достающее, пошел иным путем и дал неплохой способ решения всей зада-
чи; поэтому и мы полагали необходимым присоединить к уже написан-
ному и его решение, исправив его по мерс возможности, так как оно
вследствие людской небрежности в большей части изложения предста-
вляло большие неясности из-за значительного количества ошибок
в списках, бывших в пашем распоряжении.
Решение Д и о н и с о д о р а
рассечь плоскостью данный шар так, чтобы его сегменты находились
е заданном отношении.
Пусть оудет шар с диаметром АВ и отношение, равное тому, в ко-
тором ГД находится к ДЕ. Требуется плоскостью, перпендикулярной
к АР, рассечь jtiap так, чтобы его сег-
ГЕ
ЕД
мент с вершиной А имел к сегменту с
вершиной В то же самое отношение,
что ГД к ДЕ {рис. 32}.
Продолжим В А до точки Z, и пусть
A.Z будет равна половине АВ. Пусть
затем отношение ГЕ к ЕД будет равно
отношению ZA к АП;
ZA
лн -
пусть АП будет перпендикулярна АВ.
Возьмем для ZA и АН среднюю про-
порциональную А0;
Рис. 32.
rtfc>a = ZA-AH
конечно, А© будет больше НА. Через точку Z проведем параболу
с осью ZB и параметром АН; она пройдет через 0, так как прямоуголь-
ник между ZA и АН рапой квадрату на А0. Пусть эта парабола будет
Z0K. Через В параллельно АО проведем прямую ВК, и пусть опа
пересечет параболу и К. Через точку 11 проведем гиперболу с асимпто-
тами ZB и ВК; она пересечет параболу между точками О и К. Пусть
точка пересечения будет А. Из Л. опустим на АВ перпендикуляр ЛМ
и затем через точки II иЛ параллельно АВ проведем прямые 11N иЛЗ.
Так как ПЛ — гипербола, АВ и ВК — се асимптоты и АН, HN
ссютпетствсдпо параллельны МЛ и ЛЗ, то прямоугольник между АН,
HiM равен прямоугольнику между МЛ, ЛЗ
ЛН-Н.Ч = МЛ-Л3
согласно 8-й (12-й) теореме книги J1 «Конических сечений» Аполло-
нии. Но НК равпа ЛВ, а Л£ равна МВ; следовательно, прямоуголь-
ник между ЛМ и МВ равен прямоугольнику между НА и АВ.
ЛМ.МВ = НА-АВ
494
КОММЕНТАРИИ
Так как прямоугольник между крайними равен прямоугольнику
между средними, то четыре упомянутые прямые составят пропорцию:
таким образом, ЛМ к 11А, как АВ к ВМ;
АМ А В
НА "= ВМ
значит, квадрат на ЛМ относится к квадрату на НА, как квадрат
на АВ к квадрату па ВМ.
АМ2 АВ*
НМ2 ВМ*
Далее, так как по свойству параболы квадрат па ЛМ равен прямо-
угольнику между ZM и АН,
ЛМ2- ZM АН
то, значит, ZM относится к Л1Л, как МЛ к АН.
ZM МЛ
МЛ ' ' АН
Таким образом, как первая к третьей, так будут относиться и квад-
рат на первой к квадрату па второй, и квадрат на второй к квадрату на
третьей («Начала», кн. V); значит, ZM относится к ЛИ, как квадрат
па Л М к квадрату па ЯЛ.
7.М ЛМ*
All цд-
Но по доказанному квадрат на ЛМ к квадрату на АН относится, как
квадрат па АВ к квадрату па ВМ,
лмг АВ8
АП* ВМ*
и, значит, квадрат па ЛВ относится к квадрату на ВМ, как ZM к АП.
АВ* _ 7.М
ВМ* ’ АН
Отношение квадрата па Л В к квадрату на В М будет равно отноше-
нию кругов с радиусами ЛВ, ВМ; значит, отношение кругов будет равно
отношению ZM к АН.
Круг А н _ ZM
круг ВМ АН
Следовательно, конус, имеющий основанием круг с радиусом АВ,
а высоту ЛИ, будет равен конусу, имеющему основанием круг с ради-
усом ВМ, а высоту ZM, так как если у двух конусов основания обрат-
но пропорциональны высотам, то эти конусы равны. Но конус,
имеющий основанием круг с радиусом ЛВ и высоту ZA, к конусу, име-
ющему то же основание и высоту АН, будет относиться, как ZA к АИ,
или как ГЕ к ЕА, так как конусы с одинаковыми основаниями относят-
ся, как высоты. Таким образом, конус, имеющий основанием круг
с радиусом АВ и высоту ZA, к конусу, имеющему основанием круг
с радиусом ВМ и высоту ZM, будет относиться, как ГЕ к ЕД. Но конус,
имеющий основанием круг радиуса АВ и высоту AZ, равен шару (на
диаметре АВ), конус же, имеющий основанием круг радиуса ВМ
и высоту ZM, равен сферическому сегменту с вершиной В и высотой
ВМ, как зто будет доказано дальше. Таким образом, шар на диаметре
О ШАРЕ И ЦИЛИНДРЕ
495
АВ к конусу с высотой ZM относится, как ГЕ к ЕД.
Шар (АН) _ ГЕ
конус iZ.VI) ” ЕД
Отсюда «выделением.»
тар — конус (BM* ZM)_ГЕ — ВД
конус (ВМ8- ZM) ЬД
Значит, плоскость, проведенная через ДМ, перпендикулярная
к АВ, рассечет шар в заданном отношении,
(сегмсит ua AM): (сегмент ни ВМ) “ ГД : ДЕ
что и требовалось сделать.
А что конус, имеющий основанием круг радиуса ВМ, а высоту ZM,
равен сферическому сегменту с вершиной В и высотой 13 М, можно-
доказать так:
Сделаем, чтобы ZM относилась к МА, как ОМ к МВ,
ZM____ом_
МЛ МВ
тогда конус, имеющий то же основание, что и сегмент, и высоту ОМ,
будет равен сегменту*).
Далее, так как ZM к МА, как ОМ к МВ, и после перестановки
ZM к МО, как AM к МВ,
7.4 AM
МО — «В
по AM к МВ относится, как квадрат па ИМ к квадрату на MR или
как круг с радиусом НМ к кругу с радиусом МВ,
AM _ AM-МВ _ ИМ8 _ Круг (ПМ)
2,1 11 ' 31Вв " МВ8 — круг (МВ)
’ то значит, круг с радиусом ИМ к кругу с радиусом МВ относится,
как MZ к МО.
Таким образом, конус, имеющий основанием круг радиуса МВ,
а высоту ZM, будет равеп конусу, имеющему основанием круг
радиуса ИМ, а высоту МО,’так как у обоих основания обратно пропор-
циональны высотам. Отсюда же следует, что рассматриваемый конус
с радиусом МВ и высотой MZ будет равен и сегменту с высотой ВМ.
Решение Диокла в книге «О каустиках»
Об этой же задаче пишет и Диокл н книге «О каустиках», начи-
ная со следующего проднсаопин.
«В книге «О шаре и цилиндре» Архимед показал, что всякий сфери-
ческий сегмент равеп конусу, имеющему то же основание, что и сет-
мент, и высотой прямую, имеющую к опущенному из вершины сегмен-
та на основание перпендикуляру отношение, равное тому, которое
вместе взятые радиус шара и высота противолежащего сегмента имеют
к высоте противолежащего сегмента. Таким образом, если niap АВГ
*) Действительно, па основании предложения И книги второй «О шире и цилиндре» сегмент
ВМ будет равен конусу с тем же основанием и с высотой 11, определяющейся формулой
AM-}-2- АВ
Н=ВМ------£---
AM
MA-J-AZ
ВЫ ЛМ
496
КОММЕНТАРИИ
с диаметром АВ и центром Е рассекаются какой-нибудь плоскостью
по кругу с диаметром ГД {рис. 33}, и, если мы сделаем, чтобы отношение
ЕА вместе с ZA к ZA равнялось бы отношению 11Z к ZB,
ЕЛ -г ZA HZ
ZA “ ZB
а ЕВ вместе с BZ относились бы к ZB, как 6Z к ZA,
ЕВ -]- BZ 6Z
ZB ~ ZA
то, согласно доказанному, сферический сегмент ГД будет равен конусу,
основанием которого является построенный на диаметре ГД круг, а высо-
той ZH, сегмент же ГАД ра-
вен конусу с тем же самым
основанием и с высотой ©Z.
Затем, предложивши рассечь
данный шар этой плоскостью
так, чтобы получившиеся
сферические сегменты нахо-
дились друг к другу в задан-
ном отношении, и производя
описанное построение, Архи-
мед говорит, что будет также
дано отношение конуса, осно-
ванием которого является
круг на диаметре ГД, а вы-
сотой Z0, к конусу с тем же самым основанием и с высотой ZII. Л так
как построенные на равных основаниях конусы отвеятся между собой,
как высоты, то будет данным и отношение ©Z к ZH.
Далее, так как 0Z относится к ZA, как ЁВ вместе с BZ к ZB,
0Z ЕВ 4- HZ
ZA - ZB
то, «выделяя», ©А относится к AZ, как ЕВ к ZB.
ЕВ
AZ “ BZ
По той же самой причине НВ относится к ZB, как ЕВ к ZA.
НВ ЕВ
bz _ ля
После этого дело приводится к такой задаче:
Задав положением прямую АВ и две данные (конечные ее} точки
А, В и величиной некоторую прямую ЕВ*), рассечь АВ в точке Z так,
чтобы после добавления двух прямых 0А и В11 отношение ©Z к ZH
было данным, и кроме того, чтобы ©А к AZ было, как ЕВ к ZB и НВ
к BZ, как ЕВ к ZA;
в А ЕВ НВ ЕВ
AZ ~ ZB ‘ BZ ZA
это будет доказано далее. Архимед же, разобрав все это подробнее, свел
дело к другой задаче, которая в книге «О шаре и цилиндре» не решена.
♦) так как Диокл несколько обобщадт задачу, то эта прямая ЕВ может и не быть равной
радиусу шара.
О ШАРЕ И ЦИЛИНДРЕ
497
Заданы положением прямая АВ и две данные точки А, В и {величи-
ной некоторая прямая и) отношение, в котором, находятся прямые Г и А;
требуется рассечь прямую АВ в
точке Е и приложить ZA, НВ
так, чтобы было: как Г и А, так
и ZE к ЕН, как ZA к АЕ, так
и данная прямая к ВЕ, как НВ
к ВЕ, так и та же данная пря-
мая к ЕА {рис. 34}.
(А н а л и з). Пусть это
сделано. Нерпендинулярпо АВ
проведем ©АК и АВ М, постро-
им АК и ВМ, равные каждая z
заданной прямой, и соединяю- -
щие прямые КЕ и ME продол-
жим до А и 0. Затем соединим
К и М и проведем через А пря-
мую AN, параллельную АВ, а "
через точку Е прямую SEOII,
параллельную NK. Теперь, по-
скольку, согласно предположе-
нию, ZA к АЕ, как МВ к ВЕ, ..
ZA ._„МВ_
АЕ ~ ВЁ РИС. 34.
и, вследствие подобия треугольников, МВ к ВЕ, как 0А к АЕ,
МВ = ОА
ВЕ АЕ
то, значит, ZA к АЕ, как 0А к АЕ,
ZA _ ВА
' АЕ АЕ
откуда ZA равпа ©А.
ZA 0А
Но той же самой причине BII равна ВА.
вн вл
Далее, так как 6А вместе с АЕ относится к МВ вместе с ВЕ, как
К А вместе с АЕ к АВ вместе с ВЕ
0A + AE КА-I-АЕ
“мВ J-НЕ ’ AB-J-BE
(ибо каждое из этих отношений равно отношению АЕ к ЕВ), то, зна-
чит, прямоугольник между ©А вместе с АЕ и АВ вместе с ВЕ равен
прямоугольнику между КА имеете с АЕ и МВ вместе с ВЕ.
(0А + АЕ) (АВ + ВЕ) о- (КА + АЕ) (МВ ВЕ)
Построим АР к ВЕ, ранные каждая КА. Теперь так как ©А вместе
с ЛЕ равны ZE,AB вместе с, .НЕ раины ЕН, КА вместе. с> АЕ равны РЕ,
МВ вместе с ВЕ равны SE, и доказано, что прямоугольник, между ©А
вместо с АЕ и ЛВ вместе с ВЕ равеп прямоугольнику между КА вместо
с ЛЕ в МВ вместе с ВЕ, то, следовательно, прямоугольник между ZE
и ЕН равеп прямоугольнику между РЕ и ES; поэтому если точка Р
будет между Л и Z, то точка X попадет за Н и обратно.
32 Лркиме,!
498
КОММЕНТАРИИ
Теперь, поскольку Г к А, как ZE к ЕН
Г = ZK
А “ НИ
и ZE к ЕН, как прямоугольник между ZE, ЕН к квадрату на ЕН,
ZK ЯК КП
ЕИ еп2
•го, следовательно, Г к А будет, как прямоугольник между ZE, EII
к квадрату на ЕН.
_г _ ZE- и.п
Л ЕН8
Но, согласно доказанному, прямоугольник между ZE. ЕП равен пря-
моугольнику между РЕ, ЕЕ;
zk-eii рн-ех
значит, Г к Д, как прямоугольник между РЕ и ЕХ к квадрату ва ЕН.
РК-ЕХ
л ЕМ2
Отложим ЕО, равную НЕ, и соединяющую прямую ВО продолжим
в обе стороны; пусть восставленные из X и Р перпендикуляры пере-
секутся с этой прямой в точках Т и Г. Теперь, как как ТГ проходит
через заданную точку В, образуя с заданной по положению прямой
АВ угол ЕНО. равный половине прямого, то ТГ будет дана ио положе-
нию. Затем прямые ХТ, РГ, проведенные из заданных по положению
точек X, Р, пересекают ее в точках Т, Г; значит, ТГ будет задана
и но величине и по положению. Далее, поскольку вследствие подобия
треугольников ЕОВ, ХТВ прямая ТВ относится к 130, как ХВ к ВЕ,
тв хв
‘ BO ~ ВЕ
то, «присоединяя», ТО к ОВ относятся, как ХЕ к ЕВ,
то ХЕ
ОВ ЕВ
Но ВО к О Г относится, как ВЕ к ЕР;
ВО _ ВЕ
ОГ “ Ер
значит, «п.> равенству» ТО относится к ОГ, как ХЕ к ЕР.
ТО ХЕ
ОГ — ЕР
Но ТО относится к ОГ, как прямоугольник между ТО, ОГ к квадрату
на О Г
чо то or
ос ос2
и ХЕ к ЕР, как прямоугольник между ХЕ и ЕР к квадрату па ЕР;
ХЕ _ ХЕ КР
ЕР ~ ЕР2
значит, прямоугольник между ТО и ОГ к квадрату па ОГ относится,
как прямоугольник между ХЕ в ЕР к квадрату па ЕР;
то-or xi-> №
or2 ЕР2
после же перестановки прямоугольник между ТО и ОГ относится
О ШАРЕ И ЦИЛИНДРЕ
4'.И1
к прямоугольнику между ХЕ и ЕР, как’ квадрат на ОГ к квадрату
на ЕР. “
то-ог __ or2
ге-ер ' В1,«
Ио квадрат иа ОГ равен двум квадратам на ЕР, так как и квадрат наОВ
равен двум квадратам па 13J£; значит, прямоугольник между ТО и ОГ
равен двум прямоугольникам .между ХЕ и ЕР.
ТО • ОГ-» 2 (SR • Е1’)
Но, как доказано, прямоугольник .между ХЕ и ЕР относится
к квадрату на ЕН, как Г к А; значит, и прямоугольник между ТО и ОГ
к квадрату па ЕН относится, как 2Г к А. Далее, квадрат на ЕН равен
квадрату па SO, так как каждая на ЕП и SO равна ЛВ вместо с ВЕ;
значит, прямоугольник между ТО, ОГ относятся к квадрату на SO,
как 2Г к А,
ТО-ОГ _ 2Г
ЕО8 Л
и поскольку отношение 2 Г : А дано, то, значит, будет дано к отношение
прямоугольника между ТО, ОГ к квадрату на SO. Таким образом,
если мы сделаем, чтобы отношение 2Г : А*) равнялось отношению ТГ
к некоторой другой прямой Ф и опишем на ТГ эллипс так, чтобы
проведенные под углом SOB (то есть половице прямого) ординаты квад-
рировались па прямой Ф с недостатком, подобным прямоугольнику
ТГФ**), то этот эллипс пройдет через S согласно теореме, обратной
20-й (21-й) теореме? книги I. «Конических сечепин» Аполлония. Пусть
этот описанный эллипс, будет ГЕТ; тогда искомая точка 5 будет
находиться па эллипсе, заданном своим положением.
Далее, так как АК будет диагональю прямоугольника NM, то
прямоугольник между NE, ВН равеп прямоугольнику .между ЛВ, ИМ.
Поэтому если через точку В проведем гиперболу с асимптотами
Г)К и КМ, то опа пройдет через S; так как положения точки В,
обоих прямых АВ, В М, а значит, и асимптот ОК, КМ, являются извест-
ными, то эта гипербола будет задана своим положением. Пусть эта
построенная гипербола будет SB. Таким образом, точка S находится
на заданной споим положением гиперболе и уже находилась на задан-
ном своим положением эллипсе; следовательно, точка S дана. Так как
из псе ппущеп перпендикуляр ЗЕ, то, значит, будет дана и точка Е.
Затем так как МВ к ВЕ относится, как ZA к АЕ,
я» у. л
вк ’’ ЛЕ
и АЕ дана, то будет дана и AZ, Но той же причине будет дала и НВ.
С и н т г з я«> производится так;
Пусть на том же самом чертеже будет дана подлежащая разделению»
прямая Л В, затем другая заданная прямая ЛК и заданное отношение
*) В подлиннике ошибочно Л : 21’.
**) Но со нремеяпой терминологии это будет эллипс с диаметром ТГ и параметром Ф, орди-
латы SO in п ороги но нернендикулнрны к диаметру аллтшеа ТГ. а образуют с ним угол и 45*.
В обою ы четких ггатсг» чертежа уранкюимс итого '.шлипса будет;
ОЗ2 — ф- or — £ or8,
где Фбудет параметром. ска.ггнетстпуюиикм направлению секущих под углом в4Г»° к диаметру эллипса».
Если через Ъ' обозначим иол у диаметр, сопряженный с направленном диаметра ТГ, то
2b'i = (2Ь')г
1/2ТГ ТГ ’
•у>»»
.500
КОММЕНТАРИИ
Г : А. Перпендикулярно к АВ проведем ВМ, равную АК, затем соеди-
няющую прямую КМ, построим АР и BS, равные каждая КА, и из
точек Р и Е восставим перпендикуляры РГ и 2Т. При точке В
построим угол АВС), равный половине прямого, и пусть ВО, продол-
женная в обе стороны, пересечет прямые 2Т, РГ в точках Т и Т.
Затем сделаем, чтобы как 2Г к Л, так и ТГ относилась к Ф*),
•>г тг
’ д Ф
и опишем на ТГ эллипс так, чтобы проведенные под углом, равным
половине прямого, ординаты квадрировались иа прямой Ф с недостат-
ком, подобным прямоугольнику между ТГ и Ф. Затем проведем через
точку В построенную на асимптотах АК, КМ гиперболу ВЕ, пересека-
ющую эллипс в точке В, из Е опустим на АВ перпендикуляр ВЕ
и продолжим его до П. Далее через Е проведем ABN параллельно АВ;
придол7кмм прямые КЛ, МВ до точек ©, Л, продолжим также соединя-
ющую ME, и пусть она пересечется с KN в точке (-).
Теперь, поскольку ВЕ есть гипербола, а ©К, КМ — ее асимпто-
ты, то на основании 8-й (12-й) теоремы книги 11 «Конических сече-
ний» Аполлония прямоугольник между NB, ВП равен прямоуголь-
нику между ЛВ, ВМ,
хг-sn —ав-вм
поэтому КЕА будет прямой липнем.
Построим AZ, равную ©А, и ВИ, равную ЛВ; так как А к удвоен-
ной Г относится, как Ф к ТГ и как квадрат па ВО к прямоугольнику
между ТО, ОГ
а ф so2
2Г " тг то-or
согласно 20-й (21-й) теореме I книги «Конических сечений» Аполло-
ния. то, значит, удвоенная Г относится к А, как прямоугольник между
ТО, ОТ к квадрату па ВО. Далее, так как ТВ относится к ВО, как SB
к ВЕ
ТВ _ SB
ВО — ВЕ
и «присоединяя»- -ТО к О В. как 2Е к ЕВ.
ТО _ SB
ОВ ЕВ ’
я о ВО к О Г, как ВЕ к ЕР,
ко____ВЕ
’ог ЕР
то. значит, «по равенству» ТО к О Г. как 2Е к ЕР.
то _ ХЕ
ОГ ЕР
Таким образом, прямоугольник между ТО, ОГ к квадрату па ОГ
относится, как прямоугольник между SE, ЕР к квадрату на ЕР,
то-or ХЕ-ЕР
ОГЙ ЕР2
или, после иерестановки, прямоугольник между ТО, ОГ относится
it прямоугольнику между ЕЁ и ЕР, как квадрат иа ОТ к квадрату па
ЕР. Но квадрат на ОГ равен двум квадратам на ЕР, так как и квадрат
*) Та нее ошибка в подлиннике, что и лыше.
О ШАРЕ И ЦИЛИНДРЕ
501
на ВО равен двум квадратам на ВЕ, ибо ВЕ равна ЕО вследствие того,
что каждый из углов при точках В и О равен половине прямого. Тогда
прямоугольник между ОТ. ОТ равен двум прямоугольникам между
SE, ЕР.
то . ОГ «= 2ЕЕ-Ер
Поскольку же доказано, что удвоенная Г относится к А, как пря-
моугольник между ТО, ОТ к квадрату па ЕО
2Г тоог
д so*
то, значит, если взять половины предыдущих, Г относится к Л, как
прямоугольник между ХЕ, ЕР к квадрату па ЕО и как прямоуголь-
ник между РЕ, ES к квадрату на ЕН,
Г = хв. ЕР ХЕ-РЕ
д ЕО2 ЕН2
так как ЕО равна ЕП, вследствие того, что каждая на этих прямых рав-
на Л В вместе с ВЕ.
Теперь поскольку ОА вместе с АЕ к МВ вместе, с ВЕ откосится
как КЛ вместе, с АЕ к ЛВ вместе с ВЕ
ол АН КА -J- АК
ЯВ + Ве“ ABj-BE"
. (так как каждое из рассматриваемых отношений равно отношению АЕ
к ЕВ), то значит, прямоугольник между 0А вместе с АЕ и ЛВ вместе
с ВЕ равен прямоугольнику между КА вместе с АЕ и ЫВ вместе с ВЕ.
(ИЛ АК).(ЛВ ~ В К) ™ (КА • ле; (МВ i BE)
Но 0А-| ЛЕ равны ZE, Л13ВЕ равны ЕН, КА+АЕ равны РЕ, МВ -ь. ВЕ
равпы ES; значит, прямоугольник между ZE, ЕН равен прямоуголь-
нику между РЕ, ES.
ZE.EH = PE.ES
Но Г относится к А, как прямоугольник между РЕ, EX' к квадрату на
ЕП; значит, Г относится к А, как прямоугольник между ZE, ЕН к
квадрату па ЕН и как ZE к ЕН.
г ХЕ-ЕН ХЕ
Л ЕН2 ' ЕН
Затем так как А1В к ВЕ относится, как 0А к АЕ
мв __ ел
ВЕ ~ АЕ'
и 0А равна ZA, то, значит, МВ относится к ВЕ. как ZA к АЕ.
мв _ ZA
ВЕ “ АЕ
По той же самой причине КА к ЛЕ относится, как ИВ к ВЕ.
ка = нв
АЕ ВЕ
. . . Таким образом, если даны (величиной и положением) прямая АВ
и (только величиной) другая прямая АК и отношение Г : А, то вот на
АВ взята точка Е и прибавлены прямые ZA, НВ так, что ZE и ЕН
’• : находятся в заданном отношении; затем, если данная прямая ЛК равна
502
КОММЕНТАРИИ
МВ, то МВ к BE относится, как ZA к АЕ,
МВ _ ZA »
ИВ АВ
и КА к ЛЕ относится, как НВ к ВЕ,
к л ив
ЛЕ ВЕ
что и требовалось сделать.
После того как ото доказано, мы можем заданный шар делить в дан-
ном отношении так: пусть ЛВ{рис. 35} будет диаметр данного шара, Е
его центр, и отношение, в котором должны находиться между собой
сферические сегменты, пусть будет равно Г к А.
Рис. 35.
Берем на ЛВ точку Z и прикладываем прямые ПА, 0В так, что-
бы Г относилась к А, как HZ к Z0,
I- nz_
Л Z&
а НА относилась к AZ, как ЕВ к BZ,
на ив
" AZ “ BZ
и еВ к BZ, как ЕА к AZ;
ЙВ ЕЛ
BZ~“ “az
(и заданная прямая будет равна радиусу шара ЕВ или ЕА); доказано,
что все это выполнить возможно. Через точку Z перпендикулярно к АВ
проводим прямую KZA и рассечем шар проведенной через КЛ плоско-
стью, перпендикулярной к АВ. Я утверждаю, что получеппые сфери-
ческие сегменты будут относиться друг к другу, как Г к А.
Действительно, так как ИА относится к AZ, как ЕВ к BZ,
НА _ЕВ_
AZ ' HZ
то, значит, «присоединяя», получаем, что HZ относится к ZA, как ЕВ
вместе с BZ к BZ;
iiz ев + BZ
7.А ~ BZ
следовательно, конус, имеющий основанием круг с диаметром КЛ
и высоту ZH, будет равен сферическому сегменту с тем жо основанием
и с высотой ZA. Затем, так как 0 В относится к BZ, как ЕЛ к AZ,
ев ЕА
BZ =“ AZ
то, «присоединяя», получаем; 0Z к BZ, как ЕЛ вместе с AZ к AZ;
ez _ ел az
Bz"“ AZ ’
следовательно, конус, имеющий основанием круг с диаметром КЛ
о шаре и цилиндре
503
и высоту Z0, будет равен сферическому сегменту с тем же основанием
и с. высотой BZ. Так как упомянутые конусы, находящиеся иа одном
основании, относятся между собой, как высоты, то ость как HZ к Z0,
или как Г к Д, то, значит, ат» сферические сегменты будут находиться
между собой в заданном отношении, что и требовалось сделать.
13] При чтении этого предложения необходимо иметь л виду, что иод «двойным
отношением» Архимед подразумевает отношение, возведенное во вторую степень, а «полу-
торным!» отношением он называет отношение, возведенное в степень 3/2; таким образом,
данное предложение можно в некотором смысле рассматривать как первое появление
.дробного мокалателя степени.
Далее стоит отметить, что рассматриваемое предложение представляет единствен-
ный пример, когда изложение доказательства Архимеда может быть очень упрощено,
пи выходя из области операций, дозволенных в античной математике.
Первая часть предложения совершенно естестненно доказывается так (рис. 55 па
стр. f(i0).
Пусть HZ и AZ представляют высоты сравниваемых сегментов, причем BZ>AZ;
отношение поверхностей обоих сегментов будет равно отношению этих высот, действи-
тельно:
Л В* _ BZ -BA _ _J JZ_
ЛЛ4 ZA-BA "~ZA '
Пусть 0Z и HZ представляют высоты тех конусов, объемы которых равны объемам соот-
ветствующи х сегментов:
HZ = BZ AZ. ,
AZ
зуди ЕВ—ЕА продстанл лет радиус шара. Отношении объемов обоих сегментов равно отио-
лгшпию высот этих конусов:
8Z :'/Н_^-(ЕЛЧ AZ): “ <ИН-ВЧ-(^)*-й$£ '
Так как ЕЛ=еЕВ и BZ>AZ, то второй множитель будет меньше, единицы,
откуда сразу получается;
ez bz у
ZH ZA ) '
и первая часть теоремы доказана: отношение объемов обоих сегментов меньше возведен-
ного в квадрат отношения их поверхностей.
В наложении Архимеда встречаются все основные моменты вышеприведенного доиа-
вательетиа, ио они затушеваны привходящими второстепенными .-моментами.; п частности,
Архимед вводит точку"К, чтобы было ЕВ | BZ.= KB |-BZ = KZ.
Сначала он из исходного равенства
6Z EA+AZ ...
ZB=“A—
определяет отношение BZ/ZA;
BZ 0Z 0Z—ZB 0 В ЙВ
ZA “ ЕД-j-AZ “ “ЕД ".ЕЛ ^ЕВ’
«ли, так как ЕВ=ВК:
(2)
UK ZA •
Второе исходное равенство
HZ _ EB4-BZ
ZA BZ (
504
КОММЕНТАРИИ
сразу ему дает:
их __ kz
ZA в/, ’
пли после перестановки:
BZ KZ
-ттт—’тГГ
ZA ZI1
При этом Архимед устанавливает, что ВВ>ВЕ -факт совершенно ненужный
для доказательства первой части теоремы — из пропорции (2), так как BZ>ZA.
Определяя отношение BZ/ZA из (2) и (4), находим:
Так как
0В [iZ_0B4DZi ez
ВК — ZA BK-I-ZA EH4-ZA
и
0Z _ 0Z
ZK - EB+BZ ’
то, поскольку BZ > AZ, он на основании (5) пишет:
©Z НВ KZ
ZK it л ZH ’ { '
В правой части отношение KZ/ZB, согласно (4), представляет отношение поверх-
ностей обоих сегментов, тогда как 6Z/ZH будет отношение их объемов.
Дальнейшие операции уже вполне понятны. Из неравенства (6) мы имеем:
6Z.ZR < KZ2
и
ez_ . kz*
ziT^ hz».*
что и доказывает первую часть предложения.
Если бы оба наши сегмента были подобны, то их объемы относились бы как кубы,
а поверхности - - как квадраты сходственных сторон; следовательно, отношение объемов
равнялось бы возведенному в степень ’/», или, как сказали бы гроки, полуторному отно-
шению их поверхностей. В вашем случае, когда оба сегмента не подобны, отношение
объема большего сегмента к объему меньшего будет больше полуторного отношения соот-
ветствующих поверх постей.
Так как объемы относится, как высоты конусов 0Z/ZH, а поверхности — как
высоты сегментов BZ/ZA, и из основных формул (1) и (3)
ez BZ2 ЕД 4 AZ
ZII ~ ZA2 ’ ЕЛ 4-BZ
то после возведения в квадрат обеих частей этого ранепства мы получили бы:
Z OZ >- / BZ \S BZ (EA-|- AZ)2
< ZH ) =< ZA ) ‘ AZ(EA-|-BZ)2 ’
и для доказательства нашей теоремы нам. пришлось бы только убедиться, что последний
множитель больше единицы.
Мы имеем:
BZ (ZA-i ЕД)2 IiZ- ZA2 | BZ • ЕЛ2-J-2BZ• ZA KA
-AZ (EA-i-SzH^AZ-BZ* |-AZ-EA2-2BZ-ZA-EA '
Разность числителя и знаменателя этой дроби можно представить в виде
(BZ AZ) EA2-|-BZ ZA (ZA BZ) = (BZ —ZA) (ЕЛ2 —BZ-ZA).
О ШАРЕ И ЦИЛИНДРЕ
ЙОГ»
Так как RZ > ZA, то первый множитель положителен; что касается второго множи-
теля, то мы без труда докажем, что ЕДа > BZ-ZA. Действительно, соединим ла рис. 3(>
центр Е круга с вершиной А перпендикуляра AZ. Мы
что и доказывает выставленное положение.
Доказательство Архимеда начинается как раз с установлеяия факта, что ЕАа =
=ВЕ-ЕА > BZ-ZA. Отсюда оп получает:
ZB Ей
ВЕ" < ДТ
или на основании следствия из нашего уравнения (2), так так ВК —ЕА:
ZB ОВ
ВЕ **• BZ ‘
Отсюда оп нолучает:
ZB®<6B-BE,
или, так как.ВЕ —ВК:
ZB®<0B-BK^BN*1
где BN есть средняя пропорциональная между ОВ и ВК;
OB _ BN
BN “ ВК '
. Отсюда
ев bn®
ВК ВК*
Отношение BIN —— мы можем вычислить так: ВК BN _ 6в _ ев J-BN _r0N ВК BN NB-J-BK NK ’
и следовательно, ев ON2 ВК NK®‘
Далее, так как 6N _ 6Z+ZN NK KZ-J-ZN
и 6Z>ZK, то • eN <- eZ WK ZK
И e№ ez* NK8 C ZKa
откуда ez? ©в _ ев _ кг - - ZKS > BK BE ZH
на основании нашего равенства (5).
Б06
К ОМЫВ НТА PH И
Из неравенства
<-)Za KZ
ZK3 ZH
Архимед заключает, что
HZ / KZ у/з
ZH >\ч ZH J
без всяких дополнительных пояснений. Так как отношение 6Z/ZH равно отношению
г KZ BZ ,
объемов сегментов, а = (см- равенство (4)) — отношению их поверхностен, то
теорема доказана.
[4] К сожалению Архимед не поясняет, каким образом он получает нужное ему
неравенство с полуторной степенью
QZ z KZ у/3
ZH > k. Zlf ) ‘
Доказательство, которое даст комментатор Архимеда Евтокмй, таково:
Вообразим {рис. 37} раздельно расположенные прямые АВ, Г, А
такие, что отношение квадрата на АВ к квадрату иа Г больше отноше-
ния Г к А. .
АВ8 г
г2 Л
Я утверждаю, что отношение АВ к А будет боль-
ше возведенного в полуторную степень отноше-
ния Г к Л.
Возьмем для Г, А средшою пропорциональную Е *).
Тогда, так как отношение квадрата иа АВ к квад-
рату на Г больше отношения Г к Л
АВ8 .. Г
Г® ^~Л
и отношение квадратов на ЛВ и Г равно двойному отношению АВ к Г,
а отношение Г к А равно двойному отношению Г к Е, то, значит, отно-
шение АВ к Г больше отношения Г к Е.
_АВ_^ Г
г Е
Сделаем теперь, чтобы Е к Г относилось, как Г к BZ**).
в г
г BZ
Так как четыре прямые BZ,T, Е, А составляют непрерывную про-
порцию,
BZ _ Г _ Е
' Г ~ Е — Д •
то отношение BZ к А равно трижды взятому множителем отношению BZ
к Г, или Г к Е.
В2 _ ( Г \-1
’ А ' В '
Г Е
»> Так что = -.
**> Из атого равенства вытекает, что
О ШАРЕ И ЦИЛИНДРЕ
507
Но отношение Г к А равпо дважды ввитому множителем отношению
Г к Е.
Л \ Е >
Следовательно, отношение BZ к А равно отношению Г к А, взято-
му множителем полтора раза.
bz ( г уд-
д 'д'
Таким образом, отношение ЛВ к А будет больше отношения Г к А,
взятого множителем полтора раза.
Мы видим, что введение дробной степени для отношений произошло у греков в изве-
стной степени бсссозцатсльпо благодаря тому, что греки рассматривали умножение отно-
шений как их сложение.
Помещенное в конце, этого предложения доказательство «иным способом» вряд ли
может принадлежать Архимеду. Не говоря уже о том, что оно, как говорит Хизс, не
является пи более ясным, ни более коротким, чем предыдущее, метод доказательства,
состоящий в преобразовании искомого отношения и сведения его к уже доказанному
или очевидному, совершенно ве в духе Архимеда.
|5| В этом предложении мы видны первый пример Tait называемой изопериметри-
ческой задачи. Позднее мы имеем целое исследование «Об изолериметрических фигурах»,
принадлежащее александрийскому математику Зеиодору и освещенное в пятой книге
«Математического собрания» Паппа Александрийского.
О КОНОИДАХ и СФЕРОИДАХ
Это произведение, первое- в математической литературе, касающееся поверхностей
второго порядка, согласно первоначальному плану, изложенному во введении к трак-
тату «О спиралях», должно было быть четпертым в ряду посланий, обращенных
к Доснфею, но н действительности оно оказалось пятым.
Основной задачей рассматриваемого произведения является определение объемов
сегментов параболоида, гиперболоида и эллипсоида вращения. Эта задача была решена
Архимедом при помощи механического способа, как излагается л «Эфоде» (предложе-
ние 111, IV, V111, XI). В сочинения «О коноидах и сфероидах* дается строгое матема-
тическое обоснование решения поставленной задачи, для чего доказывается двадцать
вводных предложений.
[1] Предложении I и II носят арифметический характер, продолжая исследования,
начатые в предложениях X и XI трактата «О спиралях».
[2] Предложение III содержит вспомогательные теоремы ин теории конических
сечений..Первой является теорема, доказанная в «Началах теории конических сечений».
Доказательство этого предложения содержится
в «Конических сечениях» Аполлония (книга III,
предложение 17), пи было бы очень сложив вос-
производить всю цепь рассуждений по Апол-
лонию, привлекая все необходимые предвари-
тельные теоремы; поэтому мы дадим доказатель-
ство в современной форме, пользуясь методами
аналитической геометрии. Это тем более необхо-
димо, что в труде Хизса это предложение обхо-
дится молчанием, а в переводе Чвалинны «Ко-
ноидов» при доказательстве этого предложения
допущена грубая ошибка. Рассматриваемая тео-
рема у Аполлония формулируется так: «Если
две прямые, касательные к коническому сечению,
или я окружности круга, встречаются в одной
точке, и иэ двух произвол ьных точек, взятых па
рис £ коническом сечении, проведены прямые, парал-
лельные этим касательным, пересекающие друг
друга и коническое сечение, тн произведения
• отрезков каждой из этих прямых будут относиться, как кнадраты соответствующих
касательных».
Если взять начало координат в перпшне конического сечепня и ось абсцисс совпа-
дающей с осью последнего, то уравнение любого конического сечения может быть пред-
ставлено в форме
уя=2рх-\-кх\
где /с>0 для гиперболы, к=0 для параболы и для эллипса.
Пусть из некоторой точки А с координатами хг, yt проведены: касательные АВ, АГ
к коническому сечению (рис. 1).
Пусть а будет угол, который образует с осью Ох одна из этих касательных, напри-
мер АВ, a q — расстояние от А до точки касания В. Координаты точки В могут быть
представлены в виде
x=xj-|-o cos а,
y = ?/i4-psin<i.
О КОНОИДАХ И СФЕРОИДАХ
509
Мы можем найти координаты х и у, решив эти уравнения совместно с уравнением кри-
вой у2 — 2рх-}-/сха
(yt-|-qsin a)2--2p(xl !-Qcosa)--;-A-(xl-'-Q<:os<x)2.
Для о мы получим после нреобразонапнн квадратное уравнение
(sin® а—A- cos2 а) q2-!-2(?/j sin a—It (я, I-/,) cos a} Q-j-(y?—2pxt--kxl) — C).
Так как всякая прямая пересекается с коническим сечепием в двух точках, которые
в случае касания сливаются в одну, то рассматриваемое уравнение должно иметь равные
корпи. Для этого необходимо, чтобы
{у, sin а—к р) cos «}2=(sin2a —A cos2 а) (yj —2/wr—Attj).
Если разделим обе части последнего равенства на cos2 а, то для определения tga получится
кпадратлое уравнение: это значит, что из любой точки плоскости можно провести к кони-
ческому сечению, вообще говоря, две касательные. Если точка А выбрана так, что дли
tga получаются действительные корни, то соответствующие касательные будут ЛВ и АГ.
Таи как а случае касания для расстояния Q получаются равные корпи, то для квад-
ратов АВ и ИГ мы будем иметь выражение
. y-i-2pxt -М
” sin2 и--к cos2 a ’
где л эцаменатело вместо а нужно подставить соответственно значения углов, образуемых
•с осы» Ох каждой ил прямых АН и Л Г.
Возьмем теперь некоторую точку Л с координатами х„, у2, лежащую по другую сто-
рону кривой. Из этой точки параллельно Л В и АГ проведем прямые EZ и 011. Коорди-
наты точек, находящихся на каждой из этих прямых, могут быть представлены анало-
гичными выражениями
x=xB-|--r cos а,
г sin а.
Для г — расстояния ДЕ и AZ, или соответственно Д0 и АП, от точки Л до кривой, мы
будем иметь аналогичное уравнение
(sin2 a— A- cos2 a) г2 -] 2 {ys sin a—/с (л3 -|- р) cos a} г -|- (у4— 2рх2 - Avrs) — 0.
Но теперь корпи rlt г» этого уравнения должны иметь разные злаки, так как ДЕ к ДХ,
и соответственно Ав и АН. имеют различные направления; следовательно, произведение
абсолютных величин г., будет равняться
__ — (у а — 2рле — A-sj)
r,rs~ Siu»a-.^Cl(sea
Пусть «J представляет угол с осью Ох прямой АВ, а а2 прямой АГ; в таком случае;
Мы имеем:
У®— 2рхх -kxf
sin2aj — A-cos2 а । ’
—2pxx kx'{
si n2 aa—- к cos2 a» ’
AE-AZ=
•Д0-ДЦ--
Уъ -—2px2 —kx%
sin2aj — A-cos2^ ’
y%—2рз4—кх%
sin2 a» - A- cos2 a..
AB‘- ЛГ* _ yj—2pxt— kxj
AE-AZ "7 Д0-ЛП ~ - y'i— 2pxn — Azs ’
что и доказывает высказанную теорему. Для того чтобы правая чисть была положитель-
ной, достаточно взять точки Л и А но разные стороны от рассматриваемого конического
ссчсяия, кнк и сделано на рис. 1.
Вторая часть предложения JIJ требует преобразования уравнения параболы к косо-
угольным осям координат, началом которых служит точка Д (рис. 2), ось Ох совпадает
«прямой ЛК, а ось Оу — с параллельной В0 касательной, проведенной в точке Д. Выска-
занное Архимедом вспомогательное предложение может быть сформулировано так:
Если Пва = Л’-ВН, где Л’ = 2р параметр параболы, соответствующий прямо-
угольной системе координат, в которой ось х представляет ось параболы ВН, и ось у -
касательную к параболе в ее вершине, то AZ2 —Л/-AZ, где. /V и М связаны соотношением
Л’: Л/ = АК2 : AZ2.
510
КОММЕНТАРИИ
Пусть новая система координат представляется совокупностью прямых ЛК — диа-
метра параболы — и ТДТ, — касательной к ней в точке Д. Пусть АЕ представляет
хорду, параллельную :ггой касательной, делящуюся в точке L пополам; диаметр ЛК, как
известно, будет параллелей оси В И параболы.
Пусть ВП и IM*! будут абсциссы, с-оотаетствующие крайним точкам Л и Е хорды
АЕ; тогда по основному свойству параболы мы имеем:
BP, :ВН=ЕР?:ЛП2,
или, так как ЕР,: A1L--OP,: ОН, НИ : ВР,--=ОГ12: ОР?.
Тогда, прнмеини операцию «переворачивания», получаем:
ВП -ВР, ОПа ОР?
ВП “ ОП* ' ’
или
ВП : IIP,ОН* : (ОП-: ОР,) (ОП—ОР,),
откуда после сокращения на ПР,:
О1Р= 1Ш-(0П—ОР,).
Это равенство можно переписать
так:
(ВП -.ВО)2--ВП{.(В11 ВО)
— (ВО—ВР,)},
откуда
ВП2-|-ВО2 2В]ЬВО=
.=г Bl l«-h Ш1. ВР,—2ВП- ВО
или
ВО2-=ВПВР„
параметра параболы, соответствующего!
оси В11; тогда
Д’*. ВО*= (АГ-BII) (Л• BPt) == ДП».ЕР?,
или
ЛЕВО—= АН-ЕР,.
Уравнение параболы, отнесенной к осям ДК и ДТ, будет
у2 = Л/-аг,
откуда для точки А:
AZ2^A/-AZ.
Мы имеем:
AZ*: АК* = AZ» : (j-” ^-^^AZ*: АП-ЕР,у . д1| EpJ
Далее, так как AZ —ZE, то
ЛК = Е Р, Н- ЕД = Л11 ЕД,
откуда АП—ЕР,-—2ЕЛ; поэтому
AZ» : ЛК*=AZ2 ; (ЕА2 -j АП ЕРг).
Но ЕД* = Л’-ВЕ и АП-ЕР,— А'-В(), как было доказано выше; значит,
AZ2 : Л К*—AZ* : А (ВЕ | - ВО),
где ВЕ представляет асбцнссу точки Л касания. Так как у параболы подкасательная ЕГ
равна удвоенной абсциссе, то ВЕ+ВО—ТО= AZ, и мы имеем:
AZ2
AZ^^VAZ.
О КОНОИДАХ И СФЕРОИДАХ
511
Сравнивая эти с новым уравнением параболы, получаем параметр М".
M=N
AZ2
АК2'
131 Задачи, постаплсиные в предложениях VII--IX, могут быть формулированы
двояко. Во-иерцых, если на рис. 7 текста (стр. 179) рассматривать эллипс АпВ кап основа-
ние, а ГА как высоту колуна, который, конечно, будет, с пашей точки зрения, эллип-
тическим, то дело идет об определении круговых сечений заданного эллиптического
конуса. Во-вторых, можно рассматривать А«В как эллиптическое сечение некоторого
кругоного конуса с вершиной Г, основа нив которого требуется найти. Все говорит за
то, что Архимед рассматривал постаплсипук) задачу именно с последней точки зрения.
В предложении VII Архимед ставит такую задачу:
Дан эллипс с малой осью ЛЛ н большой уД и равнобедренный треугольник ЛВГ
(рис. 3); черен точку Л требуется так провести прямую AZ, пересекающую в В и Z
продолжении высоты ГД и боковой стороны ГН .дппного треугольника, чтобы имело
место равенство
(ЛЕ EZ) : ЕГ2=-Лу2: ЛГ2.
Архимед считает эту задачу возможной потому, что
AE-EZ АЛ АВ
> рда •
Чтобы попить значение этого условия, обратим внима-
ние на то, что н эллипсе АуВ
АД ДВ < Л у2,
п л круге AftZ
AE-EZ—Ей2,
где. Ей перпендикулярна к AZ и, следовательно, парал-
лельна Ду. Таким образом,
AE-EZ ЛД-ДВ
Ей2 •> Ду2 ’
11оскольку
Ей : Ду=ЕГ : ДГ,
полученное нами ранппстно будет эквивалентно архимедову, если только АД—ДВ <Ду„
Ti> есть если АЛ яилнется меньшей главной полуосын эллипса АуВ.
Решении поставленной задачи Архимед не дает, по оно может быть получено сле-
дующим образом.
Пусть па рис. 3 угол ГЛВ — а. Мы будем знать положение секущей п.кхжости AEZ,
сели будет известен угол BAZ=<p, или отрезок ЛЕ. Нелзиеетпая точка Е определится
из уравнении
AE-EZ Лу2
ЕГ2 " ДГ2 '
Из треугольника ЛЕГ имеем по теореме синусов:
ЕГ _sin(a--<p)
АЕ cosa
а из треугольника TEZ:
ЕГ sin (а--ср)
EZ cos а
Подставляй эти значения в ваше уравнение, получаем:
cos2 a
sin (ft -I- <p) sin (ft <p) ЛГ2
Дуа ’
512
КОММЕНТАРИИ
откуда
ЛГ2
(sin a cos <р -|- si и ф cos а) (sin а cos ф—sin ф cos а)=—^5- cos2 а.
АГ2
cos-я,
sin2 п cos2 <с — sin2 <р cos2 а — . ,
• г Ду
Л Г2
sin2 а- sin2« в1П2ф—со.ч31»»щ2ф= cos2 и.
ЛГ
S1H2U—ЙПрф
i- COS2 «,
Ду2
<и окончательна
АГ2
sin2 ф — sin2 а--cos2 а.
г Ду2
Имеем:
ГД Ад
Slba- АГ’ с05а~Лг
сл едователь но.
sin2
ГД2
Лу
ГЛ /Ду2—АЛ2
sin ф —------1----
Так как ГА > ГД
После этого
Ду > АД, то задача допускает решение.
и Ду ,> АД, то задача допускает решение.
__________ ____ Архимед доказывает, что все точки я.тлипса лежат’на поверхности
копуса с основанием A6Z и вершиной Г (этот конус, естественно, уже ле будет прямым).
Произведя описанное п тексте построение, Архимед начинает с исходной пропорции:
ЛЕ-EZ _ Да2
ЕГ2 ~ДГ2 '
Иа подобия треугольников ГАВ и ГПР получаем:
ЕГ® ГД2
ЕП-ЕР АД-ДВ ’
откуда
(АЕ EZ) : (ПЕ ЕР) = Лв«: (ЛЛ А В).
Далее, иа подобия треугольников АИЕ, ЛЕЛ, и AOZ, EPZ имеем:
АЕ : ЕП—ЛА : ЛЕ,
EZ : ЕР—-AZ : ЛО,
<<>
откуда
(ЛЕ - EZ) : (НЕ ЕР)~-= (АЛ AZ): (SA - ЛО).
Заметим но спомстпу отрезков мещду параллельными секущими эллипса
(2)
Ла2: (АД-ДВ) = ВК3: (ЛК- КВ).
Теперь, сравни пая пропорции (1) и (3), мы можем написать:
(3)
(ЛЛ-AZ): (ЕЛЛ0)=6К2 : (ЛК-КВ).
(i)
Далее, ни подобии треугольников АВГ и ЕОГ имеем:
(ЕЛ-АО) : ГЛ2—(ЛК-К В) : ГК2,
(5)
что дает нам «по равенству»:
(ЛЛ-AZ) : ГЛ2 —©К2 : ГК2.
и
.6*7
О КОНОИДАХ И СФЕРОИДАХ
513
Если в точке Л параллельно вК проведем перпендикуляр ЛМ до пересечения
с поверхностью л о п у с а, то по свойству круга получаем:
АЛ-ЛЯ=ЛМ®,
и наше равенство принимает вид
ЛМ:ГЛ=Кв: ГК.
Вто означает, что треугольники ГК0 и ГЛМ подобны или что лмнмн ГУМ есть пря-
мая. Так как точки Г и М лежат па поверхности конуса, то, значит, и принадлежащая
эллипсу произвольная точка 0 тоже будет лежать на
поверхности конуса ГЛ/.
[41 При построении фигуры дли доказательства
предложения VIII (см. рис. 8 ла стр. 183) нужно от-
метить следующий момент.
Если имеет место равенство №s=ZA-ДИ, то точ-
ки Z, Н и конец отрезка, изображающего прямую N,
будут находиться на окружности, построенной на
диаметре ZH; тогда построенная ла ЕВ подобная кри-
вая тоже будет окружностью.
Если же N2 по равно ZA-AII, то сечение конуса
плоскостью, проведенной через ZH перпендикулярно к
с плоскости чертежа, будет представлять эллипс; по-
этому на ЕВ и строится эллипс, подобный упомяну-
тому. Дальнейшее доказательство проходит вполне
аналогично предыдущему.
|5] Доказательство первого утверждения, а имен-
но что сечение параболоида нращеиия плоскостью,
параллельной оси, будет такой же параболой, как и
образующая параболоид, можно пронести так.
Пусть ОГ представляет ог.ь параболоид», Л1)В —
парабола, полученная в сечении параболоида пло-
скостью, проходящей через ось. Рассечем параболоид
плоскостью, иараялелыюй оси ОГ и перпендикуляр-
ной к плоскости чертежа. Пусть прямая ДЕ предста-
вляет след этой плоскости па плоскости чертежа
(рис. 4,а). Тогда, если смотреть сверху, сечение пара-
болоида изобразится линией ВДВ (рис. 4, б); тре-
буется доказать, что ото будет парабола, совпадающая
с первоначальной ЛОВ.
Согласно основному свойству параболы, квадра-
ты ординат возрастают пропорционально абсциссам;
если обозначим коэффициент пропорциональности че-
рез 2р, то будем иметь:
или
нооощо:
Л.Г2—2р-ОГ,
у2=2рх.
том
Нам предстоит найти соотношение между квадра-
ординаты НЕ и соответствующей абсциссой ЛЕ.
Если через точку' Е провести плоскость, перпендикулярную к осп ОГ, то мы и сече-
с параболоидом^получим картину, изображенную на рис. 4, в. Uo свойству' прямых
НИИ
в окружности мы будем имоть:
0Е2^АЕ-ЕВ = АЕ(АЕ-*-2ЕГ).
По АЕ = АГ—ЕГ; следовательно,
0ЕЛ== (АГ—ЕГ) (ЛГ+ЕГ) = АГ2- ЕГ2.
Далее,
АГ2=-2/?-ОГ, ЕГ2= AZ2—2p'OZ;
таким образом,
33 Архимед
0E2 = 2p-Or--2p-OZ = 2j?.Zr=2^-AE,
514
КОММЕНТАРИИ
или вообще
у2=2рх.
Мн получили уравнение, совпадающее с первоначальным.
Второе утверждение о том, что сечение гиперболоида вращения плоскостью, парал-
лельной оси, представляет гиперболу, подобную данной, мы доказали бы таким же образом.
Пусть ОГ представляет ось гиперболоида, К • центр его, то есть вершину асимп-
тотического конуса, АОВ — основную гиперболу. Плоскость, параллельная оси, пере-
секает плоскость чертежа (рис. 5, а) по прямой ЛАЕ и дает п сечении с гиперболоидом
линию ЛвЛ (рис. 5, б); требуется доказать, что это будет гипербола, подобная первой.
Если ОК — действительную полуось гиперболы — обозначим через и, параметр
гиперболы обозначим через /> и положим ОГ=а:, АГ —у, то гипербола (см. всту-
пительную статью) может быть представлена следую-
щим уравнением:
!?=- Х‘
Совершенно так же, как в случае параболы,
можем написать:
0Е2=АЕ*ЕВ==АГ2— ЕГ2,
или
©Е2—— (2а4-ОГ) ОГ—— (2я |-OZ) OZ »
d d
= ~{2а (ОГ—OZ)4 ОГ2—OZ2}=
=-£-(ОГ- OZ)(2«+Or+OZ}=-£ Zr{2a4-2OZ4-Zr).
Но а+О2=О1Л-{-О1Л=ЛЛ — действительной полуоси
повой гиперболы ЛЕВ; если мы обозначим эту полу-
ось через в„ то уравнение кривой сечения будет:
У2 = — (Zafj-Jjja:,
а
р Pi
или, если положить — = —:
a at
“i
это будет уравнение гиперболы, параметр Pt и действительная полуось аг которой уве-
личены в одном и том же отношении а : а(; иными словами, мы получили уравнение
гиперболы, подобной данной.
Аналогично этому можно доказать соответствующее предложение и для удлинен-
ного эллипсоида, если взять уравнение основного эллипса в виде
у2-^ ~~(2а^х) х,
где р — параметр, я 2а соответствует большой оси эллипса, вокруг которой происходит
вращение. Для сплющенного эллипсоида нужно лишь в уравнении произвести сдедую-
б2 .
щую замену: вместо у взять b—х, а вместо х взять a—у, и помнить, что р = — где и —
. >'2 е
малая полуось эллипса. Если положить р —-у» то уравнение эллипса будет.
у*=^(2Ь-х)х.
О КОПОИДЛХ И СФЕРОИДАХ
515 •
чертежа; пусть
к плоскости чертежа, образуя
Несколько сложнее обстоит дело в том случае, когда сечение гиперболоида прово-
дится через центр — вершину асимптотического копуса К. Пусть КОГ представляет ось
гиперболоида, кривая ЛОИ — сечение гиперболоида плоскостью
секущая плоскость проходит перпендикулярно
в пересечении с последней прямую КАЕ; точка
А будет представлять вершину кривой сече-
нии, расположенном в плоскости, перпендикуляр-
ной к плоскости чертежа; требуется доказать, что
ото будет гипербола, но па этот раз уже не являю-
щаяся подобной основной гиперболе ОЛВ-
Так как АВ представляет диаметр кругового
сечения, перпендикулярного к оси, то ордината у
кривой сечения будет расположена в плоскости
этого круга. Мы имеем:
у®=АЕЕВ.
Проведем через точку Е диаметр, сопряжен-
ный с прямой КЕ; пусть это будет ММ; тогда МЕ —
= NE. Возьмем прямую АЕ в качестве оси абсцисс,
а в качестве оси ординат возьмем параллель-
ную MN касательную ATS; пусть эта касательная
пересекается в точке Т с другой касательной ОТ,
проведенной в нершине О основной гиперболы.
Тогда, пользуясь первой теоремой предложения
Ш, можем написать:
АЕ-ЕВ _ ME-NE
ОТ2 ~ АТ3 ’
Рис. 6.
откуда
ОТ3
Уа-^'МЕ2.
По МЕ представляет ординату гиперболы по отпоптслию к
и АТь уравнение гиперболы в этой системе координат будет:
косоугольным осям ДЕ
У?—~~ (2я1-|-л'1)
где а.1= К А, Ж1 = ДЕ, jji = EM, а. р> -- параметр, соответствующий диаметру КЕ. Так
как ось х кривой сечения совпадает с АЕ, а ось у перпендикулярна к плоскости чертежа,
то мы можем положить х1^х и писать:
г/2==_'ДТз'77 (2й1+*)
Это будет уравнение гиперболы.
Чтобы доказать, что эта гипербола по будет подобна основной, будем рассуждать так.
Проведем через точку А плоскость, параллельную оси 01' и перпендикулярную
к плоскости чертежа; мы знаем, что и сечении получится гипербола, подобная осноппой;
пнм остается только доказать, что эта гипербола не будет подобна рассматриваемой.
Возьмем в качестве начала координат точку К. Так как AE=x( — КЕ—КА—ж- КА,
где КД есть действительная полуось п, нашей гиперболы, то уравнение гиперболы будет:
У АТ2 КА ( 1 1 '•
или, если вместо у будем писать у;:
^-КДЕ>-
Аналогично, если для гиперболы сечения AAZ возьмем в качестве начала коорди-
нат точку А — оснований перпендикуляра КЛ к прямым КГ и AZ, то ее уравнение пред-
ставится в виде
й=^-(4-АД’).
.33*
КОММКНТАРИИ
• Если бы эти гиперболы были подобны, то мы имели бы:
ОТ* Pi ~_Р
ДТ2" КД п’
Возьмем две точки Е и Z, лежащие ла прямой, нерпендикулярпой к оси: для точки Е
будет У1=АЕ-ЕВ, а для точки. Z будет y®=AZ-ZB. Мы видим, что у3 >«4- Далее,
для точки Е
г?—КД2 = К Еи— К Д2=КГ*—ЛД* [ ЕГ2— КЛ2,
а для точки Z
*5— ЛЛ2= Л Z8—ЛД* *= КГ2— АД®.
Таким образом,
ж3—КЛ2>ж£—ЛЛ2.
Отсюда следует:
УЗ Vi
%1 —ЛД2 ' rcjf —КД2 ’
иными словами, гиперболы обоих, сечений подобными яс являются.
[6] Мы видело выше, что подкасательная параболы равна удвоенной абсциссе
точки касания. Можно показать, что для гиперболы подкасательная будет меньше
удвоенной абсциссы, а для эллипса—больше.
[7] В доказательстве второй теоремы XV-ro предложения имеется некоторый не-
досмотр. Если какую-нибудь точку Л на поверхности коноида и вершину О асимптоти-
ческого конуса соединить прямой, то через эту прямую можно провести сколько угодно
плоскостей, которые, согласно второму утверждению предложения XI, будут пересекать
коноид по гиперболам. Среди этих сечений будут выделяться два: сечение плоскостью,
проведенной через прямую ОА и ось коноида, и сечение плоскостью, проведенной через
ОА перпендикулярно к первой из упомянутых плоскостей: обе эти плоскости рассматри-
ваются в комментарии [4]. Только для сечения второй плоскостью прямая ОЛ будет
осью получившейся гиперболы; в случае же сечения через ОЛ и ось прямая ОЛ будет
лишь одним из диаметров гиперболы, осью гкс юе будет ось коноида. Аналогично этому
дли всех остальных сечений плоскостями, проведенными через ЛО, эта прямая будет
лишь одним из диаметров гиперболы, получившейся в сечении.
[8] Под АГ Архимед под разуме пае г не только прямую АГ, но и кривую—сечение
эллипсоида плоскостью, проходящей через АГ и перпендикулярной к плоскости чер-
тежа. То асе самое справедливо и относительно КЛ.
[9] Положим ЕД—г, ВЛ—пг и радиус АД —Ляг. Если в качестве оси ж взять ВД,
то уравнение параболы АВГ будет у2=Л2ягх и соответствующий абсциссе ВЕ =
~(п—1)г радиус КЕ определится равенством КЕ2=Л2»» (п -1)га, так что объем самого
«ажпего вписанного цилиндра будет
Я*КЕ2-г—лЛ2я (я—1) z8,
а всей вписанной фигуры
Гвп„с=яЛ2в <1-5-2-]-... +(n-l)}z3=лЛ2п2 (п-1) z3/2.
Объем всей описанной фигуры будет:
Копие = nlt2n {1 -]-2-]- -.. -г«}г3=лЛ2па (я-1-1) г3/2.
.Мы имеем:
Гвпис яЛ2л.э2э/2 10114 с*
Объем конуса Т, равный половине объема цилиндра АВГД, будет
¥=-nfc2«2z2«z/2 = лАД2ВД /2;
он заключен между УВП.1С и УОпис« отличающимися друг от друга па величину, кото-
рую можно сделать сколь угодно малой.
[10] Пусть АЕ = 2, ВЛ-—nz и 0В=^й. Ордината КЕ определяется согласно архи-
медову «уравнению» гиперболы равенством
КЕ‘=б4^пг «гч-ь-очо- <>=>•
Объем самого нижнего вписанного цилипдра будет:
тг А А
О КОНОИДАХ И СФЕРОИДАХ
517
а всей вписанной фигуры, состоящей из (гг—1) цилиндров:
Ц l-2-i'.. .-НН-1ЛН-11Ч-2Ч ... +(«-1)г1 *3)-
Выражение и скобках можем переписать так:
rt(n--l) 1 Г , ,ч2 । ”(«—1)1 ,
2а——- z-L-r «(»— 1)2+—Ц;—i z2.
И О I Li J
Замепип (n -1) иа л, мы увеличим это выражение; таким образом,
,, л-АДах (п*( z\ । *а »1
вИнс < + ВД) ВД I 2 (. 2 + 3 ) 2 1 3 Z / ’
Объем описанной фигуры (п цилиндров) будет:
Л
=1в2+вд) вд (1 +2+ • -i (12+2S-I“ ’ • +*•»=
л-АД2х»
(BZJ-BA) ВД
Г «pi-| i) z Г . , л.(в-|-1) 11
|2a -Hj-------|- у (re - j 1) a2-j- j |
Заменив (л+1) па в, мы уменьшим это выражение
v я.ДДг2а { 1 Г z\ 1 1
и0БИС>щ2_гвд;вд {Т<2а azf-
Таким образом,
v я-КЬг(пг^ fl / . z Л . 1 1
впис < (BZ- j ВД) ВД ("2 <2л+‘3 ) +'3 "7 1 опис'
Так как z может быть сделано очень малым, то отбросим z/З н фигурных скобках.
Поскольку a = B0, nz=BA и BZ = 2B6, то средний член можно переписать так:
1 „ ллэ ш зв® 1-ВД Л
— л-АД3 ВД цд , а это и будет интересующий нас объем конуса Т.
[11] Полагаем 8E=z и B0=ztz=a. Согласно «уравнению» эллипса радиус КЕ
самого нижнего вписанного цилиндра определяется равенством
«]’2
КЕ^П^'ВЕ'ЕЛ
0Г2 0ГТ
^-(a-z)(«+z)^^(a2-z3),
л-0Гг
а его объем л-КЕ2х=——z(a2 —zs). Объем всей вписанном фигуры, состоящей из
(п—1) цилиндров, будет:
W- RV2
Т'шшс33-,- *{(»-!) (нг)8-*2 [1«<з»Ч-...+(«-!)»]}=
St-0J’2Z* Г . 1 Г , .V, 1 п(п —1)11
=—^~ («'• 1)—з [ «(« -1)’+^—' J } -
о 2 м2 л
Быражеыне, стоящее в скобках, как нетрудно ьидсть, будет равно — п3— ----------От-
15 о
бросив вычитаемое, мы можем написать:
7. 2 rt-©r2-n«zs 2 от,„
^ВПИС <С -К-~--“2---—-я- П-6Г2- В0.
о (I О
Чтобы получить описанную фигуру, надо прибавить ко пписавной только один нижний
цилиндр с радиусом a=nz, иными слонами, н скобках вместо («— 1) (rez)2 взять re(nz)2.
Тогда
Я-0Г*'3» Г 1 Г z <« । л (п — 1) 11
^опио33---cS--|п' — у [ » («—1)2Н —2-------J J
Выражение в скобках будет равно -я-—"щ- Отбросив два последние члена, мы
и 2. о
уменьшаем выражение; таким образом,
2 т • ©Г2 пя-э 2
VOI111O > 471 °* " =4 л- 0I’2- ве.
. о а • 3 .
Заключающаяся между Увшгс и величина, равная двум третям объема цилиндра
АГНМ, как раз и дает интересующий вас объем копуса
О СПИРАЛЯХ
Место, которое трактат «О спиралях» занимает и ряду произведений Архимеда,
легко устанавливается на основании посланий к Досифею, помещенных в этом трактате
и в сочинении «О шаре и цилиндре». Сочинение «О спиралях» написано после обеих
книг «О шаре и цилиндре», по до трактата «О коноидах и сфероидах», хотя по первона-
чальному плану оно должно было следовать аа «Коноидами».
Тема трактата «О спиралях» была предложена Архимеду Коионом Самосским
(Папп, Математическое собрание, кн. IV, 50). Есть основания полагать, что основной
задачей Архимеда было определение длины окружности. Действительно, Папп (там же,
кн. IV, 54). рассуждая об одной задаче, связанной с решением вопросов, поставленных
в предложениях VH1 и IX книги «О спиралях», пишет: «Этой задачей пользуется Архимед
для того, чтобы доказать, что окружность круга равна некоторой прямой». Действи-
тельно, в предложениях XVIII—XX Архимед даст способ, при помощи которого можно
построить прямую, равную по длине заданной окружности или любой ее части.
Трактат «О спиралях» интересен тем, что он представляет одно из немногих сочи-
нений греческой математики (по пе единственное), где широко используется идея движе-
ния; здесь Архимед в известном смысле предвосхищает идеи современного дифферен-
циального исчислении, генезис которого, как известно, был тесно связан с задачей про-
ведении касательной к заданном кривой. В рассматриваемом сочинении Архимед решает
задачу о проведении касательной к Архимедовой снирали — кривой, которую он опре-
деляет как происшедшую в результате некоторого движения точки на плоскости. В этой
связи уместно будет указать, что греки разделяли кривые на два класса:
1 . хаилОДси — кривые, получающиеся в результате сечения плоскостью некоторой
поверхности; классическим примером таких кривых являются конические ссчепия, для
которых, как будто, и был впервые установлен термин хадлбАаг.
2°. гХьиоеьйс’д—кривые, образуемые движением. Первым примером такой кри-
вой является квадратриса Гнпппя Элидского, которую Динострат, бывший в этой области
предшественником Архимеда, применил для определения длины окружности. Вторым
примером является Архимедова спираль, которую можно определить как траекторию
точки, участвующей в двух дппжецинх, прямолинейном и равномерном (относительном)
по прямой, равномерно вращающейся вокруг одного из своих концов (переносном).
11) Предложения I и II поеят чисто механический характер. Опп интересны тем,
'что по употребляющейся в них терминологии можно восстановить историю возникнове-
ния понятия о равномерном движении.
Первоначальной ступенью было установление понятия imrraX'Sg — равиоскортай:
так назывались д в а движения, в которых в одно и то же время проходились одинако-
вые расстояния, причем характер движении не играл большого значения: с точки зрения
греческих механиков, iooTay.Kig были бы, например, продолжаюгцпсся одинаковое времи
движения двух свободно падающих тел.
На второй ступени понятие «равноскорости» применилось уже к одному дви-
жению. Движение называлось iooraX’jg а что eawr™ — ран носко рым себе самому, если
были равноскорыми отдельные части, па которые можно было бы подразделить соответ-
ствующее движение. «Равпоскорое себе самому» движение ужо совпадает с нашим равно-
мерным движением, если определять его как такое, п котором н одинаковые промежутки
времени проходятся одинаковые расстояния. В равномерном движении пройденный путь
возрастает пропорционально времени, Архимеду приходилось доказывать зто,
что он и выполняет в предложении I по всем правилам определении пропорциональности,
которые были в свое время дацы Евдоксом Книдским и дошли до нас в книге V «Начал»
Евклида (определение 5).
[2] Предложения V—IX интересны в том отношении, что они показывают, каким
математическим аппаратом считали возможным пользоваться без всяких объяснений
Архимед и современные ему математики. Эти предложения требуют построений при
О СПИРАЛЯХ
510
помощи так называемых «стремлений» (vEiaaiS), или, как иногда говорят, «вставок*,
далеко нс пес иа которых могут быть произведены при помощи циркуля и линейки.
В предложении V речь идет о проведении такой секущей, чтобы со отрезок Z0
между касательной и окружностью был меньше любой заданной длины (рис. 1). Если
положим, что радиус ВК окружности равня-
ется 1, а угол BK0, соответствующий дуге
136, равен а, то это предложение в современ-
ной формулировке равносильно следующему.
„ »ес«—1
Предел отношения-------при а, стре-
мящемся к нулю, равен пулю.
Для решении поставленной задачи Архи-
мед издается некоторой длиной Е, которая
может быть взята сколь угодие малой, и стро-
ит равную этой длине прямую Нв так, чтобы
опа имела своп концы па окружности и на пря-
мой КП, проведенной через центр К парал-
лельно рассматриваемой касательной BZ, и
при этом «стремилась» к точке касания 13.
Это построение может быть выполнено при
помощи циркуля и линейки. Действительно,
если мы положим радиус окружности равным 11, заданную длнпу 0Н —d, обозначим
искомую хорду В0 через х и опустим перпендикуляр К.А на секущую ВП, проведенную
в точку касания В, то будем иметь;
ВКа = ВА-ВН,
или
Н).
откуда искомая длила х определится как корень квадратного уравнении х24 dx— 211-=0:
d
|-/т+2/га
- выражение, которое может быть построено при помощи циркуля и линейки. Вместо
соответствующего построения Архимед говорит просто: «отложим равную Е прямую Л 6
так, чтобы она стремилась к В», считан соответствующее построение общеизвестным;
оно, дсйстиит(!Лы1О, легко может быть выпил пени, если двигать линейку с нанесенной
па пей длиной в Ч = d так, чтобы точки виН перемещались по прямой и окружности,
а продолжение линейки проходило бы через точку В.
[3] В предложении VI ставится следующая задача (рис. 2). Если в круге радиуса В
проведена хорда АГ заданной длины 2d, то требуется так провести секущую ВК, чтобы
отношение ВЕ : ВГ — k было, заданным и
меныним отношении
d : d2 •-= tg a.
Архимед определяет прямую BN так,
чтобы /с=КГ: BN, и помещает ее так, что-
бы копцы ее скользили по окружности и
прямой KN, параллельной АГ, причем сама
прямая постоянно проходила бы через за-
да иную точку Г. Эта задача, очень близ-
кая по типу к предыдущей, уже по может
быть решена при помощи циркуля и ли-
нейки. Действительно, если опустим пер-
пендикуляр ГД на параллельный АГ
диаметр ZII и положим BN = D, КД = а,
ГД “ft н NK=s, то для определения х будем иметь уравнение (по теореме об отрезках
секущей)
BNTN = ZN-nN или jDl/rbi-r(x—«)2=(х4 Н) (® —Л),
которое может быть приведено к виду
дг {Ь24-(а:—«)*}= (х2—Ла)2,
520
КОММЕНТАРИИ
что даст пам уравнение 4-й степени, корни которого по могут быть построены при помощи
циркуля и линейки. Если положить у=ха—/I8, то искомая величина х могла выбыть
получена как абсцисса точки пересечения параболы
у=а8—Л2
и гиперболы
р2={(ж—й)24-Ь2}Л«.
Архимед п в этом случае говорит просто: «Поместим BN между окружностью и прямой
KN так, чтобы опа проходила через Г».
|41 Предложение VIГ решает такую задачу (рис. 3):
К продолжению заданной прямой АГ пронести такую секущую КЕ, чтобы ее отре-
зок IE имел к П заданное отношение к, большее того, которое Г0 имеет к 0К пли,
если провести ГЛ перпендикулярно к ГК, того,
которое ГК имеет к ГЛ.
Архимед определяет длппу 1N из соотно-
шения: к— Н: TN, где 7? по-прежнему радиус
круга, и затем помещает полученную длину IN
между окружностью и прямой КЛ так, чтобы
продолжение ее проходило через заданную точ-
ку Г — задача, сходная с той, которая разби-
рается в предложении V.
Если положим КИ = 7?, IN=£), КЛ=^а,
ГД=Ь, KN=ar, то для определения х бу-
дем иметь уравнение BN-IJN=^ri4-IN или
(7?-|-s) (ж—If) — D Vfc3-|-(a:—в)2, тождественное
с тем, которое мы имели в предыдущем пред-
ложении.
Если положить rN=^y, то для определения х и у мы будем иметь два уравнения:
у2=Ь®-|- (х—а)2,
г2—Ba=Dy.
Первое уравнение будет уравнением гиперболы, второе же — уравнением пара-
болы; таким образом, рассматриваемая задача тоже могла бы быть решена при помощи
конических сечений.
При помощи подобных же кривых может быть получено и решение ve-jot?, иа
котором основываются предложения VIII и ГХ. Дело идет о задаче такого рода:
В заданном круге проведены две взаимно перпендикулярные прямые КМ и ЛЗ:
требуется из точки К провести прямую KN так, чтобы отрезок ее IN между прямой
Л.З и окружностью имел заданную величину (рис. 4).
Решение соответствующей задачи дано в «Математической библиотеке» Паппа
Александрийского (кн. IV, 52—54).
52. «Я помещаю решение той задачи на «стремления», которой воспользовался
Архимед в книге «О спиралях», дабы у тебя пе было затруднений при чтении упомянутой
книги. Мы воспользуемся следующими геометрическими местами, которые полезны и для
многих других телесных ♦) задач.
Пусть дана положением прямая ЛВ (рис. 5), и пусть из заданной точки Г к ней про-
ведена некоторая прямая ГД и затем перпендикулярно к ЛВ восставлена ДЕ; пусть отпо-
*) Так Папп называет аэдачи на построение, решаемые при помощи конических сечений.
О СПИРАЛЯХ
521
шение ГД к ДЕ будет заданным; я утверждаю, что точка Е будет лежать па гиперболе.
Проводом через Г прямую J'Z, параллельную перпендикуляру АЕ; нянчит, точка Я будет
заданной. Затем проводим ЕН параллельно АВ и пусть отношение ГД к ДЕ будет тем
»ке самым, что у 1'Z к Z0 или ZK:
ГД : ДЕ=Г2 ; Z0 = 1’Z ; ZK;
тогда будет заданной и каждая из точек Й, К. Так как ГД2 к ДЕа относится, как Г22
к Z02:
ГД®: ДЕ2=Г2®:£0®,
то будет данным и отношение их остатков УД2, то есть ЕН2 к КН-HR:
ГД2 ГД2—rz2 ZA2 Ell2
ДЕ2 ~‘EA2-ZW2 — (ЕД-J-ZR) (ЕД — Z0) — КНИ0 ’
Точки К и 0 даны; значит, Е будет находиться па гиперболе, проходящей че-
рез 0 и Е.
53. Пусть прямая ЛВ дана величиной и положением и ЛГ перпендикулярна к пей;
пусть А Г. ГВ будет равно произведению заданной прямой <01 на ГЛ; п утверждаю, что
точка Д будет лежать на некоторой заданной своим положением параболе (рис. 6).
Разделим ЛВ пополам в Е и проведем под прямым углом EZ; Пусть ЕВ2 будет равен
прямоугольнику на заданной прямей <0) и EZ; следовательно, Течка Z будет данной.
Параллельно АВ проведем АП; тогда квадрат ЕГ, или ДН, будет равен прямоугольнику
на даппнй прямой <0) и ZH. Точка Z дапа; значит, точка Д находится па параболе, про-
ходящей через A, Z, В и имеющей ось EZ.
54. Поело этих предварительных замечаний анализ задачи, предложенной вначале,
производится следующим способом. Дан положением круг ЛВГ (рис. 7) и и пем тоже
положение»! дапы прямая ВГ и некоторая точка А па окружности; между прямой ВГ
и дугой ВЕГ вставить прямую, равную заданной (Н6) и «стремящуюся» к <Л).
Предположим, что задача решена; отложена ЕД, равная 110; перпендикулярно
к ВГ проведем AZ, равную АД. Так как к заданной положением прямой ВГ из заданной
точки Л проведена ЛД и из течки Д восставлен равный ей перпендикуляр AZ, то, значит,
точка Z будет находиться па гиперболе. Далее, так как ПД-ДГ равно ЛД-ЛЕ или ZA-AE
и нрпмап ДЕ дапа, то, значит, ВД-ДГ будет ранне прямоугольнику на заданной прямой
ДЕ и AZ; следовательно, точка Z будет и па гиперболе; значит, точка Z дана »). Этой зада-
чей пользуется Архимед дли того, чтобы доказать, что окружность круга равна некоторой
прямой. Однако некоторые ебннгиннт его в том, что он ве совеем правильно воспользо-
вался «телесной» задачей,... и доказывают, что прямую, равную окружности, можно
было бы найти и при помощи «плоских» (то есть решаемых при помощи циркуля и линей-
ки) задач, если воспользоваться упомянутыми тенремами относительно спиралей».
К токсту Паппа остается сделать очень немного примечаний. Что упомянутая
в п. 52 кривая 0Е будет гиперболой, мы можем убедиться следующим образом.
h
Положим, что заданное отношение ГД: ДЕ — к, I’Z—Л; тогда K.Z —AZ = -^-_
ГД® ЕН®
Пусть ИД — х и ЕД = р;1 пелучеппую в конце формулу -гт.-.т = ,* цд
‘ ЛЕ;“ ПП’ПР
*) Рассматриваемый теист, помешенный го 2-м томе ивдатшого Гульчем папповского «Собра-
ния*. пе Пыл полностью разобран издателем. Гульч покакал отот текст известному немецкому мате-
матику Вальперу (автор «Теории дстгркииаптово). и тот быстро нашел решение, которое было поме-
щено в приложениях к последнему (3-му) тому падания Паппа.
522
КОММЕНТАРИИ
ми можем в наших обозначениях переписать так:
№=--------------------
. G+4)(»-4)
что легко приводится к виду
Л2 гг3
J к2 Л»
В задаче Архимеда к—1; тогда исследуемое уравнение принимает вид
у2 — x2=h2.
Искомая кривая будет гиперболой с центром в Zn действительной полуосью Z0=~ ;
К
мнимая полуось будет А.
Задача п. 53 решается еще проще (рис. 6). Положим «заданную прямую» равной
р; пусть, кроме того, ZH =ги НД—у.
Ми имеем:
ЕД
ДГ-ГВ=р-ГД
отрезок
или
(АЕ- -у) (AE-p)=p(EZ-a:).
Далее, ЕВ3 — р • Е Z, или АЕ3 ~р • Е Z-
Имеем равенства
AE2 = p-EZ,
АЕ2—y2=p-(EZ—г),
из'которых после почленного вычи-
тания получаем:
— известное уравнение параболы с
вершиной в точке 7. и осью ZE.
Что касается основной задачи
и. 54, то Бальцер переделал вытпе-
приведенный чертеж следующим об-
разом (рис. 8).
Дан круг и в нем прямая ВГ =
— 2а; через заданную точку А требу-
равпился заданной прямой Н0 —р.
Ь. Если О принять
ется провести прямую АЕ так, чтобы
Опустим из Л на ИГ перпендикуляр ЛО=А и положим отрезок 01
за начало координат, то, если положить 0А=6 и ХД = ДЛ —ц, будем иметь:
АД2=ОА2-]-ОЛ2,
или
ч2=58Ч а2,
то есть точка Z лежит па гиперболе
вершина которой находится в точке Н па расстоянии ОН —ОА —А.
Затем
ВЛ-Д'Г = АД-ДЕ,
или
(2a-A-g) (Ь+£)=/Л|;
мы получили уравнение параболы, па которой находится точка Z.
Если начало координат паять в точке О' — середине прямой В Г — и положить
О'Д — х, то уравнение параболы перепишется в виде
(я -|-*)(<г—х)—ру,
О СПИРАЛЯХ
Й23
ИЛИ
4
У——-(«®—«®).
Это будет парабола, проходящая через концы заданной прямой В Г и имеющая вершину
в точке К, лежащей на расстоянии
Если рассматривать только одну ветвь гиперболы, а именно проходящую через точ-
ку Н, то поставленная задача будет иметь дна решении, соответствующие двум точкам
пересечения влитой «сягни гиперболы с упомянутой параболой.
Упреки Архимеду, что последний «ле совсем правильно поснольиовался «телесной»
(то есть решаемой при помощи конических сечений) задачей», представляют интерес, только
в том отношении, что позволяют думать, что изложенное у Паппа решение действительно
принадл ежит Л рхимеду.
(51 В этом предложении Архимед подходит к формуле, определяющей сумму
квадратов чисел натурального рядя, или, в более общем случае, сумму квадратов чисел,
составляющих арифметическую прогрессию, разность которой равпа ее парному члену.
Если через а} обозначим общий член этой прогрессии, а через п число взятых чле-
нов, то устанавливаемое Архимедом соотношение в современной формулировке может
-быть выражено так:
7t 11 7)
(л-'г1)а»=2 2 °i г( 2 "1 2 "«)»
i=i i-t i—4
откуда дан суммы квадратов получается формула
1\ п
з 2 «£=(«•;- 2 аг-
г=1
Интересно отметить, что правило суммирования квадратов чисел натурального ряда было
известно современникам Архимеда лппилолским математикам эпохи Селевкидоп (см. текст
Луврского музея ЛО (И84, опубликованный Нсйгебауаром в 1-м томе «Malhematische
KoilscbrifLtexLe». В своей книге «Архимед» С. Я. Лурье дал красивый геометрический
вывод соответствующей формулы).
Следствие из предложения X устанавливает следующие основные неравенства,
необходимые Архимеду в дальнейшем изложении:
з («?+^4-... HS-j) < < з (<>г+^+... -НЯ),
где числа щ, а»,..., составляют арифметическую прогрессию, разность которой рав-
няется ее наименьшему члену.
[61 В тексте, Гейберга доказательство рассматриваемого предложения содержит
лишнее, по существу, условие: предложение, справедливое для венкой арифметической
прогрессии, доказывается в предположении, что ее разность равпа нанменьшему члену;
так построен и чертеж, сопровождающий ато доказательство. Чтобы выяснить, в какой
степени можно считать зто условие принадлежащим Архимеду, разберем детальнее ход
доказательства.
В современной форме предложение XI мы выразили бы так:
Дана арифметическая прогрессия
^1» ^2» ^П-(> ЙП»
лв, гл. ez, не, jk, лм, №.
Обозначим через d абсолютную величину разности прогрессии. Архимед строит
ряд прямых
ОД = 01’4- ГД=Й -|-ав =«!,
HZ=IIE4-EZ*=2d-1-Лз^й!,
pe=Pii+ne=3d-i«4=e1,
SK=--XI-| IK =4d-|-ae=a1,
TM= ТЛ-{-ЛМ — =fli,
FE=rN+NS =(M-|-a7=0,.
524
КОММЕНТАРИИ
Прямая ГчТ=Г2—МЕ=6Й=«1—а-,, или я вашей формулировке а1—ап. Если
предположить, что d — аи, то выражение —ап=^а„—(п—l)d. Так как Архимед поль-
зуется бо-чсе общим выражением, то ясно, что он пе предполагал равенства между наи-
меньшим числом и разностью.
Требуется доказать справедливость неравенств
(и — 1) af ______gj_______ (n — 1) а®
«14-4+о „ , 1 1о „ч «Н«в-Г”-+ви '
Архимед говорит: «От каждой из линий, одинаково возвышающихся одна над
другой, отделим часть, равную разности» — это будут прямые ФВ =ХД = 4rZ=Q0=
=$£K = QM = NS, равные наименьшему члену. Если в тексте Гсйбсрга вместо слов»
«разности» (тййлврох?) читать «наименьшей» (га гКауюта), то мы получим более общее
выражение теоремы, исключающее предположение о равенстве an^d; в высшей степени
вероятно, что в первоначальном тексте Архимеда именно так И было.
Архимед начинает с очевидного равенства
а{ __ (п—1) nJ
- . 1 -
ахап4 у («х — ап)1 (« — ’>) |»i“n+ -у (а1—ап)*|
Для того чтобы убедиться в справедливости теоремы, нужно доказать, что
>(«—l)«i«n|-~^(ai—«11)2>п5-|-йН--”+аА,
О
где
an=at—(п—1) d.
Имеем:
(а —1) («± —cn)2=(n —1) <г£4-вп (и—1) (n—(п—l)®d®,
а 1+41' - • • -г«п-1 = (« — 1) a?x+rf®+(2d)®+... + (»—!)« d»+ 2ап {d-|-2d-|-...+(n - i)jf} =
=(« -1) «?„+ [d®+... + I)2 d®] -г n (n -1) danr
44-44- - - - +4= («—1) 44- k’4- - - (»— 2)« 1) (n—2) dan.
Сравниваем составные части всех этих выражений:
(»—1) 4=(»—!) 4 — (п — 1) а%,
п (п— 1) dan > (п — I)2 dan^>(n — 1) (п—2) dan,
fl___4
d®4-(2d)®4-... + (n—i)2 d® > (n— i)2 d®>d®4-(2«3)®4-... -H«—2)* d®
(на основании следствия из предложения X), откуда и вытекает справедливость искомых
неравенств.
[7] «13 треугольнике обе стороны будут более чел вдвое больше прямой, делящей
пополам угол между ними», так как сумма обоих сторон больше удвоенной медианы,
а медиана больше биссектрисы; действительно, нетрудно доказать, что последняя про-
ходит между медианой и высотой.
[8] В предложении XVI речь идет о касательной к сдирали, иными словами, рас-
сматриваются задачи, аналогичные тем, из которых развилось современное дифферен-
циальное исчисление. Прежде всего Архимед устанавливает, что угол касательной к спи-
рали с радиусом-вектором точки касании будет тупым, если провести касательную в сто-
рону возрастания радиуса-вектора.
Пусть (рис. 9) прямая Д1 будет касательной к спирали ДА. Требуется показать,
что прямая АД, соединяющая качало А спирали с точкой Д касания, образует с Д1 тупой
угол. Через точку А проводим окружность радиусом АД=(> с центром в А; так как со-
стороны возрастания радиуса вектора спираль лежит вне этой окружности, то угол Д1
не может быть острым, так как он больше «угла полуокружности». Под «углом полу-
окружности» греческие математики понимали криволинейный угол, вершина которого
лежала на окружности, а сторонами были диаметр п дуга окружности. Этот угол отли-
чается от прямого гг прямолинейного угла ЛД| на криволинейный угол 1ДР между каса-
тельной и дугой ДР. Эти криволинейные углы являются «исархимедовыми» величинами^
то есть такими, к которым неприложима аксиома Архимеда (повторяя любую малую вели-
О СПИРАЛЯХ
525
чипу слагаемым произвольно большое число раз, можно получить всличипу, превышаю-
щую любую заданную); поэтому из того, что угол АД1 больше угла полуокружности,
еще нс следует, что ов будет обязательно тупым, и Архимед доказывает, что од нс может
быть прямым.
Действительно, если бы оп был прямым, то касательная AI к спирали была бы одно-
временно касательной и к кругу ВДГ. В таком случае на основании предложения V можно
провести такую секущую AZ, чтобы се отрезок PZ был бесконечно малым по отношению
к дуге ДР (мы сказали бы бесконечно малым второго порядка, если считать дугу ДР бес-
конечно малой первого порядна). В действительности же дуги ДР и прямая РА меньшая,
чем ZP, являются бесконечно малыми одного порядка, так как их отношение, равное
отношению скоростей движения по окружности и по вращающейся прямой, будет конеч-
ной величиной. Таким образом, гипотеза, что угол АД1 прямой, исключается.
В связи с этим интересно разобрать ход мыслей Архимеда при доказательстве пред-
ложения V.
Для того чтобы убедиться в том, что отрезок PZ является бесконечно малым по отно-
шению к дуге АР, нужно показать, что отношение ZP : ДР может быть сделанным меньше
любого заданного числа.
Через цептр А проводим прямую А ГН параллельно касательной Д1 и продолжаем
хорду ДР до пересечения с этой прямой в точке И. Тогда
ZP <. ZP АР
др ДР РП
Но АР есть постоянная величина, равная радиусу окружности, длина же РП может быть
сделана сколь угодно большой; таким образам, отношение ZP ; ДР может быть сделано
меньше всякой наперед заданной величины.
[9] Предложении XVIII — XX являются центральными во всей книге, так как они
решают задачу о построении прямой, равной длине заданной окружности. Так как длина
окружности пропорциональна радиусу этой последней (что, конечно, было хорошо известно
Архимеду), то ясно, что задача определения длины любой окружности будет решена,
если только удастся определить длину одной какой-нибудь окружности. Эту задачу как
раз и решает предложение XVIII, которое гласит: длина окружности в ПК первого круга
равна отрезку ZA, который касательная 6Z к спирали, проведенная и точке в —конце
«первой» прямой, — отс-каог от прямой АЛ, перпендикулярной к «первом прямой» Л0
(рис. 10).
Чтобы понять основную идею доказательства этой теоремы, обратим внимание на
криволинейный треугольник, образованный дугой спирали 0Х,, дугой первого кру-
га 0Р, и отрезком радиуса-вектора Р(Х,; так как отрезок Р,Х, и дуга 0Рк проходятся
в одинаковое время (условно равномерности составных движений — прямолинейного
но Art и вращения по ©₽[), то их отношение будет равняться отношению пути А0, прой-
денного точкой по радиусу-вектору п течение одного оборота, ко всей длине окружности
КП©, описанной точкой 0 за время норного оборота. Если время прохождения дуги 0Р(
и прямой Р1Х1 мы будем беспредельно уменьшать, то в пределе получим прямоугольный
треугольник, гипотенуза которого пойдет по касательной ©N,, один из катетов нойдет
но церцс1гдикуляру к ©А, а другой станет параллельным 0Л; так как этот предельный
треугольник будет подобен треугольнику A0Z, то мы имеем:
А© Х.Р, .А 6)
окр. КЦ0 — 0Pi — AZ ’
526
КОММЕНТАРИИ
откуда
окружность KII0 = AZ.
Вот и чем заключается основная идея доказательства Архимеда; рассмотрим его-
детальнее.
Если двигаться по спирали в сторону вращении и заменить кривом инейный тре-
угольник прямолинейным, то получится треугольник (; посмотрим, как будет
изменяться отношение его сторон NjPi: Pt0. В исходном положении, когда треугольник
был бесконечно малым, это отношение равнялось отношению половины длины хор-
ды Н0 к длине перпендикуляра, опущенного из точки А па ату хорду; по мере удале-
ния Pt от 0 отношение NjPi : Pi®, как нетрудно видеть, будет увеличиваться; вот почему
Рис. 10.
в формулировке вспомогательного предложения VII говорится: отношение А^Р, к вР,
должно быть больше того, которое половина заданной в круче прямом 011 имеет к пер-
пендикуляру, опущенному на нее из центра.
Если двигаться в сторону, обратную вращению, то отрезок N|Pj обратится n NSPS,
отрезок 0N, перейдет в 6N>, а дуга 0Р( заменится хордой Рг0, которая станет теперь
гипотенузой. При движении от 0 к 11 отношение P,,N2: будет уменьшаться; началь-
ная его величина в точке 0 равнялась тангенсу угла 0ZA, то есть тому же самому
отношению, что и выше; вот почему в предложении VIII говорится, что отношение P2N.>
к N,0 или к отрезку» касательной 0Z должно быть меньше отношения половины хорды
0Н "к перпепдикулпру, опущенному на нсо из центра.
Таким образом, хотя окончательное доказательство Архимеда статично (оно изло-
жено в обычной форме приведения к абсурду), идея переменности составляет подоплеку
всех его рассуждении.
Окончательная форма доказательства Архимеда такова: 1) Пусть длина окруж-
ности (обозначим ее через С) меньше прямой AZ; возьмем прямую АА,, которая меньше
AZ, но больше С\ тогда отношение АО : AAi будет больше предельного, так что можно
провести такую прямую ANlt чтобы имела место пропорция
NiPj :0Г\ —А0 ;АЛ„
или
NtP,: А©=0Р, : AAt < HP. : С.
Затем, вспоминая, что Аб^ЛР^ «присоединением» получаем:
AP.-f-NtPt С+01»,
А0 С
AN,: А0 < (С-|-©rs): 6’—AXi ; А© (предложение XV),
О СПИРАЛИX
527
что приводит к нелепому выводу ANj-t^AX-i-
2) Пусть длина окружности С больше AZ. Возьмем прямую АА», которая больше AZ,
ио меньше С\ тогда отношение Д6 : АЛ» будет меньше предельного; следовательно, на-
основании предложения V1LJ можно провести такую прямую ЛП (рис. 17. стр. 247)..
чтобы имела место пропорции;
l\Na; П0 = А6 : ЛЛа,
Ра.\а; ЛРг=П0 : ЛЛ2 > 0Ра : С.
Тогда, «переворачивая», получаем:
АР»—РаХ8 ^~0КР8
А1’а С
ЛХ»
Ай ’
Рис. 11.
откуда AN,<AX8, что нелепо. W
Таким образом, длина окружности С должна быть равна AZ.
[10J В своих комментариях к переводу трактата «О спиралях» немецкий исследо-
ватель Чвалина предлагает следующую реконструкцию генезиса идей Архимеда при?
открытии теоремы, рассматриваемой в и] едложешш XXIV.
Предположим (рис. 11),что но осиабсциесмы откладываем угол фповорота радиуса-
вектора спирали, а по оси ординат — соответствующие величины радиуса-вектора г.
Так как длина г пропорциональна углу ф пово-
рота, то зависимость между г и q; выражается
примой линией. ()Г. Пусть ОА—2л представляет
угол, соответствующий первому ПОЛНОМ!’ обороту,
а АГ^сц — так называемую «первую прямую»—
радиус-вектор, соотвстс/гвуплций значению q: =2zt.
Разобьем ОА— 2л на п равных частей А<р и на
соответствующих радиусах Г|,г8,..., построим
прямоугольники, как показано на чертеже. К ел и
мы будем вращать всю эту фигуру вокруг ()А
как оси, то прямоугольник ОАВГ образует ци-
линдр, а треугольник ОА Г—конус. Объем этого
конуса составляет одну треть объема всего ци-
линдра, равного ()A.ji-AJ'®i=2n.л.«|. Каждым
из прямоугольничков при вращении образует
цилиндрик, объем которого равняется лгг-Дф. Эти
цилиндриЕш соответствуют круговым секторам,
из которых составляются вписанная и описан-
ная около спирали фигуры. Площадь каждого из зтпх секторов"равинстся — ra-Aq> и,
следовательно, в 2я раз меньше соответствующего цилиндрика. Таким образом, пло-
щадь 4’j, ограниченная спиралью в течение первого оборота, будет равна сумме
4 - , 11 11
У, пг®-Лф = д---ОА-п-АГ2=—’по?;
1 2п -£-1 2я .5 (3,
в этом и заключается идея, лежащая в основании рассматриваемого предложения.
ИЗМЕРЕНИЕ КРУГА
В дошедшем до лас виде вто сочинение состоит из трех теорем, первая из которых
определяет площадь круга как произведение полунериметря на радиус, третья дает отно-
шение между длиной окружности и диаметром, наконец, вторая, которую следовало бы
поместить после третьей, дает величину площади круга в виде ее отношения к квадрату
диаметра. Именно в таком виде око существовало в VI веке и. з., как показывает сохра-
нившийся комментарий Евтокия, но лс Может быть сомнений » то.м, что первоначально
это сочинение имело значительно большие размеры. На это указывают сохранившиеся
цитаты у Диофанта и Герояа*), наконец, тот факт, что Папп цитирует все первое предло-
жение, то есть иол овину имеющейся у пас книги, для того «чтобы не обращаться к сочи-
нению Архимеда из-за одной этой теоремы». За то же самое говорят и чисто внутренние
характеристики рассматриваемого сочинения: в нем отсутствует доказательство такой
-важной теоремы, как постоянство отношении длины окружности к диаметру; наконец,
•второе предложение помещено неудачно: оно определенно должно стоять после третьего.
Относительно времени нависания «Измерения круга» можно с полном достоверно-
стью утверждать только то, что оно было написано до «Псаммита». Ясна связь этого про-
изведения с трактатом «О спиралях», предложение XVIII которого даст геометрическое
построение длины окружности некоторого радиуса; об этой связи говорил н биограф Архи-
меда Гераклид. В комментарии Евтокия к «Измерению круга» мы читаем:
«Эта самая книга, как говорит Гераклид в «Жиэиеомисапия. Архимеда», необхо-
дима для житейской практики, так как она показывает, что окружность втрое больше
диаметра, причем получающийся избыток будет меньше седьмой пасти диаметра, ио более
десяти семьдесят первых частей его. Это, говорят он, дано лишь приблизительно; ври
помощи же некоторых спиралей Архимед нашел прямую, которая совершенно точно рав-
няется окружности заданного круга».
С трактатом о спиралях «Измерение круга» имеет то общее, что форма применения
метода истощении является одинаковой с использованной в последних посланиях к Доси-
фею, а именно «О спиралях» п «О коноидах». Это позволяет утверждать, что «Измерение
круги» во всяком случае написано после «Шара и цилиндра», в котором метод истощения
имеет более раннюю форму. Наконец, «Измерение круга» резко отличается от
чисто геометрических сочинений Архимеда своим вычислительным характером; равным
образом в пользу более позднего нависания «Измерения круга» говорит его связь с «Псам-
митом» и занятиями Архимеда астрономией, которые, по всей видимости, относятся
К позднейшему периоду деятельности Архимеда (Титу Лилию, описывающему смерть
Архимеда, последний известей только как астроном). Сохранившиеся у Герона фрагменты
книг «О неправильных поверхностях и телах» и «О призмах и цилиндрах» иозволяют
думать, что метрические исследования Архимеда ле ограничивались одним только «Изме-
рением круга».
[1] Первое и второе предложения «Измерения круга» касаются задачи о квадратуре
круга, интересовашпей в течение долгого времени математиков всех премия и народов.
Возможны два вида постановки этой задачи.
Во-первых, можно отыскивать квадрат, площадь которого равняется площади дан-
ного круга; так ставилась соответствующая задача и. в египетской математике, где пло-
щадь круга считалась рапной квадрату, стороны которого равнялись «/<, диаметра круга.
Во-вторых, можно было определять длину окружности круга заданного радиуса
и затем уже определять площадь круга, исходя из длины его окружности; так ставилась
задача в вавилонской математике, где отношение длины окружности к диаметру — паше
число л — нрпянмалось равным 3.
В греческой математике задача о квадратуре круга встала во второй половине
V века до и. э., после того как удалось для всякой прямолинейной фигуры найти квадрат,
’) Си. стр, 270 книги.
ИЗМЕРЕНИЕ КРУГА
529
площадь которого равнялась площади этой фигуры. Следующим шагом, естсстисвно,
была постановка задачи о нахождении квадрата, площадь которого равнялись бы пло-
щади заданного круга. Этой задачей занимались Анаксагор, Антифон и Гиппократ Хиос-
ский. О решении Анаксагора нам ничего ис известно, по решения Антифона и Гиппократа
освещены в тексте, приведенном известным комментатором Аристотеля Снмнлпкием
в его комментариях к «Физике». Этот текст нмесл очень важное значение для всей исто-
рик греческой математики; так как он по вошел еще в арсенал советских историков мате-
матики, то ми приводом его здесь как необходимый документ для освещении доархиме-
довской истории: задачи о квадратуре круга *).
«Из многих, отыскивавших решении задачи о квадратуре круга (ова заключалась
н том, чтобы построить квадрат, равный данному кругу), и Антифон, в Гиппократ счи-
тали, что нашли решение, но оба одинаково ошибались. При атом, как мы у пн дим ниже,
ошибка Антифона нс подлежит геометрическому разбору, так как он пе исходил из прин-
ципов геометрии, ошибку же Гиппократа следует разобрать геометрически, поскольку
он оставался первым принципам геометрии. Ведь нужно разбирать только те рассужде-
ния, в которых соблюдаются общепризнанные принципы научного метода и все же при-
водят к неверным зак.тючепнпм; рассуящелин же, уничтожающие и отбрасывающие
в сторону ати принципы, разбору не подлежат.
Антифон, начорттт круг, вписал в него некоторую площадь, ограниченную много-
угольной фигурой из числа тех, которые мы умеем впнсынать, например вписанный квад-
рат. Затем ои делил пополам каждую сторону квадрата и от сечений проводил под прямыми
углами .линия к окружности, которые, конечно, делили пополам соответствующие сег-
менты круга. Потом полученные точки пересечений е окружностью он соединял прямыми
с концами линий, составляющих квадрат, так что после проведения :>тих прямых иолучи-
ли ш. четыре треугольника, и вся вписанная фигура обращалась в восьмиугольник.
Следуя тому жи методу, он затем делил пополам каждую из сторон восьмиугольника,
от сечений к окружности проводил под прямыми углами линии и точки, в которых прове-
денные перпендикуляры доходи.;и до окружности, соединял прямыми с концами раз-
деленных сторон, обращая таким образом вписанную фигуру в нгестпадцатиугольник-
Затем, следуя тем же самым рассуждениям, он снова делил стороны вписанного шестпад-
цатиуголышка, проводил соединяющие прямые и таким образом снова удваивал число
сторон аниса иного многоугольник;). Так он делал все время до тех пор, пока не истоща-
лась вся площадь, заключенная внутри круга; он предполагал, что в результате в круг
будет пписан некоторый многоугольник, стороны которого, вследствие! их малости, сов-
падут с окружностью круги. Для всякого же многоугольника мы можей построить рав-
ны п ему квадрат, как мы знаем из «Начал». Таким образом, предполагай, что получен-
ный многоугольник равен кругу, п построивши квадрат, равный атому многоугольнику,
мы. тем самым сможем построить и квадрат, ранный заданному кругу.
•Это заключение, очевидно, противоречит геометрическим принципам, по, однако,
Александр *») по прав, когда говорит, что ото происходит потому, что геометр предпола-
гает, что круг касается прямой и одной точке, а Антифон ото отвергает, ведь геометр не
просто предполагает ото, п доказывает в восьмой книге ♦**). Лучше было бы сказать, что
в геометрии имеете.» основное положение!, утверждающее о невозможности совпадения
прямой с окружностью,'ибо внешняя прямая имеет с кругом только одну общую точку,
а внутренняя только две. по пи более, и касание имеют место только в одной точке. Таким
образом, рассекая все время площадь, за ключа кипу киш между прямой и окружностью
круга, он никогда не истощит :>ту площадь и ле) достигнет окружности круга, хотя бы
деление площади продолжалось до бесконечности. Если бы он мог достичь поставленной
цели, то был бы уничтожен геометрический принцип, утверждающий, что пространствен-
ные величины являются делимыми до бесконечности. Эвдсм *»**) так и говорит, что именно
••пют принцип и отвсфспетсп Антифоном •**•*).
Однако квадратура круга при помощи сегментов, помшшшо Александра, заслужи-
вает и геометрического разбора. Нод квадратурой при помощи сегментов он подразуме-
*) Текст лмтся но тигиге: С. A. D ;• е I. s с п п с 1 <1 е г. 1>)е Geometric ihiii die (reomcler vor
Enk lines. Lcip'tlK. IK'D. стр. lOO—121.
*• ) Александр Лфродаасиий — nsneCTin.iit комментатор Аристотели (первая полонии а г 11 ве-
ка п. о.).
•• •) Н действительности в третьей книге («Начала». HI, 10).
*•»*) Ученик Аристттгля. автор «Истории геометрии».
*•**•) ц сиизи с решением Аптяфоип (изкестггыЙ софист второй половины у века до и. э.) инте-
ресно вспомнить идею Анаксагора. тоже занимавшегося квадратурой круги, о так нарываемых го—
мойомерах. Анаксагор предполагал, что каждая сколь угодно малая часть данного тела но своей
сущности тождественна с отим телом; так, любая часть мяса все равно остается мясом, как бы мала
яга часть пи была. Эта идея, еовершлиио пепрапильпан с точки зрении физики, является вполне
оНрандашюИ математически — сколь угодно малая часть окружности вес-таки будет окружностью,
а не прямой линией, и нс точной. Весьма волможпо поэтому что и вся теория гсм'ойомпр зародилась
имешш ;га математической почие в противовес атомистам, точку зрения которых разделил и Аптифоп.
отрицавший возможность бесконечного деления тел. ’ ...
о I Архимед
5 Эи
КОММЕНТАРИИ
вает изобретенную Гиппократом Хиогским квадратуру при помощи луночек, так как
луночка есть некоторый сегмент круга. Доказательство этой квадратуры заключается
В следующем.
Пусть, говорит он, на прямой АВ описан полукруг АВГ (рис. 1);
разделим ЛВ пополам в Д и из Л под прямым углом к АВ проведем ДГ,
а из полученной точки Г — соединяющую прямую ГЛ; последняя будет
стороной квадрата, вписанного в тот круг,
половиной которого является АВГ. Затем
на Л Г опишем полукруг АЕГ. Так как
квадрат на АВ равняется квадрату иа АГ
вместе с квадратом па ГВ —другой стороне
квадрата, вписанного в мол упруг (ибо АВ
будет гипотенузой прямоугольного треу-
гольника), и отношение квадратов иа диа-
метрах равно отношению описанных на
них кругов и полукругов (как доказано
в XII книге «Начал»), то полукруг АГВ будет вдвое больше полукруга
АЕГ. Но полукруг АГВ вдвое больше и квадранта АГД; значит, этот
квадрант тоже будет равен полукругу ЛЕГ. Отнимем общий сегмент.
заключающийся между стороной квадрата и дугой АГ; тогда остаю-
щаяся луночка ЛЕГ будет раина треугольнику ЛГД, а последний
некоторому квадрату. Доказавши таким образом возможность квад-
ратуры луночки, он на основании вышеизложенного пытается следую
щим образом получить и квадратуру круга.
Пусть дана некоторая прямая ЛВ и па пей описан полукруг (рис.2);
возьмем прямую ГД, вдвое большую АВ, построим на ней полукруг
и впишем в пего стороны ГЕ, EZ и ZA правильного шестиугольника. На
этих сторонах опишем полукруги Г! ГЕ, E0Z и ZKA; тогда каждый из
и все четыре, взятые вместо, н четыре раза
полукругов, построенных
на сторонах шестиуголь-
ника, будет равен полу-
кругу па ЛВ, так как Л В
равна стороне шестиуголь-
ника (действительно, диа-
метр вдвое больше радиуса,
а стороны шестиугольника
равны радиусам, и ГД
вдвое больше ЛВ). Таким
образом, все четыре, полу-
круга равны между собой
больше полукруга ЛВ. Но полукруг на ГА тоже в четыре раза больше
полукруга па АВ, ибо ГД вдвое больше ЛВ, и, следовательно, квадрат
на ГЛ будет в четыре раза больше квадрата на АВ, а как квадраты на
диаметрах, так относятся друг к другу и описанные ва них круги и по-
лукруги. Итак, квадрат па ГЛ в четыре раза больше квадрата на АВ.
и полукруг на ГД будет рашш четырем полукругам: полукругу па АВ
и трем полукругам на сторонах шестиугольника. От полукруга па ГЛ
и полукругов на сторонах шестиугольника отнимем общие сегменты, .
заключающиеся между сторонами шестиугольника и дугами полукруга
ГД; тогда остающиеся луночки ГНЕ, E0Z, ZK.A вместе с полукругом
АВ будут равны трапеции TEZA; если от этой трапеции отнять разни-
цу, то есть площадь, равную трем луночкам (так как доказано, что лу-
ночка равняется некоторой прямолинейной фигуре), то в остатке полу-
ИЗМЕРЕНИ Е К РУГА
чится площадь, равнин полукругу па ЛВ; полученную в результате
прямолинейную фигуру удваиваем и, удвоив, квадрируем, то есть
строим равный ей квадрат; зтот кнадрат буде-т равен кругу, построенно-
му иа диаметре АВ, и, таким образом, квадратура круга окажется
выполненной.
Хотя изложенный способ и остроумен, но тем но менее полученное
заключение является ложным, поскольку и качестве общего положения
принято такое, которое не является и обящм случае доказанным. Дей-
ствительно, доказана возможность кпадрировапия не всякой луночки,
но только той, которая построена на стороне вписанного в круг квадра-
та, а паши луночки построены па сторонах вписанного в круг правиль-
ного шестиугольника; поэтому доказательство возможности квадрату-
ры круга при помощи луночек непригодно ине. выдерживает испытания,
так как оно содержит ложное заключение. Действительно, оно пред-
полагает. что нахождение квадратуры луночки ня сторож* квадрата
дает возможность выполнения и квадратуры круга, как будто на такие
лупочки можно было бы разложить всякий круг, и затем, взяв равный
луночке квадрат столько раз, на сколько луночек разлагается круг,
полагают, что квадрат, равный всем этим .пуночкам, вместе взятым,
будет равен и кругу. При этом дплаотся ошибочное предположение
о возможности разложения па луночки любого круга. В дойстнитель-
иости жз при составлении из луночек круга между линиями луночек
всегда остается некоторая площадь, ограниченная с обеих сторон кри-
выми линиями, которая но является пи луночкой, пи квадрируемой
площадью, так что не будет квадрируемым и любой «руг, и усилия
получить подобным образом квадратуру нс могут увенчаться успехом.
И каждому, поставившему задачу о выполнении квадратуры круга при
помощи луночек, нет надобности разделять круг на лупочки; если бы
это даже и было возможно, то п тогда нельзя было бы при помощи
луночек сквадрировать круг, ибо не доказана возможность квадрату-
ры пенкой луночки. И не разделяя круг на луночки, можно было бы
его сквадрировать, если бы оказалось возможным найти квадратуру
луночек, построенных на стороне вписанного в круг правильного
шестиугольника, а нс только на стороне квадрата. В этом именно
и заключается причина ложности заключения: после нахождения квад-
ратуры луночки только па стороне квадрата доказательство ведется так,
как будто стали квадрируемыми все какие угодно луночки, на которые
можно разделять круг.
Как говорит Александр, некоторые полагают, что если бы в области
чисел удалось найти такое число, которое было бы и квадратным
и циклическим, то и к области пространственных величин можно было
бы выполнить квадратуру круга. Как он говорит, каадратпым числом
является равноравпоо (6(Пакс-; ioo;) число, а циклическими назвали
числа, составленные из ряда последовательных нечетных чисел, иа
пример, единицы, трех, пяти,'семи, девяти. Если найти квадратное число,
которое одновременно было бы и циклическим, как, например. 3(>
(оно является квадратным, так кик получается от умножения (> на
самого себя, п циклическим, так как образуется п результате сложения
нечетных чисел 1, 3, 5, 7, 9, 11), то, по их мнению, станет найденной п
квадратура круга. Однако доказательство этого, как говорит Александр,
получается не на основании геометрических принципов, а на основа-
нии арифметических, ибо то, что такое-то число является квадратным,
а такое -- циклическим, относится к области арифметических принципов;
з»*
532
КОММЕНТАРИИ
К этим слонам Александра следует добавить, что первоначально
арифметики называли циклическими пе те числа, которые получались
к результате сложения последовательных мечетных чисел, а те, квад-
раты которых оканчивались па те же самые числа. С этен точки зрения
циклическим числом будет 25, так как пятые пять равно 25, и 36, но нс
четыре, девять или шестнадцать, хотя последние и получаются в резуль-
тате сложения последовательных нечетных чисел; такие числа будут
только квадратными, так как квадратные числа возникают путем после-
довательного прибавления почетных чисел. И может быть первый,
введший такое понятие, сказал не то, что циклическими называются
все числа, возникшие в результате последовательного прибавления
нечетных чисел, а только то, что при таком последовательном прибав-
лении нечетных могут получиться и циклические, но что это бывает не
всегда; действительно, циклическим числом будет 125, как получившееся
• из умножения 5 па 25, затем 216, как 6x36, хотя эти числа и не полу-
чаются и результате сложения последовательных нечетных чисел, если,
конечно, по считать, что эти числа являются пе циклическими, но сфе-
рическими, получившимися циклически из плоских циклических чисел.
Нужно, однако, отметить и то, что всякий, нашедший число, являв-
шееся одновременно и циклическим, и сферическим, никоим образом не
имел нрава думать, что он тем самым и в области пространственных
величин отыскал квадратуру круга, хотя возможно, что человеку,
обнаружившему среди чисел такое, которое одновременно является
и циклическим, и квадратным, пришло в голову поискать квадратуру
круга и в области пространственных величин.
Наш наставник Аммоний*) говорил, что, по-видимому, нет пик а к ай
необходимости в том, чтобы результаты, обнаруженные но отношению
к числам, были справедливы и по отношению к геометрическим величи-
нам. Прямая и окружность являются совершенно разнородными, и нет
ничего удивительного, по его сливам, в том, что не удается пайти пря-
молинейной фигуры, ранной кругу, как это и обнаруживается и отно-
сительно углов; ведь ни для угла полукруга**), пи для ого дополне-
нии до прямого угла (так называемого рогообразного угла) нельзя
найти никакого прямолинейного угла, который был бы нм равен. Воз-
можно, говори-а он, что именно вследствие этого до сих пор и пе уда-
лось найти ту теорему, которую искали такие, знаменитые люди и даже
сам Архимед. Я же отвечал наставнику, что если квадрируется луночка,
построеииан па стороне квадрата (ибо это получается вне всяких сомне-
нии), и луночка, составленная из дуг, имеет одинаковую природу
с, кругом, то что же может препятствовать тому, чтобы и сам круг тоже
оказался квадрируемым. Ведь если считать, что наличие рогов уничто-
жает подобие луночки кругу, то тем более пе может быть никакая луноч-
ка одного рода с прямолинейной фигурой; а вместе с тем луночка па
стороне квадрата вполне определенно квадрируется, тогда как пи угол
полукруга, ни ро сообразный угол м.ккду прямой и окружностью, пе
только не являются одного рода с прямолинейными углами, ио помо-
гут быть сравниваемы даже между собой.
Я пе думаю, что все вышесказанное было бы достаточным для того,
чтобы отказаться от ноископ квадратуры круга. В комментариях
*) Аммоний, сын Гермин, александриец, бывший учеником афинского неоплатоника Проклм
Га втор а известных комм ситар нс и к ««Началам» Епклила). в 480 г, н. и. м учивший позднее к Алексан-
дрии.
** ) цааыпаетсн ffpii по линейны it угод мелгду диаметром И Дугой опруишости в конце Отого
диаметра.
ИЗМЕРЕНИЕ КРУГЛ 533
к «Категориям» Л мил их*) говорит, что Аристотель может быть и не
нашел квадратуры круга, ио пифагорейцы ее пашл и; ио его словам, это
можно видеть из доказательства пифагорейца Секста, воспринявшего
метод по наследству с самого начала школы. Позднее, говорит он, квад-
ратуру круга осуществили Архимед при помощи спиральной линии,
Никомед**) при. помощи так называемой к ва др ат рисы, Аполлоний при
помощи некоторой кривой, .которую он называл «сестрой улитки»
и которая тождественна никомедовой, затем Карп при помощи некото-
рой кривой, которую он называет возникшей из двойного движения;
многие другие, говорит оп, получали разными способами решение этой
задачи, но ни один из них не получи.:! построений, отличных от меха-
нических.
Как н уже сказал, Александр в а основании изнеженных соображе-
ний. полагает, что оп обнаружил ложность за ключей ин, при помощи
которого Гиппократ, найдя квадратуру луночки, построенной только
на стороне квадрата, применяет ее так, как будто она была бы доказана
и для луночки ла стороне шестиугольника. Однако Евдем в «Истории
геометрии» говорит, что Гиппократ доказал возможность квадратуры
не только луночки па стороне квадрата, но, если можно так выразиться,
и вообще. Водь у всякой лупочки внешняя дуга или равпа полуокруж-
ности, или больше ее, или меньше, и если Гиппократ квадрирует и лу-
ночку с дугой, равной полуокружности, и луночки с дугами большими
и меньшими полуокружности, то, по-видимому, задачу можно считать
решенной и вообще. Поэтому я изложу дословно net! то, что говорит
Евдэм, добавляя лишь небольшие пояснения со ссылками иа «Начала»
Евклида, необходимые вследствие конспективного стили Евдсма,
который по древному обычаю сокращенно излагал доказательства.
Вот что он говорит во второй книге «Истории геометрии»***).
«Квадратуры луночек, считавшихся, ранее замечательными фигура-
ми вследствие своего родства с кругом, были описаны впервые Гиппокра-
том- и, по-видимому, были изложены вполне удовлетворительно**'**)-,
поэтому мы, касаясь этого предмета, будем излагать более подробно.
Начавши эти. исследования, Гиппократ, установил в качестве пер-
вого положения, необходимого для обоснования доказательства, следую-
щее: подобные сегменты кругов имеют друг к другу такое же отношение,
как квадраты их оснований. Это он доказал после того, как было уста-
новлено, что круги имеют между собой то же отношение, что и квад-
раты диаметров. Во второй раз это было доказано Евклидом в двенад-
цатой книге «Начал», где предложение было формулировано так: круги
относятся друг к другу, как квадраты на диаметрах. Действительно,
подобные сегменты имеют друг к другу такое же отношение, как и соот-
ветствующие круги, ибо подобными сегментами являются такие, какие
составляют одну и ту же часть круга; так, например, полукруг подобен
полукругу, и третья часть круга — третьей части. Поэтому подобные
*) Ямплпх сирийский irer платоник IV пекл н. занимавшийся пифагорейской математикой
ц написавший биографию Лифагсра.
** ) FTmrjihx ошибается. * надо читать Ди ио страт.
** •) Подлинный текст Пплемм можно выделить иа общего текста Сммттликил вследствие особен-
ностей математическою обозначения эпохи Аристотеля. Со времен Евклида геометрические образы
стали обозначаться, как и в настоящее время: «точки А. прямая Л Ня. но в эпоху Аристотеля писали
«точка, на которой Л (*л*Г*Л) прнман. пл которой ДВо, Ота филологическая работа пперпыс была
выполнена французским нет* рикг м математики Нолем Тали ери; в «том издании мы пользуемся
новейшей реконструкцией О. Бакнера. Текст Евцема выделен куренном. но особенности матема-
тического обозгтнчщгин у Квдема в переводе опущены.
**«*) И(7Д* TQ-jHOV g’Co^V «лебо-O^vai.
534
КОММЕНТАРИИ
сегменты, вмещают и равные углы: у полукругов эти углы являются
прямыми, у сегментов, больших полукруга, соответствующие углы
меньше.прямого, причем па столько, на сколько рассматриваемый сег-
мент больше полукруга, у сегментов иго меньших полукруга, больше
прямого па столько, на сколько сегмент меньше полукруга.
После того как это было доказано, Гиппократ начал с того, что
показал, каким образом можно квадрировать луночку, у которой наруж-
ной дугой является полуокружность', это он сделал, описав полукруг
около прямоугольного равнобедренного треугольника и построив на
основании круговой сегмент, подобный тем, которые, отсекаются боковыми
сторонами. Это положение Евклид взял в качестве 33-й теоремы третьей
книги, формулировав его так; «ла данной прямой построить круговой
сегмент, вмещающий угол, равный данному прямолинейному углу;
если иа основании построить такой сегмент, чтобы он вмещал угол,
равный том углам, которые находятся в сегментах, отсекаемых боко-
выми сторонами, то этот сегмент будет подобен боковым, ибо подобные
сегманты Евклид определил в тринадцатой книге*) как такие, которые
вмещают равные углы.
Гак как сегмент, построенный на основании, равен обоим сегмен-
там на других сторонах (ибо, согласно доказанному в предпоследней
теореме первой книги «Начал» Евклида, в прямоугольных треугольны
ках квадрат гипотенузы равен вместо взятым квадратам на сторонах,
заключающих прямой угол, а отношение квадратов па основаниях
равно отношению подобных круговых сегментов),
и в качестве общей части добавлена площадь тре-
угольника, находящаяся над построенным на осно
вании сегментам, то получившаяся луночка будет
равна взятому треугольнику, .теперь луночку,
которая., согласно доказанному, равна треуголь
нику, уже можно сквадрировать; действительно,
в одиннадцатой теореме второй книги «Начал»
Евклида показано, как строится квадрат, равный
данной прямоугольной фигуре. Таким образом.
Гиппократ легко нашел квадратуру луночки в пред-
положении, что внешняя дуга, последней есть по-
луокружность.
Вслед за этим он предполагает, что внешняя
дуга луночки больше полуокружности, и строит
трапецию, у которой три стороны равны между
наибольшего из параллельных оснований втрое
больше квадрата каждой из остальных, (рис. 3); затем около этой т.ра
пеции он описывает круг и. строит иа большей стороне сегмент, по
добный тем, которые отсекаются от круга тремя равными сторонами* *)
То, что около этой трапеции можно описать круг, ты докажешь так.
Разделив ионолам углы трапеции на основании 9-го предложения пер-
вой книги «Начал» и проведя диагонали (ВЕ и ЕД), ты найдешь, что.
так как ВЛ равна АГ, а сторона ЛЕ общая и углы равны, то... и т. д.***).
А что упомянутый сегмент больше полукруга, станет ясно, если
провести в трапеции диаметр (ВГ); та.к как он стягивает две сто
*> В действительности в третьей.
*) На рис. з атот сегмент. Опра шейный выпуклостью кверху, опущен.
*•*) Точка Е пересечения биссектрис будет центром круга, так как АК—КГ до построению
и треугольники АВЕ и ЛГЕ равны, откуда ВК“КГ=ЛЕ —ЕД.
ИЗМЕРЕНИЕ КРУГА
53ft
роны трапеции, то его квадрат необходимо будет более удвоенного квад-
рата стороны, оставшейся иг трех равных. Действительно, так как ВЛ
более АГ, то соединяющие их равные стороны ЛГ и ВА при продол-
жении встретятся в Z, ибо если ВА к ДГ равны и параллельны, и пря-
мые, соединяющие концы двух равных м параллельных прямых,
тоже, равны и параллельны, то АГ должна была бы быть равной БД.
что певозмояшо. Если же ВА к Л Г встречаются в Z, то углы ZAT
и ГАВ равны двум прямым на основании 13-го предложения первой
книги Евклида. Угол ГАВ больше угла TAZ (как внешний угол тре-
угольника по отношению к внутреннему на основании 32-го предложе-
нии первой кпиги); значит, квадрат на ВГ будет больше удвоенного
коадрата каждой из сторон ВА и АГ, а следовательно, и ГД. Значит,
квадрат наибольшей стороны трапеции необходимо должен быть мень-
ше смете взятых квадратов диаметра (ВГ) и той стороны из остав-
шихся, которая вместе с диаметром стягивает вышеупомянутую
наибольшую сторону, ибо вместе взятые квадраты на В Г и па ГЛ более
чем втрое больше квадрата на ГД, а квадрат на ВД только втрое боль-
ше последнего. Следовательно, угол, опирающийся на большую сторону
трапеции, будет острым, и сегмент, в котором он находится, будет
больше полукруга-, дуга же этого сегмента является внешней окруж
яостъю луночки.
Квадратуру этой луночки Евдем, насколько я могу судить, обошел;
она, вероятно, была следующей:
Луночка вместе с сегментом, построенным на большей стороне
трапеции, будет раина трапеции вместо, с тремя сегментами, отсекае-
мыми тремя прямыми, равными ГД,
и сегмент, построенный на большей
стороне трапеции, равен трем сег-
ментам круга, отсекаемым тремя рав-
ными сторонами, так как квадрат
большей стороны трапеции предпола-
гается ранным вместе взятым квад-
ратам трех этих сторон, и подобные
сегменты относятся друг к другу
как квадраты па основаниях; если
же от равных отпять поровну, то
будут равпы и остатки, м, следова-
тельно, луночка будет равна трапе-
ции. Еще короче ты найдешь это так.
Сегмент на большой стороне трапеции равен трем сегментам, описанным
на равных, сторонах, так как квадрат на первой втрое больше квадрата
на каждой нз последних; если к ним добавить площадь, заключающую-
ся мэжду тремя ранными сторонами и дугой большого сегмента, то полу-
чится луночка, которая будет равна трапеции. Если мы сквадрируем
эту последнюю, так как мы ведь умеем квадрировать всякую прямо-
линейную фигуру, то тем самым получится и квадратура луночки,
внешняя дуга которой больше полуокружности.
В том случае, когда эта дуга меньше полуокружности, Гиппократ
для построения такой луночки сделал следующее (рис. 4). Пусть будет
круг с диаметром АВ и центром К и линия ГД делит ВК пополам,
и под прямым углом; между ней и окружностью вставим EZ так, чтобы
она стремилась кВ, и квадрат иа EZ был в полтора рога больше квадрата
на радиусе. ![рямую ЕН проведем параллельно АВ и соединим К с Е и Z.
536
КОММЕНТАРИИ
Пусть последняя соединяющая при. своем продолжении, яа Z встретится
в точке 11 с прямой ЕП и опять соединим В с Z и И. Тогда ясно, что
прямая EZ при своем продолжении пройдет через В, ибо EZ нрсдиолн-
гается «стремящейся» к В, и ВН будет равна ЕК. Возможно, что кто-
нибудь смог бы доказать это и покороче, я же доказываю это па основа-
нии предыдущего так.
Согласно предположению, ДГ пересекает ВК пополам и нод пря-
мым углом; значит, па ДГ будет находиться центр круга, который мы
опишем около трапеции (ЕКВН) (иа основании следствия из первой
теоремы третьей книги «Начал» Евклида). Так как ЕП параллельна КВ
и их пересекла прямая ГД, то последняя образует внутренние углы,
равные вместо двум прямым (на основании предложения 2!)-го первой
кпиги); по углы при Г прямые; значит, будут прямыми и углы
при А. Проходящая через цент]» прямая ГЛ, пересекающая под
прямым углом ЕП, разделит и ее пополам ва основании третьего пред-
ложения третьей книги «Начал». Теперь, так как ДП равна ДЕ, сторона
AZ общая и углы при Д прямые, то и основание ZTT будет равно основа-
нию ZE. Также и BZ равна ZK, вследствие того, что ВГ равна ГК, a 1’Z
общая и углы при Г прямые; теперь, так как дне стороны II.Z, ZB равны
соответственно двум сторонам ZE, KZ и вертикальные углы (при Z)
равны, то основание 11В будет равно основанию ЕК.
Теперь около треугольника EZII опишем окружность, сегменты,
которой па EZ и ZH будут подобны сегментам на ЕК, КВ, В11. Если
все это так, то я утверждав;, что около трапеции ЕКВН можно описать
круг. Действительно, около треугольника КЕИ можно описать круг,
ибо в пятом предложении четвертой книги «Начал» показывается, как
описывается круг околи данного треугольника. Теперь, если я докажу,
что прямая, соединяющая центр этого круга с точкой К, равна линии,
соединяюнщн этот центр с точкой В, то описываемый круговой сегмент,
очевидно, пройдет и через ЕКН, и через В, и полученный, сегмент круга
обнимет трапецию и такой же сегмент будет, заключать и треуголь-
ник EZII. Пусть центр этого круга А — и проведем соединяющие пря-
мые ЛЕ, ЛИ, ЛК, ЛВ; так как треугольник ЕЛЯ равнобедренный (ибо
равны прямые, проведенные из центра), то будут равны и углы
ЛНЕ и ЛЕИ при основании вследствие! 5-го предложения первой кпиги
Евклида. Также и угол ВПЕ равен углу КЕИ, так как по доказанному
ВН равна КЕ; значит, и весь угол ВИЛ будет равен всему углуКЕЛ.
Но КЕ равна ВН; следовательно, и основание КЛ равно АВ; значит,
ЛВ будет равна радиусу ЛК.;такимвот образом и описывается сегмент *).
Если все это так, то получившаяся луночка, внешняя дуга которой
ЕКВН, будет равна прямолинейной фигуре, составленной из трех
треугольников ZBIT, ZBK, ZKE. Действительно, находящиеся внутри
луночки сегменты, отрезаемые от прямолинейной фигуры. (EKBHZ)
прямыми EZ и Z1I, равны отрезаемым прямыми ЕК, КВ, ВН сегментам,
находящимся вне рассматриваемой прямолинейной фигуры, так как
каждый внутренний сегмент в полтора раза больше внешнего, ибо,
согласно предположению, квадрат на EZ в полтора раза больше радиу-
са, то есть прямых ЕК, КВ, ВП, поскольку доказано, что последняя
*) Симцлпкий 3a5i.r.i понизать, что построенные на HZ п ЕК сегменты будут подобны друг
Другу.
Угол KZK вдвое больше угла ZBK. Если М сеть центр круга KZH, то и треугольнике MEZ
угол MZE--900—ЕВК; следовательли. центральный угол EMZ вдвое больше угля ZbK. который
опирается на дугу ЬЖ круга описанного около трапеции ЕКВН; это и доказывает подобие сегмен-
та EZ круга Е/ЛГ и сегмента ЕК круга ЕКЫЕ
ИЗМЕРЕНИЕ КРУГА 537
прямая ВЦ тоже равна НК. Если же квадрат на каждой из EZ, ЕП
в полтора раза больше каждой из упомянутых трех прямых, и отношение
квадратов на прямых равно отношению соответствующих сегментов, то,
следовательно, два внутренних сегмента будут равны трем внешним.
Так как эта луночка составляется из трех внешних сегментов и части
прямолинейной фигуры, лежащей вне двух внутренних сегментов,
а прямолинейная фигура с этими двумя сегментами равна луночке без
трех внешних сегментов, и два первых сегмента равны трем последним,
та луночка будет равна упомянутой прямолинейной фигуре.
Л что эта луночка имеет внешнюю дугу, меньшую полуокружности,
он доказывает, опираясь на то, что угол (ЕК11), находящийся во
внешнем сегменте, будет тупым, так как в 3-м предложении третьей
книги «Начал» Евклида доказано, что угол в сегменте, меньшем полу-
круга, будет больше прямого. Л что угол (ЕКП) тупой, он доказывает
так: поскольку квадрат на прямой EZ в полтора раза больше квадрата
на радиусе и квадрат на прямой КВ более чем вдвое больше квадрата на
прямой, BZ (ибо, как я лекажу, угол при Z будет больше (прямого) и ВК
равна КЕ), то ясно, что КЕ больше 13Z, и ВЕ в первой степени более
удвоенной BZ. Таким образом, квадрат на КЕ будет, следовательно, более
чем вдвое больше KZ вследствие подобия треугольников ВЕК и BKZ.
Действительно, как EJ3 к ВК, так будет и ЕК к ZK, и квадрат на ЕК
более чем вдвое больше, квадрата ня KZ *). По квадрат на прямой EZ
в полтора раза больше квадрата на ЕК; следовательно, квадрат на EZ
будет больше вместе взятых квадратов на ЕК и KZ**), как это имеет
место, например, для чисел В, 4, 2.
Если бы квадрат на ЕК был ровно вдвое больше квадрата на
KZ и квадрат на ZE в полтора раза больше квадрата на ЕК, то квад-
рат на EZ равнялся бы вместе взятым квадратам на ЕК и KZ. Посколь-
ку яге квадрат на ЕК более чем вдвое больше квадрата па KZ. то квад-
рат па EZ будет больше вместе взятых квадратов на ЕК и KZ. Следо-
вательно, угол при К будет тупым и, значит., сегмент, в котором он
находится, будет меньше полукруга***).
Таким образом Гиппократ нашел квадратуру для всякой луночки,
будет, ли ее внешняя дуга равна, больше или меньше полуокружности,
а но только для построенной на стороне квадрата как повествовал
Александр.
<9 EK2^JJB-KZ. I'KZ2.
*»} Е7.2 -ЕКЛ'-К?.2.
**’) Ввиду того, что «иолг,нения? Спмсликия скорее затемняют дело, полездо изложить сущ-
ность всего доказательства отдельно.
Гиппократ хочет показать, что угол ЕКН будет туп bin; длн этого нужно убедиться. что ь*под-
рат стороны KZ. лежащей против пего, будет больше суммы квадратов двух других сэсркн ЕК м
KZ. Мы им г! ем:
KZ2^- | КК«;
остистен докидать, что 4 KK2.;>KZa. В треугольнике НК.55 угол BZK будет тупой, потому что смсяс-
1гый с пим угол EZK и треугольник!! EZK >игллстсн острым, поскольку он меньше угла EKZ; следи-
и ат ел ъ ио,
KB'2/2KZ2.
откуда
и« следовательно
KZ2=| ЕК2—-КК2-, >ЕК2 I KZ2.
538
КОММЕНТАРИИ
Вместе с тем следующим образом он сквадрировал сразу и круг,
и луночку (рис. 5). Пусти около центра К описаны два круга и во второй
степени диаметр внешнего будет в шесть раз больше диаметра внутрен-
него’, вписав во внутренний круг шестиугольник АВ ГАЕЙ, продолжим
соединяющие центр (с вершинами шестиугольника) прямые КА, КВ,
КГ до окружности внешнего круга и соединим прямыми II и 0, 0 и I,
II и I; очевидно, что НО и 0.1 будут также сторонами шестиугольника,
вписанного в больший круг. На прямой Н1 опишем сегмент, подобный
тому, который отсекается прямой II©. Так как во второй степени
прямая ГП необходимо будет в три раза больше прямой 8П — стороны
шестиугольника (ибо прямая, стягивающая
две стороны шестиугольника и вместе с
третьей стороной заключающая прямом
угол — тот, который содержится в полукру-
ге —, будет во второй степени равняться
диаметру, а диаметр ио второй степени в
четыре раза больше равной радиусу стороны
шестиугольника, так как прямые вдвое
большие линейно будут вчетверо большими
во второй степени) и эта сторона ©Н во
второй степени в шесть раз больше прямой
А В, то ясно, что описанный на НI сегмент ока-
жется равным вместе взятым сегментам, от
нимаемым от внешнего круга прямыми Н0 и
©I, с добавлением тех, которые отнимают-
ся всеми сторонами
шестиугольника от внутреннего круга, ибо подоб-
ные круговые сегменты относятся друг к другу, как квадраты на
основаниях, так как подобные круги относятся между собой, как квад-
раты иа диаметрах; таким образом, если HI во второй степени втрое
больше И ©и II ©во второй степени равна ©I, и каждой из этих прямых
во второй степени равны вместе взятые все шесть сторон внутреннего
шестиугольника, ибо, согласно предположению, диаметр внешнего
круга во второй степени в шесть раз больше диаметра внутреннего.
и отношение диаметров равно отношению радиусов, а радиус равен
стороне шестиугольника, как гласит следствие из предпоследней теоре-
мы четвертой книги «Начал» Евклида, и, наконец, отношение сегментов
равно отношению квадратов на основаниях. Таким образом, луночка
1101 от отмеченного теми же буквами треугольника будет разниться
на те сегменты, которые отнимаются от внутреннего круга сторонами
упомянутого шестиугольника. Действительно, сегмент на III равнял-
ся сегментам, построенным на Н0 и 01 вместе с теми сегментами,
которые отнимаются сторонами шестиугольника; значит, сегменты IT0
и 01 будут меньше сегмента III на площадь сегментов, отнимаемых
шестиугольником. Если к обеим частям в качестве общей прибавить
часть треугольника, находящуюся выше сегмента HI, то получится,
что из нее и сегмента на III составится треугольник, а из нее же и сег-
ментов Н0 и ©1 составится луночка. Значит, луночка будет меньше
треугольника 1101 па площадь отнимаемых шестиугольником сегмен-
тов. Значит , луночка и отнимаемые шестиугольником, сегменты будут
равны треугольнику. И после добавления общего шестиугольника упомяну-
тый треугольник вместе с шестиугольником будут равны этой назван-
ной луночке вместе с внутренним кругом, ибо треугольник равнялся
луночке вместе с отнимаемым шестиугольником сегментами внутреннего
ИЗМЕРЕНИЕ КРУГА
5Ж
круга. Таким образом, «ела возможно сквадрировать упомянутые прямо-
линейные фигуры, то можно, значит, сквадрировать и круг вмесни
с луночкой.
Тан вот нужно признать, что достижения Гиппократа Хиосского
знает лучше Евдем, который был ближе it нему по времени, (чем
Александр), и является учеником Аристотеля. Что же касается
квадратуры круга при помощи сегментов, которую Аристотель отвергает
как ошибочную, или же квадратуры при помощи луночек, как он
говорит нс вполне ясно, то Александр вполне правильно оспаривает
ее, если только она та же самая, что и при помощи луночек».
Мы привели полностью весь текст Симплиция, поскольку оп характеризует поло-
жение греческой геометрии и в V веки до и. и в V веке и. э., в эпоху се упадка. Что
касается исследований Гиппократа, то нельзя но признать их очень остроумными, хотя,
как показывает текст Евдсма, Гиппократ допустил ошибку, считая, что квадратура круга
может считаться найденной, если папестиы способы квадратуры трех луночек, внешние
дуги которых равны, больше или меньше полуокружности. Это мнение, во-иидимому,
разделял и Евдем (слова y.ccri TQortov c'Sogav nnofioOTjvai.) и с шце большей степенью вероят-
ности сам Симпликий, по в эпоху Аристотеля ошибочность гишюкратовской квадратуры
была уже общепризнанной, что, конечно, хорошо было известно и Александру Афродиз-
скому. Однако принадлежащую последнему критик}' Гиппократа нельзя квалифициро-
вать иначе, чем как основанную па грубой ошибке: стоит только сравнить каши рисун-
ки 2 и 3, а также обратить внимании на роль шестиугольника в самой последней квадра-
туре Гиппократа, чтобы сказать, что Александр псе перепутал. Занятная глупость отно-
сительно квадратных и циклических чисел принадлежит, конечно, неонифагорейцаш
начала пашей эры, замечание Ендема, что Гиппократ «псриьгй» описал их, показывает'
ясно, что, вопреки Ямвлиху, первые пифагорейцы квадратурой круга не занимались.
Точно так же верх комизма представляет весь разговор Аммония с Симпликисм.
Что задача о квадратуре круга ш: считалась решенной, показывает то, что новое
ее решение дал Динострат, брат Менехма и ученик Евдокса Книдского, используя кри-
вую, которую незадолго до него изобрел софист Гшший Эаидский, по всей видимости,
для разделении угла ва три части. Эта кривая — первая в греческой математике, полу-
ченная как траектория некоторого движения, носит имя квадратрисы Дииострата. При-
водим касающийся этой кривой текст «Математического собрания» Паппа (книга IV,
30- 34), являющийся нашим первоисточником для рассматриваемой теории.
«30, Для осуществления квадратуры круга Дииоктрат, Никомед
и другие более поздние математики пользуются некоторой кривой,
получившей имя от этого ее основного свойства;
она называется квадратриной и имеет следую-
щее происхождение.
Возьмем квадрат АВГД (рис. б) и вокруг А
как центра опишем дугу окружности ВЕД;
пусть прямая АВ движется так, что точка
В описывает окружность ВЕД, а точка А
остается неподвижной; одновременно другая
прямая 13Г, оставаясь всегда параллельной АД,
перемещается так, что ее конец 13 нее, время
движется по ВА, причем в одно и то же время
прямая А13, вращаясь равномерно, проходит
угол ВАЛ (иными слонами, точка В — дугу
13ЕЛ), а прямая В Г, тоже, двигаясь равномер-
но, проходит расстояние ВА (то есть точка В
— прямую В А). Тогда
получится, что в конце движения обе прямые АВ и ВГ одновременно
совпадут с ЛД. При этом движении прямые В Г и ВЛ будут пересекать
друг друга в точке, которая все время перемещается вместе с ними и опи-
сывает некоторую, заключающуюся между прямыми ЛВ, АД и дугой
ВЕЛ, линию BZH, которая будет выпуклой в одну сторону; эта линия
оказывается очень полезной для нахождения квадрата, равного данному
540
КОММЕНТАРИИ
кругу. Ошппшое свойство этой кривой заключается в следующем:
если провести какую-нибудь прямую AZE, то вея дуга ВЕЛ будет так
же относиться к дуге ЕЛ, как прямая АВ к Z(-J; ото вытекает из самого
способа получения рассматриваемой кривой.
31. Однако эта лилия не удовлетворяет Спора,— но моему мнению,
правильно — но следующим причинам. Во-первых, эта линия уже
предполагает осуществленной ту самую цель, для достижения которой
является предназначенной. Действительно, как можно заставить дви-
гаться из В две точки так, чтобы в равное время точка, движущаяся по
прямой, пришла бы в Л, а точка, движущаяся по окружности — в Л,
если не знать сначала отношения прямом АВ к дуге ВЕД; ведь именно
в этом отношении должны необходимо находиться скорости обоих этих
движений. Затем если мы для одновременного сонертения указанных
движений пользуемся какими-то неопределенными скоростями, то
требуемый результат .может быть достигнут только случайно; а это разве
не бессмысленно? Далее невозможно определить ту точку кривой, кото-
рая необходима для выполнения квадратуры круга, а именно точку ее
пересечения е прямой АЛ. Все вышеупомянутое можно представить себе
ла прилагаемом чертике; Когда прямые ЛВ и ВГ будут при своем
движении приближаться к конечному положению, то они совпадут
с прямой ЛД и никоим образом пе дадут точки взаимного пересочемля;
они перестанут пересекаться еще до достижения совпадения с АД,
а ведь это пересечение должно быть концом рассматриваемой линии,
то есть точкой, где она встречается с прямой уХЛ. Можно, конечно,
сказать, что паша линия продолжается до прямой ЛЛ, как мы предпола-
гаем это относительно прямых линий, но это пе будет следовать из
основных предположений; да и тогда точку И можно будет взять, уже
зная предварительно отношение длин дуги и прямой. Если же это
отношение не дано, то не следует, доверяя авторитету изобретших сс,
пользоваться этой линией, скорее относящейся к механике, чем к гео-
метрии. Покажем предварительно, как при помощи этой липни решает-
ся поставленная задача.
Пусть дан квадрат АВГД и описанная около центра Г дуга окруж-
ности ВЕД (рис. 7); если образована, как сказано выше, квадратриса
BU0, то можно показать, что дуга ДЕВ так относится к прямой В Г,
как ВГ к прямой Г(-). Действительно, если это нс так, то упомянутое
отношение будет равно отношению ВГ или к большей чем Г0 прямой,
или же R мопыней.
ИЗМЕРЕНИИ КРУГА
541
Пусть сначала, если возможно, ато отношение будет равно отно-
шению ВГ к большей, чем ГМ, прямой ГК. Около центра Г опишем
дугу Z1IK, пересекающую киадратрису в точке JI, опустим перпенди-
куляр НА, и соединяющую ГП продолжим до Е(рнс. 8). Теперь, так как
дуга ДЕВ так относится к ирлмон В Г, как ВГ, или ГД, к ГК, а отноше-
ние ГД к ГК равно отношению дуг JiKA и Z.I.IK (так как отношение
диаметром кругов равно отношению соответствующих дуг), то ясно,
что дуга ZI1K будет равна прямой ВГ. И так как вследствие основ-
ного своистца кривой отношение дуг ВЕД и ЕД равно отношению пря-
мых ВГ и ПЛ, то, значит, отношение дуги ZHK к дуге НК равно отно-
шению прямых ВГ л ПА. Но доказано, что дуга ZU.K рання прмой ВГ;
значит, и дуга ПК будет равна прямой ПЛ,
что нелепо. Следовательно, отношение дуги
ВЕД и прямой ВГ не будет равно отноше-
нию ВГ к прямой, большей чем ГО.
32. Я утверждаю теперь, что оно по бу-
дет раино н отношению В Г к прямой, мень-
шой чем ге. Действительно, пусть ато отно-
шение будет, если возможно, равно отно-
шению ВГ к некоторой примой КГ; около
центра Г опишем дугу Z.MK, перпендику-
лярно к ГД проведем К 1.1, пересекающую
киадратрису в 11 и соединяющую ГП про-
должим до Е (рис. 9). Тогда, подобно пре-
дыдущему, докажем, что дуга ZMK будет
равпа прямой В Г, и отношение дуги. ВЕД
к ЕА, или дуг ZMK к МК равно отношению
Ия итого ясно, что дуга МК будет равна
Значит, отношение дуги ВЕД к прямой В Г пе будет равно отношению
ВГ к прямой, MtMjbjucjj чем Г(-). Но доказано, что оно пе может быть
равно и отношению ВГ к прямой, большей, чем ГН; следоиателыго, оно
будет равно отношению ВГ к самой прямой ГВ.
Точно так же ясно, что если мы возьмем третью пропорциональ-
ную для прямых ВГ и ГВ, то полученная прямая будет равна дуге ВЕЛ,
а учвтисрепнал — окружности всего круга. Если же найдена прямая,
равная окружности круга, то ясно, что легко построить и квадрат,
равный атому самому кругу; как Архимед доказал, прямоугольник
между прямой. ранной периметру круга, и радиусом будет вдвое больше
этого круга».
Очень tturtiptfcita it:vmrni;Mnn J кишом дальнейшая история лвадратрнсы; возможно,
что мы имеем непрерывпук) линию развития, которая от Дииострата 4epr:i К мкл ид а ведет
пеносрсдствошю к Лр.хвмеду. Нредостпиляем слово самому Ниппу.
«33. Таково про и схождение вышеупомянутой кривой, которая, как
. мы сказали, более относится к механике; геометрически поставленную
задачу можно решить следующим образом при помощи «геометрических
мест на поверхности»*).
Пусть будет дан положением квадрант АВГ круга. Проведем (ия
центра) какую-нибудь прямую ВД и опустим на ВГ перпендикуляр EZ,
который имел бы заданное отношение, и дуге АГ (рис. 10); я. утверждаю,
что TO4JWJ Е будет находиться ля лужнон нам линии.
прямых ВГ и НК.
прямил КП, что нелепо.
) Под этим именем изпсеггны ирниидлежитпе Илклцду две пинги.
542
’ КОММЕНТАРИИ
Представим себе, что на дуге ДГ построена поверхность прямого
цилиндра и на пой задана положением описанная винтовая линия
ГНВ; пусть также дана сторона ОА цилиндра. В точках В, Е восставим
(равные <ЗА) перпендикуляры FJ и ВЛ к плоскости круга, а.через (-)
проведем параллельную ВА прямую (Н)Л. Поскольку по свойству винто-
вой линии отношение прямой EI к дуге ДГ является данным, и отногае
нис EZ к ДГ тоже дано, то будет известно и отношение EZ к Е1.' Пря-
мые EZ и EJ задали положением; значит, задана положением и соеди-
няющая Z1. Опа же перпендику-
лярна к ВГ; следовательно, прямая ZI
я точка I будут находиться в плоско-
сти, секущей цилиндр, (проведенном
через .прямую ВГ), и на некоторой
линейчатой *) поверхности (так как
прямая 0Л, перемещаясь по винтовой
линии НН Г п прямой ЛВ, тоже задан-
ной положением, всегда остается парал-
лельной плоскости нижнего основания
цилиндра); следовательно, точка I. а
также и Е тоже находятся на рассма-
триваемом геометрическом месте. Таким
образом, можно получить общее реже
вне задачи; если же отношение прямой EZ к дуге АГ будет равно' отно-
шению ВА к дуге АДГ, то получается вышеупомянутая квадратрмса.
fc. 34. Поставленную задачу можно подобным же образом решать
и при помощи винтовой линии (спирали) **), построенной на плоскости.
Пусть отношение прямой EZ к дуге А Г будет одинаково с отншне
нием. прямой ЛВ к дуге ААГ; пусть за то время, в точение которого
прямая АВ, вращаясь вокруг точки В, описывает дугу АЛГ, некоторая
движущаяся по иеп н выходящая из А
точка доходит ди В в тот момент, когда
ЛВ занимает положение ВГ; эта точка j
опишет спираль ЛИВ (рис. It). Таким
образом, отношение/АВ к ВП будет
равно отношению дуги АД Г к ГА и по-
сле перестановки отношение прямой: АВ
к дуге АДГ равпо отношению ВН
к дуге ГД.
Ио в том же отношении будет и
EZ к А Г; следовательно, В И будет
равна ZE. Восстании к плоскости перпендикуляр КП, равный ВН;
следовательно, точка К. будет на поверхности цилиндроида, построен-
ного на спирали (ЛИВ). Но опа также находится и на некоторой
комической поверхности (действительно, соединяющая ВК будет на
конической поверхности, образующей половину прямого угла с, плос
костью ЛВГ и проходящей через заданную точку В); следовательно,
точка К находится на расгматрнваемом геометрическом месте. Через К
проводим прямую ЛК I параллельно ВД и опускаем па плоскость перпея
дикуляры ВЛ и EI; следовательно, ЛК1 будет находиться ва плоктп-
*> В тексте ошибочно «цилиндрической».
*’) Нужно иметь п килу. что н<> гречески и спираль, и intiiTuiiau линии (о.ч поверхности im-nni-
яря! обозначаются одним словом 005.
И ЗМ Е РЕ НД Е HP У ГЛ
543
идалыюй *) поверхности (так как прямая ЛКI. перемещается и ио задан-
ной положением прямой ВЛ и также по заданной положением кривом
линии,-на которой находится К); следовательно, на той же поверхно-
сти окажется и точка I. Но она будет также находиться и на некоторой
плоскости (действительно, ZE равпа Е I., так как опа равна ВН, и Z1,
будучи перпендикулярна к ВГ, тоже задана положением); следователь-
но, и точка 1 будет па рассматриваемой кривой, а значит, и Е. И ясно,
что если угол АВ Г прямой, то получается вышеупомянутая квадратриса».
К этому тексту необходимо сделать несъ-олько замечаний. В главе 33 рассматри-
вается линия, представляющая в известном смысле обобщение квадратрнсы (последняя
получается в частном случае!, когда отношение, прямой EZ к дуге ГД будет равно отно-
шению прямой АВ к дуги АДГ); рассматриваемое геометрическое место, описываемое
точкой 1, представляет линию пересечения некоторое! неподвижной, проведенной через
прямую В Г, плоскости е. линейчатой поверхностью, образуемой движением прямой,
скользящей по перпендикуляру ИЛ и винтовой линии Гб и остающейся все время парал-
лельной плоскости квадранта ЛВГ. Точка Е будет проекции! на плоскость АВ Г точки I;
при движении последней точка Е опишет на илоскоети квадранта АВ Г некоторую линию,
которая и иредстапляет обобщение квадратрнсы. Последняя получается, если проходя-
щая через В Г плоскость наклонена под углом н 45° к плоскости ЛВГ и шаг винтовой
линии ГС-) в четыре раза больше радиуса ГАВ.
В главе 34 рассматривается другое построение кпадратрисы, которая получается
как проекция на плоскость ЛВГ линии пересечения плоскости, проведенной под углом
в 45й к плоскости АВГ, и линейчатой поверхности, получившейся в результате движения
прямой линии, параллельной ЛВГ и скользящей по перпендикуляру ВЛ и кривой двоя-
кой кривизны, получаемой в результате пересечения конической поверхпости г, осью ВЛ
и с образующими, на клоп спеши и под углом 4.Т' к плоскости АВГ, и цилиндрической
поверхности с. образующими, параллельными ВА, построенной па Архимедовой спирали,
проходящей через точки АН В.
Кому принадлежит это остроумное обобщение квадратрнсы? Папп упоминает
о «геометрических местах на поверхности», не называя автора, но из книги VII «Мате-
матического собрания» (VII, 3) мы узнаем, что этим именем назывались дне; книги, при-
надлежавшие Евклиду, к которому, вероятно, и следует отнести построение, описанное
в главе 33; в таком случае оказалось бы, что в эпоху Евклида винтовая линия была уже
известной. Построение главы 34 уже предполагает что-то вроде Архимедовой спирали,
однако построение! соответствующей линии и довольно существенных чертях отличается
от Архимедова способа; если и это построение, относится к доархимсдопскому периоду,
тогда генезис идей Архимеда, приведший его к решению задачи о квадратуре круга
при помощи спирали, становится совершенно ясным.
Нам остается теперь взвесить все доводы pro и contra относительно принадлеж-
ности Евклиду обоих построений, описанных п главах 33 и 34. Самым серьезным доводом
является упоминание «геометрических мест на поверхности» (умолчание! Наина об Евкли-
де может объясняться тем, что принадлежность Евклиду этого сочинения была общеизве
стиой, так что Папп мог ограничиться упоминанием Евклида лишь в общем перечне
сочинений, составлявших куре высшей геометрии у греков); правда, термин «геометри-
ческих мест на поверхности» мог со временем сделаться названием геометрической дис-
циплины, вроде цитируемых Архимедом «конических сечений». Далее надо отмстить
тесную связь обоих построений с кнадратрисой; однако наличии Архимедовой спирали
по втором построении скорее говорит в пользу «Пикомеда и других более поздних
математиков», упоминаемых Паппом в начале цитируемого отрывка (глава 30). Таким
образом, принадлежщи-ть обоях построений Евклиду нельзя считать абсолютно доказан
ной. хотя она И является вполне возможной.
Если бы «Измерение круга» дошло до вас полностью, то мы, вероятно, читали бы
в нем основную теорему, утверждающую, что длина окружности пропорциональна диа-
метру (в «Началах» Евклида доказывается только, что площади кругов относятся, как
ква драты диаметров).
В качество восполнения этого недостатка даем отрывок из «Математического соб-
рания» Паппа (книга V, И--13), содержащий доказательств» упомянутой теоремы.
«11... Окружности кругов относятся друг к другу, как диаметры.
Пусть будут два круга АН, ГЛ с диаметрами АВ, ГЛ. Я утверждаю,
) Линейчатой.
544
КОММКНТЛГИИ
что отношение окружности круга АВ к окружности круга ГЛ одина-
ково с отношением прямых АВ и ГД (рис. 12).
Так как круг ЛВ относится к кругу ГД,- как квадрат ЛВ к квадра-
ту ГЛ, и учетверенный круг АВ равен прямоугольнику, построенному
на прямой ЛВ и окружности соответствующего круга, а учетверенный
к квадрату на Л В относится так'
круг ГД равен прямоугольнику,
построенному на прямой ГД и
окружности круга ГД (это уже
доказало выше), то, следователь-
но, прямоугольник между АВ и
окружностью круга АВ относит-
ся к прямоугольнику между ГД
н’ окружностью круга ГД, как
квадрат на АВ к квадрату па ГД.
1I осле перестановки прямоуголь-
ник между ЛВ л окружностью АВ
же, как прямоугольник между J Л
и окружностью 1Д к квадрату на ГЛ: следовательно, отношение окруж-
ности круга ЛВк прямой Л В равно отношению окружности ГД к пря-
мой ГД, и после перестановки окружность АВ относится к окружности
ГД так же, как Л В к ГД.
12. Это можно доказать и не применяя теоремы, что прямоуголь-
ник между диаметром круга и его окружностью вчетверо больше этого
круга. Действительно, у вписанных в круги или описанных около них
подобных многоугольников периметры относятся друг к другу, как
радиусы, так что и окружности кругов относятся друг к другу, как
диаметры.
Пусть будет опять круг АВГ с-центром Л и радиусом ДВ; проведем
из Д какую пибудь прямую ЛЕ;
относится, как круг АВГ к
сектору ВДЕ (рис. 1.3).
Теперь, если дуга BZE со-
измерима с периметром АВГ
круга, то, разделив периметр
АВГ круга на представляющие
общую меру дуги, и соединив
точки деления с центром Д пря-
мыми, мы получим совпадаю-
щие Друг с другом секторы,
число которых будет равпо чи-
слу общих мор в окружности,
и, следовательно, отношение
периметра АВГ круга к дуге BZE будет равпо отношению круга АВГ
к сектору ВДЕ. Если ясе окружность и ис будет соизмеримой с ду-
гой BZE, то все равпо отношение круга ЛВГ к сектору ВДЕ будет
равно ьтшиммшю периметра АВГ к дуге BZE.
Пусть, если возможно, отношение круга АВГ к.сектору ВДЕ будет
равно отношению периметра АВ Г к дуге BZ, которая сначала пусть
будет меньше дуги ВЕ; возьмем какую-нибудь другую дугу ВИ, кото-
рая была бы больше BZ, но менее BZE, и одновременно была соизмери-
мой с периметром ЛВГ, как это делается в леммах сфсрпки, и соединим
Л с II. Тогда на основании вышеизложенного круг АВГ будет относить-
ся к сектору ВАН, как периметр ЛВГ круга к дуге BZU. Но периметр
ИЗМЕРЕНИЕ КРУГА
545
АВГ круга к дуге BZ11 имеет меньшее отношение, чем к дуге BZ, то
есть чем отношение круга АВГ к сектору ВЛЕ; тогда круг АВГ
к сектору ВДВ будет иметь меньшее отношение, чем к сектору ВЛЕ, что
полони; следовательно, отношение круга АВГ к сектору ВЛЕ ле будет
равняться отношению его периметра АВГ к дуге BZ-, которая была бы
меньше дуги BZE.
Но я утверждаю, что оно не будет равно отношению периметра АВГ
к дуге, большей чем BZE. Пусть, если возможно, оно будет равно отно-
шению к дуге ВЕГ; точно так же возьмем какую-нибудь дугу ВЕО.
Которая была бы больше дуги BZE, но меньше, чем ВЕГ, и одновремен-
но была соизмеримой с периметром АВГ круга, и соединим Д с 0. Теперь,
так как снова отношение круга АВГ к сектору BAG равно отношении)
периметра ВАГ круга к дуге ВЕН, а периметр АВГ к дуге BE0 имеет
большее отношение, чем к дуге ВЕГ, то естг> чем отношение круга АВГ
к сектору ВДЕ, то, конечно, круг АВГ к сектору ВДО будет иметь
большее отношение, чем к сектору ВДЕ, что нелепо; значит, отно-
шение круга АВГ к сектору ВДЕ не будет равно отношению его пери-
метра АВГ к дуге, большей чем BZE.
Но уже доказано, что оно не
равно отношению и к меныпей чем .
BZE дуге; значит, круг Л ИГ отпо- /
сится к сектору ВЛЕ, как его мери- /
метр АВГ к дуге BZE. I
13. Подобные сегменты кругов \
относятся друг к другу, как квад- \
раты их основании, а их дуги отно-
сятся, как основания.
Пусть АВГ и AEZ будут подоб-
ные сегменты кругов. Я утверждаю,
что сегмент АВГ относится к AEZ, как
дуга же АВГ относится к дуге AEZ, как прямая АГ к AZ (рис. 15).
Дополним оба круга, возьмем их центры 11, 0 и соединим А с II,
1.1. с Г и Д с €), 0 с Z. Теперь, так как сегменты АВГ и AEZ подобны, то
угол при 11 равен углу при 0, треугольник ЛИГ подобен A0Z и дуга
АВГ подобна AEZ. Следовательно, круг АВГ относится к сектору
АП ГВ, как периметр круга АВГ к дуге АВГ, или как четыре прямых
угла к углу при П. Так же и круг AEZ к сектору A6ZE относится, как
периметр круга AEZ к дуге AEZ, или как четыре прямых угла к углу
при (-). По угол 0 равен углу Н; значит, круг АВГ относится к секто-
ру АН ГВ, как круг AEZ к сектору A0ZE, и после перестановки круг
АВГ относится к AEZ, как сектор АН ГВ к сектору A0ZE. Но отно-
шение одного круга к другому равно отношению квадрата на АН
к квадрату на Д0, то есть отношению треугольника АН Г к треуголь-
нику A0Z; следовательно, отношение сектора АНГВ к сектору A0ZE
равно отношению треугольника АНГ к треугольнику A0Z. Тогда
остающийся сегмент АВГ относится к сегменту AEZ, как треуголь-
ник ЛИГ к треугольнику A0Z, то ость как квадрат на АГ к квад-
рату на AZ.
Теперь я утверждаю, что дуга АВГ относится к дуге AEZ, кап
АГ к AZ.
Действительно, после тех же самых построений получится, что
отношение окружности круга АВГ к окружности круга AEZ равно
отношению дуги АВГ к AEZ. Но как окружности кругов друг к другу,
35 Архимед
546
КОММЕНТАРИИ
так относятся и радиусы АН к Л0, или АГ к AZ; слсдоватслыю, дуга
АВГ относится к дуге AEZ, как АГ к AZ».
Возможно также, чтоб «Измерении круга» заключались предложения относительно
арбелона и салинона, приводимые в «Кните лемм» и у Паппа (кц. IV, 14—20).
|2( Задача о квадратуре круга была решена Архимедом два раза: в первый раз
он решал ее геометрически при помощи Архимедовом спирали (см. трактат «О спиралях»,
предложение XVIII), о чем мы уже говорили выше; теперь нам остается разобрать второе
ею решение, приведшее к определению числового значения отношения окружности к диа-
метру; это решение и составляет третье предложение рассматриваемой книги.
Это предложение распадается на две части: в первой Архимед мри помощи описан-
ных многоугольников находит нижний предел отношения окружности к диаметру, во
второй при помощи вписанных многоугольников он ищет верхний предел того же отно-
шения.
В обоих случаях его исходная точка одна тг та же: он рассматривает прямоугольный
треугольник, в котором один острый угол равняется 30’’ (рис. 3 текста); в этом треуголь-
нике отношение большего катета ЕГ к меньшему TZ будет равняться 3. Для величины
Архимед дает следующие значения:
263 , 1351
153< 780 •
Вопрос о том, каким образом Архимед нашел эти значения, долгое время занимал
всех историков математики. Дошедший до пас комментарий Евтокия нс даст никакого
ответа па интересующий нас вопрос: Евтокия просто ссылается на труды Птолемея, Теона
и Гсрона об извлечении квадратных корней, а сам только проверяет результаты Архимеда
непосредственным умножением полученных чисел.
В па стоящее время мы находимы! в лучшем положении, чем Гейбсрг в эпоху выхода
в свет 3-го тома первого издания сочинений Архимеда (1881), так как теперь пандепа
считавшаяся в то время потерянной «Метрика» Герона. Вот что говорится там об извле-
чении квадратного корпя из 720 (ки. I, 8).
«Так как 720 нс имеет рационального корня, то корень из пего
ни найдем с. ничтожнейшей разницей так: поскольку ближайшим
к 720 квадрат будет 729, имеющий корнем 27, то разделим 720 на 27;
получается 2(5 и две трети; прибавь 27; получится 52 и две трети. От
« • 1 1
этого (возьми) иолонпиу; получится 26| — . Значит, корень из
4г О
» 1 1 11
720 будет приблизительно 2(5 Тт + т • Действительно, 26 , -т+-т»
помноженное само па себя, дает 720^, так что разница будет состав-
лять 36-ю долю единицы. Если бы мы захотели сделать разницу еще
меньшей 36-й части, то вместо 729 возьмем только что найденное число
720 и, проделав то же самое, найдем разницу, которая окажется
ut)
1
значительно меньше
зь
Исследования последних лет показывают, что этот метод, который можно иллюстри-
ровать формулой
где Ло — приближен пос значение А— имеет вавилонское происхождение. Вавилоняне
применяли его для нахождения приближенного значения Jz 2, а также для нахождения
гипотенузы по заданным катетам а и й, из которых один а значительно больше другого.
Формула, которой они пользовались, была такова
г----- Й2
Г «8 |-йа=а-|-—;
она легко получается из предыдущей, если положить .-1и рапным а
ИЗМЕРЕНИЕ КРУГА
547
Теперь мы можем непосредственно обратиться к самому сочинению Архимеда*
Каким образом были получены приближенные значения у 3:
153 780 ‘
Само произведение Архимеда не даст ответа па этот вопрос.; попробуем ответить на
него сами. Разложим па множители знаменатели обоих приближенных значений:
153 = 3.3-17 = 3.51,
780=2®. 3-5-13=3-5-52.
Если помножить на 5 числитель и знаменатель первой дроби, то мы будем иметь:
1325 г- 1351
15-51 15-52 ‘
Выбор чисел 15 и 52=2-26 не случаен; действительно,
15®=225, 262 = 676=3-225-| 1=3-1524-1.
Архимед подобрал два числа, обладающих тем свойством, что утроенный квад-
рат одного ин них только па единицу отличается от квадрата другого числа, так что
дробь могла бы быть взята в качестве приближенного значения у 3. Между прочны,
первый из. приведенных нами фрагментов к «Измерению круга» (стр. 270) прямо указывает,
что это приближенное значение у 3 было Архимеду известно. После этого дело стало- •
вптся ясным: для того чтобы получить более точное значение У 3, Архимед полагает:
о 26®- 1
3=~15®- ’
и, следовательно,
h 15
Стоящий в числителе корень легко извлекается но вавилонскому правилу:
,—=--- 1 / 26® -14
1351
~йГ'
Если умножить знаменатель ла 15, то мы получаем одной:.! архимедовых приближен-
ных значений [Л3. Нетрудно видеть, что полученное по вавилонскому правилу прибли-
женное значение корня будит всегда значением с избытком. Архимед это, конечно, знал.
Чтобы получить нужное ему второе приближение <: недостатком, он второй раз приме-
няет тот же прием — делит подкоренное выражение на уже найденный корень, иными
словами, пользуется средним гармоническим. Мы имеем:
26® - 1
26-1
О/-
26-
26
1
2-26
[2-26®— 0 ~2С
1
2-26- 1
Так лак itvtkho получить приближение с недостатком, то можно увеличить вычитае-
1
мую дробь, для чего уменьшаем знаменатель, замелив^ единицей. Таким образом, най-
денный с недостатком корепь будет:
1
26 —
1 _ 1325
51 51 ‘
2-26- 1
Указанную операцию можно вообще выразить формулой
Это привило имеется в арабской математике.
35*-
548
КОММЕНТАРИИ
X нзс ук&зыайст 1Ш арабского математика X BVK8,' аль-Кархи; автор этих строк истра-
тил его имеете с героновским и руководстве .марокканского математика XI11 века ибн
аль-Банны.
Таким образом*.
лг»_ / 262 — 1 1325 _265
* Л~: 15 > 15 -51 “153'
После этого начинается собственно процесс вычисления отношения окружности
К диаметру. Архимед заменяет окружность периметром сшнеаппого многоугольника, при-
ближая его к окружности при помощи последовательного удвоении числа сторон. Так как
у Архимеда в числителе отношения стоит диаметр (собственно говоря, радиус EZ), то
1
при замене окружности описанным многоугольником получается величина, меньшая — .
Архимед ншпет (для ясности мы заменяем неравенствами его приближенные равен-
ства) (рис. 3 текста):
EZ 306 !ЕГ 265
"zr-~ 153 ’
Разделив пополам угол ZKI’, мы по свойству* биссектрисы получаем:
ZE :Er = Z[I: НГ.
Отсюда
7.Е-ЕГ 2Г
ЕГ “ ГН ’
или
ZE-I ЕГ ЕГ .
zr “ ГН ;
следовательно,
ЕГ EZ ЕГ 306 . 265 571
TH “‘ZT-1 TZ > 153 7 153 ~' 153 •
Далее,
Е Н2 ЕГ2-|-ГН2 5712+153® 349 450
‘ТПГ1 ГН2 > 1532 ~ 1532 ’
откуда -
ЕН /349450
ПГ > 153 ’
причем корень, стоящий в числителе, надо извлечь с недостатком.
В дальнейшем Архимеду приходится извлечь три корня с недостатком и четыре
с избытком, причем подкоренное выражение получается в результате сложения двух
квадратов.
Первым таким корнем, который ему* пришлось извлекать с недостатком, был корень
из суммы 5712-р1532=349 450. Так как число 349 450 стоит в тексте Архимеда, то ясно,
что Архимед извлекал кореш, именно в этой форме.
Каким-нибудь способом (например, из таблицы квадратов чисел от 1 до 100, анало-
гичном вавилонской, дававшей квадраты чисел от 1 до 60) Архимед мог найти первое при-
ближение для корня, а именно 590, пользуясь тем, что 592—3481. Пторое приближение
он тогда мог бы найти по вавилонскому правилу*
8±
1 1
Так как 7 --- = 59-к-, то
2 2
разом, приближенное значение
(ввиду замены знаменателя это,
знаменатель можно положить равным 59
; таким об-
корпн, которое по правилу* должно быть избыточным
конечно, нужно проверить), получилось бы в виде
/349450 = 591 у .
Так как Архимеду нужно приближение е недостатком, то оп поступает по изложен-
ному памп выше правилу; только теперь ему приходится увеличить на единицу
ИЗМЕРЕНИЕ КРУГА
549
знаменатель дроби ? , поскольку опа ио пылит а е. т с. я. по прибавляет с я;
мы имеем:
У 34^450 >5911.
о
1
Собственно говоря. когда мы вместо 59 паяли 59 — , мы уже получили приближен-
ное значение с недостатком, как можно проверить лелосредственным возведением в квад-
1 1
рат числа 591 -у; одлако число 591 выгодно еще и в том отношении, что дальнейшие
расчеты помучаются более простыми с восьмеркой в знаменателе, чем с семеркой.
Разделив еще раз пополам угол ГЕН прямой ЕЙ, Архимед получает:
ПЕ : ЕГ—110: Ы’,
откуда
(ЛЕ- ЕГ):ЕГ — ПГ: 0Г,
и
ЕГ _НЕ —ЕГ
«Г HI’ ’
Мы имели
591 --
EIJ 8 EL’ 571. '
ИГ > 153 ’ ГН <153*
откуда
591 1+571 11(121
Е.1 О О
Тб > 153 ПйР •
Теперь
/7 ГТ*
~ Ев _1<ЁтЦ-Г0» I V 1162 8 ) —1532
6Г ИГ > 0Г
Заметим, что в атом месте Архимед, не произведя промежуточных вычислений,
i
просто пишет: «значит, 0Е имеет к ИГ большее отношение, чем 1172 — к 153».
О
Здесь Архимеду приходится вычислить выражение
11(121 у+ 1532.
Так как ои не дает окончательного числового значения подкоренного выражелип,
как ото он сделал в предыдущем случае, то нс будем этого делать и мы, а прямо применим
вавилонскую формулу для вычисления гипотенузы, помня, что 153s—23 409.
11621 /+ 1532 = 1162 1ч—2'И09. .
87 8 211(121
О
160
Выполнив деление, найдем, что частное равно 10------. Отбросив дробную часть
2324 1
4
(так как приближение получается с недостатком), мы получим, что искомый корень
будет
]/(j 1621 j*- 153s > 11621-j 10- 11721.
550
КОММЕНТАРИИ
Дальше Архимед делит пополам угол ©ЕГ прямой ЕК. Аналогично предыдущему
ои получает:
НЕ : ЕГ—НК :КГ,
(НЕ • ЕГ): ЕГ—НГ : ГК,
1 1 1
ЕГ _ 0Е -|- Е Г _ 11'2 7Г “! 1162 F 2334 Т
ГК — ' НГ 153 153 *
Архимеду приходится вычислять выражение
1 / 1532 - 2334 4 ‘ г 23 -
4 4 2-2334-1
4
«в а
Выполнив деление во втором слагаемом, найдем в частном 5 --т- , что после от-
46681
брасывания дроби можно принять за 5; таким образом,
. 2334 4- У’-! 153- as 2334 — 5 = 233!) 4 -
к 4 J 4 4
Теперь отношение ЕК : КГ будет болтлив 2339 —
4
примой ЕА даст пам:
153. Новое деление угла КЕГ пополам
КЕ :ЕГ = КЛ: АГ,
(КЕ -ЕГ): КГ=ЕГ : АГ,
откуда
ЕГ _ КЕ
Л Г “ КГ
• 2339-1 2334-1 4673-1
ЕГ 4 , 4 _ 2
“КГ 153” 1 153 153““
Найдено отношение радиуса ЕГ к прямой ГЛ, являющейся половиной стороны
правильного 96-уголышка. Отношение диаметра к периметру описанного правильного
96-уголышка будет больше дроби
1 .1
4673 4 4673 4
А
153-96 “ 14688 ’
Таким образом,
1 46734
л“'> 14688
14 688 (36' 2 1
л<---------т-=3-------;-<3 — ’
4673-1 4673-1 '
А
4 1
так как 667 -7 = 4672 — .
Но втором части предложения, где Архимед ищет число, меныпее л
точнее говоря.
болынее —
битном.
, ему нри извлечении корни придется брать приближенные значения с из-
ИЗМЕРЕНИЕ ЯРУГА
551
При производстве вычислений (рис. 4. текста) Архимед начинает с, изучения вписан-
лого в полукруг треугольника АЛГ, у которого гипотенуза АГ является диаметром,
а угол ГАВ но-дрежпему раней 30°. Мы имеем:
АВ -л 1351
В Г V 780
и
АГ /АН8- НГ»
ГН ГН
Проведя АН — биссектрису угла ВАГ, из подобия треугольников А]’Н и TIIZ получим:
АН ГН АГ
пг “ HZ TZ '
По свойствам биссектрисы получаем:
АГ АВ АН-I АГ АН-г АГ
TZ ' BZ - TZ-I-ZB - ГВ •
АВ _ 1351 АГ 2 1560
I ан как -Df < ?80 и rD~ t 7g() • то
АН АВ , АГ 2911
НГ — ВГ ' ГВ < 780 '
Таким образом, Архимеду приходится пайти приближенно <: избытком у^29112-г 7802,
сделаем это и мы; подкоренное число буд|’т 9 082 321. В качестве первого приближения
мы можем взять 3000; тогда
(зоощ «“«и)=± (за»+3027да)-=:тз{-
, 1321
' 2-3000'
Так как нам нужно прнилнжеино с избытком, то чвеяитоль последней дроби мы
1 1
можем увеличить до 1500, что даст нам стошцео у Архимеда число 3013 -- -т- -I- -г- .
- 2 4
.1.1
, . 3013 Tj- -J--у
е" А1 *4
Таким образом, отношение-рд-<-------.
Дальше Архимед опять делит ГАН пополам прямой АЙ. Тогда аналогично
А© _АГ+АН J01J •" 2 +“4 , 2911 _ 59“,4I’24 4
©Г — ГН 780 ~Ь 780 780
Числитель и знаменатель о'<ой дроби можно сократить па 13; после сокращения
будем иметь:
. 1 1
АО ,г>° 2 "* 4 1823
©Г 60 — 240 ‘
Теперь
АГ _ У АН2 [-©Г2 /18232J-2402
ГВ " ГВ 240
Соответствующий корень можно опить найти по вавилонской формуле для вычпе-
ления гипотенузы;
/18232-|-2402 = 1823 1-1^= 1823-1- .
Деление 28 800 на 1823 дает в частном 15 и в остатке 1455; таким образом, искомый
корень будет 1838^^. Последнюю дробь Архимед полагает равной ; действительно,
1455- 145—1600,
1823—182=1641,
552
К ОММ Е НТАРИИ
т. о. прибавление к числителю и вычитание из знаменателя их десятых долей дает прибли-
зительно одинаковые числа, в особенности если несколько уменьшит?, знаменатель, что
тоже дает приближение с избытком.
Таким образом,
п
АГ . 1838-П-
ге 240
Разделим угол вЛГ пополам прямой АК. Аналогично предыдущему будем иметь:
9 9
ЛК _ АвЧ-АГ 1823 , 1838 ЧТ 3661 ТГ
КГ «Г “Г -”>zri
Имеем: кг вг 3661 А-И 11 _ ' 240 1 3661 -11 -9 240 40280 240 1007
11-240 11-240 11-240 66
таким образом,
ЛК 1007
КГ' ' 66
и
АГ _ VZAK2 —ГК3 |G<K)7* I 66*
ГК*- ГК “ ' ’ 66
Имеем:
- »/,007'+Ю‘ = ' ™4'
сл ед ов ател ыю,
АГ , ‘“'4
ГК 66
Повое деление пополам угла КЛГ прямой ЛЛ дает:
1 1
. . Al- I 4 V AA.W 1009-х- 2016-х-
ЛЛ АК-|-ЛГ .. 101)7 , 6 6
АГ ГК < Тб 1 66 ~ 66 '
АГ _ р'АЛа—ГЛ2 2(116 6 ) 1 (>(’2
ГЛ ’ ' ГЛ < 66
Имеем
/ Л
|-662 = 2016-^
1
=2016 4
6
4356
2-2016 4-
и
323 —
1+-----
40324
l-l-4=»i71
и
АГ 2017 4
ГЛ 66
Так как ГЛ является стороной 96-уголышка, вписанного в круг, то отношение диа-
метра. круга к периметру рассматриваемого вписанного многоугольника будет меньше
отношения
АГ
96ГЛ"
2017 ~
633(5
ИЗМЕРЕНИЕ КРУГА
553-
откуда для отношения окружности к диаметру будем иметь:
6336
2017 4
4
Изложенную реконструкцию Архимедова процесса извлечения квадратных корней
приходится рассматривать лишь как гипотезу, но эта гипотеза заслуживает внимания
хотя бы по той причине, что бла пе постулирует никаких специальных алгорифмов, вроде
непрерывных дробей и т. д., существование которых у греков само ио себе еще
нуждается в доказательстве; по существу, и этом процессе применяется одна лишь фор-
мула Герока, то ость как раз та, которую уномнпает и Евтокий в своем комментарии.
,г , , 10 .
Чтобы объяснить появление числа 3^ у Архимеда, Jy-п.ч поступает так:
6336
284 4-
—-3-4
2017 4- 20174-
4 4
1137
3 8069 •
Увеличим на 1 знаменатель 8069. Тогда после сокращении на 3:
1137 _ 379
8070 “ 2690 ’
„ 1 1
Величина последнего отношения лежит между — и -=-
i 8
1 379 1
7 > 2690 > 8 '
У Паппа в книге VII «Математического собрания» доказывается теорема;
а а -|- с
п 6 с
Если — > — , >по — .
п а о о-f-d а
Па основании этой теоремы
379 379 4-1
2690 > 2690-;-8
ИЛИ
379 ^380 10 1
2690 " 2698 ”71 > 8 ’
таким образом, отношение окружности к диаметру оудет оолее чем Зу, ио менее чем Зу .
Полученные Архимедом величины, выраженные в десятичных дробях, будут;
1
3 у=3.14286,
з4?-= 3,14084.
*1
Они дают для п три верных знака.
О РАВНОВЕСИИ ПЛОСКИХ ФИГУР
Трактат «О равновесии плоских фигур» состоит из двух книг: л первой, дастся мате-
матический вывод закона равновесия рычага (предложения VI н VII) и определяются
центры тяжести параллелограмма (предложения IX и X), треугольника (предложения
XI -XIV) и трапеции (предложение XV); вторая книга посвящена определению центров
тяжести параболического сегмента (предложения И—VHI) и параболическом трапеции
(предложения IX и X). Относительно места итого трактата в ряду сочинений Архимеда
существует большое разнообразие мпеппй: ряд авторов (например, среди зарубежных
историков Хизс, а среди советских — С. Я. Лурье) — относит его к самому началу дея-
тельности .Архимеда и разбивают пл две самостоятельные части, считая, что вторая книга
представляет совершенно самостоятельное сочнпеиие. В связи с этим Хизс устанавливает
следующий порядок написания Сочинений Архимедом:
О равновесии плоских фигур, книга 1.
2е. Квадратура параболы.
3°. О равновесии плоских фигур, книга П.
Второй вопрос, связанный с трактатом «О равновесии плоских фигур», заключается
в следующем: имеем лп мы весь текст этого трактата, или же дошедшее! до пас произве-
дение представляет только часть более полного сочинения Архимеда но этому вопросу?
Дело в том, что в трактате Архимеда «О плавающих телах» имеется ссылка ла «iooggonixa»,
что вполне соответствует заглавию рассматриваемого трактата nsgi (’itijuficov iooQgoatioiv
или лер- iooQpo.nwv). Однако самая ссылка касается определения центра тяжести сегмента
параболоида, которого в трактате «О равновесии плоских фигур», конечно, не имеется.
В связи с этим можно думать, что, кроме трактата о равновесии плоских фигур, Архимед
в качестве естественного продо.тжв1П1я написал трактат и о равновесии пространственных
фигур; в это сочинение могли войти определения центров тяжести цилиндра и конуса,
цитируемые в «Эфоде», может быть, призмы н пирамиды, а затем сегментов шара, эллип-
соида, параболоида и гиперболоида вравщния; механические способы доказательства
•соответствующих теорем помещены в том же самом «Эфодс».
Клижайшее рассмотрение трактата «О равновесии плоских фигур» исключает воз-
можность отнесения ого к числу самых ранних производили^ Архимеда. Если бы мы
допустили такую возможность, то вам пришлось бы разделить указанное сочинение на
два'совершенно самостоятельных произведения. Против такого разделения можно выста-
вить ряд существенных возражении. Прежде всего мы, конечно, должны до какой-то сте-
пени считаться с традицией, рассматривающем обе эти книги как две части одного и того
же произведения. Затем нужно иметь в виду, что совершенно такую же структуру имеет
состоящее из двух книг сочинение Архимеда «О плавающих телах», первая книга которого
посвящена общим вопросам, а вторая рассматривает только одну задачу: условия равно-
весия плавающего сегмента параболоида вращения; мещду тем до сих пор еще ин один
историк не предлагал разделить трактат «О плвпавицнх телах» на два совершенно само-
стоятельных сочинения. Далее, трактат «О равновесии плоских фигур», даже в составе
первой его книги, никак не может быть отнесен к числу ранних сочинений Архимеда.
Дли згой цели достаточно сравнить механические теоремы «Квадратуры параболы» с соот-
ветствующими местами первой книги трактата «О равновесии». В первом сочинении очень
заметна конкретная, заимствованная из практики основа; говорится о рычагах (£,иусб),
о подвешенных грудях, само равновесие прсдполагяегси практически осуществимым,
то есть устойчивым. Ничего подобного ис встречается во втором, казалось бы специально
посвященном механике, сочинении: в нем отсутствует какое-либо упоминание о рыча-
гах - их место занимают простые геометрические л ними, и само равновесие стаповится
каким-то неопределенным, отвлеченно математическим; мы не можем сказать, будет ли
•оно устойчивым, неустойчивым или же безразличным. Затем нужно отметить какой-то
специально-математический чисто формальный способ доказательства теорем: они боль-
шей частью доказываются от противного, причем форма доказательства одинакова как
в первой, так и во второй книгах. Стоит хотя бы сравнить дока.;ате.'лство Теоремы
О РАВНОВЕСИИ ПЛОСКИХ ФИГУР
555
XIII первой книги и теоремы IV второй книги, оба основанные па аксиоме о том, что центр
тяжести выпуклой фигуры пе может находиться вне ее контура, чтобы почувствовать
справедливость сделанного замечания. Идея второго доказательства теоремы Х111 цер-
вой. книги, по существу, одинакова с доказательством теоремы V второй книги. Мате-
риал первой книги (центр тяжести прямоугольника, треугольника и трапеции), по суще-
•стпу, подготовляет нес необходимое для доказательства теорем второй книги (центр
тяжести параболического сегмента и параболической трапеции). Следует отмстить также
логическую связь между предложениями цервой и второй книг; так,
постулат 5 первой КНИГИ необходим дл я дока затеи ь отв а предложения III второй
книги
постулат 7 » J> » для доказательства предложений IV и VI второй книги
предложение IV » » для доказательства предложений V и. VIII второй книги
предложение VIII » » для доказательства предложении IV, VI и X второй книги
предложение Х1П » » » для до на за те; г ьств а ПреДЛОИПЩИЯ 11 вто- рой. книги
предложение XIV » » » дл я докалится ьства предложений 11 J, V и VIII второй книги
.предложение XV » » » дл я дока за гея ветвя предложений II и 111 второй книги
Особо нужно отметить предложения VI и VII первой книги и предложение I вто-
рой книги. По существу, они представляют математическое доказательство закона равно-
весия рычага, постепенно обобщаемое для различных типов фигур. В предложении VI за-
коп равновесия рычага доказывается для соизмеримых прямоугольников, в предложении
VII оп обобщается па случай несоизмеримых примоугольпиков, наконец, в предложе-
нии 1 второй книги оп распространяется па случай криволинейных фигур, но только квад-
рируемых, то есть таких, которые могут быть превращены в прямоугольники. Общего
доказательства закона равновесия рычага мы у Архимеда не находим, хотя, конечно,
Архимед был иполпе уверни в его при зольности и неоднократно пользовался нм, например,
в предложоспях «Эфода».
Точно так же пе выдерживает критики аргумент, касающийся того, что в ряде про-
изведений Архимеда имеются ссылки па первую книгу «О равновесии плоских фигур*.
Для этого стоит только более внимательно рассмотреть форму этих ссылок. Ссылка в пред-
ложении VI «Квадратуры параболы» касается центра тяжести треугольника; не говоря
уже о том, что в сохранившемся теисте «О равновесии» пет самого существенного —
не доказано, что расстояние центра тяжести треугольника от основания равно
трети высоты,— самая форма ссылки - - б»б«rztai i-v xolg [rq'Zovnzo-C — доказано в меха-
нике — показывает, что в данном месте подразумевается другое сочинение; иначе стояло
бы :v role iaooio.tixoig. В том же самом предложении доказательство опирается на то,
что при равновесии центр тяжести и точка подвеса должны лежать на одном перпендику-
ляре, причем соответствующая ссылка сопровождается словами «это тоже уже доказано».
В трактате1, «О равновесии» ничего подобного нет; очевидно, дело идет о белое раннем про-
изведении Архимеда. Ссылка па такое более раннее произведение имеется и в самом
трактате «О равновесии*. В предложении IV цервой книги говорится о том, что уже
было доказано (яройifieгитаi), что центр тяжести двух масс, лежащих па одной прямой,
тоже лежит да этой прямой. Ссылки тина ftsfieixtat ivtoig iaopionixoiC имеются только
в «Эфодо» (предложение I — центр тяжести треугольника) и в трактате «О плавающих
телах» (предложение II — центр тяжести сегмента параболоида). Таким образом,
можно только утверждать, что трактат «О равновесии* написан до «Эфода» и до трактата
«О плавающих телах».
За то, что трактат «О равновесии плоских фигур» ио был первым механическим про-
изведением Архимеда, говорит п сама форма его изложения. Трактат представляет строго
логически построенное произведение, из которого выт риале на вея конкретная физическая
основа; пе дается определения центра тяжести (оло, очевидно, уже предполагается изве-
стным), в формулировке закона равновесия рычага говорится только о равновесии па
«длинах». Особенно показателен тот факт, что в рассматриваемом произведении уже пред-
полагается известным, что центр тяжести треугольника делит медиану в отношении
1:2*); это положение, которым Архимед пользуется при определении квадратуры
параболы, необходимо должно было стоять в произведении, касающемся определения
*) Архимед псиольяует его при нахождении центра тяжести прямолинейной трапеция
<кн. I. upeR.i. 15).
556
КОММЕНТА РИМ
центра тяжести вообще. Тикам образом, мы приходим к выводу, что цель и характер-
трактата «О равновесии» таковы: Лрхпмед хотел, во-первых, математизировать меха-
нические теории определении центра тяжести, изложенные им в более ряппих со-
чинениях, и, во-вторых, применить их к нахождению центра тяжести параболического-
сегмента как целого, так и усеченного; открывши способ квадратуры параболического
сегмента, он, естественно, считал своим долгом определить и положение центра тяжести
такого сегмента.
Если считать, что первая книга содержала лишь необходимый подготовительный
материал для второй, то можно легко объяснить отсутствие в пей одной теоремы, которая
обязательно должна была бы в лей быть, если бы ота книга представляла самостоятель-
ное сочинение па тему о нахождении центров тяжести плоских фигур. Я говорю о центре
тяжести круга (соответствующее предложение находится в чпеле лемм «Эфода»).- Было бы
очень легко построить соответствующее доказательство теми же методами, которые приме-
няются в первой книге. В самом деле, предположим,
что центр тяжести круга (рис. 1) не совпадает с его
геометрическим центром О, а находится в некоторой
точке С. В рассматриваемый круг вписываем квадрат,
две стороны которого параллельны отрезку ОС; центр
тяжести квадрата совпадает с центром О круга; значит,
центр тяжести D оставшейся части будет лежать на
продолжении отрезка ОС в такой точке, дли которой
отношение расстояний ОС и CD равнялось бы обратно-
му отношению площади квадрата к площадям четы-
рех оставшихся сегментов. Если полученная точка D
будет заключаться внутри круга, то разделивши по-
полам дуги полученных сегментов, впишем в круг вось-
миугольник, центр тяжести которого будет опять сов-
падать с центром О круга, в то время как центр тя-
жести оставшихся сегментов будет находиться в не-
которой точке £, которая будет лежать на продолже-
нии отрезка ОС и на большем расстоянии от центра О
круга, чем точка 1). Так как суммарная площадь сег-
ментов, получающихся мри последовательном удвоении
числа сторон вписываемых многоугольников, может быть сделана меньше любой задан-
ной величины, то центр тяжести этой площади в конце концов может быть удален за
пределы окружности, если только центр тяжести круга пе будет совпадать с, его гео-
метрическим центром.
Но если обе книги трактата «О равновесии» представляют части одного и того же
сочинения, то время его написания может быть установлено следующим образом. Мы уже
говорили, что трактат «О равновесии» панисан до «Эфода», — что дает нам terminus ante-
quern; с другой стороны, terminus post quem определяется тем, что в предположениях
VII и VIII второй книги Архимед пользуется определением подобия криволинейных фигур,
которое дано в трактате «О коноидах и сфероидах». За это же говорит то обстоятельство,
что при доказательстве предложения V второй книги «О равновесии» Архимед опирается
на предложение 111 того же трактата «О коноидах» (о равенстве площадей двух параболи-
ческих сегментов, имеющих одну н ту же ось, но разные основания). Таким образом,,
место, занимаемое рассматриваемым сочинением в ряду произведений Архимеда, опре-
деляется совершенно точно; трактат «О равновесии» написан в промежутке между трак-
татом «О коноидах» и «Эфодом». Б связи с этим стоит отмстить, что формулировки лемм
«Эфода» (2, 3, 5, б) почти дословно повторяют формулировки соответствующих предло-
жений VIII, V, ХШ—XIV, X первом книги «О равновесии плоских фигур».
Если рассматривать обе книги трактата «О равновесии плоских фигур» как попытку
дать строго логическое обоснование системе механических теорем, то естественно выдви-
нуть вопрос, в каком мере была достигнута Архимедом поставленная им себе цель. Это-
тем более важно, что в своей «Истории механики» Мах выступ ил с критикой построения
Архимеда, указывая, что, опираясь только на постулаты, выдвинутые Архимедом, никоим
образом нельзя безупречно логически доказать основной закон равновесия рычага, содер-
жащийся в предложениях VI—VII первой книги «О равновесии». Основное его возраже-
ние сводилось к тому, что постулат Архимеда о том, что равные грузы уравновешиваются
на равных плечах еще ш: определяет формы зависимости момента силы от длины ее плеча;
мы с ранным нравом можем определять момент как произведение силы на квадрат или
куб се плеча, тогда как основной закон равновесия рычага требует только .линейной зави-
симости момента от длины плеча.
.Конечно, в общей логической схеме построения Архимеда, е пашей точки зрения,
tic хватает самого главного - - определенияцептра тяжести: это отсутствие мы можем
объяснять тем, что соответствующее определение считалось уже общеизвестным, а между
О РАВНОВЕСИИ ПЛОСКИХ ФИГУР
557
тем это определение, исходящее из того факта, что тело, подпертое в центре тяжести,
находится в без различном равновесии как бы его ни вращать вокруг центра тяжести, уже
необходимо предполагает линейную зависимость величины момента от длины плеча;
при более сложных зависимостях понятие центра тяжести теряет смысл. При наличии
этого определения архпмедовекая теория рычага становится логически вполне строгой.
Первые три постулата (равные грузы на равных плечах уравпонешиваются; на пе-
ринных перетягивает груз па болтливы плече; от прибавления (или отнятия) какого-
нибудь груза к системе грузов, уже находящихся в равновесии, послед пес нарушается)
необходимы дли доказательства первых трех предложений первой книги *).
В четвертом постулате мы уже встречаемся с ноннтием центра тяжести; если опре-
делять его как точку опоры при безразличном положении равновесия, то можно доказать,
что центр тяжести двух тел, рассматриваемых как одно, находится на прямой, соединяю-
щей центры тяжести этих тел. Это положение было сформулировало Архимедом в третьей
лемме «Эфода»; на основании его Архимед доказывает четвертую и пятую теоремы первой
книги «О равновесии» (относительно центра тяжести двух и трех равных грузов, находя-
щихся па одной примой).
Четвертый и пятый постулаты, касающиеся положения центра, тяжести подобных
и конгруэнтных фигур, употребляются Архимедом при доказательстве предложений IX,
X и XI первой книги и предложения III второй книги.
Особенный интерес представляет тестой постулат. Он читается так.
«Если тела (величины — ptiyHlevC) находятся в равновесии, то будут находиться
в равновесии п нм равные».
Если пе понимать этот постулат как простую тавтологию, то придется сказать
следующее:
Действие груза, приложенного а данной, точке, определяется только его величиной,
т. е. совершенно не зависит от его формы или ориентации.
Понимаемый так шестой постулат позволяет заменить несколько масс одной, поме-
щенном в центре их тяжести; в этом смысле
тельствс предложений VI и VL1 первой
книги и предложения I второй книги. Та-
ким образом, этот постулат как раз ц пред-
ставляет собой то положение, за «пропуск»
которого Архимеда упрекал Мах.
Теперь доказательство закона рыча-
га приобретает вполне строгую логиче-
скую форму. Идею его легче всего выя-
снить, если привести это доказательство в
той форме, которая была ему дана Гали-
леем (см. второй диалог «Механических рас-
суждений и доказательств») (рис. 2).
Пусть в точке О подвешено за середи-
ну коромысло Д/Ад имеющее длину 2(o-j-i>).
он и употребляется Архимедом при доказа-
К этому коромыслу при помощи бесконечного множества вертикальных веревочек при-
креплена однородная балка KL такой же длины 2(я-|-6). Вся система будет, очевидно,
в равновесии, которое не нарушится, если мы разрежем балку по линии СС — па два
отрезка: КС -длины 2а и CL — длины 2Ь. После этого обрезаем нее веревки, кроме
двух, .-1,1 и ЛП, находящихся в серединах отрезков KL и CL-. от этого равновесие тоже
не нлрушнтсн. Таким образом, иелнчиии КС—2а па плече АО = Ь будет урптшопешивать
величину CL~2b на плече ОБ—а-, иными словами, при равновесии приложенные в Z1 и В
грузы будут обратно пропорциональны соответствующим плечам.
Возможность поворачивания частей балки вокруг осей АЛ и ЛВ без нарушения
равновесия эквивалентна требуемому Махом закону пропорциональности моментов цер-
вой степени длины плеча и исключает всякий другой закон, например, квадратичной
зависимости, так что доказательство Архимеда, вопреки Маху, является вполне строгим.
Последний, седьмой постулат (центр тяжести выпуклой фигуры лежит внутри ее
контура) необходим Архимеду .для доказательства-предложений IX и XIII верной книги
и предложений IV и VI второй книги.
Для двух книг «О равновесии плоских фигур» мы имеем подробный комментарий,
составленный Евтокнсм Аскалопскнм, учеником знаменитого строителя св. Софии в Кон-
стантинополе Исидора Милетского (VI век и. в.). Из этого комментария мы берем наи-
более интересные места, относящийся ко второй книге (комментарии к первой книге боль-
шого интереса не представляют).
•) В переводе пришлось несколько отклониться от подлинника. У Архимеда
isirEi.v ini T'i (Нро;... — по имеют естественное стремление наклониться в сторону груза...». Ср. во
пегуичгельггой статье о смысле слов ieireiv. рбгщ.
558
КОММЕНТАРИИ
[11 Евтокяй в своем комментарии питает:
«Он (Архимед) в формулировке первой теоремы говорит:
,,Предположим площади ЛВ, ГА, ограниченные прямой и параболой п могущие
быть приложенными к заданной прямой". 11а основании доказанного здесь этого устано-
вить невозможно. По в книге «О шаре и цилиндре» оя сказал, что им было доказано, что
такая фигура составляет четыре трети треугольника, имеющего то же самое основание-
и равную высоту; так как четыре трети треугольника являются прямолинейной плоской
фигурой, то мн можем равную им площадь приложить к заданной прямой; следовательно,
ясно, что мы можем сделать то же самое и для упомянутых фигур».
Из этого отрывка следует, что в эпоху Евтокмя сочинение «О квадратуре параболы»
не было известно. Под «приложением» площади к прямой подразумевается построение
па этой примой равновеликого данной площади прямоугольника.
[2] Евтокий питает:
«Все это должно быть доказано в надлежащем месте». Поскольку высказанное-
утверждение нс вполне ясно, то необходимо несколько поговорить об этом, приведя
отрывок из «Конических сечений» Аполлония (рис. 3),
Рис. 3.
«Пусть будет фигура, ограниченная параболой АВ Г и прямом АГ;
пусть диаметр этой фнгурыбудет ВД. Ясно, что вершиной сегмента будет
точка В; ибо, вершинами линий Аполлоний . называет лежащие
па этих ли пнях концы диаметров. Если мы проведем ЛВ, ВГ, то
получится треугольник АВГ, имеющий с сегментом то же самое основа-
ние н рапную высоту, а именно опущенный из В на АГ перпендику-
ляр; ибо ВД не всегда будет осью.
Если мы, взяв вершины Е, Z сегментов АВ, ВГ, проведем через
них EG, ZK параллельно ВЛ, то они будут диаметрами сегментов АВ,
ВГ. Действительно, относительно параболы доказано,что все прямые,
проведенные параллельно диаметру, будут и сами диаметрами этого
конического сечения. Итак, Е, Z будут вершинами сегментов, и прове-
денные через Е, Z касательные параллельны АВ, ВГ. Значит, и EAZ
будет параллельна ЛАГ, так как Е0, ZK. будут параллельны и равны,
являясь диаметрами равных сегментов, и налагаются друг па друга,
как это доказано в шестой книге «Коническихсечений» (Аполлоний, VI,
19). И так как EU0 параллельна ВА, то ВН : НА—Д0 : 0А. Но ИВ- -
— АН, ибо ЕП делит ее ионолам, будучи диаметром, ..............ш
с касательной. Значит, и Д0=0Л. Па том же основании и ДК КГ.
По вся АД равна ДГ. Значит, и Д0=ДК и на основании этого EA—AZ.
Таким образом, оп правильно говорит, что соединяющая вершины сег-
ментов будет параллельна основанию главного сегмента и разделится
пополам диаметром этого сегмента.
Теперь проведем соединяющие линии ЛЕ, ЕВ, BZ, Z1’, разделим
их пополам в точках М, N, S, О, через М, А, Е, О параллельно В.Д
проведем ПМРХ, ТХ.ГФ, XE'PZ, и проведем A.U, ПЕ,
ЕТ, ТВ, ВХ, XZ, ZQ, РГ, а также Т,АХ и П,В,Г,Д,Е,22.
Из вышедоказанпого ясно, что ТХ, EZ и П£2 будут параллельны АГ
О РАВНОВЕСИИ ПЛОСКИХ ФИГУР
559'
и что Т,А=,АХ, ЕА—-AZ, П,Л“,А£2. Теперь я утверждаю, что они
делят ВД па отрезки, относящиеся, как ряд последовательных нечет-
ных чисел, то есть если В,А~1, то ,АА—3, А/\- 5 и ,ДД 7. Действи-
тельно, поскольку АН -11В и Е(-) параллельна ВД, то и А0—0Д.
Значит, АД вдвое больше АН, а также и ЕА: АД2=4ЕА2. Но АЛ2: ЕА2=
— ВД : ВЛ, согласно доказанному (Аполлоний, I, 20 — наше уравне-
ние ри—2рх); значит, ДЛ^ЗЛВ, то есть если ЛВ=1, то ЛД=3. На
том же основании если АВ^ 4, то ЛД—12. И так как EN=NB,
E,Z—,ZA и 0Ф=ФД, то ЕА вдвое больше A(Z, то есть, Т,А,.
и ЕА2—4Т,Ла; значит, ЛВ -413,А, так что AzА -3,АВ. Таким обра-
зом, если ЛВ=4, то В,А—1, ,АЛ=3, ЛД —12. Далее, поскольку
АМ=МЕ, АР=РП и AS--S0, то будут равны и ЛХ, S8, 0Ф, ФА.
Значит, если ЛД—4, то 2Д —П,Д --3, и АД2—16, а П,Д2—9. И если
ДВ—16, то В,Д=9; и, значит, остаток жАД -7. Теперь, поскольку
доказано, что если ВД---16, то В,А—1, ,АЛ—3, ,ДЛ 7 и остаток
Л,Д--5; значит, ВА рассекается параллельными на отрезки в отно-
шениях ряда последовательных нечетных чисел, если за единицу при-
нять отрезок при вершине сегмента».
[3] Евтокий пишет:
«Подобные сегменты сечений конуса Аполлоний в .книге шестой «Коинческих сече-
ний» определил пап такие, в которых при проведении в каждом одинакового числа пря-
мых, параллельных основанию, эти параллели, а также и основания будут находиться
между собой в тех же самых отношениях, что и отсекаемые ими па диаметре отрезки, счи-
тая от вершины, равно как и сами эти отрезки. Там же доказано, что и все параболы
будут подобны друг другу».
Это определенно расходится с общепринятым теперь определением подобия; так,
в смысле Аполлония подобными будут два треугольника, в которых основания будут
пропорциональны высотам, хоти бы углы в этих треугольниках и не были соответственно-
равными.
В атом определении интересны следы атомизма: подобными фигурами называются
фигуры, могущие быть разложенными па подобные элементы, хотя бы последние и были
бесконечно малыми, как это имеет место для двух параболических сегментов.
Помещаем соответствующие места из книги шестой «Конических сечений» Аполло-
ния (но переводу Ver Eccke, сделанному с латинского перевода I'аллея пятой, шестой,
и седьмой книг, «Конических сечений», дошедших до нас только в арабском переводе).
«Определение 7. Подобными сегментами мы называем
такие, у которых основания образуют одинаковые углы с диаметром,.
а также такие, г которых
при проведении одинако-
вого числа линий, парал-
лельных основанию, раз-
деляющих соотвстству 10-
щио диаметры па части,
находящиеся в одинако-
вых отношениях, будут
одипако аьтмн отношен и я
оснований и проведенных
параллелен к отсекаемым
ими от диаметра отрезкам,
считая от вершины.
Предложение 11.
Все параболы являются
подобными друг другу.
Пусть ЛВ и ГД будут две параболы с осями ЛК, ГО; я утверждаю,,
что зти конические сечения будут подобны друг другу.
560
КОММЕНТАРИИ
Пусть АП, ГХ будут параметрами этих сечений; сделаем так, что-
бы некоторая прямая ЛК так относилась к прямой ЛИ, как прямая
ГО к ГХ. Затем разделим прямую АК в каких-нибудь точках Z, О;
разделим также прямую ГО в тех же самых отношениях в точках М, 3
и перпендикулярно к осям ЛК, ГО восставим прямые ZE, ОН, КВ
и МЛ, N3, ДО. Далее, поскольку прямая КВ будет средней пропор-
циональной между I1A, АК, так же, как
прямая АО будет средней пропорциональ-
ной между прямыми ГХ, ГО, то прямая
КВ будет к КА, как ДО к ОГ* *).
Далее, так как прямая В> вдвое боль-
ше ВК, а прямая Ду вдвое больше
прямой ДО, то прямая Bg будет от-
носится к АК, как прямая Ду к ГО.
Равпым образом, так как прямая ПА
будет к ЛК, как прямая ГХ к ГО, а
прямая АК будет к АО, как прямая
ГО к ГН, то «по равенству» прямая
ПА будет к ЛВ, как ГХ к ГН. Из этого
очевидно, согласно только что доказан-
ному, получится, что прямая PH будет
относиться к АН, как XT к ГН и на
основании тех же самых рассуждений
прямая EI будет к AZ, как тЛ к ГМ.
Таким образом, отношения перпендикуля-
ров Bg, HP, EI к отсекаемым ими па
будут соответственно теми же самыми.
оси прямым АК, Л0, AZ
что отношения перпендикуляров Ду, XT, Лт к отсекаемым ими пря-
мым ГО, НГ, ГМ. Но отрезки, отсеченные па одной оси, пропорцио-
нальны отрезкам другой оси; следовательно, ‘коническое сечение АВ
будет подобно сечению ГД, что и требовалось доказать».
|4] Комментарий Евтокия:
«.Это доказывается в конце, где, знак NB»**). Вслед за этим
докажем упомянутое мы (рис. 5).
Пусть будет парабола АВГ, диаметр которой ВД. Проведем орди-
нату АД, соединим А и В, разделим ЛВ в Z пополам, и через Z ларал-
лелыкГВД проведем EZ; опа будет диаметром сегмента АВ. Затем из Е,
Z параллельно ординате проведем ЕП, Z0. Поскольку AZ равпа BZ,
то АВ вдвое больше ZB, и ДВ вдвое больше В0, и АД вдвое больше Z0,
то есть ЕП. Таким образом, квадрат АД будет в четыре раза больше
квадрата ЕП, а вследствие этот ДВ будет линейно в четыре раза боль-
ше В11 (Аполлоний, 1, 20). Так как ВД вдвое больше ВО, то и ВО
“) Действительно.
КВ-—!1Л АН, ДО*^ГХ • ГО.
ПА : АК=ГХ : ГО.
Тогда
• КВ« II4.AK ПЛАК АК«
ДО- ГХ ГО "ГХ ГО-ГО® ’
откуда
КВ : ДО—КЛ : ГО.
•*) Соотпстствующего места в аодлинипке не имеете».
О РАВНОВЕСИИ ПЛОСКИХ ФИГУР
561
вдвое больше ВН. Но ®Н равна НВ и 011 равна EZ, так как E1LZ® —
параллелограмм. Значит, ВН равна EZ и 13Д в четыре раза боль-
ше ZE».
С пашен точки зрения, это просто следует из уравнения параболы у®—2рг: если
АД — j/[ вдвое больше ЕН —у2, то отношение xL = ВД и х., — ВП будет
£L^21 = 4
[5| Самым интересным в этом доказательстве является следующее: оно по существу
мило связано с семью предыдущими теоремами, которые даже яплпются недостаточными
для строгого его доказательства. Действительно, все рассуждения в предложении VIII
опираются на следующие два положения:
1) все диаметры параболы параллельны друг другу,
2) центры тяжести всех параболических сегментов делят в одипакопом отношении
их диаметры.
Первое положение нигде по доказывается, ко поскольку оно молчаливо подразу-
мевается при доказательстве предложения V, можно думать, что Архимед считал его
общеизвестным.
Что же касается второго пункта, то у Архимеда он доказан только для п о д о б-
ны х сегментов (предложение VII), каковыми сегменты АКБ и АВГ (в пашем смысле)
не являются.
Точного определения подобия параболических сегментов Архимед но дает, считая,
по-видимому, достаточным определение, приведенное им во вппдепип к трактату «О коно-
идах» и по существу совпадающее с цитированным Евтокием гшредеяопием Аполлония.
В современном обозоачвпии доказательство предложения VIII можно провести
тап (рис. 25 текста):
Так как площадь парабол ячеек ого сегмента АВГ составляет — площа,ди треуголь-
ника АВГ, то примем последнюю на 3; тогда ллошадь сегмента АВГ будет равна 4, а сумма
площадей сегментов АКВ и ВАГ составит 1. Если примем В.А за ось ординат, то основная
формула для определения ординаты центра тяжести папшлется в пашем случае так:
4-Д0=3-ДЕ-|-1-ДЗ,
где О, Е, В представляют центры тяжести сегмента АВГ, треугольника АВГ и площади,
составленной из обоих сегментов АКВ в ВАГ. Мы имеем:
1 1
ДЕ=— ВД; Д3=AX--MZ = — ВД-S-MZ.
О —
Пусть X представляет отношение ординаты Д0 к ВД и соответственно MZ к KZ. Так
1
как KZ — -- ВД, то мы получим:
д© = X- ВД, ifZ г= X KZ=X -4- ВА.
Подставив эти пс-тпчины в основную формулу, получим:
4Х’ВД=3-4-ВД-М
V В А -1-Х
Сократив на ВД и определил из волучеппего уравцемия X, найдем:
х=4,
иными словами, В0 = — 0Д.
Л
[6| Рассматриваемое предложение играет роль леммы к следующему за ним пред-
ложению X, в котором речь вдет об определении центра тяжести усеченного параболиче-
ского сегмента, рассматриваемо™ как разность двух сегментов.
П проведении доказательства ппразипет необыкновенное искусство Архимеда в опе-
рировании пропорциями. Для нас, мзбалопаппых попрсмошгым алгебраическим апако-
положепием, ато искусство уже является недоступным.
[7] Чтобы испо представить себе ход мыслей Архимеда при доказательстве этом
теоремы, пожалуй, лучше всего будет начать ее разбор с самого конца.
36 Архимед
562
КОММЕНТАРИИ
Архимед рассматривает уссчепный сегмент ЛАЕ Г как разность двух параболиче-
ских сегментов АВГ и ДВЕ. Пусть X будет центром тяжести сегмента ВЕД, Р — центром)
тяжести АВГ и, наконец, 1 — центром тяжести рассматриваемого сегмента ЛДЕГ.
В таком случае, поскольку Р есть точка приложения равнодействующей весов обоих ссг-
ментов ДВЕ и ЛДЕГ, мы можем написать:
ХР : Р1 — сегм. ЛДЕГ :сегм. ДВЕ.
Теперь
ХР= ВР—13Х=4 BZ—A ПН = 4 (BZ - - ВЦ)=4IJZ,
а 5 ;> о
так как, согласно предложению VIII, расстояние центра тяжести параболического сег-
мента от вершины составляет 3/5 его высоты.
Далее,
се см. АДЕГ=ссгм. АВГ—сегм. ДВЕ.
Таким образом, мы можем написать пропорцию
4 HZ : Р1 = (сегм. ЛВГ—сигм. ДВЕ): сегм. ДВЕ.
О
Площадь параболического сегмента равпа 2/3 произведения основания на высоту; таким-
образом,
сегм. АВГ : сегм. ABE=(AZBZ): (ДП-ВН).
По по основному свойству параболы
BZ: ВН^=Л2«:ДЦ*.
Та чем образом,
сегм. АВГ : сегм. ДВЕ = А7.Я : A№ = ZB3/a : BIIS/s.
Полученное отношение Архимед, если можно так выразиться, линсарпауст, то есть
заменяет отношением первых степеней двух длин. Примененный им прием яплястся
обычным в греческой математике и осуществляется путем введения средних пропорцио-
нальных. Он берет:
MN —BZ; NO—ВН.
затем
2 В MX MN N3 _ / MN X2
ВИ NO No NO < N3 J '
если NS является сродной пропорциональной между MX и NO:
№=-=MNNO.
Таким образом,
/ ZB V/з MN
V У nJ ~ КЕ ’
Введение четвертой пропорциональной NT по равшетву
ZB : ВИ—MN : N0 = NS : NT
О РАВНОВЕСИИ ПЛОСКИХ ФИГУР
563
(1)
на отрезке nZ=OM =
(2)
IZ
отношение --jy
лает сам желаемый результат:
ZB3/’ ZB ZBI/a MN MN MN NS MN
BUJh “пиГ nil'/» ~ NO ' NS ’ ’ № ' NT NT ‘
Теперь, возвращаясь к исходному равенству
HZ: Р1 = (сегм. АВГ—сегм. ДВЕ): сегм. ДВЕ,
заменяем площади пропорциональными им величинами:
у HZ : PI-—(ZBS/s— BH®«) : BH3/s,
и переписываем равенство в виде
3
У112" MN —NT
“Pl “ NT
откуда
IP WT
HZ 5 MN-NT ’
Затем из предложения VIII мы з„асм, что
ZP = A BZ=-?-MN.
в 5
Так каппам желательно найти положение центра тяжести Z
= MN—NO, то находим отношение ZP ; 11Z:
ZP _ 2 MN __ 2 MN
IIZ 5 ОМ 5’MN -NO’
Теперь простым вычитанием мы можем найти нужное нам
17. _ ZP IP _1 f 2МХ 3NT
HZ “ HZ HZ “5 1 MN — NO IviN —NTj-’
Величины, входящие n правую часть равенства (3), составляют непрерывную про-
порцию
MN: ХЕ: ХЕ : NO—NO : NT.
Обозначим отношение КЗ: MN через Е; тогда
g2^ NO Bi I A IF
“AIN “ BZ “ AZ2 ’
так что
. АН
s“ AZ ’
то есть £ равно отношению ординат параболы в точках II и Z.
После этого мы можем написать:
NS = g-MN, NO—£B-MN, NT=g»MN. (4)
Если мы подставим эти значения в формулу (3), то после сокращении на MN будем
иметь:
1Z _1 Г 2 3g3 1
HZ 5'li-p 1 —Ё3 J
Выражение, стоящее в скобках, мы преобразуем так:
2 3«я 2(1 FE -H2) --ЗЕ3 (!-!-£) 2-|-2|--!-2Г-—ЗЕ3-ЗЕ4 24-4? 'г6^2-|-ЗЕа
1-£2 1-Ё3 “(1-Е)(1-£)(1 + Е-Ё2)-'(1-^(1+25+2Ё2-Ы3) 1-р2|-| 2Ё3 FE3 ’
36*
564
КОММЕНТАРИИ
Если мы теперь помножим числитель и знаменатель этой дроби па ММ и восполъ»
чуемся формулами (4), то получим имеющееся у Архимеда выражение
IZ 1 2MN4-4N3 I-6NO4-3NT
HZ"’5 MN-I-2XS+2NO4-XT *
Дальнейший ход рассуждений Архимеда может быть восстановлен почти с полной
достоверностью.
Простой взгляд на формулу (5) показывает, что
IZ 2
HZ > 5 '
2
Отложим ZK = -^-HZ и вычтем из длины IZ:
о
IZ--ZK JK 1 f 2MN4-4№-|-6.\0-I-3NT 1 2NO4-NT
ILZ “ HZ ~ 5 t MN (-2NE4-2N 6-[-NT “J" 5 MN-{-2NS-j-2NO4-NT ’
Тогда
ZU _______2N0 !-NT
K » ‘MN |-2N3-|-2NO-|-NT ’
Так как ZH = 58K, то легко получазтем, что
T_ZII _____MN+2NS
W 5 ’MN-hZNS-i-ZNO-l-NT’
откуда
IO MN-I-2NH
1K^2NO4-NT’
Теперь Архимеду нужно от вспомогательных линий MN, №, NO и NT перейти
к первоначальным линиям параболического сегмента. Он пишет:
' 10 MN4-2NS MN NT
LK MN ’ NT ‘2N0-f-NT*
Из равенств (4) видно, что
MN NO _ 1 AZ
№ ‘“'NT g — ДП ’
MN _ 1 _ AZ8
NT~|»“ ДНа ’
Таким образом,
IO AZ+2An AZ8 ДН
IK “ AZ ’ ДП» ’ 2AZ4-AH ’
или
10 _AZ2 (AZ I-2AH) /ft4
1К -ДН2 (2AZ , ДП) ’ * ’
Мы изложили вероятный ход мыслей Архимеда при получении им формулы (6).
Что касается приводимого им в предложении X доказательства, то оно развивается так.
Архимед начинает с формулы (1). Затем он от формулы ((>) идет обратным путем к фор-
муле (5). После этого он,'складывая формулы (1) и (5), при помощи вспомогательного
предложения IX доказывает, что
LZ , PZ 2 MN
1IZ HZ b HZ ’
откуда получается, что точка Р будет центром тяжести параболического сегмента АВГ,
после чего он заканчивает доказательство тем, с чего начали мы.
ПОСЛАНИЕ К ЭРАТОСФЕНУ
О МЕХАНИЧЕСКИХ ТЕОРЕМАХ
Полное заглавие рассматриваемого сочи пения таково: rteoi twv jiiqXO'viwuv flroQrjpa
tcov ngofi'ICQctTOO'tH'viqv ctpofiog (или etpiCiov). Слово ?<родоб обозначает «приступ, доступ,
вход»,' etpifiiov — деньги или .запасы, дающиеся па дорогу; очень часто переводят его сло-
вом «метод» (буквально спутник), Сокращенно принято обозначать это сочинение словом
«Эфод», или «Эфодик» (c<poSiKov), которое тоже встречается в других местах в качестве
названия этой книги.
Интересна история открытия этого сочинения. Приват-доцент Петербургского уни-
верситета Нападопуло Ксрамевс указал на имеющуюся в Константинополе рукопись
духовного содержания па пергаменте, на котором ранее был написал другой текст (так
называемый палимпсест). Отдельные места этого текста математического содержания при-
влекли внимание известного датского филолога Гейберга, который побывал в Констан-
тинополе и 190G и 1908 гг. и прочел большую часть этой рукописи, восстановленную им
при помощи фютографичсского снимка и личного осмотра. Оказалось, что рукопись,
кроме уже известных рписо сочинский Архимеда, содержала значительную часть трак-
тата «О плавающих телах», известного ранее тольковлатипском переводе, а также «Эфод»,
который ранее был известен лишь из упоминании п словаре Свиды
и цитат в Героповой «Метрике», которая и сама была открыта
и опубликована только в 1903 г. Первое издание этого текста было
сделано Гейбергом (см. [18]); с этого издания был, между прочим,
сделай русский перевод [26]. Дальнейшие чтение позволило Ггн-
бергу разобрать еще некоторую часть текста; в этом виде он и был
помещен во втором томе второго издания сочинений Архимеда,
с которого и делается предлагаемый перевод.
Время написания «Эфода» может быть определено из сле-
дующих соображений. «Эфод» написан после обеих книг «О шаре
и цилиндре», так как Р нем определяется центр тяжести сферическо-
го сегмента, объем которого дается во второй книге упомянутого
сочинения. Далее в «Эфодс» приводится лемма из трактата «О коно-
идах». Затем Архимед указывает, что две последние теоремы «Эфода»
отличаются от более ранних, л которых сегменты коноидов и сфе-
роидов сравнивались с конусами и цилиндрами, тогда как здесь
рассматриваемые тела, ограниченные кривыми поверхностями,
сравниваются с телами, ограниченными плоскостями; это показы-
вает, что«Эфод» опубликован после «Коноидов», Далее, упоминания
о трактате «О равновесии» показывают, что последний к моменту
написания «Эфода» уже был опубликован.
]1] Из помещепдых и начале «Эфода» лемм наиболее инте-
ресной является 10-я, говорящая о центре тяжести конуса. Можно
Рис. 1.
высказать следующее предположение относительно пути, которым
шел Архимед при определении центра тяжести конуса.
Архимед разбивал конус плоскостями, параллельными основанию, па очень тонкие
диски равной высоты, объемы которых были пропорциональны квадратам расстояния
до вершины. Так как ординаты параболы тоже пропорциональны квадратам соответствую-
щих абсцисс, то нахождение центра тяжести конуса можно свести к нахождению центра
тяжести сегмента параболы у = ах2, заключенного между осью абсцисс и конечной
ординатой (риг,. 1).
13 «Квадратуре параболы» было доказано, что площадь параболического сегмента
О МВД равна площади прямоугольника О АВА. В таком случае, если принять площад/
О
566
КОММЕНТАРИИ
ОАВД за 6, то плотцадь сегмента О МВ Д будет равна 4, а площадь сегмента О МВ равна I.
ЦсЕгтр тяжести сегмента ОМВ лежит на его оси ММ', делящей пополам отрезки ОБ и О А.
Мы можем рассматривать сегмент ОАВМ как разность между треугольником ОАВ и сег-
ментом ОМВ. Если дли симметрии удвоить нее эти фигуры и отсчитывать расстояния х.
центров тюкести от О (все они будут после удвоения лежать па оси ОА), то мы можем
написать следующее равенство:
миощ. ОВГ жовг=2 площ. ОМВ-хомв-|-11Л01ц. ОМВГ-комвг.
Если положить ОА = 1,то отсюда получим:
откуда искомое расстояние ОК=х будет:
_3
х "4
Таким образом, центр тяжести конуса будет лежать па оси его па расстоянии трех
четвертей от вершины.
Зятем требует разъяснений л е м м а 11-я, доказательство которой Архимед дал
в трактате «О коноидах». Понимать эту лемму надо следующим образом.
Пусть нам даны два ряда пропорциональных величин alt а», ая,...\ blt Ь2, Ья,... таких,
что
^“2 ^3 ^4
fc2 Ья 64
Отпогаепие каждой соответственной пары этих величии будет одним и тем же; обо-
значим его через а : Ь.
Возьмем затем ряд третьих величин, каждая из которых будет стоять в некотором
отношении к величинам первого ряда, причем отношения эти, вообще говоря, могут быть
неодинаковыми:
= ...
Пусть будет еще дан ряд четвертых величин, которые будут стоять в таких же отно-
шениях к соответствующим величинам второго ряда:
А.2^2, :==-
Лемма заключается в том, что сумма некоторого числа величин первого ряда к сумме
некоторого (вообще говоря, иного) числа величии третьего ряда будет иметь то же самое
с1_|“сй+с3
отношение, что сумма соответственных величин
второго ряда к сумме соответственных же вели-
чин четвертого ряда:
Ь|+Ь2-;-fc3~l Ъц
To обстоятельство, что Архимед пользуется
положением, полное доказательство которого
дается только в книге «О коноидах и сфероидах»
(предложение 1), позволяет думать, что «Эфод»
написан после упомянутого сочинения. Однако
все содержание «Эфода» характерно для более
равней стадии деятельности Архимеда, когда он
в широкой степени пользовался механическим
методом доказательства. Таким образом, дли пас
«Эфод» Архимеда имеет громадное значение в том
отношении, что позволяет заглянуть в мастер-
скую его гения, познакомиться с теми путями
его творческой работы, следы которых были
потом заглажены при опубликовании закопчен-
лых произведений.
[2] Предложения II и III касаются определения объема шара и сфероида (так
Архимед называет эллипсоид вращении).
Пусть требуется определить объем тара АБГА диаметра БД. Проводим АВ и АД
и строим конус AEZ и цилиндр HZEA (рис. 2), оси которых совпадают с диаметром АГ.
ПОСЛАНИЕ Я ЭРАТОСФЕНУ. О МЕХАНИЧЕСКИХ ТЕОРЕМАХ
567
Продолжаем последний влево, откладываем Aft — АГ и проводим сечение MN, перпен-
дикулярное к диаметру АГ; это сечение выделит в конусе круг с диаметром ПР, в шаре
крут с диаметром 03 и, наконец, в цилиндре круг с диаметром MN. Проведя все такие
сечении, мы разобьем рассматриваемые тела на ряд дисков бесконечно малой толщины;
попытаемся перетащить диски, образующие шар, па конец Н плеча А 6 рычага Гв, имею-
щего точку опоры в Л, и посмотрим, как можно будет их уравновесить. Для этого соста-
вим отношение Л£ ; Aft. Его можно будет представить в таком виде:
_AS _ АЕ _ АЕ-МЕ
Aft - М2 ~ MS2 '
Но:
ЛЕ.МЕ==АЕ-ЛГ=АЕ®^ЛЕ®4 Е2а=П22-1,ЕНг.
Таким образом,
ЛЕ _ ПЕа-’г=Е2
А« "" М22 ’
•или
АХ !I1P2-LQE2
ле ' MN*
Теперь, выражая условия равновесии рычага, будем иметь:
Л S ИГР=Aft (ИР2 -!-0Е2).
Так как круги относятся, как квадраты радиусов, то это отношение можно было бы
переписать в виде
[(круг МХ)-ЛЕ = (круг 11Р-|-круг 05)-А6.
Для получения этого равенства в современном обозначении надо было бы просто
помножить обе части па число я.
Полученный результат можно истолковать так, Что круг MN цилиндра па плече
АХ, то есть в своем положении, уравновешивает круг ПР конуса и круг OS шара, пере-
несенные па конец плеча АО. Если мы сделаем это для всех кругов, составляющих паши
тела, то найдем, что цилиндр EZHA, оставаясь в своем положении, уравновешивает пар
•и конус, перенесенные па плечо А&. Так как центр тяисестн цилиндра находится яа сере-
дине его оси, то мы имеем:
АЙ
(шар) А© | (конус)-А0—(цилиндр)—.
Но цилиндр EZIIA будет в три раза больше копуса AEZ; значит,
СЗ х 1
— -1. J конус AEZ—-р копуса AEZ.
Далее, конус AEZ будет в восемь раз больше копуса АИД; значит, шар на диаметре
ВД будет только в четыре раза больше этого конуса. Так как конус АИД в шесть раа
меньше обнимающего шар цилиндра ФХ ГТ, то отсюда заключаем, что этот последний
3
— раза больше
цилиндр будет в
обнимаемого им тара.
[3] Доказательство Архимед проводит следующим образом. Оп берет обобщенную
теорему степени точки для эллипса:
АЕЕГ_АК-КГ АК®
“ХЕ2 ' КВ* ~ КВ2 ’
которая следует из часто встречающегося у Архимеда уравнения эллипса:
ж (2-т — ж) _ a
У3 ~Р
_ &
где а — большая полуось, а р =--------параметр эллипса.
Так как ЛК : КВ —ЛХ : ХП, то мы получаем:
ЛХ-ХГ АХ2
; ЕЕ2 ~ XII2 '
568
КОММЕНТАРИИ
Далее из пропорций А2 : 2Г_= АП : ЛЕ — ЦТ : ИМ получается
А23 2П2
А2-2Г“ SU-ЛЙ '
Сравнивая обе полученные пропорции, находим:
еп-пм^ее3, ;
или
ЕП • II М -'-ПЕ2=П224-2Е2,
ХП-2М=Л12®+2Н®, -.. ;
что и требовалось доказать.
Теперь мы можем написать равенство
А2-ЕМ2 —Ае-(НЕ8 |--2Sa),
или
А2-М№=А0-(ПГ2-[-и52),
и все остальное доказательство пойдет аналогично предложению И для шара.
[4J В предложении VIII Архимед определяет объем сегмента сфероида, то есть
эллипсоида вращения. Так как Архимед не доказывает этой теоремы, то покажем, как
можно было бы осуществить это доказательство.
В сечении сфероида мы имеем эллипс (рис. 3), большая ось которого АГ — 2«..
а малая 1"Г--2/>. Откладываем ЛИ =26 и дополняем прямоугольник ЛФ так, чтобы
АФ=ЛН —26. Затем строим равноплечий рычаг с плечом Л® = ЛГ — 2а и откладываем
ГА—а. Все остальные буквы на рис. 3 имеют те же самые значения, что в на
рис. 7 (стр. 313).
Аналогично предложению III мы можем установить равенство
А 2 М№=АГ • (11Р2-|-О32),
откуда получается, что цилиндр ФЛ в своем положении уравновешивает конус AEZ
и сегмент АВА, перенесенные н точку 6:
АН
цп.т. ФЛ • ----- АН (кон. AEZ- ссгм. АВА).
Затем находим отношение цилиндра ФЛ к конусу EZ:
цп.т. ФЛ : кон. AEZ=AII2 : 4 HZ2.
<3
Имеем:
АН=26=АГ - -, КZ = А н - — .
а а
ПОСЛАНИЕ К ЭРАТОСФЕНУ. О МЕХАНИЧЕСКИХ ТЕОРЕМАХ
56»
Таким образом, для отношения упомянутых цилнпдра и конуса мы получаем то же
самое выражение, что и в предыдущем предложен ни VII:
цил. ФА А 0й А©2
кон. AEZ~= 1/яЛН2 " АХ- AT ‘ U
Так как в условиях данной теоремы справедливо равенство предложения VII
шел. ФА А« А©3 .„
коп. AEZ+сегм. АВД~ АХ — AV-АХ+ТГ-АХ ’ ( ‘
то будет иметь место и равенство
цил. ФА А©3
сети. АЙА “ ¥Г AX ’ •
Остается найти отношение цилиндра ФА к конусу ДВА. Мы имеем:
пил. ФА АП2
коп. АВА 1/3В112 1/заННГ~
так как из уравнения эллипса, если положить АП=а:, ВН —у, мы будем иметь:
х (2л — ж) л®
V3 = Ь® '
Таким образом.
пил. ФЛ _ Л03 __ А®^_
Йби/ЛЙА^ Ч^ТН НГ “ Н¥;НГ '
Окончание доказательства проводите»
аналогично доказательству предложения VII.
[6] Предложении X касается определения
центра тяжести сегмента сфероида, то есть
эллипсоида вращения. Архимед точно также
по дает доказательства сформулированной тео-
ремы; оно, действительно, п не нужно, так
как все доказательство может быть проведено
точно так же, как и для предложения IX.
В чертеже должны был. сделаны следующие
изменения. Прямая А Г будет большой осью 2а
эллипса, заменяющего круг А В ГА; прямые
ЛЕ и AZ проводятся через концы малой оси
21> упомянутого эллипса. Это отразится толь-
ко на формуле, определяющей отношение
объемов конусов АВА п AEZ, а именно мы
будем иметь:
ЕП:АП—&:а,
ВН®= ГН -АП-Дт- (ио уравнению эллипса).
Отсюда видно, что окончательная форму-
ла, определяющая отношение объемов конусов
АВА *г AEZ, остается той же самой, а следо-
вательно, останется тем яге самым и весь конец
доказательства.
|В| Предложения II—XI мы можем
Рис. 4.
рассматривать как исходную стадию работы
Архимеда над «Шаром и цилиндром» и «Коноидами и сфероидами». В дальнейшем он
освободился от чисто механических доказательств н дал строгие геометрические доказа-
тельства, опубликованные им и указанных произведениях. Сначала он сделал это только
для шара и его частей: нахождение строгих докалатс-чьстн для теорем, касающихся конои-
дов и сфероидов, оказалось более трудным; они были получены только после окончания
работы пад трактатом «О спиралях». Остальная часть книги должна была быть посвящена
разбору двух новых теорем, формулировка которых была дана в начале. Из этих теорем
570
КОММННТЛРИИ
почти полностью сохранилось доказательство первой, которому посвящены предложения
X1L—XV. Теорема эта заключается в следующем.
В призму «писан цилиндр, «снованиями которого служат круги, вписанные в верх-
нее и нижнее основания призмы. Черен центр нижнего основания и одну ив сторон верхнего
основания проведена плоскость. Требуется доказать, что отсекаемый ею сегмент цилиндра
составляет одну шестую часть объема призмы (рис. zi).
Пусть секущая плоскость будет O'P'N’M". Будем рассекать полуцилиндр вместе
с сегментом плоскостями, параллельными грани М' M"N'N" призмы. В сечениях с ци-
линдром получатся прямоугольники X' S'" Т'Т"', имеющие высоту, равную высоте
призмы; в сечениях же с сегментом будут получаться прямоугольники S'S"T'T",
имеющие с первыми одинаковые основания S'T', но меньшую высоту S'S" = TN.
Из подобия треугольников ГХГ и ГЧЪ легко заключаем, что
откуда
ГЫ : ГУ=ГГ»:¥В=ил. S'S'T'T" : пл. S'T'S"'T"',
TN пл. S' Т' SWT"= ГЧ'• пл. S'S"Т'Т".
Это значит — прямоугольник сечения полуцилиндра в своем положении уравнове-
сит прямоугольник сечения сегмента, помещенный на плечо Г1? — половине стороны
призмы. Суммируя все аналогичные равенства, получим, что полуцилиндр в своем поло-
жении уравновесит сегмент па плече, равном половине стороны призмы. Из этого следует,
что если бы нам был известен объем полуцилиндра, то есть в конечном счете площадь
полукруга, и расстояние центра тяжести полукруга от его основании, то задача была бы
решена. Остается решить вопрос, где находится центр
тяжести полукруга.
Если через р обозначим радиус полукруга, а через
П — высоту призмы, то полученный Архимедом резуль-
тат выразится так:
, к(!С1.ме=(4^-н)4(е4У
так как расстояние центра тяжести полукруга от оспова-
нпл будет . Отсюда получается
гссгм=4 (vY=4(а^2 я’
М t> \ у и
т. е. одной шестой объема нрнзмы, сторона основания
которой равна 2р.
Таким выглядело бы решение, если считать известным положение центра тяжести
полукруга. Но этого Архимед как раз не мог предполагать известным; поэтому ему приш-
лось сделать попытку определения статического момента полуцилиндра относительно
его прямоугольного основания, т. с. произведения объема полуцилиндра па расстояние
центра тяжести от основании.
|7| Б предложении X1I1 Архимед, выражаясь современным языком, определяет
статический момент полуцилиндра относительно плоскости его основания. Пусть па рис. 5
квадрат MX изображает среднее сечение призмы, а ОПР — нужный нам полукруг в сече-
нии полуцилиндра с диаметром ОР в качестве основания. Речь идет об определении суммы
произведений ординат SK на расстоянии центров тяжести этих ординат от точки S.
В наших обозначениях искомая сумма будет:
У, У, SK®=4 2pz‘-°-
Проведем диагональ Н6 и отложим 0Z=S0. Так как ZO=SP=AX, то
ЛХ.(2В.|.» )-3 лх.О+2£).
Выражение, стоящее в правой частя, представляет сумму произведений отрезков
ЛХ на расстояния SX-|- их центров тяжестей от осп ОР, т. с. взятый относительно
той же оси статический момент треугольника 0MH, или, что то же, статический момент
призмы на основании ПОМ с той жо высотой, что и полуцилиндр. Последний статиче-
ский момент мы знаем; он будет равен произведению объема треугольной призмы, т. с.
ПОСЛАНИЕ К ЭРАТОСФЕНУ. О МЕХАНИЧЕСКИХ ТЕОРЕМАХ
571
Одной четверти объема всей призмы, па расстояние центра тяжести треугольника НвМ
2 -.а
от вершины, то есть -т-SW. Если положим по-прожпему сторону основания призмырав-
<5
ной 2q, то искомый статичнекий момент полуцилиндра будет:
1 2 2
j-(2(!)^.±Q=±QW.
*± О о
Приравнивая полученную величину произведению V'cerM'Qi получаем уже известную
нам формулу
2 1
Гссги = -^еаЯ^т (2С)8Я.
Так как Архимед зпал величину площади полукруга, то рассматриваемая задача
позволила бы ему определить положение центра тяжести полукруга. Возможно, что он
и патолкиулея на :>ту задачу п своих исследованиях относительно центров тяжести
плоских фигур. Однако то обстоятельство, что он попробовал дать еще другое решение
рассматриваний задачи, в котором он сводит ее к определению площади параболиче-
ского сегмента, говорит за то, что во время создания «Эфода» ему ле был известен
момент площади полукруга.
[8] В предложении XIV Архимед, оставив в покое, полуцилиндр, сравнивает
объемы сегмента цилиндра с треугольной призмой, отсеченной от всей призмы той Же
плоскостью, и плоскости сечения проводит перпендику-
лярно к оси ОР, так что теперь в сечениях обеих фигур д
получаются Прямоугольные треугольники, высоты кото-
рых будут ранцы высоте 1J призмы. Треугольники,
составляющие отсеченную призму, все одинаковы, со-
ставлямище цилиндрический сегмент имеют основания ’
равными соответствующим ординатам М3 полукруга
(рис. 6). Таким образом, отношение искомых объемов
будет: 9
Т’пегм _V* Ма8____
^призмы MX8
НМ-WE V (НК— МК) (НК-ЬМК)
— ZJ' М№ = Л МЛ8 “
4
_ v* ПК8 - МК« у / МК8 X
" 2j мк« == < нк» ) •
Для линеаризации последнего отношения проведем параболу через точки Е, Z, Н
с осью Z0; тогда по свойству параболы:
МК8; НК-’= IZ : ZK -= AN: MN.
Мы имеем таким образом:
1'евгм VI Л ,______AN X _ у МЛ
1призмы X. MN ) MX
По все ординаты МЛ заполнят площадь параболического сегмент:* EZH, все же
MN ~ площадь прямоугольника ГДЕП. В «Квадратуре параболы» было доказано (пред-
ложение XXIV), что площадь параболического сегмента EZH составляет две трети пло-
щади прямоугольника ГЛЕН; таким образом,
т т- _ 2
“ согм ' призмы •—jj- ,
отлуди
v - 2 v ~ 1 v
' сегм —-jj- « отс.сч. приемы-jj-I всея нризмм-
[9] Рассмотренное доказательство легло в основу строгого математического доказа-
тельства по методу исчерпывания, которое Архимед дал в предложении XV. Вспомога-
тельной для него является упомянутая выше лемма И.
Возьмем каадратпое сечение А В ГД рассматриваемой призмы и впишем в одну его по-
ловину полукруг HZE, а в другую—параболу Н0Е(рис. 7). Разделим прямую НЕ нино-
лам, половины ПК и КЕ еще раз пополам, затем еще раз ионолам и т. д. до тех пор,
вика получающиеся полоски но станут меньше некоторой заданной наперед величины
(ее можно выбрать сколь угодно малой). Затем заключим полукруг и параболу между
572
КОММЕНТАРИИ
вписанной и описанной фигурами, разность между которыми, а именно два прилегаю-
щих к КВ и KZ прямоугольника, может быть сделана меньше любой заданной величины.
На прямоугольниках, вписанных и описанных около полукруга, построим треугольные
призмы, две из которых, построенные па KZ и ЕЕ, изображены па чертеже. Полоски,
да которые разделок прямоугольник ГЛЕН, являются основаниями треугольных призм
типа ЕЛ”, KZ', которые в совокуп-
ности составят треугольную призму,
объем которой равен четверти объе-
ма всей призмы.
11усть ME — ордината полукру-
га, а МЛ—соответствующая ей орди-
ната параболы. Прямая MN, равная
половине стороны квадрата, будет
одновременно радиусом полукруга и
осью параболы. Выше мы видон., что
МЕ2:М№=МЛ : MN.
Положим, что это пс имеет места: тогда мы
Это значит, что объемы призм,
построенных па прямоугольниках
типа М3-ME, будут пропорцио-
нальны площадям прямоугольников
типа МЛ-МЕ. Пусть величины ря-
да ct|, а2, иа,.„ будут представлять
объемы призм типа Ei', величины
ряда Pi, Р;, Р;г,..>—нлощади прямо-
у гол ь и и ков типа ЛЕ; далее в качестве
величии ряда уч, у«, у3,... возьмем
объемы призм типа EN', из которых
составляется большая призма, объем
которой раппяется четверти прямо-
угольной призмы, а в качестве ве-
личин ряда Лп <\, возьмем
прямоугольники типа AM, дающие
в сумме прямоугольник АВПЕ, две
трети площвди которого равны пло-
щади параболического сегмента
Ей НК. Паша задача состоит п том,
чтобы показать, что объем цилиндри-
ческого сегмента будет тоже равнять-
ся двум третям треугольной призмы,
построенной на .ЛИ.
всегда можем построить таких два впи-
санных и описанных около цилиндрического сегмента тела, составленных из треуголь-
ных призм, чтобы разность между пнми была меньше разности между объемами сегмента
II призмы.
Предположим сначала, что объем сегменте будет больше двух третей объема призмы.
Так как разность между объемами вписанного и описанного тел больше разности между
объемами сегмента и пнист пт ого в пего тела, то объем вписанного тела будет тоже больше
двух третей объема призмы. Согласно лемме 11 ряд а — сумма призм, составляющих
вписанное в сегмент тело, будет так относиться к ряду7 у — объему призмы па ЛН, как
ряд Р — сумма вписанных в параболическим сегмент прямоугольников ко всему прямо-
угольнику ЛН — ряду б. Но это равенство иепозможно, так как первое отношение
более двух третей, в то время как второе меньше двух третей. Значит, объем цилиндри-
ческого сегмента не будет больше двух третей объема призмы.
Пусть теперь он будет мепыпе двух третей объема призмы. Тогда объем тела, описан-
ного около цилиндрического сегмента, может быть сделав меньше двух третей объема
призмы; следовательно, и площадь описанной около параболического сегмента фигуры
будет мепыпе двух третей площади прямоугольника АН, что невозможно, так как две
трети последней площади уже равны площади параболического ссгмспта.
[10! Утраченный конец книги должен был содержать механическое и геометриче-
ское доказательства следующей теоремы:
Если куб «писан в цилиндр, основаниями которого служат -два круга, вписанные
в противоположные грани куба, и затем другой такой же цилиндр с основаниями на двух
других гранях, то заключающееся между поверхностями обоих цилиндров тело, т. е.
общий им обоим объем, равняется двум третям первоначального куба.
ПОСЛАНИЕ К ЭРАТОСФЕНУ. О МЕХАНИЧЕСКИХ ТЕОРЕМАХ
573
Механическое доказательство «той теоремы реконструировало Цсйтоиом *).
Для понимания доказательства следует обратят!, внимание на форму тела, объем
которою подлежит определению (рис. 8). Его сечения плоскостями, параллельными осно-
ваниям одного из цилиндров, будут представлять окружности, а сечения плоскостями,
параллельными осям ци.тнндрои, будут представлять квадраты, стороны которых при
передвижении от А до центра К возрастают от нуля до величины, равной оси каждого
цилиндра. Дальнейшее доказательство ведете» для сечения фигуры плоскостью, прохо-
дящей через ее центр тяжести, кап это обычно делается у Архимеда. К этой плоскости
относятся к все буквы л дальнейших обозначениях (рнс. 8).
Пусть будет куб Ф¥ХГ, в который вписан цилиндр с осью ВД Н боковыми сторо-
нами ФХ и Т Г. Пусть в тот же самый куб будет вписан другой цилиндр, ось которого
перпендикулярна к плоскости Ф'РХГ; эта плоскость, проходящая через ось ВД первого
дилиидря, образует в сечении со вторым цилиндром круг АВГД, касающийся в точках А,
В, Г, Д сторон квадрата ФЧГХТ; прямые АГ и ВА будут взаимно перпендикулярными
диаметрами рассматриваемого круга. Соединим А с В л А и продол жим их до пересече-
ния с прямой Г'Е в точках Е и Z; тогда ЕГ = ГХ=АГ. Дополним прямоугольник EZ0A-
Затем вообразим, что из А проведены четыре прямые к лерпшпам проходящего через ВД
и перпендикулярного к АГ квадрата; если продолжить их до пересечения с плоскостью,
проходящей через EZ и перпендикулярном к АГ, то получится пирамида, вершила кото-
рой /\, а основание— перпендикулярный к АГ квадрат со стороной EZ; дополним эту
пирамиду так, чтобы получилась квадратная призма с теми же основанием и высотой,
что и у пирамиды (на рис. 8 эти пирамида и призма пе изображены).
После этого проведем в прямоугольнике AZ какую-нибудь прямую MN, парал-
лельную EZ, и на этой прямой восставим плоскость, перпендикулярную к АГ. В пере-
сечении с интересующим нас телом, заключенным внутри обоих цилиндров, опа образует
квадрат со стороной OIL, в пересечении же с призмой и пирамидой соответственно квад-
раты со сторонами MN и ЕР (они иа рис. 8 тоже пе изображены). Продолжим ГА до Й,
отложим АН, равную АГ, п представим себе равноплечий рычаг Hi е серединой А.
Теперь, так лак АО2—АХ-АГ и АГ=М2, AS — EX, то мы можем написать:
АО2— M2-SE;
далее АО2 = ОХ2 ЕЕ2; значит,
02»-!-SSs= MS-S3.
Затем мы имеем пропорции:
ПА : АЕ = ГА : AS — MS ; SS,
MS : S3 .-(MX2): (MXX3) = (MS2): (0X24- S32) = (MN)2: (OH2-|-SP2).
*) Bibliotheca Mathematics, VII, 336 и д. (11)07).
574
КОММЕНТАРИИ
Таким образом,
НА : A3 = (MN«): (ОП® -|-SP2).
ПА : AS = (квадр. па MN): (квадр. на ОП-| квадр. па ЕР).
Это значит, что квадрат на MN, оставаясь в своем положении, будет относительно-
точки А у ран свешивать квадраты со сторонами ОП и ЕР, перенесенные и Помещенные
Спонмп центрами тяжести в точку И:
ЛН-(квадр. па ОП-f-квадр. на ЕР) = А2 (квадр. на MX).
Так как из квадратов па ОП состоит интересующее нас тело, а из квадратов па ЕР
и МК построенные нами пирамида и призма, у которых высотой является AF, а основа-
нием — квадрат со стороной MN, то просуммировав все аналогичные равенства, получим:
АП-(тело -[-пирамида AEZ)—ЛК-(призма Ев).
Таким образом, призма Е6, оставаясь в своем положении, будет уравновешивать,
относительно точки Л упомянутые пирамиду и находящееся внутри обоих цилиндров тело,
если их перенести и поместить центрами тяжести в точку Я. Так как центр тяжести призмы
находится в точке К, и АН = 2АК, то упомянутая призма будет вдьоз больше пирамиды
вместо с находящимся внутри обоих цилиндров телом:
призма — 2 (тело иирамида).
Ио пирамида равна одной трети призмы с теми же основанием и высотой; отсюда
следует, что находящееся внутри обоих
одной трети призмы или просто будет р
цилиндров тело, оудучи взято дважды, равно-
вно одной шестой призмы Et). Ио призма Е0
в четыре раза больше куба 'ГХ; значит, тело,
находящееся внутри поверхностей обоих ци-
линдров, будет равно двум третям куба УХ,
что и требовалось доказать.
Мы привели механическое доказатель-
ство рассматриваемой теоремы приблизитель-
но в тех же формах, в каких оно было бы,
вероятно, дано Архимедом (конечно, за ис-
ключением алгебраического знаколи-тожеиия
и пространственного чертежа — Архимед удо-
вольствовался бы сечением по средней пло-
скости, той, на которой у нас расставлены
буквы, как это показано па рис. 9). Чтобы
провести геометрическое доказательство рас-
сматриваемой теоремы, нужно диаметр ЛГ
разделить па достаточно большое число рав-
ных частей и через полученные точки деле-
ния пронести плоскости, перпендикулярные-
к Л Г. Эти плоскости в сечениях с кубом ФГ,
а также с рассматриваемым телом образуют
квадраты. Затем вписываем в рассматривае-
Рис. 9.
мое тело и описываем около пего телесные
фигуры, состоящие из элементарных призм и отличающиеся друг от друга менее чем на
любую заданную величину; -чти призмы будут иметь квадратные основания, а высотами
у них будут служить отрезки диаметра ЛТ. Таким образом, получится картина, подоб-
ная изображенной на рис. 7, стой только разницей, что теперь вместо треугольных призм
будут квадратные. Каждой элементарной призме вписанной или описанной фигуры будет
в кубе соответствовать элементарна» призма, основание которой будет ралич боковой
грани куба; так как отношение объемов двух таких элементарных призм с одной и той же-
высотой будет равно отношению квадратов сторон оснований, то мы можем воспользо-
ваться той же самой вспомогательной параболой что п в предложен ни XV, и провести
доказательство тем же самым способом. Это доказательство, рекоиструироваиное в стиле
Архимеда, имело бы приблизительно такой ппд:
«Пусть будет куб ФУХ Г и в него вписан цилиндр, ось которого ЕЛ и боковые сто-
роны фх и У Г. Пусть в этот же куб вписан цилиндр. ось которого будет перпендику-
лярна к плоскости ФУХ Г; пусть эта плоскость ФУХ Г, проходя через ось первого-
цилиндра, п сечении со вторым цилиндром образует круг А В ГД, касающийся в точках А,
В, Г, д сторон квадрата АВ ГД; тогда АГ и ВД будут два взаимно перпендикулярных
Диаметра этого круга. Поверхности этих цилиндров. пересекаясь друг с другом, ограничат
некоторое тело, которое в сечении с плоскостями, параллельными ФУХ Г, будет давать
Круги, в сечении же с, плоскостями, перпендикулярными к АГ, будет давать квадраты.
ПОСЛАНИЕ К ЭРАТОСФЕНУ. О МЕХАНИЧЕСКИХ ТЕОРЕМАХ
575
Я утверждаю, что ото заключенное между поверхностями обоих цилиндров тело будет
составлять две трети куба.
Прежде псего докажем, что п это заключающееся между поверх постами двух упо-
мянутых цилиндров тело можно вписать телесную фигуру и около него описать другую
такую же, причем обе они составляются из призм, имеющих равные высоты и подобные
квадратные основания, и построены так, что-
бы описанная фигура превосходила вписан-
ную, па величину, меньшую всякой наперед
заданной величины.
Будем в круге ДВГД постоянно делить
пополам диаметр ЛГ и через точки деления
проводить параллельные ВЛ прямые, пересе-
кающие окружность круга АВГД; затем че-
рез точки пересечения этих прямых с окруж-
ностью круга будем проводить прямые, нарп.ч-
лел г.ные А Г, и продолжать их в обе стороны,
пока они ио встретятся с, двумя ближайшими
прямыми, 1тпр:1.'1ле.ты1ь>мн ВЛ; далее в точках
деления диаметра АГ будем восставлять пер-
пендикуляры вверх и вниз от плоскости круга
АВГД и на каждом из этих перпендикуляров
откладывать прямые, рапные находящимся в
круге отрезкам примой, параллельной ВЛ,
проходящей через основание этого перпенди-
куляра .Затем на находящихся в плоскости
круга ЛВГД взаимно перпендикулярных пря-
мых будем строить нлоскос.тя, перпендику-
лярные к плоскости круги ЛВГЛ, а через
концы восставленных перпендикуляров будем
проводить плоскости, параллельные плоскости
круга ЛВГЛ, продолжая их в обе
стороны до пересечения с двумя плоскостями, проходящими через соседние, парал-
лельные ВД, прямые. Вес эти плоскости как внутри обеих цилиндрических поверх-
ностей, так н гпю их образуют призмы, имеющие одинаковые высоты и в качестве основа-
ний квадраты, расположен пне на прямых, параллельных прямой ВД. Будем продолжать
деление прямой ЛГ пополам до тех нор, пока две прилегающие к ВЛ призмы нс окажутся
мепыпе заданной величины; тогда составленная из призм тслес-
л пая фигура, ош'.салнай около тела, ограниченного поверхно-
стями обоих цилиндров, будет превосходить такуто же вписан-
ную на величину, меньшую заданной: действительно, первая
будет отличаться от второй па величину двух прилежащих к ВД
призм, так кик леем остальным призмам онвеаппой фигуры
будет соответствовать такое же количество ранных призм
(iiincauiroii фигуры. ("|
Затем впишем в полукруг АВГ параболу АВГ и через
if точки ее пересечения с прямыми, параллельными ВК, проведем
прямые, параллельные Л Г, продолжая нх указанным ранее-'
образом.
После этого получатся две фигуры, из которых одна опи-
сапа около сегмента параболы, о дру|ал впитана в него; обе они
составлены из параллелограммов, причем первая из пих прево-
сходит вторую на два ирижжаших к ВК параллелограмма,
причем все эти параллелограммы будут попарно соответство-
., пять упомянутым ранее призмам впнеавпой и списанном тапес-
1 вых фигур.
Теперь, если заклягчсппос между двумя цилиндрическими
понерхпостлмн тело не будет равно двум третям куба, то оно-
будет пли больше, или меньше. Пусть сначала оно будет, если
возможно, Go.ni.ine; тогда куб ФЧГХГ будет менее чем полтора раза взятое тело, заклю-
ченное между обоими цилиндрами
куб ФЧ'ХТ < 4 тела.
Впипюм в тело, как сказано, телесную фигуру и опишем другую, и притом так,
чтобы описанная фигура превосходила бы вписанную на величину, меньшую разности
между этим телом и двумя третями куба; тогда вписанная фигура будет больше двух
676
КОММЕНТАРИИ
третей куба:
вписанная фигура> — куба Ф’РХГ.
Каждой квадратной призме, вписанной в тело, половина стороны основания кото-
рой ME, будет соответствовать образующая куб квадратная призма, воловина стороны
основания которой MN, а высота одинакова с первой; ври этом первая призма будет отно-
ситься ко второй, как квадрат М3 к квадрату MN, Пусть прямая MN пересечет вписан-
ную в полукруг параболу в точке Л; было доказано (предложение XIV), что MN2 будет
к ME3, кап MN к соответствующей ординате параболы МЛ:
М№ : М5«=^МХ : МЛ.
Но как MN к МЛ, так будет построенный па MN параллелограмм к построенному
на МЛ и нмеклдему высоту, одинаковую с той, которую имеет первый параллелограмм,
а так же п с той, которую имеют квадратные призмы, из которых составляются вписан-
ные в заключенное между обоими цилиндрами тело и описанные около него телесные
фигуры. Теперь мы имеем два ряда пропорциональных величин, а именно вписанные
в цилиндрическое тело квадратные призмы ME4 н вписанные в параболу параллелограм-
мы МЛ, причем каждой из величин первого ряда соответствует имеющая ту же высоту
квадратная призма, из которых составляется куб, а соответствующей величине второго
ряда — находящийся с пей в том же самом отношении параллелограмм MN, нз которых
составляется содержащий параболу прямоугольник ЛЕ. Значит, как все параллелограм-
мы, из которых складывается параллелограмм АЕ, ко всем соответствующим параллело-
граммам, .Кроме двух, из которых складывается вписанная в параболу прямолинейная
фигура, так будут и все квадратные призмы, из которых складывается куб Ф'ГХГ, ко
всем соответствующим призмам, кроме двух, из которых составляется телесная фигура,
вписанная в заключенное между двумя цилиндрами тело:
ларалл. ЛЕ ; V паралл. МЛ=куб ФТХГ : V призм ME2,
И так как состоящая из призм ME4 телесная фигура, вписанная в заключенное
между обоими цилиндрами тело, будет больше чем две трети куба, то состоящая из парал-
лелограммов МЛ фигура, вписанная в параболу, будет больше чем две трети параллело-
грамма ЛЕ:
• я 2
5 , паралл. МЛ>-2- ларалл. АЕ,
а это же невозможно, поскольку в другом месте было доказано, что сегмент, заключаю-
щийся между параболой и прямой АГ, составляет две трети параллелограмма ЛЕ. Зна-
чит, за ключ ел ное между обоими цилиндрами тело не будет больше двух третей куба ФЧ'ХГ.
Пусть теперь оно, если возможно, будет мепыле; значит, куб ФТХГ будет более
чем в полтора раза больше тела:
л
куб Ф’ГХГ>~ тела.
Тогда, опять описав и вписав вышеуномииутые телесные фигуры так, чтобы они раз-
нились между собой па величину, меньшую той, на которую две трети куба превышают
заключенное между обоими цилиндрами тело, мы точно так же докажем, что все призмы,
заключающиеся в кубе, будут так относиться ко всем призмам, содержащимся в описан-
ной около тела фигуре, как псе параллелограммы, содержащиеся в параллелограмме АЕ,
ко всем параллелограммам фигуры, описанной около сегмента, заключенного между пара-
болой и прямой АГ:
V призм MX : V призм МЕг=У паралл. MN Упаралл. ЛМ,
то есть куб будет относиться к фигуре, описанной около заключенного между обоими
цилиндрами тела, как параллелограмм АЕ к фигуре, описанной около сегмента, заклю-
ченного между параболой и прямой АГ:
куб Ф'РХГ: У призм ME4—парэ.тл. ЛЕ ; V паралл. МЛ.
ПОСЛАНИЕ К ЭРАТОСФЕНУ. О МЕХАНИЧЕСКИХ ТЕОРЕМАХ
577
Но куб ФЧ'ХУ будет более чем и полтора раза больше телесной фигуры, описанной
около заключенного между обоими цилиндрами тела:
куб <D4FXr>-i опис. фигуры;
4U
значит, и параллелограмм АЕ будет более чем в полтора раза больше фигуры, описанной
около сегмента, заключенного между параболой и прямой АГ:
дг_ 3
паралл. At > — опис. площади;
это же невозможно, так как доказано, что параллелограмм АЕ в полтора раза больше
сегмента, заключенного между параболой и прямой АГ. Значит, тело, заключенное меж-
ду обоими цилиндрами, не будет и меньше днух третей куба. Значит, если оно не может
быть ни болыпо, ни меньше двух третей куба ФТХГ, то оно должно быть мм равно; это
и требовалось доказать».
37 Архимед
. О ПЛАВАЮЩИХ ТЕЛАХ
Произведение относится к числу поздних сочняенпй Архимеда. Оно написано опре-
деленно позднее трактата «О равновесии плоских фигур», так как в нем встречаются
ссылки на этот трактат. Оно написано позднее «Коноидов», па одно из предложений кото-
рых оно опирается, п, вероятно, позднее «Эфода», в котором содержите» теорема о поло-
жении центра тяжести сегмента параболоида. 'Го обстоятельство, что конец второй книги
по получил окончательной отделки, позволяет думать, что мы имеем дело с последним
произведением Архимеда.
Любопытна история того, как это произведение дошло до нас. Очень долго оно
было известным только в латипском переводе Вильгельма из Мербеке (1215—1282), кото-
рый сделал несколько Переводов с греческого для своего друга, известного схоласта.
Фомы Аквинского. Вильгельмом был сделан перевод всех сочинений Архимеда; руко-
пись этого перевода была обнаружена в ISM г. Валентином Розе в Ватиканской библио-
теке. Если верить словам Рожера Бэкона, написавшего про пего: «Hie Willielmus Flemin-
gus, qui nihil Hovit dignum neque in scicnlits neque in linguis (этот фламандец Вильгельм,
не знавший ничего достойного пи в науках, ни в языках)», то Вильгельм из Мербеке вряд
ли хорошо нопимал Архимеда (хотя относительно знания Вильгельмом языков Бэкон
определенно ие прав). Греческий текст был открыт только в 1905 г. Гсйбергом в Кол-
ета птипопольс.ком палимпсесте, сохранившем для нас примерно около трех четвертей
текста Архимеда; утраченный текст воеиоапнетсн по переводу Мербеке.
Сочинение «О плавающих телах» состоит из двух книг; в первой свободная поверх-
ность воды считается сферической, а во второй— плоской.
Первая книга состоит из девяти предложений. Два первых устанавливают, что сво-
бодная поверхность води, окружающей Землю, является сферическом, причем центр
сферы совпадает с центром Земли. Хотя сферичность Земли и вообще мира была признана
еще греческими философами эпохи Платона и Аристотеля, тем не менее против результата
Архимеда, по-видимому, восстал даже его друг Эратосфен Киренский, основатель мате-
матической географии. В первой книге «Географии» Страбон пишет: «Разве не смешно
теперь видеть, кап математик Эратосфен отказывается признать установленный Архиме-
дом н сочинении „О плавающих в жидкости телах" принцип, что поверхность всякой покоя-
щейся жидкости принимает форму шара, центр которого совпадает с центром Земли,
а ведь это принцип, которым теперь принимается всяким мало-мальски знающим мате-
матику» (Географии, книга I, гл. 111, 11).
Первое предложение 2-й книги формулирует принцип ареометра, а остальные
девять рассматривают условия равновесия плавающего в жидкости сегмента парабо-
лоида. Трактовка вопроса Архимедом является чисто физической. Архимед устанавливает
положение равновесия тем, что определяет, будет ли тело, отклоненное от этого положе-
ния, возвращаться в него или нет; таким образом, определенные положения будут соот-
ветствовать только устойчивому равновесию. Первые четыре предложения (Н—V) ка-
саются вертикальных положений равновесия, следующие четыре (VI—IX) — няклоллмх
положений, когда основание сегмента целиком находится или внутри, или впе Жидкости;
последнее предложение дает общий разбор вопроса о возможности положения равновесия,
когда поверхность жидкости также пересекает плоскость основания плавающего сег-
мента. Изучение последнего предложении показывает, что Архимед тлел путем, лишь
в частностях отличающимся от того метода, который был установлен во второй половине
XIX века (теоремы Дюпена — Давыдова); однако нельзя согласиться с мнением одного из
переводчиков Архимеда, Именно II. Фер-Экке, что «эти предложения удивительным образом
выражают всю ту теорию метацентра, которая должна была освободить всю теорию ко-
раблестроительства от прежнего эмпиризма»; наоборот, А рхимсл чисто физически проверял
условии устойчивости равновесия, не обращаясь пи к какому теоретическому критерию.
В новейшее время приходится слышать мнепис, что выработанная Архимедом тео-
рия по имела никакого практического применения и что было бы лучше, если бы Архимед
О ПЛАВАЮЩИХ ТЕЛАХ 57а
разработал условия равновесия бесконечно длинного параболического цилиндра, иными
словами, решил бы то, что теперь насыпается плоской задачей гидромеханики. По суще-
ству, Архимед и решал такую задачу, поскольку для тела вращения все плоские сечения
чсре.| вертикальную ось равнозначны, так что достаточно рассмотреть условия равнове-
сия для колебаний тела в плоскости какого-нибудь одного из этих сечений.
Это обстоятельство заставляет критически отнестись к старому, сохранившемуся
у Витрувия рассказу о том, как был открыт закон Архимеда. В тексте Витрувия
(«Архитектура», книга IX, гл. 3) говорится:
«Во время своего царствования в Сиракузах Гиерон, после благополучного окон-
чания всех своих мероприятий, дал обет пожертвовать в какой-то храм золотой венок
бессмертным богам. Он условился с мастером о большой цене за работу и дал ему нужное
но весу количество золота. В назначенный день мастер ирицес свою работу царю, который
нашел ее отлично выполненной; после взвешивания венок оказался соответствующим
выданному весу золота, по при испытании последнего на пробирном камне оказалось, что
мастер часть золота заменил серебром. Царь был очень раздражен этим обманом, по не
будучи в состоянии уличить мастера в сделанной им краже, попросил Архимеда приду-
мать дли этого способ. Однажды, когда целиком занятый этим делом Архимед садился
в ванну, шг заметил случайно, что ио мере погружения его тела в воду последняя псрели-
Ba.'iaci, через край. Это" наблюдение сразу позволило ему найти нужную идею, и радость
настоль 1,о наполнила его душу, что он сразу выскочил из ванны и, бегая голым по дому,
кричал, что он лашел то, что искал, говоря по-гречески: „Эврика! Эврика!"»
Если обдумать этот рассказ более внимательно, то становится ясным, что к откры-
тию закона Архимеда он никакого отношения не имеет. Чтобы уличить недобросовестного
ювелира, Архимеду было необходимо определить объем вшща и сравнить его нес с весами
соответствующих объемов серебри и золота; лак ясно из всего рассказа, объем венца был
определен по количеству вытесненной воды.
Какова бы ни была первоначальная причина зарождения закона Архимеда, нрддли
можно думать, что единственным его практическим приложением было уличение недобро-
совестных мастеров. Полибий пишет, что при обороне Сиракуз Архимед при нем ошв
крюков и рычагов приподымал и опрокидывал корабли римлян: для того чтобы построить
нужный для этого механизм, необходимо произвести его расчет, последним же невозмо-
жен без знания закона Архимеда.
(1] «Погрузившись sice, тело не будет двигаться (о'О'О^о'ета!.) вниз, так как все
части жидкости, находящиеся на одном уровне (тя =£ 'ioou иещеда), будут давить одина-
ково вследствие того, что тело является равнотяжелым с жидкостью»,— это место иногда
толковали н том смысле, что равнотяжелое с жидкостью тело будет л равновесии только
у поверхности жидкости, а не в любом положении внутри жидкости, и соответственно упре-
кали Архимеда в ошибке. Такого рода толкование нс является необходимым; дальнейшие
слова об одинаковости давления, то есть об отсутствии побудительной силы для движе-
ния, показывают, что мысль Архимеда заключалась в том, что движение вниз считалось
невозможным именно вследстние отсутствия причины для движения.
[2] Установленные уже в XIX веке теоретические положения, необходимые для
решения поставленной задачи, таковы:
Если тело легче жидкости, то плоская фигура, отсекаемая в теле продолжением
уровни жидкости, носит название плоскости плавания', так хак вес жидкости в объеме
погруженной части равняется весу всего тела и вес тела постоянен, то объем части тела,
отсекаемой плоскостью плавания, тоже будет постоянным, как бы ни наклонялось пла-
вающее в жидкости тело. Огибающая всех плоскостей плавания называется поверхно-
стью сечений: это будет геометрическое место центров тяжести плоскостей плавания.
Геометрическое место центров тяжести равных объемов, расположенных под раз-
личными плоскостями плавания, называется поверхностью центров', касательная плос-
кость к поверхности центров параллельна плоскости плавания, которой соответствует
точка касания; нормаль к плоскости плавания будет одновременно нормалью и к EOBipx-
иости центров. Так как перпендикуляр, опущенный на плоскость плавания из центра
тяжести, будет направлен по вертикали, то разыскание положений равновесия плаваю-
щего тела сводится к проведению из центра тяжести нормалей п поверхности центров;
каждой такой нормали будет соответствовать определенное положение равновесия.
Условия устойчивости определенного положения равновесия формулируются так.
Проведем через нормаль к поверхности центров плоскость, которая рассечет эту поверх-
ность центров по некоторой кривой; направления нормалей к поверхности центров будут
совпадать с нормалями к кривой сечения. Тан как сферический сегмент, рассматриваемый
Архимедом, имеет ось симметрии (плоскость плавания будет окружностью), то центры
кривизны всех таких линий сечения будут одинаковыми; бесконечно близкие к основной
(вертикал 1*11011) нормали липин действия давлений воды, совпадающие с направлениями
нормалей к поверхности центров, будут пересекаться в одном и том же центре кривизны-;
этот центр кривизны можно привить за своего рода точку подвеса для плавающего'
37*
680
Комментарии
в жидкости тела; эта точка называется метацентром. Чтобы устойчивость равновесия
была обеспечена, центр тяжести плавающего тела должен быть тике метацентра; если
центр тяжести находится выше метацентра, то равновесие будет неустойчивым.
Когда ajufpirwxvaiii сегмент плавает выпуклостью книзу, поверхность центров будет,
очевидно, шаровой поверхностью с центром, совпадающим с центром сферического сег-
мента; радиус жо равняется расстоянию ОА от центра сферической поверхности сегмента
до центра тяжести А погруженной части. В пашем случае метацентр будет в точке О,
центр тяжести Г сегмента будет находиться ниже О; слодонательво, положение равнове-
сия будет устойчивым.
Когда сегмент будет плавать выпуклостью кверху, то центр тяжести Г всего сег-
мента будет лежать выше его геометрического центра О. Пусть А будет центр тяжести
находящейся вне воды части сегмента, расстояние ОА будет постоянным; мы считаем его
известным, когда отношение плотностей плавающего тела и жидкости будет задано.
Также можно считать известным: объем погруженной части и положение ее центра тяже-
сти В. При отклонениях сегмента от положения равновесия центр тяжести А будет пере-
мещаться по окружности радиуса OA^g, который можно считать известным, а центр тя-
жести Б — по кривой Вр, которая, как легко доказать, тоже будет окружностью; поверх-
ность центров будет поверхностью вращения, образованной этой кривой вокруг оси АВ.
Пусть Г — центр тяжести всего сегмента; сели отшяцепио весов свободной и погру-
женной частей равно х (это вполне определенная величина, зависящая от соотношения
плотностей тела и жидкости), то отношение расстояний аГ и pi’ будет постоянным:
аГ :[5Г—ЛГ : ГВ=1:и.
Таким образом, кривая Вр может быть получена из окружности Аа подобным пре-
образованием, причем центром подобия служит точка Г, а коэффициент подобия отрица-
телен и равен — х, так как аир лежат по разные стороны от Г. Кривая Dp будет
окружностью, центр М которой лежит па прямой АВ так, что центр подобия Г оказы-
ваете» между М и О. Если расстояние ОГ —6, то МГ=хб. Таким образом, метацентр М
лежит выше центра тяжести Г и равновесие будет устойчивым.
Мы видим, что кривая центров (сечение поверхности центров) состоит из двух дуг
окружностей, соответствующих положениям плавания сегмента, когда плоская его часть
находится целиком в жидкости или вне жидкости. Отметим, что Архимед умел находить
объемы сферических сегментов («О шаре и цилиндре», кп. П, предложение Н) и положе-
ние центров их тяжести («Эфод», предложение IX); слсдопателыю, в обоих этих случаях
он мог при любом соотношения плотностей плавающего тела п жидкости провести все
вычисления до конца, В том случае, когда поверхность жидкости пересекала плоское
основание сегмента, уже пет оснований думать, что Архимед и теперь мог определить
объем и положение центра тяжести погруженной части тела; если бы и в этих случаях
мы построили соответствующие кривые центров, то получили бы еще два положения
равновесия, ио последнее было бы неустойчивым.
[31 Для понимания текста предложений второй книги пужпо знать некоторые свой-
ства касательных к параболе, а именно:
Если парабола отнесена к системе координат, где начало совпадает с вершиной,
ось абсцисс идет но оси параболы, а ось ординат по касательной к параболе в вершине,
•так что уравнение параболы будет у2=2рх, то для касательной, проведенной в любой
точке параболы, субтангепс будет равняться удвоенной абсциссе точки касания, а суб-
нормаль имеет постоянную величину, равную параметру р.
(4) Идея архимедова доказательства предложения II заключается в том, что
если ОР < р, то нормаль в точке касания U пересечет ось ON между Р и N, так что
угол РПЙ будет острым (рис. 11, стр. 33(i).
О ПЛАВАЮЩИХ ТЕЛАХ
581
Пусть ОК К представляет сечение параболоида плоскостью, проведеппой через его
ось ОВ (рис. 3), пусть уравнение этой параболы в координатных осях Оху будет: уг=2рх.
Пусть ось параболы ОВ будет равна -^-6; согласно доказанному Архимедом в «Эфоде»
(предложение V), центр тяжести Со всего сегмента будет лежать па расстоянии ОС0=Ь
от вершины сегмента О.
Опустим сегмент в жидкость так, чтобы его ось была вертикальна; пусть он ногру-
3
зится па глубипу ОА—а, так что прямая а'Ал' будет представлять уровень жидкости;
вес жидкости в объеме сегмента л'Аа' будет равен весу всего параболического сегмента;
центр тяжести этого сегмента будет лежать на расстоянии ОС1=л.
В предложении XXIII «Коноидов и сфероидов» доказывается, что объемы сегментов
параболоида вращения, отсеченных плоскостями, проведенными как угодно, будут рав-
вы, если равпы оси этих сегментов. Л так
как все диаметры параболы параллельны,
то поверхность сечений параболоида (оги-
бающая плоскостей плавания, отсекаю-
щих равные объемы) будет таким ясс па-
раболоидом, лишь едпипутым вдоль
па расстояние О А — — В сечении
параболоида с плоскостью чертежа
чится парабола АГУМ, уравнение которой
будет:
ОСИ X
этого
полу-
рг=2/> а
По существу, нам нужна лишь часть
АТУ этой параболы вплоть до точки D' V
касания с проведенной из К прямой; при
дальнейшем вращении параболоида угол
его К погрузите» в жидкость и следующая
часть поверхности сечений уже по будет
параболоидом АГУМ.
Так как центры тяжести сегментов
параболоида лежат на осях на расстояниях
двух третей от вершины, то поверхность
центров и пересечении с плоскостью черте-
жа даст параболу CJi'L, которая будет
представлять основную параболу, сдвину-
тую вправо на расстояние О(\ = а\ ее
уравнение будет:
^=2р(.т—«); (2)
нам нужна лишь часть ее, соответствую-
щая дуге С.А".
Так как ниже сеи Ох мы будем иметь такую же симметричную фигуру, то достаточно
рассматривать лишь полуплоскость с положительными координатами у.
Чтобы найти положения равновесия, мн должны из центра тяжести Со сегмента
провести нормали клинил центров С^Е', взнв из лих лишь те, которые пересекают дугу
С,Е', п также ей симметричную, лежащую ниже оси Ох.
Дифференцируя уравнение (2), получим:
СП
<??/
тангенс угла наклона касательной к параболе будет равен ~, а угловой коэффициент
нормали — .
Уравнение нормали, проведенной из точки Со, в текущих координатах х', у' будет:
!/'==----(=«' — Ь).
С
582
КОММЕНТАРИИ
Решая это уравнение совместно с уравнением (2), находим координаты точек пере-
сечения нормали с параболой СуЕ'. Так как в точке пересечения у=у', х=х’, то мы
будем иметь:
xg—b—р,
-xi=a, I Уг=± К2р(6—« — р).
2/1 = 0=
Первая пара решений соответствует положению равновесия при вертикальной оси
ОВ, вторая пара (или, лучше сказать, две пары) решений будет соответствовать положе-
нию равновесия, когда ось ОВ сегмента отклонится от вертикали в ту или другую сторону
на некоторый угол а. Нужно помнить, что
вторая пара решений может иметь место,
только если проведенная иа Са нормаль
пересечет параболу С,Е’ между С, и Е'.
Одно из необходимых условий суще-
ствования положения равновесия, соответ-
ствующего второй парс решений, будет
заключаться в том, что подкоренное выра-
жение для у, должно быть положительным
(если оно равно пулю, то первая и вторая
пара решений совпадают):
К
р
Рис. 4.
или
В предложении II мы
= 077—Ъ пе превышает
(3)
ОЯ =
иными
что в
имеем
3
-2-Р,
словами, Ъ^р. Это показывает,
рассматриваемом случае возможно лишь
положение равновесия, в котором ось
сегм сита верт и кал ь ла.
Будет ли это равновесие устойчи-
вым? Вместо чисто физического доказа-
тельства Архимеда мы могли бы восполь-
зоиаться понятием метацентра, определить
радиус кривизны липни центров или осповт
вой параболы у2=2рх в ее вершине, кото-
рый, как известно, равен параметру р.
Если от точки С{ отложим стрелок CtM — щ,
то расстояние ОМ метацентра будет равно
в+р» так как то при любом значении а отрезок ОМ будет больше отрезка ОСа=Ъ,
иными словами, метацентр будет лежать выше центра тяжести Сл сегмента.
[5| В предложении [11 Архимед рассматривает случай, когда сегмент плавает, имея
основание целиком погруженным в жидкость. Объемы сегментов параболоида вращении
относятся, как квадраты их осей («Коноиды и сфероиды», XXIV). Если сопостапить это
„ .. л3 ОЛ3
с первым предложением рассматриваемом второн книги, то отношение , равное
(рис. 3), даст пам отношение плотностей плавающего тела и жидкости.
Пусть сегмент опущен основанием КК в жидкость так, чтобы ось его ОВ была вер-
тикалъна, и уровень жидкости пойдет по прямой b’b' (рис. 4). Объем сегмента Ь'Ь'КК будет
равеп объему сегмента Оа'а'-, если мы обозначим отношение ^=/>2 и примем объем
всего сегмента ОКК за единицу, то
объем сегм. Оа'а'=объем сегм. Ь'Ь'КК—k1,
а объем сегм. Ь'0Ь' = 1—А3.
Рассмотрим сегмент Ob'b', находящийся над поверхностью воды. Для оси ОВ,,
мы имеем:
ОВ1 _ 1—А2
ОВ* ~~ 1
О ПЛАВАЮЩИХ ТЕЛАХ
583
’Откуда ' ......
а, наконец,
0Bt=~ / Ъг—а*.
Огибающая последовательных положений поверхности плавания будет параболой
PBjP. уравнение которой
. • f у®=2р(»---|/Ь«=^). (4)
2
Центр тяжести сегмента ОЬ'Ъ' находится па оси OBY на расстоянии ОС*~
о
= —а3; при качании сегмента около вертикального положения равновесия он будет
перемещаться по параболе AC3jV, уравнение которой будет:
уй=-- 2р (ж— /Р^а®). (5)
Теперь мы можем заняться построением линии, но которой будет перемещаться
центр тяжести сегмента Ь'ККЬ'. Абсцисса ОС.. этого центра может быть найдена из соот-
ношения
(1 — А») ОСЯ 4- А® ОС2= 1 • ОСо.
откуда
з
ь-(1..-/(2) 1/Г3^ 1-(1-AV
2----------7* ------- ь'—
3 •
<%=* (1-Kl^A5)-
Апалогично
СаС0 = 5—/Ь3—и3=б(1— /I—А2).
Отсюда видно, что отношение
--А® ’
С3С0 А2
го есть обратному отношению объемов соответствующих сегментов, как исследовало
ожидать.
Чтобы получить нужную нам ветвь ЕгСг линии центров, перестроим параболу
iVC^N около центра подобия Са так, чтобы расстояния С0С2 увеличились в отношении
<1—А®) : А2; в результате получится проходящая через точку Сг парабола, параметр
которой увеличится в том же самом отношении, то есть будет равен
Р1=Р
1 —А»
А®
Уравнение этой параболы, если пачало координат взять в точке С'с, будет
y8=2pi(C0C2—к),
то есть
Уг~2р (1-(1-*®)-. (6)
У равнение "нормали к этой параболе, проведенной из начала координат Со, полу-
чится, как и раньше:
У , ’
У " (1 —А®) ” •
.1 . Р к*
584
КОММЕНТАРИИ
Так как в точке пересечения нормали с параболой (6) у —у' и х—х', то получаем два
решения:
1) У=0,
1-ЛЕ , .
2) ^=Р~^~
Первое отвечает вертикальному положению оси ОВ, а второе — возможному на-
клонному положению. Соответствующая ордината у определится после подстановки х
в уравнение (6):
<1^ {„ Ц-.
(7>.
Условия действительности значения у требуют, чтобы
Р< b(i—
или
Р<сосг.
[6] Так как Архимед рассматривает только те положения равновесия, в которых
основание сегмента находится целиком в воде или вне ее, то нам понадобятся лишь части
СуЕу и парабол центров, которые определятся так:
Поскольку в обоих случаях плавания в наклонном положении конец основания
сегмента в пределе должен лежать ла поверх пости воды, то из Д’ нужно построить каса-
тельные к параболам /Ш и В,Р и из точки касания параллельно оси Ох провести прямые
до пересечения с параболами центров, имеющими вершины соответственно в Су и С%, точ-
ки Ёу и E-i н будут концами нужных нам дуг.
Если вершина О сегмента погружена в воду (рис. 3), то мы найдем крайнюю точ-
ку Еу липни центров, если построим касательную KD' к параболе AD'M я проведем D'E'
параллельно Ох.
Уравнение параболы AD'M будет
vt^2p(^x—~a^ ,
координаты точки К, лежащей на параболе у2—2рх,
3 г--
х—~—Ъ, у=уЗрЪ.
Л
Искомое уравнение касательной будет:
решая оба уравнения совместно и полагая, как и выше, х—х‘, у—у', будем иметь:
2 > Z 3 Л
Р2 — £Р ----j ,
У2— У pr3pb — p Чу .
Для исключения х умножаем второе уравнение на 2 и из результата вычитаем
первое:
у-—2у |/ ЗрЬ=Зра—ЗрЬ,
откуда
Ууу 2= ‘ЛрЬ ± (Зра — ЗрЬ) — ( у Ъ ± уТв).
Так как из точки К можно провести к парабол» дпе касательные — вправе-
и влево от К, а кам нужна только левая, то берем для у меньший корень:
у = - /“)
Максимальное значение квадрата ординаты, соответствующей положению равно
весия, будет:
Утах ~ Зр (*> -|- а — 2 V ab) \
О ПЛАВАЮЩИХ ТЕЛАХ
585
для точки пересечения нормали иа Со с лилией центров CEI. мы имели г=&—р. Подста-
вив ото значение в уравнение (2), получим:
yv=2jt>(6 —а—р).
Разность этих величин должна быть положительна:
Утах—у1=Р {36-[ За—6 \-rab—2b-f-2a-f-2p},
то есть
fe-|-5a-j-2p—6 /аЬ>0,
или
2p^>Gj/^ab—5а b=b(l^ab—а) (б — }Лаб)=5 a — {/а)—yrb(]/b—]/а) —
= (/&- /а)(5/а— - j/A') ^5 —•
Таким образом, если принять во внимание условно (3), то дли возможности плава-
ния сегмента в наклонном положении мы должны иметь:
Случай, когда сегмент плавает с целиком погруженным основанием, можно при-
вести к предыдущему, если вместо ОБ = -^-а па рис. 3 взять 02^ = -^- а' (рис. 4); тогда
аналогичное условие возможности плавать в паклопиом положении напишется так:
где
4'=ь/£Т».
Мы уста повили следующие возможные положения равновесия:
1) два соответствующих вертикальному положению равновесия оси ОБ,
2) два наклонных положения с вершиной О сегмента в жидкости,
3) два наклонных положения с. вершиной О вне жидкости.
Кроме этого, имеются еще два положения, когда один из углов сегмента KtK нахо-
дился вне жидкости; опи соответствуют линиям, соединяющим точки Jfj и Б2- Эти поло-
жения Архимед совершенно пе рассматривал.
Дли выяснения условий устойчивости вайдеппых положений равновесия нужно
определить радиусы кривизны линии центров в соответствующих точках. Л точках Ct
и С2 главная нормаль совпадает с осью параболы центров и равпа ее параметру; следова-
1—А?
телыго, расстояние метацентра от линии центров будет р в точке С, и р' - р f & в точке С2.
Так как при устойчивом равновесии центр тяжести Са должен лежать ниже мета-
центра, то мы будем иметь:
В положении С\ высота метацентра равпа р, высота центра тяжести Си будет
CjCg-^b—а. Условие устойчивости требует:
£>—а<^р,
то есть
3 3 I 3
Если
то это равенство будет иметь место независимо от а, то есть и от плотности плавающего
тела. В этом состоит предложение II второй книги.
В положении С2 параметр р' будет:
see.
КОММЕНТАРИИ
расстояние С„Сг центра тяжести сегмента (см. стр. 583):
сас2= ь (1 _ у 1 _ А2).
Условия устойчивости требуют, чтобы
CijCj у?,
3JJLE
Li С* Li
, Если
то равновесие будет устойчивым независимо от плотности плавающего тела Л2; в этом
состоит предложение 1П второй книги.
[7| Полое общие случаи устойчивого равновесия требуют рассмотрения плотности
плавающего тела, иными словами, глубины л его погружения. Условие устойчивости
пишем н виде
l 4“’ <10)
С и С
г , Преобразуем его так, чтобы выделить глубину а:
2
а2
Разделим обе части’ла'Ь и возведем в квадрат, помня, что —плотности пла-
вающего тела:
•. Таким образом, вертикальное положение равновесия останется устойчивым, если
плотность плавающего тела d будет равна или больше отношения, стоящего в левой части
неравенства:
В этом состоит предложение IV Архимеда.
|8| Когда сегмент плавает в вертикальном положении основанием кверху, условием
устойчивости будет:
%-ь<~р+4ьУ*=&, (io1)
& Lt Li
где -^-0 У~1—&а=-^Уб*—а2—^- а' представляет, как мы видели выше, высоту части
сегмента, находящейся вне жидкости; объем погруженной части будет, как мы видели,
равным объему сегмента параболоида с высотой-^- («—а‘).
Написанное выше равенство мы можем преобразовать так:
' 3 . 3 3 --=
О .ПЛАВАЮЩИХ ТЕЛАХ
587
Разделив оСе части
I через е. Тогда,
В левой части стоит плотность d плавающего тела по отношению к жидкости; в пра-
3 3 3
вой ~ Ъ будет ось сегмента, а — &----рпредставляет разпостьмежду осью и полу-
торным параметром.
Мы получаем результат, сформулированный в предложении V.
Положение равновесия сегмента параболоида, обращенного вершиной вверх и с вер-
тикально направленной осыо, будет устойчивым, если плотность плавающего тела будет
не больше отношении разности квадратов оси сегмента п избытка оси над полуторным
параметром к’ квадрату осн сегмента.
Доказательство V предложения у Архимеда строится совершенно аналогично дока-
зательству IV; надо только учесть, что прямая ПФ равна Ьх— а*.
Определим область устойчивости равновесия сегмента параболоида при вертикаль-
ном положении осп.
Если ось пе более полуторного параметра, то равновесие будет устойчивым в вер-
тикальном положении, будет ли основание сегмента целиком вне или внутри жидкости.
Если ось более полуторного параметра, то положение устойчивого равновесия зави-
сит и от плотности плавающего тела. Если принять плотность жидкости за единицу, то
плотность тела будет меняться от 0 до 1. Обозначим отношение
если плотность сегмента будет большее, то устойчивым будет вертикальное положение
основанием вверх; если же влотпость будет меньше 1—е, то устойчивым будет положение
равновесия основанием вниз. Можно поставить вопрос: при каких соотношениях b и р
вообще вертикальное положение сегмента будет устойчиво?
1
Если е——, то при устойчивое равновесие будет в положении основанием
вверх, а при d<^e—основанием вниз; при d=e возможны оба положения равновесия.
Если е < — , то вся область изменения d разделяется па три части: первый интервал
будет от 0 до е, второй от е до 1—е и третий от 1—е до 1. В первом интервале устойчи-
вым будем положение основанием вниз, во втором возможны оба положения равновесия,
-в третьем будет устойчивым положение основанием вверх.
1
Если е > — , то интервалы будут от 0 до 1—е, от 1—е до е и от е до 1, причем сред-
нему интервалу не будут
с вертикальной осью.
[9] В предложениях
act, сегмента расположена
всегда будет устойчивым.
Для этой цели нам нужно определить высоту метацентра, иными словами, радиус
кривизны сечения поверхности центров; как мы видели, ата линия будет параболой,
одинаковой с параболой, полученной в сечении параболоида вращения.
Если уравнение этой параболы
ya = 2pz,
то, как мы знаем из математики, радиус кривизны Q в точке, ордината которой равна у,
‘будет
соответствовать никакие возможные положения равновесия
VI—IX Архимед определяет положения равновесия, когда
наклонно. Покажем, что если равновесие возможно, то о«о
с Jpa-H/a)3/a
Р2 '
Рассмотрим положение равновесия, соответствующее случаю, когда основание сег-
мента будет целиком находиться вне поверхности жидкости (рис. 5).
Пусть APOL представляет сечение параболоида плоскостью чертежа, точка О будет
вершиной параболы, О/V — осью ее, точка Л, лежащая на расстоянии ОЙ=-^- ОЛ, будет
•J
588
КОММЕНТАРИИ
центром тяжести всего параболического сегмента. Пусть Л5' представляет сечение поверх-
ности плавания, KZ — параллельная ей касательная к параболе в Р; тогда FP предста-
вит ось погруженного в жидкость сегмента, а точка В, лежащая на расстоянии ВР =-тг PF,
О
будет центром тяжести сегмента ASOP. Точка В — центр тяжести погруженной части —
принадлежит поверхности центров, сечение которой будет параболой, одинаковой с пара-
болой АРОТ.. Прямая ВВ должна быть пер-
пендикулярна к касательной СП в В к этой
параболе, параллельной сечению поверх-
ности плавания ЛЛ; этого требуют условия
равновесия. Равновесие будет устойчивым,
если расстояние ВВ будет меньше высоты,
метацентра или радиуса кривизны параболы
АРОВ, одинаковой с линией центров.
Мы имеем:
KR2= 7?£)8-[..7Ш2.
По ВТ), как субнормаль, равна парамет-
ру Р, й BD—PB представляет ординату у-
точки В касания прямой GH и липин цент-
ров. Таким образом,
ВВ
а высота метацентра
(fl2—рМЛг’тР8
ps
„ jP2
Так как множитель ------
рг
весия обеспечена.
На чертежа видно, что
больше единицы, то о > ВВ, то есть устойчивость равдо-
ОВ >BD-^DE=RD+BP,
или в наших обозначениях
Ь > р-\-а.
что дает геометрически уже выведенное нами условие возможности равновесия при.
наклонном положении осн
Ь—а > р.
Обратимся к случаю, когда ссгмепт
плавает, имея основание целиком погру-
женным в жидкость (рис. б). Пусть при
обозначениях предыдущего чертежа та же
В представляет центр тяжести части сег-
мента SO РА, находящейся над поверхно-
стью AS жидкости, расстояние РВ~-^ PF.
Точка Л, лежащая на расстоянии 0/7 = 6,
будет центром тяжести всего сегмепта, а
точка С представляет центр тяжести по-
груженной части; опа лежит на линии
(параболе) центров ДЛЯ этой последней.
В положении равновесия точки В, В и С
должны лежать на перпендикуляре к ли-
нии плавания Я А и параллельным ей каса-
тельным К Zu СИ. Рассуждения, аналогич-
ные предыдущим, убеждают пас, что BE
есть параметр р параболы АРОВ, a RD —па-
раметр р' параболы центров (действительно,
BD-. BE— ВС". В В=от ношен ню объемов сы
ординату точки касания С прямой Gtl с линией центров погруженной части, то ВС—
О ПЛАВАЮЩИХ ТЕЛАХ
589
=Уу2+р'а, что, очевидно, будет меньше радиуса кривизны д' линии центров в точке С:
(/у2 1- д'2)3
С уа
[10] Предложения VI и VII посвящены определению наибольшей величины Ъ,
.при которой сегмент может плавать так, чтобы его основание вс пересекалось
поверхностью жидкости. При уста-
новлении этого предела Архимед
пользуется леммой, доказательство
которой не сохранилось в дошедшем
до пас тексте. Эта лемма заключает-
ся в следующем.
Пусть через какую-нибудь точ-
ку параболы В проведена секущая
В0 и параллельная ей касатель-
ная ЕЗ, через точку касания К про-
ведена прямая EZ, параллельная
оси, и в какой-нибудь точке Г оси
восставлен перпендикуляр ГА; тогда
отношение EZ: ЕД будет больше
или равно отношению АГ : ГО, где
А есть основание перпендикуляра, рис. 7.
опущенного из точки В на ось
(рис. 7).
П риводим доказательство этой теоремы, данное Хизсом. Из точки касания Е опус-
каем перпендикуляр ЕМ на ось ОЛ; тогда по свойству касательных к параболе будем
.иметь;
МО = 05,
где Е есть точка пересечения касательной ЕЕ с осью.
Нам нужно доказать неравенство
EZ:ЕД > ЛГ:ГО
или
то есть
Имеем:
Е7..Г0 > АГ-ЕЛ,
EZ-ГО —АГ-ЕД >0.
АГ —ОА—ОГ,
ЕД=01’—ОМ.
Таким образом,
EZ ОГ—АГ - ЕД = EZ ОГ—ОА • ОГ — ОМ ОГ+ОГа+О А ОМ=
= 0Г2—ОГ (0А4-0М—EZ)4-OA-OM.
По ОА-}-ОМ=ЕО-|-ОА=ЕЛ, а ЗЛ—EZ=:3A 36 = АО; следовательно,
EZ - ОГ—АГ- ЕД = 0Га—ОГ • АО+ОА • ОМ.
Затем из подобия треугольников ЕМЕ и ВАО имеем:
А0: АВ—М3: ЕМ,
или
Ав;АВ=20М:ЕМ. ’
Но 0М=я, ЕМ = у; если уравнение параболы будет у*=2рх, то АВа=2р-0А,
•а ЕМ2=2р-0М. Возведем обе части нашей пропорции в квадрат:
А08:АВ8=4ОМа:ЕМ®,
АО2 : 2р. ОЛ =4ОМ2 :2р ОМ,
•откуда после сокращений;
А02=4ОЛОМ.
590
КОММЕНТАРИИ
Теперь
Л В®
EZ-ОР—АГ-ЕД=ОГ2—ОГ-Л04---7-—
4
или
EZ ОГ—АГ ЕД = ^ОГ 4Д
что будет или больше нуля при ОГ =/= или же рапным нулю, если ОГ—.
Па основании этой теоремы Архимед находит предельную величину отношения
Ь : р, соответствующую плаванию сегмента, когда поверхность жидкости проходит черев
край основания.
Пусть APOL (рис. 8) — сечвпие сегмента плоскостью чертежа, /15" — поверхность
жидкости, ON — ось параболы. Проведем касательную ИР, параллельную и IP,
параллельную ON; точка / разделит ЛЛ' пополам. Пусть F будет центр тяжести
всего сегмента; при равновесии перпендикуляр FB к касательной должен пройти
через И —центр тяжести погруженной части. Так как HZ есть ордината точки каса-
ния, то FZ представляет параметр р. Имеем.
OF^b, РП=а,
По доказанной лемме мы имеем
PH NZ
PI > ZO •
Берем предельный случай равенства и пе-
реписываем в наших обозначениях
(' ll! =у и NF—
Рис. 8.
откуда
3
-S-а :в
и окончательно
Р=^Ь,
Искомое предельное соотношение можно получить другим путем. В мнения возмож-
ности плавания сегмента в положении, когда поверхность жидкости нс пересекает осно-
вания сегмента, мы вывели неравенство (8) (стр. 585):
Определим максимальную возможную величину правой части; для этого нам придет-
ся искать максимум выражения (1—z)(5z—1). Дифференцируя, находим
5(1—z)— (5z—1) = 0,
6 8
откуда При этом значении z наше произведение будет равно —. Таким образом,.
4 2
правая часть нашего неравенства при всякой плотности жидкости будет больше— i=-?-
. и ми получаем:
Р>^Ь
или
О ПЛАВАЮЩИХ ТЕЛАХ
•591
5 9 6
Так как 7V/'=-rp CW, то ArZ= — ОЛ’, a.ZO= — ON, иными словами, отношение
15 15 10
A’Z : ZO=3 : 2.
Поскольку Р77 : Pl^lVZ: ZO—3 : 2, а расстояние РТ центра тяжести Т погружен-
ной части удовлетворяет пропорции PT : Р1 —3 : 2,то РТ-^РН, иными славами, центр
тяжести Т будет или совпадать с 11 (случай равновесия), или лежать между Н и Р,
то есть сегмент будет всплывать так, что его основание будет над поверхностью воды.
То же самое будет иметь место, когда FZ — p будет больше иными словами,
15
15
когда О/V меньше — />; в этом заключается теорема, сформулированная в предло-
Рис. 9.
GO LМ К С N
жении VI.
Может случиться, что перпендикуляр ZH (СК. на рис. 16, стр. 542) пересечет пара-
болу правее точки касании П, a ix:i, IP погруженной части—в точке И, лежащей правее П
(второй частный случай, отмеченный Архиме-
дом), Тогда перпендикуляр ВР пересечет продол-
жение III в точке Р, лежащей ища правее П,
и очевидно, что центр тяжести В погруженной
части, находящийся левее Р па расстоянии
ТП =Ац], будет и подавно левее нормали ФР,
так что течка А подымется над поверхностью
жидкости. По существу, эти равносильно тому,
что при малых плотностях плавающего тела
наклонпос положение равновесия, ври котором
угол А лежит па поверхности жидкости или
ниже ее, является невозможным.
[И] Предложение VI] доказывается совер-
шенно аналогично; второй упомянутый Архи-
медом случай равносилен тому, что при плот-
ности плаваштсго тела, приближающейся к единице, невозможно положение равнове-
сия, когда верхний, конец основания сегмента будет находиться на поверхности воды
или выше се.
Не представит большого труда найти предельный угол, мри котором тело будет
плавать, касаясь поверхности жидкости лишь одпой точкой основания; для этого тре-
буется определит!, угол наклона оси сегмента к поверхности жидкости при пла-
вании.
Пусть (рис. 9) ОЕВ будет парабола сечения сегмента с осью Ъ, точка С пред-
ставляет центр тяжести сегмента (ОС=Ъ), расстояние СМ равно параметру р, а кривая
3
LDL" представляет параболу плавании; отрезок ED — OL—— а, а точка F— центр
тяжести сегмента ВЕП ) ; через точку F проходит парабола центров. В поло-
жении равновесия CF должна быть нормалью к параболе центров, а параллельная ей пря-
мая DN — нормалью к параболе плавания {1>И — сечение поверхности жидкости).
Прямую LK — абсциссу точки касания — обозначим через х. Так как KN — CM — пара-
метру р, то, обозначая угол KDN череп q>, можно написать:
t KN p ^4—KD—y-
II о так же t KD у ^-CK^GK- ’
Отсюда
. ... p
Ho GK—2LK, a
LK^ON—KN—OL=OC \-FD—KN — OL= F —T a—b—p—a.
• - -
592
КОММЕНТАРИИ
Таким образом, окончательно
tg * *₽ — у 2(6—р—и) ’
(Н)
Эта формула даст величину .угла наклона оси, при котором сегмент будет плавать
с основанием, находящимся вне Поверхности жидкости. Она одинаково применима и к слу-
чаю, когда сегмент плавает, будучи погружен основанием в жидкость; только в этом слу-
чае под а нужно подразумевать две трети оси сегмента, находящегося над поверхностью
жидкости.
Предельная величина угла наклона оси к поверхности жидкости при плавании сет-
мента, когда основание его касчется поверхности жидкости только в одной точке, опре-
делится очень просто. Мы имеем:
*вФ=-~
Но мы видели выше (стр. 584), что наибольшая величина ординаты р, соответ-
ствующая плаванию в указанном положении, равна
У=/¥ (/б-/а).
Следовательно,
1g «йпто — , —-7^г- •
3(|/ 6— а)
[12] В предложениях VIII и IX Архимед определяет величину тангенса угла пла-
вания.
Для возможности: плавания в наклонном положении: необходимо неравенство
Ь—а~> р, или а<6— р.
п , °2
Плотность d плавающего тела по отношению к жидкости равна , но
а
3
(Ь-Р)2
6®
2
•2
3
или, поскольку ось сегмепта ОЛ'=—6:
3
оЛ“2
Необходимое построение на оси Архимед производит отдельно. Отрезок PD—O/V
представляет ось сегмента, К — центр его тижести, КР — параметр р, отрезок TD=
3 3
=— р *); тогда отрезок BT—OJV —~р представит линию, стоящую в числителе пра-
вой части неравенства для d. 'Гак как плотность тела относительно жидкости d опреде-
ляется формулой
2
(Ф4-Х)2
“ ОЛ'2
ОЛ'2
и ВТ—^г ВР, то отсюда следует, что Ф<^ВР. Архимед полагает Ф равной отрезку РЧ?;
это будет наше а.
3 3
*) Это нетрудно получить из следующих соображений. Если 117’=—ВР= — (BD—KD—КР)=
2> 2
= 5 (0>V——j---КР)=ОЛ—К'Р, то Tf)=BD—ВТ, естественно, будет равняться ^КР. Точку Т
проще получить, исходя из точки В, при помощи вычитания полуторного параметра КР.
О ПЛАВАЮЩИХ ТЕЛАХ
593.
Затем Архимед стрсшт угол ф по формуле
1 11
уКРВЧ' i/CP Ip
to2 ф=-ДД-—.—£---—=—f_____________f______
Ь * и1уг в^а ВР—РФ (Ь—р)—а *
После этого Архимеду остается лишь доказать, что при таком угле наклона равно-
весие будет иметь место и что оно будет устойчивым. Он достигает обеих целей, доказы-
вая, что равновесие не может иметь места пи при больших, ни при меггылих значениях
угла наклона. Его доказательство сводится к тому, что центр тяжести Z погруженной
части пе может лежать ни правее, ни левее перпендикуляра ГН, опущенного из центра
тяжести Г па касательную ИГ, параллельную поверхности жидкости SZ.
113] Предложение IX является аналогичным предложениям V и VII; в нем также
фигурирует предельная величина плотности
(3 \2
<W—J р)
ол» ~
с той только разницей, что теперь плотность плавающего тела должна .быть не меньше,
а больше этой величины:
d>
3 \2
ON3 — {ON—~ р j
В соответствии с этим произойдут некоторые изменения в формулировке теоремы.
Так как теперь плотность плавающего тала предполагается равной
то иен», что Ф представляет, как и выше, длину я, соответствующую двум третям оси
сегмента, выступающего пад поверхностью жидкости. Если вести рассуждения примени-
тельно к этому сегменту, то все доказательство будет развиваться аналогично доказатель-
ству предложении VIII.
[14] Обширное предложение X рассматривает положения равновесия при
4
параметре р, меньшем оси сегмента,— значении, при котором еще возможно плава-
ние с оснотшиисм, касающимся поверхности жидкости л одной точке. В этом случае
в зависимости от плотности плавающего тела возможны следующие шесть положений
равновесия, обозначенных в пашем переводе Архимеда цифрами:
(1) Ось сегмента стоит вертикалыю.
(2) Ось сегмента наклонна; основание вне поверхности жидкости.
(3) То же; основание пне поверхности жидкости, касается последнем в одной точке.
(4) То же, основание рассекается поверхностью жидкости.
(5) То же; основание вне жидкости н касается поверхности последней в одной точке:
(в) То же; основание целиком вне жидкости.
[15] Для понимания дальнейшего важно представить собе физический смысл обо-
значений рис. 22 текста (стр. 348). Точка К представляет центр тяжести сегмента АОВА
4
(ВК—2КД); прямая КТ, равная ВД, представляет наибольшую величину параметра р.
Если положить ВД — 15, ДК.=5 я КТ=4, то ТВ будет равна 6; иными словами,
ВТ—-~ВД. Точка S получается при помощи построении BS —В1‘; отрезок 2Д=-
=ВД—вх=у (ВК—ВР)
4уКР или полуторному параметру р. Таким образом, BZ
представляет величину — (1 -р), входящую в выражение
если птношение
38 Архимед
594
КОММЕНТАРИИ
плотностей сегмента и жндкостг-г больше этого значения, то возможно плавание сегмен-
та п вертикальном положении (случай 1). Параболы Л0А и AEI представляют некоторую
аналогию с современными параболами плавания (сечений) и центров; одпако не нужно
забывать, что точка А предполагается лежащей па повврхпостя жидкости и проведенные
через псе прямые ЛЛ, ЛХ и другие представляют основания сегментов, обт.емм которых,
будучи наполнены жидкостью, могут уравновесить вес плавающего сегмента нри раз-
личных величинах отношений плотностей сегмента и жидкости.
Так как параметр р — КР меньше КТ, то проведенная через Р горизонталь пере-
сечет параболу центров в двух точках 1’ и У; проведенные через них вертикали опреде-
ляют в пересечении с параболой плавания точки 2 н Ф, а с параболой АНОЛ точки (г
и П. Прямые АХ и ЛФ (последняя на рис. 22 пе проведена) определят соответствующие
сечения сегмента поверхностью жидкости; точки О и 1'1 будут верншпами погруженных
сегментов АОХ и 11АФ, а проведенные в них касательные OQ н 1.1¥ определят соот-
ветствующие равновесию углы наклона (случаи 3 и 5).
Идея определения положений равновесии сегмента очень проста: отношение и
плотностей сегмента и жидкости Архимед выражает в виде квадрата отношения некоторой
примой ¥ к оси сегмента ВЛ н определенную таким образом прямую вставляет между
параболами ЛПОЛ и ЛОЛ, Если Чг будет больше BS, то, согласно теореме IV, сегмел'|
будет плавать в вертикальном положении (случая 1); если ¥ равняется ОГ или ПФ, то
сегмент будет плавать, имен одну точку (Л) ла поверхности жидкости (случаи 3 и 5).
Остальные три случая будут соответствовать таким значениям ¥: . ..
мучай 2: В2>¥>ОГ,
случай 4: ОГ > ¥ > ПФ,
случай 6; НФ > ¥.
Доказательство во всех случаях производится обычным для Архимеда методом — иссл<-
довапием действия приложенных к сегменту сил.
(1(5] Текст Архимеда для последних трех случаен не является вполне сохранив
шимсн. Прежде всего это отражается па порядке изложения; после 3-го случая разби-
рается не 4-й, а 6-й; кроме того, не все обстоит в порядке и па чертежах. Тик па рис. 28
точка Г, а с пей н вся прямая MX, должны быть передвинуты так, чтобы Г попала в пе-
ресечение прямой 5Р с параболой центров. Равным образом прямая N0 должна
быть сдвинута влево так, чтобы она претила через точку пересечения прямой HP с па-
раболой цонтроп; тогда опа будет соответствовать прямой 11Ф рис. 22 и рассматрива-
емая прямая ГП окажется левее ПФ. В таком случае угол Ф рис. 28 соответствует
углу ¥ рис. 22.
Доказательство Архимеда сводится к тому, что теперь угол й оси сегмента с поверх-
ностью жидкости будет меньше предельного угла ¥ рис. 22.
Рис. 28 относится и к изложению случая 5, где встречается та же прямая 6N, соот-
ветствующая ПФ рис. 22.
117] Последним разбирается случай 4, соответствующий такому положению пла-
вающего тела, при котором основание сегмента разрезается поверхностью жидкости. Для
того чтобы это имело место, необходимо, чтобы плотность плавающего тела была болыш,-
отношения (ФП : ВА)2, по меньше чем (0=-: ВА)2, если пользоваться обозначениями
рис. 22 текста. В таком случае между параболами АЙД и АВА придется вставлять пря-
мую, меньшую 05, но большую чем 11Ф. Доказательство Архимеда сводится к тому,
что сегмент не может находиться в равновесии ни тогда, когда его основание находится
вне жидкости (рис. 32 текста), пи когда его основание только в одной точке касается
поверхности жидкости (рис. 33), по должен наклониться еще более так, что угол его оси
с горизонтом будет меньше предельного угла </ рис. 22.
(18] В зависимости от плотности плавающего тела Архимед устанавливает две
области, в которых возможно плавание тела с основанием, находящимся вне жидкости.
Физически объяснить появление этих областей можно таким образом.
Начнем со случая, когда плотность тела, или, лучше сказать, ваша величина л,
3
2*
или
a — длина оси вегмепта погруженной части тела, будет равпа пулю; тогда тело
будет просто лежать на поверхности жидкости, причем ось его будет образовывать
с горизонтом-угол ср, тангенс которого мы получим, положив «—О в общи) формуле
7»
2(Ь—р—«)
Если мы будем увеличивать плотность тела, или величину а, то тело начнет погру-
жаться в жидкость н одновременно увеличивать угол наклона своей оси с горизонтом.-.
В первую очередь увеличение объема погруженной части пойдет за счет погружения сег-
мента и приближения поверхности жидкости к нижнему углу основания; это будет про-
o' ПЛАВАЮЩИХ ТЕЛАХ
595
исходить до тех пор пока угол ср, определяемый ио вышеприведенной формуле, не сде-
лается равным минимальному углу фга1п> которым удовлетворяет формуле
дометим, что этот угол томе возрастает г, увеличением а. Дальнейшее увеличение плот-
ности тела повлечет за собой увеличение затопления основания и увеличение угла ф.
Затопление основания пс будет продолжаться беспредельно, но после достижения некото-
рой максимальной величины будет уменьшаться вследствие увеличении угла наклона
оси до тех пор, пока нижний угол основания не покажется па поверхности жидкости;
после этого увеличение объема погруженной части будет происходить исключительно до
счет увеличения угла наклона оси - - мы по.:;учим вторую область плавания тела с осно-
ванием вне поверхности жидкости. Это будет продолжаться до тех пор, пока а нс сделает-
ся равным 1>--р\ п этот момент тело станет отвесно; при дальнейшем увеличении а тело
будет просто погружаться в жидкость, причем ось остается псе время вертикальной.
Когда а сравняется с Ь, то есть плотность тела сделается равной плотности жидкости,
то плоскость основания опить совпадет с поверхностью жидкости.
После предложения X в переводе Мербеке стоит; «Archimeilis de insidentibus in
humido liber sccundus explicit» — «Кончается вторам книга Архимеда о телах, плаваю-
щих в жидкости». Также па этом кончается греческий текст Константинопольского
палимпсеста.
Мы ожидали бы, что после предложении X последует аналогичный разбор поло-
жений рашювссия при плавании сегмента с полностью погруженным основанием, как это
сделано п предложениях II J, V, VII, JX сохранившегося текста. Это обстоитслг.стло,
а также и необычный характер изложения предложении X, по существу объединяющего
минимум пять самостоятельных теорем, позволяет думать, что рассматриваемое про-
изведение Архимеда но было им закопчено и, может быть, является самым последним
его сочинением. Оно представляет высшую точку линии развития, которая началась
в «Коноидах и сфероидах» и продолжалась в «Эфоде», В трактате «О плавающих телах»
Архимед далеко обогнал свою эпоху. Об этом свидетельствует полное отсутствие в сохра-
нившейся античной литературе сведений об этом сочинении Архимеда, если но считать
короткого упоминания во введении к восьмой книге «Математического собрания» Паппа
Александрийского, где механик Карп Антиохийский говорит о нем как о «математиче-
ской игрушке». Не лучше обстояло дело и йо время наивысшего развития культуры исла-
ма, как можно видеть из сохранившегося арабского изложения трактата Архимеда,
которое мы приводим ниже.
К и и г а Л р х п м е д а о т я ж е с т и и л о г к о с т и
Некоторые тела и жидкости тяжелее других. О теле говорят, что
оно тяжелее (другого) тела, или о жидкости говорят, что она тяжелее
другой жидкости, или же о теле говорят, что оно тяжелее жидкости,
если, когда берут их количества одинакового объема, а затем взвешивают,
то одно окаяьшается тяжелее другого (то ость вес одного больше веса
другого). Если их вес одинаков, то не говорят, что одно из пих тяжелее
другого. То, о чем говорят, что оно тяжелее,— большее по весу.
Мы полагаем, что природа жидкости такова,, что се смежные час-
тицы гладкие; поэтому то, что давит больше, вытесняет то, что давит
меньше. На всякую частицу жидкости давит то, что находится верти-
кально над пен, если только жидкость не заперта в чем-нибудь, что
заставляет ее частицы давить на другие предметы. Всякая стоячая
жидкость не движется и со форма — форма шара.
Если некоторое тело равно по весу некоторой жидкости и бро-
сить тело в эту жидкость, то оно погрузится в ное только до тех пор,
пока его поверхность не сравняется с поверхностью жидкости. Если
же некоторое тело легче некоторой жидкости и бросить тело в эту жид-
кость, то оно не погрузится в нее целиком и часть его выступит над
повер хпостью жидко сти.
.38*
596
КОММЕНТАРИИ
Если некоторое тело легче некоторой жидкости и бросить его в эту
жидкость, так что погрузится только часть его, и если взять некоторое
количество жидкости, равное по объему том части (тела), которая погру-
жена в нее, то оказывается, что вес этого количества жидкости равен
весу этого тела.
Если некоторое тело легче некоторой жидкости и утопить его в этой
жидкости, то оно будет подниматься с силой, равной силе избытка веса
количества жидкости, равного по объему этому телу, над весом этого
тела.
Если некоторое тело тяжелее некоторой жидкости и бросить его
в эту жидкость, то его вес в жидкости равен избытку веса тела над
весом количества жидкости, равного по объему этому телу.
Если тело легче жидкости и имеет форму сегмента шара и бросить
тело в эту жидкость, то оно всплывет, причем его основание не сопри-
коснется с жидкостью и тело будет стоять прямо, так что ось сегмента
круга будет вертикальной, а если ее наклонить, то после соприкоснове-
ния основания (сегмента шара) с жидкостью ось не останется наклон-
ной, а напротив, возвратится к прямому положению.
Если некоторое тело легче некоторой жидкости и бросить тело
в эту жидкость, то вес этого тела будет относиться к весу количества
жидкости, равного но объему этому телу, как вес части этого тела,
погруженной в жидкость, к весу всего этого тела.
Книга Архимеда окончена*).
Манускрипт дает изложение первой книги «О плавающих телах» вместе с первым
предложением второй книги. Весь конец последней, относящийся к сегменту параболоида
вращения, выпущен; удивляться этому ие приходится, поскольку «Коноиды» остались
арабам иепзвссгиг.гми.
В Западной ГСврэпс трактат «О плавающих телах» по явился в XIII веке в переводе
Вильгельма in Мербеке, использованном также в изданиях Луки Гаврика и Тартальи.
Вопрос о том, насколько они понимали это произведение, лучше оставить открытым.
Впсрлые зто «оиимание мы встречаем во второй ио.-П'ягигге XVI лека у Федериго Иомшш-
дипо (1503 —1575) в ого латинском издании Архимеда, где он сделал попытку восстано-
вить места, недостающее в переводе Мербеке; как стало видно в дальнейшем, реставра-
ции Коммапдипо оказалась правильной. Полное понимание мы встречаем у Христиана
Гюйгенса, одно из юношеских произведений которого, увидевшее свет только в конце
Х1Х века в национальном издании его сочинений, было посвящено определению поло-
жения равновесия плавающего параллелепипеда. Продолжателями Гюйгенса в XVIII ве-
ке оказались авторы теории корабля Буге и Эйлер, а в XIX — Дюпен во Франции и про-
фессор Московского университета А. 10. Давидов, давшие полное теоретическое реше-
ние рассматриваемого вопроса. Мы уже имели возможность видеть, насколько близко
оказалась современная теория к методике Архимеда при определении плавания сегмента
параболоида
Было бы, однако, неправильным доводить модерлизацшо до полного отождествле-
ния обеих мегодик — Архимеда и современной. Основное различие между математикой
Архимеда и современной заключается п том, что мы стремимся получить наиболее общее
решение вопроса, нее же произведения Архимеда представляют решения частных задач.
Правда, эти решения настолько гениальны, что Архимеда можно .назвать родоначальни-
ком классической математики XVII и XVIII воков, но том не мепое попыток создания
общих теорий мы у Архимеда почти по замечаем. 'Гак в трактате «О плавающих телах»
обе задачи на равновесие сегментов шара и параболоида решаются совершенно незави-
симыми друг от Друга методами. В предложении П второй книги Архимед близко под-
ходит к понятию метацентра (но существу, ому осталось сделать только предельный
мореход), по примененный им физический метод определения устойчивости полностью
исключает мысль о возможности его применения. Одна из парабол Архимеда очень
близка к современной поверхности сечений; однако возможность использования Лрхи-
*) Книга Архимеда о тяжести и легкости (Макала ли Лршимияис Фи-л-сикл ва-л-уиффа)
перевецепа с рукописи 2457/4 (листы 22 об.—23) Парижской Папионалытой библиотеки. Микрофильм
втой рукописи был прислан г-жой И. Мейер-Шагал. Перевод произведен Б. А. Розенфельдом при
консультации М. А. Салке.
О ПЛАВАЮЩИХ ТЕЛАХ
597
медом настоящей поверхности сечений является исключспиой хоти бы ио той причине,
что Архимед нс был в состоянии построить сс полностью (в случаях плавания с полу-
затопленным основанием), а для греческой математики суш,сствующими считались только
тс образы, которые так или иначе могли быть построены.
Вышесказанное является справедливым пе только для рассматриваемого произве-
дения. В посланиях к Досифею Архимед занимался задачами, которые в настоящее время
решаются при помощи интегрального исчисления, но тем нс менее общего понятия об
интеграле у пего не было; определение площадей сегмента параболы и объема парабо-
лоида вращения, с пашей точки зрения, могут быть сведены к вычислению одного и того
же интеграла, но Архимед решает их совершения пкигпяеммыми друг от друга методами.
Архимеду два раза пришлось решать задачу иа максимум и минимум — в предложениях
IV и IX второй книги «Ошаре и цилиндре» и в предложении VI второй книги «О плава-
ющих телах», по примененные им методы в сохраненном Евгением тексте решения и при
нахождении предельной величины отношении параметра параболы сечения сегмента него
оси («О плавающих телах», II, 6) нс имеют друг с другом ничего общего. В трактате «О спи-
ралях» Архимед определяет касательную методом, который, по существу, одинаков
е робервалсвским методом сложении скоростей, по только у Робервалл метод мог быть
применен ко многим кривым, а у Архимеда только к специально построенной кривой.
Однако все ото показывает только, что Архимед, несмотря па всю свою гениальность,
псе же был греческим математиком, а разница между греческой и современной математи-
кой может быть охарактеризована следующим замечанием. Ла жалобы царя Птолемея
по поводу трудности геометрии Евклид отвечал, что в геометрии царской дороги не суще-
ствует. После открытки анализа бесконечно малых Лейбниц писал;
*Мы открыли ту царскую дорогу, на отсутствие которой жаловался Птолемей».
ПСАММИТ
Слово «псаммит» (фарр-тт]? от i|:ajipog — песок) ле имеет на русском языке себе адэ
«ватного; передать его еловом «песочник» значило бы просто выдумать новое слово.
Поэтому обычно принято переводить его по содержанию книги «Исчисление песчинок».
Рассматриваемое сочинение является одним из самых поздних в ряду известных
нам сочинений Архимеда. Оно написано после «Измерении круга», по до смерти Гелопа
(216 г. до п. э.) — сына и соправителя сиракузского царя Гмерона.
Особенностями этого сочинения, поставившего своей целью определить число пес-
чинок в объеме шара, являются астрономическое содержание и арифметический харак-
тер — создание нумерации для очень больших чисел. Обе эти отличительные черты тесно
связаны между собой. Передача па Запад достижений вавилонской вычислительной
астрономии, находившейся в III веке до и. э. в апогее своего развития, поставила вопрос
о способах изображения больших чисел, для чего существующая греческая нумерация
была абсолютно не приспособлена. Способу изображения таких чисел посвящепо пе дошед-
шее до пас послание к Зевксиппу, о котором упоминается в тексте «Псаммита». Около
того ate времени другой большой математик Аполлоний Пергский написал «Быстросчет»
(Qkvtoxiov — точнее «сродство для быстрого разрешении от бремени»), в котором ой
излагал новую систему счисления больших чисел и правила действий с ними; возможно,
что результатом полемики Архимеда с Лио.тлонием или, как думают некоторые, с Эрато-
сфеном было появление «Задачи о быках», принадлежность которой Архимеду очень
вероятна.
В тесной связи с астрономией лежит еще одна особенность этого произведения —
употребление отношений между углами и прямыми линиями; вместе с дошедшим до пас
сочинением Аристарха «О величинах и расстояниях Солпца и Луны» рассматриваемая
книга Архимеда является своего роди предтечей греческой тригонометрии, пад которой
в дальнейшем работал ряд астрономов, начиная с Гиппарха.
[1] Упоминаемый здесь Аристарх Самосский, творец первой гелиоцентрическом
системы мира — «Коперник античного мира» — был знаменитым греческим астрономом
первой половины III века до н. э. До нас дошло только одно сочинение Аристарха
«О величин о и расстояниях Солнца и Луны», в котором имеются данные о сравнитель-
ных величинах диаметров и расстояний Солнца и Луны. В этом сочинении Аристарх
еще стоит на почве геоцентрической теории строения солнечной системы. Указание
Архимеда на то, что, по мнению Аристарха, орбита Земли относится к сфере неподвиж-
ных звезд, как центр к окружности, вернее всего было бы понимать в том смысле, что
Аристарх считал мир бесконечным; Архимед несколько извращает его мысль, по всей
вероятности стой целью, чтобы сделать теорию Аристарха доступной для математических
вычислении, хотя и с очень большими, но все же конечными числами.
1'2) Так как величина греческой стадии составляет около 150 метров, то 3 000 000
стадий будут равняться примерно 430 тысячам километров, что примерно и десять раз
больше истинной длины земного экватора, составляющей только 40 228 км.
[3] В действительности диаметр Солнца в 109 раз больше диаметра Земли и в 436 раз
больше диаметра Лупы.
[4] Сторона правильного тысячсугольпика соответствует центральному углу
в 0,36°, то есть равна 21'6". Истинная величина видимого диаметра Солнца колеблется
между 31'28" (в апогее) и 32'37" (в нернгес). Аристарх считал видимый диаметр Солнца
равным 30'.
[5 J Мы имеем здесь очень редкий в сохранившейся литературе греков пример экспе-
риментального определения физической величины, сопровождающегося поправкой на
неточность наблюдения (Архимед принимает в расчет величину зрачка).
Как следует из комментируемого текста, а также из сохранившихся фрагментов
«Катоптрики», Архимед рассматривал процесс зрения как совершающийся при помощи
выходящих из глаза и как бы ощупывающих наблюдаемый предмет лучей зрения. Теория
ПСАММИТ ;
59V
)С0 опыта по различному толковалась комментаторами; следующее описание, по-види-
мому, будет наиболее соответствующим действительности.
Архимед наблюдает Солнце вблизи горизонта, когда на пего можно смотреть гла-
нами. Он берет горизонтальную линейку, обращай последнюю к восходящему Солпцу.
На эту пластинку он помещает круглый цилиндр (слово ытОь£ - • прямой — в тексте -
гюэполпет думать, что этот пнлипдр ставился портика;!г,по, хотя некоторые «оммелтаторы.
Данная Рнпо реконструкция прибора Архимеда для определения
диаметра Солнца.
ншрпмер второй издатель Архимеда француз Рино, полагают, что цилиндр был положен
па Липецку горизонтально); затем, поместив глия у конца линейки, он передвигает
цилиндр до тех пор, пока последний не закроет диск Солнца (но мнению Рино, Солнце
за к рыпается не боковой поверхностью, по круглым основанием цилиндра); в этом поло-
жении он измеряет угол между прямыми, идущими от глаза к цилиндру и касающимися
его боковых сторон (рис. J); полученная пелнчипа дает верхний предел значения угла,
под которым видимо Солнце.
Архимед янаот, что найденная величина угла будет больше истинной вследствие
того, что па самом деле крайние зрительные лучи выходили ке из одной и той «кв точки
глаза, ио из двух различных точек, находившихся по краям горизонтального диаметра
>рачда; можно было бы получить более точное значение угла видимости Солнца, если
учесть, что на самом деде вершина угла ц является не точкой, но некоторым диском,
диаметр которого равняется горизонтальному диаметру зрачка, как это покапано па рис. 2;
если вставить этот диск па место, занимаемое глазом, и найти угол 0 между крайними
лучами, соединяющими кран цилиндра и зрачка, то этот угол 0 даст нижний предел для
угла видимости Солпца.
Таким образом, дело сводится к тому, чтобы определить диаметр зрачка. Для этой
цели Архимед делает следующее.' считая, что если лучи выходят из глаза параллельным
пучком, то ширина пучка лучей будет равна горизонтальному диаметру зрачка; оц устраи-
вает так, чтобы параллельность зрительных лучей была обеспечена. Для этой цели он
берет два тонких цилиндра одинакового диаметра (рис. 3); если последний равен диа-
метру зрачка, то зрительные лучи идут параллельным пучком и задний цилиндр будет
600
КОММЕНТАРИИ
полностью заслонен передним (рис. 3 вверху); если же диаметр цилиндров меньше диа-
метра зрачка, то лучи от зрачка пойдут сходящимся пучком и задним цилиндр будет или
полностью виден (рис. 3 внизу), или лишь отчасти заслонен передним (рис. 3 н ссрсдипе).
Таким образом, задача состоит в том, чтобы найти два одинаковых цилиндра такой тол-
щины, чтобы задний полностью заслонялся перед-
ним, если последний приставлен к самому глазу.
Наименьшая толщина цилиндров, вызывающая
такое явление, и даст размеры горизонтального
диаметра зрачка.
|61 В результате поставленных опытов Архи
мед пашел следующие значения углов;
верхний предел а
1
164
rf=32'55".5.
нижний предел р
1
2Й0 rf=27'-
Истинпая величина видимого диаметра Солнца
колеблется между 31'28" и 32'37", то есть в сред-
нем 32'; таким образом, верхний предел, полученный
Архимедом, достаточно близко подходит к истинно-
му. Коперник считал видимый диаметр» Солпца рав
ими 31'48".
[7| Диаметр Земли меньше диаметра Солнца. Такого мнения держались большин-
ство астрономов :>иохи Архимеда. Мы находим его у Аристарха Самосского; вероятно,
зто обстоятельство и было причиной принятия последним гелиоцентрической теории.
По-видимому, впервые стал держаться итого мне-
ния знаменитым математик Евдокс Книдский
(середина IV века до н. а.). Такое представле-
ние поручилось из наблюдений над затмениями;
диаметр зампой топи на расстоянии орбиты Зем-
ли меньше» диаметра Земли, что может получить-
ся лишь в том случае, если диаметр Солпца боль-
ше диаметра Земли. Если известны отношения
расстояний Луны и Солнца от центра Земли, ви-
димые диаметры Солпца и Лупы и видимый диа-
метр земной тени на расстоянии орбиты Лупы
(он может быть установлен по времени продол-
жительности луппого затмения), то могут быть
определены и отношения истиппых величин
диаметров Солнца, Земли, Луны и земной тспи
на расстоянии лунной орбиты.
[81 Архимед рассматривает прямоугольные треугольники ©КР и АКТ, у которых
катеты К.Р и КТ одинаковы, а гипотенуза ©К больше, чем АТ, и следовательно, из остаю-
щихся катетов 0Р бо.чыпе, чем АТ. Он хочет показать, что отношение угла КАТ (поло
В1ша измеренного утла видимости Солпца) к углу КвР (половина угла видимости Солнца
яз центра Земли) будет заключаться-между отношениями ©К : АК и <-)Р : АТ
©К Z ТАК ©Р
АК < Z К©Р < ДТ
Если перепишем :>то соотношеппе в виде
АК. Z КЙР ДТ
©К > Z ТАК " 0Р ’
АК ВК Z K0P AT . ©Р
КТ ’ КР~> Z ТАК > КТ ' КР
(отрезки КТ и КР равны, как радиусы), то неравенство будет равносильно следующему:
sin КОР Z КОР LgKBl’
sin ТАК > Z ТАК > 1g ТАК *
Для пас -чти неравенства являются простым выражением факта, что угол растет быстрее
своего синуса, но медленнее своего тангенса.
ПСАММИТ
601
Дли Архимеда эти псравенстиа вытекали из следующей теоремы.
Если, у двух прямоугольных треугольников имеются одинаковые «горизонтальные»
катеты и неравные «вертикальные», то больший из углов, прилежащих к неравным кате-
том, имеет я меньшему отношение, большее соотношения соответствующих еипоте-
нуз, но меньшее отношения соответствующих катетов.
Эту теорему Архимед сообщает без доказательства, считая //оследнее, очевидно,
общеизвестным. Приводим доказательство этой теоремы, помещенное в сочинениях Архи-
меда, изданных в 1615 г. учителем Людовика XJI1 французом
Давидом 1’ипо в его издании трудов Архимеда.
«Пуглъ будут треугольники АВС и BDC с прямым углом
при D, построенные па одном и том же катете DC, и имеющие
неравные катеты AD и BD, причем AD > BD’, в таком случае
и гипотенуза АС будет больше: гипотенузы ВС.
Архимед утверждает, что больший угол DBC будет иметь
к меньшему углу Л отношение, которое больше отношения
АС-. СИ, ио меньше отношения AD-.BD.
Параллельно АП проводим прямую CG-, откладываем
СЕ=ВС и этим радиусом из центра С описываем дугу ВИР.
Затем точки В и Е соединяем прямом ВЕС, пересекающей ли-
нию CG в точке С, лежащей вис окружности ВЕЕ. Далее из
точки В проводим прямую ВП, параллельную АС, и из центра В
радиусом BLL описываем дугу JHK. Так как сторона ВП более
BL), то эта окружность пройдет пне треугольника ВИП, но рас-
сечет треугольник ВНС, так как лежащая против тупого угла
ВИС сторона ВС будит более ВП.
В треугольниках А ЕВ и С EG равны углы при Е, также
угол Л равен ACG, как внутренние накрест лежащие, а следо-
вательно, равны и остальные; значит, стороны этих треугольников пропорциональны
Рис. 5.
BE GE
ЕА ~ ЕС ’
после нерестанопки
BE _ АЕ
EG ~ ЕС ’
откуда «присоединением»
BE-\-EG АЕ+ЕС BG АС
EG ~~ ЕС ’ то ость EG ЕС '
Но отношение BG к EG будет равно отпошентгю треугольников BGC и ECG', следова-
тельно, так же. будет относиться сторона АС к стороне ЕС или к рапной ей стороне ВС-.
АС : СС^Тр-к ВСС : 'Гр-к ECG.
По сектор ВСЕ содержит треугольник ВСЕ, так как ирпмаи BE пересекает круг; следо-
вательно, сектор ВСЕ к треугольнику ECG имеет большее отношение, чем треугольник
ВЕС к тому же треугольнику ECG
тр-к ЕСС tj>-k ECG
Ио сектор ИСЕ к сектору EFG имеет отношение большее, чем к треугольнику EGC
сект. ВСЕ сект. ВСЕ
сект. EEC ' тр-к ECG
Следовательно, отношение сектора ВЕС к сектору ECF будет больше, чем отношение тре-
угольников ВЕС и ECG
сект. ВСЕ тр-к ВЕС
сект. ЕСЕ тр-к ЕСС
Отсюда «присоединением»
сект. ВС Я+сект. ECF „ тр-к АА’С+тр-к ECG
. - сект. ЕСЕ тр-к ECG
602
КОММЕНТАРИИ
то есть весь сектор BCF к сектору ECF имеет большее отношение, чем треугольник BCG
к треугольнику ECG
сект. ВС F тр-к BCG "
сект. ЕСЕ тр-к ECG ’
и это влачит, что отношение углов BCF и ЕСЕ будет больше отношений линий /«,’ к ЕС
или АС к ВС, как показано выше
угол BCF АС ' ' ‘
угол ECF ВС
Но угол BCF равеп углу DBC, а угол ECF ранен углу /1; следовательно, угол DBC
к углу НАС имеет большее отношение, чем большая гипотенуза АС к меньшей ВС.
Вторая половина предложения устанавливается следующим образом. 'Треуголь-
ник ВПС имеет к треугольнику BDH отношение большее, чем сектор ВПК к тому же
треугольнику
тр-к ВНС сект. ВПК
J . тр-к BDH > tp-к ВВП '
Но этот сектор к сектору BJH имеет мепыпес отношение, чем к треугольнику HDH
сект. ВНК
сект. BJTI
сект. ВПК
тр-к BDH
Следопательпо, треугольник ВИС к треугольнику ВВП имеет большее отношение, чем
сектор ВПК к сектору BJH
тр-к ВНС сект. ВНК
тр-к В Dll сект. BJH
И после «присоединения»
тр-к ВНС-1-тр-к ВВН .. сект. /?/771-|-сект. BJH
тр-к BDH сект. BJII
получается, что весь треугольник BDC и своей части BDH, то есть ВС к ВН, или AD
к BD (вследствие подобия треугольников ДОС и BDU, обусловленного параллельно-
стью ВН основанию АС), будет иметь большее отношение, чем сектор JBK к сектору JBH
или угол DBH к углу DAC
тр-к ВВС ВС _ AD сект. JBK __ A DBH
тр-к BDH‘—~tXH'~~ВО‘> сект.ЛйГ '' T'DAC~ ’
как и было предложено
Z DBH AD
Z. DAU BD ’
«[9] Рассуждения, изложенные в конце этой главы, позволяют лам составить пеко
торос представление об астрономических работах Архимеда. Непосредственный предше-
ственник Архимеда Аристарх Самосским при определении расстояний Солпца и Лупы
от Земли считал иоеледтою точкой, Архимед же, выражаясь современным языком, про-
водит свои наблюдения к центру Земли, иными словами, имеет понятие о том, что мы
теперь называем параллаксом. Обычно считают, что введение п астрономические расчеты
пара л .такса было сделано знаменитым астрономом Гипиархпм приблизительно через
пятьдесят .тот после смерти Архимеда».
{101 Архимедова нумерация чисел такова:
Все числа от 1 до 10s, кроме последнего, называются первыми *), число ;кс 10“ назы-
вается единицей вторых чисел; числа от 10“ до 10s'2, кроме последнего, называются вто-
рыми**), число же 10s'2— единицей третьих чисел, числа от 10й’2 до 10й’л, кроме
последнего, называются трвтымш, число же 10s'3—единицей четвертых чисел и
т. д.; числа от ю8‘(108—О до Ю8’10 , щюме последнего, называются мириа&о-мириад-
пыми.
•) Или числами nepaoil октады. поскольку числа 1, 10. 10s, 103. 10*. 10®. 10®. t О7'образуют' .
первую «октаду» в бесконечной непрерывной пропорции
I ; ю : 10®: 10s : 10* : 10s : 10® : 107 : 10” ...
*») Или числами второй октады (108> 10®, 101и, .... 10й).
ПСАММИТ
ЮЗ
Все яышеуказанные числа составляют б совокупности первый период. Но такой же
схеме строятся первые, вторые и т. д. чпсла.торого периода, только б качестве исходном
единицы для второго периода борется число Я=10®’101!; все числа от Л до Л-108, кроме
последи ею, называются первыми числами второго периода, число яке Л -10“ - - единицей
вторых чисел этого периода, числа от Л-10к до Л-108’3, кроме последнего, называются
чторыми числами старого периода, число же А-10"’8— единицей третьих чисел этого
периода и т. д.; числа от А-ю8 <* °*—1) д0 Кр0МС последнего, называются мириадо-
мириадными числами второго периода, число же А- берется в качестве основной единицы
для построения чисел третьего периода от А2 до Л5, причем А' берется единицей для
чисел четвертого периода и т. д. и т. д.
Архимед доводит это построение до мириадо-мириадного периода, единицей ко-
торого служит число А10Я_|, и заканчивает [ свою классификацию числом А1 °8—
= 10®' ,8®,|88=е40®'*®1Л. Впрочем, для решения той конкретной задачи, которую ста-
илт собе Архимед в рассматриваемом сочинении, ему нс требуется выходить даже за
пределы первого периода, поскольку он устанавливает’, чго число песчинок, заполняющих
сферу неподвижных звезд, заведомо не превосходит тысячи мириад единиц восьмых
чисел первого периода, то есть числа 103-104-108’7=10“3.
111] Во всем расчете Архимеда поражает необычайная (мы сказали бы излишняя)
осторожность в оперировании с большими числами, покаэыяаюкцт, что пользование ими
еще было новинкой для громадного большинства. То, что было необходимым и эпоху
Архимеда, в настоятцее время скорее является помехой мри чтении; поэтому пе будет
липшим представить все расчеты Архимеда в более наглядной, привычной для пас форме.
Число песчинок в объеме макового зернышка = 10 000 песчинок. Один дюйм содерякит
10 маковых зернышек; следовательно,
Шар диаметром в один дюйм будет содержать 403х1(Н)0()---64-107
песчинок или меньше чем 10е песчинок
Шар диаметром в 100 дюймов будет содержать пе более (100):* 10”
— 10’6 песчинок
Шар диаметром в 10 000 дюймов будет содержать меньше (100)3-10,ь
— 10s1 песчинок
Стадия равпа 0600 дюймов; следовательно, шар диаметром в одну ста-
дию будет содерякать менее —1031 песчивок
Диаметр Земли содержит не более миллиона (10е) стадий; следователь^
по, число песчинок в объеме Земли будет не более 1О6’а-Ю21 —10:в песчинок
Диаметр мира В 10 000 раз больше диаметра Земли; следовательно, чис-
ло песчшток в объеме: мира будет 104’3-10зв —10м песчинок
Диаметр сферы неподвижных звезд в 10 000 раз больше диаметра мира;
следовательно, число песчинок я сфере неподвижных звезд будет
104-3-1061 —1003 песчинок
Полученное число, равное 107'817, но нумерации Архимеда будет
равно Ю’-Ю7’3, то есть тысяче мириад единиц восьмых чисел (107’8).
КНИГА ЛЕММ
«Книга лемм» сохранилась только в виде арабской обработки и латинского перевода
этой обработки. Несомненно принадлежат Архимеду предложения IV и VI вместе со
вспомогательным предложением I, относящиеся к фигуре, названной Архимедом «арбо-
доп», и также предложение VIII, дающее способ трисекции угла, и предложение XIV,
определяющее площадь фигуры, названной Архимедом «салинон».
Сочинение было издано впервые С. Фостером в сборнике «Смесь» (Miscellanea),
вышедшем в Лондоне в 1659 г. в латинском переводе с арабского. В 1661 г. этот перевод
был переиздан Ворелли. Текст, изданный Борелли, был переиздам в классическом падании
сочинений Архимеда, опубликованном Гейбергом.
Три арабские рукописи итого сочинении, с. которых производился перевод Фостера,
хранятся в библиотеке Медичи во Флоренции.
[1] Тебитом бен Корой (Thcbit ben Kora) латинский переводчик называет Абу-л-Ха-
сана Сабита ибн Курру ал-Харранй (836—901) — одного из крупнейших ученых сред-
невекового Востока. Сабит ибн Курра был уроженцем месопотамского города Харрана,
выходцем из семьи апездопоклоппикоп — сабпеп, потомков вавилонских жрецов. Сабит
ибн Курра был не только астрономом, как его предки, по и математиком и механиком.
Сабит ибн Курра работал главным образом в Багдаде, ему принадлежит перевод и коммен-
тарии к «Альмагесту» Птолемея, перевод «Конических еёчеяий» Аполлония, комментарии
к «Началам» Евклида, механический трактат о рычажных весах и большое число тракта-
тов но геометрии, арифметике, теории отношений, тригонометрии и астрономии, а также
переводы многих научных сочинений с греческого и сирийского па арабский. Три книги
«Конических сечений» Аполлония и три сочинении Архимеда сохранились до нашего
времени только в переводах или обработке Сабита ибн Курры.
[2J Ученым Альмохтассо Абильгасапом Гали бен Ахмадом Насуэнским (doctor
Almoclitasso Abilhasan Hali ben Ahmad Nasiiensis — латипский переводчик называет
Абу-л-Хасана 'Алй мбн Ахмада ан-Насавй (умер около 1030 г.), уроженца Пасы в Хора-
сане (около ныпепгпего Ашхабада Туркменской ССР). Слово Almochtasso — транскрип-
ция арабского слова ал-мухтас — «выдающийся» (слова ductor Almochtasso соответст-
вуют арабским словам, означающим «выдающийся ученый»). Ап-Насави работал n Pet-
ri Исфахане при дворе бупдеких султанов, а затем п Газпе при дпоре Махмуда Газневи
Ап-Насави - - автор нескольких математических трактатов, наиболее крупным из кото-
рых является арифметический трактат, где излагаете» ряд математических приемов
индийского и китайского происхождения.
|3] Абусахлем Алькухи (Abusahl Alkuhi) латипский переводчик называет Абу
Сахла ал-Кухй, уроженца Табаристама, работавшего в Багдаде около 988 г. Ал-Кухи был
большим знатоком греческой математики.
Таким образом, историю «Книги лемм» можно представить так. Сабит ибн Курра
перевел ряд лемм, принадлежавших Архимеду; через сто лет ал-Кухи систематизировал
их, еще через пятьдесят вп-Иасави комментировал их, а следующий за ним автор руко-
писи (если под ним скрывается во сам ан-Ыасави) сократил их. Такая длинная история
объясняет то, что в целом рукопись пе стоит па достаточной математической высоте, ие
все теоремы интересны, а про второе предложение приходится сказать, что его можно
и должно было доказать лучше.
[4] Словами «присоединение отношения» здесь переведены латинские слова сош-
pcisitio proportionis. Пенено, идет ли здесь речь о так называемом «присоединении» отно-
шений (componendo—ovvOe'vri), равносильном образованию из пропорции a: b=c : d
производной (а [-&) ; &=(c-|-d) : d или о «сложении» отношений, равносильном нашему
умножению их.
[5| По-видимому, пл книги ал-Кухи взяты предложения I и IV.
КНИГА ЛЕМЫ
605
[6] Как правильно заметил ап-Пасави, предложение остается верным и в том слу-
чае, когда оба круга имеют внешнее касание; именно в такой форме оно и употребляется
я предложении VI (стр. 395).
[7] При доказательстве предполагается, что обе касательные BD и DC являются
перпендикулярными друг к другу, о чем не говорится пи слова в формулировке предло-
женин. Эта ошибка ученых-арабов была обнаружена
ужо Фостером; Торелли показал, что предложение
остается верным и в том случае, когда касательные BD
и DC не будут взаимно перпендикулярными.
Доказательство в атом случае пойдет так:
Пусть мы имеем полукруг ЛВС с центром О,
к которому проведены касательные BD и CD. Фигу-
ра OBDC будет так называемым дельтоидом; BD—DC,
как касательные, проведенные к кругу из одной точки,
DB—OC, кик радиусы, иуглы OBb—OCD, как прямые.
Отсюда легко заключаем, что прямая OD — ось симмет-
рии дельтоида будет перпендикулярна к ВС. Вследствие
того, что угол ЛВС будет прямым, как угол .в полукру-
ге, заключаем, что прямая ABG будет параллельна OD,
из равенства же прямых АО и ОС убеждаемся в равен-
стве прямых CD и GD. Значит, точка D является сере-
диной прямой CG\ тогда, если опустить перпендикуляр
ВЕ на АС п провести /II), из подобия треугольников
АВЕ и AGC заключаем, что ВЕ^=ЕК, т. к. GD = DC.
В примечании Гомберг приводит доказательство
ан-Пасави в предположении, что BD перпендикулярна
к (CD; так как BD — DC, то угол DC В ранен углу
ЛВС; но углы DBC и DBG составляют в сумме прямой
угол, так же кик и углы DCB и CGB', следовательно,
угол DBG равняется CGB, или BD — DG—DC.
Книга Архимеда «О прямоугольных треуголь-
никах», ссылка на которую дана в тексте доказатель-
ства этого предложения, упоминается только у арабов.
предложение используется в «Альмагесте»
предложение, равно
Название «арбелон»
[8 ] Это
[9] Это
к Архимеду.
1, КП-
Нтшемся (книга
лак и оба последующих, без сомнения восходят
произошло от греческого слова, обозначающего
скребок для выделки кожи, па который походит
рассматриваемая фигура.
[10] «Проведем соединяющие линии НС и СС',
тоеда ПС будет тоже прямой».—Это следовало бы
из предложения I, если бы носледнее было доказано
и для случая ннстиого нз.саиня кругов. Соогвегету-
ющее доказательство можно провести так:
Пусть АСС и НСЕ будут два круга, внешне
касающихся друг Друга в точке G; пусть АС и ПЕ
будут взаимно параллельные диаметры этих кругов.
Требуется доказать, что липин АСЕ и CGI1, соеди-
няющие точку касания G с концами обоих диа-
метров АС и Л//, будут прямыми.
Пусть К и Q будут центрами обоих кругов;
соединяющая их прямая пройдет через точку касания
С. Вследствие параллельности ПЕ и АС замечаем,
что угол TTKG равеп углу GQC, откуда следует,
что равнобедренные треугольники HKG и GQC подобны и угол T1GK равен углу QGC.
Но угол ИСК составляет два прямых е углом HGQ, поскольку' KGQ есть прямая
линия; следовательно, будет равна двум прямым и сумма углов HCQ и QGC, то есть
липин HGC тоже будет прямой.
Аналогично докажем и то, что линия AGE будет прямой.
[11] «Как мы показали е предложениях, написанных е комментарии в трактату
о прямоугольных треугольниках» — Доказательство ап-Г1асави основывается на том, что
высоты в треугольнике мересекатотеи в одной точке.
Действительно, пусть BID (рис. 3) пе будет прямой; проведем тогда прпмую через В
и D, которая пересечет АТ в точке т, пе совпадающей с I; тогда угол АтВ будет прямой,
так как АТ будет высотой для третьей стороны BD треугольника. По угол АТВ тоже
будет прямым, как опирающийся на диаметр; следовательно, угол АтВ равен АТВ, что
невозможно.
606
КОММЕНТАРИИ
(12] В «Математическом собрании» Паппа (кп. IV, 14—20) имеются еще теоремы,
касающиеся арбелопа.
14. «В некоторых книгах нрмподитсп древнее предложение такого рода:
Возьмем три. касающиеся друг друга полуокружности АВГ, АДЕ, EZr
и в заключающуюся между их окружностями фигуру, которую называют
арбелон, впишем, несколько кругов,
касающихся друг друга и основные
полукругов' пусть центры, этих кру-
гов будут Н, в, К, А (рис. 4). Тре-
буется показать, что опущенный и.,
центра II на АГ перпендикуляр бу-
дет равен диаметру круга, описан-
ного около Н, далее, что перпенди-
куляр, опущенный из (-), будет вдвое
больше диаметра круга около 0,
а перпендикуляр из К. втрое больше
соответствующего диаметра, и вооб-
ще. последовательные, перпендикуляры
будут кратными соответствующих
диаметров в прогрессии натурального ряда чисел, причем- вписывание кругов
может продолжаться до бесконечности.
Пусть АВГ и АДЕ будут, полукруги (рис. 5), опишем касательные к их
окружностям круги с центрами 'L, 11, 0, а также следующие га ними
вплоть до точки А. Теперь то, что опущенный из Z на АГ перпендикуляр
будет равеп радиусу круга Z, является очевидным-, еще я утверждаю, что
перпендикуляр, опущенный из II, будет втрое больше радиуса круга 11,
опущенный из 0—в пять раз больше {радиуса круга 0) и. все следующие,
перпендикуляры будут больше соответствующих, радиусов в кратностях
последовательных нечетных чисел».
Хотя Папп не называет имени Архимеда, нее же авторство последнего является
очень пероитным; ла это указывают:
1) получившая at Архимеда свое название фигура арбелон,
2) ссылка я доказательстве на предложение Т «Книги лемм», связанное с несо-
мненно принадлежащими Архимеду теоремами 4—6, и, наконец,
3) вполне достойное Архимеда изящество основной доказываемой теоремы (гл. 14).
Однако и в этом случае к Архимеду можно относить самое большее лишь основную
идею доказательства, его подробности в данном тексте наверняка принадлежат Паппу
или другим комментаторам.
[13] В этой теореме мн встречаемся с третьей из знаменитых задач древности,
а именно разделением угла на три части. Возникновение этой задачи было, конечно,
связано с построением правильных многоугольников; для се решения, по всей видимости,
была придумана знаменитым софистом Гинпиом Элидским (вторая половина V века до
КНИГА ЛЕММ
607
и. ».) та самая квадратриса, котором мы занимал мел. в комментарии к «Квадратуре круга».
Решение задачи при помощи квадратрисы является очевидным.
Пусть в круге ЛОВ требуется разделить натри части угол ЛОМ (рис. 6). Проведем
квадратрису ВКЛЕГ, через точку К ее пересечения со стороной ОМ угла ироиодим ДЕ
параллельно ОА, полученный отрезок ОД делим на три равные части AZ, ZH, ПО, через
точки деления Z, И параллельно ОЛ проводил! ZO, III и точки Л, S пересечения этих
прямых с киадрзтрисой соединяем с. вершиной О угла
прямыми OAN и 0EI1; тогда заданный угол ЛОМ раз-
делится па три равные части MON, NO11 и НОЛ.
Подобно тому, как мы это сделали относительно
удвоения куба и квадратуры круга, приводим основной
текст, каеакпцийся истории трисекции угла в древности
(Папп, кв. IV, 36—44).
36. «Когда древние геометры захотели данный
прямолинейный угол разделить па три равные чисти,
то им встретились затруднения последующей причине.
Мы говорим, что геометрические проблемы разделяются
на три вида: одни из анх называются плоскими, другие
телесными, третьи же линейными. Те задачи, которые
могут быть разрешены при помощи прямых линий и
окружностей круга, виол нс законно можно назвать
плоскими, так как лилии, при помощи которых
отыскивается решение таких задач, имеют свое про-
исхождение на плоскости. То же задачи, решение которых требует применения одного
или нескольких конических сечений, называются телесными, так как для их построения
необходимо пользоваться п б верхи остями тел, а именно коническими. После них остается
третий вид задач, так называемых линейных; для построения <в этом случае), кроме упо-
мянутых, берутся и другие кривые, имеющие очень разнообразное и даже очень искус-
ственное происхождение, получаясь от сечений менее правильных поверхностей и в ре-
зультате сложных движений. Такими являются линии, изучаемые в так называемых
«геометрических местах на поверхности», а также другие более сложные, чем упомянутые,
и. в большом количестве, найденные. Деметрием Александрийским в «Линейных построе-
ниях» (iv tois yi>ap,urxoig :?tioTiued) и Филоном Тияпскпм при соединении (eg f лшХсицс)
плектоидальных и других разнообразных поверхностей, обладающие многими удиви-
тельными основными характеристиками. Некоторые из этих кривых удостоились больших
исследований со стороны новейших геометров: одной из них пил летел линия, названная
Менелаем «парадоксальной». К этому же роду принадлежат н другие кривые — спирали
и винтовые линии, квадратрисы, конхоиды и циссоиды. По-видимому, у геометров счи-
тается по малой ошибкой, если кто-нибудь из них плоскую задачу решает при помощи
конических сечений, или еще болео сложных линий, или вообще при помощи несвойствен-
ных классу данной задачи кривых, как, например, задача о параболе в книге V «Коничес-
ких сечений» Лноллопия *) пли то, что деласт Архимед в книге «О спиралях» для доказа-
тельства предложенной им теоремы, что окружность описанного при нервом обращении
круга равна прямой, проведенной из начала спирали до касательной ♦•), где он восполь-
зовался «стремлениями» и задаче, решаемой при помощи конических сечений и кругов.
При наличии такого существенного различия в классах задач первые геометры и не
смогли данную задачу относительно угла, являющуюся но природе телесной, решить при
помощи плоских построений; таг? пак они еще пе были знакомы с коническими сечениями,
то по этой причине и затруднялись; позднее ;кс при помощи конических сечений оказа-
лось возможным разделить угол на три равные части при использовании описанного ниже
«стремлении».
Дан прямоугольный параллелограмм АВ ГД и продолжена
сторона В Г; требуется провести прямую АЕ так, чтобы отрезок EZ был
равсп заданному {рис. 7}.
Пусть это уже сделано; проведем ДИ и HZ параллельно EZ и ЕД.
Теперь, так как EZ дана, то будет данной и равная ей АН. Затем дана
*) И книге V Аполлонии ничего подобного не имеется. Монет быть, следует читать «первой
«нн1«». где к предложении Ь2 говорится о построении параболы на плоскости. Ijosmowho также» что
Аксллппй кап и ниже Архимед, порицаетен совершенно незаслуженно.
**) Ото предложение XVIII книги «О спиралях». Для доказательства этого предложения тре-
буется использовать предложения VH и VIII, которые действительна получаются при помощи
«стремлений». причем едко из них (предложение VIII) требует применения построения, оквивалентного
нахождению пересечения гиперболы и параболы. Приведенный нами в примечаниях к соответствую-
щему jvccTy анализ показы вист, что без применения конических сечений решение задачи невозможно.
Вероятно мысль Паппа выключалась в тем, что если задача решается при помощи копичесних сечений,
то нет смысла польясвятьсл «стремлениями»» • ....
608
КОММЕНТАРИИ
точка Д; следовательно, II будет находиться па окружности заданного
своим положением круга. Далее дана {величина) прямоугольника
между ВГ и ГД; поскольку он равен
прямо угольнику между BZ и ЕД, то
будет данным и прямоугольник меж-
ду BZ и ЕЛ, или прямоугольник меж-
ду BZ и ZH; следовательно, точка Н
находится на гиперболе. Но она на-
ходится также и на заданной, поло-
жением о к руяшости; с л ед овате л ьпо,
будет данной и точка II.
37. После этого синтез задачи
производится следующим образом.
Пусть заданный параллелограмм бу-
дет АВГД, а заданная по величине
прямая — М {рис. 8}. Пусть ДК будет равна М; через точку Д прове-
дем гиперболу ДН© с асимптотами АВ, В Г (это мы разберем позд-
нее), а через точку
К — окружность круга
КН с центром Д, пере-
секающую гиперболу в
II; затем, проведя HZ
параллельно Д Г, про-
ведем соединяющую
прямую ZA. Я утверж-
даю, что EZ будет рав-
на М.
Действительно, про-
ведем соединяющую пря-
мую НА и ПЛ парал-
лельно К А; следователь-
г
а
я
Рис. 8.
К
ZB
ВГ
по, прямоугольник меж-
ду ZH и ИЛ или прямоугольник между BZ и ZII будет равен прямо-
угольнику между ГЛ и z\A или между ВГ и ГЛ. Значит, как ZB к ВГ
или как ГД к ДЕ, так будет относиться и ГД к ZH;
гл гл
ДЕ ’ ZH
лелограмм TZ, продолжим сторону ZA
следовательно, ЕД будет равна ZII; значит, AZ1IE — параллелограмм;
значит, EZ равна ДИ или
z\.K, или М.
38. После того как это
/(оказано, заданный прямо-
линейный угол делится на
три части следующим обра-
зом.
Пусть заданный угол
АВГ будет первоначально
острым {рис. 9}; из некото-
рой точки опустим перпенди-
куляр Л Г и, дополнив парад-
но направлению к Е. Затем,
имея прямоугольный параллелограмм TZ, проведем между ЕЛ и АГ
стремящуюся к В прямую ЕД, которая была бы равна удвоенной АВ
КНИГА ЛЕММ
609
(что это возможно, показано выше). Я утверждаю, что угол ЕВГ
является третьей частью заданного угла АВГ.
Действительно, разделим ЕД пополам в Н и соединим А и Н;
тогда три прямые ДН, НА и НЕ будут равными*); значит, ДЕ вдвое
болыне АН. Но ДЕ также вдвое больше и АВ; значит, ВА равна АН
и угол АВД равен углу АНД. Но угол АНД вдвое больше угла ЛЕД,
или ЛВГ: следовательно, угол АВД вдвое больше угла ДВГ. Если
теперь разделить пополам угол ЛВД, то угол АВ Г будет разделен на
три ранные части.
39. Если бы заданный угол был прямым {рис. 10), то, отло-
жив какую-нибудь прямую В Г, построим на ней равносторонний
затем угол ДВГ пополам, получим раз-
треугольник ВДГ; разделив
деленный на три части угол АВГ. *
40. Пусть теперь заданный угол АВГ будет тупым {рис. 11}; про-
недем ВД перпендикулярно к В Г; затем отделим ABZ — третью часть
угла ДВГ и ЕВД —третью часть острого угла АВД (это уже показано
нами выше); тогда угол EBZ
будет третьей частью угла ЛВГ.
Если при каждой из сторон АВ
и ВГ построим по углу, равно-
му EBZ, то и разделим задан-
ный угол па три равные части.
41. Теперь займемся реше-
нием оставленной нами ранее
задачи. Пусть даны положони-
. см две прямые АВ и В Г и ка-
кая-нибудь точка Д; требуется
провести через Д гиперболу с
асимптотами ЛВ, ВГ {рис. 12}.
Пусть это сделано и про-
ведена гипербола EAZ; из точ-
ки Д проведем к пей касатель-
ную АДГ, диаметр ИВА и пря-
мую z\0, параллельную В Г.
Так как IIД и Л0 даны положе-
нием, то будет данной и точка 0.
Затем, так как АВ н В Г являются асимптотами гиперболы, а АГ —
касательной, то АД будет равпа АГ, и квадрат на каждой из них будет
*) Если \Н — НЕ и угол ЕЛА яримой, то Н будет центром круга на диаметре ЛИ, окруж-
ность которого проходит через А.
39 Архимед
610
КОММЕНТАРИИ
равен четвертой части фигуры, построенной на ДН *), (это доказывает-
ся в предложении 3 книги II Аполлония «Конические сечения»). Так
как Г/\ равна ДА, то и В0 будет равна О А. Но В0 дана; следователь-
но, будет данной и ОА. Затем дана точка О; следовательно, будет дан-
ной it А; значит, будет дана положением и прямая ДГ. Далее, АГ дана
и по величине, так что будет данным и квадрат на АГ. Но последний
равен построенной на НА фигуре; значит, будет данной и эта фигура.
Затем дана НД (она будет вдвое больше прямой ВД, заданной по вели-
чине, так как дана каждая из точек В и Л); следовательно, будет дан-
ной и прямая сторона (Jalus rectum — параметр) кривой. Таким обра-
зом, получилась такая задача; заданы величиной и положением две
прямые — ПД и параметр; требуется построить на диаметре НД гипер-
болу, у которой прямой, на которой квадрируются ординаты **) была бы
другая заданная прямая, и соответствующие НД ординаты были бы
параллельны заданной положением прямой АГ. Все это разрешено
в первой книге «Конических сечений» (предложение 53).
42. Синтез задачи производится так. Пусть АВ, ВГ будут задан-
ные положением прямые, а Д — заданная точка. Проводим Д0 парал-
лельно ВГи 0А, равную В0, затем соединяющую АД продолжаем к Г,
а соединяющую ВД продолжаем (назад) и откладываем B1I равной
ВД; пусть квадрат на АГ будет равен прямоугольнику па ПА и неко-
торой другой прямой К; затем на диаметре НД и параметре К строим
гиперболу EAZ так, чтобы проведенные к НА ординаты были парал-
лельны АГ; тогда АГ будет касательной к построенному коническому
сечению. Затем АД равна ДГ (так как В0 равна 0А), и ясно, что квад-
рат каждой из прямых АД и
НД фигуры; следовательно,
ДГ будет равен четверти построенной на
АВ, В Г будут асимптотами гиперболы
EAZ; таким образом, построена прохо-
дящая через точку Д гипербола, име-
ющая заданные прямые асимптотами.
43. Если не пользоваться «стремле-
ниями», то третью часть заданной дуги
можно будет получить и иначе, при
помощи следующего «телесного» гео-
метрического места.
Пусть положением задана прохо-
дящая через точки А и Г прямая; через
проведем ломаную АВГ так, чтобы угол Л ГВ
заданные точки А и Г
был вдвое больше угла ГАВ; тогда точка В будет на гиперболе (ряс. 13}.
Проведом перпендикуляр ВД и отложим ДЕ равной ДГ; тогда
соединяющая BE будет равна АЕ. Отложим EZ равной ДЕ; тогда
TZ будет втрое больше ГА. Пусть АГ будет втрое больше Г11; тогда
точка Н будет заданной, и остающаяся прямая AZ втрое больше
НД. И так как разность квадратов иа BE и EZ ость квадрат на ВД
BE9 - EZ2 = ВГ2 - ГД2 = ВД1
и этой же самой разности будет равен прямоугольник между ДА и AZ,
BE9 - Е22 = АЕ2 - ЕЛ2 = (АЕ + Ей) (АЕ - EZ)
*) Произведению &Н не параметр h.
••) Эта прямая, на которой квадрируются ордипати, соответствует нашему параметру.
КНИГА ЛЕММ
611
то, значит, прямоугольник между ДА и AZ, то есть трижды взятый
прямоугольник между АД и ДН, будет равен квадрату на ВД;
зал-лк = вд2 > . •.
следовательно, точка В будет на гиперболе, действительная ось
которой АН, а параметр втрое больше АН*). Далее ясно, что
точка Г при вершине Н конического сечения отсекает прямую ГП,
равную половине действительной оси АП гиперболы.
Синтез задачи очевиден; требуется прямую АГ разделить так,
чтобы АН была бы вдвое больше ГН и на оси АН построить проходящую
через точку Н гиперболу, параметр которой был бы втрое больше АН,
и затем показать, что эта гипербола действительно производит задан-
ное отношение углов при Г и А, равное двум. Легко видеть, что начер-
ченная таким образом гипербола отсекает третью часть заданной дуги
окружности, крайними точками которой являются Л и Г.
44. Некоторые анализ задачи о делении па три части заданного
угла или дуги излагают другим способом, тоже не пользуясь «стремле-
ниями». Пусть рассуждение будет касаться дуга, поскольку пот никакой
разницы, делить ли дугу или угол. Пусть это будет сделано, и от
заданной дуги ЛВГ отсечена третья часть ВГ [рис. 14}. Проведем
соединяющие А с В, В с Г и Г с А; тогда угол АГВ вдвое больше угла
ВАГ. Разделим угол АГВ пополам прямой ГД и опустим перпенди-
куляры BZ и ДЕ; тогда АД будет равна ДГ, а значит, и АЕ равна ЕГ;
следовательно, точка Е дана. Теперь, так как отношение АГ к ГВ равно
отношению АД к ДВ или ЛЕ к EZ,
АГ АД АЕ
ГВ °” ЛВ - EZ
то, значит, после перестановки ГЛ так относится к АЕ, как ГВ к EZ.
га гв
АЕ ° EZ
Но ГА вдвое больше АЕ; значит, и В Г будет вдвое больше EZ; следо-
вательно, квадрат на ВГ, или квадраты на EZ и ZT, (вместе взятые),
будут в четыре раза больше квадрата на EZ.
ВГ2 = BZ2 + Zl’2 = 4EZ®.
“) Если доложить ВЛ=у и ЛП=х, то уравнение гиперболы будет:
•у2 = 2рх 4- я* = ЗА Нх 4- -Ag„ х«.
39*
'612
КОММЕНТАРИИ
Теперь, поскольку являются заданными точки Е и Г, проведен
перпендикуляр BZ и задано отношение квадрата на EZ, к сумме квад-
ратов на BZ и ZT, то точка В будет, следовательно, находиться на
гиперболе. По она находится также и па заданной положением окруж-
ности; следовательно, точка В дапа. Синтез
задачи является очевидным.
45. Деление на три части заданного угла
или дуги является, как мы показали, «телес-
ной» задачей; деление же заданного угла или
дуги в данном отношении будет уже «линей-
ной» задачей. Это доказано новейшими гео-
метрами; мы опишем два способа ее решения.
Пусть Л0 (рис. 15) будет дугой круга
КА©; требуется разделить ее в заданном
& отношении.
Проведем к центру прямые ЛВ, В© и
восставим ВК — перпендикуляр к В©; за-
тем через К проведем квадратрису КАД Г и
опущенный перпендикуляр АЕ разделим в Z
отношение AZ к ZE равнялось заданному отношению,
К
В
Е
Рис.
квадратрисьг АЕ так отно-
так, чтобы
в котором мы хотим разделить данный угол; далее проводим ZA парал-
лельно ВГ, соединяющую прямую ВД(М) и опускаем перпендикуляр
АН. Так как вследствие основного свойства —
сится к АН, пли ZE, как угол АВГ к
Л В Г, то после «выделения» получится;
что AZ так относится к ZE, как угол
ДВА к углу АВГ,
AZ _ Z АВА
ZE Z АВГ
то есть заданное отношение равняется
отношению углов АВА и АВГ или дуг
AM и М0.
46. Иначе дуга АГ*) окружности АНГ
(рис. 10) может быть разделена так. Точно
так же проводим к центру прямые ЛВ ц
В Г и описываем из В спираль BZAT, на-
чальным положением вращения которой
является прямая ГВ; пусть заданное отно-
шение равняется отношению АЕ к ЕВ. Через точку Е около центра В
описываем дугу окружности EZ, пересекающую спираль в Z; соеди-
няющую BZ продолжаем до Н; тогда ио свойству спирали АВ будет
относиться к BZ или к ВЕ, как дуга АНГ к ГН
ДВ _ АНГ
ВЕ " гн
и после «выделения»— как ДЕ к ЕВ, так и дуга АН к НГ.
ЛЕ ’ АН
») Волыиан полуокружности.
КПИГЛ ЛЕММ (513
Но отношение ДЕ к Е13 равному данному; следовательно, и отношение
дуги АН к НГ равно данному; следовательно, дуга разделена в задан-
ном отношении».
Переходя к Архимеду, нужно отмстить, что он, по всей видимости, как и в квадра-
туре круга, тоже дал два решения поставленной задачи: в самом общем случае деление
угла па любое число равных частей может быть выполнено При помощи Архимедовой
спирали, в частном же случае деления угла иа три части он дал решение, изложенное
в предложении VII «Книги лемм»; эту красивую теорему известный историк математики
Морнц Кантор с полным правом считает принадлежащей Архимеду.
{М1 Ото предложение без всякого сомнения тоже восходит к Архимеду. Значение
слова «салмнои» в точности неизвестно. М. Кантор производит его от aakoQ (морское)
волнение, качка, толкуя его как «ватнообразную лилию», Хизс считает, что здесь скрыто
испорченное латинское слово salinum - солодка; издатель Архимеда Гейберг сближает
его со словом acAivov — сельдерей, па лист которого эта фигура будто бы похожа.
[15J Это предложение, касающееся пятиугольника, представляет естественный
переход к следующей, тоже восходящей к Сабиту ибп Курре «Книге о семиугольнике;).
КНИГА 0 ПОСТРОЕНИИ КРУГА, РАЗДЕЛЕННОГО НА СЕМЬ
РАВНЫХ ЧАСТЕЙ
«Книга о построении круга, разделенного на семь ранных частей», посвященная
построению правильного семиугольника, сохранилась только в виде арабской обработки,
принадлежащей тому же Сабиту ибп Куррс, которому принадлежит обработка «Книги
лемм».
Изложение этого сочинения было опубликовано в книге Карла Шоя ([22], стр. 74—
84) и в статье И. Тролфкс [44], стр. 636—651).
Единственная сохранившаяся рукопись «Книги» хранится в Каире в Египетской
Национальной библиотеке (Аг 7805/15, лл. 105—110). Микрофильм этой рукописи был
любезно прислан переводчику директором Национальной библиотеки Фуадом Сайидом
и передан ио время XXV Международного конгресса востоковедов в Москве каирским
профессором Амином ал-Холи. Перевод рукописи осуществлен Б. Л. Розенфельдом.
[1) См. комментарий к «Книге лемм».
[2] Переписчик и редактор рукописи Мустафа Сиддикй жил в XVIII веке (в копцо
рукописи указано, что опа переписана в 1740 г.).
[3] Предисловие написано Сиддики (это очевидно из слов «желая переписать эту
книгу»; Сабит пбп Курра сказал бы: «желая перевести эту книгу»). Добавленные Сиддики
доказательства некоторых теорем Архимеда принадлежат средневековым комментаторам
Архимеда, жившим в X—XI веках. Все добавления Сиддики к тексту, который он счи-
тает восстановленным текстом Архимеда, начинаются словами «я говорю».
[4] Выражение «плоскость из А на В» (здесь: сатх а фи б) означает прямоугольник,
построенный па отрезках А и И, то есть равносильно выражению «прямоугольник между
А и В» в переводах сочинений Архимеда, сохранившихся на греческом языке. Однако
Здесь предлог фи между обозначениями отрепков — тот же, что между сомножителями
при умножении чисел.
[5] Абу’Алй ал-Хасап ибн Харис ал-Хубубй— уроженец Хорезма, автор изве-
стного математического трактата о разделе наследств. Доказательства ал-Хубуби неко-
торых теорем Архимеда сохранились в «Трактате об определении хорд в круге» ал-Бпру-
пи. В рукописи вместо «Хубубй» палисано «Джуйуби» (эти имена отличаются только
диакритическими точками).
[б] Предложение 111 можно представить в следующей алгебраической форме:
если ни b - - катеты прямоугольного треугольника, с — его гипотенуза, а р — полупе-
риметр, то
2(а-[-с) (Ь4-с) = (2р)*.
17] Предложение 1V в алгебраической форме, может быть выражено так: если h —
высота, опущелпая на гипотенузу того же треугольника, то
(2р)»=2с (2р-| А).
Предложение V — другое доказательство предложения IV.
[8] Абу’Абдаллах Мухаммад ибн Ахмад аш-Шапни— египетский математик, автор
нескольких геометрических трактатов. Доказательства аш-Шанни некоторых теорем
Архимеда также сохранились в «Трактате об определении хорд в круге» ал-Бируни.
[9] Предложение VI может быть выражено в виде
(2р)»+(« - Ь)»=(а -Н)2+(б- <=)2 •
Предложение VII — другое доказательство предложения VI.
КНИГА О ПОСТРОЕНИИ КРУГА. РАЗДЕЛЕННОГО НА СЕМЬ РАВНЫХ ЧАСТЕЙ 615
110] Предложение VIII может быть выражено следующим образом: если
х-]-у-|-г—2s и 2sy—Ж2,
то
4sy = (a:4-y) (у_|_=),
[11] Это утверждение вытекает из обобщенной теоремы Пифагора для треуголь-
ника АНН', высота итого треугольника, опущенная из вершины А на продолжение сто-
роны ЕП, пересекает эту прямую в середине отрезка DE, и в силу обобщенной теоремы
Пифагора Ati2=AEs-^-EUt-\-2EH• , откуда следует, что А11*=АЕг-[ HD-IIE.
[12] Предложения IX и X являются, по существу, подготовительными к выводу
«формулы Герона» для прямоугольного треугольника. Беля мыположш ЕС—-а и ЛВ=Ъ,
то в силу предложения IX И£)= р—а, а и силу предложения X DC-=j>—h. Поэтому пред-
ложение XI равносильно указанному частному случаю «формулы Герона» в виде
£=(р—°) (/>—&)»
где S — площадь треугольника.
Предложения XII и XIII—другие доказательства предложения XI.
|13] Предложение XIV дает второй вид «формулы Герона» для прямоугольного
треугольника:
S=p(p—с).
Если перемножить формулы предложений XI и XIV, то мы получим «формулу
Герона»
<У2=р(р—а)(р—Ь) (р—с),
которая, таким образом, доказала для прямоугольного треугольника.
В передаче ал-Бируни сохранилось доказател ьстпо общего случая «формулы
Герона», которую ал-Бирупи также приписывает Архимеду (см. «Теоремы Архимеда,
сохранившиеся в передаче ал-Бцруни», стр. 419—420
настоящего издания).
[14] Это предложение представляет большой
интерес; ово по существу равносильно известной
тригонометрической формуле
1 — cos а
2 ’
которую обычно считали известной только для эпо-
хи Птолемея (11 век и. :>.).
[15] Предложение XVII в нашей формулиров-
ке сводится к следующему. Возьмем квадрат ABCD
(рис. 1) со стороной а, проведем диагональ ВС и
прямую DF.F так, чтобы площадь треугольника С ВТ
равнялась площади треугольника ' AEF\ мы имеем здесь пример построений типа
veioeig, которые по времена Архимеда принадлежали к числу уиитреблиомых элемен-
тарных построений. Через точку Г пересечения проведенной прямой DF с диагональю ВС
проведем прямую КЕ параллельно АС и обозначим через у и 2 отрезки, на которые зта
прямая рассекает противоположные стороны квадрата:
у—АК, z=BK. : . .
Если через х обозначим отрезок АР':
AF—x,
то для упомянутых отрезков будут иметь место отношения:
(1) ABKB=AF» или «z=z2,
(2) FKAK^KB* или (z-[-y) у—z2,
к которым присоединяется еще очевидное уравнение
(3) у-гг=а.
Предложение XVII и заключается в установления первых двух отношений.
me
КОММЕНТАРИИ
Из равенства треугольников AFE и CDT согласие построению заключаем:
х-АЕ=ау
или
а : х—АЕ : у.
И» подобия треугольников AFE, DLT и ЕКТ заключаем:
AE'.TL^-AFtLD
или
АЕ : у=х : г,
откуда
а : х=х : z,
что равносильно равенству (1).
Далее,
TL : DL— ТК : FK
или
y.z—z:(y-\-x),
что доказывает равенство (2).
Если исключить из уравнений (1), (2) и (3) неизвестные у и г, то дли определения х
мы придем к уравнению третьей степени:
х2 (х-]-2л) = аг (х-| -а).
[16] Предложение XVIII посвящено непосредственному построению семиугольника.
Здесь (рис. 17 текста) берется некоторая прямая АВ — хорда будущего круга, и который
будет вписан семиугольник. Эта прямая, которая предполагается известной, делится
в точках С и D так, чтобы
АВ-CD—BD2, CBBD=AC2.
Если положить AC =х, CD—у, DB = z, то эти равенства равносильны следующим:
(у-;-г)2=ж2,
то есть уравнениям (2) и (1) предшествующего предложения. Затем строится треуголь-
ник CED, в котором СЕ — С А и DE=DB\ полученная точка Е будет третьей вершиной
треугольника АВЕ, около которого мы описываем круг: прямая ВЕ будет стороной семи-
угольника, вписанного в этот круг.
Продолжаем ЕС и ED до пересечения с окружностью в точках G и И, проводим
ВС, пересекающую НЕ в точке F, и соединяем Сй’.*
Вследствие равпобсдреппости треугольника АСЕ легко убеждаемся в том, что.
дуга ЛС равна дуге ЕВ. Затем по построению ADCD—BD2, или Е1)\ то сеть
AD-.DE = DE-.CD,
а это значит, что треугольники AED и CED, имеющие общий угол при Е, будут подобны;,
отсюда следует равенство углов СЕВ и САЕ и таким образом дуга НС оказывается рав-
ной дугам АС и ЕВ,
Затем из параллельности ЛЕ и ВС следует равенство углов АЕС и ABG, а так
как угол CED=CEA, то мы заключаем о равенство углов CEF и СВР. Поело этого из
равнобедренности треугольника BED мы заключаем, что фигура ВЕСЕ представляет
равнобедренную трапецию, около которой может быть описана окружность. Из равен-
ства треугольников ЕВС и EBF следует, что
BF=EC=CA=x, BD=ED,
DF—CD — y,
FE=CD+DB=y+z.
Из соотношения СВ-BD~EC2=АС2 следует, что
СВ: ЕС= ЕС : BD,
что в нашем случав может быть переписано так:
EF •, FC — FC'.ED,
КНИГА О ПОСТРОЕНИИ КРУГА, РАЗДЕЛЕННОГО НА СЕМЬ РАВНЫХ ЧАСТЕЙ 617
а ото равносильно тому,что треугольники ECDv ECF с. общим углом при Е будут подобны:
FE-ED^EC*
или
Затем угол 1)С£=углу О7? = углу EFC (из подобия треугольников EDC л EFC),
а это значит, что угол ЕРС или /?ВС’= углу ECD, или удвоенному углу САЕ; иными сло-
вами, дуга ЕА будет вдвоо больше дуги ЕВ; разделив дугу ЕЛ пополам, мы получим
еще две дуги, равные. ЕВ. Затем из равенства углов DEB и DBE заключаем, что дуга НВ
будет тоже равна дуго АЕ, или удвоенной дуге BE. Таким образом, разделив ВН попо-
лам, мы получаем еще дне дуги, равные. BE, и значит, весь круг разделился па семь рав-
ных частей.
Обо последние теоремы доказываются совершенно самостоятельно и независимо
от предыдущих предложений, с которыми их роднит лишь то обстоятельство, что на
продолжениях одной стороны CD откладываются две другие стороны СЛ=СЕ и DB—DE.
Наличие этом чисто внешней связи показывает, что перед нами не подлинное сочинение
Архимеда, а сочинение того же. типа, что «Книга лемм», которая восходит к тому же
Сабиту ибн Куррс. Однако в том, что в основе обоих сборников лежат подлинные работы
Архимеда, вряд ли возможно сомневаться.
[1.71 Дата переписки рукописи — 31 июля 1740 г.
В книге Шоя [22] помощеп еще (стр. 85 и ел.) трактат о семиугольнике ибн ал-Хай-
сама (Альхазсп), рукопись которого хранится в библиотеке India Office в Лондоне-
(Jft 734/21).
ТЕОРЕМЫ АРХИМЕДА» СОХРАНИВШИЕСЯ
В ПЕРЕДАЧЕ АЛ-БИРУПИ
Формулировки трех геометрических теорем Архимеда, принадлежащие самому
Архимеду, и принадлежащие ему доказательства одной из этих теорем сохранились и гео-
метрическом трактате средневекового среднеазиатского ученого Абу-р-Райхана Ахмада
ибн Лухаммода ал-Бйрупй (973—1048) «Трактат об определении хорд в круге при помощи
свойств вписанной в пего ломаной линии» (Рисала фй пстрихрадж ал-автар фй-д-даира би
хавасс ал-хатг ал-мупхапй ал-ваки' фйха). Этот трактат сохранился до нашего времени
в виде четырех рукописей: в Банкипуре (Восточная публичная библиотека, № 2468/42),
Лейдене (Университетская библиотека. Со<1. от. 513/5), Каире (Египетская Националь-
ная библиотека, № 7805/11) и Стамбуле (Библиотека Мурада Моллы, № 1396/14); бап-
кипурская рукопись была издана Осмапийским университетом в Хайдарабаде в 1948 г.
(стр. 1—108), немецкий перевод лейденской рукописи был издан Г. Зутером в 1911 г.
[21] (стр. 11—78).
Приводятся переводы отрывков из трактата ал-Бируни, посвященных теоремам Архи-
меда. Переводы выполнены С. А. Красновой под редакцией Б. А. Розенфельда; переводы
осуществл епы с хайдерабадского издания банкипурской рукописи; пробелы в этой руко-
писи восполнены по изданию .Зутера лейденской рукописи. Эти дополнения приведены
в квадратных скобках.
[1] Формулировка этой теоремы приведена на стр. 4—5 хайдерабадского издания
и на стр. 12 перевода Зутера. Доказательства Архимеда приведены па стр. 7—8, 18—19
и 20—21 хайдерабадского издания и на стр. 13—15 перевода Зутера. Кроме трех доказа-
тельств этой теоремы, принадлежащих самому Архимеду, в банкипурской рукописи при-
ведено еще 18 доказательств, а в лейденской — еще 20 доказательств этой теоремы, при-
надлежащие различным ученым средневекового Востока — Ибн ал-Хайсаму, ал-Хубуби,
аш-Шаиии, ал-Джурджапи, ас-Спджизи, Азархуру Джашниеу, учителю ал-Бируни Ибп
Ираку и самому ал-Бируни. Эта же теорема под названием «предпосылка Архимеда»
приведена в тригонометрической книге сочинении ал-Бирупи «Канон Мас'уда по астро-
номии и звездам» (ал-Кануп ал-Мас'уди фи-л-хайа ва-п-пуджум, стр. 273).
Теорема состоит в том, что если ломаная ЛИС вписана в дугу ЛВС и нз середины
этой дуги опущен перпецдикуляр на большее звено ломаной, то основание этого перпен-
дикуляра делит ломаную пополам. И в банкипурской и в лейденской рукописях указано,
что доказательства Архимеда взяты из его книги, которую ал-Бируни называет «Книгой
кругов» (Китаб ад-данаир), и что третье, из этих доказательств перевел с греческого на
арабский Юханна ибн Юсуф (Иоанн, сын Иосифа), известный также под именем ал-Касс
(православный священник). В банкипурской рукописи указано также, что эти доказа-
тельства были воспроизведены в книге «Начала геометрии» александрийского матема-
тика IV века Серена Финского. Очевидно, что «Книга крутой» — сокращенное название
«Книги о касающихся кругах». В обработке «Книги о касающихся кругах», перевод кото-
рой приводится па стр. 421—439 этого издания, указанные доказательства изложены
в предложениях XXIV—XXVI в несколько другой редакция; чертежи в трактате
ал-1>ирунв являются зеркальными отражениями соответствующих чертежей «Книги о
касающихся кругах».
[2] Эта теорема приведена в хайдсрабадском издании па стр. 58—59, в лейдспской
рукописи эта теорема отсутствует. Ал-Бирупи ие указывает нм автора доказательства, пи
в каком сочинении Архимеда доказана эта теорема.
Теорема состоит в том, что если основание треугольника а (рис. 1 и 2), а его
остальные стороны Ь и с, а прямоугольные проекции сторон Ь и с иа основание или его
ТЕОРЕМЫ АРХИМЕДА, СОХРАНИВШИЕСЯ В ПЕРЕДАЧЕ АЛ-БИРУНИ
619
продолжение — Ь' и с', и если Ь>с, то
_ i_ Г Ьй- с1 1 = Д I а №— с* | _ I а2 - !>2-)-с2 I.
2 [ а ' a J 2а * С 2 | а | | 2а | ’
эта теорема равносильна «обобщенной теореме Пифагора», которую можно записать фор- -
мулами Ь2=а2-|-сг—2ас’ 62=а2-|-с2-Ь2ас' В > J, с2=а2-|-£>2—2ab', до- .
казанной Евклидом в предложениях 12 и 13 книги II «Начал».
[3] Ота теорема состоит в том, что площадь А произвольного треугольника со сто-
ронами а, Ъ, с и лолупсриметром р равна
J= Yp (/>—а) (д—6) (р— с).
Эту теорему обычно называют «теоремой Геропа», так как европейцы впервые позна-
комились с ней ия сочинений Геропа. В хайдарабадском издании эта теорема приведена
па стр. 61—64, в переводе Зутера — на стр. 39—40. В банкипурской рукописи автор
доказательства пе указал, в лейденской рукописи доказательство приписывается аш-
Illaiiuu. Ал-Бирупи ие указывает, в каком сочинении Архимеда доказана эта теорема.
О принадлежности этой теоремы Архимеду свидетельствует и хорасанский математик
Абу-л-Вафа ал-Бузджапи (940—998), который также приводит дпа доказательства этой
теоремы (см. письмо Шоя к Троифке от 16 сентября 1925 г. на основании анализа араб-
ской рукописи Thurston 11.1 Оксфордской университетской библиотеки.
В «Кпигс о семиугольнике», как мы видели, доказан частный случай этой теоремы
для прямоугольного треугольника (стр. 400).
Общее доказательство (формы Герона содержится в Вороновой «Метрике» (кни-
га I, 8). Несмотря па то, что доказательство носит общий характер, чертеж в книге
Герона воспроизводит прямоугольный треугольник; таким образом, весьма возможно,
что приводимое Геропом доказательство восходит непосредственно к Архимеду; поэтому
воспроизводим относящийся сюда текст Геропа.
«Дапы три стороны треугольника; найти его площадь.
Это возможно сделать, проведя одну высоту, и, найдя ее величину,
определить площадь треугольника, но пусть будет нужно определить
площадь помимо нахождения высоты.
Пусть будет дап треугольник ЛВС и пусть каждая из ЛВ, ВС, С А
будет данной; найти его площадь.
Впишем и треугольник круг DEF, центром которого пусть будет Я;
соединим Л и Н, В и Н, С и II, D и II, Е и 11, F и Н. Тогда ВС-ЕН
будет вдвое больше, треугольника ВИС, CA-FII вдвое больше треуголь-
ника АСН, {АВ-DIl вдвое больше треугольника АВН)\ значит, про-
изведение периметра треугольника АВС на ЕН, то есть на радиус кру-
га DEF, будет вдвое больше треугольника ЛВС. Продолжим СВ и от-
ложим ВС равной AD\ значит, CBG будет половиной периметра тре-
угольника ЛВС, вследствие того, что ЛВ равна -4F, DB же равна ВЕ
и FC равна СЕ\ значит, CG EH будет равно треугольнику ЛВС. Но
620
КОММЕНТАРИИ
CG-ЕН будет квадратным корнем из квадрата СС, помноженного на
квадрат ЕН:
CGEI1 = VcG2EH2;
значит, площадь треугольника ЛВС, помноженная на самое себя, будет
равна квадрату GC, помноженному ла квадрат ЕН.
Проводом HL перпендикулярно таСНиВС перпендикулярно к СВ и
соединим Си В. Поскольку каждый из углов, СНВ и CBL будет прямым,
то четырехугольник СНВ Л
будет вписанным в круг; зна-
чит, углы СНВ и CLB будут
вместе равны двум прямым.
Но также и углы СНВ и AHD
будут раины двум прямым
вследствие того, что приле-
жащие к Н углы разделены
пополам прямыми АН, ВН,
СП, и углы СНВ, AHD вме-
сте будут равны ЛИС, DHB,
и все они в сумме равны
четырем прямым; значит,
угол АНН будет равен углу
CLB; также и прямой угол
ADH равен прямому углу
СВ С-, значит, треугольник"
АН D будет подобен треуголь-
нику CBL. Значит, как ВС
к В В, так и АН к НН, то
есть BG к ЕН:
ВС : BL = AD : DH “ BG : ЕН,
и обратно *), как СВ к ВС,
так и BL к Elf, то есть В К к КЕ:
СВ : BG = BL: ЕН = ВК : К Б
вследствие того, что BL параллельна ЕН; затем, «присоединяя», —
как CG к BG, так и BE к ЕК:
{СВ -) BG) : BG = (ВК -J- КЕ) : КЕ,
СО : BG = БЕ : ЕК,
таким образом, как квадрат на CG к прямоугольнику между CG и GBT
тан и BE-ЕС к СЕ-ЕК, то ость я ЕНг:
CG* : (CG • GB) = (ВБ • ЕС) : (СБ БК),
CG2 : (CG- GB)=(BE-EC): ЕН2,
так как в прямоугольном треугольнике из вершины прямого угла опу-
щен на основание перпендикуляр ЕН; таким образом, CG2, помножен-
ный на ЕН2, откуда квадратный корень давал площадь треугольника
АВС, будет равеп прямоугольнику CG-GB, помноженному на СЕ ЕВ:
CG* • ЕН2 = (CG • GB) {СЕ ЕВ).
И каждая из CG, GB, BE, СЕ является данной; действительно, CG
есть половина периметра треугольника ABC, BG есть избыток, на
который половина периметра превосходит СВ, а BE есть избыток, на
') Читай «переставляя».
ТЕОРЕМЫ АРХИМЕДА, СОХРАНИВШИЕСЯ В ПЕРЕДАЧЕ АЛ-ЕИРУНИ
R21
который половина периметра превосходит АВ, так как ЕС равна СЕ,
а ВС равна АЕ, поскольку опа же равна и Л1):
ас - са, bg = af.
Значит, будет данной и площадь треугольника АВС.
[4] Теорема о том, что площадь треугольника ACD равпа сумме площади тре-
угольника АВС и произведении DR-ICI3, также доказываемая и трактате ал-Бируни,
янлнстся следствием теоремы Архимеда о ломаной линии: если АЕ—ЕВ—ВС и F.M=BE,
то треугольник AMD ранен треугольнику BDC, так как АМ—ВС, DM=DB и AD—DC
и треугольник ADC равновелик пятиугольнику AMDBC, состоящему иа треугольников
АВС и BDM, а площадь треугольника BDM равна произведению DE.EB.
DG DE DG3 DGGA DE* DF.-EB
[а] Мы имеем сл —5 отсюда l)G,GA ~~ DE-EB~ ЕВ2
_DGGA~DREB
” DGGA—DE.EB СА*~ ЕВ2
Далее, TFTAtS = Ag> Ле£ “ ЛВС=У(В&-ВЕ») (АСР-ЕВ2)^
= /Л’Я (ЙЛ-ЬЛС) (АК-СК).
Если через р обозначим нолулсриметр треугольника АВС, то
ЕН > - ВЛ - AG = Л- (АВ + ВС) + AG - 2AG ~ Р - ЛС,
АК = AG - GK - ЕВ = ~- (АВ - ЕА) =--• ЕА + - ЛВ р - ЛВ,
ЕА + AG = Д- (АВ + ВС) + Л- АС = Р,
а
СК ^~ + ЕИ=Л^-1 ЛВ - АЕ - Ав -L 4г - 4- <АВ ВС) -=
АВ . АС ВС (АВ + ВС + AC) n„ Rr
" Т ’ Т“ 2 ” 2 .
Таким образом,
пл. ЛВС = Vp (Р — АС) (р — АВ) (р — Вс).
КНИГА О КАСАЮЩИХСЯ КРУГАХ
«Книга о касающихся кругах», так же как «Книга лечим» и «Книга о иостроении
круга, разделенного па семь равных частей», сохранилась только в виде арабской обра-
ботки, принадлежащей, по-видимому, тому же Сабиту ибн Курре, которому принадле-
жали обработки этих сочинений. Единственная сохранившаяся рукопись этого сочинения,
озаглавленная «Китаб фй-д-даваир ал-мутамасса», хранится в Банкипурской Восточной
публичной библиотеке (Ав 2468/28). Эта рукопись опубликована Османийским универ-
ситетом в Хайдарабаде (part 2). Перевод, осуществлен Б. А. Розенфельдом с хайдера-
бадского издания.
Вместе с «Книгой о касающихся кругах» в хайдарабадском издании опубликована
рукопись As 2468/29 той же библиотеки (part 1), озаглавленная «Книга о началах
геометрии Архимеда, переведенная с греческого на арабским язык Абу-л-Хасапом’Али
ибн Яхьей, клиентом поаелителя правоверных, Сабитом ибн Куррой, умершим в двести
восемьдесят восьмом году хиджры». Эта книга содержит доказательства 19 геометрических
предложений, 5 из которых относятся к свойствам круга, а остальные 14 — к свойствам
треугольников (из них 4 относятся к свойствам равностороннего треугольника и 4 —
к свойствам равнобедренного треугольника). Элементарный характер этих предложений'
(например, предложение VII о равенстве высот равностороннего треугольника) пе даст
возможности включить эту кпигу в собрание сочинений Архимеда.
(1) Здесь имеется в виду предложение 32 книги III «Начал» Евклида. В арабском
тексте «11ачала>> названы словом «ал-устуксат», означающим «стихии, элементы», являю-
щимся транскрипцией греческого названия «Начал» (SToQ^in).
Предложение 32 читается так: «Если некоторая прямая касается круга и от точки
касания внутри круга проведена некоторая секущая круг прямая, то углы, которые эта
прямая образует с касательном (ААР и ого дополнение до 180°), будут равпы углам в па-
крест лежащих сегментах крута».
[2] Здесь в арабском тексте пропущено слово «квадратов»; аналогичный пропуск
произведен и при формулировке примера, а и доказательстве вместо слов «двойному
отношению» написано «отношению». Систематический характер этих пропусков указы-
вает па ошибку одного из переписчиков этого сочинения. Нужно отметить, что в класси-
ческой математике грекоп четвертые степени линий не употреблялись, как не могущие
быть построенными геометрически; таким образом, эта и теорема XI, в которой встре-
чается двойное отношение площадей, пс могут восходить к Архимеду.
(31 См. примечание (4j к «Кпиге о построении круга, разделенного на семь рав-
ных частей». Здесь слово «плоскость» передано пе словом сатх, а равнозначным словом
мусаттах. Разнобой в терминологии объясняется, вероятно, вкусами переписчиков трак-
тата, которые, как видно из предисловия переписчика к «Кинге о построении круга»,
довольно свободно обращались с текстами переписываемых имя сочинений.
[41 Рис. 24 отсутствует в рукописи, по для пего оставлено пустое место.
(51 Это предложение Архимеда играло очень важную роль в развитии тригономет-
рии па средневековом Востоке. В тригонометрической кпиге своего «Канопа Мас'уда
по астрономии и звездам» среднеазиатский ученый Абу-р-Райхан ал-Бируни основывает
па нем доказател ьства многих теорем тригонометрии, называя его «предпосылкой Архи-
меда». В своем «Трактате об определении хорд в круге» ад-Бирупи приводит три дока-
зательства этого предложения, данные Архимедом в «Кпиге о касающихся кругах» (кото-
рую ал-Бнруци называет «Книгой кругов»), а также приводит многочисленные доказа-
тельства этого предложения, принадлежащие средневековым коммептагорам Архимеда
(см. «Теоремы Архимеда, сохранившиеся в передаче ал-Бирунн»).
—1^—g
ПРИЛОЖЕНИЯ
СПОСОБЫ ЗАПИСИ ЧИСЕЛ И ВЫЧИСЛЕНИЙ
В ДРЕШШ’РЕЧЕСКОЙ МАТЕМАТИКЕ
У греков были в употреблении дна способа обозначении чисел: алфавитный и при
помощи так называемых геродиановских знаков.
В следующей таблице) даны числовые значения отдельных букв греческого алфавита
вместе с греческими и семитическими (еврейскими) названиями этих букв.
ЧИСЛОВЫЕ ЗНАЧЕНИЯ ВУКВ ГРЕЧЕСКОГО АЛФАВИТА
Число Буква греческо- го алфа- вита Греческое название буквы Семитическое название буквы
1 гс альфа алеф (бык)
2 Л бета бет (дом)
3 Y гамма гимель (верблюд)
4 б дельта далет (дверь)
5 в эпсилон хе (he)
6 S виу (дигамма) вау (столб, па котором стояла
палатка)
7 дзета вайи
8 ч эта (Н) хет (плетень)
0 0 тета тет
10 1 йота иод (РУ«а)
20 X каппа каф
30 ламбда ламед (острый стержень, кото-
рым подгоняли быков)
40 р- МИ мим (вода)
50 V пи пун (рыба)
60 £ КСИ самок
70 О омикрон айи (глаз)
80 % 1111 не (рот)
90 Q копии коф (затылок)
100 0 ро рот (голова)
200 <7 сигма глин (зуб)
300 тау тку (крест)
400 ю
500 Ф фи
600 X хи
700 1b пси
800 ’ омега
900 сампи*)
*) Этот внак не входил в алфавит и употребляется только для обозначения
числа 900. Ок представляет слинпис двух букв: сигмы (дорийское название «сан»)
и пи, откуда произошло и плавание.
Порядок цифр следует семитическому алфавиту, кончавшемуся на букве «тау»,
за единственным исключением: между буквами «не» и «коф» у семитов стояла еще «цаде» —
40 Архимед
626
ПРИЛОЖЕНИЯ
твердое th; все буквы, стоящие после т—300, являются специфически греческими. Более
того, указанный алфавит является восточно-греческим (ионийским); западный (халкид-
ский алфавит), от которого произошла современная латинская азбука, имел некоторые
отличи». Это показывает, что упомянутый способ изображения чисел при помощи букв
мог возникнуть только в восточной Греции (Ионии.) и представляет специально греческое
изобретение. Если бы греки заимствовали ого с востока вместе с азбукой, то он обяза-
тельно появился бы и в западных алфавитах и, в частности, вместе с латинским алфавитом
и у римлян. Что касается времени создания рассматриваемого обозначения чисел, то
наличие дигаммы (позднее опа была заменена буквой S — знаком для сигмы в конце
слова) и коппы (Ср, исчезнувших очень рано, показывает, что щхшикновепие алфавитной
системы обозначения чисел относится к самым начальным стадиям развития греческой
культуры. Документально »та система засвидетельствована лишь для середины с V века,
но мы пе очепь ошибемся, если отнесем ее возникновение к VI. или даже VII векам до
п. э. В тсчопие классического периода эта система употреблялась преимущественно
в восточной Греции; с конца IV века она распространилась по всему греческому миру
и была перепита и семитическими народами.
При помощи указанных знаков можно было писать все числа от 1 до 999. Для обо-
значения тысяч (от одной до девяти) перед буквой ставился слева внизу значок; так
число 1851 греки записали бы так:
,шго<х.]
Для обозначения десятков тысяч употреблялся знак М (начальная буква
слова [jloqioi — мириада, то есть десять тысяч), причем соответствующее число десят-
ков писалось вверху:
М£₽=21.0 062.
Дроби с числителем единица обозначались цифрой знаменателя с штрихом справа
вверху:
если числитель по равнялся единице, то его значение писалось пад знаменателем или
слева от пего. Половила обозначалась специальным знаком Z, очень похожим
на египетское обозначение половины. Точно так же египетским можно назвать способ
представления дробной части числа в виде суммы нескольких дробей с числителями, рав-
ными единице. Для того чтобы выделить в тексте числа от обыкновенных букв, пад ними
сверху ставилась черта. Вот примеры, заимствованные из Архимедова «Измерения круга»:
г.б_
M,{)v............349450,
______ 1
Ч^ал'.............о!И К ’
,fiXoy Z'........... 4673 4-.
/л
дчуЛ'б' ...... 3013 4-+4-=3(ИЗ 4 ,
2 4 4
,шоЛ.Т) ОиГ........... 1838 2 ,
- , 10
Другой способ обозначения чисел при помощи геродиаповских *) знаков заключался
в следующем.
Единицы обозначались черточкой |, пятерки буквой П или Г (начальной буквой
слова (juvxe — пять), десятки буквой Д (ДЕКА — десять), сотни — Н (HEK.ATON —
сто), тысячи X (x<Xtoi), десятки тысяч — М (popioi — мириада). При помощи «умноже-
ния» пятерки на десятки, сотпи и т. д. получались знаки для 50, 500, 5000, 50 000:
F* = 50 , F =500 , Р-5000 , F =50000
*) По имени описавшего его грамматика II века и. а. Геродиаяа, сына анамсиитого Аполло-
Ния Дискола, который является твирцОл! греческого синтаксиса.
ЗАПИСЬ ЧИСЕЛ И ВЫЧИСЛЕНИИ В ДРЕВНЕГРЕЧЕСКОЙ МАТЕМАТИКЕ 627
Вычисления производились при помощи абака — счетных досок, вроде наших сче-
тов, ва котором единицы различных разрядов обозначались жетонами — пссфами (ф^ф01>.
Самос раншзо упоминание о счетных жетонах встречается в «Афипской политип» Аристо-
теля при объяснении процедуры выборов и подсчета голосов. Греческий абак (само наз-
вание обозначает «доска») дошел до пас в виде так называемой саламинской доски,
относящейся примерно к 111—II векам до я. э.,
рисунок которой помещен ниже. Помещеинк»
сбоку знаки соответствуют изображениям по
геродиаповой системе следующим числам:
Т—талант (6000 драхм),
Р-5СОО , X - 1ПСЮ , Iя-ИО , Н - ИЮ ,
Р - 50 , Д-1!» , Г -5 , h -1
1-1 . С -| . Т-1 , Х--1
£ 7 ' U
ХГИРДГМСТ
Саламинская доска.
Нижние, не разделенные пополам полоски
соответствуют драхме и се долям'. Очень инте-
ресно, что основная часть доски представляет
полосы, разделенные пополам. Для десятичной
системы счисления подобное разделение является
немного странным, по оно упорно повторяется и
па римском абаке, и на китайском суаппапе, по-
казывая, что когда-то это деление имело смысл.
Мы можем объяснить это, если предположим,
что прототип сазамипской доски был выработан
в стране, гдо каждый разряд числа требовал для
своего обозначения двух знаков; такой страной
была как раз Вавилония с ее шести десятеричной
системой счисления, где каждый разряд состоял
из десятков и единиц. Вторым признаком вави-
лонского происхождения саламинской доски яв-
ляется обозначение на вей таланта — специфиче-
ски вавилонской единицы веса, равной 60 минам
или 6000 драхм, так как греки, когда они перепи-
ли вавилонскую монетную систему замелили де-
ление мины па 60 шекелей более подходящим для
их системы счисления делением па 100 драхм.
Мн обладаем более чем скудными сведениями о том, какими способами греки про-
изводили арифметические вычисления. Конечно, сложение и вычитание настолько просты,
что ,пе требуют вообще никаких комментариев. Относительно умножения мы имеем при-
меры, приведенные Евтокием в его комментарии к «Измерению круга» Архимеда.
Греки пользовались тем же способом умножения, что имг.т, с той только разницей, что
мы начинаем умножение с низших разрядов множителя и множимого, а греки начинали
<: высших. Интересно, что совершенно так же, кап греки, поступали средневековые
абацистьт эпохи Герберта (X—XI века) и вавилонские вычислители, начиная с третьего
тысячелетия до н. э. Это сходство даст право предположить, что вообще греческие способы
арифметических вычислений мало отличались от методов, изложенных в самом раннем,
принадлежащем Герберту трактате об абаке, тем более, что последним наверняка пред-
ставляет собой лишь переработку античных методов арифметических вычислений.
Об античных способах деления мы имеем гораздо более скудные снедения. В гре-
ческих источниках мы не имеем ни одного примера производства деления.
Зато относительно методики извлечения квадратного корня у Архимеда мы теперь
знаем гораздо больше, чем исследователи, трудившиеся пятьдесят лот тому назад. Откры-
тая в начале XX века «Метрика» Герона Александрийского вместо с вавилонскими мате-
матическими текстами дала нам твердое основание для восстановления методики извле-
чения квадратного корня Архимедом.
Способ извлечения квадратного корня, изложенный в «Метрике» Герона и в вавилон-
ских математических текстах, состоял в том, что если известно какое-нибудь приближен-
ное значение /10 квадратного корня из некоторого числа А, то более точное его значение
можно найти по следующей формуле:
628
ПРИЛОЖЕНИЯ
Числа /10 и -т~ представляют собой два приближенных значения квадратного кор-
ня, из которых одно является значением с недостатком, а другое — с избытком. Так как
истинный корень заключается между ними, то вполне естественно, что арифметическое
среднее обоих этих значений дает более точную величину искомого квадратного корня.
_ . Л
Положим Ив=:а: и-у- =у; тогда
"о
и искомый кадратпый корень представляет геометрическое среднее для х и у
УА=Уху.
Мы можем приближенно представить его в виде арифметического среднего
Еслибымыхотслинолучитыю вавилонскому способу следующее значение квадрат-
ного корня, то должны были бы разделить Л на полученное приближенное значение
,<-г «л/
уА=~----------, откуда
у М У)
1 Г1 1 14i
|/'у| 2ху '2 \х' у)’
Мы получаем третье «среднее», употреблявшееся в греческой, математике, а именно
среднее гармоническое. Таким образом, все три греческих «средних» оказываются свя-
занными между собой в операции извлечения квадратного корня: если среднее геометриче-
ское У ху дает точную величину квадратного корня из произведения ху, то сроднее ариф-
метическое — («+#) дает, как нетрудно видеть, приближение с избытком, а среднее гар-
моническое — приближение с недостатком. Как показывает книга X «Начал» Евклида,
первичное значение р’от] — медиа ль — относилось именно к среднему геометрическому,
называвшемуся просто «средним» без всяких прилагательных; таким образом, вполне
естественно нредноложить, что и два других «средних» возникли первоначально в связи
с операцией извлечения квадратного корня. То обстоятельство, что все эти три средних
встречаются в совместном комбинации уже у Архита Тарантского, позволяет предполо-
жить, что указанный способ извлечения квадратного корня был уже известен грекам
еще в знаку Платона в IV веке до н. з. Каким образом при его помощи Архимед мог
вычислить встречающиеся в «Измерении круга» квадратные корни, показано нами в ком-
ментарии к названному сочинению (стр. 547 и сл.).
ОКОНЧАНИЕ ВТОРОЙ КНИГИ «О ПЛАВАЮЩИХ ТЕЛАХ»
л
В комментарии ко второй книге «О плавающих телах» мы указали на незакончен-
ность этого произведения Архимеда. В связи с этим пе может не представить интереса
вопрос, что могло бы стоять в ненаписанной части книги.
В конце предложения X Архимед рассматривает вопрос о положении равновесия
сегмента параболоида, когда параметр р меньше оси сегмента. В зависимости от
плотности плавающего тела Архимед устанавливает две области, в которых возможно
плавание сегмента с основанием, находящимся
ляс жидкости, а именно когда плотность тела
будет или близка к нулю, или же почти равна
плотности жидкости. В качестве меры плотно-
сти мы можем взять величину оси погружен-
ной части сегмента, которую мы обозначали
через а. Определенно предельных значении а
мы можем произвести по методу Архимеда.
Пусть па приложенном рисунке ABL бу-
дет парабола, получающаяся в сечении тела
плоскостью, проходящей через ось, парабо-
ла .4(767 представляет параболу центров, а
парабола A VQD соответствует пашей параболе
плавания. Центр тяжести' сегмента будет в
I
точке А'(А'/)—— 7JA); отрезок К К равеп па-
£»
рамстру р параболы ABL, a ID составляет
две пятых AL,
Через В проведем параллельную AL
прямую до пересечения в С и U с параболой
AI; отрезки СН и Uli будут ординатами, соответствующими плаванию с нижним углом
основания на поверхности жидкости, a OQ и PV дадут папш -^-а—длины оси погружен-
ных частей сегмента, соответствующих искомым предельным положениям. Значения
отношений плотности тела к жидкости для этих положений мы получим, возведя и лвад-
OQ PV
рат отношения и .
Возьмем начало координат в точке В, пусть ось абсцисс пойдет по BD, а ось орди-
нат перпендикулярно к ВТ) влево. Уравнение параболы ABL будет:
„ AD-
У BD
X.
Уравнение параболы АС! будет;
( . 2 ,
Наконец, уравнение последней параболы
1
1 V
у AD )
8 3 AD2 f 1
AQ1) будет:
AD2 А 1
2 BD
630
ПРИЛОЖЕНИЯ
2
Расстояние ВВ—х будет равно — BD—р. Подставляя это выражение в уравнение
параболы АС1, получаем:
/ 2
( у--к
3 АП3
5* BD
что может быть приведено к виду
, 4 ,3 ЛЯ» л
откуда получаются корпи:
Таким образом,
У Архимеда тангенсы соответствующих предельных углов наклона будут:
в УА
5 Р
2 AD
1
4 BD
G Р_ — L Р ____?______
’ СВ 2 AD
1 Г 1 4 BD
Переходим к определению предельных величин OQ и PV погруженных осей. Для
итого нам нужно найти разность абсцисс парабол AB.L и AQD, соответствующих опре-
деленным ординатам i/i и
Уравнения этих парабол будут: •
У
, AD*
у BD
Умножим первое уравнение ла два и вычтем из него второе, помня, что ординаты у
(в обоих уравнениях одинаковы, по абсциссы различны. Если обозначим абсциссу пара-
болы AQD через т3, а абсциссу параболы ЛВ1- через х1г то будем иметь:
Cl АП*
y-TAVj -у^^-^-х,)
Остюда определится нужный нам отрезок Д — х2—
АВ
.г 1-5?=^.
Г 1 2 AD'2
2у AD-2-}
, BD
*)
Если вместо I/ вставим пайдсниую величину
?го после очевидных упрощении получим:
4t.,=®(0,52-<1.G0^±0.4S
ОКОНЧАНИЕ ВТОРОЙ КНИГИ «О ПЛАВАЮЩИХ ТЕЛАХ»
631
Таким образом мы приходим к следующему выводу:
1Q. Если плотность тела по отношению к жидкости меняется в пределах от 0 до
QO.52—0,60-j~—0,48 J/ 1—, то тело плавает с основанием, находящимся пад
жидкостью.
2°. Если плотность тела лежит в пределах
"(0,52-0,60^-0,48 4- д» (о.52-0,№^<0,48 /1-ЭД".
то тело будет плавать с полузатопленным основанием.
3°. Если нлотпость тела мспиется в пределах
„ (о.И-О.Ю^+О.в/Г^)' до (1. 4й>)’.
то тело будет плавать в наклонном положении, имея основание пад поверхностью
жидкости.
,, ' с. з р v . ,
4 . Если плотность тела меняется в пределах от I 1 J до 1, то тело будет
плавать, имея ось вертикальной.
Для случаи плавания сегмента с погруженным основанием надо вместо погружен-
ной части рассматривать часть сегмента, находящуюся вис поверхности жидкости и заме-
нить относительную нлотпость тела ее дополнением до единицы. В таком случае мы полу-
чили бы предложении, аналогичные 3, 5, 7 и 9 сохранившейся части второй книги. Нет
никакого сомпепии, что Архимед был в состоянии сделать это; мы же ограничимся лишь
формулировкой окончательных результатов.
1“. Если плотность тела изменяется от 1 до
1 -( 0,52-0,60^-0,
то сегмент плавает в наклонном положении, имел основание полностью под поверхно-
стью жидкости.
2°. Если плотность тела меняется в пределах
да 4 -(0,52 -0.60 ^5+0,48 /1—
то сегмент плавает с полузатопленным основании!.
3°. Если плотность тела меняется в пределах
" l-(o,52 - 0,60 7fB1-0,48 /
да l-A-^Y,
А V 2 BD J ’
то сегмент плавает в паклонпом положении с основанием, находящимся полностью под
поверхностью жидкости.
4°. Накопоц, если плотность тела меняется в пределах от 1—^1—Тн)) я°
нуля, то сегмепт плавает с вертикальной осью, имея основание нише поверхности
жидкости.
Соответствующие углы наклона могут быть определены по той жо формуле
Ч?4>=/ ^Ъ-р-а)'
если только вместо а брать величину оси сегмента, находящейся вне поверхности жидкости
632
ПРИЛОЖЕНИЯ
Окончательные результаты исследования Архимеда могут быть сформулированы так:
3
1°. Если ось сегмента не превышает -у параметра р, то сегмент может плавать
с вертикальной осью, имея основание безразлично над или под поверхностью жидкости.
Плавание ссгмепта в наклонном положении невозможно.
2 . Если длина оси сегмента заключается в пределах от ~^р до -^-р, то плавание
в наклонном положении становится возможным, но основание сегмента должно
быть или над, или под поверхностью жидкости. Предельными значениями плотности
являются
V1 2 Вп) 1 2 В1))
ГТ Р 2 Р
При эти пределы равны пулю и единице; если , то мы получаем
IjU <5 ijJ.) 3-0
И
16.
25’
р 2 р 4 „
во всем промежутке от рг.=-т до -.тг.— тр первый предел будет ниже второго. Таким
15U & £>J_J 10
образом, мы замечаем следующие три области изменения плотности тела.
. _ f . 3 р V
а) Если плотность тела заключается в пределах от нуля до f 1—j , то воз-
2
можно или плавание тела в вертикальном положении с погруженным основанием, или же
в наклонном положении с основанием вне жидкости.
б) Если плотность тела заключается в пределах от
1 Р ‘
2 BJ).
то возможно плавание только в вертикальном положении, причем основание может бе:
различно находиться над и под поверхностью жидкости.
в) Если плотность тела заключается в пределах от 1
3 р V .
2BD) Д0 11 ТОВОа’
можно пл а ватт и с тела или в вертикальном положении с основанием вне жидкости, или
в наклонном положении с основанием внутри жидкости.
3°. Теперь рассмотрим случай, когда отношение будет больше В таком
случае возможно совпадение обеих предельных величин плотности; зто будет, если
или
Отсюда
1
что можно положить равным примерно — .
•> 15 з-
Таким образом, если длина оси сегмента изменяется в пределах от — р — 3-^р
и приблизительно до 5р, то мы будем иметь по-прежнему три области: к
а) При небольших плотностях плавание возможно в вертикальном положении
основанием вниз или в наклонном положении основанием вверх, причем последнее может
быть или целиком вне поверхности жидкости, или отчасти.
б) При плотностях тела, несколько отличающихся в ту или другую сторону от поло-
вины, возможно плавание только в вертикальном положении.
в) При плотностях, приближающихся к единице, возможно плавание в вертикаль-
ном положении основанием вверх или в наклонном положении основанием вниз, причем
последнее или целиком, или отчасти находится ниже поверхности жидкости.
Если BD более 5р, то средняя область пропадает совсем, а две крайние начинают
отчасги налагаться одна па другую.
БИБЛИОГРАФИЯ
БИБЛИОГРАФИЯ
Издание трудов Архимеда основывается на следующих рукописях:
1. К о д е к с Георгия Валл ы. Сам кодекс утерли, но его содержание может
быть восстановлено па основании следующих рукописных копий:
a) Codex Laurcntianus (XV в.) во Флоренции,
b) Codex Marcianos (XV в.),
с) Codex Parisinus 2360 (XVI в.),
d) Codex Parisinus 2361 (1544 г.)
2, Константинопольский палимпсест (X в.), найденный в иеруса-
лимском монастыре и прочтенный Гейбергом в 1906—-1908 годах.
3. Л а т и и с. к и й перевод сочинений Архимеда Вильгельма
из Мербеке (XII век), сделанный настолько буквально, что па его основании
можно восстановить греческий оригинал. Хранится в ватиканской библиотеке.
1. II е ч а т п ы е издания сочинений Арх и л» е д а
4. Archiniedis орста, quae quidem exstant. oinniii (с комментарием Евтокия), Basileae,
Joh. llervagius, 1544.
5. Archiniedisopera nonnullaa Fed. Commandinonuperin latinuin converse, Vencliis, 1523.
V>. Archiniedis de iis quao vebunlur in aqua Jibri duo a Fed. Conimandino restituti cl illust-
rati, Bononiae, 1565.
7. Archiniedis opera quae exstant, novis demonstrationibus illustrala per Dav. Hivaltum.
Paris, 1615.
8. Lemmata Archiinodia apud Graecos et Latinos jumpi-idem desiderata о vetusle codice
M. S. arahico a Joh. Gravio traducta et nunc primuin cum arabum scholiis publicata...
a Sanio cl e Forster, Londini, 1657.
9. Admirandi Archiniedis Syracusani -monumenta omnia matbomatica quae exstant ex
traditiono D. Fr, Matirolici, Panormi, 1685.
10, Archiniedis opera, Apollonii Pergaei Coniconini libri IV..., London, 1675 (Barrowius),
11. Lessing G. E., Bcitriige zur Geschichte iind I.iteraLur, Braunschweig, 1773 (первое
издание задачи о быках, стр. 421 и ел.).
12. Archiniedis quao supersunt- oninia cum Eutocii Ascalonilac comiricntariis ex versionc
Jos. Torclli, Oxoriii, 1792.
13. Peyra rd F., Oeuvres d’Arcliiiriedo, traduites litl.cralcitient. avec. un common taire,
Paris, 1807.
11. Archimedes von Syrakus Vorhandcne VVerkc, aus dent gricchischcn iihersetzt... von
Xizze, Stralsund, 1824.
15. Archiniedis opera omnia cum commentariis Entocii, od J. L. Ileiberg, I—III. Leipzig,
Teubner, 1880—1881, 2-o изд., I (1910), II (1913).
16. Heath T. L., The works of Archimedes edited in modern notation wilh introductory
chapters Gambridge, 1897. (Немецкий перевод с. дополнениями Fr. Klin m’a,
Berlin, 1914.)
636
БИБЛИОГРАФИЯ
17. Suter И., Ein Fragment <‘шк Archimedis Sloinachion. Abhandlungen sur Geschichte-
der Mathematik, IX, 491 с ил. (1899).
18. Heiberg J. L., Eine nene Schrift des Archimedes. Hermes, ХЫ1, 235—297 (1907),
19. Ver В веке P., Les oeuvres completes tl’Arehimede t-radniles du grec en francais,
Paris—Bruxelles, 1921.
20. Czwal ina A., Archimedes Cbersetzungen mit Kommentar. Ostwald’s Klassiker
der exakten Wissenschaften. 5 выпусков, Leipzig, 1922—1925.
21. Suter H., Das Buck der Auffindung der Sehnen ini Krelso von al-Binini. Bibliotheca
Mathematics, 3 Folge, XI, 12—26 (1910/11).
22. S c h о у C., Die trigonometrischon Lehren dos persischen Astronomen... ai-Biruni,
Hannover, 1927 (перевод «Книги о семиугольнике», ст. 77—84).
П. Русские переводы трудов Архимеда
23. Петрушевский, Архимеда две книги о шаре и цилиндре, измерение круга
и леммы, Сиб., 182?
24. II е т р у ш е в с к и и, Архимеда «Псаммит», Спб., 1824.
25. Трактат Архимеда «Об измерении круга». Перев. В а щ о в к о-З ахарчепко
(в его переводе «Начал» Евклида), Киев, 1880.
26. Гейборг И., Новое сочинение Архимеда. Послание Архимеда к Эратосфену
о некоторых теоремах механики, Изд. Mathesis, Одесса, 1909.
27. Архимед, Гюйгенс, Ламберт, Лежандр. Четыре сочппспия
о квадратуре круга,- Matheris, Одесса, 1911. (Переизданы 1934, 1936.)
28. «Псаммит» Архимеда, Перев. Г. Н. Попова, Птгр., 1922 (Переиздан 1932.)
29. Начала гидростатики (Архимед, Стевии, Галилей, Паскаль). Перев. A. II. Долго-
в а, 1932, 2-е изд., 1933. (Переведена первая книга «О плавающих телах» и первое
предложение из второй.)
III. Сочинения греческих авторов, содержащие
упоминании о математических трудах Архимеда
30. Герои А л о к с а и д р и й с к и й. Метрика, Hero Alexandrines Opera, Lipsiao,
III, 2—252, 1903.
31. Его же «Механика», парен, с арабского, L. Nix. Opera, Lipsiae, IV, 2—252, 1900,
32. Папп Александрийский, Математическое собрание, Изд. Гульча.
Перлин, I—III, 1876—1878.
IV. Общие работы и биографии Архимеда
33. Heiberg J. L., Quaestiones Arcliimedcao, T-Iauniae, 1879.
34. II u I t sch F., Статья «Archimedes» в Real-Encyclopadic der Irlassischen Altertums-
wisscnschaften, Pauly-Wissowa, II, 507—539.
35. Heat- h T. I.., Archimedes, London, 1920.
36. Czwalin a A., Archimedes, Leipzig—Tenbner, 1925 (есть русский перевод, ГТТИ,
1931).
37. К I i с iu Fr — Wolff G., Archimedes, Berlin, 1927.
38. I) i j k s L о r h n i s E. I., Archimedes, Groningen, 1938; «Euclidos», XV—XVII,
XX, 1938—1944. Англ, перевод: Copenhagen, 1956.
39. Л у p i. с С. IL, Архимед, Изд. Акад, паук, 1945 (имеется дополненный румынский
перевод).
40. К а г а н В. Ф., Архимед, Гостехиздат, 1949.
41. Веселовский 11. II., Архимед, Учпедгиз, 1957.
библиография
637
V. Исследован пл о Б отдельных работах Архимеда
А. М а т е м а т и к а
42. W i е 1 е 11 п с т, Das Fortlcben der Archimcdischcn Infinitesimal Methodon bis sum
Beginn des 17 Jahrhunderts. Quellen ui>d Studicn zut Geschichtc dor MaLhematik, J,
201—220 (1931).
43. Mnil er C., Wio 1'and Archimedes dio voii ihm gegcbcncn Naherungswcrtc dcr |/”3,
Quellen und Stndien, II, 281—285 (1932).
44. Tropfke I., Die Siebcueckahhandlting des Archimedes, Osiris, I, 636—651 (1936).
45. Башмакова И. Г., Дифференциальные методы в работах Архимеда, Историко-
математические исследования, VI (1953).
Б. М е х а и и к а
46. М а с h Е., Die Mechanik in ihrer Entwicklung, Leipzig, 1—17 (1904).
47. D и h c in Р.» Les origines de la Statiquc, I, Paris, 1—12, 61—98 (1905).
48. Stein W., Der Begriff des Sch-werpunktes hei Archimedes, Quellen u. Stndien, I,
221—224 (1930).
49. Reimann Dora, Historlsche SLudien iiber E. Nadi’s Darstellung der Entwick-
lnng des Hcbelsatzes, Quellen u. Studien, III, 554—592 (1936).
СОДЕРЖАНИЕ
ПРЕДИСЛОВИЕ ПЕРЕВОДЧИКА ............................ 3
ВСТУПИТЕЛЬНАЯ СТАТЬЯ К. И. «есг.'швского ........... Ь
АРХИМЕД, сочинения
МЕХАНИЧЕСКИЕ ФРАГМЕНТЫ............................. б»
КВАДРАТУРА ПАРАБОЛЫ................................ 77
О ШАРЕ И ЦИЛИНДРЕ................................ 85
О КОНОИДАХ И СФЕРОИДАХ.......................... IBS
О СПИРАЛЯХ............ ...... ..... .......... 227
ИЗМЕРЕНИЕ КРУГА .............................. 266
О РАВНОВЕСИИ ПЛОСКИХ ФИГУР, ИЛИ О ЦЕНТРАХ ТЯЖЕСТИ
ПЛОСКИХ ФИГУР ............................... 272
ПОСЛАНИЕ К ЭРАТОСФЕНУ. О МЕХАНИЧЕСКИХ ТЕОРЕМАХ . . 298
О ПЛАВАЮЩИХ ТЕЛАХ ......................... ..... 328
ПСАММИТ ......................................... 358.
КАТОПТРИКА ..................................... 368
ОБ УСТРОЙСТВЕ НЕБЕСНОЙ СФЕРЫ.................... 370
ЗАДАЧА, КОТОРУЮ АРХИМЕД НАШИЛ В ЭПИГРАММАХ И ПОСЛАЛ
НА РАЗРЕШЕНИЕ ЗАНИМАЮЩИМСЯ ПОДОБНЫМИ ВОПРО-
САМИ АЛЕКСАНДРИЙСКИМ УЧЕНЫМ В ПОСЛАНИИ К ЭРА-
ТОСФЕНУ КИРЕНСКОМУ ........................... 372.
СТО.МАХИЙ ........................................ 378
О МНОГОГРАННИКАХ ................................ 383.
ТРАКТАТ ЛБУ-Л-ХАСАНА СЛЕЙТА ИБН КУРР.Ы О ПОСТРОЕНИИ
ОПИСАННОЙ ОКОЛО ШАРА ТЕ ЛЕСНОЙ ФИГУРЫ С ЧЕТЫР-
НАДЦАТЬЮ ОСНОВАНИЯМИ.......................... 387
КННГЛЛЕММ АРХИМЕДА В ПЕРЕВОДЕ ТЕБИТЛ БЕН КОРЫ С РАЗЪ-
ЯСНЕНИЯМИ УЧЕНОГО ЛЛЬМОХТАССО АБИЛЬГЛСАНА ГАЛИ
КЕН АХМАДА НАСУЭНСКОГО ....................... 391'
КНИГА АРХИМЕДА О ПОСТРОЕНИИ КРУГА. РАЗДЕЛЕННОГО НА
СЕМЬ РАВНЫХ ЧАСТЕЙ. ПЕРЕВОД АБУ-Л-ХАСАПА САБИ-
ТА ИБН КУРРЫ АЛ-ХАРР АНИ................... 401
ТЕОРЕМЫ АРХИМЕДА, СОХРАНИВШИЕСЯ В ПЕРЕДАЧЕ АЛ-ЕИРУНИ 41С.
КНИГА О КАСАЮЩИХСЯ КРУГАХ АРХИМЕДА, УБИТОГО В ДВЕСТИ
ДВЕНАДЦАТОМ ГОДУ ДО РОЖДЕСТВА................ 422.
КОММЕНТАРИИ
КВАДРАТУРА ПАРАБОЛЫ ....................... 443
О ШАРЕ И ЦИЛИНДРЕ................................. 451
О КОНОИДАХ И СФЕРОИДАХ............................ 508
СОДЕРЖАНИИ
639
О СПИРАЛЯХ ................................ - - 518
ИЗМЕРЕНИЕ КРУГА . . . .................... .... 528
О РАВНОВЕСИИ ПЛОСКИХ ФИГУР........................ 554
ПОСЛАНИЕ К ЭРАТОСФЕНУ. О МЕХАНИЧЕСКИХ ТЕОРЕМАХ . . 565
О ПЛАВАЮЩИХ ТЕЛАХ ................................ 578
ПСАММИТ ........................................ &»8
КНИГА ЛЕММ........................................ 604
КНИГА О ПОСТРОЕНИИ КРУГА. РАЗДЕЛЕННОГО НА СЕМЬ РАВ-
НЫХ ЧАСТЕЙ................................ 614
ТЕОРЕМЫ АРХИМЕДА. СОХРАНИ НШИЕСЯ И ПЕРЕДАЧЕ АЛ-ВИ-
РУНИ ....................................... 618
КНИГА О КАСАЮЩИХСЯ КРУГАХ......................... 622
ПРИЛОЖЕНИЯ
СПОСОБЫ ЗАПИСИ ЧИСЕЛ И ВЫЧИСЛЕНИЙ В ДРЕВНЕГРЕЧЕСКОЙ
МАТЕМАТИКЕ ............................... 625
ОКОНЧАНИЕ ВТОРОЙ КНИГИ «О ПЛАВАЮЩИХ ТЕЛАХ-........ G2S
БИБЛИОГРАФИЯ...................................... 635
АРХИМЕД. СОЧИНЕНИЯ
М.» Физматгия, 1962 г.» 640 стр. с млл.
Редактор Л. Ю. Чернышева
Оформление художника В. А. Селенгинского.
Художественный редактор И* И. Рр.мяшев.
Техн, редакторы А. И. Колесникова и П. Я. Мураш св а
Корректоры Е. В. Кузнецова и О. А. Сигал.
* * *
Сдано в набор 3/1Л 1062 г. Подписано к печа-
ти 13/X 1062 г. Бумага 70X108i/i6< Физ. неч. л. 40.
Условн. печ. л. 54.8. Уч.-изд. л. 50. Тираж 4000 экз.
Цена книги 2 р. 70 к. Заказ 200.
* * »
Государствен нос издательство
физи1со-матсматич<!С1;о й литерату ры.
Москва, В-71, Ленинский проспект, 15.
* * »
Московская типография ?Ji 5 Мосгорсовнархоза,
Москва, Треклрудцый пер., 9.