*м ♦
' . ' 'Л- v.\
POL SKA AKADEMIA N A U K*I N S TY T U T M ATEM AT YQZ NY
ft
• ••?.>•
ROZPRAWY
MATEMATYCZNE
KOMITET REDAKCYJNY
Karol Borsuk redaktor
Andrzej Mostowski Marceli Stark
Stanislaw Turski
XII
J. Mikusinski and R. Sikorski
THE ELEMENTARY THEORY
OF DISTRIBUTIONS (I)
W A RSZ A W A 19 5 7
PAN3TWOWE WYDAWNICTWO NAUKOWE

БИБЛИОТЕКА СБОРНИКА «МАТЕМАТИКА»
Я. МИКУСИНСКИЙ и Р. СИКОРСКИЙ
ЭЛЕМЕНТАРНАЯ ТЕОРИЯ
ОБОБЩЕННЫХ
ФУНКЦИЙ
I
Перевод с английского
ф. в. шир око в А
С предисловием
И. М. ГЕЛЬФАНДА
ИЗДАТЕЛЬСТВО
ИНОСТРАННОЙ ЛИТЕРАТУРЫ
Москва. 1959

Этой монографией Издательство иностранной литературы
начинает выпуск серии брошюр под общим названием «Библиотека
сборника Математика». Имеется в виду включать в эту серию
переводы математических монографий небольшого объема, обзорных
статей и отдельных работ, представляющих широкий интерес.
АННОТАЦИЯ
Уже сравнительно давно физики и инженеры
применяют различные «незаконные» математические приемы,
пользуясь расходящимися рядами и интегралами, дельта-
функциями типа функции Дирака и т. п.
В последние годы математиками (главным образом
советскими и французскими) разработана так называемая
теория обобщенных функций, в рамках которой указанные
выше приемы становятся вполне законными. В брошюре
польских математиков Я. Минусинского и Р. Сикорского
дается элементарное введение в теорию обобщенных
функций. На базе очень простого определения обобщенных
функций авторы развивают основные понятия анализа этих
функций: алгебраические действия, дифференцирование,
интегрирование, сходимость последовательностей и
рядов и т. п.
Для чтения брошюры достаточно знания
математического анализа в объеме основного курса технических
вузов.
Брошюра представляет интерес для широкого круга
лиц, сталкивающихся с различными приложениями
математики и желающих ознакомиться с новыми мощными
средствами математического анализа.
Редакция литературы по математическим наукам

ПРЕ ДИ СЛО ВИЕ
К РУССКОМУ ИЗДАНИЮ
«Элементарная теория обобщенных функций»,
написанная известными польскими математиками Я. Минусинским и
Р. Сикорским, содержит прозрачное изложение основ теории
обобщенных функций. В этой книжке изложено
большинство основных понятий теории обобщенных функций и имеется
ряд полезных примеров.
Обобщенные функции авторы определяют как «пределы»
последовательностей непрерывных функций и как
формальные производные от непрерывных функций, доказывая
эквивалентность этих определений. Этот подход к теории
обобщенных функций требует от читателя знания только
простейшие понятий анализа. Показав, что класс обобщенных
функций содержит не только непрерывные функции, но и
обширный класс разрывных функций, а также такие
сингулярные функции, как дельта-функция Дирака, авторы
устанавливают основные правила действий над обобщенными
функциями: дифференцирование, интегрирование, замену
переменного и т. д. В последних параграфах рассматривается
понятие значения обобщенной функции в точке и
устанавливается необходимое и достаточное условие существования
такого значения. В заключение авторы рассматривают
периодические обобщенные функции и их разложения в ряды
Фурье; к сожалению, одна из важных сторон теории
обобщенных функций — теория преобразований Фурье — осталась
здесь незатронутой.
Эту книгу можно рекомендовать как хорошее введение
в теорию обобщенных функций.
Я. М. Гельфанд. ч
26 февраля 1958 г.

ВВЕДЕНИЕ
Цель данной брошюры — изложить теорию обобщенных
функций столь просто, чтобы эта теория стала доступной
физикам и инженерам. Для того чтобы достигнуть этой
цели, мы не будем пользоваться методами функционального
анализа и не будем определять обобщенные функции как
функционалы. В прикладной математике обобщенные
функции, например S-функция Дирака, рассматриваются как
обычные функции. Однако, по существу, обобщенные
функции не являются обычными функциями, но могут быть
аппроксимированы в некотором интуитивном смысле обычными
функциями. Такая, уже строго определенная аппроксимация
является нашей отправной точкой при определении
обобщенной функции. Это определение естественным образом
приводит к тем же самым обозначениям для обобщенных
функций, что и для обычных функций, позволяет сохранять ту
же самую форму аналитических формул и пользоваться
нашими выкладочными навыками.
Другие авторы также испытывали потребность в более
простой трактовке теории обобщенных функций, в
трактовке, основывающей определение обобщенной функции на
более простых понятиях. Это можно видеть во многих работах
по основаниям теории обобщенных функций (Гальперин [3],
Кёниг [6], Коревар [7], Микусинский [10, 11], Сикорский [13],
Словиковский [14, 15], Темпл [17]).
^Каждая обобщенная функция является в известном
смысле производной некоторой непрерывной функции. Мы
доказываем это свойство в начале нашей брошюры и
развиваем остальную часть теории на основе двух точек зрения
на обобщенные функции: как на предельный случай
непрерывных функций и как на производные от непрерывных
функций. Это помогает сделать доказательства всех теорем
элементарными и очень простыми.

8
Введение
В этой брошюре мы имеем дело с теорией обобщенных
функций конечного порядка, которые играют основную роль.
В § 21 мы показываем, как распространить основные
определения и теоремы на случай ' обобщенных функций
бесконечного порядка.
Хотя основной задачей этой брошюры и является
изложение теории обобщенных функций для целей
преподавания, мы включили в нее некоторые ноЕые результаты. Они
являются продуктом работы семинара, который авторы
вели в Математическом институте Польской Академии Наук
в 1954—55 и в 1955—56 учебных годах. Для написания
брошюры особенно полезными оказались результаты С. Лоясе-
вича, К. Урбаника, И. Влеки и 3. Железного.
В данной работе мы занимаемся обобщенными
функциями одного переменного. Дальнейшие разделы этой теории
и теория обобщенных функций многих переменных будут
изложены в последующих выпусках.

§ 1. Метод абстракции
Метод абстракции состоит в отождествлении предметов
(математических объектов), имеющих некоторое общее
свойство. Он часто применяется в математике для построения
ноеых понятий. Поясним этот метод на примерах.
Направленные отрезки х и у называются
эквивалентными, если они параллельны и имеют одинаковую длину и
ориентацию. В этом случае мы пишем
х^у.
Легко видеть, что определенное выше отношение
эквивалентности обладает следующими свойствами;
(£i) х ^ х {рефлексивность),
(£г) если х ^ У* то У Гч х (симметричность),
(6з)3 [еслих^ у и y^z, то х^ г (транзитивность).
Отождествляя эквивалентные направленные отрезки/гмы
приходим к понятию свободного вектора. Разъясним
математический смысл этого отождествления. При помощи
отношения эквивалентности мы получаем такое разбиение
множества всех направленных отрезков на непересекающиеся
классы, при котором отрезки из одного и того же класса
эквивалентны, а отрезки из различных классов не
эквивалентны. Таким образом, с логической точки зрения, каждый
свободный вектор является классом эквивалентных
направленных отрезков.
Другим примером метода абстракции служит канторово
определение действительного числа. ОтпраЕной точкой здесь
является понятие фундаментальной последовательности
рациональных чисел. Под фундаментальной последоЕатель-
ностью мы понимаем последовательность { ап }, удовлетворяв

10
§ 1. Метод абстракции
ющую условию Коши: для любого (рационального) числа
£>0 существует такой номер п0> что
I ат — ап | <£ при туп>п0.
Фундаментальные последовательности { ап } и ( Ьп }
рациональных чисел называются эквивалентными, если
последовательность {ап — Ьп } стремится к нулю. В этом случае
мы пишем { ап ) ^ { Ьп ). Легко проверить, что4 это
отношение эквивалентности обладает свойствами ($^), ($2) и ($s).
Отождествляя эквивалентные фундаментальные
последовательности, мы приходим к понятию действительного
числа. Таким образом, в теории Кантора действительное число
является классом эквивалентных фундаментальных
последовательностей.
Метод абстракции можно применять к множествам,
состоящим из произвольных элементов, при условии, что
имеется некоторое отношение эквивалентности ~,
удовлетворяющее условиям (SJ, ($2) и ^з)-
Для каждого элемента у обозначим через [у] класс
элементов х, удовлетворяющих соотношению х ^ у.
Полученные таким образом классы [у] будем называть классами
эквива/Сентности. Из условий (^), (£2) и . (£3) вытекает
следующее:
(a) у принадлежит [у];
(b) если y^z, то [у] = [г], т. е. классы [у] и [z] со
стоят из одних и тех же элементов;
(c) если соотношение у^гне выполняется, то классы
[у] и [z] не имеют ни одного общего элемента.
Свойство (а) следует из (£^.
Для того чтобы доказать (Ь), предположим, что у ^ z.
Если х принадлежит классу [у], то х ^ у и в силу (<£3)
x^z, т. е. х принадлежит классу [z]. С другой стороны,
z^y в силу ($2). Поэтому, если х принадлежит классу
[г], т. е. х ^ zy то х ^у в силу (<о3), т. е. х
принадлежит классу [у].
Для того чтобы доказать (с), предположим, что
соотношение у ^ z не выполняется, но существует элемент ху
принадлежащий классам [у] и [г]. Это значит, что х^у и
х ^ г, а тогда в силу (£,) и (<£3) У^г, что
противоречит предположению.

§ 2. Фундаментальные последовательности
11
Из (а), (Ь) и (с) видно, что все множество разбито на
классы без общих элементов так, что два элемента принадлежат
одному и тому же классу в том и только в том случае,
когда они эквивалентны. Отождествление эквивалентных
элементов Состоит в переходе от элементов
рассматриваемого множества к классам эквивалентности. При этом
отношение эквивалентности превращается в обычное равенство.
§ 2. Фундаментальные последовательности
непрерывных функций
Множество обобщенных функций является расширением
множества обычных функций. Мы выведем обобщенные
функции методом, аналогичным методу, используемому в
теории Кантора при расширении множества рациональных
чисел до множества действительных чисел. Введение
действительных чисел преследует цель сделать всегда
выполнимыми определенные операции, например вычисление
корней или логарифмов. Введение обобщенных функций
преследует цель сделать всегда выполнимой операцию
дифференцирования. Для обычных функций, даже в предположении
непрерывности, это не имеет места.
Тогда как отправной точкой в теории Кантора являются
рациональные числа, отправной точкой в развиваемой здесь
теории будут непрерывные функции, определенные в
фиксированном интервале А < х < В (— о^ ^ А <Г В ^ ею).
Последовательность { fn(x) } непрерывных функций,
определенных при А < х < В, называется фундаментальной,
если существуют некоторая последовательность функций
{Fn(x)} и целое число k ^ О, такие, что
(FJ F£)(x)=fn(x),
(F2) последовательность { Fn(x)} сходится почти рае-
номерно.
Мы говорим, что последовательность { Fn(x)} сходится
к функции F(x) почти равномерно в интервале Л<х<5
и пишем
Fn(x)^F(x),
если она сходится к F(x) равномерно на каждом конечном
замкнутом интервале, содержащемся в интервале А < х < В.

12 § 2. Фундаментальные последовательности
Например, х/п ~Х 0 в интервале — оо < х < оо. Немного
труднее установить, что (1 + х/п)п it ех при — оо < # < оо.
Последовательность частных сумм любого степенного ряда
так^е сходится почти равномерно в его интервале
сходимости.
Каждая равномерно сходящаяся последовательность,,
очевидно, сходится и почти равномерно. Предел почти
равномерно сходящейся последовательности непрерывных
функций является также непрерывной функцией.
Запись
означает, что [[последовательность {Fn(x) } сходится почти
равномерно к некоторой функции, а запись
Fn(x) U 3= Gn(x)
означает, что последовательности { Fn(x)} и { Оп(х)}
сходятся почти равномерно к одной и той же функции.
Непосредственно из определения (при k = 0) вытекает:
2.1. Каждая почти равномерно сходящаяся
последовательность непрерывных функций является
фундаментальной.
Другие примеры фундаментальных последовательностей
будут даны после следующих лемм.
2.2. Если { fn(x)} —фундаментальная
последовательность функций с непрерывными производными т-го порядка
1(пт){х)у то последовательность { j{nm)(x)} также является
фундаментальной.
Так как последовательность { fn(x)} удовлетворяет уело-
виям (FJ и (F2), то последовательность { f(nm)(x)}
удовлетворяет [условию F{%+m)(x) = j{nm)(x) и условию (F2).|3to и
доказывает, что последовательность { f(nm)(x)}
фундаментальная.
2.3. *) Если последовательность { fn(x)} непрерывных
функций ограничена и если fn(x) zt f(x) в .интервалах
г) Эта лемма является частным случаем менее элементарной
теоремы из теории интеграла Лебега.

§ 2. Фундаментальные последовательности 13
х х
А < х < х0 и х0 < х<В, mo f /„(/)<# =^ f /(/)d/ в интервале
Xq Xq
A < x < В. Поэтому последовательность { fn (x\}
является фундаментальной.
Пусть |/я(х)| <Л1. По заданным s>0 и интервалу
а^х^Ь (Л <Г а < *0 < 6 < В) подберем номер я0 так, чтобы
в интервалах а^х^х0 — г/4М и х0 + в/4М ^ х ^ 6 при
л > А20 выполнялось неравенство | /„ (#) — / М К £/2 (6 — а)1).
Тогда, при я >я0 интеграл от | fn (х) — f (х)\ по каждому
из этих интерзалоз будет меньше г/2. Та же оценка имеет
место для интервалов х0 — е/4М ^ х ^ х0 и х0 ^ х ^
^ *о + £/4М. Следовательно,
| f fn (t) dt — f / (/) й|<е при a < x ^ 6 и ft > я0,
Xq Xq
что и доказывает лемму.
Примеры фундаментальных
последовательностей
Г. Последовательность
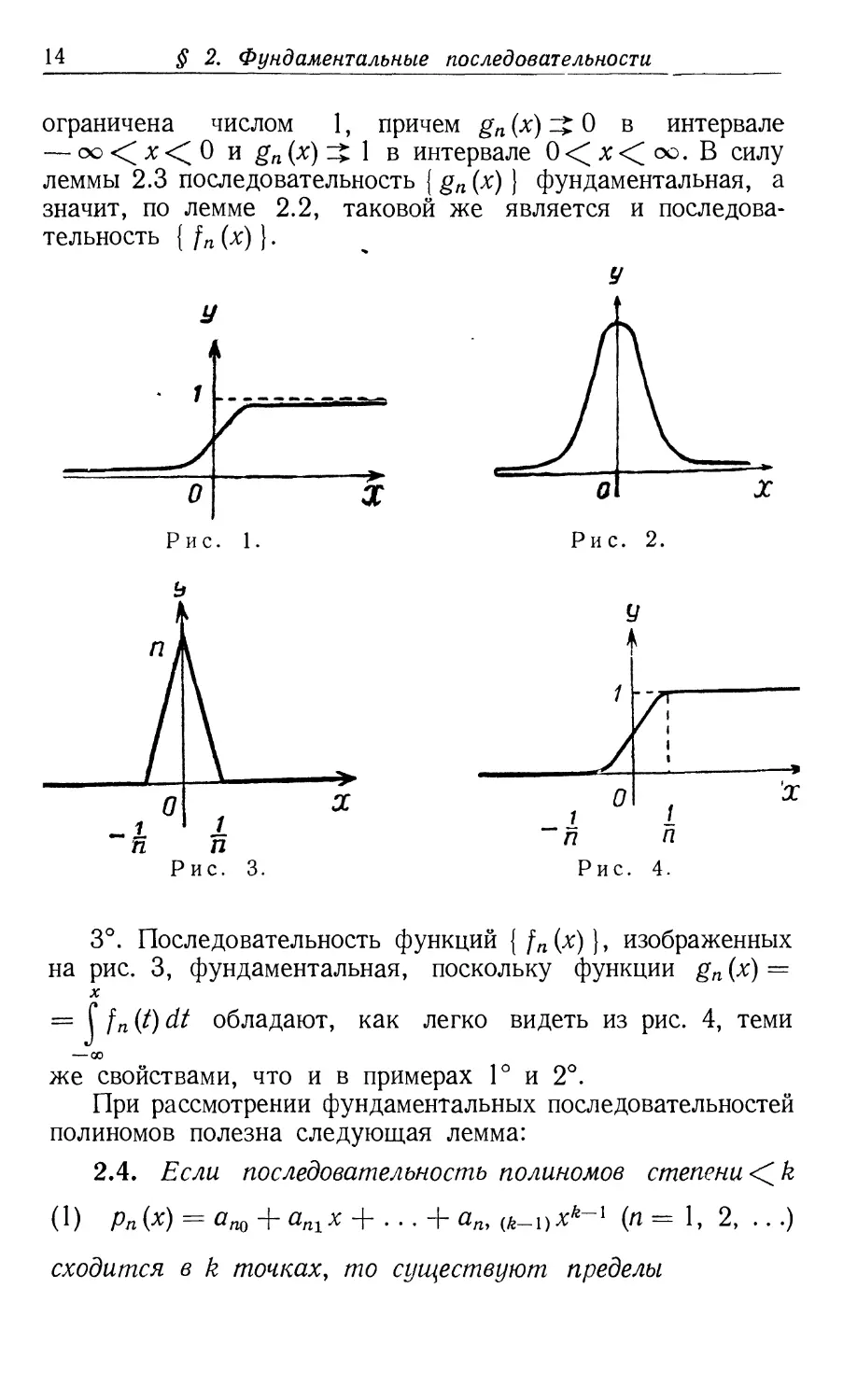
ограничена числом 1, причем g„ (х) ^t 0 в интервале
— оо < х < 0 и gn (х) з£ 1 в интерзале 0 < х < оо.
Согласно лемме 2.3, эта последовательность фундаментальная.
2°. Последовательность
является фундаментальной. Действительно,
последовательность
gn(x)=ffn(t)dt
J) Число М предполагается настолько большим, что a<*0—г/AM
и х0 -\- е/4/И < 6. —Прим. персе.

И § 2. Фундаментальные последовательности
ограничена числом 1, причем gn (х) zj 0 в интервале
— оо < х < 0 и gn (х) zt 1 в интервале 0 < х < оо. В силу
леммы 2.3 последовательность {gn (х) } фундаментальная, а
значит, по лемме 2.2, таковой же является и
последовательность {fn(x)}.
У
1
• /
У
0
i
/^
■■-■■— ,>
Рис. 4.
3°. Последовательность функций {/л(л:)}, изображенных
на рис. 3, фундаментальная, поскольку функции gn (х) =
х
— f fn (t) dt обладают, как легко видеть из рис. 4, теми
— со
же свойствами, что и в примерах 1° и 2°.
При рассмотрении фундаментальных последовательностей
полиномов полезна следующая лемма:
2.4. Если последовательность полиномов степени <^k
(1) рп(х) = апо + аП1х + ... + апу {k-\)Xk~x (п= 1, 2, ...)
сходится в k точках, то существуют пределы

§ 2. Фундаментальные последовательности
15
(2) ау = lima. (/ = 0,1,...,6-1).
Обратно, если пределы (2) существуют, то рп (х) z£ р(х), где
р(х) = а0 + а1х + ... а^_! л:*-1.
Пусть xv...,Xk — различные числа. Тогда, подставляя
их в полином (1), находим, что
Vnj= 4" (Аи Рп (*l) + -"+Akj Рп (xk)),
где
А =
1 *х ... х*-1
1 ** . . . **->
=£0,
а Л/у — алгебраическое дополнение элемента x'f1
определителя А. Следовательно, если пределы limpn(Xj) (i= 1,2,.. .,k)
существуют, то и пределы (2) также существуют.
Равномерная сходимость в любом интервале — с ^ х ^ с
вытекает из оценки
k-\
IM*) —/Ч*)|<2 \anj — aj\d.
/
2.5. Последовательность { рп (х)) полиномов степени
< т является фундаментальной в том и только в том
случае, когда она сходится почти равномерно.
Ввиду леммы 2.1 достаточно доказать необходимость.
Пусть {рп(х)}—фундаментальная последовательность;
тогда существуют целое число k^O и последовательность
{ Рп(х)} полиномов степени <^m-\-k, такие, что PW (х) =
= рп (х), причем последовательность { Рп (х)} сходится
почти равномерно. В силу леммы 2.4 коэффициенты
многочленов Рп(х) стремятся к пределам, следовательно,
стремятся к пределам и коэффициенты многочленов рп{х).
Отсюда, в силу леммы 2.4, вытекает, что {рп (х)} сходится
почти равномерно.
Полезно отметить, что целое число /г, фигурирующее в
определении фундаментальной последовательности, можно в
случае необходимости заменить любым большим целым
числом. Это вытекает из следующей леммы:

16
§ 3. Определение обобщенной функции
2.6. Если последовательность { Fn (х)) удовлетворяет
условиям (F^ и (F2), то последовательность функций
Fn(x)=^dt^dt2... ^Fn(tt)dtlt
Xq Xq Xq
где I—некоторое целое положительное число, также
удовлетворяет условиям (FJ и (F2) с заменой k на k -{- L
Кроме того, если Fn(x) ^F(x), то Fn{x)zt F(х), где
х U *1-\
F(*)=Jd/Jd/2... $ F^di,.
Xq Xq Xq
§ 3. Определение обобщенной функции
Мы говорим, что две фундаментальные
последовательности { fn (х)} и { gn (х) \ эквивалентны и пишем
(fn(x)}^[gn(x)},
если существуют последовательности { Fn (х)} и { Gn (х)} и
целое число k ^ О, такие, что
(Е,) Fp (х) = fn (х) и G<*) (х) = gn (х),
(Е2) Fn(x)^t:Gn(x).
.Из леммы 2.6 следует:
3.1. Целое число k, фигурирующее в определении
эквивалентных последовательностей, может быть в случае
необходимости заменено любым большим целым числом.
Для этого достаточно заменить функции Fn (х)
функциями Fn{x), а функции Gn(x) — аналогично определяемыми
функциями Gn(x) .
3.2. Фундаментальные последовательности {fn(x)} и
{gn (х)} эквивалентны в том и только в том случае,
когда последовательность
(1) h(x), gM, f2(x), g2{x),...
является фундаментальной.

ff 3. Определение обобщенной функции 17
Если последовательность (1) фундаментальная, то
существуют целое число k > 0 и непрерывные функции Fn (х)
и Gn{x), такие, что F^(x) = fn(x) и Gnk> {х) = gn(х),
причем последовательность
(2) /ч(*), вг(х), Fa(x), G,(x)f...
сходится почти равномерно. Следовательно, условия (Ех) и
(Е2) выполнены.
Обратно, пусть условия (Е2) и (Е2) выполнены. Тогда
последовательность (2) сходится почти равномерно, т. е.
последовательность (1) удовлетворяет условиям (F^ и (F2).
Легко видеть, что введенное нами отношение ~ обладает
свойствами ($г) и (<£2). Докажем, что оно обладает также
и свойством (<£3). Пусть [fn(x)}^{ gn (х)} и { gn (х)} ^
^ {hn(х)}; тогда существуют целое число ^0 и после
/довательности {Fn(x)\ и {Gn(x)}y удовлетворяющие
условиям (Ех) и (Е2), и, кроме того, существуют целое число
//^0 и последовательности {Gn(x) } и [Нп(х)},
удовлетворяющие аналогичным условиям:
G<'> (х) = gn (х) , HW (Х) = hn (х), Gn(х) 3 Л Нп(х).
Ввиду леммы 3.1 можно считать, что k = l. Тогда, полагая
Лп (х) = Gn (х) — Gn (х) + Нп (х), получаем
Fnk) (х) = fn (х), W (х) = К (*), Fn (х) ~Х^Нп (х) ,
т. е. {fn(x)}^{hn(x)}.
Ввиду того что условия (^), (<£2) и (<£3) выполнены,
множество всех фундаментальных последовательностей
{ fn (х)} (определенных на интервале А < х < В)
разбивается на классы эквивалентности без общих элементов так,
что две фундаментальные последовательности лежат в
одном и том же классе тогда и только тогда, когда они
эквивалентны. Эти классы эквивалентности мы будем
называть обобщенными функциямиг) (на интервале А < х < В).
Таким образом, понятие обобщенной функции возникает
путем отождествления эквивалентных фундаментальных
последовательностей.
х) Термин distribution —распределение — мы переводим принятым
в русской литературе термином обобщенная функция. —Прим. перев.
2-439

18
§ 4. Расширение понятия функции
Обобщенную функцию, определяемую фундаментальной
последовательностью {fn(x)}, т. е. класс всех
последовательностей, эквивалентных последовательности |/„U)), мы
будем обозначать символом [fn(x)]. Последовательности
{}п(х)} и [gn(x)} определяют одну и ту же обобщенную
функцию тогда и только тогда, когда они эквивалентны.
Иначе говоря,
lfn(x)] = lgn(x)] тогда и только тогда,
когда {/„(*)} ^ {gn(x)}.
Фундаментальные последовательности примеров 2° и 3°
(§ 2) определяют одну и ту же обобщенную функцию,
называемую дельта-функцией Дирака.
Действител ьно, пусть {fn (х)} — последовательность
функций примера 2° или примера 3°; тогда, в силу леммы
2.3, последовательности
х t
§dt^fn(z)dz
— оо —оо
сходятся почти равномерно к одной и той же функции
F{x)= (0 при *<0,
I х при х ^ 0.
Значит, последовательности { fn (х)} примеров 2° и 3°
эквивалентны.
§ 4. Обобщенная функция как расширение
понятия функции
По лемме 2.1 постоянная последовательность {/(#)},
т. е. последовательность, все члены которой равны
непрерывной функции f(x), фундаментальна. Таким образом,
она определяет обобщенную функцию [/(#)].
Различные функции f (х) и g (х) определяют различные
обобщенные функции [/(#)] и [g{x)].
Действительно, пусть [f(x)] = [g(x)], т. е. пусть
существуют функции Fn (х) и Gn (х) и целое число k ^ О,
такие, что
FТ (х) = / (х), GT (х) = g (х), Fn (х) ^tzGn (x).

§ 4. Расширение понятия функции
13
Тогда функции рп (х) = (Ft (х) — G1 (х)) — (Fn (х) — Gn (х))
представляют собой полиномы степени < k, поскольку
pnk)(x) = 0. Кроме того, pn(x)^t {F1(x)— G1(x)). Из
леммы 2.4 вытекает, что функция F1(x)—G1(x) является
полиномом степени < k. Поэтому ее k-я производная f(x) — g(X)
равна нулю, т. е. функции f (х) и g (х) совпадают.
Рассмотрим множество всех обобщенных функций вида
lf(x)]. Только что установленное взаимно-однозначное
соответствие между функциями f (х) и обобщенными
функциями [f{x)] позволяет не различать эти два понятия.
В дальнейшем мы будем отождествлять обобщенные
функции [f(x)] с функциями f(x) и писать [f (х)] = f(x).
Однако не все обобщенные функции могут быть
представлены в виде [/(#)], т. е. не все обобщенные функции
могут быть отождествлены с непрерывными функциями.
Например, дельта-функцию Дирака нельзя отождествить ни
с какой непрерывной функцией. Это будет доказано в § 8.
Поэтому понятие обобщенной функции можно
рассматривать как существенное расширение понятия непрерывной
функции. Позднее мы покажем, что это расширение
содержит также обширный класс разрывных функций.
С логической точки зрения это расширение в точности того же
самого типа, что и расширение множества рациональных чисел до
множества действительных чисел в теории Кантора. В самом деле,
рациональное число а отождествляется в этой теории с классом [а]
фундаментальных последовательностей, эквивалентных постоянной
последовательности {а}.
4.1. Если Ы*) =£/(*), mo [fn(x)] = f(x).
Для доказательства достаточно заметить, что f (х)
непрерывна и что последовательности {fn(x)} и {/(#)}
удовлетворяют условиям (Ех) и (Е2) с k = 0.
Поскольку обобщенные функции представляют собой
расширение понятия функции, мы сохраним для них
обычные функциональные обозначения. Обобщенные функции мы
будем обозначать символами /(#), g(x) и т. п. Следует
заметить, что это обозначение — чисто символическое и что,
в общем случае, недопустимо* подставлять вместо
переменного х числовые значения.
Дельта-функция Дирака будет обозначаться
символом Цх).
2*

20
§ 5. Алгебраические действия
§ 5. Алгебраические действия над обобщенными
функциями
Теперь мы определим сложение и вычитание
обобщенных функций и умножение обобщенной функции на число.
Определения этих действий обобщают аналогичные действия
над функциями, иначе говоря, в том случае, когда
обобщенные функции оказываются обыкновенными функциями,
вводимые ниже действия совпадают с обычными действиями
над функциями.
Под суммой f(x) + g (х) обобщенных функций / (х) =
= [/«(*)] и g(x) = [g"n(;c)] мы понимаем обобщенную
функцию [fn{x) + gn(x)].
Чтобы проверить корректность этого определения, мы
должны доказать следующее:
Г. Если последовательности {/„(#)} и {gn(x)}
фундаментальные, то такова же и последовательность (fn (х) +
+gn(x)}.
2°. Обобщенная функция [fn(x) +gn(x)] не зависит от
выбора последовательностей {}п(х)} и \gn{x)},
представляющих обобщенные функции f(x) и g(x), т. е. если
Unix)} ^ {fnW И JgnW ~ {gn(x)}, ТО [fn (X) +
+ 8n(x)}^{fn{x) + gn(x)}.
Свойство 1° обеспечивает выполнимость сложения, а
свойство 2° — единственность результата.
Для доказательства 1° предположим, что существуют
целые числа k, kx^0 и функции Fn(x) и Gn(x) со
свойствами
F{n)(x) = fn(x)9 Fn(x)^,
.G{nki)(x) = gn(x), Gn(*)=t .
В силу леммы 2.6 можно считать, что k = kv Поскольку
(Fn (х) 4 Gn (*))<*> = fn (x) + gn (x) и Fn (x) + Gn (x) zt ,
последовательность {fn (x) + gn (x)} является
фундаментальной.
Пусть теперь выполнены предположения пункта 2°.
Тогда, по лемме 3.2, последовательности
fi(x), 7i(*). Ш> J2(x) , • • • ,
gi(x), gi(x), g2(x), ~g2{x) , ...

§ 5. Алгебраические действия
21
фундаментальны, а значит, по пункту 1°,
последовательность
fi(x)+gi(x), 7i(*) + £iM, /2(*)+&(*). h(x)+g2{x) .-
также фундаментальна и, снова по лемме 3.2,
{fn(x) + gn(x)}^{fn(x) +gn(x)}.
*
Под разностью f(x) — g (х) обобщенных функций / (х) =
= ifn{x)] и g(x) = lgn{x)] мы понимаем обобщенную
ФУНКЦИЮ [fn(x)—gn(x)].
Под произведением \f (х) обобщенной функции f (х) =
= [/«(*)] на число X мы понимаем обобщенную функцию
Корректность этих определений можно доказать
аналогично доказательству корректности определения суммы.
Непосредственно из определений только что введенных
действий вытекает, что для обобщенных функций, так же
как и для обычных функций, выполняются следующие
свойства действий:
(1) f(x)+g(x) = g(x)4-f(X),
(2) (f(x)+g(x)) + h(x) = f(x) + (g(x) + h(x)),
(3) разность g(x) — h {x) — f (x) является
единственным решением уравнения f (х) + g (х) ■■= h {х),
(4) Hf(x) + g{x)) = b f(x) + \g(x),
(5) (* + |1)/(*) = Ь/(*) + 1*Д*),
(6) XW(*)) = (W(*),
(7) \-f(x) = f(x).
Обозначая символом 0 обобщенную функцию,
определяемую функцией, тождественно равной нулю, имеем
0 + f(x) = f(x) и 0.f(x) = 0.
Символ 0 в последней формуле имеет два различных
значения: в левой части он обозначает число нуль, а в
правой — нулевую обобщенную функцию. Эта
двусмысленность не приводит к неправильному пониманию,

22
§ 6. Дифференцирование
§ 6. Дифференцирование обобщенных функций
Для определения дифференцирования обобщенных
функций нам нужны следующие леммы:
6.1. Если функции fn(x) и gn{x) имеют непрерывные
производные т-го порядка и если {fn(x)} ^ {gn(x)}, то
(ЛИ - {gim)(x)}. .
Действительно, так как функции fn (х) и gn (х)
удовлетворяют условиям (Ех) и (Е2), то f{nm) (х) и g-„m) (х)
удовлетворяют условию (Ех) с заменой k на k -f- т и условию (Е2).
6.2. Для любой непрерывной функции F (х) существует
такая последовательность полиномов {Рп(х)}, что
Pn(x)^F(x).
Пусть \ап)—убывающая, а \Ьп)—возрастающая
числовые последовательности, причем ап -> А и Ьп-> В. По
хорошо известной аппроксимационной теореме Вейер-
штрасса х), существует полином Рп(х), удовлетворяющий
условию
\F(x) — Рп (х) | < \/п при ап < х < Ьп.
Отсюда Рп (х) :J F (х) в интервале А < х < В.
6.3. Всякую обобщенную функцию можно представить
в виде [рп (#)], где рп(х) —полиномы.
Действительно, пусть [fn(x)] — обобщенная функция,
т. е. существуют некоторое целое число ^Ои почти
равномерно сходящаяся [к некоторой функции F (х) ]
последовательность {Fn(x)}7 такие, что F{nk\x) = fn(х). Положим
Рп(х) = Pnk\x), где {Рп(х)\—последовательность
полиномов, сходящаяся почти равномерно к F (х). Тогда
{РпШ^{Ш}, т. е. [pn(x)] = [fn(x)l
Под т-й производной обобщенной функции f(x),
представленной в виде / (х) = [рп (х)], где рп (х) — полиномы, мы
понимаем обобщенную функцию [рТ\х)]. Это определение
г) См., например, книгу И. П. Натансона, Теория функций
вещественной переменной, изд. 2, Гостехиздат, М., 1957, стр. 119—
1Щ • — Прим. перев.

§ 6. Дифференцирование
23
корректно, поскольку, в силу леммы 2.2,
последовательность {рпт){х)} фундаментальная и обобщенная функция
[рпт) {х)]У в силу леммы 6.1, не зависит от конкретного
представления f (х) в виде [рп(х)].
Из леммы 6.3 вытекает:
Теорема I. Каждая обобщенная функция имеет
производные любого порядка.
В определении т-й производной обобщенной функции
можно заменить полиномы рп (х) функциями fn (х) с
непрерывными m-ми производными. Это вытекает из следующей
леммы:
6.4. Если фундаментальная последовательность {fn(x)}
состоит из функций с непрерывными m-ми производными,
то обобщенная функция [f{nm){x)] является т-й
производной обобщенной функции [fn(x)].
В самом деле, согласно лемме 2.2, последовательность
{fnm) (х)} фундаментальная и, если [ /„ (х) ] = [ рп (х) ], где
рп(х)— полиномы, то в силу леммы 6.1 lfnm\x)] =г
6.5. Если обобщенная функция является обычной
функцией с непрерывной т-й производной, то ее т-я
производная в обобщенном смысле совпадает с ее т-й
производной в обычном смысле.
Действительно, согласно лемме 6.4, m-й производной
обобщенной функции f (х) = [/ (х)] является обобщенная
функция [f{m)(x)] = f№(x).
Таким образом, понятие производной обобщенной
функции является расширением понятия производной для
непрерывно дифференцируемых функций. Поэтому можно
применять обычные обозначения: т-ю производную
обобщенной функции f(x) = [fn(x)] мы будем обозначать
посредством /(т)(х) или [fn(x)]{m)- В частности, первая
производная обобщенной функции f (х) = [ fn (х) ] будет обозначаться
посредством f'(x) или [fn(x)]'. Если функции fn(x) имеют
непрерывные га-е производные, то, по лемме 6.4,
[/ffWl(m)= lf»m)(x)).

24
§ 6. Дифференцирование
Из определения производной обобщенной функции
непосредственно вытекают следующие формулы,
встречающиеся в обычном дифференциальном исчислении:
(1) (f(x) + gWm) = fm(x) + gW(x),
(2) (X f (х)Ут) = X /С")(я') (\ — число),
(3) (fW(x))W - ftm+P>(x).
Теорема II. Равенство f(m)(x) = 0 имеет место тогда
и только тогда, когда обобщенная функция f (х)
является полиномом степени < га.
Достаточность очевидна. Для доказательства
необходимости предположим, что /(m)(x) = 0. Мы можем
представить / (х) в виде lfn(x)] с непрерывными fT\x)\ тогда
{fnm)(x)}"^[0}. Это значит, что существуют некоторое
целое число k^m и последовательности {Fn(x)\ и {Gn(x)}>,
такие, что
/ {пт) (х) = F™ (х), G(nk)(x) = 0, Fn (х) zt Р (х), Gn (х) U Р (х)..
Но тогда {fn (х) — f{nk~m) (х) j является фундаментальной
последовательностью полиномов степени < т. По лемме 2,5
эта последовательность почти равномерно сходится к
некоторому полиному р(х)> а по лемме 4.1 [fn(x) — F{nk~m^ (х)] =■
= р(х) и, следовательно,
(4) f(x)=[fn(x)] = [F{fM\x)] +р(х).
Согласно лемме 2.4, функция Р (х) представляет собой
полином степени < k, поскольку таковыми являются
функции Gn(x). Но, по лемме 4.1, [Fn(x)] = Р(х), а потому
обобщенная функция [F*%~m)(x)] = P^k~m) (х) представляет
собой полином степени < т. Отсюда, согласно формуле (4),
заключаем, что f(x) является полиномом степени <^т.
Из теоремы II, в частности, вытекает:
6.6. Равенство f'(x) = 0 имеет место тогда и
только тогда, когда обобщенная функция f (х) является
постоянной функцией.
Заменяя в лемме 6.6 обобщенную функцию f(x) на
f(x) — g (х), получаем;

§ 6. Дифференцирование 25
6.7. Равенство f'(x)-=g'(x) имеет место тогда и
только тогда, когда обобщенные функции f{x) и g(x)
отличаются друг от друга на постоянную функцию.
В дальнейшем будет полезна следующая лемма:
6.8. Если производная fW(x) обобщенной функции
f(x) — непрерывная функция, то и сама f(x) является
непрерывной функцией, a fW(x) — ее обычной производной.
Положим
х tx * т—1
g(x) = J dtx j div .. J /<»> (tm) dtm, где A < a < B.
a a a
Из теоремы II и леммы 6.5 вытекает, что р{х) =
= f(x) — g (х) — полином степени < т. Таким .образом,
f(x) = g(x)+p(x) — обычная функция, a f{m)(x), в силу
леммы 6.5, — ее обычная т-я производная.
Согласно теореме I, каждая непрерывная функция
имеет производную. В общем случае эта производная
является не функцией, а обобщенной функцией. Например, недиф-
ференцируемая функция Вейерштрасса в теории
обобщенных функций дифференцируема, однако ее производная не
является функцией.
Теорема III. Каждая обобщенная функция является
обобщенной производной некоторого порядка от
непрерывной функции.
В самом деле, если f(x) = [fn(x)]y т. е. fn(x) = Fnk)(x),
причем Fn(x)^Z F(х), то, по лемме 4.1, F(x) = [Fn(x)] и
f(x) = [F{nk)(x)] = [Fn(x)]M = FM(x).
В дальнейшем нам понадобится также следующая
лемма *):
6.9. Пусть обобщенная функция f (х) является k-й
производной в обобщенном смысле от непрерывной функции
F(x):
1) Добавлена переводчиком.—Прим. ре$.

26 § 7. Определение при помощи производных
Построим непрерывную функцию
х ty fi—i
F(x) = jd/J dtv.. j F(tddtlt
a a a
где A < a < B\ тогда f (x) будет обобщенной производной
(k + l)-ao порядка от F (х):
f(x)= ?«+1Цх).
Действительно, по формуле (3) имеем, в силу леммы 6.5,
Л*+0 (х)= (Я'> (*))<*> = (F(x))W =f(x).
Эта лемма показывает, что число k в случае
необходимости можно увеличить.
§ 7. Определение обобщенных функций
при помощи производных
Теорема III наводит на мысль о другом, эквивалентном определении
обобщенных функций. Это определение также использует метод
абстракции, однако иным способом. В качестве отправной точки мы берем
здесь не фундаментальные последовательности, а упорядоченные пары
(F(x),k), где F(x) — непрерывная функция в интервале А < х < В,
a k — целое число > 0. Мы говорим, что пары (F(x),k) и (G(x)J)
эквивалентны и пишем
(F(x),k)~(G(x),l),
если выполнено хотя бы одно из следующих двух условий:
1°. k < /, а разность \—1 —F (х) существует и является
многочленом степени < k.
2°. /<&, а разность Szl—G (х) существует и является
dxk — l
многочленом степени < /.
Под многочленом степени < 0 мы понимаем функцию,
тождественно равную нулю.
Легко видеть, что введенное нами отношение -х/ обладает
свойствами (<£\) и (<^2)- Докажем, что оно обладает также и свойством
(<£з). Пусть (F(x),k)^(G(x)J) и (G(x),l)^(H(x),m). В силу
симметрии ((^г) можно считать, что 0 < k < т. Тогда для / имеются
три возможности: 0 < / << &, k < / < т и m < /.
В любом из этих трех случаев доказательство основывается на
Том, что при каждом дифференцировании степень полинома снижается

§ 7. Определение при помощи производных 27
по крайней мере на единицу, а при каждом интегрировании она
повышается на единицу. Разберем, например, второй случай k < I < т.
Имеем
^-*с*> -м*> и *£££>--*<*> =*<*>,
где Pi(x)—полином степени < k, a p2(^) — полином степени < />
Отсюда
dm-kH(x) _F(X)_ S-*Pt{x) (х)
$—* Do(x)
причем ~t~^ + Pi(x) — полином степени <&, что и доказывает
dx п
эквивалентность (F (x)fk) -^ (# (х),т).
Поскольку условия (($4), (^2) и (сгрз) выполнены, множество
всех пар (F(x)fk) разбивается на классы эквивалентности без общих
элементов так, что две пары лежат в одном и том же классе тогда
и только тогда, когда они эквивалентны. Эти классы эквивалентности
назовем обобщенными функциями, В этой новой формулировке мы
получаем обобщенные функции путем отождествления эквивалентных
пар.
Обобщенную функцию, определяемую парой (^(л:),^), т. е.
класс всех пар, эквивалентных (F(x)fk), будем обозначать символом
F(k)(x), который в настоящий момент еще не имеет смысла
производной. Мы вводим это обозначение потому, что обобщенную функцию
Fk(x)f как будет показано ниже, можно интерпретировать как k-ю
производную функции F(x).
Из определения эквивалентности вытекает, что (F(x)fi) ^
r>~ (G (х) ,0) в том и только в том случае, когда F(x) = G(x).
Таким образом, класс эквивалентности типа F^(x) содержит в
точности один элемент вида (G(x),0), а именно, элемент (F(x),0).
Следовательно, мы можем отождествить обобщенную функцию F^ (х)
с обычной функцией F(x) и написать
F{0)(x) =F(x).
Под т-й производной обобщенной функции Fk(x) мы понимаем
обобщенную функцию F№ + m) (*). в частности, k-й производной
обобщенной функции F^(x) является обобщенная функция F^(x).
Если обобщенная функция является обычной функцией с
непрерывной т-й производной, то ее производная в определенном выше
смысле совпадает с ее производной в обычном смысле:
t (X) - dxm
В самом деле, пара (F(x),m) эквивалентна паре I. ^-, 0
I dxm
Здесь теорема III становится очевидной: обобщенная функция
f^ (х) является k-й производной функции Fix). Этот факт onpag-

28
§ 8. Локально интегрируемые функции
дывает способ записи обобщенных функций, примененный в этом
параграфе .
Всякую обобщенную функцию F(k)(x) в новом смысле можно
отождествить с обобщенной функцией [/7 (*)] в прежнем смысле:
FW(x) = [F(x)](k)-
Это отождествление корректно, поскольку F(k)(x) = G(l)(x) тогда
и только тогда, когда [F (*)](&)= [G (x)](l). Действительно, пусть
Fib)(x)=GV)(x) и k<l, иначе говоря, пусть F(x) = d'~~ /Ц^+
+ р (л:) , где р (х) — полином степени <&. Интерпретируя эти функции
как обобщенные функции в прежнем смысле, получаем, в силу
леммы 6.5,
Щ) + [Р (*)]<*> = [<? (*)]№.
№»1»-[^Д-И
Пусть, -наоборот, [F(x)](b) = [G (x)](D и k < L Тогда ([£(*)] (*-*> —
-^(^)1)(^)=0^ значит, [G (л:)] (/ -Л) =/■ (*) +р (*), где р(х) —
полином степени <&. Следовательно, по лемме 6.8,
что и доказывает соотношение F^k)(x) =G^(x).
Отождествив обобщенные функции в прежнем и нынешнем
смысле, обнаруживаем, что дифференцирование в обоих случаях дает одно
и то же, ибо
(F(ft(x)){m) = f{k + m)(x) = [F(x)\ib + m) = {[F(x) ]{k) )(m) .
Для обобщенных функций в смысле этого параграфа можно очень
просто определить действия сложения, вычитания и умножения на
число, а также и другие действия, вводимые в дальнейших
параграфах.
§ 8. Локально интегрируемые функции
В § 4 мы видели, • что множество обобщенных функций
в интервале А < х <^ В является расширением множества
функций, непрерывных в этом интервале. Теперь мы
увидим, что обобщенные функции охватывают также и
некоторый более широкий класс функций.
Пусть / (х) — непрерывная функция; тогда, как хорошо
известно,
х
О) (§f(t)dt)' = f(x).

§ 8. Локально интегрируемые функций 29
ч Если функция f(x) кусочно непрерывна или (более
общий случай) если она интегрируема по Риману, то
соотношение (1) также справедливо всюду, кроме, быть может,
точек разрыва функции f(x). Читатель, знакомый с
интегралом Лебега, может интерпретировать формулу (1) в еще
более широком смысле, а именно как равенство,
выполняющееся почти всюду.
В упомянутом выше случае левую часть формулы (1)
можно также истолковать как обобщенную функцию,
которая является производной в смысле теории обобщенных
х
функций от непрерывной функции J f(t)dt. При этом ра-
а
венство (1) позволяет отождествить обобщенную функцию,
стоящую в левой его части, с функцией f(x). Посредством
такого соглашения мы включаем в множество обобщенных
функций на интервале А < х < В некоторый класс
разрывных функций. Обширность этого класса зависит от
принимаемого определения интегрируемости*), а именно, этот
класс является множеством всех локально интегрируемых
функций, т. е. функций, интегрируемых в каждом
интервале а<х<6(Л<а<&<£).
Интерпретация подобных функций как обобщенных
требует следующего соглашения: локально интегрируемые
функции f(x) и g (х) считаются равными в том и только в том
случае, когда они равны как обобщенные функции, т. е.
X X
когда j f(t)dt=\g (t) dt для всех х. В частности, если
а а
эти функции кусочно непрерывны или (более общий случай)
если они локально интегрируемы по Риману, то они
считаются равными, если их значения во всех общих точках
непрерывности равны. Функции, интегрируемые по Лебегу,
считаются равными тогда и только тогда, когда они почти
всюду имеют одинаковые значения. Следует заметить, что
г) Практически интегрируемость достаточно понимать в смысле
Римана или в смысле Лебега. Но ничто не мешает ввести и интеграл
Данжуа, если дифференцирование в формуле (1) считать
асимптотическим. (По этим вопросам см. книгу И. П. Натансона, Теория
функций вещественной переменной, изд. 2, Гостехиздат, М., 1957,
стр. 452 и след. —Прим. перев.)

30 § 8. Локально интегрируемые функции
это определение равенства обычно и принимается в теории
интеграла Лебега.
Класс неопределенных интегралов Лебега локально
интегрируемых функций совпадает с классом абсолютно непрерывных функций.
Обычная производная абсолютно непрерывной функции существует
почти всюду и совпадает с ее производной в смысле теории
обобщенных функций.
Если / (х) и g (х) — локально интегрируемые функции,
то выражение / (х) + g (х) имеет один и тот же смысл,
интерпретируем ли мы f (х) и g (х) как функции или как
обобщенные функции. Это замечание относится также к
вычитанию и к умножению на число.
Введение локально интегрируемых функций позволяет
нам усилить лемму 6.8, не меняя ее доказательства.
8.1. Если производная f (m> (х) (m > 0) обобщенной
функции — локально интегрируемая функция, то сама
обобщенная функция f(x) является непрерывной функцией,
a fW(x)—ее обычной т-й производной.
В приложениях часто встречается так называемая функ*
ция Хевисайда:
0 при x<0,
1 при х ^ 0.
Ее интеграл
G (х) = Г Н (t) dt = {
о *
0 при х < 0,
х при х ^ 0
непрерывен при всех х. Функция Хевисайда Н (х) является
обобщенной производной функции G(x); всюду, кроме
точки х = 0, она является также обычной производной от G(x).
Так как G (х) — предел интегралов
§gn(t)dty
гАе gn (х) — функции примера 1° (§2), то мы имеем
lgn(x)] = G'(x) = H(x);

§ 9. Последовательности и ряды
31
иначе говоря, фундаментальная последовательность { gn (х))
представляет функцию Хевисайда.
Фундаментальные последовательности { gn (х)} примеров
2° и 3° (§ 2) точно так же представляют функцию
Хевисайда. Поэтому для функций fn (х) примеров 2° и 3° (§ 2)
имеем
Цх) = [/„(*)] =lgn(x)] = H'(x).
Таким образом, функция Дирака § (х) является обобщенной
производной функции Хевисайда.
Функция Дирака 8 (х) служит примером обобщенной
функции в интервале —оо<^х<^ооу которая не является
локально интегрируемой функцией. Действительно,
предположим, что 8 (х) — интегрируемая функция. Из формулы
Н'(х) — Ь(х)у согласно лемме 8.1, вытекало бы, что
функция Н (х) непрерывна, а это неверно.
Стоит отметить, что обычная производная функции Хевисайда
Н(х) равна нулю всюду, кроме точки # = 0, в которой она не
существует. Этот пример показывает, что обычная производная не всегда
совпадает с производной в смысле теории обобщенных функций, даже
если обычная производная существует всюду, за исключением одной
точки х).
§ 9. Последовательности и ряды обобщенных функций
Мы говорим, что последовательность {fn(x)}
обобщенных функций сходится к обобщенной .функции / (х) и
пишем
fn (х) -> / (х) или lim fn(x) = f(x),
П-fCD
если существуют це^ое число k ^ 0, непрерывная функция
F(х) и последовательность [Fn(x)} непрерывных функций,
такие, что
(1) Fn(x)zZF(x), F<*>(x) = fa(x) и Я*>(*) = /(*)*).
х) Обычная производная функции Н(х) существует почти всюду
(всюду, кроме точки 0) и является локально интегрируемой
функцией, однако обобщенная производная с этой локально интегрируемой
функцией не совпадает.—Прим. перев.
2) В этом определении производные понимаются в обобщенном
смысле. — Прим. перев.

32
§ 9. Последовательности и ряды
Предел f(x)> если он существует, единственен.
Действительно, соотношения fn (х) -+ f (х) и fn (х) -> g (х)
означают, что существуют последовательности непрерывных
функций Fn (х) =t F (х) и Gn (х) =£ G (х) и целые числа k, I
со свойствами:
Fm{x) = Gjp(x) = Ш, FW(x) = /(*) и G<D(*) = г(д).
Можно считать, что £<:/. Согласно леммам 6.9 и 2.6,
существуют такие функции Fn(x) и F(x), что
Разности Fn (х) — Gn(x) образуют последовательность
полиномов степени < /, поскольку FW(x) — G^(x) = 0. По
лемме 2.4 предел F (х) — G(x) этой последовательности
также является полиномом степени </, а поэтому
FW{x) — GW(x) = 0, т. е. f(x)=g (х).
Теорема IV. Для любой последовательности
обобщенных функций {fn(x)} и для любого целого т > 0 из
сходимости fn(x)->f (х) вытекает сходимость f^m)(x)-^f^(x).
Иначе говоря, каждую сходящуюся последовательность
обобщенных функций можно дифференцировать почленно.
Действительно, если имеют место ее отношения (1), то
F£+m)(x) = f^ (х), Fn(x) XF(x) и Fik+m>(x) = р>(*).
Из определения сходимости (при k = 0) непосредственно
вытекает лемма:
9.1. Последовательность {fn(x)\ непрерывных функций,
сходящаяся почти равномерно к функции f(x), сходится
к f(x) также и в смысле теории обобщенных функций.
Более общая лемма:
9.2. Последовательность {fn(x)} локально
интегрируемых функций, сходящаяся почти всюду к функции f(x)
и ограниченная некоторой локально интегрируемой функ-

§ 9. Последовательности и ряды 33
циейу сходится к f (х) также и в смысле теории
обобщенных функций.
Эта лемма вытекает из почти равномерной сходимости
X X
последовательности интегралов J fn (/) dt к интегралу J f (t) dt.
a a
Теорема V. Последовательность {fn(x)} непрерывных
функций сходится к обобщенной функции f(x) тогда и
только тогда, когда она является фундаментальной
последовательностью обобщенной функции f(x).
Иными словами,
fn{x)—►/(*) тогда и только тогда, когда [fn(x)] = f(x).
Из условия fn(x)—>f(x) вытекает, согласно равенствам
(1) и лемме 6.8, что последовательность {fn(x)}
фундаментальная. Кроме того, в силу первого из этих равенств
и леммы 4.1, [Fn(x)]=F (х). Отсюда, по лемме 6.4, получаем
[Я*) W] = Я*> (*), т. е. [fn(x)] = f(x).
С другой стороны, если [fn(x)] = f(x), то
последовательность {fn(x)} фундаментальная, т. е. выполняются два
первых равенства (1) и, в силу леммы 4.1, имеет место
соотношение F (х) = [Fn (х)]. Дифференцируя последнее
соотношение k раз, получаем F^k)\x) = [F^(x)] = f(x). Таким
образом, имеет место также и третье равенство (1) и,
значит, доказано, что fn (х) -> / (х).
Аналогичная теорема имеется в теории действительных чисел
Кантора, в которой доказывается, что последовательность
рациональных чисел сходится к действительному числу а тогда и только тогда,
когда она является фундаментальной последовательностью числа а.
Ввиду теоремы V последовательности [fn(x)} примеров
2° и 3° (§ 2) сходятся к 8 (х) в смысле теории обобщенных
функций. В классическом анализе рассматривалось много
последовательностей функций, сходящихся к 8 (х) в смысле
теории обобщенных функций, например:
sin пх /тт ч
^- (Дирихле),
__яе-л1*1 (Пикар),
\ п 1ГЛ
-^' епх+е-пх (Стильтьес) -
3-439

34 $ 9. Последовательности и ряды
Из теоремы V и леммы 2.5 следует лемма:
9.3. Последовательность полиномов степени <С k тогда
и только тогда сходится в обобщенном смысле, когда
она сходится почти равномерно.
В частности:
9.4. Последовательность постоянных функций тогда
и только тогда сходится в обобщенном смысле, когда
она сходится в обычном смысле.
Из определения сходимости непосредственно вытекает,
что арифметические действия над пределами
последовательностей обобщенных функций можно выполнять так
же, как и над пределами последовательностей обычных
функций:
9.5. Если fn(x)-*f(x) и gn{x)-*g{x), то
fn(x) + gn(x)-+f(x)+g{x) U fn(x)—gn(x)-*'f(x)—g(x).
Если fn(x)->fix) и ХЛ->Х, то Kfn(x)->^f(x).
00
Ряд обобщенных функций ^ gn (х) называется сходя-
щимся, если сходится последовательность его частных сумм
fn (х) = gi (*)+... + gn (х). Предел g (х) = lim fn (х) назы-
П-+СО
вается суммой этого ряда. В этом случае мы пишем
со
g(*) = Eg«(*)-
/1=1
Из теоремы IV следует
Теорема VI. Для любого сходящегося ряда
обобщенных функций
(оо \ / оо
л=1 / л=1
Иначе говоря, всякий сходящийся ряд обобщенных
функций можно дифференцировать почленно.
Теоремы I, IV и VI дают поразительные преимущества
в практических применениях теории обобщенных функций.

§ 10. Случай непрерывного параметра 35
Они позволяют без каких бы то ни было ограничений
дифференцировать любую функцию и переставлять
дифференцирование и переход к пределу.
Теоремы IV и VI значительно проще аналогичных
теорем дифференциального исчисления, в котором необходимы
некоторые дополнительные предположения. Таким образом,
введение обобщенных функций, обобщенных производных и
обобщенной сходимости облегчает и автоматизирует
выкладки, что подтверждает целесообразность этих - понятий.
Определение сходимости можно распространить на
последовательности обобщенных функций, определенных в
различных интервалах.
Мы говорим, что последовательность функций Fn(x),
определенных в интервалах Ап <[ х <[ ВПу сходится к
функции F (х) почти равномерно в некотором интервале А<^х<СВ,
если всякий конечный замкнутый интервал а ^ х ^ 6,
содержащийся в А < х <] В, содержится при достаточно
больших п также и в интервалах Ап<^х<^ВПУ а функции
Fn(x) сходятся к F (х) равномерно на а^х^Ь. В этом
случае мы пишем: Fn(x) -=$F(x) в интервале Л<х<£.
Высказанное определение обобщает понятие почти
равномерной сходимости § 2.
Далее мы говорим, что последовательность fn(x)
обобщенных функций, определенных в интервалах Ап < х < Вп,
сходится к обобщенной функции / (х) в интервале Л < х << В,
если выполнены условия (1), приведенные в начале этого
параграфа. При этом почти равномерная сходимость
Fn (х) =£ F (х) понимается в только что указанном более
общем смысле.
В этом случае мы пишем fn (х) -> / (х) в интервале
Л<х<В.
Теорема IV и леммы 9.1—9.5 остаются справедливыми.
§ 10. Обобщенные функции, зависящие от непрерывного
параметра
Сходимость обобщенных функций, зависящих от
непрерывного параметра, удобно определить сразу в общем
случае, т. е. в случае, когда обобщенные функции определены
в интервалах, также зависящих от этого параметра.
3*

Зё § 10. Случай непрерывного параметра
Мы говорим, что функция Fa(x), определенная в
интервале А* < х < Ва , стремится при а -* а0 к функции F(#)
почти равномерно в интервале Л <] х < В, если всякий
конечный замкнутый интервал *а ^ х ^ 6, содержащийся в
А < х < В, содержится также и в интервалах Аа < х < 5«
при а, достаточно близком к а0, а функции /v (л:) стремятся
к F(#) равномерно на а^х^Ь при а-*а0. В этом
случае мы пишем
(1) Fa(x)^ZF(x) при а->а0.
Мы говорим, что обобщенная функция /а (#),
определенная в интервале Аа < х <Г Ва, стремится при а -> а0 к
обобщенной функции /(#), определенной в интервале
А <^х<^В, и пишем
fa(x)-»f(x) при а->а0
или
(2) Нт/.(*) = /(*).
а-*а0
если существуют целое число k ^ О, непрерывная функция
jF(x), определенная при А<^х<^В, и непрерывная функция
Fa(x), определенная (при а, лежащем в некоторой
окрестности а0) в интервале Аа < х < Ва , удовлетворяющие
условиям:
Fa(x)=zF(x) при а_>а0, F^(x) = fa(x) и Л*>(*) = Д*)1).
Если предел / (а:) существует, то он" единственен.
Доказательство аналогично доказательству для
последовательностей.
Равенство (1), как хорошо известно, выполняется тогда и только
тогда, когда
Fan(x) zj F(x) для любой последовательности ап -> а0.
Мы докажем сейчас аналогичное утверждение для обобщенных
функций.
10.1 (Влёка [1] )• Равенство (2) выполняется тогда и только
тогда, когда
(3) fa (х) -*■ /(-О для любой последовательности ал-* а0.
Необходимость условия (3) очевидна.
При доказательстве достаточности будем писать fn(x) k f (х),
х) Здесь, как и в начале § 9, производные понимаются^ в
обобщенном смысле. —Прим. пер ев,

§ 10. Случай непрерывного параметра
37
если существуют функции Fn(x), F(x) и номер я0, такие, что
~ (k) ~
(4) Fn(x) = fn(x) при п>п0, Fn(x)z$F{x) и F^(x) = f(x).
Исходя из соотношения (3), докажем существование такого
целого числа k > О, что
п (х) Л /(-О Для любой последовательности ал-*► а0.
Предположим противное. Тогда существует возрастающая
последовательность целых чисел kmy а при каждом фиксированном m —
последовательность атп -> а0, такие, что соотношение
(6) /««»(*)-UW (л-оо)
выполняется для / = km и не выполняется при / < km. Не
"ограничивая общности, можно считать, что все числа атп могут быть
расположены в простую последовательность {ап}, сходящуюся к а0
(в крайнем случае для этого достаточно пренебречь конечным числом
начальных членов в каждой из последовательностей {ain} ,'{а2п],...).
Из соотношения (3) следует существование такого целого числа
k0>0, что fan (х) bj(x), а значит, и famn(x) ^ f (х) при
любом т. Это противоречит предположению, что кт -> оо и что
соотношение (6) не выполняется при I <Ckm.
Пусть, в дальнейшем, k — фиксированное целое число со
свойством (5). Функция F(x), фигурирующая в соотношениях (4),
определена с точностью до полинома степени <Ск. Эту неоднозначность
можно устранить, прибавляя такие полиномы ко всем функциям
Fn(x), и поэтому мы будем считать, что F (х)—одна и та же для
всех последовательностей {Fn (х)}.
Пусть {ап}—убывающая, а {Ьп}—возрастающая числовые
последовательности, причем ап -> А и Ъп-+ В. Докажем, что для любого
целого т> О существует число f\m^> 0 со следующим свойством:
При \а — а0\ <v]m существует,функция Fa (х), удовлетворяющая
соотношениям
~ (к)
(7) F а (х) = /а (х) в интервале Ла < х <Ба ,
(8) \F (х) — F (х)\ < \/т при ат < х < Ът.
Действительно, в противном случае существовала бы такая
последовательность ал -> а0, что при а = ап (п = 1, 2,...) любая функция,
удовлетворяющая соотношению (7), не удовлетворяла бы неравенству
(8). Но, с другой стороны, в силу соотношения (5) существуют такие
функции Fam(x), что для достаточно больших п
F«n (х) = hn (*) и F*n (*) ^F(x)-
ЭпГфункции удовлетвэряют соотношениям (7) и (8) при достаточно
больших п. Противоречие!

38
§ 10. Случай непрерывного параметра
Можно считать, что y\m + i <^m (/я= 1, 2,...) и ч\т -> 0.
Согласно предыдущему рассуждению, мы можем определить Fa(x) так,
чтобы
(9) F^{x) = fa{x) в интервале Аа <х <Ва
и \рЛх) — F{<x)\ <х1т ПРИ ^т<х<Ьт
для а, удовлетворяющих условию Y)m + i<la— а0| <Y]m (т = 1,
2,...). Этим способом функции /^(х) определены при 0< | а — а0| <тг)!.
Пусть задано произвольное фиксированное целое число #> 0. Для
т > q имеем
\РЛЛХ) — F (х)\ < х1т ПРИ ctq<x<bq,
*
если0<]а— а0\ < тг)т. Таким образом, функции /^(л:) стремятся
к функции F (х) равномерно на интервалах aq<x<bQ (q = 1, 2,...),
т. е. Fa (х) r£ F (х) при a-+a0. Последнее, вместе с равенством
(9), означает, что * (х) -> f(x) при а ->- а0, и доказательство для
случая конечного а0 завершено.
Для а0 = оо или — со нужны лишь очевидные изменения в
доказательстве.
Следующие утверждения об обобщенных функциях,
зависящих от параметра, можно доказать аналогично тому,
как это делалось в случае последовательностей
обобщенных функций.
Теорема VII. Если fa (х) -+f(x) при a ->a0, то
fW(x) ->/C")(.v) при a -+a0 и m^O.
• 10-2. Если Fa(x) -=tF(x) при а—+а0,тои Fa(x)-+F(x)
при a—>a0. Иначе говоря, из почти равномерного
стремления к пределу функции, зависящей от параметра,
вытекает стремление к пределу в смысле теории
обобщенных функций.
10.3. Полином степени <^k с коэффициентами,
зависящими от параметра а, стремится к пределу при
а ->а0 в обобщенном смысле в том и только в том
случае, когда этот полином стремится к пределу почти
равномерно.
10.4. Если fa(x) -+f(x) и ga(x) -+g(x) при а ->а0,
то fa(x) + ga(x) -+f(x)+g (х) и Цх) — ga(x) - / (х) —g (х)
при а—>а0. Если К -> X и fa{x) -+f (х) при а->а0, то
Kfa(x)^lf(x) при а->а0.

§ 11. Умножение на функцию
39
§ 11. Умножение обобщенных функций на функцию
В данной работе мы ограничимся умножением
обобщенной функции f(x) на бесконечно дифференцируемую
функцию о)(х). Под произведением u>(x)f(x) мы понимаем
обобщенную функцию [ш (х) fn(x)], где [fn(x)] = f(x).
Для проверки корректности этого определения достатоя-
но показать следующее:
1°. Последовательность {<»(x)fn(x)} является
фундаментальной.
2°. Из соотношения (Мх)1^(&(х)1 вытекает, что
{v(x)fn(x)}^<{u(x)gn(x)}.
Существуют функции Fn(x) и целое число k ^ 0, такие,
что Fn(x) =$ и F (*)(#) = fn(x). Последовательность
«(*) F'n(x) = (<° (х) Fn(x))' -- ш' (x) f n(x)
фундаментальна как разность двух последовательностей,
фундаментальных в силу лемм 2.2 и 2.1. По той же
причине фундаментальна и последовательность {о/ (х) F'n (#)},
а тогда фундаментальна также последовательность
ш (х) F; (л) = (ш (х) F'n (X))' - *'{x)F-n (х).
Тем же самым рассуждением убеждаемся в том, что
последовательности { и>(х) F^(x)), ..., { ш(а:) F^(x)}
фундаментальны. Таким образом, последовательность {v>(x)fn(x)}
фундаментальная.
Для. доказательства 2° заметим, что из эквивалентности
фундаментальных последовательностей
М*). М*). ••• и £i(*)> £2(*)> •••
по лемме 3.2 вытекает, что последовательность
fi(x), gx(x), Ш, g2(x), ...
фундаментальна. Тогда, по пункту Г, будет
фундаментальной последовательность
со (х) №), со (х) g^x), со (*) /2(х), со (*) g2(*),
а значит в силу леммы 3.2 последовательности
0) (х) fx (х), со (х) /а (х), ... и со (х) gx (х), о) (*) g2 (*), . ..
эквивалентны.

40
§11. Умножение на функцию
Непосредственно из определения вытекают следующие
обычные свойства умножения:
^(х) (ш2(*) f(x)) = К (х) ш2 (х)) {(х)9
((О, (х) + <»2 (*)) / (х) = «)х (х) f (х) + о>2 (*) / (*),
<° (*) (/ W + ^ (*)) = «>(*)/ М + <»(*)£ (*)•
Если /(а:) является функцией, то определенное выше
произведение оказывается обычным произведением функций.
Кроме того, если о> (х) — постоянная функция, a f(x) —
произвольная обобщенная функция, то введенное здесь
произведение совпадает с произведением, определенным в § 5.
Предполагая, что функции fn(x) в определении
умножения являются полиномами, легко доказать формулу
(1) ^(x)f(x))'^^(x)f(x) + ^(x)f'(x).
Эту формулу можно рассматривать как частный случай
(при k = 1) формулы
k
(2) ш (х) /<*>(*) - 2 (- \Ш (<о<л(*) /(*))<* - л,
/ = о vy/
которая может быть доказана по индукции, как и для
обычных функций.
Из последней формулы, заменяя / (х) непрерывной
функцией F(x), получаем
k
(3) ф) f(x) = 2(- 1/(^)(0)(/) (х) F (*))<*-/>,
/=о vy;
где
f(x) = FW(x).
Поскольку под знаком суммы стоят произведения непрерывных
функций, правая часть последней формулы имеет вполне
определенный смысл, даже если не введено понятие умножения обобщенной
функции на функцию. Поэтому формулу (3) можно использовать
как другое определение произведения m(x)f(x).
В качестве применения формулы (1) докажем формулу
(4) а>(*)8(х) = ш(0)8(*).

§ 11. Умножение на функцию
41
Действительно, легко проверить, что
х
J о/ (/) я (о л = (ш (*) — о. (0)) вд.
о
Дифференцируя в обобщенном смысле, получаем
а/(х) Я (х) = а)' (х) Я(х) + (со (х) — ш (0)) 8 (х),
откуда и вытекает формула (4).
Полагая в формуле (2) / (х) = § (х), получаем, согласно
формуле (4):
k
ш(*) 8<*>(*) = Yi (— iy(4 0)(/)(0) 8<*-/) (х).
11.1. Если fn(x) -> /(х), ШО «>(х) f„(x)-^ ш (х) f (х).
Более общий случай: если со^7*) (х) =^ш(т) (л:) для т=0, 1, 2,...
и /„ (х) -> / (х), то а>я (х) /„ (х) ->со (х) / (х).
Действительно, в силу формулы (3) имеем
k
*n(x)fn(x) = %(-\y(b)(oW(x)Fn(x)«-»),
/= о w/
где f„(*) = Я*> (х), F„(x) zt> (x) и / (д) = Я*>(х). Выра-
жение в правой части этой формулы стремится к
выражению в правой части формулы (3), а следовательно, то же
самое имеет место и для левых частей. Таким образом,
второе утверждение леммы 11.1 доказано. Первое
утверждение является частным случаем второго.
11.2. Формула
00 00
°>(x)yifa(x)=y£la(x)fa(x)
/z=l /z= 1
справедлива всякий раз, когда сходится ряд обобщенных
функций в левой части.
Эта лемма вытекает из 11.1.
Следующая лемма является непрерывным аналогом
леммы J 1.1,

42 § 12. Замена переменных
11.3. Если fa(x) -* / (х) при а -+ а0 (— сю < а0 < ос), ]
то а) (х) fa (х) -* и> (#) / (л:). Более общий случай: если i
а>(«>(*) z$ a>W(*) (т *= 0, 1, 2, .. .) и fa(x) — / (х) при }
а -* а0, то а>№(х) /а(х) -> а>(х) / (х).
§ 12/ Замена переменных
Пусть ср (л:) — бесконечно дифференцируемая функция,
определенная в интервале А0< х< Б0, и пусть Л <^ ср (#)< Б
и ?'(*) =£ О ПРИ любом х. Пусть, наконец, /(х) = [fn(x)] —
обобщенная функция в интервале А<^х<^В. Под
суперпозицией f (ср (а:)) обобщенной функции / (х) и функции ср (х)
мы убудем понимать обобщенную функцию [/„(? (*))],
определенную в интервале Л0< \х:<Б0.
Для проверки корректности этого определения мы должны
показать следующее:
Г. Если \fn(x)}—фундаментальная последовательность,
то такова же и {/я (<р (*))} •
2°. Из соотношения {fn(x)}~[gn(x)} вытекает, что
{fn(<?(x))}~[gn(<?(x))}.
Заметим сначала, что если функции gn{x) непрерывно
дифференцируемы, а последовательность {gn (?(*))}
фундаментальная, то в силу леммы 2.2 и свойства 1° § 11
фундаментальной будет и последовательность функций
я; (?(*»=-^,-&.(?(*)»'•
Пусть \Fn(x)}—почти равномерно сходящаяся
последовательность таких непрерывных функций, что FW (х) = fn (х).
Тогда последовательность {Fn(<p(x))} также сходится почти
равномерно, а потому является фундаментальной. Значит,
фундаментальны и последовательности [F'n(y(x))}, . . .
...» [F^k) (<р (#))}. Последняя из них совпадаете {f п (ср (х))},
что и доказывает пункт 1°.
Свойство 2° можно доказать тем же самым
рассуждением, каким доказано свойство 2° § 11.
Выкладки с суперпозициями обобщенных функций можно
производить так же, как и с суперпозициями обычных
функций. В частности, имеем формулу

§ 12. Замена переменных
43
поскольку
• (f (? (х))у = Un (ср да = [/;(? (*» cp'Mi =
Из формулы (1) вытекает, в частности, соотношение
8 (*(*» = ^ (Я (*(*»)'•
Если ср (х) Ф О всюду, то функция Н (ср (я)) или всюду
равна 0, или всюду равна 1. Поэтому
8(Т(*)) = 0.
Если же ср (х) обращается в 0 в некоторой точке х°
[единственной, поскольку ср' (х) ф 0], то Я(ср (л;)) = Н(х — х0)
для возрастающей ср (х) и Н (ср (х)) = 1 — Н (х — х0) для
убывающей ср(х)1). Следовательно,
(2) 8и*)) = 7тЬ75(Мо)-
12.1. Если последовательность обобщенных функций
fn(x) сходится к f(x), то последовательность /л(<р(*))
сходится к f(y(x)). Более общий случай: если
yW(x) U <fW(x) для т = 0, 1, 2, . . . м /„ (х) -> / (х), то
Действительно, возьмем такие функции Fn(x) и F(x),
что /^(х) = fn (х), F{k)(х) =f(x) и Fn (х) ^ZF(x). Тогда
Fn(9n(x))':tF((f(x)). Отсюда, дифференцируя, получаем
(3) ^(TnWJ^W-^HTWJT'W.
Легко проверить, что
(4) {-г—\ =t(-77-v) (m = 0, 1,2, ...)•
г) Равенство tf(cp(jt)) = l—Н (х— х0) при убывающей ср (л:)
выполняется всюду, кроме точки x0t в которой левая часть равна 1,
а правая 0. Однако как обобщенные функции левая и правая части
равны, поскольку они кусочно непрерывны и имеют одинаковые
значения во всех общих точках непрерывности. См. § 8, —Прим. перев.

44
§ 12. Замена переменных
Из (3) и (4), в силу леммы 11.1, вытекает
Р'пЫ*)) -^ч?(*)).
После k таких шагов получаем
ff'feW) - ^*>(<р(*)),
Следующая лемма является непрерывным аналогом
леммы 12.1.
12.2. Если fa(x)->f{x) при а->а0(—оо^а0^оо),
то fa(<p(#))->/(<р(#)). Более общий случай: если
?(">(*) =tcp(^)(x) (m = 0, 1, 2, ...) и /«(х) -> /(*) Агра
а->а0, mo /.(?«(*)) -> /(? (*))•
Доказательство такое же, как и для леммы 12.1.
Особенно важен случай линейной замены.
12.3. Для любой обобщенной функции f(x) при любом
целом k^O имеет место формула
(f {ах + р))(*> = ak /(*> {ах + Р) (а ф 0).
Действительно, пусть полиномы рЛ(л:) образуют
фундаментальную последовательность обобщенной функции f(x)\
тогда
(/(« + р))№ = [/7>Х+Р)](*> =
= [a*/?<*>(«* + Р)] = a* /<*>(« + Р).
Применяя лемму 12.3 к очевидному соотношению
получаем формулу
(5) 5(** + p)=JL-8(x + L),
являющуюся частным случаем формулы (2). Дальнейшим
дифференцированием формулы (5) получаем
(6) . ^)(ax + P)=|^8(m)(-V+{).

$ 13. Равенство на интервалах
45
Из леммы 12.3 сразу же следует:
12.4. Если обобщенная функция f(x) является
производной k-го порядка непрерывной функции F(x), то
/ (ах + (3) будет производной k-го порядка функции
(\/ak)F'(ax + $).
§ 13. Равенство обобщенных функций на интервалах
Любую обобщенную функцию f(x) в интервале А<С х<СВ
можно в случае необходимости рассматривать как
обобщенную функцию в некотором меньшем интервале а <С х < Ъ,
поскольку функции любой фундаментальной
последовательности, представляющей /(#), можно рассматривать как
функции в этом меньшем интервале.
Например, в разности f(x + a) — / (*), гДе f (х) —
обобщенная функция в интервале А < х < В, обе обобщенные
функции / (х + а) и / (х) следует рассматривать как
обобщенные функции в общей части интервалов А — а<^х<^В— а
и А<^х<^В. Тогда разность будет обобщенной функцией
в этой общей части. Если интервалы не имеют общей
части, то разность не имеет смысла.
Вообще, сумма f (х) + g (х) и разность / (х) — g (х)
являются обобщенными функциями в общей части
интервалов, в которых определены f(x) и g(x). Аналогичное
замечание относится и к произведению w(x)f(x).
Если мы записываем одно лишь равенство
f(x)=g(x)>
то мы всегда подразумеваем, что обобщенные функции в
обеих его частях определены на одном и том же интервале
и равны. До сих пор мы поступали таким образом и так
же будем поступать в дальнейшем.
Записывая же
f(x) = g(x) в интервале а<^х<^Ь,
мы будем подразумевать, что интервал а < х < b
содержится в каждом из интервалов, в которых определены
f(x) и g(x), и что f(x) и g(x), рассматриваемые как
обобщенные функции при а<^х<^Ьу равны.

46 . _ _ § 1$- Равенство на интервала*
Например, мы имеем
Ь(х) = 0 в интервале — ос <[ х < О
и
Ь(х) = 0 в интервале 0<л:<оо.
В самом деле, фундаментальные последовательности
{/Л(а:)} примеров 2° и 3° (§ 2), если их рассматривать на
каком-либо из интервалов — ос<Гл:<0 или О^ж^ос,
сходятся почти равномерно к нулю и определяют поэтому
нулевую обобщенную функцию.
Более общий случай:
(1) ъЪ(х~х0) + ^'(х-х,) + ... + akW(x-x0) = О
при X ф х0;
это означает, что предыдущее равенство справедливо в
интервалах — оо<^х<^х0 и х0<^х<^оо.
Теорема VIII. Если f(x) = 0 при х Ф х0, то
обобщенная функция f(x) имеет вид
(2) f(x) = ax,b(x—x0) + OL1b'(x—x0) + ... + ak№(x-x0).
Действительно, существует такая непрерывная функция
F(x), что FM(x) = f(x). В силу теоремы II функция F(x)
является полиномом степени < / в каждом из интервалов
— оо<^х<С.х0 и х0^х<^ос, т. е.
(F(x0) + a1(x — x0) + ... +ai-i(x — xoy-1
FM = I ПРИ — ^<^<%
W №) + М*-*о) + • • • + Vi^-^o)'"1
I при х0 < а: <^ оо.
Функцию /7^) можно записать в виде
F(x) = F(x0) + M*)+---+b-i(x)>
где
\^{х — х0)1 при — оо<х<л:0,
1 I bi (х — x0)' при х0 < х <" оо.

§ 13. Равенство на интервалах
4?
Легко видеть, что
^i4x) = il(ai + (bi-ai)H(x-x0))
и
W(x) = i\(bi-at)b«-*-»(x-x0),
что и доказывает теорему, причем k = l — 2.
Если / (х) = 0 при х ф х0, то представление обобщенной
функции f(x) в форме (2) единственно. Это вытекает из
следующей леммы:
13.1. Пусть g(x)—некоторая функция1) и
(3) g (х) +«0Ъ(х-х0) + ...+ ak№(x-x0) = О
на всей оси —оо<я'<оо. Тогда g (х) = 0 и а0 = . . . = а&=0.
Будем рассуждать по индукции. Случай k = 0 очевиден,
поскольку обобщенная функция Ь(х — х0) не является
обычной функцией. Предположим, что утверждение
справедливо для k — 1.
Из соотношения (3) вытекает, что g(x) = 0 при х ф х0.
Таким образом, функция g(x) является обобщенной
функцией, равной О2). Применяя лемму 6.6 к соотношению (3),
получаем
с + а0Щх - х0) + а1Цх — х0)+ ... +акЫ*-1)(х — х0) = 0.
Отсюда, по предположению индукции, заключаем, что
аг = . .. = <xk = 0 и с + а0 Н (х — х0) = 0, . а потому и
а0=0.
На примере формулы (1) мы видим, что обобщенные
функции, равные друг другу в интервалах — оо < х < х0
и л:0<л:<оо, т. е. отличающиеся только в одной точке,
не обязательно равны. Из теоремы VIII следует, что их
разность является конечной линейной комбинацией
обобщенной функции Ь(х — х0) и ее производных. Тем не менее
обобщенные функции, отличающиеся самое большее в одной
точке и являющиеся обычными функциями, равны.
г) Локально интегрируемая.—Прим. перев.
2) Поскольку g(#) локально интегрируема и равна 0 при хфх0.—
Прим. перев.

48
§ 14. Функции с полюсами
§ 14. Функции с полюсами
Функция \/х является обобщенной функцией в
интервалах — со < л: <; О и 0 << л: < оо. Однако ее нельзя
непосредственно отождествить ни с какой обобщенной функцией
в интервале — оо < х < оо, поскольку она не интегрируема
ни в какой окрестности точки х = 0.
Но, с другой стороны, в интервале — ос <] л; <[ со
существуют такие обобщенные функции f(x), что
(1) /W = t при хф0-
Например,
(2) (1п|*|)' = 1 при ХФО,
где производная понимается в обобщенном смысле.
Равенство (1) останется справедливым, если к левой части
соотношения (2) прибавить произвольную линейную комбинацию
дельта-функции 8 (х) и ее производных.
В качестве дополнительного соглашения можно принять,
что равенство (2) отождествляет функцию \/х с
обобщенной функцией (In \х\У. Такое отождествление можно
распространить на достаточно широкий класс функций, которые
в отдельных точках имеют полюсы, а в остальных точках
локально интегрируемы. Именно, мы будем рассматривать
в интервале А<^х<^В функции f(x), которые в
окрестности любой точки х0 можно представить в виде
k
(3) /w = /oW+Sriv.
v=1(*-*o)
где f0(x) — интегрируемая функция. Это разложение на
интегрируемую функцию /0 (х) и дополнительную сингулярную
часть однозначно. Сингулярная часть может отсутствовать.
Точки х0, в которых по меньшей мере один из
коэффициентов cv отличен от нуля, называются полюсами функции
f (х). Во всяком конечном замкнутом подинтервале с
концами а и Ъ имеется самое большее конечное число полю-

§ 14. Функции с полюсами
49
сов. Поэтому можно написать
т k
(4) /w=m*)+E2
[1.= 1 v=l Ч ^ 7
где /х(л:) — интегрируемая функция, а л^, ..., хт— полюсы
из этого интервала. Это разложение однозначно. Пусть
а и b не являются полюсами; определим интеграл в
пределах от а до b формулой
b . Ь т
\т<и = ушл + X см in |*-*„
о а ц— 1
m А
1*\
+
+
v v
#Ы ('-'Х'-^г
которая получается из формулы (4) формальным
интегрированием. Под неопределенным интегралом от f(x) будем
понимать всякую функцию вида
lf(t)dt + c,
где а не является полисом, а С — произвольная постоянная.
Только что описанный неопределенный интеграл, заданный
с точностью до постоянной, также является функцией с
полюсами, однако порядки этих полюсов по крайней мере
на 1 меньше.
В дальнейшем мы будем иметь дело только с
функциями, у которых число k в разложении (3) не зависит от х0г).
Интегрируя k раз в вышеуказанном смысле функцию f(x),
получаем локально интегрируемую функцию F(x),
определенную с точностью до полинома степени < k. Ее
обобщенная производная F^k)(x) однозначно определяется
функцией f(x). Мы отождествляем обобщенную функцию F^(x)
с функцией f(x).
Таким образом, в анализ обобщенных функций
включаются все рациональные функции; в частности, функцию
г) Точнее, у которых порядки полюсов ограничены и
максимальный порядок равен k. —Прим. перге.
4-439

50 § 15. Производная как предел отношения
\/(х— x0)k следует отождествить с &-й обобщенной
производной функции
(k — \)\ 1х х°\'
Кроме того, включаются также все рациональные функции
от синуса и косинуса; в частности, имеют место формулы
tg* = (— In | cos л: |)', ctgx = (In | sinх |)'.
Многие другие функции, весьма полезные с
практической точки зрения, например эллиптические функции,
гамма-функция Эйлера и т. п., также включаются в анализ
обобщенных функций.
§ 15. Производная как предел разностного отношения
Производную обобщенной функции можно определить
тем же самым способом, что и производную обычной
функции. Действительно:
15.1. Для любой обобщенней функции f(x)
f'(x) = \imf{x+a)-l{x) .
а-0 , а
Существует такая функция F (х) с непрерывной первой
производной, что F{k)(x) ==■ f(x). Так как
Fix+a) — Fix) г,, у. п
—v ^ ; *—£- ztF {х) при а->0,
то мы имеем в силу теоремы VII
f(x + a)-f(x) _ ( F(x+*)-F(x) ) <*> _^ {F, {х)) {k) = ff{x^
15.2. Для любой обобщенной функции f (х)
/1\ с// \ 1- f(x + ax)—fix)
(1) xff(x) = lim — '—l^-J— .
Существует такая функция F (x) с непрерывной первой
производной, что Fik)(x) = f(x). Дифференцируя
соотношение
F(x+ax)-F(x) ^хГ{х) при a_+0i

§ lS. Производная как предел отношения 51
получаем
F'(x+ax)^-F'(x) + р,^ + ^ ^хГщ + р^х)
В силу леммы 12.2 имеем F'(x + olx) -+F'(x), и, значит,
F'(x + ax) — F'(x) .^ xF'\x).
а
После k подобных шагов получаем
F«(x+<uQ-F№(,) _>xF(k>u{x)
a v '
т. е. формула (1) справедлива.
Умножая формулу (1) на 1/х, получаем, в силу леммы
11.3,
(2) /'(*) = lim /(*+"*)-/(*) при х ф о.
а-*0 аХ
Если /(а:) является обобщенной функцией в интервале
Л<х<£, причем Л<0<В, то, согласно § 13,
формулу (2) нужно понимать как равенство на интервалах
Л<х<0 и 0<x<fi.
На обобщенные функции можно также распространить известную
теорему Пеано.
15.3. Для любой обобщенной функции f(x) в интервале А < х <Б
и для любого целого числа т^> 0 в общей части интервалов
А —а < л: < £ — а и А < л: < £ имеет место формула
f(x + a) = f(x)+^r(x) + ...+ £]f(m)(x)+a'*ra(x)9
причем обобщенная функция га(х) определена в этой общей части,
и при а -+ 0
га (*)-»- 0 в интервале А <# <£.
Существует такая функция F(x) с т непрерывными
производными, что для некоторого целого k F(k)(x) = /(х). Имеем
F(x + i)^F(x) + yiF'(x) + ...+ a™F(m\x) f a"Ra(x),
где Ra (x) rtO при a -> 0. Дифференцируя & раз, получаем
требуемое равенство с ra(x) = R^(x).
4*

52 § 16. Значение в точке
§16. Значение обобщенной функции в точке
Докажем сначала следующую лемму:
16Л (Железный [5]). Если обобщенная функция g(x)>
определенная в интервале —оо < л: <; ос, удовлетворяет
уравнению
(1) g"(^)=gM для любого Х=£0,
то она является постоянной функцией.
Из равенства (1) вытекает, согласно формуле (2) § 15,
что g'(x)=0 при х^О, а тогда, по теореме VIII,
g\x) = a0b(xHa1b'(x) + ...+QLkbW(x).
Следовательно, по лемме 6.7,
g(x) = c+aQH(x)+a1b(x) + ...+akb^)(x)9
где с — некоторая постоянная. Из равенства (1), применяя
формулу (6) § 12, получаем
а0(Н(\х)-Н(х))+^-щ -\)Цх)+ . . .
а отсюда, в силу леммы 13.1, следует, что ^=^=...
...=а£=0. Этим доказано, что g(x)=c.
16.2. Если предел
(2) g(*)=lim f{ax+x0)
<х-»0
существует, то он является постоянной функцией.
Действительно, обобщенная функция g(x) удовлетворяет
условию леммы 16.1.
Значение функции, определяемой формулой (2), будем
называть значением обобщегшой функции f(x) в точке х0.
Если значение обобщенной функции в точке х0 существует,
т.е. если существует предел (2), то точка х0 называется
регулярной. В противном случае она называется
сингулярной.

§ 16. Значение в точке
53
16.3. Если обобщенная функция f(x) является локально
интегрируемой функцией, непрерывной в точке х0, то
f(ax-\x0)zZf(x0) при а->0. Следовательно, х0—регулярная
точка, а значение f(x) в точке х0 в смысле теории
обобщенных функций равно f{x0).
16.4. Если функция F(x) имеет в точке х0 обычную
производную, то последняя равна значению обобщенной
функции F'(x) в этой точке.
По предположению, существует предел
F(a-\-x0)— F(x0) n
—v u/ ^-^- -> с при а->0
(здесь все символы понимаются в классическом смысле).
Следовательно, при а->0
F(ax-\-Xn) — F(Xn) .^ ~ .
— ■ Л сх в интервале —ос<^л:<.ос.
Дифференцируя в обобщенном смысле эту формулу,
получаем
Ff(ax+x0)-> с при а->0,
что и доказывает лемму.
Обратное утверждение неверно. Может случиться, что
обычная производная в данной точке не существует, хотя
обобщенная производная и имеет в этой точке некоторое
значение. Например, функция F(x)= 3x2s'm— — xcos—не
имеет обычной производной в точке 0. Однако обобщенная
производная F'(x) имеет в точке 0 значение 0. В самом
деле, имеем
axhin— zt 0 при а->0.
ОХ -* Г
Отсюда, последовательно дифференцируя, получаем
—^-*0 и F'(ax)-+0 при а->0.
Следующая лемма является частным случаем леммы 16.4»

54
§ 16. Значение в точке
16.5. Пусть f(x)—локально интегрируемая функция,
X
причем функция F(x) = U{t)dt имеет обычную производную
а
в точке х0; тогда значение этой производной является
значением обобщенной функции f(x) в точке х0. '
Значение обобщенной функции f(x) в толке х0 будем
обозначать символом f{x0), как и в случае обычных
функций. Такая запись не приводит к недоразумениям.
Действительно, если обобщенная функция f(x) является непрерывной
функцией, то значения f(x0) в обоих смыслах совпадают в
силу леммы 16.3. Если же f(x) только локально
интегрируема (или, в более общем случае, является функцией с
полюсами), то, согласно лемме 16.5, значения обобщенной
функции f(x) существуют почти всюду. Значения f(x0) в
обоих смыслах при этом совпадают почти всюду, но, вообще
говоря, не всюду. В случае несовпадения мы условимся
обозначать символом f(x0) значение в смысле теории
обобщенных функций.
Примеры. Г. Согласно лемме 16.3, всякая точка х0ФО
является регулярной точкой функции Хевисайда Н(х),
причем значение в точке х0 в обобщенном смысле совпадает
со значением в обычном смысле. Точка х0 = 0 является
сингулярной, поскольку предел выражения
(3) Н(ах)=^(щх)-^)+±
при а->0 не существует.
2°. Функция Дирака Ь(х) имеет значение 0 в каждой
точке х0Йи не имеет никакого значения в точке х0=0.
Действительно, дифференцируя формулу (3), получаем
|а|8(а*) = 8(х).
Из существования предела lim Ь(ах) вытекало бы, что Цх)
является обычной функцией, тождественно равной нулю.
3°. Из леммы 16.5 следует, что значение (в
обобщенном смысле) функции sin(l/#) в точке 0 равно 0.
Действительно, выполнив замену переменного /=±1/т
(где знак + берется при х>0, а злак — при х<0) и применяя

§ 17. Теоремы существования значений
55
вторую теорему о среднем значении, находим
1 р . 1 ,. 1 р 1 sim , '|*| г» sin т , / 1 .«. . \
0 1/1*1 1/1*1 ^ *
а отсюда
Г sin -i-dt\ =lim — f sin-7-^= 0.
I * K-o -o - J <
Можно доказать, что в случае, когда значение
обобщенной функции f(x) равно нулю всюду, эта обобщенная
функция f(x) является нулевой функцией (Лоясевич [9]). Таким
образом, обобщенная функция однозначно определяется ее
значениями, если таковые существуют всюду.
§ 17. Теоремы существования значений обобщенных
функций
В приложениях очень важна следующая теорема:
Теорема IX (Лоясевич [8, 9]). Обобщенная функция f(x)
имеет значение с в точке х0 тогда и только тогда, когда
существуют целое число k^O и непрерывная функция
F(x), такие, что F{k)(x) = f(x) и
Достаточно доказать эту теорему в случае^х0=0. Пусть
Л *>(*) = /(*) и
х-0 х л*
тогда, при а->0, a~kF(zx)i5cxk/k\ в интервале —ос<л:<оо.
Так как f(ax) = (a~kF(ax))(k\ то Umf(oLX) — c, т.е. f(x) имеет
а->0
значение с в точке 0.
Предположим теперь, что f(x) имеет значение с в точке 0.
Тогда существуют целое число fe>0 и функция Fa (х),
зависящая от параметра а, такие, что
сх
Fik> (х) = ({ах) и Fa (х) г? йГ при а -+ 0.

56
§ 17. Теоремы существования значений
В частности,
Я*> (*) = /(*).
Поскольку (akFa(x/(x)—F1(x)Yk)=0, функции akFa(x/oi)
и F^x) отличаются друг от друга только на полином
степени < k:
«kF« (£) = ^М + М«) + Ьг(*)х + ...+ bk^(a)x^ .
Мы собираемся доказать, что пределы 6/=lim 6/(а)
(/=-0, 1, ..., &—1) существуют и что функция
F(x)=F1(x)+b0+b1x+...+bk_1xk'1
обладает требуемым свойством.
Так как
Fa(x) = a'HF1(ax) + b0(a)+oib1(a)x+
то, полагая
G(x)=F1(x)—^r у
получаем
a"*(G(oa)+60(a)+a61(a)x+...+a*"16^„1(a)x*"1)z^O при а->0.
Следовательно, существует возрастающая функция г (а)
параметра а>0 со свойствами: г(а)->0 при а->0 и
(2) \G(ax)+b0{a)+ab1(a)x+... +^'1bk^1(a)xk'1\<:ah(oL)
при —1<ж1.
Фиксируем k точек —1^:^...-0^^1. В силу
неравенства (2) имеем
|G(«i)+M«)+afti(a)^+-••+a*~%-iW~l| <сЛ(а).
Заменяя в неравенстве (2) а на р ф>а) [и л: на л:/а/р,
получаем

§ 17. Теоремы существования значений
57
Из двух последних неравенств следует, что
(3) |(60(а)-6оФ)) +«0i(«)-*i(P) )*+ •• •
...+^-^.^)-6^^))^-11< 2р*еф)
При Х = ХХ, ..., Xfc .
Обозначая через p(#) полином, стоящий под знаком
модуля в левой части неравенства (3), имеем
*1Ы*)-Ь№)= 4 (AMxJ+-+AkiP(4))>
где ЛУ7—алгебраические дополнения элементов определителя
1 xk ... ^-1
как это было в доказательстве леммы 2.4 (стр. 15). Отсюда
вытекает, что при некоторой постоянной К выполняются
неравенства
«'1м«)-мр)кадр)р*.
При а < [3 <: 2а имеем
(4) Ма)-6«(Р)|<2'+1/(е(|})р*Ч
Из неравенства (4), полагая а=2-/2"1 и р = 2"л, находим
| &/(1/2я + 1) — 6/(1/2Л) К 2/+1/Се(1/2Л) (1/2л<*-'>)
(л=1, 2, ...).
Записывая эти неравенства для п, я+ 1, ..., га— 1 и
складывая их, получаем оценку
(5) |fy(l/2«)—6/(1/2л)|<2/+2/С£(1/2л)(1/2«(^)) (т>/г).
Подберем для произвольных а и (3 ( 0 < а < (3 ^ -^-
целые положительные числа тип так, чтобы
<х<1/2"^2а и 1/2"<р<2/2",

58 § 17. Теоремы существования значений I
Заменяя в неравенстве (4) число (3 на 1/2т, получаем
(6) | b£(a) — bi(l/2m) | < 21+1Щ\/2т) (1/2т<*-'>).
Заменяя в неравенстве (4) число а на 1/2Л, получаем
(7) | 6Д1/2«) — 6ДР) | < 2'+1/Се(Р) p^-i.
Из неравенств (5), (6) и (7) находим
|6«(«)-6ДР)|<2' + 8/Се(Р)Р*-' (0<а<(3<4-)_
Это неравенство доказывает, что пределы
bi = НтбДа) (/= 0, 1, ..., k—\)
а-*
сосуществуют, причем
(8) |fy—&Да)|<2' + 8/Се(а)а*-' (/= 0, 1, ..., k—l).
Из неравенств (2) и (8) вытекает, что при —1 <;#s^ 1
(9) | 6(«) + b0+ abxx 4-...+ аЬ-Ч^х*-1 | < ^ (а)а*.
где /^ = 1 -{-k2k+3K' Докажем, что функция
F(x) = G (х) 4 604 V +•••+ Vi^_1+ -fr^
удовлетворяет соотношению (1). Действительно, в силу
неравенства (9), при х = 1 имеем
<*!*(«)•
Поэтому правый предел отношения F(a)/ak равен с/£!.
Аналогично при х = —1 проверяем, что и левый предел равен
тому же.
Для завершения доказательства достаточно отметить,
что F^(x) = f(x).
Теорема X (Лоясевич [8, 9]). Если обобщенная
функция f'(x) имеет в точке х0 некоторое значение, то и
обобщенная функция f(x) также имеет в точке xQ некоторое
значение.

§ 17. Теоремы существования значений
59
Действительно, пусть непрерывная функция F(x) и целое
число fe^O таковы, что F{k)(x) = \'(х) и предел
1- F(x)
существует. Если k = 0, то f'(x)—непрерывная функция,
а значит, f(x) также непрерывная, и теорема справедлива.
Если же &>0, то
х^ (x~xo)k х
Из теоремы IX вытекает, что обобщенная функция F<fc-^(x)
имеет в точке х0 значение, равное нулю. Обобщенная
функция f(x) отличается от F^'^ix) на постоянную, а потому
f(x) также имеет в точке х0 некоторое значение.
Пусть ш(лг) удовлетворяет условию §11.
17.1. Если обобщенная функция f(x) имеет в точке х0
значение f(x0); то обобщенная функция &(x)f(x) имеет в
точке х0 значение &{x0)f(x0).
Действительно, при а -> 0 имеем Дал; + л:0) -> f(x0),
со (ах +х0) =t ш(х0) и (u(oiх + х0) Ут) ^Z 0 (т=1, 2, ...).
Отсюда, по лемме 11.3, заключаем, что
о)(ах + X0)f(ax + X0)->ta(x0)f(x0).
Пусть ср(лг) удовлетворяет условиям §12.
17.2. Если обобщенная функция f(x) имеет некоторое
значение в точке х = у(х0), то обобщенная функция f(<?(x))
имеет в х0 то же самое значение.
Действительно, по теореме IX существуют непрерывная
функция F(x) и целое число fe^O, такие, что
где с — значение f(x) в точке у(х0). В силу равенства
F(<?(x)) = FMx)) I ?(*)-?(*„) \*
(х-х0)" (?(*)-<f(*o))ft \ х-х9 J

60
§ 18. Значение в бесконечности
имеем
Ьт7^^-=1Г(?'(*о))*."
Следовательно,
*(,(«+*.)) ^№о))^.
Дифференцируя в обобщенном смысле, получаем
Т7' (ср(осл:
Но, поскольку
^±^- *'<«+*)- ^ <*'(*> )* ** -1-
1 _ 1
<р'(а*+*о) ~* <р'(*о)'
^ <?'(ах+х0) у V 7
в силу леммы 11.3 имеем
После fe подобных шагов окончательно получаем
F№(<f(ax+x0)) ->с, т.е. /(<р(«*+*Ь)) -> с при а+ 0.
§ 18. Значение обобщенной функции в бесконечности
Докажем лемму
18.1. Для любой обобщенной функции f(x) предел
(1) Нт/(* + Р)
(если он существует) является постоянной функцией.
Обозначим предел (1) символом g(x). При произвольном
а имеем
g(x + а) = \imf(x + а + р) = limf(* + р) = g(*).

§ 18. Значение в бесконечности 6]
Отсюда
g'(x) = lim ^v ; *v ; = 0
a-0 a
и, следовательно, g(x)—постоянная функция.
Значение функции, определяемое равенством (1),
называется значением обобщенной функции f(x) в ос и
обозначается символом /(ос).
Аналогично определяется значение /(—оо) обобщенной
функции f(x) в —ос.
Символы /(ос) и /(—оо), очевидно, имеют смысл в том
и только в том случае, когда существуют соответствующие
пределы.
18.2. Пусть обобщенная функция f(x) является
непрерывной функцией, имеющей обычный предел с в оо
(соответственно ъ — оо); тогда f(x+$)7*c при [3-*^о
(соответственно при (3->—оо). Следовательно, f(oc) = c
(соответственно /(—оо)=с).
Следующая лемма непосредственно вытекает из
определения /(ос) и из теоремы VII.
18.3. Если /(ос) существует, то /'(оо) —0. Если
/(—ос) существует, то /'(—оо)=0.
X
Отсюда, как частный случай, при f(x)= Г g(t)dt полу-
а
чаем:
18.4. Если g(x) — локально интегрируемая функция,
00
для которой сходится несобственный интеграл Г g(t)dt
а
то g"(oo)= 0.
Из этого замечания вытекает, что существуют
непрерывные функции g(x), имеющие обобщенное значение g(oo), но
не имеющие обычного предела в точке оо.
Пусть ю(х) удовлетворяет условию §11.
18.5. Если обобщенная функция f(x) имеет в со
значение Дос) и если о)(л:+р)=г^(оо) и а)(т)(л:+Р)=>0 (т=\, 2,...)

62
§ 19. Интеграл
при [3->оо, mo обобщенная функция &(x)f(x) имеет в точке
оо значение a)(cv)/(cx).
Эта лемма непосредственно вытекает из леммы 11.3.
§ 19. Интеграл от обобщенной функции
Под неопределенным интегралом обобщенной функции
f{x)y заданной в интервале Л<х<£, мы понимаем всякую
обобщенную функцию ф(х), определенную в интервале
Л<х<£, для которой ty'(x) = f(x). Из леммы 6.7 и теоремы
III следует, что неопределенный интеграл от любой
обобщенной функции существует и определяется с точностью
до постоянной (так же, как и для обычных функций).
В случае, когда обобщенная функция является обычной
функцией, данное нами определение совпадает с обычным.
Из теоремы X вытекает лемма
19.1. Всякая регулярная течка обобщенной функции
f(x) является также регулярней точкой неопределенного
интеграла от f(x).
Введем следующее обозначение:
ь
(1) ^fi<x + t)di = ^x + b)-ty(x-ha)t
а
где <1>'(х) = f(x)f а точки а и Ь принадлежат интервалу
А<Сх^В. Обобщенная функция (1) определена в общей части
интервалов А — а < .v < 5 — а и А — 6 < л: < J3 — b и не
зависит от выбора неопределенного интеграла <1>(х). Если
f{x)—локально интегрируемая функция, то выражение (1)
имеет обычный смысл.
Справедливы следующие формулы:
а ь
U(x + t)dt = — U(x + t)dty
b а
b b
§bf(x + t)dt=\\f(x + f)dt,
a a

§ 19. Интеграл
63
j(/(* + t) + g(x + t) )dt - J f(x + f) dt + j g(x + t)dt9
a a a
j (f(x + t) -g(x + t))dt=$f(x + t)dt-§ g(x + t)dt,
a a a
b с с
Г f(x + t)dt+ {f(x + t)dt= f /(л: + /) dt,
aba
/ b у b
П f(x + t)dt \= j/'(x + t)dt = f(x + b) - f(x + a).
Теорема XI. Если fn{x)-> f{x)y mo
ь ь
{2) $fn(x + t)dt-+ \f{x + t)dt.
a a
Действительно, существуют целое число k > 0 и
непрерывные функции Fn(x)^Z F(х), такие, что F^\x) = fn(x)
и F{k)(x) = f (х). Следовательно, Fn(х + Ь) — Fn{x -\- а)^
=£ F(x + Ь) — /7^ + а). Дифференцируя k — 1 раз,
получаем в силу теоремы IV формулу (2).
Следующая теорема является прямым следствием
теоремы XI.
Теорема XII. Для любого сходящегося ряда
обобщенных функций имеет место равенство
b со оо b
j ( %gn(x + t) )dt = £ §ga(x + t)dt.
a n~1 n-\ a
Можно дать эквивалентное определение интеграла (1) как
предела сумм
J т
Е/(* +ту) (/,— /;_,)
(где a =s t0 </г «^ ... </от = 6*и /y_t < ту < /у), взятого по
последовательности разбиений, аналогично тому, как эго делается в теории
интеграла Римана. Чтоэы доказать экзизаленгность этих определений,
b
дсстагочно представить интеграл J ^(л: + t) dt, где F(x) —непрерыв-
ik) а
ная функция и F (*) = /(*)> в виДе предела аналогичных сумм и
продифференцировать этот предел k раз.

64 § 19. Интеграл
Значение обобщенной функции j f(x-\-t)dt при х = О,
а
если таковое существует, будем обозначать символом
ь
(3) \f(t)dt.
а
Этот символ, если он имеет смысл, всегда является
числом. Если обобщенная функция локально интегрируема, то
(3) — ее обычный определенный интеграл.
Непосредственно из определения вытекает, что*в
случае, когда а и Ь — регулярные точки неопределенного
интеграла ф(лг) обобщенной функции f(x), имеет место
формула
ь
(4) \f(t)dt = №-b{a).
а
Равенство (4) примем за определение определенного
интеграла в случае, когда а или Ь бесконечно. В частности,
имеем формулы
оо Ь
\ /(0 dt = ф(оо) - 4(c), j / (t) dt = <#) - «К - оо) ,
а —оо
со
(5) j f (f) dt = у (оо) — ф(— оо).
Заменяя х на л: + t в формуле (1) § 11 и интегрируя,
находим
(6) §o>(x + t)f'{x + t)dt+ ^f(x + t)f{x + t)dt^
а а
= (o(x + b) f(x + b) — аь(х + a) f (х + а).
Это соответствует классическому интегрированию по частям.
Полагая х = 0, получаем, согласно лемме 17.1,
ь ъ
(7) J со (0 /'(/) Л + jo>'(0 f (О Л = co(b) f(6) - ш(а) Да)

§ 19. Интеграл
ее
в предположении, что соответствующие значения
существуют и что по меньшей мере один из интегралов в
левой части имеет смысл. Формула (7) остается
справедливой, когда а или Ь бесконечно, если о) (х) удовлетворяет
условиям леммы 18.5 или аналогичным условиям при
X = — ос.
Применяя формулу (7), легко показать, что
ь
(8) J о) (/) 8 (t — х0) dt = <!>(х0), если а < х0 < Ь.
а
Действительно,
ь
j а) (0 H'(t — *0) dt = ш(6) Н(Ь — х0) — а) (а) Я (а — *0) —
а
Ь Ь
— |о>'(/)Я(/ — xQ)dt = ш(6) —Ju)'(/) Л ='o>(jc0).
Аналогично можно доказать формулу
(9) J 0)(/)8(/—х0)<# = 0, если *0<а<6 или a<6<x0.
a
Пусть функция <р(х) удовлетворяет требованиям §12;
тогда имеет место оэычная форма замены переменного
9Ф) ъ
(10) \ f(t)dt= J/(t(0)t40*
<P(a) а
при условии, что в точках ср (а) и ср (6) существуют
значения неопределенного интеграла от f(x).
Действительно, пусть F(x) — неопределенный интеграл
от / (х), т. е. F'(x) = f{x). Полагая фх(х) = F (ср (Ь) + х) —
— F(<?(a) + x), видим, что левая часть равенства (10)
равна фх(0). С другой стороны, полагая ф2(х) = F(y(b + х)) —
— F(<p(a + х))у для правой части равенства (10) получаем
ь ь
\ /"'(? (0) ?'(0 dt = J (f (ср (0))' Л = ф2 (0).
a . a
5-439

66 § 20. Периодические обобщенные функции
Поскольку в точках ср (а) и ср (Ь) существуют значения F(x)>
имеем фх(0) = ф2(0) в силу леммы 17.2. Таким образом,
правая и левая части равенства (10) равны.
Заметим, что равенство (10) может нарушиться, если
значения F (х) в точках ср (а) и ср (Ь) не существуют.
Положим, например, /(х) = (In | х2— 2х\)', ср (х) = х2 + х
(— ^< х<оо) иа=0,Ь = 1. Тогда F (х) = In | л:2 — 2х} и, как
легко подсчитать,
фх (х) = In | (2 + х)/(2 - х) |, ф2 (х) = In [ (3 + х)/(\ - х) |.
При этом фх(0) = 0 =£ ф2(0) = 1пЗ, а значит, правая и
левая части формулы (10) различны.
§ 20. Периодические обобщенные функции
Обобщенная функция / (х) в интервале — ос < х <^ оо
называется периодической (с периодом 2тг), если
f(* + 2*)=f(*).
Докажем следующие утверждения:
20.1. Для любой периодической обобщенной функции
f(x) существует интеграл
it
20.2. Для всякого сходящегося ряда периодических
обобщенных функций имеет места формула
TZ 00 00 ТС
—тс П-\ П-\. —тс
20.3. Если интеграл (I) от периодической обобщенной
функции f (х) обращается в нуль, то существует
периодическая обобщенная функция ф(х), для которой
тс
f(x)=/(x) и |ф(/)Л = 0,

$ 20. Периодические обобщенные функции 6?
Пусть ty'0(x) = f(x)\ тогда
тс
(2) I f(x + f)dt = %(x + «) — %(x-«).
—тс
Поскольку производная этой обобщенной функции
равна f(x 4- к) — f (х — тс) = 0, интеграл (2) является
постоянной функцией. Таким образом, в точке 0 он имеет
значение
тс тс
(3) J/(0<«= $f(x + f)dt,
—тс —тс
что и доказывает лемму 20.1.
Лемма 20.2 следует из формулы (3) и теоремы XII.
Пусть интеграл (1) обращается в нуль и ty'0(x) = f(x)\
тогда, согласно формуле (2), ф0 (х + тс) — ф0 (х — тс) = 0.
Это означает, что обобщенная функция %{х) периодична.
Обобщенная функция
1 к
Их) = Ых) — с, где с = ^ J Фо(0 л»
—тс
обладает всеми свойствами, требуемыми в лемме 20.3.
Теорема Х^Н (Шварц [19]; см. также Влёка,
Железный и Лоясевич [2]). Всякая периодическая обобщенная
функция f(x) является суммой тригонометрического
ряда в
(4) f(x) = -^-+ 2j ian cos nx + bn sin nx),
где
(5)
i
an = — f f(t) cos ntdt (n = 0,- 1, 2, . . .),
—TC
&„= -i- f f(t)smntdt (n=l,2,...).
—TC
Разложение (4) единственно.

68 § 20. Периодические обобщенные функции
Теорема XIV (Шварц [19]). Ряд
00
(6) ^] (ап cos пх + bn sin пх)
/2=1
сходится в обобщенном смысле тогда и только тогда,
когда для некоторого целого k
ап Ъп
(7) -jjf -*•() и -пь -> 0 при п->ос.
Предположим, что ряд в равенстве (4) сходится и
притом к f(x). Умножая обе части равенства (4) на cosmx и
интегрируя, получаем в силу леммы 20.2
тс тс
Г f(t) cos mtdt = ~y a0 f cos mt dt +
-—к —тс
со тс тс
+ У (ап f cos nt cos mt dt +bn ^ sin nt cos mt dt) = nam,
n - 1 —TC —TC
поскольку, как известно, все фигурирующие здесь
интегралы от тригонометрических функций обращаются в нуль,
кроме интеграла при атУ равного тс. Таким образом, мы
получили первую из формул (5). Аналогично получается и
вторая.
Отсюда вытекает, что представление f(x) по формуле
(4), если таковое существует, единственно.
Пусть теперь f(x) — произвольная периодическая
обобщенная функция. Интеграл от обобщенной функции g (х) —
к
= /(^) о~ао равен нулю; ^ g(t)dt = 0. Применяя k раз
—тс
лемму 20.3, находим, что существует периодическая
обобщенная функция G0(x), для которой G^{x) = g(x). С другой
стороны, при достаточно большом k существует
непрерывная функция G(x), для которой GW(x) =g(x). Можно
считать, что k кратно 4 и что G (х) непрерывно
дифференцируема. Обобщенные функции G0(x) и G(x) отличаются друг

§ 20. Периодические обобщенные функции
69
от друга на полином степени <f k, а поэтому G0 (х)
является периодической функцией с непрерывной производной.
По элементарной теореме о рядах Фурье, G0 (х) пред-
ставима суммой равномерно сходящегося
тригонометрического ряда
1
(8) G0 (х) = -уа0 + ^ (ал cos пх + ря sin aw),
п=\
у которого
(9) ап -*0 и рп -0.
Дифференцируя в обобщенном смысле формулу (8)
k раз и прибавляя к обеим частям а0/2, получаем
равенство
1
f(x) = -б- а0 + V (л* an cos azx + п* $п sin ллг),
/2=1
причем сходимость ряда в правой части понимается в
смысле теории обобщенных функций.
В силу единственности представления f(x) в виде (4)
заключаем, что
(10) ап = nkan и bn = nk ря {п = 1, 2, . . .),
где ап и Ьп даются формулами (5). Этим завершается
доказательство теоремы XIII.
Свойство (7) вытекает из соотношений (9) и (10). Для
доказательства теоремы XIV достаточно показать, что из
соотношений (7) вытекает обобщенная сходимость ряда (6).
Пусть k0 кратно 4 и fc0>fe+l. Тогда ряды
аз оо
у Еп и у^п
абсолютно сходятся, а значит, ряд
00
У (~-cosnx-] ^smnx\
п- 1
сходится равномерно.

70 § 20. Периодические обобщенные функции
Дифференцируя последний ряд k0 раз, получаем ряд (6),
который в силу теоремы VI сходится в смысле теории
обобщенных функций.
В классическом анализе принято различать тригонометрические
ряды и ряды Фурье. В теории обобщенных функций это различие
исчезает, поскольку всякий сходящийся тригонометрический ряд
является разложением некоторой периодической обобщенной функции.
Отметим, что тригонометрический ряд, являющийся разложением в
классическом смысле некоторой периодической функции, является
разложением и в смысле теории обобщенных функций. Это вытекает из
того, что коэффициенты разложения подсчитываются по одним и тем
же формулам (5).
Пример периодической обобщенной функции, не
являющейся обычной функцией, дает ряд
со
(И) Ь2к(х) = £ Ъ(х + 2кп).
п = —00
Обобщенная функция Ь2г.{х) является производной функции
Е(х/2к), где символ £(а) означает наибольшее целое
число, не превосходящее а. Действительнз, функцию Е (х/2к)
можно выразить при помощи функции Хевисайда:
(12) £(-^)= £ Н(х + 2*п) + % (Щх+2кп)-\).
П- — 00 /2 = 0
При дифференцировании этой формулы ее правая часть
превращается в правую часть формулы (11).
Для нахождения коэффициентов разложения обобщенной
функции Ъ2к{х) воспользуемся формулами (8) и (9) § 19:
ап= — Г 8 2к (0 cos ntdt = — f 8 (t) cos nt dt = — cos 0 = —
и, аналогично,
Ь« = 0.
Таким образом, согласно теореме XIII,
(13) 82к (х)= — [ у + cos л: + cos 2л; + • ♦ • ).

§ 20. Периодические обобщенные функции
71
Отсюда получается формула для суммы косинусов:
cos х + cos 2х + ... = т: Ь 2п (х) — у .
Этот ряд не сходится в обычном смысле ни в одной точке.
Обобщенную сходимость можно доказать двукратным
интегрированием или же вывести из теоремы XIV.
Аналогично, ряд синусов
sin х + sin 2х + ...
сходится в обобщенном смысле. Для отыскания его суммы
будем исходить из известной формулы
,л .. cos л: , cos2л: , л
(14) —т—+-^— +... = — In
. х
sin у
— In 2
Функция в правой части локально интегрируема, поэтому
она является обобщенной функцией. Дифференцируя в
обобщенном смысле ряд (14) и меняя знак, получаем,
согласно § 14,
1 х
sinx -f sin 2х + ... = — ctg у .
Отсюда получается разложение ctgx:
ctgx = 2 (sin 2х -f sin \х + sin 6х+ . ..).
Заменяя х на тс/2 — х, получаем разложение tg*:
tg х = 2 (sin 2х — sin Ах + sin 6х — ...) .
Поскольку 1/sinx = tg (х/2) + ctgx, имеем
—-. = 2 (sin х + sin 3x + sin Ъх + . ..) .
sin* v ' ' ' '
Заменяя x на rc/2— x, получаем
-J— = 2 (cos x — cos 3a; + cos Ъх —...).
cos* v ' '
Интересно отметить, что предыдущие формулы остаются
справедливыми, если понимать суммирование не в смысле
теории обобщенных функций, а, например, как
суммирование методом средних_арифметических.

72 § 21. Обобщенные функции бесконечного порядка
Хорошо известно, что п-я частная сумма ряда (13)
является не чем иным, как ядром Дирихле
sin in + ~2 1 х
71 X
2 sin -у
Согласно формуле (13), ядро Дирихле стремится в
обобщенном смысле к Ъ2к(х). Другие ядра, рассматриваемые
в теории тригонометрических рядов, например
1 / 01П 2
2тт
sin тг пх \
sin -о- X
(ядро Фейера),
У
Л/ — cos2" -2 а: (ядро Балле-Пуссена),
обладают тем же свойством.
В некоторых случаях бывает выгодна комплексная
форма тригонометрического ряда
(15) V Спе
1ПХ
i-J
Из теоремы XIII вытекает, что всякую периодическую
обобщенную функцию можно представить как сумму ряда (15)
с коэффициентами
тс
-intdt
:п = ЦШ)е~^
Согласно теореме XIV, ряд (15) сходится тогда и только
тогда, когда для некоторого целого k выполняется
соотношение: c+n'nk —»-0 при п ->оо.
§ 21, Обобщенные функции бесконечного порядка
Понятие обобщенной функции было введено в
математику С. Д. Соболевым (16) в 1936 г.; Л. Шзарц [18, 19, 20]

§ 21. Обобщенные функции бесконечного порядка 73
назвал эти функции «distributions»г) и развил их
теорию в 1945 и последующих годах. Определение Соболева
отлично от приведенного в данной работе.
Обобщенные функции, рассмотренные в данной работе,
называются обобщенными функциями конечного порядка,
ибо они являются производными конечного порядка от
обычных функций. Обобщенные функции Соболева и
Шварца являются производными непрерывных функций только
локально, а не на всем рассматриваемом интервале. В
настоящем параграфе мы собираемся изменить наше
определение с тем, чтобы получить понятие, эквивалентное
понятию Соболева—Шварца.
Последовательность непрерывных функций fn(x),
определенных в фиксированном интервале А < х < В (конечном
или бесконечном), называется фундаментальной, если
для любого конечного замкнутого интервала а <;#<;■ 6
(Л<а<Ь<В) существуют целое число k^O и
последовательность непрерывных функций [Fn(x)}, определенных при
а^ х ^ Ъ, такие, что:
Г. F{nk)(x) = fn (х) при а < х < Ъ .
2°. [Fn[x)\ равномерно сходится.
Мы говорим, что фундаментальные последовательности
\fn(x)} и [gn(x)} непрерывных функций, определенных в
интервале А<^х<^В, эквивалентны, если для любого
конечного замкнутого интервала а^х^Ь (Л < а < 6 <В)
существуют целое число k ^ О и последовательности
непрерывных* функций {Fn(x)\ и {Gn(x)}, такие, что:
\°.F^(x) = fn(x) и G{*4x) = gn(x) .
2°. Последовательности { Fn (х)} и { Gn (х)} сходятся
к одному и тому же пределу равномерно на интервале
а^х^ Ь.
В этом новом определении существенно, что выбор
целого числа k зависит от интервала а^х^Ь.
Классы эквивалентных последовательностей
называются обобщенными функциями.
Последовательность, фундаментальная в прежнем смыс-*
ле, является, очевидно, фундаментальной и в новом
смысле. Обратно, если последовательность фундаментальна
]) Буквально «распределения», — Приц, черен ,

74 § 21. Обобщенные функции бесконечного порядка
в новом смысле и если можно выбрать целое число fe, общее
для всех интервалов а^х^Ь (1<а<Ь<£), то можно
также выбрать и функции Fn(x), общие для всех
интервалов; таким образом, последовательность является
фундаментальной в прежнем смысле. Обобщенные функции в
новом смысле, определяемые подобными последовательностями,
называются обобщенными функциями конечного порядка.
Последовательности, фундаментальные в прежнем смьсле,
эквивалентны в новом смысле тогда и только тогда, когда
они эквивалентны в прежнем смысле; доказательство мы
здесь опускаем.
В силу предыдущих замечаний обобщенные функции в
прежнем смысле можно отождествить с обобщенными
функциями конечного порядка.
Для новых обобщенных функций можно определить
сложение, вычитание, умножение на число или на
функцию, замену переменного, дифференцирование,
интегрирование и т. п. При этом основные свойства этих действий
сохраняются.
Для любого интервала а^х ^Ь (Л <Г а<^Ь<^В)
существует такое целое число k ^ О, что данная обобщенная
функция является производной /г-го порядка некоторой
непрерывной функции на этом интервале. Целое число k
можно выбрать общим для всех интервалов а ^ х ^ Ь тогда и
только тогда, когда обобщенная функция имеет конечный
порядок. В этом случае обобщенная функция оказывается
k-й производной непрерывной функции во всем интервале
А <С х <С В. В противном случае обобщенная функция
имеет бесконечный порядок.
Определение сходимости нужно изменить, ввиду того
что новые обобщенные функции не являются, вообще
говоря, производными никакого порядка от функций,
непрерывных в А <^ х < В.
' Именно, мы говорим, что последовательность
обобщенных функций [fn(x)} сходится к обобщенной функции f(x),
если для любого конечного замкнутого интервала
а^х ^ Ь (Л < а < & < В) существуют целое число
^Ои непрерывные функции F(x), Fn(x) со свойствами:
f (*) (х) = fn (х), Л*> (х) = /(*), и последовательность
I К (х)} равномерно сходится к F(х).

§ 21. Обобщенные функции бесконечного порядка 75
Остаются справедливыми все предыдущие теоремы,
касающиеся сходимости. Сходимость в прежнем смысле
влечет сходимость в новом смысле, но не наоборот.
Например, ряд
8(*) + 8'(*—1) + 8*(* —2) + ...
сходится в новом смысле, но не сходится в прежнем
смысле. Этот ряд представляет обобщенную функцию
бесконечного порядка.

ЛИТЕРАТУРА
[1]Влёка И. (W 1 о k a J.), Uber die Gleichwertigkeit zweier Stetig-
keitsdefinitionen (в печати).
[2] Влёка И., Железный 3. и Лоясевич С. (Lojasie-
wicz S., Wloka J. und Zielezny Z.), Uber eine
Definition des Wertes einer Distribution, Bull. Acad. Pol. Sc.
CI. Ill, 3 (1955), 479—481.
[3] Гальперин И. (Halperin I.), Introduction to the theory
of distributions, Toronto, 1952. [Русский перевод: Введение в
теорию обобщенных функций, Изд. ин. лит., М., 1954.]
[4]1) Гельфанд И. М. и Шилов Г. Е., Обобщенные функции.
Выпуск I: Обобщенные функции и действия над ними, Физмат-
гиз, М., 1958.
[5] Железный 3. (Zielezny Z.), Sur la definition de Lojasi-
ewicz de la valeur d'une distribution dans un point, Bull. Acad.
Pol. Sc. CI. Ill, 3 (1955), 519—520.
[6]Кёниг Г. (Konig H.), Neue Begrundung der Theorie der
«Distributionen» von L. Schwartz, Mathcmatische Nachrichten,
9 (1953), 130—148.
[7] Коревар Я. (Korevaar J.), Distributions defined from the
point of view of applied mathematics, Proc. Kon. Nederl. Akad.
Wetenschappen, Ser. A, No 2 и Indag. Math., 17.2 (1955),
368—383; там же Ser. A, 58.4 и 17.4 (1955), 463—503; там же
Ser. A, 58.5 и 17.5 (1955), 563—674.
[8] Лоясевич С. (Lojasie.wicz S.), Sur la valeur d'une
distribution dans un point, Bull. Pol. Acad. Sc. CI. Ill, 4
(1956), 239—242.
[9] » — .» Sur la valeur et la limite d'une distribution dans
un point, Studia Math., 16 (1957), 1—36.
1 Добавлена переводчиком, — Прим . ред.

Литература ft
[10] Минусинский Я. (Mikusifiski J.), Sur la methode de
generalisation de M. Laurent Schwartz et sur la convergence
faible, Fund. Math., 35 (1948), 235—239.'
[11] » — » Une definition de distribution, Bull. Acad. Pol.
Sc. CI. Ill, 3 (1955), 589—591.
[12] Мышкис А. Д. и Лепин А. Я*, Об определении
обобщенных функций, Машем, сборник, 43(85): 3 (1957), 323—348.
[13] Сикорский P. (Sikorski R.), A definition of the notion
of distribution, Bull. Acad. Pol. Sc. CI. Ill, 2 (1954),
209—211.
[14] Словиковский В. (Slowikowski W.)> A
generalization of the theory of distributions, Bull. Acad. Pol. Sc. CI.
Ill, 3 (1955), 3—6.
[15] » — » On the theory of operator systems, Bull. Acad. Pol.
Sc. CI. Ill, 3 (1955), 137—142.
[16] Соболев С. Л., Methode nouvelle a resoudre le probleme de
Cauchy pour les equations hyperboliques normales, Машем,
сборник, 1(43) (1936), 39—72.
[17] Темп л Дж. (Temple G.), Theories and applications of
generalized functions, J. London Math. Soc, 28 (1953),
134-148.
18] Шварц Л. (Schwartz L.), Generalisation de la notion de
fonction, de derivation, de transformation de Fourier, et
applications mathematiques et physiques, Annates Univ. Grenoble,
21 (1945), 57—74.
[19] » — » Theorie des distributions I, Paris, 1950 (второе
издание: Paris, 1957).
[20] » — » Theorie des distributions II, Paris, 1951.
[21]1) Шилов Г. E., Обобщенные функции и их приложения, УМН,
11, вып. 6 (72) (1956), 217—226.
) Добавлена переводчиком. — Прим. ред.

ОГЛАВЛЕНИЕ
Предисловие к русскому изданию 5
Введение 7
§ 1. Метод абстракции 9
§ 2. Фундаментальные последовательности непрерывных
функций И
§ 3. Определение обобщенной функции 16
§ 4. Обобщенная функция как расширение понятия функции 18
§ 5. Алгебраические действия над обобщенными функциями 20
§ 6. Дифференцирование обобщенных функций 22
§ 7. Определение обобщенных функций при помощи
производных 26
§ 8. Локально интегрируемые функции 28
§ 9. Последовательности и ряды обобщенных функций ... 31
§10. Обобщенные функции, зависящие от непрерывного
параметра 35
§11. Умножение обобщенных'функций на функцию 39
§ 12. Замена переменных 42
§13. Равенство обобщенных функций на интервалах 45
§14. Функции с полюсами 48
§ 15. Производная как предел разностного отношения .... 50
§ 16. Значение обобщенной функции в точке 52
§ 17. Теоремы существования значений обобщенных функций "55
§18. Значение обобщенной функции в бесконечности .... 60
§ 19. Интеграл от обобщенной функции . . . , , 62
§ 20. Периодические обобщенные функции . , . , 66
§21. Обобщенные функции бесконечного порядка 72
Литература , 76

Я. Микусинский и Р. Сикорский
ЭЛЕМЕНТАРНАЯ ТЕОРИЯ
ОБОБЩЕННЫХ ФУНКЦИЙ I
Редактор Е. Д. СОХОМЕНЦЕВ
Художественный редактор Е. И. Подмарьковъ
Технический редактор М. П. Грибова
Корректор Р. Я- Новик
Сдано в производство I3/V 1958 г.
Подписано к печати 2 7/XI 1958 г.
Бумага 84 X 108732 =1,3 бум. л.
4,1 печ. л.
Уч.-изд. л. 3,5. Изд. № 1/4422'
Цена 2 р. 45 к. Зак. 439
ИЗДАТЕЛЬСТВО
ИНОСТРАННОЙ ЛИТЕРАТУРЫ
Москва. Ново-Алексеевская. 52.
20-я тип. Московского городского
совнархоза
Москва, Ново-Алексеевская, 52.