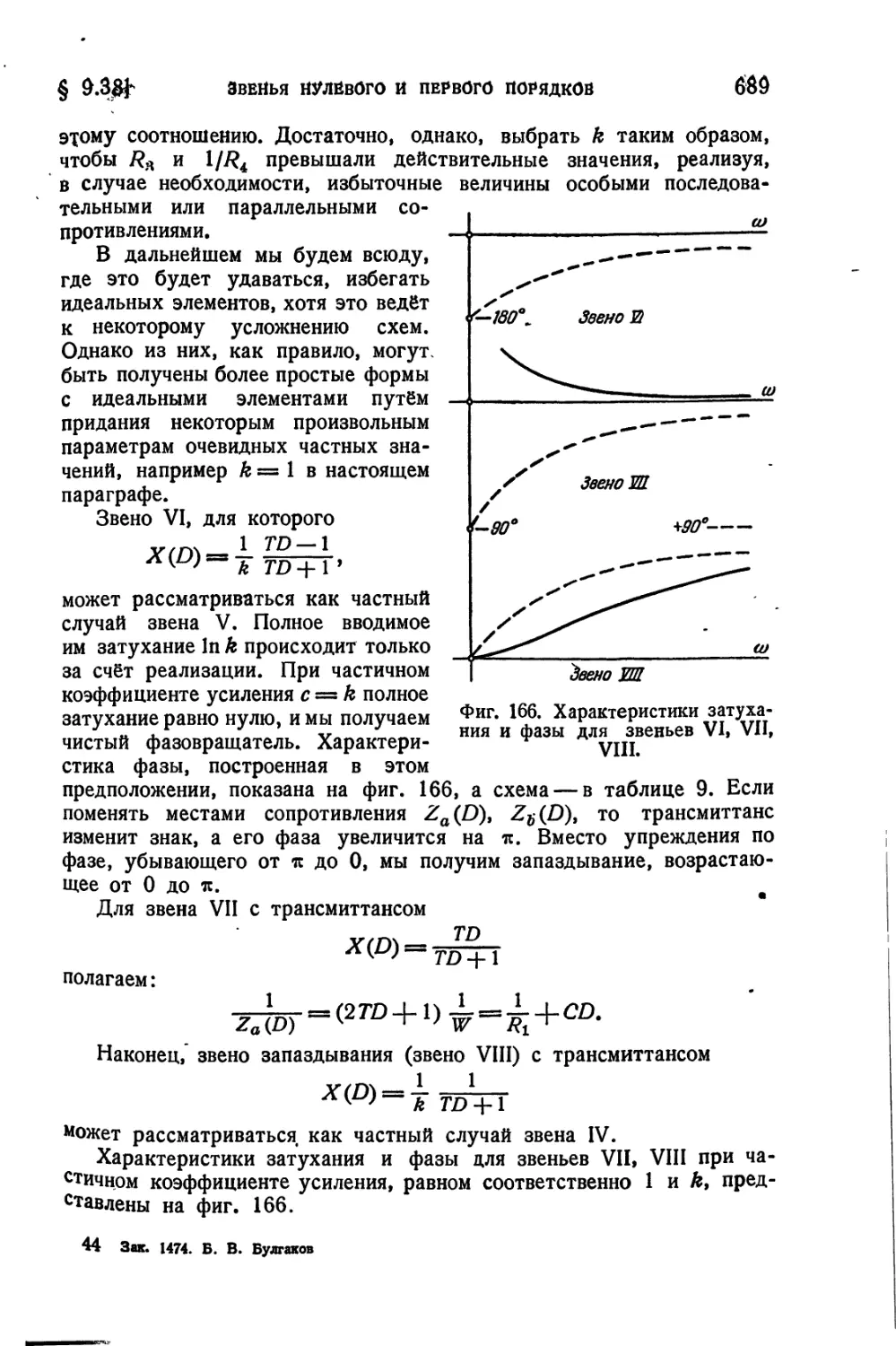
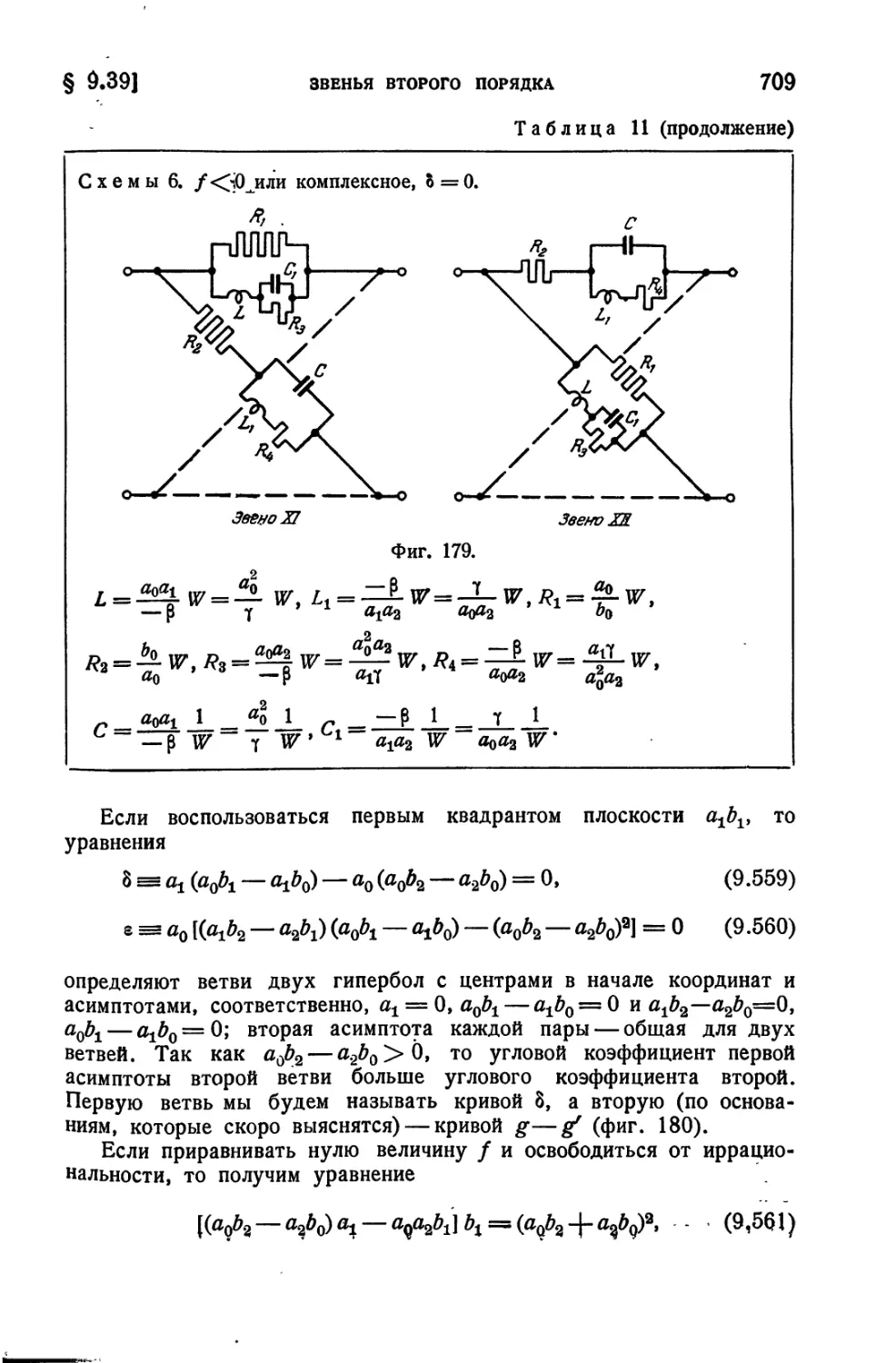
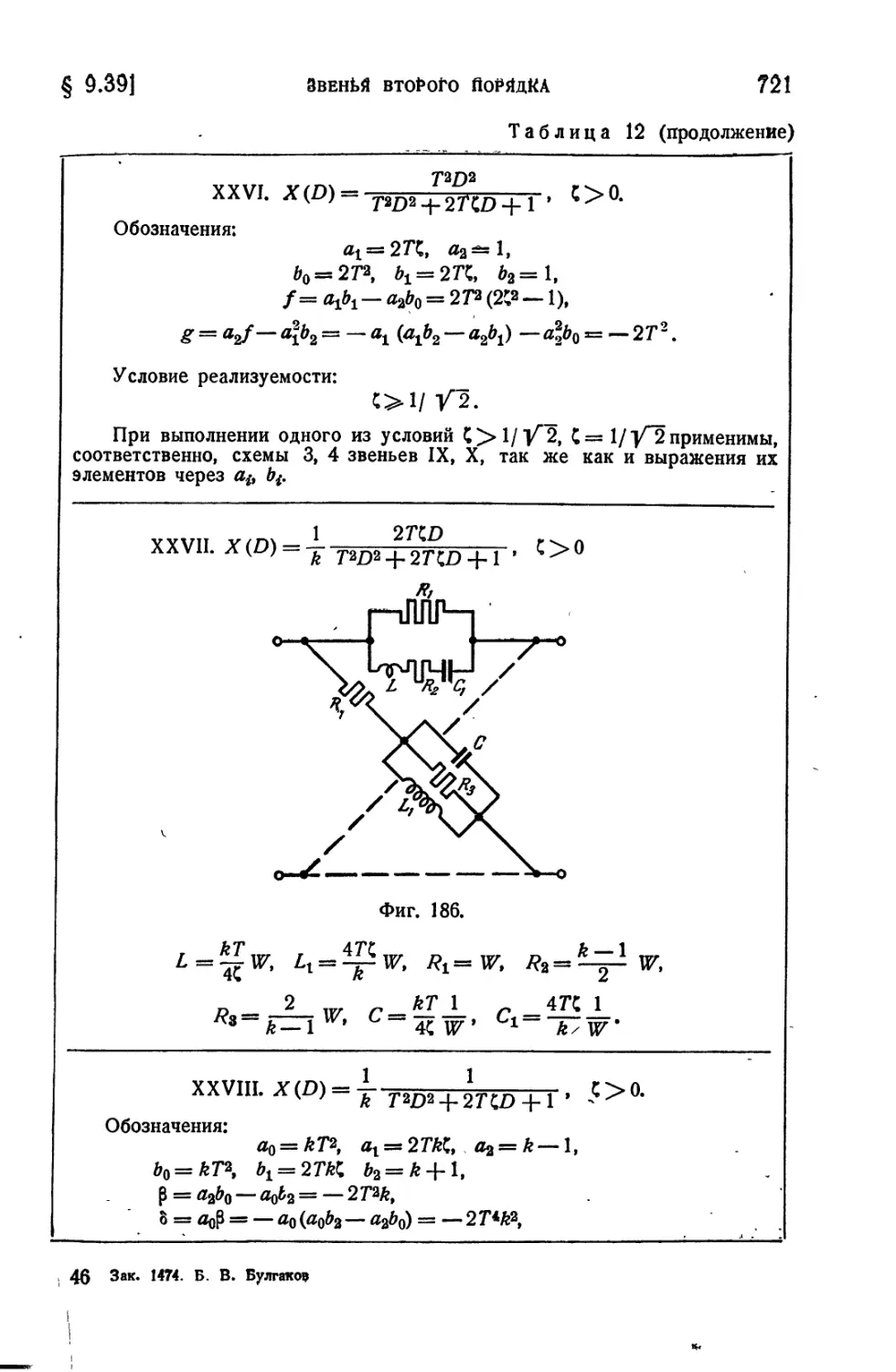
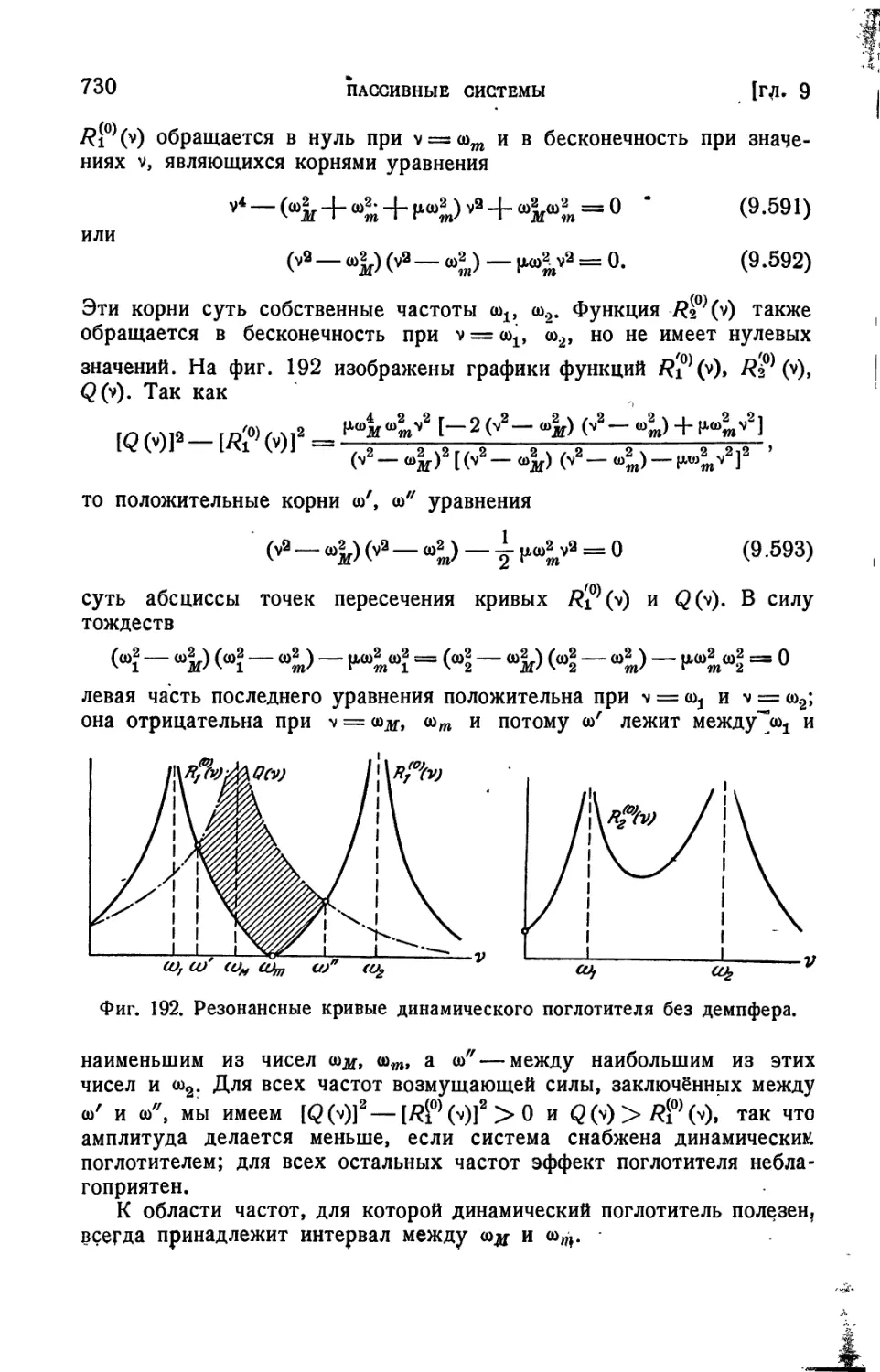
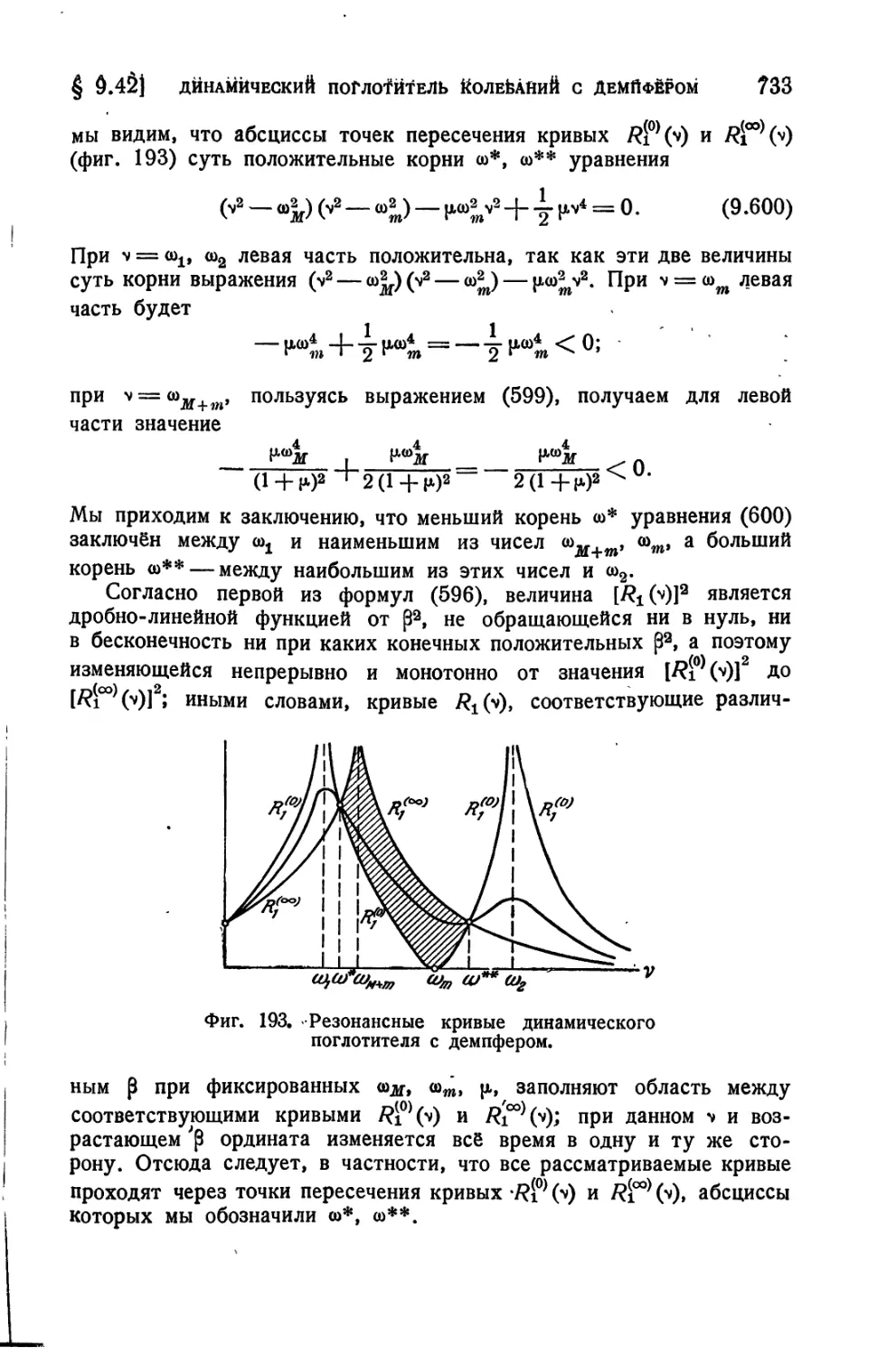
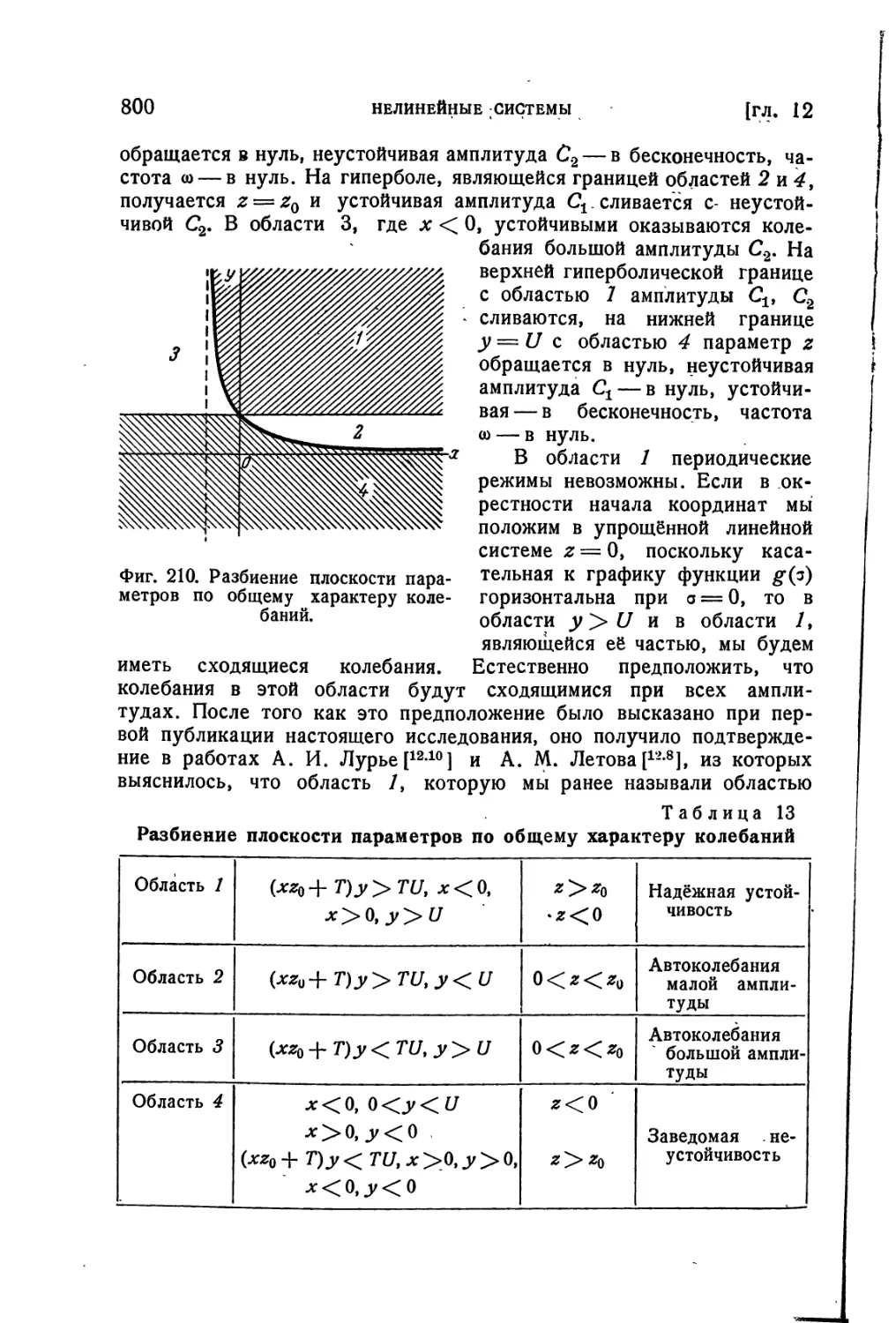
Текст
Й.В.иуЛГАКОВ
КОЛЕБАНИЯ
Б. В. БУЛГАКОВ
Б. В. БУЛГАКОВ
ОЛЕБАНИ
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО ТЕХНИКО-ТЕОРЕТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1 954
12-5-4
ОГЛАВЛЕНИЕ
От издательства....................................... 11
ЧАСТЬ I
СМЕЖНЫЕ ВОПРОСЫ МАТЕМАТИКИ И ОБЩЕЙ МЕХАНИКИ
Глава 1. Элементы матричного исчисления........................ 15
А. Основные определения
§ 1. 1. Матрицы. Ранг...................................... 15
§1.2. Сложение, вычитание и умножение матриц.............. 17
§1.3. Единичная матрица.................................... 22
§ 1. 4. Сложные матрицы. Коагуляция........................ 23
§1.5. Присоединённая и обратная матрицы. Деление матриц ... 26
§ 1. 6. Степени матриц..................................... 32
§1.7. Элементарные преобразования........................ 35
§1.8. Приведение матриц к канонической форме............. 40
§1.9. Теорема Сильвестера о ранге произведения двух матриц . 40
§ 1.10. Евклидово и эрмитово метрические пространства...... 41
§ 1.11. Преобразование координат......................... 44
§ 1.12. Взаимный репер..................................... 45
§ 1.13. Линейная вектор-функция. Подобная матрица.......... 47
§ 1.14. Матричные единицы . ............................... 48
§ 1.15. Рациональные функции матриц........................ 49
§ 1.16. Матрицы Кейли...................................... 51
Б. Полиномные матрицы
§ 1.17. Полиномные матрицы. Эквивалентность................ 56
§ 1.18. Инвариантные множители и элементарные делители .... 57
§ 1.19. Получение эквивалентных полиномных матриц путём умножения на квадратные матрицы с постоянными определителями ..................................................... 59
§ 1.20. Преобразования коагулированных полиномных матриц ... 60
§ 1.21. Умножение и деление полиномных матриц.............. 60
§ 1.22. Треугольные полиномные матрицы..................... 64
§ 1.23. Элементарные делители диагональных, квазидиагональных и некоторых треугольных полиномных матриц................... 70
§ 1.24. Эквивалентность и канонические формы полиномных матриц первой степени.............................................. 73
§ 1.25. Дифференцирование матриц........................... 76
g 1.26. Характеристические числа........................... 77
§ 1.27. Уравнение Гамильтона-Кейли......................... 81
1*
4
ОГЛАВЛЕНИЕ
В. Аналитические функции матриц
§ 1.28. Пределы и ряды матриц............................... 85
§ 1.29. Интерполяционные полиномы........................... 89
§ 1.30. Формула Сильвестера для матричных полиномов и степенных рядов................................................... 94
§ 1.31. Аналитическое продолжение функции от матрицы....... 99
§ 1.32. Умножение степенных рядов со скалярными коэффициентами .......................................................100
§ 1.33. Формула Сильвестера для матричных рядов Лорана .... 101
§ 1.34. Характеристические числа скалярных полиномов, степенных рядов и рядов Лорана . . . .-...............................102
§ 1.35. Дробные рациональные функции матриц.................104
§ 1.36. Элементарные делители функций от матриц.............105
§ 1.37. Свойства модальных столбцов.........................108
§ 1.38. Интегрирование матриц. Матрицант.....................ПО
Глава 2. Элементы операционного исчисления......................113
§ 2. 1. Общая идея........................................113
§ 2. 2. Преобразование Карсона............................114
§ 2. 3. Соответствие единиц...............................115
§ 2. 4. Линейность........................................116
§ 2. 5. Интегрирование оригинала..........................117
§ 2. 6. Дифференцирование оригинала.......................118
§ 2. 7. Линейные дифференциальные выражения...............119
§ 2. 8. Дифференцирование изображения.....................119
§ 2. 9. Теоремы запаздывания и упреждения.................120
§ 2.10. Конечная сумма и разности оригинала.................122
§ 2.11. Теорема смещения....................................123
§ 2.12. Интегрирование по параметру.........................124
§ 2.13. Дифференцирование по параметру......................124
§ 2.14. Умножение изображений.............................. 125
§ 2.15. Теорема подобия................................... 126
§ 2.16. Начальное значение оригинала........................126
§ 2.17. Конечное значение оригинала..........................126 *
§ 2.18. Изображения простейших функций......................127
§ 2.19. Теоремы разложения..................................132
§ 2.20. Линейные дифференциальные уравнения с постоянными коэффициентами..............................................133
§ 2.21. Приложение к скалярным уравнениям...................136
§ 2.22. Ступенчатые функции.................................141
§ 2.23. Конечная сумма и разности ступенчатой функции......142
§ 2.24. Умножение изображений ступенчатых функций...........143
§ 2.25. Изображения некоторых ступенчатых функций . *.......143
$ 2.26. Линейные разностные уравнения с постоянными коэффициентами ...................................................144
§ 2.27. Абсцисса сходимости.................................146
§ 2.28. Спектральное представление функций действительного переменного ....................................................148
§ 2.29. Определение оригинала по изображению................151
§ 2.30. Вычисление интеграла в формуле обращения............153
§ 2.31. Умножение оригиналов.............о..................156
§ 2.32. Интегралы от квадратов и произведений оригиналов в интервале (0, оо).................................... • • • • 157
Глава 3. Уравнения аналитической динамики.......................168
§ 3. 1. Связи и виртуальные перемещения механической системы . 168
§ 3. 2. Реакции связей и их работа..........................170
/
I
ОГЛАВЛЕНИЕ
5
§ 3. 3. Уравнения Лагранжа первого рода и основное уравнение
аналитической динамики............................170
§ 3. 4. Обобщённые координаты...........................173
§ 3. 5. Уравнения Лагранжа второго рода.................174
§ 3. 6. Геометрическая интерпретация....................178
§ 3. 7. Уравнения Лагранжа, разрешённые относительно вторых
производных..................................; • • 182
§ 3. 8. Распространение уравнений Лагранжа на электромеханические системы..............................................185
§ 3. 9. Уравнение энергии.................................187
§ 3.1 0. Преобразование Рауса.............................188
§ 3.1 1. Канонические уравнения...........................190
§ 3.1 2. Вариационное уравнение Гельмгольца...............192
§ 3.1 3. Контактные преобразования .......................193
§ 3.1 4. Выражение контактных преобразований с помощью производящих функций 195
§ 3.1 5. Теорема Гамильтона-Якоби.........................197
§ 3.1 6. Случай, когда функция Гамильтона не зависит явно от времени .....................................................198
часть п
СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
Глава 4. Постановка задачи. Линейные системы..................203
А. Уравнения движения
§ 4. 1. Канонические уравнения и фазовая диаграмма........203
§ 4. 2. Собственные колебания.............................204
§ 4. 3. Линейные системы..................................206
§ 4. 4. Приведение общей задачи к интегральным уравнениям . . . 209
Б. Линейные системы с постоянными коэффициентами
§ 4. 5. Колеблющаяся система как линейный фильтр..........212
§ 4. 6. Автоматическое регулирование......................213
§ 4. 7. Следящая система с линейным законом включения.....214
§ 4. 8. Общее решение уравнений движения..................216
§ 4. 9. Устойчивость положения равновесия.................219
§ 4.1 0. Затухание колебаний после мгновенных возмущений .... 221
§ 4.1 1. Вынужденные колебания.......................... 225
§ 4.1 2. Выбор параметров регулятора по коэффициенту устойчивости ....................................................231
В. Линейные системы с постоянными коэффициентами и запаздывающими силами
§ 4.1 3. Постановка задачи ✓............................. 235
§ 4.1 4. Общее решение уравнения движения.................236
§ 4.1 5. Определение корней характеристического уравнения . . . 241
§ 4.1 6. Система без естественных демпфирующей и восстанавливающей сил...................................................242
§ 4.1 7. Система без искусственного демпфирования ‘.......245
6
ОГЛАВЛЕНИЕ
Глава 5. Собственные колебания нелинейных систем............250
А. Консервативные системы
§ 5. 1. Интегрирование канонических уравнений...........250
§ 5. 2. Общие свойства движения.........................251
§ 5. 3. Угловые переменные и переменные действия........256
§ 5. 4. Метод Ньюкома и Линдстедта......................259
Б. Диссипативные системы
§ 5. 5. Общие свойства движения.........................263
§ 5. 6. Кулоново трение.................................265
§ 5. 7. Кулоново трение вместе с линейным...............272
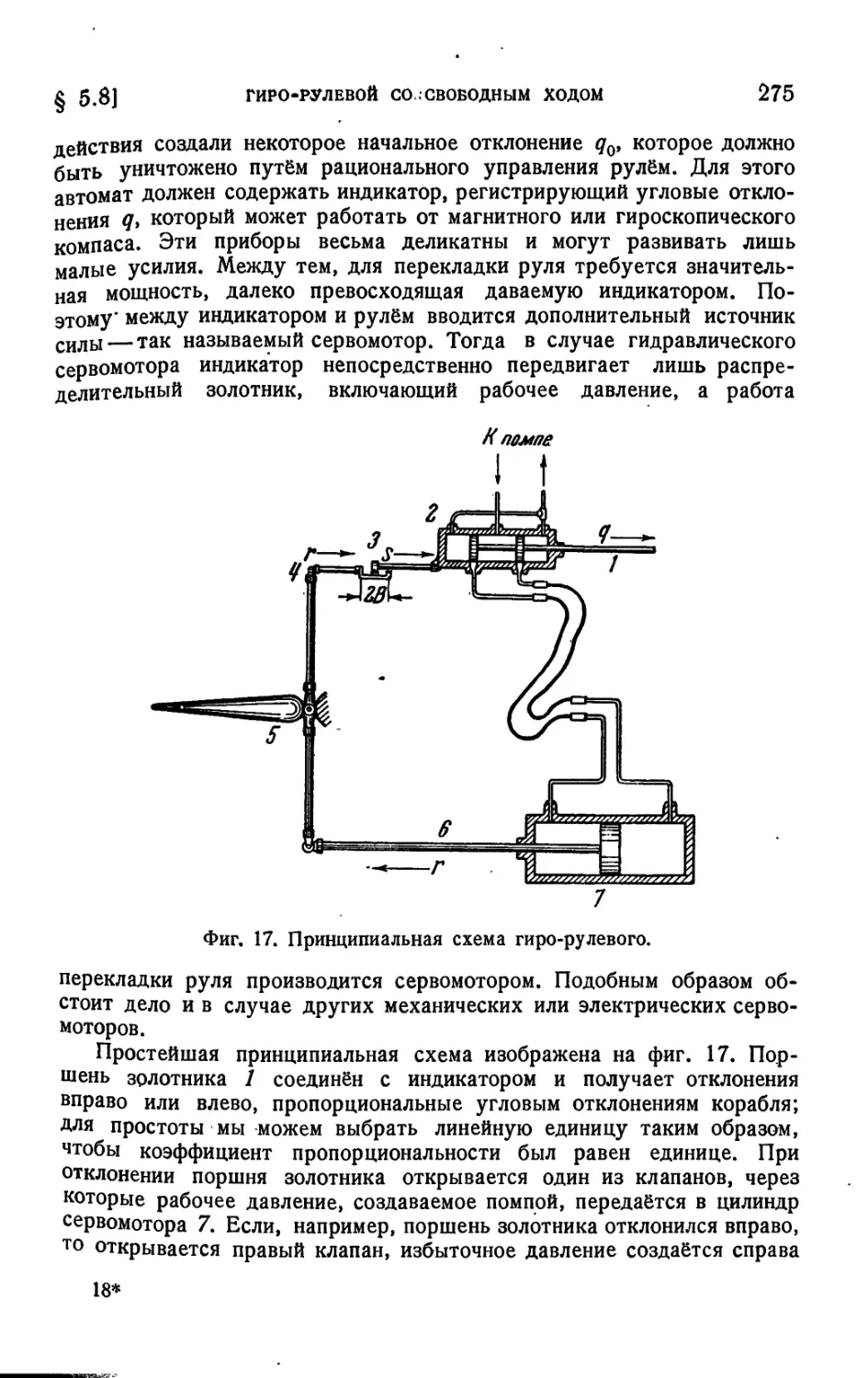
§ 5. 8. Гиро-рулевой со свободным ходом................ 274
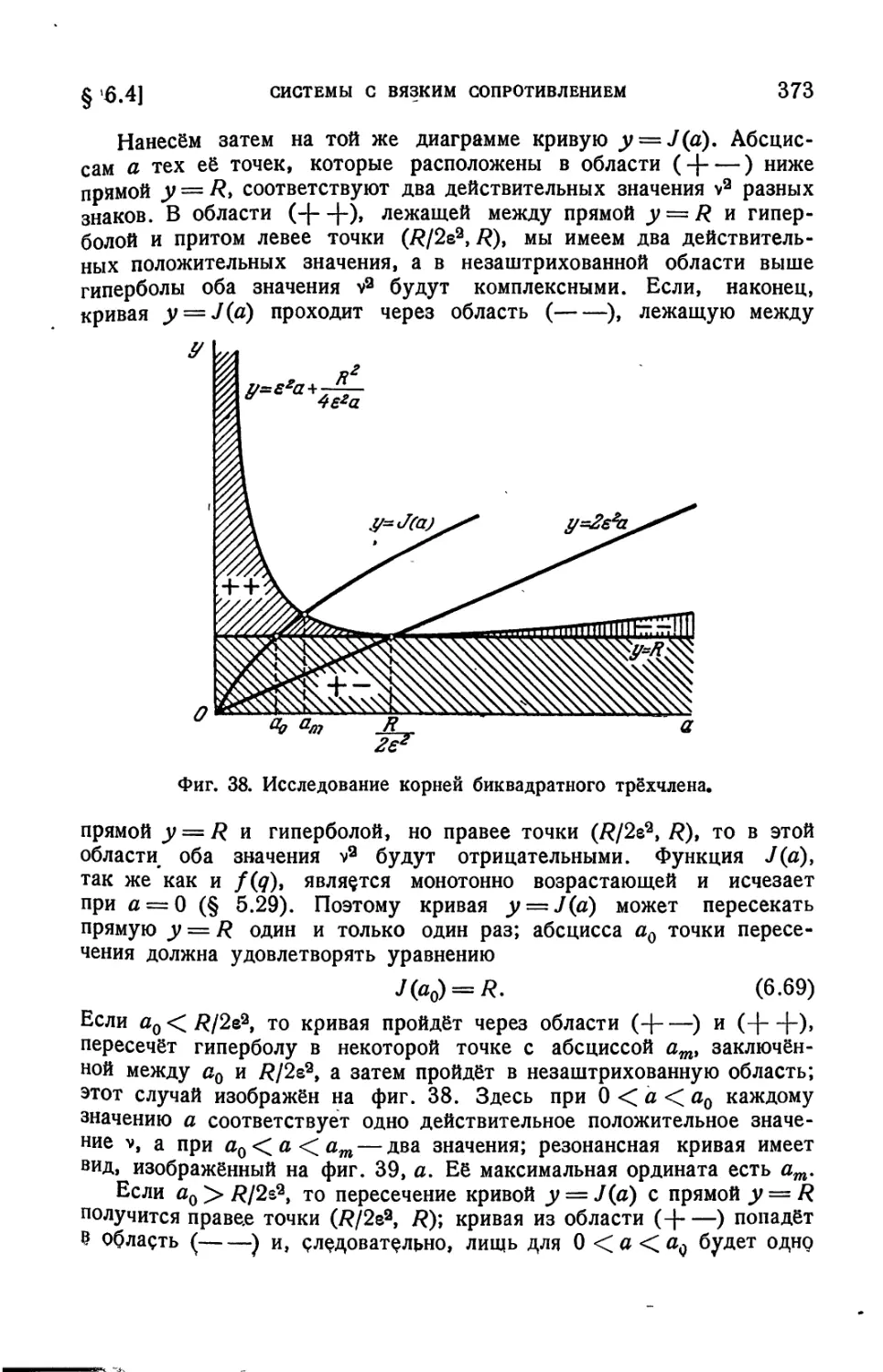
§ 5. 9. Кулоново трение вместе с квадратичным...........277
В. Автоколебательные системы
§ 5.10. Общие замечания.................................284
§5.11. Часы............................................285
§ 5.12. Графическое определение стационарных амплитуд и проверка устойчивости......................................294
§ 5.13. Электронный генератор........................ . . 296
§ 5.14. Следящая система с люфтом ......................299
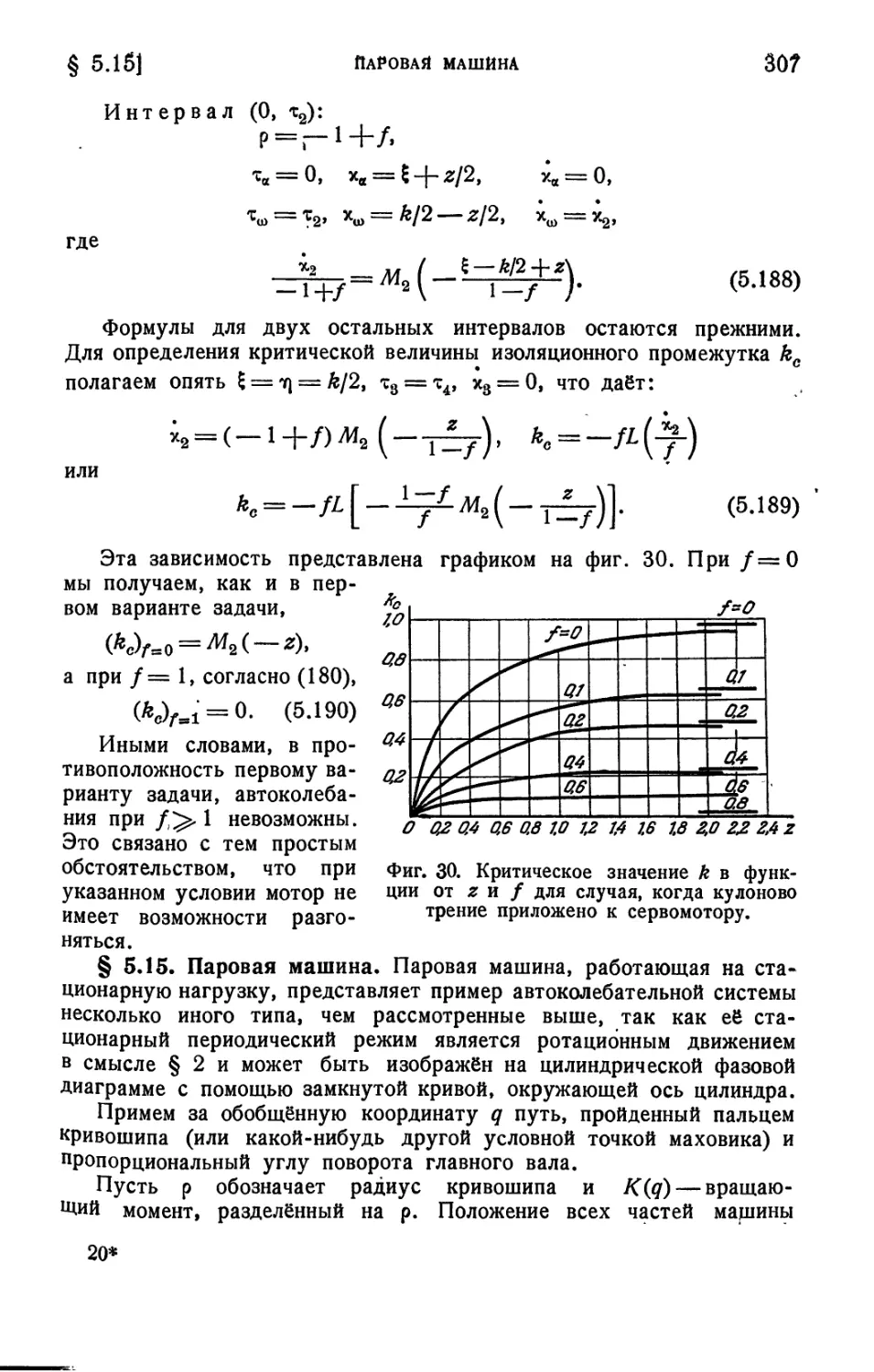
§ 5.15. Паровая машина..................................307
Г. Метод Пуанкаре
§ 5.16. Периодические решения уравнений собственных колебаний, содержащих малые параметры..............................311
§ 5.17. Системы, близкие к линейным.....................313
§ 5.18. Первое приближение..............................315
§ 5.19. Второе и высшие приближения..........*..........317
§ 5.20. Линеаризирующая частота.........................321
§ 5.21. Приложение к консервативным системам............322
§ 5.22. Приложение к электронному генератору............324
§ 5.23. Случай, когда правые части уравнений движения зависят явно от времени.........................................329
§ 5.24. Приложение к паровой машине. Расчёт маховика....330
Д. Метод осреднения
§ 5.25. Основная идея...................................336
§ 5.26. Укороченные уравнения...........................337
§ 5.27. Выбор линейного приближения.....................339
§ 5.28. Стационарные режимы.............................341
§ 5.29. Приложение к консервативным системам............345
§ 5.30. Система с нелинейной позиционной силой и вязким сопротивлением ..............................................349
§ 5.31. Переходный процесс в электронном генераторе.....352
Глава 6. Вынужденные колебания, нелинейных систем...........355
§ 6. 1. Постановка задачи и получение укороченных уравнений . . 355
§ 6. 2. Установившиеся колебания с частотой возмущающей силы и их устойчивость................................: . . . 359
§ 6. 3. Системы с нелинейной восстанавливающей силой.362
§ 6. 4. Системы с нелинейной восстанавливающей силой и вязким сопротивлением..........................................^371
ОГЛАВЛЕНИЕ
7
ЧАСТЬ III
СИСТЕМЫ С КОНЕЧНЫМ ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ
Глава 7. Малые колебания около данного состояния................377
§ 7. 1. Уравнения в вариациях ...........................377
§ 7. 2. Приведение к уравнениям первого порядка..........382
§ 7. 3. Малые колебания и устойчивость...................383
§ 7. 4. Влияние переменных параметров....................385
§ 7. 5. Переходный процесс в паровой машине с регулятором . . 387
§ 7. 6. Статика центробежного регулятора............... 390
§ 7. 7. Влияние инерции регулятора.......................395
§ 7. 8. Центробежный регулятор с фрикционным изодромом .... 399
§ 7. 9. Малые колебания натуральной системы около состояния установившегося движения....................................401
§ 7.10. Линейная пассивная цепь.............................405
§ 7.11. Активная цепь.......................................409
Глава 8. Линейные системы с постоянными коэффициентами . 411
А. Общие свойства уравнений
§ 8. 1. Однородное и неоднородное уравнения.................411
§ 8. 2. Линейные преобразования уравнения...................412
§ 8. 3. Линейные преобразования неизвестной.................414
§ 8. 4. Условие совместности................................414
§ 8. 5. Неособые уравнения .................................417
§ 8. 6. Пример приложения к пассивному четырёхполюснику . . 418
§ 8. 7. Исключение неизвестных..............................419
§ 8. 8. Непрямое регулирование..............................419
§ 8. 9. Приведение к форме Коши.............................423
Б. Собственные колебания
§ 8.10. Собственные колебания системы с линейными элементарными делителями.............................................426
§ 8.11. Общий случай собственных колебаний..................430
§ 8.12. Комплексные корни; собственные формы и модальная матрица . .*................................................. 435
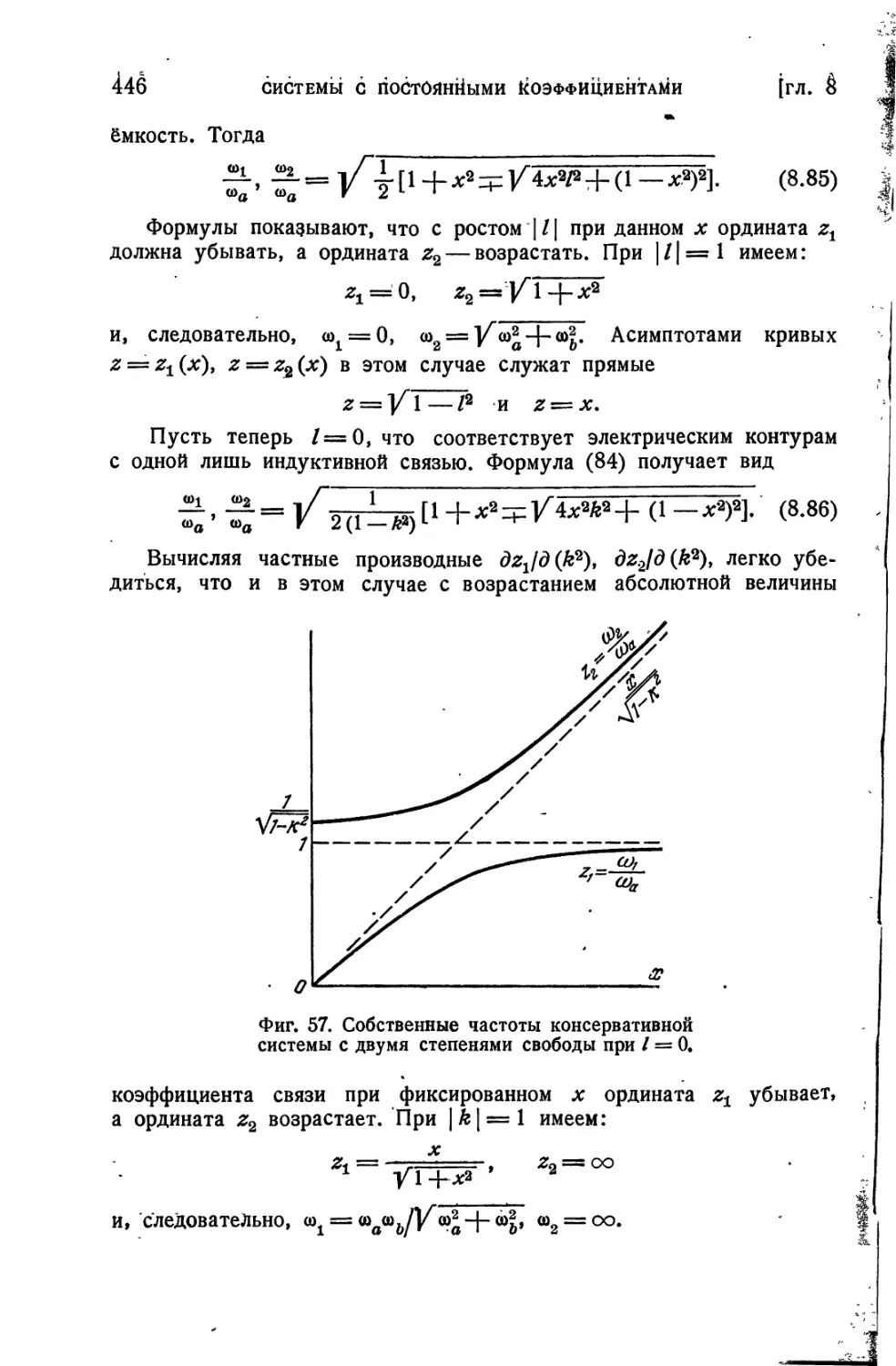
§ 8.13. Собственные частоты консервативной системы с двумя степенями свободы..............................................441
§ 8.14. Собственные колебания консервативной системы с двумя степенями свободы...........................................447
§ 8.15. Различные виды связи двух электрических контуров . . . 452
В. Устойчивость и быстрота затухания собственных колебаний
§ 8.16. Критерии Рауса, основанные на свойствах квадратичных форм.........................................................453
§ 8.17. Линейная устойчивость. Случай любых элементарных’ делителей .......................................................457
§ 8.18. Асимптотическая устойчивость данного движения.......457
§ 8.19. Область устойчивости в пространстве коэффициентов . . . 458
§ 8.20. Области устойчивости в подпространствах.............463
§ 8.21. Системы ,с ненадёжными параметрами..................464
§ 8.22. Быстрота затухания. Критерий Цыпкина-Бромберга .... 465
§ 8.23. Устойчивость следящей системы.......................475
§ 8.24. Линии равной устойчивости для следящей системы при
^езинерционном сервомоторе.......................... 482
8
ОГЛАВЛЕНИЕ
§ 8.25. Разбиение плоскости параметров в случае характеристического уравнения с комплексными коэффициентами. Метод
Неймарка............................................485
§ 8.26. Диаграммы Вышнеградского......................... 489
§ 8.27. Дискриминантная кривая и область апериодической устойчивости 491
Г. Вынужденные колебания и волны при гармонических возмущениях
§ 8.28. Установившиеся колебания......................... 492
§ 8.29. Уравнение энергии..................................499
§ 8.30. Проводимость электрической цепи....................501
§ 8.31. Двухполюсники......................................592
§ 8.32. Четырёхполюсники...................................596
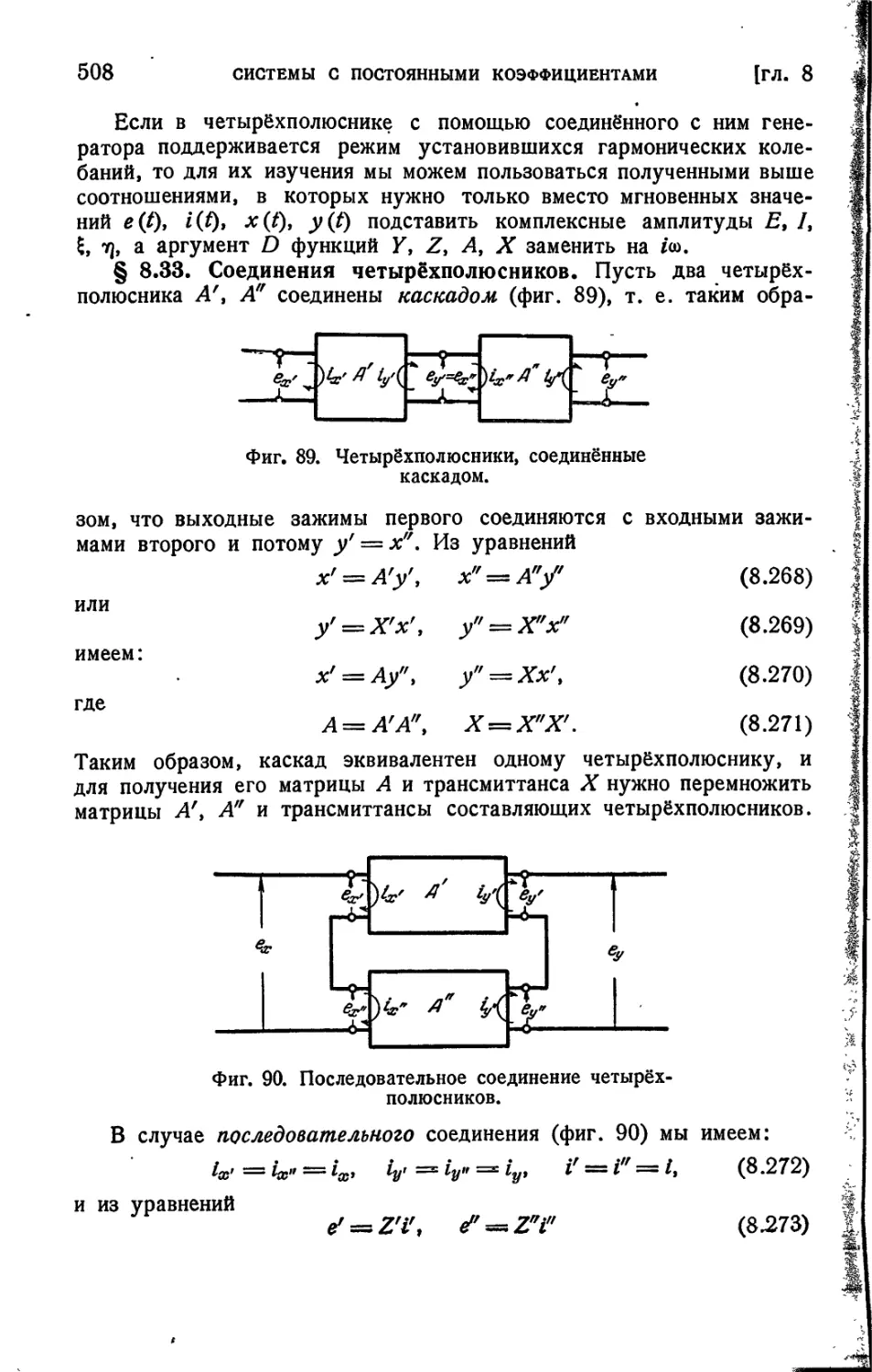
§ 8.33. Соединения четырёхполюсников.......................508
§ 8.34. Волновые параметры четырёхполюсника ...............509
§ 8.35. Четырёхполюсники, составленные из одного двухполюсника 514
§ 8.36. Трансформатор......................................515
§ 8.37. Четырёхполюсники, содержащие триоды................517
§ 8.38. Решётчатый четырёхполюсник.........................519
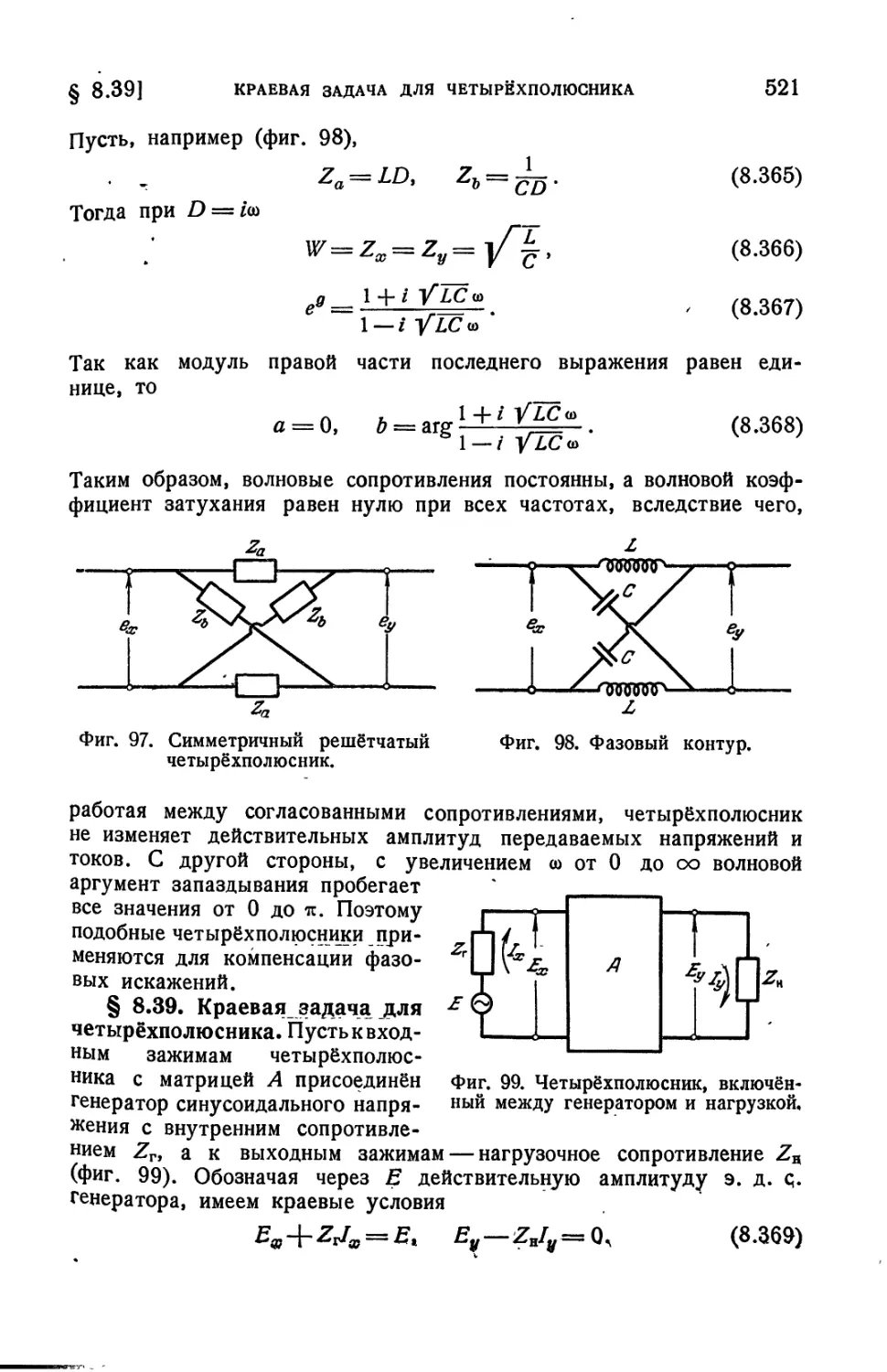
§ 8.39. Краевая задача для четырёхполюсника................521
§ 8.40. Краевая задача для каскада четырёхполюсников с согласованными волновыми сопротивлениями...........................522
§ 8.41. Повторные параметры четырёхполюсника...............525
§ 8.42. Г-образные и Т-образные четырёхполюсники...........528
§ 8.43. П-образный четырёхполюсник ........................531
§ 8.44. Т-образная мостовая схема..........................532
§ 8.45. Двойная Т-схема....................................533
§ 8.46. Краевая задача для каскада четырёхполюсников с одинаковыми повторными сопротивлениями...........................534
§ 8.47. Вносимые параметры.................................535
§ 8.48. Рабочие параметры................................ 537
§ 8.49. Вносимые и рабочие параметры каскада четырёхполюсников 539
Д.Общий случай вынужденных колебаний. Нормальные координаты
§ 8.50. Общий случай вынужденных колебаний............541
§ 8.51. Вариация постоянных...........................543
§ 8.52. Нормальные координаты.........................548
§ 8.53. Приложение к системам первого порядка; приведение ма-трйц к нормальной форме...............................553
Е. Устойчивость при длительных возмущениях
§ 8.54. Накопление возмущений в линейных колебательных системах ...............................................562
Глава 9. Пассивные системы...............................573
А. Линейные консервативные системы с постоянными коэффициентами
§ 9. 1. Постановка вопроса............................573
§ 9. 2. Элементарные делители и общее решение.........575
§ 9. 3. Представление билинейных и квадратичных форм с помощью матриц..........................................578
§ 9. 4. Теорема Сильвестера...........................580
§ 9. 5. Ортогональность собственных форм..............583
ОГЛАВЛЕНИЕ
9
§ 9. 6. Колебания натянутой нити с закреплёнными концами, загруженной сосредоточенными массами.........................588
§ 9. 7. Та же задача при иных пограничных условиях....................594
§ 9. 8. Экстремальные свойства характеристических чисел .... 596
§ 9. 9. Теорема Рейли об изменении характеристических чисел при наложении новых связей и увеличении инерции или жесткости системы............................................601
§ 9.10. Обратный метод; предельный переход к интегральному уравнению..............................................602
§ 9.11. Функция влияния натянутой нити...........................605
§ 9.12. Коэффициенты влияния закрученного вала...................607
§ 9.13. Колебания балки, загруженной сосредоточенными массами 607
§ 9.14. Собственные формы рациональных функций от матриц . . . 610
§ 9.15. Развёртывание характеристического определителя по Ле-веррье и Крылову...........................................611
§ 9.16. Крутильные колебания вала авиационного мотора......613
§ 9.17. Оценка Данкерли и обобщение ван ден Дунгена и Пап-ковича ....................................................616
§ 9.18. Метод последовательных умножений..............................618
Б. Синтез пассивных двухполюсников
§ 9.19. Уравнение энергии для вынужденных колебаний...................622
§ 9.20. Уравнение энергии для внешних степеней свободы .... 623
§ 9.21. Энергетические соотношения и связанные с ними свойства пассивных систем. Реактивные цепи .................625
§ 9.22. Функции Бруне.................................................629
§ 9.23. Теоремы о положительных функциях..............................630
§ 9.24. Функции Мин Най-да............................................634
§ 9.25. Построение двухполюсника по импедансу Z (£>), имеющему один нуль и один полюс в левой полуплоскости. Реализация некоторых других видов Z (D)...........................638
§ 9.26. Двухполюсник, импеданс которого Z (D) имеет два нуля и два полюса в левой полуплоскости...........................652
§ 9.27. Общая процедура построения двухполюсника по заданному импедансу..................................................654
В. Син тез четырёхполюсников и его приложения
§ 9.28. Реактивные четырёхполюсники...................................657
§ 9.29. Фильтры нижних частот.........................................659
§ 9.30. Фильтры вёрхних частот........................................666
§ 9.31. Полосовые фильтры.............................................668
§ 9.32. Заграждающие фильтры..........................................672
§ 9.33. О реализуемости заданной рациональной функции как транс-
миттанса симметричного решётчатого четырёхполюсника, не содержащего идеальных элементов..............................673
§ 9.34. Корректирующие цепи. Каскад симметричных решётчатых четырёхполюсников с постоянным волновым сопротивлением 677
§ 9.35. Согласующие Г-полузвенья......................................679
§ 9.36. Условия реализуемости трансмиттанса пассивного четырёхполюсника ...................................•.............681
§ 9.37. Реализация трансмиттанса каскада пассивных четырёхполюсников ................................................683
§ 9.38. Звенья нулевого и первого порядков............................684
§ 9.39. Звенья второго порядка...................................... 691
§ 9.40. Преобразование к симметричному мостовому Т-образному
четырёхполюснику................................................724
10
ОГЛАВЛЕНИЕ
Г. Некоторые другие приложения пассивных систем
§ 9.41, Динамический поглотитель колебаний без демпфера .... 727
§ 9.42. Динамический поглотитель колебаний с демпфером . . . . . 731
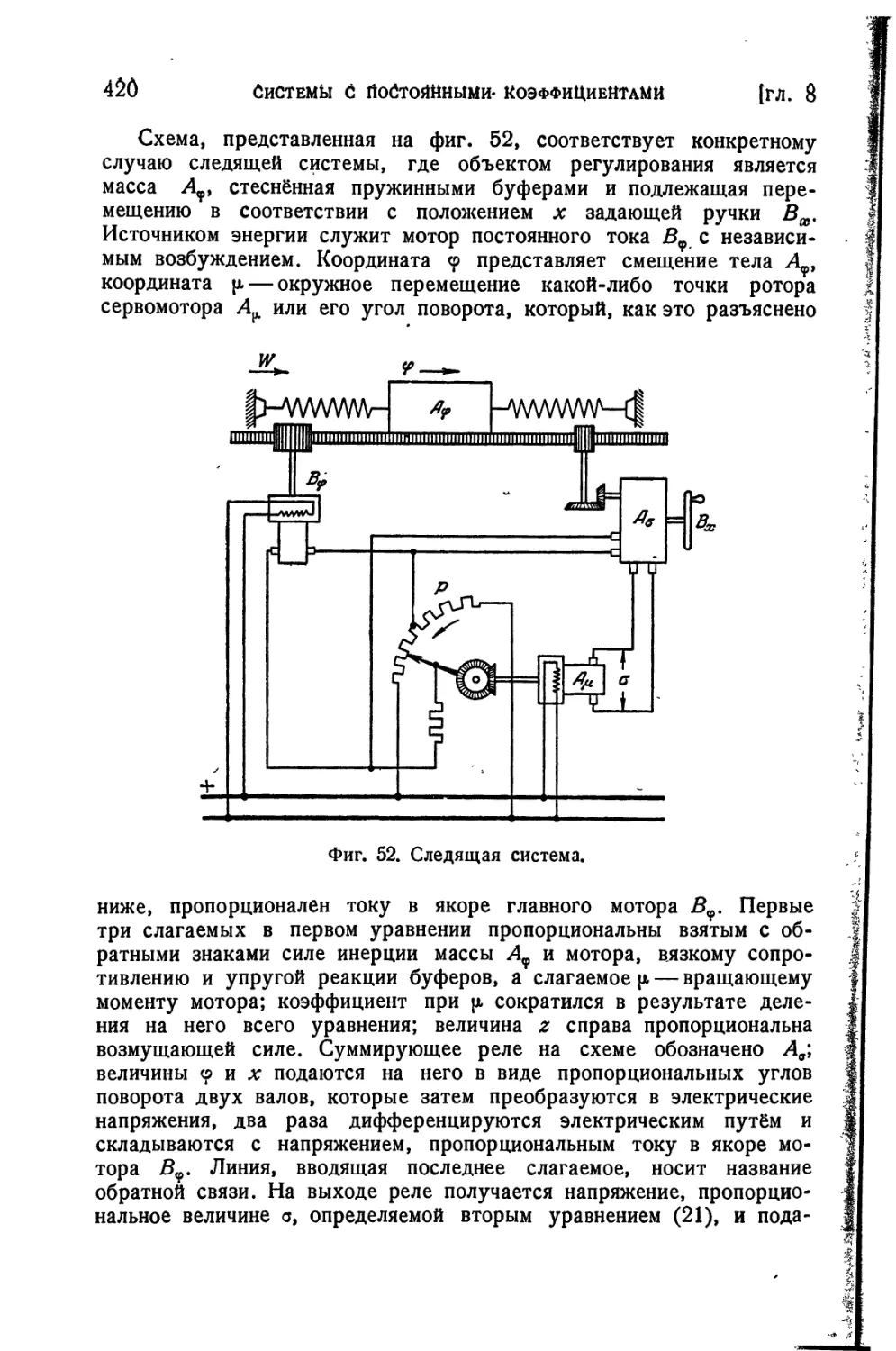
Глава 10. Линейные регулируемые системы..........................735
§ 10.1. Разомкнутая и замкнутая цепь регулирования......735
§ 10.2. Одноконтурная замкнутая цепь ........................736
§ 10.3. Характеристическое уравнение одноконтурной замкнутой
цепи............................................741
§ 10.4. Автоматическое управление курсом корабля........742
§ 10.5. Гироскопический стабилизатор....................746
§ 10.6. Характеристическое уравнение изменённой системы .... 748
§ 10.7. Критерий устойчивости Найквиста.................750
§ 10.8. Применение критерия Найквиста к системам с нейтрал ь-ными и неустойчивыми звеньями..............................752
§ 10.9. Частотная диаграмма для оценки быстроты затухания и логарифмического декремента................................756
Глава 11. Линейные системы с периодическими коэффициентами . ....................................................759
§ 11.1. Общая форма решения..................................759
§ 11.2. Случай нелинейных элементарных делителей.............762
§ 11.3. Характеристические показатели........................764
§ 11.4. Соотношение между характеристическими показателями . . 765
Глава 12. Нелинейные системы...................................767
А. Метод Пуанкаре
§ 12. 1. Периодические решения уравнений, содержащих малые параметры.................................................767
§ 12. 2. Системы, близкие к линейным.........................770
§ 12. 3. Первое приближение..................t...............773
§ 12. 4. Второе и высшие приближения.........................776
§ 12. 5. Уравнение в вариациях и устойчивость периодических решений .....................................................779
§ 12. 6. Решение уравнения в вариациях с помощью ряда по степеням параметра............................................780
§ 12. 7. Выбор упрощённой системы в случае одной нелинейности 784
§ 12. 8. Случай двух нелинейностей...........................788
§ 12. 9. Периодические движения следящей системы.............790
§ 12. 10. Устойчивость периодических движений следящей системы и общий характер движения....................................795
Б. Метод осреднения
§ 12. 11. Приведение уравнений нелинейной колебательной системы к нормальной форме...........................................801
§ 12. 12. Укороченные уравнения. Квазипериодические и периодические режимы..............................................805
§ 12. 13. Регулирование положения^ системы, обладающей естественной направляющей силой.....................................807
§ 12. 14. Влияние сил сухого трения на движение гироскопического маятника.....................................................827
Приложение. О движении, возмущаемом силами большой частоты .....................................................840
Литература.......................................................877
Предметный указатель.......................................... 887
ОТ ИЗДАТЕЛЬСТВА
Борис Владимирович Булгаков, один из крупнейших советских учёных в области механики, родился 6 августа 1900 года. В 1928 году он окончил физико-математический факультет Московского государственного университета им. М. В. Ломоносова. Педагогическая и научная деятельность Б. В. Булгакова в Московском государственном университете продолжалась без перерыва с 1928 года до самой его смерти, последовавшей 29 апреля 1952 года.
В Московском государственном университете Б. В. Булгаков состоял профессором и заведующим кафедрой на механико-математическом факультете. В течение ряда лет он читал курсы теоретической механики, прикладной механики, теории гироскопов, теории колебаний.
Б. В. Булгакову принадлежит ряд выдающихся работ в области общей механики, теории колебаний, теории упругости.
В 1946 году Б. В. Булгаков был избран членом-корреспондентом Академии наук СССР.
Над книгой «Колебания», подытоживающей многочисленные собственные исследования, Б. В. Булгаков работал последние шесть лет своей жизни. Первые две части были им закончены в 1949 году и тогда же вышли в свет в виде первого тома книги; работа же над третьей частью, посвящённой системам с конечным числом степеней свободы, длилась до последних дней жизни Б. В. Булгакова, но осталась не вполне законченной. По поручению Учёного совета механико-математического факультета Московского государственного университета им. М. В. Ломоносова обработку оставшихся материалов и их подготовку к печати выполнил проф. Я. Н. Ройтенберг.
Настоящее издание, выпускаемое в виде одной книги, содержит все три части работы; первые две даны без изменений (исправлены только замеченные опечатки и неточности); третья часть выпускается в свет впервые.
Первая часть книги содержит основы матричного и операционного исчисления и изложение некоторых вопросов аналитической механики, теснейшим образом связанных с теорией колебаний.
Во второй части рассматриваются свободные и вынужденные колебания систем с одной степенью свободы, главным образом нелинейных,
12
ОТ ИЗДАТЕЛЬСТВА
В первых двух главах третьей части (главы 7 и 8} рассматриваются собственные и вынужденные колебания линейных систем со многими степенями свободы. Наряду с обстоятельным и оригинальным изложением общей теории уделено большое внимание приложениям, в частности, вопросам быстроты затухания колебаний, накопления возмущений при произвольно изменяющихся внешних силах, а также теории электрических цепей (раздел Г главы 8).
Глава 9 посвящена пассивным системам, т. е. системам, не содержащим источников энергии. В разделе А дана теория линейных консервативных систем; в разделах Б и В рассмотрены вопросы синтеза пассивных двухполюсников и четырёхполюсников и синтеза корректирующих цепей.
Глава 10 посвящена линейным регулируемым системам.
В главе 11 рассматриваются вопросы теории линейных систем с периодическими коэффициентами.
Глава 12 содержит теорию колебаний нелинейных систем со многими степенями свободы.
В приложении помещён перевод статьи автора книги, опубликованной им в 1940 году в журнале «Compositio mathematica»; содержание этой статьи непосредственно примыкает к вопросам, изложенным в последней главе книги.
Список литературы в конце книги не претендует на полноту и содержит либо то, что непосредственно использовано автором, либо работы, которые могут ввести читателя в более детальное изучение вопросов, лишь коротко изложенных в тексте или с ними смежных.
Цифры в круглых скобках представляют номера формул, а цифры в квадратных скобках относятся к списку литературы. В обоих случаях, а также при нумерации параграфов первая цифра, отделённая точкой, указывает на главу. Однако при ссылках на параграфы и формулы в пределах той же самой главы её номер не указывается.
Ббльшую часть вычислений, необходимых для построения таблиц и графиков первой и второй частей книги, выполнил И. 3. Пирогов. В подготовке к печати третьей части книги приняла участие кандидат физико-математических наук И. А. Балаева.
ЧАСТЬ I
СМЕЖНЫЕ ВОПРОСЫ МАТЕМАТИКИ
И ОБЩЕЙ МЕХАНИКИ
ГЛАВА 1
ЭЛЕМЕНТЫ МАТРИЧНОГО ИСЧИСЛЕНИЯ
А. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
§ 1.1. Матрицы. Ранг. Теория матриц принадлежит к числу основных глав классической алгебры, но лишь в последние десятилетия получила широкое применение в физике и инженерных науках. Вместе с тем эта теория приобретает характер исчисления, символика которого позволяет систематизировать и сократить выкладки при линейных преобразованиях систем переменных и при решении систем линейных алгебраических, дифференциальных, интегральных и конечноразностных уравнений.
Матрицей называется совокупность комплексных или, в частности, действительных чисел, образующих прямоугольную таблицу, при записи которой будет применяться двойная черта слева и справа:
#12 • • • ат
#21 #22 • • • а'2П
• • • &тп
(1.1)
Числа ajk называются элементами матрицы, причём первый индекс есть номер строки, второй — номер столбца. Приведённая матрица состоит из т строк и п столбцов. Мы будем также писать коротко:
«=ИМ («X») (1-2)
и говорить, что имеем матрицу типа т X
При п = 1 'получаем матрицу-столбец
г/=
при т= 1 —матрицу-строку
а»“Il«i ••• ™п\\>
(1.3)
(1-4)
16
ЭЛЕМЕНТЫ МАТРИЧНОГО ИСЧИСЛЕНИЙ
)
(гл. 1
при т = п— квадратную матрицу n-го порядка. Если матрица не является или необязательно является квадратной и мы желаем подчеркнуть это обстоятельство, то будем называть её прямоугольной. В частности, при /п>п имеем укороченную, при т < п— удлинённую матрицу. Для отличия от матриц комплексные (в частности, действительные) числа именуются скалярами} они могут рассматриваться как матрицы типа 1 X !•
Таблица
J1 ••• Ju k± ... kv
а , ... а.,
(1.5)
а., ... а. ,
состоящая из элементов некоторых и строк и v столбцов матрицы а, называется её субматрицей} очевидно, что и^т, v^n. Если и = v, т. е. субматрица — квадратная, то её определитель
называется минором й-го порядка матрицы а.
Говорят, что матрица имеет ранг г, если по крайней мере один из её миноров r-го порядка отличен от нуля, тогда как все миноры более высоких порядков исчезают. Разность между наименьшим из чисел т9 п и рангом называется дефектом. Если дефект равен нулю, то ранг матрицы — наибольший возможный для данного типа.
Единственный минор квадратной матрицы, имеющий тот же порядок, что и она сама, есть её определитель
A = deta = |a^|; (1.7)
если он равен нулю, то матрица называется особой, в противном случае — неособой. Ранг неособой квадратной матрицы равен её порядку, а её дефект — нулю.
Матрица считается равной нулю тогда и только тогда, когда = 0 для всех J и k*9 это обозначается обычным образом:
а = 0. (1.8)
Пусть имеем, кроме а, вторую матрицу
Ь — IIЫ (РХ9). ' (1.9)
Матрицы а, Ъ считаются равными тогда и только тогда, когда они одного и того же типа (т = р, п = q) и а$к = bjk для всех j и k} в этом случае пишут:
а = Ь. (1.10)
Если строки матрицы а превратить в столбцы и наоборот, то полученная новая матрица называется транспонированной по отно-
§ 1.2] СЛОЖЕНИЕ, ВЫЧИТАНИЕ И УМНОЖЕНИЕ МАТРИЦ 17
шению к а и обозначается ат, так что
a]k = akj. (1.11)
В частности, транспонированная для матрицы-строки есть матрица-столбец, и наоборот. Квадратная матрица а называется симметричной, если она тождественна со своей транспонированной, так что а = ат и
ajk = (1*^2)
Через а будем обозначать матрицу, элементы которой суть комплексные числа ajj., сопряжённые с
Матрица а* = ат с элементами
a*ik = akj (1.13)
называется сопряжённой для а по Эрмиту. Если же для квадратной матрицы а мы имеем а = а* и
= &к 0*14)
то она называется эрмитовой. Если все элементы а^к действительны, то матрица, сопряжённая по Эрмиту, не отличается от транспонированной, а определение эрмитовой матрицы совпадает с определением симметричной.
§ 1.2. Сложение, вычитание и умножение матриц. Суммой матриц а, b одного и того же типа т X » называется матрица с = lc# II того же типа, для которой Cjk = ajk-]~bjk при всех J и fe; при этом пишут:
с = а-]-Ь. (1.15)
Если же bjk = sajk, то говорят, что матрица b есть произведение матрицы а на скаляр s, и пишут обычным образом:
b = sa. (1.16)
Если s = —1, то пишут:
(— 1)а = — а. (1.17)
Сложение матриц и умножение матриц на скаляры подчиняются коммутативному, ассоциативному и дистрибутивному законам, а именно: обозначая через а, Ь, с матрицы и через s, t скаляры,
имеем:
а-уь = Ь-}-а, (1.18)
а -{- (Ь -|- с) = (а -|- ^)-|" с> (1*19)
sa = as, (1.20)
s(ta) = (st)a, (1.21)
s(a-f-^) = + (s-\-f)a = sa-}-ta. (1.22)
2 Зак. 1474. Б. В. Булгаков
•i
I
18
ЭЛЕМЕНТЫ МАТРИЧНОГО ИСЧИСЛЕНИЯ
[ГЛ. 1
Вычитание определяется равенством а — Ь=а-^-(— Ь).
(1.23)
Пусть а и b определены, как и выше, с помощью (2), (9) и пусть п = р\ мы будем называть тогда эти матрицы, взятые в указанном порядке, конформными. Их произведением называется матрица с — Цс^И типа с элементами
п
cjk — 2
(1.24)
Иными словами, Cjk есть сумма произведений элементов у-й строки первой матрицы на соответственные элементы fe-го столбца второй; обозначение применяется обычное:
c — ab. (1.25)
Матрицы а, b конформны и могут быть перемножены в любом порядке -лишь в том случае, когда они будут типов т X л и n X ^5 в частности, этому условию удовлетворяют квадратные матрицы одного и того же порядка.
Произведение двух матриц может быть нулём и тогда, когда ни один из сомножителей не равен нулю; например,
О О
g 0 h О
О О
= 0.
Однако если b есть удлинённая или квадратная матрица с дефектом, равным нулю, то с помощью теоремы о системах линейных однородных уравнений легко показать, что из ab = 0 должно еле- ' довать а = 0 аналогично тому, как это имеет место для чисел. • Аналогичным образом, если а есть укороченная или квадратная матрица дефекта нуль, то из ab = 0 вытекает b = 0. Если можно ' найти такую матрицу Ь, отличную от нуля, что ab = 0 или Ьа — 0, то а называется делителем нуля.
Легко проверить, что для матриц имеет место ассоциативный, закон умножения
a (be) = (ab) с (1.26)
и дистрибутивный закон
a (b -f-с) = ab ас, (а-\-Ь)с = ас^-Ьс, (1.27) но, вообще,
ab ф Ьа,
если даже конформность .имеет место как в том, так и в другом порядке.
Если для двух квадратных матриц мы имеем ab = ba, то они называются коммутативными.
§ 1.2]
СЛОЖЕНИЕ, ВЫЧИТАНИЕ И УМНОЖЕНИЕ МАТРИЦ
19
Если c = ab, то == Cfcj bjlClu,
I I
или cT = (aby* = Z>TaT; аналогично (abcy* = cT (ab)* = c*b*a* и, вообще, (axa,2... ap)r = ap... alaf, (1.28)
t. e. матрица, транспонированная для произведения нескольких данных матриц, равна произведению транспонированных матриц, взятых в обратном порядке.
Каждая субматрица произведения с = ab, где а — матрица типа т X п, а Ъ — типа n X может быть сама представлена в виде произведения субматриц, взятых из а и Ь:
причём
u^mt v^q.
(1.29)
Если а, b — квадратные матрицы одного и того же порядка, то, на основании правила умножения определителей
det (ab) = det а • det b. (1.30)
Чтобы получить более общее предложение, воспользуемся теоремой Бине-Коши *), состоящей в том, что если т п, то для матриц а, b типов т X л и п X я* имеет место разложение
det (ab) = У а ( .
где сумма распространяется на все сочетания j\.. .jm по т из п чисел 1, ..., п; если же т > ть9 то det(a&) = 0.
Пусть теперь а, b обозначают опять какие угодно матрицы типов т X л, P'Xq, конформные в написанном порядке, так что п = р. Предполагая, что и = v /п, nf q, и применяя теорему Бине-Коши к произведению субматриц (29), имеем:
где сумма распространяется на все сочетания ... 1и из п элементов. Эта формула даёт выражения миноров произведения двух матриц через миноры сомножителей; при и > п все эти миноры равны нулю.
*) См., например, А. К. Сушкевич [1Л], § 36.
20 ЭЛЕМЕНТЫ МАТРИЧНОГО ИСЧИСЛЕНИЙ [гл. 1
Из последней формулы вытекает также, что если га, гъ, гс обозначают ранги матриц a, b, с — ab, то
ге<га, гь, (1.32)
т. е. ранг произведения не может быть больше ранга каждого из сомножителей.
Квадратная матрица, у которой все элементы, не принадлежащие главной диагонали, равны нулю, называется диагональной.
Пусть а — диагональная, ай — какая угодно прямоугольная матрица с тем же числом строк. Тогда a^ — G при /=/=/, и элементы произведения c = ab будут
Cjk = == ajfijk»
z
таким образом, матрица с получается из b путём умножения её строк соответственно на а22, ... Аналогичным образом, если Ъ является диагональной, то матрица c = ab получается из а умножением её столбцов на соответствующие элементы &П, й22, ...
Отсюда следует, в частности, что произведение двух диагональных матриц одинакового порядка есть диагональная матрица того же порядка, элементы которой получаются перемножением соответственных элементов данных. Поэтому диагональные матрицы коммутативны.
Пусть имеем некоторое конечное или бесконечное множество квадратных матриц данного порядка п. Любые две из нцх конформны при умножении, и если, сверх того, их сумма, разность и произведение также являются всегда матрицами множества, то это последнее замкнуто в отношении трёх действий и на языке современной алгебры называется кольцом. Если при этом все матрицы попарно коммутативны, то и кольцо называется коммутативным. Например, множества всех вообще квадратных матриц данного порядка и всех квадратных матриц данного порядка с целочисленными элементами суть кольца. Множества одних только диагональных матриц Данного порядка с любыми и с целочисленными элементами суть коммутативные кольца, входящие в два названных раньше.
Пример 1. Предполагая, что J есть одно из чисел 1, ..., п — 1, назовём у-м косым рядом квадратную матрицу п-го порядка
О ... Тл 0 о ... о
О ... 0 ° ... °
0 ... 0 0 0 ... Yj, n—j
о ... о о о ... О
(1.33)
СЛОЖЕНИЕ, ВЫЧИТАНИЕ И УМНОЖЕНИЕ МАТРИЦ
21
которой равны нулю все элементы, кроме тех, которые расположены по прямой, параллельной главной диагонали, но сдвинутой на j
мест вправо; индексы расставлены здесь по иному принципу, чем раньше, а именно: первый обозначает номер косого ряда, а второй — номер элемента в этом ряду. Косой ряд для значений / = — 1, .. __получается, если наклонная прямая сдвинута на |/| мест влево; наконец, под нулевым косым рядом 70 будем понимать диагональную матрицу. Непосредственным перемножением убедимся, что если задан ещё косой ряд 8fc и если — п < j -|- k < п, то произве
дение
8j+fc — Т.А
будет (j-|-fe)-M косым рядом, если же — п или
то ^4 = 0.
Например, при -\-k <п имеем:
sy+fc, 1 — SJ+fc, 2 — ^+2* • • • >
(1.34)
Пример 2. Составляя сумму n косых рядов от нулевого до (п—1)-го, получим матрицу
с = 7о + 71+---+Тп-1==
7oi Tn l2i- • 0 I()2 712 ‘ * 7п-2,2
0 0 0 ... у0№
(1.35)
у которой равны нулю все элементы по одну сторону главной диагонали. Такие матрицы называются треугольными. В данном случае это будет правая треугольная матрица. Если дана вторая такая матрица
= 80 + 8i+ ... “Ь8№_1,
то сумма и разность end суть также правые треугольные матрицы. Затем, перемножая, можем написать:
= + • • • + 7n-i)(&o4" . +8W-1) =
= 8o + 8i + • • • ~bsn~l>
где матрицы
s° 8i= Т(А ~Ь Ti^o» • • • > еп-1 — ~Ь Т1^м-2 Ч“" • • • ~Ь Тп-1^0
сУть косые ряды. Таким образом, произведение двух правых треугольных матриц есть также правая треугольная матрица. Множество всех правых треугольных матриц данного порядка является некоммутативным кольцом.
22
ЭЛЕМЕНТЫ МАТРИЧНОГО ИСЧИСЛЕНИЯ
[ГЛ. 1
Аналогичным образом, пользуясь косыми рядами с индексами 7 = 0, —1, ..., —/г —1, построим левые треугольные матрицы.
§ 1.3. Единичная матрица. Диагональная матрица
1 0...0
0 1...0 • • • •
0 0...1
(1.36)
все диагональные элементы которой равны единице, носит название единичной, так как она обладает легко проверяемыми свойствами:
Еа = а, ЬЕ — Ь\ (1-37)
здесь а и b обозначают любые прямоугольные матрицы, конформные с Е в указанном порядке. Если же а — квадратная матрица, то
Еа — аЕ = а. (1.38)
В том случае, когда нужно определённо указать порядок п единичной матрицы, можно пользоваться символом Еп.
Диагональная матрица
s 0... 0
0 0... $
где s — какое-нибудь число, называется скалярной. Так как .
(Es) a = sa, b (Es) — bs,
то умножение любой матрицы на скалярную приводится к умножению на её скаляр 5, и все правила умножения матриц на скаляры могут быть выведены из правил умножения матриц. Очевидно также, что скалярная матрица коммутативна с любой квадратной матрицей того же порядка.
Рассмотрим ещё, в качестве упражнения, матрицу £(wn) типа т X п,
у которой элементы с равными индексами равны единице, а все прочие — нули.
Например,
£(23) =
1 0 0
0 1 0
При т = п получаем единичную матрицу
£(nn) = (1*40)
Легко проверить, что если а — какая-нибудь матрица типа т X л, то при < т произведение b = Е{^ я представляет субматрицу, состоящую из первых строк матрицы а, между тем как при > т матрица b получается из а добавлением ц — т строк, все элементы которых равны нулю.
§ 1.4]
СЛОЖНЫЕ МАТРИЦЫ. КОАГУЛЯЦИЯ
23
Аналогичным образом, произведение b — aE(nj при n < п представляет субматрицу, состоящую из первых v столбцов матрицы а, между тем как при матрица b получается из а добавлением v—п столбцов, все элементы которых — нули.
Отсюда вытекает, что если мы имеем конформные матрицы £(wn), Е(nQ) и если п не меньше наименьшего из чисел т, q, то
Е(тп) E(nq) —
Если же n<Cw, n<^qt то
(1.41)
(1.42)
где g'mnq) есть матрица типа т X <7, У которой первые п элементов с равными индексами суть единицы, а все прочие — нули. В частности,
Е(тп)^(пт) Em (^ ^(тп) ^(пт) = £(тпт)
Например,
§ 1.4. Сложные матрицы. Коагуляция. Можно представить себе матрицы, элементами которых служат не числа, а какие угодно другие объекты. Нужно только, чтобы те операции с элементами, которые, согласно определениям, приходится производить для установления равенства матриц, для их сложения, вычитания и умножения, были определены и возможны. -
В частности, можно рассматривать сложные матрицы, элементы которых сами являются матрицами. Для того чтобы * можно было образовать сумму и разность двух таких сложных матриц, нужно, чтобы они имели одинаковое число строк и столбцов как в целом, так и в соответственных элементах. Для перемножения необходима конформность как в целом, так и в тех элементах, которые приходится перемножать. Например, для
G = ||g, й'||,
k I
т п,
конформность в целом имеет место, так как число столбцов первой матрицы и число строк второй равны двум. Конформность в элементах будет иметь место, если положить
§11 §12 1 ^12
g= §21 §22 , h — 9 k = ^2 , Z — Zji Zq2
/ra = || m||, n = || > ^2 | 9
так как тогда все перемножения, нужные для составления элементов произведения
GK= || gk -Ц- hm,
24
ЭЛЕМЕНТЫ МАТРИЧНОГО ИСЧИСЛЕНИЯ
[ГЛ. 1
возможны и дают:
gk hm =
Sit ”Ь Si 2^2
S-2\kl+g^k2
hxm h2m
gi2kiA-him
htnv h±n2 h2n^, h2n2
S‘1141 512^21 ’ 511*12 + 512*22
521*11 4“ 522*21’ 521*12 4~ S22*22
Будем называть коагулированными сложные матрицы, получающиеся путём разделения обыкновенных матриц горизонтальными и вертикальными перегородками. Так, в предыдущем примере
5*11 S‘12
S21 S22
т
(1.43)
Л1
Л2
Нетрудно показать, что конформными в элементах при умножении могут быть только коагулированные матрицы, вследствие чего мы и ограничимся их рассмотрением.
Основное правило при этом состоит в том, что, перемножая две коагулированные матрицы, заменяя матрицы-элементы их полными таблицами, производя все необходимые действия с ними и убирая перегородки, мы получаем тот же результат, что и при непосредственном перемножении первоначальных матриц, из которых произошли данные коагулированные. Так, в случае приведённых выше матриц
GK=[gk-\-hm, gl~\~hn^ =
gllkl + gl2k2 + him gnlll + gl2l-21 + Ml> £hZ12 + gl2l22 + М2 .
g-21kl + g22k2 + h2m g-21lU + g-22l21 + Ml- gllll<2 + g-22l22 + ft2«2
если здесь убрать перегородку, то получится тот же результат, что и при непосредственном перемножении матриц (43) с убранными перегородками.
В качестве первого приложения рассмотрим коагулированные диагональные матрицы
Л
§ 1-4]
СЛОЖНЫЕ МАТРИЦЫ. КОАГУЛЯЦИЯ
25
в которых элементы Jx являются квадратными матрицами
одного и того же или разных порядков. Такие коагулированные матрицы носят название квазидиагональных. Если матрица
имеет ту же структуру, что и J, элементов и одинаковые порядки
т. е. равное число диагональных соответственных элементов Л, J9
1 —
т
г
т. е. сумма, разность и произведение J и У суть квазидиагональные матрицы той же структуры. Отсюда следует, что всевозможные квазидиагональные матрицы данной структуры образуют некоммутативное кольцо.
В качестве второго приложения возьмём какие-нибудь матрицы v, иг соответственно типов т X Л г X л и обозначим через ..., vr столбцы первой, рассматриваемые как отдельные матрицы-столбцы, и через ..., wr— строки второй:
«’.= ||«’Р1...............Wp»|| (р=1»
Мы можем представить v и w в форме
v = ||^р ..., vr||, w =
где первая матрица коагулировала в строку, вторая — в столбец. Перемножая, получим:
г
а = vw = 2 (1.44)
г Г
Р=1
при этом как vw, так и каждое слагаемое есть матрица типа т X я. Так как
г
ajk=== S ^/р^рЛ» / 1
р = 1
то fe-й столбец матрицы а есть линейная комбинация столбцов , vr со скалярными множителями ...» wrk, образующими
26 ЭЛЕМЕНТЫ МАТРИЧНОГО ИСЧИСЛЕНИЯ [ГЛ. 1
&-й' столбец матрицы w. Если г не превосходит наименьшего из чисел т, п и если столбцы г/р и строки wp линейно независимы, так что матрицы v, w имеют ранг г, то среди линейных комбинаций, о которых была речь, найдётся г независимых, вследствие чего матрица а будет ранга г. Путём аналогичного рассуждения мы могли бы представить строки матрицы а как линейные комбинации строк wp. Что касается отдельных матриц гуа/р, то каждая из них имеет лишь один независимый столбец и одну независимую строку и потому её ранг равен единице.
Очевидно, что каждая матрица типа т X л и ранга г может быть представлена в виде произведения укороченной матрицы v типа т X Л составленной из г независимых столбцов, на удлинённую матрицу типа г X я, составленную из г независимых строк, или же в виде суммы г матриц vpwp первого ранга.
В дальнейшем мы будем изучать, главным образом, матрицы с числовыми элементами и всякий раз, когда понадобится ввести коагулированные матрицы, будем это особо оговаривать.
§ 1.5. Присоединённая и обратная матрицы. Деление матриц.
Пусть а есть квадратная матрица и Akj (обратить внимание на порядок индексов!) обозначает алгебраическое дополнение элемента Ujk в определителе det а. Матрица
называется присоединенной к матрице а. Её можно получить, если ’ заменить в а каждый элемент его алгебраическим дополнением, а затем транспонировать полученную матрицу. По известному свойству определителей,
, Yi ( det а при j = I,
^jkAkl 2dAjkakl— | Q при
1 fc=l
(1.45)
что можно записать в виде
2 a^Aki S ^jk^ki ~ Eji det fc = l Л=1
где Eji — элементы единичной матрицы, так что | 1 при j = l, Е*1 | 0 при J =# /.
Отсюда получается соотношение аА = Аа = Ед&а, (1.46)
выражающее основное свойство присоединённой матрицы.
4
§ 1.5] ПРИСОЕДИНЁННАЯ И ОБРАТНАЯ МАТРИЦЫ. ДЕЛЕНИЕ МАТРИЦ 27
Если а есть,неособая матрица, то
det а
(1-47)
называется матрицей, обратной по отношению к а. Из (46) путём почленного деления на det а получается соотношение
аа~г = а~га = Е,
(1.48)
выражающее основное свойство обратной матрицы и вполне аналогичное такому соотношению, как
5х4 = тХ5=1.
О о
Обратная матрица, когда она существует, является единственной обладающей этим свойством. В самом деле, из соотношения ах = Е, умножая его слева на а"1, мы получаем а~Аах = а~уЕ, или х = а~1, и то же самое вытекает из ха = Е.
Мы имеем из (48):
det а • det а-*1 = 1, или
det а-1 == (det а)-1, (1.49)
т. е. определитель обратной матрицы равен обратной величине определителя данной.
Пусть av а.2, а3, ..., ар — неособые матрицы; мы имеем:
(а-1 ... a-^a-^Ca^ag ...ар) =
= (а-х ... a^a-^ia-^ia^a-g ... ар) =
= (ар1 • • =
= (ар1 • • • «Г1) («ГЧ) («з • • • ар) =
= (.арг • • • «з-1)(а3 ар) = ... = а~'ар = Е.
Следовательно,
(a&a-g ... ар)~* = ... а^а^а-1, (1.50)
т. е. матрица, обратная по отношению к произведению нескольких данных, равна произведению обратных матриц, взятых в обратном порядке.
Если для неособой матрицы а транспонированная и обратная совпадают, ат = а~1, то а называется ортогональной матрицей. Для неё
аа? — а?а = Е, (1.51)
т. е.
2 a^aik = 2 а^а-^ = E^t
28
ЭЛЕМЕНТЫ МАТРИЧНОГО ИСЧИСЛЕНИЯ
[ГЛ. 1
ИЛИ
S a3lakl = 2 "W = EJk- (1-52)
I 7
Деление матрицы а на неособую квадратную матрицу b можно определить как умножение матрицы а слева или справа на &-1. Если а есть квадратная матрица того же порядка, что и то обе операции возможны, но дают, вообще, разный результат. Для избежания двусмысленности мы можем различать левое и правое частные: b\a = b~1a, a/b = ab"1; (1.53)
сокращение дробей должно производиться по формулам: cb\ca==b\a, ас/Ьс = а/Ь. (1-54)
Если матрицы а и b коммутативны при умножении, то левое и правое частные равны между собой. В самом деле, умножая соотношение ab~ba слева и справа на &-1, найдём:
b-^abb-1 = Ь-ЧаЬ"1, или b~xa = ab~1.
Если же принять, что имеет место это последнее соотношение, то, умножая его слева и справа на Ь, получим: ab = ba. В рассматриваемом случае мы можем применять без различия оба обозначения частного или же пользоваться горизонтальной дробной чертой:
6\а = а/й=-|-. (1.55)
Пусть теперь имеем некоторое коммутативное кольцо квадратных матриц одинакового порядка. Левое и правое частные b \а, а/Ь тождественны для любой матрицы а и любой неособой матрицы Ь, принадлежащих кольцу. Кроме того, легко убедиться, что для всех таких дробей имеют место правила сокращения сл ас са ас a \ /л
— = — — (Ь и с — неособые), (1.56)
cb be be cb b 4 / . 4 7
правила приведения к одному знаменателю и умножения дроби на дробь
-r-zt —= —r-z—, -r--7==7Z7 (fi и — неособые) (1.57) b d bd ’ b d bd ' 7
и правило деления дроби на дробь
(&, с и d— неособые). (1.58)
В каждой из четырёх формул можно заменить Ъ или d на £*. Правила (57) показывают, что, складывая, вычитая или перемножая
§ 1.5] ПРИСОЕДИНЁННАЯ И ОБРАТНАЯ МАТРИЦЫ. ДЕЛЕНИЕ МАТРИЦ 29
в любом порядке такие дроби, мы всегда получаем в результате одну из дробей того же вида. То же самое относится к сложению, вычитанию или умножению дроби и одной из матриц кольца. Отсюда следует, что если среди рассматриваемых дробей есть такие, которые сами не принадлежат к кольцу, то присоединяя их к нему, мы получим расширенное множество матриц, также представляющее коммутативное кольцо.
В числе присоединяемых матриц ajb особыми будут те, для которых а — особая матрица. Деление в расширенном кольце возможно и однозначно во всех случаях, когда делитель не является особой матрицей. Кроме того, как показывает (58), не только сложение, вычитание и умножение, но и деление матриц расширенного кольца даёт опять некоторую матрицу этого кольца. Можно сказать также, что расширенное кольцо замкнуто в отношении четырёх действий.
Примером может служить кольцо диагональных матриц п-го порядка с целочисленными элементами. Расширяя это кольцо по предыдущему, получим кольцо диагональных матриц, у которых диагональными элементами могут быть всевозможные рациональные числа.
В случае диагональных матриц п-го порядка с действительными или комплексными элементами расширение кольца излишне, так как все дроби alb уже содержатся в нём.
Пример 1. Если ни один из элементов Хр ..., диагональной матрицы
(1.59)
не равен нулю, то и det А = Хх ... Х№ =# 0. Матрица А является в этом случае неособой и, как легко проверить,
(1.60)
Пример 2. Пусть теперь матрица А в предыдущем примере — квазидиагональная и Хр ..., кп суть её субматрицы. Пользуясь теоремой Лапласа о разложении определителей, получим:
det А = det Хх ... det Xw,
(1.61)
и если ни одна из субматриц не является особой, то и А будет неособой. Выражение для А-1, полученное в предыдущем примере, остаётся верным, так как, умножая на него матрицу А, мы получим, согласно § 4, квазидиагональную матрицу, субматрицы которой суть единичные матрицы и которая поэтому сама будет единичной.
30
ЭЛЕМЕНТЫ МАТРИЧНОГО ИСЧИСЛЕНИЯ
[гл. 1
Примерз. Пусть имеем квадратную матрицу порядка 4-представленную в коагулированной форме
аи а12
а21 а22
(1.62)
где суть соответственно субматрицы типов tij X пк* Если квадратные матрицы ап, а22 и
Р1 = ац а12а22 а21> ?2 === а22 а21аИ а12 G .63)
являются неособыми, то обратная для а будет
Pi1 — Pi
---^2 Р2 1 .
(1.64)
Чтобы убедиться в этом, нужно
лишь составить произведение
Р1 (а11 а12а22 а21)» (а12 а12а22 ^22)
р2 ( а21аИ а11 4“ а21)» ( а21аИ а12 4“ а22)
которое оказывается, как мы видим, единичной матрицей.
Можно получить другие выражения для а-1, менее симметричные, но зато более удобные для некоторых приложений. Например, пользуясь выражениями (63) для рх, р2, найдём:
Р1вГ11а12 = а12 — а12а2-21а21аи а12>
<Х12а221?2 = а12 а12а221а21ац1а12’
откуда
, Pxaix1<xi2 = ^ха^га^а’
Рх"1 (Рхах"х1ах2) Р2-1 = Рх"1 (“хг^Рг) Рг"1’'
ах?а12р2-1 = Pl"1<X12a^ > С1 -65)
а с другой стороны,
Рх ai2a221<3t2X = ахх* Pl'1 (Рх+ «Х2а2-21а2х) а7хХ = Рх"1аххаГх1> а-1 + Рг1а12а^1а21а1-11 = Pf1
и, согласно (65),
“х"? + ах"х1а12р2"1а21аХ_Х1 = Рх"4 С1 -66)
v
§ 1.5] ПРИСОЕДИНЁННАЯ И ОБРАТНАЯ МАТРИЦЫ. ДЕЛЕНИЕ МАТРИЦ
31
С помощью (65) и (66) выражение для а-1 может быть представлено в следующей форме [1Л]:
а-1 =
аГ11 + аГ11«12р2"1«21аи
Г2 2111
— 8-1
11 12Г2
(1.67)
которая удобна тем, что она содержит только две обратные матрицы а-1 и р"1. Эта форма сохраняет поэтому смысл и в том случае,
когда а22 или оказываются особыми, так как хотя мы получили её из (64), но можно было бы и непосредственным умножением на а убедиться, что (67) представляет обратную матрицу для а.
Пример 4. Формулами предыдущего примера удобно пользоваться при нахождении обратных матриц для матриц с заданными цифровыми значениями элементов. Например, в случае матрицы чет-
вёртого порядка
берём сначала верхний левый элемент «1 = 2,
а затем, добавляя по одной строке и
одному
столбцу, составляем
матрицы
О
Обратная для а2 матрица вычисляется непосредственно по фор-
муле (47):
2
32
ЭЛЕМЕНТЫ МАТРИЧНОГО ИСЧИСЛЕНИЯ
[ГЛ. 1
Для определения а”1 полагаем
«ц — ^2’ «12 —
а
откуда
«Н = а2-1 =
«22 —
«На12 =
2 ’
^22 «21«11 «12 — 1»
=
аГ1
2111
— а~ ‘2 21 11
и по формуле (67)
Переходя к а4,
аз-1 =
полагаем
«й — —
» «21
«22
О
и после вычисления, вполне ходим:
аналогичного
проделанному для а3, на-
6
5
1
а-1 =
О
2
О
этим методом встре-
Единственное затруднение при пользовании чается в том случае, когда одна из тех вспомогательных матриц, об- ч ратные для которых входят в формулы для аг1, оказывается особой. Но это затруднение может быть легко преодолено (§ 7, пример 4).
§ 1.6. Степени матриц. Произведение р матриц, равных квадратной матрице а, называется её р-й степенью и обозначается а?. Это определение может быть дополнено соглашением: а° = £’. Обо
§ 1.6] СТЕПЕНИ МАТРИЦ 33
значая через а$ элементы ар, мы имеем при р > 1 редукционные формулы:
£ Если а есть неособая матрица, то пишут = а-Р,
и степени матрицы, таким образом, получают определение для всех целых показателей. Обычные правила
= = (1.68)
являются следствиями ассоциативного закона и сохраняют силу для всех матриц, если р и q суть целые неотрицательные числа; если же а — неособая матрица, то р и q могут быть любыми целыми числами.
Из первого правила следует, что степени одной и той же матрицы коммутативны при умножении.
Пример 1. Для диагональной матрицы Д (59) мы имеем при целом неотрицательном р*.
(1.69)
если же ни один из элементов Xt, ..., \п не равен нулю, то эта формула с помощью (60) обобщается на все целые р.
Пример 2. Пусть матрица Л в предыдущем примере — квази-диагональная и ..., kn— её субматрицы. Формула для Ар остаётся верной для целых неотрицательных р, как-это вытекает из правила перемножения квазидиагональных матриц (§ 4). Если же ни одна из субматриц Лр ..., кп не особая, то, принимая во внимание § 5, пример 2, заключаем, что формула для Ар и в данном случае обобщается на все целые показатели р.
Пример 3. Рассмотрим матрицу
0 1 0 0 0 ... 0
0 0 1 0 0 ... 0
00000 ... 1
00000 ... 0
(1.70)
представляющую первый косой ряд (§ 2, пример 1), составленный из единиц. Из правил перемножения косых рядов вытекает, что при
3 Зак. 1474. Б. В. Булгаков
34
элементы Матричного исчисления
{гл. 1
возведении v в квадрат, куб и т. д. должны получаться второй, третий и т. д. косые ряды, также состоящие из единиц:
00 1 00 ... 0
0 0 0 1 0 ... 0
00000 ... О
00000 ... О
00000 ... 1
00000 ... о ........., V»
о о о о о ... О 00000 ... о
с другой стороны,
1 0 0 0 0 ... О
О 1 0 0 0 ... О vo = Е ................
О 0 0 0 0 ... О 00000 ... 1
Отрицательные степени не могут быть образованы, так как v есть особая матрица. Но транспонированная матрица vT есть, очевидно, (— 1)-й косой ряд, составленный из единиц; аналогично (vT)2.
суть (—2)-й.......(—п-|-1)-й косые ряды, также составленные из
единиц, а все степени ('£)”, (vT)n+1, ... суть нули.
Пример 4. Рассмотрим правую треугольную матрицу
с — Еа.-\~ч,
(1-71)
где а обозначает скаляр, отличный от нуля, а т — сумму косых рядов от 1-го до (п—1)-го:
1 = 71+ •••+?»-!•
(1.72)
Так как при р^п все члены развёрнутого выражения степени
(1Г1+-.-+Ъ»-1)₽
обращаются в нуль по правилу перемножения косых рядов, то уп — yW+l — ... — 0.
Пользуясь этим, можно получить формулу для вычисления обратной матрицы с-1. Применяя сначала совершенно формально правило бинома
ЗлеМейтарйЫе ПРЕОБРАЗОВАНИЯ
35
Ньютона, имеем:
= £,a“1 — a-2^-|_a-^2— .. • +(— ly^a-^-i. (1.73)
Умножая затем это разложение, почленно на c — Ea-\~^t получаем единичную матрицу, откуда следует, что написанная формула и на самом деле даёт обратную для с.
Так как det£ = an, то присоединённая для с будет
С = с-1 det с =
= fa™-1 — aw-2^ -|- aw“872— ... -J-(— l)n-i^n-i# (1.74)
В силу непрерывности эта формула остаётся Для числового просчёта возьмём
верной и при a = 0.
10 3 1
О 1 11 6
00 >Г8
0 0 0 1
Здесь a = 1 и
0 0 3 1
0 0 116
о о 0 1
1о
о 0. о о
0 0 0 1
0 0 0 й 1о
0 0 0 0
О 0 0 0|
0 0 0 0
0 0 0 0
-0 0 0 0
0 0 0 0
3___
1
о
1
о
о
е = с-1.
§ 1.7. Элементарные преобразования. Следующие преобразования матриц носят название элементарных*
1) перестановка двух строк или столбцов;
2) умножение всех элементов какой-либо строки (столбца) на одно и то же число, отличное от нуля;
3) прибавление к элементам какой-либо строки (столбца) соответственных элементов другой строки (столбца), умноженных на одно и то же число.
3*
36
ЭЛЕМЕНТЫ МАТРИЧНОГО ИСЧИСЛЕНИЙ
[гл. 1
Две матрицы называются эквивалентными, если одна получается из другой с помощью конечного числа элементарных преобразований. Такие матрицы не являются, вообще, равными, но, как можно Доказать *), имеют один и тот же ранг.
Легко убедиться, что каждая матрица, связанная с матрицей а одним из элементарных преобразований, может быть получена также путём умножения а на некоторую неособую квадратную матрицу; при этом, если преобразование производится над строками (столбцами), то квадратная матрица должна быть левым (правым) множителем и связана с единичной матрицей тем же преобразованием, которое мы желаем произвести над а.
В самом деле, например, для матрицы
^2 а3
^2
мы имеем:
О 1
1 О
s О
О 1
1 S
0 1
^2 а3
^2 ^3
^2 ^3
Oj а2 а^ ^2 ^з
sa± sa2 sa3
^2 ^3
a1 a*
Ь'2 &3
Определитель квадратной матрицы, на которую множится а при этих трёх элементарных преобразованиях, равен, соответственно, — 1, s и 4- 1.
Если для получения из а эквивалентной матрицы а± требуется несколько элементарных преобразований над строками и столбцами, то мы имеем соотношение вида
at = up... uxav±... v* или
at = uav. (1-75)
При этом матрица и получается из единичной путём тех же элементарных преобразований, которые производятся над строками матрицы а, и в том же порядке, между тем как v получается из единичной путём тех преобразований, которым подвергались столбцы матрицы а.
Нетрудно проверить, что следующие преобразования над коагулированной формой матрицы сводятся к элементарным преобразованиям первоначальной матрицы:
1К) перестановка двух строк (столбцов);
*) См., например, [1Л], стр. 58.
§ 1-7]
ЭЛЕМЕНТАРНЫЕ ПРЕОБРАЗОВАНИЯ
37
2К) умножение всех субматриц какой-либо строки (столбца) слева (справа) на конформную им неособую квадратную матрицу а;
Зк) прибавление к субматрицам у-й строки (столбца) соответственных субматриц fe-й строки (столбца), умноженных слева (справа) на одну и ту же конформную им и, вообще, прямоугольную матрицу, число строк (столбцов) которой должно быть таким же, как число строк (столбцов) в субматрицах у-й строки (столбца) коагулированной формы.
Для получения соответствующей матрицы и в случае одного или нескольких преобразований над строками нужно взять единичную матрицу, конформную с данной матрицей в порядке £*, а, и разбить как её строки, так и её столбцы на такие же группы, что и строки коагулированной формы матрицы а\ после этого надлежит произвести над полученной квазидиагональной единичной матрицей те же преобразования, которые мы желаем произвести над строками а. Аналогичным образом получается матрица v в случае преобразований над столбцами; здесь нужно разбить строки и столбцы единичной матрицы на те же группы, что и столбцы коагулированной формы.
Если производится только одно из трёх преобразований, то определитель матрицы и или v при первом преобразовании равен положительной или отрицательной единице, при втором преобразовании — определителю Матрицы а, при третьем преобразовании — единице.
Пример 1. Рассмотрим, как и в § 5, пример 3, коагулированную квадратную матрицу
а12
а22
где а3-к суть субматрицы типов tij X пк- Если квадратная матрица otn — неособая, то, прибавляя к субматрицам второй строки субматрицы первой, умноженные слева на — а21ай1, имеем эквивалентную коагулированную правую треугольную форму
аи а12
О а22 а12
ч если же а22— неосо'бая, то аналогичным путём получаем эквивалентную матрицу
ОСц ^Х2^22 ^21 6
а21 а22
Так как определители соответствующих матриц и равны единице, то, пользуясь теоремой Лапласа и применяя обозначения (63), мы имеем в первом случае
det а = det аХ1 det р2, (1.76)
а ио втором
(1.77)
det а = det det а22.
38
ЭЛЕМЕНТЫ МАТРИЧНОГО ИСЧИСЛЕНИЯ
[ГЛ. 1
Эти формулы дают пример вычисления определителя квадратной матрицы с помощью её коагулированной формы. Если ни одна из матриц аи, а22— не особая, то оба выражения пригодны и, разумеется, равны между собой. Но если обе матрицы an, а22— особые, то ни одна из двух формул непригодна.
Проведём вычисления для
О
О
а =
Полагая
’и =
О
ai2 —
2 О
а21 —
а22 —
имеем:
О
az1 =
«21 «Н =
О —2
’21аГ11а12 =
det a
Пример 2. В качестве обобщения задачи предыдущего примера вычислим определитель коагулированной квадратной матрицы
detp.a=15, det а = 15.
~83
81 О о
(1-78)
Чп-1
где суть неособые квадратные субматрицы порядков /Пу(/=1, ...,п), 8t— субматрица типа а остальные 8j— субматрицы типов
(7 = 2, ...» я). Умножая последнюю строку на —5д-1
и складывая с первой, получим эквивалентную форму
а —
О
О
О
О
О
О
О О О
О О
О О
§ 1.7] ЭЛЕМЕНТАРНЫЕ ПРЕОБРАЗОВАНИЯ
где матрица
39
« = 77 — 1
г., 0 0 ... 3 y-1o
•1 n
— 82 72 0 ••• 0
0 —8з Ъ ••• 0
0 0 0 ... и.!
имеет тот же вид, что и а; при этом, по теореме Лапласа, det а = det det ап_±.
Преобразуя матрицу ап_± так же, как а, и продолжая эту процедуру, получим после п — 2 шагов:
det а = det ... det det а2, где
наконец, после последнего (п—1)-го преобразования, det а = det 72 ... det det . W (1.79)
Пример 3. Формулой (76) примера 1 можно пользоваться при одновременном вычислении обратной и определителя квадратной матрицы а по способу, указанному в § 5, пример 4. Для этого нужно образовать, начиная с л1==а11, последовательность вспомогательных
матриц
и для вычисления а*1 и det di принять
аи — #4-1, а12 —
^14
ai-l, i
, а21— || d^ ... djt ||, «22
Если — неособая матрица и скаляр {32 = а22— a2iaiilai2 отличен от нуля, то из (76) получается отличное от нуля значение определителя матрицы dit которая оказывается поэтому также неособой, а формула (67) даёт а-1. Переходя, таким образом, от I—1 к Мы вычислим обратные матрицы и определители для всех d^ включая
40 ЭЛЕМЕНТЫ МАТРИЧНОГО ИСЧИСЛЕНИЯ [гл. 1
ап = а> предполагая, что имеем нормальный случай, когда все эти матрицы — неособые.
Так, для матрицы, рассмотренной в § 5, пример 4, находим: det ^ = 2, deta2=l, deta3=l, det а = 7.
Пример 4. Предположим теперь, что, применяя метод предыдущего примера, мы встретили первую особую матрицу Это. обнаружится при вычислении благодаря тому, что соответствующее р2 окажется равным нулю. В этом случае можно, например, в матрице а поменять местами 7-ю и одну из следующих строк, что приводится к умножению а слева на неособую матрицу и.
Если для изменённой матрицы Ь = иа при дальнейшем вычислении не. встретится затруднений, то мы получим матрицу = и определитель det#. Обратная матрица и определитель для а будут а-1 = й“1м, deta = det&/detw;
таким образом, а-1 получится из Ь~г умножением справа (не слева!) на а, а так как в данном случае det#==—1, то deta = — det&. В случае необходимости перестановку строк следует произвести несколько раз, учтя это при составлении матрицы и.
§ 1.8. Приведение матриц к канонической форме. Покажем, что.любая матрица ранга г эквивалентна матрице g того же типа, у которой элементы gn, . ..,grr равны единице, а все прочие — нули.
Если матрица равна нулю, то её ранг также будет нулём и она уже имеет требуемую каноническую форму. Если она не равна нулю, то мы можем путём указанных в § 7 элементарных преобразований типа 1) поставить на верхнее левое место какой-либо ненулевой элемент и путём преобразования типа 2) обратить его в единицу. Затем путём преобразования типа 3) приведём к нулю все остальные элементы первой строки и первого столбца. Если теперь среди элементов второй и следующих строк есть такие, которые не равны нулю, переместим один из них на второе место второй строки и обратим в единицу, после чего приведём к нулю все остальные элементы второй строки и второго столбца, причём всё это может быть сделано без изменения первой строки и первого столбца. Очевидно, что, продолжая такие преобразования, мы получим эквивалентную матрицу, у которой отличны от нуля и равны единице только несколько элементов gn, g22, ... Но так как ранг матрицы не изменяется при элементарных преобразованиях, то этих элементов будет ровно г.
§ 1.9. Теорема Сильвестера о ранге произведения двух матриц. Приведём несколько предложений о ранге матриц.
1°. Образуем субматрицу из каких-нибудь р строк матрицы а типа тп X я и ранга г; ранг субматрицы не может быть меньше, чем р. — Если же взять v столбцов, то ранг полученной субматрицы будет не меньше, чем v — п-\-г. Доказательство предоставляется читателю.
§ 1.10] ЕВКЛИДОВО И ЭРМИТОВО МЕТРИЧЕСКИЕ ПРОСТРАНСТВА 41
2°. Пусть имеем три матрицы а, Ь, с рангов ra, rbi гс, причём ab = c.
В § 2 мы уже установили, что rc^.rai rb.
Если а — неособая квадратная матрица, то Ь — а~1с, а так как ранг а-1 равен га, то гь га, гс и, следовательно, необходимо rb—rc. Аналогичным образом, если Ъ — неособая квадратная матрица, то га = гс. Таким образом, при умножении какой-либо матрицы на неособую, её ранг не меняется.
3°. Пусть теперь а, b — какие угодно конформные матрицы типов /п X11X Я- Мы можем, согласно предыдущему параграфу, представить одну из них, например вторую, в виде b = ugv, где и, v — неособые квадратные матрицы порядков n, qt a g—матрица типа п X Чу У которой гъ элементов gn, g22, • • • Равны единице, а остальные — нули. Тогда.
с — ab = augv.
Матрица аи типа т X 11 имеет тот же ранг rQi что и а. Матрица (аи) g представляет субматрицу, состоящую из первых гь столбцов матрицы аи и, согласно 1°, её ранг не может быть меньше, чем гь— п-{-га. Так как при умножении на неособую матрицу v, ранг не изменится, то rQ>ra-\-rb — п.
Итак, если п— число столбцов матрицы а, равное числу строк матрицы Ь, то ранг произведения c = ab удовлетворяет неравенствам
ra + r6 —ГЪ- (1.80)
В этом состоит теорема Сильвестера, сформулированная им для квадратных матриц.
4°. Если, в частности, га = п, то т не может быть меньше чем.п, а из неравенств (80) вытекает: гь = гс\ если же гь = п, то q^n и га — гс. Иными словами, ранг матрицы не меняется, если её умножить слева на укороченную или квадратную матрицу дефекта нуль или же справа — на удлинённую или квадратную матрицу также дефекта нуль. Это предложение является обобщением 2°.
§ 1.10. Евклидово и эрмитово метрические пространства. Определения основных понятий и операций матричного исчисления возникли в связи с некоторыми геометрическими представлениями, которые остаются наилучшей их иллюстрацией. Поэтому мы должны остановиться на этой связи.
Определим вектор х в n-мерном пространстве как линейную форму
(1.81) j=i
от п координатных векторов elf ..., еп, совокупность которых II£п|| будем называть фундаментальным репером (герёге—
ESV
42
ЭЛЕМЕНТЫ МАТРИЧНОГО ИСЧИСЛЕНИЯ
[гл. 1
метка). Действительные числа хэ называются компонентами вектора, причём j обозначает не степень, а порядковый номер. Координатные векторы ev . . еп предполагаются линейно-независимыми; это значит, что х равен нулю тогда и только тогда, когда все х$ равны нулю. Пока п 3, мы располагаем для векторов и операций над ними общеизвестными геометрическими определениями. Линейная независимость при п — 1 сводится к тому, что координатный вектор должен быть бтличен от нуля; при п = 2 нужно ещё, чтобы ev е2, будучи проведены из начала координат, не были направлены по одной прямой, а при п — 3 три вектора ev е$ не должны лежать в одной плоскости. Если п — какое угодно, то мы можем заменить наглядное представление алгебраической моделью, определяя вектор просто как упорядоченную совокупность п действительных чисел х$ или матрицу-столбец
(1.82)
Принимая за координатные векторы матрицы
будем иметь представление
х=2
Мы, однако, примем другой метод, который позволяет не отказываться от наглядного представления там, где это возможно. Он состоит в том, чтобы стать на более общую точку зрения современной алгебры и считать, что при операциях с векторами нет дела до их природы, если только мы потребуем, чтобы они подчинялись обычным формальным правилам при сложении и умножении на скаляры. Точки пространства определяются их радиусами-векторами, проведёнными из начала координат, причём координаты точки равны компонентам радиуса-вектора. Если же имеем две точки (х1, ...» хп) и (у1, ...» yn)t то компоненты вектора, проведённого из первой во вторую, равны разностям у1— х1, ..., уп— хп.
Правило, по которому порядковые индексы ставятся в одних случаях снизу, а в других — сверху, будет разъяснено ниже, а пока этот способ, обозначения может бмт^ принят как простая условность,
§ 1.10]
ЕВКЛИДОВО И ЭРМИТОВО МЕТРИЧЕСКИЕ ПРОСТРАНСТВА
43
Пользуясь матрицей-строкой ||^р •..еп|| с векторными элементами и матрицей-столбцом х, можем записать разложение (81) в виде
* = ki> .... еп\\х. (1.83)
Пусть g —1| g^ || обозначает некоторую фундаментальную симметрич-ную квадратную матрицу n-го порядка с действительными элементами, а у так же как и х,—какой-нибудь вектор:
9
п
скалярным произведением ху векторов х, у называется величина
ху =ух = x'gy = y*gx = g(x, у) = 2 (1-84)
являющаяся билинейной формой от х</, у*. Квадратичная форма
х2 — x*gx = g(x, х) = 2S gjkXjxk (1.85)
3 &
принимается за квадрат модуля вектора х; матрица g поэтому предполагается такой, чтобы эта форма была определённой положительной. Пространство с указанными определениями скалярного произведения и квадрата модуля вектора называется метрическим евклидовым.
Если х ф 0, у Ф 0, ху — 0, то векторы х, у называются взаимно ортогональными. Мы имеем:
e^ = gjK, (1.86)
так что фундаментальный репер является, вообще, косоугольным, а длины координатных векторов не равны единице. Но если g = E, то
ху = ух = х*у — У^Х = 5 х3УЕ & — х*х — 2 3 3
и векторы Cj являются взаимно ортогональными и единичными.
Предыдущие определения распространяются на векторы с комплексными компонентами и точки с комплексными координатами с той разницей, что скалярное произведение и квадрат модуля целесообразно определить с помощью формул
ху = х*Ну = Я(х, у) = 2 2 Hjkxiy\ (1.87) з ъ
X* = х*Нх = Н(х, х) = 2 2 Н^хк, (1.88)
44 ЭЛЕМЕНТЫ МАТРИЧНОГО ИСЧИСЛЕНИЯ [гл. 1
где Н—эрмитова матрица (§ 1), а знак * применяется, как и раньше, для обозначения матриц, сопряжённых по Эрмиту. В этом случае пространство может быть названо метрическим эрмитовым.
Мы имеем:
ух=2 2 fy, yjxk = 22 nk^>kxi = 22 j k k j ' jk
так что скалярное произведение обладает свойством
ух = ху. (1.89)
С другой стороны, полагая здесь j = имеем:
у2 — у2
т. е. квадрат модуля всегда действителен.
§ 1.11. Преобразование координат. Введём п векторов с помощью формул
.^-=2,»5'ел> с1-90)
к
коэффициенты которых образуют неособую матрицу
»=И‘°М (»х«)-
При этом, хотя штрихи стоят при индексах, а не при буквах, но они служат для обозначения новых векторов, отличных от и таких величин, связанных с ними, как v3jc’. Первый индекс элемента матрицы будет всегда обозначать, как и раньше, номер строки, а второй — номер столбца, независимо от того, стоят ли эти индексы снизу или сверху, причём пустующее место первого индекса снизу занимает точка.
Система векторов е? может служить координатным репером взамен фундаментального. В самом деле, объединяя п формул (90) в одно матричное соотношение
|| &1Г » • • • > || ‘ || • • • i || ^ ( 1 .9 1)
и вводя столбец х' с элементами х? при помощи соотношения
x = vx', (1.92)
однозначно разрешимого относительно х\ получим:
X — || , • • •, || X —- || , • • •, || VX ,
или
х = || й1>, ..., еП’ || х' = 2 (1.93)
з
Но это разложение имеет тот же вид, что и разложение по координатным векторам фундаментального репера. Числа х? суть компоненты х относительно новой координатной системы.
§ 1.12]
ВЗАИМНЫЙ РЕПЕР
45
Обозначая
w-v-1, (1.94)
получим из (91) и (92)
рр <?J|== 1|w, (1.95)
V = (1.96)
Таким образом, обратная матрица есть матраца обратного преобразования.
Соотношения (92), (96), записанные в элементах, получают вид xj = 2 Ф\к'*к' > х? = ^^кХк. (1-97)
к к
Так как y = vy't то скалярное произведение преобразуется следующим образом:
ху = ух = x^gy = y^gx = х' ^goy' = y'Wgvx'-, это можно записать в виде
ху =ух = x'*g'y' =y'*g'x' = g' (х', у') = 3 s >
j к J
где
gr = v’tgvi (1.98)
gyv = S S . (1.99)
I m
Так же как и для фундаментального репера, мы имеем: ерек'~§3'к’* 1
Не представляет затруднения получить аналогичные формулы для эрмитова пространства.
§ 1.12. Взаимный репер. Репер
и,.... ^||=1К. .... ^Ilg-1. (1.100)
получающийся из ||et, .. еп^ с помощью преобразования, в котором роль v играет матрица g“\ носит название взаимного для ||et, ...» е№||. Обозначая элементы g*”1 через gi\ мы имеем вследствие симметрии этой матрицы:
?=2A(/=i..............»). (i.ioi)
к
Составляя скалярное произведение
esek = 3 = 2Л»
I V
и пользуясь основным свойством обратной матрицы, получаем соотношения
j 1 при j = k,
е ек к 0 При J=£k.
(1.102)
46
Элементы Матричного ибчибЛЕйий
[гл. 1
Таким образом, каждый из векторов е3 ортогонален к векторам е19 ..., ej+i> .фундаментального репера.
Компоненты Xj вектора х, отнесённые к взаимному реперу, называются ковариантными в отличие от ранее рассмотренных компонент х3> называемых контравариантными. Индексы ковариантных
компонент пишутся внизу, индексы контравариантных — наверху. Обозначая
(1.103)
имеем по аналогии с (92), (93), (96)
х = ||е1, ..., еп\\^=^х^3, з
(1.104)
(1.105)
откуда получаются формулы для перехода от ковариантных компонент к контравариантным, и обратно:
Xj = ^g}\, х, = 2&Х (J=l> (1.106)
k 3 k 3
а скалярное произведение и квадрат модуля получают вид
ху — ух = ?у = rfx = (1.107)
3 3
д.2 = рх = 2 XjXi (1.108)
или также
ху = ух = = rfg-Ч = s 5 (1.109)
з fc
Х2=^-ч = S 5 g^XjXK. (i.iio)
3 к
Взаимный репер и ковариантные компоненты могут быть определены для нового координатного репера ||^г, ..., еп> [| по формулам
Це1'.....е”'|| —Цвр.......еп> ||(g')_1,
х' = (^)-Ч', ? = g'x'-,
с помощью соотношений (92), (98) имеем: .
5 = gx = goxr = go (g')~\r = gvv-'g-* (^Т)“Ч' = (^Т)""Ч\ откуда, пользуясь тем, что (^т)-1 = (^“1)т = гДе полу-
чаем формулы преобразования ковариантных компонент:
6 = ^4', S'=v4. (1.1П)
§ 1.13] лийеййай ёЕЙто^-ФУНйция. п6добйай Матрица 47
Сравнивая с (92), (96), мы видим, что ковариантные компоненты связаны преобразованием, транспонированным по отношению к обратному. Отсюда самые термины ко- и контравариантный, т. е. со- и противопреобразующийся.
§ 1.13. Линейная вектор-функция. Подобная матрица. Пусть л = ||яМ (ftX4
Вектор у, связанный с переменным вектором х соотношениями / = (1.112)
к
ИЛИ
у = ах, (1.113)
носит название линейной вектор-функции. Если трактовать х$ и у* как координаты двух точек, то рассматриваемые соотношения определяют точечное преобразование пространства.
Если имеем второе преобразование
z-=by, где
Ь=11^11 («Х«)>
a z— матрица-столбец, составленный из компонент вектора z, то
z = b (ах) или
z = сх, где
с = Ьа.
Таким образом, два последовательных преобразования эквивалентны одному преобразованию с матрицей, равной произведению матриц этих преобразований. Этим оправдывается целесообразность принятого определения умножения матриц.
Пусть теперь мы переходим к новым координатам. Тогда компоненты вектора-аргумента х и вектор-функции у преобразуются согласно формулам:
x = vx', y = vy'\
подставляя в (113), имеем:
vy' = avxr или
у' = а'х', (1.114)
где
a' = v~'1atv. (1.115)
Линейное соотношение (114) определяет то же самое геометрическое соответствие между векторами или точками, что и (113), но
48 ЭЛЕМЕНТЫ МАТРИЧНОГО ИСЧИСЛЕНИЯ [ГЛ. 1
выраженное в новых координатах. Мы видим, что матрица а при этом должна быть заменена матрицей а'9 которая определяется формулой (115) и называется матрицей, подобной матрице а. Полагая опять = и переходя к элементам, получим из (115):
m^Wk- (1.116)
I т
Следует подчеркнуть, что этот закон преобразования получен нами для вектор-функции, связывающей контравариантные компоненты двух векторов; совокупность величин преобразующихся по этому закону, носит вообще название смешанного тензора второй валентности. Нетрудно было бы получить формулы преобразования для вектор-функций, переводящих ковариантные компоненты одного вектора в контравариантные компоненты другого, или наоборот; эти формулы характеризуют дважды контравариантный или дважды ковариантный тензор второй валентности. Можно сказать вообще, что тензор второй валентности есть квадратная матрица плюс закон преобразования. '
Из формулы (115) вытекает:
det ar = det Ф~г det a det ф — det а,
так что подобные матрицы имеют один и тот же определитель. Легко проверить, что матрицы, подобные сумме, разности, произведению, левому и правому частному двух данных матриц а, Ь, равны, соответственно, сумме, разности, произведению, левому и правому частному матриц, подобных данным:
ф-1 (а±Ь)ф = Ф~гаФ ± ф^Ьф, ф"1 (ab) ф = (ф-^аф) (ф-^Ьф), ф~х (Ь\а)ф = ф-1Ьф \ Ф~хаФ, ф~у (а Ь)ф = / ф~'1Ьф.
(1.117)
(1.118)
(1.119)
(1.120)
Аналогичное правило имеет место для суммы и произведения нескольких матриц, а также для их степеней:
v-1apv = (v~1av)p. (1.121)
§ 1.14. Матричные единицы. Назовем квадратную матрицу ejk, у которой элемент j-й строки и й-го столбца равен единице, а все остальные элементы суть нули, матричной единицей.
С помощью таких единиц мы получим для произвольной квадратной матрицы а данного порядка разложение
а = 2 2 ajkejk> (1.122)
J *
| 1.15] Рациональные функций матриц 49
аналогичное разложению вектора по координатным векторам фундаментального репера. Легко убедиться, что для матричных единиц верна следующая таблица умножения:
^jk^km === 0 (fe Z), (1.123)
отправляясь от неё, мы могли бы, обратно, вывести общее правило умножения для квадратных матриц.
Можно себе представить, что, в случае преобразования координат, элементы а^к матрицы а и единицы преобразуются таким образом, что мы имеем для той же матрицы а новое разложение
а = 3 к
\ Определим закон преобразования единиц таким образом, чтобы элементы а^к, образовали подобную матрицу, так что z
4 J к
Заменяя здесь а предыдущим выражением, найдём:
= 1(^^aj,ktejrk'^V=^i^aj,kf(V le3rk,V^ j к 3 к j к
сравнивая коэффициенты при одинаковых a^w, которые должны рассматриваться как произвольные величины, находим искомый закон преобразования:
ejk = ej’w = vejkv~'. (1.124)
Из этого закона следует, в частности, что для новых единиц верна та же таблица умножения, что и для старых.
§ 1.16. Рациональные функции матриц. Пользуясь определениями сложения и умножения матриц, а также степени квадратной матрицы z, мы можем образовать правый матричный полином
f (z) = a^L а^-1 *4- ... +^^4-^, (1.125)
। коэффициенты которого — прямоугольные матрицы одного и того же типа, конформные с z в указанном порядке:
' ч «4 = й^|1- (1.126)
Этот полином является матрицей того же типа, что и коэффициенты, и элементы его суть .
/л == S да + aW-1) + • • • + (1 • 127)
где через Е1к обозначены элементы матриц Е. Аналогичным образом определяется левый полином
g(z) = zLaQ 4- z^a^ + ... + zaL_1 + aL. (1.128)
4 Зак. 1474. Б. В. Булгаков
I
50
элементы Матричного исчисления
[гл. 1
Следует заметить, однако, что правыми и левыми полиномами не исчерпываются все возможные формы. Наиболее общим матричным полиномом будет
L
• • • zai, 7, i-i.i.zat h L-i- (1.129)
1=0 Л
Если коэффициенты полиномов f{z) или g(z)— скалярные матрицы = где — числа, то при подстановке этих выражений множитель Е может быть опущен во всех членах, кроме свободного, и мы получаем скалярный полином от матрицы z
P(<z)^k{izL + k1zL^+ ... -\-kL_tz-\-kLE. (1.130)
Он является квадратной матрицей того же порядка, что и zt с элементами
Р* = _1) + ... + kL.1Zjlc + k^. (1.131)
Так как степени данной матрицы z коммутативны при умножении, то это верно и для всех скалярных полиномов от неё, которые образуют поэтому коммутативное кольцо. Согласно сказанному в § 5, деление в этом кольце возможно и однозначно во всех случаях, когда z не обращает знаменатель H(z) в особую матрицу; в дальнейшем (§ 35) мы найдём простое условие, при котором последнее требование выполняется. Присоединяя дроби
получаемые путём деления, мы расширим кольцо скалярных полиномов до кольца скалярных рациональных функций от данной ‘ матрицы z. Для действий с этими дробями имеют место обычные правила арифметики (56), (57), (58).
Из правил сложения, умножения и деления матриц, подобных данным (§ 13), вытекают следующие формулы для скалярных полиномов и рациональных функций:
v-'P (z)v = P (y~'zv), (1.133)
v-xR(z)v = R(v~1zv), (1.134)
при обычном условии, что П(з) должно быть неособой матрицей.
Пусть ещё Л —диагональная или квазидиагональная матрица с диагональными элементами Лх, ...» Из формулы (69) для степени вытекает:
Р(Х1)
Р(Л) =
(1.135)
>(ХЯ)
§ i.iSj
Мат^иЦы Кейли
&
Если же матрица
n(Ai)
П(А) =
является неособой, то
% = П(Л)=
(1.136)
Я (Х„)
§ 1.16. Матрицы Кейли. В качестве упражнения на применение правил умножения читатель легко проверит, что для матриц
имеют место такие же соотношения
как для действительной и
Р = — Е, Е1 = 1Е = 1, (1.138)
мнимой единиц 1, L Перемножая матрицы
8
0)
----О)
8
(1.139)
е'
(1)
----СО
8
получим:
88-------(0(0 ,
— ео/— (ое', ее' — (0(0 = (ее' — oxo') Е -|- (ео/ -}- <os'
(1.140)
Таким образом, если образовать две матрицы вида (139) из действительных и мнимых частей двух комплексных чисел е -1-f(o, s'-}-до', то после перемножения получится матрица того же вида, образованная из действительной и мнимой частей произведения этих чисел (е -}- /со) (е' /о/).
Заметим, что рассматриваемые матрицы являются частной формой тех, с помощью которых Кейли представил кватернионы Гамильтона. Мы будем условно называть их матрицами Кейли, Этим наименованием мы будем пользоваться и для матриц немного более общего вида
4*
вайв&лг*'-
(1.141)
эЛейейты матФичйого ИСЧИСЛЕЙИЯ
являющихся квазидиагональными. Если
О О е' <о' — <о' е'
то
хх' О О
О ее' — о)о)'
О — ео)' — о)е'
80)'
ее' — о)о)'
(1.142)
х и х' перемножаются, а е, е', о), о/ комбинируются попрежнему как действительные и мнимые части комплексных чисел. Это правило верно и для произведения нескольких матриц рассматриваемого типа.
В частности, для целых неотрицательных р
Qp—
уР О
О Re (е 4~
О — Im (e
О
Im (е te)p
Re (е 4- i^)p
(1.143)
Если, далее, х, е-Ц-^о, а значит, то мы имеем обратную матрицу
и det Q = х (е2 4~ <*>2) не равны нулю,
(1.144)
причём её выражение „может быть получено из предыдущего при р=—1. Поэтому формула (143) для Qp тотчас распространяется на все отрицательные р. Из этой формулы вытекает также, что если P(Q) есть многочлен от Q с действительными коэффициентами, то
P(Q) =
Р (х) О О
О Re Р (е 4~ ю) Im Р (е /со) *
О — Im Р (е 4“ to) Re Р (е 4- to)
(1.145)
если же П (Q) есть второй многочлен, представляющий неособую матрицу, так что
П(х)=#0, П(е4-¥= О,
то
р — Р (Q)________
A: (У) — п (Q) —
/?(х) О О
О Re (е 4-й») Im (е 4- 1&)
О — Im R (a-j” to) Re Z? (е -|- /о»)
(1.146)
§ 1.16]
МАТРИЦЫ КЕЙЛИ
53
Мы можем, далее,’ рассматривать коагулированные матрицы Кейли Q вида (141), где х суть уже некоторые прямоугольные матрицы, а е и о? — другие прямоугольные матрицы с одинаковым числом строк и столбцов. Для того чтобы такие матрицы были конформны в элементах при умножении в любом порядке, мы ограничимся случаем, когда х суть квадратные матрицы некоторого данного порядка s', а е и со— квадратные матрицы порядка матрицы Q будут тогда также квадратными порядка s =* s' -f- 2s". Формулы (142), (143), (145) для произведения, целой неотрицательной степени и многочлена с действительными коэффициентами, полученные выше, немедленно обобщаются и для данного случая на оснований правила умножения коагулированных матриц. Переходя к формуле (144) для Q-*, заметим, что если е, со коммутативны и е 4-to— неособая матрица, то е— to и (е 4“to) (е — /со) = е2 4~ также будут неособыми и
(е 4~ /со)"1 = (е 4~ to)\£ = (s2 4~ <о2)\(е — /со) =
= 2?/(е 4“ to) = (г — to) /(s2 + <°2)«
Сравнивая действительные и мнимые части, найдём:
(е2 + ш2)\е = е/(е2 со2) = >
(S2 _|_ ш2)4^ = щ/(е2 «2) == _2L_)
вследствие чего выражения элементов в формуле для Q"1 сохраняют смысл в случае, если ещё и х есть неособая матрица. Умножая затем матрицу, определяемую этой формулой, на' Q, непосредственно убедимся, что получающаяся матрица — единичная. Поэтому матрица, принятая нами за Q"1, есть действительно обратная для Q. Формула (143) обобщается на все отрицательные р с сохранением предположения, что х и е 4- /со суть неособые матрицы.
Для выяснения смысла последнего предположения, а также некоторых последующих применений, заметим, что Q подобна квази-диагональной матрице
х О О
А = О е 4~ to О О 0 s — /со
В самом деле, полагая
(1.147)
ПОД-..
О
1Еа» 1 Eait
54
ЭЛЕМЕНТЫ МАТРИЧНОГО ИСЧИСЛЕНИЯ
[ГЛ. 1
где Е8/, Е8„— единичные матрицы порядков s', s", непосредственным перемножением убедимся, • что обратная для этой коагулированной матрицы будет:
/ 2Ев, 0 0
V~* = 0 ~2 ~ 2”
0 ~2 iEa" ~2 Еа"
v~*Qv — А.
и что
Отсюда вытекает det Q — det А или
det Q = det x det (e-J-Zco) det (e — Zco) = det x | det (e Zco) |2; (1.148)
поэтому предположение, что x и СУТЬ неособые матрицы,
которое служило условием применимости формулы для Qp при отрицательных р, эквивалентно предположению, что Q — неособая.
Формула для R(Q) может также применяться к коагулированным матрицам Q при условии, чтобы П(х), II(s4~z<u)» а значит, и H(Q) были неособыми.
Совокупность всех коагулированных матриц Кейли Q при заданных порядках субматриц х, е, со является некоммутативным кольцом.
Совокупность многочленов P(Q) и совокупность рациональных функций R(Q) данной матрицы Q образуют два коммутативных кольца.
Для последующих приложений в теории колебаний представляют интерес частные случаи коагулированных матриц Кейли Q, в которых х, в и со являются диагональными и квазидиагональными матрицами. В первом случае
(1.149)
Очевидно, что все матрицы Q с такими субматрицами образуют коммутативное кольцо со всеми вытекающими отсюда последствиями (§ 5).
Рассмотрим произведение
w = Qw
(1.150)
коагулированной матрицы Кейли Q на какую-нибудь матрицу w типа s X п. Разбивая последнюю горизонтальными линиями на три матрицы соответственно цз s', s" и s" строк и поступая
§ 1.161
МАТРИЦЫ КЕЙЛИ
55
так же с w, перепишем предыдущее соотношение в виде
откуда
Wx = XWx, W£ — SWe -J- = COWg + s%*
Эти формулы верны для случая любых квадратных матриц х, е, со; но если они являются диагональными, то, обозначая через отдельные строки w и аналогично для w, найдём:
^ = х^ (а=1, ..., s'), (1.151)
W +А = + h + +8"+Л»
Wdr+s//+Zl — — <ttA^j'+fc4-eA‘aV+«''+A (A=l, ..., s").
Две последние формулы могут быть объединены в одну:
W +ft — iwj +8*+л = (eft + /сой) (wdr+л — +а»+п) (1.152)
(ft=l, ...,s").
Аналогичным образом в произведении v — vQ
(1.153)
какой-нибудь матрицы v типа п X5 на коагулированную матрицу Кейли Q разбиваем v вертикальными линиями на матрицы г/х, v&, соответственно из s', s", s" столбцов и так же поступаем с v, тогда
X О
О
II 11 = 11 ||Х
О О
8 О)
----СО 8
откуда для общего случая каких угодно квадратных матриц х, е, со имеем:
и. = -их, А А —
Ve = *>е® — Чо = + ЧА
Если же х, е, со суть, в частности, диагональные матрицы, то, обозначая через vv ..., vs отдельные столбцы v и аналогично для v, найдём:
= (а=1, s'), (1.154)
/
+h~Va' 4.^-------Ч,'+8"+Ла)А>
^'+8"+* = ^8'+Л0)л + 1С'8'+з''+й®Л (Л=1, ...» S"),
56 ЭЛЕМЕНТЫ МАТРИЧНОГО ИСЧИСЛЕНИЯ [ГЛ. 1
Две последние формулы объединяются в следующую:
+Ч+8-'+й=Ч' +»+Ч-+8«+л) Ч+Ч) <1 •155>
(Л = 1, s").
Б. ПОЛИНОМНЫЕ МАТРИЦЫ
§ 1.17. Полиномные матрицы. Эквивалентность. Мы дали выше (§ 15) определение полинома f(z) от матрицы и рассматривали частный случай, когда коэффициенты суть скаляры. Другой частный случай имеет место, когда коэффициенты остаются прямоугольными матрицами ai общего вида, но z — скалярная матрица, так что ^ = ЕХ, z2 = £’Xa, ..., где X — скаляр. При подстановке этих выражений в правый или левый полином множитель Е можно не писать, и мы получаем матричный полином от скалярной переменной X:
/(X) = + О1ХЬ-1 + ... + ai_ix + aL. (1.15.6)
Полагая
/Ю= 114* WII >
||а$||, Л1= ||<$11..<Ъ-1= 11<$-1)1Ь ^=11^11.
имеем:
• • • +«^-1)x+4i), (i.i57)
так что элементы прямоугольной матрицы /(X) — скалярные полиномы от X. Поэтому матричные полиномы от скалярной переменной называются также полиномными матрицами или X-матрицами (ламбда-матрицами).
Миноры полиномной матрицы являются, очевидно, полиномами от X. Рангом г полиномной матрицы называется порядок её самых старших, не обращающихся тождественно в нуль миноров. Следует заметить, что при подстановке вместо X какого-либо определённого его значения а ранг р получающейся числовой матрицы может быть равен, но может быть и ниже, чем г. Квадратная полиномная матрица, ранг которой равен порядку, называется неособой, в противном случае— особой.
Элементарными преобразованиями полиномной матрицы называются следующие:
1) перестановка двух строк или столбцов;
2) умножение всех элементов какой-либо строки (столбца) на одно и то же число, отличное от нуля;
3) прибавление к элементам какой-либо строки (столбца) соответственных элементов другой строки (столбца), умноженных на один и тот же полином от X.
Две полиномные матрицы называются эквивалентными, если от одной можно перейти к другой с помощью конечного числа элементарных преобразований.
§ 1.18] ИНВАРИАНТНЫЕ МНОЖИТЕЛИ И ЭЛЕМЕНТАРНЫЕ ДЕЛИТЕЛИ 57
Общий наибольший делитель D^(X) всех миноров Z-ro порядка (Z^r) полиномной матрицы называется детерминантным делителем. Для определённости будем предполагать, что коэффициент старшей степени X в £)ДХ) приведён к единице. Нетрудно показать*), что ранг и детерминантные делители не меняются при элементарных преобразованиях или, как говорят, являются инвариантами относительно этих преобразований.
§ 1.18. Инвариантные множители и элементарные делители. Выберем один из миноров Z-ro порядка полиномной матрицы и разложим его по элементам какой-либо строки или столбца. Каждый член разложения содержит множителем один из миноров (Z—1)-го порядка, а потому делится на О^_х(Х). Следовательно, взятый нами, а также всякий другой минор Z-ro порядка, делится на £^_х(Х). Поэтому и ОДХ) делится на Di_1(X), так что частное
Е^Х) = Di(k)/ (1.158)
представляет собою полином, в котором коэффициент старшего члена равен единице и который не меняется при элементарных преобразованиях. Полиномы Ei(K) носят название инвариантных множите -лей. Если положить < условно Do (А) = 1, то Е{ (X) определяются для всех Z от 1 до г. Перемножая соотношения типа (158), получим формулу
Di(X) = E1(X) ... ЕДХ) (Z=l, ...,.г), (1.159)
которой оправдывается самое наименование инвариантных множителей.
В случае неособой квадратной матрицы n-го порядка её определитель
A (X) = det/(X) (1.160)
может лишь постоянным множителем отличаться от старшего детер-минантного делителя О№(Х); в этом, случае инвариантные множители являются множителями определителя А(Х).
Можно доказать**), что каждый инвариантный множитель делится на все предыдущие.
Пусть а, а', ... — различные между собою корни старшего детер-минантного делителя Dr(X), так что
£>Г(А) = (А —а)®(А —а')4' ... (1.161)
Линейные множители А. — а, А. — aS •. • называются также линей-иыми множителями матрицы.
*) См. А. И. Мальцев [L5], стр. 158, где доказательство проведено для квадратных матриц, но применимо и к прямоугольным,
’**) См, А. И, Мальцев [E5J, стр. 154, 161,
58
ЭЛЕМЕНТЫ МАТРИЧНОГО ИСЧИСЛЕНИЯ
[ГЛ. 1
Так как, согласно (159),
Dr(X) = E1(X) ... ЕГ(К), (1.162)
то, сравнивая (161) и (162), убеждаемся, что каждый из полиномов ЕДХ) представляет произведение вида
£.(Х) = (Х — а)е*(Х — а'/* •••> (1.163)
причём
е2^ ... ег\ ... (1.164)
Те из степеней (X — а)% ..., (X — а)\ которые не приводятся к единице, называются элементарными делителями, соответствующими корню а. При у > О элементарные делители (X — а)Ч (X — а)6*4’*7 считаются различными даже и в том случае, когда = eiJrj. Сумма степеней элементарных делителей, соответствующих корню а, равна, очевидно, его кратности:
е1+---+ег = 9- (1.165)
Аналогичным образом определяются элементарные делители для других корней.
Инвариантные множители вполне определяют элементарные делители; обратное также верно, если ранг известен.
Из предыдущего вытекает, что для того, чтобы две полиномные матрицы одного и того же типа были эквивалентны, необходимо, чтобы они имели одни и те же инвариантные множители или, что то же, один и тот же ранг и одни и те же элементарные делители. Достаточность этого условия может быть также доказана *), вследствие чего заданием ранга и элементарных делителей матрица определяется с точностью до элементарных преобразований.
Пример. Пусть
__ Х2 — 2Х+1 X —1 X —1
X- 1 Х2 —2X4-1 X—1
Здесь
Di (X) = X -1, D2 (X) = (X -1)2 (X -2),
£1 (X) = X — 1, £2 (X) = (X — 1) (X — 2)
и элементарные делители суть А — 1, X—1, X — 2; все они линейны.
Для последующих приложений рассмотрим подробнее вопрос о соотношении между рангом г полиномной матрицы и рангом р той числовой матрицы /(а), которая получается при каком-либо определённом значении X = а. Очевидно, что р не может быть больше г, но для того, чтобы было р = г, нужно, чтобы по меньшей мере один из
#) См, А. И, Мальцев [1Л], стр. 162, 167,
§ 1.19] ПОЛУЧЕНИЕ ЭКВИВАЛЕНТНЫХ ПОЛИНОМНЫХ МАТРИЦ 59
миноров r-го порядка матрицы f(K) не обращался в нуль при Х=-а; иными словами, для равенства рангов г и р необходимо и достаточно, чтобы а не было корнем старшего детерминантного делителя Dr(X).
Поэтому если теперь а будет корнем полинома Dr(X) некоторой кратности q, то р должен быть меньше г. Все миноры/(X) порядков р-]-1, •••> г обращаются в нуль при Х==а, и детерминантные делители Dp+1(X), ..., Dr(X) содержат степени линейного множителя X—а, между тем как в детерминантные делители низших порядков этот множитель не входит. Поэтому степени двучлена X — а входят только в инвариантные множители £р+1 (X), ..., Er (X). Отсюда следует, что ранги г, р матриц /(X), /(а) и число ъ элементарных делителей, соответствующих корню а, связаны соотношением
г — р = т.
Можно отметить, что а будет не менее чем ер+1-кратным корнем миноров (р—[-1)-го порядка матрицы /(X), не менее чем (^р+1 + ^р+2)" кратным корнем миноров (р -j- 2)-го порядка и т. д. Кроме того,
Т = г — р=^гр+1-|- ... -\-er = q, (1.166)
так как ни одно из чисел гр+1, ..., ег не меньше единицы. Точное равенство т —г — р = 7 имеет место лишь при гр+1 = ... = er = 1, т. е. в случае, когда все элементарные делители, соответствующие корню а, линейны.
Если, в частности, мы имеем неособую полиномную квадратную матрицу /(X), то дефект матрицы /(а) равен числу элементарных делителей, соответствующих значению а.
§ 1.19. Получение эквивалентных полиномных матриц путём умножения на квадратные матрицы с постоянными определителями. Тем же способом, что и в случае матриц с постоянными элементами, нетрудно показать, что эквивалентные полиномные матрицы /(X), /1(Х) могут быть получены друг из друга путём умножения слева и справа на неособые квадратные матрицы, причём определители последних оказываются в данном случае не зависящими от X:
/1Q) = a(X)/(X)^(X), /(Х) = И-1(Х^/2(Х)х»-1(Х).
(1.167)
Матрица и(Х) получается из единичной путём тех же элементарных преобразований, которые производятся над строками матрицы /(X) и в том же порядке, a t>(X) получается из единичной путём тех преобразований, которым подвергаются столбцы матрицы /(X).
Если, обратно, мы имеем соотношения (167), то матрицы /(X), /1(Х) эквивалентны. В самом деле, согласно (32), из первого соотношения вытекает, что ранг матрицы Д(Х) не превосходит ранга /(X), а из второго соотношения следует, что ранг /(X) не превосходит ранга Д(Х). Поэтому эти ранги одинаковы. Затем из формулы (31)
60 ЭЛЕМЕНТЫ МАТРИЧНОГО ИСЧИСЛЕНИЯ [ГЛ. 1
для миноров произведения двух матриц вытекает, что если миноры Z-ro порядка матрицы /(X) имеют общий множитель, то он будет также множителем всех миноров того же порядка матриц /(X)t>(X) и и (^) f W о (М- Поэтому каждый детерминантный делитель матрицы Д (X) делится на детерминантный делитель того же порядка матрицы /(X). Обратное заключение также' верно, вследствие чего все эти детерми-нантные делители совпадают. Инвариантные множители и элементарные делители обеих матриц будут также одинаковы, и согласно сказанному в § 18 эти матрицы эквивалентны.
Итак, для того чтобы две полиномные матрицы одного и того же типа были эквивалентны, необходимо и достаточно, чтобы они были связаны соотношениями вида (167), в которых я(Х), — неособые квадратные матрицы с определителями,
не зависящими от X.
§ 1.20. Преобразования коагулированных полиномных матриц. Как и в случае матриц с постоянными элементами, можно указать преобразования коагулированной формы полиномной матрицы, эквивалентные ряду элементарных преобразований первоначальной формы. А именно: 1к) перестановка двух строк (столбцов); 2К) умножение всех субматриц какой-либо строки (столбца) слева (справа) на конформную им квадратную полиномную матрицу а(Х) с отличным от нуля и не зависящим от X определителем; Зк) прибавление к субматрицам у-й строки (столбца) соответственных субматриц fe-й строки (столбца), умноженных слева (справа) на одну и ту же конформную им полиномную матрицу, число строк (столбцов) которой равно числу строк (столбцов) в субматрицах у-й строки коагулированной формы.
Матрицы и(Х) и г>(Х), соответствующие этим преобразованиям, могут быть найдены тем же способом, что и в случае матриц с постоянными элементами (§ 7).
§ 1.21. Умножение и деление полиномных матриц. Пусть имеем две полиномные матрицы соответственно степеней L и М:
/(X) = а0Ах + а/"1 + ... 4-ал_1 X + aL (а0 #= 0),
= (*0У=°)-
Если они конформны в порядке /(X), g(X), то произведение
, = 14~ •••
может быть вычислено по тому же формальному правилу, что и для скалярных полиномов, так что
^0 === == а А’ • • •»
= “Ь aTpM-V CL+M = а1рМ*
Если, сверх того, /(X) — укороченная или квадратная матрица и а0 имеет дефект нуль или же если g’(X)— удлинённая или квадратная
1.2i] умножение и Деление Аблиномнык матриц 61
матрица и bQ имеет дефект нуль, то произведение с0 = а0&0 не может быть нулём (§ 2). В этом случае степень произведения /(X)g(X) будет L-j-Af, так же как и при перемножении скалярных полиномов.
Переходя к делению, предположим /(X) неособой квадратной матрицей п-го порядка, конформной с g(X) в порядке /(X), g(X). Частное f(ty\g(ty не будет, вообще, полиномной матрицей, но мы покажем, что
/(Х)\ g(X) = S(X)+/(X) \ Т(Х), (1.168)
где целая часть S(k) и остаток Т(к) — полиномные матрицы, причём все элементы матрицы f(k) \ 7*(Х)— правильные дроби.
В самом деле, обозначая через F(k) присоединённую для /(X), а через Д(Х)— определитель /(X), имеем:
Ж\£(Х) = Р(^(к), и элементы этой матрицы суть
(Ч
Ц1) — W "Г Тог ’
где Sjfc(X) — полиномы, a (Х)/Д (X) — правильные дроби. Поэтому
/(X)\g(X) = S(X)+^ (1.169)
И
g(X)=/(X)S(X)+T(X), (1.170)
где матрица
Т(Х) = ^^ (1.171)
является полиномной, поскольку она равна разности g(X) и /(X)S(X). Так как
ia = /W\7-W.
то мы получаем соотношение (168), которое хотели вывести. Матрицы S(X), Т(Х) определяются единственным образом, й из выражения (171) для второй матрицы видно, что её, степень ниже степени /(X).
Если не только /(X), но и а0 есть неособая матрица, то мы получим те же S(X), Т'(Х), что и выше, ограничиваясь требованием, чтобы степень Т(Х) была ниже степени /(X). Это объясняется тем, что в данном случае из указанного требования уже вытекает, что все элементы матрицы /(Х)\ 7'(Х)== F(X) Т(Х)/Д(Х) суть правильные Дроби, так как коэффициент при старшей степени kLn в Д(Х) равен deta0=£ 0.
Мы можем также в этом случае непосредственно определить S(X) и следующим путём.
62
Элементы МатФиФюГо ис^идлЕЙий
[гл. 1
Если 7И < Z, то, как показывает (170), единственное тривиальное решение есть S(X) = O, T(Z) = g(A). Если Л4^Л, то S(X) должна иметь степень М — L, так как степень Т(Х), самое большее, равна L— 1:
S(X) = S^-b+S1XM-i-1+ ... +
Подставляя выражения для /(X), £(Х), S(X), Т(Х) в соотношение (170), имеем:
ьй\х+ь^-1 + ..'•+ ьи_г =
= (a(/b 4” ai 14~ ••• + 4” °е) X
Х(50Х
•• 4’5м-б-Л4~5л/-б)4~
• • • 4- Л;-2^4~ ^L-l’
а затем, перемножая и приравнивая коэффициенты при одинаковых степенях X, получим: х
4~ Мо =
а0 4~ 4“
и
Л) 4- ai$M-L 4~ a2^M-L-l 4~ • • •
4- a2$M-L 4” a3^M-L-l 4" • • •
^ЛГ-Ь+1’
4~ aL^M-L bjXL'
Из первой группы уравнений последовательно и однозначно определяются So, Sx, ..., SM_L, а из второй 7^, Tv ..., Тх_г Очевидно, что этот метод тождественен элементарному правилу деления полиномов.
Если данные матрицы конформны в порядке g(X), /(X), то так же, как и выше, покажем, что
g(X)==Q(X)/(X) + /?(X).
Пример 1.
(1.172)
^(Х) = £,
Д (X) = 2 (X 4-1).
§ i.2i]
Умножейие И Деление полиномйых матриц
63
Выделяя целые части элементов матрицы F (X) g (Х)/Д (к), находим: 1 1
2 2
Так как л л
то из соотношения Е =/(Х) S + Т получается:
Матрицы S, Т оказались тельно К.
в данном случае нулевой степени относи-
Пример 2.
/(*)==
2X2 — х —1
2Х
X —1
К+ 2
Н Х2
+-Х Х2 —х
Д (X) = X (X — 1),
а2 — X
\2— X
/(k)S =
Пример 3.
/М =
Х2 — 2Х—1 X —1
£(*) =
Матрицы Q (к), R (X), удовлетворяющие соотношению
QW =
Пример 4.
/?(Х) =
А—— 1
1
О *
£(k) = Q(XW) +
— 1
1 ‘
Г = £—/(Х)$ =
X О
X —1 х —1
— 1
— 1
— 1 о
1
1
1
1 О 1
О
— 1
— 1
1
1
О
О
О
О
О
g W = Е,
О
О
О
О
О
О О
2Х —2
О 1
О О
— 1
— 1 О
Применяя правило деления
полиномов, получаем матрицы
О -1
О 1
64
ЭЛЕМЕНТЫ МАТРИЧНОГО ИСЧИСЛЕНИЙ
[гл. 1
Пример 5.
/W =
$(к) =
2к — 2 к 4- 2
ЗА —1 к
— к + 7 —1
Зк — 22 3
Г(к) =
л2 4- 1 х
3 1
59 —8
10 0
§ 1.22. Треугольные полиномные матрицы. Покажем, что любая квадратная полиномная матрица путём элементарных преобразований над строками может быть приведена к эквивалентной треугольной матрице
£nW £12W •• • £i»W 0 £22 (*)••• £2п (*)
(1.173)
0 0 ...gnn(\)
В самом деле, рассмотрим первый столбец заданной матрицы /(А) и возьмём в нём какие-нибудь два элемента /р1(А), /^(А); если степень второго больше или равна степени первого, то можно написать:
А1(А)=Л>1(*)<?(*) + Ш.
где степень полинома ф(А) ниже степени /^(А) или же ф(А)==О. Умножая р-ю строку на полином ©(А) и вычитая из ^-й, мы получим эквивалентную матрицу, в которой Д1(А) заменён полиномом ф(А) более низкой степени или нулём. Очевидно, что такие операции мы можем продолжать до тех пор, пока в первом столбце будут оставаться хотя бы два полинома, не равных тождественно нулю; если, в частности, один из них окажется нулевой степени, т. е. приведётся к постоянной, то второй после указанной операции обязательно заменится нулём. В результате после конечного числа преобразований в первом столбце останется не более одного элемента, не равного тождественно нулю. Ту строку, в которой окажется этот элемент, мы поставим на первое место и этим закончим приведение в желаемый порядок первого столбца.
Теперь во всех строках, кроме первой, на первых местах стоят нули. Оперируя прежним способом над этими п—1 строками, мы достигнем того, что в числе их вторых элементов останется не более одного, не равного тождественно нулю. Соответствующую строку поставим на второе место и тем закончим приведение в нужный порядок второго столбца. Продолжая таким образом, мы и получим треугольную форму (173).
Совершенно так же покажем, что путем элементарных преобразований над строками укороченные а удлинённые прямоугольные полиномные матрицы могут быть приведены соответственно к экви-
s л
§ 1.22]
ТРЕУГОЛЬНЫЕ ПОЛИНОМНЫЕ МАТРИЦЫ
65
валентным формам
git (*) £12 (X) gin (Л) о &2 (*)••• £>»(*)
g(X) =
gllW gl2 W ••• glmW 0 g-22<M ••• g-lmtK)
gnn (^) о
(1-174)
gl, m+1 (A) ... gi„(X) ^2,771+1 (^) ’ ’ * S*.n(^)
(1.175)
0 0 ... SmW(X) gm,
m+1 (X) . •. gmn (x) И
Имеет место также следующая теорема Н. Н. Лузина [1Л]:
Если полиномная матрица имеет ранг г и один из её неисчезающих миноров г-го порядка принадлежит первым г столбцам, то для неё существует единственная, получаемая путём элементарных преобразований над строками, каноническая форма
gnW gi>(V ... glr(V glt r+1 (X) .
0 g-M $2r (*) g2, r+1 (X) .
• «mW
• gtnO^
g(M =
grAK) gr>
r+1 (X) .
0 0
• gm (^) . 0
(1.176)
О О
О О
О
О
О
и
0 0
о 0
1
О 0 ... О 0 ... О
которая отличается тем, что коэффициент старшего члена в каждом элементе gkk(K) (& = 1, ..., г) равен единице и что этот полином является старшим в своём столбце.
При доказательстве будем представлять себе, что матрица, по предыдущему, приведена к одной из трёх форм (173), (174), (175). Так как ранг субматрицы, образованной первыми г столбцами, не мог при этом измениться (§ 17), то и после преобразования эта субматрица должна заключать неисчезающий минор r-го порядка. Этим минором может быть только тот, который образован из первых г строк субматрицы, поскольку все элементы остальных её строк исчезают. Рассматриваемый минор равен произведению элементов glt (X), ..., grr (X), и потому ни один из них не может быть тождественно равен нулю. С другой стороны,, все элементы, не принадлежащие ни первым г строкам ни первым г столбцам, исчезают, так как если бы хоть один из них был отличен от нуля, то, добавляя соответствующие строку и столбец к первым г строкам^ и г столбцам, мы построили бы неисчезающий минор (г-[- 1)-го порядка, что невозможно.
5 Зак. 1474. Б. В. Булгаков
^ЛеМеЙТЫ МАТРИЧНОГО ИСЧИСЛЕНИЯ г
[гл. 1
Итак; матрица уже имеет вид (176). Остаётся выполнить остальные условия, входящие в определение каноническрй формы. Для этого представим элементы первых г столбцов в виде
S$k (X) = gkk (X) (А) + tyjk (Л);
при этом степень полинома tyk (Л) ниже степени gkk (X) или же ^а,(а) = 0. Вычитая й-ю строку, умноженную на <р^А (X), из у-й и проделывая это при данном k для j = 1, ..., k— 1, мы достигнем того, что полином gkk(\) станет старшим в своём столбце; коэффициент его старшего члена можно обратить в единицу путём деления й-й строки на этот коэффициент. Всю процедуру нужно. провести последовательно для всех столбцов от первого до r-го, в результате чего мы и получим каноническую форму.
Допустим теперь, что, оперируя со строками, мы получили для данной матрицы/(X) две эквивалентные канонические формы g(X), й(Х). Тогда таким же способом одна из двух последних матриц может быть преобразована в другую. Согласно § 19, найдётся такая квадратная матрица и (X) с определителем, отличным от нуля и не зависящим от X, что
. *(X)g(X) = A(X),
или, выписывая подробно,
Йц (X) (X) • • • (X) • • • и1т (X)
W21 (X) U22 (X) * • • П2г (*•) ••• (X)
^rl (X) иГ2 (X) . . . Urr (X) . . . Urm (X)
Wr+1,2 (X) ...
ttr+l,r (X) ... (X)
I ( J
I j
1 I
I I i ♦
।
w • • • (X) ... (Л) II
gn W Sa W • • • gir (*) gi,r+i(M • • • sin(X)
0 ^22 (*) • • • g-2rW g‘2,r+l U) • • • g2n (*)
• • grr (^) gr,r+l(^) • • • grnO^
0 0 ... 0
0 0 ... 0 0 ... 0
fill W a12 (X)... Л1г (X) ht ,r+l (X) ... hln (X) II
О й22 (X) ... й2г (X) - h 2,r+l (X) ... ^2П w
0 0 .../^(X) ЛГ>Г+1(Х) ... ЛГИ(Х) .
о о ... о о ... о
о о ... о о ... о
§ 1-221
ТРЕУГОЛЬНЫЕ ПОЛИНОМЙЫЕ МАТРИЦЫ
67
Умножая все строки матрицы и (Л) на первый столбец в найдём:
йц (^) Sit (^) = Й21 (^) Sii (^) = • • •» #mi W Sii W = О*
Первое из этих соотношений показывает, что степень ЛП(Х) больше или равна степени £*ц(Х). В силу равноправия матриц g(X), ^(Х) мы могли бы получить и обратное неравенство, откуда следует, что степени полиномов g,lt(X), /гц(Х) в точности равны между собой; а так как коэффйциенты их старших членов равны единице, то
#п = 1
и, следовательно, g1± (X) = (X). Остальные т—1 из предыдущих т
соотношений дают;
#21 = ... = #Ш1 = 0.
Если все строки #(Х) умножить на второй столбец в g*(X), то
S12 (^) "I" W12 (^) S*22 (^) = ^12 (^)» W22 W S22 (^) = ^22 (^)»
#3*2 W S22 W = 0, • • • > Um2 (^) S22 W = 0*
Из второго и следующих соотношений заключаем, что
#22 — 1 > #32 — • * * — ит2 — ®
и S22 W = ^2-2 W* Первое соотношение показывает, что так как степени полиномов g12(X), ^12 W должны быть ниже степени полинома S22 (X) = Й22 (X), Т0
#12 = 0-
Продолжая таким образом, убедимся, что
#(Х) =
1 0 ... 0 #1>Г+1 (X) . . . #17/2. (X)
0 1 ... 0 #2,г+1 (^) • • • #2w (^)
0 0 ... 1 иг> 1 (X) ... urm (X)
0 0 ... 0 #г+Ъг+1(Х) . •. #г+1,1»(^)
0 0 ... 0 #ш,г+1 (^) • • • Нтт (^)
и> следовательно, g(X) = /?(X), что и доказывает единственность канонической формы, полученной путём элементарных преобразований над строками.
Аналогично предыдущему, можно доказать, что путём элементарных преобразований над столбцами любая квадратная полиномная матрица может быть приведена к эквивалентной треугольной матрице (173), а укороченная и удлинённая — соответственно.
5*
68
ЭЛЕМЕНТЫ МАТРИЧНОГО ИСЧИСЛЕНИЯ
[гл. 1
к формам'.
£(А) =
g^ =
£и0-) 512 (*) ••• 5i»(*)
о ••• g2n(V
о О ... ^(Х)
gn+V 1 (^) g-n+l, ••• Sn+l.nO’)
gml (^) gm2 • • • gmn
И
gnW giz(M - • • gimW 0...0
0 g22(.V • • • ?2m(X) 0 . . . 0
(1.177)
(1.178)
0 0 ... gmm(K) 0 ... 0
Если, в частности, имеем неособую квадратную матрицу или удлинённую матрицу, ранг которой равен числу её строк, то эквивалентная форма может быть выбрана таким образом, чтобы коэффициент старшего члена в каждом полиноме gjj(k) был равен единице, а сам этот полином был старшим в своей строке*, в этом случае эквивалентная форма определяется единственным образом.
Оперируя, по предыдущему, как над строками, так и над столбцами, можно, очевидно, привести любую полиномную матрицу ранга г к эквивалентной форме
guW 512 W • • • glr W 0...0
o ^(X) ... feW 0 ... 0
g(v=
0 0 ... grr(X) 0 ... 0
0 0 ... 0 0 ... 0
(1.179)
0 0 ... 0 0 ... 0
где коэффициент старшего члена в каждом из полиномов gtl (X), ..., grr (X) равен единице. Произведение этих полиномов равно старшему детерминантному делителю Dr(X) заданной матрицы*).
В нижеследующих примерах элементарные преобразования записаны как умножения на квадратные матрицы с определителями, отличными от нуля и не зависящими от X.
*) Относительно дальнейших упрощений см. А. И. Мальцев [1Л], стр. 154.
§ 1.22]
ТРЕУГОЛЬНЫЕ ПОЛИНОМНЫЕ МАТРИЦЫ
69
Пример 1. Для матрицы
/(М =
2X^ + 3 2X4-1
Х2 —2 Х4-2
имеем каноническую треугольную форму
а(Х)/(Х) =
причём
«(Х) =
Пример 2.
/(Х) =
где
det«(X) = -5-. О
«(Х)/(Х) =
det а (X) = — i.
О
9
1 О О 1 о о
Здесь миноры второго порядка в/(Х) не имеют никаких общих множителей, кроме 1, а потому D2(X) и элементы ^ц(Х), ^22 М канонической формы равны единице.
Пример 3.
/(*) =
Здесь D2 (X) = К — 2, а потому каноническая форма будет
причём
«(Х)/(Х) =
1 О О
а(Х) =
О .1
О X —1
I -X
det а(Х) = — 1.
О
—1
1
70
ЭЛЕМЕНТЫ МАТРИЧНОГО ИСЧИСЛЕНИЯ
[гл. 1
Пример 4.
Х2 X +1 1 о Х2 + х х к х + 1 1
Ранг матрицы равен 2, старший
детерминантный делитель D% (X) = X.
f(k) =
—1 — 1 X + 1
X О
/(*) =
X X —1 —Х2
О 1 О
О О
X о о
о о 1 о о о
§ 1.23. Элементарные делители диагональных, кваеидиаго-нальных и некоторых треугольных полиномных матриц. 1°. Рассмотрим диагональную полиномную матрицу
(1.180)
* fnW
и обозначим через а, а', ... различные между собой корни полиномов (X), ..., fn (X); тогда
4(X) = fe/X-ap(X-a'p ..., (1.181)
причём, в отличие от (163), мы здесь не предполагаем, что числа е$ связаны неравенствами (164). Однако элементарными делителями матрицы /(X) будут те и только те из степеней линейных множителей X — а, X — а', ..., которые входят в /ДХ), но не приводятся к единице. Для доказательства достаточно проследить процесс образования детерминантных делителей D± (X), D,2 (X), ...
2°. Пусть теперь /(X) есть квазидиагональная полиномная матрица и Л(^) обозначают, вообще, уже не элементы, а квадратные субматрицы. Тогда совокупность элементарных делителей матрицы /(X) состоит из элементарных делителей всех субматриц Для доказательства достаточно привести каждую субматрицу к какой-либо диагональной форме с теми же самыми элементарными делителями. Такое приведение всегда может быть выполнено с помощью элементарных преобразований, которые, благодаря виду матрицы /(X), могут рассматриваться как элементарные преобразования всей этой матрицы в целом.
3°. Рассмотрим далее треугольную полиномную матрицу первой степени
£(Х) = ЕХ — с, (1.182)
§ 1.23] ЭЛЕМЕНТАРНЫЕ ДЕЛИТЕЛИ НЕКОТОРЫХ МАТРИЦ
где с есть постоянная треугольная матрица с равными диагональными элементами:
а 711 Tai • • • 7n-i,i
— 0 а 712 •• • 7п—2,2 /1 1 оол
0 0 0 ... а
Обозначая через у1} представить с в виде
• •» 7n-i косые ряды (§ 2), мы можем
с = £«-{-7’
где
7 = 7i+ — +7n-i-
Покажем, что если ни один из элементов (й = 1, 2, ..., п:— 1) первого косого ряда 7, не равен нулю, то матрица g(k) имеет единственный элементарный делитель (X— а)п.
В самом деле,
0 X — а — у12
g(X) = £(X — а) — 7 =
0 0 0
7n-i,i 7п—2,2
X — а
откуда видно, что
и, следовательно,
det g(X) - (X — а)” D№(X) = (X-a)w.
Затем, согласно (74), присоединённая матрица для g(X) может быть представлена в виде
Отсюда
G (X) = Е (X — a)”-1 + (X — a)”"2f + ... + 7*-1.
G (а) = f1 = (71 + • • • + Tn-i)”’1 = 7?" Х>
так как при развёртывании (п—1)-й степени выражения в скобках все члены, за исключением y*-1, обратятся в нуль по правилу умножения косых рядов (§ 2, пример 1).
Применяя повторно формулу (34), найдём:
0 0
G (а) = 7”-1 =
711712 • • •‘71, п-1 0
0 0
0 0 ... О
72
ЭЛЕМЕНТЫ МАТРИЧНОГО ИСЧИСЛЕНИЯ
[ГЛ. 1
т. е. все элементы матрицы G(a), кроме того, который расположен в правом верхнем углу, равны нулю. Так как этот последний равен Тп • • *11,п-1 и» в СИЛУ сделанного предположения, отличен от нуля, то и G(a)=£0. Следовательно, элементы матрицы G(X),- а значит, и миноры (п—1)-го порядка матрицы g(k) не имеют общим множителем никакую степень бинома X — а. Поэтому
и инвариантные множители матрицы g(k) будут
Зд)=1........
Еп (X) = = (X - «)*.
ип-1 КК)
Отсюда вытекает, наконец, что единственным элементарным делителем будет (X — a)w, что и требовалось доказать.
4°. Пусть имеем теперь полиномную матрицу первой степени
g’(X)=EX —А, (1.184)
где А есть постоянная треугольная квазидиагональная матрица
1
А =
(1.185)
т
с субматрицами
о
г
Ъ1(<) •••
Т12(<) ••• Тег-2,2(<)
(1.186)
О
о о
при этом Хг- суть постоянные, — порядки субматриц, —треугольные матрицы, у которых все элементы нулевого косого ряда равны нулю.
В этом случае матрица g(X) может быть представлена в виде
gi<A)
g,(X)
и сама будет треугольной и квазидиагональной; её порядок есть п = + ... exi
а субматрицы имеют форму
gi (X) = Еч (X — X,) — 7 «> (i = 1.........Т),
§ 1.24] ЭКВИВАЛЕНТНОСТЬ ПОЛИНОМНЫХ МАТРИЦ ПЕРВОЙ СТЕПЕНИ 73
которую мы уже рассматривали выше. Поэтому если ни один из элементов первых косых рядов субматриц Ь* не равен нулю, то элементарными делителями матрицы g(k) будут степени (X— ki)&i (1=1......*)•
§ 1.24. Эквивалентность и канонические формы полиномных матриц первой степени. Пусть имеем две квадратные полиномные матрицы первой степени
f (X)= яХ “4“ fi (^)== ^1»
через a, av b, Ьг обозначены квадратные матрицы того же п-го порядка с постоянными элементами, причём первые две предполагаются неособыми. Матрицы /(X), /t(X) также являются неособыми, так как коэффициенты при старших степенях кп в развёрнутых выражениях определителей А (X) == det/(X) и Дх (X) = detj^ (X) равны, очевидно, det а и detat. Если полиномные матрицы /(X), /t(X) эквивалентны, то, согласно общей теории (§ 19), можно найти такие неособые полиномные матрицы с определителями, не зависящими от X, что путём умножения на них слева и справа матрица /(X) преобразуется в ДСХ).
Можно доказать*), что в рассматриваемом специальном случае найдутся, в частности, матрицы и, v с постоянными элементами, . осуществляющие это преобразование, так что
А (X) = Uf(k) v,
откуда
ar — uav, b1 — ubv. (1.187)
Иными словами, матрицы и, v решают задачу об одновременном приведении а и b к аг и bv Необходимым и достаточным условием такой приводимости является, как сказано, эквивалентность матриц /(X), А(Х) или, что сводится к тому же, совпадение их инвариантных множителей или элементарных делителей.
В частности, за /х(Х) можно принять треугольную квазидиаго-нальную матрицу g(X), рассмотренную нами в п. 4° предыдущего параграфа и имеющую те же элементарные делители (X — к^е* (Z= 1, ..., т), что и /(X):
a±k -\~b1 = g(k) = Ek — А.
Отсюда
а1 = £’, Ь± =—А и
иа*о = Е, ubv — — А, (1.188)
*) См. рл], стр. 255 и след.
74
ЭЛЕМЕНТЫ МАТРИЧНОГО ИСЧИСЛЕНИЯ
[ГЛ. 1
так что в данном случае матрицы я, v решают задачу об одновременном приведении аи&кЕи —А.
Пользуясь произволом в выборе недиагональных элементов матрицы А, можно брать её в различных частных формах. Возьмём, например, А = J, где J есть каноническая квазидиагональная матрица Жордана
(1.189)
с субматрицами
Ь 1 ... О О
V
О Xi ... о о
“1“
(Z=l, ...,т); (1.190)
Xi 1
О Xi
о о о о
при этом ve^ обозначает первый косой ряд порядка составленный из единиц. В этом случае, при надлежащем выборе матриц и, v,
uav = Е, ubv = — J,
(1.191)
Докажем, что если все элементы матриц а, b действительны, то можно выбрать и и v также и таким образом, чтобы
uav = Е, ubv = — Q,
(1.192) .
где Q есть матрица Кейли (§ 16) с действительными элементами. В самом деле, в этом случае мы можем разбить все элементарные делители матрицы f(X) на группу из ч/ элементарных делителей, соответствующих действительным корням ха(з=1, т') уравне-
ния Д (X) = О и на две группы по т" делителей, соответствующих комплексным сопряжённым корням Qh±i<&h (Л=1, ...» т"). При данном способе нумерации каждый корень повторяется столько раз, сколько ему соответствует элементарных делителей: Субматрицы, из которых, согласно (185) и (186), построена матрица А, также разобьются на три группы:
(I) Ах, ..., Ax'j (II) A/j'-j-i, ..., Ах'4-х";
(III) Ат' ^-х"-}-!» • • • > Ах' -j-2T,r,
при этом соответственные субматрицы второй и третьей групп можно путём надлежащего выбора недиагональных элементов сделать сопряжёнными друг другу. Поэтому, образуя из этих групп три квазидиа-
§ 1.24]
ЭКВИВАЛЕНТНОСТЬ ПОЛИНОМНЫХ МАТРИЦ ПЕРВОЙ СТЕПЕНИ 75
гональные
матрицы, мы можем написать:
(1.193)
где е и со составлены из действительных и мнимых частей элементов
матриц, стоящих в правых частях второго и третьего равенств. Матрица Д представится теперь в новой коагулированной форме
х
О
О
О
О
О
8-----40)
Но мы показали в § 16, что эта форма подобна матрице Кейли
(1.194)
и потому найдётся такая матрица v%, что
^^ = Q.
С другой стороны, при некоторых 44t,
uxavr = Е, u1bvl = — Л и, следовательно,
= —Q.
Обозначая
zz = ^1rz1, ^ = ^2,
мы и получим соотношения (192), которые хотели вывести.
Можно показать, что матрицы и, ф в этих соотношениях всегда могут быть выбраны таким образом, чтобы их элементы были действительны. При построении матрицы Q можно, в частности, предполагать, что Д = J.
Если все элементарные делители линейны, то их общее число равно числу п корней уравнения A (X) = 0, субматрицы Д$ сводятся к корням Х$ и матрица Д получает простую диагональную форму
к
76 ЭЛЕМЕНТЫ МАТРИЧНОГО ИСЧИСЛЕНИЯ [ГЛ. 1
выделяя группу действительных корней xff(a = 1, ..s') и две группы комплексных сопряжённых ± (Л = 1, s"), мы можем, по
предыдущему, образовать матрицу Кейли (194), причём её субматрицы будут также иметь простую диагональную форму (149).
§ 1.25. Дифференцирование матриц. Пусть
/(*)= 114*(*)II («Х»)
есть матрица, элементы которой являются полиномами или, вообще, какими-нибудь непрерывными и дифференцируемыми функциями скалярного аргумента X. При переходе от X к ХЦ-ДХ элементы получают приращения
Д4й=4«^+ДА)-4*(х),
и мы можем написать:
д/=/(х+дл)-/(Л)= П4* (Х+ДХ)|| -114^)11 = цд/^п.
i
£
Производная от /(X) определяется обычным образом как предел отношения Af/kk при ДХ->0, и потому df dfjk
dk dk '
Для производной от суммы мы имеем обычную формулу d । ч df i dg
(1.196)
<1
(1.197)
но, вследствие некоммутативности умножения,
(1.198)
и аналогично для произведения нескольких матриц. Для производных от степеней квадратных матриц мы имеем такие формулы, как
i(/8) = f/2+/f/+/2f- (1.199)
Дифференцируя соотношение
ff~x = E, находим:
df 1 fdf-i~ dkJ dk
откуда получается формула для производной от обратной матрицы
= (1-200)
5
§ 1.261
ХАРАКТЕРИСТИЧЕСКИЕ ЧИСЛА
77
Рассмотрим теперь случай, когда квадратная матрица а играет роль аргумента при дифференцировании.
Если Р(а) есть скалярный полином от а, то естественно понимать под Р^(а) матрицу, которая получается из /n-й производной р»(Х) полинома Р(Х) путём замены X через а. С помощью этого определения можно обобщить на матрицы формулу Тейлора для полиномов, а именно: если а, b суть коммутативные квадратные матрицы одного и того же порядка, то алгебра полиномов, содержащих только эти две и единичную матрицу Е, формально тождественна со скалярной алгеброй. Поэтому если Р(а) есть полином степени 5, то
= P(a) + lp'(a)d + lp"(a)^+... 1(1.201)
Эта формула, в частности, всегда применима, когда а или b есть скалярная матрица, так как в этом случае коммутативность обеспечена.
§ 1.26. Характеристические числа. Вернёмся к рассмотренному в § 13 линейному преобразованию пространства
✓ у = ах,
производимому квадратной матрицей а с постоянными элементами, и будем искать точки х, которые после преобразования лежат на той же прямой, проходящей через начало координат, что и до преобразования. Для таких точек мы имеем, очевидно, у — кх, где X — скалярный множитель; подставляя в предыдущее соотношение, получаем:
где
f(k)==Ek — а =
/(Х)х = 0,
а11 #12 * * * #1П
#21 #22 • • • #2п
#П1 #п2 • • • #пп
(1.202)
(1.203)
Так как каждый элемент матрицы-столбца /(Х)х должен быть равен нулю, то мы имеем систему п скалярных уравнений
п
2 /Л(Х)** = 0 0=1.............я). (1-204)
fc=l
эквивалентных матричному уравнению (202). Они линейны и однородны относительно хк и допускают решения, отличные от тривиального х± = ... = хп = 0, тогда и только тогда, когда определитель
78
ЭЛЕМЕНТЫ МАТРИЧНОГО ИСЧИСЛЕНИЙ
[гл. 1
системы
X ап а12 ... а1п
Д (X) = det (EX — а) =
a2i X а22 ... а2№
^пп
1 =Xn+fetxn-i4_ ... +kn_^kn (1.205)
I ! равен нулю. Таким образом, X должно удовлетворять уравнению
Д(Х) = О.
Матрица /(X) называется характеристической матрицей для а, определитель Д (X) и последнее уравнение — характеристическим определителем и характеристическим уравнением, а его корни Хр ...» Хт — характеристическими числами матрицы а. При этом мы пока сохраняем применённый ранее способ нумерации, состоящий в том, что характеристическое число Хв, которому соответствует элементарных делителей, записывается раз, так что Xff = Xff+1 =
• • • ~ —1*
Пусть х есть какое-нибудь нетривиальное решение уравнения
/(U * = 0,
(1.206)
получаемого из (202) при X — Xff. Очевидно, что столбец сх, где с — произвольный скаляр, также будет решением. Это значит, что если мы нашли одну точку, удовлетворяющую поставленному в начале геометрическому условию, то тотчас находим бесчисленное множество таких точек, заполняющих прямую, проходящую через начало координат. Эта прямая инвариантна относительно преобразования. Согласно общей теории линейных однородных уравнений *), число линейно независимых решений предыдущего матричного уравнения, эквивалентного системе
п
(/=1, .... п), (1.207)
fc=l
равно дефекту её матрицы /(ХД Так как, согласно § 18, этот дефект равен та, то мы можем обозначить линейно независимые решения через Va, Va¥1, ..., Ув+Т р мы будем называть их модальными столбцами. Общее решение уравнения (206) может быть представлено в виде
г,-1
х=5^+РК+р> (1.208)
р=0
♦) См., например, М. Б о х е р рл], стр. 54.
§ 1.26)
ХАРАКТЕРИСТИЧЕСКИЕ ЧИСЛА
79
где с9, св+1, •••’ — произвольные постоянные. Если есть
простое характеристическое число или кратное, но с одним единственным элементарным делителем, то ему соответствует один модальный столбец и одна инвариантная прямая. Если же есть кратное характеристическое число и та> 1, то мы имеем модальных столбцов и линейное инвариантное многообразие с таким же числом измерений. Так как t9^q9, где q9 есть кратность характеристического числа Хв, то общее количество т модальных столбцов не превосходит п.
Заменяя f(K9) в (206) его выражением и х через V9, получим:
(ЕЛа — а)Уа = 0 или
aVff=VA •••> *)• (1.209)
Обозначая через V матрицу типа п X Ъ составленную из модальных столбцов, и через d — диагональную матрицу порядка т
(1.210)
мы можем заменить предыдущие т соотношений
(209) следующим
эквивалентным им уравнением:
aV = Vd,
которому должна удовлетворять матрица У.
Характеристическая матрица f (Л) может быть приведена к треугольной форме, как это было сделано в § 24. Для этого нужно лишь в полученных там результатах заменить а и b соответственно через Ей —а. Тогда формулы (188) дают
uv = Е, — uav = — А, откуда и — ст-1 и
v-'av = A. (1.212)
Таким образом, каждая квадратная матрица с постоянными элементами подобна треугольной квазидиагональ ной матрице с теми же элементарными делителями. В частности, за матрицу А можно взять каноническую матрицу Жордана J и тогда при надлежащем выборе v
y-iav — J. (1.213)
Если все элементы матрицы действительны, то она подобна также некоторой матрице Кейли с действительными элементами,
80 ЭЛЕМЕНТЫ МАТРИЧНОГО ИСЧИСЛЕНИЯ [гл. 1
так что при надлежащем выборе матрицы v, которую можно при этом предполагать действительной, мы получим:
v^1av = Q. (1.214)
Геометрический смысл последних теорем состоит в том, что, согласно сказанному в § 13, всегда можно найти такую систему координат, в которой уравнение линейного преобразования будет иметь вид
т] = AS или, соответственно,
'0 = ^.
Если, в частности, все элементарные делители характеристической матрицы линейны, то для каждого характеристического числа мы имеем = qg, и потому t = п. Тот способ нумерации характеристических чисел, который мы применяли, совпадает теперь с .обычным, при котором каждое число выписывается столько раз, какова его кратность. Подобная матрица Д получает в данном случае простую диагональную форму (195); если же все элементы матрицы а действительны, то и субматрицы х, е, со подобной матрицы Кейли Q имеют простую диагональную форму. Матрица V, составленная из модальных столбцов, будет квадратной и, как можно показать, неособой, а матрица d совпадает с А. Поэтому уравнение (211) принимает вид
аУ=1/Д, (1.215)
откуда
у-1аУ = А.
Таким образом, если элементарные делители линейны, то мы можем в качестве матрицы, осуществляющей подобное преобразование а к форме А, принять матрицу V, и обратно.
В этом случае для вычисления столбцов Vg, можно кроме непосредственного разрешения уравнений (207), пользоваться ещё следующими соображениями. Вследствие линейности элементарных делителей, многочлен Dn_1 (X) будет заключать множитель (X — Этот множитель войдёт в каждый минор (п— 1)-го порядка матрицы f (X) и, следовательно, в каждый элемент присоединённой матрицы F (X). При X = Xff матрица F (X) будет обращаться в нуль вместе с производными до порядка qg— 2 включительно. Пользуясь соотношением /(X)F(X) = F(X)/(X) = E,A(X), дифференцируя его qg—1 раз, полагая Х = Хв и замечая, что (Xff) = 0, найдём:
/(у (Ь.) = 0, (U f (А.) = 0.
Сравнивая первое соотношение с (206), убедимся, что независимые столбцы матрицы (Хс) могут быть приняты за модальные. Можно показать, что этих столбцов будет как раз столько, сколько
§ 1.271
УРАВНЕНИЕ ГАМИЛЬТОНА-КЕЙЛИ
81
нужно, т. е. q„. Принимая во внимание, что матрица Р'Яя (Хв) имеет, таким образом, ранг q„, мы можем также согласно § 4 представить ей в виде
F(a’-i)(Xe) = K(s)r(e), (1.216)
где У(а, матрицы соответственно типов п X и q9 X я и
ранга q9. Подставляя в предыдущие соотношения, имеем:
f М V(ff) W(9) = 0, У(в) T(ff) f (Xff) = О,
откуда (§ 2)
f (К) = о> w(a) f (х.) = о.
Если же обозначить через Ул> ..., Уа+За_1 отдельные столбцы матрицы У(а) и через Wgi ...,' ITa+ga_i—отдельные строки W&, то
/(U% = o, = o (р = о> b ...» ^-1).
Из первого соотношения видно, что мы можем принять столбцы Vg, полученные описанным путем, за модальные*
В заключение параграфа покажем, что подобные матрицы имеют одни и те же характеристические числа одинаковых кратностей, а соответствующие характеристические матрицы — одни и те же элементарные делители.
В самом деле, если
а± — v^aV) то мы можем написать:
Д (X) ==г Ek — а± — v~xEvk — = (Ek — a) v — ^-1/(X)
Дх (X) = Д (X), где
Дх (X) = det Д (X).
Таким образом, характеристические определители матриц а, а± одинаковы, а характеристические матрицы подобны и, следовательно, эквивалентны. Отсюда и вытекает предложение, которое мы хотели доказать.
§ 1.27. Уравнение Гамильтона-Кейли. Для любого скалярного многочлена
п
Д (X) = X” + k^-1 + ... + kn_^ + kn = П (X - X.) (1.217) ст = 1
мы имеем по теореме Безу
ф (X, |Х) == = X™-1 + (н + *x) X”-2 4- • • • +
А ' [Л
_|_ (и^1 + б1Ип-2 +йл1) (1.218)
и
Д(Х) — Д(|л) = (Х — р)Ф(Х, |а).
6 Зак. 1474 Б. В. Булгаков
ЭЛЕМЕНТЫ МАТРИЧНОГО ИСЧИСЛЕНИЯ
[ГЛ. j
Заменяя pt квадратной матрицей а, получим матричное соотношение Д(Х)Е — Д(а) = (£Х — а)Ф(Х, а), которое также будет верным. Переписывая его в виде
Д(Х)£ = (ЕХ — а)Ф(Х, а)4-Д(а),
мы заключаем, что Ф (X, а) есть частное, а Д (а) — остаток при делении полиномной матрицы Д (X) Е слева на характеристическую матрицу
/(X) = FX —а.
Если, в частности, Д (X) есть определитель матрицы f (X), a F (X) обозначает её присоединённую, то из формулы
Д (X) Е = /(Х) F(X)
вытекает, что при делении, о котором шла речь, частное есть F (X), а остаток — нуль, так что
F(X) = Ф (X, а) = ЕХ*'1 + (а 4- ktE) 4~ ...
... 4-(а«-1-|-Л1ап-2+ ... 4- kn_xE), (1.219)
Д(а) = 0. (1.220)
Первое из этих двух соотношений даёт выражение присоединённой для характеристической матрицы в виде полинома от X и а, а второе носит название уравнения Гамильтона-Кейли и показывает, что каждая квадратная матрица с постоянными элементами удовлетворяет своему собственному характеристическому уравнению.
В случае, когда не все элементарные делители'характеристической матрицы первые между собой, многочлен Д (а) в уравнении Гамильтона-Кейли может быть заменён другим многочленом более низкой степени. В самом деле, в этом случае найдётся по меньшей мере одно характеристическое число Xff, которому соответствует более одного элементарного делителя, вследствие чего детерминантный делитель (X) будет отличен от единицы. Он будет множителем всех элементов матрицы F (X) и определителя Д (X), так что
F(X) = Dn_. (X) F. (X), Д (X) = Dn_± (X) Ared (X), откуда
/(X)F1(X) = EAred (X);
если степень OW-1(X) есть g, то Fx(X) будет полиномной матрицей степени п — g— 1, a Ared (X) — полиномом степени п — g, причём этот многочлен, очевидно, есть не что иное, как старший инвариантный множитель характеристической матрицы. Исходя из последнего соотношения, мы можем рассуждать совершенно так же, как в начале параграфа, заменяя лишь Д(Х) через Ared (X), и в результате получим
§ 1.27] УРАВНЕНИЕ ^аМиЛЬТОЙЛ-ЙеЙЛЙ §3
приведённое уравнение
Ared(a) = 0, , (1.221)
которые хотели вывести. По аналогии с выражением п
Д(А)=П(Х-Лв)
3 = 1
мы можем представить матричный многочлен А (а) в виде
А (а) = П (« — = (~ О” П /(U С1 -222)
3=1 3=1
так как перемножение линейных двучленов в обоих случаях производится по одним и тем же формальным правилам. Уравнение Гамильтона-Кейли примет вид п
П/(Х,) = 0; (1.223)
3 = 1
множитель /(ХД соответствующий ^-кратному характеристическому числу Хв, входит здесь q9 раз. Но если мы представим в такой же форме приведённое уравнение (221), то множитель /(XJ войдёт
лишь е9 раз, где е9 есть степень старшего элементарного делителя, соответствующего характеристическому числу Ха.
В заключение параграфа мы выведем некоторые необходимые в дальнейшем формулы, относящиеся к присоединённой матрице Л(Х)и её производным.
Если X остаётся произвольным, то мы имеем для F (X) выражение (219). Но если X совпадает с одним из характеристических чисел Xff, то, из (218),
и, согласно (219),
/?(и=
Д(|О 1
И ^з_|р.->а
(1.224)
где нужно сначала произвести сокращение дроби, а затем подстановку так как иначе в знаменателе получится особая матрица; в результате находим:
F(X.) == U (« — = (— О”-1 П /(хр. (1.225)
Р-#® РГ®
Эти формулы верны для всех характеристических чисел Xff, простых и кратных.
6*
84
5ЛеМей1ы Мд^РичйоГб ИСЧиСЛеЙиЯ
[гл. 1
С другой стороны, дифференцируя (218) по правилу Лейбница, имеем:;
^Ф(*. н) =
Ofc
_(_iyp|i!W-;W+P(_1y-(l>_1),-^a-+...+.^W;
. (к—n)p+1 V г (х—И)Р ‘ ~ х—и
если же Аа есть ^-кратное характеристическое число, то при р = О,
др - п х . Д(р.)
—- Ф (Ав, ц) = р!-------
ах? (и - ktf)p
откуда в качестве обобщения формулы (224) 1 Ыр)/^ Г Д(Н) 1 л
•» Ча
Если здесь произвести сокращение дроби и затем замену р. —> а, то получим:
-1- F(p) (А.) = {а - Ек^~ ₽-х Д. (а) =
= (—1)”-р-1 [ДАв)]«'_р_7(Х1)- • •/(^-1)/(Х4+7в).'. .f(kn)
(р = о, 1.......1), - (1.227)
где
= (Х-Х1) ... (Х-А^ИА-А^) ... (к — АД (1.228)
Следует заметить; что если степень старшего элементарного делителя, соответствующего характеристическому числу Aff, есть еа, то (А—Аа)^-’е» будет множителем детерминантного делителя DW-1(A) и матрицы Е(А). Поэтому значения производных Fp)(Aff), определяемые предыдущими формулами, исчезают при р= 1, ..., q9— е9— 1, что вытекает также из приведённого уравнения Гамильтона-Кейли. Ввиду этого достаточно было бы давать индексу р значения qa — e9i ..., q9 — 1.
Если воспользоваться соотношением /(А)Е(А) = ЕД(А), продифференцировать его и заметить, что f (А) = Е, то получится
/7(Х)+/(А)Е'(А)==ЕД'(А).
Если же теперь . полученное, соотношение умножим слева на F(A) и положим А = Аа, где Aff — простое характеристическое число, то найдём следующее выражение для [F(kff)]2:
[F(A,)p=F(A,)A'(X,). (1.229)
§ 1.28] ПРЕДЕЛЫ И РЯДЫ МАТРИЦ 85
С другой стороны, каковы бы ни были характеристические числа Х„ X., мы имеем из (223) и (225):
F(X,)F(XT) = 0 (а=£т). (1.230)
Пользуясь опять соотношением /(X)F(X)==F(X)/(X) = EA(X) и дифференцируя его р-{-1 раз, находим:
(р + 1) Ffr)(X)+/(X) F(p+1)(X) = ЕД(₽+1)(Х),
(р 4-1) F'9} (X) + Ffp+1) (X) /(X) = ЕД(р+1) (X).
Отсюда, умножая первое уравнение слева, а второе справа на F(k) и полагая X = Xff, где есть ^-кратное характеристическое число, получаем:
F (X.) F^ (X.) = Fр) (Хо) F (Хв) = 0 )
(р = 0, 1, ..., 9,-2), I
^P)(U-= ^р)(Ха) F(Xa) = -Ь Ури> (Xe) F(Xay (1’231)
' Г I 1
(р === Я<3 • • •)•
В. АНАЛИТИЧЕСКИЕ ФУНКЦИИ МАТРИЦ
§ 1.28. Пределы и. ряды матриц. Если элементы переменной матрицы стремятся к соответствующим элементам некоторой постоянной матрицы, то естественно назвать вторую пределом первой.
Бесконечный ряд из матриц одного и того же типа
ai + аз + • • • (1.232)
называется сходящимся, если сумма его т первых членов, представляющая матрицу того же типа, стремится к некоторой предельной матрице при zn-> oo; эта предельная матрица будет суммой ряда. Если элементы матрицы а действительны и меньше соответствующих элементов другой матрицы b того же типа, то будем писать я < Ь. Если элементы четырёх матриц a, b, с, d действительны и неотрицательны, то из а < b, с <d следует ас < bd, а из а Ь, с <d следует ас bd.
Матрицу с элементами, равными модулям соответствующих элементов матрицы а, будем обозначать | а | и называть модулем матрицы а. Очевидно, что
| а + b |< pa | +1 b |, | ab | < \а | • | b |. ! (Г.233)
Пусть ещё Ia, 1Ь, /с обозначают матрицы соответственно тех же типов, что и матрицы a, b, c = ab, причём все элементы матриц 1а, равны единице, а и |3 — положительны^ скаляры, — чцсдр
86
ЭЛЕМЕНТЫ МАТРИЧНОГО ИСЧИСЛЕНИЯ
[ГЛ. 1
столбцов в а, равное числу строк в Ь, и пусть
IйI < «4» IЪ | < р/ь; тогда
\ab\<a$nlc. (1.234)
Если вместе с рядом (232) сходится и ряд
|^11 + |л21 + 1азИ" • • •> ' (1.235)
то мы будем называть первый абсолютно сходящимся. Если | ai | где bi — матрицы с действительными неотрицательными элементами, образующие сходящийся ряд
+ ^2 + ^з • • •»
то ряд (232) сходится абсолютно.
В качестве обобщения матричного полинома мы можем построить правый ряд по степеням квадратной матрицы z с матричными коэффициентами а0, av а.2, ...; его сумма будет аналитической функцией от z в той области матриц, где ряд сходится:
ф (z) = a0-j- a^z -j- a2z2 ... (1.236)
Аналогичным образом можно образовать левый ряд
ф (z) — а0 + za± + z*a2 + ... (1.237)
Заменяя z скалярной матрицей ЕХ, получим матричный ряд по степеням скаляра
ф (X) = а0 + ахХ + а2Х2 + ..., (1.238)
являющийся обобщением полиномной матрицы. Каждый элемент ©(X) представляет скалярный ряд по степеням X; наименьший из радиусов сходимости этих рядов г и соответствующий круг сходимости назовём радиусом и кругом сходимости матричного ряда (X).
Покажем, что ряды ©(z), ф(з) сходятся абсолютно в области
где п — порядок матрицы z, а I—квадратная матрица, все элементы которой равны единице. Для этого заметим прежде всего, что г есть также радиус сходимости ряда
I ао I Н“ I | X -|-1 а21X2 • • •
Обозначая через г' какое-нибудь число, заключённое . между наибольшей из величин |^|я и г, где z^k— элементы одной из матриц, принадлежащей области (239), получим для этой матрицы;
1
§ 1.28] ПРЕДЕЛЫ И РЯДЫ МАТРИЦ 87
отсюда, с помощью (233) и (234),
Таким образом, общий член ряда
не больше соответствующего члена сходящегося ряда
что и доказывает наше предложение для Аналогичным образом проводится доказательство для
В дальнейшем (§ 30) мы получим более сильный критерий сходимости, связанный с характеристическими числами матрицы z.
Частным случаем матричного степенного ряда является скалярный ряд по степеням матрицы
Ф (z) = + ktz + k.2z* + ..., (1.240)
коэффициенты которого — числа.
Если соответствующий степенной ряд от скалярного аргумента ф (X) = kQ + ftxX + fe2X2 + ... (1.241)
представляет целую функцию, т. е. сходится при всех X, то г = оо и, на основании предыдущей теоремы, ряд Ф(г) сходится абсолютно для всех матриц z.
Поэтому мы можем, с помощью тех же рядов, что и в случае скалярного аргумента, определить для всех квадратных матриц функции
cos z=E — .... (1.243)
sin.? = .?—-i- z8 + -gj- &—..., (1.244)
причём
eiz — cos z 4- i sin z. (1.245)
Предельным переходом из формулы (133), относящейся к скалярным полиномам от матрицы, подобной данной, получается:
. 4У"1Ф(^)^==:Ф(<У"1^)- (1.246)
88
ЭЛЕМЕНТЫ МАТРИЧНОГО ИСЧИСЛЕНИЯ
[гл. Г
Пример 1. Если Л — диагональная (квазидиагональная) матрица с диагональными элементами (субматрицами) ..., лп, то, так же как в § 15,
Ф(АХ)
Ф(А) =
(1.247)
Пример 2. Если коэффициенты ряда &0, kr, ... действительны и Q — матрица Кейли (141), то
Ф(х)
Ф(С) =
Re Ф (в ta Ф (в Ц- zo>)
О Re Ф (в 4“ta Ф (в +1®) О — Im Ф (в zoo) Re Ф (в z‘oo)
(1.248)
Эта формула остаётся верной для случая, когда х— квадратная субматрица порядка s', а в, оо — квадратные субматрицы порядка s".
В частности, обозначая через t какое-нибудь действительное число, имеем для всех таких коагулированных матриц Q
(1.249)
О —Re^'84*^)^
при этом, если х, в, оо — диагональные матрицы (149), то три субматрицы, из которых образована , сами являются диагональными и выражаются следующим образом:
е 3 e^f cos
Re — e9t cos w/ =
> (1.250)
8 .nt j.
e, ° cos t
sin (b±t
Im f sin go/ =
e.»>Z . i e 3 sin
Пример 3. Пусть 7 есть треугольная матрица n-го порядка, определяемая согласно (72). Так как её степени, начиная с n-й, рав-
ны нулю, то все аналитические функции от неё сводятся к полиномам;
§ 1.291
ИНТЕРПОЛЯЦИОННЫЕ полиномы
89
например,
₽Т = ^+т1Т+ (1-251)
1п (Е+Т) = Т 7 - j I2 + • • • + Т”"1’ С1 -252)
(Е4-7)от=^+т7+/”(г-71) 12+ - •• +
. т(т— 1)...(от— л + 2) , „„ч
Н1.2... (п-1) * ’ (к2&<5)
где т— какой-нибудь скаляр.
Приведение к полиномам аналитических функций других матриц будет рассмотрено ниже (§ 30).
Если z— неособая матрица, то можно рассматривать правый и левый ряды Лорана
<?(z) = ... + + ..., (1.254)
6(2)=... + £“9я_2 + + z<*a.2-\- ... (1.255)
Заменяя z скалярной матрицей Ек, получим ряд
ф(Х) = ... -р 4“ а2^2 + • • • (1.256)
Каждый элемент о (А) есть скалярный ряд Лорана по степеням X; общая часть колец сходимости этих рядов, если она существует, представляет собой также кольцо в плоскости комплексного переменного X, которое мы назовём кольцом сходимости ряда ф(Х).
Частным случаем матричного ряда Лорана является скалярный ряд Лорана по степеням матрицы
Ф(г)= ... +k_2z^^k^1z-1 + kQE + k1z^k^+... (1.257)
§ 1.29. Интерполяционные полиномы. Эти скалярные полиномы понадобятся нам при изучении матричных полиномов и других функций от матриц.
Пусть r плоскости комплексного переменного X задано п точек ^х» • • •» кп. Если предположить сначала, что все они различны, то полином (п— 1)-й степени
п
Г()Л . V' /1 \ (^ Xj) ... (X Xff_t) (X Xff.f_t) ... (X Xn) .. neo\
(Л) ~ 9 (А, ~ М ... (X.- Х^) (X. - W ... (Aff — Х№) <1’258)
принимает в этих точках заданные наперёд значения ф (Xff). В самом деле, например, при X = Хр тот члей суммы, для которого а = р, приводится к .ф (Хр), а все остальные обращаются в нуль. Полисом L (X) называется интерполяционным полиномом Лагранжа.
90
ЭЛЕМЕНТЫ МАТРИЧНОГО ИСЧИСЛЕНИЯ
[ГЛ. 1
Обозначая
Дв (X) = (X—X,) ... (X—Х,_^ (к — Хв+1) ... (X — ХД (1.259)
ев(Х) = Д,(Х)/Д.(Х,), (1.260)
представим £(Х) в виде
L (X) = S ф (X.) е. (X). (1.261)
ст=1
Обратимся теперь к общему случаю, когда не все п точек обязательно различны. Мы можем тогда разбить их на N групп так, чтобы qa точек, составляющих какую-либо из этих групп, совпадали между собой и только между собой: Xff = Xff+1 = ... = X(Xfaff_1. Пусть с?(Х) есть скалярная аналитическая функция комплексного переменного X, регулярная в некоторой области, заключающей все точки Xff. Выразим эту функцию через посредство значений, принимаемых ею и её производными до (qQ—1)-го порядка в точках Хв.
Если
Д(Х) = (Х —Хх) ... (X —Х„), то функция <р(Х)/Д(Х) не имеет в рассматриваемой области других особых точек 'кроме полюсов и может быть представлена в виде
<L262>
а
При этом S(X) есть функция, регулярная в области; штрих при 5 указывает, что суммирование распространяется лишь на индексы
0^=1, •••> “Ь • • • (7®#—1 “Н 1 > (1.263)
соответствующие N различным точкам; Оо (й—г-) — бесконечная часть, относящаяся к полюсу X = Х9. Мы можем представить её в виде в.-1'
° ° (х=х;)= S (x—ljp+i =oi> • • •»aN>’
если подставить это выражение в (262) и полученное соотношение умножить на (X — Xff)% то
р=0
где Дв(Х) определяется согласно ности точки Хв и обращается в водными до (q9—1)-го порядка.
“ Дв(X) У*
(228), а фа(Х) регулярна в окрест-этой точке в нуль вместе с произ-Поэтому Г ?(Х) ‘
! L Ла (A) J
<5
ИНТЕРПОЛЯЦИОННЫЕ полиномы
91
§ 1.29]
Таким образом,
<р(Х) =
Д(Х)
у,-1
= S(A) + 2 S(?s —р —1)!
9 Р = 0
ню] 1 эх4’_р_1 дв(Х)]х=х (х—ха)р+1'
а
(1.264)
Мы можем написать также
<р(Л) = Д(Х) + 5(Х)Д(Х), (1.265)
где выражение
Д(А) =
1 (^-р-1)!
' Л"р 1 <? (X)
dxe»_p_1 д,(Х)
Дв(А)(Л-Л>-Р-х
(1.266)
представляет собою полином (п—1)-й степени. Функции S(X), Д(Х) регулярны в области, причём вторая исчезает при X = Xff вместе с производными до (q9— 1)-го порядка. Из соотношения (265) следует поэтому, что при том же значении X должны совпасть как значения функций ©(X), А(Х), так и значения их производных до (q9—1)-го порядка. Таким образом, это соотношение даёт искомое представление функции ©(X), а А(Х) есть интерполяционный полином, принимающий, вместе с производными до (q9—1)-го порядка, заданные наперёд значения в каждой из точек Xff. Мы будем называть его конфлюенпъ-ным интерполяционным полиномом или конфлюентной формой полинома Лагранжа.
Он может быть также преобразован следующим образом:
'«=Г
<Л~Р 1 ? (X,) 1 Д(Х) д* 1 ах^-р-1 Д, (X.) J (- 1)рр! ЭХР X - х„
р 1 ?(Х,) 1 д? 1 .dx^-p’4(UJ U₽x-x,
S' Д(Х) Л 1 <?(ХД)
(^-l)!dXg’-1 Д,(Х0)(Х-Ха)
«а-1 а -р-1
_ у' у А<х> М а) А2____________________________1______
Zl ЛрЦ^-р-!)!* Д,(Хд)(Х-Х,)-
g р=0
92
ЭЛЕМЕНТЫ МАТРИЧНОГО ИСЧИСЛЕНИЯ
[ГЛ. 1
Пользуясь тем, что при |л = Ха все производные до (qa—1)-го порядка от Д(|л) исчезают, вводя Ф(Х, у.) согласно (218) и обозначая
% (X) =
Д(Х) (9, - 1)1
Л"1 I
Д,(Хв)(Х-Х.)
“ (9,-1)!
(1.267)
Д(М dg° Р 1 1
l’₽W (9,-p-l)l^«,-P-1 Д,(Хв)(Х-Х,) а
1 (9,-р-1)! (Р=1>
' а9» р 1 ф (х, и) ~
• • • > 9, 1)>
(1.268)
получим окончательную форму
в,-1
L (X) = £ [© (Хв) в, (X) + J] -L ?'р) (X.) т)ар (X)] , ' (1.269)
а р = 1
в которой выделены множители при задаваемых наперёд значениях функции ?(Х) и её производных. В случае, когда все различны, мы имеем qa=l, ев(Х) = Да(Л)/Дв(Ха) и конфлюентный полином обращается в полином Лагранжа.
Для последующих приложений выведем некоторые свойства функций eff(X), TQop(k). При этом будем писать:
П1О(1Д(Х)
и говорить, что /(Л) сравнимо с g(X) по модулю Д(Х), если разность f(k) — g(k) делится на Д(Х), так что
/(X) = ^(X) + S(X)A(X).
Если дано второе сравнение
А (X) Si (X), mod Д (X),
то, как легко проверить, modA(X), /(X)/1(X)sg(X)a(X), modA(X), т. e. сравнения можно складывать и перемножать.
Формула (265) может быть написана в виде
©(Х)==А(Х), modA(X). (1.270)
Предполагая сначала все X, различными, применим эту формулу к функции © (X) = 1,
§ 1.2§] ИЙТЕ^ПОЛЙЦИОНЙЫЕ ЙОЛИЙ0МЫ §3
В рассматриваемом случае А(Х)— полином Лагранжа и потому
S e„(X)=s 1, modA(Z), 0 = 1
а так как eff(X)— полиномы (п—1)-й степени по X, то лева# и правая части не только сравнимы, но и тождественны; применяя знак s без указания модуля для обозначения сравнимости по любому модулю, т. е. тождества, получим: -
п
(1.271) 0 — 1
Из выражения для еа(Х) видно, что если то произведение sa(X)eT(X) делится на Д(Х), так что
еЖ(Х>0, modA(X) (з^=т). (1.272)
Умножая обе части тождества (271). на еа(Х) и пользуясь только что полученным сравнением (272), найдем:
К (X)]2 = е, (X), mod Д (X). (1.273)
Обращаясь к общему случаю, когда не все Xto различны, мы, так же как и выше, получим тождество
(1-274) а
Развертывая производную в формуле (267) для функции еа(Х), убедимся, что эта функция есть линейная комбинация выражений
д W Йг Г=Г = Р!Д ~ Х«)Р+1 = Р!Д‘ <Х> -1
Оку, ла о
(.Os^psg^—l),
т. е. представляет произведение Да(Х) на полином от X — Хв не более чем (q9—1)-й степени. Следовательно,
ee(X) (X) = О, modA(X) (Ха=#Хт), (1.275)
откуда, так же как и выше, выводим:
[Stf (X)]2 = etf (X), modA(X).
Очевидно, что во всех сравнениях, относящихся к случаю, когда не все Хв различны,, мы могли бы вместо modA(X) написать ftiod Дгеа (X), где Дгеа(Х) есть полином, состоящий из тех же множителей X — Xff, что и Д (X), но в степенях е9, меньших или равных q0.
Если <р(Х) — полином, то мы имеем вследствие (274)
?(х) = 2'<?(Х)8а(Х)= а , «а"1
= 2 [<? (U + 2 тг?<₽) <х’)(Х “ Х’)Р]8»(Х)+R (х)’
а р = 1
§4 ЗлеМейТы МатРичноРо исчисления [Гл. 1
где /?(Х) имеет вид
S'(x-xa)e’Ce(X)8e(X), ff
а Св(Х)— полиномы. Поэтому
z е*-1
? (Л) S £'[<? (X.) + 2 7Г ?(Р) - V J е, (A), mod Дге1 (X).
а р=1
Сопоставляя со сравнением (270), в котором мы заменим кон-флюентный полином L (X) его выражением (269), а вместо mod A (X) напишем modArea(X), получим:
/а"1 ea-i
2' 2 к (z) К 2 тг <х -raod Дге*(Х)-
СТ р = 1 СТ р = 1
а так как значения <?(р\Ха) произвольны, то можно сделать одно из них равным единице, а другие нулями, что даёт:
т|вр (X) = (X — Xff)p (X), mod Ared (X)
(p = 1, ...» в9 1), mod Are!i (X) I
(p = e9, • ••> 1)* ]
(1.276)
§ 1.30. Формула Сильвестера для матричных полиномов и степенных рядов. Пусть имеем сначала п различных комплексных чисел Хр ..., Xw. Применяя формулы (261), (265) к функции ср(Х) = Хр, найдём:
п
F-2$,(a)+S(W
ст=1
Если заменить здесь X квадратной матрицей z, имеющей своими характеристическими числами Хр Х№ и своим характеристическим полиномом А(Х), то получаемое соотношение
п
2 (*)+$(*) де?)
ст=1
останется тождеством, так как S(z), A(z) суть полиномы со скалярными коэффициентами и их перемножение производится по тем же формальным правилам, что и при скалярном аргументе. Но так как z удовлетворяет уравнению Гамильтона-Кейли A(z) = 0, то
§ 1.30] ФОРМУЛА СИЛЬВЕСТЕРА ДЛЯ МАТРИЧНЫХ ПОЛИНОМОВ И РЯДОВ 95 предыдущее соотношение получает вид:
п
? = (1.277)
а=1
где se = eff(z) или, согласно (224) и (260),
8. = Д. (г)/Д, (Xff) = F(X,)/Aa (X.), (1.278)
причём F(X) обозначает присоединённую характеристической матрицы /(X) = FX:—z.
Если теперь ©(х) есть какой-нибудь правый матричный полином © (z) = а0 + a±z4-a2z24" • • • 4" aiZL,
то, полагая в (277) р — 0, 1, 2, ...» Л, умножая обе части хлева на а0, av ..., aL и складывая, получим формулу Сильвестера
п
?(*)=S?(Ue„ (1.279)
Ст=1
которая сводит любой правый матричный полином к такому же полиному (п—1)-й степени.
Эта формула не является, конечно, тождеством относительно z, т. е. коэффициенты полинома в правой части зависят от элементов матрицы z.
Аналогичным образом, для левого полинома <p(z) получим:
п
(1-280) ст=1
Пусть теперь имеем правый матричный степенной ряд
© (г) = а0 -j- a±z 4- a2z2 -J- • • • (1.281)
Формула Сильвестера может быть применена к сумме ©m(z) его ^4~1 первых членов, так как эта сумма есть полином /n-й степени
9m (^) s= S 9 m (^а) а=1
При этом матрицы е* не зависят от т. Поэтому если все ©w(Xa) стремятся к определённым пределам при zn—>оо, то и <?m(z) будет иметь предел.
Следовательно, правый матричный степенной ряд (281) сходится и представляет функцию матрицы z, если все её характеристические числа лежат внутри круга сходимости
96
Элементы Матричного исчийлёний
(гл. 1
соответствующего ряда по степеням скалярного аргумента
?W = ^0 + alX + a2^+ • •
(1.282)
и расходится, если хотя бы одно из характеристических чисел лежит вне этого круга. В первом случае на ©(з) распространяется формула Сильвестера (279), которая позволяет, таким образом, представить аналитическую функцию матрицы полиномом; бесконечными рядами выражаются только значения -© (Хв).
Предыдущая теорема верна также для левого ряда
Ф(г) = Ло + ^1 + *Ч + •••»
(1.283)
и если ряд сходится, то формула (280) распространяется на <p(z). Пусть теперь не все характеристические числа различны. Поло-
жим eff = sa(z), 7|S==7kp(z), причём р в левой части второго равенства должно пониматься пока как индекс, а не как степень. Заменяя в (267), (268), (276) аргумент X на z, учитывая, что, вследствие приведённого уравнения Гамильтона-Кейли, сравнения по модулю Агеа(Х) переходят при этом в точные равенства, и пользуясь формулой (219), найдём:
Д (z) dqa 1
1 F(k,)
(яв - i)i д, (к) ’
(1.284)
А (г) Г
Gz.-P-iyLxe.-p-1
= (.г-£Хя)Ч
1 /--(хя)
Ч-Р-1)! ^«,-Р-1 Д (X,)
(Р !,•••» в9 1),
^ = 0 (р = е,.?,— !)•
(1.285)
(1.286)
Под q9 нужно понимать здесь кратность характеристического числа, а под е9 — степень , старшего элементарного делителя, относящегося к этому числу.
Рассуждая затем так же, как и в случае простых характеристических чисел, получим формулу Сильвестера для правого матричного полинома
а , р = 1
§ 1.30] ФОРМУЛА СИЛЬВЕСТЕРА ДЛЯ МАТРИЧНЫХ ПОЛИНОМОВ И РЯДОВ 97
и, аналогично, для левого полинома %-!
Ф (*) = % [«.I (А,) + 2 -п^(р) (Ч)] • а р=1
(1.288)
Эти формулы, как и теоремы о сходимости, распространяются на правые и левые матричные ряды.
Обратимся к свойствам полиномов ев, Опять предполагая сначала, что характеристические числа простые, и заменяя в (271) X на z, найдём:
Ssa==E. (1.289)
<7=1
Если сделать ту же замену в сравнениях (272) и (273), то они обратятся в точные равенства
еА = 0 (а=М), (1.290)
^ = в,; (1.291)
из второго вытекает, что и для любого целого положительного р
р =
Поэтому матрица sa, так же как и все другие матрицы, обладающие подобным свойством, называется идемпотентной (idem—тот же самый, potentia — степень); она называется также идемпотентным элементом матрицы z, соответствующим характеристическому числу Хв.
Матрицы линейно независимы. В самом деле, если где — скаляры, то
0 Тт®т == Tar®® s= Та®а»
а так как еа является полиномом от z более низкой степени, чем характеристический, и, следовательно, не может обращаться в нуль, то 7а = 0.
Если не все Ха различны, то мы имеем для матриц sff, которые называются в этом случае главными идемпотентными элементами матрицы z, относящимися к характеристическим числам Ха, соотношения
2Ч = £. (1.292)
<7
8^ = 0 (Хв¥=Лт), 8? = 8«-. (1.293)
Зак. 1474. Б. В. Булгаков
98
ЗлеМейты Матричного исчислений [гл. 1
Пользуясь последней формулой, коммутативностью матрицы z с полиномом ев и третьим выражением (285) для находим:
(nl)2 = К*—£Л,) в,]2 = (Z—Е'к^ = (z — ЕЛ,)2 в. =
и вообще
= ('П«)Р = (^ — Екв)9ев (р = 1...............е„— 1),
/
где 'qe = 'qi, или
__ Д (г) Г agg~2 1 1 _
(дв - 2)! 1дХ«з-2 Д. (Ха) (X - Хв) 1х=г “
(1.294)
1 Р(\я)
(^-2)!дХ«з~2Д,(Ха)
= (г — ЕЛ,) 8,.
(1.295)
Таким образом, верхние индексы величин tjp могут теперь пониматься как показатели степени, поскольку эти величины оказались действительно степенями матрицы Так как гв-я степень по-
линома (X — Xff)eff(X) является первой, которая содержит множителем Дгеа (Х)> то все степени т)а, начиная с и, только с неё, равны нулю. Поэтому является нильпотентной матрицей (nil — нуль, potentia — степень) индекса называемой также главным нильпотентным элементом матрицы z, относящимся к характеристическому числу Ха. Из выражения (294) для 7$ вытекает, что
='п»®»='•& «X s ( п₽+р' Р р' I
W =( 0
7]Р-Г]Р' = О
Матрицы е,, 7], линейно независимы. В самом деле,
(р+р (р+р
(1.297)
(1.298)
если
г
где Y,p — постоянные, то, умножая на ц®» \ получаем:
wny1 = °>
откуда y0o = 0; затем, умножая на т]*®”2» имеем:
TalV"1 = 0.
откуда = 0 и так далее.
§ 1.31] АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ ФУНКЦИИ ОТ МАТРИЦЫ 99
§ 1.31. Аналитическое продолжение функции от матрицы. Пусть комплексное число р принадлежит кругу сходимости К матричного ряда по степеням скалярного аргумента
^(Х) = а0+а1Л-|-а2Ха+ ...
Заменяя А суммой р + (X — Р) и располагая по степеням А — р, представим © (^) в виДе- ряда
?W=x(W)=UMWm(M)2+ •••.
сходящегося в некотором новом круге с центром в р. Естественно назвать оба ряда, как и в скалярном анализе, аналитическими, элементами функции ф(А), а процесс получения одного из другого — аналитическим продолжением. Совокупность аналитических элементов, получаемых путём продолжения всеми возможными способами некоторого исходного элемента, составляет полную аналитическую функцию ф(А).
Если теперь имеем правый ряд по степеням матрицы
?(*) = 0o+ai* + a2*2 + •••> (1.299)
то^ полагая z — E$-\-(z— Ер), мы можем, как и выше, представить <!>(z) в окрестности скалярной матрицы Ер рядом
который представляет аналитический элемент, являющийся продолжением элемента (299). Этот новый ряд сходится для матриц z — Ер, характеристические числа которых по модулю меньше радиуса круга Кр. Но, как легко убедиться, характеристические числа матрицы z — Ер равны Ао — р и потому аналитический элемент %(z — Eft) определяется для всех .матриц z с характеристическими числами, принадлежащими кругу Очевидно также, что мы можем выразить Х(я—Ер) с помощью формулы Сильвестера через значения х(Аа— Р). Таким образом, аналитическое продолжение правого ряда <?(z) будет одним и тем же, определим ли мы его непосредственно располагая по степеням z—Ер или с помощью формулы Сильвестера. Совокупность всех аналитических элементов, получаемых ’ аналитическим продолжением, можно назвать полной правой аналитической функцией матрицы z. v
Аналогичным образом определяются аналитическое продолжение левого ряда и полная левая аналитическая функция.
Если бы, по аналогии со скалярным анализом, мы положили £==£0--|-(£ —£0), где Zq — какая угодно, а не обязательно скалярная млтрйца, то вследствие некоммутативности матриц zQ и z — z0 мы получили бы при подстановке в правый ряд по z не правый ряд
7*
Элементы матричного исчисления
[гл. 1 •
юо
по z — zQi а более общий ряд с членами такого же типа, как в полиноме (129). Поэтому в определении, данном выше, мы продолжали функцию от матрицы лишь с помощью аналитических элементов в окрестности скалярных матриц.
§ 1.32. Умножение степенных рядов со скалярными коэффициентами. Пусть имеем два скалярных ряда по степеням комплексной переменной
Ф1 (А) = + fc^A + + ...,
ф2 (А) = + А^А + й(22)А2 + ...,
а .
Ф(А) = Ф1(А)ф8(А)
— ряд, получаемый их перемножением по обычному правилу:
Ф (А) = + (й?^2) -h й?^2)) А +
+ А2 + ... (1.300)
Скалярные ряды Фх(£), Ф2(^), Ф(^) по степеням квадратной матрицы z заведомо сходятся, если все её характеристические числа лежат внутри наименьшего из кругов сходимости для Фх(Х) и Ф2(Х). Но будет ли Ф(г) равно ФХ(^)Ф2(^)?
Чтобы ответить на этот вопрос, предположим сначала все характеристические числа простыми и воспользуемся формулой Сильвестера и свойствами (290), (291) матриц ©0, что даёт
Ф1 Ф2 (?) = [ДФх (А.) 8J [ Д ф2 (А.) 8 J =
=S Ф1 (и ф2 (а,) в,=2 ф (U е,=ф (z). asi ст=1
Если не все характеристические числа различны, то нужно, кроме свойств матриц sff, воспользоваться и свойствами матриц т|Р:
V1
Фх (г) Ф2 (г) = {2' [фх (А,) 8, + 2 тг ф1Р) IX
9 р=1
в.-1
X { 2' [ф2 (А,) в, + 21 ф£» (X.) } =
в Р=1
в-1 в -1
(У Q -1
= % [ф1 (А,)8, + 2 Ф1Р)(Аа) [ф2 (А,) 8, + 2 И Я =
в Р=1 Р=1
§ 1.33] ФОРМУЛА СИЛЬВЕСТЕРА ДЛЯ МАТРИЧНЫХ РЯДОВ ЛОРАНА
101
== 2' { (^) $2 (U 8. + 1ФХ (U *2 (V + «) ф2 (м -*1, + +[1 фх (х,) ф:(х,)+ф: (и Ф2 (А»)+4- ф; (v ф2 <а. >] + • • •}= =2/{ф1(л’)ф2(Х’)®а +
+ 4 (Ф1 (Аа) ф.2 (А,)]' 7], + 4 [ф1 <л«> ф2 <Х’> 1" •*!« + • • •} =
Таким образом, в обоих случаях сумма ряда Ф(г), полученного формальным перемножением рядов cpj (z) и Ф2 (г), действительно равна произведению ФхСг) Ф2(^) или, короче, ряды со скалярными коэффициентами по степеням одной и той же матрицы можно перемножать по обычному правилу. Из приведённого доказательства видно также, что функции Ф^з), ФгС2)» как и полиномы, коммутативны.
§ 1.33. Формула Сильвестера для матричных рядов Лорана. Пусть z есть неособая квадратная матрица, так что detz =# 0. Так как свободный член её характеристического полинома A (X) — det (EX — z) может лишь знаком отличаться от detz, то ни одно из характеристических чисел Ха не может быть равно нулю. Предполагая сначала, что все эти числа простые, т. е. среди них нет кратных, напишем формулу Сильвестера для <?(z) = z:
п •••
z = Sa,ss. - -
а=1
Принимая затем в качестве гипотезы
п
— У I-*
а=1 * , -ч
и перемножая оба выражения подобно тому, как это делалось в предыдущем параграфе, получим единичную матрицу. Это доказывает, что принятое выражение для z-1 действительно даёт обратную матрицу. Умножая его самого на себя один, два, ... раз, получим- для всех целых отрицательных р то же самое выражение
п
zp = 5 А?8в>
а=1
что и для целых неотрицательных. Рассуждая так же, как в § 30, распространим формулу Сильвестера (279) или (280) на правые и левые матричные полиномы ©(г), ^(з), содержащие не только положительные и нулевую, но и отрицательные степени z. Применяя
102 ЭЛЕМЕНТЫ МАТРИЧНОГО ИСЧИСЛЕНИЯ [гл. 1
формулу к частичным суммам матричного ряда Лорана
(*) = + • • • + + aQ+axz 4- .. . +
и переходя к пределу при /п—>оо, получим следующую теорему: Правый матричный ряд Лорана
?(^) = • • • 4-a_2£“2+a-iz~1 + ao+A^ + a2z2+ • • • сходится и представляет функцию матрицы z, если все её характеристические числа лежат внутри кольца сходимости соответствующего ряда по степеням скаляра
ф(Х) = ... 4-а^2Х-2 + л-1^"1 + ао4“лЛ + ^2+ • • • »
и расходится, если хотя бы одно из характеристических чисел лежит вне этого кольца. В первом случае на <f(z) распространяется формула Сильвестера (279). Аналогичную теорему имеем и для левого ряда Лорана
Все результаты этого параграфа шаг за шагом распространяются на случай кратных характеристических чисел, и конфлюентные формулы Сильвестера (287) и (288) оказываются применимыми к правым и левым матричным полиномам с отрицательными степенями и правым и левым матричным рядам Лорана; для этих последних остаётся в силе основная теорема о сходимости.
Теорема об умножении рядов распространяется на ряды Лорана со скалярными коэффициентами.
§ 1.34. Характеристические числа скалярных полиномов, степенных рядов и рядов Лорана. Пусть обозначает полином, степенной ряд или ряд Лорана со скалярными коэффициентами по степеням матрицы z. Предполагая сначала характеристические числа этой матрицы простыми, напишем формулу Сильвестера
Ф(г) = 2Ф(ХвК.
а=1
Обозначив w = $(z), р = Ф(Х), образуем какой-нибудь полином A (w) со скалярными коэффициентами и соответствующий полином A(|i). Так как эти полиномы после подстановки выражений w и р. обращаются в полиномы, степенные ряды или ряды Лорана по z и X, то к ним может быть также применена формула Сильвестера
п
A (w) = 5 А (Н«)
а=1
где р,в = Ф(ХД а матрицы q9 — те же самые, что и выше. Вследствие линейной независимости .этих матриц отсюда вытекает, что если A(w) = 0, то и все А(ра) обращаются в нуль; обратное также справедливо. Поэтому, если понимать под A(w) пока неизвестный приведённый характеристический полином матрицы w, то каждое pff
§ 1.34]
ХАРАКТЕРИСТИЧЕСКИЕ ЧИСЛА
103
должно быть корней А(р-). Если же положить
А(Ю = (Н — Hi) ... (Р — Fr)> (1.301)
где ...» Ну—различные значения п чисел |лв, то все А([ха) будут нулями, а значит^ и А(^) = 0. Вследствие этого последнее выражение и является приведённым характеристическим полиномом матрицы w = Ф (з), a Hi> • • • > Hr — е6 различные характеристические числа.
Пусть теперь матрица z имеет кратные характеристические числа.
Умножая обе части формулы Сильвестера
ф (2)=2Г [ф s‘+SIф(₽) (Хя)
а р=1
на ев, получим:
Ф (г) = Ф (\,) еа-{-Св, где
•«Г1.
С, = £ £ ф(₽) (Ш, Р=1
или же
= НА +
Очевидно, что — нильпотентная матрица, и если s9 обозначает порядок первой не обращающейся в нуль производной в её выражении, a k9— индекс нильпотентности, то (k9—l)se < e9^k9s9, или
(1.302)
откуда целое число k9 вполне определяется. Затем ,
А (то) = А (те) Е = A (w) 2 8,= ^/A(w)es= A(wsa)ea =
а а а
=2'а(на+о9=2' [д(ю^+2^л(р)<^Ч’ a a р=1
так что A(w) обращается в нуль в том и только в том случае, когда величины являются йа-кратными корнями А(|л). Отсюда следует, что приведённый характеристический полином для w есть
Л(Ю=П"(н-1*а)й’. (1-303)
где знак П" обозначает, что нужно, во-первых, дать а значения °1» • • • > согласно (263) и, во-вторых, в тех случаях, когда различные о из этой последовательности дают одно и то же = Ф (Хв),
104
ЭЛЕМЕНТЫ МАТРИЧНОГО ИСЧИСЛЕНИЯ
[гл. 1'
сохранить в произведении лишь тот множитель (р—для К0Т0‘ рого ka— наибольшее.
Как часть полученных выводов, мы имеем теорему: если Ф(^) — скалярный полином, степенной ряд или ряд Лорана и z — квадратная матрица, характеристические числа которой лв принадлежат кругу или кольцу сходимости, то характеристические числа матрицы Ф(з) суть Ф(лв).
§ 1.35. Дробные рациональные функции матриц. Из последней теоремы предыдущего параграфа вытекает, что если скалярный полином 11(A) не имеет общих корней с характеристическим полиномом Д(Л) матрицы z, то П(з) будет неособой матрицей, так как её характеристические числа отличны от нуля. Предполагая это условие выполненным, можем немедленно распространить формулу Сильвестера на обратную матрицу П_1(г), а затем на любую дробную рациональную функцию
К — п (zy
Остаётся верной и теорема о характеристических числах функции от матрицы.
Под P(z), П(з) можно также понимать не полиномы, а сходящиеся степенные ряды или ряды Лорана со скалярными коэффициентами при условии, что П(л) не имеет общих нулей с Д(^). ч
Прим е р.
Xi =1, = 2,
₽(Х2) = -|.
Непосредственным вычислением находим:
1 3
— 2 6
С другой стороны, по формуле Сильвестера
R (г) = R (КО + R Z\7-\' =
12 2 1
= -l(z-2£) + -|-(*-£) =
_ 1 , 5 1 13
- 8 8 8 _2 6 ’
t
Характеристические числа 7? (z) равны Pi = R (/4) = 1/2 и |х2 = /? (Х2) = %
§ 1.361
ЭЛЕМЕНТАРНЫЕ ДЕЛИТЕЛИ ФУНКЦИЙ ОТ МАТРИЦ
105
§ 1.36. Элементарные делители функций от матриц. Займёмся теперь вопросом об элементарных делителях функций от матриц.
Пусть, сначала, Р(г)— скалярный полином от матрицы z. Из (213) получаем при a~z\
z = 'vJ‘V~1,
так что, согласно § 15,
P(z) — P (yJv~ *) = vP (J) v~x,
где
।
P(J)=
(1.304)
(1.305)
' P (Л)
Далее, применяя формулу Тейлора для полиномов и принимая во внимание, что Р (Ее X J = Ее Р (X.J, Р' (Ев кА = Ее Р'(кА, ..., находим: - i i i i
Р(Л) = Р(Де^ + уе<) =
= ЕеР(^ + Tt Р'(м)\+ + (1.306)
так что P{J^ есть треугольная матрица, у которой все диагональные элементы суть P(XZ), все элементы первого косого ряда равны и т. д.
Так как матрица P{J) подобна Р(г), то, принимая во внимание сказанное в § 23, пункт 4°, приходим к заключению, что если ни одно из значений Р' (Х.£) не равно нулю, то элементарные делители характеристической матрицы для P{z) суть
[\ — P^]ei (Z=l, т); ' (1.307)
их общее число г и степени е{ — те же, что и для матрицы z {теорема Лаппо-Данилевского).
г Эта теорема распространяется и на дробные рациональные
функции
р (~\ Р (*) п {z)
) при обычном условии, что П(г) не должно быть особой матрицей, В самом деле, так же как и для полинома, мы можем написать:
I *
P(z) = R(vJv~') = vP(J)v-\ (1.308)
Я (А)
/?(•/) =
(1.309)
106
ЭЛЕМЕНТЫ МАТРИЧНОГО ИСЧИСЛЕНИЯ
[ГЛ. 1
и затем
Ев Р (М + ± р/ М ч + ,.. + ^-2^- (Х<) Si~'
£е<п (М + 4г п' Ч + • • • + ^1)Г п(в,’1) (Х<) "Г1 *
Так как при этом П(г) есть неособая матрица, то подобная ей квазидиагональная матрица П (J) и её субматрицы П (Л) также являются неособыми и дробные функции R (J), R (J£ действительно существуют.
Кроме того, ни одно из характеристических чисел П(ХЭ матрицы П(г) не равно нулю, и мы можем применить формулу (73) для получения обратной по отношению к треугольной матрице Л (Ее^ ve<): [п (Еех{+vCf)i -1=вв п-1 - л-® (ха [4г п' <ха *ei +. • •+
+7^1), п^-^сха*:*-1] + п-»(ха [.. .р—.. =
=е0<п-1 <ха—и-2 <ха п' <ха \ +...; отсюда
r (Л)=1Евр <ха+р' <ха \ . j х
х [£е п-1 <ха - п-2 (ха п' (ха ^ + • • • 1=
=5ep(xan-i(xa+i/x(xan-i(xa-p(Mn-3(xan'(xaive.+..
х я(/а=2ця(ха+4г*'(х*)ч+--- (L310>
С помощью' этого соотношения доказательство заканчивается совершенно так же, как и выше для полинома P(z).
Пусть теперь имеем аналитическую функцию Ф(Х) комплексного скалярного аргумента X, определяемую внутри круга | X | < г степенным рядом
Ф (X) = к§ -|- -j~ к^№ -|- ...,
и пусть Фш (X) обозначает сумму его tn Ц- 1 первых членов, так что lim Фш (X) = Ф (X). ш->со
Так как ФОТ(Х) есть полином, то для Фта(г) верны все полученные выше выводы. Если все лежат внутри круга | X | < г, то при т -> оо величины Фт (Ха, Ф» (Ха> • • • стремятся соответственно к Ф (Ха, Ф'(Ха, ... Из формул (304), (305), (306) вытекает, что при этом
§ 1.36] ЭЛЕМЕНТАРНЫЕ ДЕЛИТЕЛ ФУНКЦИЙ ОТ МАТРИЦ 107
Фш(/Д и будут стремиться к пределам
Ф(А)
Ф(У)==
Ф(Л)
Ф(хг) = ^Ф(7)о“’1.
Мы приходим к выводу, что если
Ф(2') = й0Е-]-й1^ + й22:2+ ..
причём все характеристические числа матрицы z лежат внутри круга сходимости соответствующего ряда по степеням скалярного аргумента, то на функцию Ф(^) распространяется теорема об элементарных делителях, ранее доказанная для полиномов.
Пусть ещё имеем скалярную аналитическую функцию, определяемую в кольце г± < | X | < г2 рядом Лорана
ф (X) = ... + /г_2Х-2 + й^Х-1 + fe0 + k±k + fc2X2 -j- ...,
и пусть Фш (X) обозначает сумму его 2т -f-1 членов от A_WX-W до &ШХШ, так что
Ига ФМ(Х) = Ф(Х).
Если предположить, что все Х^ лежат внутри кольца, то ни одно из этих чисел не равно нулю, матрица z будет неособой и к дробной рациональной функции Фш(я) могут быть применены все полученные выше выводы. Кроме того, при т -> оо величины Фот (ХД Фт (ХД .. . будут Стремиться соответственно к Ф (ХД Ф' (ХД ... Далее можно повторить то же самое, что и для ряда, расположенного по положительным степеням, и мы приходим к заключению, что если имеем ряд Лорана
Ф(^)= ... +*_2г~2-}-А:_1г-1 + й04-А!1гг4-А!2г2+ ..
причём все характеристические числа матрицы z лежат внутри кольца сходимости соответствующего ряда по степеням скалярного аргумента, то на функцию Ф (z) распространяется теорема об элементарных делителях.
.Пример. Матрица
имеет двойное характеристическое число 1, а её характеристическая матрица — единственный квадратичный элементарный делитель (X—I)2.
ЮЗ
ЭЛЕМЕНТЫ МАТРИЧНОГО ИСЧИСЛЕНИЯ
[ГЛ. 1
4
Матрица
также имеет двойное характеристическое число = а её характеристическая матрица — квадратичный элементарный делитель
Но если взять
то
S'(l) = 0.
Поэтому, хотя характеристическое число .S (1 )„==1/о матрицы 5(г) и будет попрежнему двойным, но её характеристическая матрица имеет не один квадратичный, а два линейных элементарных делителя
§ 1.37. Свойства модальных столбцов. Пусть имеем неособую полиномную матрицу n-го порядка и первой степени f(k) — ak-\-b и пусть Хв есть простой корень определителя Д (X) = det/(X). Дифференцируя соотношение/(X) F(X) == £Д(Х), замечая, что /'(Х)==^, и полагая Х = Ха, найдем:
аР (М+Ж) F' (U = EV (V.
умножая полученное соотношение слева на F(Xff) и воспользовавшись тем, что'F(Xff)/(Xff) = О, получаем:
F(Xff)aF(Xff) = A'(Xe)F(Xa). (1.311)
Так как детерминантный делитель Dn_r(K) матрицы /(X) не может делиться на X — Xff, то ранг /(Ха) равен п—1, а ранг F(Xff) больше нуля; с другрй стороны, из соотношения F(Xa)/(Xff)=O и теоремы Сильвестера вытекает, что ранг F(Xff) не больше единицы. Следовательно, этот ранг в точности равен единице, и мы можем представить F(Xff) в виде произведения V9W9, где V9i W9 суть соответственно столбец и строка, имеющие, по меньшей мере, по одному ненулевому элементу. Так как W9aV9 есть скаляр, то
F(Xff) aF(Xff) = V9W9aV9W9 = (W9aV9) V9W9 = W9aV9F(ХД
Сравнивая с предыдущим соотношением, получаем следующую формулу:
Г;лУа = Д'(Ха). (1.312)
Если, в частности,/(X) = £*Х — а есть характеристическая матрица для а, то мы должны заменить а, b соответственно через Е,
§ 1.37]
свойства модальных Столбцов
109
— а, и тогда
1ГХ=д' (х,).
(1.313)
С другой стороны, если Х„, Хх суть два простых характеристических числа, то, заменяя в соотношении (230) матрицы F(Xa), F(Xx) выражениями V9W9i VxWxi получим.:
yffireyxiyx = o,
а так как W9VX есть скаляр, то
(W)(VffITT) = 0;
поскольку матрицы V9, Wxi а значит, и имеют хотя бы по одному ненулевому элементу, отсюда вытекает:
= 0 (о¥=т). (1.314)
Из формул (313), (314) следует, что если все характеристические числа простые, то матрицы У, W\ составленные соответственно из столбцов V9 и из строк W9> удовлетворяют соотношению
(1.315)
А'(^п)
Пусть теперь среди характеристических чисел матрицы а есть кратные, но все элементарные делители для f(k) — E(K) — а линейны. Производные до порядка q9 — 2 включительно от Г(Л) исчезают при Х = Ха так же, как все матрицы nqp, входящие в формулу Сильвестера (287); полагая ф (Л) — Л, ф (а) — а, мы найдём с помощью этой формулы, а также (44), (216) и (284):
а - у\ с _ у' =
а~ 21 — 44 (q,- 1)!Д,(X.)
а а
_ У' у ХаУдЯ7, _
“ 44 {д,- 1)! Дд (X,) Х4 (да - 1)! Да (лд) “
а а=1
_________£(р (?., - 1)! Д31 (X.J
= VA
Здесь А есть диагональная матрица (195), ар ...,, а^.-и-номера различных характеристических чисел и Е^........ Е^} -п- единичные
110
ЭЛЕМЕНТЫ МАТРИЧНОГО ИбЧИСЛЕЙИЙ
(гл. i
матрицы порядков q9, ..., q9 . Сравнивая с выражением
а = УДУ-*
получаемым из (215), найдём:
1)! Дв(Хв)Е(1)
(1.316)
(^-1)^,^
Это соотношение является обобщением (315).
§ 1.38. Интегрирование матриц. Матрицант. Интеграл от матрицы /(X), элементы которой являются однозначными и непрерывными функциями от X, определяется обычным образом, как предел
суммы
i
i
так что
(1.317)
В случае, когда X — действительное переменное, предполагается, что однозначность и непрерывность имеют место в некотором йнтер-. вале (а, Р), заключающем интервал интеграции (Хо, X), а числа Х^ образуют возрастающую или убывающую последовательность во втором интервале. Если же X —комплексное, то однозначность и непрерывность должны иметь место в некоторой области О плоскости комплексного переменного X, заключающей кривую интеграции, а X* суть точки, расположенные вдоль этой кривой. Для того чтобы во втором случае интеграл не зависел от пути, соединяющего Хо и X, следует предположить, что элементы /#(Х) суть не только непрерывные, но и аналитические функции в области О и что эта область односвязна или превращена в односвязную путём построения некоторого числа барьеров.
Для обозначения интеграла мы будем иногда пользоваться символом Г, так что
r/ = j’/(X1)dX1, (1.318)
где, в отличие от верхнего предела, Хг обозначает переменную интеграции. Если, во избежание двусмысленности, нужно определённо указать пределы интеграции, то можно Писать I*. Оператор Г может
§ 1.38]
ИЙТЕ^РИ^ОВАЙИЕ МАТРИЦ. МАТ^ИЦАЙТ
быть применён повторно, например,
х х2
Г/Г/= f /(Х^ J
Xq х0
л «з л»
г/г/г/ = J/<х3) dks J /(Х2) dX2 J /(Хх) dX, Xq Xq Xq
и так далее. С помощью таких выражений мы можем построить матрицу
Й = ^ + Г/+Г/Г/+Г/Г/Г/+ ..(1.319) называемую [4-12] матрицантом и применяемую при интегрировании линейных дифференциальных уравнений.
Предполагая для определённости, что Л — действительное переменное, покажем, что ряд в правой части (319) сходится абсолютно и равномерно, пока Хо и X остаются внутри ; интервала (а, р). Для этого обозначим через U наибольшую из верхних границ модулей элементов /д-(Х) в интервале (а, £), а через /—квадратную матрицу л-го порядка, все элементы которой равны единице. Замечая, что
|/| Р = получим:
|Г/Г/К^2^Л|Л—Лор/.
| Г/Г/Г/1 < иу |Х - Хо |3 /
и так далее. Таким образом, абсолютные значения членов ряда (319) не превосходят соответствующих членов сходящегося ряда
/Н-11/[ ₽-а |Z + 11/2„| р_а|2/+^ W|р_а |8/_|_ ... =
= /-{-— [еРте|Р-а1 — = — 1)/,
откуда и вытекает, что ряд (319) сходится абсолютно и равномерно.
Аналогичным образом можно доказать сходимость для случая, когда /(X) есть аналитическая функция комплексного переменного X.
Дифференцируя 2, находим:
§=Г+/г/+/г/г/+-------------/(£+г/+г/г/+...),
*) Так как (//л)2 = I/п, то //л есть идемпотентная матрица.
112
ЭЛЕМЕНТЫ МАТРИЧНОГО ИСЧИСЛЕНИЯ
[ГЛ. 1
так что матрицант обладает свойством
Другим важным соотношением является следующее:
х
det 2 = еК ..
(1.321)
Мы проверим его для п = 2, хотя метод доказательства является вполне общим. Дифференцируя, имеем:
(det 2)' =
2ц 212
2.ji 220
2П
2,1
212
222 ’
а так как 2' = /2, то
(det 2)' =
(det 2)' = (/п +/22) det 2.
212
/21^12 /22^22
или
Интегрируя это линейное уравнение первого порядка относительно det 2 и принимая во внимание, что при Л = мы имеем 2 = £, det 2 = 1, получаем:
х
In det 2 = J (/n +/22)dX-
Xo 4
Отсюда и вытекает, что
х
j (Ai+/22)
det 2 = eK
ГЛАВА 2
ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ
§ 2.1. Общая идея. Пусть х обозначает функцию независимого переменного t. Вводя оператор дифференцирования
D = (2.1)
представим производные dx d*x dt’ d&’ ‘ ‘ ’ как символические произведения степеней оператора на х: Dx, D~x, ...
Линейное дифференциальное выражение dKx . dK-*x ] । dx .
e0 +е1 + • • • ~reK-idt-\~eKx
может быть записано в виде
или
е (D) х,
где е (D) есть операционный полином
е (D) = + е^-1 + ... + ек_, D + ек. (2.2)
Таким образом, с помощью этой символики дифференцирование и составление линейных дифференциальных выражений сводятся к сложению и умножению, вследствие чего естественно стремиться свести обратную задачу квадратур и решения некоторых линейных дифференциальных и интегро-дифференциальных уравнений также к алгебраическим вычислениям с операторами. Совокупность правил такого рода, распространяющихся также на уравнения в частных производных и уравнения в конечных разностях и позволяющих, в известной
8 Зак. 1474. Б. В. Булгаков
114
элементы операционного исчисления
[гл. 2
его части, алгебраизировать анализ, составляет операционное исчисление. Его-истоки восходят ко временам создания исчисления бесконечно малых, но основные методы построены Хевисайдом в работах, относящихся к 1893—1894 гг. Недоверие, которым вначале было встречено новое исчисление, объяснялось, с одной стороны, представлением, что оно не даёт ничего, кроме стенографии, служащей для записи результатов, легко получаемых классическими методами, а с другой стороны — отсутствием строгих обоснований. Первое возражение изживается по мере того, как развитие и разнообразные физические и гехнические приложения обнаруживают плодотворность принципов и силу формального аппарата операционного исчисления. Второе возражение было устранено, когда Джорджи, Бромуич, Вагнер, Карсон, ван дер Поль, Игнатовский, Эфрос и Данилевский и другие установили связь операционного исчисления с интегральным преобразованием Лапласа, которую предвидел ещё Коши.
§ 2.2. Преобразование Карсона. Для краткости мы не будем воспроизводить первоначальный ход рассуждений Хевисайда, а введём сразу преобразование Карсона
со
р
X (t) e~i* dt'9
(2.3)
с помощью которого действительной или комплексной функции х (f) действительной переменной t ставится в соответствие функция В(р) комплексной переменной р. Первая называется оригиналом, вторая — её изображением или трансформацией по Хевисайд у-Карсону. Обе функции могут быть либо скалярами, либо матрицами и притом одного и того же типа. При первом чтении можно предполагать, что все матрицы, которые встречаются в общих теоремах, принадлежат к типу 1X1, т. е. являются скалярами.
Соответствие между х (/) и $ (р) выражают символическим соотношением
(2.4)
причём остриё стрелки обращено к оригиналу.
Интеграл в правой части (3) называется интегралом Лапласа или трансформацией функции х (/) по Лапласу. Когда предпочитают непосредственно пользоваться этой трансформацией, её обозначают обычно через £ [х (/)], и мы имеем, таким образом, следующую формулу для перехода от одной системы обозначений к другой:
1^2 = 2 [X (01. (2.5)
Jr
Функция х (0 предполагается однозначной, конечной и непрерывной для всех неотрицательных значений t, кроме тех, которые соответствуют точкам разрыва первого рода, причём таких точек может
§ 2.3] 4 СООТВЕТСТВИЕ ЕДИНИЦ ilS
быть лишь конечное число в каждом конечном интервале. Эти предположения достаточны для приложений, хотя они и не самые общие, которые можно сделать. Так как интеграл Лапласа берётся от О до оо, то значения х (f) при £<0 не влияют на изображение..
Изображение определено лишь для тех значений р, где интеграл Лапласа сходится. Можно показать, что это имеет место в полуплоскости Rep>ac, где ае — некоторое действительное число, называемое абсциссой сходимости для х (/). Аналогичным образом, абсолютная сходимость интеграла Лапласа имеет место в полуплоскости Rep > <за, где аа называется абсциссой абсолютной сходимости для х (/). Нам понадобится также теорема, состоящая в том, что если
° >°с
И t y(f) = j x(f)dt, о то
lim y(t)e~at = O. (2.6)
t->oo v <
Иными словами, функция у (t) возрастает при > оо медленнее, чем е9*. Доказательства этих теорем мы дадим ниже, в § 27, чтобы не откладывать вывод основных операционных свойств трансформации Хевисайда-Карсона.
Может случиться, что для данного оригинала <зс = — оо или ос = = -|-оо. В первом случае интеграл Лапласа сходится всюду, а во втором он не сходится нигде. Если ос равно — оо или конечно, т. е. ае < оо, то функция х (0 называется трансформируемой.' Аналогичным образом, для некоторых оригиналов аа =— оо или оа = -]”°о; если < оо, то функция х (t) абсолютно трансформируема.
Можно доказать, что $ (р)!р является аналитической функцией от р в полуплоскости Re р > ое. Во многих случаях $ (р) может быть аналитически продолжена и влево от прямой Rep = ас, но для таких значений она не представляет изображения х (f), связанного с этой функцией уравнением преобразования (3). Можно показать также, что если два изображения тождественны, то их оригиналы могут отличаться только своими значениями при t < 0 или в точках разрыва; иными словами, если такие оригиналы не считать различными, то соответствие между функциями х (t) и 5 (р) взаимно однозначно.
§ 2.3. Соответствие единиц. Полагая х (/) = Е, имеем из уравнения Карсона (3):
оо
= Е e~ptdt = E lim ‘
Р j £->оо Р
8*
116
ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. 2
Предел существует при a = Re/?>0 и равен 1/р. Поэтому как абсцисса сходимости зс, так и абсцисса абсолютной сходимости равны нулю и $(/?) = Е. Иными словами,
Е-~>Е. (2.7)
Введение делителя р в
левой части уравнения Карсона и имеет
целью получить это соответствие.
Изображение не изменится, если в качестве оригинала взять единичную ступенчатую матрицу
( 0 при t < О, Е«> = Ь при o<t (28)
Если порядок матрицы равен единице, то она приводится к скалярной единичной ступенчатой функции
Фиг. 1. Единичная ступенчатая функция 1 (t).
при при
(2.9)
график которой изображён на фиг. 1.
§ 2.4. Линейность. Пусть
п
х (О == 2 (О»
где aj — постоянные, которые, так же как и могут быть
скалярами или матрицами; если и те и другие являются матрицами, то должна, разумеется, иметь место конформность в написанном порядке.
Положим
Тогда
л? w п п е г \
Mr = | S (0 e~pt dt=^ а3- f Xj (t) e~pt dt=^ a5 ,
o j=i d J=i
так что
Цр)= S «Л(р) j=l
ИЛИ ’
S «А (p) S ajxj (£). (2.10)
J=1
Таким образом, изображение линейной комбинации есть линейная комбинация изображений.
§ 2.5] ИНТЕГРИРОВАНИЕ ОРИГИНАЛА 117
Если при матричных постоянных и функциях имеет место конформность в противоположном порядке, то
п п
S (р) 2 (t) (2.1 Оа)
J=1 J=1
§ 2.5. Интегрирование оригинала. Положим
t y(f) = f x(f)dt.
6
Обозначая через т|(р) изображение этой функции и применяя интегрирование по частям, находим:
оо оо
I У (/) di = — - y(t)e-i>f ”+ - [x(f)e-pfdt.
p 0 P 0 P
Так как, согласно (6), проинтегрированный член равен нулю, то оо
•q(p) = f = jT О
или t
X(t)dt. (2.11)
0
Таким образом, интегрирование оригинала приводится к делению изображения на р.
Повторно применяя формулу (11), найдём: t t
\x(t)(dt)™. (2.12)
О о
Если нас интересует изображение неопределённого интеграла t
x(t) = f x(t)dt = ( x (t) dix (O'), (2.13)
0
где x(0)— произвольная постоянная, то с помощью теоремы о линейности и формулы (11) находим:
ц. х (0) -н- x(t). <2-14>
Если применить эту формулу повторно, заменяя в ней x(f), «(Р) соответственно функцией x(t)n её изображением, определяемым
ь
ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. 2
118
той же самой формулой, то получим:
ИЛИ
Е (р) . х (0) р2 ‘ р
и вообще
где
5(Р)
|7П I пт—1 I
х(0)
х (0)
W —1
(2.15)
т
т
3
t t
>)
т
(2.16)
о о 1
+ х(0)-^----Пт + *(0) 7 - -ox t + > .. +х
1 . 4 7 (>77 — 1)! 1 .. 4 7 (ттг —2)! 1 1 т
§ 2.6. Дифференцирование оригинала. Пусть x(f) непрерывна и дифференцируема при £>0, а при /=0 имеет, по крайней мере, производную справа. Полагая здесь т| (р) -?-> х (0, имеем согласно предыдущей теореме
t
о
где х(ОЦ-) обозначает предел, к которому стремится x(t), когда t неограниченно убывает, оставаясь положительным. В дальнейшем мы будем писать просто х(0), понимая под этим именно х(ОЦ-).
Согласно теореме о линейности, имеем:
Е(р) —x(0)-F*x(f) —х(0)
и сравнение с предыдущим уравнением даёт:
•п (р) = р (р)— *(0)1
или
При наличии дальнейших производных эту формулу можно применять повторно. Например,
или
рЧ О)—р*х (0)—р'х (0) -4-* х (0
и вообще
PmW~р^х^т-р^хСО)— ...— р™х (0)-г->х(0. (2.18)
§ 2.8]
ДИФФЕРЕНЦИРОВАНИЕ ИЗОБРАЖЕНИЯ
119
Вводя согласно (1) оператор D, а также . ...
D — (^\
можно представить предыдущую формулу в виде pml(j>) — P(P’“-1 + pw-2O0+ ...
или
(Р) -Р - д -°- X (0) -4-> Dmx (0. (2.19)
Р — . т—1
Если, в частности, х (0) = х (0) = ... = -х (0) = 0, то
рт1 (Р) Dwx (0, (2.20)
и, следовательно, дифференцированию оригинала соответствует умножение изображения на степени р.
Две последние теоремы имеют фундаментальное значение и объясняют связь формально-операционного исчисления Хевисайда с исчислением трансформаций Лапласа-Карсона.
§ 2.7. Линейные дифференциальные выражения. Найдём изображение выражения e(D)x(f), где e(D) — операционный полином (2) с постоянными коэффициентами eQi ev ..., ек. Эти коэффициенты, так же как и х(/), могут быть скалярными или матричными.
Полагая’в формуле (19) предыдущего параграфа
т = К> К— 1, ..., 1, 0, * •* ь»
умножая получаемые соотношения соответственно на ♦ 1
и складывая, получим:
е(р)Цр) — pP(P)++e(D)x(t), (2.21)
где . - - - .
Р(р) = ~ е х (0). (2.22)
Р — и о
Легко написать аналогичные формулы для случая, когда при матричных коэффициентах и функции x(t) имеет место конформ^ ность в противоположном порядке.
§ 2.8. Дифференцирование изображения. Дифференцируя уравнение Карсона (3) по р, имеем:
оо
£ [Цт] = (- l)m f (0dt,
r L г J d
0 . -
120
ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. 2
откуда
dm [£(/>)' dp™ р
±+t™x(t). (2.23)
Если мы хотим найти оригинал для то следует применить только что полученную формулу к функции x(t) и её изображению 'П(Р):
dm h(p) p
По теореме о дифференцировании
•n(p) = pU(p)—*(0)1, и потому при т > 0
оригинала
''l (P)/P = (p) — X (0),
(— О Pd^n~^t х®’ отсюда, применяя теорему об интегрировании оригинала, имеем: t
w [t™x(t)dt о’
dpm
и, наконец, после интегрирования по частям t
(— 1)*[(0 — т ftm-lx(0dt\. (2.24)
UP е/ J
0
Таким образом, дифференцирование в области изображений эквивалентно умножению оригинала на степени — t и некоторым дополнительным операциям.
Эта теорема аналогична теореме о дифференцировании оригинала, и мы встретим в дальнейшем другие примеры подобной двойственности. Её причины выяснятся, когда мы получим интеграл Бромуича, позволяющий вычислять оригинал по данному изображению.
§ 2.9. Теоремы запаздывания и упреждения. Обозначая через т некоторое положительное число, найдём изображение $_х(р) функции
X _х (f) = х (t т), которая имеет то же множество значений, что и х(/), но принимает их с опозданием на т. С помощью замены tr — t—т находим:
Е_т (р) = р J x(t—т) е-Р*dt — p $ x(f)e р(t'+т)dt' = 0 — х
§ 2.9]
ТЕОРЕМЫ ЗАПАЗДЫВАНИЯ И УПРЕЖДЕНИЯ
121
Отсюда, полагая о ф(р) = f хфе-РШ, (2.25)
—т
получаем теорему запаздывания
[5 (р) + (р)] Н-> х (t—т). (2.26)
Если применить её не к x(t—т), а к функции x(t—т), то о
(р) = Г х (0 7 (0 е-Р* dt=O —Г
И ( р) -?> х (t — т) 1 (t—т). (2.26а)
Изображение Ех(р) функции
хт(0 = х(/+т)
даётся теоремой упреждения, для получения которой нужно только заменить в предыдущем выводе постоянную т через —т. Обозначая при этом
а (р) = р f х (0 е~Р* dt, (2.27)
О найдём:
(р) — а (р)] -Н> х (t+т).
Введём ещё оператор упреждения Т, преобразующий х (f) в х(/-[-т), так что
х(/-}-т)= Tx(f), х^+2т)=Г2х(/), . тогда
ерх [5 (Р) — а (р)] Н-> Тх (f). (2.28)
С другой стороны, заменяя т через лп, где m — целое положительное число, имеем:
ертх [В(р) — р (р)] -Н- х (t + тт), где
»»т Ш_1 (/+1)т
р(р) = р j* x(f)e-Pfdt— 2 Р j* x(t)e~Ptdt=
т—1 * ш—1 т
= 2 Р Г х (f -I- j'-c) е~р dt' — 2 е~Р^р f Т*х (/) е~Р* dt.
j=o J j=0 J
122 ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО исчисления [гл. 2
Поэтому, полагая т
(р) = р СTjx (f) e~Pf dt, (2.29)
О
получаем в качестве обобщения формулы (28):
т—1
Л(р)— S ер{т~^аЛр) 4-> 'Гх (0, (2.30)
з=о причём «о(р)=«(р)-
§ 2.10. Конечная сумма и разности оригинала. Зададимся изо-бражением
оо
ч (р) = -LLpL = = $ (р) V е-рк
ерх— 1 1 — е~рх
3=1
Интерпретируя отдельные члены ряда с помощью теоремы запаздывания, находим оригинал оо
3 = 1
Если обозначить через J t/x наибольшее целое число, заключающееся ь Цх, то при данном t
l(t—j-i) =
1 при у Sg J t/т, 0 при j > J t/x.
Поэтому мы можем написать:
Е(/0
^т—1
%X(t-h). 3=1
(2.31)
Выражение, стоящее справа, называется суммой функции x(f). Она играет в теории конечных разностей такую же роль, какую определённый интеграл — в непрерывном анализе. При 0^/<т она обращается в нуль. Функция
Дх (/) = х (/+ х) — х (0 (2.32)
при фиксированном т называется первой разностью от х (f). Мы можем написать:
Дх(0 = Tx(t) — x(f) = (T— l)x(f),
так что операторы Т и Д оказываются связанными простым соотношением
Д=Т—1. . (2.33)
ТЕОРЕМА СМЕЩЕНИЯ
Пользуясь формулой (28), находим изображение первой разности: (ерх — 1) $ (р) — е рха. (р) -Н- Дх (О- (2.34)
Разность от разности называется второй разностью
№х (0 = ДДх (0 = (Т— 1)ах (О,
Д2х (0 = х (t + 2т) — 2х (t+т) + х (t).
Вообще
д»»х(0 = (7’—1)’»х(0 = х(^+т) — у-х(^+(т—1)т) +
+ -^=-^-x(f+(m_2)T)— (2.35)
1 ’ Z
Заменяя x(t)f t(p) в формулах (27), (34) первой разностью и её изображением, определяемым этими же самыми формулами, найдём:
(ерх — 1) [(<?*” — 1) $ (р) — ерха ( р)] — ерх^ (р) -4-> ДДх (t), где
Pi(P) = /’j* Дх(0е~Р#Л,
О или же
(^ _ 1)2 $ (р) _ ерх [(ерх - 1) а (р) Ц- (р)] Д2х (/).
Продолжая этот процесс, получим изображение т-й разности
(е2>г_1)1»^(/?)_ерт 2 (е^_ 1)п‘--'-1й.(р)-^->Дтх(/), (2.36)
J=0
причём
(р) = Р / (f) е-р* dt (2.37)
и, в частности,
₽о(Р) = а(/>)-
§ 2.11. Теорема смещения. Заменяя в уравнении преобразования (3) р через где X—действительное или комплексное
число, имеем:
оо
j* х (t) dtt
6
р + х
оо
124
ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. 2
откуда
+ (2.38)
jf/ I rv
Это соотношение составляет теорему, двойственную для теоремы запаздывания, так как оно показывает, как изменяется изображение при умножении оригинала на показательную функцию.
По теореме об интегрировании оригинала получаем соотношение
t
—^(p-f-X)-;-* $x(f)e~»dt, О
а умножая его на X и складывая с предыдущим, найдём:
t
. е (р X) -4-> е~™х (0 + X Гх (0 е-» dt. (2.39)
О
Эта форма теоремы показывает, как изменится оригинал, если аргумент изображения увеличить на X.
§ 2.12. Интегрирование по параметру. Пусть оригинал и изображение содержат параметр 5, не зависящий от t и р:
Цр, 5)-4->х(А $),
оо
У 6(р, s) = Г х (t, s)e-pt dti (2.40)
О
Интегрируя по $, имеем:
8 8 СО
— s)ds= ds Jx(Z, s)e~v*dt =
So So 0
co 8
= f e~?f s)dsjd£ 0 So
ИЛИ
j*£(A s)ds j* x(t, s)dSi (2.41)
Sq
так что интегрирование по параметру и преобразование Карсона коммутативны.
§ 2.13. Дифференцирование по параметру. Дифференцируя
(40) по s, найдём:
Ацр, s)-4->^x(t, s), (2.42)
т. е. дифференцирование по параметру также коммутативно с пре
§2.14]
УМНОЖЕНИЕ ИЗОБРАЖЕНИЙ
125
образованием Карсона. Эта теорема позволяет применить операционное исчисление к уравнениям в частных производных, где, кроме /, имеются и другие независимые переменные.
§ 2.14. Умножение изображений. Выведем теорему, которая позволяет построить оригинал произведения двух изображений, если известны оригиналы сомножителей^
Пусть
^(рЭ-^ЯО-
Из преобразования
оо
1 г
= x(u)e~Pudu
о
получаем:
оо
у (Р) “О (р) = J X (а) 7] (р) е~?и du.
О
Но по теореме запаздывания
е ~Рич\ (р) —у (t — и) 1(1 — и), откуда х (и) т| (р) е-^и -4-> х (и) у (t— и) 1 (t— а).
Так как правая часть равна нулю при то теорема об
интегрировании по параметру даёт оо t '
J х (и) 7) (р) е~Ри du -т-> J х (и)у (t— и) du, о • о
откуда получается соотношение t
— ? (р) V (Р) [ х (и)у (t—u) du, (2.43)
Л V
о
которое вследствие равноправия x(f), y(t) может быть написано также в виде
t
5 (р) 1Q (р) Г x(t— и) у (и) du. (2.44)
О
Применяя теорему о дифференцировании оригинала, получаем ещё одну форму:
$ (Р)-n (р)J x(u)y(t—u)du = О t
~ f х (*— w)У (?) (2.45)
о
дающую непосредственное решение поставленной вначале задачи.
126
ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЙ
[гл. 2
§ 2.15. Теорема подобия. Положим
. Ч (р) -г* X (at).
Так как оо
— т| (р) — Jх (at) e~vf dt,
? о
то, полагая tr = at, находим:
оо
Ч (р) = £ I •* (^)е 'а dt'> о
ч(р)=^(4), \ <4* /
ИЛИ
(2.46)
§ 2.16. Начальное значение оригинала. Вводя в уравнение преобразования вместо t новую переменную
u = pt,
найдём:
ОО
(» ^e~udu. о
При неограниченном возрастании р множитель х(и!р) стремится к х(0), если же x(t) имеет при /=0 разрыв, то этим пределом будет х(0-|-). Вынося этот множитель из-под знака интеграла, найдём в пределе
£(оо) = х(0+). (2.47)
§ 2.17. Конечное значение оригинала. Пусть % < 0. Полагая в уравнении преобразования р~>0, получим:
оо
= | х (0 dt.
L р W
(2.48)
Если же применить эту формулу к изображению р{Ъ(р) — х(0)] и его оригиналу x(f), то
$(0) —х(0) = J x(t)dt - о
или
в (0)=х (оо).
(2.49)
§ 2.18]
ИЗОБРАЖЕНИЯ. ПРОСТЕЙШИХ ФУНКЦИЙ
127
§ 2.18. Изображения простейших функций. Полагая x(f)—$(р)=1 в (12), находим при целом положительном т:
1 рт
(2.50)
Аналогичным образом из (38), после замены X на — X, где X — любой скаляр:
(2.51)
если же применить (23) к функции е™ и только что найденному её изображению, то
_____Р______^2 52\
Если а есть квадратная матрица, то, полагаяи x(t) = eat, имеем: со оо 4
£(p) = pj e^e-ptdt^p I t = _ e-(Ep-a)t\t
о о
Пользуясь формулой Сильвестера, легко убедиться, что второй член в скобках стремится к нулю, если Rep>oc, где ас есть наибольшая из действительных частей характеристических чисел матрицы а. Поэтому ас является абсциссой сходимости для eatt и мы получаем в качестве обобщения (51)
Ер Ер — а
(2.53)
Заменяя в (51) X через е±Х, находим:
<2-54>
если же заменить здесь X на /ш, то 2 ezt cos 1--------------------------------. о —sin (2.55)
(р — е)2-|-(о2 \Р — e)2 4-oj2 • 4 '
В частности, при е = 0 получим:
—£L_-j->chX/, -^—-++shM, (2.56)
/М — К * pt — №
—„ -i-> cos wt, -T-> sin mt. (2.57)
р2 pl _|_ 4
128
ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. 2
Полагая в (26а) х (f) = $ (р) = Е, имеем при положительном т Ее~Рх -т->Е(£— т), (2.58)
где E(t — т) обозначает матрицу, равную нулю при /<т и совпадающую с единичной при
Отсюда
Е (е~Р* — е-Р?) Е (t— а) — Е (t — р), (2.59)
причём оригинал есть матрица, равная Е в интервале а^/<р и исчезающая вне его.
Рассмотрим далее операционное соотношение
п п
2 kj/ft—т,-);
J=0 3 = 0
(2.60)
если »здесь fy(/ = 0, 1, ..., ri) суть действительные скаляры и 0 < < Ti < т2 < • • • < Tn-i < т0 график оригинала имеет вид
лестницы с п -|- 2 ступенями шириною Tq, Tq, ^2 ,
тп--00 И ВЫСОТОЮ 0, fe0,
kv ..kn_v kn (фиг. 2). В част-
& Ъ V; тг .
Фиг. 2. Ступенчатая функция.
Фиг. 3. Пилообразная функция.
ности, при бесконечном множестве ступеней одинаковой ширины и высоты 1 имеем ту = т0-|-/т, fy=l (/==0, 1, 2, ...) и
оо оо
е-рт. е-рл-Н- 2 l{t——Л) 3=0 ^=0
или оо
(2.61) 1 -^=0
Если J^/т есть наибольшее целое число, заключающееся в £/т, то, очевидно, 3=0
§ 2.181
ИЗОБРАЖЕНИЯ ПРОСТЕЙШИХ ФУНКЦИЙ
и (61) даёт
(2.62)
что получается также из (31) при х(/) = $(р)=1.
Отсюда, с помощью (50),
где оригинал есть пилообразная функция (фиг. 3).
Пусть имеем скалярную или матричную функцию а(/)> исчезающую вне интервала (0, т). Её изображение есть
а (/?) = р j* a (t) dt. (2.64)
о
Сдвигая интервал на dr т, dr 2т, ..., образуем периодическую функцию
A(t) = a(t— (Jt/x)x)= S a(t—jz). (2.65) — CO
При построении её изображения имеют значение только те члены ряда, для которых J^>0. Поэтому, согласно теореме запаздывания, это изображение будет
со
V а (р) е~^х = ——.
Х4 1— е~Рх
о
Таким образом, мы имеем для любой скалярной или матричной периодической функции операционное соотношение
а (р)
(2.66)
С его помощью легко показать, например, что неизвестная функция определяется по своей первой разности лишь с точностью до произвольной периодической функции. В самом деле, если оригиналы связаны уравнением
Aj/(0 = x(0, (2.67)
то ему соответствует, согласно (34), уравнение (ерт _ 1) т] (р) _ еР’а (р) = Е (р), связывающее изображения. При этом a (f) совпадает с неизвестной j/(f) на интервале (0, т). Разрешая относительно т|(р), находим: . 71 (р) =-1^-+---“ (Р) , еРх—\ ерт—1
9 Зак. 1474. Б. В. Булгаков
130
ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. 2
откуда, согласно (31), (66), Я
-Г tlx 1
у (0 = 2 х (t—Jt) + A (t). (2.68)
j=i
Функция у (f) носит название неопределённой суммы функции х (f) ?
и играет в теории конечных разностей ту же роль, что и неопреде- ;
лённый интеграл в непрерывном анализе. Вместо произвольной постоян- J
ной здесь появляется произвольная периодическая функция. Определённая сумма, являющаяся первым слагаемым справа, есть та из ] неопределённых сумм, которая исчезает при 0 t < т.
В приложениях операционного исчисления к теории конечных разностей приходится интерпретировать также изображение, немного более общее, чем (66), а именно:
5 (р) “ =2«(р) ।
ерх — X ** 1
0 I
причём а(р) имеет прежнее значение (64) и 1
Rep>^l. I
За оригинал можно принять функцию
х(/)=2 Ma(t—J-), — СО
которая получается из a(f) путём сдвига интервала определения последовательно на ±т, ±2т, ... и умножения на X*1, Х±2, ... Поэтому
x(t} = A(f)kxt'\
где A(t)— та же периодическая функция, что и выше. Итак, -^а(Р^ -Ь> А (0 kxt,\ (2.69)
При X =/= 1 эта формула отличается от (66) множителем Х"1"^. Пусть далее
Так как
&У (0 = А (Г) [( J tfz + 1) kxtfx+1 — ( J f/т) AJ’^] =
= (X - 1) А (0 ( J t/т) kxt/T + АЛ (0 кх* = = (X—lV(0+Ax(0,
где x(f) обозначает опять оригинал в (69), то
(А - 1) 7) (р) + А -н- bytf);
а л
§ 2.18]
ИЗОБРАЖЕНИЯ ПРОСТЕЙШИХ ФУНКЦИЙ
131
с другой стороны, по общей формуле (34)
(ерх — 1) ц (р) — ер^ (р) -j-> Ду (О,
где Р (р) = так как J = О при 0 <7 < т. Сравнивая два последних соотношения, находим:
ер —л
так что
i->4(O(J^)X^
или, разделив изображение и оригинал на X,
_£^_^>^(O(Jf/T)X-r#/t“1. (2.70)
Для функции г(0 = л(0(1^х-г,/г имеем:
bz (t) = А (/) [(J t/r-j-1 )2 XTf/x+1 — ( f //т)2 Ал/1 =
= (Z—1)Л(0( f//T)2X-ri/x+2X2X(f)( fZ/-c)Z-ri/T_1 + X Л(0 Kxtft,
(X — 1) С (р) + 2Х2 еР-а 4- X (р)—^^z(t);
4 7 (вР’_х)2~ е?'_х ' .
но по (34)
(ер-' — 1) С (р) — ер\ (p)-i-> (0,
где опять 7 (р) = 0. Отсюда путём сравнения найдём:
С(р) = 2Х2
ер"а(р) J. ерха(р) (ерх — Х)»-*” (е^т —Х)2
или, интерпретируя второй член справа с помощью (70), 2X2 (PL~^ А 1( -Г ~ < -Г кХ #/’J — X)3
Окончательно еута (р) — X)3 ‘ и вообще
грта(р) (е^х_X)wl+1 ‘ х
^->Л(0
т
(2.71)
9*
132
^леМейть! ойеРаЦиойнсФо ИСЧИСЛЕНИЯ
[гл. 2
§ 2.19. Теоремы разложения. Предположим, что 5(р) регулярна в бесконечности, так что
Е(р)-«.+^+а+..„
где ряд сходится при |р| > р. Обозначим через элементы матриц at и через р' — какое-нибудь положительное число, большее р.
Каждый из рядов
сходится абсолютно при р — р'. Поэтому при любом I и фиксированных у, k
I I
| 1 < М^'1,
так что
1 ^ | < Мр",
где М — матрица с элементами Mjk. Вследствие (50) ряд х(О = ао + т|-«1< + 4а2^+---
формально является оригиналом для £(р). Абсолютное значение его общего члена меньше общего члена ряда
м/|*| = мГ1+^рЧ/|+Ау2|г|2+.,1
сходящегося при всех |/|. Поэтому ряд x(t) сходится при всех t. Таким образом, при Rep>p
“o + f+$+...(2.72)
что составляет первую теорему разложения Хевисайда.
Найдём теперь оригинал дробной рациональной функции
Р* (р)
Д(р)’
где е(р), Д(р)— полиномы от р, первый из которых может быть матричным, а второй — скалярным. Предполагается, что дробь £(р)/Д(р) — правильная, т. е. степень её числителя меньше степени знаменателя. Вследствие этого мы можем разложить её на элементарные дроби. Обозначая корни знаменателя Д (р) через (а = 1,..., их кратности через qa и полагая
А, (Р) = (Р\ (р-Х.Г’
(2.73)
§ 2.20] ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 133
имеем по образцу (1.264): г* п _ р-j -|
е(р) = V' У 1______________8 е(р) 1
Г ₽t4o(^“P“1)’l
Умножая обе части на р и пользуясь операционной формулой (52), получаем отсюда вторую теорему разложения Хевисайда'.
р ре(р) • у' у г ехрка<
Д(р) * 2л
ст р=0
(2.74)
Она даёт интерпретацию любой дробной рациональной функции от р вида г(р)/Д(р), где степень числителя не выше степени знаменателя. В самом деле, чтобы в этом убедиться, достаточно положить Д(р) = /?Д(р), написать
е (р\ = Ре (Р)
Д(Р) *(/>)
и поступать по предыдущему.
§ 2.20. Линейные дифференциальные уравнения с постоянными коэффициентами. Операционное исчисление даёт удобный аппарат для получения решений линейных дифференциальных уравнений с постоянными коэффициентами и систем таких уравнений,— в особенности в тех случаях, когда нужно удовлетворить заданным начальным условиям. Мы покажем в следующем параграфе, что все эти задачи могут быть сведены к одному уравнению
/(О)у(0==е(О)х(0, (2.75)
в котором х (f) обозначает заданную возмущающую функцию, y(t) — неизвестную, a e(D) и f(D) — полиномы с постоянными коэффициентами от оператора £) = ^-, причём все четыре величины являются, вообще, матрицами; в частности, f(D) предполагается квадратной и неособой, так что её определитель
A(D) = det/(D) (2.76)
не равен тождественно нулю. Правую часть уравнения (75), представляющую известную функцию, можно было бы обозначить одной буквой, однако мы предпочитаем принятую выше форму, симметричную относительно х(/), y(t), так как в прикладных задачах возмущения иногда зависят не только от какой-либо функции, но и от её производных.
Полагая
е (р) -4-> х (t), 71 (р) (t),
134 ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО исчисления [гл. 2
имеем по формулам (21), (22)
« (р) £ (р)—рР (р) -г-* е (D) х (О,
f (р)'»! (р)—PQ (р) -г* / (D) у (О, где
Р(р)= e{p}~eD(Do)x(O), Q(p)=Z-(;2~<(Po) J(O). (2.77) Р — Р — LJq
Изображение уравнения (75) будет
/ (р) 'П (р)—PQ (р) = * (р) $ (р)—рР (.р), откуда, разрешая относительно т|(р), получим:
*1 (Р) = /(Р) \ Р [Q (Р) - Р (Р)] +/(Р) \ е (р) $ (р),
или, обозначая через F(p) матрицу, присоединённую для f(p), P(PnQ(p)-P(p)} . Р (Р) е (р) £
^Р)~Р Д(р) “Г д(?) ЧР)-
Положим
^(Р)+н(Р), FMe(P) <2-78>
^^=5(p) + v(p), ]
причём —R(p), S(p) обозначают целые части рациональных функций, стоящих слева, а |х(р), v(p) — правильные дроби. Операционное решение принимает вид
7] (р) = рр (р) + S (р) В (р)—pR (р) + j- pv (р) В (р). (2.79) Интерпретируем сначала второй и третий члены справа, для чего воспользуемся выражениями (77), (78), тождеством Л(р)/(р) = Д (р)Е и соотношением /(D0)y (0) = е(£)о)х(О), получаемым путём подстановки в заданное уравнение начальных значений. Тогда
_ р (п\ _1_... (п\ — р <?>~ <°> ~ Iе W ~ е (роИ х <°> > —
/?(Р) + |*(Р) Д(р)(р-Д0) —
_ F(P)[/(p)y(0)~e(p)^(0)] _j(0)-S(p)x(0)-v(p)x(0) д (Р) (Р — F>o) P — Do
= _ S(p)-S (Dp) f(n , ^-[ЧТМ + ЧрЛ-уО))
Р — Do ' -'“г р — Do
Так как —R(p) представляет, по условию, целую часть последнего выражения, а второе слагаемое является правильной дробью, то P(P)=S ~SD {Do) х (0).
р — Uq
Мы видим, что R(p) связано с S(p) и начальными значениями x(f) и его производных таким же соотношением, как Р(р) с е(р), и
§ 2.20]
ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
135
теми же начальными значениями. Поэтому
5 (р) 5 (р)—pR (р) -r+S(D)x (0, (2.80)
что и даёт искомую интерпретацию второго и третьего слагаемых в (79).
Займёмся теперь интерпретацией первого и четвёртого членов.
Если к0 (з = 1, 2, ..., у) суть корни Д (/?), a q, — их кратности, то, по образцу разложения (1.264),
Р-(Р) =
_ у' V 1 ^(р)[<?(р)~^(р)1 1
Т р=0(^“Р-1)!^ Мр) J₽=\(P-MP+1’
откуда, умножая на р и интерпретируя по формуле (52), имеем: рр(р)-^Л4(0, (2.81)
где
Л4(0 =
у' у tf exp ( cfr"1*-1 F(p)[Q (p)-P(p)] a " P! (4,- P - 1)! I др^-^1 Д, (p)
Мы не воспользовались прямо второй формулой разложения Хевисайда только для того, чтобы ввести под знак производной не дробную часть |*(р), а всю рациональную функцию. Можно написать также
Р (Р) [Q (Р) - Р (P)J 1 Д«(р)
Аналогичным образом
(2.83)
где
pv(p)-H»N(0,
S' exp X/ ( Э \ga 1 F(p) e (p) 1 (4» — 1)! I \ dp ) Д, (p) a ff
По теореме об умножении изображений
t
J N(t— и)х (и) du. о
(2.84)
(2.85)
(2.86)
71 ’ (р) ’ Ср) -т*
'1
) •... ла
136 ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ . [ГЛ. 2
Вследствие (80), (81), (86) операционному решению (79) соответствует в области оригиналов соотношение [2-7]
t
J (/) = м (04- S (D) х (0 + f N(t— и) х (и) du. (2.87)
о
Это и есть решение уравнения (75). Оно принимает, вместе с производными, заданные начальные значения при £ = 0, в каком именно смысле — будет выяснено в следующем параграфе.
§ 2.21. Приложение к скалярным уравнениям, а) Предположим сначала, что x(t), y(t\ e(D), f(D) в (75) являются матрицами типа 1 X 1, т. е« скалярами. Мы имеем тогда одно скалярное уравнение с одной неизвестной. В этом случае
A(D)=/(D), F(D)=1.
Полином S(D) определится как целая часть дроби
Г(О) = у{^-; (2.88)
полиномы Р(р), Q(p) вычисляются по общим формулам (77).
Пусть в числе s корней f(D) имеется s' действительных, которые мы обозначим через ха(з==1, ..., s'), и s" пар комплексных сопряжённых, которые мы обозначим (Л=1, ..., s"). По-
ложим
А(Р) =-(’ = 1.S'),
(Р-*вГв
=(Л=1, ..
(2.89)
А
Чтобы представить M(t), N(t) в действительной форме, объединим члены, соответствующие сопряжённым корням; тогда
М(О= yz*^rfr+* +
Ла (?.—1)1 [\ “др/ f„(p) L=x
exp tht
(t -l +й'1
/>+Л(Р)
^=*л+,ил
cos <oft£—
— Im
sin
§ 2.2Ц
ПРИЛОЖЕНИЕ К СКАЛЯРНЫМ УРАВНЕНИЯМ
137
уУ ехр
— Im
ехр х/
д \9а 1 е (рУ
J® = x а
ннг
е(р)
fs' + n^P) 'p='h+io3h
л । JLVd'+h 1
\'др) /^+ft(P)
sin <ол/
(2.91)
COS (Ол/ —
Штрих при 2 обозначает, как и раньше, что суммирование ведётся лишь по индексам, соответствующим различным корням. Если мы предпочитаем не выделять комплексные корни, то нужно
распространить первые суммы в правых частях на все различные корни и выбросить вторые. Если все корни — простые, то нужно
вычеркнуть степени скобки
(<+£)•
Вычислив S(p), УИ(р), N(/?),
получим решение по формуле (87). Вторая из формул (77) показывает, что решение содержит начальные значения неизвестной и её
производных до порядка, на единицу меньшего, чем порядок уравнения. Эти значения действительно принимаются при £=0.
б) Пусть теперь имеем систему п скалярных уравнений
п п*
2 /ул (О) ук (f) = 2 ejk• (D) xv (0 (/ = 1.........n), (2.92)
fc=l fc'=l
1
где xk> (/)(&'=!,..., n') Обозначают заданные, yk (f) (k = 1,..., n) — неизвестные функции, e^'(P), fjk(D)— полиномы от D с постоянными коэффициентами. Наивысшую степень полиномов (D) при данном k обозначим через тк, это — порядок старшей производной от Л» фигурирующей в уравнениях. Полагая
x(t) =
У 1(f)
Уп®
e(D)=\\eilc,(P)\\ (пХп'У, /(D) =||/. (D)|| («Х«).
Jnf
(2.93)
(2.94)
;(0 =
можем заменить предложенную систему эквивалентным матричным Уравнением (75). Его решение (87) после перехода к элементам даёт решение системы
t
yj (0 = М, (f)+2 Sw (D) xp (t) + f 2 Njv (t — «) xv («) du. (2.95) fc' * к*
138
ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. 2
При этом Sjw (D) суть целые части дробей
Затем
(О) к Д(О)
к'
Q, W ~ л (0).
к
(2.96)
Наконец, пользуясь теми же, что и выше, обозначениями для действительных и комплексных корней Д(/?), имеем:
expV ГV(/_1_AV’ 1 р (п\Qk(p)—Pk(p> (?, — 1)! L\ "Г" др) г*W &,(р)
к
.. /п FV Л । Vs'4 Л-1 о / ч
X | Re X “Ь др)
L к
Qk (.р)—Рк (рУ
^в'+к(р) Jp=»)i+ia>^
COS —
Qk (P> — Pk (/01
bj+ntp)
sin <0fti
(2.97)
p=th+imh
S' exp zbt
n
^.+h(p)
ekk' (p) .
cos ------
^=«л+<шд
екк'(рУ
. sin <aht
к
Вторая формула (96) показывает, что решение содержит начальные значения каждой неизвестной у^(0 и её производных до порядка тк — 1; общее число этих значений есть
т == 2 Мк- (2.99)
§ 2.21] ПРИЛОЖЕНИЕ К СКАЛЯРНЫМ УРАВНЕНИЯМ 139
Если определитель коэффициентов при старших производных в уравнениях системы (92) отличен от нуля, то она разрешима относительно этих производных и может быть представлена в форме Коши. В этом случае все т начальных значений независимы и действительно принимаются при f = 0, как бы они ни были заданы. Степень s полинома А (О) также равна т, так как определитель старших производных является, очевидно, коэффициентом старшего члена в развёрнутом выражении A (D) и степень этого старшего члена как раз равна т»
Если теперь определитель старших производных равен нулю, то $ < т\ мы можем исключить старшие производные из заданных уравнений и получить т — s других уравнений, не содержащих этих производных, причём новые уравнения должны удовлетворяться, разумеется, и в начальный момент. Таким образом, в этом случае т начальных значений, фигурирующих в решениях, связаны т — s соотношениями; только s из них являются независимыми и действительно принимаются, как бы они ни были заданы.
в) В самом общем случае четыре матрицы e(D), x(f), f(D), y(f)9 входящие в уравнение (75), будут соответственно типов пХп', п' Xг, п X
Общие формулы предыдущего параграфа остаются верными, и этот случай не представляет ничего нового, поскольку пг скалярных уравнений, которые получаются, если перейти к элементам, распадаются на г частных систем по п уравнений
2 А» Ф)ук1 (0 = 2 (D) хкЧ (0 и = 1, , п), (2.100)
к кТ
причём в каждую входит только п неизвестных ykl(f) (6=1,..., п), образующих Z-й столбец в y(t). Относительно начальных условий, которым удовлетворяет решение каждой частной системы и их независимости, можно повторить всё сказанное в пункте-б). *
Мы можем также обозначить здесь через х^(/), ^j(0 не элементы, а строки матриц х(/), y(t) и тогда формулы (93) остаются в силе, но дают коагулированное представление этих матриц. Поэтому сохраняются также уравнения (92) и вся - группа формул (95), (96), (97), (98), дающих решение, причём S;k> (D) и (f) остаются теми же скалярами, что и раньше, между тем как Pj(p), Qj(p) и
будут теперь не скалярами, а матрицами-строками. Ничего не стоит также получить выражения для отдельных элементов урф9 но мы- позволим себе их не выписывать.
Пример. Пусть имеем систему '
{D^^y^ + Dy^xtt),
(D24-D —3)^ + (D+1)j/2 = 0.
140
ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. 2
Она эквивалентна одному матричному уравнению вида (75), в котором
У1
У2
e(D) =
f{D) =
D* — 2 D
D^+D — 3 D-M
1| о г
a x (f) есть скаляр. Здесь n = 2, n' = 1 и
A(D) = D —2, s=l, Xx = 2, ft=l, A1(D) = 1,
F(D) =
Поэтому
— —D4-3
— D
Z)2 —2
P (P) = o>
9
J1(O) ^(0)
P (P) e (p) =
откуда
c/rn « F(D>e(D)
S (D) = целой части —- =
1
— D — 3 ’
M (/) = ea
— e2*
P+1
- -рЗ-р + З
(0) + У2 (0)
-У1 (0) - y> (0)
1
1
Jt(0)
ja(0)
j9 = 2
>
AT(if) = e2*
0
x (и) du.
у = e®
yt (0) + ja (0)
-ji(0)-j2(0)
Так как в данном случае
= 2, т2 = 1, m = mi -j- т2 = 3, т — s = 2,
то из данных уравнений можно вывести два других, в которые не входят старшие производные. А именно, вычитая первое уравнение из второго, имеем:
(D — 1)_У1 +у2 = —х (0;
если же из первого вычесть только что полученное, умноженное на D, то
AD-2)yi=(D + \)x(t).
Эти соотношения должны удовлетворяться и в начальный момент, так что мы имеем из первого:
Л<°)+Л(0)=л(0)”-*(0).
$ 2.22]
Ступенчатые фУнкЦий
141
Пользуясь этим, получаем следующее решение:
t
~ LVi (0) — х (0)] e2t -J- х (t) -J- 3 J* e2 X (ti) dut
о
t
У2 = [ — У1 (0) 4" X (0)] e2t — X (0 — 3x (0 — 3 J e2tt-u> x (a) du, о
содержащее одно независимое начальное значение у± (0).
§ 2.22. Ступенчатые функции. Пусть скалярная или матричная функция h(f) определена для всех или, по крайней мере, для неотрицательных t и пусть т — положительная постоянная.
Ступенчатая функция
х (0 = h (0) 1 (t) + 2 Ыг ((j — 1) т) 1 (t—j-z) (2.101)
J=1
принимает при равноотстоящих аргументах £ = ут(У = О, 1, 2, ...) те же значения, что и 7г (£), и мы будем писать, обобщая смысл символа J:
x(t) = (2.102)
Имея в виду рассмотреть несколько подробнее приложения операционного исчисления к теории конечных разностей, мы ограничимся в основном ступенчатыми функциями такого типа.
Изображение x(f), согласно (60), есть
оо
В (р) = Л (0) + s Дй (С/ — 1) г) е~РК, (2.103)
J=1
можно написать также:
В (р) = h (0) + 2 [й (/т) - й ((/ - 1) т)] е~Р3' =
J=i
оо оо
= А (0) + 2 й С/т) е~р^ — 2 й С/т) е~р w+1)t =
j=l J=0
= й (0) е-рт (е*т — 1) + 2 й С/т) е~р y+1)t (еГ — 1)
У=1 или оо
= У х С/т) (2.104)
J=0
Это уравнение аналогично уравнению Карсона, причём роль делителя р в левой части последнего здесь переходит к двучлену — 1, а справа вместо интеграла с бесконечным верхним пределом входит бесконечный ряд.
142 элементы операционного исчисления [гл. 2
Так как х (I) = х (0) при 0 t < т, то величина а (р), определяемая формулой (27), принимает вид
а(р) = х(0)(1— (2.105)
и для изображения функции Tx(t) мы получаем из (28) формулу еЩр)— 1)х(0)<-> Tx(t). (2.106)
Таким же образом, из (29) и (30)
а/р)==7^х(0)(1-е-П,
еЧ>т^(р)-~{е^— 1) 7^х(0)-н> Tmx{f). (2.107)
j=o
Полагая
7 == е?\ (2.108)
можно представить предыдущее соотношение в форме, аналогичной (19):
(Р) — х (0) Ттх (/). (2.109)
Если же е(Т) есть полином от Т, то
«(Т)5(р)-(7-1)Р(7)н->^(Пх(О. (2.П0)
где
Р(1)=-е{^~ет(Т)х(0). (2.111)
§ 2.23. Конечная сумма и разности ступенчатой функции. Формула (31) для конечной суммы может быть, в случае ступенчатой функции, написана в виде
Ti/x-l
Пользуясь выражением (105) для а(р), получаем из (34) изображение первой разности:
(^ — 1) [В (р) — х (0)] Дх (0. (2.113)
Аналогичным образом из (36), (37):
(р) = Д'х(0)(1—«’*")>
(?* _ 1 )”Ч (р) — m^(epx — 1 )”-'д'х (0) Ьтх (t),
j=0 что можно представить в виде
- D- Е(Р)- -(0)А*-<0. (2.114)
§ 2.25] ИЗОБРАЖЕНИЯ НЕКОТОРЫХ СТУПЕНЧАТЫХ ФУНКЦИЙ
143
Это соотношение вполне аналогично формуле (19) для wi-й производной; роль, которую там играли р и операторы D и £)0, здесь переходит к двучлену — 1 и оператору Д.
§ 2.24. Умножение изображений ступенчатых функций. Найдём оригинал произзедения изображений t(p); т|(р) оригиналов x(f), y(t), первый из которых является ступенчатой функцией. Умножая обе части (104) на -q(p), имеем:
Е (р) (р) е^— 1
ОО
= У X (Л) Т) (р) е-РV *
J=0
Но по теореме запаздывания
(р) —ft — т) 1 (t—jx — т),
так что
оо
S x{j-z)y{t—jx — т) i=o j=o
и, следовательно,
Е (р) •>! (Р) — 1
Т//г-1
г* У ХМУ$-jx — т);
(2.115)
J=0
если же y(f) есть ступенчатая функция, то
Е (Р) •») (р)
1
Tt/T-l '
3=0
(2.116)
Так как оригинал исчезает при t < т, то, согласно формуле (34) для первой разности, имеем соответственно:
Т#Л-1
Е (р) -П (р) -?> Д 2 x(Jx)y(t—Л —
з=о
Xth-i.
Е(Р)“»1(Р)-г*д 2 x(f—jx—x)y(jx).
Последние формулы представляют конечно-разностные аналогии обеих форм общей теоремы об умножении изображений. Как и раньше, роль делителя р переходит к двучлену ерг—1, а интегрирование заменяется суммированием.
§ 2.25. Изображения некоторых ступенчатых функций. Предположим, что функция a(t), фигурирующая в формулах (64), (65), равна единице в интервале (0, т) и исчезает вне его. Тогда
а(р)=1— Л(0=1;
144
ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ [ГЛ. 2
применяя символ f в общем смысле, принятом в начале § 22, получим из (71)
1 ~~ (W - 1) ... (^ - /к + 1) .th_m ,211П
(е^ —k)w+1 ’ • _ 1-2.../П V ‘ 7
В частности, при Х=1 имеем:
1 . Г№)
— -^J 1-2...т
(2.118)
С помощью (117) можно найти оригинал для изображения, представляющего любую дробную рациональную функцию от у = еРх, степень числителя которой не выше степени знаменателя. В самом деле, такую функцию можно написать в виде (у—1) Н*(т), где Н(к) — правильная дробь, которую можно разложить на элементарные. В результате получится линейная комбинация выражений вида (7—1)/(^ — X)w+1, интерпретируемых по формуле (117). Мы немедленно применим этот приём к решению линейных конечно-разностных уравнений с постоянными коэффициентами.
§ 2.26. Линейные разностные уравнения с постоянными коэффициентами. Пусть имеем уравнение в конечных разностях
d (А)у (0 = с (А) х (0, (2.119)
где x(t), y(f) суть ступенчатые функции, первая из которых задана, а вторая является неизвестной; с (A), d(A) обозначают полиномы с постоянными коэффициентами от оператора А. Все четыре величины могут быть скалярами, и тогда мы имеем одно скалярное уравнение с одной неизвестной. Или же эти величины являются матрицами, и тогда мы имеем матричное уравнение, Эквивалентное системе скалярных уравнений; дело обстоит таким же образом, как и для дифференциальных уравнений, и потому мы на этом не останавливаемся. Относительно б/(А) предполагается, что это либо скалярный полином, не равный тождественно нулю, либо квадратная неособая полиномная матрица. Так как оператор А связан с Т соотношением (33), то предложенное уравнение может быть представлено в форме
/(Т)ХЭ = *(7Эх(а (2.120)
где е(Т),/(7') — полиномы, легко вычисляемые по с (A), б/(А). Можно искать решение как для той, так и для другой формы, но вторая, повидимому, удобнее, вследствие чего мы ею и ограничимся.
Так как по формуле (ПО)
е (7) 5 (р) - (Т — 1) Р (7) -Н- е (Т) х (Q,
/(7) *1 (Р) - (7 — 1) Q (7)
§ 2.26]
ЛИНЕЙНЫЕ РАЗНОСТНЫЕ УРАВНЕНИЯ
145
где у = и
Р(1) = е^_ет-Х(°)’ Qd)=-/(^_r(r) J(O)« (2Л21)
то изображение уравнения (120) будет
/СО 'П (Р) — (7 — 1) Q (l) = « (7) £ (Р) — (7 — 1) р (7);
отсюда
*1 (Р)=/(7)\(7 - О К? (7) - Р (7)1 +/(7)\г (7) * (Р)
или
•П (Р) = (7 — 1)-------------------F д(т) « (Р)>
причём Г (7), Д(у) обозначают присоединённую матрицу и определитель для /(f). Положим
FW19<^PMI=-«W + HW, I
(2.122)
где — /?(l), 5(7) и p-Cf), v(f) обозначают, соответственно, целые и дробные части выражений, стоящих слева. Операционное решение принимает вид
Ч (Р) = (7 -- 1) И (7) + 5 (7)«(Р) - (7 — 1) я (7) +
(т —1)Чт)^(Р). (2.123)
Совершенно так же, как в § 20, покажем, что
Р (7) = (T)TZ г( П * (0) и, следовательно,
S(7)*(P)-(7— l)/?(7)H->S(T)x(0. (2.124)
С другой стороны, обозначая через 7а(о=1, ..., $) корни определителя Д(ч), через q9 их кратности и через Aff(?) полиномы А(т)/(Т— 7<у)д<,> имеем разложение на элементарные дроби:
Н(7)^
у 1 J д% Р~х Р(т)[О(т)-Р(т)]1 1
» р^(9в~Р~1)! * ^"₽_1 Аа(Т) |т=Та(т_Тв)₽+1 ’
10 Зйк. 1474. Б. В.- Булгаков
146
ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. 2
Отсюда, пользуясь операционной формулой (117), находим:
где
(I— 1)р(7)-г>Л4(0,
(2.125)
а р=0
(WW*- !)...( Pl (?» —Р-
г А-р-1
х I
Мт)
. (2.126) о
Аналогичным образом,
(I—
(2.127)
yt/n-p
По теореме об умножении изображений ступенчатых функций (§ 24) имеем:
-Т—-Ь» S N(/—/т —т)х(/т).
J=0
(2.129)
Пользуясь (124), (125), (129), можем интерпретировать выражение (123) и получить искомое решение
Т*Л-1
j(O = >W(0 + S(T)x(O+ S 7V(f——т)х(/с). (2.130)
J=O
Аналогия с решением (87) линейного дифференциального уравнения с постоянными коэффициентами очевидна. Относительно начальных условий и их независимости можно повторить то же самое, что и там, с той разницей, что вместо производных в этих условиях фигурирует несколько функций Tmy(t).
Если x(t) не является ступенчатой функцией и неизвестная не предполагаётся заранее таковой, то решение будет содержать не произвольные начальные значения, а произвольные периодические функции. Это было установлено выше для простейшего уравнения (67).
§ 2.27. Абсцисса сходимости. В § 2 были приведены некоторые теоремы, доказательство которых мы отложили и дадим здесь. Положим p = a-]-fa и покажем прежде всего, что если интеграл Лапласа сходится в точке р0 = о0 Ц- /<о0, то он сходится во всех точках р, для которых а > <з0.
§ 2.27]
АБСЦИССА СХОДИМОСТИ
Г47
В самом деле, пусть
t
zQ (t) = j* x (f) e~PQt dt.
о
Так как zQ(f) имеет конечный предел при t->oo, то существует такая матрица М с положительными элементами, что | zQ (f) | Л4 при 0 t оо. Полагая
t
z(f) = J х (t) e~pt dt о
и интегрируя по частям, имеем:
t
z(t) = J [x (t) e~*oi] e~(p~Po) * dt = о
= (f)<,-«-«' + (,-Pi) j(0 at,
0 откуда
z(t") — z (f) = e[Zo (t") (r-n — z0 (f)] +
tn
+ (.P ~Pq) J z0 (0 e~(p~Po)t dt.
t'
Если 0<^'<^'<оо, то
— z(t')\<£
<C 2Me”I I P -Pol м ^*-*0) (£"—^')i
вследствие чего |z(£") — £(f)| стремится к нулю, когда f и f стремятся к бесконечности. Согласно известной теореме анализа (признак Коши) отсюда вытекает, что z(f) имеет конечный предел при >оо, что мы и хотели установить.
Из доказанной теоремы следует, чго для данной функции x{t) возможны лишь следующие три случая: 1) интеграл Лапласа всюду расходится, 2) интеграл всюду сходится, 3) существует такая конечная абсцисса сходимости ос, что интеграл расходится при о = Rep < ос и сходится при o = Rep>ac.
Совершенно аналогичные соображения в отношении интеграла f\x(t)\e-Ptdt
О
приводят к определению абсциссы абсолютной сходимости <за.
10*
14$ ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЙ [ГЛ. 2
Докажем теперь формулу (6), характеризующую порядок роста интеграла
t
y(f) = $X(f)dt о
при £->оо. При этом будем предполагать, что o = Rep>0, ос. Мы имеем, понимая под z(t) тот же интеграл, что и выше:
* *
у (t) = J е?и [х (и) е~^и} du — J ери [z (и) — z(f)]du =
о о
a t
= z(f)-\-p J е1** \z(t)— z(u)\da-\-p \z(f)— z(if)\du',
o a
предполагается, что 0 < а. Так как функция z(f) имеет конечный предел при >оо, то она ограничена, и, кроме того, а может быть выбрано таким образом, чтобы при a, t>a удовлетворялось неравенство
\z(f)—Z(u)\<e,
I
где s — заданная наперёд матрица с положительными элементами. Тогда
\y(f> I const. eat [1 —£-*(*-<»)], | у (t) e~ot | (const.) e~at + J
а так как все элементы в в могут быть взяты сколь угодно малыми, то отсюда и вытекает соотношение (6).
§ 2.28. Спектральное представление функций действительного переменного. Для получения формулы обращения, позволяющей построить оригинал по данному изображению, нам придётся воспользоваться интегралом Фурье. Привлечение этого аппарата важно также и для раскрытия существа соответствия, которое устанавливается преобразованием Хевисайда-Карсона.
Начнём с комплексной формы ряда Фурье. Пусть x(f)— периодическая функция действительного переменного t с периодом Р. Как известно, при выполнении некоторых условий (например, условий Дирихле) эта функция разлагается в ряд Фурье
х(t) (= 2 (ап cos ^sinА, (2.131)
П = 1
где символ ( = ) обозначает, что в точках непрерывности мы имеем точное равенство, а в точках разрыва вместо x(t) нужно писать
)+*(*+)]•
§ 2.28] СПЕКТРАЛЬНОЕ ПРЕДСТАВЛЕНИЕ ФУНКЦИЙ 149
Коэффициенты а0, ап, bn определяются формулами 4-Р/2 6Zq = х (t) dt, ~Р/2 +Р/2
ап= [ х (0 cos t) dt>
-Р'2 +PI2
Ьп— [ х (f) sin i\ dt.
-Р/2
(2.132)
(2.133)
Функция x(f) может быть не только скаляром, но и матрицей, что не влечёт каких-либо осложнений и будет, вообще, предполагаться в дальнейшем.
Так как
то
/и2гс “п COS Нг
(aw —tfjexp
а из (133) получается
4-Р/2
[ х (f) exp (qz i i] dt
—P/2 или же
a„ cos t + bn sin t = 1 [X(a>) + X(— a>) e-*»*],
ЛГ к л»
где
ш = (2.134)
+P/2
л»= f (2.135)
-P/2
Разложение (131) может быть теперь представлено в виде ряда Лорана »
4-со
*(0(=)^- 2 <2-1S6>
150
ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ
[гл, 2
в котором со пробегает бесконечную в обе стороны последовательность значений
2 • 2те 1 • 2те п 1 • 2те 2 • 2те • • • > р > ~р » и, р > р , • ..
Ряд (136) называется комплексной формой ряда Фурье.
Если x(f) действительна, то Х(ы) и Х(—оо) суть сопряжённые величины, и
4 [X (<») + Х(— ш) e-^t] = Re Х(ш) e{a>t.
Если, кроме того, х(/) есть скаляр, то -¥(оо) является комплексной амплитудой двучлена, стоящего слева, так как этот последний представляет проекцию на ось абсцисс вектора А’(<*>), вращающегося вокруг начала координат с угловой скоростью (о (если рассматривать t как время). Гармоническая составляющая функции х(/), соответствующая частоте (о, отличается от рассмотренного двучлена лишь множителем 2/Р и её комплексная амплитуда есть 2yV(oo)/P. Если х(7) и -Y(oo) суть матрицы, то это истолкование применимо к их элементам.
Соотношения (135), (136) могут рассматриваться как взаимно обратные функциональные преобразования, устанавливающие соответствие между функциями действительного переменного x(f) и их частотными спектрами A'(oo), определяемыми на дискретном множестве значений аргумента
Пусть теперь функция x(f)—непериодическая. Если применить предыдущие формулы, то получится ряд Фурье, сумма которого будет периодической функцией с периодом Р, совпадающей с x(t) лишь на интервале (—Р/2, 4-^/2), а вне его повторно пробегающей те же значения. Чтобы получить выражение, пригодное при всех /, представим (136) в виде
+оо
<о = —оо
и будем стремить Р к оо. Величина
. «о 2тс Да) =— = --п Р1
/ представляющая разность последовательных значений переменной оо, стремится при этом к нулю, и ряд Фурье переходит в интеграл Фурье
Ч-оо
*(9(«=)Л I ЛГ(ш)^Ло. (2.137)
§ 2.29] ОПРЕДЕЛЕНИЕ ОРИГИНАЛА ПО ИЗОБРАЖЕНИЮ 151
Выражение комплексных амплитуд (135) приводится к подобной же форме
Х(щ)= f x(f)e~iwtdt. (2.138)
— ОО
Преобразование, определяемое этим соотношением, будем называть двусторонним преобразованием Фур'е, а .¥(<*>)— трансформацией Фурье для х (/). Эта трансформация представляет непрерывный частотный спектр функции x(f). Формула (137) определяет обратное преобразование.
Проведённый нами предельный переход не является строгим. При строгом доказательстве нужно предположить, что х(0 абсолютно интегрируема в интервале (—оо, +оо), т. е. интеграл
+ оо
f\x(t)\dt
—СО имеет конечное значение.
§ 2.29. Определение оригинала по изображению. Условие абсолютной интегрируемости не выполняется для многих весьма простых функций, например для единичной ступенчатой функции. Чтобы устранить это затруднение, можно применять преобразование Фурье не к х(/), а к произведению х(/)г“с*, где с есть положительное число, выбранное так, чтобы интеграл
ъ
J | х (f) e~ct [ dt а
сходился при Ь-> + °о. Однако при — оо добавленный множитель будет ухудшать сходимость. Ввиду этого можно сделать следующий шаг и представить интегралом Фурье не саму функцию x(t)e~ct, а некоторую вспомогательную функцию, совпадающую с ней при 0и равную нулю при t < 0.
Выражение получаемого таким образом одностороннего преобразования Фурье будет
со
Х(у>) = $ [х (/) e-cf] di о
и для обратного преобразования
+*°°
x(/)e-cf( = )^- | XWe^dv (0</), —со
152 ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО исчисления [гл. 2
или, окончательно,
оо
х (ш) = f х (0 е~ <«+*“>) t dt,
О
4-со
х(0( = )^- I ЛГ(ш) <?(«+*»)* Ж» (()</)•
— ОО
В правой части первого соотношения стоит интеграл Лапласа, и условие абсолютной интегрируемости приводится к следующему:
Незначительное изменение ведёт к обобщённому преобразованию Фурье. А именно, принимая за аргумент трансформации не со, а г —|—Zco, получаем:
оо
•¥(с-|~гю)= j* dt {за<.с),
о
с-М’со
1 f
*(/)( = ) п-j X(c-\-i<s>)e (с+*«>)#£цс_|_/(В) (О-СА ао < с),
с—гео
Наконец, заменяя с действительной переменной а и полагая р ==а-|-/а),
1(р)=рХ(р), найдём:
00
Ц^= \x(f)e~ptdt (0o<a = Rep),
О
с+гсо
х(О( = )йЬ f (°<^> %<с)- (2.139)
С—гм
Первое соотношение есть уравнение преобразования Карсона, и потому второе даёт искомое явное выражение его обращения; входящий в него интеграл называют интегралом Бромуича.
Следует, однако, дать себе ясный отчёт, в каком смысле последняя формула решает задачу обращения.
В противоположность прямому преобразованию, определяемому непосредственно уравнением Карсона, задача обратного преобразования формулируется лишь косвенным образом: найти оригинал по заданному изображению $(р) значит найти функцию х(0, которая бы воспроизводила Е(р) с помощью уравнения Карсона, иными словами, разрешить
§ 2.30]
ВЫЧИСЛЕНИЕ ИНТЕГРАЛА В ФОРМУЛЕ ОБРАЩЕНИЯ
153
последнее, как интегральное уравнение относительно x(f). Результат, полученный выше, решает эту задачу лишь в следующем смысле: если заранее предположить, что оригинал для данного $(р) существует и обладает некоторыми свойствами, которые были приняты при выводе, то он может быть вычислен с помощью интеграла Бро-муича. Этим можно удовлетвориться для приложений, но принципиально было бы естественнее не предполагать ничего заранее об оригинале и установить, каким условиям должна удовлетворять функция $(р), чтобы для неё существовал оригинал, и как его вычислять,
если эти условия выполнены.
Мы не можем, однако, на этом останавливаться.
§ 2.30. Вычисление интеграла в формуле обращения. Интеграл в формуле обращения (139) берётся в плоскости комплексной переменной р по прямой, параллельной мнимой оси и лежащей в области Rep>oc, т. е. правее всех особых точек функции Ъ(р)!р. Мы
покажем, что вместо этого за путь интегрирования можно принять некоторый замкнутый контур. Для этого нам понадобится следующая лемма Жордана.
Пусть Г есть часть окружности радиуса R с центром в начале
координат, расположенная левее прямой Rep = с, где 0 < с (фиг. 4). На этой дуге р = Re*9 (it/2 — а Зтг/2 а). Если при R оо функция $ (р)/р стремится к нулю равномерно относительно о в интервале (гс/2 — 8, Зтг/2-Ц- 8), где & — малый заданный угол то, при 0 < t
lim
В->оо
^eptdP = o. р - г
<(2.140)
В самом деле, условие леммы означает, что для любой матрицы s с положительными элементами можно найти такое /?0, что при R^>Ro и тт/2— 8 ^3^/2 +§ мы бу-
дем иметь |£(р)/р|<еД Предположим, что большим, что а < 8. Так как на Г
Фиг. 4. Дуга Г.
R взято при этом столь
е
tR cos <р
| dp | = | iRe1* d<?\ = R d<o,
то
f ^le^dp I p p
Вк/24-а
et
•J i?/2—a
/B°O8<P7?
154
ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. 2
или, полагая © = д-|-тс/2,
^eptdp
Р *
ic4-a л/2
j' e-tR= 2.tR Г e~tRsinФ
—a —a
Но, как видно из фиг. 5,
а из фиг. 4:
sin
sin > 2^/к
при —а^ф<0, при 0 < ф < it/2,
sin a
с
поэтому О те/2
<2stf?( e~tRil dty + f d^—
г -a o
= 2e Г(е#в’ — 1) -|- (1 — e~ts)
ИЛИ
’ dp
s (2£#crc/2 -{- t: — 2).
Так как все элементы s могут быть взяты произвольно малыми, то лемма доказана.
Фиг. 5. Оценка функции sin<p.
Обозначая теперь через С замкнутый контур, образованный дугой окружности Г и отрезком длины 2/? cos а, отсекаемым ею на прямой Rep = c, имеем:
c + iR cos a
1 f ^^р = ±№£е^р-± f ^eptdp. 2tcZ J p r J p J p
§ 2.30]
ВЫЧИСЛЕНИЕ ИНТЕГРАЛА В ФОРМУЛЕ ОБРАЩЕНИЯ
155
В пределе при R —> оо интеграл слева переходит в интеграл Бромуича, а второй интеграл справа обращается в нуль по лемме Жордана, вследствие чего
Х(0(=)2^Л™ хъ—>оо
J dp (0 =sS /)•
С
Если функция имеет лишь конечное число особых точек
в каждой конечной области, то, применяя теорему Коши, мы можем написать:
<2Л41>
где интеграл берётся теперь по любому замкнутому контуру, заключающему все особые точки, лежащие на конечном расстоянии, a Res %(p)ept/p— вычеты функции ^{р)^1р по этим точкам. Эта форма уравнения обратного преобразования удобна для вычисления многих оригиналов.
В дальнейшем нам понадобится аналогичная формула для интегралов с несколько более общей подъинтегральной функцией $(р), на которую, однако, приходится накладывать более жёсткое условие. А именно, пусть $ (р) имеет в каждой конечной области слева от прямой Rep = с лишь конечное число особых точек и пусть при R —> оо произведение р* (р) стремится к нулю равномерно относительно угла © в интервале (к/2 — 8, Зк/2 -Ц- 8). Тогда при достаточно большом А?,
Зя/24-а Зк/24-а
J” 5 (р) dp j | $ (р) | • | | d<o < е j d<o < в (it Ц- 23),
Г тс/2—а тс/2—а
так что
£(p)dp = 0.
~~ г ~ г
С другой стороны,
c+iBcosa
i j e(P)rfP=2^^(P)rfp-^-j5(p)dp, c—iR cos а С Г
откуда, переходя к пределу при R —> оо, получаем желаемую формулу:
с4-<оо
2ST J 5(P)<*P = ^^(P)<*P==SRese(P). (2.142)
с—too
в которой второй интеграл берётся по любому замкнутому контуру, заключающему все особые точки функции 5 (р)> лежащие на
г 1 11Ш
156
ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. 2
конечном расстоянии слева от прямой Rep = c, и никаких других, a Res$(p) суть вычеты относительно этих точек. В отличие от предыдущей теоремы, функция £(р) может иметь особые точки справа от прямой Reр = с, но они не принимаются во внимание при вычислении интеграла.
§ 2.31. Умножение оригиналов. Найдём изображение произведения двух функций х(0, y(f) по их изображениям ?(р), т|(р). Пусть °а1» аа2> обозначают абсциссы абсолютной сходимости соответственно для х(0, и x(t)y(f). Мы имеем:
оо
О
ОО Cg+ioO
= p\x^^dt J = rt'Q co
C2+ioo оо
J \ x^e-^-^dt ^-dq (<зо < o, aa2 < c.2), c2—ico 0
где a = Rep. Ho
oo
f x (fl
4 ' p — q
0
при
°ai < °—или — aal. Итак,
P 2nl
c2—too
E (p — 9) *l (g) (p—q)q
dq -j-* x (0 у (i)
(°a> °al + °a2 < °>
°a2<c-2<° —°<й)-
(2.143)
Теорема, выражаемая этой формулой, является двойственной для теоремы об умножении изображений (§ 14).
Если применить формулу (142) предыдущего параграфа, то получится
р SRes е %-У } х ® у <2-144)
где вычеты берутся относительно всех особых точек функции т|(^)/^; при этом \q рассматривается как аргумент, а р — как постоянный параметр.
Пример. Положим
^(0 = “£т, v 1 т\ ь
y(f) = e^ch kt.
§ 2.32] ИНТЕГРАЛЫ ОТ КВАДРАТОВ И ПРОИЗВЕДЕНИЙ ОРИГИНАЛОВ 157
Изображения этих функций даются формулами (50), (54) и потому
р У Res-----Ц—1--------ch М.
(Р— Q) +1 (Я — е)2 — X2
Особыми точками, которые должны быть приняты во внимание, являются два полюса ^ = 8zpX. Так как эти полюсы — простые, то, применяя для вычисления вычетов известную формулу *)
Resa/(*) = lim (* — я)/(Д (2-145)
получаем в левой части предыдущего соотношения сумму
Р
Ар - чГ+1 (ч -«- X) J а=._х+Р
______ч—*______
.(P-?)w+1(?-« + X)Je=.+x'
Поэтому
1
(р-е-Х)™*1
Р Г 1
2 L(/> —e + X)m+1
— f*?* ch \t. т\
(2.146)
Аналогичным образом,
£ Г-----------1------ J---------1------- н->1 — tine^ sh Xt
2 L (P —e + X)w+1 (p — e — X)w+1 J m\
(2.147)
Если же заменить X на Zw, то
pRe
(р —£ + Z<0)W+1 [(р__е)24.ш2]»» + 1
-i- cos co/, m\
т (P — £-l-Z<o)W+1 p Im—--------------------r
[(p — e)2 + (o2]W»+i
-Ь> — tmezt sin ooZ, m\
(2.148)
(2.149)
где при определении слева действительной *и мнимой частей буква р формально трактуется как действительное число.
§ 2.32. Интегралы от квадратов и произведений оригиналов
в интервале (0, оо). Применим формулу (48) к функции
и её изображению, определяемому согласно (143), (144). Это даёт:
ОО Сл + ^СО
[ x(f)y(f)dt= J
О сг,—гоо
5 (— ?) ц (?)
?(—?)•»! (?)
(2.150)
причём вычеты берутся относительно всех особых точек функции
п (?)/?•
*) См., например, И. И. Привалов, Введение в теорию функций комплексного переменного, Гостехиздат, 1954, гл. VII-
158
ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЙ
[гл. 2
Полученная формула позволяет вычислить интеграл от произведения x(t)y(f) в интервале (0, оо) непосредственно по изображениям сомножителей. В частности, при x(t)=y(t)
оо 4-г’со
/= J [х(0Р^=2^- [ ач =
О -Лоо
= Res-^=4^-. (2.151)
В качестве примера вычислим интеграл
[x(t)^dt
О
для функции x(f), изображение которой есть
5= k0(/>24- 2сХ + ’ <2‘152)
где С, со — действительные положительные числа.
В данном случае
€(—?)£ (?)______— ад + Ь ад+ Ь
— Я2 (?2 — %*<ng -f- <о2) k0 (д% 2&>д ш2)
Если С>1, то корни знаменателя второй дроби суть л2 = —ш(с±/(;2—1)<о.
Эти корни представляют полюсы функции Hg)lq> лежащие слева от мнимой оси. Вычеты по этим полюсам по формуле (145) будут:
lim (q — Xt)
— a2q2 + №
и
у / 1ч — aq -\-b aq + Ь ______
ДW 2J М?2-2Са>?+<*2) ’ Ы?2 + + “2) “
— а2д2 + ^2
_2k* (q2 — 2С»? 4- “а) (q 4- С“)
Х2
Вычисляя выражения
(_ 4- Ха = азшз (— 2Сз +1 зй 2С / С^Т) 4- Ь\
(q* — 2^q 4- ш*)а=Х1> Ха = 4ш*С (С ±
(? + ^)д=11.х2 = ^“К^Л
§ 2.32] ИНТЕГРАЛЫ ОТ КВАДРАТОВ И ПРОИЗВЕДЕНИЙ ОРИГИНАЛОВ 159
и составляя сумму вычетов, находим:
/ — 1 Г (2С2 — 1 + 2С V С2 — 1) —
2 — 8£0<Л L с +
Д2щ2 (—2С2 4-1 + 2С Vca— 1) Ч- &2 с—
или
_ ^2(d2 ^2
2== 4й0ш3С ’
(2.153)
Это выражение остаётся верным и при 0 < С 1.
В качестве обобщения рассмотрим случай, когда t(p)[p есть какая угодно скалярная правильная дробь
Р Н(рГ
Интеграл (151) принимает вид
4 ioo
____L ° d<! — V Ррч G(y)
- 2«Z . H( — q)H(q)~~ A*™ H(-q)H(q)’
где
О(р)= U(—p)U(p).
(2.154)
(2.155)
(2.156)
Функция G(p), так же как и Н(р), является полиномом. Если степень Н(р) равна s, то степень О(р) не выше 2s — 2, причём второй полином не меняется при замене р на —р', поэтому можно положить
Я(р) = kop* + А^р8"1 + ... + ka, G(p) = l0P2s-2 + lip2s-i+ • • • +4-1-
При $=1 вычисление весьма просто и даёт:
I ___ !°
1 “ 2Mi‘
При s = 2 мы имеем из (152):
И(.Р) _ U(P) ар + Ь
р Н (р) ko (р* + 2C<u/> + ш2)
(2.157)
(2.158)
и можем положить
U (р) = арb, Н(р) = k0 (J? + 2>р + со9),
G (р) = — а2р2 Ь2, так что
Zjji -- 2Z?q^(o, • Z?q(o2,
Zo = —a2,
160
ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. 2
Формула (153) для Z2 может быть выражена через эти коэффициенты:
__/ ^2 I /
flW + ^2 _ ° 1
4^<Л “ 2^2
или
2^1^2
(2.159)
При s > 2 вычисление настолько усложняется, что оказывается необходимой разработка общей методики. Мы изложим с некоторыми упрощениями процедуру, которая предложена Филлипсом [418] и даёт для I выражение, рациональное относительно коэффициентов kj, lj. Это оказывается возможным потому, что хотя при вычислении вычетов и участвуют корни pj полинома Н(р), но в силу равноправия всех полюсов I зависит от этих корней только через посредство их симметрических функций, а эти последние, как известно, выражаются рационально через коэффициенты.
Предполагая сначала все корни простыми и применяя для вычисления вычетов формулу (145), находим:
у G(PP) 2<Я(-рр)//'(Рр)’ p=i
где И' (р) — производная от Н(р). В дальнейшем будет доказано, что метод распространяется и на случай кратных корней.
Так как
3 Я(р) = й0П(Р—Pi)> г = 1
ТО
н(—Рр) = 2*о ( — 1)’ р? П (Pi+Рр)-
Общее наименьшее кратное сумм Pi-\-р? есть произведение
Пм(а+л),
где индекс Ю обозначает, что берутся все сочетания индексов 1, ..., s по два. Мы имеем:
(-1)® у О(л)
2MI (А+а) Г1. PfH' <Р₽>
Р=1
Ц(с)(р«+рА
Дальнейший вывод состоит из двух частей. Во-первых, будет получено выражение произведения всех парных сумм корней какого-нибудь полинома
(?(«)=2v^ (2.160)
з=о
2.32] ИНТЕГРАЛЫ ОТ КВАДРАТОВ И ПРОИЗВЕДЕНИЙ ОРИГИНАЛОВ
161
через его коэффициенты. Это выражение послужит для вычисления ц(с; _}_ рх), а также и величины H(CJ которая является
произведением парных сумм корней полинома
(р)=
Н(р) p—pf
+(М-1+МГ2+ • • • + Vi) (2.161)
и выразится в виде полинома Р(/?р) от pf с коэффициентами, зависящими от kj. В результате выражение для / получит вид
(_1)8 yG(pt)P(pt) 2АоП(е) (Л+А) Zi PfH' (Pf) ’
(2.162)
Произведение G(pp)P(pp) есть опять полином относительно рр с коэффициентами, зависящими от fy, /у, но не от р. Так как часть предыдущей суммы 2» происходящая от каждого члена полинома О(рр)Р(Рр), может вычисляться отдельно, то вопрос сведётся к вычислению сумм типа
V
Н' (Рр)
(Г = — 1, 0, 1, 2, ...).
(2.163)
Это составит содержание второй части вывода.
Пусть все корни z? полинома* Q(z)^—простые. Считая индексы р, о фиксированными, положим:
« = -§-(гр+А)«
Так как
Q(zp) = Q(z,) = 0,
a—^(^ — Zf) = zp, a + l(zG —zp) = ze,
то Q(a—у) и рассматриваемые как полиномы относитель-
но переменной у, имеют общий корень (z0— z?)l2. Если обозначить
. ,(2.164)
где О<«-Л(г) есть (s—у)-я производная от Q(z), то по теореме Тейлора
Q (а + у) = К^у3 + К1У»-' + Kay8"2 + +К(У3~* Н-
11 Зак. 1474. Б. В. Булгаков
162
ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. 2
и, предполагая сначала s чётным,
Q («—у) = V—+V"2—tfsj'8"3 + J
+к^-к^+...-к3_1У+ка. I
Складывая и вычитая уравнения
Q(«+j') = O> Q(«— У) = 0 и полагая i
X = у*, ?
получим два уравнения относительно х: ' \
(х) = К-х^ + + К4х^2-2 + ... + К8 = 0, ?
Г2 (х) = Ktx^ + + /<5х^-з + ... + Xs-i = О,
которые должны иметь общий корень x* — (za— zp)9/4. Условием для этого служит равенство нулю результанта, который может быть получен классическим методом. А именно, заметим, что ITt(x), 1Г2(х) имеют вид
Wr1(x) = ^(x)(x-x*), IF3(x) = N2(x)(x —х*), 1
где ^(х), N.2(x)—полиномы, степени которых на единицу ниже, < чем степени W1(x), IF2(x):
(*) — + и.2х^~2 + «Зх8/2-8 -|- а3/2.
ЛГ2 (х) = у1х8/2-2 -J-^x8/2-3 + a3x8/2-4-{- • • • + ^/2-1. i
Мы имеем: I
— W2 (x) (x) + Wt (x) N2 (x) = 0 j
-'ft
или, подставляя вместо четырёх полиномов их выражения, перемно- 1 жая, делая приведение и приравнивая нулю коэффициенты при сте- 3 пенях х: г}
— ~Ь KqUi = ;
-4“ --K1U2 4“ ^0^2 “ ;
^5^14- К1У1 Xg^2 4~ ^^2 ^1^3 4~ ^0^3= 0’ *
1
Х^/2-1--= 0. J
1
Мы получили s — 1 уравнений, линейных и однородных относительно ' 1 5 — 1 неизвестных - I
-~ ‘l/j, £Z2, ‘Уд» ^3’ *^8’ • • • > ^d/2—1, ж
2 32] ИНТЕГРАЛЫ От КВАДРАТОВ И ПРОИЗВЕДЕНИЙ ОРИГИНАЛОВ 163
Условием существования нетривиальных решений является равенство нулю следующего определителя Гурвитца (s—1)-го порядка:
А.-1= Кь К4 КА Ъ Кх Ко ... 0U) , (2.165)
о о о о о о ... к8 к8^
который, с точностью до знака, и представляет искомый результант. Повторяя вычисление, получим то же выражение и для нечётного s. Закон составления определителя Гурвитца состоит в том, что индексы диагональных элементов образуют натуральный ряд, а индексы элементов каждой строки — убывающую последовательность, причём вместо элементов с отрицательными индексами или с индексами, большими s, ставится нуль. Таким образом,
(а) — ^1»
Д2(*) = *Л2 —*№
А3 (а) = К&К* — KQKl —
(2.166)
Суммы индексов при К в каждом члене этих выражений равны соответственно 1, 3, 6, ...; для Ag_1(a) эта сумма будет s(s—1)/2. А так как из формул (164) для /Cj(a) видно, что каждая из этих величин есть полином относительно а степени, равной у, то, приравнивая нулю результант As_t, мы получим уравнение для а степени s(s—1)/2. В силу сказанного выше, это уравнение должно удовлетворяться, если принять для а значение (zp-f-ze)/2, причём, очевидно, безразлично, какие именно значения приписать индексам р и аг Так как общее число различных комбинаций (^р-|-^)/2 как раз равно s(s—-1)/2, то ими исчерпываются все корни результанта. Поэтому свободный член результанта, делённый на коэффициент старшей степени а, равен
П Ц>+г»)-
Свободный член есть А8_г(0), а так как, очевидно, Kj(f)) — Aj9 то ^e-i(O) получается путём замены в определителе (165) всех- Kj через Aj. Старший член в каждом Л} (а) есть где
есть обычное обозначение биномиальных коэффициентов. Поэтому коэффициент старшего члена в Л8_1(а) есть произведение До”1 на определитель Г8_19 получаемый из (165) заменой Kj на
11*
164
ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЙ
[гл. 2
Пользуясь (166), находим:
и вообще
Можно отметить, что эта величина есть определитель Гурвитца для
полинома Су+О8.. .
Итак,
1 П(с> (Z 4- z ) = А*~г (0)
или
1 ло
Д8-1 (0) =
А± Ао 0 0 0 0 ... О
Л3 А2 Ai Ао 0 0 ... О
А ^4 А А А 4> • • • О
О о о
(2.167)
О 0 0 0 0 0 ... As Ая *
Применяя эту’ формулу к полиному Н(р) и заменяя Ai через kif
вычислим произведение . .
стоящее в знаменателе выражения (162).
Для вычисления Р(/?р) нужно применить формулу (167) к полиному Нр(р) и заменить s на s— 1 и на
Vp + M-1+•••+*<. (2.168)
Этим закончена первая часть вывода по намеченному выше плану, и мы должны перейти к вычислению выражений (163), представляющих, очевидно, суммы вычетов функций ръ!Н(р) по их полюсам рр. Если степень числителя на две или более единиц меньше степени знаменателя, то вычет относительно бесконечно удалённой точки, а потому и сумма вычетов относительно полюсов, лежащих на конечном расстоянии, равны нулю *). Точка р = 0 является полюсом только для L = —1, и поэтому
Spp/y'Cpp =: — = — (2Л69)
Р=1
8 ръ
(£ = 0,1,2..........5-2). (2.170)
Р=1 ₽
*) И. И. Привалов, Введение в теорию функций комплексного переменного, Гостехиздат, 1954, гл. VII, § 1, п. 4.
§ 2.32] ИНТЕГРАЛЫ ОТ КВАДРАТОВ И ПРОИЗВЕДЕНИЙ ОРИГИНАЛОВ 165
Чтобы получить аналогичные формулы для L>s — 2, напишем: kop3 _ р3 _ 1 __
2
оо
Г=0
где Гг суть симметрические функции
о
р’
Умножая обе части предыдущего соотношения на pL~8lk^ имеем:
—• 1-У Г р-г+Ъ-а Н(р) г=0
откуда видно, что вычет относительно бесконечно удалённой точки *) есть —Гь_а+1/й0, а так как в сумме с вычетами по полюсам, лежащим на конечном расстоянии, он должен давать нуль, то
Ь‘ Т, «
^0
С другой стороны, мы имеем:
оо
г=о
>
откуда, перемножая и приравнивая коэффициенты при одинаковых' степенях р9 получаем следующие рекуррентные формулы для Гг:
Vr + MV-i+ — +Vo==0 ('>1); (2.172)
*) И. И. Привалов, Введение в теорию функций комплексного переменного, Гостехиздат, 1954, гл. VII, § 1.
166
ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ
[гл. 2
при i > s входящие в них должны быть заменены нулями. Вычисляя последовательно, получаем рациональные выражения
(2.173)
Можно также совсем избежать необходимости вводить функции Гг, если воспользоваться соотношениями
koPf = — М?-1 — k2Pf~2 — • • • — ksPf~S > S)
и постепенно понижать степень числителей в суммах (163) или непосредственно в выражении / до ($—1)-й.
Этим заканчивается вторая часть вывода.
Легко освободиться теперь от сделанного в начале предположения, что корни рр — простые. В самом деле, так как коэффициенты kj представляют непрерывные функции корней, то полученное для / выражение и подинтегральная величина будут также непрерывны, пока корни остаются в левой полуплоскости. Это выражение равно интегралу, если корни различны; оно останется таковым и в том случае, когда некоторые корни, изменяясь непрерывно, сольются.
Проведём описанную процедуру для s = 3. В этом случае
Н (р) = + k-LP* -f- k2p 4- k.3,
G(p) = /0^ + /1p* + /2
И
nt (p) = kop*4-(kopf 4- kj p4-4- krPf+*2).
С помощью выражений
A2(a) = K1/<2 — KOKS, Ai(a) = K, и формулы (167) получаем:
* Rq
§ 2.32] ИНТЕГРАЛЫ ОТ КВАДРАТОВ И ПРОИЗВЕДЕНИЙ ОРИГИНАЛОВ 167
согласно (162)
так что,
£о А> +
2 (Мз
Р?Н' (рр)
Далее из (169), (170), (171), (173)
и, следовательно, Г ______________________ kok^ -- ,д 1 уДх
По вычислениям Филлипса и Мак Лейна в цитированном выше сочинении
У . ^0 (^1^2 — ^О^з) ^3 — Ч~ kffaklh + (kikj — Iq /2 1 yg\
* 2^4(va-Ms-W 1 ’
Тот же источник даёт ещё выражения /5, /в> Л> ^^ми соот-
щие в них коэффициенты aj, bj можно считать ветственно с применёнными выше kjt lj. „пмпшыо'или без
Различные способы вычисления интегралов д д кра-
помощи операционного исчисления дали Г. Б. р Фельдбаум [*•"! совскийМ, Ф. А. Михайлов, Н. Д. Моисеев М» А. А. Фельдбаум! 1 и А. К. Холл (*•«].
УРАВНЕНИЯ АНАЛИТИЧЕСКОЙ ДИНАМИКИ
§3.1. Связи и виртуальные перемещения механической системы. Пусть имеем систему h материальных частиц, массы которых обозначим через Шр а прямоугольные координаты через Хр у?, z?(f= 1, ..., Л).
Движение системы может быть стеснено некоторым числом связей, выражаемых уравнениями
Фа С^р У1’ • • •» О === 0 === 1 > • • •»
И
(*^1> У1> • • • > ^h’ У1> • • • f Zip ty === 0 (т == 1, • • •, £),
которые содержат, соответственно, либо только координаты и время t, либо также и проекции скоростей Хр ур Zp Можно применить также более краткую условную запись
Фа(х, у, z, 0 = 0 (а=1, (3.1)
(х, у, z, х, у, z, f) = 0 (у=1, ..., с).
Связи первого типа называются геометрическими, второго типа— дифференциальными. Мы ограничимся чаще встречающимся и лучше изученным случаем систем, у которых уравнения дифференциальных связей линейны относительно проекций скоростей и имеют поэтому вид
S + d'fyr + + С, = 0 (7=1........с), (3.2)
где С^р С^р С"р могут зависеть от координат и времени, а знак S обозначает суммирование от 1 до h.
Если функции Фа, C^f, Ctf, не зависят явно от г, а свободные члены равны нулю, то связи и сама механическая система называются склерономными относительно данной системы координат, в противном случае—реономными.
Дифференцируя уравнения геометрических связей, получим:
аФ«(- ' А4-^2 — П \dxf Xf ""Г" dyf dzf I )' dt ’
§ 3.1] СВЯЗИ И ВИРТУАЛЬНЫЕ ПЕРЕМЕЩЕНИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ 169 что можно записать в форме
S (A^Xf-|- Ал — 0 (а = 1, .. ., а), (3.3)
сходной с (2), если положить
л' _дФа у/ _ дФа dXf ' dyf
4 <м
ЛаГ ' dzf’ Я“— dt ’
Однако же геометрические связи отличаются от дифференциальных тем, что уравнения последних, как мы будем предполагать, неинтегрируемы и не могут быть представлены в конечной форме.
Если дифференциальных неинтегрируемых связей нет, то система называется голономной, в противном случае — неголономной.
Умножая на dt, получим уравнения связей в форме
§ (Arf dXf -f- Atf dyf Aaf dzf) -|- Aa dt = 0 (3.5)
(oc —— 1, • • •, tz),
S (CyfdXf-\- c"fdyf-\-C%fdzf) -^-Cxdt=Q (3.6) (7=1..................0-
Входящие сюда дифференциалы dXf, dyf, dZf представляют проекции элементарных действительных перемещений частиц. В отличие от них, виртуальными перемещениями называются векторы, проекциями которых служат вариации §Xf, Zyf, Взу, удовлетворяющие уравнениям
Аа (8) = $ (A'f 8xf + X>8jy+ A"'ftef) = 0 (3.7)
• (а= 1......«)>
C7(8) = S(C;r8x/.+</8^+e;;8zf) = O (3.8)
(7=1,..., с).
Эти уравнения отличаются от (5), (6) только для реономной системы, так что в этом случае виртуальные перемещения должны согласоваться со связями, остановленными в данный момент, и действительные перемещения, вообще, не принадлежат к числу виртуальных. В случае склерономной системы действительные перемещения обязательно будут в то же время и виртуальными. Мы могли бы также назвать виртуальные перемещения пробными. Принято считать их малыми, однако вариации 8х^, Zyf, Zzf не перестают удовлетворять последним соотношениям, если их все умножить на одно и то же число.
170
УРАВНЕНИЯ АНАЛИТИЧЕСКОЙ ДИНАМИКИ
[ГЛ. 3
§ 3.2. Реакции связей и их работа. Связи влияют на движение системы, и потому их механический эффект может быть представлен некоторыми силами с проекциями Nf, Nf, Nf't называемыми реакциями, в отношении которых принимается фундаментальная гипотеза или постулат. Он разъясняется на примерах в статике и выражается уравнением
А (8) = S (N'f bCf+Nf Nf' = 0, (3.9)
согласно которому реакции связей не препятствуют виртуальным перемещениям и не совершают при этих перемещениях никакой работы.
С помощью этого постулата реакции могут быть выражены аналитически с точностью до некоторых неопределённых множителей. В самом деле, виртуальные перемещения должны удовлетворять линейным соотношениям (7), (8) и потому среди вариаций 8лу, 8jy, 8гу будет лишь 3/г— а — с независимых. Соотношение А(8) = 0 также линейно и не может быть независимо от (7), (8), так как иначе число независимых вариаций было бы меньше, чем 3/г— а — с. Поэтому линейная форма А (8) должна быть линейной комбинацией форм Аа (8), СД8), составленной с помощью некоторых множителей j , *
ха, •
А (8) = 2 «.А, (8) + 2 лтСт (8) = а у
= S KS *вА/+ 2 Xy^^y/*) 8jCy* 4“ (5 xaAxf 4“ 5 4“
a Y « T
4“ (2 xa^af4“ S * а Г
Сравнивая c (9), находим искомые выражения сил реакции:
А/у = 2 xaAxf4“* 2 a Y
^==2хХ>+2^ (/=i, .
a y
(3.10)
Появление неопределённых множителей естественно и обусловлено тем, что связи, которые мы учитываем, являются идеальными, поскольку они выражаются уравнениями, точное выполнение которых постулируется а priori, вне зависимости от сил, приложенных к системе. Силы реакции должны обеспечить выполнение этих условий, и их величины должны быть такими, какие для этого потребуются.
§ 3.3. Уравнения Лагранжа первого рода и основное уравнение аналитической динамики. Пусть проекции заданных сил, приложенных к частицам т? и называемых активными в отличие от пас-
171
«
§ 3.3]
УРАВНЕНИЯ ЛАГРАНЖА ПЕРВОГО РОДА
сивных сил или реакций связей, суть
Первые слагаемые представляют проекции консервативных составляющих, происходящих от потенциальной функции U(х, у, z), а вторые слагаемые — проекции добавочных неконсервативных составляющих. Такое разбиение на составляющие неоднозначно, но удобно; в частных случаях все или некоторые из первых или вторых составляющих могут быть, разумеется, равны нулю.
Уравнения движения будут
dU mfXf = dTf 4 •• dU ™М = д^
А);
(З.И)
т
пользуясь выражениями проекций сил реакции, найденными в предыдущем параграфе, получаем так называемые уравнения Лагранжа первого рода:
Вместе с а-^с уравнениями связей (1), (2) они достаточны для определения ЗА + a -f- с неизвестных координат х?> у?, z? и множителей ха,
Если умножить уравнения (11) соответственно на Злу, Ъу?, 8^, сложить и принять во внимание (9), то получится основное уравнение аналитической динамики
выражающее принцип виртуальных перемещений.
Иногда удобно рассматривать координаты ^, yfi zf или, лучше, числа
(/=1, ..., А),
172
УРАВНЕНИЯ АНАЛИТИЧЕСКОЙ ДИНАМИКИ
[ГЛ. 3
где тс есть некоторая условная масса, как декартовы прямоугольные координаты «изображающей» частицы массы тс в Зй-мерном евклидовом пространстве E._>h. В частности, можно взять за тс суммарную массу системы или положить для простоты /пс = 1. Полагая также в уравнениях Лагранжа
получим уравнения движения изображающей частицы
Вместо (1) будем иметь соотношения вида
<paG, 0 = 0 (а = 1, ..., а), причём, вследствие (4), (14), (15), А«) i = д<?а/д^.
Обозначая п = Зй— а,
(3.15)
(3.16)
(3.17)
(3.18)
(3.19)
можно рассматривать (17) как уравнения n-мерной поверхности Rn, форма и положение которой в случае склерономной системы постоянны, а в случае реономной системы меняются с течением времени. Частица mG должна всегда оставаться на Rn и, кроме того, её движение стеснено дифференциальными связями.
Принимая, что в отношении величин с индексом i символ S должен здесь и в дальнейшем обозначать суммирование от 1 до Зй, представим уравнения этих связей в виде:
S С(й i d\i + dt = ° (7 = 1............с) (3.20)
§ 3.41
или
ОБОБЩЁННЫЕ КООРДИНАТЫ
173
Sc(T)<e + CT==O (7-1..........с). (3.21)
Основное уравнение (13), после перехода к координатам получает вид
S (- + Si) = 0. (3.22)
Применённое здесь истолкование в* терминах многомерной геометрии мы сохраним и для некоторых дальнейших выводов, поскольку это вносит в них единый план и своеобразную наглядность. С другой стороны, не следует опасаться уйти от механической реальности, так как величины лишь постоянными множителями отличаются от координат частиц у?, и потому ничего не стоит на любом этапе рассуждения вернуться к этим последним.
§ 3.4. Обобщённые координаты. Число неизвестных в уравнениях движения может быть уменьшено, если перейти от декартовых координат к так называемым обобщённым.
С этой целью заметим, что так как а уравнений геометрических связей (17) можно предполагать независимыми, то среди 3/г координат всегда найдутся а таких, относительно которых эти уравнения разрешаются, в результате чего а координат выразятся через /г = = 3/г— а остальных, которые останутся независимыми.
Или же можно добавить к а уравнениям геометрических связей какие-нибудь п независимых соотношений
fjtt, 0 = 0 (/=!> ")> (3.23)
содержащих 3/г декартовых координат п новых независимых параметров д1, ..., qn и время причём в этой главе верхние индексы обозначают не степени, а порядковые номера. Разрешая полученную совокупную систему a-]-n = a-\-(Sh-—д) = 3/г уравнений относительно 3/г декартовых координат, найдём:
= 0 (*=1> ..•> 3/г). (3.24)
Эти выражения определяют все положения системы, совместимые с геометрическими связями, через независимые параметры которые и называются обобщёнными координатами или координатами Лагранжа. Их число п называется числом степеней свободы системы. Можно также рассматривать предыдущие соотношения как параметрические уравнения поверхности Rn.
Действительные перемещения и виртуальные перемещения, совместимые с геометрическими связями, суть соответственно
<3-25>
8t<=S <3-26>
174 УРАВНЕНИЯ АНАЛИТИЧЕСКОЙ ДИНАМИКИ [ГЛ. 3
где вариации Sqi произвольны. Подставляя выражения в уравнения дифференциальных связей, получим:
Sc№(2^^+>«)+c,«=o
И
^Е(т)^+ЕтЛ = 0 (7=1........с) (3.27)
2 £(т) j = 0 (7=1.......с), (3.28)
3 где
Е^ = S Qr) i • Е. = S + Сг (3.29)
Аналогичным образом, для виртуальных перемещений
С. (8) Е= 2 Е(М 8^ = О (7=1.с), (3.30)
3
так что если виртуальные перемещения должны быть совместимы как с геометрическими, так и с дифференциальными связями, то вариации обобщённых координат bqi должны удовлетворять с линейным соотношениям.
§ 3.5. Уравнения Лагранжа второго рода. Заменяя в основном уравнении (22) вариации 8^ их выражениями (26) и складывая с уравнениями (30), умноженными на получим:
S (- “Л<+йг+s<) 2 + 2 Ч 2 W=0.
3 Т 3
Если же заметить, что
QdUdZ{ _dU
^dtidq3-dq3’ (3‘31)
и обозначить
<з.з2)
<з.зз>
ТО
2 (- meWj + + 2 \Еи Л W = 0. (3.34)
3 У 1
Суммы -|- Qj j носят название обобщённых сил, соот-
ветствующих координатам qi.
§ 3.5]
УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА
176
С помощью уравнений (30) мы можем выразить какие-нибудь с из числа п вариаций bq3 через остальные п — с, которые останутся независимыми. Заметив это, определим множители приравнивая нулю в (34) те с круглых скобок, которые умножаются на зависимые вариации; полученные выражения подставим в остальные . круглые скобки. В результате левая часть (34) будет представлять линейную комбинацию только п— с независимых вариаций, коэффициенты которых должны исчезать в отдельности в силу этой независимости. В итоге все круглые скобки будут равны нулю, и мы получим п уравнений
эд = +Qj+2х А> * (7 =1 • • • • > «)• (3.35)
q т
Чтобы преобразовать выражения Wj, перепишем соотношения (25) в виде
<336>
откуда
dt dq3 ~ dq3 dqk К
dq3 dqj ’
& _l = ± ( У = •
dq3 dt dq3\^dqk J dq3 ’
К
поэтому
и
d dT dT м -г?-------------------
3 dt fig!
(3.37)
(3.38)
где
Так как сумму S (^)2 можно интерпретировать как квадрат скорости, изображающей частицы тс, а -f- (^)а -|- С*/)2 есть квадрат скорости одной из частиц т? механической системы, то Т представляет одновременно как кинетическую энергию частицы тпс, так и суммарную кинетическую энергию системы.
Подставляя выражения для в (35), получим уравнения Лагранжа второго podaz
^ДГ_дТ = а[/_|_^ |у КЕ (3 39)
dtdq3 dq3 dq3'1^ 7 4
176
УРАВНЕНИЯ АНАЛИТИЧЕСКОЙ ДИНАМИКИ
[ГЛ. 3
t Входящие в них величины Т, U, Qp Е^ j должны быть выражены через q3, q3, t с помощью соотношений (24), (36), и тогда эти уравнения, вместе с с уравнениями дифференциальных связей, достаточны для определения rt — Zh — а обобщённых координат и с множителей Лу, через которые выражаются реакции дифференциальных связей. Реакции геометрических связей не входят; поэтому если такие, связи существуют (а =f= 0), то уравнения Лагранжа .второго рода содержат на 2а меньше неизвестных, чем уравнения первого рода.
Всё сказанное сохраняет силу, если в числе а.связей с?а = 0, учитываемых при введении обобщённых координат, фигурирует лишь часть геометрических связей. Тогда остальные войдут в группу с связей, определяемых уравнениями (28), некоторые из. которых будут поэтому интегрируемыми.
При такой точке зрения уравнения Лагранжа первого рода получаются как частный случай из уравнений второго рода, если положить а = 0, п = З/z и принять за q* декартовы координаты частиц ntf. Это легко проверить, замечая, что
дТ dXf
= ТП^Хр
дТ • дТ
—- = mfyfi -т- = ntfzf,
dyf ' ' dzf '
дТ = дТ дТ dXf dyf dzf
Для получения явного выражения кинетической энергии в координатах Лагранжа в общем случае, заметим, что элемент дуги траектории изображающей частицы /пс- есть
2 4
= /S У У —1 ^dq3dqk-\-2 \\^L^Ldq3'dt-j-f—tfdt*\,
Г ^dq3 dq* 4 4 dqJ dt 4 '\dtJ J’
2 k 2
откуда
== 2 5 gjk dq3 dq*-^^ gjt n+1 dq3 dt-\- gn+1> n+1 dt*, ; к з
(3.40)
где
dq3 dqk ’
dq3 dt ’
(3.41)
Sn'+l, n+1
Поэтому искомое выражение, получаемое из (38), может ставлено в форме
быть пред-
о»
(3.42)
§ 15j
уравнений лаграйжа Второго рода
177
где Г', 7*, TQ суть однородные полиномы
Тг = ^2 а$кЧ^к* А 1 ?o 2 ^n+1» (3*43)
j к j
относительно обобщённых споростей qit а коэффициенты их суть
ajk = ^cSjk =
q / dXf dXf dyf dyf dZf dz? \
\ dqk &qk dqf tyk / *
ajt n+1 ^cSj, n+1 =
____Q / dXf dXf dyf dyf dzr dzf \
#П+1, П+l = ^cSn+1, n 4-1 =
_ Q m [ (dxf^ , (dyf^x( dZf f
-Omf \~3F) +{~дг) +\ГдГ) •
(3.44)
Мы будем называть систему склерономной в координатах qi, если кинетическая энергия и левые части уравнений (28) дополнительных связей суть однородные полиномы относительно обобщённых скоростей qf соответственно второй и первой степени, с коэффициентами, не зависящими явно от времени, т. е. если
Sjk = gjk ((?)> Sjt n+1 = gn+l9 п+1 “
^(i) J == ^(т) 1 (?)* ^ == 0.
Для того, чтобы это имело место, достаточно, чтобы система была склерономна в декартовых координатах и чтобы обобщённые координаты были определены склерономно, т. е. соотношения (23) не содержали явно времени.
Вводя функцию Лагранжа или кинетический потенциал
L=T+tr=T—V, (3.45)
где V = — U есть потенциальная энергия, и замечая, что
= dL — дТ I ди
dq^ dqf ’ dq^ dqi dq^ 9
получим другую форму уравнений второго рода
+ 0 = 1......»> <з-4в)
Если нет никаких дополнительных связей кроме тех геометрических, которые учтены при введении обобщённых координат, то ура-
12 Зак. 1474. Б. В. Булгаков
178 У1>АВЙЕНИЯ АЙАЛИ1И^ЕСК0Й ДЙНАМИЙИ [гл. 3
внения не содержат членов с множителями и обобщённые скорости не связаны никакими соотношениями.
Если же система консервативна, то исчезают все Qj и уравнения принимают вид
= С/=!.......«)• <3-47)
dt dq3 dq3 ~ 1
При изучении некоторых аналитических свойств достаточно предполагать, что L есть какая угодно однозначная, непрерывная и дважды дифференцируемая функция от q3, qi и t с отличным от нуля определителем Гесса, составленным из вторых производных д2А «т» ~ ..
—:——. Такие системы носят название обобщенных лагранжевых dq3 dqK
систем в отличие от рассматривавшихся до сих пор натуральных систем, у которых L есть полином второй степени относительно обобщённых скоростей.
§ 3.6. Геометрическая интерпретация. Координаты могут рассматриваться как компоненты радиуса-вектора г изображающей частицы тс, движущейся в пространстве Е311. Так как, согласно (24), r = r(q, t)9 (3.48)
То на поверхности Rn, соответствующей некоторому данному t, этот вектор будет функцией обобщённых координат. Если изменять какую-нибудь одну из них q3, фиксируя остальные, то мы получим координатную линию на поверхности. Вектор
=тт (3-49)
dq3
с компонентами , ..., направлен по касательной к этой dq3 dq3
линии. Через каждую точку поверхности проходит п координатных линий и соответствующие могут быть приняты за координатные векторы локальной декартовой системы координат, определяющие касательную плоскость поверхности.
Вектор
(3.50) j W
представляет виртуальное перемещение частицы тс, причём, если не принимать пока во внимание дополнительных связей, определяемых уравнениями (28), то Zq3 остаются произвольными.
Согласно обычному правилу тензорного исчисления, установленному Эйнштейном, будем в этом и следующем параграфах пропускать знак 2 и подразумевать, что по каждому индексу, который
?еоМетРйческая йй^еййретаЦия
может принимать все значения от 1 до п, должно производиться суммирование всякий раз, когда он встречается в каком-либо произведении два раза: один раз сверху, другой раз снизу. Тогда
8г = ^8^; (3.51)
мы видим, что виртуальное перемещение 8г является линейной комбинацией векторов е3- и потому принадлежит касательной плоскости. Числа 8^‘, являющиеся множителями при называются контра-вариантными компонентами вектора 8г в локальной системе координат. В случае перехода к новым обобщённым координатам qi'f связанным со старыми соотношениями
qj = qj{qVt ..., qn'> t), (3.52)
мы имеем закон преобразования
(3.53) dqK
который остаётся верным и для контравариантных компонент других векторов, проведённых через данную точку.
Вычисляя квадрат модуля виртуального перемещения, получим его в виде квадратичной формы
8$2 = gjk Iqi bqk, (3.54)
причём величины gjk совпадают с теми, которые входят в выражение квадрата действительного перемещения и определяются первой формулой (41); они могут быть также представлены в виде скалярных произведений
gjk = ^j^k» (3.55)
Скалярное произведение двух различных виртуальных перемещений 8г(1) 8г(2) = в- bq^ ek 87^ выражается билинейной формой
<3-56)
зная его, можно найти косинус угла между векторами 8г(1), 8г(2).
Таким образом, величины gjk определяют длины и углы в данной точке поверхности Rn, остановленной в данный момент, и рассматриваются как компоненты фундаментального метрического тензора поверхности.
Введём матрицу
к £=11Ы (3.57)
и обратную матрицу
g-1 = ||g./*||. (3.58)
Векторы связанные с соотношениями
= gjkP1** & = gjkCk> (3.59)
называются обратными по отношению к
12*
180 Уравнения аналитической динамики
Мы имеем:
= g^k = gflglk или, по свойству обратной матрицы,
е3ек = El, где величины
j _ 1 При J = kt
0 при j =/=k
(3.60)
суть элементы единичной матрицы.
Пусть «г есть какой-нибудь вектор, проведённый из данной точки поверхности и принадлежащий касательной плоскости. Так как такой вектор может быть представлен в виде линейной комбинации
= (3.61)
то, умножая скалярно на е3 и принимая во внимание (60), получим следующие формулы для контравариантных компонент ф3:
Ф3 = Фе^. (3.62)
Вектор ф может быть также выражен через обратные векторы е3:
Ф = Ф^е3; (3.63)
при этом множители ф^ носят название ковариантных компонент. Так как свойство двух пучков по п векторов быть обратными между собой является, очевидно, взаимным, то, рассуждая аналогично предыдущему, получим формулы для ковариантных компонент
ф^ = фе^ (3.64)
Умножая соотношение (61) скалярно на и пользуясь (55), находим выражения ковариантных компонент через контравариантные:
= gjkVk; (3.65)
отсюда обратно
= Л- (3.66)
Если вектор не лежит в касательной плоскости, то он может быть представлен в виде
ф = (3.67)
где ф' принадлежит плоскости и вычисляется по прежним формулам ф' = Ф3ез = Фзв3> ф3 = фз3\ Ф] = Фвр (3.68)
а ф" есть добавочная составляющая. Подставляя последние выражения в (67), находим:
ф = (фе^) -j- ф" = (фе$) е3 + о", (3.69)
§ 3.6]
ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ
181
откуда, умножая, например, второе выражение скалярно на ек, v"ek = vek —(vej) Eb или
o"efc = 0. (3.70)
Таким образом, составляющая ф" перпендикулярна к каждому вектору ек, а значит, и к касательной плоскости, вследствие чего ф' есть ортогональная проекция вектора ф на эту плоскость, а вели-j
чины <г, ф$— её контравариантные и ковариантные компоненты.
Применим эти общие правила к векторам действительного перемещения и скорости. Если система склерономна, то мы имеем для dr формулу
dr = e^dqi
того же вида, что и для 8г, и потому действительное перемещение dr лежит в касательной плоскости и дифференциалы dqf являются его контравариантными компонентами.
Скорость изображающей частицы есть
dr
и производные qi являются её контравариантными компонентами. Но если система реономна, то, очевидно,
dr = eidqi-\-en^ldt, (3.71)
«> = erf+en¥V (3.72)
где
еп+1 = %- (3.73)
и, благодаря наличию вторых слагаемых в выражениях dr и ф, ни тот ни другой вектор, вообще, не лежит в касательной плоскости. Пользуясь вектором мы можем представить величины w+1, Sn+it n+i> которые входили в выражение (40) для ds2, в виде
или
Затем
И аналогично
gj, n+i — gn+i, n+i — \^n+i) •
dr = (dr)' + (dr)" = (dre^) ej + (dr)" = = [(efe dq1* + en+ j dt) (dr)" =
= (Eldq*+en+1dtg*ek)ej+(dry
dr = (dqt 4- g*gk> n+l dt) Cj + (dr)"
(3.74)
(3.75)
v=(q1+gjkgk. n+i)
(3.76)
182
УРАВНЕНИЯ АНАЛИТИЧЕСКОЙ ДИНАМИКИ
[ГЛ, 3
Таким образом, контравариантными компонентами тангенциальных составляющих действительного перемещения и скорости являются в данном случае не dql и q^ а выражения
= + (3-77)
Мы в состоянии теперь дать геометрическую интерпретацию уравнений Лагранжа для натуральной системы. Вторые производные суть компоненты вектора ускорения w изображающей частицы в декартовых координатах пространства Z?s7l, и уравнения Лагранжа первого рода (16) могут быть представлены в виде векторного уравнения
OTew = grad 1/+Л”+2 хвА«+ 2^, (3.78)
a y
выражающего второй закон Ньютона для этой частицы. При этом четыре вектора в правой части имеют своими компонентами соответ-
ственно и МОГУТ рассматриваться как
консервативная сила, добавочная неконсервативная сила и реакции поверхности Rn и дифференциальных связей. Формулы (29), (31), (32), (33) могут быть переписаны в виде
Wj =
dU dqf
— grad U - ej,
Qj — Xty, Ety j —
(3.79)
и показывают, что
поненты проекций тельную плоскость
Wj, yj, Qj и суть ковариантные ком-
ускорения w и сил grad U, X и 2 на каса-поверхности Rn. Таким образом, уравнения Ла-
гранжа второго рода выражают тот же второй закон Ньютона, но
только в ковариантных компонентах относительно локальной системы поверхности связи Rn. Реакция поверхности в эти уравнения не входит, так как из уравнений (7), которые можно представить в форме
Да8г = 0 (а=1, ..., а), (3.80)
видно, что векторы А* нормальны к любому виртуальному перемещению, совместимому со связью, а следовательно, и к касательной плоскости поверхности Rn.
Геометрический смысл уравнений (30) дополнительных связей заключается в том, что виртуальные перемещения должны быть перпендикулярны к тангенциальным составляющим векторов Сг
§ 3.7. Уравнения Лагранжа, разрешённые относительно вторых производных. Покажем, что если написать уравнения движения не в ковариантных, а в контравариантных компонентах, то они оказываются разрешёнными относительно вторых производных от обобщённых координат,
§ 3.7]
УРАВНЕНИЯ ЛАГРАНЖА, РАЗРЕШЁННЫЕ ОТНОСИТЕЛЬНО ф 183
Ограничиваясь при этом случаем склерономной натуральной системы-, для которой
т= Г = у mcgjkqtyk, gjk = gj1c (q), (3.81)
напишем развёрнутое выражение ковариантной компоненты ускорения, меняя обозначение индексов суммирования так, как это будет удобно по ходу вычисления:
1 / d дТ дТ \ d , 1 dg-^i
mc \dt dq™ dqm)~ dt 2 dq™ ? ~
=+ту8- i‘i‘—4 i ki‘ =
=s--?+j (-^ iV+й») —у W.
или же
= gm^k + Гот, klqkql, где величины
p __ Г kl 1 _ 1 / dgim । dgmk dgki\ m 2 \ dqk dq1 dtp*1 /
(3.82)
(3.83)
носят название скобою Крисшоффеля первого рода и рассматриваются как компоненты объекта или экстенсива Кристоффеля; они обладают очевидным свойством
— (3.84)
Контравариантные компоненты ускорения будут
wi=gimwm = ffmgmlflk + gim Vm>klqkql или
=q3-[~Tklqkql, где величины
±к1 j j g
(3.85)
(3.86)
суть скобки Кристоффеля второго рода, обладающие свойством
Гы = Г/й. (3.87)
Вводя далее контравариантные компоненты rd_____________( dU । п \ jjj _______ jm с
\dqm ' Qmj > Ат) — s Rt)»»
тангенциальных составляющих активной силы grad U-[-X и вектора Ср мы получим, умножая уравнения (35) на gimt суммируя по т и восстанавливая для ясности знак S:
т^ = Qj Т
184 УРАВНЕНИЯ АНАЛИТИЧЕСКОЙ ДИНАМИКИ [ГЛ. 3
ИЛИ п п с
«в(? +22 = QJ' + 2 *Д) (3.88)
Л=1 1=1 у = 1
(/= 1, . . п).
Это и есть искомые уравнения, разрешённые относительно вторых производных.
В предыдущем преобразовании основное значение имели выражения контравариантных компонент ускорения. Мы дадим ещё другой их вывод с помощью абсолютного дифференцирования, представляющего одну из фундаментальных операций тензорного исчисления.
Для этого рассмотрим сначала векторы
д2г деъ
-r-Г = —г = -4. (3.89)
dq^dqk dqk dq3
Они, вообще, не принадлежат поверхности, но ковариантные компоненты их проекций на касательную плоскость могут быть найдены по общему правилу и равны
де$
~dq*ei'
Эти компоненты можно связать с фундаментальным метрическим тензором, если продифференцировать соотношение
gij =
что даёт:
dgij _ dej dei
dq* ~~ dq* T" 6i dq* *
Совершая здесь два раза круговую подстановку индексов J, k, I, находим:
dgjk _ дек dej dql — е1 dq1 6* dq1 ’
dgki dei dek
dql к dql 1 dq>
откуда
г — 1 I dg4 _ dgl*\ =
l,ik 2 \ dql dq* dq1 )
1 / dek dei \ 1 / dei dej \ 1 / dej de^ \
~ *2 \ ~dq*j ek \ dql^dq^J ~dq*^~ ~dql J
или, пользуясь тождествами (89),
d^kel =
(3,90)
§ 3.8] ЭЛЕКТРОМЕХАНИЧЕСКИЕ СИСТЕМЫ 185
Пусть имеем теперь какой-нибудь вектор ф, проведённый в некоторой точке поверхности Rn, предполагаемой неподвижной, так как мы условились ограничиться склерономными системами. При бесконечно малом перемещении точки приложения вектора по поверхности тангенциальная составляющая ф'= <uie* изменяется на и
d<or = dv3e^ ф3 de у
.Этот дифференциал, вообще, не лежит в касательной плоскости; его проекция на эту последнюю и носит название абсолютного дифференциала. Обозначая абсолютный дифференциал через Dv, а его контравариантные компоненты через Dvi, имеем:
(3.91) и, используя (90),
Dv 3 — dve3 = (dvkek + vk dek) e3 = dvke3ek + vk dqle3 =
= dv^o* dq^mem = dv* + dql
или же
Dvj = dvs dql. (3.92)
Если под <u понимать скорость изображающей частицы mQi то, в случае склерономной системы, она совпадает со своей тангенциальной составляющей о' и dvjdt = dv'jdt будет ускорением; его тангенциальная составляющая есть Dvjdt, а контравариантные компоненты, согласно предыдущим формулам, равны
-LrW'
dt dt dt ‘
Пользуясь тем, что ф3 = q3, получаем опять выражения (85), что мы и ставили своей задачей.
§ 3.8. Распространение уравнений Лагранжа на электромеханические системы. Максвелл в своём трактате об электричестве и магнетизме [ЗЛ2] применил уравнения Лагранжа к системе тел, заключающей проводники с токами; эти проводники могут образовать несколько индуктивно или кондуктивно связанных контуров.
Обозначим через q\ ..., qu геометрические обобщённые координаты системы и через Lm— механический кинетический потенциал. В качестве электрических координат qu+*9 ..., qn примем по Максвеллу количества электричества, протекшего через поперечные сечения проводников с некоторого начального момента; соответствующие обобщённые скорости i = q^ (J — и-\-1, ..., п) будут представлять контурные токи. Электромагнитная и электростатическая энер-
186
УРАВНЕНИЯ АНАЛИТИЧЕСКОЙ ДИНАМИКИ
[ГЛ. 3
гии системы суть
п п п п
^=-^=42 (3.93)
^'=u4-l fc=u+l j=u+l ft=u+l
где мы обозначили через Ljk, bjk электромагнитные и электростатические коэффициенты индукции. Мы также восстановили для ясности знаки 2*
Положим
L = Lm+Te + Ue (3.94)
и заметим, что 7в и Ue могут рассматриваться как потенциальные функции пондеромоторных сил, т. е. механических сил, действующих на проводники; поэтому движение системы должно определяться уравнениями Лагранжа, составленными по общему правилу для у = 1, ..., и, если учесть возможные неконсервативные силы . ,QM и дифференциальные связи.
При составлении электрических уравнений воспользуемся тем, что выражения
п п
= = (3-95)
U = ^+ 1, . . п)
равны, соответственно, потокам индукции через контуры токов I3 и напряжениям в их ёмкостях. Обозначим также через R&, fy(y, = = ..., п) омические сопротивления и приложенные напряже-
ния; тогда потеря энергии на джоулево тепло и работа напряжений ej в элемент времени dt будут
— S Zj dt-\- 2 eji?dt= 2 Qjdq*, j=u+lk=u+l j=u+l j=u+l
где
Qj = — 2 + (/ = « + !, .... ti). (3.96)
Величины QM+1, ..., Qn мы примем за электрические неконсервативные обобщённые силы. Тогда уравнения Лагранжа, составленные по общему правилу для у = и-|-1, ..., п, имеют вид
uJ = ej = «) (3.97)
§ 3.9]
УРАВНЕНИЕ ЭНЕРГИИ
187
и выражают действительный баланс электродвижущих сил в контурах, так как---суть электродвижущие силы индукции, а — 2j Rjkt
— потери напряжения в сопротивлениях.
§ 3.9. Уравнение энергии. Умножая уравнения Лагранжа (46) на dq^ суммируя по j и применяя знак имеем:
2(^ # 2%^+ 2(2
з 4 * з J . т ,
или
«2 ‘2 О > М - 2 % +2'-. 2 *
3 3 3 т 3
Но
Я dqi\ = dL — ^ dt, dql ) dt
2 E(y) } dqi -dt.
3 f
Поэтому, обозначая
H=2$’’,*j£’ <3'98)
Q, = -^-S\e,. (3.99)
мы получаем соотношение
+ (3.100)
з
которое остаётся верным при любой функции L(q9 q, t). В частности, для натуральной системы мы имеем:
L= T-{-U=T'^T1+T(>—V= Т'+ Т\— V', (3.101)
где
V' = — То+ V, (3.102)
и, по теореме Эйлера об однородных функциях,
так что
Я== Г+Г.
(3.103)
Если же система, сверх того, склерономна, то Т' — Т, = Т0 = 0, Vr=V и
fi=T^Vt (3.104)
188
УРАВНЕНИЯ АНАЛИТИЧЕСКОЙ ДИНАМИКИ
[ГЛ. 3
т. е. Н есть сумма кинетической и потенциальной энергий или полная энергия системы; кроме того, в этом случае = и уравнение (100) принимает вид
dH=W(d), (3.105)
где
= (3.106)
Таким образом, для натуральной склерономной системы (105) есть уравнение энергии, согласно которому изменение полной энергии Н равно элементарной работе W(d) сил Qj. Что же касается уравнения (100), то оно может быть названо обобщённым уравнением энергии.
Пусть теперь имеем обобщённую лагранжеву систему (Qj = 0) с функцией L, не зависящей явно от времени и склеро-
номными дифференциальными связями (Е^ = 0). Тогда Qt = 0 и, согласно (100), dH—Q, откуда получается обобщённый интеграл энергии, или интеграл Якоби*.
Н= const. (3.107)
В частном случае натуральной консервативной склерономной системы мы получаем обычный интеграл энергии
Т-]- У== const., (3.108)
выражающий закон сохранения механической или электромеханической энергии системы.
В некоторых задачах механики, например в так называемой ограниченной задаче трёх тел, приходится иметь дело с натуральной консервативной системой без дифференциальных связей или со склерономными дифференциальными связями, которая не является склерономной потому, что её кинетическая энергия Т не представляет однородного полинома от обобщённых скоростей. Если, однако, Т не зависит явно от времени, то интеграл энергии будет существовать, но это* будет интеграл Якоби Т' V' = const., а не закон сохранения механической энергии ТV= const.
§ 3.10. Преобразование Рауса. Все уравнения Лагранжа или некоторые из них могут быть заменены двойным числом уравнений первого порядка, если ввести обобщённые скорости qj в качестве вспомогательных неизвестных.
В преобразовании Рауса, которое представляет обобщение рассматриваемого в дальнейшем преобразования Пуассона и Лагранжа, та же цель достигается путём разбиения обобщённых координат на две группы q1, ..., qn-m и ..., qn и использования
в качестве добавочных неизвестных не обобщённых скоростей,
$ s.idi
Й^ЕОЁ^АЗОВАЙЙЕ ЙЛУСА
а величин
dL
(у = п —/п+1, ..п),
(3.109)
которые носят название обобщённых импульсов. Так как£ = L(q, q, f), то, рассматривая последние соотношения как уравнения относительно qn-m+it ,.,tqn и разрешая их, мы можем выразить эти обобщённые скорости через импульсы рп~т+1> .Рп, а также координаты и время.
Обозначая символом 8 какие-нибудь малые приращения переменных, найдём:
п—т п
8£=2(В8*'+ВМ)+ 2И1^+В8++
\oqJ oqJ / 2e" \oqJ oqJ / ot
1 * * n-mi v *
Поэтому, вводя функцию Рауса
п
(3.110)
имеем:
п—т п
8*=2(A8^+S8+ 2 (-л+1+h
если же предположить, что обобщённые скорости qn-m+i.........qn,
входящие в R, выражены через соответствующие импульсы, координаты и время, <так что R = R(q1, qn~m; pn_m+i........рп;
q\ ..., qn't t), то
n—m n
Сравнение обоих выражений для 8/? даёт соотношения
dL = dR dq^ dqf1
dL ^dR dqJ dq$ dL _dR dqi dq^
(y = 1, . . ., n —/n),
dt “ dt ’
190
^РАЙЙЕНЙЯ АЙАЛИТИЧЕСкоЙ ДИЙАЙЙкЙ
(гл. <4
которые вместе с уравнениями Лагранжа
с
(7=1.......ri — ni),
С
+ (/=»-«+!.......................«)
приводят к следующей системе (п— т)~\-2т = п-\-т уравнений: с
= (у = ‘............(3-112)
oqJ oqj •
с
^ = —^2= Д + Qj+V (3.113)
dt dpj' dt dq^'3 ' 1 W3 4 7
(j = «— m-f-1......re);
вместе с с уравнениями дополнительных связей они определяют re-|~/ге + с неизвестных рп_т^.....рп, q1, .... qn, Xt.....Хс.
Уравнения первой группы имеют тот же вид, что и уравнения Лагранжа, но с заменой L на /?. Вторая группа заключает вдвое больше уравнений, чем до преобразования, но все они первого порядка, что мы и имели в виду. Приём, применённый Раусом, обладает тем преимуществом, что обе группы уравнений составляются с помощью одной и той же функции R.
Кроме того, уравнения Рауса весьма удобны в том частном случае, когда координаты ..., qn являются циклическими,
т. е. входят в L, а значит, ив/?, только своими первыми производными. Предполагая сверх того, что все Qj и E^j равны нулю при j = n— zn-j— 1, •••> а остальные Qj и E^j не зависят от dpj
qn-m+i, . qn, Мы имеем: -тг = 0, откуда получаются т первых С* С'
интегралов
Pj = cj U = n — (3.114)
где Cj — произвольные постоянные. Заменяя этими постоянными импульсы pj в функции Рауса, мы сведём задачу к системе, состоящей из п— т уравнений первой группы, имеющих ту же форму, что и первоначальные уравнения Лагранжа, и из с уравнений связей.
§ 3.11. Канонические уравнения. Если т = п, то преобразование Рауса обращается в преобразование Пуассона и Лагранжа, при котором все импульсы
pj=^- (7 = 1.........и) (3.115)
°<Н
используются в качестве вспомогательных неизвестных.
§ 3.11] ЙАНОЙИЧЕСЙИЕ 1ГРАвЙЕЙЙЙ 1Э1
Так как мы больше не имеем в виду систематически применять геометрическое истолкование в пространстве Rni то будем писать здесь и в дальнейшем все индексы внизу. В рассматриваемом случае функция Рауса, очевидно, лишь знаком отличается от функции Н, которая входит в обобщённое уравнение энергии и определяется формулой (98). При этом, если все обобщённые скорости исключены с помощью последних соотношений и выражены через импульсы, координаты‘и время, то получаемое выражение
H=H{q,p,t) (3.116)
носит название функции Гамильтона. Переменные pj носят название сопряжённых канонических переменных. Первой группы уравнений (112) в данном случае не существует, а из (ИЗ) путём замены R на — Н получаются следующие 2п уравнений относительно неизвестных qj, pj,
с
dt др,’ dt да,-Г -Г v 1
J Л * yzsl
(J 1 Э • • • > Л)» они называются каноническими.
Уравнения дополнительных связей могут быть написаны в виде
................................с)- <3-118) J 3
Если система консервативна и дополнительных связей нет, так что все Qj, E^j и Еу равны нулю, то мы получаем канонические уравнения в форме, данной Гамильтоном:
dqj _дН dpj_ дН . 1Q
(7 = 1.....">• <ЗЛ19>
Возвращаясь к общему случаю, выведем для контроля обобщённое уравнение энергии из канонических уравнений и уравнений связей. Для этого нужно воспользоваться последними при преобразовании дифференциала dH, что даёт:
3
- УравйенЙя Айалй^Йчесйой дйнАмйкй [гл. 3
или
dH = 2 Qj . (3 Л 20)
где
^=^-2ха- (ЗЛ21)
т
Принимая во внимание опять, что R = — /7, мы получаем из последнего соотношения (111):
!=-" <з122>
Отсюда тотчас же следует, что выражение для Qt и уравнение (120) тождественны с теми, которые мы получили в § 9.
Если система является лагранжевой (Qj = 0) и функции Z, а зна-/ д Н \
чит, и Н не зависят явно от времени = 0 L а дополнительные
связи склерономны (Е^ = 0), то, как мы уже видели, имеет место обобщённый интеграл энергии Н = const.
§ ЗЛ2. Вариационное уравнение Гельмгольца. Пусть
W) = SW (3-123)
3
Покажем, что канонические уравнения для промежутка времени (70, /х) эквивалентны вариационному уравнению Гельмгольца
f [8 £&ЦР{ -H} + W(5)] dt = ^pfa 1, (3.124)
/ 3 3
в котором (ty связаны соотношениями
(8) S3 S ZWtfj = 0 (7=1, .... C),
3
a произвольны.
В самом деле, в силу коммутативности операций 8 и мы имеем, применяя интегрирование по частям:
/ 3 2 ^р*dt = J* 2 fap3 + р*1й dt =
3 3
= J S (я^р,— 12 >
r0
§ 3.13] КОНТАКТНЫЕ ПРЕОБРАЗОВАНИЯ . 193
вследствие чего уравнение Гельмгольца может быть представлено в виде
f [S Лч-) —SH+ W)] dt= °- сз.125)
to 3
Если здесь развернуть выражения ЗЯ, IF (о) и сложить с очевидным соотношением
f SX/?(8)<ft=O, tc, Т
то получится:
J 2 [( “ — + Qj + S Х A) Ч] dt = °-
#0 3 3 К 3
Рассуждая затем так же, как при выводе уравнений Лагранжа в § 5, и пользуясь основной леммой. вариационного исчисления, заключаем, что все круглые скобки, являющиеся множителями при 8^-, Зр^, должны исчезать в отдельности для любого t в интервале (£0, £*). Таким образом, из вариационного уравнения вытекают канонические уравнения. Всё рассуждение может быть обращено, и тогда теорема об эквивалентности оказывается полностью доказанной.
Вследствие этого при изучении различных свойств канонических уравнений мы можем оперировать не с ними, а с вариационным уравнением, что позволяет упростить многие выводы.
§ 3.13. Контактные преобразования. Обычный приём, применяемый при разрешении канонических уравнений, так же как и всяких других, состоит в том, что их стремятся упростить, вводя новые зависимые переменные. Обозначая эти последние через Vj, будем предполагать, что уравнения преобразования
• • • > Qn* Pi» • • •» Рп» ty*
Vj = Vj (^р • . ., qnt ру ...» рп} t)
(У=1, ..., п)
(3.126)
разрешимы относительно qv ..., qn, pv ..., рп, и ограничимся здесь и в дальнейшем, голономными системами без дополнительных связей, вследствие чего канонические уравнения будут иметь вид
da, дН dpj дН z
’dtz=dpj> ~dF = — Q 0==1>’ •> ft)- (3.127)
Начнём с преобразований, которые Ли назвал контактными.
Они удовлетворяют условию
<3-128)
3 3
13 Зак. 1474. Б. В. Булгаков
194
УРАВНЕНИЯ АНАЛИТИЧЕСКОЙ ДИНАМИКИ
[ГЛ. 3
где S—г какая-нибудь функция старых и новых переменных и времени; при вычислении вариаций время, как и раньше, не варьируется. Чтобы получить аналогичное соотношение в дифференциалах, мы .’должны учесть добавочные члены, происходящие от изменения А совокупность которых мы представим как — Ht dt, так что
2iPjdqj= ^Vjdiij-[-dS—Htdt. (3.129)
3 3
Пользуясь (128), (129) и обозначая?
= (3.130)
найдём:
и, таким образом, - . .
Л :
Л* (2 -H)+w (S)] dt — 2 It =
t0
= f Я')+Г(8)]Л-Н$£ -(2^+8S)£.
to ' . . , . .
Так как левая часть последнего соотношения равна нулю в силу вариационного уравнения Гельмгольца, то равна нулю и правая, т. е.
Л8(2^-и')+1г(8)1Л=2.л|;:<
to
Мы получили вариационное уравнение в новых переменных, причём нужно только иметь в виду, ,что форма 1Г(8)^ выраженная в этих же переменных, будет вообще иметь вид
(8) =• А+W)- (3.1 з 1)
§ 3.14] ПРОИЗВОДЯЩИЕ ФУНКЦИЙ ПРЕОБРАЗОВАНИЙ
195
В остальном можно рассуждать совершенно так же, как в § 12, что даёт:
t;
v L to
дН<
to
и приводит к преобразованным уравнениям в новых переменных:
du* дН' dv; дН*
....n). (3.132)
Как мы видим, их форма является лишь немного более общей, чем у исходных уравнений (127), хотя, в случае натуральной системы, новые переменные не сохраняют физического значения координат и импульсов. Новая функция Гамильтона Н' вычисляется с . помощью соотношения (130).
Мы можем теперь вообще писать канонические уравнения системы без дополнительных связей в виде
dqj дН dp л дН
= + <' = 1...............»>• <здзз>
и эта форма уже не меняется при дальнейших контактных преобразованиях, в чём легко убедиться, повторяя все предыдущие вычисления для этих уравнений.
Если все Pj равны нулю и исходная система имеет гамильтонову форму (119), то все Up Vj также исчезают, и преобразованные уравнения будут
du; dj-u dv; дН'
-2. = — ™ (7=1.....й). (3.134)
Таким образом, гамильтонова форма канонических уравнений консервативных систем сохраняется при контактных преобразованиях, что составляет важнейшее их свойство.
§ 3.14. Выражение контактных преобразовании с помощью производящих функций. 1°. Предположим, что S — S^q, и, t). Условие (129) получает вид
2+2 dqj+ё+Sdt~ н* dt>
и сравнение коэффициентов при^дифферёнциалах даёт:
W=1.......“>• <3J3S>
„ _dS п*~ dt ’
13*
196 Уравнения аналитической динамики [гл. 3
откуда с помощью (130)
Н' = Н+^. (3.136)
Соотношения (135) дают выражение контактного преобразования через производящую функцию S(q, и, t).
Разрешая первую серию этих соотношений относительно Uj и подставляя решения во вторую серию, получим уравнения преобразования в форме (126).
2°. Пусть теперь условие контактного преобразования представлено в виде
2 Pj = 2 dai + d (s — 2 «л) — fitdi,
где S = S(q> v, t). Развёртывая дифференциал от круглой скобки справа, получаем:
2 Pj d4j = - 2 dvi + 2 dqf + Й > dt - Ht dt'
if 3 *
откуда
(7-1. ••..») (3.137)
J
с прежним выражением для H'.
3°. Третью форму с производящей функцией S(p, и, f) получим из условия
2Pjd<h = 2 VjduJ-]-d(S + 2l — Htdt или
0 = ^qjdpj-{- 2 vj duj + 2 dfy~^~daJ dui)~^ ~5tdt H^dt,
что даёт:
%=-£ й=-э£ <'=>......................”)• <3-138>
* J 3
4°. Для S(p, v, t) полагаем
5 Pj dqj = 2 4 duj + d^S-}-^ qjPj — 2 —Htdt
и находим:
“7-^- W-l.............») (3-139)
5°. Можно рассматривать ещё более общую производящую функцию S(r, х, гДе каждое есть одна из двух старых сопряжённых переменных q^ pj того же номера, а —одна из новых сопряжённых переменных Uj, Vj. Условие контактного преобразования
§ 3.15]
ТЕОРЕМА ГАМИЛЬТОНА-ЯКОВИ
197
представляем в виде
2 Pj dqj = 2 duj + d (S + S(i>) — S’> V>./) — Ht di,
причём сумма z» берётся лишь по тем j, для которых г3- = pj, по тем J, для которых Xj = Vj. Определяя аналогич-ным образом суммы z> , Zj , находим:
+ —^) + -зг^—Htdt.
1 Л4\дг3- э 1 дх^ 1 dt 1
Отсюда, обозначая через Sj, yj переменные, сопряжённые соответственно для и Xj, получаем:
s>=±'^' Л = W=‘.......»>• <3-14<»
И J
причём верхние знаки берутся при дифференцировании по координатам qj, Uj, а нижние — при дифференцировании по импульсам pj9 Vj.
6°. Нетрудно построить контактное преобразование, в котором одна из двух серий старых переменных связана лишь с одной из серий новых и притом наперёд заданными соотношениями. Пусть, например, мы хотим, чтобы
Vj =fj (Pl> • • •. Рп) (J = 1> .... «)• Полагая
5 = ....рп) (3-141)
и применяя формулы (138); найдём:
^=2Ий|г’ V/=Z/(A’ •••> Р») (/=1...............п). (3.142)
it 3
§ 3.15. Теорема Гамильтона-Якоби. Эта теорема устанавливает эквивалентность задач об отыскании общего решения канонической гамильтоновой системы и полного интеграла некоторого уравнения в частных производных. Так как вторая не проще первой, то значение теоремы заключается не в како^-либо прямом продвижении в решении задачи, а скорее в той удобной форме, в которой она даёт решение, когда его вообще удаётся найти.
Вывод теоремы можно получить, если задаться целью найти такое контактное преобразование
л=^. У = >....................’) <ЗЛ43>
198
УРАВНЕНИЯ АНАЛИТИЧЕСКОЙ ДИНАМИКИ
. [гл. 3
с производящей функцией S(q, v, f), чтобы новая функция Гамильтона Н' была равна нулю. Тогда преобразованная каноническая система будет ....
du,; dvx ___t = о — = 0 dt U’ dt
и новые неизвестные Uj, Vj постоянны. Соотношения (143) определяют, следовательно, канонические переменные qj, pj в функции времени и 2п произвольных постоянных и дают общее решение заданных канонических уравнений. С другой стороны, приравнивая нулю выражение (136) для Н' и исключая импульсы pj, входящие в Н(д,р, f), с помощью первой группы формул (143) найдём:
<3-144>
Это уравнение в частных производных, которому должна удовлетворять функция S, носит название уравнения Гамилыпона-Якоби. Искомое контактное преобразование будет вполне определено, если удастся найти полный интеграл этого уравнения, т. е. функцию S (q, v, t), тождественно удовлетворяющую уравнению и зависящую от п-|-1 переменных t, рассматриваемых как независимые, и от п произвольных постоянных Vj. Так как в уравнение входит не сама функция S, а только её частные производные, то, собственно, можно ввести ещё (п-|- 1)-ю аддитивную постоянную vn+t и написать полный интеграл в виде S(q, v, O + но эта постоянная выпадает при составлении соотношений (143).
§ 3.16. Случаи, когда функция Гамильтона не зависит явно от времени. Если H—H(q, р), то можно положить
$ = ,— ht^W, (3.145)
где h есть постоянная, a W—новая неизвестная функция, не зависящая от Л Тогда
dS _ dW dS _ h
dq< ~dq^ dt~ П
и уравнение Гамильтона-Якоби принимает вид
я(?, ^) = Л. ' (3.146)
Полный интеграл будет содержать п—1 постоянных vt, ..., vn_lf не считая аддитивной постоянной и h.
Уравнения (143),. определяющие общее решение канонической системы, принимают вид: .
§ 3.16]
СЛУЧАЙ, КОГДА ФУНКЦИЯ Н НЕ ЗАВИСИТ ОТ t
199
При этом первые п—1 уравнений в последней строке не содержат t и позволяют выразить какие-либо п — 1 координат q$ через п-ю, т. е. найти траекторию в пространстве Rn\ п-е уравнение определяет закон движения по этой траектории.
Пуанкаре предложил другую процедуру. Предположим, что нам удалось найти такую функцию W(q, v), содержащую п постоянных щ, •••> чт0 после подстановки в соотношение (146) его левая часть получает постоянное значение Л; это значение будет функцией от v19 ..., vn:
h = h(v). (3.148)
Примем за производящую функцию контактного преобразования не S, а Г:
Pi~dqj> U2~dvj С/~ Л)- (3.149)
Так как в этом случае ^^ = 0, то новая функция Гамильтона согласно (136), будет равна старой, выраженной в новых переменных, т. е.
Н' = Н (q, = h (у).
Преобразованные канонические уравнения будут
du л dh dv;
—L—— —- = 0.
dt dvj ’ dt
Отсюда, обозначая
.... (3-150)
получаем:
= •••> Vj = const., (3.151)
где 0^, так же как и Vj, суть произвольные постоянные.
ЧАСТЬ II
СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
ГЛАВА 4
ПОСТАНОВКА ЗАДАЧИ. ЛИНЕЙНЫЕ СИСТЕМЫ
А. УРАВНЕНИЯ ДВИЖЕНИЯ
§4.1. Канонические уравнения и фазовая диаграмма. Канонические уравнения системы с одной степенью свободы имеют вид (§ 3.13):
dp____dH_,Q (4 п
dt ~ др Г’ dt— dq^^ ' ' '
ИЛИ
= р. ^=?2(?> р> 0- (4.2)
Условия, при которых соответствующий процесс носит колебательный характер, могут быть выяснены только после исследования или разрешения уравнений для отдельных систем или отдельных классов систем.
Каждая пара значений qt р определяет , мгновенное состояние или фазу, т. е. положения частиц и распределение скоростей механической системы или заряд конденсатора и ток в электрическом контуре. Эти значения могут быть истолкованы как координаты некоторой изображающей точки в фазовой плоскости qp. Уравнения (2) опре-. деляют поле, каждой точке которого в каждый момент отнесён вектор фазовой скорости с проекциями q, р. Если время t действительно входит в и ?2, то поле нестационарно и скорость изменения состояния не определяется вполне самим состоянием. Мы будем в этом случае называть колебания вынужденными.
Каждое решение
? = Р=Р(О (4.3)
, I
уравнений движения определяет в плоскости qp кривую, называемую фазовой траекторией. Не следует смешивать фазовые скорости и траектории со скоростями и траекториями материальных частиц механической системы. Чертёж, получаемый с помощью подобного истолкования, называется фйзцво^ диаграммой. ‘
204 ПОСТАНОВКА ЗАДАЧИ. ЛИНЕЙНЫЕ СИСТЕМЫ [ГЛ. 4
Для натуральной системы мы имеем:
L = i [т (q, f) q* + (q, t) q-\-m2 (q, f)] — V(q), (4.4)
£
p =^ = tn(q, t) q-^-n^^q, f), (4.5)
dq
H=^q-L = [p - 7 Щ <4, 0 + V (?). (4.6)
dq w» l) *
P = 0,
и канонические уравнения принимают вид:
dq _р — тх (q, t)
dt m (q, t) ’
dp \p — mi (q, Q]2 dm t p — mx (q, t) dm\ t dt 2 [m (q, t) p dq m (q, t) dq '
+ 2-^-^+^’ P’f)-
(4.7)
§ 4.2. Собственные колебания. Если время не входит явно в и ©2, так что
' itt = Р)' %F = <?2 (q> Р) > (4.8)
то поле скоростей на фазовой диаграмме стационарно и скорость изменения состояния системы вполне определяется самим состоянием. Колебания, описываемые при этих условиях каноническими уравнениями, мы будем называть собственными.
В случае натуральной системы собственные колебания могут иметь место, если связи склерономны и силы не зависят явно от времени.
Предполагая, как это естественно, что определение обобщённой координаты также склерономно, мы получим m = m{q)t т± = т.2 = 0 и
L — у т (q) — V (q), p = ^- = m(q)q, (4.9)
z dq
Т/=о^7-т+^(?). (4.Ю)
2m (q) ' ™ 4 7
Положительная функция m (q) может быть названа приведённой массой системы. Канонические уравнения принимают вид:
dq _ р dt т (q) ’
dp_____ mr (q) p^
~dt~2\m (?)]2
-V'(^)+Q(?.p).
Уравнение энергии
2^) + V(?)] = Q(^p)^,
(4.И)
(4.12)
d
§ 4.2]
СОБСТВЕННЫЕ КОЛЕБАНИЯ
205
или
не содержит А а потому представляет дифференциальное уравнение первого порядка относительно переменных q и р. Его общее решение
р=р(д, V), (4.14)
в котором v есть произвольная постоянная, определяет семейство интегральных кривых. Это семейство стационарно, так же как и поле скоростей. Если изображающая точка при изменении t от —оо до 4- оо пробегает всю интегральную кривую, то эта кривая является в то же время и фазовой траекторией. Но может случиться, что интегральная кривая состоит из нескольких фазовых траекторий.
В уравнении (12) можно ввести в качестве зависимой переменной
вместо р живую силу
Р2 2т (д)
(4.15)
и представить это уравнение в форме
^ + V'(g)-Q(?.l<2m(?)T) = 0. (4.16)
Тогда, найдя общее решение 7’== T(q, v)t получим:
р = У 2т (?) Т (q, v).
(4.17)
Если уравнение интегральных кривых разрешено тем или иным путём, то определение времени требует лишь одной квадратуры. В самом деле, пользуясь, например, первым из канонических уравнений, получим:
t = f ^£)^ + и> (4.18)
J p(q, v) 7
где и — вторая произвольная постоянная.
Для выяснения свойств интегральных кривых, как мы увидим далее, важно знать те точки фазовой диаграммы, в которых обе проекции фазовой скорости обращаются в нуль. Их координаты q*f р* удовлетворяют конечным уравнениям
— V'(^) + Q(?, 0) = 0, р = 0, (4.19)
и потому все они лежат на оси абсцисс.
Легко видеть, что уравнение энергии (13) получается также путём деления одного из канонических уравнений на другое, а потому не определяет угловой коэффициент интегральной кривой в точках (<7*> р*). Поэтому по терминологии, принятой в теории дифференциальных уравнений, эти точки являются особыми для уравнения (13).
206
ПОСТАНОВКА ЗАДАЧИ. ЛИНЕЙНЫЕ СИСТЕМЫ
[гл. 4
Они соответствуют положениям равновесия системы, так как постоянные значения q = q*, р = р* являются, очевидно, решениями канонических уравнений.
Вне оси абсцисс скорость всегда отлична от нуля, и изображающая точка движется по интегральной кривой без остановки, причём, в силу т(^)>0, из первого уравнения (11) следует, что в верхней половине фазовой плоскости движение . происходит слева направо, а в нижней половине — справа налево.
Фазовая скорость не обращается в нуль также и при пересечении интегральной кривой с осью абсцисс, если только точка пересечения не является особой. В такой точке мы имеем:
2m (q) р
Фиг. 6. Пересечение интегральной кривой с осью абсцисс вне особой точки.
— V'W + Qtq, 0)¥=0, р = 0, и соотношение dq_______________
+ (<7)]2 [- V' (q) + Q (qt р)] ’
получаемое из (13), даёт^ = 0; следовательно, касательная вертикальна и кривая пересекает ось под прямым углом. Если же продифференцировать предыдущее соотношение ещё раз по р, рассматривая q как функцию от р, а затем положить р =. 0, то получится:
dp2 т (д) [_у/ (Q) + Q (qt 0) ]
Отсюда вытекает, что в окрестности точки пересечения интегральная кривая располагается обязательно по одну сторону от своей вертикальной касательной (фиг. 6). Координата q, возрастая (убывая), достигает в течение конечного вре-
мени значения, соответствующего точке пересечения, после чего нает убывать (возрастать).
Дело обстоит иначе при прохождении интегральной кривой особую точку.
§ 4*3. Линейные системы. Если р, t) и ©.,(^, р, t) в нениях (2) линейны относительно q и р, то мы имеем:
начи-
через
урав-
^+А1(0?+/12(0р=л(0>
+/21 (0 я Ч"/22 (0 р=(0-
(4.20)
Многие уравнения этого типа весьма подробно исследованы и решены в связи с задачами механики деформируемой среды и других разделов математической физики. Мы займёмся далее теми из
§ 4.3]
ЛИНЕЙНЫЕ. СИСТЕМЫ
207
них, которые представляют особый интерес для теории колебаний, а пока сделаем некоторые общие замечания.
Вводя матрицы
(4.21)
ложем представить систему (20) в виде одного матричного уравнения
^+7(0*=Я0-
(4.22)
Предполагая сначала, что д>(/) = 0, имеем однородное уравнение
£+/(<> •»=<>
(4.23)
Всякая матрица
е„(0 в12(0
МО 022 (0 ’
(4.24)
столбцы которой представляют линейно независимые решения уравнения, называется фундаментальной. В силу этого определения
«ik(0 o2fc (0
+7(0
0« (0
02fe (0
Я
0(0+7(00(0 = 0,
или причём detO(Q#=0.
Если не представляется более удобного пути, то фундаментальная матрица может быть найдена методом последовательных приближений. А именно, образуя из —f(t) матрицант- (§ 1.38) ... .
2 = Е— Г/+ Г/Г/—Г/Г/Г/+ ..., (4.26)
мы имеем, заменяя в уравнении (1.320) X на t и / на—/:
2(0+7(02(0 = 0-
Так как, кроме того, t - /[Г,, («)+/»»(*)]<« det 2 = е =#0,
2(/0) = Е, (4.27)
то 2(f) представляет фундаментальную матрицу, обращающуюся в Е при t=t0.
208
ПОСТАНОВКА ЗАДАЧИ. ЛИНЕЙНЫЕ СИСТЕМЫ (ГЛ. 4
С помощью матрицы 2(0 мы можем немедленно получить решение, принимающее при £ = заданное начальное значение
Это решение будет
х = 2(0х(^о), так как
i -|_/(0 х = 12 (0 +/(0 2 (01X (/0) = 0,
а при / = ^0 столбец х обращается в
(^о)% (А))= (zo) = * (А))‘
Если мы желаем иметь фундаментальную матрицу, принимающую при / = заданное значение
к /?> ;ч’ ’•
в 21 (*0> ®-22 («
(detO (£0) =/= 0),
то достаточно положить
6 (0 = 2 (0 6 (*0), (4.28)
так как при этом4 уравнение (25) удовлетворяется, а определитель
t
- fiAiW+лио]^ ;
det 6 (t) = det 0 (t0) e
отличен от нуля. i
Решение, принимающее при t = начальное значение х(/0), пред-, ставится теперь в виде
x = (4.29)
ГДе c = 0-’(Qx(fo). (4.30)
После того как фундаментальная матрица однородного уравнения найдена тем или иным путём, решение неоднородного уравнения может быть получено методом вариации постоянных; неизвестная х ищется в форме
х = 0(^)х(О.
отличающейся от (29) тем, что постоянная с заменена матрицей-
столбцом
х(0=
Xi(0
XJ0
представляющей неизвестную функцию времени. Подставляя в (22), имеем:
9 (0 X (0+9 (0 х (0 +/(09 (0 х (0=У (0.
а так как, в силу (25),
9 (0 X (0+/(0 9 (0 X (0 = 19 (0 +/(0 ° (01X (0 = О,
!ж:
§ 4.4] ПРИВЕДЕНИЕ ОБЩЕЙ ЗАДАЧИ К ИНТЕГРАЛЬНЫМ УРАВНЕНИЯМ 209
НО х (0=^(0. x(o=0-1a)j(O. t j*6 “1 СО-У (т) rfz-J—с ^0
и
t
х = 0 (/) с + f О (0 е-1 (х)у (г) dx.
(4.31)
Если здесь с имеет значение (30), то это решение принимает заданное значение х(/0) при
§ 4.4. Приведение общей задачи к интегральным уравнениям. Полученное в предыдущем параграфе решение линейного уравнения позволяет привести общую задачу о свободных или вынужденных колебаниях к интегральным уравнениям.
Полагая
напишем уравнения (2) в форме
®1 (?. р> t) ®2 (?• Р> О
= р, f)
(4.32)
и предположим, что мы тем или иным способом представили функ-ции ©t (q, р, t), ©2 (q, р, t) в форме
®i(?. Р> 0 = —/и(0^—А2(0р+л(0 + ^(?> р. 0.
®2(?> р> 0 = —Л1(0?—/22(0р+з'2(0+Ф2(?> р> О»
т. е. в виде сумм некоторых аппроксимирующих трёхчленов, линейных относительно канонических переменных, и нелинейных поправок 4ч(?, Р, 0> %(?> Р» 0« В матричной форме мы запишем это следующим образом:
®(?. Р> t)=--^f(t)x-\-y{f)-\-^{q, р, 0;
при этом f(f), х и у (t) определяются согласно (21), а
р, f) =
Ф1 (?. р> О % (?> р« О
Подставляя предыдущее выражение для ©(<?, р, t) в (32), получаем: $+/(0 *=J (0+4- (?. р. о. (4.33)
Это соотношение отличается от уравнения (22) предыдущего параграфа только тем, чтоу(/) в правой части заменено через у(0 + + Р> О’ Поэтому, рассуждая совершенно так же, как и там, мы придём к уравнению, которое можно прямо получить путём
14 Зак. 1474. Б. В. Булгаков
210
ПОСТАНОВКА ЗАДАЧИ. ЛИНЕЙНЫЕ СИСТЕМЫ
(гл. 4
указанной замены из (31), а именно, t t
x = 0(Qc+ J 0(0О"1 (?)^(?)d? + J 0(00-1 (*)ф(?(*)• P(O> *)<*• ^0 «0
Предполагая, что с имеет значение (30) и обозначая t
g(f) = О (/) 0-1 (Q х (t0) + J о (0 0-1 (?) j (?)(к, (4.34)
to
K(t, ?, q, р) = 0 (0 0-1 (0 ф (q, р, 0, (4.35)
имеем матричное интегральное уравнение t
х (0 = g(0 + J K(t, ?, q (0, p (0) dz, (4.36)
^0
эквивалентное исходному дифференциальному уравнению вместе с начальным условием. В скалярной форме мы получим систему двух вообще нелинейных интегральных уравнений относительно q{t) и p(f):
<7(0 = &(0 + f q,(y)> Р($)<К, \ (4.37)
p (0=& (0 + J ^2 (A ъ q CO, p (O)
выражения для gj, Kj (y = l, 2) легко получить из (34) и (35):
gt (0 = {1®11 (0 «22 (У - ®12 (0 021 (Q1 $0 +
+ [— 0ц (0 012 (*0>+012 (0 0ц (QI Pol X
X [^11 (9 ®22 (9 ®12 (?()) ®21 (91 4“ t
+ / {[6ц (О %2 СО - «12 (О «21 (01 У1 (О +
Ч" I 0Ц (О 012 (О, Ч" ®12 (О 0Ц (т)1 У2 (Т)} X X [0Ц (т) 0-22 (Т) 012 (Т) 0*21 (т)]
Й2 (0 = { [®21 (0 ®22 (^о) ®22 (0 021 (^о)1 ^0 Ч~
4“ I ®21 (0 012 W Ч~* 022 (О 0Ц (^o)l Ро J X
X [0Ц а0) 022 (Q 012 (fo) 021 (91 Ч~ t
Ч- J {[021(0 022 СО—022(0 021 +
#0
+ I- 021 (0 012 СО + 022 (0 0ц (О] л (*)} X X [0ц (т) 022 (т) — 012 (?) 021 (?)] -1 d?, ,
(4.38)
§ 4.4] ПРИВЕДЕНИЕ ОБЩЕЙ ЗАДАЧИ К ИНТЕГРАЛЬНЫМ УРАВНЕНИЯМ £11
t,q,P)={ [0Ц (О 022 СО — 012 (О 0-21 СО) Ф1 (?’ Р’^) + + [-011(О012(О + 012(О0ц(ОП2(^ л 0}Х
Х[0ц(О022(О-012(О021(О]Л
^2 (Л Т, q, р) — { [021 (О 022 (О 022 (О 021 (О] Ф1 (я» Р* О 4"
+ [--^21 (О ^12 СО + 022 (О 0Ц (01 ^2 (q» А т)} X
X [0ц (О 022 (О ^12 СО 021 (О] •
(4.39)
Приведение к интегральным уравнениям само по себе является, разумеется, лишь изменением формы постановки задачи. Однако эта форма может быть более удобной для применения различных приближённых методов.
Можно показать, например, что при некоторых ограничениях точное, решение даётся пределами последовательных приближений
9(°) (0 = gt (t),
p«Hf)=g^t),
t
9(1) (0 = Si (0 + JX Ц, z, q& (z), pM (?)) dz,
^0 t
P(1) (0 = & (0 + JX (t, z, q^ (z), p(0) (t)) dz,
^0 t
Я™ (0 = Si(0 + j* «л (t, z, (T), рЫ (x)) dz, tu
t
P® (0 = & (0+ f '^2 (t. <7(1) (y), P^ W) dz,
^0
Недостаток этого метода состоит в быстром усложнении функций q^(t), p^(f) при возрастании L В этом случае можно применить числовой метод, разделяя интервал интеграции на малые интервалы = —10, — ... и заменяя интегральные урав-
нения системой конечных рекуррентных соотношений
J-i 1
Я (0) = & (^) + S (t3, h, q (Ы, р (ffe)) A/ft,
<4-40>
р (tj) = (fj) + 2Х (fj> я (Ы> р (4)) д4» fc=0
из которых последовательно определяются приближённые значения Я(*1)> P(ti)> я(^2)> Р(?2)< •••
14*
212
йостлйовкА Задали. линёЙныё системы
(гл. 4
Б. ЛИНЕЙНЫЕ СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
§ 4.5. Колеблющаяся система как линейный фильтр. Рассмотрим массу fe0, движущуюся поступательно и прямолинейно под действием упругой силы пружины и неконсервативной силы Q. По закону Гука, упругая сила равна —&>_у, где k2— постоянная, а у — координата, отсчитываемая от положения, в котором пружина не напряжена. Силу Q будем предполагать состоящей из вязкого сопротизления — k±y, пропорционального скорости у, и некоторой добавочной возмущающей силы x(t). Мы имеем, следовательно,
(4.41)
Q = — V + (4.42)
и канонические уравнения будут
Если же исключить р или составить уравнение Лагранжа второго рода, то получится:
(fc0D2 + + k2)y (0 = х (f), (4.44)
где
Система может рассматриваться как линейный филыпр, на входе которого действует сила x(f), а на выходе получается соответствующее смещение y(f).
Вместо y(f) можно ввести в качестве зависимой переменной давление пружины
z = k2y (4.45)
на ту неподвижную точку, к которой она прикреплена. Уравнение фильтра принимает вид
(kQD^-^k1D + k.2)z(f) = k2x(t) (4.46)
и связывает теперь две величины одного и того же рода (две силы). В качестве электрической аналогии рассмотрим контур, составленный из последовательно включённых источника напряжения £*(/), самоиндукции L, сопротивления 7? и ёмкости С. Положим для единообразия
k0 — L, ki — R, k2 — ^, х — Е (4.47)
. dv
и обозначим через у заряд конденсатора, а через i = — силу тока
в контуре. Согласно (3.93), (3.96) выражения (41), (42) определяют
§ 4.6] АВТОМАТИЧЕСКОЕ РЕГУЛИРОВАНИЕ 213
теперь электромагнитную и электростатическую энергии системы и электрическую неконсервативную обобщённую силу. Колебательный процесс в контуре определяется поэтому уравнением Лагранжа (44). Мы можем также придать ему форму (46), и тогда оно будет связывать два напряжения, так как переменная
Z = ^У (4.48)
представляет, очевидно, напряжение на обкладках конденсатора.
Многие другие задачи теории колебаний приводят к уравнению типа (44). Его элементарное решение излагается во всех курсах механики. Поэтому мы ограничимся ещё одним примером из теории регулирования, после чего обратимся к изучению некоторых общих свойств движения.
§ 4.6. Автоматическое регулирование. Регулятором называется устройство, присоединяемое к какой-либо физической системе и воздействующее на неё таким образом, что одна или несколько её координат qu ..., qn остаются всегда вблизи некоторых желаемых значений ..., #*. При этом под координатами разумеются вообще величины, характеризующие состояние системы; они могут быть длинами, углами, давлениями, температурами, электрическими токами или напряжениями и т. п. Совокупность систем значений координат
• • •> Яп мы будем называть полем регулирования. Одной и той же регулируемой системе могут соответствовать различные поля регулирования. Например, в одном и том же трубопроводе можно регулировать либо давление, либо температуру; в первом случае мы будем иметь пьезометрическое, во втором — тепловое поле регулирования.
Простейшие регуляторы управляются машинистом, причём исполнительный орган может приводиться в действие либо непосредственно за счёт физического усилия. машиниста, либо с помощью вспомогательных машин или сервомоторов; примером может служить управление паровозом или штурвалом корабля. В этих случаях машинист непрерывно наблюдает за состоянием поля регулирования, сравнивает его с желаемым и действует в соответствии с результатами этого сравнения. Регулятор осуществляет лишь функцию передаточного механизма, либо также усилителя мощности. Этот способ регулирования связан с постоянной нагрузкой машиниста и, кроме того, ввиду невозможности поддержания его внимания на одном и том же уровне не позволяет достичь большой точности.
Поэтому во всех случаях, где это возможно, стремятся перейти к автоматическому регулированию, при котором регистрация состояния поля регулирования производится не с помощью органов чувств машиниста, а измерительными приборами (чувствительными элементами). Сравнение фактического мгновенного состояния с желаемым и: у правление сервомоторами также осуществляются автоматически с помощью органов, которые носят общее название реле.
214 ПОСТАНОВКА ЗАДАЧИ. ЛИНЕЙНЫЕ СИСТЕМЫ [ГЛ. 4
Чувствительные • элементы, реле, сервомоторы и исполнительные органы являются основными элементами автоматического регулятора. Регулятор вместе с полем регулирования образует систему регулирования. Следует заметить, впрочем, что задача создания единой чёткой терминологии теории регулирования не может считаться решённой.
Желаемые значения координат q*. могут быть либо постоянными, либо заданными функциями времени q^(t). В последнем случае регулирование обычно называется программным.
§ 4.7. Следящая система с линейным законом включения. Следящей системой [4Д9] называется система автоматического регулирования положения, в которой некоторое следящее тело S должно повторять все движения задающего тела S*. При этом источником энергии следящего движения должно служить не задающее тело, .а сервомоторы, которые лишь, управляются задающим телом. Это необходимо либо потому, что благодаря большой массе. следящего тела оно вообще не может быть приведено в движение задающим, либо потому, что хотя такое непосредственное воздействие и возможно, но вызвало бы значительное и нежелательное искажение движения задающего. Эти требования легко понять, когда задающим телом является, например, какой-либо деликатный регистрирующий или измерительный прибор.
На фиг. 7 представлена простейшая принципиальная схема, в которой, благодаря надлежащим направляющим, как задающее, так и следящее движения поступательна и прямолинейны. Смещение задающего тела обозначим через #*, смещение следящего тела, которое можно в то же время рассматривать и как координату сервомотора Q — через q. Множество значений q представляет позиционное поле регулирования.
Тело S* снабжено реостатом (потенциометром), три точки которого соединены с полюсами генератора постоянного тока G, как показано на схеме. Тело S снабжено контактными роликами, связанными с сервомотором Q. Начало отсчёта для q* может быть назначено произвольно, начало отсчёта для q выбирается так, чтобы при q = q* каждый ролик стоял на середине одной из двух ветвей потенциометра; эти средние положения показаны на чертеже пунктиром.
Потенциометр и ролики образуют контактную систему, с помощью которой происходят включение й реверсирование сервомотора. Пока q = q*t потенциалы на роликах равны между собой вследствие симметрии системы, и ток в цепи якоря сервомотора не возникает. Но если следящее тело обгоняет задающее, то между роликами получается напряжение
и= — a(q— q*)>
•где а — постоянная. В цепи якоря возникает ток и мотор передает на тело S усилие, имеющее тенденцию уменьшать расстояние q -— q*.
§ 4.7] СЛЕДЯЩАЯ СИСТЕМА С ЛИНЕЙНЫМ ЗАКОНОМ ВКЛЮЧЕНИЯ 215
Если следящее тело отстает от задающего, то напряжение U, ток в якоре и усилие мотора меняют знаки. Вследствие инерции тело S, следуя за телом S*, совершает около него колебания, изучение которых и составляет нашу задачу.
Уравнение движения следящего тела с сервомотором и уравнение электродвижущих сил в цепи якоря суть
k*i-R°dt~
— Щ
U—cq~ RL
При этом I обозначает силу тока в цепи, kQ— постоянную приведённую массу следящего тела с сервомотором, R— омическое сопро-
Фиг. 7. Принципиальная схема следящей системы с линейным законом включения.
тивление цепи якоря, X и с — постоянные коэффициенты; —kq, ci в первом уравнении представляют, соответственно, вязкое трение и усилие, передаваемое сервомотором, член —cq во втором уравнении — противоэлектродвижущую силу, возникающую при вращении якоря. То обстоятельство, что в выражении усилия сервомотора и противоэлектродвижущей силы мы имеем один и тот же коэффициент с, вытекает из простых энергетических соображений. Самоиндукцией цепи мы пренебрегаем.
Заменяя U его выражением, находим из второго уравнения
. — a(q —q*) — cq .
f " d >
216 - ПОСТАНОВКА ЗАДАЧИ. ЛИНЕЙНЫЕ СИСТЕМЫ [ГЛ. 4
если же воспользоваться этим соотношением для исключения силы тока I из первого уравнения, то получится уравнение вида (46)
(fe0D3 -|- ktD -|- fe2) q =
в котором
, ' t с2 г ас
А1— л + -у, h — -R-
Это уравнение следует ещё исправить, замечая, что величина q*9 зарегистрированная контактной системой, представляет сумму
q* = xi+x2,
где характеризует основное движение задающего тела, воспроизведение которого составляет задачу следящей системы, а х2 — ложный сигнал, происходящий от добавочных случайных движений задающего и от ошибок контактного устройства. В качестве зависимой переменной, целесообразно ввести рассогласование
y = X1 — q9
характеризующее погрешность системы. С помощью двух последних соотношений уравнение движения получает вид:
(V>2 + kxD + й2)у (0 = (kQDL^kxD) х± (0 - k х2 (0. (4.49)
Мы имеем здесь линейный фильтр с двумя величинами x±(f) и x.2(t) на входе.
§ 4.8. Общее решение уравнений движения. Все линейные системы в предыдущих примерах представляют "частные случаи линейного фильтра, характеризуемого уравнением
= 2(^+«1Р + ау)^(0 (4.50)
с п координатами xt(t), ..., xn(t) на входе. Мы, однако, ограничимся получением общего решения для системы (44), так как методы исследования, продемонстрированные на этом примере, могут быть, без . существенных затруднений, перенесены и на другие.
Воспользуемся операционным исчислением, полагая
•’ 5 (р)(0. ЯрЭ-н-ЯО-
Согласно (2.21), (2.22) имеем:
(М2 + М + Мп (Р) ~ Р КМ + Й1).Уо + Мо1 -=->
—(A0Da AsjZ) -J- k2~) y(t), -
где yQi yQ обозначают начальную координату и начальную скорость. Изображение уравнения (44) будет
(М2+*1Р + “Ч (Р) = Pj(M + *1) у0 + Mol +1 (р)>
§ 4.8] ОБЩЕЕ РЕШЕНИЕ УРАВНЕНИЙ ДВИЖЕНИЯ 217
из него получаем операционное решение
т| (/?) = (р) + Y (р) $ (р), (4.51)
где
<4-52>
(4-53>
Выражение У(р), характеризующее влияние $(р) на т|(р), может быть названо передаточной функцией, или операционным транс-миттансом системы. Полагая
ри (р) М (0, р Y (р) N (0 (4.54)
и применяя теорему об умножении изображений, получаем общее решение
у (t) = М (0 + Г N(t—U)x («) du. (4.55)
О
Входящий в него интеграл называется интегралом Дюгамеля\ он выражает влияние внешних возмущений за всю историю системы. При этом элементарный импульс x(a)da, действовавший на t—и секунд ранее данного момента t, входит с множителем N(t—и) и производит в этот момент элементарное отклонение N(t—u)x(u)du. Таким образом, функция ЛГ(/ — и) характеризует относительное влияние предшествующих импульсов и. может быть названа функцией последействия. Если начальные значения yQ, yQ, а следовательно, и М (/) равны нулю и если сила х (и) бесконечно велика и, действуя в течение бесконечно малого промежутка времени (и, и-[-du), сообщает системе конечный ударный импульс x(u)du = l, то y(t) = N(t—и). Иными словами, функция последействия N(t—и) при переменном t и фиксированном и есть частное решение, соответствующее единичному начальному ударному импульсу в момент и.
С другой стороны, обозначим через A(t) оригинал для Y (р):
Y{p)^A(t). (4.56)
Так как (§ 2; 16)
Л (0) = У (оо) = 0, (4.57)
то из второго соотношения (54) вытекает:
?/(/)=: Л(/). (4.58)
Принимая во внимание ещё, что (§ 2.14) в интеграле Дюгамеля можно поменять ролями аргументы и и t—и, получим:
' t
у (t) — (^) —}— J A(u)x{t—и) du, (4.59)
о
218 ПОСТАНОВКА ЗАДАЧИ. ЛИНЕЙНЫЕ СИСТЕМЫ [ГЛ. 4
Если, в частности, j/o = j/o = 0 и сила действует по закону ступенчатой функции
х(0 = /(0,
то j>(/) = ?1(/). Таким образом, A(t) представляет частное решение, называемое также переходной функцией, при внезапном приложении единичной силы. Согласно предыдущему, переходная функция является оригиналом для операционного трансмиттанса, а её производная A (t) равна функции последействия.
Форма явных выражений для N(f), A(t) зависит от вида корней характеристического уравнения
+ kiP + k-г — 0* (4.60)
Они действительны при kf > 4fe0&2> и мы представим их в этом слу-
чае в виде —тх, —f2, где
71» Ъ =
(4.61)
Известные соотношения между коэффициентами и корнями дают: = *о (li “Ь* Тг)» k’2 = ^оТГ1Т2»
и с их помощью мы можем написать:
PH (Р)=Р
(Р + Tt + Т2) +.Уп (Р + 71) (Р + 72) ’
pY^ Mp+ti) (Р + Тг) или
рр- (Р) = — (Т2Л+jo) ^7 + (Т1Л +л) >
II L I 11 Jr I |А J
pY (р) ~ — (“р + Т1 ^"р + ъ)’
Пользуясь операционной формулой (2.51), находим оригиналы этих изображений:
М (0 = HWo+jo) + jo)«-Ta#l> (4.62)
11 i A
Интегрируя N(p) и принимая во внимание (57) и (58), получаем:
1 /. ъе —ъе T>t' МП А ' 71— tz
(4.64)
§ 4.9]
УСТОЙЧИВОСТЬ ПОЛОЖЕНИЯ РАВНОВЕСИЯ
219
Если < 4feofe2, то корни характеристического уравнения будут комплексными и могут быть представлены в форме —sz+z/oo, где
8_ Ь. ш—
2ЙО’ m~V Йо 4йГ
<* V
В этом случае
(4.65)
(Р + 2£)Jo+Уо р(р+е) I Уо+*Уо Р">
(р -j" •'О (р -|- е)2' ш (р 4" е)2 “Ь *
PY^ £0(1>(p-J-e)2 4-<o2’
откуда, интерпретируя с помощью (2.55),
М (f) = е~а \yQ cos sin oj/J , (4.66)
N (0 = i е“е4 sin (4.67)
Вводя вспомогательный угол 0 с помощью соотношений
sin 0 = —=^=, cos 0 — --- ш , (4.68)
у е2 ш2 у е2 -|~ 0)2
получим переходную функцию в виде
Л(0 =
#0<о )/*е2 -|- 0)2
[—cos (art— Ь)4“ cos 0].
(4.69)
Пусть, наконец, fef = 4fepA?2. Характеристическое уравнение имеет действительный двойной корень —s; с помощью предельного перехода при (о -> 0 из формул (66), (67) получается:
затем, интегрируя, найдём:
#ог
(4.70)
(4.71)
(4.72)
§ 4.9. Устойчивость положения равновесия. Пусть, в частности, внешняя сила x(t) равна нулю. Если при этом колебания затухают и координата у стремится к нулю при t—>оо, каковы бы ни былй начальные условия, то положение равновесия у = 0. называется асимптотически устойчивым. Оно считается устойчивым и в том случае, когда координата у остаётся ограниченной, не стремясь к нулю, но такая устойчивость не является асимптотической.
220 ПОСТАНОВКА ЗАДАЧИ. ЛИНЕЙНЫЕ СИСТЕМЫ [ГЛ. 4
Общее решение приводится к М (f) и выражения этой функции, полученные в предыдущем параграфе, показывают, что затухание имеет место, когда 72 или е положительны и, следовательно, действительные корни или действительная часть комплексных корней характеристического уравнения (60) отрицательны. Будем предполагать, что коэффициент kQi представляющий приведенную массу системы, положителен. Из формул (61), (65) вытекает, что для положительности ft, или s необходимо, и достаточно, чтобы
> 0, ft2>0. (4.73)
Эти неравенства представляют условия асимптотической устойчивости. Если при фиксированном fe0 трактовать klt k2 как прямоугольные координаты в некоторой плоскости параметров, то последние неравенства определяют первый квадрант этой плоскости, который будет областью устойчивости для рассматриваемой задачи. Её граница состоит из положительных координатных полуосей; на полуоси положительных абсцисс (fej > 0, k.2 = 0) характеристическое уравнение имеет нулевой корень, между тем как второй корень — отрицателен; на полуоси положительных ординат (kt = 0, k,2 > 0) уравнение имеет пару чисто мнимых корней zt i ]Лй2/А0. Таким образом на границе устойчивость сохраняется, но она уже не будет асимптотической. Парабола
kl = 4fe0fc2 (4.74)
делит область устойчивости на две части. В нижней части корни действительные и неравные, в верхней — комплексные, на самой параболе— действительные равные.
Если условия асимптотической устойчивости выполнены, то каковы бы ни были корни характеристического уравнения, функция A (I) стремится к l/fe2 при ^->оои характеризует непрерывный переход системы от положения равновесия, соответствующего силе х = 0, к положению, соответствующему силе х= 1. Если, в частности, корни характеристического уравнения действительны и различны, то функция последействия
АГ/л л /а 1 -(Т1+Х2)4-Г -(Т1-Ь)4 I
N(t) = A(t) = -r~7------гв 2 —е 2 4-е 2
w 4 7 £о(Т1 —Т2) L J
положительна при всех t и функция A(t) изменяется монотонно. То же самое будет и при действительных равных корнях, между тем как при комплексных корнях скорость бесчисленное множество раз меняет знак, а переходная функция имеет бесчисленное множество максимумов и минимумов. Решение, соответствующее переходу от начального положения x^jk^ соответствующего какой-нибудь постоянной силе к положению равновесия x2/fe2, соответствующему любой другой внезапно приложенной силе х2, есть
. . У (0 = (Х2 — Xi) A (t).
§ 4.10] ЗАТ^ХАНЙЕ КОЛЕБАНИЙ ПОбЛЕ МгНОЙЕНЙЫк ВОЗМУЩЕНИЙ 221
§ 4.10. Затухание колебаний после мгновенных возмущений. Проверка устойчивости представляет первый необходимый шаг при анализе колебательного процесса в любой физической или технической задаче. В самом деле, если, например, уравнение (44) относится к какой-либо системе регулирования и если колебания после начального возмущения не затухают,, то система, разумеется, непригодна. Однако наличие асимптотической устойчивости не является ещё достаточной характеристикой системы, так как действительный корень или действительная часть комплексных корней характеристического уравнения могут быть отрицательны, но очень малы, и тогда колебания затухают столь медленно, что практически не отличаются от незатухающих. Необходимы поэтому. какие-либо критерии, дающие общую оценку колебательного процесса; в теории регулирования их называют критериями качества регулирования. Единого принципа в настоящее время не существует, что объясняется, быть может, тем, что проблема отчётливо и во всей общности поставлена лишь недавно. С другой стороны, возможно, что и по существу дела не следует требовать установления критерия, одинаково пригодного для всех систем и всех возможных условий.
Очень простая оценка предложена Я. 3. Цыпкиным и П; В. Бромбергом [4-9]. По их определению за коэффициент устойчивости а, т. е. меру затухания, в случае действительных отрицательных корней — 71 > —7-2 принимается наименьшая из их абсолютных величин подобно тому, как скоростью эскадры считается скорость самого тихоходного корабля:
“ = V <‘> > ». »>>»•*? > (4-75)
U ▼ T’/vQ V
ч
В случае двойного отрицательного корня — е или пары комплексных корней—ez±z/co с отрицательной действительной частью коэф-фицициент устойчивости равен е:
а = А (/гх > 0, й2 > 0, kf > 4 W (4-76)
Фиксируя а, получим линии равной устойчивости в плоскости Каждая из них состоит из двух полупрямых
fe.2==afe1 — fe0a2 (ftx>2fe0a, fe2>fe0a2), (4.77)
= 2feoa (&2 > fe0a2), (4.78)
лежащих в первом квадранте и пересекающихся на параболе (74), причём первая полупрямая касается параболы, а вторая параллельна её оси fex = 0.
В приведённой оценке не учитывается суперпозиция нормальных колебаний, соответствующих двум корням характеристического уравнения. Это можно сделать, принимая за меру затухания
• » * I t
222 постановка задачи, линейные системы (гл. 4
интегральную абсолютную величину отклонения
Z=J|j/(Z)[^ (4.79)
О
такая оценка была применена Б. В. Раушенбахом [4-6]. Мы предположим при этом, что системе при t = 0 сообщён единичный ударный импульс; тогда, согласно § 8, у (t) будет равна функции последействия N(f) = A (f).
Если характеристическое уравнение имеет различные или равные действительные отрицательные корни, то Af(Z) всегда положительна и знак абсолютной величины излишен:
l=J A(f)dt (4.80)
О или
/=Л(оо)-Л(0) = ^.
Если корни характеристического уравнения комплексные с отрицательной действительной частью, то
/= Г |Л (t)\dt. о
(4.81)
Функция АГ(£) = Л(£), определяемая формулой (67), меняет знак при аргумента^ tn = тгп/со (п = 0, 1, 2, ...), и потому
со л (П+1)/<о
Z=S(—Т)” f A(t)dt=
= [Л(4) —Л(0)1 —И(4) —Л(^)1 + [4(/3) —X(Z2)1—...
Вводя декремент 8 с помощью соотношения
8 = = ехр ( \ ,
' V Ufa — k?
получим из (69):
Л(/„) = 1ц— 1)«+13”+1Ь
и, следовательно,
/=^[(8 + 1)-(-83-8)+(88+83)—...] =
1 (1 । п* । । \ 1 / < । 28 \ 1 1 -|“о
=г/1+2о+28 г
§ 4.10] затуханйе Колебаний после мгновенных возмещений 223
Так как затухание тем слабее, чем больше /, то за коэффициент устойчивости при ударе можно принять величину Р = у или
k,2 при
при k* < 4^2.
(4.82)
Фиксируя р, получаем линии равной устойчивости в плоскости ktk.2\ каждая из них состоит из полупрямой
62 = р (^>2/й0р)
(4.83)
и кривой
1п
0^2
Itl
(^2
(4.84)
пересекающихся на параболе (74).
Ещё одну оценку устойчивости можно получить по Н. Д. Моисееву [4Л] и А. А. Фельдбауму [4Л] с помощью интеграла
оо
/= j* {МЯЭР+МХОРИА о
(4.85)
где 0р 02 — неотрицательные постоянные. Как и выше, мы предположим, что системе при £=0 сообщён единичный ударный импульс, вследствие чего она, оставаясь в начальном положении
у$ = 0, получает начальную скорость Уо=-г~-Kq
Если в дальнейшем
возмущающая сила не действует, то $(р) = 0 и формулы (51), (52) дают:
где
*4(/0 = h Я(р) = й0Р2 + *1Р + й2-
С другой стороны, обозначая через С(р) изображение y(t)t имеем по формуле (2.17):
где
1^ = ^(„)_0 = ^ р ^р> Н(р) ’
им—р-
Образуя, согласно (2.156), полиномы
Gi (р) = Ц (—р) £4 (р) = 1, О2 (р) = £72 (—р) U2 (р) = —р’,
* £
224
Постановка задачи, линейные системы
(гл. 4
получаем с помощью (2.155):
4-too +«оо
, f в1°1 (g) + 0,0, (g) 1 f G(p)dp
2iti J ff( — q)H(q) 4 ~ 2vi J H(— p)H(p)’
— too ~~ico
где
G (p) = OtOt ( p) + в2Оа (p) = /OP9+ly
Iq = 62> /j = 6p
Поэтому, согласно (2.159),
j Mo 4~ ^2^2
2kQktk2
Обобщая определение А. А. Красовского [4*3], принимаем за коэф-. 1 фициент устойчивости величину ^1 = 97 или
•'=«тЬг (4-86)
В отличие от р, это выражение рационально относительно kQi kv k2. Линиями равной устойчивости будут ветви гипербол
(Mi 7i®a) = 71Мо» (4*87)
лежащие в первом квадранте.
Для сравнения применим квадратичный критерий к следящей системе, описываемой уравнением (49). Так как правая часть (49) содержит xt и но не хх, то мы можем считать, что роль первой возмущающей функции играет истинная скорость хг задающего тела. Предположим, что при /-=0 она внезапно получает бесконечно большое значение, которое удерживает в течение бесконечно малого времени dt, причём х19 а с ним вместе и у — х±— q получают конечное изменение x±dt~l. Если в дальнейшем x±(t) и x2(t) равны нулю, то операционное решение будет
71(Р) = Р|*(Р).
где |л(р) определяется опять формулой (52), в которой нужно только положить у0 = 1, j/o = O. Поэтому
где
lL£L = а (о) = М)
Р ^Р) Н(р) •
Ц ( Р) = К р + kv Н(р) = kop* 4- kxp 4- k.2.
Обозначая вновь через С(р) изображение .у, имеем: .U2(p) —-------------------------^Р)~1-тц^
§ 4.11]
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
225
где
^(Р) = ^2*
Та же процедура, что и выше, даёт:
-|- 62^2 + ®1^Ь^2
*
Определяя коэффициент устойчивости соотношением = > имеем:
7 о = —-----ft— • (4.88)
4“ *"Ь ^1Ло^2
Линиями равной устойчивости .будут ветви гипербол
ТоМ? — М-2 + ТоМ! + То МА = 0. (4.89)
лежащие в первом квадранте и получающиеся при
° > 70 < 2‘
Когда коэффициент устойчивости обращается в нуль, линии всех четырёх рассмотренных выше семейств сливаются с границей области устойчивости.
§ 4.11. Вынужденные колебания. При выводе коэффициентов устойчивости а, р, 70, 41 принимались во внимание импульсивные возмущения, создающие начальное отклонение yQ и скорость yQ.
Предположим теперь, что у0 и yQ равны нулю, но система подвергается непрерывным возмущениям x(t), относительно которых известно, что они ограничены по абсолютной величине:
IX (01 1. (4.90)
В остальном x(t) может быть любой однозначной функцией, непрерывной и дифференцируемой всюду, кроме точек разрыва 1-го рода, число которых в каждом конечном интервале будет предполагаться конечным.
Определим накопленное, т. е. максимальное возможное отклонение системы, описываемой уравнением (44), при этих условиях [410].
Мы имеем /И (£) = О и, согласно (59), t
y(t) = J* А (и) х (t— и) du. о
Пусть характеристическое уравнение имеет различные или равные действительные отрицательные корни. Тогда функция N(t) = A (t) положительна и абсолютная величина интеграла при данном t будет наибольшей, если x(t—и) сохраняет во всём интервале интеграции
15 Зак. 1474. Б. В. Булгаков
bsss;
226 ПОСТАНОВКА ЗАДАЧИ. ЛИНЕЙНЫЕ СИСТЕМЫ [ГЛ. 4
предельное значение 1 или — 1 • Эта наибольшая величина, следовательно, равна
t m(t)= j* О
с ростом t она будет возрастать, и при t=oo мы получаем maximum maximorum (максимум всех максимумов)
оо
т (оо) = J A(t) dt о
или, сравнивая с (80),
zn(oo) = Z. (4.91)
Если корни характеристического уравнения комплексные с отрицательной действительной частью, то при данном t абсолютная величина интеграла будет наибольшей, когда абсолютная величина функции x(t—и) всё время равна предельному значению 1, а её знак меняется так, чтобы подинтегральная функция в целом оставалась положительной. Иными словами, x(t—и) должна менять знак при u = tn, где tn — корни функции N(t) — A(t). Величина y(t) при этом будет равна
t т (/) = J | А (Z) | dt, « о
и для соответствующего maximum maximorum находим:
оо
т (оо) = у | A (t) | dt. . о
Сравнивая с (81), получаем опять соотношение (91). Поэтому, определяя коэффициент устойчивости р соотношением р= l/zn(oo)= 1/Z, получаем для него формулу (82).
Таким образом, коэффициент устойчивости по накоплению тождественен с коэффициентом устойчивости при ударе, вычисленным с помощью интегрального абсолютного значения. Он характеризует поведение системы при наихудших возможных условиях. Если, однако, иметь в виду средние, наиболее вероятные условия, то следует пользоваться коэффициентами добротности; полученными с помощью статистических характеристик возмущений [4-18]. *
Обычно считают достаточным рассмотреть простейшие гармонические возмущения
x(t) = Р cos v/,
которые могут передаваться системе колеблющейся средой, например воздухом или упругими опорами. Постоянство амплитуды Р
| 4.11] вынужденные колебания 227
должно обеспечиваться при этом за счёт какого-либо источника энергии.
Решение уравнения движения
(fe0D2 + kxD + k2) у (f) = P cos v/
может быть получено с помощью выведенных выше общих формул. Однако проще и поучительнее рассматривать выражение x(t) как действительную часть функции Реы. Частное решение ^(0 уравнения движения может быть получено тогда, как действительная часть частного решения изменённого уравнения
+ kxD + k2)y (0 = Ре™.
Это последнее ищем в форме y = he™\ подстановка в уравнение даёт:
h [fe0 (Zv)2 fe1Zv + й,2] e™ = Ре™, откуда
А = < ,.-<о 1^. .-г—г- = Y (Zv) Р>
и, следовательно,
yt (0 = р Re Y (Zv) е™.
По свойству линейных уравнений, общее решение будет
где у2 (0 — общее решение однородного уравнения, представляющее некоторое собственное колебание. Но если, как мы будем предполагать, имеет место асимптотическая устойчивость, то собственные колебания будут затухать, вследствие чего yt(f) характеризует стационарное колебательное состояние, к которому стремится система; это состояние поддерживается энергией, передаваемой возмущающей силой.
Величина h является комплексной амплитудой вынужденного колебания, так как смещение у1(0 = РеАеы может рассматриваться как проекция на действительную ось вектора he™ в плоскости комплексного переменного; этот вектор вращается вокруг начала с угловой скоростью v, и h есть его начальное значение. Полагая Ь = Ае~^, где А— модуль, а — аргумент с обратным знаком, имеем:
Д = Р|У(/у)|, ф = — arg У (Zv)
А—± Р “ Я ’ cos4>= —k^+kLj sin<J> = -^r,
или
где
*=/(-V+*2)2+^2;
15*
228
постановка ЗадАчй. Линейные системы
[гл. 4
при этом ' :
У1 (0 = cos (У*—Ф)*
Действительное число А представляет амплитуду вынужденного колебания, а — сдвиг фазы по отношению к фазе возмущения или аргумент запаздывания. Комплексная функция Y (fv), получаемая из операционного трансмиттанса Y (D) заменой оператора D на /у, называется частотной характеристикой линейного фильтра. Как видно из предыдущих формул, её модуль даёт отношение амплитуд Л/Р, которое может быть названо коэффициентом усиления фильтра; аргумент частотной характеристики лишь знаком отличается от аргумента запаздывания.
Представляя графически зависимость отношения Л/Р от угловой частоты возмущения у, получим резонансную кривую, известную из курса механики. Мы имеем:
^ = 2й0(*0>2-*2) + ^ и если
то Р с ростом v сначала убывает, достигает при
,2 =________________
2^ *0.
минимума
а затем возрастает. Если же
то Р всё время возрастает вместе с у и минимальным будет его значение при v = 0, а именно,
& =
Минимальному значению Р соответствует максимальное значение Р/& амплитуды вынужденного колебания. Чем больше &, тем эта амплитуда будет меньше, и потому мы можем принять & за коэффициент
устойчивости при гармонических возмущениях.
Задавая &, будем получать линии равной устойчивости в первом квадранте плоскости параметров определяемые уравнениями
При эти линии
. №kg 4kg "I
& сливаются
при . kt .< К2М» (4>92) при k± > ]/*2й0&.
с границей области устойчивости.
§ 4.11] ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ 229
г
Рассмотрим теперь более общую задачу о вынужденных колебаниях под действием произвольной периодической силы х(/) с периодом т. При этом будем следовать Дуффингу [611] и Лурье [2б] и ограничимся случаем, когда вязкое сопротивление отсутствует (fe = 0), a fe.2, так же как и fe0, положительно. Характеристическое уравнение имеет тогда два чисто мнимых корня ztzw, где
"=/v
Согласно (2.64) и (2.66) имеем:
где
а (р) = р J х о
Поэтому если предположить для простоты, что у (0) = у (0) = 0, то изображение уравнения движения будет
w+^(p)=T^^, •
откуда
Ч__ а (р)
~ k0 (р* + <о2) (1 —
и, согласно (2.141), /а 1 Vo <*(p)ept
УУ)— kQ 2uReS р(р2 4-0,2) (1—У
где вычеты берутся относительно всех особых точек функции а(р)^р7/?(Р2“Ьа)2)(1—*-*’)> лежащих на конечном расстоянии. Числитель представляет функцию, регулярную во всей плоскости, и потому нужно принять во внимание только простые полюсы, соответствующие нулям знаменателя.
Вычет относительно полюса р = 0 есть
ар , . 4 со2 ’
где
230
ПОСТАНОВКА ЗАДАЧИ. ЛИНЕЙНЫЕ СИСТЕМЫ [ГЛ. 4
Вычеты относительно полюсов dzZco будут
1 е± м I*
—----------x(u)e^iaiUdu =
2/ю 1— J } о
±i (ш/+^) J
—---------—__ х (и) (— cos ти ± i sin соя) du —
4<оsin№-\ о
= (cos <о/± I sin mt) ( ctg-^J- z±z ij ( — c ± is),
причём
т
c = J* x (u) cos mu du, о
T
s = j x(u) sin mu du. о
Наконец, для вычетов относительно полюсов
±2тъ1ъ (п=1, 2, ...)
получаем выражения
-с
f х (и) е* ‘itnrM!r- du
о_________________________g± 2<nitf/T _____ /yw) [cos (‘Inidl’z) zfc Zsin (2z»tZ/i:)]
0)2 — 4л2тс2/т2 т 2 (co2 — 4л2л2Д^)
где
2
’ 2 С
x (и) cos (2п^и/х) du, ^п = — х (и) sin (Яппи/х) du. J т .
о о
Соединяя попарно вычеты, относящиеся к сопряжённым полюсам, и суммируя, представим y(t) в виде
^(0=Л(0+л(0>
причём
оо
л= й + 2 I?» cos + Ь sin (2«^)Ь
п=1
sin mt
Первое слагаемое yx(t) представляет ряд Фурье, выражающий вынужденное колебание с тем же периодом т, что и врзмущающая сила. Второе слагаемое имеет частоту собственных колебаний со.
§ 4.12]
ВЫБОР ПАРАМЕТРОВ РЕГУЛЯТОРА
231
Так, как, согласно (55) и (67), при е = 0 мы имеем:
t •
у = I х wsin “
б
то вынужденное колебание может быть также представлено в форме (0 = ^(0—Л (0 иди
х (и) sin со (t— и) du +
^s-j-cctgcos sin
куда бесконечный ряд не входит.
Вычисления по этой формуле достаточно сделать для промежутка времени (0, т), после чего полученную функцию нужно лишь периодически продолжить на промежутки (т, 2т), (2т, Зт), ... и т. д.
§ 4.12. Выбор параметров регулятора по коэффициенту устойчивости. Синтез регуляторов составляет основу их рационального проектирования и заключается в решении двух задач: составлении принципиальной £схемы, соответствующей поставленной технической задаче и имеющимся в распоряжении средствам, и выборе наивыгоднейших количественных характеристик, которые должны быть выдержаны при конструировании и наладке. Эти задачи могут быть решены, разумеется, лишь при полном учёте физических свойств элементов регулятора и поля регулирования. Можно, однако, наметить, в очень общей форме, схему вычисления в том случае, когда вторая задача о выборе параметров решается ♦ с помощью коэффициентов устойчивости или добротности [4Л»418], причём имеются в виду попреж-нему системы, характеризуемые одним линейным уравнением второго порядка, например уравнением (44).
Как мы видели, условия устойчивости ограничивают при данном возможные значения остальных коэффициентов первым квадрантом плоскости k±k2. Но и из этих значений не все будут допустимыми, так как, с одной стороны, усилия, развиваемые сервосистемой, не могут быть сколь угодно большими, а с другой стороны, мы можем поставить дополнительные условия из динамических соображений. Можно потребовать, , например, чтобы частота о> не превосходила некоторого предельного значения ww, что исключает, на основании второго выражения (65), все точки первого квадранта, лежащие внутри параболы
&1 — 4^q/^2 “Н == 0*
(4.93)
В результате мы будем иметь область В допустимых значений kY и составляющую лишь часть первого квадранта и. ограниченную
232 ПОСТАНОВКА ЗАДАЧИ. ЛИНЕЙНЫЕ СИСТЕМЫ [ГЛ. 4
некоторой линией S. Коэффициент устойчивости или добротности о, определяемый тем или иным способом, представляет функцию от и задача состоит в том, чтобы найти точку (fet, AQ области В, кото-рой соответствует максимум этой функции. Если она лежит внутри области, то её окружает система замкнутых и вложенных друг в друга линий равной устойчивости, которые стягиваются к ней при некотором o =
Может случиться, однако, что максимум достигается в точке границы S. Так как эта точка должна лежать на той из линий равной устойчивости, проходящих через область В, которой соответствует наибольшее значение о, то в рассматриваемом случае она будет либо точкой касания граничной кривой и линии равной устойчивости, либо такой их общей точкой, которая является угловой для одной из них, но не служит их точкой пересечения.
Пусть, например, параметры и системы, описываемой уравнением (44), заданы и положительны, а параметром k2 можно располагать с условием, однако, чтобы имела место асимптотическая устойчивость и чтобы частота о> не превосходила заданного предела (лт, В этом случае область В представляет отрезок прямой fe1== const., параллельной оси ординат, заключённый между осью абсцисс и параболой (93); на этом отрезке
О
ki 2
^2 < 4^ +
(4.94)
Если применить коэффициент устойчивости а, то из отрезка В выделится часть В', отсекаемая параболой (74) и определяемая, следовательно, неравенствами
£2 ^2
<4-95>
для ординат, удовлетворяющих этим неравенствам, коэффициент а имеет одно и то же значение йх/2й0, между тем как для меньших значений k,2 он будет меньше.
Если применить коэффициент устойчивости р или же коэффициент 7! при = 1, 62 = 0, то, как легко видеть, среди соответствующих линий равной устойчивости не найдётся такой, которая бы касалась отрезка В или имела с ним общую точку, являющуюся для неё угловой, но не точкой пересечения с отрезком. Поэтому наибольшие значения того и другого коэффициента получатся в наивысщей точке отрезка, где k2 = А?/46о +
Таким образом, при учёте суперпозиции с помощью обоих крИ’ териев мы получаем определённую и притом одну и ту же точку отрезка В',
Тот же результат получится и для следящей системы, описывае-мой уравнением (49), если сохранить определение отрезка В и при
§ 4.12] ВЫБОР ПАРАМЕТРОВ РЕГУЛЯТОРА 233
менить коэффициент устойчивости при 1, О2 = 0, предполагая, что начальная скорость yQ создана единичным ударным импульсом какой-либо возмущающей силы/Можно, однако, при прежнем основном предположении k± = const, ограничить скорость не условием (о < а путём применения коэффициента ч0 при и 6.2, отличных от нуля; начальные условия пусть будут те же самые, которые были приняты выше при вычислении 70. Чтобы найти линию равной устойчивости, касающуюся прямой k± = const., представим уравнение (89) в виде
~Ь (ТоМо &1) k'2 =Р
и потребуем, чтобы оно имело двойной корень при разрешении относительно fe2. Это даёт коэффициент устойчивости
10 01*о + 2/ОЛА
и ординату точки касания
*2 = 1/"!- kV (4-96)
Г 02
9 которая и представляет оптимальное значение fe2.
Вторая пара значений, соответствующая знаку минус перед радикалом, должна быть отброшена, так как при k± > 0 ордината k,2 получилась бы в этом случае отрицательной.
При переменных k2 уравнение (96) представляет прямую, проходящую через начало координат. Абсциссы её точек пересечения с параболой (93) определяются уравнением
*12 — 4Й0 *1 + 4*o®m = О,
из которого
При У61/Ь2 < <лт корни будут комплексными и прямая проходит под параболой, при Укорни действительны и положительны и дают две точки пересечения в первом квадранте.
Во всех сделанных оценках мы получаем при заданном коэффициенте вязкости k± конечное оптимальное значение коэффициента восстанавливающей силы k.2 только в силу налагаемых нами ограничений на скорости. Если этих ограничений не делать, то ответ получился бы весьма тривиальным: отклонение тем меньше, чем больше k2.
Пусть теперь й0 и k.2 заданы и положительны, а коэффициентом kt можно располагать при условии сохранения устойчивости. Область В представляет в этом случае полупрямую, параллельную Реи абсцисс и лежащую в первом квадранте» Применим сначала
234
ПОСТАНОВКА ЗАДАЧИ. ЛИНЕЙНЫЕ СИСТЕМЫ
[ГЛ. 4
коэффициент устойчивости а. При а = V^k,2/k0i где — заданное значение, получаем линию равной устойчивости, имеющую угловую точку на прямой В. Абсцисса этой точки есть
^ = 2/^; (4.97)
она представляет оптимальное значение k± и даёт для коэффициента демпфирования критическое значение 1.
Коэффициент р для системы, описываемой уравнением (44), при данном k2 будет расти вместе с пока k± < 2 ^kQk2i при больших значениях k± получается одно и то же значение р = й2. Если же рассмотреть линии равной устойчивости по коэффициенту при 01 = 1, 62 = 0, то абсциссы их точек пересечения с прямой В будут тем больше, чем больше иными словами, с точки зрения этого критерия, чем больше kv тем лучше.
Иной результат получается для следящей системы (§ 7) с помощью коэффициента ч0 при том же предположении: 0х= 1, О2 = 0. Уравнение линии равной устойчивости (89) получает вид
^1^2 7оМ2 = О*
Если
где fe2 — заданное значение, то соответствующая кривая касается прямой В в точке с абсциссой
= Vk^, (4.98)
которая представляет оптимальное значение kr и даёт для коэффициента демпфирования ^/2]^kQk2 значение 1/2.
Эти результаты, на первый взгляд столь противоречивые, легко объяснимы и вполне соответствуют физической сущности явлений.
При выводе коэффициентов р и мы исходили из рассмотрения импульсивных или длительных возмущений системы § 5, описываемой уравнением (44), и так как коэффициент восстанавливающей силы задан, то увеличение не может быть невыгодно, поскольку вязкость препятствует раскачиванию системы.
Иное дело — следящая система, к которой естественно применять коэффициент f0. Здесь вязкость должна быть достаточна для демпфирования собственных колебаний, но не должна мешать следящему телу догонять задающее. Поэтому этот критерий и даёт некоторое конечное оптимальное значение kt. Аналогичный результат получается путём расчёта по коэффициенту а, так как при его определении учитывается лишь затухание собственных колебаний после начального отклонения, вследствие чего этот критерий, в сущности, также естественнее применять не к системе § 5, а к следящей сйстемеч
§ 4.13] ЗАПАЗДЫВАЮЩИЕ силы 235
Следует заметить, что эти примеры, которые мы привели, чтобы показать применение критериев качества к простейшим системам с одной степенью свободы, могут служить лишь для первой ориентировки, так как реальные системы регулирования обычно могут быть сколько-нибудь полно трактованы лишь как системы с одной степенью свободы и запаздывающими силами или же как системы со многими степенями свободы.
В. ЛИНЕЙНЫЕ СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ И ЗАПАЗДЫВАЮЩИМИ СИЛАМИ
§ 4.13. Постановка задачи. Рассмотрим массу й01, движущуюся поступательно и прямолинейно под действием линейной восстанавливающей силы —k21y (f), пропорциональной координате, и неконсервативной силы Q. Для Т и V мы имеем выражения
T=^koiy4t), V = ±k.21y*(t)-, (4.99)
что же касается Q, то мы предположим, что
Q = — *ц у (0+х (0—*02 У$—т) —
— х) — *22 У (*—“О» (4.100)
где т — некоторый постоянный промежуток времени.
Первые два члена справа, как и в предыдущем разделе, представляют линейное трение и возмущающую силу, а три последних — запаздывающую силу, исходящую от автоматического регулятора, присоединённого к системе для того, чтобы удерживать её, возможно более жёстко, вблизи положения у — 0. Чувствительные элементы регулятора регистрируют перемещение, скорость и ускорение массы fe01, а сервомотор передаёт на неё усилие, линейно зависящее от этих величин. Но так как для срабатывания чувствительных элементов, реле и сервомотора нужно некоторое время, то и получается, что все три величины в выражении усилия относятся к некоторому предшествующему моменту t—т. Предположение о том, что т постоянно и что других искажений нет, хорошо отражает действительные явления в тех случаях, когда запаздывание связано с передачей звукового сигнала, гидравлическим ударом или другим волновым процессом. В остальных случаях сделанные предположения описывают реальный регулятор лишь приближённо, но представляют • шаг вперёд по сравнению с моделью «идеального» регулятора, которая получается, если предположить для первой ориентировки, что срабатывание происходит мгновенно.
Уравнение Лагранжа имеет вид
fe01 У (О + *11У (0 + к21У (0 + *02^ (* — “О +
+ *12У (t—-с) + k22y (t—т) = х (0. (4.101)
236
ПОСТАНОВКА ЗАДАЧИ. ЛИНЕЙНЫЕ СИСТЕМЫ
, [гл. 4
Для идеального регулятора т = 0, и мы -получаем уравнение вида (44), в котором
== *01 ^02’ === ^11 4“ ^12» ^2 == ^21 Н” ^22* (4.102)
Распоряжаясь здесь параметрами регулятора kQ2, k12, k>2, .мы можем дать коэффициентам kQi ku k2.любые значения, и с этой точки зрения, собственно, и следует рассматривать те .соображения о выборе параметров регулятора, которые мы привели в § 12. Одна из задач настоящего раздела должна состоять в исправлении этих соображений путём учёта запаздывания.
Коэффициенты fe01, будут, естественно, предполагаться положительными, а для fe21 можно допустить как положительные, так и отрицательные значения соответственно тому, будет ли V иметь минимум или максимум при у = 0. В первом случае регулятор должен лишь помочь естественной восстанавливающей и демпфирующей силам; во втором случае дело сложнее, так как сила — fe2]у (t) является уже ~не восстанавливающей, а дестабилизирующей, и задача регулятора состоит в том, чтобы превратить естественно неустойчивую систему в устойчивую.
Вводя в качестве новой независимой переменной безразмерное время
= (4.103)
имеем:
XL —ХХ1
dt du ’ di* du* *
причём мы также будем обозначать дифференцирование по и штрихом. Преобразованное уравнение будет
(и) “X (tt)+1'21У +Ъ&у" (а — 0 4“
+ W' (« — О + 1>*У О* — 1) = х (а), где
А)1 = ^01’ ^11 = ^21 = ^21^9 1
А)2 == ^02’ ^12 === ^12***’ ^22 == ^22***9» J
(4.104)
(4.105)
а у (и) обозначает координату y(f), рассматриваемую как функция нового независимого переменного и, между тем как х(и) отличается от x(t) множителем т2.
§ 4.14. Общее решение уравнения движения. С математической точки зрения уравнение (104) является дифференциально-разностным, и для его решения мы применим операционное исчисление, полагая в (р)X («)> “П (р)-Н-J («)• (4.106)
По теореме о дифференцировании оригинала (§ 2.§)
Р h (р) — У (0)1 —г*-у' (а),
Р IP’l (Р)—РУФ)—У (0)] (и).
-i-Wi
§ 4:14]
ОБЩЕЕ РЕШЕНИЕ УРАВНЕНИЙ ДВИЖЕНИЯ
237
Если же применить теорему запаздывания (§ 2.9) к функциям у (и), У 'У"(и)> учитывая, что по отношению к независимой переменной и запаздывание равно единице, то получится:
е~Р h (р)+рФ (P)J -Ь*У (« 1)
е~рР Ь| (Р) —У (0) + ф,(р)] -г*/ (и — 1),
' е~рр [рц (р)—ру (0) — у' (0)+ф2 (р)] ~^у" (и — 1), где
ф(р) = $ ytuy'e-^du, (4.107)
-1
*Ь\Р) = J у’ (u)e~pudu,
-1
ф2(Р) = f у" (а) du.
-1
Интегрируя по частям, мы имеем также:
Ф1 (Р) = У (0)—у (— 1) ер+рф (р),
ф2 (р) = РУ (°) + У' (У)~РУ (— О ер—у' (— 1) ер-\-р^ (р),
так что
в_^р[-п(р)+рф(р)1—РУ(— 1).
е~рР I Р*! (Р)+Р3Ф (Р) ] — Р [РУ (— О+У' (— О) У' (« — 1 )•
Изображение уравнения (104) будет
/ (р) -n (р)—PQ (р) = (р).
где
/(р) = V3+41Р+Ь+е~р ('огР3+42р+Q. (4. iOS)
Q (Р) = ('oiP + 'nW) + l0Jy' (0) + ('ойР+112)У (- О +
+ 1^У (- 1) - е~Р (/02ра + /12р + /22) Ф (р). (4.109)
Разрешая относительно т|(р), найдём:
,п(р) =
PQ (.Р) + 6 (Р) /(Р)
Оригинал этого изображения представим интегралом Бромуича:
Р(«) =
c+ioo
1 f PQ (Р) + S (Р)
2”Z J P/(P)
С--lOO
epudp,
238 ПОСТАНОВКА ЗАДАЧИ. ЛИНЕЙНЫЕ СИСТЕМЫ [ГЛ. 4
который может быть также (§ 2.30) заменён выражением Я
У («) = 2 Res ери, (4.110) I
где вычеты берутся по всем особым точкам подинтегральной функ-ции, лежащим на конечном расстоянии. Это выражение и даёт общее J
решение при любых начальных значениях функций у (и), у' (и) |
в интервале — 1 и 0. |
Нас будут интересовать, естественно, главным образом асимпто- I тически устойчивые системы, для которых координата у (и) при собственных колебаниях, т. е. при отсутствии возмущения х(и) и I любых начальных значениях, стремится к нулю, когда и —> оо. f
В этом случае интеграл Лапласа
оо |
§y(u)e~pudu Л
О
заведомо сходится при Rep>0 и абсцисса сходимости не больше Т
нуля, вследствие чего левая часть последнего соотношения, которая *
при £(р) = 0 приводится к
q(p) ;
f(p) 9
должна быть регулярной функцией в правой полуплоскости. Числи- |
тель Q(p) есть целая функция, так как в состав её входят лишь р, |
р2, е~р, постоянные и ф(р), а эта последняя, согласно (107), может |
рассматриваться как лапласова трансформация функции, исчезающей |
вне конечного интервала; эта трансформация остаётся конечной при &
всех р, имеет поэтому абсциссу сходимости — оо и является целой |
функцией. Отсюда следует, что Q(p)!f(p) не имеет других особых i
точек, кроме полюсов, соответствующих нулям знаменателя f(p), 'I
т. е. корням трансцендентного характеристического уравнения |
4if+417+41+(W3+42Т+4г) = 0; (4.111) /
ни один из этих корней не может лежать в правой полуплоскости.
Никаких особых точек, кроме этих корней, не приходится учитывать 4. также и при вынужденных колебаниях, если только изображение 5 (р) <
является целой функцией, как это будет, например, когда возму- |
щающая сила действует лишь в течение конечного промежутка |
времени. Предполагая, что это имеет место и что все корни — простые, представим (ПО) с помощью формулы (2.145) в виде разложения I Хевисайда
«"*> I
j 3 3
§ 4.14]
ОБЩЕЕ РЕШЕЙИЕ УРАВНЕНИЯ ДВИЖЕНИЯ
239
Иными словами, как и в случае линейных систем без запаздывающих сил, решение выражено через нормальные колебания ехр разница состоит в том, что в данном случае этих нормальных колебаний будет бесчисленное множество и сумма в последнем выражении представляет бесконечный ряд.
Если какой-либо корень окажется двойным, так что — = f (^.) = 0, то, согласно известной формуле для вычета относительно кратного полюса *), мы должны заменить соответствующий член ряда через
(£ (P~Tj)2[pQ (Р) + Е(Р)] еРи\ \dp pf(p) е
Значение этого выражения, получаемое путём выполнения дифференцирования и повторного применения правила Лопиталя для раскрытия неопределённостей, есть
< 2/'"(Т;) ЪС(Т;.) + 6(Ъ.) 2 d + (
I 3[/"(ъ)]2 ь- ь- +
2 + а (4Л 13)
Tj I
Аналогичным путём можно получить выражения, относящиеся к корням высшей кратности.
Более общие случаи вынужденных колебаний, когда изображение $(р) имеет особые точки на конечном расстоянии, нуждаются в особом рассмотрении.
Пример 1. Предположим, что постоянно действующей силы x(t) нет и y(f)=y(t) = 0 при £<0, причём y(t) остаётся равным нулю и при /=±=0, а скорость под действием единичного ударного импульса мгновенно получает значение 1/А?01. Соответствующее значение у'(и) будет у' (0) = т//01. Поэтому
Q(p) = *, 5(Р) = 0 и
= (4.114)
i *
а выражение общего члена ряда для случая двойного корня обра-Щается в следующее:
(4.115)
*) И. И. Привалов, Введение в теорию функций комплексного переменного. Гостехиздат, 1954, гл. VII, формула (9).
ива»?,г
240
ПОСТАНОВКА ЗАДАЧИ. ЛИНЕЙНЫЕ СИСТЕМЫ
♦
[гл. 4
Пример 2. Пусть имеем теперь постоянную силу 1/а, которая производит единичный импульс, действуя в течение конечного интервала 0 t < а.
Относительно новой независимой переменной а величина интервала будет
а постоянное значение х(и) равно
т2 __ т
а b ’ так что
*(«) = у [/(e) — <(« — ад.
(4.116)
Изображение этой функции, согласно (2.59), есть
*(Р) = у(1— е **), (4.117)
откуда, в частности, £(0) = (К Если, кроме того, значения у (и), а значит, и у' (и) в интервале— 1 и < 0 равны нулю, откуда в силу
непрерывности следует также v(0)=/(0) = 0, то
Q(P)hbO.
Решение (112) получает вид:
(4.118)
Выделяя члены ряда, соответствующие действительным корням ха, и соединяя попарно члены, соответствующие комплексным сопряжённым корням найдём:
V («) = S
О
+ 2 2 bhe**u cos (<ohH -|- 6ft), л
где
_ S Ю г. _ S (£Л +
’ Л (еЛ + (SA + Z<UA) ’
0 — are- £
h S (£a+z“a)/'(£a + z“a)‘
(4.119) ?
(4.120)
Выражение (113) общего члена для случая двойного корня обращается в следующее:
( 2/^(ь) ВЫ , 2 d Ц1) 2 Цъ) .. .......
) .._____1____L. J__________i_ J__________ и\е} (4 1211
I 3[/"(Т,)Р ъ ^/"(T,)d-rj Tj ь Г • 1 '
</ J J J J J J
4.15] ОПРЕДЕЛЕНИЕ КОРНЕЙ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ
241
Заметим, что если в формулах (118), (121) положить £(р) = /п,
то мы вернёмся к решению, полученному в предыдущем примере
для случая ударного импульса.
Пример 3. Рассмотрим ещё случай, когда х(и) равномерно возрастает от 0 до х/b при 0 J и равномерно убывает от z/b до 0 при b и < 2&, а при всех остальных значениях и равно нулю. Полный импульс силы х (/) равен единице, как и в предыдущих примерах. Так как
т/&2 при О С и
— и/Ь2 при ь и
ь,
2Ь,
то мы можем написать:
= ^ [/ 00 — 2 • Z (« — &)+Z (# — 2&)1;
изображение этой производной есть
pt (Р) = G — 2е~рЬ + е-2^6),
откуда
= е~рЪ^ (4.122)
При сохранении тех же начальных условий, что и в предыдущем примере, формулы (118) — (121) остаются в силе.
§ 4.15. Определение корней характеристического уравнения.
Перепишем характеристическое уравнение (111) в виде
W2 + 42Т + 42 = (41? + lilt + 41). (4.123)
положим
у = S —/(О
(4.124)
и приравняем отдельно действительные и мнимые части:
^02 (®2 °*2) (12® Ч" 4г —
= н — [/(Я (в2 — а>2) 4- /ив 4 /21] COS Ш 4 О) (2/адв 4 4j) sin to),
<0 (2/02е 4 42) —
= — е‘ { 141 (s2—ш3) + 41s + 411 Sin w 4 ш (2/01s 4 /ц) cost»}.
Эти уравнения определяют две кривые в плоскости ©со, координаты точек пересечения которых (их будет, вообще, бесчисленное множество) дают действительные и мнимые части корней характеристического уравнения. Обе части первого уравнения являются чётными, а обе части второго — нечётными функциями от <о, так что если характеристическое уравнение имеет корень то оно имеет
также и корень — i&Hi что и следовало ожидать. Поэтому достаточно вычертить кривые лишь в верхней полуплоскости. Кроме того,
16 Зак. 1474. Б. В. Булгаков
(4.126) . Так как
(4.127)
(4.128)
(4.129)
242 ^ПОСТАНОВКА ЗАДАЧИ. ЛИНЕЙНЫЕ системы [гл. 4
если система устойчива, то заранее известно, что в правой полуплоскости нет корней.
Таким образом, в итоге достаточно вычертить кривые во втором квадранте (е < 0, <о > 0)..
Этими замечаниями об определении корней мы пока и ограничимся, намечая лишь общий ход вычислений, которые более подробно развиты для частных случаев в следующих параграфах.
§ 4.16. Система без естественных демпфирующей и восстанавливающей сил. Случай
= 41= А)2 ~ о
был рассмотрен Каллендером, Хартри и Портером [< при этом
Zq = Zqj, Z-£ = Z^2> Z2 = Zg2>
то уравнения (123), (125) получают вид:
4т+4=—Ал2**’
4е + к = I— — ш3)cos ш + 2еоо sin ш], - Z^co = — Zo£® [(s2 — со2) sin go -j- 2soo cos 00].
Начнём с выяснения области устойчивости, интерпретируя отношения
Р = |, а = | (4.130)
как координаты точек плоскости параметров. Три коэффициента Zo> 4» 4 бУДУт, следовательно, однородными координатами этих точек. Мы видели в § 14, что в случае устойчивой системы корни характеристического уравнения не могут лежать справа от оси ординат плоскости sou, и потому на границе области устойчивости в плоскости параметров мы должны иметь либо нулевой корень (^ = 0), либо пару чисто мнимых (© = 0).
В первом случае из (128) получается Z2 = 0 или
<5 = 0, (4.131)
т. е. уравнение оси абсцисс.
Во втором случае подстановка в (129) даёт соотношения
р = GO sin GO, о = GO2 cos go, (4.132)
представляющие параметрические уравнения кривой, которая имеет вид спирали. Областью устойчивости является часть первого квадранта, ограниченная отрезком оси абсцисс и дугой кривой, на которой 0 < со < тс/2 (внешний контур на фиг. 8). В самом деле, согласно (102), (105)
К _ р k2 _ _О_ kQ т ’ х2 *
§ 4.16]
СИСТЕМА БЕЗ ЕСТЕСТВЕННЫХ СИЛ
243
kb
Если интерпретировать и как декартовы координаты в другой плоскости, то с помощью отображения (133) мы получаем в этой плоскости область (фиг. 9), зависящую от параметра т и, при т —> 0 распространяющуюся на весь первый квадрант, а этот последний является, как мы знаем (§ 9), областью устойчивости для системы без запаздывания.
Фиг. 8. Область устойчивости и линии равной устойчивости в параметрах Z при Zlt = Z21 = Ав = О*
Механический смысл полученного результата заключается, очевидно, в том, что, поскольку демпфирующая и восстанавливающая силы создаются искусственно и связаны с запаздыванием, коэффициенты этих сил р, а не могут быть взяты сколь угодно большими без нарушения устойчивости. Область устойчивости тем меньше, чем больше запаздывание.
Построим теперь линии равной устойчивости по Цыпкину и Бромбергу. Каждая такая линия служит границей области, в которой
Фиг. 9. Область устойчивости в параметрах k.
наименьшая из всех абсолютных величин отрицательных действительных частей корней характеристического уравнения больше данного значения р. На самой линии мы имеем либо действительный корень — р, Либ° пару комплексных сопряжённых — pziz/oo. .
16*
244
ПОСТАНОВКА ЗАДАЧИ. ЛИНЕЙНЫЕ СИСТЕМЫ
[ГЛ. 4
В первом случае, полагая в (128) 7 =— р, получаем:
т. е. уравнение прямой в плоскости ро.
Во втором случае полагаем в (129) з = — р, оставляя вольным, что даёт по разрешении относительно р, о:
р = е 2р cos оо
sin <0
>
(4.134) со произ-
Q = e
(4.135)
Отрезки прямых и части кривых, определяемых двумя последними уравнениями, в которых со рассматривается как переменный параметр, составляют линии равной устойчивости (фиг. 8). Они образуют систему вложенных друг в друга контуров и в конце концов стягиваются в точку (р*, о*), которая соответствует наибольшему возможному коэффициенту устойчивости р*.
Каждый контур имеет две угловые точки, в которых прямолинейная часть контура смыкается с криволинейной, причём левая точка получается при а) = 0 и координаты её суть
р0 = (2р — р2), а0 = е~ф (1 — р). (4.136)
Пока р < р*, угловой коэффициент криволинейной части в этой точке больше углового коэффициента прямолинейной, но при р = р* эти угловые коэффициенты, очевидно, становятся равными, а точка (р0, °о) совпадает с точкой (р*, а*), чем мы и воспользуемся для определения последней.
Пользуясь тем, что
(sin ш\' __~ /sin <о\" __ 1
I ' V, I I г, , • • • ,
/<»=0 \ /<0 = 0 3
где штрихи обозначают производные по о>, дифференцируя (135) и полагая о> = 0, находим:
(pZ)u) = O == О’ (° )ш=0 =
Поэтому точка (р0, о0) является точкой возврата кривой, и приходится дифференцировать ещё раз:
(р")и>=0==е"?(-2р + 2-|-£),
(°X=o = е [2 (1 - р) + рз (-1 + 1Y .
Угловой коэффициент в точке (р0, о0) будет
(°"\ _ ₽3 — 3₽2 — 6р + 6
. \ 9" Л»=о ~ р2_6р + 6 ’
§ 4.17] СИСТЕМА БЕЗ ИСКУССТВЕННОГО ДЕМПФИРОВАНИЯ
245
Приравнивая его угловому коэффициенту р прямой (134), получаем: р-2 —4р^2 = 0. -
Меньший корень этого квадратного уравнения
£* = 2-/2 = 0,58579 (4.137)
представляет искомое значение коэффициента устойчивости. Подставляя его в (136), находим:
р* = 0,46116; о* = 0,07913. (4.138)
Параметры
—-Из-
будут с точки зрения применённого критерия наилучшими. Они имеют конечные значения, между тем как при т = 0 эти формулы дают fe1 = oo, &2 = оо; это согласуется с анализом систем без запаздывания в предыдущем разделе, где конечные значения получались только в силу предварительных условий, наложенных на допустимые значения параметров.
§ 4.17. Система без искусственного демпфирования. Случай
*02 = 42 = 0 (4.139)
был рассмотрен А. А. Андроновым и А. Г. Майером [4Л]. условиях
4= 41» 4 = 41’ 4 = 41 + 4г»
При этих
(4.140)
если воспользоваться обозначениями (130) и положить ещё
= К (4.141)
то уравнения (123), (125) получат вид:
(а — Х)е"т = — (7з+рТ + Х), (4.142)
(а — X) £”е = (— s2 —<о2 — pa — Л) cos оо -j- оо (2s -j- р) sin оо, 0 = — (— е2 оо2 — ps — X) sin оо —J— оо (2е р) cos оо.
(4.143)
Для определения границы области устойчивости требуем сначала, чтобы характеристическое уравнение имело нулевой корень (7 = 0), и находим <5 = 0, т. е. уравнение оси абсцисс в плоскости рз. Если же потребовать, чтобы характеристическое уравнение имело пару чисто мнимых корней (s = 0), то из (143) вытекает:
откуда
о — X = (оо2 — X) cos 00 рсо sin 00,
0 = — (оо2 — X) sin 00 pen cos <0,
(<о2 — X) tg <о
<о2 + X (cos <0 — 1) COS CO ’
(4.144)
246
ПОСТАНОВКА ЗАДАЧИ. ЛИНЕЙНЫЕ СИСТЕМЫ
[ГЛ. 4
рассматривая здесь со как переменный параметр, получаем кривую в* плоскости ра. В частности, при Х = 0
P = “tge>, ° = (4-145)
и мы имеем область устойчивости, показанную на фиг. 10 (внешний контур).
Механический смысл полученного результата заключается в том, что так как восстанавливающая сила создаётся искусственно, то её коэффициент о при данном р не может быть сделан сколь угодно большим без нарушения устойчивости. Наоборот, в направлении оси абсцисс область устойчивости не ограничена, поскольку демпфирование обусловливается только естественной силой сопротивления.
В цитированной выше работе Андронова и Майера можно найти построение области устойчивости для Х= 16 (в наших обозначениях).
Ограничиваясь опять случаем X = 0, построим линии равной устойчивости. Полагаем сначала в характеристическом уравнении (142) 7 = — р и получаем
а = ' (4.146)
т. е. уравнение семейства прямых в плоскостищараметров. Если же положить в (143) 8 = — р, то
= (ц)2--р2 _[_ рР) c0s О) _[_ О) (-2р 4” р) sin СО,
0 = — (со2 — Р2 + рр) sin со (— 2р -|- р) cos со,
откуда, разрешая относительно р, о, имеем:
2р<0 COS со (со2 — Р2) sin <0 (О COS <0 — р Sin СО
СО (со2 -|~ р2)
СО COS СО — р Sin со *
(4.147)
Полагая здесь со = 0, получаем после раскрытия неопределённостей
р (2 — р) р2
Ро = ±т=р ’ ^ = е Т=Т
(4.148)
Эти значения представляют координаты общей точки прямой (146) и кривой, определяемой параметрическими уравнениями (147), если считать р фиксированным. При этих значениях величина р является двойным действительным корнем характеристического уравнения. Каждая линия равной устойчивости состоит из частей прямой и кривой, пересекающихся в точке (р0, а0), которая является, таким образом, угловой. Изменяя р, получаем семейство линий равной устойчивости (фиг. 10).
§ 4.17]
СИСТЕМА БЕЗ ИСКУССТВЕННОГО ДЕМПФИРОВАНИЯ
247
Пусть р* есть заданное значение отношения IJIq, определяемое естественной инерцией и демпфированием системы и запаздыванием регулятора. Значение коэффициента р, соответствующее той из линий равной устойчивости, । которая имеет угловую точку на
Фиг. 10. Область устойчивости и линии равной устойчивости в координатах I при = Zj.2 = 0.
прямой р = р*, получается из первого соотношения (148) и равно
р* = 1+4 — /" 1+-^. (4.149)
Если взять, например,
йх/й0 = 2 сек-1, т = 0,1 сек, то
Р* — 4/А) = (fel/feo) т =: °>2>
P# = 0,095.
Соответствующее значение о, определяемое из второй формулы (148), будет
а* =0,00907;
248 ПОСТАНОВКА ЗАДАЧИ. ЛИНЕЙНЫЕ системы [гл. 4
для k2 получается значение
Й2==й0о*/т2 = (0,907 секГ2)к^
которое будет с точки зрения данного критерия наилучшим, так как оно даёт, очевидно, наибольший коэффициент устойчивости р при данном
Перейдём теперь к определению корней характеристического уравнения. Возводя в квадрат и складывая уравнения (143), находим:
(to2 _ е2 _ р8 _ Х)2 _|_ 0)2 (2е р)2 = (0 — к)2 £-2е
или, разрешая относительно о>2,
со2 = i [— s2 — (е -j- р)2 “h 2Х qz £
у (2s + р)2 (р2 — 4Л) + 4 (а — X)2 е~*].
С другой стороны, разрешая второе уравнение (143) относительно е, имеем:
е = [— (р -[- 2cd ctg go) zjz ]Лр2 -|- 4to2 cosec2 to — 4А].
£
Дальнейшее вычисление проведём для к = 0; тогда две предыдущие формулы принимают вид: *
1 [— е2 — (S + р)2 4- /р2 (2е + р)2 -у 4а2е-2е],
1 _________________ (4.150)
s = -н- [— (р Ц- 2to ctg to) zjz ]/ p2 4~ 4to2 cosec2 to].
x* )
Так как каждая из них разрешена относительно одной из неизвестных s, с», то с их помощью удобно строить определяемые ими кривые в плоскости ео). Координаты точек пересечения этих, кривых дают корни характеристического уравнения, если только при подстановке в первое из исходных уравнений (143) его правая часть получает положительное значение. Знак минус перед радикалом в первой формуле (150) брать не нужно, так как это даёт отрицательные значения о>2.
Если р и о принадлежат области устойчивости, то, как мы уже указывали, достаточно вычертить обе кривые во втором квадранте (е < 0, оо > 0).
Вторая кривая состоит из бесчисленного множества ветвей, по две в каждой полосе со < (п-|-О *4 к этим ветвям нужно ещё присоединить ось абсцисс о> = 0, которую мы потеряли при разрешении относительно е.
§ 4.17]
СИСТЕМА БЕЗ ИСКУССТВЕННОГО ДЕМПФИРОВАНИЯ
249
В таблице 1 приводятся значения нескольких корней для случая = 0,2, о = 0,00907, который мы рассматривали выше. Так как.
Таблица 1
Коэффициенты затухания и угловые частоты для системы с параметрами р = 0,2; а = 0,00907
1«М со/т
Действительный двойной корень 1-я гармоника 2-я гармоника 3-я гармоника 4-я гармоника 5-я гармоника 6-я гармоника 0,9501 93,10 101,15 107,64 112,73 116,84 120,27 0 39,52 110,97 177,67 242,70 306,93 370,76
нормальные колебания, выраженные через натуральную переменную tK имеют вид
= = ц. = [CQS . s.n
то мы даём для каждого корня коэффициент затухания | е/т | и угловую частоту go/т при *£ = 0,1 сек.
СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
А. КОНСЕРВАТИВНЫЕ СИСТЕМЫ
§ 5.1. Интегрирование канонических уравнений. Канонические уравнения консервативной системы имеют гамильтонову форму
dq__дН dp________дН п
dt ~ др9 dt~ dq *
Интеграл энергии
H(q,p) = v, (5.2)
где v — постоянная, представляет конечное уравнение семейства интегральных кривых. Координаты, q*, р* особых точек, в которых фазовая скорость обращается в нуль, удовлетворяют конечным уравнениям
f=°> <5-3)
и потому эти точки являются также особыми точками интегральных кривых (2) в смысле, принятом в дифференциальной геометрии.
Ограничиваясь при дальнейшем анализе натуральными системами со склерономными связями и склерономным определением обобщённой координаты, мы будем иметь для L и Н формулы (4.9) и (4.10), а канонические уравнения примут вид:
*1____Р_ „ -
' dt~ m(q)> dt ~~2[m (q)P ' ' '
Заменяя в функции Гамильтона Н канонический импульс производной и приравнивая Н постоянной, получим (§ 3.16) уравнение Гамильтона- Якоби
1 (dW^fi | V/ \ /К
о—I +V(?) = v; (5.5)
2m (7) i » \ j
представляя его в виде
=/2/и(9) — V (<?)] ,
ДВИЖЕНИЕ КОНСЕРВАТИВНОЙ СИСТЕМЫ
251
§ 5.2]
найдём:
W = j* У 2т (q)\v — V (9)] dq + const. (5.6)
W{qt vy за производящую функцию контактного пре-
Примем образования
dW _dW dq 1 U dv
к новым элементам и, v. Выписывая подробно, имеем:
р = у 2/и (?) [о — У (?)],
а~ J У
(5.9)
Из формул (7) и уравнения (5) вытекает, что гамильтонова функция, выраженная через a, v, будет Н' (а, v) — v*, преобразованные канонические уравнения получают вид:
f=0- (5Л°)
Из них вытекает:
а = v = const., (5.11)
где 0, так же как и ф, есть произвольная постоянная. Формулы (8), (9) вместе с (11) дают общее решение канонических уравнений.
§ 5.2. Общие свойства движения. Уравнение (2) интегральных кривых получает для натуральной системы вид
п2
sh)+',<’)=»; <5Л2>
так как оно не меняется при замене р на — р, то интегральные кривые симметричны относительно оси абсцисс фазовой диаграммы. Разрешая относительно р, получаем соотношение (8), в котором радикал может, как всегда, иметь два значения, соответствующих двум ветвям интегральной кривой.
Действительные точки кривой, соответствующей данному значению ф, получаются лишь для тех qt которые удовлетворяют неравенству
V(^)<v.
Последовательно строя графики функции V (q) и функции Р2 (я) = 2т (q) — V(q) ] при различных v, можно получить затем (фиг. 11) фазовую диаграмму со спектром интегральных кривых.
Дифференцируя (8) по q, получим выражение углового коэффициента интегральной кривой
dp _ т' (д) [v — V(g)] — m (д) V' (д) (5 13)
dq V2m(g) [v—V(g)] ’ '
252 СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ [ГЛ. 5 fl
Мы уже рассмотрели в § 4.2, что происходит, когда интеграль- fl
ная кривая пересекает ось абсцисс в точке, не являющейся особой. Я
Пусть теперь имеем особую точку (#*, р*), в которой фазовая я скорость обращается в нуль, так что fl
У'(9) = 0, р = 0. (5.14) *
Эти точки лежат на оси абсцисс и соответствуют стационарным # значениям потенциальной энергии V(q). Если V* есть значе- -J ние константы v для интегральной кривой, содержащей особую 1 точку, то, как видно из (8) и (14), JI
= Vy(^*) = 0. (5.15) I
Мы предположим, что при q = q* существует первая не обра- | щающаяся в нуль и непрерывная производная V(#). Тогда j
У(?) = 'у*+^[У(11)(Г) + 8(9)](?-9*Г, । |
. И > (5.16) I
^(^) = (7^I)-!(VW(9*) + 'r1(?)](^- I I
где e(^), T\(q) стремятся к нулю при II
Пусть сначала ц чёт.но. Если при этом V^(q*) положительно, то для значений q, достаточно близких к q*, мы будем иметь V (q) >г/* |
и подкоренное выражение в (8) будет отрицательным. Потенциальная энергия имеет минимум при q = q* (фиг. 11, а, точка Д), а ветвь #
интегральной кривой, содержащая особую точку, сводится к самой /Этой точке, которая будет, таким образом, изолированной точкой кривой (фиг. 11, в, точка 2). Если, при чётном Уи)(#*) отрица- _ тельно, то потенциальная энергия имеет максимум при q = q* (фиг. 11, а, ? точка В), и через особую точку проходят две действительные ветви ? интегральной кривой, совокупность которых называется в этом случае разделяющей. Пользуясь формулами (13), (16), мы представим 5 выражение углового коэффициента разделяющей кривой в виде dp _ — т' (q) [Ии) (q*) + е (7)] (q — q*) — у<т (q) [У(и) (q*) + g (?)] у d<i V— 2^.m (q) [V-W (?*) + e (g)]
^-1 X(<7 — <7*)2 • (5.17)
При = 2 предел этого выражения для q -> q* есть |
(g) = /-m(<7*) Г'(<?*), I
\a4 Jq=q* f
а при > 2 он будет равен нулю. Таким образом, при уь = 2 раз- j деляю'щая имеет в особой точке самопересечение (фиг. 11, 8, fl точка 4), а при рь = 4, 6, ... —самосоприкосновение. Время I t*—tQ = u*— uQ, необходимое изображающей точке для достижения jr
§ 5.2]
ДВИЖЕНИЕ КОНСЕРВАТИВНОЙ СИСТЕМЫ
253
положения равновесия q = q*> выражается интегралом
Г ,/' т (?) ~ d(f.
J V 2[v-V(q)]aq’
(5.18)
так как вблизи q = q* подинтегральная функция может быть представлена в виде
/~ р.!т (<?) 1 t
г 2 [— Vw (q*) — s (?)](? — 9*)^
где [а/2^1, то по известной теореме о сходимости несобственных интегралов время это будет бесконечным. Таким образом, изображающая точка, будучи помещена на разделяющей в начальном положении (qQi pQ) на конечном расстоянии от особой точки, будет приближаться к
ней лишь асимптотически при или t->— оо со скоростью, стремящейся к нулю.
Если теперь у нечётно, то разность v* — V (#) меняет знак при q = q*, и при этом аргументе нет ни минимума ни максимума потенциальной энергии. Кривая V (q) имеет здесь точку перегиба с горизонтальной касательной (фиг. 11, я, точка С). Две действительные ветви разделяющей располагаются лишь по одну сторону положения равновесия (фиг. И, в, точка 7). Так как в данном случае р.^3, то угловой коэффициент (dp/dq) & равен нулю и положение равновесия является точкой возврата разделяющей. Время, необходимое для достижения этого положения, остаётся бесконечным.
Фиг. 11. Графики функций V (q), p2(q) и фазовая диаграмма консервативной системы.
Из фиг. 11, в видно, что интегральные кривые 3, близкие к изолированной особой точке, соответствующей минимуму А потенциальной энергии, представляют бесконечное множество вложенных
254 СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ [ГЛ. 5
друг в друга замкнутых контуров, окружающих особую точку 2» которая в этом случае называется центром. При малом начальном отклонении от особой точки фазовая траектория остаётся во всех своих точках на малом расстоянии от особой. Положение равновесия называется поэтому устойчивым.
Интегральные кривые, близкие к разделяющей кривой с точкой самопересечения 4, соответствующей максимуму В потенциальной энергии, располагаются таким образом, что изображающая точка, приблизившись к особой, затем удаляется от неё, не оставаясь в её окрестности. Особая точка называется в этом случае седлом. Положение равновесия неустойчиво. Подобным же образом обстоит дело и в случае, когда особая точка служит точкой самосоприкосновения разделяющей (на фиг. 11 не изображена), а также для положений равновесия, соответствующих точкам перегиба С на графике потенциальной энергии^
Мы видим, что при сделанных предположениях отсутствие минимума потенциальной энергии влечёт за собою неустойчивость положения равновесия, что представляет для данного случая теорему Ляпунова, обратную теореме Лагранжа об устойчивости равновесия.
Резюмируя сказанное, мы можем дать следующую классификацию возможных движений консервативных систем.
Мы имеем, во-первых, состояния устойчивого и неустойчивого равновесия;*во-вторых, движения, фазовые траектории которых совпадают с разделяющей или составляют её часть. В этом случае координата q может при I -♦ -{- 00 стремиться к конечному пределу, соответствующему положению неустойчивого равновесия, а при — оо неограниченно убывать или возрастать (траектории 1", 4т) или» наоборот, при t-> — оо стремиться к конечному пределу, а при t —> -|~ 00 неограниченно убывать или возрастать (траектории 4"). Наконец» мы можем иметь стремление к конечному пределу как при /—>-|~ оо» так и при — оо (траектория 4'). Такие движения носят название лимитационных*, три указанных частных движения можно назвать» соответственно, инфинитно-лимитационным, лимитационно-инфи* нитным и дважды лимитационным движениями.
В числе движений с фазовыми траекториями, не сводящимися и не стремящимися к особым точкам, отметим, как третий тип, движения с замкнутыми фазовыми траекториями, окружающими одно или несколько положений равновесия (траектория 3). Так как фазовая скорость зависит только от q и р и потому будет одной и той же при повторном прохождении изображающей точкой одного и того же положения на фазовой траектории, то эти движения будут периодическими. Они называются либрационными. Во время такого движения координата q системы колеблется между двумя крайними значениями q19 q%, соответствующими точкам пересечения фазовой траектории с осью абсцисс.
§ 5.2]
ДВИЖЕНИЕ КОНСЕРВАТИВНОЙ СИСТЕМЫ
255
Период колебания (туда и обратно) есть «2 __________
Р = 2 J V-2[v-V(<f)l d<1 &
ИЛИ
Q2 _________
Р- I P-W
Всё остальные фазовые траектории без особых точек имеют ветви, уходящие в бесконечность при — оо и (траек-
тории 2', 3', 5); соответствующие движения мы отнесём к последнему, ^четвёртому, классу дважды инфинитных движений, при которых координата q неограниченно убывает или возрастает, когда t-+— оо и /
Дважды инфинитные движения могут также быть периодическими, хотя и в ином смысле, чем либрационные. Это имеет место, когда т (q) и V (д) сами являются периодическими функциями от q с некоторым периодом 2с. Пример графиков, построенных для этого случая прежним способом, см. на фиг. 12. Дважды инфинитным движениям соответствуют здесь фазовые траектории типа 4, 4'ь на которых координата q является монотонной функцией от £ возрастающей или убывающей на 2с за промежуток времени
J V 21» - И(,)1 “Ч- (5.20) ~С
Иными словами, функция q(f) обладает свойством
q (t + Р) = q (t) 4- 2с. (5.21)
Что касается канонического импульса, то он будет просто периодической функцией, так что
р(^+Р)=р(0. (5.22}
Движения этого типа носят названия ротационных.
Периодичность по q функций m(q)9 V(q) может иметь место». апРимер, для системы, в которой значениям обобщённой коорди-
Фиг. 12. Графики функций V (q),p2 (q) и фазовая диаграмма для случая* когда т (q) и V (а) периодичны по q.
256
СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
[гл. 5
даты qQ, qQ 4- 2с, qQ 4с, ... соответствуют одна и та же конфигурация и одни и те же силы. В этом случае, чтобы сделать соответствие между точками фазовой диаграммы и состояниями системы взаимно однозначным, мы можем вырезать из фазовой диаграммы полосу, заключённую между ординатами qQ и #04-2с и наклеить её на прямой круглый цилиндр с длиной параллели 2с, причём ось абсцисс должна расположиться по этой параллели. В силу свойств (21), (22) фазовые траектории ротационных движений на полученной цилиндрической фазовой диаграмме обратятся в замкнутые кривые, так же как и траектории либрационных движений. Разница состоит лишь в том, что в первом случае фазовые траектории окружают ось цилиндра, а во втором — особые точки.
Либрация и ротация являются колебательными движениями, между тем как все остальные движения консервативных систем таковыми считаться не могут.
Пример. Рассмотрим физический маятник. Обозначая через / момент инерции относительно оси подвеса О, через М массу, через h расстояние от оси до центра тяжести С и через q угол отклонения (фиг. 13), имеем:
Г = 1V, (5.23)
-так что т = 1= const. Так как расстояние центра тяжести от горизонта оси подвеса есть zG — h cos q, то элементарная работа веса Mg равна
— dV = Mgd (h cos q)t и можно принять
V = — MgL^osq. (5.24)
Таким образом, мы имеем здесь пример системы, положение которой, а также обобщённая сила — V' (q) и потенциальная энергия не меняются при увеличении q на 2с, где с = тс.
Уравнение интегральных кривых есть
р = У2/ (Mgh cos q 4- v). (5.25)
Графики функций V (q)t p2(q) и фазовая диаграмма на фиг. 12 построены как раз для данной задачи. Особые точки соответствуют устойчивому и неустойчивому положениям равновесия, когда центр тяжести распола-
гается в вертикальной плоскости, проходящей через ось подвеса. Если поместить маятник в положение устойчивого равновесия и дать ему лёгкий толчок, то получится либрационное движение, т. е. обычное качание маятника. При более энергичном толчке маятник достигает положения неустойчивого равновесия, минует его и начинает совершать ротационное движение с угловой скоростью q, постоянной по знаку и периодически меняющейся по абсолютной величине. В качестве промежуточной формы возможно дважды лимита-дионное движение.
z мд
•Фиг. -13. Физиче-ский маятник.
§ 5.3. Угловые переменные и переменные действия. Мы видели в § 1, что вместо переменных q, р можно ввести новые канонические элементы и, v таким образом, что и будет линейной функ
§ 5.3]
УГЛОВЫЕ ПЕРЕМЕННЫЕ И ПЕРЕМЕННЫЕ ДЕЙСТВИЯ
257
цией времени, а~т>— постоянной. Однако эти элементы определяются неоднозначно, так как в W(qt v) можно было бы заменить v любой функцией от другой произвольной постоянной.
В квантовой теории для либрации и ротации применяется специальная система новых канонических элементов ft, J.
В случае либрации J определяется соотношением *
J=^&pdq=f(v), (5.26)
в котором криволинейный интеграл берётся по всей замкнутой фазовой траектории и равен площади, ограничиваемой ею в плоскости qp. Отсюда
У = ?(/). (5.27)
W(9> v) = W(q, ф (J)) = Г* (q, J), (5.28)
где функция W*(qt J) остаётся полным интегралом уравнения Гамильтона-Якоби, в котором лишь иным способом введена произвольная постоянная. Поэтому мы можем, совершенно так же, как и выше, принять W* за производящую функцию контактного преобразования
dW* а dW* r dq * dJ
(5.29)
к новым элементам ft, J. Гамильтонова функция, выраженная в этих элементах, будет
Я*(&, J) = ?(J)
и потому новые
канонические уравнения имеют вид
di = Q’
где
Интегрируя,
a)(J) = ?'(J). находим:
& = со (У) f —|— 8, J— const., есть произвольная постоянная.
(5.30)
. (5.31)
где 8, как и J, есть произвольная постоянная.
Элемент J равен делённому на 2к приращению «действия» W при однократном прохождении координатой q полного цикла изменения:
J==2S (5-32)
поэтому J называется переменной действия. С другой стороны, р . р d2W* . де dW* .
У dqdq~ § dqdJdq~ dJ§ dq dq ~ _d(&W*)_d -----------dJ----=57 (2^-2^
С другой
17 Зак. 1474. Б. В. Булгаков
258
СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
[ГЛ. 5
так что & при прохождении координатой q полного цикла изменения увеличивается на 2к и называется поэтому углозой переменной. Эта переменная связана с и соотношением
dW* dWdv „
или
& = GO (J) и.
(5.33)
Из (31) видно, что <o(J). есть угловая частота, а 8 — начальная фаза» В случае ротации J определяется формулой
+с z 1 f Й 7=2^ J Pd(l’
-С
(5.34-)
/
а в остальном преобразование к угловой переменной и переменной действия делается так же, как и для либрации.
Пример. При гармонических колебаниях массы т, удерживаемой пружиной, материал которой подчиняется закону Гука, восстанавливающая сила есть
— V' (q) = - aqt (5.35)
где а — жёсткость пружины. Отсюда
V (?) = у °?2 (5.36)
И
причём т = const. Интегральные кривые 1 2 I
суть подобные эллипсы с полуосями
а = у/~ , b = У 2mv.
Поэтому все движения, кроме состояния устойчивого равновесия q = р = О, являются либрационными.
Так как площадь эллипса есть
jzab = 2iw ,
то переменная действия J связана с постоянной энергии v соотношением
Уравнение Гамильтона-Якоби, в котором v выражено через J, имеет вид 1 (dW*\2 , 1 2 Т 2т у dq / 2 г т
г I
§ 5.41
МЕТОД НЬЮКОМА И ЛИНДСТЕДТА
259
и даёт
W*
Yma q* dq + const
Принимая
преобразования
имеем:
или
При этом
где
так что
UZ« за производящую функцию контактного dW* „ dW*
= shift, р = V™ /2 J cos ft.
& = W 4- S, J = const., _ Г Q v-dJ- V m'
a = I/ sin (ш/ + 8), 1 F
p — YCOS (w/ -f' &),
§ 5.4, Метод Ньюкома и ведённая масса т постоянна.
Линдстедта. Предположим, что при-Уравнения движения (5.4) принимают
вид или где
mq — р, р + V/ (q) = О,
9+/(9) = 0>
(5.37)
/И";»"»
Если функция /(?) является аналитической я окрестное™ поло-жения устойчивого равновесия q > так
f (fl) = k?q(1 + М + Ма + сз^ + • • •)• ’
t_i .п и Пинпгтелта даёт решение, описывающее либра-то метод Ньюкома и Линдстедта дае н auMniIim, Лоому ряда по ционные движения в этой окрестности и «“^еФ?Р”УеГ3Дначе. степеням амплитуды а, сходящегося при 40 одной из двух
ниях. При этом под амплитудойк Р^У“еес00ТВ1тствующая замкнутая точек фазовой диаграммы, в которых У
фазовая траектория пересекает ось абсцисс, т
д = о, ^ = Опри^=^
где tQ есть момент прохождения через точку пересечени
17*
мяипжди."
260 собственный колёвайия йелийеЙныХ систем
(гл. 5 J
Одно тривиальное частное решение q = 0, соответствующее самому 1 положению равновесия, нам известно; мы будем называть это решение j порождающим. Так как при малых q уравнение движения близко | к линейному и период колебания близок к р __________________________
^0—Т’
(5.41)
то этот период, как предельный, должен быть приписан порождающему решению.
Вводя новое безразмерное «время»
& = k (t— /0) /1 + 8 , (5.42)
где 8 — постоянная, мы представим уравнение движения в форме
(1 + 8) + Ч = — Ма — ОД3(5.43)
и будем искать общее решение в виде ряда
Я (&) = 41 (») а + q2 (&) а2 + q3 (&) а3+(&) а4 + ..., (5.44)
представляющего аналитическое продолжение порождающего решения и приводящегося к нему при а = 0. Из (40) вытекают начальные условия для функций ^(&):
91(0)=1, ^2 (0) = ?з (0) = (0) = •• • =0, 1
. . . . Г (5.45)
<71 (0) = (0) = (0) = ?ДО) = ... = 0. J
Постоянную 8 мы определим так, чтобы период колебания по отношению к & был всегда равен 2гс. Тогда период по t будет
поэтому 8, так же как и Р, должно зависеть от амплитуды. Сравнивая выражения Р и Ро, заключаем, что 8 должно обращаться в нуль вместе с а\ поэтому мы будем искать 8 в виде ряда
8 = 8^ + 82д2 _|_ 8^4 . (5.47)
Подставляя ряды (44), (47) в уравнение (43) и обозначая теперь точками производные по &, получим:
(1 8i<z -j- 82а2 -j- 83а3 -J- 84а4 -J- ...) (д^о, -j- q3cft -j- q3(fi -j-
+ ?# + .. .) + fta + ?2a2-|- ?3fl8 + ?4a4+ • • • =
= — ci K<78«8++ (2ад + ф a4 + ... ] —
— c2(^«8 + 3?^2«4+ • • •) —c3(^4+ .••)—•••
^яа
§ 5.4] МЕТОД НЬЮКОМА И ЛИНДСТЕДТА 261
Отсюда, располагая обе части по степеням а и сравнивая коэффициенты, имеем:
+ = о»
^2 + ?2 = — Ml —
5з + ^ = ——Ma” 2W2 —Mr (5.48)
= — Mt — М2 — Мз — С, (29^3 + —
^^2^1 ^2 С3?1>
Решение первого уравнения, удовлетворяющее начальным условиям (45), есть
= cos ft. (5.49)
Поскольку q (ft) должна быть периодической функцией с периодом 2к, мы будем требовать, чтобы и все ^(ft) были такими же функциями. В частности, для того чтобы #2(^) удовлетворяла этому условию, правая часть второго уравнения (48) не должна содержать cos ft, так как иначе при разрешении уравнения ft войдёт множителем вне знаков тригонометрических функций. Следовательно,
8t = 0, (5.50)
и второе уравнение будет л
?2 + ?2 = — -§ С1 U + C0S 2!0. откуда
ц.2 = —у С1 0 —cos ^2 cos ^4~^2 sin Если же принять во внимание начальные условия, то
<h = с,
(5.51)
Уравнение для д3 получает вид
Ч- <7з = — i с? + -|- 4- с? — 4- с2^ cos О — О \ О 4 /
— 4 С1 cos 2ft — (4 С1 4- 4* COS 3ft, 3 \ 6 * 4 /
ОткУда в качестве условия периодичности находим:
(5.52)
262 СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ [ГЛ. 5
и затем, принимая во внимание начальные условия,
tfs —
29 2
144 C1
cos 3ft.
Аналогичным образом,
озо 1 \ л «к
144 С1 32 С1С2 IT ) C0S 4’ ’
откуда
(5.54)
25 з , 21
48 C1 32 С1С2
/2 .з 1
119 з_
432 C1
cos 2ft
и так далее.
Если расположить ряд для q не по степеням а, а по косинусам кратных дуг, то получится
<1 = — -г, сха —
119 3_
432 С1 /2 з
Период колебания, согласно (46), есть
Р = ^(1+8)-*/’==5(1-±8+...),
cos 2&4"
(5.56),
CiC2 —
C1C2
§ 5.5J
ДИССИПАТИВНЫЕ СИСТЕМЫ
263
так как
5 =
5 2 I 3 л \ 2 I / ОЗ|1 \ 3 I
— б'С1“^ТС2)а +(“ *9C1 (5.57)
то
I / 5 2 3 \ 2 I / 5 з 1 \ 3 I
“Н \12 С1 8 С2) а \Д8 С1 ~4 С1Су а + •
(5.58)
Пример. Рассмотрим опять физический маятник. Применяя те же обозначения, что в примере § 2, имеем уравнения движения
q 4- № sin q = О,
Поэтому
<?£ = О, = 0, ..
и для Р получается формула
(5.59)
(5.60)
(5.61)
которая могла бы быть получена также из известного точного решения в эллиптических функциях. Удерживая только те члены, которые написаны, мы найдём, например:
при 10° Р = ^х 1,001,
» а = 20° Р=^-Х 1.006,
» а = 30° Р = X 1.014.
к
Б. ДИССИПАТИВНЫЕ СИСТЕМЫ
§ 5.5. Общие свойства движения. Рассмотрим натуральную систему со* склерономными связями и склерономным определением обобщённой координаты qt для которой неконсервативная добавочная сила Q{q, р) имеет характер сопротивления, так что её элементарная работа
Q dq = Qq dt = Q(g,/.)p dt
V m (q)
отрицательна или равна нулю при положительном dt\ при этом Q(7, р) не обращается в нуль при р#=0. Такая система носит название диссипативной.
Уравнение энергии (4.12) принимает вид:
Q (<1, Р) Р m(q)
dt
264
СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
[ГЛ. 5
ИЛИ
dH_ _ дН-'дН- _0&1РГР< dt dq ’ др Р т (q)
(5.62)
где
Я
2т (q)
+ V (?)•
Линии
H(q, p) = v
не являются теперь интегральными кривыми, но мы воспользуемся ими в качестве топографических кривых, позволяющих следить за изменением полной энергии р) во время движения, которое мы будем изучать в области фазовой плоскости, заполненной замкнутыми топографическими кривыми, окружающими точку (q*, 0), где q* соответствует минимуму потенциальной энергии V(q). Путём простой замены переменной можно сделать q* нулём, и тогда цент-
ром колебания будет начало координат. Частные производные
дН dq *
дН др
представляют собою проекции вектора градиента функции H(q,p),
направленного нормально к топографической кривой в сторону возрастания H{q, р). А так как эта функция, очевидно, имеет минимум в начале координат, то градиент направлен по внешней нормали, и уравнение энергии (62) показывает, что вектор фазовой скорости образует тупой или прямой угол с градиентом. Иными словами, фазовые траектории либо пересекают топографические кривые снаружи внутрь, либо касаются их, причём касание может иметь место только на оси абсцисс (см., например, фазовую диаграмму на фиг. 14 для случая кулонова трения, который мы рассмотрим ниже).
Если начальное состояние (qQ, р0) принадлежит рассматриваемой области, то Н будет для данного движения монотонной’убывающей функцией от /. Эта.функция ограничена снизу и потому при возрастании t она стремится к некоторому пределу <ul9 а фазовая траектория— к предельным точкам, лежащим на соответствующей топографической кривой = Но так как вне оси абсцисс
dH
производная остаётся отрицательной, то единственной предельной
точкой будет одна из точек пересечения рассматриваемой топографической кривой с осью абсцисс. Эта точка должна быть, очевидно, положением равновесия, так как в других положениях фазовая скорость отлична от нуля.
Таким образом, движение стремится к состоянию равновесия и является, как говорят, затухающим.
§ 5.6]
КУЛОНОВО ТРЕНИЕ
265
§ 5.6. Кулоново трение. Предположим, что
а сопротивление происходит от кулонова трения и
Q(<1> Р) =
— F при р > О, + при р < О,
(5.63)
причём а и F суть постоянные. При р = 0 трение уравновешивает восстанавливающую силу — V' (д) = — cq, если она по абсолютной величине не превосходит F, и противодействует ей в противном
случае:
(5.64)
Таким образом, Q (</, р) оказывается однозначно определённой также и на оси абсцисс фазовой диаграммы, но только после того, как задана V(q).
Полагая
B = Fj<3, (5.65)
мы видим, что все точки отрезка оси абсцисс от q— — В до q = -|~ В являются состояниями равновесия и образуют зону застоя.
Уравнение энергии имеет вид
d «-А—aBdq, 2т (q) 1 2 * J ’
причём здесь и в дальнейшем мы берём верхний знак для хода слева направо (р>0) и нижний для хода справа налево (р <0). Интегрируя, получаем уравнение
Р2 1 1 9 | - о .
о----/--.- 4- -к- <зя 2 ± aBq — const., 2т (q) 1 2 * *
или
(S.66)
которое представляет кривую в верхней или нижней полуплоскости, пересекающую ось абсцисс в двух точках, симметричных относительно точки (zjzB, 0).
Если в некоторый момент мы имеем | q | = aj > В, р = ®, так что q(t) проходит через максимум или минимум, то изображающая точка будет двигаться затем по интегральной кривой до следующей точки пересечения с осью абсцисс. Эта точка получится по другую сторону от начала, если
а<—В>В, или 3
^>2В, (5.67)
266 СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ [ГЛ. 5
и абсолютная величина её абсциссы определится из уравнения В (aj В) = #j+i>
так что
aj+i = aj — 2B. (5.68)
Из этой рекуррентной формулы видно, что последовательные амплитуды образуют убывающую арифметическую прогрессию и
aj = ао — 2Bj. (5.69)
Формула остаётся верной, пока при некотором j = п мы не получим амплитуду ап = а0 — 2Вп, (5.70)
для которой 0<aw^2B. Если при этом 0 < ап^В, то n-е полуколебание будет последним и движение прекратится. Если же В < ап^2В, то произойдёт ещё одно полуколебание, но изображающая точка достигнет после него оси абсцисс с той же стороны от начала, что и после n-го полуколебания. Поэтому
В В) = + откуда
ап+1 = 2В — ап (5.71)
и ап+1 < В, так что (пЦ-1)-е полуколебание будет последним.
Дуги интегральных кривых, лежащие в верхней и нижней полуплоскостях и соответствующие отдельным полуколебаниям, смыкаются
Фиг. 14. Колебания под действием линейной восстанавливающей силы и кулонова трения.
на оси абсцисс и образуют спиральную фазовую траекторию, оканчивающуюся в одной из точек зоны застоя. Так как продолжительность каждого полуколебания и число п конечны, то движение затухает в течение конечного времени.
§ 5.6]
КУЛОНОВО ТРЕНИЕ
267
Если, в частности, т = const., то дуги интегральных кривых, как видно из (66), будут половинами эллипсов с центрами в точках 0) и полуосями У^С/а, 2Ст (фиг. 14). Для периода колебания мы получаем ту же величину
(5.72)
что и при отсутствии сопротивления. В самом деле, эффект трения состоит лишь в том, что дуги эллипсов, получающихся так же и при простом гармоническом колебании, смещаются на zpB в направлении оси абсцисс, а так как dt = ntdq/p, то время, необходимое для прохождения каждого элемента дуги, остаётся тем же самым.
Пример [бЛ]. Карманные часы при начальном отклонении aQ = 135° = = Зтс/4 рад. останавливаются без завода через 40 сек. Период равен 0,4 сек. Найти В.
Так как число колебаний до остановки равно
то из уравнения
и/2 = 40/0,4 = 100, ап = aQ — 2Вп = Зтс/4 — 400В 0
находим с достаточной точностью
В = Зтс/1600 = 0,006.
Большинство карманных часов имеет в незагрязнённом состоянии постоянную В такого порядка.
Допустим теперь, что V (q) — какая угодно функция, имеющая минимум при 9 = 0, а сопротивление попрежнему происходит от • кулонова трения; но в качестве обобщения мы предположим, что абсолютное значение силы трения не обязательно одно и то же при ходе слева направо и ходе справа налево, так что
' — FL при . + ^2 ПРИ
р>0, р< 0;
(5.73)
при р == о мы должны положить
[ —^1 при V' (я) < — Flt .
Q(q, 0) = | V'(q) при — Ft sg V (q) ==S + F2> (5.74)
' + ^2 ПРИ + ^2 < v' (Я)-
Точки оси абсцисс фазовой диаграммы, для которых — Fr С С V' (Я) + F%, являются состояниями равновесия и могут образо-
вать одну или несколько зон застоя.
Уравнение энергии
d [Tt + V (q)] = ^Fi dq, (5.75)
268 СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ [ГЛ. 5
в котором I = 1 при р > 0 и i = 2 при р < 0, даёт
= (5.76)
где %(?) = V(q)±Fiq. (5.77)
Уравнение интегральных кривых будет
Р=-± у 2m (9) Tt (q). (5.78)
Для определения последовательных амплитуд можно применить следующее построение. Выделим на оси q отрезок, заключающий начало координат и принадлежащий той области фазовой плоскости, которая заполнена замкнутыми топографическими кривыми p) = v. Для всех значений q на этом отрезке, отличных от q = 0,. производная V' (q) также отлична от нуля и имеет тот же знак, что и q. Построим для этих значений графики функций V(9), (9), о2 (q)
(фиг. 15). Так как
(?)=у (?)+
?;<?)=v'(^ - f2>
(5.79)
то (д) заведомо положительна при q 0, а (д) заведомо отрицательна при q 0. Зоны застоя, где — Fr С V' (q) 4- F2, харак-
теризуются на графике тем, что в них одновременно
о <?'(?), ?;(?)<о.
Эти зоны показаны жирной линией на оси абсцисс.
Пусть в некоторый момент мы имеем значения q = а > 0, р = = Т= 0. Если а не принадлежит зоне застоя, то <?'2(а) > 0, так как иначе мы имели бы одновременно о'(а)>0, ©'(аХО, что может
иметь место только в зоне застоя. Для следующего за этим состоянием полуколебания справа налево мы должны принять для Т(д) выражение
^2 (?)= ^2 ?2 (?)’
где
=
этому значению постоянной соответствует на фиг. 15, б горизонтальная прямая, пересекающаяся с кривой <?2(?) в т°чке (а, <?2(а)). Левее этой точки обязательно найдётся другая точка пересечения прямой и кривой <?2(#), так как иначе Т оставалось бы отличным от нуля и изображающая точка на фазовой диаграмме, двигаясь налево, вышла бы из области замкнутых топографических кривых или удалилась в бесконечность. Во второй точке пересечения величины р и Т обращаются в нуль, а ©', как видно из чертежа, обязательно
I
§ 5.61
КУлоново тРенйе
269
отрицательна^ или нуль. Поэтому либо мы попадём здесь в зону застоя и движение прекратится, либо <р' будет также отрицательной. В последнем случае соответствующая абсцисса не может быть положительной или нулём, так как это влекло бы за собой ср' > 0; по
этому эта абсцисса может быть представлена как — Ь, где b > 0, и мы имеем ср2(—Ь) = С2 или
?2 (а) = ?2 (—^)- <5-80)
Для следующего полуколебания слева направо переходим к точке кривой <?* (д) с той же абсциссой — Ь, для которой, как мы установили, ф' (— Ь) < 0.
Принимая затем для Т(д) выражение
Т1 (?) = Ci — <Pi (?)>
вдаюге.
276 СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ [ГЛ. 5
где
Cj = {pj ( &),
проводим горизонтальную прямую через точку (— &, <рх (— &)) и ищем следующую направо точку (с, ©х (с)) её пересечения с кривой фх (#), для которой
= (5.81)
Очевидно, что таким образом мы можем строить последовательные амплитуды a, b, с, d, ... до тех пор, пока соответствующая абсцисса не попадёт в зону застоя. Так как разности ординат горизонтальных прямых и кривых <рх (^), <р2(^) Дают значения T(q), то мы ’ можем затем с помощью формулы (78) получить и фазовую траекторию, которая также должна строиться отдельными дугами, лежащими попеременно в нижней и верхней полуплоскостях и смыкающимися на оси абсцисс. J
Для определения продолжительности полуколебаний мы имеем 1
формулы |
-Ъ а ______________________________ Я
__ {m(q)dq_ f Г m(q) , |
“с (5-82) J
z т (q) dq _ /~ т (д) . f
6 .1 р (q) .1 V 2Ti(q) dq- 1
-ъ -ъ В
Рассмотрим, например, маятник с кулоновым трением, для кото- j рого, согласно примеру § 2, 1
т = /, V (q) == — Mgh cos q, 1
V' (q) = Mgh sin q. 1
Зоны застоя определяются неравенством I
— Mgh sin q ^2» |
и мы предположим, что Fx, В2 < Mgh, так как иначе маятник, пре- 1 доставленный самому себе без начальной скорости слева или справа 1 от наинизшего положения, не будет колебаться. S
Полагая I
sin Bi — . (5.83) g
мы получим из предыдущего неравенства f
— sin Вх sin q sin В2, (5.84) 11
откуда видно, что ширина зон застоя около наинизшего и наивыс- Ц
шего положений равна В1-[гВ.2. ж
§ 5.6]
КУЛОНОВО ТРЕНИЕ
271
В данном случае
(q) = — Mgh (cos q — q sin B^), ?2 (?) = — Mgh (cos Я + Я sin B2). Если же Bj = B2 = В, то, полагая
®(g) = cos q-\- q sin B, можем написать:
?i (?) = — Mgh <o (— q),
®2 (?) = — Mgh ® (?)•
(5.85)
(5.86)
Графики на фиг. 15 построены как раз для данной задачи. Последовательные амплитуды связаны зависимостью
?(«) = ? (— h). (5.87)
Отдельное исследование соотношения между амплитудами Ь, с при полуколебании слева направо излишне, так как, в силу симметрии кривых (q)t <?%(<]) относительно оси ординат, оно имеет вид
<р (6) = <р (—С),
т: е. не отличается от предыдущего. Из уравнения (87) можно определить b как функцию от а. Таблица 2 и график на фиг. 16 дают значения этой функции для В = 5°.
Таблица 2
Зависимость между последовательными амплитудами для маятника с кулоновым трением
а 6(a) а 6(a) а 6(a) а • 6(a)
5° — 5° 50° 38°55' 95° 79°43' 140° 112°40'
10° 0 55° 43°40/ 100° 83°55' 145° 115°06'
15° 4°57' 60° 48°20' 105° 88°01' 150° 117°22'
20° 9°53' 65° 52°59' 110° 92°03/ 155° 119°18'
25° 14W 70° 57°32' 115° 95°51' 160° 120°51'
30° 19°44' 75° 62°09' 120° 99°34' 165° 121°59'
35° 24°33' 80° 66°38z 125° 103°06' 170° 122°40'
40° 29°21' 85° 71°04' 130° 106°27' 175° 122°54'
45° 34°10' 90° 75°26' 135° 109°35'
Кривая Ь = Ь(а) пересекает ось абсцисс при а = В', где В'= 10°01'— отличный от нуля корень уравнения
cos В' В' sin В = 1.
(5.88)
272 СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ [ГЛ. 5
Если то ординаты кривой отрицательны; при этом
условии система оказывается в конце полуколебания не с другой, а с той же стороны от начала отсчёта, что и в начале полуколебания. На фиг. 16 показано также графическое построение последовательны^ амплитуд а, а', а", ... Получив b как ординату точки
Фиг. 16. Зависимость между последовательными амплитудами для маятника с кулоновым трением.
кривой с абсциссой а, проводим через эту точку горизонтальную прямую до пересечения с биссектрисой угла между координатными осями. Абсцисса точки пересечения есть ar = b и соответствующая ордината кривой даёт третью амплитуду и т. д. Построение имеет вид лестницы, заключённой между кривой и биссектрисой. Процесс заканчивается, как только лестница доходит до зоны застоя.
§ 5.7. Кулоново трение вместе с линейным. Рассмотрим систему с постоянной приведённой массой, потенциальной энергией V (q) = у ыр и силой Q, которая происходит как от кулонова трения, так и от сопротивления, пропорционального первой степени скорости, и может быть представлена в виде
— F—2msq при я > О,
. . (5.89)
+ F—2meq при q < 0.
Исключая р из уравнений движения
inq — p, р — — aq^F—2imq и полагая
F = aB, (5.90)
КУЛОНОВО ТРЕНИЕ : ВМЕСТЕ С’ ЛИНЕЙНЫМ
273
найдём:
q2zq№ (q ± В) = О (5.91)
или
< (q =t В) + 2е ± (q =t В), + (q ± В) = 0. €44 ***’
?
Рассматривая, например, ход справа налево, берём нижний знак и начальные значения q = q — 0. При этом должно быть dj > В, так как иначе система будет в зоне застоя и движение не начнётся. Предполагая, что е < fe, находим следующее решение, удовлетворяющее начальным условиям:
q — B = — В) e~9t \cos sin art), (5.92)
где _______
u) = /^_£-2; (5.93)
отсюда • Ь2
q =------(aj — В) e~zt sin wt (5.94)
После /=0 скорость q обращается в нуль в первый раз при /=к/о); вводя декремент затухания
8 = e-’t?/to < 1, . (5.95)
получаем соответствующее значение q:
q = B — (dj — В)8 = -— а^ + В(1 -J-8). , ' (5.96)
Если
dj> В(1 + 1/3)>2В, (5.97)
то это значение отрицательно, и мы представим его как:где dj+1 — — 8), (5.98)
причём dj+1 < dj. Поэтому полученная рекуррентная формула даёт последовательность убывающих амплитуд и остаётся верной др тех пор, пока для некоторого j~n .не окажется 0 < dn ^.В(\ 1/8).
Если при этом 0<ап<^В, то п-е полуколебание будет последним и система остановится. Если же В < dn^ В(1 -|- 1/8), то произойдёт еЩё одно (n-(-l)-e полуколебанйе, причём att+1 нужно определить прямо из (96), так что i ь
ап+1 = — ап^ + В (1 -J- 8).
Так как мы можем написать: dn+1 = В — (dn — В) о < В, то l это vn~rl)-e полуколебание будет последним.
18 Зак. 1474. Б. В. Булгаков
j -
274 СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ [ГЛ. 5 1
Мы имеем из (98): j
— 5(1 —[-8), 1
о.2 = 4Zj8 — 5(1-{-8), ।
ai-l = flJ-28 —В(1+8).
а3 ~ aj-l^--5 (1 д). I
Отсюда, умножая соответственно на 8;”\ 8;”2, ..., 8, 1 и скла- 5 дывая, имеем: *
^ = а08; —5(1+8)(1+8+ ... +8--1)= '
= ^ — 5(1+28+ ... +2о^“1 + 8;), \
откуда получается следующее выражение для /-й амплитуды:
а/ = (а0 — — 2В _ в. (5.99)
Продолжительность двух полуколебаний будет ?
2тс______ 2тс
со "У № — е2 ’
(5.100)
так же как при действии одного только сопротивления, пропорционального первой степени скорости. Поэтому и здесь колёбанйе затухает в течение конечного времени.
§ 5.8. Гиро-рулевой со свободным ходом. В качестве примера приложения решения, полученного в предыдущем параграфе, рассмотрим автоматическое управление кораблём с помощью гиро-рулевого со свободным ходом; подробное описание и анализ этого устройства даны Чалмерсом [4-16].
Ограничиваясь простейшей приближённой постановкой задачи, представим уравнение углового движения корабля вокруг вертикальной оси, проходящей через его центр тяжести, в виде
Iq = — Mq — Кг, (5.101)
где q есть угол отклонения продольной оси корабля от желаемого курса, г — перемещение тяг руля, пропорциональное углу его поворота, I — момент инерции корабля относительно вертикальной оси, УИ и К—постоянные коэффициенты. Произведение —Mq представляет момент сопротивления, пропорциональный угловой скорости q, а — Кг есть момент воздействия руля, который мы принимаем пропорциональным его отклонению. Обычно корабль находится также под воздействием ветра, волн и течения, что мы должны были бы учесть дополнительным возмущающим моментом в правой части уравнения. Мы, однако, представим себе для простоты, что возмущающие воз
§ 5.8]
ГИРО-РУЛЕВОЙ СО.«СВОБОДНЫМ ходом
275
действия создали некоторое начальное отклонение qQ, которое должно быть уничтожено путём рационального управления рулём. Для этого автомат должен содержать индикатор, регистрирующий угловые отклонения q> который может работать от магнитного или гироскопического компаса. Эти приборы весьма деликатны и могут развивать лишь малые усилия. Между тем, для перекладки руля требуется значительная мощность, далеко превосходящая даваемую индикатором. Поэтому* между индикатором и рулём вводится дополнительный источник силы — так называемый сервомотор. Тогда в случае гидравлического сервомотора индикатор непосредственно передвигает лишь распределительный золотник, включающий рабочее давление, а работа
/7 помпе
Фиг. 17. Принципиальная схема гиро-рулевого.
перекладки руля производится сервомотором. Подобным образом обстоит дело и в случае других механических или электрических сервомоторов.
Простейшая принципиальная схема изображена на фиг. 17. Поршень золотника 1 соединён с индикатором и получает отклонения вправо или влево, пропорциональные угловым отклонениям корабля; для простоты мы можем выбрать линейную единицу таким образом, чтобы коэффициент пропорциональности был равен единице. При отклонении поршня золотника открывается один из клапанов, через которые рабочее давление, создаваемое помпой, передаётся в цилиндр сервомотора 7. Если, например, поршень золотника отклонился вправо, то открывается правый клапан, избыточное давление создаётся справа
18*
276 СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ [ГЛ. 5
от поршня сервомотора, его шток 6 перемещается налево и поворачивает руль 5. Под действием момента, создаваемого рулём, корабль начинает возвращаться на курс и для того, чтобы он не получил затем большого отклонения в противоположную сторону, автомат должен ограничить отклонение руля, как это делает рулевой при ручном управлении, а также велосипедист или водитель автомобиля. Для этого в системе предусмотрена обратная связь 4, представляющая систему стержней, с помощью* которой корпус золотника 2 получает одновременно с рулём продольное перемещение вправо, вслед за поршнем 7. Благодаря этому следящему движению корпус золотника догоняет поршень, нейтральное относительное положение того и другого восстанавливается, клапаны перекрываются и дальнейшее движение сервомотора прекращается. Аналогичным образом происходит дело и при отклонении поршня золотника налево. Для завершения процесса нужно, разумеется, некоторое время, вследствие чего корпус золотника будет следить за поршнем с некоторым отставанием. Однако в первом приближении мы пренебрежём этим запаздыванием, считая, что сервомотор срабатывает бесконечно быстро. Тогда, не принимая сначала во внимание свободный ход и предполагая, что в точке 3 мы имеем жёсткое соединение, мы можем считать, что смещения штока сервомотора г и корпуса золотника s равны смещению q его поршня:
r = s = q. ’ (5.102)
Из (101) получается
lq = — Mq — Kq или
£ + 24 + #ty = 0, (5.103)
где
2е = -у, /г2 = у. (5.104)
Таким образом гиро-рулевой создаёт искусственный восстанавливающий момент — Kq, заставляющий корабль возвращаться на курс, совершая около него согласно (103) затухающие колебания.
Так как, однако, естественное сопротивление может быть слишком мало, чтобы обеспечить достаточно быстрое затухание, то в гирорулевом Сперри вводится свободный ход. На фиг. 17 он представлен в виде детали 3, состоящей из шпонки, имеющей возможность свободно скользить в скобке длиной 2В и заменяющей жёсткое соединение стержня обратной связи с корпусом золотника. Благодаря этому корпус золотника отстаёт на величину ±В от того положения, которое он занимал бы, если бы шпонка была жёстко закреплена в середине скобки. Поэтому теперь
г В — s = q,
(5.105)
§ 5.91
КУЛОНОВО ТРЕНИЕ ВМЕСТЕ С КВАДРАТИЧНЫМ
277
где верхний знак берётся при ходе слева направо (q > 0), а нижний — при ходе справа налево (q < 0). Из уравнения (101) теперь получается:
или
Iq = — Mq — K(q±B)9
q+2eq±k*(q±B)==Q.
Это уравнение тождественно с (91) и, следовательно, эффект свободного хода эквивалентен кулонову трению между управляемым объектом и внешней средой.
Поэтому после затухания колебаний корабль приводится на желаемый курс лишь с точностью до некоторого остаточного отклонения q, принадлежащего интервалу (—В, В), причём удержание его в этом положении сопровождается перекладками руля,-при которых г изменяется в интервале (q — В, q-[-B). С точки зрения принятой нами приближённой постановки задачи эти перекладки нужно считать бесконечно быстрыми, тогда как на самом деле они могут происходить лишь с конечной скоростью. Но для полного выяснения этих обстоятельств нужно было бы учесть инерцию индикатора и сервомотора, которыми мы пренебрегли.
§ 5.9. Кулоново трение вместе с квадратичным. Рассмотрим теперь систему с силой Q, которая происходит от кулонова трения и сопротивления, пропорционального квадрату скорости, например сопротивления воздуха, и может быть представлена в виде
или
I + ^ + (<7Й9
при q > 0, при q < 0
Q{4> Р) =
, ___Oi(q)p*
1 И (<7)12
• । С2(д)р* 2'[т (?)Р
при р > 0,
при р < 0;
(5.106)
при этом F{ суть положительные постоянные, a G{(q) — положительные функции.
При р = 0 мы должны, как и в § 6, ввести дополнительное условие (74) и вытекающее из него определение зон застоя.
Уравнение энергии (4.16) будет
। тг/ z х 1 у' fq) ±
da 1 ,
или
7 | 2(7* G?) *7* 1 _
m(q)
а1\± 2Gy (у) m (?)
(5.107)
278
СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
[ГЛ. 5
Интегрируя это линейное уравнение первого тельно Tit находим:
Г 2G{ «П
Tdq) = e^J «(«> ®[С{ —
где (q) имеет одно из значений:
порядка относи-
Сб. 108)
С , J т(е> *
?i (q) = I iv (?)+^ii е° dq при
-feu
/• J т (q) 4
®2(?) = Г W'tq) — Е>]е 0 dq при
(5.109)
Интегральные кривые определяются уравнением (78).
Производные <?'((?), <?2(q) получаются из выражений V'(^) + /i и V'(д)— F2 умножением на показательные функции и имеют, следовательно, те же &аки. Поэтому/как легко убедиться, то построение, которым мы пользовались в § 6 для определения последовательных амплитуд в случае кулонова трения без квадратичного и произвольной V{q), применимо и здесь вместе с его обоснованием. Нужно только понимать под T^q), ^(д) полученные только что выражения.
При этом условии остаются верными уравнения (80), (81), связывающие последовательные амплитуды и формулы (82) для определения продолжительности полуколебаний.
Пусть, например, восстанавливающая сила линейна, так что
V(q) = ±°q*, 1 а т и = G2 = тг суть постоянные величины. Если
Ft = qBv F2 = оВ2» (5.110)
то зона застоя будет —Мы имеем:
Tt{q)^=e^^ [С} — <?/?)], где
/
®< (?) = о J (.q e**dq =
= (q ± f e±«« dq =
§ 5.9]
КУЛОНОВО ТРЕНИЕ ВМЕСТЕ С КВАДРАТИЧНЫМ
279
так что
Л (?) = [С, — з ~1 ~ ~ Bt) *±,а] =
= i {ТС< +11 + 6 e±,q}•
Вводя новую переменную
х = е(?±Вг), представим 7^ в виде .
= г г’1”’4т с. + <1 1'
где
,^ = 35,=^. р2=вВ2=ф; или же
Т{ = е** [vt + (1 qz х) е±ж],
(5.111)
(5.112)
(5.113)
причём vf суть новые постоянные.
Пусть в некоторый момент q = а > О, Т = 0. Если при этом а > В.» так что система находится вне-зоны застоя, то для следующего за этим состоянием полуколебания справа налево мы должны положить
х = &(д—В2), .
вследствие чего значение
е = 8 (а — Я2) = еа — р2 (5.114)
переменной х, соответствующее q = а, будет положительным. Чтобы удовлетворить начальным условиям, мы должны взять для v значение ®2=—(1+$)еЧ и тогда
г2 = J е® [/(X) -/(£)] = £ (X + 1 - ($ 4-1) где
/(х) = (х-4-1)е‘-< (5.115)
Так как
/(-1) = 0, /(0)=1, /(оо) = О,
Г(0) = 0,
то график /(х) имеет форму, изображённую на фиг. 18. Из этого графика видно, что всегда найдётся такой отрицательный аргумент х = — т), при котором /(х) примет то же значение, что при х = В, так что
($_|_1)е-« = (_ (5.116)
280 СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ [ГЛ. 5
Кинетическая энергия Т при этом опять обратится в нуль. Если соответствующее значение
п— R
положительно, то оно будет меньше и система попадёт в зону застоя справа от начала отсчёта q = 0. Если же это значение отрицательно, то оно может быть представлено как — Ь, где b > 0, так что
q = s (р + = eb + ?2-
Но чтобы система не оказалась в зоне застоя слева от начала, нужно ещё потребовать, чтобы b > Вх. В этом случае после рассматривае-
мого состояния будет иметь место полуколебание слева направо, при котором
а значение х, соответствующее q = — b, будет —S', где величина ^ = е(&_В1) = е6 —рх, (5.117)
или
= “П - (01 + Р2) (5.118)
положительна. Значения х = 7|', q — c в конце второго полуколебания связаны соотношением
< = е(с + Вх),
а для получения зависимости между %, т/ нужно, как и выше, воспользоваться формулой (ИЗ), которая даёт
(£' + 1) = (— vf + 1) гч'. (5.119)
Для исходного значения х = при третьем полуколебании находим: Г = е(с —B.j) -
§ 5.9]
КУЛОНОВО ТРЕНИЕ ВМЕСТЕ С КВАДРАТИЧНЫМ
281
Г = 7!'- (рх + р2). (5.120)
Так как соотношения (119), (120) вполне аналогичны соотношениям (116), (118) для первого полуколебания, то общую закономерность можно считать выясненной.
Найдя т| как функцию от $ с помощью уравнения (116) или графического построения, показанного на фиг. 18, мы можем изобразить эту функцию на графике (фиг. 19), который может служить также для определения последовательных значений ?, Г, . Для этого нужно, кроме кривой т] = т] (Е), нанести ещё прямую Е = т| — (Pi + Р2), параллельную биссектрисе угла между координатными осями. Построение имеет вид лестницы, заключённой между кривой т) = т) (?) и упомянутой прямой. Процесс заканчивается, как только одна из ступенек выйдет в область отрицательных абсцисс.
Величины Е, Е', ... согласно (114), (117) пропорциональны отклонениям от края зоны застоя, а сами амплитуды найдутся по таким формулам, как '
а==кЕЁ2 (5.121)
для отклонений направо и
6 = (5.122)
для отклонений налево.
Из графика /(х) непосредственно усматривается, что
7|(0) = 0, 7|(ОО)=1,
как это показано на фиг. 19. Поэтому большие значения Е убывают очень резко, а меньшие более плавно, что представляет специфи-
Фиг. 19. График функции (5).
ческий эффект квадратичного сопротивления. Кривая т| s= т|(Е) касается биссектрисы Е = т|, так как т/ (0) = 1, что легко установить, если построить, например, степенной ряд для (В), который может служить также для вычисления этой функции при малых Е. Мы имеем:
/(х) = (1 4-х) (1 хЦ-2* х2 -g- х34"24 12б‘ *) ~
1 - A- v*2 I -А уЗ - .. ± | _А v*5 —
2 ’3 8 30 ” ’
282
СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
[гл. 5
и уравнение (116) или /(?)=/(—-т|) может быть написано в виде Полагая
11 = ^+^3+с8В8+с4Е<+..., •
подставляя в уравнение и сравнивая коэффициенты при одинаковых степенях 5, определим clf с2, с3, с±, ... Таким образом, получим:
=*-I $з+4 • • • <5-123)
Значения т|0) для некоторых $ приводятся в таблице 3.
Таблица 3
Функция 12(g)
5 4 (В) 5 е 4(5)
0,0767 0,0808 0,0854 0,0906 0,0964 0,1030 0,1106 0,1194 0,1298 0,0730 0,0767 0,0808 0,0854 0,0906 0,0964 0,1030 0,1106 0,1194 0,1420 0,1570 0,1753 0,1986 0,2290 0,2704 0,3301 0,4240 0,5936 1 0,1298 0,1420 0.1570 0,1753 0,1986 0,2290 0,2704 0,3301 0,4240 0,5936 1,5 2 2,5 3 4 5 6 8 10 оо 0,7316 0,8214 0,8809 0,9207 0,9651 0,9849 0,9936 0,9989 0,9998 1
Первые две колонки даны по В. Либишу [б-26] и дают возможность вычислить двадцать последовательных убывающих значений 5, начиная с ё = 1.
Для вычисления времени мы имеем, предполагая, например, что изображающая точка движется справа' налево:
dt = — '[/r ^JL-dq = — -\/'— dx ^(q) F 2a i l)e-^-a>)
Поэтому времена, необходимые для прохождения от крайнего положения х = В до х = 0 и отсюда до следующего крайнего положения х = — т], определяются соотношениями
(5.124)
§ 5.9] КУЛОНОВО ТРЕНИЕ ВМЕСТЕ С КВАДРАТИЧНЫМ 283
Эти времена также были вычислены В. Либишем для ряда значений Е и даны в таблице 4.
Таблица 4
Времена полуколебаний при квадратичном законе сопротивления
5 4(0 1/-'1 г т 1/"— г т
0 0 я/2 = 1,571 те/2 = 1,571 к = 3,142
0.330 0,270 1,627 1,527 3,153
0,424 0,330 1,643 1,517 3,160
0,594 0,424 ’1,673 1,502 3,175
1 0,594 1,747 1,475 3,222
2 0,821 1,941 1,442 3,383
5 0,985 2,579 1,419 3.998
10 1 3,612 1,414 5,026
20 1 5,28 1,41 6,70
40 1 7,80 1,41 9,21
80 1 11,42 1,41 12,84
200 1 18,71 1,41 22,12
1000 1 48,36 J.41 49,77
оо 1 оо 1<2 = 1,41 ОО
Для малых 5 период полуколебания стремится к пределу
гс V’ соответствующему незатухающему гармоническому коле
банию. Это объясняется тем, что сопротивление, пропорциональное квадрату скорости, мало заметно при малых х и х, а кулоново трение, как мы видели раньше, не влияет на период.
Рассмотрим теперь случай маятника:
т = /, V (д) = — Mgh cos q.
Полагая
sin Gi=.y/Si’ (5.125)
имеем:
Tdq) = e*W[C{ —
Tt
sin B^) е***4 dq =
Mgh
——r,e
sin BA.
ei 7
В частном случае, когда = В2 = В, = е2 = ©, можно написать:
М?) = ~?-а(9) = —
284
СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
[ГЛ. 5
где
?(?) = *~tff(cos ?-|-8 sin q — sin в). (5.126)
Последовательные амплитуды связаны соотношением
?(«)==? (— Ь).
Значения функции b (а), определяемой этим уравнением, вычислены
Фиг. 20. Зависимость между последовательными амплитудами для маятника с квадратичным сопротивлением.
для В = 0, s = 0,4 и даны в таблице 5 и на графике (фиг. 20).
Таблица 5
Зависимость между последовательными амплитудами для маятника с квадратичным сопротивлением
а b (а) а &(«) а *(«) а Ь(а)
0° 0° 50° 40°12' 100° 64°28' 150° 75°33'
5° 4°37' 55° 43°16' 105° 66°09' 155° 76°02'
10° 9°31' 60° 46°13' 110° 67°40' 160° 76°25/
15° 14°01' 65° 48°59' 115° 69°04' 165° 76°43/
20° 18°16/ 70° 51°38' 120° 70°18' 170° 76°55' .
25° 22°21' 75° 54°08' 125° 71°31' 175° 77°02'
30° 26°15' 80° 56°31' 130° 72°33' 180° 77°04/
35° 30°00' 85° 58°40' 135° 73°28'
40° 33°33' 90° 60°45' 140° 74°16'
45° 36°56' 95° 62°40' 145° 74°58'
В. АВТОКОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ
§ 5.10. Общие замечания. Изучая консервативные системы, мы видели, что при известных условиях они могут совершать либра-ционные и ротационные колебательные движения. Эти колебания
§ 5.11]
ЧАСЫ
285
обладают периодичностью в том или ином смысле и могут быть представлены замкнутыми кривыми на плоской или цилиндрической фазовой диаграмме.
При этом для консервативных систем характерно, что если для них вообще существуют возможные периодические колебательные режимы, то таких режимов будет бесчисленное множество, точнее, множество мощности континуум, и соответствующие замкнутые фазовые траектории непрерывно заполняют конечную или бесконечную часть фазовой поверхности.
В противоположность этому автоколебательные системы, к изучению которых мы переходим, характеризуются конечным или, вообще, дискретным множеством возможных либрационных или ротационных колебательных движений. При этом об автоколебаниях в собственном смысле мы будем говорить лишь в случае, когда соответствующий стационарный режим асимптотически устойчив по Ляпунову, т. е. когда близкие непериодические колебания стремятся к нему при
Широким развитием теории автоколебательных систем мы обязаны московской школе теории колебаний, созданной Л. И. Мандельштамом, Н. Д. Папалекси и А. А. Андроновым. В результате работ этой школы отдельные известные ранее решения были дополнены новыми, приведены в общую систему и связаны с общей качественной теорией дифференциальных уравнений.
§ 5.11. Часы. В качестве первого примера рассмотрим движение часов. Пусть регулятором хода служит система баланс — спираль, т. е. твёрдое тело, качающееся на оси, проходящей через его центр масс и удерживаемое вблизи некоторого положения равновесия спиральной пружиной. Предполагая, что восстанавливающая сила спирали подчиняется закону Гука, положим:
где о — постоянная, a q — отклонение баланса от положения равновесия. Это выражение пригодно в качестве приближённого и для часов с маятником, если считать размахи малыми. Основной силой сопротивления является кулоново трение
Если бы, однако, кроме восстанавливающей силы и трения на систему не действовало никаких других сил, то она была бы диссипативной и часы, будучи приведены в движение, через некоторое время остановились. Поэтому для пополнения энергии колебаний Регулятору передаются усилия от часового хода, приводимого в действие гирей или заведённой пружиной. Это происходит на некотором конечном угле поворота баланса или маятника, называемом углом
286
СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
[ГЛ. 5
импульса. Мы, однако, сначала примем для простоты, что при прохождении регулятором некоторого определённого положения ему сообщается толчок, при котором он мгновенно получает конечное приращение энергии ДЯ.
Чтобы учесть инерцию различных деталей, связанных с регулятором, будем считать приведённую массу переменной; тогда для любого промежутка времени, не заключающего момента толчка, имеем уравнение энергии
2m(q) ’ 2 ’ j *
где верхний знак соответствует ходу слева направо (р > 0), а нижний — справа налево (р < 0).
Интегрируя, находим, как и в § 6:
2^)+у = + а5? + const.
или
1 п2
4 <3'(q±В)2 + я- = const.
2 7 1 2т (q)
Пусть в начальный момент q = а > 0, р = 0, причём должно быть
а > В,
(5.128)
Фиг. 21. Фазовая диаграмма движения часов.
так как иначе система будет в зоне застоя и часы не пойдут. Если это условие выполнено, то регулятор начнёт двигаться к положению равновесия (/? < 0). Определяя постоянную интегрирования из начальных условий, будем иметь:
= 1в(а_В)2.
Это уравнение определяет в фазовой плоскости qp кривую (фиг. 21), симметричную относительно оси абсцисс и пересекаю
щую эту ось в двух точках, симметричных относительно q — Bt причём движение изображающей точки начинается от Ло по той ветви, которая лежит в нижней полуплоскости (р < 0). Разрешая относительно р, находим:
p = — V<im{q) [(а — В)2 — (q — В)2].
§ 5.И1
ЧАСЫ
287
Значение р в точке А19 соответствующей положению q — f> где регулятору сообщается толчок, будет:
А = — /а/» (/)[(« — В)а — (/— В)2] =
=—/ а/» (/) (а —/) (а — 2В+/). ' (5.129)
Время, необходимое для прохождения от q = а до q =f, есть f а ____
Г Vn, M
1 J r j
а /
Для того чтобы система могла фактически дойти до положения q = f и р± было действительным, должны выполняться неравенства а>/, В — (a — B)<f
или
а > 2В—
(5.131)
так как иначе часы остановятся, ещё не получив толчка.
Предположение а < /, а < 2В — f, достаточное для действительности радикала в (129), должно быть отброшено, так как из него вытекает: 2а < 2В, что противоречит (128). Если В <f, то 2В < 2/, 2В—f<f, т. е. f будет наибольшим из двух чисел /, 2В—и второе условие (131) может быть отброшено как следствие первого; условие (128) также излишне. Если, наоборот, B>f, то 2В > 2/, 2В—f > /, и первое условие (131) может быть отброшено как следствие второго; так как В < В Ц- (В—f) = 2B —f, то условие (128) и в этом случае оказывается излишним. Таким образом, условия (128) и (131) приводятся к следующему:
а
(5.132)
Обозначая через pi значение канонического импульса с диаграммы после толчка при q~f, имеем:
_2 1
Pi 1
фазовой
точке Ai
/2
L 2m (/)
. 2m (/)
= ДЯ,
-тг а
в
или
Pi2 — Pi = 2m (/) ДЯ,
где
Pi = —И #-|-2т(/)ДЯ =
= — /от (/) К» — В)‘ — </— В)а + Л|,
(5.133)
а
(5.134)
ВИЛп?-. -
288 СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ [гл. 5
После толчка изображающая точка в фазовой плоскости движется по кривой, определяемой уравнением
i ° <’ - в>3+i °- 8)3 +
которое может быть с помощью (133) представлено в виде
Р = — V от. (?) [(а — В)3 + Л — (? — В)3].
Кривая пересекает ось абсцисс в двух точках, из коих абсцисса левой точки А2 есть
q = — b = В — —
откуда
£ = /(а —В)34-Л —В. (5.135)
Условия, при которых b будет действительно положительным, a q =— b отрицательным, выяснятся ниже.
Время, необходимое для прохождения от q = f до q = — b> есть
-ь f ___
Г т (д) dq _ Г_______Ут (q) dq___-
) Р J /О[(а-В)2+Л-(^-В)2]'
(5.136)
Если, в частности, т = const., то
— arc sin
lf—B\
\а — В )’
q-B
V(a-B)2-\-h
q-B
V(a — B)2+h .
/
t
f—В । . b+B
— arc sin— - -4- a resin —- —--
Via — B)*+h V(a — B^ + h
к . . f—B
= 7Г + arcsin • >/.. -г
2 ’ V(a — B)2 + h
ЧАСЫ
289
Продолжительность полуколебания (одного размаха) будет
т а
it — arcsin ---к- 4- arcsin 7 .. .
а —В 1 /(a — B)* + h
л — arcsin
/-В / (а-В)2 + /г_(/-В)2
—В V (a — B)*+li
V(a — B)2—(f — B)z f—B
а— В
V(a — By*+h J 1 .
или
« —
— arcsin
(а —В) V(a — B)* + h
(5.137)
При отсутствии толчка (Л = 0) эта величина была бы равна половине периода гармонического колебания it /п/з. Поэтому второй член в фигурных скобках представляет изменение продолжительности полуколебания вследствие толчка; он отрицателен, когда /—В и h одного знака, и положителен в противном случае.
Мы получаем, таким образом, следующую теорему Эри. надлежащим образом модифицированную для учёта влияния трения: толчки, направленные к границе зоны застоя, ближайшей к началу раз-маха, уменьшают период*, толчки, направленные от этой границы^ увеличивают период*, толчки на самой границе оставляют период без изменения. При этом мы, для краткости, назвали периодом двойную продолжительность полу колебания, не предрешая вопроса о том, будут ли колебания действительно периодическими, затухающими или нарастающими. К выяснению этих вопросов мы сейчас обратимся.
Формула (135) устанавливает зависимость между амплитудами а> b в начале и в конце хода справа налево. Эта формула будет верна для двух любых последовательных амплитуд, если регулятор, как мы предположим, получает толчок в положении # = -}-/при каждом ходе справа налево и в положении q = —f при ходе слева направо, причём энергия АН, сообщаемая при этих толчках, одна и та же;' величина / может быть как положительной, так и отрицательной.
Выясним, при каких условиях амплитуды будут расти.
Требуя, чтобы было Л
b = — + й — В> а,
19 Зак. 1474.
Б. В. Булгаков
290
СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
к л. s
получаем:
(а — В)3 + h. > (а -|- В)3, h > 4аВ
или
а < А,
Где
h__ЬН
“ 4В “ 2В<з ’
Совершенно аналогичным образом получим» что амплитуды будут
убывать, если
а > А.
Наконец, если а = А, то и Ь — а = А\ мы получаем в этом слу- 1 чае периодическое движение со стационарной амплитудой Л. Для | того чтобы оно могло действительно иметь место, нужно ещё, чтобы |
f при В
2В — f при В
(5.139) I
откуда
2Вз/ при В . 2Вз(2В—f) при В
(5.140)
т. е. мы получили условие, которому должен удовлетворять механизм гири или заводной пружины. Как и следовало ожидать, из него выте- i кает, в частности, что Д77 должно быть положительно. 1
Так как F= В<з есть сила трения, то формула (138) может быть 1 переписана в виде I
(5.141)
или F • 2А = ДЯ. Она выражает тот простой факт, что при стационарных колебаниях работа трения на пути 2А равна работе часового хода.
При В < а < А мы имеем также:
b < V(A — В)3 4- h — В = V(A — В)3 4- 4 АВ — В
ИЛИ
Ь< Л.
Поэтому, если амплитуда была меньше Л, то, возрастая, она и | в дальнейшем будет оставаться меньше этого значения. Она должна, 1 следовательно, стремиться к некоторому пределу, не превосходя- J
§ 6.111 *1А6Ы 291
тему Л. Остаётся доказать, что этот предел в точности равен А. Для этого заметим, что
b - а = V(a-B^h- (а + В) = =
у (а — И)л -у (а -у о)
__________к — 4аВ_______________4В (А — а)____ ~~ Y(a — B^+h 4- (а + В) У(а — В)^±Ь + (а + В) *
При В < а < А отсюда вытекает, что
ь_а>__________4В(Л —я)______
Я> У(Л-В)з + Л.+1(Л}+ В)|
ИЛИ
, 2В(Л —а).
b~a> А+В '
а так как а и b стремятся к одному и тому же пределу, то b — а-+ О, вследствие чего А — а—>0 и а->Л, что мы и хотели доказать.
Аналогичным образом можно показать, что если амплитуды больше Л, то они стремятся к А убывая.
Следовательно, периодическое движение со стационарной амплитудой А орбитно-устойчиво, т. е. его замкнутая фазовая траектория является предельной для фазовых траекторий всех близких движений. Отсюда уже можно вывести устойчивость по Ляпунову, но на этой тонкости мы позволим себе не останавливаться.
Итак, если неравенство (140) выполнено, то существует автоколебательный режим качаний регулятора, соответствующий нормальному ходу часов. Стационарная амплитуда А не зависит от начальных условий и определяется только конструкцией и трением. Зависимость от начальных условий сводится к тому, что качания не затухают и стационарный режим устанавливается лишь в том случае, когда начальная амплитуда не слишком мала и удовлетворяет неравенству (132). Такое возбуждение автоколебаний носит название жёсткого в отличие от мягкого, когда автоколебания устанавливаются при сколь угодно малом начальном отклонении. Если неравенство (140) не выполнено, то качания будут затухать при любых начальных условиях.
Переписывая соотношение (135) в виде
(а-В)2 t (Ь + В^_^ ~ h ' h
мы можем рассматривать его как уравнение кривой в координатной плоскости ab (фиг. 22).
Эта кривая — равнобочная гипербола с центром в точке (В, — В) и асимптотой Ь = а — 2В. Проведя биссектрису а = Ь угла между координатными осями, мы можем с её помощью строить последова-
19*
идол
292
СОБСТВЕННЫЕ ЙОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
[гл. 5,
тельные амплитуды, так же как мы это делали раньше для диссипативных систем, например для маятника с одним лишь кулоновым
Фиг. 22. Зависимость между последовательными амплитудами для часов с балансом.
Уравнение энергии при движении
трением. В пересечении гиперболы и биссектрисы получается точка с координатами hj^B, hf^B или А, А.
Рассмотрим теперь в общих чертах более сложную задачу, когда V (q) — какая-нибудь функция, имеющая минимум при q = 0, а энергия колебаний пополняется путём затяжных импульсов, сообщаемых силой Gx (д) > 0, действующей на некотором конечном угле импульса при ходе слева направо, и силой — ^2 (в) < О ПРИ ходе справа налево. Абсолютную величину силы трения мы можем также для общности предполагать различной для того и другого хода и обозначить, соответственно, через и F2.
справа налево будет
или
4®ГЙ) +''(?)] = ft-
2^5) 4- Vft) — Fa? — J,(4) = const-,
где
+co
•4 (?) = ]*
Q.
(5.142)
.Максимальное значение J2(q) равно полной работе импульса +оо
ДЯ2= j O2(q)dq, —CO
причём в обеих последних формулах мы можем, разумеется, вместо пределов —оо, -[-оо взять левую и правую границу угла импульса. Подставляя в уравнение энергии значения q = a, р — 0 и q = —?b, р=0 для начала и конца размаха и вычитая почленно, найдём:
/2(а, &) = 0, (5.143)
§ 5.1U
ЧАСЫ
293
где
/2(а, *) = V{d)-V(—b) — f2(a + ^)-J2(a) + J2(-&); (5.144)
при этом начальная координата q = a должна лежать вне зоны застоя
i^V'(9) + O2(9)^F2.
(5.145)
Аналогичным образом для хода слева направо имеем уравнение энергии
+ У (.Я) + Р1Я — Ji (Я) = const.
и соотношение между последовательными амплитудами
А (!>, с) = о,
(5.146)
причём
Л (?) = J* °1 (?) аЯ>
(5.147)
fi(P> c)=V(-b)-V(c)-F1(b-[-c)-J1(-b)-i-Jl(c). (5.148) Максимальное возможное значение J^(q) есть
f G^q)dq\
начальное положение q — — b должно лежать вне зоны застоя
\ У (.4) - 01 (?) f2.
(5.149)
Если вместо затяжных импульсов на регулятор действуют мгновенные толчки в точках q=f19 f%, то Jx(9), J2(9) обращаются в ступенчатые функции
4 (?) =
О при q
Д77х при q
v
i>
_АН2 при q
Для стационарного движения мы должны положить а = с и определить а, b из уравнений
/х(&, а) = 0, /2(а, &) = 0.
(5.150)
При некоторых упрощающих обстоятельствах решение получается очень легко. Пусть, например, V(q) есть чётная функция, как это будет в случае простейшей системы баланс — спираль, для которой V(q)=^^ или в случае маятника, для которого V(д) = === — Mgh cos q.
294
СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
[ГЛ. 5
Пусть, кроме того, ДЛД = ДЯ, = ДЯ, Ft = F2 = F. Попытаемся найти симметричное решение а = Ь = А, где А и —А лежат вне углов импульса и зон застоя. Так как, очевидно,
— А (- А) 4- Л (Я) = f Gt (q) dq = АН,
-A
+4
— J2(X) + J2(—Л)= f O.2(q)dq = ^H,
-A
то подстановка принятых значений в оба уравнения (150) даёт один и тот же результат
— 2Л^ + ДЯ=0, откуда для А вновь получается выражение (141). Если Д/7 настолько велико, что это значение А действительно лежит вне углов импульса и зон застоя, то оно и является амплитудой автоколебаний.
Для строгой проверки устойчивости, а также и для определения амплитуд автоколебаний в случае, когда упрощающие обстоятельства не имеют места, следует обратиться к общей процедуре, изложенной в следующем параграфе.
Определяя канонический импульс р в функции координаты q из уравнения энергии, мы можем найти период колебания с помощью квадратур, которые, однако, могут не выражаться в элементарных функциях и должны в этом случае выполняться , числовым путём.
Дальнейшее усложнение задачи заключается в учёте потерь от ударов в механизме, в результате которых при прохождении через некоторые положения канонический импульс р претерпевает конечные изменения Д^, Др2. Пользуясь уравнением энергии и принимая во внимание эти изменения, можно и здесь получить соотношения вида (143), (146).
§ 5.12. Графическое определение стационарных амплитуд и проверка устойчивости. Предположим, что, так же как в первой задаче предыдущего параграфа, мы применили к какой-либо системе интегрирование по интервалам и получили соотношение между последовательными амплитудами
/(а, &) = 0, (5.151)
пригодное, вследствие симметрии, как для хода справа налево, так и для хода слева направо. При симметричных периодических колебаниях мы должны иметь а = b = Л, и стационарные амплитуды А являются положительными корнями уравнения
/(Л, Л) = 0. (5.152)
В случае системы с кулоновым трением амплитуды Л должны ещё лежать вне зон застоя. Проверим, будет ли стационарное движение орбитно-устойчивым.
5.12] ГРАФИЧЕСКОЕ ОПРЕДЕЛЕНИЕ СТАЦИОНАРНЫХ АМПЛИТУД 295
Для этого положим . cl = А —Ъ = ^4. —J— 8Z^, где 8а, ЬЬ — малые возмущения. Подставляя в (151), разлагая в ряд Тейлора и ограничиваясь малыми первого порядка, имеем:
где круглые скобки при частных производных обозначают, что они берутся для значений а = Ь = А. Принимая во внимание (152), получаем:
84=_m/mi8«,
i\daj/ \ob /
откуда видно, что возмущения будут убывать и стремиться к нулю при условии
(I)/(I)l<h <5-,5з>
Если интерпретировать (151) как уравнение кривой в плоскости ab, то стационарные амплитуды найдутся как координаты точек пересечения кривой с биссектрисой угла между положительными координатными осями. Условие (153) означает, что угол наклона касательной в точке пересечения должен быть заключён между —45° и -|-45о.
Из фиг. 22 видно, что в задаче предыдущего параграфа это условие выполняется. Тот же вывод получается и путём вычисления, так как, согласно (135),
. /(а, Ь) = /(а-В^ + Л-(й + В), А =
ba У(д,~-ВУ+Ь ’ А-±В' bb \db)
в силу условия (139) последняя величина положительна и меньше единицы.
Изложенная процедура применима также и в том случае, когда а, b в соотношении (151) обозначают амплитуды в начале и в конце Целого колебания, состоящего из двух размахов.
Предположим теперь, что для хода справа налево и слева направо мы получили, как во второй задаче предыдущего параграфа, различные соотношения (143), (146)
&) = 0„ Д(&, с) = 0.
Пусть а = с = д, Ь — В суть величины амплитуд, соответствующие стационарному режиму. Тогда
Д(В, Л) = 0, /2(Л, В) = 0,
296
СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
[ГЛ. 5
так что А и В могут быть определены как координаты тех точек пересечения кривых (150)
А (6, а) = 0, /2(а, 6) = 0, которые лежат в первом квадранте.
Для исследования устойчивости полагаем а = А-\-Ъа, Ь — В-^-ЪЬ, с = и представляем уравнения (143), (146) в виде (= о, \ db J 1 \ да J (^}ba+(-^-}bb=Q> \ да / * \ до /
где под /х, /2 мы разумеем Д (6, а), /2(а, 6), а круглые скобки обозначают подстановку а = Л, b = В. Отсюда, исключая 86,
\ да )\ db / \ db )\ да J
Условие устойчивости будет - -
(dfA(dfa\ /( dfi\( dfo\ 1
k db Д да ) / \ да )\ db ) или с
(» / (4г) | < I (» / (4г)I <5-154>
что можно интерпретировать геометрически как соотношение между угловыми коэффициентами кривых (150).
Этот способ применим также для разыскания несимметричных периодических решений при симметричных зависимостях
/(а, 6) = 0, /(6, с) = 0. (5.155)
§ 5.13. Электронный генератор. Рассмотрим колебательный процесс в электронном генераторе, изучение которого имело большое значение для развития теории автоколебательных систем. Это устройство служит для получения переменных токов высокой частоты и основное своё применение находит в радиотехнике. Оно состоит из трёхэлектродной электронной лампы (триода), соединённой с колебательным электрическим контуром (фиг. 23), заключающим батарею (для более мощных генераторов — машину постоянного тока), сопротивление R, ёмкость С и самоиндукцию L. Электронная лампа представляет баллон, воздух из которого откачивается до глубокого вакуума. Тремя электродами являются катод /С, накаливаемый специальной батареей и испускающий свободные электроны, анод А,
§ 5.13]
ЭЛЕКТРОННЫЙ ГЕНЕРАТОР
297
служащий приёмником этих электронов, и сетка О, помещённая ближе к катоду и потому весьма сильно воздействующая на поток электронов и служащая для управления им. Лишь небольшая часть электронов захватывается сеткой, создавая в ней ток, которым мы будем пренебрегать при составлении уравнений. Основная масса электронов направляется к аноду и создаёт анодный ток /д, который, как показало исследование, может с достаточной точностью рассматриваться как нелинейная функция /(а) от так называемого управляю-
Фиг. 23. Схема электронного генератора.
щего напряжения
u = Ug + iUa. (5.156)
При этом Ua обозначает напряжение между анодом и като-
Фиг. 24. Аппроксимация f(u) ступенчатой функцией.
дом, a Ug— между сеткой и катодом; 7 есть малая величина, называемая проницаемостью лампы. Поэтому мы примем приближённо и = Ug и ia = f(Ug). (5.157)
t
Функция f(u) носит название характеристики лампы. Примерный вид её графика, полученного из опыта, изображён ниже на фиг. 33 (стр. 327) здесь мы аппроксимируем её ступенчатой функцией (фиг. 24) :
/(«) =
' 0 при и S при и
(5.158)
Для того чтобы система могла служить генератором колебаний, вводится обратная связь между анодной цепью и цепью сетки; на схеме, представленной на фиг. 23, это осуществлено с помощью катушки, включённой в цепь сетки и индуктивно связанной с анодной цепью; коэффициент взаимной индукции пусть будет Л4.
Обозначая ещё через U напряжение на обкладках конденсатора и через q ток в ветви анодной цепи, содержащей катушку L и сопротивление 7?, имеем:
и = J (ia~q)dt, U-L-^- = Rq,
298
СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
[ГЛ. 5
откуда
Lq + Rq + q = ia.
Так как
U = М — ив dt 9 то с помощью (157), (158) получается
Й Н-Я? + 4- Я =
И
<? + + =[ ° при ? < °- (5.159)
fe9S при ?>0,
где
—fr- '‘“РЖ- (S160)
При (7 < 0 мы имеем:
q -f- 2s(7 4" — О’
и последовательные амплитуды а, b связаны зависимостью
Ь = Ъа, (5.161)
где 8 обозначает не символ вариации, а декремент
8 = rw>, (5.162)
причём
Ш = ]Ла>2 — е2. (5.163)
Если же q > 0, то получается уравнение g + 2eg + ft2(g —S)=0,
которое отличается от уравнения затухающих колебаний с линей-
ным и кулоновым трением (§ 7) при том же условии q > 0 только
Фиг. 25. Определение стационарного режима электронного генератора.
знаком перед постоянной S. Мы получаем поэтому, следующее соотношение между последовательными амплитудами Ь, с, аналогичное (98):
c = 5&4-S(1+8). (5.164)
Применяя вторую процедуру предыдущего параграфа, мы должны положить
/2 (а, Ь) = 8а — b, j
ft(b, с) = 86 —c + S(1+8)/(5-165)
и для определения стационарного режима решить уравнения /,(/»> а) = 0, /2(д, ^) = 0>
J § 5.14] СЛЕДЯЩАЯ СИСТЕМА С ЛЮФТОМ 299
у
которые представляют две прямые в плоскости ab (фиг. 25), пересекающиеся в точке с координатами
Л=-[^Г, 5 = -^-. (5.166)
Так как 3 < 1, то абсолютная величина углового коэффициента для прямой /2 = 0 меньше, чем для А = 0. Поэтому, согласно (154), / стационарный режим устойчив.
§ 5.14. Следящая система с. люфтом. .Автоколебания могут возникать от разных причин в системах автоматического регулирования, где они обычно весьма вредны, так как ухудшают точность работы. В этом случае практическая цель изучения автоколебаний заключается в выяснении условий для их подавления. Одна из задач
Фиг. 26. Схема следящей системы с люфтом.
этого типа решена Краутвигом I5*24] и относится к следящей системе с люфтом, простейшая схема которой представлена на фиг. 26.
Как и в § 4.7, задающее и следящее движения являются, благодаря направляющим, прямолинейными и поступательными. Смещение задающего тела S* обозначим через s*, смещение следящего тела S — / через s, координату сервомотора — через q.
Тело S* несёт контактные ламели Lv L2, L3, разделённые изоляционными промежутками одинаковой ширины /С, а тело S — контактные ролики г2* Начало отсчёта для s выбирается так, чтобы j при $ = $* каждый ролик стоял в середине соответствующего изоля-1 Ционного промежутка. Ламели и ролики образуют контактную систему, 1 с помощью которой, как видно из схемы, происходят автоматическое i включение и реверсирование постоянного напряжения U, получаемого сервомотором Q с независимым возбуждением от генератора G.
300 СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ ’ [ГЛ. 5
Если следящее тело отстаёт от задающего, то ролики r19 на- |
катываются, соответственно, на ламели Л1} и генератор подает мотору напряжение имеющее тенденцию заставить его передавать на тело S усилие, направленное таким образом, чтобы оно догоняло тело S*. Если следящее тело опережает задающее, то ролики rt, г2 накатываются на ламели и знак напряжения
меняется. Между мотором и телом S имеется люфт 2В, который в реальной конструкции получается обычно за счёт неизбежной игры в зубчатых передачах. Начало отсчёта для q выбирается так, чтобы при q — s шпонка А стояла на середине люфта 2В. Инерцией следящего тела мы будем пренебрегать. Вледствие люфта и инерции сервомотора тело S, следуя за телом S*, совершает относительно него колебания. Координата может, вообще, изменяться по любой заданной программе s*=s*(2), но мы здесь ограничимся простейшим* случаем, когда $* = 0 и задающее тело неподвижно.
Предположим сначала, что в некоторый момент следящее тело, двигаясь вслед за мотором, достигает крайнего положения направо и останавливается. Принимая этот момент за начальный и учитывая люфт, имеем начальные значения
Если а<^-, то ролики останутся на изоляционных промежут-ках, напряжение не будет включено и движение прекратится. Поэтому мы предположим, что
В этом случае ролики гх, окажутся на контактных ламелях Z2, Z,3, генератор будет давать напряжение —U и мотор начнёт вращаться по часовой стрелке. Тело S при этом будет оставаться на месте до тех пор, пока в некоторый момент t[ мотор не выберет весь люфт 2В (фиг. 27) и мы получим:
q = a — В, s = а> q = qv
Так как мы считаем тело S лишённым инерции, то следует представлять себе, что в момент оно без удара входит в зацепление с мотором и движется с ним с той же скоростью налево до некоторого момента /2, когда контактные ролики отрываются от ламелей, так что
Так как в этот момент напряжение выключается, то система продолжает затем двигаться по инерции, пока в момент t* ролики не пройдут изоляционных промежутков и
К о К
q 2 $ <2 * Q
§ 5.14] СЛЕДЯЩАЯ СИСТЕМА 6 ЛЮФТОМ V 301
После этого ролики rt, г2 накатятся на ламели £*, Л2 и генератор даст на зажимы сервомотора напряжение -}- U, в результате чего торможение мотора усилится и в некоторый момент t± он остановится, причём
q =— (b-^B), s = — b, q = 0. t
Описанные явления. составляют одно полуколебание, и затем всё начинает повторяться в обратном порядке.
Случай, когда скорость сервомотора обращается в нуль в течение второго или третьего из указанных четырёх промежутков врет
Фиг. 27. Диаграмма движения следящей системы
* с люфтом.
мени, мы можем не рассматривать, так как тогда система остановится, совершив одно полуколебание.
Очевидно также, что если в начальный момент q не равно а -|- В, а имеет любое другое значение в интервале (а — В, a -j- В), то либо система остановится, совершив одно полуколебание, либо для второго полуколебания мы будем иметь начальное расположение
q =— (b-\-B), s = — b, <7 = 0, тождественное рассмотренному выше.
Уравнение движения сервомотора и уравнение электродвижущих сил в цепи его якоря суть
т = — \q и,
± U—cq — Rit
где I обозначает силу тока в цепи, т — приведённую массу сервомотора, F—момент кулонова трения, R — омическое сопротивление Депи якоря, X и с — постоянные коэффициенты. Члены — X q, ci в первом уравнении представляют, соответственно, момент линейного
302 СОБСТВЕННЫЕ кОЛЕБАНИЯ НЕЛИНЕЙНЫк СИСТЕМ (гл. В
трения и вращающий момент сервомотора, член —cq во втором уравнении— противоэлектродвижущую силу, возникающую при вращении якоря. Из энергетических соображений мы имеем один и тот же коэффициент с в выражениях момента и противоэлектродвижущей силы. Кулоново трение мы сначала будем считать приложенным только к телу S, и потому знак перед F зависит от направления его движения; если же тело S и мотор не находятся в зацеплении, то F нужно заменить нулём. Знак перед U зависит от того, на каких ламелях находятся контактные ролики; если они движутся по изоляционным промежуткам, то U должно быть заменено нулём.
Исключая силу тока Z, имеем:
dq . , • г, । ± U — cq
M-£ + bl = + F+c-------1
ИЛИ
— !L
dt 4 в ’ где
т—Я™
1 ~ СВ ’ с ’
FR
С
Введём безразмерные величины:
t Bq
*- —-— - у — . — —=—
• т ’ и Т ’
то уравнение (167) принимает вид
_=-х + р,
(5.167)
(5.168)
(5.169)
(5.170)
(5.171)
(5.172)
(5.173)
где точка применяется теперь для обозначения дифференцирования по
# = (5.174)
ат
Путём почленного деления двух последних уравнений находим:
rfx _ Р— х dx х .
§ 5.141
Следящая система С люфТом
303
или
ах =----г.
р —х
Отсюда, интегрируя между начальными ними значениями хш, хш,
значениями ха,
и конеч-
%<*>
Вводя функцию
и её обращение
можем написать:
Так как
x-f-ln(l —х)
х = м су),
ц>
при X при X
(5.175)
(5.176)
(5.177)
(5.178)
*ш — Х« =
^ = £(х)
м
а
%
X,
£(0) = 0, £(2) = 2,
(х) = 1 —
0 при х < О, О при 0 < х О при 1 < х.
(х) = —
0.
то график L(x) имеет вид, изображённый на фиг. 28. Обратная функция М (у) имеет ветви (у), 2И2Су), М4(у), которые берутся в формуле (178) соответственно при ха/р, хш/р < 0; 0 < хв/р, хш/р< 1; 1 < хв/р>*ш/р. Ветвь М3(у) мы определим позже.
Так как
то
lim я?->—оо
41п(1 - х)1 = 0, I
lim
X -> — ОО
±£(х)1=1»
и мы получаем необходимую нам в дальнейшем формулу
(5.179)
где х стремится к нулю по положительным значениям.
304
СОБСТВЕННЫЕ КОЛЕБАНИЙ НЕЛИНЕЙНЫХ СИСТЕМ
(гл. 5
С другой стороны, при у > 0 величина Л42(—^/^ представляет тангенс угла наклона к оси —у радиуса-вектора кривой х — М2(—у)\ поэтому, как сразу видно из чертежа,
Нш Г±М2(-^)1 = 0, t/->oo L У J
и мы получаем другую нужную формулу
lim
хМ2
(5.180)
Формулы (177), (178) непригодны при хв = р; в этом случае мы имеем из (173) решение
и, в частности, хш = р. Это значение может быть получено из общей формулы (178), если ввести в качестве третьей ветви для Af(.y)
функцию
M3CV)=1,
изображаемую на фиг. 28 прямой, параллельной оси ординат.
Обозначая
S = -FT’ 1> = Zr4-’ <5Л81>
‘ мы получаем для четырёх частей полуколебания, охарактеризованных выше с качественной стороны, нижеследующие значения.
Интервал (0, rj:
р= 1,
т« = о> xa = $4-z/2, хв = 0,
== ^/2, Хц) •—• Хр
где, согласно формуле (178),
—- хх = М2 ( z),
так что
— 1 < ^ < 0.
Интервал (тх, т2):
Р = —1 +Л
== ^1» = Ё ^/?» Хв = Хр
= т.2, хш = А?/2 #/2, хш = х2,
(5.182)
§ 5*14j СЛЕДЯЩАЯ СИСТЕМА С ЛЮФТОМ
305
где Х2 определяется из условий
Е —£/21
М, L
при 1
при О
iW4 L
при
Интервал (т2,
а — ^2»
— т3’
где х3 определяется из
х, = k/2 — z/2,
v.w = — k/2 — zl2,
уравнения
(5.184)
ц>
хв — — й/2 £/2, хв — х3,
хш = —tj —^/2, хш = 0,
где т| определяется, согласно (177), из уравнения
(5.185)
А
X
1
Пользуясь полученными формулами, можно, считая £, zt f заданными, выразить т) через х3, затем х3 — через х2 и Хд — через Е. А так как хр в свою очередь, выражается через’ z, то в итоге мы получим соотношение между последовательными безразмерными амплитудами вида
"П = ? (5).
Для стационарного периодического режима 5 = 7) и
5 = <?(&)»
откуда определяется Е. Например, считая z, f фиксированными, выразим Е как функцию от £; так как изоляционный промежуток проходится системой по инерции, то эта функция будет определена лишь на некотором конечном интервале (0, £с), вне которого
20 Зак. 1474. Б. В. Булгаков
306 СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ систем [гл. S
автоколебания невозможны. Критическое значение kc определится, если потребовать, чтобы $ = ц = k/2, так как тогда ролики в крайних положениях системы будут находиться как раз на границе изоляционных промежутков. В этом случае = т2, т3 = т4, х3 = 0, и из (182), (184) получается
— *2 — ' ^2 ( ^)> — fL
или
(5.186)
Эта формула даёт критическую величину приведённого изоля-
ционного промежутка k в функции приведённого люфта z и приве-
дённой силы трения /. На фиг. 29
О Q2 Q4 0.6 ад 1,0 1,2 14 1,6 1,8 2,0 2,2 2.4 Z
Фиг. 29. Критическое значение &k в функции от z и f для случая, когда кулоново трение приложено к следящему телу.
эта зависимость представлена графически. В частности, при /=0, применяя формулу (179), имеем: (*с)л=о=^2( —*)• (5.187)
Из графика усматривается следующее:
1) Если люфта нет, z = О, то критическая величина изоляционного промежутка также равна нулю при всех / и автоколебания невозможны.
2) При данном z критическая величина изоляцион-
ного промежутка тем меньше и потому точность следящей системы тем больше, чем больше /. Таким образом, кулоново трение действует стабилизирующим образом.
3) При сколь угодно большом /, в частности при /> 1, суще-
ствуют такие конечные, хотя и малые величины изоляционного промежутка, при которых автоколебания возможны. Это связано с тем, что при пробеге люфта мотор разгоняется, будучи свободен от куло-нова трения.
4) При увеличении z критическая величина изоляционного промежутка стремится к конечному пределу.
Рассмотрим теперь второй вариант задачи, когда кулоново трение приложено не к следящему телу, а к мотору. В этом случае система может совершить более одного полуколебания только при /< 1, что мы и будем предполагать. Интервалы (0, (тх, т2) могут быть объединены в один.
§ 5.161
Паровая машина
30?
Интервал (0, т2):
Р = —1 +/>
та = 0, ха = $-|-г/2, ха = 0,
Тф = т2, Ху, = fe/2 £/2, хш = х2, где __*2 _ л* ( е—^/2+г\
—1+/_ 2\ 1—/ г
(5.188)
Формулы для двух остальных интервалов остаются прежними. Для определения критической величины изоляционного промежутка ke полагаем опять $ = -q = &/2, т3 = т4, х3 = 0, что даёт:
;2 = (-1+/)Л42(—г47), ke = -fL(^
или
к~-fL [ - м2 (- з4у)
(5.189) ’
Эта зависимость представлена графиком на фиг. 30. При /=0
мы получаем, как и в первом варианте задачи,
(^c)f=0 = ^2 ( ^)>
а при /= 1, согласно (180),
(*е)лл = 0. (5.190)
Иными словами, в противоположность первому варианту задачи, автоколебания при /^>1 невозможны. Это связано с тем простым обстоятельством, что при указанном условии мотор не имеет возможности разгоняться.
Фиг. 30. Критическое значение k в функции от z и f для случая, когда кулоново трение приложено к сервомотору.
§ 5.15. Паровая машина. Паровая машина, работающая на стационарную нагрузку, представляет пример автоколебательной системы несколько иного типа, чем рассмотренные выше, так как её стационарный периодический режим является ротационным движением в смысле § 2 и может быть изображён на цилиндрической фазовой диаграмме с помощью замкнутой кривой, окружающей ось цилиндра.
Примем за обобщённую координату q путь, пройденный пальцем кривошипа (или какой-нибудь другой условной точкой маховика) и пропорциональный углу поворота главного вала.
Пусть р обозначает радиус кривошипа и K(q) — вращающий момент, разделённый на р. Положение всех частей мащины
20*
ЗЬ8 Собственные кСлеёаНий нелинейных Систем (гл. 5 восстанавливается при увеличении q на 2с = 2гср и K(q) является периодической функцией от q с периодом 2с. Мы мржем положить /С(#)== — D-\-F(q)> где D — среднее значение вращающего момента за один оборот, a F(q)— его переменная часть со средним значением, равным нулю: +с +с
D = i J dq' I = -c -c
Пусть ещё = EG(q) обозначает разделённый на р момент нагрузки, причём Ё есть его среднее значение, а О (р) — периодическая часть. При этом здесь и в дальнейшем имеется в виду вращение машины в одном определённом направлении, например в сторону роста q, что соответствует верхней половине фазовой плоскости. Полная обобщённая сила будет Q — D — Е—V'(д'), где
в
V(.^ = f[-F(q) + O^]dq. О
Масса машины, приведённая к пальцу кривошипа, есть
т (q) = тх + 4- /п3 + a (q), (5.191)
где и т2 обозначают приведённые массы маховика и других вращающихся частей, а +<*((?)— приведённую массу всех остальных частей, кроме вращающихся, причём т3 есть её среднее значение, a a(q)— периодическая часть.
Предполагая сначала, что D = E, так что вращающий момент в среднем уравновешивает нагрузку, и обозначая через р канонический импульс m(q)q, получаем консервативную систему с полной энергией
4-У(д);
при достаточно большом значении константы энергии v система будет совершать ротационное движение.
Если D=f=E, то функция Гамильтона будет
Так как V(q)— конечная периодическая и потому ограниченная функция, то интеграл энергии H' = v или
P2 = 2m(9)[v + (D — E)q — V(q)\ .
показывает, что при некоторых начальных условиях скорость будет либо неограниченно возрастать, либо убывать до нуля.
§ 5.15] , \ ПАРОВАЯ МАШИНА „ 309
Чтобы этого избежать, ставят регулятор, который делает вращающий момент зависящим не только от q, но и от скорости r = q по такому закону:
^,p) = D(r) + F(^r), (5.192)
что K(q, р) при данном q монотонно убывает с возрастанием г или, что то же, с возрастанием р, предоставляя нагрузке притормаживать машину. Мы можем при этом включить* в нагрузку возможные сопротивления, зависящие от скорости, так что момент нагрузки обращается в функцию
L(^p) = E(r) + O(^,r), (5.193)
которая должна быть, очевидно, монотонной возрастающей по отношению к р. Полная обобщённая сила
Q{q,p) = K(q, р) — L(q,p) (5.194)
будет монотонной убывающей функцией от р, так же как и K(q, р). Система не является теперь консервативной, и мы имеем уравнение живой силы
dT .dq
dt ~Q(q'p>dt' где
- л- __ - рз - ........ :
. ’ 2т (q)'
или же дТ • . дТ • • .
Уравнение — . ,..
Q(p,p) = Q ' - *
представляет некоторую кривую в фазовой плоскости, состоящую из конгруентных кусков, отсекаемых прямыми, проведёнными параллельно оси Ординат на расстоянии 2с друг от друга. Увеличивая, если нужно, значения /С(д, р), мы можем, по свойству этой функции, увеличить все ординаты кривой Q и достичь того, чтобы она лежала выше оси абсцисс; в этом случае система не будет, очевидно, иметь никаких положений равновесия. Если - построить ' топографическую систему кривых
Т'(9.р) = ® или - ~
р = + V 2отп (?),
состоящих также из конгруентных кусков, и выбрать две кривые.^, касающиеся кривой Q снизу и сверху, то получится полоса,
заключающая .кривую Q. При значениях константы энергии v' топографические кривые проходят ниже кривой Q, функция Q(q, р)
ваг
310
СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
[гл. 5
на них положительна и
о, м дТ р . п дТ
Так как в верхней полуплоскости > 0, то ,
дТ
ъ ПР°-
порциональны направляющим косинусам обращённой кверху нормали топографической кривой. Последнее неравенство показывает, что фазовые траектории образуют острый угол с этой нормалью. Проводя аналогичное рассуждение для v" > -у2, убедимся, что все фазовые траектории, пересекая топографические кривые -у', -у", проходят с обеих сторон внутрь образуемой ими полосы. Если разрезать фазовую плоскость параллельно оси ординат на ленты шириною 2с и наклеить на цилиндр, как в § 2, то кривая Q и топографические кривые обратятся в замкнутые циклы, окружающие ось цилиндра.
Согласно сказанному выше, фазовые траектории только входят внутрь полосы между циклами v' и -у", но ни одна не выходит. Так как эти циклы могут быть проведены сколь угодно близко к циклам vlf
v2, то в полосе между последними должна заключаться некоторая предельная траектория.
Полоса лежит выше оси абсцисс и фазовые скорости на ней всюду положительны, вследствие чего предельная траектория может быть только предельным циклом, окружающим ось цилиндра. Этот цикл
определяет стационарное ротационное движение, для которого
<7(f+P) = 9(0 + 2c, p(t-\-P)=p(f).
Остаётся доказать единственность этого режима. Для этого 1°*Ч напишем уравнение живой силы в виде dT . .
Jq— P)dcl
и допустим, что существует два периодических режима, соответствующих циклам А == А (?), ==/2 (?)• Интегрируя от qQ—с до
получим:
1711^°0 = °= f Ш M)dq,
Зо-С
во+с
= J <?(?, 4(?)И?.
«0-с
откуда
ffu+C
J [Q(?. А (?))—<? (?,/>(?)) И? ==0.
§ 5.16] ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ 311
Но так как два цикла не могут пересекаться, то разность —р2 имеет определённый знак; вследствие монотонности функции Q(q, р) то же самое можно утверждать и относительно разности Q(#, р^) — — Q(q> А)* Поэтому последний интеграл не может равняться нулю, так что предположение о существовании двух периодических решений привело нас к противоречию.
Приближённый метод нахождения периодического решения и расчёта необходимого веса маховика изложен ниже (§ 24).
Г. МЕТОД ПУАНКАРЕ
§ 5.16. Периодические решения уравнений собственных колебаний, содержащих малые параметры. Будем рассматривать собственные колебания натуральной склерономной системы с постоянной приведённой массой т, находящейся под действием сил, зависящих от каких-либо параметров р^, ..., рьг, которые мы желаем выделить, так что
— V' + Q = — q, |х]............М-
Уравнения движения будут
.....>4 <5л95>
В настоящем разделе мы займёмся получением периодических решений по методу Пуанкаре. Такие решения соответствуют стационарным периодическим процессам, которые нам уже приходилось неоднократно рассматривать при изучении консервативных и автоколебательных систем. С математической точки зрения главная ценность метода состоит в том, что при известных условиях он даёт возможность представить искомые функции сходящимися рядами по степеням параметров р^, ..., рьг и получить, таким образом, хотя и частные, но точные решения нелинейных уравнений (195).
Предположим, что при некоторых определённых значениях параметров удалось найти частное решение q = q* (f), р = р* (£), которое удовлетворяет соотношениям
<7* (А)+ Р) = ?* Р* ('о + Р) = Р* %)> (5-196)
где tQ, Р — постоянные. Мы будем называть это решение порождающим. Очевидно, что оно будет периодическим с периодом Р. В самом деле, в момент мы имеем те же условия, что и в момент tQ. Поэтому, в силу основной теоремы о существовании и единственности решений, удовлетворяющих заданным начальным условиям, мы имеем при любом t:
q*(t+P) = q*tf)> Р* Р) = Р* (0> (5.197)
и, следовательно, Р есть период, а величина
$ = %kIP (5.198)
312
СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
(гл. 5
— угловая частота стационарного колебания. Очевидно? что функции q*(t— т), p*(t—т), где т — постоянная, описывают тот же стационарный процесс, лишь запаздывающий на время т. Так как дифференциальные уравнения не содержат явно А то эти функции также образуют решение, зависящее от одной произвольной постоянной; такую более общую форму мы в дальнейшем и примем за порождающее решение.
Для простоты можно предположить, что уравнения, которым удовлетворяет порождающее решение, соответствуют нулевым значениям параметров пр •••> Hr и имеют вид
s-0......°)- (О-1")
Мы будем называть эту систему упрощённой, так как она, обычно, действительно проще обшей системы (195), благодаря чему для неё и удаётся получить точное периодическое решение q*(t — т), p*(t—т). Физически переход к упрощённой системе обозначает пренебрежение какими-либо второстепенными факторами и, в частности, в механической задаче, отбрасывание каких-нибудь малых сил.
Основной вопрос заключается теперь в том, существуют ли периодические решения при значениях параметров, отличных от нуля, т. е. при полном учёте всех обстоятельств явления.
Так как время не входит явно в уравнения (195), то общее решение может быть представлено в виде
Hi»
Н1»
• э
• >
(5.200)
причём мы предполагаем, что для порождающего решения, которое получается при . = нУ = 0, постоянная С имеет значение С*, так что
т, С*, 0,
fz(t—т, С*, 0,
ty = q*(f—т), | 0)=р*(/—т). J
(5.201)
Искомые периодические решения должны заключаться в (200), но будут, вообще, иметь период Р = Р-|-ДР, отличный от Р. Условия периодичности, аналогичные (196), имеют вид:
ft (A) Ч~ Р ~~~ ’с» Hi> • • • > Hr)
fi (^о Q Hi> • • • > Hr) === 0» т» ^» Hi» •••> Hr)
/2(^0 ^» Hi> •••> Hr) = -
(5.202)
и поставленный выше вопрос сводится к тому, можно ли найти величины
Р'= Р'(уп ,,., Hr)» С=С(Нр ••» Hr)» (5,203)
§ 5.17] СИСТЕМЫ, БЛИЗКИЕ К ЛИНЕЙНЫМ 313
удовлетворяющие этим конечном уравнениям. При ==...= = О
такими значениями будут Р' = Р и С=С*, так как тогда условия периодичности принимают вид:
?*0о+^ — '') = «'* 0О—г)> Р* 0о + р ~ т) = Р* 0о —"')•
Поэтому, согласно основной теореме о неявных функциях, решения (203), близкие к Р, С*, существуют и для ненулевых, но достаточно малых значений параметров, если только будет отличен от нуля функциональный определитель, составленный известным образом из частных производных от левых частей уравнений (202) по Р' и С. Если же это условие не выполняется, то искомых решений не существует или же Р' и С не определяются в отдельности, а связаны лишь одним соотношением, содержащим также 14, ..., р.г. В том случае, когда значения (203) удаётся найти, подстановка второго из них в общее решение даёт искомое периодическое решение, которое оказывается зависящим от t—т и параметров 14, ..., |лг и имеет период Р’> также зависящий от этих параметров. Зная это, мы будем в частных задачах прямо искать периодическое решение в виде системы функций только что указанной формы, без предварительного составления общего решения.
§ 5.17. Системы, близкие к линейным. Мы ещё вернёмся к общим вопросам существования периодических решений в части III, а сейчас займёмся частным типом систем, близких к линейным, содержащих один параметр рь, для которых ф имеет вид:
? (я> Я> н) = <^Я — Я< и). (5.204)
Этот случай был исследован А. А. Андроновым. Исключая р из уравнений (195), находим:
<7+ ?(?>?> Н) = о (5.205)
или
(D2 + о>2) q = нФ (?, н)> (5.206)
где
При н = 0 получаем упрощённое линейное уравнение (02^0)2)^^ о, (5.207)
решения которого
q* = A cos со (t—т) (5.208)
являются периодическими с угловой частотой со и периодом
Р = ^-. (5.209)
Мы, однако, увидим в дальнейшем, что, вообще, лишь при некоторых определённых значениях А* постоянной А решение будет
314 СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ (ГЛ. 5
действительно порождающим, т. е. представляющим предел, к которому стремится при р —> 0 некоторое периодическое .решение нели--нейного уравнения (206). Мы обозначим это последнее череву (я, р), где и есть новая независимая переменная, связанная с t соотношением й = со (1 —|—ос) (t—т), (5.210)
а через а обозначена некоторая постоянная. Мы будем определять её j вместе с искомой функцией q {и, р) из условия, чтобы период по и 1 этой функции был всегда равен 2-гс. Тогда период по t будет, оче- 1 видно, I
p'-vn-.-nr <5-21» |
а так как он должен зависеть от параметра р и обращаться в Р при р = 0, то а есть функция от р, обращающаяся в нуль вместе с аргументом: а == а (р), а(0) = 0. Угловая частота искомого перио- \ дического решения будет i
а/ = 2те/Р' = со (1 + а), (5.212) j
так что 1
и, следовательно, а есть относительное изменение частоты, или по-
правка на частоту. Полагая >
°. = Е. <5-213) |
получаем из (210) , 1
О = О„ш(1+а). (5.214) |
Если разуметь под q* (и) порождающее решение, то I
q* — q(u, 0), (5.215) I
Л
а так как при р = 0 соотношение между и и t принимает вид | й = со(/—т), то, согласно (208), <
q* = Acosu. (5.216)
В дальнейшем понадобится ещё выражение q*' = — A sin й, (5.217) |
У-
где штрих обозначает дифференцирование по и. Мы займёмся теперь вычислением значений А* и производных
• э
(5.218)
(5,219) j
§ 5.18]
ПЕРВОЕ ПРИБЛИЖЕНИЕ
315
что позволит затем представить #(а, у.) и а (у.) в виде конечных или бесконечных рядов по степеням у.. С помощью (214) имеем:
i(D= + »>) = 2OD„»|,
(02 4- 0)2) = 2 Г ОО„ш + 0^0)3 (^l,
ф2 \ । / Iм Ф3 \«F / J
(5.220)
С другой стороны, если заменить q через q (и, рь), то
“ ♦« sj+Ъ “(1+'‘)+ж " Я+*
и аналогично для второй и высших производных от ф по |л. Поэтому, делая подстановку q = q(u> р) в уравнении (206), дифференцируя один, два, ... раз по у. й полагая затем рь = 0, получим следующие уравнения для г, &, с, ...:
0)2 (Z)2_|_i)r==_ 2«Ж£9* -|-ф, (5.221)
о)2 (О® + 1) $ = — ^bDur — 2<о9 (с _|_ b'*) Dig* +
4-2[фвг + ф-ш(г' + ?*'£) + %.]> (5.222)
. При этом мы условимся, что всякий раз, когда здесь или в дальнейшем функция ф или её частные производные написаны без указания аргументов, под последними нужно понимать соответственно q* = Acbsu, q* — — Лео sin и и 0.
§ 5.18. Первое приближение. Заменяя в уравнении (221) функцию q* её выражением (216), получаем:
(А)®4-1)г = 2Мсози + ^. (5.223)
Для того чтобы это уравнение относительно функции г допускало периодическое решение с угловой частотой 1 по независимой переменной к, нужно, чтобы коэффициенты при cos и, sin и в разложении правой части в ряд Фурье были равны нулю:
cos а, — A® sin а, 0) cos с da = О,
^(4)^
— Am sin а, 0) sin a da = 0.
316 СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ [ГЛ. 5
Через о здесь обозначена переменная интеграции. Второе из двух последних соотношений представляет конечное уравнение относитель-
но Л; его решения Л*,
Фиг. 31. Определение порождающих амплитуд.
если они существуют, мы будем называть порождающими амплитудами. Они могут быть определены графически (фиг. 31) как абсциссы точек пересечения кривой, изображающей функцию Я (Л), с осью абсцисс. Заметим, что функция Я (Л) нечётна; в самом деле,
Н(-А) =
~ ф (— Л cos о, Лео sin о, 0) sin о do
или, после замены переменной а —р-|-к, о ' '
Н(— Л) = J (Л cos р, — Ло> sin р, 0) (— sin р) dp =
—2я ’
4-тс
= —-i- J (Л cos р, — Л(о sin р, 0) sin р dp = — Н (Л).
—«
После того как порождающие амплитуды определены, из первого уравнения (224) можно найти первую поправку на частоту Ь.
Общее решение для г будет . . ............ .
с -- г — В cos и Bt sin м-|-г*, (5.225)
где г* есть частное решение неоднородного уравнения, так что в . * « * Ь »
/*'=-^'(«)> (5.226)
причём
- и
Р (а) — J (2о)9 ЬА cos а -|- ф) sin (и —,а) do, (5-227)
о ‘ /
<. k - S а. , L / - * •
и ь t ' ......- ;
р' (м) = £ (2ы*ЬА cos а -|- ф) cos (и— а) da. - ; (5.228) о
Так как В,.ВХ на данном этапе вычисления; не могут быть определены, то пока в качестве приближённого выражения для q может служить лишь функция (м), в которой Л есть, одна из порождающих амплитуд; для а мы имеем приближённо:
(5.229)
§ 5.19]
ВТОРОЕ Й ВЫСШИЕ ПРИБЛИЖЕНИЯ
§ 5.19. Второе и высшие приближения. Заменяя в уравнении (222) функции г их выражениями, получаем:
1) = 4о)ай (В cos и 4~ В± sin и) 4~
+ 2ш2 (с + 62) A cos и 4~ 2В (ф? cos и — ф^со sin а) 4~
4- 2ВХ (фа sin и + ф^а) cos и) — 2ф^соМ sin и — 4ш2ьЬ1г* 4»
+ 2 (Фе'* + Ф .«г*' + Фи.)-
Пользуясь дифференциальным уравнением (223), имеем:
Dlr* = 2bA cos и -|- — г*,
и уравнение для s принимает вид:
(Di4" l)s = 4Ь (В cos и~]~В1 sin и) 4-2 (с— 3№)А cos и -|-
—• М Ф^ sin а+— ф)+(фдГ* + Ф^<иг*/ + Фи). (5.230)
Так же, как и в первом приближении, мы получим условия периодичности для $, приравнивая нулю коэффициенты при cos а, sin и в разложении правой части в ряд Фурье:
2ш26В + со2 (с — 3&2) А +--
—те
—те
q sin а 4“ ф.<° cos °) cos a da--------J
—те
j [2b (оо2/** — ф) 4- ф^* 4- Ф^г*7 4“ ф|1] cos a da = О, —те
—те
(ф^ cos о — ф^<о sin a) sin a da 4~
~ (ф3 sin а ф .а) cos о) sin a da —
—те
— те
<
—те
318 Собственные Колебания Нелинейных систем (гл. 5
<
Интегралы, входящие в эти условия с множителем могут быть с помощью уравнений (224) преобразованы следующим образом:
—«
cos a da = —
дФ , cos a da =
да
—те
—тс
_^№cosa]i;
sin <з d<3 — О,
(5.231)
—те
sin a da =
a
—тс
— ~л 1Ф sin
—тс
J cos a da = — 2o)2&k. — TC
Обозначая далее
и
у (и) — J* (Л cos a, — До) sin a, 0) cos a — о
— cos °> — A® sin °» 0) ш s^n °1 sin — a) da =
и
= I ф (Д cos o, — До) sin a, 0) sin (a — a) da, (5.233) OA J
0
и
8 (a) = J (Д cos a, — До) sin a, 0) sin a sin (a — a) da, (5.234) о
и
e (и) = J* {2&a)2 [p (a) — ф (Д cos a, — Да> sin a, 0)] о
-Ц- фд (Д cos a, — Да) sin a, 0) p (a) -|-
ф • (Д cos a, — Да) sin a, 0) a)^ (a) -|-
-|- ф„ (Д cos a, — Да) sin a, 0) a)2} sin (a — a) da, (5.235)
* 3'
§ 5.19]
ВТОРОЕ И ВЫСШЙЕ ПРИБЛИЖЕНИЯ
319
мы имеем:
и
Y (а) = J (Л cos о, — Аш sin а, 0) cos а — о
— (Л cos а, — Лео sin а, 0) со sin а] cos (и — а) da =
и
= J <J> (Л cos о, — Лоо sin а, 0) cos (и — а) da, о ,
и
8' (*) = J (Л cos а, — Лоо sin а, 0) sin a cos (и — a) da, о
и
гг (ц) — J* {2&со9 [р (о) — (Л cos а, — Лоо sin а, 0)] -|-о
+ cos °> — Ла> sin °> 0) р (а) 4“
+ Фд (A cos °> — si*1 °> 0) (°) +
+ %. cos °> — A® sin °> 0) о*2} cos (# — °) da.
(5.236)
(5.237)
(5.238)
Условия периодичности могут быть теперь записаны в виде
2<оаЛ 4--1 / (2 л)
ш2 (С _ 3£2) _ J- (2л)
А + е' (2л) = О, 1 TWO2 х '
(5.239)
_ JL 7 (2л) В + -1- (2«) А - ± е (2л) = 0.
Мы видим, что исключилось из этих условий и потому остаётся произвольным. Второе условие разрешимо относительно В, если
cos а, — Лоо sin о, 0) sin a da =/=0
—тс
или
Я'(Л)=/=0.
(5.240)
Это неравенство означает, что в точках, соответствующих порождающим амплитудам, кривая Н (Л) на фиг. 31 должна пересекать ось абсцисс, а не касаться её.
После того как В определено, мы из первого условия (239) найдём вторую поправку на частоту с.
Пользуясь интегралами р(я), Т(я)> 8 (и), 8 GO и их производными, легко написать и общее решение для $, которое будет содержать Две новые постоянные С, Ct.
320 СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ [ГЛ. 5
Отметим ещё следующие тождества, получаемые сложением у (2it), 7'(2it) соответственно с интегралами (231) и (232):
4” к + «
7(2я) = j* tynda, (2и)— 2ю2&тс = j* фд da. (5.241)
— тс — тс
Как мы убедимся ниже, во многих задачах имеем:
4-тс ' ' 4 . '
Ь — — 2м#А f (A cos а’ — A® sin °’ 0) cos ° = (5.242)
♦ *
—тс » ,
в этом случае и
cos а, — A<a sin а, 0) sin (а — о) da, (5.243)
о
© (а) = j* [фд (A cos а, — Лю sin а, 0) р (а) -[-о
+ ф • (Л cos а, —- Лю sin а, 0) юр' (а) al
+ фр, (Л cos а, — Лю sin а, 0) ю2] sin (а — a) da,
и
Р' (а) = J* ф (Л cos а, — Лю sin а, 0) cos (а — a) da, о
(5.244)
(5.245)
а' (а) = J [фв (Л cos а, — Лю sin а, 0) Р (а) -ф-о
4“ Ф^ cos а, — Лю sin а, 0) юР' (а) -|-
-ф“ Фр, (Л cos а, — Лю sin а, 0) ю2] cos (а — a) da. (2.246)
Для 7 (я), Y Си) остаются в силе прежние выражения, но мы можем написать:
'Г(«) = ^?(«). /(«) = Д ?'(«)• (5.247)
Условия периодичности принимают вид:
7' (2и) В 4“ оРпАс 4- е' (2^) = 0,
и дают:
1 е (2к) ___ Y (2тс) е (2тс) — у (2гс) е' (2тс)
<о2 у (2те) ’ С <о4кЛ7 (2^)
(5.248)
(5.249)
§ 5.20]
ЛИНЕАРИЗИРУЮЩАЯ ЧАСТОТА
321
Если функция ty(q9 q9 |л) является аналитической по всем трём аргументам, то мы можем, по образцу второго приближения, вычислить и дальнейшие приближения сколь угодно высокого порядка. При этом постоянные Сх, . будут оставаться произвольными; мы можем либо приравнять их нулю, либо определить из какого-либо начального условия при и = 0, так как решение уже содержит произвольную фазовую постоянную т, введённую при замене независимой переменной. С другой стороны, как можно убедиться, условие (240) обеспечивает однозначное определение остальных постоянных С, D, ... и поправок на частоту d, е9 ... Сходимость рядов
? = ?* +jj-'lt+sj-sP’2+ • • а=-йи-|--ср,2+...
(5.250)
при достаточно малых р., а следовательно, и действительное существование формально вычисленного решения, вытекает из общих теорем Пуанкаре [5-30] и Мак-Миллана [s-nJ.
Следует заметить, однако, что определение порождающих амплитуд, представляющих нулевое приближение для амплитуд искомого периодического решения, не зависит от сходимости рядов.
§ 5.20. Линеаризирующая частота. Пусть уравнение рассматриваемой системы имеет вид:
?+/(?> ?) = 0, (5.251),
где /(0, 0) = 0, так что q = Q есть положение равновесия. Если при этом f(q, q) не содержит натурального параметра, с помощью которого эта. функция могла <5ы быть непосредственно представлена в форме (204), то мы будем исходить из некоторой линеаризирующей частоты со, которая должна быть определена в дальнейшем таким образом, чтобы порождающее решение, удовлетворяющее упрощённому линейному уравнению (207), возможно лучше аппроксимировало искомое периодическое решение. Положим
4» (q, q) = rfq—f (q, q) (5.252)
И рассмотрим вместо данной задачи более общую, вводя безразмерный параметр р и определяя <р(^, q9 р) соотношением
? (?> Ч, И) = — НФ (?> 9) = С1 — н) ^Ч + Н/(?> Ч)- (5.253)
При р = о мы получим тогда упрощённую систему, для которой ?(?> q9 р) обращается в о>2#, а при р=1—заданную первоначальную систему, для которой <р(у, q9 р) приводится к /(^, q).
21 Зак. 1474. Б. В. Булгаков
322
СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
[гл. 5
Чтобы найти линеаризирующую частоту, потребуем, например, чтобы первая поправка b была равна нулю и оо представляла частоту а/ искомого решения с точностью до членов, содержащих р.2.
Заменяя в (224) функцию ty(q, q) её выражением через /(#, q), получим два уравнения:
®9 = -Т «Л J
—те
cos о, — А(й sin о) cos a da,
(5.254)
а, — Аа> sin a) sin о da = О,
—тс
из которых (о определяется вместе с порождающей амплитудой А.
§ 5.21. Приложение к консервативным системам. В качестве примера рассмотрим консервативную систему, описываемую уравнением
?+/(?) = О-
Для определения А и со мы имеем соотношения (254) или
со2 (Л) =
cos a) cos о da,
+ тс
f(A cos a) sin а da = 0.
(5.255)
(5.256)
—те
Второе из них удовлетворяется тождественно, так как, обозначая через F(q) первообразную функцию для f(q), мы имеем:
4-те 4-те
J /(Л cos о) sin a da = —J f(A cos a) d (Л cos о) — —тс —тс
=—4 cos »)]+:=о.
Таким образом, Л остаётся неопределённым, и уравнение допускает семейство периодических решений, зависящих от двух произвольных постоянных Лит. Это семейство представляет общее решение в соответствующей области фазовой плоскости. Изменяя Л, мы получаем континуум различных замкнутых интегральных кривых, а изменяя т, вводим лишь постоянное упреждение или запаздывание в закон движения по данной кривой. Всё это вполне согласуется с результатами качественного исследования в разделе А настоящей главы.
Уравнение (255) даёт частоту линейного приближения в зависимости от амплитуды Л.
§ 5.21]
ПРИЛОЖЕНИЕ К КОНСЕРВАТИВНЫМ СИСТЕМАМ
323
Полагая
^(q) = ^q —f(q)
и вводя параметр р. так, как указано в предыдущем получим из (243), (245)
и
р (я) = У ф (Л cos о) sin (и — a) da, о
►
и
р' (я) = У ф (Л cos a) cos (и — a) da. о
Первая из этих функций чётная, так как
—и
Р (— и) = J ф (Л cos a) sin (— tt — a) da о
параграфе,
(5.257)
и, после замены а = — р,
и
р (— и) = J $ (Л cos р) sin (и — р) dp == р (а);
о
функция р' («), наоборот, нечётная.
Далее,
ф' (Л cos a) cos a sin {и — a) da = p (й),
O/i
4(a) = € 0
8(й) =0, и
ъ(ц) — j* ф' (Л cos a) р (a) sin (и — a) da,
• о i
и
Y (и) = J Ф' (Л cos a) cos a cos (и — a) da = p' (a), о
8'(a) = 0,
и
e' (a) = у ф' (Л cos a) p (a) cos (a — a) da. о
(5.260)
(5.261)
Так как cos a, ф'(Лсозй) и Р(и) суть чётные функции, а sin и нечётная, то
4-те
Y (2и) = — у ф' (Л cos a) cos a sin a da = 0,
8 (2ic) = — У ф' (Л cos a) p (a) sin a da = 0
—те
21*
324 СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ [ГЛ. 5
и второе условие (248) обращается в тождество. Вследствие этого не только но и В не определяется из условий периодичности. Однако эти, а также и другие постоянные С, Сх, Z), Dv ... могут быть найдены, если задать какие-либо начальные условия, например,
г = s— ... = г' = 5' = ... = О при и = 0, откуда
q = At q' = Q при « = 0.
Таким путём получаем:
В = В± = 0, вследствие чего
? = Лсоза+-^-р(а){».+-... (5.262)
Из первого условия (248) находим:
. _ (2к)
и поправка на частоту будет
а = (5.263)
2<о4яД г 1 4 7
Рассмотрим ещё диссипативную систему с линейным трением, описываемую уравнением (251), в котором
/(?> ?)=/(?) +2е?.
Так как колебания в этом случае являются, как мы знаем, затухающими, то стационарные периодические движения невозможны. К этому же выводу приводит и метод Пуанкаре. В самом деле, если написать уравнения (254), то первое будет иметь тот же вид (255), что и для консервативной системы, а второе сведётся к
— 2еДште = 0,
откуда А = 0. Иными словами, единственным возможным периодическим движением является равновесие, что формально верно, так как всякая постоянная, в том числе и нуль, может рассматриваться как периодическая функция с любым периодом.
§ 5.22. Приложение к электронному генератору. Рассмотрим электронный генератор с колебательным контуром в анодной цепи, схема которого представлена на фиг. 32. Если ia, iL, iQt iR обозначают соответственно силы анодного тока и токов в трёх разветвлениях, содержащих самоиндукцию £, ёмкость С и сопротивление R, то, по первому закону Кирхгофа,
Zi+Zo+ZB = Za- (5-264)
§ 5.22]
ПРИЛОЖЕНИЕ К ЭЛЕКТРОННОМУ. ГЕНЕРАТОРУ
325
С другой стороны, напряжения в трёх разветвлениях равны между собой, так что
dlL 1 Г
с I= (5.265)
где Ua—анодное напряжение, а Еа— постоянная электродвижущая сила, создаваемая батареей или другим источником постоянного тока, включённым в анодную цепь. Обозначая, наконец, через Ug напряжение на сетке, найдём:
dlT
Ug = M-±. (5.266)
Из предыдущих уравнений получается:
_ . _ . . . . diL
dt* ~lc~ la lL lR> *R~ # dt ’
так что
L dtL .
LC + * ~dF + = ‘a = f («)> (5-267)
где функция f представляет характеристику лампы, величина
u^Ug + ^Ua есть управляющее напряжение, а 7 — проницаемость. Пользуясь соотношениями (265), (266), находим : или
• tl •— Eq —|— где
Е0 = ^Еа, (5.268) dlT q = (M-4L)-± (5.269) так что Eq будет постоянной, а q—переменной слагающей упра
вляющего напряжения, зависящей от колебаний силы тока в колебательном контуре. Производя над обеими частями (267) операцию (7И—у£) —, получим:
LCq + £ ?+Ч = (М- yL)f (Ео + q) q.
Полагая
--Cq
Фиг. 32. Схема электронного генератора.
(5>270)
Г Aw
326
СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
[ГЛ. 5
представим уравнение в виде q^vPq =qF' (д), (5.271)
так что, в обозначениях § 20, Ш q) — F'{q)q. (5.272)
Применяя в дальнейшем метод Пуанкаре к более общей системе, определяемой уравнением
? + = (5.273)
мы всегда сможем вернуться к первоначальной задаче, полагая |л=1. Первое уравнение (224) принимает вид:
+«
2о>96Л -|“ ~ [ F' (A cos о) (— Л<о sin a) cos а ds = 0, —«
а так как интеграл обращается в нуль по той же причине, что и интеграл в левой части (256), то
6 = 0.
Функция Н (Л), входящая во второе уравнение (224), может быть путём интегрирования по частям представлена в виде — ДЛ)<о, где +«
У(Л) = -^ J F(A cos о) cos a rfs; (5.274)
поэтому порождающие амплитуды определяются уравнением
У(Л) = 0. (5.275)
Будем предполагать, что Ео равна как раз абсциссе точки перегиба характеристики f (a) и что
= F' (0) > 0. (5.276)
Тогда график F(g) имеет вид, изображённый на фиг. 33. Нетрудно показать, что график функции У(Л) (фиг. 34), связанной с F(q) интегральным преобразованием (274), будет того же типа. В самом деле, F(q) исчезает при q~Q и ещё при одном отрицательном и одном положительном значениях q\ первая производная* F' (д) имеет положительное значение при ^ = 0, а вторая производная F" (д) неотрицательна при #<0, исчезает при д — 0 и неположительна
§ 5.22] ПРИЛОЖЕНИЕ К ЭЛЕКТРОННОМУ ГЕНЕРАТОРУ 327
при # > 0. Из выражения (274) и из соотношений
J(0) = 0, (5.277)
J' (А) = 1 \ F' (A cos о) cos2 a da, J' (0) = F’ (0), (5.278)
—те
+«
J" (А) = 1 J F" (A cos a) cos8 a da, J" (0) = 0 (5.279)
—л
видно, что У(Л), J'(A), J (А) имеют аналогичные свойства по
Фиг. 33. Характеристика f (и) эле-^ ктронной лампы, графики функций [(Af—iL)ILC] (/(£о + ^)—f(fo)] и F (?).
отношению к аргументу А. Кроме того, так как функция J(A) = — Н(А) нечётна, то два ненулевых значения А, при которых она обращается в нуль, отличаются лишь знаком; их общая абсолютная величина А* представляет единственную порождающую амплитуду. Мы убедимся ниже (§ 31), что соответствующее периодическое решение устойчиво, так же как и решение, полученное нами ранее для ступенчатой характеристики
Фиг. 34. График функции J (Л).
(§ 13). Поэтому Л* есть приближённое значение амплитуды автоколебаний электронного генератора. Неравенство (276), обеспечивающее существование автоколебатель ного режима, называется условием самовозбуждения.
Для того чтобы получить явное выражение для Л* и второй поправки на частоту, разложим f(EQ-]-q) в ряд Тэйлора, пренебрегая членами брдее чем третьего порядка относительно Так как? по
328 СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ [ГЛ. 5
предположению, /"(Ео) = 0, то
/(Ео+9) -/ (Ео) = f (Ео) 9 +1Г (Ео) q*.
F(q) = *q — ^q*. (5.280)
где .
X = F' (0) = f (Ео) - *,
1 M-tL ' (5-281>
Л = -4г"(О) = -^^Г(Ео)- j
В силу условия * самовозбуждения (276) мы имеем х > 0, а из отмеченных выше свойств второй производной F"(q) вытекает, что к > 0.
Мы имеем теперь
4-те
У(Л) = ^- J (кА cos2 о — •— ХЛ3 cos4 о) di
—те ИЛИ
7(Л) = хЛ— |U3, так что
А* = 2 ]/"у .
(5.282)
Затем, пользуясь полученными выражениями для ty(qt q), Л* и выполняя вычисления, находим:
р (и) = сох3/^-1^ sin3 а, р' (и) = Зсох’/гХ-1/’ cos и sin2 а,
(2те) = — 2ка>х, (<Ь ?) = -
в (2л) — 0,
7' (2л) = 0,
Фв- (Я> ?) = * — W, (q, q) = 0, е' (2л) = i ЛшЗх’/гЛ“‘/а,
Из формул (249) получается
В = 0,
%2 8(1)2*
Для определения а также С1} Dlt ... потребуем, чтобы г' = sf= = ... = 0 при и — 0, что даёт: q' = 0 при и = 0. Из условия г' = 0 находим = 0, так что
q = 2 j/*cos и -|- j/*~ (3 sin и — sin Зи) р» -J- ..., (5.283)
где
(5.284)
§ 5.23] СЛУЧАЙ, КОГДА ПРАВЫЕ ЧАСТИ ЗАВИСЯТ ЯВНО ОТ ВРЕМЕНИ 329
§ 5.23. Случай, когда правые части уравнений движения зависят явно от времени. Этот случай относится, собственно, к теории вынужденных колебаний, но мы рассмотрим его здесь потому, что к нему, после преобразований, могут приводиться некоторые задачи о собственных колебаниях. Уравнения движения возьмём в общем виде
(?. Р> t, Pj, ..., Pr), = ©2 (я, Р, t, Vi..Рт) (5.285)
и предположим, что по отношению к t функции <?*, <?2 являются периодическими с периодом Р.
Так же как и раньше, докажем, что если для упрощённой системы, получающейся при ^ ==...= р.г = О, удалось найти частное решение q — q* (t), p = p*(t)t удовлетворяющее условиям
Г (4) + Р) = (^о)> р* ('о + Р) = Р* (4>)>
то оно будет периодическим с периодом Р и мы можем принять его за порождающее. В данном случае функции q* (t—т), р* (t—т) не образуют решения, если -и ¥= 0.
Общее решение для произвольных значений параметров имеет вид
Я—flit’ Рр ^2’ Pi ^*2’ Hi
Hr)’
Hr)’
(5.286)
причём порождающее решение получается при С± = С*, С2 =
Hi= • • • =Нг = 0:
fi (t, с1г с2> о.....0) = г (0,
sis sis
/2(/, сх, С2, О, ..., 0)=р*(0-
(5.287)
Для того чтобы выделить периодические решения при значениях параметров, не равных одновременно нулю, составляем условия периодичности:
^1 % I'' ^1’ ^2’ Н1’ • • • ’ Hr) fl (^Q’ ^1’ ^2’ Hl’ • • •» Hr) *—’ 0’1 z- r»on\
в которых, в отличие от случая собственных колебаний, мы берём прежний период, предопределённый самими уравнениями движения, без поправки. Вместо этого можно было бы только задаться периодом, составляющим целое кратное от Р, но такими периодическими решениями, рассмотренными Пуанкаре, мы не будем заниматься. При выполнении обычного условия, наложенного на функциональный определитель, можно найти выражения
: Сг (|Хр . .., рг), б?2 — С2 (|ip •.., р»г), (5.289)
330
СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
[ГЛ. 5
удовлетворяющие уравнениям (288) при малых значениях параметров и обращающиеся в С2 при Р4= ... =цг = 0. Если же Эти выражения подставить в общее решение, то получится искомое периодическое решение, зависящее от t и параметров ..., рьг и имеющее период Р.
§ 5.24. Приложение к паровой машине. Расчёт маховика. Приложим предыдущую теорию к паровой машине с регулятором, возвращаясь к постановке задачи и обозначениям § 15 и лишь для простоты предполагая, что периодическая часть вращающего момента и нагрузка не зависят от скорости r = q> так что
D (г) + F (?), L = Е + G (?), (5.290)
Q = D (г) — Е — V' (9), (5.291)
причём а
v (?) = J* [— F(?) + О (?)] dq, (5.292)
О
а О (г) есть будет
Так как
где
монотонная убывающая функция. Уравнение Лагранжа
d дТ дТ Т7// \ । п/ \ г?
m{q) = М + «(?)»
(5.293)
М '= 4- Щ + тез>
(5.294)
то уравнение движения может быть представлено в форме
т ® %+i т' ra=- v' +D<r)~E <5-295)
или в виде системы двух уравнений первого порядка
dq___
dt ~~
агрг® [ - 4 - V' (9) + О (г) - S]
(5.296)
Если масса маховика, а вместе с ней и Ж бесконечна, то мы имеем решение q = а, г = гт, где
Q = rm{t— т), (5.297)’
а гт и т — произвольные постоянные. При конечном М принимаем а за новую независимую переменную и вводим вместо q неизвестную функцию ф ПРИ помощи соотношения
(5,298)
§ 5.24] ПРИЛОЖЕНИЕ К ПАРОВОЙ МАЩИНЕ. РАСЧЁТ МАХОВИКА 331
Первое уравнение обращается в следующее:
и мы можем написать преобразованную систему в виде
*Lr =__________1_____
d<s Гт Л4 + а(а + Ф)
(5.299)
х Г — | а' (а + 4») /-3 — V (а + ф) + D (г) — Е &
Так как правая часть первого уравнения не содержит независимого переменного а, а правая часть второго является периодической функцией от о с периодом 2с, то мы можем применить общую теорию, изложенную в § 23.
При Л4 = оо система имеет тривиальное решение
Ф = 0, r = rmi (5.300)
которое можно рассматривать как периодическое с периодом 2с и принять за порождающее; период по t будет
(5.301)
При большом, но конечном М ищем периодическое решение с тем же периодом в виде рядов по степеням малой величины 1/М:
r = rm + r1(a)^ + r2(a)-^+ ...
(5.302)
Если условиться писать а, а', а".гр . .., V', V", ...
без указания аргументов вместо а (а), а'(а), • ••>
ri(°)..У" (°).........а под D, D', ... разуметь постоянные
значения D(rm), D'(rj, ...» то
Л* + а(а + ф) -~м L1 + *•*]“““Af\ aAf+ "*/’
a/(®+ ’!’)= а'+ а"Ф1^+ • ••>
r2 _ r2 _|_ 2r r — -4-' — ’ m ~T m'1‘ ’
a (a 4- ф) r2 = fa' _|_ rm(rma\ + 2а'Г1) -|- ....
У'(° + ф)=У'Н-У"ф11+ .... *
P(r) = D-|-D'r1l+ ...
332 СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ [ГЛ. 5
Поэтому,, обозначая
/(0) = - ± [ у (а) + dj —L Гта (а), (5.303)
г Ш *
где Ь± — постоянная, имеем:
— 1 а' (о + ф) /-a — V (а + <{-) + D (г) — Е =
= rmf + D — Е + (/-„Л — гтагГ1 + D'rJ ^4- ...,
и уравнения (299) принимают вид
I г 1 | j г 1 I _ Г 1 1_| 1 |
V1 мТ"?2Д42“Г ••• — 7^м“ГЛ42-Г •••>
(5.304)
Приравнивая коэффициенты при 1/Л4, получаем соотношения = ri = f' + ^> (5.305)
гт гт
второе из которых даёт:
причём постоянная интеграции уже включена в /. Функция г± должна быть периодической, и потому D— E = Q или
D (гт) = Е, (5.306)
откуда однозначно определяется гт. Следовательно, гх=/(а), (5.307)
= 7"/i + «р гт где а
А(°) = J7(°)<b. (5.308)
о
a av так же как и bv есть постоянная интеграции. Так как, по предположению, средние значения F и Q равны нулю, то V не со-держит линейного члена и является периодической функцией, так же как и а. Поэтому и г1=/ будет периодической. |
Для того чтобы то же самое было верно в отношении Д и 1
нужно, чтобы >
+с 11
j* /(a)da==0, I
5.24] ПРИЛОЖЕНИЕ К ПАРОВОЙ МАШИНЕ. РАСЧЕТ МАХОВИКА
333
а так как среднее значение а равно нулю, то это приводит к условию +с
*i = —i f V^)da, (5.309)
— С
благодаря которому функция f оказывается вполне определённой.
Приравнивая в (304) члены с 1/Л42 имеем:
Ф2 = ?» = + (5’310)
гт гт
или, заменяя во втором уравнении ф], г± найденными выражениями,
Интегрируя по частям, находим:
J fif' = fif' — J ff' d° + const
j* ff' da—f2—j* ff' da-|-cons^> так что
J ff'da = -1 /2 + const., J da = faf' — у /2 + const.
Отсюда, принимая во внимание, что D' есть постоянная, имеем:
rz = —fa +ffif ~2ТГ2 + “if + ^fi — b2’
где b.2— постоянная интеграции. Так как функции Д, /, а, по предыдущему, периодические, то и г2 является таковой. На а± не налагается никаких условий; мы можем определить эту постоянную так, чтобы, например, обращалось в нуль вместе с а. Но так как Д, по определению, также исчезает вместе с а, то
= 0»
и мы получаем окончательные выражения:
= 7-А (°), (5.311)
г т
(а) + (а) f (а) —-£-[/(о)р + (а) - Ь2. (5.312)
гт гт
Для того чтобы функция ф2, определяемая первым уравнением (310), Оыла периодической, нужно сделать среднее значение г2 равным
334 СоёствейИЫе колебаний нелинейных систем [гл. 5
/
нулю; из этого условия получаем: +с
i J {-Я°)а (°) + /1 (°) -
—с
-27-|/(в)1а + ^А(а)ра. (5.313)
Входящая в /'(о) производная а'(о) от приведённой массы может быть найдена по способу И. И. Артоболевского [бЛ].
Намеченное здесь последовательное вычисление функций (о), ri(<s) может быть продолжено.
Для определения колебаний скорости машины найдём её минимум и максимум, полагая
= ••• =0.
Соответствующие значения аргумента о ищем в виде рядов
Подстановка в предыдущее уравнение даёт: r^(a)4-r" • ♦ -1 • • • = 0,
, <
<И+<-(»)’7я+-"]ж+1'-;<6>+=° 5
или, приравнивая нулю коэффициенты при степенях 1/М, г'(д) = 0, rj0) = O, (5.314)
, гг(л) " Z \ " zb\ ’
(д) rt (b)
У • •••••••••••••• £
Из первых двух уравнений видно, что а и b суть значения аргу- | мента, при которых rt(o) имеет минимум и максимум. J
Неравномерностью называется отношение 8 колебания скорости г (о**) — г (а*) к её среднему значению rw:
g__ г (q**) — г (q*) _
r т
__гi (q**) — ri (ст*) । r2 (g**) — г2 (а*) » _ W
A W —Г1(Я) ri W 4* — Г1 (д) (Ь) — га (д) I
ГтМ гтМ^ “г ' ‘ ” I
4 5.24] приложение К паровой машине. Расчет маХовйка 335
или
8 =
ft (6) — г^а)
|- — г, (Ь) г2 (Ь) г'[ (а) + г{ (д) r2 (a) r't (fr)
+ L ^i(fl)r"(b)
+ >2 (!>) — r2 (a)
1 r„,Afa m
При проектировании машины допустимая неравномерность задаётся сообразно с условиями эксплоатации и задача состоит в том, чтобы рассчитать необходимую массу маховика. Поэтому, рассматривая величину 1/М в предыдущем уравнении как неизвестную, ищем её в виде ряда с неопределёнными коэффициентами по степеням 8:
А = qg с282 .
Подставляя в уравнение и приравнивая коэффициенты при одинаковых степенях 8, находим:
гх (а) г'2(а) г" (6) - (Ь) г' (6) г" (д) д 1_
т
< (а) г’[ (0
9 Ml
С1 ~ П(Ь) — rt(a) ’
Ci~ [ГХ (&) — rt (Д)]8 tr2 W r2 (a) +
П (д) r'2 (д) r" (b) - r{ (b) r'2 (b) г" (д) -г" (д) r" (6)
Для массы M = -f- m.2 -|- m3 получается выражение
1 11
CjS -4- ... ^18 1 . /<?2 \> ।
1 "4“ I — 16 ~Т“ • • •
или
Л4 • • •>
где . 1 gW-rifr)
-1 ci rm ’ в° в---th\ 1--------7*\ [Г2 W r2 (°) +
C? ^l(b) — 2 2
r{ (д) r'2 (д) r" {b)—r[(b) r2 (b) r[ (a) r'i («) r'[ (b)
(5.315)
(5.316)
EG6W ’
Г
гт
336
СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
[ГЛ. 5
Отсюда находим, наконец, массу маховика
д_
/п1 = — /п2 — /п3 + -^-1 + ^0 4-^34-... (5.317)
Заметим ещё, что уравнение г' (о) = 0, из которого определяются а и Ь, может быть с помощью (292), (303), (307) представлено в виде
F(a)— 0(a) — |rs/(a) = 0. (5.318)
Если же ограничиться в (317) первым членом ряда, то получится формула
т± — — т2 — /^з +
ь
f [F(a) — О (a)] da —1 [а (Л) — a (a)]}, (5.319)
a
не отличающаяся от той, которая была предложена Радингером [б-31]. Ход его рассуждений заключался, примерно, в следующем.
Пренебрегая переменной частью приведённой массы т(д) в первом члене левой части уравнения (295), имеем:
^=-la'G7)r9 + Fta)-GG7) + D(r)-E;
если же заменить справа г через то
(1 Mr*) — F{q) — G{q) — ^ a' (q)r2m,
откуда для получения значений а, Ь, соответствующих минимуму и максимуму скорости г*, г**, получается уравнение (318). Затем, интегрируя по q, найдём:
ь
| /И (г **2 — r*2) J [Л (а) — О (a)] da — 14 [а (£) — а (а)].
а
Если же принять
то и получится формула (319).
Д. МЕТОД ОСРЕДНЕНИЯ
§ 5.2S. Основная идея. Излагаемый здесь метод — приближённый и может применяться лишь для первой ориентировки. В отличие от метода Пуанкаре, он позволяет изучать не только стационарные
§ 5.26]
УКОРОЧЕННЫЕ УРАВНЕНИЯ
337
периодические состояния, но и другие процессы в колебательных системах, получающиеся при произвольных начальных условиях и называемые переходными или процессами установления. Основная идея заключается в замене некоторых членов в дифференциальных уравнениях системы их интегральными средними; в сущности, она уже давно применялась в небесной механике. В физику этот метод введён ван дер Полем и развит московской школэй теории колебаний, начиная с Мандельштама и Папалекси, которые дали свою формулировку и первое исследование его точности. Здесь излагается приложение метода в одном из простейших случаев, но, как и метод Пуанкаре, он может быть применён также ко многим другим задачам.
§ 5.26. Укороченные уравнения. Будем рассматривать опять натуральную склерономную систему с постоянной приведённой массой Tn, находящуюся под действием какой-нибудь силы
— V' + Q == — mf(q, q), (5.320)
зависящей от положения и скорости. Гамильтоновы канонические уравнения будут
~ = — (5.321)
dt т ’ dt J v’ m /’ 4 7
путём исключения p они могут быть приведены к уравнению (251) ? + /(?. ^) = 0.
Предположим, что т/(д, р/т) может быть аппроксимировано линейным выражением
4"М- (5-322)
Вопрос, о том, как выбрать коэффициенты g, klf й2, мы, рассмотрим ниже, а пока предположим, что это уже сделано. Тогда система (321) близка к упрощённой линейной системе
dt т
где постоянная q* определяется соотношением
— = £ (5.323)
Упрощённая система эквивалентна линейному уравнению второго порядка
(mD* + kxD + fe2) (q — q*) == 0,
и если его характеристическое уравнение, как мы предположим, имеет комплексные корни —eztz'co, то
k± = m2®, k,2 =>-т (в2 °>а)> (5.324)
22 Зак. 1474. Б. В. Булгаков
336 СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ систем [гл. S
а общее решение может быть представлено, в виде q — q* = Ae~zt cos (otf 4~ 8),
где А и 0 — постоянные. Отсюда
р = — ntAe~zt [со sin ®)."Ь 8 cos/ (<^+ 0)].
Если же положить
a = Ae~*ti #==а)/-}-0> то
q — q* = a cos ut р = — та (со sin и 4~ е cos и),
(5.325)
(5.326)
так что а и а представляют амплитуду и полную фазу колебания. Пока эти величины определяются формулами (325), последние выражения представляют общее решение упрощённой системы и не будут, разумеется, удовлетворять точным уравнениям (321). Но этого можно потребовать, если рассматривать а и и как новые неизвестные, вводимые вместо q и р. Тогда (326) будут просто формулами замены переменных. Подстановка в (321) даёт:
a cos и — аи sin и = — aoosin и — аг cos и,
— а (о> sin и е cos и) — аи (со cos и — sisin и) -(-
+/[<7* + а cos я, — а (<° sin и + е cos и)] = О,
где выражения в квадратных скобках представляют аргументы функции /. Разрешая относительно производных а, и, имеем:
(ьа — а (— aw cos2 и 4~ sco sin2 и — со2 sin и cos и -}-
+ е2 sin и cos и) -f- sin uf [... ],
<&au — а (2ео) sin и cos а 0)2 sin2 и + ®2 cos2 w) + cos #/!•••]»
что можно представить в виде
ыа — — юга — sin uty [q* 4“ а cos и, —а (со sin и 4- е cos а)], <ьаи = оРа — cos uty \q* 4~ л cos а, — а (со sin и 4* е cos а)],
(5.327)
где
Ф (?> Я) = 2&Я + (“a+S2) (? — ?*) — f (Я> Я>- (5.328)
Уравнения (327) являются точными, так как они получились путём преобразования исходных уравнений, при котором мы использовали | лишь форму решения упрощённой системы. Выражение 1
2* £+(<°3+«3) (?—?*) (б-329> I
представляет линейное приближение для f(q, р/т), так как, умно- « I
м Д’
§ 5.27]
ВЫБОР ЛИНЕЙНОГО ПРИБЛИЖЕНИЯ
339
жая его на т и пользуясь (323), (324), получаем выражение (322). Поэтому ф(?,рМ) есть разность между линейным приближением и самой функцией/^, pfin). Эта разность мала в силу сделанных предположений, и мы можем в этом пункте вывода приближённо заменить в (327) величины sin аф [...], cos иф[...] их интегральными средними значениями за одно колебание, что даёт:
^ = — аФ(е, ш, q*, а), ^ = Ф(е, <о, ?*, а), (5.330)
где
ф(е, ?*> «) =
-и тс
= •+»/* +
a cos и,— а (ш sin м 4" 8 cos tt)l sin u du,
Ф(е, <o, ?*, а) =
w J — TC
a cos zz, —a (co sin cos и)] cos и du.
(5.331)
Если же под интегралами подставить вместо функции ф [...] её выражение (328) через то получится:
Ф(е, со, а) =
4-тс
=_________!_[
— тс
а (со sin и е cos я)] sin и du,
a cos и, — а (со sin и -|~ s cos я)] cos и du.
— тс
При вычислении интегралов амплитуда а трактуется как постоянная.
Уравнения (330) носят название укороченных. Они нелинейны, так же как и исходные, но представляют то преимущество, достигнутое ценою сделанного осреднения, что могут быть решены двумя квадратурами. В самом деле, общий интеграл первого уравнения может быть найден путём разделения переменных, после чего разрешается и второе уравнение.
Функции Ф(е, со, q*, а), Ф(е, со, ^*, а) могут рассматриваться как мгновенный коэффициент затухания (или нарастания) и мгновенная угловая частота.
§ 5.27. Выбор линейного приближения. Рассмотрим вопрос 0 выборе величин е, со, q*. Так как трудно надеяться получить пРиближение, одинаково удовлетворительное при всех аргументах, то
340 СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ [гл. $
ограничимся окрестностью какой-либо выбранной расчётной амплитуды а*. Заметим, что функция + cosu, —а* sin и г cos л)] является периодической относительно и и может быть разложена в ряд Фурье Ограничиваясь в нём тремя членами, получим:
П?* л* cos а, —а* (со sin а -|- з cos #)]
—к
sin и du^sxn. и
или, пользуясь соотношениями (326) между q, р и а, и,
f (9* + cos — а* (ш sin и 4“ 8 cos #)] ~
4-я 4-я
j/[...]d« + (4 j/[...] cos +
—я —я
4-я
4~(— f /Ь .. 1 sin gdu\ (У~
1 \” J / та*а>
— Я
Если же потребовать, чтобы это было равно
2в£ + (<»2 +в2) (?-?*),
то, приравнивая свободные члены и коэффициенты при р, q — q*t найдём:
4-я
—я
--Я
1 г
2е —-------г- /[...] sin и du,
—я
4-я 4-я
1 £ Г*
u)2-Ue2 = —х /[...] cos и du-----------/[.
1 тиа* J J 1 J J J 1
— я —я
.] sin и du,
или, исключая второй интеграл в третьем соотношении при помощи
§ 5.28]
СТАЦИОНАРНЫЕ режимы
341
второго,
--Я
л
f yq* _|_ д* cos и, — а* (со sin и -J- s cos а)] du = О,
(5.333)
1
4-я
X [/[?*+«* «
—я
cos и, — а* (<о sin и -}- е cos я)] sin и du,
► (5.334)
0)2----©2
j / [Я* + a* cos — a* (w sin и -f- © cos и}} cos и du.
Этими тремя уравнениями при заданном а* определяются три величины ©, <о, q*.
Пользуясь .функциями Ф, Ф, можно представить второе и третье уравнения в форме
е = Ф (©, со, q*> а*), со = Ф (е, о, q*, а*). ,
Таким образом, коэффициент затухания, и. угловая частота аппроксимирующей линейной системы равны мгновенным значениям .соответствующих величин для нелинейной системы при (г=а*.
§ 5.28. Стационарные режимы. Пусть постоянная а = а* является частным решением первого укороченного уравнения. Предполагая, что она принята за расчётную амплитуду, мы .должны вследствие "Л- = О иметь:
а*Ф(©, со, q*, а*) = 0.
Если при этом а* = 0, то уравнения (326) дают
р = 0, J
(5.336)
т. е. состояние равновесия. При этом уравнение (333) приводится к следующему:
/(?*> °) = 0’ (5.337)
откуда определяется q*.
Если а* у= 0, то мы должны иметь:
Ф(в, ш, q*, а*)=0 /
342
СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
[ГЛ. 5
и, согласно первому соотношению (335), е = 0.
Формулы (332) принимают вид:
Ф(со, ?*> а) =
2п<оа . —я
ХР" (со, ?*, а) =
/(?* + а cos — а ш s^n и) sin и du,
2^<оа
•»
f(q* -|~а cos sin tt) cos и du;
—я
аргумент е слева не указан, поскольку он равен нулю. Уравнения (333), (335) получают вид:
+к
J* f(q*+а*cos — °*05 sin #) du = о,
Ф(ш, q*> а*) = О, (о = ЧР‘(ш, q*, а*),
(5.339)
откуда определяется одна или несколько систем значений ф, q*, а*.
Уравнения (326) и второе укороченное уравнение дают для стационарной амплитуды а*:
q = q*-j-a* cos и, р = — zna*cosina, >
и = со/ -|— UQt
(5.340)
так что мы имеем в этом случае периодический процесс. Кривая, представляемая первыми двумя уравнениями, есть эллипс в плоскости qp с центром в точке (?*, 0).
Чтобы исследовать устойчивость периодического режима, положим а — а*-\-Ъа, где функция 8а представляет малое отклонение амплитуды а от её стационарного значения а*. Подстановка в первое укороченное уравнение даёт:
— = — (а*-}-8а) Ф (со, q*t а*-|-8л)
илц
= — я*Ф(<°> ?*> а*)— ^-аФ(<о, q*t а) Ль ол
8а— .. а=а*
§ 5.28]
СТАЦИОНАРНЫЕ РЕЖИМЫ
343
Если же принять во внимание второе соотношение (339) и ограничиться малыми первого порядка, то получится линейное однородное дифференциальное уравнение относительно 8а:
d (6а)
8а = 0; а=а*
оно'легко интегрируется и даёт:
Г.
— а^Ф(о>, q*,
a) f.
7 Ja=a*
Таким образом, всё зависит от знака величины
Г^Ф(о>, q*, а)1 * =
Lda 4 * а*
ДаФ(ш, д* а)]вжв*
а cos а, — а о sin а) sin а du
ass а*
— К
— 5=F J </.<«•+“•
cos а, — а*<о sin и) cos а —
—(?* + а* cos — а* со sin а) со sin а] sin а du.
• ф
где /ff, обозначают частные производные от f(q, q) по первому
и второму аргументам. Обозначая
X(q, q) = fq{q, ?)(<7~ ?*)+/,/(?• ?)?. (5.341)
мы можем написать также:
[^ф(ш, q*, a)]e=e,=
2я<оа*2 J
—к
a* cos а, — а*о> sin а) sin и du. (5.342)
Если эта величина положительна, то периодический режим асимптотически устойчив, а если отрицательна, то неустойчив.
Закончим параграф следующим замечанием, которое позволяет иногда упростить определение q*. Если для некоторого q* функция f(q*-\-x, у) нечётна по х или по у или же состоит из слагаемых, обладающих этим свойством, то это q* удовлетворяет первому уравнению (339) при всех а* и о>. В самом деле, в случае нечётности
344
СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
[ГЛ. 5
по х, мы имеем, пользуясь заменой и = ~— v:
4-тс
J /«#* + л* cos я, —- а* оо sin и) du —
—тс
4-тс/2
= j* /(^* 4~ а* cos и, — а*ы sin и) du 4-
-ТС/2
+Зтс/2
“h f /(<7* ~Ь л* cos а,—а*а> sin и) du =
+тс/2
= J /(</*-|-а* cos а, —0*0) si” u)du-\-
—тс'2
—тс/2
4- j /(<7* — а* cos v,—0*0) sin-у) (— dv) =
4-тс/2
4-тс/2
= j* /(<7*4-a* cos я,—а*о) sin u) du— x
—tc/2
+fS
— I /(<7* 4“ a* cos v, — 0*<o sin v) dv — 0.
—tc/2
В случае нечётности по у нужно применить замену и — —v:
+«
J*/(?*4-я* C0Stt, —0*0) sin 0)^0 =
—тс
О
= J* f(q* 4- a* cos 0, — 0*<о sin и) du 4~ —тс
А нтэоь
те
4- J f(q* 4- 0* cos 0, — 0*<о sin и) du = о о
j*/(<7* 4“ °* cos —0* °) sin и) du 4~
-тс
—тс
4-J /(<7* 4~ cos г/, 0*o)sin<y)( — dv) = о о
J* f(Q* + cos 0, — 0*о) sin и) du — к О • -
— J cos v, —а* « sin v)dv = 0.
§ 5 29]
ПРИЛОЖЕНИЕ К КОНСЕРВАТИВНЫМ СИСТЕМАМ
345
§ 5.29. Приложение к консервативном системам. Если действующая сила — позиционная, так что f зависит только от qt то Q = 0 и мы’можем написать:
/W = ^-V'(?). (5.343)
Выражение для Ф принимает вид:
1
+ к
[ /(?* + а cos я) sin и du\
так как подинтегральная величина представляет произведение sin и на функцию от cos и, то интеграл обращается в нуль при всех а по тем же соображениям, что в § 21. Первое укороченное уравнение даёт:
^ = 0, а = const., (5.344)
так что каждая амплитуда будет стационарной и может быть принята за расчётную. Поэтому звёздочка при а в этом случае может быть отброшена.
Первое и третье уравнения (339) могут быть с помощью второй формулы (338) написаны в виде
где
Г /(9* + ° cos а) = о* —тс
a cos и) cos ttdu =
—те
4-
(5.345)
(5.346)
(5.347)
—тс
Соотношение (345) даёт возможность выразить q* через а, после чего«и J будет зависеть только от а. Тогда (346) даёт зависимость частоты собственных колебаний от амплитуды. Если функция А?* (л), а) представлена графически в виде кривой, то <о2(а) будет угловым коэффициентом радиуса-вектора, проведённого из начала координат в какую-нибудь точку (a, J) кривой.
Второе укороченное уравнение даёт:
и = со (a) t+(5.348)
346
СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
[гл. 5
Подставляя это выражение и q* (а) в (326), найдём закон движения в координатах q, р. Изменяя а, получим бесчисленное множество замкнутых интегральных кривых.
Если f(q) нечётна, то, как было показано в конце предыдущего параграфа, уравнение (345) удовлетворится, если взять q* = 0. В этом случае для J получается выражение 1
J(a) = 2- /(a cos и) cos и du, (5.349)
—л
не отличающееся от выражения (274) в § 22. Как мы там видели, функции f(q) и J(a), связанные такого рода преобразованием, не будучи, конечно, тождественными, обнаруживают в некоторых случаях сходные свойства. Можно получить и другие, аналогии, которые оказываются полезными при изучении консервативных систем. Пусть, например, V(д) имеет минимум при q = 0, так что в окрестности q — Q функция f(д) — Vr (?)/w имеет тот же знак, что и аргумент q, что можно выразить условием qf(q) > 0. Пока оно выполняется, сила — V' (д) является восстанавливающей. Пользуясь соотношением (349), легко показать, что найдётся такая окрестность значенияч а — 0, в которой J(a) обладает аналогичным свойством: aJ(a) > 0. Если свойство qf(q) > 0 имеет место при всех значениях аргумента (кроме нулевого), то это будет верно и в отношении свойства aJ (а) > 0.
С помощью соотношения
/' (a cos и) cos2 и du .
—л
докажем, что J'(d) есть чётная функция и что если f(q) монотонно возрастает (убывает), то это же имеет место и для J(a).
Пользуясь соотношением между вторыми производными
+«
= I /"(a cos я) cos3a da,
убедимся, что J"(a) нечётна и что если в некоторой окрестности значения ^ = 0 верны неравенства ?/z,(^)>0 или qf'(qX®> то в некоторой окрестности значения а — 0 будет соответственно aJ/z(a)>0 или aJ"(a)<0. Если f(q) одновременно имеет свойства /(0) = 0, f (д) > 0, qf'(q) < 0, то мы имеем так называемую мягкую силовую характеристику, так как, например, в области положительных q функция /(д) будет меньше линейного выражения /'(0)^, которое получилось-бы, если бы восстанавливающая сила следовала закону Гука. При /(0) = 0, /'(<?)> 0, получается жест
§‘6.29J
ПРИЛОЖЕНИЕ К КОНСЕРВАТИВНЫМ СИСТЕМАМ
347
кая характеристика, поскольку /(?)>/'(0)^ при q > 0. Функция J(a) в обоих случаях имеет аналогичные свойства.
Пример 1. Пусть имеем массу, удерживаемую вблизи положения равновесия ‘пружинами с начальной затяжкой, благодаря которой восстанавливающая сила получает конечное значение при сколь угодно малом отклонении от положения равновесия. Для такой системы
/(?) = b sign q + cq, (5.350)
где b, с — постоянные. Так как f(q) нечётна, то можно взять ^* = 0. Для функции J(a) получаем согласно (349)
j (а) = i f(a cos и) cos и da =
—тс
—тс/2 ' +тс/2
(•— b) cos a du 4- ( + b) cos и du +
—тс —тс/2
(— b) cos и du +
тс
4-тс
са cos2 udu~
cos и du +
—тс
cos3 udu =------k ca,
к 1
и, следовательно,
“(«)=]/ с+™-
(5.351)
Период колебаний в зависимости от амплитуды выражается формулой
Пример 2. Пусть
х . 2Е . (1 — т \ f (Я) = rnq + — arctg I-gg- ,
(5.352)
где — положительные постоянные. Так как
- f (q) = т +
то с возрастанием q от 0 до оо угловой коэффициент кривой С=/(^), представляющей график f (q), монотонно изменяется от /' (0) = Z до /' (оо) — т. кривая проходит через начало координат, и та её часть, которая соответствует положительным q, имеет при 1">т асимптоту С = mq 4- Е, а при — асимптоту ^ = mq— Е. В первом-случае мы имеем мягкую, а во втором — жёсткую силовую характеристику.
348
СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
[гл/ 5
Так как f(q) нечётна, то = 0. Поэтому +тс
J(a) = — /(a cos a) cos и du =
те »
—тс
4е тс
— т \ J
ъа cos и) cos udu =
2Е )
— тс
—тс
Z — т
ка cos а) sin а
—тс
тс/?
I — т -----------а те
sM&udu
I — т \2
теа cos и 1 2Е /
тс/2
Z — т > f ------------а
те J
. о
tg2 ц d (tg ц) //— т \2
2£
00
Z — т -----------а те
x^dx
Z — m \2 2£
о
Вычисляя интеграл, находим:
... , 4Е V(l — m)W + 4Е2 — 2Е
J \Uj — ига ~ ,. . ,
те (Z — m) na
откуда получается следующая зависимость угловой частоты от 4£ /(/ — т)Ъ№ + 4£3 — 2Е теа
(5.353)
амплитуды:
(О'
(Z — т) ка
(5.354)
Как легко убедиться,
Пример 3. Ю. И. Иориш [6.2] исследовал колебания массы, снабжённой амортизатором с экспоненциальной характеристикой
_ f(q) = №(e*— 1). (5.355)
Так как график f(q) несимметричен, то нельзя ожидать, что q* будет нулём. Мы имеем:
-f-TC ’ ”{”ТС
/(#* + а cos и) j* &а C0S U — 2те t
— тс - - —тс
4-тс +тс
еа cos и CQS и £и —
—ТС —Тс
. 4-я
COS и
= ^а» f e“«»s“cos«rf«.
§ 5.301
Система С вязким сопротивлением
349
Чтобы привести эти выражения к гралом Гансена *)
/-п
л»(г)=—
известным функциям, воспользуемся инте-
«
г**008 ? cos nep о
где Jn(z} обозначает функцию Бесселя первого рода и n-го порядка. Полагая п = 0 или 1, я = — 1а и вводя модифицированные функции первого рода
А) — *А) (^)> А. 00 — О-^О»
получим:
/0( — а) = 1 [ в°008’^ = 1 | eacoaudu, О —Тс
(5.356)
тс 4-тс
Z/j (—а) = i еа cos ф cos 9 dy = J еа cos и cos и du.
0 —тс
Так как 1&(а) есть чётная функция, а 1±(а)— нечётная, то
J* / (0* + а cos и) du == 2л&2 [^Zo (а) — 1J, J (д*, а) = 20е**11(а).
Уравнения (345), (346) получают вид
е«*/0 (а) — 1 = 0,
<о (а) =
= •»/ 2№е^(а}к(а) ' а
откуда
<7* (а)----1п/0(а),
, ч ь,/"2/i(a) ь
<о (в) = kA/ = k
’ Г alo(a)
8 Я2+ 192
64
(5.357)
§ S.30. Система с нелинейной позиционной силой и вязким сопротивлением. Предположим, что, кроме позиционной силы —= —mf(q)9 имеется ещё сопротивление, пропорциональное первой степени скорости
Q = — 2m^q.
io *) Е. ЯнкеиФ. Эм де, Таблицы функций. Гостехиздат, М. — Л., 1У48, стр. 239. Там же другие формулы и таблицы функций Бесселя.
350 СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ [гл^ б
Тогда
Ш <7)=/(?) + 2р?.
(5.358)
Уравнение (333) получает вид +«
J [/(9* + °* cos и) — 20а* (оо sin и + s cos и)] du = 0 —л
или
Jcos «)</а = 0, —«
т. е. совпадает с уравнением (345) предыдущего параграфа. Затем Ф (е, о), ?♦, а) =
1
2ода
+те
[/((7* + а cos и) — 2ра(оо sin и 4~£ cos я)1 sin и du
или
и
Ф(е, со, а) = р
(5.359)
Ф(в, ®, д*, а) =у(1+-^) +
4-те
[/(^* Н~а cos и) — 2ра (со sin и -|- е cos я)] cos udu~ V 7С
“ Л I е2 \ I / (?* а)_______sft
2 \ ** <»2/—’ 2юл 1
где J{q*^ а) определяется согласно (347). Так как функция Ф не обращается в нуль, то никаких стационарных состояний, кроме равновесия, не .существует. Составляя соотношения (335), имеем:
(5.360)
и
или
Л _____Р2 \ । У (q*t а*)
2 \ с«2/ ‘ 2<оа*
(5.361)
W (s, ш, д*, а) =
Выражение Ф может быть поэтому написано в виде г (д*> Д*) [ J _______________________________________202
а* * а Р
1 J" J (q^t а)_J (д*, а*)'
2<о
а
а*
к
- тава
§ 5.30]
СИСТЕМА С ВЯЗКИМ СОПРОТИВЛЕНИЕМ
351
Первое укороченное уравнение немедленно интегрируется и даёт а = айе~'^. (5.363)
Пример. Рассмотрим затухающие колебания физического маятника. Так как для него (§ 2, пример) т = /, V = — Mgh cos q, то
/(?) - —sin ?,
где
Если предположить, что сопротивление сводится к силе, пропорциональной скорости, то
/(?, £) = *2 sin q 4- Qftq, (5.364)
так что /(<?, q) представляет сумму двух слагаемых, нечётных соответственно по первому и по второму аргументу. Вследствие этого можно взять д* = 0, и тогда 4-те те/2
if 4 Г
j (а) = — Z?2 sfn (a cos и) cos и du — №— I sin (a sin <p) sin dy.
7C J 7U J
• -к 0
Сравнивая это соотношение с формулой*)
«/2
Л («) = 4 J sin (a sin <р) о
sin ? d<?9
которую можно написать для функции Бесселя J± (а) первого рода и первого порядка, имеем:
J (а) = 2Wi (а) = Л» (а — 4- а» + i а® — ... У (5.365) \ о 1Ул /
Если принять за расчётную амплитуду а* = 0 и воспользоваться второй формулой (278), то
со
— р2=у>(0) —р2 =уу/(О) —£2
или
(D = ₽2.
Формула (362) для ЧТ получает вид
(5.366)
^•(е, «о, <?*, «) = «о-}-^(О)
. & I 1 , . 1 . \
—в, ( 16® 384я
(5.367)
*) См. И. М. Рыжик, Таблицы интегралов, сумм, рядов и произведений, ИзД. 2, Гостехиздат, 1948.
352 СОБСТВЕННЫЕ колебаний нелинейных систем . [гл. 5 1
Выражение (363) для а, полученное из первого укороченного уравнения, $ остаётся, разумеется, в силе. Второе укороченное уравнение может быть g с помощью первого написано в форме
du . № (\ 1 „ . \da |
dt~ “ + 384a+”Jrf/‘ !
Отсюда, интегрируя и полагая и$ = 0, имеем:
. . Л3 / 1 Q 1 > । \ Л2 / 1 2 1 4 I \ /к о«о\
« — в>/+рй)(з2а 1536Л +”•) £<о(з2а° 1536 е° ‘ ’ (5<368)
причём под а нужно разуметь а^е
§ 5.31. Переходный процесс в электронном генераторе. Вернёмся к задаче о колебаниях электронного генератора (§ 22), определяемых уравнением (271), в котором мы будем только во избежание недоразумения писать k вместо <о:
В данном случае
q + k*q==qF'(q).
f{q, q) = kfiq — F'(q)q,
(5.369)
и если принять за расчётную одну из стационарных амплитуд, то согласно сказанному в § 28 первое уравнение (339) удовлетворяется при
q* = О,
так как f(q, q) состоит из двух слагаемых, нечётных соответственно относительно первого и второго аргументов.
Затем, согласно (338),
Ф (со, а) = —
+«
Д- f i*2«
/
cos и + F' (a cos и) a® sin и} sin udu =
--ТС
2теа е
sin и d{F (a cos а)] =
s 2S7lsin “ F(-a C0S И)1-„ - 2тш J
—те
ИЛИ
ф(ш, а) = -<Д,
(5.370)
353
§ 5.31] Переходный процесс в электронном генераторе где мы обозначили, так же как и в (274),
J(a) =
4-тс
F(a cos и) cos и du.
7С — тс
Далее,
ч со । 1
ф(<о, а) = -о+г5-2— v 7 2 1 2™#
+ тс
J \№а cos и + F' (a cos и) а<л sin и] сгз и du = — тс
-J-TC
Ш I 1 Г Q л <0 . Л2
= 0-+ й— я2 cos2я du = —4- —.
2 1 2iw> J 2 1 2<о
—тс
Второе уравнение (339) приводится к
J(d) = 0;
как мы видели в § 22, оно имеет корень а = 0, соответствующий состоянию равновесия, и два корня a = z±za*, соответствующих периодическому режиму. Третье уравнение (339) даёт со = fe, вследствие чего
Ф(со, a) = k. (5.371)
Для выяснения устойчивости периодического режима нужно, согласно § 28, определить знак величины
1 д ч /'(«*)
= —г т-аФ(о), а) =*-------------
Но, как показывает один взгляд на график функции J(a) (фиг. 34), величина J' (а*) отрицательна, вследствие чего > 0 и перио-
дический режим асимптотически устойчив.
С помощью укороченных уравнений
>=р(»), = к (5.372)
можно получить не только стационарные, но и переходные режимы. При этом квадратура, необходимая для разрешения первого уравнения, должна, вообще, выполняться каким-либо численным методом. Чтобы этого избежать, воспользуемся приближённой формулой (280), с помощью которой для J(a) и а* получаются явные выражения
J(a) = ъа— --- Ла3, а* = 2]Лс/Л.
23 Зак. 1474. Б. В. Булгаков
354
СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
[ГЛ. 5
Первое укороченное уравнение (372) получает вид da 1 / 1 л п\
_ = )м
Умножая обе его части на 2а, имеем:
4^ (<0) _ ..
а» (4х — Х«2) — ’
(Л + л \ d (»3) = * dt, \а2 1 4х— Ха2/ 4 7
что можно также переписать в виде
, t 4х — Ха2 d In-----X----= — х dt.
а*
Если же обозначить через а0 значение а при /=0 и проинтегрировать, то
4х Ха2 «Q 2а0 Ух
1п------------------у = — х/, а = - - =
а 4х— Ха‘ V\a2n + (At.—l
Пользуясь выражением а* через х, X и интегрируя второе укороченное уравнение, получаем окончательно:
___________atfi*__________ /«о + (л*2 — e~xt
' и = kt-^-Uq.
(5.373)
Отсюда видно, что если aQ равно нулю или а*, то это постоянное значение сохраняется при всех t. Если же а0 имеет любую другую величину, то а стремится к а* при t —>оо. Таким образом, состояние равновесия неустойчиво, а периодический режим асимптотически устойчив и представляет режим автоколебаний электронного генератора, в чём мы, впрочем, уже убедились раньше.
ГЛАВА 6
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
§ 6.1; Постановка задачи и получение укороченных уравнений. Мы будем рассматривать в этой главе вынужденные колебания системы с постоянной приведённой массой т под действием обобщённой силы
— ^'(?)+Q = m[-f(q, я)+4-(VOL (6.1)
где q попрежнему обозначает лагранжеву координату системы, v — постоянную, /(#, q) и — заданные функции, причём первая представляет силу, зависящую от положения и скорости системы, как в ранее рассмотренных задачах, а вторая характеризует возмущающую силу и предполагается периодической с периодом 2тс по отношению к своему аргументу
& = (6.2)
период по t будет
P = V« (6-3)
вследствие чего v есть угловая частота возмущения.
Обозначим через С свободный член ряда Фурье для функции <р(&):
с=w J *(!)) м (6-4)
—тс
и положим:
23*
&S6 ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ [ГЛ. 6
Тогда совокупность членов нулевого и первого порядков в ряде Фурье будет
2те J
— тс
— тс
те j
— тс
$ (&) sin & sin & = С-Ц- R cos (& 4“ ?)•
Гамильтоновы канонические уравнения суть
ntq = р, р = т
(6.7)
и
может быть аппроксимирована линейным выражением
а <р(8) суммой C4"^cos(0 + t)> т0 мы получим «упрощённую» линейную систему
d(q — q*) _ Р dt т 1
W Й) + <ш3 + е2> (? - <7*) + 2s £ = * cos
где постоянная q* определяется соотношением
z — (со2 -{- s2) q* = g — С. (6.10)
Путём исключения р упрощённая система может быть заменена уравнением
d2 (q — q*) d&
d(q — q*)
dt
и имеет поэтому частное решение , вида
q— q* =.acos(&4~7 — ®)> Р =— тау sin (& 4~ 7 — ®)> (6.11) представляющее вынужденное колебание, которое устанавливается после затухания собственного. При этом а и 6 обозначают амплитуду и сдвиг фазы (запаздывание), выражения которых нетрудно найти. Пока а и 0 остаются постоянными, найденное частное решение не будет, разумеется, удовлетворять точным уравнениям (7); но этого можно потребовать, если применить метод вариации постоянных и и рассматривать а и 0 как новые неизвестные функции, . вводимые вместо q и р. Производя эту замену переменных в уравнениях (7),
§ 6.1]
ПОЛУЧЕНИЕ УКОРОЧЕННЫХ УРАВНЕНИЙ
357
находим:
— av sin и
a cos и — а (у — 6) sin и = — av sin я,
t (v — 0) cos и -\-f(q* + a cos ut — av sin и) = ф (&),
где
(6.12)
или же, разрешая относительно производных,
va =
— ф (&) sin а — av2 sin и cos и
vaO =
ф (&) cos и я*3 cos2 и.
(6.13)
При этом q и р в правых частях предполагаются заменёнными по формулам
<7 = <7*4-0 cos я, р = —ш\пи, (6.14)
Уравнения (13) являются точными, так как мы использовали лишь форму решения упрощённой системы. Чтобы продвинуться дальше, мы применим приближённый метод осреднения. Если уравнения (7) и (9), а также и начальные условия для рассматриваемых решений мало отличаются друг от друга, то новые неизвестные а и 6, не являясь более постоянными, будут, однако, меняться медленно. Поэтому мы можем позволить себе заменить правые части уравнений (13) их средними значениями по и за период 2к и написать:
• г - - >
4-тс . ,
v ж=i .1 [/(?’ £) - * <а)]sin«du>
4-тс
— тс
рассматривая при интеграции величины а и 0 как постоянные.
Из (6) вытекает:
+ тс 4“ тс
1 г if*
~ | (0) sin a du = — ф(&) sin [0-4-(7— 0)]dO =
— ТС —ТС
= — 7? sin 7 cos (7 — 0) 4- 7? cos 7 sin (у — 0) =;— 7? sin 6
и» аналогично,
+ тс э
ф(&) cos udu = R cos 0.
— к
*>
358
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
[ГЛ. 6
Поэтому, вводя ещё обозначения
2rcwz J — тс
Ч₽’(>, q*, а) =
— va sin и) sin и du,
(6.15)
V | 1
2 ’ 2те^а J
— тс
a cos и, — ча sin и) cos и du,
мы можем написать укороченные уравнения в следующей окончательной форме:
^- = — аФ(ъ q*, a)-|-Asin0, М dt — v
2va
(6.16)
Величина q* может быть определена для всех а в окрестности некоторого данного расчётного постоянного значения а* следующим образом. Напишем приближённое разложение + тс
1 г f(q*-j-a*cosu,—^a*sina)^ — | f(...)du-j-
— тс + тс 4- тс
sin и
И те
..) sin и du
— тс
и, пользуясь формулами (14), приравняем его выражению (8): 4- тс 4- тс
J- f + f /(...)cos и du] -------------------------
2те J 7 v 7 1 [ те J 7 4 J a*
— TC — TC
+ TC
— — f /(.. .) sin и dul—^г = g*+(^2 + s2) 9 4“ •
те J J 4 7 J тча* & ‘ v 1 7 1 m
Сравнение свободных членов и коэффициентов при q и р даёт: 4- тс 4- тс
g = -±- f(q* -|-a* cos и,—^a*s\nu)du — J /(...) cos и du, — тс — Тс
-- тс
1 f
_L_ £3 = —— f (а* 4- a* cos u, —va* sin u) cos и du, (6.17)
1 тел* . 7 1
— тс
—-ar f(q* 4-a* cos u, —va* sin u) sin и du. (6.18)
wca* J 7 1
— TC
§ 6.2]
УСТАНОВИВШИЕСЯ КОЛЕБАНИЯ И ИХ УСТОЙЧИВОСТЬ
359
Если же из первого уравнения исключить второй интеграл с помощью второго уравнения и воспользоваться формулой (10), то получится:
/((?* 4-я* cos а, —va* sin и) du = С. (6:19) Ztc , I — к
Это и есть искомое соотношение, из которого может быть найдено q*.
§ 6.2. Установившиеся колебания с частотой возмущающей силы и их устойчивость. Чтобы получить такие колебания, мы должны предположить, что а и 0 в формулах (11) имеют постоянные значения а*, 0*. Укороченные уравнения обращаются в конечные
соотношения
а*Ф(^, а*) =sin 0*,
#*pF(^, q*t а*) — ч] =cos 6*, & г
а если исключить 6*, то получится:
F(v, q*. а*) = 0,
(6.20)
(6.21)
где
Г(^, ?*, а) = а2([Ф(., a)]2 + F(^ <1*> «) — Ч2} — (6.22)
Из двух уравнений (19), (21) определятся q* и а*, если принять искомую постоянную а* за расчётную амплитуду, как это естественно сделать в данном случае; 6* найдётся затем из (20).
Чтобы иметь возможность судить об устойчивости установившихся состояний, рассмотрим колебание, немного отличающееся от установившегося, для чего заменим а и 6 в укороченных уравнениях через и 6*-|“ЭД. Считая приращения 8а, 80 малыми, разложим правые части в ряды Тейлора:
~а dt = — а*Ф(^ tf*) + -^-sine* —
— -^-1а*Ф(у, q*, а*)] 8а + -^- cos 0* 86 -f- ....
(6*4-89) * I Я
— ---------= V _ ф (V, q*, а*) + 2^ cos 6* —
— Я*> а*) + 'тг^» cos 0*1 8а — sin 0* 80-f~ • ••;
да* \ ч » /I 2va*2 2va* . *
невыписанные члены будут второго и высших порядков относительно оа,-80. Так как значения а*, 0* постоянны и удовлетворяют соотношениям (20), то производные от них, а также группы членов в правых
360
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
[ГЛ. 6
частях последних уравнений, не содержащие 8а, 60, равны нулю. Исключая ещё sin 6*, cos 0* при помощи тех же соотношений (20) и пренебрегая членами второго и высших порядков, найдём:
d (За) =q*, а*)] 8а + а* рГ(v, q*, а*)— ч] 86, di он
d(60) dt
д да*
Ф(ч, q*, а*)+* (у. <!*>“*)—фа —Ф(м, q*t а*)88> а
Приращения 8а, 80 являются неизвестными функциями времени, и мы имеем для них систему двух линейных дифференциальных уравнений с постоянными коэффициентами. Полагая
8а = 80 — с2е™, (6.23)
получим для с2 однородные уравнения
9*’ a*)]|q-[-a* pF(v, #*)— 4^2 = 0,
- g*. a*)+ *(v’ ]q- •
— [X-]-<E>(\>, q*, a*)]c2 = 0 с определителем
Д (X) = X2-|- M± (v, j7*, a*) X -j- M2 (y, q*, a*\ где
Afi(v, q*, a) = $(v, q*, а) + -^-[аФ(у, q*, a)],
4J2 (v, q*. a) — Ф (v, q*, a) [аФ (v, q*, a)] +
~|- pF (v, q*> a) — v] T(v, q*, a) — v-[“ +а-^'(у, 4*' a)
(6.24)
Для того чтобы q, c2 не были равны нулю одновременно, должен быть равен нулю Д(Х), и мы получаем для X квадратное характеристическое уравнение
Х2-}-^^, q*, a*)X4-Al2(v, q*> a*) = 0.
Устойчивость установившихся колебаний зависит от характера изменения величин 8a, 80, которые можно представить в виде сумм выражений вида (23), относящихся к двум корням характеристического уравнения. Если эти корни действительные и отрицательные или комплексные с отрицательной действительной частью, то 6a и 80 будут стремиться к нулю, а не возрастать со временем. Изменённое движение a*-[-6a, 6*-[-69 стремится к установившемуся режиму
§ 6.2] УСТАНОВИВШИЕСЯ КОЛЕБАНИЯ И ИХ УСТОЙЧИВОСТЬ
361
I а*, 0*, который в этом случае будет асимптотически устойчивым. Если корни характеристического уравнения действительные и один или оба положительны или если корни комплексные с положительной действительной частью, то мы будем иметь неустойчивость. Наконец, если характеристическое уравнение имеет один отрицательный и один нулевой корень или два нулевых или два чисто мнимых, то мы имеем так называемый критический случай/ когда уравнения в вариациях не решают вопроса, так как, хотя в первом приближении 8а и 89 с возрастанием t не стремятся ни к нулю ни $ к бесконечности, но отброшенные в дифференциальных уравнениях члены высших порядков могут изменить это положение в ту или другую сторону. Нетрудно убедиться, что для того, чтобы корни характеристического уравнения были действительными и отрицательными или комплексными с отрицательной действительной частью, необходимо и достаточно, чтобы
Mt(v, а*) > О, М2(у, q*> «*) > 0.
(6.25)
Эти неравенства и представляют собою условия устойчивости по первому приближению [6-8].
В дальнейшем, если нет противоположных указаний, мы будем предполагать возмущающую силу симметричной (С = 0), а функцию f(q, q) нечётной по крайней мере по одному из своих аргументов или состоящей из слагаемых, обладающих этим свойством. При этом условии можно взять q* = 0, так как тогда, согласно § 5.28, интеграл в левой части (19) обращается в нуль при всяком а*.
Как и в случае линейных колебаний, мы будем графически представлять зависимость амплитуды вынужденного колебания от частоты возмущения с помощью резонансной кривой UZ(v, а) = 0 в плоскости va (фиг. 35); при этом W(y, а) определяется формулой. (22)* а звёздочку у а мы будем при изучении резонансной кривой опускать. С этой кривой можно связать второе условие устойчивости Л12>0. В самом деле, из (22), (24) мы имеем:
= 2аФ (v, а)-^[аФ (у, а)] +
H-2a[T(v, a) — v] fa(v, а) — уa(у, а)1,
<6-26>
Резонансная кривая отделяет ту область (заштрихованную на фиг. 35) плоскости ча, где функция W(y, а) отрицательна, от той, где W(yt а) положительна. Если при перемещении вверх по прямой, параллельной оси .ординат и пересекающей резонансную кривую, нам
362
Вынужденные колебания нелинейных систем
[гл. 6
r(v, а) с резо-
приходится переходить из первой области во вторую, то меняет знак минус на плюс и в точке пересечения прямой „ лх dW
нансной кривой производная —положительна, в противном слу-
чае— отрицательна. Вследствие (26) в первом случае будет удовлетворяться также и условие устойчивости М2 > 0; соответствующие
Фиг. 35» Резонансные кривые систем с нелинейной восстанавливающей силой,
части резонансной кривой показаны на фиг. 35 более жирной линией. Изменение знака может иметь место только при ' dW в нуль , а так как dW . dW да д'* • да д'* 9
обращении
то это может случиться либо в точках с вертикальной касательной /3U7 ЭГ А да \ л л fdW dW а\
(-з— =# 0, — = 0, -з- = оо), либо в особых точках (-3— = -3— = 0 |,
\ д'* да д'* ) \ д'* да / ’
если таковые существуют.
§ 6.3. Системы с нелинейной восстанавливающей силой. Начнём Со случая, когда функция f совпадает с V' (9)/m, а потому зависит только от q и притом кусочно-непрерывна и нечётна. Предположим ещё, что V(q) имеет минимум при q = 0, так что это значение соответствует положению устойчивого равновесия системы при отсутствии возмущающей силы. Вследствие этого f(q) обращается в нуль при 9 = 0, а в окрестности этого значения или даже при всех q #= 0 имеет тот же знак, что и 9, так что qf(q) > 0. По формулам (15) мы имеем:
ФММ, 4r(,|fl)=’+1Lj(fl)1
где +тс + тс
, d Г 1 паи — -j— — da \_тп
— тс —Тс
J I/(acosw)dtt . (6.27)
j(a)==— /(a cos я) cos
тс
§ 6.3] СИСТЕМЫ С НЕЛИНЕЙНОЙ ВОССТАНАВЛИВАЮЩЕЙ СИЛОЙ
363
Укороченные уравнения (16) принимают Вид:
^=2Tsitl0> + 2^7 cos 6) (6.28)
а в случае установившихся колебаний с частотой возмущающей силы
О = -5-sin О*, а* Г—2-4--!^ j (а*) 1 = A cos 6*. (6.29)
2v 2 ’ 2va* 4 71 2v 7
Первое уравнение даёт
sin 6* == 0, cos 0* = ± 1,
(6.30)
и потому второе может быть переписано в виде
(6.31)
Отсюда, опуская звёздочку у а, получаем уравнение резонансной кривой >
Если существуют такие положительные а, при которых Дя)^>А?, то под радикалом можно брать оба знака и резонансная кривая состоит из двух ветвей, расположенных левее и правее кривой собственных частот v~k(a) (§ 5.29), где
fc(a)= (6.33)
Фиг. 35, а относится к рассматриваемому подслучаю. Кривая собственных, частот изображена пунктиром. Её абсциссы действительны по меньшей мере для некоторых а, так как из #/((?)> 0, согласно § 5.29, вытекает аДа)> .0 и, следовательно, J (а)/а> Если J (а) < R при всех а, то под радикалом в (32) можно брать только нижний знак и левой ветви не существует (фиг. 35, б). Правая ветвь асимптотична к оси абсцисс. При R -> 0 резонансная кривая стягивается к фигуре, которая может быть названа скелетной [6 ‘-31 и состоит из кривой собственных частот и положительной части оси абсцисс. Необходимость присоединения оси абсцисс можно объяснить тем, что при отсутствии возмущения (/? = 0) мы получаем положение равновесия q = 0 при а = 0 и любой частоте v.
На левой ветви резонансной кривой сдвиг фазы 6* равен нулю, а на правой он получает значение it.
В случае линейной системы k есть константа и кривая собственных частот обращается в прямую, параллельную оси ординат; поэтому каждому v соответствует единственная ордината а резонансной кри-в°й. Наоборот, в случае нелинейной восстанавливающей силы, как видно из фиг. 35, а, одной и той же частоте возмущения иногда
364 ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ [ГЛ. 6 f
В
$
соответствует несколько возможных амплитуд установившихся колебаний. В реальных системах удерживаться могут только те, которые соответствуют устойчивым колебательным режимам, причём от начальных условий зависит, какой из них будет действительно избран системой. Экспериментально эти факты, весьма характерные для нелинейных систем, были впервые обнаружены О. Мартинсе-ном р-22] и затем хорошо проверены другими исследователями.
Пользуясь формулами (22), (24), (26), (31), находим:
W Ь й) = {и («) — ^й]а - Я2}.
7И1 (^, а*) = О,
dW _ [J (а*)-- 'Яа*] [J' (а*) — ^] да* 4^2а*
/? [Л (а*) — 4^2а*
Так как 7(0) = 0, то
^«0) = —g-,
(6.34)
(6.35)
(6.36)
Л42 (^> а*)
2 \ > / 2а*
и I^(v,la), будучи отрицательной на оси абсцисс, сохранит, в силу непрерывности, отрицательный знак во всей области между осью абсцисс и резонансной кривой (заштрихована на фиг. 35). Пользуясь правилом, изложенным в конце § 2, легко указать те части резонансной кривой, где М2 > 0 (изображены жирной линией), и те, где М2 < 0. Однако вопрос об устойчивости решается сразу и притом в отрицательном смысле только во втором случае, так как при Мх — 0, М2 < 0 корни характеристического уравнения А (Л) = 0 действительны и имеют разные знаки; частное решение уравнений в вариациях, соответствующее положительному корню, неограниченно возрастает вместе с t и даёт заведомую неустойчивость. Что касается тех частей резонансной кривой, которые изображены жирной линией, то для них = 0, Л42 > 0 и корни характеристического уравнения чисто мнимы. Таким образом, в рассматриваемой простейшей задаче мы встречаемся как раз с тем критическим случаем, когда уравнения в вариациях не решают вопроса об устойчивости. В дальнейшем мы преодолеем это затруднение.
Полагая
х — a cos 6, у = a sin 6, (6.37)
мы получаем из (11) при ^* = 0
^ = xcos(& + 7)+jsin(n-|-7), }
= —xsin(& + Y)+^cos(& + 7). j ///» V J
§ 6.3] СИСТЕМЫ С НЕЛИНЕЙНОЙ Восстанавливающей СИЛОЙ
365
Эти соотношения можно рассматривать как преобразование, связывающее координаты q> р/т\ в фазовой плоскости с координатами х, у относительно второй вращающейся системы осей, имеющих то же самое начало и образующих с осями первой переменный угол Величины а, 6 представляют полярные координаты во
вращающейся плоскости.
Мы имеем:
х = a cos 6 — аб sin 6, у = a sin 9 -Ц- аб cos 6
и, .вследствие уравнений (28),
— —
2va da ’
(6.39)
2 2ча
2ч 2ча da. ’
где
(6.40)
Функция получить
Замечая, что
/С(а) чётна, так как ЛГ(— а) = К(а).
----V (a cos и) da. тп I v 7 —тс
с помощью замены и = v + тс легко
*(<0 =
х да у да
а дх 9 а ду ’
имеем:
или
dx 1 дК
dt 2v dy
dy _ 1 (дК
dt 2ч \дх
dx___дН
dt ду
dy___
дН дх *
(6.41)
>
где
Н=±^(а) — Ях] =
1
~ 2v
тк
—
V (a cos и) da .
—тс
возмущающей силы соответ-
(6.42)
, Установившиеся колебания с частотой ствуют положениям равновесия (х*, j*) во вращающейся плоскости, Для которых поэтому
(6.43)
дн_ п дх* ду*
Благодаря канонической форме, к которой мы привели укороченные уравнения, мы можем легко исследовать также и все другие виды колебаний. В самом деле, так как гамильтонова функция Н
Збб ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ [ГЛ. 6
не зависит явно от времени, то можно тотчас написать обобщённый интеграл энергии Н = const., или
К (а)
где h = const. Отсюда
= К(а)
. ,/“ К(а) 7 / J Г/ / ч К (я)
У = у — 4 («)J [4 (а)---
к(а)~ — а~\~ К («) = « + h.
или
где
(6.44)
(6.45)
(6.46)
(6.47)
Уравнения (45), (46) могут рассматриваться как параметрические уравнения интегральных кривых в плоскости х, у. Они симметричны относительно оси х.
Умножая (39) на 2х, 2у и складывая, найдём:
d (а2) _ Ry dt ~ V ’
если же заменить у его выражением (46), то получится уравнение
= 'ф)-/,(а)1Ь („)_£»
dt nV R 1 v / 2 \ / r
(6.48)
в котором переменные могут быть разделены, в результате чего определение закона движения по интегральной кривой приводится к квадратуре.
Поскольку J(a) есть нечётная функция (§ 5.22), мы можем представить (31) в виде
— v2a* zt J(± а*) = zt /?, а так как
х* = a* cos 0* = ± а*, у* = а* sin 0* = 0, (6.49)
то
J(x*)==v2x* + /?. (6.50)
Таким образом, при данном v значения х* могут быть получены по Г. Дуффингу [611] как абсциссы точек пересечения кривой С = J(x) и прямой C = v2x-(~7? (фиг. 36, верхняя часть). Дифференцируя (40) и сравнивая с выражением (27) для J(a), имеем:
К' (a) = J(d) — v2a, К" (а) = J' (а) — v2. (6.51)
§ б.З] СИСТЕМЫ С НЕЛИНЕЙНОЙ ВОССТАНАВЛИВАЮЩЕЙ СИЛОЙ 367
Разность J(a) — '^а можно взять из построенного графика; то обстоятельство, что теперь мы берём аргумент а, а не х, не имеет, разумеется, значения. Прямая, изображающая линейный член v2a, проходит через начало координат и параллельна ’той, при помощи которой мы находим амплитуды установившихся колебаний. Зная К' (а), можно
составить представление и о течении функции /С(а) (фиг. 36, нижняя часть). Экстремумы этой функции соответствуют абсциссам точек пересечения кривой С = 7(х) и прямой С = v2x, точки перегиба на кривой l=K(a)IR имеют общие абсциссы с теми точками кривой С = J(x), где её касательная параллельна прямой С = v2x.
Как показывает (46), действительные значения у получаются только при тех положительных а, при которых соответствующая часть кривой l=K(a)IR заключена внутри прямого угла, образованного прямыми I = = 4 (а)’ = 4 (°)* Эта часть кривой может состоять из одной или нескольких от-
дельных дуг, а значения а фИГе 3g Диаграмма Дуффинга и график образуют один или несколько функции К (а).
сплошных интервалов, огра-
ниченных корнями подрадикального выражения в (46); интегральная кривая в плоскости ху будет также состоять из одной или нескольких отдельных ветвей.
Пусть Л* будут значения постоянной h, соответствующие положениям равновесия (х*, у*). Mbj имеем:
К(а*) * । /<'(«*) J(a*) —. 1е
следовательно, h* суть те значения h, при которых число а* обращает в нуль один из множителей подрадикального выражения в (46) вместе с его производной и является двойным корнем этого выражения. При этих значениях h кривая Z = K(a)IR касается одной из прямых Z = 4(a), Z=Z2(a) в точке с абсциссой а*.
вею?
368
ВЫНУЖДЕННЫЕ ЙОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
[tVI. 6
С помощью соображений подобного рода, рассматривая малые изменения Л*, можно было бы решить и вопрос об устойчивости. Мы, однако, предпочтём другой путь.
Пользуясь формулами (51), находим:
= а даГ дх‘* дх \_da дх
-Ц-\-К (а)1=— К'(а)-\-х 4--(°)14 =
дх La v 7J а \_da a v 7J a
a x ' 1 a a x a2 7
J (a) — Pa I x2 a ‘ a
jr (g) _ v2 j (a) _ у2д a cP
«=—v3+~|j(a)(l — + —
1 a L \ я2 / v 7 a _
— v2 + i +
и, аналогично,
d^K xy
дх dy a2
2M+j'(a)
Замечая, что вторые производные от К и Н отличаются только множителем 2v, и пользуясь соотношением (31), а также чётностью Jf (а), мы имеем для положений равновесия х = х* = ±а*, у =у* = 0:
д*Н _ J' (а*) — \2 _ J' (х*) — у2
дх*2 2\* 2v
д2//
ду*2 2va* 2vx*
д2Я дх* ду*
(6.52)
Так как, согласно (43), первые производные
дН дН
-ч—, ~s“ в положе-дх ’ ду
ниях равновесия обращаются в нуль, то функция Н имеет в этих положениях стационарные значения, характер которых зависит от знаков вторых производных, т. е. от знаков величин J' (х*)— v2 и х*. Если эти знаки различны, то мы не будем иметь ни минимума, ни максимума; величина М2 (v, а*), выражение которой (35) можно
написать в виде
M2(v, = (6.53) I
будет отрицательной, а колебательный режим, как мы уже знаем, f неустойчивым. Если обе величины J' (х*) — v2 и х* положительны 1 или обе отрицательны, то Н имеет минимум или максимум и М2 > 0. j Интегральные кривые могут рассматриваться как сечения поверх- ч| пости z = K(a)IR — х или
z=^-H(x,y) (6.54> 1
ж
§ 6.3] СИСТЕМЫ С НЕЛИНЕЙНОЙ ВОССТАНАВЛИВАЮЩЕЙ силой
369
плоскостями з = й. В положениях равновесия плоскость касается поверхности, и если это положение есть минимум или .максимум для z, то при малых изменениях h мы получаем в сечении малые замкнутые кривые, окружающие положение равновесия. Следовательно, это положение устойчиво. Мы доказали, что в рассматриваемой задаче вопрос об устойчивости ’ полностью решается условием М2 > 0, так что те части резонансной кривой, которые показаны жирной линией на фиг. 35, действительно соответствуют устойчивым колебательным режимам.
Критерий устойчивости можно связать также с диаграммой на фиг. 36. Для этого представим себе две области плоскости X, которые примыкают к кривой С = J(x) снизу и сверху. Разность J' (х*)—v2 будет положительна, если, ведя прямую C = v2x-|-^ слева направо и пересекая кривую, мы переходим из верхней области в нижнюю. Поэтому при отрицательных х*. устойчивые колебания получаются в тех случаях, когда прямая переходит из нижней области в верхнюю, а при положительных х* в тех случаях, когда имеет место переход из верхней области в нижнюю. Если переход совершается в противоположном смысле, то соответствующий колебательный режим неустойчив.
В качестве примера возьмём характеристику Г. Дуффинга /(<7) = Х?-|м8. (6.55)
Здесь (§ 5.22)
J(a) = Ха — — |ла3, (6.56)
так что, с помощью (51),
К' (а) = (X — V2) а — 1- |ia3, К (а) = у [(А — v2) а2 — | Иа4]
Уравнения резонансной кривой и абсцисс положений равновесия (50) для данного случая будут
,= ]/" х—G—2)*-|н*3 = Я. (6.57)
Если взять числовые данные
4=15, 4=1°>р-=1б> <6-58)
Уравнение абсцисс положений равновесия получает вид:
4х3 — 5х + 1 = (х — 1) (4х2 + 4х — 1) = 0. (6.59)
Параметрические уравнения интегральных кривых будут
х = Ааа_ai—h, .
У = ]/ a2 — (у <z2 — а4 —/г? =
= — j^a4—у а9-|-а-|-/Л(—а4-|-.у — h\.
24 Зак. Б. В. Булгаков
370 ВЫНУЖДЕННЫЕ КО ЛЕБ АН ИЯНЕ ЛИНЕЙНЫ ХСИСТ EM 6
Уравнение (59) имеет корни "
^ = — -+^ =—1,207, х2 = ~ -4-— = 0,207,
" *8 = “ЬЛ ” . - -
определяющие положения равновесия Alf А2, А.3 (фиг. 37)/
График на фиг. 36 вычерчен как раз для данного случая; применяя сформулированный выше критерий, видим, что корни х1# х2 соответствуют устойчивым, а корень х._> — неустойчивому колебательным режимам, "
Если взять h = 1/2, то подкоренное выражение в формуле для у делится на (d2—1)'2 и мы можем написать:
x =-a9—-a4 —-g-,
y — dzfa2— 111/~— a4 + 3a2— -j’
Интегральная кривая, определяемая
I/
Фиг. 37. Интегральные кривые во вращающейся плоскости.
этими уравнениями, есть так называемая разделяющая кривая, проходящая через неустойчивое положение равновесия Л8, которое соответствует значению а=1; эта кривая показана на фиг. 37. Для получения ее действительных точек нужно давать а все значения, • при которых подрадикальное
выражение — -|~ За2 — остаётся положительным; эти значения заключены между корнями
J/Q —/2 = 0,293,
у/ | +]/ 2 = 1,707.
Разделяющая ограничивает заштрихованную на чертеже серпообразную область значений х, у, где поверхность , * '
z = у (Х9 + у*) — (х9 + у*)* — X
лежит выше плоскости .г = 0,5. Вершина этой «возвышенности» лежит над точкой Af, её высота равна
’ •+ = g + /2 =-2,727. •
\ л* 1о * г
§ 6.4] сйсТемы d вязкйм Сопротивление^
При 0,5 < h < 2,727 интегральные кривые проходят в заштрихованной области и окружают точку А±. Внутри этой области имеется другая незаштрихованная область, где Поверхность лежит под плоскостью z = 0,5. Наинизшая точка этой «низменности» лежит под точкой А2 на глубине
гт = ^-/2 = -0,102.
Для точек, лежащих снаружи заштрихованной области, поверхность также лежит ниже плоскости £ = 0,5. При —0,102 <Л< 0,5 каждая интегральная кривая состоит из двух ветвей, одна из которых лежит во внутренней низменности и окружает точку Д2, а другая проходит снаружи серпообразной области. При h<Z — 0,102 остаётся лишь одна наружная ветвь.
Так как все интегральные кривые, за исключением приводящихся к точкам равновесия, а также разделяющей, являются замкнутыми и всюду .пробегаются изображающей точкой с конечной скоростью относительно плоскости ху, то эти относительные движения будут периодическими с периодами, вообще различными для различных кривых и отличными от 2n/v. Функции q, р> характеризующие само изучаемое движение, будут квазипериодическими. Так называются, вообще, функции от п аргументов = периоди-
ческие по отношению к каждому и с одним и тем же периодом 2к; при этом суть фундаментальные частоты, которые можно предполагать линейно независимыми, т. е. такими, что не существует никакого соотношения
= o (6.60)
I '
с целочисленными коэффициентами git не равными нулю одновременно. В самом деле, если бы v* были линейно зависимы, то все можно было бы выразить через меньшее число п' линейно независимых аргументов = v7. В рассматриваемой задаче мы имеем две фундаментальные частоты.
§ 6.4. Системы с нелинейной восстанавливающей силой и вязким сопротивлением. Рассмотрим теперь случай
/(?>
где J (Q), как и в предыдущем параграфе, — нечётная функция.
Определяя опять J(a) формулой’(27), получим при С=0;
ф0« а) = е,’ Wfv;
tlZ(v, а) = ±{482а^ + [у9а——/?3}, • (6.61)
24*
вввь**^*
3?2 ВЫНУЖДЕННЫЕ коЛЕЙАЙИЯ нелинейных систем |гл. 6
и уравнение резонансной кривой может быть написано в виде
a2v4 — q v2 с2 (а) = О, (6.62)
где
с± (а) = 2а [J(а) — 2а&\, с2 (а) = [J (а)]2 — /?2. (6.63)
Дискриминант этого уравнения, квадратного относительно v2, есть
d (а) = 4а2 {Я2 — 4е2а [J(a) — е2а]}. (6.64)
Разрешая относительно v и беря только положительные имеем:
значения
(6.65)
Далее
1 dW
[Az* — /'(«*)], (6.66)
4v2a# 5 .
первое условие устойчивости удовлетворяется, если в положительно и сила — представляет собою сопротивление, что мы будем всегда предполагать.
Кроме того, что f(q) нечётна и потому исчезает при q = 0, допустим, что это — непрерывная монотонно возрастающая функция, так что Отсюда уже будет следовать, что qf (q) > 0.
Рассмотрим, как изменяется v в зависимости от а. Действительные точки резонансной кривой могут получаться в интервалах тех значений а, для которых трёхчлен в её уравнении, квадратный относительно V2, имеет один или два действительных положительных корня, а также на границах таких интервалов. В первом случае (а) < 0 или
J(a)</?,
откуда следует, что d (а) > 0. Во втором случае должно быть С1 (а) > с2 (°) > 0, d (а) > 0 или
J 2e2a < J(fl) < Ч^4е2Л •
Исследование удобно вести графическим путём, строя в некоторой плоскости ау (фиг. 38) прямые
4е2д ’
и гиперболу
(6.67)
(6.68)
в точке (/?/2е2, R) первая прямая пересекает вторую и касается гиперболы.
§ 6.4]
СИСТЕМЫ С ВЯЗКИМ СОПРОТИВЛЕНИЕМ
373
Нанесём затем на той же диаграмме кривую у = J(d). Абсциссам а тех её точек, которые расположены в области (-|---) ниже
прямой у = R> соответствуют два действительных значения v2 разных знаков. В области (++), лежащей между прямой y — R и гиперболой и притом левее точки (/?/2s2, R)t мы имеем два действительных положительных значения, а в незаштрихованной области выше гиперболы оба значения v9 будут комплексными. Если, наконец, кривая y = J(a) проходит через область (-----), лежащую между
Фиг. 38. Исследование корней биквадратного трёхчлена.
прямой у = R и гиперболой, но правее точки (Z?/2e2, R), то в этой области оба значения v9 будут отрицательными. Функция J(a), так же как и /(#), является монотонно возрастающей и исчезает при а = 0 (§ 5.29). Поэтому кривая y — J(a) может пересекать прямую y = R один и только один раз; абсцисса а0 точки пересечения должна удовлетворять уравнению
J(a0) = R. (6.69)
Если а0 < /?/2е9, то кривая пройдёт через области (-|-----) и (-|- +),
пересечёт гиперболу в некоторой точке с абсциссой ат, заключённой между aQ и /?/2е2, а затем пройдёт в незаштрихованную область; этот случай изображён на фиг. 38. Здесь при 0 < а < aQ каждому значению а соответствует одно действительное положительное значение v, а при a0<a<aw — два значения; резонансная кривая имеет вид, изображённый на фиг. 39, а. Её максимальная ордината есть ат.
Если fl0>/?/2s2, то пересечение кривой y = J(a) с прямой у = R получится правее точки (Z?/2e2, /?); кривая из области (-|--) попадёт
8 область (-----) и, следовательно, лищь для 0 < а < будет одно
374 ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ [ГЛ.6
действительное положительное значение v; резонансная кривая имеет вид, изображенный на !фиг. 39, б. Максимальная ордината есть а0.
Фиг. 39. Резонансные ^кривые систем с нелинейной восстанавли-
Неограниченные ординаты у резонансной кривой могут получиться только в том случае,когда. J.(a) при всех а остаётся меньше /?, так .как тогда конечного числа а0 не существует (фиг. 39, в).
При а = 0 коэффициенты биквадратного трёхчлена при v4 и v2 обращаются в нуль и потому оба значения v2 обращаются в бесконечность; следовательно, резонансная кривая асимптотична к оси абсцисс.
Кривая собственных частот v = = k (а) пересекает правую ветвь резонансной кривой (в случаях, соответствующих фиг. 39, б и в, эта ветвь будет единственной) при а, удовлетворяющем уравнению
__________2s2 -4-
а а________~
+ 1Л—4еа№1— га2 а
или
4eW(a) = /?2. (6.70)
вающей силой и вязким сопроти- Так как левая часть есть неогра-влением. ниченная монотонно возрастающая
функция, то это уравнение имеет единственный корень ап. Замечая, что
R . л* R д* иг/ &2(а*)—ч2
-—- sin 0* — ©, fr—z cos 0* = Ф (v, — v = —,
мы видим, что левее кривой собственных частот сдвиг фазы О* принадлежит первой четверти, а правее кривой — второй четверти.
Вследствие того, что 7(0) = 0, мы имеем:
0) = -^<01
и, в силу непрерывности, функция 1У(>, а) сохраняет отрицательный знак во всей области (заштрихованной на фиг. 39) между осью абсцисс и резонансной кривой. Пользуясь общим приёмом, выделим те дуги кривой, которые соответствуют устойчивым колебательным режимам; эти дуги показаны жирной линией. Отметим, в частности,’ что точке пересечения резонансной кривой с кривой собственных частот всегда соответствует устойчивый режим, так как при v = fe(a*) мы цмеем Л42 = 82>0.
\ bj "1 I . '1? »—
ЧАСТЬ III
СИСТЕМЫ С КОНЕЧНЫМ ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ
ГЛ’АВА 7
МАЛЫЕ КОЛЕБАНИЯ ОКОЛО ДАННОГО СОСТОЯНИЯ
§ 7.1. Уравнения в вариациях. Мы начнём с линейных задач, к которым приводит обычно метод малых колебаний. Так как этот метод широко распространён в математической физике и технических науках, то он будет нами сформулирован также в весьма общей форме.
Пусть будет
9j(?v 4i> •••> 4i> ч±> ^2» •••> Чп> 0 = о (7 = •••> #0 (7.1)
— система тп обыкновенных дифференциальных уравнений, описывающих какие-либо физические процессы. Зависимыми переменными являются п обобщённых координат qt> ...» qn, характеризующих состояние рассматриваемой физической системы; они могут быть длинами, углами, давлениями, температурами, электрическими токами или напряжениями и т. п. Условие zn = n необязательно, если на это не сделано указания; есть порядок самой старшей производной qt от q^ встречающейся в уравнениях, /п2 — порядок старшей производив
ной q2 от q2 и т. д.
Вводя матрицы-столбцы
со «т
<h
СР I
(тХ О.
(Я XI)
(7.2)
Чп
и обозначая через L наибольшее из чисел ..., mni мы можем записать систему (1) в форме одного матричного уравнения
<?(?, О = °- (7.3)
Часто случается, что уравнения (1) представляют значительные трудности для исследования и найти их общее решение не удаётся, HQ зато известна система функций ^(/)(А = 1, ..., п), образующих
378 МАЛЫЕ КОЛЕБАНИЯ около данного состояния [гл. 7
частное решение либо самих уравнений (1) либо некоторых упрощённых уравнений
)
Ф/(91» 91» • ••> 91» 91» ^2» •••> 9п» 0= 0 (7===1> •••> (7*4)
получающихся путём пренебрежения второстепенными обстоятельствами явления; например, в механической задаче мы можем отбросить какие-либо малые силы. Матричное упрощённое уравнение, соответствующее скалярной системе (4), будет:
Ф(<7> q......q, 0 = °> (7.5)
а через q(t) мы обозначим его известное частное решение, т. е. матрицу-столбец с элементами q^t), Это частное решение, определяющее некоторый выбранный процесс или состояние, мы будем называть порождающим.
Можно попытаться, отправляясь от порождающего решения, иссле^-довать, хотя бы приближённо, процессы, близкие к выбранному. Как сказал по другому поводу Пуанкаре, мы постараемся превратить светящуюся точку в светящийся диск, большей .или меньшей величины. Для этих процессов мы положим
q = q<f)-\-y>
где матрица-столбец
У1
выражает отклонение от выбранного процесса, которое мы будем
рассматривать как новую неизвестную.
Совершая эту замену в заданном уравнении (3), имеем:
<р(<7(О+.у> ?(0+ у> •••> q(f)+y> 0 = °>
L Б-1
а так как зависимость левой части от матриц у, у, у сводится
к зависимости от их элементов, то мы можем разложить её в конечный ряд Тейлора по степеням этих элементов:
<р(<7(0. ?(/).....?(0>/) +
” L Г-1
+ S (afc0)№ + afc У к +. •• • +4Ь)3'й) + остаточный член = 0.
Л = 1
При этом
а'к.=а'н = d<?id "" 4Ь)=d^d<Jic’
§ 7.1]
УРАВНЕНИЯ В ВАРИАЦИЯХ
379
а элементы этих матриц-столбцов суть
= d^/dqk, а$ = д^/д qk.........= д^дд*,
после вычисления частных производных все их аргументы, кроме tt должны быть заменены известными функциями qk(f) и их производными по t.
Полагая
L L-1 w = —<D(q(f), q(f), ..., q(t), f), ll/r'0) z/0)ll Л —7»(1)n Пт— ИлФ Л<£'п 1 ’ }
Uq — Il > • ••» ||> — I* » •••> Ц» •••> &L —’ || » • ••> ||> .
можем написать преобразованное уравнение в виде
L Ь-1
* аоУ^га1 У + ••• + аъУ + остаточный член = ад(£). 9
Очевидно, что предыдущие выражения для а0, av ...» суть коагулированные формы прямоугольных матриц
ao = |la$ll’ а1 = Иа$11..ал = ||<4»)1 («X»).- (7.9)
Вводя оператор дифференцирования
(7.Ю)
и образуя матричный операционный полином
/(D).= aoob + fliDb_1+ ••• +«£> (7?11)
получим преобразованное уравнение в форме
f (D) у -|- остаточный член = w (t).
Будем предполагать, как это естественно, что функции Ф и <р мало отличаются друг от друга в окрестности порождающего решения. .Так. как это решение должно обращать в нуль Ф, то •wit) будет мало. Рассматривая лишь малые отклонения у и пренебрегая остаточным членом, получим линейное уравнение
= (7.12)
при этом мы ещё можем допустить, что при вычислении величин частные производные берутся от функций Ф^, а не
о а($ = <ЭФ^; (7.13) такая-замена также, сводится к пренебрежению в предыдущем лицей-ном уравнении членами высших порядков малости, , .
380
МАЛЫЕ КОЛЕБАНИЯ ОКОЛО ДАННОГО СОСТОЯНИЯ
1гл. 7
Если упрощённое уравнение (5), для которого найдено порождающее решение q(t), в частности не отличается от заданного, так что Ф== ©, то w(t) = Q и мы получаем однородное линейное уравнение
f(D)y = 0. (7.14)
Переходя к элементам, имеем соответствующие скалярные системы:
п
^f3ic(D)yk = 'w3(f) = (7.15)
k — i » »4
и ч
п 1
= 0 (/=1,.... т). (7.16) |
fc=l -I
Эти уравнения или предыдущие матричные носят название уравнений в вариациях, так как мы могли бы писать bqk, Zq вместо у^, у. М
Величины суть операционные полиномы *
/,.,(О) = а^Оь + а^7/-1+ ... + <$. (7.17) !
Заметим, что можно было бы ограничиться рассмотрением случая, I когда упрощённое уравнение не отличается от заданного, сводя к нему £ общий случай путём введения добавочной координаты Для этого Л нужно только вместо заданной скалярной системы (1) рассматривать | новую систему: t
+ —$j) = ° (7= 1> .... rn), |
>y причём включение последнего уравнения необязательно. Если совокуп- | ность функций q^it), ..., qn(t) представляет порождающее решение j упрощённой системы (4), то функции q^t), ..., qn(f), 0 образуют j| порождающее решение новой. Решениями заданной системы (1) являются | те решения новой, для которых qn+1 = 1. Уравнения в вариациях Д получаются путём сохранения членов первого порядка в разложениях > левых частей новой системы по степеням уг, ..., уп, уп+1 и их Л производных, так как хотя интересующее нас значение уп+1 = qn+1 = Г J и не мало, но коэффициентами при нём в первых т разложениях д служат малые разности ©j— Ф^, а коэффициенты при произведе- j ниях уп+1 на остальные ук пропорциональны частным производным ; тех же разностей по qki причём в выражениях всех коэффициентов f нужно положить = (/=1, ..., n). j
Этим замечанием мы воспользуемся при случае, а пока сохраним I прежнюю точку зрения, допуская несовпадение заданного и упрощён- 4 ного уравнений. Коэффициенты аг уравнения в вариациях являются, 1 вообще, функциями времени, и интегрирование уравнения связано 1 поэтому с обычными трудностями. Если, однако, функция Ф не зави- f Сит явно от времени и матрица q (t) есть постоянная, характеризую-
§ tij
уРавнёййя в варйаЦййх
щая состояние равновесия физической систомкг ™ „л„
будут также достоян™. Это будет “к и i б„ ° «оаффиинедть, «J-i функция Ф и , и, не 6уд"ГобЯзате^об°„2
обладают, однако, тем саойстаом, что I исключается S” "обо» „з
выражения
L ъ Д-1 Д-1
Ф(?(0+^> ?(0+ .У.
> /).
(7.18)
Выбранный процесс, характеризуемый порождающим решением, называют в этом случае установившимся. Физически установившийся процесс характеризуется тем, что при отсутствии возмущений, т. е. при Ф = % закономерность, которой подчиняется отклонение у от выбранного процесса, не зависит от начала счёта времени.
Другим важным случаем является тот, когда Ф представляет собой периодическую функцию по отношению к явно входящему t или вовсе его не содержит и функция q(t) также является периодической; при этом, если t входит в Ф, то период для этой функции и для q(f) должен быть один и тот же. При этих условиях коэффициенты уравнения в вариациях будут, очевидно, периодическими. Это имеет место и в том более общем случае, когда выражение (18) оказывается периодическим по t, хотя бы сами функции Ф и q(t)n не были таковыми.
Будем теперь. предполагать, что т = п.
Пусть, кроме того, скалярная система, соответствующая матричному упрощённому уравнению, разрешима относительно старших тк
производных qk и пусть известно не только частное, но и общее решение упрощённого уравнения, содержащее полное число s = 2 произвольных постоянных cl9 ..., с8. Тогда интегрирование уравнения в вариациях сводится к квадратурам, независимо от того, будут ли коэффициенты постоянными или переменными.
В самом деле, пусть общее решение есть
q = q(t, с), (7.19)
где
(s X О-
ci
(7.20)
При некотором определённом значении с должно получаться
щее решение g<if); предположим, Что это будет при с —0. Подставим выражение (19) в уравнение (5), продифференцируем получившееся тождество по одной из постоянных св и положим затем Q ... в По правилу дифференцирования сложной функции получим:
ве^ъ***
п L L—1
Малые колебаний окблб данного состояния
[гл; j
где •
40) = дФ/д^, 4Х) = дФ/dq^,..., 4Е) = дФ/ддк, (7.21) причём в выражениях частных производных все qk должны быть заменены функциями qk (t), а символ ( )0 обозначает подстановку с± = = ... = cs = 0. Пользуясь коммутативностью дифференцирования по t и по сс и производя те же преобразования, что и при выводе уравнения в вариациях, получим:.
/(О)(^-)=0. , \UCqJQ
Мы видим, что производная , вычисленная-с помощью (19), * представляет частное решение уравнения в вариациях без правой части. Полагая а=1, ..., s, получим s решений, с помощью. которых можно построить и общее решение
8
у - <7-щ>
а=1
/ f
Если уравнение в вариациях в рассматриваемой задаче неоднородно, то, пользуясь соответствующей скалярной системой (15), мы получим затем общее решение квадратурами по известному методу, вариации постоянных.
§ 7.2. Приведение к уравнениям первого порядка. Система обыкновенных дифференциальных уравнений любых порядков может быть приведена к системе первого порядка путём введения добавочных неизвестных и уравнений. Мы проделаем это для уравнений (3) или (1), предполагая, что А^2.
С этой целью будем трактовать L матриц
Ь-1 L-2
>q, q
как самостоятельные неизвестные. Уравнение (3) может быть представлено в виде
Ч.....q, *) = о. (7.23)
Присоединим к нему L—1 тривиальных соотношений
Е—1 Ь—2
; - я -Ц--------0,,.., q-g = O. (7.24)
« О» X
Общее число матричных уравнений тогда будет равно числу неизвестных матриц L. Соответствующая скалярная- система содержит Ln неизвестных и состоит из nt-\-(L — 1)п уравнений.
§ 7.31
МАЛЫЕ КОЛЕБАНИЯ И УСТОЙЧИВОСТЬ '
383
Если порядки тк старших производных от неизвестных qk в скалярных уравнениях не все равны между собой, то мы получим меньшее число уравнений первого порядка, вводя отдельные группы скалярных неизвестных
/ /
- Як» • • •» Як
для каждого индекса fe;. при , этом т'к равно наибольшему из чисел 1 и тк или им обоим (при дел=1). Общее число неизвестных будет:
к к
_ f *
где I—число тех mkj которые равны нулю, если такие существуют. Что касается уравнений, то мы прежде всего выразим в новых неизвестных заданные т уравнений. Кроме того, для тех индексов k, для которых тк^2 и только для них, мы добавим группы уравнений
a —0 'п —
Як dt —. • • • > Як — dt ’
число добавляемых уравнений для каждого k есть тк—И. Общее число уравнений равно —я.
Полученная по первому или второму способу расширенная, система первого порядка может быть вновь представлена в виде одного матричного уравнения . '
(7;25)
где и q имеют, разумеется, иные значения, чем раньше. Уравнение в вариациях будет иметь вид
{A(t\D-\-H(t)\y = w(f), (7.26)
Если, в частности, для исходного' уравнения т = п, то в случае приведения по первому способу число скалярных неизвестных и уравнений расширенной* системы равно Ln, а по второму способу В обоих случаях матрицы A(t) и H(t) будут квадратными.
§ 7.3. Малые колебания и устойчивость. Предположение о малости отклонения у, которое служило основанием к тому, чтобы отбросить члены высших порядков в уравнении в вариациях, .может быть, оправдано в общем случае лишь для ограниченного промежутка времени Т. Для определённости предположим, что в заданной скалярной системе число неизвестных равно числу уравнений и что'она Разрешима относительно старших производных,-, вследствие чего, .по к уравнениям первого, порядка, она: может быть;
МАЛЫЕ колеЬаний около ДАННОГО СОСТОЯНИЯ [гл: 1
представлена в форме матричного уравнения
^ = <?(?> 0. (7.27)
*
а упрощённая система — в форме уравнения
g = Ф (?, 0; (7.28)
при этом q, <р и Ф суть столбцы с одним и тем же числом элементов, которое мы обозначим опять через п.
Рассматривая сначала случай. Ф==еф и пользуясь общей теоремой о непрерывной зависимости решения от начального значения неизвестной qQ, мы можем предположить, что оно выбрано столь близким к начальному значению q(tQ) для порождающего решения, что от начального момента t0 до момента отклонение y = q— q(t) остаётся меньшим сколь угодно малого положительного столбца е. Этого предположения, вообще, нельзя сделать, если промежуток времени Т неограничен, а те выбранные физические процессы и описывающие их порождающие решения, для которых это всё же возмож-, но, являются исключительными и, согласно определению А. М. Ляпунова [б1°], называются устойчивыми по отношению к координатам qk.
Итак, выбранный процесс или состояние равновесия устойчивы при начальных возмущениях, если для любого положительного столбца е можно найти такой другой столбец т|, что, выбирая |йУ01<т1> мы по" лучим IjH < е ПРИ всех А больших tQ\ в противном случае мы имеем неустойчивость. Если, выбирая достаточно малое мы имеем д/->Опри £оо, то устойчивость называется асимптотической. Таким образом, понятие об устойчивости выбранного процесса связано со свойствами соседних процессов. Устойчивый процесс стремится удерживать свои свойства, так как соседние процессы имеют тенденцию стремиться к совпадению с ним или, по крайней мере, не удаляться от него. Этим и объясняется важное значение устойчивых процессов в общей физике, несмотря на их исключительность. В технике, в частности в технике регулирования, их значение ещё больше, так как, в терминах математической теорий, задача всякого регулятора состоит в том, чтобы, управляя потоками энергии в системе, подлежащей регулированию, сделать устойчивым некоторое желаемое её состояние или происходящий в ней процесс или же усилить уже существующую устойчивость. Этим объясняется роль техники регулирования как источника задач для теории устойчивости и теории колебаний. Только для устойчивых процессов соседние процессы имеют характер колебаний около выбранного.
Можно сказать также, что лишь в случае устойчивых процессов математический аппарат линейных уравнений в вариациях вполне адэкватен физике явления для неограниченного промежутка времени.
ВЛИЯНИЕ ПЕРЕМЕННЫХ ПАРАМЕТРОВ
385
§ 7.41
Поэтому задача установления признаков устойчивости имеет важнейшее значение не только для изучения самого данного процесса, но косвенным образом и для суждения о законности метода уравнений в вариациях при изучении соседних процессов. Простейший путь к решению состоит здесь в изучении самого линейного уравнения в вариациях и его интеграла; в этом случае мы будем говорить о линейной устойчивости. Однако выводы, получаемые этим путём, не вполне надёжны, так как мы пользуемся здесь тем самым линейным приближением, законнность которого ещё только предстоит проверить. При строгой постановке, основанной на анализе точных уравнений, проблема устойчивости принадлежит к числу труднейших; в её общей классической постановке она разрешена А. М. Ляпуновым. Результаты, полученные им для частных, но достаточно широких и важных классов задач, оправдывают метод уравнений в вариациях: оказывается, что суждение об устойчивости или неустойчивости, составленное на основании решения линейного уравнения, подтверждается и при строгой трактовке. В особых, или «критических», случаях линейное приближение не решает задачи: при наличии линейной устойчивости действительная устойчивость может иметь, а может и не иметь места. Для изучения действительных свойств изучаемых явлений ещё важнее то, что во многих случаях линейное приближение хотя и подтверждается теоретически в указанном смысле, но лишь в очень малой области, так что для сколько-нибудь значительных начальных отклонений, которые в действительности всегда могут иметь место, качественная картина явления уже сильно отличается от .той, которую даёт линейная трактовка. Именно эта категория проблем в теории регулирования и радиотехнике вызвала за последние десятилетия настойчивые поиски методов исправления и улучшения линейных приближений.
Аналогичные проблемы возникают и при Фф«. В этом случае q(t) не является решением заданного уравнения, так что, полагая у0 = О, мы не будем иметь у — 0 при tQ < t. Для получения малых отклонений у на конечном или бесконечном интервале времени нужно как-либо ограничить разность ©— Ф. Выбранный процесс или состояние равновесия называются устойчивыми при длительных возмущениях, если для любого положительного столбца в можно найти такой другой столбец С, что, полагая yQ — 0 и требуя, чтобы при t0 < t и 1-У| < 8 длительные возмущения удовлетворяли неравенству |©—Ф| < С, мы имеем |,у| <е при всех t, больших tQ [7-3].
Можно, наконец, исследовать устойчивость в самом общем слу-чае» когда имеют место как начальные, так и длительные возмущения рб]
§ 7.4. Влияние переменных параметров. Во многих случаях Уравнение физического процесса целесообразно писать в виде
LL-1 k fc-1
<?{q, q, ..., q, р, р, ..., р, /) = 0, (7.29)
25 Зак. 1474. Б. В. Булгаков
386 малые колебания около данного состояния [гл. 7 1
4 $
где 9 и q имеют прежние значения и выражаются формулами (2), |
в которых, однако, нужно обычно полагать = матрица-столбец р содержит п' элементов являющихся заданными функциями / и i характеризующих внешние факторы, которые воздействуют на систе- | му, но испытывают лишь весьма малое обратное воздействие с её I стороны, которым мы пренебрегаем. - J
Если, например, дело идёт об измерительном приборе, то р мо- 1 жет характеризовать действительные значения измеряемых величин, j a q — показания прибора. В классической теории регулирования угло- | вой скорости машины матрица р может определять нагрузку машины J и установочные параметры регулятора, которые считаются постоян-ными в течение процесса регулирования. В новейших задачах теории регулирования, относящихся, например, к автоматическому управлению кораблём или самолётом или к следящему силовому приводу, ; р характеризует команду, осуществляемую перестановкой какой-либо задающей ручки; в этом случае р может меняться и притом по за- . кону, в отличие от программного регулирования, неизвестному зара-нее. Вследствие этого различия соответствующему разделу теории i регулирования иногда дают специальное название теории сервоме- ; ханизмов, хотя мы безусловно имеем здесь один и тот же круг идей \ и единую дисциплину, новые ветви которой вряд ли что-нибудь выиграют, отказываясь от родства со старыми. В качестве даль- ? нейшего примера можно указать механические или электрические с усилители, для которых р есть сигнал на входе, a q — сигнал на ) выходе, причём эта терминология часто применяется также для при- 4 боров и систем регулирования. Во всех случаях физическая система играет роль фильтра, преобразующего сигнал на входе, рассматриваемый как заданный, в сигнал на выходе, который подлежит опре-делению из уравнения (29).
Пусть p(t) — некоторый выбранный сигнал на входе. Допустим . сначала, что он постоянен и что t не входит явно в уравнение (29). Если предположить, что и q постоянно, то последнее принимает вид |
9(0, 0, ..., q, 0, 0, ..., р) = 0. (7.30) |
f
Матрица-столбец, составленная из данного ^постоянного сигнала р f и решения конечного уравнения (30) относительно q, если оно суще- J ствует, должна рассматриваться как порождающее решение.. В этом М случае упрощённое уравнение тождественно с заданным уравнением (29). Если теперь p(i) не постоянна, но меняется медленно в сравнении < с изменением q, определяемым внутренней структурой системы, то | в качестве порождающего решения естественно принять матрицу- । столбец, составленную из заданного сигнала p(f) и матрицы q(f)> £ получаемой разрешением относительно q упрощённого уравнения || ф(о, 0....................q, 0, 0, .... p(f), /) = 0, (7.31)|
§ 7.5] ПЕРЕХОДНЫЙ ПРОЦЕСС В ПАРОВОЙ МАШИНЕ С РЕГУЛЯТОРОМ 387
аналогичного предыдущему, но теперь уже не совпадающего с заданным. Матрица q(t) представляет «статическое» решение заданного уравнения, но оно не является, конечно, его действительным точным решением.
При получении уравнения в вариациях целесообразно варьировать всю совокупность переменныхр19 ..., pnr, q19 ..., qn , объединенных в матрицу-столбец, которая может быть записана в коагулированной форме:
к
L (я'4-nXi).
Заменяя р и q через p(f)-\-x и q(f)-\-yt мы получим линейное уравнение относительно неизвестной
У
с операционной матрицей типа тХп'-^-п (как мы уже указали, обычно т = п). Представляя последнюю в коагулированной форме || — е (D), f (О) ||, где е (О), / (D) — субматрицы типов m X л' и будем иметь:
II -е (D), /Ф) ||Х
= (О,
или
/(D)у = е (D) х + W (0. (7.32)
Если же возмущающая функция w(t) равна нулю, то
f(D)y = e(D)x.
(7.33)
Ту же форму получим и при w(t), неравной нулю, если присоединим эту функцию к х и положим
е1 (£0 = II (£>)» *JI> xi = w »
так как тогда j
е (D)х w = (D) xt.
Матрицы х и у входят в (33) вполне равноправно.
§ 7.5. Переходный процесс в паровой машине с регулятором.
В качестве примера рассмотрим движение паровой машины, снабжённой регулятором.
Центробежный регулятор предложен Уаттом в четвёртом патенте его паровой машины в 1784 году. Основы теории и методики расчёта даны в 1876 году И. А. Вышнеградским р-2].
Уравнение движения машины мы возьмём сначала в его простейшей форме
№ = К- L, (7.34)
at „
25*
Малые колЕБАния около данного состояний (гл. 7
где J—момент инерции вращающихся частей, <о— угловая скорость главного вала, К—вращающий момент, L — момент, происходящий от нагрузки, на которую работает машина, и от различных сопротивлений. Дальнейшее исследование существенно не изменится, если понимать под со производную от любой обобщённой координаты, определяющей положение машины, а под J, К, L — массу и обобщённые силы, приведённые к этой координате.
Движение будет равномерным (da>/d^==0), если K=L, но если нагрузка изменится, а вращающий момент останется прежним, то вращение машины будет неограниченно ускоряться или замедляться. При наличии регулирующего клапана, положение которого характеризуется координатой а, вращающий момент будет зависеть от и, причём вид функции
определяется устройством клапана. Положение д могло бы устанавливаться машинистом, который для целесообразной координации своих действий должен оценивать угловую скорость, со или, лучше, иметь перед глазами измерительный прибор (тахометр). Если z обозначает показание тахометра, то его устройство характеризуется зависимостью
•г = /3(<о).
Задача машиниста состоит в установлении целесообразного соотношения
«=/2 (^)> t что с успехом может быть осуществлено и с помощью автоматического регулятора.
В результате, К оказывается функцией от о>:
/С=ЛГ(а)). (7.35)
Стационарный режим равномерного вращения машины будет иметь место при угловой скорости о>*, определяемой из уравнения
K(a) = L. (7.36)
Таким образом, машина, снабжённая реулятором, получает определённую характеристику, т. е. однозначную зависимость между нагрузкой и стационарной угловой скоростью. Вторая задача состоит в обеспечении устойчивости стационарных режимов: р - случае отклонения действительной угловой скорости со от величины ^^соответствующей данной нагрузке, регулятор должен приводить машину к стационарному режиму. Для этого при со* < со должно : быть dm/dt <О или
/С(ш) — L = Л» — А>*) < 0, а при о> < со* должно иметь место противоположное неравенство. Иными словами, /С(<о) должна быть монотонно убывающей функцией
§ 7.5] ПЕРЕХОДНЫЙ ПРОЦЕСС В ПАРОВОЙ МАШИНЕ с РЕГУЛЯТОРОМ 389 в области рабочих угловых скоростей и
< 0. (7.37)
асо
Переходный процесс характеризуется соотношением
J f_________= t—t
. . K^-L 1 -°’ - -
<D0 - -
получаемым из уравнения машины путём разделения переменных.
Чтобы получить более простое соотношение, рассмотрим малые колебания около стационарного режима. Для этого заменим в уравнении через со -J- понимая под со стационарную угловую скорость со* и опуская звёздочку; © должно обозначать малое отклонение от стационарного значения. Разлагая /С(со-]-©) в конечный ряд Тейлора и ограничиваясь малыми первого порядка, имеем:
#(а> + <р)«#(со)4-/С'(со)©;
если же подставить в уравнение машины и принять во внимание (36), то J d (?+.?) = +к, (ш) ? _ L
или
У9 = Г(а))?.
Полагая
можно написать это уравнение в виде
(ГО+1)© = 0; (7.39)
его решение будет
Так как в силу неравенства (37) постоянная Т положительна, то <р стремится к нулю с возрастанием t и стационарный, режим, как мы и ожидали, асимптотически устойчив.
Постоянная Т имеет размерность времени; величины такого рода введены в теорию регулирования А. Стодолой [7Л] и носят название постоянных времени.
Так как второй член в уравнении (39) получился из разности вращающего момента и момента нагрузки, то постоянной Т в данной задаче можно дать следующее истолкование. Пусть отклонение © получило начальное значение © = 1, после чего мы заставляем машину работать при постоянном вращающем моменте, соответствующем этому значению, для чего можно, например, отключить клапан от тахометра. Уравнение движения получит вид
Ту = — 1,
390
МАЛЫЕ КОЛЕБАНИЯ ОКОЛО ДАННОГО СОСТОЯНИЯ
[гл. 7-
откуда, в силу начального условия, t Т — 1 р >
так что Т есть время, необходимое для того, чтобы привести отклонение ф к нулю.
§ 7.6. Статика центробежного регулятора. Регулятор прямого действия состоит из центробежного тахометра, регулирующего клапана и соединяющей их передачи. Центробежный тахометр представляет собой систему с одной степенью свободы, состоящую из масс, которые могут перемещаться параллельно некоторой плоскости, вращающейся вместе со шпинделем, связанным с главным валом машины зубчатой или червячной передачей. Если плоскость проходит через шпиндель, то регулятор называется коническим, если же она перпендикулярна к шпинделю, то мы имеем
J 2е к плоский, или инерционный, регу-
ляшор. Характеристики z = /3 (со) / \\ \ изучаются в статической теории, ос-
\ х е* нованной на рассмотрении равнове-\\ \ сия масс тахометра относительно ко-1 z \ \ ординатной системы, связанной с \Х г / вращающейся плоскостью'.
W Будем понимать под z обобщён-
| НуЮ координату, определяющую по-
R L ложение масс тахометра в относи-
’ ’ I ’ тельном движении. В случае кони-
Фиг. 40. Регулятор Уатта. ческих регуляторов, с которых мы начнём (фиг. 40), z может обозначать, например, подъём муфты. Если считать, что все массы расположены в самой плоскости, то тангенциальные переносные ускорения и ускорения Кориолиса перпендикулярны к ней и соответствующие силы инерции не дают работы при элементарном перемещении в относительном движении. При вычислении обобщённой силы Q, отнесённой к координате z, мы должны, следовательно, учесть лишь силу тяжести, упругость пружин, которые часто ставятся, и центробежные силы, пропорциональные со2.
Обозначим через E(z) часть обобщённой силы, происходящую от тяжести и упругости и взятую с обратным знаком; она иногда неправильно называется энергией регулятора. Для Q получается выражение вида
,Q = ^ = -£(*) +Л(з)ш2, (7.40)
где U(z) есть потенциальная функция относительного движения:
U(z) = UE (z) +1 а (г) шЗ; (7.41)
§ 7.6]
СТАТИКА ЦЕНТРОБЕЖНОГО РЕГУЛЯТОРА
391
при этом
Если потенциальная энергия растёт вместе с г, то 5(г)>0.
(7.42)
(7.43)
Это имеет место, например, когда z обозначает подъём муфты; в этом случае Е (z) может быть определена взвешиванием при невращаю-щемся шпинделе. Уравнение относительного равновесия есть
Q = —E(z) + A(z)e>* = О,
откуда
(О
Е(г) A(z)'
(7.44)
Полученное -соотношение и представляет характеристику тахометра. Разрешая его относительно z, получаем уравнение г = /3(а)), дающее значения координаты z в положении относительного равновесия, соответствующем угловой скорости со. При этом мы опять позволили себе обойтись без звёздочек или других значков, указывающих на то, что эти величины относятся к положению равновесия.
Для того чтобы равновесие было устойчивым, необходимо и достаточно, чтобы потенциальная энергия —U(z) имела в соответствующем положении минимум (§ 5.2). Это условие выполняется при
= Е' (z) — А' (z) а>2 = Е' А (г) ~£(г) А'^ > О
или
‘ E'(z) — A'(z)mQ- = A(z)^)>0. (7.45)
Так как Е (z) и A (z), согласно (44), имеют один и тот же знак, то из последнего неравенства вытекает, что du/dz должно иметь тот же знак, что и Е (г). Сопоставляя с (37), заключаем, что dKIdz inE(z) должны быть противоположных знаков. Если вместо (45) имеет место противоположное неравенство, то равновесие неустойчиво. Наконец, если d4J!dz* = О, то нужно принять во внимание дальнейшие производные или воспользоваться тем, что устойчивость должна иметь место, если при возрастании z в окрестности рассматриваемого значения первая производная от потенциальной энергии — U' (z) = Е (г)— A(z)(d* меняет знак минус на плюс.
Определение положений равновесия и проверка устойчивости могут ыть также выполнены графически с помощью характеристик энергии и центробежной силы, т. е. кривых, представляющих функцию E(z) и Функцию Л^ш2 при различных значениях <о2 (фиг. 41). Если z есть подъём муфты, то ось абсцисс удобно расположить вертикально
392 МАЛЫЕ КОЛЕБАНИЯ ОКОЛО ДАННОГО состояния [гл. 7
в соответствии с направлением действительного отсчёта аргумента z по шпинделю. Абсцисса точки пересечения кривой E(z) и кривой Л(г)о)2, соответствующей данному <о2, определяет положение равновесия. Если угловой коэффициент Е' (z) первой кривой в точке пересечения больше углового коэффициента второй кривой А (z)<o2, то равновесие устойчиво, в противном случае — неустойчиво. Если характеристики касаются друг друга, то устойчивость имеет место тогда и только тогда, когда с ростом z кривая Е (z) переходит с левой стороны от кривой Л(^)а)2 на правую.
Заметим, что суждения об устойчивости, получаемые описанным путём, могут считаться лишь предварительными, так как в статиче-
Фиг. 41. Характеристики регулятора Уатта.
ской теории угловая скорость <о рассматривается как заданная и её изменения в результате малых отклонений тахометра от положения равновесия и связанной с этим перестановки исполнительного органа не принимаются во внимание. Более полное изучение взаимодействия между регулятором и машиной составляет задачу динамической тео-рии (§ 7).
Пример 1. Регулятор Уатта. Схема этого регулятора изображена на фиг. 40. Обозначая через z подъём муфты от ее наинизшего положения и применяя другие обозначения, указанные на чертеже, имеем:
z = 2а (1 — cos ср).
Элементарная работа веса муфты и шаров есть (9/2______________________________________________z\
^5—?) = — £ (z) 6z, где
E(z)=Q+P^-;
Элементарная работа центробежных сил шаров будет:
(7.46)
§ 7.61
СТАТИКА ЦЕНТРОБЕЖНОГО РЕГУЛЯТОРА
393
ле о/ == сю есть угловая скорость шпинделя. Так как 2а— z *
cos^-^-, 8<? = 2ЖР
где
то предыдущее выражение получает вид
— (е + b sin <?) ю'2 & (S'*. = A (z) ю2 §z,
2л2 g 1 sin <f
(7.47)
Характеристики изображены на энергии Е (z) представляет вертикальную прямую, а все характеристики центробежных сил проходят через точку (2а, 0) и имеют общую асимптоту z = 0/Все положения равновесия. определяемые пересечениями характеристик, устойчивы, так как угловой коэффицйент характеристики Е (z) равен нулю, а угловые коэффициенты характеристик A (z) ю2 отрицательны. '
Пример 2. Регулятор Ф а р к о (фиг. 42). Этот регулятор отличается от регулятора Уатта только перекрещёнными тягами. Поэтому для Е (z) остаётся в силе выражение (46), а формула для A (z) получается из (47) путём замены е на —е:
фиг. 41. При этом характеристика
/?2 Р h2
А^ = тт~^(2а~г)
Фиг. 42. Регулятор Фарко.
(7.48)
Характеристики представлены на фиг. 43. Как нетрудно подсчитать, кривые Е (z) и' A (z) ш2 пересекаются лишь при ю > где
если ю = то имеет место касание в точке с абсциссой
zm — 1 у 1 \^/ *
Положения равновесия устойчивы, если в точках пересечения характеристик имеет место неравенство z>zmt и неустойчивы при z<^zm. Положение z = zmt соответствующее точке касания, также неустойчив?, так как в её окрестности характеристика E(z) располагается справа от характеристики A (z) ш2, а не переходит с левой стороны на правую, как это должно °ыло бы быть в случае устойчивости,
Рассмотрим теперь плоский регулятор* (фиг. 44), состоящий из Центробежной массы т и инерционной массы mlt которые могут поворачиваться вокруг осей С, Cv параллельных шпинделю О и
394 МАЛЫЕ КОЛЕБАНИЯ ОКОЛО ДАННОГО состояния [гл. 7
вращающихся вокруг него как одно целое с угловой скоростью са>. Обе массы связаны спарником, благодаря чему они имеют лишь одну
Фиг. 43. Характеристики регулятора Фарко.
степень свободы. Движение центробежной массы стеснено пружиной LG. Центр тяжести инерционной массы лежит на оси СР В статической теории угловая скорость оо предполагается постоянной, и
Фиг. 44. Плоский регулятор.
потому мы должны учесть лишь силу натяжения пружины и центробежную силу массы т. Масса т1 учитывается в динамической теории.
Примем за обобщённую координату угол поворота центробежной массы z = / OCS. Если s = LG есть длина пружины, $0 — та же длина в ненапряжённом состоянии, о — жёсткость, то сила натяжения
§ 7.7] ВЛИЯНИЕ ИНЕРЦИИ РЕГУЛЯТОРА 395
будет a(s — $0)/$0; её элементарная работа равна
—Е (z) Ьг=> — о —hbz,
Sq
где h — плечо. Так как
sh = 2 пл. Д COL = el sin
s = ]/ е2 Z2 —2el cos у,
X = * —*о>
где zQ— значение z в том положении, когда / = 0, то
Е(г) — аh = ael(^---------sin у,
7 \ so s) A
или
E(z) — aelsin(z— гп) —------r 1 . (7.49)
4 V °L^ Уг2_|-/2__ 2elCQS(Z — ZQ)\ '
Центробежная сила F массы m приложена в её центре тяжести S.
Фиг. 45. Характеристики плоского регулятора.
Её момент относительно оси С можно написать в виде
/пс2оо2 • 2 пл. Д OCS = тс2ы2гр sin z.
Этот момент, делённый на оо2, представляет, очевидно, функцию Л (г):
A (z) = mc2rp sin z. (7.50)
На фиг. 45 представлены характеристики для случая г0 > 0. При этом условии положения равновесия, для которых
< z <
устойчивы, а остальные неустойчивы.
§ 7.7. Влияние инерции регулятора. Начнём опять с конического регулятора и учтём то обстоятельство, что, при изменении угловой скорости' оо, массы регулятора не принимают мгновенно рав-
ЧЕА
396
МАЛЫЕ КОЛЕБАНИЯ ОКОЛО ДАННОГО СОСТОЯНИЯ
[гл. 7
новесного положения во вращающейся плоскости, а совершают колебания, связанные с колебаниями угловой скорости. Мы должны, следовательно, рассмотреть систему с двумя степенями свободы, обобщёнными координатами которой являются угол поворота главного вала & и координата регулятора z. При этом о> — &.
Выражения кинетической..и потенциальной энергий абсолютного движения и элементарной работы неконсервативных сил имеют вид
Т=1 J®3+y[a(z)a>8 + T(z)i3J, (7.51)
V(z) = — Ue(z)l
W (8) = К(г) — А] 8& — R t>z. (7.52)
Кроме величин, уже введённых в двух предыдущих параграфах, сюда вошёл коэффициент ^{z) при z2 в выражении кинетической энергии и приведённая сила сопротивления регулятора R. Произведение &z в составе Т не фигурирует, так как скорость ~ каждого элемента массы тахометра есть геометрическая сумма переносной скорости, перпендикулярной к плоскости относительного движения, и относительной скорости, лежащей в плоскости, вследствие чего квадрат скорости частицы равен сумме квадратов этих составляющих, которые пропорциональны, соответственно, обобщённым скоростям ш и z.
Полагая ещё
. <7-53’ имеем:
дТ г Т I / дГ П
аг=l-Н-«(*)1 ^г=°-
л
= ^=A(z)^-}-C(z)z*,
dz dz
f ’ ~
и уравнения Лагранжа будут:
[J+a(^)l <*> + 2Л (z)(oz = K(z)— £,
7 (z)z + C(z)z* — A (z) co9 E (z) = — R.
Упрощённые уравнения получаем, пренебрегая сопротивлением R, а в качестве порождающего выбираем решение, характеризующее стационарный режим, для которого о> и z постоянны и оо = г = z = 0. Это даёт:
K(z) = A (z) с»9 = Е (z\ (7.54)
откуда определяются значения чо и z, соответствующие данной постоянной нагрузке L.
При изучении малых колебаний около этого состояния ограничимся случаем сопротивления R — k (z)z, пропорционального первой
।
£ f f ] ВЛЙЯНЙЕ ЙНЕРЦЙЙ РЕГУЛЯТОРА 09?
степени скорости.' Заменяя ю, Z через w -J- <?, z -|- р, где <р и р — малые приращения, разлагаем в ряды Тейлора, ограничиваясь малыми первого порядка:
[J-f- a (z)] <р 2 A (z) ш р = К (г) -j- К' (z) р — £,]
7(г)р — И (-г) + ^'(^) р] (а>2+2ш<р)-|-£ (г) + £'(г) р = — fe(z)p.
Если же принять во внимание уравнения стационарного режима (54), то получится:,
[J + а (г)] <р + 2 А (г) юр — К' (z) р = О,
— 2A(z) ш<р 7 (z) р -|- k,(z) р [ Е' (z) — A' (z) ш2] р = О,
или
где
£/£)<? + (.¥£>4-1)р = 0, — (p_|_(I/2£)2_|_U7£)_|_8)p=0, .
. J + g (z) у _ 2 A (Z) О>
U~—K'(z)' Л~—К'{гу
IZ2 — 'Т (g) \W — k (г)
2X(z)o> ’ 2X(z)m ’
8 Е' (z) — A' (z) о>2 _ dm .
2А (z) <о dz '
(7.55)
(7.56)
при преобразовании последнего выражения, называемого неравномерностью регулятора, мы приняли во внимание (45). Величина a(z) в выражении U и величина X получились в результате учёта того слагаемого -x-a(^)w2 в составе Т, которое происходит от масс ре-£
гулятора и мало в сравнении с у’ЛА При написании первого уравнения (55), характеризующего движение машины, разумно пренебречь указанными величинами и принять
*-«• <7-57’
I ’
В настоящей главе мы вынуждены ограничиться выводом уравнений малых колебаний, откладывая их исследование до следующей главы, так как там в нашем распоряжении будет необходимый для этого критерий линейной устойчивости.
Остановимся ещё на случае плоского регулятора. Так как здесь переносные и относительные скорости частиц могут образовать любые углы, то выражение кинетической энергии содержит слагаемое с произведением обобщённых скоростей со, z:
Т=.^ Jop + у [a (z) ша -|- 20 (z)wz + 7 (z)z2].
398
МАЛЫЕ КОЛЕБАНИЯ ОКОЛО ДАННОГО СОСТОЯНИЯ
[ГЛ. 7
Выражения (52) для V (z) и U7(8) остаются в силе. Полагая
<7-58>
и проводя вывод по тому же плану, что и для конического регулятора, получаем прежние уравнения стационарного режима (54) и уравнения малых колебаний
Ш)<р + СТО+1)|л==0, 1 — (№О+1)<р + (У2О2+ГО + 8)|л==0; J
при этом
дг =______Р
2А (г) <и ’
(7.59)
(7.60)
а остальные коэффициенты определяются попрежнему формулами (56),
Фиг. 46. К определению живой силы центробежной массы.
(57). Значение добавочного слагаемого — ND® мы выясним при исследовании устойчивости.
Найдём функции а(з), ((te), 4(2) для плоского регулятора. Начнём с центробежной массы т (фиг. 46), относя её к связанным с нею осям Ет| с началом на оси вращения С, причём ось £ должна проходить через центр тяжести S. Координаты элемента массы dm относительно неподвижных осей ху с началом на шпинделе О будут:
x — r cos eft 4~
4~ Е cos (eft -j- z) — т] sin (eft -|~ ^)>
у == г sin eft -|“ £ sin ~Ь z) + *4 cos + *)*> отсюда
х = — г coo sin eft (ссо *) I— £ sin z) — *4 cos *)1»
у = гсш cos eft 4~ (С(Л z) № cos + z) — sin ~Ь ^)1»
х2 + J'2 = + (£<° + я)2 (S2 + 'G2) + 2гсш (сю 4“ z) cos z —*4 sin z)-
Но так как координаты центра тяжести суть = — р, 7|s = 0, то для кинетической энергии имеем выражение
1 Г • • 1 1
*2 (х3 + У2) dm тг^ш2 + у ® (са) + z)2 — тге^ (с<о 4~ cos z>
где В обозначает момент инерции массы т относительна оси С.
§ 7.8] ЦЕНТРОБЕЖНЫЙ РЕГУЛЯТОР С ФРИКЦИОННЫМ ИЗОДРОМОМ 399
Для инерционной массы получим аналогичное выражение, но без третьего слагаемого, так как центр тяжести массы лежит на её оси вращения:
1J (х2 + j2) 1 + 4 <сю + *i)2-
Ограничиваясь случаем, когда обе массы соединены шарнирным параллелограммом, так что z = zlf получим выражение суммарной кинетической энергии:
4 [ a (z) ®2 + 2 Р (*) + 7 (-г) -г2],
£
где
а (z) = с2 (znr2 -|- /n/J + 0 + 0t — 2/nrp cos z), p (z) = c (0 -}- 0* — znrp cos z), Т(г) = 0 + 01.
Из первого соотношения вытекает:
Д (z) = i = Лпгр sin z
(7.61)
в согласии с полученной ранее формулой (50).
§ 7.8. Центробежный регулятор с фрикционным изодромом. Уравнения (54) стационарного режима центробежного регулятора показывают, что при различных постоянных значениях нагрузки L подъём муфты z и угловая скорость со будут, вообще, различны. В § 3 мы видели также, что Для затухания колебаний системы необходимо, чтобы dKIdw < 0.
Однако по условиям эксплуатации во многих случаях необходимо, чтобы машина приспосабливалась к изменениям нагрузки, сохраняя постоянную угловую скорость. Регуляторы, с помощью которых решается эта задача, называются изодромными\ они появились в восьмидесятых годах прошлого столетия.
Обычно изодромные устройства применяются в схемах непрямого регулирования, в комбинации с сервомоторами, но основной принцип может быть разъяснён на простейшем примере фрикционного изодрома в системе прямого регулирования (фиг. 47).
В этом регуляторе муфта тахометра М не соединяется непосредственно со стержнем R исполнительного органа. Между ними вводится гайка N, составляющая одно целое с фрикционным диском Р, получающим вращение от другого диска Q, связанного зубчатой передачей со шпинделем. Гайка и стержень имеют винтовую нарезку.
Обозначим через <р отклонение угловой скорости от желаемого значения ш, через rj смещение гайки, через р. смещение стержня исполнительного* органа. Пренебрегая инерцией тахометра, можно
400 Малые колЕЁлйия около данного состояния [гл. 7
положить т|даа<р. Пока т] = 0, диск Р стоит против центра диска Q и гайка не вращается. Но как только она получит смещение т| =/= О, диск Q начинает её навинчивать с угловой скоростью, пропорциональной произведению ?| (со 4“ ~ аа)?> а стержень R получает ли-
Фиг. 47. Регулятор прямого действия с фрикционным изодромом.
нейную скорость bawp относительно гайки, ние стержня будет:
Поэтому полное смеще-
р, = atf 4- ab& J © dt.
Движение машины может быть охарактеризовано первым уравнением (55), в котором мы, согласно (57), положим ^=0. Вводя ещё изменение нагрузки х, получим уравнения движения
р, = а© -р йЬ<мр. Полагая
и умножая первое уравнение на 1/U, второе на T‘2/U, найдём:
Г2 •
или же, дифференцируя первое и исключая р, (Т2Д2+2T(.D + 1) <р = -П х.
(7.63)
(7.64)
§ 7.91 КОЛЕБАНИЯ ОКОЛО СОСТОЯНИЯ УСТАНОВИВШЕГОСЯ ДВИЖЕНИЯ 401
Из уравнений (63) видно, что при уменьшении нагрузки на постоянную х мы имеем частное решение
? = о, |Л = Х.
(7.65)
Таким образом, стационарная угловая скорость действительно остаётся одной и той же при всех постоянных значениях нагрузки, так как перестановка исполнительного органа за счёт винтового движения изодрома достаточна для изменения вращающего момента в соответствии с изменением нагрузки, и потому муфта тахометра по окончании переходного процесса возвращается на прежнее место.
Если при t < 0 мы имели х = О, <? = = О и изменение нагрузки на постоянную х произошло внезапно при £=0, то мы получаем, согласно первому уравнению (63), начальное значение производной
• х
Переходный процесс в машине определяется уравнением (64) с правой частью, равной нулю, и потому сводится к затухающим колебаниям с начальными условиями ср = 0, ср = <р0. Длительные возмущения угловой скорости могут иметь место лишь при
х = х (f), х (t) Ф 0.
§ 7.9. Малые колебания натуральной системы около состояния установившегося движения. В теории центробежного регулятора угловой скорости мы имеем пример малых колебаний механической системы, описываемой уравнениями Лагранжа, около состояния установившегося движения.
Рассмотрим эту задачу в общем случае.
Обозначая опять через ^обобщённые координаты, через q^tt)— их значения для установившегося движения, через у$— малые приращения, мы можем для вывода уравнений малых колебаний заменить в выра-
жениях кинетической энергии T{q. q, t) и обобщённых сил -|-+ 0 координаты qj суммами ^(0+jZy и разложить их
в ряды по степеням у^ у^. После этого нужно составить уравнения Лагранжа в переменных yj, рассматривая их как новые обобщённые координаты.
В разложении Т (q(t)-\-y, q i) достаточно сохранить члены
второго порядка относительно у^ у^ так как тогда частные производные по этим величинам, фигурирующие в уравнениях, будут линейны относительно них. Итак,
26 Зак. 1474. Б. В. Булгаков
402
малые Колебаний около данного состояний
(гл. 7
где
^2 — 2 ^зкУзУк~\“ 2 В$кУэУк “1“ 2 ^^кУзУк^ j к j к j к
т\=ЪАм+Ъвм. . i з
T0=T9(q(f), q(t). t\
При этом Ajk = Akj* Bjk = &kj* но, вообще,
Cjzc =h Ckj.
(7.66)
(7.67)
(7.68)
Кинетическая энергия T не будет, вообще, однородным квадратичным полиномом относительно новых обобщённых скоростей, хотя бы это и имело место до преобразования переменных.
Разложения обобщённых сил достаточно продолжить лишь до линейных членов:
+ Qj = Q;P + 2 (АйЛ Mjkyk); к
(7.69)
а так как
то, предполагая, что все Ajk, Bjk, Cjk, Ljk, Mjk постоянны, получим уравнения Лагранжа в виде
— Bj + I ^кУк + (Cjk — Ckj) У к — Bjkyd =
к
= Q'P + S (^ЭкУк ~Ь М^кУк) (J = 1 > ...» П)-к
Для установившегося движения (ук = 0) мы должны иметь тождества
- Bj = Q(?) . (7.70)
которые, конечно, представляют собой результат подстановки функций qj(t) в уравнения Лагранжа для этого движения, так как
Л=(® — У»
B=(—\ дТ°
j ^9pqj=qj(t);
§ 7.9] кОЛЕБАЙЙЙ около СОСТОЯЙЙЯ УС^АЙОВЙВШЕГОбЯ ДВИЖЕНИЯ 403
Учитывая тождества (70), имеем:
2 1^кУк + (Cjk — ^к^Ук — В$кУк\ = 2 ^кУк'У^зкУк) к к
(/=1, ..п).
Так как коэффициенты этих линейных однородных уравнений постоянны, то при сделанных предположениях движение, определяемое порождающим решением q = q(t), действительно является установившимся.
Силы типа 2 ^кУк называются скоростными, а силы2^а:№— позиционными. Каждая группа может быть в свою очередь разбита на две:
^ЗкУк ~ ^кУк ~Ь ^кУк> где
Jjk == ~2 ( ,
Jjk=-2 -j- Mjfj),
М&Ук = — ЬкУк + J;kyk ,
Nfa = 2 ^jk “Ь ^kj)* 1
1 ( (7*71)
Njk = ”2* (Ljk Lfrj), j
причём
/ffc — Zfcj»
Jjk == J kjt
Njk — Nkjt
Kjk = — Nk;>
(7.72)
так что, в частности,
Jjj 0,
Jjj = Mjj,
Njj ^ = 0.
(7.73)
Силы Rj~ — 2 Jjkyk не консервативны, так как соответствующие им компоненты вихря
= Jkj + Jjk — ^Jjk = ^jk ~Ь Mkj,
вообще, отличны от нуля. Можно назвать эти силы «искусственными», так как при прохождении системой какого-либо замкнутого цикла конфигураций С в n-мерном пространстве координат у$ работа этих сил Ср 2 Rj ctyj имеет определённое значение, вообще, отличное о j
от нуля; при повторных прохождениях цикла совершённая работа будет неограниченно возрастать, что предполагает наличие некоторого, теоретически неограниченного, источника энергии.
Силы
2 ^Ук = -^7 у S 2 -ЪкУ1Ук к J j к
являются консервативными.
26*
464
МАЛЫЕ КОЛЕБАНИЯ ОКОЛО ДАННОГО СОСТОЯНИЯ
[гл. 7
Силы —ZjNjkyic можно представить в виде
к Э
где 2V(jz, у) есть квадратичная форма
N(y, У) 2 2 (7.74)
к
Работа этих сил есть
Она отрицательна, если N(y, у) является определённой положительной формой, что имеет место, когда рассматриваемые силы происходят от вязких сопротивлений, пропорциональных абсолютным и относительным скоростям частиц системы. Эти силы обусловливают тогда рассеяние энергии.
Наконец, силы 2^^ называются гироскопическими. Силы такого же рода, представляемые членами (— Gjk-\-Ckj) yki вошли уже в левые части уравнений вследствие неоднородности Т относительно скоростей у^. Наименование этих сил связано с теорией циклических систем (§ 3.10), в частности таких систем, которые заключают симметричные твёрдые тела, вращающиеся с постоянными угловыми скоростями. Работа этих сил всегда равна нулю:
2 (S dyj = 22 dt = 0. j k j k
так как каждому члену М^кУзУк соответствует другой- член ЫкзУкУз — =— М^кУзУк противоположного знака.
Полагая
Gj/c= * @кЗ = Cjk Cjfj -|- Hjk = Hkj = Bjk J^kt
получим уравнения малых движений в виде
S [^ЗкУк + (Njk + Gjk) ук 4- (Н/л + ^Зк)Ук = 0 (у = 1, ..., п). (7.75) к
Если же ввести формы
А(у, У) = 22^(;, ;) = 22 Н^уу^, i к j 1с
. . [(7.76)
о (у. у) s 2 2 01кУ1Ук< J(у. v) s 2 2<»Лл>
j к к
§ 7.10]
ЛИНЕЙНАЯ ПАССИВНАЯ ЦЕПЬ
405
то можно написать также
= 0
dt dyj dyj
U=l, .... n).
(7.77)
Уравнение энергии будет:
d(A + И) = — 2 (J±N)dt.
Вводя квадратичные операционные трёхчлены
fjk (D) = Ajk& + (Д^ + Ojk) D + (Hjk -f- Jjk), мы приведём уравнения к форме (16).
Если же образовать матрицы
л=1М^П> w=WII> н=\\н:к\\, о=цад ii^ib
то получится матричное уравнение
МО2 + (МЦ- G) D Ц- (Я 4- /)] у = 0.
(7.78) f А
(7.79)
(7.80)
(7.81)
§ 7.10. Линейная пассивная цепь. Рассмотрим разветвлённую электрическую цепь, не содержащую нелинейных элементов, как, например, электронных ламп или катушек с железом. Точки разветвления цепи называются узлами, части цепи между узлами — ветвями. Например, цепь на фиг. 49 содержит 4 узла и 6 ветвей. Каждая ветвь х (фиг. 48) может, вообще, содержать последовательно включённые постоянные индуктивность Lx, омическое со- »--------- i
противление Rx и ёмкость Сх, & ] 4г |
которые мы объединим в полное —О °"Ги II । ° сопротивление Zx, а также источ- I zx 1
ник напряжения ех. Пусть число 1 1
ветвей равно В, а число узлов IV. Фиг. 48. Ветвь электрической цепи. Мы можем написать В уравнений, согласно которым алгебраическая сумма падений напряжения в сопротивлениях каждой ветви равна сумме приложенных электродвижущих сил и разности потенциалов на концах. Из первого закона Кирхгофа вытекает N уравнений, согласно которым алгебраическая сумма токов, текущих по направлению к каждому данному узлу и от него, равна нулю. Таким образом, получается B-\-N уравнений, содержащих В токов ветвей и N узловых потенциалов. Однако если цепь состоит из К блоков, связанных лишь индуктивно (в частности, /С=1), то среди IV уравнений узлов будет лишь N—К независимых. В самом деле, ток каждой ветви войдёт в два уравнения, относящихся к узлам в начале и в конце неё и притом с противоположными знаками. Поэтому сумма левых частей уравнений узлов каждого блока равна
406
МАЛЫЕ КОЛЕБАНИЯ ОКОЛО ДАННОГО СОСТОЯНИЯ
[гл. 7
нулю и одно из этих уравнений является следствием остальных. С другой стороны, среди N узловых потенциалов будет лишь N—К существенных переменных, так как уравнения ветвей каждого данного блока не изменятся, если из всех узловых потенциалов вычесть один из них. Итак, окончательно мы имеем B~\~N—К независимых уравнений относительно такого же числа неизвестных *).
Уравнениями узлов можно воспользоваться, чтобы исключить N— К токов, выразив, их через
п = В — N+K (7.82^
остальных. Тогда из В уравнений ветвей определятся п независимых токов и А/ — К независимых потенциалов.
Дальнейшее упрощение может быть достигнуто, если вместо токов ветвей ввести, по Максвеллу, п контурных токов, текущих по п замкнутым контурам, выбранным в цепи. Назначая как-либо положительное направление в каждом контуре, следует рассматривать действительный ток в каждой ветви, общей для двух или большего числа контуров, как алгебраическую сумму соответствующих контурных токов. Так как контуры не имеют незамкнутых концов, то мы можем написать, что алгебраическая сумма падений напряжений в каждом равна сумме приложенных электродвижущих сил е$. Узловые потенциалы не войдут, и мы получим, таким образом, п уравнений относительно п контурных токов ij.
При записи этих уравнений удобно применять I/O как символ неопределённого интегрирования, например
± = [ ij (f) dt-, (7.83)
в этой связи мы будем иногда называть D неопределённым оператором для отличия от «определённого» оператора Хевисайда-Карсона р.
Уравнения контурных токов получают вид п
S Zjk (D) ik = e^f) (j = 1........n), (7.84)
k=l
где выражения
(D) = LjkD + Rjk + 4- (7-85)
называются собственными (/ = k) и взаимными (J =# k) сопротивлениями или импедансами контуров (в операционной форме); L& R& Cjj представляют полную самоиндукцию, омическое сопротивление и ёмкость /-го контура; Ljk, Rjk} Cjk(j Ф k) обозначают, соответственно, самоиндукцию общей ветви /-го и 6-го контуров вместе
♦) Заметим, что для блока, состоящего из одного простого замкнутого контура, нужно и число ветвей и число узлов считать равными единице.
§ 7.10]
ЛИНЕЙНАЯ ПАССИВНАЯ ЦЕПЬ
407
с их взаимной индуктивностью, омическое сопротивление и ёмкость обшей ветви. При этом самоиндукция, сопротивление и ёмкость входят в Rjk> Qk со знаком плюс, если положительные направления токов ij и ijc в общей ветви совпадают, и со знаком минус в противном случае. Что касается взаимной индуктивности, то она входит в Ljk со знаком плюс, если э. д. с., индуктируемая при возрастании 1к, вызывает падение напряжения в положительном направлении /-го контура; в противном случае соответствующее слагаемое войдёт со знаком минус. По самому определению
T'jfc = Lfcj) Rjk = Rfcj, Cjk = Ckj (7.86)
и, следовательно,
Z^(D) = ZfcJ(D). (7.87)
Эти условия выражают принцип взаимности Максвелла. Член Zjk(D)ik в (84) представляет падение напряжения в /-м контуре за счёт тока а вся левая часть /-го уравнения — полное падение напряжения за счёт всех токов, протекающих через этот контур.
Если мы хотим получить решения, удовлетворяющие определённым начальным условиям, то следует представить (84) в виде системы интегро-дифференциальных уравнений
(/=1, ..., п), где обозначает алгебраическую сумму начальных ^напряжений во всех ёмкостях /-го контура. Таким образом, начальные условия в отношении этих напряжений включаются в сами уравнения. Начальные значения токовм/(0) должны быть заданы особо.
Интегралы #
^ij(t)dt (7.89)
о
суть заряды, переносимые контурными токами начиная с момента /=0, и мы можем также написать (88) в виде системы дифференциальных уравнений
п
S fJkФ) qk = ej(t) + (7=1.......«), (7.90)
Л = 1 где
fjk ф) = DZJk ф) = + RJkD + (7.91)
При этом для координат задаются начальные значения ?Д0) = 0, а для производных — какие-нибудь значения ?Д0) =/ДО); условия з отношении начальных напряжений в ёмкостях выполняются в силу Дифференциальных уравнений.
408
МАЛЫЕ КОЛЕБАНИЯ ОКОЛО ДАННОГО СОСТОЯНИЯ
[гл. 7
В некоторых задачах, может быть, удобно понимать под всеми или некоторыми qk в (90) заряды конденсаторов, выбранных по одному в соответствующих контурах. В этих случаях нужно озаботиться тем, чтобы значения постоянных вообще, отличные от тех, которые они имели выше, правильно учитывали начальные заряды.
В рассматриваемых нами пассивных цепях, матрицы, составленные из элементов Rj}., оказываются симметричными в силу условий (86). Поэтому, если ввести квадратичные формы
Л(<7, q) =
. 3 к
N(q> , (7 92)
q) = J] qjqk,
3 к
представляющие соответственно (§ 3.8) удвоенные электромагнитную энергию, функцию рассеяния и электростатическую энергию, то уравнения (90) могут, быть представлены в виде уравнений Лагранжа:
d дА . дН л г /а । i 1
7.т^ + т- = 2[«Л0+ъ1 — (J = l. •
dt dqj dqj dqj
Если же ввести симметричные квадратные матрицы /(D)= (D)||, Z(D) = ||Z^(D)||
и матрицы-столбцы qi
г"1
«1(0
«„(0
(7.93)
(7.94)
(7.95)
Яп
п
, е(0 =
то мы можем записать уравнения цепи в матричной форме
f{D) q=e(0 + 7 (7.96)
ИЛИ
Z(D)i = e{t). (7.97)
Матрица Z (D) может быть названа {матричным) сопротивлением, или импедансом цепи.
Фиг. 49. Мостовая схема. В качестве примера составим уравне-
ния контурных токов для мостовой схемы на фиг. 49. Согласно сказанному выше, для этой схемы
и, согласно (82),
0=6, АГ =4,
1
§ 7.111
АКТИВНАЯ ЦЕПЬ
409
За независимые контуры принимаем Z±ZGZB. ZnZBZB. ZAZBZBZGt где порядок букв указывает и выбранные условные положительные направления. Уравнения контурных токов iMt ty, lz будут:
Zr 1<в + zc (l№ - is) 4- ZB (Z* + iy - za) = e (Z),
ZJ,4-ZB (ty 4- z* - zp 4- ZB (Iy - z,) = o,
Z^+z» V, - V + ZB <4 - - 9+ZC (4 ~ У = °>
• (Zr 4- ZB 4-ZG) lx + ZBiy- (ZB 4- ZG) l9 = e(t): zBia!+(zB+zB+zD)fy-(zB + zB)i9=o, - (ZB 4- ZG) i* - CZB 4- ZB) iy 4- (ZA 4- zB 4- zG 4- ZB) lt = 0. .
(7.98)
Коэффициенты при Z^, ZF ls в последних уравнениях суть собственные и взаимные импеданеы.“
§ 7.11. Активная цепь. Цепи,, содержащие электронные лампы (§ 5.13), принадлежат к активным цепям. Пусть у-й контур есть цепь сетки, а fe-й контур — цепь анода (фиг. 50). При выбранных положительных направлениях имеем нелинейную зависимость
Фиг. 50. Трёхэлектродная лампа в электрической цепи.
где it, е* е* — постоянные составляю-/ь у Qf щие fe-го контурного тока, сеточного и анодного напряжений, происходящие от источников постоянного напряжения, включённых в цепь. Буквы ik, ед, еа
мы сохраняем для обозначения переменных составляющих.
Разлагая в ряд Тейлора и учитывая, что
имеем:
df * df — — - P I— J p
* и ~ n * ea’ deg dea
или, вводя с помощью соотношений
_L=_3£ и. — sr deg dea
(7.99)
величины S, р, называемые крутизной характеристики, внутренним сопротивлением и коэффициентом усиления лампы:
еа ===
Таким образом, анодное напряжение представлено как разность между приложенной э. д. с. — \№д и потерей напряжения Rво внутреннем
410 МАЛЫЕ КОЛЕБАНИЯ ОКОЛО ДАННОГО СОСТОЯНИЯ [ГЛ. 7
сопротивлении лампы. Поэтому уравнение fe-го контура может быть записано в виде
2 Zftl (Р) h = &к (?) №д Rihe* Z=1
где обозначают, как и раньше, импедансы пассивных элементов. Если сопротивление сетка-катод обозначить через Zgi то ед = Zgij и
••• ~Ь (^kj + У^д) h ~Ь ••• + (%кк + Ri) he + ••• — ек (?)-
(7.100)
Это уравнение примет тот же вид, что и для пассивной цепи, если суммы Zjfj-^pZg, Zjfc-]-#,} обозначить опять через Zkji Zkk. Изменение первой из этих величин имеет своим результантом потерю симметрии матрицы Z. Наоборот, изменение второй величины не имеет существенного значения, так как оно означает лишь присоединение пассивного сопротивления лампы к сопротивлению контура; аналогичное исправление нужно сделать и в уравнении /-го контур
ного тока.
Итак, уравнения контурных токов для активной цепи с триодами отличаются тем, что принцип взаимности для них не имеет места. Так как утрата симметрии получается лишь за счёт коэффициентов при /у = то эти уравнения могут быть написаны
в виде
(Я+ 20) = 2
dqj dqj
(7.101)
(/ — 1, . • •, ri)t
где A, N, H суть квадратичные формы, определяемые согласно (92), a Q — билинейная форма
0(9. = (7.102)
3 к
в которой
Gjk = — Ow.
ГЛАВА 8
ЛИНЕЙНЫЕ СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ А. ОБЩИЕ СВОЙСТВА УРАВНЕНИЙ
§ 8.1. Однородное и неоднородное, уравнения. Так как линейные дифференциальные уравнения с постоянными коэффициентами со времён трактата Рауса [°-14], повидимому, прочно перешли в ведение теории колебаний, то мы изложим в настоящем разделе общие теоремы, необходимые для строгого обоснования методов интеграции, развитых в дальнейших разделах *).
Будем рассматривать линейное матричное уравнение вида
f(D)y = w(t), (8.1)
где f(D)— матричный полином
/(О) = (О) II = a0DL + . + aL (т^п) (8.2)
с постоянными коэффициентами, а у и w(f)— матрицы-столбцы
^1(0
У1
Уп
(«ХО» w(f) =
(m X 1)>
первая из которых представляет неизвестную матричную координату, а вторая — заданную функцию времени t. В предыдущей главе мы получили (1) как уравнение в вариациях некоторой, вообще нели-нейной, колебательной системы.
Соответствующая скалярная система уравнений будет: п ^fdk(D)yk = ^(t) (j = l, ..., /ц). (8.3)
в начале раздела мы будем рассматривать общий случай т^п так как первая важная проблема совместности системы не упрощается существенно при т = п.
с *) Поскольку, однако, формальная рецептура интеграции сама по себе мало связана с общими теоремами, они могут быть в первом чтении опущены.
412
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
[гл. 8
Переходя к новой неизвестной v' при помощи преобразования
У=У'+У*> (8.4)
в котором у* есть какое-нибудь частное решение, немедленно убеждаемся, что у' удовлетворяет уравнению без правой части
f(D)y = 0. (8.5)
Таким образом, общее решение неоднородного уравнения есть сумма общего решения однородного и какого-нибудь частного решения неоднородного.
Матрицу f(D) будем называть операционной, а матрицу
11/(0), ®(0|| =
ll
/11(0) .../1И(О)
/»1 (О) ... fmn (О)
«*1(0
(mXn+1), (8.6)
получаемую добавлением столбца свободных членов,—расширенной.
Все миноры операционной матрицы и те миноры расширенной, в которые не входит столбец свободных членов, являются полиномами по D. Те миноры расширенной матрицы, в которые входят i— 1 столбцов операционной матрицы и столбец свободных членов, мы будем всегда сокращать на общий наибольший делитель всех миноров (Z—1)-го порядка, содержащихся в данных I—1 столбцах расшйренной матрицы, и называть в этой форме изменёнными минорами* они должны рассматриваться как функции от /, получаемые путём развёртывания по элементам последнего столбца и выполнения дифференцирований, соответствующих степеням D в операционных полиномах, на которые множатся эти элементы.
Ранги операционной и расширенной матриц определяются обычным Ьбразом как наивысшие порядки их неисчезающих миноров, но исчезание или неисчезание, о котором идёт речь, должно пониматься как тождественное по D для миноров, в которые не входил столбец свободных членов, и как тождественное по t для изменённых миноров.
§ 8.2. Линейные преобразования уравнения. Матричное уравнение (1) может подвергаться преобразованиям, которые, однако, не должны влиять на искомое решение.
Умножая обе части слева на конформную полиномную матрицу и (D) типа (т' X #0, получим преобразованное уравнение
f1(D)y = ^1(t), (8.7)
операционная и расширенная матрицы которого суть
A (D) =, и (т X п),
||/1 (О),®, (0|| = «(Р>||/(О), да(О[| (т' X «+1). (8 8)
§ 8.2] ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ УРАВНЕНИЯ 413
Из определения умножения матриц вытекает, что связь между скалярными системами, соответствующими заданному и преобразованному матричным уравнениям, заключается в том, что /-е уравнение второй системы получается путём умножения тп уравнений первой на операционные полиномы яд(О), ..., Ujm(D) и сложения результатов. Поэтому каждое решение первого матричного уравнения удовлетворяет и второму. Если, в частности, m — mf и и есть квадратная матрица, а её определитель deta(D) отличен от нуля и не зависит от О, то обратная матрица и~г(р) существует и является полиномной; мы можем написать тогда:
f(D) = «-1 (D)A (D); II/(D), w (Oil = «"» (D)||/i (D), Wi (Oil • (8.9)
Таким образом, если u(D) — неособая квадратная матрица с определителем, не зависящим от D, то два уравнения равносильны, т. е. каждое решение одного из них есть в то же время решение другого.
Отметим также, что две различные операционные или расширенные матрицы, получающиеся друг из друга путём умножения слева на неособые квадратные матрицы с определителями, не зависящими от D, эквивалентны в смысле алгебры матриц (§ 1.17) и, как легко показать, могут быть получены друг из друга путём элементарных преобразований над строками. В самом деле, по теореме Лузина (§ 1.22), мы можем привести u(D) путём элементарных преобразований над строками к канонической треугольной форме. Так как произведение диагональных элементов этой формы может лишь постоянным множителем отличаться от постоянного определителя det и (D), то все эти элементы равны единице. Недиагональные элементы должны быть нулями по определению канонической треугольной формы. Следовательно, u(D) путём элементарных преобразований над строками приводится . к единичной матрице и обратно. Производя обратные операции над матрицами f(D)=Ef(D) и ||/(D), w (t)[] = Е||/(О),г|(/)||, получим /t(D) и ||/i(D), щ (0Ц» что и требовалось доказать.
Если, обратно, две операционные или расширенные матрицы получаются друг из друга путём элементарных преобразований над строками, то их можно также (§ 1.19) получить друг из друга путём умножения слева на неособые квадратные полиномные матрицы с определителями, не зависящими от оператора D.
Ранг и детерминантные делители операционной матрицы, как и всякой полиномной, не меняются при умножении слева на неособую квадратную полиномную матрицу с определителем, не зависящим от D. Ранг расширенной матрицы при этом также сохраняется, в чём легко убедиться, если применить обычное рассуждение (§ 1.19), пользуясь, однако, данными выше специальными определениями изменённых миноров и ранга расширенной матрицы.
s
414 СИСТЕМЫ С ПОСТОЯННЫМИ кбЭф4»ИЦИЕЙТАМЙ
(гл. 8
§ 8.3. Линейные преобразования неизвестной. В процессе решения может оказаться полезным ввести вместо у новую матричную неизвестную у± типа n' X 1 с помощью линейного преобразования
y = v(D)ylt
(8.10)
где v (D) — полиномная матрица типа п X Подставляя в уравнение (1), получаем преобразованное уравнение
А(^)Л = «’(0»
(8.11)
операционная и расширенная матрицы которого суть
A(D) = /(D)t»(D)
НА (D), W (t) II = 11/(0), IIX
(m X «')>
(i»X«'+D-
(8.12)
Если yi(t) есть некоторая определённая функция, удовлетворяющая второму уравнению, то соответствующая функция y(t), определяемая с помощью, формулы преобразования, удовлетворяет первому уравнению. Пусть, в частности, ф(Р)— квадратная матрица, а её определитель deto(£)) отличен от нуля и не зависит от О; тогда обратная матрица (D) существует и является полиномной, причём
У1 = V-1 (Р)у,
/(D)=A(D)v-X(D);
11/(0), -W(011=НА (£>), w(Оих
(8.13)
•О-1 (О) О
О '1
(8,14)
Таким образом, если — неособая квадратная матрица с определителем, не зависящим от D, то два уравнения равносильны в том смысле, что каждое решение одного из них превращается после преобразования в решение другого.
§ 8.4. Условие совместности. Если матричное уравнение имеет хотя бы одно решение, то соответствующая скалярная система называется совместной, в противном случае — несовместной.
Покажем, что для существования решений необходимо и достаточно, чтобы операционная и расширенная матрицы имели один и тот же ранг г. Если это условие выполнено, то общее решение содержит п — г произвольных функций и некоторое число произвольных постоянных.
В самом деле, если ранг операционной матрицы равен г и если мы занумеруем неизвестные у1с таким образом, чтобы один из неисчезающих миноров r-го порядка принадлежал первым г столбцам, то с помощью теоремы Лузина мы можем привести скалярную систему путём элементарных преобразований над строками к канонической
§ 8.4]
Условие совместности
415
форме:
Й1(Р)Л + &2(Д)Л+ ••• +&г(°)л +
“1“ &,г+1 (^) Ут+1 -{"•••= (О»
£22 (^) У* ~Ь • ‘ ‘ + &2г (®)Уг + £2,7+1 (^) Уг+1 + • • • = *2 (О’
ёгг Ф)Уг + £г,г+1 (£>) Ут+1 + • • • = Хг (О’
О = xr+i (0>
(8.15)
О — хт (f).
Ранги операционной матрицы этой формы и субматрицы, состоящей из первых г столбцов, равны г. Единственный неисчезающий минор первых г столбцов есть £и(О) ... £^(0); он может только постоянным множителем отличаться от общего наибольшего делителя миноров первых г столбцов. Система может быть совместной только в том случае, если
•^г+1 (0 — • • • хт (?) О*
(8.16)
Но тогда все миноры (г-Ц-1)-го порядка расширенной матрицы равны нулю и её ранг равен г. Таким образом, равенство рангов операционной и расширенной матриц необходимо для совместности.
С другой стороны, изменённый минор (г-[-1)-го порядка расширенной матрицы, образованный из первых г и (г4-у)-й строк (у = 1, ,.щ — г) и из первых г столбцов и столбца свободных членов, равен xr^(f) или, отличается от этой величины постоянным множителем. Если ранг расширенной матрицы равен г, то все её миноры (г-Ц-1)-го порядка должны исчезать и мы имеем соотношения (16). Таким образом, равенство рангов не только необходимо, но и достаточно для совместности, как мы и утверждали.
Если это условие выполнено, то последние т — г уравнений преобразованной системы имеют вид 0 = 0 и могут быть отброшены. В первых г уравнениях можно считать координаты уг+1, ..уп произвольными функциями от t и перенести содержащие их члены в правые части. В результате мы получаем для остальных неизвестных у19 ..., уг систему г скалярных уравнений с квадратной неособой операционной матрицей r-го порядка, определитель которой равен (D) ... grr (D). Последнее r-е уравнение содержит только одну неизвестную уг и может быть разрешено по известному правилу, причём в общее решение войдёт столько произвольных постоянных, какова степень vr полинома grr(p). Подставля найденное выражение Ут в (г—1)-е уравнение, которое содержит две неизвестные уг_± и Л, можем разрешить его относительно уг^ причём общее решение будет содержать, кроме прежних, ещё постоянных. Продолжая таким образом, получим общее решение системы, содержащее п—г
416
Системы-с постоянными коэффициентами
[гл. 8
произвольных функций и v = Vj-]- ... -|-vr произвольных постоянных, причём v равно также степени общего наибольшего делителя миноров r-го порядка, образованных из первых г столбцов операционной матрицы f(D) заданного уравнения.
Пример. Пусть имеем скалярную систему
У i—2yt — +У2—У2 + Уз — Уз — 4^з = 2г(0, •
У1 — 2yt + у2 + Уз — 2Уз = % (О,
—У1 —У2 +Уз — 4.Уз = — * (О,
где z(t) — заданная функция.
Операционная и расширенная матрицы суть
'Р) =
||/(О). w (01| =
02 —20—1
0 — 2
— 1
02 — 20 —1
0 — 2
— 1
2z (О
— *(0
Ранг операционной* матрицы равен двум. Для трёх неизменённых миноров третьего порядка расширенной матрицы, содержащих столбец свободных членов, получаем выражения
2(0 —3)(О-Ь1)^(0, (О-2)(О-3)(О4-1)^(0, —(О —3) (0 4-1)хг (О-
Принимая во внимание, что общие наибольшие делители миноров второго порядка операционной матрицы, заключённых, соответственно, во 2-м и 3-м, в 1-м и 3-м и, наконец, в 1-м и 2-м столбцах, суть
0 — 3, (О —2)(О —3), 0 — 3, находим три изменённых минора третьего порядка:
2(04-1)^(0. (04-1)^(0, - (О 4-1)^(0-
Для того чтобы ранг расширенной матрицы был равен двум, нужно, чтобы все эти миноры исчезали, и условием совместности будет:
(О + 1)г(/) —0.
Поэтому скалярная система совместна в том и только в том случае, когда z(t) имеет вид
z (0 = ce~ti где с — постоянная.
Пользуясь символом ~ для обозначения эквивалентности в отношении элементарных преобразований над строками и приводя к канонической форме, имеем;
02 — 20 —1 0—1 02—О —4 2Dz (f)
0 — 2 1 0 — 2 z(0
— 1 — 1 0 — 4 — *(0
О о
I
£>(D — 2)(D — 3)
— (D —2)(D —3)
— D4-4
( —£>a + 4D + l)z(0 CD-3)z(f) г(0
ЮТ
§ 8.5]
НЕОСОБЫЕ УРАВНЕНИЯ
417
0 0 о
О D — 3 — (О —2) (0 — 3)
1 1 —D+4
1 1
0 D — 3
О О
— 04*4
— (О—2)(D —3) О
(О 4*1)* (О
(D-3)z(0
z(0 (О — 3)z(0 (0 4-1)2(0
Если условие совместности выполнено, то третье уравнение преобразованной скалярной системы имеет вид 0 = 0 и может быть отброшено, а первые два мы напишем в виде
У14* У2 = (D — 4) Уз 4- се-*,
(D — 3) у2 = (О — 2) (О — 3) уз 4- (О — 3) се~*.
Считая произвольной функцией ср (t), можно разрешить полученные уравнения относительно уь у$.
= — <7*3* — 2ср (0,
Уъ = С& + (D — 2) с? (0 + се-К
На этом примере можно убедиться, что формулировать определение ранга расширенной матрицы и теорему совместности с помощью неизменённых миноров нельзя.
В самом деле, если бы мы приняли такую формулировку, то для того, чтобы обратить в нуль полученные выше выражения трёх неизменённых миноров, мы могли бы положить (D — 3) z {f} = 0 и z (0 = сё^. Очевидно, однако, что при такой форме функции z(f) система несовместна.
На этом же примере можно видеть, что, вообще, непозволительно в самой исходной системе выбирать г уравнений и разрешать их относительно г неизвестных, хотя бы операционная матрица получившейся усечённой системы и была неособой. Возьмём, например, третье и первое из заданных уравнений и представим их в виде
Ji4-J'2 = (O-4)<?(04-^(0.
— (D2 — 2D — 1)Л — (О — 1) Уз = (02—D — 4) (0 — 2Dz (t).
Умножая первое на 02 — 2D — 1 и прибавляя ко второму, а затем, принимая во внимание, что в силу условия совместности (О 4* 1)^(0 = 0 и (D2 — 4D —!) z (fl = [(D2 — 40 — 1) 4- (О 4- 1)] z (0 = D (D — 3) z (t), получаем правую каноническую треугольную форму
У14* Уг = (О — 4) <? (О 4- се-*,
D (О —3)_у2 = О (0 — 2) (D —3) ? (04-О (О — 3)се~*, откуда
у2 = Сё& + С' + (D — 2) ср (0 + се~*.
Но если С' Ф 0, то это решение неверно, в чём легко убедиться путём подстановки во второе из заданных уравнений.
§ 8.5. Неособые уравнения. Будем в дальнейшем предполагать, что т = п и что определитель
A(D) = det/(D) (8.17)
27 Зак. 1474. Б. В. Булгаков
418
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
1гл. 8
не равен тождественно нулю, так что f(D) — неособая квадратная 1 матрица. Матричное уравнение (1) мы также будем называть в этом 1 случае неособым. Эти предположения не влекут существенного огра- ж ничения общности, так как в предыдущем параграфе мы показали, каким образом самый общий случай может быть сведён к рассма- 1 триваемому. -Определитель A (D) и уравнение 1
A(D) = 0,
(8.18)
в которых D рассматривается просто как скалярный аргумент и 1 может быть заменён любой другой буквой, называются характера- । стическим определителем и характеристическим уравнением.
Так как ранги операционной и расширенной матриц равны п, то J из общего условия совместности следует, что неособое уравнение 5 всегда имеет решения и что эти решения не содержат произвольных функций. Кроме того, очевидно, А(О) может лишь постоянным множителем отличаться от произведения диагональных элементов эквива- • лентной треугольной формы; поэтому порядок скалярной системы, j т. е. число произвольных постоянных в ее общем решении, равен | степени s характеристического уравнения. Он равен также числу линейно-независимых частных решений; при этом каждому корню характеристического уравнения соответствует столько произвольных
постоянных и частных решений, какова ] его кратность. 1
пллг
§ 8.6. Пример приложения к пас-сивному четырёхполюснику. Четы-рёхполюсником, вообще, называется f система каким-либо образом соединён^ 1 ных сопротивлений, индуктивностей и 1 ёмкостей, имеющая две пары зажимов. 1 К одной паре может быть приключён, 3 например, генератор, а к другой— J нагрузка. Если четырёхполюсник не Ж
содержит источников энергии, то он Фиг. 51. Пассивный четырёх- называется пассивным.
Обозначая через их, иу напряжения на входных и выходных зажимах пас-
полюсник.
сивного четырёхполюсника, изображённого на фиг. 51, и через q заряд конденсатора, можем написать, предполагая выходные зажимы 1 разомкнутыми: |
или
+ “у
—(ТХО+ 1)9 = 0,
(7\P+\)q = Cux, .
(8.19)
I
§ S.81
Непрямое регулирование
410
где
Л = ся2, г2 = с(/?1+л2).
Если рассматривать uyi q как неизвестные, то система уравнений имеет правую треугольную форму. Приводя к левой треугольной форме с помощью элементарных преобразований над строками, получаем:
(T^D+l)», =(,T1D+l)ux> '
С Т2иу (Т2 Тх) q = CTtux.
(8.20)
Первое уравнение непосредственно связывает входное и выходное напряжения, а второе даёт возможность в конечном виде выразить через них заряд конденсатора q.
§ 8.7. Исключение неизвестных. Элементарные преобразования над строками, применяемые для приведения операционной матрицы к треугольной форме, могут быть выполнены лишь частично и в разных вариантах, например так, чтобы в последнем столбце были равны нулю все элементы, кроме последнего, в предпоследнем столбце — все, кроме двух последних, и так далее до (п— /?4"1)‘г0 столбца, в котором могут быть отличны от нуля только последние р элементов (р<и). В результате первые п — р уравнений будут содержать лишь п — р неизвестных у19 ..., уп_р, а р неизвестных Уп-р+1> •••» Уп окажутся из них исключёнными.
§ 8.8. Непрямое регулирование. Рассмотрим автоматически регулируемую систему, в которой управление источником энергии, воздействующий на поле регулирования (§ 4.6), требует столь больших усилий, что не может быть осуществлено непосредственно чувствительными элементами, а ведётся с помощью сервомотора. В этом случае реле, в котором производится сравнение действительного состояния поля регулирования, зарегистрированного чувствительными элементами, с желаемым, служит лишь для управления сервомотором. Такое регулирование называется непрямым. Предполагая, что поле регулирования, реле и сервомотор имеют по одной степени свободы, которые характеризуются скалярными координатами ср, о, р, будем рассматривать общий случай, когда и поле регулирования и сервомотор обладают инерцией и вязким сопротивлением, а поле регулирования, сверх того, — восстанавливающей силой. Обозначая через х команду, подаваемую на регулятор, будем считать открытие реле а линейной комбинацией разности х — ср, её первой и второй производных и координаты сервомотора |л. Тогда уравнения регулирования будут:
(T2D2 UD + &) © — ji = z (поле регулирования),
° == (А2О2 MD + Z) (х — ср) — пр. (реле),
(V 2/)2 WD) pt = Лз (сервомотор).
(8.21)
27*
420 Системы с йоётоййными- Коэффициентами (гл. 8
Схема, представленная на фиг. 52, соответствует конкретному случаю следящей системы, где объектом регулирования является масса Л,?, стеснённая пружинными буферами и подлежащая перемещению в соответствии с положением х задающей ручки Вх. Источником энергии служит мотор постоянного тока с независимым возбуждением. Координата © представляет смещение тела Дф, координата рь— окружное перемещение какой-либо точки ротора сервомотора 4^ или его угол поворота, который, как это разъяснено
Ж
Фиг. 52. Следящая система.
ниже, пропорционален току в якоре главного мотора Первые три слагаемых в первом уравнении пропорциональны взятым с обратными знаками силе инерции массы и мотора, вязкому сопротивлению и упругой реакции буферов, а слагаемое — вращающему моменту мотора; коэффициент при рь сократился в результате деления на него всего уравнения; величина z справа пропорциональна возмущающей силе. Суммирующее реле на схеме обозначено Ла; величины и х подаются на него в виде пропорциональных углов поворота двух валов, которые затем преобразуются в электрические напряжения, два раза дифференцируются электрическим путём и складываются с напряжением, пропорциональным току в якоре мотора Линия, вводящая последнее слагаемое, носит название обратной связи. На выходе реле получается напряжение, пропорциональное величине а, определяемой вторым уравнением (21), и пода-
§8.81
НЕПРЯМОЕ РЕГУЛИРОВАНИЕ
421
ваемое на якорь сервомотора с независимым возбуждением; при этом коэффициенты второго уравнения мы определим так, чтобы а имела, так же как ср и р, размерность длины. Первое и второе слагаемые в последнем уравнении (21) пропорциональны взятому с обратным знаком главному моменту сил инерции сервомотора и про-тивоэлектродвижущей силе,* а величина ha в правой части — напряжению, приложенному к цепи якоря. Сервомотор поворачивает движок потенциометра Р, включающего напряжение, питающее главный мотор Если пренебречь самоиндукцией, то ток в якоре последнего будет пропорционален напряжению и, следовательно, координате сервомотора р., как мы и утверждали выше.
При х = const, z = 0 мы имеем статическое решение
/у Ъ1х
<?да==/ + лА’ °® = 0’ l + nk'
а при х = 0, z = const — статическое решение nz л lz
l^nk' — V-t — — T+Hk'
При п = 0 это последнее обращается в следующее:
— 0, — Z',
таким образом, при отсутствии обратной связи поле регулирования не реагирует на постоянные возмущения и система регулирования оказывается изодромной.
Операциойная матрица есть
f(P) =
TW^UD-^k
О
п
V^-j-WD
Очевидные элементарные преобразования над строками приводят её к виду
T*D*-]-UD + k 0 — 1
(£3 + пТ*) D*+(М -l-nU)D + (/+»&) 1 О
(ТаОа + UD + К) (У2/)2_j_ WD) —h о
и
(ТаО2+УОЧ-£)(Уа£>2 4-№7)) — h
(£a + nra)Da4-(M + «£J)D-|-(/-|-nA!) 1
— (7'aZ)2_|_t7£)_|_£) о
(8.22)
Если остановиться на последней форме, то, очевидно, два первые Уравнения будут содержать только ф и на, а и. окажется из них исключённым.
422 СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
[гл. 8
Умножая теперь вторую строку на h и прибавляя к первой, получаем левую каноническую треугольную форму
TW (ЛГ+ UV'2) + + + О О
+ + т 1 0 ,
— (T4)2+UD-\-ft) 0 1
где
$ = ^ = h^-\-Wk) l = |
а = А24-пТ2 р = /И4-п[7, 7 = /+»£. )(8,23)
Преобразованная система уравнений при x = z = 0 будет: i(D)? = 0, 1
<з =— (а£>2-|“ Р+ Т) ?> г (8.24)
^=^(ТЮ2-\-ий-Ук)Ъ J
где Д(£>) есть характеристический определитель
Д(О)== T2V2D^(T2W^UV2)D^^D2^^D + ^ (8.25)
Заметим, что так как координаты о, а, р. имеют одну и ту же размерность длины, то все те постоянные в уравнениях (21), которые обозначены малыми буквами, безразмерны. Постоянные, обозначенные большими буквами, имеют размерность времени; это — различные постоянные времени, которые могут быть истолкованы подобно тому, как это было сделано в § 7.5 для постоянной Т в уравнении движения паровой машины, управляемой центробежным регулятором.
Для облегчения изучения влияния постоянных параметров их число может быть уменьшено путём целесообразного преобразования переменных. Например, введём безразмерное время f и новые зависимые переменные а', р/ при помощи соотношений
, T*f u*w , и* , / U t > а 7*4 ° > Р*
и заметим, что
(8.26)
где
Преобразуя уравнения (21), найдём при x = z = Q: (D'2 + D' + k') © — = О, а' = — (L'SD'2 + M'D'.+ /') © — «У,
§ 8.9]
ПРИВЕДЕНИЕ К ФОРМЕ КОШИ
423
где все постоянные
/2 = -1 Л2 М' = Л4
UW * WW v ’
nr = п V2 = I/2
UW ’ T*W* V
(21) с преобразованными, мы видим, что не
л U2
1 LFW ’ безразмерны.
Сравнивая уравнения
штрихованные и штрихованные постоянные входят в обе системы совершенно аналогичным образом, за исключением того, что постоянным Т> U, W в первой системе соответствуют единицы во второй.
Поэтому мы можем просто предположить, что рассматриваемое преобразование уже сделано, и положить в первоначальных уравнениях
§ 8.9. Приведение к форме Коши. Как мы видели (§ 7.2), любая скалярная система может быть приведена к уравнениям первого порядка. В частности, матричное линейное уравнение с постоянными коэффициентами приводится к уравнению вида
(AD + H)y = w(f).
Если А — неособая квадратная матрица, то, деля на неё слева, представим уравнение в форме Коши
разрешённой относительно производной. Но если А — не квадратная или квадратная, но особая, то для этого необходим другой приём. Это приведение представляет теоретический интерес для выяснения структуры общего решения, хотя применять его к каждой конкретной задаче, разумеется, нет нужды *).
Пусть условия совместности выполнены и пусть А — матрица типа тХли ранга s1(sl^.nt9 п). Если s1=^m9 то> выделяя из А неособую квадратную субматрицу а порядка перенося в правые части скалярных уравнений п — неизвестных, соответствующих тем столбцам, которые не вошли в а, и считая их произвольными Функциями, получим:
(aD + &)Л = w (О — (л'О +
При этом матрицы-столбцы yv у2 состоят из и п — неизвестных. Полученное матричное уравнение немедленно приводится к форме Коши путём деления слева на a. j
*) Метод и формула для порядка приведённой системы, указанные
У Фрезера и др. ([1,10]v стр. 163, 164), в общем случае неверны, в чём легко Убедиться, применяя их к примеру в крнце настоящего параграфа.
424
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
[гл. 8
Если < т, то среди строк матрицы А найдётся линейно независимых; путём надлежащих элементарных преобразований эти строки могут быть поставлены на 5t последних мест и объединены в субматрицу B.2i а остальные строки приведены к нулю. В резуль
тате операционная матрица получит вид
Zr (AD-\-H) =
B.2D+K.2
где Z'— матрица преобразования.
Если ранг матрицы есть i\ (г^^т — st)9 то из неё можно выделить неособую квадратную субматрицу К и порядка rv а строки, не вошедшие в Ли, привести к нулю путём элементарных преобразований. Передвигая Ли в левый верхний угол, а строки, приведённые к нулю, — вниз, получим:
Z"(XD + H)V(1) =
О
Разделим, далее, первую строку слева на её слева на В^Э + Лгь вычтем из второй:
Ли, а затем, умножив
Л12
г(1)(О)(ло+н) у(1)=
о о
Если ранг s2 матрицы В22 равен числу её строк $х, то приведение заканчивается, как об этом будет сказано в следующем абзаце. Вообще же, s2 < st и с матрицей B^D + Л22 нужно поступить так же, как с данной операционной матрицей AD-\-H, что позволит выделить субматрицу B^D-\-K33 из $2 строк и т. д.
В результате, после некоторого числа v — 1 шагов, получим:
Л12 • • • Лх. Лх, v+x
О ЕГа ... Л2. Л2, v+x
Z(^1)(D)HD + H)V= .................................
О 0 ... aD-\-h a'D-\-h'
.0 0 ... 0 0
где a, h — квадратные матрицы порядка 5 = sv_x, первая из которых — неособая, a a', h' — матрицы типа s X (я — г — s)t причём г = г± + . • • + Число последних строк, заполненных нулями, равно т—г—s. В частности, может быть 5 = 0, т— г — 5 = 0,
§ 8.9]
ПРИВЕДЕНИЕ К ФОРМЕ КОШИ
425
п—-г—$ = 0. Применяя более компактную запись, имеем:
г(,_1)(Р)(ЛД + Я)У =
Hi Нг
О dD —|— h
О О
или, после деления первой строки слева на Hit
Z (D)(AD-\-H)V =
Er Н2 Hs
О aD-j-Л a'D-\-h' ООО
Совершая в первоначальном уравнении замену
умножая его слева на Z(D) и полагая
•^1(0
Z(D)w(t) = ,
5
С
э
w3(0
получаем преобразованное
матричное уравнение
Я8
a'D + h' . О
Ег Н2
О ч aD h
О О
которое сводится к трём следующим:
(aD 4“ ti) т| (afD + h') С = (0>
0 = w3(/).
Последнее уравнение должно быть тождеством в силу условий совместности и может быть отброшено.
Матрица-столбец С существует только в том случае, когда Л — г— s > О, и в этом случае состоит из п — г — s элементов, которые должны считаться произвольными функциями от t.
Первому уравнению соответствует г конечных скалярных соотношений между неизвестными; из него можно выразить С через т] и произвольные функции; Второе уравнение относительно т] приводится к форме Коши путём деления слева на неособую квадратную матрицу а J с°ответствует s скалярным уравнениям. В частных случаях одно или два.из трёх уравнений могут отсутствовать.
426
СИСТЕМЫ с постоянными коэффициентами [гл. 8
Полученный результат можно, очевидно, формулировать и так, что существует преобразование
у — S (D) w (0 и? (О + trq,
содержащее, вообще, произвольную матрицу ©(/), с помощью которого для новой неизвестной т] получается уравнение в форме Коши.
Пример.
О
— 1
У1
У'2
Уз
О
О
Умножая слева на
—1
Z(D) =
О
и совершая преобразование
О
О
О
О
О
О
У1
Уз
Уз
находим:
о
1 о
1
О О
1
У1
Уз
Уз
-(D + 2)x(0
т. е. два конечных соотношения между неизвестными
_У1 — 2j2 = (D +1) х (0, Уг + Уз = — (D + 2) х (/)
и уравнение первого порядка относительно у%
Б. СОБСТВЕННЫЕ КОЛЕБАНИЯ
§ 8.10. Собственные колебания системы с линейными элементарными делителями. В § 2.20 было дано общее решение линейного матричного уравнения с постоянными коэффициентами методами операционного исчисления. Это решение удобно в тех случаях, когда нужно исследовать колебательный процесс при заданных начальных условиях. Здесь мы займёмся построением решения неособого однородного матричного уравнения (5), которому соответствует система скалярных уравнений
п
S= ° (7 = 1, • • •> «)» fc=l
с помощью так называемых нормальных колебаний. Эта форма обладает своими преимуществами при общем анализе структуры и устойчивости системы и в других вопросах.
Мы имеем:
(a0Z/ + + ... аъ) еи = а^е* -J- А
“УЗИ
§ 8.10] СИСТЕМА С ЛИНЕЙНЫМИ. ЭЛЕМЕНТАРНЫМИ ДЕЛИТЕЛЯМИ 427 что можно записать короче:
/(О)^ = /(л)^, (8.28)
причём эта формула верна и при п==1, т. е. для любого скалярного полинома.
Пользуясь этим, будем искать частное решение в виде y = ueXi, где и есть матрица-столбец с постоянными элементами,
и1
(* XI).
Подстановка в уравнение и
сокращение на дают:
/(Х)я = 0, или, в скалярной форме,
S/,fc(x)«fc=o (/=1.........»)•
к
Мы получили для определения постоянных ..., ип систему линейных алгебраических уравнений. Они однородны и* допускают решения, отличные от тривиального . = ип = 0, лишь при условии, что их определитель равен нулю; иными словами, X должно быть корнем характеристического уравнения (18). Если степень s полинома Д(Х) равна нулю, так что он приводится; к постоянной, то характеристическое уравнение не имеет корней и мы не можем* получить никаких решений, кроме тривиального. Если же s больше нуля,, то характеристическое уравнение имеет корни (а = 1, ..., $). Значение и для одного из них определяется матричным уравнением
/(Ч) и = 0, (8.29)
соответствующим скалярной системе
(8.30)
2М)«* = °
к
с особой матрицей /(Xff). Мы имеем: дД _ F tfjk -
ГДе есть алгебраическое дополнение элемента fjk в Д. Поэтому
^Д.(Х) VVf
~dT= huFli^K) ~Т> з »
ТаД что если все Ffcj(X) обращаются в нуль, при Х = Хв, то.не только W» но. и Д' (X) обращается в нуль и есть кратный корень характеристического уравнения. Отсюда мы заключаем, что если предпо-
428
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
[гл. 8
дожить, напротив, что есть простой корень, то среди алгебраических дополнений F^(X) должны найтись такие, которые не обращаются в нуль при Л = Лв. Ранг матрицы /(Аа) в этом случае равен п—1, её дефект — единице, и если
(л ХО (8.31)
V v па есть какое-нибудь нетривиальное решение уравнения (29), то общее выражение решения будет и = V9C9, где С9— произвольная постоянная. С помощью найденного значения и получим искомое частное решение дифференциального уравнения У/^ехрл/.
Для получения V9 можно воспользоваться матрицей
F(D)=||^fc(D)H (яХ4 (8.32)
присоединённой к f(D), т. е. транспонированной матрицей алгебраических дополнений P^D). Замечая, что все элементы квадратной матрицы /(Aa)F(Aa) = Д(лв)£ равны нулю, примем за V9 любой столбец F(Xff), среди элементов которого есть отличные от нуля. Тогда произведение f(k9)Ve будет представлять собой один из столбцов матрицы /(Ae)F(Xff) и потому
F(y у. = 0.
(8.33)
Таким образом, взятый нами столбец V9 действительно удовлетворяет уравнению (29). Можно было бы также принять за У9 матрицу-столбец, отличающуюся от выбранного столбца матрицы Г(Ла) постоянным ненулевым множителем.
Пусть теперь = ... = есть ^-кратный корень;
числоq9 может быть также представлено любым из символов q9+i, ...»
Пусть, далее, ра есть ранг матрицы /(Хв) ит9 = п— рв — её дефект, который равен числу элементарных делителей, соответствующих данному корню (§ 1.18); при разрешении уравнения (29) войдёт t9 произвольных постоянных и число линейно независимых решений также будет равно та. Вообще, t9^qa и точное равенство x9 = q9 имеет место лишь при условии, что все элементарные делители линейны. В этом случае для и мы получаем q9 линейно независимых значений V9, ..., K+g -1, которым соответствуют частные решения V9C9№9 ..., Ve+Q'-iCo+q дифференциального уравнения. Число произвольных постоянных в этой группе решений равно кратности корня. В частности, каждому простому корню (<7а=1) соответствует единственный линейный элементарный делитель; но и при q9 > 1 элементарные делители могут оказаться линейными.
Если все, вообще, элементарные делители, относящиеся ко всем корням, линейны, то частные решения, найденные с помощью описан* ,
§ 8.10] СИСТЕМА С ЛИНЕЙНЫМИ ЭЛЕМЕНТАРНЫМИ ДЕЛИТЕЛЯМИ 429
ного элементарного приёма, будут содержать столько произвольных постоянных, какова степень 5 характеристического уравнения. По фундаментальной теореме § 5 это есть полное число постоянных, которые должны содержаться в общем решении
8
У = S V'C'K (8.34)
а=1
получаемом суммированием всех частных. Столбцы V9 мы будем называть модальными.
В общем случае при наличии кратных корней для всех или некоторых из них может иметь место неравенство т0 < q9 и тогда среди элементарных делителей будут встречаться нелинейные. В этом случае элементарный приём не даёт полного числа произвольных постоянных; для этого нужно прибегнуть к методам, изложенным в следующем параграфе.
Пример 1. Пусть имеем систему скалярных уравнений
Dbzi + (D2 + D + l)j2 = 0,
(D3 + D) У1 + (да + D + 2) = О,
соответствующую матричному уравнению f(D)y~0 с операционной матрицей
f(D}= D3 /?2+D + 1 .
} D^+ D D^+D + 2 ’
характеристический определитель
Д (D) = det/ (D) = — D (D + 1) имеет корни
= 0, kg = — 1.
Для первого из них система уравнений, которым должны удовлетворять иь есть -
= 0, 2«2 = 0;
второё уравнение может быть отброшено как следствие первого, и мы можем взять, например, = 1, = 9 или и = где
Аналогичным образом для второго корня
—-»-] ^2== 9, -“ 2#2 = 9
Можно было бы также вычислить
430
Системы с постоянными коэффициентами
[гл. 8
и заметить, что оба столбца в F (0) пропорциональны Vh а оба столбца в F (—1) пропорциональны V2.
Общее решение будет:
У = VtCx + V&e-t или
yi= О. + У2 =
Пример 2. Рассмотрим следующее матричное уравнение:
D D — 1
D 2D + 1 —1
2 2 D + 3
Здесь
J'i
У2
Уз
A(D) = (D + l)2(D + 2),
Xi = к2 = — 1, = — 2, qx = ^2 = 2, ^з=1.
Заменяя D через —1, получаем матрицу
—1
—1
—1
имеющую ранг 1 и дефект 2, а это показывает, что двойному корню —1 соответствуют два линейных элементарных делителя. Из трёх уравнений
— Й! — й2 — = 0’ —.И1 — и2 — Из = 0, 2йх + 2«2 + 2й3 = 0,
относящихся к этому корню, два последних могут быть отброшены, и мы можем принять в качестве двух линейно независимых значений и столбцы
Полагая D = — 2, получаем:
и
—1
—1 1
Уз =
0
2
Общее решение:
У1 = (- Сх + С2) e-t- С&-*,
У2 = Схе^,
' Уз ~ — Ctf $ 4” 2Сз# 2^.
§ 8.11. Общий случай собственных колебаний. Если есть простой корень характеристического уравнения, то, согласно сказан- . ному в предыдущем параграфе, каждый столбец матрицы удовлетворяет алгебраическому уравнению f (Xff) и = 0, а каждый столбец матрицы является частным решением дифференци-
ального уравнения собственных колебаний. Чтобы решение было
§ 8.11) , дикций случай собственных Колебаний 431
нетривиальным, нужно только взять столбец, в котором не все элементы равны нулю. Этот вывод может быть следующим образом обобщён на случай ^-кратного корня XG = ... = -i с какими угодно соответствующими ему элементарными делителями. Образуем q* матриц
[д? П
(р = 0, .... qe~ 1) (8.35)
и заметим, что
/(D) Т, (А X) =/(D)-^ e«F(X) = -^/(D) e*F (X) =
= e*F w = Sv<X> E = ОКУ о№
= eKt [ Д (A) t9 + Д' (X) Zp-1 + Д" (X) t9~2 + ... + Д(р) (X)]E.
Так как A (XG) = A' (Xe) = ... = A^-1) (XG) = 0, то, полагая в предыдущем соотношении X = Xff, получим:
/(D) Тр(/, Ха) = 0 (р = 0, ..., ^-1).
Это соотношение остаётся верным, если в качестве второго множителя взять вместо Тр (/, Хв) какой-либо столбец этой матрицы, который оказывается, таким образом, частным решением матричного дифференциального уравнения. Решением будет также и сумма
(0 Н” • • • ~Ь (0
где •••> -i суть какие-нибудь столбцы матриц Тр(/, XG) или их линейные комбинации, a Cff, ...» C9+q ±— произвольные постоянные. Общее число столбцов во всех q9 матрицах Тр(/, XG) ерть q^n; но за ..., &ff+g _i мы возьмём лишь линейно независимые столбцы или их линейные комбинации, а таких будет ровно q9. Это следует из того, что, определяя в дальнейшем постоянные из начальных условий, можно убедиться, что в общем решении каждому кратному корню соответствует группа членов вида С9, образованных с помощью линейно независимых столбцов &e (t) матриц Тр (t, Aff), а по общей теореме § 5 число независимых частных решений, соответствующих каждому корню, должно быть равно его кратности.
Мы можем написать:
Т(Л = X), (8.36)
где ир (t, X) = F (X) t9 + 4- ? (х) е~1 + е F" (х) *Р'2 + X 1*4
+ ... + ?Р)(Х) = (-^+*)₽ (8-37)
432
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
[гл. 8
Тогда каждому корню Ха соответствует решение
v, (о +ve+1 (о с.+1Л* +... + v,^ (t)
где V9(f), ..., Va+q -i(0 суть линейно независимые столбцы матриц С/р(А А3) или их линейные комбинации. Мы будем, как и в предыдущем параграфе, называть их модальными столбцами.
Пусть будет е9 степень самого старшего из элементарных делителей, соответствующих корню Aff. Все Fkj(D) делятся на (D— Аа)*«“в« и при D = Aff исчезают вместе с производными до (q9— е9—1)-го порядка. Поэтому первые неисчезающие из матриц /^(АД С7р (/, Аа) будут порядка p^ = qa— еа. Наименьшее значение р' = 0 получается в том случае, когда корню Aff соответствует единственный элементарный делитель, так как тогда e9 = q9. Другой крайний случай получается при qa линейных элементарных делителях; тогда е9=1, p^ = q^ — 1, и для образования модальных столбцов мы располагаем единственной неисчезающей матрицей (Aff) = U^_± (t, Aff) с постоянными элементами, вследствие чего и все модальные столбцы будут также постоянными.
При наличии нелинейных элементарных делителей некоторые из модальных столбцов V9 могут быть полиномами от t. Это и составляет существенное отличие рассматриваемого случая, хотя форма частных решений остаётся той же, что и в предыдущем параграфе.
Для общего решения получается прежняя форма (34).
Замечая, что для любой функции <р(£) имеют место соотношения
De^> (0 = е™ (D + А) ? (О, Dme\ (0 = е*(D + Х)т<р(f),
(0 = e*f (D + X) <? (0.J.
(8.38)
где f(D)— скалярный или матричный полином, мы получаем: /(£)) e^V, (0 = Л7(Р + Л.) V, (0.
Отсюда следует, что модальные столбцы V9 (t) удовлетворяют дифференциальным уравнениям
/(О + УУо(0 = О, (8.39)
которые для постоянных V9 обращаются в полученные ранее конечные уравнения (33).
Отыскание модальных столбцов, соответствующих кратным корням, может быть иногда ускорено с помощью следующего предложения.
Теорема. Если линейное однородное уравнение f(D)y = Q имеет решение u(f)ext, где u(t) есть матрица-столбец, то u(t)eu также будет решением.
ОЫЦЙЙ СЛУЧАЙ СОБСТВЕННЫХ КОЛЕБАНИЙ
433
В самом деле, дифференцируя тождество
/(D) а (0^ = 0,
находим:
Df(D) и (t) е™ =f(D) Du(f) e^=f(D) и (f) и (t) e™ = 0.
Так как второй член исчезает сам по себе, то мы получаем соотношение
(8.40)
/(D) а (0^ = 0, которое и доказывает теорему.
В связи с этим можно отметить, что, как легко проверить,
X).
Поэтому, если не принимать в расчёт несущественные постоянные множители, то столбцы матриц U9(t, Ха) могут быть получены друг из друга, в соответствии с теоремой, путём дифференцирования по t.
Пример 1 (Т. J. Bromwich). Рассмотрим матричное уравнение 2D2 —3 —1
1 2D2—1
J'l
У'2
= 0.
Характеристический определитель
A (D) = 4 (D —1)2 (D + 1)2.
Корни характеристического уравнения A (D) = 0 будут:
Кратность этих корней qt = q% = q$ = q± = 2. Присоединённая матрица
2D2 — 1 1 II
— 1 2D2 —з
F(D) =
и
4D 0
' ' 11 0 4D
2X2—1
£/0(/, Х) =
2X2 — 3 ’
Uitt, Х) =
U^t, 1) = ^Ш
t
£/i(4-l) =
Можно принять оба столбца матрицы Ui (tt 1) за модальные или же можно заметить, что они представляют собой комбинации Vi, Vi — 414
28 Зак. 1474. Б. В. Булгаков
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
[гл. 8
434
столбцов
и принять эти последние за модальные. Столбцы матрицы Uaif, 1) совпадают с Аналогичным образом выбираем два столбца, соответствующих корню—1:
V3 =
У4= '
Общее решение
Vi = [Cl У + 4) + С2] е* + [Cs (t - 4) + C4J е-\
Пример 2 (T. J. Bromwich).
-1 02 —20
- О 02
kj = k2 == 0,
Д (D) = D2 (D + 3),
„ ~ D2
"W--№-D
0)
x л Уз
^з = — 3, q± = q2 = 2, q^ = 1,
11 20 F' (O) =
} Ц — 2О — 1
0 2
= 0.
2D
0 0
0 1
Vi=
о
14 =
U0(t, ~3) =
9 —15 — 6 10 ’
3
У1
П р и м е р 3 (Е. J. Routh).
3(0—1)2
(О -1)2
— (£> — 1) (£> — 2) О —1
— (D —1)(D —3) 2(D—1)
Д(О) = (О-1)<
J'l
J's =0-
J's
3
2 = — (^> — 1)6,
М. = k2 — ^3 ~ — ^6 — Ъ
Яг — Яя — Яз — Яг = Яь — Яъ =
F (D) = (D —1)3 — 1
^(1) = F'(1) = ^(1) = O,
СОБСТВЕННЫЕ
ФОРМЫ
Й МОДАЛЬЙАЯ МАТРЙЦА
1
о о О
О
О О
О
О
= 60
— f2 — f2
— /2 f2-|-2f —f2_ztf
&+2t — — /24-6/ —2
Обозначая три столбца последней матрицы — 60 а’ Т20 "*
О
О
— 2
О
3
через a, b, ct составим комбинации
—(« + 2Я-С)
и примем их за модальные столбцы Vi, V4:
О
V2 =
о о
В качестве V3, Vg, Vq можно взять комбинации
*K+Vi
dt 41
1 dVr
2 dt
2_ 2
dW± dV2 dt* dt ’
или
t
Уз= О о
V5 =
О
О
V6= 0 0
Общее решение
У1 = (^i^2 + Ctf + Cq) e\
У% = (^V2 + C2t + Cg) ett
Уз = [Cl (- - 20 - CJ + C4] e*.
§ 8.12. Комплексные корни; собственные формы и модальная матрица. Пусть характеристическое уравнение ймеет s' действительных корней Xff = xcy (о= 1, ..., s') и s" пар комплексных сопряжённых V+ti, A8'+^+A = eftz±f(o^ (Zt=l, s"). Мы можем, если желаем, избавиться от мнимостей и путём простого преобразования общего решения выразить его в действительной форме.
Для этого следует модальные столбцы и произвольные постоянные, соответствующие корням Х8'+л, взять взаимно сопряжён-
ными, полагая
> 3
Vs'+h* +8''+h — v8' — ,f+(8.41)
C^l'+h, <'^'+s''+^ = 2"(csz^-л-t::l<:B'+в"+л)• (8.42)
28*
4S6 СИСТЕМЫ С ЙОСТОЙННЫМИ кОЭФФиЦЙЕЙТАМЙ [гл. §
Мы назовём v8'+fc, собственными модальными столбцами
или собственными формами} при будем считать модальные столбцы в то же время и собственными, полагая
V, = »., С„ = с, (о < s').
Общее решение (34) переписывается в виде
У = 2 V.C.S'-'+ 2[V.4A4l«,,'‘+‘"",' + g=1 Л=1
। • » —9—
“h ^s'+s"+&£s'+s,'+b e ] ~
8r s"
- %vs+‘ 2R=[v..+1c,+ie(,*t‘-*,'i= cr=l Л=1
8'
G = 1
матрицу-
(8.44)
(8.45)
—P Re [(^з' +Л ~H ^8' Ч-з^+й) (^з' +h LCs' +e"+ft) ^ ]*
Л=1
Назовём матрицу
*’=II‘M (nXs), (8.43)
образованную из s = s'-|-2s" собственных модальных, столбцов * ^1, .v8, модальной матрицей и обозначим через $ столбец из 5 элементов определяемых формулами
= е9* -с, (о = 1, ..., s'),
^З'+Л ^8'+8" + Л в (С8'+Ъ lC8’+8tt+l)
(/Z=l, /'),
вторая из которых эквивалентна двум следующим: S8'+7> = (С8’+Л C0S <U^+C8'+8’+h Sin Шь0.
- ^+8,+Л =/ft< (— ce,+bsina>^+cg,+8W+ftcosM (Л=1........................s"). J
Введём также матрицу
& =ПЫ («х^.
образованную из s столбцов &в, определяемых соотношениями
&, = v„ eat (а = 1«..., s'), (8.48)
&«'+л + ^в<+8»+л = +л + Ч’ +«"+»)в * А (8.49)
(Л=Г, .... s")
(8.46) »
>
(8.47)
§ 8.12] СОБСТВЕННЫЕ ФОРМЫ И МОДАЛЬНАЯ МАТРИЦА 437
и составляющих систему 5 независимых частных решений; последняя формула эквивалентна двум следующим:
&8,+fc = eh* (vt,+h cos »в,+8«+л sin
d8'+s-+ft = e,A#(^'+ftsin<0^+®e'+8>-+ftcos<0»0 (8‘50)
(A=l.......s").
Наконец, обозначим через с матрицу-столбец из 5 постоянных с±, ...» с8. Общее решение принимает вид
8' в"
У~ S S (®в'+л^'+д4"®а'+8"+л£8'4-8"+л) =
8=1 Л=1
8Г 8"
— 2 4“ S (^8'+А' +Л 4“ ^8' +»”+ЪСа'+вя+1)
8=1 Л=1
или, проще,
j=i^9=iv,. (8.51)
а=1 а=1
Если же перейти к элементам, то
8 8
= (7=1.......п), (8.52)
ff=l 8 = 1
так что
у = = 9с. (8.53)
Это и есть искомая действительная форма общего решения.
Выполненное нами преобразование применимо независимо от того, будут ли элементарные делители линейными или нелинейными, но в первом случае можно дать простое истолкование результата. Каждый столбец г/Д, называемый нормальным колебанием, можно представить графически, откладывая по оси абсцисс целые числа у, а по соответствующим ординатам — элементы столбца v^9 и соединяя концы этих ординат прямолинейными отрезками; получающаяся стоячая волна изменяется с течением времени, но её ординаты остаются пропорциональными ординатам неизменяемой фигуры, получаемой подобным же построением из элементов постоянного столбца
Таким образом, собственный модальный столбец действительно определяет форму, или модус, нормального колебания. Как видно из (44), (46), нормальные колебания будут затухающими при хв < О, гл < 0 и нарастающими в противном случае. Первые s' колебаний, соответствующие действительным корням, апериодичны. Числа а)д, называемые собственными частотами, представляют угловые частоты остальных 2s" нормальных ’колебаний.
Другое истолкование состоит в представлении у как переменного вектора в n-мерном пространстве, определяемого, согласно (51)? как
438
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
[гл. 8
геометрическая сумма s составляющих векторов численная величина каждого из этих последних переменна, но направление совпадает с направлением постоянного «собственного вектора» vg.
В связи с этими истолкованиями следует отметить, однако, что в общем случае нормальное колебание относящееся к одному
из комплексных корней, может существовать только вместе с парным колебанием ^г+8^+ЛЕ8г+8„+ь, так как лишь сумма
<71 ? —1— <71 £ —— Я С Л (*
Оз'ЧЛз'+з'ЧЬ з'+Л у'+Л 1 s'+s"+fc%'+s''+7i
является, сама по себе, частным решением. Иными словами, нормальные колебания* соответствующие комплексным корням, вообще, не могут быть возбуждены изолированно на при каках начальных условиях', но это возможно в частных случаях, когда У8г+Л= V3^3»^ действительно и 1>8,+8(Г+Л равно нулю.
Предполагая опять элементарные делители какими угодно, выведем ещё зависимости между. матрицами v, ft, Е, с, получающиеся с помощью матрицы Кейли (§ 1.16)
(8.54)
построенной из трёх диагональных матриц
(8.55)
(8.56)
Согласно
Кейли:
сказанному в § 1.28,
функция е& также будет матрицей
* 0 0
eQt = 0 ezt cos mt e*1, sin ml
0 — ezt sin mt cos mt
(8.57)
причём ё*&, ezt cos оо/, ezt sin mt суть
диагональные матрицы:
(8.58)
§ 8Л2]
СОБСТВЕННЫЕ ФОРМЫ И МОДАЛЬНАЯ МАТРИЦА
439
м**
cos m^t
cos mt =
e s" cos т3Л
eet sin mt =
S.f . /
e 1 sin mxt
(8.59)
e 8 sin msnt
настоя-
Развёртывая произведения е&с, ve®* по образцам произведений Qw, vQ в § 1.16 и сличая с соотношениями (44), (45), (48), (49) щего параграфа, получим:
Е = е&с, & = veQt.
(8.60)
Общее решение (53) может быть представлено
Qt у = с.
Пример 1. Рассмотрим матричное
уравнение
в виде
(8.61)
У1
У1
= 0.
Характеристический определитель
откуда
Присоединённая матрица
F(D) =
и
Первый столбец получается из второго умножением на [Ь — 1 zt i (b +1)]. Полагая
V2 =
о ’
»i =
»2 =
имеем:
v =
0
2Z
eif, 0 =
— 2 sin t
2 cos t
У1 = ci (cos t + sin t) + (— cos t + sin 0?
у 2 = — sin t + 2<?2 cos
440
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
Пример 2. Рассмотрим задачу о непрямом регулировании (§ 8), пре* небрегая инерцией сервомотора по сравнению с сопротивлением и движущей силой (У=0). Пользуясь выражением (22) операционной матрицы и предполагая, что команда х и возмущение z равны нулю, получим уравнения движения в виде
IF(T2£>3+ UD^+kD)^ — йо = 0, ) [(L2 + пТ2) + (М + nU)D + (I + nk)] <f + = 0. J
Умножая их на 1/T2W, h/T^W и полагая
У1 = Ъ = находим:
(пз + ^О2+^о)^-Л = 0,
[Л(L2 + пТ2) D2 + h (М + nU) D + h(l + nk)]yt+y2 = 0.
Пусть параметры поля регулирования имеют, численные значения Т= Уо,1 сек, U = 0,2 сек, k = 1,
(8.62)
(8.63)
(8.64)
а параметры управления удовлетворяют соотношениям
^(£2 4-пТ2) = о,2 сек,
^(М + nU) = 0,6, Vr
^ (/+«£) = 6,4 сек-Х Vr
Операционная матрица будет:
/Ф) =
£)3_p2D2+10Z) —111
2D2 + 6D + 64 . 1 j ’
откуда
Д (D) = D3 + 4D2 + 16D + 64 = (D + 4) (D2 16) (8.65)
и корни характеристического уравнения суть = — 4 и k2, Х3 = rt 4Z. Затем
Вычисляя матрицу частных решений
_ в-** ' cos 4^ sin4£
— 72е~и — 32 cos 4t -f- 24 sin 4f — 32 sin 4t — 24 cos 4t
сейчас же напишем и общее решение
/ = »(<)₽,
§ 8.13] СОБСТВЕННЫЕ ЧАСТОТЫ КОНСЕРВАТИВНОЙ СИСТЕМЫ 441
§ 8.13. Собственные частоты консервативной системы с двумя степенями свободы. Рассмотрим более детально консервативную систему с двумя степенями свободы и постараемся проследить зависимость собственных частот от постоянных параметров, характеризующих структуру системы.
Выражения кинетической и потенциальной энергий имеют вид
Т=+2ЖЛЛ+W ]
. , } (8.66)
причём не только первая, но и вторая из этих квадратичных форм будет предполагаться определённой положительной, вследствие чего L > О, ЛГ>0, LN— М2>0, Д>0, С>0, АС — В2>0; (8.67)
при этих условиях положение равновесия ^1=^2 = О будет устой-
чивым. Уравнения Лагранжа имеют вид Lyi + ^2 + АУ1 + = Qv
МУ1 + Ку2 + ВУ1 + Су2 = q.2,
(L&+А) У1 + (ЛЮ2 + В) у2 = (MD* + В)У1 + (ЛЮ3 + С) у.2 = Q2.
Фиг. 53. Связанные
маятники. Первое нормальное колебание.
Демонстрационной моделью системы рассматриваемого типа могут служить два маятника, связанных пружиной (фиг. 53). Принимая за коорди
наты у19 у2 перемещения тех точек маятников, к которым прикреплены концы пружины, и обозначая через h расстояние этих точек от точек подвеса, через g ускорение силы тяжести, через с жёсткость пружины, через ша9 тъ массы маятников и через ha, hb их длины, найдём:
ад=—У1 (л — л)>
(8-'
тьУь = — У*~^3~ (Л — Л)-
«6 Аь
Эти уравнения получаются из (68), если положить = Q2 = 0 и
h hr
i = Л = 0,
Л = '^+е, В = —с, +
442 СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [гл. 8
Уравнениями такого же вида, что и для связанных маятников, определяются колебания двух масс на валу с закреплёнными кон-
Фиг. 54. Две вращающиеся массы на валу с закреплёнными концами.
няется закону Гука, получаем
цами, имеющих возможность немного поворачиваться за счёт крутильной деформации вала (фиг. 54). За координаты yif у2 здесь нужно принять углы поворота двух масс. Обозначая через Jv J2 их моменты инерции, через с0, ct, с2 крутильные жёсткости трёх частей вала и предполагая, что его материал подчи-уравнения движения
АЛ----соЛ + (л—Л)’
•/аУ2 = — — С1(У2— Л); •
(8.70)
ни приводятся к виду (68), если положить Q1 = Q2= 0 и
L — Jit Л4 = 0, N = J2, А = В = — С = с1-|-с2.
Примером электрической
системы могут служить два контура с индуктивной и ёмкостной связью (фиг. 55). Обозначим через qfl, qb, qc заряды трёх конденсаторов, через La, Ьъ коэффициенты самоиндукции, через Л4 коэффициент взаимной индукции, через Са, Сс ёмкости конденсаторов. Очевидно, что
Яе = Яе (0) + Я а — Я а (0) — 1Яъ—Яъ (°)1 •
Фиг. 55. Электрические кон- Применяя второй закон Кирхгофа, туры с индуктивной и ёмкост- согласно которому сумма падений на-нои связью. пряжения в каждом контуре, отсчи-
танных в каком-либо определённом направлении обхода, должна быть равна нулю, найдём:
^•аЧа ^Чь 1 Q& Я a i (.Ча 4 b) 7»
^Ча~\г ^ъЧъ~А Чъ--------Ь
где
°C
Уравнения (71) получаются из общих уравнений (68), дожить
(8.71)
если по
Л = ^2.= ^. Qi =—^2 = Т
§ 8.13]
СОБСТВЕННЫЕ ЧАСТОТЫ КОНСЕРВАТИВНОЙ СИСТЕМЫ
443
представим общие уравнения в форме
(D2 + 4)у j + (kaD2 — la<s>awb) у2 = Qv (kbD2 — lb^b) У1 + (D2 + ш|) Л = Q2.
(8.73)
Из неравенств (67) вытекает действительность величин <оа, <о6. Введём ещё коэффициенты связи
k = vfe = (slsn k°kb' у Li /V
I = - у==- = - (sign В) VlJb>
(8.74)
где sign есть символ функции сигнум, определяемой соотношениями ( — 1 при t < О, I sign£= < 0 при f = 0,
I 4“ 1 при t > 0;
. тогда
0<й2 = *Л<1> 0</а = /о/ь<1, 1 == ^а/'Ъ == 1 •
(8.75)
При = Q2 = 0 мы имеем собственные колебания и характеристическое уравнение будет:
(X2 4- (0^) (X2 4- <»ь) — (&дХ — === 0»
оно может быть также написано в виде
(X2 + Ш2) (X2 + со2) — (Кк2 — 1^ь)2 = О, или
(I — k2) X4+(4+4 4- 2Ш^) X2+(1 — Z2) ш2 <о| = О, (8,76)
4.44 СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [гл. 8 i
У?
I Все коэффициенты этого биквадратного уравнения положительны t в силу неравенств (75). Дискриминант может быть представлен в форме f
(4 -4-44- 2Й/шо(»ь)2 — 4 (1 — й2) (1 — /2) 44 =
= (<оа — <о6)2 [(шо — <и6)2 4“ 4 (1 4" ^0 “Л] “1“ 4 (k -j- /)2 44
и, следовательно, не может быть отрицательным. Поэтому из биквадратного уравнения получаются два действительных отрицательных значения X9. Если же положить X = /со, то характеристическое уравнение принимает вид 5
/ (<о) а (— со9 сор (— о)9 -|- о)9) — (feo)2 /о)ло)ь)2 = 0 (8.77) f
или
(1 — 69) О)* — (0)2 + 0)2 -|- 2ШЛО)Ь) О)2 + (1 — Р) 0)20)2 = 0 (8.78)
г
и даёт для о)2 два действительных положительных значения
4 “I = 2(1 — ^) [“«+шъ +
V К + Ч + — 4 (1 - Й2) (1 _ /2) „2^ ]. (8.79)
Абсолютные величины а)р ах2 корней квадратных из этих значений представляют собственные частоты системы, так как четыре корня характеристического уравнения суть z±rfo)p zt/o)2.
Если оба коэффициента связи fe, I равны нулю (М = В = 0), то о)р о)2 обращаются, соответственно, в min {о)а, о)&} и max {о)Л, о)д}, ; т. е. в наименьшую и наибольшую из двух величин о)Л, о)ь. Поэто-му эти величины представляют собственные частоты тех двух частей, на которые распадается рассматриваемая система при отсутствии связи.
Если |fe|, |/| стремятся к единице, то о^ стремится к нулю, а о)2 — к бесконечности.
С другой стороны,
/(0)= (1-/2)ш>2ь >0,
Ж)=-“а(Ц + Ч)<0’ ;
/ (“ь) = — ®2 < 0 >
/(ОО)= (1-^2) (4-00) >0.
Поэтому о)р вообще, меньше или равна наименьшей из частот о)Л, а <о2 больше или равна наибольшей из них. Равенства <о1 = min {ооЛ, со©} или а)2 = тах{(о0, в отдельности имеют место только, если одна из величин
—(МА
lVna
(8.80) ;
(MC—NB)
§ 8.13] СОёСТЙЕЙИЫЕ ЧАСТОТЫ кОЙСЕ^ВАТИВНОЙ сйстеМы 44б
Mt
равна нулю, т. е. при совпадении отношения В/Л4 с наименьшим или наибольшим из отношений Л/L, С/ЛГ.
Равенство = возможно только при
соа = ш&> й-(-/== 0 (8.81)
или Т=ГТ1- <8-82)
Вводя величину * = », ’ (8.83)
которую можно назвать настройкой, получим следующие выражения отношений собственных частот к соа:
<*>1 <°2 _- ’ " >
“а <°а ь * \
= У2(1^) [1 + /(1 +х2+2Ш)2-4 (1-Й2) (1-/”) х2].
. “ \ ; (8.84)
Зависимость отношений zx = z2 = <ь%1<йа от настройки при различных k и I удобно представить графически с помощью кривых
Фиг. 56. Собственные частоты консервативной системы с двумя степенями свободы при k = 0. \
' . S
(фиг. 56 и 57). При й=7=0 эти кривые обращаются в ломаные, составленные из отрезков прямых z — 1 и z = х.
Пусть, в частности, £ = 0. Это соответствует случаю упруго связанных маятников или электрических контуров/связанных через
446 системе! с постоянйыми Коэффициентами [гл. §
ёмкость. Тогда
= /Ъ1 +-^2 /4x2/2Н-(1-^2)2]- (8.85)
Формулы показывают, что с ростом |Z| при данном х ордината zr должна убывать, а ордината z2— возрастать. При |Z| = 1 имеем:
21 = 0, г2=У1+х2
и, следовательно, <о =0, <л =]/го>2_|_(02> Асимптотами кривых z — z1(x), z — z2(x) в этом случае служат прямые
z = '|Zrl—Z2 и z — x.
Пусть теперь 1—0, что соответствует электрическим контурам с одной лишь индуктивной связью. Формула (84) получает вид
Z ъ <8-86>
Вычисляя частные производные dzjd(j^), dz.2/d(k2), легко убедиться, что и в этом случае с возрастанием абсолютной величины
Фиг. 57. Собственные частоты консервативной системы с двумя степенями свободы при Z = 0.
коэффициента связи при фиксированном х ордината zt убывает, а ордината z2 возрастает. При |fe| = l имеем:
^ = —7“=-, Zn = OO
1 /1+*2 2
и, следовательно, <о1 = (оло>&ДЛсо2 -|- со2, о>2 = оо.
§ 8.14] СОБСТВЕННЫЕ КОЛЕБАНИЯ КОНСЕРВАТИВНОЙ СИСТЕМЫ 44?
При х = 0 получается:
z< =0, z2 = -у
1 2 Vl — №
Асимптотами кривых z = zt(х), z = z.2(x) в этом случае служат прямые z = 1 и z = х/У 1 — А2.
§ 8.14. Собственные колебания консервативной системы с двумя степенями свободы. Элементы uv и,2 модального столбца, соответствующего одной из двух пар корней характеристического уравнения ± (h — 1, 2), удовлетворяют уравнениям
4 п * 1 х а п * а а о' 2 ’
— (Мл 4- «!.+ (— Ч + “Р «2 = 0-
Выясним прежде всего знак отношения который суще-
ственно влияет на характер нормальных колебаний. Мы сейчас убедимся, что решение этого вопроса зависит от того, удовлетворяется ли неравенство
(МА — LB)(MC — NB) > 0, (8.87)
как это имеет место, например, для упруго связанных маятников или вращающихся масс или для электрических контуров с одной лишь ёмкостной или одной индуктивной связью.
В самом деле, предполагая неравенство выполненным и представляя его в форме
+ /шь) (Ыь + /шв) > 0, (8.88)
мы видим, что оно исключает возможность одновременного исчезания величин k и Z, а также, согласно сказанному в предыдущем параграфе, возможность совпадения <о1 или <о2 с о>л или со&. Заметим, кроме того, что если Z =# 0, то и 1а, 1Ъ отличны от нуля и имеют тот же знак, а если k =/= 0, то и ka, kb отличны от нуля и имеют тот же знак. Поэтому мы можем написать либо
«1 = '(^л + Ч^б) _ la (— 4 + юб) (1 , 0)
а2 (— “Л + 1 (Й<ОЛ +
либо
_ k = , QX
z М““ю&+Ша)
причём входящие сюда отношения Z/Zd, Za/Z, /г/йь, kjk положительны. Кроме того, согласно сказанному в предыдущем параграфе,
соь < о)2, вследствие чего разности —+ —Ш1Ч~Ш6
положительны, а разности —<°|4-®2, —+ отрицательны. Таким образом, для установления знака отношения остаётся выяснить знаки сумм Z<oa<oft, Для этого> предполагая
44$ системы с побтояййыми Коэффициентами [гл. 8
сначала й #= О, положим
а = йсо2 /<оа<оь, выразим <о2 через о и, подставляя в (77), получим для а квадратное уравнение
ft9/ (Ш) = (1 - ft2) а2 — [ft («: + «Р + 2А»л] а +
+ <“А (*% + 1<»ь) (йв»Ь + 1ша) = 0.
Два его корня а, а„ связаны с ш2, ш2 линейным соотношением с действительными коэффициентами и потому также действительны. Они имеют один и тот же знак, поскольку свободный член уравнения положителен в силу (88). Так как, кроме того, коэффициент при первой степени о равен сумме величин о>а (йшл -j- ^°ь)» (^шь + /саД взятой с обратным знаком, то знаки этих величин, совпадающие между собой в силу (88), совпадают также и с общим знаком корней ах, о2. Иными словами, ограничиваясь в дальнейшем системами, для которых выполняется неравенство (87) или (88), мы должны считать знак выражений = йо)2-|“ о2 = й<о2-|-/а)а(о& тождественным со знаком выражений йюо—зависящих только от параметров системы. Это верно, конечно, и в частном случае k — 0, который мы выше исключили. Отношение будет положительно для одной из двух пар корней и отри-
цательно для другой. Иными словами, если имеет место неравенство (87), то одна из собственных форм будет знакопостоянной, а другая знакопеременной.
Обозначая
е = sign (Ыа -|- 1<аь) = sign (ka>b -f - /<ов) (8.89)
и предполагая, что Z #= 0, можем написать
и положить ^21 = 81^11Ь I С- “1 + ®|)’ Если же ft #= 0, то примем «1 = - . «2 •^ц =/1 ft« 1 (— + ®21 = 8 /| 1 (— “1 + <»„)• ;+«. (89О) > . 1 f Г Й&(— (Ofc + 0)2) - О —— 8/|ftJ(—“лЧ-10»/ ' ' « =/lfe. |(— «2+«>2). ” ‘ 22 ». 1 q 1 \ д 1 2* ।
§ 8.14] СОБСТВЕННЫЕ КОЛЕБАНИЯ КОНСЕРВАТИВНОЙ СИСТЕМЫ
449
Так как модальные столбцы = v19 V2 = v2 действительны, то v3, v± равны нулю и общее решение в обоих случаях будет:
Л = V11 (С1 C0S “#+ С3 sin “10 + ®12 (С2 C0S + С4 sin “гО- | /8 92ч
Уз = ^21 (С1 C0S + С8 Sin “10 + ®22 (С2 C0S W2Z + Sin <».£). /
Полагая с2 = с4 = 0 или с± — с3 = 0, получаем нормальные колебания, при которых координаты уг, у2 остаются пропорциональными элементам одного из двух модальных столбцов:
и всегда имеют поэтому в одном случае одинаковые, а в другом — различные знаки (фиг. 58).
Если при t = 0 координаты ух, у2 имеют начальные значения 3^(0), у2(0), а начальные скорости yt(0), у2(0) равны нулю, то, определяя постоянные cit имеем:
с = ^22^1 (0) — ^12^2 (0) с = — ^21У1 (0) + ^11 (0) /8 93ч
1 ^11^22 — ^12^21 ’ 2 ^11^22 — ^12^21 * V ’ /
массам начальные откло-
Фиг. 58. Связанные маятники. Второе нормальное колебание.
Отсюда следует, в частности, что нормальные колебания упруго связанных масс можно осуществить, сообщая нения одного и того же или разных знаков, пропорциональные элементам соответствующего модального столбца, и предоставляя их самим себе без начальных скоростей. В случае электрических контуров нужно надлежащим образом распорядиться начальными зарядами конденсаторов при нулевых начальных токах. Если мы имеем маятники с равными массами и длинами или электрические контуры с одинаковыми параметрами, так что .а)а = а)ь и 1а = 1Ъ = I или ka = kb = k, то элементы модальных столбцов и значения
координат при нормальных колебаниях одинаковы по абсолютной величине и лишь по знаку либо согласуются либо взаимно противоположны.
Если теперь начальные условия не соответствуют ни одному из нормальных колебаний, то имеют место биения, которые особенно резко выражены в случае близких собственных частот <о2, т. е. при малых | (оа — <о& | и Чтобы исследовать это явление,
29 Зак. 1474. Б. В. Булгаков
450 СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [гл. 8
напишем:
Л = ®Л
Q ( COS <°1~^<°2 t COS-----yi + rca. I _j_ sin
t sin
+ Сз ( sin ^21+^ t cos - V- cos ^4^
t cos
+ sinMpMsin
/
/cos
Z^l+^2 t + COS t Sin
yj = Aj cos ^1 + (°2 0^ (7=1, 2),
где
Aj cos Qj = (q cos —<°1g^~ °*2 t— cs sin —_|_
+(c-2 cos ~Ю12+ Ю2 <+c4 sin ~<O12+”2.,
(8.94)
исключая Q1t находим:
•F
(8.95)
л| = (fji)2 <ci+ф+W (C1+Ф+
+ 2^,2 KC1C2 + C3C1) COS ( — <»! + «2) * 4- (CA — C2CS) Sin ( — 0>1-|-<02) fl
(J =1,2). (8.96)
Величины Aj9 Qj переменны, но меняются медленно вследствие малости— а)1-[-а).2. Поэтому обе координаты yj совершают, согласно (94), почти гармонические колебания с амплитудами, которые медленно модулируют между некоторыми нижними и верхними пределами. Эти пределы соответствуют тем моментам /, когда
sin ( — <о1 -4- <о2) t — ± - С1<?4 _
/(^ + с2)(с| + ^
и равны I г/д и с? + 4 — ^*2 ' с 2 + |. Из этих выражений выясненного выше закона чередования знаков величин следует, что
т1 v* X
« Зй?
6.14] СОБСТВЕННЫЕ КОЛЕБАНИЯ КОНСЕРВАТИВНОЙ СИСТЕМЫ 451
когда одна из амплитуд Aj достигает максимума, то другая минимальна, и наоборот, так что мы имеем перемежающиеся колебания, сопровождающиеся обменом энергии между двумя частями системы.
Если начальные скорости равны нулю, то с3 = сА — 0 и пределы изменения амплитуд Aj будут | Пользуясь выражениями
(90) или (91) и (93) и предполагая у2(0) = б, находим:
^11^1 “F ^12С2 —Л (®)> ^21^1 Н” ^22^2-------0’
^11^1 ^12^2
^11^22 4~ ^12^21
^11^22 ~ ^12^21
У1 (0) =
( — Ш1 ~Ь ш&) ( — ШО + ш2) — У( — Ш1 + шр) (-+ ш2) (Q)
У(-^ + “й)(-‘“а + «>|)+/(-‘»! + ^(-‘“б + 0,2) 1
Vq1c1 ®22С2 =-----------— 2t^-------- V, (0) «
21 1 22 2 »11»22 —»1^21 ’ '
л (0).
Отсюда видно, что если мы желаем продемонстрировать, биения связанных маятников, отклоняя лишь один из них и предоставляя оба самим себе без начальных скоростей, то амплитуда второго
Фиг. 59. Биения настроенных связанных маятников.
будет модулировать между нулём и некоторым верхним пределом, между тем как для первого маятника, получившего начальное отклонение, нижний предел изменения амплитуды будет, вообще, отличен от нуля, а верхний предел равен абсолютной величине начального отклонения; таким образом, обмен энергией будет, вообще, неполным. Но если маятники настроены (/na = rnb, ha = h^t то нижний
29*
4Й2 СИСТЕМЫ С ПОСТОЯННЫМИ кбЭФФиЦйЕНТАМИ [гл. 8
предел модуляции амплитуды первого маятника будет также равен нулю, а верхний предел модуляции второго станет равным абсолютной величине начального отклонения первого; обмен энергией будет полным (фиг. 59).
§ 8.15. Различные виды связи двух электрических контуров. Для электрических контуров с индуктивной и ёмкостной связью, рассмотренных в начале § 13 (фиг. 55), мы имеем следующие выражения частот <оа, а)ь и коэффициентов связи через параметры контуров:
<8-97>
Для некоторых других систем связанных контуров, применяемых, например, в радиотехнике, получаются дифференциальные ура-
Фиг. 60. Электрические контуры с авто-' трансформаторной связью.
внения того же типа, что и для рассмотренной, и потому для их рас- | чёта нужно только получить формулы приведения, аналогичные напи- | санным.
В случае автотрансформаторной связи (фиг. 60), как верить, 1 1 4 (О _ = —г— - ---- ' ----- ,
V(La + Le)Ca VlLb + LJCt,
легко про- ; f
(8.99)
«
(8.100),
« 4 * 1.
г
* " V
1
§ 8.16]
КРИТЕРИИ РАУСА
453
В случае сложной ёмкостной связи (фиг. 61) мы имеем, обозначая через qa, Яс заряды трёх конденсаторов и применяя второй за-кон Кирхгофа к первому, второму контурам и к контуру связи:
А~Чс)-\-^Яа = О’ (Яъ + Яс) + ~Q~b Яь =
__Qa ЯЬ_]_Яс_ л С а Съ^Сс U’
или, исключая qG,
•• I 1 • Са Сс •• п
Яд Z (С -4- С ) + СЙ С -4- С О’ ьа\ьат^с) ьЬьатьс
Га с^+се + Lb (Сь + Се) ^ = °‘
Эти уравнения приводятся к (73), если положить:
1
VLa (Са + Сс)
________1
ь~ УLb (Сь + Се) ’
(8.101)
откуда
Ь —_____ _________ /— А
V<ca+c0)(cb + cc)’
(8.102)
Таким образом, коэффициент k выражается здесь не через ин-дуктивности, а через ёмкости. С помощью полученных формул можно
Фиг. 61. Электрические контуры со • сложной ёмкостной связью.
пользоваться графиком фиг. 57, а также полученными ранее результатами, относящимися к собственным .колебаниям.
В. УСТОЙЧИВОСТЬ И БЫСТРОТА ЗАТУХАНИЯ СОБСТВЕННЫХ КОЛЕБАНИЙ
§ 8.16. Критерии Рауса, основанные на свойствах квадратичных форм. Вернёмся к уравнениям (7.75) малых колебаний около состояния установившегося движения и предположим, что к, х' суть Два корня характеристического уравнения и и, и' — соответствующие
454 СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [гл» 8
им постоянные модальные Столбцы. Подставляя выражения ук = ике** в уравнения (7.75), получим:
2 [^fc*a + (^ + 0Jfc)x + (^fc + ^)] “fc = 0 (J= 1......Й). (8.103)
к
Отсюда, умножая на и суммируя по J, найдём:
А (и', a)x3-]-[(W(a', u)-\-Q(u', «)1 к-J- Н(и', а) = 0,
(8.104) где А (и', и) есть билинейная форма
А (и', 4) = ^^ A^u'jUj, (8.105)
J к
и аналогично для форм ЛГ(а', a), О (а', и),...; напоминаем, что матрицы A, N, Н симметричны, а матрицы G, J антисимметричны.
Пусть сначала х есть действительный корень. Тогда мы положим х — х', и = и' и заметим, что по свойству коэффициентов Gj7c, Jjk
О (и, u) = J(u, u) = Q, (8.106)
так что
Л (а, и)х24-ДГ(я, и) х 4- 77(и, и) = 0. (8.107)
При действительном корне х числа Uj также действительны, не все равны нулю, и мы приходим к следующим выводам, указанным Раусом.
1°. Для отрицательности действительных корней, если они существуют, достаточно, чтобы три квадратичные формы А (и, и), N(u, и), Н(и, и) были знакопостоянными одного знака, а Н(и, и), сверх того, знакоопределённой, т. е. не только знакопостоянной, но и неособой и, следовательно, не обращающейся в нуль при значениях Uj, не разных нулю одновременно.
Это следует из того, что если бы было х^>0, то при сделанных предположениях левая часть уравнения (107) не могла бы быть нулём.
Если допустить, что три квадратичные формы знакопостоянные одного знака, причём какая-нибудь одна из них заведомо неособая (в механической задаче такой всегда будет А (и, и)), то можно утверждать лишь, что действительные корни не могут быть положительными.
2°. Если А (и, и), Н(и, и) попрежнему знакопостоянные формы одного знака, но N(u, и) тождественно равна нулю, так что сопротивления нет, а Н(и, и), сверх того, неособая, то никаких действительных корней быть не может. Если известно только, что одна из двух форм неособая, то можно утверждать лишь, что не может быть никаких действительных корней, кроме нулевых.
3°. Если А (и, и), Н(и, и) суть знакопостоянные формы одного знака, a N(u, и) — знакопостоянная форма противоположного знака, причём Н(и, и) — неособая, то действительные корни, если они существуют, обязательно положительны. Если же из
§ 8.16]
КРИТЕРИИ РАУСА
455
вестно лишь, что одна из трёх форм неособая, то можно утверждать, что действительные корни могут быть только либо положительные, либо нулевые.
Заметим, что эти теоремы, относящиеся к действительным корням, совершенно не связаны со свойствами коэффициентов Gjk, Jjk.
Пусть теперь х есть комплексный корень, а х'— сопряжённый
С НИМ • __ । • f . /л . ло\
X==7|-f-ZO), Х=7]------Z<o, (8.108)
причём о)=#0. Модальные столбцы и, и' также будут комплексными сопряжёнными:
ui = аз + u'i = — ify- (8 •1 °9)
Уравнение (104) получает вид
Л (я', и) (т| &»)2 + \N(u', и)-\-О{иг, ii)\ (т| -f- Z<*>) +
-\-H(uf, u)^-J(u', w) = 0; (8.110) при этом
Л (й , U) = 2 2 Ajk (aJ (afc Ц- tfk) = j k
= 2 2 Ajk (aj4 + РД) +1S 2 Ajk (afa - 0,afc). (8.111)
3 fc j k
Если же принять во внимание симметрию коэффициентов Ajk, то
А(и', и) = А(а, а)~|-Л(р, р) (8.112)
и аналогично для N(u', и) и Н(и', и). Но
G(u', u) = 2iG(a, р) (8.113)
и аналогично для J(u', и). Подставляя эти выражения в (ПО) и отделяя там действительную и мнимую части, найдём:
И (а, а) + Д(р, PW — «>2)+[ЛГ(«, а)+ЛГ(р, ?)И~ — 2О(а, р)а> + Я(а> а) + Я(р, р) = 0,
2 [Я (а, а)-)-Д(р, 0)]-ф» + [ЛГ(<х, «) + ^(Р> ?)]» + + 20 (a, p)7i + 2J(a, 0) = О,
1(8.114)
откуда, исключая G(a, Р),
[Л (а, а) + Л(р, p)]7i(7i2 + <o2) + [N(a, а)-}-ЛГ(р, pW + <”2) +
+ [Я(а, а)4-Я(р, Р)]71 = —2Да, р) ш. (8.115)
Из последнего соотношения вытекают дальнейшие теоремы Рауса.
4°. Для отрицательности действительных частей комплексных корней, если они существуют, достаточно, чтобы А(и, и), N(u, и), Н(и, и) были знакопостоянными квадратичными формами одного знака, N(u, и) была, сверх того, неособой, а форма J(u', и) тождественно равна нулю\ форма G(u', и) может быть
456
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
[гл. 8
какая угодно» Если известно только, что какая-нибудь одна из трёх форм А (и, и), N(u, и), Н(и, и) неособая, то можно утверждать лишь, что действительные части комплексных корней не могут быть положительными.
5°. Если А(и, и), Н(и, и) суть опять знакопостоянные формы одного знака, причём по крайней мере одна из них — неособая, но N(u, и) тождественно равна нулю, так же как и J(u', и), а О (и', и) какая угодно, то действительные части yj должны быть равны нулю; иными словами, комплексные корни могут быть только чисто мнимыми.
По теореме 2° в этом случае действительные корни могут быть только нулевыми, а если неособой формой является именно Н(и, и), то и нулевых корней быть не может.
Это предложение может рассматриваться как обобщение теоремы Сильвестера, изложенной ниже (§ 9.4).
Пусть теперь не только форма J(u', и), но и G(u', и) тождественно равны нулю; соотношение (114) даёт, по сокращении на о>, формулу
2[А(а, а) + Л(Р, Р)И + ЛГ(а, а) + ЛГ(р, р) = 0, (8.116)
из которой вытекает следующая теорема.
6°. Для отрицательности действительных частей комплексных корней достаточно, чтобы А (и, и), N(u, и) были знакопостоянными формами одного знака, N(u, и), сверх того, знакоопределённой, а О(и', и) и J(u', и) тождественно равны нулю; свойства формы Н(и, и) при этомуже не имеют значения. Если известно только, что одна из форм А (и, и), N(u, и) неособая, то можно утверждать лишь, что действительная часть не можещ быть положительной. Если же А (и, и) есть знакоопределённая форма, a N(u, и), О (и7, и), J(u', и) тождественно равны нулю, то комплексные корни могут быть только чисто мнимыми.
Сохраняя условия О (и', u) = J(u', и) = Ъ и исключая из (8.115) сумму N(a, я)-|-ЛГ(р, р) с помощью (116), найдем:
[Л(а, а) + Л(р, рЭК^ + шЗ)— [Я(а, а) + Я(р, р)] = О, откуда вытекает следующее предложение.
7°. Если А(и, и), Н(и, и) суть знакопостоянные формы противоположных знаков, причём по крайней мере одна из них знакоопределённая, а О(и', и), J(u', и) тождественно равны нулю, то комплексных корней быть не может; свойства формы N(u, и) при этом не имеют значения.
Изложенные теоремы дают достаточные условия, которые позволяют в некоторых случаях вывести заключение о природе корней характеристического уравнения и о линейной устойчивости или неустойчивости данного движения. Например, если А(и, и), N(u, и), Н(и, и) суть знакопостоянные формы одного знака, причём N(u, и),
§ 8.18] АСИМПТОТИЧЕСКАЯ УСТОЙЧИВОСТЬ ДАННОГО ДВИЖЕНИЯ
457
/у(и, и) знакоопределённые, G(a', и) какая угодно, а У(и', и) тождественно равна нулю, то, комбинируя теоремы 1°, 4°, мы заключаем, что данное движение асимптотически устойчиво.
Если ни один из критериев не может быть применён, то остаётся лишь обратиться к общим неравенствам Рауса-Гурвитца, приведённым ниже.
§ 8.17. Линейная устойчивость. Случай любых элементарных делителей. Линейная устойчивость данного движения, описываемого порождающим решением, имеет место, когда интегралы линейных уравнений (уравнений в вариациях) выражаются суммами членов вида Се™, где С суть постоянные, а комплексные числа X имеют отрицательные или нулевые действительные части.
Как показано выше, если в числе элементарных делителей, соответствующих некоторым кратным корням характеристического уравнения, имеются нелинейные, то в общем решении появятся члены вида С1?е \ где р > 0.
Поэтому критерий устойчивости для общего случая будет: действительные части всех простых корней характеристического уравнения и тех кратных, элементарные делители которых линейны, должны быть отрицательными или нулями, а действительные части остальных кратных корней — строго отрицательными .
§ 8.18. Асимптотическая устойчивость данного движения. Если действительные части всех вообще корней строго отрицательны, то линейная устойчивость будет асимптотической, так как в этом случае при t -э- оо значения всех неизвестных и их производных стремятся к нулю. Э. Раус [0-14] и А. Гурвитц [81°] дали критерии, которые позволяют, не решая характеристического уравнения, установить, имеет ли место этот случай. Если это уравнение имеет вид
*0Х* + М8"1 + • • • + ks-^ + *s = 0, (8.117)
то, по Гурвитцу, следует составить s определителей
(8.118)
0 0 0 ... k8
о
Если fe0 > о, то для того, чтобы все действительные корни и действительные части комплексных корней были отрицательны, необходимо и достаточно, чтобы все эти определители были положительны.
458 СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [гл. 8
Заметим, что, принимая во внимание предпоследнее условие As_* > О, можно _ заменить последнее условие более простым неравенством k8 > 0.
§ 8.19. Область устойчивости в пространстве коэффициентов. Если трактовать действительные коэффициенты klf ..., k8 при заданном k$ > 0 как декартовы координаты некоторой («изображающей») точки ^-мерного пространства В, то условия Рауса-Гурвитца (118) определяют некоторую открытую область С этого пространства, которую можно назвать областью устойчивости *). В каждой точке граничной поверхности Тпо меньшей мере одно из неравенств Д^> 0 (Z= 1, ., s) должно обратиться в равенство. С другой стороны , в этой точке по меньшей мере один действительный корень или действительная часть одного из комплексных корней должна обращаться в нуль. Для того чтобы имело место первое, необходимо, чтобы в данной части 1\ границы было k8 — 0. Поэтому, если feg>0, то первая возможность исключается и мы должны обязательно иметь пару чисто мнимых корней. Иными словами, в каждой точке той части Т% границы, где k8 > 0, система дифференциальных уравнений обязательно имеет по меньшей мере одно периодическое решение. Для того чтобы дать уравнение этой части границы, обратимся к результатам § 2.32.
Согласно формулам (2.160), (2.167), необходимым условием наличия у характеристического уравнения (117) пары чисто мнимых корней zt Zo> является равенство нулю предпоследнего определителя Гурвитца Д8_!.
Из соотношения (2.167) следует, однако, что в случае, когда Д8-1 = 0, характеристическое уравнение имеет по крайней мере либо два чисто мнимых корня z±zfco, либо два действительных корня zta, либо две пары комплексных сопряжённых,корней: a ±Zo> и —aztZo).
Вследствие этого не вся гиперповерхность Д8_^ = 0 является частью Т2 границы области устойчивости. Эта часть Т2 характеризуется тем, что на ней должны соблюдаться 5 — 1 неравенств
Ai 0, А2 0, ..., Д8_2 > 0, k8 > 0.
Если изображающая точка пересекает гиперповерхность As_x = 0 в случае корней ztZoo, то это означает, что действительная часть некоторой пары комплексных корней изменила знак или что общее число пар комплексных корней с положительными действительными частями изменилось на' единицу.
Аналогичным образом не вся гиперплоскость k8 = 0 составляет часть 7^ границы области устойчивости. Эта часть 1\ характеризуется 5 — 1 неравенствами At > 0, А2 > 0, ..., ^8_± > 0. Вообще же при пересечении изображающей точкой гиперплоскости = 0
*) На важность такой точки зрения для прикладных задач обратил внимание акад. А. А. Андронов.
8.19] ОБЛАСТЬ УСТОЙЧИВОСТИ В ПРОСТРАНСТВЕ КОЭФФИЦИЕНТОВ 459
число действительных положительных корней меняется по крайней
мере на единицу.
Если отбросить часть Ть поверхности = 0, соответствующую корню или корням zt(aztZco), то части Т2, Т4 этой поверхности вместе с частями Т19 Т3 гиперплоскости k8 — 0 делят всё пространство параметров на области, в какой-нибудь из которых g (г', /') имеется одинаковое число г' действительных положительных корней и одинаковое число /' пар комплексных с положительными действительными частями. Область устойчивости С есть не что иное, как область §(0, 0).
Выход из области устойчивости всегда связан с нарушением
одного из двух последних условий Рауса-
Гурвитца.
Область устойчивости С составляет лишь часть более широкой области Г, определяемой только двумя неравенствами > 0. Однако переход из С в остальную часть области Г по внутренним точкам невозможен, так что С представляет всегда обособленный «отсек» в Г.
Это видно на примерах ниже.
1°. Пусть $ = 2. Условия Рауса-Гур-
| | Затухающие колебания
^/^Апериодическое движение
витца суть
i > 0»
— ^1^2 >
или
> 0,
&.2
0.
Фиг, 62. Область устойчивости при <9 = 2.
0
Этими неравенствами определяется первый квадрант плоскости причём при пересечении оси k.2 должны получаться чисто мнимые корни;
они равны ±1 у На оси мы имеем корни 0,— Парабола
fei — 4^0^
отделяет области действительных и комплексных корней (фиг. 62). 2°. При $ = 3 имеем следующие условия Рауса-Гурвитца:
0
kQ
— k^k,2 0,
0
k2
0*
Заменяя последнее неравенство через k3 > 0, имеем: kt > 0, k3 > 0, k±k2 — kQk3 > 0;
460
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
[гл. 8
из этих неравенств получаем ещё условие 62>0.
Условиями k± > 0, k2 >0, k3 > 0 определяется первый октант трёхмерного пространства. Условием ktk2 > из этого октанта выделяется область С, ограниченная сверху седлообразной поверхностью
Фиг. 63. Область устойчивости при «у = 3.
второго порядка
Так как в пересечении поверхности плоскостями, параллельными координатным плоскостям k± = 0, fe2 = 0, получаются прямолинейные образующие, то эта поверхность есть гиперболический параболоид, для которого эти две плоскости служат направляющими. Снизу область устойчивости ограничена координатной плоскостью k,3 = 0 (фиг. 63).
На части границы Т, принадлежащей поверхности гиперболического параболоида, мы имеем, по предыдущему, пару чисто мнимых и, конечно, один действитель-
ный отрицательный корень, которые нетрудно найти. Заменим для этого в характеристическом уравнении k3 через и напишем:
V»+М’+м + = Vs (*+>М‘ +х)=
=Мх+-й>+~£)-
Отсюда видно, что три корня уравнения суть:
На плоской части границы Т мы имеем корни
Построим ещё дискриминантную поверхность, отделяющую область действительных /корней. Её уравнение может быть получено непосредственным приравниванием нулю дискриминанта*):
kfkl — X-4О| 4.1800 — 27O| = 0. (8.119)
Л а X О X. V « 1 U X & о Uo '
*) См., например, Э. Ч е з а р о, Элементарный учебник алгебраического анализа и исчисления бесконечно малых, ОНТИ, 1936, стр. 435.
§ 8.19] ОБЛАСТЬ УСТОЙЧИВОСТИ В ПРОСТРАНСТВЕ КОЭФФИЦИЕНТОВ 461
Так как это уравнение 4-й степени, то для облегчения исследования полезно также получить его в параметрической форме.
Для этого найдём сначала геометрическое место точек пространства параметров fe2, fe3, где характеристическое уравнение имеет данную пару комплексных сопряжённых корней — 8 + и действительный отрицательный корень —(& + н) (предполагается 8 > О, > — 8). По формулам Виета,
^ = (38 + ^0,
= [82 + 0)2 + 28 (8 + И)] ft0, fe3 = (82 + o)2)(8 + |x)fe0
или
kx = (38 + И) ft0, й2 = (382 + о)2 + 28и)й0, fe3 = (82 + 0)2) (8 + и) fe0, откуда найдём:
—38Л0 ^2 — (332 + <о2)Л0 k3 — 8 (о2-|-0)2) л0 .
1 “ 28 “ 32 4-0)2 •
Эти уравнения определяют прямую, которая и будет искомым геометрическим местом.
Если, в частности, о> = 0, то пара комплексных сопряжённых корней обращается в двойной действительный корень. Уравнения . прямой могут быть записаны в виде
^ = (38 + |1)ЙО, k2 = (38228И)k0, 63 = 83(8 + |*)Л0, (8.121)
или
— 38Л0 ^2 — 382А?о Лз — 83#о /о i
1 = 28 — 82 (8.122)
Таким образом, геометрическим местом точек, в которых характеристическое уравнение имеет данный двойной корень —8, является прямая п с направляющими косинусами, пропорциональными 1, 28, 82, проходящая через точку L с координатами
fe1==38fe0, fe2 = 382fe0, feg = 8%0. (8.123)
При изменении 8 точка L описывает кривую Z, а прямая п — линейчатую поверхность, которая и будет геометрическим местом точек, в которых - характеристическое уравнение имеет какой-либо двойной корень, т. е. дискриминантной поверхностью.
Уравнения (121) являются параметрическими уравнениями дискриминантной поверхности, а 8 и р служат её гауссовыми координатами. На кривой Z имеем р = 0, а характеристическое уравнение принимает вид 6о(л-|-8)3 = 0 и имеет тройной корень .— 8.
Часть дискриминантной поверхности, на которой 8 > 0, р>— 8, лежит внутри области устойчивости С и вместе с частью координат-
462 системы с постоянными коэффициентами [гл. 6
ной плоскости = 0 выделяет из неё подобласть Е апериодического затухания парциальных движений (фиг. 64).
Фиг. 64. Область устойчивости и подобласть апериодического затухания колебаний.
Неустойчивость
пзгзз Апериодическое движение
| \3атухающие колебания
Фиг. 65. Сечение плоскостью
= const.
Неустойчивость
Апериодическое движение | | Затухающие колебания
82Й8
Неустойчивость
1^51 Апериодическое движение | | Затухающие колебания
Фиг. 67. Сечение плоскостью Л3 = const.
Фиг. 66. Сечение плоскостью • &2 = COBS! .
Чтобы составить лучшее представление о форме рассматриваемых поверхностей, мы дадим их сечения плоскостями, параллельными координатным (фиг. 65—67). При этом область устойчивости даёт
§ 8.20]
ОБЛАСТИ УСТОЙЧИВОСТИ В ПОДПРОСТРАНСТВАХ
463
в сечениях плоские области С19 С.2, С3, ограниченные кривыми Т*, 7^*, Т***, а область Е— плоские области Et, Е.„ Е$> ограниченные кривыми У*, У**, У***. Последняя из трёх диаграмм впервые получена И. А Вышнеградским р-2].
Приведём уравнения кривых Т*, Т** Г*** и V*, V*** для
этих случаев.
1°. fe1==€onst>0 (фиг. 65).
^1^2 Мз= 0, k^ = 0, (71*)
*2 = 8(2^ —38й0), |
= 82 _ 28fe0), I (V*)
fe3 = 0. ]
2°. fe,2 = const > 0 (фиг. 66).
fexfe2 —feofe3 = O, fe3 = 0, (Т**)
_ л2 + З^о 23 ’
и ___£ ^2
«з —0 2 »
£3 = 0.
3°. &3 = const > 0 (фиг. 67).
^1^2 = ^0^3’
г ^3 4” 23ЭДо §2 >
* 2fe3 -|- B3feo
«2— & •
§ 8.20. Области устойчивости в подпространствах. Вместо того чтобы строить область устойчивости в s-мерном пространстве коэффициентов, можно делать это в /n-мерном пространстве
= •••> = (8.124)
получаемом при фиксированных значениях q, ..., с8_т, каких-либо — т координат fey ...» мы назовём его подпространством В'.
Можно также взять более общее подпространство В', определённое — т линейными независимыми уравнениями
5fe$jfej = *< (Z=l, ...,s— /п). (8.125)
Z»i
Например, понижение числа измерений до т 3 может быть важно при исследовании конкретных задач, так как при числе измерений, большем трёх, мы имеем лишь геометрический язык, между, тем как наглядное представление, как метод исследования, пусть только эвристический, несомненно отказывает, хотя мы и склонны иногда
464 СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [гл. 8
об этом забывать.. Вместо линейного w-мерного многообразия можно пользоваться и нелинейным, на чём мы, однако, сейчас не будем настаивать.
Областью устойчивости С в подпространстве Вг будет сечение первоначальной области устойчивости С с подпространством. Границей области будет (т—1)-мёрная поверхность Т', определяемая уравнениями Д8-1 = 0 и fe8 = 0 и 5 — т уравнениями (124) или (125) вместе с s—1 неравенствами. Пользуясь s — т уравнениями подпространства, можно выразить 5 — т координат через т остальных независимых координат или других линейно связанных с ними параметров |лх, ..., так что
(»=1......«)• (8.126) •
Такие формулы могут получаться непосредственно как выражения коэффициентов уравнения через какие-либо параметры р*, ..., - колебательной системы. Эти параметры являются гауссовыми координатами подпространства. Если выразить ki через pj в уравнениях Д8_1 = 0 и fe8 = 0 и неравенствах, то мы получим уравнения {т—1)-мерной поверхности, части которой T'v Т'2 составляют границу области устойчивости в подпространстве. Кроме того, эти поверхности содержат части Т', Т', отделить которые можно только с помощью неравенств. Поверхности T'-j-T' и Т'Т'делят подпространство на области (г', г") с одинаковым числом г' положительных действительных корней и одинаковым числом г" пар комплексных к корней с положительными действительными частями.
Поверхность Т' соответствует парам действительных корней z±za и корням ±(а±гш).
§ 8.21. Системы с ненадёжными параметрами. Иногда приходится иметь дело с системами, из ш учитываемых параметров которых jj^, ..., первые п более или менее постоянны или допускают точную регулировку, между тем как остальные ш — п ненадёжны, так как их значения могут сильно меняться или не точно известны. В этих случаях естественно пытаться искать условия, которым должны удовлетворять основные параметры, чтобы обеспечить устойчивость при любых значениях ненадёжных параметров или же при значениях последних, принадлежащих некоторой области.
Все коэффициенты характеристического уравнения и определителей Гурвитца предположим выраженными через ш величин р.1, ..., При этом основные параметры р.х, ..., будем трактовать как декартовы координаты в n-мерной плоскости В", между тем как Hn+i> •••» ISn рассматриваются как постоянные. Каждой системе значений этих последних соответствует некоторая область устойчивости Cff в плоскости В". Общая часть (на языке теории множеств — пересечение) областей С" при всевозможных v значениях ненадёжных
§ 8.22] БЫСТРОТА ЗАТУХАНИЯ. КРИТЕРИЙ ЦЫПКИНА-БРОМБЕРГА 465
параметров в их области G есть область надёжной или гарантированной устойчивости С*. Совокупность точек, ни при каких значениях ненадёжных параметров в О не попадающих в одну из областей С" (пересечение областей В"— С!\ составляет область заведомой или гарантированной неустойчивости С\ Наконец, точки подпространства В", не принадлежащие ни к С"+ ни к С”_, образуют область ненадёжной устойчивости С" _ ( = В — С* — С")\ при некоторых значениях параметров р.№+1, ..., этим точкам соответствуют устойчивые колебания, при других — неустойчивые. В частных случаях любая из трёх областей может не существовать (быть пустой).
§ 8.22. Быстрота затухания. Критерий Цыпкина-Бромберга. Проверка устойчивости представляет первый необходимый шаг при анализе колебательного процесса в любой физической или технической задаче.
Однако наличие асимптотической устойчивости не является ещё достаточной характеристикой системы, так как действительный корень или действительная часть комплексных корней характеристического уравнения могут быть отрицательны, но очень малы и тогда колебания затухают столь медленно, что практически не отличаются от незатухающих.
Очень простая оценка предложена Я. 3. Цыпкиным и П. В. Бромбергом (§ 4.10). По их определению за коэффициент устойчивости 8, т. е. меру затухания, принимается меньшая по модулю действительная часть всех корней характеристического уравнения (117):
Д(Х) = + ••• +fe8 = 0.
Для определения коэффициента устойчивости преобразуем характеристическое уравнение посредством подстановки
Х= — 8 + х, (8.127)
где 8 > 0, к виду
Д( —8 + х)==/Сох« + Я1х«-1+ ... +^_хх + ^ = 0. (8.128)
Здесь
7^(~8) = 7^-!-аГд('_Л< —8> <-/ = 0’ 1...........(8.129)
и, в частности, всегда KQ = kQ.
Корни уравнения (128) смещены относительно корней характеристического уравнения (117) влево от мнимой оси на величину 8. Тогда, если при 8 = 80 и й0 > 0 коэффициенты /С- удовлетворяют условиям
К» ...)>0; Д2(^, К2, ...)>0; ...1 „
(o.lou)
К» Лз>0,
где ДД/Q, /<2, ...) суть определители Гурвитца, то все действитель-НЫе корни и действительные части всех комплексных корней харак-
I
30 Зак. 1474 б. в, Булгаков
466
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФЙЦИЕЙТАМЙ
|тл. 8
теристического уравнения (117) будут по абсолютной величине больше, чем 80.
Определители К2, •••) и /^являются функциями коэффициентов fe0, k19 ..., k8 и величины 8, или функциями т незави-' симых параметров |х2, ..., рт и величины 8, если сами коэффициенты k0> klf .ks зависят от этих параметров.
В пространстве коэффициентов k±i k.2, ..., ks при заданном Ао > 0 (или в пространстве параметров |лг, р2, ..., p,w) условия (130) определяют открытую область во всех точках которой, очевидно, 8>8О. Границей области С$(Сб) при фиксированном 8 является гиперповерхность Те (7в), определяемая условиями
K&v К» ...)>0; Д2(^, ...)>0; ...;)
Д8_1(Хр ...)>0; /С, = 0; J ( }
ДД/Сх, К2, ...)>0; Д2(^, К» ...)>0; ...;)
МК1Л,...)>0; /Q>0; Д8_!(^, К2, ...) = 0.р * }
Эту поверхность можно назвать поверхностью равной устойчивости, так как во всех её точках коэффициент устойчивости равен 8.
При этом в точках поверхности Cs(Cg), где выполняются условия (131), характеристическое уравнение (117) имеет действитель-ный корень, равный — 8; в точках поверхности С§(С§), где выполняются | условия (132), характеристическое уравнение (117) имеет пару ком- | плексных сопряжённых корней, у которых действительная часть | равна —8. |
При 8 = 0 поверхность равной устойчивости обращается в гра-ницу области устойчивости. ]
С возрастанием 8 поверхность равной устойчивости деформируется | и при некотором значении 8 = 8тах вырождается в многообразие мень-1 шего числа измерений, причём при 8 > 8тах условия (130) невыпол-1 нимы. Таким образом, это значение 8 = 8тах является максимальным! значением коэффициента устойчивости, который можно получить, | выбирая коэффициенты klt k.2, ..., k8, при заданном feo>0 (или| независимые параметры |л2, ..., |iw) внутри области устойчи-1 вости С (или, соответственно, С'). 1
Переходим к частным примерам. Я
Случай 5 = 2 был рассмотрен в § 4.10. При этом 1
д (х) = ж
и, согласно (129), 1
/<о ( 8) = -gi • = kQ, j
/C1(_g) = _2ft08 + *1, f
/С2(-8) = й082-й18 + &2. J
§ 8.22] Быстрота затуханйя. Критерий цыпкИна-ёромберБа 467
При s = 3 имеем:
Д (X) = *0Л8 + М2 + V + *з и, согласно (129),
Ло(-«)=43!Й0 = Й0, ^i(-S)=4( — 6М + 2Й1), К2 ( — 8) = 3*082 — 2*,8+k.2, *з (— 8) = — *088+М2 — М + *з-
Таким образом, в рассматриваемом примере
*о ~ &о»
Ki — — 3МЧ“А« (8.133)
/С2 = 3*082 — 2*t8 4- *2>
^ = —й088 + М2 —М + *з- .
Из (130) для данного случая получаем следующие неравенства:
/Q > 0; К±К2 — К(Л3>0; К3>0. . (8.134)
Подставляя выражения (133) во второе из неравенств (134), находим:
— 28*2 + kfa + 88a*0*i — 28*0*2 — 883jfeo — > 0.
Окончательно неравенства (134) представляются в виде — 38fe0 > 0,
— 28&14- ktk2 4- 882*o*i — 28*0*2 — *о*3—88®*о > 0, 82*. — 8*„ 4- *3 — 88*О > 0. X a I U V
В пространстве эти неравенства определяют область С§,
лежащую по одну сторону плоскости — 38fe0 = 0 ниже поверхности второго порядка
28*1 — ^1*2 — 882*o*i 4- 28*0*2 + Мз + 8sSfeo = 0 и выше плоскости
82fex — 8Aj2 + fe3 — 8s&0 = 0. (8.135)
Представляя уравнение поверхности в форме
28 (*? — 48*o*i 4- 482*?) — *2 (*i — 28*О) 4* *0*3 = 0 или
(*! — 28*О) ]28 (*i — 28*О) — *2] 4~ *0*3 = 0. (8.136)
30*
468 СйстеМЫ с йобтояйиымй коэффициентами (гл. 8
можем рассматривать его как результат перемножения уравнений
° (^i — 28fe0) = kQ, 23 (kx — 28fe0) — fe2 = — ой3
или
x (ki — 28fe0) — k.3, 28 (k± — 28fe0) — k,2 = — xk0.
Эти две пары уравнений определяют два семейства прямолинейных образующих, параллельных плоскостям k± = 0 и 28 — 28fe0) —
— fe2 = 0 соответственно. Поэтому поверхность (136) является гиперболическим параболоидом. На параболоиде характеристическое уравнение имеет пару комплексных корней с действительной частью — 8, на плоскости (135) — действительный корень —8.
Найдём линию сечения параболоида и плоскости. Для этого умножим уравнение плоскости (135) на &0 и вычтем почленно из уравнения параболоида (136). Будем иметь:
(fei — 38£О) [8 (2/гх — 38fe0) — k.2] — 0. (8.137)
Если приравнять нулю первый множитель (137) и подставить получающееся выражение для в уравнение плоскости (135), то получим:
k± = 38й0, 8&2 — k.3 = 23ай0.
Эти уравнения определяют некоторую прямую т с направляющими косинусами, пропорциональными неотрицательным величинам 0, 1, 8.
Если же приравнять нулю второй множитель в (137)
28 Ац — — 382fe0 = О Л a U
и использовать ещё раз уравнение плоскости (135), то получится:
— 38ЛО ^2 — Зо2Л0 А?з — 83£О 1 = 28 = 82 ’
т. е. уравнения прямой п с направляющими косинусами, пропорциональными положительным величинам 1, 28, 82. Эту прямую мы уже рассматривали в § 22 как прямолинейную образующую дискриминантной поверхности.
Совокупность прямых т, п образует линию сечения параболоида и плоскости. Обе прямые являются прямолинейными образующими параболоида, принадлежащими двум различным семействам. Они пересекаются в точке L с координатами
fe1 = 38fe0, fe2 = 382fe0, fe3 = 8sfe0; (8.138) с
эта точка представляет остриё, которым заканчивается область Сз (фиг. 68). В этой точке, как мы видели, характеристическое уравнение имеет тройной корень —8.
При изменении 8 остриё L описывает кривую /, определяемую параметрическими уравнениями (138); она проходит через начало координат. Так как направляющие косинусы её касательной пропор
§ 8.22] БЫСТРОТА ЗАТУХАНИЯ. КРИТЕРИЙ ЦЫПКИНА-БРОМБЕРГА 469
циональны величинам 1, 26, 82, то этой касательной является образующая п. В начале координат касательная совпадает с осью k±.
Рассмотрим теперь некоторые различные постановки задачи о подборе наивыгоднейших значений параметров k±i k.2, k3 по коэффициенту устойчивости 8.
а) Предположим, что мы хотим найти навыгоднейшие значения kif ko, k$ в области В[ допустимых значений, ограниченной плоско-
Фиг. 68. Область устойчивости и поверхности равной устойчивости.
стями kL = k± = k*. Кривая I (138) пересечёт вторую плоскость при 8 = 8Р где 8Х определяется из соотношения
ki = 361й0. (8.139)
Это значение коэффициента устойчивости является наиболь-шим возможным в области Оно соответствует поверхности 7§, имеющей остриё на плоскости k±^kit и достигается как в точке (381&О» 381й0, 8i&0), так и во всех точках той части образующей поверхности
k. = 38,^, SA, — k* = 28i&0, A A U л. 4 О U
которая направлена в сторону возрастания fe2. Если, однако, мы хотим при заданном k± иметь максимальное 8 при минимальных k.2 и то нужно брать именно точку (381Л?О, 38ife0, 8?fe0), координаты которой и представляют наивыгоднейшие значения параметров k19 k.2t ke>. При этих значениях характеристическое уравнение имеет тройной корень —6Х.
470
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
[гл. 8
Аналогичным образом, ограничивая допустимые значения параметров klf fe2, fe3 областью В2, где 0^k.2^k2i и определяя число 8.2 с помощью соотношения
*2 = 38^0, (8.140)
мы получим наибольший возможный коэффициент устойчивости 82 в точке (382й0, 38|fe0, 8|fe0), где кривая (138) пересекает плоскость
&2 —
В области В3, где .0^й3<^йз, наибольшим возможным коэффициентом устойчивости будет число 83, определяемое из соотношения
= (8.141)
причём оно достигается в точке (3S3fe0, 33|fe0, §з&0).
б) Если область В допустимых значений ограничена одновременно неравенствами
то нужно определить три числа 8Х, 82, 83 с помощью соотношений (139), (140), (141). Наименьшее из них 8* будет наибольшим возможным коэффициентом устойчивости, достигаемым в точке (38Д), 38*fe0, 8|fe0), лежащей на плоскости = Характеристическое уравнение имеет в этой точке тройной корень —8^.
в) Предположим теперь, что фиксировано и подлежат выбору только k,2 и fe3. Иными словами, рассмотрим сечение пространства параметров плоскостью k± = const.
Гиперболический параболоид (136) и плоскость (135) пересекаются с плоскостью k± = const по прямым 4, 4’ определяемым уравнениями
(ftt — 28fe0) fe2 — fe0fe3 = 28 (kx — 28fe0)2, 8fe2 — fe3 = 82 (k± — 8fe0).
Эти прямые ограничивают область Сц плоскости k± == const, где действительные части корней по абсолютной величине больше 8. Прямые пересекаются в точке с координатами
й2 = 8 (2йх — 38£О), fe3 = 82 (fex — 28й0), (8.142)
которая представляет след прямой п на плоскости kt = const.
Угловые коэффициенты прямых /2 суть:
k-t —— 2ВА?п л
C1 = -L^-0., с2 = 8, причём в силу первого из условий (134) имеют место неравенства k± — 38fe0 > 0,
0 < ^1*
& 8.22] БЫСТРОТА ЗАТУХАНИЯ. КРИТЕРИЙ ЦЫПКИНА-БРОМБЕРГА 471
Проводя в плоскости сечения оси, параллельные координатным осям (и расположенные в координатных плоскостях fexfe2 и
имеем для точек пересечения прямых /х, /2 с осью fe2:
№ = 28 (*! — 28й0), = 8 (k± — 8fe0).
Из k± — 38fe0 > 0 вытекает:
2fex — 48&O > — 8A?0 или
0 < A22) <
Взаимное расположение прямых Zt, Z2 показано на фиг. 69. При изменении 8 их точка пересечения описывает кривую, определяющуюся
параметрическими уравнениями (142) и представляющую линию сечения дискриминантной поверхности с плоскостью k± = const. Дифференцируя (142) по 8, имеем:
^ = 2(^-38fe0),
= 28 - 38АО),
откуда dk^dk2 = 8, так что прямая Z2 касается кривой.
Обе производные положительны, пока 38fe0 < и обращаются в нуль, когда коэффициент устойчивости 8 достигает значения 8Х), определяемого уравнением
k± = 38xfe0.
Неустойчивость
Апериодическое движение | | Затухающие колебании
Фиг. 69. Сечение плоскостью ^1= const.
Соответствующая точка М имеет
следующие координаты:
* = 38^О = —, k, = 8^0 = -J-.
2 °' 3k0 3 0 27^q
В точке М мы имеем с± = с2 и область С15 стягивается в полупрямую. г
Две ветви ОМ, MN кривой (142), соответствующие интервалам (°, kJZkJ, (kJSk0, ^х/2^0) параметра 8, ограничивают область апериодического затухания (фиг. 69), где все корни характеристического Уравнения действительны и отрицательны.
Наибольшее возможное значение коэффициента устойчивости 8 в плоскости k± = const равно 8Х и достигается в точке М, а также во всех точках идущей из неё вправо полупрямой с угловым коэф
472 СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ . [гл. 8
фициентом 8Х. Координаты точки М дают также наивыгоднейшие значения А2 и А3 в том случае, когда область их допустимых значений В ограничена прямоугольником 5, образованным координатными осями и прямыми А2 = А*, А3 = Аз, если только точка М лежит в этой области, т. е. если 8Х меньше чисел 82, 83, определяемых соотношениями
== 382&Q, Аз = 83А0.
Если же 8Х превышает по меньшей мере одно из чисел 82, 83, то нужно найти точку пересечения кривой (142) с периметром прямоугольника; её координаты и будут представлять наивыгоднейшие значения А2, А3, а соответствующее значение 8 будет наибольшим возможным коэффициентом устойчивости.
Может случиться также, что область В допустимых значений А2, А3 ограничена не прямоугольником, а каким-либо другим контуром 3, и тогда наивыгоднейшие значения будут соответствовать (§ 4.12) точке касания контура S и одной из линий равной устойчивости, состоящих из полупрямых Zx, /2, или же такой общей точке контура и линии равной устойчивости, которая служит угловой для одной из них, но не является их точкой пересечения.
г) Предположим теперь, что А2 фиксировано, т. е. рассмотрим сечение пространства kv k2, k3 плоскостью А2= const.
Параболоид (136) даёт в сечении параболу
28 (Ах — 28А0)2 — А2 (Ах — 28АО) = — А0А3, или
28 (k! 28feo 4I) — *о(*з
Вершина параболы расположена в точке с координатами
k2
= Й + 28ЙО’ *3 = Ж?
Парабола пересекает ось Ах при
й1 = 28£0, 28*0+§.
Плоскость (135) даёт в сечении прямую р
8^+А;3=8(£2+82й0) с угловым коэффициентом —8а, отсекающую на осях klt k3 отрезки -1(^ + 8^), 8 (k2 + 8ай0).
Область С25, где действительные части корней по абсолютной величине больше 8, представляет сегмент параболы, отсекаемый прямой р
§ 8.22] БЫСТРОТА ЗАТУХАНИЯ. КРИТЕРИЙ ЦЫПКИНА-БРОМБЕРГА
(фиг. 70). Парабола и щих следы прямых /п, точек суть:
473
прямая пересекаются в точках, представляю-п на плоскости k2 = const. Координаты этих
= 38АО,
fe3 = 5(fc2 — 28%)
и
, __ «2 ~Г
х“" 26 *
5» k‘2 — 62Z?q
3 = 8------9----
(8.143)
быть левее,
Первая точка должна лежала бы левее прямой k± = что противоречит усло-0. Разность абс-
так как
= 38£О, вию kx — 38fe0 цисс
н.
ляемом соотношением k.2 = 38Х-£ — и
При этом значении область С
I ipjri □Аиш □патиппн uvviaLiD ^*2^ стягивается в точку М с коорди-натами
= 3o2A?j = 3&0^2,
__ ^3 t _ 1 1 / ^2 3_о2ло — -у у .
иначе вся область С2Ъ
k% — 3o2Z?o
26
Фиг. 70.
Сечение плоскостью = const.
Она имеет две ветви,
Неустойчивость
Апериодическое движение
Правая точка пересечения паря-Г {Затухающие колебания болы и прямой описывает при изменении 8 кривую, определяемую параметрическими уравне-
ниями (143); эта кривая представляет линию сечения дискриминантной поверхности с плоскостью k2 = const.
уходящие в бесконечность при 8 = 0, оо. Так как
~ 38%),
= 4 (*2 - 382&о),
то точка М служит точкой возврата для кривой. Мы имеем dk.Jdk^ = 82, т. е. касательной к кривой служит прямая
474
СИСТЕМЫ с постоянными коэффициентами [гл. 8
д) Рассмотрим, наконец, сечение пространства параметров плоскостью fe3 = const. Параболоид (136) даёт в сечении гиперболу
(fex — 28£О) [— 28 — 28й0) + fe2] = fe0fc3,
асимптоты которой
_ 28 (kr — 28fc0) + k,2 = 0, kr — 28fe0 = 0
имеют угловые коэффициенты 28, оо. Координаты центра, определяемого пересечением асимптот, суть:
k± = 28fe0, fe2 = 0.
Плоскость (135) даёт в сечении прямую /, определяемую уравнением
82fex — 8fe2 = — fe3 + 8»fe0,
с угловым коэффициентом 8, отсекающую на осях отрезки ^3 — *3*0 ^3 —
противоположных знаков.
Гипербола и прямая I пересекаются в точках, представляющих следы прямых т, п на плоскости k3 — const; координаты этих точек:
= 38fc0> k.2 =
и
= *з+2^, = 2fe3 -НА _ (8.144)
Область Сз8, в которой действительные части корней по абсолютной величине больше 8, представляет сегмент, отсекаемый на верхней ветви гиперболы прямой Z. Первая из двух точек пересечения гиперболы и прямой должна быть левее второй, так как иначе вся область Сз8 лежала бы левее ординаты kx — 38fe0, что противоречит условию — 38feo>O.
Разность абсцисс
&з + 2о3Л0 за;. __^з —
оол0 — р
убывает с ростом 8 и обращается в нуль при значении 83, определяемом соотношением
= ^з&о-
При этом значении область С35 стягивается в точку М с координа-
тами
или
&х — 38<jZ?q,
°з^о 4”
k2 = 338fe0 == 3 /A&3,
§ 8.231
УСТОЙЧИВОСТЬ СЛЕДЯЩЕЙ СИСТЕМЫ
475
Правая точка пересечения гиперболы и прямой / описывает при изменении 8 кривую, определяемую параметрическими уравнениями (144);
эта кривая представляет линию сечения дискриминантной поверхности с плоскостью k3 — const. Она имеет две ветви, уходящие.в бесконечность ПрИ 8 = 0, оо. Так как
то точка М служит точкой возврата для кривой. Так как 6Zfe.2/d&1 = 6, то касательной к кривой служит прямая /, образующая хорду гиперболы. Расположение кривых показано на фиг. 71.
§ 8.23. Устойчивость следящей системы. Приведённые в § 8 уравнения движения (21) следящей системы при Т= U = 1 сек и / = 1 в случае, когда команда х и воз-
tWi HpcmoUVUSOCmA
Периодическое движение 1 I Затухающие колебания
Фиг. 71. Сечение плоскостью = const.
мущающая сила z тождественно равны нулю, можно представить в таком виде *):
(D2 + D + ^)o — |л=0, о = — (ZAD2 + М£>+1)<р — П|1, (VWD* + WD) р — о = 0.
(8.145)
а) При V = 0, т. е. при безанерционном сервомоторе, система дифференциальных уравнений (145) имеет следующее характеристическое уравнение:
Л* + (1 +
Ц^ = 0. (8.146)
Так как буквы х и z теперь свободны, то обозначим
__£2 п x~\+kn>
М + п
1 + kn ’
1 + kn W
и Уравнение (146) запишем в следующей форме:
б *) Здесь V и W — величины, не совпадающие с обозначенными теми же уквами в уравнениях (21).
476 СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [гл. 8
где
fe0=l, k1 = xz-\-\, k% = yz-\-k,. k3 = z. (8.147)
Условия Рауса-Гурвитца в рассматриваемой задаче будут: (х^+1)>0> (xz-}-\)(yz-\-k)— z > 0, z > 0.
Уравнение
V)(yz-\-k) = z (8.148)
вместе с неравенством (хг-[~1)>0 определяет в качестве границы области устойчивости в плоскости ху ветвь гиперболы с центром
в точке
Фиг. 72. Область устойчивости и дискриминантная кривая для следящей системы.
__ 1^ __А
хс~ z' уа~~ Z
и асимптотами, параллельными координатным осям (фиг. 72). Отрезки, отсекаемые гиперболой на координатных осях х и у, будут:
1 — 1 1—А
k z ’ z ‘
При z = оо уравнение гиперболы получает вид ху~0 и она распадается на пару координатных осей.
Область устойчивости расположена выше верхней ветви гиперболы.
Дискриминантная кривая может быть получена из уравнения кривой I/***, изображённой на фиг. 67.
В рассматриваемом сейчас случае коэффициенты характеристического уравнения fe0, k19 fe2, определяются формулами (147). Поэтому параметрическое уравнение дискриминантной кривой
имеет вид
Дифференцируя по 8, получим:
rf(xz+l) _ 2(83 — Z) db 8з
'd(yz + k) =2(83 — z) db o2
(8.149)
Отсюда
АСУ£+_А_ = й
d (xz + 1)
УСТОЙЧИВОСТЬ бЛЕДЙЩЕЙ СИСТЕМЫ
47?
Для точки пересечения с гиперболой имеем: 2о34~^ о3 + 2з_
откуда
8б_|_2г33 + ^2 = 0,
(Зз-^з^о.
Это уравнение имеет двойной корень 8 = — /Сг, которому соответствует точка касания с нижней ветвью гиперболы х^4-1=—//з, yz-\-k =— zf\
При 8 = ^, как видно из (149), дискриминантная кривая имеет точку возврата, для которой
(хг + 1) = ^ = зА _уг-|-Л = у = зА
(8.150)
(8.151)
так что эта точка лежит внутри области устойчивости.
Если рассматривать параметр z> зависящий от характеристики сервомотора, как ненадёжный, то для отыскания области надёжной устойчивости ищем огибающую семейства гипербол, рассматривая z как параметр. Развёртывая уравнение (148) и дифференцируя по z, имеем:
xyz*-\-(kx-\-y—l)z-|_fe = 0, 1
2xyz -J- kx Ц- у—1=0, J откуда
xyz* = k\ исключая z при помощи соотношения
4x2y2z2 = (kx -|- У — I)9 = 4fexy, получим:
fe2x3 — 2kxy-\-y* — 2 (&x_y)1 = 0.
Это уравнение представляет параболу. При у = 0 мы имеем двойной корень х = 1 /А, а при х = 0 — двойной корень у = 1.
Следовательно, парабола касается координатных осей в точках
, о), (0. 1). (8.152)
f \ к /
Так как из (150), (151) вытекает:
kxy = ^ kx-\-y=\ — 2-|,
ТО kx и у для точки касания одной из гипербол с параболой суть корни квадратного уравнения
4?8
системы С постоянными Коэффициентами
(гл. 8
т. е.
1 k
И1> 1*2 — 7
k
Z.
k/z
ОМ
Область надёжной-устойчивости
Фиг. 73. Область надёжной устойчивости
Так как можно положить йх = |4, у — или йх=р.2, У = \ё1> то мы имеем, вообще, две точки касания.
Пусть сначала k > 0 (фиг. 73). Тогда центры всех гипербол расположены в третьем квадранте. Отрезки, отсекаемые гиперболой на осях, отрицательны при z < й, обращаются в нуль при z = k и положительны при k < z. Огибающая парабола лежит в первом квадранте. Однако при $<4й действительных точек касания гипербол с огибающей не существует. При z = 4k две точки касания сливаются в одну точку (1/4й, 1/4). При4й<з< < оо имеем две действительные точки, причём с ростом z одна перемещается по параболе вниз, другая — вверх и при z — оо они достигают координатных осей, сливаясь с точками касания (152) параболы с осями х и у. Последнее обстоятельство становится совершенно понятным, если вспомнить, что при z = оо гипербола обращается в пару координатных осей.
Область надёжной устойчивости состоит из внутрен-расположенных, соответственно,
А
i
&
Й
4
.4. у*
'Л*
ности параболы и двух областей, между параболой и осью х правее их точки касания и между параболой и осью у выше точки касания. Вся остальная часть области -устойчивости составляет область ненадёжной устойчивости. Области гарантированной неустойчивости не существует.
Пусть теперь й< О (фиг. 74). Центры всех гипербол расположены во втором квадранте. Отрезки, отсекаемые гиперболой на оси х, отрицательны, а на оси у положительны при всех z> однако первый принадлежит нижней ветви и лишь второй — верхней ветви гиперболы, которая служит границей области устойчивости. Огибающая парабола лежит во втором квадранте и действительные точки касания существуют при всех z. Но лишь одна из них принадлежит верхней ветви гиперболы и расположена выше точки касания огибающей с осью у\ вторая принадлежит нижней ветви. С возрастанием z от Q до оо первая точка касания движется по верхней части параболы И3|
4‘
| 8.231
УСТОЙЧИВОСТЬ СЛЕДЯЩЕЙ СИСТЕМЫ
бесконечно удалённой точки (—I/O, —fe/О) вниз и при г = оо достигает оси ординат в точке касания параболы с этой осью.
В область гарантированной v
неустойчивости входит внутренность параболы, все точки второго квадранта ниже неё, а также вся нижняя полуплоскость. Остальные точки плоскости ху составляют область ненадёжной устойчивости. Области надёжной устойчивости не существует.
Предположим, наконец, что & = 0 (фиг. 75). Центры всех гипербол располагаются на отрицательной части оси абсцисс., Отрезки, отсекаемые гиперболами на оси у, равны единице. При z = 0 гипербола распадается на прямую у = 1 и бесконечно удалённую прямую; при z = оо, как всегда, — на пару координатных осей. Огибающая сводится к точке (0. 1).
Область надёжной устойчивости состоит из части первого квадранта выше прямой У—1. Область ненадёжной устойчивости состоит из части
Область гарантированной неустойчивости
первого квадранта ниже прямой у = 1 и части второго выше той же прямой. Остальные точки плоскости составляют область заведомой неустойчивости.
Область гарантированной неустойчивости
Область надёжной устойчивости
| | Область ненадёжной устойчивости
Фиг. 75. Случай k = 0.
б) Вернёмся теперь к общему случаю V#=0. В этом случае характеристическое уравнение системы дифференциальных уравнений (145) имеет вид
—J— —J— —J— fegX. —|— = 0,
где
&o=V; Aj1 = V-}-1; k2 = xz-\- 1;
k3 = yz-^k\ k4 = z.
(8.153)
480
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
[гл. 8
Условия Рауса-Гурвитца имеют вид
0, > 0, 0, 0, (kjk.} ; 0.
Так как k.2, k3 линейны относительно x и у, то можно принять первые временно за декартовы координаты.
Уравнение
, f Мз) ^1^4 ==: 0
вместе с неравенством > 0 определяют в качестве границы области устойчивости верхнюю ветвь гиперболы. Координаты её центра определяются из соотношений
'a£'=feA = o> 2Мз = °>
что даёт:
Уравнения асимптот будут:
й3 = 0, kxk.2 — kjz.^ = 0.
Возвращаясь к координатам х, у, согласно формулам (153), имеем координаты центра
и уравнения асимптот уг-|-й = 0, (УН-1)(хг+га+1) — V(yz-^k) = 0 или
= z[(V+l)x— Уу] + (У% + У+1) = 0.
Уравнение самой гиперболы может быть представлено в виде
(^ + *) {г:[(У+1)х —Vyl + ^+y+i} —(Vr+1)3z = 0.
Область устойчивости есть внутренность верхней ветви.
При z — оо уравнение гиперболы получает вид у [(V 1) х —
— 1/у] = 0, т. е. гипербола распадается на пару прямых
^ = 0, (У+1)х— Уу = 0.
Асимптоты всех гипербол, соответствующих различным z, параллельны этим прямым. Поэтому последние целесообразно принять за оси косоугольной системы, а величины (У-Ц-1)х— Vy, у — за координаты по этим осям, причём, как нетрудно подсчитать, масштабные единицы будут, соответственно,
§8.231
УСТОЙЧИВОСТЬ СЛЕДЯЩЕЙ СИСТЕМЫ
481
Координаты центра в косоугольных координатах будут: r/т/ 11ч I/ 1 V^k+V+\ k •
[(У4-1)х — Vy] =------т t у _
&
а отрезки, отсекаемые гиперболой на новых осях, равны (У4-1)2 i/2£+V+l (K+l)2 k
k z * V^+V+1 z*
Если рассматривать параметр z, зависящий от характеристики сервомотора, как ненадежный, то для определения области надежной устойчивости следует найти огибающую семейства гипербол, рассматривая z как параметр. Развертывая уравнение гиперболы и дифференцируя по z> имеем:
[(У+ 1) х _ Vv]yz* + {k [(V + 1) х — Уу] 4-
У+ 1) v —(У-L 1)2} zA~k(V*k + У+ 1) = О, 2[(IZ+l)x-Vjljz+{*[(y+l)x — VyJ+ (8Л54)
+ (K2A: + — (V+ I)9} = 0..
Отсюда
[(V+ l)x— Vy]yz* = k(V*k + V4-1) (8.155)
и, исключая z,
{k [(V+1)X— V>]4-(IZ2fc_|_ У-Р)^ — (У —|—1)2}2 —.
= 4k [(У+1)х—Уу]<у(У2* + У+1) или
{Aj[(y+l)X—y3,]—(y2ft+y+l)^}2_
-2(У+1)2{й[(У+1)х—Уз/1 + (У^+У+1)^ + (У+1)^0.
Так как совокупность старших членов представляет полный квадрат, то огибающая — парабола.
При у = 0 имеем двойной корень (У-j- 1) х — Vy = (У + 1)2/&, а при (У-|- 1)х — Vy = 0 — двойной корень^/ = (У-[-1)2/(У2й-|-У-|-1)-Поэтому парабола касается косоугольных осей в точках
Z(^+D2 0\ (^+1)2 V
\ k ’V \ ’ У2^+ v+v
Так как из (154), (155) вытекает:
k [(У4- 1)X — Vy] + (V9fe + V + 1) j = (V+ I)9 — 21&±±+±) t
k [(V+ 1)x_ Vy](V*k + V+ 1)у = fe2(V^+V+l)2, f
то величины £[(У-|-1)х — Уу] и (У‘2А?-|-У-}-!)^, пропорциональные косоугольным координатам точки касания одной из гипербол с оги-
31 Зак. 1474. Б. В. Булгаков
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [ГЛ. §
бающей, должны быть корнями уравнения
т. е.
Р1>
= (K+D* k(V2k+V+l)_ у : n /(V-Ц)2 *(у^+у+1)
‘ 2 2 z -+-\ *Т 4 z
Поскольку мы можем положить k [(V-J- 1)* — Vy] = Hi» (V2ft-j-V+l)y = |a,2 или й1(У4-1)х— V>] = h2, (V2A?-t-V+l) j/ = Hi»
то при
4k(V*k + V+l) (V+l?
имеем две точки касания. При меньших значениях z действительных точек касания или пересечения не существует. При
z = 4fe(Vr2£+l/+ 1)/(У+1)2
мы имеем Hi = На = 0^+ 1)2/4 и две точки сливаются в одну точку А с косоугольными координатами
rfi/4-.nv—i/vi v О'+Р2 *
[(U-f-l)X Vy]A— 4k , Уа~4(у^+У+1)‘
При дальнейшем росте z одна точка перемещается по огибающей вниз, другая — вверх и при z = оо они достигают косоугольных осей в точках касания огибающей с этими осями. Последнее обстоятельство становится совершенно понятным, если вспомнить, что при z = оо сама гипербола распадается на пару косоугольных осей.
§ 8.24. Линии равной устойчивости для следящей системы при безинерционном сервомоторе. В случае безинерционного сервомотора имеем характеристическое уравнение 3-й степени. Его коэффициенты *0, **, *, и *3 определяются формулами (147). Коэффициенты k± и *2, линейно зависящие от х и у, примем временно за декартовы координаты. Так как k3 = z считается фиксированной величиной, то построение области С8, в которой действительные части всех корней по абсолютной величине больше, чем 8, можно провести по данным § 22, п. «д».
Принимая во внимание, что, согласно (147), сейчас *0=1 и kQ = z, перечислим полученные ранее результаты. Область является сегментом гиперболы, расположенным между гиперболой
*х (— 28*! + *2) + 88‘2*х — 28*2 — 88» — z = О и прямой
8% — Sfe2 — 83 + z = 0.
Координаты центра гиперболы будут:
= 28, (^2)0 = О*
§ 8.24] ЛИНИЙ РАВНОЙ Устойчивости ДЛЯ СЛЕДЯЩЕЙ СИСТЕМЫ 433 уравнения асимптот гиперболы
— 28 = О, — 28^ + ^4-482 = 0.
Точки пересечения А и В гиперболы с прямой имеют следующие координаты:
(6^ = 38, (k.2)A = 282 +1,
(fe1)s = 28 +, (fe2)B = 82+^-.
При № = z обе точки совпадают и прямая касается гиперболы.
При 83 > z мы имеем О^в < (fe2)^ и точка В лежит
левее точки А\ весь гиперболический сегмент, отсекаемый прямой, расположен левее вертикальной прямой k± = 38, что противоречит первому неравенству Рауса-Гурвитца (134)^ которое при = 1 имеет вид k± — 38 > 0.
При 83<z мы получаем (йх)А < (fex)B, (k.2)A < (fe2)B и точка А лежит левее точки В, вследствие чего указанное неравенство Рауса-Гурвитца теперь удовлетворяется.
Предыдущее неравенство представляет, таким образом, условие существования конечной области С$. При 8s = z она стягивается в точку М с координатами
(*1)м = 38 = 3^.,
(й8)м = 382 = Зд
Величина 8 = есть максимальная возможная степень устойчивости при данном z9 а величины (k2)M — наивыгоднейшие значения fe2.
Возвращаясь к координатам х, у, согласно (147), имеем уравнение гиперболы
(zx + 1 _ 28) [z (— 28х + у) + 483 _ 28 + k\ = z.
При z = oo оно принимает вид
(— 28х +_у) х = 0, т. е. гипербола распадается на пару прямых — 28х+ву = 0, х = 0, проходящих через начало. Можно принять их за косоугольные оси, а величины х, —28x+j, в этом именно порядке, — за отсчитываемые по ним координаты. Масштабные единицы для этих осей, как нетрудно подсчитать, будут ]/* 1 + 489, 1.
31*
Фиг. 76. Линии равной устой-‘ чивости для следящей системы.
E7CCU
4§4 СИСТЕМЫ С ПОСТОЙНЙЫМЙ КОЭФФИЦИЕНТАМИ [гл. 8
Отрезки, отсекаемые гиперболой на косоугольных осях (фиг. 76), в их масштабах определяются уравнениями
«тр + 1 -23) (48^ _ 28 -j- k) = z, (1 — 28) [z (— 28х +Х'Т Р + 432 — 28 + k] = z или
гхотр = 482 _ 2о + k — (1 — 2о)>
z (_ 2Sx +<р = - (43-2 - 23 + *),
откуда окончательно „ __ 1 1— 26
хотР — 432 — 23 + k . z (_28х4-v)" =—i___________432-23+А
zox -t- J9OTP t _ 2В z
Косоугольные координаты центра определяются из соотношений
1 = 2о, z [Су— 28х)с4” 28хс] + & = О,
откуда
О-28*)„ = .
Уравнение прямолинейной границы области С8 имеет вид
— 8Чгх — 8г СУ — 28х) — 83 82 — &8 4“ z = 0.
Отрезки, отсекаемые этой прямой на косоугольных осях,
, = 1 62 —B + Z?
ХотР““ 62 6г ’ .
О'-2йЧтР = Т----------
При z > 83 имеем косоугольные координаты угловых то.чек границы
1 1-26 . k + 362 -26
хв = ^---------- =---------------------z-----
Координаты точки Л1, к которой при г = о3 стягивается область С8 (значение 8 дано), будут:
__ 1—36
63 >
§ 8.25]
МЕТОД НЕЙМАРКА
485
Если z рассматривается как заданное, то удобнее подсчитать прямоугольные координаты
__ 1— за __ з&2
> Ум ьз »
так как угол и масштаб косоугольной системы зависят от 8. Тогда последние формулы выражают значения х, у, дающие при данном z
Фиг. 77. Формы траекторий точки М при различных значениях k.
максимальную степень устойчивости 8 = z'K Чтобы исследовать траекторию точки М при изменении 8, вычисляем:
dxM __ 3(1—28)
~db~~ 8? ’
_3(k- 82)
rf8 8« ’
dyN __ k — &
dxM 1 — 28
Формы траекторий изображены на фиг. 77 с отметками, выражающими значения 8.
§ 8.25. Разбиение плоскости параметров в случае характеристического уравнения с комплексными коэффициентами. Метод Неймаркц. Предположим [8-3], что у рассматриваемого хардктеристц-
486 СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [гл. 8
ческого уравнения s-й степени
Г(Х) = Л0Х8 +• • • + V1*4A = ° (8.156)
коэффициенты являются комплексными величинами и линейно зависят от двух параметров р. и у, так что
F(X) = P(X)|i + Q(X)v + /?(X). (8.157)
Каждой точке плоскости рьу соответствуют определённые значения коэффициентов характеристического уравнения, а следовательно, определённые значения s корней. Значения координат (рь, у) точек плоскости jAv, соответствующих точкам плоскости комплексной переменной X, можно определить так. Полагая
X =
(8.158)
Р (е -|- /со) = (s, o>) + ZP2(e, со), ]
Q (е+ *<*>) = Qi (s, <*>) + /<2з(8> <°)>
R (е z<o) = R± (е, o)) + //?2(8> ш) 1
(8.159)
и разделяя в уравнении (156) действительную и мнимую части, имеем:
4~ QtV 4“ Ri — О, л2 = р2р. 4- q2v 4~ /?2 = о. < Отсюда
Др. Д7
Н = ~д-’ У==Д"’
где
(8.160)
(8.161)
(8.162)
Таким образом, каждой единственная пара
паре значений е, со значений |л, у;
но,
соответствует при А #=0 уже сказано выше, каж-
(л)
плоскости параметров (|Л, у).
Фиг. 78. Разбиение
как дой паре значений |л, v соответствует s пар значений в, <о, где s обозначает степень алгебраического уравнения (156).
Если фиксировать © и изменять О) от —оо до 4"°°» ТО В ПЛОСКОСТИ 80) получим прямую 8 = const, параллельную мнимой оси, а в плоскости |лу — некоторую кривую Ге
(фиг. 78), определяемую параметрическими уравнениями (161). При пересечении кривой Те точкой (ji, у) точка X в плоскости ео> переходит с одной стороны прямой 8 = const на другую. Следовательно, кривая 7\ разбивает плоскость pv на области Cf(/), в каждой из
§ 8.25] метод неймар к а 487
которых имеется данное число j корней с действительной частью большей, чем в. В частности, Се(0) есть область, где нет корней, действительная часть которых больше, чем з.
Если выбрать значение е = 0, то Со(0) будет областью, где нет ’ корней, действительная часть которых положительна, т. е. Со(О) есть область устойчивости.
Будем штриховать кривую Те так, чтобы при переходе с нештрихованной стороны на штрихованную число корней с действительной частью большей, чем е, убывало на единицу.
Перейдём к установлению правила штриховки кривой 7^, которое удовлетворяло бы указанному требованию. Пусть (р, у), (р4-8р, v4~6v) — координаты двух бесконечно близких точек на плоскости pv, a e-j-zco, е 4-8е4-г(со4-8(о)— соответствующие им точки на плоскости X. Для второй из указанных пар точек уравнения (160) принимают следующий вид:
где невыписанные слагаемые являются величинами второго и высших порядков малости и в дальнейшем отбрасываются. При этом уравнения (163) можно переписать так:
(8.164)
Обозначая
8s 8<о
1 00)
8 со
(8.165)
дг 0ю
получим для 8|л и 8у следующие выражения:
Ago, ~
8v = --y.
(8.166)
Рассматривая теперь на плоскости ру две точки с координатами (н + 8рх, v + ^vi)> (Н“М|л2, у4~8у2), которым на плоскости X соответствуют точки е 4~ 8е( Ц-1 + Sco-J и s 4~ 8е2 4~ * (<*> 4” 8<о2), и определяя 8^, 8vp согласно (166), найдём после несложных пре-
488
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
[гл. 8
образований:
Обозначая согласно (160), а также
Svi
8у.2 £
dA2 de
дЛ.1 day
дЛ,2 dm
8sx ScOj
8s2 8(0.2
имеем:
dA.i____dA%______
de day ’
dAt_____дЛ,2
day de
Подставляя в (167), получим:
8si 3oox
8s.2 8o)2
(8.167)
(8.168)
(8.169)
(8.170)
(8.171)
8Р1
дЛх
“ д
SjAj 8vt
8^2 Sv2
Рассматривая определитель в левой части соотношения (171) как векторное произведение двух векторов, проекции которых суть, соответственно, 8р, 8vx и 8р2, 8у2, а начало расположено в точке (р, v), и, аналогично, определитель в правой части (171) как векторное произведение двух векторов, проекции которых суть 8^, 8сох и 8г2, 8оо2, а начало расположено в точке (в, оо), можно заключить,
Фиг. 79. Правило штриховки в
случае Д^ = Д^ = Д = 0.
что правило штриховки кривой должно быть следующим: при движении по кривой в направлении возрастающих значений оо следует штриховать левую сторону при А > 0 и правую при А < 0. Тогда при переходе с нештрихованной стороны на штрихованную число корней с действительной частью большей, чем е, будет убывать на единицу.
Штриховка может меняться только при обращении А в нуль, т. е. при прохождении кривой через одну из несобственных точек проективной плоскости р, или при особых значениях оо, для которых одновременно А =Д^==А = О. При этих значениях одно
§ 8.26]
ДИАГРАММЫ ВЫШНЕГРАДСКОГО
489
и3 уравнений есть следствие другого, и поэтому мы имеем лишь одно уравнение между [*, v, определяющее прямую:
Лн + ^ + ^1 = 0- (8.172)
Правило штриховки может быть получено в этом случае предельным переходом, т. е. части прямой должны быть заштрихованы навстречу смежным частям кривой (фиг. 79).
Фиг. 80. Правило штриховки для случая, когда ш является двойным корнем уравнения Д = 0.
Если со — двойной корень Д, то Д знака не меняет и мы имеем расположения, показанные на фиг. 80, из которых видно, что прямая
в этом случае не штрихуется вовсе.
§ 8.26. Диаграммы Вышнеградского. Разбиение плоскости
в случае действительных коэффициентов полиномов Р, Q, R Неймарк
предложил называть диаграммой Вышне-градского. В этом случае при наличии корня г-1—Zcd имеется и сопряжённый корень е — /со, так что значениям -рсо, —со соответствует одна и та же точка кривой Те. Это можно видеть также и из того, что Рх, Qi> Pi в этом случае — чётные функции от со, а Р2» ^2» ^2 — нечётные и потому Др Д^, Д также нечётны, а
(со2), v=v (со2)—чётные функции. Кривая Тв пробегается дважды, а так как Д, будучи нечётной функцией от со, меняет
Фиг. 81. Диаграммы Вышнеградского.
знак при со = 0, то штри-
ховка наносится с одной стороны (фиг. 81).
Прямые
Р (в) у. 4- Q (в) v + Р (в) = 0, (8.173)
Р С?) р. + Q (z) у + /? (г)
(8.174)
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
[гл. 8
получающиеся при со = О и <о = оо, здесь всегда будут особыми и
правило их однократной штриховки — прежнее. Для особых значений <о,
Фиг. 82. Правило штриховки диаграммы Вышнеградского в случае особых значений <о, не равных 0 и оо
не равных 0 и оо, пример штриховки показан на фиг. 82.
Пример (К). И. Неймарк). Рассмотрим характеристическое уравнение 2-й степени
(к^ -|- К) -J- 1) *7 —— к 2 2 = 0.
Полагая е = 0, т. е. принимая к = /со, имеем:
— со2р, -|- ( — w2 + 1v = — 0)2 — 2, <о|Л = 0.
Для рассматриваемого примера
А = со (со2 — 1),
Параметрическое уравнение кривой То имеет вид
откуда также следует, что
=....-3.....<0.
d (<о2) (со2— 1)2
Из полученных выражений видно, что кривая То представляет собой пробегае-
Фиг. 83. Пример диаграммы Вышнеградского.
мую два раза часть оси ординат, отмеченную двойной штриховкой на фиг. 83. При к = 0 и к = оо имеем:
^ + 2 = 0,
р. + —1=0.
Это — уравнения особых прямых, отмеченных на фиг. 83 однократной штриховкой,
§ 8.27]
ДИСКРИМИНАНТНАЯ КРИВАЯ
491
В точке р, = у = О имеем:
_ к2 + 2 = 0,
Х = ± /2,
и следовательно, эта точка принадлежит области Со(1).
В точке р. — у = 1 имеем:
\2 -f. к + з = О,
Эта точка принадлежит к области Со(О), т. е. к области устойчивости.
§ 8.27. Дискриминантная кривая и область апериодической устойчивости. Вернёмся к алгебраическому уравнению (156), у которого будем полагать коэффициенты вещественными, но попрежнему линейно зависящими от двух параметров р. и v. Поставим себе целью выделить область плоскости р.у, в которой все корни вещественны, и ту её часть, где они отрицательны. Последнюю будем называть областью апериодической устойчивости, так как если (156) есть характеристическое уравнение линейной колебательной системы с постоянными коэффициентами, то в указанной области все парциальные колебания затухают по показательному закону. Поставленную задачу нужно решать во многих вопросах синтеза регуляторов.
Пары комплексных корней могут появляться или исчезать при перемещении изображающей точки в плоскости рьу только при условии предварительного обращения в двойной действительный корень л = е [8-7]. Это может случиться лишь в точках (рь, у), где уравнение (156) и уравнение
F'(X) = 0 (8.175)
имеют общий корень X = s, так что
^О)н + <?(е)*4-Я(е) = 0, Р'(в)н + <?'(е)* + Я'(8) = 0. (8.176)
Условием этого является, в свою очередь, обращение в нуль результанта этих уравнений, т. е. дискриминанта уравнения (156). Обозначая
(8) =
<2 (8) ₽(8)
Q'(S) fl'(s)
Г(8) =
Г, (в) =
Q(8)
Р'(е) Q'(s)
/?(а) Р(з)
Я'Ф Р'(е)
(8.177)
(8.178)
получим параметрические уравнения дискриминантной кривой Y:
^(е) Г(е) ’
(8.179)
492 СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [гл. 8
в которых е должен пробегать все действительные значения от — сю до -[-оо.
Кривая Y разбивает плоскость р на такие области E(j), что во всех точках E(j) полином F(X) имеет j пар комплексных корней. Целое число j может иметь все значения от 0 до [$/2], т. е. наибольшего целого числа, заключающегося в s/2. В частности, Е(0) есть область, где все корни вещественны. Кроме точек, получающихся из (179) при действительных значениях е, дискриминантная кривая может содержать конечное число изолированных точек, соответствующих кратным комплексным корням, но такие точки не входят в состав границ областей E(j) и потому не будут рассматриваться.
Для того чтобы правильно наименовать области E(j), т. е. указать, сколько пар комплексных корней имеет полином F(X) в точках каждой из них, нужно, во-первых, каким-нибудь путём, например численным разрешением уравнения, установить характер корней в какой-либо одной точке плоскости р и, во-вторых* установить такое правило штриховки кривой У, которое позволяло бы утверждать, что при переходе с нештрихованной стороны на штрихованную два комплексных сопряжённых корня обращаются в действительные. Если окажется, что число областей, образуемых кривой У, — наибольшее возможное, т. е. [s/2] -[-1, то правило штриховки достаточно для наименования областей и фактическое определение корней даже и для одной точки излишне.
Общая часть области F(0) и области устойчивости Со(О) (§ 25) есть область апериодической устойчивости.
Правило штриховки можно установить методом, аналогичным изложенному в § 25. Это правило состоит в следующем: при Г(е)>0 следует штриховать ту сторону кривой У, которая лежит по левую руку от наблюдателя, странствующего по кривой в направлении убывания е; при Г(е) < 0 штрихуется правая сторона. При переходе с нештрихованной стороны на штрихованную теряется одна пара комплексных корней.
Г. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ И ВОЛНЫ ПРИ ГАРМОНИЧЕСКИХ ВОЗМУЩЕНИЯХ
§ 8.28. Установившиеся колебания. Предполагая, что уравнение системы имеет вид
f{D)y^e{D)x(t), (8.180)
рассмотрим некоторые случаи, когда заданный переменный параметр x (t) выражается показательными и тригонометрическими функциями, а также степенями t. Как и в § 7.4, через e(D), f(D) обозначены полиномные матрицы типов п^п, а через х, у —
Столбцы из ti' и /г элементов; при этом, вообще, п ¥=
£ g 28] УСТАНОВИВШИЕСЯ ИолеЬанйй 493
Пусть сначала
J х = ^>Л (8.181)
где ____столбец из пг постоянных элементов, а л — постоянный
скаляр. Полагая j/==7]^, (8.182)
подставляя в уравнение, пользуясь формулой (28) и сокращая на еи, имеем: отсюда 7] = ЛГ(л)е, (8.183)
где
X(k)=/(X)\e(X) = ^LW (8.184)
и д(а) = det/(A). Искомое частное решение будет: j/ = X(X)^4 (8.185)
Мы могли *бы также поступить следующим образом. Разрешая (180) формально относительно у, находим:
y = X(D)x(t), (8.186)
где
X(D)=f(D)\e(D) = ^±^. (8.187)
Уравнение (186), разумеется, выражает не больше того, что первоначальное уравнение (180), но мы имеем удобное правило: если х = то для получения частного решения достаточно заме-
нить D через X. Матрицу X(D) типа n X п' мы будем, обобщая определение § 4.8, называть передаточной функцией (передачей) или трансмиттансом системы.
Складывая частное решение с общим решением однородного уравнения, получим общее решение неоднородного уравнения; поэтому можно считать, что интерпретация формального решения при х = выражается соотношением
Х(Р) = Х(л) &« + 2 (0 с.. (8.188)
ff=1
где Ba(Q — частные решения однородного уравнения, а с9— произвольные постоянные. Эта формула представляет обобщение (28) на случай, когда матричное операционное выражение является дробной рациональной функцией. Существенное различие состоит в том, что теперь интерпретация даётся лишь с точностью до собственного колебания с неопределёнными коэффициентами с9, причём парциальные колебания определяются корнями знаменателя.
ЯБК
4Й4 6йСТеМь1 с йостояййыми Коэффициентами [гл. 8
В дальнейшем мы ограничимся получением частных решений, так как способы построения общих решений однородных уравнений были изложены раньше.
Пусть
х cos (arf-|- fy') (/' = L • • • > и')> (8.189)
3 3
так что мы имеем нарастающие или убывающие колебательные возмущения одной и той же частоты, но различных амплитуд и фаз. Мы можем написать:
-<(»#+•;')] _ (8.190)
3
и
х = [5г(е+М * *] = Re |е(«+М *,
(8.191)
где
(8.192)
Этот столбец может быть назван матричной комплексной амплитудой возмущения, так как значения переменных параметров х^ равны проекциям на действительную ось векторов * в пло-
скости комплексного переменного. Каждый вектор вращается вокруг начала с угловой скоростью со, а его длина в то же время возрастает или убывает по показательному закону; начальное значение вектора при £=0 есть fy.
Метод комплексных амплитуд был развит в теории переменных токов, но с неменьшей пользой может быть применён в общей теории колебаний, тем более, что с ним связана физическая интуиция методов операционного исчисления.
Частные решения, соответствующие слагаемым могут быть найдены по предыдущему, а полному возмущению х будет соответствовать полусумма
У = 1 + (8.193)
где величина
^ = ^(8+ f(o) 5 (8.194)
есть комплексная амплитуда матричной координаты у. Выражения её элементов суть:
п’
= 2 (е+ *№ • (8.195)
V=1
Остановившееся колебания
495
Так как
Xjk, (S + xw) = I Xjk, (s + Z®) I e~^'ю), (8.196)
где (s> <°) — аргумент комплексного’ числа Xjk> (e—|—Zoj), взятый с обратным знаком, то мы можем написать:
п'
у<— 2 ReXflf (s +«О 5fc'e(,+<u>) * — fc‘=l
n'
= 2 I Xjk' (в+*»)I Pk' e*f COS (®Z + Ofc' — fyk’) (8.197)
fc'=l
С/ —— 1 > • • • 9
k'-e слагаемое в* правой части у-го уравнения выражает влияние fe'-го переменного параметра хк> на у-ю координату. При этом амплитуда изменяется в отношении \Хк' (г —Zco) а фаза запаздывает на оо). Поэтому мы можем назвать эти величины коэффициентами усиления и аргументами запаздывания.
Если
х? = sin (oof —р (/ = 1, ..., n') (8.198)
или
х = 4- = Im 5e(‘+i”)f, (8.199)
^£4
то аналогичным путём получим частное решение у = ~ = Im (8.200)
w4
или п'
Уз = S Im Xik' (s -j- Zw) L ,*(•+<<»)# =
к’ =1 K
n’
= 2 \Xjk' (e-|-Zw)|Pfe,e‘* sin (<oZ-|-6fc- — <^.) (8.201)
С/ ==:: 1 > • • • Э n).
Если, в частности, e = 0, то мы имеем чисто гармонические возмущения. Соответствующие частные решения определяют установившиеся колебания, так как они поддерживаются за счёт внешнего источника энергии, между тем как собственные колебания в случае асимптотически устойчивой системы затухают. Матрица Л’(Zoo) может быть названа в этом случае частотной характеристикой.
Отметим следующее свойство, которое понадобится в дальнейшем: так как числители и знаменатели всех элементов Х^> (Zoo) — полиномы От Zo), то действительные части этих элементов и матрицы X(Zoo) являются чётными, а мнимые части — нечётными функциями от оо.
496
системы с постоянными коэффициентами
(гл. 8
Графики, представляющие зависимость коэффициентов усиления I от частоты возбуждения со, носят название резонансных кривых. * При их построении иногда предпочитают выделять статические коэф- j фициенты усиления |ЛГ^(О)|, не зависящие от частоты (если только 1 они не обращаются в 0 или оо); тогда ординаты резонансных | кривых представляют безразмерные динамические коэффициенты |
(0) |. В строительной механике величины Xjk> (0) носят название коэффициентов влияния^ так как, очевидно, (0) Pk> есть значение координаты у$ при равновесии в случае постоянного возмущения х# = Pkf.
При построении резонансных кривых можно также вместо числового принять логарифмический масштаб, т. е. откладывать по ординатам значения величин
= In | Xjk’ (teyX# (0) |.
Если символ In обозначает натуральный логарифм, то эти значения считаются выраженными в неперах (неп) в отличие от чисел (а*'), = 21g | Xjk. (i^/X^ (0) |
(1g — десятичный логарифм) или
{ajk.)dS = 201g | Xjk. (i^lXjk’ (0) I, которыми иногда также пользуются и которые считаются выраженными соответственно в белах (<5) или децибелах (дб). Так как In = 2,302591g, то, очевидно,
1 дб = 0,11513 неп.
Гармонические возмущения представляют лишь очень частный случай, но его значение заключается в том, что почти любое периодическое возмущение может быть разложено в ряд Фурье и каждой гармонике будет соответствовать в частном решении слагаемое, вычисляемое по правилам, которые мы только что установили.
Рассмотрим ещё некоторые другие формы возмущающих функций.
Так как Л'(Х)^ есть частное решение уравнения f (D)y== = e(D)&xt, то, дифференцируя обе части т раз по А и обозначая т-ю производную от неизвестной опять через у, мы найдём, что частным решением уравнения
f(D) у = е (D) №е™ будет д™ v/xr У = -д^х <А>ie Иными словами, если X =
(8.202)
(8.203) f
(8.204)1
§ 8.28]
УСТАНОВИВШИЕСЯ КОЛЕБАНИЯ
497
то
у = Вд t (8.205)
Отсюда вытекает и ещё более общий результат: если
х = e™Q (0 = е™ + ... + Ат),
(8.206)
где коэффициенты полинома Ло, Av ..., Ат—- матрицы-столбцы, не зависящие от Д то
(8.207)
где действие оператора д/дк распространяется на -¥(Х), но не на что отмечено квадратной скобкой. При действительных отрицательных л матрицы x(t) только что рассмотренного вида представляют группы переменных параметров, которые могут иметь по нескольку максимумов и минимумов при конечных значениях tt а затем стремятся к нулю.
Полученные выше решения становятся непригодными, если л (или е-}-^) оказывается равным одному из корней характеристического уравнения, так как тогда знаменатель выражения Х(к) обращается в нуль. Пусть, например, опять х = ^еи и степень кратности А как корня характеристического уравнения равна q. Ищем частное решение уравнения (180) в форме
Та(А Х)Л, где, как и в § 11,
Л Х) = "S? eUF & Х)’ (8 -208)
4 ок*
a h— матрица-столбец, подлежащая определению. Имеем:
/ (D) Tg (t, (D) eltF (O) e™F (X) =
* OK* OK*
= — f(k) e^F(K)^= — e™ Д (X) E,
а так как
Д (X) = Д' (Л) = ... = Дй-1) (X) = о, то
. f(D) Tq(t, Х)=Л(«>(Х)Е.
Подстановка выражения Tg(t, Х)Л в уравнение поэтому даёт: Д<®(Х)Л = е(Х)£,
откуда
g(X) Д(«> (X)
32 Зак. 1474. Б. В. Булгаков
498
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
[гл. 8
Частное решение будет:
——-------
(к)
(8.209)
Пример 1.
D2 + 2D4-1
D* + (— b + l)D + b + 2
D — 1
D+b
У1
У2
Р sin со/.
F(D)==
— D + l
D2 + 2D + 1
1 0
х = Р sin tof,
Д(Р)=2(* + 1)(£>2+1),
X ~ Д (D)
D + b
— D* + (b — 1)D — (b + 2)
>
Х(йо)— 2 4-1) (_ <.2 4-1)
b -J” /to
<d2 — (b + 2) + i(b — l)to
Частное решение неоднородного уравнения есть
J —Im 2(*4-l)(— «>24-1)
b -j- /to to2 —(^ + 2)+ /(&—!) to
Pgiwt _
to cos tof -f“ b sin to/
(b — 1) co cos to/ -|- (to2 — b — 2) sin to/
Присоединяя сюда общее решение однородного уравнения, вычисленное в § 12 (пример 1), находим:
_ <о cos to/ + b sin to/ . .
Ji = P 2 (й 4-1) (— шх 4-1) + C1 (cos + sin +‘c2 cos * + sin *)’
‘ {b — 1) to cos to/ -f- (to2 — b — 2) sin to/
Пример 2.
У1
У*
0
F(D) =
0
^(D) =
Д (D) = 1.
Уравнение энергии
499
Характеристическое уравнение не имеет корней и общее решение у = 0 однородного уравнения не содержит произвольных постоянных..
(О2 — 1 — /со
_£)2 —d —1
или
*
Частное решение неоднородного уравнения есть
II 0)2 — J — /со
Pftiwt — р
(—. ш2 1) cos
У1 = Р [(<о2 — 1) COS со/ 4“ ш sin
оно является также и общим.
§ 8.29. Уравнение энергии. Рассмотрим натуральную скую систему, характеризуемую матричным уравнением
f(P)y = <0(f),
механиче-
в. котором (§ 7.9)
f(D) = AD* -j- (N+О) D + (Я + J),
(8.210)
&
имеем также
где
С = /(07|.
Элементарная работа силы «ь будет:
причём A, N, Н—симметричные, О, J—кососимметричные матрицы, 10(f)— столбец синусоидальных возмущающих сил. Представляя 10(f), у в виде
(8.212)
(8.213)
(8.214)
Wjdyj = 40jyj dt = -^r (^ем -]-5je_,<“f) (C,ew -|- ^je~i<ot) dt =
= | + +¥^"2W) dt> (8-215)
а средняя мощность за период 2tc/<d:
4-к/со
J адл=4-(еЛ+^). (8.216)
—тс/со
Вводя, так же как и для электрических цепей, матричное сопротивление
Z (D) =f (D) = ADNG, (8.217)
32*
500
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
[гл. 8
находим среднюю мощность всех сил Wj:
1 +Го = | =
= -г к7« -п + с7(— *») й =
= [iTZ (/со) с 4- Crz (— гш) С] =
= 1U(CTX —СТЛС)+1Г^+О) С+ тг I
-Нт(ЛН-ОК + т- [Г(#+•/) С — CT(H4-J)C]l. (8.218)
Но в силу симметрии матриц A, N, Н и косой симметрии матриц G, J
= Чта1, = Сгк, 1ТНГ. = Стж,
-т т - -т т - (8.219)
стос=—;гос, сгл=—
вследствие чего
I (^ +ёГС) = у С т (n — С. (8.220)
Величины
4-те/со
Л/ер = £ J N(j, y)dt =
—к/ы
4-тс/со
= J ± (Сге«<»« ZTe-i<»t) N + 1е~^) dt
—iz[a>
ИЛИ
4<ic/o>
J У) dt == ± ± N (Ъ Q (8.221)
— n[<a
И
4-тс/со
= i J •'O. >)-«—E> (8'222)
—tc/o>
представляют средние значения квадратичной формы N(y, у) и билинейной формы J(y, у) за период 2ir/<o и в то же время взятые с обратным знаком средние мощности диссипативных и искусственных сил. Поэтому уравнение (220) выражает тот факт, что при гармонических колебаниях работа, сообщаемая системе возмущающими силами, в среднем затрачивается только на преодоление сопротивлений
§ 8.30]
ПРОВОДИМОСТЬ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
501
и искусственных сил, поскольку средние значения кинетической и потенциальной энергий остаются постоянными. Удвоенные значения
этих средних суть:
4-тс/со
Лор = ^? f А (у, у) dt = | ?А? = ± А (С, С),
*—тс/со
4-тс/о>
н = -£- f Н(у, y)dt=^ Q.
СР 2ти J 2(о* 2(о*
—к/со
(8.223)
Гироскопические силы, как известно, не совершают работы.
§ 8.30. Проводимость электрической цепи. Рассмотрим линейную электрическую n-контурную цепь (§ 7.10), характеризуемую матричным уравнением
Z(D)i = e(f), (8.224)
в котором I и e{t)— матрицы-столбцы контурных токов и приложенных э. д. с., a Z(D)— матричное сопротивление.
Разрешая алгебраически относительно I и полагая
y(D) = Z-i(D), (8.225)
находим:
i=Y{D)e(t). (8.226)
Первоначальное уравнение (224) или только что полученное уравнение (226) выражают в матричной форме закон Ома для цепи. Y (О) может быть названа {матричной) проводимостью или адмиттансом, а элементы этой матрицы Yjk(D)— собственными (J = k) и взаимными (J k) проводимостями или адмиттансами контуров . Для пассивной цепи матрица Z (D), а следовательно, и Y (D) являются симметричными и мы имеем соотношения взаимности
Уд(П) = Уад(0). (8.227)
Обозначим
<8228>
и предположим, что все приложенные э. д. с., кроме е$(1), равны нулю; тогда
= Wjj(D) • (8.229)
вследствие чего W^{D) носит название входного сопротивления цепи со стороны /-го контура. Если же равны нулю все э. д. с., кроме ek{i),
(8'23tl)
и потому Wjk{D) называется сопротивлением передачи от й-го к /’Му контуру. •
502 СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
[гл. 8
Если электродвижущие силы ej (Z) создаются генераторами синусоидального тока одной и той же частоты <о, но, вообще, разных амплитуд и фаз, то мгновенное значение e(t) может быть представлено как действительная (или мнимая) часть выражения в котором Е обозначает матричную комплексную амплитуду, а I—мнимую единицу. Соответствующее мгновенное значение матрицы-столбца контурных токов при установившихся колебаниях будет действительной (или мнимой) частью выражения причём комплексная амплитуда I связана с Е соотношением
I — Y (Zoo) E = Z (Zoo) \ Е.
(8.231)
Так как мы в дальнейшем будем оперировать главным образом комплексными амплитудами, то путаницы от применения одной и той же буквы Z для обозначения матрицы токов и мнимой единицы можно не опасаться.
Матрицы Y (Z<o), Z(Zoo) являются частотными формами матричной проводимости и матричного сопротивления. Их действительные части— чётные, а мнимые части — нечётные функции от оо.
Для цепи переменного тока можно также получить уравнение энергии (§ 29). Средняя или активная мощность приложенной э. д. с. ej(f) есть
+ тс/ш
£ / <8-232)
—тс/со
Для пассивной цепи
Zjl( (D) = -* fjk (D) = LjkD + Rjk + - , (8.233)
где элементы Ljk, Rjk, 1/Cjk образуют три симметричные матрицы. Так как величины, аналогичные в уравнении энергии (220) в данном случае отсутствуют, то это уравнение получает вид
где
1(£'7+е7)=|лГ(7, 7),
NU, Ъ = S ВД4-
(8.234)
(8.235)
В случае активной цепи форма уравнения энергии будет зависеть от того, в какой мере учитываются проводимости сетка-катод в электронных лампах.
§ 8.31. Двухполюсники. Предположим, что один из контуров цепи не замкнут и заканчивается двумя зажимами (фиг. 84). Присваивая этому контуру номер 1, заменим действие отключённой его части, которая может быть соединена с другими цепями, электро
§ 8.31]
ДВУХПОЛЮСНИКИ
503
движущей силой ех((). Если в остальных контурах приложенных э. д. с. нет (г2= ... = г№ = 0), то полученная система называется двухполюсником.
Ток в разрезанном контуре будет
. i1 = y;i(D)e1. (8.236)
Так как Y (О) — матрица, обратная матричному сопротивлению
Z(D)=1-/(0), (8.237)
где /(D) —матричный квадратный трёхчлен, то
(D)
<8-238>
при этом A(D) есть определитель матрицы f(D)9 a — эле-
менты её присоединённой.
Обозначая через Za(D) входное сопротивление цепи со стороны первого контура, имеем:
Z'<P)=-&$>) (8'239>
а если применить вместо е19 обозначения #А, iA, то соотношение между этими величинами примет вид
Фиг. 84. Двухполюсник.
Функция ZA (р) называется также сопротивлением двухполюсника и вполне характеризует его поведение в отношении всех других цепей, с которыми он может быть связан через свои зажимы. С этой точки зрения два двухполюсника называются эквивалентными, если их сопротивление Z^(D) одно и то же, хотя их внутренняя структура может быть различной.
Пусть имеем второй двухполюсник с сопротивлением Zb(D), так что
1в = zB (Р) • (8.241)
При последовательном соединении обоих двухполюсников (фиг. 85) — iB == I и
е = еА + ев = Z (D) Z, (8.242)
где
Z (D) = ZA (D) + ZB (D). (8.243)
При параллельном соединении (фиг. 86) еА = ев = е и
= ^ + ^ = Z(D) ’ (8.244)
504
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
[гл. 8
где
1 — 1 4- 1
Z(D) — Za(D) ' Zb(D) •
(8.245)
Таким образом, мы получаем обобщение известных элементарных правил: при последовательном соединении складываются сопротивления, а при параллельном — проводимости.
Соединяя несколько двухполюсников, можно получать новые двухполюсники или, вообще, новые цепи. Мы можем предположить, напри-
Фиг. 85. Последовательное соединение двухполюсников.
Фиг. 86. Параллельное соединение двухполюсников.
мер, что п контуров цепи, определяемой матричным уравнением (224), состоят из любых последовательно включённых двухполюсников, а не только простых индуктивностей, омических сопротивлений и ёмкостей; при наличии взаимной индукции контуров и электронных ламп их эффект учитывается обычным образом. В этом случае собственные
а) б)
*
Фиг. 87. Эквивалентные двухполюсники.
и взаимные сопротивления (D) будут, вообще, уже не полиномами, а дробными рациональными функциями.
В качестве примера рассмотрим сложные двухполюсники а), б) на фиг. 87 и постараемся определить положительные числа с, d> е9 / таким образом, чтобы двухполюсники были эквивалентны при любых сопротивлениях Zt(P)t Z^(P) и положительных числах а, Ь,
§ 8.31]
ДВУХПОЛЮСНИКИ
505
Составляя выражения сопротивлений и приравнивая их, имеем: t 1 f- + aZx + Z>Z2 =-------------j------1-----j---, (8.246)
Zj Z2 cZj -j- </Zg eZ\ 4*fZ2
(8.248)
df из двух
(8.249)
или *
[a(c + <0 — <*]Z|4-[£(d-]-/) — df]z’-J-
+ [(1 + a + b) (c + e) + a (d-]-/) — ce — (c/+de)] zfz2 +
+ P (c + *) + (1 + a + b) (d+/) — df—(cf+ de)] Z,Z22 = 0. (8.247)
Приравнивая нулю коэффициенты при степенях и произведениях Z19 Z& находим:
а (с е) = се, b(d-\-f) = df, (1 -f- ci -|~ b) (c -|- e) -|- a (d 4- /) = ce -p cf b(c-^re) + (l + a^rb)(d+f) = df-^cf+de.
Если с помощью первых двух уравнений исключить се, последних и положить
x* = cf-{-de,
(1 + b) (с + е) + a (d+/) = х2,
^(с + е) + (1+а)(^+/) = х2, откуда
с 4-е — 1+а+6>
ах* bjfl
Ce~l + a + b’ df ~ 14a-j-6;
следовательно,
“ ^=2<i+*+»>l*=i=/*’l~'‘i'(1+°+i')l'
Подстановка этих выражений в (249) даёт для х уравнение, из которого
х=У\-\-а-\-ЬВ, (8.251)
где
В = / (1а 4-й)2 — 4aft. (8.252)
Для с, d, е, f получаются окончательные формулы:
(8.250)
с, е = ±В[В + (1 — а-\-Ь)], &
. d, f=^B\B + (\-\-a — b)].
(8.253)
506
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
[гл. 8 I
При этом можно взять либо верхний знак для с и нижний для е, 3 либо наоборот, и аналогично для d и /. В итоге получаются два || существенно различных решения. ж
§ 8.32. Четырёхполюсники. Предположим теперь, что два из п I контуров электрической цепи не замкнуты и заканчиваются двумя 1 парами зажимов, которые мы назовём входными (х) и выходными (у), 1 Действие отключённых частей двух контуров, которые могут быть | соединены с другими цепями, заменим электродвижущими силами ех, 1 eyi а токи в этих контурах обозна- 1 чим через ix, iy. Полученная си- f стема называется четырёхполюсни- | ком (фиг. 88). Во многих электротехнических расчётах нас интересует не внутренняя структура четырёхполюсника сама по себе, а лишь определяемые ею соотношения между
напряжениями и токами на входе и выходе. Эта точка зрения лежит в основе теории четырёхполюсников. В качестве таковых могут рассматриваться линии электропередачи, трансформаторы, электрические фильтры, измерительные схемы и т. д. Теория четырёхполюсников может быть приложена и к механическим задачам.
Присваивая входному и выходному контурам номера 1 и 2,
имеем из общих уравнений цепи, разрешённых относительно токов (§ 30): 1
Фиг. 88. Четырёхполюсник.
5
к а-1
й if-
Лр S'
У'
(8.254) |
Следует заметить, однако, что так как при показанных на схеме > направлениях отсчёта напряжений и токов положительное напра- 1 вление для еу противоположно положительному направлению тока iy 1 в выходном контуре, то величины К12(£>), К22(О) отличаются знаком 1 от тех, которые были обозначены теми же символами в общей теории 1 /г-контурной цепи. Поэтому, например, в случае пассивного четырёх- Ц полюсника мы имеем условие взаимности Ж
12 — 1 21
X*
Иногда приходится пользоваться соотношениями, полученными 1 путём разрешения относительно ех, еу и ext I
&Х = ^11^^) ^Х "F ^12 (^)
&у “ ^21 (^) ^х ^22 (^) 1у>
У*
(8.257) 1
у*
§ 8.32] четырёхполюсники 507
При этом
А1 Аг Аг
(8.258)
Так как
(8.259)
то соотношения взаимности для пассивного четырёхполюсника, выраженные через или Ajk, будут:
Аг = Ах» (8.260)
Ах Аг Аг Ах = 1 • (8.261)
Отметим, что все эти условия необходимы, но недостаточны для того, чтобы четырёхполюсник был пассивным.
Четырёхполюсники, удовлетворяющие условиям взаимности, для которых Уп = — У22 и, следовательно, Ztl = — Z22, Alt = А22, носят название симметричных.
Вводя матрицы
еу
Y (D) = || Yjk (D) ||, Z (D) = || Zjk (D) ||,
Л(О)=||Л/Й(О)||(2Х2),
(8.262)
(8.263)
представим основные соотношения (254), (256), (257) в форме i=Y(D)e, ]
e = Z(D)i, I (8.264)
х = A(D)y. j
При этом
y(D)±=Z-i(D). (8.265)
Можно было бы ввести также матрицу
ЛГ(П) = Л-1(О), (8.266)
представляющую трансмиттанс четырёхполюсника в смысле § 4.8, и написать
у = Х(Р)х. (8.267)
Однако матрица' A(D) более употребительна.
508
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
[гл. 8
Если в четырёхполюснике с помощью соединённого с ним генератора поддерживается режим установившихся гармонических колебаний, то для их изучения мы можем пользоваться полученными выше соотношениями, в которых нужно только вместо мгновенных значений е(0, /(0, x(f)9 y(t) подставить комплексные амплитуды Е, Ц 5, т], а аргумент D функций У, Z, Af X заменить на fa.
§ 8.33. Соединения четырёхполюсников. Пусть два четырёхполюсника Д', Д" соединены каскадом (фиг. 89), т. е. таким обра-
Фиг. 89. Четырёхполюсники, соединённые каскадом.
зом, что выходные зажимы первого соединяются с входными зажимами второго и потому у' = х". Из уравнений
или
имеем:
где
х' = ДУ, у = Х'х', х' = Ду", А = Д'Д",
х" = Д'У у" = Х"х” у” = Хх\ Х = Х"Х'.
(8.268)
(8.269)
(8.270)
(8.271)
Таким образом, каскад эквивалентен одному четырёхполюснику, и для получения его матрицы А и трансмиттанса X нужно перемножить матрицы Д', Д" и трансмиттансы составляющих четырёхполюсников.
Фиг. 90. Последовательное соединение четырёхполюсников.
В случае последовательного соединения (фиг. 90) мы имеем:
/гр/ = 1 Zjjj, 1уг —* iyu —“ I ——1 — Z, (8.272)
и из уравнений
е' = Z'Z', У'«ZV (8.273)
§ 8.34] ВОЛНОВЫЕ ПАРАМЕТРЫ ЧЕТЫРЁХПОЛЮСНИКА
509
получается:
e = (Z' + Z")Z,
(8.274)
где элементы матрицы е — ег-\-еп представляют напряжения на входе и выходе* четырёхполюсника, эквивалентного двум данным. Таким образом, при последовательном соединении матрицы сопротивлений складываются.
Фиг. 91. Параллельное соединение четырёхполюсников.
Наконец, при параллельном соединении (фиг. 91)
eX'~ex» = exi ey’=ey>'—eyi ef = ef/ — e (8.275) и из уравнений
/' = Y'e’, i" = Y"e" (8.276)
получается:
/ = (У' + У")е, (8.277)
где элементы матрицы / = суть токи на входе и выходе эквивалентного четырёхполюсника. Таким образом, при параллельном соединении складываются матрицы проводимостей.
Все эти правила немедленно обобщаются на случаи соединения п четырёхполюсников.
§ 8.34. Волновые параметры четырёхполюсника. Предположим, ЧТО зажимы (у) четырёхполюсника замкнуты на сопротивление Zy, а к зажимам (х) присоединён генератор переменного тока, с помощью которого поддерживается режим* установившихся гармонических колебаний, определяемый уравнениями
(8.278)
^х у ^12^’
Лс == ^21 ^у ^22^у* .
Так как Еу = то
(8.279)
510
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
[гл. 8
Отношение
X
(8.280)
представляет входное сопротивление на зажимах (х), и мы имеем:
(8.281)
Аналогичным образом, если левые зажимы замкнуты сопротивление ZXi то, учитывая принятые направления
—Г _ пряжений и токов, имеем —EX = ZXIX или
на внешнее отсчёта на-
Входное сопротивление у правых зажимов будет:
7Г___ Еу
ЛУ — 7
*У
или
12
у —
(8.284)
Если потребовать, чтобы при Zx — Zx было z'y = Zy, то
Разрешая это уравнение относительно Zx и подставляя результат в предыдущее, находим:
Zx=Wlq, Zy=Wq, (8.286)
где ___ ______________
v=V^- <8-287>
Каждый из радикалов УAjk должен иметь здесь и в дальнейшем одно из двух возможных для него значений *). Величины Zxi Zy по основаниям, которые .выяснятся позже, называются волновыми сопротивлениями четырёхполюсника.
Если зажимы (у) замкнуты на внешнее сопротивление Zy, равное волновому, то в силу соотношений Ey = ZyIyi Ex = ZaJx находим из второго уравнения (278)
== Ч" ^22) 1у (8.288)
*) Значения радикалов выбираются так, чтобы действительная часть волнового коэффициента распространения gx, определяемого согласно (290), была положительной.
г
§ 8.34] волновые параметры четырёхполюсника 511
Фг=14=4 г+='
£Л zy'y q __________ _________
= (/Л1Л2 +/Л12Дц)2- (8.289)
Полагая _____ ________
• = е я = /ЛиЛ22 + /А2Аа, (8.290)
имеем:
= (8.291)
* Ьу'у
Комплексное число gx, равное половине натурального логарифма отношения кажущихся комплексных мощностей ЕХ1Х, Еу1у на входе и выходе четырёхполюсника, называется волновым коэффициентом распространения в направлении от зажимов (х) к зажимам (у).
Действительная часть
=i1П <8'292)
называется волновым коэффициентом затухания и определяется однозначно как половина натурального логарифма отношения кажущихся мощностей и |£^| • |/^|. Этот коэффициент выра-
жается в неперах или децибелах.
Мнимая часть Ьх волнового коэффициента распространения называется волновым аргументом запаздывания и выражается в радианах или градусах.
При замыкании левых зажимов на внешнее ’ сопротивление имеем, согласно предыдущему, —Ex = ZxIxi —Ey = ZyIyi так чт0
/« = ( - +А2) 4. (8-293)
^У^У _ Zy^ У _________1.
ZA (-AxWq + Aa)* (-Л211Г+Л22/7)2
= ----- 1 - (8.294)
( V Л11Л22 — V A^A^i)
Волновой коэффициент распространения в направлении от (у) к вводится с помощью соотношения
е вУ^е {аУ+ у} =VАпА.^ — VА12А21
или
Л23ц__ zy?y
е Е Т ’
Sy = ау + = у In gA".
(8.295)
(8.296)
512
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
[гл. 8
Полагая имеем:
и
gB = g’+8> gy = g— 8> g=^(gx-\-gy\ ^ = ^(gx — gy)
е8chg = -i-{ева> + e By)=VЛ1л22»
e8 sh g= у (/®—e~Sy) = VЛ12Л21 , •
»28 — <?Х~ОУ — A A _A A
e — e — Л12Л21-
Отсюда следует, что для пассивного четырёхполюсника
(8.297)
(8.298)
(8.299)
(8.300)
и коэффициенты распространения в обоих направлениях одинаковы: gx = gy- (8-301)
Для симметричного четырёхполюсника
9=1, Zx = Zy=W. (8.302)
Полученные соотношения (287), (299) дают возможность выразить ; четыре элемента матрицы А через четыре волновых параметра W, q, 8, g или W, q, gx, gv:
= +« v)>
Л12 = e*W shg= 4- W(ea — е~ву),
z>S 1 д^ — д
^ = vsh^=2^(A-e Ч
(8.303);
Л22 = e*q ch g = (ел -j- e 3y).
(8.304)
Уравнения четырёхполюсника могут быть, следовательно, выражены через волновые параметры следующим образом:
Ех = е8 ("7 ch g ЕУ+11/811 ^4) > 4=«8 (-^sh %еу+?ch ^4) •
Пусть имеем каскад из дву^ четырёхполюсников с параметрамй| ^1» <71» Si и ^2’ ?2> ^2’ Si и согласованными волновыми сопро^] тивлениями, т. е. волновое сопротивление Z± = W1q1 на выходе|
§ 8.34]
ВОЛНОВЫЕ ПАРАМЕТРЫ ЧЕТЫРЁХПОЛЮСНИКА
513
первого равно волновому сопротивлению W2/q2 на входе второго:
= (8.305)
Перемножая матрицы
sh gt
ch gl
F2 sh g2
42 ch g2
, (8.306)
получим каскаду,
для матрицы А = А1А.2 четырёхполюсника, эквивалентного
выражение
rshg-
?chg
(8.307)
в котором
Г=И71?2 =
1Г2
41 ’
Г2 ) 4^=4142 = -^, g=gi + gi- I
(8.308)
О — Oj —Og,
Отсюда
5+ 8 = (& + 81) + (& + 82). g — 8 = (& - М + — 82), (8.309)
т. е. коэффициенты распространения эквивалентного четырёхполюсника равны суммам соответствующих коэффициентов распространения составляющих четырёхполюсников.
Входное и выходное волновые сопротивления эквивалентного четырёхполюсника будут:
Z2=Wq=W2q2, (8.310)
Ч VI
Т. е. они равны соответственно входному волновому сопротивлению первого и выходному волновому сопротивлению второго.
Пусть теперь имеем каскад из п четырёхполюсников с параметрами Wj, gj (J = 1, ..., ri) и согласованными волновыми сопротивлениями Zj на выходе j-го четырёхполюсника и входе (/~|-1)-го:
= C/=1..........*-!)• <8-311)
Из этого условия вытекает:
^+1 = Щц, = ^14141... q^14j = zoqf... (8.312)
Каскад эквивалентен одному четырёхполюснику с параметрами U7, A, G. при этом
Zo = -^, Zn=Wq (8.313)
v
33 Зак. 1474. Б В. Булгаков
514
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
[гл. 8
и, в качестве обобщения второго соотношения (308),
Следовательно,
W, = W qi'“qj~1 , (8.314)
1 4j+l---4n 1
т. е. если все q$ выбраны, то в силу условий согласования п величин Wj выражаются через один независимый параметр W.
Для А, О имеем формулы п п
Д = 2 Ч G = (8-315)
4=1 4=1
а волновые сопротивления Zj выражаются через W, q'lt . дующим образом:
Zj=W
Vj+1
., qn еле-
(8.316)
§ 8.35. Четырёхполюсники, составленные из одного двухполюсника. Рассмотрим в качестве простейших примеров четырёхпо-
Фиг. 92. Четырёхполюсники, составленные из одного двухполюсника.
люсники, составленные из одного двухполюсника (фиг. 92). Для схемы а),
очевидно, имеем:
так что
(8.317)
(8.318)
(8.319)
(8.320)
(8.321)
(8.322)
(8.323)
I
§ 8.361
Для схемы б):
и
ТРАНСФОРМАТОР
515
(8.324)
(8.325)
(8.326)
(8.327)
(8.328)
(8.329)
(8.330)
§ 8.36. Трансформатор. Пусть первичная обмотка соединена с входными зажимами, вторичная — с выходными. Из схемы (фиг. 93)
выводим уравнения
ех = (LAD + Ra) ix — MDiy, 1
— ey — {LBD Rb) iy — MDix, J откуда
(8.331)
Zu(D) = LaD + Ra, Z^D) = -MD,
Z21 (D) = MD, Z22 (D) = — (LBD + RB), .
ZUZ22 — Z12Z21----(LALB — М2) № _ (LaRb 4. LbRa) D—
— RaRb,
A<‘ & =
. m. «>>ОЧ-(АЛ + £В^>О-Я^В
Л12 \U) =
MD
Л21 (D) = -±-, Л22 (D) = - - . '
Ali^22 Аз Aa — 1 •
Четырёхполюсник является пассивным.
Имея в виду установившиеся гармонические колебания, находим, вменяя D через Zw:
w=V- (lalb—м2) <i>2+RaRb -i- гш (larb 4- lbra) ,
Ra + ^a^ '
33*
(8.334)
516
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
[гл, 8
Если пренебречь потерями и рассеянием, то Ra и Rb следует считать равными нулю, а коэффициент связи k = M/V LaLb— единице; тогда
(^) = ^12 (^) = V LaLb (g 335)
Z21 (О) = /ZIZT Dt Z22 (D) = — LBD,
An(P) = ±, Л12(Я) = 0,|
i 1 (8.336)
-^21 (^)= i/r 7~“ n * ^22 (D)=q ’ ।
г lalbu J
r=0, q=y^, (8.337)
8 = g- = 0. (8.338)
Для коэффициента трансформации, т. е. отношения комплексных амплитуд Ех, Еу, имеем выражение
Еу _ ^21Ав + ZzJy _ У LB VLB !У ,g qqqx
E06 ZtfJai + ZvJy У La У La Л» — У LB Iv
или
= q. (8.340)
Таким образом, при отсутствии потерь и рассеяния коэффициент трансформации не зависит от нагрузки и от частоты.
Фиг. 93. Схема трансформатора.
Пусть вторичная обмотка замкнута на сопротивление ZH, так что Ey — ZJy. Тогда
zJy х ~Ь ^22^у = (1^ LaLb Iх Ев!^) (8.341)
и отношение комплексных токов на входе и выходе будет:
ty ^У^^а^в
Zh "h ^^в
(8.342)
§ 8.37]
ЧЕТЫРЁХПОЛЮСНИКИ, СОДЕРЖАЩИЕ ТРИОДЫ
517
Если сделать дополнительное предположение, что £л<о, LB& беско-
нечно велики по сравнению с ZH , то мы получим идеальный трансформатор, для которого
(8.343)
т. е. отношение комплексных амплитуд токов постоянно и обратно . такому же отношению для напряжений. Матрица А будет:
О
Ч
(8.344)
Четырёхполюсник с диагональной матрицей А такого вида, где q, однако, не обязательно действительно и постоянно, а может быть любой функцией от D, называется идеальным преобразователем} он не может быть точно физически реализован. Волновой коэффициент распространения идеального преобразователя равен нулю. Любой несимметричный четырёхполюсник эквивалентен симметричному, соединённому каскадом с идеальным преобразователем:
е*
1 .
Tchg
№shg
<7 dig
ch g Zyshg
1 1, и
т-shg chg
(8.345)
Соединим произвольный четырёхполюсник каскадом со стороны входных зажимов с идеальным преобразователем, имеющим коэффициент трансформации fe; для полученного нового четырёхполюсника входное волновое сопротивление будет уже не Zxi a Zx= Zx!k\ между тем как Zy не изменится; если идеальный преобразователь присоединить со стороны выходных зажимов, то Zx не изменится, а Zy обратится в Zy — Zy№. Постоянные распространения g ± 3 остаются в обоих случаях без изменения. Мы можем таким способом изменять волновые сопротивления, если только удаётся с достаточным приближением реализовать идеальный преобразователь.
§ 8.37. Четырёхполюсники, содержащие триоды. Начнём с триода (фиг. 94), цепь сетки которого связана с входными зажимами, а анодная цепь — с выходными. При этом пренебрежём как сеточным током, так и всеми межэлектродными ёмкостями. Согласно § 7.11, усиление лампы можно учесть, вводя в анодную цепь приложенную э. д. с. — pegi
ец— напряжение ца сеткеЦо ц нашей схеме ед есть входное
518
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
[гл. 8
напряжение и потому
в у = &&у>
где Rt — внутреннее сопротивление лампы. А так как
и мы условились пренебречь сеточным током, то
Следовательно,
откуда
i
(8.346)
(8.347)
(8.348)
(8.349)
(8.350)
Рассмотрим теперь схему (фиг. 95), представляющую ступень лампового усилителя со связью между анодом и сеткой через сопроти-
Фиг. 94. Идеальный триод.
Фиг. 95. Ступень лампового усилителя.
вление Zb- Сопротивления Za, Zg представляют межэлектродные ёмкости. В качестве четырёх контурных токов примем входной ток ix, выходной ток iy1 сеточный ток i' и анодный ток контуры отмечены на схеме. Вводя в анодную цепь э. д. с. — представляющую эффект усиления, получим следующие уравнения контурных токов:
(Zb + ZG) — ZGiy — (Zb + ZG) i' + ZGi" = ex, ZGix ZGiy —ZGi ZGi —- Cy,
4—{Zb ZG) ix-\-ZGiy -j- (Za -f-Zb^-Zq) i'—ZGi" — 0,
ZGix — ZGiy — ZGir (R$ ZG} i!r = —^ZAir-
(8.351)
§ 8.38]
РЕШЁТЧАТЫЙ ЧЕТЫРЁХПОЛЮСНИК
519
Если отсюда исключить i коэффициенты при ех, еу будут
у/ и выразить ix, iy через элементами матрицы
еу> ТО
где S = ^!Ri. Отсюда
R*ZB
12 “ Ri
21 —
22 —
д а А —
11л22 л12л21 — J
(8.354)
§ 8.38. Решётчатый четырёхполюсник. Схему, представленную здесь (фиг. 96) в двух вариантах, можно получить из цепи, рассмотренной в § 7.10, полагая
&Х --- е Zplgp £в.1у*
(8.355)
Фиг. 96. Решётчатый четырёхполюсник.
л —
И
с
Тогда уравнения (7.98) принимают вид
(^в -Jr Zc) 4~ Z&y (Zb -Н Zo) 1g &х*
Zblx “Ь С^в “Ь ^в) iy — (Zb 4~ Zb) ie = — еу9
{Zb Zq) ix — (Zb Ц- Zb) iy -|-
Ч- (Za 4“ Zb + Zq 4- Zb) 4 = 0.
(8.356)
520
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
[гл. 8
Исключая L, находим:
еу
(8.357)
где
Z =
(Za + Zd)(Zb+Zg)
(ZA + ZC)(ZB+ZB)
(8.358)
откуда
ZBZCZD~^ZCZDZ A +ZDZAZb+ZAZВ ZC
(ZX+ZD) (ZB+ZC)
ZAZB ~ ZCZB
С^д 4" Z(^ (ZB + ZD$ ZaZb — ZcZT)
(8.359)
^11^22 Al2^21 — 1 *
В частном случае симметричной Zg— Zj) = Zb И
схемы (фиг. 97) Za==Zb = Zo,
(8.360)
^11^22 ^12^21 —
(8.361)
(8.362)
(8.363)
Для вычисления g можно также пользоваться формулой
§ 8.39] КРАЕВАЯ ЗАДАЧА ДЛЯ ЧЕТЫРЁХПОЛЮСНИКА
Пусть, например (фиг. 98), - = Zb= •
Тогда при D = Zo> _
w=zx = zy=^^,
д__ 1 + I УLC (D
1 — i УLC ад
521
(8.365)
(8.366)
(8.367)
части последнего выражения равен еди-
b = arg . (8.368)
1 —Z
сопротивления постоянны, а волновой коэф-
Так как модуль правой нице, то
а = О,
Таким образом, волновые
фициент затухания равен нулю при всех частотах, вследствие чего,
Фиг. 97. Симметричный решётчатый Фиг. 98. Фазовый контур, четырёхполюсник.
работая между согласованными сопротивлениями, четырёхполюсник
не изменяет действительных амплитуд передаваемых напряжений и токов. С другой стороны, с увеличением со от 0 до оо волновой
аргумент запаздывания пробегает все значения от 0 до к. Поэтому подобные четырёхполюсники применяются для компенсации фазовых искажений.
§ 8.39. Краевая задача для четырёхполюсника. Пусть к входным зажимам четырёхполюс
ника с матрицей А присоединён Фиг. 99. Четырёхполюсник, включён-генератор синусоидального напря- ный между генератором и нагрузкой, жения с внутренним сопротивле-
нием Zr, а к выходным зажимам — нагрузочное сопротивление ZH (фиг. 99). Обозначая через Е действительную амплитуду э. д. q. генератора, имеем краевые условия
(8.369)
522
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [гл. 8
Сопротивления Zr> ZH можно рассматривать (§ 35) как четырёхполюсники с матрицами
Матрица каскада
из трёх четырёхполюсников будет:
(8.370)
•^21
1
О
ZH
Лп
Л21
1
^12
•^22
(8.371)
А’ = ЛГЛЛВ =
1
О
Напряжение и ток на входе каскада суть Е, 1Х, а на выходе 0, /„ и потому
(8.372)
Заменяя Ajk их выражениями (303), находим:
+ Zy) (е8 — г^Гув-8),
(8.373)
где величины
(8.374)
носят название коэффициентов отражения.
Из второго краевого условия и первого соотношения (372) получаются следующие выражения для напряжения и тока на выходе
2ZHUZ£e-S
(Zr + Zx) (Za + Zy) (eS-r^e-S) '
____________2WEe~*__________
(Z„ + Z ) (ZH + Z„) (e« — rjrf8) • ' r * ' H • Jr' X у 'J
(8.375)
§ 8.40. Краевая задача для каскада четырёхполюсников с согласованными волновыми сопротивлениями. Пусть имеем каскад из п четырёхполюсников с согласованными волновыми сопротивлениями, который мы уже рассматривали в конце § 34. Предположим, что к входным зажимам первого звена присоединён генератор с внутренним сопротивлением Zr, а к выходным зажимам последнего звена — нагрузка ZH. Будем обозначать через Е
§ 8.40] КРАЕВАЯ ЗАДАЧА ДЛЯ КАСКАДА ЧЕТЫРЁХПОЛЮСНИКОВ 523
действительную амплитуду напряжения генератора, через Ij — комплексные амплитуды напряжения и тока на выходе у-го звена и входе C/-f-l)-ro. Согласно формулам предыдущего параграфа,
где
(8.376)
2Z„U7Ee-A
(Zr + ZQ) (ZH + zn) - r^e-0) ’
(8.377)
Часть каскада, состоящая из четырёхполюсников с номерами от (/-]- 1)-го Д° и-го включительно, эквивалентна одному четырёхполюснику с параметрами Wf, д', Д', G', где
ч п * п
Д'=2Х о'=2&. ^+1 J*+l
Поэтому
Ел = *д' O'ch °' • £n + 4 sh O' • In], v \qr * qt njf
= (-y- sh G' • En-^-q' ch O' •
(8.378)
(8.379)
Подставляя выражения En, In, имеем:
2ЖЕе"д+д'
(Zr + ZQ) (ZH + Zw) (eG - rxrye-G) q'
(ZHchG'+ZnshG'),
_________21Г£е~д+д'^_______
(Zr + Z.) (Z_ + Z„) (eG — rje-0)
4 sh G' + ch G'
(8.380)
если же воспользоваться тем, что, согласно (316),
то
W Z< IF 1 er ___ _
Я' 71 * • • 7/ 71 • • • Яп
(8.381)
(8.382)
524
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
[гл. 8
(8.383)
(8.384)
(8.385)
получим для мгновенных значений (f) = Re Ejei,ot, ij (Z) = Re 1$ем формулы
= cos «(*—$) +cos ш (£+£}), 3gg
= costa(t—У3' cos ш
Чтобы дать кинематическую интерпретацию, рассмотрим сначала частный случай, когда числа t~., t~ монотонно возрастают вместе с /; легко убедиться, что это будет иметь место, например, в том случае, когда каскад составлен из п одинаковых фазовых контуров по схеме фиг. 98. При указанных условиях первые слагаемые в выражениях ^(0, представляют волны напряжения и тока, распространяющиеся по каскаду в направлении роста индекса /, так как мы имеем одну и ту же фазу напряжения на выходе 1-го, 2-го, 3-го,... четырёхполюсников в моменты Т-4-/+,
• • • и °ДНУ и ТУ же фазу тока в моменты
Т-Ь4з’ ••• Распространение волн может сопровождаться нарастанием или затуханием амплитуд. Аналогичные соображения показывают, что вторые слагаемые в выражениях ^(0, *j(0 представляют отражённые волны, распространяющиеся в направлении убывания индекса у, причем амплитуды могут также нарастать или
§ 8.41] ПОВТОРНЫЕ ПАРАМЕТРЫ ЧЕТЫРЕХПОЛЮСНИКА 525
затухать. Величины д$ ® ± (byj+©7—©/.о,
д^.=1(^— Ф/+ФМ Д^=|(^-+Ф7-Ф7-1) (8’387)
представляют времена распространения падающих и отражённых волн в у-м четырёхполюснике.
В общем случае кинематика будет более сложной, так как те значения индекса у, при которых нарастание чисел одной из последовательностей t+-, 1~ сменяется убыванием или наоборот,
являются такими точками сходящегося или расходящегося движения соот
ветствующих волн, в которых направление этого движения меняется на обратное. Наименования падающей и отражённой волн могут быть сохранены за составляющими напряжений и токов лишь в качестве условных.
Отношение комплексных амплитуд напряжения и тока для падающих волн равно Zj, т. е. волновому сопротивлению на выходе у-го четырёхполюсника. Для отражённых волн соответствующее отношение отличается лишь знаком. Таким образом, закон Ома верен в отдельности для падающих и отражённых волн, если только иметь в виду волновое сопротивление, в чём и состоит мотивировка этого наиме
нования.
Если ZH равно Zn, то коэффициент отражения гу и все Сг равны нулю. Иными словами, при замыкании выходных зажимов каскада на внешнее сопротивление, равное волновому, отражённых волн не существует.
§ 8.41. Повторные параметры четырёхполюсника. Пусть зажимы (у) четырёхполюсника замкнуты на внешнее сопротивление Z'; вычисляя, так же как в начале § 34, входное сопротивление на зажимах (х), потребуем, чтобы оно было равно Z':
Отсюда
21Z' (Лц
^12 —
(8.389)
2А21 ' 11 22 I Г V ‘11 л ‘22/ I “ 12 ‘21 / * J
Радикал должен иметь одно из двух возможных для него значений *).
Аналогичным образом, замыкая зажимы (х) на сопротивление Z" и требуя, чтобы входное сопротивление на зажимах (у) имело
*) Значение радикала выбирается так, чтобы действительная часть повторного коэффициента распространения s', определяемого согласно (393), была положительной.
526 СйстМмы С постоянными Коэффициентами [гл. 8
то же самое значение, найдём:
Z" = i <Л22 - Ах + /(Ах - А2)9 + 4Д12Ал). (8.390)
Величины Z', Z" носят название повторных сопротивлений четырёхполюсника .
Если зажимы (у) замкнуты на повторное сопротивление Z', то в силу соотношения Е.. — Z'L. имеем:
J У У
Так как E^ = Z'K и м/ м/
(8.392)
то, полагая
ев> = +ib' = | (Ли _|_ Л22 _|_ у (Аи _ А^ + 4Л12Лл), (8.393)
находим:
s' = a'-\-lb' = 1п> = 1п> = 11п<ф. (8.394)
Число s' называется повторным коэффициентом распространения в направлении от (х) к (у), а его действительная и мнимая части а', Ь'— повторными коэффициентом затухания и аргументом запаздывания. Выражение для а' можно написать в виде
= In
(8.395)
Таким образом, а' равен половине натурального логарифма отношения как кажущихся, так и средних или активных мощностей.
Повторные коэффициент распространения, коэффициент затухания и аргумент запаздывания для направления от (у) к (х) определяются формулой
= = 1 (Ли _|_ л22 _ /(Д11-Л92)-з+4Л12Ал) (8.396)
§ 8.41]
ПОВТОРНЫЕ ПАРАМЕТРЫ ЧЕТЫРЁХПОЛЮСНИКА
527
s" = а" + lb" = In = In ф- = 1 In , (8.397)
*х * £х1х
где имеются в виду направления и токи, получающиеся при замыкании зажимов (х) на повторное сопротивление Z".
Полагая
= /' = ^ — 3, (8.398)
имеем:
s = 1 (s' -]- $"), 8 = 1 (S' — s") (8.399)
М &
и
s8 ch s = 1 (е* + е~8") = 1(ДП -|- Д22),
в8 sh s = 1 (<*' - е~»') = 1/(Ди — Д22)3 -j- 4Д12Д21, <8 -400)
— All ^22 А12^21*
Таким образом, величина 3 здесь та же самая, которую мы ввели ранее вместе с остальными волновыми параметрами.
Для симметричного четырёхполюсника (Ди = А22) мы имеем Zr = Z" — Zx — Zy — W и s = g, так что все повторные параметры совпадают с волновыми.
Полученные соотношения • (389), (390), (400) дают возможность выразить Ajk через четыре параметра Z', Z", 8, 5 или Z', Z", s', s":
. \ Z'ee' sh s I —------=
и
(8.401)
(7t___ ?ГГ
chs —
Уравнения четырёхполюсника, выраженные через повторные пара-метры, получают вид
(8.402)
Пусть имеем каскад из двух четырёхполюсников с одинаковыми повторными сопротивлениями Z', Z"; остальные параметры имеют значения 81э Sj и 32, s2. Перемножая матрицы четырёхполюсников Alt Аа,
528
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
[гл. 8
получим матрицу А = А±А.2 четырёхполюсника, эквивалентного каскаду, для которого Z', Z" имеют те же значения, а остальные параметры будут:
3 = 8Х 82, s = ^ + $2. (8.403)
Отсюда
s' = 4 + s'2, s" = s" + 4. (8.404)
В случае каскада из п четырёхполюсников с одинаковыми повторными сопротивлениями мы имеем для эквивалентного четырёхполюсника п п
Д = 23., 5 = 2^. (8.405)
1 1
Приведём ещё решение краевой задачи § 39, выраженное через повторные параметры. Вводя в качестве коэффициентов отражения величины
(8.406)
мы имеем при краевых условиях (369) следующие выражения для комплексных амплитуд напряжения и тока на выходе:
, = ZH (Zz + Z") Ее-*
у (ZT + Z') (Zn + Z") (е8 - r'r"e~s) ’
(8.407)
§ 8.42. Г-образные и Т-образные четырёхполюсники. Элементы Т-образной схемы представляют какие угодно пассивные или активные двухполюсные цепи с сопротивлениями Z^, Z^, Zq (фиг. 100).
Фиг. 100. Т-образный четырёхполюсник.
Составляя уравнения контурных токов для входного и выходного контуров, отмеченных на схеме, имеем:
(Zj.—Zp) /д» Zj^iy — &х*
— Zb^x + (Zb -]~Zc)iy = — eyi
(8.408)
§ 8.42]
Г-ОБРАЗНЫЕ И Т-ОБРАЗНЫЕ ЧЕТЫРЁХПОЛЮСНИКИ
так что
(8.409)
откуда
Zb —(Zb-(-Zc')>
ZnZ22---^12^21 = V(^11^22 ^12^21) =
= — (ZBZ С+% qZa -|- ZjZb)>
(8.410)
A1^22 ^12^21 — 1 •
Фиг. 101. Г-образный четырёхполюсник.
Волновые параметры:
W— ZqZa ZaZb>
Фиг. 102. Обращённый Г-образ-ный четырёхполюсник.
8 = 0,
(Za + Zb) (/в + Zg) ZbZq + Z qZa + ZaZb
(8.411)
Повторные параметры:
cths =
34 Зак. 1474. Б. В. Булгаков
(8.412)
530
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
[гл. 8
Для частного случая Г-схемы (фиг. 101) имеем Z^ = 0, ZG = Zb, ZG=Za и
(8.413)
Zp 4~ ____
У ZO(Z„ + 4Z6) '
Za Za
Фиг. 103. Симметричный Т-образный четырёхполюсник.
Для обращённой Г-схемы (фиг. 102) Zj. = Za, Zs = Zb, Z(y = 0 и
8 = 0, cthg-=|/'Z° + Zb ,
Z', zn = (=t V Za+l/za4-4zb),
(8.414)
П-ОБРАЗНЫЙ ЧЕТЫРЁХПОЛЮСНИК
631
§ 8.431
Для симметричной схемы (фиг. 103) ZA'=ZG = Zai ZB = Zbl2 и 1 | ^Zg
Zb
‘ Zb 2Za
3.^» <t>«• "M *HW^^^?V^V^r^T>v«?e4’$«Pj»435fW^W<
Zb
(8.415)
8 = 0, cth 4
a
четырёх-
П-образный ПОЛЮСНИК.
X i i
§ 8.43. П-образный четырёхполюсник. Эта схема (фиг. 104) получается как частный случай четырёхполюсника, рассмотренного в § 37, если положить -> оо, так как тогда электронная лампа не рабо- -тает. Совершая этот предельный переход в выражениях (352),"(353) элементов матриц У, А и обозначая через У а, Уд, Yq обратные величины сопротив- —-—-о лений ZA, Zb, Za, т. е. соответ- фиг 104 ствующие проводимости, имеем:
(
J I-i i
£
J ? t
111 22
YB
(8.416)
1_£ G
^11^2’2 ^12^21
Волновые параметры:
Zq(Za -f- ZB)
ZA(ZB + Z0) ’
(8.417)
8 = 0, cthg = Повторные параметры:
2(Za+Zb + Zg)
(8.418)
ZBZg-\-2ZgZa + ZAZB
cth s = ..... - ---------------.
/ZB (ZA + zc) [ZB (ZA + ZG) + 4ZaZc1
»
34*
ИЯЙ’' 4.
532 СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
[гл. 8
Для симметричной схемы (фиг. 105) 2д = Zq = Zb, Z# = <lZa и
8 = 0, cth|=]/"Zg+ Zb .
(8.419)
§ 8.44. Т-образная ставленный на фиг. 106,
мостовая схема. Четырёхполюсник, пред-применяется в радиотехнике и технике ре-
Фиг. 105. Симметричный П-образ- Фиг. 106. Т-образная мостовая схема, ный четырёхполюсник.
гулирования. Его можно рассматривать (фиг. 107, а) как параллельное соединение Т-образного четырёхполюсника и четырёхполюсника,
Фиг. 107. Параллельное и последовательное соединения, эквивалентные мостовой схеме.
состоящего из одного последовательно включённого сопротивления Z^ или же (фиг. 107, б) как последовательное соединение П-образного
§ 8.45]
ДВОЙНАЯ Т-СХЕМА
533
четырёхполюсника и четырёхполюсника, состоящего из параллельно включённого сопротивления ZB. Поэтому матрицы Y, Z мостовой схемы можно получить суммированием соответствующих матриц, составляющих четырёхполюсников:
ZazB+zAzC+zBzc+zBzD +ZgZb -(ZaZB ±ZAZG+ZBZC±ZBZD)
ZAZB +zAzC+zBzO+zBzD______~(ZAZB+ZAZG+ZAZD+ZBZG±ZBZD)
ZD (ZAZB+ZAZG+ZBZG) 9
yaYg+ Ya Yd+ybyg+ yb yb+ygyb -<Гдya+ yayb+ybyd+ygyd
Ya yg+ YaYd+ybyd+ygyd -{yayb+ya yg+ yayd+ybyd+YGYD)
z ~ YB(YAY0+ yayd+YGYd)
(8.420).
§ 8.45. Двойная Т-схема. Эта схема (фиг. 108), также применяемая в системах регулирования, может рассматриваться как парал-
Фиг. 108. Двойная Т-схема.
Фиг. 109. Параллельное соединение двух Т-образных четырёхполюсников.
Дельное соединение двух Т-образных четырёхполюсников (фиг. 109),
534
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
[гл. 8
Поэтому
11
3(8.421)
(8.422)
22—
Фиг. 110. Т-образный нуль-четырёхполюсник.
2s'*CD j 82/?
12- /21- zBz0i+z0zAi+zAzBi
Пусть, например (фиг. ПО),
Предыдущие формулы дают:
v _ v _ sW&D* + 2 (1 + 82) PCD + 1
41 — У22 —
<2.R(s*RCD + 1)
_ 82/?2C2D2^_l
12 121 OP 4. 1 Г
(8.423)
четырёхполюсников
§ 8.46. Краевая задача для каскада с одинаковыми повторными сопротивлениями. Рассмотрим подробнее (ср. § 41) каскад из п четырёхполюсников с одинаковыми повторными сопротивлениями Z', Z". При тех же краевых условиях, которые мы принимали для одного четырёхполюсника, имеем на выходе каскада:
£
-д
Ж
п
(8.424)
п —
В
кл
§ 8.47]
ВНОСИМЫЕ ПАРАМЕТРЫ
535
С другой стороны, обозначая
• ’ A* = S8ftI S* = isy,
J+l J+l
получаем на выходе /-го звена и входе (/-f- 1)-го:
Ej = е*' [(ch S* 4- g-pg sh $*) Еп + sh S*/„], h = еД*[~Z' + Z" sh+ (chs*- Zz~+1" shs*);«]♦
Подставляя сюда выражения En, In, находим:
Zn (Z'+Z") ch S* + [ZB (Z'—Z")+W"\ sh S* o tK
(Zr + Z') (Z„ + Z") (es - r'r"e~8)
(Z' + Z")chS* + (2ZH-(Z'-Z")]shS* o м дт
---------------------------------£ Q—(Д — Д*)
(Zr + Z') (ZH + Z") (es — r't^e-8)
(8.425)
(8.426)
(8.427)
или
где
(8.428)
(8.429)
—2 = S (afc+^)> Sj = 2 sk—2 (ak 4“ ^)« (8.430)
ii ii
Как и в случае каскада с согласованными волновыми сопротивлениями, нетрудно было бы получить мгновенные значения напряжений и токов и представить каждое как результат суперпозиции Двух волн. Закон Ома верен в отдельности для той и другой волны, сопР°тивления, вообще, различны и равны, соответственно,
§ 8.47. Вносимые параметры. Волновые и повторные параметры характеризуют поведение четырёхполюсника при специальных краевых условиях на выходных или входных зажимах. В практике телеграфно-телефонной связи обычно стремятся, насколько возможно, Удовлетворить этим условиям и неизбежные погрешности в согласо
глг-чт'-'
536
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
[гл. 8
вании сопротивлений требуют лишь незначительных, поправок в расчётах. Исправленные характеристики, учитывающие любые условия замыкания, носят название вносимых и рабочих параметров. Они получаются из решения краевой задачи § 39.
Так как W = 1/Z^Z.., то, полагая г w ]f в
0ВНОО е
Лвноо+г&вноо_"Ь + % у
~ 2/Z^
!—Vyg 2g
(^г + А)/(2/ЛА)
_’ -^я ~Ь % у (1 га>гуе
” 22(Zr4-ZH)/(2 VZX) ’
(8.431)
где A?r = ReZr, 7?H = ReZH суть активные сопротивления генератора и нагрузки, мы можем переписать формулы (375) в виде
”0внос е
____ Е “^вноо у~~Zr + ZH
(8.432)
Если выключить четырёхполюсник и присоединить нагрузочное сопротивление непосредственно к генератору, то напряжение и ток посылаемые в сопротивление, будут:
Ef =
(8.433)
они равны первым множителям в выражениях Еу, 1у. Поэтому ехр (— gBEQG) характеризует эффект включения четырёхполюсника и gBH0C называется вносимым коэффициентом распространения, а Лвносэ ^внос — вносимыми затуханием и аргументом запаздывания. Первым слагаемым выражения
(8.434)
является волновой коэффициент распространения, а остальные связаны, соответственно, с отражением на входе, отражением на выходе, взаимодействием этих отражений и несогласованностью внутреннего сопротивления генератора и сопротивления нагрузки.
Так как
внос
>
(8.435)
§ 8.48]
РАБОЧИЕ ПАРАМЕТРЫ
537
то, зная ехр(—авнос), и —Явное» как функции от частоты, легко построить резонансные кривые для Еу9 1у в числовом или логарифмической масштабе.
§ 8.48. Рабочие параметры. Полагая
#раб___ араб+г&раб
е е
9fl),
(8.436)
имеем из (375)
о “0раб г Е “0раб
Еу — В , 1 лг — ---- В
у 2/7?г/?в у 2/^
где
(8.437)
(8.438)
(8.439)
Величина gpa6 носит название рабочего коэффициента распространения, а яраб и йраб—рабочего затухания и рабочего аргумента запаздывания. Для выяснения физического смысла яраб найдём максимальную мощность, которую генератор может передать непосредственно подключённой к нему нагрузке, предполагая сначала, что 7?н— не зависящие от частоты омические сопротивления.
Напряжение и ток в нагрузке при таком включении выражаются, вообще, формулами (433), а потребляемая мощность будет:
- (Е'Т 4-Ё'Г) = ^^н+З) _ == ^(Zs+zB)
4l } 4(Zr + ZB)(Zr + ^H) 4|Zr+ZH|2
Если же положить
2 (/?г 4- Ян)2 + (Хг + Хв)2 •
то
Считая /?г, Хг фиксированными, вычисляем производные
дР' _Е2 /?2 - RB + (Хг+Хн)2
dRB — 2 [(7?Г + ^В)2 + (Х1, + ХВ)212 ’
дР' м ЯН(ХГ4-ХВ)
дхв — [(/?г + /?в)2 4- (Хг+Хв)2]2
И приравниваем их нулю. Это даёт значения
— /?г»
(8.440)
(8.441)
(8.442)
(8.443)
(8.444)
538
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
[гл. 8
при которых Р' получает максимальное значение
(8.445)
Так как мощность, развиваемая генератором, при этом равна
(8.446)
то мы имеем неблагоприятный баланс
к.п.д. = Ртах/Ро = О,5, (8.447)
что, однако, при тех малых мощностях, с которыми приходится иметь дело в технике связи, не имеет большого значения.
Обозначая теперь через Р мощность, фактически потребляемую в нагрузочном сопротивлении, соединённом с генератором через четырёхполюсник, найдём с помощью (437)
р=4 ад+ад=(Zh+Zb) 1 е'9раб |2 (8 -448) или
Р = . (8.449)
Следовательно,
араб = In |/ (8.450)
Таким образом, рабочее затухание характеризует степень использования генератора и для пассивных четырёхполюсников не может быть отрицательным.
Всё сказанное остаётся верным и в случае, когда Zr и ZH суть сопротивления каких угодно пассивных двухполюсников, так как Rv == Re Zr, Рн = Re ZH положительны при всех частотах; строгое доказательство этого дано ниже, в § 9.21.
Отметим, что величина
„ |Z1,4-Z„|
^oTP = L_EX=aL (8.451)
не может быть меньше единицы, вследствие чего яотр^>0 и
#вноо=== Яраб ЯотР Яраб» (8.452)
Коэффициент Явное может быть отрицателен даже и для пассивного . четырёхполюсника, и тогда этот последний как будто играет роль усилителя; это, однако, должно пониматься лишь таким образом»
§ 8.49]
ПАРАМЕТРЫ КАСКАДА ЧЕТЫРЁХПОЛЮСНИКОВ
539
что четырёхполюсник, изменяя согласование сопротивлений» способствует отдаче генератором большей мощности, чем при непосред-ственйом подключении нагрузки.
§ 8.49. Вносимые и рабочие параметры каскада четырёхполюсников. Чтобы получить формулы для каскада, мы должны начать с преобразования выражения вносимого коэффициента распространения одного четырёхполюсника.
Обозначая попрежнему через ZH сопротивление нагрузки, присоединённой к зажимам (у), и пользуясь соотношением Еу = ZJy и формулами (304) и (286), имеем:
Е* = 27 (<* + е~^ + <-еа — е~9>>
е*
(8.453)
х = \ZJy (ев — е~9) 4- IyWq (ев + е~е)] =
Г 1 Ч „ Ч
Отсюда получаем входное сопротивление
= Еу (Zn + Zy)e9 + (Z^Zy)e^ Ix qZн / (ZH+Z ) ев - (Z„ - Z ) е-в
о и
(-8.454)
или
® 1 — Гуе-*9'
(8.455)
где коэффициент отражения гу определяется попрежнему согласно второй формуле (374). Разрешая относительно гуе~^> имеем также:
Затем
я у
_ ^2 (S4-0)
(8.456)
улу
вх
вх
(8.457)
Н у
е®
У
— е х
540 СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
Поэтому, если ввести коэффициент передачи
то
[гл. 8
(8.458)
(8.459)
Выражение для вносимого коэффициента распространения можно, согласно (432) и (433), представить в виде
где
(8.460)
(8.461)
а Е, Zv обозначают э. д. с. и внутреннее сопротивление Так как
то, обозначая
или
генератора.
(8.462)
(8.463)
(8.464)
получаем искомое выражение для одного четырёхполюсника
5^00 = То+ т- (8.465)
Пусть имеем теперь каскад четырёхполюсников Aj {j = 1, ..., ri) с какими угодно, хотя бы и несогласованными волновыми сопротивлениями Zxj, Zyj. Через Ejt Ij обозначаем попрежнему комплексные амплитуды напряжения и тока на выходе у-го четырёхполюсника и входе (у-{-1)-го, через ZBxy— входное сопротивление у-го четырёхполюсника со стороны его зажимов (х). Мы имеем тогда, согласно (456), формулы
по которым можно последовательно вычислить все ZBX^.
§ 8.50] ОБЩИЙ СЛУЧАЙ ВЫНУЖДЕННЫХ КОЛЕБАНИЙ 541
Вносимый коэффициент распространения каскада будет:
____„ I 1„ ZBXJ+1 + Zyj ZBij+Zxj
Sio/-!- 2VZ . Z 21/Z Z-
U= 1.......«)•
(8.467)
(8.468)
(8.469)
(8.470)
Отсюда имеем также, согласно (468),
(8.471)
(8.472)
(8.473)
Рабочее затухание каскада может быть вычислено по формулам (451) и (471)—(473) с учётом того, что
Яраб — ^внос ^отр-
(8.474)
д. ОБЩИЙ СЛУЧАЙ ВЫНУЖДЕННЫХ КОЛЕБАНИЙ.
А НОРМАЛЬНЫЕ КООРДИНАТЫ
§ 8.50. Общий случай (180) Псу?ь°какие-
□X’ ₽= *« Воспользуемся опять а—ескям
выражением F(D)e(D) (f} (8.475)
У— Д(5) 4
получающимся путём формального^®^pa”34eдр^би Р F (D) е (О)/Д (О) нения (180) относительно у. выделя г бь на эле.
«лук, часть S(D), разложим оста.шуюся "Р“а"“ Sai’no , , 2.20. ментарные; аналогичное вычисление бь Р
542 СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
{гл. 8 4
Часть разложения, относящаяся к корню — Ха+1 = ...== х кратности q9i будет:
(D —kff)P+i ’ р=0
где
Н = 1 Г F(D)^(D)(D —
’+Р («Za-p-n’I-dD^-P-1 A(D) Jp=x
(P 0,1, ..., 1),
и, следовательно, «а-1
’ Л-P-1 F(D)e(D)(D—Ха)«а'
A(D) x(0
а
(8.476)
Штрих при 2 указывает, что суммирование распространяется лишь на индексы
°1 — 1, а2 — qO1 + 1, <*з = (Zaj + ?а2 1, ...»
°^ = + • • • +1» соответствующие W различным корням. Интерпретация символического выражения
<8Л77)
получается, если заметить, что эта функция при действии на неё оператора (О — Ч)р+1 Должна воспроизводить x(t)\ это значит, что она удовлетворяет дифференциальному уравнению
(D — A,)p+1j = x(0. (8.478)
По формуле (38) мы имеем:
/)Р+1е-М?а+р (0 = (D _ V+1 ?,+р (0;
если же положить t
?,+|> (0 =• J £ {t-(т) dT, (8.479) о
(D - Ч)р+4+р (0 = AfD₽+1e-X’4+p (0 = t
\ t dp+1 Cl,, Xp -X T z к .
= ea T>e ex(z)dx.
§ 8.51]
ВАРИАЦИЯ ПОСТОЯННЫХ
543
Применяя правило дифференцирования под знаком имеем для любой функции
. . _ t
интеграла, мы
d^+1J pl о
(8.480)
и, следовательно,
действительно
так что взятое нами выражение (479) для ?а+р(0
является частным решением уравнения (478).
Частное решение, соответствующее внутренней сумме в (476), будет:
р" р! (^а —Р— 1)!
а
р Л
0
• Л р 1 f (D) g (D) (D — х/« . д (°) в,-1 Jf V f Л(*~х) (?а——Р) Л) р=0 0 d Р (£)) е (р) (D _ Ав
ID) Д (£>)
х (т) dx = а
exp —т
о
d \«»-1 F (D) е (D) (О — X,)5’
\D) Д (D)
а
интерпретация всего символического решения в целом может быть представлена в виде
t
j = a(f)4-S(D)x(0+ f p(f—T)x(T)dx, (8.481)
o
где первое слагаемое
a(0 = 2vec,eV (8.482)
есть общее решение однородного уравнения, а Р(£) определяется формулой
В (А == V' е*р М (f I d f.'1 Р (D) е (О) (D - \в)% ] 4ft,
Р U Т^-ijf IV + dD) ------------------Д(О)-------J D=х • (8’483>
а а
Выражение (481) и представляет собой общее решение неоднородного уравнения.
§ 8.51. Вариация постоянных. Общее решение неоднородного уравнения, так же как и общее решение однородного уравне-я» может быть освобождено от мнимостей, получающихся благо-Ря комплексным корням. Мы проведём это вычисление, ограничи
544
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
[гл. 8
ваясь системами с линейными элементарными делителями, так как для них возможно весьма важное преобразование к нормаль-ним координатам, получение которого будет нашей следующей задачей.
Если = Ха+1 ==...= есть ^-кратный корень характеристического уравнения такой системы, действительный или комплексный, то F(D) должно делиться на (D— Поэтому, как мы
уже отмечали в § 11, F(D) исчезает при D = k9 вместе с производными до (q9— 2)-го порядка:
= F' (U = ... = ^"2) (X,) = 0. (8.484)
Матрица F^ х) (Ха) = Uq (A Xff) должна быть ранга q9— по числу линейно-независимых модальных столбцов v9, v9+l, ..., vo+3ff_i, которые можно из неё получить. С помощью этих столбцов и q9 линейно-независимых строк
У
^а+р II -Ь р, 1* •••> ^а+р, nil (Р ‘ 1, ...» qa
матрица /^®»-1)(Хд) может быть представлена в форме а,-1 ^va+ we+ ₽=о
(8.485)
(8.486)
“г
ч
Пользуясь соотношениями (484), (486), мы можем переписать выражение (483) для Р(/) в виде
У
Л(£>)
S' expV ₽<«,-!) n Je(D)(D — X,)®’ (* -1)1 а
а
ИЛИ
8
у Ч . v у
(q, -1)1 W ff=l
[е (£>)(£) —Xa)g»~
. л=х а
Д(О)
(8.487)
г/
^4
где суммирование ведётся опять подряд по всем о.
В дальнейшем нам понадобятся выражения не только самого у, но и его производных у, у, ...; например, в механической задаче нас могут интересовать, кроме положений частей системы, также J скорости и ускорения. Дифференцируя (481) м раз, находим: ;1
'Э
(8.488) ’1
0
$ 8.511
ВАРИАЦИЯ ПОСТОЯННЫХ
545
где
3м (D) \= D’S (D) + р (0) D7-1 + р (0) ZT-2 + ... + У (0), (8.489)
V а л
«(0=2 VaK,C<,e 3, а=1
сг = 1
Wa
(д, - i)i
[ е (D) (D - ХаЛ1
L А (О) "J
е °
При v = 0 из этих выражений опять получаются те, которые соответствуют самому решению у.
Так же как в § 12, выделим действительные и комплексные корни и применим те же обозначения и то же преобразование, что и там.
Вводя, кроме того, матрицы типа пХ$, составленные
из столбцов, определяемых формулами
*4° = (а = 1, ...» /), (8.490)
— iv$+8i'+h= V8'+^(e^-|-^h)v> Vs'+*»+h(Qn — *<»лУ (8.491)
(/*=!,...,$")
(/) = v‘V’# (а = 1...., s'), (8.492)
$+»(Н<.м(0 = l^+h+^+s’+fc]>(8.493) (Л = 1...................s'),
получим: v s' .
а (0 = 5 S +/i(eb4~ Си'
ff=l n=l
+ Vs'+8"+&(8& — Csr+8rr+he(e* =
8' S"
= +2 SRelV8, + h(eft + fa)hyC8,+hA+^K] =
*=i h=i
8' S"
= 2 в?’ (i) c, + 2 Re [»<?+h (0 + i№<.,„+k (f)l (csr+ft — =
’=1 Л=1
’ 8' g№
2 (0 Ca -j- 2 (0 + h -J- (f) ^8r +8"+hl =
®=1 ft=l
^2е(0св=&(1,)фС.
35 Зак. 1474.
Б. В. Булгаков
546
системы с поСтояннымй Коэффициентами
Если ещё ввести матрицу Кейли (§ 12), то, совершенно так же как в § 12 при выводе выражения для S, найдём:
= (8.494)
и
а (0 = 8(’> (/) с = М. (8.495)
Для преобразования р(/) обозначим через матрицы-строки, аналогичные wff, но соответствующие комплексным корням ед zt /<оЛ, и введём матрицу b типа s X составленную из строк, определяемых формулами
Р(Р) (Р-%ДЛ1
L А(£>) J
(а=1, .... s'), (8.496)
1 ,h .. . We,+h Ve(D)(D-4-i^’^
2(рл'+Н ibj+e'+b)— ,+R_l)| [ Д(£>)
(Л=1..s").
(8.497)
Вычисление, отличающееся от проведённого выше для a(f) только тем, что строки матрицы b входят там, где раньше фигурировали элементы столбца с, даёт:
р (0 = (0 b = v^e^b. • (8.498)
Отсюда получаем, в частности, величины
р (0) = v^b, (8.499)
входящие в формулы (489) для ^ (£)).
Выражение у может быть теперь представлено в виде
t
у = 5м (D) х (0+8м (0 с + f 8м (/—т) Ьх (т) d-z (8.50 0)
о
или
у = (D) X (t) + (0 = (D) x (0 + 8(,) (0 В (0, (8.501)
где
t
B(t) = c-[-f e~^bx(t)d-z. (8.502)
В частности, при v = 0 мы имеем искомое выражение общего
§ 8.51]
ВАРИАЦИЯ ПОСТОЯННЫХ
547
решения •
• ‘^ = S(D)x(O + &(0c+ f&(/— z)bx(z)<h =
О
= S (D) х (0 + & (О В (0, (8.503)
не содержащее никаких мнимостей. Второе слагаемое отличается от общего решения однородного уравнения лишь заменой с на 0(0. Оно получается, следовательно, вариацией постоянной.
Так как &х(т) есть столбец из s элементов ^х(т) s),
то e~&bx(x) и B(t) суть такие же столбцы. С помощью формул, относящихся к умножению произвольной матрицы слева на матрицу Кейли, нетрудно установить, что элементы столбца B(f) определяются выражениями t
В, (0 = С, + b, J е~dz (а = 1...............s'), (8.504)
о
В в’ (0 1Вв' +в*+Л (0 = Сь' +Л ^в' +8"+Л
t
“h +h ibs*+««+&) J* (t) dx
0 Пример.
(A= 1, ..., s"). (8.505)
О3 4.202 _|_ юр 2D24.6D +64
J't
J2
0 IOO
X(0.
Для этого уравнения
г(О) =
° II
loo |г
Пользуясь результатами, полученными в примере 2 § 12, имеем:
Wi = ||l, 1П, Г2= Г3 = ||1, 1П,
X(0SX(O‘
V’2r2 = /?(4Z),
так как эти строки удовлетворяют соотношениям
^1w1 = F(—4), принимающим здесь вид
1 — 32 — 24Z
ХЦ1 И1 =
— 32
Дале$, по формулам (496), (497) . /II О
*‘ = 41 10D
=иЦ| 1q°d
1 1
-24/ —32 — 24/
1 1 _ 5
£>2 + 1б Ь=_4- 4’
1 1 ? 5(1-/)
(D + 4) (D + 4/) Ь=4Г 2<4 ’
35*
548
СИСТЕМЫ С ПОСТОЯННЫМИ ЙОЭФФЙЦЙЕНТАМЙ
[гл. 8
так что
^2 — #8 = >
Затем
F(D)c(D) =
10D
10D4 + 20£>3 4- 100D2
и первое выражение (503) с помощью ранее найденной матрицы 0 даёт “общее решение
У1 = + с2 cos 4t + с3 sin 4t +
Y
t
+ J [— e-4 + cos 4 (t — c) 4- sin 4 (t — -t)J x CO dt,
о
у2 = 10x (0 — 20x (0 — 72c1c“4^ + c2 (— 32 cos 4t + 24 sin 4t) 4-
+ сз (— 32 sin 4t — 24 cos 4t) + t
4- 5 f [18e“4 (*"T) —14 cos 4 (t — t) — 2 sin 4 (t — t)] x CO dt.
0
Мы могли бы также по формулам (504), (505) найти: t
Bi (0 = Cl — J e*t CO dt, о t
B2 (0 = c2 + J (cos 4т — sin 4x) x (t) dt, о
t
5 Г
B3 (0 = <?з + ~т (cos 4т sin 4т) % (т) dt
•/ о
и вычислить уь у2 с помощью второго выражения (503).
§ 8.52. Нормальные координаты. Введём матрицу-столбец
е = (8.506)
которая в случае однородного уравнения приводится к матрице, обо- J знаменной той же буквой в § 12. При 1=0 мы имеем £ = с. Эле-.^ менты $ определяются формулами t'
-VJ
= (а=1......s'), ] <
+Ж — Йу+s-+h = [В.'+л (0 — iBj +8<+ft (01
.507)
§ 8.52] нормальные координаты 549
а выражения (501) могут быть представлены в виде
• < ; J/ = S(v)(D)x(0 + v(v)t (8.508)
С другой .стороны, дифференцируя (506) и пользуясь выражением (502) для B(f), найдём:
= Qe&B (0 + е* = (?* + е& • e~<»bx (t)
или
(DE — Q)* = bx(f). (8.509)
Переходя к элементам, получаем:
Формулы (508) дают линейное преобразование к новой неизвестной В, причём, давая индексу ч значения 0, 1, L—1, где L есть старшая степень D в f(D), мы выразим через В всю совокупность неизвестных расширенной эквивалентной системы уравнений первого порядка, получающейся по первому способу § 7.2. Элементы новой неизвестной матрицы ?1, ..., Bs носят название нормальных координату линейные уравнения первого порядка (510), (511), которым они удовлетворяют, отличаются тем, что каждое из первых содержит только соответствующую координату а остальные 2s" уравнений разбиваются на s" пар, содержащих по две координаты
Из (508) вытекают следующие соотношения между элементами матриц v т 8
Л = 2 5^(£>)хи(0+ 2 (8.512)
1Х = 1 ®=1
Пусть ntj обозначает порядок старшей производной D^y^ от у^ фигурирующей в заданных уравнениях. Если в последних формулах придать индексу для каждого j значения
0, 1, ..., т';— 1,
гАе m'j есть наибольшее из чисел т$ и 1, то мы выразим через НоРмальные координаты^1 всю совокупность скалярных неизвестных
550 СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [гл. 8
расширенной системы первого порядка, получающейся по второму способу § 7.2. Число этих неизвестных есть M-j-e, где
M = (8.513)
а е есть число тех у$, для которых tzzj = 0 и которые мы будем называть е-координатами. Остальные М неизвестных расширенной системы назовём М-фуакциями.
Если число нормальных координат s меньше суммы М-[-е, то УИ-функции и я-координаты должны удовлетворять Л4Ц-2— 5 конечным линейным соотношениям с постоянными коэффициентами, содержащими также и функции x*(t) и их производные. Тем же соотношениям должны удовлетворять,' разумеется, и начальные значения.
Для того чтобы было s = М -|- г и число соотношений было равно нулю, необходимо и достаточно, чтобы определитель коэффи-циентов при старших производных D 3yj в заданных уравнениях и все числа ntj были отличны от нуля. Это условие вытекает из того, что указанный определитель равен, очевидно, коэффициенту члена степени ^mj== М в выражении A (D) в виде полинома относительно D. Можно показать, что если условие выполнено и e(D) = E, то все (О) при данном j и v = 0, 1, ...» т$—1 тождественно равны нулю.
Чтобы получить другую форму нормальных координат, которая иногда оказывается полезной, положим:
(#з'+h — iB*’ +«"+а) (8 514)
так что
—h> = ahe \ (8.515)
Отсюда получаются формулы
^•'+л—i^+8"+h = afteUn (Л = 1.........s"), (8.516)
выражающие вторую серию координат через пар новых переменных ah, uh. Мы будем называть ah, ип, соответственно, амплитудами и угловыми переменными*, к амплитудам мы будем причислять также и первую серию координат соответствующую значениям а= 1, ..., s'.
Если положить ещё
Vj, + s'+s"+a = Njhe (8.517)
+ = = (8.518)
§ 8.52]
НОРМАЛЬНЫЕ КООРДИНАТЫ
551
s' +*''+?£*’ +8"+h ~
* = Re [^\гФЛ + /^)йг+и,,+л1 (^р+л +«"+&) =
" = Re Njhe^^ne^naheiUh = N$ah cos (un + yh + ^n) и формулы (512) могут быть представлены в виде
У • = 2 (/) 4" 2 + 2 ^;hah COs (uh “F* Ijh “h VW* (8.519)
|1=1 а=1 fc=l
Затем, дифференцируя (515) и умножая на e~iu\ имеем:
ехр |(ч + »,)«-«,) I И»*» C4I*
~Ь (sfc + *шл) (Д>' +л-+ь"+л) =
4-/а
dun л dt ’
или же, используя (505) и (515),
^3r+iah^ = (.^’+h — ^’+S''+h)x(f)e ittft + (eh + i<»h)ah.
Отсюда, отделяя действительную и мнимую части, получим: Ш
= Чаь + 2 +п, р. cos «„ — ^+s-'+ft. р. Sin «л) Xp (0,
IX=1
m
(fis +Л, p. Sin «ft + ds'+e“+».p. COS «ft) x* (t) h 11=1
(/1=1, ..., s").
(8.520)
Таким образом, если принять за новые неизвестные амплитуд
?1> •••, Es', •••> и sr/ угловых переменных их, ..., то будем иметь формулы преобразования (519). Дифференциальные уравнения, которым должны удовлетворять новые переменные, суть уравнения (510) и (520).
Пример!. Л+Л = КО.
У1 + .У1+ J'i+J'a = 0>
D2 1 Ф(О
/(D)= D2 + D D+1 ‘ *(D) = £’ X(Z)= 0 >
A(D) = D(D — 1)(D4-1), s = 3. >4 = 0, ^=1, x-3 = —1,
552
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
[гл. 8'
Обозначая через w матрицу, составленную из строк wgt имеем:
W =
ь=-
о
1
о
• • •
Так как определитель из коэффициентов при старших производных ух> у^ есть
и тп± = 2, тп2 = 1, то должно быть
S1(l (D) = S« (О) = S2(I (О) = о при (Л = 1, 2,
что можно проверить и непосредственным вычислением.
Преобразование к нормальным координатам есть
У1 = £1 + ?2 + ?3» У1 = ?2 — ?3» У 2 — — ^2 ?3*
С помощью матрицы b получаем по общим формулам (510) уравнения в этих координатах
>=-Н0.
То же самое мы могли бы получить, образуя расширенную эквивалентную систему первого порядка
-5Г+Л - • ~dt~yi-Q’ ~dt +j 1 + ~dt +y* ~ °’
заменяя Л4-функции ух, ylt y-z их выражениями через £2, и разрешая относительно £2* £з«
Пример 2.
Ух — 2.У1 ~Ух + Л —У2 = Х1 (0.
„ jt—+ J2 = х2 (0.
Здесь ^ = 2, m2=l, М = 3, е = 0,
А (D) = D— 3, <9—1, %1 = 3, М-\~е— <9 = 2.
Л4-функции ух> Уь У2 связаны двумя соотношениями:
+ У2 = — (0 + Х2 (0, У! — 2У1 + У-2 = Х2 (0,
' первое из которых получается вычитанием первого из заданных уравнений из второго, предварительно продифференцированного по t\ второе соотно-
шение совпадает со вторым уравнением. Далее:
е (D) = Et х (0 =
р (О) ₽
— 0 + 2
Хх (0 х2 (0
-0 + 1 02 —20 —1
/’(3) =
§ 8.53] ПРИВЕДЕНИЕ МАТРИЦ К НОРМАЛЬНОЙ ФОРМЕ
553
V =
V^ =
3
-3 ’
»(0 =
е3* — est
Зе3*
— Зе3* ’
&(1) (0 =
₽(0 = »(0 Ь =
е™, р (0) =
О
S (D) = целая часть —>
1
Д(£>) -1
S(1) (£)) = DS (D) 4- р (0) =
Выражения Af-функций через единственную нормальную координату £ == £1 суть
У1 = — ^2 (*) + ?.
У1 = А (0 — *2 (*) — 2х3 (0 + 3;,
л=—Х1 (t)+х2 (о+х2 (ty—е.
Так как
bx(t) = xi (0 — 2х2 (О, то дифференциальное уравнение для 6 есть
^—3-. = x1(t)-2x2(t);
мы могли бы получить его, переписывая первое из данных уравнений в виде
^У1 nL v t &У'2 v v /а\
-dF — + ~dt - -*1
и заменяя УИ-функции yt, ylt у2 их выражениями через 5, Xi (t), х2 (0; второе уравнение после такой замены обращается в тождество.
§ 8.53. Приложение к системам первого порядка; приведение матриц к нормальной форме. Мы видели в § 7.2, что любая система путём введения добавочных неизвестных и уравнений может быть преобразована в систему первого порядка. Здесь мы рассмотрим приведение такой системы к нормальным координатам; её уравнение пусть будет:
(AD + Н) у = е (D) х (Г), (8.521)
где А и Н обозначают квадратные матрицы n-го порядка с постоянными элементами.
Введём матрицу z типа s X строки которой определяются Формулами
*Z” = (qa — 1)! _( Д(D) .o=xs (а= 1, ..s'), (8.522)
JD = gft+ia>ft
(Л = 1, .... s"),
(8.523)
554 СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [гл. 8
и предположим сначала, что п = т, е (D) = Е. Тогда матрица b совпадает с z. Заменяя у в уравнении (521) выражением
у = S (D) х (0 + < (8.524)
имеем:
(AvD + Hv) S = [— (AD + H)S (D) + £] x (/);
если же умножить слева на z, то
(zAvD + zHv) Е = [— z (AD (D) Ц-z] x (/).
Сравнивая это уравнение с (509) и пользуясь тем, что b = z, получаем: zAv = E, zHv = A, (8.525)
где
А = — Q (8.526)
и z(AD-±H)S(D) = 0.
Первые два соотношения могут быть выражены в виде следующей алгебраической теоремы:
Пусть А и Н суть две матрицы с постоянными элементами, причём все элементарные делители полиномной матрицы AD-\-H линейны\ тогда найдутся такие матрицы z, v с постоянными элементами, что после умножения матриц А, Н слева на z и справа на v матрица А приводится к единичной матрице Е, а Н—к матрице Кейли А.
Способ вычисления z и v выяснен выше. Теорема иллюстрируется рядом примеров в конце параграфа.
Если, в частности, А есть неособая матрица, то полином Д(£>) будет n-й степени, без понижения, так как коэффициент при Dn есть, очевидно, detA#=0. Поэтому n = s и v есть квадратная матрица, также неособая в силу линейной независимости частных решений, образованных с помощью её столбцов. Первое соотношение (525) даёт
z = v-'A"1.
Можно независимо и вполне строго доказать, что в данном случае v-'A-1 и v являются приводящими матрицами. А именно, будем исходить из уравнений модальных столбцов
(— Л?), + Я) V, = 0 (а = 1.....s'), (8.527)
[— Л (|ЛЙ + ivft) + Я] (®s-+h4-i4,+i.M+h) = 0 (А=1, ..., s"), (8.528) где мы положили
(о = 1 > • • •, 5 ), pjj = = (0^ (h = 1, . • ., )•
(8.529) Если в Д(Х) сделать замену
Л = — т], (8.530)
то корнями характеристического уравнения Д(—т|) = 0, выраженного через новую переменную т), будут как раз числа v]g,
§ 8.53]^ ПРИВЕДЕНИЕ МАТРИЦ К НОРМАЛЬНОЙ ФОРМЕ 555
(8.531)
Разделяя в (528) действительную и мнимую части, найдём: — А (Vj + №h — Vj +s"+bvh) “h Hvj = О, — A (vS' +hyh + Ч/ +е"+мч) + #4/ +8"+Л = О-
Если теперь воспользоваться формулами (1.153), (1.154), то соотношения (527), (531) могут быть представлены в виде
— + = 0 (з= 1, ..., $'),
+ + = 0’ ^/8'4-у''+л+ ^8'4-8''+Л = О
(А=1, ..., 5"),
где v', ..., у'8'+2*>' сУть столбцы матрицы ^' = vA.
Последние соотношения в свою очередь эквивалентны одному матричному уравнению
— Avr -Ц- Hv = О,
ИЛИ AvA = Hv. (8.532)
Принимая за z произведение v^A-1, мы получаем немедленно: zAv = (у М-1) Av = Е
и с помощью (532)
zHv = (уМ-1) (А^А) = А,
что и требовалось доказать.
Отбросим теперь условия п = т, е (D) = Е и предположение, что матрица А — неособая. Производя опять преобразование к нормальным координатам (524) в уравнении (521), найдём:
(AvD + Hv) $ = [— {AD + Н) S (О) + е (D)] х (t),
или после умножения слева на z:
(zAvD + zHv)% = z[-(AD-]-H)S(D) + e(£))]x(t). .
Сравнивая c (509), мы, кроме найденных выше соотношений (525), получаем тождество
z{-{AD-\-H)S{D)-\-e{D)\ = b. (8.533)
Пример 1.
Dyi + 2Dy3 = хг (О,
(D -1) + (D - 1)у> + (D -1) у3 = х2 (0.
e(D) = E. A(D) = D(D-1), — 2D^ + 2D D* £>2—d
2D2 —D —1
— 2D2 4-2D
*2=1,
. F(D) =
0 0
0
0 0
0
0
0 0
^(0) =
0
о 0
1 0
о- 0
- - *.
0
v =
0
0
556
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
[гл. 8
Обозначая через w матрицу, составленную из строк wat имеем:
о
W =
z = b =
о 1 о
о
о о ’ о о ’
€
5(D) =
— 1
1
Преобразование к нормальным ние должны удовлетворять, суть:
У1 = 2X1 (0 — 2хг (0 — 2х3 (0 4- 5Ь
У2 = — xj (0 + х2 (0 + х3 (0 — 514
координатам
и уравнения, которым послед-
•я
dF ~~ Xi (0’
dt ,
•JF $ I 1 i
Мы можем на этом примере нимающие
проверить тождества
zAv = Et zHv = А, при-
вид
1 о
О
О
О
о
1
О
О
О
О
о о
О —1 о
- 1 -
О
О
Равным образом,
убедимся, что
Пример 2.
V =
О
О
о о
О
вычисляя предварительно произведение
z(AD+H) =
z (AD + H)S (D) =
е (D) = £,
2=6 =
dt
О
о о
О
О
2D
О о
о о
о о
= 0.
У1
У*
5=1,
О ,
S(D) = 1
1
§ 8.ЙЗ] ПРИВЕДЕНИЕ МАТРИЦ К НОРМАЛЬНОЙ ФОРМЕ Й5?
Пример 3.
— — Х1 (0 + х2 (0 + хз (О,
—е2 = (о—-g- х2 (о,
dt +^3““ 2 Х2^’
ООО
zAv =
О
О
1
zHv = 0 — 1
О О
О
1
Пример 4.
1
A (D) = D2 (D _
О
2
1
О 1 1
У1
У2
Уз
х2 (О , хз (О
О О
О О
е (D) = £,
1), 5 — 3, ‘Х>1 — %2 — О, Xg — 1)
= 02 = 2,
Яз = Ь
558 СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
[гл. 8
Так как /(0) имеет ранг 1, дефект 2, то элементарные делители, соответствующие двойному корню D = 0, линейны.
0
F(D) = D
0
О
— 2D
О О О
/?(0) = 0, F'(0) =
F(l) =
О
W =
То же самое выражение для z = b
мы получили бы, вычисляя
det (Av) = — 1
и пользуясь соотношением
Далее,
z — v-lA-1 = (Av)-1,
S (D) = О,
У1 = 51 + 5з> У2 = ?2» = А (0. $ = -*2(0+ А (О,
Уз — 51
$-е8=-*1(0+*8(0.
Пример 5.
F(D)e(D) = (D-l)
S(D) =
1
— 1 о
О
О
О
О
О
О
2 = Ь =
О
О
У1 = Х2 (0 + 51 + ?2» У2 — Х2 (0 + 51 + 252, $ - - а (о+а (0, $ - е2=2а (о+*2 (0.
Сф ф СфС'
zAv =
1 О
О 1
1
О —1
§ 8.33]
ПРИВЕДЕНИЕ МАТРИЦ R НОРМАЛЬНОЙ ФОРМЕ
559
ч
— (AD + Н) S (D) + е (D) =
= 6.
Пример 6.
z [- (AD + Н) S (D) + е (О)] =
A(D) = (D4-1)[(D4-1)2 4-1],
s — 3, Xi = — 1, Х.2, Xg = — 1 zfc Z,
Wi = ||-1 О 1Ц =
*1 = ^1, 7^2“^8) = — у * =
Iztz
— 1 О
О —1
О 1
*1 = ще (- 1), 1 (fa- ib$ = -~ w2e (-1 + Z),
Р (D) е (D) =
1
1 О
— D^ —2D2 —2D 2D3-J-4D2+6D + 2 — D3 — D2 — D
D2 + 2D+2
— D2 — 3D — 4
1
S(D) =
О О
О
------*1 (О + ?1> = 2X1 (О — 2?! ^2 + ?3> Уь = — (Z) + ?1 — ^2»
-^1 + $1 = Х1 (О 4- Х2 (О, — 5з = — Х1 (О + -^2 (О»
+ ^2 + £з = *1 (О>
560
driCTEMbt с йобтбяйныМи Коэффициентами
(гл. 6
zAv =
1 О О
О о 1 — 1 1 1
1 О О
О О
1 о
О 1
zHv =
— 1
— (AD +H)S(D) + e (D) = 1
О О 1
О
1
zHADW(D) + *(D)] = -1
1 Ч О
1
Пример 7. Для системы, рассмотренной в примере 1,
М = 3, е = 0, 5 = 2, М-±-е— 5=1.
Поэтому между неизвестными и заданными функциями должно существовать конечное соотношение; и действительно, умножая уравнения на — 1, 4~ 1> + 1 и складывая, получаем:
Л = — xi (0 + х2 (0 + хз (О*
С помощью этого соотношения можно, например, исключить у$ из первого и третьего уравнений, отбрасывая второе. Это приводит к системе
Dyt = (2D + 1) xt (0 — 2Dx2 (0 — 2Dx3 (/),
-J'i+(D-1)j/2 = -(D + 2)x1(0 + (D + 2)x2(0 + (D + 1)a:3(0
с прежним определителем
A(D) = D(D —1).
Для этой системы
0
F (D) е (D) =
(D—1) (2D 4-1) — (D2 —1)
— 2D(D —1) —2D(D —1)
D2 D(D —1)
S(D) =
1
, Выражения для уь у2 через нормальные координаты, которым должны удовлетворять последние, получаются те же, что и в примере 1. Можно также на данном примере проверить тождества (525), (533).
§>. 8,531
ПРИВЕДЕНИЕ МАТРИЦ К НОРМАЛЬНОЙ ФОРМЕ
561
Обобщение. Рассмотрим уравнение
(AD* + Н)у = е (О) х (0, (8.534)
где о £сть любое целое число; вычислим матрицы -у, z> bt S(D) так, как если бы было а=1, и предположим, что S(D) = 0. Тогда, совершая преобразование к нормальным координатам
y = vi (8.535)
и умножая преобразованное уравнение слева
на
z, получим:
Пример 8.
D2
D2
D3
У*
Уз
*2 (О
*з (О
При замене 1 А = 1 О
D2
1
на D получаем систему
первого порядка, для которой
, e(D) = £,
—1
О
О О
1
о О
О
1
— 1
3
Д (D) = (О + 1)2 (О + 2), ?1=?2=2.
5 = 3.
1 о
О
Из F(—1) = 0 следует, зают при D = элементарные делители линейны.
Далее:
что
все
1; матрица /(—1)
1 0 — 1
о ' чг ; " о .
второго порядкав /(Д) :исче-имеет ранг 1, дефект 2,-и потому-$се
миноры
3
— 1
1 о
1 о
— 1
4
У1 — 51 + ^2 + 5з» у 2 = — 51, Уз = — 5а <— 25g,
+ Si = (0 — хг (О,
+ 5g = 2хх (0 + *з (О»
^4-25, = -х1(0-х,(О.
36 Зак. 1474. Б. В. Булгаков
И»Ч“? -5
562' СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [ГД. 8 I
ц
Е. УСТОЙЧИВОСТЬ ПРИ ДЛИТЕЛЬНЫХ ВОЗМУЩЕНИЯХ |
§ 8.54. Накопление возмущений в линейных колебательных f
системах. Если внешние силы конечны, то демпфированная линей- ?
ная система с постоянными параметрами не может получить неограниченных вынужденных колебаний. Однако при неблагоприятных условиях возмущения могут накапливаться и отклонения становиться значительными.
Целью этого раздела является подсчёт верхних пределов отклонений в предположении, что внешние силы х^< (t) (k' = 1, ..., п!) связаны условиями
(8.537)
(fa постоянны); в остальном они могут быть любыми однозначными и непрерывными функциями t, имеющими достаточное число производных; точки разрыва 1-го рода допускаются, но число их в любом конечном интервале должно быть конечным.
Такую задачу приходится решать, например, при отыскании максимальной погрешности измерительного прибора или максимального отклонения автоматически регулируемой системы от желаемого состояния.
Мы предположим, что дифференциальные уравнения системы имеют тот же вид, что и в §§ 2.20, 2.21:
п п*
S f* (О) У к (0 = S eilc, (D)xk,(f) 0=1........п), (8.538)
fc=l fc'=l
где xw (f) (k'=l, ..., n') обозначают заданные, а ук(/) (k= 1, ..., ri) — неизвестные функции, е,к, (D), f$k (D) — полиномы от D с постоянными коэффициентами.
Наивысшую степень полиномов fjk(P) при данном k обозначим через тк,. это— порядок старшей производной от yki фигурирующей в у равнениях. Полагая
у1(f)
(8.539)
е (D) = ||^' (D)|| (« X «')> f(D) = ||/л(D)|| (n X «). (8.540)
можно заменить систему скалярных уравнений (538) эквивалентным матричным уравнением
f(D)y(t) = e(D)x(t). (8.541) ,
•J
Матрица f(D) предполагается неособой, так что её определитель
Д (£)) = det/(D) не должен тождественно равняться нулю. |
33& ж
§8.64] НАКОПЛЕНИЕ ВОЗМУЩЕНИЙ В ЛИНЕЙНЫХ СИСТЕМАХ
563
Сделаем ещё следующие добавочные предположения: •
. а) действительные части всех корней определителя Д (D) отри-цательны;
б) определитель коэффициентов при старших производных и отличен от нуля;
в) матрица e(D) линейна относительно £):
^(О) = &0О + ^; . (8.542)
г) степень F(p)e(p) по р не превосходит степени Д(р).
В § 2.20 через Р(р) была обозначена следующая матрица (2.77):
р (р) = £(£>—х (0). p — D0 4 '
Из условия в) вытекает, что для рассматриваемого сейчас вида (542) матрицы e(D) матрица Р(р) будет:
Р(р) = &ох(О). (8.543)
Там же (§ 2.20) функция F была представлена в виде
(2.78)
^l£M = S(p) + v(p),
причём S(p) обозначало целую часть этой рациональной функции, a v(p)— правильную дробь.
Из условия г) вытекает, что в рассматриваемом сейчас случае S (р) есть постоянная матрица
S(p) = S. (8.544)
Ниже нам потребуется выражение оригинала, изображением которого является • Чтобы его построить, рассмотрим функцию
F(p)e(p) рА(Р) ’
В силу условия г) эта функция является правильной дробью. Её разложение на элементарные дроби, согласно (1.264), будет следующим:
f (Р) е (р) у' у 1
РА(р) ~ Zl 2d (^ — р — 1)!Х р. р=0
г _ Г (Р) е (р) (Р1 45
XL/<p_1 ^0») -1=^ (p-Mp+1 ’
гДе суть корни уравнения рД(р) = 0. Это уравнение имеет нулевой корень (р == 0) первой кратности. В разложении (545) ему соответствует
36*
564
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
(гл. 8
слагаемое
' F(p)e(PY\ 1 Р (0) е (0) „(0) Д
. Л (р) Jy=0 р ~ А (0) р р'
(8.546)
Выписывая это слагаемое отдельно и попрежнему обозначая через Хв (р) корни уравнения А (р) = 0 и A Z X А (р) д. (р) = —. (р-м’°
(8.547)
можно представить разложение (546) в таком виде:
Р(р)е(р) _ рД (Р) «а-1
д*' Р 1 Р(р) е (р)
•d —Р—1)1 а р=0
Ldp °
Рд0(р) .]«=) (Р~ Ч) ст
(8.548)
1
Умножая левую и
правую части на р, будем иметь:
Р (Р) е (р) Д(р) '
«а"1
d (я,—
а р = 0
дЧ° р 1 F(p)g(p)' ®’"р"1 рА,(р) _
idp
р=Х (Р ^ст)
<з
(8.549)
Отсюда, согласно (2.52), получим:
Р (Р) е (р) Д(р)
г/ъ1 Г^а~р-1 P(P)g(P)
U 2d р!(?,~р—1)! [dpie р 1 РД»(Р) ст р=0
а
(?«-!)! L
1 /?(р)^а рД« (р)
Ji>=\
е а '
Таким образом,
Р (р) е (р) Д(Р)
(8.550)
где
«а"1
РДа(Р)
(8.551)
_/Л_ V' gа' Г(t\±Xa ~ r(p)g(p)'
О 2d (q, —1)1 L\ "I др / рДа(Р) а 9
Согласно изложенному в § 2.20, оригинал, изображением кото-, (р) е (р)
рого является функция —д (р) ~ > можно представить и в другом
§ 8.54] НАКОПЛЕНИЕ ВОЗМУЩЕНИЙ В ЛИНЕЙНЫХ СИСТЕМАХ 565
виде^В, рассматриваемом сейчас случае
=5 + Чр), (8.552)
где. S— постоянная матрица, a v(p) — правильная дробь. Согласно (2.84) и (2.85),
р(р)-Н-Лф), где в г а
По теореме об интегрировании оригинала отсюда получим:
о
и, следовательно,
t
В(о) + а (0 = S + f W(-c) dz, о
W(0 = 4 а (0.
(8.553)
(8.554)
Предположим теперь, что искомые функции (/=1, ..., п) должны исчезать при t = 0 вместе со своими производными до 1П . —1 '
D 3 yj(f) включительно. Иными словами, ограничимся сейчас случаем нулевых начальных условий. При этом ограничении фигурирующая в § 2.20 матрица Q(p) (2.77)
Q(p)=/(pZgPn'^(0) р
обращается в нуль:
Q(p)s0. (8.555)
Дробно-рациональная функция
„Р(р> [Q (р)-Р(р)]
Р А (р)
входящая в качестве одного из слагаемых в изображение (2.79) искомой матрицы у (f), в силу соотношений (543) и (555) принимает вид
Р(р)[О(р) -Р(р)] = _р ь^. (0) (8.556)
г Д (р) г Д (р) 0 4 7 4 7
Изображение tj(р) искомой матрицы y(f) при этом будет следующим:
+ m (8,557)
где Е(р) является изображением, матрицы заданных возмущающих сил 5(/?)-г*л(0. (8.558)
566
. СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
[гл. 8
Оригинал для изображения нетрудно построить
предыдущему. Он будет следующим:
г
аналогично
где
Учитывая выражения (553), (554), по теореме об умножении изображений получим оригинал для второго слагаемого в выражении (557) в таком виде:
t
- (Д)(р)(Р) * ® x(t—x)dx.
О
(8.561)
Таким образом, для y(t) получаем следующее выражение:
t
у (t) = Sx (0 — 8 (0 х (0) Ц- | Г А 0 (Т)1 х (t—т) dx. (8.562) о
Отсюда, обозначая через 8jfe, (О, (f) элементы матриц S,
8(0> а(0> получим элементы матрицы y(t) в таком виде:
пг
У] (0 == [Sjk'Xk1 (0 fyk1 (f) %kr (0)1 k’=l
n
0 fc'=l
(8.563)
Вьедём теперь вместо особые обозначения: (а= 1, ..., s') для действительных корней и ей ± (Л = 1, ..., s") для пар сопряжённых комплексных корней. Обозначая через Ffc^(D) алгебраические дополнения элементов /Jfc(D)B A (D), получаем из (551):
i)i[2 з Й =
2S (^+ft-l)! {Re
q° 1 (Р) ew (/>)
п
/>М/0 Ji>=x,
®8' + ь-1 Fjn (Р) eKk' (р)!
P^s’+h^ -*^=,Л+1шЛ
х cos <oht — Im
ee'+b-1 Fjk (P) ekk’ (/>) j
(8.564)
§ 8.54] НАКОПЛЕНИЕ ВОЗМУЩЕНИЙ В ЛИНЕЙНЫХ СИСТЕМАХ 567
Здесь
(Р) =--—------7771 (А = 1......<8-565)
- (p-4-i^-+h
Для Njk'(t), согласно (2.98) и (554), имеем следующее выражение:
Njk' ^~~dt 0 jk’ (О ~
Pjk (Р) екк- (Р) 1
А» (.₽) Jp = x с
Fjk (Р) ^к' (Р) 1
А«' + л(Р) =
V е 9
(?»—!)!
х cos — Im
Г V 6 I d \8’+lt 1 Fjk(.P)ekk'(PY[ . „ ; ISv + dp) Ad-+ft(p) -L=.ft+<«fc A
(8.566)
Обращаемся к подсчёту наибольшего возможного отклонения по координате у^ имеющего место, когда лишь одна из сил хк, (f) отлична от нуля. При данном t абсолютная величина выражения
xw (0 хк' (®) “Ь J aik' хъ9
6
получает своё максимальное значение м^к, (0, если абсолютная величина функции xk,(t—т) всё время равна /л,, а её знак меняется так, чтобы все элементы интеграла, а также два других слагаемых были положительны. Иными словами, хк,(1—т) должна менять знак при т = 4»^2’ • • • и, возможно, при т = 0, А причём суть последовательные положительные корни уравнения №к, (0 = 0.
Если t<Zf, то интервалам (0, 0, (0, f) соответствуют два бесконечных множества допустимых определений функции ук, (т), причём первое является частью второго. В самом деле, каждое определение, соответствующее (0, t}t может быть отнесено к равному интервалу (Г— Д f) и дополнено предположением, что хк, (т) = 0, noKg t принадлежит (0, tr — 0; таким образом, первоначальное, определение может фррмально считаться относящимся также и к (0,?/'). Отсюда следует, что т^к, (0 тп.к, (f). Заставляя t стремиться к до, мы получим maximum maximorum т^к, (оо). Как видно» . иа;(560), функция 8^, (0 при этом стремится к нулю, и т^, (оо) будет
568
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
[гл. 8
суммой сходящегося ряда
(°°) = 4') — { , 2т Н“
6
#2
Знаки следует брать так, чтобы оба слагаемых были положительны. Можно написать также
mjk, (оо) = Ajk, 1к,, (8.568)
где
=^S/ft,±(a^(0)-2a^(#1) + 2a^(^-...]. (8.569)
Так как функции хк, (/) независимы, то наибольшее отклонение Ну(оо) по координате у^ при одновременном действии всех возмущающих сил может быть теперь вычислено с помощью коэффициентов влияния *) Ajjcf:
п'
Е(оо)=2 (8.570)
к'=1
Это и есть решение поставленной общей задачи.
Случай ненулевых начальных условий. Выше мы ограничились случаем, когда все yAt) вместе со своими производят .—1
ными до D 3 yj(f) включительно обращались в нуль при £=0. Отказываясь теперь от этого ограничения, рассмотрим вновь систему уравнений (538) или эквивалентное ей матричное уравнение (541), изменив, оДнако, предположения в) и г). Именно, будем считать:
в') матрица >е (D) имеет вид
^(7)) = ^, (8.571)
т. е. bQ = 0;
г') степень F(p)e(p) по р меньше степени Д(р).
*) В случае, когда степепь F (р) е (р) по р строго ниже степени Д (р), оо
коэффициент влияния А$к, = J* | Njk, (0 [ dt. Однако и при этом ограниче-о
нии получение в аналитической форме выражения для А;к, остаётся затруднительным. В связи с этим для определения значений параметров колебательной системы, при которых величина Ajkf снижается, может представить интерес изучение условий минимума квадратичного интеграла от функции
со
последействия J* [Njk, (t)]2dt, выражение для которого можно получить в о
общём виде при помощи метода, изложенного в § 2.32.
§ 8.54] НАКОПЛЕНИЕ ВОЗМУЩЕНИЙ В ЛИНЕЙНЫХ СИСТЕМАХ
569
..Из .условия в') вытекает, что матрица Р (р), для которой выше было получено выражение (542), теперь обращается в нуль:
Р (р) = Ь^х (0) = 0. (8.572)
В силу ограничения г') теперь является правильной
дробью и, следовательно,
Решение рассматриваемой предположениях, согласно
5 = 0. (8.573)'
системы уравнений (538) при сделанных (2.87) и (573), будет следующим:
t
(8.574)
4 о
где функция М (£), согласно (2.83), имеет вид
41(Q_yz 7' I d X^Fip) [Q(p)-p(p)1 v
а
СУ
При ненулевых начальных условиях матрица
отлична от нуля. Так как, согласно (572), Р(р) = 0, M(f) принимает вид
1P(p)Q (pY А су (Р) _ p=k
TQ фуНКЦИЯ
(8.575)
а г «
Вводя те же специальные обозначения, что и выше, для действительных и комплексных корней, можно представить элементы матрицы Л4(0 в таком виде: ___________. х t =2
п
а-1 (р) Qk (р);
(Р) - = х
л J
к=1
п
а
1 (р) Qk (Р) ~|
&з' 4-Л (Р) =
в. е »
П
fc=l
Л'+л-i ?>(p)Qfc(p)i -----------------r—--- Sin O)hr.
7 A^ + fc(P)
(8.576)
570 СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [гл. 8
Из (574) получим для искомых функций yj(/) следующие выражения: f п'
^(0 = ^(0+ 2 ('-*)* (8-577)
О fc’=l J
С/ = 1, ..re).
I
'Здесь, как и выше (554),
= . (8.578)
Л t
где Njk, (t) и Gjk, (t) определены формулами (566) и (564).
Наибольшее возможное отклонение по координате yj (J фиксировано) получится, если функции xk,(i— т) (й'= 1, ..., п'), оставаясь по модулю равными /^, будут менять знак вместе с Л^'(т) так, чтобы каждый из п' интегралов в выражении (577) имел тот же знак, что и Л4Д0.
В результате такого выбора функций x~(t—i) будем иметь при /ь возрастании t монотонное нарастание абсолютной величины всех интегралов в выражении (577) и получим следующую максимальную абсолютную величину отклонения по координате у$ в момент времени t при одновременном действии всех возмущений
п'
H,(O = I^(QI+S . (8.579)
"к* — 1
где
(0 = I > (0) - ($,) Н- 2, .к, да - ... +
+ 2 (- 1) зк ojk, ) + (- 1) ад, (01. (8.580)
При этом суть корни уравнения ty# (f) = 0, а п^ — число корней внутри интервала (0, t).
Так как | Л4<(0|, а-с-ним вместе и имеет, вообще, колебательный характер, то момент времени £*, которому соответствует наибольшее отклонение на бесконечном или конечном интервале (0, Т), может лежать как в конце, так и внутри этого интервала.
Замечание. Полученные результаты можно обобщить на линейные колебательные системы с переменными параметрами [8-Ч. Так, например, если матричное дифференциальное уравнение колебательной системы имеет вид
(8.581)
§ 8.54] НАКОПЛЕНИЕ ВОЗМУЩЕНИЙ В ЛИНЕЙНЫХ СИСТЕМАХ 571
где7(С — Ц/# (О И (n X л), а у и х (0 — матрицы-столбцы типа (пХ 1)> то, обозначая через 9 (0 фундаментальную матрицу однородного уравнения, получаемого при x(0=sO (см. § 4.3) и вводя матрицу последействия
т) = 9 (09-1(0 (8.582)
и матрицу-столбец
W t0) = 0(09"1 tf0)y(to) = ДЦА ^0)^(у, (8.583)
можно, согласно (4.31), представить решение матричного уравнения (581), принимающее при t = t0 заданное значение у(£0), в следующем виде:
t
у (0 = M (t, /0) 4- f W (А т) х (т) dx. (8.584)
to
Элементы матрицы у(1) в случае, когда лишь одна из возмущающих сил x9(t) отлична от нуля, будут:
t
Я (0 = Mj (t, t0) + J ДА, (A ?) xf (?) dx. (8.585) to
Аналогично предыдущему, при данных t, t0 абсолютная величина у3-получает своё максимальное значение /0), если абсолютная величина функции хр(т) всё время равна /р, а её знак меняется так, чтобы все элементы интеграла в выражении (585) имели тот же знак, что и Mj(t, t0). Иными словами, хр(т) должна менять знак при т == 4р\ ...» ..., где суть последовательные корни урав-
нения typ (t9 т) = 0 по аргументу т на интервале (t0, f) при заданном t.
Поэтому
(A t0) = IМ,(А QI(A Q lf> (8.586) где
t
А>)= J |ty₽(A ?)|d? = to
= I % to) - 2«/p (A $) + 2 3jf (t, ^) - 2Э/Р (A 4^) + • •. I. (8.587) Здесь
(t, X) = J (t, x) dx. (8.588)
Наибольшее абсолютное отклонение по координате у$ в момент i При одновременном действии вд^х возмущающих сил, очевидно.
572
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
[гл. 8
будет:
п
Hj (t, t0) = I Щ (t, 1+ S ajf (t, t0) lf. (8.589)
P=1
Первый член справа представляет собой отклонение вследствие начальных возмущений, второй член — наибольшее отклонение за счёт непрерывно действующих сил.
Если состояние системы у = 0 асимптотически устойчиво, то первый член стремится к нулю при t—> оо.
Как и выше, наибольшее возможное отклонение по координате yj в заданном конечном или бесконечном интервале времени может благодаря наличию начальных возмущений иметь место как на границе, так и внутри этого интервала времени.
ГЛАВА 9
ПАССИВНЫЕ СИСТЕМЫ*)
А. ЛИНЕЙНЫЕ КОНСЕРВАТИВНЫЕ СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
§ 9.1. Постановка вопроса. Задача о малых движениях склеро-номной консервативной механической системы около положения равновесия может естественно возникать в связи со многими повседневными явлениями, например качаниями всяких систем так или иначе связанных тяжёлых твёрдых тел. Однако же основным классом явлений, питающих интерес к общей задаче, следует считать колебания упругих тел, с которыми приходится постоянно встречаться как в природе, непосредственно предстоящей нашему опыту, так и в технике. Колебания с частотами от 16 до 20 000 герц (т. е. колебаний в секунду), передаваемые нашему уху какой-либо проводящей средой, обычно воздухом, ощущаются как звук; периодические колебания воспринимаются как музыкальные звуки или тоны, непериодические — как шумы. Поэтому акустика, по крайней мере с принципиальной точки зрения, не имеет объекта исследования, отличного от теории механических колебаний. Самостоятельное значение она получает благодаря специфическим экспериментальным методам, связи с физиологией уха, с архитектурой (строительная акустика), с теорией музыки, музыкальных инструментов и усилителей звука. Другой пример — это колебания упругих элементов сооружений, машин и приборов, которые возникают под действием переменных нагрузок и должны учитываться при расчётах на прочность, вследствие чего относящиеся сюда методы составляют важный раздел строительной механики.
Сказанным объясняется то, что рассматриваемая задача исторически была первой в теории колебаний систем со многими степенями свободы. В первой половине XVIII века Б. Тейлор, Ж. Даламбер, Л. Эйлер и Д. Бернулли изучали колебания натянутой струны, причём Д. Бернулли высказал в 1753 году принцип разложения сложных колебаний на простые. Общая теория была дана Лагранжем в 1762—1765 годах и воспроизведена в виде одной из глав его «Анали
*) Пассивными называются системы без источников энергии.
574 ПАССИВНЫЕ СИСТЕМЫ (гл. §
тической механики» (1788 г.). Развитие этой теории в течение долгого времени и составляло содержание позднейших исследований и соответствующих глав в курсах механики, пока новые вопросы, поставленные теорией регулирования, не привели к более общей точке зрения.
Трактовка упругой системы как агрегата конечного числа материальных частиц, связанных упругими силами, является во многих случаях целесообразным первым приближением, с помощью которого может быть и был выяснен ряд фундаментальных свойств колебательных процессов. При неограниченном увеличении числа частиц, с одновременным уменьшением размеров и массы каждой, мы приходим к непрерывной упругой среде, и, как будет показано ниже, системы обыкновенных дифференциальных уравнений, которыми описываются колебательные процессы, переходят в пределе либо в уравнения в частных производных с соответствующими граничными условиями, либо в интегральные уравнения. Задачи, связанные с этим аппаратом, составляют, однако, большую самостоятельную область, которой мы не можем касаться в настоящей книге.
Уравнения движения могут быть получены из уравнений главы 7 (§ 7.9), если положить:
п п
&зк ((71> • • • > Яп) ЯзЯк^ Qj == , ^(?i> • • • > *7п)>
3=1Л=1 3
так что
Xj = Bj = 0, Aj^ = Afcj = ajk (^i, ...» Qn)i Bjk = Cjk = 0,
Ljk = = Mkj = >
дя^Як Jjk === 0’ jk == = 0,
@jk== Hjk Jjk= Mjk-
С точностью до малых высших порядков
^п== ^/кУ^Ук» 3=1 Л = 1
V = — U = const + 722 НяУзУк‘
3=1 к=1 Обозначая
fjk(D) = AjkD* + Hjk (9.1)
и вводя квадратные симметричные матрицы
А = ЦЛД||, Н=||ЗД /(О)= 11^(0)11=^ + //,
§ 9.2] ЭЛЕМЕНТАРНЫЕ ДЕЛИТЕЛИ И ОБЩЕЕ РЕШЕНИЕ 57б
мы ^можем записать уравнения движения в форме
f(D)y = 0 . (9.4)
ИЛИ
{AD^-^H)y = ^. (9.5)
§ 9.2. Элементарные делители и общее решение. Легко показать, что если квадратичная форма Н{у, у) неособая, то элементарные делители матрицы (3) или, если угодно, несколько более общей матрицы
/(Р) = ЛР’ + Я, (9.6)
где а — любое натуральное число/всегда линейны. Для этого произведём в матрице /(х) замену
х* = —X (9.7)
и положим
/(х) = Л(Х), (9.8)
так что
/ЦХ) = — ЛХ4-Я. (9.9)
Выраженное через переменную X характеристическое уравнение
det/г (X) = О (9.10)
имеет п корней, называемых характеристическими числами.
Матрица h (X) является матрицей пары квадратичных форм А (у, у), Н О> у) и её элементарные делители линейны, поскольку первая форма знакоопределённая (т. е. знакопостоянная и неособая).' Отсюда тотчас вытекает и линейность элементарных делителей матрицы /(х). В самом деле, она отличается от h(k) только тем,:что за аргумент принято х, а не X. Поэтому каждому элементарному делителю X — Xfc матрицы Л(Х) соответствует з элементарных делителей матрицы /(х),
а именно, х —у—Xfc , ..., х — у— Хь где т)т, ..., суть
корни з-й степени из единицы, а под]/—Xfc разумеется какое-нибудь одно из значений корня. Написанные з линейных элементарных
делителей могли бы слиться в один з-кратный делитель х® лишь в том случае, когда Xfc = 0. Но так как матрица /7 неособая, то определитель det 7/ отличён от нуля. С другой стороны, он является, очевидно, свободным членом в разложении det h (X) по степеням X и, следовательно, свободным членом характеристического уравнения. Поэтому
ни одно характеристическое число не может быть равно нулю и линейность элементарных делителей матрицы /(х) обеспечена.
Вследствие этого общее решение уравнения (4) всегда выражается в показательных и тригонометрических функциях, между тем как при нелиЦейных элементарных делителях решение должно было бы содержать также и степени t.
Эту последнюю возможность при наличии кратных корней допускал Лагранж и, следуя ему, некоторые позднейшие исследователи. Ясность была внесена Вейерштрассом, который в 1858 году развил
576
ПАССИВНЫЕ СИСТЕМЫ
[гл. 9
теорию элементарных делителей, ранее открытых Сильвестером, и приложил её к задаче о колебаниях. На ошибку Лагранжа в этом вопросе часто указывают, хотя рассматриваемая задача, особенности которой не были учтены Лагранжем, является, в сущности, весьма частной и невыполнение хотя бы одного из перечисленных выше усло
вий действительно влечёт за собой при наличии кратных корней по-
явление в решениях степеней t (см. пример в конце параграфа). Вводя матрицу-столбец
и =
(9.Н)
п
полагая у = подставляя в (4) и применяя замену (7), получим уравнение модального столбца
+ Н)и = 0. (9.12)
Сохраним предположение, что матрица И неособая. Поскольку матрица h(k) = — зависит только от X, можно брать один
и тот же модальный столбец и = для группы корней
'nil/'-Xft....(9.13)
соответствующих одному и тому же характеристическому числу Xfc, и считать, что каждому простому характеристическому числу соответствует единственный модальный столбец, а каждому кратному — столько столбцов, какова его кратность. Общее число модальных столбцов будет тогда равно числу неизвестных п, а модальная матрица образованная из столбцов vk, будет квадратной.
Общее решение может быть записано в виде
W а ___ а _________________________
J = S •Wfe l4’expOi-t)/ —Afc*)4- ... 4-c£’exp С»]а ]/— Xfcf)]. (9.14) fc=l
Пример. Пусть имеем консервативную систему, для которой
А (у, у) = 2 У2> н (У> У> = S 2 <1 ~ 2£Л) У№
j 3 к
где Ejk суть элементы единичной матрицы; уравнения малых движений будут:
J't —У1 +у-2 + Уз + • • • + Уп = о*
У* +J1 —Уъ +^3 + • • • + Уп = О»
Уп + У1 +j2 + Уз + • • • —Уп = 9,
'<4
««зя
ЭЛЕМЁНТлРНЫЕ дёЛитёЛи и оёщеё ёёшёниё
577
§ 9.2]
Так как матрица *> W
h (—2) =
1 1 ... 1
1 1 ... 1
1 1 ... 1
имеет ранг 1, дефект п — 1, то — 2 есть характеристическое число, которому соответствует п — 1 элементарных делителей h (л); кратность этого характеристического числа не меньше чем п — 1. Она и не выше чем п — 1, ибо легко найти ещё одно простое характеристическое число.
В самом деле,
Л (п — 2) =
— (л —1) 1 ... 1
1 — (л — 1) ... 1
1 1 ...-(л-1)
Прибавляя к первой строке все остальные, убедимся, что определитель этой матрицы равен нулю, так что п — 2 есть характеристическое число. Ему соответствует оказывается Однако,
один элементарный делитель матрицы h (к), а общее их число равным и. Поэтому все они если п = = 2, матрица
должны быть линейными.
оказывается особой, а элементарные делители матрицы
/(х) =
%2—1 1
суть X — /2, х + '|/ 2, х2. Последний из них нелинеен.
Так как
2х О
О 2х
F(x) =
F'(*) =
F' (0) = 0,
то общее решение
.У1 = + с2е~^ 2 ь + c$t + сь
У2 == — 2 * — С2в 2 4* C$t + С4,
составленное по правилам раздела Б главы 8, содержит t линейно.
Если теперь п =/= 2, то нулевых характеристических чисел нет, определитель матрицы Н отличен от нуля и линейность элементарных делителей матрицу/(х) обеспечена. Возьмём для определённости л = 3; как показывает выражение h (—2), уравнения, которым должны удовлетворять и2, и%, для двойного характеристического числа — 2 тождественны между собой и имеют вид
4“ из= о.
Поэтому мы можем взять для этого характеристического числа модальные
37 Ззк. 1474. Б. В. Булгаков
578
ПАССИВНЫЕ СИСТЕМЫ
[гл. 9
столбцы
Матрица h (п — 2) при п = 3 будет:
алгебраические дополнения элементов первой строки суть 3, 3, 3, и мы можем для характеристического числа 1 взять модальный столбец
Общее решение есть
г V2£ н —V2t , i it , if —it
y1 = c1e 4-c e +c3e + c3e ,
r V2t . if —1^2t r it if —it
У‘2. == ^2 & "Ь ^2 & “1“ ^3 & ^3 »
, 1 , r V2t , n , —V2,t i it , a —it
Уз = — f^ + c^e —(cx+c2)^ +c3e +cse
или
Ji = ajch (/2 14-0t) 4-«зcos(t + 03),
y* = cl3 ch (1^2* 14- B^) л3 cos (t 4* 03),
J3=—«iCh(]<2 £4-0!) —«2 ch (/2 £4-02) +«з cos(£4-03),
где ab a*t a& 0j, 02, СУТЬ новые постоянные
§ 9.3. Представление билинейных и квадратичных форм с помощью матриц. Пусть будут х и у матрицы-столбцы с элементами Xj и yj. Так как для х транспонированная матрица х' есть матрица-строка, то мы можем представить билинейную форму
в виде
А (X, у) = 2 2 AjkXjyk j к
А (х, у) — х'Ау = || Хр
Л
Уп
(9.15)
(9.16)
В самом деле, произведение х'А есть матрица-строка
2 • • •» S »
з з
если же ещё умножить на матрицу-столбец у, то получится матрица с одной строкой и одним столбцом, т. е. скаляр
х'Ау = 2 х}А51у± + •. • + 2 х^пуп = 22 XjA^.
3 3 j к
§ <).3j ПРЕДСТАВЛЕЙИЕ ЙИЛИНЕЙНЫХ ФОЙМ С ПОМОЩЬЮ МАТРИЦ
Если переменные х и у подвергаются линейным преобразованиям y = где w — квадратные матрицы, а Ё, 7) — матрицы-столбцы новых переменных, то, пользуясь известным правилом, мы имеем: ы
xr = (vS)' = t'v', а затем
х'Ау = ¥v'Avrf\ = Е'ат|, где
a = (9.17)
есть матрица билинейной формы, выраженной в новых переменных. В случае квадратичной формы
А (х, х) = 2 S AjkXjXk (9.18)
i »
матрица А будет симметричной, так что А = А', а обе серии переменных совпадают:
А(х, х) = х'Ах; (9.19)
путём линейного преобразования x = v£ получаем новую квадратичную форму Ъ'а*9 матрица которой '
a = v'Av (9.20)
будет, конечно, также симметричной, так как
а' = (vr Av)' = vrAr (vry = vr Av = a.
В качестве примера рассмотрим единичную билинейную форму
х'Еу = 2 S EjkXjyk = S зд J j
и потребуем, чтобы преобразованная форма была того же типа:
3 3
v'Ew = Е
<
v'w = Е 1 *
• -
и, переходя к транспонированным матрицам, vfv = Е.
Из двух последних соотношений вытекает
т- е. матрица v является транспонированной по отношению к матрице, обратной для V), и наоборот. Преобразования v, V) называются в этом случае контраградаенпгными.
37*
Это значит, что или, проще,
§80
ЙЛбСЙВЙЫЕ СИСТЕМЫ
[гл. 9
§ 9.4. Теорема Сильвестера. Уравнение /n-го модального столбца имеет вид
(- Акт + Н) vm = 0 (9.21)
ИЛИ
S ^jkVkm^m “1“ S ^jk^km == 0 •
к к
Вводя диагональную матрицу
A=||Ajft|| =
р „р,у=*. (9 22) [ 0 при у #= fe,
можно переписать предыдущее соотношение в виде
S 2 Ajk^klAlm 4“ S fijk^km = ® к I к
ИЛИ
— Av&-]-Hv = 0. (9.23)
Мы получили уравнение, которому удовлетворяет модальная матрица v.
Совершим теперь с помощью этой матрицы преобразование
^ = ^7) (9.24)
к нормальным координатам т^ есть столбец, образован-
ный из этих координат. Подставляя в уравнение (4), найдём:
(AvD5 4- Hv) т| = 0;
если же умножить слева на транспонированную матрицу г/', то (Л*О* 4- Н*) т| = 0, где
Л* = УАу, H* = v'Hv, (9.25)
это суть матрицы квадратичных форм , Н* (т|, т|), полу-
чаемых из А (4^, 4^), Н(У>У) путём линейного преобразования (24). Если уравнение модальной матрицы (23) также умножить слева на vf, то оно примет вид
— Л*А4-Я* = 0.
Из выражений для Л*, Н* вытекает:
А*т = ViAvm = A (tip vm) = 2 2 Ajk^km>
3 к
Hlm = ЧНит = Н (VU Vm) = 22
(9.26)
(9.27)
§ 9.4] ТЕОРЕМА СИЛЬВЕСТЕРА 581
' * . Покажем, что все характеристические числа действительны (теорема Сильвестера). Это будет означать, что модальная матрица и преобразование к нормальным координатам действительны.
Для доказательства воспользуемся уравнением (26), написав его в виде
А
— Ат1кг-]-Нт1 = 0. (9.28)
Пусть теперь кт есть характеристическое число, сопряжённое с соответствующие модальные столбцы т4акже естественно взять сопряжёнными:
+ $1' vim = а3 —
По первой формуле (27),
Ami == 2 2 AjkVjmvki “22 А^ (а^ — ify) (ak fpft) — 3 k 3 k
=r 2 2 Ajk (ajak PjPfc) i 2 2 A& (a^ — Pjafc)«
3 k 3 k
Так как вторая сумма с множителем i исчезает вследствие симметрии матрицы Л, то мы получаем:
Ж?
Лы = Л(а, а) + Л(р, р)
и аналогично
Поэтому
Н*тг = Н(а, а)4-Я(Р, ₽).
— [Л (а, а)4-Л(₽, р)] [Н(а, а) + Я(р, p)J = O,
а так как форма Л (у, у) знакоопределённая, то
, _ Я(«, «) + Я(р, р)
1~ Л (а, а) + Л(₽, р)
и характеристическое число должно быть действительным, что и требовалось доказать.
Вследствие действительности характеристических чисел естественно и все модальные столбцы взять действительными; тогда все равны нулю и предыдущая формула приводится к соотношению
Н (vi, vi)
А (уъ ’
(9.29)
Которое, впрочем, непосредственно вытекает также из (28). Отсюда видно, что если Н(у> у) является знакоопределённой формой того же знака, что и А(у, у), как это и будет при а = 2 для натуральной механической системы, потенциальная энергия которой имеет в положении равновесия минимум общего типа, то все характеристические
582
ПАССИВНЫЕ СИСТЕМЫ
[гл. 9
числа положительны, корни характеристического уравнения чисто мнимы и имеют вид ztZ<ofc, где — Общее решение будет:
У = 5 vk {с'к ехр W+4 ехр (— Za)ft^] = п
= 2 kfc cos a>kt 4- сп+к sin Л=1
или
У — 2 vkak cos (<s>kt 4- 6Л), (9.30)
к
Уз = S v3kak cos (®fc#4- Ofc) (9.31)
1c
Малые движения имеют, следовательно, колебательный характер; в рассматриваемом случае можно на основании точных уравнений строго доказать, что положение равновесия устойчиво. Сравнивая (24) и (31), найдём:
7lfc = afccos(a)^+0fc) (й=Ь 2, •••> л). (9.32)
При каждом нормальном колебании, определяемом частным решением
Уз = Vjkftk = cos + 0fc) (/ = 1, 2, ..., n), все координаты yj остаются пропорциональными постоянным vllc, ... •••>vnk> образующим модальный столбец vk. Эти столбцы, как уже упоминалось в § 8.12, называются собственными формами колебаний] они определяют стоячие волны. Числа суть угловые частоты нормальных колебаний или собственные частоты. Полное колебание является результатом наложения, «суперпозиции», нормальных колебаний, как это было установлено Д. Бернулли.
При звуковых колебаниях нормальные колебания определяют простые тоны, или ноты; собственные частоты определяют высоту этих тонов. Нормальное колебание наименьшей частоты соответствует основному тону, остальные называются обертонами. Те обертоны, частоты которых представляют целые кратные частоты основного тона, называются гармоническими*, они образуют с основным тоном приятные для уха комбинации («консонанс»). Сила звука простых тонов зависит от амплитуд нормальных колебаний. Полное колебание даёт, строго говоря, музыкальный звук или тон только в том случае, если оно также является периодическим, а для этого нужно, чтобы все обертоны были гармоническими. В этом случае частота основного тона определяет высоту звука, а состав и относительная сила офертонов — его тембр,
§ 9.5] ОРТОГОНАЛЬНОСТЬ СОБСТВЕННЫХ ФОРМ 583
••Пример (А. Н. Крылов)., Рассмотрим консервативную систему, для
А (у, у) = 6у% + 11у* + 22>з + 28_у2у3 + 22_у3 +12угу2, Н (У, У) = + 38^ + 49уд + 82j2у3 + 40у3yt + 30ух_у2.
Уравнения малых движений будут:
(6D2 + 9) yt + (6D2 4.15) у2 + (11D2 + 20) у3 = 0, (6D*+ 15) + (11D2 4. 38) у2 + (141)2 + 41) у3 = 0, (11D2 + 20) + (1402 + 41) у2 + (2202 4- 49) у3 = 0,
* (X) =
-6X4-9
— 6X4-15
-11X4-20
— 6X4-15
— 11X4-38
-14X4-41
— 11X4-20
— 14Х + 41
— 22Х 4- 49
det(X) = — (X—1)2(Х —4), Xi = X2=l, Х3 = 4,
Л(1) =
9
27
27
9
27
27
М4) =
— 15 —9
— 9 - 6
— 24 —15
— 24
— 15 ,
— 39
3
9
9
10 1
0 1 1
Ji = ^1 cos (t 4- Oi) 4- а3 cos (2f 4- 03),
j2 = а2 cos (t + 02) + a3 cos (2/ + 03),
J3 = — ai cos + 0i) “ a2 cos & + 02) — аз cos (2* + 08).
§ 9.5. Ортогональность собственных форм. Из симметрии матриц А, Н вытекает «ортогональность» собственных форм. Чтобы убедиться в этом, поменяем в (28) ролями Хг, Xw:
^1т == 9.
С другой стороны, вследствие симметрии матриц А, Н, а значит, и Л*, Н*
1 I и* Л — AiHi^i 4~ = 0.
Вычитая почленно, находим:
(^7 == 0»
так что, если* характеристические числа кр различны, то
Xm = A (vJt ©от) = S 2 А^рью = 0 {14= т) (9.33)
J к
и» следовательно,
= Н {Vj, vm) = 2 2 = 0 {14= ni). (9.34)
) к
дае •*
584
ПАССИВНЫЕ СИСТЕМЫ
(гл. 9
Таким образом, в n-мерном пространстве с метрикой, определяемой формой А {у, у) или Н(у, у), векторы, относящиеся к различным характеристическим числам, будут взаимно ортогональны. Если потребовать ещё, чтобы для каждого простого характеристического числа собственная форма была «нормирована», т. е. удовлетворяла условию
Ап = A (vlt = 2 2 AjkVn<>id — 1 > (9-35)
J к
из которого вытекает также
Hn = H(vlt = (9-36)
J к
то коэффициент пропорциональности, заключающийся в числах будет вполне определён. Вектор будет тогда единичным.
В случае ^-кратного характеристического числа различные, относящиеся к нему и как-нибудь выбранные, независимые модальные столбцы могут оказаться не только не нормированными, но и не ортогональными между собой. Однако того и другого можно достичь, если об этом позаботиться.
Пусть, в самом деле, qr < q и мы уже получили q' нормированных и ортогональных столбцов vk (k = l, ..., l-\-qr—1). Пусть, далее, и есть какой-нибудь линейно-независимый от них столбец, относящийся к тому же характеристическому числу. Тогда столбец
и' —и.— 2 'skvk’ (9.37)
к=1
где
ък = А(и, vtt), (9.38)
не равен нулю и ортогонален к столбцам V}, . .., vl+q'_lt ибо для какого-нибудь из них мы имеем:
r+q'-l
А (и', ъ^ — А(ц, — S ™kA(vki = — ^ = 0.
Столбец
Vl+q' = ---7\ (9.39)
у A и')
будет не только ортогонален к ранее найденным, но и нормирован. Так как один нормированный столбец всегда можно образовать, то, переходя от q'— \ к q'=2, от q = 2 к q' = 3 и т. д., мы достигнем желаемого результата.
Таким образом, мы всегда можем получить систему п ортогональных, а если угодно, то и нормированных собственных форм. В этом случае, переходя к нормальным координатам при помощи преобразования (24), мы приведём формы А (д/, у), Н(у, у), выражающие
§ 9.5] ОРТОГОНАЛЬНОСТЬ СОБСТВЕННЫХ ФОРМ 585
удвоенные кинетическую и потенциальную энергии, к виду
л* (7), 7]) = 2 “nS Я*(71, Т]) = 2М}. (9.40)
Мы можем сказать, что полная кинетическая или потенциальная энергия равна сумме энергий соответствующих отдельных нормальных колебаний.
Рассмотрим ещё неоднородное уравнение
+ = (9.41)
получающееся при е (D) = Е из уравнения, приведение которого к нормальным координатам мы рассматривали в § 8.50. Предыдущая теория, основанная на предположениях, что матрицы Л, Н симметричны, а первая из них, кроме того, неособая, позволяет дать для этого случая специальный метод приведения. Совершая преобразование к нормальным координатам (24) и умножая преобразованное уравнение слева на v', полечим:
или с помощью (26)
Л* (EDa —A) nq = vx (t).
Если же модальные столбцы ортогональны и нормированы, то Л* = Е и
(EDa 4- А) т| = vx (0 (9.42)
или, переходя к элементам, п
= S V» (0 и = 1..............«)• (9.43)
/с=1
Пример 1. Вернёмся к примеру § 2, предполагая опять п = 3. Полученные там модальные столбцы не нормированы, а первые два и не ортогональны между собой, вследствие чего, пользуясь матрицей v для линейного преобразования, мы получим независимые уравнения в новых переменных, но не сможем привести формы
А (у, у)=у[ + У% + у1
Н (У, у) = — —Уз + ЯУ2>з + 2УзУ1 + 2лЛ
к нормальному виду. Но если нормировать первый и третий столбцы, а взамен второго построить по изложенному выше правилу нормированный столбец, ортогональный как к первому, так и к третьему, то мы получим преобразование
586
ПАССИВНЫЕ СИСТЕМЫ
[гл. 9
приводящее формы А (у, у), Н (у, у) к виду л* (•»>, i) = i?+’)2+is> Н* (*), *)) = — 2i)i — 2v)| +
Пример 2. Две массы ть т2, соединённые пружиной, могут колебаться по прямой (фиг. 111). Если с есть жёсткость пружины, I — её длина в
Фиг. 111. Две массы на пружине, ненапряжённом состоянии, то силы, действующие на массы, суть
Поэтому
Qi = с (у2 — /),
q2 = — <?Су2— St — О-г = 4 (т1У1 + т2У2>>
Принимая за пружины
новые переменные 5, т] координату
центра масс и удлинение
^1 + ^2 ’
V] = —yi -j-y2— Л
^ij't + т2у2
приведём Т и V к виду
Z7Z1/?/•> • о
, , <]2,
У=уСТ)2.
Поэтому I, т] суть нормальные координаты. Уравнения Лагранжа суть
(тих + т2) ? = О,
./Wt/772 tfzi -f- т2
^4-^ = 0,
а их решения
где
$ = c't -f- с", т] = a cos («of -J- 6),
J Гс + ffl2)
V mim2
Таким образом, решения все же содержат t в первой степени. Причина заключается в том, что потенциальная энергия является здесь особой формой, поскольку её определитель по £ и т) равен нулю. Положение равновесия £ = т] = 0 не является изолированным, так как равновесие будет иметь, место и при любом 5 = const и т| = О,
§ 9.5]
ОРТОГОНАЛЬНОСТЬ СОБСТВЕННЫХ ФОРМ
587
Матрица
— (7И1 + ^2)
О
О m\tn^ mt + т%
имеет лишь линейные элементарные делители к, к — оА Но элементарные
делители матрицы
/(*)=
(«! + /И2) X2 О
О ^_Х2 + С
т1 "Г т2
Л(к) =
суть %— Z<o; первый из них нелинеен.
Пример 3 Р•1П]:
А (у, у) = 32у® 4- 32>| + 11 у1 + 8>2>8 + 8у3уг — 32^j2,
Н (у, у) = 48^ 4- 48у14- 12j|,
h (X) =
— 32Х 4- 48 16k — 4л
— 4Х
— 4к
— 11М-12
det h (к) = — 2833 (к —1)2 (к — 4), Xi = к2 = 1, к3 = 4,
16 16
16 16
— 4 — 4
Л(4) =
— 80 64 —16
64 —80 —16
— 16 —16 —32
Двойному характеристическому числу 1 соответствует уравнение
/г(1)=-
и мы можем взять модальные
столбцы
5
^1 =
^2 =
Характеристическому числу уравнений
4tti — 5«2 — «з = 0, и мы можем взять
4 соответствует система двух независимых
1
1
Однако столбцы Vi, v2, v3 не нормированы, а первые два не ортогональны. Так как
Л (vb = Н (vit v^ = 2160,
то» нормируя Vi, получим столбец
* v.
1
V1
588
ПАССИВНЫЕ СИСТЕМЫ
[гл. 9
Вычисляя ещё
A (vlt v2) = Н (уь v2) = — 1728, получаем столбец
л / * \ ♦ A (уь v2) Vi - 9
и = VQ — A (V<, Vo) v< = Vo-у~Г—2-r-1 == -=
2 4 1 2 1 2 A(vb v^ 5
О 1 4
ортогональный к v*. Нормируя его, находим
* и 1
2 YA (а, а) 4/15
а нормируя v3, — столбец
О 1 4
Таким образом, мы получаем новую модальную матрицу
Формы А (у, у), И (у, у) и уравнения движения
(32D2 4- 48) yt - 16D2y2 + 4D2y3 = (О,
- 16D2J! + (32D2 + 48)у2 + 4D2y3 = х2 (f), 4D2Jt + 4D2y2 + (1Щ2 + 12) y3 = x3 (t)
после преобразования у = v*t] получают вид
. Л* (т), *)) = + ill + (*b *1) = *1? + *12 + 4y&
+ *11 = — 1/ —' X1 (0 —--------7= -^2 (0 +-----^3 (0»
dt^ 12' 3 3 /15 3 /15
^2y12 I 1 ! 1 /ЛЧ
---L + ^2 =------= X2 (0 4 7= X3 (t)t dt* 4 V15 /15
d^> 1 1 1
+ 4^ =-------— Xi (t) 4----x2 (0------------— x3 (t).
dt* 6/3 6/3 6/3
§ 9.6. Колебания натянутой нити с закреплёнными концами, загруженной сосредоточенными массами. Рассмотрим в качестве примера классическую задачу о колебаниях натянутой нити с прикреплёнными к ней п массами mjt делящими нить на участки, длины которых суть hp концы нити закреплены неподвижно. Поперечные
§ &.&] Колебаний йатйнУтоЙ Нити С закрепленными концами 68$
смещения у$ предполагаются столь малыми, что можно не принимать во внимание удлинение и связанное с ним изменение силы натяжения Р.
Кинетическая энергия системы есть
п
j=i
(9.44)
Сила, действующая на каждую массу ntj в поперечном направлении, найдётся, если натяжения Р в частях нити, примыкающих к этой
Фиг. 112. Нить, загруженная сосредоточенными массами.
массе слева и справа, спроектировать на направление нити и сложить (фиг. 112); таким образом, получаются уравнения движения
п^Уз Р h-^1 ~h • (7—!»•••> л), (9.45)
з з
причём, разумея под yQ, yn±i смещения концов нити, мы в силу сделанного предположения полагаем в первом и последнем уравнениях
?о = 3'ге+1 = °- (9.46)
Правые части могут быть представлены как — дУ/ду^ где функция
или
(9.47)
есть потенциальная энергия.
Полагая, как всегда, у^=и^ехЪ, х2 =— X, получим:
^из и j-i) nijkitj Uj) — 0 (у— 1, ..., я); (9.48)
* * *.4
если же разделить каждое уравнение на Р(htx^hj)l2h*th. значить
и обо-
Р/==2 —
2П<
2/Ь
(9.49)
5Йб
Пас6ивУЫе СЙСтеМь!
[гл. §
то
— r3ui-i +Pjaj—4juj+i = ° (J = 1 > • • • > «); (9.50)
при этом в соответствии с (46) мы полагаем:
#Q:=ttw+i = 0. (9.51)
Определитель полученной системы линейных уравнений относительно п неизвестных ult ..., ип, есть Д№, если, вообще, обозначить
р! — Qi 0 . . . 0 О
— r2 р.2 — q2... О О
Л,
О 0 0 ... р,_± —q„_i
О 0 0 ... — г, /?,
(9.52)
Разлагая этот определитель по элементам последней строки, получим редукционную формулу
^=/»A-i-WA-8> (9.53)
причём, чтобы сделать её применимой при
v= 1, 2, 3, ...,
следует положить условно
A_t = 0, До=1. (9.54)
Доведём до конца все вычисления для случая равных масс /пх = = ... = тп = т, помещённых на равных расстояниях /г0 = =
= ... = /г„ = Л; здесь ... =рп = С, q1 — r1= ... =?„ = = rn = 1, где
rnh
Полагая
0=2 cos О,
(9.56)
где 0 есть действительное или комплексное число, мы удовлетворим редукционной формуле
Д., = 2 cos 9 Д.-! — Д._2, (9.57)
если возьмём
Д., = р sin (v -|- 1) 6, (9.58)
так как
sin (у —1) 9 = 2 cos 9 sin у9 — sin (у — 1) 9. (9.59)
Принятое нами выражение даёт Д_х = 0, как и должно быть, а чтобы получить
До =s р sin 9 = 1, (9.60)
§ 9.6] КОЛЕБАНИЯ НАТЯНУТОЙ НИТИ С ЗАкРЕПЛЕННЫМИ КОНЦАМИ §91 нужно взять
Р = Е1, (9.61)
так что окончательно
А, = 81П°-6 (* = -Ь О’ Ь 2. ...)• (9.62)
Характеристическое уравнение есть
д = sin£i + l)e = 0 9 63
п sin 6 7
или
(пЦ- 1)0 = kit (fe=l, ..., п),
откуда для 0 получается п значений
0» = 7ТТ (* = 1> •••««)• (9-64)
Сравнивая выражения (55) и (56) для С, получаем характеристические числа и соответствующие собственные частоты:
2Р н х 4Р . q kit
Aft = —7- (1 COS 6fc) = —Г Sin2 ,
л mhv mh 2 (п 4-1) ’
k (9.65)
= 2 1/ sin 6 - (k = 1, ..., n).
л V mh 2(л + 1) v 7 J
Уравнения собственных форм (50) принимают вид
— uj-i + Сио — uj+i = 0 (/ == 1, ..., ^); (9.66)
они удовлетворяются, если положить С = 2 cos 6 и взять
= a cos у‘0 b sin (9.67)
так как, подставляя, получим тождество
а [ — cos (7— 1) 0 -|~2 cos 6 cos у’О — cos (у + 1)0] +
Ь [ — sin (у— 1) 0 —2 cos 0 sin у’О — sin (у 4- 1) 0] = 0.
Что же касается пограничных условий (51), то они дают а = 0 и sin (n-]~ 1) 0 = 0 при произвольном Ь. Получившееся уравнение для О —то самое, которое мы уже имели раньше (63). Собственно говоря, последние соображения относительно чисел iij совершенно Достаточны для их нахождения и вычисление определителя Aw было приведено лишь с целью установления связи с общей теорией. Заменяя в формуле для угол 0 его значениями, найдём при а = О, 1 элементы п модальных столбцов
vik = sin (9.68)
Пассивны в систем ы *
Переходя к вопросу об ортогональности собственных форм, что
п
S. х/я
Sin —Vv sin п 4-1 п
\>&я _ ( (п-]-1)/2 при y = fe, О при y#=fe.
Для этого заметим, что, пользуясь тождеством
sin a sin р = A- [cos (а — Р)—cos (а -1- р)],
мы можем написать:
докажем,
(9.69)
1 (у — k) я . о (] — k) я । . (У — Л) я
n COS —--р-=----1- COS 2 —--Н . . . + COS п ---—
2 L п +1 1 п +1 1 1 и +1
if U + k) я . п (j + £) I t ( / + k) я
— -тг cos - ---f- cos 2 w—1, \-k ... + cos n v \ -
2 n +1 1 n +1 1 1 n +1
Вычислим затем сумму
5 = cos <p + cos 2<p —... —cos n<p; умножая её на 2 cosep, имеем:
2S cos <p = 2 cos ср cos ср -|- 2 cos 2cp cos cp —... —2 cos nep cos cp. Если же воспользоваться тождеством
2 cos a cos р = cos (а — р) -|- cos (а -}- Р),
то получится:
25 cos ср = 1 cos ср ... + cos (п — 1) ? +
4~ cos 2ср 4~ cos Зср —... 4“ cos (Л + О ? — = [5 4“ 1 — COS пер] 4-» [5 — COS ср 4~ cos (п 4" 1) ?] = = 254-1 — cos ср 4~ cos (п4- 1) <р— cos пер.
Рассматривая последнее соотношение как уравнение относительно 5, найдём:
25(1 — cos ср) =
— cos ср) — cos
sin (2л + 1) -J-2sin-X-£
§ 9.6] КОЛЕБАНИЯ НАТЯНУТОЙ НИТИ С ЗАКРЕПЛЁННЫМИ КОНЦАМИ 593
Теперь мы можем написать:
где
Так кзк
(9.70)
(9.71)
то знаменатели в St и S2 отличны от нуля, если j=f=k. предположении
При этом
или
Sin (J — k) л — У/ . П
и, аналогично,
S2 = — 4- [I + cos (у + fe) л] — — (I -j- cos уте cos kity (9.73)
отсюда
St— S2 = 0 при j=f=k.
CC другой стороны, при j =к c 1 । 2» + l Si = —y H------------------§— = “’
1 sin (2n 4-1) —/
Q __ I. «4-1 _
— "о" i 7Z —'
2 SIH —< «4-1
, zn. /те \
•1 . sinF-rM) _;
2 2,sin4r-r
n-P 1
Si — S2 = n4"l при y = fe.
♦
(9.74)
(9.75)
38 Зак. 1474. Б. В/ З^УЛгаков
п . (j — Ф *
2sin~T7---гАт
594
пассивные системы
[гл. 9
Таким образом, соотношения (69) доказаны; мы можем переписать их в виде
” f(rt-J~l)/2 при j — k,
Л *_£. А (9.76)
i=i 7 I 0 при j=/=k. 4 7
Первое из них может служить для нормировки, а второе показывает ортогональность собственных форм.
Заметим теперь, что абсциссы п масс, отсчитываемые от левого закреплённого конца, суть
lj=jh b ...» я).
Откладывая в качестве соответствующих ординат отрезки, пропорциональные элементам v1Jt, ..., vnk какой-нибудь fe-й собственной формы, и соединяя полученные точки отрезками прямых, можно построить изображение стоячей волны, соответствующей этой форме. Так как при изменении j от 0 до и фиксированном k аргумент синуса в формуле (68) изменяется от 0 до feir, то fe-я собственная форма состоит из k полуволн. При принятой нами системе нумерации собственные частоты 04, ..., по формуле (65) образуют возрастающую последовательность, так что есть частота основного тона, а>2, ..., <лп — частоты обертонов. Поэтому если назвать узлами те точки, где ломаная, изображающая собственную форму, пересекает ось абсцисс, то выходит, что собственная форма основного тона не имеет узлов, а форма fe-го обертона (k — 1,..., п—1) имеет k узлов (не считая, конечно, закреплённых концов /о = О и ^п+1)*
Общее решение есть
п
а* sin7rprcos<“^+sfc) (/= 1, .... л); (9.77) fc=l
если же заметить, что Z = ZW+1 = (п-|-1)/г есть общая длина нити,
то
j __ Ч_________Ч_
п +1 h (п + 1) Z
(9.78)
и
Л = S аъ sin ~Г cos ®fc) U = 1.....................»)• (9.79)
А=1
§ 9.7. Та же задача при иных пограничных условиях. Если положить
Pi = £ («Ли — «/) (9-80)
и написать о>а вместо X, то соотношение (48) примет вид
pj-i — m-jiijW2 — Pj=0 (/=1, ..., n) (9.81)
§ 9.7] ТА ЖЕ ЗАДАЧА ЙРИ ИНЫХ ПОГРАНИЧНЫХ УСЛОВИЯХ
и- может рассматриваться как уравнение равновесия трёх «сил». Если бы вместо и3- и Uj+1 стояли yj и yj+1, то Р$ действительно представляло бы силу, с которой (J—|— 1)-я масса через посредство части нити воздействует на j-ю; мы будем называть Pj амплитуд-ними силами. Они могут быть применены для формулировки различных пограничных условий.
Например, вместо того чтобы считать оба конца нити закреплёнными, предположим, что это имеет место лишь в отношении одного из них, хотя бы левого. Правый конец мы предположим свободным, так что уравнение движения n-й массы имеет вид
<Уп = -РУ\Уп~Г\ (9.82)
в последней из уравнений (45) мы должны, следовательно, положить J'n+i—Уп~^ и в соответствии с этим считать n-ю амплитудную силу, действующую на правом конце нити, равной нулю: Рп — = (P//zw) (и№+1— а№) = 0. То же получится, если предположить правый конец нити прикреплённым к невесомому колечку, свободно скользящему по проволоке, перпендикулярной к нити в положении её равновесия. Рассматривая колечко как (/г-[-1)-ю массу, напишем для неё уравнение
™п+^=~РУп\~Уп, ’ (9.83)
а затем положим znw+1 = O, что даёт уп+±—Уп~® и потому Pw = 0.
Итак, в данном случае мы имеем вместо (46) пограничные условия
.Уо ~ Уп^Уп-ь!9 (9.84)
а для собственных форм — условия
^0 = 0, (9.85)
Выражение потенциальной энергии может быть переписано в виде n—1 2 п-1
<9-86>
Чтобы довести до конца все вычисления, предположим опять все # масс равными т±= ... = тп = т и помещёнными на равных расстояниях hQ = hx = ... = hn_x = h. Тогда мы имеем уравнение собственных форм (66), являющееся, в сущности, линейным уравнением в конечных разностях с постоянными коэффициентами; формула (67) представляет его общее решение с двумя постоянными а, Ь,
Комбинируя её с пограничными условиями (85), находим;
а = 0, sin пб — sin (п-Ц-1) 6; (9.87)
38*
596
ПАССИВНЫЕ СИСТЕМЫ
[гл. 9
так как
sin ® — sin пО = 2 sin
0,
то мы должны иметь:
cos (п + 6 = 0, (п +4") в = — 1),
для 6 получается п значений
t\ 2 А? 1 / х. 1 \
0/с = it । i~ («:=:: 1, •. •, я).
Соответствующие собственные частоты будут:
Ш* = 2У ssin2W (А=1’ ">•
(9.88)
(9.89)
(9.90)
а элементы модальной матрицы (при 6=1) определяются лами
. j(2k— 1)л = sin 9„4.1
форму-
(9.91)
Заметим, что для основного тона (k = 1) мы имеем на свободном конце С/ = я, п+1):
= ®п+1,1 = sin -ь oZ2 । j ~2 • (9.92)
При достаточно большом п аргумент синуса близок к к/2, так что, в то время как при закреплённых концах собственная форма основного тона представляет одну стоячую полуволну, здесь мы имеем, приближённо, четверть волны с максимумом на свободном конце.
Общее решение есть
п
®in ТГИГ" cos 8*>
*=i
(9.93)
(/=!,. .... n).
§ 9.8. Экстремальные свойства характеристических чисел. Независимо от того, являются ли собственные формы нормированными или нет, мы имеем соотношение (29) или
22 HjkVjlVul
Н и____ j 1с
4, “22 ^jkvjlvkl ’ J к
(9.94)
Оно не может, разумеется, служить для нахождения характеристических ।чисел, так как собственные формы заранее неизвестны, но, отправляясь от него, можно установить важные экстремальные
§ 9.8] ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА ХАРАКТЕРИСТИЧЕСКИХ ЧИСЕЛ
597
свойства этих чисел. Прежде чем обратиться к этому, заметим, что если Н(у> У) есть знакоопределённая положительная форма, то мы можем написать также:
9 ни
(9.95)
При Z-м нормальном колебании = cos (со4/-Ц-6г) мы имеем для кинетической и потенциальной энергий выражения
4 = 4 Auaimi sin2 (®i*+ ег)>
1 * 2 1 . , (9-96)
- Hnt\i = uai cos2 (<o^+1)г),
M At I
1 2 2 1 rr* 2
так что их максимальные значения суть Аца^г и -кНца^ мы мо-At At
жем сказать, что в рассматриваемом случае предыдущее соотношение (95) выражает равенство этих максимумов.
Вернёмся теперь к общему случаю и рассмотрим величину X, определяемую в функции матрицы-столбца и формулой
22
х (#х, ...» ww) = ,
A jkU’jU'k 3 к
Переписывая её в виде
^22 Азкизик 2 S ^jkujuk = О
3 к 3 к
и дифференцируя, найдём:
(9.97)
2 2Х 2 Ajk du3uk 2j 2j Hjk dttjUk 0»
3 к j к 3 ,k
откуда
(2 2 AjkW) dX = 2 5 [S ( - XAJk + Hjk) uk] dUj. (9.98)
3 k 3- к
Если и есть одна из собственных форм vb то соответствующее значение X = \г будет характеристическим числом и внутренняя сумма в правой части последнего соотношения обращается в нуль при всяком j. Так как А(у, у) есть неособая форма, то мы получаем сГК = 0. Таким образом, характеристические числа суть стационарные значения функции X (и19 ..., aw), что было отмечено ещё Лагранжем.
Величина X (ах, ..., #w) может рассматриваться как характеристическое число той системы с одной степенью свободы, которая получится, если мы нашей первоначальной системе «навяжем»
598
ПАССИВНЫЕ СИСТЕМЫ
[гл. 9
собственную форму и, т. е. введём такие связи, чтобы было
Уз = и&. (9.99)
В самом деле, тогда
Т = i S 2 AikaiuK^> V = cons! + i 2 Н*ази^> (9.100) j fc j' к
и единственное уравнение Лагранжа для связанной системы при учёте (97) может быть написано в виде
£4-Х9 = 0, (9.101)
откуда и видно, что X есть характеристическое число; если оно положительно, то оно равно квадрату собственной частоты связанной системы.
Пусть теперь имеем какую-то систему постоянных ulf ..., ип, которую можно рассматривать как первое грубое приближение для собственной формы. Эту систему а можно себе представить разложенной по точным собственным формам vk:
= (9.102)
к
Коэффициенты этого линейного преобразования образуют модальную матрицу, вследствие чего системы постоянных и и к находятся в таком же отношении друг к другу, как какие-нибудь первоначально данные и нормальные координаты системы. Поэтому
А (и, и) = ^А&т$, И (и, и) = 2 = 2 A*jkjify (9.103)
J J J
отсюда, обозначая через Xt, Xw наименьшее и наибольшее из характеристических чисел, мы имеем при любых значениях этих чисел:
j____и) j
«л
3 3
или
(9.104)
(9.105)
Таким образом, мы можем теперь дать более определённую формулировку высказанному выше принципу в отношении наименьшего и наибольшего характеристических чисел Хх, Xw, принадлежащую Рейли: число X, определяемое согласно (97) в функции столбца я, заключено между числами Хх> Хп, которые являются для X точным абсолютным минимумом и максимумом. Эти extrema действительно достигаются, когда и совпадает с одной из собственных форм v19 vn.
Пример. Рассмотрим частный случай задачи § 7 — колебания трёх равных масс, помещённых на равных расстояниях на нити, один конец которой закреплён, а другой свободен.
§ 9.8] ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА ХАРАКТЕРИСТИЧЕСКИХ ЧИСЕЛ 599
Лолагая в формуле (90) л =3, Л= 1, получим точное значение частоты основного тона
Wi — 0,44504
Посмотрим теперь, что может дать принцип Рейли. В данном случае Л (и, «) = m (а® 4-а® 4-и^), (9.106)
Н {и, и) = ^- [и* 4- («2 — aj2 4- («з — «г)2] =
= -j— (2«t 4“ 2вг 4" из 2и^а2 <2и2и.^). (9.107)
В качестве приближённого выражения для собственной формы возьмём: «/=/ — аД (9.108)
где а — некоторая постоянная; в координатах у, и это соотношение представляет параболу, проходящую через начало координат. Подставляя (108) в выражения для А (л, л), Н (и, и), находим:
А (и, и) = 2m (7 — 36а + 49а2),
Н (и, а) = £• (3 — 18а 4- 35а2).
Величина
H(ut и) _ Р 1 3—18а + 35а2 “Л (а, и)~ mil 2 7 —36а-р49а2 ’
рассматриваемая как функция от а, имеет при значениях этого параметра at = 0,119273 и а2 = 0,399246
минимум
V = 0,198487 Аг mh
и максимум
= 2,7847 -Д-.
Минимуму соответствует частота а/ = ук или
а/ = 0,44552
которая может рассматриваться как приближённое значение частоты основного тона. Оно немного превышает точное значение ошибка составляет всего 0,1%. Этот результат получен с помощью приближённого выражения собственной формы в виде квадратичного двучлена, между тем как точное решение выражается тригонометрической функцией.
Перенумеруем теперь все характеристические числа в порядке возрастания, так что Х2 Х№, и предположим условия
нормировки (35) выполненными, что имеет целью лишь упрощение вычислений, но нисколько не ограничивает общности выводов. Тогда можно доказать ещё более общую теорему Фатера-Куранта'.
600 ПАССИВНЫЕ системы [гл. 9
Характеристическое число является наибольшим значением, которое может принять минимум отношения \(ux, ..., я№), определяемого согласно (97), при добавочных условиях* :
%a,kak = 0 0=1, .... j— 1), (9.109) J
k “ i
г если рассматривать этот минимум как функцию параметров а^.
Чтобы пояснить прежде всего самый текст этой теоремы, заметим, что ..., ип) является обратной величиной квадрата расстояния р от центра гиперповерхности Н (у, у) = 1 до точки её пересечения с линией действия вектора и. В самом деле, в «нормальной» системе координат *%, ..., т)п, получаемой линейным преобразованием = формы А (у, у) и Н(у, у) получают вид
= • • • +^> Н* (7], 70 = + . . . + (9.110)
и координаты указанной выше точки будут pitfc/]Z тг^—f— • •.
(& = 1, . . ., п). Подставляя эти выражения вместо в уравнение Ь мы и получим:
Уравнения (109) можно рассматривать как уравнения гиперплоскостей, проходящих через начало координат и определяющих линейное мно- £ гообразие п—у—|— 1 измерений. В пересечении с гиперповерхностью \ получается многообразие п — J измерений и дело идёт сначала о ~ максимуме радиуса-вектора р на этом многообразии, а затем о наи- - } меньшем значении этого максимума при всевозможных положениях линейного многообразия. Например, в трёхмерном пространстве при | пересечении эллипсоида плоскостью (п = 3, у = 2) получаетсг эллипс и наименьшая величина его большой полуоси равна средней полуоси || эллипсоида р.2. ‘ fl
Переходя к доказательству, предположим, что в «нормальной» | системе мы получили вместо (109) новые условия 1
2«л = о 0=1,.... j— 1). (9.111)1
k ‘ I
Полагая = ... = к№ = 0, мы будем иметь J—1 однородных 11 уравнений относительно у неизвестных irx, . ♦., Всегда можно II найти системы значений, удовлетворяющие этим уравнениям, и для II них 1
я*(к, к) = х^4- • • • j(Ki+ • • • +к?), II
, Л* (и, -к) = . . . -Ц- тс?»
Н(и, и)/А(и, и) = Н* (к, it)/A* (it, ^)<С^у 1
як
W
(9.И2)
§ 9.9]
теорема Рейли
601
. Цоэтому и искомый минимум при любых не превосходит к^ Но этот минимум становится как раз равным kj, если в качестве условий (109) взять 74= ... = ^._1 = 0, так как
этим и завершается доказательство.
Теорему можно также формулировать таким образом: j-e харак-меристическое число данной системы является наибольшим из минимальных характеристических ' чисел различных систем* получаемых путём наложения на данную каких-нибудь j—1 связей.
С другой стороны, так же как и выше, можно доказать, что характеристическое число kn_j+1 является наименьшим значением, которое может принять максимум отношения k (ulf ..., ип) при j—1 добавочных условиях (109), если рассматривать этот максимум как функцию параметров.
§ 9.9. Теорема Рейли об изменении характеристических чисел при наложении новых связей и увеличении инерции или жёсткости системы. Пользуясь доказанными в предыдущем параграфе теоремами о характеристических числах, можно выяснить, как они изменяются, если на систему вновь налагаются с независимых связей. С той же точностью, с которой составлялись уравнения движения, уравнения связей можно считать линейными:
2М = ° (Т = 1, (9.114)
к .
коэффициенты мы предполагаем постоянными. Обозначим через. (Ь) линейное многообразие значений^, удовлетворяющих уравнениям (114). Какие-нибудь п — с из числа этих переменных можно принять за независимые координаты новой механической системы, получаемой из данной путём наложения новых связей.
Пусть ещё (а) есть линейное многообразие значений п переменных, удовлетворяющих j—1 уравнениям (109), зависящее от параметров и (ab) — общая часть многообразий (а), (&). у-е характеристическое число kj первоначальной системы получается путём Решения задачи о наибольшем значении минимумов функции ...» ип) на различных многообразиях (а), у-е характеристическое число Л', новой системы получается путём решения такой же задачи для различных линейных многообразий, определяемых внутри (fi) пУтём наложения на п — с независимых координат системы j— 1 добавочных линейных условий. Всегда можно рассматривать эти частичные
602 ПАССИВНЫЕ СИСТЕМЫ [гл. 9
многообразия как пересечения (ab) многообразия (Ъ) с некоторыми (а). Следовательно, при разыскании минимумов для определения X'. мы имеем дело с частями (ab) тех многообразий (а), которыми поль-зовались для определения Х^; поэтому отдельные минимумы, а вместе с ними и характеристическое число для новой задачи не меньше, чем для прежней.
С другой стороны, Xc4_j есть наибольшее из значений, которое получает минимум функции Х(я1} ..., ип) на линейных многообразиях (#c+j_i), определяемых заданием c-[-J—1 линейных однородных условий при различном выборе коэффициентов. Поэтому Хс+^ ; не может быть меньше, чем X'., для которого с из этих условий 5 суть уравнения связей с фиксированными коэффициентами. |
Таким образом, Х^ Х^ Хс+у, и мы получаем следующую тео- 1 рему Рейли.
I. Если на систему налагаются с независимых связей, то j характеристические числа Хх, ..., Xw_c получаемой системы ] с п — с степенями свободы не меньше соответствующих чисел ] ряда Xt, ..., Xw_c и не больше соответствующих чисел ряда | Хе+1, ..., Хм. Если Н(у, у) есть знакоопределённая положительная 1 форма и положение равновесия устойчиво, то приведённое предложение | формулируется как теорема об изменении собственных частот системы, 1 т. е. частоты её основного тона а>1} и обертонов о>2, ..., oow. 1
Рассмотрим, далее, эффект изменения инерции или жёсткости 1 систем, удовлетворяющих тому же условию относительно Н(у, у). 1 При этом под увеличением инерции, которое может быть достигнуто Ж путём введения в систему новых масс, мы понимаем замену квадра- 1 тичной формы А {у, у) такой новой формой А'(у, у), что разность В А'(у, у) — А (у, у) сама является знакоопределённой положительной Ж формой. Увеличение жёсткости, которое можно себе представить Цм осуществлённым путём увеличения восстанавливающих сил, опреде- Ж ляется аналогичным образом в связи с формой Н(у, у). Так как при Ж] этих изменениях увеличивается или числитель или знаменатель отно- >1 шения X(wt, ..., rzw), то мы получаем две дальнейшие теоремыSI Рейли. JI
II. При увеличении инерции системы собственные частоты^®! уменьшаются или, по крайней мере, не увеличиваются. 11
III. При увеличении жёсткости системы они увеличиваютсяШ или, по крайней мере, не уменьшаются. В!
§ 9.10. Обратный метод; предельный переход к интеграль-ж| ному уравнению. Рассмотрим неоднородную систему уравнений >1
Ay-\-Hy = Q, (9Л15)1|
где Q обозначает матрицу-столбец добавочных обобщённых сил приложенных к механической системе. Предположим, что матрица #11
§ 9.10] ПРЕДЕЛЬНЫЙ ПЕРЕХОД К ИНТЕГРАЛЬНОМУ УРАВНЕНИЮ 603 неос(Тбая, так что обратная матрица
ф^/7-i (9.116)
существует. Полагая ещё К= А = Ф А, Р = H"1Q = $Q, (9.117)
найдём, разрешая относительно у. y = — D^Ky + P. (9.118)
Заметим, что матрица К, вообще, не будет симметричной, хотя бы А и Н являлись таковыми. В механической задаче А будет неособой матрицей, но для существа дальнейшей теории достаточно, чтобы А не была равна нулю. Тогда и К будет отлична от нуля, поскольку Н—неособая матрица.
В случае равновесия мы имеем у = 0 и
3/ = Ф(? (9.119)
или п
Уз = S *ikQk и = 1. •. •. «)• (9.120)
Zc=l
Ф называется матрицей влияния, а её элементы ФуЛ — коэффициентами влияния', Ф^ есть статическое смещение в координате у$ от силы Qk = 1 при остальных силах, равных нулю: Мы имеем Ф# = Ф^ (теорема взаимности Максвелла).
Рассматривая опять собственные колебания, предположим, что Р = 0, и возьмём, как всегда, y = uexpvt', обозначая Х =— х2, найдём:
и = ХКи (9.121)
или, переходя к элементам,
= (/=!,...,«). (9.122)
к
Вводя монотонную последовательность чисел
O = Zo<Z1<Z2< ... <ZM<ZM+1 = Z, (9.123) будем трактовать Uj и ик как значения некоторой скалярной функции от одного непрерывно меняющегося переменного
= и (ty, ик = и (1к) (9.124)
и аналогичным образом будем считать числа Kjk пропорциональными значениям некоторой функции двух переменных:
Kjk = КЩ, 1к)Мк, (9.125)
гДе AZfc — малая величина. Тогда
И ((/) = А. 2 K(ljt 1к) и Д/й U= L....«)• (9.126)
к
604
ПАССИВНЫЕ СИСТЕМЫ
1гл. 9
При большом п уравнение (126) можно считать за приближённое г выражение соотношения 4
* « ®
' * I
K(s, а) и (a) da, (9.127) I
п ’ <
0 $ которое носит название однородного линейного интегрального урав- | нения Фредгольма 2-го рода с неизвестной функцией u(s)\ K(s9 а) | называется его ядром. • |
Предельный переход такого рода, поскольку его молено отнести | и к самой колебательной системе, означает переход к механике | сплошной среды. В отношении аналитического аппарата этому coot- 1 ветствует, как мы видим, переход от матриц к скалярным функциям | и от системы линейных алгебраических уравнений к интегральному | уравнению. |
Возвращаясь к системе (118), заметим, что так как |
Е — кК~Е — Ш-Ы = Ф(— ЛХЦ-Я),
то характеристический определитель
Dn (X) = det (Е - = det || Ejk - KKjk ||
(9.128) j
(9.129)
преобразованной системы отличается от прежнего характеристического t определителя det (— А к Ц- Н) = det |[ — А$к\ tyk II только постоянным Л множителем det Ф, вследствие чего характеристические уравнения, выраженные через X, имеют одни и те же корни Xfc. Эти корни называются > собственными значениями матрицы К. Иногда удобно ввести вместо X ;; обратную величину 4
(9.130) f
и переписать уравнение (121) в форме uz = Ки
(9.131)
или
b(z)u = 0,
где
Так как
то определитель
b(z) = Ez — K.
b(z) — ^-(E — kK),
Г (г) = det b (г)
(9.133)
(9.134) I
(9.135) )
связан с Dn(k) соотношением
Г(г) = 1оя(Л),
(9.136) |
вследствие чего корни zk уравнения Г(^)==0 суть обратные значе- | ния величин корней определителя Dn(ty величины zk суть j
§9.П1
ФУНКЦИЯ ВЛИЯНИЯ НАТЯНУТОЙ нити
605
характеристические числа матрицы К-Уравнение модальной матрицы _ дуД _1_ Hv = 0 по умножении слева на Ф примет вид — KvA -J- v = О или, 'умножая справа на Z = А-1,
vZ = Kv, (9.137)
причём
' (9.138)
п
Мы могли бы рассматривать матрицу К и задачу об определении собственных форм и из уравнения (131) вне зависимости от связи К с матрицами А и Н. Тогда и уравнение модальной матрицы (137) будет непосредственно вытекать из (131). Если при этом матрица К симметрична, то последнее уравнение можно считать частным случаем уравнения (—ЛХЦ-//)а = О при А = Е, Н=К, Х = все характеристические числа zk будут действительны, согласно теореме Сильвестера, а собственные формы взаимно ортогональны:
2 Эдт = 2 S = 0 (/¥=/»). (9.139)
J 3 *
Соотношение
2 w=1 <2 * * * * * * 9 * * * * •14°)
J 1 i к
может служить для нормировки.
Уравнения обратного метода представляют лишь иную форму первоначальных; однако во многих вопросах, особенно в задачах строительной механики, обратный метод очень удобен, так как коэффи-
циенты влияния Ф;А. могут быть получены из непосредственных меха-
нических соображений. Если рассматривать коэффициенты влияния как значения некоторой функции Двух переменных
ФЛ = Ф(//,/*), (9.141)
то эта функция носит название
Функции влияния.
§ 9.11. Функция влияния на-
тянутой нити. Если оба конца
нити закреплены и на расстоя-
нии от левого приложена, сила
Q=l, то нить принимает форму, показанную на фиг. 113. Так как натяжения Р в частях нити, примыкающие слева и справа к точке приложения силы, должны уравновесить эту силу, то
Фиг. 113. Нить с двумя закреплёнными концами.
Р (sin а sin р) = 1,
(9.142)
боб
причём
пассивные системы
|гл. 9
(9.143)
где f обозначает поперечное смещение под силой. Мы
Pf ,/-^- = 1,
7 a (Z — а)
S . I
J ~ Pl ' I
получаем:
(9.144)
Для смещения у = Ф (s, о) на расстоянии s от левого конца мы имеем из подобия треугольников:
при
при s а,
(9.145)
так что функция влияния будет:
( s(Z-g)
I pl
Pl
при S < а,
При S <5.
(9.Г46)
Если в точках с абсциссами /х < 1.2 < ... < 1п помещены дискретные массы, то коэффициенты влияния будут:
Pl hAl-lj)
Pl
при
при j^k.
(9.147)
Если левый конец закреплён, а правый свободен, то нить примет
Фиг. 114. Нить с левым закреплённым и правым свободным концами.
форму, показанную на фиг. 114; путём вычисления, аналогичного проделанному выше, получим функцию влияния
-р при s а,
Ф(5, а) = { с (9.148)
-g- при $ а
“-Г<
9.13] КОЛЕБАНИЯ БАЛКИ, ЗАГРУЖЕННОЙ СОСРЕДОТОЧЕННЫМИ - МАССАМИ б07
и коэффициенты влияния
* I ПРИ
I 1к и
( при J>fe.
(9.149)
§ 9.12. Коэффициенты влияния закрученного вала. Если воспользоваться известной аналогией задач о поперечных отклонениях натянутой нити и закручивании вала, то мы должны заменить отношения hj/P длин отдельных участков нити hj к натяжению Р крутильными податливостями 1/су, следовательно, сумма
должна быть заменена суммой
(9.150)
(9.151)
которая представляет крутильную податливость части вала от закреплённого сечения до у-й массы. Формула (147) предыдущего параграфа для случая закреплённых концов заменится следующей:
(А — ак) А
(А — а^) ак А
при y^fe,
при J k,
(9.152)
причём ар ак суть крутильные податливости частей вала от левого закреплённого конца до сечения 1р где вычисляется угол закручивания ср, и до сечения Zfc, где прилагается единичный момент М = 1; А есть крутильная податливость всего вала.
Если один конец закреплён, а другой свободен, то мы имеем коэффициенты влияния
(9.153)
§ 9.13. Колебания балки, загруженной сосредоточенными массами. В сопротивлении материалов*) доказывается, что прогиб у балки с опёртыми концами на расстоянии s от левой опоры под действием груза Q, приложенного на расстоянии с от правой опоры,
*) См., например, С. П. Тимошенко, Сопротивление материалов, Перев. с англ., ч. I, Ленинград — Москва, 1933, стр. 160.
608
ПАССИВНЫЕ СИСТЕМЫ
1Гл. О
равен
при S I-cf
при s^l—c,
$.154)
причём В есть так называемая жёсткость на изгиб, зависящая от упругих свойств материала балки и формы её поперечного сечения.
Полагая здесь Q = 1,
с ~1 — з, получим функцию влияния
i 6/В g) (~ — з2 + 2/з) при $ < а, Ф(5> =) = < а-.), (9-155)
j - (-----S2---02-|-2&) при $>5
и коэффициенты влияния 1^^ z *2 Л । л»j х •
“4“ 2/Zjt) при j
(9.156)
k.
I 6ZB
Пример (Лойцянский и Лурье). Рассмотрим колебания
= mt т2 = 2т, т$ = т, расположенных в четвертях пролёта балки с опёртыми концами (фиг. 115).
Матрица инерции есть
Фиг. 115. Балка, загруженная тремя массами.
т О О
О 2т
О
О О т
= т
трёх масс
О О
О О
2 О
О 1
Полагая в формуле (156) Zj = -^-j7, получим:
(^.j2_^2 + 8^) /3
768В
Вычисляя, найдём матрицу влияния
Отсюда
Полагая
768В m/з Zi
L =
9 22 7
11 32 11
7 22 9
§ 9.13] КОЛЕБАНИЯ ЙАЛКЦ, ЗАГРУЖЕННОЙ СОСРЕДОТОЧЕННЫМИ МАССАМИ 609
мы'заменим уравнение модального столбца uz — Ku следующим:
мС = Lu.
Вычисляя определитель матрицы
— 22 — 7
С —32 —И
— 22 С — 9
находим:
det (ЕС — L) = С3 — 50С2 + 1245 — 56;
приравнивая его нулю, находим корни
Так как
q = 47,4095; С2 = 2,0000; С3 = 0,5896.
1768 В z Ст/3’
то соответствующие собственные частоты будут:
= 4,025 1/ -4г, <02= 19,59 1/ , <о3 = 36,10 1/
1 V ml3 V ml3 V ml3
Определяя нормированные собственные формы, соответствующие этим числам, получим модальную матрицу
v =
0,498
0,710
0,498
0,707 0
— 0,707
0,634
— 0,444
0,633 а
Если же отложить на чертеже ординаты, пропорциональные элементам каждого столбца, то мы получим изображения собственных форм (фиг. 116),
Фиг. 116. Собственные формы колебаний балки с тремя массами.
состоящие из одной, двух и трёх стоячих полуволн. Иными словами, собственная форма основного тона вовсе не имеет узлов, а собственные формы первого и второго обертонов имеют, соответственно, один и два узла.
39 Зак. 1474. Б. В. Булгаков
610
ПАССИВНЫЕ СИСТЕМЫ
[гл. 9
§ 9.14 Собственные формы рациональных функций от матриц. Нижеследующая теорема послужит нам в дальнейшем для обоснования некоторых методов решения характеристического уравнения. Пусть и есть одна из собственных форм матрицы К и z — соответствующее характеристическое число; умножим обе части уравнения
uz = Ки
на z и заменим uz справа его выражением из этого же самого урав-
мг9 = ЛГ-zzz = /<.= (9.157)
Если продолжить этот процесс, то получится, вообще,
uzm = Kmu> (9.158)
откуда видно, что каждая собственная форма и матрицы К является также собственной формой и для /n-й степени Кт этой матрицы, a zm есть соответствующее характеристическое число. Эта теорема, по существу, высказана Леверрье [915] в 1839 году.
Из полученной формулы вытекает, далее, что если P(z) есть какой-нибудь полином, то
= (9.159)
иными словами, и является собственной формой и для любой матрицы Р(К)> а соответствующее характеристическое число есть P(z).
Эта теорема легко распространяется и на дробные рациональные функции. Пусть Q(z) есть ещё один полином, для которого мы можем написать также
uQ(z)==Q(K)uK (9.160)
откуда
a = Q"i(/<)aQ(z). (9.161)
Подставляя в (159), находим:
иР (z) = Р (К) и Q(z) (9.162)
или
aR(z) = R(K)u, (9.163)
где
R(z) = P(z)/Q(z), (9.164)
причём при составлении по этой формуле R(K) мы разумеем под Р (K)/Q (К) результат умножения Р (К) на Q-1 (К) безразлично слева или справа, так как полиномы от матриц коммутативны в отношении умножения, а значит, и деления.
Формула (163) и даёт обобщение, которое имелось в виду: и будет также собственной формой для любой дробной рациональной функции от К, причём соответствующее характеристическое число определяется значением той же самой функции аргумента z.
§ 9.16] РАЗВЕРТЫВАНИЕ ХАРАКТЕРИСТИЧЕСКОГО ОПРЕДЕЛИТЕЛЯ 611
§*9.15. Развёртывание характеристического определителя по Леверрье и Крылову. Для получения характеристического уравнения необходимо развернуть определитель (135)
Г (z) = det || Ejkz — Kjk || и представить его в виде многочлена
Г(z) s zn + a^z*-1 + ... + (9.165)
в котором, как это важно заметить для последующего, ^==-(^1+...+^). (9.166)
При сколько-нибудь значительном п процедура развёртывания весьма тягостна, и задаче об её упрощении посвящён ряд работ. Мы обязаны А. Н. Крылову [9-2] тем, что он вновь обратил внимание на элегантный метод Леверрье и дал своё усовершенствование.
Если sm обозначают степенные суммы корней любого многочлена Г(-г) степени п
sm = Zl+---+Zn> <9-167)
то они связаны с коэффициентами ат формулами Ньютона *), которые были даны им в «Arithmetica universalis» (1707):
5m + al$m-l+• • •+Si-l5l + wam = ° (^=h •••> >*)• (9.168)
Первое из этих соотношений (m=l) совпадает с формулой Виета — сопоставляя её с (166), имеем:
«1 = ^1+ (9-169)
Если же составить матрицы №, ...» Кп и воспользоваться тем, что по теореме предыдущего параграфа их характеристические числа суть степени характеристических чисел матрицы то мы получим, вообще,
sm = хЦв)+ ... +№, (9.170)
где т=1, ..., п. Все степенные суммы, входящие в формулы Ньютона, будут теперь известны, и из этих формул можно будет определить.коэффициенты, что позволит написать развёрнутое выражение Г(з). В этом и состоит метод Леверрье.
Степени матрицы К, которыми здесь приходится оперировать, связаны формулами
Кт = ККт-1 (9.171)
или
(9.172)
*) См., например, А. К. Сушкевич [1,7Jстр.207. 39*
612
пассивные системы
(гл. 9'
если считать элементы этих матриц пропорциональными значениям некоторых функций двух переменных
= Л™ 4) Д4, (9.173)
то при переходе к интегральному уравнению мы получим соотношения
z
А'ж(S, о) = J K(s, т) Km.t (т, a)dz, (9.174)
О
благодаря которым функции Km(st а) называются итерированными (повторными) ядрами.
Можно добавить, что для достижения цели достаточно вычислить п п 1
полностью матрицы Л?" лишь до № при п чётном и /С2 2 —при п нечётном. Перемножая их по две, можно получить остальные матрицы до Кп, но в каждой из них достаточно фактически вычислить лишь диагональные элементы, так как это всё, что нужно для составления степенных сумм.
Метод А. Н. Крылова состоит в следующем. Выпишем п матричных соотношений
uz™ == Кти (т = 1, ..., п) (9.175)
и приравняем в каждом /-е элементы матриц-столбцов, стоящих слева и справа; это даст:
«,г«» = 2 Ку? uk (т = 1.........п), (9.176)
к
ИЛИ
• • • + (Kj~z) uj-\~ • • • + ип =0>
г”)и/+^^+1и^+14* • • • ~Г^пип— 0- • (9.177) Определитель этой однородной системы линейных уравнений есть Дд ••• z ~т~•••
№ ... *fi-i -+k%> Kft,, ... K$
C(z) = . (9.178)
rXn) Hw). _________ n I ИФ H№).
A;1 ... Лд,4-1 --z -j-A# A4, 4+1 ... A^n
£ 9.16] КРУТИЛЬНЫЕ КОЛЕБАНИЯ ВАЛА АВИАЦИОННОГО МОТОРА
613
Полагая
Со= С(0) =
• • • к$п lA?) Ад . . . Ajn
• •••••
АД . . . Ajn
(9.179)
и обозначая через Ct, ..., Сп алгебраические дополнения элементов у-го столбца в C(z), получим путём разложения определителя характеристическое уравнение
- С (г) » Cnzn + Cn_1Zn-i + ... 4- C1Z - Со = 0. (9.180)
Сличая с (165), найдём: ат=А^- (яг=1..............................О-
_______Со ап с •
(9.181)
Способ этот имеет то преимущество, что он требует вычисления лишь тех из величин К$\ которые соответствуют данному фиксированному J и связаны друг с другом рекуррентными соотношениями
К*
(9.182)
Фиг. 117. Вал шестицилиндрового авиационного мотора.
в которых k, т = 1, . •«. Если обозначить/-ю строку матрицы К*, рассматриваемую как особую матрицу-строку, через К) , то рекур-рентное соотношение может быть написано в виде
/С^) = КУП-1)К. (9.183) Когда характеристические числа найдены, уравнения (177) позволяют определить собственные формы.
§ 9.16. Крутильные колебания вала авиационного мотора. Пусть имеем л-цилиндровый мотор, связанный с пропеллером очень большого момента
инерции, так что вращение последнего разуметь моменты
можно считать равномерным (фиг. И*)* Под Jj °У Р ппгтгпятельно инерции вращающихся масс с учетом '°™. “ „их меха
движущихся масс соответствующих кривошипно-шатунных низмов.
614
ПАССИВНЫЕ СИСТЕМЫ
(гл. 9
Матрица инерции есть
Д =
(9.184)
формулы (153) для коэффи-
матрицу влияния составим с помощью
циентов влияния:
(9.185)
Отсюда
ЛГ=ФА =
(9.186)
Для численного примера возьмём п — 6,
(9.187)
ct = ... = с5 = с. Тогда
где
2 2 2 2 2 2
2 3 3 3 3 3
2 3 4 4 4 4
2 3 4 5 5 5
2 3 4 5 6 6
2 3 4 5 6 7
(9.188)
§ 9.16] КРУТИЛЬНЫЕ КОЛЕБАНИЯ ВАЛА АВИАЦИОННОГО МОТОРА 615
Уравнение модального столбца uz = Кй принимает вид «£ = £«, (9.189)
где •
Чтобы применить метод Леверрье, вычисляем:
24 34 42 48 52 54
34 49 61 70 76 79
42 61 77 89 97 101
48 70 89 104 114 119 ’
52 76 97 114 126 132
54 79 101 119 132 139
508 738 934 1088 1194 1248
738 1073 1359 1584 1739 1818
£8 =
934
1088
1359 1723 2010
1584 201.0 2347
1194 1739 2208 2580
1248 1818 2309 2699
2208 2309
2580 2699
2838 2970
2970 3109
Для матриц Z4 = (Z2)2 и Z6 = £2£3 ограничиваемся нахождением элементов главных диагоналей, а именно:
11420, 24195^ 38 945, 53 098, 64185, 70264;
258216, 547234, 881 073, 1201 383, 1452176, 1589595.
Составляя суммы диагональных элементов, имеем:
s1 = 27, sa = 519, s3 = U598, «4 = 262 107, «Б = 5 929 677, откуда по формулам Ньютона получаем последовательно:
«1 = — 27, а2=105, Од = —140, а4 = 81, а6 =— 21.
Чтобы не вычислять Z6, последний коэффициент а6 можно искать не по формуле Ньютона, а непосредственно из выражения ав = (—)• det Ц определитель det L легко вычисляется, если предварительно его упростить, вычитая пятую строку из шестой, четвёртую из пятой и т. Д. и, наконец, первую из второй. Это даёт:
а6=2.
Таким образом,
Г (С) = det (ЕС — Z) =
= ;« —27C6-J-105C4—140C8-J-81Ca—21C-J-2; (9.191)
616
ПАССИВНЫЕ СИСТЕМЫ
[гл. 9
приравнивая это выражение нулю, получим характеристическое уравнение. При взятых нами численных данных оно совпадает с тем, которое получено в работе Картера. Его старший корень будет найден ниже, в следующем параграфе.
Для этого нам потребуется значение $6, которое находим по ранее вычисленным величинам $ и а из формулы Ньютона, соответствующей т = 6:
$6= 134 162 280.
§ 9.17. Оценка Данкерли и обобщение ван ден Дунгена и Папковича. Если нумеровать собственные значения так, чтобы
то модули характеристических чисел образуют убывающую или по крайней мере не возрастающую последовательность
Предположим, что характеристическое число z± с максимальным модулем будет единственным, а потому и действительным; тогда в предыдущем ряде неравенств первое будет |^|>|г2|.
Так как z™ тем более доминирует над z™> z™, ..., чем больше mt то мы можем представить формулу (167) в виде
zl (1 + 8m) = sm> lim em = ° ' (9.192)
m->oo
и ’V—
lim Vsm, (9.193)
m->oo
tn _
вследствие чего числа у sm могут служить приближёнными значениями для zx.
Если известно, что все характеристические числа положительны, то можно получить две последовательности величин, сходящиеся к zr и дающие его приближённые значения, соответственно, с недостатком и с избытком. Это даёт возможность судить о достигнутой степени приближения.
Для указанной цели заметим, что если т.2, ... есть последовательность каких-нибудь возрастающих положительных чисел, взятых из натурального ряда, то из формулы (192) вытекает:
(9.194)
§9.17]
ОБОБЩЕНИЕ ВАН ДЕН ДУНГЕНА И ПАПКОВИЧА
617
так .ч?о. последовательность • • • также
имеет пределом zt. Затем вследствие положительности всех zk из (192), следует:
z^<smt. (9.195)
С другой стороны, выписывая подробно, мы имеем:
1 1 + teMl) + • • •
а так как zr есть наибольшее из всех чисел zki то
1 + (ZzlzJ™* + ... < 1 + (z^z^ + . .
— < ^2-^1 . smx
• f
(9.196)
(9.197)
Продолжив этот процесс, получим ряд неравенств
(9.198)
которые мы имели в виду. Приближённое значение с избытком z^ получаемое при т1 = 1 и. вообще, ещё очень грубое, было найдено экспериментальным путём Данкерли Оценки (198) при » т2 = 4, /п3= 8, ... предложены ван ден Дунгеном |°-9] и П. Ф. Нап-ковичем Р Я, и для их получения достаточно последовательными умножениями составить матрицы К2 = КК, К4 = /С2/^2, К8 = К К » • • •
Заметим ещё, что если найдены все sm до sn, то можно определить коэффициенты ат характеристического уравнения. Поэтому если требуются суммы sm более высоких порядков, то их можно также найти с помощью второй группы формул Ньютона *):
Sm alsm-l
— ^п-1^т~п+1 “Г ^п^т-п
(/п = я-[-1> ^ + 2, ...).
(9.199)
Пример 1. Возвращаясь вновь к задаче о колебаниях трёх масс на невесомой балке (§ 13), вычислим квадрат матрицы L:
372 1056 368
А2 = 528 1508 528 }
368 1056 372
*) См. А. К. Сушкевич рл], стр. 207.
618
ПАССИВНЫЕ СИСТЕМЫ
[гл. 9
для матрицы £8 = £2£ ограничиваемся определением элементов главной диагонали, а именно:
17 540, 71 488, 17 540.
Составляя суммы диагональных элементов, получаем:
$х = 50, 2252, $з = 106 568
и, по первой группе формул Ньютона, находим коэффициенты характеристического уравнения
= — 50, а2 = 124, а3=* — 56,
которые, впрочем, были нами уже получены раньше непосредственным развёртыванием определителя. Пользуясь второй группой формул Ньютона, находим далее:
$4 = 5 051 952, $б = 239 509 280
и составляем две последовательности:
$1== 50, s2ls± = 45,04, VX = 47,46, $з/$2 в 47,321, ^$3 = 47,411,
s4/«3 = 47,4059, ]Л4 = 47,4094,
в,— S&/S4 = 47,4093, V s6 = 47,4094.
Так как s^st и ]/s6 отличаются лишь на 0,0001, то мы можем принять Ci = 47,4094, что практически совпадает со значением, найденным выше (§ 13). Пример 2. В задаче о крутильных колебаниях вала шестицилиндрового мотора (§ 16) нами были вычислены величины $t, $2, ^з, $4, ^б» Пользуясь ими, составляем;
$2/$t = 19,222,
=s 22,347,
sjs3 =s 22,599,
= 22,623,
$б/^в = 22,626,
= 27, <$? = 22,752,
= 22,636, yTi = 22,627, У* = 22,626, У «в = 22,626.
Значение наибольшего корня характеристического уравнения с пятью точными десятичными знаками будет поэтому = 22,626.
§ 9.18. Метод последовательных умножений. Предположим опять, что имеется одно характеристическое число с максимальным модулем, которое поэтому обязательно действительно. Для приближённого определения этого старшего характеристического числа и соответствующей собственной формы может быть также применён следующий метод. Пусть будет и некоторое исходное приближение
§ 9.18] МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ УМНОЖЕНИЙ 619
ддя . Образуем матрицы и(1) = Ки, и(2) = Ка^ = №а,
«О») = /СиИ-i) в к™и> ....................1
Пусть будет, далее, tt=VK
(9.200)
(9.201)
— выражение и через собственные формы, в котором v обозначает попрежнему модальную матрицу, а те — некоторую матрицу-столбец. Пользуясь уравнением модальной матрицы, получим:
#(*) = /ft/те — vZic,
^(2) = /ft/Z-n: = vZZit = vZ^n,
(9.202)
м(«») = KvZm~^ = t>ZZ”*-Iit = ©Zmit,
причём, очевидно, Z есть диагональная матрица
т
1
Zn
Для элементов получим выражения
=2 w">
к
в которых первое слагаемое при большом т будет больше остальных, так что можно написать:
^ = ЗД^(1+^0»)), lim sk^ — O.
»»->со *
(9.203)
(9.204)
значительно
(9.205)
Поэтому
(9.206)
620
ПАССИВНЫЕ СИСТЕМЫ
[гл. 9
т. е. отношение соответственных элементов двух последовательных «итерированных» форм и стремится к наибольшему характеристическому числу zr и может служить для его приближённого определения. Исключение представляет тот случай, когда, для взятого нами исходного приближения, 14, а может быть, и нескольких следующих чисел гс2, тс3, ... оказываются равными нулю; тогда мы придём, очевидно, не к наибольшему характеристическому числу z±i а к одному из следующих.
Мы можем написать также
или
<7» + 1)
(9.207)
(9.208)
1 „
Таким образом, и&Ь удовлетворяет уравнению, которое в пределе совпадает с уравнением для vt. Следовательно, итерированные формы имеют своим пределом первую собственную форму.
Впервые данный метод был применён Вьянелло [9Л0] к одной задаче об устойчивости стержней.
Пример 1. Вернёмся к задаче о колебаниях трёх масс
= т, т2 = 2m, т
на невесомой балке с опёртыми концами (§ 13) и применим к уравнению модального столбца метод последовательных умножений (на матрицу £). Принимая за исходное приближение числа
= 1/2, и2 = 1, и3= 1/2,
будем после каждой итерации приводить к единице один из элементов итерированного столбца, например второй. Результаты вычисления приведены в таблице 6.
Таблица 6
Итерированные формы в примере 1
ai «(1) “j из ui и<2) 3 i № и № №
0,5 30 0,6977 60 33.16 0,7004 47,53 33,21 0,7004 47,41
1 43 1 43 47,35 1 47,35 47,41 1 47,41
0,5 30 0,6977 60 33,16 0,7004 47,53 33,21 0,7004 47,41
Мы видим, что при взятом числе десятичных знаков третья итерированная форма уже совпадает со второй. С другой стороны, отношение и^/и№
§ 9.181
метод последовательных умножений
621
ещё‘зависит от j, между тем как и^/и^ при том же числе знаков имеет для всех j одно и то же значение 47,41, совпадающее также с точным значением Ci, найденным выше (стр. 609).
Пример 2. Применим метод последовательных умножений к задаче о крутильных колебаниях вала шестицилиндрового мотора (§ 16), принимая за исходный столбец
0 0 0 0 0 1
и приводя к единице, после каждой итерации, последний элемент полученного итерированного столбца. Результаты вычисления приведены в таблице 7 [1Л0].
Таблица 7
Итерированные формы в примере 2
из а(?) “л
0 0 0 0 0 1 2 3 4 5 6 7 0,29 0,43 0,57 0,71 0,86 1,00 7,72 11,29 14,43 17,00 18,86 19,86 0,389 0,568 0,727 0.856 0,950 1 8,980 13,081 16,614 19,420 21,370 22,370 0,4014 0,5848 0,7427 0,8681 0,9553 1 9,1046 13,2555 16,8216 19,6450 21,6003 22,6003 0,40285 0,58652 0,74431 0,86924 0,95575 1
и. 3 ifl?) из и(6) и3 и У) из
0 0 0 0 0 1 9.11734 13,27316 16,84246 19,66745 21,62320 22,62320 0,40301 0,58671 0,74448 0,86935 0,95580 1 9,11870 13,27504 16,84467 19,66982 21,62562 22,62562 0,40303 0,58673 0,74450 0,86936 0,95580 1 9,11884 13,27523 16,84489 19,67005 21,62585 22,62585 0,40303 0,58673 0,74450 0,86936 0,95580 1
Мы видим, что седьмая итерация до пяти значащих цифр повторяет шестую, вследствие чего мы можем принять = 22,626; это значение в тех же пяти цифрах совпадает с наибольшим корнем характеристического Уравнения.
622
ПАССИВНЫЕ СИСТЕМЫ
[ГЛ. О
Б. СИНТЕЗ ПАССИВНЫХ ДВУХПОЛЮСНИКОВ
§ 9.19. Уравнение энергии для вынужденных колебаний.
Так же как и в § 8.29, обратимся к натуральной системе, характеризуемой матричным уравнением
/(D)ey = w(0. (9.209)
Для теории электрических цепей имеет значение общий случай
w = (9.210)
&
При этом матрицу у можно представить в таком виде:
у = 1 (О?*ш# + (9.211)
Мгновенную мощность всех этих сил, сохраняя обозначения § 8.29 и предполагая для общности О=/=0, но J=0, можно вычислить так:
У Wjjj = W1 у = yTw = J e2tt (&eiwt + CTe-1<ot) =
= 1 еы (?$ 4- СЧ 4- C4- ?ie~2i<ot) =
=_L e2ti [Cz (s 4- io) c 4- Cz (S—/®) c 4- Cz (s 4- /<4 &2М 4-
») Ce-2<“*] = 1 e2tt I (s w>) C 4- CT A (s — iw) t
4- cT (N 4- о) c 4- c’ 4- 0) i+-ст + -S
Выражение (212) можно привести к следующему виду:
w’j) =1 e2tt I e (Ст ДС 4- С’ДС) + Z<o (СТДС — С’Д Q 4-
4-c1 (w+o)c+c’^4-0)с4-^фз [СТМ+СТЯС]4-
+ict(-^c+ctW)4-
4- 2 Re [сж (8 4- /Ш) 4- c’ (N4- 0) c 4-
(9.213)
Вследствие симметрии матриц A, N, H и косой симметрии матрицы G на основании формул (8.219) получим:
Т * 1 2в^
w У
{в?дс+Стм+V fK +
4- Re С’ДС (s 4- гш) 4- С’М +
(9.214)
е
е -|- /а>
§ 9.20] УРАВНЕНИЕ ЭНЕРГИИ ДЛЯ ВНЕШНИХ СТЕПЕНЕЙ СВОБОДЫ 623
ИЛИ • •
<?•= 4 (С, Q + N (С, С) + И (С, Q +
+ Re [Л (С, Q (е+/ш) + N (С, С) + е™ }.
(9.215)
Назовём условно средней мощностью часть мгновенной мощности, не зависящую от периодической функции exp2zW,
(да’Лр = у^Гд(С, C)e+W(C, Q+H(C, С)
(9.216)
Так как форма Л (С, С) положительна, а ЛГ(С, С) и Н(С, ^неотрицательны, то для пассивной системы средняя мощность положительна при нарастающих силах (а > 0); при синусоидальных силах (s = 0) она также положительна для строго диссипативной системы (С, С) > 0] и равна нулю для консервативной системы [ЛГ(г, С) = 0],
§ 9.20. Уравнение, энергии для внешних степеней свободы. Для механической системы с п-\-р степенями свободы, у которой только первые п возмущающих сил отличны от нуля, или же для эквивалентной электрической 2п-полюсной цепи имеем:
{D)y±+ ... + zlt п+руп+р = (/),
^П1(^)У1 "4“' ••• “Н^п, п+рУп+р-^п(0>
(9.217)
%n+pt 1 Ф)У1 Ч* • • • Т zn+pk п+рУп+р 0»
причём в случае электрической цепи Wj = ej.
Разрешая относительно у, имеем для внешних координат у19 ..., уп (токов внешних контуров):
Л = S Yjk Ф) (о и=1.............«)>
fc=l
или в матричной форме y=Y(D)w(t), Z(D)y=w(f), .
(9.218)
(9.219)
причём Zjk(D) являются, вообще, дробными рациональными функциями и не совпадают с Zjk(D), если р > 0. Так как z{D) (п-}-р X л + Р)
624 пассивные Системы [гл. 9
и Y (D) (п X являются симметричными матрицами, то
Z(D) = ZT(D). (9.220)
Уравнение энергии может быть получено тем же вычислением, что и для исходной натуральной системы в предыдущем параграфе:
^yTw — yFZ (D) у =
= -i- ezt (ремCTe“*w) Z (D) e9t -4- —
= е^а (ре™** -|~ Ст£~ги>*) [Z (е Zoo) -4- Z (s — Zoo) =
= 4 е™ [?Z (в —1«) С + CTZ (в + го») С + ТГ
+ ?Z (в + iw) 4-ZTZ (в — гш) Се-2«<»#]. (9.221)
Так как r-?Z (s-{- z<o)C есть скаляр, то
CrZ (в + й>) С = [PZ (в + гю) Ср =
= C’Z’ (в + гш) С = CTZ (в + z<o) С (9.222)
и слагаемые в wTy, не зависящие от периодических функций exp2ZooZ, ехр (— 2ZooZ), суть:
(wTj>)op = 4 е2^(? [Z (в — гш) Ц- Z (в -f- Z<n) ] С (9.223)
ИЛИ
(w’Ap = 1 IRe Z (в+fo)] С =| J 2[Re (s + 'w)1 =
J
=42 2[Re (s+to)1 (w*+(9 -224)
j s
где
+ % = (9.225)
Пользуясь свойствами (^ту)ср, установленными в предыдущем параграфе, заключаем, что квадратичная форма
2 2lReZ^(e + «w)]Wfc fc=l
должна быть положительной при е > 0; при е = 0 она также положительна для строго диссипативных систем > 0) и равна нулю для консервативной системы (АГ=О).
Для п = 1, когда Z (D) является скалярной рациональной функцией, предыдущие свойства были установлены Фостером и Бруне. После этого обобщение на любое п не представляло затруднений.
§ 9.21]
РЕАКТИВНЫЕ ЦЕПИ
625
§,§.21.. Энергетические соотношения и связанные с ними свойства пассивных систем. Реактивные цепи. В рассматриваемом в § 8.29 уравнении f{D)y = w{t) матрица f(D)9 которую мы можем назвать матрицей динамической жёсткости, при G = J=0 имеет вид
f (D) = ЛД2 + ND + Н. (9.226)
Если, как и в § 8.29,
w ==Re£e<u>*, &
I
у = ~ — Re7)e<u)*,
4W
У =-л (Ce<u>f-j- Ce~w) = Re Celu>i, £
• •
то среднее значение формы A (у, у)
Аналогично
WCp=yW, С),
(9.227)
(9.228)
(9.229)
M=p=2^W. Q- (9-230)
Средняя кинетическая и средняя потенциальная энергии суть •^•Д5р, -^Нср, а средняя диссипативная функция есть NGp.
Уравнение энергии (8.220) получает вид
' = 0-231)
3
Пусть отлична от нуля только одна из приложенных сил L. Тогда (§ 8.30)
0-232)
где Wjj= l/Yjj есть входное сопротивление со стороны /-го контура. Согласно уравнению энергии (231),
или
^+V/=2M(C, Q (9.233)
W W=22 +W
3 к
(ГЛ- + ^у) = 2 2 N* Re СД,
J Л
| I2 2 Re wsj = 2 2Njk +рД).-
з к
(9.234)
40 Зак. 1474. Б. В. Булгаков
б2ё ПАССИВНЫЕ CHCtEKlM (гл. § >
С®
Средняя мощность, затрачиваемая на преодоление активных сопро- | тивлений, есть 1
4|tj|2Re^.= |[W(<x, а)+АГ(₽, ?)], (9.235) f
£
й следовательно, ReW^>0. (9.236)
Отсюда получаем следующую теорему Боде:
Действительные части входных сопротивлений контуров пассивной цепи не могут быть отрицательны. Входные сопротивления реактивной цепи чисто мнимы.
Это верно также в отношении собственных проводимостей цепей и сопротивлений пассивных и реактивных двухполюсников.
Пусть теперь имеем пассивный четырёхполюсник. Для него
(9.237)
Принимая во внимание, что направление отсчёта Еу противоположно направлению отсчёта 1у, имеем, согласно уравнению энергии:
+ —(^Х+^Л)>°- (9.238)
•4/U/I w М 'Ни* о о' ’
Затем, так как Ylt и —К22 суть собственные проводимости входного и выходного контуров, то
Re Гп > 0, ReF22<0 (9.239)
или
Re ф? > 0, Re ф-1 < 0. (9.240)
>112 -4ц 4
Пример. Для изображённого на фиг. 118 четырёхполюсника, согласно (8.410), имеем:
1
CD
__ 1 CD
K>+LD+S
1 CD
CD
LD + Я ’ CD
(1 + £CD^ + /?CD),
^22 =
„ I — LC^ + IRC^
K« (/<0) =-------R + Тй,-----’
«TVS'
§9.211
РЕАКТИВНЫЕ ЦЕНИ
627
илн-
/? (1 — LCufi) + RLC<& +1 U&Cu — £<>(! — LC«fi)]
K22 (/<>>) =
Re Yu (/<>) > 0, Re Y& & < 0,
как это и должно быть, согласно (239).
ляянйяМ^ДДр-о
О
Фиг. 118. Схема четырёхполюсника к примеру.
Рассмотрим теперь ещё некоторые установленные Фостером р*11] свойства реактивных цепей, т. е. цепей, составленных из чисто реактивных элементов. Уравнения реактивной цепи можно представить в виде:
Н” ^nrJn
(9.241)
A “F
Принимая во внимание, что в уравнениях (241) Е± постоянно и дифференцируя по D, получим:
где
(9.242)
^11/1 “Ь* • • • ~Н ' п
^21^ 1 Ч" • • • Ч~ п = ^2»
п
S ^4-fc=i
Разрешая относительно находим:
(9.243)
40*
1А-Р)Нк
Е1
(9.244)
628
ПАССИВНЫЕ СИСТЕМЫ
ибо при отсутствии сопротивления> I^IEt = УЛ1 функция от D. Итак,
п
E^^H^-D).
Й=1
Так как
/к—у —_L
Ei и —ТГц’ то
jf = — El t/ТГц
1 Wh dD ’
есть нечётная
(9.245)
(9.246)
(9.247)
(9.248)
(£i\2rfwrii
171 W dD
n
fc=i
Отсюда, подставляя значение Нк, получим:
dIFn _ dD
п п
- Сй1)2 2 2 <- D> а(О)=
7 Л=1 Z=1
п п
=- (^)2 2 2 4 (~ D)Ii (D)- (9-249)
fc—1 Z=1
При D = Zo), учитывая (228) и (230), будем иметь:
(9.250)
Для пассивной системы, согласно (8.238),
rn ____ А (D) _____у (D) ___ арР2п-|~ Д1^2п 1 + * *«+ a2n-+ а2п
11 DFn (D) “ ф (D) d0D2«-i + ь^п-2 + ... + *2м_2Р
(9.251)
Так как Д(О) стоит в таком же отношении к квадратичным формам А (у, У)> N(y> у)9 И{у, у) от п переменных, в каком /711(D) стоит к формам Дх (у, у), (у, y)f Нх (j, у) от п — 1 переменных, то
корни Fn(D) будут такого же характера, как и корни A(D).
Входное сопротивление 1Г31 со стороны контура, к которому приложено внешнее напряжение, можно рассматривать как импеданс двухполюсника. Будем его далее обозначать через Z(D). При отсутствии сопротивления корни Д(О) и EU(D) чисто мнимы, так что функция Z(D) может быть представлена в таком виде:
(D2 + 0>f) (D2 + <>*)... (D2 + <4-s) (д2 + D(D2 + <»2)...(D2+<02n_2)
(9.252)
§ 9.22]
ФУНКЦИИ БРУНЕ
629
где^<&?—положительные числа. Если же положить D = fa>, то J
/2 2\ / 2 2\ /2 2 \ / 2 2 \
(ф — Ф..) (ф — Ф«) . . . (ф — Ф«„ «) (ф— ФО(И Л
z (/<») = 3---------------- 2/ 2 3 „ 2 2Я~23 \-----------------—
<о2 (<о2 — ш2) ... (<о2 — 0>2п_2)
Из формулы (250) следует, что ^и_2И(<о)Гм + н
где Л’(а)) обозначает реактанс
Z (Zco) (ф2 — ф2) (ф2 — ф2) ... (ф2 — ф|п_3) (ф2 — ^2n-i)
-----= /2(1)-------------------------------------
; 2 / 2 2\ / 2 2 \
I ф (ф — ф2) ... (ф — ф2п_2)
(9.253)
(9.254)
(9.255)
Из изложенного следует, что нули и полюсы реактанса, должны перемежаться (фиг. 119), и мы предположим, что они занумерованы в порядке возрастания:
0 < (Dj < оо2 < ... < <0.2П-1 < 00 •
Кратные нули и полюсы невозможны, так как ©(D), ty(D) получаются из Д(О) и DF1±(D) в результате возможного сокращения. Величины % — 0 и <o2w = оо также оказываются полюсами.
Фиг. 119. График реактанса X.
Знак h должен согласоваться с теоремой о производной, согласно которой при o>2fc_2 <ш < а)2й_! (k = 1, ..., п) должно быть ЛГ(о>)< 0. При этом множители <о9— <о| (/ = 0, 1, ..., 2k— 2) положительны, а — о)2 ^j = 2k—1, ..., 2п—1) отрицательны, и их — нечётное число. Поэтому должно быть
Л>0.
§ 9.22. Функции Бруне. Будем называть функцию Z (D) комплексной переменной D «положительной», если её действительная часть положительна при положительной действительной части D; очевидно,
630
ПАССИВНЫЕ СИСТЕМЫ
[гл. 9
что на мнимой оси действительная часть функции Z (D) неотрицательна. Если положительная функция действительна при действительном D, то будем называть её «действительной положительной». Если она, кроме того, рациональна^ то назовём её функцией Бруне. Далее будет доказано, что для всякой такой функции может быть построен двухполюсник, для которого она является импедансом.
§ 9.23. Теоремы о положительных функциях. Согласно определению положительная функция Z (р) осуществляет конформное преобразование правой полуплоскости £) на всю или часть правой полуплоскости Z. Например, функция
4 ' cD + d ’
для которой a, b, с, d суть действительные, одного и того же знака числа и ad — bc=£Q, является действительной положительной и преобразует правую полуплоскость D во внутренность круга на плоско-
~ ~ I / а 1 b\ lab
сти Z с центром в точке Z = y (y+'j) и радиусом -% —— — .
Теорема I. Если Z(D), z(D) суть положительные функции, то Z[z(D)] будет также положительной функцией.
В частности:
Следствие 1. Проводимость Y(D) =1[Z(D), соответствующая положительному сопротивлению Z(D), положительна.
Следствие 2. Сопротивление W (D) = Z , получаемое преобразованием обратных частот из положительного сопротивления Z(D), положительно.
Если предположить реализуемость действительных положительных функций уже установленной, то эти следствия доказывают существование обратного двухполюсника Zt (D) = R^jZ (D) и двухполюсника W(D) = z(±^. Общий же текст теоремы утверждает, что если Z(D), z(D) суть сопротивления двух двухполюсников N, п, то и Z [z(D)] будет сопротивлением некоторого двухполюсника.
Займёмся теперь рассмотрением нулей и полюсов положительных функций. Если D-с есть n-кратный нуль, то в окрестности этого нуля
(D-су. (9.256)
4 ' n\\dDn)D=c 4
Полагая
(S)D=0 = ae<T1 D — c = pei6, (9.257) имеем:
Z (D) « ар»е* (?+»’), (9.258)
Re Z (D) = apn cos («О Ц- <?), (9.259)
§ 9.23] ТЕОРЕМЫ О ПОЛОЖИТЕЛЬНЫХ ФУНКЦИЯХ 631
т. е.^действительная часть при обходе вокруг с меняет знак 2п раз. Следовательно, наличие нуля в правой полуплоскости противоречит положительности. На границе, т. е. на мнимой оси, возможны две перемены (п = 1) при условии ср = 0. Иными словами, нули на мнимой оси должны быть простыми с положительным значением производной a = (dZldD)D^e.
Аналогичные выводы могут быть сделаны в отношении полюсов. Во внутренних точках правой полуплоскости никакие полюсы невозможны; на мнимой оси возможны простые полюсы, причём из представления
(9.260)
ReZ(D)Aa-cos(0 —ф), (9.261)
р
где Ье^ — вычет, вытекает ф = 0, т. е. вычет должен быть действительным положительным числом.
Таким образом, установлена следующая теорема:
Теорема II. В правой полуплоскости не может быть нулей или полюсов положительной функции. Нули или полюсы на мни-мой оси должны быть простыми, причём в случае нуля значение производной dZfdD, а в случае полюса вычеты должны быть действительны и положительны.
Особый интерес представляют нули или полюсы рациональных положительных функций при D = 0, оо. Эти точки лежат на границе и соответствующий полюс или нуль должен быть простым. Если 0 = 0 есть простой нуль или полюс, то D должен быть множителем числителя или знаменателя. Если О = оо есть простой нуль или полюс, то степень знаменателя будет на единицу выше степени числителя, или наоборот.
В качестве резюме можно сформулировать:
Следствие. Степени числителя и знаменателя рациональной положительной функции относительно D или 1/D не могут отличаться больше чем на единицу. Следовательно, общий вид рациональной положительной функции есть - : .
7(П\ _ ДрОп+г + + ... +ап+1 (а олоч
b^-\-bxD^^bzD^^- ... +bn ’
Воспользуемся теперь известной теоремой *) о том, что функция, гармоническая в открытой области и непрерывная в замкнутой области, полученной включением границы, достигает своего минимального и максимального значений только на границе. Если имеются полюсы на границе, то они могут быть выключены дугами окружностей сколь угодно малого радиуса и теорема применена к оставшейся области.
*) См., например, С. Л. Соболев, Уравнения математической физики, изд. 2f Гортехиздат, J950; стр. 14/.
632
ПАССИВНЫЕ СИСТЕМЫ
[гл. 9
Применим теорему к действительной части рациональной положительной функции и воспользуемся также тем, что точка D = оо может быть причислена к мнимой оси. Отсюда вытекает:
Теорема III. Действительная часть рациональной положительной функции достигает максимума на мнимой оси.
Следствие. Если меньше или равно минимуму действительной части Z(Zgo), то
(О) = Z (О) — (9.263)
есть положительная функция.
Мы немедленно применим это следствие для устранения из данной положительной функции полюсов на мнимой оси.
Если D = oo есть полюс, то с помощью деления получим:
z 0>) = .++Х* - LD+<D> <9-264>
, (^о ^0» 0)>
где
I
7 . CqD” + CtP""1 + ... +сп > (9.265)
1 k ~ b0Dn + btPn-i
(cn = ап+1У'
Отношение L — aJb^ представляет, очевидно, вычет в полюсе и потому положительно.
Так как действительная часть LD на мнимой оси равна нулю, то • Re Zx (Zo>) = Re Z (Zo>) > 0. (9.266)
Но так как Re Zt (О) есть регулярная гармоническая функция в конечных точках правой полуплоскости, то •она там больше, чем на границе, т. е. больше нуля. Поэтому функция Z1{D\ получившаяся после выделения LD, есть положительная функция.
Если, теперь, 0 = 0 есть полюс-, то Ьп — 0 и
7(Г)\__ + axDn + ... — I 4-Z (D\ (9 267}
Z “ b$Dn + blDn-i + ... + Fn^D ~CD^ (U)
(^n+l 0» ®)>
где 4
C = (9.268)
an+l
7 rr^ - CoD"*1 + <\Pn 4- ... Ц- C№P 1 — doDn + diDn-i _|_ _ +dn-^D,
^hPn—i . _____
co~-^7’ Cl-^> ai~~^
§9.23]
ТЕОРЕМЫ О ПОЛОЖИТЕЛЬНЫХ ФУНКЦИЯХ
или> *
Z1 (D) =
сорп-РС1рп-1-р ... +сп dQDn-l^dtD^+ ... +
633
(9.269)
величина С представляет собой обратную величину вычета по полюсу р= 0 и потому положительна. Z1(D) является положительной функцией по тем же основаниям, что и выше?
После выделения возможных полюсов в обеих точках D = 0, оо положительная функция имеет вид
::: °- <В 9-27о>
Пусть теперь действительная положительная функция имеет полюс в точке D = Za. По условию действительности дблжен существовать полюс и при D = — /з, так что, пользуясь разложением на элементарные дроби, имеем:
z (°)=oh+d^T.+A <°)=STS+z< <D>' <9-271 >
где k — действительный положительный вычет по полюсам D = ±ia. Дробь 2&D/(D’a-|-з2) будет чисто мнимой на мнимой оси, откуда, как и раньше, вытекает, что Re Z (Zoo) = Re Z± (Zoo) и что ZX(D) есть действительная положительная функция.
Теорема IV. Если Z (D) есть действительная положительная функция, имеющая полюсы ±hr и оо с вычетами kr/2 и L (г = 0, 1, ..., т), то
т
Z(D) = LD + \ +Zx (D), (9.272)
где Zt (D) — действительная положительная функция uXteZ (Zoo)= ==ReZ1(Zoo); в частности, может быть ао = 0.
Следствие 1. Если Z(D) есть действительная положительная функция, имеющая нули (r=0, 1, т) и оо, то
т
(9.273)
где Zt(D) — действительная положительная функция и
В частности, может быть о0 = 0.
Разность Z(D) — LD в основной теореме имеет, согласно пре-ДЫдущему, числитель степени п или п—1 и знаменатель степени п. Поэтому степени числителя и знаменателя ZX(D) будут, соответ-
634
ПАССИВНЫЕ СИСТЕМЫ
[гл. 9
ственно, п — (2т -f- 2), п — (2т 2) или п — (2т -|- 3), п — (2т Ц- 2); если же ао=0, то п— (2т-\-\), п— (2т-\-\) или п— (2т2), п— (2т-1- 1). Во всех случаях общее число нулей и полюсов уменьшается после преобразования.
Аналогичным образом обстоит дело с преобразованием проводимости согласно следствию 1 из теоремы IV.
Отсюда вытекает, в частности, ещё одно следствие из теоремы IV.
Следствие 2. Если все полюсы действительной положительной функции лежат на мнимой оси, mq Zt (D) в теореме IV есть положительная постоянная. Аналогичный вывод получается из следствия 1 в случае, когда все нули лежат на мнимой оси.
Теорема III, очевидно, связана с тем известным фактом, что гармоническая функция определяется своими значениями на границе,, и, следовательно, с возможностью сформулировать определение положительной функции с помощью значений ReZ(Z)) на мнимой оси. С другой стороны, регулярность ReZ(D) в правой полуплоскости требует отсутствия там полюсов Z (D). Затем, как вытекает из теоремы IV, ReZ(D) совсем не зависит от полюсов на мнимой оси, условия в отношении которых должны быть сформулированы отдельно. Из этих соображений вытекает следующая теорема, которую легко доказать ссылкой на теорему III.
Теорема V. Функция Z(D) будет действительной положительной, если она удовлетворяет условиям: а) в правой полуплоскости нет полюсов; б) полюсы на мнимой оси должны быть простыми, а их вычеты действительными и положительными; в) Re Z (&>);> 0. £
Функция Z(D), в частности, не будет иметь нулей в правой по- | луплоскости. |
С помощью следствия 1 теоремы I выводим следующее следствие j из теоремы V: ;
Следствие. Функция Y(D) будет действительной положи- | тельной, если она удовлетворяет условиям: а) в правой полупло- £ скости нет нулей; б) нули на мнимой оси являются простыми, f а соответствующие им значения dYfdD действительны и поло- j жител+ны; в) Re Y (iti) 0. i
Функция Y (fo>), в частности, не будет иметь полюсов в правой Д полуплоскости. |
§ 9.24. Функции Мин Най-да. Функцией Мин Най-да [9-16] 4 или М-функцией будем называть рациональную функцию Z(D), $ действительную при действительном D, у которой действительная ? часть положительна при. ReD> — р, где р — положительное число . |
Совершая над Z (D) импеданс-преобразование
D = D* —р, (9.274) z
получим функцию ; 1
Z*(D*) = Z(D*-p), - (9,275)^
$ 9.24]
ФУНКЦИИ мин НАЙ-ДА
.635
которая будет, очевидно, функцией Бруне (В-функцией) от О*. Обратно, если Z*(D*) есть В-функция от О*, то
Z(D) = Z*(D+p) (9.276)
будет М-функцией от D. Для Л4-функций имеет место следующая теорема:
Теорема. Для того чтобы функция Z(D) могла быть сопротивлением двухполюсной цепи без взаимоиндуктивностей, в которой каждая индуктивность L связана с последовательным сопротивлением RL и каждая ёмкость С связана с параллельной проводимостью 1//?с, необходимо и достаточно, чтобы Z(D) была М-функцией, для которой р меньше всех чисел рь = RTJL и pa=l/RaC.
M-функции могут быть охарактеризованы своими свойствами на прямой Re D = — р, совершенно аналогично тому, как В-функции характеризовались их свойствами по отношению к мнимой оси. Однако полную характеристику этого последнего типа полезно дать и для М~функций.
Покажем, что для того чтобы Z(D) была Л4-функцией, необходимы и достаточны следующие условия: a) Z(D) рациональна и действительна при действителных D; б) она регулярна в правой полуплоскости и на мнимой оси; в) если при D = оо имеется нуль или полюс, то и тот и другой должен быть простым; г) Re Z (Zco) >0; если при D = оо есть полюс, то Re Z (Zoo) должна стремиться к положительному конечному пределу или к -}- оо при оо —> оо, если же D = оо есть нуль, то это должно быть верно по отношению к Re Z”1 (Zco).
Необходимость первых трёх условий и первой половины четвёртого совершенно очевидным образом вытекает из соответствующих условий по отношению к прямой ReD = — р. Затем, если О = оо есть простой ‘ полюс Л4-функции, то, располагая числитель и знаменатель по степеням О-}-р и выделяя член с первой степенью, получим:
Z (О) = L (D + р) + Zx (D), (9.277)
где L > 0, откуда
Z (D) = Z* (D*) = Z (D* — р) = LD* + Z* (D*). (9.278)
Так как Z*(D*) есть В-функцйя и её действительная часть при £*==Zco неотрицательна и совпадает с действительной частью Z*(D*), то Z*(D*) есть В-функция, a Z±(D) — М-функция. Действительная часть последней положительна при D = и при со —> оо может стремиться только к неотрицательному конечному пределу или к -роб. Отсюда следует, что Re Z (Zoo) при со—>оо стремится либо к конечному положительному пределу, либо к -}-оо, т. е. мы доказали Необходимость второй половины условия г).
636
ПАССИВНЫЕ СИСТЕМЫ
[гл. 9
Пусть теперь условия а), б), в), г) выполнены. Предположим также сначала, что О = оо есть обыкновенная точка Z(D). Так как в замкнутой, правой полуплоскости нет полюсов, а число всех полюсов конечно, то можно провести прямую Re D — — р (р > 0) так, чтобы все полюсы оставались слева и на ней самой или даже только слева. Так как D = oo есть обыкновенная точка, то степени числителя и знаменателя одинаковы и ReZ(Zco) при со—>оо стремится к положительному пределу а0/&0. Так как Z(D) регулярна в замкнутой правой полуплоскости, то ReZ(D) достигает на границе положительного наименьшего значения ар, а во внутренних точках подавно ReZ(D) > ар. В силу непрерывности можно взять р настолько малым, чтобы справа от Re£) =— р функция Z(D) была регулярна, a ReZ(D) положительна, или даже чтобы эти свойства имели место и на самой прямой. Поэтому Z(D) или даже Z*(D*) = Z(D* — р) будут Л1-функциями.
Пусть теперь D = oo есть полюс. Так как на мнимой оси и в правой полуплоскости полюсов нет, то можно попрежнему провести прямую ReD =— р так, чтобы Z(D) была регулярна справа от неё или даже и на ней самой. Так как, по условию, ReZ(Z<o) стремится к конечному положительному пределу или к -[-оо при о> оо, то Re Z (D) положительна на замкнутой мнимой оси и достигает на ней положительной нижней границы /?0. Полагая 0 < R < /?0, отделим от Z(D) вместе с главной частью XD постоянную R:
Z (D) = XD + R + Zj (D); (9.279)
так как действительная часть остаточной функции Z1(D) всё ещё положительна на мнимой оси, то она является Л4-функцией, регулярной при D = oo. Функция
Z*(D*) = Z(Z)* — р) = ЛО* + (/? — АГр) + А(О* — р) (9.280) будет В-функцией, если взять р столь малым, чтобы, во-первых, по предыдущему, Z*(D*) = Z1(D* — р) была ещё В-функцией и,; во-вторых, чтобы R — Лр^>0. Можно даже сделать Z*(D*) Л4-функцией, если выбрать р столь малым, чтобы Zj (О*) была ; УИ-функцией. 1 |
Если, наконец, D = оо есть нуль для Z (D), то нужно только j повторить предыдущее рассуждение для Z”1 (D), которая имеет полюс при D = оо. Кроме того, поскольку Z (D) регулярна в замкну^ той правой полуплоскости, ReZ(D) имеет минимум — нуль на границе и положительна во внутренних точках; поэтому Z(D) не имеет нулей нигде, кроме D = оо, a Z”1 (D) регулярна на мнимой оси в правой полуплоскости. Её действительная часть ReZ(D)/|Z(P)l7 положительна на мнимой оси. 7
Итак, мы доказали, что условия а), б), в), г) во всех случая?! достаточны, чтобы Z (О) была Л1-функцией, и что Z* (О*) = Z (D* — р)1 .«и*
*
§ 9.24]
ФУНКЦИИ МИН НАЙ-ДА
637
может\быть сделана не только В-функцией, но даже Л4-функцией. Разумеется, в последнем случае, увеличивая р, мы можем сделать 2*(Р*) В-функцией с полюсами или нулями действительной части на мнимой оси, если только таковые, вообще, существуют левее ReZ) = 0.
Пример 1.
Z(D) =
Oq D -|-bQD + b^
ReZ(Z<o) =
~F”
Если Ьь bi > 0, то единственный полюс D == — b^b^ лежит слева от мнимой оси. Если также ai>0, то ReZ(Zw)>0 и В = со не является ни полюсом, ни нулём; действительная часть стремится к при <о->оо. Полагая
В = В* — р, где р < min , получим функцию Бруне:
Z* (D*) = Z(D* — р) = fo"*—~ Аг\
Пример 2.
z т\ — + _ «о п , fD + «2*1
biD + b-i “*i + *i(*iD + *2) ’
—|-
2 ~i t.2 ’
*1“ + *2
где
В = оо есть полюс; действительная часть ReZ(Zw) будет положительной, если а0, ai, a2f b% положительны и /:>0. Но так как предел ReZ(Zw) при <о -> оо есть f/bp то Z (D) будет функцией Мин Най-да лишь при строго положительном /. Полагая опять D = В* — р, имеем:
Z* (D*) = Z (D*_____о) = "Ь + (а°р2 — а1Р + ,
' / \ Г/ h. Г\* —1— ( л —1— h Л
и это будет В-функцией при
— *1Р + *2 > О,
0,
или
Рbi' рao^i ’
•эким образом, для р надо принять: «0*1
р = min
а1
Ч —4У2 2oq
а1 — 4 у2 2о0
638
Пассивные Системы
1гл. 9
§ 9.25. Построение двухполюсника по импедансу Z (Z>), имеющему один нуль и один полюс в левой полуплоскости. Реализация некоторых других видов Z(Z>).
1°. Пусть функция Z (D), которую мы хотим реализовать в качестве импеданса некоторого двухполюсника, имеет вид
При D = Zw получим:
2(D) =
Z(Zo>) =
(а± + /дрсо) (bx — ?дош) Ф>24А2
(9.281)
(9.282)
do D + *
Действительная часть функции Z(Zoo) имеет следующий вид:
Re Z (Zoo) =
ардрсо2 4~ .
(9.283)
Чтобы нуль и полюс были расположены так, как предполагается, ни один из коэффициентов не должен обращаться в нуль и а0, между собой и Ьо, Ь± между собой должны быть одного знака. Из выражения числителя Re Z (Zoo) и требования его положительности вытекает, что все четыре коэффициента должны быть одного знака. Без ограничения общности можно принять, что общий знак есть плюс.
При обращении в нуль одного коэффициента имеем случай вырождения, когда реализация очевидна.
. Построим график функции у = Re Z (Zoo) по аргументу х = со2, включая и отрицательные значения последнего, хотя они, собственно, не имеют смысла. Уравнение
(Ь*х + bl) у — aQbQx + ci1b1
или
(blx+$ (.у — =ф (^0 - а^) (9.284)
\ и0 /
представляет гиперболу с асимптотами
(9.285)
и центром
При х = 0 имеем:
&*9.2Ji] построение Двухполюсник А По ИМПЕДАНСУ 2. (£)) бЗЙ
Две формы соответствуют случаям а0&х — (фиг. 120). В слу-
чае aG&i — fli&o > 0 наименьшее значение Re Z (w>) для действительных «>, равное получается для <о = 0. Если это значение вычесть
Фиг. 120. График функции Re Z (Zoo).
из Z (D), то получится всё ещё положительная функция Zx (D) (следствие из теоремы III § 23):
Z(D) = /?1 + Z1(D),
где
р _
—V
7 /Г}\_ W1 В
^U)~ b^D + bJ ‘
(9.287)
(9.288)
(9.289)
Так как Zt(D) имеет нуль в начале, то, по теореме IV § 23,
1 = M*op + *i> = ьхь ь*
zi(£>) (0Q&1 — «1М7) aQbt — atbt •" («0^i — а^0)D
или
1 — 1 I 1
Z^D) — LD 9 где n _________________________1
I
т__— #iA) f
~ J
Таким образом, мы получили (фиг. 121):
Z (£) = /?!+ -У--Ц-
^2 ’’’
(9.290)
(9.291)
(9.292)
640
ПАССИВНЫЕ СИСТЕМЫ *
{гл. 9
\
Совершенно такая же процедура возможна и при ~:
где
Отсюда
или
где
Z(D) = ₽1 + Z1(D),
р ____д0
7 (Г)х __ ^1
^1{-U) ~ b0(b0D + bir
1 в , Ух
Zi (D) а^о — Oobi ' а^о—«А
1 = CD -4__-
ZX(D)
„ %
atb0 — ааЬг ’ , _ ajbn — anbj 2 bobt
(9.293)
(9.294)
(9.295)
(9.296)
Окончательно получаем (фиг. 122):
Z (О) = /?! -|-J—(9.297)
CD + b
Если тг = тг, то Z (D) сводится, очевидно, к омическому сопротив-лению R = а0/60 =
Фиг. 121. Схема двухполюс- Фиг. 122. Схема двухполюсника к формуле (292). ника к формуле (297).
Другие эквивалентные реализации дробно-линейной функции получаются, если оперировать вышеуказанным образом не с Z(D)» а с \IZ(D).
При а0/&0 > имеем:
1 — 1 । 1
Z(D)“R1+Z1(D)’
(9.298)
§ 9.25] ПОСТРОЕНИЕ ДВУХПОЛЮСНИКА rid ИМПЕДАНСУ Z(D) 641
где •
•>
или где
Z^D)^^*"0.
1 «0*1—«1*0 J
Z1(D) = LD + ^2>
л2
“о р «0«1
«0*1 — «1*0 ’ 2 «0*1 — «1*0 *
(9.299)
(9.300)
4
(9.301)
При этом Z(D) принимает вид (фиг. 123)
Z(D) =
При получается:
1 _ 1 , 1 Z(D) R^ZiiDY
где
D ___а1
Z (D}____ ~Ь
1 A — 0(A) D ’
или
1 CD’
где
__#1^0 ——
2 «7
(9.302)
(9.303)
(9.304)
(9.305)
(9.306)
ajOo a^o — aobi
Фиг. 123. Схема двухполюсника к формуле (302).
Фиг. 124. Схема двухполюсника к формуле (307).
и функция Z(D) принимает вид (фиг. 124) Z(D)_t—Ц-------------------------------------
7?t + Я2 + VCD
41 Зак. И74. Б. В. Булгаков
(9.307)
642
ПАССИВНЫЕ СИСТЕМЫ
[гл. 9
2°. Теперь мы можем легко реализовать такие формы, как
' z(D) = hr^£tnt-u/, - (9.308)
UqL)a -f- v^LJ -f- Pg '
Выделяя нуль в бесконечности, имеем:
Z(Dr = CD + zT(Dj’ (9.309)
где
__^0
«о’
При этом, кроме положительности всех и bi9 должно соблюдаться
условие
d^ajbr — а±Ь0 > 0. (9.311)
Если ещё
Оо&2 + a%bQ — a^ibi > °* (9.312)
то
A (D) = J , (9.313)
где
п О-i п “Ь а1^а йой1^1
R*~ — ’ (9.314)
t ►
«Х + Фо—ао«Л
*1.2 ’
и для \jZ(P) мы получаем (фиг. 125):
Если же то
Фиг. 125. Схема двухполюсника к формуле (315).,
(9.315)
(9.316)
(9.317)
§ 9.25] ПОСТРОЕНИЕ ДВУХПОЛЮСНИКА ПО ИМПЕДАНСУ Z(D)
643
где. *
ъ________а0 р ___gOal^l Д0^2 Фо
Ki afa— aibQ ’ 2 b2 (a0&i — atbQ) ’
с (аА—дчМ2 ао (лол1^1 Л0^2 л1Ао)
и функция \!Z(D) принимает вид (фиг. 126) _1 = cd J________________________1_____
Z(D) №+^1+—L_
r+c'd
Если, наконец, ciob^ “и CL^d — О, то
Zx (D) = R, где
(9.318)
(9.319)
(9.320)
(9.321)
(9.322)
и для функции Z(D) получаем (фиг. 127):
2(D) =
(9.323)
НШЛг-г-тЛПР—1
Фиг. 126. Схема двухполюсника к формуле (319).
Фиг. 127. Схема двухполюсника к формуле (323).
Можно также для реализации сопротивления Zx (D) использовать Дуальные цепи *), применённые выше (фиг. 123 и 124). Если ф2 — (9.324)
то
А (О) = --------Ц------, (9.325)
*) См.» например, М. Р. Гарднер и Д. Л. Бэрнс [2Д8]/ стр. 62. 41*
644
ПАССИВНЫЕ СИСТЕМА
(гл. 9
где
(9.326)
и функция Z(D) принимает вид (фиг. 128)
Фиг. 129. Схема двухполюсника к формуле (331).
Фиг. 128. Схема двухполюсника к формуле (327).
и для. функции Z(D) получаем (фиг. 129):
(9.331)
2
При — 0^ = 0 имеем ранее полученную реализацию.
§ 9.25] ПОСТРОЕНИЕ ДВУХПОЛЮСНИКА ПО ИМПЕДАНСУ Z (D) 645
•3°. Далее рассмотрим форму
Z(D) =
-j- a^D -|- ^2 bQD 4» b±
Выделяя полюс в бесконечности, имеем:
Z(D) = W + Z1(D), где
г _^0
Ь h 1
7 /Г)\ ___ (#зА) — D + #2^0
1 {U) bQ (b»D + bj
(9.332)
(9.333)
(9.334)
Кроме положительности всех ai и b< должно соблюдаться условие
«А—«<А>°-
Если ещё то
где
о о
— й2Ь0 — aQbi > 0
A (D) = д—- —
L^D У?2
(9.335)
(9.336)
(9.337)
(9.338)
э __лфо—«0*1
<1------->
"о
(а^р — яо&рз
*о («1М1 — «2*о — «0*1) ’
д2 (^1^0 — #0^1)
«1*0*1 — «2*0 — «0*1
Фиг. 130. Схема двухполюсника к формуле (339).
и функция Z(D) принимает вид (фиг. 130)
Если же
Z (D) = LD + -j--------l—j------
^+£1О-Ь7?2
— аз^о — «о <0»
(9.339)
(9.340)
646
ПАССИВНЫЕ СИСТЕМЫ
[гл. 9
то
Zi (D) =
CD
где •
р ___ #2 (д1^0 —
Ь1 ’ 2 — «1М1 + «а&о+ а0Ь1’
— fljMt + + а01>1,
^0Л2
и для функции Z(D) получаем (фиг. 131)
Фиг. 131. Схема двухполюсника к формуле (343).
Фиг. 132. Схема двухполюсника к формуле (347).
«1V1 — а2*о — aobl = О,
(9.343) <
Если, наконец, то где
А (И) = R,
—^2
и Z(D) принимает вид (фиг. 132)
Z(D) = LD + /?.
4°. Рассмотрим ещё импеданс
7 (гу\— а^2 "Ь boD^+b^ + b^
Выделяя нуль при D — 0, имеем:
(9.344) 5
(9.345) 4
I
(9.346) I
'ж
(9.347) I
(9.348) I
-
(9.349) 1
§ 9.25] ПОСТРОЕНИЕ ДВУХПОЛЮСНИКА ПО ИМПЕДАНСУ Z(D)
647
где*
Zi (D) =
~Ь #1) atb$D 4- (atbx — ‘
(9.350)
Из условия реализации дробно-линейной функции вытекает, что все коэффициенты при степенях D в Z±{D) должны быть одного знака;
Фиг. 133. Схема двухполюс* ника к формуле (355).
а так как а± > 0, то этот общий знак должен быть плюсом. В частности, а1Ь0 > 0, т. е. все ai9 bi должны быть одного знака и
Если теперь то где
d = а±Ь± — а0Ь.2 > 0.
а^ (aQd а± Ь^) 0,
1 — ~
-а1 ~ а ’
«I (М — rf2 >
_ М — «1Ь0, ----------
(9.351)
(9.352)
(9.353)
(9.354)
и для функции Z(D) получаем (фиг. 133):
Если же то
Z?2 L^D
2
fli (ао^ — ai®o) < О,
(9.355)
(9.356)
(9.357)
ПАССИВНЫЕ СИСТЕМЫ
[гл. 9
6,48 где
. л0
1— Ьо ’
_ «А М
2= М
: • А»о
Я1 й0 — а<^
(9.358)
и функция Z(D) принимает вид (фиг. 134): Z (D) = —j-------------------------L---------
Если, наконец, ai Ц/* — <&о) = О»
то
Z± (D) = Я, где
й для Z(D) получаем (фиг. 135):
Z<P) = 1 .
~r+~ld
(9.359)
(9.360)
(9.361)
(9.362)
(9.363)
Фиг. 134. Схема двухполюс- Фиг. 135. Схема двухполюсника к формуле (359). ника к формуле (363).
Используем теперь для реализации сопротивления Z±(D) дуальные цепи.
.Если
«1 (aQd — albQ)> 0, (9.364)
то
ZT(D)в + LiD+^a’ (9.365)
§ 9.25] ПОСТРОЕНИЕ ДВУХПОЛЮСНИКА ПО ИМПЕДАНСУ Z(D) 649
где.. * .
♦ * *
л2 ~ _ а0 а1
1 aod — a\b0 ’
, _ «о
1 ~ Ьо ’
, ___ а0 а1
2 A J ’
aQa *—
(9.366)
и функция Z(D) принимает вид (фиг. 136):
(9.367)
Фиг. 136. Схема двухполюсника к формуле (367).
Фиг. 137. Схема двухполюсника к формуле (371).
Если же то
где
2
а1 — ai^o) < О’
1 1
Zi (D) — 7?1
9 а:
D ___ 01
i\2 — 9--------
aQ^
ai^o—
(9.368)
(9.369)
(9.370)
а функция Z(D) имеет вид (фиг. 137)
Z(D) = -X--j-
7?z+zd
‘ CD
При — а%Ъо) — Ъ имеем найденную выше 5°. Пусть теперь
7 (jy\ + а1^ ~Ь а2
У ) ~ + bxD
(9.371)
реализацию.
(9.372)
650
ПАССИВНЫЕ СИСТЕМЫ
[гл. 9
Выделяя полюс при D = 0, имеем:
Z (D) = -А + Zx (О),
где
с=А, «2
у (г\х_ а^Р +
b^D + bJ
(9.373)
(9.374)
Аналогично предыдущим случаям заключаем, что все at и бить одного знака и
d =5 a^bi — a2bQ > 0.
Если теперь
a0&i — bQd > 0, то
Zx (D) = п-------Ц------,
+ Z.D +/?а где
L _ Ф1 ao^i bod
П ___ ^0 D ______
Kj — *7” , — Tg —',
°о а0 — bod
Фиг. 138. Схема двухполюсника к формуле (379).
Ь{ должны
(9.375)
(9.376)
(9.377)
(9.378)
и функция Z(D) принимает следующий вид (фиг. 138):
Если же то
(9.379)
(9.380)
(9.381)
§ 9.25] ПОСТРОЕНИЕ ДВУХПОЛЮСНИКА ПО ИМПЕДАНСУ Z(D) 651
* где4
л
р __
R1~ ь* ’
n _ М
"2—r~i
Uq<* —
n _ ^(Ы —«о61)
4—
(9.382)
а для функции Z(D) получаем (фиг. 139):
z (D) = -gL + -J-----Ц-------. (9.383)
^1+ _L , p
(\D +/?2
6°. Пусть ещё
Z(D) = ^^P + a2, (9.384)
где все положительны. Выделяя полюсы D = ±iy b2/bQ на
Фиг 139. Схема двухполюсника к формуле (383).
мнимой оси, имеем:
Z(D) =
D —Z У^/Го
где
___ У b$b2 4~ z (#0^2 — ^2^о) — zr: , -i- >
ьо
k ~ a^Vbob* — z 0*062 — а2ьо) ==----------—--—==--------
При этом Z{D) принимает вид
Z(D) =
0.
ЯВ0»
&2
2
о
652
ПАССИВНЫЕ СИСТЕМЫ
[гл. 9
или
у / Г)\ 4~ (^2^0 — Др&2)
к } b^bQD^+b2)
где
’ ( гу\ flpfrg __ «о Л bQ(b0p^ + b2) —
Реализация возможна только при
^2&о ^0^2 ===
и тогда для функции Z(D) получаем (фиг. 140):
(9.387)
(9.388)
(9.389)
где
Фиг. 140. Схема двухполюсника к формуле (390).
(9.390)
(9.391)
§ 9.26. Двухполюсник, импеданс которого Z(D) имеет два нуля и два полюса в левов полуплоскости. Пусть теперь функция Z(D), которую надлежит реализовать в качестве импеданса двухполюсника, имеет вид
ClftP^ С1]Р Л2 b$P% -|~ Ь-\Р -|- Ь2
Z(D) =
При D = to будем иметь:
Z (Z<o) =
Действительная часть Z(zco) имеет следующий вид:
Re Z (Zw) =
—|— (л^Ь^ — a$b2 — bod2) <o2 -|- a2b2
*o‘“4+(*i-2M2)“2+*2
(9.392)
(9.393)
(9.394)
(— -|- 6Z2)
(— —|— £>2) -|~
Детальное исследование условий, которым должны удовлетворять коэффициенты ait Ьг для того, чтобы функция (392) была действительной положительной аналитической функцией в смысле Бруне, приводится ниже, в § 39, в котором рассмотрены звенья второго порядка корректирующих цепей.
§ 9.26) два нуля и Два йолюСа в левой полуплоскости
653
.Эти условия состоят в том, что все коэффициенты aif bi должны быть неотрицательными и должны удовлетворять неравенству
(9.395)
Случаи вырождения, при обращении в нуль отдельных коэффициентов, рассмотрены в предыдущем параграфе, и здесь мы будем предполагать, что все коэффициенты положительны.
Исследование общего случая реализации Z (D) дано ниже, в упомянутом уже § 39. Укажем лишь на два частных случая реализации.
Фиг. 141. Схема двухполюсника к формуле (396).
Фиг. 142. Схема двухполюсника к формуле (398)?
а) Функция Z (D) может быть представлена в таком виде (фиг. 141)
Z (D) = /?! Ч------j-i-----J.
(9.396)
При этом
Др
»р’
^2 — ~h~
1 ф __________(Ojbn — Др&1)2__________
Ьй ” bt (atb0 — «o&j) — bQ (a2b0 — a0b2) ’
_ J____________________(aibp — apfri)2 (д2»р— Др»г)________________
3 »o ’ b2 (Д1*р—ДрМ2 + («2»о~Др»а) [»p («а»р—Др»г)—»i (<?i»p—«p»i)] ’
£_ J_e___________________________(Д1&Р — flp^i)3_____________________
»p’ b2 (ДА—Др»1)24-(Д2»р—Др»а) [»p(«2»p—Др»г)—»i («1»р—Др»1)] ’
(9.397)
А2 _____ __
#1^0 —
б) Другое представление функции Z(D) (фиг. 142) будет следующим:
(9.398)
654
ПАССИВНЫЕ СИСТЕМЫ
[гл. 9
где Rlt R2, Rs, L и С имеют такие значения:
р *0 V
D #п[#1(#0*1—#1М —#п(#0*2 —#2*п)]
К2 --
р —
8 а^Ь2— aj>o
(#0*1—#1*0)3 ’
#0#2 ’ *0 ( #0#1*1 Ч” #0*2* — *1*0 — *0*2)
(«о*1—«1*о)2
(9.399)
#o*i—*i*o ’
__ 1 и арЬ1 — gt&0 7?3 #0^2 — #2*0
При этом предполагается ещё, что выполнены следующие условия:
#о*х— aibo> °>
(9.400)
*0*2 *2*0 > 0 ’
§ 9.27. Общая процедура построения двухполюсника по заданному импедансу. Переходим к общей задаче о реализации произвольной рациональной действительной положительной функции.
Мы будем решать её шаг за шагом, выделяя простые непосредственно реализуемые элементы, причём остающаяся часть должна быть опять действительной положительной функцией, но с меньшим числом нулей и полюсов.
Прежде всего, по теореме IV и следствию 1 из неё (§ 23) можно выделить все полюсы, а затем все нули, лежащие на мнимой оси, в частности в точках 0 = 0, оо. Не исключено, что после второй операции опять появятся полюсы на мнимой оси. Но так как при каждой операции число нулей и полюсов уменьшается, то, повторяя операции по выделению полюсов и нулей попеременно достаточное число раз, мы получим либо положительную постоянную (теорема IV, следствие 2), реализуемую как сопротивление, либо действительную положительную функцию Zt(D), не имеющую ни нулей, ни полюсов на мнимой оси.
Пусть 7? есть неотрицательный минимум ReZ1(Zo>), достигаемый при со = ztz а, и
Z2(D) = ZX(D) — R. (9.401)
Так как минимум ReZ2(Zo>) равен нулю и Z2(D) регулярна в правой полуплоскости, то эта функция действительна и положительна. Кроме того,
Z2(Zg) = ZAT (9.402)
есть чисто мнимое число. Если при этом а = 0 или оо, то Z2 (Zg) действительно и Л = —Х=0. В этом случае 0 = 0 или оо будет
§ 9.271 ОБЩАЯ ПРОЦЕДУРА ПОСТРОЕНИЯ ДВУХПОЛЮСНИКА 655
нудбм Z^fD), вследствие чего, согласно процедуре теоремы IV,
1
или
Z2 (D) ~ D
ZS(D)
(9.403)
Z2(D)~LD + Zs(D)'
(9.404)
Переходим к случаю, когда с не равно ни 0, ни оо. При этом вместо процедуры Бруне, требующей идеального трансформатора *), мы применим процедуру Ботта и Даффина [9-8], состоящую в следующем.
Назовём рангом п функции Бруне сумму степеней числителя и знаменателя. Пусть теперь Z(D) есть функция Бруне, не имеющая полюсов и нулей на замкнутой мнимой оси, и Z(ti) = iX.
Пусть сначала Х>0, так что можно положить:
Z (и) = ibs.
(9.405)
Как показано Ричардсом функция
**), если Z(D) есть функция Бруне, то и
Z(D) — DZ(1) Z (1) — DZ (D)
(9.406)
будет таковой, причём её ранг не выше ранга Z(D). Если k есть положительное число, то Z(kD*) есть, функция Бруне от D*. По теореме Ричардса функцией Бруне будет также и функция
р* (г)*\ — % (W*) D*Z (k) 407)
К ~ Z(k) — D*Z (kD*) ’ A >
Поэтому и R (О) = /?* (D*/fe) или
RW = kkZW-DZ(P) (9>408)
есть функция Бруне от D. Так как Z(D) остаётся конечной и отличной от нуля при 0 = 0, оо, то при изменении k от 0 до оо отношение Z (А)/й изменяется от оо до 0 (не обязательно монотонно) и мы можем выбрать k так, чтобы
L = Z(kyk. (9.409)
Тогда
р /.• \_(Zcr) hZ (k)______ IkL# toZ (k) ___q f о 41
' kZ (k) — laZ (lo) ~~ kZ{k) — blLi u> ('У' '
*) Боде стр. 220.
D **) P. J. R1 c h a r d s, Duhe Math. J. 14, 777—786 (1947); P. J. R1 c h a r d s, Proc- I. r, E. 36, 217—220 (1948).
656
ПАССИВНЫЕ СИСТЕМЫ
[гл. 9
Разрешая соотношение (408) относительно Z(p), получим:
или
где
й _ kz (*) R (D) I DZ(k) __
k + DR(D) k 4- DR (D)
1 i 1
~~D 1 k R(D)
kZ (k) + Z (k) R(D) Z(k)D+Z (k)
z (D) =--L_—_—L__,
CD + z1(O) ld+шр}
Zx (D) = Z (A) R (D) = LkR (D),
Z (D)= % ___
' /?(£>) /?(£>)’
= _J—= _1—
u kZ (k) №L 9
(9.411)
(9.412)
(9.413)
(9.414)
(9.415)
причём ранги функций Zt(D), Z2(D) не выше ранга Z(D). Так как
(fo) = 0, то Zt (О) имеет нуль, а Z2(D)— полюс на мнимой оси, и потому эти функции могут быть приведены к функциям низшего ранга.
Таким образом, Z (О) реализуется по-
следовательным соединением двух двух-Фиг. 143. Схема двухполюс- полюсников (фиг. 143). Первый предста-ника к формуле (412). вляет параллельное соединение ёмкости С и сопротивления Z^ (D), а второй — параллельное соединение индуктивности L и сопротивления Z2(Z>).
Аналогичным образом при X < 0 и
Z (Za) =
1 ZCa
(9.416)
рассмотрим функцию 1/Z(D). По теореме Ричардса k D
S(D) = ?-W R U
ZAK}~'Z(P)
есть функция Бруне, причём если
kZ (k)9
то
k _ fo ..r____________________
s (Z0) e . -y> = e 0.
Z (k) Z (fo) Z (k)
(9.417)
(9.418)
(9.419)
§ 9.28] реактивные четырехполюсники
Разрешая соотношение (417) относительно получим:
657
1 feS(D) . D
Z (D) ~ kZ (k) + DS (D) Z (k) kZ (A) + DS (£>) Z (Й) “*
^-D +^) + ^T^ + ZWS(D)
(9.420)
или
(9.421)
где
. _Z(k)_ 1 . -L~ k ~~Ck^
Z1 (n) = f$)> z2(D) = z (*)5 (D)-
(9.422)
(9.423)
Итак, в случае, когда X < 0, функция Z (D) реализуется параллельным соединением двух двухполюсников (фиг. 144).
Фиг. 144. Схема двухполюсника к формуле (421).
Таким образом, описываемая процедура последовательно приводит к функциям Бруне, ранг которых ниже ранга заданного импеданса. Следовательно, повторяя этот процесс, мы в конечном счёте составим цепь с заданным импедансом.
В. СИНТЕЗ ЧЕТЫРЁХПОЛЮСНИКОВ И ЕГО ПРИЛОЖЕНИЯ
§ 9.28. Реактивные четырёхполюсники. Пассивные четырёх-
полюсники, не содержащие активных сопротивлений, носят название реактивных. Как показывают формулы (8.233) для Zik(P), эти величины являются нечётными функциями от D. Поэтому в матрице А элементы Ли, А.& будут чётными, а элементы Д12» ^21 нечётными функциями.
В формуле
cth g
1/ AtAa
и а12а21
(9.424)
8 её частотной форме подкоренное выражение
всегда действительно,
42 Зак. 1474. Б. В. Булгаков
658
ЙАСбИВЙЬ^Е СИСТЕМЫ
[гл. 9
а потому cthсможет быть только чисто мнимым или действительным. Из известной формулы
cth g = cth (а 4- ------п;--- (9.425)
ь * 7 ch2 а — cos2/? v 7
видно, что в первом случае
а = 0, ctg b = i cth g, (9.426)
т. е. волновой коэффициент затухания равен нулю, вследствие чего соответствующие диапазоны частот <о носят название полос пропускания. Волновые сопротивления
^=^=/8! (э-427»
в полосах пропускания действительны, так как подкоренные выражения будут, очевидно, действительными числами противоположного знака по сравнению с подкоренным выражением в формуле для cth g.
Вне полос пропускания должно быть либо
/> = 1т/2, th а = cth g, (9.428)
либо
b = 0, cth а = cth g, (9.429)
т. е. мы имеем здесь некоторый положительный волновой коэффициент затухания, что показывает, что вне полос пропускания четырёхполюсник более или менее гасит все частоты. Задерживание будет наиболее полным в окрестности тех частот, где cth g = 1 и коэффициент затухания обращается в бесконечность; эти частоты носят название полюсов затухания. Волновые сопротивления вне полос пропускания мнимы. Эти предварительные соображения показывают, что реактивные четырёхполюсники ведут себя, как фильтры, пропускающие одни частоты и задерживающие другие.
Для вычисления рабочего затухания реактивных четырёхполюсников можно дать удобные специальные формулы. Мы имеем, согласно (8.449), (8.445), (8.448),
_ £2 _ 1
- 47?г7?н^/^ 47?г7?н
(9.430)
Но, согласно (8.372),
я»
(9.431) .
$
у
§ 9.29]
ФИЛЬТРЫ йижник ЧАСТОТ*
Предположив, что Zr = Rr, = Rh суть активные сопротивления, имеем:
Ref-y—V—^22^г> Itn (7“) === ”~Н (9.432)
А^/ \iyJ
е2“₽аб = 4^ 1(Л11/?Я + ^г)2 ~ (Л12 + Л з^гЯн)2! =
(•^и^н (^12 Л217?г7?н)2
4/?г*н
(9.433)
>
так как АцА22— А12А21 = 1. Если же воспользоваться выражениями (8.303) для Ajk через волновые параметры (при 8 = 0), то
1 /7? \2 1 ✓ 7? 7? \2
'!"’“=‘+4«a(7-^) V) sh“i' <9'434>
или
. -(/fe-/W8h’4 (9лз5)
г
§ 9.29. Фильтры нижних частот. Электрические фильтры, широко применяемые в технике связи, автоматике и телемеханике, предста-
Фиг. 145. Звенья фильтров нижних частот.
вляют каскады реактивных четырёхполюсников, предназначенные для того, чтобы пропускать переменные токи в некоторых желательных
42
660
ЙАбЙИЁНЫЕ СИСТЕМЫ
(гл. §
диапазонах частот и задерживать другие! Рассмотрим сначала некоторые употребительные схемы звеньев фильтров нижних частот. Для схемы lb (фиг. 145), составленной из сопротивлений
Zb == £3D +
1
C2D’
(9.436)
находим, согласно § 8.42
£2C2Z)2+1
(9.437)
Имея в виду дальнейшие так называемые реактанс-преобразования, выражаем W, д сначала также через D, а не через Z®
(9.438)
и далее, рассматривая данную схему как полузвено и обозначая поэтому волновой коэффициент распространения не через g, а через g/2,
: > (9.439)
2 YLiCzD
Вводя величины
(9.440)
получаем:
(9.441)
§ 9.29] фильтры нижних частот
Полагая теперь D = й», мы видим, что в полосе частот
661
О < со < <о0
величина cthg/2 будет чисто мнимой, а вне.этой полосы — действительной.
Пользуясь известной формулой
,« g .. а 4- ib cth = cth —i— =
.а . . b b sh ch — i sin-и- cos
ch2 %- — cos2 ~
(9.442)
9
мы видим, что в первом случае
(9.443)
т. е. волновой коэффициент затухания равен нулю, вследствие чего интервал (0, ш0) носит название полосы пропускания. Волновые сопротивления Zx, Zy в этой полосе действительны.
Вне полосы пропускания должно быть либо
(о)0 < О) < (Ооо),
(9.444)
либо
(9.445)
т. е. мы имеем здесь некоторый положительный волновой коэффициент затухания, что показывает, что вне полосы пропускания фильтр более или менее гасит все частоты. Задерживание будет наиболее полным в окрестности частоты cdqq, называемой полюсом затухания, так как при этой частоте коэффициент затухания обращается в бесконечность. Волновые сопротивления Zx, Zy вне полосы затухания мнимы. -
662
ПАССИВНЫЕ СИСТЕМЫ
[гл. 9
Разрешая соотношения (440) относительно L2, С2, получаем формулы
(9.446)
которые позволяют подобрать элементы четырёхполюсника по заданным наперёд <о0, а>оо и /?.
Предположим теперь, что два полузвена только что рассмотренного типа, первое из которых должно быть обращено, соединены каскадом; тогда получается симметричное Т-звено If, для которого, очевидно,
Уо2+«>0
W = Zx — Zy — R-----, (9.447)
а выражения для R, <оо, Шоо и cth i будут прежними, если только £
под g понимать коэффициент распространения получившегося целого звена.
Комбинируя полузвенья в обратном порядке, получаем симметричное П-звено Ig с волновым сопротивлением
W‘=ZX = Z„ = R ж и
(9.448)
и прежними выражениями для Rr ш0, ojqo, cth
Формулы (446) для подбора коэффициентов самоиндукции и ёмкости также остаются в силе для обоих симметричных звеньев.
Полузвено, рассмотренное вначале, можно упростить, выкидывая катушку в параллельном плече и полагая = L, L2 = 0, С2 = С. Для получившейся схемы 1а имеем:
ell, е _£1С№+1
(9.449)
§ 91291
ФИЛЬТРЫ НИЖНИХ ЧАСТОТ
663
^причём опять коэффициент Если же положить
распространения обозначен
через g/2.
ТО
W=R,
В полосе пропускания
“о =
(9.450)
(О0
/о2
<7 =
OJ0
(D0
(9.451)
“о
0 < со < <о0
величины cthи g—ib будут чисто мнимыми, причём
со
(9.452)
2 О
у
>
cth -7Г =
b
вне полосы пропускания cth действительно и = 4W
причём
th 4 =
(О
(9.453)
четырёхполюсник может служить полюс затухания здесь удаляется мы получаем менее совершенное
Таким образом, рассматриваемый звеном фильтра нижних частот; в бесконечность, вследствие чего задерживание частот, немного превосходящих со0.
Формулы для подбора индуктивности и ёмкости принимают вид
с»о ’
Из двух полузвеньев рассматриваемого типа мы можем опять образовать симметричное Т-звено Id с волновым сопротивлением
(9.454)
(9.455)
и симметричное П-звено 1е с волновым
сопротивлением
V D2
«о
2 о
(9.456)
ИВГГ-'
664
ПАССИВНЫЕ СИСТЕМЫ
[гл. 9
Коэффициентом распространения будет в обоих случаях величина g, определяемая согласно (451).
Для полузвена 1с проводимость последовательного плеча 1/Za вычисляется, как сумма проводимостей и CJD, вследствие чего
cth4 = ^-<cyt£->g,+1,
2 Yl,C,D
где опять коэффициент распространения обозначен через g/2, Полагая
получим:
так как для cth g/2 получается то же самое выражение, что и для полузвена 1Ь (441), то все выводы о полосе пропускания и полюсе затухания, сделанные выше с помощью этого выражения, остаются
в силе.
Формулы для подбора элементов четырёхполюсника будут:
(9.460)
§ 9Д9]
ФИЛЬТРЫ нижних ЧАСТОТ
665
Пример*) (фиг. 146). 1 10“6 1 ГТ
L = с = ~^г- “o=V7F = 2”-100()’ * = V Т= 10°0’ 2те х&те у LCf r С
IF=Za) = Z!,= 1000 /Г=7^, cth 4 = . * = -7Г-
X COq
В полосе пропускания 0 < х < 1 имеем: .. л , b У1—х2 g = lb, а = 0, ctg у = ---»
cos = У1 — х2, Sin = X, ch 8g = cos 8b.
с----ПШЙЯЙП у— НЯЯШШП О—
Z L
ZC
Фиг. 146.
Звено фильтра нижних частот.
Вне полосы пропускания
a
2
th
b = те,
ch 8g = ch 8а.
Полагая, что число звеньев (фиг. 146) в каскаде п = 4 и Zr = 7?г = 1500 ом, = = 500 ом,
будем согласно (434) и (8.315) иметь:
2
ch2 4g —
Г2
(1Г2 \2
7?Л_1) Sh2^_
, , 1 Г4 з 1 /4 1—х2 у 1
= 1 + 4g~ 4Ь=^(Т—--------9 Sh34gj
или
ег«раб = j о,16667 Г1 + 0,0625 (1.
+ 0,1666711—0,0625
В полосе пропускания (0<д:<1)
(1 —4x2)2 ]
Г-Х2 СЬ 8^
/°Рав = 1 -I- 0,16667 Г1 + 0,0625
(1 4x2)2 -1—х2
+ 0,16667 1 —0,0625
(1 _ 4x2)21
-Ц-----cos 8b.
1 —х2
*) Е. A. Guillem in, Comm. Netw., т. II, стр. 287.
666
ПАССИВНЫЕ СИСТЕМЫ
[гл. 9
Вне полосы пропускания (1 х)
,2«раб = j 0>1б667 Гj _00б25 (4Хз I)2] I «Л* А
+ 0,16667
1 + 0,0625 ---РЛ ch 8л.
-- I
§ 9.30. Фильтры верхних частот. Звенья, представленные на фиг. 147, можно было бы исследовать непосредственно, как это было сделано для фильтров нижних частот. Проще, однако, приме-
Фнг. 147. Звенья фильтров верхних частот.
нить реактанс-преобразование, что позволит, к тому же, познакомиться с этим методом.
Если положить
2
= (9.461)
то индуктивные и ёмкостные сопротивления, которые могут входить в состав звена, преобразуются по формулам
LD =
г 2
D'
= L'D't
где
1
C'D' ’
(9.462)
(9.463)
1 _ D' CD • Cwq
§ 9.301 ФИЛЬТРЫ ВЕРХНИХ ЧАСТОТ 667
. А. ' <
т. че. каждая индуктивность L переходит в ёмкость С', а каждая ёмкость С—в индуктивность L'.
Полагая D = до, D' = /со', находим формулу преобразования частот 2 соп
“ = (9.464)
отображающую интервал — <оо < со < 0 на интервал <оо < о/ < оо, который и будет новой полосой пропускания.
Применяя преобразования к полу звену 1b (фиг. 145) и полагая
о
о/— <о, а/ =—(9.465)
О 0’ оо /о ’ 4 7
оо
получаем из формул (441), (446) и (463):
668
ПАССИВНЫЕ СИСТЕМЫ
[гл. 9
если же опустить теперь акценты, то мы получим схему полузвена ПЬ (фиг. 147) и формулы
Таким образом, интервал (о>0, оо) будет полосой пропускания для полузвена ПЬ, Комбинируя полузвено ПЬ с обращённым полузвеном, аналогично изложенному в § 29, получим звенья фильтров верхних частот, показанные на фиг. 147. Легко видеть, что звено Пс (фиг. 147) будет также фильтром верхних частот.
§ 9.31. Полосовые фильтры. Эти фильтры получаются из фильтров нижних частот путём реактанс-преобразования'
D Df2 4- (о<ф2 z .
--- = ------—<. %)• w0 (<°2 — ш1) 41 27
Индуктивные сопротивления преобразуются по формулам
(9.468)
(9.469)
(9.470)
(9.471)
(9.472)
где т <°о г*' 1
= Ь---------, Cl = -J----------
<о2-L,
а ёмкостные проводимости — по формулам
где
— Г—Lr = — Ш2— 2 ’ 2 б? (Do<Dj(02
Следовательно, каждая индуктивность L заменяется последовательным соединением индуктивности L± и ёмкости Ci, а каждая ёмкость С— параллельным соединением индуктивности 12 и ёмкости С2. Полагая D = Z(o, D' = /а/, находим закон преобразования частот
со а/2 — a>t<t)2 со0 (со2 — (ot) и' ’
(9.473)
§ Oij йоЛобойЫЁ ФйлЬТРУ
л If
согласно которому частоты w = — w0, —J—<o0 переходят в go' — сор <о2, а частота о> = 0— в среднюю геометрическую о/ — Интервал
__о)0 < < + а>0 переходит в интервал < а/ < ш2, ограниченный конечными частотами а^, а>2, который и будет полосой пропускания преобразованного четырёхполюсника.
Полузвено Ша (фиг. 148) получается из соответствующего полузвена Id фильтра нижних частот (фиг. 145). Применяя преобразова-
Фиг. 148. Звенья полосовых фильтров.
ние к (451), а также учитывая (470), (472) и .(454) и отбрасывая штрихи, по окончании вычисления, имеем:
(9.474)
Т — п — 1 1
* — Ш1 9 • R 9 I
Г — D w2 —_ 1 1 |
До -- •*\ —————, Un --- “7Т" * .1
- 03^2 * . /? )
Полюсами затухания здесь будут <о = 0 и = оо.
Расчёт будет несколько сложнее, если мы хотим получить затухания при конечных частотах а)'=’а)100, а)2оо. Эти частоты соответствовать значениям о> = — а>оо, для фильтра
частот, так что 2
Лоо ш1оо“ш1ш2 «мм. - -----
. ®0 ’ (®2~
®оо_ ю2со — “0 (®2 — “1) ®2оо ’
(9.475)
полюсы должны нижних
(9.476)
670
Пассивные системы
|гл. О
или, складывая и вычитая эти соотношения,
^1оо^2оо>
(D (Dn_— СО.___
оо _ 2оо loo
(Oq ш2 — W1 *
(9.477)
Применяя теперь реактанс-преобразование к полузвену /Ь фильтра нижних частот (фиг. 145), получаем прцмежуточную форму (фиг. 149), состоящую из последовательного контура С' в последовательном плече и последовательного соединения параллельного контура Z.J, С{
Фиг., 149. Полузвено полосового фильтра, полученное реактанс-преобразованием.
и последовательного контура £2> С2 в параллельном плече.
Так как
(<d2 —a^D'2
2 2 ~ '"loo-' <
co----- % 2
(<o2 — COj^ D'
то мы получаем из формул (440), (477), опуская штрихи чании вычисления:
л (D2 + "loo) (D2 + “L) x a (<02TO - ш1оо) D V (D* + (D2
_ /(О2 + ш2) (D2+<02)
>
(9.478)
по окон
(9.479)
Л и*-
i
.. g 2/(7>2 cth — =----==
Индуктивности и ёмкости преобразованной схемы, согласно (470),
9 Ж •X.
>FV-
§ §.3J1
ЙОЛОбОВЫЕ ФЙЛЬТРЫ
671
(472), (446), будут:
А со2 — сох 1 С02--(Ох
£1 <О()СОХСО2 7? yQ2—1сохсо2 1 <02 — <01 п “200—“1ОО
-С2 ш0<«>1Ю2 У Й2—- 1(0^2
__ 1 /aaZTi
R “2со — “loo ’
со.-» — со. ’
2оо loo
<02оо ш1оо
(9.480)
«>0
<О2 —(О.
ю0
ш2 — Ш1 У У
, 1 <о2 —<ох 1
2 £2 Я
2оо Ю1оо)
2оо 03 loo)
<ох<О2
Оказалось технически целесообразным заменить двухполюсник в параллельном плече параллельным соединением двух последовательных контуров L_, С_ и £+, С+. В итоге получается полу звено ШЬ (фиг. 148). Для пересчёта индуктивностей и ёмкостей мы отношение (8.246), в котором следует положить:
имеем со-
(9.481)
вследствие чего
a = b= -4
<°1<°2
1
2 (ш2оо —wloo)2’
В =/Г+4^ 032000)100 1 СО — со,
2оо loo
и мы можем принять, согласно (8.253), 1
(9.482)
щ1оо foloo + щ2оо) '
(<0о — со. )2 ’
\ 2оо loo'
“2со (“1со + т2со)
(“a»—“loo)2 ’ -
Опуская штрихи у L', С' и вычисляя С_, L., С+
1
по
(9.483)
формулам
d ’
4-
(9.484)
6?2
ПаСЙивйЫе СИСТЕМЫ
Гл. 9
получаем окончательно:
Т — Г _ 1 Ш2оэ~ “loo 1
/ О ^«,4-^ Г (Мгю_а11оо)/5^11
<°2оэ (“гео — “loo) V&— 1’ " К “гоо (“loo + “200)
£ “loo + “2со 1 (“2оо~“loo) 1
+ “loo (“2оо ~“1оо) V 23 “ 1’' + R “loo (“loo + “2оо) ‘ .
(9.485)
Можно также поменять местами С_ и С+. Формулы (479), (485) дают выражения волновых сопротивлений, коэффициенФа распространения и всех индуктивностей и ёмкостей схемы ШЬ через проектные границы полосы пропускания <о1, <d2 и полюсы затухания <oi0o, <»2со.-
§ 9.32. Заграждающие фильтры. Эти фильтры (фиг. 150) получаются из фильтров нижних частот путём реактанс-преобразования
— (®i<“2)- (9.486)
Полагая D = zw, О' = го/, находим преобразование частот — — (°*2 — 031 (9.487)
<oq — а/2
согласно которому частоты — со0, % переходят в а/ = <о2, <0р а частота
Фиг. 150. Звенья заграждающих фильтров.
ш = 0 переходит в а/ = 0,оо. Следовательно, интервал — о>0 <<о< переходит в интервал —оо < < <ох, <о2 < а/ < -}-оог ограниченный
§.*9.33] О РЕАЛИЗУЕМОСТИ ЗАДАННОЙ РАЦИОНАЛЬНОЙ ФУНКЦИИ 673 4
конечными частотами а^и о>2 и zt оо, который и будет полосой пропускания преобразованного четырёхполюсника.
Индуктивные проводимости преобразуются по формулам
где
(9.488)
£(о0 (ю2 — (ot)
<0^2 ’
(9.489)
а ёмкостные сопротивления — по формулам
где
CD оз0 (ш2 —
CD'
(9.490)
Сшр (со2 — <°1) О)1(О2
Са)0(а)2—ац) ’
(9.491)
Следовательно, каждая индуктивность L заменяется параллельным соединением индуктивности и емкости С19 а каждая емкость С— гг Л последовательным соединением индуктивности ь2 и С2.
Полузвено IVа (фиг. 150) получается из соответствующего полузвена 1а фильтра нижних частот (фиг. 145). Применяя преобразование к (451), учитывая (489), (491) и (454) и отбрасывая штрихи, по окончании вычисления имеем:
’ (9.492)
Полюсом затухания здесь будет ^00 = ]/ Комбинируя полузвено IVa с обращённым полузвеном, аналогично § 29, • получим звенья заграждающих фильтров IVd, IVe (фиг. 150).
§ 9.33. О реализуемости заданной рациональной функции как трансмиттанса симметричного решётчатого четырёхполюсника, не содержащего идеальных элементов. Пусть имеем симметричный решётчатый четырёхполюсник с постоянным действительным волновым сопротивлением W, замкнутый на внешнюю нагрузку с тем же сопротивлением W (фиг. 151).
43 Зак. 1474. Б В. Булгаков
674
Пассивные системы
[гл. 9
Если, как и выше, положить D — d/dt и обозначить через Z (D) сопротивления последовательных плеч, то, как известно, диагональные плечи должны представлять обратные двухполюсники < сопротивлениями Zfl (D) = UZ2/Z (О), а трансмиттанс четырёхполюсника, т. е. отношение изображений напряжений и токов на выходе и входе, будет:
Еу _ Iy _ W-Z Ь* 1Л — W+Z ’
(9.493)
Как установил Мин Най-да (§ 24), для того чтобы пассивный двухполюсник не содержал идеальных элементов, т. е. индуктивностей без последовательных сопротивлений и ёмкостей без параллельных
Фиг. 151. Симметричный решётчатый четырёхполюсник.
проводимостей, необходимо и достаточно, чтобы его импеданс Z (D) был УИ-функцией.
Как было показано в § 24, если Z (D) есть УИ-функция, то и 1/Z (О) является таковой.
Из результатов Ботта и Даффина [9-8] вытекает, что установленные Мин Най-да условия остаются в силе, если мы поставим дополнительное требование, чтобы двухполюсник Z (О) не содержал взаимо-индуктивностей.
Известны также (§ 36) условия, накладываемые на функции Z (О), X(D) в более общем, но и более абстрактном случае, когда требуется только, чтобы двухполюсники были пассивными, но идеальные элементы не запрещаются.
Две нижеследующие теоремы имеют целью выяснить аналитические свойства трансмиттанса четырёхполюсника, не содержащего идеальных элементов и взаимоиндуктивностей без рассеяния.
Теорема I. Для того чтобы рациональная функция Х(р) могла быть реализована как трансмиттанс симметричного решётчатого четырёхполюсника без взаимоиндуктивностей и идеальных элементов и с постоянным волновым сопротивлением W, необходимо и достаточно, чтобы её значения в замкнутой правой полуплоскости могли быть заключены в одном из кругов
ХХ±-ъ^(Х+Х) — Xz4 = 0, (9.494)
§ 9;33] О РЕАЛИЗУЕМОСТИ ЗАДАННОЙ РАЦИОНАЛЬНОЙ ФУНКЦИИ 675
проходящих соответственно через точки X = zp 1, причём 8 есть положительное число} значения qz 1 могут приниматься только при D = оо.
В самом деле, если X(D) реализуемо, то импеданс
— * Х(Р)
(9.495)
и W*IZ(D) являются Л4-функциями. Действительная часть ReZ(/<o) положительна при конечных <о, а если D = оо есть полюс или обык-
новенная точка для Z (D), но не нуль, то Re Z (fo>) при <о —> оо стремится к конечному положительному пределу или к -J-оо. В этом
случае ReZ(D) положительна на замкнутой мнимой оси (т. е. дополненной точкой D = оо) и имеет на этой оси и в замкнутой правой полуплоскости положительную нижнюю границу 8(р) (фиг. 152).
При конформном преобразовании Z=-^-=-ylV (9.496)
Фиг. 152. Область значений функции Z (О).
прямая ReZ = 8 или
Z^Z — 28 = 0
(9.497)
переходит в окружность, так как, подставляя выражение Z, находим:
—1=) W— 28 = 0, (9.498)
откуда
^+тЬг('¥+Х)+1ту = <)' <м99>
Если же положить Х=$.-\-1ч\, то получим:
£2X^2 1__??_g I .5 ~ = О
’ w с-Г 8_|_ w
_L । (9 500)
1Г + 8/ T7 + 8 (1Г+&)2 }
Это уравнение представляет окружность с центром в точке с координатами
w'-j- в > 1* 'По 0
и с радиусом
_ w .
Г ~ IF-Н ’
(9.501)
(9.502)
окружность проходит через точку — 1 (фиг. 153).
43*
676
Пассивные Системы
[гл. 9
Если теперь Ю = оо есть нуль для Z (D), то предыдущие отображения могут быть повторены в отношении Л4-функции W^jZ (D), для которой Re W'2fZ (Zoo) должно стремиться к конечному положительному пределу или к -|-оо при <о—>оо. Трансмиттанс четырёхполюсника с последовательным плечом W2IZ(D) будет —X(D) и по доказанному выше его значения лежат внутри окружности (499), а значения Х(р) — внутри окружности, симметричной первой относительно мнимой оси.
Значениям X — qz 1 в силу формулы (495) соответствуют значения Z=oo, 0, которые могут приниматься только при £) = оо. Этим
Фиг. 153. К отображению прямой Re Z = 8.
доказана необходимость условий теоремы.
Пусть теперь, обратно, Х(р) регулярна в замкнутой правой полуплоскости и значения этой функции могут быть заключены в одном из кругов (494), где 8 > О, причём значения — 1 или -f-1 могут достигаться только при О = оо. Тогда в случае первого круга значения функции
Z(D)= W
в замкнутой правой полуплоскости Re О
должны заключаться в замкнутой полуплоскости ReZ^>8, причём полюс может быть только при D = oo, а нулей нет совсем. Поэтому найдётся такое р, что ReZ положительна в точках D правее прямой Re D = — р и является поэтому Л4-функцией. В случае круга второго семейства рассуждение может быть повторено в отношении —Х(р) и W^/ZtZ)). Этим доказана
достаточность условий реализуемости.
Теорема II. Если рациональная функция P(D)/Q(D) регулярна в замкнутой правой полуплоскости, то для реализуемости функции
х <D> “ i wy • <9-503>
как трансмиттанса симметричного четырёхполюсника без взаимо-индуктивностей и идеальных элементов, необходимо и достаточно, чтобы k>m, где т — максимум модуля P(D)IQ(D), а при k = т,— чтобы максимум модуля достигался только при D = оо.
В самом деле, при k > т максимум модуля X(D) будет < 1 и область значений Х(р) будет заключена в круге с центром в начале и радиусом, меньшим единицы (фиг. 154). А этот последний можно заключить в одном из кругов (494). Значения Х= — 1 или Ц-1 не достигаются.
। Если k = т, то область значений X(D) будет заключена в единичном круге. Эту область невозможно будет заключить также и в один из
§ 9.34] КОРРЕКТИРУЮЩИЕ ЦЕПИ 677
:Л* •
кругов (494), если на границе имеются точки, отличные от X = — 1 или X = 1, но лежащие на единичном круге, или же если обе эти
точки принадлежат границе. Необходимо, следовательно, чтобы одна и только одна из этих точек была общей точкой границы и единичного круга. А так как эти точки соответствуют Z = oo и Z = 0, то значение X —— 1 или +1 должно достигаться лишь при О = оо. Затем, для того чтобы можно было провести круг (494), заключающий область значений Х(р), необходимо ещё, чтобы радиус кри-
Фиг. 154. Область значений функции X(D) при k^>m.
Фиг. 155. Область значений функции X (D) при k = т.
визны границы при X = — 1 (возьмём для определённости один из двух случаев) был меньше 1. Но это так и будет (фиг. 155), так как если
Х= 54-/7), (9.504)
то на границе D = до и $ = $(/), т) = т| (/), где через t обозначено /=1/со. Затем, при со—>оо
5 = —1, 7) = 0, |
На4-т)2 = 1, J |40а+^)=к+^=°. I 4-й<’а+7>9) = ^+7>;>+^+;12<0’
откуда следует, что
5 = 0, 5 > и
, ($2 _1_ ^2)а/г is is
радиус Кривизны I = = ----v-тг = < 1.
И — ' —Т) £ 5
(9.505)
(9.506)
(9.507)
(9.508)
§ 9.34. Корректирующие цепи. Каскад симметричных решётчатых четырёхполюсников с постоянным волновым сопротивлением. В последние годы корректирующие цепи находят применение
678
ПАССИВНЫЕ СИСТЕМЫ
[гл. 9
в автоматических регуляторах и сервомеханизмах для улучшения их частотных характеристик.
Ниже (§§ 34—40) рассматриваются вопросы синтеза корректирующих цепей. При этом учитываются интересы указанных отраслей техники, хотя задачи ставятся в обШей ферме. Это представляется нелишним, поскольку, например/диссертация А. Холла [4ЛЛ] содержит много схем, но не ставит общей задачи синтеза; что же касается соответствующей главы книги Боде р-1], то, при вполне общей постановке задачи, в ней для некоторых элементов цепей приводятся расчётные формулы без полного указания условий их применимости, а в отношении других элементов имеются лишь беглые замечания без расчётных формул. В настоящем разделе ставилась цель избегать взаимоиндуктивностей и, по возможности, идеальных элементов, т. е. индуктивностей без последовательных сопротивлений и ёмкостей без параллельных проводимостей, как это делали для частных задач А. Холл и Мин Най-да |9-17].
Корректирующую цепь мы будем предполагать включённой между некоторыми другими цепями, входные сопротивления которых равны одному и тому же действительному постоянному числу W; случай различных постоянных активных оконечных сопротивлений рассмотрен отдельно ниже (§ 35). За основную форму корректирующей цепи примем каскад симметричных решётчатых четырёхполюсников с одинаковым волновым сопротивлением W (фиг. 156). Наименование «сим-
Фиг. 156. Каскад решётчатых четырёхполюсников.
метричный решётчатый» будем в дальнейшем заменять буквами PC. Принятая форма с согласованными волновыми сопротивлениями может, в частности, заменить применяемый в системах регулирования и сервомеханизмах каскад [4-17* 4Л4], в котором вследствие отсутствия | согласования последовательные четырёхполюсники должны быть | изолированы буферными усилителями. I
Четырёхполюсник PC благодаря своей общности обладает извест-ными расчётно-теоретическими преимуществами. Для непосредствен- j ной реализации он не очень удобен, так как, с одной стороны, пред- % ставляет схему, сбалансированную относительно земли, а с другой— требующееся число отдельных элементов (индуктивностей, омических Ц сопротивлений и ёмкостей) не всегда получается наименьшим. Однако $
§9.35]
СОГЛАСУЮЩИЕ Г-ПОЛУЗВЕНЬЯ
679
Фиг. 157. Симметричный решётчатый четырёхполюсник (PC).
после того как параметры PC найдены, он может быть, во многих случаях, преобразован в другие, практически более приемлемые формы. Вопрос этот — общий и рассматривается в руководствах по теории цепей. Некоторые преобразования указаны в § 40.
Обозначим (фиг. 157) через Za'D), Zy (D) составляющие сопротивления четырёхполюсника PC, причём че-рез D мы будем, как и выше, обо-значать «неопределённый» оператор дифференцирования djdt. Пунктиром на фиг. 157 и в дальнейшем обозна
чены сопротивления последовательного и диагонального плеч, идентичных с показанными более подробно. Назовём передачей или трансмиттансом четырёхполюсника
и обозна-
чим через X отношение напряжений и токов на выходе и входе. Тогда, согласно известным соотношениям,
При этом величина
X(D) = e~9 —
g=a-[-ib
(9.509)
(9.510)
(9.511)
есть коэффициент передачи, а а и b — коэффициенты затухания и фазы. Исключая из (509), (510) сначала Zb, потом Za, находим:
(9.512)
(9.513)
Так как корректирующая цепь представляет каскад четырёхполюсников, то её трансмиттанс равен произведению трансмиттансов всех звеньев.
Общая задача синтеза состоит в том, чтобы выбрать число и структуру звеньев таким образом, чтобы трансмиттанс корректирующей цепи представлял по возможности с малым искажением некоторую заданную наперёд функцию.
§ 9.35. Согласующие Г-полугвенья. Пусть оконечные сопротивления, между которыми включена корректирующая цепь, представляют различные действительные положительные постоянные Ry; Для их согласования можно воспользоваться Г-полузвеньями.
680
ПАССИВНЫЕ СИСТЕМЫ
[гл. 9
Если Rx > Ryi то вводим на входе каскада обращённое Г-полу-звено (фиг. 158) с составляющими сопротивлениями
Ra=V R^R*—Rv)> ' я
Rb =
(9.514)
По общим формулам теории четырёхполюсников волновые сопротивления Zx, Zy на входе и выходе полузвена и коэффициент пере-
Фиг. 158. Входное обращённое Г-полузвено.
-ЛЛР
-о
Фиг. 159. Выходное Г-полузвено.
дачи, равный в данном случае коэффициенту затухания а0, определяются формулами
cth aQ
откуда
£а0 =
X
(9.515)
X Г J'X Г'У
Если Rx<Ry, то вводим на выходе каскада Г-полузвено (фиг. 159) с составляющими сопротивлениями
Ra = VRy(Ry — Rx), RxRy
(9.516)
Волновые сопротивления определяются формулами
и коэффициенты затухания полузвена
Js
х VRM+Rb)
а» % у — l^~Ra (Ra Ry
?!
и
4
О
<
У
У
X
а
У
ч
&
$ %
§ 9.36] О РЕАЛИЗУЕМОСТИ ТРАНСМИТТАНСА ЧЕТЫРЁХПОЛЮСНИКА 681
И 4
откуда
(9.517)
В обоих случаях волновые сопротивления полузвена равны оконечным сопротивлениям Rx, Ry, и если наименьшую из этих величин принять за волновое сопротивление W четырёхполюсников PC, то мы будем иметь полное согласование как внутри, так и на концах каскада. Согласование достигается ценой дополнительного затухания а0.
§ 9.36. Условия реализуемости трансмиттанса пассивного четырёхполюсника. Для того чтобы функция Za(D) могла быть реализована как сопротивление некоторого пассивного двухполюсника, она должна быть действительной положительной аналитической функцией в смысле Бруне [9-9*9ДЗ], т. е. она должна быть действительна при действительных значениях D, а её действительная часть должна быть положительной при положительных значениях действительной части D; например, D, (D-{-V)lD, ln(14“^)> thD.
Указанные выше условия равносильны следующим: функция должна быть аналитической в правой полуплоскости значений аргумента D, полюсы на мнимой оси должны быть простыми, а их вычеты— действительными и положительными и, наконец, должно удовлетворяться неравенство ReZa(Z<o)^>0; точка D = oo причисляется к мнимой оси; если там есть полюс, то он должен быть простым и коэффициент при D в соответствующем ряде Лорана—действительным и положительным. Оставляя общий вопрос о возможности существенно особой точки при D — оо открытым, ограничимся случаями, когда таковой не существует и Za(D) является рациональной. Этого достаточно для цепей с сосредоточенными постоянными. Транс-миттанс X(D) будет в этих случаях также рациональной функцией.
Если Zt есть действительная положительная функция, то, очевидно, \jZ\ будет такой же. При двух действительных положительных функциях Zx, Z2 такими же будут:
Zx [Z2 (0)1, zt + z2> z ==
Если же Zx, Z2, Z3 действительны и положительны, то это будет верно не только в отношении функции Z± {Z2 [Z3(D)]} и суммы ^i4~Z2-|-Z3, но и в отношении выражения
У___ Z| -|~ Zg Ч~ Z3 Ц- ZtZ2Z3
1 + Z%Z% -f- Z3Z1 -|- ZjZ2
И Т. д.
682
ПАССИВНЫЕ ’ СИСТЕМЫ
[гл. 9
Первая формула (512) определяет конформное отображение правой полуплоскости Zn на внутренность единичного круга с центром в начале плоскости X (фиг. 160). Поэтому мы должны иметь:
|Х(О)|<1 при ReD>0. (9.518)
Фиг. 160. Конформное отображение X=(IT-Za)/(r+Za).
Обратно, при выполнении этого условия функция Za(D) будет действительной положительной.
В силу этого условия кривая ^=Л'(za)), т. е. частотная характеристика, должна лежать в единичном круге. С другой стороны, функция X' D) должна быть аналитической в расширенной правой полуплоскости D (т. е. включая точку О = оо) и на мнимой оси, так как при наличии там особых точек значения X(D) не могли бы быть ограничены единичным кругом.
Пусть, обратно, частотная характеристика лежит в единичном круге и X(D) аналитична в расширенной правой полуплоскости и на мнимой оси. В силу теоремы о максимальном модуле *) максимальное значение | X (D) | на мнимой оси будет также максимальным для всей правой полуплоскости D. Условие (518) будет выполнено и Za (О) будет действительной положительной функцией.
Таким образом, для реализуемости функции X(D) как трансмит-танса пассивного четырёхполюсника PC необходимо и достаточно, чтобы она была регулярна в расширенной правой полуплоскости и на мнимой оси и чтобы её частотная характеристика К = X (z<o) лежала в единичном круге.
Физический смысл условия | X (zoo) | = | | 1 заключается,
очевидно, в том, что при передаче через пассивный четырёхполюсник мы можем иметь при всех частотах о> только затухание а 0, а не усиление амплитуд напряжений и токов.
Если мы имеем какую-нибудь рациональную функцию Р (D)/Q (D), удовлетворяющую только первому условию регулярности в указанной выше области, то максимум её модуля на мнимой оси будет конечным числом zn, но оно может оказаться ббльшим единицы. Мы
можем положить
т при т > 1, 1 при т С 1
(9.519)
*) См., например, И. И. Привалов, Введение в теорию функций ком* , плексного переменного, изд. 9, Гостехиздат, 1954, стр. 204.
§ §.37] РЕАЛИЗАЦИЯ ТРАНСМИТТАНСА КАСКАДА 683
и реализовать функцию
Х(Р) = е~аг^> (9.520)
Итак, для того чтобы функция P(D)/Q(D) могла быть реализована* как трансммиттанс пассивного четырёхполюсника PC с точностью, быть может, до постоянного затухания, необходимо и достаточно, чтобы она была регулярна в расширенной правой полуплоскости и на мнимой оси.
§ 9.37. Реализация трансмиттанса каскада пассивных четырёхполюсников. Так как трансмиттанс каскада равен произведению трансмиттансов всех звеньев, то только что сформулированное условие реализуемости немедленно распространяется на всю корректирующую цепь. Если P(D)IQ(D) есть рациональная функция, удовлетворяющая этому условию и подлежащая реализации, то для этого представляются, вообще, два пути;
Мы можем пытаться реализовать заданную функцию одним PC. и одним согласующим полузвеном. Определяя трансмиттанс PC из (519), (520) и сопротивление Za(D) из первой формулы (513), мы должны будем реализовать последнее пассивным двухполюсником. Для этого можно воспользоваться методом Бруне. Не говоря уже о возможной сложности расчёта и самого двухполюсника, который при этом получится, вообще нельзя будет избежать появления взаимоиндуктив-ностей без рассеяния, что составляет известное слабое место метода. С другой стороны, кроме затухания согласования мы будем иметь только затухание реализации PC и окончательный трансмиттанс цепи будет
е~(а°+аг> (9.521)
где аг определяется согласно (519).
Другой путь состоит в том, чтобы представить Р (D)/Q (D) в виде произведения
Р(Р) _РХ(Р)Р2(Р) Рп(Р)
Q (Р) ~ Qx (D) Q2 (Р) ’ ’ * -Qn (Р)
и реализовать каждый множитель Pj{D)IQj(D) отдельным PC.
Так как Р (D)/Q (D) не может иметь при D = оо полюса, но может иметь там нуль любого порядка, то степень Р(Р) не превосходит степени Q(D). С другой стороны, комплексные нули и полюсы входят попарно и их при разбиении на множители нельзя разделять. Поэтому очевидно, что поставленная задача будет разрешена, если составить реализации всех дробей со знаменателями первой и второй степени и степенью числителя, не превосходящей степени знаменателя.
При этом, как будет показано, цепей Бруне с взаимоиндуктив-ностями без рассеяния можно избежать ценой введения для некоторых множителей P^(D)IQj{D) второго PC,
684
ПАССИВНЫЕ СИСТЕМЫ
[гл. 9
С другой стороны, при реализации каждого множителя будет иметь место потеря arj и окончательный трансмиттанс корректирующей цепи будет:
QW’
где
при 1, при nij 1.
(9.523)
(9.524)
Так как максимумы модулей звеньев т$ достигаются, вообще, при различных частотах, то
О
следовательно, реализация получается, вообще, с большим затуханием, чем при одном PC.
Во всех случаях для компенсации затухания от согласования и реализации можно ввести в конце каскада пропорциональный усилитель, с коэффициентом усиления, большим или равным ехр (а0Н~ 2 arj)* Этот коэффициент усиления можно теоретически представлять себе разложенным на множители, приписанные отдельным дробям Pj(D)IQj(D).
В следующих параграфах даны реализации звеньев PC первого и второго порядков. Интересы теории регулирования отражены в условных наименованиях звеньев и в значениях частичных коэффициентов усиления; ни те, ни другие не обязательны для остальных приложений.
При этом рассматриваются обычно только трансмиттансы, в выражениях которых старшие члены числителя и знаменателя имеют положительные коэффициенты. Для изменения знака трансмиттанса, как видно из формул (510), (512), достаточно поменять местами сопротивления Za, Zb.
§ 9.38. Звенья нулевого и первого порядков. Начнём с единственного звена нулевого порядка (звено I) с трансмиттансом
*(£>) = 4“’
где k — постоянная, большая единицы. Это звено вводит постоянное затухание a = lnfe, не меняя фазы сигнала. Мы имеем:
za фу=w •
Соответствующий двухполюсник и обратный двухполюсник Zb(D) позволяют построить схему звена PC, показанную в таблице 8 (стр. 687).
§ 9.381 ЗВЕНЬЯ НУЛЕВОГО И ПЕРВОГО ПОРЯДКОВ 685
.Далее рассмотрим звено упреждения (звено II) и стабилизирующее звено (звено III), для которых
*(О) =
Т2 TXD±1
Tt T2D -f-1 ’
Л
2>
причём как здесь, так и в других формулах верхний знак относится к звену II, а нижний — к звену III. Постоянные времени Тх, Т2 предполагаются, разумеется, положительными.
Выбирая для частичного коэффициента усиления значение
мы можем с помощью функции сХ(р) звена II обратить трансмиттанс 1/(7\Z>—|— 1) одного из основных звеньев системы регулирования
Фиг. 161. Характеристики затухания (сплошная кривая) и фазы (пунктир) для звеньев II и III.
в 1 /(T2D -1- 1), т. е. уменьшить его постоянную времени; таким же образом звено III позволяет заменить трансмиттанс l/^D—1) статически неустойчивого звена на 1/(T2D-J-1). Этим мотивируются принятые наименования звеньев. /
Формы характеристик затухания а — — In | сХ | и фазы ==='—arg \сХ(Z(o)] представлены на фиг. 161. Оба звена дают отри-
Пассивные системы
[гл. О
686
цательный сдвиг фазы, т. е. опять упреждение на всех частотах. Звено упреждения мало влияет на амплитуду и фазу сигнала при низких частотах и более сильно — на средних и высоких; благодаря упреждению по фазе это звено может применяться для улучшения диаграмм Найквиста регулируемых систем:
Для Za(D) имеем выражение
Za{D) =
W,
которое можно представить также в виде
^a(D) =
Соответствующий PC показан в таблице 8 вместе со значениями электрических параметров, получающимися путём сравнения коэффициентов.
Пусть имеем теперь звено запаздывания (звено IV) и стабилизирующее звено (звено V), для которых
Ъ < т2.
Формы характеристик затухания даны для
с = kT2/Tt
на фиг. 162. Звено IV даёт запаздывание по фазе, а звено V — упреждение на всех частотах. Звено запаздывания обусловливает более или менее значительное усиление сигнала при низких частотах и весьма мало влияет на него при высоких; поэтому оно иногда применяется для уменьшения статической ошибки и улучшения характеристик следования сервомеханизмов. Если обозначить
CLq ==— k 7*2 _-1.- , СЬ-у — k 1,
&о == kT2 —5— 7^, = k —|— 1,
то обратную величину Za(D) для звена IV можно выразить в виде
1 ^bQD + bl 1 1 . 1
Za (D) aQD +at W 'LD +
и совершенно так же можно представить 1/Z6(D) для звена V. Это даёт реализации, указанные в таблице 8.
§ 9.38]
ЗВЕЙЬЙ НУЛЕВОГО И ПЕРВОГО ПОРЯДКОВ
687
Таблица 8
Звенья I, И, III, IV, V
I. X(D) = 4-к
688
ПАССИВНЫЕ СИСТЕМЫ
[гл. 9
Таблица 8 (продолжение).
Фиг. 165.
_ (A»T2zpTt)2 kT2^Tx _ kT2±Tx
~’2k(T2^Tl) Wi kT2±Ti' Н2~~ kT2+ TtW’
(k-\)(kT2+l\) 2k(T2^Tx)
<3” 2k(T2^T1) W' (k— 1) (kT2^ ?i) Wi
(kT2^Tx)* 1 ь”“2Л(Т2^Л) W
При k—\ сопротивление 7?3 и проводимость l//?4 обращаются в нуль, соответствующие элементы выпадают и схемы упрощаются. Они становятся, однако, менее удовлетворительными, поскольку индуктивность без последовательного сопротивления и ёмкость без параллельной проводимости, которые мы будем называть идеальными элементами, можно рассматривать лишь как приближения. Поэтому лучше брать й> 1, хотя благодаря этому вводится затухание реализации ar = In k > 0. (9.525)
Отметим, что с возрастанием k от 1 до оо сопротивления Rt для • звена IV и R2 для звена V возрастают, a Rr для V и R2 для IV убывают от своих значений при k = 1 до W. Что касается последовательного сопротивления и параллельной проводимости 1//?4, то они возрастают, оставаясь связанными линейным соотношением
Можно было бы возразить, что омическое сопротивление реальной J индуктивности и проводимость ёмкости могут совсем не удовлетворять >
§
Звенья нулевого и первого порядков
683
величины особыми последова-
Фиг. 166. Характеристики затухания и фазы для звеньев VI, VII, VIII.
этому соотношению. Достаточно, однако, выбрать k таким образом, чтобы /?д и 1//?4 превышали действительные значения, реализуя, в случае необходимости, избыточные тельными или параллельными сопротивлениями.
В дальнейшем мы будем всюду, где это будет удаваться, избегать идеальных элементов, хотя это ведёт к некоторому усложнению схем. Однако из них, как правило, могут быть получены более простые формы с идеальными элементами путём придания некоторым произвольным параметрам очевидных частных значений, например k = 1 в настоящем параграфе.
Звено VI, для которого
может рассматриваться как частный случай звена V. Полное вводимое им затухание In k происходит только за счёт реализации. При частичном коэффициенте усиления с = k полное затухание равно нулю, и мы получаем чистый фазовращатель. Характеристика фазы, построенная в этом
предположении, показана на фиг. 166, а схема — в таблице 9. Если поменять местами сопротивления Za(D), Z&(D), то трансмиттанс изменит знак, а его фаза увеличится на я. Вместо упреждения по фазе, убывающего от тс до 0, мы получим запаздывание, возрастающее от 0 до тс.
Для звена VII с трансмиттансом
TD
полагаем:
тлзг = (2ГО+1)^=^+са
Наконец, звено запаздывания (звено VIII) с трансмиттансом
X(D) = ~k TD-{-\
может рассматриваться как частный случай звена IV.
Характеристики затухания и фазы для звеньев VII, VIII при частичном коэффициенте усиления, равном соответственно 1 и ft, представлены на фиг. 166.
44 Зак. 1474. Б. В. Булгаков
690
Пассивные системы .
Звенья VI, VII, VIII
(гл. 9
Таблица 9
VL
Фиг. 167.
^v.
n , (^+1)2T 1 '
C~ 4k W
TD
VII. X(D) = y~^T.
Та же схема, что для звеньев II, III (табл. 8).
2Т
£ = 2ТГ, = С = ^.
ГУ
L = ^W, Ri=W, ??, = *—*IF, jfs=TL.W,
§ 9.39]
Звенья второго порядка
691
. § 9.39. Звенья второго порядка. Для звена PC с трансмит-тансом
A^D* АуГ) А%
BqD2 ByD -f- В%
Х(О) =
сопротивление последовательного плеча есть действительная положительная функция такого же вида:
<9-526’
Если сначала иметь в виду общий случай, когда ни один из коэффициентов не обращается в нуль, то для регулярности функции в правой полуплоскости необходимо, чтобы й0, b19 b2 имели один и тот же знак; без ограничения общности можно считать, что этот знак — плюс..
Мы имееда:
Re Z. (Ы) = + + w (9.527)
где
= ^o^o» = йфр nt2 = #2^2» /Л enO\
.2 OA A a2 (9.528)
/l>0 - “ ^0» ‘ "^O^X’ ^2 ' ^2*
A > Г « *
Так как знаменатель ( — -|- &2)2 -f* всегда положителен,
то для положительности ReZa(f(o) при о>2 = 0, оо необходимо, чтобы /п0, т2 > 0 й а0, Oj > 0. При этих условиях числитель, рассматри-
Два действительных корня разных знаков
Фиг. 169. Распределение корней квадратного трёхчлена.
ваемый как квадратный трёхчлен от х = о>2, сохранит положительный знак при всех положительных х, если его корни — отрицательные или комплексные. Из диаграммы распределения корней в зависимости от отношений (фиг. 169) легко усмотреть, что
Этб может быть либо при
/Пх/лп0 > 0, гп2/тп0 > 0,
44*
692
йассйвйые СИСТЕМЫ
(гл. 9
либо при
< °> (wiMo)a < 4/п2//п0;
если т0, т2 > 0, то можно объединить в одно условие
''П Г
Подставляя значения /п0, ntv m2t получим простое неравенство *
aji > (/«А — (9.530)
Как легко проверить, оно в то же время выражает требование, чтобы модуль JV(fw) не превосходил единицы. Из него также следует, что афх >0, а± > 0, так что в итоге все коэффициенты ait должны быть положительны.
Предположение о необращении в нуль ни одного из коэффициентов может быть отброшено, и из соображений непрерывности вытекает общее условие реализуемости: коэффициенты должны быть неотрицательны (неположительны) и удовлетворять неравенству (530).
Возможны, следовательно, различные случаи вырождения, когда некоторые коэффициенты обращаются в нуль. При любой дробной рациональной функции ZO(D) мы имеем ограничения, связанные с требованием, чтобы нули и полюсы при D = 0, оо были простыми; в самом деле, из этого требования вытекает, что показатели старших степеней в числителе и знаменателе не могут отличаться больше чем на единицу, так же как и показатели младших. Нетрудно убедиться, однако, что в случае сопротивления вида (526) последнее условие есть следствие (530).
С одним из случаев вырождения мы имеем дело при рассмотрении звена упреждения (звено IX) и стабилизирующего звена (звено X) второго порядка, для которых
*ф)=
2> ^2 > О’
3
£
где Т19 Т29 разумеется, положительны; то же предположение в отно шении Cg обеспечивает регулярность функции X(D) в правой полу плоскости.
Сопротивление последовательного плёча будет:
Za (°) = W> (9.531) I
а ' OqDa + btD -Ь ь2 1
где значения коэффициентов ai9 bt приведены в таблице 10 (стр. 695). । Из неё видно, что а.2, bQ9 b2 положительны. Из (530) при ао = 0 получается:
где выражение для f также приведено в таблице 10. С его помошы0 получаем вследствие чего Ьг должны быть также
положительны.
'S& у &•. >
У
Л? .f.
•Л/ '&•
л
§ 9.39]
ЗВЕНЬЯ ВТОРОГО ПОРЯДКА
693
4 Следуя Бруне [*Л], выделяем из 1/ZO(D) член, соответствующий полюсу при D = oo, и получаем:
zh = CD+^B-r (9'533)
где
С = (9.534)
1 __ fD *4- 1
Z^D) “ M^ + *2) >’
(9.535)
Первый член в правой части (533) можно истолковать как проводимость ёмкости С, а второй — как проводимость параллельно соединённого с ней двухполюсника. Так как
Re 1 /Zx (Z<o) =
1 a?<o2 + a! IF1
X 1 6
то проводимость 1 IZ± (D) является действительной положительной функцией.
В случае g>0, где выражение g дано в таблице 10, минимальное значение Re l/Z1(Z(o), достигаемое при <о = 0, есть d2/a2lF. Если эту величину представить как проводимость 1//?х и вычесть из 1/Z1(D)9 то получится всё ещё действительная положительная функция, но её реализация будет заключать идеальный элемент. Чтобы избежать его, полагаем:
1 — 1 । 1
где за мы принимаем величину, меньшую минимума Re 1/Z^Zoj):
Ri> г w-
Затем 2
g ([)\ ==____дt ~~F" ^2) Ri W .
(fRi-alWyD+a^b^-a^'
эта действительная положительная функция легко реализуется, если заметить, что
(Mi — a2lF) — йа (JRt — = -Rlg< Q,
И принять
z2(D)=/?8+z8(D),
_ e^RiW ,
Z8 (D) _____________________________________W
tfRj.-<%W) [tfRt-eflT) D 4-(ад—eglT)]
[гл. 9
694 . ПАССИВНЫЕ . СИСТЕМЫ
»
Полагая затем Z8(D)= 1
найдём Сх и 7?б.
Если g=0, то
/ 1 =агЬ2 1 _ 1 = _1_
a{W a&W Z^D) /?/
Если f > 0, g < 0, то минимальное значение Re 1 /Z± (ш>)9 достигаемое при о) = оо, равно fla^W и мы можем положить:
1 _ 1 । 1
Z2(D) ’ где а?
вычисляя Z2(O) и полагая
Z2 (D) = LJ) + /?8, найдём Zj и /?8.
, Наконец, при /=0 функция
Z\ (D) = Д1£>,+ W о2
легко реализуется, но ёмкость С не имеет параллельной проводимости.
1 Сопоставим четыре представления проводимости (535), соответствующие четырём найденным реализациям двухполюсника ZX(D):
#з +
Zt(D) ~ Rt
при g=0;
(9.536)
} Z^D) ~ +
4)_Д______ 1
ЬПЛ.1>.
при
Читатель может избежать деталей метода Бруне, непосредственно проверяя путём подстановки, что выражения индуктивностей, омических сопротивлений и ёмкостей через bit приведённые в таблице 10, удовлетворяют предыдущим соотношениям. Условия пригодности, указанные для каждого соотношения, необходимы и достаточны, чтобы все эти^элемецты оказались положительными.
л
§ 9.39]
ЗВЕНЬЯ ВТОРОГО ПОРЯДКА
695
Звенья IX, X
Таблица 10
IX, X. X(D) = -^
Обозначения^ общие для четырёх схем:
„ ___f}T т /т f тг \ „ ___ »г2__»г>2
2»
2
60 = 2ВД b^ZTJ^T^ /=аД-а/о = 2Т^]2(-
Л>Т2,С2>0.
2»
2
Общее условие реализуемости:
До W*
/?<>-— UZ, в остальном произвольно, /?2 = -77— ,
W _ (fR'-a; W)W______________glfi________
“ //?! Ri~ a2^ 6 “ (/7?!-a*IF) a2W)’
(f^-alwyib^-a^W) Ьй 1 _ _ 1
«вЛ----------—75 С — „ wr> С1 — п api ЦТ
&Q 1 at Г’
696
ПАССИВНЫЕ СИСТЕМЫ
[гл. 9
Таблица 10 (продолжение)
Схема 2. g=0.
Та же схема, что для звеньев II, III (табл. 8).
§ 9-3PJ ЗВЕНЬЯ ВТОРОГО ПОРЯДКА 697
Схемы четырёхполюсников PC, соответствующие четырём формам Zt(D), приведены в таблице 10. При этом обратный двухполюсник Zb(D) получается из ZO(D), если, по известной теореме, заменить все последовательные соединения параллельными и наоборот, а вместо всех индуктивных, омических и ёмкостных сопротивлений подставить сопротивления, обратные им относительно W.
Так как v^g^a^f— a*b2 0 вытекает f > 0, то четыре схемы (536) исчерпывают область реализуемости (532) сопротивления (531) с положительными а.2, bQi д2, а следовательно, и принятой нами формы трансмиттанса звеньев IX, X. При f= 0 не удалось избежать идеальных элементов; однако этот случай — граничный, и если мы желаем пользоваться только схемами без идеальных элементов, то нужно будет лишь заменить общее условие реализуемости /^>0 через />0, что не имеет большого значения. Для /<0 мы не имеем, вообще, никаких схем, но в конце параграфа будет указано, как обойти это ограничение, не прибегая к цепям с взаимоиндуктивностями без рассеяния.
С помощью выражений для f и g можно представить геометрически области применимости четырёх схем звеньев IX и X.
Если воспользоваться сначала первым квадрантом плоскости (ах >0, Ь± > 0), то уравнения
f = — 0,
(9.537)
^Л1(—*2а1 + а2й1) —а^о = ° (9.538)
определяют ветви двух гипербол с асимптотами соответственно Ох = 0, &х = 0 и at = 0, — d2ax + а.2Ь± = 0, причём первая асимптота каждой пары — общая для двух ветвей. Мы будем называть эти ветви кривыми / и g (фиг. 173).
Область g> О.есть внутренность кривой g, область g= 0 состоит из точек самой этой кривой, область />0, §*<0 лежит между двумя кривыми и, наконец, область /=0 состоит из точек кривой f и образует границу общей области реализуемости звеньев IX, X. Соотношенйя
могут рассматриваться как уравнения аффинного преобразования плоскости Ох&х в плоскость С^. Так как определитель преобразования есть — 47172, то все сходственные углы имеют противоположные знаки.
Вторая из формул обратного преобразования
— Д1 +
__+fri 4Т2Т2
47?2 ’
&
698
ПАССИВНЫЕ СИСТЕМЫ
. [гл. 9
показывает, что так как для кривых /, g в плоскости аАЬ± обе координаты положительны, то преобразованные кривые должны
лежать
Звено и
Фиг. 174. Кривые / и g для звеньев IX, X в плоскости С1С2.
в верхней полуплоскости Cg > 0. Это будут ветви гипербол р2 р2
«а ’ *2
(9,540)
___2 2То
4^7/7^ (- Т& + 7^) = (7^ 7^)9. (9.541)
Общая асимптота — TJ^ Ц- Т\Ъ = 0 представляет преобразование оси ординат ах = 0 (фиг. 174). Мы видим, что область реализуемости
Л 4
§ 9.39]
ЗВЕНЬЯ ВТОРОГО ПОРЯДКА
699
в плоскости СгС2 ограничена снйзу, так что коэффициенты затухания С2 не могут быть слишком малы. Области нереализуемых значений параметров отмечены на чертежах штриховкой.
Обращаемся к звену запаздывания (звено XI) и стабилизирующему звену (звено XII), для которых
ЛО)= Т1<т„ с_>0.
k T2-D2 + 2Г2С2Р +1
Делитель k > 1 вводится для того, чтобы избежать идеальных элементов. Если принять обозначения ai9 bi согласно таблице 11, то сопротивление последовательного плеча звена XI определяется общей формулой (526) и совершенно так же выражается через ait bt сопротивление диагонального плеча звена XII.
Для определённости будем сначала иметь в виду звено XI.
Так как изменение функции ReZ0(/co), определяемой формулой (527), не будет, вообще, монотонным, то её минимальное значение не должно совпадать , со значениями при о> = 0 или <о = оо. Это верно и ,в отношении действительной части
Re 1 /Z_ (to) = ^*+(«Ау^2-«з&о)^Л.Д2»2. 1 (9>542)
+ (а{ — 2а0а2) ш + а2 ™
Поэтому, если положить 1 — 1 । 1
Za(D)~ а0 Z(D) ’ где
1 уР — р_____1_
Z(D) До (#oP2-|--|- д2) W 9
(9.543)
(9.544)
а значения 0, у указаны в таблице 11, то i/Z (D) не является, вообще, действительной положительной функцией. Но это будет так, если при всех <о
Re *
ИЛИ
8со2 — а20 0, (9.545)
где значение 8 также указано в таблице 11. Она показывает, кроме того, что а.2 для звеньев XI, XII всегда положителен, так же как о0, ^о> ^2» а ? отрицателен. Поэтому единственным существенным условием законности выделения bJa^W будет:
8>0.
Предполагая, что оно выполнено, полагаем
R1 = Г. х Оо
(9.546)
(9.547)
700
3
ПАССИВНЫЕ СИСТЕМЫ
(гл. 9
и замечаем, что из —р = а062 — и условия г (530) следует ai> ^1 > 0, а из 8 = яор Ц-у О вытекает т > 0.
Поэтому задача о реализации проводимости \IZ(D), которую мы должны теперь разрешить, вполне аналогична задаче о реализации сопротивления Za(D)t рассмотренной в начале параграфа; выражения обеих функций (531) и (544) имеют одну и ту же форму. Решения будут также вполне аналогичны.
Выделяя из Z(D) полюс при О = оо, находим:
где
Z (О) = LD + Zx (D), (9.548)
(9-549)
А (°) = (9-550)
Вводя обозначение в согласно таблице 11, предполагаем W е > 0. Тогда минимальным значением ReZt(fo) будет а0а2 — полагая
сначала однако,
^i(D) = /?3 + Z2(D),
мы во избежание появления идеальных элементов принимаем:
оставляя А?3 в остальном произвольным. Тогда Z (р\ W—7а#з) 4~ Т ОМз 1^ + Р#з)
Так как
Та (*о^+ ?Яз) + ? (*о^— №%) = - < 0>
то можно представить 1/Z2(O) в виде 1 - 1 । 1 Za(D) Z3(D) ’
где г> ________________________Т2^?з .
>
если вычислить затем Z3 (D) и положить
то 11, /?7 также легко определятся. ' jp
§ 139]
ЭвЕНьЯ ВТОРОГО ПОРЯДКА
701
Пусть теперь е = 0. Пользуясь выражением е, находим:
IF = IT = Z! (D) = Я3.
В двух рассмотренных случаях из е = — а2%9 — [38 ; 0 вытекает 8 > 0.
Если 8 > 0, е < 0,
где
О и а.2 > О,
то полагаем:
Z1(D) = 7?3-J-Z2(D),
/?8 = ^ W,
а функцию. Z2 (Р), после ее вычисления, можно представить в форме
Z2 (D) =
*5
Если, наконец, 8 = 0, то из (550)
А(О) = ^р- w=
1 1 /?3
Сопоставим результаты для четырёх исследованных случаев, которыми исчерпывается область З^О, где реализация сопротивления Za(D) приводится к реализации вырожденной формы \IZ(D)*.
|«> b J,
Z(D) —
При 8 > О,
/?г, LD+fy
2а)
ьп 1 1
Z(D)~£D + ^s
при 8 = 0,
За)
Z(D)“
(9.551)
4а)
__L 1_____
Oq W~ /?t’ Z(D)~
К6
при 8 = 0.
' 1 Я3
Пусть теперь знак 8 — какой угодно, форме может быть невыполнимым и именно Бруне ввёл взаимоиндуктивность без рассеяния. Мы построим несколько схем без таких элементов, области применимости которых частью входят в область 8 < 0, хотя и не исчерпывают её.
Сведение к вырожденной в этом последнем случае
702
ПАССИВНЫЕ СИСТЕМЫ
[ГЛ. 9
Величина d0/a0 W может теперь не совпадать с минимальным значением Re 1/Za(io>), и если это минимальное значение или величину, меньшую него, обозначить через 1;/^, то можно положить:
= . (9-б52)
где 1//?з — некоторая добавочная проводимость. Функция
1 1 1 _ 1 / 1 । 1 \ '
Z(D) Za(D)
может не являться действительной положительной, но
1 I 1 _ 1 1
Z(D)"^/?3“ Za(D) /?х ’ ‘
обязательно будет таковой.
Пусть />0, g<0, где значения /, g указаны в таблице. Очевидные дополнительные предположения, которые нужно сделать в данном, а также в других случаях, будут выписаны по рассмотрении их всех.
Полагая
или
Т(р) = LD + Ri ~~ 1 , 1 \ ’ (9 553)
воспользуемся выражением (544) для \jZ{D) и будем поступать, как при разложении этой функции на элементарные дроби; при этом примем:
где значения Лх, Х2 приведены в таблице И. Представляя соотношение (553) в виде
умножаем его один раз на W-|~R6, другой раз на CXD +
и полагаем затем, соответственно, D = — Х2, D = — Это даёт:
^(Xt-X2) _ _ a?(Xt-X2) W
s —SRt
где значение g' указано в таблице.
g 9.39] Звенья второго порядка 703
- /
Три проводимости 1/Я1> 1/Я3, 1/Т?7 связаны соотношением (552) и соотношением '
1 , 1 _ _ , _ aoxiV «i— 4л0л2 W rs~4~ ~g М’
О
из которых 1/R» ЦК? определяются через 1//?8:
___J_ 1 __ Г (а\ V W Л .
/?1 Oq W 7?з ’ /?3 \ — g /?3 '
а? — 4алао JL-----0_2. W9
R3 остаётся связанным лишь неравенствами Л
. ^W<RS<^
которым, однако, можно удовлетворить лишь при условии
S if af — 4а0а2 > 0
или />0, что мы уже приняли выше.
Если f > 0, g' < 0, где значение f приведено в таблице, то можно, как и в предыдущем случае, принять для 1/Z(D) выражение (553), но положить
Ф = + = (9-555)
L, Ci \/<з /<7/
тогда
£___ go(*i q __ до(Ч М W
~ g 9 1~- — g' R%*
Формулы
_____1_ 1 1 Г а1— 4аоаг W Л
Ri W 7?з ’ /?7 Z?8 \ ~~ gr '
получаются прежним путём и дают положительные значения 1/Rlf 1/Т?7, если удовлетворяет неравенствам
Эти последние
ал . d&zV ал—
pW<R^< — - /-------
Ьо 3 — g1
возможны лишь при условии s' -4- cicJbAc. Vai — 4алал > 0
или f' > 0.
Пусть ещё /=0. Из вычислений, проделанных выше для />0, g< 0, в данном случае получается:
704
ПАССИВНЫЕ СИСТЕМЫ
(гл. 9
переименовывая R3 в R± и /?в в R3, получим: ЬЛ1________________________________1.
OoW~ Rt’
1
(9.557)
ai у «7 —
° t——w, R9 = I\,
6
О
Если f = 0, то из вычислений для случая f опять:
О получается
0;
переименовывая Rs в Rt и /?5 в Rlt получим:
Ьо _1___1_
во W —R^
1
ао V af —4а0ао
——1----®-2 w, R. = и
Ct О
aoV а1 — 4«о«2 w
Для того чтобы полученные формулы имели смысл, при f > 0, g<0 должны выполняться дополнительные условия g'>0, а*— 4а0а2>0. Но, как показывает приводимый ниже геометрический анализ, это условие является следствием двух основных:/> 0, g<0. Аналогичным образом обстоит дело с дополнительными условиями g*> 0, а%— 4а0а2>0 при /'>0, g' < 0. Сопоставляя результаты для последних рассмотренных случаев, получаем:
^±-1x1 1.11 I 1
°' «о W Ri /?з’ , 1
при J > и, g < и ИЛИ J' > I
&0_1____1_ 1____.1 1
Др W R±* Z[D) Ri
0.
§: 091
Звенья второго порядка
705 ' t
Таким образом, ё двух граничных случаях 4а, 26 не удалось избежать идеальных элементов, что, однако, не имеет большого значения по тем же соображениям, что и для четвёртой схемы звеньев IX, X.
Для построения схем реализации звеньев XI, XII используются все шесть представлений 1а, 2а, За, 4а, 16, 26. Из дальнейшего геометрического анализа вытекает окончательная формулировка условий
применимости.
Схемы четырёхполюсников PC приведены в таблице 11. Так как всё сказанное в отношении сопротивления Za(D) последовательного плеча звена XI может быть повторено для диагонального плеча звена XII, -то схемы реализации для этого последнего (вторая схема каждой пары в таблице) получаются из схем для звена XI путём простой перестановки двухполюсников Za(D), Zb(D). Выражения для индуктивностей, омических сопротивлений и ёмкостей через а$, —
одни и те же для двух звеньев, хотя сами ai9 bi выражаются различно через Т19 Т%, Q, С2, k.
Таблица И
Звенья XI, XII
1 T^ + 2T^lD± 1
F ^£)2 + 2%Р + 1
Обозначения, общие для схем 1—6:
аа = kT% Tf, at = 2 (ЛТаСа qr %), оа = k — 1, b0 = kTl±Tl bl = <2(kT^±TM, b9 = k+\, ot = oxfta — ла&£ = 4ft (й- TjCi "I- ТзСз), p= oaft# — ^0^2= — 2ft (7*2 *“ 7*x), 7 = o#&x— «^0 = й: 4Г1Гай (TaCt— 7iCa)>
8 = a& + «п = ox (Offii — афд) — a0 (afa — a2bg) =
= 2ft [+ 47iTa (ft% T&) (%- %) - (7*1 + 7*) (kT& Г“)], e = — 0372 — p8 = — o#p2 — ajfc — arf = o0 (ay — p2) =
= a0 [(afy — a2bj) (aobt — a^bg) — (a0b2 — o2ft0)2] =
= 4ft2 (ftT* й: [± 4^ (TA- TA) (+ TA + %) -(7*1 й= T*)2], 11 = "2o# (ai + У a^ — ^agOi ), x2 = '2^‘ («1 — V a2— 40003), f = 7^1 + ? + V ai — 4a(/l2, f' — — 7X3 — а1.— 4agOg,
^' = o0(7X1 + P) = 8—007X3 = 0#/—Oo&oXiK о2 —4ооОз, ^ = _ a0 (7X3 + p) = — 8 4- o#7Xx = agf— O0V3 V ai — 4адОз.
Общее условие применимости: 8>0 или />0.
45 Зак. 1474 Б. В. Булгаков
?об
ПАССИВНЫЕ СЙСТЕЙЫ (гл. Q
Таблица 11 (продолжение)
г
Схемы 1. е>>0.
Фиг. 175.
—^3)2 aQ^W
Rx=^-W, 7?2 = AWr ^0 «о
W\ в остальном 7?3 Произвольно, /?4 = , /?5 = У „1^8.
— р *<3 V
__ _ (Др$ W _ Т2#3) (Дрд2г^ + р^з)
a^W — 72Я9’ Кч
(«о» W— fM?3) (a^W + р/?3) ’
_ «о 1 г _ (a<)8lF —т2Я8)2 “ у W > С1“ «о-relF»
Схемы 2. е=0.
Те же схемы, что для звеньев IV, V (табл. 8).
«о
/?2 = -^17, VQ ^0
7?, = ^. 17=-^ IF, /?4=7TW=^i
° Y2 —В OqO ; «0^2
т W’
ЗВЕНЬЯ ВТОРОГО ЙОРЙДЙА
Таблица 11 (продолжение)
45*
ВИГЛ
108
U W<Rs<
ПАССИВНЫЕ СИСТЕМЫ [ГЛ. §
Таблица 11 (продолжение)
4до$а ----------PZ, в остальном Ro произвольно,
1ГЗ
Rs ’
*5 =
,2
w, J?e = s - w, «0Х2 V al ~
af — Aa^aa W + gRi'.JXrz a" ’ в
/?8 =
«0*1 V af — 4oo«a W + gRs
aoV ai~4ao«a 1 _ «ol^ a? —4«o«2 W
P W> Cl “T?*
w= a?V a"- W, Z1=-^1F=--V.aia~4^3- w, ь<№ g' 1 «0*1 — g
K.-^w, R,-^V. r^=^Aw-bo Oo b^g' g'
== w=-----------w,
ofa V al— Aa^
” w g' W
bo 1 b“V —W2 i aoXilF” — g W
§ 9.39J
ЗВЕНЬЯ ВТОРОГО ПОРЯДКА
709
Таблица 11 (продолжение)
Схемы 6. /<гр_или комплексное, В = 0.
Если воспользоваться первым квадрантом плоскости a^bv то уравнения
8 (^о^2 ^2^0)== 0* (9 .559)
8 = Oq [(#i&2 &2^1) (^0^1 (^0^2 ^2^о)2] === 0 (9.560)
определяют ветви двух гипербол с центрами в начале координат и асимптотами, соответственно, а1 = 0, aQb± — a±bQ = Q и a±b2—й2&0=0, аф1— 0^0=0; вторая асимптота каждой пары — общая для двух ветвей. Так как а0&2— а2&0>0, то угловой коэффициент первой асимптоты второй ветви больше углового коэффициента второй. Первую ветвь мы будем называть кривой 8, а вторую (по основаниям, которые скоро выяснятся) — кривой g—£ (фиг. 180).
Если приравнивать нулю величину / и освободиться от иррациональности, то получим уравнение
((#2&2 ^2^о) (^Q^2 “Н (9,561)
гз
710 ПАССИВНЫЕ СИСТЕМЫ [гл. 9
которое определяет в первом квадранте плоскости агЬ^ ветвь гиперболы с центром в начале координат и асимптотами (а0&2 -f* ci2bQ) ах— — a(a.2b1 = Q и &х = 0. Так как (aQb.2 + а2&0)/а0а2 = 4-
то угловой коэффициент первой асимптоты больше угловых коэффициентов обеих асимптот кривой g—g'. Рассматриваемую ветвь
Фиг. 180. Кривые В, /—g—g' для звеньев XI, XII в плоскости
гиперболы будем Называть кривой f—f (см. фиг. 180).
' Мы получили бы ту же кривую, если бы приравняли нулю величину f (табл. 11), отличающуюся от f только знаками членов, не содержащих радикала.
Легко убедиться также, что если приравнять нулю g или gri то получится уравнение кривой, названной нами выше кривой g— g'9 на которой исчезает также величина е. Кривые f—f и g—gr касаются в точке с координатами
ас = 2 /аоа2, )
~|~ ^2^0 I (9.562)
Ьс = ’
Общая касательная - а± — ае вертикальна и является границей области действительности радикала Уа*— 4aQa2. Тщательное исследование показывает, что ниже точки соприкосновения на кривых f—f', g—gr исчезают, соответственно, величины f и g, а выше этой точки — величины /' и g'.
Для точки пересечения общей касательной с осью абсцисс мы
имеем аг = 2 а0а2, Ь± = 0 и 7 < 0, так что /< 0, /' > 0 и g < 0, £•'>0. Отсюда следует, что внутри кривой f—f' мы имеем />0, /' > 0, а внутри кривой g—g' будет g> 0, g' > 0.
Области 1—6 на фиг. 180 и на фиг. 181 соответствуют схемам 1—6 звеньев XI, XII.
Область © > 0, есть внутренность кривой g—g'\ область е —0 состоит из точек самой этой кривой; область 8 > 0, е < 0 заключена между кривыми 8 и g—gr\ область />0, 8<;0 лежит между кривыми f—f' и 8 правее их точки пересечения Е и заключает также точки своей верхней границы. Наконец, область /=0, 8<0 есть часть кривой f—fr правее точки а область, где 8 = 0, а /<0 или комплексное, есть часть кривой 8 левее той же точки; эти две дуги образуют границу общей области применимости схем таблицы 11.
§9.39]
ЗВЕНЬЯ ВТОРОГО ПОРЯДКА
711
Граница лежит внутри кривой, определяемой соотношением (530) при его обращении в точное равенство. Последняя кривая является гиперболой и ограничивает наибольшую возможную область реализуемости трансмиттанса рассматриваемого вида. Обе границы имеют асимптотами оси alf b±.
В таблице мы пользовались тем, что если f > 0, 8 0, то
af— 4а0а2>0, g<0, g7 > 0; доказательство легко получается с помощью приведённого геометрического истолкования.
Аффинное преобразование к плоскости будет:
a1 = 2(kT^^T1^1)> b1 = 2(kT^± %); „(9.563)
его определитель равен вследствие чего для звена XI
сходственные углы имеют противоположные знаки, а для звена XII — одинаковые.
Фиг. 181. Кривые 6, f—g— g, для звеньев XI, XII в плоскости
Вторая из формул обратного преобразования
<. = =тит <9-564'
показывает, что преобразованные кривые 8, f—f, g—g' должны лежать в верхней полуплоскости Сз > 0. Это будут ветви гипербол
±4Т1Т2(ЙТ2С2^ %)(%— ад = (71й= Т[), (9.565)
{hz[3T|A!2 —(Ti=L 71)*=й Г?] Т1С14-[Т^2 +
+ (Tl ± Т?) k zjz 3 Th k%) (± T& + kад = (A2Tl zp Г?)2. (9-566)
±47'17’2 (% — ад (zjz 7^ + ЭД = qz Tl)2. (9.567)
Так как уравнение кривой g—gr не зависит от k и она касается всех кривых f—f, образующих семейство с одним параметром fe. То оца является огибающей этого семейства,
712
- ПАССИВНЫЕ СИСТЕМЫ
[rh. 9
Общая область применимости схем таблицы в плоскости СЛ2 ограничена снизу, вследствие чего коэффициенты затухания С? не могут быть слишком малы, так же как и для звеньев IX, X. Граница состоит из частей кривых 8, f—f'9 пересекающихся в точке Е. Для звена XI точка Е лежит в первом квадранте, поскольку этому квадранту принадлежит целиком кривая 8.
Различные другие свойства, относящиеся к взаимному расположению кривых и установленные выше для плоскости будучи аффинно-инвариантны, сохраняются и для преобразованных кривых.
Отметим ещё предельные формы уравнений кривых 8 и f—f при k = оо:
±4% (% — T^)=T^Tt (9.568)
Са=1. (9.569)
следует изучить случай равных Tv
Рассмотренные четыре звена второго порядка — основные. Далее То и различные случаи вырождения, когда один или два члена в числителе X(D) отсутствуют. Звено XIII с трансмиттансом
у п _ 1 T2D2 + 2TCtD + l
k T^D^ + 2T^D + 1 9
Фиг. 182. Области применимости звеньев XIII, XIV, XV в плоскости CiC2.
нельзя рассматривать как частный случай звеньев IX или XI из-за появления при-’7^ = 7\ идеальных элементов. Поэтому для построения схемы и формул, приведённых в таблице 12, мы ограни
чиваемся использованием обоих вариантов представления 16, полученного выше при рассмотрении звеньев XI, XII. Областью применимости (фиг. 182) будет вся внутренность кривой f-—
Для. той же формы трансмиттанса известны [94] схемы с идеальными элементами, применимые во всей верхней Головине плоскости СХС2. Для одной из них полагаем k = и
1 _ Г2(С1 + С2)П2 + 4ТСАП + (С1+С2) 1_
Za (D) “ . Т2 (Ct - С2) D2 + (Сх - Q W
_ Ct + C2 1 f 4TC&D 1 — 1 I 1 /о 57(П
“ Ci —С2 (Ci-C2)(T2D2+1) rn. 1 * k }
LU±'C^D
При условиях Ci > 0, 0 < C2 < Ср . или < 0, . О < C2 .< —CP которые можно объединит^ в одно, Q < С2 < | С^ отсюда получаются
§ 9.39] звенья второго порядка I 713
схема и выражения элементов, указанные в таблице 12 под рубрикой звена XIV. Из области её применимости мы ещё выключаем часть, лежащую выше кривой /—так как там мы имеем схему звена ХШ без идеальных элементов; Благодаря условию _0<С2<|С1| данное звено XIV может быть названо звеном ослабления затухания. Важно отметить, что Cg может быть здесь сколь угодно малым, лишь бы оно было отлично от нуля.
При fe=l, 0|| Сг можно написать:
1 T2D2+r(c2 + Ct)D + i j t j ,____i_
Za(D)~ Г(С2 —QD LtD ’
откуда получаются схемы и выражения элементов, указанные в таблице под рубрикой звена XV (звено усиления затухания).
Области применимости звеньев XIV, XV показаны на фиг. 182 вместе с кривой f—f для звена XIII. Для этого последнего кривая g— g' обращается в пару слившихся полупрямых, направленных по биссектрисе координатного угла первого квадранта. Эта биссектриса в данном случае не касается, а пересекает кривую f—f\ касательной в точке пересечения является прямая а± = 2 Уа0а2 или
1)»
на которой обращается в нуль радикал а*— 4аоаз. Левее точки касания на кривой f—f исчезает величина /, а правее исчезает
Наличие идеальных элементов в схемах звеньев XIV, XV не имеет большого значения, так как случай точного равенства 1\ = является предельным; стоит несколько расстроить это равенство, как мы получаем возможность применять реальные схемы с потерями в индуктивностях и ёмкостях. Если, например, немного меньше то можно воспользоваться схемой 3 звена XI, область применимости которой в плоскости CjCg ограничена кривыми 8 и g—gf. Первая из них при достаточно большом k близка к кривой Sqo, определяемой уравнением (568), а кривая g—gf определяется уравнением (567), причём в обоих уравнениях нужно взять верхние знаки. Так как, кроме того, разность Т2—7\ мала, то область между 8оо и g—gr, в свою очередь, мало отличается от нижней половины первого квадранта между биссектрисой и осью которая составляет также половину первоначальной области применимости звена XIV.
Аналогичным образом можно было бы подыскать реальные схемы для другой половины этой области и для звена XV.
Из числа других звеньев, указанных в таблице, звенья XVIII, XIX, XXV, XXVI могут рассматриваться как частные случаи звеньев IX, X; звенья XVI, XVII, XX, XXI, XXII, XXIV, XXVIII —как частные случаи XI, XII и звено XXIII — как частный случай XV. Мы приводим для- этих звеньев лищь окончательное данные И таблице.
714
ПАССИВНЫЕ СИСТЕМЫ
*(£») =
Наконец, для звена XXVII с трансмиттансом
1 27W г п
k T2D2 + 2TCD + 1 ’ ’
мы можем написать:
1 kT‘^+2Ti;(k+l)D + k 1 _
Za(D) ~ kT2D* + 2П(£ — 1)£> + £* W~
_ 1 j 47W
~ W~^ kT2D2 + 2Tt:(k— l)D + k
1
(9.572)
в таблице 12.
Отсюда получаются схема и формулы, приведённые
Области применимости, кроме трёх наиболее важных случаев, не показаны, так как они легко могут быть построены по образцу этих трёх. Следует отметить только, что лишь для звеньев XIV, XXIII, XXVII коэффициент С2 (при Ct = О мы полагаем = С) может быть сколь угодно малым, хотя и большим нуля. Для всех остальных звеньев второго порядка границы областей применимости лежат выше оси Ср
Таблица 12
Звенья XIII—XXVIII
XIII X (D) - ± га>2 + 2П1Р + 1 ,
ХН1. Л (и) — k w + 2K2D + 1 ’ > °*
Обозначения:
а0=ТЦ1г — 1), ^ = 27(^2 —Ct), a2 = k — 1, 60=T2(A:+l), &i = 27 (AC2 + Ci), Z>2 = *+1,
a = iZi^2 — #2^i = 47ft (— Ci *4~ C2),
7 = «o&i — = 47% (Ci — C2),
X,='257 ("1 + ^«1 —4ЛьЛ2)» X2 = -2^(«i — Va? —4a0a2), f = xi G + bo V — 4a0a2 ), f = X2(— 7 + ba у — 4a0a2 ),
g - Mxi = «о/ — ao6oxi И «1 — 4яоа2 •
S' = — «оТХ2 = «о/7 — ao*0Х2 v Я1 — 4aoa2 •
1
Условия применимости: />0, /z>0.
Та же схема, что и схема 4 звена XI, но при С1<Са — те же выражения элементов, а при > С2 следующие:
§ 9.39]
ЗВЕНЬЯ ВТОРОГО ПОРЯДКА
715
Таблица 12 (продолжение)
Др/?з
^3 — *0^ дет
Ло#з ’
Лл ЛлХ.л ”»
— W < /?з <----------------7------- UZ, в остальном /?з произвольно,
^0 — g
XIV х(DI - 2^!±2Щ£±1 ( >~ ^ T2D2 + 2ТС2О + I •
Условия применимости:
О < С2 < I £11» /< 0, или f < 0, или ft f' комплексные; при этом /, f' определяются так же, как для XIII.
А?
Фиг. 183.
L-----^~~w> ’ ^_1Г+СГ^’
> _ С1 + С2 w . r(Ct-C2) 1 47^2 1
(2~ q—c2 ’ w 1 q—c2 w‘
716
ПАССИВНЫЕ СИСТЕМЫ
[гл. 9
Таблица 12 (продолжение)
XV X(D} : PO3 + 2ntD+l AV. л. +2niD + ! .
Общие условия применимости:
0<|С1|<С2, /<0 или комплексное;/—то же, что и для XIII.
L
/?2
Схема 2
= с2—cj w' С1 = Т(^~?1)'wF<
. с1 = —с2<о.
§ 9.39j
ЭВЁНЬЯ ВТОРОГО ЙоРЯДкА
Таблица 12 (продолжение)
XVI. X(D) =
1 T2D2 * *4-2TCiD —1 k ПОЗ 4.2TC2D +1
Ca>0.
Обозначения:
Oq = (А -|- 1), = 2Т (АСа 4" С1), л2 = А 1,
b0=T*(k — 1), *i = 2T(«2 —Ci), А2 = А4-1, а = — лА = 4ТА (Ci + Са), р = aJ>0—а^>1 = — 4Т2А,
1 = Оо&1 — «А = 4Рй (— Ci + Сг), 8 = лор + «1Т — а1 («А—в А) — «о («А — аА) =
= 4Г<* [2 (Кг + Ct) (-Cj + Са) - (А +1)1,
« = — л2т2 — Р8 — — Лор2 — «1Рт — лат2 — Ло (“I — Р2) = = По [(а^а — оА) (а^—а^о) — (ОдЬц — дА)2] = = 16ТвА2 (А + 1) [(- Ci + Са) (Ct+Са) -1],
\ = 2ло^л14* 4л0л3 ), Xg = V ai ) >
/=lX1 + p + &0XiV<ai —4л0л2, / = — Тх2~ Р + *оЦ/л2 — 4д0л2, g = Ло (тХг 4- Р) = 8 — доТХ2 = aaf—aQb0\ у а{ — 4ааа2, g' = — л0 (тХ2 4- Р) = — 8 + «ОТ\ = л,/' — л0 V-г / л2 — 4а0л2,
Общее условие применимости: В >> 0 или />-0.
Схемы, условия их применимости и выражения, элементов через ai9 те же, что для звена XII (табл. 11).
XVII. X(D)— k 7^£)2 4_27’(;2D4-1 » ^>0.
Обозначения:
Oo=AT2, ai = 2T(^Ca — Ct), a2 = A—1,
bo^k-П, 6i = 2T(ACa + Ci), &a=A+l,
a = Л|Аз —— ЛаА^ = 4TA (— Ci 4“ ^з)> P = Ла^о — HqA, = —- 2Г2А,
T — a^bi^—atb9 — 4T®ACv
8 = вор 4- Л1Т = лх (oqAi—л^о) — ло (ло&а—«а&о) = = 2ra[4Ci(ACa —СО—А],
е = — ла!2 — Р5 = — ЛоР2 — лхРт — л2т2 = Ло (ат — Р2) =
= Ло {(л^а — Ла^х) (aobt — лА) — («о^з — Ла^о)2] =
= 4ra8[4Ci(-C14-Ca)-lJ,
*1= "2л^ — )> ха = 2^ (.at~^ai — 4аоаг ) >
/ = т\ + ₽ + V1V л2 —4л0л2, /' = — тХ2 — р 4- АюХ2 V д2—4Д0Л2, g = Ло (т\ 4- ₽) = 8 — йотк2 — aof~ДО& *ОХ1 У а1 — »
£'= —л0 (тх2 + Р) = — 8 4- лот\ = Ло/' — л0А0Х2 V al — 4д0л2.
718
ЙаССЙВНЫЕ СИСТЕМЫ
(гЛ. 9
Таблица 12 (продолжение)
Общее условие применимости:
8 >. О или />. 0.
Схемы, условия их применимости и выражения элементов через те же, что и для звена XI (табл. 11).
XVIII, XIX. %(£>) =
•2
2
T1 2 * * 5D2 ± 1
Т2 Т|Ог + 2Г2СО4-1
Г1>Т2, С>0.
Обозначения:
а1 = 2Г2Т2С, а2=Т2^Г2,
*0=2Т2Т2 ЬГ = 2Т*Т£,
f = «Л - azb0 = 27® Т2 [27fС2- (7* + Т2)], g = atf—a\b2 = — at (ax62 — a2&x) — л2*0 = = 2Г2Tz [ip 47'2TfC2 — (72 T2)2].
, / rfqz T2
Общее условие реализуемости: C> I/ -----2.
< 2 Tу
Для звена XVIII при выполнении одного из условий о/ (Г|- 7|)/2Т2', С=/(Т2-Т2)/2Т2 схемы вместе с выражениями их элементов через ait bi совпадают, соответственно, со схемами 3, 4 звеньев IX, X (табл. 10).
Для звена XIX при С>(72 + Т2)^^, С = (Т2 +
(Т2 + Tl)ftTx Т2 > С > V (Tf+ T‘z)pTf, С = V(r2+ Т2)/2Т2,
соответственно, те же четыре схемы и выражения их элементов через ait Ь& что и для звеньев IX, X.
XX, XXI.
1 Т 2D2 rt 1
Г T2D2 + 2T2ZD + 1 a I А 1
Т\<Т* С>0.
Обозначения:
«о = АТ2 Tl at = 2kT^, а2 = k -1,
• b0 = kTf ± 1^, bt = 2AT2C, bz = k +1.
a = л^&2 л2^ = 4AT2C, P = = 2A(T2^
T = «0*1 — Я160 = 471 Г2^>
5 = aoP + (aQb1a^) — a0 (a0b2 — agM =
= 2A[4=4T2rX-(^ ?i)].
§ 9.33]
ЗВЕНЬЯ ВТОРОГО ПОРЙДЙА 71 §
Таблица 12 (продолжение)
е = — = — Лор2 — «1Рт — «212 = («7 — р2) =
= «о [ (а^2 — а2М (лА — — (V2 — л2М2] =
= 4k2 (kT2 qz Т2) [йз 4Т2 Т2? — (Т2 дз Т2)2],
\= 2а7 + V* «£ — 4а0а2 ), Х2 = (ai “ V «J —4а0а2),
f = + Р + Vi У al ~ 4а0а2 > /' = — Тх2 — ₽ + а1 — 4аоа2’
g=+ Р) = 8 — а0тХ2 = aj — а0*0ХхУ af — 4а0а2, g' — ~ «о (Тх2 + ₽) = — 5 + = aof' — Vox2 V А. — ^2 •
Общее условие применимости: 8>-0 или />0.
Для эвена XX — схемы 4, 5 звена XI с теми же условиями применимости и выражениями элементов через а& Для звена XXI — те схемы звена XII, условия применимости которых могут удовлетворяться; те же выражения элементов через
1 Т2£)2 Д- 1
ХХП. X (О) = j 7'2£>2_|_2Ш> +1 Обозначения:
а0=Т2(& — 1), at = 2T^C, «2 = ^—1» bQ = Т2(k +1), д! = 2Т«, д2=Л+1, а = а^Ьъ — aj}1 = 47Ж, Y = — б/1^о = — 47Ж,
Xi=i (ai+ai -4а^ х2=2^ к - .
f = \ G + Ьй /«? - 4д<«2)> f = Х2 (— Ч + >оК а1 — 4«о®2) •
g = = «(/“ aoVi V а1 — 4аоа2>
g' = — a0TfX2 = а0/' — а0&0Х2 J/af—4а0в2 .
Условие применимости:
k V £4-3*
Та же схема, что и схема 4 звена XI, с теми же выражениями элементов.
XXIII. X (D) ргра-]^ 2TW +1 * £> О-
Условие применимости: k V k+з'
Схема совпадает со схемой 1 звена XV, причём
L=^W, Li=TiW, Rt = Rz=W. C = <?1=Tci.
че > IV W
720
пассивные Системы (гл. 9
Таблица 12 (продолжение)
1 уадг—1
XXIV. X (D) = 2 др + j ,
Обозначения:
а0=Та(А+1), лх=2Ж, aa = k — 1, 60=Т2(й —1), 6Х=2Ж, 63 = й + 1, а = atb3 — = 4ТАС,
Р = &2pQ — Лд&2 = — 4 T^k, 7 = аД — ах&0 = 4ТЖ,
8 = аор 4- ад = лх (а0^1—й1^о) — «о («о^з — аз&о) = = 4ЛА[2Ю —(А4-1)],
е = — O2Y2 — Р8 = — Лор2 — Л1Рт — Л2Т2 = Ло (ат — Р2) =
= «о [(«1^2—Л2&1) (00*1—ахА0) —(Offa—Л2&0)2] = 16Т®Й2 (А 4-1) (С2— 1)»
\ i (Й1+ Х2 = 27о (а1 “У 4-^«2).
/ = + Р “h fyAi V^i — 400^2, У' = — уХ2 — р ^2 Л1 — 4а0а2,
g = ЛО СгХх + Р) = ь — ОоТ*2 = «о/— «О^ОХ1 V А —- 4«оа2»
£, = — а0 (Тх2 + Р) = — & + = а0/' — й0^2 V — 4а0а2.
Общее условие применимости:
&>0 или /;>о.
Те из схем звена XII, условия пригодности которых могут быть удовлетворены, с теми же самыми выражениями элементов через
XXV. X (D) =
T3D2 + 2TCXD Т2£>з + 2ГСз£>+1 ’
Сз>0.
Обозначения:
Л1 = 2Т(Сз — Ci), 02=1, bQ = 2T^t ^^гТСз + Сх), &2=1,
f = - a2b0 = 2Т2 [2 (- ^ 4- Ф ~1J.
g = a^f- а*Ьг = - лх (лх&2 - л2*х) - л|&0 = 2Т2 [4С, (- 4- С2) - М-
Общее условие реализуемости:
/>0.
Схемы, условия применимости и выражения элементов через ait те же, что и для звеньев IX, X (табл. 10).
§ 5.39]
ЗвенЬЯ второго АоРЯдКА
721
Таблица 12 (продолжение)
XXVI. X(D) =
Г2£)2
Г2£)2 + 2ТСЛ+1 *
С>0.
Обозначения:
а1 = 27'С, #2—1,
&0=27Ч ^ = 2П, д2=1, /= а1Ь1 — = 2Т2 (2С2 — 1),
S = Л1^2 = (^1^2 Л2^1) ^2^0 = ""* 2Т “ .
Условие реализуемости:
С>1/ У2.
При выполнении одного из условий С> 1/ У 2, С== 1/У”2 применимы, соответственно, схемы 3, 4 звеньев IX, X, так же как и выражения их элементов через ty.
XXVIII. X(D) k ^2jd2_|-2TCD + 1 ’ '
0.
Обозначения:
а0 = kT*t ar =» 2ТМ, = k — 1, bQ=kT\ b1 = 2TkZ b2=k + lt p = ^2^0 — #0^2 = — 2 T^kt
s = oqP = — aQ (aQb2— a2bQ) = —2T^k\
46 Зак. 1474. Б. В. Булгаков
ПАССИВНЫЕ СИСТЕМЫ (гл. §
Таблица 12 (продолжение)
Х1 = 2^ («1 + — 4а0а2) • Х2 = (а1 — — 4«о«2 ) •
f = ₽ + Mi У— 4аол2> /' = — ₽ + Мг V«i — 4«0Л2>
S ~ = ° = aj 4л0а2,
S' ~ ~ & — aof' ~ ®о^оХ2 ’ ®1 4аоа.,.
Общее условие применимости:
с>/ ГТг
При выполнении одного из условий С> Vkj(k 1), С= V &/(£-|-1) применимы, соответственно, схемы 4, 5 звена XI, так же как и выражения их элементов через ait
Из изложенного можно сделать следующий вывод. Если задан любой трансмиттанс второго порядка
P(D) _ T2D2 + ZT^D ± i
Q(O) T^2+2T2C2D+1 ’ аналитический в замкнутой правой полуплоскости, то в таблицах всегда найдём форму, отличающуюся от него, может быть, только постоянным делителем. Если при данном второй коэффициент затухания С2 достаточно велик и удовлетворяет условиям применимости соответствующего звена, то задача отыскания схемы решена. |
В противном случае подставляем вместо С2 какое-нибудь С3,' большее и удовлетворяющее условиям применимости, например минимальное значение при данном Таким образом, получаем реализацию трансмиттанса
1 T2D2+ZTiLD± 1
X. (D) = - > Т—L1-------.
1 k r2D2 + 2T2LD4-1 а 1 а О *
Далее, чтобы изменить £3 на С2, строим звено ослабления затухания Х1\ с трансмиттансом
С2 Т2Р2+2Т2С3Р + 1
С, T2D2 + 2^ +1 •
Каскад из двух четырёхполюсников реализует трансмиттанс <¥1(D)A2(D) = C2P(D)/feC3Q(D), пропорциональный заданному.
Сказанное распространяется, разумеется, и на вырожденные транс-миттансы, формально не содержащиеся в общем выражении. /
§ 9.3$j
звенья второго по^ядкл
Этим завершается доказательство реализуемости любой функции P(D)/Q(D), аналитической в замкнутой правой полуплоскости, с помощью каскада пассивных четырёхполюсников PC без взаимоиндук-тивностей их элементов:
Если поставлено дополнительное условие отсутствия идеальных элементов, то сопротивления Za (D), Zb (D) должны быть «функциями потерь» по Мин Най-да [9Д6], а класс реализуемых трансмиттансов P(D)IQ(D) будет также, соответственно, ограничен в отношении величины коэффициентов С2, причём степень этого ограничения будет зависеть, очевидно, от допускаемых величин отношений
_ 1
L ' С—
последовательных сопротивлений Rl к соответствующим индуктивностям и параллельных проводимостей к соответствующим ёмкостям. Задача установления точных условий реализуемости ещё подлежит разрешению.
Процедура подбора реализующей цепи в этом случае может быть изменена следующим образом. Если второй коэффициент затухания С2 некоторого заданного трансмиттанса второго порядка не удовлетворяет условиям применимости соответствующего звена, то вместо Т% подставляем немного меньшее Т3 и вместо С2 — несколько большее С3, удовлетворяющее условиям применимости; реализуем трансмиттанс
1 T*D2 + 2T^D± 1
Затем для реализации трансмиттанса
пользуемся схемой 3 звена XI, которая, как мы выяснили раньше, даёт возможность при большом fe2 и малой разности Т2—Т2 получить весьма малые С2. Каскад из четырёхполюсников с трансмиттан-сами Xt (D), Х2 (D) реализует функцию Xt (D) JV2(D) — Р {Djlk^Q (D), пропорциональную заданной.
Если встретится звено XXVII, то для исключения идеальных элементов его можно заменить каскадом звеньев VII и XVII с трансмит-тансами
X х m С 2KiD + l
' —27X1D + 1 ’ 2k T2D2 + 2TCD + 1 ’
произведение которых при < £ равно трансмиттансу звена XXVII
^(О)^2(О) =
1 27W
k Г2£>2-|-2ГСП + 1 ‘
46*
йАдсйвйкЁ ёЙс/шШ
§ 9.40. Преобразование к симметричному мостовому Т-образ-ному четырёхполюснику. К этой схеме (фиг. 187), которую мы будем сокращённо именовать ТМС, могут быть приведены многие из рассмотренных выше четырёхполюсников PC.
Для эквивалентных между собой четырёхполюсников PC и ТМС имеем известные соотношения:
о
(9.573)
О--- — А
Фиг. 187. Симметричный мостовой Т-образный четырёхполюсник.
Za заключает параллельное
Отсюда, пользуясь тем, что во всех рассматриваемых нами схемах Zb — = W2/Zai находим:
7 _ IF2
^2 —~7~
* (9.574)
Следующий приём, указываемый у Гийемена [9-14], позволяет во многих случаях произвести преобразование. Пусть омическое сопротивление /?, так что -=4+4- (9-575)
и
"2“~z Z*~ Z^\R zj' w ' 7
В качестве Zt можно также принять любое омическое сопротивление, удовлетворяющее неравенствам
„ IF2
(9.577)
если только /?2 W* или
R<W. (9.578)
При этих условиях формулы (576) определяют действительные положительные функции Z2, Z3. Итак, данный приём преобразования ведёт к цели, если Za заключает параллельное омическое сопротивление, не превосходящее W. В частности, при Zt = R*
ДОЗ . IF2 — /?2
(9.579)
если же Z = W*!R, то „ IF*
(9.580)
Изложенный приём распространяется, очевидно, на случай, когда Za заключает последовательное омическое сопротивление, не меньшее
§ 9.40] ПРЕОБРАЗОВАНИЕ К Т-ОБРАЗНОМУ ЧЕТЫРЁХПОЛЮСНИКУ 725
чем IF, так как тогда Zb будет заключать параллельное сопротивление, не превосходящее IF. Меняя местами Za и Zb и производя преобразование по предыдущему, получим четырёхполюсник ТМС, трансмиттанс которого лишь знаком отличается от заданного, а это легко исправить переключением концов.
Обращаясь к схемам, построенным в предыдущих параграфах, и просматривая таблицы звеньев первого порядка, легко установить, что преобразование к форме ТМС, по предыдущему, возможно для звеньев Г, II, IV, VII, VIII и невозможно для III, V, VI.
Для звена IX преобразование возможно в случае схем 1, 2 и не-возмойсйо в случае схемы 4. Что касается схемы 3, то из приведённого в таблице выражения вытекает условие преобразуемости f—которое обращается в равенство при
или
#1 (^1 а1) — ^2^0
4 Т& ( % — ВД = Т{ — Tl
(9.581)
(9.582)
Эти уравнения определяют две гиперболы, соответственно, в плоскостях arbt и СХС2. Нас опять будет интересовать ветвь, лежащая
в первом квадранте, которую назовём кривой ТМС (фиг. 188). Эта кривая лежит между кривыми f и g и имеет с ними общую асимптоту а± = 0 или Т^2—7^ = 0. Так как области применимости схем 1, 2 оказываются внутри кривой ТМС, а область применимости схемы 4 — вне её, то окончательно областью преобразуемости к форме ТМС является внутренность кривой ТМС. Область, где преобразование невозможно, на чертеже заштрихована. Аналогичное исследование показывает, что для
Фиг. 188. Кривая ТМС для звена IX в плоскости СХС2<
звена X преобразование невозможно ни при каких значениях
параметров.
Для звена XI преобразование возможно в случае схем 1, 2, 3, 6 и невозможно в случае схемы 5. В случае схемы 4 условие преобра-зуемостц С IF с помощью приведённого в таблице выражения Для через /?3 получает вид
OqW
726
ПАССИВНЫЕ СИСТЕМЫ
[гл. 9
Сопоставляя с имеющимся в той же таблице неравенством, ограничивающим Rq сверху, имеем:
aQ
&о — #0
Л0Х1 V а1 — 4а0Л2
или где
h = + ₽ + (й0 ~ ао) & — 4^002- (9.583)
Легко убедиться, что h получается из f путём замены й0, Ьг и Ь2 разностями й0— а0, Ь±— %, Ь2 — а.2. Поэтому результат уединения радикала в неравенстве и возведения в квадрат получается путём той же замены из уравнения (561) кривой f—ft -)
( ^0^2 #2^0 ^0^2) (^0^2 4“ ^2^o)
(^0^2 “"H ^2^0
Левая часть разлагается на рациональные множители, и уравнение
Фиг. 189. Линия TMG для звена XI в плоскости а^.
о
Фиг. 190. Схема 1 звеньев IX, X, преобразованная к форме ТМС.
кривой h — h' в плоскости получаемое при обращении неравен ства в равенство, будет: ч
[(^o&2 "J“ ^0^2) (pi
.?= —2 (9.584)
§ 9.41] ДИНАМИЧЕСКИЙ ПОГЛОТИТЕЛЬ КОЛЕБАНИЙ БЕЗ ДЕМПФЕРА 727
Кривая имеет ту же вертикальную касательную с той же точкой касания (ас, ZQ, что и кривые f—f и g—£ (фиг. 189).
Угловые коэффициенты асимптот кривой h — hr суть:
при этом для XI оба отношения а следовательно, и пер-
вый угловой коэффициент больше единицы. Так как угловые коэффициенты асимптот кривых f—f и g— gf равны, соответственно,
। b2 n . b2 bQ aQ ' а2 а2
то угол между асимптотами кривой h — h' лежит внутри такого же угла для f—f и объемлет аналогичный угол для g—gf. Поэтому кривая h — h' проходит между кривыми g — g' и f—Область преобразуемости звена XI к форме ТМС в плоскости а±Ь± ограничена снизу линией ТМС, которая состоит из части кривой 8, лежащей слева от её точки пересечения Е' с кривой h — h'9 и части кривой h—h' правее этой точки.
Аналогичным путём убеждаемся, что для звена XII преобразование с помощью изложенного выше приёма невозможно.
Мы не будем продолжать этих вычислений для других звеньев второго порядка, так как ход их достаточно выяснен, и ограничимся приведением в качестве примера схемы 1 звеньев IX, X, преобразованной к форме ТМС (фиг. 190). Экономия в числе отдельных элементов, достигаемая в результате пре-образования, здесь совершенно очевидна.
Г. НЕКОТОРЫЕ ДРУГИЕ ПРИЛОЖЕНИЯ ПАССИВНЫХ СИСТЕМ
§ 9.41. Динамический поглотитель колебаний без демпфера. Это устройство предложено Фрамом в 1909 году. Главная масса М на упругой связи
с жёсткостью С схематически представляет машину ---------------
или её часть, которую нужно предохранить от воз- фиг Дина-мущающей силы Psinv^ (фиг. 191). Поглотитель мичёский поимеет массу т, малую в сравнении с главной мае- глотитель коле-
сой, и присоединён к ней при помощи упругой связи
баний.
с жёсткостью с.
Обозначая смещение масс М и т от их положений равновесия через уг и имеем:
= — Суг Ц- с (у2 —У1) + р sin 'it, | ту2 = — с yt), j
(9.585)
728
ПАССИВНЫЕ СИСТЕМЫ
[гл. 9
так что
/(О) =
ЛЮ-аЦ-С + с — с
—' с
e(D) =
1
x(t) — P sin \t,
Д (D) = MmDi -j- (mC 4“ Me mc) D2-[-Cc,
mD2 Ц- с c c MD^-^C^c ’
ф,о>-!й
/nD2 + c c
Обозначим через = у собственную частоту главной массы /" с л
при отсутствии поглотителя, через o>w = 1/-----собственную частоту
— т
поглотителя при неподвижной главной массе; И =
Если разделить A(D) на Мт, то характеристическое уравнение примет вид
D* + +< + Н<) D* + = 0; (9.586)
его корни суть ±i(a2, где величины
“1> “2 = ^2/"шлг+шжU +р4+4/'«—<°м)94-2н-<(“m+O+r2<
(9.587)
суть собственные частоты, причём <о1 < а>2. Отсюда
Ю2 — “1 = V(®1 — «t)2 4- 2н«>1 (<о„ + ) 4- И2®4 х г 4 т М7 » г тv М • ш7 » 2 т
и
*
^(ш1) d (<>>2) ___ 1 ( ад2 —fojf ~Ь шот О 4~И)]
rfp. ’ ф — 2 | т~^ <4—<4
или
(9.588)
§ 9.41 J ДИНАМИЧЕСКИЙ ПОГЛОТИТЕЛЬ КОЛЕБАНИЙ БЕЗ ДЕМПФЕРА 729
При р. = 0 собственные частоты совпадают в о>м> Если же при фиксированных и <ом отношение ji возрастает и стремится к бесконечности, то, как показывают последние формулы, меньшая частота убывает и стремится к нулю, а ббльшая частота о>,2 возрастает и стремится к бесконечности.
Переходя к вычислению коэффициентов усиления и аргументов запаздывания, получаем:
(V) = I ФХ (*)/Ф1 (0) I =
№ (v) = I ф2 (й»)/ф2 (0) | =
С (— tw'j2 + с)
— (тС -f- Me -j- тс) -f- Сс
_____________Сс_____________
Мт^ — (тС-уМС + тс) va + Сс
<р(°> (V) = (V) = 0.
Верхние индексы (0) напоминают, что все величины относятся к системе, в которой трение между главной массой и поглотителем равно
нулю.
Если числители и знаменатели выражений A?i0)(v), /?20) (>) поделить на Мт, то
Я10) (V) =
(9.589)
Мы видим, что если поглотитель настроен на ожидаемую частоту возмущающей силы hgow = v, то= 0; главная масса не получает никаких вынужденных колебаний и вся энергия, передаваемая системе внешней силой, направляется в поглотитель.
Так как, однако, частота внешней силы обычно не бывает одной и той же, то следует подробнее рассмотреть ход функций /?i0)(v), Z?20)(v). Прежде всего заметим, что
/?1°\0) = ^0)(0)=1,
/?10)(+ оо) = № (+ оо) = 0.
При т = 0 мы в функцию
имеем —оо, а ра)^ = с/Л4 и /?i0)(v) обращается
Q(v) =
(9.590)
Которая имеет бесконечное значение при v = <0^. Если w =# 0, tq
730 пассивные системы [гл* 9
>
«
Z?i0)(v) обращается в нуль при v = co7n и в бесконечность при значениях v, являющихся корнями уравнения
v4 — 4-ay*--4-aw2) V2со2 _ о • (9.591)
v Лх * ш » » m7 I М т к '
ИЛИ
(V2 — <*& (V3 — <И) — риф2 = о. (9.592)
Эти корни суть собственные частоты о)х, о),2. Функция также обращается в бесконечность при v = o)t, со2, но не имеет нулевых значений. На фиг. 192 изображены графики функций /?i0)(v), (v),
Q(v). Так как
[Q(v)]2 — [^(v)]2
н4<у2 2 (у2- «&) (у2 — <) + н<4*2] (у2 - 4)2 [ (^2 - 4) - “«) - нЧг2]2 ’
то положительные корни о/, со" уравнения
(V9 — (V9—О - у = 0 (9.593)
суть абсциссы точек пересечения кривых и Q(v). В силу
тождеств
О2—О?—<)—нЧХ=И—<”#) —<)—^<*1 = о
левая часть последнего уравнения положительна при и = о).2; она отрицательна при \ = w#, <лт и потому о/ лежит между^со1 и
Фиг. 192. Резонансные кривые динамического поглотителя без демпфера.
наименьшим из чисел со#, а)ш, а а/'— между наибольшим из этих чисел и <о2. Для всех частот возмущающей силы, заключённых между о/ и со", мы имеем [QC012—[A?i0) СО]2 > 0 и Q (у) > Z?i0) (v), так что амплитуда делается меньше, если система снабжена динамическим поглотителем; для всех остальных частот эффект поглотителя неблагоприятен.
К области частот, для которой динамический поглотитель полезен* всегда принадлежит интервал между со# и со^.
§ 9.42] ДИНАМИЧЕСКИЙ ПОГЛОТИТЕЛЬ КОЛЕБАНИЙ С ДЕМПФЕРОМ
731
§ 9.42. Динамический поглотитель колебаний с демпфером. Рассмотрим теперь, как изменится эффект поглотителя, если ввести демпфер, включённый между массами М и параллельно пружине поглотителя. Демпфер является источником силы взаимодействия 2/пРСу2—уД пропорциональной относительной скорости у%—yt двух масс. Уравнения движения теперь будут:
МУ1 = — Cyi + 2m? (Л —л) + с (Л—Л) + Р sin )
5- (9.594) ту\ = — 2тР (Л —У1) — с (Уэ—Л)> J
так что
mD' 2zn(3Z) -|~ С 4“ с — 2m$D — с
_2m^D — c + ’
Д (£>) = MznD4 4-2^9 (M+^) D^~\-(inC-yMc-{-inc) D*^2in$CD-\-Cc,
mD* 4-2/n^O 4“ c 2m$D-\-c
*<d>-T7o>
mD* 4~ 2znpD 4“ c
4- c
а выражения e(D), x(t) остаются прежними. Далее,
W = I $! (0) I =
(— 4- c)2 + 4zn2p2\2
[Mmv4—(mC+Mc+mc) \2+Cc]2+4m2p2^2 [—(M+/n) v2+C]2’
Ъ w = IФ2 (Zv)/$2 (0) I =
(9.595)
c2 -p 4/n2p2^2
[Mmv4—(mC+Mc-hmc) v24-Cc]2+4m2p2v2 [— (Af4-m) ^2+C]2
или, пользуясь обозначениями о>д£, сош, р,, введёнными в предыдущем параграфе,
р М _ 1Л 4к-^+О2+4рУ] )
1 w г ь4-(»м+<+1А<) ^+^2т]е+^е [-(i+to *4-412 ’
>
р о = У.Л 4(4-ь^2)
(9,596)
732
ПАССИВНЫЕ СИСТЕМЫ
(гл. 9
У (0) = /?2 (0) = 1, /?1(+оо) = /?2(+оо) = 0.
Если положить здесь р = 0, то R± (v), /?2 (v) обращаются в функции /?2°\v), рассмотренные в предыдущем параграфе; при
Р = оо функция R± (у) принимает вид
М^О)» п 4- Л 2 (1 + р.р —0)^
(9.597) .
она обращается в бесконечность при v = ®м+т, где
(О,- , = ----- --
м+т УТ+й
(9.598)
Если в уравнении (592) сделать подстановку м = ®м+от» то левая часть получает значение
( 4 2 V 4 2 \
\14-H “м) \ 1 -|_ р. ®т) l-f-p. —
= (1 qrjx)2 {— н414—О + н) 41 — н (1+н) 44) =
= —лта-<0’ (9-599)
Так как при n = 0 левая часть положительна, то мы приходим к заключению, что меньший положительный корень уравнения не только меньше, чем &м и как это было установлено в предыдущем параграфе, но также меньше, чем
Вычисляя разность
(Мо)о)]2—[M°°W=
4 - 4) 1(1 +^2 - 412 - (о2 - 4) ft2 - 4) - v^i2 _
Wjlr 1(1 + Р-) ч2 — <4f]2 [(V8 — 4) (ч2 — 4) — J2
4 - 4) ((1 ч- р-) —41 - (у2 - 4) - 4)+^2
((1 + и) "*2—41
, (у2 - 4) ((1 + ^) ^2—41+(^2 - 4) - 4) - н4 _
х 1(ч2-4)(^2-4)-|Чг2]
4t^* (2 (»2—4) (у2—4)+>*^2 (?г—24)
- ((i4-i*)v8-4]8[(va-«>8r)(v8-4)-^8]8 ’
| динамический поглотитель КолеЬайий С ДЕМЙФЁРОМ ?33
мы видим, что абсциссы точек пересечения кривых /?1О)С0 и (фиг. 193) суть положительные корни оо*, оо** уравнения
О2 — шм) О2 — — НЧ?2 + у = 0 • (9.600)
При = со1э <о2 левая часть положительна, так как эти две величины суть корни выражения С2— <*>м)(у2 — — Н0^2* При = левая
часть будет
—к»+4 к»=—4 к. <0;
при v = a)j|f+w, пользуясь выражением (599), получаем для левой части значение
р-"4 . _ l1'0® 0
(l + |x)2"1~2(l+t»)2— 2 (1 +(л)2 и>
Мы приходим к заключению, что меньший корень оо* уравнения (600) заключён между oot и наименьшим из чисел а больший
корень <о** — между наибольшим из этих чисел и о>2.
Согласно первой из формул (596), величина [/?х СО]3 является дробно-линейной функцией от р2, не обращающейся ни в нуль, ни в бесконечность ни при каких конечных положительных р2, а поэтому изменяющейся непрерывно и монотонно от значения [/?х0^ О)]2 До [М00) СО]2; иными словами, кривые /?хС0, соответствующие различ-
Фиг. 193. Резонансные кривые динамического поглотителя с демпфером.
ным р при фиксированных о>^, р», заполняют область между соответствующими кривыми /?1О)С0 и Ях^СО; ПРИ данном \ и возрастающем 'р ордината изменяется всё время в одну и ту же сторону. Отсюда следует, в частности, что все рассматриваемые кривые проходят через точки пересечения кривых 7?х0) СО и СО» абсциссы которых мы обозначили со*, о>**.
?34'
пассивные СибтЕйь!
|гл. 9
В интервале частот (о>*, о>**) кривые /?х (v) проходят выше кривой и, если есть уверенность, что частота внешнего возмущения лежит в этом интервале, то выгоднее делать поглотитель без демпфера.
Если, одйако, мы хотим приспособить поглотитель для всех внешних частот v, то следует принять во внимание, что при крайних значениях р = 0, оо резонансная кривая имеет две или одну бесконечные ординаты, между тем как для остальных р все ординаты конечны. Поэтому необходимо должно найтись такое значение р, при котором максимальная ордината резонансной кривой имеет наименьшее возможное значение при данных шдг, o>w, |л. Вычисление этого наивыгодиейшего коэффициента демпфирования можно найти в книге ден Гартога [°-3].
ГЛАВА 10
ЛИНЕЙНЫЕ РЕГУЛИРУЕМЫЕ СИСТЕМЫ
§ 10.1. Разомкнутая и замкнутая цепь регулирования. Наряду с колебаниями упругих тел и колебательными явлениями в электрических цепях процессы регулирования всегда служили источником проблем и полем приложения теории колебаний. Отдельные вопросы уже рассматривались в качестве примеров и то, что мы имеем в виду добавить здесь, — это некоторые методы, связанные со специфической структурой линейных регулируемых систем и ряд новых примеров.
Мы ранее дали определение регулятора как устройства, присоединяемого к физической системе и управляющего воздействующим на неё источником энергии таким образом, чтобы одна или несколько её координат оставались всегда вблизи некоторых желаемых значений.
Обычно регулируемая система представляет простую или разветвлённую цепь, звеньями которой являются поле регулирования и такие части регулятора, как чувствительные элементы, усилители, органы управления, сервомоторы и исполнительные органы. Взаимодействие между смежными звеньями, указываемое на структурных схемах (фиг. 194) соединительными стрелками, можно с достаточной точностью представлять себе как одностороннее, если только два данных звена не образуют сами по себе замкнутого контура. Если регулятор
действует вне зависимости .от состояния поля регулирования, то цепь регулирования не замкнута; пример — автомат, включающий осветительный прибор на определённый промежуток времени. В большинстве случаев, однако, регулятор, воздействуя с помощью источника энергии на поле регулирования, сам функционирует в соответствии с его состоянием, регистрируемым чувствительными элементами; в этом случае мы имеем одноконтурную или многоконтурную замкнутую цепь регулирований (фиг. 195).
Все или некоторые звенья могут иметь по нескольку степеней свободы. Схематическое представление структуры регулируемой системы заключает элемент произвола постольку, поскольку мы можем
Фиг. 194. Смежные звенья цепи регулирования.
736 линейные Регулируемые системы [гл. 10
при её анализе объединять смежные звенья в один блок, рассматривая его как одно звено. Поэтому, если какая-нибудь регулируемая система не может быть представлена в виде одноконтурной цепи с более чем двумя звеньями, то к двузвенному замкнутому контуру она может быть сведена во всяком случае. Для этого нужно только каким-нибудь образом разбить все координаты и скалярные уравнения на две группы и отнести одну группу к первому, а другую — ко второму звену.
Рассмотрим (фиг. 194) два принадлежащих цепи смежных звена с матричными координатами yt, у.2 типов 1, /п2Х 1; пусть эти звенья соединены каскадом, т. е. первое звено подвергается только внешнему для системы двух звеньев воздействию, характеризуемому матрицей-столбцом х типа тшХ1> а второе звено — только воздействию первого. Матричные уравнения двух звеньев пусть будут:
fi(D)yi = ei(D)x, f2(D)y2 = e2(D)ylt
где /1(0), /2 (О) — неособые квадратные полиномные матрицы порядков тх, /п2, а #1(0), e2(D)— вообще прямоугольные полиномные матрицы типов ^Х^, /n2Xwi« Разрешая относительно^,^, имеем:
У1 = (D) х, у2 = X? (О) у±,
где каждая из матриц
Ъ (D) = Ъ (D) \ et (D), X* (£>) = /8 (D) \ е2 (D)
представляет передачу или трансмиттанс соответствующего звена. Исключая уг, имеем:
у.2 = Х(Р)х, где матрица
X(D) = X2(D)Xx(D)
играет роль трансмиттанса системы двух звеньев.
Таким образом, трансмиттансы звеньев, соединённых каскадом, перемножаются. При этом порядок сомножителей в произведении, считая справа налево, соответствует порядку следования звеньев в цепи в направлении одностороннего воздействия. Если каждое звено имеет по одной степени свободы и тх = 1, то трансмиттансы Хх (D), Х2 (О) являются скалярами и порядок их перемножения несущественен.
Установленное правило представляет обобщение соответствующего закона для четырёхполюсников.
§ 10.2. Одноконтурная замкнутая цепь. Пусть имеем одноконтурную . замкнутую цепь регулирования из п звеньев ...,«» (фиг. 195). Первым звеном может быть поле регулирования, остальные звенья — различные элементы регулятора. Число степеней свободы звена aj пусть равно ntj. Возмущение приложено к первому звену, команда — к (г-|“1)-му.
§ 10.2)
ОДНОКОНТУРНАЯ ЗАМКНУТАЯ ЦЕЙЬ
737
Матричные уравнения в вариациях для системы п звеньев имеют вид
Л <Р)у! = (D)уп + elg (D) z,
/2 (£0 У 2 — е2 (^)Л>
Л (Р) У Г &т (^) Уг-1»
(10.1)
fr+1 (Р) Ут+1 ^г+1 (^) Ут ^г+1, х (Р) %*
fn (^) Уп--еп (^) Уп -1 •
Фиг. 195. Одноконтурная замкнутая
При этом матрицы у^> х, z типов X h X 1, тпя X 1 характеризуют, соответственно, состояние звеньев, команду, изменение нагрузки и помехи; fj(D) — неособые квадратные полиномные матрицы порядков a ^(D), e2(D), ..., en(D), er+lt p(D), (D) — вообще
прямоугольные полиномные матрицы типов щ X mn, w2Xwi> •••> ' тп х ^г+1 X тх, т1 X
Обозначения выбраны таким образом, чтобы в одном уравнении, а именно, перед операционной матрицей er+1(D), стоял минус; этим имеется в виду выразить, что регулятор должен противодействовать нарушению желаемого режима.
Умножим матричные уравнения, начиная со второго, слева на матрицы
— е± (Djfn1 (£>) еп (D).. ./Г1 (D), • ••••••••••••
и сложим с первым. После приведений получим:
(А Ф) + Ч (D) f-1 (D) еп (D).. е.2 (D)] У1 =
== e^Dyfn^Dye^D).. ./r"+i Ф)er+1, ? (D)х + е1г(D)z. (10.2) Полагая
A/D) = det/^D), ГДО) = adj (D),
где символ adj обозначает присоединённую матрицу, введём транс-миттансы односторонних воздействий между смежными звеньями
Л}(О)=//(П)\еДП) = ^^-) (j= 1, ..п) (10.3)
47 Зак. 1474. Б. В. Булгаков
738
ЛИНЕЙНЫЕ РЕГУЛИРУЕМЫЕ СИСТЕМЫ
[гл. 16
и трансмиттансы команды и возмущений
V f /Л\\ л ГП\ ^ГЧ-1 (^) ^Г-Ь1, х (D)
Xu(D)=A(D)\eu(D) =
. (10.4)
Тогда после деления слева на /Х(О) уравнение (2) получает вид [E,Bi + X (D)] Л = Х+ (D) х+Хи (D) z, где
X (D) = Хх (D) Хп (D)... X* (D), Х+ (D) = Хг (D) Хп (D)... Хг+1, х (D), или же
У1 = (°) * + Хг (D) z,
причём
Хх (D) = [£,„. + X (£>)] \ Х± (D), Хг (D) = [EW1+X(D)\ \ Xle (D). /
(10.5)
(10.6)
(Ю.7)
Квадратная матрица -
X(D) = ||X,fc(D)|| (WiX^) (10.8)
представляет трансмиттанс разомкнутой цепи a2...analf получаемой путём разрыва связи между первым и вторым звеньями, как показано на схеме. Если х = z = 0, то, подавая, например, на вход первого звена а2 этой цепи вместо ух какой-нибудь синусоидальный сигнал и (0, мы снимем на выходе последнего звена crt сигнал — X(PjU (t) (минус получился благодаря наличию такового в (г-|~ 1)‘м уравнении). Если [^1}] обозначает размерность скалярной координаты у^ звена то размерность Xjk(D), очевидно, будет [у{/}] -1;
если, в частности, все координаты у^ безразмерны, то и все Xjk(D) будут таковыми. Матрицу Е)П1 -Ц-X(D) мы будем, несколько обобщая терминологию Боде [9Д], называть возвратной разностью, так как [E„h -ЬАЧ£))] #(0 есть разность между сигналами u(t) и —X(D)u(f).
Матрицы Xx(D), XZ(D) представляют трансмиттансы поля регулирования с включённым регулятором по отношению к команде и к возмущениям.
Часть цепи между полем регулирования и местом подачи команды, состоящая из звеньев а2, ..., аг, может быть названа обратной связью, так как с её помощью осуществляются регистрация состояния поля регулирования и передача соответствующего сигнала для его сличения с командой, которая происходит в звене аг+1. Если обратную связь выключить, то, очевидно, будет:
Л = ^+(О)х + Х1г(О)2!, (10.9)
т. е. трансмиттансы Xx(D), Xe(D) приводятся к Х+ (£)), Х1г(D). Сла-
I 1б.£] ОДНОкОНТУРЙАЯ ЗАМкйУТАЯ Цейь 730
«
гаемое X(D) в знаменателях правых частей формул (7) выражает поэтому влияние обратной связи. Уравнение (9) характеризует управление типа незамкнутой цепи, уравнение (6) — автоматическое регулирование.
Если Ад,(0) конечно, то мы имеем при х = const, z = 0 статическое решение
У\х = (0)
если притом условия асимптотической устойчивости выполнены, то это решение характеризует состояние, к которому стремится поле регулирования в ответ на постоянную команду; рассогласование у1х—ух при этом стремится к нулю. Аналогичным образом, если АГДО) конечно, то при х = 0, z = const мы получаем частное решение
Уи = ^0 (0) z, характеризующее статическую реакцию поля регулирования на постоянное возмущение, например уменьшение нагрузки паровой машины на постоянную величину. Если
А*(0)== 0, то эта статическая реакция равна нулю; при внезапном приложении постоянного возмущения происходит переходный процесс, по окончании которого поле регулирования возвращается в прежнее состояние, так что мы имеем изодромное регулирование.
Изодромными системами регулирования целесообразно называть также и такие, в которых не все, а лишь некоторые, наиболее важные координаты имеют нулевые статические значения при постоянном возмущении; этот случай, . однако, сводится к предыдущему, если' сузить определение поля регулирования и считать, что оно определяется лишь значениями тех координат, которые нас особо интересуют.
Совершая замену D -> /о, мы можем обычным образом перейти от трансмиттансов, входящих в предыдущие уравнения, к соответствующим частотным характеристикам. Эти характеристики могут определяться не только вычислительным, но и экспериментальным путём, для чего нужно поочередно задавать синусоидальные возмущения каждому скалярному элементу матричной координаты на входе и замерять соответствующие элементы матричной координаты на выходе.
В частности, некоторые или все звенья «j могут иметь по одной степени свободы, так что т$ — 1; тогда соответствующие будут скалярными полиномами. Полиномная матрица е^(р) и трансмиттанс Xj(D) будут скалярами только в том случае, когда оба смежных звена «х имеют по одной степени свободы; аналогичные замечания можно сделать в отношении er+i, х (D), eiz (^)> ^*+1» ® (^)> (D).
47*
(гл. 10
(10.10)
(10.11)
?40 лйнеЙные ЁЕгёлЙЁУЭДЫЁ сибТЁМы
W
Обозначая
l(D) = X(D)\X+(D),
мы можем написать:
X+(D) = X(D)l(D), Хх (D) = [Emi + X (D)] \ X (О) I (D).
В элементах каждого столбца матрицы Eilh-\-X(p) отметим члены, содержащие степень О, старшую для данного столбца, и предположим, что определитель коэффициентов этих членов отличен от нуля. Рассмотрим затем регулируемые системы, для которых в некотором диапазоне частот элементы матрицы Х(1<л) велики. В этом случае матрица
. к adj [Ет + X (до)]
Хг (in) = [Emi + X (Йо)] \ Х1г (ia>) = det х Х1й (Йо)
мала, так что помехи мало чувствительны. Что же касается матрицы
Х„ (гш) = [Emi + X (1Ш)] \ X (Йо) I (Йо) =
= [£»>, + X (йо)] \ [ЕТО1+X (йо) — EWJI
то она близка к Z(Zco) и, следовательно, в рассматриваемом диапазоне приближённое значение частотной характеристики команды есть Z(Zgo). Чтобы сделать рассматриваемый случай более конкретным, предположим ещё, что т± = тг = тх и ег^9 х (D) = ег+1 (D), вследствие чего трансмиттанс обратной связи
X_(D) = ^r(D)...^2(D) (10.12)
является квадратной матрицей /пг-го порядка, так же как и матрица
Х+(Р) = X^D)Хп(Р) ... ХГ^(Р). (10.13)
При этом
X(D) = Х+ (D) Х_ (D) = X(D)l (D) Х_ (D) и
l(D) = XZ1(D), (10.14)
так что частотная характеристика команды определяется в основном обратной связью; иными словами, ответ системы на команду зависит только от настройки измерительных, передающих и счётно-решающих элементов, составляющих линию обратной связи. Характеристики элементов аг+1, ..., <*№, 04, образующих вторую половину цепи с трансмиттансом Х+(р), и даже их постоянство не имеют при этом особого значения, лишь бы X(fa) оставался в рассматриваемом диапазоне частот достаточно большим. Этим свойством совсем не обладает управление типа незамкнутой цепи, которое получается, если выключить обратную связь.
§ 10.3] ХАРАКТЕРИСТИЧ. УРАВНЕНИЕ ОДНОКОНТУРНОЙ ЗАМКНУТОЙ ЦЕПИ 741
§ 10.3. Характеристическое уравнение одноконтурной замкнутой цепи. Уравнение (2) было получено из заданных уравнений (1) путём почленного сложения первого с ^остальными, умноженными слева на некоторые матрицы. Это имеет своим результатом элементарные преобразования третьего типа в смысле § 1.7, производимые над строками коагулированной формы операционной матрицы. Поэтому, если заменить уравнением (2) первое из заданных уравнений и оставить без изменения остальные, то матрица полученной системы, которую можно представить в виде
fl(D)-]-e1(D)Xn(D)...X2(P) 0 ... 0 0
— е2(О) /2(О) ... 0 0
0 0 ...-e„(D) Д(Д)
имеет тот же определитель Д(£>), что и операционная матрица f(D) первоначальной. Пользуясь теоремой Лапласа, находим:
Д (D) = det (A (D) + et (D) Хп (£>)... Х2 (£>)] det/2 (£>)... det A, (D) =
= det {A (D) [EOT1 + X(D)]} Д2 (D) ... bn (D)
ИЛИ
Д (D) = До (D) det [Emi + X (£))], где величина
До (D) = Дх (D) ... Д„ (D)
(10.15)
(10.16)
представляет характеристический определитель разомкнутой цепи. Развёртывая определитель возвратной разности
1+^U(D)
«^1, ?»/! (Р)
Emi-]-X{D) =
представим его в виде
Хт» 1 (Р) 1 (^)
det [Emi + X(D)] = 1 + tf(D),
(10.17)
где
W)=2^(£»)+S
i i3
ijk
Xu (D)
Xji (D)
Xki (D)
Xu (D)
Хц (P)
Xi} (D)
Хн(Р)
X^D) Xik(D) X^D) Xjk(D) Xkj(D) Xkk(D)
+ ... -l-detA'(D).
(10.18)
Так как, согласно (5),
X\D) =
Pi (D) (£>) Fn (D) en (D)... (O) e2 (D)
At (D) Дп (D)... Д, (D)
742
ЛИНЕЙНЫЕ РЕГУЛИРУЕМЫЕ СИСТЕМЫ
[ГЛ. 10
то вс*е Xjk(D) имеют делитель Д0(О), и К(Р) после приведения к одному знаменателю получает вид
ЦР)
^‘(D) ’
где L(D)— полином. Но выражение
Д (D) = det/(D) = Д0(О) [1 + tf(D)] =
= До (О) +
L(D)
(D)
должно быть целой рациональной функцией, так как это есть операционный определитель системы. Следовательно,
= М (D),
где М (D) — полином, откуда
£(D) = M(D)A»>--1(D),
*<d>=Sb>- <10J9>
Такой вид должно иметь К(Р) после вычисления и возможных сокращений. Характеристический определитель замкнутой цепи будет:
Д (D) = До (D) [ 1 + tf(D)] = До (D) + М (D); (10.20)
зная его, можно написать характеристическое уравнение
Д(О) = 0. (10.21)
Так как при вычислении характеристического определителя внешние воздействия х и z не имеют значения, то мы можем получить другие выражения для /((£)), разрывая цепь после второго звена, после третьего и т. д.:
1 + K(D) = det [E„h + X2 (D) Xr (D) Xn (D)... X3 (D)] = = det [Етз + X3 (D) X2 (D) Xt (D) Xn (D)... X, (D)] и T. Д.
Обычно бывает выгодно делать разрыв после звена а?, для которого nij — наименьшее, всего лучше — единица, так как тогда и трансмиттанс разомкнутой цепи и соответствующая возвратная разность получаются скалярными. В этом случае
*(£>) = Xj (D) ... Xt (D) Хп (D) ... Xj+1 (D).
§ 10.4. Автоматическое управление курсом корабля. Принцип действия гиро-рулевого и вывод его простейшего уравнения изложены в § 5.8. Здесь в качестве примера теории, развитой в предыдущие
§ 10.4] АВТОМАТИЧЕСКОЕ УПРАВЛЕНИЕ КУРСОМ КОРАБЛЯ 743
параграфах, мы рассмотрим хорошо известные уравнения, которые полнее описывают динамику управления и могут быть найдены, например, у Басина [10д ], Ведрова []0-2], Вейсса [10-13 ] Граммеля [1(Ш ]. Мак-Колла [10-5], Чалмерса [4-16]; эти уравнения применимы и к самолёту.
Уравнение моментов относительно вертикальной оси корабля, проходящей через центр тяжести, и уравнение боковых сил могут быть в случае малых отклонений от прямолинейного курса написаны в виде
(Г2£)2_|_ [/£)) 0 ka — р = 0,
—/?D9+(SD+l)a —^р = 0.
Здесь 6 обозначает угол рыскания (фиг. 196), т. е. угол продольной оси корабля с заданным курсом, а — угол дрейфа, т. е. угол продольной оси с вектором v скорости центра тяжести, р — отклонение руля. Остальные буквы обозначают коэффициенты, которые при данной скорости могут считаться постоянными.
Уравнения автомата управления и рулевой машины будут:
□ = (£2D2+ MD + 0 (х — 6) — пр,
(У2О2+Г£>)р = Ь,
Фиг. 196. Корабль при малых отклонениях от прямолинейного курса.
где а — координата автомата, х — команда; через £2, М, I, п обозначены параметры настройки автомата, через V’2, W, h — параметры рулевой машины. Согласно первому уравнению, автомат, вообще, реагирует на угол рыскания, угловую скорость и ускорение, регистрируемые чувствительными элементами, и на сигнал, пропорциональный углу отклонения руля, передаваемый обратной связью.
Чтобы уменьшить число постоянных параметров, введём новые переменные a', o', при помощи соотношений
и заметим, что
где
0 = ^0', 1 *
744
ЛИНЕЙНЫЕ РЕГУЛИРУЕМЫЕ СИСТЕМЫ
[ГЛ. 10
Преобразуя уравнения, найдём:
(О'2 + О') 6 + k'a' — 0' = 0,
— S'O'O + (S'O' + 1) а' — m'p' = 0, а' = (А'2 О'2 + M'D' +Г) (х — 0) — п'Р', (V'2O'2 + O') 0' = а',
причём
7? Л
SU2
, SU2 т = ~RT^ '
Ny =----/И
U2W ’
гь
UW ’
U*W ’
, T*h
п ~ UW П’
2 — U V2
T%W ’
Постоянные без штрихов и со штрихами входят в первоначальные и преобразованные уравнения совершенно аналогичным образом,, за исключением того, что постоянным Т, U, W, R, h в первой системе соответствуют величины 1, 1, 1, S', 1 во второй. Поэтому мы можем просто предположить, что рассматриваемое преобразование уже сделано и, опуская штрихи, положить в первоначальных уравнениях
. t=U=W=1, R = S, Л = 1.
Разрешая первые два уравнения формально относительно 0, а, а два последних относительно а, 0, получим матричные уравнения
в которых
Ai(D)
0
0
SD —J— 1 — km ffiD2+(m + S)D ’
X2 (О) =
£2£)2 + MD + I
MO)
У2£)2_|_о о
1 0 ’
1
• z _ A2D2 + MD +1 Д2 (О)
Д t (£>) = SD» + (S + 1) О2 + (Sk + 1) D, Д3(О)=
§ ЮЛ]
АВТОМАТИЧЕСКОЕ УПРАВЛЕНИЕ КУРСОМ КОРАБЛЯ
745
Трансмиттанс разомкнутой цепи будет:
X{D) = Xt (D) Х2 (D) = £2P2^znf+ /
SD-\-(\—km) 0
mD* J-(Sт) D 0
bJD) = bJp)b.JD).
Отсюда
(Л2О2+ЖО+/) [SD+(1 — km)]
^(D)
Д(О) = Д0(О)[1+/С(О)] =
= 4- kJ)* + k.J)* + kJ)* + kJ) + fc6,
k0 = SV'2, kr = S (V2 + 1) + V'2, k.2 = 3 (A2 + n 4- V'2k -P1) + V2 + 1, fc3 = S(Af4-«4-fc)4-£a(l — km) + n 4-1, ki = 3 (/4- kri) 4- M (1 — km) 4- n, k5 — l(l —km).
При исследовании устойчивости ограничимся частным случаем
£ = Л4 = У=0,
т. е. предположим, что автомат реагирует только на угол рыскания, а инерцией рулевой машины можно пренебречь. Тогда характеристическое уравнение Д (X) = 0 может быть написано в виде
P(X)» + Q(X)Z+#(a) = O,
Р(Х) = за» 4- (s 4-1 j х2 4-, (Sfc 4-1) а, Q(X) = SX4-(1 —km), r (X)=sx4 4- (3 4-1) X» 4- (Sfe 4-1) x2.
Полагая X = /ш, отделяем в характеристическом уравнении действительную и мнимую части и разрешаем два получившихся уравнения относительно п, I. Это даёт параметрические уравнения кривой Т в плоскости nl:
__А»(ш) > _ А; (ю) А(<о) ’ А(<а) ’
причём
Д п (<о) = ш2 [— S2®2 4- 32й 4- km (3 4-1) — 1 ], дг («) = «а [_ з2®4 4- (гз2*—з2 — 1) в»2—(Sk 4-1)2], л ((О) = — 3 (3 4- km) <оа — (1 — km) (Sk 4-1).
746
ЛИНЕЙНЫЕ РЕГУЛИРУЕМЫЕ СИСТЕМЫ
[ГЛ. 10
Штриховку кривой производим по правилу Неймарка (§ 8.25). Особыми прямыми, соответствующими значениям со = 0, оо, являются ось абсцисс и бесконечно удалённая прямая (фиг. 197).
Если в характеристическом уравнении и в уравнении
положить л = s и разрешить относительно n, Z, то получатся параметрические уравнения дискриминантной кривой (§ 8.27):
Г(е) ’ Г(е) ’
где
Гм (е) = 3S2e4 + 2S (S + 3 — 2km) в3 +
[52* + 4$4- 3 — 3km (S+ 1)J S2-I-2 (S&+1) (1 — km) в, Гг(в) = — 82[5е2Ц_(5+ i)e_|_-(S*+1)]2>
Г (е) = — 2$3ё8+ $(—$— 4 + 3km) в2— 2 (1 — km) (S+ 1) е —
— (1— km)(Sk-\-\).
Принимая, например, для натуральных параметров корабля численные значения, приводимые в главе VIII книги А. М. Басина [101], получим следующие значения параметров уравнений (до преобразования переменных):
Г2 = 0,6601; 5= 1,295;
R = 0,6009; й = —0,5281;
U = 2,007; w = 0,2331.
После преобразования:
k = — 0,04016; 5 = 3,938;
т = 3,066.
I
Кривая Т и дискриминантная кривая для этих параметров показаны на фиг. 197. Кривая Т и положительная часть оси абсцисс, заштри-
хованные по правилу Неймарка, выделяют область устойчивости. Дискриминантная кривая выделяет подобласть апериодического затухания (показана сплошной штриховкой).
§ 10.5. Гироскопический стабилизатор. В качестве второго примера, которым автор обязан Я. Н. Ройтенбергу, рассмотрим гироскопический стабилизатор, исследованный в его статье [10Д], откуда мы заимствуем уравнения. Прибор предназначен для удержания в гори
Фиг. 197. Область устойчивости для корабля, управляемого гирорулевым.
§ Ю.5]
ГИРОСКОПИЧЕСКИЙ СТАБИЛИЗАТОР
747
зонтальном положении платформы, которая может качаться на горизонтальной оси. Он представляет собою гироскоп с тремя степенями свободы, кожух которого играет роль внутреннего карданова кольца, между тем как внешнее кольцо жёстко связано с платформой, так что ось платформы является в то же время и осью внешнего кольца. С этой осью при помощи зубчатой передачи соединён вал электромотора постоянного тока, который должен преодолевать действие внешних сил на платформу. Электромотор имеет независимое возбуждение, а ток в его якоре регулируется усилителем. Напряжение на вход усилителя поступает с потенциометра, укреплённого на оси кожуха гироскопа.
При воздействии на платформу внешних возмущающих сил, создающих момент относительно её оси, гироскоп прецессирует вокруг оси своего кожуха, а установленный на кожухе потенциометр подаёт напряжение на вход усилителя. Полученное после усиления напряжение подводится к цепи якоря мотора, который развивает момент, противодействующий моменту внешних сил. Гироскоп, помимо управления мотором, выполняет ещё и функцию прямой стабилизации платформы, так как непосредственно после приложения внешнего момента, когда токи в усилителе и якоре электромотора, а значит, и вращающий момент последнего, ещё не достигли нужной величины, уравновешение внешнего момента происходит не только за счёт момента мотора, но и за счёт гироскопического момента, развивающегося в результате прецессии гироскопа.
Уравнения системы при линейном законе включения потенциометра можно представить в виде
ДОсо — HDfi — Ri = 0,
ро) (^ +1) *—pJ = о — 5^ + (аО+ 1)7=0
(гироскопическая система),
(мотор), (усилитель).
Здесь со — угловая скорость платформы, р — угол прецессии кожуха гироскопа относительно платформы, I и 7 — токи в цепи якора мотора и в усилителе, А — момент инерции платформы и гироскопической системы относительно оси платформы вместе с приведённым моментом инерции якоря мотора, В — экваториальный момент инерции гироскопа, Н—его кинетический момент, р, т, р, R, S, о — параметры мотора и усилителя.
Принимая за первое звено цепи гироскопическую систему с мотором, а за второе звено — усилитель, имеем матричные уравнения
О)
I i
(О
= X1(D)/,
i
748
ЛИНЕЙНЫЕ РЕГУЛИРУЕМЫЕ СИСТЕМЫ
[ГЛ. 10
в которых
р
Д1Ф)
*1 (D)=
BRD* — HR D (ABD^ + //2)
^<D>=dc>i° -1
At (D) = AB [tD* + D3 + (h + q%) D* + q*D
Д2 (D) = aD + 1,
n = ^
H
Ч~ VZ4B'
Трансмиттанс цепи, разомкнутой на выходе второго звена, будет:
X(D) = Х2 (D) X, (D) =
где
Д0(О) = Д1(О)Д2(О).
Так как здесь Х(р)— скаляр, то
К(Р) = Х(Р),
и характеристический определитель будет:
Д (D) = До (D) [ 1 + /С (£>)] = До (D) + т№ или
Д (О) = АВ [otD6 (а -|~ т) В* + (1 + “h q2(yt) & “h
+ (n + q^ -Ц- qfy) D* q*D mq*].
§ 10.6. Характеристическое уравнение изменённой системы.
В качестве обобщения задачи § 3 рассмотрим следующую: зная характеристический определитель Д0(О) линейной системы
/o(D)j = 0,
найти определитель Д(£>) изменённой системы
/(D)j/ = 0.
При этом, имея в виду дальнейшие приложения к частотным методам исследования устойчивости, требуется дать такое правило, которое позволяло бы определять отношение Д(/о>) к До (fa>) как вычислительным, так и экспериментальным путём.
Предполагается, что /0(^)’ /(^) — квадратные матрицы одного И того же порядка п, и что матрица 8/(0) = /(О)—/р(7)) имеет
§ 10.6] ХАЙАЙТЕРЙСТЙЧЕСЙОЕ ^РАЙНЕНЙЕ ЙЗМЕНЕННОЙ СЙСТЕМЫ 74§
ненулевые элементы только в строках с номерами j\, ..., Jp и столбцах с номерами klt ..., kq.
Полагая
Укх
и представляя второе матричное уравнение в форме /о(0).У==-8/(0).у, можем заменить его эквивалентной системой
fQ(D)y — &vt и — ^у, V — —X2(D)u, (10.22)
где s есть матрица типа пХр» У которой элементы ©дд..........р
равны единице, а прочие — нули; затем & есть матрица типа qXn, у которой элементы ...» &q, к равны единице, а прочие — , нули, и, наконец,
X (О) =
(Р) ... 8/^(D)
8ЛрЛ(О) ... 8/^(0)
(10.23)
Три уравнения (22) можно рассматривать как уравнения звеньев замкнутой цепи. Операционные матрицы звеньев суть /0(D), Eq, Ер и характеристический определитель разомкнутой цепи будет Д0(О). Разрешая первое уравнение относительно у, получим:
-у = Х(О)4У, и = $у, v = — Х%(Р)и, (10.24)
где
Л*
ЛГ
*
a E$(D) суть элементы матрицы EQ(D), присоединённой к fo(JD). Определитель замкнутой цепи, согласно (20), есть
A(D) = Д0(О)[1 +/<(£)], причём 1 /C(Z>) равен определителю любой из двух матриц
Eq + $х[ (D) Х2 (D), Ер + Х2 (D) gX (D),
представляющих возвратные разности, получаемые при размыкании цепи после звена ам или после звена %.
?6б
лйнеЙные РЕГУЛИРУЕМЫЕ СИСТЕМЫ
[гл. 16
Полагая Х± (D) = $Xi (D)
*‘(D)=^S>
или
FZ\ (О) • • • fZv (d) с *
... i л. ЛГ
>
представим возвратные разности в более простом виде +Хг (D) Х2 (D), Ер + Х2 (О) Хх (D) и тогда
Д (D) = До (D) det [Eq + Х± (D) Х2 (D)] = = До (D) det [Ер + Х2 (D) Х± (D)].
(10.25)
(10.26)
(10.27)
Г
Фиг. 198. К вычислению характеристического определителя изменённой системы.
Можно также исключить у из системы (24). Получающиеся таким путём уравнения
и =X1(D')v, V — — X2(D)u (10.28) следует рассматривать как уравнения двухзвенной цепи.
Размыкая цепь на выходе звена *ам, можно экспериментально замерить элементы матрицы Eq -|- (zoo) Х2 (zoo), сравнивая синусоидальные сигналы, подаваемые на вход звена с ответными сигналами, снимаемыми на выходе звена ам. Замкнутая цепь и место размыкания показаны на фиг. 198, где звено аи, составляющее часть неизменной системы а0,
изображено внутри последней. Звено av представляет совокупность тех элементов, которыми система а0 отличается от изменённой системы а.
§ 10.7. Критерий устойчивости Найквиста. Излагаемый ниже критерий был предложен Найквистом [10-12] для усилителей с обратной связью и применён А. В. Михайловым [10-6] и др. к регулируемым системам.
Предположим, что степень числителя 7H(D) в выражении /C(D) (§ 3) не выше степени знаменателя A0(D). Это условие, в частности, заведомо удовлетворяется, если оно выполнено для всех Xi(D). В точках комплексной плоскости D, лежащих на конечном расстоянии, нули дробно-рациональной функции
1 + K(D) = А° (10.29)
суть нули числителя Д(О) = Д0(Л)-[-711(D), а полюсы — нули знаменателя. Если все звенья в отдельности асимптотически устойчивы, то их определители АДР), произведением которых является A0(D),
§ lO.f]
КРИТЕРИЙ УСТОЙЧИВОСТИ НАЙКВИСТА
751
не имеют нулей в правой полуплоскости и на мнимой оси. Поэтому, если проинтегрировать в направлении движения стрелки часов по замкнутому контуру С в этой полуплоскости, то, согласно теореме Коши,
Slj TPW = -N+₽ = -N’ <10-30>
с
где N есть число нулей функции 1 -{- К(В) внутри контура, а Р = 0 — число полюсов. С другой стороны, переходя в плоскость К с помощью конформного отображения
К= К(Р),
получим:
(10.31)
(10.32)
где Г — контур, получаемый отображением С, направление обхода которого определяется отображением и не может быть выбрано произвольно. Так как коэффициенты полиномов Л1(О), Д0(О) действительны, то действительным точкам D соответствуют действительные точки K(D), точке 0 = 0 и бесконечно удалённой точке О = оо— также действительные точки /С(0), /С(оо). Точкам D = s-|-zco, О = е — /со, симметричным относительно действительной оси, соответствуют также симметричные точки /С(е -|- zco)> К (е — /<») = = К (е -р &>)• Поэтому, если контур С симметричен относительно действительной оси, то достаточно вычертить лишь половину контура Г, так как другая получится путём зеркального отображения.
Так как
l-^/CI^-argd^), in(!+/<) = In | l + K| + /arg(l+^ = dln (1 4-K) = din 11 + К |-J-id arg (1+ K),
то выражение (32) принимает вид
d arg (1A").
(10.33)
Иными словами, N равно числу S полных оборотов вектора l-f-K(D) вокруг точки —1, когда D описывает контур С по стрелке часов, причём обороты считаются положительными также по стрелке часов
5 = АГ. (10.34)
Пусть, в частности, контур в окружности L большого радиуса диаметра С -|~ С', расположенного
плоскости D составлен из подуть с центром в начале и из её по мнимой оси; направление
752
ЛИНЕЙНЫЕ РЕГУЛИРУЕМЫЕ СИСТЕМЫ
[гл. 10
обхода — по стрелке часов (показано на фиг. 199 стрелками). Когда D изменяется от Z0 до -|-/оо, точка К(Р) пробегает путь Г от точки /С(0) до /<(оо). Вместе с зеркальным отражением Г' этого йути относительно действительной оси получаем замкнутый контур Гт|-Г', изображённый сплошной линией на фиг. 199. Полуокружности L от £) = -]-//? через D = R до D = — iR соответствует дуга А от /С=/C(-|-z7?) через #=/((/?) до К=К{ — iR). Эта .дуга А представляет ответвление контура Г-|-Г'. Если /?—>оо, то контур в плоскости D в пределе охватывает всю правую полуплоскость. В плоскости К ответвление А стягивается к точке /С(оо) и остаётся только замкнутый контур Г-рГ'. Число оборотов S этого
Фиг. 199. Диаграмма Найквиста.
контура по стрелке часов вокруг точки (—1,0) равно числу нулей N определителя А(О) в правой полуплоскости. Если число обо-ротов равно нулю, то замкнутая цепь асимптотически устойчива. В частности, асимптотическая устойчивость имеет место в случае, когда точка (—1,0) лежит вне контура. В этом и состоит критерий Найквиста.
Заметим, что А0(0)иД0(оо) всегда имеют одинаковые знаки, так как иначе Ао (D) имел бы по меньшей мере один положительный действительный корень, что противоречит предположению. Если система устойчива, то и До (0) -f-М (0), А (оо) -f- М (оо) должны иметь одинаковые знаки; отсюда следует, что знаки у действительных чисел 1-)~7<(0), 1-|-^(оо) также должны быть одинаковыми. Иными словами, точки /С(0), /С(оо) должны лежать на действительной оси по одну сторону от точки (—1,0).
Найквист доказал свой критерий и для распределённых систем, предполагая,, .однако, в обоих случаях /С(оо) = 0. На возможность более общего предположения /С(оо) < оо указал в 1944 году Энь Лун-чжу I10-10].
§ 10.8. Применение критерия Найквиста к системам с нейтральными и неустойчивыми звеньями. Пока критерий Найквиста
применялся к электрическим усилительным системам, для исследования которых он первоначально был изобретён, ограничивались
§ Ю.8]
ПРИМЕНЕНИЕ КРИТЕРИЯ НАЙКВИСТА
753
рассмотрением устойчивых звеньев и все дело было в том, чтобы избежать неустойчивости при соединении их в замкнутую цепь. Однако поля регулирования могут быть нейтральными или неустойчивыми (паровая машина, корабль, нейтральный или статически неустойчивый самолёт), и задача регулирования состоит в превращении их в устойчивые системы. Среди элементов регулятора также встречаются нейтральные (сервомоторы).
/>Лри наличии нейтральных элементов нуль будет полюсом для К(Р) и при построении контура в плоскости D его нужно обойти по £малой полуокружности I радиуса г (фиг. 200). Если полюс —
Фиг. 200. Диаграмма Найквиста для системы с нейтральными звеньями (простой полюс при D = 0).
первого порядка, то в окрестности 0 = 0 функция К(D) ведёт себя примерно как 1/0, и аргументам Ц-/0, —/О функции /С(/ш) соответствуют ветви кривых Г, Г', уходящие в бесконечность вдоль мнимой оси. Полуокружность Z отображается на кривую X, близкую к полуокружности большого радиуса, описываемой по стрелке часов, и смыкающуюся с бесконечными ветвями кривых Г, Г\ Когда А?—>оо, г—>0, дуга Л, отображающая большую полуокружность Л, стягивается к точке /С(оо), а дуга Л, отображающая малую полуокружность Z, уходит в бесконечность. В итоге опять остаётся кривая. Г Г', бесконечные ветви которой нужно представлять себе замкнутыми полуокружностью бесконечно большого радиуса в правой полуплоскости. К. полученному замкнутому контуру попрежнему
48 Зак. 1474. Б. В. Булгаков
754
ЛИНЕЙНЫЕ РЕГУЛИРУЕМЫЕ СИСТЕМЫ
[гл. 10
применяем критерий Найквиста. Можно написать S+—= ДГ или
Фиг. 201. Диаграмма Найквиста для системы с нейтральными звеньями (двойной полюс
(10.35)
Фиг. 202. Диаграмма Найквиста для системы с неустойчивыми звеньями.
Если полюс n-го порядка, то кривая Г^-Г' должна быть замкнута бесконечно удалённой линией, состоящей из п полуокружно-
§ 10.8]
ПРИМЕНЕНИЕ КРИТЕРИЯ НАЙКВИСТА
755
стей, пробегаемых по стрелке часов; в этом случае
S = W—4. • (10.36)
Фиг. 201 относится к случаю п = 2.
При наличии неустойчивого элемента К(Р) будет иметь п-крат-ный полюс в точке D = a (Rea>0). Мы предположим для опреде-
Фиг. 203. Примеры диаграмммг*Найквиста для устойчивых и неустойчивых систем: а — полюс при D = 0; б — двойной полюс при D = 0; в — один полюс при D = 0 и один полюс в правой полуплоскости.
лённости, что а действительно. При построении контура в плоскости D нужно выключить полюс а с помощью малого кружка I
48*
756
ЛИНЕЙНЫЕ РЕГУЛИРУЕМЫЕ СИСТЕМЫ
[ГЛ. 10
радиуса г, проходимого против, стрелки часов. В плоскости К ему будет соответствовать кривая X, близкая к окружности большого радиуса, описанной п раз по стрелке часов (фиг. 202 относится к случаю п = 1).
При применении критерия Найквиста нужно дополнить контур Г + Г' бесконечно большой окружностью, описанной п раз по стрелке часов. Можно написать для этого случая
5 = /г. (10.37)
Во всех рассмотренных случаях формула
S = W—р, (10.38)
или
W=$ + P, (10.39)
оказывается верной, если простые полюсы во внутренних точках правой полуплоскости считать за единицу, а на мнимой оси — за половину; кратные, — соответственно, за п и п/2.
Для систем, которым соответствуют графики на фиг. 199—202, мы имели M=S-|-P = 0, вследствие чего соответствующие замкнутые цепи устойчивы. Дальнейшие примеры диаграмм Найквиста для устойчивых и неустойчивых систем приведены на фиг. 203 [414].
§ 10.9; Частотная диаграмма для оценки быстроты затухания и логарифмического декремента. Сделаем в К(Р) замену переменного
D = — <* + £>', (10.40)
где а — действительное положительное число, и построим частотную
характеристику К=К{ — a-j-zw), рассматривая а как постоянный
Фиг. 204. Конформное отображение D = — а -|- D'.
параметр. Каждый нуль или полюс функции
1+#(£))= 1 4-К( — «+£'), лежащий в правой полуплоскости переменной О', будет лежать правее прямой Re D = — а в плоскости D (фиг. 204). Поэтому, если S обозначает число оборотов частотной характеристики — a —}—/а») вокруг точки К= — 1 плоскости К и Р — число полюсов К(Р)9 лежащих
правее прямой Re D = — а плоскости О, то N = S -|- Р есть число нулей 1-1-К(Р)9 лежащих правее той же прямой. При
наличии n-кратного полюса правее прямой или на ней самой он обычным образом считается, соответственно, за п или п/2. Если 7У = 0,.то все нули лежат левее прямой. ReD — — а.
§ 10.9] ЧАСТОТНАЯ ДИАГРАММА ДЛЯ ОЦЕНКИ БЫСТРОТЫ ЗАТУХАНИЯ 757
Вместо вертикальной прямой можно брать другие контуры в плоскости D, причём положительное направление на таком контуре мы будем брать так, чтобы «хорошая» (желаемая) область оставалась по левую руку от наблюдателя, странствующего по кривой в этом направлении.
Например, для того чтобы, согласно А. А. Фельдбауму [10-8], получить оценку корней по их логарифмическому декременту, возьмём отмеченную штриховкой на фиг. 205 угловую область, ограниченную контуром
/зе<е = а ( — sin О -Ц- i cos 6), — = а (— sin 6 — i cos 6)
(0 < а < оо). (10.41)
Корням характеристического уравнения, расположенным в этой области, соответствуют парциальные колебания, для которых логарифмический декремент больше или равен ictgO. (Например, для корня, располо
Фиг. 205. Области допустимых значений корней характеристического уравнения.
женного на границе угловой области на фиг. 205, а, при 6 = 25° имеем tg 6 = 0,466; логарифмический декремент к tg 6 =1,46; декремент затухания парциального колебания, соответствующего »этому корню, tgQ = 0,232).
При построении ветви частотной характеристики /С(/з£<9) мы имеем:
D3 = = (гз/ (cos/6 -|-i sin /0), (10.42)
так что действительная и мнимая части определителя разомкнутой
цепи
Ао (D) = й0О* + + ... + k^D + ka (10.43)
758 ЛИНЕЙНЫЕ РЕГУЛИРУЕМЫЕ системы [гл. 10
i будут: Re До = . .. — sin + o4feg_4 cos 40 4“ '
4-o3&s_3 sin 39 — a2Zjs_2 cos 26 —a&g-! sin 6-|-Zjs, Im До(foe*9) — ... 4- a6feg_6 cos 59 4" s^n 49 —
— o3fes_3 cos 39 — a2fes_2 sin 20 4~ a^s-i cos 9. ,
Аналогичным образом получим действительную и мнимую части полинома 7И(О).
Частотная характеристика состоит из ветви /С= K(heih) и её зеркального отображения К=К(— foe~*,f); если число её оборотов вокруг точки К=— 1 равно нулю и K(D) не имеет полюсов внутри и на границе угловой области, то все нули 1 лежат внутри
этой области, т. е. логарифмические декременты всех корней больше irtg9.
Н. А. Картвелишвили [10-3] и Н. Т. Кузовков [10-4] берут в плоскости D контур согласно фиг. 205, б.
ГЛАВА 11
ЛИНЕЙНЫЕ СИСТЕМЫ С ПЕРИОДИЧЕСКИМИ КОЭФФИЦИЕНТАМИ
§ 11.1. Общая форма решения. Мы отмечали раньше (§ 7.1), что уравнения в вариациях для периодических решений нелинейных уравнений являются линейными уравнениями с периодическими коэффициентами. Поэтому к таким уравнениям приводят некоторые механические задачи о малых движениях вблизи данного состояния равномерного вращения. Уравнение Хилла в теории Луны также принадлежит к этому классу. Если главным предметом исследования является само периодическое решение, то для суждения об его устойчивости нужно знать форму общего решения уравнения в вариациях, что уже само по себе достаточно для объяснения значения изучения линейных уравнений с периодическими коэффициентами.
Напишем уравнение в виде
A(t)y +Я(/)^ = 0, (11.1)
где А(/), H(f)— квадратные матрицы n-го порядка, элементы которых являются периодическими функциями от t с периодом Р, так что
А (/+ Р) = А (0, H(t+ Р) = H(fy, (11.2)
у обозначает, как всегда, столбец из п неизвестных у$.
Пусть 6 (£) есть квадратная матрица, составленная из п столбцов 6fc) (/), являющихся линейно независимыми решениями:
6(0 =|| 6t) (/).6И)(О||;
всякая такая матрица называется фундаментальной. Очевидно, что Л(0 б (0 + Н(0 & (О = 0, а также
A (t+Р) б (/+Р) + Р) 6 (t + Р) = 0,
откуда на основании (2)
A (f) 6 (t + Р) 4- H(f) 0 (f + Р) = 0.
760 ЛИНЕЙНЫЕ СИСТЕМЫ С ПЕРИОДИЧЕСКИМИ КОЭФФИЦИЕНТАМИ [ГЛ. 11
Таким образом, 0(£-|-Р) является также фундаментальной матрицей, вследствие чего каждый её столбец 0^(^+В) Должен быть линейной комбинацией решений 0Z) (f) первой фундаментальной системы:
п
Ч) (*+ Р) = 5 0») (0 Blk (k = 1.....п).
1=1
Эти п соотношений эквивалентны следующему:
0(^+Р) = 0(ОВ, (11.3)
где
Я=||Я#|| (ЯХ4
Соотношение (3) может рассматриваться как линейное 1 уравнение в конечных разностях относительно 0(0 с постоянным /матричным коэффициентом В и основным интервалом р.
Матрица 0(0 принимает при t = tQ начальное значение 0(£о). Если мы хотим получить начальное значение, равное любой другой неособой матрице 0*(^о), то следует взять фундаментальную матрицу '
6*(0 = 0(0?, где
9 = О(^\0*(^.
Каково будет уравнение в конечных разностях для О*(0? Чтобы ответить на этот вопрос, напишем:
Q*(t-\-P) — b(t-^-P)q = 4(t)Bq, '
а так как
0(О = 0*(О/^, то
0*(*+Р) = 0*(ОВ*, (11.4)
где I
В* = q^Bq = О*-1 %) 0 (/0) ВО"1 (tQ) 0* (tQ) = *
= 0*-1 (0 0(0 ВО”1 (0 о* (0. (11.5)
Таким образом, любая матрица 0* (0, как и следовало ожидать, удовлетворяет уравнению в конечных разностях того же вида, что и для матрицы 0(0, но коэффициент В* будет матрицей, подобной В. 1 Поэтому В и все В* имеют одни и те же характеристические числа одних и тех же кратностей, а соответствующие характеристические матрицы ХЕ— В, ХЕ— В* — одни и те же элементарные делители. В настоящем параграфе мы будем предполагать пока все эти элементарные < делители линейными. В этом случае можно выбрать матрицу q или, |
в конечном счёте, начальное значение 0*(£о) таким образом, чтобы В* 1
была диагональной матрицей, составленной из характеристических
ОБЩАЯ ФОРМА РЕШЕНИЯ
§ 11.1]
чисел
Обозначая
найдём:
где
Подставляя в (4), имеем:
0*(/+Р) = 0*(О^, 0*(^P)e-3(*+P)
Если же положить то
V(f) = 0*
У(0=У(/+Р),
761
(И.6)
(11.7)
(11.8)
(11.9)
(11.10)
так что матрица V(t) представляет периодическую функцию от t с периодом Р.
Фундаментальная матрица 6*(/) выражается через V (t) формулой
B*(t) = V(t)e?t, (Н.П)
аналогичной второй формуле (8.60) для уравнений с постоянными коэффициентами и отличающейся только тем, что в ней матрица в случае линейных элементарных делителей, является постоянной, а эта согласуется с тем, что постоянная может рассматриваться как периодическая функция с произвольным периодом.
Аналогия с уравнением с постоянными коэффициентами сохраняется, естественно, и для общего решения
у = 0* (t) с = V(f) е&с, (11.12)
где с обозначает столбец произвольных постоянных. В скалярной форме имеем:
(плз)
762 ЛИНЕЙНЫЕ СИСТЕМЫ С ПЕРИОДИЧЕСКИМИ КОЭФФИЦИЕНТАМИ [ГЛ. 11
Формулы (12), (13) определяют форму общего решения матричного линейного уравнения с периодическими коэффициентами и составляют содержание теоремы, Флоке [11л].
§ 11.2. Случай нелинейных элементарных делителей. Предположим, что среди элементарных делителей характеристической матрицы ЕХ— В имеются нелинейные. Обозначим попрежнему через характеристические числа, через ек — степени элементарных делителей. При этом, если, например, характеристическому числу л1 = Х2== = — Аб соответствует один кубический и один квадратичный
элементарные делители, то мы положим et = е2 = е3 = 3, е± = е& = 2. Все элементарные делители могут быть записаны в виде (X — Xa)0» (0=^, .ат), где т — число всех элементарных делителей и
1 “4" 1, — &cL “4”" 1 > • • • >
= "Ь е°2 Н" • • • Ч" 6о . 1 •
х — 1
Рассуждение предыдущего параграфа должно быть изменено с того места, где мы преобразовали матрицу В с помощью матрицы q к подобной канонической форме. Теперь таковой будет квазидиаго-нальная форма Жордана
(П.14)
в которой субматрицы
X, 1 0 ... О
О X, 1 ... О
• • • • • • • • • о о о ...
(^Х^) (0 = ^, ат) (11.15)
•соответствуют отдельным элементарным делителям. Обозначая через ve* первый косой ряд (§ 1.2) порядка составленный из единиц, можем написать:
4 = Е<Л, -j- Vaa = (Еев + -уу)
я если ввести числа с помощью (7), то
A = (XJ+vL)expM’.
Разбиваем фундаментальную матрицу 6*(f) вертикальными линиями на субматрицы 0*СТ1) (£), ..., 6*вт) (Q, содержащие, соответственно, еа столбцов, в результате чего f)*(0 коагулирует в строку 1 т
ЛИЯ
§ 11.2] СЛУЧАЙ НЕЛИНЕЙНЫХ ЭЛЕМЕНТАРНЫХ ДЕЛИТЕЛЕЙ
763
и соотношение (4) может быть представлено в виде
Л(*+Р)........С)(Н-Р)II ==Pw(9>.. •> 6(,Т)^)ПХ
откуда
Матрица
б*а) Р)=б*а) (о ja, f)*a) (о в: </+Р)
(0 = О’.) (О V</P = 9(а) {t+Р) J-(t+P)IP
является поэтому периодической функцией от t с периодом Р и 0;,)(o=z(a)(oj//p или
* ( . че \t/P
9<o)(0=Z(a)(0(£ea+-^-) ехррЛ (11.16)
Так как v6ff нильпотентна (§§ 1.6, 1.30), то, полагая
sg,(О =
(( = 2,3,...) (11.17)
и пользуясь правилом возведения в степень косых рядов (§ 1.6),
I
находим конечный ряд
Обозначая через 0*> (t), ZO) (f) отдельные столбцы матриц 0*e)(f), Z(a) (f), имеем:
<С)(0= 1Р’)(0.......O*+ea-l)(QH
z(a)(0 = ||Za)(0......za+ee_1)(0||
(a = 01, .... aT)
И из (16), (18)
CP)(0= Va+₽)(0A‘.
j ^«+p)(0 = (0Sf (0АзЧ~^а+1)(0s’p-i(ОМ® -|-...-|-zo+p)(Z) (i 1.19) (0 = ^......................ax; p = 0, 1, ..., e,— 1).
764 ЛИНЕЙНЫЕ СИСТЕМЫ С ПЕРИОДИЧЕСКИМИ КОЭФФИЦИЕНТАМИ [ГЛ. 11
Таким образом, в данном случае в состав Уа+Р) (0 кроме периодических функций входят и степени t. Если обозначить через V (t) (пХ^) матрицу, составленную из всех п столбцов Vff+p)(0, соответствующих всем элементарным делителям, то можно опять написать матрицу 6*(0 и общее решение в формах (11), (12), (13), хотя для V9) (0 сохраняются выражения (19). Этот вывод составляет обобщение теоремы Флоке на случай любых элементарных делителей.
§ 11.3. Характеристические показатели. Из формулы (11) получаются следующие выражения частных решений, составляющих фундаментальную матрицу 6*(0:
О?) (О = V.) (О е (а = 1.......п). (11.20)
Решение будет стремиться к нулю при оо, если действительная часть числа [За отрицательна, и неограниченно возрастать, если она положительна. Если же действительная часть равна нулю, то решение будет оставаться конечным, не стремясь к нулю, когда все элементарные делители матрицы Ек — В*, соответствующие корню линейны, и неограниченно возрастать, когда среди них есть нелинейные. Величины (Зв, от которых, таким образом, существенно зависит поведение решений, названы Пуанкаре характеристическими показателями, Они известны с точностью до целых кратных от 2ir//P, если известны характеристические числа матрицы В. А так как, согласно (3),
В = 9(0\6(^+Р), (11.21)
то матрица В в свою очередь будет известна, если тем или иным способом удалось построить фундаментальную матрицу 6 (0 на интервале, равном периоду Р. Таких способов известно несколько, но ни один из них, вообще, не избавляет от длительных вычислений, а так как в основе всегда лежит тот или иной бесконечный процесс, то - в действительности можно получить лишь приближённый результат
с достаточно малой ошибкой. Например, матрицант 2 (§ 1.38) от — А (0\Н (0, вычисляемый последовательными интегрированиями, представляет собой, очевидно, фундаментальную матрицу, обращающуюся в Е при t = t0; вследствие этого мы имеем просто
В = 2(^0 + Р). (11.22)
С характеристическими показателями связана следующая теорема, вытекающая из выражения общего решения: положение равновесия у = 0 системы, определяемой линейным матричным уравнением с периодическими коэффициентами, асимптотически устойчиво, если действительные части всех характеристических показателей отрицательны, и неустойчиво, если хотя бы одна из них
положительна.
§ 11.4] СООТНОШЕНИЕ МЕЖДУ ХАРАКТЕРИСТИЧЕСКИМИ ПОКАЗАТЕЛЯМИ 765
Этой теореме, можно дать ещё одну геометрическую формулировку. Из общего решения (12) и из (4) вытекает:
у (£-|- Р) = 0* (£4-Р) с = 0* (0 =
= о*(ОВ*о*-1(Ову(0 или
У (tР) = Т (t) у (t). (11.23)
При этом на основании (5), (8), (И) и ввиду коммутативности матриц е$р, мы можем представить матрицу T(t) выражениями
T(t) = 0 (/) ВО-* (0 = 0* (О В0*-1 (0 = 1/(0 В* У-* (0, (11.24)
из которых видно, что Т подобна В*, не зависит от выбора фундаментальной матрицы и является периодической функцией от t, вследствие чего можно написать также:
y(t-\-2P) = T(f)y(t-\-P), ,y(H-3P)=7W(H-2P).
Если столбец у интерпретируется как радиус-вектор точки п-мерного пространства, то соотношение (23) представляет линейное преобразование, связывающее точки у (/) фазовых траекторий, соответствующие моменту /, с их же положениями к моменту t-\-P. При этом, как показывают последние соотношения, то же самое преобразование связывает ,у(^ + Р) с y(t-\-(2P'), затем y(t-\-2P) с у (/-]“ ЗР) и т. д. При любом начальном t стремление точки у к началу координат или же неограниченное удаление от него после большого числа повторных преобразований, разумеется, совершенно так же зависит от характеристических показателей, как и в приведённой выше теореме об устойчивости положения равновесия. Но данная формулировка может быть перенесена на повторные преобразования, определяемые матрицей Т, заданной вне связи с каким-либо уравнением с периодическими коэффициентами.
§ 11.4. Соотношение между характеристическими показателями.
Обозначая
/(О = Л(0\Я(О, (11.25)
мы имеем, согласно § 1.38, t
-JVn + ...+fnn)^ det 2 = е ,
где 2 — матрицант, т. е. фундаментальная матрица, обращающаяся в Е при t—10. Для любой другой фундаментальной матрицы
е (о=2 (0 е (4)
766 ЛИНЕЙНЫЕ СИСТЕМЫ С ПЕРИОДИЧЕСКИМИ КОЭФФИЦИЕНТАМИ [ГЛ. Ц
мы получим: t
...+fnn) at det 6 (f) = e det 9 (/0),
t+P
- J (fu+-+fnn)at
det Ь (tP) = e det9(f0)==
f+p
- J (fu+...+fwn)^
= det 6 (/) e *
и, согласно (3),
t+P
- J (fu+...+fnn)at-det В = e *
Характеристические числа матрицы В удовлетворяют уравнению det || кЕ — ВЦ = 0, свободный член которого есть ( — l)n det В, а с другой стороны, по формуле Виета, равен (—1)лХх..Дл или
Учитывая ещё, что вследствие периодичности коэффициентов fa интеграл в предыдущем соотношении может быть взят по любому интервалу длиною Р, получим:
п п
к=1 —Р/2 Л=1
Это и есть искомое соотношение между характеристическими показателями.
ГЛАВА 12
НЕЛИНЕЙНЫЕ СИСТЕМЫ
А. МЕТОД ПУАНКАРЕ
§ 12.1. Периодические решения уравнений, содержащих малые параметры. Периодические решения изучались в небесной механике Г. В. Хиллом [12-25] в 1877 году, а их основная теория принадлежит А. Пуанкаре [12-28]. Об общем значении периодических решений мы уже говорили в разделе Г главы 5.
Пусть имеем систему нелинейных уравнений
Уу (У1> • • • > Уп* Р1» • • • > Ну) С/ = 1> • • • > я) (1^.1)
с п, неизвестными уп и г параметрами Р4, ..у.г. Время t
не входит явно; правые части ср^ предполагаются в некоторой области аналитическими функциями всех аргументов.
Вводя матрицы-столбцы ср, у и у., можно написать в матричной форме
j = [*). (12.2)
При некотором определённом значении у. будем называть уравнение упрощённым и предположим, что оно допускает тогда частное решение у* (t), для которого
^(^=^(^0 + Р). (12.3)
Это решение будет периодическим с периодом Р, так как в момент мы имеем те же условия, что и в момент tQ. Иными словами, при любом t
у*(Г) = У*(*+Р)- (12.4)
С другой стороны, функция y*(t—tQ) при произвольном постоянном t0 будет также периодическим решением. Таким образом, если для уравнения рассматриваемого вида констатировано наличие одного периодического решения, то должно существовать семейство таких решений с одной произвольной постоянной. Поскольку время не входит явно, общее решение при любом у. имеет вид
У —^1» • • •» ^п-1* Р)>
(12.5)
768
НЕЛИНЕЙНЫЕ СИСТЕМЫ
[ГЛ. 12
где С19 ...» Сп_±— произвольные постоянные; мы будем предполагать, что найденное семейство периодических решений получается при значениях С* , ..., Cn-i, а соответствующее значение столбца рьестьО.
Основной вопрос в теории Пуанкаре заключается в том, можно ли путём подбора постоянных выделить периодические решения из общего также и для р. #= 0; при этом ставится ещё условие, чтобы эти решения при р,—>0 обращались в найденные ранее периодические решения упрощённого уравнения, которые в этом случае можно назвать порождающими. Так как нет оснований ожидать, что период искомых решений при р ¥= 0 будет тот же, что и для порождающих, то обозначим его через Р'. Тогда условие периодичности, аналогичное (3), будет:
Ср..., Сп_19 р)-/(0, Ср..., С№_р р) = 0. (12.6)
При частных значениях Р' = Р, Ct = С* , ..., Сй-1 = C^-i, р = 0 это уравнение обращается в у*(Р)—д/*(0) = 0, т. е. совпадает с (3) при ^о = О и, следовательно, удовлетворяется. Поэтому, если функциональный определитель п функций фр ...» по п аргументам Р', С19 ..., Cn_t при вышеуказанных частных значениях отличен от нуля, то вблизи этих значений уравнение может быть, согласно общей теореме о неявных функциях, разрешено относительно совокупности п аргументов и они могут быть выражены как аналитические функции от 14, ..., ру. Если же выражения для Сх, ..., Сп_х подставить в общее решение, то мы получим искомое периодическое решение в виде аналитической функции от t—tQ и р.
Различные случаи обращения в нуль функционального определителя, когда по крайней мере один из его миноров (п—1)-го порядка ютличен от нуля или же когда все эти миноры также исчезают, служили предметом исследований самого Пуанкаре и позднее Мак Миллана [12-26 ], причём обнаружилось, что в этих случаях периодические решения могут получаться в виде рядов не по целым, а по дробным степеням р. И. Г. Малкин [12ДЗ] исследовал случай упрощённого уравнения, допускающего семейство периодических решений с несколькими произвольными постоянными при условии, что период от этих постоянных не зависит.
Мы ограничимся изложением случая, когда имеется семейство, зависящее кроме tQ ещё только от одной постоянной А:
У*=У*(?—*о> А). (12.7)
Это семейство должно получиться из общего решения при р = 0 с помощью соотношений вида
С^С^А)........Cn_t = Сп_х (Л); (12.8)
периоды решений семейства будут также зависеть от А:
Р = Р(А). (12.9)
1
§ 12.1] ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЙ 769
Порождающее решение или решения (так как их может быть несколько) и их периоды Р* будут соответствовать некоторым специальным значениям А = А*9 которые дают:
Р* = Р(Л*), 0?=^^*), ..., С*^=С№_Х(Л*). (12.10)
Если р. = 0, то функциональный определитель должен обращаться в нуль при значениях Р*9 С* , ..., C^-i, так как иначе точка с такими координатами была бы изолированной точкой пространства Р, Ci,..., Cn_lt удовлетворяющей при р. = 0 условию периодичности (6), а между тем мы знаем, что таких точек имеется бесчисленное множество, заполняющее кривую, определяемую п уравнениями (8) и (9).
Предположим, что по крайней мере один из миноров (п—1)-го порядка функционального определителя отличен от нуля при р. = О, например минор
д ......Фп)
d (Pf, С2, •.., Cn—i)
Тогда из уравнения = 0, ..., = 0 можно выразить Р', С.2, ..., Сп_±
в виде функций от Сх и р. и подставить в = 0, что даёт уравнение
Ф(СХ, И) = 0
для определения Сх через р.. При р. = 0 это уравнение должно удовлетворяться тождественно по Ct, так как иначе мы опять имели бы изолированное периодическое решение. Следовательно, Ф (Ср р) должно иметь вид
|х)^И[Ф(С1) + Т1(С1)н+ ...1
и Сх при р. = О либо должно рассматриваться как произвольная величина, либо быть выражено через другую произвольную постоянную А. Пользуясь ещё выражениями для Р', С.2, ..., Cn_t через С± и р, мы получим при р» = О уравнения кривой вида (8) и (9). Если, однако, иметь в виду не всю совокупность решений (7), а лишь порождающие решения, являющиеся пределами периодических решений первоначального уравнения при р —> О, то для них должно удовлетворяться уравнение
(Ct) = О,
а после перехода к постоянной А — некоторое уравнение
О(Л) = 0. (12.11)
Это уравнение даёт, если не принимать в расчёт исключительные случаи, лишь изолированные значения А*.
Во всяком случае, как мы убедились, порождающими решениями будут лишь те из периодических решений семейства (7), для которых А имеет одно из значений Л*, удовлетворяющих уравнению (11).
49 Зак. 1474. Б. В. Булгаков
770
НЕЛИНЕЙНЫЕ СИСТЕМЫ
[гл. 12
В качестве упрощённых уравнений, допускающих семейства периодических решений с двумя постоянными Д, применяются линейные уравнения с постоянными коэффициентами и уравнения консервативных систем. В первом случае при всех вычислениях, связанных с упрощённой системой, к нашим услугам детально разработанная и широко известная процедура. Во втором случае семейство периодических решений упрощённой системы может быть получено квадратурами или построено в виде рядов Ляпунова по степени амплитуды. Несмотря на большую трудность метода, следует ожидать развития его приложений к задачам, в которых упрощёнными являются уравнения систем с нелинейными восстанавливающими силами, например силами упругости.
Что касается систем регулирования, то они неконсервативны и притом не от случая к случаю, а как правило, так как всегда предполагают включение малыми силами более мощных потоков энергии, источники которой не принадлежат собственно системе. Поэтому применение здесь консервативных систем, даже в качестве упрощённой модели, затруднительно.
§ 12.2. Системы, близкие к линейным. Обратимся к более детальному рассмотрению уравнений, близких к линейным с постоянными коэффициентами («псевдолинейным»), которые широко применялись к физическим задачам Л. И. Мандельштамом, Н. Д. Папа-лекси, А. А. Андроновым и рядом других исследователей, более или менее близко связанных с созданной ими школой. Мы изложим здесь метод Пуанкаре в форме, удобной для отыскания периодических решений рассматриваемых уравнений при любом порядке п соответствующей скалярной системы. Эта форма, опубликованная нами [12-и], применялась в некоторых работах |1216’12Л], главным образом к задачам теории регулирования.
Параметр рь будет предполагаться скалярным. Вместо того чтобы сначала строить ряды по степеням произвольных пострянных и параметра рь, с тем чтобы потом выражать произвольные постоянные через |л, все разложения ведутся сразу по степеням у..
Исходное матричное уравнение зададим в виде
f(D)y = ^(y, |л), (12.12)
где
f (D)=\\fik(D)\\ = \\a^Dp + . + а$’|| (»Х«).
^(У> Н) =
Мл н)
'Ьп(У> н)
(п X 1).
(12.13)
J
§ 12.2] СИСТЕМЫ, БЛИЗКИЕ К ЛИНЕЙНЫМ 771
причём |л) представляют данные нелинейные функции от неизвестных у19 ..., уп и от [I.
Предположим, что определитель
A(D) = det/(D) (12.14)
имеет пару простых чисто мнимых корней Zo> и что никакое их целое кратное ztZznw не является корнем.
Упрощённая система, получаемая при р. = О,
f(D) у = 0 (12.15)
допускает семейство периодических решений с периодом
Р=2л/<о, (12.16)
которое получается следующим образом. Полагаем
у =
где Д, 9 — скаляры, а У—пока неизвестный модальный столбец. Подставляя в уравнение, имеем:
/(Zto)V=O.
Так как, с другой стороны,
/(Zto) F(Zco) = EL (Zto), где F(D)— присоединённая матрица, то за V можно принять любой столбец Fw)(fto).H3 F (Zto), в котором есть хотя бы один элемент Fz?n(Zto), отличный от нуля:
• > п).
Разумеется, если это удобно, какой-нибудь постоянный общий
Полагая
то в правых частях можно ввести множитель.
(12.18)
берём действительную часть от у^:
= ^.cos(to/4-9 + Tj) (/=1, п). (12.19)
Совокупность этих п функций должна также составлять решение. Точнее говоря, поскольку А и 6 остались произвольными, мы имеем семейство периодических решений с двумя постоянными.
Как мы обнаружим дальше, при некоторых определённых значениях А = А* эти решения будут порождающими и вблизи них при И =# 0 будут существовать периодические решения нелинейного уравнения. Периоды Р' этих последних будут, вообще, отличаться от Р
49*
772
НЕЛИНЕЙНЫЕ СИСТЕМЫ
[ГЛ. 12
и зависеть от р.. Поэтому, полагая
(12.20) «
мы должны считать как Р', так и а функциями от р», принимающими при |л = 0 значения Р и 0. Но если ввести новую независимую переменную
т = [1+«(н)1^, * (12.21)
то периоды относительно неё будут всегда равны (l-j-a)Pz = Р. Обозначая
= (12.22)
/ \
с \ ф2 4=о
/ da\
wV
(12.23)
имеем:
О = От(14-а),
£/(С)=Г(О)О,£,
^/(D) =/-(D) О,^+Г (D) оЦ£)’,
(12.24)
L “Iх Jp,=o
^/P)] =/'Pr) dxc +/"(DT)DX '
Если же теперь понимать под у искомое периодическое решение заданного нелинейного уравнения и положить
(12.25)
то все функции г, s, ..., так же как и у*, будут периодическими по отношению к новому «времени» ъ с периодом Р.
Дифференцируя данное уравнение один, два, ... раз по р и полагая в данном и в полученных уравнениях р = 0, найдём:
/(DT)_y* = 0,
/Рт) г = -f (DT) DJy* + Ф (у*, 0),
/Рт) s = — If (DT) Dxc +f" (DT) DX] У* — n
- 2f (Dt) Djr + 2 Щ r, + ,
ду*
s-i
(12.26)
j
§ 12.3]
ПЕРВОЕ ПРИБЛИЖЕНИЕ
773
При этом мы условимся, что всякий раз, когда здесь или в дальнейшем аргументы функции ф или её производных не указаны, то этими аргументами являются у* и 0.
§ 12.3. Первое приближение. Из первого уравнения (26) имеем:
y* = ±A(Vei«-]-Ve-^), (12.27)
где
и = шт + 6, (12.28)
а V определяется согласно (17).
Заменяя у* во втором уравнении (26) полученным выражением, имеем:
f(PJr = — + 0),
£
или, разлагая в ряд Фурье в комплексной форме,
/(От)г=^ш_^ 9 (12.29)
где
р = —~Л&/'(/о))го)У-|--^- I ф(з/*, 0)e~iudu,
—и
а многоточием заменён член pe~iu и члены второй и высших кратностей.
Так как по условию ни одна из целых кратностей ±inw> не является корнем характеристического уравнения, то соответствующие члены в правой части дают в частном решении периодические функции той же самой частоты. Что же касается членов peiu, pe~iu> то они, вообще, могут дать в частном решении периодические функции, умноженные на степени t. Чтобы этого не было и решение было чисто периодическим, необходимо и достаточно, чтобы уравнение, получаемое из (29) отбрасыванием справа всех членов, кроме первого, удовлетворялось функцией вида
Г = We*”, так что
/(/ш)Г = р.
Мы получим относительно столбца W линейное неоднородное алгебраическое уравнение с матрицей /(Zw) ранга п,—1. Для существования решений необходимо и достаточно, чтобы расширенная матрица ||/(/<*>), р|| имела тот же ранг-. А для этого в свою очередь требуется, чтобы соотношение
2^ («•>)/# (*»)== о,
3
774
НЕЛИНЕЙНЫЕ СИСТЕМЫ
[ГЛ. 12
которому удовлетворяют элементы fjk любого fe-го столбца матрицы /(Zoo), удовлетворялось и элементами Pj столбца р:
2^(to)/>j = 0. (12.30)
При этом, согласно прежнему соотношению, предполагается, что в Z-й строке матрицы F(Z<o) имеется элемент (/<»), отличный от нуля.
Замена коэффициентов pj их выражениями
Рз =—у Аbia> S &Vk+i J • • > Уп’ °) e~iu du к —тс
даёт:
АЫш 2 S Рц (to) fjk (to) У к = . к
=ч2г«(/ш) J ^e'iuda- <12-31)
Но, согласно известной теореме теории определителей, из A (Zoo) = 0 следует:
Fkj <Р°) Fkm (i°>) _
^(to) ~
так что
Fk; (Zto) Flm (Z<o)
Fij (to) У к = F* » = Fv (/(°) Fi™ (z“)-
Затем
5 2 Fu (i^fik (to) Vk = Fim 2 2 Fk3 W fjk (to) =
3 к 3 k
= Fto(z«) A' (to), (12.32)
<oA' (z®) = 2zwa
= 2Zoo2
A(D) (D — Z«) (D + Z<o)
D-i<o
= 2Z(o2 Ax (Zoo),
(12.33)
где
Ai (D) =
A(D) £)2Ц_<о2»
ПЕРВОЕ ПРИБЛИЖЕНИЕ
775
§ 12.3]
и потому
— = J W*> tye-^du. (12.34)
J —те
Если же разделить обе части на (fo>) Flm (/со) и отделить действительные и мнимые части, то
тс
2Л£ф9 = — - Re -дД-ч У У „ Т f Ъ (У*> °) e~iu du’ я ' Дх (z<o) Л4 Flm (Z“) J ‘3
3 -те
1 1 Fiл (Z<o) С
— Im . , V p J . %• (j*, 0)e~iudu = 0.
я Дх (йо) MJ Flm (z<o) J V v 3 -те
(12.35)
Фиг. 206. Определение порождающих амплитуд.
Обозначая левую часть второго уравнения через О(Л), представим его в форме (И); значения Л*, удовлетворяющие этому конечному уравнению, если они существуют, мы будем называть^ порождающими амплитудами. Решение может быть проведено графически (фиг. 206) или другими специальными приёмами. После определения порождающих амплитуд первое уравнение (35) даёт соответствующие значения первой поправки на частоту Ь.
Наиболее общее периодическое решение для г с частотой со по т будет:
Г = г* + 4 В (Veiu-\-Ve~iu) + 4- В, (Veiu—Ve~iu), (12.36)
где г* — решение неоднородного уравнения.
Произвольные постоянные В, В± не могут быть определены ца данном этапе вычисления, и в качестве приближённого выражения искомого периодического решения у может пока служить лишь столбец у* (27), в котором Л заменена одной из порождающих амплитуд Л*. Приближённым выражением поправки на частоту а будет:
а
(12.37)
Во многих технических задачах эти приближения оказываются достаточными, если удалось удовлетворительным образом выбрать упрощённую линейную систему; последняя должна аппроксимировать данную нелинейную систему не при всех её режимах, что, вообще, и невозможно, а лишь в режиме периодического процесса. Мы вернёмся к этому в § 9 в связи с примером следящей системы.
776
НЕЛИНЕЙНЫЕ СИСТЕМЫ
[гл. 12
9
§ 12.4. Второе и высшие приближения. Подставляя в правую часть уравнения (26) вместо у*, г их выражения (27), (36), находим:
/(Dt) s = — \f (DT) Dxc +f' (DJ D*t?\ 1A (Veiu + Ve~<*) —
— 2f' (Dx) DJ Ir* + -i- В (+ Ve~*«) + 4- si (Vetu — Ve~<*) £ &
n
+2S#- [<+Ts<y‘e‘“+v>e',“H fc=l
Разлагая правую часть в ряд Фурье в комплексной форме и замечая, что
^,м+Пе-*“= 2-^, Vke*»- Vke-iu — — (12.38)
получаем:
f(Dx)s = qe^+ ..., где
q = — i A [f' (/со) шс (до) (/ш)2 &2] V—f (Zoo) ЫЬ {В Ц- /Вх) V -|-
4W
А так как
§ 12.4] ВТОРОЕ И ВЫСШИЕ ПРИБЛИЖЕНИЯ
777
то, подставляя в выражение для q и переходя к элементам qp по* лучим: п
qj = — у А tfjk О) «»с +/Л (1’“) (г’ш)^2] Ук —
fc=l
п
— (В + iBi) 2 &к iwb Vk +
к=1
4- тс 4-тс
Д- — 4т I du +-^г | ф,е-<айа +
1 . те дА J TJ 1 теЛ J
г. ।
к дц I
e~iu du~
Условие периодичности, аналогичное (30), имеет вид
п
S О*0*) 4j = о»
j=i
а коэффициент при iBx в этом условии, согласно (31), будет:
п п п Т»
— J fye~iudu = (i
J=1 fc=l j=l —тс
Коэффициенты q', q" при В и с выражаются следующим образом:
п п п "кЛ
q'=— 2 2 f 'ik imb Vk~^~h.^HiFu J ^e~iu da*
^=lfc=l J=1 —тс
П П
я" =—-^ Ai<° 2 ’S FU (j^fik У к
J=1 fc=l
или, согласно (32),
Я’ == — bim Д' (io>) Flm (fa) +
d dA
n +"
-j 2^^ J fye-tuda j—1 — TC
q'' = — у A fa Д' (fa) Flm (fa).
Условие периодичности и сопряжённое ему уравнение могут быть представлены в виде
+ ... =0, q'B+q"c-\- ... =0, (12.39>
778
НЕЛИНЕЙНЫЕ СИСТЕМЫ
[ГЛ. 12
тде невыписанные члены не содержат ни В, ни с. Эти два уравнения дают определённые значения для В и с, если отличен от нуля определитель
q'q" — q'q" = 2Z Im (q'q") = 2/ Re (—iq'q") или
Re jАш Д' (— i<o) Flm (— iw) I — biw Д' (z<o) Flm (i<o) + n
+ ^4 I 2 (Z<0) J ^je~iuda
J=1 —тс
Величина
Д' (— 1<о) Flm iw) Д' (zw) Flm (iw)
действительна и отлична от нуля, вследствие чего, принимая во внимание (33)
Д' (Zw) = 2Zo> Дх (Zoo),
можно написать:
d dA
1 Г . 11
л л < У /• ч be~*“du ИО.
J=1 —«
А так как выражение в фигурных скобках было в § 3 обозначено через О (Л) и решения строятся для А = А*, то мы имеем окончательно:
G'(A*)=#0. (12.40)
Геометрически это условие обозначает, что кривая, изображающая функцию О (Л), не должна касаться оси абсцисс при А = Л*. Если условие выполнено, то мы можем определить В и с из (39). Что касается Вх, то, как мы убедились, коэффициент при этой постоянной в условии периодичности равен нулю, вследствие чего она остаётся произвольной. Для s может быть найдено решение, которое будет периодическим и будет содержать две постоянные С, Ср о значении которых, однако, пока ничего нельзя сказать. Поэтому второе приближение будет:
у = -у А (Veiu -Ve~iu
а = IF СН9-
Если функции аналитичны по всем аргументам, то это вычисление может быть продолжено до приближений сколь угодно высо-
1
§ 12.5] УРАВНЕНИЕ В ВАРИАЦИЯХ И УСТОЙЧИВОСТЬ РЕШЕНИЙ 779
кого порядка. Коэффициенты при С, Сх, d в третьем условии периодичности будут пропорциональны аналогичным коэффициентам во втором условии, вследствие чего третье условие достаточно для однозначного определения С и d, между тем как Сг остаётся неопределённым. Аналогично обстоит дело и для дальнейших приближений. В результате мы получаем периодическое решение и поправку на частоту в виде рядов
у =4 (Л* + тг 4-сн2+ . •+ Уе-<«) + X У 1 • j
• + i (ттi + • • •) (VV“— +
+ nV*r+^V+---> (12.41)
1 . I 1 „ .
« = bV- + 2f + • ♦ •
Постоянные можно приравнять нулю или определить из
какого-либо условия при и = 0, так как решение уже содержит произвольную постоянную 6 в составе и.
• Сходимость рядов и, следовательно, действительное существование формально вычисленного решения при достаточно малых р вытекает из общих теорем Пуанкаре и Мак Миллана. Однако порождающее решение-, представляющее приближение нулевого порядка для искомого периодического решения, вовсе не зависит от сходимости рядов.
§ 12.5. Уравнение в вариациях и устойчивость периодических решений. Для исследования устойчивости найденных периодических решений заменяем в (12) у через ЧУ, где Зу— малое прираще-
ние (вариация). Разлагая в ряд по степени Ъук и ограничиваясь членами первого порядка малости, находим:
I
f (D) су+8у) = и
п
(12.42)
Ограничимся частным случаем систем первого порядка, для которых f(D) = AD Ц- Н, где Л, Н—постоянные квадратные матрицы, и заметим, что так как у есть решение, то тождественно
(AD^H)y = ^(y, И). (12.43)
Уравнение в вариациях тогда будет:
где
или же
(ЛО + Я)оу = р.Ф(у, и)3у,
ч'О'.
(n X «),
[AD + H— уХ(у, |л)]8у = 0.
(12.44)
(12.45)
780 НЕЛИНЕЙНЫЕ СИСТЕМЫ [гл. 12
Мы получили линейное уравнение с периодическими коэффициентами относительно by; его характеристические показатели называются также характеристическими показателями периодического решения нелинейного уравнения.
Покажем, что для рассматриваемого уравнения, так же как и в других случаях, когда время не входит в уравнение явно, действительная часть по крайней мере одного из характеристических показателей равна нулю. В самом деле, время входит в периодическое решение в комбинации t—tQi где — произвольная постоянная. Подстановка решения в уравнение даёт тождество по t и £0, которое можно дифференцировать по £0. А так как это дифференцирование с точностью до знака совпадает с дифференцированием по /, то мы имеем:
[ДО + Я— рйГСу, h)1J = 0.
Сличая с (45), заключаем, что Dy является решением уравнения в вариациях. А так как столбец Dy и его элементы представляют периодические функции, то, сравнивая ещё с формой (11.12) решения уравнения с периодическими коэффициентами, заключаем, что характеристический показатель данного решения равен нулю или OknilP.
А. М. Ляпунов показал, что если действительные части всех характеристических показателей отрицательны, то периодический процесс устойчив и притом асимптотически; если же хотя бы одна из действительных частей положительна, то — неустойчив.
А. А. Андронов и А. А. Витт [12-2] показали, что если время не входит явно в уравнение и если характеристический показатель с нулевой действительной частью не является кратным, а действительные части всех остальных характеристических показателей отрицательны, то периодическое решение устойчиво. Эта теорема была ещё обобщена Н. Ф. Строковым [12Дб] и И. Г. Малкиным [1212].
§ 12.6. Решение уравнения в вариациях с помощью ряда по степеням параметра. Предположим, что 6, а значит, и Ф не зависит явно от р.. Разлагая Ф(у) в ряд Тейлора, имеем:
> (j)=т~ 2 (^-jp +
3
... =
* 3
= ,г+т! S(itV+5№+ +
3
+ 2! Zj(if+ 2Г••• =
i
= — ....
§ 12.6]
РЕШЕНИЕ УРАВНЕНИЯ В ВАРИАЦИЯХ
781
где
яз ю=- i S ад;-1 2 2 гл <ад; J J fc
(12.46)
При этом аргумент у* функции ЧР* и её частных производных опущен. Вводя переменную т и оператор Dx = dfdx по формулам
т = (1 + 4 СН2 + •••)/•
D = (l+1^4-1 СН3+
получим уравнение в вариациях в форуме
ADX (1 +1 ftp +1 С|*2 + ...) 4-Я-Ь^ (г) И+Я2 (г) р^+.
или
(12.47)
= О
0.
Пусть 0(т) есть некоторая фундаментальная матрица этого уравнения; будем искать её в виде ряда
0(т) = »(г)Ш)|4Ша + ...» (12.48)
причём
М*о) = 02(Ч>= ••• =0. (12.49)
так что
0 (То) = 0 (т0). (12.50)
Подставляя в уравнение и приравнивая нулю коэффициенты при степенях р, имеем:
(ADX + Н) & = 0,
(ADX + Н) = — {AbDx + Нг (?)]»,
(ADX + И) в2 = — Ц AcDx + Я2 (г)
0 —(ЛЮ. + ЯДт)] 0t>
(12.51)
Первое уравнение показывает, что & — фундаментальная матрица упрощённого линейного уравнения с постоянными коэффициентами.
Полагая
СО = » W »< (т),
(12.52)
имеем:
0 (т) = & (т) [Е + &х (т) |* + &2 (?) рз + ... ].
(12.53)
782
НЕЛИНЕЙНЫЕ СИСТЕМЫ
[ГЛ. 12
А так как
(ЛОТ + Я) f){ = (ADX + Я) (&»<) = (а£ + Я») + А» g =
то полученные выше уравнения для 0р 02, ... переходят в следующие:
А» = — АЬ — ЯД
dz rfx 1
А & ± А с % — Я2& + (—А Ь g—Нх Я) О, — А ЬЪ ,
dz 2. az \ аъ 1 / dz
или же, исключая производные от &, &р ... в правых частях,
(— йа + 4с)я + я1г> — Я2 & Д (Я6 — Ях)
Отсюда
&!= f 871А-1(Я6 —Я^&йт,
= | &-1а-1/ (_&2_|_±с)я+Я1й—Я2 &+
(12.54)
+ (Hb — Hj)
Матрица В будет:
В = 0 (т0)\6 (т0 + Р) = 0 (т0)\0 М-Р)
= 0 (т0) \ » (т0 + В) IE + 0! (ТО + Р) И +1% (т0 + Р) . I.
Обозначая через \ (з = 1, ..., s') и ^h± (Л=1, ..., s") дей-
ствительные и комплексные корни характеристического уравнения det|| ДЛЦ-ЯЦ = 0 упрощенной системы, введём матрицу Жордана J (§ 1.24). Каковы бы ни были элементарные делители, мы можем затем с помощью подобного преобразования привести её к матрице Кейли Q (§ 1.16). Обозначая ещё через v модальную матрицу, получим (§ 8.12):
D (т) = {р1 (т) =
(12.55)
"ОЛЯШШШ
§ 12.6J
РЕШЕНИЕ УРАВНЕНИЯ В ВАРИАЦИЯХ
783
откуда
Выражение матрицы В получает вид
B = e<?P + /fy4-Sy.2+ ...,
(12.56);
где
₽ = ^P&1(x0 + P), 5 = Л2(*0 + -Р).
(12.57)
Для получения характеристических чисел Ха матрицы В нужно решить уравнение
det J ЕХ — В || = О, которое при р = 0 принимает вид
(12.58)
det || Ек — eQP || = 0.
(12.59)
Заметим теперь, что так как уравнение det|| ДХ-|-#11 = О, по предположению, имеет пару простых чисто мнимых сопряжённых корней, то мы можем положить ± ± /оо == z±z 2rijP. При указан-
ном выше способе получения матрицы Q её субматрица, образованная пересечением и (s'О“й строк с (s'-|~l)‘M 11
(s' 1)-м столбцами, будет:
О 2г/Р — 2r.jP 0 |
причём на остальных местах в указанных строках и столбцах стоят нули. Для соответствующей субматрицы в составе матрицы е®р найдём:
Поэтому уравнение (59) имеет двойной корень X = 1, а получающиеся из него при рь =# 0 два корня уравнения (58) можно искать в форме ряда
Л = 1 -J- .
После подстановки выражений (56), (61) находим:
(12.61)
det||(£ —ееР) + (^ —Я)р + (Дт] —«5)Н9+ ...|| = 0. (12.62)
784
НЕЛИНЕЙНЫЕ СИСТЕМЫ
[ГЛ. 12
Благодаря наличию в составе е®Р субматрицы (60) мы получим при развёртывании последнего определителя ряд по степеням р. вида
В — 8'4-1
^?d'4-s"4-l, s'4-1
---4-1, s'4-8"-HL
$----^?s'4-s"4-l, s'4-8"+l
H2 + ... = 0, (12.63)
где К не зависит от рь и . Приравнивая нулю коэффициент при рь2, получаем квадратное уравнение относительно »
---(R*’ 4-1, 8' 4-1 R*’ 4-з"4-1, s' 4-8"4-1) 5 “h
+ (#8'4-1, s' 4-l#s' 4-8"4-1, 8'4-8"4-1—#s'4-l, s’ 4-s*4-l #8' 4-8"4-1, s'4-1) = 0* (12.64)
Для вычисления $ из этого уравнения преобразуем матрицу 7?. Подставляя с этой целью выражение (55) для &(т) в первое уравнение <51), имеем:
(ЛОТ+Н)^ = 0,
(AvQ 4- Hv) — 0,
Q = — v~1A~1Hv, и для матрицы &х(т):
(г) = f {e~^v~xA~xHbveqz — ^~1А~ГН^~) d-c =
•Со
= — J (fT&Qe^b + а'ЪГ1#!») dt.
Отсюда, пользуясь коммутативностью матриц Q, е&> е & и выполняя интегрирование первого слагаемого, получаем:
R = — eQP bQP + j & -1 (т) (т) & (т) dx .
(12.65)
Можно не продолжать этих вычислений, если мы желаем удовлетвориться определением В.
§ 12.7. Выбор упрощённой системы в случае одной нелинейности. Во всём предыдущем, и в частности при построении порождающих амплитуд согласно фиг. 206, упрощённая система предполагалась вполне определённой самим способом введения параметра рь и представления нелинейной системы в форме (12).
Мы покажем, как в простейших случаях одной или двух нелинейностей можно графическим путём не только найти порождающие амплитуды и первую поправку на частоту, но определить также основную частоту о> и некоторые коэффициенты упрощённого уравнения таким образом, чтобы уже при у. = 0 иметь удовлетворительную
§ 12.7] ВЫБОР УПРОЩЁННОЙ СИСТЕМЫ В СЛУЧАЕ ОДНОЙ НЕЛИНЕЙНОСТИ 785
аппроксимацию нелинейной системы в-режиме периодического процесса. Для систем регулирования с одной нелинейностью Л. С. Гольдфарб [12-4] разработал графический приём, основанный на методе гармонического баланса Н. М. Крылова и. Н. Н. Боголюбова и на применении диаграмм Найквиста. Такие^ же системы рассматривал А. И. Лурье [1л91; так как он произвёл также сравнение результатов^ получаемых по методу гармонического баланса и по методу, Пуанкаре, то мы ограничимся графическими построениями,, соответствующими второму из них.
Упрощённое линейное уравнение будем писать . попрежнему в виде (15).
Первоначальная система скалярных нелинейных уравнений пусть будет
Ai (£>)л +
• • "Ь/п (^)л
+ • • • (£0Уп=®>
fmi(D)yi+ ... +/Ы(Д)Л + ^(Л)+ ... +/^(0)^=0, (12.66)
fnl +
• • (Р)У1
+ ... +fnn (D)yn=0.
т. е. отличается от упрощённой системы тем, что в zn-м уравнении вместо ftnlSP)yi стоит сумма fml (D)yi-\-gtyj), где ё(Уг) — нелинейная функция от одной неизвестной Ур удовлетворяющая условию
J g(A cos u)du = 0. (12.67)
При образовании матрицы f(D) за элемент /n-й строки и Z-ro столбца берём /wZ(D)-(-/z, где h — постоянный коэффициент линеаризации, а на остальных местах должны быть попрежнему fatD). Элементы столбца определяем соотношениями
Ф1 • • • ФтП-1 Ф/П + 1 • • • Фп О»
(12.68)
Вместо первоначальной системы рассматриваем более общую, описываемую уравнением (12) с параметром |i. При = 0 оно приводится к упрощённому линейному уравнению, а при рь = 1 получается уравнение, соответствующее первоначальной скалярной системе.
Если /0 (О) есть матрица, получаемая из f(D) при 6 = 0 и
A0(D) = det/0(D), (12.69)
то, полагая
= ' (12.70)
имеем:
Д(О) = Д0(О).П+Л/С(О)]. (12.71)
50 Зак. 1474. Б. В. Булгаков
MS*
786
Нелинейные системы
[гл. 12
Определим теперь коэффициент линеаризации h таким образом, чтобы упрощённое уравнение ймело периодическое решение. Для этого строим частотную характеристику К=К(1ы) в плоскости комплексного переменного К и ищем точку (или точки) пересечения характеристики с действительной осью. Обратные величины абсцисс этих точек, взятые притом с обратным знаком, будут искомыми значениями /г, а соответствующие значения <о — частотами периодических решений. Значения h получаются конечными, только если Flm (Zo>) #= 0. При небольшом числе п выгоднее вместо графического построения определить /г, приравнивая нулю предпоследний определитель Гурвица, а оо — из разложения Д(О) на множители.
Заметим теперь, что в суммах, фигурирующих в уравнениях (35), отличны от нуля только слагаемые, соответствующие j = т. Второе уравнение имеет поэтому вид
Im т-у.-х Ф (У,) e~iu du — 0.
—к
Далее, полагая
At = ANl9 иг = и + Ъ9 (12.72)
имеем, согласно (19):
у* = Аг cos иг (12.73)
и
+ те 4-те
j К (Я)*-*" du = eni j (Аг cos «г) е~ tui dut.
Обозначая ещё через Ф (уг) первообразную для функции (уг) и
найдём:
+ w
J фт (Ai cos «г) cos ut dut =
—те
—тс
— TC
cos яг) cos иг dul9
(12.74)
[hAi cos U] — g(Ai cos izz)] cos и^иг=
= hAl —
(12.75)
cos izz) sin и^иг = — J УГ' (Аг cos kz) d (Лг cos иг) =
—те
— -^-[Ф(ДгсО5Нг)]- = 0. (12.76)
— к
§ 12.7] выбсФ Упрощенной системы в Случае Одной нелинейности 787
Следовательно,
4-тс
—тс
и второе уравнение (35) может быть представлено в виде
(Zw)
У(Лг)] = 0.
Так как в силу (18)
то мы приходим к заключению, что если
Im [^w(Zo>) Дх(— Zu>)] =/= О, (12.77)
то Аг должно удовлетворять уравнению
ЬАг — J(A) = 0, (12.78) которое при уже известном h может быть разрешено графически согласно фиг. 207 (на чертеже индекс I опущен). Первое уравнение (35) даёт тогда
& = 0. (12.79)
Фиг. 207. Графическое определение порождающих амплитуд.
Соотношение (78) может быть получено и из таких же соображений, что и в § 5.27; разлагая в ряд Фурье
/yz — Y1___
. Ыг
4-п
g(Az cos иг) =
g(A, cos az)daz
—тс
4-тс
—тс
g(A cos uj) cos Kj dat
cos ZZj -|-
+U J м — TC
cos Ui) sin иг dat
sin иг + ...
и учитывая, что первый интеграл исчезает в силу (67), а третий — по той же причине, что и (76), можем написать приближённо g(y*) = hy*, где коэффициент линеаризации h определяется
50*
?88
НЕЛИНЕЙНЫЕ СИСТЕМЫ
(Гл. 12
следующим образом:
1 Г
J g<Ai cos нг) cos аг da
—«
(12.80)
Это соотношение эквивалентно (78).
Мы не останавливались здесь на исключительных случаях, когда конечных значений h не существует или когда неравенство (77) обращается в равенство. Но такие случаи и их физический смысл, пови-димому, лучше выясняются на конкретных задачах. Пример такой задачи рассмотрен ниже, в §§ 9, 10.
§ 12.8. Случай двух нелинейностей. Пусть первоначальная система скалярных уравнений
• • +/1г1(О)д+ ... +/п (Я)д+ ... +
+/1мФ)уп = 0,
/шд (D)л + • • • +4л (D)У\ + £1 (д) + • • • +
+4л (°) Д + • • • +/Win Уп = °’
(^)л + • • • +4л(°) Д + • • • +-U (°) Д+
(12.81)
+ g2 (Ур + • • • +41№(°) Уп = °’
(п)л + • • • +WV • • • +4Ж+ • • • +
“"Н fnn (Р) Уп 0 ‘
содержит две нелинейные функции gx (yzx), g2 (yQ, которые входят в качестве добавочных слагаемых при выражениях (D) у^ fmJt(P)yh в упрощённой системе. Предполагается, что gi и g2 удовлетворяют условиям симметрии вида (67). При образовании матрицы f(D) за элементы я^-й строки /t-ro столбца и ап2-й строки /2-го столбца принимаем:
(Р) + (D) й2,
где hv h2— коэффициенты линеаризации, а на всех остальных местах оставляем f^iPY Элементы столбца ф определяем соотношениями
k = .. К = М*. —&(№)• Z.OOOX
у <12-82>
С помощью f(D) и ф образуем уравнение вида (12), определяющее нелинейную систему, более общую, чем первоначальная, и приводящуюся к ней при =х 1.
' Форма образованной нами матрицы f(D) такова, что её определитель Д (D) содержит h± и h2i во-первых, линейно, во-вторых,
§ 12.8]
СЛУЧАЙ ДВУХ НЕЛИНЕЙНОСТЕЙ
789
в виде произведения hyh2. Поэтому, если отделить действительную и мнимую части A (Zoo), приравнять их нулю и обозначить временно hAh2 через h, то мы получим два линейных уравнения относительно трёх величин й2, h. С помощью этих уравнений можно получить линейные выражения для двух величин через третью и подставить эти выражения в уравнение
hrh2 = h,
которое тогда обращается в квадратное относительно третьей величины. Путём разрешения этого уравнения получим соотношения
hr = hx ((о), h2 = й2 (ш)» (12.83)
правые части которых будут, вообще, состоять из двух ветвей. Эти соотношения определяют в плоскости hxh2 кривую Неймарка Clt выделяющую область устойчивости (§ 8.25).
Предположим теперь, что коэффициенты линеаризации й2 связаны с амплитудами Л?р Л?2 периодических колебаний в координатах у1$ у1з соотношениями
(Л^) — 0, *4 (A? = , .(12-84)
где
1 i*
71(XZ.)==V .1 & cos ui) cos dut,’
} (12.85)
-{-тс
A = Т j & (Ala C0S C°S UhdUh-
— ТС
Эти соотношения выводятся по тем же соображениям, что и в конце предыдущего параграфа. Из них можно для каждой пары значений /ц, h2 найти соответствующую пару Ait, Ai£ и с помощью соотношений (83) построить в плоскости A?tA?a кривую С2 с числовыми отметками о>, определяемую соотношениями вида
Аг, — (°0> Ah = <?2 (<“)• (12.86)
С другой стороны, согласно (17), (18), (72),
Аг ANr
A^~A*ht~
*\т (*°)
= k (со),
что даёт возможность для каждого « построить в плоскости AitA^ луч
Ah -= k (°>) Аг,,
проходящий через начало координат, Если теперь Аг, есть значение,
[гл. 12
790
НЕЛИНЕЙНЫЕ СИСТЕМЫ
*
получаемое при данном о> из первого уравнения (§6), то в пересечении луча и вертикальной прямой с абсциссой получим некоторую точку. Совокупность таких точек для разных о> составит кривую С3, определяемую уравнениями вида
А = Х1(<°). л?а = Х2(“)- (12.87)
Точки пересечения кривых С2, С3 дадут нам амплитуды Aj2 и частоты w порождающих решений, а кривая С± даст соответствующие значения коэффициентов линеаризации ht, h2.
Если учесть, что из такого же вычисления, что и в предыдущем параграфе, вытекает
4-тс
J 4ч (X? e~iU da = ехР ^г) — А (А)1>
— тс
+тс
v J 'UsO'*? e~iU da = ехР (A?s) — h G4)b
—Л,
(12.88)
то второе уравнение (35) при найденных Д^, Д^ удовлетворяется тождественно, а первое даёт первую поправку на частоту bt которая здесь опять будет, вообще, равна нулю.
Как и в предыдущем параграфе, мы не останавливались на исключительных случаях.
Пример системы с двумя нелинейностями можно найти в уже цитированной работе Я. Н. Ройтенберга, который также одновременно определял коэффициенты линеаризации, частоты и амплитуды порождающих решений, хотя его процедура отличается от только что изложенной.
§ 12.9. Периодические движения следящей системы. В качестве примера с одной нелинейностью рассмотрим следящую систему, которая отличается от описанной в д(о) § 8.23 только тем, что напряже-------------------------------- ние, приложенное к цепи якоря сервомотора, является нелинейной функцией g*(o) от входного напряжения о. Примерный график этой функции представлен на фиг. 208. Эта частная задача ------------------------------~ типична для многих вопросов теории регулирования, что имелось
Фиг. 208. Функция ^(а). в виду при первоначальной публикации решения [12»20J, Первое приложение методов нелинейных колебаний, а именно методов Н. М. Крылова и Н. Н. Боголюбова, составляет заслугу В. А. Котельникова и руководителя его кандидатской диссертации В, С, Ведрова.
§ 12.9] ПЕРИОДИЧЕСКИЕ ДВИЖЕНИЯ СЛЕДЯЩЕЙ СИСТЕМЫ 791
Уравнения рассматриваемой системы при x = z = Q будут*): TO(fyD4-l)9'==v, р = — (£2D2-|-ЛЮ + 1) ©,
(12.89) о = р — nv, 4 7
D(VD+l)v = g(o).
С помощью первого и второго уравнений исключаем р, v из третьего и четвёртого:
(А2 -|~ TUri) © -|~ (М “F Тп) ? 4" ? ~Ь 0 =
iv
TUVv + + У) ? + Тф = g(o).
(12.90)
(12.91)
Положим
g(a)==^a—ф(а)>
где 1/W—коэффициент линеаризации, и, как в § 8, обобщим задачу, вводя параметр р при нелинейной поправке ф(о):
(Z2 -|- TUri) ср -р (М ~Ь Тп) ? + ? Н“ ° ~ о, I
iv ..... < (12.92)
TUV<o +?*([/+ V) ? + Т?] + А а = нФ (’)• IV z
Очевидно, что W есть постоянная времени сервомотора в линеаризованной задаче.
Поскольку буквы х, z теперь свободны, введём обозначения: «
x = £2-j-7Vn, y = M-j-Tn, z = -^. (12.93)
Характеристическое уравнение упрощённой системы тогда будет: Д (D) ==е kQ& + kJF + + k3D + = 0, (12.94)
где
ka-wv. k^Tiu+vy. I (12 96)
k2 — XZ + Tt k3 —yz,» й4 = z. J
Сначала -пренебрежём инерцией сервомотора (V = 0). Тогда
Д (О) = k±D^ + = 0, (12.96)
kx=TU, k.2 = xz+Ty k3=yz, k^z. (12.97) Условия Рауса-Гурвитца могут быть представлены в виде x^+T>0, (xz+T)y— Т47>0, z>&, (12.98)
*) В отличие от уравнений (8.145), приведённых в § 8,23, здесь ^=^0, д коэффициенты Т и U не считаются равными I сек,
792
- , НЕЛИНЕЙНЫЕ СИСТЕМЫ
следствием из них является неравенство v>0.
Предпоследнее условие обращается в равенство Т)У — TU при коэффициенте линеаризации z, равном Т(Ц—у) --------------------------------W ’
[гл. 12
(12.99)
(12.100)
(12.101)
Упрощённая система имеет тогда периодическое решение, причём из разложения на множители
Д(О) = raD3 + (xz+7)D2+y?D + z =
_ TUD* 4. D 4-=
1 у 1 X .. 1 ху
= ти (D Ц- Д + П#—у). М 1 \ в
\ ~У/~ X \ 'у)
= ти (d 4- 1) (D2-4- = 0 (12.102)
определяется квадрат частоты
о>9=^=Л (12.103)
Коэффициент линеаризации z и квадрат частоты будут положительны,
если
✓
Лри этом
^>0.
X
f22(D) = xD2 4->D4-i,
Д1 (D) = 02^2 =TU(D-]-
1 х 7 2)2 -U 0)2 у у /
и
F22(Za)) =-X0)2-pl + iy<S— у(~--\-ил
* / • х_ TU * 1 . х
Д1 (—(1 — У'®)» ч
. Im [F22 (й) Дх (— гш)] == Тш (U—у).
(12.104)
(12.105)
(12.106)
(12.107)
’ (12.108)
(12.109)
При условии (104) эта величина будет действительна и отлична от нуля, вследствие чего первая поправка ца частоту t> окажется равной нулю, а для определения амплитуду периодических колебаний С В координате <? мы будем иметь обычное уравнение
гС==/(С), (12.110)
§ 1-2.91
ПЕРИОДИЧЕСКИЕ ДВИЖЕНИЯ СЛЕДЯЩЕЙ СИСТЕМЫ
793
где
J (С) = g(C cos и) cos и du.
— ТЕ
(12.111)
Однако для действительного существования периодических движений нужно, чтобы уравнение амплитуд имело решения. Но по свойству функций типа о которых была речь в § 5.29, их графики или, как мы будем говорить, интегральные характеристики (фиг. 209) имеют тот же общий вид, что .и графики функций g(y). Поэтому условие существования решений будет:
0 < z < z0,
(12.112)
где z$— угловой коэффициент луча, проведённого из начала координат на фиг. 209 и касающегося интегральной характеристики.
Фиг. 209. Интегральная характеристика.
При данном z, удовлетворяющем неравенству, уравнение (100) определяет в плоскости ху -гиперболу с центром
х =___Г 1
° г’ \ (12.113)
У =0 |
и асимптотами, параллельными осям координат. В силу условия (99) рассматривается только верхняя ветвь. Отрезок гиперболы на оси ординат при всяком z0 равен U. При z = Q гипербола обращается в прямую y = U, параллельную оси абсцисс.
При изменении z в интервале, определяемом неравенством (112), получается семейство гипербол, зависящее от одного параметра. В плоскости ху мы должны выделить три области: одна из них оме-тается верхними ветвями гипербол семейства и в ней возможны периоди-» ческие движения, другая остаётся внутри всех этих ветвей, а третья—< вне их, так что ни во второй, ни в третьей области периодические
794
НЕЛИНЕЙНЫЕ СИСТЕМЫ
[ГЛ. 12
движения невозможны. Но эти области уже рассмотрены нами в § 8.23 (фиг. 75) в связи с вопросом о ненадёжных параметрах, каковым в данном случае является z. Окончательное механическое истолкова-ние полученных сейчас выводов возможно только после рассмотрения вопроса об устойчивости периодических режимов; при этом выяснится, в частности, что поведение системы в двух областях несуществования периодических решений совершенно различно.
Вернёмся теперь к общему случаю, когда инерция сервомотора учитывается (У=£0).
Неравенства Рауса-Гурвитца могут быть представлены в виде
T(U-}~ V) > 0, у > 0, |
l(U-\-V){xz-\-T) — UVyz}y — T(i/+V)2>0, I (12.114) z > 0; ]
следствиями из них являются неравенства (У+ V)(xz-\-T) — UVyz>Q, xz-\-T>Q. (12.115)
Предпоследнее условие обращается в равенство
I(tf + V) zx-\-(U + V) Т— UVyz]y — T(U+ 1Z)2= 0 (12.116) при г = (12.117)
_y[(t/+V)x—uvy]
Из разложения на множители
Д (£>) =э TU VD* + T(t7+ V) D* + (xz + Т) D2 +yzD + z = = TUVD^-Y T(U-\- V)Z)3_|_riWJO_|_ t^.1 Da_|_
(12.118)
определяется квадрат частоты
, Q О-ГК -J
~~ (U^V)x-UVy
И выражение
At(D)=
(12.119)
(12.120)
§ 12.10] УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ движений
795
Коэффициент линеаризации z и квадрат частоты будут положительны, если
(U+V)x — UVy > °’
(12.121)
Так как для F22(D) имеем прежнюю формулу (105), то
F22 (Z<o) = — ха)2 +1 + Zyo> = у
x — UV _(U+V)x — UVy
Ц- Z<o
(12.122)
Д1 (—zw) = - [ — t/v>2+г/4- v— i (f/+ v) j<o] =
T[ —2C/V(t/+y)j/+l/yy2+([/+V)2x jL (У+Ю-*— UVy
— i(U-\-V)y<s>
(12.123)
Im [F22 (i<o) At ( — za>)] = V) xy +
+ UV(U + V)у — 4UV (U 4- V) у + UVy* 4- (LT4- У)3 x]
ИЛИ
Im (F22(Zco) Ax( —Zco)] = T^(U^V—y). (12.124)
Это выражение действительно и отлично от нуля при условии (121), вследствие чего, по общей теории, первая поправка на частоту равна нулю и порождающие амплитуды должны определяться аналитически или графически из уравнения (НО).
Для выяснения условий действительного существования таких амплитуд мы опять должны воспользоваться неравенствами (112) и выделить в плоскости ху область, ометаемую гиперболами семейства (116) с параметром z, где периодические решения существуют, и две области, где они невозможны. Это опять приводит нас к ранее решённой задаче (§ 8.23), к которой мы и отсылаем.
12.10. Устойчивость периодических движений следящей системы и общий характер движения. При проведении исследования устойчивости периодических движений следящей системы, согласно § 5, нужно иметь её уравнения в форме системы первого порядка. Чтобы при этом не слишком увеличивать число уравнений, ограничимся случаем, когда инерцией сервомотора можно пренебречь (V =0), и, пользуясь обозначениями (93), добавим к уравнениям (92) ещё одно путём дифференцирования первого. В результате получим систему
0
TU
(12.125)
геяь
796
НЕЛИНЕЙНЫЕ СИСТЕМЫ
[ГЛ. 12
исключая отсюда ср и ср, будем иметь:
— тих(<р+<з) — 7\х—Uy)(y®+с?+о) + х3 [ — 4- (°) ] = о*
Производя упрощения и комбинируя это уравнение с первым из (92) и с тривиальным соотношением Оср==ср, получим окончательно:
(xD+j/) <р-|-ср-|-<5 = 0,
ср — D© = О,
— Т (ху — Uy2 Ux) ср — Т(х — Uy) © +
+ [— TUxD — Т(х — Uy) — хЧг] а = —[лх9 (а).
(12.126)
Если рассматривать здесь ср как самостоятельную неизвестную, то мы имеем систему первого порядка, приводящуюся даже к форме Коши путём деления уравнений, соответственно, на х, —1, —TUx.
Нам в дальнейшем понадобятся элементы третьего столбца присоединённой матрицы
F13(D) = D, F23(D)=1, F88 (D) = — xD3 —jD — 1. (12.127)
Вычисляя для проверки операционный определитель упрощённой системы, найдём х9Д(О), где Д(£>) определяется согласно (94) и (95).
Если z имеет значение (101), то упрощённая система кроме двух мнимых сопряжённых корней ±Zo> имеет ещё действительный отрицательный корень —х; как видно из разложения на множители (102),
х = у. (12.128)
Три независимых частных решения упрощённой системы при этом будут:
&1) = &2) = Re (V2) еш), ’%) = Im (I/2) егш*)>
где V^, У2)—модальные столбцы, соответствующие корням —х, Zco. За элементы этих столбцов мы можем принять:
= ^13 (Z<0)> = ^23 <»’ М/Тз = F33 (Za))
^ = -у = -х, V2=4, V3 = -jJ, (12.129)
= гад, = —у -f- ко j, (12.130)
откуда
^ = <о, Ъ = «/2, N8=l, Т8 = 0, (12.131)
1
§ 12.16] устойчивость Периодических движений 797
Фундаментальная матрица будет:
«(0 =
Vte-^
V2e“x#
V z> —X#
V 3е
cos (mt-J- -fi) /V2cos (erf 4-72) W3cos (w/4-73)
Nt sin (<0/ —f— 7i) Mi sin (“*+ T2) W8sin(arf+73)
(12.132)
Матрицы eQp, A, в данном случае будут:
е<??=
2тсх
е
о
о
о
о о 1 О ’
о 1
(12.133)
0
—1 0
где
—TUx
.0
Ht (?) = ха
о о Z—g' О*)
(12.134)
о о
о о о
а* (?) = С COS (ак 6 -|- 7g).
(12.135)
Поэтому, обозначая через V (?) определитель фундаментальной матрицы и через Wjfc(?) — элементы присоединённой, найдём следующее выражение для подинтегральной функции в R:
(?) Д-i Я1 (?) »(?) = - *-
013^81 023^31
0 33^31
013^82 028^82
®33%2
Далее, полагая
sin р = х/]Лх2 -|~ с°2»
cos р = со/)/ х2-|- со2 ,
013^83
®23^83 ’
® 83^33
(12.136)
имеем:
013 = ^1^2 sin (72 — 71) = —
023 = [^1^2 Sin (<°Т Ч- 71) — ^2 V1 Sin (ш * + 72)1 =
= е~хг х2 -f- о2 (cos р cos sin Р sin сот) =
— ]/ х2 4“ со2 cos (сот — р),
033 = *~хх [^2^1 cos (<°- + 72) — А/1V2 cos (<°т + 71)] =
= в“хт ^Лх2 -|- СО2 (-sin Р COS СОТ -|- COS Р sin 0>т) =
= в“хт j/"x2 -|т со2 sin (сот — р),
V W = &31013 + »32028 + »880зз = V (0) (12.137)
где
v (0)=+ ЛГ8 /х2 + а>2 cos (Тз + Р). (12.138)
798
Нелинейные системы
[гл. 12
Так как & = 0, то матрица R, согласно формуле (65), будет:
TUV (0) J
*0
«13* р*&зх 0-23^31 033^31
13G v32
Я 23v32 33^32
©is* ~Рх®зз 023^33 033^33
(12.139)
где
(12.140)
Из этой матрицы нам для составления уравнения (64) потребуются элементы
—тс
_____ +w
# 23 = J* lz — s' (C cos -У)] cos (on — 0) sin (ok:+dv,
—тс
4-тс
^32 = f [^ — g-'(Ceos®)] sin (шт — P) cos (ar: + 73)
— TC
_____
# 33 = ^rXviof2 ,( [z~ g' (Ccos©)] sin (m —p) sin (шт+ 73) di». — TC
Пользуясь обозначением J(С) и замечая, что 4-тс 4-тс
— g'(Ccos^) cos2^6fo== Дг— g(C cos v) cos vdv = J'(С), 7C I uC 7C eJ
— тс —тс
имеем на основании (ПО): 4-тс 4-тс
-i- g' (С cos v) sin2 vdv = — J sin v gr (C cos v) d (C cos v) =
—те —те
кС
i vg(C cos-y)] I g(C cosv).cosvdv =J(C)=zt
—тс
<OT — — (Р + 'Гз + 6)> ‘“• + 7з = ® — е»
gr (C cos v) cos2 v dv = z—J' (C)t
—тс
л J
—тс
g' (С cos v) sin2 v dv = z — z = 0.
§ 12.10] Устойчивость Периодических движений 799
Отсюда
*22 = * ~ J' C°S Ф + ТЗ + 0) C0S 9>
*23 = — ,t ^rXvio)012 [z~J'(С)1 cos (Р + 'Гз + 9) sin 9>
Я32 = — It [Z _ У (QJ sin (Р + 73 4- 0) cos 0,
*зз = я I* — Г sin (? + 7з + 9) sin 9-
(12.141)
Квадратное уравнение (64) для $ имеет в данном случае вид
-. - (*22 + *ЗзН + (*22*33 — *23*32) = 0.
причём
*22 + *33 = —^~J>^ C0S (Р + Тб)-
^22^33 ^23^32 ~ 0*
Таким образом, один характеристический показатель будет равен нулю не только в нулевом, но и в первом приближении в соответствии с общей теорией, а от второго зависит устойчивость периодического решения, поскольку третий, бывший отрицательным при |л==0, останется таковым при достаточно малых рь.
Так как
ЛГ8)/ х2 ai2 cos (Р -}- 73) = —у<а — х = <о—- = оАг,
V(0) = ^(1+jAo2), то
*22+ *33= TU1T+№{Z-J'{C}}' (12Л42)
•>
В случае х > 0 периодическое решение, соответствующее точке пересечения луча zC с интегральной характеристикой ДС), устойчиво, если точка, перемещающаяся по лучу от начала координат, переходит из части плоскости, лежащей выше интегральной характеристики, в часть, лежащую ниже неё; в случае х < 0 мы имеем противоположное условие.
Как мы видели в § 9, периодические решения возможны только Для тех значений параметров х, у, где z, определяемое соотношением (101), удовлетворяет неравенству (112), т. е. в областях 2, 3 (фиг. 210 и таблица 13). В области 2 мы имеем х > 0 и, согласно только что сформулированному правилу и фиг. 209, устойчивыми будут колебания малой амплитуды Cv На прямой у = U, являющейся границей области 7, будет z — О, устойчивая амплитуда С±
НЕЛИНЕЙНЫЕ СИСТЕМЫ
• 11ч
[гл. 12
800
обращается в нуль, неустойчивая амплитуда С.2 — в бесконечность, частота со — в нуль. На гиперболе, являющейся границей областей 2 и 4, получается z = z0 и устойчивая амплитуда ^ сливается с- неустой-
Фиг. 210. Разбиение плоскости параметров по общему характеру колебаний.
, устойчивыми оказываются колебания большой амплитуды С2. На верхней гиперболической границе с областью 7 амплитуды Clt С,2 сливаются, на нижней границе y — U с областью 4 параметр z обращается в нуль, неустойчивая амплитуда Ct— в нуль, устойчивая — в бесконечность, частота оо — в нуль.
В области 1 периодические режимы невозможны. Если в окрестности начала координат мы положим в упрощённой линейной системе z = 0, поскольку касательная к графику функции g(y) горизонтальна при о = 0, то в области y>U и в области 7, являющейся её частью, мы будем
иметь сходящиеся колебания. Естественно предположить, что
колебания в этой области будут сходящимися при всех амплитудах. После того как это предположение было высказано при первой публикации настоящего исследования, оно получило подтверждение в работах А. И. Лурье (1210] и А. М. Летова [12Л], из которых выяснилось, что область 7, которую мы ранее называли областью
Таблица 13
Разбиение плоскости параметров по общему характеру колебаний
Область 1 (xzo+T)y>TU, х<0, х>0, _у> U t? о bl Надёжная устойчивость
Область 2 (xza+T)y>TU,y<U 0<*O0 Автоколебания малой амплитуды
Область 3 (xzQ + Т) у <TU, у > U 0 < z < z§ Автоколебания большой амплитуды
Область 4 хсо, о<у<и х>0,У<® (xz0 + Т)у < ГУ, х >0, у > 0, х < 0, у < 0 Z<0 £>*0 Заведомая . неустойчивость
§ 12.11] ПРИВЕДЕНИЕ УРАВНЕНИЙ К НОРМАЛЬНОЙ ФОРМЕ 801
надёжной устойчивости, есть та самая, где можно по методу А. И. Лурье построить функцию Ляпунова и доказать устойчивость системы «в большом», т. е. при любых начальных отклонениях.
Аналогичным образом в области 4 или области заведомой неустойчивости периодические режимы невозможны, но колебания являются расходящимися при всех начальных отклонениях.
Б. МЕТОД ОСРЕДНЕНИЯ
§ 12.11. Приведение уравнений нелинейной колебательной системы к нормальной форме. Пусть некоторый колебательный процесс в системе с п степенями свободы определяется уравнениями
п
S W1> • • •. Уп> 0 (7=1.......»)> (12.143)
А- — 1*
где, как и выше, символ D = -~ есть дифференциальный оператор, а у19 ..., уп обозначают неизвестные обобщённые координаты, зависящие от времени t\ и tyCXi, • • •> Уп> *) СУТЬ заданные функции своих аргументов, причём являются просто полиномами
любых конечных степеней с постоянными коэффициентами. Пусть тк есть самая старшая степень D в полиномах fjk(D) с данным фиксированным k; мы допустим, что функции могут содержать про-. изводные от каждого ук до (тк—1)-го порядка включительно; они не указаны явно лишь во избежание усложнения обозначений. Пусть, далее, Д(/Э) есть определитель матрицы \\fJk(D)||, a Fkj(D)— алгебраическое дополнение элемента fjk(D) в Д(О).
Предположим, что а) определитель Д(О) не равен тождественно нулю, б) все элементарные делители линейны, в) определитель коэффициентов при старших производных Dmkyki представляющий коэффициент старшего члена степени M = в разложении Д(О), отличен от нуля; г) все дроби Fjk(p)l&(D) с такими индексами /, й, для которых соответствующее есть нуль, а не равно тождественно нулю, являются правильными.
Воспользуемся результатами раздела Д главы 8 о нормальных координатах.
Первая группа основных соотношений—это преобразование (8.495), с помощью которого вводятся нормальные координаты. В данном случае таковыми будут амплитуды ..., а/, ..., а8н и угловыа пере-
менные ..., iLjft а преобразование (8.495) в силу сделанных предположений принимает вид
N а' с"
У} = 2 <6? So + X cos (а л + + vCft) (12.144)
а=1 Л=Г
(У г 1, • • • > И>, V —— 1, ••, fflrj)•
51 Зак. 1474. Б. В. Булгаков
802
НЕЛИНЕЙНЫЕ СИСТЕМЫ
[гл. 12
При этом ^ обозначает производную D^y^ и, в частности, само у$ при v — 0; wj равно наибольшему из чисел 0 и —1.
Нормальные координаты !ja, ah, ип, рассматриваемые как новые неизвестные, должны удовлетворять уравнениям, получаемым из (8.486) и (8.496) путём замены функций x^(t) через ^0^, .уп, t).
Заменяя в уравнениях (8.486) и (8.496) элементы &вл, р.» bj + 67/+h, и матриц Ьд, Ьб'+8"+п их выражениями согласно (8.472) и (8.473) и учитывая, что входящая в эти выражения матрица e(D) теперь, согласно (143), является единичной матрицей, можно представить уравнения (8.486) и (8.496) в следующем виде:
dah
dt
Д(П)
п
Хе )t=i
(12.145)
— 8Л+
I I 2 X
dt — Ш*_Г(9в,+й-1)!айШ’Ц Д(О) b=.ft+^ n
X e +Л, ktyk (.У1> • • • > Уп’ ty 1
fc=l
(A=l, ...,s").
Величины yk и их производные в правых частях уравнений (145) нужно представлять себе заменёнными их выражениями (144).
Напомним, что согласно обозначениям, принятым в разделе Д главы 8, yff(a= 1, ..., s')— действительные корни характеристического уравнения A (D) = 0, а z+z (h = 1, ..., s") — пары сопряжённых комплексных корней этого уравнения. Среди выписанных здесь действительных и комплексных корней могут быть и одинаковые; кратность таких корней обозначена, соответственно, через qa1 q^+h,-
Величины v$ в формулах преобразования (144) суть, согласно (8.466), элементы матриц-столбцов
0=1, ...» s'),
§ 12.11] Приведение уравнений к нормальной форме S03
<
где v9— модальные столбцы, соответствующие действительным корням ха. Так как по предположению б) все элементарные делители линейны, то для кратного корня хв модальные столбцы ф~ представляют собой линейно-независимые столбцы матрицы (ха). Эле- • менты всех столбцов v9 действительны и постоянны.
Величины w9k в уравнениях (145) суть элементы матрицы-строки '“’а = II«'«V да»2........i (° = 1............О-
Для каждого корня хв, кратность которого равна q9, имеем q9 линейнонезависимых строк we+p (р = 0, 1, ..., q9— 1), которые вводятся так, чтобы удовлетворялось соотношение (8.462) ' ' «а"1
р=0
где vff+p— только что упомянутые модальные столбцы. Матрица (хв) является квадратной матрицей и ранг её равен q9, поскольку модальными столбцами ф9±9 являются её линейно-независимые столбцы, то матрицы-строки wa+p определяются единственным образом.
При q9=l, т. е. для простого корня xff, соотношение (8.462) принимает простой вид
(*.) =?= V,-
Через W8r^ Ws^8ff^ обозначены матрицы-строки, аналогичные Ф)9, но соответствующие комплексным корням
Модальный столбец, соответствующий комплексному корню обозначен так (8.493):
. > * * пп
т. е. Njh — модули, а —аргументы элементов матрицы-столбца Vs'+h-
Согласно (8.494), через р и С обозначены модуль и аргумент комплексного корня ел-|-/а)л, т. е.
SA — Phe^h>
а величины в формулах (144) определяются так:
Мы перечислили все величины, входящие в формулы преобразования (144) и в дифференциальные уравнения (145).
Если среди корней характеристического уравнения Д (D) = 0 нет кратных, как это чаще всего бывает в приложениях, то величины
51*
804
Нелинейные системы
[гл. 12
yh, w9kt Wsr+ktki входящие в (144) и (145), можно определить следующим образом.
В случае простых корней по меньшей мере одна из величин Fkj (ха) при данном а и одна из величин Fkj (ел -|~ ПРИ данном h должны быть отличны от нуля; пусть
Z(a)(^e) ¥=0, F(2ft *4~ K°ft) 0. (12.146)
Так как ранг присоединённой матрицы F (xff) равен единице, то имеет место соотношение
Frn (а), I (а) (^а) Fjk (^а) Рj, I (а) С^а) Рт (ff), к (^а) =s 0,
и мы можем написать
PjM = V^ (12.147)
где
(12.148)
Г т (а), I (а) se
a s0 есть какой-либо определённый коэффициент пропорциональности. Сравнивая выражение (8.462) с (147), мы видим, что только что полученная величина есть та самая, которая входит в преобразование к нормальным координатам.
Аналогичным образом,
Fjk + ‘Ч) = W8,+h. к, (12.149)
Njifi 3 $h р (~ I , \ ’
гт (h), I (ft) V8h + 1<*W (12 150)
W«' + л, к = -7- ?т (Л), к (Sft + Ч) •
6ft I
Дифференциальные уравнения (145) принимают в случае отсутствия кратных корней следующий вид:
п
+уЪ S ....................<12Л51)
° к=1
(о = 1.....s'),
-iu п
= вЛ4- 2 Re [д/ toft)- 2 WS'+K к ..............уп, о], (12.152)
fc=l
-i п ............................°] (12-153)
ft=l
(6=1, ..., s").
Входящие сюда величины W8f+ktk определяются из (148) и (150). Переменные и их производные в правых частях уравнений
§ 12.12]
УКОРОЧЕННЫЕ УРАВНЕНИЯ
805
(151)—(153) нужно представлять себе, как и выше, заменёнными их выражениями (144).
При ^ = ...==6^ = 0 уравнения (143) будут линейными дифференциальными уравнениями с постоянными коэффициентами. Уравнения (151), (152), (153) становятся тогда независимыми друг от друга, что и показывает, что новые переменные uh имеют характер нормальных координат. Интегрируя, получим:
, ап = Ahe*if, иъ = <о^+
Подставляя найденные выражения в формулы (144), соответствующие v = 0, получим общее решение исходных уравнений (143) для этого случая.
§12.12. Укороченные уравнения. Квазипериодические и периодические режимы. Мы произвели пока лишь замену переменных, и (151), (152), (153) суть точные уравнения. Чтобы получить более простые приближённые уравнения, мы к условиям а), б), в), г), принятым в § 11, добавим новые. А именно, предположим, что: д) частоты линейно-независимы, так что не существует никакого соотношения вида2ййшл = 0» где gh СУТЬ целые числа, не равные нулю Л
одновременно; е) линейные члены shah в уравнениях (151), (152) малы в сравнении с ж) нелинейные поправки
•••’ Уп> 0 также малы для рассматриваемых значений аргументов (псевдолинейные системы) и з) при изменении А если оно действительно входит явно в fy(y19 ...» уп, t), эти функции меняются медленно в сравнении с их изменением, происходящим от аргументов
При этих условиях амплитуды ah будут расти или убывать медленно в сравнении с самими колебаниями, и мы можем применить осреднение по, угловым переменным
+(2к)8<> д/ К) 2 .(• • • J • • • dMs" >
806
НЕЛИНЕЙНЫЕ СИСТЕМЫ
[гл. 12
Это и есть «укороченные» уравнения. Первые две группы этих уравнений не содержат неизвестных главное преимущество заключается, однако, в том, что мы получили уравнения в медленно изменяющихся переменных. Угловые неизвестные uh найдутся путём квадратур из уравнений третьей группы после определения $в, из уравнений первых двух групп.
Если функции не зависят от Д то мы найдём, в частности, квазипериодические режимы, если потребуем, чтобы амплитуды $в, ап были постоянны. То же самое предположение нужно сделать и
в отношении производных и если представить их в виде
Ън— постоянные, подлежащие определению, то мы получим вместо (154):
Из этих конечных, но, вообще, нелинейных уравнений
можно определить s'4-s" стационарных амплитуд ah и s" поправок на частоты
Выражения (144) для в этом случае принимают следующий вид:
8^ 8^
Л = 2 SMKcosK(l+^K+8ft + u + vCft] (12.156)
а=1 h=l
(/= 1, 2, ..., п),
8Л суть произвольные постоянные.
Уравнения (155) могут рассматриваться как прямое обобщение уравнений для простых периодических колебаний, полученных с помощью метода Пуанкаре в предыдущем разделе настоящей главы. Рассматривая здесь этот случай, заметим, что если все кроме некоторого
§ 12.13] РЕГУЛИРОВАНИЕ ПОЛОЖЕНИЯ СИСТЕМЫ 807
исчезают, то получаем:
Уэ + Njhah cos [а)л (1 + (12.157)
ст=1
(7=1.2........n)
И
4-тс 4-тс
[ ... f ^k6~tut dux ...dua» = 0 при l^h. (12.158)
Формулы (157) определяют простое периодическое решение; при следующих
этом величин £р . .., ah> bh определяются из уравнений (число'которых также равно $'4“2)‘-
п
+ 2яД' (х0) ju W’fc J " fc=l —тс
tyk d^h — О
П
--ТС
1
a-=i
— ТС
П
duh
= 0,
(12.159)
Д'(ч + ^)^ fc=l
— тс
^ke~iuhdah =0.
В ещё более специальном случае, когда характеристическое уравнение не имеет действительных корней, а, кроме того, вл = 0, остаются только две величины ап = Ап и bh, которые необходимо определить. Заменяя элементы матрицы-строки их выражениями
согласно (148), легко видеть, что последние два уравнения (159) могут быть получены из уравнения
п
\^-iu^duh (12.160) ' Jx/ —<
л fc=l —тс
при отделении в нём действительной и мнимой частей.
Уравнение (160) совпадает с уравнением (34) [в последнем заменяем Д^до) при помощи (33)], полученным в разделе 12, А по методу Пуанкаре.
§ 12.13. Регулирование положения системы, обладающей естественной направляющей силой. 1°. Исходные уравнения движения. Рассмотрим колебания системы, определяемой уравнениями
Т’2© = — Lfo— йф— Н~Ьх (регулируемый объект), ]
. / . .. 1 ч 1 (12.161)
-}-Н ( /ф -1- Х<? -1~ К2ф-у \ (сервомотор),
\ / J
808
НЕЛИНЕЙНЫЕ СИСТЕМЫ
[ГЛ. 12
причём <р есть отклонение от желаемого состояния, рь — координата органа управления, приводимого в действие сервомотором, /—внешнее возмущение; ©, / предполагаются безразмерными. Заглавные
буквы Т, U, V, W‘, X, Y обозначают постоянные, имеющие размерность времени, a k, I, т — безразмерные коэффициенты. Эти уравнения, с точностью до некоторых обозначений, совпадают с уравнениями (8.21), приведёнными в § 8.8.
Периодические движения аналогичной системы были рассмотрены в § 9. Обобщение по сравнению с изложенным состоит в том, что здесь учитывается естественная направляющая сила — feo и рассматриваются не только установившиеся колебания, но и переходные процессы в их окрестности; эффект силы инерции сервомотора—У2р. и внешней силы у рассмотрен лишь частично. Характеристика сервомотора — обычная и представлена на фиг. 211; параметры V2, W выбираются так, чтобы максимум функции /7(6) был равен единице, а параметры У2, Х> I, т — таким образом, чтобы аргумент
+ 1-н (12.162)
tf £>
пропорциональный открытию реле,
Фиг. 211. Характеристика сервомотора.
принимал некоторое стандартное значение ф* (например, 0,1) в середине области быстрого возрастания //(ф).
Постоянные времени Т2, (/, У2, W и передаточное число обратной связи т предполагаются положительными; k положителен для естественно устойчивой системы, но он равен нулю для нейтральной и отрицателен для неустойчивой. Отрицательные значения по-
фирования X и коэффициента I сами
стоянной искусственного демп-по себе неинтересны, но нам
нет нужды заранее исключать их из рассмотрения, так же как и отрицательные значения постоянной У2.
Основная задача состоит в получении граничных линий, отделяющих области допустимых значений параметров, которые обеспечивают
удовлетворительное течение процесса регулирования.
С помощью первого уравнения (161) исключаем из выражения (162) и из второго уравнения (161) и находим:
(т2+/пУ2) ф 4- (^+/п^г) ?+(k+?—^Ф = X»
T^vZ^(UVi+WT^'i + (V^k+UW)’<?+Wk^-\-H(:b)= (12.163)
§ 12.13] РЕГУЛИРОВАНИЕ ПОЛОЖЕНИЯ СИСТЕМЫ / 809
В случае идеального управления без инерции (V = 0) и сопротивления (UZ=O) второе уравнение даёт /7(ф) = 0 и мы должны иметь всё время ф = 0, так как Н($) не обращается в нуль при других аргументах. Первое уравнение принимает вид
(Т2 + /пУ2) ? + (^+^ЛЭ? + (й + //п)с? = х; (12.164) оно определяет линейные затухающие колебания, возмущаемые силой х» причём T*-\-mY\ измеряют полную инерцию,
демпфирование и статическую устойчивость. Первые слагаемые в этих двучленах характеризуют соответствующие естественные свойства, а вторые представляют приращения, привносимые регулятором. Мы будем предполагать, что
Т2 + апУ2>0, А?Ц-7/п>0. (12.165)
Для значений ©g, и соответствующих положению равновесия при постоянной силе ysi мы имеем, согласно первому уравнению (161) и уравнениям (163),
*Гв + нв = Х8> (* + Ьи) — Не = Ъ> #(ф8) = 0;
последнее из этих трёх соотношений даёт = 0, а из первых получается:
т. = ^. = <l2-166>
В общем случае мы можем обозначить через у8 некоторое постоянное среднее значение внешней силы (в частности, нуль) и представить уравнения движения (163) в виде
[(7'2_|-ту2)О2_]-(У-(-тлГ)О4-(й-4-/т)](?-<р8) —/и<р= ' = х—Xs-
[ T^Di -4- (UV* + ITT2) D3 + (V2k + UW) D2 +
+ WkD] (? - ?s) + H (Ф) = + WD) (X — Xs).
Из этой формы можно получить вывод, относящийся к роли сигнала У2<р. Обозначим
_/Г2 —А»у2 тТ2 _ХТ2— UY*
72 ’ — 72 _|_ ту%' 72 ’
так что
7__I (^ ~~ те) I U ~ ^е)
е ‘ тпте ’ е * тте ’
уд___ т?)
тте
(12.168)
(12.169)
810
НЕЛИНЕЙНЫЕ СИСТЕМЫ
[ГЛ. 12
Тогда при постоянной внешней силе Х = первое уравнение (167) может быть написано в виде
[Т-ЗО2 _|_ (у+ теХе} D + (ft + zeWe)J (? — ?в) - твф = 0;
то же самое получается из того же уравнения, если рассмотреть другую систему, у которой параметры /, т, X, Y имеют изменённые значения /е, те, Хв и 0. Так как и второе уравнение (167) будет одно и то же для обеих систем, то динамика колебаний около положения равновесия будет та же самая. Мы видим, что в этом смысле регулирование по ускорению эквивалентно изменению параметров /, т, X в системе, не имеющей такого регулирования. Мы можем сделать даже т —> оо и всё же получить любые желаемые значения /е, те, Хв эквивалентных параметров, давая /, X» У2 конечные предельные значения
. k .и
/=Ч + —, Х=Хв + —, /2 = — , (12.170)
е * те ’ в 1 те тпе 4 7
получающиеся из (169). В этом случае регулирование по ускорению вполне заменяет отсутствующую материальную обратную связь, обеспечивая обычное «сдерживание» слишком энергичного функционирования регулятора; с другой стороны, как показывает первая формула (166), статическое отклонение <ps равно нулю при любом постоянном Одновременное достижение обеих целей оказалось возможным только благодаря регулированию по ускорению.
Чтобы уменьшить число постоянных параметров в уравнениях, введём вместо неизвестных <р, <J>, заданной функции / и независимой переменной t новые переменные, определяемые формулами
в которых р, q, г суть
постоянные. Обозначая
г = уА (12.171)
(12.172)
dt ’
мы приведём уравнения
движения (167) к виду
(7’2 + тУ2)^Е2 + (г/+тЛГ)^Е + (А! + /т)р x — my = qz,
TW^EL-^fJJV^+WT*) Е^(V2kUW) Е^Wk Е *+
+ н (у) = ( V2 ± Е2 4- е) Z.
Если же положить
тп
Т2 -J, zn/2
(12.173)
г =
§ 12.13} РЕГУЛИРОВАНИЕ ПОЛОЖЕНИЯ СИСТЕМЫ
и ввести обозначения
811
U ГT* + mY* _ k (T* 4- mY%)
T2 V k + lm ’ a~ T'+k + lm) ’
ft_ _ U + mX
r V(k + Im) (T* + mY*)’
(Г2Ч-отУ2)а/« _ У2 / k+lm' gF3
Г31Гт(й4-/т)^’ — m‘ W V Т^т^' ° ~ T2 ’
то получится:
(£2Ц_реЦ_1)х— =
[р£4 + (1Ц-Л4р)ЕЗ + (Л1-|-ар)Е2 + аЕ]х + 'ГЯ(зО==
= (А + а)(рЕ2 + £)г. .
(12.174)
(12.175)
Полагая q = ni' или q-T^Y2, можно обратить X или о в единицу. Сделанная нами замена переменных связана с тем новым условием, что при Z == 0 или У\= О нельзя рассматривать предельный случай т —> оо.
2°. Приближённая линеаризация. Сделаем первое ограничение постановки нашей задачи, предполагая внешнюю силу постоянной х = х8, откуда вытекает, что £ = 0.
Постараемся аппроксимировать Н(у) в рассматриваемой области значений аргумента биномом g-\-hy, т. е. заменить часть характеристики надлежащим образом выбранной секущей. Это приближение должно быть приспособлено прежде всего для изучения периодических колебаний, поскольку их возможность и свойства являются определяющими для движения .системы вообще; фактическое определение амплитуд и коэффициентов бинома будет сделано ниже. Рассматривая пока gt h как известные, напишем уравнения (175) в виде
(£2 _|_ ! ) (х _ _ (у _j*) =
[рЕ4 + (1 + Мр) Е3 + (М + ар) Е2 4- аЕ] (х — х*) + • +тЛ(.у—>*)=*2>
где
х ~ h’
(12.176)
(12.177)
= 0, % = 7 [g+ hy—H (у)] = 7 {h {у — у*) — Н Су)]; (12.178)
ф2 есть малая нелинейная поправка.
Вычёркивая Фх, ф2, мы получаем линейные однородные уравнения с постоянными коэффициентами относительно неизвестных х — x*t у—у*. Будем называть эти уравнения упрощёнными; их операционный
812 НЕЛИНЕЙНЫЕ СИСТЕМЫ . [гл. 12
определитель есть
+ -1 _ pE* + (l+Mp)E8 + (2M-4-aP)E2-|-aE —
==d0E1+d1E8-j_</2£2_)_d3£_)_j4> (12.179)
причём
d0 = p. dx= 1 +Л4р, d2 = + Л14-ap, 1
d3 = M + a> d4 = 7A- I ( • )
Условия Рауса-Гурвитца для характеристического уравнения Д = 0 могут быть написаны в виде
dx =51 Л4р >0, d3 = рчй -|- а > 0, 2 2 2.. (12.181)
4t^3----------^1^4 = ^Й + e±h 4- ^2 > ^4 = ?й > 0, J
(12.181)
где
e0 = (W+(M—₽)р),
e1 = 7(a-f--'WP — 1+(—ap + Ala Ц-Л12Р — 2Л4)р-|- • + Ж(ар — Al)p2], j е2 = Ma (1 -р Л4р + ар2).
(12.182)
Корни трёхчлена суть
*1’ (12.183)
причём
/?21== [а — 1 4- (— ар 4-Ма + Л42р—2М) р±М (ар—М) р2]2—
— 4Л4ар[1 4-(Л4 — р)р] (1 4-Л4р4-ар2), (12.184)
a R есть положительное значение радикала
Упрощённые уравнения допускают периодические решения в том случае, когда характеристическое уравнение имеет пару чисто мнимых корней. Для этого необходимо, чтобы предпоследнее неравенство Рауса-Гурвитца обратилось в равенство, т. е.
— d^d^ = е0й2 4- (12.185)
и, следовательно, й имело одно из значений й^ (/=1, 2). При этом условии имеем, применяя его для исключения d2 из выражения ДГ dtd,A = + d\d3E3+(<Мз + Е*+^lE + djd.^ =
— d±E2 (dQd3E2 4- drd3E 4~ d±d^ 4~ ^з (^о^з^2 + d\d^E 4~ d±d^, '
или же
где
d^ = (d0^2 + 4- d±d^ (E^ + u>2), (12.186)
ds fahj + a _ dxd^ d^ 1 -|- Л4р djd‘> ——
\ 12.187)
§ 12.13] РЕГУЛИРОВАНИЕ ПОЛОЖЕНИЯ СИСТЕМЫ 813
Если полученное выражение для действительно и положительно, то оо действительно и представляет угловую частоту периодического движения по отношению к безразмерному «времени» т. В следующем разделе мы выясним, при каких условиях значения пригодны для построения удовлетворительного линейного приближения для функции Н(у)} в этом случае периодическое решение упрощённых уравнений будет приближённо представлять такое же решение точных нелинейных уравнений.
Рассмотрим предельный случай самотормозящегося сервомотора, когда его инерцией можно пренебречь (V — 0, р = 0). Тогда
с?о = О, dx=l, = + ^3 = ₽7^ + а> — (12.188)
ео = ₽Т2> = Т (а + W—1), е2 = Ма, (12.189)
= а —Л4₽+11р^), (12.190)
#2 = (а_1)2_2(а4-1)Л40-|-(Лф)2, (12.191)
ш2 = рт/г<+а=^ = у(а — Н- 1 /?); (12.192)
при этом djd% == 7^/(7^ -|- М) заведомо действительно и положительно при действительном положительном Первый квадратичный множитель в правой части (186) обращается в линейный двучлен d3E-\~d4i и характеристическое уравнение имеет три корня —х, ±гсо, где в силу (185)
>'• = § = +М = 1(-а+ Мр + 1=р/?). (12.193)
Для выяснения механического смысла формулы (192) сделаем постоянную естественного демпфирования регулируемого объекта у, а следовательно, и 7И, равными нулю. Тогда для <о получаются значения 1 и ]Ла, причём второе действительйо лишь при а > 0. Для получения угловых частот по отношению к натуральному времени t нужно, согласно (171), делить на г. Пользуясь (173) и (174), получаем частоты
Первая из них есть частота внешнего колебательного цикла, образуемого регулируемым объектом и регулятором и характеризуемого полной инерцией и полным коэффициентом восстанавливающей силы [ср. уравнение (164)]; вторая частота соответ-
ствует естественно устойчивой системе с выключенным регулятором. Затухание при этом не учитывается.
Другой предельный случай получается, если сделать равной нулю силу сопротивления сервомотора (117=0; р = оо, 7 = оо). Отноше-ние р/7 при этом остаётся конечным. Из формул (182), (183) видно, что
814
Нелинейные системы
[гл. 12
один из корней А* обращается в нуль, а другой получает предельное значение
р М (ар — 7И)
Y Р(Р-М) ’
Имея в виду только это последнее, мы должны при вычислении <о2 с помощью второго выражения (187) пренебречь в числителе величиной а по сравнению ffyA, а в знаменателе — единицей по сравнению с Мр. После деления на г получаем с помощью (173), (174) частоту периодических колебаний
pTA 1 __ /~1Г Г . тХ Мр г “ V mV* V ‘ U ’
(12.195)
Первый множитель справа представляет частоту внутреннего колебательного цикла, образованного сервомотором и реле, отключённым от регулируемого объекта. Соответствующее уравнение движения есть
н);
аппроксимируя, как и выше, характеристику Н линейным выражением, мы и получим линейную.систему с угловой частотой (h/niV'2)\ 3°. Установившиеся колебания и уравнения переходных процессов в их окрестности. Мы сделаем теперь для упрощения второе ограничение условий задачи, имея в виду во всём дальнейшем случай безинерционного сервомотора (У = О, р = 0). Операционный определитель принимает вид
£2 + р£-|-1
— 1
7А
= E34-d2F2 + d3E-|-d4, (12.196)
причём мы имеем относящиеся к этому случаю формулы (188) — (193).
Применим с указанным ограничением общее преобразование к нормальным координатам и укороченные уравнения к псевдолинейной системе (176), беря для А одно из значений А$ и полагая
х± = х— х*9 х2=у—у*9 (12.197)
sz = sz/=l, xi ——®2 = 0> — = (12.198)
Если принять ^=$2=1, Z(l) = Z(2) = 1, то из (147), (148) получается: __ 1 _ 1
V11~ «м- Q ’ где, согласно (192), (193),
z»(l) = m(2) = 2, (12.199)
ti21 = l, (12.200)
(12.201)
§ 12.13] Регулирование Положений системы 815
Аналогичным образом
А/12 ехР *112 = = ___ш2 -f_ 1 -|- /рсо ’ ^22 еХР ^22 = I • (12.202)
Так как условия в), г) из § 11 выполняются, то, полагая
51==а, а2 = Ь, и2 = и = сот-]-0, (12.203)
имеем согласно (144) преобразование
х — X* 4~ + М.2& COS (U + 712)»
х = — — N12&b sin (и 4- Т12)>
х = vn^a — N12M cos (u 4- Ti2)> у = у* 4- a 4~ b cos и
к новым неизвестным а, b, и. Далее заметим, что
А (Е) = (Е 4- х) (Е — Z(o) (Е 4- Zo>),
Д' (х) = х2 4~ <°2, . Ал (*°>) = 2(0 (— (о 4~ Zx),
(12.204)
(12.205)
1^22 _______(— to2 + 1 + Zpto) (— а> — Zx)
Д' (Zco) 2<о (х2 -f- ш2)
и вспомним, что ^ = 0; тогда уравнения (151), (152), (153) для данной задачи примут вид
db р, (со (о>2—l-|-6x)+Z Гх (в>2—1)—Всо2] . . . А । , Л
-т- = Re {—------- - । ох-----—-—4 е~гиФо (у* + а -4- b cos а)},
ат j <о (х2 + w2) i » /j ’
I 1Т (<° (<о2“1 -bBx)+Z[х((о2-1)-ра)21 . * . . 1
-г-=ш+-г1т{—---------- /-о- .- ох—- в-шФо(у*4-а+&с05м)>.
4/т b I <0 (х2 + (О2) I I /J
(12.206)
Чтобы получить укороченные уравнения, находим с помощью формулы (178):
^2 (J'* 4~ а + b cos и) cos и du
4-те
= ------ [ Н(у*4-^ + b cos и) cos и du
—те
816
НЕЛИНЕЙНЫЕ СИСТЕМЫ
[ГЛ. 12
а также, полагая ф2 (у) = ЧГ (у):
4-тс
J Ф-2(Д,*_Ьа + ^ cos и) sin и du =
—тс
+тс
1 f
= — I ЧТ' (у* 4- а b cos и) d (у* -j- a -j- b cos и) =
—тс
= 4-« + bcos«)]1: = 0.
Пользуясь этим, замечая, что, согласно (201),
о)2 — 1 4- рх = zp R,
и заменяя правые части уравнений (206) их средними значениями, получаем:
^ = А(а,д), % = В(а,Ь), (12.207)
4-тс
du dx
те
—тс
(12.208)
где
h^a—
—тс
те J
—тс
cos и) du ,
► (12.209)
В (а, Ь) =
В качестве первого приложения мы воспользуемся этими уравнениями для определения состояний установившихся колебаний, соответствующих решениям а = а*, &==&*, где а*, А*— постоянные. Для этих значений мы должны иметь Л (а*, А*) = В(а*, А*) = 0. Кроме того, чтобы обеспечить наилучшую местную аппроксимацию для искомых состояний и в их окрестности, потребуем, чтобы все средние значения в (209), происходящие от тех членов точных уравнений, которые содержали 62, исчезали при а = а*, А = А*:
+тс
А^* — [
2те J —тс
н (у* 4- л* 4“ cos и) = о.
+тс
А^А*------- I Н(у* 4~ и* 4" cos и) cos udu = 0.
§12.13]
РЕГУЛИРОВАНИЕ ПОЛОЖЕНИЯ СИСТЕМЫ
817
Отсюда следует, что ха* = 0; из (191), (193) вытекает, что х не может обращаться в нуль при конечном р и ТИ > 0. Поэтому должно быть а*=0 и
4~ тс +тс
J Н (у* b* cos и) du — 0, — -i- J Н(у* b* cos и) cos и du—0.
—тс
тс
Так как Н(у) есть нечётная возрастающая функция, то первое соотношение возможно лишь при j/* = 0, хотя в случае несимметричной характеристики дело обстояло бы иначе. Второе соотношение может быть написано в виде
/(&*) = й^*, (12.210)
где
4-тс
/(&) = — H(b cos и) cos и du. (12.211)
Из конечного уравнения (211) определяются стационарные амплитуды й*. Значениям а — а* = 0, й = й* соответствует, согласно (208), постоянное значение ш производной Соотношения (204) показы
Фиг. 212. Определение стационарных амплитуд.
вают, что в переменных х, у при этом получается периодическое решение. Оно определяет установившиеся незатухающие колебания; если они устойчивы, то это будут автоколебания.
Мы могли бы получить периодические решения также по методу Пуанкаре, пользуясь теми же упрощёнными уравнениями, что и выше, и полагая в них g= х* —у* = Q, h — h^ «порождающие» амплитуды совпали бы с й*, а первая поправка на частоту была бы равна нулю. Сравнение с точными решениями для простейшей ломаной характеристики дано ниже, в 6°.
4°. Граничные лин и и. Уравнение (210) можно разрешить графически (фиг. 212), определяя стационарные амплитуды как абсциссы точек пересечения кривой c = J(b) и секущей c = hjb. Эти точки могут быть отличны от начала координат только при 0<й^<Л*, где h* есть угловой коэффициент проведённой через
начало касательной к кривой с~ J(b). Таким образом, существование и поведение периодических решений зависят от характера корней трёхчлена Чтобы изучить их зависимость от
52 Зак. 1474. Б. В. Булгаков
818
НЕЛИНЕЙНЫЕ СИСТЕМЫ
[ГЛ. 12
параметров системы* будем интерпретировать величины
~ T*(k-\-lm)’ Г2 (k + 1т)
= (12.212)
как координаты точки на диаграмме (фиг. 213). Параметры т, М считаются при этом фиксированными.
Вследствие (191) уравнение /?2 = 0 представляет коническое сечение; переписывая его в форме * «ч '
' (— 5 + 'Г))9— + |) = о, (12.213)
* \ ~ /
видим, что это — парабола, ось которой —£ + '*) = О является биссектрисой угла между координатными осями. Кривая касается этих осей в точках (1,0) и (0,1); при переходе через оси меняются знаки коэффициентов е$ = (т3/Ж) т| или е2 = ЖЕ. Коэффициент ех меняет знак на прямой
^/7 = $ + ^—1=0, (12.214)
проходящей через точки прикосновения (1,0) и (0,1).
Найдём ещё геометрическое место точек, в которых один из корней принимает значение /г.., так что = или,
согласно (189),
(TA + 41)(M + 7M) = ^- (12-215)
Это уравнение представляет прямую, касающуюся параболы в точке с координатами
(12.216)
При 7Й* = 0, оо эта касательная совмещается, соответственно, с осями т| и Е, а точка касания совпадает, соответственно, с. точками (0,1) и (1,0). Поэтому на оси Е один из корней h обращается в бесконечность, а на оси ?| — в нуль.
Парабола, две координатные оси и касательная (215) разделяют плоскость Ет| на одиннадцать областей, которые показаны нафиг. 213. В таблице 14 приводим знаки величин е0, ev е2> R3 и характер корней в этих областях.
Мы видим, что установившиеся незатухающие колебания возможны лишь в областях 6, 7, 8, 9\ их свойства существенно связаны с их устойчивостью, которая исследуется в п. 5. В частях плоскости, образованных группами областей /, 2, 3, 4, 5 и 10, 11 (на чертеже заштрихованы), периодические колебания невозможны. В первом случае а > 0 и, следовательно, k > 0, так что система статически устойчива; поскольку никакие установившиеся состояния, кроме равновесия, невозможны, колебания затухают при всех начальных отклонениях;
§ 12.13] РЕГУЛИРОВАНИЕ ПОЛОЖЕНИЯ СИСТЕМЫ
819
регулирование может считаться, вообще, удовлетворительным, хотя его качество будет зависеть от быстроты затухания, различной в разных точках данной части плоскости. Во втором случае k < О, колебания расходятся и регулятор негоден. Существование промежу
точной (незаштрихованной) части'плоскости параметров, в которой возможны установившиеся колебания, характерно для нелинейных систем. В самом деле, сохраняя предположение V=0, сделаем IF—> оо и, следовательно, эффективность регулирования бесконечно малой; второе уравнение (161) даёт в пределе р = 0, и мы можем принять рь= О, так
Фиг. 213. Разбиение плоскости параметров по общему характеру колебаний.'
что. движение определяется линейным уравнением Т2ф
£7© *-1” ft© = X- С Другой стороны, вследствие (174)
имеем *(->0, и касательная (215) стремится к совпадению с осью Незаштрихованная часть плоскости стягивается к этой же оси и
в пределе заштрихованные области покрывают всю плоскость.
В приложениях необходимо возвращаться к естественным параметрам. Мы можем, например, зафиксировать Т, U, V, X, Y, k, I
и давать передаточному числу т непрерывный ряд положительных
Таблица 14
Знаки величин eQ, е19 е2, № и характер корней hi
1 1 е0>0 21' >0 >0 /?2>0 Л1<о, h2 < 0
2 «о>0 7?2<0 hit h2 комплексные
3 е0>0 *1< /?2>0 hlt h* h2 Сходящиеся колебания
4 е0>0 >0 >0 7?2>0 /*1<0, Л2<0
5 е0<0 t >0 > о о *8* *8? * 4
6 <?0>б СО >0 ЯЗ>0 * О •X-*8* <8? О
7 е0>0 СО >0 /?2>0 о *^С Лх < < ^2 I Установив-} шиеся коле-
8 е0<0 - - >0 0 й2<0
9 ё>0>0 е2< со /?*>0 й1<0. 0<Л2<й# | бания
10 е0>0 е2< СО /?2>0 hi < 0, Ji* < h2 I Расходящиеся
11 е0<0 СО е2< СО /?а>0 Zfcx < 0, Zr2 < 0 • j колебания
52*
' 820
НЕЛИНЕЙНЫЕ СИСТЕМЫ
[гл. 12
значений. Точка (5, ?|) при этом опишет отрезок прямой, определяемой уравнением
T*U(IU — kX) 5 + ЙТ2 (kY* — IT*) т) -|- kU(Т*Х— UY*) = 0, (12.217)
которое получается путём исключения ш из (212). Мы должны проследить за перемещением точки по отношению к областям плоскости, принимая во внимание, что положение касательной (215) также меняется вместе с ш,
5°. Устойчивость установившихся колебаний. Для того чтобы решить вопрос об устойчивости установившихся колебаний, исследуем возмущённое движение а = а*-|-6а, b = Ь* -|-8&.
Укороченные уравнения (207) дают готовый аппарат для этого.. Так как достаточно рассмотреть лишь малые возмущения 8а, 8&, то воспользуемся уравнениями в вариациях
(12.218)
которые получаются, как обычно, путём разложения в ряды Тейлора и отбрасывания членов высших порядков. Символ ( )* указывает на подстановку значений а = а* = 0, b = b*, а именно:
<м\*
да )
h,—
— тс
От
I H'(b* cos и) cos и du, —тс
cos и) cos и du,
—тс
| Hr (b* cos и) cos2 a du
—тс
(12.219)
Дифференцируя (211) по Ь, интегрируя по частям и принимая во внимание(210), находим:
/(£) = -!• [ Hr (b cos и) cos* и du,
<M\* дЬ )
дВ\* да )
*
г
§ 12.13]
РЕГУЛИРОВАНИЕ ПОЛОЖЕНИЯ СИСТЕМЫ
821
4-тс 4-тс
(Р* cos и) du = -i- Н' (b* cos и) (cos2 и + sin2 и) du =
—я —я
= J' (£*) — [Я (b* cos и) sin и]+* +
* cos и) cos adu = J' (£*) -}-Лг,
—К
так что
*
Qi
дА да
— ... . гД__j' (£*)]
db) 2(x2+<o2)1^ J
(12.220)
С другой стороны, так как Н(у) есть нечётная функция, то Н' (у) будет чётной и интеграл, входящий во второе и третье выражения (219), исчезает:
М \* = / дВ_ \* = db ) \ да )
(12.221)
Корнями характеристического уравнения системы в вариациях будут поэтому действительные числа (дА/да)*, (дВ/db)*, и если оба ’ они отрицательны, то состояние установившихся колебаний устойчиво.
Принимая во внимание (193), (201), мы видим, что сумма
|~(д&\ —__х । (Q -1-7?) 7 гд_Jr (b*W—
\да) ‘\db) ~~ ^2(х2+<оЗ) 1л< J IP )1 —
= — СгЛ< + АГ)[ht—Jf (b*)] = — М — % {hi + J' (b*){ (12.222)
всегда отрицательна, так как для установившихся состояний > 0, /'(#*) ^>0. Поэтому условием устойчивости будет неравенство
(#)’ (-У Г - 4 № - 7' (f)l IS + W (»*)1 > о, <12.223)
где вследствие (193), (201)
S = 2х (х2 + о>2) — = (2-f^ + 2 Л4) (х2 + о>2) — (х2+а>2± /?) =
= (Х2 _|_ Ш2) + 2Ж) +
Если условие (223) выполняется, то, по классификации Пуанкаре, особая точка (а*, 5*) уравнений (207) есть устойчивый узел; в противном случае она будет седлом, но никогда не может быть фокусом1, “ ;
822
НЕЛИНЕЙНЫЕ СИСТЕМЫ
[гл. 12
Пользуясь формулами (190), (191), (192), (193), можно выразить S через 44, а, р. В результате вычислений находим:
. 2p8S = Af(—a + 2Af3 — 2)Ps + [a2 — (5/W2-|-3)a4-21p2 + 4-Af(a—l)(4a —1) ₽ + (—«+1)3^:
=й К— « + 2Ма + 2) р2 + М (— За + 2) р + (a — I)2] (12.224)
Q помощью полученных формул вопрос об устойчивости всегда может быть решён для данных численных значений; при общем рас-смотрении ограничимся простейшим случаем малых положительных и отрицательных а. Определив знаки нужных нам величин при а = 0, будем затем пользоваться тем, что в силу непрерывности знаки должны оставаться теми же самыми и в некоторой окрестности этого значения.
Начнём со следующего случая.
I. Значение | а | мало, 44|3 > 1 (граница областей 1 и 9 и её окрестность, фиг. 213):
Применяя систематически индексы 1, 2 для значений, соответствующих корням h± (верхний знак перед /?) и й2 (нижний знак), имеем при а = 0
R — — 1, -At = —2fc±<0, ^ = 0.
Поэтому на оси не существует периодических решений, так же как и в области /, где й2 становится отрицательным. . ,
Но в области 9 этот корень удовлетворяет неравенству 0 < й2 < й* и из фиг. 212 видно, что здесь мы имеем два периодических решения с амплитудами й* = .#2, для которых, соответственно, У (й2) > й2,
У'(йр<й2 (чертёж относится, собственно, к следующему случаю II, а здесь мы должны брать только верхнюю секущую с = й2й). Полагая опять а = 0, находим:
x2 = 7ft2-|-44 = 44, Q2 = 442 —РЛ4+1, S2 = 2443>0.
Если 1 < 44₽ < 1 + 442, т0 Q2 > (V S2 + Q^J' (й2) > 0, S2-{-Q2^J'(bQ > 0 и эти неравенства остаются в силе в части области 9, примыкающей к оси т|. Условие (223), в котором мы должны взять нижний знак, удовлетворяется для й2, но не для Первая амплитуда устойчива, вторая — неустойчива. Мы имеем, таким образом, автоколебания малой амплитуды,} существование неустойчивого режима с большей амплитудой указывает, как всегда, ца то, что при соответствующих отклонениях регулятор не справляется со своей задачей.
Если 1 442 < 714(3, то Q2 становится отрицательным при a = 0.
С другой стороны, пока а отрицательно, но достаточно мало по абсолютному значению, корень й2 и обе величины У (#g), У (ftp также
§ 12.13] РЕГУЛИРОВАНИЕ ПОЛОЖЕНИЯ СИСТЕМЫ 823
малы. Поэтому первые положительные слагаемые в S.2 + (^2)
и S2-^Q2^J' (/>') оказываются преобладающими и предыдущие выводы в отношении устойчивости остаются в силе. Однако дальше от оси ?| амплитуды Ь2, Ь2 могут быть обе неустойчивы.
Предполагая теперь, что ТИр < 1, полагаем а = 0; находим: - - * - * ... _ • /?=1 —^ = 0, A2 = 1=^L,-
Xj = 7Й! 4-М =.Л4, Q1 = Af2 — Mp+l, St = 2M\
х2 = 7й2 + Л1 = 1, Q2 = i, р»52 = 2р2 (1 - MP) + 1 + Мр и рассматриваем отдельно следующие случаи.
II. Значение [а | мало, М/(М-|-< 44$ < 1 (граница областей 9 и 6 и её окрестность).
При а = 0 получаем:
й1 = о, <?1>0, 5х>0, о < *2 < Л*. Q2 > 0, S2>0 и, следовательно, на оси имеем стационарные амплитуды #2, 4', соответствующие h2. Так же как и выше, Ь2 устойчива, Ь2 неустойчива и система получает автоколебания малой амплитуды. То же самое имеет место в прилежащей частя области 9, где hr становится отрицательным.
Но по другую сторону оси т], в области 6, корень h± также удовлетворяет неравенству 0 < hr < h*. Следовательно, кроме такой же пары b2, Ь2, как и выше, имеем другую пару стационарных амплитуд bv b[ (фиг. 212). Для этих последних берём верхний знак в (223) и заключаем, что Ьх неустойчива, а устойчива. Таким образом, в части области 6, прилежащей к оси ?|, имеем два' возможных состояния автоколебаний. Которое из них будет устанавливаться В'действительности — зависит от начальных условий.
III. Значение |а| мало, 44$ < (граница областей
10, П и 7, 8 и её окрестность).
При а = 0 имеем:
/г1 = 0, ^>0, 5х>0,
h*< h.2 при 0 < *2 <0 при Аф <0.
Периодических решений не существует ни на оси т|, ни в областях 10, 11, где hY становится отрицательным.
Две стационарные амплитуды bv b[ в областях 7,8, где 0<^1<ЛИ:. При малых положительных а амплитуда Ь± неустойчива, Ь'± устойчива. Итак, в частях областей. 7, 8, прилегающих к оси т|, имеем
824
НЕЛИНЕЙНЫЕ СИСТЕМЫ
[ГЛ. 12
автоколебания большой амплитуды. Процесс регулирования мало отличается от неустойчивого.
В заключение отметим, что чрезвычайно поучительно проследить за изменением рассмотренных величин и свойств при переходе из одной области в другую.
6°; Точные периодические решения. Если представить характеристику сервомотора ломаной линией, то можно найти точные симметричные периодические решения и сравнить результаты с теми, которые получены выше приближённым путём. Примем простейшую идеализацию
Н(у) — sign (12.225)
пригодную для хорошего сервомотора без заметной зоны застоя.
Если х = Хз, ‘2’ = 0 и р = 0, то уравнения (175) принимают вид
х + Р* + х —у = О,
х 4- Мх + ах 7 = 0 при у > 0, j х4-Мх4~а* — 7 = 0 при < 0, J
(12.226)
(12.227)
где точками обозначено дифференцирование по т. Последнее уравнение может быть также представлено в форме
х 4- Мх 4- ах ± 7? 4- А = 0, (12.228)
где А — постоянная. Из (226), (228) находим:
А = (1 — а) х (0) + (р — М) х (0) — у (0) (12.229)
и, предполагая а < Л42/4,
при этом
(12.233)
а Р, Qt S суть постоянные интеграции. Постараемся определить их, а также некоторое положительное значение о аргумента т так, чтобы
§ 12.13]
РЕГУЛИРОВАНИЕ ПОЛОЖЕНИЯ СИСТЕМЫ
825
было
х (о) = — х (0),
х (о) = —х (0), у (о) = у (0) = 0 (12.234)
и чтобы внутри интервала (0, о) переменная у имела тот же знак, который стоит перед у в (228). Условия (234) в развёрнутом виде будут:
е 2 (
М
Ма
2
2
ЛГа v Ма
е 2 ch со I------------ft- е
а— М>—х—
е 2
2 sh со Q-|-2/? = 0, (12.235)
sh со
отсюда и могут быть найдены четыре величины Р, Q, S, а, после чего нужно проверить знак у. С другой стороны, уравнения (235) линейны и однородны относительно Р, Q, Pt S. Поэтому, если им удовлетворяет некоторая система значений Р, Q, S, о при данном /?, т. е. при данном знаке перед у, то им же удовлетворяют значения — Р, —Q, —S,. а при замене этого знака на противоположный. Иными словами, меняя знаки у Р, Q, Р, S, получим решение, удовлетворяющее уравнениям (226), (228) и условиям (234) с изменённым знаком перед 7; при этом если в первом решении у положителен, то во втором он отрицателен, и наоборот. Второе решение описывает непосредственное продолжение движения на второй интервал а, причём лишь для удобства переменная т опять считается от нуля. В конце второго интервала три переменных х, х, у принимают те же значения, что и в начале первого; ъш имеем, следовательно, периодическое решение с периодом 2з, удовлетворяющее соотношениям
х (т —|—о) =— х(т), х(т4-а) = — х (т), у (т + а) = —д/(т), (12.236)
где т теперь считается от одного определённого нулевого значения.
Если рассматривать (235) как четыре линейных уравнения относительно Р, Q, S, то для их совместности нужно, чтобы их определитель Г (а) был равен нулю. Вычисление даёт:
е -%- Г (о) = аса ( ch -у + ch со) — 2с (Л4 — ар) sh -
— [2а (1—а) —Л4(М —ар)] sh со, (12.237)
826
НЕЛИНЕЙНЫЕ СИСТЕМЫ
[ГЛ. 12
и мы имеем трансцендентное уравнение для а: *
= ЩМ ар) Sh (Л4а/2) + [2а (1 - а) - М(М - ар)] sh си
ch (Ма/2) + ch сс . ’ '
Для существования искомых периодических решений необходимо, чтобы это уравнение имело действительные положительные корни.
Если а = 0, то мы имеем из (228):
х-]~Мх±^-^-\-Ах-[-В==0, В = — Мх(0) — х (0), (12.239)
4W
и формулы (230), (231), (232) должны быть заменены следующими:
X =Pe~ih-JrQzi + Rx + S, х = — MPe~x’t^-2Qx-\-R, (12.240)
У = р (Л1'з _ р/И _|_ 1) е~Мх + Q + 20т + 2)+/? (s-^+S; (12.241)
«.
при этом •
Q = (12-242)
а Р, R, S—постоянные интеграции. Условия (234) получают вид (1_|_е-лг’)РЦ_02(2 + а/?4-25 = 0, ’ -Ж(1+^)Р + 2з<2 + 2/? = 0> 1224
е-Ж(Л12—рЛ44-1)Р+(а2+2₽зН-2)С?-|-(a + p)/? + S= 0,
(М2 —l)P4-2Q + p/? + S = 0.
Вычисляя определитель Г (з) этих четырёх форм, линейных относительно Р, Q, /?, S, находим:
-±в’2Г(а) =
= Л4а(1 —Afp)ch^ —2(Ж2 —+ l)sh^, (12.244).
*
так что уравнение Г (а) = 0 может быть представлено в виде
th ’^g_/19 945ч
th 2 “ 2 —pAf-f-l* (12.246)
Рассматриваемый случай a = 0 при Y — 0 исследовали А. А. Андронов и H. H. Баутин [121], которые указали, что последнее уравнение имеет положительные корни при УИр < 1. Если же /Ир > 1, то искомых периодических решений не существует. Этот вывод совпадает с тем, который получается из приближённой теории. В самом "деле, q = /Hp=l есть ордината точки касания параболы на фиг. 213
на движение льные ура виде второго
Фиг. 214. Плоский гироскопический маятник.
§ 12.14] ДВИЖЕНИЕ ГИРОСКОПИЧЕСКОГО МАЯТНИКА 827
с осью 7|; . но из-сказанного в пп. 4°, 5° следует, что для тех систем значений параметров, которые изображаются точками оси, лежащими выше точки касания, установившиеся колебания невозможны.
Заметим ещё, что уравнение (245) может быть получено с некоторыми предосторожностями путём предельного перехода из (238). Если в последнем уравнении сделать просто а = О, то оно обратится в тождество; то же самое будет и в том случае, если предварительно продифференцировать обе части по а. Но если дифференцировать по а два раза и затем положить а = 0, то, как нетрудно убедиться, получится уравнение (245).
§ 12.14. Влияние сил сухого трения, пического маятника. 1°. Дифференци; гироскопического маятника. В приложения метода осреднения рассмотрим задачу о влиянии сил сухого трения на движение гироскопического маятника. Для сокращения рассуждения будем отправляться от известных дифференциальных уравнений малых движений гироскопического маятника с горизонтальным средним положением гироскопической оси (фиг. 214), которые приводятся, например, в* нашей книге f12?22]:
Ла -р La Н$ = О,
Вр + Жр — На = 0; (12.246)
> f
в этих уравнениях а обозначает .угол отклонения маятника от вертикали; р — угол, на который повернулся кожух гироскопа от своего среднего положения относительно маятника на своих цапфах, расположенных в направлении стержня маятника; А — момент инерции всей системы относительно оси качания маятника; В— момент инерции гироскопа с кожухом относительно оси цапф;
циент момента Ла силы веса всей системы; — коэффициент восстанавливающего момента Л4р, развиваемого пружиной, которая стремится удерживать кожух гироскопа у его среднего положения относительно маятника; Н—постоянный главный момент количества движения гироскопа относительно его оси вращения, так что —Н$ и -|- На суть гироскопические моменты.
Уравнения (246) верны также и для гироскопического маятника с вертикальным средним положением гироскопйческой оси. К той же форме приводятся уравнения простого маятникового гирокомпаса, если
гироско-внения примера
L обозначает
828
НЕЛИНЕЙНЫЕ СИСТЕМЫ
[ГЛ. .12
учесть постоянный наклон его гироскопической оси к горизонту, * происходящий от вращения Земли [12-22].
Разделим все члены первого уравнения на А, все члены второго -— на В, введём обозначения
1
I
} (12.247)
и будем писать yv у2 вместо а, р. Затем пополним уравнения членами— рру-р —МУ& выражающими такие вязкие сопротивления, как сопротивление воздуха, и членами —— мСУа)» происходящими от трения в опорах. Через jr обозначен малый параметр;
и ^(Уо) определяются с помощью функции Кронекера сигнум, а именно:
$(ji) = Ai signup Ti(y2) = /z2signy2. (12.248)
В результате получаем уравнения
У1 + Wt + Р2 Л + СУ1). 1
— Vi + Л + мЛ+°2№ = ^- FG (j2)- J
При |л = 0 имеем упрощённую линейную систему
Уг+р2л+=°> — ^1+л+°2^2=°;
(12.249)
(12.250)
её операционный определитель
х£)
О2 4-а2
= Di 4- (р2 + о2 + я2) D2 + р2<з2
(12.251)
имеет две пары чисто мнимых сопряжённых корней ±i<ult± 1<и2, причём угловые частоты ш2 определяются формулами
t 4 = 4 (Р24-°2-+ «2—/2)> 4 = 4(р2 + °2 + «2+/2)> (12.252)
в которых
/2= 4- У (р2 4- а2 4- я2)2 — 4р2а2 = + ]Ля4 4-2(р24-а2)я2 4-(р2—а2)2.
(12.253) Обозначая
.. и[₽л+£(л)1. (122И)
fc &>=—i* । +nw i
§ 12.14J движение гироскопического Маятника
запишем уравнения (12.249) так:
Ф2+р2)л+*^з=Ф16'1). V
- Wyt + (О2 + а2)л = ф2 СУз) • J
829
(12.255)
Эквивалентное матричное уравнение имеет вид f(P)y=^(ylryJ, где
Z)2 р2 х£)
— № О2-|-а2 ’
Ф (Ji> Л) =
Ф1 (Л) Фз (.Уз)
(12.256)
Матрица F(D), присоединённая для матрицы f(D), щий вид:
имеет следую-
(12.257)
F(D) =
£)2Ц_О2 _ ХО
W О2 + р2
Преобразуем рассматриваемые уравнения движения (249) к нормальным координатам. Корни операционного определителя (251), т. е. определителя матрицы обозначим так:
zt zojj = p1e±i^ , • z±z Z<o2 = p2 e±<c«.
(12.258)
Здесь, очевидно,
Pt — p«2 — ^2» — ^2 — 2 • (12.259)
Присоединённая матрица F(D) при О = /шх и Z) = Zoo2 принимает следующий вид:
F(i<i>i) =
F(iw2) =
—
— <“i + P2
---/х(О2
— “г + р2
(12.260)
Выбирая матрицы-столбцы
1
/Хсо2
(12.261)
830
НЕЛИНЕЙНЫЕ СИСТЕМЫ
и матрицы-строки
= II + °2> *%a)l ||» ^2 = || ш2 4" °2’ /хСОд || ,
(12.262)
имеем очевидные соотношения
V2W2 = F(zo>2). (12.263)
Для согласования с обозначениями, принятыми в общей теории, запишем матрицы-столбцы Vt и V2 так:
У. =
1 II
N12e^
(12.264)
Сравнивая матрицы (261) и (264), получим:
(12.265)
В случае отсутствия у Д (О) действительных корней формула (144) преобразования к нормальным координатам принимает вид
&=1 .
(у — 1, 2, ..«, /1, v — 0, 1, 2, ..., z/ij).
Здесь, согласно (8.490), ип заменено его значением
Для нашей задачи формулы преобразования к нормальным координатам будут следующие:
у± = а± cos (ох/ + 0!) -}- а2 cos (o>2f + 62)>
О[ cos +-g-)Ч~
X<d2
2 I 2 — “2 + °
Л =------ 2_Г~ а1Ю1 C0S (®1#+ 61 + Я) +
--(Dj 4“ °
----(О
а2<о2 cos (ш2< + в2 + гс).
2 2
§12.14] ДВИЖЕНИЕ ГИРОСКОПИЧЕСКОГО МАЯТНИКА 831
Обозначая
= АХФХ, #2== -^Фз» |
а __ 4 р ^2____а — 4 р } (12.267)
_<о*+7Й1 “ liv -Ч 4-°2 2 “ 2 2’ I
представим выражения (266) в таком виде: г I • .
Л = C0S К* + 61) + A-2$2 C0S + 02> > )
У1 = — Sin W+ 91) — ЛФ2Ш2 Sin (0>2f + e2), I
y2 = — АГ1 sin («1^ + 01) — A2^2 Sin (»./+ 62)>
У2 — — А11ш1 cos (<°/+ ®i) — cos (<*>2/-j-
Здесь теперь Alf A2, 0X и 62 — новые неизвестные (нормальные координаты), между тем как Фх, Ф2, 1\ и Г2 обозначают некоторые вполне определённые коэффициенты пропорциональности, которые должны удовлетворять соотношениям
2 । 2
Г1 __ — ^1 + Р _____ kwj '
Ф7 — -ю^+а2 ’
Г2 _ — юг+р _ Х<02
Ф2 *<°2 — со* 4- а*
« - Л I
(12.269)
Если заметить, что
р2_ Ш2 = | (/2 _|_р2 — 02 — ft2) > 0> 02 — О)* = 1 (/2 — рЗ + 02 — П2) > О,
ш2---Р2 = -у (/2-----Р2 + °2 + Л2) > 0>
— °2 == V </2 + Р2 — °2 + я2) > О,
4W
и предположить для определённости, что х > О, X > 0, то можно написать также:
Н > 0, и, следовательно,
Х(р2-^) х(а2^со2) ’
(12.270)
Первые члены в выражениях (268), имеющие меньшую угловую частоту <ох, соответствуют более медленному парциальному колебанию, которое носит название прецессии*, вторые члены с большей частотой <о2 выражают более быстрое колебание:—нутацию. .
832
НЕЛИНЕЙНЫЕ СИСТЕМЫ
[гл. 12
Из (252) имеем:
d (п2) /2 ’
d(«fy d (и2)
так что, когда угловая скорость вращения гироскопа, а с нею вместе и число п возрастают, меньшая угловая частота убывает ещё более, а большая частота <о2 возрастает. Следует, однако, помнить, что для законности нашего приближения силы сопротивления должны предполагаться столь малыми, чтобы обусловленное ими убывание амплитуд происходило достаточно медленно в сравнении с прецессией.
2°. Укороченные уравнения. Дифференциальные уравнения, которым должны удовлетворять новые неизвестные А19 Д.2, 0х и 62, можно, согласно (152) и (153), представить в следующем виде:
(ад,<л)+адь(л)1.
^+,Лф * =
dt 1 * * di
= (л)+
(12.271)
где W'nk— элементы матриц Wh (/г =1,2), введённых выше (262). В уравнениях (271) аргументы у{ и у2 функций и ф,2 предполагаются заменёнными их значениями (268); они не выписаны явно лишь для сокращения записи.
Как легко видеть из выражений (251) и (252),
Д' (/со*) = [Д' (D)]p=t4 = 2Zo)x /2,
Д' (/о>2) = [Д' (0)1.0=^= — 2/о)2/2. ,
(12.272)
Подставляя вместо Whk их значения из (262), а вместо фх и ф2 выражения (254) и возвращаясь к обозначениям
я.2 = . (12.273)
приведём уравнения (271) к виду
ta^+*Mi^)24/2 =
=—((—uy а2) (РЛ + ’ (ji)) — '2Ш1+ *1 (Л)11 >
U . л, л ( *
\ 2 dt ""I- ^2^2 dt j 2tw.2f
= — {( — <1)2 + а2) [р’уг+Ь (A)l—«ш2 М'А+'П (A)l)• •
§ 12.14]
ДВИЖЕНИЕ ГИРОСКОПИЧЕСКОГО МАЯТНИКА
833
Укороченные уравнения будут следующими:
(ф^+гад 5)2гш1/-з= )
4-тс +тс
= — 2^2 J J e~iUl {(—<°?+а2) 1РУ1+* (Л)1 — — к —тс
— «®1(Л)] }duldu2, J 2 275)
(ф,^+»И.^)2ЧЛ=
4-тс 4-тс
= 2& f J e-iM4( — <“| + о3) [РЛ + ^(Л)] — — ТС —тс
— «“2 [?Л + 'П (Л)] 1 J
Подставляя в уравнения (275) вместо ух и у,2 их значения (268) и вычисляя входящие в правые части уравнений (275) интегралы (при вычислении интегралов амплитуды А± и А.2 трактуются как постоянные), приведём эти уравнения к виду
W ^14- Ф1Л1 {- 2шх/2 +
+ К - Р2 + =>2) (Р — Я) + (/2 - »3) (Р + 9)1} =
=—2^1» (-«>? +°2) Ai + «V2iL (12.276а)
Ф 2/а» | ф А I___2<п /2 ^2 I
Ф2 AIW.J d{ -j- Ф2Л21 2«>2у -|-
4- Кр3 - 53) (Р - я) 4- (/3 4- «3) (р 4- 9)]} =
= 2^5 ( ^(ю2 °2) А.2 4~ > (12.2766)
причём
4-тс 4"л
ZJ11 = J J Ц — А1Ф1(о1 sin «j, — А2Ф2а>.2 sin и2) e~iu^ du^u.^ — тс —тс 4-тс 4~л
— *41 = J / *4 (— ЛЛ00! cos ui — cos я2) e-iu^ du± du2,
—тс —тс 4-тс 4-тс iV12= J f $( — Л1Ф1<о1йпа^ — А2Ф2ш2 sin а2) e~iu‘ dut du2, —тс —тс 4-« 4-л
— -4-2= J У 'Ч (— 4J1C4 cos и± — А2Г2<о2 cos м2) e^iu» dut du2.
—тс —тс
53 Зак. 1474 Б. В. Булгаков
834
НЕЛИНЕЙНЫЕ СИСТЕМЫ
[ГЛ. 12
Для того чтобы привести уравнения к симметричному виду, заметим, что из (269) следует:
о»! = У(р2 — (о2) (а2 — ш2),
V хХ а>2= У (<и2 — р2) (ш2 — а2);
отсюда
_ °2— <»i
У х(р2 —а»2) У\(а2—ш2)
2 9
__ ш2 а
V —р2) V х(<°2—д2)
где, согласно (270),
(12.277)
(12.278)
Далее примем во внимание, что, как интегралы, представляющие мнимые части нулю и что $ и т| — нечётные функции; ния (248), имеем:
нетрудно убедиться, все 41» Л1> Ла и Ла» Равны
подставляя их выраже-
Л1 == ^й^а^а)»
Л1 =3 16/z2O (Д^л, Да-^а^а)»
Ла== 16/ZjO (ДдФз^а» ^i^i^i)»
Ла = 16й2О С^Га^а» .
(12.279)
где функция О(х, у) определяется с помощью формулы
—ТС —тс
sign (х sin ut sin и2) sin dut du2 =
—тс — тс
cos ut у cos я2) cos dat du2.
(12.280)
Отделяя в уравнениях (276) действительные и мнимые части,
§ 12.14] ДВИЖЕНИЕ friPOCkOftH4EdKOtO Маятника 835
с помощью формул (277) и (279) получим:
tZQi л d&2
'~dF~Ui ~di
“i/2 К- P2+°2) (P - 9)+(/2-«2) (P + <7)1 =
= - HST \G (A^, Л2Фа<02) +
+ (p2_ Ш2) hzQ (Л^, Л2ГЛ)],
<V2^-2+l(P2 ~ °2) (P ~ ?)+(Z2+«2) (P+9)1 Л = =- ^ l]AH-°2) \q (л2фл, лхфЛ) -
— /х (0)2 — p2) h.fi (Л2Г20)2, ЛХГЛ)].
(12.281)
В силу первых двух уравнений 0! = const, 02 = const. Приближённое решение рассматриваемой задачи даётся формулами (268), в которых 4lt А2 — функции от Д определяемые уравнениями (281).
Из определения (280) вытекает:
0(0, 0) = 0,
(12.282)
О(х, —y) = G(x, у), О(—х, у) =— G(x, у). (12.283)
С помощью двух последних соотношений G(x, у) всегда может быть приведена к неотрицательным значениям х и у. Предполагая, что это преобразование уже выполнено, двойной интеграл в (280) можно выразить через полные эллиптические интегралы первого и второго рода К и Et как это было сделано при аналогичных обстоятельствах Н. В. Бутениным [12-3]; получаем, таким образом:
при х^д/>0,
где
О (х, у) =
при О
*(7)--[(Я-‘К)<М)
(12.284)
(0<х<О)- (12.285)
Найденные выражения верны и в том случае, когда один из аргументов х, у исчезает, в то время как другой остаётся положительным, а именно:
G(x, 0) = £,
0(0, .у) = 0.
(12.286)
53*
836
Нелинейные системы
[гл. 12
Второе соотношение могло бы быть также получено формальным путём'из второго уравнения (283).
3°. Исследование укороченныхуравнений. Для того чтобы рассмотреть эффект таких демпфирующих сил, как сопротивление воздуха, сначала пренебрегаем сухим трением, вычёркивая члены, стоящие в правых частях уравнений (281), так что
^г + М1 = 0. 4г+ ^2 = 0, (12.287)
где оба числа
С1 = 4^ К- Р3+°2) (р - <7) + (У2—«*) (Р+?)Ь с2 = 47? Кр3—°2) (р—?)+(У2+л2) (р+9)]
положительны. Решение (287) есть
Л* — , Д2 — ^20^
Если
п2
(12.288)
(12.289)
то первый из показателей clt с% меньше второго и, следовательно, под действием вязких сопротивлений нутация должна затухать быстрее прецессии} это хорошо известно из опыта.
Предыдущее неравенство, разумеется, несущественно, если его правая часть отрицательна или равна нулю; если же она положительна, то неравенство будет выполнено при условии, что скорость собственного вращения гироскопа не слишком мала.
Переходя теперь к эффекту сухого трения, положим:
р = ? = 0, (12.290)
и, чтобы избежать осложнений, не имеющих существенного значения, ограничимся в дальнейшем симметричным устройством, для которого
р = а, х = Х, /^=/z2 = /z.
Отсюда следует, что
со2 = р2 —
2
и можно положить
так что
(12.291)
(12.292)
(12.293)
(12.294)
§ 12.14]
ДВИЖЕНИЕ ГИРОСКОПИЧЕСКОГО МАЯТНИКА
837
Пользуясь также нения (281) в виде
вторым соотношением (283), представим урав-
dt к2 (Oi/2 U V1!0*!’ Я2да2?»
dA% 4&h + л2
=------° (АШ2> Аш1)-
dt л2 <o2/2 v 11/
С помощью формул (284) и вводя обозначения 4рй , Т---------------------------------------------""л2”
(12.295)
получим:
• (12.296)
—f1 +-J-)ТВЙ) ПРИ *>_У>0
ИЛИ X > у — О,
Zi I п2\с(х\ л
-- 1 При 0<х<^у
\ 1 У2/ \У ! Г
или X = 0 < у.
Отсюда, деля второе уравнение на первое, найдём:
(12.298)
(12.297)
В таблице 15 даны значения B(yjx) и R(ylx), вычисленные с помощью (285), (298) для различных значений отношения у/х.
Из уравнений (296) видно, в частности, что оси х и у — интегральные кривые в плоскости ху. Далее заметим, что, согласно таблице, R(y/x) заключено между х/з и 2, и с помощью (297) получим уравнение
(У\ 1 У (1 + П2//2) /? (у/х) (1 - Л2//2)
dx \х) х х L—л3//2
(12.299)
838
НЕЛИНЕЙНЫЕ СИСТЕМЫ
[гл. 12
Таблица 15
Значения В(у)х) и R(y!x)
у \ X / У X
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 я/4 0,786 0,789 0,795 0,802 0,813 0,827 0,846 1/2 0,502 0,508 0,518 0,533 0,554 0,583 0,624 0,8 0,9 1 2 5 10 оо 0,872 0,912 1,000 0,683 0,778 1,000 1,806 1,970 1,992 2,000
При
1 + л2//2
1 —Л2//2
угол, образуемый касательной к любой интегральной кривойу — у(х) с осью х, будет, согласно (297), больше угла, образуемого радиусом-вектором точки ^касания, если эта точка лежит в первом квадранте вне координатных осей. Отсюда или, более непосредственно, из уравнения (299) вытекает, что, когда т возрастает, а х убывает, у/х, а вместе с ним и отношение А2/Лх, будет также убывать и что все интегральные кривые, кроме одной, касаются оси х в начале координат. Кривая, представляющая исключение, есть та; которая совпадает с осью у. Поэтому расположение интегральных кривых вблизи начала будет того же типа, что и в окрестности устойчивого узла.
Предыдущее неравенство удовлетворяется, когда
1
П > -7=Р. у 2 г
(12.300)
Таким образом, если скорость собственного вращения гироскопа не слишком мала, то нутация должна затухать быстрее прецессии, как это было и в случае вязкого сопротивления. Это избирательное действие сил сопротивления, быстро гасящее. колебания высокой частоты,. и является истинной причиной того, что обычно во всех технических приложениях гироскопа нам приходится иметь дело только с прецессией, между тем как нутация возникает лишь при запуске или стопорении гироскопа, при толчках и вибрации опор и т. п.
Характерной особенностью рассматриваемого случая сухого трения является то, что полное погашение как прецессионного так и нутационного движений завершается в конечное время.
§ 12.14] ДВИЖЕНИЕ ГИРОСКОПИЧЕСКОГО МАЯТНИКА 839
Чтобы убедиться в этом, заметим прежде всего, что в случае интегральных линий, совпадающих с координатными осями, имеем соответственно:
dx /1 л2\о/п\ л2\ Л
и
х = 0, £__(1 + *)Е(0)=_’(. + *),
Таким образом, представляющая точка движется по этим линиям с конечными постоянными скоростями. Если, далее, ни одно из начальных значений х0, yQ не равно нулю, так что точка (х0, yQ) лежит внутри первого квадранта вне координатных осей, то отношение х/у будет увеличиваться вместе с т и х/у > xQ/yQ. В нижней половине квадранта (1 < х/у < оо) имеем:
х0
dx . / . л2 \ г? / уn \ 1 л2
>11-----75-)п(— )>1------То-.
\ /2 / \ *0 / /2
С другой стороны, если точка (х0, у^) лежит в верхней половине (0 <х /у < 1), то для всех других точек кривой, лежащих в той же угловой области, имеем:
Jo
dx dt
f4 Jo 4-
Таким образом, в каждой из двух областей абсолютная величина скорости убывания абсциссы х больше некоторого положительного числа. Отсюда следует, что эта координата действительно обратится в нуль по истечении конечного промежутка времени.
О ДВИЖЕНИИ, ВОЗМУЩАЕМОМ СИЛАМИ БОЛЬШОЙ ЧАСТОТЫ*)
§ 1. Дифференциальные уравнения задачи. Рассмотрим систему дифференциальных уравнений
= А Я, И) (7 = 1, (1)
W> If где
fj • • •» р)= (*^1» • • •» % %» А р) *4“
+ 2 (*1......XL ’ *' н) cos т ft -|- (*1......XL н) sin т ft], (2)
Ш = 1
& = + (3)
г
причём xv ..., xL — неизвестные функции времени t\ р.— малый параметр. Указывая переменные, входящие в функции
мы имеем в виду время t, лишь явно входящее в эти функции, но не через посредство &, хотя этот аргумент и является линейной функцией t.
Форма такой явной зависимости ничем не ограничена: так, например, все указанные здесь величины могут быть периодическими функциями времени t, имеющими период, независимый от 2-iqjb.
К рассматриваемому типу относятся уравнения движения системы, подвергающейся действию пульсирующих сил, а также некоторые уравнения, встречающиеся в задачах небесной механики. В такой же
*)* Настоящее приложение является переводом статьи автора: «Sur 1е mouvement troubte par des forces de haute frequence», опубликованной в журнале «Compositio mathematica» (vol. 7, fasc. 3, pp. 390—427, 1940). Перевод выполнен A. H. Обморшевым.
О ДВИЖЕНИИ, ВОЗМУЩАЕМОМ СИЛАМИ БОЛЬШОЙ ЧАСТОТЫ
841
форме получаются уравнения в результате применения метода вариации постоянных в некоторых задачах нелинейной теории колебаний. Эппльтон и Ван-дер-Поль *) указали способ интегрирования этих уравнений с помощью так называемых «укороченных уравнений». Однако лишь П. Фату**) и Л. И. Мандельштам и Н. Д. Папале-кси***) дали достаточно глубокий анализ этого метода.
Продолжим исследования указанных авторов и укажем сходящийся процесс, который позволит отыскать последовательные приближения решения рассматриваемых уравнений, иначе говоря, привести задачу к построению «укороченных уравнений» различных порядков. Эти последние значительно проще для исследования и позволяют определить вековые члены вариаций, порождаемые возмущающими функциями ..., xTji t, р), а также найти эффект накопления возмущений от импульсов высокой частоты.
Предположим, что все функции
• • •» А Iх), • • •» XL н)> ’ *L’ и)
являются непрерывными и имеют частные производные по xv..., xL, t до некоторого определённого порядка, причём эти переменные изменяются внутри пространственно-временной замкнутой области S, а параметр р. удовлетворяет неравенству
(4)
Допустим, кроме того, что при тех же условиях ряды
оо . оо
сходятся равномерно, так же как и аналогичные ряды с частными производными. Отсюда следует, что ряды Фурье, стоящие в правых частях заданных уравнений, коэффициенты которых не постоянны, сходятся абсолютно и равномерно внутри S для всех значений 8.
Суммы f3(xv ..., xL, t, ft, p.) сами по себе являются непрерывными функциями, допускающими частные производные по xv ..., xL и по А входящему явно в эти выражения; эти производные получаются почленным дифференцированием рядов.
Допустим, наконец, что найдены числа Aj столь большие и числа ау, а0 столь малые, что при указанных выше условиях функ-
*) Phil. Mag. (6) 43 (1922), 177—193 и 700—719.
**) Bull. Soc. Math. France 56 (1928), 98—139.
***) Журнал технической физики J (1935), 415—428.
842
ПРИЛОЖЕНИЕ
ции fj(xv ..., xL, t> ft, |л) и их производные, которые эти функции допускают, удовлетворяют следующим неравенствам:
• • •> И*) I
^a+...+x+со j
t, н)
а!...у !<о!--------.
а 1 • • • аЪ
(6)
(7)
Для более ясной постановки задачи рассмотрим какую-либо систему обыкновенных дифференциальных уравнений первого порядка, разрешённых относительно производных.
Если правые части этих уравнений достигают по абсолютной величине очень больших значений или если их изменения происходят быстро и по сложным законам, то непосредственное применение методов численного интегрирования по большей части оказывается мало эффективным. Классический метод вариации постоянных, как это указано, например, Лагранжем в «Аналитической механике», имел главной целью преодоление этих трудностей путём перехода к медленно изменяющимся переменным, определяемым дифференциальными уравнениями, правые части которых достаточно малы по абсолютной величине.
В рассматриваемой нами задаче абсолютные величины правых частей и их производных по ..., t ограничены предыдущими неравенствами, вследствие чего главное препятствие обусловлено наличием членов высокой частоты. По этой причине полные производные правых частей по времени £, входящем явно и через посредство ft, могут достигать по абсолютной величине очень больших значений.
В этих условиях замена данных уравнений уравнениями «укороченными», правые части которых полностью освобождены от членов высокой частоты, представляется средством для преодоления затруднений.
§ 2. Образование последовательных приближений. Дадим параметру некоторое значение, удовлетворяющее неравенству (4), и разделим, всю область изменения Д начиная с tQi на частные интервалы (^-1> *<)> гДе /= 1, 2, ... Величины последних должны быть целыми кратными 2к|л, не превосходящими t* = 2А?кр., где k — фиксированное целое число. Это условие, наложенное на протяжённость интервалов, связано со специальной формой функций fj(xv ..., xL, t, ft, |л) и будет использовано только в § 4.
Обратимся к рассмотрению общего процесса построения функций которые определяют собой приближения искомых неизвестных Xj. Определим эти функции в г-м интервале с помощью
особой формы метода последовательных приближений, применяя конечное число Q итераций, При t=tQ функции должны принимать
О ДВИЖЕНИИ, ВОЗМУЩАЕМОМ СИЛАМИ БОЛЬШОЙ ЧАСТОТЫ
843
начальные значения = х^0, тождественные начальным значениям
ИСКОМЫХ фуНКЦИЙ Xj.
Значения Si, Ejd, i-i этих функций в конце (/—1)-го ин-
тервала (/ = 2, 3, ...) служат в то же время начальными значениями их для следующего, Z-ro интервала. При этом мы делаем совершенно естественное предположение, что указанный вычислительный процесс для функций при возрастающих значениях Q продолжается лишь до тех пор, пока точка (Bj, t) остаётся в области S.
Напишем функции в Z-м интервале в таком виде:
(8)
где — функции от Z, которые мы считаем величинами порядка р\ их определение будет указано ниже. Для указания в явном виде порядка членов напишем предыдущее уравнение в несколько изменённом виде:
Р=1
(9)
где X обозначает вспомогательный параметр, который мы положим равным единице по окончании всех вычислений.
Введём вспомогательное переменное f, которое равно t при Z = Zi_1. Введём также параметр X в систему заданных уравнений, которые напишем в виде
, Xjfj (Хр ..., х^., t, fl, ji), dt' __ 1 dt — Л-
(Ю)
При X = 1 приходим к первоначальной системе.
Рассмотрим теперь подробно процесс построения функций в интервале (Z^, Q, для чего выполним вычисление приближённого решения порядка Q через посредство решения порядка Q — 1:
p=i
Прежде всего разложим в конечные ряды Тейлора правые части уравнений (10) ₽ окрестности точки
844
ПРИЛОЖЕНИЕ
Далее уравнения (10) заменим приближёнными уравнениями:
Здесь возведение в степень q выражения, стоящего в квадратных скобках, мыслится как символическая операция; обозначает частное дифференцирование по /, входящему явно в функции. Для простоты не будем в дальнейшем указывать переменные, от которых зависят функции и их производные, если этими переменными являются
£1, i—1, • • •, i— 1, ti—1, P**
Первые L-p 1 из этих величин обозначают соответствующие начальные значения для Z-ro интервала; аргумент & есть величина быстро изменяющаяся, вследствие чего в выражение функции входит именно этот аргумент, а не его начальное значение.
Заменим теперь искомые функции Xj в правых частях предыдущих уравнений приближёнными решениями (Q—1)-го порядка. В соответствии с основным принципом метода последовательных приближений определяем приближённые решения Q-ro порядка посредством уравнений
«=1 1?=1
' 4- о2'»
— 4 -к
Последнее уравнение (12), которое здесь не выписано, приводит нас с помощью начального условия для f к выражению
? — = (13)
посредством которого исключается t'. Штрих, поставленный у знака суммы в уравнении (12'), напоминает, что после разложения по степеням выражения, стоящего в квадратных скобках, следует удерживать члены, порядок которых относительно X не превышает Q—1.
о Движений, возмущаемом силами большой частоты 845
Q-я итерация заканчивается квадратурами, с помощью которых определяются из ^предыдущих уравнений. В начале интервала, при £ = значения приближённых решений всех' порядков должны быть тождественны между собой и равны В/.
Внося выражения (9) в левые части уравнений (12') и приравнивая коэффициенты при всевозможных, но одинаковых степенях X в левой и правой частях уравнений, получим рекуррентые формулы
(И)
Zc= 1
Здесь U<f\p >2) — полиномы с положительными коэффициентами относительно функций и их производных до (р—1)-го порядка включительно, вычисленных в точке ((^ <_i, ..., *-i, ^-i), относи-
тельно функций до (р — 2)-го порядка включительно и относительно разности t—Все функции ф^ должны обращаться в нуль в начале интервала при / = Легко убедиться, что рекуррентные формулы не зависят от порядка приближений, образованных с помощью функций ф^\
Полагая Х= 1, мы получим окончательные выражения в форме (8) для которые и определят приближённые решения Q-ro порядка для /-го интервала. Заметим, что целое число Q не обязательно должно быть одним и тей же для всех интервалов; оно может быть вполне определено как функция номера i интервала.
В следующем параграфе мы оценим близость аппроксимации точных решений посредством функций Однако для этого необходимо найти верхние границы величин ф^\
Имея это в виду, заметим, что вследствие неравенств (7)'тем более выполняются неравенства
дх*.. .дх}де*
• 9 9 А Р*)
(15)
Отсюда следует, что абсолютные величины коэффициентов конечных рядов в правых частях уравнений (12) меньше соответствующих
846
ПРИЛОЖЕНИЕ
величин, получаемых тем же методом из вспомогательной системы уравнений
или, тем более, из системы
(16)
где А и а — некоторые числа, удовлетворяющие неравенствам
Aj<A, aj>a. . (17)
Для неотрицательных значений приращений Л} — i-i, f — ряды в правых частях сходятся в полиэдрической области
*4 *1, г-1 I I Ь 'L, г-1 I __2-1 1
Л "Г • • * Т а ’ Йо
Предположим, что начальные значения, соответствующие = выбраны для вспомогательной системы таким же образом, как и прежде. Можно легко показать, что функции вспомогательной системы, аналогичные функциям 6^, мажорируют эти последние (являются их доминантами); иначе говоря, || < для всех значений t в интервале (^_lf
В самом деле, например, функция Ф^ удовлетворяет уравнению
.Л dt ~Л
и обращается в нуль при Обращаясь к аналогичным уравнениям для убеждаемся, что di}/1)
—и ФУ являются доминантами для • и Эти рассуждения могут быть последовательно продолжены; тогда приходим к выводу, d№
что для всех значений р функции J и Wjr' мажорируют —тт- и ill ut
л,(*)
О ДВИЖЕНИИ, ВОЗМУЩАЕМОМ СИЛАМИ БОЛЬШОЙ ЧАСТОТЫ
847
Очевидно, что все функции Ф^, имеющие один и тот же верхний индекс, равны между собой; таким образом, проще можно напи-
сать:
dV№ if
dt *
(18)
Можно видеть также, что все Ф^ являются полиномами относительно t—Их выражения мы получим, воспользовавшись тем обстоятельством, что вспомогательная система выбирается таким образом, чтобы она легко интегрировалась посредством элементарных функций.
Положим
(19)
*1 Si, г-1 । I — ^L, У-1 1
a 4 • • • ~t~ a ’T'
и напишем уравнения (16) в виде
d(t'~t) _ х dt
Из этих уравнений выводим:
или
do ___L_
~dt а
d<3 _ а ‘ «о dt~—K 1 — а ’
причём о = 0 при f = Переменные разделяются, и мы имеем: 1|(1 - =)’ -11 = - - i V -
где в силу условия о = 0 при i = перед радикалом взят знак минус.
Если А удовлетворяет неравенству
то предыдущая формула может быть представлена в виде ряда Oe(^+±)(/_/4_0 А+ + (*-4-1)9А9+ • • • +
\ и UQ J £, \ Ц, UQ /
. 1 • 1 • 3.. ,(2р —3) ILA . _1_у* (t_ t ..
848
ПРИЛОЖЕНИЕ
С другой стороны, очевидно, что
^1 ^1, 1 “ • • • Xl ^L, i—1 f
вследствие чего соотношения (13) и (19) дают:
Эти ряды представляют решения Xj, если выполнено условие (20). , Напишем их в виде
оо
+ (2i)
Р=1 где
W) = ,ЬЬЗ...(2/>-3) a ILA t ур р > 2. } (22)
Функции не зависят от X, а поэтому неравенства (18) и выражения (22) для 4PW, которые мы только что получили, не зависят от сходимости рядов (21). Таким образом, мы получили искомую оценку функций
В случае, когда функции fj(xv ..., xL, t, ft, |i) допускают частные производные всевозможных порядков, удовлетворяющие условиям (7) в каждой точке области S, эти функции могут быть разложены в бесконечные ряды Тейлора, которые сходятся внутри каждого призматоида
I xj i-l I < H ^i—1 I < a0
или его части, содержащейся в S. Принципиально процесс определения приближённых решений в каждом интервале (^_1Э tt) может быть продолжен до бесконечности. Полагая Х=1 и, кроме того,
(23)
можно убедиться, что ряды
t . if л/*)
Р=1
О ДВИЖЕНИИ, ВОЗМУЩАЕМОМ СИЛАМИ БОЛЬШОЙ ЧАСТОТЫ 849
а также ряды, получаемые отсюда путём почленного дифференцирования, сходятся равномерно и абсолютно в интервале (^_1Э /<). В самом деле, они имеют в качестве мажорирующих сходящиеся ряды с постоянными положительными членами, которые можно образовать, полагая t=ti в функциях и их первых производных. Отсюда в свою очередь следует, что w заданных начальных значений решение в каждом частном интервале может быть представлено посредством сходящегося ряда функций
*В действительности, однако, мы можем получить для каждого интервала! лишь приближённые решения некоторого конечного*{'порядка. Значения неизвестных в конце каждого интервала, которые являются в то же время начальными значениями для следующего, имеют ошибки. Эти ошибки идут в процессе вычисления, всё увеличиваясь по мере перехода от одного интервала к следующему.
§ 3. Оценка точности и исследование сходимости приближённых решений. Из сказанного выше следует, что мы должны теперь отдать себе отчёт о характере накопления ошибок при переходе от одного интервала к другому^ и вычислить разности между*'приближёнными решениями и точными Xj во всей области изменения г.
Поскольку мы, вообще, будем рассматривать одновременно приближённые решения какого-либо одного определённого порядка Q, будем для упрощения отбрасывать верхний индекс исписать вместо
Предположим,, что призматоид
принадлежит области S, и ограничимся вычислением функций в наибольшем интервале (/с, tQ-\-E—0), где точка (^, ..0 остаётся внутри другого призматоида
| Cj Cp t (25)
причём числа Cj удовлетворяют неравенствам
О < < ‘1 Cj. (26)
Символом (/0, £0-f-E— 0) обозначена совокупность значений /, для которых
Как только функции определены, можно найти число Е, соответствующее каждой системе сколь угодно малых чисел
Отбросив верхний индекс у можно написать4 уравнения (12')> в таком виде:
db
= •••• н) —МО. .
54 Зак. 1474. Б. В. Булгаков
ИГ
850
ПРИЛОЖЕНИЕ
где
•••• В . i'. Н)— fj—
-z4[ 2^+ • +2
3=1 j)=l 0 = 1 < '
Используем теперь конечную формулу Тейлора , .
/j(^l> • • • 9 t 9 И, Р*) —f j *-J__
Q-l
+2 i h“;’ • ->) A + • + S41 +:V-‘ -«>a] f> +
3=1
| 1 /► _£ \ & | | /£ ______ {; \ ‘ f /j.r_J. \
‘ Q! ’*1’*“!'0JQ ‘ * * * | Gb '•L, i —1) “i \ i-1) Jj*
где
Z — Zf(’l, i-1 4“ ® G1 ’1, i-l)> • • • 9
^.^1), A-l + 6(/'—^г-l), &, Д 0<0<1.
Заменяя разности — V, г-t и их выражениями из фор-
мул (9) и (13), находим:
- 2'А + + <fc+ 2=1 р=1
+(*—л+^г 2^)xF Д-+-*-+
Р=1
Р=1
Два штриха у 2 обозначают, что после разложения по степеням выражений, стоящих в скобках, следует отбросить все члены порядка Q—1 и ниже относительно Л.
Пользуясь неравенствами (15), (17) и (18), получим:
1хдэ| < [2^1,+• • • + £]’л
Q = 1 р = 1 pzsl
< А> 2' [т 2 V<rv+к11
pt=l
О ДВИЖЕНИИ, ВОЗМУЩАЕМОМ СИЛАМИ БОЛЬШОЙ ЧАСТОТЫ
851
Если положить
LA а
(27)
, _ 1-1.3... (2/> — 3) А! у* а
Р 1 .2.3 .. .In \ 2 ) L
(Р = 2, 3
(28)
то выражения для могут быть написаны в виде
+-±)Р (f - С/ . (Р = 1. 2, ...). (29)
\ и* ^**0 /
Обозначая буквой х число, удовлетворяющее неравенству
Поскольку выражение в квадратных скобках не больше единицы, находим:
Полагая А = 1, получаем далее уравнения
(51 л-•.> t, а. |1)-(0, (31)
в которых для функций 7^(0 имеем оценку
(32
54*
852
ПРИЛОЖЕНИЕ
где
a=i
p=i
2л0
(33)
Q
Q
я
Два штриха у 2 напоминают нам, что следует из данного выражения вычесть члены порядка Q—1 и ниже относительно х.
В случае, когда
(34)
можно положить х = 1; тогда получим:
(35)
СО
Мы 'замечаем, [кроме того, что ряды которые мы
получаем из рядов (21) при условии
сходятся; их суммы равны выражениям
i-1 + £, ° [(*— ti-1) Х ,
в которых положено t—t- , =-----------------------------
’-1 гх(—4-—V
\ а а0 /
Иначе говоря, имеем соотношение
и тогда
или
Итак, для аппроксимирующих функций ij имеем дифференциальные уравнения (31)/ правые части которых отличаются от правых частей точных уравнений на члены Величины, оценивающие верхние границы абсолютных значений этих членов, позволяют срав
О ДВИЖЕНИИ, ВОЗМУЩАЕМОМ СИЛАМИ БОЛЬШОЙ ЧАСТОТЫ 853
нить решения двух систем уравнений, т. е. функций Zj и точных решений Xj. Как уже указывалось, соответствующие функции двух групп принимают при t=tQ одни и те же начальные значения. Для осуществления указанного сравнения можно воспользоваться методом последовательного приближения, приняв за приближение нулевого порядка функции В данном случае применение этого метода более просто для всей области изменения /, имея конечной целью вычисление разностей — Xj. Однако это всё же не есть эффективный вычислительный метод, который можно рекомендовать для применения в конкретных задачах.
Уравнения (31) могут быть написаны в таком виде: t t
Ъ Я, —J
Л)
первые приближения новой последо-правых частях точных уравнений:
x?)==xio + •••> А
Из последних двух уравнений следует, что
t
С другой стороны, мы получим вательности, заменяя Xj на в
или в силу соотношения (32)
Далее мы имеем:
Для того чтобы точка (х^, ..., х£), /) оставалась внутри призматоида (24), достаточно выполнения условия
(t—^<с, (38)
где с удовлетворяет неравенству
Cj > с (39)
для всех значений у.
364
ПРИЛОЖЕНИЕ
Предполагая, что условие (38) выполнено> вычислим вторые приближения
t
= Хзо + J fj И0» • • • ’ х№> I1) dt'
откуда вытекают формулы t
*0 t
+ f A &. I*)— //41’......ХУ> *> (*)MA
A)
Обратимся к тем из неравенств (/)/которые относятся к первым . производным; из этих неравенств следуют условия Липшица
Ы А
f j (5-р • • •, ’L> Iх) “~"fj • • •» Iх) I < I ^к ’ Хк | 9
К
Л=1
(40) где (Ер .Еь, /) и (х1, xL, t) — дйе точки области S, имею-
щие общую (£+ 1)-ю координату Д
Отсюда имеем для рассматриваемого случая:
и для того чтобы точка (х£2),t) оставалась внутри призматоида (24), достаточно выполнения условия
с.
(42)
Тогда неравенство (38) удовлетворяется само собой.
. Аналогичные вычисления дадут нам следующие приближения до некоторого порядка г. Если г стремится к оо, величины х?*) имеют
своими предельными значениями точные решения Xj.
О ДВИЖЕНИИ, ВОЗМУЩАЕМОМ СИЛАМИ БОЛЬШОЙ ЧАСТОТЫ
855
Таким образом, получаем искомую оценку
или
Эти оценки применимы, если
Согласно допущенной гипотезе, переменнее t должно в то же время принадлежать большему интервалу (/0, /0-[~Е-—0), для которого точка (?!, /) остаётся внутри призматоида (25).
Число Е, посредством которого мы ограничили область изменения Д зависит от системы аппроксимирующих функций Sj заданного порядка. От этой зависимости можно освободиться следующими рассуждениями.
Пусть F есть число, удовлетворяющее неравенству
(45)
В интервале (/0, Ц- F — 0) точные решения х$ существуют, и точка (xv ..., t) остаётся внутри призматоида
IXj <^0(46)
Следовательно, в интервале (/0, —0) неравенство (44) всегда
удовлетворяется.
Если t принадлежит как интервалу (£0, /04-£— 0), так и интервалу (/0, Z0-j-F— 0), то неравенства (43)" и (44) имеют место одновременно, откуда следует, что
(47)
Докажем теперь, что вследствие непрерывности условие является тогда излишним и может быть отброшено.
В самом деле, когда переменнее t начинает возрастать от своего начального значения /0, то оно неизбежно остаётся сразу в двух ин* тервалах: {tQi — и (tf0, — 0). В то же * время
856
ПРИЛОЖЕНИЕ
точка (Jp t) движется внутри призматоида (25), тогда как*
точка (х , ..., xL, t) остаётся в призматоиде (46); при этом абсолютные значения разностей соответствующих координат и Xj будут меньше с.
Кроме того, невозможно, чтобы момент наступил прежде момента Действительно, в этом случае точка ($t, ..., t)
достигла бы впервые поверхности призматоида в момент и
тогда, поскольку обязательно должно быть <£0 + по крайней мере одно из условий — Xj0| < Cj— Cj было бы нарушено. Что касается точки (xv ...» xL, t), то она в этот момент находилась бы ещё внутри своего призматоида и мы имели бы I XjQ | < Cj •
Далее следует, что, по крайней мере, для одного индекса J удовлетворялось бы неравенство | — Xj\ > Cj > с. В силу непрерывности это неравенство имело бы место также в некоторый предшествующий момент времени А очень близкий к рассматриваемому, для которого £< < *o + F- С Другой стороны, в соответствии с тем, что
было сказано выше, для такого момента должно быть — х^|<с. Вследствие этого указанный момент времени принадлежит двум интервалам (£0, — 0) и (^0, —0). Мы пришли к противоречию,
что заставляет нас принять соотношение ^0 + ^>*^0 + /7.
Итак, условие
влечёт за собой неравенство вследствие чего это по-
следнее может быть отброшено. Таким образом, можно применить для расчёта оценки (43) и (45).
После получения указанных результатов можно показать, что приближённые решения сходятся равномерно к точкам решения Xj и притом двумя различными путями, именно: абсолютные значения разностей — Xj могут быть сделаны сколь угодно малыми либо уменьшением /*, либо увеличением порядка приближения Q.
Для доказательства первой части этого предложения рассмотрим произвольный интервал (/0, tQ -|~ О Ц- 0) и выберем так, чтобы удовлетворялись неравенства
(48)
Здесь с сохраняет свой прежний смысл, а т| — сколь угодно малое положительное наперёд заданное число. Всегда возможно выразить число t* = указанным образом, для чего можно начать с умень
О ДВИЖЕНИИ, ВОЗМУЩАЕМОМ СИЛАМИ БОЛЬШОЙ ЧАСТОТЫ 857
шения целого числа К, положив его, если это необходимо, равным единице; далее, если указанная операция окажется недостаточной, продолжить уменьшение t* путём уменьшения числа у..
11 Пусть теперь F есть число, не превосходящее G и притом такое, что в интервале (/0, — 0) существуют точные решения х$,
соответствующие принятому значению у., и что точка (хр ..., /)
остаётся всё время внутри призматоида (46). В этих предположениях неравенство (/5) выполняется и число F удовлетворяет всем условиям, наложенным на него выше (стр. 855).
В интервале (tQ, — 0) мы имели оценку (43). Принимая
во внимание условие и неравенство (49), получаем:
<-»!, (50)
что доказывает первую часть нашего предложения.
Для доказательства второй части предположим, что t* удовлетворяет неравенству
SLA
\ а «о
(51)
Этого условия достаточно, чтобы достигнуть любой желаемой степени точности путём увеличения порядка аппроксимации Q без изменения величины, t* в сторону её уменьшения. В самом деле, в этом случае можно положить х = 1 и, в соответствии с неравенством (36), заменить ©^ через AQ. Доказательство выполняется таким же образом, как выше, с той лишь разницей, что теперь, увеличивая число Q, следует всё время удовлетворять неравенствам
Это всегда возможно, так как последовательность чисел
имеет своим пределом нуль при безграничном возрастании Q.
Итак, мы. видим теперь, что можно числа К и у. выбирать столь малыми, иначе говоря (при условии (51), порядок аппроксимации Q столь высоким, что функции будут представлять собой точные решения Xj с произвольной заданной степенью точности в заданном интервале — 0), по крайней мере, в части этого
интервала, где точка (х±, ..., xL, f) остаётся внутри призматоида (46).
Толщина 2cj каждой стенки призматоида может быть взята сколь угодно малой в предположении, что его внешний контур —xj0]=Cj принадлежит области S.,
858
приложение
Условие (51) сходимости процесса не зависит от величины интервала, что представляет существенное отличие изложенного метода от непосредственного разложения по степеням малого параметра, которому соответствует теорема Пуанкаре.
§ 4. Эффективный метод нахождения приближённых решений первого и второго порядков. Воспользуемся выражениями (2) и (3) для функций ..., xL, t, ft, |л) и для Я, первой формулой (14) и условием, согласно которому все функции должны обращаться в нуль при Z = f0; кроме того, примем во внимание сделанную выше гипотезу (начало § 2) относительно величины интервалов (Zi-t, Q. Поскольку ряды, представляющие Д, сходятся абсолютно и равномерно для всех значений &, их можно почленно интегрировать.
Итак, для Z-ro интервала ti) получим следующие разложения функции
оо
№ = Fj — ti- i) +1* S i (?*» cos m&o—fjm sin m»0) +
4BH ffC
m-1
co
+1* S i (— cos тЬ +Л»sin OT&)- (54)
m=l
Каждый из четырёх рядов в правой части этих выражений в свою очередь представляет собой ряд, абсолютно и равномерно сходящийся, так как эти ряды имеют своими мажорантами сходящиеся ряды
(55)
Обозначая через ^(Z) приближённое решение первого порядка и обозначая подробно переменные, входящие в состав функций, получаем для рассматриваемого интервала
(0 — i-1 + 4-1» • • • ’ i-l* ti-1’ н) (*-------*4-1) +
оо
~Ь Н Ул •••’ 4-1» *4-1» H)cos^o
г/4
т-1
— fjmtrl, 4-1» •••» 4-1» h-V Iх) sin Ч"
оо
- - <
Ул“^7 t ?/т(^,4-1» •••» *4-1» и) cos “Ь*
ш=1
“Ь/jm ($1, 4-1» • • • > 4-1» *4—1» Iх) s^n w^]*» (56)
О Движении, возмущаемом силами большой частоты $59
в конце интервала при t=^t^ ряды справа исчезают, и тогда значения, принимаемые функциями будут таковы:
^j,i ~ 'j, i-1 (^1, i-l> •••> г-1» ^-1» Н*)(^г ^-1)« (57)
С помощью этих формул можно определить последовательно все что позволяет написать по формуле (56) выражения для приближённых решений первого порядка внутри каждого интервала. Этот алгорифм немедленно же применяется к числовым расчётам.
Заметим, что необходимые для определения 4 вычисления не отличаются от тех, которые приходится выполнять при оперировании с «укороченной системой»
dX;
= ..., Ajq, А |л) (/= 1, • ••> £), (58)
в которой искомые неизвестные Xlt ..., Xi*) при t = t^ должны принимать те же значения Х^ = х^ что и х$. Эти соображения позволяют получить некоторые новые результаты. В самом деле, воспользовавшись принятой системой интервалов (^_х, Q для образования приближённых решений
&j(f) = i-1 “Ь ^/(^1, г-1» •••> i-l> ^i-l* И*) (f ^i-l)* (59)
находим:
&ji == i-l Fj (^1, i—1» • • •» ti-1* Iх) (fi (50)
Сравнивая соотношения (57) и (60) и учитывая начальные условия SJ0 = XjQ = = х^, видим, что
&ji=
для всех значений I и /, что и требовалось доказать.
Вследствие этого можно написать:
оо
^’(О^3 (0 “Н Н (^1» i—1» • • •» i—li ^i—lt Р») COS W&q
m=l
<—1> • • • 9 i—1, ^i—li Р») Sin —|—
co
+ И У m (Sl, i-19 • • •, Sx, i-19 ii-l> p) COS mb +
H~~ fjm (^1» i—1» • • •> i—1, ^i—1, P«) Sin /И.0]. (61)
Так как «укороченная система» не содержит членов высокой частоты, то, вообще, её легче проинтегрировать соответствующим образом, чем систему заданную.
Допустим, что решения этой системы Х$ (t) найдены; тогда предыдущие формулы указывают на возможность написать приближённое
•*
*) Само собой разумеется, что эти Xj не имеют ничего общего с величинами, обозначенными теми же буквами в § 2.
860
ПРИЛоЖеЯЙЁ
решение в виде функций
со
У$> (0 = + Н 2 f- (Ai.................Хт., t, |1) cos /п» +
+ /}m(Ai........Xi,, t, p.)sin/re&], (62)
где функции со
К,- (0 = X,(f) +1* У J- ................Xi, t, ,0 cos
JHHH •fl'
—fjm (Ai> . • Xi, t, |i) sin m%] (63)
представляют собой секулярные части y'P(t). Эти выражения имеют силу во всей области изменения Д а не только лишь в одном интервале.
В следующем параграфе мы дадим непосредственный и более строгий вывод, а также оценку точности этой формы приближённых решений.
Определяющие соотношения (56) и (57) или же (58), (62) и (63) дают всё, что необходимо для приложения предыдущего анализа, если мы желаем ограничиться решением в первом приближении.
Обращаясь теперь к решению во втором приближении, воспользуемся выражениями функций fj (xt, ..., t, ft, |i) и величины ft, второй рекуррентной формулой (14) и выражениями (54) для полученными в начале этого параграфа. Имеем:
<*!><?) dt
dxjc дхк т=1
fc=i
00 л
дхк «1=1
оо
п=1
оо
п-1
п=1
df?j । V4 &f jm
-ЗГ-+ 7i COS
dt ' dt m-1
sin шЪ (t—
m=l
где все ряды в квадратных скобках сходятся абсолютно и равномерно в интервале (^-i, ty. Перемножая их почленно, получим двойные ряды, которые также сходятся абсолютно согласно классической теореме Коши.
О ДВИЖЕНИИ, ВОЗМУЩАЕМОМ СИЛАМИ БОЛЬШОЙ ЧАСТОТЫ
861
Итак, мы можем написать:
+ И S i 2 § (<pfeOT cos w&0—fkm sin Wl&o) + m=l й=1
co co
[G(zn, n, m 4- n) H (nt, n, m— «)], m=l n=l
где
„ , . v 1 V Г (dfjm I dtjm . \ , . . „ ,
G(m, n, = — 2j + An) cos(/» + «)& +
fc=l k 7
Я(/п, nt m — =
. ,fc=iL
“ fkn ~ <?kn) sin (^ + П) & , (66)
£ \ f x n
r"?fcn fknj cos (m
Fm ,: I m \ . . л1 ______
fkn~{" dx-fc sin L (67)
862
ПРИЛОЖЕНИЕ
причём функции G (т, п, Н(т, п, т — п) определены лишь
для целых значений т, п.
Двойные ряды, образованные с помощью указанных функций могут быть преобразованы следующим образом.
Полагая в рядах О (пъ, п,
т-]-п = tnL,
и, следовательно, п — получаем:
ОО ОО CO wij —1
2 2 О (т, п, = 2 2 О (nv т1 — nlt (68) m = l П = 1 Wj = 2 Пх = 1
В рядах Н (пъь п, т — п) можно сделать преобразование
т— п, = т2> п = п2,
т = т2-\-п2
в случае т — п = т2>® и преобразование
т — п = — т3, т = /г3,
п = 4- %
в случае т— п —— < 0. Находим:
2 3 Н(т, п, т — п)= 2 т, 0)-[~
т=1п=1 т-1
+ 22 H(m2 + n2, п.2, т2)+ 2 2 ^(«3- даз + лз> — тз>- (69) т2=1 п2-1 m3=l п3=1
В формулах (68) и (69) можно отбросить индексы у т и п и приме-»
нить эти формулы для преобразования выражений производных ;
все простые ряды, расположенные по косинусам и синусам аргумента zn&, входящие в преобразованные выражения, сходятся абсолютно и равномерно. В самом деле, эти ряды имеют своими мажорантами аналогичные ряды с постоянными положительными членами, которые получим, если функции F, /, <р и их производные заменим их абсолютными значениями, заменим t—на и отбросим
все тригонометрические множители. Полученные мажорирующие ряды сходятся на основании теоремы Коши.
Из приведённых рассуждений следует, что ряды для ф}2) можно интегрировать почленно с учётом начальных условий.
Получаемые таким образом выражения для распадаются на две группы членов, а именно: во-первых, члены непериодической части,
О ДВИЖЕНИИ, ВОЗМУЩАЕМОМ СИЛАМИ БОЛЬШОЙ ЧАСТОТЫ
863
содержащие множителями биномы (t—и его квадраты; во-вторых, члены периодической части, содержащие только постоянные и тригонометрйческие функции &.
Непериодическая часть может быть написана в виде
оо
"* И S i cos wfto—Sin /»%)+
?п=1
оо
। X1 1 / ' t— h-t g । Z t— k-t
+ H 2j m W™ Г“ C0S ------------------T^*
m=l
sin znB),
где
°° L
= S i - s %»)cos + m=l fc=l
dxk
n 1 VI (dfjm , \
sin —у ( dx ?»m— fkm) >
k=l
(70)
причём функции fjm, ф/и» определяются по формулам (65). Периодическая часть имеет вид
1 г v / т(т—дхк'к'т к-1
CO W—1
ш = 2 п = 1
^tjn дхк
(cos тЪ — COS /П&0) —'
Тй» т-п
864
ПРИЛОЖЕНИЕ
?n=l п=1 к=1
(cos mb — cos zn&0) +
л = 1
mb—sin mb^)
(71)
После приведения она упрощается, принимая вид
оо
И9 У cos /»% — /$, Sin ffl&0) +
ляЛ TH
m=l
оо
+ Р-9 У cos +Ж sin «П)>
ЛЯЛ ffC
т=1 *
(72)
где и имеют очевидные значения.
Итак, имеем:
со
W = 1
cos mb
sin mb
(73)
О ДВИЖЕНИИ, ВОЗМУЩАЕМОМ СИЛАМИ БОЛЬШОЙ ЧАСТОТЫ 865
(
Пользуясь выражениями (54), найденными выше, и обозначая теперь через .приближённые решения второго порядка, получаем:
со
+ н 2 i [(**»+cos т*<> ~ т-1
со
т=1
Ряды в правых частях этих уравнений исчезают в конце интервала t=t^ Приходим к рекуррентным формулам
tji = Ь < -1 + {Pj + И) + p'i (ti !. 2~1)2 ’ (75)
которые могут служить для последовательного вычисления всех и затем для нахождения числовых значений коэффициентов в выражениях (74), определяющих вторые приближения в каждом интервале.
Как и в рассмотренном выше случае первой аппроксимации, мы 1 видим, что необходимые вычисления для определения те же самые, что при нахождении приближённого решения уравнений
= Fj (Хъ.... Xl, I, Ю + V-P'P (Ai.Хъ, t, j*), (76)
если ограничиться членами второго порядка относительно рь (приращения t—t* = 2А/тс<х при этом должны рассматриваться как величины первого порядка).
Будем называть уравнения (76) укороченными уравнениями второго порядка. Если бы удалось их каким-либо способом проинтегрировать, было бы совершенно естественно попытаться в качестве вторых приближений во всей области изменения t использовать функции
°°
уТ (О = Yj (0+н 2 i (^1. • • •. xL, t, н) 4-т=1
....Xl, t, |1)1 cos mb + [fjm (Xi.XL, t, p) +
+{Xi........Xi,, t, |x)l sin (77)
55 Зак. 1474. Б. В. Булгаков
MSB. *
866
ПРИЛОЖЕНИЕ
где функции
оо
4“ Н zj “ZT {[<?jm G^l» • • •» Д н) *”1“ GVp • • • > р»)] COS TH^q—
ЯШЯк 99V
т=1
\fjm(-^ii* • •> Xl> н) C^i> • • •> t> p)psin w%} (78)
представляют собой секулярные части yf.
В следующем параграфе будет дан прямой вывод также и этих приближённых решений.
Определяющие соотношения (74) и (75) или же (76), (77) и (78) вместе с выражениями для F(/\ <р$> образуют алгорифм для
получения приближённого решения второго порядка конкретно взятой задачи.
Чтобы закончить этот параграф, укажем на одно важное обстоятельство. Предположим, что непостоянные коэффициенты
*•” XL> н)> •••’ XL> н)
рядов Фурье содержат один и тот же постоянный множитель е.
Обращаясь к формулам (70) и (71), легко замечаем, что F/\ /Ф, делятся на этот множитель. Тогда члены типа
р— <fjm cos /п&0, pF^ оказываются порядка ре, между тем как члены типа р -- р<?Ф cos делятся на р2е.
Ещё более частный случай — тот, когда величины Fj содержат также множитель е, а все частные производные от Fj, fjm, <?jm по t обращаются в нуль или имеют порядок величины е2.
Тогда Fj\ делятся на е2. Члены типа р — cos /пВ0
содержат, как и в предыдущем случае, множитель ре. Но уже члены pFj4 имеют порядок ре2, тогда как порядок членов типа р yrf/m cos есть H2s2-
Последнее замечание находит своё приложение в некоторых задачах о движении твёрдого тела.
§ 5. Приближённые решения, вычисленные с помощью «укороченных уравнений». Когда речь идёт лишь о вычислении и оценке некоторых приближённых решений, но не о их сходимости при возрастании порядка аппроксимации Q, можно, вводя разбиение времени движения на интервалы, применить метод, аналогичный методам П. Фату, Л. И. Мандельштама и Н. Д. Папалекси.
О ДВИЖЕНИИ, ВОЗМУЩАЕМОМ СИЛАМИ БОЛЬШОЙ ЧАСТОТЫ 867
Кроме гипотез, введённых в начале данной работы, допустим, что в области S при у. < рь* имеем:
и что суммы рядов (5) меньше Н. Вводимые далее величины В, Ь, bQ, Я, h, hQ обозначают некоторые постоянные положительные числа. Допустим, что при указанных условиях суммы рядов, аналогичных (5) и образованных первыми производными по xt,..., xL, t, меньше чисел
/У //
— , -г-; положим: h hn
Призматоид
I I < A) < A) + D
должен принадлежать, как и выше, области S.
Пусть теперь Х19...9 — некоторые функции t9 t допускающие
непрерывные первые производные и принимающие при t=t$ значения Х^ = х^0. Мы их примем в качестве начальных функций последовательности аппроксимаций. Мы предполагаем, что < |л* и что t принадлежит большему интервалу
когда точка (Xi,..., Лх, 0 остаётся внутри второго призматоида
где — положительные произвольно малые числа, удовлетворяющие неравенствам
Два призматоида образуют «ящик», а каждое из чисел Cj обозначает толщину соответствующей его «стенки».
Первые приближения последовательности определяются формулами
t
Xj — "^jo § fi , XL) 0, dt,
$0
55*
868
ПРИЛОЖЕНИЕ
Условимся в дальнейшем писать обозначения функций /j, F^ fjm, без указания на переменные, от которых они зависят, если этими последними являются Х±,..., Х^, tt ft, рь.
Пользуясь выражениями (1) и (2) и применяя интегрирование по частям, находим:
* t
Xj > = XjQ -|- f Fj dt
#0 co
+ H У — [— (cos mb — cos + fjm (sin mb — sin zn&0)] — •ЯМВ f 9 Ъ
m—1
00 I b 3
V 1 Г /V dXlt I d^\ z (Y Q 4 .
lim I (1 ~d^ ~dT + ~дГ) (c°s mb - cos mbj Ц-
m=l #0 Ar=l
+ ( V(sin — sin znft0)l dt.
1 \^J dxfr dt 1 dt 0/J
fc=i
Здесь все преобразования сделаны на законных основаниях. В самом деле, если рь < рь*, ряды (2) сходятся абсолютно и равномерно в S при всех значениях ft; следовательно, разложения fj (Xi,..Xl, t, ft, рь) могут быть проинтегрированы почленно. Каждый из рядов оо
cos /nft), так же как и другие ряды того же типа в выра-т=1
жениях для Xj\ сходится абсолютно и равномерно. Отсюда следует, что сходимость рядов, образующих неггроинтегрированную часть также обеспечена. Для сокращения формул следует теперь положить
что даст для Xj «укороченные уравнения» (58). Используя эти уравнения, мы получим:
Xj — Кд И» (04)
где у'У являются именно приближёнными решениями первого порядка, 3 1)
написанными в форме (62), a Rg' имеют вид со L ~
FH“»»)+
т-1 t0 fc=l
sinOT5>°)dt' \ rV / 4
6 ДвиЖейий, ЙойМУЩаеМоМ СиЛаМи ёолЬшой частоты
869
Для абсолютной величины R^ можно написать неравенство
t0 Л=1 т=1
dfjm дхк'
т=1
dfjm дхк
wi=l
dfjm "дТ
Ш = 1
dt
так как все ряды под знаком Н их сумма меньше величин
интеграла равномерно сходятся, причём
и — . Следовательно, Ло
1^’1<4жга—/0),
I ур - х? I < -ЦА,
(84)
(85)
где
С другой стороны,
= £Д .______1_
‘ ft “г h0 '
(86)
ОО
x(j)—А- = (I У (<Pjm cos sin m&0) +
v ЛЛ fit
Ш = 1
CO 1 /•
+ >* Ът cos sin m&) — m=l
co co
l4>-X,| < 2И (211^1+ +
m=l m—1
ИЛИ
14* — А}|<4|*я{1 + £-Ц^}. (87)
Для последующего существенно, чтобы внутри области S оставалась не только точка (Xv ..., XL, t), но и точка (х^1), ..х£\ f). Так как
Л)_ v Г-Д-Г г
^3'Qi
14} - Xjo I < 4ря{1.++ q - Cj, (88)
то указанное условие выполняется, если
4ИЯ{1 + Q-Ц-^} + С} — Cj < Cjt
4|xtfh <с,
(89)
870
Приложение
где Cj удовлетворяет неравенству
Cj > с
для всех значений индекса у.
Для вторых приближений х^ мы имеем соотношения t
Х^ — Х^}= J [/'(хГО,..., хф, t, &, |Х)—........XL,t, ft, |*)]<й;
^0
далее, в силу (81) и условий Липшица
f l I
xf—ху>|< | уА|4>_хк|^<М4|*я I {1+qIzAI^ * * J U И J II
t о 7с=1
или же, наконец,
Iхр — х/) I < 4|Ш -И ('-у.2 I. (90)
•/ J I с* 1 u> 1 * J
Из тождеств
выводим, что, во-первых, + + (91)
и что, во-вторых, точка (х<2>, ..., х'£\ f) остаётся внутри области S, если
4|1Я{1+^^+<?[-Ц-^ + ^-^Ц=^]}<С. (92)
При выполнении этого условия предыдущее неравенство (89) оказывается также выполненным.
Продолжая указанные рассуждения, мы получим аппроксимации хФ произвольного порядка г и соответствующие неравенства. При г—>оо функции х<р стремятся к точным решениям х.-, и мы по-•г *
лучим следующие оценки приближённых решений у'Р:
J
+ «[— (LA\*(t-№ \ а ) Ь2 “Г ’ * г "Г ^0 I ^о)2 I 1 /по\ 1 ' а Ь2 +•••/•
О ДВИЖЕНИИ, ВОЗМУЩАЕМОМ СИЛАМИ Большой ЧАСТОТЫ
871
Эти оценки сохраняют свою силу до тех пор, пока выполняется неравенство
} < с. (94)
Кроме того, согласно сделанной вначале гипотезе, переменное t должно оставаться внутри интервала (£0, £04-£ — 0).
Из двух предыдущих неравенств следует, что
Ij?) — хА<с — 4[хН < с. (95)
•/ •/
Оценка (93) и условие (94) могут быть записаны также с помощью показательных функций
1ЛХ)-^ I < + zr) [- 1 +ехР > (96)
4|*Я {exp (t - Q + [- 1 + exp (t- } < с. (97)
Отсюда следует, что поскольку ряды (5), а также аналогичные ряды, образованные частными производными, равномерно сходятся в замкнутой области S, то, перемножая их попарно в произвольном порядке, получим ряды, также равномерно сходящиеся.
Это вытекает из доказательства теоремы Мартенса *) об умножении рядов и из того факта, что равномерная сходимость простого или кратного ряда с положительными членами сохраняет свою силу, если произвольно изменить порядок суммирования.
Обращаясь к приближённым решениям второго порядка, примем во внимание сделанное замечание. На этот раз, для краткости, ограничимся формальным вычислением.
Примем функции
со
= X. + р. У Д- (<pJOT cos /п»0—fjm sin m&0) +
m=l co
+ И У (— <?jm cos mb sin m&) (98)
m—1
за начальные функции новой последовательности аппроксимаций. Входящие в эти формулы функции Xj не предполагаются идентичными с величинами, обозначенными выше теми же буквами. Эти функции при t = tQ должны принимать начальные значения XjQ = Xj0 и
*) Journ. fiir reine u. angew. Math., t. 79 (1874), стр. 182—184 или E. Picard, Traite d*Analyse, т. 1 (1922), стр. 252.
872
ПРИЛОЖЕНИЕ
' допускать непрерывные первые производные относительно t, в остальном же они заранее не определены. Уточнение выбора этих функций может быть осуществлено лишь в процессе последующего расчёта.
Величины Х19 ...» Xl, р, которые входят в функции ©jm, здесь не указываются.
Согласно конечной формуле Тейлора имеем:
, (4Х)..........Н) = fj + У IН У (?*» cos —
fc=l n = l
со
—fkn sin Л&о) + р- 2 (— ?fcn cos »9 +/fen sin »9)
n=l
+н —(2 <c°s n9—cos n9°)+
n=l fc=l
fc=l
Чтобы установить принцип, позволяющий упорядочить расположение членов в наших вычислениях, условимся рассматривать функции и их производные по хх, ..., как величины
порядка е, а их первые производные по /, — как величины порядка е2. Члены, не выписанные в предшествующей формуле, а также в последующих и обозначенные через (...), имеют порядок |л2е3.
Сформулированное условие не влечёт за собой какого-либо ограничения в общности рассуждений.
Произведя интеграцию, получим аппроксимирующие функции которые назовём вторыми приближениями новой последовательности:
t t
xj2)=xjo+ J/г <ЧХ>....л9> (fjdt+
to t0
Гц n=l Л=1
?fcn) (cos —cos n%) +
. .)dt.
О ДВИЖЕНИИ, ВОЗМУЩАЕМОМ СИЛАМИ БОЛЬШОЙ ЧАСТОТЫ
873
Заменяя здесь функции fj их выражениями, находим:
ОО
to
оо £
Ш = 1 to
m=l t0
/3\ dFf \
- ( 2j д^^т) (cos тЪ — cos /w»0) + fc=l
+ ( 2 Й Am) (sin — sitl m&o) dt+
л=1
V
L dxk
f0 m-1 n=l fc=t
$ оо со
fc=i
л=1
fc=l
sin
Выделяя интегралы, содержащие cos /n&0, sin произведём гт интегрирование по частям. Предполагая, что производные являются Сф с
величинами порядка в, получим:
ч?)=^»+ J {^я-н 2 i [(2 cos т^~
to т=1 fc=l
L дР
—(2 ~д^^т)sin от&о]}dt+ fc — 1 ф
оо
+н 2 "т <cos ~cos (sin ~sin +
т=1
I V 1 f Г (V d<tJm TdX^ I a OS
+«12i^'. IQ4^t+t)(C0SOT&—cosmao)-mxsl fo Л=1
“ IL ~d^ ~dF +-5Г") <sin mb — sltl dt—
874
ПРИЛОЖЕНИЕ
~ Н2 2 i [(2 ~дх^ ?кт) (cos т?> ~ cos +
m=l fc=l
?fem) (sin т» — sin m»0) U-
co oo L _
4- F-2 2 2 2 &kn cos n^—fkn sin П%) X
m=l n=l fccl
X(cos m & — cos mf>0) -|-
(?fcn cos — fkn sin л%) (sin — sin! +
$ co oo
+11 2S [G(zn, n, t0 m=ln=l
t
n, m — n)]4#+ j* (. ••)<&, ^0
где функции \G(mt n, H(m, n, m — ri) определяются по-
средством формул (66) и (67); невыписанные величины, от которых зависят эти функции, суть Х19 ..., Xl, t, |л. Знаком (...) обозначена, как и прежде, совокупность членов порядка |л2з3.
Выделяя интегралы, содержащие Н(т> п, т — п) при т — п, и производя опять интегрирование по частям, имеем:
(9\ । f I с 1 <i V 1 /V dXk ,
42)=^о+ .| ^+^2-5г[-(2-^й-5г+-д?----------
t; 1Л-1 к~1
dxk ?*»»)c0sw% + \2 dxk dt 4- dt к=1 Л=1
— 2 bxk ^ktn) ?in 2 2 \ дхк dxk fkm) If dt~^ k=l k=l
oo oo
4- и 2 C0S w&0—Лт sin /»%) + H 2 m cos wft 4-
w=l W = 1
1
I x , n V4 1 И 1 /V dfim dxk ! V t \
4-Zfr»Sin»i&) + |i9 2/m Vm (2 dxk dt 4- dt 2ddxk^)
m=l k-l k=l
О ДВИЖЕНИИ, ВОЗМУЩАЕМОМ СИЛАМИ БОЛЬШОЙ ЧАСТОТЫ
875
п-1 к—1
(.Ъп cos Sin га»0)
dX-fc d^jm дхъ dt * dt
(cos тЪ — cos Ы>0) -j-
('?kn cos —fkn sin n%) (sin /и» — sin
CO co
O(m, n>
m=l n=l
ft Г v-i f
+-y | 2 1 #(m>n> m—»)<#+ J
to w = l W = 1 f-
где совокупность (...) состоит только из членов порядка рь2©3, а через Xj, для сокращения, обозначено выражение
причём функции /L, сохраняют свои значения в соответ- .
ствии с формулами (65) и (70).
Функции Xj должны тогда удовлетворять «укороченным уравнениям» второго порядка (76). Легко также убедиться, что мы пришли именно к решениям УЖ0> определяемым формулами (77), вследствие чего можно написать:
t
t.
Итак, «укороченные уравнения» первого порядка могут быть заменены уравнениями более точными. Решения этих последних могут
876
ПРИЛОЖЕНИЕ
быть сейчас же применены для уточнения непостоянных коэффициентов рядов Фурье, представляющих приближённые решения заданных уравнений.
Указанный процесс есть не что иное, как специальное видоизменение метода последовательных приближений; принципиально он может быть продолжен и далее, но при этом вычисления неизбежно-становятся всё более и более громоздкими.
Этим замечанием мы заканчиваем изложение метода. Примеры его приложений могли бы быть даны в теории движения твёрдого тела около неподвижной точки и в теории нелинейных колебаний.
ЛИТЕРАТУРА
Сочинения общего характера
0.1. Андронов А. А. и X айкин С. Э., Теория колебаний (1937).
0.2. Гантмахер Ф. Р. и крейн М. Г., Осцилляционные матрицы и малые колебания механических систем (1941).
0.3. Ден Гартог Дж. П., Теория колебаний, перев. А. Н. Обморшева (1942).
0.4. Крылов А. Н., О некоторых дифференциальных уравнениях математической физики, имеющих приложения в технических вопросах, изд. 5 (1950).
0.5. Крылов Н. М. и Боголюбов Н. Н., Введение в нелинейную механику (1937).
0.6. Релей (Стрэт Дж. В.), Теория звука, перев. П. Н. Успенского и С. А. Каменецкого, т. I (1940).
0.7. Теодорчик К. Ф., Автоколебательные системы, изд. 2 (1948).
0.8. Тимошенко С. П., Теория колебаний в инженерном деле (1931).
0.9. Van den D u п g е n, Cours de technique des vibrations. Bruxelles (1926).
0.10. Fdppl O., Grundziige der technischen Schwingungslehre, Berlin (1931).
0.11. Hort W., Technische Schwingungslehre, Berlin, изд. 2 (1922).
0.12. Klotter K., Einfiihrung in die technische Schwingungslehre, Berlin, т. I, Einfache Schwinger (1938).
0.13. Lehr E., Schwingungstechnik. Berlin, т. I (1930); т. II (1934).
0.14. Routh E. J., Dynamics of a System of Rigid Bodies, ч. II, London and New York, изд. 6 (1905).
К главе 1
1.1. Б о x e p М., Введение в высшую алгебру, перев. под редакцией А. Г. Куроша (1933).
1.2. Гельфанд И. М., Лекции по линейной алгебре, изд. 2 (1951).
1.3. Лаппо-Данилевский И. А., Теория функций от матриц и системы линейных дифференциальных уравнений (1934).
1.4. Лузин Н. Н., К изучению матричной теории дифференциальных уравнений. Автоматика и телемеханика, № 5, стр. 4—66 (1940).
1.5. Мальцев А. И., Основы линейной алгебры (1948).
1.6. Смирнов В. И., Курс высшей математики, т. Ш, ч. I, изд. 6 (1954);
т. 111, ч. II, изд. 4 (1953).
1.7 Суш к ев и ч А. К., Основы высшей алгебры, изд. 4 (1941).
1.8 Широков П. А., Тензорное исчисление, ч. 1 (1934).
1.9 Aitken А. С., Determinants and Matrices, Edinburgh and London, изд. 5 (1948).
JO, Frazer R. A., D;.un.can W. J. and Collar A. R., Elementary Matrices and some App'icatlons to Dynamics and Differential Equations, Cambridge — New York (1947).
JL Fantappie L., Le calcul des matrices, Comptes rendus, t. 186, стр. 619—621 (1928).
878 литература
1.12. Mac Dutfee С. C., The Theory of Matrices, Berlin (1933).
1.13. Michal A. D., Matrix and Tensor Calculus, New York (1947).
1.14. Wedderburn J. H. M., Lectures on Matrices. American Mathematical Society Colloquium Publications, т. XVII, New York (1934). |
К главе 2
2.1. Диткин В. А., Операционное' исчисление. Успехи математических наук, т. II, вып. 6 (22), стр. 72—158 (1947).
2.2. И г н а т о в с к и й В. С., По поводу лапласовской трансформации. Доклады Академии наук, т. 2, № 1, стр. 5—11 (1935); т. 2, № 5, стр. 169— i
172 (1936); т. 4, № 3, стр. 107—110 (1936). j
2.3. Карман Т. и Био М. А., Математические методы в инженерном । деле, перев. с англ., гл. X (1946).
2.4. Курант Р. и Гильберт Д., Методы математической физики, т. II, 1 перев. Ю. Рабиновича и 3. Либина (1945). Дополнения к гл. III.
2.5. . Лурье А. И., Операционное исчисление в приложениях к задачам механики (1938).
2.6. Эфрос А. М. и Данилевский А. М., Операционное исчисление и контурные интегралы (1937).
2.7. Булгаков Б. В., Об операционных решениях систем линейных дифференциальных уравнений с постоянными коэффициентами. Доклады Академии наук СССР, т. 41, № 6, стр. 248—251 (1943). 1
2.‘8 . Berg Е. J., Heaviside’s Operational Calculus, New York and London (1936).
2.9. Bromwich T. J. ГА, Normal Coordinates in Dynamical Systems, Proceedings of the London Mathematical Society, Second series, t. 15, стр. 401— ।
448 (1916).
2.10. Bush V., Operational Circuit Analysis, New York (1929).
2.11. C a m p b e 11 G. A. and F о s t e r R. M., Fourier Integrals for Practical Applications (1942).
2.12. Car si aw H. S. and Jaeger J. C., Operational Methods in Applied Mathematics, New York (1941). (Имеется русский перевод: К ар с л оу X. и Егер Д., Операционные методы в прикладной математике, 1948.)
2.13. Carson J. R., Electric Circuit Theory, and Operational Calculus, New York (1926). Немецкий перевод: Elektrische Ausgleichsvorgange und Ope-ratorenrechnung, erweiterte deutsche Bearbeitung von Ollendorff F. und Pohlhausen K., Berlin (1929). Русский перевод: Карсон Д. Р., Электрические нестационарные явления и операционное исчисление, Харьков— Киев (1934).
2.14. Churchill R., Modern Operational Mathematics in Engineering, New । York (1944). I
2.15. Da hr K. A., A Course of Integrational and Operational Calculus, Stock- I holm (1935). I
2.16. Doetsch G., Theorie und Anwendung der Laplace-Transformation, Berlin (1937).
2.17. Doetsch G., Tabellen zur Laplace-Transformation und Anleitung zum Gebrauch, Berlin und Gottingen (1947).
2.18. Gardner* M. F. and Barnes J. L., Transients in Linear Systems, t. I, New York (1942). (Вышел русский перевод: Гарднер М. Ф. и Б э р н с Дж. Л., Переходные процессы в линейных системах с сосредоточенными постоянными, 1949.)
2.19. Heaviside О., Electromagnetic Theory, т. I (1893), т. II (1899), т. Ill (1912), New York. Новое издание — London (1922).
2.20. Humbert Р., Le calcul symbolique, Paris (1934).
2.21. Humbert P. et Colombo S., Le calcul symbolique et ses applications a la physique mathematique. Memorial des sciences math&natiques, вып. 105, Paris (1947).
Vi
Ли1еЬаТ$г?а 87§ I
§
цзд* V (f931)H ’ OperationaI Methods in Mathematical Physics, Cambridge, $
2.23. Mac Lachlan N. W. et Humbert P., Formulalre pour le calcul symbolique, Memorial des sciences math^matiques, в,ып. 100, Paris (1941).
j 2.24. MacLachlan N. W., Modern Operational Calculus with Applications in Technical Mathematics, New York (1948).
2.25. Van d e r Pol B., On the Operational Solution of Linear Differential Equations and an Investigation of the Properties of these Solutions. Philosophical Magazine, cep. 7 t. 8, стр. 861—898 (1929).
2.26. Van der Pol B. and Nlessen K. F., Symbolic Calculus. Philosophical Magazine, cep. 7, t. 13, стр' 537—577 (1932).
2.27. Prager W., Uber Verwendung symbolischer Methoden in der Mechanik.
j Ingenieur-Archiv, t. 4, стр. ,16—34 (1934).
' 2.28. Stephens E., Elementary theory of Operational Mathematics, New York
(1937).
2.29. Wagner K. W., Operatorenrechnung nebst Anwendungen in Physik und Technik, Leipzig (1940).
2.30. Widder D. V., The Laplace Transform, Princeton (1941).
2.31. Wiener N., The Operational Calculus. Mathematische Annalen t. 95, стр. 557—584 (1926).
К главе 3
1 3.1. Бухгольц Н. Н., Основной курс теоретической механики, ч. I
(1945); ч. II (1945).
3.2. Зомм.ерфельд А., Механика, перев. Т. Е. Тамма (1947).
3.3. Каплянский А. Е., Введение в общую теорию электрических машин (1941).
3.4. Лойцянский Л. Г. и Лурье А. И., Теоретическая механика, ч. 1, ч. II, (1933), ч. Ill (1934).
3.5. Суслов Г. И., Теоретическая механика, изд. 3 (1946).
3.6. Уиттекер Е. Т., Аналитическая динамика, перев. И. Г. Малкина (1937).
3.7. Булгаков Б. В., .О преобразовании уравнений движения неконсерва-
1 тивных систем. Доклады Академии наук СССР, т. XLIV, № 3,
стр. 104—107 (1944).
3.8. Andoyer Н., Cours de mScanique celeste, т. I, Paris (1923).
3.9. Chazy J.. Sur urie generalisation des equations canohiques. Comptes rendus de 1’Acad. des Sci. Paris, t. 226, стр. 19—23 ,(1948).
3.10. Levi-Civita T. e Am al di U., Lezioni di meccanica razionale. Bologna, т. I, изд. 2 (1930), т. II, ч. 1 (1926), ч. 2 (1927).
3.11. Mac Millan W. D'., Dynamics of Rigid Bodies, New York and London (1936).
3.12. Maxwell C.,A Treatise on Electricity and Magnetism, Oxford ,(1873).
3.13. Osgood W. F., Mechanics, New Vork (1937).
К главе 4
4.1. Андронов А. А. и Майер А. Г., Простейшие линейные системы с запаздыванием. Автоматика и телемеханика, т. VII, вып. 2—3, стр. 95—106 (1946).
4.2. Боднер В. А., О динамических погрешностях приборов, предназначенных для измерения быстроизменяющихся величин/ Труды Военно-воздушной йнженерной академии, вып. 233 (1947).
4.3. Кр ахсовс к ий А. А., О степени устойчивости линейных систем. Труды Военно-воздушной инженерной академии, вып. 281 (1948).
4.4. Моисеев Н. Д., Квазиинтегральный вывод прямого коэффициентного критерия асимптотической устойчивости для обыкновенной системы
I Кл
880
ЛИТЕРАТУРА
однородных линейных дифференциальных уравнений с постоянными коэффициентами. Записки Семинара по теории устойчивости движения Военно-воздушной инженерной академии, вып. 3, стр. 41—69 (1948).
4.5. Моисеев Н. Д;, Коэффициентный критерий асимптотической устойчивости для обыкновенной системы, эквивалентной одному линейному однородному дифференциальному уравнению с постоянными коэффициентами. Там же, стр. 71—85.
4.6. Раушенбах Б. В., О выборе рациональной меры продольной динамической устойчивости самолёта. Труды ЦАГИ, вып. 533 (1941).
4.7. Ф е л ь д б а у м А. А., Интегральные критерии качества регулирования. Автоматика и телемеханика, т. IX, вып. 1, стр. 3—19 (1948).
4.8. X а рк е в и ч А. А., О применении критерия квадратичной погрешности к оценке линейных искажений. Журнал технической физики, т. VII. вып. 5 (1937).
4.9. Цыпкин Я. 3. и Бромберг П. В., О степени устойчивости линей ных систем. Известия Академии наук СССР, ОТН, № 12, стр. 1163(1945).
4.10. Бу л г ак о в Б. В., О накоплении возмущений в линейных колебательных системах с постоянными параметрами. Доклады Академии наук СССР, т. LI, № 5, стр. 339—342 (19'46).
4.11. Baker Н. F., On the Integration of Linear Differential Equations. Proceed. of the London Mathematical Society, t. 35, стр. 333 (1903).
4.12. В 6 d e w a d t U. T., ‘ Schwingungen bei periodisch veranderJichen Ohm-schen Widerstand. Zeitschrift fiir angewandte Mathematik und Mechanik, t. 19, вып. 3, стр. 146 (1939).
4.13. Brillouin L., A practical Method for Solving HiTs Equation. Quarterly of Applied Mathematics, t. 6, № 2, стр. 167—178 (1948).
4.14. Brown G. S. and Campbell D. P., Principles of Servomechanisms, New York (1948).
4.15. Callender A.,Hartree D. R. and Porter A., Time-Lag in a Control System. Phylosophical Transactions of the Royal Society, cep. A, t. 235, № 756, стр. 415—444 (1936).
4.16. Chalmers, The Principles and Practice of Automatic Control. The Engineer, t. CLXIII, № 4228-4241. стр. 94—95, 122—124, 150—151, 176^-177, 201—205, 236—237, 268—269, 294—295, 322—323, 352—353, 380—382, 408—409, 438—439, 467—469 (1937). Русский перевод под названием «Автопилоты», под ред. Г. В., Щипанова Москва—Ленинград (1939).
4.17. Hall А. С., The Analysis and Synthesis of Linear Servomechanisms. Massachusetts Institute of Technology (1943).
4.18. James H. M., N i c h о 1 s N. В., P h i 11 i p s R. S. (ed.), Theory of Servomechanisms. Massachusetts Institute of Technology, Radiation Laboratory Series, kh. 25, New York — Toronto — London (1947).
4,19. L a u e г H., L e s n i k R. and Matson L., Servomechanisms Fundamentals, New York and London (1947).
4 20. Obradovic J., Die Abweichungsfiache bei Schnellregelvorgangen. Arch I v fGr Elektrotechnik, т. XXXVI, стр. 382—390 (1942).
К главе 5
5.1. Аксельрод 3. М., Часовые механизмы. Теория, расчёт и проектирование (1947).
5.2. Андронов А. А., Предельные циклы Пуанкаре и теория колебаний. VI съезд русских физиков, стр. 23—24 (1928).
5.3 А р т е м ь е в Н. А., Качественная теория дифференциальных уравнений (1941).
5.4. Артоболевский И. И., Об определении маховых масс в машинах. Доклады Академии наук СССР, т. XL1V, № 5, стр. 198—202 (1944).
ЛИТЕРАТУРА
881
5.5. Асеев Б. П., Основы радиотехники (1947).
5.6. Дородницын А. А., Асимптотическое решение уравнения ван дер Поля. Прикладная математика и механика, т. XI, вып. 3, стр. 313—-328 (1947).
5.7. Дроздов Ф. В., Приборы времени (1940).
5.8. Кокурин С. Н., Релаксационные колебания, ч. I (1938).
5.9. Крылов А. Н., О применении способа последовательных приближений к нахождению решения некоторых дифференциальных уравнений колебательного движения (1933).
5.10. Ляпунов А. М., Общая задача об устойчивости движения, изд. 3 (1950).
5.11. М а н д е л ь ш т а м Л. И., Па па лек си Н. Д., Андронов А. А., Витт А. А., Г о р е л и к Г. С., X а й к и н С. Э.» Новые исследования нелинейных колебаний (1936).
5.12. Немыцкий В. В. и Степанов В. В., Качественная теория дифференциальных уравнений 2 (1947).
5.13. Папалекси Н. Д., Андронов А. А., Горелик Г. С., Рытое С. М., Некоторые исследования в области нелинейных колебаний, проведённые в СССР, начиная с 1935 г., Успехи физических наук, т. XXXIII, вып. 3, стр. 335—352 (1947).
5.14. Ван дер Поль Б., Нелинейная теория электрических колебаний. Перев. Я. А. Копиловича (1935).
5.15. П у а н к а р е А., О кривых, определяемых дифференциальными уравнениями, перев. Е. Леонтович и А. Майер (1947).
5.16. Стрелков С. П„ Маятник Фроуда. Журнал технической физики, т. III, вып. 4, стр. 563—573 (1933).
5.17. С уза нт А. Е., Введение в нелинейную радиотехнику (1934).
5.18. Ф о р х г е й м е р Ф., Гидравлика, перев. А. А. Черкасова (1935), § 139.
5.19. Чета ев Н. Г., Устойчивость движения (1946).
5.20. Под ред. Шулейкина М. В., Нелинейные системы. Сборник (1939).
5.21. В i 1 h ar z Н., RoHstabi’itat eines urn seine Langsachse freien Flugzeugs bei automatisch gesteuerten, Intermittierenden, konstanten Qnerrudermo-menten. Luftfahrt-Forschung, t. 18, вып. 9, стр. 317—326 (1941).
5.22. В i 1 h a r z H., Ober eine gesteuerte eindimensionale Bewegung. Zeitschrlft fttr angewandte Mathematik und Mechanik, t. 22, № 4, стр. 206—215 (1942).
5.23. Haag J., Ann. Sci. Ecole Norm. Sup. (3) 60, стр. 35—64, 65—111 (1943); 61, стр. 73—117 (1944).
5.24. К r a u t w i g F., StabiHtatsuntersuchungen an unstetigen Reglern, darge-stellt an Hand einer KontaktnactVaufsteuerung. Archiv ffir Elektrotechnik, т. XXXV, № 2, стр. 117—126 (1941).
5.25. Lefschetz S., Lectures on Differential Equations. Princeton (1946).
5.26. Lieb is ch W., Zeitschrift des Osterreichischen Ingenieur- und Architek-ten-Vereines, 63, стр. 280 (1911).
5.27. Llndstedt A., Beitrag zur Integration der Differentialgleichungen der Stdrungstheorie. Mdmoires de 1’Acad£mie des Sciences de St.-P6tersbourg, VII сер., т. XXXI, № 4 (1883).
5.28. Mi nor sky N., Introduction in Non-linear Mechanics (1947).
5.29. Picard E., Traite d’Anatyse, Paris, t. Ill, изд. 3 (1928).
5.30. Poincar£ H., Les methodes nouvelles de la mecanique cdleste. Paris, т. I (1892), т. II (1893), t. Ill (1899).
5.31. P б s c h 1 Th., Technische Anwendungen der Stereomechanik. Handbuch der Physik herausgegeben von Geiger u. Scheel, т. V, Berlin, стр. 520 (1927).
К главе 6
6.1. Бата М. И., Вынужденные колебания в системе с гистерезисом. Прикладная математика и механика, т. IV, вып. 3, стр. 13—30 (1940),
§6 Зак» 1474- Б. Ц. Булгадод
882
ЛИТЕРАТУРА
6.2. И о р и ш Ю. И., Равночастотные амортизаторы вибраций для самолётного оборудования. Труды НИ Института самолётного оборудования № 7 (1945).
6.3. И ори ш Ю. И., Субгармонический резонанс в системе с упругими ограничителями хода. Журнал технической физики, т. XVI, вып. 6, стр. 681—694 (1946).
6.4. К а ц А. М., Труды Ленинградского индустриального института, стр. 102 (1939).
6.5. Лурье А. И. и Чекмарёв А. И., Вынужденные колебания в нелинейной системе с характеристикой, составленной из двух прямолинейных отрезков. Прикладная математика и механика, т. I, вып. 3, стр. 307—324 (1938).
6.6. Лурье А. И., К задаче о вынужденных нелинейных колебаниях. Учёные записки Ленинградского гос. университета. Серия математических наук (механика). Вып. 8, стр. 25—33 (1939).
6.7. Мандельштам Л. И. и Папалекси Н. Д., О явлениях резонанса л-го рода. Журнал технической физики, т. II, стр. 775—811 (1932).
6.8. Натанзон В. Я., Крутильные колебания валов с муфтами, обладающими нелинейной характеристикой, Москва (1943).
6.9. Булгаков Б. В., К задаче о вынужденных колебаниях псевдолинейных систем. Прикладная математика и механика, т. VII, вып. 1, стр. 31—40 (1943).
6.10. Appleton Е. V., On the Anomalous Behaviour of a Vibration Galvanometer. Phil. Magazine, t. 47, стр. 609—619 (1924).
6.11. Duffing G., Erzwungene Schwingungen bei verMnderlichen Eigenfre-quenz und ihre technische Bedeutung, Braunschweig (1918).
6.12. E с k о 11 W., Uber erzwungene Reibungsschwingungen. Zeitschrift fur technische Physik, t. 7, стр. 226 (1926).
6.13. Friedrichs К. O. and Stoker J. J., Forced Vibrations of System with Non-linear Restoring Force. Quarterly of Applied Mathematics, т. I, № 3, стр. 97—115 (1943).
6.14. Hamel G., Uber erzwungene Schwingungen bei endlichen Amplitudes Mathematische Annalen, t. 86, стр. 1 (1922).
6.15. Den Hartog J. P., Forced Vibrations With Combined Coulomb and Viscous Friction. Transactions of the American Society of Mechanical Engineers. Paper АРМ-53-9, стр. 107—115 (1931).
6.16. Den Hartog J. P. and Mi kin a S. J., Forced Vibrations with Nonlinear Spring Constants. Там же, Paper APM-54-15 (1932).
6.17. Den Hartog J. P., The Amplitudes of Non-Harmonic Vibrations. Journal of the Franklin Institute, t. 216, стр. 459—473 (1933).
6.18. Den Hartog J. P. and Hei 1 es R. M., Forced Vibrations in Non-Linear Systems with Various Combinations of Linear Springs. Journal of Applied Mechanics, t. 3, № 4, стр. 126—130 (1936).
6.19. Horn J., Uber kleine, endliche erzwungene Schwingungen. Archiv fur Math, und Phys. (1920).
6.20. I g 1 i s h R., Die erste Resonanzkurve beim Duffingschen Schwingungspro-blem. Mathematische Annalen, t. 112, стр. 221—246 (1936).
6.21. Jacobsen L. S., Steady Forced Vibrations as Influenced by Damping. Transactions of the American Society of Mechanical Engineers. Paper АРМ-52-15, стр. 169—181 (1930).
6.22. Martienssen O., Uber neue Resonanzerscheinungen in Wechselstrom-kreisen. Physikallsche Zeitschrift, год. изд. 11, № 10, стр. 448—460 (1910).
6.23. Rauscher M., Steady Oscillations of Systems with Non-Linear and Unsymmetrical Elasticity. Journal of Applied Mechanics, t. 5, № 4, стр. Д-169—Д-177 (1938),
ЛИТЕРАТУРА
883
6.24. Rfldenberg R., Einige unharmonische Schwingungsformen mit grosser Amplitude. Zeitschrift fQr angewandte Mathematik und Mechanik, t. 3, № 6, стр. 454—467 (1923).
6.25. Ziegler H., Erzwungene Schwingungen mit konstanter Dampfung. Ingenieur-Archiv, т. IX, № 3, стр. 163 (1938).
К главе 7
7.1. Артемьев И. А., ' Осуществимые движения. Известия Академии наук СССР, серия математическая, № 3, стр. 351—367 (1939).
7.2. Вышнеградский И. А., О регуляторах прямого действия. Известия СПБ Практического технологического института, т. I, стр. 21—62 (1877).
7.3. Дубошин Г. Н., К вопросу об устойчивости движения относительно постоянно действующих возмущений. Труды ГАИШ, т. XIV, вып. 1, стр. 153—164 (1940).
7.4. Лагранж Ж. Л., Аналитическая механика, перев. В. С. Гохмана, т. I, изд. 2 (1950).
7.5. Малкин И. Г., Об устойчивости при постоянно действующих возмущениях. Прикладная математика и механика, т. VIII, вып. 3, стр. 241—245 (1944).
7.6. Ч е т а е в Н. Г., Об устойчивых траекториях динамики. Сборник научных трудов Казанского авиационного института, № 5, стр. 3—18 (1936).
7.7. S t о d о 1 a A., Ueber die Regulferung von Turbinen. I, II. Schweizerische Bauzeitung, т. XXII, № 17, стр. 113—117; № 18, стр. 121—122; № 19, стр. 126—128; № 20, стр. 134—135 (1893); т. XXIII, № 17, стр. 108—112; № 18, стр. 115—117 (1894). Русский перевод в сборнике: Д. К. Максвелл, И. А. Вышнеградский, А. Стодола, Теория автоматического регулирования. Под редакцией А. А. Андронова* и И. Н. Вознесенского (1949).
К главе 8
8.1. Акул ьшин П. К.,. К о щ е е в И. А., К у л ь б а ц к и й К. Е., Теория связи по проводам (1940).
8.2. М е й м а н Н. Н., Некоторые вопросы расположения нулей полиномов. Успехи математических наук, т. IV, № 6 (34), стр. 154 (1949).
8.3. Н е й м а р к Ю. И., Об определении значений параметров, при которых система автоматического регулирования устойчива. Автоматика и телемеханика, т. IX, № 3, стр. 190 (1948).
8.4. Неймарк Ю. И., Устойчивость линеаризованных систем (дискретных и распределённых) (1949).
8.5. Булгаков Б. В., О равносильности и совместности систем линейных дифференциальных уравнений с постоянными коэффициентами. Прикладная математика и механика, т. XVI, вып. 1, стр. 15—22 (1952).
8.6. Булгаков Б. В., О нормальных координатах. Прикладная математика и механика, т. X, вып. 2, стр. 273—290 (1946).
8.7. Булгаков Б. В., Дискриминантная кривая и область апериодической устойчивости. Доклады Академии наук СССР, т. LXXIII, № 6, стр. 1143—1144 (1950).
8.8. Булгаков Б. В., О накоплении возмущений в линейных колебательных системах с постоянными параметрами. Доклады Академии наук. СССР,-т. LI, № 5, стр. 339—342 (1946).
8.9. Булгаков Б. В. и К у з о в к о в Н. Т., О накоплении возмущений в линейных системах с переменными параметрами. Прикладная математика и механика, т. XIV, вып. 1, стр. 7—12 (1950).
8.10. Hurwitz A., Ober die Bedingungen, unter welchen eine Gleichung nur Wurzeln mit negativen reelen Teilen besitzt, Mathematjsche Апда1епг т. 46, стр. 273 (1895).
56*
/
884 ЛИТЕРАТУРА
8.11. Routh Е. J., A treatise on the stability of a given state of motion . ch. Ill, London (1877).
8.12. S t г e с к e г F. und Feldtkeller R., Grundlagen der Theorie des allgemeinen Vlerpols. Elektrische Nachrichtentechnik, t. 6, стр. 93—112 (1929).
К главе 9
9.1. Боде Г., Теория цепей и проектирование усилителей с обратной связью. Перев. А. А. Колосова и Л. А. Мееровича (1948).
9.2. Крылов А. Н., О численном решении уравнения, которым в технических вопросах определяются частоты малых колебаний материальных систем. Известия Академии наук СССР, отделение математических и естественных наук, № 4, стр. 491—539 (1931).
9.3. Лузин Н. Н., О методе академика А. Н. Крылова составления векового уравнения. Известия Академии наук СССР, отделение математических и естественных наук, № 7, стр. 903—958 (1931).
9.4. П а п к о в и ч П. Ф., Об одном методе разыскания корней характеристического определителя. Прикладная математика и механика, т. I, вып. 2, стр. 314—319 (1933).
9.5. Ш и Т. Е„ Четырёхполюсники и электрические фильтры (1939).
9.6. Эфрос А. М., Новый метод электрических аналогий. Журнал технической физики, т. X, вып. 14, стр. 1189—1196 (1940).
9.7. Булгаков Б. В., Вопросы синтеза корректирующих цепей. Известия Академии наук СССР, ОТН, № 1, стр. 21—40 (1952) и № 5, стр. 699—723
9.8. Bott R., Duffin R. J., Impedance Synthesis without Use of Transformers. Journal of Applied Physics, t. 20, № 8, стр. 816 (1949).
9.9. Brune O., Synthesis of a finite two-terminal network, whose driving-point impedance is a prescribed function of frequency. Journal of mathematics and physics (MIT), т. X, № 3, стр. 191—236 (1931).
9.10. Dtinkerley S., On the Whirling and Vibration of Shafts. Phi’osophical Transactions of the Royal Society of London, t. 185 (А), стр. 279—360
9.11. Foster R. M., A Reactance Theorem. The Bell System technical Journal, t. 3, стр. 259 (1924).
9.12. Frahm H., Neutige Schlingertanks zur Abdampfung von Schiffsrollbe-wegungen. Jahrbuch d. Schiffbautechnischen Gesellschaft, t. 12, стр. 283—365 (1911).
9.13. Guillem in E. A., The Mathematics of Circuit Analysis, New York (1949).
9.14. Guillemin E. A., Communication Networks, т. I, II, New York (1931, 1935).
9.15. Leverrier C., Sur les variations seculaires des Elements des orbites. Прибавление к Connaissance des Temps (1843).
9.16. Nai-Ta Ming, Verwlrklichung von linearen Zweipolschaltungen vor-geschriebener Frequenzabhangigkeit unter Beriicksichtigung der Verluste von Spulen und Kondensatoren. Archiv fiir Elektrotechnik, t. 39, № 6, стр. 359—387 (1949).
9.17. N ai-T a Ming, Verwlrklichung von linearen Vieipolschaltungen vor-geschr’ebener Frequenzabhangigkeit unter Beriicksichtigung iibereinstim-mender Verluste aller Spulen und Kondensatoren. Archiv fiir Elektrotechnik, t. 39, № 7, стр. 452—471 (1949).
9.18. Sylvester J. J., On homogeneous quadratic polynomials. The Philosophical Magazine and Journal of Science, t. 4, cep. 4, стр. 138—142 (1852).
9.19. V i a n e 11 о L., Graphische Untersuchung der Knickfestigkeit gerader Stabe. Zeitschrift des Vereines deutscher Ingenieure, t. 42, № 52, стр. 1436—1443 (1898).
9,20, Weierstrass К.» Gesamjnelte Werke, т, 1 (1894),
ЛИТЕРАТУРА
885
К главе 10*)
10.1. Басин А. М., Теория устойчивости на курсе и поворотливости судна (1949).
10.2. Be др о в В. С., Динамическая устойчивость самолёта (1938).
10.3. Картвелишвили Н. А., Об условиях качества автоматического регулирования. Доклады Академии наук СССР, т. LXI, № 1, стр. 21—23 (1948).
10.4. Кузовков Н. Т., Об оценке степени устойчивости и максимальной частоты линейной системы. Научно-технический сборник НИИ МПСС, № 1, стр. 1—16 (1949).
10.5. М а к - К о л л Л. А., Основы теории сервомеханизмов. Перев. под редакцией Я. 3. Цыпкина (1947).
10.6. Михайлов А. В., Метод гармонического анализа в теории регулирования. Автоматика и телемеханика, № 3, стр. 27—81 (1938).
10.7. Ройтенберг Я. Н., Автоколебания гироскопических стабилизаторов. Прикладная математика и механика, т. XI, вып. 2, стр. 271—280 (1947).
10.8. Фельдбаум А. А., О распределении корней характеристического уравнения. Автоматика и телемеханика, т. IX, № 4, стр. 253—279 (1948).
10.9. Булгаков Б. В., Цепи регулирования со звеньями, имеющими по нескольку степеней свободы. Прикладная математика и механика, т. XIV, вып. 6, стр. 619—634 (1950).
10.10. Е n-L u n g-C h u, Notes on the stability of linear networks. Proceedings of the Institute of Radio Engineers, t. 32, № 10, стр. 630 (1944).
10.11. Gramm el R., Der Kreisel. seine Theorie und seine Anwendungen, Braunschweig (1920). (Имеется русский перевод: Граммель Р., Гироскоп, его теория и применения, т. 1, 2, перев. Г. А. Вольперта, 1952.)
10.12. Nyquist Н., Regeneration Theory. The Bell System technical Journal, т. XI, № 1, стр. 126—147 (1932).
10.13. Weiss H. K., Constant Speed Control Theory. Journal of the Aeronautical Sciences, t. 6, № 4, стр. 147—152 (1939).
К главе 11
11.1. Floquet G., Sur les £quations, diferentfelles lin£aires a coefficients рёНо-diques. Annates scientifiques de ГЁсо1е Normale superieure, t. 12, стр. 47—48 (1883).
К главе 12**)
12.1. АндроновА. А. и Баутин Н. Н., Движение нейтрального самолёта, снабжённого автопилотом и теория точечных преобразований поверхностей. Доклады Академии наук СССР, новая серия, т. 43, № 5, стр. 197—202 (1944).
12.2. А н др о н о в А. А. и Витт А. А., Об устойчивости по Ляпунову. Журнал экспериментальной и теоретической физики, т. III, вып. 5, стр. 373—374 (1933).
12.3. Б у т е н и н Н. В., Об одной задаче Кельвина, относящейся к теории часов. Журнал экспериментальной и теоретической физики, т. X, вып. 11, стр. 1283—1292 (1940).
12.4. Гольдфарб Л. С., О некоторых нелинейностях в системах регулирования. Автоматика и телемеханика, т. VIII, № 5, стр. 349—383 (1947).
12.5. Котельников В. А., Продольная динамическая устойчивость самолёта с автопилотом. Техника воздушного флота, № 1, стр. 27—31 (1941).
12.6. Крылов Н. М. и Боголюбов Н. Н., Новые методы нелинейной механики в их применении к изучению работы электронных генераторов (1934).
12.7. Л е т о в А. М., К задаче об автопилоте. Вестник Московского университета, № 1, стр. 123—129 (1946).
*) См. также список литературы к главе 4.
**) См, также список литературы к главе 5,
886
ЛИТЕРАТУРА
12.8. Летов А. М., К теории изодромного регулятора. Прикладная мате, матика и механика, т. XII, вып. 4, стр. 363—368 (1948).
12.9. Лурье А. И., Некоторые нелинейные задачи теории автоматического регулирования (1951).
12.10. Лурье А. И., Об автоколебаниях в некоторых регулируемых системах. Автоматика и телемеханика, т. VIII, № 5, стр. 335—348 (1947).
12.11. Лурье А. И. и Постников В. Н., К теории устойчивости регулируемых систем. Прикладная математика и механика, т. VIII, вып. 3, стр. 246—248 (1944).
12.12. Малкин И. Г., Об устойчивости периодических движений. Прикладная математика и механика, т. VIII, вып. 4, стр. 327—331 (1944).
12.13. Малкин И. Г., Методы Ляпунова и Пуанкаре в теории нелинейных колебаний (1949).
12.14. Мандельштам Л. И. иПапалекси Н. Д., Об обосновании одного метода приближённого решения дифференциальных уравнений. Журнал экспериментальной и теоретической физики, т. IV, вып. 2, стр. 117 (1934).
12.15. Отроков Н. Ф., К устойчивости периодических интегралов. Учёные записки Горьковского государственного университета, вып. 6, стр. 125—128 (1939).
12.16. Ройтенберг Я. Н., Автоколебания силовых гироскопических стабилизаторов. Приборостроение, № 3, стр. 3—26 и № 4, стр. 3—24 (1948).
12.17. Булгаков Б. В., О применении метода А. Пуанкаре к свободным псевдолинейным колебательным системам. Прикладная математика и механика, т. VI, вып, 4, стр. 263—280 (1942).
12.18. Б у л г а к о в Б. В., О применении метода ван дер Поля к псевдолинейным системам со многими степенями свободы. Прикладная математика и механика, т. VI, вып. 6, стр. 395—409 (1942).
12.19. Б у л г а к о в Б. В., Автоколебания регулируемых систем. Доклады Академии наук СССР, т. XXXVII, № 9, стр. 283—287 (1942).
12.20. Булгаков Б. В., Автоколебания регулируемых систем. Прикладная математика и механика, т. VII, вып. 2, стр. 97—108 (1943).
12.21. Булгаков Б, В., Некоторые задачи теории регулирования с нелинейными характеристиками. Прикладная математика и механика, т. X, вып. 3, стр. 313—332 (1946).
12.22. Булгаков Б. В., Прикладная теория гироскопов (1939).
12.23. Appleton Е. V. and van der Pol В., On a type of oscillation — Hysteresis in a simple triode generator. Philosophical Magazine and Journal of Science, t. XLIII, cep. 6, № 253, стр. 177—193 (1922).
12.24. В a rk h aus e n H., Lehrbuch der Elektronen-ROhren uud ihrer tech-nischen Anwendung, t. 2, 2 изд., Leipzig (1926).
12.25. Hill G. W., On the Part of the Motion of the Lunar Perigree, wich is a. Function of the Mean Motions of the Sun and Moon. Acta Mathematica, t. 8, стр. 1 (1886). (Работа Хилла была впервые опубликована в 1877 г.)
12.26. Mac М i 11 а п W. D., An Existence Theorem for Periodic Solutions. Transactions of the American Mathematical Society, t. 13, стр. 146—158 (1912).
12.27. Moller H., Die ElektronenrOhren und ihre technische Anwendungen. Braunschweig (1920).
12.28. P о 1 п c a r e, Les methodes nouvelles de la mecanique celeste, Paris, т. 1 (1892), т. II (1893), t. Ill (1899).
12.29. Tolle M., Die Regelung der Kraftmaschinen, 3 изд., Berlin (1921).
12.30. Van der Pol B., On oscillation hysteresis in a triode generator with two degrees of freedom. Philosophical Magazine and Journal of Science, t, XLIIL, cep. 6, № 256, стр. 700—719 (1922).
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абсцисса сходимости 115, 146
Адмиттанс 502
— контура 502
Амплитуда 551
— комплексная 150
----матричная 494, 502
— порождающая 316,’ 775
— расчётная 340
Аргумент запаздывания 228, 495
----вносимый 536
- — волновой 511
----повторный 526
----рабочий 537
Балка, загружённая сосредоточенными массами 607
Боде теорема 626
Ботта и Даффина процедура 655
Бромуича интеграл 152
Бруне функция (В-функция) 630, 656
Быстрота затухания собственных колебаний '53
Вектор с комплексными компонентами 43
Вектор-функция линейная 47
Векторы ортогональные 43
Ветвь электрической цепи 405
Возбуждение автоколебаний жёсткое 291 ----мягкое 291
Возмущение гармоническое 226, 493 и д.
— периодическое 229
Волна стоячая 237, 582
Вход 506
Выход 506
Вышнеградского диаграмма 489
Гамильтона функция 191
Гамильтона-Кейли уравнение 82
Гамильтона-Якоби теорема 197
----уравнения 198
Гельмгольца вариационное уравнение 192
Генератор электронный 296, 324, 352
Гиро-рулевой со свободным ходом 274
Гурвитца определитель 163
Данкерли оценка 616
Движение, возмущаемое силами большой частоты 840 и д.
— дважды инфинитное 255
— либрацирнное 254
— лимитационное 254
— орбито-устойчивое 291
— ротационное 255
Движения периодические 311, 767, 790,807
Двойственность теорем операционного исчисления 120
Двухполюсник 503
— пассивный 621
Двухполюсники эквивалентные 503
Действие 257
Декремент логарифмический 756
Деление матриц 28, 61
Делитель детерминантный 57
— нуля 18
— элементарный 58, 70, 575
----линейный 426
Демпфирование, коэффициент 234
Дефект матрицы 16
Диаграмма Вышцеградского 489
— Дуффинга 367
— фазовая 203
— частотная для оценки быстроты затухания н логарифмического декремента 756
Дифференциал абсолютный 185
Дифференцирование абсолютное 183
— изображения 119
— матриц 76
— оригинала 118
— по параметру 124
Дюгамеля интеграл 217
Единица матричная 58
Жордана лемма 153
— матрица 74
Зажим входной 506
— выходной 506
Закон сохранения энергии 188
Запаздывание 120
Затухание вносимое 536
— колебаний 221
— рабочее 537
Значения собственные матрицы 604
Зона застоя 265
Изображение 114, 127, 143
— линейной комбинации 116
Импеданс контура 406
— цепи 408
Импульс обобщённый 189
Интеграл Бромуича 152
— Дюгамеля 217
— Лапласа 114, 146
— Фурье 150
— энергии 188
— Якоби 188
Интегрирование матриц ПО
— оригинала 117
— по параметру 124
Карсона преобразование 114
Каскад четырёхполюсников 508
----симметричных решётчатых 678
Кейли матрицы 51
Коагуляция 24
Колебания вынужденные 203, 225, 355 и д,
888
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Колебания малые около данного состояния 377 и д.
— нормальные 426, 437, 582
— собственные 204, 250 и д„ 426 и д.
----консервативной системы с двумя степенями свободы 447
— установившиеся с частотой возмущающей силы 359
Компоненты вектора 42 ----ковариантные 46, 180 -----контравариантные 46, 179
Контур электрический 212
Конформность матриц 18
Координаты нормальные 544, 548, 549, 801
— обобщённые 173
— циклические 190
— электрические 185
Коэффициент влияния 297, 603
-----закрученного вала 607
— демпфирования 234
— добротности 226
— затухания повторный 526
— отражения 522
— распространения вносимый 536
----- волновой 511
-----повторный 526
----- рабочий 537
— трансформации 516
— усиления лампы 409
-----системы 495
-----фильтра 228
— устойчивости по абсолютному интеграль ному отклонению 222
----по квадратичному интегральному отклонению 223
----по наименьшему характеристическому показателю 221. 465
-----по накоплению 226
Кривая дискриминантная 491
— разделяющая 252, 370
— резонансная 228, ЗоЗ, 497
— собственных частот 363
— топографическая 264
Кристоффеля скобки 183
— экстенсив 183
Критерий качества регулирования 221
— Найквиста 750
— Рауса 453
' — Рауса-Гурвитца 457
— Цыпкина-Бромберга 465
Круг сходимости матричного ряда 86
Крутизна характеристики 409
Крылова метод Ы2
Лагранжа координаты 173 — полином интерполяционный 89 — уравнения второго рода 175 -----первого рода 171 "1 — функция 177 Ламбда-матрица 56
Лапласа интеграл 114
Лаппо-Данил.вского теорема 105
Леверрье метод 611
Лемма Жордана 153
Либрация 25 , 257
Лорана ряд матричный 89, 102
Лузина теорема 413
Люфт 299
Максвелла принцип взаимности 407
— теорема взаимности 603
Масса приведённая 204
Масштаб логарифмический 496
Матрица 15
— влияния 603
— диагональная 20 . .
— динамической жёсткости 6£5
Матрица единичная 22
— Жордана 74
— идемпотентная 97
— квадратная 16
— квазидиагональная 25
— Кейли 51
— коагулированная 24
— модальная 436
— неособая 16
— нильпотентная 98
— обратная 27, 45
— операционная 412
— ортогональная 27
— особая 16
— подобная 48
— полиномная 'Х-матрица) 56
неособая 56
особая 56
треугольная 64
— приводящая 554
— прис единённая 26
— прямоугольная 16
— расширенная 412
— симметричная 17
— скалярная 22
— сложная 23
— сопряжённая по Эрмиту 17
— транспонированная 16
— треугольная 21
— удлинённая 16
— укороченная 16
— фундаментальная 207, 759
— характеристическая 78
— эрмитова 17
Матрицант 111
Матрицы коммутативные 18
— конформные 18
— равные 16
— эквивалентные 36
Машина паровая 307, 330, 387
Маятник гироскопический 827
— физический 256, 263, 270, 351
Метод Крылова 612
— Леверрье 611
— Неймарка 485
— Ньюкома и Линдстедта 259
— осреднения 336 и д„ 801
— Пуанкаре 311 и д„ 767 и д.
Мин Най-да функция (Л4-функция) 634
Минор 16
— изменённый 12
Множитель инвариантный 57
— линейный матрицы 57
Модуль матрицы 85
Модус нормального колебания 437
Найквиста критерий устойчивости 750
Напряжение управляющее 297
Настройка 445
Неймарка метод 485
Неравн,мерность регулятора 397
— хода машины 334
Неустойчивость заведомая (гарантированная) 465
Ньюкома и Линдстедта метод 259
Обертон 582
— гармонический 582
Область неустойчивости заведомой 465
— устойчивости апериодической 492
-----ненадёжной 4б4
Обмен энергии между частями системы 451
Обобщение ван ден Дунгена и Папковича 61
Оператор дифференцирования неопределённый ИЗ, 406. 493
— упреждения 121
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
-1
Определитель Гурвитца 163
— характеристический 78, 418
Орган исполнительный 213
Оригинал 114
Осреднение 336 и д.
. Оценка Данкерли 616
Параметр вносимый 535, 539
— рабочий 537, 539
Передача системы 493
— четырёхполюсника 679
Переменная действия 257
— угловая 258, 550
Переменные сопряжённые канонические 191
Перемещение виртуальное (пробное) 169 — действительное 1ь9
Плоскость фазовая 203
Поверхность дискриминантная 46Q
— равной устойчивости 466
Подобие, теорема 12о
Показатель характеристический 764
Поле регулирования 213
Полином интерполяционный Лагранжа 89
----конфлюентный 91
— матричный 49
— операционный ИЗ
Полоса пропускания 658, 661
Полюс затухания 658, 661
Поправка на частоту 314
Последействие, функция 217
Постоянная времени 389
Потенциал кинетический 117
Предел матрицы 85
Преобразование Карсона 114
— контактное 193
— контраградиентное 579
— координат 44
— матрицы коагулированной 36, 60
— — элементарное 35, 56
— Пуассона и Лагранжа 190
— Рауса 1ь8
— Фурье двустороннее 151
----обобщённое 152
----одностороннее 151
Преобразователь идеальный 517
Принцип взаимности Максвелла 407
— виртуальных перемещений 171
Проводимость взаимная 501
— матричная 501
— собственная 501
Продолжение аналитическое 99
Произведение матриц 18
— скалярное 43
Проницаемость лампы 297
Пространство метрическое евклидово 43
— — эрмитово 44
Процедура Ботта и Даффина 655'
Процесс переходный (процесс установления)
----в паровой машине с регулятором 387
— установившийся 381
— устойчивый по отношению к координатам 384
----при длительных возмущениях 385
Прямая инвариантная 78
Пуанкаре метод 311
Пуассона и Лагранжа преобразование 190
Равновесие асимптотически устойчивое 219
— неустойчивое 254
— устойчивое 219, 254
----при длительных возмущениях 385
Радиус сходимости матричного ряда 86
Разложение, теоремы 132, 133
Разность возвратная 738
— конечная оригинала 122
Разность конечная ступенчатой функции 142
Ранг матрицы 16, 56
----расширенной 417
— функции Бруне 655
Рассеяние энергии 404
Рассогласование 216
Рауса-Гурвитца критерий 457
Рауса преобразование 188
— функция 189
Реактанс-преобразование 660
Рейли теорема о01
Регулирование 213
— изодромное -739
— непрямое 419
— программное 214
Регулятор 213
— изодромный 399
— центробежный 390
---- конический 390
----плоский (инерционный) 390, 393, 397
----с фрикционным изодромом 399
---- Уатта 392
----Фарко 393
Режим квазипериодический 806
Реле 213
Репер фундаментальный 41
— — взаимный 45
Решение порождающее 311, 378
Решения периодические 311, 767, 790, 807
Ротания 255, 257
Ряд косой 20
— матричный 85 и д.
----Лорана 89, 102
----степенной 100, 102
----сходящийся 85
— скалярный по степеням матрицы 87
— Фурье, комплексная форма 148
Самовозбуждение, условия 327
Связь автотрансформаторная 452
— геометрическая 168
— дифференциальная 168
— обратная 420, 738
— реономная 168
— склерономная 168
— сложная ёмкостная 452
Седло 254
Сервомеханизм 386
Сервомотор 213, 419
— без инерционный 475 , 482
Сила амплитудная 595
— возмущающая 22ь, 229, 359
— восстанавливающая нелинейная 362, 371
— гироскопическая 404
— искусственная 403
— обобщённая 174
— позиционная 403
— пондеромоторная, её потенциальная функция 18о
— скоростная 403
Сильвестера теорема 456, 580
----о ранге произведения матриц 40
— формула 95, 101
Синтез пассивных двухполюсников 621
— регуляторов 231
Система автоколебательная 285 и д.
— близкая к линейной 313, 770
— голономная 169
— диссипативная 263 и д.
— консервативная 250 и д., 322, 345, 573
-~ лагранжева обобщённая 178
— линейная 206, 212 и д.
----консервативная с постоянными коэффициентами 573
----колебательная 562.
----регулируемая 735
ИКЙ
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Система линейная с периодическими коэффициентами 759 '
----с постоянными коэффициентами 235, 411 и д.
— натуральная 178
— неголономная 169
— нелинейная 355, 767
—• обладающая естественной направляющей силой 807
— пассивная 573 и д.
— регулирования 214
----изодромного 739 *
— реономная 168
— скалярная несовместная 414
----совместная 414
— склерономная 168, 177
— следящая 47, 214, 790
» — с люфтом 299
— с ненадёжными параметрами 464
— с одной степенью свободы 203 и д.
— упрощённая 312
— циклическая 404
— электромеханическая 185
Скаляр 16
Скобки Кристоффеля 183
Скорость обобщённая 177
— фазовая 203
Случай критический 385
Соотношение взаимности 501
Сопротивление взаимное 406
— внутреннее 409
— входное 501
— вязкое 371
— двухполюсника 503
— матричное 408
— передачи 501
— собственное 406
— четырёхполюсника волновое 510
----повторное 526
Стабилизатор гироскопический 746
Степень свободы 173
— матрицы 32
Столбец модальный 78, 108, 429
Субматрица 16
Сумма конечная 122
----неопределённая 130
----ступенчатой функции 142
— матриц 17
— ряда матричного 85
Схема мостовая Т-образная 532
Тахометр центробежный 390
Тело задающее 214
— следящее 214
Тензор второй валентности 48
Теорема Боде 626
— взаимности Максвелла 603
— Гамильтона-Якоби 197
— Лаппо-Данилевского 105
«— Лузина 413
— подобия 126
— разложения вторая 133
— — первая 132
— Рейли 601
— Сильвестера 456, 580
— - о ранге произведения матриц 40
— смещения 123
— совместности 417
— - упреждения 121
— Флоке 764
— Эри 289
Теория сервомеханизмов 386
Тон основной 58
— простой 58
Траектория фазовая 203
Трансмиттанс системы 493
Трансмиттанс системы операционный 217, 218, 228
— цепи разомкнутой 738
— четырёхполюсника 507, 676
Трансформатор 515
Трансформация по Лапласу 114
— по Хевисайду-Карсону 114
— Фурье 151
Триод 517'
Трение 265 и д„ 272, 276 и д„ 824
Уатта регулятор 392
Угол дрейфа 743
— импульса 285
- т- рыскания 743
Узел 405
Умножение изображений 125, 143
— матриц 17, 60
— оригиналов 156
— степенных рядов 100 -,,
Управление.автоматическое курсом корабля 742
Упреждение, оператор 121
Уравнение вариационное Гельмгольца 192
— в вариациях 380
— Гамильтона-Кейли 82
— Гамильтона-Якоби 198
— интегральное Фредгольма второго рода 604
— матричное неособое 418
----в форме Коши 423
— основное аналитической динамики 171
— разностное 144
— скалярное 136
— характеристическое 78, 418
— энергии 188
----обобщённое 188
Уравнения канонические 191
— Лагранжа второго рода 175
----первого рода 171
— псевдолинейные 770
— укороченные 339
----второго рода 865
— упрощённые 811
Условие самовозбуждения 327
Устойчивость 359
— апериодическая 492
— асимптотическая 361, 384
----по Ляпунову 285
— линейная 385
— надёжная (гарантированная) 464
— ненадёжная 465
— при длительных возмущениях 385, 562
— следящей системы 475
Фаза 203
Фарко регулятор 393
Фигура скелетная 363
Фильтр заграждающий 672
— линейный 212
— нижних частот 659
— полосовой 668
Флоке теорема 764
Форма билинейная 578
— квадратичная 578
— каноническая матрицы ,40
-------полиномной 65, „73
— комплексная ряда Фурье 148
— колебаний собственная 582
----нормальная ч37
Формула Сильвестера 95, 101
Функция аналитическая полная 99
— Бруне 630, 655
— влияния 605
----натянутой нити 605
— Гамильтона 191
— действительного переменного, спектральное представление 148
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Функция квазипериодическая 371
— комплексной переменной положительная 629
----------действительная 630
— Лагранжа 177
— матрицы 49 — Мин Най-да 634 — передаточная 217 — переходная 218 — пилообразная 128 — последействия 217 — потенциальная 171 ----пондеромоторных сил 186 — потерь 72 — производящая 195 — Рауса 189 — ступенчатая 141 — трансформируемая 115 Фурье Интеграл 150 — преобразование двухстороннее 157 ----обобщённое 152 ---- одностороннее 151 — ряд, комплексная форма 150 —- трансформация 151
Характеристика интегральная 793 — лампы 797 — силовая (мягкая, жёсткая) 346 — частотная 228, 496, 739 — тахометра 391 Хевисайда теоремы разложения 132, 133
Центр 254
Цепь активная 409 — корректирующая 677 — реактивная 625, 627 — регулирования замкнутая 735 ----одноконтурная 736 ----разомкнутая 735
Цепь электрическая 405
Цыпкина-Бромберга критерий 465
Частота линеаризирующая 321
— собственная 437, 582
— фундаментальная 371
Частоты собственные консервативной системы с двумя степенями свободы 441
Часы 285
Четырёхполюсник 418, 506
— Г-образный 528
— пассивный 418
— П-образный 531
— реактивный 657
— симметричный 507
----мостовой Т-образный 725
----решётчатый 679
—, содержащий триоды 517
—, составленный из одного двухполюсника 514
— Т-образный 528, 725
Число степеней свободы 173
— характеристическое 78, 102, 575
----матрицы 605
Эквивалентность матриц 36
Экстенсив' Кристоффеля 183
Элемент аналитический функции 99
— идеальный 688
— идемпотентный 97
— матрицы 15
— нильпотентный 98
— чувствительный 213
Энергия электромагнитная и электростатическая 185
Эри теорема 289
Ядро интегрального уравнения 604
-------итерированное (повторное) 612
Б. В. Булгаков. Колебания. Редактор В. И. Левантовскай и П. М. Раз. Техн, редактор Н. А. Тумаркана.
Корректор А. С. Баку лова.
Сдано в набор 3/VI 1954 г. Подписано к печати 2ё/Х 1954 г. Бумага 60 ХОД* Физ. печ. л. 55,75 +1 вклейка. Условн. печ. л. 55,75. Уч.-изд. л. 54,74. Тираж 10000 экз. Т-0/758. Цена книги 29 руб. 40 коп. Заказ № 14/4.
Государственное издательство технико-теоретической литературы.
Москва, Б. Калужская, 15.
Министерство культуры СССР. Главное управление полиграфической промышленности. 4-я тип. им. Евг. Соколовой. Ленинград, Измайловский пр., 29.
1
Опечатки
Стр. > Строка Напечатано -Должно быть
129 • 11 сн. ^«(р) ер—1 1 % ъ <» <1 1 R
237 4 св. (а 1)
239 1 » =/(Ту)
240 7, 11, 15 сн. V у
302 1 св. — cq —cq
368 5 /Св. (2 раза) К (а)
578 9 св. /Л С
639 8 сн. bib Mo
661 9 св. 2 0 -20
708 1 сн. 1 - W . 1 _ W —
751 9, 25 сн.
788 И св. V t fu
• 825 1 2 сн. M<s e~ Me 2
829 8 » (У1. ja) (уъУ2)
Зак. 1474.
I