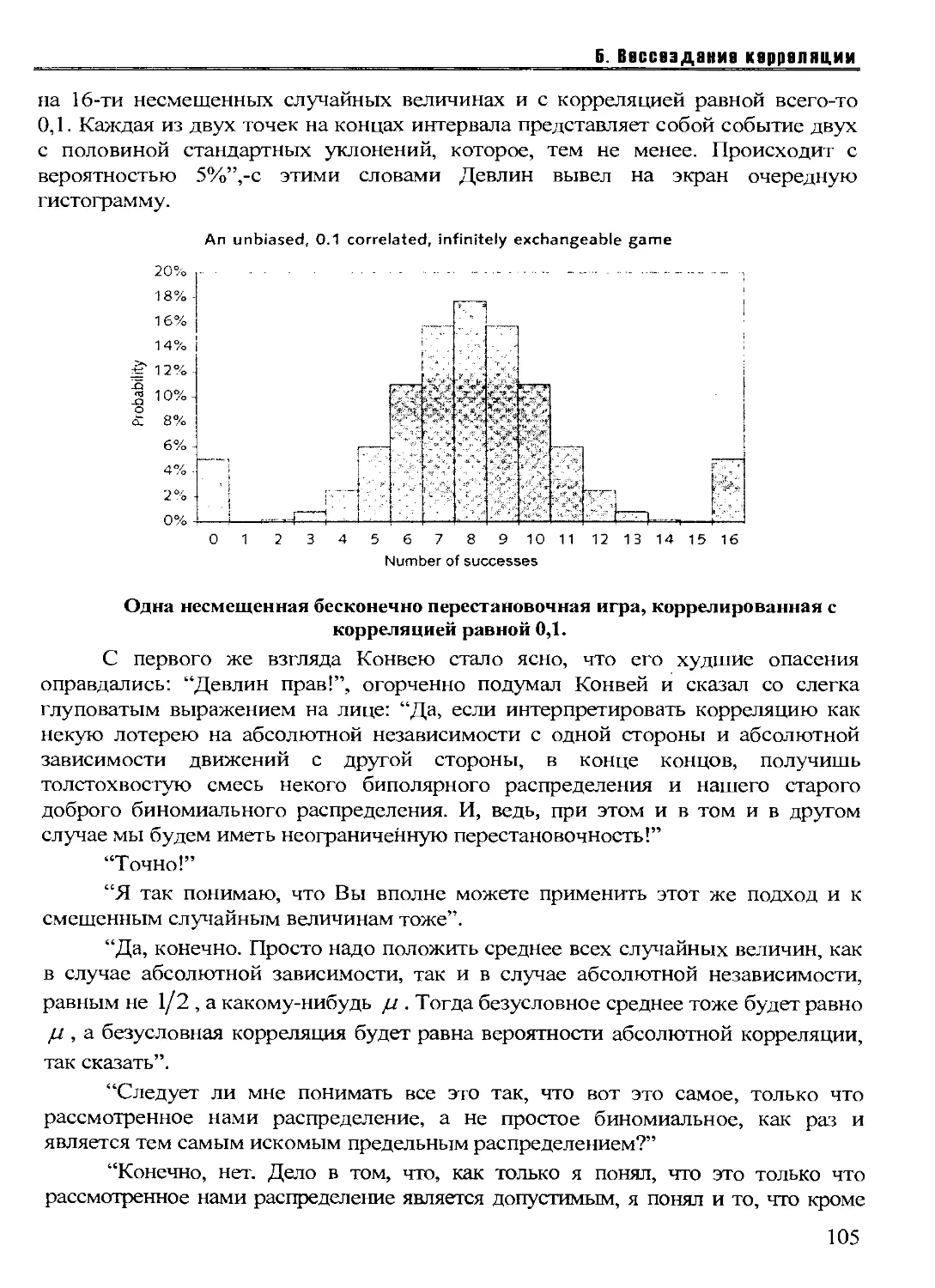
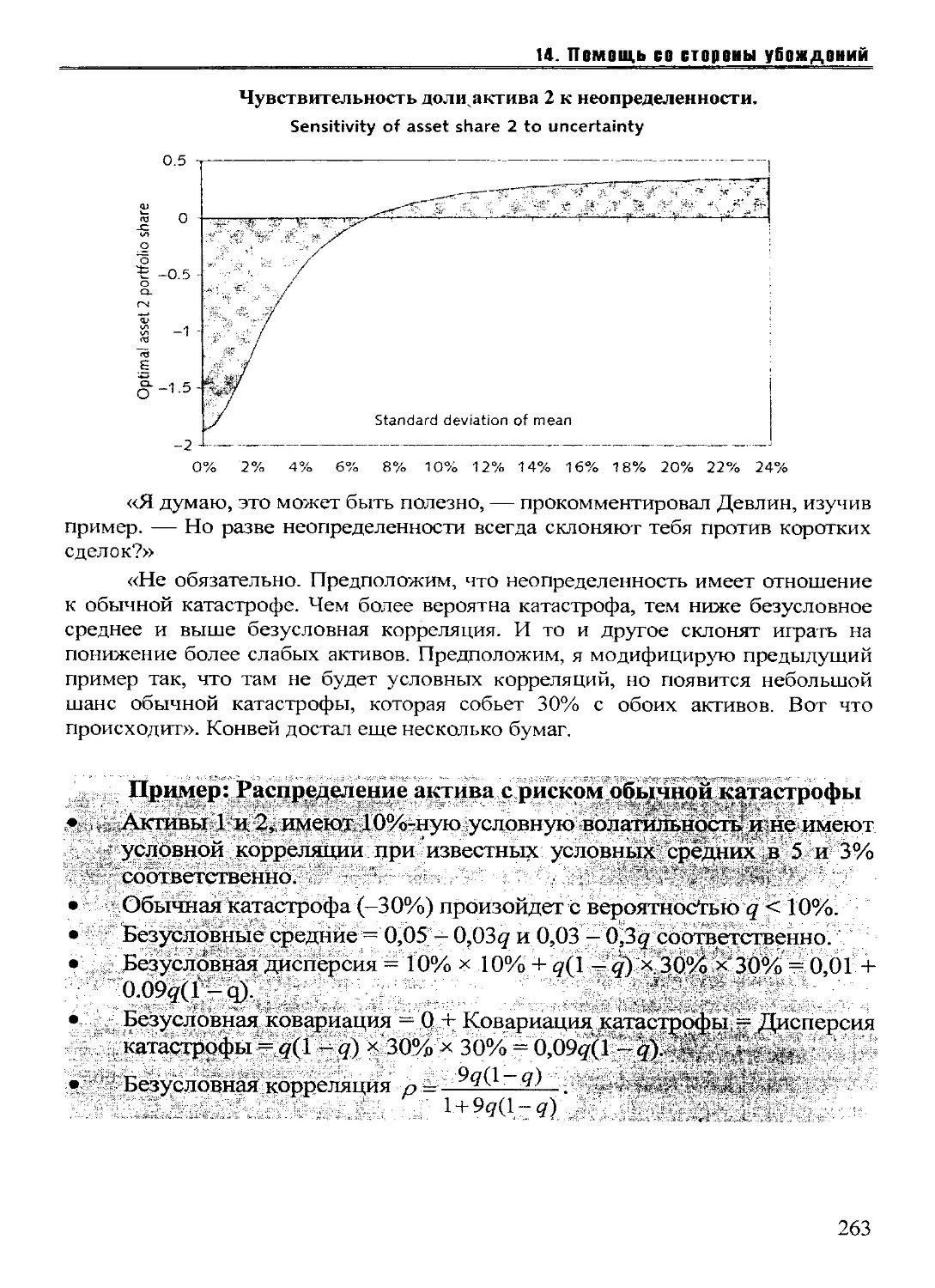
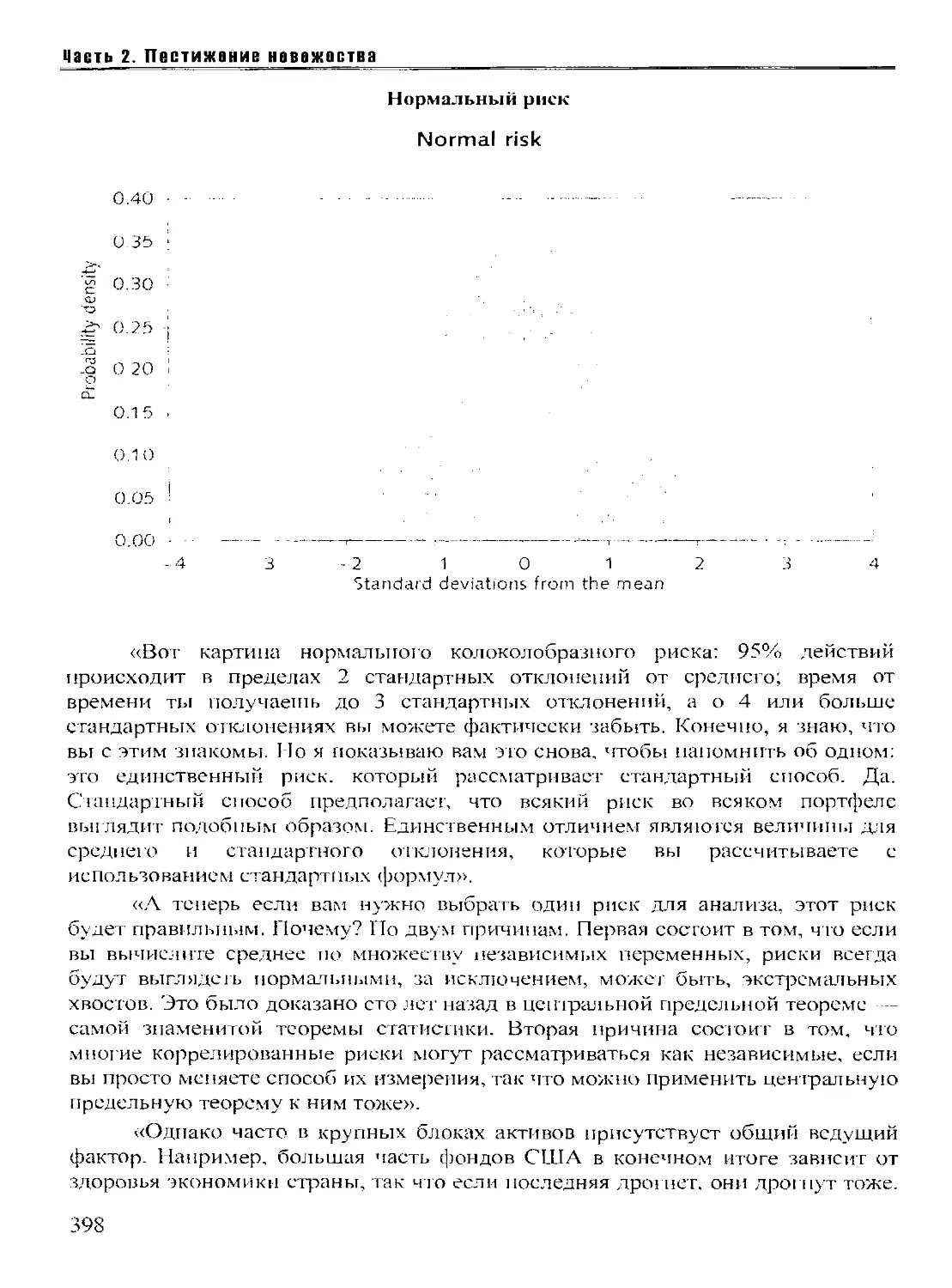
Текст
Кент Осбанд
РИСК JL Л Л Д\ АЙСБЕРГА
Рискованная экспедиция в Теорию управления портфелем
£@ОМЕГА-Л
Издательство "И-трейд"
Москва, 2007
Осбанд К.
Айсберг риска. Рискованное путешествие в Теорию управления портфелем/ Осбанд Кент. - М.:Изд-во Омега-Л: И-трейд,, 2007. - 422с.
ил.,табл. - ISBN 5-365-00653-4
Книга посвящена анализу портфеля ценных бумаг и нахождению компромисса между риском и вознаграждением на множестве различных наборов финансовых активов. Автор использовал метафору "айсберга" для обозначения срытого риска непривычной, широкомасштабной катастрофы, который не принимается в расчет при стандартной оценке инвестиционных рисков. О границах применимости Центральной предельной теоремы, когда нормальность не может быть хорошим приближением коррелированных рисков, которые невозможно разложить на множество мелких, независимых составляющих. О принятии иррациональных инвестиционных решений.
Каждая глава книги поделена на две части. В первой части все объясняется на интуитивном уровне и "на пальцах”. Первая часть обычно включает в себя один-два иллюстративных рисунка, либо графика. Вторая же часть содержит все строгое математическое обоснование первой части. При этом математическая информация нарезана на “сгустки смысла”, каждый из которых можно разбирать отдельно от других.
Эта книга нацелена на широкую аудиторию и будет полезна студентам, изучающим финансы и смежные дисциплины, а также частным инвесторам и спекулянтам, самостоятельно выходящим на мировые финансовые рынки. Её читателями также будут и управляющие капиталовложениями, и инвестиционные консультанты, и менеджеры пенсионных фондов, и отделы по управлению капиталовложениями страховых компаний, а также банки, осуществляющие валютные операции и операции с ценными бумагами.
ISBN 5-365-00653-4
© Zakaryan Publishing 2006-2007
© ООО "И-трейд” 2006-2007
Оглавление
ВВЕДЕНИЕ.......................................9
ВВЕДЕНИЕ: “...СЧИТАЯ АЙСБЕРГ СКОПЛЕНИЕМ МЕЛКИХ ЛЬДИН...” 19
1. ПРИЧУДЫ ШАНСОВ.............................33
2. ДОПОЛНИТЕЛЬНЫЕ УГЛЫ ДЛЯ ТРЕУГОЛЬНИКА ПАСКАЛЯ..53
3. ЭТИ ЗАБАВНЫЕ ХВОСТЫ РИСКА..................69
4. ЕЩЕ О ЗАНИМАТЕЛЬНЫХ ХВОСТАХ РИСКА..........83
5. ВОССОЗДАНИЕ КОРРЕЛЯЦИИ....................101
6. ОПРЕДЕЛЯЕМ МОМЕНТЫ С ПОМОЩЬЮ ДЕ ФИНЕТТИ...119
7. БОЛЬШИЕ РИСКИ VAR.........................134
8. ПЛОХОЕ ПОВЕДЕНИЕ ХОРОШИХ АППРОКСИМАЦИЙ....147
9: НЕНОРМАЛЬНОСТЬ НОРМАЛЬНОСТИ...............163
10: ЗАВИСИМАЯ НЕЗАВИСИМОСТЬ..................183
11: HAPPY END, ЧЕРТ ПОБЕРИ!..................201
ВВЕДЕНИЕ: «БОЛЬШЕ ДОЛЛАРОВ, ЧЕМ ЗДРАВОГО СМЫСЛА».216
12. КАК НАУЧИТЬ СЛОНА ТАНЦЕВАТЬ..............225
13. СТАВКА НА БЕТА...........................243
14. ПОМОЩЬ СО СТОРОНЫ УБЕЖДЕНИЙ..............259
15. ОЦЕНКА РИСКОВ БЕЗ СОЖАЛЕНИЙ..............275
16. НЕОБЫЧАЙНО ПОЛЕЗНАЯ ПОЛЕЗНОСТЬ...........289
17. ОПТИМАЛЬНЫЕ НАЛОЖЕНИЯ....................301
18. ОТКОРРЕКТИРОВАННЫЙ СОВЕТ.................315
19. УЛОВКИ ВЫСОКИХ ПОРЯДКОВ..................330
20. ВОПРОС ПЕРЕНАСТРОЙКИ.....................345
21. ВЗВЕШИВАНИЕ ОПЦИОНОВ.....................360
3
Оглавление
22. ЗАКРЕПЛЕНИЕ ФОКУСА...........................377
23. ПРИНЦИП ПЕТУХА...............................396
РЕКОМЕНДУЮ ПРОЧИТАТЬ.............................412
ОБ АВТОРЕ........................................416
О КОМПАНИИ «ЦЭРИХ КЭПИТАЛ МЕНЕДЖМЕНТ»............417
4
Вступительное слово
Уважаемые читатели!
Эта книга содержит чрезвычайно важную информацию. «Важную информацию» мы принимаем в любом виде - пусть это просто набор цифр на квитанции по оплате телефона. Важная информация интересна нам сама по себе, независимо от формы ее подачи. Уникальность этой книги состоит в том, что важная информация о рисках при инвестировании на фондовом рынке представлена тут в удивительно живой и понятной форме. Причем, от формы подачи содержание не страдает: «Риск айсберга» будет интересен и профессиональному трейдеру, и начинающему инвестору.
Отличие опытного инвестора от неопытного заключается в том, что первый глубоко осознает существующие на рынке риски и обладает моделями их оценки. Не раз я встречал начинающих инвесторов, которые бросались в «биржевую игру», забыв о рисках. Или тех, кто считал управление рисками делом скучным и недостойным «настоящего» биржевого игрока. В итоге, получив убыток, они все-таки начинали задумываться о собственном «риск-менеджменте». Однако большинство моделей оценки рисков, которые используют даже опытные инвесторы, далеко не идеальны. Их применение на реальном рынке не дает возможности адекватно выявить и оценить все потенциальные риски. Обходя лишь верхушку айсберга, инвесторы часто пользуются интуицией вместо продуманной системы защиты своих инвестиций.
Вероятно, автор книги также встречал инвесторов, которым очень не хотелось заниматься оценкой рисков собственных инвестиций. Поэтому он попытался (и преуспел в этом!) написать о «скучных» рисках живым образным языком вперемежку с математически обоснованными выкладками. Такая книга особенно актуальна именно сейчас, когда инвестиционные продукты перебираются из бутиков в финансовые супермаркеты.
На фондовом рынке созданы все условия для работы большого числа частных инвесторов. Не составит труда и привлечь этих инвесторов - за счет
5
Вступительное слава
грамотной рекламы и информационно-просветительской работы. Важная функция этой книги состоит в том, чтобы научить инвесторов правильно управлять своими вложениями в рынок ценных бумаг. Ценность этой книги в том, что она не ставит знак равенства между правильным и неинтересным, а, наоборот, дает оригинальное и живое описание рискам фондового рынка.
Желаю приятного чтения!
Александр Щеглов, Исполнительный директор Инвестиционной компании «ЦЕРИХ Кэпитал Менеджмент»
Москва
6
Предисловие научного редактора
Несмотря на предполагаемую научную изощренность и точность количественных моделей оценки инвестиционного риска, по крайней мере один, но очень существенный вопрос все еще остается без удовлетворительного теоретического ответа и по сей день “терзает” финансовых менеджеров и аналитиков, практикующих управление портфелем ценных бумаг. Вот этот “проклятый” вопрос: “Почему все-таки пограничные или, как еще говорят, нестандартные события типа краха происходят на рынке ценных бумаг гораздо чаще, чем это предполагается в общепринятой теории управления портфелем?”.
А между тем, ответ на этот вопрос обескураживающе прост: “Стандартная теория построена на нормальности распределений вероятностей, что выводит нестандартные события за рамки анализа”. Конечно, стандартный подход очень удобен, ведь он радикально упрощает вычисления и позволяет без труда генерировать успокаивающие и солидные на взгляд неискушенного потребителя отчеты аудитора. Однако, несмотря на всю свою простоту, стандартный подход имеет крупный и неустранимый изъян: за исключением ничтожного числа очень специальных случаев, стандартная теория не в состоянии ни предсказывать катастрофические события одновременного роста, либо падения значительной части портфеля, ни как-либо оценить риск такого одновременного резкого изменения котировок.
“Риск Айсберга” достаточно четко обозначает и помогает осмыслить указанный недостаток общепринятой теории. Для этого автор применяет интересный дидактический подход: текст книги представляет собой занимательную историю из жизни аналитиков, занимающихся инвестиционным риском, близкую к повседневной практике оценки этого риска, иллюстрированную строгой математикой и графическими методами. В этой схеме «история», изложенная живо и интригующе, играет роль некой “наживки”, которая должна поддерживать интерес читателя и побуждать его вникать в математические тонкости. А идеи математической статистики сначала излагаются автором “на пальцах” и по большей части интуитивно, но затем автор приводит строгие математические выкладки, организованные в виде неких “сгустков сухой теории”, легко ассоциируемых с конкретными
7
П|вдислввив научного редактора________==______===_=^_
идеями. В результате книга может быть в равной мере привлекательна для всех, желающих критически пересмотреть традиционную теорию, - и для неискушенных студентов, только приступивших к изучению анализа инвестиционных рисков, и для опытных аналитиков.
Но критика теории мало что дает для практического применения. Именно поэтому вторая часть книги является попыткой построить теорию оценки инвестиционного риска на более прочном по сравнению с существующей теорией портфеля фундаменте. При этом предлагаемая автором модель не только соответствует принципу экономической целесообразности, но и отвечает здравому смыслу. Так, в полном соответствии со здравым смыслом автор ни явно, ни косвенно не призывает к “стратегии дебютанта” (в отличие, кстати сказать, от некоторых конкурирующих теорий оценки инвестиционного риска). В то же время новая теория достаточно гибкая: с ее помощью можно анализировать любой инвестиционный риск и любые активы, включая опционы. Наконец, эта теория технологична. Иными словами, ответы на поставленные вопросы можно легко рассчитать на персональном компьютере с помощью стандартных электронных таблиц. И эти ответы легко выразить в терминах доходности с поправкой на риск, т.е. с помощью естественной, но, к сожалению, слишком редко применяемой на практике, меры эффективности портфеля.
И все же настоящая книга, хотя и удачное, но только начало большой работы по построению новой фундаментальной теории анализа инвестиционного риска. Образно выражаясь, “Риск Айсберга” предлагает читателю совершить нечто вроде “набега” на неизведанную территорию анализа риска. Экспедиция стартует там, где остановились Марковиц и Шарп и имеет своей целью определить новое направление в разработке теории анализа портфеля.
Иван Закарян, Генеральный директор ООО "И-трейд" Руководитель консалтинговой группы "Ицтернет-трейдинг”
8
Введение
Диалог автора и читателя
Читатель: Да... “Риск «айсберга»”... “Экспедиция в теорию портфеля”... замысловатое, надо сказать, названье. Так о чем книга-то?
Автор: Об анализе портфеля ценных бумаг. О поиске компромисса между риском и вознаграждением на примере подборок ценных бумаг или финансовых активов.
Читатель: Ну а при чем здесь айсберги?
Автор: Я использовал термин «айсберг» как метафору скрытого риска широкомасштабной катастрофы, который не принимается в расчет стандартной практикой оценки инвестиционных рисков и не может быть оценен в рамках стандартной теории.
Читатель: Этот риск принципиально нельзя оценить или все-таки можно, но этого почему-то не делают?
Автор: В том то и дело, что нельзя. Главный постулат общепринятой модели — нормальность. Отсюда неизбежность моделирования общего риска в виде колоколообразной кривой.
Читатель: А я всегда считал, что портфель обязан быть нормально распределен. Разве не об этом говорит центральная предельная теорема?
Автор: Об этом. Но центральная предельная теорема применима, если составляющие риски независимы.
Читатель: Минуточку! Но нормальность вполне может быть приближением и коррелированных рисков.
Автор: Конечно, но при условии, что каждый из этих рисков можно разложить на множество мелких, но независимых составляющих, так сказать “строительных блоков”. К сожалению, очень часто такая декомпозиция принципиально невозможна.
Читатель: Можете привести пример?
Автор: Легко. Допустим, вы владеете портфелем акций NASDAQ и NASDAQ рушится. Иными словами, представьте, что некий постоянно развивающийся процесс, характерный для значительной части вашего портфеля ценных бумаг, который даже отдаленно не может быть смоделирован каким-либо нормальным распределением, воздействует на эту часть вашего портфеля.
9
Вваданиа ======^======
Читатель*. Ну, это очевидно. Я-то думал, вы мне расскажете о чем-то более значительном.
Автор: Значительность этого примера в том, что стандартная теория не в состоянии его смоделировать.
Читатель: Вы все время говорите, что общепринятая теория бессильна, но я вам не верю. Вот недавно мне попались на глаза сразу несколько книг о стоимости риска. Разве эти методы неприменимы к «айсбергам»?
Автор: Применимы, но, как и всякие прочие эвристические методы, они не имеют ничего общего со стандартной теорией.
Читатель: Ну и что? Черная кошка, белая кошка... какая мне разница какого она цвета, если исправно ловит мышей?
Автор: Это плохая аналогия. Дело в том, что никакой риск-менеджер не стремится устранить вообще риск инвестиций. Он просто стремится разумно сбалансировать риски и вознаграждения. Но все типичные методы типа стоимости риска или никак не измеряют ожидаемые вознаграждения, или включают в себя некоторые иррациональные инвестиционные решения.
Читатель: Что именно вы понимаете под термином “иррациональный”?
Автор: Иррациональными я считаю решения, которые при любых обстоятельствах ведут к потере денег.
Читатель: Назовите мне такого инвестора, который никогда не бывал иррациональным!
Автор: Я таких не знаю. Но это вовсе не основание для того, чтобы советовать применять иррациональные инвестиционные решения на практике. Теория должна помогать, а не усложнять жизнь инвестора.
Читатель: Согласен. Значит, ваша книга учит тому, как встроить риск «айсберга» в стандартную теорию?
Автор: Этим я занимался в первой части книги, но потерпел полный провал.
Читатель: Что Вы имеете в виду под провалом?
Автор: То, что «айсберг» нельзя встроить в стандартную теорию. Дело в том, что стандартная теория вся построена на нормальности, а «айсберг» изначально ненормален.
Читатель: Но, если неудача неизбежна, зачем пытаться?
Автор: Чтобы помочь читателям избавиться от иллюзий. Необходимо, чтобы и Вы поняли, что нормальность ненормальна.
Читатель: И для этого Вам потребовалось исписать полкниги?
Автор: Я вовсе не уверен, что и половины книги достаточно. Нормальность — очень глубоко укоренившийся предрассудок, его придерживаются даже те теоретики, которые на практике отвергают это предположение.
10
Вввданиа
Читатель: Интересно. И почему, как Вы думаете?
Автор: Да потому, что нормальность — это просто. Только предположите нормальность, и Вы сможете легко и просто найти для любых активов компромисс между риском и вознаграждением по данным о средних, дисперсиях и корреляциях между активами.
Читатель: Ну, я бы не сказал, что это просто! Сотня активов порождает чуть ли не 5000 различных корреляций!
Автор: Так-то оно так, но без нормальности даже триллиона параметров недостаточно, чтобы смоделировать хвостовые риски разных портфелей. Ведь, сколько параметров не заводи, все равно невозможно найти ответ на вопрос типа: “Если 50 активов моего портфеля рухнут, какова вероятность того, что все остальные активы этого портфеля не рухнут тоже?”.
Читатель: А что, если я соберу дополнительную информацию по хвостовым рискам каждого актива?
Автор: Толку от этого будет меньше, чем кажется на первый взгляд. Дело в том, что из активов даже с очень толстыми хвостами можно составить устойчивый портфель, и, наоборот, почти нормальные активы могут генерировать огромный хвостовой риск.
Читатель: Так что же тогда имеет значение?
Автор: То, о чем я Вам уже говорил. Общие факторы, которые могут «заставить» ваши активы рухнуть одновременно.
Читатель: И как же Вы предлагаете моделировать эти факторы?
Автор: Единственным поддающимся количественному анализу образом. С помощью условной нормальности.
Читатель: Минуточку! Вы только что доказывали мне, что нормальность не работает.
Автор: Не работает безусловная нормальность. Условная нормальность — другое дело.
Читатель: И в чем тут разница?
Автор: Рассматривайте безусловное — как среднее значение котировок за конкретный период времени, а условное — как среднее за тот же период, но с поправкой на состояние рынка — например, “бычий ” или “медвежий ’’рынок.
Читатель: Послушайте, Вы можете объяснить все-таки, описывают или нет колоколообразные кривые инвестиционные риски? Просто скажите “Да” или “Нет”.
Автор: Да, для условных рисков, Общий же риск является наложением, или суперпозицией, или взвешенным средним различных колоколообразных кривых. И эта суперпозиция похожа на обычную колоколообразную кривую, так же как горный хребет похож на отдельную гору.
11
Вваданиа
Читатель: Вы хотите сказать, что если Вы построите достаточно много колоколообразных кривых, то сможете смоделировать любой пучок взаимодействующих рисков. Верно?
Автор: Верно. При этом можно моделировать и отдельные риски. Просто в этом случае придется использовать довольно много режимов. На практике, конечно, лучше действовать поэтапно: выделить несколько режимов, построить аппроксимацию и перейти к следующему шагу, опять выделить несколько режимов и т.п.
Читатель: Я что-то недопонимаю...
Автор: Когда Вы прочтете первую половину книги, поймете...
Читатель: Простите за нескромный вопрос, но на каком уровне я должен знать математику, как Вы думаете?
Автор: На таком, на каком Вы сами захотите остановиться.
Читатель: Разве такое может быть?
Автор: Я разделил каждую главу на две части. В первой части я все объясняю на интуитивном уровне и “на пальцах”. В ней, как правило, есть пара рисунков либо графиков — просто для иллюстрации. Вторая же часть содержит все строгое математическое обоснование первой части. При этом математическая информация нарезана на кусочки, каждый из которых можно разбирать отдельно от других.
Читатель: Значит, если у меня есть мозги, мне следует сосредоточиться на математике, да?
Автор: Это значит, что, если Вы имеете какое-то представление о тех материях, о которых идет речь, Вам следует сосредоточиться на интуиции. Как только Вы поняли, о чем я хочу сказать, все остальное становится простым. Математика — здесь просто язык для выражения интуитивных идей. С помощью математики я объясню Вам непонятные, но интересные мысли даже в том случае, если Вы туго соображаете. Если же интуитивно Вам та или иная мысль понятна, или кажется Вам не очень важной, или просто Вы не интересуетесь математикой, то соответствующую математическую составляющую легко можно опустить.
Читатель: Спасибо, Вы укрепили мою уверенность в себе. Теперь знаю, что как минимум смогу прочесть вашу книгу. Постараюсь не забыть этих ваших объяснений.
Автор: Но я вовсе не хотел укреплять вашу уверенность в себе. Как раз наоборот, я хотел радикально ее ослабить! Представьте, что Вас попросили проанализировать некие инвестиционные риски и вдруг Вы понимаете, что эти риски, которые надо проанализировать и управлять которыми Вы должны помочь, скорее всего, гораздо больше, чем Вы думали, но при этом их гораздо труднее идентифицировать и описать, а те математические модели, с которыми Вы работали раньше, теперь не работают, и Вы не можете найти разумную замену этим моделям. Каково?
12
Ввадавиа
Читатель: Вы думаете, это привычная ситуация при управлении финансовыми рисками?
Автор: Нет. Но у многих вошло в привычку скрывать такие ситуации, когда они возникают. И таким образом управлять не самим риском, а некой видимостью риска.
Читатель: Звучит цинично...
Автор: Увы, так оно и бывает. Между прочим, управлять видимостью риска тоже надо уметь. По крайней мере, если Вы не хотите вылететь со своей работы...
Читатель: Если я должен притворяться, зачем понижать мою уверенность в себе?
Автор: Для того чтобы с помощью второй части данной книги Вы смогли восстановить уверенность, но уже на более прочном фундаменте.
Читатель: Как?
Автор: Посредством такой модификации существующей теории, чтобы она включала в себя риск «айсберга».
Читатель: Эти изменения просты?
Автор: Настолько просты, насколько возможно.
Читатель: Просты настолько, что обычные люди смогут использовать модифицированную теорию?
Автор: По правде говоря, этим обычным людям, скорее всего, юнадобится помощь квалифицированного математика.
Читатель: Мне помнится, вы недавно говорили, что математика не шляется критически важным фактором...
Автор: Понять, что и как пошло не так, можно и без математики. Но чтобы выправить положение, математика необходима.
Читатель: А если я все-таки не смогу понять вашей математики?
Автор: Тогда поручите разобраться в деталях кому-нибудь, кто понимает. А Вы сосредоточьтесь на интуиции.
Читатель: Очень хорошо. Между прочим, не могли бы Вы в двух словах резюмировать те изменения, которые предполагаете внести в действующую теорию?
Автор: Конечно. Функции разбиения.
Читатель: Никогда о таких не слышал.
Автор: Ничего удивительного. Они пришли из термодинамики, где их называют термодинамическими суммами, и их применение в теории портфеля неочевидно...
Читатель: И каково же их назначение в теории портфеля?
Автор: Мы используем их способность переключения с режима на режим при работе с опционами.
13
Введения
Автор: Потому, что мои контрпримеры вовсе не являются
несущественными исключениями, как эго показано в последующих главах первой части.
Читатель: Но Вы обещали, что вторая часть книги поможет мне разобраться с вашими контрпримерами, не так ли?
Автор: При наличии некоторой дополнительной информации, да,
поможет.
Читатель: Под дополнительной информацией Вы подразумеваете информацию об условных колоколообразных кривых?
Автор: Да, но не только ее. Еще надо знать, какова ваша склонность к риску. Например, неплохо бы знать, готовы ли Вы рискнуть, скажем, четвертью своего состояния, чтобы получить колоссальную прибыль.
Читатель: И каким же образом Вы намерены связать условные колоколообразные кривые с моей склонностью к риску?
Автор: Я же сказал: функции разбиения.
Читатель: Как я уже сказал, это название мне ничего не говорит.
Автор: Ну, хорошо, хорошо. Функции разбиения — это взвешенные суммы экспонент, причем каждому режиму соответствует одна и только одна экспонента, а веса зависят от вероятностей соответствующих режимов.
Читатель: Интересно.... А что, Вы говорите, определяет показатели степени этих экспонент?
Автор: Скорректированные на риск ожидаемые вознаграждения, помноженные на некий множитель, связанный со склонностью к риску.
Читатель: Почему Вы осуществляете коррекцию на риск дважды?
Автор: Один фактор осуществляет коррекцию внутри режима, а второй — при переходе между режимами.
Читатель: Как именно Вы проводите коррекцию на риск внутри
режимов'
Автор: Вычитаю некий член, кратный условной дисперсии, из соответствующего условного матожидания.
Читатель: Насколько велик это член?
Автор: Это тоже зависит от склонности к риску... простите, но мне не хотелось бы сейчас входить во все тонкости новой теории и расставлять все точки над i.
Читатель: Конечно, конечно... я лишь хочу понять, почему Вы не можете просто взять, да и усреднить различные вознаграждения с коррекцией на риск.
Автор: По сути, именно это и делается. Просто веса в моей формуле зависят нс только от того, каковы шансы реализации соответствующих режимов, но и от того, насколько плох или хорош каждый режим. Чем хуже
15
Вввдвнив ^^=======
ожидаемое вознаграждение, скорректированное на риск, тем больший вес получает соответствующий режим.
Читатель: Какой в этом смысл?
Автор: Такой подход сделает Вас более осторожным.
Читатель: А я привык думать, что более осторожным делает штраф дисперсии.
Автор: И это тоже. Но важно, что член, учитывающий склонность к риску, штрафует за риск как внутри данного режима, так и при переключении с режима на режим.
Читатель: Хорошо, в этом, похоже, действительно есть некий смысл. Есть ли еще что-нибудь, о чем мне неплохо бы знать заранее?
Автор: Довольно много. Но самое важное: в мою схему можно встроить опционы и прочие нелинейные активы, не прибегая к методу Монте-Карло.
Читатель: Как Вы это делаете?
Автор: Посредством коррекции вознаграждений, скорректированных на риск, по дельта- и гамма-вклада от опционов.
Читатель: Удивительно, как это Вам удалось вместить все это в единую формулу....
Автор: Ну, она вовсе не проста, а, точнее говоря, проста по мере возможности. И еще в отличие от стандартной теории “среднего и дисперсии” моя теория не дает замкнутого набора форм решений. Тем не менее решение на практике можно очень быстро найти с помощью компьютера.
Читатель: Если ваша теория верна, она совершит переворот в управлении инвестиционным риском.
Автор: Моя теория верна. Но я сомневаюсь в том, что она сильно изменит существующую практику управления риском.
Читатель: Почему же?
Автор: Потому что практикующие менеджеры гораздо больше заинтересованы в управлении видимостью риска, нежели в управлении собственно риском. А моя теория благодаря тому, что в явном виде включает в себя возможность изменения режима, делает настоящие риски, я бы сказал, более видимыми.
Читатель: Но мне кажется, если бы кто-нибудь доходчиво объяснил финансистам пороки существующей системы оценки инвестиционного риска и то, как преодолеть эти пороки, его приняли бы “на ура”.
Автор: Я вижу, что Вы пока не знакомы ни с Конвеем, ни с Девлином.
Читатель: А это кто такие?
Автор: Неважно. Не будем забегать вперед и портить приключение. Добро пожаловать в "Риск «айсберга»"!
16
Часть 1
СТАНДАРТЫ ОТКЛОНЕНИЯ
Введение: "...считая айсберг скоплением мелких льдин..."
Вторник, 09 апреля 1912 года
Капитан Смит вышел в приемную из своего тесного кабинета в здании штаб-квартиры пароходной компании White Star Line, что на Саутхэмптон-док. Он был раздражен и ворчал: “Смотрите, если вы отвлекаете меня на ерунду...”. Бумаг было много, и прочитать их надо было до завтрашнего утра. На глупости отвлекаться было некогда. Секретарь капитана, который пару мгновений назад, поборов внугреннес сопротивление, постучал-таки в дверь кабинета шефа, нервно кивнул в сторону молодого человека потертого вида, сидевшего в приемной и курившего вонючую сигарету. “Мне очень жаль, сэр. — оправдывался секретарь. — Я все утро пытаюсь объяснить этому молодому господину, что Вас нельзя обрывать от работы, но он не отстает и твердит, что должен непременно Вас видеть и что не уйдет, не повидав Вас, потому что якобы ваше судно в большой опасности”.
“Мое судно в опасности”, — машинально повторил капитан. “Это «Титаник»-то! — подумал он про себя. — Самое большое, самое быстрое судно из всех, когда-либо построенных», — и как отрезал: “У меня нет времени на глупости".
Клерк улыбнулся посетителю с издевкой: “Видите, я говорил вам. что капитану вряд ли будут интересны ваши предложения. Теперь будьте любезны покинуть офис, нам надо работать”, — закончил клерк уже уверенным гоном.
Молодой человек встал со стула: “Капитан, пожалуйста, дайте мне пару минут на объяснение. Клянусь, я пришел сюда нс для того, чтобы подвергать сомнению тактико-технические данные вашего великолепного судна. К тому же наши эксперты сходятся во мнении, что «Титаник» и вправду — самый лучший представитель судов этого класса. Но потерять его было бы трагедией,-воскликнул молодой человек. —Я пришел, чтобы это предотвратить”.
“Ваши эксперты? — угрожающе пробасил капитан. — Вы пытаетесь угрожать мне?”.
Молодой человек энергично сунул капитану руку для рукопожатия . “Никоим образом! — воскликнул он. — Пожалуйста, разрешите мне объясниться. Меня зовут Жак Башелье, и я представляю один из консорциумов страхователей морских судов. Мы готовы застраховать «Титаник» на очень
19
Часть 1. Стандарты отклонении
выгодных для Вас условиях, если Вы согласитесь на проведение на вашем судне научных процедур, снижающих риск столкновения с айсбергами”.
“Айсберги! — воскликнул капитан. — Бросьте, молодой человек. Я плаваю по Северной Атлантике вот уже двадцать лет, — продолжил он снисходительно, — и не могу припомнить, чтобы за все это время я хотя бы раз слышал о столкновении судна с айсбергом, не говоря уж о том, что со мной никогда такого не происходило ”. “Действительно, — продолжал капитан, — айсберги достигают время от времени морских торговых путей, но мы не игнорируем даже этот ничтожный риск и приняли все необходимые меры предосторожности. В команде «Титаника» шесть наблюдателей, если кто-либо увидит айсберг, мы его просто обогнем. Вы удовлетворены?”, — сказал капитан с видом превосходства.
Тем не менее система безопасности «Титаника», по всей видимости, не произвела на Башелье особого впечатления: “Великолепная система, капитан, — сказал молодой человек, — при условии, что Вы вовремя заметите айсберг”.
“«Титаник», как Вы только что заметили, очень быстр, но габариты не позволят ему совершить какой-либо резкий маневр”.
Но и капитана не так просто было смутить: “А еще «Титаник» очень высок, мсье. Наблюдатели смогут увидеть айсберг издалека, и у нас будет много времени, чтобы принять меры предосторожности”.
Но мсье не унимался: “Даже в тумане, даже безлунной ночью?”
Снисходительность капитана к настырному посетителю прошла, и Смит опять почувствовал раздражение: “Вы что, думаете, я дурачок? В таких условиях я сделаю то, что моряки делали столетиями — сбавлю ход! А теперь, молодой человек, не оставите ли вы меня в покое, много работы, знаете ли”.
Однако Башелье ничуть не смутился: “Снизите ход, — чуть-чуть поддразнил он капитана. —- Правда? Неужели Вы намерены снижать ход всякий раз в условиях плохой видимости? Но тогда вы пересечете Атлантику не так быстро, как все того ждут, не так ли? Будете слишком часто снижать ход и, как следствие, сделаете в год гораздо меньше рейсов туда и обратно, чем это запланировала White Star Line. Подумайте о своих работодателях, капитан. Мы понимаем, что Вы не в состоянии полностью исключить всякий риск. Мы просто хотим предложить Вам управлять этим риском на научной основе”.
Капитан посмотрел на часы. Время было дорого, но капитан был заинтригован: “Управлять риском на научной основе? А что, конкретно, Вы имеете в виду?”.
Башелье перевел дух: “Я предлагаю применить на практике теорию, разработанную моим братом Луи более чем десять лет тому назад. Эта теория работает со статистикой взаимодействия миллионов плавающих частиц. Хотя индивидуальные взаимодействия предсказать практически невозможно, большинство индивидуальных отклонений взаимоуничтожаются при агрегации. В сухом остатке получается некое случайное движение, которое является нормально распределенным со средним отклонением и дисперсией, растущими линейно по времени”.
20
Введении
Вот теперь капитан его, наконец, понял. Он мысленно снисходительно улыбнулся, а вслух сказал: “Как я понимаю, вы имеете в виду теорию броуновского движения, открытую, как мне помнится, Альбертом Эйнштейном в 1905, вроде бы, году. Что-то я не припоминаю, чтобы слышал имя вашего брата в этой связи”.
Капитан оказался начитанным. Но, по сути, все было просто. Дело в том, что часы, дни, месяцы и годы, проведенные на морской службе, дают массу времени для чтения и самообразования. К тому же наш капитан, как и большинство моряков во все времена, имел склонность к азартным играм. Поэтому и читал кое-что по теории вероятностей.
Жак Башслье выглядел одновременно и удивленным и оскорбленным: “Уверяю Вас, капитан, что мой брат самостоятельно разработал эту теорию за пять лет до господина Эйнштейна и изложил ее в своей докторской диссертации, которую защитил во время учебы в Сорбонне. Его “Теория спекуляций” предлагает новое понимание законов, управляющих случайным движением котировок ценных бумаг. Но профессора Сорбонны не проявили должного внимания к разработкам моего брата, и его труды были забыты. Я хочу отдать ей должное, проверив ее на деле”. Тут тон молодого человека смягчился: “Независимо от только что сказанного, я потрясен глубиной ваших знаний, капитан. Потрясен и приятно удивлен. Ясно, что вы, как никто другой, способны по достоинству оценить мою новую систему предсказания встречи с айсбергами. Я назвал ее «АйсМетрика»”.
Жак нащупал-таки слабое место капитана. Дело в том, что капитан был очарован математикой и преклонялся перед математиками. Поэтому с последней фразой Жака капитан почувствовал к нему внезапное расположение: “Будьте так добры, молодой человек, пройдите в кабинет и расскажите мне о своем предложении поподробнее”.
Почувствовав себя в своей тарелке, Жак еще больше воодушевился и проследовал за капитаном, не переставая говорить: “В своей основе «АйсМетрика» оценивает средние частоты столкновений с крупными и мелкими частицами льда в океане, дисперсии этих частот и опарные корреляции между большими и малыми льдинами. Предполагая, что движения льдин можно моделировать многомерными нормально распределенными случайными величинами, мы можем вычислить искомую вероятность встречи с айсбергом”.
Капитан все-таки сомневался в том, что все так уж просто: “Но, разве Вы не предполагаете, что вероятности встреч с айсбергами должны быть разными для различных географических точек и времен года?”
Жака, однако, это не смутило: “Конечно. Именно поэтому я и предлагаю каждый час делать выборочные замеры количества и размеров льдин в океане, а также корректировать оценки соответствующих средних частот и корреляций на основе вновь полученной информации. Естественно, встреча с айсбергом — исключительно редкое явление, но имейте в виду, что айсберг можно представлять себе, как высококоррелированное множество льдин гораздо
21
Часть 1. Стандарты отклонения
меньшего размера. При таком подходе можно построить оценку частоты встречи с очень большими льдинами, т.е. с айсбергами, по данным соответствующих измерений для малых льдин”.
Капитану идеи понравились, но все-таки доля скептицизма осталась: “Все это прекрасно в теории, но насколько точными, если, конечно, Вы применяли эти методы на практике, оказались Ваши прогнозы?”.
Башелье слегка покраснел и опять закурил: “Результаты выглядят вполне достойно. Но замечено и то, что редкие явления имеют стойкую тенденцию происходить значительно чаще, чем это предсказывает моя теория. К счастью, мои коллеги из Международного бюро страхования морских судов нашли практическое решение, исправляющее эту неприятность”.
Капитан вскинул брови вверх: “И какое же?”
Башелье выпалил: “Они умножают оценки моей «АйсМетрики» на некий коэффициент, равный трем или чуть больше”.
Капитан удивился: “Почему на три?”
Башелье смущенно улыбнулся: “Честно говоря, я не знаю. Мне кажется, что Бюро хотело, чтобы система оценки риска была максимально простой и персоналу было легче с ней работать. Поэтому они решили выбрать корректирующий множитель в виде натурального числа. В то же время они не хотели бы недооценивать риск и поэтому, не рассматривая двойку, остановились на тройке”.
Капитан не унимался: “А почему не на четверке?”
Башелье выкручивался, как мог: “Как я уже говорил Вам, капитан, мы, страховщики, вовсе не стремимся устранить весь риск подчистую, а стремимся грамотно этим риском управлять. Коэффициент четыре применяется только для тех кораблей, управление которыми нельзя назвать удовлетворительным. Так или иначе средство оказалось эффективным, и все наши страховщики вполне освоились с «АйсМетрикой» и теперь работают с ней без проблем, страхуя риск айсберга”.
Капитан был разочарован: “И Вы называете это наукой, мсье Башелье?”
Однако Жак не сдавался: “Капитан, «АйсМетрика» является научной основой для мониторинга риска айсберга, но не претендует на то, чтобы выдавать точные оценки. Скорее, она является практическим инструментом. С одной стороны, «АйсМетрика» доводит до страховщиков порядок величины того риска, который они страхуют. А с другой — помогает отбивать критику наших акционеров, когда и если несчастье все-таки произойдет. Мы обозначили эту ипостась «АйсМетрики» буквами ПСЖ — от ‘Прикрой Свою Задницу’, простите за грубое слово. И уж поверьте мне, капитан, эта вторая сторона «АйсМетрики» не менее важна и эффективна, чем первая, сугубо научная. Я имею в виду, что в наше время ни один уважающий себя менеджер не обходится без солидной научно обоснованной ПСЖ, т. е. индульгенции своих ошибок”.
Но капитан не был склонен к юмору в обсуждаемых вопросах: “Почему-то я не уверен, что потомки простят мне столкновение «Титаника» с айсбергом, 22
Введения
даже если моя индульгенция будет обоснована самым научным и наилучшим образом ”.
Почувствовав настроение капитана, Башелье тоже посерьезнел: “Капитан, я вполне понимаю ваш скептицизм, но, прошу Вас, дайте мне шанс убедить Вас в моей полезности. Просто позвольте мне и моей помощнице Флер принять участие в вашем плавании, которое начинается завтра. Мы будем ежечасно предсказывать концентрацию льда, и Вы сможете лично сравнить наш прогноз с тем количеством льда, который Вы реально встретите. Наш интерес состоит в том, что, если Вы будете удовлетворены результатами, мы попросим Вас рекомендовать компании White Star Line применять «АйсМетрику» в качестве инструмента управления риском, а также позволить нам приводить вас в пример предлагая свои услуги другим клиентам. Если же вы не будете удовлетворены результатами, никаких проблем с нами у Вас не возникнет. В любом случае, наш консорциум намерен застраховать ваше первое плавание на «Титанике» по самой низкой ставке”.
Капитан был заинтересован, но возражения у него все-таки были: “Ваше предложение представляется мне очень заманчивым, не скрою, но мне необходимо подумать и о пассажирах. В первом плавании среди пассажиров будет много влиятельных лиц типа Асторов и им подобных. Я не могу позволить вам проводить на палубе замеры льда и вызывать тревогу у этих людей”. Но Жак уже почувствовал успех и дожал капитана: “Капитан, я полностью разделяю вашу заботу о комфорте пассажиров, и поэтому обещаю, что мы с Флер будем крайне деликатны и не станем привлекать к себе никакого внимания”.
Однако, попав на борт, Флер и Жак с таким энтузиазмом принялись за дело, что не заметить их усилий мог бы только слепой. Нередко они балансировали на самой кромке борта огромного корабля, чтобы как можно лучше забросить и вытащить свои сети для ловли льда. Понятно, что такая отчаянная храбрость поначалу произвела настоящий переполох среди пассажиров, но потом о странных занятиях молодых людей стали говорить как о выходках юных любовников, и на них перестали обращать внимание.
Меж тем ежечасные замеры «АйсМетриков» не отличались разнообразием результатов. Единственной более или менее мудреной процедурой была модификация прогноза. Первоначально прогноз был основан на простой скользящей средней 20 выборок, но Жак очень скоро заметил, что лед попадается островками или кластерами, из чего следовало, что более поздние наблюдения должны иметь больший вес. Тогда он применил метод так называемого экспоненциально взвешенного скользящего среднего, который со временем уменьшал вклад наблюдений. Анализируя результаты наблюдений, Жак отметил волнообразное поведение дисперсии. Он учел и это с помощью метода, который назвал методом льдоохранной авторегрессивной условной гетероскедастичности. Капитан ежился от подобных названий, но млел от результатов. Почасовые прогнозы на каждый следующий час оказались очень точными, что нельзя было приписать игре случая. Правда, «Титаник» находился в плавании всего-то четыре дня, и пока что в океане им не попадались места с большой концентрацией льда.
23
Часть 1. Стандарты иткланиния _____________________________
Однако Башелье заверил капитана, что результаты, которые могли бы быть получены в экстремальных условиях, можно экстраполировать из результатов экспериментов, проведенных в нормальных условиях. Он, даже доказал это утверждение строго с привлечением многомерных нормальных распределений. Наконец, ни в одной из выборок отношение фактически измеренной частоты экстремальных событий (т. е. больших льдин) к прогнозной величине этой же частоты даже близко не подошло к балансирующему коэффициенту, применяемому страховым бюро (т. е., тройке).
В тот злосчастный вечер квартирмейстер Хитчин доложил капитану, что на море густой туман. Поскольку Хитчин был моряком старой школы, он предложил капитану сбавить ход. В тот момент, когда капитан уже был готов согласиться с Хитчиным и отдать соответствующие распоряжения, к нему обратился Башелье с последними результатами и прогнозами. Жак доложил, что последние 24 часа концентрация льда были пренебрежимо малой и, соответственно, все оценки средних и стандартных уклонений оказались исключительно малыми.
Капитан выслушал это и сказал: “Мсье Башелье, вот и наступил момент практической проверки вашей теории! Каковы, по-вашему, шансы налететь на айсберг, настолько большой, чтобы «Титаник» пошел на дно?”.
Жак бодро ответил: “По моим расчетам, капитан, событие, состоящее в появлении фатального для «Титаника» айсберга, отстоит от среднего не менее чем на десять стандартных уклонений, что означает, что с практической точки зрения вероятность появления айсберга равна нулю”.
Капитан выслушал и переменил решение: “Тогда сохраним нашу скорость на прежнем уровне”, — а потом добавил с ноткой патетики: “Начиная с этого момента, для замеров и оценки риска встречи с айсбергом на «Титанике» будет применяться «АйсМетрика». Я верю, что решение сохранить скорость войдет в историю — как самого «Титаника», так и науки оценки риска!”.
Через несколько часов стало ясно, что пророчество капитана оправдалось с максимальной полнотой.
Однако не будем слишком строги к злосчастному Жаку Башелье. Тем более, что научный вклад его брата и на самом деле получил-таки заслуженное признание, а семья — заслуженную славу. К тому же увлекательная и трагическая, хотя и сильно измененная история отношений Жака и Флер послужила основой для самого популярного в мире кинофильма. Наконец, даже научная ошибка Жака принесла свои плоды. Морские суда теперь оснащены оборудованием, которое максимально снижает риск налететь ночью на айсберг, как и на другой крупный предмет.
С морским судоходством — все ясно, но меня заботит, что мир до сих пор не извлек более глубоких уроков из «АйсМетрики». Никаких, образно
24
Ввидинии
выражаясь, финансовых радаров до сих пор не существует, чтобы просвечивать туман, окружающий риск больших финансовых катастроф, а уж если такое крушение произошло, почему-то под рукой всегда слишком мало спасательных шлюпок. Но что еще неприятнее, хотя и профессиональные менеджеры, и завсегдатаи разного рода крупных финансовых площадок постоянно отслеживают и прогнозируют свою уязвимость по отношению к внезапному массовому обрушению/росту котировок, методологии, которые они используют и на которые всецело полагаются, пугающе близки к той самой «АйсМетрике». Взгляните, например, на стандартную практику, в которой средние, стандартные уклонения и попарные корреляции между активами используют для того, чтобы оценить риск масштабных потерь большого портфеля ценных бумаг. Технически это означает, что априори все активы портфеля многомерно нормальны, т.е. портфель как единое целое хорошо моделируется многомерной нормально распределенной случайной величиной. Подчеркнем: применение стандартного подхода к оценке риска оправдано, если предположить, что любой портфель нормально распределен.
Однако, и к этому мнению склоняются все большее число профессионалов, нормальность распределения портфеля — явление исключительно редкое. В настоящее время особое внимание уделяют определению и оценке альтернативных распределений. И все для того, чтобы научиться оценивать толстые хвосты отдельных активов. Но, к сожалению, никто не прилагает столь же значительных усилий к разработке техники применения этих альтернативных распределений при оценке рисков не отдельного актива, а целого портфеля. Этому кажущемуся парадоксу есть несколько серьезных причин:
• Во-первых, хотя на практическом уровне модные методы стоимости риска используют примерно так, как пьяница — уличный фонарь: не для освещения, а для опоры, когда вам надо будег лишь “для вида” обосновать уже принятое решение, скорее всего, не станете напрягать аналитические способности и использовать новомодные методы, потому что старые добрые нормальные аппроксимации в данном случае вполне сгодятся. Например, Банк международных расчетов неявно стимулирует такой подход в банковском деле, требуя, чтобы все оценки риска умножались для верности на множитель, равный 3. В этом случае даже вполне добросовестный риск-менеджер будет искать способ указать только треть истинной стоимости риска.
• Во-вторых, отказ от предположения о многомерной нормальности порождает целый клубок взаимосвязанных проблем. Дело в том, что большинство альтернативных моделей или теоретически несостоятельны, или их трудно, если вообще возможно, использовать в компьютерных приложениях. Иными словами, даже в тех случаях, когда аналитики признают неадекватность предположения о многомерной нормальности, в практической работе они применяют все те же нормальные распределения просто потому, что ничего другого пригодного для работы нет. Рассматриваемая ситуация особенно характерна для финансового сектора, потому что здесь особенно приветствуется решительность менеджеров.
25
Часть 1. Стандарты птклпниния ___________________
• В-третьих, большинство почему-то наивно полагает, что портфели обязаны нести меньшие риски потерь, чем отдельные активы, при появлении неординарных событий, отстоящих от среднего в нормальной модели на множество стандартных уклонений. Это предположение не соответствует действительности. Конечно, центральная предельная теорема утверждает, что портфели, составленные из множества независимых одинаково распределенных активов, имеют асимптотически нормальное распределение, даже если хвосты составляющих распределений очень толстые. Однако мало кто принимаег в расчет, что даже слабая зависимость между активами портфеля может сделать центральную предельную теорему неприменимой.
Теперь попробуем разобраться с вышеизложенным более подробно. В настоящее время единственная количественная мера финансового риска, о которой можно уверенно сказать, что она применяется повсеместно, — это волатильность, или стандартное уклонение в годовом выражении. Такое положение в значительной мере объясняется двумя факторами. Во-первых, тем, что волатильность — очень удобная мера, поскольку волатильность любого портфеля зависит только от волатильности составляющих активов, от весов этих активов и их корреляций. Во-вторых, тем, что мы всегда можем аппроксимировать все риски нашего портфеля как единого целого каким-нибудь нормальным распределением, имеющим в качестве параметров все те же среднее и стандартное уклонение, т. е. волатильность. Но здесь, конечно, со всей остротой встает вопрос: “Насколько хорошей окажется аппроксимация портфеля по сравнению с аппроксимацией отдельного актива?”.
Несмотря на всю очевидность и важность этого вопроса, его очень редко ставят явно. Зато неявно он возникает очень часто. И всякий раз, когда для портфеля применяют нормальную аппроксимацию, и в том случае, когда составляющие активы явно не нормальны, считается, что нормальная аппроксимация относительно хороша. И в самом деле, нормальная аппроксимация хороша, ведь большинству других распределений для того, чтобы измерить риски портфеля, только среднего и волатильности не хватило бы.
При практическом применении нормальной аппроксимации надо помнить, что в действительности она справедлива только для центральной области рисков портфеля, поскольку только в этой области выполняется утверждение, что чем больше активов входит в портфель, тем лучше сама аппроксимация, т. е. точность приближения. Но на хвостах приближение гораздо хуже. Известно, что даже для очень больших портфелей так называемые “события больших стандартных уклонений”, т. е. события, отстоящие от среднего на расстоянии множество стандартных уклонений, происходят гораздо чаще, чем следовало бы, исходя из нормальной аппроксимации. И чаще всего такое происходит на медвежьем рынке, чего инвесторы боятся более всего. Тем не менее хвостовой риск очень сильно варьирует от сценария к сценарию, и не для каждого портфеля так уж он велик. Я назвал этот дополнительный риск риском «айсберга», потому что по большей части он вообще не попадает в поле зрения аналитиков, но грозит катастрофическими последствиями. Его можно было бы назвать “Ноев риск” в
26
Ввидинии
память о библейском потопе, но тогда на слух этот риск воспринимался бы как риск всего чрезвычайного, в то время как я хотел бы сосредоточить ваше внимание исключительно на хвостовом риске портфеля ценных бумаг. Специфика рассматриваемого случая, кроме всего прочего, состоит и в том, что любой портфель может нести в себе большой риск «айсберга» даже в том случае, когда локальный хвостовой риск каждого из составляющих его активов такой же, как и у нормального распределения или даже тоньше. А потом, как мы все помним из библии, Господь ясно предупреждал людей о потопе, но не был услышан, в то время как айсберги люди всегда стараются разглядеть или каким-либо иным способом обнаружить, но им это далеко не всегда удается. Так что название “Ноев риск” тут явно не подходит.
Введение в рассмотрение риска «айсберга» помогло мне провести для себя четкую грань между теорией портфеля ценных бумаг и практикой управления таким портфелем. Например, теория часто советует компоновать портфель таким образом, чтобы массивные длинные позиции по значительному количеству активов уравновешивались не менее значительным количеством почти таких же массивных коротких позиций. Однако эти портфели подвержены настолько очевидному и громадному риску «айсберга», что никакой практикующий менеджер даже не будет рассматривать подобные стратегии в чистом виде, если, конечно, он не хочет моментально вылететь с работы. Поэтому разработчики моделей управления риском, дорожащие своей репутацией и рабочим местом, научились ограничивать риск «айсберга» с помощью наложения довольно жестких верхних и нижних границ на размеры позиций портфеля. В таком виде портфели выглядят гораздо лучше, но в частных разговорах профессионалы не скрывают своей тревоги по поводу этих самых “полов-потолков”. Дело в том, что эвристические методы определения нижних и верхних границ на практике становятся из вспомогательных основными, меняя до неузнаваемости тот опорный результат, который рекомендует теория, и сводя тем самым роль этой теории до, так сказать, “оформления витрины”, используя его для проведения презентаций, дабы произвести хорошее впечатление на клиента и т. п.
Интересно, что в естественных науках подобный разрыв между теорией и практикой неизбежно привел бы к радикальной ревизии теории. Так, квантовая теория появилась в частности и потому, что, как заметил Макс Планк, согласно предположениям классической физики абсолютно черное тело должно выжигать наблюдателю глаза рентгеновскими лучами. И конечно же, классическая физика подверглась ревизии. Но с теорией портфеля ничего подобного, как это ни удивительно, не происходит. Может быть, теория портфеля не падает потому, что у нее есть мощный костыль, на который она, в отличие от естественных наук, может опираться. Этот костыль принято заворачивать в разные красивые и оригинальные упаковки, но суть его в том, что люди просто глупы. Почему рынки не ведут себя так, как говорит теория? Потому, что люди глупы. Почему управляющие портфелями не принимают всерьез рекомендаций теории? Потому, что люди глупы. При этом трудно с порога отмести аргументы типа “Люди дураки” потому, что люди и в самом часто ведут себя как дураки. Ну вот вы
27
Часть 1. Стандарты птклпниния=____________________________________________
видите, я и сам впал в этот грех и опираюсь на тот же костыль... Что я, собственно, хотел бы прояснить относительно этого костыля? Да то, что обвинения в тупости отупляют того, кто их раздает направо и налево. Представьте себе, что ребенок выбегает на проезжую часть за мячиком и попадает по машину. В этом случае моментально находят кандидатов в придурки. Это и те взрослые, кто должен смотреть за ребенком, и сам ребенок, и, наконец, водитель. Но, может быть, честнее назвать то, что произошло, просто несчастным случаем? Я имею в виду, что всякое обвинение в тупости неявно предполагает, что на самом деле у придурка была возможность принять мудрое, а не дурацкое решение. Просто ему надо было воспользоваться информацией, которая практически валялась у него под ногами. Но наш тупица очевидной возможностью не воспользовался.
В этой книге я, рискуя, что меня объявят глупцом, отказываюсь от концепции тупости и заменяю ее парадигмой невежества и обучения. Поэтому в отличие от классической теории финансов не стану предполагать, что все рыночные риски и выигрыши выставляют видимые дорожные знаки и сигналы, которым разумный инвестор просто должен следовать и все. Вместо этого я допущу возможность внезапных изменений, причем без всяких уведомлений о том, что такое изменение должно произойти либо только что состоялось, о том, что на что должно поменяться либо только что поменялось, и о том, когда и как все изменившееся должно вновь измениться. Иными словами, я предполагаю, что инвесторы редко когда точно знают, каковы реальные риски и реальные выигрыши рынка в каждый конкретный момент. Вместо этого инвесторы вынуждены полагаться на свои догадки, основанные на своих представлениях о прошлом поведении рынка и своих теориях, объясняющих мир.
Я подозреваю, что большинство найдет мои соображения и комментарии банальными и в силу этого не заслуживающими внимания. А некоторые подумают, что последние из приведенных соображений уже встроены в общепринятую теорию управления портфелем. А кое-кто посчитает, что их просто нельзя встроить ни в какую теорию. Так вот, настоящая книга призвана доказать, что все эти читатели не правы. И докажет! По крайней мере тем из них, кто прочитает книгу до конца, а может быть, и тем, кто просто пролистает ее. Но, если вы, как я, сильно загружены работой, то, скорее всего, не захотите тратить столь свое время и усилия на чтение книги без предварительного “железобетонного” доказательства того, что предлагаемый мной подход имеет смысл. Поэтому позвольте привести всего два примера.
Первый из них касается одного явления, которое известно всем. Оно состоит в том, что инвесторы почти всегда остро реагируют на данные о доходах эмитентов. Точнее, вы можете считать, что они реагируют неадекватно, если предполагаете, что эти инвесторы в общих чертах понимают те рынки, на которых они делают свои инвестиции, и те риски, которым они себя подвергают, делая свои инвестиции. Некоторые экономисты всерьез считают такое поведение инвесторов доказательством их экономической иррациональности (читай — тупости). Однако, если вы допустите, что параметры рисков могут
28
Вввдвнив
эволюционировать (причем я даже не требую, чтобы сами параметры изменялись, я лишь требую, чтобы инвесторы могли думать, что эти параметры могут измениться), вы легко найдете объяснение рассмагриваемое избыточной волатильности.
Второй пример — уже из моего личного опыта. Я впервые начал присматриваться к явлениям, на которых построил то, что назвал “теорией невежества”, еще в начале 80-х гг. прошлого века, когда учился в аспирантуре, когда написал и защитил диссертацию по проблемам мотивации и оценки создателей экономических прогнозов. И хотя меня интересовали явления невежества, в конце концов я, как говорится, женился на той подружке, которую знал лучше всех остальных, а именно занялся советской экономической реформой, которая плавно переросла в постсоветскую. Потом некие ничтожества — лощеные советники — увели у меня мою милую, и я, познав, что ни одно доброе дело не остается безнаказанным, тоже изменил ей и ушел на Уолл-стрит. Но в 1994 г. я вновь встретился со «старой знакомой» и втюрился еще с большей силой. Дело в том, что моя новая визитная карточка делала меня признанным экспертом по постсоветским долговым рынкам точно так же, как диплом волшебника страны Оз сделал чучело мудрецом. Жаль только, что мне не досталось немного той мудрости. Например, через пару недель после того, как я появился на Уолл-стрит, мне было поручено оценить будущий риск дефолта по государственным облигациям Болгарии, которые в тот момент готовились к выпуску (облигации Брэйди). Несмотря на то что я долго занимался вопросами экономической реформы и в МВФ, и во Всемирном Банке и был близко знаком с некоторыми ключевыми игроками на этом поле, я понятия не имел, как подойти к решению поставленной мне задачи. В то время я был настолько неопытен в методах оценки риска, принятых на Уолл-стрит, что не знал даже, что аналитик Уолл-стрит не должен позволять себе где бы то ни было говорить о том, что он чего-то не знает. В общем, первый блин на Уолл-стрит у меня вышел комом. Можете себе представить, как я завидовал коллегам, работавшим по Латинской Америке. По сравнению с постсоветским блоком любая страна типа Мексики имела гораздо более стабильный политический режим, намного более длительную историю обслуживания долга, гораздо больше достоверных экономических данных, etc. Так вот, на основе консультаций с МВФ и основными инвесторами, а также с правительством Мексики мои гениальные коллеги уверенно предсказали, что мексиканский песо будет держаться в пределах объявленного коридора его обменного курса к доллару США. Ах, как они были правы! Правда, лишь до того дня, когда оказалось, что они совершили огромную непоправимую ошибку. И мексиканский «айсберг» стал для меня откровением. Я подумал: “Ага! А некоторые из этих гуру еще тупее меня!” На более продуктивном уровне я осознал, что те рынки, на которых я специализировался, движутся, главным образом, благодаря восприятиям инвесторов и изменениям в этих восприятиях, и только изредка реальность вторгается в этот сон. С тех пор (и навсегда) я сосредоточился на том, чтобы понять, как работает невежество на финансовых рынках как в теоретическом, так и в практическом аспектах. Можете назвать это путешествием в
29
Часть 1. Стандарты втклвнвния____________________________________________
невежество. Данная книга, если вы, конечно, дадите ей такой шанс, отправит и вас в такое же путешествие.
Первая часть книги исследует математические основы риска «айсберга». Ее основное назначение — разрушение. Я имею в виду разрушение того предрассудка, что риск «айсберга» в большинстве случаев является небольшим. Она начинается с нескольких очень простых примеров, настолько простых, что некоторые читатели, сильно привязанные к устоявшимся взглядам на оценку риска, сочтут эти примеры исключениями, не стоящими в силу их исключительности серьезного внимания. Но призываю этих скептиков подождать захлопывать дверцу в свой разум, поскольку эти простые примеры будут неуклонно развиваться по ходу первой части книги и разрастутся-таки до такой степени, что окажется, что именно эти, первоначально казавшиеся исключениями, примеры как раз и являются нормой, а общепринятая модель, первоначально считавшаяся нормой, наоборот, составляет исключение.
К счастью, в самой середине разрушительного процесса начнет проклевываться некий более надежный, чем общепринятый на сегодня, подход к моделированию. Он основан на идее разбиения сложной зависимости на составные части, одни из которых являются независимыми, а другие — общими. Получающиеся в результате этого подхода распределения вероятностей известны в математической теории как смешанные (условные) многомерные нормальные. Привлекательность нового подхода состоит в том, что, допустив к рассмотрению даже в очень ограниченных пределах эти самые смешанные распределения, мы получим гораздо более правдоподобные (более адекватные) модели риска.
Вторая часть книги посвящена приложению нового подхода, намеченного в первой части, к анализу портфеля ценных бумаг. Здесь, после анализа силы и слабости нескольких вариантов, я выскажусь в пользу некой “гибридной” системы, прививающей, образно говоря, новые черенки переключения между режимами на ствол общепринятой теории. Я покажу, что эти дополнительные детали, хотя и добавляют головной боли в виде существенных математических усложнений, сделают теорию более адекватной практическому применению, хотя бы потому что результаты приложения модернизированной теории никогда не будут приводить к рекомендациям, абсолютно нереализуемым или безумным с точки зрения здравого смысла.
Тем не менее, если вы думаете, что моя новая теория полностью оправдает все существующие на сегодняшний день экспертные методы, то вы ошибаетесь. Условности, традиции, общепринятые мнемонические правила и тот же здравый смысл превратили управление риском, так сказать, в хромого слона. А мой новый подход говорит, что этот слон должен танцевать! Ну, а если говорить серьезно, управление финансами нуждается в сглаживании финансовых рисков в дополнение к уже внедренному и модному процессу сглаживания валютных рисков. Методы такого сглаживания должны будут непрерывно меняться не только вместе с изменением информации о неустанно меняющемся мире, получаемой риск-менеджерами, но и с изменением позиции этих менеджеров по отношению к риску.
30
Ввадапиа
Но прежде чем, как говорится, поднять паруса, позвольте сделать несколько предостережений по поводу предстоящего путешествия. Дело в том, что моя книга — это не вылизанный академический трактат и не исчерпывающее руководство типа “сделай сам”. Моя книга — это попытка предложить новое направление в управлении инвестиционным риском. При этом мне следовало бы сказать “непривычное направление” вместо “новое направление”, потому что, строго говоря* ничего радикально нового в моем подходе нет. Точнее говоря, нет ничего нового на уровне составных частей. Но способ соединения элементов в единое целое — безусловно новый, хотя и с этим утверждением можно при желании поспорить. Так вот, о предостережениях. Вы, читатель, беретесь за изнурительную работу. Дело в том, что, независимо от того, нов мой подход или всего лишь непривычен, одна из основ привычного подхода состоит в том, чтобы отмахиваться от всякой критики просто потому, что эта критика, дескать, неинтересна или непрактична. Так вот, мы в этой книге отмахиваться от критики не будем. А критика означает математику. Поэтому моя проблема при создании книги состояла в немалой степени и в том, что, если я слишком уж углублюсь в математическую сторону модели риска «айсберг», слишком мало потенциальных читателей смогут последовать за мной, если я сокращу математику до уровня деклараций, весь новый подход будет выглядеть пустой болтовней, если я приналягу на критику существующей практики оценки риска, буду выглядеть критиканом, не предлагающим ничего конструктивного, наконец, если я уделю слишком много внимания методам улучшения ситуации, читатель спросит, а есть ли, вообще, болезнь, которую лечит автор. Аналогичная проблема показана в старом прелестном анекдоте: “Сколько нужно священников, чтобы поменять электрическую лампочку?” Ответ: “Всего один, но лампочка сама должна глубоко и искренне хотеть измениться”. К сожалению, подавляющее большинство практикующих аналитиков финансового риска встанут на дыбы от предположения, что их лампочка или давно перегорела, или светит в пол накала. Скорее всего, они привыкли с удобством работать в полутьме, а может быть, отказываются принимать новые лампочки взамен старых на том основании, что цена замены неоправданно высока по сравнению с возможными улучшениями ситуации.
В силу серьезности вышеуказанной проблемы, я не знал, как наилучшим образом построить книгу и пребывал в тяжелых раздумьях. Но тут, на мое счастье, встретил двух старых друзей, которые в тогда работали в отделе управления риском одного крупного инвестиционного банка. Мы разговорились на профессиональные темы и, пока они рассказывали мне о проблемах, с которыми они сталкивались в своей практической деятельности, и тех “лекарствах”, которые они разрабатывали для решения этих проблем, я понял, что их интеллектуальная эволюция шла параллельно моей собственной. А между тем, их приключения и забавные дебаты воспринимались гораздо живее и интереснее моей сухой теории. Однажды меня осенило, что мои читатели, скорее всего, подумали бы то же самое, послушай они моих приятелей. Видимо, поэтому у меня родилась гениальная идея ввести двух моих друзей в самую суть
31
Часть 1. Стандарты отклонения_=__==^=_^_==_=_===_ книги и использовать их, чтобы создать второй план и некую сюжетную зацепку для сухой теории. К моей радости, друзья дали мне свое милостивое разрешение на такой ход при условии, конечно, что я надежно скрою их истинные имена и всякие идентифицирующие подробности, имеющие отношение к их бизнесу.
Итак, без дальнейшего промедления, позвольте, читатель, представить вам моих друзей и начать знакомство с ними с того инцидента, который стал первым, поколебавшим их прежде несокрушимую веру в случайный выбор.
Общее замечание о ссылках
Хочу сделать одно общее замечание об отсутствии ссылок на литературные источники. Как ни печально, но ссылок на другие печатные работы по рассматриваемому предмету в моей книге действительно нет. Тому есть по крайней мере две причины. Во-первых, я весьма далек от академических кругов и просто не знаю, кто, когда, где и что сказал в самый первый раз. Конечно, это — моя проблема и вовсе не причина отказывать коллегам в привычной возможности попастись на той же полянке, что и автор. Поэтому книга заканчивается неким списком литературы для дальнейшего чтения. Я надеюсь, что в рекомендованных книгах вы, читатель, легко найдете ссылки на литературу, причем на любом уровне математической подготовки. Это должно частично восполнить отсутствие таких ссылок в моей книге. Во-вторых, большинство тех потенциальных читателей, до которых мне хотелось бы дотянуться в первую очередь, так же как и я, не слишком озабочены тем, кто, что, когда и где сказал в самый первый раз.
32
1. Причуды шансов
Конвей, начальник отдела управления риском крупного инвестиционного банка “МегаБакс”, в очередной раз перелистывал последний отчет аудиторов по его подразделению. Тревожное чувство не проходило. Хотя на первый взгляд все было не так уж плохо. Например, аудиторы сильно похвалили в своем отчете новую информационную систему мониторинга риска, которую Конвей недавно ^пробил” для своего отдела. Благодаря этой новой системе банк для каждого актива своего портфеля ценных бумаг мог в режиме реального времени получить не только информацию о среднем и стандартном уклонении, но и о их асимметрии и эксцессе. Кроме этого, команда Конвея методично отслеживала с помощью новой системы корреляции между активами портфеля. Но и в этом случае аудиторы не преминули подложить “ложку дегтя”: они обвинили подразделение Конвея в разгильдяйском отношении к великолепной новой системе и в недооценке отдельными специалистами ее возможностей. В качестве вопиющего примера в отчете описывался случай, когда один из подчиненных Конвея осмелился оспаривать то, что некие три абсолютно некоррелированных актива не несли в себе какого бы то ни было риска одновременного краха. Даже в сухом отчете его авторам не удалось скрыть раздражения по поводу невежества и нерадивости этого аналитика.
Отчет не называл этого нерадивого аналитика по имени, да в этом и не было нужды: только Девлин в подразделении Конвея был настолько безрассуден, чтобы открыто спорить с аудиторами. Вообще-то, казалось бы, в этом не было ничего нового. Девлин и раньше демонстрировал, что он — типичный “адвокат дьявола”, т.е. пессимист, зануда и спорщик из любви к искусству. Все верно. И на первых порах Конвей даже невзлюбил Девлина за его упрямство, но со временем начал высоко ценить его «закидоны», приносившие большую пользу его отделу по управлению риском. По крайней мере они мешали благодушной самоуспокоенности, которая могла воцариться в отделе, а это уже немаловажно. И к тому же Девлин, как это ни странно, в большинстве случаев оказывался прав, хотя его предположения, на первый взгляд, казались фантастическими.
Так-то оно так, но на этот раз Девлин, похоже, достукался. За каким чертом, на самом деле, с таким упорством защищать то, что защитить нельзя в принципе? Конвей вздохнул и сокрушенно покачал головой. Он ведь пришел в управление одновременно с Девлином. Это было уже довольно давно, еще в то время, когда разразился Азиатский кризис. Тогда они оба увлекались управлением риском, и Конвей в те времена часто думал, что они с Девлином будут подниматься и падать в своих карьерах параллельно. Но не тут-то было. Жизнь распорядилась по-другому, и карьера сложилась только у Конвея. Может быть, дело было в том, что Девлин всегда стремился к совершенству, а это всегда
33
Часть 1. Стандарты отклонвнин
мешает получению быстрых результатов. К тому же люди, как правило, не любят педантов. По правде говоря, Девлина держали в отделе только благодаря Конвею. И он невесело подумал: “Теперь они опять захотят его крови... И крови всякого, кто будет солидарен с ним... Черт, надо разобраться с этой проблемой, а то, как бы не было поздно!”
Конвей нашел Девлина там, где и предполагал, — за его рабочим столом. Девлин выглядел даже более озабоченным, чем обычно. Он не заметил Конвея: Девлин был занят. “Как всегда занимается ерундой!” — подумал Конвей, взглянув на стол из-за плеча Девлина. Девлин играл в кости, только вместо костей использовал монеты. Он тряс их в стаканчике, а потом выбрасывал на стол, раскладывал их по три монеты и яростно чиркал что-то в тетрадь, затем собирал монетки обратно в стакан, тряс его и снова бросал монетки на стол. Пронаблюдав эти ним минут пятнадцать, Конвей, наконец, решился отвлечь «маэстро» от важного дела: “Девлин, я, конечно, восхищен вашей погруженностью в самую суть управления риском, но, боюсь, эти изыски никак не влияют на прибыль нашего банка...” Девлин подскочил как ужаленный: “А, это ты, Конвей! Твои шутки, как всегда, в точку... Но, представь, я занят сугубо практическим вопросом. Я ставлю имитационный эксперимент над нашим опционным портфелем”.
“При помощи трех монеток?”
“Конечно, это грубовато. Но я решил начать с азов, с простейшей схемы. Такой подход всегда обостряет мою интуицию”.
“Подумать только! А туг я влез со своим глупым страхом, что у моего старого друга-спорщика окончательно съехала крыша! Девлин, тебе надо все-таки постараться выглядеть хоть малость повеселее, а то начинаешь напоминать мне того молодого психиатра из известного анекдота...”
“Какого анекдота?”
“Как, ты его не слышал? Так вот, молодой и старый психиатры принимали пациентов в соседних кабинетах. Каждый вечер старый психиатр, уходя домой, проходил мимо кабинета молодого коллеги, излучая энергию и хорошее настроение, и на ходу предлагал составить ему компанию в каком-нибудь интересном занятии на вечер, будь то теннис, пробежка по парку, посещение концерта или что-либо другое в том же духе. Но молодой психиатр уставал до изнеможения и всегда отклонял предложения старика. Наконец, однажды он не выдержал и сорвался: ‘Весь день люди говорят мне об их проблемах. О невероятных проблемах! Меня это изматывает до последней степени. А вы на тридцать лет старше меня, целый день выслушиваете те же проблемы, что и я, и, несмотря на это, веселы, свежи и полны энергии. Я не могу понять, как вам это удается?’ Старый психиатр ответил очень спокойно: ‘Никакого секрета у меня нет. Просто я не слушаю этих придурков”.
Девлин рассмеялся, но не повеселел. Он устало подумал, как это бывало и раньше, что Конвей озабочен тем, чтобы иметь, так сказать, отлаженную систему развешивания ярлыков на риски, а не тем, чтобы построить, наконец, систему,
34
1. Причуды шансов
которая точно взвешивала бы эти риски и проставляла бы на конвеевские ярлыки, продолжая аналогию, достоверные точные данные.
Мысли Девлина о Конвее потекли в привычном направлении: “Он думает, что если какое-то утверждение часто повторяют люди, обладающие авторитетом, оно обязано быть истиной. Господин ‘Общепринятый здравый смысл’...” По мнению Девлина, при встрече с серьезной проблемой первым, вторым, третьим и сто третьим побуждением Конвея всегда будет следовать общепринятому авторитету или сразу нескольким, что было бы еще лучше. Тем не менее, со временем Девлин стал уважать Конвея за прагматизм. Дело в том, что с годами Девлин осознал, что Конвей вовсе не сделал общепринятый здравый смысл своим идолом, он просто полагал, что вероятность того, что общепринятая точка зрения окажется правильной, гораздо больше, чем то, что она окажется неправильной. В частности, если Девлину, а равно кому бы то ни было еще удавалось продемонстрировать Конвею, что его любимый здравый смысл ошибается, Конвей менял свое мнение. Девлин считал, что именно это свойство характера Конвея стало причиной его карьерных успехов.
В отличие от Конвея, Девлин был рожден сомневаться. Чем больше он изучал финансовые случайные величины, тем больше у него возникало вопросов и сомнений. И чем больше Девлин сомневался, тем более разочарованным, усталым и даже подавленным он выглядел. Именно так он и чувствовал себя, по правде говоря. Иногда ему хотелось бросить анализ риска и заняться чем-нибудь вроде теории происхождения Вселенной, где доля строгой научной обоснованности и уверенности была значительно выше, чем в теории портфеля.
Такие невеселые мысли бродили в голове Девлина, но Конвей вывел-таки его из задумчивости: “Да, Девлин, между прочим, здравствуй”. Девлин слегка смутился: “Прости, я несколько замечтался. Да не крути, Конвей, скажи, о чем ты всс-таки хотел со мной поговорить?” Девлин почувствовал неприятности. Вообще, надо сказать, что Девлин демонстрировал хороший нюх на неприятности всякий раз, когда он в них попадал. Однако он никогда не чувствовал беды до того, как попадал в нее.
Конвей, наконец, перешел к делу: “Аудиторы до небес «расхвалили» тебя в своем отчете за необоснованные оценки риска”. “Ах, эти уроды... Я пытался растолковать тупицам, что я имел в виду, но они не стали слушать”, — сказал Девлин с видимым облегчением. Но Конвей не был склонен перевести разговор в шутку: “Если ты говорил с ними в таком же стиле, как со мной, их отношение меня не удивляет. Почему бы тебе прямо не рассказать, что у тебя с ними вышло?”
Девлин перешел к деталям:“Помнишь те проблемы, на которые я натолкнулся при оценке верхней границы совокупного риска трех различных бинарных опционов нашего портфеля? Ты тогда посоветовал мне прислушаться к здравому смыслу, и я в кои-то веки послушался твоего совета”.
В голове Конвея появилось некое смутное воспоминание: “Мир полон чудес! Сейчас я припоминаю... Если я не ошибаюсь, ты тогда оценивал
35
Часть 1. Стандарты отклонония ___________________________________
доходность независимо от фиксированных выплат на уровне ±10 млн. долл, дж каждого опциона с шансами на успех 50 на 50 при нулевых корреляциях, верно?”
“У тебя хорошая память..
Конвей был польщен и слегка развил тему: “Как я мог забыть? Опционщики подняли визг и просили сохранить эти опционы, в то время как сверху пришла строгая директива не допускать риска совокупных потерь большего, чем 20 млн. Но, по правде говоря, я в тот момент не мог понять причины всей суматохи, ведь суть дела казалась тривиальной”.
Девлин как бы закончил фразу Конвея в той же благодушной манере: “Воз и я так подумал. Поэтому позволил сектору опционов сохранить эти позиции...”
С Конвея при последних словах Девлина все благодушие как ветром сдуло. “Что?!” — заорал он. Ему наконец-то стало ясно, что Девлин перешел от своей обычной неудобоваримой наукообразной чуши к весьма опасным действиям по реализации его сумасшедших идей. Впрочем, Конвей мгновенно взял себя в руки: “Девлин, прости мою несдержанность, ради бога. Ты серьезно болен. Тебе нужен врач. Ты переутомился. Иди-ка домой, а я пока посмотрю, как можно поправить дело и уменьшить ущерб”.
Однако Девлин совсем не чувствовал себя ни больным, ни ущербным: “Конвей, сбавь-ка, пожалуйста, обороты, — сказал он абсолютно спокойно. — И просто выслушай меня. Я вовсе не сумасшедший. Во всяком случае, пока не сумасшедший”.
Но Конвей уже больше не мог сдерживать своей ярости: “Значит, ты тогда меня одурачили! Нет, это ты послушай! Разве можно вообразить более простую задачу, чем та, которая стояла перед тобой? Слушай, ты, любитель подбрасывать монетки, ответь-ка: ‘Если выброс орла и решки равновероятен, каковы шансы, что при бросании монет три раза подряд выпадут три решки?”
Девлин ответил с ледяным спокойствием: “Зависит от обстоятельств. Если монетки, участвующие в бросаниях, независимы, то 1/8. Во всяком случае, именно так ответило бы большинство”.
“Конечно, — саркастически подтвердил Конвей. — Разве может быть какой-то другой ответ? Ведь если вероятность двух решек равна 1/4, а третья некоррелированная монетка выпадает на решку с вероятностью 1/2, вероятность зрех Решек обязана быть равна 1/8”.
Но Девлин не проявил никакого смущения и ответил назидательно, как учитель: “Но это не единсзвенная возможность. Предположим, что наши монетки чеканят в двух одинаково законных и общеупотребительных формах, причем одна форма такова, что при подбрасывании сделанной в ней монетки, всегда выпадаез орел, а при другой — всегда выпадает решка. Тогда, ставя этот эксперимент и наудачу выбирав форму монетки, вероязность трех будет равна ’Л”.
Но Конвея пример не смутил. Он посчитал его притянутым за уши: “Прекрати свои штучки, Девлин! У меня нет времени на эту ерунду. Мы решаем серьезные вопросы, а не показываем математические фокусы школьникам”. Конвей для себя решил, что уж на этот раз он не даст опять втянуть себя в так
36
1. Причуды шансов
называемые “великие теоретические дебаты гениального Девлина”. Но внезапно в голове Конвея появилась блестящая, как ему показалось, мысль. И он не смог отказать себе в удовольствии осадить спесивого теоретика: “К тому же твои теории не имеют никакого отношения к нашему случаю. В твоем последнем гениальном примере все три бросания были бы абсолютно коррелированными, в то время, как опционы, о которых мы спорим, некоррелированые. Так что все-таки тебе придется согласиться на 1/8”.
Наконец-то и Девлин смог позволить себе торжествующую улыбку. Ведь Конвей только что сам загнал себя в ловушку. Тем не менее он ответил вполне миролюбиво: “Подожди-ка, Конвей. Всем известно, что, хотя независимые активы не могут быть коррелированными, некоррелированные активы могут, тем не менее, быть зависимыми. Правда, известно, что, если бернуллиевых активов всего два, некоррелированность будет эквивалентна независимости, т.е. вероятность двух решек равна квадрату вероятности одной решки. Но с этими опционами — особый случай. А кроме того, вообще концепция корреляции имеет смысл только для пар активов, но не для больших групп”.
Конвей был смущен, но не подал виду: “А что такого уж особенного в этих опционах? Каждый из них некоррелирован по отношению к любому из двух оставшихся, что дает нам три пары некоррелированных активов против единственной такой пары в случае рассмотрения только двух активов. Неужели это не равносильно независимости?”
“Нет, не равносильно!, — отчеканил Девлин. — И позволь мне привести еще один поясняющий пример”. Девлин в возбуждении начал, как слепой, ощупывать поверхность своего заваленного всякой всячиной стола, пока не нашел, наконец, ту тетрадку, в которой писал, когда к нему подошел Конвей. В процессе поисков Девлин смахнул в мусорное ведро недоеденный бутерброд, успев подумать По-привычке: “Интересно, это — случайный выбор или рассчитанное действие?” Наконец, Девлин смог перейти к собственно примеру: “Допустим, для начала, что мы бросаем три независимые правильные монеты, но налагаем на этот эксперимент такое условие: всякий раз, когда появляется нечетное количество решек, вся тройка локальных исходов, соответствующая макроисходу, не принимается к учету и монеты бросаются снова. В таком эксперименте допустимыми макроисходами будут такие тройки локальных исходов: ООО, РРО, POP и ОРР, причем все эти допустимые тройки равновероятны. Конвей, ты можешь сам сосчитать и убедиться, что вероятности появления орла и решки для каждой монеты, участвующей в эксперименте, равны, но при этом для любой наперед заданной пары этих монет вероятность выпадения двух решек равна
Конвею стало по-настоящему интересно: “Скажи-ка, а почему ограничение ‘без нечетных решек’ не влияет на корреляцию?”
Девлин был готов к этому вопросу: “Предположим что в макроисходе на третьей монете выпал орел. Тогда, очевидно, две первые монеты обязаны выпасть или обе на орла, или обе на решку. Аналогично, если третья монета выпала на решку, обязательно одна, неважно, первая или вторая, из двух первых 37
Часть 1. Стандарты втклонвния
монет выпадет на орла, а оставшаяся — обязательно на решку. Отсюда следует, что попарная корреляция двух первых монет равна или +1 или —1 в зависимости от локального исхода на третьей монете. Но, поскольку локальные исходы на третьей монете равновероятны, общая безусловная корреляция есть ноль. Понятно?”, — и Девлин вопросительно посмотрел на Конвея.
Конвей переживал шок. Он посмотрел на часы и стал как-то суетливо оглядываться по сторонам. Дело в том, что Конвей должен был через пару минут встречаться с руководством банка. Наконец он тяжело вздохнул, сел за стол Девлина и начал играть с монетами и стаканом. Поиграв минут десять, он встал и сказал: “Замечательно! Я сам ни за что не догадался бы, что такое возможно. А сколько, вообще, существует таких некоррелированных схем с правильными монетами?”
“Не сосчитать! — ответил Девлин. — При этом, заметь, схема ‘без нечетных орлов в тройках’ — тоже допустимое решение. Это следует из соображений симметрии. А теперь предположи, что при каждом бросании трех монет случайным образом налагается ограничение или ‘без нечетных орлов’, или ‘без нечетных решек’. Выбор в пользу первого отграничения делается с вероятностью 0 < А < 1, в пользу второго — соответственно, с вероятностью 1 — Я . Тогда, независимо от того, какие конкретно ограничения будут наложены на эксперимент, мы будем иметь некоррелированное несмещенное решение, т.е. некоррелированную схему испытаний с правильными монетами. Отсюда следует, что всякая рандомизация наших схем ‘без нечетных решек’ и ‘без нечетных орлов’ обязана тоже быть некоррелированным несмещенным решением. При этом вероятность трех решек будет в этой схеме равна ”.
Конвей в очередной раз тяжело вздохнул: “Хорошо! Я признаю глубину и правильность твоих теоретических построений. Но наши трейдеры опционов играют на очень серьезные деньги, а не на мелкие монетки. Несмотря на всю красоту этих примеров, я по-прежнему не вижу, почему ты из всех возможных решений выбрал наименьший возможный хвостовой риск для рынков опционов. Ведь это невероятно! Почему бы не проявить разумный консерватизм и не предположить максимальный хвостовой риск или средний, что, кстати, соответствовало бы гипотезе независимости?”
Девлину стало скучно, но он не подал виду: “Когда я пытался теоретически ответить на этот вопрос, мне стало ясно, что у меня недостаточно информации. Тогда я стал разговаривать с трейдерами. Оказалось, что эти три опциона относились к трем компаниям, которые жестко конкурировали за право установить новый промышленный стандарт в компьютерных сетях. В плане установления этого нового стандарта наши трейдеры посчитали возможными и равновероятными все четыре исхода— от ‘один из конкурирующих проектов’ до ‘никакого промышленного стандарта, т.е. status quo’. При этом трейдеры ожидали, что каждая из компаний будет процветать в том случае, если конкурирующий стандарт не будет принят в качестве промышленного. Легко можно проверить, что эта ситуация прямо соответствует только что рассмотренному нами сценарию ‘без нечетных решек”.
38
1. Причуды шансов
У Конвея отвисла челюсть, и он тупо уставился на монеты, разбросанные по столу Девлина...
Позвольте мне, пока бедняга Конвей собирается с мыслями, прояснить некоторые из тех терминов, которые Девлин использовал в вышеприведенном замечательном разговоре. Это важно, поскольку за каждым из этих слов стоит целый строительный блок того, образно говоря, здания, которое я строю настоящей книгой. Все эти блоки, тем не менее, вполне элементарны, и вы спокойно можете пропустить страницы, оставшиеся до следующей главы. В любом случае несколько трудным может оказаться лишь материал о смешанных моментах высших порядков.
Одномерные случайные величины
Когда мы моделируем доходность некой инвестиции с помощью подбрасывания монеты, мы абстрагируемся от всех аспектов, составляющих суть этой инвестиции, кроме риска. Математически такая модель формализуется определением случайной величины X , которая может принимать различные значения к из некого множества допустимых исходов К. При этом случайная величина X называется одномерной, если каждому исходу к можно поставить в соответствие единственное число хк е А1 .
Произвольная скалярная функция h от произвольной одномерной случайной величины X также является одномерной случайной величиной, принимающей значения {h(xk)} для различных к е К .
Случайные величины Бернулли
В наших примерах с бросанием монет случайная величина X соответствует одной отдельной монете, а множество К •— паре исходов орел и решка. По установившейся традиции мы будем обозначать орла цифрой 1, а решку — 0, хотя можно и наоборот.
Любую случайную величину, которая принимает только значения 0 и 1, принято называть случайной величиной Бернулли в честь Якобы Бернулли, одного из основателей теории вероятностей. Если бернуллиева случайная величина не является моделью монеты, то исход, соответствующий 1, принято называть “успех’', а исход, соответствующий 0, принято называть “неуспех”.
Вероятностные меры
Любому подмножеству множества исходов К соответствует некое возможное событие. Для произвольного наперед заданного события говорят, что оно произошло тогда и только тогда, когда реализовался по крайней мере один
39
Пасть 1. Стандарты отклонения
исход того подмножества множества К, которое поставлено в соответствие этому рассматриваемому событию. Из этого определения, в частности, следует, что можно обозначать и событие, и соответствующее ему подмножество исходов одинаково. Для V7L g К вероятностью Pr{ZJ события L называют предел частоты появления этого события в несмещенных (правильных, т. е. нс содержащих систематической ошибки) выборках или испытаниях при предположении, что этот предел существует. Вероятность, таким образом, соответствует интуитивному понятию “правдоподобности” события L или так пазыйаемьт1и“шансам” появления этого события в некой игровой схеме. Несмотря на свою интуитивную привлекательность, приведенное определение вероятности не является адекватным хотя бы потому, что понятие несмещенности выборки само определяется с использованием понятия вероятности, т. е. мы, определяя вероятность, воспользовались тем понятием, которое хотим определить. Однако для целей настоящей книги достаточно, если у читателя будет сформировано некое правильное представление о вероятности, а строгое аксиоматическое теоретико-множественное определение вероятности мы здесь только упомянем, но приводить не станем. Скажем лишь, что по формальному определению вероятности она является некой мерой подмножества относительно того множества, которое это подмножество содержит, и что эту меру принято связывать с предельным правдоподобием. Фундаментальным свойством вероятности, следующим из ее канонического определения, является то, что О < Pr{ L} < 1У£ е К, Рг{К} = \. Другое не менее важное свойство вероятности — ее аддитивность на несовместных, т. е., взаимоисключающих событиях. Для произвольного события, являющегося объединением счетного множества несовместных событий (произвольная пара событий называется парой несовместных, или взаимоисключающих, событий, если не существует ни одного исхода, соответствующего одновременно обоим событиям из этой пары), вероятность этого события равна сумме вероятностей несовместных событий, входящих в это объединение.
Дискретные распределения вероятностей
Для произвольного дискретного множества исходов К распределение вероятностей является некой функцией р, заданной на множестве всех подмножеств К и ставящей в соответствие каждому значению х g К некую вероятность у?(х) = Рг{х} . Из определения вероятности легко видеть, что (р(х) > 0 Vx) & (X р{хк) = Рг {К} = 1) . ЕслиЭ£ G К такой, что, у?(хА ) — 1 кеК
говорят, что исход к является достоверным, а само распределение вероятностей — вырожденным (т.е. исход, по сути, всего один). Вырожденные распределения — самые простейшие. Следующим простейшим распределением является распределение Бернулли, которое полностью характеризуется значением вероятности “успеха” /?(!) , поскольку вероятность единственного оставшегося
40
1. Причуды шансов
исхода, т. с. “неуспеха”, в этом случае однозначно определена: р(0) = 1 — р(1) •
Для УХ,х е 7?1 вероятность Рг{Х < х} называется интегральной вероятностью в точке х и обозначается как /^(х). Если рассматривать интегральную вероятность как функцию от х, можно сказать, что /^(х) неотрицательна, монотонно не убывает и имеет в качестве максимального значения 1. Для произвольного дискретного распределения вероятность произвольного события х можно записать так: р(х) = /^(х) — max ^(>0 -
Носитель распределения
Распределение вероятностей может быть устроено так, что оно приписывает нулевой вес (т. е. нулевую вероятность) некоторым исходам из множества исходов К. Подмножество множества исходов таково, что каждый исход этого подмножества имеет положительный вес, а любой исход, не входящий в это подмножество, имеет нулевой вес и называется носителем данного распределения. Произвольное распределение, носителем которого являются п исходов, называется л-точечным дискретным распределением.
Хвостовой риск
Понятие хвостового риска введено для того, чтобы характеризовать исходы, которые отличаются исключительно малыми или исключительно большими значениями некой случайной величины. Хвостовой риск определяется с помощью так называемого порога Т с R1, задаваемого большим числом, и в первом случае интегральной вероятности F(T) = Pr{JV < Т} того, что случайная величина X лежит левее порога, т. е. попадает в так называемый “левый” или, как еще говорят, “нижний” хвост. Когда же во втором случае интерес представляют исходы, характеризуемые исключительно большими значениями случайной величины X, рассматривают интегральную вероятность \ — F(T) — Pr{JV > Т} того, что случайная величина X попадает в “правый” или “верхний” хвост.
Многомерные случайные величины
Определения вероятности нетрудно распространить на переменные, являющиеся векторами. В этом случае каждому исходу ставится в соответствие не единственное число, как это было в случае одномерных случайных величин, а единственная точка в многомерном пространстве, причем соответствующая вероятностная мера опять определяется на множестве К всех возможных исходов. Такое распределение вероятностей называется многомерным, или совместным, распределением вероятностей. Если многомерные исходы дискретны, совместное распределение вероятностей задается некой функцией р ,
41
Пасть 1. Стандарты атклвнвнин
связывающей каждый дискретный исход, т. е. вектор (хи ,х2Л xfjk ) — х с R” с неким неотрицательным числом /?(х) = p(xlk, x2kxnk ) е /?' таким образом,
что =
Условная вероятность
Условной называют вероятность Рг{/,, |Z,2} того, что произойдет событие Ll при условии, что произойдет некое второе “обеспечивающее” событие Ь2. Условную вероятность определяют как частное от деления безусловной (т. е. обычной) вероятности того, что произойдут оба события одновременно, на безусловную вероятность того, что произойдет обеспечивающее событие, т.е.
Во многих практических приложениях вероятность обеспечивающего события неизвестна, но может быть вычислена по данным о совместном распределении вероятностей неких двух случайных величин. Например, пусть X и Y — это две случайные величины, характеризующиеся совместным распределением вероятностей у) . Тогда распределение вероятностей одной случайной величины можно вычислить так: p(xk , у) . Подставив
это в формулу для условной вероятности, получим:
_ р(х,у)
РгМ
Обратно, если нам дано распределение случайной величины Y и условное распределение случайной величины X при известном значении случайной величины Y, т. е. р{х | д;) , мы можем вычислить совместное распределение случайных величин X и Y : р(х,у) = p(x\y)pY(y) .
Смеси распределений
Последнюю формулу предыдущего параграфа можно интерпретировать как некий способ генерировать новые распределения вероятностей из уже известных. Конкретно, я имею в виду, что любая взвешенная сумма Дл(^) распределения вероятностей < i < п G Nx3n : 1 < п < оо} тоже является
распределением вероятностей, при условии что (Д > ОУг) & Д- ~ 1). Для того чтобы это понять, достаточно ввести в рассмотрение такое вспомогательное множество исходов Y, что Д = р(у} ДОЯ пЗу Y . Тогда можно считать,
42
1, Причуды шансов
что Pj (JV) = P(Ajy) для у и из вышеупомянутой формулы следует, что Л.р(ф) = р(х> y)Vx е X соответственно. Но тогда для Vx е Х^/?(х, у) — Рх (х) . Иными словами, смешение вероятностей задает Y
неотрицательную функцию на множестве исходов X . Осталось показать, что ZPv(x) = l. Поскольку в конечных суммах можно менять порядок суммирования, имеем: ^г(х) = 2^(х). Внутренняя сумма в
последней двойной сумме равна 1, по определению распределения вероятностей, значит и вся двойная сумма равна 1 по условию смешивания, наложенному на коэффициент {Д}.
Любое распределение вероятностей, построенное так, как мы только что рассмотрели, принято называть смесью распределений. В специальной литературе смеси распределений часто называют выпуклыми комбинациями распределений, потому что таково общее название взвешенных сумм с неотрицательными весами, где сумма весовых коэффициентов равна 1. Есть и третье распространенное название для смесей распределений. Их еще называют рандомизациями. При этом то дискретное распределение вероятностей, которое определяет веса и используются в процессе рандомизации, называют смешивающим распределением.
Независимость
Интуитивно понятно, что, если каждая случайная величина из некоторой пары случайных величин является детерминистической функцией другой случайной величины из этой же пары, эти случайные величины будут полностью зависимыми. На другом полюсе находятся пары независимых случайных величин. Говорят, что две случайные величины независимы, если и только если исходы одной случайной величины не оказывают никакого воздействия на исходы другой случайной величины. Иными словами, если эти случайные величины обозначить как X и Y, условная вероятность Рг(х|у) должна быть функцией только х, а условная вероятность Рг(у|х) должна быть функцией только у . Таким образом, произвольные случайные величины X и Y независимы тогда и только тогда, когда для произвольной пары их исходов Vx е ХуХ/у е Y справедливо, что . Отсюда
следует, что, если случайные величины X и Y независимы, то функцию их совместного распределения можно представить в виде произведения двух множителей, где первый зависит только от X, а второй — только от Y. Легко видеть, что справедливо и обратное, т. е., если функцию совместного распределения можно представить таким образом, то случайные величины независимы.
43
Часть 1. Стандарты отклонвния
Иначе говоря, независимость математически эквивалентна мультипликативной отделимости совместных вероятностных мер.
Математические ожидания
По сути, математическое ожидание Е случайной величины X , — это взвешенное среднее исходов этой случайной величины, где весовые коэффициенты соответствуют вероятностям соответствующих исходов. Согласно этому определению, математическое ожидание произвольной дискретной случайной величины X можно записать как Е[Х] =
Интересно отметить, что математическое ожидание вовсе не обязано существовать. Например, рассмотрим случайную величину X , распределенную
на множестве натуральных чисел № так, что р(к) =-------—\/к е № . Ясно,
к к +1
что в этом случае мы имеем легитимную дискретную случайную величину, СО Х |
поскольку / р(^) = 1. Ясно также и то, что 7Г[А] = / ,— представляет собой 4 = 1 4=1 к
гармонический числовой ряд, который, как известно, расходится. В тех случаях, когда математического ожидания некой случайной величины не существует, в качестве приближений этого несуществующего значения рассматривают средние значения выборок этой случайной величины, которые называются выборочными средними. Выборочные средние, конечно, являются ограниченными величинами при фиксированной величине выборки, но имеют тенденцию к неограниченному росту с ростом самой выборки.
Математические ожидания функций
Поскольку любая функция h произвольной случайной величины X тоже является случайной величиной, мы можем вычислить математическое ожидание h как E[h(X)\ = )р(хк ) . Например, математическое ожидание
всякого аффинного преобразования произвольной случайной величины равно аффинному преобразованию этой случайной величины, т.е. для \fa^R\\fb^Rx и произвольной случайной величины X математическое ожидание случайной величины A(JV) — аХ + b определяется формулой E\h(X)\ = аЕ\Х] + b. Аналогично, мы можем определить и условное
Eix и -
математическое ожидание
лг.р(х.|У). Заметьте,
что условное
математическое ожидание является уже не числом, как безусловное математическое ожидание, а функцией случайной величины Y, т.е. случайной величиной. Это значит, что мы можем найти безусловное математическое
ожидание условного математического ожидания относительно распределения обеспечивающей случайной величины, т. е. случайной величины Y в наших
1. Причуды шансов
обозначениях. При этом легко показать, что Еу [£’[%|У]] = £?[%], т.е. математическое ожидание условного математического ожидания равно безусловному математическому ожиданию.
Понятие математического ожидания нетрудно применить и к смесям распределений. При этом интересно отметить, что для того, чтобы найти вероятность любого отдельного исхода смеси распределений, следует найти вероятности этого исхода в соответствии с составляющими распределениями и математическое ожидание вероятности этого исхода по смешивающему распределению рх (х) = Еу [/7(х|У)]. Это прямо следует из нашего определения Рх (х) для смеси распределений (см. выше). На самом деле верно и более общее утверждение — то, что математическое ожидание любой функции от произвольной смеси распределений равно смеси математических ожиданий, каждое из которых берется от той самой функции от соответствующей случайной величины, распределенной в соответствии с ее индивидуальным распределением.
Смещение и несмещенность в сравнении с правильностью и справедливостью
Для того чтобы обозначить монету с несмещенным центром тяжести, которая, по идее, должна с равной вероятностью падать на любую из своих сторон, Конвей и Девлин употребляли термины, производные от прилагательных “несмещенный” и “правильный”. По аналогии они будут употреблять термин “несмещенный”, чтобы обозначать любую бернуллиеву переменную, характеризуемую 50%-ной вероятностью успеха. Однако, строго говоря, употребление этого термина несет в себе некую двусмысленность. Дело в том, что смещение не является строго объективным свойством чего бы то ни было. Скорее, а в математической статистике и чаще, смещение обозначает разницу между предполагаемыми и фактическими величинами. И в самом деле, если некая бернуллисва случайная величина такова, что предполагается, что она никогда не реализуется в неуспех, и именно это и происходит на практике, в ней, по сути, нет ничего смещенного.
В теории Hip, а это особенно имеет отношение к азартным играм, правильность интерпретируют более адекватно, как справедливость игры, которая, в свою очередь, означает некую эквивалентность между ожидаемым выигрышем и ставкой, т. е, платой за вступление в игру. Точнее говоря, справедливая игра должна быть таковой, чтобы, приняв в расчет величину ставки и состояние текущей и возможной информации игрока, мы должны однозначно получить, что ожидаемый выигрыш этого игрока есть 0. А в теории финансов концепция справедливости положена в основу понятия “мартингала”.
Поскольку я не готов отвергнуть ни общепринятые, в том числе и разговорные, термины, я прошу читателей просто смириться с двусмысленностью несмещенности, правильности и справедливости. Договоримся, что справедливость будет в большинстве случаев означать 50%-
45
Пясть 1. Стандарты отклонения
ную вероятность успеха для бернуллиевых игр и нулевой ожидаемый выигрыш для всех остальных.
Первый момент
Математическое ожидание Е\_Х"] называют п -ном моментом произвольной одномерной случайной величины X, где и е N1 . Первым моментом, соответственно, называется математическое ожидание самой этой случайной величины X. Первый момент в специальной литературе часто обозначается как // .
Заметьте, что для любой бернуллиевой случайной величины // — это вероятность успеха, а кроме того, любой момент, а не только первый, тоже равен ll .
Заметим также, что среднее произвольной взвешенной суммы любых случайных величин равно взвешенной сумме их средних. Иными словами, если {с?.} - это произвольные константы, то Е[^ 67. JV. ] — aiE\^Xj ] для V/7 е Az 1 .
Второй момент
Второй момент E[JV2] дает дополнительную информацию о рассеянии значений случайной величины X относительно ее среднего значения (чаще всего). Поэтому очень часто под вторым моментом имеют в виду так называемый второй центральный момент, или дисперсию
Уак[Х] = Е\(Х — //)2] = Е[Х2] — р1, где jd — это по прежнему математическое ожидание случайной величины X и ее первый момент, т. е. Е[Х], Дисперсия положительна для всех распределений, кроме вырожденных, для которых она равна нулю. Дисперсия произвольной бернуллиевой случайной величины равна //(1 — /л) .
Квадратный корень из дисперсии называется стандартным, или среднеквадратичным, отклонением и обозначается Std\X}. Стандартное отклонение измеряется в тех же единицах, что и сама случайная величина X, что полезно при оценке риска. Стандартное отклонение часто обозначают как ст или сух , и соответственно дисперсию в этом случае обозначают как ст2 или ст2 .
Если к произвольной случайной величине прибавить или от нее отнять произвольную константу, дисперсия модифицированной таким образом случайной величины будет в точности равна дисперсии исходной случайной величины. Но, если любую случайную величину умножить на любую константу, ее дисперсия модифицированной будет равна квадрату этой константы, умноженному на дисперсию исходной случайной величины. Это можно записать следующим образом: для VX, где X — случайная величина, при
46
1. Причуды шансов
V<7 е R',\/b е /?' выполняются условия Уаг[аХ + £>] = а2Уаг\Х] и Std[aX + b]~ а • Std[X].
Моменты высших порядков
Для того чтобы подчеркнуть ценность информации о характере рассеяния значений случайной величины относительно среднего значения, моменты высших порядков случайной величины X обычно выражают в виде моментов другой случайной величины, которая является так называемой “нормализацией”, или стандартным преобразованием, исходной случайной величины X , а именно X — Е[Х~\ Х-ц
---------=-------, которое имеет нулевое среднее и стандартное отклонение, Std[X] ст
равное 1. Моменты стандартного преобразования любой случайной величины называются стандартными моментами этой случайной величины. А третий стандартный момент случайной величины X, а именно Е[(——“)3L называется асимметрией случайной величины X .
Важно отметить, что асимметрия, как и все остальные стандартные моменты нечетных порядков выше третьего, будет равна 0 для тех случайных величин, чьи распределения являются симметричными относительно средних. При этом асимметрия случайной величины стремится к отрицательным значениям, если значения этой случайной величины сгруппированы, главным образом, слева от среднего значения, и к положительным значениям, если значения этой случайной величины сгруппированы, главным образохм, справа от среднего значения.
Четвертый стандартный момент случайной величины Е[(-----—)4] — 3
называется эксцессОхМ случайной величины X . Значение эксцесса состоит в том, что с его помощью измеряют, так сказать, “относительную толщину” хвостов распределений. Отметим такие свойства эксцесса, как то, что его минимальное значение по всем возможным распределениям равно —2 и достигается на двухточечном распределении, где обе точки имеют равные веса, и то, что эксцесс близок к нулю для среднего арифметического большого числа независимых одинаково распределенных случайных величин. Распределения с отчетливо положительными значениями эксцесса называют “островершинными” или “толстохвостыми”.
Смешанные моменты
В общем случае многомерным моментом называется математическое ожидание вида EfJV*5Х22...Хкп” ], где все различные показатели степени
47
Часть 1. Стандарты отклонония _______=_==_^==^_
kt являются неотрицательными целыми числами, такими, что ki > 0, причем эта сумма показателей степеней (ki называется порядком многомерного момента. Предположим, что Е[ХхХ3 , Е[Х^Xэ] и являются моментами третьего порядка. Если не менее двух показателей степеней момента положительны, такой момент называется смешанным. Все остальные моменты высших порядков (т. е. моменты, чей порядок не меньше 2) являются по сути одномерными и называются собственными моментами высших порядков.
Вообще, смешанные моменты естественно возникают при расчете моментов взвешенных сумм случайных величин. Так, каждый член математического ожидания ! ai Xi У ] представляет собой или
собственный, или смешанный момент порядка J .
Ковариация
Любой смешанный момент второго порядка имеет вид . Как это
было показано для собственных моментов второго порядка, измерение случайных величин по отклонению их значений от среднего помогает получить дополнительную информацию о поведении этих случайных величин. В результате такого подхода и применения смешанных моментов второго порядка получается квант информации, который назвали ковариацией. Ковариацию принято обозначать Cov[X, У] и можно выразить в разных формах. Например, обозначив средние случайных величин X, Y через //х и /лу , получаем такое выражение для ковариации
Cov[X, У] = Е[(Х - E[X])(Y - E\Y])] = E[XY] - jux/aY .
Отметим также, что, если к любой из двух случайных величин, ковариацию которых мы вычисляем, прибавить произвольную константу, ковариация не изменится. Но, если любую из двух случайных величин, ковариацию которых мы вычисляем, умножить на произвольную константу, ковариация модифицированной пары случайных величин будет равна ковариации исходных случайных величин, умноженной на эту константу. Иными словами, для произвольных случайных величин X и У и для Ча е R' yb R' ,Чс & R' ,4d <= R' Cov[aX + b,cY + d] = ac- Cov[X, У].
В специальной литературе нередко пользуются сокращенным обозначением ковариации случайных величин X и У, а именно вместо Cov[X, У] пишут стху . Поскольку ковариация любой случайной величины равна дисперсии этой случайной величины, вместо о~хх употребляют сгх .
48
1. Причуды шансов
Корреляция
Корреляция — это смешанный момент второго порядка, содержащий еще более концентрированный элемент информации о паре случайных величин, чем ковариация. Иногда корреляцию называют попарной или частичной корреляцией, но суть дела от этого не меняется. По определению, корреляция — это ковариация между парой нормализованных случайных величин, т.е. корреляция — это стандартный момент. Следовательно, корреляцию можно записать в виде:
Cor[X, Y] = Е[(Х ~ )(Y ~ )] = Га Гу
O“v СТу СТу СТ у СТ у СТ у
Корреляция, иногда ее называют коэффициентом корреляции, — это безразмерная величина. Отметим также, что, если к любой из двух случайных величин, корреляцию которых мы вычисляем, прибавить произвольную константу, корреляция не изменится. Но, если любую из двух случайных величин, корреляцию которых мы вычисляем, умножить на произвольную константу, корреляция модифицированной пары случайных величин будет равна или корреляции исходной пары случайных величин, если знак рассматриваемой константы положительный, или корреляции исходной пары случайных величин, но с противоположным знаком, если знак рассматриваемой константы отрицательный. Это значит, что для произвольных случайных величин X и Y и ДЛЯ Xfa е R1,\/Ь е ,Х/с е ,\fd е Z?1 => Сог[аХ + b,cY + d] = sign(ас) Cor[X, Y] .
В специальной литературе часто применяют сокращенное обозначение корреляции случайных величин X и У, а именно вместо Cor[X,Y] пишут pXY' Подобно ковариации, корреляция инвариантна относительно перестановки аргументов, т.е. pXY — pYX . Заметьте, однако, что в отличие от ковариации корреляция любой случайной величины с собой равна 1, т. е. рхх — 1X/JV .
Если корреляция пары случайных величин равна нулю, говорят, что эти случайные величины некоррелированы. Важно понимать, что, хотя корреляция любой пары независимых случайных величин равна нулю, не все некоррелированные случайные величины независимы. Собственно, именно в этом состояла суть того, что Девлин показал Конвею. Но можно привести пример и попроще, нежели монеты Девлина. Пусть случайная величина X распределена симметрично относительно начала координат. А случайная величина Сбудет детерминированной функцией случайной величины X , т.е. Y — X2. Тогда случайные величины Хи Y — зависимые, но — обратите внимание! — некоррелированные.
Основное применение концепций ковариации и корреляции
Практическое применение и ковариация, и корреляция нашли в задаче вычисления дисперсии суммы случайных величин. Дело в том, что, как легко
49
Часть 1. Стандарты втклвнвния
видеть, дисперсия произвольной суммы случайных величин равна сумме дисперсий слагаемых и ковариаций между всеми возможными парами несовпадающих случайных величин — слагаемых. Эту формулу легко распространить и на взвешенные суммы случайных величин:
п
Иш'ГУ , а,ХЛ =V. , ст2ст2 + У. , У а-а-О'.- , где ст,2 и ст.. обозначают 7=1
соответственно Pzc7r[X] и Cov[Xt., Xj ]. Если обозначить Cor[X t , Xy], как р~ , и учитывать, что = p~, рассматриваемую формулу можно переписать так: Истг[У"=|а,.Х,.] = Уа,.сг2 +2£^^Я(.Яуст.ст7.
/ = 1 / = 1 у=1
Корреляция и дисперсия средних
Интересный с практической точки зрения частный случай взвешенной суммы -—- среднее арифметическое п случайных величин, каждая из которых характеризуется одной и той же дисперсией ст2 , при условии, что любая пара этих случайных величин характеризуется одним и тем же коэффициентом корреляции р . В этом частном случае последняя формула предыдущего параграфа сильно упрощается:
= (— + р——-)<т2 — (-—— 4- Х?)сг2 . Другими словами, п п п п
дисперсия среднего равна общей дисперсии слагаемых, умноженной на некий множитель (-—— + р) , зависящий от числа слагаемых и общего коэффициента п
корреляции так, что существует предел этого множителя при неограниченном росте числа слагаемых, равный этому общему коэффициенту корреляции. Важность этого частного случая в том, что он показывает в явном виде, что диверсификация по переменным, имеющим положительную корреляцию, может уменьшить совокупный риск, но лишь до некоторого отличного от нуля предела.
Существенно, что та же самая формула получается, если построить иную модель частичной зависимости и предположить, что исходы рассматриваемых случайных величин идентичны с вероятностью р и независимы с вероятностью 1 — р. Это значит, что по крайней мере в некоторых приложениях можно рассматривать корреляцию, как некую меру независимости в ситуациях, когда нет ни независимости, ни полной зависимости. Однако понятие корреляции шире, чем вероятностная смесь или рандомизация абсолютной зависимости и полной независимости, к тому же в отличие от вероятностной меры корреляция допускает и отрицательные значения р .
50
1. Причуды шансвв
и
0,ЗЛ еТ?1. А значение корреляции говорит о полной отрицательной корреляцию веяичины X и Y связаны неким
Ограничения, налагаемые на корреляцию
Если каждой случайной величине из пары случайных величин X и Y поставить во взаимно однозначное соответствие некий вектор, т. е. иаправленный отрезок прямой, то pXY будет соответствовать косинусу угла между этими двумя векторами. Отсюда следует, что корреляция — это всегда число от —1 до +1, причем +1 говорит о полной положительной корреляции и означает, что случайные величины Хи Y связаны неким аффинным 1 и означает, что случайные аффинным отображением:
попарные корреляции любого наложены некие ограничения что вектор, соответствующий которое в точности
Заметьте, что в векторной модели на жгоожесгва случайных величин должны быть ^Нравого смысла”. Например, предположим, случайной величине X, смотрит в направлении,
противоположно направлениям и того вектора, который соответствует случайной величине У, и того вектора, который соответствует случайной величине Z . Это зваачит, что X является полностью отрицательно коррелированным и с У, и с Z. Но тогда вектора, однозначно соответствующие случайным величинам У и Z, обязаны быть коллинеарными и одинаково направленными, т.е. случайные величины У и Z будут полностью положительно коррелированными.
The geometry of correlation
cos(t/) = р
= -1
= 1
Геометрия корреляции.
Эти геометрические ограничения на корреляцию имеют непосредственный статистический смысл, показывающий, что у взвешенных сумм случайных величин не может быть отрицательной дисперсии. Например, если п штук случайных величин таковы, что у каждой пары из этих случайных величин одна
и та же общая корреляция, эта корреляция не может быть меньше чем-------
Условные ковариации
Условную ковариацию случайных величин X, Y при наступлении некого общего события Z можно записать следующим образом:
Cov[X, YZ] = E\XY Z] - E[X Z] • E[Y\Z}.
51
Часть 1. Стандарты отклонония _______=_=====^=__
Если взять математическое ожидание обеих частей этого равенства и провести некоторые преобразования с тем, что в результате получится, то будем иметь: Cov[X,Y] = Covz[E[XZ],E[YZ]] + Ех[Сог[Х,Г^]] . Иными
словами, “безусловная ковариация равна ковариации условных средних плюс математическое ожидание условной ковариации”. В частном случае, когда X — Y, мы получаем, что безусловная дисперсия равна дисперсии условного среднего плюс математическое ожидание условной дисперсии: Var\X] = Varz\E{X\ZY\ + Ez{Var[X\Z]].
Существенно, что приведенные в этом параграфе формулы применимы и к смесям вероятностей, что легко видеть, если предположить, что Z — это смешивающее распределение вероятностей. Рассмотрим, например, сценарии Девлина “Без нечетных решек” и “Без нечетных орлов”. Каждый из них характеризуется средним 1, дисперсией 1/4 и ковариацией 0. Вышеприведенные формулы означают, что любая смесь этих сценариев соответствует тем же значениям среднего, дисперсии и ковариации и поэтому является допустимой в той схеме, которую Девлин предложил Конвею.
Смешанные моменты высших порядков
Считается, что средняя по произвольному множеству нормализованных случайных величин корреляция в первом приближении является мерой того, насколько случайные величины этого множества в среднем изменяются в линейной синхронности. Однако эта средняя тенденция может формироваться различными способами. Например, наше множество случайных величин может оказаться таким, что его случайные величины будут переключаться между идентичными и независимыми изменениями, но может оказаться и таким, что его случайные величины будут изменяться более однообразно. Эти смешанные моменты высших порядков как раз и должны фиксировать отклонения от синхронности.
Нормализованные смешанные моменты третьего порядка называются коасимметриями. Существует два типа коасимметрии:
Е[(Х-~ )(Ez2Al)(Z - V?)] и
СУу СУz су х СУ Y
Нормализованные смешанные моменты четвертого порядка называются коэксцессами. Существует четыре типа коэксцессов:
£[( х -/л х yY-^z-jj^ w - , £[( X - Их )2 ( ,
X &Z &W & X ^Y & Z
Е^Х~ И Е\Х ~ X ~ )]
СГд. сгг ст, стг
52
2. Дополнительные углы для треугольника Паскаля
После долгого молчания Конвей, наконец, заговорил: “Прости меня, Девлин. Мне не следовало делать скоропалительных оценок твоей работы. Но теперь надо растолковать все аудиторам, чтобы они могли изменить свой отчет...”
Девлин, однако, отнесся к своей победе без видимого энтузиазма: “Я не думаю, что это — хорошая идея. По крайней мерс па данный момент. Дело в том, что, скорее всего, наши аудиторы верят в то, что нашу систему оценки риска вполне безопасно и даже полезно внедрять в практику”.
Конвей, тем не менее, не понял, куда клонит Девлин: “Совершенно верно! Именно это они и сказали. Теперь надо просто объяснить им ситуацию и добиться от них, чтобы они смягчили свою критику”.
Девлин понял, что нужны пояснения: “Видишь ли, Конвей, я думаю, что этим разговором ты ничего не добьешься. Дело в том, что этот неприятный инцидент с аудиторами явно показывает серьезный и принципиальный изъян в нашей системе оценки риска. Поэтому не стоит, по-моему, заострять внимание аудиторов на моих теориях. Строго говоря, данный случай явно демонстрирует, что даже тогда, когда мы точно знаем распределение каждого актива портфеля и все попарные ковариации и корреляции активов, мы все равно не всегда можем правильно оценить совокупный хвостовой риск этого портфеля. В конце концов мы с тобой только что видели, что всего-то при трех несмещенных, некоррелированных, бинарных активах вероятность их одновременного падения может меняться в интервале от 0 до 25% в зависимости от обстоятельств, которые наша система не отслеживает”.
“Так что же мы упустили?”
“Начнем с того, что мы упустили коасимметрию. Например, коасиммсзрия между нашими тремя некоррелированными, несмещенными бернуллисвымн активами может принимать значения от +1/8 до -1/8. Тогда вероятность одновременно трех неудач будет равна +1/8 минус эта самая коасиммегрия...”
Но Конвей все еще не осознал масштаба проблемы и искал простое решение: “Ничего страшного, слегка модифицируем систему и начнем регистрировать коасимметрии между тройками активов... Я составлю спецификации на дополнительное программное обеспечение, а ты пока посмотри, что надо изменить в наших формулах оценки стоимости риска... в приложении к нашим портфелям”.
53
Часть 1. Стандарты стклонония
Но Девлин не выказал энтузиазма по отношению к попытке Конвея исправить все “по быстренькому”: “Я не могу этого сделать. Понимаешь, Конвей, для того чтобы написать общую формулу для трех небинарных активов, мне понадобится информация по коасимметриям пар этих активов. Конечно, Конвей, мы можем добавить в спецификации системы мониторинга нужный нам модуль, и система станет-таки выдавать данные по коасимметриям, но даже в этом случае, мы не сможем специфицировать риск одновременного падения на четверках активов. Для чегверок нам понадобилась бы информация о коэксцессах, которые бывают четырех сортов... А для пятерок активов нам станет нужна информация о смешанных моментах пятого порядка, которые бывают шести различных сортов и т.д. ...”
“Стоп!, — закричал Конвей и поднял вверх руки. — “Наконец-то я понял. Но не подошла бы нам какая-нибудь более простая аппроксимация? Почему бы нам не остановиться на том, что у нас есть. Ты все-таки должен признать, Девлин, что эта троица бинарных опционов — специфический частный случай”.
“И то верно, специфический! Но частные случаи имеют обыкновение порождать неожиданные взгляды на вполне обычные, казалось бы, вещи. А за неожиданным взглядом обычно следует неожиданная догадка... Что касается нашего частного случая, он заставил меня осознать, что агрегированные портфели могут нести в себе как невероятно меньшие, так и катастрофически большие риски, чем предполагает наша действующая система оценки риска”.
“О, боже, только не это! Девлин оседлал своего конька и сейчас начнет мудреные мысленные эксперименты. Ис хочу втягиваться в эту бодягу”, — мысленно запаниковал Конвей, но вслух произнес: “Я так понимаю, что конструктивных предложений у тебя нет?”
“Какие у меня могут быть конструктивные предложения... Я пока даже толком не знаю, с чем мы имеем дело. Иногда думаю, что, когда в одном портфеле объединяют много одинаково зависимых активов, исходы должны тяготеть к некой центральной тенденции, т.е. должны вести себя так, как если бы эти активы были независимыми... С другой стороны, вроде бы отклонения в этом случае становятся более отчетливыми... Вообще, одна вещь предельно ясна: при таких ставках, как наши, на прояснение вопроса не жалко никаких затрат. Ия уже начал проводить кое-какие мысленные эксперименты”.
“Типа игры в кости? — Конвей кивнул на стакан с монетками.
“Да, конечно. Говоря строгим математическим языком, это многомерные бернуллиевы игры. С монетками все не очень хорошо в том смысле, что трудно не принять одно из двух предположений, а именно, что монетки или идентичны, или независимы. А я пока не готов налагать на свои эксперименты какие-либо ограничения”.
“Но какие-то ограничения ты все-таки собираешься наложить?”
“Всего два, но принципиальные. Первое ограничение — это, собственни-говоря, бернуллиевость, т.е. у каждой случайной величины есть всего два исхожг1 А второе ограничение — перестановочность, т.е. все вероятности зависят тольжиг
54
2. Дополнительные углы для треугольника Паокаля
от общего числа успехов и неуспехов, но не от порядка следования во времени этих успехов и неуспехов. Эти ограничения задают самый простой из возможных фундамент для рассмотрения зависимости. Они облегчают вычисления, и маловероятно, по-моему, что они направят нас в сторону от коренных закономерностей этой зависимости, т. е. от целей исследования”.
Конвей слушал рассуждения Девлина и размышлял. Дело в том, что Конвею, конечно, не хотелось позволять Девлину заниматься своим любимым делом и двигать науку, в то время как все остальные члены коллектива должны будут взять на себя рутину, которая раньше падала и на Девлина. С одной стороны, Конвей не хотел озлоблять коллектив и боялся обвинений в фаворитизме. Но с другой стороны, то, чем планировал заняться Девлин, заняло бы его на какое-то время и он удержался бы в стороне от скандала с аудиторами, предоставив дипломатию Конвею... “А еще я мог бы необидно выставить его в смешном свете и помочь ему избавиться от слепой привязанности к бредовым идеям и тем самым снова обрести уверенность в себе”, — подумал Конвей, а вслух сказал: “Звучит разумно. А есть ли у тебя конкретные предложения, как сыграть в эти шры побыстрее? Девлин, я ведь не могу позволить тебе целыми днями раскладывать монетки по кучкам”.
“Конечно, — кивнул Девлин. — Я только что нашел очень удачный, точный и производительный метод. Этот метод состоит в том, чтобы строить треугольники, дополнительные к знаменитому треугольнику Паскаля. Помнишь еще, что такое треугольник Паскаля, Конвей?”
Конвей не обиделся на очевидную подначку и отбарабанил: “Да, помню. Это равнобедренный треугольник из натуральных чисел, стоящий на основании, с единицей в вершине, а каждое число, включая вершину, равно сумме чисел, ближайших к рассматриваемому числу и находящихся слева и справа от него, но в строке, находящейся над рассматриваемым числом. При этом элемент, находящийся на к Ч-1 -м месте, считая слева, в п + 1 -ый, считая сверху, строке представляет собой число сочетаний из и по к , которое принято обозначать С„ ”.
Треугольник Паскаля
1
1 1
1 2 1
13 3 1
1 4 6 .4 1
1 5 10 Ю 5 1
1 6 15 20 15 6 1
• • • • • • * ♦ • • • • • » • 4 «
“Правильно. Мои дополнительные треугольники построены так же, с той разницей, что каждый элемент дополнительного треугольника равен сумме ближайших соседей слева и справа, но не в соседней верхней строке, как это
55
Пасть 1. Стандарты отклвнония=в=====
было в треугольнике Паскаля, а в соседней нижней строке. Оказалось, что любую перестановочную бернуллиеву игру можно однозначно и адекватно отобразить треугольником, дополнительным к треугольнику Паскаля, притом, что элемент дополнительного треугольника, стоящий на к + 1 -м месте, считая слева, в п + 1 -ый строке, считая сверху, представляет собой число, равное вероятности того, что первые к из и испытаний этой игры будут успехом, а остальные, соответственно, неуспехом. Правило построения треугольника, которое я назвал ‘правилом суммирования’, говорит о том, что если в п испытаниях произошло к успехов, из этого неизбежно следует, что в п + 1 испытаниях будет или к + 1 успехов, или к успехов”.
“Что, кроме дополнительного треугольника, необходимо, чтобы однозначно характеризовать произвольную перестановочную бернуллиеву игру?”
“Ничего. Мой треугольник содержит всю необходимую и достаточную информацию. На самом деле любое, взятое отдельно, ребро этого треугольника содержит всю необходимую и достаточную информацию, поскольку все остальные вероятности можно вычислить, применяя правило суммирования”. Конвей выглядел обескураженным, поэтому Девлин подумал, что необходимо обсудить с Конвеем какой-нибудь простенький пример. И он набросал на бумаге такой треугольник:
Пример Девлина
1
V2 Уг
% % %
1/8 1/8 1/8 , 1/8
5/64 3/64 5/64 3/64 5/64
Закончив выписывать числа, Девлин объяснил смысл своего примера: “Первая строка устанавливает меру достоверного события, т.е. вероятностную меру множества всех исходов, равную 1 . Вторая строка задает вероятности успеха и неуспеха в одном испытании так, чтобы игра получилась несмещенной. Третья строка определяет вероятность получить в двух последовательных испытаниях ни одного успеха, один успех, за которым следует неуспех и два успеха подряд, т.е., как мы видим, эта игра — некоррелированная. Из четвертой строки становится ясно, что игра не является асимметричной (далее мы будем говорить ‘неасимметричная’). Тем не менее те бернуллиевы случайные величины, розыгрыш которых и составляет рассматриваемую игру, не являются независимыми, поскольку, если бы они были независимыми, каждая четверка исходов имела бы вероятность 1/16, что, как мы видим, не имеет места в нашей
56
2. Двпвлнитвльныо углы для троугольника Паскаля
игре. На самом деле четверки, содержащие четное число успехов, на две трети вероятнее1 четверок, содержащих нечетное число успехов”.
Конвей снова стал проявлять интерес: “Ты говоришь, что правило суммирования дает возможность построить весь треугольник но одному ребру?”
“Суди сам. Если начать с нижней строки, то получишь элементы четвертой строки как 5/64 + 3/64 = 1/8, затем так же тривиально элементы третьей строки: 1/8 +1/8 = 1/4 и т.д. Если же начать с того ребра, которое соответствует нулевому количеству успехов, то придется по правилу генерации элементов треугольника заменить суммирование на вычитание и двигаться слева направо. Например, вероятность ровно одного успеха в пяти испытаниях равна вероятности ни одного успеха в четырех испытаниях минус вероятность ни одного успеха в пяти испытаниях, т.е. 1/8 — 5/64 = 3/64”.
Тут Конвей запутался и был вынужден попросить дополнительных пояснений: “Девлин, прости, я опять что-то недопонимаю. Если в строках этого треугольника вероятности, почему их сумма в строке может быть меньше единицы?” Но здесь Конвея осенило: “Подожди, подожди... Ну да! Я понял! Вероятности в вашем треугольнике представляют собой вероятности конкретных перестановок успехов и неуспехов, в то время как, за исключением нескольких вырожденных случаев, сразу несколько различных перестановок одного и того же числа успехов могут порождать одно и то же событие, состоящее в появлении этого числа успехов в данном числе испытаний... Поскольку эти случайные величины перестановочны, каждая из таких перестановок будет иметь ту же самую вероятность, верно?”
“Верно. А число различных перестановок к успехов в наборе из п испытаний как раз и равно С* , т.е. задается треугольником Паскаля. Это значит, что, для того чтобы вычислить полную вероятность к успехов в п испытаниях, надо умножить элемент, стоящий в п + 1 строке моего треугольника на к + 1 - м месте, на соответствующий элемент треугольника Паскаля”.
Конвей обрадовался, что он до чего-то додумался и почувствовал азарт: “А ну-ка, дай я проверю этот пример... В четырех испытаниях существует ровно одна перестановка, соответствующая четырем неуспехам подряд, ровно шесть разных перестановок, каждая из которых содержит два успеха, и ровно одна
1 Здесь надо понимать, что, говоря: . .на две трети вероятнее,, Девлин имеет в виду не вероятность в общепринятом смысле, а шансы наступления события, что четверка, выбранная в игровой схеме, реализующей указанные вероятности четверок, окажется четверкой с четным числом успехов. Надо иметь в виду, что, если вероятность некого события А равна Р(А), то шансы этого события равны по определению /*( Л) . Ниже будет показано, что вероятность четверки с четным числом успехов 1-Р(Л)
равна 5/8, что означает, что шансы выбрать наудачу четверку с четным числом успехов равны 5 : 3 (говорят “пять к трем”), что на 2 : 3 больше, чем 3 : 3, когда шансы выбрать четверку с четным числом успехов были бы равны шансам выбрать четверку с нечетным числом успехов. Вот это и имел в виду Девлин, когда говорил . .на две трети вероятнее...”. — Прим, перев
57
Часть 1. Стандарты отклононня____________________________________________
перестановка, соответствующая четырем успехам подряд. Поэтому вероятность получить в результате четырех испытаний, производимых над бернуллиевыми случайными величинами по схеме дополнительного треугольника, какое-нибудь четное число успехов равна 5/64, умноженному на 1 + 6 + 1, что дает 40/64 = 5/8. Аналогично, существует ровно четыре перестановки, соответствующие одному успеху, и ровно три перестановки, соответствующие трем успехам. Поэтому вероятность получить в результате четырех испытаний, производимых над бернуливыми случайными величинами по схеме дополнительного треугольника, какое-нибудь нечетное число успехов равна 3/64, умноженному на 4+4, что дает 24/64-‘3/8. И эти вероятности, действительно, дают в сумме единицу, как и положено, и четные успехи действительно на две третьих вероятнее нечетных... Но что ты всем этим доказываешь?”
"'Ну, теперь тебе ясно, что могут существовать такие четыре случайные величины, которые будут несмещенными, некоррелированными и неасимметричными, причем каждая тройка этих случайных величин будет вести себя, как тройка независимых в совокупности случайных величин, а в результате портфель может обладать более толстыми хвостами, чем если бы эти четыре случайные величины были независимы в совокупности. А если обобщить этот пример, то вполне может найтись такое конечное множество, состоящее из п. < оо случайных величин, что любое конечное множество, состоящее из Vw < п элементов и являющееся подмножеством этого конечного множества, состоящего из п. случайных величин, окажется подмножеством независимых в совокупности случайных величин, но эта независимость не будет распространяться на какие-либо конечные подмножества вес того же множества, насчитывающих больше, чем т элементов. Это значит, что в отсутствие каких-либо дополнительных ограничений хвостовой риск просто нельзя вывести из информации о моментах низших порядков..
“Неплохо, — с задумчивым видом протянул Конвей, но про себя подумал, что все это, напротив, очень плохо, однако виду не подал. — Ты хочешь сказать, что произвольный треугольник, составленный из неотрицательных чисел так, что в вершине треугольника стоит единица, а каждый элемент этого треугольника равен сумме двух соседних элементов справа и слева из соседней нижней строки, может однозначно представлять какую-нибудь многомерную бернуллиеву игру?” “Да”.
Конвей, между тем, продолжал допытываться: “Значит, если я возьму и начну строить какой-нибудь треугольник сверху вниз, просто добавляя строки в соответствии с этим правилом суммирования, то создам некую вероятностную меру для бернуллиевой игры на десяти, двадцати, пятидесяти случайных величинах?”
“Возможно, но, скорее всего, ты наделаешь ошибок и для того, чтобы игра была физически реализуемой, придется эти ошибки сначала найти, а потом исправить...”
На этот раз Конвей не стерпел обиды: “Я бы настоятельно рекомендовал тебе, Девлин, воздержаться от подобных высказываний в мой адрес, по крайней
58
2. Дополнитольныо углы для треугольника ТТасколя
мере на текущем этапе. По сути дела у тебя сейчас практически нет других друзей в нашей организации”.
Девлин слегка смутился: “Ах, прости, Конвей! Я вовсе не имел в виду тебя лично. Просто построение моих треугольников довольно хитрое. Генерировать новые строки и. правда, очень легко, но еще легче сгенерировать такие строки, иоторые через несколько шагов вниз приведут к строкам с отрицательными значениями. У меня было много таких заморочик. Так что дело, конечно, не в тебе лично.. .Простейший пример такого сорта с несмещенными и некоррелированными случайными величинами возникает, когда мы пытаемся дописать строку к нашему сценарию ‘Без нечетных решек в тройках’. Пусть q обозначает вероятность не получить ни одного неуспеха в четырех испытаниях. Тогда наш треугольник должен выглядеть в соответствии с правилом суммирования следующим образом”.
Недопустимые расширения игры
1
/2
/2
О
q
О
посмотрим, какими должны быть ограничения на чтобы получающаяся бернуллиева игра была
-Ч
“А теперь давай, Конвей значения переменной q, допустимой”.
Конвей внимательно посмотрел на рисунок Девлина: “Ни одного допустимого значения q не существует. Или само q, или -1/4 - q обязано быть отрицательным. Чушь какая-то... Ну и что это значит, Девлин?”
“Если произвольное множество, состоящее из элементов, являющихся четверками монет таково, что в нем не может быть подмножества с такой подборкой монет, в которой на трех первых местах находятся одна решка и два орла, то исходное множество обязано содержать только четверки монет типа ‘ни одной решки’, или ‘три решки’, или ‘четыре решки’. Если же это исходное множество еще и таково, что в нем нс может быть такого подмножества, то в этом подмножестве обязательно есть четверка монет, в которой на трех первых местах находятся три решки, это исходное множество обязано не содержать четверок монет типа ‘три решки’ или ‘четыре решки’. Следовательно, наше исходное множество должно состоять из таких четверок монет, в которых вообще нет ни одной решки, а значит оно не может быть несмещенным”.
Конвей шумно издал вздох облегчения: “Хорошая работа и великолепный результат, Девлин! Ты решил проблему”.
Девлин был обескуражен: “Что?”
“Твой треугольник показывает, что угроза экстремальных событий резко уменьшается с ростом числа перестановочных случайных величин. Поэтому, поскольку в большинстве больших портфелей большинство предназначенных
59
Часть 1. Стандарты отклонония _________
для перепродажи активов перестановочны с другими активами, мы можем для подавляющего большинства наших задач полагаться на старый добрый метод анализа среднего отклонения. А эти наработки оставим для анализа специальных случаев”.
Девлину показалось, что он сходит с ума. Нет, не потому, что Конвей не понял даже приблизительно глубины проблемы, а потому, что Конвей, по всей видимости, и не хотел ничего понимать. Поэтому Девлин простонал: “Я вряд ли вообще что-либо доказал или решил. Я всего-то показал тебе один-единственный пример, в котором область риска сужается по мере роста числа перестановочных случайных величин, а ты уже готов прекратить дальнейшие исследования!”
Но такие стоны уже не могли изменить хорошего настроения Конвея: “Я просто, в отличие от некоторых моих друзей, пытаюсь быть практичным. Только и всего. Но ты прав, что не позволяешь мне останавливать исследования. Во всяком случае, если ты натолкнешься на какой-либо частный случай, когда хвостовой риск не уменьшается с ростом объема и номенклатуры портфеля, обязательно дай мне знать об этом”.
“Тогда позвольте мне показать тебе кое-что прямо сейчас”,- торопливо проговорил Девлин, пытаясь поймать Конвея на слове.
Конвей решил проявить великодушие к причудам Девлина: “Ради бога, я готов”, — а про себя подумал: “Боже, сделай так, чтобы вся эта кутерьма оказалась ‘ложной тревогой!”
Девлин между тем приступил к объяснению следующего примера: “Рассмотрим еще раз игру на четырех несмещенных некоррелированных бернуллиевых случайных величинах, но теперь мы не будем ограничены сценарием ‘без нечетных решек в тройках’. Пусть теперь г обозначает вероятность того, что в трех испытаниях не будет ни одного успеха. Тогда в соответствии с правилом суммирования треугольник вероятностей будет выглядеть так:
Игры на четырех случайных величинах
% г
q r-q
1
%
%
!4 -г
% -2r +q
72
74
г 74 - г
-l/4+3r-q Уг -4r+q
Этот треугольник тогда и только тогда представляет собой некую допустимую вероятностную меру некой физически реализуемой бернуллиевой игры на четырех перестановочных случайных величинах, когда ни один из его элементов не отрицателен. Из четвертой строки мы видим, что г обязано
принадлежать отрезку
о,-4
Из второго элемента пятой строки ясно, что г
обязано быть верхней гранью для q, а из последнего элемента пятой строки видно, что 4r-7г обязано быть нижней гранью для q. Иными словами,
60
2. ДОПОЛНИТОЛЬНЫО углы ДЛН ТРОУГ8ЛЬНИК8 П8СК8ЛЯ
4г---< q < г => Зг < — => к < — - Аналогично, из первого и четвертого элемента
2 2 6
пятой строки имеем, что г > — . Мы видим, что дополнительный параметр q
сужает-таки интервал допустимых значений параметра г. Однако допустимые
значения для параметра q существуют для любого допустимого значения
1 Г 12'6
г е
а именно, допустимые значения параметра q можно выбирать из
отрезка
min\ г,3г-----1;тах1 0,4г------
I 4 J I 2
Оказывается, что абсолютный минимум
допустимых значений q равен в этих условиях нулю, что приводит к следующему решению:
Решение при минимальном значении q
1
72 72
74 74 74
1/12 1/6 1/12 1/6
О 1/12 1/12 0 1/6
А максимальное допустимое значение q оказывается тогда равным 1/6, что дает решение, являющееся зеркальным отображением вышеприведенного треугольника. Это значит, что экстремальный хвостовой риск в этом случае выглядит весьма необычно и гораздо более непривычно, чем в предыдущем примере”.
Конвей, надо отдать ему должное, на этот раз слушал Девлина очень внимательно, вник и думал, что вполне его понял. Видимо, поэтому Конвей опять почувствовал себя неуверенно: “Прости меня, Девлин, но в случае трех случайных величин экстремальный риск менялся в интервале от 0 до %, а сейчас опять для трех же случайных величин он меняется в интервале от 1/12 до 1/6, так почему же, по-твоему, теперь положение хуже?”
Девлин ответил, как на духу: “Потому что вероятность 1/6 для четырех хвостов более чем вдвое больше того, что мы имели бы в случае независимости случайных величин. Обрати внимание, что в случае трех случайных величин мы имели вероятность наихудшего случая ровно вдвое больше того значения вероятности наихудшего случая, которое получилось бы при независимости. Это значит, что при переходе от трех к четырем случайным величинам положение ухудшилось, ведь вероятность наихудшего случая стала более чем в два раза больше вероятности наихудшего случая при независимости”.
Конвей несколько минут внимательно изучал последний треугольник Девлина. В конце концов, он сказал: “Мне кажется, твой вывод о хвостовом риске зависит от того, как ты определяешь хвост. Допустим, что хвостовое событие определяется как ‘три или более неуспехов’. Тогда твое решение для
61
Часть 1. Стандарты отклолония
минимального q дает хвостовую вероятность равную 0+(4х 12)=1/3, а для
максимального q - 1/6. Интервал
_б’ з
лучше, чем интервал 0;— , который мы
4
имели в случае трех случайных величин”.
Девлин почувствовал благодарность к Конвею. Ему стало приятно, что Конвей, наконец, отнесся к его треугольникам серьезно и потратил силы и время на серьезное обдумывание этой проблемы. Кроме того, Девлин очень ценил поддержку Конвея, когда, конечно, мог ее получить... И Девлин высказал Конвею свою благодарность, единственным доступным ему способом: “Конвей, не следует полагать, что те экстремальные значения q , которые определяют риск четырех неуспехов, дадут нам экстремальные значения риска трех или более неуспехов. Дело в том, что этот последний риск определяется формулой q + 4(r — q) или 4г — 3q . Поиск экстремальных значений этого риска означает решение соответствующей задачи линейного программирования. Вот, посмотри:
1 л 1
• если г> —, минимально допустимое значение q=^4r--------------, а
8 2
максимальное значение величины 4г — 3q есть тогда максимальное 3
значение величины---8г , которое очевидно равно У * * * * ХА при г = 1/8;
1
• если г < — , минимально допустимое значение q = О, а максимальное 8
значение величины 4г— 3q есть тогда максимальное значение величины 4г, которое очевидно равно '/г при г = 1/8;
1
• если г > — , максимально допустимое значение q = г, а минимальное 8
значение величины 4r — 3q есть тогда минимальное значение величины г, которое очевидно равно 1/8 при г = 1/8;
1 о 1
• если г < —, максимально допустимое значение q = Зг — —, а
минимальное значение величины 4r -3q есть тогда минимальное значение 3
величины----5г , которое очевидно равно 1/8 при г = 1/8”.
У Конвея закружилась голова: “Ну хорошо, хорошо, Девлин! Я тебе верю. Но не мог бы ты сразу перейти к выводам и опустить промежуточные
выкладки?”
“Я как раз и собираюсь это сделать. Вероятность трех и более неуспехов в
четырех перестановочных испытаниях может быть минимальной и равной 1/8
или максимальной и равной в соответствии со следующими треугольниками
вероятностей:
62
2. Дополнитольныо углы для троугольникя Паскаля
Экстремальные вероятности трех и более неуспехов в четырех испытаниях
Минимум
1
1/8 7> % 1/8 72 1/8
74 1/8 %
1/8 0 1/8 0 1/8
Максимум
1
72 72
1/ 1/ 1/
/4 /4 /4
1/8 1/8 1/8 1/8
0 1/8 0 1/8 0
Конвей снова оживился: “Как интересно! Оба случая симметричны относительно среднего, значит, ни в одном нет никакой асимметрии...”
Девлин подхватил: “Они и не предполагают какой бы то ни было зависимости, пока не доберешься до последней строки. Каждая тройка независима в совокупности. Поэтому, если поторопиться с выводами, то вполне можно предположить, что все четыре случайные величины в совокупности тоже независимы и оценить в 5/16 риск трех и более неуспехов. А на самом деле эта оценка может оказаться или завышенной, или заниженной на 3/16. И опять моменты низших порядков дают мало информации о хвостовом риске. Я считаю, это очень настораживает”.
Конвей сдался: “Я тоже теперь так думаю. Мне кажется, следует посмотреть, как обстоят дела в ситуации с большим количеством случайных величин. Кажется, ты только что сказал, что поиск экстремальных хвостовых вероятностей — это задача линейного программирования? Мне хотелось бы, чтобы ты составил задачу для компьютера, тогда мы сможем получить нужное нам решения. Давайте снова встретимся, когда ты с этим закончишь. А я тем временем подразберусь с математикой этих треугольников...”
“Я немедленно займусь линейным программированием”.
Конвей вяло улыбнулся: “Мне бы очень хотелось, чтобы решение было ХфОСТЫМ. ..”
Пока мы ждем результатов Девлина, поможем Конвею разобраться с математикой.
Треугольник Паскаля
Начнем с того, что выпишем полностью формулу для числа сочетаний из п элементов по к элементов:
63
Часть 1. Стандарты отклонония
_ п\ _ п(п — 1)(л — 2) ... 2 1 п(п — 1) ... (п — к + 1)
" “ к\(п — к)\ ” к(к - 1) •• 1 • (и - к)(п - £ - 1) •• 1 ” £(£-1)-...-1
Правило сложения, по которому строится треугольник Паскаля, означает, что: С* + С*+1 = С**/. Это правило на самом деле является теоремой, которую легко доказать. По определению числа сочетаний имеем для \7п е 7V, \/к < и : +^+i _ Zr + 1^ п—к_п\-(к + \ + п—к)_ (гг + 1)! _£*•*!
"+ " ~ kl(n-ky"k + \ + (к + }у.(п-к-1у.' п-к~ (А + 1)!(и-Аг)! ~ (£ + 1)!(и-£)! “ ’
что и требовалось доказать.
Треугольники Девлина
Теперь нам надо показать, что произвольный треугольник Девлина, все элементы которого неотрицательны, представляет собой некую законную вероятностную меру.
Для доказательства зафиксируем Vw е < со, и обозначим к+1, считая слева, и п+1, считая сверху, строки треугольника Девлина как р(гцк) и положим, чток) есть вероятность произвольной перестановки к успехов в п испытаниях, которая одинакова для всех таких перестановок (когда в п испытаниях произошло ровно к успехов). Согласно этому определению, множество {р(п, = 0, п}
состоит из неотрицательных элементов, является замкнутым и удовлетворяет тому свойству, что вероятность объединения несовместных, т. е. взаимоисключающих событий, равна сумме вероятностей тех событий, которые составляют это объединение.
Для того чтобы {р(п, к) к = 0, >?} было распределением вероятностей, надо только проверить, что вероятность объединения всех допустимых и различных перестановок или n-векторов, составленных из единиц, обозначающих успехи, и нулей, обозначающих неуспехи, т.е. вероятность полного множества исходов равна единице. Это значит, что нам надо доказать, что равенство С^р{п^к) = \ справедливо для Х/л е {№ +0} . Докажем это методом математической индукции. Поскольку в вершине треугольника Девлина стоит единица, доказываемое равенство справедливо для п=0. Предположим, что равенство справедливо для некого п=т>1 и докажем, что из этого следует справедливость доказываемого равенства для n=m+l. Итак, имеем QC^p(m,k') - 1 - Вспомним правило суммирования Девлина и тот факт, что по определению С”1 = С ° = 0 . Тогда можем записать:
SZ=o к"> = ХГ=0 с^р(т + !,£) + + 1л+1)] =
= + УР(т + !>*) = П-о + к>
Что и требовалось доказать.
64
2. Дополпитольныо углы для троугольнико Поскаля
О биномиальном распределении
Рассмотрим п независимых в совокупности бернуллиевых случайных величин, вероятность успеха каждой из которых равна одному и тому же числу ц. Тогда вероятность любой наперед заданной перестановки из к успехов в п испытаниях равна произведению вероятностей тех событий, которые являются составляющими этой конкретной перестановки, т.е. /э(лг, А:) =/Z (1 —. Правило суммирования Девлина в этом случае проверяется в лоб*. р{п +1, к) + р(п + 1, £ +1) = рк (1 - + рк+' (1 - рГк = (1 - рГк [(1 - р) + р\ =
Поскольку наши случайные величины независимы в совокупности, для е {7V1 о 0}, к < п < оо
1 1 ’ вероятность того, что в п испытаниях произойдет
Ск ик г} _ Li\n к
ровно к успехов, равна v . Набор вероятностей
{с:л/(1-аГ’> = оГ^} .
1 называется биномиальным распределением вероятностей
порядка п.
Решение треугольников Девлина “сверху вниз”
Как мы видели выше, любой треугольник Девлина обязан содержать неотрицательные элементы, удовлетворяющие разнообразным ограничениям типа равенств и неравенств. При этом все эти равенства и неравенства линейны, значит, и выражение для хвостового риска, по вероятности, тоже линейно. Отсюда следует, что поиск экстремальных значений хвостового риска однозначно ведет к некой задаче линейного программирования. На первый взгляд соответствующая постановка задачи линейного программирования неизбежно должна быть громоздкой, поскольку общее число переменных решения и ограничений превышает п2. Но, к счастью, здесь возможны радикальные упрощения. Дело в том, что, если заданы все элементы некой строки треугольника Девлина и всего один элемент следующей строки этого же треугольника, все остальные элементы следующей строки вычисляются по правилу суммирования. Поэтому каждая новая строка вводит ровно одну дополнительную степень свободы, которую мы можем однозначно связать с первым элементом этой строки р(ш,0). В свою очередь, каждый предопределенный элемент, напротив, уменьшает общее количество степеней свободы задачи на единицу. Первый элемент треугольника обязан быть единицей, чтобы вероятность достоверного события была равна единице. Элемент р( 1,0) является предопределенным, т. е. заданным, фиксированным, если задано среднее; элемент р(2,0) будет предопределенным, если задано не только среднее, но и корреляция и т.д. Это значит, что для игры, построенной на п бернуллиевых случайных величинах, в которой специфицированы среднее и корреляция, оставшиеся п-2 переменные являются свободными в рамках ограничений неотрицательности. Что касается ограничений неотрицательности,
65
Часть 1. Стандарты отклонония___________________________________________
то здесь тоже все просто. Нам надо всего лишь проверить, что ни один из п+1 элементов последней строки неотрицателен, потому что, если все элементы последней строки неотрицательны, то в строках выше последней уже не может быть отрицательных элементов. Этот метод “сверху вниз” обладает значительной интуитивной привлекательностью. В частности, такой подход делает наглядным двойственный характер введения в треугольник дополнительной строки, так как появляется дополнительная свободная переменная решения при дополнительных ограничениях неотрицательности.
Как и для любой задачи линейного программирования, симплекс-метод с легкостью найдет решение, если ему задать допустимый исходный план, т. е. первоначальное, хотя и далеко не оптимальное, но допустимое решение. Выше мы уже видели, что допустимое первоначальное решение существует всегда и известно для случая некоррелированных игр: это биномиальное решение, соответствующее независимости в совокупности. В следующей главе Девлин представит нам допустимое решение для коррелированных игр.
Решения методом подгонки по моментам
Еще один метод строит треугольники Девлина с нижней строки вверх. Поскольку, как мы знаем, сумма случайных величин Бернулли равна к тогда и только тогда, когда среди суммируемых случайных величин есть ровно к успехов, идущих в неважно каком порядке, то (п+1)-я строка треугольника Девлина полностью определяет вероятностное распределение суммы п случайных величин Бернулли. Более того, благодаря правилу суммирования каждая строка однозначно определяет предыдущую строку. Тогда, если у нас есть нижняя строка, у нас есть и весь треугольник, но для того, чтобы этот треугольник был допустимым, нам надо проверить три вещи: во-первых, что в вершине треугольника стоит единица (вероятность достоверного события, под которой можно понимать момент нулевого порядка, равна единице), во-вторых, что в нижней строке нет отрицательных элементов и, в-третьих, что нижняя строка не противоречит тому, что у всех случайных величин, на которых построена данная игра, одно и то же математическое ожидание ц и у каждой пары этих случайных величин одна и та же корреляция р, которую должна определять вторая строка. Для того чтобы формализовать ограничения третьего типа, применим формулы, выведенные в предыдущей главе, и потребуем, чтобы на нижней строке первый и второй моменты были равны соответственно пц и
Таким образом у нас возникают п+1 переменных решения, п+1 ограничений-неравенств на неотрицательность и три ограничения-равенства на моменты. Ограничения-неравенства и ограничения-равенства на нулевой и первый моменты линейны и с ними легко разобраться в рамках модели линейного программирования, но ограничение-равенство на второй момент — квадратично. Это значит, что без дополнительных упрощений симплекс-метод применить не удастся.
66
2. Дополнительный углы для треугольника Паскаля
Однако, несмотря на отмеченные трудности, метод подгонки по моментам имеет свои преимущества перед методом “сверху вниз”. Дело в том, что, поскольку метод подгонки по моментам устраняет промежуточные строки треугольника Девлина, он упрощает процесс формальной постановки задачи условной оптимизации и уменьшает ошибку округления, столь характерную при работе с большими массивами данных. Наконец, если заранее известно, что оптимальное решение содержит ровно два положительных элемента, метод подгонки по моментам даст очень простое аналитическое, а не численное решение.
Гибридные решения
Существует и третий метод решения, который является гибридом двух рассмотренных. Подобно методу подгонки по моментам, гибридный метод помещает все переменные решения на последнюю строку треугольника Девлина. Подобно методу “сверху вниз” гибридный метод использует только линейные ограничения и, следовательно, сводим к симплекс-методу линейного программирования.
Этот гибридный метод задает линейные ограничения в виде равенств на три элемента последней строки треугольника Девлина, выражая каждый из этих элементов через остальные п-2 элементов этой последней строки. Эти формулы (т. е. ограничения-равенства) гарантируют, что вероятность достоверного события есть единица и что первый и второй моменты соответствуют некоторым предварительно заданным значениям. Коль скоро все эго гарантировано, мы можем искать решение нашей задачи среди тех допустимых решений, что удовлетворяют ограничениям неотрицательности.
С геометрической точки зрения гибридные решения основаны на интуитивно прозрачной идее, что отсечение любой части треугольника прямой линией, параллельной ребру, дает трапецию и треугольник, который отвечает всем требованиям треугольника Девлина за исключением того, что в его вершине теперь стоит не единица. В терминах теории вероятностей операция отсечения параллельно ребру просто означает, что, если исходы m случайных величин из общего числа п случайных величин Бернулли известны, то оставшаяся игра — та же игра Бернулли, но на n-m случайных величинах.
Срезы треугольника Девлина
МЫ!
р(2,о)
/7(3,0) /7(3,1) >Я2) ХЭД
/7(4,0) /7(4,1) /7(4,2) ВЖ
В частности, самый верхний элемент и элемент^! нижней строки треугольника, оставшегося после отсечения, связаны линейным уравнением,
67
Часть 1. Стандарты пткпонпния
которое не зависимо от отсеченных элементов. При этом конкретные веса конкретных элементов в этом уравнении определяются только длиной последней строки и позициями этих элементов в строке. Например, как ясно видно из вышеприведенного треугольника, = р(4,0) + 2р(4,1) + р(4,2) подобно
тому, как /2(0,0) — /2(2,0) + 2/2(2,1) + р(2,2) . Если обобщить это наблюдение, то получим следующий результат: для Х/и е TV1, Vz е {TV1 kjO},V/ е {№ ljO} , при i < j < п, имеем С^р(п, к + Z) = р(р i)
Отсюда ясно, что, если нам задано некое предопределенное значение р(2,0) и если через р(п,к} обозначены искомые значения первых п-2 элементов последней строки, мы можем выразить из только что полученного уравнения (п-1)-й элемент этой строки, т. е. р(гцп — 2). После этого мы можем совместно задействовать предопределенное (т. е. предварительно заданное соответствующим ограничением) значение для р(1,0), с одной стороны, и первые п-1 элементов последней строки, с другой стороны, чтобы выразить p(n,n — 1) , т. е. п-й элемент последней строки. Наконец, мы используем предопределенное значение для р(0,0) и первые п элементов все той же последней строки для того, чтобы выразить последний элемент этой строки, т. е. р(пу п) . Мы знаем, что любое решение треугольника Девлина будет допустимым в том случае, если ни одно из значений {р(гц£)} не является отрицательным.
Для того чтобы уменьшить число элементарных операций при вычислениях и снизить тем самым риск нарастания ошибки округления, проще работать не с вероятностями{/?(/?,£)}, а с вероятностями = С^р{п,к) ,
которые являются вероятностями к успехов (причем неважно в каком порядке) в п испытаниях. Тогда соответствующие формулы принимают более простой вид:
р(„, „ _ 2)=р(2,о) - хх: к >;
Р(п, п -1) = п /2(1,0) - о(п - к)Р(п, к);
Р(п, и) = 1 - 22" ° Р(п, к) .
68
3. Эти забавные хвосты риска
На другой день с утра Девлин сделал попытку энергично войти в кабинет Конвея, но подвели усталые глаза. Видимо, поэтому Девлин споткнулся о порожек в дверях, потерял равновесие и разбросал по всему кабинету те компьютерные распечатки, которые он, собственно, и хотел показать Конвею. Конвей удивленно поднял глаза от своей утренней газеты: “Ах, это ты, Девлин! Ты сегодня очень энергичный. Это совсем на тебя не похоже. Что это ты принес?”
Девлина, наверное, эти слова не задела, и он ответил, демонстрируя некоторое воодушевление: “Такие занимательные хвосты... Лох-Несское чудовище околеет от зависти!” После этого он аккуратно собрал бумаги, перевел дух и сказал совсем спокойно: “Ты только погляди на эти гистограммы, Конвей. Заметь, каждая из них есть представление некой несмещенной, некоррелированной бернуллиевой игры на 16 перестановочных случайных величинах. В каждом случае математическое ожидание общего числа успехов равно 8, а соответствующее стандартное уклонение не превышает 2 ”.
Unbiased, uncorrelated 16-variable Bernoulli games
Несмещенные некоррелированные бернуллиевы игры на 16 случайных величинах.
69
Часть 1. Стандарты отклонония
0 30 . .. <
! 1
По горизонтальной оси откладывается число успехов. По вертикальной оси откладывается соответствующая вероятность. Заметьте, что шкала вероятности для разных гистограмм различна.
Конвей внимательно просмотрел диаграммы: “Интересно... Рисунок слева и сверху — это та колоколообразная форма, которую я ждал. Правая верхняя фигура — прямоугольник. Нижняя правая фигура напоминает экспоненциальное распределение, смещенное вправо. А вот левый нижний рисунок я даже и не знаю, как назвать, может быть, ‘костел’? Да-а-а, не знаю, как оценят это название у нас в банке, если не подразумевать, что имеется в виду храм поклонения Мамоне... Но пойдем, конечно, дальше. Это что, твои экстремальные случаи?”
“Только самый первый. Он относится к стандартному биномиальному распределению, которое является адекватной моделью, когда случайные величины независимы в совокупности. Остальные случаи — не экстремальные. Я решил показать их потому, что они весьма интересны”.
“А как же тогда выглядят экстремальные случаи?”
“Они различны, что зависит от применяемого определения хвоста и от того, является экстремизация максимизацией или минимизацией. Однако все они схожи в одном: плотность вероятности сконцентрирована в каждом экстремальном случае в двух или трех точках. При этом одна из точек обязательно лежит на пороге, а вторая — на другой стороне среднего от порога и отстоит от среднего на расстояние меньшее одного стандартного уклонения, тогда и только тогда, когда порог отстоит от среднего на расстояние, превышающее одно стандартное уклонение”.
“А третья точка?”
“Эта третья точка, если, конечно, она существует, обычно примыкает ко второй точке словно это оптимизирующее решение нацелено на то, чтобы сконцентрировать две вероятностных массы в некой промежуточной области. Но так бывает не всегда. Иногда вторая и третья точки отмечают собой два полюса — абсолютного успехи и абсолютного неуспеха, так сказать”.
Конвей попытался нарисовать различные формы экстремальных распределений, но запутался: “Мне было бы проще разобраться в этом на примерах”.
70
3. Эти забавные хввсты риска
“У меня есть кое-что получше. Вот восемь гистограмм, из которых с помощью зеркала мы получим все шестнадцать, т. е. все возможные экстремальные хвостовые риски при заданных 16 перестановочных переменных Бернулли и 50%-ной вероятности успеха. Для того чтобы сделать эти результаты более наглядными, я напечатал поверх каждой гистограммы график биномиального эталона”.
; h i j к d ЛI; ;il И шШШН
Probability distributions yielding extreme tails
Распределения вероятностей, дающие экстремальные хвосты.
71
Часть 1. Стандарты втклвнвния
T
о *? - Г”-
Ли
рЛ рт 0 Й - U -;
j г * • : i ; f £
О 4 ’ Ь-Л
06 L.!
* .;
0 i ~ k!,S o* k
Л йй Г..Л
□ 4 - . 4
• • • ^4
С 7 - t " * о з - ;J
c ? -
O’ ' ГД i. -i
* 11
0 1 |
~ j L—.. „ g L
0 t 7 3 4 5 6 7 в 9 W И П В 14 »5 14 0 i J 3 4 5 6 ? S J 10 11 12 H U 15 u
Все исходы ограничены набором целых чисел от 0 до 16, при том что среднее равно 8, а стандартное уклонение равно 2. Тонкая кривая представляет биномиальное распределение.
09 j
OE j *7
□ 7 ,
a 6
05 i
Q 4 •
О 3 ;
07 !
a 1
о i-----—
il 5 J
Mirror image distributions
Распределения зеркального отображения.
“А для чего нужно зеркало? И почему среди этих картинок нет картинки за номером семь?”
“Если бернуллиева игра на случайных величинах устроена так, что вероятность успеха в одном испытании равна 50%, и если некое распределение суммы этих случайных величин в игре является допустимым, то и распределение сумм случайных величин, чей график плотности совпадает с симметричным отображением первого графика плотности относительно среднего, тоже будет допустимым. Это значит, что, если некое распределение суммы дает исключительно тонкий хвост и при этом допустимо, допустимо и то распределение суммы, плотность которого будет симметричным отображением плотности первого распределения, несмотря на то, что хвост его исключительно толстый. Поскольку симметрия — достаточно простое преобразование графиков, я не стал печатать зеркальные отображения. Правда, распределения №7 и 8 сами симметричны относительно среднего, поэтому их зеркальные отображения совпадают с ними же. Но я не нарисовал распределение №7 именно потому, что оно является зеркальным отображением распределения №4. Но раз ты им заинтересовался, то вот оно”.
72
3. Эти забавные хвосты риска
“Да, теперь я это понял. Распределение №/С показывает максимальную вероятность того, что будет не более К успехов, а его зеркальное отображение показывает максимальную вероятность того, что будет не менее 1 6 — К успехов. Иными словами, распределение №4 показывает максимальную вероятность того, что будет не менее 9 успехов, а его зеркальное отображение показывает вероятность того, что будет не более 7 успехов”.
“Абсолютно верно. А еще мы на этих распределениях легко можем выразить минимальные хвосты. Не желаешь попробовать?”
Конвей снова внимательно просмотрел гистограммы: “Посмотрим, посмотрим... Любой из первых шести графиков показывает, что вероятность числа успехов, равного либо превышающего 10 равна нулю, в то время как зеркальные преобразования тех же распределений показывают, что вероятность любого числа успехов, не превышающего 6, равна нулю. Распределение №8 показывает минимальную вероятность события, состоящего в наступлении или не более 7, или не менее 9 успехов. Распределение №4 показывает минимальную вероятность события, состоящего в наступлении не более 8 успехов, а его зеркальное отображение показывает минимальную вероятность события, состоящего в наступлении не менее 8 успехов”.
“Снова верно, — Девлин передал Конвею очередную распечатку. — А вот таблица, в которой я собрал данные по верхним и нижним границам. Для того чтобы сравнение с биномиальным распределением было более наглядным, я включил в таблицу две графы, одна из которых показывает значение числа успехов, измеренное в стандартных отклонениях от среднего, а другая — соответствующие вероятности в биномиальном случае, т. е. то, если бы случайные величины Бернулли, на которых построена игра, были независимы в совокупности”.
Вероятностные границы для сумм 16 несмещенных, некоррелированных переменных Бернулли
Число успехов Стандартных отклонений от среднего Минимальная вероятность Максимальная вероятность Вероятность в случае независимости
0 -4,0 0 0,056 0,00002
1 -3,5 0 0,071 0,0003
2 -3,0 0 0,095 0,002
3 -2,5 0 0,133 0,011
4 -2,0 0 0,200 0,038
5 -1,5 0 0,300 0,105
6 -1,0 0 0,500 0,227
7 -0,5 0,031 0,800 0,402
8 0 0,200 0,969 0,598
Диапазон очень большой. И что, все промежуточные значения тоже допустимы?”
73
Часть 1. Стандарты отклонения
“Да. Любая смесь этих допустимых распределений тоже допустима, поскольку у нее будут те же самые первые моменты, что и у компонентов, составляющих эту смесь. Но у этой смеси вероятности любых событий будут промежуточными по отношению к вероятностям тех же событий, задаваемым составляющими распределениями. Поэтому, регулируя веса распределений, представляющих наибольший и наименьший хвостовые риски, мы можем генерировать любое промежуточное значение”.
“А как меняются эти вероятностные границы, когда увеличивается число случайных величин, участвующих в игре?”
“Это очень интересно. Граница меняются очень незначительно при условии, что мы измеряем риск в стандартных отклонениях. Давай договоримся использовать термин ‘5-хвост’, под которым будем понимать множество таких исходов, которые лежат на 5 либо больше стандартных отклонений левее среднего, т. е. любое событие 5-хвоста означает не более успехов, чем 5, умноженное на стандартное отклонение. Возвращаясь к асимптотическому поведению наших вероятностных границ, отмечу интереснейший факт: при условии неограниченного роста числа случайных величин Бернулли при X7s > 0,5 < оо минимальный риск соответствующего 5-хвоста стремится к 0, но максимальный риск этого же 5-хвоста и в тех же условиях стремится к ——”.
52 + I
“Почему ты разделяешь положительные и отрицательные 5? Разве для отрицательных 5 отмеченные пределы не имеют места?”
“Имеют, при условии, что мы измеряем наши хвосты правильно, т.е. по направлению от среднего, а не к нему. Но, видишь ли, Конвей, математически удобнее измерять хвосты так, как я, т.е. всегда влево. Тогда, если 5 < О, соответствующий 5-хвост по пути в отрицательную бесконечность переходит через среднее. Такой 5-хвост можно назвать неправильным или несобственным, потому что его дополнение — привычный нам правильный или, как бы лучше сказать, собственный хвост. Очевидно, что никакое распределение не может порождать нулевую вероятность попадания не правее своего среднего”.
“Мне кажется, я все понял. Ты хочешь сказать, что максимальный риск произвольного неправильного хвоста равен 1 минус минимальный риск дополнительного правильного хвоста, а минимальный риск произвольного неправильного хвоста равен 1 минус максимальный риск дополнительного правильного хвоста. Отсюда следует, что, если 5 < 0, границы риска есть границы 2
интервала от —т-- до 1. Так?”
S + 1
“Почти. Дело в том, что дополнение произвольного верхнего хвоста не включает сам порог. Этот факт, вообще говоря, необходимо учесть. Но, поскольку неправильные хвосты нас непосредственно не интересуют, об этой тонкости можно не беспокоиться, за исключением строгих доказательств, где, конечно, ‘каждое лыко в строку”.
74
____________3- Эти забавимо хвосты риска
Хотя Конвей и не подал виду, он был польщен, что догадался до чего-то, ае лежащего на поверхности, и подумал: “Ну, сегодня хоть одна хорошая новость. Чем меньше сложностей, тем лучше”. Однако спросил: “Насколько хорошо эти асимптотические границы риска аппроксимируют реальные границы выборках малых размеров?”
“На удивление хорошо. Но проблема здесь не в законе больших чисел, а в целочисленности ограничений. Большинство границ, соответствующих предыдущим графикам плотностей для игр на 16 случайных величинах Бернулли, или достигают пределов или подходят к ним достаточно близко”.
“А что будет, если вероятность успеха не равна вероятности неуспеха?”
“Тогда по сравнению с несмещенным случаем среднее сместится, а стандартное отклонение сожмется, что, конечно, сместит порог любого 5-хвоста. И до тех пор, пока некий положительный 5-хвост включает в себя допустимые исходы, вероятностные границы этого хвоста продолжают быть границами интервала от 0 до —— ”, 5^+1
“Иными словами, до 4% вероятности пяти стандартных уклонений, до 1% десяти стандартных уклонений? Здорово отличается от всего, к чему мы привыкли и что обычно предполагается по умолчанию!”
Девлин заметил без тени торжества: “То-то и оно... ”, — и положил но стол еще одну диаграмму. “Затененная область показывает допустимые хвостовые риски для значений 5, изменяющихся в интервале от 2 до 10 стандартных отклонений. Жирная черная линия показывает те хвостовые риски, которые мы получаем из предположения независимости в совокупности”.
Конвей какое-то время внимательно разглядывал график и, наконец, выдал: “Эта диаграмма означает, что, если мы придерживаемся стандартных аппроксимаций общепринятого подхода ‘стандартного уклонения’, то с гораздо большей вероятностью недооцениваем реальный хвостовой риск, чем переоцениваем его. Это, как показывает практика, действительно имеет место, и меня всегда интересовало, почему так”.
Девлин развил последнюю мысль Конвея: “Мне тоже всегда было это интересно. Конечно, про значения из серой области нельзя даже приблизительно сказать, что они одинаково часто встречаются на практике. Скорее всего, те значения, которые действительно часто встречаются на практике, должны группироваться вблизи дна... Но ведь общепринятый анализ риска никак не показывает этого. Просто стандартный подход игнорирует без всяких объяснений огромную часть области допустимых значений”.
Как раз в этот момент раздался голос секретарши Конвея по внутренней связи: “Шеф, сожалею, но вынуждена прервать ваши занятия. Вас срочно ждут в зале заседания Совета директоров на собрании Комитета контроля риска...”
75
Часть 1. Стандарты отклонония
Assumes large finite number of exchangeable, uncorrelated variables.
Допустимые хвостовые риски для бернуллиевых сумм.
По горизонтальной оси откладывается число стандартных уклонений, соответствующее расстоянию события от среднего. По вертикальной оси откладывается соответствующая вероятность. Заметьте, что игра предполагает конечное, но большое количество перестановочных некоррелированных бернуллиевых случайных величин. Серая область определяет допустимые значения в отсутствие независимости в совокупности. Черная линия определяет допустимые значения в предположении независимости в совокупности.
Конвей торопливо ответил: “Спасибо, Карен. Я бегу...”, — и обратился к Девлину: “Прости, надо идти. Продолжим, когда я вернусь, хорошо..
Давайте, пока Конвей сидит на совещании, я попробую обосновать представления Девлина об области допустимых значений сумм некоррелированных бернуллиевых случайных величин. Однако, до того как мы углубимся в математические тонкости, мне хотелось бы сделать одно предостережение и одно ободряющее замечание. Начну с плохой новости. Она состоит в том, что работа с целочисленными ограничениями будет означать привлечение неприятных математических выкрутасов типа “почти двухточечных” решений. Хорошая новость состоит в том, что как показывают строгий анализ и практика, целочисленные ограничения не имеют такого уж большого значения, так что в большинстве случаев целочисленность можно просто игнорировать.
Вводные замечания, обозначения и договоренности
Рассмотрим п перестановочных некоррелированных бернуллиевых случайных величин, среднее каждой из которых равно одному и тому же числу ц.
76
==s=^=_______3- Эти эдбявныв хввсты риска
Как мы видели выше, сумма этих случайных величин будет иметь среднее p5tZA/ и дисперсию сг57;л/, соответственно, числа лгц и wp(l — ц), т. е. ц5г7А/= лгр, o2Sum = пц(1 — ц). Здесь я буду считать, что рассматриваемые случайные величины — невырожденные, откуда следует, что дисперсия их суммы положительна и монотонно возрастает по п.
Как мы знаем, минимальное допустимое значение суммы рассматриваемых случайных величин равно 0. Точка 0 лежит на действительной оси левее точки среднего на расстоянии, равном величине стандартного (т.е. среднеквадратичного) уклонения, умноженной на величину yfn/d /(1 — /л) . Максимально допустимое значение суммы рассматриваемых случайных величин равно п. Точка п лежит на действительной оси правее точки среднего на расстоянии, равном величине стандартного уклонения, умноженной на величину д/п(1 — //)/// ‘ Легко видеть, что обе вышеприведенные величины неограниченно растут с ростом Vw -
Я также намерен воспользоваться условным термином “5-хвост”, введенным Девлином. А именно: я буду называть левым 5-хвостом совокупность всех исходов, которые будут лежать на действительной оси левее среднего на расстоянии, равном или превышающим величину стандартного уклонения, умноженную на коэффициент 5, а правым 5-хвостом совокупность всех исходов, которые будут лежать на действительной оси правее среднего на расстоянии, равном или превышающим величину стандартного уклонения, умноженную на коэффициент s. При 5 > 0 мы имеем собственный (правильный) левый (или правый) 5-хвост, так как его исходы, действительно лежат левее (или правее) среднего суммы случайных величин, а для отрицательных значений s мы имеем несобственный левый (или правый) 5-хвост, так как его исходы в действительности лежат не левее, а правее (или не правее, а левее) среднего (т. е. переходят вправо или влево за точку среднего значения, поскольку по определению должны идти в отрицательную сторону на некое отрицательное расстояние, что эквивалентно движению в положительную сторону на положительное расстояние).
Двухточечные распределения
Рассмотрим некую дискретную случайную величину, принимающую ровно два значения и распределенную таким образом, что некоторой точке действительной оси, лежащей левее среднего нашей суммы случайных величин на расстоянии, равном величине стандартного уклонения, умноженной на некий коэффициент 5, приписана вероятность q, и некой второй точке, лежащей на действительной оси левее среднего нашей суммы случайных величин на расстоянии, равном величине стандартного уклонения, умноженной на некий отрицательный коэффициент s' (т.е. справа от среднего нашей суммы случайных величин на расстоянии, равном величине стандартного уклонения, умноженной
77
Часть 1. Стандарты сткланания
на коэффициент —1^'|), приписана вероятность q' = 1 — q . Допустим, далее, что эта случайная величина, которую мы будем называть двухточечной, стандартизована. Тогда, поскольку среднее и дисперсия любой стандартизованной случайной величины должны быть равны 0 и 1 соответственно, введенные нами выше числа q,s и s' должны удовлетворять следующей системе уравнений:
qs + (1 — q)sf = О,
^2+(l-?)(s')2 =1,
которая имеет следующее решение:
1. 1
5 , д — ? •
5 № + 1
Для того чтобы проверить симметричность этого решения, достаточно заметить, что:
1 gl - 1
1 Я 1.2 -2
s'2 + 1 4 ’
Хвосты нулевого риска
В тех случаях, когда для суммы случайных величин можно применить двухточечное распределение, структура которого рассмотрена выше, убытки не превышают величины, численно равной значению соответствующего стандартного уклонения, умноженному на коэффициент 5. Отсюда следует, что, если мы для произвольного положительного, но сколь угодно близкого к нулю 5 сможем найти допустимое двухточечное распределение, минимальный риск собственного хвоста будет равен нулю.
Допустим теперь, что 5 выбирается так, что — s^sum в точности равно наибольшему целому числу, меньшему Тогда, просто увеличивая число /?, мы можем сделать значение 5 сколь угодно малым при сохранении условия, что будет превосходить и. Более того, выбирая эту большую величину л?, мы всегда сможем добиться такого положения, что вторая точка нашего двухточечного распределения или будет равна некоему целому числу, или сколь угодно близка к некоему целому числу.
Предположим, например, что /1-А в точности равна некой рациональной V А
дроби — , где к \л / являются целыми. Тогда, если п = /2(у~ + &2)Bz е N, где TV-
множество натуральных чисел, то и piSUM = i2j'2(J2 + к2) , .и crSUM = ijk , и Msum ~ s*&sum = /2 j2 С/2 + 2£2) все будут целыми при том, что, если i будет
78
3. Эти забавные хвосты риска
достаточно большим, s = — окажется достаточно малым.
Цк
Интуитивно понятно, что все рассмотренные экстремальные величины должны быть непрерывны по ц всюду за исключением границ интервала возможных значений ц. Это значит, что, если мы знаем те / и у , которые определяют j 1 - а как рациональную дробь, то знаем, что наше ц не попадет на V Х'
границу своего интервала и, значит, все в порядке. Таким образом, если у нас есть достаточно много некоррелированных перестановочных бернуллиевых случайных величин, риск собственного хвоста может быть сколь угодно малым.
Хвосты максимального риска
Результаты предыдущего параграфа проливают некоторый свет на то, как устроен 5-хвост максимального риска. Для произвольного большого числа некоррелированных перестановочных случайных величин Бернулли значение точной нижней грани верхней границы риска не может быть существенно меньше —!---
S'2 + 1
Но может ли сама эта верхняя граница риска быть больше? Нет. Дело вот в чем. Интуитивно попятно, что, если есть возможность увеличить дисперсию суммы, можно добавить побольше плотности вероятности хвосту, не изменяя среднее. Но, если нет возможности увеличивать дисперсию, т.е. если надо, так сказать, сэкономить на дисперсии, а плотности хвосту (пусть это будет собственный, т. е. правильный хвост) желательно все-таки добавить, остается только один путь: поместить всю добавляемую плотность на порог, поскольку порог — это ближайшая к среднему точка хвоста. И вообще, для заданной вероятности хвоста лучше всего экономить на дисперсии и поместить всю плотность в одну какую-нибудь точку этого хвоста, если только точка является допустимой.
Почти двухточечные решения для минимального риска
Теперь я намерен более строго сформулировать выводы предыдущего параграфа. Для этого введем такое понятие, как “почти двухточечные решения”. Почти двухточечным решением мы будем называть решение, которое приписывает некоторую плотность вероятности, не равную 1, точке, находящейся вблизи порога либо совпадающей с порогом 5, а всю остальную плотность вероятности двум не совпадающим точкам, которые лежат рядом друг с другом.
Пусть D = {£>*} обозначает множество двухточечных распределений, что для У к, при котором Dk eD, соответствующее распределение Dk таково, что его среднее равно /JSUM и приписывает некую положительную, но меньшую 79
Часть 1. Стандарты отклонении
единицы вероятность некой точке, отстоящей от среднего на 5 стандартных уклонений, а остальную плотность вероятности другой точке к > /JSUM . Обратите внимание, что Var\Dk ] монотонно возрастает по к. Заметим, что, если число п будет достаточно большим, величина Var[Dk ] будет меньше <т2им при малых значениях но больше сг^им при больших значениях к. Это значит, что такое, что Var[D}(] < < Var[Dj^x ], j -единственно. Тогда
некоторая смесь Dj и DJ+X могла бы иметь средним /JSUM > а дисперсией — с2им > те- Риск потерь, не превышающий 5 стандартных отклонений.
Почти двухточечные решения для максимального риска
Если мы обозначим величины j и j +1, выраженные в стандартных отклонениях, как У и sff соответственно, то / _ ~ _ 1/ .А обозначив /^SUM
соответствующие вероятности как q, q' и q” соответственно, получим, что ограничения на среднее и дисперсию равны:
qs 4- q's' 4- q\sf--—) = 0 ,
qs2 + q'(s')2 + q"(s'-—) = 1,
что, конечно, гораздо труднее для анализа, чем рассмотренный выше “чистый” двухточечный случай. Однако не все так плохо. Дело в том, что мы можем оценить структуру искомого решения, хотя и не имея его в явном виде.
Обозначим г = 1 ~ r , £ s . Тогда вышеприведенные
1 Я &SUM &SUM
ограничения на среднее и дисперсию будут следующими:
qs + (1 - q)s — О,
qs2 + (l-q)s2 =1 - 8,
что, очевидно, гораздо ближе к двухточечному случаю. Интересно, что произведенные нами преобразования легко интерпретировать статистически. Наше решение пытается уравновесить плотность вероятности, приходящуюся на 5, плотностью вероятности, приходящейся на точку s. Однако, поскольку точка s - это не целое число, наше решение распределяет эту балансирующую плотность не на s, а две точки s' и s" , являющиеся приближениями s. Необходимость использовать в искомом решении эти приближения влечет появление некой дополнительной дисперсии 8, которую необходимо “финансировать” из общей стандартизованной дисперсии, равной 1, что оставляет свободным для вариации только остаток этой стандартизованной дисперсии, равный 1 - 8.
80
3. Эти забавный хвосты риска
Если теперь сделать еще пару подстановок:
можно еще больше упростить выражения для ограничений на среднее и дисперсию:
qs + (1 — qys’ = 0,
qs2 + (1 -<7)(S")2 =1,
которые соответствуют уравнениям для двухточечного случая. Это значит, мы имеем решение:
s &SUM
1 _
<7 1 2 t ’
5 +l 5 +1-6Г
которое, конечно, неявное, поскольку 8 — функция q .
Хотя оно и неявное, но зато с его помощью можно определить некие явные границы, внутри которых это неизвестное q должно-таки находиться. Дело в том, что для \/q => 8 > 0 при произвольном наперед заданном и фиксированном q величина 8 достигает своего наибольшего значения по г, \ — q 1
равного ----— при г = —. Откуда следует, что
4бТя.'л/ 2
1 . 1 - £ 1 /1 1 - Я \ 1 /1 1 ч
—-----> q > ---(1----г3-) > ”3---О-----5--) *
+ 1 s + 1 s2 + 1 4cr2 м s + 1 4сг2
Последние неравенства, в свою очередь, означают, что, поскольку q не превосходит , для любой наперед заданной точности приближения всегда s + 1 можно подобрать настолько большое значение п , которое сделает эту величину 1
q равной величине —----- с этой самой точностью. Это значит, что q может
5+1
быть сколь угодно близким к .
S + 1
Несобственные хвосты
Лучше всего представлять себе несобственный хвост как дополнение собственного хвоста. Поэтому очевидно, что для того, чтобы минимизировать некий несобственный хвост, надо максимизировать соответствующий собственный хвост. Отсюда следует, что нижняя грань для вероятности
81
Ость 1. Стандарты отклаюдия_______________________________________
1 52 ~
несооственного 5-хвоста равна 1------------- и что к этой нижнеи грани
? + \ s2 +1
можно подойти сколь угодно близко с ростом п. Аналогично, верхняя грань для вероятности несобственного хвоста равна 1.
Пояснения
Хотя в общем случае целочисленность ограничений сильно осложняет поиск решения при малых значениях л/, бывает так, что целочисленность несущественна даже при небольших значениях п. Например, мы видели, что для сумм 16 некоррелированных, несмещенных, бернуллиевых случайных величин “чистые” двухточечные решения приложим для пороговых значений, равных 4, 6, 7, 9, 10 и 12, что соответствует событиям ±2, ±1 и ±0,5 стандартных уклонений. Значит в этом случае вероятности левых и правых 2, 1 и 0,5 хвостов могут достигать асимптотической верхней границы, несмотря на небольшие значения /г
Еще одна проблема с двухточечными распределениями, не лежащая на поверхности, состоит в том, что в принципе может существовать такое сочетание достаточно малых положительных и и 5, что вторая точка нашего двухточечного распределения, а именно s' ~ 1 / 5, вполне может означать какое-нибудь отрицательное число успехов или неуспехов. К сожалению, в этом случае какое бы то ни было двухточечное или почти двухточечное решение не смогут быть допустимым. Обсуждение этой проблемы мы отложим до следующей главы, где рассматриваются случаи ненулевых корреляций и малых п.
82
4. Еще о занимательных хвостах риска
С заседания по оценке риска Конвей вернулся непохожим на самого себя. Он казался взволнованным и даже несколько растрепанным. Устало подошел к столу и плюхнулся в кресло. Потом промямлил: “Лучше бы я туда не ходил... Мы пересматривали основные положения по кредитному риску. Начальство желает, чтобы мы закрыли на 100% риск потерь и на 99% риск неопределенности по времени. Мы обсуждали, является ли наше текущее покрытие риска потерь вплоть до трех стандартных уклонений от среднего достаточно осторожным решением и не будет ли оно сверх осторожным... Они захотели, чтобы я привел в связи с обсуждаемыми вопросами какие-нибудь соображения, основанные на математической статистике... Хорошо еще, что мы с тобой поговорили как раз перед этой встречей. А, может быть, мне было бы лучше и вовсе тебя сегодня не видеть...,- вдруг без всякой связи с предыдущими словами пробормотал Конвей, помолчал какое-то время и продолжил: — Во всяком случае, я сказал им, что правильные пределы в стандартных отклонениях могут быть от 2 до 5”.
“Иными словами, от 0 до 10, не так ли? — педантично заметил Девлин. — Ведь для некоррелированных бернуллиевых случайных величин нижний предел равен 0, а верхний — 9,95”.
6'Давай! Давай крути пируэты со своей статистикой, —- раздражен но подумал Конвей. — Как будто это хоть что-то решает!” Но вслух сказал примирительно: “Да знаю я, знаю... Но у меня просто духу не хватило сказать им это. Даже 5 и то очень много! При сохранении всех прочих параметров нам и так по-хорошему пришлось бы процентов на 40 уменьшить области риска... Директор по кредитным операциям просто взбесился, и мне пришлось использовать все свое красноречие, чтобы уговорить его отказаться от этой идеи..
Девлин оставался бесстрастным, по крайней мере, внешне: “Ты убедил его отказаться от представлений о пределах для 99%-ной уверенности? Прекрасно!”
Но Конвею было не до шуток: “Нет, я уговорил его повременить с моим увольнением! Мне удалось убедить его, что все эти изменения, — всего лишь теоретические построения и я не стану предлагать никаких радикальных изменений без того, чтобы все еще раз перепроверить”.
Девлин почувствовал тревогу и укол совести. Он вовсе не хотел подвести Конвея под неприятности. При этом, как Девлин понял с предельной ясностью, процесс зашел далеко и спустить его на тормозах уже не удастся. Положение Конвея осложнилось. Но вслух Девлин произнес: “И что же, по твоему мнению, нам следует предпринять?”
Конвей уныло смотрел в окно. Он, было, задумался, что можно предпринять
83
Часть 1, Стандарты отклонения
в пожарном порядке, но быстро понял, что всякая суета бесполезна: раз уж ты схватил тигра за хвост, отпускать его теперь опаснее, чем не отпускать. Вслух Конвей изрек: “Думать!”
“Ты хочешь сказать, что нам следует подумать о том, чтобы прекратить исследования?”, — со страхом спросил Девлин. Конечно, ему хотелось разобраться в поднятых им же вопросах, но принуждать к этому Конвея он, по совести, не мог.
“Хотел бы хотеть! — изрек Конвей глубокомысленно. — Но, нет, на самом деле я хочу знать, что происходит с хвостами риска, когда переменные становятся коррелированными. Насколько шире может стать область допустимых значений?”
Девлин облегченно вздохнул. Они по-прежнему оставались партнерами. Поэтому и ответил без своего обычного педантизма: “Она не может стать намного шире. Дело в том, что неравенство Чебышева устанавливает для событий, отстоящих от среднего на расстоянии, равном либо превышающем s стандартных уклонений, верхнюю границу, равную 1/s2. Иными словами, здесь имеются в виду оба собственных хвоста, и левый и правый, являющиеся зеркальными отображениями друг друга. А для любого из них эта верхняя граница не может быть выше ——”.
S2 +1
“Так значит, — Конвей произнес с досадой, — корреляция не влияет на хвостовой риск. Почему же ты не сказал мне об этом с самого начала?”
“Потому что это справедливо только для частного случая: если мы агрегируем по всем возможным невырожденным средним. Но для любого конкретного фиксированного среднего ненулевая корреляция сужает область допустимых значений по сравнению со случаем нулевой корреляции”.
У Конвея в голове все перемешалось, и он закричал: “Как сужает!? Разве хвосты не растут при росте корреляции?”
Но Девлин не обратил внимания на возбуждение Конвея: “В абсолютных единицах — да. Но в стандартных уклонениях — нет. Дело в том, что любая положительная корреляция ограничивает то число ,v стандартных уклонений, на которое могут отвалиться экстремально далекие от среднего события. А кроме того, может так случиться, что положительная корреляция заставит нас одновременно дать некую плотность и очень далеким влево, и очень далеким вправо суммам. Другими словами, для некоторого 5 и двухточечные, и почти двухточечные распределения останутся допустимыми. Отсюда и получаем полные интервалы от 0 до l/(s2+l) для собственных хвостов и от s2/(s2+l) до 1 для несобственных. Однако при s, близких к 0, экстремальные распределения начинают выглядеть как распределение №8, которое я тебе показывал для 16 случайных величин”.
Конвей вспомнил: “Это там, где весь положительный вес на каждом из концов и на пороге?”
“Точно. Я бы назвал распределения этого сорта три полярными. Обрати внимание, что, если мы имеем дело с три полярным распределением, положительная плотность на левом конце делает минимальный риск строго
84
4. Еще о занимательных хвостах риска
положительным и вынуждает нас поместить больше плотности вне хвоста, чтобы это уравновесить, ведь распределение-то должно остаться три полярным. Такая механика понижает верхнюю и повышает нижнюю границы, что сужает, конечно, область допустимых значений. Однако, если ни двухточечные, ни почти двухточечные распределения не являются допустимыми, самое лучшее, что нам остается — это три полярные распределения”.
“И как велика разница?”
“Зависит от других параметров вариационной задачи. Если при этом не требуется, чтобы и среднее, и корреляция были велики, ты можешь не думать об этой разнице. По крайней мере по отношению к тому типу хвостов, которым ты, скорее всего, станешь интересоваться. Например, если тебя интересуют области событий, отстоящих от среднего по меньшей мере на 2 стандартных уклонения, три полярные распределения не повлияют на область допустимых значений, если только не будет наложено дополнительное условие, что среднее должно быть не меньше 0,8. Но, если и среднее, и корреляция должны быть большими, нижняя и верхняя границы сильно поджимаются друг к другу. Взгляни-ка на эту диаграмму. Она отображает допустимые хвостовые риски, когда среднее и корреляция одновременно равны 0,9”.
Tail risks when mean = correlation = 0.9
-3.5 -3.0 -2.5 -2.0 -1.5 -1.0 -0.5 0.0
Standard deviations from mean
Assumes large finite number of exchangeable Bernoulli variables.
Хвостовые риски для бернуллиевых сумм, когда среднее и корреляции равны 0,9.
По горизонтальной оси откладывается число стандартных уклонений, соответствующее расстоянию от среднего. По вертикальной оси откладывается соответствующая интегральная вероятность. Заметьте, что игра предполагает конечное, хоть и большое количество перестановочных некоррелированных бернуллиевых случайных величин. Серая область определяет допустимые значения в отсутствие независимости в совокупности. Черная линия определяет допустимые значения в предположении независимости в совокупности.
85
Часть 1. Стандарты отклонении
Конвей какое-то время рассматривал рисунок, стараясь понять его смысл, потом, видимо ничего не поняв, спросил Девлина раздраженно: “Как, черт возьми, вы все это насчитали?’*
Девлин предпочел опять не заметить раздражения Конвея: “Я рассматривал двух- и трехточечные распределения, которые представляли бы собой экстремальные решения при различных ограничениях на допустимость. Однако я предлагаю пока оставить в стороне математику, а то мы в ней увязнем, и продолжить обсуждение 'на пальцах’, т.е. сосредоточиться на выводах. Подумай, что тебе кажется самым неожиданным на этом рисунке, кроме, естественно, самой формы допустимой области?”
На этот раз Конвей ответил мгновенно: “Резкое отличие допустимой области от тех оценок, которые дает стандартная теория ‘среднего и дисперсии’. Например, шансы хвоста, отстоящего на 2,5 стандартных уклонений, лежат в пределах от 5 до 11%, что резко отличается от 1%, который дает предположение о том, что наша сумма составлена из независимых случайных величин”.
“Верно! Мне это тоже бросилось в глаза прежде всего. Ведь за исключением всего-то двух коротеньких интервалов аппроксимация методом среднего и дисперсии целиком лежат вне нашего множества допустимых значений”.
“Насколько типичен этот пример?”
“Такие вещи встречаются не часто. Ведь надо, чтобы и среднее, и корреляция были велики”.
“Ну, слава богу! Не все, значит, то, что, я считал твердо знаю, является полной чушью. Но я по-прежнему озадачен твоим заявлением о том, что область допустимых значений уже для любой ненулевой корреляции по сравнению с нулевой ... Разве не должна отрицательная корреляция расширять область допустимых значений, раз уж положительная корреляция ее расширяет?”
“Для любого фиксированного среднего и некоего конечного допустимого числа случайных величин это так и есть, но геометрия ограничивает сверху максимальное число случайных величин с общей отрицательной корреляцией. Дело в том, что в противном случае наши суммы имели бы отрицательную дисперсию. А при ограниченном числе случайных величин целочисленность ограничений начинает играть существенную роль и сильно сокращает область допустимых значений для событий, далеко отстоящих от среднего в стандартных уклонениях”.
В тот момент какое-то смутное беспокойство зашевелилось в душе, и Конвей полуосознанно вытащил из-под других бумаг гистограммы Девлина для хвостов 16 случайных величин, стал снова их внимательно изучать, а насмотревшись, проворчал: “Эти твои экстремальные распределения такие вычурные... их не встретишь на практике. Они просто невозможны. Или ты специально придумал эти распределения, чтобы они были под стать распределению ‘без нечетных решек в тройках’, а?”
86
4-Ещ, о о эаним а т ильных х в остах ри ска
Девлин улыбнулся: “А как насчет простого и вполне вероятного объяснения для распределения №4? Допустим, что Департамент торговли нашего банка владеет 16 бинарными опционами 16 компаний, занимающимся электронными сетями. Допустим, что с вероятностью 1 из этих 16 компаний будут выбраны несколько, которые создадут новый отраслевой стандарт, причем с вероятностью 0,8 это будут 9 каких-то компаний, а с вероятностью 0,2 — 4 каких-то компании. Допустим, наконец, что все сочетания из 16 компаний по 9 равновероятны, как и все сочетания по 4. Каково?”
То ли Конвей не понял смысла последних слов Девлина, то ли они на него непроизвели впечатления. Во всяком случае, он остался при своем мнении: “Так, значит, ты признаешь, что это распределение практически невозможно. Более того, точно так же, как это имеет место в сценарии 4 без нечетных решек в тройках’, эти случайные величины нельзя рассматривать как случайные выборки из какого-то более широкого перестановочного множества. Скажи-ка, что будет, если исключить из рассмотрения такие треугольники вероятностей, к которым нельзя добавить еще одну строку снизу?”
“Это, конечно, сузит область допустимых значений и сблизит границы. Кстати, мы это уже наблюдали. Чем больше мы добавляли строк к моим треугольникам, тем уже становились пределы допустимых значений на нижнем уровне”.
Но Конвей, казалось, добивался чего-то более конкретного и развивал какую-то четкую идею: “Теперь скажи мне прямо, добавление новых строк сильно сжимает область допустимых значений или только слегка?”
Девлин должен был признаться, что вопрос Конвея поставил его в тупик, по крайней мере на данный момент: “Сходу я этого сказать не могу. Мне надо поработать над этим”.
“Ну так и работай. Никто тебя не подгоняет. Но я хочу знать, что происходит с границами области допустимых значений, когда мы рассматриваем только те распределения, которые можно расширить добавлением большего числа строк. Например, каково множество допустимых значений для суммы 16 перестановочных случайных бернуллиевых величин, выбранных из некого множества, состоящего из 32 перестановочных случайных бернуллиевых величин?”
У Девлина опять не было ответа, поэтому он попытался подвергнуть сомнению смысл самого вопроса: “Зачем это знать? Ведь в конце концов, если мы возьмем 32 случайных величины и решим задачу для них, мы все равно получим именно ту широкую область допустимых значений, которую только что рассматривали для хвостовых рисков. Зачем ограничивать себя рассмотрением результатов, усредненных по подмножествам равного веса, состоящим из 16 случайных величин?”
Но Конвей почувствовал свою правоту и упрямо гнул свое: “Послушай, Девлин. Я, ведь, не утверждаю, что твои результаты не верны или вообще не имеют смысла. Напротив, я признаю, что они показывают, что теоретически
87
Часть 1. Стандарты отклонения ______________
может произойти, даже если активы перестановочны и некоррелированы. Однако, я уверен, что расширяемые распределения ближе, так сказать, к коренному явлению, породившему все наши задачи. Например, вообрази, что департамент производных ценных бумаг нашего банка приобрел множество несмещенных, некоррелированных бинарных опционов и что никому из нас не известно о каком бы то ни было конкретном событии, связывающем эти опционы. Никаких, словом^ грядущих стандартов в сетевой обработке данных или чего-либо подобного в обозримом будущем. Ну, и как ты собираешься это моделировать?”
Девлин сказал то, что первым пришло на ум: “Тогда я предложил бы считать все эти опционы взаимозаменяемыми не только друг с другом, но и со всеми другими существующими несмещенными некоррелированными бинарными опционами. В пределе мы даже могли бы считать, что наши опционы выбраны из некого бесконечного набора перестановочных бернуллиевых случайных величин”.
“Вот и прекрасно. Ты разберешься с этим?”
“Я попробую. Но мне придется разработать некий новый аппарат... Как я могу добавлять бесконечные строки к моим треугольникам?”
“Маэстро, не сомневаюсь, что тебе эта задача по зубам! — сказал Конвей весело, а про себя подумал: По крайней мере мне бы очень этого хотелось”.
Давайте, пока Девлин борется с бесконечностью, проверим справедливость его заявлений относительно хвостовых рисков, связанных с суммами коррелированных конечно перестановочных бернуллиевых случайных величин. В этой связи я намерен показать, что двухточечные, почти двухточечные и три полярные распределения определяют область допустимых значений для хвостового риска. Потом я подсчитаю те величины, которые определяют границы этой области допустимых значений.
Здесь я вновь должен сообщить одну хорошую и одну плохую новость. Плохо то, что математика будет еще более сложной, чем в предыдущей главе, а хорошо то, что кроме границ экстремального интервала от 0 до 1/(52 + 1) вам нет никакой необходимости запоминать какие-либо еще числа или формулы. Положитесь на свою интуицию и расслабьтесь: того, что останется в голове, будет достаточно.
Связь с неравенством Чебышева
Неравенство Чебышева показывает, что вероятность попасть в положительный или отрицательный 5-хвост не превышает I/52 . Доказать его просто. Пусть z обозначает такой исход, который, будучи измерен в стандартных уклонениях, находится левее среднего. Пусть p(z) обозначает вероятность события z (z — стандартизованная случайная величина). Тогда справедлива следующая цепочка рассуждений:
88
4. Еще о занимательных хвостах риска
где последнее равенство следует из определения стандартного уклонения.
Это распределение, для которого имеет место строгое равенство:
p(s) = p(-s~) =
2s s
всех остальных распределений
неравенство Чебышева — строгое. Аналогичный подход можно использовать, чтобы определить границы риска, связанного с одним-единственным 5-хвостом:
Поскольку первый момент z равен нулю, а второй момент z равен 1, последнее выражение можно переписать так:
2 1 ( 2 1V ( 1 1
5 +1 >pr[z> у} 5 + •> откуда следует, что Pr\z > 5) < —5-.
s2 \ S ) 5+1
Из последнего неравенства ясно, что, даже если допустить корреляцию, возможности выйти за те границы, которые мы раньше определили для сумм некоррелированных бернуллиевых случайных величин, нет. Наоборот, эти границы могут стать значительно ближе друг к другу, если только никакие двухточечные распределения по точкам 5 и — 1/s нельзя будет считать ни допустимыми, ни почти допустимыми.
Условная оптимизация
Для область допустимых значений определяется максимальным и
минимальным хвостовыми рисками, где минимум и максимум ищется по множеству всех дискретных распределений по п + 1 точкам, таким что каждое из этих распределений имеет среднее и дисперсию, равными некоторым наперед заданным числам. Отсюда следует, что вычислить область допустимых значений можно с помощью традиционного аппарата условной оптимизации и вариационного исчисления. Определим искомый левый хвост максимальным числом Т успехов, которое все еще квалифицируется как событие хвоста (здесь Т соответствует числу 5 из определения 5-хвоста, но измеряется в абсолютных единицах, а не в стандартных уклонениях). Обозначим далее через 1Т некую индикаторную случайную величину, которая принимает значение 1 на хвосте и значение 0 вне хвоста, а через рк — вероятность события, состоящего в появлении ровно к успехов. Тогда вероятность произвольного события хвоста, а именно она является нашей целевой функцией, которую мы намерены максимизировать и/или минимизировать, можно записать так:
Pr{k<T}^Pll^PkITW-к-Л~) к~<)
89
Часть 1. Стандарты отклонения____________________________________________
Вот наши три ограничения, а именно ограничение на вероятность достоверного события и на первый и второй моменты соответственно:
52 Рк = 1; 52 — PsUM ^52^ Рк = PsUM + °"SUM '
А=0 А'=0 А=0
Еще есть п + 1 ограничений на неотрицательность вероятностей: рк > OVk е [0; п\ .
Теперь из нашей целевой функции и ограничений следует построить лагранжиан:
Л ““ 52 Рк^Т (^) +" ^0 (52 Рк “ D + t^'.Pkk “ PsUm) +" ^2 (52 Рк PsUM ~ ^SUm) 52 к Рк »
А=0 А=0 А=0 А=0 А=0
где весовые коэффициенты {rm; m = 0,2} и {у к; к = 0, п} принято называть множителями Лагранжа. В данном случае множители Лагранжа имеют содержательную экономическую интерпретацию теневых цен. Дело в том, что в точке оптимума каждый из них измеряет так называемую “цену шанса” или уменьшение оптимального значения целевой функции от маржинального ужесточения соответствующего ограничения.
Условия Куна — Такера
В соответствии с теоремой Куна — Такера в точке условного экстремума все частные производные лагранжиана по переменным решения обязаны быть равными нулю. Более того, каждый из коэффициентов у к, к = 1, гг, соответствующих ограничениям на неотрицательность вероятностей, обязан отвечать так называемому условию “дополнительной нежесткости”, состоящему в том, что, во-первых, vkQ — G\fk^ = 1, /7, если ограничение рк >0 не является жестким, т. е. не обращается в ноль в точке экстремума, а, во-вторых, для V&| : ~ 0 знак соответствующего коэффициента ул должен быть таким, что
элемент vk рк будет штрафовать лагранжиан за нарушение соответствующего неравенства. Совместно все вышеперечисленные условия образуют так называемые условия Куна — Такера для точки условного экстремума.
А для нашей вариационной задачи условиями Куна — Такера как раз являются три ограничения на моменты плюс условия, которые должны выполняться для всех целых Аг между Ойл:
Т / 1 \ . 9
0 = -— = 1т(к) + т0+т1к + т2к + vk, дРк
(УкРк =0)<£(п <0),
если наша вариационная задача является задачей минимизации, или
90
4. Еще в занимательных хввстах риска
О =-— = 1т(к) + т0 +Т}к + Т2к2 +vk, аРк
(УкРк =0)<&(Л7 ^О)>
если наша вариационная задача является задачей максимизации.
Оптимальные распределения для задачи максимизации
Теперь я намерен применить условия Куна — Такера для определения форм оптимальных распределений. Начнем с максимизации. Необходимые условия, налагаемые на множители Лагранжа для произвольного допустимого к, в этом случае равны:
- т0 — т\к — v2k2 = Q(ky
(Л >0)&(0<£<Т) (РА=О)&(О<Л<Т) (рк > 0) & (Т < к < 7?) (рк = 0)&(Т<к<п)
Обратите внимание, что квадратичная функция заключена в некотором ограниченном пространстве и, для того чтобы генерировать какое-либо допустимое распределение, обязана касаться границ этого пространства, по крайней мере, в двух точках. Если вы возьмете карандаш и нарисуете несколько графиков, то быстро убедитесь, к своему удовольствию, что не существует других способов добиться вышесказанного, кроме тех трех, что я изобразил ниже. (Конечно, можно было бы все это доказать строго, но уж больно скучное это доказательство.)
Feasible shapes for Q in maximization
Допустимые конфигурации для Q в задаче максимизации
Обратите внимание, что график слева соответствует некому двухточечному или почти двухточечному распределению. Он отвечает некому
допустимому случаю, когда порог лежит значительно левее среднего pSUM -Поскольку Q — выпуклое множество, т2 обязано быть отрицательным, чтобы
91
Часть 1. Стандарты отклонения
как можно больше увеличить дисперсию и, как следствие, получить возможность положить на точку Ткак можно большую плотность вероятности.
Средний график соответствует случаю, когда мы помещаем всю плотность в хвост. Это допустимо только в том случае, когда среднее превосходит Г, тогда одно из допустимых распределений будет устроено таким образом, что помещает всю плотность на порог Т и еще либо на одну, либо на две соседних точки. Поскольку теперь Q — прямая, т2 обязано быть нулем, что означает, что одним лишь увеличением дисперсии нельзя сколько-нибудь нарастить хвост.
Правый график соответствует три полярному распределению. Он соответствует тому случаю, когда Т лежит левее среднего, но близко к нему. Поскольку теперь Q представляет собой вогнутое множество, любое увеличение дисперсии будет означать перенос большей плотности на две крайние точки распределения от порога 7", что, в свою очередь, будет означать сжатие хвоста как единого целого.
Оптимальные распределения для задачи минимизации
Максимизация вероятностной меры Pr{k < т} произвольного левого хвоста эквивалентна минимизации вероятностной меры Рг{Л>Г + 1} дополнительного правого хвоста. Более того, любой правый хвост эквивалентен какому-нибудь левому хвосту, если при этом поменять местами определения успеха и неуспеха. Это значит, что результаты, полученные для задачи максимизации, определяют решение задачи минимизации при одном маленьком, но важном изменении: мы должны помещать все плотность вероятности внутри хвоста в точку Г, а нс снаружи хвоста в точку Г +1. Тогда мы немедленно получим три следующих решения:
• Т слева: поместить положительную вероятность только на Т и еще или на одну, или на две соседние точки справа; если при этом дисперсия уменьшится, вес хвоста тоже уменьшится;
• Т рядом с /лSVm : поместить положительную вероятность только на О, Г и п\ если дисперсия уменьшится, вес хвоста возрастет;
• Т справа: поместить всю положительную вероятность только на Г и еще или на одну, или на две соседних точки слева либо применить любое другое решение, когда весь вес сидит в хвосте; если дисперсия уменьшится, вес хвоста останется равным единице.
Интуитивная интерпретация результатов
Из всех распределений таких, что их среднее равно заданному значению, хвостовой риск можно максимизировать, если одной из точек этого распределения является Г, и минимизировать, если одной из точек этого распределения будет Т + 1. При этом, если увеличение дисперсии может двинуть целевую функцию в нужном направлении, наиболее рациональным применением
92
4. Еще о занимательных хвостах риска
дополнительной дисперсии будет поместить всю ту плотность, которая уже не помещается на порог, на одну или на пару целочисленных соседних с порогом точек. Но, если дополнительная дисперсия, наоборот, будет двигать целевую функцию в ненужном направлении, следует погасить как можно больше дисперсии тем, что разбить всю плотность, не помещенную па порог, между двумя экстремальными значениями.
Взаимоисключающий характер типов решений
Оказывается, что для произвольного фиксированного набора значений //, р и п допустимым будет ровно одно двухточечное, почти двухточечное или три полярное распределение. Здесь я тоже не дам строгого математического доказательства этого факта, а вместо этого приведу интуитивно более понятную геометрическую иллюстрацию.
Итак, допустим, что по оси абсцисс координатной плоскости мы откладываем значение Л, а по оси ординат той же координатной плоскости величину k2\/k^N} . Обозначим через Lk точку (Л,Л2). Обозначим далее через L множество {Lk к = 0,оо} . Если теперь предположить, что сумме наших случайных величин приписано распределение вероятностей к — 0,п}, первый и второй моменты этого распределения взаимнооднозначно к-п к=п п
отображаются точкой М= крк рк) — . Это значит, что Мявляется
А'=0 Л--О А=0
выпуклой комбинацией (неотрицательным средневзвешенным значением) различных элементов квадранта L и, следовательно, должна лежать где-то внутри выпуклой оболочки этих элементов, которую я обозначу как Соп\’(к) . Геометрически L — это наименьшее множество, содержащее и Д и все отрезки прямых, соединяющих различные пары точек в Conv(L) .
Теперь проведем пунктирные линии между парами точек LT hL, для некого заданного порога Т и всех возможных значений к, не являющихся соседними с порогом. Ясно, что пунктирные линии LTLk разделяют Conv(L) на п — 2 смежных треугольников с общей вершиной LT. Поскольку L — это выпуклое множество, каждое значение Lk лежит строго на границе Conv(L) , и, следовательно, внутренности этих треугольников не пересекаются. Отсюда следует, что:
• произвольное двухточечное распределение является допустимым при заданных значениях Тик тогда и только тогда, когда точка Мтежит строго между Lr и Lk\
• произвольное почти двухточечное распределение является допустимым при заданных значениях Т, к и к + 1 тогда и только тогда, когда точка М лежит
93
Петь 1. стандарты отклонения
внутри треугольника LTLkLkVi;
произвольное строго три полярное распределение является допустимым при заданных значениях Т и п тогда и только тогда, когда точка М лежит внутри треугольника L^LtlLT;
если точка М лежит на границе Conv(L) , существует ровно одно допустимое распределение, причем такое, что оно размещает всю ненулевую плотность вероятности в одной-единственной точке к и либо в двух соседних точках к и к + 1, либо в двух крайних точках п и 0.
Convex huh (feasible moment-pairs) for n = 5
25 !
-Ф5
7, s . Convex hull of L
• L for л-5
--- Partitions for Г=1
0 *0 0
2 3
First moment
Выпуклая оболочка (допустимые пары моментов) для п — 5
Для того чтобы облегчить дальнейшие теоретические построения, мне придется несколько расширить определение вырожденного распределения, чтобы под него подходили все распределения, лежащие на границе Conv(L) .
Три полярные решения
Теперь надо немного потерпеть и изучить несколько нудных, трудоемких, но необходимых выкладок. Ну, если вы сильно устали или вам так скучно, что читать дальше невмоготу, пропустите этот текст и переходите сразу к выводам в конце главы.
Итак, пусть величины q0 и qn обозначают те вероятностные веса, которые размещены, соответственно, в точках Т, п и 0 . Ограничения среднего и дисперсии тогда таковы:
Tq + nqn = ^SUM,
2 „ 2 2 2
T q + n qn — + •
94
4. Eiub а занимательных хввстах риска
Ясно, что эти ограничения представляют собой систему линейных уравнений по q и qn , которая имеет единственное решение:
^PsUM PsUM & SUM .
Т\п — Т)
Яп
PsUM + &SUM TjJ,SuM п(п — Т)
А поскольку qQ = 1 — q — qn , из вышеприведенного решения системы
линейных уравнений находим решение для qQ :
п _ Psum & sum ~(Т + rT)pS!JM чо “
Тп
Для того чтобы представить полученное распределение вероятностей в стандартных уклонениях, надо сделать две вещи, а именно: во-первых, подставить Psum ~ sctsum вместо Т, а во-вторых, сделать замену
2^2 ~ 1-Р
стандартизации: pSUM ~пр и &SUM - рп р(\ - р) , где р =-h р . В
п
результате нехитрых преобразований получаем:
=_____(1-р)7аО~А)____=____(1-Р)УаО~А)___,
q (Та-а))(71-а С1 - р^ЭТаС1 - а) + (2 а - 1)ТЭ
q„ = а • ( ----7=-) = а
д/1- A +S-VAA
(1-р)а(»-а)
1 - А + 5ТрР(1-Р)
При этом, если некое три полярное распределение допустимо, вероятность произвольного л-хвоста будет находиться в промежутке от q^ до + q .
Область допустимых решений для три полярных решений
Ясно, что произвольное строго три полярное распределение допустимо тогда и только тогда, когда все три вероятности, определяющие это распределение, будут строго положительны. Отсюда ясно, что при максимизации хвостового риска: _2 2
и______Zsum_<t < и . U SUM
Psum _ РSUM
п ~ Psum Hsum
Аналогичный результат справедлив и при минимизации хвостового риска, надо только заменить Т на Т + 1. Если теперь перейти от абсолютных единиц к стандартным уклонениям и заменить на 5 на Т или Т + 1 в зависимости от того, 95
Часть 1. Стандарты вткпвнвния
рассматриваем ли мы задачу максимизации или минимизации хвостового риска, то получим такие ограничения:
IpG-p) с , I рр
V А
Maximum s for tripolar distribution
Максимальное s для три полярного распределения
Событие, состоящее в том, что некое три полярное распределение не является допустимым, на самом деле означает, что это три полярное распределение таково, что по какую-то сторону от порога Т (по левую или по правую) совсем нет никакой плотности вероятности, т.е там ноль вероятностного веса. Поэтому ту область допустимых значений, которая определяется только что рассмотренными ограничениями, логично назвать “областью ненулевых хвостов”. График, приведенный на рис. 12, показывает верхнюю границу этой области ненулевых хвостов как набор линий уровня в плоскости /л и р . Ясно, что для того, чтобы эта граница проходила низко, надо, чтобы или р или р было мало.
Двухточечные и почти двухточечные решения
В предыдущей главе мы показали, что для произвольного s-хвоста всегда найдется такое строго двухточечное решение для сумм некоррелированных
• 1
случайных величин, что на нем будет достигнута вероятность —-. Если же мы
s2 +1
будем рассматривать почти двухточечные решения, аналогичная предельная вероятность будет равна q - —---, где г = —-———, аг — это такое число
s +1 — £ °-sum
ГЛ11 '
из интервала [U;lJ, которое превращает в целое s =-I-----. Существенно,
5 ^SUM
96
4. Ещв о эвниматвльных хввстах риска
что все эти равенства остаются в силе даже в том случае, когда составляющие случайные величины становятся коррелированными. Отсюда следует, что максимальный риск левого 5-хвоста всегда меньше для почти двухточечных решений, чем для строго двухточечных. Меныпе-то он меньше, но на практике разница очень невелика, что в абсолютных, что в относительных единицах (т.е. когда сумма случайных величин измеряется и в абсолютной шкале, и в шкале стандартных уклонений). Исключения из этого правила возникают только в одном случае, а именно, когда наша сумма бернуллиевых случайных величин имеет почти вырожденное распределение. Эта почти вырожденность может состоять в том, что /л будет очень близко к 0 или 1, или/и в том, что п очень мало, или/и в том, что р — большое по модулю отрицательное число.
Очевидно, что аналогичные соображения справедливы для минимального риска и несобственных (правых) хвостов, поскольку минимальный риск просто равен единице минус максимальный риск собственного (левого) хвоста. А
1
дальше надо просто заменить s на — , что приведет к тому, что вероятность
1 1 s2
—---- превратится в —---= -----.
52+1 5~2 +1 s2 +1
Область допустимых значений для двухточечных и почти двухточечных решений
Для того чтобы произвольное чисто двухточечное решение было допустимым, необходимо, чтобы две его точки, а именно 5 и / = -—, лежали между 0 и п (см. определение двухточечного решения в предыдущей главе). Отсюда для левых (собственных) и правых (несобственных) хвостов возникают следующие ограничения:
О <---= / - < s < --—--— для левых хвостов
s„ VpG-^)
и, соответственно,
— <0 для правых (несобственных)
*0
хвостов.
1 1
Тогда интервал между-------и-------и есть в точности область ненулевых
So s„
хвостов.
Наконец, чисто двухточечное решение обязано удовлетворять ограничениям целочисленности. Это значит, что для достижения максимального хвостового риска следует выбирать 5 соответствующим наибольшему целому Т в
97
Часть 1. Стандарты отклонения
хвосте, т.е. в этом случае 5т должно соответствовать
И SUM * а) пр — Т
Аналогично для достижения минимального хвостового риска на двухточечных решениях следует так выбирать значение s, чтобы оно соответствовало наименьшему целому Т + 1, лежащему вне хвоста. Поэтому для того, чтобы определить надо просто поставить Т + 1 вместо Т в вышеприведенной формуле.
Наконец, если окажется, что Т' — не целое число и если при этом все остальные ограничения будут выполнены, то придется обратиться к почти двухточечным решениям. Дело в том, что, если поставить такой эксперимент, что параметры наших случайных величин генерируются неким случайным механизмом, то окажется^ что по сравнению с чистыми двухточечными решениями почти двухточечные решения приложим в огромном большинстве случаев. Оно и понятно, ведь легко представить, что для неких р и // величина Т' вполне может оказаться нецелой для любых возможных значений п, что, конечно, вообще исключает для этих р и р применение строго двухточечных решений. Тогда, очевидно, надо переходить к почти двухточечным.
Максимальные значения нижней границы хвостового риска
Теперь можно обобщить максимальные нижние границы хвостового риска (те значения, выше которых нижняя граница риска быть не может) в следующем виде, имея в виду, что Т означает максимальное целое число, все еще находящееся в хвосте:
2
О, если Т + 1 < nSUM-;
п “ Msum
п(Т + 1) + pZslJM +
^SUM (Т + 1 + м)Р$им
, если
п(Т +1)
2 2
—5^^ < т +1 < ;
п Msum №sum
(Т + 1- р )2
---------—- плюс малое положительное число обычно, если
(Т + 1 — pSUM ) + &sum
2
pSUM+-^<T + \<n-
Msum
1, если T > п .
98
А. Еще а занимательных хвастэх риска
Минимальные значения верхней границы хвостового риска
Аналогично можно обобщить минимальные верхние границы хвостового риска (те значения, ниже которых верхняя граница риска быть не может) в следующем виде:
• 0, если Т < 0;
/ rri х 2
• ---------—-— минус малое положительное число обычно, если
(Т ~ Psum ) + &SUM
' < // — SUM .
— PSUM >
n ” №sum
№sum + & SUM ~ ____ . & SUM
>eCJIH Hsum
n ~ № SUM
2
Vsum + P-SUM
п(п — Т)
^2
1, если Т > pSUM +
№sum
Область допустимых значений для случая неограниченности п
Используя те формулы, которые мы вывели ранее для преобразований в шкале стандартных уклонений и которые применяют в качестве составляющих величин , /5 > и> собственно, стандартное уклонение, выраженное величиной Т или Т 4-1, можно преобразовать все вышеприведенные величины. При этом, если допустить, что п может неограниченно возрастать, что, конечно, исключает возможность появления отрицательного р , область допустимых значений для х-хвостов станет такой:
О, если 5
(1-Р- }
Р - SyJppO. - р) I-p + s^pp(l-р)
I рр . „. _ \p<X-p) . \ p
[-A- ’1] ’ ec™ - 5 > ;
1 + 5 у p V pp
99
Часть 1. Стандарты аткланания
1, если s<~
Границы для того случая, когда может меняться
Те границы, которые мы вывели выше, применимы только в том случае, когда величины р и р фиксированы. Но, если допустить, что р может
I р , /1-^
меняться, то /.— и/ил и j------ может стать или неограниченно малой, или
\ /л
неограниченно большой величиной. Тогда границы будут определяться независимо от р и двухточечных распределений, что возвращает нас обратно к некоррелированному случаю. В этом случае областью допустимых значений 1 s2
будет [0,------т] для произвольного левого хвоста и [---------- ,1] для
1 + 5 1 + 5"
произвольного правого хвоста.
100
5. Воссоздание корреляции
Поскольку на следующее утро Девлин не пришел в офис Конвея, после обеда Конвей сам отправился на поиски Девлина. Поиски продолжались недолго. “Как дела с бесконечными треугольниками?”,- первым делом в слегка шутливом тоне спросил Конвей. “Продвигаются, но с конечной, к сожалению, скоростью”,- ответил Девлин тоже, вроде бы, с намеком на шутку,- “Пока что я не могу сказать, что я с ними полностью разобрался. Но кое-какой прогресс, безусловно, имеется. Во всяком случае, по крайней мере, на один из ваших вопросов я уже могу ответить”.
“О каком вопросе речь?”
“Ну, помните, Вы спросили меня, сильно или нет исключение из рассмотрения тех распределений, которые нельзя продолжить добавлением следующих строк в треугольник снизу, сужает допустимую область хвостового риска. Так вот, я обнаружил, что в случае несмещенной некоррелированной игры сужение очень значительное”.
“Ну, слава богу! Кажется, после обеда пошли хорошие новости..подумал про себя Конвей, но вслух сказал другое, как всегда: “Можете привести конкретный пример?”
“Я анализировал экстремальные хвосты различных наборов из 16-ти случайных величин при условии, что каждая случайная величина каждого рассматриваемого набора выбиралась без возвращения из множества, состоящего из 32-х бернуллиевых некоррелированных случайных величин. Другими словами, я просто начал с нашей первоначальной некоррелированной несмещенной бернуллиевой игры на 16-ти случайных величинах и отсеял те распределения, которые нельзя было бы продолжить до игры на 32-х случайных величинах. Оказалось, что границы допустимых распределений гораздо плотнее прилегают к нашему родному биномиальному распределению, по сравнению с тем случаем, когда никакого дополнительного сита на распределения 16-ти случайных величин не налагалось. Вот, взгляните на это...”,-с этими словами Девлин вызвал на экран своего монитора соответствующий график.
Конвей ликовал, по крайней мере, в душе: “Слава тебе, Господи! Вы уж было совсем заставили меня поверить, что хвостовые риски и, правда, подобны щупальцам огромного спрута. Но теперь я вижу, что главные риски таки пришиты к биномиальной модели. Значит мы можем применять все наши привычные случаи в общем случае!”
“Вы и вправду так думаете? Я, все-таки, не стал бы делать столь категоричных заявлений. Начнем с того, что для меня вовсе не очевидно, что этот график ‘пришивает’, как Вы изволили выразиться, хвостовой риск к биномиальной модели. Да, вот, взять хоть область изменения хвостового риска. Она остается значительной. Ведь худший случай дает 29-процентный шанс того, что произойдет событие аж четырех стандартных уклонений”.
101
Часть 1. Стандарты отклонения
Extreme tail risks for 16 unbiased, uncorrelated Bernoulli variables
Maximum successes
Экстремальные хвостовые риски для 16-ти несмещенных, некоррелированных, бернуллиевых случайных величин.
Extreme tail risks for 16 unbiased, uncorrelated Bernoulli variables
Экстремальные хвостовые риски для 16-ти несмещенных, некоррелированных, бернуллиевых случайных величин.
102
б.Весс аз д ян ин корреляции
Эйфория у Конвея, конечно, прошла, но он, как всегда, цеплялся за удобную благополучную картину мира: “Ну и что ж, что существенна? Она еще сожмется, если добавить случайных величин, наверняка!”
“Ваша правда. Область изменения, и правда, сожмется. Вот, посмотрите, еще одна схемочка. Она имеет, так сказать, обобщающий характер. Речь идет о хвостовом риске для 16-ти штук несмещенных, некоррелированных, бернуллиевых, перестановочных случайных величин, выбираемых из конечного множества, состоящего из последовательно 16, 32 и 48 таких случайных величин. Интерес представляли хвостовые риски двух и более стандартных уклонений”.
Конвею графики определенно понравились: “Так, значит Вы, все-таки, согласны. Та гора, которую вы мне вчера нарисовали, теперь сжалась до размеров холмика над кротовой норой, не так ли?”
Последние слова Конвея показались Девлину незаслуженной обидой: “Нет, я не согласен! Несмотря на определенное сжатие области допустимых значений даже в рассматриваемом примере хвостовые риски, все равно, могут оставаться очень большими, даже при увеличении генеральной совокупности”.
“А если генеральная совокупность вообще не ограничена?”
“Ответа на этот вопрос я пока не знаю. Сейчас могу только сделать предположение, впрочем, лежащее на поверхности, о том, что область допустимых значений должна сократиться до биномиального распределения. Но не спешите радоваться. Дело в том, что, даже если это предположение удастся доказать, его практическое значение, по всей видимости, не будет сколько-нибудь существенным, поскольку неограниченная перестановочность- это очень сильное ограничение, которое в практическом применении методов анализа риска всегда нарушается, так как никогда не имеет места в практике инвестирования. Вот, например, неограниченная перестановочность не разрешает отрицательных корреляций. Но, даже если мы все-таки примем это допущение, мы, все равно, не избавимся от экстремально небиномиальных хвостов”.
“Бедный Девлин!”,- подумал Конвей о коллеге с жалостью,- “Он так привязан к этой задаче, что не хочет решить ее, чтобы, не дай бог, не расстаться с ней...”. Однако, вслух Конвей, как всегда, сказал другое: “Вы, Девлин, хотя бы себя послушайте. Вы только что признали, что увеличение масштаба перестановочности сжимает, а, возможно, и вообще сводит на нет абнормальные хвосты в случае некоррелированных случайных величин. А вчера Вы внедряли мне в подкорку идею, что для коррелированных случайных величин границы риска имеют тенденцию быть уже, по сравнению с аналогичным случаем, но некоррелированными случайными величинами. Сопоставьте эти две ваших идеи. Разве неясно, куда мы в итоге придем? В бесконечность и даже дальше!”. С последними словами Конвей посмотрел в лицо Девлина в ожидании отклика на его удачную, как ему показалось, шутку.
Но Девлин, почему-то, шутки не понял и спросил туповато: “Как это Вы можете пойти дальше бесконечности?”.
Пришлось пояснять, тоже, впрочем, не вполне грациозно: “Это была шутка.
103
Часть 1. Стандарты отклонония_____________________________________________
Точнее говоря, слова одного персонажа из популярного фильма. Это- комедия, вообще-то. Вам, Девлин, тоже очень не помешает посмотреть этот фильм как-нибудь”.
Девлин был смущен, но старался не подать виду: “Кино? Может быть... Последний фильм, который я посмотрел, был ‘Титаник’, и там сюжет был слишком уж надуманный. Те двое ребят, которые все перегибались через ограждения бортов на носу корабля... они просто выглядели нереально... Ну, кроме шуток, я так понимаю, что Вы намекаете, что неограниченная перестановочность покончит-таки с теми распределениями, у которых слишком толстые хвосты, не так ли?”.
“А Вы, что же, думаете по-другому?”.
“Я не знаю. Может да, а может и нет. Но хотел бы напомнить, что мои результаты относительно соотношения границ риска в коррелированном и некоррелированном случае имеют отношение только к нижней строке моих треугольников. Мне пока не удалось распространить эти результаты на строки в середине треугольника”.
“Ну, наверно, это не просто. Но, мне кажется, Вам не следует слишком уж углубляться в теорию. Лучше поработайте опять со своей моделью линейного программирования и найдите снова границы риска для разных п. Я уверен, эти границы сойдутся, когда п станет достаточно большим”.
“Я так и сделал, а границы так и не сошлись”.
“Наверняка Вы где-нибудь ошиблись”.
“Я сначала так и подумал. Потом я проверил все свои действия. Потом перепроверил. Потом меня осенило”.
“Девлин, Вы не могли бы, наконец, перейти к делу, черт возьми? Что именно Вас осенило?”
“Один очень простой способ генерировать симметрично коррелированные бернуллиевы случайные величины, независимо от того, являются ли они конечно или бесконечно перестановочными. Причем, такой способ, который всегда порождает толстые хвосты”.
“Ну и что это за способ?”
“Представьте себе, что природа раз за разом осуществляет один и тот же случайный выбор между двумя своими состояниями, а именно, в первом ее состоянии, которое наступает с вероятностью р, наши бернуллиевы случайные величины являются абсолютно коррелированными, во втором же ее состоянии, наступающем с вероятностью 1 — р, наши случайные величины независимы в совокупности. При этом, заметьте, что в каждом из этих состояний природы среднее равно 1/2 . Легко видеть и нетрудно проверить ‘в лоб’, что безусловная корреляция в рассматриваемом случае будет равна р, и что сумма этих бернуллиевых случайных величин будет иметь хвосты гораздо более толстые, чем это допустимо, если считать биномиальное распределение адекватной моделью. Вот, взгляните, гистограмма моего сценария ‘двух состояний природы’
104
6. Вассазданиа карраляции
на 16-ти несмещенных случайных величинах и с корреляцией равной всего-то 0,1. Каждая из двух точек на концах интервала представляет собой событие двух с половиной стандартных уклонений, которое, тем не менее. Происходит с вероятностью 5%”,-с этими словами Девлин вывел на экран очередную гистограмму.
Ап unbiased, 0.1 correlated, infinitely exchangeable game
Одна несмещенная бесконечно перестановочная игра, коррелированная с корреляцией равной 0,1.
С первого же взгляда Конвею стало ясно, что его худшие опасения оправдались: “Девлин прав!”, огорченно подумал Конвей и сказал со слегка глуповатым выражением на лице: “Да, если интерпретировать корреляцию как некую лотерею на абсолютной независимости с одной стороны и абсолютной зависимости движений с другой стороны, в конце концов, получишь толстохвостую смесь некого биполярного распределения и нашего старого доброго биномиального распределения. И, ведь, при этом и в том и в другом случае мы будем иметь неограниченную перестановочность!”
“Точно!”
“Я так понимаю, что Вы вполне можете применить этот же подход и к смещенным случайным величинам тоже”.
“Да, конечно. Просто надо положить среднее всех случайных величин, как в случае абсолютной зависимости, так и в случае абсолютной независимости, равным не 1/2 , а какому-нибудь // . Тогда безусловное среднее тоже будет равно /л , а безусловная корреляция будет равна вероятности абсолютной корреляции, так сказать”.
“Следует ли мне понимать все это так, что вот это самое, только что рассмотренное нами распределение, а не простое биномиальное, как раз и является тем самым искомым предельным распределением?”
“Конечно, нет. Дело в том, что, как только я понял, что это только что рассмотренное нами распределение является допустимым, я понял и то, что кроме
105
Часть 1. Стандарты отклонанин ______________=я=_
него существует еще много других аналогичных и допустимых, но не совпадающих с ним. Ну, в качестве примера набора из п штук неограниченно перестановочных бернуллиевых случайных величин подойдет любая смесь биномиальных распределений порядка п. Существенно, что эта смесь потенциально является допустимой. Вам просто придется как-то гарантировать, ч тобы два первых момента этой смеси соответствовали заданным значениям // и р”.
“Откуда следует, что эти смеси будут допустимы?”
“Это легко видеть с помощью моих треугольников. Мы, ведь, знаем, что любое биномиальное распределение вероятностей можно неограниченно расширять, не нарушая при этом ни правила суммирования ни неотрицательности вероятностей. Поэтому мы всегда можем неограниченно продолжить любое биномиальное распределение посредством того, что будем осуществлять смесь каждого из его расширений. Любая такая смесь будет полноправной вероятностной мерой и при этом будет сохранять правило суммирования. Так что все условия допустимости будут соблюдены... Однако, строгое математическое доказательство,- не самый лучший способ интуитивно воспринять рассматриваемый результат.”
“А конкретнее, что Вы имеете в виду?”
“Условную независимость. Представьте себе, что все наши случайные величины независимы для любого фиксированного значения их общего среднего. Теперь представьте, что природа случайным образом сдвигает это среднее. Ясно, что такие случайные величины будут неограниченно перестановочны, и что некое биномиальное распределение будет являться результатом каждого шага природы. Тогда распределение смеси- это просто смесь этих распределений”.
“Ну, и откуда же здесь появляется корреляция?”
“От изменения общего среднего. Вспомните, что безусловная ковариация равна сумме средней условной ковариации и ковариации условных средних. Первое слагаемое этой суммы равно нулю, благодаря условной независимости. Второе слагаемое положительно благодаря перестановочности, если только это самое среднее не фиксировано. Наша безусловная корреляция показывает, какая доля совокупной вариации любой из наших перестановочных переменных проистекает от вариации ее условного среднего”.
“Не могли бы Вы привести какой-нибудь конкретный пример?”
“Я уже это сделал. Все что нам теперь нужно,- это по новому интерпретировать этот уже приведенный мной пример. Заметим, что абсолютно коррелированные бернуллиевы случайные величины можно рассматривать как отражение процесса смешивания двух вырожденных условно независимых биномиальных распределений таких, что у одного успех является достоверным, а у другого- неуспех. Поэтому вышеприведенную гистограмму можно понимать как некую смесь биномиальных распределений, имеющую среднее равным нулю с вероятностью 5%, единице с вероятностью 5% и одной второй с вероятностью 90%”.
“Вырожденные распределения - это слишком заумно. Как насчет примера с нормальными биномиальными распределениями?”
106
6. Вассазданив каррвляции
Девлин молча кивнул и щелчком мыши вызвал на экран очередной график: “Вот еще одна смесь. Она дает то же самое результирующие среднее и корреляцию, что и предыдущая смесь, но выглядит совершенно по-другому. Она есть взвешенное среднее двух биномиальных распределений, имеющих средним, соответственно, 4 и 9,6. Вы можете интерпретировать ее следующим образом. С вероятностью 28,6% все наши 16 штук бернуллиевых случайных величин независимы в совокупности с общим средним, равным JL = o25, в противном 16
случае они тоже независимы в совокупности, но с общим средним равным 9,6 / 16-0,6”.
Another unbiased, 0.1 correlated, infinitely exchangeable game
Еще одна коррелированная, несмещенная, бесконечно перестановочная игра с корреляцией тоже 0,1
Конвей впечатлился результатами Девлина и проговорил уважительно: “Да... Без ваших объяснений я ни за что не догадался бы, что эта гистограмма представляет собой некую допустимую бесконечно перестановочную игру”.
“Не переживайте. Никто не смог бы догадаться. Между прочим, какова здесь вероятность 16 успехов, не подскажете?”
“Почти ноль. Настолько близко к нулю, что мне и не разглядеть”.
“Мне тоже не разглядеть. Но, вот, если бы эта вероятность была в точности равна нулю, данная гистограмма не была бы гистограммой бесконечно перестановочной игры”.
“Почему?”
“Потому, что, если любая выборка, состоящая из 16-ти случайных величин, обязана быть такой, что она всегда содержит, по крайней мере, один неуспех независимо от размеров генеральной совокупности, вся эта генеральная совокупность не может содержать более 15-ти успехов. Единственным типом
107
Часть 1. Стандарты атклононин
неограниченно перестановочных случайных величин, удовлетворяющих этому ограничению,- это вырожденные неуспехи”.
“Ну хорошо. А не можем ли мы на глаз хотя бы сказать, соответствует или нет та или иная гистограмма какой-либо биномиальной смеси?”
“Иногда можем. Это просто, если, скажем, Вы заведомо знаете, что случайные величины некоррелированы. Дело в том, что, если средние биномиальных случайных величин, составляющих смесь, различны, дисперсия смеси будет положительна и, следовательно, корреляция между такими случайными величинами будет положительной. Поэтому единственной допустимой биномиальной смесью для некоррелированных случайных величин является какое-нибудь чистое биномиальное распределение”.
“Ну, ладно. Допустим теперь, что я не знаю, что случайные величины коррелированны, и должен выяснить это из гистограммы. Что мне тогда делать?”
“Тогда Вам надо посмотреть насколько резкими являются колебания результирующего графика. Если некая биномиальная смесь отводит большой кусок плотности вероятности какой-нибудь такой точке к, которая не является крайней точкой интервала, она обязана отвести тоже значительный кусок плотности вероятности, по крайней мере, одной из соседних точек к+1 или к-1, а, чаще всего, обоим сразу. Поэтому за возможным исключением крайних точек гистограмма биномиальной смеси слишком резко колебаться не должна”.
“Но и слишком слабо она колебаться тоже не должна, как мне кажется, не так ли, Девлин? Ведь биномиальные смеси геометрически напоминают линию, огибающую горный хребет. Поэтому они и не должны, вроде бы, быть уж слишком гладкими. Я не прав?”
“Вы удивитесь, но взгляните на это”,- с этими словами Девлин вывел на экран очередную гистограмму,- “Ну, и где здесь ваши горные пики? А ведь это-биномиальная смесь из 50 случайных величин”.
Binomial mixture without peaks
Number of successes
Биномиальная смесь без пиков.
108
5. Воссоздании квррвляции
“Очень смешно. Вы, Девлин, шутите, конечно? Это не может быть биномиальной смесью”.
“Тем не менее, это- биномиальная смесь. Вы получите эту биномиальную, повторяю, смесь, если положите все возможные условные средние одинаково вероятными. При этом ваши безусловные бернуллиевы случайные величины получатся несмещенными и коррелированными с коэффициентом корреляции 1/3. Ровно это же самое распределение Вы можете сгенерировать с помощью моих треугольников, даже не думая при этом ни о какой биномиальности, а просто положив, что вероятность нулевого числа успехов равна для каждого и в точности \/ и + 1. Все остальные элементы каждой строки треугольника будут однозначно следовать из правила суммирования”.
“Знаете, что? Может быть математически все, действительно, так как Вы говорите, но с точки зрения здравого смысла это распределение выглядит нелепо. Вы сами посмотрите. Допустим, у нас есть 50 штук монет. Это значит, ровно СЦ способов реализовать выпадение 25 орлов”,- с этими словами Конвей перегнулся через Девлина и быстро произвел вычисления на компьютере Девлина,- “Это значит больше чем 126 триллионов способов! А получить 50 орлов- всего один способ. И получить 50 решек тоже можно ровно одним способом. Но ваше распределение считает эти события равновероятными. Это же абсолютно противоестественно! ”
“Это вовсе не противоестественно. Более того, без этого распределения вся наша вселенная развалилась бы на атомы или на нечто более мелкое”.
“Что это Вы такое несете, Девлин? Нам надо ‘по взрослому’ обсуждать реальные проблемы и, значит, реальные распределения, которые встречаются в жизни, а не в псевдонаучной фантастике для тинейджеров! И, пожалуйста, уберите театральность из наших рабочих разговоров, будьте серьезнее и ближе к насущным делам”.
“Но это распределение имеет отношение к абсолютно реальным вещам. Оно касается фотонов, а также ионов, имеющих четное общее число протонов и нейтронов. Смотрите, допустим, у Вас есть 50 таких идентичных частиц, которые со страшной скоростью носятся себе по двум одинаковым половинам одного куска ограниченного замкнутого пространства. Вероятность того, что ровно к частиц окажутся в первой половине этого куска, задана моей последней гистограммой. Обобщение этого результата на большее чем два число частей куска пространства называется распределением Бозе-Эйнштейна. Это распределение делает равновероятными сочетания, а не перестановки”.
“Но это - очень странно!”
“Да, очень. И, надо сказать, многие физики были, по всей видимости, просто шокированы, когда этот. результат был впервые обнародован. Что неудивительно, ведь он тогда показался им настолько же неестественным, насколько он представляется неестественным Вам сейчас. Но им пришлось смириться, поскольку экспериментальные данные постоянно подтверждали его
109
Пасть 1. Стандарты отклонения
справедливость в том, конечно, контексте, для которого это распределение было введено. Вообще, надо сказать, что вряд ли возможно описать поведение элементарных частиц в каком-либо содержательном аспекте каким-либо одним единственным биномиальным распределением или какой-либо аппроксимацией к одному какому-то биномиальному распределению. Может быть, поэтому физики и были вынуждены вводить в рассмотрение все более и более сложные распределения вероятностей...”
“Спасибо, Девлин, за интригующую вводную лекцию в квантовую механику, но, должен заметить, она хоть и вправду интересна, не имеет к нашим скорбным делам никакого отношения, квантовая механика, то есть. Вы сами, кстати, подумайте, ведь физики осуществляют свои измерения и производят обработку этих своих измерений во все более и более контролируемой среде. Даже та неопределенность, с которой они неизбежно имеют дело, становится все более и более строго определенным понятием. А мы, Девлин, как Вам, может быть, тоже известно, имеем дело с активами, которые несут в себе, причем, в качестве принципиально неотъемлемой составляющей, неопределенные и, даже, неизвестные факторы, которым и имени-то нет, всех мыслимых сортов. И определенность в нашем деле не увеличивается. При этом Вам, должно быть, известно и то, что релевантные причинно-следственные связи в наших задачах непрерывно меняются, почему нам и трудно до невозможности их воспроизвести или смоделировать”.
“Простите, Конвей, но что, собственно, Вы имеете в виду? Не то ли, что менеджерам риска нужны такие измерители финансового риска, которые были бы устойчивы к ошибкам людей, являющихся источниками информации, и к принципиальной неопределенности среды принятия решения?”
“Точно! Наконец-то мы говорим о деле. Именно поэтому я и хотел, чтобы Вы разобрались с неограниченно перестановочными случайными величинами. Мне надо было разобраться не с тем, как моделировать реальность, а с тем, как адекватно моделировать нашу неопределенность по отношению к этой самой реальности. Ясно, ведь, что, когда мы не можем отличить одну случайную величину от другой, мы можем предположить все, что угодно, например, симметрическую зависимость. А, если нам не известно матожидание, нам придется как-то догадаться, каким оно может быть, то есть, сделать экспертную оценку”.
“А что, разве так бывает, что Вы настолько понятия не имеете о том, какова может быть величина среднего, что можете предположить, что любое число является равновероятным кандидатом?”
“Навряд ли, но я не стал бы с порога отвергать такое предположение, как недопустимое при построении наших моделей. И оно, уж во всяком случае, является гораздо более реалистичным, чем те экзотические распределения, которые Вы мне постоянно подсовываете. Бозе-Эйнштейн! Мозги свихнуть можно!”
“Я рад, что распределение Бозе-Эйнштейна пришлось Вам'по душе. Кстати сказать, оно должно быть близко Вам по духу, так сказать, ведь, если Вы предполагаете симметрическую зависимость при том, что общее среднее
НО
5. Воссоздании коррвляции
рассматриваемых случайных величин распределено равномерно, Вы ровно распределение Бозе-Эйнштейна и получите в качестве распределения суммы!” После этого Девлин накарябал на бумаге несколько уравнений. Потом он какое-то время объяснял Конвею смысл этих уравнений. Потом Конвей засмеялся. Потом Девлин засмеялся над Конвеем. Потом они весело посмеялись какое-то время вдвоем по-американски, так сказать.
“О’кей! Вы победили”,- сказал Конвей, отсмеявшись сколько положено,-“Я снимаю шляпу перед стариной Бозе-Эйнштейном и поклоняюсь всякой прочей биномиальной смеси, какую Вы только умудритесь выдумать. Но в настоящий момент мне надо передохнуть. Идеи носятся в моих мозгах, как фотоны, и я не хочу, чтобы какая-нибудь из них затерялась... Можно мне сбросить на дискету копию вашей последней ЕхсеП-таблицы, чтобы я мог самостоятельно поиграть с разнообразными распределениями?”
“Да ради бога! Вы, кстати, можете поработать прямо здесь, если хотите. А я пойду в библиотеку. Может быть, мне придет на ум еще какая-нибудь догадка относительно неограниченно перестановочных случайных величин Бернулли. Я, кстати, так и не знаю, покрывают ли биномиальные смеси весь спектр возможной зависимости..
Давайте, читатель, используем эту паузу на то, чтобы подразобраться с некоторыми из свойств биномиальных смесей распределений вероятности. Поскольку такие смеси могут содержать бесконечное число составляющих, я намерен начать с повторения “стандартных правил обращения” с подобными смесями. Потом я выведу формулу, связывающую моменты произвольной биномиальной смеси с моментами тех бернуллиевых случайных величин, которые эту смесь составляют. В конце этих наших рассмотрений я проверю, что некая равномерная смесь биномиальных распределений порождает некое равномерное распределение Бозе-Эйнштейна. Несмотря на путающий вид некоторых интегралов, математика здесь проще, чем в двух предыдущих главах, но, в отличие от математики двух предыдущих глав, математику этой главы надо понять досконально, поскольку материал будущих глав будет во многом построен именно на ней.
Вероятностные меры на континууме
До сих пор мы имели дело только с дискретными исходами, то есть, с такими, которые можно перенумеровать с помощью натуральных чисел. Но, если множество элементарных событий представляет собой континуум, то вероятность /?(х) Pr{JT = х}того, что одна какая-то точка этого континуума окажется исходом и реализуется, должна почти наверняка быть равна нулю (или “равна нулю почти всюду”, говоря строгим математическим языком). И в самом деле, понятно, что, даже в том случае, если вероятностная мера некого интервала,
111
Пасть 1. Стандарты отклонония ____________________
соединяющего какие-нибудь две несовпадающие точки нашего континуума, строго положительна, /?(х) вполне может (и должна в огромном большинстве случаев) быть равна нулю для любой точки х из этого интервала. В таких случаях теория занимается не вероятностями элементарных исходов р(х), а т.н., “функциями плотности распределения вероятности”, обозначаемыми как f(x) .
Для т. н., “чисто непрерывных” вероятностных мер f (х) > OVx, и, кроме
4-СО
того, J f (x)dx = 1 . В этом случае математическое ожидание определяется как
+оо
2ДХ] = ^xf(x)dx . Соответственно, для произвольной функции Л(Х) от такой —оо
непрерывной случайной величины X, математическое ожидание этой функции +оо
£[/?( АД] будет равно Jh(x) f (x)dx.
— QO
Смешанные вероятностные меры
Всякая т. н., “Смешанная” вероятностная мера означает ровно то, что она есть некая смесь какой-то чисто дискретной вероятностной меры и какой-то чисто непрерывной вероятностной меры. Это, в частности, значит, что при заданных дискретном распределении вероятностей {рк к G К с: Аи} , с одной стороны, и плотности распределения вероятности f(x),x g [—qo;-fqo] , с другой
стороны, задано еще и число A G [0;1] такое, что для нашей смешанно распределенной случайной величины X ее математическое ожидание 4-00
выражается так: Е[Х] = Л.У'хкрк + (1 - Я) \xf(x)dx • Аналогично,
кг-К
£[/?(%)] = Я]Г Ыхк)рк +(1-Я) |/?(х)/(х)б£г-
Единый подход к исчислению вероятностных мер
Существует единый подход к дискретному распределению плотности вероятности по отдельным точкам и непрерывной функции плотности вероятности, а именно, обобщенная функция распределения случайной величины X, которая определяется как /^(х) = Рг{Х < х} . Обратите внимание, что определение функции распределения не зависит от того, имеем ли мы дело с дискретной или с непрерывной случайной величиной. Заметьте, также, что функция распределения любой случайной величины всегда или достигает нуля или асимптотически приближается к нулю при неограниченном уменьшении
112
5. Воссозданий корреляции
аргумента этой функции распределения. Аналогично, функция распределения любой случайной величины всегда или достигает единицы или асимптотически приближается к единице при неограниченном увеличении аргумента этой функции распределения. Я в дальнейшем буду записывать это как 77(—со) = 0 и К(+со) — 1 , соответственно. Более того, функция распределения любой случайной величины монотонно возрастает. Это значит, что для любой пары точек действительной оси: Xj > х0 => F(x,)>F( х0).
Для смешанных и непрерывных вероятностных мер имеем:
]
F дифференцируема почти всюду, причем, если в некоторой точке л е д
существует производная функции распределения F(x) случайной величины X,
обозначаемая как У(х) =----
---- х=х ’то она неотрицательна; dX
если в некоторой точке х0 е R1 функция распределения F(x) случайной величины X разрывно, скачок вероятности р(х0) = F^Xq) — /^(х^) является строго положительной величиной, где под F(x$ ) понимается предел функции
распределения при х стремящимся к х0 слева;
• ^р(хк) = 1.
-ОС
Вообще говоря, мы можем доопределить f и р , чтобы они покрывали все действительные числа, включая точки разрыва функции распределения, если определим функцию плотности вероятности f и дискретную вероятность р для Vx е R1 вот так: f (х) а= f (х“) , р(х) = F(x) - F(x~). Тогда, очевидно, наша плотность распределения будет совпадать с производной функции распределения во всех точках, в которых эта производная определена, а в тех точках, где функция распределения недифференцируема, будет определено дискретное распределение вероятностей в виде скачков вероятности. При этом сумма интеграла плотности и суммы скачков будет строго равна 1. Таким образом, мы получили, что плотность f и дискретное распределение р совместно определяют некую вероятностную меру. Для того чтобы завершить определение этой объединительной меры нам осталось определить производную функции распределения так:
dx\ F(x) — дифференцируема в х dx
dF(x) — <--------—:------------------------------,
F(x) — F(x ) F(x) разрывна и имеет скачок в х
Из
последнего
определения
следует,
что
113
Часть 1. Стандарты отклонения
J/7(.v)6//7(.v) = /?(х)(/7(х) — /^(х”)) + j*A(x)-2—dx для любых
j j j dx
интервалов J и любых измеримых функций h. При этом тот интеграл, который стоит в вышеприведенном уравнении слева, называется интегралом Римана-Стилтьеса,
Заметим, что теперь любая монотонно неубывающая функция F такая, что
pF(x)= 1
является функцией распределения для некого распределения
вероятностей. Наконец, если нам задана некая вероятностная мера F, мы имеем, что для любой измеримой функции h определено математическое ожидание этой
функции по этой мере: [/?(X)] — J/z(x)tZF(x).
Условные и безусловные вероятности на континууме
Пусть нам дана функция /"(х, у) = Pr(% < х, Y < у) совместного распределения вероятностей случайных величин X и Y. Если при этом
совместная плотность f (х, у>) =
определена и конечна всюду, мы
можем определить:
• безусловную плотность распределения случайной величины „г YiY _ dF(^,y} .
условную плотность распределения случайной величины
£(у)
условную
распределения случайной величины
6F(oo,y)
—<30
По смыслу, вышеприведенные формулы соответствуют тем, которые определяют те же условные и безусловные вероятности в дискретном случае, просто интегралы теперь используются вместо сумм, а частные производные-вместо разностей. Строго говоря, для смешанных распределений нам следовало бы писать суммы там, где есть скачки вероятностей, или записать вышеприведенные формулы через двумерные интегралы Римана-Стилтьеса, но, поскольку обозначения в этом случае стали бы очень громоздкими (надо было бы
114
__________________________________________________5. Воссоздании корроляции
различать приращения по X и приращения по Y), я ограничусь только формулами для непрерывного случая. Кстати, принципиальной разницы между непрерывными и смешанными распределениями в рассматриваемом аспекте все равно нет.
Смеси биномиальных распределений
Как мы видели выше, произвольная сумма п штук независимых бернуллиевых случайных величин таких, что вероятность успеха для каждой из них одинакова и равна некому числу О е [0;1], распределена биномиально, то есть, вероятность того, что эта сумма будет равна некому натуральному числу к<п, равна Ск0к (1 — 0)”~к. Теперь пусть это 0 будет не фиксированным числом, а случайной величиной с функцией распределения G. Это значит, что каждый исход в виде суммы неких чисел мы теперь будем моделировать за два следующих шага:
♦ некий случайный механизм, реализующий функцию распределения G, где G(x)-это, напомним, вероятность того, что случайная величина 0 не превосходит х, разыгрывает нам какое-нибудь число 0 е [0;1] в качестве общей для каждой из п штук наших бернуллиевых случайных величин вероятности успеха;
♦ другой случайный механизм разыгрывает нам исходы п экспериментов с этими самыми случайными величинами Бернулли, распределенными так, что вероятность успеха в каждом из экспериментов равна в точности тому самому 0,
Мы будем считать, что получившаяся сумма п чисел (каждое из которых, конечно же, равно или 0 или 1) является исходом розыгрыша случайной величины, которая является по определению смесью биномиальных случайных величин, при условии, что смешивающим распределением является именно G. Тогда вероятность того, что в случайном эксперименте с этой смесью появится 1
ровно к штук успехов, равна Р(п> к) = JСк0к (1 — 0)”'к dG(&) .
о
А соответствующий элемент треугольника Девлина, то есть, вероятность р(гг,к} того, что реализуется данная перестановка из к успехов, будет такой: 1
^0к (1 — 0)п~к dG(0) . Тогда правило суммирования проверяется “в лоб”: о
1 1
р(/7, к) + р(л, к + 1) = р* (1 - оу~к dG(0) + (1 - dG(O) =
о о
1 1
= J[1 - 0 + &\0к (1 - б’)'”*-1 c7G(6») = jff* (1 - 6>)" 0G(0) = р(п-1, к)
о о
115
Часть 1. Стандарты отклонония________________________
Среднее и дисперсия произвольной смеси биномиальных распределений
Мы знаем, что “чистое” биномиальное распределение имеет средним пО , а дисперсией /7 0(1 — /7 0). Произвольная же смесь биномиальных распределений- это смесь, соответствующая некому произвольному распределению смешивания G . Такая смесь, очевидно, имеет средним nEG[O]. А дисперсию этой смеси мы можем выразить как сумму среднего условной дисперсии и дисперсии условного среднего, то есть: Ес[п9(1 - 0)] + n2Vara[0} = пЕс[0] - пЕс[02} + n2Varc[0] =
= иЕа[0] — и{Еа[0]}2 — иЕагс;[0] + n2VarG\ff\ =
= nEG[0](l - EG[0]) + (и2 - n)EarG[0]
п
Теперь вспомним, что сумма X. перестановочных, бернуллиевых /=1 случайных величин, среднее каждой из которых равно р, а коэффициент корреляции каждой пары которых равен р, будет иметь средним величину пр , а дисперсией- величину /7//(1 — р) + (и2 — п)рр{\ — р) . Наконец, заметим, что два полученных нами результата для среднего и дисперсии не будут противоречить друг другу, тогда и только тогда, когда
£G[0] =//; P27rG[0] = рр{\ — р) = pVar[X]. Иными словами, мы показали, что, если сумма перестановочных бернуллиевых случайных величин распределена как некая смесь биномиальных случайных величин, то смешивающее распределение будет обязано иметь средним наше бернуллиевское среднее (т. е. Общее среднее наших случайных величин Бернулли), а дисперсией-коэффициент корреляции, умноженный на нашу же бернуллиевскую дисперсию.
Альтернативная интерпретация корреляции
Из последнего из вышеприведенных равенств элементарно следует, что
К?гг[0] ъ-
р —----и--- Теперь представим себе, что X - это некая случайная величина,
Уаг[Х]
равная сумме нашего условного среднего 0 и некого случайного уклонения, которое равно 1 — 0 с вероятностью 0 и — 0 с вероятностью 1 — 0. Тогда р будет показывать, какой “вклад” делает дисперсия случайной величины 0 в безусловную дисперсию случайной величины X .
Обратите внимание, что первый пример допустимого смешивающего распределения, приведенный Девлином, был устроен так, что значению О приписывалась вероятность /7(1 — //), значению 1 приписывалась вероятность рр, а значению р приписывалась вероятность 1 — р. Это можно
116
Б. Воссоздания коррид я и. и и
интерпретировать как то, что прямолинейная корреляция имеет вероятность р , а нулевая корреляция имеет вероятность 1 — р при том, что оба состояния имеют средним р .
Распределение Бозе-Эйнштейна
Допустим, что смешивающее распределение в смеси биномиальных распределений является равномерным так, что G(0) = 0. Тогда соответствующие случайные величины Бернулли будут иметь среднее равным 1/2 , а корреляцию равной 1/3 . Тогда будем иметь для \7к е (0; п — 1) :
1
Р(и, £) = /С* вк (1 - 6»)""* dO = о
1 1
о о
0м
d0 = 0+ Jc* о
—- вк+'(\ - еу-к-х d 6 к + \
(к - и)(1 - 0)п~к']
1
= Jcy вм (1 - do = Р(п, к +1).
о
Это значит, что гистограмма должна представлять собой прямую, параллельную оси абсцисс, и проходящую на высоте 1/(л? +1) . Существует и интуитивно более прозрачное доказательство этого же факта. Предположим, что из интервала [0;1] выбираются п+1 чисел в соответствии с неким случайным механизмом, реализующим равномерное распределение на этом интервале. Если теперь последнее выбранное число равно 0, вероятность того, что ровно к штук выбранных чисел окажутся меньшими, чем 0, и ровно n-k штук выбранных чисел окажутся большими 0, равна Ск0к(1 — 0)п~к. Тогда безусловная вероятность того, что последнее выбранное число будет иметь ранг, равный к+1, 1
считая снизу, будет равна ^Ск0к (1 — 0}п~к d0. Но из соображений симметрии о
имеем, что любая аранжировка должна иметь одну и ту же вероятность. Поэтому последний интеграл обязан быть равен 1/(;7 + 1) .
Интерпретация распределения Бозе-Эйнштейна
Допустим, что рассматривается серия испытаний Бернулли, порождающих распределение Бозе-Эйнштейна. Допустим, что первые к испытаний из п испытаний дали к успехов подряд. Тогда вероятность того, что исходом следующего испытания будет успех, равна:
117
Часть 1. Стандарты ятклянонин
(Ar + l)!(w-Ar)!
р(и + 1,£ + 1) = Р(>?+ !,£ + !)/С**1 = (>7 + 2)! = £ + 1
р(п,к) Р(п,к)/Ск„ к\(п-к)\ п + 2
(п +1)!
к превосходит —.
п
что всегда
Таким образом, распределение Бозе-Эйнштейна представляет собой некую модель механизма “успех порождает успех”, или, по крайней мере, можно его так себе представлять в рамках более общей модели последовательных выборок. И в самом деле, некая игра, представляющая собой схему выборки с возвращением, известную как “Урановая схема Пойа”, дает именно такое распределение. Предположим, что в некой урне первоначально лежат один красный и один черный шары. Предположим, далее, что всякий раз, когда один шар вынимают из этой урны, обратно кладут два шара того же цвета. Тогда условная вероятность вынуть в таком эксперименте еще один красный шар при условии, что уже к +1
вынуты к красных шаров и n-k черных шаров, равна -----. Таким образом, мы
77 + 2
получаем еще одну возможную интерпретацию распределения Бозе-Эйнштейна, а именно, притяжение некоторыми частицами к себе некоторых других частиц.
Однако, модель смеси биномиальных распределений вовсе не требует к + 1 привлечения какой бы то ни было причинности. И в самом деле, величину --
77 + 2 можно рассматривать как корректируемую оценку среднего, получаемую из первоначальной равномерной оценки и последующих к успехов в п испытаниях.
118
6. Определяем моменты с помощью Де Финетти
Второе утро подряд Девлин не попадался на глаза Конвею. “Должно быть ничего пока не выудил. Иначе уже давно махал бы тут своими гистограммами. Ну что ж, если гора не идет к Магомету...”,- подумал Конвей и после ленча сам отправился искать Девлина. Девлин обнаружился быстро, в предсказуемом месте и в предсказуемом состоянии. Он сидел за рабочим столом и с видом помешанного бормотал: “Определенно, определенно...”1.
“Что о пределе!шо-то, Девлин?” — спросил Конвей.
“Да не ‘определенно’, а ‘де Финетти’. Бруно де Финетти, помнишь... Он идентифицировал все допустимые распределения бесконечно перестановочных случайных величин Бернулли. Его основная теорема хорошо известна профессионалам в статистике... Но большинство стандартных учебных курсов математической статистики ее игнорируют, да и сам я ее подзабыл...”
“А я и вообще не знаю, то ли забыл напрочь, то ли совсем никогда не знал... Ну, и какие же допустимые распределения существуют, кроме уже обсуждавшихся биномиальных смесей?”
“Таковых нет! Все совместимые распределения обязаны быль биномиальными смесями. Иными словами, если задано условное среднее О, случайные величины Бернулли обязаны быть независимыми. Но это условное среднее может меняться по некоторому множеству своих состояний в соответствии с неким смешивающим распределением G”.
“Не мог бы ты объяснить мне ‘на пальцах’, почему биномиальные смеси — единственно допустимый тип распределения?”
“Доказательство этого факта не является, к сожалению, интуитивно прозрачным. По крайней мере таковы те доказательства, которые я видел относительно недавно. Поэтому я начал снова играть с моим треугольником и треугольником Паскаля, и так продолжалось до тех пор, пока меня вновь не осенило. Дело в том, что мы можем использовать эти треугольники, чтобы моделировать это самое распределение <7”.
“Как это?”
“Начнем с того, что станем собирать информацию по вероятностям полного успеха, т. е. по р(пъп) для разных значений п. Эти значения определяют правое ребро одного из моих треугольников, скорее, мне следовало бы сказать ‘правый угол’, поскольку этот треугольник простирается в бесконечность. Заметьте, поскольку каждая новая строка добавляет ровно одну дополнительную степень
1 Здесь игра слов: Definitely (определенно) звучит по-английски как Де Финетти. — Прим, перее.
119
Часть 1. Стандарты отклонения
свободы, значения р(п,п) однозначно определяют и весь треугольник. Поэтому, для того чтобы доказать теорему де Финегги, необходимо всего лишь определить некое смешивающее распределение G, которое будет правильно специфицировать это самое правое ребро..
“А что, собственно, такого особенного в этом правом ребре?”
“Ну, например, то, что для всякой биномиальной смеси р(п,п) представляет собой /7-й момент смешивающего распределения G. А рассчитать такое распределение, которое генерирует заданный набор моментов, довольно просто. Например, мы могли бы непосредственно построить производящую функцию моментов, а потом обратить ее и получить G”.
“Нет, нет, нет... Не так быстро. Откуда следует, что это ваше G будет распределением вероятностей на единичном интервале?”
“По построению, каждый из элементов p(n^k) определяет математическое ожидание 0к (1 — 0)п~к . Если G не было бы распределением вероятностей или было бы но таким, что какая-то часть плотности размещалась бы за пределами единичного интервала, то по крайней мере один из этих элементов был бы строго отрицательным”.
“Как-то все это меня не слишком убеждает... И потом, что, если я не знаю, как мне следует обращать эту производящую функцию?”
“Ну, тогда ты мог бы построить соответствующие аппроксимации, используя строки моего треугольника. Для этого надо для каждой строки с номером п вычислить распределение вероятностей Gn как некую ступенчатую функцию относительных частот. Я имею в виду, что Gn(&) по определению равно вероятности появления не более п 0 успехов в п испытаниях. Эта функция по виду должна быть ступенчатой со скачками в точках, кратных 1/п . Так вот, Gn должны сходиться к той самой функции распределения G, которая нам и нужна”.
“Может быть, для тебя это очевидно, но я по-прежнему ничего не понимаю... Может ты разберешь со мной какой-нибудь пример? И поподробнее, если можно”.
“Конечно. Да вот возьмем хоть наш пример с абсолютно плоской гистограммой, помнишь? Там Р(п,п) - р(п,п) = —5— для Ун- Так вот, и +1
единственным распределением вероятностей, чей и-й момент равен 1/(лг + 1) для любого /7, является равномерное распределение G(6) = в. С другой стороны, посмотри на приближенное распределение
G (0) = , где £*(п#) - это наименьшее целое, превосходящее п0.
" 72 + 1
Ясно, что при /7, стремящимся к бесконечности, Gn(&) стремится к О ”.
Конвей нарисовал на бумаге несколько строчек треугольника Девлина и на какое-то время углубился в размышления. Наконец он нехотя сказал: “Поздравляю. Тебе все-таки удалось продолжить свой треугольник в бесконечность”.
120
В. Определяем моменты с помощью До Финотти
"Спасибо, но заслуга в этом вовсе не моя, аде Финетги”.
"Ах, чтоб меня! Значит и у тебя есть-таки авторитеты?”
Девлин даже обиделся: “А что, у тебя был повод усомниться в этом?”
"Я просто подначивал тебя, Девлин, - миролюбиво сказал Конвей, хотя он вовсе не думал шутить. — Но вот, что я действительно хочу знать, — это что же все-таки происходит с областью возможных значений хвостового риска, когда ты задвигаешь свои треугольники в бесконечность. Мне кажется, эта область должна все-таки быть уже, чем в случае конечной перестановочности, ведь накладываются же дополнительные ограничения..
“Ты прав, дополнительные ограничения, конечно, есть. Дело в том, что те распределения, которые ограничивают хвостовые риски неограниченно перестановочных случайных величин Бернулли, являются смесями двух или трех биномиальных распределений, а не двух- или трехточечных распределений. Таким образом, дополнительное ограничение, о котором ты говоришь, зависит от того, насколько хорошо или, наоборот, плохо некое отдельное биномиальное распределение может аппроксимировать некое одноточечное распределение. Иногда из-за этого допустимая область сужается весьма значительно..— с этими словами Девлин вывел на дисплей очередную гистограмму.
Maximizing the odds of < 2 successes for n = 16, p. = 0,5, p — 0.1
Максимизируем шансы не более чем 2 успехов для п = 16, [Д, — 0.5, р = 0.1.
“Каждая из этих гистограмм, — пояснил Девлин, — изображает 16 несмещенных перестановочных случайных величин Бернулли с коэффициентом корреляции равным 0,1. При этом светлая гистограмма имеет максимальный риск двух и менее успехов без дополнительных ограничений. Этот риск представляет собой хвост 1,9 стандартных уклонений. А темная гистограмма дает тот же максимум, в том случае если случайные величины условно независимы. Видишь, хвостовой риск во втором случае более чем в два раза меньше: 10,8 против 21,4%”.
“Почему же такой большой разрыв?”
121
Часть 1. Стандарты откпопопия
“Потому, что каждое из биномиальных распределений, составляющих смесь, потребляет намного больше дисперсии, чем любое дискретное распределение, сконцентрированное вокруг двух условных средних. Соответственно, гораздо меньше дисперсии остается на то, чтобы ‘финансировать’ плотность вероятности в хвосте”.
“Я заметил, что условные Средние, или пики этих распределений, тоже не одинаковы по высоте. Почему так?”
“Тот биномиальный пик, что пониже, сдвинут влево, так что меньше плотности вероятности попадает вправо за порог. Хотя на это уходит больше дисперсии, оно, в определенном смысле, того Стоит. В рассматриваемом примере оптимальное среднее нижней биномиальной составляющей равно 1,27, что дает нам 75%-ную условную вероятность не вылететь за порог, против 50%-ной условной вероятности, которую мы имели бы, если бы это среднее было равно 2,00”.
“А высокий пик?”
“Ясно, что, если низкий пик сдвигается влево от среднего, то, чтобы соблюсти ограничения на среднее и дисперсию, высокий пик должен все-таки сдвинуться к среднему и стать несколько более вероятным. Это значит, что в результате оба пика сдвигаются влево”.
“Вы сказали, что границы риска сблизились приблизительно вдвое, не так ли? Это, что, общий результат?”
“Нет. Значения зависят от конкретных параметров. Например, по сравнению со случаем ‘умеренных’ хвостов границы риска в случае экстремальных хвостов подвержены сравнительно меньшим изменениям. Все дело в том, что биномиальные составляющие биномиальных пиков не создают много дисперсии. Вот взгляни на границы хвостового риска, связанные с тем сценарием, который мы сейчас рассматриваем...”, — с этими словами Девлин вывел на дисплей очередную гистограмму.
Extreme tail risks for n = 16, /х = 0.5, p — 0.1
Экстремальные хвостовые риски для п = 16, JLL — 0.5, =0.1.
122
В. Вярвдвлявм моменты с нвмвщъю Де Финвтти
“На этой схеме.. .событием скольких стандартных уклонений будет событие 4ни одного успеха’?”
“Немногим более 2,5. Максимальная вероятность сжимается с 13,3 до 9,1%. А минимальная вероятность, наоборот, вырастает от 0 до 1 из 16 000. Заметьте при этом, что общепринятый анализ риска по методу ‘среднего и дисперсии’ оценивает вероятность осуществления события 2,5 стандартных уклонений в 0,6%”.
Конвей вздохнул разочарованно: “Вероятно, мне все-таки надо быть благодарным, что событие 2,5 стандартных уклонений происходит всего лишь в 15 раз чаще, чем принято считать, а не в 20...”
“К сожалению, и этого нельзя исключить. Дело в том, что, когда число п случайных величин растет, ограничение биномиальности смеси играет все меньшую и меньшую роль. В пределе оно уже совсем ничего не значит, при условии, что корреляция р положительна”.
“Разве такое возможно? Ведь мы только что видели, что биномиальные смеси расточают больше дисперсии, чем точечные распределения при тех же самых условных средних, и что эта повышенная расточительность уменьшает область допустимых значений для хвостового риска? Короче, мы знаем, что с ростом п дисперсия любой биномиальной составляющей растет, почему бы тогда не усилиться заодно и ‘расходу’ этой дисперсии?”
“В абсолютных терминах все так. В биномиальных смесях, действительно, рассеивание дисперсии прямо пропорционально п. Однако в выражение для общей дисперсии любой бернуллиевой суммы входит еще и член, зависящий от рп~. Это значит, что если р > 0 , рано или поздно он начнет доминировать с ростом п. Откуда следует, что с ростом п рассеяние дисперсии уменьшается примерно пропорционально ”.
“Слушай, я не опровергаю твои выкладки, но, скажу тебе, не вижу смысла сосредотачивать все внимание на относительном рассеянии, а не на абсолютном количестве”.
“Ну тогда давай нарисуем еще одну картинку. Пусть она отражает только успехи, но при этом ширина диаграммы все время должна оставаться постоянной независимо от и. Тогда увидишь, что каждый раз стандартное уклонение любой биномиальной составляющей со средним числом успехов, равным О, будет
иметь ширину -------j=—. Откуда следует, что, если п растет, каждая
V п
биномиальная составляющая будет выглядеть все более и более сосредоточенной вокруг своего пика. Это значит, что при достаточно большом п мы сможем разместить произвольную биномиальную составляющую на несколько стандартных уклонений под порогом, что позволит нам свести ‘перехлест’ за порог к весьма малым величинам и при этом без значительного рассеяния дисперсии”.
123
□ Exchangeable and conditionally independent
□ Exchangeable but not conditionally independent
<т£Г[ТГ1
Часть 1. Стандарты атклонвния
“Ага, я, кажется, начинаю понимать. А не мог бы ты для закрепления, так сказать, разобрать со мной еще один пример?”
“Да ради бога! Только договоримся придерживаться несмещенных и 0,1-коррелированных случайных величин и увеличим их общее число до 64. Это уполовинит стандартное уклонение произвольной биномиальной составляющей по отношению к области допустимых значений. А еще, выберем в качестве хвостового события получение 11 или меньшего числа успехов. Это даст нам хвост в 1,94 стандартных уклонений, т. е. довольно близкий аналог хвоста в 1,90 стандартных уклонений из предыдущего примера. Вот смотри, какими будут распределения, максимизирующие хвостовой риск”, — и Девлин вывел на дисплей очередную диаграмму.
Maximizing the odds of < 11 successes for n — 16, /x — 0.5, p = 0.1
45% 40% -35% -30% 25% -20% -15% -10% -5% -
0% -I
0 4 8 12 16 20 24 28 32 36 40 44 48 52 56 60 64
Максимизируем шансы не более чем 11 успехов для п = 64, Р = 0.5, р — 0.1.
“Ты же обещал, что биномиальные составляющие будут более концентрированными. Что же тогда пики стали ниже, чем раньше?”
“Пики стали ниже, потому что теперь стало в 4 раза больше допустимых исходов. В новой схеме аналогом события на предыдущей схеме, состоявшего в получении 9 успехов из 16 исходов, будет что-нибудь вроде получения от 36 до 39 успехов из 64 исходов. И, хотя вероятность 9 успехов на предыдущей гистограмме была равна 17%, вероятность получить от 36 до 39 успехов из 64 исходов равна 33%. Чтобы убедиться в большей концентрации, просто сравни ‘ущелья’ между пиками. В рассматриваемом случае пространство между 14 и 24 успехами практически пусто, поскольку вероятность попасть в этот интервал равна всего 0,5%. А на предыдущей диаграмме биномиальные составляющие практически перекрывали друг друга в точке, соответствующей 4 успехам из 16 исходов”.
“Да, и, кажется, перехлест за порог тоже уменьшился...”
124
8. Определяем мвмвнты с пвмвщью Дв Финетти
“Совершенно верно. И условная вероятность того, что сумма превзойдет порог при условии, что более низкая биномиальная составляющая останется под порогом, теперь меньше 9%. Сравни-ка это с теми 25%, которые мы имели для аналогичной вероятности в случае 16 случайных величин. Увеличение числа случайных величин до 64 позволяет той биномиальной составляющей, что пониже, иметь слегка больший вес по сравнению с предыдущим случаем, т.е. 14,9 вместо 12,4%. И это потому, что меньше рассеивание дисперсии1’.
“Ладно. Но все-таки насколько ближе мы теперь к неограниченному диапазону?”
“Ну, при шестидесяти четырех 0,1-коррелированных случайных величин и при условии неограниченной перестановочности максимальная вероятность попадания под порог 1,94 стандартных уклонений равна 13,6%, в то время как та же вероятность равна 20,9%, если неограниченная перестановочность отсутствует. Это значит, что теперь неограниченная перестановочность съедает максимально чуть больше трети этой вероятности по сравнению с тем, что было раньше — более половины при 16 случайных величинах и аналогичном пороге”.
“Но и одна треть — это существенно. Сколько же нужно случайных величин, чтобы ты мог сказать, что и конечная, и бесконечная перестановочность дают примерно одни и те же границы хвостового риска?”
“Строго говоря, это зависит от конкретных параметров, но, если нам задана положительная корреляция, то, скорее всего, речь идет о сотнях тысяч, а не о десятках. Дело в том, что сходимость здесь — очень медленная, примерно такая, как сходимость к 0 последовательности у t— ”.
/ уп
“А что будет, если корреляция отрицательна или равна нулю?”
“С этим вопросом мы уже разбирались. Корреляция — это некое положительное кратное дисперсий условных средних, поэтому она не может быть отрицательной. Если же она равна нулю, то этому условию удовлетворяет только безусловная независимость”.
“Значит, некоррелированный случай — это некая выколотая точка, исключение...”
“Именно. Причем отличие здесь очень резкое. Скажем, совершенно неважно, сколько независимых в совокупности бернуллиевых случайных величин у нас есть, хвостовые риски все равно обязаны быть биномиальными. Но для любого сколь угодно малого возможного значения корреляции эти хвостовые риски могут варьировать в неком интервале, который в пределе превращается во 1 „ все тот же интервал от 0 до —--’.
s +1
В этот момент Конвей почувствовал, что было наметившийся у него в голове порядок опять рушится: “Но ты же раньше говорил, что именно этот интервал задает границы s-хвостового риска для любого
s +1
125
Часть 1. Стандарты отклонении______________________________________
распределения вероятностей! Неужели бесконечная перестановочность ничего не может сделать, чтобы сузить-таки эти проклятые границы?” — тон Конвея стал откровенно унылым.
“Нет, — бесстрастно отчеканил Девлин. — Если, только, у тебя не абсолютно некоррелированные случайные величины или ограниченный набор строго подобранных коррелированных случайных величин”.
“И как же я на практике узнаю, так это или нет?” — спросил Конвей, уже предчувствуя ответ.
“Да никак. У тебя даже теоретически нет такой возможности, поскольку любые оценки всегда будут иметь ненулевое значение предельной погрешности”.
1
“Итак, мы опять вернулись к тем же общим границам [0; —--] ”, — вбил
5' + 1
последний гвоздь Конвей.
“Боюсь, что да”.
Конвей нахмурился и с мрачным видом стал курсировать взад-вперед перед столом Девлина. Мысли его при этом были весьма безрадостными: “Ужасно! Как, скажи на милость, я все это объясню Комитету контроля риска?"
Оставим Конвея на какое-то время мучиться с его непростыми и не вполне математическими вопросами и разберемся с теоремой де Финетти и ее приложениями.
Теорема де Финетти
Теорема де Финетти утверждает, что, если некоторое множество бесконечно перестановочных случайных величин Бернулли таково, что все эти случайные величины имеют средним одно и тоже число, то эти случайные величины будут условно независимыми.
Формально же, вероятность k) получить к успехов в п испытаниях
1
должна быть равна (1 — 0)”~к dG(0) для некого распределения
о
вероятностей на [0;1]. Тогда соответствующий элемент треугольника Девлина 1
будет равен )0* (1 - 0)п~к dG(0) и, в частности, о
1
р(и,и) = \0ndG{0) = Ec[0n}. о
Строгое доказательство теоремы де Финетти приведено в учебнике У. Феллера по теории вероятностей. В ходе доказательства Феллер строит нечто 126
8. Определяем мвмонты о помощью До Финотти
вроде ступенчатых функций Gn, определяемых как
dGn(~) = Р(п,к) — Скр(п^к). Потом применяет некую разновидность п
треугольника Девлина, чтобы доказать, что моменты Gn сходятся к множеству {/?(0,0);...; /?(и, и);...} . А потом Феллер показывает, что эти моменты однозначно определяют G .
Вслед за Девлином заметим, что для распределения Бозе — Эйнштейна Р(п, к) не зависит от к. Если Int(n 0) — это наибольшее целое, не
/Э z- /zj, Intend) + 1
превосходящее пи , то Gn(tr) становится равным ----------- и, следовательно,
п + 1
сходится к равномерному распределению. В качестве еще одной иллюстрации заметим, что, если р(п^к) = 0к (1 — 0)п~к Для всех п и всех Л, то Gn соответствует некому биномиальному распределению с п переменными и средним п0 , если, конечно, принять во внимание, что те вероятности, которые в обычном биномиальном распределении были бы приписаны событию, соответствующему к успехам, в нашем случае, т. е. в рамках распределения Gn, будут приписаны значениям %. Теперь, если п растет, Gn будет сжиматься в точечное распределение над 0, что корректно определяет G .
Демонстрация сходимости к G
Пусть Рп (п, Ап) обозначает вероятность появления Ап успехов в п испытаниях при условии, что соответствующее распределение вероятностей генерируется смесью Gn . Тогда имеем:
р„(п,лп)= ^0^ {1- е)п-^ (1- Р(п,дп)=
о е
А(п^ Л, 0)Р(п, 0п) , где суммирование осуществляется по величинам 0, е
1 2
которые принадлежат конечному множеству {0, —, —Теперь я намерен п п
применить формулу Стирлинга, согласно которой мы имеем
п! 1
—,= = 1 для п у[2тт
больших п. Отсюда следует, что, если ни Ап, ни п — Ап не малы, то
• (Ап)! (п — Ап)!
127
Часть 1. Стандарты откпонания
л/2л7Ь • • 72л-(1-Л)и • (1 - Л)(1’А)'’гХ''"'е-^п
= [2л2(1-А>Г^ •
6»Y< 1-6» У *
л; li-л
= 5(и,Л)[С(А,6»)]".
Теперь рассмотрим член С(Л,0). Эта величина меньше 1, если только О не равно Л , что легко проверить максимизацией 1п(С) по 0. Отсюда получаем, что Сп сходится или к 1 при 0 ~ Л , или к 0 при 0 Ф Л , Более того, В{п, Л) — это нечто вроде интегрирующего множителя, который предназначен для случаев, когда 0 лишь инфинитезимально, отличается от Л . Отсюда имеем, что, поскольку В не зависит от значений Р, и, поскольку Рп обязано всегда иметь ту же самую агрегированную меру, что и Р, то В обязано на самом деле быть равным 1. Это показывает, хотя и нестрого, конечно, что Рп(п, Лп) сходится к Р(и, Лп),
Производящие функции моментов
Математическое ожидание М(/) случайной величины егХ , где / — независимая переменная, а X — случайная величина, называется производящей функцией моментов случайной величины X. Легко проверить, что и-ная производная М(/) при у = 0 в точности равна я-ному моменту случайной величины X, а именно:
dyn
п dF(X) = ЕF[X”}.
Если заданы эти значения производных функции моментов М , мы можем реконструировать ее с помощью ряда Тейлора. При соблюдении некоторых ограничений функцию М можно будет обратить и вычислить ту функцию F , которая и породила эту производящую функцию моментов М . Если положить, что Мл(0) = 1, функция F будет иметь меру 1. Однако эта функция F не будет все-таки полноправной функцией распределения (потому, что dF сможет время от времени принимать отрицательные значения), если только рассматриваемые моменты не будут внутренне непротиворечивы. А для внутренней непротиворечивости необходимо, чтобы второй момент был не меньше, чем квадрат первого момента, иначе дисперсия будет отрицательной.
Если применить производящие функции моментов к доказательству теоремы де Финетти, то для того, чтобы построить соответствующую производящую функцию моментов для G и потом инвертировать ее, следует использовать элементы р(п, п). При этом неотрицательность соответствующего
128
6. Опрвдвлявм мвмвпты с пвмвщью Дв Финвтти
треугольника Девлина будет гарантировать монотонность получающейся функции этого распределения G.
Однако все вышеприведенное “доказательство” никак не затронуло ни возможного несуществования производящей функции М, ни возможного несуществования ее обратного преобразования. Для того чтобы исследовать вопросы, связанные с теоремой де Финетти более строго, следует переключиться с производящей функции моментов на какой-нибудь ее близкий аналог, например на преобразование Лапласа или на характеристическую функцию. Но я хотел бы заметить, что основная идея доказательства будет той же самой.
Типы биномиальных смесей, генерирующих экстремальные риски
Для произвольной биномиальной смеси хвостовой риск для Т или меньшего числа успехов в п испытаниях равен: Т 1
Рг(А: < Т) = JС* 6^(1 — 0)п~к dG(0) . Если для соответствующих
*=0 о
бернуллиевых случайных величин заданы среднее д и положи тельная корреляция р , то, как известно из предыдущей главы, смесь G обязана иметь средним д , а дисперсией будет дд(1 — д) , что означает, что второй момент G будет равен рр 4- (1 — д)д2 . Отсюда по аналогии с конечно перестановочными случайными величинами Бернулли задача определения области допустимых значений для хвостовых рисков биномиальных смесей может быть поставлена как задача условной оптимизации, в которой соответствующий лагранжиан
равен:
p(6»)c7G(6>)
О
, где {rz} — множители соответствующих моментов, a —-
множитель, отвечающий для каждого dG(3) условию дополнительной нежесткости v(3) > 0, dG(3) > 0, v(3)dG(3) = 0 .
Решение этой задачи условной оптимизации требует, оптимального G и каждого 3 :
чтобы для
^Ск0к(1-ЗУ~к
+ г0 + тх0 + г2(92 = Q(&) =
0|<Л7(<?) > О < О|Г>6(0) = О
Это полиномиальное уравнение и-ной степени выглядит устрашающе. Тем не менее мы можем выудить из него весьма существенную информацию, достаточную для того, чтобы установить, что решениями задачи оптимизации для G могут быть либо двух-, либо трехточечные распределения. Для того чтобы
129
Часть 1. Стандарты втклвпвпип
в этом убедиться, продифференцируем Q три раза:
Q’ = -пс;~' 6>г(1 - + г, + 2г,6>;
Q" = пс;-''0т~[ (1 - 0)п-т~2 [(и - 1)6» - Г] + 2г2 ;
Q"' = пС;~{ 6>r“2(1 - 6»)"~т~3[(л - 1)(и - 2)6»2 - 2Т(п - Т)0 + Т(Т - 1)].
Заметим, что каждый внутренний ноль Q должен представлять собой некий локальный максимум, а каждая пара локальных максимумов должна разделяться каким-нибудь локальным минимумом. Отсюда следует, что, если какое-нибудь распределение G, являющееся решением, назначает положительные вероятности двум каким-нибудь внутренним точкам и еще одной или нескольким другим точкам, то функция Qf должна быть такой, что она меняет знак как минимум четыре раза. А это значит, поскольку все наши производные непрерывны, что функция Q” должна будет поменять знак как минимум три раза, а функция Q’” будет иметь по меньшей мере три внутренних нуля. Однако анализ функции Qtu показывает, что она может иметь не более двух внутренних нулей. Это значит, что поддержка любого оптимального распределения G должна состоять либо из двух внутренних точек, либо из одной внутренней точки плюс полюса.
Геометрическая интерпретация
Как вы, наверное, помните, я представлял пары первых и вторых моментов для сумм п конечных перестановочных случайных величин Бернулли как выпуклую оболочку Conv(L) некоего множества Л, состоящего из п + 1 точек, представляющих вырожденные распределения. Теперь для пар моментов можно сделать то же самое с той разницей, что множество L будет соответствовать квадратичной кривой (6?, О2) между точками (0,0) и (1,1). Предположим, что для некоего специфицируемого хвоста распределение G генерирует экстремальный риск в классе распределений Ф(М) , имеющих моментами некую пару М. Предположим далее, что G имеет в классе Ф(М) предельно тонкую поддержку. Я намерен продемонстрировать, что в этом случае G имеет в этой поддержке самое большее три точки.
Обозначим через Н то подмножество в А, которое соответствует рассматриваемой поддержке распределения G. Поскольку М G Conv(H), то, как следствие предыдущего обсуждения, М обязана принадлежать выпуклой оболочке Н* cz Н , такой, что ||/7|| < 3 . Отсюда следует, что Ф(Л/) обязан включать в себя некое распределение G , такое, что его поддержкой будет г! . Более того, должно найтись такое третье распределение G , что G будет смесью распределений G и G . Легко проверить, что G е Ф(7И) , а также то, что хвостовой риск распределения G является неким взвешенным средним
130
6 Опрвдвлявм момвпты с помощью Дв Финвтти
хвостовых рисков распределений G и G**. Поскольку мы условились, что хвостовой риск распределения G является экстремальным в классе Ф(уИ) , G* и G* обязаны иметь ровно тот же самый хвостовой риск, что G, а распределение С7, в свою очередь, обязано не иметь большей поддержки, чем G*.
Выпуклость дает нам и некоторое интуитивное понимание того, почему оптимальные распределения, состоящие из трех точек, являются три полярными. Ниже на графике О обозначает начало координат, С обозначает другой полюс (1,1), Л/— ограничение на моменты, а А и В — две точки на L, причем такие, что ОРВ и АРС являются прямыми линиями. Пусть далее X обозначает произвольную точку (О, 0г), являющуюся кандидатом на оптимальное распределение. Эта точка должна быть связана с одной или двумя другими точками из L, такими, что М содержалась бы в их выпуклой комбинации. Для того чтобы рассеять наименьшую дисперсию, выберем такую точку JV* = , чтобы линия ХМ пересекала L. Любое двухточечное
распределение будет допустимым для любой точки, лежащей в сегментах О А или 2?С, принадлежащих L. Однако, если X лежит в сегменте АВ, никакое двухточечное распределение не будет допустимым, и наилучшим способом максимизировать или минимизировать хвостовой риск будет связать это распределение с точками О и С.
Convex hull for binomial mixture
Оцениваем область допустимых значений
Вышеприведенные геометрические построения связывают каждое внутреннее О с одной двухточечной или трехточечной биномиальной смесью GQ, удовлетворяющей ограничениям на моменты. На самом деле достаточно
131
Часть 1. Стандарты атклснвпил _________________________
рассмотреть только те О ъ которые соответствуют точкам области ОВ. поскольку у каждой точки области ВС есть эквивалентный аналог в виде какой-нибудь точки из области ОВ. Тогда соответствующее смешанное распределение является
решением для:
dGa{0) =
рр((-р)
- ]Ll) + (JLI -
dGe{0*) = dGg{ =
tz V Z tf ул
I p -° )
(p~0)2 pp(\- p) + (p~0)2
= \ — dGe(0*)
всякий раз, когда 9 <(\ — p)p.
Область АВ соответствует условию (1 — р)р <0 < р + (1 — р)р, где dGB (0) = ((- Р))в-(Х- Р)Р\ ;
О
dGg(O) =
(\-р)р(\-р) _ О(\ - 0) ’
dGg (1) = A[1 9 ° P)(1 Л)] = 1 - dGe (O') - dGg (0) .
C7
Мы можем теперь вычислить хвостовой риск, связанный с каждым кандидатом Ge и поискать экстремальные значения. И, хотя нельзя выписать аналитическое решение, справедливое для всех Т и всех п, соответствующие численные решения найти легко.
Асимптотические пределы области допустимых значений
Поскольку дисперсия условного среднего каждой случайной величины рр(У — р) , дисперсия суммы этих условных средних будет ycv?2 //(1 — р) . Но полная дисперсия бернуллиевых сумм равна (1 — р + рп)пр(\ — р) . Остаток р)пр(\- р) — это ожидаемая условная дисперсия. Для того чтобы это доказать, заметьте, что условная дисперсия суммы равна п9(\ — 9) и посчитайте математическое ожидание при условии распределения G. Отсюда следует, что на дисперсию условного среднего независимо от р приходится доля полной дисперсии, равная Рп . Таким образом, при растущем /7, если G 1- р + рп
не выродится, доля дисперсии условного среднего будет сколь угодно близкой к 100%. На интуитивном уровне это означает, что, если п очень велико, мы можем представлять себе хвостовой риск так, словно все суммы были сконцентрированы в точках, значение каждой из которых равнялось бы числу, равному /7, умноженному на соответствующее значение в поддержке распределения G, т.е. так, как если бы все суммы были сконцентрированы в 77-кратных точках поддержки G.
132
6. Опрвдвлявм мвмвнты с помощью Дв Финвтти
Девлин определил асимптотический допустимый интервал как q 1 .
L ’52 +1_
Это правильно, если мы хотим получить пределы, которые были бы справедливы для Vа . Те границы, которые справедливы для случая, когда р и а известны, уже приведены в конце гл. 4. Здесь я повторю их для левого 5-хвоста:
• 0, если ;
V р(1-а)
О,——- , если [...А > 5 > - \-BiL. ;
1 + 5" J у p(i — р) у 1 — А
1 _ _ (1 - Р)Р(1 - Р) j _ + (l-p)p(l-p)
р - рр(\.~ р) ’ 1 - р + рр(\- р) j
> 5 > 0 •
Одна физическая аналогия
Из курса физики известно, что, если абстрагироваться от квантовых эффектов, в произвольном неподвижном герметичном контейнере с газом фактически любое пространственное распределение молекул этого газа будет допустимым. Тем не менее, если только этот газ не является сверхразряженным, вероятность того, что плотность газа окажется существенно выше в какой-либо одной части контейнера по сравнению с другими частями, исчезающее мала, хотя и не ноль. Иначе говоря, гигантское подавляющее большинство всех возможных распределений сгруппировано вокруг среднего распределения, которое есть равномерное распределение частиц газа по всему пространству контейнера. Более века назад Людвиг Больцман доказал этот очевидный факт теоретически и тем самым открыл для исследований новую область теоретической физики, называемую статистической термодинамикой, достижения в которой сыграли ключевую роль не только в развитии физики, но и современной химии и средств коммуникации.
“В чем же здесь аналогия?” — спросите вы. А в том, что наши случайные величины Бернулли соответствуют молекулам идеального газа, а условное бернуллиево среднее соответствует равномерному распределению молекул внутри того контейнера Продолжая аналогию, заметим, что распределение вероятностей G соответствует набору вероятностей того, что наш контейнер ’’сидит’ в различных возможных положениях. Физика обычно игнорирует это С7, поскольку экспериментатор может легко контролировать местоположение и окружение контейнера либо просто измерить расположение контейнера относительно системы координат.
Если бы портфельные инвесторы могли контролировать ту среду, в которой они делают свои инвестиции, им тоже можно было бы не обращать никакого внимания на G.
133
7. Большие риски VAR1
Из всех манер, которые в Конвея вколотили в детстве в английской школе-интернате, наиболее полезной оказалась тактичность. Спору нет, очень трудно оставаться тактичным в хулиганской среде торгового зала биржи, да и просто по жизни необходимо уметь использовать крепкое словцо, чтобы не прослыть слабаком. Как известно, если хочешь выжить на пиратском корабле, умей изрыгать проклятья и раздавать пинки. Но несмотря на все, Конвей старался изо всех сил оставаться тактичным. И, надо сказать, его потуги щедро вознаграждались. Правда, для того чтобы во всех случаях сохранять тактичность и спокойствие, необходимо некая хладнокровность, а в этом-то и главная трудность. Но Конвей научился хранить спокойствие в разных ситуациях. В частности, чтобы сохранять спокойствие на совещаниях, он заранее прокручивал в голове возможные сценарии каждого совещания, стараясь предугадать спорные вопросы и будущее конфликты, чтобы заблаговременно найти выход из затруднительных положений. Но сейчас Конвей чувствовал глубокое смятение. Дело в том, что раз за разом он пытался вообразить, как будет докладывать Комитету контроля риска о последних откровениях Девлина, но все его экзерсисы заканчивались тем, что он мысленно видел, как его за ухо выводят из зала заседаний. И как, скажите на милость, объяснить Зевсу-громовержцу, для которого амброзия — это финансовый рычаг, что его банк «Мегабакс» должен, видите ли, иногда придерживать оборотные средства на 10 стандартных уклонений в качестве резерва, чтобы держать риск внезапной неплатежеспособности ниже 1%? Да никак! Нельзя это объяснить! В этот момент Конвей осознал, что любой его доклад на эту тему обречен на провал. И дело было вовсе не в том, что его не стали бы слушать или отнеслись к его сообщению предвзято или невнимательно, а в том, что Конвей ясно себе представил очевидную контратаку, от которой у него, о ужас, не было защиты. “Девлин! — в озарении воскликнул Конвей. — Здесь явно чем-то попахивает!”
“Не обращай внимания, Конвей. Это, должно быть, остатки моего сэндвича с рыбой. Мне следовало бы его завернуть поплотнее”.
“Сэндвич с рыбой? Девлин, выбрось его немедленно. А потом завещай свой желудок науке. Где-нибудь там, в отложениях, наверняка найдут заменитель асбеста или что-то в этом роде... Но я, вообще-то, имел в виду не твою еду третьей свежести, а твои научные откровения”.
“Опять мои откровения! Но, ведь мы все это уже по многу раз разбирали и, кажется во всем разобрались”.
1 VAR (Value At Risk) — стоимость сопряженная с риском.
134
7. Большие РИСКИ VAR
“Но ты сказал, что большие высоко диверсифицированные портфели могут представлять собой почти 4%-ную вероятность хвоста пяти стандартных уклонений! А я твердо знаю, что подавляющее большинство аналитиков с железобетонной уверенностью заявили бы, что такое невозможно. Скажи-ка, Девлин, может быть, они видят что-то такое, чего ты не замечаешь?”
“Конечно, такое возможно. Мои оценки предполагают минимум информации. Дополнительная информация могла бы ограничить хвостовой риск поточнее. В одних случаях выбросы за пределы пяти стандартных отклонений — редкое явление, в других — не редкость. Но те, кто утверждает, что такие выбросы — большая редкость, говорят так не потому, что очень проницательны или у них есть какое-то особое понимание наших проблем. Они просто невежественны или сами не знают что несут”.
“Вот за что я тебя всегда люблю, Девлин, так это за уважительное отношение к коллегам... Скажи, их непременно нужно колесовать и четвертовать или, может быть, повешения вполне достаточно?”
“Я не критикую кого-то персонально. Я просто говорю об общей ситуации в нашем деле, только и всего”.
“Ситуация с точки зрения теоретика, так. Но, возможно, на практике существует какой-то мощный фактор, который остался незамеченным и который существенно подавляет хвостовой риск. Иначе я не могу рационально объяснить, почему тысячи всесторонне образованных и тщательно подготовленных аналитиков могут так ошибаться, если ты прав, конечно”.
“Ну и что здесь такого невероятного? Они и могут ошибиться всем скопом, да и ошибаются, не так ли. Ты не забыл, что случилось с нашими предшественниками в этом замечательном банке. Они прозевали азиатские кредитные риски в 1997 г. В противном случае они до сих пор сидели бы на своих местах, а мы, напротив, сейчас не вели бы этих дискуссий, во всяком случае, здесь”.
“То другое дело, Девлин. Они пользовались правильной моделью. Просто ввели в нее неправильные параметры. А риск дефолта и корреляция оказались гораздо выше, чем они думали”.
“Дело не только в конкретных оценках, Конвей. Причина была еще и в том, как они понимали постановку задачи. Я думаю, что общепринятый метод среднего и дисперсии одел смирительные рубашки на их мозги, так сказать”.
“Что ты имеешь в виду, поясни?”
“Ну, кризис дестабилизирует фундаментальные параметры, и их становится трудно предсказывать. Если брать в расчет эту неопределенность, т.е. рассматривать ее в качестве дополнительного фактора, то следовало бы резко поднять уровень отчислений в резерв на покрытие возможных потерь. Но общепринятый анализ ничего подобного не предполагает. Традиционный анализ интересуется только оценками, желательно максимально точными, среднего, дисперсии и корреляции. Традиционный анализ не принимает во внимание уверенность или неуверенность в тех данных, которые ему предоставляют”.
135
Часть 1. Стандарты отклонения________________________________________
“А не могли бы мы обойтись без явного введения более высокого риска в модель, а просто повысить значение средней частоты дефолта?”
“Этого было бы недостаточно. Вот, например, значения корреляции имеют тенденцию к росту во время кризиса. А это — шило в заднице общепринятого анализа...”
“Не мог бы ты объяснить свою мысль с шилом поподробнее?”
“Не уверен, что могу объяснить все свои интуитивные догадки, но точно знаю, что частично проблемы с корреляцией проистекают от неопределенности. Вспомни, для бесконечно перестановочных случайных величин Бернулли корреляция прямо пропорциональна дисперсии среднего риска дефолта. Чем больше неопределенность, тем большей стремится стать дисперсия, значит, и оценка корреляции нарастает”.
“Интересно. Следовательно, надо пересмотреть оценки корреляции в случае изменения среднего и дисперсии условного риска дефолта, правильно я понимаю?”
“К сожалению, этого все равно недостаточно. Дело в том, что, даже используя правильные значения первого и второго моментов, стандартная модель недооценивает риски внешних хвостов. На самом деле, если только дисперсия традиционно оцениваемого условного риска дефолта не является очень малой величиной, эта недооценка будет очень серьезной. Вот смотри, я построил таблицу, которая сравнивает фактические и оцененные хвостовые риски при различных привходящих условиях. Не хочешь посмотреть мою модель при разных условиях?”
“Конечно. Допустим, у нас есть 1000 различных начинающих молодых азиатских корпораций. Пусть, далее, каждая займет у нас по 1 млн. долл, сроком на 1 год. В случае дефолта любой из них мы в конце концов вернем только половину того, что они нам должны. В обычные времена частота дефолта составляет приблизительно 3% в год, но во время кризиса, который случается в среднем раз в двадцать пять лет, частота дефолта подскакивает до 50%. За исключением общих вероятностей дефолта, выплаты нам от этих корпораций некоррелированы. Какой будет величина VAR с вероятностью 99%? Это значит, что я хочу знать, где лежит порог левого хвоста, несущего 1%-ный риск”.
“Каковы твои допущения относительно протяженности кредита до кризиса? — спросил Девлин. -Мне это надо знать, чтобы вычислить чистые потери прибыли”.
“Забудь об этом. Предположи самый наихудший сценарий, когда дефолт происходит сразу после того, как деньги выданы, а не в день, когда должен быть возвращен основной долг. Хотя такое предположение и не слишком реалистично, именно так наши проверяющие и начальство оценивают VAR по банковским кредитам”.
Девлин молча кивнул, открыл на компьютере свою таблицу, ввел нужные данные и прочел результаты вслух: “В стабильные времена наш банк будет иметь 1%-ный шанс потерять 21 млн долл, или несколько больше, если включить
136
___________________________________________________7. Большие риски VAR
прибыли. В условиях кризиса соответствующее значение VAR будет равно уже 268 млн долл. Если бы мы не знали, что надвигается кризис, но оценили бы его вероятность не в 3%, а в 4%, то величина VAR составляла бы 255 млн”.
True 1%-ile values at risk
Истинный l-процентильный VAR.
Предполагается, что эти 1000 условно независимых активов, каждый из которых при дефолте теряет половину своей стоимости, таковы, что в стабильные времена риск дефолта каждого из них равен 3%, а во время кризиса возрастает до 50%.
“255 млн долл, очень близки к 268 млн... Почему так мала разница между ситуациями 4%-ной и 100%-ной вероятности кризиса?”
“В твоих предположениях шанс потерять более 100 млн в стабильные времена исчезающее мал. Это значит, что, по сути, каждое событие в нашем 1-процентильном случае происходит именно во время кризиса. Если мы знаем, что приближается кризис, нам следует обратить внимание на 1-процентильное кризисное распределение. А если существует всего лишь 4%-ная вероятность наступления кризиса, то нам следует обратиться к 25-процентильному кризисному распределению. Эти точки лежат слева от условного среднего на расстоянии, соответственно 2,33 и 0,67 стандартных уклонений. При условии наступления кризиса стандартное уклонение мало по сравнению со средними потерями: 8 млн долл, против 250 млн. Вот почему с практической точки зрения между этими двумя оценками разница невелика”.
“Иными словами, если я тебя правильно понял, если нам дан 4%-ный шанс наступления кризиса, то 3,9-процентильная оценка VAR тоже будет лежать где-то вблизи 250 млн долл., не так ли?”
“Совершенно верно. Поскольку 3,9% равно 97,5% от 4%, то 3,9-процентильная оценка будет лежать правее условного среднего примерно на 2 стандартных уклонения. Ну кА, посмотрим...”, — с этими словами Девлин быстро произвел на компьютере какие-то вычисления. — Мы получаем 235 млн долл., что немного больше чем на 4,5 безусловных стандартных уклонения левее безусловного среднего и близко к 4,6%-ному максимально возможному риску для такого выброса”.
137
Пасть 1. Стандарты атклалвния _===^^==
“Интересно. Эти верхние границы, оказывается, не выглядят такими уж дикими, как казалось поначалу... А каковы тогда соответствующие VAR, получаемые с помощью общепринятого метода среднего и дисперсии?”
“Если ты точно знаешь, в какое именно состояние попадешь, то и традиционным методом получишь правильные ответы: 21 млн в условиях стабильности и 268 млн в условиях кризиса, что покрывает 1-процентиль. Но уже 4%-ная вероятность кризиса сильно меняет эти оценки. Начнем с наивного подхода, при котором предполагается, что мы правильно предсказали вероятность кризиса, но корреляция осталась постоянной и равной нулю. Тогда 1-процентильные потери дают 32 млн, или что-то около одной восьмой их истинного значения”.
“А что будет, если безусловная корреляция будет подсчитана правильно?”
“Для 4%-ной вероятности кризиса безусловная корреляция составляет 0,183. Стандартный метод среднего и дисперсии, получив эту информацию, пересчитает VAR и выдаст его 1-процентильное значение, равное 132 млн долл. Это гораздо лучше, но все-таки едва дотягивает до половины того, что нужно”.
“Да, расхождение очень серьезное... Может, мой пример слишком жестко определенный? — сказал Конвей. — Ведь на практике мы никогда не знаем истинных значений риска дефолта. Поэтому давай предположим вместо среднего 3%-ного риска дефолта в стабильное время, что этот средний риск равномерно распределен в интервале от 0 до 6%. И вместо среднего риска дефолта в кризисные времена равного 50%, будет риск равномерно распределенный на интервале от 25 до 75%. Как это повлияет на наши замечательные 1-процентили?”
Estimated 1%-ile values at risk
100°/
300 250 200 150 100 50 0
1 % -lie value at risk
LjNaive method
EjStandard method
Q True VAR
Оценки 1-процентильных VAR.
Все исходные предположения такие же, как и ранее. Стандартный метод использует истинные значения первого и второго моментов. Наивный метод не учитывает корреляцию.
138
7. Большио риски VAR
Девлин ввел в компьютер новые параметры и через секунду получил результат: “Истинные 1-процентили составляют, соответственно, 40 млн долл, в стабильное время, 383 млн — в кризисное время и 313 млн — с 4%-ной вероятностью кризиса. VAR теперь больше, а также больше разрыв по VAR между достоверным кризисом и 4%-ной вероятностью кризиса”.
“Почему?”
“Каждый 1-процентильный VAR слегка превышает средние потери в силу того, что задан соответствующий 1-процентиль среднего риска дефолта. Поэтому дополнительная неопределенность порождает более высокие, но и более разнообразные пределы риска. Удивляться тут нечему”.
“А как насчет оценок по традиционному методу, стали они сколько-нибудь ближе к истинным значениям или нет?”
“Нет, если Вы игнорируете корреляцию, порождаемую неопределенностью. Но такое игнорирование привело бы нас к тем самым наивным оценкам из предыдущего примера, т. е. к 21 млн при стабильности, 268 млн при кризисе и 32 млн — при 4%-ной вероятности кризиса. Наивные оценки недооценивают истинные VAR на величину от 30 до 90%”.
“А что будет, если мы правильно посчитаем два первых момента?”
“Если мы точно знаем, в каком состоянии находимся, т. е. кризисе нас ждет или стабильность, то традиционный анализ работает вполне удовлетворительно. Для стабильного времени он оценит VAR в 36 VAR, а для кризиса — в 419 млн. Эти данные на 9% соответственно недооценивают и переоценивают VAR. Но, подчеркиваю, традиционный подход среднего и дисперсии дает плохие результаты в случае скошенного риска. Он оценивает VAR при 4%-ном риске кризиса в 139 млн долл. Это чуть-чуть больше, чем в предыдущем примере, но меньше половины истинной величины”.
Re-estimated 1%-ile values at risk
Скорректированные оценки 1-процентильных VAR.
Предполагается, что средний риск дефолта равномерно распределен в интервале от 0 до 6% в стабильные времена и от 25 до 75% в кризисное время. Все остальные предположения — те же самые.
139
Часть 1. Стандарты отклонония
“Так что же получаем в сухом остатке, а, Девлин?”
“У меня, пока что нет окончательных выводов, Конвей, Я еще очень многого не понимаю”.
“Это бодрит, конечно... Но у меня на руках бизнес, который требует ответов, причем немедленно!”
“Ерунда, у тебя в запасе сколько угодно ответов! Твой классный метод среднего и дисперсии строгает ответы непрерывно и круглосуточно... Правда, это все больше ответы на вопрос: ‘Что есть самое плохое, что может со мной случиться при текущем состоянии Вселенной?’, не так ли?”
“А чем, собственно, тебе не нравится этот вопрос?”
“Нравится, нравится... Пока кризис далеко, все в порядке. Но, если риски кризиса существенны, тогда то, что происходит непосредственно сейчас, т. е. ‘текущее состояние Вселенной’, не имеет для нашего 1-процентиля никакого значения. Тогда нам надо переключить внимание на большие риски”.
“Но, как быть, если ты даже не уверены, что знаешь, что это такое, эти самые ‘большие риски’?”
“Тогда тебе следует как-то учесть неопределенность. Хотя неопределенность сама по себе среднего не меняет, она порождает более высокую корреляцию. А корреляция — ключевой фактор при оценке VAR сильно диверсифицированного портфеля”.
Конвей вяло кивнул и впал в задумчивость. Одна вещь по крайней мере становилась прозрачнее. Он стал яснее понимать, почему все было таким нечетким. А дело было в том, что главное правило в “Мегабаксе” гласило: никогда не признавать малейшего непонимания природы каких угодно рисков, наоборот, надо делать вид, что ты все и всегда лучше всех понимаешь... Покупай риски, продавай риски, шинкуй их, играй в них, как в кости, перекладывай их из одного пакета в другой, но, если ты открыто признаешь, что чего-то не знаешь или не понимаешь, ты потеряешь авторитет у клиентов и у коллег, и тогда кто-то все знающий о рисках легко займет твое место. Поэтому гораздо безопаснее прикидываться знатоком и объяснять непредвиденные выбросы причудами природы. Не надо, конечно, быть Девлином, чтобы додуматься до этой истины. Но, все равно у Конвея не было ответа, почему эти выбросы стремились стать все выше и выше... А методы Девлина предлагали по меньшей мере два, но зато весьма реальных объяснения. Во-первых, объективные границы риска проходят гораздо выше, чем предполагает стандартная аппроксимация. Во-вторых, невежество способствовало тому, что эти границы воспринимались, катастрофически высокими.
После долгого молчания Конвей, наконец, спросил: “Девлин, а существует ли какой-нибудь способ уменьшить неопределенность хвостовых рисков?” И не дожидаясь ответа, продолжил: “Дело в том, что мы могли бы сделать высокие риски 5-хвостов более «съедобными» для Комитета контроля риска, если бы нашли способ исключить их из рассмотрения”.
“Тебе нужны рекомендации типа: ‘Покупай побольше акций страхователей от природных катастроф’ или ‘Продавай права на те активы, что демонстрируют
Вводонио_________________________________________===_=======^_
Читатель: Они сложные?
Автор: Да, достаточно сложные. Но я буду строить их медленно и шаг за шагом, чтобы Вы смогли разобраться, как соотносятся и работают их составляющие.
Читатель: Разве я могу доверять теории, которую я понимаю только наполовину?
Автор: Конечно, можете. Любые электронные таблицы легко смогут выполнить все вычисления. Вы или самостоятельно получите все ответы, причем почти мгновенно, или кто-либо сделает это для Вас.
Читатель: Как Вы думаете, эти ответы будут сильно отличаться от тех, что дала бы старая система?
Автор: Это зависит от того, какую информацию Вы подаете на вход и о чем спрашиваете. Ясно, что чушь на входе даст чушь на выходе...
Читатель: Допустим, я подал на вход обычную информацию: риск и ожидаемые вознаграждения различных активов и их полные корреляции, сможет ли новая система показать мне, какими будут хвостовые риски всего портфеля?
Автор: Как я уже сказал, этого сделать нельзя.
Читатель: Чепуха какая-то. Эксперты постоянно отвечают на подобные вопросы, имея даже меньше исходной информации.
Автор: Я не говорил, что эксперты не смогут ответить на ваши вопросы. Просто они не могут ответить на них правильно.
Читатель: Приближенные ответы тоже годятся...
Автор: Но ответы, которые Вы получите, не будут даже приблизительно правильными. Вернее, они не будут правильными, если отказаться от некоторых неявных, но очень существенных ограничений старой модели.
Читатель: Вы преувеличиваете, конечно!
Автор: Нет, я не преувеличиваю. Допустим, у Вас есть три монеты. Какова вероятность того, что при одновременном бросании выпадут три решки?
Читатель: Конечно, одна восьмая. Одна вторая, умноженная на одну вторую, умноженную на одну вторую.
Автор: А вот и нет! В главе 1 я привожу некоторые контрпримеры.
Читатель: Не представляю себе, как можно построить контрпример очевидному!
Автор: Очень хорошо! Это значит, что книга как минимум поколеблет систему ваших интуитивных восприятий.
Читатель: Почему нельзя пренебречь вашими контрпримерами как несущественными исключениями, даже если окажется, что они верны?
14
7. Больший риски VAR
неконтролируемый иррациональный рост’?”
“Нет, я имел в виду не то, как справиться с существующим хвостовым риском, а то, как бы это сказать, как показать, что он есть такое, этот хвостовой риск”.
“А ты не хочешь узнать, как измерить моменты старших порядков?” — спросил Девлин с ядовитой усмешкой.
“Ну, как мне помнится... — начал, было, Конвей, но внезапно осекся и подумал: Всякий раз, когда у него такая хитрая рожа, надо держать ухо востро. Надо думать, в этом вопросе какой-то подвох... — и продолжил вслух: Постой-ка! Я помню, что нам понадобятся еще и смешанные моменты”.
“Конечно, понадобятся, — сказал Девлин, улыбаясь еще шире, и добавил: Теперь машинное время дешево, а эти моменты — как раз то самое, что нужно бюрократу-буквоеду: много цифр”.
“Так-то оно так, но только вряд-ли кто-нибудь из них поймет, зачем все это надо, и что все эти смешанные моменты означают”.
“А им и не надо ничего понимать. Ты просто дай компьютеру задачу рассчитать максимальное и минимальное из допустимых значений риска х-хвоста, совместимые с неким заданным множеством смешанных моментов. Доложи Комитету только этот интервал, а сами эти моменты никому не показывай”.
“Хорошая идея! Ну, и какие нужны вычислительные мощности для того, чтобы ограничить риски х-хвостов портфеля, содержащего, скажем, 1 000 кредитных активов?”
“Хм-м-м-м. Для того чтобы ограничить любой риск как следует, при условии, что ты не определил заранее, являются эти активы перестановочными или нет, нам понадобится измерить вероятность каждой пары исходов. А вероятность того, что только два первых актива объявят дефолт, не обязательно равна вероятности того, что объявят дефолт только два последних и так далее. Так что число различных парных исходов равно 21000, или 1 с 434 нулями. Конечно, мы предполагаем, что каждый из этих активов моделируется случайной величиной Бернулли, что само по себе является очень сильным упрощением. Но вопрос о том, слишком или не слишком большое упрощение представляет собой бернуллиевость, не имеет большого практического значения, поскольку то количество машинной памяти, которое нам понадобилось бы при рассматриваемых предположениях, намного превышает общее количество элементарных частиц в изученной части нашей Вселенной”.
“Ну знаешь, Девлин, — сказал Конвей, сдерживая улыбку, — порой ты бываешь жутким занудой!” И они оба весело рассмеялись.
Отсмеявшись, Конвей уже серьезно сказал: “Ладно, давай упростим постановку задачи. Предположим, что различные кредитные активы так перестановочны с другими активами, что у нас есть всего лишь 40 классов активов для работы. Ограничимся далее только моментами порядка не выше пятого. Сколько в этом случае существует моментов, которые мы должны держать в поле зрения?”
Девлин быстро ввел что-то в компьютер и почти мгновенно прочитал ответ: “1221758”.
141
Часть 1. Стандарты отклонония
“Опять более миллиона! Почему?”
“Дело в том, что каждый отдельный момент ?и-того порядка изоморфен некой уникальной комбинации из т чисел, такой, что каждое число этой комбинации чисел изоморфно некоему из наших классов. Это число, кстати говоря, может повторяться в этой комбинации, а может и не повториться ни разу. Теперь посчитаем количество возможных комбинаций. Начнем с того, что всего существует С40 > 650000 комбинаций, состоящих из 5 чисел, таких, что каждое число выбрано без повторений из некого набора из 40 чисел. Аналогично, существует С40 > 90000 комбинаций, состоящих из 4 чисел, таких, что каждое число выбрано без повторений из некоего набора из 40 чисел. Далее существует 4 х С44о > 360000 комбинаций, состоящих из 5 чисел каждая, таких, что в каждой комбинации только 4 числа разные, а пятое число является повторением одного числа из этих четырех. Таким образом, у нас уже набежало более 1,1 млн вариантов, а мы еще не посчитали комбинации, в которых только тройки чисел уникальны, только двойки уникальны и комбинации, каждая из которых составлена из одного числа, повторенного 5 раз”.
“Ну, хорошо. Скажи, наконец, как нам подсократить количество классов и уменьшить порядок моментов, чтобы ситуация стала, наконец, стала реально обозримой?”
“Это зависит оттого, какой смысл ты вкладываешь в понятие ‘обозримость’. Послушай, давай-ка, я сделаю для тебя одну табличку”. И через несколько минут Девлин ее распечатал.
Number of distinct mth-order moments given n assets
Л1 - 2 m — 3 т = 4 m = 5 т — 6
п — 5 15 35 . 70 126 210
п — 10 55 220 715 2,002 5,005
п — 15 120 680 3,060 11,628 38,760
л -- 20 210 1,540 8,855 42,504 1,77,100
л = 30 465 4,960 40,920 278,256 1,623,160
п - 40 820 11,480 123,410 1,086,008 8,145,060
п ~ 50 1,275 22,100 292,825 3,162,510 28,989,675
including lower-order moments (except m = 0)
л = 5 20 55 125 251 461
л = 10 65 285 1,000 3,002 8,007
п - 15 135 815- 3,875 15,503 54,263
л = 20 230 1,770 10,625 53,129 230,229
л = 30 495 5,455 46,375 324,631 1,947,791
л - 40 860 12,340 135,750 1,221,758 9,366,818
л - 50 1,325 23,425 316,250 3,478,760 32,468,435
Число различных моментов /и-го порядка для п активов.
Конвей быстро просмотрел данные и сказал разочарованно: “Их слишком много!”
142
7. Большие риски VAR
“Да, к сожалению, скорее всего, их действительно слишком много. Например, если у нас есть 20 активов и если не рассматривать ничего, старше эксцесса и коэксцесса, то все равно придется присматривать примерно за 10 000 моментов. При сегодняшней технологии это допустимо, а завтра, может быть, станет совсем простым делом. Но даже в этом случае мы встречаемся с проблемой другого сорта, напрямую не связанной с вычислительной сложностью”.
“И в чем же эта проблема?”
“В точности наших вычислений. Дело в том, что, как говорит классическая статистическая теория, чтобы достоверно оценить какое-то количество параметров, число наблюдений, которые следует провести для получения этих оценок, должно существенно превышать число этих параметров. Но по современному состоянию финансовых данных мы вряд ли наберем данных, соответствующих одному дню, на 10 000 наблюдений..
Конвей поднял руки: “Итак, моментов так много, что их и не упомнить, и даже если мы ухитримся уследить за ними, то, скорее всего, не сможем их измерить... Сдаюсь! Комитет контроля риска никогда не воспримет это всерьез, — сказал Конвей, а про себя подумал: Во всяком случае, они уж точно не вникнут в проблему за те 30 секунд, которые они мне дадут, перед тем как повесить меня на просушку... Пойду-ка я, лучше, в офис, да выпью пару таблеток аспирина. 2 таблетки из бутылки, в которой 100 таблеток... Уж с этими-то числами я как-нибудь справлюсь!”
Ну, пока Конвей борется с головной болью, подразберемся с формулами, которые использовал Девлин.
Воздействие неопределенности
В общем случае можно считать, что с ростом неопределенности растет дисперсия VarG, а математическое ожидание EG не меняется. Однако
____—____ — это корреляция соответствующих случайных величин Бернулли и,
eg(\-eg)
следовательно, должна расти с ростом неопределенности, что, в свою очередь, должно резко увеличить оценку VAR.
Для того чтобы построже вывести этот результат, рассмотрим следующие соображения:
• для перестановочных случайных величин безусловная корреляция ри равна безусловной ковариации Covu , разделенной на безусловную дисперсию Varu ;
• Covu всегда равна средней условной ковариации E\Covc] плюс ковариация соответствующего условного среднего Cov[EG ], что включает в качестве
143
Часть 1. Стандарты втклонония ==__s__=_==== частного случая тот факт, что Varu = E\Varc ] + Var\EG ];
• из условной независимости имеем, что Covc = 0 ;
• для перестановочных случайных величин Cov[EG] равна дисперсии VarG условного среднего;
• для случайных величин Бернулли Уак(; равна вероятности успеха, умноженной на вероятность неуспеха, т. е. EG (1 — EG ) .
Отсюда следует, что для условно независимых случайных величин Бернулли ------ХЕЕ---. Это значит, что чем выше воспринимаемый уровень
дисперсии распределения G при фиксированном значении математического ожидания, тем выше воспринимаемая корреляция.
Применяем моменты высших порядков для демаркации хвостового риска
Как непосредственно следует из треугольника Девлина, для того чтобы полностью определить хвостовой риск произвольного портфеля, содержащего N бернуллиевых активов, в общем случае надо знать N моментов. Если наши случайные величины не являются случайным величинами Бернулли, т.е. исходы этих случайных величин не бинарные, нам могут понадобиться моменты более высоких порядков. Чем больше активов, тем больше надо знать моментов и более высокого порядка, но при этом достоверная информация даже об одном моменте высокого порядка может сильно сузить область допустимых значений хвостового риска. В качестве наглядного, хотя и довольно экстремального примера заметим, что информация о том, что, скажем, эксцесс очень близок к -2, означает, что риск хвостов отстоящих от среднего более чем на 2 стандартных уклонения, пренебрежимо мал, поскольку существует единственное распределение, которое имеет эксцесс равный —2, и оно распределяет всю плотность вероятности поровну между точками ±1 стандартное уклонение от среднего.
Для того чтобы максимизировать или минимизировать хвостовой риск при ограничениях на моменты, мы можем просто добавить ограничений в те лагранжианы, которые мы вывели в гл. 4. Ну, например, если эти ограничения относятся к асимметрии и эксцессу, то, обозначая соответствующие этим ограничениям множители Лагранжа как т3 и т4 соответственно, мы получим следующие необходимые условия экстремума функции Лагранжа:
- т0 - тхк - т2к2 - т3к3 - т^Е = Q(k) = <
144
7. Больший РИСКИ VAR
Итак, мы видим, наши ограничения, как и раньше, требуют, чтобы некий полином Q лежал не ниже неких двух отрезков прямой, параллельных оси абсцисс и находящихся на, соответственно, уровнях 1 (в этом случае мы имеем хвост) и 0 (в этом случае мы находимся вне хвоста), причем, полиному должна быть приписана ненулевая вероятность только в тех точках, где он касается этих отрезков. Есть в данном случае и еще одно отличие. Оно состоит в том, что теперь Q — не квадратичная форма, а форма четвертой степени. Все интересующие нас решения бывают двух видов в зависимости от того, является ли эта форма четвертой степени выпуклой вверх или вниз, как показано на трафике, приведенном ниже.
Maximal supports given restrictions on first four moments
! Outside tail i Tail ! Outside tai!
"J !
I Value —1 ।
I : :
’ * i Q (quarttc) (
Value = 1 q (quartic) - ! 5
I . ' ? :
! • . Z Value = O ; i Value—О т
I . -—--I .--------------1
ОТ n 0 T n
Максимальные поддержки при заданных ограничениях на первые 4 момента.
Очевидно, что максимальные риски 5-хвоста при заданных ограничениях на третий и четвертый моменты будут характеризоваться некой поддержкой, которая не будет шире, чем три или четыре точки, а именно: точка Г, точка между Т и п, или точки О и /?, или еще одна точка между О и Т. В любом случае мы имеем 5 степеней свободы. Но и ограничений — тоже пяты 4 момента и ограничение на 0-й момент или на сумму вероятностей. дают пять штук ограничений. Отсюда следует, что нам остается найти два множества параметров и определить, какое из этих множеств является допустимым и будет увеличение эксцесса ослаблять или ужесточать соответствующее ограничение. Аналогичная процедура позволяет нам определить искомый минимум или наивысшую из нижних границ, если определенного минимума не существует. Для полноты замечу, что, если экстремальные вероятности могут принимать только значения 0 или 1, оптимальная Q может быть прямой линией и обычно на практике бывает больше степеней свободы.
Все эти технические приемы легко распространить на моменты более высоких порядков. При этом Q становится неким полиномом, степень m которого равна степени самого старшего момента из тех, на которые наложены ограничения. Существует два вида кандидатов в решения в зависимости от знака ограничения на m-й момент. Но в любом случае m + 1 ограничений исчерпывают m + 1 степеней свободы. Иными словами, существует самое большее 2 решения, но только одно из них является допустимым.
145
Насть 1. Стандарты отклонения
Предварительные соображения: Почему смешанные моменты имеют значение
Весь вышеприведенный вычислительный аппарат держится на знаниях моментов, соответствующих данному портфелю. Для каждого заданного портфеля эти величины можно подсчитать, если, конечно, есть в наличии достаточное количество необходимых и достоверных данных по портфелю как единому целому. В этом случае никакие смешанные моменты не нужны. Но, как быть в том случае, если мы захотим для некого портфеля, состоящего из активов
посчитать момент
Заметим,
что выражение,
стоящее в квадратных скобках, очевидно, полином m-й степени, и, как таковой, включает в себя много одночленов типа | J Xj - Это значит, что, для того
к
чтобы подсчитать все т-е моменты портфеля по тем данным, которые есть, нам понадобится знать смешанные моменты по этим активам.
Считаем моменты и смешанные моменты
Сколько вообще существует различных моментов т-го порядка, включая смешанные? Благодаря Феллеру, есть способ их подсчитать. Упорядочим натуральный ряд чисел от 1 до п по возрастанию слева направо. Теперь разместим между этими числами произвольным образом справа от единицы т нулей, не обязательно подряд. Поставим в соответствие каждому нулю слева ближайшее положительное число. Тогда нашему ряду нулей будет соответствовать некое покрытие из т положительных чисел. Так, серию из 4 нулей, размещенную среди ряда натуральных чисел от 1 до 5, -1200304450 — будет представлять следующая четверка чисел: {2, 2, 3, 5}. Оказывается, что каждому такому m-покрытию можно поставить в соответствие некий момент m-го порядка, причем это соответствие будет взаимнооднозначным с точностью до перестановки. Поскольку у нас ровно т нулей и ровно п + т -1 мест, на которые эти нули можно разместить, число возможных размещений равно С™+тЧ .
Для того чтобы сосчитать все различные моменты порядка не выше т, несколько расширим метод Феллера с тем, чтобы ситуация, когда нули стоят левее единицы, была разрешена. Например, мы тогда можем свернуть серию натуральных чисел: 0, 1, 2, 0, 0, 3, 4, 5, 0 в четверку: {0,2,2,5}. Таким образом, мы сможем однозначно идентифицировать и моменты порядка меньше т тоже. Дело в том, что, поскольку теперь у нас есть п + т мест, куда мы можем размещать нули, число различных комбинаций становится равным С„+т • Однако надо, конечно, иметь в виду, что одна из этих дополнительных комбинаций с нулями впереди относится к моменту нулевого порядка, который обычно не рассматривается.
146
8. Плохое поведение хороших аппроксимаций
Спустя несколько дней Конвей сказал Девлину как-то за ланчем: “Ты меня убедил. Больше никакого анализа риска по принципу ‘Всяк ботинок на одну колодку’ не будет. Теперь мы будем различать кредитный риск и краткосрочный рыночный риск. Я назову этот подход ‘Разделение Девлина’, каково? Для кредитного риска величина (l/s2+l) теперь будет представлять верхнюю границу. И мы будем априори предполагать нормальность распределения только для рыночного риска”.
Девлин был так поражен тирадой Конвея, что чуть не подавился сэндвичем, который он в тот момент жевал. Чтобы вновь обрести дар речи, ему пришлось залпом выпить стакан воды. Наконец он выдавил: “Конвей, не дай бог! Не прицепляйте мое имя к своим откровениям, будьте так добры”.
“Не скромничай! Ты заслужил эту порцию почета. И потом, нам же надо как-то восстанавливать твой авторитет в нашей замечательной организации, так ведь? И уж если быть предельно честным, я сам никогда не догадался бы, что кредитный риск фундаментально отличается от всех остальных видов риска. Имей в виду, что я вовсе не намерен противопоставлять себя Комитету контроля риска без поддержки с твоей стороны: камикадзе летают парами... и мы -команда, черт возьми!”
Конвей все больше и больше воодушевлялся, поэтому, чтобы прервать его речь, Девлин был вынужден повысить голос: “Но, ведь, я никогда не говорил тебе, что кредитный риск так уж фундаментально отличается от других!”
“Как это? Еще как говорил! Ведь все случайные величины, которые мы анализировали, платят нам, как мы предполагали, или фиксированную сумму, или ничего. А это не что иное, как кредитный риск”.
“Это не только кредитный риск. Из случайных величин Бернулли можно построить и другие процессы риска, как дом из кирпичей... Например, среднее большого числа независимых перестановочных случайных величин Бернулли сходится к некоему нормальному распределению. Это непосредственно следует из центральной предельной теоремы и значит, что при желании, ты можешь моделировать рыночный риск как набор исходов испытаний, каждое из которых имеет всего два возможных исхода — 0 или 1”. В конце этой тирады Девлин так неудачно раскусил маринованный огурчик, что залил соком подбородок.
“Ага! — подумал Конвей и улыбнулся. — Хоть раз, но ты попался! Здесь-
147
Часть 1, Стандарты отклонония ____________====^__=_=
то я тебя и прижму”. Но вслух Конвей с притворным почтением произнес: “Может, ты забыл чего-нибудь, профессор? Что-то очень важное...”
“Твоя правда. Я куда-то засунул свою салфетку. Подожди, пожалуйста, минуту. Я сейчас раздобуду себе новую...”
“Вот, возьми мою, — Конвей протянул Девлину салфетку. — Ты же всегда забываешь взять салфетку, поэтому я всегда беру запасную... Но я, конечно, имел в виду не салфетку, говоря о том, что ты кое-что забыл. Я имел в виду фундаментальное различие между рыночным и кредитным рисками”.
Девлин неспеша вытер подбородок и спросил притворно наивно: “И в чем же состоит эта разница, позволь тебя спросить?”
“Это очевидно. В области определения. Среднее суммы независимых случайных величин Бернулли всегда распределено биномиально. И хотя биномиальное распределение может очень походить на нормальное распределение для большей части области определения, на хвостах это сходство всегда нарушается. Всякая биномиальная распределенная случайная величина принимает только положительные значения. Никакая нормально распределенная случайная величина не может быть ограничена”.
“Ты прав. Центральная предельная теорема не подходит для экстремальных хвостов. Оказывается, ты помнишь больше из нашего курса статистики, чем я думал... ”
Конвей удовлетворенно кивнул. Не так уж часто ему удавалось поймать Девлина на ошибке. Поэтому он решил не обращать внимания на несколько издевательский характер комплимента. Но в этот момент Девлин испортил Конвею радость его маленькой победы: “Но, по большому счету все это не имеет никакого значения. Когда стандартное уклонение становится достаточно малым, вероятность того, что некое нормальное распределение с положительной средней доходностью породит отрицательную валовую прибыль становится исчезающее малой, и мы вполне можем ей пренебречь”.
“Пытаешься выкрутиться, не так ли?” — со злостью подумал Конвей, а вслух сказал: “Подождите-ка, Девлин! Не ты ли неделями твердил мне, что мы не должны судить о хвостах какого бы то ни было распределения только по двум первым моментам этого распределения? А теперь, что? Теперь ты утверждаешь обратное, не так ли? Я не вижу здесь никакой логики”.
“С этой логикой мы недавно разбирались. Даже в случае кредитного риска существует один случай, когда мы можем обоснованно игнорировать моменты высших порядков. Я имею в виду бесконечно перестановочные случайные величины Бернулли с нулевой корреляцией. По теореме Де Финетти такие случайные величины должны быть независимы в совокупности”.
“Не значит ли это, что ты хочешь провести грань не между кредитным и рыночным рисками, а между зависимыми и независимыми рисками?”
“В принципе, это имело бы смысл. На практике всегда приходится принимать волевое решение на каком-то этапе. Независимость в совокупности — это миф, но иногда миф полезный”.
148
8. Плохоо ппвпдпнип хороших аппроксимаций
“Миф? При чем здесь мифы? Я говорю об абсолютно реальных вещах. Допустим, что мы с тобой играем в рулетку за соседними игорными столами одного и того же казино. Какова может быть связь между исходами наших игр?”
“Может быть много связей. Ну, во-первых, по дороге мы можем попасть в аварию и не приехать в казино вообще. Во-вторых, может вырубиться электроэнергия посреди игры, и в этом случае вероятность того, что я не буду играть, меньше, если я буду знать, что ты тоже не будешь играть, и наоборот, т.е. исходы наших игр не независимы”.
“Давай игнорировать события нулевой вероятности”.
“Вы налагаешь ограничение...”
“Тривиальное”.
“Как посмотреть... Но, если ты так уж хочешь наложить это ограничение, пожалуйста! Вернемся в казино. Предположим, что мы с тобой делаем ставки на соседних игровых столах. Допустим, что внезапно полиция врывается в это казино, арестовывает меня и мои деньги. Скорее всего, в этом случае тебя тоже арестуют. И это делает наши потенциальные выигрыши зависимыми”.
“Но вероятность такой полицейской операции крайне мала...”
“Да, но не во всех странах мира и не во все времена. Откажись рассматривать эту возможность, и ты наложишь еще одно условие...”
“Ну, это уж выливается в какой-то маразм: полиция, дорожно-транспортные происшествия... все явно должно закончиться вторжением инопланетян...” — раздраженно думал Конвей. Но вслух он выразился помягче: “Ну вытаскивай кролика из шляпы, Девлин. Я говорю о справедливых играх, в которые играют по правилам!”
“Таких игр в реальности немного. Вот, скажем, и без всяких рейдов полиции ожидаемый выигрыш всех клиентов от игры в казино отрицателен. Ясно ведь, что проигрыш клиентов — это доход оператора казино, а этому оператору надо покрывать издержки его бизнеса, да и прибыль хочется получить. Поэтому в некоторых казино цены за игру более высокие, чем в других, а в некоторых берут с выигрыша более высокий процент в пользу казино... Все это говорит о том, что даже, если мы играем за соседними столами и если шансы вашего стола стоят сильно против игрока, то, скорее всего, и шансы моего стола тоже будут сильно стоять против игрока”.
“Опять отговорки и увертки... Большинство колес для рулетки стандартны, за исключением криминальных случаев...”
“Ты продолжаешь налагать одно ограничение за другим. Но, согласен, иногда их следует игнорировать. Я же говорил, что придется наложить независимость волевым порядком или волевым же порядком от нее отказаться. Вот и все, что я имел в виду”.
Конвей какое-то время обдумывал последние слова Девлина, а потом сказал более примирительным тоном: “А, разве мы не можем провести тестирование на независимость?”
149
Ысть 1. Стандарты отклонении_____________________________________________
“Мы можем. Если у тебя есть репрезентативная выборка и если ты можешь провести несколько достоверных экспериментов, в которых все параметры, за исключением немногих, будут оставаться постоянными. Но и здесь есть некая ’заноза’. Дело в том, что в финансовой практике значимые факторы почти всегда непрерывно меняются, и, следовательно, эксперимент, строго говоря, невозможен. Вот, например, даже самая тщательная, обработка фактических данных по прошлым котировкам акций молодых азиатских компаний сама по себе не смогла бы подготовить нас к обрушению азиатского рынка в 1997 г. Нам следовало бы сначала осознать, что молодые азиатские компании уже вступили в кризис переинвестирования, а потом сравнить с тем, как развивались аналогичные ситуации в Японии в конце 80-х и в Британии и в США в начале 90-х”.
“Насчет Азии твоя мысль мне понятна. Дело в том, что мы или видим кризис и подстраиваем под него свои модели, или не видим кризиса и получаем пинок...”
“Или мы и кризис видим, и пинок получаем... Даже очень хорошие модели могут привести к большим убыткам”.
Конвей согласно кивнул, но, тем не менее, нашел, что возразить: “Я все же никак не могу взять в толк, как отличить хорошую модель от плохой. Допустим, большая часть активов нашего портфеля такова, что эти активы и, вправду, независимы в совокупности. Можем ли мы спокойно применять для этого портфеля как для единого целого нормальную аппроксимацию?”
“Для центральных тенденций такой подход вполне оправдан, а для хвостов — нет. Дело в том, что отклонение от нормальности на хвостах может быть огромным”.
“Даже если 95% активов независимы в совокупности?”
“Даже в том случае, если пропорция выше. Рассмотрим для ясности один пример”. С этими словами Девлин достал из кармана ручку и начал что-то быстро писать на чистом уголке своей многострадальной салфетки. Наконец он сказал: “Допустим, что мы владеем 2500 чисто бернуллиевыми активами, каждый из которых несет в себе риск дефолта в 2%. Допустим также, что группа, составляющая 98% этих активов, представляет собой набор независимых в совокупности случайных величин. Допустим, наконец, что остальные 2% этих активов представляют собой набор абсолютно коррелированных случайных величин. Теперь представь, что ожидаемое число дефолтов тогда равно 50, а стандартное уклонение — немного меньше 10. И при всем этом 2% своего времени общее число дефолтов будет находиться в окрестности 100, что отстоит от среднего на 5 стандартных уклонений”.
“Ой! Это слишком много для нормальных распределений...”
“Ты не прав. Дело в том, что это слишком много для одного нормального распределения, поскольку на одном нормальном распределении такой фокус не построить, но на двух можно”.
“Что ты имеешь в виду?”
150
8. Плохое поводаниа хороших пппрокоимоций
“Я хочу сказать, что для того, чтобы получить результат, который я только что разрекламировал, нам нужно взвешенное среднее двух нормальных распределений. Первое, которое несет 98% веса, является условным распределением в том случае, что ни одного дефолта не произойдет в группе абсолютно коррелированных активов. Оно будет иметь среднее, равное 49 дефолтам, при стандартном уклонении слегка меньше 7, т.е., квадратному корню из среднего количества дефолтов. А второе нормальное распределение, которое несет всего лишь 2% веса, будет тоже условным при условии, что в группе абсолютно коррелированных активов случится-таки дефолт. Это второе распределение будет иметь среднее, равное 50 + 49 = 99 дефолтам, опять же при стандартном уклонении слегка меньше 7”.
“Боюсь, что ты опять запутал меня...”
“Ты закончил есть? Если закончил, пойдем в мой офис, и я покажу тебе соответствующий график”. Конвей и Девлин сдали подносы с грязной посудой в мойку и вернулись к компьютеру Девлина. Девлин быстро вывел обещанный график.
“Теперь вижу,- сказал Конвей,- что очень небольшое количество высококоррелированных активов могут радикально изменить хвостовые риски. Нам, действительно следует рассматривать их поведение как условный сдвиг в среднем значении всего портфеля. Но что получится, если в портфеле не будет высококоррелированных активов вовсе? Сможем мы тогда использовать аппроксимацию одним-единственным нормальным распределением?”
“Не факт. Вот, допустим, у нас есть 50 активов. Предположим далее, что доходность каждого из этих активов представляет собой среднее 50 различных бернуллиевых факторов, с общим математическим ожиданием, равным 0,98. Допустим, что из этих 50 факторов все, кроме одного, попарно независимы друг от друга и от факторов, влияющих на другие активы. Допустим, наконец, что последний фактор является общим по всем активам. Какова, по-вашему, корреляция между любыми двумя активами этого портфеля?”
“0,02. Но это практически невозможно отловить большинством наших тестов. Они просто укажут его как нечто, явно отличающееся от нуля”.
“Верно. А между тем, для агрегированного портфеля мы получим то же самое распределение, что мы имели в предыдущем примере. Все что мы сделали, чтобы из предыдущего примера получить теперешний, — это назвали 2500 изначальных активов факторами и перегруппировали их в 50 перестановочных активов”.
“Ясно. Отсюда следует, что маленькая корреляция по активам большого портфеля может принести столь же большие разрушения, что и большая корреляция, но в маленьком субпортфельчике того же портфеля”.
“Да, но при условии, что этой маленькой корреляцией управляет некий общий или в значительной мере общий фактор”.
Конвей вдруг почувствовал себя скаковой лошадью, которую заставляют взять барьер. Всякий раз, когда он одолевал очередной барьер, Девлин поднимал
151
Часть 1. Стандарты отклонении _________________________________________________
планку. Вот и сейчас оставалось лишь тупо спросить: “А в чем, собственно говоря, разница?”
“Этот общий фактор не позволяет диверсификации размыть совместный вклад в риск”.
Probability distribution of defaults
Распределение вероятностей для числа дефолтов.
Рассматривается 2500 бернуллиевых активов, каждый из которых имеет вероятность дефолта, равную 2%. Подмножество этих активов составляет 2% от общего числа рассматриваемых активов, причем входягцие в него активы абсолютно коррелированны. Остальные активы независимы в совокупности.
“А, разве, не это же самое делает корреляция?”
“Совсем не обязательно. Если мы слегка изменим условия предыдущего примера и оставим 50 перестановочных активов с их общим средним, равным 0,98, и корреляцией, равной 0,02, но избавимся от общего фактора, доходность такого портфеля станет неотличима от нормального распределения”.
“Разве можно избавиться от общего фактора, не меняя корреляции?”
“Легко. Пусть фактор т, воздействующий на актив w, будет тем же самым, что и фактор и, влияющий на актив т. И пусть так будет для каждой пары п \\ т. А во всем остальном пусть все факторы будут независимы. Среднее будет по-прежнему равняться 0,98. Вы можете легко проверить, что корреляция и в этом случае будет равна 0,02, но ни единый фактор не влияет больше чем на 2 актива”.
Конвей позаимствовал у Девлина бумагу и ручку и начал бормотать, одновременно делая подсчеты: “Значит, теперь вместо 50 х 49 — 2450 факторов, таких, что появляются 2450 раз, и одного фактора, появляющегося 50 раз, у нас есть (50 х 49) -ь 2 = 1225 факторов, появляющихся дважды, и 50 факторов, появляющихся строго один раз. Дисперсия портфеля обязана остаться той же самой, поскольку зависит только от дисперсии и корреляции факторов. Отсюда следует, что 2450 х 1 + 1 х 50 х 50 обязано быть равно 1225 х 2 х 2 + 50 х 1... Да, оба выражения равны 2950. Все сходится”.
152
8. Плохоо поводонио хороших аппроксимаций
“А как с хвостовыми рисками?" — спросил Девлин тоном учителя.
“Они должны уменьшиться, — отрапортовал Конвей как примерный ученик, — поскольку раньше нам для того, чтобы получить 50 дефолтов хватало одного фактора, а теперь нам нужно никак не меньше 25”.
“Абсолютно верно. И агрегированное распределение портфеля теперь должно выглядеть гораздо глаже, без второго пика,” — с этими словами Девлин вывел очередной график.
Alternative probability distribution of defaults
Альтернативное распределение вероятностей для числа дефолтов.
Рассматривается 2500 бернуллиевых активов, каждый из которых имеет вероятность дефолта, равную 2%, а корреляция каждой пары равна тоже 2%. Ни один фактор не действует больше чем на 2 актива.
“Глаже? Да это дикобраз под одеялом! Ты уверен, что все подсчитал правильно?”
Девлин рассмеялся: “Я совсем забыл! Теперь дефолты ходят парами, поэтому график слегка скачкообразен. Но он гораздо ближе к нормальному распределению на правом хвосте. Раньше мы имели 1%-ную вероятность 100 и более дефолтов, т. е. событие 5 стандартных уклонений! А сейчас нет и 1%-ной вероятности для 75 и более дефолтов, т. е. события 2,5 стандартных уклонений”.
“Да, это замечательно, конечно. Даже в том случае, когда два первых момента и соответствующие смешанные моменты все время остаются постоянными, присутствие или отсутствие некого общего фактора радикально меняет хвостовой риск. Скажи, а почему никто раньше мне этого не говорил, как ты думаешь?”
“Не знаю. Может быть, никто раньше этого просто не замечал, а может, это явление, о котором мы говорим, для тех распределений, с которыми работают другие аналитики, не имеет значения...”
“Нет, правда? Кроме шуток? Правильно ли я понимаю, что существуют такие портфели, на которые эти самые общие факторы никакого влияния не оказывают, а влияют только волатильность и корреляция?”
153
Часть 1. Стандарты отклонония_______________
“Правильно. Такими замечательными портфелями являются нормально распределенные портфели. То есть те, в которых два первых момента их независимых и общих факторов обязаны определять агрегированное среднее и агрегированную дисперсию. Поэтому ничто из остального значения не имеет”.
“Ага, понятно. А другие хорошие портфели существуют?”
“Других не бывает. Все дело в том, что всякое другое распределение портфеля было бы чувствительно к наличию общего фактора в гораздо большей степени, чем к попарной корреляции. Это легко доказать с помощью производящих функций моментов. Хочешь, чтобы я это строго доказал?”
“Пока я готов принять это утверждение без доказательства. Но не кажется ли тебе все это странным с точки зрения здравого смысла?”
“Что странного в том, что некий общий фактор в гораздо большей степени влияет на хвостовой риск, чем это предполагает корреляция? По мне, так это совершенно естественно. Корреляция — это в конце концов всего лишь мера попарных взаимодействий, а общий фактор влияет на все сразу”.
“Да нет, я имел в виду, что мне кажется странным то, что нормальное распределение, — это единственный вариант сведения одного к другому. Я всегда думал, что нормально распределенные случайные величины должны быть, ну... более нормальными, что ли... Зачем, скажите, называть распределение нормальным, если оно на самом деле такое исключительное?”
“Термин 'нормальный’ изначально означал некий тренд в совместном поведении больших количеств независимых в совокупности случайных величин. Но фактор, общий для всех этих случайных величин или для части этих случайных величин, есть именно то, что эту независимость рушит, а когда независимость в той или иной мере разрушена, гипотеза нормальности вполне может и не быть асимптотически корректной. В общем, как я уже говорил, существует гигантский разрыв между полной независимостью и отсутствием независимости хоть в какой-то мере!”
Конвей помрачнел. Дело в том, что, если то, что говорил Девлин, было правдой, большая часть курса статистики, которому их учили в университете, не имела отношения к проблемам, с которыми сталкивался его банк в настоящее время.
“Но, может быть, все не так уж плохо. Может быть, просто Девлин не видит леса за деревьями?” — тоскливо подумал Конвей, а вслух сказал: “Успокойся, Девлин. Я верю, что во всем, что ты говорите есть рациональное зерно. Я просто думаю, что различия не так уж велики, как ты их представляешь. Давайтс-ка изучим повнимательнее твое доказательство этого утверждения”.
Прежде чем пытаться понять доказательство, Конвею неплохо было бы освежить свои знания о нормальном распределении, не так ли? Я думаю, что Девлин мог бы прочитать ему что-то вроде лекции, примерный конспект которой я привожу ниже.
154
8. Плохоо поводонио хороших аппроксимаций
Нормальность
По определению случайная величина X имеет стандартное нормальное распределение, что обозначается как 7V(0, 1), если плотность ее вероятности может быть записана в виде f(x) = . -.- е 2 . Это та самая плотность, график
72^
которой имеет хорошо известную колоколообразную форму, что и показано на нижеприведенном рисунке.
Standard normal distribution
Стандартное нормальное распределение
Кривая плотности 7V(0, 1) симметрична относительно начала координат так, что среднее соответствующей случайной величины и все ее моменты нечетных порядков (которые в рассматриваемом случае оказываются хорошо определенными) равны нулю. Для произвольного четного п момент рассматриваемой случайной величины порядка п равен произведению (п — 1) х (л-З)х ... х5 хЗ х 1 всех нечетных натуральных чисел, меньших п. В частности, дисперсия этой случайной величины равна 1, а эксцесс равен нулю. Строгий способ вывода этих величин я покажу несколько позднее.
Теперь же заметим, что, если случайная величина X распределена как 7V(0, 1),
то случайная величина X' = сгХ + // распределена с плотностью—-— ° > ,
л/Зд'сг
которая имеет средним /л, а дисперсией ст2. Распределение такой случайной величины принято называть общим нормальным, или распределением Гаусса. Последнее несколько вычурное распределение применяют, если хотят избежать недоразумений, связанных с другими возможными смысловыми наполнениями прилагательного “нормальный”. Обозначают общее нормальное распределение как о*2). Обратите внимание на важный факт, что, измеряемая в стандартных уклонениях, любая нормально распределенная случайная величина становится случайной величиной, распределенной по закону Az(0, 1).
155
Часть 1. Стандарты отклононин
Хвостовые риски нормальных распределений
Известно, что риск s-хвоста нормального распределения, а именно
несобственный интеграл вероятности
е 2 dx ’
нельзя вычислить аналитически
ни для каких значений s, за исключением конечного числа значений верхнего предела. Однако, не менее хорошо известно, что для Vs интеграл вероятности легко вычислить с помощью численных методов с любой степенью точности. Вот несколько выборочных значений интеграла вероятности.
Normal tail risks for s = О to s — 6
Standard Tail risk 1/Tail risk
0 0.500000000 2.0
0.5 0.308537539 3.2
1.0 0.158655254 6.3
1.5 0.066807201 15
2.0 0.022750132 44
2.5 0.006209665 161
3.0 0.001349898 741
3.5 0.000232629 4.3 thousand
4.0 0.000031671 32 thousand
4.5 0.000003398 294 thousand
5.0 0.000000287 3.5 million
5.5 0.000000019 53 million
6.0 0.000000001 1.01 billion
Хвосты риска нормально распределенной случайной величины для s G [0, 6] -
Заметьте, что чем дальше от среднего, тем больше скорость уменьшения хвостового риска. Так, передвижением порога, скажем, с точки 1 на точку 2 мы уменьшим хвостовой риск, соответствующий этому порогу, в 7 раз, а передвинув порог с точки 5 на точку 6, уменьшим хвостовой риск, соответствующий этому порогу, уже в 300 раз, т. е., получим уменьшение риска в 40 раз большее.
Центральная предельная теорема
Скорее всего, своим названием нормальное распределение обязано тому факту, что именно нормально распределенные случайные величины лучше всего аппроксимируют суммы и средние большого числа независимых одинаково распределенных случайных величин для громадного большинства классов распределений случайных величин — слагаемых. Наиболее яркой, классической и красивой формализацией этого факта является так называемая центральная предельная теорема, которая гласит, что все s-хвостовые риски любых сумм п независимых в совокупности и одинаково распределенных случайных величин с конечными средним и дисперсией сходятся к s-хвостовому риску стандартного нормального распределения при неограниченно стремящимся к ос .
156
8. Плохой поводонип хороших апнроксимаций
Оказалось, что центральную предельную теорему можно распространить на суммы таких случайных величин, которые не являются одинаково распределенными, при условии, что никакая ограниченная подгруппа этого набора случайных величин не доминирует над остальными случайными величинами. Существуют и такие аналоги центральной предельной теоремы, которые допускают неограниченность дисперсии слагаемых.
При этом надо отметить существенный факт. Дело в том, что, хотя вид распределения случайных величин- слагаемых не влияет на то распределение, к которому сходится, в конце концов, сумма, скорость этой сходимости, и это один из важных результатов применения теоремы, зависит-таки от вида распределения слагаемых. Чем сильнее индивидуальный хвостовой риск отличается от нормального, тем медленнее соответствующая сходимость к аппроксимирующему нормальному хвостовому риску. И различие в скоростях сходимости может быть значительным. Поэтому, то количество слагаемых, которое в одном случае более чем достаточно для адекватности нормальной аппроксимации, в другом случае может оказаться слишком малым.
Примеры сходимости сумм биномиальных случайных величин к нормально распределенной случайной величине
Вот несколько примеров, которые демонстрируют, как саму сходимость к нормальности, так и возможные различия в скорости этой сходимости. Я начну с плотности распределения вероятностей исходов 13 бросаний правильной монеты. График распределения выглядит настолько колоколообразным, насколько это вообще можно сказать о каком-либо 14-точечном распределении. Разница между соответствующими нормальным и биномиальным интегральными распределениями нигде в точках полу целых чисел не превышает 20 базисных пунктов (я выбрал полу целые числа в качестве своего рода компенсации различия между непрерывными и дискретными распределениями).
Probabilities of heads with 13 independent coin tosses
0.40
0.35
0.30
025
0.20
0.15
0.10
0.05
0.00
01 23456 789 10 11
Вероятности появления гербов в 13 бросаниях правильной монеты
Теперь ограничим вероятность хвостов величиной 0,1. Тогда нормальная
157
Часть 1. Стандарты отклонении
аппроксимация 13 бросаний монеты получается менее успешно. Дело в том, что среднее нашей суммы равно 1,3 и лежит настолько близко к началу координат, что колоколообразную кривую необходимо очень сильно прижать к оси, проходящей через среднее. Даже если мы произведем в 5 раз больше бросаний, чтобы среднее значение, как раньше, было равно 6,5, результирующее распределение все равно будет перекошено направо, и это будет видно невооруженным глазом. Для того чтобы продемонстрировать это более наглядно, я построю огибающую дискрегно-нормальной аппроксимации, ступеньки которой вычисляются как интегралы от соответствующей нормальной плотности между нижним пределом, равным к — 1/2, и верхним пределом, равным к + 1/2, и предположу, что моя огибающая совпадает с осью абсцисс для числа гербов, превышающего 16, на том основании, что шансы, соответствующие этому, меньше, чем 0,02%.
0.18 t
Binomial distribution versus normal approximation for // - 0.9, n — 65
0.16 4
0.14
0 12;
0.10 ;
0.08 i
0.06 I
0.04 !
0.02
0.00 -
01 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Биномиальное распределение в сравнении с нормальной аппроксимацией для
м—0,9 и п 65-
Производные моментов нормального распределения
Особенностью производных моментов распределения ) является
I & I
ее красивый вид: М(у) = е Чтобы доказать ее справедливость, вычислим:
+О0 ( С*"/')2 1 +оо Г-х2+2/£с-р2+2/стМ +а0 ( -(х-р-/ст2)2+2/рс72+,Дсг-И
Г ис 1 I 2cr2 J J fl I 2cr: J 1 f 1 I 2<г' J j
| ---------е v dx ~ |----------т= • е dx = I-----.---с dx =
сгДл- Х<т72л- _^сгл/2л-
'’ст2
~ е''
1 2
При этом надо, конечно, понимать, что последнее из вышеприведенных равенств следует из того, что вероятность достоверного события равна единице. Для стандартного нормального распределения N(0, 1) производная моментов будет f—х2
выглядеть следующим образом: М(/) = с-2 < Для проверки вычислим четыре
первых момента:
158
8. Плохоо поводонин хвроших аппроксимаций
М"(у) = е~
Mw(y) — е
М(4\/) - е ~ ; • (/ + 6у2 +3)=> М(4)(0) - 3.
Отметьте, что все производные моментов, соответствующие стандартному нормальному распределению, должны иметь квадратичные экспоненты, в противном случае М(0) не будет равно I.
Производные моментов простых портфелей
Увеличить произвольный актив в сс раз в терминах производных моментов означает умножить / Hatz . Сложить независимые активы в терминах
производных моментов означает перемножить производные соответствующих
моментов. Для производной МД/) портфеля X
состоящего из активов xt,
каждому из которых соответствует его производная мы получаем:
г г (f(X \ (с ( i \
МД/) = J... '=' Jt/F1(x1)t/F2(x2)...t/F„(xw) = (je^'^Cxj)}...- (j e(w")6/Fi(xj)=
= M.Ccr.y) • M2(a2y) •... • M„(a„y).
Верно и то, что логарифм производной моментов любого портфеля независимых активов аддитивен по логарифмам производных моментов, соответствующих отдельным активам, составляющих этот портфель, при том, конечно, условии, что / в каждом случае отражает индивидуальную количественную меру.
Случай, когда среднее и дисперсия выражают общие факторы портфеля
Предположим, что доходность актива можно линейно разложить по некоторой общей группе независимых факторов^ }, таких что для каждого /-го фактора из этой группы нам известны его среднее //. и дисперсия ст2. Тогда любой агрегированный портфель, очевидно, может моделироваться как линейная комбинация ^az со средним и дисперсией г = .
/=i f=i i=i
Предположим, что эти общие факторы не могут влиять на наш портфель никоим образом, кроме как через среднее и дисперсию. Что это говорит нам об этих общих факторах?
Для ответа на поставленный вопрос обозначим через {tzj тот набор параметров, который для любого заданного у экстремизирует (максимизирует
159
Часть 1. Стандарты птклпнпния
или минимизирует) логарифм производной моментов всего портфеля при условии, что среднее М и дисперсия V постоянны. Соответствующий лагранжиан выглядит тогда так:
Е 1 n (М, (4 у )) + г, (м - £ ) + т2 (и - £ arf ),
а условия первого порядка как:
г,//, + 2г3<7,2 .
<7^ у у
Мы видим, что, когда задано не менее трех общих факторов, мы будем иметь целый континуум допустимых {г//}, связанных с любой парой заданных М и V. Каждый отдельный вектор {л,} из этих допустимых наборов обязан удовлетворять нашим условиям первого порядка, что означает, что производная от ln[Mz (^О] обязана быть линейна по а. Только производные моментов нормальных распределений обладают этим свойством. Отсюда следует, что каждый общий фактор из {Zi} обязан быть нормально распределен.
Характеристическая функция как резервное средство обоснования всеобщности
Все вышеприведенные построения красивы, но страдают одним недостатком, а именно они относятся только к таким распределениям, чьи производные моментов вполне определены. Но эти наши замечательные выкладки не относятся к плотностям типа /(х) = 2х~3 для Vx > 1, чьи третий момент и моменты старше третьего неограниченны. Поэтому, для того чтобы вполне корректно доказать вышеприведенный результат, нам следовало бы призвать на помощь, так сказать, “старшего брата” производной моментов, а именно характеристическую функцию.
Характеристическая функция, которую я буду обозначать как С, оказалась бы действительно хорошим подспорьем в нашем деле, поскольку она применима ко всем распределениям вероятностей. При этом все, что могут делать производные моментов, может делать и характеристическая функция, только лучше. Однако сложность применения характеристических функций состоит в том, что они определены над полем комплексных чисел, а именно:
с = M(/z) ЕЕ e[cos(/v)]+ z£’[sin(ja)], где, конечно же, i = -УЛ.
Для людей, неискушенных в математических тонкостях, работать с комплексными числами довольно затруднительно, хотя технически это не намного сложнее, чем работать с более привычными действительными числами. Поэтому я отказался от подробного рассмотрения характеристических функций и применил производные моментов как нечто вроде “заменителей” характеристических функций. Если вы, читатель, ‘^упертый” сторонник достижения математической строгости любой ценой, тогда самостоятельно подставьте iy вместо у и посмотрите, что получится.
160
8. Плохой повпдпнип хпрпших анироксимаций
Нормальные компоненты нормальных портфелей
Вообще говоря, нет никакой необходимости предполагать существование трех или большего числа общих факторов. Дело в том, что можно в любой момент разложить любую наперед заданную нормально распределенную случайную величину на независимые компоненты — факторы, так что эти факторы будут нормально распределены. Правда, строгое доказательство и этого замечательного факта тоже потребует тонкого анализа характеристических функций и, следовательно, далеко превосходит тот уровень сложности математической теории, которого я решил не переходить в настоящей книге.
Я хотел бы подчеркнуть следующее. Имейте в виду, что, если первый и второй моменты дают всю необходимую и достаточную информацию обо всех не лежащих на поверхности общих факторах, то и весь портфель и все его общие факторы обязаны быть нормально распределены. Но тогда верно и то, что, если ваш портфель не является нормально распределенным, вам не удастся однозначно определить все общие факторы активов, входящих в этот портфель, просто анализируя два его первых момента.
161
9: Ненормальность нормальности
Спустя несколько дней во время утреннего бритья Конвея осенило. Это было так просто... Настолько просто, что Конвею захотелось дать самому себе пинка за то, он не додумался до этого раньше. “Я же чувствовал, черт возьми, что мы за деревьями не видим леса!” — думал Конвей со смесью злости, удовольствия и восхищения собой. “Теперь главное не спешить! - предвкушал он удовольствие от того, как огорошит Девлина. — Пусть сначала этот чертов сноб получит порцию моего обычного унижения!” Окрыленный, как ему казалось, собственной небесталанностью, Конвей быстро собрался и пулей вылетел на работу.
Заглянув в офис, где было рабочее место Девлина, Конвей неспешно подошел к нему и деланно спокойно обратился к нему: “Девлин, если у тебя сегодня найдется свободное время, не зайдешь ли ко мне. Нет-нет, ничего срочного. Просто пара мыслей, которые я хотел бы обсудить с тобой...” И мысленно закончил фразу: “Парочка колоссальных контрпримеров ко всем твоим заморочкам!”
Когда Девлин, наконец, пришел, Конвей, слегка переигрывая, проводил его к столу, закрыл дверь и сказал ласково: “Пожалуйста, устраивайся поудобнее... Может быть, кофе?”
“Кончай играть в стюардессу, Конвей. Какую гадость ты мне приготовил?”
“Что это ты такой нервный? Просто, я хотел продолжить наш последний разговор, но в более спокойной обстановке... Ну, ладно, на чем тогда мы остановились?”
“Да все на том же, зависимость или независимость — наш ‘великий водораздел’, что же еще...”
“Ну да, великий водораздел... Скажи, Девлин, правильно ли я понял, что ты поместил нормальность в независимую часть Вселенной относительно вашего водораздела?”
“Совершенно верно. Нормальность в своей основе — статистика независимых случайных величин”.
“Ага, теперь приступим к разгрому! — подумал Конвей и сказал кротко: Тогда, зачем мы, вообще, подсчитываем корреляции между активами, которые, как предполагается, являются нормальными?”
“Да все по той же причине, по которой нам интересны корреляции между любыми другими активами: чтобы поспособствовать вычислению дисперсии портфелей”.
“Но если уж активы коррелированны, они не могут быть независимыми. Значит, наш водораздел не так уж и ‘велик’. Нормальность является мостиком
163
Часть 1. Стандарты отклонения _______^=_==
через него, — закончил Конвей все тем же кротким тоном, а про себя подумал: Наконец-то я тебя подцепил!”
Девлин начал было возражать, но потом спохватился. Подумав минуту, он продолжил, более тщательно подбирая слова: “Я вижу, на какой ‘мостик’ ты намекаешь... Но дело обстоит вовсе не так, как ты его представляешь. Та зависимость, которую якобы отменяет нормальность, — это просто скрытая форма независимости, вот так-то!”
Конвей почувствовал острое раздражение: “Скажи-ка, Девлин, почему всякий раз, когда я начинаю выигрывать в споре, ты тут же меняешь терминологию и границы наших рассмотрений? И перестань, наконец, корчить из себя гуру! Говори нормальным языком, а то используешь только тебе одному понятный жаргон. ‘Скрытая форма независимости’, изволите видеть!”
“Ладно, ладно... Тогда начнем, как всегда, с простого примера, хорошо? Допустим, ты делишь свой портфель пополам между двумя чокнутыми трейдерами — Панчем и Джуди. Допустим, далее, что каждая из этих половин приносит нормальный, некоррелированный, идентично распределенный доход со средним 0, с доходом, превышающим норму по модели оценки активов, тоже 0, и с дисперсией 1/2. Каковы шансы, что потери портфеля превысят 4?”
“Ну, это просто. Наш портфель будет нормально распределен со средним О и дисперсией 1. Поэтому искомые шансы — это 1 из 30 000”.
“Неверно. Ты забыл об общих факторах”.
“А зачем мне этим интересоваться? Ты же сам вчера сказал, что эти факторы для нормально распределенных портфелей значения не имеют, не так ли?”
“Так. Но нормальные активы вовсе не всегда дают нормальные портфели. И уж точно они не дадут нормальных портфелей в случае наших друзей — Панча и Джуди”.
“Почему?”
“Потому что существуют странные отношения между Панчем и Джуди. Ровно половину времени они соглашаются друг с другом в оценке активов своих портфелей и, следовательно, согласны иметь одинаковые портфели. А в оставшуюся половину времени они абсолютно во всем не согласны и ‘воротят нос’ друг от друга. Так что ни один из них не имеет устойчиво доминирующего мнения”.
“Это сильно напоминает мне кого-то...”
“Ну, я изменил, конечно, имена... — Девлин ядовито улыбнулся Конвею, — но в любом случае Панч совместно с Джуди зарабатывают или ничего, или вдвое больше того, что зарабатывает каждый в отдельности с равными шансами каждого исхода. Это значит, что вероятность совместной потери 4 равна половине вероятности того, что Джуди потеряет не меньше 2. Последняя вероятность - это 2,8-хвост для одной Джуди, поскольку для ее портфеля стандартное уклонение равно 0,7. Посчитай теперь шансы — они выше, чем 1 из 1000, и, очевидно, в 30 раз превосходит нашу предыдущую оценку”.
164
8. Нвнврмальлвсть нврмальнвсти
“Понятно. Совместное распределение является равновзвешенной смесью двух нормальных распределений, одно из которых вырождено. Но, ведь, 4-хвостый риск, все равно, мал. Вообще, насколько можно еще ухудшить ситуацию?”
“Она может стать хуже примерно в 10 раз. Представь себе, что ты делишь свой большой портфель между тысячей Панчей и Джуди, каждый из которых постоянно держит стандартные нормальные портфельчики. С вероятностью 9% наши трейдеры делятся друг с другом информацией и соображениями по ведению портфеля, так что их портфели становятся одинаковыми. В противном случае они действуют независимо. Дисперсия при условии совместного принятия решений составляет почти всю совместную дисперсию, так что грубо совместная дисперсия будет равна (9%)хЮ002 = 90 000, а совместное стандартное уклонение — 300. В 4-хвостом случае, когда почти наверняка у наших трейдеров портфели будут идентичны, потери каждого будут равны 4x30^-1000^1,2. Умножьте теперь 9%-ную вероятность сговора на примерно 11%-ную вероятность индивидуально потерять 1,2 и получите общий риск равным примерно 1%. Это, я думаю, максимально большой 4-хвостый риск из всех, который мы могли бы получить на смеси нормальных распределений с общим средним”.
“Ну и что? Ведь 1%-ный 4-хвостый риск никак не больше 6%-ного риска, который мы имели бы, если бы средние могли меняться”.
“Все равно, и этот риск весьма велик. Большой он или маленький — в конце концов не в этом дело, а в том, что для нормальности портфеля необходимо, чтобы составляющие активы были нормальными, а дисперсия портфеля была стабильной. Этим условиям удовлетворяет только многомерное нормальное распределение”.
“А я-то всегда считал, что многомерное нормальное распределение — это просто несколько нормально распределенных случайных величин, возможно, коррелированных”.
“Ну, что ж, так думает и большинство местных парней. Они либо никогда нормально не занимались статистикой, либо напрочь забыли все контрпримеры из своих учебников. Ничего, вообще-то, удивительного. Формула многомерной нормальной плотности выглядит достаточно невинно. В ней нет никакого намека на то, что всякая коррелированность исключается. Для того чтобы понять, какие на самом деле ограничения налагает многомерная нормальность, надо мыслить геометрически. Можно воспользоваться твоим компьютером, чтобы нарисовать пару графиков?”
“Да, ради бога...”
“Тогда вернемся к нашему примеру с Панчем и Джуди и попытаемся понять, как в этом случае будет выглядеть совместная плотность. Если мы будем откладывать доходы Панча по оси X а доходы Джуди по оси У, то вся ненулевая плотность, как видите, будет ‘сидеть’ в двух диагоналях. Одна из этих диагоналей представляет собой одинаковые доходы, а другая --противоположные. На каждой из диагоналей плотность нормальна, значит, совместная плотность — это просто пересечение двух сплющенных колоколов”.
165
Часть 1. Стандарты птклпнпния
“А что означают эти линии сетки?”
“Вертикальные зигзаги ничего серьезного не означают. Они изображают нечто вроде «нашеста», на котором ‘'сидит’ плотность. Вот вертикальные линии — важны. Это линии уровня, или линии равной вероятности. Вдоль этих линий плотность вероятности имеет одно и то же значение. Каждая линия уровня состоит из 4 разных, но симметрично расположенных точек, по одной в каждом квадранте. Кроме этих точек, там ничего нет”.
“Хорошо. Я понял схему. Правильно ли я считаю, что все линии уровня многомерного нормального распределения непрерывны?”
“Правильно. А еще они симметричны. Вот, взгляни на совместную плотность распределения двух стандартных нормальных независимых случайных величин, т. е. на так называемый ‘стандартный двумерный случай’. Она выглядит как обычный двумерный колокол, а линии уровня — это окружности”.
Probability density for 1st Punch-and-Judy example
Плотность распределения вероятностей для 1-го примера с Панчем и Джуди.
“Она абсолютно симметрична относительно вертикальной оси...”
“Вот именно. Это называется ‘осевая симметрия’. В частности, это замечательное свойство означает, что вероятность любого заранее заданного отклонения зависит единственно от соответствующего расстояния до начала координат. А от направления отклонения эта вероятность не зависит”.
166
8. Нвнврмальнвсть нврмальнвстн
“Скажи, правильно ли я понял, что для п стандартных, независимых в совокупности, нормально распределенных случайных величин кривыми уровня совместной плотности распределения будут на самом деле не кривые, а поверхности, точнее, /7-мерные сферы, что означает, что наша плотность и в этом случае будет обладать свойством осевой симметрии?”
Probability density for standard bivariate normal
Плотность распределения вероятностей для стандартного двумерного нормального распределения.
“Браво, Конвей! Ты начинаешь соображать... Теперь вообрази, что каждое наблюдение — это фиксация некого случайного движения одновременно в п ортогональных направлениях. Тогда, если это движение является стандартным, многомерным, нормальным, согласишься ли ты со мной, что любые движения в ортогональных направлениях должны быть независимы друг от друга?”
“Соглашусь. Иначе график плотности зависел бы от ориентации этих ортогональных движений относительно системы координат, и у нас не было бы этой осевой симметрии...”
“Точно! А теперь напрягись и скажи, какая физическая система ведет себя подобным образом?”
“Ну, не знаю! Может быть, курица, которой отсекли голову? Она, уж точно, слишком безмозгла, чтобы бежать в каком-то одном направлении!”
167
Часть 1. Стандарты втклонвния
Девлин улыбнулся: “Это правильно. Точный ответ — изолированный сосуд с газом. Молекулы газа статистически ведут себя точно так, как микроскопические безголовые куры, которые носятся по всему сосуду. Поэтому, если задать правильный масштаб времени, движение молекул газа можно считать моделью стандартного многомерного нормального распределения”.
“Минуточку! Почему это движение молекул газа должно подчиняться именно многомерному нормальному закону, разве не существует других многомерных распределений независимых в совокупности случайных величин, компоненты которых обладали бы свойством осевой симметрии?”
“Именно, что нет. Ну, могут быть различия в шкалах измерения составляющих одномерных случайных величин, но это не принципиально, ты же понимаешь... Именно так, между прочим, Максвелл и вывел свое распределение скоростей молекул газа...”
“Ладно, ладно... Но, даже если осевая симметрия и кажется разумной для газов, если, конечно, не принимать в расчет гравитационные асимметричные эффекты, для финансов это предположение кажется слишком ограничительным, не так ли?”
“Да? А я бы этого не сказал... Ведь, когда вам надо, его можно всегда сдвинуть, куда надо, растянуть, как надо, и перекосить, как надо... ”
“Что ты имеешь в виду?”
“Это просто. Начните измерять каждую составляющую каждого движения, являющегося симметричным относительно некоторой оси, своей линейкой с ее собственным масштабом, потом сдвиньте, растяните и наклоните по своему усмотрению некоторые из этих линеек. Сдвиг начальной точки, т.е. ‘нуля’ линейки, меняет математическое ожидание соответствующей случайной величины, растяжение или сжатие линейки в некой постоянной пропорции — дисперсию соответствующей случайной величины, т. е. ее ‘волатильность’, а наклон линейки — и среднее, и дисперсию, и корреляцию соответствующей случайной величины по отношению к другим случайным величинам. Но сами многомерные случайные величины, изначально- соответствовавшие движениям сразу в нескольких направлениях, остаются многомерными нормальными. Они просто начинают иметь средние, дисперсии и ковариации, отличные от стандартных нулей и единиц”.
“Как насчет какого-нибудь примера, профессор?”
“Легко. Начнем со стандартного, двумерного, нормального закона. Теперь сдвинем начало оси X на 2 единицы вправо, сожмем линейку Y вдвое и повернем ось ¥ вокруг начала координат на 45° по часовой стрелке”. Девлин быстро нарисовал на бумаге два. набора линеек. Закончив рисовать, он продолжил: “Наши новые линейки определяют X ~ X — 2 и Y = ^2Х + ^lY. Теперь X имеет средним —2, a Y — среднее 0, дисперсию 4 и ковариацию с X равную а/2”.
168
8. Ненормальность нормальности
Original and revised rulers for example
(0,0) ------* X
втттгтттттт: 1
(2,0) X'
Модификация линеек.
“А что стало с нашим замечательным стандартным колоколом после преобразования измерений?”
“Он стал похож на старый пластмассовый колпак, который используют для сигнализации на дорожных работах. Линии уровня вытянулись, и из окружностей превратились в эллипсы. В многомерном случае сферы превратились бы в эллипсоиды. Вот, как теперь будет выглядеть плотность”.
Конвей какое-то время рассматривал новые графики и потом сказал: “Спасибо, конечно, Девлин, но я несколько разочарован тем типом зависимости, который они собой представляют. Произведя обратное преобразование, ты, конечно, сможешь все объяснить в терминах независимых случайных величин, и эти независимые случайные величины будут теперь портфелями, а не отдельными активами, но это бухгалтерский вопрос...”
“Абсолютно верно. Вот, например, обратное преобразование: Y = yl(l/2)Y~X-2 и X = X + 2 даст то, что нужно. Однако ты же понимаешь, что здесь подойдут и другие преобразования. Просто поверни оси Хи Yвокруг начала координат на один и тот же угол, чтобы сохранить прямой угол между ними... Поскольку нам важна осевая симметрия, результат этого преобразования системы координат вновь даст независимые случайные величины”.
“Ага... Это-то мне и не нравится... Мне нужны примеры многомерной нормальности, которую нельзя было бы с такой легкостью интерпретировать через независимые случайные величины”.
“Понятно. Но вынужден тебя огорчить. Таких примеров не существует. Любой портфель, составленный из многомерных нормальных активов, можно разложить на независимые нормальные кирпичики”.
“И никаких исключений?”
“Никаких”.
Последнее заявление Девлина не оставляло Конвею никаких шансов на “триумф”. Поэтому он сказал: “Ну ладно, я согласен с твоими теоретическими построениями. Каковы расхождения этой теории с практикой нашей работы?”
“С ходу7 не скажешь. Почему бы нам не проанализировать какие-нибудь практические данные?”
“Хорошая мысль. Но только давай не будем слишком усложнять наш анализ. Я предлагаю рассмотреть данные по месячной доходности рынка акций США, Англии, Франции и Японии за последние 30 лет. Мы с этим справимся?”
169
Часть 1. Стандарты отклонения
“Вполне. Я могу достать эти данные. Доходность валовая или чистая тебя интересует?”
Density and fevef curves for revised measure
Плотность вероятности и линии уровня после преобразования
“Надо будет включить дивиденды и исключить доходы по национальной валюте. Таким образом, мы максимально исключим из рассмотрения флуктуации дивидендов, инфляции и обменного курса”.
170
а. Ненормальность нормальности
Пока Девлин готовил графики и расчеты, Конвей спросил о том, какой именно эксперимент он собирался ставить.
Девлин ответил: “Ну, во-первых, я намерен вычислить вектор средних и матрицу ковариаций. Эти данные я планирую использовать для того, чтобы стандартизировать исходные данные в терминах набора из пяти случайных величин, имеющих нулевые средние и единичные дисперсии и некоррелированных. Потом я посчитаю квадрат расстояния от начала координат до каждого стандартизованного наблюдения, который равен сумме квадратов компонент этого расстояния. Затем проверю статистическую гипотезу о многомерной нормальности. Дело в том, что, если гипотеза о многомерной нормальности верна, то этот квадрат расстояния должен быть такой случайной величиной, которая соответствует распределению ‘хи-квадрат’ с пятью степенями свободы”.
“Ну, и если данные пройдут проверку критерием ‘хи-квадрат’, можем мы считать, что имеем дело с многомерным нормальным распределением?”
“Не совсем. Дело в том, что критерий ‘хи-квадрат’ работает только с расстоянием от начала координат. Он ничего не говорит об осевой симметрии. Если бы, например, наши данные все лежали в одной плоскости, они бы прошли тест ‘хи-квадрат’, но некоторые портфели при этом остались бы резко ненормальными. Правда, я предлагаю на время забыть об этой тонкости. Понимаешь, мне кажется, что данные и близко не лежат с тем, чтобы пройти через ‘хи-квадрат’ ”.
Конвей понимающе кивнул и пошел по своим делам, предоставив Девлину возможность заниматься его задачей.
Когда Конвей вернулся, Девлин со словами “А что ты на это скажешь?” гордо указал Конвею на экран своего компьютера, на котором в этот момент висел очередной график.
Comparative histograms
Сравнительные гистограммы.
171
Часть 1. Стандарты втклононин
“Да ничего хорошего. Если сравнить с гистограммой стандартного многомерного нормального распределения, то согласия не слишком много. На глаз видно, что у нас слишком много плотности вблизи начала координат, слишком мало в середине и очень много вдали от начала координат. А, вообще, насколько дальше 24 забираются ваши значения?”
“На январь 1975 г. мы доходили почти до 80. Тогда английские акции выросли почти вполовину за месяц, французские поднялись почти на 22%, а все остальные индексы изменились незначительно. При этом имейте в виду, что шансы на то, что в течение 360 замеров пятимерного нормального распределения будет отмечен выброс такого масштаба, равны 1 из 3 трлн.”
“Очевидно, что январь 1975 г. — или ошибка, или нехарактерное явление. Проигнорируем эти данные. Каков ваш второй нехороший всплеск?”
“35 в октябре 1987 г. Если бы мы смогли наблюдать пашу пятимерную нормально распределенную случайную величину в течение ближайших 40 000 лет, скорее всего, мы столкнулись бы не более чем с одним всплеском подобного масштаба”.
“Тот обвал был несистемной аберрацией. Проигнорируем и его тоже”.
“Конвей, ты не можешь постоянно отсекать всплески. Формировать таким образом нормальное распределение — то же самое, что создавать женщину посредством кастрации мужчины. Имей в виду, что иногда те шероховатости, которые ты срезаешь под тем или иным предлогом, являются отражением некой фундаментальной причины, пока еще не известной”.
Конвей ответил со смехом: “Да брось, Девлин! Ты же знаешь, что те два месяца были артефактами... Я хочу, чтобы ты исключил их из рассмотрения и снова оценил соответствие экспериментальных данных и нормального закона”.
Девлин сделал, как просил Конвей. А через какое-то время сказал: “Теперь наихудший всплеск имеет значение 46,6. В пятимерном нормальном мире такое может случаться раз в 12 млн. лет... А еще есть выбросы в районе 33 и 27, которые должны бы произойти 1 раз в 200 000 и 1 раз в 20 000 месяцев соответственно. Вероятность того, что три выброса такого масштаба произойдут при наблюдении за пятимерной нормальной случайной величиной меньше чем 1/16 000”.
“Единица из 16 миллиардов? И это после того, как мы отсекли два наихудших выброса?”
“Да, я еще не отметил другие всплески, представляющие собой события, которые должны бы происходить один раз на 1000 испытаний. Если бы мы рассмотрели и их...”
“Может быть, если я закрою глаза и помедитирую, этот кошмар сам собой рассосется?” — подумал Конвей с горькой иронией, а вслух сказал: “Хватит! Я и не предполагал, что соответствие настолько плохое... Как это выглядит на фоне шансов, если каждая одномерная выборка соответствует одномерному нормальному закону?”
“Ну, если мы проигнорируем январь 1975 и октябрь 1987, наихудший всплеск в каждой выборке лежит в пределах от 3,6 до 4,3 стандартных уклонений
172
В. Нонормальность нормальности
от среднего. Если бы одномерная случайная величина была нормально распределена, шансы такого события лежали бы в интервале от 1/18 до 1/318. А шансы того, что одномерное нормальное распределение продемонстрирует три всплеска худших, чем те три всплеска, которые мы наблюдали, лежат в интервале от 1/2000 до 1/200 000”.
‘Значит, если одномерная нормальность соответствует шансу получить целый солнечный месяц в Лондоне, многомерная нормальность соответствует шансу выживания для снеговика в аду?”
“В физике — нет. В финансах — да!”
“Ну, и что ты предлагаешь со всем этим делать?”
“В аккурат после обеда я переключаюсь на физику... Хочешь составить компанию?”
“Я ничего не понимаю в физике...”
“Я не имел в виду составить мне компанию в изучении физики, я хотел предложить пообедать вдвоем?”
“Конечно! Мне кажется, что существует даже некий шанс, что я оплачу твой чек...”
“Нормальный шанс?”
“Скорее, многомерный нормальный шанс...”
Ну, будем надеяться, что Девлин не забудет захватить деньги, отправляясь в столовую. А мы пока быстренько повторим математику многомерной нормальности. Начать мне придется с азов теории матриц, поскольку ее нам больше избегать не удастся. Если вы освоитесь с матрицами, польза от этого будет большая, взять хотя бы резкое упрощение в формализации математических выражений. Ну и, кроме всего прочего, матрицы обостряют интуицию, которая так важна в нашем деле. Поэтому, имея в виду прежде всего интуицию, я намерен особое внимание уделить геометрической интерпретации матриц.
Матрицы
По определению матрицей А порядка т х п называется произвольная прямоугольная таблица чисел, имеющая т строк и п столбцов:
а\ 1 а\2 ... *!("-!)
<721 а22 ... 1) а2 п
А = ... ► » • ... ...
а(т-1)2 ► » • а{т~\}п
< ат\ ат2 ...
Иногда такую матрицу сокращенно обозначают как А = ]. Всякая
173
Часть 1. Стандарты стклснония
матрица порядка т х п такая, что все ее элементы суть нули, называется нулевой матрицей и обозначается 0. Две произвольные матрицы А = \а~ J и В = [бу] называются равными тогда и только тогда, когда они являются матрицами одного и того же порядка и когда i\fj , т. е. элементы этих
матриц, стоящие в двух матрицах на одинаковых местах, равны. Если число т строк произвольной прямоугольной матрицы равно числу ее столбцов, такую матрицу называют квадратной матрицей порядка т. Элементы {<7/7} квадратной матрицы, стоящие на ее диагонали, проведенной из левого верхнего угла, называются диагональными элементами квадратной матрицы. Если все элементы произвольной квадратной матрицы, не являющиеся ее диагональными элементами, равны нулю, такую квадратную матрицу называют диагональной. Если все диагональные элементы произвольной диагональной матрицы порядка т равны единице, такую матрицу называют единичной матрицей порядка т и обозначают как I.
Матрица как совокупность векторов
Произвольную прямоугольную матрицу, состоящую из единственного столбца, называют вектором-столбцом или просто вектором. Произвольную прямоугольную матрицу, состоящую из единственной строки, называют вектором-строкой. Заметьте, что всякую прямоугольную матрицу можно рассматривать и как строку векторов-столбцов, и как столбец векторов-строк.
Всякую строку и всякий столбец, если они содержат т элементов, называют w-вектором. Геометрически произвольный /д-вектор взаимнооднозначно соответствует направленному отрезку в /д-мерном метрическом пространстве. При этом Z-я компонента всякого w-вектора равна z-й координате соответствующего направленного отрезка. Отсюда возникает представление о матрице как о совокупности направленных отрезков. Иными словами, всякая прямоугольная матрица порядка т х п представляет собой или совокупность т векторов zz-мерного пространства или совокупность п векторов w-мерного пространства. Тогда векторные компоненты квадратных матриц можно рассматривать как ребра некого параллелепипеда (многомерного параллелограмма).
Матричные операции и макросы
Производить вручную вычисления, связанные с операциями в поле матриц достаточно больших порядков, может быть очень утомительным и долгим делом. К счастью, в наше время для большинства таких операций разработаны подпрограммы-макросы, так что чаще всего вам потребуется нажать только пару “горячих” ‘ клавиш, чтобы заставить компьютер произвести эти вычисления.
174
8. Ненормальность нормальности
Сложение матриц и умножение матрицы на скаляр
Складывать можно только матрицы одного порядка. Для трех матриц А = В = (by) и С = ) одного порядка матрица С будет суммой матриц
А и В тогда и только тогда, когда а у + by = Cy\fi\fj . Геометрически сложение матриц означает попарное сложение векторов первой матрицы-слагаемого с соответствующими векторами второй матрицы-слагаемого по известному правилу сложения векторов (или по правилу треугольника, когда первый вектор перемещают параллельно самому себе так, чтобы второй вектор начинался в точности в конце первого вектора, а потом проводят новый третий вектор с началом в начале первого вектора и концом в конце второго вектора; или по правилу параллелограмма, когда векторы-слагаемые перемещают параллельно самим себе так, чтобы совместились их начала, потом строят параллелограмм на этих векторах и новый третий вектор, совпадающий с диагональю, проведенной в этом параллелограмме из общего начала векторов-слагаемых).
Для того чтобы произвольную матрицу умножить на произвольный скаляр надо каждый элемент этой матрицы умножить на этот скаляр. Геометрически умножение матрицы на скаляр означает увеличить длину каждого вектора этой матрицы в число раз, равное этому скаляру, но без изменения направлений этих векторов.
Заметьте, что все свойства операций умножения и сложения действительных чисел сохраняются при замене аддитивной операции на сложение матриц, а мультипликативной операции — на умножение матрицы на скаляр.
Простейший случай умножения матрицы на матрицу
Умножение в поле матриц — это довольно противная операция, в которой легко запутаться. Поэтому с ней следует разбираться не спеша. Начнем с простейшего примера, а именно с правила умножения вектора-строки
R = гт] на вектор-столбец
того же самого размера. По
т определению в этом случае результатом умножения матриц будет скаляр z;cf . 1=1
Если отвлечься от того правила, что можно умножать строку на столбец, но нельзя умножать столбец на строку, мы здесь имеем скалярное произведение двух векторов. А скалярное произведение векторов R и С равно, как мы знаем, произведению длины вектора R на длину проекции вектора С в направлении вектора R. Эта проекция говорит нам, какова длина вектора С в направлении вектора R. Понятно, что эквивалентным выражением для скалярного произведения будет произведение длин векторов, умноженное на косинус угла между ними.
175
Часть 1. Стандарты отклонония
Vector projections
Проекции векторов
Общее правило умножения матриц
Для того чтобы одну матрицу можно было умножить на другую, у первой матрицы должно быть ровно столько столбцов, сколько есть строк у второй матрицы. Далее, если произведение двух матриц А и В определено, то результирующая матрица АВ будет иметь столько строк, сколько есть у матрицы Л, и столько столбцов, сколько столбцов у матрицы В. Элемент (^АВ^ матрицы АВ стоящий на пересечении ее Z-й строки и j-го столбца вычисляется как произведение Z-й строки матрицы А и /-го столбца матрицы В, которое, как мы
п
только что выяснили, равно '^\taik^kj » где, конечно же, к--\
(Z = 1,...,^)&(/ =
С геометрической точки зрения операция умножения одной матрицы на другую вращает, растягивает и сплющивает каждый вектор по отдельности, но так, чтобы сохранить вышеприведенные линейные ограничения масштабирования. Этим я хочу сказать, что, хотя, фигурально выражаясь, линейка в результате операции умножения матриц может стать длиннее или короче, даже может получить другое направление, чем раньше, она по-прежнему будет линейкой, измеряющей длины отрезков прямой, а ее деления будут, как и раньше, отмечать отрезки равной длины на этой прямой. Математическое название для трансформаций такого рода — “линейное отображение”.
Отметим также, то свойство операции умножения матриц, что, умножая произвольную квадратную матрицу А и слева, и справа на единичную матрицу того же порядка, мы получим все ту же матрицу А. Можно доказать и ассоциативность операции умножения для тех матриц, для которых определены соответствующие операции умножения: Л(5 + С)= АВ + АС;
(АВ)С — А(ВС) . Но умножение матриц не коммутативно, даже когда оба сомножителя — квадратные матрицы одного и того же порядка: АВ не обязательно равно ВА .
176
а. Нонормальность нормальнооти
Транспонирование
По определению перемена мест строк и столбцов, такая, при которой элемент у) матрицы А становится элементом (j,/) матрицы Л, так что V/, V/, называется транспонированием, а матрица А — транспонированной матрицей.
Вообще, транспонирование матриц можно себе представлять как их отражение в “хитром” зеркале: только симметричные относительно главной диагонали квадратные матрице равны своим транспонированным. Но зато все матрицы равны транспонированным своих транспонированных. Транспонированная сумма матриц равна сумме соответствующих транспонированных: (А + 5) = А' + В', а транспонированное произведение двух произвольных матриц равно произведению соответствующих транспонированных матриц, взятых в обратном порядке: (АВ) = В'А'.
Произведения матриц и их транспонированных матриц играет в поле матриц ту же роль, которую в поле действительных чисел играет возведение числа в квадрат, и, следовательно, имеет весьма широкое применение. Например, для произвольного вектора-столбца X произведение XX равно квадрату длины этого вектора в среднеквадратической метрике, а XX дает квадратную матрицу, элементами которой являются все возможные попарные произведения компонент исходного вектора X. Обратите внимание, что в поле матриц квадрат — всегда симметрическая матрица.
Ортогональность
По определению два ненулевых вектора-строки В и С называются ортогональными, если и только если косинус угла между ними равен нулю, что эквивалентно тому, что их скалярное произведение равно нулю: ВС = СВ - 0. Если к тому же каждый из этих векторов еще имеет и длину равную 1, эти векторы называются ортонормальными. Можно доказать, что для произвольной матрицы А все ее векторные компоненты будут ортонормальными тогда и только тогда, когда А А = /. Вы, наверное, думаете, что такие матрицы называются ортонормальными? Совсем нет, в литературе их называют ортогональными. По правде говоря, я сначала хотел исправить это очевидное неудобство, но потом отказался от этой идеи. Поэтому будем называть такие матрицы так, как называют их все, — ортогональными.
Геометрически умножение на произвольную ортогональную матрицу соответствует совместному согласованному вращению того, объекта, который соответствует умножаемой матрице, поскольку все углы и расстояния между векторами в таком случае остаются неизменными:
t 1 '
(AYj ) ЛХ2 - Х} Л!АХ2 = Х{ Х2, где Л — ортогональная матрица.
177
Часть 1. Стандарты отклононин_
Отсюда следует, что любая математическая структура является симметричной относительно вращения вокруг начала координат, если и только если она не меняется от умножения на ортогональную матрицу.
О п редел ител и
Заметим, что определитель существует только у квадратной матрицы. Неквадратные матрицы не имеют определителей. Определителем |Л| квадратной матрицы А порядка т называется алгебраическая сумма т\ одночленов. Каждый одночлен является произведением ровно т сомножителей — элементов матрицы и включает в себя ровно по одному элементу каждой строки и столбца: а2 • • • ат , где (zt, /2,..., im ) есть перестановка упорядоченного по П *2 !т
возрастанию набора натуральных чисел от 1 до т. В зависимости от того, сколько пар элементов этого исходного набора надо поменять местами, чтобы получить заданную перестановку натуральных чисел, эта перестановка называется четной или нечетной. Определитель суммирует с положительным знаком все одночлены, соответствующие четным перестановкам индексов, и с отрицательным знаком все одночлены, соответствующие нечетным перестановкам индексов.
Определитель произведения квадратных матриц равен произведению определителей матриц-сомножителей. Транспонирование произвольной квадратной матрицы не меняет ее определителя. Отсюда определитель всякой ортогональной матрицы должен быть равен 1.
Геометрически, если отвлечься от знака, определитель произвольной квадратной матрицы измеряет объем того параллелепипеда, который связан с этой матрицей. Этот объем будет равен нулю, если и только если не менее чем один из векторов матрицы лежит в гиперпространстве, перекрываемом гиперпространствами других векторов той же матрицы, т.е. является нетривиальной линейной комбинацией других векторов.
Обращение матриц
Если для произвольной пары матриц А и В определено произведение АВ, причем АВ = /, говорят, что матрица В является правым обращением матрицы А, а матрица А — левым обращением матрицы В. Имея дело с квадратными матрицами, мы будем называть обращения произвольной квадратной матрицы А обратной матрицей и обозначать А~1. Дело в том, что для всякой квадратной матрицы правое обращение является одновременно и левым обращением: А"'А = АА~* = I. Для УДЭД’1 |j| * О, т. е. у всякой квадратной матрицы, такой, что ее определитель не равен нулю, существует обратная. Это свойство матриц согласуется с представлением об определителе как об объеме. Дело в том, что равенство определителя нулю означает, что соответствующее линейное преобразование уничтожает по меньшей мере одно измерение информации и вы
178
а. Ненормальность нормальности
не сможете из ничего восстановить нечто. Однако, если информация все-таки существует, можно восстановить ее через инверсию линейного преобразования. Алгебраически, инверсия легко выражается в терминах детерминантов и суб-детерми нантов.
Квадратичные формы и положительно определенные матрицы
По определению произведение со’А со произвольной симметрической квадратной матрицы А и вектора со соответствующей длины называют квадратичной формой. Если о матрице А известно, что все ее возможные квадратичные формы положительны (неотрицательны), такую матрицу называют положительно определенной (положительно полуопределеиной). Но если некая квадратная матрица А не является .симметрической, симметрическая квадратная матрица (А + А )/2 даст ровно те же квадратичные формы, что и исходная матрица А. Любая симметрическая положительно определенная матрица А имеет положительный определитель |Л|, и у нее заведомо существует положительно определенная обратная матрица А'\ Плюс к этому у такой матрицы А будет 1/ существовать обратимая матрица-квадратный корень А/2 .
Многомерные моменты в матричной форме
Наконец мы подошли к тому, ради чего затеяли всю возню с матрицами, а именно к тому, как невероятно упростить с помощью введения матриц все наши обозначения и выкладки.
Пусть X = ,..., х„ J — некий вектор, такой, что его компонентами
являются п скалярных случайных величин. Пусть М == обозначает вектор
соответствующих математических ожиданий. Тогда можно показать, что соответствующую матрицу ковариаций X = [сг^ ] можно получить как
S — Е {X — М\Х — А/) . Рассмотрим теперь вектор
со , составленный из о
произвольных чисел. Покажем, что дисперсия линейной комбинации со’Х будет равна квадратичной форме сХЕсо :
со
Поскольку дисперсия не бывает отрицательной, X обязана быть положительно полуопределенной. Если теперь предположить, что никакой компонент вектора X не является линейной комбинацией остальных компонент того же вектора, мы получим, что его дисперсия не может быть нулем за исключением тривиальных случаев, что означает, что S будет положительно определена.
179
Часть 1. Стандарты отклонания
Многомерная нормальность
По определению произвольный w-мерный вектор X, компонентами которого являются случайные величины, называется многомерной нормально распределенной случайной величиной, если его плотность можно записать как:
2л7г"|Е|
е" 2 7, где через М и У обозначены вектор
средних и матрица ковариаций соответственно.
Стандартным многомерным нормальным распределением называется такое многомерное нормальное распределение, вектор средних которого есть нуль-вектор, а матрица ковариаций — единичная матрица, т.е. М = О, У = I. Легко видеть, что любое многомерное нормальное распределение можно превратить в стандартное многомерное нормальное распределение преобразованием
Стандартная многомерная нормальность есть независимость плюс осевая симметрия
Предположим, что одномерные случайные величины {хД, являющиеся компонентами многомерной случайной величины X, независимы в совокупности. Тогда мы можем записать плотность распределения многомерной случайной величины А как произведение плотностей распределения одномерных компонент
этой многомерной случайной величины: f(X) = I I /j(xz). Допустим теперь,
что наша многомерная случайная величина X еще и обладает свойством осевой симметрии, т.е. что для произвольной ортогональной матрицы А выполняется: уравнение /А)=/(А¥). Эго значит, что, поскольку независимы в
совокупности, Здесь опять
хорошей наглядной физической аналогией является идеальный газ в отсутствие гравитации, молекулы которого совершают независимое движение вдоль трех осей пространства вне зависимости от того, как именно эти оси в этом пространстве проведены. Если мы теперь объединим все эти уравнения, прологарифмируем и введем обозначение то получим:
Если теперь продифференцировать это дважды —
п п
сначала по переменной х}, а потом по переменной хк, мы получим
« « tf л
° = ЕЕ/г.ai\aikaax! =В'Ак , где В,= Уад а,..
180
а. Нанармальнаоть нармальнасти
Далее, поскольку вектор В ортогонален каждому вектору Ак, а значит, и вектору то В с необходимостью есть произведение вектора Д на некий
(Г
скаляр. Это может иметь место, только если hi принимает некое фиксированное значение, независимое ни от %, ни от/, что, в свою очередь, означает, что каждая одномерная плотность f. является нормальной с одной и той же дисперсией. Более того, из осевой симметрии следует, что fi обязана быть центрирована на начало координат, поскольку в противном случае она имела бы несколько пиков. Из всего вышесказанного ясно, что случайная величина X обязана быть стандартной многомерной нормальной случайной величиной, умноженной на некий скаляр.
Конечно, вышеприведенное рассуждение во многом основано на предположении о дифференцируемости соответствующих плотностей. Тем не менее это доказательство можно распространить ина общий случай посредством сравнения характеристических функций. Наконец, полная осевая симметрия тоже не является необходимой. Нужна просто симметрия относительно одного достаточно сложного вращения.
Критерий “х- квадрат” для многомерной нормальности
По определению статистика z равная сумме квадратов п независимых в совокупности стандартных одномерных нормально распределенных случайных величин называется статистикой “хи-квадрат”, или статистикой (п), плотность которой равна
J и
где Г — — гамма-функция, определенная
таким образом, чтобы, во-
во-вторых, ее значения для
первых, интеграл плотности по всей оси давал 1, а п
---1 , а для каждого нечетного п равны
каждого
четного п были равны
1 3 5 и-1 г
--------...------V п .
2 2 2 2
Легко видеть, что произвольную многомерную нормальную случайную величину X можно превратить в вектор S 2 (Х — Л/) со стандартными
независимыми в совокупности нормально распределенными компонентами,
181
Часть 1. Стандарты отклонения
сумма квадратов которых будет равна (А" — М) S ’(Af — Это именно та статистика, которую Девлин использовал при проведении проверки на многомерную нормальность.
Вывод формулы плотности статистики “х-квадрат”
Начнем с того, что любая независимая в совокупности ^-мерная нормальная плотность будет прямо пропорциональна величине [1 я А , ч
(1 А
2“' / I 2Г J
е ,=l 7 = е , где г обозначает расстояние от начала координат. Ясно, что точки, которые лежат от начала координат на расстоянии, равном г, образуют поверхность ^-мерного сфероида, а значит, имеют меру, пропорциональную г”-1 . Это означает, что вероятность попасть в слой между сферой радиуса г и сферой
радиуса г + dr будет пропорциональна гп хе 2 dr. Чтобы найти вероятность того, что квадрат расстояния от начала координат попадает между z и z + dz, подставим
- -1 „21
z вместо г и dz вместо 2л7г, что даст z'"1' •€ 2dz. Это значит, что сумма и квадратов подчиняется распределению ^2(w).
Применение критерия “х- квадрат”
Девлин, как вы помните, вычислял вероятность того, что выборка из пяти независимых наблюдений из распределения ^2(5) будет давать равные или худшие всплески. Для нескольких наблюдений вычислять такие вероятности довольно затруднительно. Поэтому Девлин аппроксимировал эту вероятность произведением хвостовых рисков, соответствующих каждому из всплесков, умноженным на число допустимых перестановок этих всплесков. Но это слишком грубая оценка сверху. Так, для всплесков на уровнях 46, 33 и 27 Девлин на самом деле сосчитал комбинацию (46, 34, 34) дважды, потому что сосчитал ее один раз как (>46,>33,>27) и один раз как (>46,>27,>33).
Но с другой точки зрения, Девлиновская категоризация на “худшие всплески” является серьезной недооценкой. Вот, например, он не посчитал (27, 32, 50) как хуже чем (27, 33, 46), хотя плотность распределения первого меньше. Вспомните, однако, что очищенная выборка содержала еще 4 всплеска, хвостовые риски которых были такими, что каждый из них имел вероятность меньшую чем 1 к 1000. Вставьте это в свои подсчеты и поймете, что шансы были даже меньшими, чем это утверждал Девлин.
182
10: Зависимая независимость
Просветление? Разочарование? Конвей не мог объяснить словами те противоречивые эмоции, которые сейчас испытывал. Наконец, его успокоила мысль, что все его неясные переживания на самом то деле крутились вокруг очень простого факта, который состоял в утрате веры в чудо — не больше и не меньше. Итак, Конвей утратил слепую, иррациональную, в чем-то даже каббаллистическую веру в математическую статистику, но не почувствовал ни радости, ни особого разочарования. Разве что почувствовал, “по здравом размышлении”, некое облегчение. Конечно, это чувство было бы куда большим, если бы Девлин прекратил, наконец, жадно глотать спагетти, чавкая при этом совершенно непристойно. Уловив мгновение, когда Девлин замер, чтобы перевести дух, Конвей сказал почти скороговоркой: “Разреши мне отдать тебе, Девлин...”
“О, не трудись, мой друг! Я вполне смогу дотянуться до стакана и сам остоятел ьно...”
“Как бы мне хотелось, чтобы это было шуткой!” — подумал Конвей, но вслух невозмутимо пояснил: “Хорошо, но я имел в виду... в общем, спасибо, что показал мне ‘ великий водораздел ’. На одной стороне — норм альность и независимость — башни-близнецы, на которых держится современная статистика. На другой — тот сорт зависимости, с которой мы имеем дело в своей работе. Плохо только, что между этими мирами нет моста...”
Девлин был настолько смущен тем, что Конвей согласился с его выводами, что сначала даже не нашел, что сказать и какое-то время просто молча жевал спагетти. А потом вдруг засомневался в своей правоте и прервал неловкую паузу словами: “Может, не так уж я прав... Может я сгустил краски и преждевременно сделал слишком радикальный вывод... — бормотал он растерянно, вытирая брызги соуса со своей рубашки. — Может, этот мост у нас под носом... Эдакий ‘мост Чеширского кота’...”
Конвей театральным жестом постучал по часам: “Знаешь, Девлин, мой универсальный переводчик сломался. Поэтому, пока не починю его, прошу тебя, пожалуйста, говори по-английски... Ты только что сказал что-то вроде ‘мост Чеширского Кота’, не так ли?”
183
Часть 1. Стандарты атклпнанил
Но Девлин его не слышал, углубившись в свои мысли, что, впрочем, с ним бывало довольно часто. Девлин вспоминал свое детство в Нью-Мексико, точнее, горы недалеко от дома, в котором жил маленький Девлин, и чуть ли не ежедневные прогулки в горах. И ту тропу, петлявшую по краю обрыва, что вела на вершину. Иногда тропа выписывала столь крутые виражи, что, казалось, следующий поворот ведет в пропасть... Но на самом деле каждый поворот открывал новые горизонты, и лучше виден был путь, что лежал впереди. “Да, — ответил Девлин механически, — именно мост Чеширского кота...”
“Черт побери! — не сдержался Конвей. — О чем ты говоришь?”
“Я говорю о мосте, который то появляется, то исчезает, то снова появляется, но уже в другом месте, вроде Чеширского кота из ‘Алисы в стране чудес' Кэррола”.
“Ну, слава богу. По крайней мере ты теперь говоришь на нормальном английском языке. Плохо, правда, что я все равно не понимаю, что это значит с точки зрения математической статистики”.
“Да нет же! Ты должен знать, о чем идет речь. Ведь мы уже наблюдали этот мост Чеширского кота. По-другому он называется теоремой де Финетти. Припоминаешь?”
“Не уверен. Погодите-ка, ты говоришь о теореме, которая связывает зависимые случайные величины Бернулли с условно независимыми случайными величинами. Тогда условность служила чем-то вроде моста между зависимостью и независимостью. А! Теперь я понял! Мост Чеширского кота — это условный мост, как и теорема де Финетти, да?”
“Совершенно верно. А что является непрерывным аналогом независимых бернуллиевых сумм?”
“Нормальные суммы. Так, значит, ты предлагаешь моделировать зависимые непрерывные случайные величины смесями нормально распределенных случайных величин?”
“Для точности: смесями условно многомерных нормально распределенных случайных величин”.
“Это и произнести-то трудно, а понять, и вообще, уму не постижимо...”
“Брось, с идеей здесь по крайней мере все прозрачно. Идея состоит в том, чтобы разделить сложную зависимость на две составляющих, а именно на абсолютно зависимую и независимую”.
“И в чем состоит абсолютная зависимость?”
“В общем кондиционирующем событии или режиме. По определению это событие или режим одно и то же для всех случайных величин. И как только режим будет установлен, эти самые случайные величины считаются многомерными нормальными, которые, как мы только что видели, уже можно разложить на независимые компоненты”.
“Здорово. И какие же классы зависимых случайных величин можно моделировать подобным образом?”
184
10. Зависимвя независимость
“Любые. А может, это я так думаю, что любые”.
“Секундочку, профессор. Теорема де Финетти относилась только к симметрично зависимым случайным величинам Бернулли. Так почему же непрерывный ее аналог должен относиться ко всем вообще зависимым случайным величинам?”
“Потому что в отличие от теоремы де Финетти я вовсе не требую, чтобы мои компоненты были симметричными. И, хотя у меня нет строгого доказательства справедливости этой идеи, я не могу найти и содержательного контр примера. Геометрически моя идея — не более чем моделирование заданного ландшафта смесью смятых определенным образом колоколообразных холмов и гор”.
“Ну, допустим... А как быть с теми распределениями, чьи плотности имеют острия и острые грани?”
“Ну один такой пример мы уже видели...”
“Мы?”
“Конечно. Припомни-ка равномерное распределение Бозе — Эйнштейна для сумм случайных величин Бернулли. Мы же видели, что можно выразить его как равномерно распределенную смесь биномиальных сумм, не так ли? Теперь обратите внимание, что, когда число случайных величин неограниченно растет, каждая из биномиальных составляющих стремится к некому нормальному распределению, согласен?”
“Согласен. Но все это требует целого континуума условных состояний. Как ты намерен достичь хорошей аппроксимации, имея на руках всего-то считанное число состояний?”
“Ну пока не знаю. Но вопрос мне нравится. Давай, я над этим поработаю пару часов, а потом подойду к тебе с результатами. Ты не против?”
Они сдали подносы с грязной посудой и пошли каждый по своим делам...
Конвей с самого начала думал, что Девлин не справится с задачей за два часа, и был прав. Он не видел Девлина часов до 11 утра следующего дня, когда он ввалился в офис Конвея, прижимая к груди ворох распечаток.
“Ты что, не спал всю ночь, а Девлин?”
“С чего это ты взял?”
“А у тебя до сих пор спагетти на рубашке...”
“Наплевать... Слушай, я, кажется, получил несколько тонких очень нетривиальных результатов. Так, что? Хочешь взглянуть на результаты или будешь меня воспитывать?” — Девлин мог решать математические задачи сутками, но сохранять вежливость после бессонной ночи ему было трудно.
“Хорошо, хорошо... Конечно, я хочу на них взглянуть, не кипятись”.
Девлин передал Конвею первую из своих распечаток со словами: “Вот, начнем, пожалуй, с аппроксимации стандартного равномерного распределения восемью нормальными...”
185
Часть 1. Стандарты вткнанвния
Approximating a uniform distribution with 8 normals
Аппроксимация равномерного распределения восемью нормальными.
“Неплохо... Нет, это совсем даже неплохо! Только что-то уж слишком волнистой получилась эта аппроксимация... Я могу насчитать 8 пиков. Но и стенки при 0 и 1 тоже не вполне вертикальны”.
“Твоя правда. Вот тебе улучшенный вариант с 16 случайными величинами”.
Approximating a uniform distribution with 16 normals
Аппроксимация равномерного распределения шестнадцатью нормальными
“Да... Это впечатляет... Пики и неотвесность вертикалей почти незаметны”.
“Я знал, что тебе понравится”, — Девлин и сам был доволен, как малыш, который только что научился рисовать квадрат... Поэтому продолжил: “А теперь перейдем к равномерному двумерному распределению на единичном квадрате. Моделировать это в виде смеси условных двумерных нормальных распределений с геометрической точки зрения означает аккуратно напихать колоколов в куб и плотно утрамбовать. По сравнению с одномерным случаем это не так-то просто
186
10. Завиоимая независимость
сделать, особенно трудно выдержать ровные углы. К тому же нам понадобится примерно /72 нормальных распределений, если мы хотим добиться той же гладкости при покрытии единичного квадрата, что и в случае и одномерных случайных величин при покрытии единичного отрезка прямой”.
“Значит, 64 двумерных нормально распределенных случайных величин недостаточно для того, чтобы достичь той же аппроксимации, что мы имели па восьми одномерных нормальных случайных величинах...”
“Точно. И это в предположении реализации наилучшего сценария, считая, что мы выбираем лучшие параметры. Поскольку я пока не разработал формулу наилучшего приближения, мне пришлось воспользоваться методом проб и ошибок. Ясно, конечно, что, чем больше случайных величин надо подобрать, тем дальше от оптимального будет решение, которое этим методом можно построить”.
Конвей слушал его вполуха, поскольку производил в уме некоторые арифметические подсчеты. По получении некого промежуточного результата он спросил удивленно: “Постой-ка, каждая из двумерных случайных величин характеризуется двумя средними, двумя дисперсиями, одной ковариацией и одной плотностью вероятности. Значит, ты просмотрел методом проб и ошибок комбинации 384 непрерывно измеряемых параметров?”
“Вообще-то я использовал 80 двумерных нормальных случайных величин. Хотелось добиться лучшего приближения... Но не пугайся. Это оказалось проще, чем кажется на первый взгляд. Начнем с того, что я воспользовался симметрией. Дело в том, что квадрат симметричен относительно горизонтальной и вертикальной осей, а также обоих диагоналей. Это значит, что мне нужно было рассматривать только те распределения, которые обладали свойством симметрии по всем этим осям одновременно. Это оставило меня с задачей найти 10 двумерных нормальных распределений при условии, что, во-первых, каждое из этих распределений должно перейти в себя 8 раз посредством отражения относительно осей симметрии, и, во-вторых, вероятности тех 10 нормально распределенных случайных величин должны при сложении дать 1/8. Это сводит общее количество степеней свободы к величине 6 х 10 - 1 = 59”.
“Этого все равно слишком много для тотального перебора. Как же ты справился?”
“Секс с компьютером...”
Конвей побледнел. Него в голове возникли совершенно нелепые мысли: “Господи, это неизлечимо... Меня учили математике, а не психиатрии... Это уже слишком...”. Однако, собравшись с духом, Конвей сказал Девлину мягко и нежно, как ребенку: “Слушай, Девлин, я высоко ценю твои усилия и понимаю важность и сложность того, чем ты занимаешься, но, согласись, у каждого человека есть предел возможностей. Мне кажется, что ты слишком устал... Знаешь что? Возьми-ка отпуск на несколько дней... Попробуй изменить свою личную жизнь... Кстати, у меня есть знакомый психоаналитик, хочешь дам тебе его телефончик...”
187
Часть 1. Стандарты отклонения
“Ты не заткнешься? — Девлин довольно грубо прервал Конвея. — Я не удовлетворял свои сексуальные потребности с помощью компьютера, как ты подумал! Я имел в виду одну современную компьютерную игру с сексуальным подтекстом. Компьютер случайным образом отбирает несколько решений-кандидатов, потом выбирает из них наилучшего и позволяет ему ‘произвести потомство’ посредством обмена ‘генами’, под которыми понимается набор кодов различных параметров. Компьютер допускает мутации... В общем, идея здесь в том, чтобы улучшить поиск методом ‘тыка’ некоей имитацией биологической эволюции... Этот подход называется ‘генетическим алгоритмом’. Оказывается, весьма эффективно! Мне хватило всего одной ночи, чтобы породить многотысячное потомство...”
Конвей слушал эту тираду Девлина и думал: “Да... Похоже, компьютер получил больше кайфа, чем бедняга Девлин... Хотя он заводится все больше и больше день ото дня...” Но сказал он, как обычно, другое и деланно равнодушным тоном: “Ну, я вижу, что так или иначе, но проблему ты решил”.
“Ну да! Я сильно в этом сомневаюсь! Конечно, с генетическими алгоритмами ни в чем нельзя быть до конца уверенным, но с потомством, насчитывающим всего несколько тысяч, нельзя надеяться решить задачу такого масштаба..
“Ну и к чему же ты, или мне лучше сказать ‘матушка-компьютер’, в итоге пришел?”
В ответ Девлин передал ему распечатку очередного графика со словами: “Вот, разрез первого квадранта при условии, что единичный куб центрирован в начале координат”.
Approximating a uniform bivariate with 80 bivariate normals
Аппроксимация двумерного равномерного распределения восьмьюдесятью двумерными нормальными
188
ID. Зависимая независимость
“Выглядит как-то по-дурацки, тебе не кажется? Напоминает смятую скатерть или больной коренной зуб, каковым его видит дантист, нет?”
“Мне очень жаль... Но, правда, я и сам надеялся на что-нибудь более привлекательное”. Лицо Девлина как-то все обмякло и стало чем-то напоминать последний из графиков. Может быть, все дело было в том, что недосыпание всегда сказывалось на Девлине не лучшим образом.
Конвею стало жаль друга, и он сказал успокаивающе: “Да брось ты, Девлин! Не принимай все близко к сердцу. Плохая или хорошая аппроксимация получилась, ты уж никак не виноват в этом”.
Но такое простое лекарство не помогло. Оно и понятно. В последние несколько недель Девлин головой ушел в разработки, да и Конвей не давал ему потерять интерес к исследуемому вопросу. Но теперь он, похоже, выдохся: “Ах, я так надеялся, что условная многомерная нормальность окажется полезной... Я устал раз за разом находить решения, которые каждый раз оказываются практически неработоспособными..
Да, Девлином явно овладевало уныние, если не депрессия. Но в этот момент сработал тот довольно часто встречающийся факт, что удачно подобранные партнеры неосознанно стремятся компенсировать недостатки друг друга. Возможно поэтому уныние Девлина породило вспышку энтузиазма у Конвея: “Но, ведь, это работает! И не забывай, мы рассматриваем крупный план. А всякий крупный план всегда привлекает внимание к частным недостаткам и некрасивостям. Однако главное все же в том, что значение плотности внутри квадрата близко к единице, тогда как ее значение вне квадрата близко к нулю. Это и есть то, что нам нужно. Только на границах мы имеем некоторые неприятности”.
“Рассказывай! Даже при 80-компонентной смеси, которая загрузила работой компьютер на всю ночь, мне не удалось получить идеального результата. Что-то сопротивляется... Боюсь, мы чего-то важного не понимаем!”
“Но послушай, Девлин! Разве мы на практике часто имеем дело с такими плотностями, которые имеют идеально плоские вершины и идеально отвесные стенки? За исключением попадающихся нам изредка бинарных опционов я ни одного практического примера привести не могу ”.
“Твоя правда. Выпуклые макушки и клиновидные хвосты гораздо проще приблизить условно многомерными нормальными плотностями. Но на этом вся правда и кончается... Дело в том, что никакую выпуклую макушку и никакой клиновидный хвост не удастся хорошо приблизить малым количеством таких плотностей. Результат всегда будет выглядеть, как жеваная простыня, или кариозный зуб, или как что-нибудь похуже”.
“Ну и ладно! Пусть некрасиво, зато, может быть, такой точности вполне достаточно, как думаешь, Девлин? Ведь дело вовсе не в красоте, с практической точки зрения нам вовсе не нужно идеальное приближение, не так ли? Мне, например, вполне достаточно, если результат подойдет, что называется, 'для косого глаза’”.
189
Часть 1. Стандарты отклонения______________________________________________
“Мне неизвестно, что такое тест косоглазого...”
“О, это нечто! Нарисуй на листе эмпирические частоты и предсказанные вероятности. Потом зажмурь один глаз, а другой прищурь и скосите так, чтобы частоты и плотности совместились. Если удалось, то и хорошо!”
“Очень научно!” — заметил Девлин с сарказмом.
“Можешь модифицировать этот метод, чтобы он выглядел более научно. Вот, скажем, вчера ты проверял правдоподобность многомерных нормальных всплесков, используя ‘хи-квадрат’. По сути, это тоже разновидность теста косоглазого. Ты, ведь, неспроста уверял меня, что удовлетворение критерию ‘хи-квадрат’ не гарантирует осевой симметрии... Так что я бы трактовал все наши сомнения по части многомерной нормальности, как говорится, ‘в пользу обвиняемого’, т.е. образца, прошедшего тест”.
“Ну а я бы не стал торопиться...”
“Ну, что ж... Я это знаю. Знаю и то, что ты в статистических критериях разбираешься лучше меня. Но именно высокая квалификация и делает тебя таким педантом на практике. А в нашей практике трудно быть педантом”.
“Ну вы-то, ребята, уж слишком непеданты!”
“Опять верно! Мы прищуриваем и скашиваем глаза порой слишком сильно, а иногда вообще держим их ‘широко закрытыми’. Спасибо, что раскрыл мне глаза, Девлин! Нет, кроме шуток, я тебе чрезвычайно признателен. Но теперь мне надо снова зажмурить и скосить глаза, чтобы посмотреть, как ты будешь проводить еще один из своих тестов”.
“О каком тесте ты говоришь?”
“Я хочу, чтобы ты попытался приблизить те практические данные об индексах биржевых котировок, которые мы рассматривали вчера, каким-нибудь смешанным многомерным нормальным распределением”.
“Удачно тебе закосить! Те данные представлены в пяти измерениях. Поэтому тебе понадобиться косить при сверхъестественном зрении!”
“Нокаут! У меня, конечно, самое обычное зрение... Слушай, мне просто хочется понять, сколько компонентов надо смешать, чтобы никакой всплеск не казался уж слишком ‘кричащим’”.
“Что значит ‘кричащий’?”
“Вот ты мне и скажешь”.
“Как это я могу тебе сказать, если это ты прищуривается, а не я? — Девлин вдруг покраснел и заорал: Ты что издеваешься! С меня хватит!”
Конвей ответил сдержанно, но не скрывая сарказма: “Мне жаль, Девлин, что ты считаешь, что преобразовывать твои хитроумные теории в нечто применимое на практике ниже твоего достоинства”.
“Может быть, это выше моего понимания..
“А может быть, тебе просто следует завести привычку попытаться сделать то, о чем тебя просят, прежде чем утверждать, что ты этого не можешь...”
190
ID. Завиоимая независимость
‘‘Может быть, тебе самому следует отвечать на свои идиотские вопросы...” “Хватит! — заорал было Конвей, но оборвал себя, потому что подумал: “Не забывай, что он всю ночь бился над этой задачей!” Немного успокоившись, Конвей сказал в своей обычной мягкой манере: “Позволь мне напомнить тебе, дорогой Девлин, что я не только коллега, но еще и твой начальник. Однако, поскольку я все же считаю себя твоим другом, то эту стычку просто ‘вычеркиваю из протокола’. В общем, ступай-ка ты домой и ложись спать. Завтра утром мы и думать забудем о сегодняшнем скандале”.
На следующий день умиротворенный, посвежевший и благоухающий Девлин объявился в новом костюме и даже при аккуратно повязанном галстуке. Нигде никаких пятен от спагетти. Так он выглядел только в свой первый рабочий день в «Мегабаксе», ибо уже на второй день он пришел на работу совсем другим. Выбрав момент, Девлин подошел к Конвею и сказал как бы в продолжение вчерашнего разговора: “Конвей, я забрал данные по индексу домой и аппроксимировал их многомерными нормальными распределениями. Наилучший ответ, который я могу дать, это ‘два’”.
“Ты хочешь сказать, что смог приблизить всю ту фактуру всего двумя многомерными нормальными случайными величинами? И это, включая данные января 1975-го и октября 1987-го?”
“А, да... Все, все, включая... Во всяком случае, я смог это сделать настолько хорошо, чтобы пройти тест ‘косоглазого’. Видишь ли, я разделил все исходные данные на два режима. Если бы исходы в каждом режиме были сгенерированы каким-нибудь условно многомерным нормальным распределением, которое характеризовалось бы теми же значениями средних и ковариаций, что и выборка, квадраты радиусов в каждом режиме должны были бы соответствовать распределению ‘хи-квадрат’ с пятью степенями свободы. Вот, изволь прищуриться на эти гистограммы...”
Конвей посмотрел на распечатки. Немного подумав, он проговорил: “Ну вот, теперь гораздо лучше, чем вчера. А что это во втором режиме такие дыры?”
“Проблема малой выборки. .Во второй режим я отнес только 24 из 360 наблюдений. При таком малом объеме выборки неудивительно, что есть дыры”.
“Почему ты не поделил наблюдения более равномерно?”
“Потому что так было удобно. Дело в том, что я просто искал какой-нибудь способ сократить число выбросов. Поэтому начал с того, что определил максимально большую выборку, такую, чтобы она не содержала уж слишком резких пиков. Граница ‘хи-квадрат’, на которой я таким образом остановился, была равна 16, что соответствует хвостовой вероятности, равной 0,7%. Шансы того, что ни одно из 360 наблюдений за многомерной нормальной случайной величиной не попадет в такой хвост равны всего лишь 10%, так что я, по крайней мере, хотя бы в одном аспекте консервативен”.
191
часть 1. Стандарты втклвнвния
“А с чего ты взял, что все всплески и выбросы можно отнести ко всего одному дополнительному режиму?”
A crude mixed multivariate normal fit
0.18
0.16
0.14
c 0.12
J o.w
0.08
3 0.06
0.04
0.02
0.00
Histogram for Regime 1
0 5 10 15
Histogram for Regime 2
Грубая смешанная многомерная нормальная аппроксимация.
“Я ничего заранее не предполагал. Напротив, даже был готов повторить операцию, т.е. снова по максимуму исключить всплески и завести третий режим и т. д. Но делать этого мне просто не понадобилось. Если предположить, что все наблюдения второго режима действительно отражают некие фундаментальные вектор средних и матрицу ковариаций некоего многомерного нормального распределения, то даже самые резкие пики представляют хвостовую вероятность, превышающую 5%. А шансы на то, что 24 наблюдения не принесут ни одного всплеска, в таком хвосте равны всего лишь 28%. Это значит, что два режима и в самом деле уничтожили толстые хвосты”.
“Фантастика! Даже на тебя это должно было произвести впечатление. Я имею в виду точность аппроксимации”.
“В определенном смысле я и вправду поражен. Это на световые годы опережает обычный подход. Но..
192
10. Зависимая нваависимвсть
“Какое еще ‘но’?”
“Не важно”.
“Девлин, я знаю, о чем ты думаешь. Ты считаешь, что я не хочу слышать никаких критических соображений. Но это неправда. Мне просто не хочется, чтобы твои критические соображения парализовали нас. Но теперь, когда ты принесли некий результат, ты не только можешь, но и должен указать на его недостатки. Итак, в чем состоит плохая новость?”
“Ладно... Во-первых, второй режим вполне аморфен. Главный его ‘общий знаменатель’, если так можно сказать, это высокая волатильность, которая меняется в интервале от 29 до почти 58% в годовом исчислении. Может быть, для некоторых задач, как, например, оценка хвостовых рисков, некий ‘дикий’ режим ‘хватаю все подряд’ типа нашего второго вполне бы и подошел, но для других целей, мне кажется, нам надо было бы провести дополнительные подразбиения. Ну, например, если бы мы просто переклассифицировали наблюдение, соответствующее октябрю 1975-го, как некий отдельно стоящий выброс, максимальная волатильность второго режима упала бы ниже 45%. И потом, может быть, нам следует различать сценарии улета вверх и сценарии обвала вниз...”
“Правдоподобно. Тебе еще что-нибудь не нравится?”
“Да. Я, видишь ли, вовсе не думаю, что эти гистограммы говорят об очень хорошем приближении. В третьем и восьмом подинтервалах мало плотности вероятности по сравнению с другими под интервалами. А это еще одно указание на то, что нам следовало бы рассмотреть больше режимов...”
“Но почему бы просто не переклассифицировать несколько наблюдений из первого режима во второй?”
“Конечно, поначалу я так и сделал. Просто это не сработало. В этом случае появляется все больше и больше наблюдений с ненормально низкими статистиками ‘хи-квадрат’, да и к тому же статистики ‘хи-квадрат’ разбухали все сильнее и сильнее для выбросов второго режима. При этом, как ни странно, получалось, что я все время стремился опустошить средний диапазон гистограммы второго режима, причем в большей мере, чем я заполнял этот диапазон для первого режима. Вог так”.
“Ну и сколько же режимов оптимально, как ты думаешь?”
“Не знаю. Я вовсе не уверен, что двух режимов недостаточно. Может, я просто неправильно рассортировал наблюдения. Или слишком жестко требовал, чтобы параметры режима отвечали значениям соответствующих средних и ковариаций? Не знаю”.
“А ты не пытался просто максимизировать общее правдоподобие наблюдений выборки? Тогда не понадобилось бы сортировать наблюдения по режимам или подгонять какой-нибудь конкретный параметр...”
“Конечно, пытался, неоднократно! Но всегда это была катастрофа. Оценка правдоподобия упорно лезла в бесконечность. Потом я понял почему”.
193
Часть 1. Стандарты отклонения_________________________________________
“Компьютерный глюк, очевидно?”
“Если бы... К сожалению, с компьютером все в порядке. Все дело в том, что я пытался приписать нулевую дисперсию одному из условных режимов, со средним, равным одному из наблюденных исходов. Тогда плотность в точке этого наблюдения должна была бы стать равной бесконечности, максимизируя, конечно, правдоподобие”.
“Очень странно! — сказал Конвей, ничего, впрочем, не понимая, что именно странного в таком результате. — Почему же ничего подобного не происходит с обычными распределениями?”
“Потому что в случае любого одноточечного распределения выигрыш от точного приближения одного наблюдения уравновешивается проигрышами от неточного приближения других наблюдений. В противоположность этому некая смесь одноточечного распределения и какого-нибудь распределения, которое натянуто на все пространство, может достичь бесконечного правдоподобия на одном исходе без того, чтобы где-либо еще залезть в минус бесконечность”.
“Понятно. Тебе надо наложить несколько новых ограничений, чтобы исключить нелепые решения”.
“Да, если, конечно, мы пытаемся максимизировать правдоподобие. Но я вовсе не уверен, где, как, почему и от чего следует абстрагироваться. И как, вообще, измерить адекватность или, иначе говоря, нашу уверенность в правильности построенной модели? И как можно быть уверенным, что примененные нами алгоритмы поиска не прошли мимо какой-нибудь гораздо более адекватной модели? И как..
“Хорошо! — прервал его Конвей. — Хорошо! Я понял. Еще очень во многом надо подразобраться. Обычное дело. Но я по-прежнему думаю, что мы сделали значительные успехи. Большое тебе спасибо за это, Девлин”.
“Это за что же? Не за то ли, что я нахожу все больше и больше дьявольски запутанных проблем?”
“Ну, хотя бы за то, что ты подсказал мне идеи, которые могут иметь большое значение в нашем мире. А потом, те проблемы, на которые ты натолкнулся, не исключают переключения режимов. Твой результат не противоречит практике. И при этом не заставляет нас напрямую оценивать все центральные и смешанные моменты старших порядков. Твой подход даже включает традиционный метод, хотя и как частный случай”.
“Так-то оно так, но моя работа порождает больше вопросов, чем дает ответов”, — сказал Девлин уныло.
“А мне всегда казалось, что ты любишь трудные вопросы!” — бодро брякнул Конвей.
“Любил. Теперь бы для разнообразия мне хотелось бы получить хоть немного ответов. В настоящий момент мне кажется, что я больше ничего не знаю наверняка...”
“Не сходи с ума, Девлин!”
194
10. Зависимая нвэависимвсть
“По всей видимости, так оно и есть...” Девлин потоптался и поплелся к двери.
Ошарашенный Конвей какое-то время безуспешно пытался взять в толк, что произошло. Потом заторопился, побежал за Девлином, догнал его и затараторил тоном медсестры из психушки: “Послушай, я вовсе ничего такого не имел в виду, ну не буквально же...”
Боюсь, что Девлин впал в глубокую депрессию. Однако, пока Конвей героически пытается привести его в норму и успокоить, мы можем заполнить кое-какие теоретические пробелы в их дискуссии.
Условная многомерная нормальность
Допустим, что некий л-мерный случайный вектор X таков, что мы знаем вероятности {р*|(* того, что X попадет в А-й режим из К
возможных режимов. Это значит, что {/?*[(& G задает
смешивающее распределение на множестве режимов. Предположим далее, что в каждом режиме к наш случайный вектор X является многомерной нормально распределенной случайной величиной с вектором средних Мк и матрицей ковариаций . Тогда безусловная плотность задается следующим матричным
уравнением:
Когда говорят о какой-нибудь смеси условно многомерных нормальных режимов, ее называют смешанным многомерным нормальным распределением.
Степени свободы смешанного многомерного нормального распределения
Каждый многомерный нормальный режим будет характеризоваться одной смешивающей вероятностью, п значениями компонент вектора математических ожиданий и !4(л + 1)(и) различных компонент матрицы ковариаций, т. е. различных дисперсий и ковариаций, что в итоге даст !4(л + 1)(л +2) степеней свободы. Если теперь допустить, что у нас есть К различных режимов, то количество степеней свободы нашей системы увеличится в К раз, за исключением того, что одна степень свободы “расходуется” на то, что сумма всех смешивающих вероятностей должна быть равна 1. Это значит, что мы будем иметь У1К(п + 1)(л +2) — 1 степеней свободы для всей системы.
Для того чтобы представить себе, много это или мало, соотнесите вышеприведенное выражение с тем фактом, что для того, чтобы непосредственно
195
Часть 1. Стандарты отклонения ________________
специфицировать все три первых момента многомерного нормального распределения и соответствующие смешанные моменты, нам надо знать С^+3 — 1 параметров. Смешанное многомерное нормальное распределение будет гораздо более “бережливым” по отношению к степеням свободы, если и только если К < (w/3) + 1. Аналогично для спецификации смешанного многомерного
распределения потребуется меньше степеней свободы, чем для спецификации первых четырех моментов и соответствующих смешанных моментов многомерного нормального распределения, если и только если К < ((л/3) + 1) ((ц/4)+ 1).
Наука и искусство аппроксимации
Приближение, деликатно выражаясь, эмпирических данных неким распределением вероятностей, иными словами, подгонка распределения под эмпирику, всегда порождает массу непростых вопросов, которые обычно крутятся вокруг выбора критерия оптимальности приближения и на которые неочевидно, как отвечать. Вот некоторые из них: должны ли мы измерять близость приближения в терминах плотностей или интегральных функций распределения? Должны ли мы минимизировать максимальную дивергенцию, среднюю абсолютную дивергенцию, квадрат средней дивергенции или что-нибудь еще? Следует ли дивергенции на хвостах придавать большее значение, чем дивергенции вблизи среднего? При этом у каждого конкретного ответа на конкретный вопрос есть свои плюсы и свои минусы, но ни на один из этих вопросов не существует ни стандартного, ни даже статистически предпочтительного с практической точки зрения ответа. Вот, например, когда Девлин приближал равномерную плотность смешанной многомерной нормальной плотностью, он использовал в качестве меры близости этого приближения некую смесь абсолютной дивергенции и квадрата дивергенции просто потому, что ему понравился внешний вид того, что в итоге получилось. На практике же эстетичность внешнего вида обычно гораздо менее значима, чем удобство аналитической и компьютерной обработки.
Максимальное правдоподобие
Наиболее удобным способом аппроксимировать сложное распределение чаще всего является максимизация правдоподобия. По определению правдоподобием называют совместную вероятность наблюдений как функцию параметров выбора 3. Это значит, что, если Xj — вектор исходов у'-го наблюдения (а не j-я компонента вектора А), правдоподобие, соответствующее этой схеме наблюдений, равно где, конечно, предполагается, что
j
наблюдения независимы. Заметим, что на практике удобнее работать не с самим правдоподобием, а с его логарифмом, или “логарифмическим правдоподобием”. При переходе к логарифмическому правдоподобию мы преобразуем произведение в сумму, не меняя оптимального значения 3.
196
10. Зависиман независимость
К сожалению, метод максимального правдоподобия не работает в случае смешанных многомерных нормальных распределений. Дело в том, что, выбрав одно из наблюдений выборки в качестве среднего Мк одного из режимов и уменьшая определитель соответствующей матрицы ковариаций |S*|, любой алгоритм максимизации сможет сделать плотность в точке Мк сколь угодно большой. И этот эффект будет доминировать над всеми остальными элементами смеси постольку, поскольку они будут ограничены этой смесью. Поэтому, чтобы получить более реалистичный результат, нам следует ограничить каждый снизу или наложить какие-то другие ограничения, но с тем же эффектом.
Случайный поиск на решетке
Представьте, что вы возглавляете некую команду исследователей, перед которой стоит задача найти в условиях крайне ограниченной видимости (скажем, из-за густого тумана) на неком достаточно обширном участке местности самую высокую сопку. Конечно, если вам заранее известно, что в этом районе есть ровно одна сопка, то надо выбрать то направление движения, где подъем самый крутой, только и всего. Однако, если на вашем участке местности есть несколько сопок, велика вероятность, что вы со своим простым подходом окажетесь на какой-нибудь второстепенной стопочке, не дойдя до самой высокой. Поэтому как разумный руководитель поисковой партии, особенно если у вас много подчиненных, вы, скорее всего, организуете то, что принято называть “случайным поиском на решетке”. Иными словами, вы методично разделите свой участок на сектора-клетки и в каждую клетку пошлете небольшую группу исследователей, которым поручите измерить высоту в некой случайно выбранной точке. Потом, скорее всего, вы сосредоточите внимание на той клетке или на нескольких клетках, где высоты окажутся максимальными. Эти клетки вы вновь поделите на подклетки и снова пошлете туда исследователей. В конце концов вы почувствуете, что нашли-таки клетку, где можно, как вам кажется, без опаски применить метод самого крутого подъема.
Так вот, максимизация сложной функции во многом напоминает поиск наивысшей сопки в тумане, что математики часто называют применяемые методы алгоритмами "карабканья на бугры". Как и в рассмотренных нами гипотетических поисках самой высокой сопки, эти методы прекрасно работают, если у максимизируемой функции есть только один локальный максимум, который и будет в этом случае глобальным. Если же локальных максимумов больше одного, нашему математику придется-таки организовать нечто вроде поиска на решетке. Но при этом надо понимать, что более-менее серьезный поиск на решетке в реальной ситуации, скорее всего, будет практически нереализуем, поскольку каждая новая независимая переменная добавляет в таких случаях новое измерение для поиска. Таким образом, если мы, скажем, позволим найти по четыре варианта для каждой из двадцати случайных величин, мы получим триллион комбинаций. Клеток в сетке быстро становится слишком много.
197
Пасть I. Стандарты откнонвния ____________________________________
Генетические алгоритмы
Генетические алгоритмы — это некая альтернатива нереализуемому тотальному поиску на решетке. Этот подход имитирует дарвинистское представление об эволюции природы на планете Земля, основной смысл которого, как вы знаете, состоит в так называемом естественном отборе. Вот и любой генетический алгоритм по своей сути устроен так же. Сначала каким-то случайным образом выбирается несколько (чем больше, тем лучше) первых кандидатов на решение проблемы. Потом алгоритм оценивает эффективность каждого кандидата и отсекает самых неэффективных. Оставшихся первых кандидатов мы назовем “пращурами”. Пращуры дают потомство, которое тестируется алгоритмом на эффективность, и из него выбираются наиболее успешные варианты и т. д. Тонкий момент здесь — произведение потомства. В алгоритме следует соблюсти аналогию с половым размножением особей биологического вида, когда потомки имеют параметры, в каком-то смысле являющиеся смесью параметров родителей. Существенно, что смешивание параметров родителей должно допускать случайные мутации.
Подобно естественной эволюции генетические алгоритмы насколько непредсказуемы, настолько же и чудотворны, т. е. способны приносить немыслимо хорошие результаты, но без всякой гарантии. Порой тысячи поколений могут пройти, сменяя друг друга, без какого-либо существенного приближения к оптимуму, так что достижение даже локального оптимума не может быть в общем случае гарантировано. С другой стороны, генетические алгоритмы являются, несомненно, гигантским улучшением чисто случайного поиска оптимума, время от времени выдавая результаты, которые иначе чем “гениальными” и не назовешь.
На практике наиболее успешно показали себя схемы поиска, в которых генетические алгоритмы работают в связке с другими более предсказуемыми методами. В простейшем случае такого подхода генетический алгоритм должен выделить некое “ядро” решения, т. е. набор протовариантов, из которого окончательное решение будет выделено уже методом локальной оптимизации. При этом нелишним оказывается и некий творческий волюнтаризм лица принимающего решения, которое в таких схемах является некоей аналогией бога. Вспомните, например, как Девлин создал смешанную двумерную аппроксимацию равномерного распределения с помощью генетических алгоритмов. Вы можете попытаться улучшить результат Девлина, добавив новые режимы на границах, консолидировав некоторые почти совпадающие режимы и проведя локальную оптимизацию. Ниже я привожу разрез одного такого улучшения, которое демонстрирует гораздо меньшую волнистость, по сравнению с волнистостью, которую имеют все остальные полученные мной улучшения и сам исходный вариант Девлина.
Хвостовые риски — реальные и оцениваемые
Как вы помните, Девлин отметил, что даже грубые модели смешанных многомерных нормальных распределений способны давать весьма разумные оценки хвостовых рисков. Нижеприведенный плоский график представляет
198
10. Зависимая независимость
собой как раз такой пример, использующий некую равновзвешенную корзину (перевзвешиваемую каждый месяц) тех пяти индексов акций, которые исследовал Девлин. На этом графике серая кривая линия показывает реальные частоты хвостов с порогами, изменяющимися в интервале от 2,5 до 5,0 стандартных уклонений левее среднего. Пунктирная линия показывает риски для некого нормального портфеля. Жирная кривая линия — это Девлиновская грубая смешанная нормальная аппроксимация.
Approximating a uniform bivariate: revised version
Аппроксимируем двумерное равномерное распределение: улучшенный вариант.
Tail risks for an equal basket of five equity indices
Хвостовые риски для равновзвешенной корзины пяти индексов.
199
Часть 1. Стандарты отклонении
Как видите, грубая смешанная нормальная аппроксимация выглядит гораздо лучше чисто нормальной аппроксимации в том диапазоне хвостовых рисков, который обычно представляет интерес на практике. Однако наша грубая смесь слишком сильно переоценивает риск очень больших всплесков. Поэтому, хотя этот пример, может быть, и не самым яркий, он все-таки показывает основные преимущества и недостатки грубого смешанного многомерного оценивания.
200
11: Happy end, черт побери!
Хотя в течение всей следующей недели напряженность в отношениях Конвея и Девлина постепенно уменьшалась, они столь же постепенно отдалялись друг от друга. Как это ни казалось странным, учитывая их род занятий, они больше ни разу не обсуждали теоретические вопросы с глазу на глаз. При этом оба считали, что условная многомерная нормальность — это гигантский шаг вперед в постулатах построения модели по сравнению с традиционным подходом, основанном на безусловной нормальности. Их расхождения касались применения этих основополагающих принципов.
Так, Конвей видел огромное поле возможностей для применения этих принципов к практическому оцениванию. Поэтому он сказал однажды Девлину с некоторым душевным подъемом: “Не понимаю, почему ты, Девлин выглядишь таким мрачным. Ну, если два режима не дают нужной точности аппроксимации, примени три или даже четыре. Всего и проблем-то. Если с одним методом подгонки и коррекции смеси не удается достичь приемлемого приближения, возьми другой. Так или иначе, но мы выберемся на ‘столбовую дорогу’”.
А Девлин, напротив, никакого энтузиазма не испытывал. На пути применения идеи условной многомерной нормальности ему всюду мерещились подвохи. Поэтому он ответил, как обычно, с известной долей сарказма: “Да уж, ты выберешься на большак, еще бы! Точно так же, наверное, думают лемминги, когда идут к океану... Ну скажи на милость, как мы можем идентифицировать разнообразные режимы или даже просто понять, какой из выбранных режимов в настоящее время является главным? Ведь все наши доверительные интервалы — всего лишь гипотезы! Неужели ты не понимаешь, что основываться на существенно неполных знаниях, хотя и имеющихся в ‘достаточно приличном количестве’, опасно?”
“Да-да: ‘Солидное образование опасно...’Это, кажется, Александр Поуп. Как я мог забыть?” — ответил Конвей и тут же пожалел о своем самодовольстве, но вида не подал и продолжил: Скоро ты начнете убеждать меня, что невежество — это благодать!”
“Нет, невежество — это маразм, это идиотизм, и знаешь почему? Потому что глупые люди таким путем просто находят псевдорациональную причину прикидываться, что знают больше, чем на самом деле!”
“Спокойно, спокойно... У него опять крыша едет”, — подумал Конвей и сказал: “Хорошо, хорошо! В этом я с тобой полностью согласен! Именно здесь и сидит причина того, что традиционный анализ ‘среднего и дисперсии’ так часто и с такими тяжелыми последствиями подводит нас именно на хвостах. Дело в том, что с точки зрения этого анализа его методы дают нам большее понимание
201
Пасть 1. Стандарты втклвнвмим____________________________________________
существа происходящих процессов, чем этот анализ на самом деле может дать... Но ведь условная нормальность снимает шоры с наших глаз, не так ли?”
"В принципе, да. Но как ты сможешь корректно применить на практике нечто такое, что сам не можете адекватно и надежно оценить?”
“Да? А насколько надежными были, как теперь выясняется, все наши традиционные оценки, которыми мы пользовались долгие годы и пользуемся до сих пор? Ведь все эти оценки во многом основаны на допущениях о стабильности режимов, которые, как ты успешно показал, невозможно обосновать. Поэтому я предпочитаю быть более-менее правым, чем наверняка неправым”.
“И я тоже. Тогда почему бы нам просто не объявить, что риски 5-хвостов могут изменяться в интервале от 0 до (1А2 + 1)?”
“Конечно, мы обязательно об этом объявим. Но не только это! Этот интервал слишком большой. И ты прекрасно понимаешь, что нам надо дать некоторые направляющие рекомендации”.
“А я думаю, что в данный момент мы не можем дать никаких направляющих рекомендаций. И давай не будем делать вид, что такие рекомендации у нас есть!”
“Неправда! Кое-какие рекомендации мы можем дать уже сейчас. Но значит ли это, что нам не понадобится в будущем улучшить нашу способность управлять риском? Нет, не значит. Так что давай не будем делать лучшее врагом хорошего!”
“И давай не будем судить об этом твоем ‘хорошем’ по фасаду!”
После этого они договорились остаться каждый при своем мнении. Однако Конвей решил не ждать развития событий и заставил-таки Девлина прочесть остальным сотрудникам подразделения лекцию о последних результатах, полученных Девлином.
К чести Девлина надо сказать, он не стал упрямиться, а прочел лекцию четко, ясно и занимательно так, что в группе оценки риска только и разговоров было, что о переоценке границ и пределов риска. Мнения, как и следовало ожидать, разделились. Некоторые, подобно Конвею, с энтузиазмом оценивали перспективы применения смешанной многомерной нормальности. Другие же, как и сам Девлин, оказались пессимистами. Но, несмотря на это, все были едины в том, что по сравнению со стандартным методом ‘среднего и дисперсии’ новый теоретический подход оказался гораздо более адекватен тем процессам, которые имели место на практике. И это при том, что каждый без исключения член группы был ‘воспитан’ именно на традиционном подходе.
Конвей тихо радовался вспышке энтузиазма в рядах своих сотрудников. И, хотя он пока что не чувствовал себя готовым с ходу переубедить весь состав Комитета контроля риска, но надеялся завербовать пару топ-менеджеров из членов Комитета в свои союзники и, следовательно, в союзники нового подхода. “А потом они со временем переубедят остальных”, — думал Конвей.
Через несколько дней Конвею представился шанс привести в исполнение его
202
11. Happy and, март паВари!
нехитрый план. В тот момент Конвея не было на рабочем месте, потому что он был на торговой площадке. Там в компании главного трейдера он пересматривал основные внутрибанковские ограничения по позициям, сделкам и операциям. За этим занятием его и отловила секретарша: “Конвей, я весь день вас ищу! Звонил сам контролер. Он хочет вас видеть”.
“Это еще зачем?”
“Он не сказал. Вы же знаете, что он никогда этого не говорит... Он просто попросил меня передать, чтобы вы зашли, как только освободитесь”.
“А! В переводе с языка контролера это означает ‘ брось все и лети немедленно ко мне!’”.
“Именно поэтому я и ищу вас повсюду..
Конвей извинился перед трейдером и заторопился в свой офис. Схватив кипу распечаток графиков Девлина, он пулей помчался к лифтам.
По прибытии на этаж высшего руководства он назвал себя секретарше и сел ждать. От нечего делать Конвей стал думать о том, что всегда приходило ему на ум, как только он попадал на этот этаж, а именно о том, почему этот этаж так сильно отличался от остальных помещений банка. И то сказать: богатые чехлы на креслах, персидские ковры и дорогие картины на стенах красного дерева... Но больше всего ему нравилась тишина. Это так отличалось от гула и шума торгового зала...
“Контролер вас сейчас примет”, — прервала его мысли секретарша и с глубоким чувством собственного достоинства поправила безупречную прическу. Через пару минут она пригласила Конвея пройти в самый тихий, по всей видимости, уголок этажа руководства. Там она мягко постучала в дверь кабинета, а потом полуоткрыта ее, приглашая Конвея войти.
В просторном кабинете за столом, не отягощенном бумагами, сидел аккуратно и дорого одетый человек с тщательно причесанными седыми волосами. Вся его поза и выражение лица излучали властность. Он неспеша оглядел Конвея с ног до головы и проговорил со спокойствием, не предвещавшем, как правило, ничего хорошего: “Добрый день, Конвей. Рад видеть вас снова”, — с этими словами контролер выдавил из себя улыбку, которая, казалось, растворилась в тишине кабинета вместе с его словами.
“Добрый день, господин Форд! Я тоже рад вас видеть...” — Конвею определенно становилось все более и более не по себе. И он замер в нерешительности, не дойдя трех метров до великолепного стола контролера.
“Надеюсь, я не прервал ваших занятий”.
“Вовсе нет, сэр. У меня была обычная беседа о границах риска. Ничего особенного”.
“Беседа с Девлином?”
“Нет, не с Девлином. Не знал, сэр, что вы знакомы с ним”.
“Я не знаком с ним. Я просто наслышан о нем. Присаживайтесь, Конвей, и устраивайтесь поудобнее”.
203
Часть 1. Стандарты отклонония_________________________________________
Пока Конвей усаживался в роскошное кресло, его внимание привлекло роскошное пресс-папье на столе контролера, а точнее, гравировка на этом пресс-папье, которая гласила: “Невежество — это благодать!” Конвей прочел надпись и поежился.
“Я так понимаю, что вы это видели?” — с этими словами контролер протянул Конвею отчет аудиторов.
“Да, сэр, — быстро ответил Конвей, сдерживая волнение. — Но я не припоминаю, чтобы в этом отчете упоминалось имя Девлина, сэр”.
“Оно здесь и не упоминается. Немного ума не надо, чтобы понять, кого именно аудиторы имеют в виду. Вы знаете, они хотят его голову... Впрочем, если и не знаете наверняка, то догадываетесь”.
Все, что смог сказать в ответ Конвей, было глуповатое: “Да, сэр!” Потом он спохватился и добавил торопливо: “Но я хотел бы заявить со всей ответственностью, что насчет Девлина они абсолютно неправы! Он был абсолютно прав в том споре с аудиторами. И вообще Девлин — самый толковый из моих подчиненных”.
“Конечно, ваш Девлин был прав. Я это понял сразу, как только узнал о том, что аудиторы затаили на него злобу”, — с этими словами контролер вдруг остро посмотрел прямо в глаза Конвею и продолжил: “Посредственность вроде наших аудиторов легко прощает ошибки, но она никогда ни за что не простит правоты”.
Конвей был шокирован. Он никак не ждал услышать таких слов от контролера. И уж во всяком случае, представить не мог, что контролер примет сторону Девлина. Возможно, в силу некоторой ошарашенности Конвей спросил опять-таки глуповато: “Значит ли это, что вы согласны с Девлином, сэр?”
“В отношении риска того, что не будет ни одного выигравшего из трех несмещенных некоррелированных случайных величин Бернулли? Конечно. Этот риск вовсе не обязан быть равен 1/8. В зависимости от смешанного момента он может быть равен любому числу между 0 и 1/4”.
“Конечно, сэр! Это именно то, что открыл Девлин. Вы себе не представляете, какое облегчение, что высший руководитель, как вы, до тонкостей разбирается в этом вопросе”.
“Но почему вы придаете столь большое значение этой, в общем-то, частной проблеме?”
“Потому что эта проблема — только верхушка айсберга. Того айсберга риска, который стандартный метод ‘среднего и дисперсии’ обнаружить не в состоянии”.
Контролер вскинул брови вверх: “Вы уверены?”
“Видите ли, я и сам поначалу не поверил, но Девлин объяснял ее мне, приводя все больше и больше примеров, что в конце концов я проникся значимостью этого вопроса”.
“Что есть такого особого в Девлине, что он увидел то, что не заметили другие профессионалы?”
204
11. Happy end, чёрт псВври!
“He могу ответить точно, сэр. Лучше бы вы спросили его самого... Но, что касается моего видения, я могу сказать, что он подходит ко всякой задаче так, как отнесся бы к ней, я бы сказал, ребенок, что ли... Он достаточно прост, чтобы признать, что чего-то не понимает, но зато очень настойчиво старается разобраться во всем и ликвидировать свое незнание”.
“И это при прямой вашей поддержке?”
"Не с самого начала, сэр. Вначале я в этом не участвовал, и Девлин самостоятельно проделал значительную часть работы. Но мало-помалу Девлин убедил меня, что большая часть привычного подхода к анализу риска крайне ненадежна. В большинстве случаев сжечь отчет по анализу риска — значит, пролить на вопросы, анализируемые в этом отчете, больше света, чем если внимательно его прочитать”.
“Прекрасно! Приятно, черт побери, что кто-то еще думает так же, как я думал всегда. Как-то зимой я, знаете ли, взял домой несколько этих отчетов именно на растопку”. Контролер весело рассмеялся, но глаза его при этом оставались настолько холодными и лишенными всякого веселья, что Конвей не решился посмеяться за компанию, а счел за лучшее вежливо промолчать. Отсмеявшись, контролер продолжил: “Но, как я понимаю, Девлин предложил-таки вам более количественную оценку ценности этих отчетов. Не поделитесь, что же он все-таки накопал?”
“По сути, Девлин доказал, что риски произвольного хвоста, отстоящего от среднего на s стандартных уклонений, или то, что мы называем ‘5-хвостами’, могут варьировать от 0 до (1/(5~+1)). Это, в частности, означает, что произвольный 5-хвост вполне может иметь 4%-ную вероятность”.
“А хвост 10 стандартных уклонений вполне может иметь вероятность в районе 1 %. Я припоминаю, что однажды читал об этом в одной старой книге по математической статистике. Но, ведь это же чисто теоретические построения, не так ли? Эти внешние границы отражают некие весьма частные, очень особенные распределения. На практике мы в основном все же должны иметь нормальность, разве нет?”
“И я поначалу так думал, сэр. Но эти границы упрямо продолжали возникать даже после того, как Девлин по моему распоряжению предпринял ряд действий, которые должны были исключить из рассмотрения причудливые малореальные случаи”.
“Действия какого сорта?”
“Ну, я начал с того, что велел Девлину рассматривать только суммы или средние перестановочных бернуллиевых активов. При этом каждый такой актив мог принимать значение только ‘успех’ или ‘неуспех’ и был обязан быть статистически перестановочным с любым другим активом. Тогда каждая схема, или ‘игра’, становится однозначно определяемой числом активов в генеральной совокупности и фиксированным внутренне состоятельным набором вероятностей, заданных на множестве исходов”.
“Как это понять: ‘внутренне состоятельным’?”
205
Пасть 1. Стандарты аткланания____________________________==___^=_
“Какого черта ты меня экзаменуешь как первокурсника?” — озлобленно подумал было Конвей, но контролер спрашивал по делу и с неподдельной заинтересованностью, так что Конвей отбросил опасения и продолжил рассказ: “Ну, внутренняя состоятельность — это просто стандартный набор ограничений. Всякая вероятность должна быть неотрицательна, вероятность любого набора исходов должна быть равна сумме вероятностей исходов, составляющих этот набор, и вероятность достоверного события — равна 1 ”.
“И все равно у вас останется слишком много возможных вариантов, чтобы с ними управиться...”
“Ваша правда, сэр. Каждый новый актив добавляет новую степень свободы. Девлин это доказал с помощью построения особых треугольников, являющихся своего рода дополнениями треугольника Паскаля. Разница между треугольником Девлина и треугольником Паскаля состоит в том, что соседние элементы строки треугольника Девлина дают в сумме ближайшего соседа сверху, а не ближайшего соседа снизу, как это было в треугольнике Паскаля. Так вот, оказалось, что любой неотрицательный треугольник Девлина определяет некую перестановочную бернуллиеву игру, и наоборот, поскольку к-п элемент /?-й строки треугольника Девлина задает вероятность того, что в игре первые к — 1 исходов будут успехами, а все остальные п — к исходов — неуспехами”.
“Ну, и для чего вам все эти степени свободы?”
“Мы использовали их для того, чтобы максимизировать и минимизировать хвостовые риски при целом многообразии ограничений: общее число активов, средние, корреляции и т. п. С помощью треугольников Девлина мы поняли, что можно сформулировать наши вариационные задачи в виде соответствующих задач линейного программирования. Но поначалу нам было непонятно, как следует интерпретировать решения”.
“Почему?”
“На самом деле это моя вина. Дело в том, что я дал указание Девлину сосредоточить внимание только на некоррелированных активах, поскольку считал, что с некоррелированными активами проще работать. Но оказалось, что, когда вы неограниченно расширяете генеральную совокупность некоррелированных бернуллиевых активов, проявляются две разнонаправленные тенденции. Первая из них предполагает очень узкую область хвостового риска, а вторая, наоборот, очень широкую”.
“Что это за тенденции?”
“Видите ли, с одной стороны, для любого фиксированного числа случайных величин распределение вероятностей сходится к некому биномиальному распределению с тем же самым средним. Например, если мы наудачу выберем три монеты из некой генеральной совокупности, состоящей из четырех несмещенных некоррелированных перестановочных монет, вероятность получить в таком эксперименте три решки будет варьировать от 1/12 до 1/6, что, конечно, уже, чем интервал от 0 до 1/4, который мы имели бы, если бы наша генеральная совокупность состояла из трех таких монет. Ясно, что, когда
206
11. Happy end, чёрт пвВври!
генеральная совокупность расширяется, вероятность трех решек сходится к 1/8”.
“И это значит, что проблема широких областей хвостового риска есть просто проблема недостаточно больших чисел, так?”
“С одной стороны, да, это так и есть. Однако, если мы сосредоточим свое внимание на последней строке треугольника Девлина, что изоморфно рассмотрению одновременно всех случайных величин генеральной совокупности, мы получим ответ, который будет абсолютно другим, а именно: чем больше наша генеральная совокупность, тем шире пространство, куда может ‘шлепнуться’ хвостовой риск”.
“А что, если управлять этими вариациями через средние и стандартные уклонения?”
“Тогда область допустимых значений для некоррелированных 5-хвостов всегда будет интервалом от 0 до 1/(52+1), что, конечно, отличается от целочисленных ограничений на число успехов и неуспехов. Последние, как правило, не имеют большого значения до тех пор, пока наши хвосты охватывают лишь небольшое количество исходов”.
“Ладно. Так что же происходит, когда вы разрешаете корреляцию?”
“В общем и целом ничего. Область не становится ни уже, ни шире. Если вы вместо средних зафиксируете корреляцию, область допустимых значений опять-таки не изменится. Но при условии, что эта корреляция является допустимой, конечно”.
“Как это корреляция может оказаться недопустимой?”
“Геометрически, сэр. Например, три случайных величины не могут быть так устроены, чтобы одна всегда будет абсолютно негативно коррелированна с другой. Это как если бы одновременно приказать трем людям ‘смотреть в абсолютно противоположном направлении’...”
“Ясно. Мне кажется, это похоже на ограничение, состоящее в том, что никакой портфель не может когда-либо иметь отрицательную дисперсию, разве не так?”
“Фактически это то же самое требование. Очевидно, вы очень серьезно изучали статистику, сэр”.
“Слишком серьезно. Тогда я еще не знал, насколько прав был Марк Твен”.
“Простите, сэр, но прав в чем?”
“Ну как же, это ведь он сказал, что ‘существует три типа лжи, а именно ложь, наглое неприкрытое вранье и статистика’”. Заметив, что Конвей побелел, контролер поспешил добавить: “Очевидно, что у Марка Твена не было возможности поучаствовать в такой дискуссии, вроде нашей с вами. Ваше исследование захватывающе”.
“Это все заслуга Девлина, сэр. Я передам ему ваш комплимент, если только вы не решите сами поговорить с ним”.
“Ну, в этом нет никакой необходимости. Ваши объяснения исчерпывающи. Но простите, мне кажется, я потерял нить нашего разговора. Что-то я не пойму,
207
Пасть 1. Стандарты атклананин _____________________________________________
если допустимая корреляция никакого значения не имеет, зачем вы выделили ее в отдельное исследование?”
“Потому что корреляция начинает играть роль, если среднее фиксировано. Дело в том, что тогда корреляция ограничивает то наибольшее расстояние от начала координат, выраженное в количестве стандартных уклонений, где может быть всплеск. А это, в свою очередь, запрещает целые области допустимого хвостового риска. В зависимости от других параметров оценки хвостового риска, основанные на нормальности, могут оказаться слишком малыми или, наоборот, слишком высокими, чтобы быть допустимыми”.
“Все это очень интересно... Я не разу так и не собрался проверить это”.
“И я тоже, сэр. Это как раз та штука, для которой Девлин годится лучше всего. Но, сэр, даже у него в этом деле были трудности, я имею в виду при проверке допустимости в том случае, когда размер генеральной совокупности неограничен”.
“Да, я подозреваю, чего это стоит.,. Но, как, скажите мне, вы анализировали последнюю строчку, которой, по сути, и нет вовсе?”
“Это просто, сэр. Вместо последней строки треугольника мы анализировали его боковое ребро, которое взаимнооднозначно определяет весь зреугольник. Но Девлин поначалу думал не об этом. Он был счастлив, когда ему удалось найти один класс бернуллиевых активов, относительно которых смог доказать неограниченную перестановочность”.
“И что же это оказался за класс?”
“Активы, которые независимы.при заданном их общем среднем, даже если это среднее может флуктуировать. Видите ли, их распределения вероятностей — это биномиальные смеси. А их допустимые хвостовые риски покрывают весь интервал, о котором я сказал выше. За исключением того случая, когда корреляция нулевая”.
“А что особенного в нулевой корреляции?”
“Она допускает только одну тривиальную смесь, состоящую ровно из одного чисто биномиального распределения, такого, что его риски 5-хвостов такие же, как и у нормального распределения”.
“Понятно. Биномиальные смеси привели к абсолютно раздвоенному результату. Удалось ли Девлину найти какие-нибудь другие бесконечно перестановочные случайные величины Бернулли?”
Конвей отрицательно покачал головой: “Нет, сэр. Но ему удалось найти нечто лучшее. Он нашел доказательство того факта, что других таких случайных величин, кроме тех, что он уже нашел, не существует. Этот результат называется теоремой де Финетти, сэр. Но и это еще не все. В ходе изучения доказательства этой теоремы Девлин выяснил, что оно есть просто выполнение таких преобразований, которые в неявном виде уже ‘сидят’ в его треугольниках”.
“И какая от того польза?”
“С одной стороны, эстетическая, сэр. Теперь мы знаем, что существует
208
11. Happy end, чёрт побери!
единая, простая для понимания модель. А еще, мы знаем, как посредством производящей функции моментов считывать параметры смешивающего распределения, двигаясь по вероятностям правого ребра треугольника Девлина”.
“Вы углубляетесь в детали. Думаю, я не смогу их запомнить”.
“Вам и не надо, сэр. В принципе, достаточно помнить всего лишь две вещи. Первая — это резкая бифуркация в областях допустимых значений хвостовых рисков при выборе между чистыми биномиальными распределениями и биномиальными смесями. Вторая — это интерпретация чистых биномиальных распределений и биномиальных смесей как независимости и условной независимости соответственно ”.
“Да, это резкое различие. Но как все это связано с активами, чьи выплаты строго бинарны?”
“По форме — кардинально. По существу — всего лишь значительно”.
“Не говорите шарадами. Что, конкретно, вы имеете в виду?”
“Всякое биномиальное распределение предполагает портфель, состоящий из идентичных независимых активов. Но, для того чтобы мы могли рассматривать континуум исходов и более широкое многообразие активов, нужно более гибкое распределение. Однако чистое распределение по-прежнему привязано к независимости, а смесь — к условной независимости, при том что последствия перехода от одного к другому для хвостовых рисков — гигантские”.
“На какое это более гибкое распределение вы намекаете? На нормальное?”
“Не совсем, сэр. Многомерное нормальное. Это будет просто означать, что все портфели состоят из независимых нормальных компонент”.
“Эй, эй! Постойте-ка”, — контролер впервые с начала разговора выглядел озадаченным. — “Многомерные нормальные активы вовсе не обязаны быть независимыми. Они могуг иметь любую допустимую ковариационную матрицу”.
“Хотите верьте, хотите нет, сэр, но моя первоначальная реакция была ровно такая же! Но Девлин потом объяснил мне, что эти независимые компоненты вовсе не обязаны быть активами по сути. Они могут быть полноправными портфелями”.
“Допустим. Но ведь многие случайные величины могут быть разложены на независимые компоненты. Чего такого особенного в многомерных нормальных?”
“А то, что их можно преобразовать в независимые скалярные компоненты, причем разными способами. Более того, каждый из этих скалярных компонентов будет нормальным, и, следовательно, его можно рассматривать как предел некой суммы независимых случайных величин со специфическим общим средним и дисперсией. Многомерные нормальные распределения независимы по своей сути, сэр”.
“Какая здесь связь с реальностью?”
“Ответ зависит от того, на какую часть этой реальности вы смотрите. Если вы способны полностью стабилизировать внешнюю среду, как это делает, скажем, физик, изучающий газ в бутыли, то многомерная нормальная модель
209
Часть 1. Стандарты отклонания _______________________________________
вполне реалистична. В противном случае вам придется делать различия между общими и независимыми влияниями. Это тот случай, когда нужна условная многомерная нормальность”.
Контролер деланно удивленным взглядом оглядел свой кабинет, якобы в поисках бутылей с газом, и сказал все тем же ровным тоном: “Ну вот я смотрю на финансовую реальность. Отвечайте, какой подход к построению модели вы считаете лучшим и почему”.
“Ответ, как ни странно, зависит от точки зрения. Гораздо проще делать далеко идущие выводы, предполагая чистую многомерную нормальность. Практически все результаты классической финансовой теории основаны на этой модели. Могу сказать, что я, наверное, до конца своей жизни буду первым делом искать ответы именно там, потому что меня очень долго учили именно этому. Но я уже никогда не смогу настолько доверять ответам, получаемым в рамках модели чистой многомерной нормальности, насколько доверял им раньше. И уж, во всяком случае, не буду доверять этой модели в ее приложении к анализу риска”.
“Короче говоря, вы считаете, что для анализа финансового риска условная многомерная нормальность лучше, верно?”
“Она должна быть лучше. Чистая многомерная нормальность — это неадекватная модель”. В этот момент Конвей вспомнил о терзаниях Девлина и, скрепя сердце, добавил: “Но, можете быть уверены, в этой модели хватает практических проблем, в которых еще предстоит разобраться”.
“Да!? И в чем же состоят эти практические трудности?”
“Да просто непонятно, как подобрать такое многомерное условное нормальное распределение, чтобы приближение было не хуже, чем в случае чистой многомерной нормальности. Мы даже не знаем наверняка, как определить доверительные интервалы, сэр”.
“Значит ли это, что если бы вы задались целью исключить недооценку s-хвостовых рисков, то выбрали l/(s2+l)?”
Конвей попытался уклониться от прямого ответа на щекотливый вопрос: “Нет, сэр, не значит. До тех пор пока у меня были бы хоть какие-нибудь надежные данные, я пытался бы построить на них смешанную многомерную нормальную аппроксимацию и выжать из нее хвостовые риски”.
“Но вы же только что сказали, что трудно построить хорошую аппроксимацию на смешанном многомерном нормальном распределении и трудно оценить доверительные интервалы. Разве не так?”
Конвей замешкался, но потом, собравшись с духом, выпалил :“Да, сэр, это правда... Но, несмотря на это, мы всегда смогли бы найти несколько смешанных многомерных нормальных распределений и подсчитать их средний риск 5-хвоста или их наихудший риск, если вам так больше нравится!”
Контролер какое-то время молчал, пристально глядя в глаза Конвею, который затаил дыхание и замер как кролик перед удавом. В кабинете повисла звенящая тишина. Наконец, контролер медленно и раздельно проговорил;
210
11. Happy and, чйрт поВари!
“Конвей, сегодня у меня была самая захватывающая беседа о риске за всю мою практику. Видите ли, я всегда удивлялся тому, что события многих стандартных уклонений на практике случаются гораздо чаще, чем должны были бы по предсказаниям стандартной теории. Теперь, благодаря тому, что вы просветили меня относительно открытий Девлина, я знаю, почему это так”.
Конвей облегченно перевел дух и впал в некое подобие радостной эйфории: “Я очень рад, сэр, что вы так смотрите на проблему!”
Но контролер невозмутимо продолжил все тем же ровным голосом: “Ваш доклад к тому же укрепил меня в моем интуитивном понимании того, как мне следует поступить в отношении намечающегося дисциплинарного дела против Девлина”, — с этими словами контролер открыл скоросшиватель, подписал какой-то документ и сказал по селектору: “Госпожа Стефенсон, не могли бы вы зайти?”
Конвей похолодел от дурного предчувствия и спросил хрипло: “Какого дисциплинарного дела?”
“Я же говорил вам, что аудиторы требуют головы Девлина, разве нет? При этом они рассчитывают на статус Девлина, все еще проходящего свой бесконечный испытательный срок, который постоянно продлевается из-за стычек с начальством и скандалов с коллегами. В общем, аудиторы предлагают понизить Девлина в должности. Обычно они добиваются своего. Однако кое-кто из дисциплинарного комитета считают Девлина интеллектуальным провокатором и человеком оригинально, хотя и поперек, мыслящим. Они считают, что Девлина следует сберечь, поскольку он очень ценен для ‘Мегабакса’. В результате мне поручено принять окончательное решение в вопросе о том, что делать с Девлином”.
“Как хорошо, что нам удалось вовремя переговорить, сэр!” — облегченно выдохнул Конвей, и в этот самый момент вошла госпожа Стефенсон. “Какие будут указания, господин Форд?”,- спросила она деловым бодрым тоном.
Контролер передал ей скоросшиватель со словами: “Госпожа Стефенсон, возьмите личное дело Адвогадо Девлина и передайте его в службу безопасности. Дело содержит все документы, необходимые и достаточные для увольнения этого господина. Я хочу, чтобы его немедленно выкинули с территории банка”.
“Как прикажете, господин Форд!” — каркнула Стефенсон, не теряя бодрости и делового тона.
Конвей почувствовал себя так, как, по его мнению, должен был чувствовать себя паралитик. Правда, он ощущал-таки тошноту где-то в желудке и нечто вроде холода кожей лица.
“Я так понимаю, что вы удивлены, не так ли?” — спросил контролер.
Внутренне сжавшись в кулак, Конвей заставил себя неопределенно кивнуть в ответ.
А контролер, казалось, не заметил состояния Конвея и продолжил все тем же ровным участливым голосом: ‘^Поверьте, мой друг. Я принял чисто деловое решение. Ничего личного. Я вовсе не желаю Девлину зла”.
211
Пасть 1. Стандарты отклонения
Конвей, наконец, справился со своими голосовыми связками и прохрипел: “За что?’1
“За неоднократное злостное неисполнение своих служебных обязанностей аналитика риска".
Вспышка ярости окончательно привела Конвея в чувство: “Я категорически не согласен, сэр! Девлин всегда показывает риски так, как он их видит".
“У меня нет никаких сомнений в этом... Но его служебные обязанности состоят в абсолютно другом. Видите ли, Конвей, его дело видеть риски именно так, как он их называет, а не наоборот!"
“Как прикажете вас понимать? Что значит "видеть риски так, как называть’? В чем здесь смысл, черт меня побери?"
“Это значит, уважаемый, что аналитик риска обязан грамотно, доходчиво и правдоподобно обосновывать третьим лицам те аранжировки риска, которые он налагает. Если аналитик сам не в состоянии принять однозначное решение или если он выдвигает в качестве обоснования своего решения слишком мудреную теорию, он способствует повышению воспринимаемого риска или чего-то еще, что он там замеряет и контролирует... Ни один уважающий себя инвестиционный банк терпеть такое не будет, так-то вот!"
“Но, ведь, это не вина Девлина, что он вскрывает дополнительные трудности, сэр!"
“Конечно, его вина вовсе не в этом, Конвей. Он может открывать столько дополнительных трудностей, сколько его душе угодно. Но его задача состоит в том, чтобы умело спрятать все эти трудности. Или полностью разрешить все проблемы, если он, конечно, может. Вот что бы вы сказали об архитекторе, который так спроектировал дом, что все туалеты и ванные без дверей были бы на самом виду? Представьте себе это!"
Конвей был взбешен, что его друга выставляют придурком, и ляпнул сгоряча: “Если вы такого мнения о Девлине, можете выгнать и меня вместе с ним!"
Но Форд был невозмутим: “Это было бы непрофессионально, уважаемый. Хотя Девлин не справился со своими обязанностями аналитика, вы определенно справляетесь со своими обязанностями менеджера".
“Как это может быть, чтобы я справился, если я толком не понимаю, где мы находимся в плане риска?"
Контролер с досадой покачал головой, в первый раз обнаруживая признаки раздражения: ‘"Я вижу, что вы так ничего и не поняли, Конвей! Я ведь не сказал, что вы хорошо управляете риском. Но вы умудрились сделать вид, что с риском в «Мегабаксе» все в порядке. Это и есть ваша наиглавнейшая обязанность".
""Не верю, что я слышу это от вас, сэр... Вы ведь контролер! Вы призываете катастрофу на «Мегабакс»!"
"‘Не давайте своим чувствам затмить ваш разум, — сказал контролер
212
11. Happy and, чйрт побори!
невозмутимо. — За хорошие деньги мы всегда провоцируем катастрофу. В особенности, если все остальные делают то же самое. Поймите, если мы упадем все вместе, Гринспен нас выкупит! А подход Девлина, между прочим, провоцирует катастрофу, за которую будет платить только «Мегабакс» и никто больше, так-то..
“Каким же образом?”
“Ну, начнем, с того, что Банк международных расчетов все время делает попытки заставить нас расширить страховое покрытие наших рисков раза в три. Допустим теперь, что вы с Девлином успешно проводите свои исследования условной многомерной нормальности и бодренько докладываете, что БМР прав. Хороший результат?”
“Может быть”.
“Ответ неверный. Даже один только факт появления отчета, в котором оценка риска возросла в три раза, заставит «Мегабакс» принять на вооружение вашу более осторожную систему. Указание БМР не заставит себя долго ждать, и нас принудят-таки увеличить страховое покрытие. Поскольку активы ограничены, мы будем вынуждены уменьшить риски, а, следовательно, сократить бонусы, что вынудит топ-менеджеров искать другие места приложения их талантов. Акции «Мегабакса» начнут падать, а инвесторы потребуют сменить команду топ-менеджеров. Это что, справедливо? И заметьте, все потому, что Девлин не смог, видите ли, справиться с внезапной вспышкой честности!”
“БМР не может подходить к делу так механически. А инвесторы не могут быть так близоруки”.
“Да вы, оказывается, оптимист... Возможно, Вы и правы, но зачем подвергать себя риску, когда грибная гидропоника работает так хорошо?”
“Грибная гидропоника?”
“Корми их жидким дерьмом и держи в темноте”, — здесь контролер изобразил полуулыбку.
Конвей, наконец, разобрался в своих чувствах. Он чувствовал, главным образом, омерзение: “Господин Форд, вы самый циничный человек из всех, кого я знаю!”
“Я реалист, — сказал контролер усталым голосом учителя школы для дефективных детей. — А еще я очень богат. И это благодаря долгим годам верной службы «Мегабаксу»”.
“И вы ждете, чтобы я тоже служил «Мегабаксу» из этих же принципов?”
“Нет, не жду. В какой-то мере болезнь Девлина заразила и вас”.
“Понятно. Вы все-таки намерены уволить и меня тоже!”
“Нет. Это было бы слишком явно. А принимая во внимание ваш великолепный послужной список, ваше увольнение выглядело бы крайне неприятным. Поэтому я распорядился перевести вас с повышением”.
“Перевод? Куда?”
“В систему доверительного управления. Я думаю, вам там понравится. Там
213
Пасть 1. Стандарты атклананин
вы сможете разрабатывать свои теории без риска для собственного капитала «Мегабакса». Но, конечно, бонусы там будут существенно ниже... Мелкая разношерстная клиентура мелкая маржа, сами понимаете”.
“И когда должен произойти перевод? Немедленно вслед за увольнением Девлина?”
“Нет, через два месяца. Но свои обязанности вы перестанете исполнять прямо сегодня. Я уже распорядился, чтобы вам продолжали в течение двух месяцев выплачивать жалование, и хотел бы предложить вам длительный отпуск. Всегда полезно приступать к новой работе хорошо отдохнувшим, не так ли?”
“Вы все это продумали задолго до нашего разговора, правда?”
“Я старался. В конце концов, это моя работа”.
Конвей не стал отвечать на вежливую улыбку контролера и сказал устало: “Если вы закончили со мной, сэр, можно мне уйти?”
“Рад, что вы оказались понимающим человеком. Желаю удачи, Конвей!”
В течение первых минут после выхода из кабинета контролера Конвей чувствовал себя как водолаз, которого слишком быстро подняли на поверхность. Наконец он сделал глубокий вдох, и вспомнил о Девлине. Бегом бросившись в свой офис, Конвей надеялся увидеть Девлина до его ухода из банка. Но Конвей опоздал. Сотрудники службы безопасности даже умудрились прибраться в закутке Девлина. Единственным предметом, напоминающим о прежнем хозяине этой каморки, была надпись черным маркером поперек стола:
'Невежество — это маразм /"
214
Введение: «Больше долларов, чем здравого смысла»
Пока психиатрическое сообщество продолжает спорить по поводу эффективности новейших методов лечения доктора Дональда Дементи, никто не отрицает его маркетингового дара. Нарезав традиционную психотерапию по фразам и приправив ее дополнительными товарами и услугами, он завоевал долю рынка товаров и услуг для умалишенных, которым большинство отраслевых аналитиков прописали «Прозак» на постоянной основе. Доктор Дементи впервые привлек к себе внимание публики в 1992 г., когда он запустил Mad Donald’s™ — первую сеть закусочных, в которой предлагали дополнительные консультации, пока клиент ждал своего заказа. Отзывы были восторженными, особенно по комбиобедам; «двойной чизбургер, картофель фри, газированный напиток и терапия утробного крика». Несмотря на высокую цену 49,95 долл., The Big Mad™ стал бестселлером, после того как страховые компании приняли его в качестве допустимого расхода на медицину.
К сожалению, когда была зарегистрирована одна сотая франшизополучателей, британское правительство подтвердило, что несколько коров — убежденных вегетарианок — совершенно сошли с ума, после того как их накормили потрохами больной овцы, и возникла угроза инфицирования хищников, занимающие свое в пищевой цепи. Возникшая в результате истерия заставила закрыться всю сеть Mad Donald’s, несмотря на образцовые показатели по здоровью. Журнал Forbes позднее опишет ситуацию, сказав, что «она пала жертвой сумасшествия толпы и коров».
Может кто другой уже сдался бы, проклиная европейские стандарты, применяемые к сельскохозяйственной продукции. Но только не доктор Дементи. Отдыхая на Карибах со своей женой и любовницей и будучи неспособным удержать эту парочку от постоянных пререканий, на него нашло озарение. Легионы зажиточных, измотанных стрессом беби-бумеров выбрасывали огромные деньги на отдых и восстановление сил, в итоге не получая в достаточном количестве ни того, ни другого. Совмещение отдыха с лечением будет более привлекательным, не говоря уже о прибыльности, чем совмещение обедов и лечения.
Спешно вернувшись домой, доктор Дементи быстро нашел несколько венчурных капиталистов, которые рискнули поддержать его идею. Club Mad™ оказался потрясающе успешным. Ни один человек, желающий получить статус толстосума, не мог устоять перед рекламным соблазном местечка «Для тех, у кого долларов больше, чем здравого смысла™». Иски со стороны стареющей
Введение: "Больше долларов, чем здравого смысла
французской сети схожей направленности были улажены с помощью выкупа контрольного пакета акций за счет кредита, после чего французские инвесторы остались довольны и наводнили курортами Club Mad весь мир.
Критики утверждают, что Club Mad — это всего лишь хитрая уловка, чтобы заставить медицинское страхование субсидировать отпуска богатеев. Но даже тайные сыщики телекомпаний не обнаружили никаких признаков мошенничества. Всемирный бухгалтерский концерн PriceEmstDeliotte & Others проводит аудит всех платежей и выставляет страховым компаниям и организациям, ответственным за правительственную программу медицинской помощи, счета только за те услуги, которые отвечают их требованиям. Все психиатры имеют полный набор рекомендаций и проходят постоянное обучение.
Более того, лист предварительных заявок длиннее всего на тех двух курортах, которые предлагают меньше всего традиционных отпускных услуг. The Palm Beach Club Mad, открытый в декабре 2000 г., не может похвастаться даже выходом к морю. Вместо этого бывший старый склад поделен на комнаты, имитирующие избирательные участки, офисы окружных предвыборных комиссий, залы суда и конференц-залы. Каждому гостю предоставляется возможность проконтролировать по меньшей мере одну имитацию выборов, с правом не только точно отрегулировать подачу избирательных бюллетеней, но и установить количество отметок, необходимых для того, чтобы голос был засчитан. Это неотъемлемая часть знаменитой терапии Club Mad под названием «Забудьте о неудачах™», которая позволяет гостям проигрывать болезненные ситуации до тех пор, пока они с ними не примирятся.
Другой Club Mad, пользующийся высочайшим спросом, находится на берегах Гудзона, принадлежащих штату Нью-Джерси, куда легко добраться на пароме с Уолл-стрит и из финансового района. Терапевтический гвоздь программы — огромный торговый зал, заполненный привычной трейдерам техникой — экраны Bloomberg, терминалы Reuters, компьютеры. На самом деле машины искусно перепрограммированы, так позволяют повернуть время вспять и вернуться в прошлые времена, используя новые данные. Например, можно заново проиграть октябрь 1987 г., так чтобы избежать обвала рынка. Причем возможны два варианта: катастрофы вообще не будет или же она произойдет, но пользователь может обратить крах в свою пользу, перейдя на короткие сделки. И все это — с видом на Манхэттен.
Результаты впечатляют. Согласно независимым медицинским исследованиям, опубликованным в New England Journal of Medicine^ до 25% испытывавших жестокую депрессию бывших трейдеров восстановили нормальный уровень серотинина в мозгу за один месяц. А за три месяца более 80% из них вновь почувствовали себя хозяевами Вселенной. Спрос на игру с экранами, BloomAgain™ настолько высок, что имитационный торговый зал держат открытым 24 часа в сутки и для всех гостей действует ограничение до 30 минут за сессию в периоды обострений.
217
Часть 2. Пестижение невежества
Критики утверждают, что поклонники курса «Забудьте о неудачах» путают суррогат излечения с реальным. Однако, как объяснил доктор Дементи ведущим ток-шоу Лари Кингу и Опер Уинфри, аргументация критиков основана на неуважении к людям, испытывающим психические трудности. Если человек, который считал себя сумасшедшим, больше таковым себя не считает, то кто может судить, прав ли в обоих случаях, ошибается ли в обоих случаях или прав в одном случае и ошибается в другом?
К сожалению, некоторым так и не удается забыть о своих неудачах. Конечно, «никогда» — это слишком страшный диагноз. Оптимистично настроенный доктор Дементи считает, что некоторые орешки просто сложнее расколоть, чем другие. В частном разговоре штатные сотрудники Club Mad, правда, допускают, что возможны срывы.
Чтобы лучше оценить, что делает человека «полным неудачником», давайте перенесемся в Club Mad на Гудзоне и подслушаем терапевтический сеанс...
«Не знаю», — говорит знакомый голос.
«Но если вы не знаете, то кто может знать?» — спрашивает врач.
«Не знаю».
Врач, делающий записи, гневно постукивает карандашом. «Если Вы не можете придумать какой-нибудь хорошей альтернативы, — говорит он настолько мягко, насколько это только возможно, — может быть, попробуем BloomAgain еще раз? Тридцать минут, больше я ни о чем не прошу. Вечером, если хотите, когда нет народу».
«Это не поможет. Это совсем другое».
«Вы можете настроить программу так, что все будет так же, как тогда. Или совсем по-другому. Смысл именно в этом. Все шансы контролирует пользователь».
«Все равно это будет иначе, чем тогда. Я буду знать шансы, а в реальной жизни не знал».
«Поэтому так лучше. Это поможет вам отточить навыки заключения сделок, проигрывая шансы».
«Но я не был трейдером. Я был аналитиком по рискам. Моя работа в том и заключалась, чтобы угадывать шансы. Если я знаю, каковы они, что еще может улучшить качество моих догадок?»
«Тогда просто раскрутите колесо риска, и, не глядя, попытайтесь угадать, каковы риски, исходя из результатов».
«Это слишком просто. Я ведь буду знать, когда я раскрутил колесо риска. Это говорит о том, что мне следует отбросить предшествовавшие данные за ненадобностью. В реальности никогда не бывает так просто. Было ли почти удвоение NASDAQ в 1999 г. признаком того, что NASDAQ продолжит стремительно расти в 2000 г., или того, что он, скорее всего, отступит, а может, это вообще не признак? Я тогда не знал. На самом деле я и сейчас не знаю».
218
Вввдвнив: "Большв двлларвв, чвм эдраввгв смысла"
«Девлин, пожалуйста, не преувеличивайте. Конечно, сейчас вы не знаете. Но NASDAQ отступил». Доктор очень хорошо это помнил, наблюдая за своими усыхающими счетами.
«Но я не знаю, почему. То есть я хочу сказать, это всегда очень заманчиво при прочих равных, благоприятствующих гипотезе, которая лучше всего предсказывает данные... Но это не всегда срабатывает. Вы верите в слепую удачу, доктор?»
«О, да». Конечно, он верит в слепую удачу. Но особенно слепо невезение: именно оно привело к нему Девлина. «Но, боюсь, мы слишком отклонились от дела. Вы не возражаете, если мы сменим тему? Я бы хотел задать вам несколько вопросов о вашем детстве».
Девлин плюхнулся на диван: «Конечно. Начинайте».
«В последний раз вы сказали, что идентифицируете себя со всеми и ни с кем. Что вы имели в виду, когда это говорили?»
«В жилах моей матери смешалась кровь невероятного числа национальностей. Апачи, наваха, китайцы, мексиканцы, англичане — все национальности, которые только можно придумать. Она научила меня считать себя частью большой мировой семьи. Но все остальные в нашем маленьком городке, казалось, идентифицировали себя с какой-то конкретной национальностью. В некотором роде это сделало меня изгоем».
«А ваш отец?»
«Не знаю».
«Вы не знаете его национальности?»
«Я не знаю своего отца. Он бросил нас до моего рождения. Но я думаю, что он, возможно, был евреем, поскольку мне очень нравятся еврейская кухня».
Доктор поморщился, но продолжил писать. «Что-то еще, что вы знаете или о чем догадываетесь относительно вашего отца?»
«У него было хорошо с математикой. По крайней мере так говорит моя мама. Она сказала, что он мог складывать счета клиентов быстрее любого калькулятора».
«Ваш отец работал в баре?»
«Нет, мама. Она была официанткой, разносившей коктейли. Она должна быть так говорить с мужчинами, чтобы они покупали больше. И время от времени она встречалась с ними вне работы. Именно так я и появился на свет».
«Вы когда-либо пытались что-то выяснить о своем отце?»
«Нет, у меня было недостаточно информации о нем».
Доктору показалось, что он нащупал ключ. «Вы ничего не упускаете, Девлин?»
«Например?»
«Ну, например, то, что вы могли бы найти своего отца? Еврей, который прекрасно умеет считать, вряд ли затерялся бы в маленьком городке?»
219
Чаоть 2. ТТвстижвнив нвввжвства__
«Мы жили недалеко от Лос-Аламоса. На расположенной там лаборатории по производству оружия работает несколько сотен физиков. И я не знаю, сколько еще сотен проходит через нее в качестве посетителей. Там никому ни при каких условиях не предоставляют информацию о кадрах, если, конечно, вы не выслеживаете китайского шпиона».
«Ладно, не важно, — сказал доктор. — Итак, что вы чувствуете, когда думаете о том, что ваш отец вас бросил?»
«Он не бросил. Вернее, не совсем бросил. Ежегодно нам под дверь подбрасывали толстый конверт с деньгами с надписью: «На образование Девлина». Моя мать относилась к этому серьезно. Она тратила их только на книги, репетиторов и тому подобное, а когда мне исполнилось 12, мы переехали в Лос-Аламос, чтобы я мог ходить в хорошую школу. По окончании школы я получил стипендию в Стэнфорде. Тогда-то я и познакомился с Конвеем».
«Вашим бывшим начальником».
«Моим бывшим другом. Я почти не оставил ему шансов остаться моим другом. Слишком уж он Зим».
«Зим?»
«Ну да. Белый поселенец в Зимбабве. Его родители были зажиточными фермерами; это было в те годы, когда в Зимбабве еще существовали зажиточные фермеры. Родители послали Конвея в английский пансион в надежде, что он продолжит свое образование в Оксфорде или Кембридже. Но Конвей решил, что ему нравятся приключения, и вместо этого пошел учиться в Беркли. Когда я впервые с ним встретился, то подумал, что это простой белый парень из колонии. Но я ошибся. Внешность обманчива».
«Так почему вы называете его бывшим другом?»
«Это произошло по моей вине. Я серьезно его подвел. Это стоило ему работы».
«Как у вас это получилось?»
«Я слишком часто говорил: «Не знаю». Пока он и сам не перестал что-либо понимать».
Доктор тал же почувствовал большую симпатию к Конвею: «А зачем вы это делали?»
«Не знаю. Полагаю, у меня было слишком много сомнений».
Врач взглянул на часы. Слава богу, уже 4:30. Через 15 минут у него по расписанию был теннис. «Девлин, боюсь, на сегодня нам придется закончить. Увидимся на занятиях по самбо вечером».
«Простите, но меня там не будет. Я записался на ночное погружение в Гудзон. До завтра, до групповой терапии».
Тем временем за Гудзоном и на полпути к Ист-Ривер бывший друг Девлина проходил собеседование на новой работе.
220
Вввдвнив: "Бвльшв долларвв, чвм эдравогв смысла
«Добро пожаловать в «Мегабакс Эссет Менеджмент», Конвей. К нам не часто переводят людей из отделения продаж, но я рад, что вы с нами. Мой брат очень вас хвалит. Ваш опыт управления рисками мог бы стать нам хорошим подспорьем».
«Спасибо, господин Форд». И что он на самом деле обо мне сказал?
«Пожалуйста, называйте меня Джимом. У нас нет нужды в соблюдении формальностей, за исключением периодических конференций для инвесторов. Жизнь в нашем отделении покупок более спокойна. Вам почти не придется задерживаться или работать по выходным».
«Я рад работать здесь, сэр».
«Хорошо, но зовите меня Джимом. И надеюсь, вы не будете путать меня с моим братом». Он тепло улыбнулся Конвею.
Конвей сдержанно улыбнулся в ответ: «Возможно. Постараюсь это запомнить. Просто скажите мне, под какую дудку плясать».
Джим рассмеялся: «Мой брат действительно вас достал, да? Послушайте, независимо от того, что там с вами произошло, попытайтесь об этом забыть. Здесь ребята не привыкли плясать под чью-то дудку. Они просто скачут в ногу».
«Ну и как успехи?»
«Неплохо. У нас ценных бумаг на 100 млрд долл., рост примерно 12% в месяц. Средние заработки управляющего среднего звена примерно 200 базовых пунктов — где-то 600 млн долл, «грязными». Конечно, большая часть из этого уходит брокерам, которые заставляют колесики вертеться, другие накладные расходы тоже довольно высоки, но все равно остается приличная прибыль».
«Я хотел сказать: насколько высока эффективность фонда?»
«Неплохая. Менеджеры обычно превосходят стандартные индексы на процент или около того».
«Это чистыми или включая гонорары?»
«Чистыми. Послушайте, Конвей, давайте я попытаюсь угадать, о чем вы думаете, и если я выиграю, вы расслабитесь. По рукам?»
Конвей кивнул.
«Думаю, вас удивляет, почему люди в нас инвестируют, несмотря на то что без учета гонораров мы не превосходим индекс».
Конвей рассмеялся: «Хорошо, Джим, Вы выиграли. Так почему люди в нас инвестируют?»
«В основном из-за контроля. Людям, как правило, необходимо, чтобы кто-то убеждал их следить за их долгосрочными вложениями, и им нужна некоторая помощь при взвешивании рисков и прибыли. Вот почему для того, чтобы продавать страховки или взаимные фонды, нужна сила продаж. Нельзя просто раздавать проспекты на полке или вывешивать баннеры на веб-сайте».
«Вас не беспокоит конкуренция?»
«Очень беспокоит. Прибыли со временем становятся более скудными, а
221
Часть 2. Постижвнив нвввжвства
наши клиенты — более требовательными. И несмотря на рост, мы потихоньку теряем свою долю рынка. Я полагаю, что следующий медвежий рынок потреплет нам нервы. Вот почему и хочу воспользоваться вашим опытом».
«Послушайте, Джим, но я не эксперт по предсказанию медвежьих рынков. Я просто старался управлять людьми, которые были экспертами или по крайней мере позиционировали себя именно так».
«Я все равно считаю, что вы можете нам помочь».
«Как? Вы же сказали, что люди здесь шагают в ногу. Я даже не знаю, в каком направлении вы хотите, чтобы они двигались».
«Честно говоря, я и сам этого толком не знаю. Все пользуются разными картами, так что с коммуникацией у нас не очень, и я не знаю, как определить, идет ли человек верным путем или нет. Я хочу, чтобы вы мне дали совет».
Конвею понравилась эта идея — работать напрямую с начальником и не влезать в офисную политику.
«Какой совет Вы хотите получать?»
«Я хочу, чтобы вы извлекли несколько полезных практических уроков из теории портфеля о том, как управлять нашими фондами».
«Я уже не уверен в том, что стандартная теория настолько полезна. Ее предположения слишком экстремальны».
«Всегда?»
«Нет, не всегда».
«Тогда просто скажите мне, какие из них полезны и почему. Если вы считаете, что нужно изменить предположения, чтобы они стали более реалистичными, отлично. Именно поэтому я и взял на работу вас, а не какого-то умника. Просто не усложняйте чрезмерно. У меня очень быстро устают глаза».
«Честно говоря, у меня тоже. И раньше мне помогали, к сожалению, я теперь лишен этой помощи».
«Тогда вперед. Мне нравятся люди, которые знают, что их возможности не безграничны. Кое-кто из моих инвестиционных менеджеров не отличаются этим свойством».
Конвею все больше нравился Джим. Возможно, в конечном итоге этот перевод не так уж и плох. «Вы только что сделали мне предложение, от которого невозможно отказаться. С чего вы хотите, чтобы я начал?»
«С одной-единственной меры, которая, по вашему мнению, лучше всего резюмирует компромисс между риском и вознаграждением в портфеле. Я хочу, чтобы вы разъяснили эту меру и сообщили нам, как ей пользоваться, чтобы лучше управлять нашим распределением активов».
«Ну, это очень просто. Я могу сказать вам прямо сейчас. Это...»
Но Джим прервал его: «Не сейчас. Завтра в 3:00 дня. На совещании старших инвестиционных менеджеров. Это даст мне возможность вас представить».
222
Введение: "Больше долларов, чем здравого смысла
Конвей поперхнулся: «Вы не считаете, что мне сначала следует рассказать об этом только вам?»
«Не вижу для этого причин. Вы сказали, что это просто, а они не кусаются. Я уверен, что все у вас будет хорошо».
Конвей не разделял уверенности Джима, но аргументов для возражений у него не осталось. Он извинился и удалился, чтобы подготовиться к выступлению.
Сейчас вы вступили в новую стадию нашего приключения. Вы можете назвать это стадией проверки остроты ума. Конвею придется проверить свой ум, в то время как Девлину придется привести в порядок свой. Но я предпочитаю называть это реконструкцией. Иногда жизнь заставляет нас перестраиваться еще до того, как готов генеральный план. Как нам следует реагировать? Лучший ответ, который я могу дать, звучит так: «Экспериментируйте!»
Экспериментировать нравится не всем. Эксперимент подразумевает условность, беспорядок и сдвиги. Против этого протестуют не только конформисты. Вторая мировая война вызвала гораздо больше разрушений в Советском Союзе, нежели в любой другой стране, и тем не менее Советский Союз встал на ноги первым. Как оплоту мировой революции удалось совершить этот удивительный подвиг? В основном в результате восстановления всех имевшихся до войны заводов, точно следуя букве исходных чертежей. Эти чертежи, датирующиеся обычно 30-ми годами, сами собой нередко являли имитации американских и британских заводов, построенных за 20-х годах или ранее. По контрасту, Западная Германия и Япония восстанавливались с использованием новейших технологий. Неудивительно, что к 1960-м годам Советский Союз потерял темп, в то время как Западная Германия и Япония устремились вперед.
Но я все равно должен отдать должное Советам за то, что они в итоге все же «выбросили полотенце». Сопоставьте это, скажем, с лондонским общественным транспортом, который, как мне кажется, погружается на еще более и более глубокие уровни бесчестья. Не то чтобы власти этого хотели, они просто попали в ловушку споров о том, как приватизировать, сколько инвестировать, откуда взять деньги, как избежать срывов, но главное — как переложить вину за бездействие на кого-то другого. То, что началось как битва между лучшим и хорошим, не привело к триумфу ни того, ни другого. Страх перед экспериментом вызвал паралич.
Итак, я прошу читателей не судить Конвея слишком строго. Он ищет ответы, которых он не видит, и иногда ему приходится довольствоваться тем, что получилось. Я лично остаюсь оптимистом, поскольку работа Конвея заставляет его твердо стоять ногами на земле, в то время как настрой Девлина заставил его устремиться к звездам. Но звезды слишком далеко. Лучшее, на что мы можем надеяться, это найти немного звездной пыли.
223
Часть 2. Постижение невежества__________________________________________
Что же касается Девлина, надеюсь, он переживет свое ночное погружение. Но он никогда не был хорошим пловцом.
224
12. Как научить слона танцевать
Управляющие портфелем ценных бумаг собрались на следующий день, чтобы познакомиться с новым начальником отдела управления риском портфеля. Оставаясь учтивыми, они были несколько подавлены, несмотря на попытки Джима создать теплую атмосферу. Конвея это не удивило. Никто не хочет, чтобы стрелка «неисправность» указала на него. Конвей вертел в руках провода своего ноутбука и проектора, которым намеревался воспользоваться.
Представив всех друг другу, Джим сказал: «Как вы знаете, я попросил Конвея провести семинар по самому важному вопросу управления портфелем ценных бумаг».
«О, это я уже знаю, — выпалил один из менеджеров. — Как переложить вину на другого». Все рассмеялись.
«Возможно, это самый важный вопрос, — сказал Конвей. — Но я не могу сказать, что я его полностью изучил. В противном случае я бы все еще занимался продажами». Все еще раз рассмеялись, атмосфера явно стала теплее. Выдержав паузу, Конвей продолжил: «Итак, сегодня я расскажу о втором по важности уроке в моей жизни, о том, чему я научился, несмотря на то что не всегда хорошо это применяю. А теперь, если мне удастся заставить этот проектор работать, я спроецирую изображение на экран». Он нашел правильный переключатель и всеобщему обозрению предстал слайд:
225
Часть 2. Постижение невежества
«Это еще что за черт?» — спросил кто-то.
«Ой, ошибся, секундочку. — Конвей перевернул слайд. — Вот так уже
лучше».
226
______________________________________________12. Как научить слана танцевать
«Генри, гляди-ка, на тебя похож!» - сказал кто-то сзади. Снова раздался смех.
«Отличный слайд, — сказал Джим. — И что он значит?»
«В основном две вещи. Во-первых, что стандартное распределение портфеля напоминает неуклюжего слона. Движения требуют много энергии, для того чтобы после одного неуклюжего шага сделать второй неуклюжий шаг. Однако, как только движение началось, вернуться назад не так-то просто. Шаги, как правило, стирают с лица землю любые ростки возражений».
«Почему вы так считаете?»
«По разным причинам. Теория портфеля воспринимается лучше всего при охвате больших периодов, когда закон крупных чисел пересиливает краткосрочные отклонения. Большинство консультантов по инвестициям предостерегают своих клиентов, чтобы последние придерживались определенно стабильных распределений, чтобы не потерять опоры и не стремиться до бесконечности к наилучшим прошлогодним сделкам. Инвестиционные менеджеры также склонны придерживаться знакомых моделей, отчасти потому, что знают, как работать с ними, а отчасти потому, что именно этого от них и ждут и клиенты, и начальство. В итоге возникает некий консенсус, который тянет за собой распределение активов».
«Это изображение кажется правильным, — сказал один менеджер. — И я не понимаю, что в этом плохого. Это лучше, чем метаться из стороны в сторону как мотыльки вокруг лампы. Это прямой путь к тому, чтобы подпалить крылышки».
«Я не критикую стандартное распределение. И согласен, что стабильность — это плюс. Но считаю, что прогнозы рисков следует обновлять гораздо чаще, чем это кажется нормальным большинству, и что новая информация иногда требует существенных изменений в распределениях. Это второе, что я хотел подчеркнуть. Слон должен не шагать, а танцевать».
«Нет никакого смысла стремиться к тому, что невозможно. Слоны не танцуют».
«Отчасти я с вами согласен. Танцевать им непросто, и они никогда не будут настолько гибкими, насколько нам этого хочется. Но верно и другое. Без хороших стимулов и культуры обучения вы не увидите и малейшего следа танго, не говоря уже о всех деталях танца».
Менеджеры задумались. Конвей произвел хорошее впечатление, но они не совсем были уверены в том, что именно он имеет в виду. Один из них заговорил: «А где музыка?»
«Простите?»
«Я спросил, где музыка? Мы, слоны, не можем танцевать без музыки. Как мы узнаем, когда делать движения? А когда станем двигаться, как мы узнаем, твист это или вальс?»
«Прекрасные вопросы. Хотел бы я, чтобы у меня было хотя бы половина столь же прекрасных ответов. Все, что я могу вам предложить, — это основы.
227
Часть 2. Постижение невежества
Наша музыка состоит из оценки рисков и вознаграждений. Наша хореография — это оптимизация, основанная на этих оценках».
«Вот незадача. А я то надеялся на «Лебединое озеро»!»
Конвей улыбнулся и покачал головой: «Мы никогда и близко не подойдем к «Лебединому озеру». В нашей музыке слишком много фонового шума, да и хореография слишком небрежна. Сомневаюсь, чтобы во время представления наши танцоры не столкнулись друг с другом и не упали со сцены. К счастью, наша аудитория терпимо относится к ошибкам, пока они не слишком велики».
«А какую оптимизацию вы имеете в виду?» — спросил еще кто-то.
«Я еще не отработал все детально. Но есть один базовый критерий, которым мы можем пользоваться для грубой прикидки. Он также показывает необходимость танцевать. Он называется коэффициентом Шарпа».
«Это случайно не средняя доходность портфеля, разделенная на стандартное отклонение?»
«Не совсем. В числителе здесь средние чрезмерные доходы относительно без рискового эталона, за который обычно принимают краткосрочные казначейские векселя. Более того, предлагаю использовать ожидаемую избыточную доходность, а не историческую доходность, которую мы обычно варьируем в зависимости от случайных ошибок или изменений режима».
«Как мы должны измерять эту ожидаемую избыточную доходность?»
«Мы не можем ее измерить. Мы должны ее спрогнозировать. И предсказываете вы ее так же, как предсказываете все остальное — смешивая исторические данные с субъективными суждениями по поводу того, какие данные имеют значение и как, возможно, будет меняться ситуация».
«А если наши данные или суждения недостаточно верны?»
«Тогда прогноз, вероятно, будет отвратительным. Если вкладываешь мусор, на выходе тоже получаешь мусор. Это основной закон прогнозирования. Игра с коэффициентами Шарпа не может его отменить. Самое большее, что она может, — это помочь нам хорошо воспользоваться хорошими прогнозами».
Конвей сомневался, что он сказал что-то новое, то, что менеджеры еще не знали. Они просто проверяли, знает ли он основы своей профессии. Оглядев слушателей в поисках признаков возражений, он решил, что можно продолжать. «Теперь позвольте мне задать вам всем вопрос. Почему, как вы считаете, я остановил свой выбор на коэффициентах Шарпа, а не на каком-то другом критерии?»
После короткой паузы начали поступать ответы. «Это просто». «С ним легко работать». «Его нельзя надуть с помощью левереджа». «Это самая лучшая цель для максимизации».
«Отлично», сказал Конвей. — Все вы правы. Чтобы помочь вам оценить почему, давайте взглянем на этот график». Он продемонстрировал другой слайд.
228
12. Как научить слона танцевать
Максимизация коэффициента Шарпа
«Давайте сначала взглянем на эту могильную плиту. Каждая затененная точка, — продолжил Конвей, — указывает на комбинацию риска и вознаграждения для некоего допустимого портфеля, где горизонтальные координаты обозначают стандартное отклонение, а вертикальные координаты — ожидаемую избыточную доходность. Но это не единственные допустимые точки. Может кто-то сказать мне почему?»
Никто не ответил, но Конвей видел, что многие ответ знали. В конце концов, парень по имени Генри заговорил: «Пока ты можешь инвестировать в безрисковые ценные бумаги, ты всегда можешь двинуться радиально к началу координат. Поскольку инвестиция срезает избыточную доходность и стандартное отклонение в одной и той же пропорции, коэффициент Шарпа не меняется. А если вы можете одолжить безрисковые ценные бумаги, то можете пойти радиально за пределы начала координат».
«Спасибо, Генри. Коэффициент Шарпа портфеля равняется его вертикальной координате, разделенной на горизонтальную, что является точкой наклона линии от начала координат. Следовательно, луч, проведенный от начала координат по касательной к могильной плите, представляет собой самый высокий допустимый коэффициент Шарпа. Левередж может завести вас в любую точку ниже этого луча, но никогда не выше его».
«Что представляет из себя этот смайлик?» — спросил Джим.
«Радость инвестора. Нормальным инвесторам нравится вознаграждение и не нравится риск. Итак, если среднее и стандартное отклонение — это единственная информация о портфеле, которой мы располагаем на настоящий момент, они предпочтут пакеты, расположенные северо-западнее других. Это означает, что из всех допустимых расположений портфелей инвесторы всегда предпочтут диагональ, где коэффициент Шарпа выше всего».
«Где это на диагонали?»
229
Пасть 2. Постижение невежества
«Мы не знаем. Все зависит от того, насколько привлекательно вознаграждение в сравнении с риском, а этот критерий у каждого инвестора свой. Для инвестиционных менеджеров привлекательность ситуации в том, что все это не имеет значения. Они могут просто сконцентрироваться на том, чтобы коэффициенты Шарпа были высоки и ждать нужных координат. Отдельные инвесторы могут воспользоваться поддержкой или разводнить, его пожелают».
«А если у инвесторов будет больше информации, чем только планируемое и стандартное отклонение?»
«Тогда этот подход может не сработать. И, честно говоря, я не уверен в том, что есть такой, который сработает. Я же сказал вам, что это грубая прикидка».
«Справедливо, — заметил Джим. — Давайте пока будем придерживаться лишь коэффициента Шарпа. Предположим, мы стараемся его максимизировать. Что это даст для нашего распределения активов?»
«С математической точки зрения существует очень простой рецепт для максимизации коэффициента Шарпа, - Конвей вновь сменил слайды. - Вот он».
МАКСИМИЗАЦИЯ КОЭФФИЦИЕНТА ШАРПА
ДЛЯ РИСКОВЫХ АКТИВОВ
Установите веса портфеля пропорционально обращенной ковариационной матрице, умноженной на вектор ожидаемой избыточной доходности.
«Здесь «обращение» означает обращение матриц, а «умножение» относится к перемножению матриц. Если воспользоваться алгебраическими символами, рецепт еще короче и наглядней. Теперь может ли кто-нибудь сказать мне, какое очевидное практическое следствие можно получить из этого рецепта?».
Конвей окинул взглядом аудиторию, но на этот раз, казалось, идей ни у кого не возникло. «Хорошо. И вот мы снова пришли к согласию. Никакое следствие не кажется очевидным, кроме того, что теория, которую легко показать математически, может быть сложна для интуитивного понимания. Итак, давайте попробуем потренировать наше воображение на более простых примерах. Какая часть формулы наиболее страшна? Обращение матриц, правильно?»
Все кивнули. Конвей продолжил: «К счастью, она не всегда является устрашающей. Предположим, что все активы некоррелированные. Тогда как ковариационная матрица, так и ее обращенный двойник будут диагональными. Каждый диагональный элемент в инверсии равен другому по относительной дисперсии. Итак, чему будет пропорционален оптимальный вес каждого актива в этом случае?»
«Его ожидаемой избыточной доходности, разделенной на его дисперсию», — сказал кто-то.
«Совершенно верно. А эта хореография намекает уже на весьма живой танец. Предположим, что ваш портфель содержит два некоррелированных 230
12. Как научить слона танцевать
актива и вы повышаете свою прогнозируемую долларовую доходность по одному из этих активов до 9% среднего от 6%, не изменяя никакой другой прогноз. Максимизация коэффициента Шарпа предлагает грубо удвоить относительный вес этого актива в вашем портфеле».
«Почему удвоить? Доходы выросли всего на треть».
«Потому что нам следует проверять избыточную доходность в добавление примерно к 3%-ному доходу по казначейским векселям».
«Простите, Конвей, — прервал его Джим, — но мне это не кажется столь впечатляющим. В крупном портфеле некоррелированных активов я могу представить небольшие изменения в прогнозах, которые могли бы вызвать значительные колебания в весах портфелей, если бы не операционные издержки. Конечно, я не уверен. У нас бывает немного случаев, где корреляции можно не принимать в расчет».
«Я это признаю. На данном этапе мы всего лишь получаем подсказки. Позвольте мне предложить вам другой пример, который, возможно, произведет на вас большее впечатление. Предположим, единственным рисковым активом инвесторов будет мега-фонд, управляемый одним инвестиционным менеджером — звездой. Предположим также, что статистический анализ выявил надежную альфу, бету и остаточную погрешность против NASDAQ и что вы оптимально корректируете подверженность риску, покупая и продавая фьючерсы NASDAQ. Это кажется вам более реалистичным?»
«Да, хотя, возможно, мне следует предупредить вас, что мы не делаем много хеджирования. Я мог бы переложить вину за это на инспекторов, но, по правде говоря, мы могли бы делать намного больше, если бы хотели, прямо или косвенно».
«Возможно, нам следует больше этим заниматься. Посмотрим, что нам скажет анализ. Возвращаясь к примеру, позвольте мне попросить всех мысленно разбить отдельные пакеты акций и длинные или короткие позиции по фьючерсам NASDAQ на два некоррелированных компонента. Первый компонент — это чистая подверженность NASDAQ риску. Второй — это комбинация альфы менеджера и остатка. Следите за мыслью?»
«Вы измеряете альфу, включая или исключая номинальные ставки?» — спросил Генри.
«Исключая. Начиная с этого момента, давайте измерять все в терминах избыточной доходности, так, чтобы нам не приходилось помнить, что нужно вычесть ставку казначейского векселя. Теперь представим, что мы управляем распределением активов для этого мега-фонда с середины 1999 г., когда NASDAQ падал, до середины марта 2000 г., когда NASDAQ вырос, но переживал большую турбулентность. Как изменятся наши прогнозы в этот период?»
«Сложный вопрос, — сказал Джим. — Теперь, когда мы знаем, что произошло, сложно вспомнить, что в тот момент казалось разумным. Очень хочется подменить настоящий прогноз ретроспективным».
231
Часть 2. Постижонио новожвства==
«Конечно. Но позвольте мне спросить следующее. Будет ли разумно занять более бычью или менее бычью позицию по перспективам NASDAQ при том условии, что NASDAQ взмыл вверх на 75% за 5 месяцев?»
«Конечно, менее бычью».
«Будет ли разумно со стороны аналитиков изменить свой взгляд на волатильность фьючерсов NASDAQ в соответствии с подразумеваемой волатильностью по опционам NASDAQ?»
«Это кажется таким же хорошим предположением, как и любое другое».
«А вы помните, что произошло с волатильностью опционов NASDAQ в тот период?»
«Она выросла, насколько я помню, но ненамного».
«До 1500 базисных пунктов, на 50% вместо и без того высоких 35%. Предполагаемая дисперсия удвоилась. Так что максимизация коэффициента Шарап подскажет по крайней мере вполовину сократить относительную подверженность риску по NASDAQ в середине марта 2000 г. по сравнению с предшествовавшим полугодием, даже до того, как вы подготовите свой прогноз среднего. Конечно, это подразумевает, что альфа менеджера и остаточная дисперсия остаются постоянными».
«Ух-ты, — сказал Джим. — Это был бы громадный скачок. Жаль, что тогда вас с нами не было. О чем еще говорит нам теория?»
«Она говорит о маржинальных прибылях различных некоррелированных ценных бумаг или суб-портфелей и их доле в общей эффективности. Результаты могут быть резюмированы и сведены к четырем правилам». Конвей высветил следующий слайд:
ВОЗВЕДЕННЫЕ В КВАДРАТ ПРАВИЛА ШАРПА ДЛЯ НЕКОРРЕЛИРОВАННЫХ АКТИВОВ
1. Оптимальные веса прямо пропорциональны коэффициентам Шарпа на единицу риска (волатильности).
2. Квадрат коэффициента Шарпа по оптимальному портфелю равняется сумме квадратов отдельных коэффициентов Шарпа.
3. Каждый оптимально взвешенный актив вносит свой вклад в среднюю доходность портфеля в прямой пропорции к квадрату его коэффициента Шарпа.
4. Каждый оптимально взвешенный актив вносит свой вклад в среднее отклонение портфеля в прямой пропорции к квадрату его коэффициента Шарпа.
«Это подтверждает, что диверсификация по некоррелированным активам или стратегиям заключения сделок всегда помогает в мире среднего/дисперсии. И, что более важно, она показывает, насколько сильно она помогает. Удвоение коэффициента Шарпа некоррелированного актива или суб-поргфеля гарантирует в целом учетверение его справедливой доли риска. Некоррелированный актив, у которого коэффициент Шарпа в три раза больше, чем у других, грубо стоит девяти последних».
232
12. Как научить слона танцевать
«Очень интересно. Плохо, что это не очень полезно. Я никогда в реальной жизни не встречал портфелей без нескольких высоко коррелированных активов. Чаще всего мы хотим, чтобы высоко коррелированные активы помогли нам отследить эталон».
«На самом деле портфели, сильно сориентированные по рыночным индексам, — это именно те, где возведенные в квадрат правила Шарпа пригодятся больше всего. Нам просто следует пересчитать коэффициент Шарпа для каждого актива или стратегии, чтобы сконцентрироваться на том компоненте, который не является коррелированным с эталоном, как мы делали в предыдущем примере. Коэффициент Шарпа остатка часто называют «информационным коэффициентом» актива, поскольку он измеряет сигнал относительно шума. Но, если вы не возражаете, я бы лучше назвал его «резкостью», поскольку это позволяет запомнить, что он означает».
«Да, ради бога. А как этим пользоваться?»
«Все просто. Предположим, что остатки независимы друг от друга. Тогда мы воспользуемся возведенными в квадрат правилами Шарпа, чтобы построить портфель, который максимизирует совокупную резкость. Затем играем на повышение или на понижение достаточного количества фьючерсов индекса, чтобы достичь желаемой эталонной подверженности риску».
«Мы всегда можем найти некоррелированный остаток?»
«Да. Представьте себе гиперпространство, где каждое измерение определяет возможное множество рыночных доходностей. Опустите перпендикуляр из вектора, который представляет актив на гиперплоскости, представляющей линейные комбинации эталонных индексов. Тогда перпендикуляр описывает остаток, в то время как вектор, продленный на гиперплоскость из начала координат до перпендикуляра, описывает наилучшее размещение индекса. Вот как это выглядит для трех измерений и двух эталонных индексов».
Разложение активов на ортогональные компоненты
Decomposing assets into orthogonal components
233
Пасть 2. Постижвнив нвввжвства
«Насколько сложно это рассчитать?»
«Совсем несложно, если у вас есть репрезентативные данные. Просто вычислите коэффициент регрессии избыточной доходности актива из избыточной доходности индексов и константы. Бета-оценки покажут наилучшее линейное расположение, в то время как резкость -— это просто пересечение, разделенное на стандартную ошибку расположения».
«Как мы можем быть уверены, что остатки для различных активов будут независимы друг от друга?»
«Никак не можем. Но чем больше рыночных механизмов осуществляет эталон, тем менее разумным становится обращение с остатками, как с нормальными и независимыми. Это немного похоже на отбеливание: чем больше цветов вымываешь, тем белее выглядит вещь. Только здесь мы говорим о статистическом белом шуме. Если остатки сводятся к этому, то портфель, который максимизирует совокупную резкость, скорее всего, будет эффективнее эталона, который его отслеживает. Хотите, я рассмотрю гипотетический пример?»
«Давайте».
«Предположим, осенью 2000 г. вы управляете всемирным взаимным фондом с техническим и нетехническим субпортфелями. При регрессии против процентной доходности NASDAQ и рыночного заместителя процентной доходности MSCI World ваша доходность по субпортфелю дает следующую декомпозицию в годовом выражении», — с этими словами Конвей вывел на экран новый слайд.
ГИПОТЕТИЧЕСКИЕ ТЕХНИЧЕСКИЕ И НЕТЕХНИЧЕСКИЕ СУБПОРТФЕЛИ
Технические = 0,06 + 0,5 NASDAQ + 0MSCI + 0,20 Стехн; 5техй= 0,4
Нетехнические — 0,03 — 0,1-NASDAQ + 0,8-MSCI + 0,1- €HeiexiI; ^негехн = 03 Стехни Снетсх11 независимые, стандартные, нормальные переменные
«Иными словами, у вашего технического субпортфеля есть альфа в 6%, бета NASDAQ равная 0,5, бета MSCI равная 0 и остаточная волатильность 20%. У вашего нетехнического субпортфеля альфа 3%, бета NASDAQ — 0,1, бета MSCI — 0,8 и остаточная волатильность 10%. Резкость S составляет 0,4 для технического и 0,3 для нетехнического субпортфелей. Это дает совокупную резкость 0,5, что подразумевает 69%-ный шанс превзойти эталон в одногодичном диапазоне».
«Независимо от эталона?»
«Эталон не имеет значения, пока он представляет из себя некую смесь NASDAG и MSCI, которую вы можете купить или закодировать на рынке. В том-то и прелесть анализа резкости. Он позволяет вам отвечать на некоторые вопросы даже тогда, когда вы все еще воюете с другими».
234
12. Как научить слсна танцевать
«И как же построить оптимальный портфель?»
«Начните с желаемого эталона индекса. Перераспределите 25 единиц из свободных денег в 16 единиц технического субпортфеля и 9 единиц нетехнического. Затем нейтрализуйте сдвиг по NASDAG и подверженность MSCI, продав 16 х 0,5 + 9 х (—0,1) = 7,1 единиц NASDAG и 16x0 + 9* (0,8) = 7,2 единиц MSCI. Это поможет пополнить ваши денежные запасы».
«О какой величине сделок вы говорите?»
«Она может варьироваться в зависимости от того, какой объем риска и левереджа для вас приемлем. Резкость сама по себе не может вам этого сказать».
«Но, тем не менее, может оно принять решение об относительном распределении между техническими и нетехническими су б портфеля ми?»
«Да, при условии, что вы отслеживаете эталон и если считаете, что остатки белым шумом».
Джим откинулся на спинку стула и потер подбородок. «Знаете, в этом есть кое-что интересное относительно управления. В пределах, в которых эти предположения верны, мы могли бы разделить группу на альфа-, бета- и омега-команду. Каждая альфа-команда могла бы сконцентрироваться на максимизации своей резкости. Команда бета старалась бы отслеживать желаемый эталон. Команда омега могла бы распределять активы между командами, чтобы улаживать вопросы риска и левереджа. Хотя мы по-прежнему заинтересованы во взаимодействии команд между собой, оно смогли бы работать относительно автономно, не задерживаясь уровнем самых медленных и не переполняясь незначимой информацией».
«Вы имеете в виду, что у нас будет меньше собраний, где мы будем говорить обо всем и ничего не решать?» — спросил кто-то. Все засмеялись.
«Да, — сказал Джим. — Но тогда нам придется не засыпать на тех, где мы все-таки будем присутствовать. Не похоже, чтобы здесь кто-либо спал, так что это хорошее начало, спасибо Конвею. Это очень хорошая помощь».
«Подождите минуточку, разве вы не хотите послушать о распределении с коррелированными активами?»
«Я думал, что вы рассказали обо всем с разбивкой на общие и независимые компоненты».
«Так оно и было, но это работает только для команды альфа. Если ваша команда бета управляет как подверженностью NASDAG, так и MSCI, и нацелена скорее на наибольшую эффективность, чем просто на пассивное отслеживание, вам следует принять во внимание корреляции между NASDAG и MSCI».
«Понятно. Но, боюсь, мне не осилить сегодня еще больше информации. Как насчет того, чтобы снова встретиться завтра? В этом же месте в тот же час».
Остальные согласно кивнули, и собрание разошлось. Конвей был вне себя от радости. Никаких айсбергов. Никаких профессиональных сомневающихся.
Просто отличное рабочее обсуждение.
235
Часть 2. Постижвнив нвввжвства
Какое это облегчение — найти простые модели, которые, кажется, работают! Вот несколько замечаний, рассматривающих основные расчеты максимизации коэффициента Шарпа, чтобы помочь читателю поближе ознакомиться с результатами. Я также указываю на некоторую свойственную им неопределенность в измерении, но не с тем чтобы разочаровать потенциальных пользователей, а для того чтобы помочь им отличать хорошие аппроксимации от плохих.
Избыточная доходность
Избыточную доходность обычно определяют как номинальный процентный доход по активу за вычетом без рисковой ставки процента — так, словно инвесторы взяли взаймы деньги по без рискованной ставке, купили актив, выплатили займы из выручки, а затем измерили чистую прибыль как акцию изначальной инвестиции. Это правильная мысль, за исключением того, что лучше измерять чистую прибыль в терминах текущей стоимости до того, как мы взяли ее соотношение к изначальной инвестиции:
_rrj. _ ~ 1 Е\Уьдоход\--БезрисковаяСтавка
Е\ИзоыточнаяСтоимостъ\ ~ —----------------------------
1 + БезрисковаяСтавка
Этот подход делает соотношение почти независимым от валюты, используемой для его измерения. Например, когда турецкие казначейские векселя приносили 100%-ный доход в связи с высокой инфляцией, актив, обещающий 110% в турецких лирах или 1000 базисных пунктов (б.п.) в номинальной избыточной доходности, не был таким уж привлекательным, как актив, обещающий 600 б.п. избыточной доходности в долларах или марках. Конечно, ни один разумный инвестор не считал подобные казначейские векселя без рискованными активами! Но проблема возникает в игре более мелкого масштаба на еще более развитых рынках. На самом деле концентрация на избыточной доходности подразумевает, что инвесторы хеджируют весь внешний информационный и валютный риск, за исключением того случая, когда они прямо покупают этот риск в качестве актива.
Если измерить ожидаемую избыточную доходность логарифмически, т.е. как ln( 1 + Е[% доходности]), она должна определяться линейно во времени (пока режим не меняется). Процентная доходность должна быть составной. В любом случае она обычно выводится в годовом исчислении.
Волатильность
Волатильность (vol) относится к стандартному отклонению в годовом исчислении. Чтобы перевести стандартное отклонение инвестиции, измеряемое каждые Т торговых сессий, в годовое исчисление, следует умножить его на
236
12. Как научить слана танцевать
л/252/7", где 252 представляет из себя среднее количество торговых сессий в году. В то время как нет ничего особенного в числе 252 или исключении дней, когда торги не проводятся, умножение на квадратный корень базируется на простом, сильном и зачастую правдоподобном предположении о том, что доходности по периодам удерживания являются некоррелированными. Это заставляет стандартное отклонение логарифмических доходностей (и в большинстве случаев процентных доходностей) быть соизмеримыми с квадратным корнем времени.
Когда доходности являются сериально-коррелированными, использование стандартных формул пересчета в годовое исчисление может оказаться обманчивым. Возможно, наиболее крайний пример касается валютной торговли в узком диапазоне вокруг некоего инвалютного якоря. Внутридневные колебания могут соперничать с колебаниями плавающего обменного курса, что подразумевает высокую волатильность, несмотря на то что действительное стандартное отклонение годовых движений будет ничтожно, пока удерживается диапазон. К счастью, помимо валют, очень мало ценных бумаг демонстрируют большое количество сериальных корреляций при заданных периодах удержания, варьирующихся от нескольких дней до нескольких месяцев, которым уделяет внимание эта книга.
Меры портфеля
Допустим, М обозначает вектор ожидаемой избыточной доходности, а со обозначает вектор весов портфеля, определяемых как доли базовой инвестиции. Ожидаемая избыточная доходность ц по портфелю может быть рассчитана как со'ц при условии, что М измеряется за весь период и портфель по ходу дела не корректируется.
Если забыть о предостережениях, это может вызвать массу недоразумений. Возьмем крайний пример: предположим, что ваш портфель стоимостью 100 долл, изначально поровну разделен между нал ичными деньгами и рисковым активом, который каждые шесть месяцев либо утраивается, либо почти уничтожается. Ясно, что у вас есть равные шансы как заработать 100 долл., так и потерять 50 долл, за первые шесть месяцев, при ожидаемой 25%-ной доходности. Как насчет вашей годовой доходности? Если вы восстановите доли исходного портфеля на вторые полгода, вы получите годовую ожидаемую доходность в размере 1,25 * 1,25 — 1 = 56,25%. Напротив, если вы будете продолжать удерживать исходный пакет весь год, то у вас будет 25%-ный шанс заработать 400 долл, и 75%-ный шанс потерять 50 долл, при ожидаемой доходности в +62,5%.
Если обозначить ковариационную матрицу избыточной доходности символом Е, то дисперсия о2 избыточной доходности портфеля будет равняться юТсо. И снова, эта формула точна только для единичного периода удержания.
237
Часть 2. Пвстижвнив нввожвствв
Коэффициент Шарпа
Коэффициент Шарпа, названный по имени профессора финансов, который с ним мир, указывает, сколько стандартных отклонений доходности должно упасть ниже своего среднего перед тем, как инвестор заработает меньше без рискованной процентной ставки. Я обозначу его .S’. Он равен ожидаемой избыточной доходности ц портфеля, разделенной на стандартное отклонение о этой избыточной доходности:
и vv’f Л/
Коэффициент Illapna(S) = — — . .
О' y/w'£a)
Коэффициент Шарпа обычно грубо сопоставим с квадратным корнем времени. Подобно среднему и стандартному отклонению его обычно рассчитывают в годовом исчислении, чтобы избежать недоразумений.
Инвариантность к левереджу
Обратите внимание, что доля портфеля, отведенная под безрисковый актив, не затрагивает ни среднего, ни стандартного отклонения, за исключением случаев, когда она ограничивает сумму остальных долей. Итак, левередж или спад при без рискованной ставке не оказывают влияния на коэффициент Шарап.
Если предположить неограниченную потенциальную инвестицию или займу по без рискованной ставке, тогда в наших расчетах матрицы удобно игнорировать безрисковые инвестиции. Это позволяет опустить любое ограничение по сумме оставшихся акций портфеля. Мы все еще можем отклонить подразумеваемую без рискованную долю как 1 — со'1; т.е. как единицу минус сумма оставшихся акций.
которая
Любая функция g среднего и стандартного отклонения, инвариантна к левереджу, является функцией коэффициента Шарпа. Заметим, что я(ц, о) = ко) для всех к = l/о. Таким образом, мы определим новую
Матричные производные
Чтобы вывести веса портфеля, которые максимизируют коэффициент Шарпа, удобно воспользоваться матричным исчислением. Матричное исчисление — то же самое, что и обычное исчисление, за исключением того, что оно использует матричное счисление, чтобы отслеживать результаты. Основное правило состоит в том, чтобы производная столбца ш-вектора относительно ряда w-вектора являлась матрицей т х л, чей <4 у> элемент равняется производной z-го вектора-столбца относительно у-го элемента вектора-строки. Нам нужно принимать во внимание производные стандартных матричных произведений и квадратичных форм:
238
12. Как научить слона танцовать
— х'М = М , dx
— x'Sx = 2Sx
dx
для любого вектора М или симметричной матрицы S. Единственная сложность включает в себя слежение за транспонированием и порядком умножения.
Максимизация коэффициента Шарпа
А теперь давайте применим все эти формулы, чтобы максимизировать коэффициент Шарпа. Поскольку коэффициент Шарпа инвариантен к левереджу, ограничим избыточную доходность так, чтобы она равнялась или превосходила некую цель /л , и поищем портфель с минимальной дисперсией в этом классе. Сформируем лагранжиан
cdY со - 77 (W М - Д
с положительной г/ (поскольку ограничение всегда будет связывающим) и продифференцируем относительно а), чтобы получить матричное условие первого порядка:
2£й) — т]М = 0.
Это уравнение имеет единственное внутреннее решение, только если Е является обратимой (так, чтобы ни один портфель рискованных активов никогда не был полностью без рискованым). В таком случае:
И’* - .
Следовательно, любое положительное число, кратное Е-1М, — это точка покоя для некоторого /л . Аргументы выпуклости (если вы строите график дисперсии в «-пространстве, касательные к кривой должны располагаться ниже ее) подтверждают, что точка покоя минимизирует дисперсию. Максимальный коэффициент Шарпа выражается следующим образом:
- гм:^м
у/со'Хс» л/М'Х~'М
Коэффициент Шарпа и период удержания
В той степени, в которой период удержания изменяет относительное среднее, он изменяет и оптимальную стратегию. Возможно, это покажется странным, поскольку формулы Шарпа не относятся явно к периодам удержания. Но противоречия в этом нет. Помните, что оптимизация портфеля
239
Часть 2. Постижение невежества
проверяет все возможные стратегии. Скорее она выбирает из тех стратегий, которые перенастраивают портфель настолько часто, насколько сложными будут доходности. Также изменение периода удерживания косвенным образом меняет определение средних и ковариаций. На практике неопределенность относительно периода удержания — это пустяк по сравнению с неуверенностью прогнозистов в рисках портфеля, которых следует ждать в будущем.
Квадратичные правила Шарпа для некоррелированных активов
Если активы некоррелированные, L будет диагональной матрицей, в случае чего оптимальный вес каждого актива будет пропорционален как //. S.
—- = — . Вклад актива i в ожидаемую совокупную избыточную доходность сг/ ст.
будет пропорционален /л
в то время как вклад в совокупную
волатильность — пропорционален
В конце концов квадрат
А*2
совокупного коэффициента Шарпа будет равен > —1-
Эталонные сравнения
Рассмотрим портфель, состоящий из эталона плюс субпортфеля многомерно нормальных активов. Предполагается, что субпортфель обычно распределен с ожидаемой избыточной доходностью /л и волатильностью о, которая зависит от весов субпортфеля со. Риск, что портфель будет работать
с хуже эталона, равняется совокупной нормальной вероятности------= —о .
ст
Чтобы минимизировать этот риск, прибегните к правилам для коэффициента Шарпа, приведенным выше, чтобы максимизировать S.
Регрессии
Регрессия Y по Af аппроксимирует Y с помощью линейной комбинации Ар. Здесь Y — J- вектор, X— матрица J * т (эквивалентно, т — вектор У-векторов), а [3 - /д-вектор, где J — количество наблюдений, а т —число каузальных величин. Остаток R= Y—X /3 измеряет соответствие.
Обычная среднеквадратическая регрессия минимизирует сумму возведенных в квадрат остатков. Дифференциация относительно [3 дает следующее решение:
240
12. Как научить слонатанцппать
X'Y - Х'Х/7 = О <=> (3 = (Х'Х)’1 X'Y .
Если X и Y измеряются как отклонения от их соответствующих средних или если одна из каузальных величин является константой, R — (I — Х(Х'Х)”1 X')Y будет некоррелирована с %, gjcijkmre
Cov [X, Л] = ^[ХК] - Е[Х'] £[/?] = Е [х'(/ - Х(Х'ХГ’ Х’)У] - Е[Х'] О = Е[(Х’ - ХХ(ХХ)~’ Х’)У1 = E[(X'-X’)Y] = о
Резкость («Информационный коэффициент»)
Предположим, что Y состоит из линейной комбинации товарных индексов X и некоррелированного остатка со средним ос и волатильностью v . Резкость относительно X определяется как коэффициент Шарпа ос / v этого остатка. Ни общий левередж, ни хеджи по компонентам X не могут изменить взвешенной резкости. Но изменение X обычно меняет резкость и может даже сменить ее знак на обратный. Стандартный коэффициент Шарпа — это особый случай резкости с чистым без рискованным эталоном.
Возведенные в квадрат правила Шарпа также применимы к резкости. Например, если резкости актива являются некоррелированными, сумма их квадратов равняется квадрату’ оптимальной резкости портфеля. Стандартная финансовая литература использует фразу «информационный коэффициент» в более общем смысле, как его употребляют в статистике для названия статистического свидетельства, имеющего отношение к гипотезе. Однако, я считаю, что термин «резкость» сильнее напоминает о том, чем она является. Но поступайте по собственному вкусу. Статистике все равно...
Смеси идиосинкразических и коррелированных эффектов
Если все построенные остатки, включая подверженность ключевым торговым индексам, независимы друг от друга, мы можем прибегнуть к возведенным в квадрат правилам Шарпа, чтобы установить оптимальные относительные веса. Если мы можем избавиться от некоторых подверженностей, но не от других, мы все равно можем прибегнуть к возведенным в квадрат правилам Шарпа для части портфеля. Предположим, что реконструированные субпортфели имеют ковариационную матрицу
где D — это диагональная матрица, а остаточная ковариация £R — нет. Тогда инверсия переработанной ковариационной матрицы принимает форму
у-1 _ О
I 0
241
Часть 2. Постижение невежества
Поскольку матрица также диагональная, отсюда следует, что
квадратичные правила Шарпа применимы для активов, которые входят в D Однако обратим внимание на то, что реконструированные активы должны быть независимы от любого другого актива, а не только от тех, что входят в D.
242
13. Ставка на бета
«Спасибо всем, кто пришел, - сказал Джим, открывая собрание на следующий день. — Вчера, как вы помните, Конвей представил нам видение портфельных слонов, раскачивающихся под музыку Шарпа. Но он сконцентрировался на том случае, где каждый слон слышит свою независимую музыку. Сегодня он рассмотрит более продвинутую хореографию, где основные мелодии коррелированы. По крайней мере, я так считаю. Начинайте, Конвей».
Отлично, поехали. Надеюсь, вчера это не было просто везение новичка. «Спасибо, вы правильно резюмировали, Джим. Но я должен предупредить всех: я буду водить вас кругами. Сначала я расскажу о ключевых отличиях анализа коэффициента Шарпа для коррелированных и некоррелированных активов. Потом, чтобы воспользоваться предлагаемой Джимом схемой управления, я объясню, чем команда бета должна отличаться от команды альфа. Затем покажу один фокус, который позволит вам обращаться со всеми активами как с некоррелированными, так что команда бета превратится в конечном итоге в команду альфа. Готовы?»
Все согласно кивнули. «Хорошо. Давайте начнем с рассмотрения двух основных методов сокращения риска без снижения вознаграждения. Первый метод — это диверсификация, или раскладывание яиц по разным корзинам. Второй - длинное или короткое хеджирование, где вы играете на понижение одного актива против другого. Какие факторы влияют на ваш выбор метода?»
«Прежде всего, коэффициент Шарпа, - сказал Генри. — Очень сложно получить прибыль, играя на понижение или приобретая актив с высоким или отрицательным коэффициентом Шарпа».
«Верно. Что еще?»
«Корреляция. Диверсификация лучше всего срабатывает, когда корзины растут в разных средах или, если это невозможно, растут более-менее независимо друг от друга. Это означает отрицательную или низкую корреляцию».
«Снова верно. Чтобы это проиллюстрировать, я построил график совокупного коэффициента Шарпа для портфеля из двух активов при корреляции от -0,4 до +0,9. Каждый график предполагает избыточную ожидаемую доходность в 4% для первого актива и 8% для второго, при 20%-ной волатильности для каждого». Конвей включил проектор и продемонстрировал слайд. «Кстати, спасибо тому, кто оставил инструкцию по пользованию проектором на моем столе вчера вечером. Это мне очень помогло».
243
Часть 2. Постижение невежества
Влияние корреляции на портфель из двух активов
Werght on asset 1
Mean, - 0.06, Mean2 - 0.12, Vol, - Vol2 == 0 20.
Среднее! = 0,06. Среднее2= 0,12. Волатильность! = Волатильность2= 0,20.
«В любом случае, как видите, все графики пересекаются в трех точках: там, где вы удерживаете только первый или второй актив или там, где вы удерживаете портфель с нулевым средним. И все графики выравниваются в точках экстремума с одним внутренним максимумом. Но в противном случае форма значительно варьирует. Когда корреляция низка, всегда стоит удерживать немного актива 1, несмотря на то что это дает только половину вознаграждения актива 2 при том же риске. Однако при высокой корреляции лучше сыграть на понижение актива 1 и сделать упор на актив 2».
«Теперь при первом взгляде на вчерашнюю формулу максимизации коэффициента Шарпа, которая устанавливает веса портфеля кратно обратной ковариационной матрице, умноженной на ожидаемую избыточную доходность, ничего нельзя сказать ни о коэффициентах Шарпа, ни о корреляциях. Но мы можем переписать ее так, чтобы она заговорила». Конвей высветил следующий слайд:
ПЕРЕФРАЗИРОВАННАЯ МАКСИМИЗАЦИЯ
КОЭФФИЦИЕНТА ШАРПА
Установите вес портфеля, умноженный на волатильность, пропорциональный обращенной корреляционной матрице, умноженной на вектор коэффициентов Шарпа.
244
13. Ставка на бота
Квадрат максимального коэффициента Шарпа равен квадрату коэффициента Шарпа актива и обращенной корреляционной матрицы.
«Теперь мы очень ясно видим, что корреляции и коэффициенты Шарпа являются центральными в схеме распределения. Но их взаимодействие сложно. Чтобы лучше его понять, нам следует погрузится в расчеты. Вот результат для двух активов.
МАКСИМИЗАЦИЯ КОЭФФИЦИЕНТА ШАРПА ДЛЯ
ДВУХ АКТИВОВ
Установите вес портфеля, умноженный на волатильность, пропорционально собственному коэффициенту Шарпа актива минус р (корреляция), умноженная па коэффициент Шарпа другого актива.
Повышение коэффициента Шарпа актива улучшает совокупный коэффициент Шарпа тогда и только тогда, когда оптимальный вес портфеля является положительным.
«Неплохо, не так ли? При заданных коэффициентах Шарпа повышение корреляции усиливает стимулы к длинному/короткому хеджированию в противоположность диверсификации. При заданной корреляции повышение коэффициента Шарпа актива помогает в том случае, если вы уже играете на повышение этого актива, но если вы сьнраете на понижение, результаты могут быть не самыми приятными. А если корреляция нулевая, у нас снова начинают действовать вчерашние правила. Невозможно придумать более простую формулу, которая дает такие результаты».
«А если у нас больше двух активов? — спросил Джим. -- Что в этом случае дает нам максимизация коэффициента Шарпа?»
«Что полезность диверсификации сокращается относительно длинного/короткого хеджирования, когда вы сталкиваетесь с большим количеством коррелированных активов. Если вы не можете сыграть на понижение, но уверены в параметрах риска, тогда, несмотря на то что корреляции малы, не стоит удерживать более дюжины активов».
«Да? Большая часть взаимных фондов США основаны на совершенно противоположных принципах: инвестируйте в дюжину умеренно коррелированных активов без коротких хеджей».
«Я это понимаю. Однако с математической точки зрения результат сомнений не вызывает. Если вы удерживаете вероятностно взаимозаменяемые активы с общей корреляцией р, то, можег быть, вы никогда не умножите свой изначальный коэффициент Шарпа более чем на / 1/ ».
245
Масть 2. Постижение невежества
«Что если р отрицательно или равно нулю?»
«Такого не может быть, чтобы у вас было слишком много активов с отрицательным р. Если р равно нулю, тогда, как мы видим, квадрат совокупного коэффициента Шарпа продолжает расти за счет квадрата коэффициента Шарпа следующего покупаемого вами актива. Но, как показывает следующий слайд, с ростом р предел очень быстро вносит свой вклад.
Пределы на доходы из простой диверсификации
Limits on gains from simple diversification
«При p — 0,25 вы можете в лучшем случае удвоить свой изначальный коэффициент Шарпа. При р = 0,7 вы не сможете улучшить изначальный коэффициент Шарпа на 20% даже при бесконечном количестве активов. Более того, чем выше корреляция, тем быстрее сокращаются доходы, несмотря на то что вы прибавляете и прибавляете активы. Взгляните на таблицу, где приведены размеры портфеля, при котором маржинальный доход по коэффициенту Шарпа от добавления еще одного актива падает ниже 1%. Здесь хорошо видно, насколько близок этот портфель к получению максимально возможной прибыли от диверсификации».
Когда портфель взаимозаменяемых активов достаточно велик?
Корреляция Размер портфеля, при котором Улучшение коэффициента Шарпа маржинальное улучшение Шарпа <1% (процент от максимума)
0 50 0
0,1 17 81%
0,2 12 84%
0,3 10 89%
0,4 8 91%
0,5 7 93%
0,6 5 93%
246
13. Ставка на бита
0,7 4 94%
0,8 3 95%
0,9 2 97%
«Это намного меньше, чем я предполагал, - сказал Джим. — И что делать с интуицией после этого?»
«Считайте, что каждый актив содержит два компонента. Один компонент, отвечающий за долю р дисперсии (или д/р волатильности), генерирует одну и ту же доходность для всех активов. Другой компонент независим. В крупном портфеле независимые компоненты вымываются, но общий компонент -никогда. Поэтому их комбинация никогда не сокращает дисперсии до значения менее исходного р, а коэффициент Шарпа никогда не улучшается более чем на . К тому же, чем больше р, тем меньше независимые компоненты, так что
то, что вы остановили диверсификацию на пригоршне активов не принесет вам много работы».
«Что если корреляция происходит не от одного-единственного общего компонента?»
«Пока мы делаем анализ среднего и дисперсии, результаты будут одними и теми же. И мы с таким же успехом можем предположить самую простую из возможных причинных структур. Обратите внимание, каузальная структура может изменить третий и более высокие моменты».
«Хорошо. Думаю, я понимаю, почему диверсификация не сильно помогает, когда корреляции высоки. Но не понимаю, чем длинные или короткие хеджи могут в данном случае помочь. Как можно заработать деньги, скупая абсолютно взаимозаменяемые активы?»
«Никак. Активы должны иметь, по крайней мере, несколько отличные коэффициенты Шарпа. Но если так оно и есть, то длинные или короткие хеджи могут создать новый ряд прибыльных, некоррелированных групп активов. Чем больше таких групп у нас есть, тем лучше, особенно при отсутствии потолка по совокупному коэффициенту Шарпа».
«Можете привести пример?»
«Конечно. Предположим, к нам поступают активы двух типов. Каждый тип имеет волатильность в 20%, при этом он сильно коррелирован с другим. Однако, если у первого типа на 100 б.п. выше ожидаемая доходность, чем у второго, тогда пакет из одной длинной единицы по первому типу и одной короткой единицы по второму типу будет иметь ожидаемую доходность в 1% при отсутствии волатильности».
Джим наконец-то увидел проблему: «Один объединенный актив с бесконечным коэффициентом Шарпа? Безусловно, это крайность».
«Так оно и есть. Я просто хотел продемонстрировать эффект длинных и коротких сделок в полную силу. Если бы в предыдущем примере у различных
247
Часть 2. Постижвнив нвввжвства
активов имелась только 50%-ная корреляция друг с другом, у каждого длинного/короткого объединенного пакета волатильность равнялась бы 20% при коэффициенте Шарпа 0,05. Но все пакеты по-прежнему были бы некоррелированны друг с другом, так что распределяя свой портфель между все большим и большим количеством ему подобных, вы смогли бы повышать свой совокупный коэффициент Шарпа до бесконечности».
«Возможно, понадобится громадный портфель, прежде чем эта комбинация длинных и коротких сделок победит коэффициент Шарпа по лучшему активу».
«Согласен. Как я уже сказал, для заданной корреляции более вероятно, что крупные, а не маленькие портфели отдадут предпочтение длинному/короткому хеджированию перед другой простой диверсификацией. Но на практике, где корреляции по крупным рыночным индексам превышают 0,7, а отдельные коэффициенты Шарпа отклоняются на сотни базисных пунктов, запреты на короткие или связанные деривативны убьют вашу способность управлять риском».
«Возможно, Вам следует написать письмо в Комиссию по ценным бумагам и биржам, — сказал Джим. - Хотя, я бы не поручился за быстрый ответ. Общество ассоциирует деривативны в большей степени с риском, нежели с сокращением риска, и Комиссия по ценным бумагам и биржам, как кажется, больше тяготеет к управлению внешней стороной риска, нежели самим риском. Поэтому давайте просто предположим, что у нас есть одобрение регулирующих органов. Как в этом случае нам управлять бета-командой?»
«Первый подход — заставить бета-команду максимизировать совокупный коэффициент Шарпа для портфеля, состоящего из различных рыночных индексов, одновременно проинструктировать альфа-команду нейтрализовать любую чистую подверженность риску по индексу. Команда омега затем распределит фонды командам альфа и команде бета прямо пропорционально их резкостям на единицу волатильности риска. Команда омега также приобретет эталонный индекс или какой-то его заместитель».
«Не слишком ли это расточительно, когда различные команды играют на повышение и понижение одних и тех же индексов?»
«Просто договоритесь определить нетто-позицию внутри компании, прежде чем заключать сделки на внешнем рынке. Например, если у команды альфа 0,2 единицы коротких сделок по NASDAG 100, а у команды бета 0,1 единиц коротких сделок, эталон составляет 0,3 единиц длинных сделок, то на внешнем рынке не следует приобретать или продавать фьючерсы NASDAG».
«Потребуются дополнительные расчеты, чтобы отслеживать различные уязвимости. Возможно, даже внутренний аудит». Замечание Джима вызвало общий стон.
«Но это несложно, -- сказал Конвей. — С предыдущим примером легко справиться любой трейдер, работающий по всем фьючерсам Nasdaq. Это не душит инициативу, а всего лишь повышает вашу ответственность. Ни одна фирма не может развиваться децентрализовано в отсутствии ответственности».
248
13. Ставка на бета
Джим улыбнулся. «Нам, инвестиционным менеджерам, нравится это в компаниях, в которые мы инвестируем. Я не уверен, что нам понравится, когда вопрос ответственности коснется нас самих. Но продолжайте. Что вы имели в виду, говоря об отличиях в управлении бетой и альфой? Принимая во внимание все вышесказанное, они кажутся одинаковыми».
«Если вы управляете множественными коррелированными индексами, вам придется принимать решения относительно относительных совокупной подверженностей. Это требует решения нескольких уравнений одновременно, что и происходит при умножении обратной прогнозной ковариационной матрицы на ожидаемую избыточную доходность. Но вам придется прогнозировать индексы более тщательно, поскольку высокие корреляции повышают чувствительность взвешивания к ошибкам».
«Почему бы не разбить команду бета на множество команд, чтобы каждая могла управлять одной-единственной подверженностью риску индекса?»
«Это мало поможет при коррелированных индексах, поскольку каждой команде бета все равно понадобятся другие прогнозы, чтобы принять решение относительно собственной доли. Но существует способ заставить этот подход работать».
«А именно?»
«Разложите индексы на некоррелированные компоненты. Тогда команды бета действительно будут напоминать команды альфа».
«И как вы предполагаете раскладывать индексы?»
«Есть один способ, причем довольной простой. Проаранжируйте индексы в порядке воспринимаемой важности для вашего портфеля. Первым обычно будет индекс по рынку в целом, скажем, MSCI World, если вы управляете всемирным фондом. Закрепите управление им за первой командой бета. Затем регрессируйте второй индекс относительно первого индекса и константы, и закрепите управление им (включая константу) за второй командой бета».
«Подобно предложенному вами закреплению остатка сектора за командой альфа?»
«Именно так, — согласился Конвей. — Затем регрессируйте третий индекс против первых двух индексов и константы, и закрепите управление остатком (включая константу) за третьей командой бета. Продолжайте в том же духе, пока у вас не закончатся индексы. По построению компонент каждой команды бета будет исторически некоррелирован со всеми остальными компонентами команды бета или альфа. Если повезет, индексы останутся некоррелированными и, возможно, даже будут взаимно независимыми».
«А если нет?»
«Тогда настраивайте их до тех пор, пока вы они станут некоррелированными, ищите имеющие к этому отношение параметров и инвестируете свое распределение так, как планировали. Вот это и означает управление компонентами альфа и бета».
249
Часть 2. Постижение невежества
«Что если некоторые остаточные резкости настолько малы, что они вряд ли будут оказывать влияние на совокупный коэффициент Шарпа?»
«Тогда расформируйте команды, управляющие этими остатками. Например, если вы управляете всемирным фондом акций и ожидаете, что французские и немецкие индексы будут двигаться в основном синхронно, тогда одной команды достаточно, чтобы управлять и теми и другими. Другой команде, возможно лучше поручить управление, скажем, азиатскими подверженностями риску против европейских».
«Это звучит очень субъективно».
«Так оно и есть. Но существует инструмент, которым вы можете воспользоваться, чтобы действовать более объективно. Это анализ основных компонентов. Чтобы понять мотивацию, взгляните на этот график избыточной доходности французского и немецкого фондовых рынков с 1986 по 1999 г. Несмотря на то что на том и другом рынке доходности сильно варьируются, большая часть вариаций идет вдоль построенной мной диагональной оси. Если вы определили, что один индекс будет измеряться вдоль этой оси и если сохраняются прошлые тренды, это охватит 88% общей дисперсии этих двух рынков».
Избыточные доходности рынка в 1986—1999 гг.
«Я воспользовался анализом основных компонентов, чтобы выбрать ось. Правда, рассматривая график, я и сам бы выбрал ее примерно такой же. Но глаза не работают так же хорошо при большем количестве измерений. Анализ основных компонентов использует собственные значения и собственные векторы, чтобы идентифицировать ортогональные оси, которые объясняют большую часть дисперсии между ними. Если хотите, можете приписать первый основной компонент первой группе бета, второй — второй группе бета и т.д., пока не охватите большую часть дисперсии».
250
13. Ставка на бета
«Почему вы изначально этого не предложили?»
«Я почти предложил. Но боюсь, что в некоторых случаях у аналитиков это может вызвать опасения, а масса деталей многофакторного индекса показаться им каким-то фундаментальным изменением. Также управление по дробным нестандартным индексам может повлечь за собой значительные транзакционные издержки».
«И как вы предлагаете использовать принципиальные компоненты?»
«Как факел. Освещайте основные тренды и старайтесь найти некий индекс, который охватывает их суть, но с которым будет проще работать. Например, совокупный мировой индекс почти всегда очень высоко коррелирован с первым основным элементом государственных индексов и индексов, относящихся к разным экономическим секторам. Вот почему я решил приписать его к ведущей группе бета. Другие основные компоненты демонстрируют тенденции «США против не США», «Европа против Азии», «новая технология против старой технологии» и т.п. Я бы предложил использовать последние как заменитель основных компонентов, а не заменять их основными компонентами».
«Итак, если я правильно вас понимаю, вы предлагаете создать некоррелированные команды альфа и бета с помощью некой комбинации того, что люди считают удобным прогнозированием и того, что, как кажется, объясняет большую часть дисперсии».
«Верно».
«А что, если люди будут чувствовать себя неловко, прогнозируя некоррелированные остатки?»
«Тогда, возможно, нам придется разделиться на команды по другим признакам. Но я бы предпочел сначала испытать этот метод. На моей предыдущей работе мне как-то пришлось прогнозировать премию по процентной ставке для долларовых облигаций развивающегося рынка. Как обычно, я сконцентрировался на анализе развития отдельной страны. Но скоро стало ясно, что колебания на фондовых рынках США подталкивали более чем половину общей дисперсии. Большая часть того, что делаем мы, аналитики развивающихся рынков, является просто предсказанием эффективности остатка. Думаю, это справедливо в отношении многих аналитиков».
Джим кивнул. «Я понимаю, что вы имеете в виду, — сказал он. — И думаю, что я понимаю, как управлять командами альфа и бета, используя одни те же принципы. Возможно, нам следует попробовать. Но позвольте мне сначала задать вам вопрос».
«Конечно. Приятно иметь дело с думающим человеком».
«Что вы предлагаете делать с риском айсберга?»
У Конвея внутри все похолодело.
«Я....э..не уверен, что я понимаю, что вы имеете в виду», —
пробормотал он.
251
Часть 2. Постиженио новожоствя
«Я имею в виду крупные опасности, которые явно никогда не видны, но которых нельзя себе позволить проигнорировать. Типа рыночных крахов, которые, как кажется, пренебрегают законами среднего».
«Или внезапных смен режимов», — сказал Генри.
«Или параметров риска, которые стабильны, но только ты не уверен, каковы они», — заметили с задних рядов.
Конвей почувствовал себя ребенком, застигнутым в тот момент, когда он только залез в коробку с конфетами. Лучше сразу покаяться и просить о пощаде. «Да, я знаю об этих типах рисков. На моей прошлой работе был сотрудник, который только об этом и говорил. Довел себя до сумасшедшего дома».
«Но если о них не думать, можно довести себя до банкротства, — сказал Джим. — Я хочу, чтобы мы соблюдали баланс. Может ли подход, связанный с коэффициентом Шарпа, это обеспечить?»
Конвей сделал паузу, подыскивая нужный ответ. И не нашел его.
«Не знаю. Надеюсь, что да».
«Задумывались ли вы о том, как это обеспечить?»
«В некотором роде, но недостаточно».
«Ну что ж, я предлагаю вам подумать об этом. Я ценю то, что вы уже сделали, Конвей. Правда. Но я не готов решиться радикально изменить нашу систему, если не получу более полной информации относительно того, куда мы направляемся».
Все согласились с этим. «Я тоже. Согласен. Зачем торопиться?» - звучали голоса. Собрание закончилось, и все разошлись, оставив Конвея зализывать раны. Можно убежать, но спрятаться нельзя.
Пока Конвей думает, что делать дальше, давайте еще поработаем над матричной математикой.
Диагональный оператор
Диагональный оператор преобразует вектор или квадратную матрицу А в диагональную матрицу. Если А — это вектор, тогда i-й элемент А становится /1’. z \
элементом 4 7 диагонали (А). Если А - квадратная матрица, диагональ (А)
просто «обнуляет» недиагональные элементы Я. Эти операторы полезны при
определенных видах умножения. Например, если А — .....а В =
.......вектор с элементами может быть выражен либо как diag(y4)Z? или diag(Z?)y4.
252
13. Ставка на бета
Переформулировка максимизации коэффициента Шарпа
Допустим, что Р обозначает матрицу корреляционных коэффициентов, а Н- diag(X) — диагональную матрицу дисперсий. Обратите внимание, что Е =Н,/аРН'/\ где 1//г обозначает диагональную матрицу волатильностей. Также FT IZ2M равняется вектору 5 коэффициентов Шарпа. Следовательно, оптимальные веса портфеля со пропорциональны £~!М = Н~1/2 Р’'Н”1/2М = H~1Z2P~’5, а веса, умноженные на волатильности, пропорциональны H1/2H'I2P-1S, Максимальный возведенный в квадрат коэффициент Шарпа M’E^N может быть переписан как МЪГ/2 = s'p-’s.
Максимизация коэффициента Шарпа с двумя активами
При двух активах обратная корреляционная матрица Р-1 равняется
1 Г1 -р\
1-х?2 |_-х? 1 J
су, ст, что подразумевает, что —t—!-
су2 ст2
Максимальный коэффициент
Шарпа составляет
Геометрия максимизации коэффициента Шарпа
Вспомним, что корреляция между двумя векторами может быть истолкована геометрически как косинус угла между ними. Максимизация коэффициента Шарпа с двумя активами может быть интерпретирована геометрически следующим образом. В приведенной ниже диаграмме АВ и АС — это отрезки линии с длинами Sj и соответственно с углом 0 = cos-1(p) между ними. BD — это перпендикуляр от В к АС, в то время как СЕ — это перпендикуляр от С к АВ. Поскольку длина равняется 51, умноженной на cos 0 = р, CD должен иметь длину S2~ р5]. Сходным образом BE должен равняться по длине 51 — р52, так чтобы две длины были пропорциональны оптимальным вкладам волатильности.
253
Цяоть 2. Поотижонио новожоотвя
Отрезок СЕ имеет длину S2, умноженную на sint? = л/1 — cos2 О = 92 . По теореме Пифагора сторона СВ должна иметь длину
д/с*?! - д5*2 )2 р2 )^2 = V5' • Теперь продлим СЕ до
точки F так, чтобы СТ^имел такую же длину, что и СВ. Постройте линию через F параллельно АВ и продлите СА до тех пор, пока отрезок не пересечет эту линию в точке G. Поскольку угол между GAC и GF равняется 0, CG должен иметь длину, равную длине СВ, деленной на sin0, что равняется максимальному коэффициенту Шарпа.
Пределы диверсификации с взаимозаменяемыми активами
Согласно правилу симметрии, оптимальный портфель из п взаимозаменяемых активов будет вмещать в себя \/п долю каждого актива. Среднее портфеля будет равняться ц, в то время как дисперсия портфеля | 1 ~ + р |о-2, которая ограничена снизу 0 или рсГ. Если р положительно, то
коэффициент Шарпа портфеля никогда не превзойдет ^/1 / /9 , умноженного на
отдельный коэффициент Шарпа S.
Более того, если р не слишком близко к нулю, маржинальный доход будет быстро снижаться вместе с и. Логарифм совокупного коэффициента Шарпа
равен его верхней границе In 5-In р минус щ 1ч
2 I
рп J
, который при р?7 > 5
близок к -----. Например, если р - 0,5, то 10 активов приведут к 5%-ному
2/977
максимальному коэффициенту Шарпа, достигаемого через диверсификацию, а удвоение количества взаимозаменяемых активов — до 50 с 25 повышает коэффициент Шарпа только на 1%. На практике понижение качества вторых 25 активов, скорее всего, поглотит доходы от диверсификации, если только активы не являются почти некоррелированными. К сожалению, для клиентов, среди менеджеров взаимных фондов очень немногие играют только на повышение.
Оптимальность длинных/коротких хеджей в крупных портфелях
Если Р — это матрица и х /7 со всеми недиагональными элементами, равными р, то легко все диагональные элементы Р-1 будут равны 1 + (и ~ 2)р
-----Ь----LL---, в то время как все недиагональные элементы равняются (1 +
-------£---------------И снова р должна превосходить ———, чтобы дисперсии (1 - р)(1 + (лг - 1)р)-и-1
254
13. Ставка на бета
оставались положительными, так что если п может безгранично расти, р не может быть отрицательным.
Если обозначить через Д,- разность между отдельным коэффициентом Шарпа $ и средним коэффициентом Шарпа для всех активов, оптимальный вес, умноженный на волатильность, должен быть пропорционален:
(1 + (и - 2)р) 5 - Sj = (1 - p')Si + p(nS, - £5.)
J
= (I - p)S, + pn^.
Следовательно, если n достаточно велико, стратегия оптимального портфеля будет всегда играть на понижение положительно коррелированных активов с коэффициентами Шарпа ниже среднего.
Безграничные доходы от длинного/короткого хеджирования
Продолжая пример, предположим, что активы могут иметь два равно распространенных коэффициента Шарпа S\ и S2. Тогда максимальный возведенный в квадрат коэффициент Шарпа составляет:
2
(1 - р) (S,2 + S2 ) + р (5, - S2 )2
(1 - р)(1 + (и - 1)р)
что при условии, когда п становится большим, приближается к:
S2 + S; n(St -S2y-
2 + 4(1-р)
В отличие от диверсификации, максимальный коэффициент Шарпа от хеджирования безгранично растет по мере того, как растет п. Чтобы понять почему, представьте, что вы владеете активами высшего и худшего качества в оптимальных длинных/коротких парах, с одинаковой волатильностью для каждого владения. Коэффициент Шарпа каждой пары будет составлять |5. -S2|
—' , а поскольку п/2 пары некоррелированны, совокупный возведенный
>/2(1 - Р)
ntS.-Stf
в квадрат коэффициент Шарпа будет составлять -!----—, что охватывает
4(1 - р~)
большую часть допустимых доходов.
Генерирование некоррелированных компонентов при помощи регрессий
Пусть {-AS} обозначает ряд случайных переменных из J величин. Определим, что Хо— 1, и рассмотрим остатки Rj, формируемые последовательно
255
Часть 2. Постижвнио невежества
от i = 1 до /л?, путем регрессии X, по Х-ь ...» AJ). Согласно правилам линейной регрессии каждая R, будет линейной комбинацией Ао, ..Xi9 некоррелированной с Xi, ..., Х^]. По структуре она также некоррелированна с любыми предшествовавшими остатками. Следовательно, ни один остаток не будет коррелирован с любым другим.
Собственные векторы и собственные величины
Ненулевой вектор z — это собственный вектор квадратной матрицы А, со связанным скалярным собственным значением X при Az = te. В то время как любой скалярный член, кратный собственному вектору, также является собственным вектором (с тем же связанным собственным значением), обратим внимание на собственные вектора единичной длины, где z'z — 1. А также рассмотрим вещественную симметричную матрицу А. Чтобы преобразовать несимметричную матрицу в симметричную, дающую такие же квадратичные формы, усредните ее с ее транспозицией.
Отношение собственного вектора к собственному значению может быть переписано как (А — 7J)z = 0, которое имеет ненулевое решение для z тогда и только тогда, когда определитель |Л — Л/| исчезает. Это дает полиномиальное уравнение по X в степени и. Предположим, что п решений являются четкими, игнорируя незначительные осложнения, которые представляют из себя удвоения.
Портфель с весами, пропорциональными собственному вектору z ковариационной матрицы X актива, будет иметь дисперсию, которая является положительным членом, кратным z', т.е. Ez — z"kz = 'kz'z — k, Следовательно, ни у одной ковариационной матрицы не может быть отрицательных собственных значений. И ни одна ковариационная матрица не может быть корреляционной.
Собственные векторы и собственные величины вещественных симметричных матриц
Пусть А — это вещественная симметричная матрица с четкими собственными значениями {X/} и собственными единичными векторами (z,}. Тогда любой собственный вектор будет ортогонален любому другому, поскольку
Zizizj — Z;A Zj — z.tA z . ~ <=> zzzy ~ 0 .
Пусть A = diagQXj ... XJ) обозначает диагональную матрицу собственных значений, a Z = [zi ... z„] обозначает квадратную матрицу связанных собственных векторов. Ортогональность четких собственных векторов подразумевает, что Z'Z ~ Ц a Z'AZ = А. Более того, Z1XZ' = ZZ'AZZ' — А. Другие результаты включают:
• Л и Z должны быть вещественными. Сложные собственные векторы, подобно сложным собственным значениям, появляются сопряженными
256
13. Ставке ва бета
парами в форме А±Ву/—\. Но (А + Ву/—1)'(А — Ву/~Т) = А ’ А 4- В1В , что не может равняться нулю, если только А и В не равны нулю.
• А будет положительной (полу-) определенной тогда и только тогда, когда все собственные значения будут положительными (неотрицательными). Поскольку w'Aw = w'ZAZ'w, любая квадратичная форма в векторе w и А может быть переписана как квадратичная форма в w'Z и Л. Эта форма является положительно взвешенной суммой собственных значений, а следовательно, может быть отрицательной тогда и только тогда, когда по крайней мере одно из собственных значений будет отрицательным.
• Если А является определенно-положительной, у нее будет определенноположительная инверсия и квадратный корень. Инверсия А~1 равняется ZA-1Z', поскольку ZA“*ZZAZ' = ZA-1AZ' = ZZr — L Квадратный корень АУг равняется ZA/2Z', поскольку ZA*/aZ'ZAl/’Z' = ZA/2A/2ZZ = ZAZ' = А. Это подтверждает выдвинутое ранее утверждение.
Идентификация базового основного компонента
Для множества векторных величин X со средним М, компоненты в направлении z задаются X’z с дисперсией z'E[(X - М)(% — М)^ = z'Zz. У основного компонента имеется максимум дисперсии, контролирующей длину z. Чтобы ее идентифицировать, решите задачу условной максимизации с лагранжианом z'XX’z — X^z'z — 1). Условие первого порядка 2Lz - 2Xz = О показывает, что z должен быть собственным вектором X. Почему так? Поскольку дисперсия z’XX'z = zXz = Xzz = X, основной компонент должен быть собственным вектором, связанным с максимальным собственным значением X.
Если X измеряется в стандартных отклонениях от среднего, то, чтобы контролировать отличия в единицах измерения, Е[(Х — М)(Х - М) '] будет соответствовать корреляционной матрице Р, а не X. Основные компоненты могут быть рассчитаны относительно любой из них.
Другие основные компоненты
Среди компонентов единичной длины у, которые не коррелированны с первым основным компонентом z, объясняющим большую часть дисперсии, интерес вызывает второй основной компонент. Соответствующий лагранжиан y'Zy — г{(у'у — 1) — v(y'z — 0) отвечает условию первого порядка:
2Zy -• 2ry —vz~ 0
помимо ограничений допустимости. Предварительно умножьте это уравнение на z и воспользуйтесь информацией по ортогональности и единичной длиной собственного вектора для следующего упрощения:
О = Zz'Zy — 2qz 'у — vz'z = 2Xmaxz у’ — 0 — v = —v.
Следовательно, v = 0, а условия первого порядка указывают, что у должен являться собственным вектором X, отличным от z. Ограниченная максимальная
257
Часть 2. Постижение невежества
дисперсия есть т|, так что у должен быть связан со вторым по величине собственным значением. Сходная логика применима и к другим основным компонентам.
258
14. Помощь со стороны убеждений
Каждую субботу в Club Mad день посещений. Дети и родители, супруги и любовницы, друзья и деловые партнеры могут прийти на несколько часов или на весь день. Они могут посплетничать с выздоравливающими или подремать с ними, сходить на лекцию или воспользоваться спортивными площадками, а также от души закусить- и выпить. Все это за скромную плату в 100 долл., при этом для маленьких детей вход бесплатный.
Не всем нравится эта политика. По субботам намного больше криков, чаще случаются драки, вскрываются вены и предпринимаются попытки самоубийства. Сотрудники Club требуют тройную оплату за работу по субботам. Страховщики предложили сократить наполовину расходы по страхованию, если посещения будут отменены. Наиболее строгие критики такой политики — это те, к кому приходят посетители. «Пусть тайный приют останется тайным», — кричат они. В качестве уступки в Club Mad появились зоны «спасения», куда посетителям вход воспрещен, охраняемые громилами, набранными из местных ночных клубов. В этих зонах очень людно и уныло по субботам, что заставляет обитателей сравнивать их с лагерями беженцев в Боснии.
Почему, несмотря на все сопротивление, Club Mad продолжает практику дней посещений? Рекламная брошюра Club подчеркивает терапевтическую цель: чтобы сохранить связи обитателей Club с «материком» — таков клубный термин, означающий весь остальной мир. Однако, беседуя за коктейлем с аналитиками Уолл-стрит, готовящихся первичное размещение акций Club Mad, доктор Дементи однажды открыл реальную причину. «Это невероятно эффективный маркетинговый инструмент, -— сказал он. — Наши записи показывают, что гости, которые принимают посетителей, в среднем остаются в клубе на 25% дольше тех, кто не принимает. Полагаю, это напоминает тем, кто скучает по родным, почему они так плохо чувствуют себя дома. Еще один плюс: когда посетители видят все прелести Club, многие из них решают зарезервировать номерок для себя. А некоторые остаются в тот же день!»
Аналитики отнеслись к его словам скептически, и в следующую субботу просочились в Club под видом посетителей. По пути они прошли мимо матери с дочерью, которые уезжали. «Это было так здорово, мамуль, — говорила девочка, сверкая от счастья. — Можно я тоже буду ездить в Club Mad, когда вырасту?» «Если будешь хорошо себя вести и зарабатывать много денег», — сказала мама. Аналитики пересмотрели свои рекомендации, отметив для себя «Обязательно купить», и первичное размещение акций вполовину превысило намеченную сумму.
259
Часть 2. ТТсстижанив наважаства______________и__=та_=_==^=_=^=
Конвей не знал, почему в Club Mad разрешаются посещения, но был этому рад. «Добро пожаловать, — сказала администратор. — Позвольте, я запишу ваше имя. Как зовут человека, к которому вы приехали».
«Конвей Уисдон. Я пришел к Девлину Адвогадо».
Администратор проверила свой список посетителей. «Да, он вас ждет. Он даже внес плату за ваш визит. Шерри сейчас вас проводит».
Шерри оказалась стройной блондинкой, что-то между стоматологом и брокером рынка недвижимостью. На ес пиджаке блестела крупная желтая пуговица с надписью сиреневого цвета: «Мы исцеляем людей с деньгами». «Принести вам что-нибудь выпить? — спросила она. — Стакан апельсинового сока?»
«Нет, спасибо. Я только что позавтракал».
«Жаль. Девлин, должно быть, забыл сказать вам о нашем позднем завтраке с шампанским. Записать вас на массаж или маникюр, пока вы здесь?»
«Нет, спасибо. У меня нет времени».
«Даже на быстрый осмотр предлагаемых услуг?»
«Может быть, в другой раз. Я хочу повидаться с Девлином. Я не видел его уже несколько месяцев. Как он?»
«О, он быстрыми темпами идет на поправку, — выпалила Шерри. — У него чрезвычайно высокая мотивация, и, тем не менее, он чутко относится к потребностям других и никогда не навязывает своих взглядов».
«Рад это слышать». Неужели это о Девлине!? Они вошли в большой, со вкусом обставленный холл. Народу было довольно много. Одни читали, другие сидели за компьютерами, третьи просто разговаривали. Конвей заметил взмах руки. Это был Девлин. Конвей поблагодарил Шерри и пошел дальше. «Рад тебя видеть, Девлин».
«Я тоже». Они обменялись рукопожатиями.
«Я слышал, дела у тебя идут отлично».
«Неплохо. Я стараюсь никому не мешать и потихоньку изучаю квантовую механику. Если кто-то что-то спрашивает или просит, я говорю «не знаю», «мне все равно» или «как хотите»».
Так вот что Шерри имела в виду. Конвей рассмеялся: «Я горжусь тобой, Девлин. Наконец-то ты овладели социальными навыками».
Девлин улыбнулся: «Это облегчает жизнь. Мне нравится читать об ученых, которые признали неопределенности в сердце того, что, по их мне, они знали наизусть, и построили на этой основе интересные теории».
«Как ты?»
«Хотелось бы верить. Пока у меня отлично получилась только первая часть».
«Откуда ты знаешь?»
260
14. Памащь са стнрнны убвжданий
«У меня начисто отсутствуют идеи. Есть такая присказка: из репы крови не выжмешь».
«По мне, так ты совсем не смотришься репой. Как ты отнесешься к тому, что я подброшу тебе пару идей на пробу?»
Девлин попытался сдержать улыбку: «Не обижайся, Конвей, но я никогда не считал тебя богатым на идеи».
Конвей рассмеялся: «В цель! Спасибо, что напомнил мне о преимуществах отсутствия необходимости ежедневно ходить на работу. На самом деле я пришел с несколькими острыми идеями, или, по меньшей мере, идеями относительно резкости. Я надеялся, что ты поможешь мне их отточить».
Девлин, изголодавшийся по серьезным разговорам, не смог устоять перед наживкой: «Какое отношение резкость имеет к финансам?»
Конвей притворился, что не расслышал: «Конечно, если ты слишком увлечен физикой, я пойму...»
«Если только ты не имеешь в виду что-то типа коэффициентов Шарпа. Очень полезно в мире среднего и дисперсий. Плохо только, что они не могут справиться с риском айсберга».
«Я тоже об этом подумал. В конце концов, коэффициенты Шарпа являются функциями только первых двух моментов, в то время как риск айсберга прячется среди моментов более высокого порядка».
«О чем ты думаешь сейчас?»
«Что мы можем внедрить, по крайней мере, часть риска айсберга, проводя различия между условными и безусловными коэффициентами Шарпа».
Девлин оживился: «Что ты имеешь в виду?»
«Большую часть риска айсберга составляет неопределенность. Мы не совсем уверены в оценках для первого и второго моментов, действительно применявшихся в прошлом. У нас еще больше сомнений относительно того, применимы ли они в будущем. Но стандартные процедуры просто основываются на лучших оценках. Они не принимают в расчет степень наших сомнений».
«И как ты предлагаешь принять это в расчет?»
«Путем моделирования сомнений как вероятностных распределений по параметрам. Каждое убеждение «исход» представляет условно вескую оценку параметра».
«В этом нет ничего дурного. Даже лучшие экономические оценки допускают ошибки. Но чего мы, таким образом, добьемся?»
«Это позволит сформировать безусловные оценки, которые соединят условные оценки и неопределенности».
«Велико дело. Независимо от того, равна ли средняя избыточная доходность точно 4% или она просто нормально распределена в районе 4%,
261
Часть 2. ТТвстижвнив новожоства
безусловное среднее все равно составляет 4%».
«Конечно. Но безусловная ковариационная матрица — это больше, чем средняя условная ковариационная матрица. Так что следует прибавить ее к ковариационной матрице условных средних. Для любого портфеля безусловная дисперсия всегда будет равна или больше условной дисперсии».
«И что? Как это помогает справиться с риском айсберга?»
«Ну, прежде всего, это может избавиться от распределений, которые хорошо выглядят на бумаге, но не являются разумными».
«Например?»
«Предположим, что ты выбираешь между двумя активами, которые в целом одинаковы, за исключением небольших отличий в налогообложении. Поскольку корреляция в каждом налоговом режиме составляет почти 100%, традиционная теория предлагает играть на повышение актива с более высокой ожидаемой доходностью и на понижение второго».
«А чем отличается твой подход?»
«Неопределенность относительно налогового режима увеличит безусловную волатильность каждого из активов, но не сильно изменит ковариацию. Итак, безусловная корреляция упадет, сделав пару длинная/короткая сделка более рискованной. Если она упадет достаточно, ты не станешь играть на понижение меньшего актива, а вместо этого купишь его для диверсификации».
«Ты не мог бы продемонстрировать мне расчеты? Я хочу быть уверенным, что все правильно понимаю».
Господи, спасибо! Конвей вытащил какие-то бумаги из своей сумки и вручил их Девлину. «Я надеялся, что ты так скажешь. Вот пример, который я проработал».
Пример: Распределение актива с высокой неопределенностью
• Активы 1 и 2 имеют 10%-ную условную волатильность и 90%-ную
*-
<Среднйе йёопределе Убеждения ? мотугу^Ь^ как
независимые распределения вероятностей со средним и 5 и 3% соответственно и стандартным отклонением 5. •. — уу.'У уу.у..
• Безусловная дисперсия — 10% х!0% + 32= 0,01 +
• Безусловная ковариация = 0,9 х 10% * -.10% 0,009*
У 9 ; X- \ л . %%%'
10 + 1000J2 ’ ;
............ . У ; У уу -V
• Оптимальный коэффициент распределения актива — , так что играйте
.. ’ . • . : .. У' » .-У " л. . у'5/7 y^-y;v:. ;
на понижение актива 2 тогда и только тогда, когда р = 0,6, что, в свою у очередь, справедливо тогда и только тогда, .когда'5:S3?Q7%*jyjy:.г.
• Безусловная корреляция р =
' --у;у'уу -’ х .у - . ' у
у: \у. y.ysy -J4 :Jу. У sт:. . <
262
U. Помощь св стороны убождоний
Чувствительность доли актива 2 к неопределенности.
Sensitivity of asset share 2 to uncertainty
«Я думаю, это может быть полезно, — прокомментировал Девлин, изучив пример. — Но разве неопределенности всегда склоняют тебя против коротких сделок?»
«Не обязательно. Предположим, что неопределенность имеет отношение к обычной катастрофе. Чем более вероятна катастрофа, тем ниже безусловное среднее и выше безусловная корреляция. И то и другое склонят играть на понижение более слабых активов. Предположим, я модифицирую предыдущий пример так, что там не будет условных корреляций, но появится небольшой шанс обычной катастрофы, которая собьет 30% с обоих активов. Вот что происходит». Конвей достал еще несколько бумаг.
Пример:Распределение активах рискомобь^нойтсадастрофь!
^и-стий^^
условной корреляции при известных. условщ^
Обычная катастрофа (-30%) произойдет с вероятностью #< 10%. Безусловные средние = 0,05 - 0,03# и 0,03 - 0,3# соответственно.
Безусловная дисперсия = 10% х 10% + #(1 -#) к30*Й'к ЗЙ% = 0,01 4-
БезуслОвнаяковариация = 0 + Ковариациякатайр^ы;??Дисперсия х'зо% х зо%
Безусловная корреляция р '<
. -<;.... х XX л' 1+9?(1-?)'. . :••• л.
263
Пасть 2. Пвстижвнив нвввжвства
•Д. 'ЛЖ Оптималыпяй коэффициснт распределения актива = 5-30^-р(3-30)^ - ;_
-^——-..ЖЖ'..: , так что играйте на понижение актива 2, если
3 —30<? '
р > 3 , что требует <7 > б,4%- . ЖЖ;,-
5 - ЗОг/ / ' ' . • Ж'ЖЖЖЖЖ' , "
Чувствительность доли актива 2 к риску катастрофы
Sensitivity of asset share 2 to disaster risk
Девлин посмотрел расчеты и покачал головой: «Цифры верны, но у меня есть сомнения относительно самой схемы».
«Уверяю тебя, невозможно точно знать, насколько велика будет катастрофа. Но можно сделать допуск на неопределенность в этом отношении тоже».
«Я не это хотел сказать. Я имел в виду фокус на среднее и дисперсию в чрезвычайно ненормальной среде. Подозреваю, что большинство инвесторов с радостью пожертвуют частью коэффициента Шарпа, чтобы сократить риск катастрофы. Но в твоей системе показателей это не имеет значения».
Конвей кивнул: «Ты прав. Я и сам увидел проблему, но не знал, что ей противопоставить. Тогда я пошел в библиотеку и стал прочесывать литературу, чтобы узнать, какие предлагаются меры борьбы с этим».
«Ну и?»
«Ничего. Я все еще не нашел ответа. Но нашел отличный способ внедрения неопределенности, когда все является многомерно нормальным. Это называется подходом Блэка — Литтермана».
«Что в нем такого замечательного?»
264
14. Помощь со стороны уВождоний
«Ну, прежде всего, тебе не нужно иметь свое мнение обо всем. Совершенно нормально быть невежественным».
«Мне это нравится. А если у тебя нет своего мнения, то чье же мнение используется?»
«Рынка. Или, скорее, обзор рынка, подразумеваемый моделью».
«Как ты это подсчитываешь?»
«Считай рынок объединено принимающей решение субстанцией, выбирающей оптимальные веса для рискового портфеля с целью максимизировать коэффициент Шарпа. Избыточные доходности будут прямо пропорциональны ковариационной матрице, умноженной на взвешивающий вектор. Правда, рыночный взвешивающий вектор — просто относительная капитализация активов. Но если предположить, что мир — устойчиво многомерно нормален, то ковариационную матрицу тоже легко идентифицировать. Мы можем сделать вывод о коэффициенте пропорциональности из других данных, например из долгосрочного коэффициента Шарпа. Перемножь эти три величины и получишь подразумеваемую избыточную доходность».
«А что если рынок ждет, когда ковариационная матрица изменится?»
«В принципе, можно было бы использовать подразумеваемые волатильности для рынков опционов, чтобы идентифицировать дисперсии. Если в наличии есть достаточно разнообразные комплексные опционы, мы могли бы идентифицировать ковариации. В противном случае, полагаю, нам придется проводить исторические корреляции».
«Почему бы не использовать исторические данные по средним, чтобы вменить ковариации?» — ухмыльнулся Девлин.
Приятно видеть, что он приходит в норму. «Ну, Девлин, ты отлично знаешь, почему нет. Относительных рыночных потолков п различных активов достаточно, чтобы идентифицировать только п других переменных. Этого достаточно для того, чтобы идентифицировать относительные избыточные доходности, но не ковариации. А в любом многомерно нормальном мире необходим намного более длинный исторический ряд, чтобы идентифицировать средние, чем ковариации. Так что Блэк и Литтерман просто предполагают, что оценки ковариации являются действительными».
«Мне это не очень нравится, но продолжай. Что еще хорошего в подходе Блэка — Литтермана?»
«Он позволяет более гибко подходить к своим убеждениям. Вместо того, чтобы по отдельности предсказывать европейский и японский рынки, например, та можешь просто спрогнозировать, что Европа, скажем, скорее всего, будет работать эффективнее Японии в среднем на 5% при стандартном отклонении в 5%. Или можешь сказать, что существует 16%-ный шанс, что Европа будет эффективнее Японии на 10% — из этого можно извлечь и подразумеваемое среднее, и стандартное отклонение в 5%».
«А если твое убеждение касается средневзвешенной корзины?»
265
Часть 2. Пастижанив нвавжастаа
«Не проблема. Убеждение просто должно относиться к линейной комбинации доходностей актива, с неопределенностью, выражаемой как нормальное распределение».
«Как насчет сложных убеждений?»
«С этим тоже никаких проблем при условии, что каждое убеждение относится к линейной комбинации, а совместная неопределенность может быть выражена в терминах многомерно нормального распределения».
«А как ты совмещаешь рыночный консенсус с убеждениями предсказателя?»
«Для ожидаемых избыточных доходностей ты просто берешь взвешенное среднее, где веса пропорциональны инверсии ковариационной матрицы, известной как прецизионная. Интуитивно, чем менее расплывчатой будет оценка, тем сильнее хочется ее взвесить».
«Зачем взвешивать по точности, когда можно использовать чего-то еще?»
«Вот единственный способ логично все объяснить. Рассматривай каждое убеждение точности j как основанное на j независимых наблюдений, или мер, где каждая мера имеет точность единицу».
«Что измеряют эти наблюдения?»
«Настоящее среднее, которое никто из нас не знает наверняка. Так думать об убеждениях не обязательно, но полезно».
«Хорошо, продолжай».
«В любом случае, соединяя два убеждения, каждая базовая мера должна быть взвешена в равной степени. Это означает, что каждое убеждение взвешивается по его точности, а совокупная точность равняется сумме отдельных точностей».
«Ясно. И это все, что нужно, чтобы выработать оптимальные веса портфеля при заданных разнообразных убеждениях?»
«Абсолютно. Хотя расчеты несколько путают, они достаточно просты. Лучше всего они дают гибкость в том случае, когда изначальные рекомендации выглядят нелепыми. Надо просто урезать точность собственного убеждения и сократить рекомендуемые веса до эталона».
«Почему бы просто не усреднить рекомендации с эталоном напрямую?»
«Это не так уж сложно. Кроме того, сокращение не всегда линейно. Если хочешь взглянуть, я подготовил пример».
«Пожалуйста».
«Консалтинговая группа Вахта сводит в таблицы отдельные индексы для компонентов S&P 500 «Рост» и «Стоимость», где активы «Роста» определяются как имеющие более высокие соотношения цена/прибыль, нежели активы «Стоимость». С 1993 г. доходности по «Росту» и «Стоимости» были на 80% коррелированны с волатильностями в 18,4 и 14,4% соответственно. Чтобы равное распределение было оптимальным при предполагаемом долгосрочном коэффициенте Шарпа 0,3, рынок должен ожидать избыточных доходностей в
266
14. Помощь св стороны уВвждвний
5,3% по «Росту» и 4% по «Стоимости» с разностью в 1,3%. Теперь предположим, что ты лично на 95% уверен, что на самом деле разность по ожидаемым доходностям находится между —3 и +5% при среднем в 1% и стандартном отклонении 2%. Как будут варьироваться распределения активов, исходя из доверия, которое ты оказываешь мнению рынка относительно твоего мнения?»
«Давай-ка посмотрим. Если я не уважаю собственное мнение, то, вероятно просто буду удерживать эталон 50/50. Если взять другую крайность, когда я считаю, что согласие с рынком ничего не стоит, то меня вообше не будет волновать его мнение. Вместо этого я положу в портфель те активы, за которые готов поручиться, а именно комбинацию длинные сделки по «Росту»/короткие по «Стоимости»».
«Что если ты не слишком сильно доверяешь собственному мнению?»
«Полагаю, что, возможно, придаю слишком низкий вес активам «Роста», поскольку моя оценка средней разности по доходностям ниже рыночной. Но если я обрету большую уверенность в своей правоте, то в итоге начну концентрироваться на длинной/короткой позиции».
«Точно! Вот график. На самом деле кривая начинает становиться более крутой, если ты даже на одну десятую так же уверены в собственном мнении, как и в мнении рынка. И как только она становится более крутой, рост становится почти линейным в относительном весе, приписываемом твоему частному убеждению. В то время как не все ситуации демонстрируют поворотную точку, почти линейность для высоких степеней уверенности является типичной. Приписывание равных весов своим личным убеждениям и убеждениям рынка — неплохо для приближенных подсчетов и позволяет избегать крайностей, не имитируя рыночное распределение».
Оптимальная доля актива «Роста» в примере Блэка —Литтермана
Optimal growth stock share in Black-Litterman example
267
Пасть 2. Постижонио новожоства
«Умно, — сказал Девлин, кивая. — Но, с моей точки зрения, слишком сложно. Твой взгляд на то, как взвешивать свое убеждение против рыночного, тоже является личным убеждением, так что я не очень уверен в том, что ты сохранишь различие. И хотя приближение к эталону вытаскивает нас из беды, это не объясняет, почему нас туда затягивает».
«И почему же, по-твоему, нас туда затягивает?»
«Потому что Блэк-Литтерман сводит всю нашу неопределенность к одной колоколообразной горе условных средних. А что, если рынки скинут нас с одной горы на другую, так как сделали это в время технологического бума, который вот-вот прикажет долго жить? От нас и мокрого места не останется задолго до того, как кто-нибудь заметит предполагаемый 2%-ный выход рабочих характеристик за установленные пределы условных средних».
«Я согласен. Первая модель, которую я тебе показал, справляется с изменением режима, но теряет оптимальность максимизации коэффициента Шарпа. Подход Блэка — Литтермана идеально подходит к максимизации коэффициента Шарпа, но исключает крупные смены режима. Как нам их примирить между собой?»
Девлин не ответил. Он сидел молча, все больше и больше погружаясь в свои мысли. Секунды перетекали в минуты.
«Девлин, ты со мной?» По-прежнему нет ответа.
Я его потерял. Конвей уже собрался уходить, когда он почувствовал, что кто-то хлопнул его по плечу. Он обернулся и увидел женщину с волосами цвета воронова крыла, одетую в черное. У красавицы были самые печальные глаза, какие Конвей когда-либо видел. «Извините, но я подслушивала, — сказала она. — Если доктор Ничего-не-знайка не может вам помочь, возможно, это удастся мне».
«Уходи, Плакса, — вдруг вспыхнул Девлин. — Мы не нуждаемся в твоей помощи».
«Да нет, полагаю, нуждаетесь», — сказала она.
Пока Девлин отражает нападение, давайте проработаем математику корректировки убеждений.
Убеждения как вероятности
Вероятности — это меры объективного риска. Убеждения — меры субъективной неопределенности. Вопрос того, может ли последнее быть идентифицировано с первым является в течение многих лет единственным вызывающим острые разногласия вопросом в статистике. Ортодоксальные статистики утверждают, что это невозможно. Они решительно настроены искоренить субъективность, которая, как они считают, может только загрязнить
268
14. Помощь со стороны убеждений
науку. Они признают, что наблюдатель может получить только несовершенные наблюдения относительно меры вероятности. Но сама по себе мера должна быть точной, неподверженной причудам человеческого суждения.
Сторонники субъективной вероятности известны как байесовцы, названные так в честь преподобного Байеса, который положил начало этому подходу более двух веков назад. Байесовцы часто агностически относятся к существованию объективной меры риска. Они скорее сфокусируются на процессе умозаключения для соединения старой информации с новой и формирования суждений при неопределенности.
Чтобы навязать свою структуру, оба лагеря требуют, чтобы были удовлетворены определенные аксиомы по самой мере вероятности. Байесовцы либо налагают на убеждения сходную структуру, либо выводят ее из аксиом о разумном поведении при игре в азартные игры, основанных на том, что игроку не нравится проигрывать деньги.
Признание неопределенности
Пятьдесят лет назад байесовская статистика казалась обреченной. Но некоторые адепты этой теории не сдавались. Они показали, как в принципе обращаться с неопределенностями, присущими различным наукам, и постепенно стали получать поддержку. На практике они могли решать только относительно простые задачи, поскольку байесовская корректировка весьма требовательна к расчетам. Их последователи использовали растущую компьютерную мощь для того, чтобы значительно расширить диапазон байесовского анализа.
Книжные полки университетов несут в себе свидетельство растущей приемлемости субъективной вероятности. Сейчас намного больше, чем десятилетие назад, написано учебников, объясняющих баейсовский метод. Более того, все чаще появляются одобрительные отзывы о байесовском подходе.
Финансы, конечно, — эго все для людей, которые считают, что их инвестиции следуют определенным законам вероятности, при этом не уверены, каким именно, и пытаются угадать. Кажется, что такое положение дел сделает их самой удобной территорией для приложения байесовского метода. Тем не менее большая часть академических разработок в сфере финансов остается в браке с классическим подходом. Странно, не так ли?
Байесовское правило
Наиболее важное равенство в байесовской статистике известно как баейсовское правило. Оно описывает, как воспользоваться наблюдениями х, чтобы откорректировать убеждения о феномене У/, который вы напрямую не наблюдаете. Путем повторного применения правила условной вероятности, мы можем написать:
269
Часть 2. Постижение невежества
= IHW='
/ i
Здесь jP(y,) обозначает (субъективную) вероятность, что событие У/ произошло до или при отсутствии знания о том, что произошло событие х. А P(idx) обозначает откорректированную вероятность при условии, что
событие х возникает. Например, предположим, что в деревне всегда косят сено, когда светит солнце, и косят сено четверть обычно времени, когда пасмурно. Если вы начали с того, что сочли солнечную и пасмурную погоду равновероятными, тогда вероятность того, что погода солнечная при условии, что в деревне косят сено, задается следующим равенством:
Р ( Сено | Солнце} Р ( Сол нце} Р(Сено\Солнце} Р^Солнце} -г Р(Сено\Тень}Р(Тень}
2 4 2
4 .
5
Ни один ортодоксальный статистик не возражает против байесовского правила самого по себе. Они просто возражают против использования байесовского правила для описания убеждений и других вещей, которых не считают объективными мерами риска. И снова байесовцы утверждают, что это не имеет значения. И действительно, может ли когда-нибудь какой-либо наблюдатель полностью провести грань между объективными рисками и убеждениями.
Внедрение неопределенности в ковариации
При расчете оптимальных относительных весов портфеля с помощью правила ХМ’1 большинство пользуются наилучшими объективными точечными оценками для среднего М, обусловленного дисперсией, и дисперсии X, обусловленной средним. Конвей хочет пересмотреть это, сделав допуск на неопределенность, которую он моделирует в байесовском стиле как вероятностное распределение по среднему и дисперсии.
Шаткая дисперсия обычно не меняет оценку среднего (более формально «безусловное среднее условного среднего»), если только веса по различным наблюдениям не меняются. Однако шаткое среднее все-таки изменяет общую или безусловную дисперсию даже тогда, когда она не меняет условной дисперсии. Разность этих двух величин —- дисперсия условного среднего, которое никогда не бывает отрицательным.
Соответствующая формула матрицы выглядит так:
Covu [X] = Еи [Cov. [X]] + Cov„ [Д [X]],
270
14. Помощь со стороны убвждоний
где X —вектор, а индексы и и с обозначают безусловность и условность соответственно. Для недиагональных ковариаций безусловная стоимость может упасть ниже соответствующих ожидаемых условных стоимостей. Однако для любого портфеля безусловная дисперсия должна равняться или превосходить ожидаемую условную дисперсию, поскольку:
crj - сН = w’Cc% [JV] w — w’ En [Covc [ Aj w = w’Covw [X] vv > 0
Влияние на корреляции, коэффициенты Шарпа и веса портфеля
Предположим, что у двух активов равные условные дисперсии сг^, равные дисперсии сА их условных средних, корреляция рс их условных дисперсий и корреляция р,н их условных средних. Безусловная корреляция рг/ составляет:
Ри
2 2 2
= А А + рЕт = оР;_. + (1 - ё) Рт, где е = -2 сГ\ст~ СГ + О’
ст с т
У™-, [X]
Г<7ги[Х]’
Другими словами, р„ — это взвешенное среднее рг и рт, с весами, определенными соотношением условной дисперсии к безусловной. Если неопределенности в отношении условных средних независимы друг от друга, то рт= 0, а ри < рс. Если общий базовый фактор управляет всеми неопределенностями об условных средних рт— 1, a ptJ> рс.
Неопределенность сокращает коэффициенты Шарпа отдельных активов,
поскольку она поднимает их воспринимаемую дисперсию, не меняя избыточных доходностей. Чтобы определить относительные веса портфеля, нам нужно учесть также и их корреляцию. Примеры Конвея демонстрируют, что это влияние может быть потрясающим.
Предостережение для применения анализа коэффициента Шарпа
Как только вы внедрите неопределенность в среднее или дисперсию, распределение доходностей обычно перестает быть многомерно нормальным. При отсутствии многомерной нормальности в целом будет невозможно проранжировать желательность портфелей в терминах только среднего и дисперсии. Тем не менее, лучше быть примерно правым, нежели точно ошибаться. Корректировки, предложенные выше для неопределенности, могут предостеречь от экстремальных рисков.
Подход Блэка — Литтермана
Подход Блэка — Лиг германа покоится на пяти принципах:
271
Часть 2. Пвстижвнив нвввжвства
1. Мир избыточных рыночных доходностей является многомерно нормальным с неизвестным средним М и известной ковариационной матрицей
2. У аналитиков, делающих прогнозы, имеются убеждения относительно различных линейных комбинаций ожидаемых доходностей М. Так, Q имеет столько рядов к, сколько у специалиста имеется убеждений, и столько же
-10
3 3
, то у аналитика
есть два убеждения о трех переменных, из которых первое касается разности первых двух ожидаемых доходностей, а второе — простой средней ожидаемой доходности.
3. Убеждения могут быть выражены как многомерно нормальные распределения для QM, имеющие среднее q и ковариационную матрицу Q. Обычно Q считается диагональной, подразумевающей нулевую корреляцию между убеждениями, но это не главное.
4. Вектор рыночного эталона весит ww, рассчитанный с помощью текущих капитализаций, может считаться оптимальным выбором портфеля при заданном рыночном представлении R„}. Следовательно, ют должен быть пропорционален так чтобы R,„ = для некоего масштабного
коэффициента к. Этот коэффициент может быть рассчитан как:
wm'Rm РыночнаяИзбыточная Доходность _ Рыночный Коэффиицент Шарпа.
/С —— " । — 4 — _ 1 4 — —' 1 -
Рыночная Дисперсия Рыночная Волатильность
5. Рыночное представление R„, само по себе является случайным, со средним, равным ожидаемой доходности М и дисперсии тХ для некоего положительного скаляра т. Масштабный коэффициент указывает, насколько сильно аналитик оценивает свои личные убеждения относительно консенсуса.
Оставшаяся часть главы рассматривает последствия этих принципов.
Условная многомерная нормальность средних доходностей
Байесовское правило гласит, что плотность вероятности р\ от М при заданном рыночном консенсусе R}„ прямо пропорциональна плотности р? рыночных убеждений об Rm при заданном М, умноженном на плотность р? убеждений аналитика об М:
Рх К-) х Рг (К,„ \МУр-АМ)
f"1Rm ~ М' ^R"' ~ М) • exp Г -1 ( QM - q ) ’ Q -1 ( QM - q )
272
U. Помощь co стороны убеждений
ж ехр[ ~(Ят -M)'(rS)’’ (Я„, -М)
\ 7
+(еЛ/-9)’О-1(0Л/-^))) = ехрЦг .
Чтобы установить многомерную нормальность ру со средним М* и дисперсией V, нам необходимо показать, что Y не больше, чем на константу, отличается от квадратичной формы Y = — к/Г^'У } . (Константа
сдает, поскольку в любом случае плотность вероятности должна интегрироваться к 1.) Теперь У минимизируется при М = М*, в то время как Y может быть минимизирована в том случае, если:
-(zS)-1 (/?„, - M') + Q'£Y' (QM* -g) = О
<=>((£)' =(rS)'' R,„ +Q'CL-'q
M’ =((rZ)’' +2'Q-‘0)((zS)’1 R,„ +2'Q-y) .
Более того, Y и Y должны иметь одинаковые вторые производные относительно М, так чтобы
При этих условиях Y и У действительно согласуются так, как требуется.
Интерпретация в терминах отдельных средних и погрешностей
Если Q является обратимым, убеждения аналитика могут быть пересмотрены как среднее Q~q для М с погрешностью Q'£1~XQ. Совокупное среднее М* тогда действительно является взвешенным средним рыночного представления Rm и убеждения аналитика Q~xq с весами, равными точностям (обратите внимание, что Q'QT'QQ~xq = Q'£l~}q). Более того, точность совместной оценки является суммой отдельных точностей, поскольку для двух независимых оценок, взвешенных по их точностям УУХ, она должна всегда быть такой:
Var
+V2-'Vaf[X1/2
V2 ' + ковариации ) (PJ 1 + V2 1)
= GT’ + r TW + i;-' +о)(г-1 +Г’1) ’ = (У+УУ-
Иными словами, Q не обязательно должна быть обратимой, но мы все
273
Пасть 2. Постижение невежества
равно можем провести такую интерпретацию путем наращивания Q дополнительными рядами, которые делают ее обратимой, проводя расчеты, а затем отбрасывая дополнительные ряды.
Оптимальные веса портфеля при заданных убеждениях
Безусловная ковариационная матрица доходностей актива равняется сумме условной ковариационной матрице Z и ковариационной матрицы V из М при заданном Rm. Чтобы максимизировать коэффициент Шарпа, установите веса портфеля пропорционально (S + K) умноженному на безусловное среднее М*. Подставляя это выражение в формулу и упрощая, получаем:
(s + и)' М' =(S + K) 1 к((т£)Rm +2'Q 'g)
= + ' ((rSf1 kZwm +Q’£Y'q}
-((r-'E’1 +e'Q-1e)L + z)(r-1^v,„ +Q'CT]q) =((i+r-,)z+e'Q-iev)‘l (т-’А^+е’п-'я)
Это резюме формулы Блэка — Литтермана. Стандартная максимизация коэффициента Шарпа — это частный случай, где Q = /, q = М, Q = Е, а т = оо.
274
15. Оценка рисков без сожалений
Девлин приготовился к нападению со стороны незваной гостьи. «Уходи, Плакса. Мы говорим не о неудачах во взаимоотношениях, так что тебе будет с нами неинтересно».
«Очень умная мысль, доктор Ничего-не-знайка. Мои поздравления. Жаль только, что она ошибочна».
О, нет! Я попал в мыльную оперу. Пожалуйста, вы, оба, поубавьте свой пыл. «Я так полагаю, вы друг друга знаете», — с милой улыбкой сказал Конвей.
«Мы вместе ходим на групповую терапию, — сказала женщина. — Два раза в неделю по два часа».
«Дважды в неделю - это целая вечность. Так будет правильнее, — сказал Девлин. — Словно сцена из пьесы Сартра об аде».
«Вы читали «Выхода нет»? Я потрясена, Ничего-не-знайка. Там же нет ни единого уравнения».
«Что вы, Плакса, имеете против уравнений?»
«Ничего. Я просто считаю, что групповая терапия — это не то место, где их нужно обсуждать. Предполагается, что ты будешь говорить о том, что тебя беспокоит».
«Ну, неопределенность беспокоит меня так же, как вас беспокоит потерянная любовь. По крайней мере, я сконцентрирован на настоящем, чего о вас не скажешь».
Глаза девушки наполнились слезами. Конвею стало ее жалко. «Не обращайте внимания на моего друга, — сказал он мягко. — Иногда его заносит. Меня, кстати, зовут Конвей. А вас?»
«Регретга, — сказала она. - К сожалению, ваш друг прав. Я действительно слишком сосредоточилась на прошлом. Именно поэтому я больше не торгую на бирже. Но знаю, по каким принципам следует торговать. Думаю, они могут помочь вам в распределении активов».
«Типа «покупай дешево, продавай дорого»?»
«Это только часть. Но я имею в виду нечто более общее. Это теория экономической рациональности».
«Что вы можете об этом знать?» — с подозрением спросил Девлин.
«Больше, чем вы думаете. Я два года училась в докторантуре, специализировалась в области экономики бихевиоризма, а потом решила, что стезя ученого не для меня. Но я нашла хороший способ приложения своих знаний, а именно - заключение сделок против тех, у кого нет таких знаний».
«Что же вы такого знали, чего не знали они?»
275
Часть 2. Постижение нвввжвства________________________
«Это очень просто — делать ставки как трус. И очень важно этого не делать. Нужно быть хладнокровно рациональным».
«Вы хладнокровно рациональны? Ха!» — фыркнул Девлин.
Глаза Регретты приобрели стальной оттенок.: «Я вам уже говорила, Ничего-не-знайка, что больше не заключаю сделок. Точно так же, как вы больше не отвечаете ни на какие вопросы. Но, к вашему сведению, меня раньше называли Снежной королевой. А теперь, вы будете меня выслушать или этот разговор только для мальчиков?»
Девлин мгновенно съежился, уши его покраснели. Она попала в точку. И Девлин это знал. «Поскольку вы столь тонко выражаете свой выбор, — сказал Конвей после паузы, — мы с удовольствием вас выслушаем. Не так ли, Девлин?» Девлин бросил на Конвея сердитый взгляд, но ничего не сказал.
«Спасибо, — сказала Регретга. — А теперь — о том, что, по моему мнению, вам следует сделать. Во-первых, измеряйте каждый исход в терминах валовой процентной доходности: например, 1,05, если у вас 5%-ная доходность. Во-вторых, возведите эту доходность в квадрат и возьмите отрицательную инверсию. В-третьих, сформируйте вероятностно взвешенное среднее различных отрицательных инверсий. В-четвертых, выберите портфель, который генерирует самое высокое вероятностно взвешенное среднее. Я понятно выражаюсь?»
Девлин с Конвеем были в нокауте. «Она соображает в математике», — проворчал про себя Девлин. «Возможно, даже слишком понятно, — ответил Конвей. — А откуда вы получаете квадрат?»
Регретга улыбнулась. «На самом деле я не знаю насчет квадрата. Просто теория гласит: используй степень, которая изменяется с твоим неприятием риска. Возможно, два — это не самое верное число. Я просто полагаю, что оно не сильно ошибочное».
«А зачем вообще использовать степенную функцию? И зачем взвешивать с помощью вероятностей?»
«Первое зависит от того, чего вы нс знаете. Второе — от того, что вы не хотите выяснять».
«Я потерял нить рассуждений, Регретга. А я-то думал, что это Девлина сложно понять. Не возражаете против того, чтобы начать все с начала?»
«С экономической рациональности?»
«Почему бы и нет? Она сильно отличается от обычной рациональности?»
«Я не уверена в этом. Я просто хочу сконцентрироваться на принятии экономических решений в условиях неопределенности: рациональных азартных играх, если вам так больше нравится. А здесь рациональность сводится к одному простому правилу: не трусь».
«Не трусь? Что вы под этим имеете в виду?»
«Не делайте ставок или рядов ставок, которые могут привести к тому, что вы окажетесь в более затруднительном положении, чем были».
276
15. Оценка рисов баз свжалвний
«А как вы определяете «более затруднительное положение»?»
«Довольно либерально. Больше — это всегда лучше, чем меньше. Но синица в руках может быть больше или меньше, чем два журавля в небе. Все зависит от вашего отношения к риску».
«Если определение настолько либерально, то почему я не могу просто определить «более затруднительное положение», чтобы сделать все ставки рациональными?»
«Хороший вопрос. Существует совсем немного недозволенных вещей. Во-первых, вы должны стремиться оценить каждую ставку — под ставкой я имею в виду любой выбор с неопределенным исходом — против любой другой. Если вы строго предпочитаете ставку А ставке В, то не можете сказать, что вы предпочитаете В ставке А при тех же условиях. Нужно определяться. В противном случае хитрый трейдер может подвигнуть вас заключить сделку по А вместо В, а затем заплатить лишние деньги, чтобы выкупить А. Это аксиома полноты».
«Это очевидно, — сказал Конвей. — Что еще?»
«Ваш выбор должен быть транзитивным. Если вы предпочитаете ставку А ставке В, а ставку В ставке С, то не можете строго предпочесть С ставке А при тех же условиях. В противном случае трейдер может продать вам В в обмен на С, потом продать А в обмен на С, а затем заставить вас доплатить, чтобы снова выкупить С вместо А».
«Это тоже очевидно. Что еще?»
«Ваш выбор должен быть выпуклым. Выпуклость означает, что неопределенность сама по себе не изменит ваших оценок. Поэтому если вы предпочитаете А ставке В как при заданном вероятностном распределениир, так и при вероятностном распределении q, значит вы предпочтете А ставке В, если применимо р или 7, но вы не уверены, какое именно. В противном случае трейдер может быстренько устроить лотерею между р и 7, заставить вас заключить сделку по А плюс обналичится по В, а затем заставит вас купить В вместо А, когда лотерея завершится».
«У меня с этим нет проблем. Но почему Вы называете это выпуклостью? Разве это не геометрическое понятие?»
«Геометрическое. Позвольте, я нарисую. У вас случайно нет с собой цветных ручек?»
«У меня в сумке есть синий фломастер и желтый маркер». Конвей достал их вместе с листом бумаги.
Регретта рисовала и тут же давала комментарии. «Давайте предположим, что у природы есть только три возможных состояния. Тогда я могу построить график пространства допустимых вероятностных мер как прямоугольный треугольник протяженностью в одну единицу по горизонтали и одну единицу по вертикали от начала координат. Горизонтальная координата измеряет первую вероятность /?], вертикальная координата измеряет pi, а р3 задается
277
Часть 2. Пвстижвнив невежества
неявно, как 1 — р\ — р2 . Теперь предположим, что я закрашу все точки, в которых А слабо предпочтительнее В синим, а все точки, в которых В слабо предпочтительнее А желтым. Тогда зеленый цвет будет отмечать все точки, в которых А индифферентна по отношению к В. Насколько грубой может быть итоговая модель?»
«Не знаю. Полагаю, это зависит от предпочтений».
«Неправильно. Если они являются выпуклыми, то модель вообще не может быть грубой. Зеленый кусок обязан быть отрезком прямой, разделяющей треугольник на синюю и желтую части. А любой отрезок прямой, соединяющий две точки одного и того же цвета, должен оставаться в пределах этого цвета».
Предпочтения между двумя действиями в трех состояниях.
Preferences between two acts in three states
«И это справедливо независимо от того, сколько состояний и выборов есть?»
«Совершенно верно. Нам понадобится намного больше цветов и измерений, чтобы выделить каждую область предпочтений. Но если предпочтения являются выпуклыми, то любая область должна содержать прямолинейный отрезок, соединяющий две точки».
«Ясно. Итак, полнота, транзитивность и выпуклость — это все, что значит «не быть трусом»?»
«Почти все. Теоретики обычно ставят более сильное условие, а именно то, что обмен одного приза лотереи на что-то, что вам нравится в той же степени, не снижает вашего мнения о лотерее в целом. С философской точки зрения это более противоречиво, чем выпуклость, поскольку многие утверждают, что оценку не следует отделять от контекста».
«Я склонен с этим согласиться. Что плохого в том, чтобы предпочитать соленые крендельки воде, когда ты голоден, и воду кренделькам, когда хочется пить?»
278
15. Оценка рисквв бвэ свжалвний
«Ничего. В реальной жизни предпочтения почти всегда находятся в состоянии изменения. Тем не менее, говорить об этом полезно, поскольку они моментально стабильны и четко определены. В противном случае не работает даже аксиома порядка».
«Конечно. Я по-прежнему не уверен, разумно ли сравнивать призы лотереи вне контекста».
«Так считаете не только вы, но и многие другие. Однако вы все-таки приняли выпуклость, а на практике между ними не такая уж большая разница. По существу, если у тебя имеются полностью упорядоченные, транзитивные, выпуклые предпочтения и ты знаешь соответствующие шансы, тебя невозможно заставить струсить, и наоборот. Я понятно объясняю?»
Конвей нахмурил брови. «Относительно экономической рациональности? Думаю, да. Но какое это имеет отношение к системе оценки портфеля, которую вы предлагаете?»
«Все очень просто. Экономическая рациональность позволяет вам присваивать балл полезности каждому исходу и ранжировать ставки по их ожидаемой полезности. Это ключевая часть моей системы оценки».
«Вы предлагаете количественно выражать каждый исход?»
«Конечно, нет. Но экономически рациональные люди должны действовать так, будто они это делают. Это называется «поведением согласно теории ожидаемой полезности»».
«Замечательно. Спасибо, Регретга. Я и не знал, насколько просто это оправдать».
«С одной стороны, да. К сожалению, существует масса свидетельств того, что теория ожидаемой полезности не верна, а Барнум был прав».
«Барнум?»
«Ф.Т. Барнум — знаменитый цирковой импресарио. Более века назад он сказал, что ежеминутно на Земле рождается по трусу. А еще он сказал, что в иногда можно обмануть всех людей, а некоторых людей можно обманывать всегда».
«И какую же аксиому рациональности нарушают люди?»
«Выбирайте сами. Например, люди очень чувствительны к тому, как формулируются выборы. Это называется «эффект обрамления». Если вы собираете мнения о новом медицинском препарате, вы получите больше поддержки, если вы сформулируете вопрос в терминах ожидаемого количества спасенных жизней, а не в терминах ожидаемого количества погибших, несмотря на то, что представляемые вами вероятности являются идентичными. Вряд ли кто-то может оставлять все свои выборы транзитивными, имея дело с малыми шансами очень крупных доходов или штрафов».
«Кажется, будто они падают жертвой эмоций в первом случае и арифметических ошибок в последнем».
«Возможно, но это очень широко распространено. Без этого в деловом
279
Часть 2. Постижение навожоства
мире намного меньше людей занимались продажами, а публичные мегалотерии не продавали бы так много билетов».
«Как насчет нарушений выпуклости?» — спросил Конвей.
«Они более трудноуловимы, но, возможно, в той же степени распространены. Например, розничные продавцы считают, что покупатели, столкнувшиеся со слишком большим выбором часто отказываются от покупки, несмотря на то что те же артикулы по отдельности продаются очень хорошо».
«Возможно, покупатели просто хотят отложить свое решение, чтобы получить больше информации».
«Иногда так и происходит. В других случаях они ведут себя так, будто хотят получить меньше информации. Например, людям обычно не нравится слышать об успехе инвестиций, которые они могли бы сделать, но не сделали. На самом деле некоторые люди утверждают, что страх будущего сожаления — когда человек обнаруживает, что он мог бы приобрести, но не приобрел — это более важный мотивационный фактор, чем удовлетворение от покупки».
«Разве это не может быть улажено с помощью теории ожидаемой полезности?»
«Не все так просто. Выпуклость в основе своей отрицает любую ценность информации, отличной от той, что повышает потребление. Теория сожалений дает информации ценность по собственному праву».
«Но что если информация о том, чего вы не купили, поможет вам отточить свои потребительские выборы в будущем?».
«Хорошее замечание. Я уверена, что вы можете объяснить очень много очевидной иррациональности подобным образом. Например, представьте себе мать двоих детей, у которой есть только один леденец на палочке, который она может им дать. Она может разумно принять решение с помощью справедливого подбрасывания монеты, а не предвзятого подбрасывания монеты, чтобы не продемонстрировать предпочтения первому или второму ребенку. В краткосрочном периоде подобный выбор явно нарушает выпуклость. Но мать, возможно, извлекает долгосрочную ценность в плане дисциплины и создания теплых взаимоотношений, культивируя восприятие справедливости».
«Итак, вы считаете, что принятие в расчет будущих доходностей упрощает процесс защиты экономической рациональности?»
«Защиты — да. Но в деле опровержения альтернативных точек зрения — нет. Гораздо сложнее проверить теории, связанные с долгосрочными исходами, во-первых, потому, что на это уходит больше времени, а во-вторых, потому, что предпочтения могут эволюционировать с течением времени».
«А как вы оправдываете теорию ожидаемой полезности в финансах?»
«Двумя способами. Первый — эволюционный. Рациональные трейдеры, которые изучают иррациональных трейдеров, должны добиться некоторого успеха в том, чтобы ободрать последних как липку. Я знаю, что сама так поступала. С течением времени это должно принести благосостояние
280
15. Оцонка рисксн боэ сожалений
экономически рациональным инвесторам, хотя здесь может быть некоторое рассеяние».
«А второй?»
«Фидуциарная ответственность. Когда вы управляете фондами, предполагается, что вы будете наилучшим образом защищать интересы своих клиентов. Предположительно, эти интересы не включают в себя чрезмерно осторожную политику или отношение к клиенту как к трусу, даже если клиент действительно трус. На самом деле именно поэтому наши инвесторы сами пришли к управляющему фондами, чтобы их не считали трусами».
Конвей задумался над аргументами Регретты. Звучит разумно. Но, возможно, я что-то упускаю. «Довольно убедительно, Регретта. Настолько убедительно, что я диву даюсь, почему этим подходом так редко пользуются».
«Но пользуются, Конвей. Конечно, вы знакомы с VAR-анализом-анализом риска стоимости».
«Конечно. Мы все время пользовались им в «Мегабаксе». Приходилось. Нас заставляли контролеры».
«Ну, VAR — самое простое из всех возможных применений теории ожидаемой полезности, где балл полезности имеет только две возможные стоимости. Вот, взгляните на это». Регретта быстро что-то нарисовала. «Какова ожидаемая стоимость для этой функции полезности?»
VAR функции полезности.
VAR utility function
Utility »
t k !
। । Value^
I
*
.... ♦ -1
I I I
Threshold
«Позвольте-ка. Она составляет минус один, умноженный на вероятность падения на уровень порога или ниже. Я понял. Максимизация ожидаемой полезности срабатывает для минимизации хвостового риска».
«Точно. Просто, не так ли? И несколько глупо. Я хочу сказать: почему крупные убытки не должны волновать вас больше мелких или крупные доходы приносить вам душевный покой? И почему такой скачок на пороге?»
«Думаю, контролеры просто пытаются охватить риск необходимости общественной ссуды».
«Но VAR этого не охватывает. Общественная ссуда необходима только в том случае, если другие частные кредиторы не вступят в игру через кредитные линии или вливания акций. А это существенно зависит от размера убытков и перспектив крупных прибылей».
281
Часть 2. Постижение невежества
«Возможно, другие потенциальные кредиторы тоже будут находиться в кризисном состоянии, и не смогут вступить в игру. Думаю, контролеров больше всего беспокоит именно это».
«Тогда почему они не сконцентрируются на убытках, которые высоко коррелированны с убытками других банков или, скажем, с фондовым рынком, если им нужен заместитель? Они в меньшей степени должны способствовать неприятию риска. Агрегированный портфель никогда не должен стоить больше своего среднего, но по критериям VAR это возможно. Это просто обязательно стимулирует дополнительный риск и манипуляции с бухгалтерией».
«Не знаю, Регретга. Я всегда поражался силой бюрократии при трансформации уймы ярких индивидов в коллективного идиота. Но какая функция полезности необходима для того, чтобы способствовать неприятию риска?»
«Она должна быть вогнутой. Знаете, в которой первая производная положительна, а вторая — отрицательна, без скачков. Например, такой». Она построила еще одну кривую.
Вогнутая функция полезности.
Concave utility function
Девлин, который молчал с того момента, как Регретга его отругала, в конце концов, все же вмешался в разговор. «Послушай, Конвей, я покупаю ее подход ожидаемой полезности. Но это самая простая часть. Я все равно хочу услышать, как она оправдает свой выбор отрицательного обратного квадрата».
«Послушайте, Ничего-не-знайка. Если не все понимаете, о чем я говорю, почему бы не спросить у меня напрямую? В любом случае вы ошибалась. Оправдание подхода ожидаемой полезности — это самое сложное. Остальное просто. И если вы уделите мне полчаса своего времени, чтобы сделать некоторые расчеты, я вам все покажу. Извините, ребята». И с этими словами она удалилась.
Конвой смотрел, как уходит Регретга. «Хорошая фигурка, да?» — спросил он у Девлина.
Девлин, чьи уши резко покраснели, покачал головой. «Поверить не могу, что я никогда раньше ее не замечал».
282
15. Оценка рисков fioa сожалений
«Вы никогда раньше не замечали, насколько она привлекательна?»
«Я никогда не видел, чтобы она писала математические символы. Знаешь, Конвей, возможно, я ее недооценил».
Конвей рассмеялся: «Возможно?»
«Она умеет говорить. Посмотрим, как она покажет себя на деле. Между прочим, как насчет того, чтобы прогуляться?»
Пока Конвей с Девлином осматривают окрестности, давайте вспомним теорию ожидаемой полезности.
Рациональная игра в азартные игры
Люди по-разному относятся к риску и не всегда ведут себя так, как чувствуют. Это значительно усложняет моделирование предпочтений риска. Чтобы все это обрабатывать, следует исключить из рассмотрения только поведение. В финансах это означает исключить трусов. Трусы время от времени заключают сделки, которые непременно принесут убыток. Все остальные являются «рациональными игроками». Я не знаю никого, включая меня самого, кто никогда не оказывался трусом. Тем не менее, это подходящее исключение для теории финансов, так как рынок имеет тенденцию выжимать трусов насухо, к тому же вы вряд ли оказываете трусам добрую услугу, уважая их предпочтения.
Максимизация ожидаемой полезности
Рассмотрим другую группу людей, известных как максимизаторы ожидаемой полезности. Они ведут себя так, словно они присваивают балл полезности любому из возможных исходов, рассчитывают ожидаемый балл или полезность для каждого рискованного выбора, и выбирают то, что обещает наиболее высокий ожидаемый балл. Какое отношение эти люди имеют к рациональным игрокам?
Ясно, что максимизаторы ожидаемой полезности должны быть рациональными игроками. Ставка труса или ряд ставок труса снизят их ожидаемую полезность, поэтому они откажутся от нее. Менее очевидно, что рациональные игроки должны вести себя так, будто они максимизируют ожидаемую полезность. Но в основном именно так они и поступают. Это один из наиболее поразительных результатов микроэкономической теории.
Выбор между лотереями
Чтобы оценить эту почти равнозначность, давайте переформулируем рациональную азартную игру в терминах нескольких аксиом, выбора. Давайте начнем с выборов между лотереями. Лотерея определяется доходностями и
283
Часть 2. Постижение новожоства
вероятностями получения этих доходностей. Пусть для любых двух лотерей А и М выражение L>M обозначает «L слабо предпочтительнее М». Также пусть L > М обозначает «L строго предпочтительнее М», где верно отношение L>-M , но не обратное. Пусть L~ М обозначает индифферентность, где L>M , a M>L . Самые базовые аксиомы гласят:
Полнота: Либо L>^M , либо M>^L
Транзитивность: Если L >- М , a M>-N , то L >- N .
Эти аксиомы необходимы, чтобы последовательно распределять предпочтения. И ясно, что без них нельзя стать рациональным игроком. Но ни одна из них не обращается непосредственно к риску. Чтобы это сделать, стандартная обработка предлагает аксиому подстановки, сформулированную в терминах сложных лотерей. Сложная лотерея предлагает окупаемость
L с вероятностью X и М с вероятностью 1 — X. Аксиома подстановки гласит, что замена одного из обоюдно эксклюзивных призов в лотерее более хорошим призом может только улучшить лотерею в целом.
Подстановка: Если L>M, то для любой положительной
вероятности X.
Стандартное дифференцирование теории ожидаемой полезности
Предположим (это не обязательно, но упрощает дифференцирование), что набор лотерей содержит наиболее предпочтительный элемент Lbest и наименее предпочтительный элемент Lworst. Припишем балл полезности 1 наилучшему и О — наихудшему; т.е. U(Lhcs!) = 1, а С(Аи^) = 0. Для любой другой лотереи М полнота и транзитивность подразумевают, что существует точно одна вероятность Хд/, для которой LbestLworst; ~ М. Определим = Хд/. Теория
ожидаемой полезности будет в силе тогда и только тогда, когда для любых двух лотерей L и М и любой вероятности X справедливо UL,M\k = kC/(Z) + (1 — Х)С/(ЛУ). Теперь по аксиоме подстановки мы можем заменить как L, так и М лотереями и Lworst, так чтобы
Z, М, А — Lbest, Lwors(, Ял, LbesJ, Lwors{, , Я — Lbest , Lwors!, ЯЯ£ + (1 — •
Но это подразумевает, что UL^M^A, = АХд + (1 — X)XW = + (1 —
Х)£7(ЛУ), что и требовалось доказать.
Выборы между действиями
Как сказала Регретга, аксиома подстановки подвергается серьезной критике, поскольку кажется, что она отделяет оценку от контекста. Чтобы этого
284
15. Оцанкя рисков Два свжалвний
избежать, можно сравнивать действия, а не лотереи. Действие устанавливает исходы в различных состояниях мира, не устанавливая при этом вероятностьр = (pj, р2, ---) этих состояний. Поэтому, предпочтете ли вы одно действие или другое, это будет варьироваться вместе ср.
Пусть для любых двух действий А и В выражение А>РВ обозначает отношение «А слабо предпочтительнее В при вероятности р». Сходным образом, если А >- В , а А ~ р В, то это обозначает соответственно строгое предпочтение и индифферентность. И снова самые основные аксиомы гласят:
• Полнота: Либо А>РВ, либо В>^ А .
• Транзитивность: Если А >~р В , а В^рС, тогда А >р С .
В этих рамках никогда не просят оценить одну вероятностную меру относительно другой или действия в одном контексте вероятности относительно действий в другом контексте, но какая-то аксиома необходима, чтобы связать различные риски. Наиболее естественной аксиомой является выпуклость:
• Выпуклость: Если А >-р В, а А>^В, то А >~Лр+(]_Л)д В для любой вероятности X.
Считайте X вероятностью того, что при подбрасывании монеты выпадет орел. Если исход — орел, то будет применима вероятностная мера р и вы строго предпочтете А. Если исход решка, то будет применима вероятностная мера 7, но вы все равно слабо предпочтете А. Выпуклость означает, что вы захотите выбрать Л, а не В даже до того, как узнаете исход подбрасывания монеты. Другими словами, если знание чего-то не окажет влияния на ваше поведение, тогда незнание также не окажет на него влияния.
Геометрия выпуклости
В геометрии множество является выпуклым тогда и только тогда, когда оно содержит все прямолинейные отрезки, выходящие из одной точки этого множества. График Регретты демонстрировал выпуклость между двумя действиями в трех состояниях. Продление к пространствам, имеющим больше измерений, было прямолинейным. При п + 1 состояний допустимые вероятности составляют «-мерное субпространство, известное как единичный симплекс. Если предпочтения являются выпуклыми, области строгого предпочтения для каждого действия будут выпуклыми и «-мерными, если только они не пустые (в таком случае вы можете проигнорировать это действие, поскольку оно никогда не будет выбрано).
Строгие предпочтения между любыми двумя действиями будут отделены (« — 1)-мерными гиперплоскостями, чьи пересечения с единичным симплексом представляют индифферентность. Без ущерба для общей применимости мы можем продлить эти отделяющие гиперплоскости через начало координат, сделав их «-мерными. Каждая продленная гиперплоскость является полностью
285
Часть 2. Постижение невежества
определенной ортогональным ей единичным вектором vAB. Иными словами, q'vAB ~ 0 всегда, когда А — q В .
Применение выпуклости для построения меры полезности
Меры ожидаемой полезности всегда являются полными, транзитивными и выпуклыми. Чтобы проверить последнее свойство, обратите внимание, что, если Uл и Uв обозначают векторы баллов полезности для А и В соответственно, то р'ил > p'UB> а q'UA q'UB подразумевает, что (Л/? + (1 — Л)#)'UA > (stp + (1 — Л)#)' Uв для любой вероятности X.
Теперь предположим, что есть отображение предпочтений и нас просят найти меры ожидаемой полезности, с ним согласующиеся. В любой точке где А ~ цВ, мы должны иметь q'Ua ~ q'Ub или q'(UA - Ub) ~ 0. Мы знаем, что это сработает, если Ua — UB кратно vAB. И это не может работать по-другому, поскольку в противном случае Ua — UR, vAB и различные q не охватят п + 1 измерений — на одно больше, чем допускает симплекс. Итак, мы можем построить меры полезности следующим образом:
• Установите UA = 0 для некоего А.
• Если vAB определяет гиперплоскость индифферентности между А и 5, установите UB, равное плюс или минус vAB, где знак выбирается так, чтобы сделать p\UA- UB) положительным в точке, где А >р В .
• Если vAB определяет гиперплоскость индифферентности между В и С и если q — некая точка, где А рассматривается индифферентно к С, но не к п тг тт q'UR
В^ тогда установите Uc = Uв----~vbc •
Qvbc
• Продолжайте в том же духе до тех пор, пока векторы полезности не будут определены для всех действий.
Применение транзитивности, чтобы установить существование
Я еще не показал, что этот метод построения работает. А что если некоторые из областей индифферентности и предпочтения определены неправильно? Вот тут-то в игру вступает транзитивность.
Чтобы это проиллюстрировать, давайте вернемся к миру, в котором существует три состояния, с предпочтениями между Я, В и С. (Для упрощения не будем обращать внимания на границы симплекса.) Метод построения, описанный выше, правильно определяет все предпочтения между А и В, линию индифферентности В — С и точку q на линии А — С, которая не находится на двух других линиях индифферентности. Согласно транзитивности, пересечение
286
15. Оценка рисков Воз сожалений
А - В и В ~ С также лежит на А ~ С, а сравнение ожидаемой полезности называет эту вторую точку тоже правильной. Поскольку ожидаемая полезность — это выпуклая мера, она должна правильно определять всю линию А ~ С.
Выпуклость с транзитивностью и без нее.
Convexity with and without transitivity
Полная транзитивность
Нарушенная транзитивность
Затем давайте проверим, не ошибочно ли построение полезности определяет строгие предпочтения между В и С. При заданной выпуклости и правильном размещении линии В — С построение полезности должно либо принять все эти предпочтения, либо все не принять. Но в любой точке линии А — С оно должно получить предпочтения между В и С принятыми, поскольку оно получает предпочтения между А и В принятыми и не нарушает транзитивности. Сходный аргумент показывает, что построение полезности правильно определяет все строгие предпочтения между А и С.
Когда состояний более трех, проверка того, действительно ли построение полезности подразумевает правильную гиперплоскость индифферентности, является более сложной задачей. Однако, я ее здесь не исследую, частично из-за того, что логика похожа, а частично из-за того, что логика некорректна.
Пороки аргументации
Что если в предшествовавшем графике пересечение линий А ~ В и В — С выпадает за пределы единичного симплекса? Тогда транзитивность не заставит А ~ С пройти через это пересечение, несмотря на то что на этом будет настаивать теория ожидаемой полезности. Итак, в некоторых случаях предпочтения могут быть полными, транзитивными и выпуклыми, не подчиняясь ожидаемой максимизации полезности.
Эти случаи могут иметь некоторое значение для выборов между несколькими дискретными альтернативами, подобные таким: стоит строить
287
Часть 2. Постижение невежества
атомную электростанцию или нет. Однако, когда дело доходит до оптимизации финансовых портфелей, каждый выбор обычно имеет соседей с очень сходными доходностями. Это размещает гиперплоскости индифферентности очень близко друг к другу, так что нарушения транзитивности за пределами симплекса почти наверняка вызовут нарушения транзитивности в пределах симплекса. Конечно, ни одна из условно неясных альтернатив теории ожидаемой полезности не соблюдает выпуклости в пределах симплекса. На практике полнота, транзитивность и выпуклость являются почти равносильными максимизации ожидаемой полезности.
Неприятие риска
Давайте представим, что мы — убежденные рациональные инвесторы, которых ничто так не заботит, как финансовое благосостояние W. Если больше — всегда лучше, чем меньше, наш балл полезности U будет расти в ГК Если мы оцениваем риск хуже, чем определенность при заданной равной ожидаемой доходности, любой отрезок линии 5, соединяющий две точки на U должен пройти ниже U. Так происходит потому, что при заданной лотерее с двумя исходами, связанными с этими точками, высота 5 в ожидаемом благосостоянии будет равна ожидаемой полезности. Напротив, если нам нравится риск, множество выше U будет выпуклым, что делает U выпуклой функцией.
Обратите внимание, что выпуклость и вогнутость функций полезности не имеют ничего общего с выпуклостью предпочтений. Выпуклость предпочтений относится к множествам, определяемым в вероятностном пространстве, без явного упоминания количественных доходностей. Выпуклость и вогнутость функций полезности относятся к множествам, определяемым количественными доходностями безотносительно вероятности. С экономической точки зрения, это всего лишь различие между • максимизацией ожидаемой полезности и поиском или уходом от риска.
С алгебраической точки зрения, любящая материальный достаток и неприемлющая риск U является непрерывной и почти повсеместно бидифференцируемой, с положительной U и отрицательной U". Чтобы выверить последний пункт, давайте рассмотрим лотерею, которая выплачивает W + 6 или W - 6 при равных шансах для некоего малого положительного 5. Если провести разложение в ряд Тейлора второго порядка, ожидаемая
полезность составит примерно U(W) + — С7”(ГК), так что U' должна быть
отрицательной, чтобы стоить меньше математического ожидания W.
288
16. Необычайно полезная полезность
Регретта вернулась час спустя, сжимая в руках несколько диаграмм. «Извините, что заставила вас ждать. Оказалось, что мои знания таблиц устарели в большей степени, чем я думала».
«Ничего, — сказал Конвей. — Это дало нам с Девлином немного времени на то, чтобы во всем разобраться. И один из нас заработал немного денег, поставив на то, что вы вернетесь. Не так ли, Девлин?»
«Буду должен, — пробормотал Девлин Конвею. — У меня с собой нет бумажника».
Регретта повернулась к Девлину. «На самом деле? — спросила она с интересом. — Еще одно твердое мнение? А я-то думала, что сеансы групповой терапии вам не помогли».
«Те, на которых присутствуете вы, мне не помогают».
«Забавно. Мне тоже так кажется. В конце концов, у нас есть что-то общее».
Не знаю, стоит ли по разным углам или закрыть их вместе в одной комнате. «Пожалуйста, — сказал Конвей. — не могли бы мы вернуться к функциям полезности? Регретта, что заставляет вас выбирать степенную функцию валовой процентной доходности?»
«Я с радостью рассмотрю более широкий диапазон, если вы хотите отследить общее благосостояние клиентов».
«Благосостояние клиентов? Не думаю. И какое это имеет значение? Инвестиционные менеджеры просто берут фонды, инвестированные с их помощью, и распределяют их между различными активами».
«При этом каждый клиент получает распределенную пропорционально часть фонда с одинаковыми процентными кризисами, как и все остальные инвесторы».
«Конечно. Любое другое деление было бы чрезвычайно сложным и привело бы к постоянным визитам в суд. Но я уверен, что вы об этом знаете, Регретта. К чему вы ведете?»
«Один лишь вид функции полезности подразумевает оптимальные относительные распределения портфеля, которые не зависят от благосостояния, независимо от распределения доходов. Так что вы могли бы предположить, что она здесь применима. Она характеризуется неким фактором, называемым постоянным относительным неприятием риска, или CRR, который указывает, какой кратный процент благосостояния Вы хотите уступить за малый процент сокращения в дисперсии».
289
Часть 2. Пастижаниа невежества
«Иными словами, CRR этой функции равняется валовой процентной доходности, возведенной в степень?»
«Не совсем. Вам следует отметить результат, чтобы убедиться, что больше лучше, чем меньше. CRR равно единице минус степень, поэтому если людям не нравится рисковать, степень не может превосходить единицу. CRR нуля соответствует логарифмической полезности. Более того, как и в случае с функцией ожидаемой полезности, вы всегда можете прибавить константу или умножить на положительную константу, не меняя подразумеваемых предпочтений. Я тут подготовила два графика.
Два взгляда на функции CRR.
Two views of CRR functions
Регретта пояснила. «Слева я построила CRR как имеющие знак степенные функции. CRR нуля обозначает индифферентность к риску и соответствует прямой линии. Когда CRR положительно, но меньше нуля, инвестор хочет рискнуть всем за достаточно многообещающую доходность. С любым более высоким CRR отрицательная полезность общих убытков безгранична, поэтому агент никогда по своей воле не станет рисковать всем. Действительно, с CRR больше единицы полезность положительных доходностей строго ограниченна, так что даже бесконечный доход не может компенсировать риск заданного конечного убытка. Справа я ввела другую шкалу, так чтобы нулевые доходности давали полезность, равную нулю и маржинальную полезность, равную единице. Это объясняет, что более высокое CRR соответствует растущей выпуклости, т.е. стремительно снижающейся маржинальной доходности».
«Я не знаю ни одного инвестора, кто бы захотел рискнуть обанкротиться, — сказал Конвей. — Если действительно надо рисковать всем».
«Я тоже. Это говорит в пользу CRR, по меньшей мере, в единицу».
«Но что заставляет вас считать, что два — это хорошее число?»
290
18. НААбЫЧАЙНА НАЛАЭНАЯ НАЛАЭНАСТЬ
«Я не сказала два. Я сказала повысить доходность до минус второй степени, что соответствует CRR, равному трем».
«Хорошо, почему три?»
«Я мысленно провела несколько экспериментов. Первый состоял в том, чтобы рассмотреть максимальный риск заданного убытка, которому ты готов подвергнуться, даже если повышение будет безграничным. Например, какую величину риска потери половины своего состояния, на Ваш взгляд, охотно перенесет большинство?»
«Не знаю. Думаю, больше 5%, но меньше 50%. Полагаю, это не дает серьезной наводки».
«Вы будете удивлены. Ваши оценки охватывают CRR между двумя и несколько выше пяти. Вот график».
Максимальный допустимый риск с функциями CRR.
Maximum tolerable risk with CRR functions
«Интересно, — сказал Конвей. — Но у меня появляются другие мысли. Не знаю, насколько надежно я могу сравнивать огромные убытки с бесконечными доходами».
«Справедливо. Тогда давайте проведем еще один эксперимент. Предположим, что людям предлагаются равные шансы удвоения их общего благосостояния. Какой частью своего состояния, на Ваш взгляд, они захотят рискнуть, чтобы воспользоваться этой возможностью?»
«В этом вопросе я тоже не чувствую себя достаточно уверенно. Ну, может быть, что-то около 20-40%».
«Что ж, это говорит об CRR между 1,5 и 3,8. Вот еще один график, если вам интересно. Если сопоставить эти исследования, то окажется, что CRR заслуживает коэффициента 2 или 3».
291
Часть 2. Пастижаниа нааажаствэ — " ~ » —— ———
Желание рискнуть при равных шансах удвоения благосостояния.
Willingness to risk for even odds of doubling wealth
Relative risk aversion (CRR coefficient)
Тут заговорил Девлин: «Вы имеете в виду благосостояние фондового рынка или общее благосостояние?»
«Хороший вопрос. В теории сюда следует включать все благосостояние, включая человеческий капитал. Но на практике нам интересна отдача на изменение в финансовых активах. Что думаете, Конвей?»
Потрясающе. Ты не набросилась на Девлина, «Извините, я отвлекся. Думаю о чем, Регретга?»
«О чем вы думали, когда давали свои оценки? Об общем благосостоянии или просто о финансовом благосостоянии?»
«О финансовом благосостоянии. Полагаю, я имел в виду инвесторов, чье благосостояние в основном является финансовым. Кажется, именно они доминируют на рынках».
Регретга кивнула: «Некоторые источники оценивают CRR на уровне выше десяти. Но эти оценки сцеплены с общим благосостоянием. Если ваше нефинансовое благосостояние некоррелированно с вашим финансовым благосостоянием и имеет сравнимый размер, тогда CRR, рассчитанное только для финансового благосостояния примерно равно четверти общего CRR. Я предлагаю сконцентрироваться на изменениях в финансовом благосостоянии, которое представляет сбой все, что мы хотим измерить. И это приводит нас ко второму способу оценки CRR».
«Какому?»
«Использовать данные по долгосрочной эффективности финансового рынка, чтобы исключить профили риска инвесторов. Инвесторы предположительно корректируют свои портфели до тех пор, пока их маржинальная ожидаемая полезность от приобретения или продажи ценных
292
16. Необычайно нолоэнан нолоэность
бумаг не перестает покрывать транзакционные издержки. И если в долгосрочном периоде рынки ведут себя примерно так, как и ожидали инвесторы, средняя историческая полезность должна представлять ожидаемую полезность. Тогда мы можем просто найти CRR, которое обнуляет среднюю историческую маржинальную полезность».
«Какая история? Средние избыточные доходности относительно волатильности намного выше, если концентрироваться на рынках США после Второй мировой войны, если, конечно, включить в расчеты Великую депрессию или мировой опыт в целом».
«Согласна. Скорее всего, рынок США работал эффективнее, чем от него ждали в послевоенные годы, из-за того, что угроза мировой войны, гиперинфляции или депрессии так и не материализовалась. И безусловно, он работал значительно хуже в годы Великой депрессии. Так что я предпочитаю включать как большой бычий, так и большой медвежий рынок».
«Как вы определите, что среднее неприятие риска было стабильно в течение такого длительного времени?» — снова вмешался Девлин.
«Я этого не утверждаю. Я выступаю только за то, чтобы считать это приблизительной оценкой. Вы считаете, что оно того не стоит, Ничего-не-знайка?»
Ну вот, она опять начинает раздражаться. Все возвращается на круги своя. На этот раз Конвей решил не вмешиваться.
«Это зависит от того, насколько широко вы понимаете приблизительность», — сказал Девлин.
«В принципе, я предполагаю, что приблизительность — достаточно широкий термин. На практике я не видела, чтобы он изменял оценку CRR больше чем на пару единиц. Если я правильно помню, подразумеваемое CRR для чистого портфеля S&P 500 выдерживалось с начала ряда в 1871 г. и составляет примерно 2,1. Если взять только послевоенный период, подразумеваемое CRR будет около 3,5».
«Я полагал, что ваша базисная оценка CRR равна трем».
«Это потому, что я считаю, что портфель S&P слишком узко сосредоточен. Если сделать допуск на какое-то количество наличных и облигаций, то подразумеваемое CRR выше».
«А почему только на единицу выше?»
«По кочану. Послушайте, я же вам сказала, что не утверждаю, что три — цифра правильная, я только сказала, что она не сильно ошибочна».
Конвей утвердительно кивнул. Женщина моего сердца. Жаль, что я женат. «Итак, Девлин, что вы думаете?»
«Не уверен насчет оценок параметров...»
«Не удивительно, Ничего-не-знайка, — сказала Регретга. — И это все, что Вы можете сказать?»
«Нет, не все, Регретга. Пожалуйста, можно мне закончить?»
293
Пасть 2. Постижннин нввожвстаа
Регретту это застало врасплох. Девлин никогда прежде не звал ее по имени, не говоря уже о том, чтобы говорить с ней вежливо. «Конечно, Девлин, вперед».
«Я не уверен в оценках параметров, но мне нравится математика. Жаль, что я не могу смешать полезность CRR с нормальными вероятностными распределениями».
«Почему нет? — спросил Конвей. — Разве матоожидание настолько сложно решить?»
«Хуже, — сказала Регретта. — Оно не определено для нормального распределения. Нормальные распределения неограниченны, в то время как полезность CRR не позволит благосостоянию упасть ниже нуля. Если вы все же попытаетесь рассчитать матожидание, то получится минус бесконечность».
«Как насчет того, чтобы сократить нормальное распределение так, чтобы благосостояние никогда не падало так низко? Это более реалистично в любом случае!»
«Полагаю, это можно, — сказал Девлин. — Но не уверен, где сокращать, и даже если я это сделаю, расчет будет сложным. Хотелось бы иметь что-то получше».
«Ну, — сказала Регретта, — существует семья полезностей, называемая CAR, у нее отрицательная экспонента в доходности. Это позволит работать с отрицательным благосостоянием. Более того, это превращает математическое ожидание в функцию, генерирующую момент, расчеты по которой вести цплг/гл»
«Отлично, — сказал Девлин. — А что означает CAR?»
«Постоянное абсолютное неприятие риска. Оно означает, что вы хотите уменьшить величину константы в обмен на небольшое сокращение в дисперсии, независимо от своего базового благосостояния».
«Не очень похоже на правду, не так ли? Чем я богаче, тем больше я хочу потратить миллион долларов на то, чтобы сократить риск. А если у меня нет миллиона долларов, я могу об этом забыть».
«Я это понимаю. И это еще одна причина, почему следует отдать предпочтение CRR полезности».
«Как насчет компромисса? —1 осмелился сказать Конвей. — Используйте форму экспоненты, но пользуйтесь процентной доходностью вместо абсолютной».
«Мысль хорошая, — сказала Регретта, — но забудьте о ней. Это может выглядеть как формат ожидаемой полезности, но на деле таковым не является. И не может являться. Если предпочтения зависят только от относительных доходностей, функция полезности будет иметь CRR. А это исключает нормальность».
«Плохи дела. Но, полагаю, нам придется приспосабливаться. Если бы желания были бы лошадьми, то нищие ездили бы верхом».
Некоторое время все молчали. Затем Регретга заговорила. «Что если допустить другое распределение помимо нормального? Что-то такое, что генерирует простую форму для ожидаемой CRR полезности».
«Хорошо бы, но я такого не знаю. Что вы предлагаете?»
«Я тоже не знаю. А вы, Девлин? Есть идеи?»
«Ну да, есть. Это...» Внезапно глаза Девлина покрылись поволокой, и он начал говорить сам с собой. «Постойте, сработает ли это для портфелей?... Полагаю, нет. Плохи дела... А какие распределения у этих портфелей?... Посмотрим. Если мы возьмем простой ряд Тейлора... Так, оно такое же, как ... Возможно, в конечном итоге это сработает... И еще раз, возможно, аппроксимация не ...»
Регретга помахала графиком перед носом Девлина, тщетно пытаясь привлечь его внимание. «Мы утратили с ним контакт, — сказала она Конвею. — Как вы думаете, может, позвать сестру?»
«Нет, для Девлина это нормально. Должно быть, он приходит в норму. Оставьте его в покое».
Через некоторое время Девлин пришел в себя, и его взгляд снова обрел ясность. «Интересно. Думаю, возможно, Вы оба правы».
«В отношении чего?»
«В отношении того, как сделать матожидание CRR удобным в обработке».
«Но мы не знаем, как. Поэтому мы к вам и обратились».
«Слушайте, я сейчас не хочу с вами спорить. Возможно, я ошибаюсь. Дайте мне немного времени для того, чтобы тщательно все продумать. Конвей, ть! сможешь приехать в следующую субботу?»
«Конечно. Регретга, вы к нам не присоединитесь?»
«Мне нужно свериться с ежедневником, не запланировано ли у меня что-то другое, — сказала Регретга с улыбкой. — Но думаю, мне удастся вписать туда эту встречу».
«Хорошо. Тогда и увидимся. Удачи, Девлин. Я на тебя рассчитываю».
Пока Девлин углубился на работу, давайте исследуем эти CRR и CAR функции полезности.
Эквивалентность по функциям полезности
При любой заданной функции полезности U, любом скалярном а и любом скалярном b выражение а + bU определяет те же рисковые предпочтения при ожидаемой максимизации полезности, что и U. Так происходит потому, что для любых двух действий А и В величина 2Г[£7(Д)] > тогда и только
тогда, когда а + ЬЕ [£7(/4)] > а + ЬЕ [L7(5)] •
295
Часть 2. Постижанио новажаство___________________________
Справедливо и обратное. Предположим, что для любых двух действий А и В, двух множеств функций полезности U и V ряд предпочтений одинаков, независимо от базового распределения. Иными словами, Е[Е(А)] > Е[И(В)] тогда и только тогда, когда . Определим и и v как
векторы, чьи компоненты — величины U(A) — U(B) и И(Л) — И(В), соотнесенные с различными исходами, в этом случае v'р = 0 тогда и только тогда, когда и 'р — 0. То есть v будет ортогональным всем векторам, которые ортогональны и, а следовательно, должен быть скалярным кратным b к и. Более того, Ъ должно быть положительным, чтобы сохранить знак неравенства. Отсюда следует, что И(В) — bU(B) = V(A) — bU(A), независимо от исхода. Поскольку это справедливо для любой пары действий, V—bU должны быть постоянными.
Следовательно, функции полезности появляются в равнозначных семьях, где каждый член семьи равен скаляру плюс положительному кратному каждого второго.
Кривизна и неприятие риска
Из предшествующей главы ясно, что для малых рисков гэп между ожидаемой полезностью Е [£7(И)] и полезностью £7(В[И]) ожидаемого исхода составляет примерно — . Итак, на первый взгляд, неприятие
риска варьируется прямо с U". Однако поскольку умножение U на положительное число не меняет подразумеваемые предпочтения риска, неприятие риска должно скорее варьироваться с коэффициентом U” и производными высшего порядка к U\ нежели чем напрямую с U". Это меры кривизны, контролирующие масштаб. Чем более изогнута U, тем большее неприятие риска она подразумевает.
Эквивалентность надежности
Чтобы исследовать отношения между кривизной и неприятием риска более тщательно, давайте измерим, сколько гарантированного дохода дает лотерея L. Это так называемый эквивалент надежности. Он может, в свою очередь, быть разложен на две части: ожидаемая доходность и рисковая
премия R. Правда, R варьирует не только в зависимости от свойств лотереи, но и в зависимости от другого благосостояния И7, поскольку другое благосостояние оказывает влияние на способность человека переносить риск. Основная формула такова: L/(FK + JE7[7L] — 2?) = E^l/(FK + Л) .
Этой формулой пользоваться проще, чем кажется. К примеру, рассмотрим четно-нечетную ставку получения или утраты небольшой суммы 5. Ожидаемая доходность равна нулю, следовательно, мы можем написать:
296
U(W-R) = ^U(W + $) + l-U(W-<5).
Взяв разложение в ряд Тейлора второго порядка и упростив, получаем
-RU '(W) + - R2U "(W) = - <52U"(W").
2
По мере того как 8 приближается к нулю, R становится грубо линейной в 82, в то время как R2 приближается к нулю намного быстрее. Поэтому мы можем в аппроксимации проигнорировать член R\ и написать:
2 иХЮ
Это подтверждает зависимость R от неприятия риска в соотношении — IT'IU\ что известно как коэффициент абсолютного неприятия риска.
Постоянное абсолютное неприятие риска
U ” d In U ’
Если R не зависит от РЕ, то -—------ должно быть константой —к, где
U' dW
к — положительное заданное неприятие риска. Если проинтегрировать, то In(U') будет равняться —к РЕ плюс некая константа, такая чтобы IT была пропорциональна ехр(—кИЭ. Отсюда следует, что U должно давать ту же классификацию, что и —ехр(—кИ7). Это называется полезностью CAR для постоянного абсолютного неприятия риска. Вот несколько графиков разных значений к.
Функция полезности CAR.
CAR utility function
297
Пасть 2. Пнстижннин нвввжвстнз
Так как параметры к полезности CAR на этих графиках не превышают нескольких процентов, они не существенны. В зависимости от единицы измерения W, их использование может быть даже неуместным.
Относительное неприятие риска
Если рисковая премия R выражается как доля г от IV, а риск 6 как доля е от W, равенство, определяющее отношение рисковой премии к риску может быть сформулировано следующим образом:
1 2 -WU\W)
Г = — G---------- -
2 U\W)
-WU"
Соотношение -----;— известно как коэффициент относительного неприятия
риска.
Если г не зависит от И7, то ... === должно быть константой —с, где
U' dinV
с всегда положительно при заданном неприятии риска. Если проинтегрировать, то ln(t7') будет равняться —с*1п(^Е) плюс константа, такая, чтобы U' была пропорциональна Отсюда следует, что U должна давать ту же
W^c
классификацию, что и ----, когда с 1, или что и ln(W), когда с = 1. Это
1 — с
называется CRR полезностью.
Когда значение имеет только относительное благосостояние
При полезности CRR, делящей все исходы благосостояния на скаляр, это не оказывает влияния на относительные классификации лотерей или действий. В частности, вы можете делить на базовое благосостояние так, чтобы все доходности благосостояния стали бы валовыми процентными доходностями: например, 1 + х, где х — процентная доходность. Изменение масштаба формулы CRR так, чтобы полезность и маржинальная полезность в .г = 0 равнялись нулю тт, . (1 + ^-1 и единице соответственно, дает нам выражение U (х) ----------, что
1 —с
технически не определяется при с = 1, но приближается к ln( 1 + х). В большинстве случаев, представляющих из себя практический интерес, с превосходит единицу, в связи с чем мы можем просто рассмотреть выражение U(x) = -(1 + х)‘“с .
На самом деле CRR — это единственная функция полезности, которая производит все сравнения в процентах. Чтобы в этом убедиться, обратите внимание, что если значение имеет только относительное благосостояние, то для любого положительного скаляра m U(nV) и U(•) должны определять те же
предпочтения риска. Это означает, что U (jnW) = a(rri) + b(jn)U(W) для некоторых функций а и Ь, которые зависят от т, но не от W. Дифференциация обеих сторон относительно т и W и оценка при т = 1 показывают, что
= £>'(1)для всех W. Следовательно, относительное неприятие риска
должно быть постоянным.
Максимальный приемлемый риск с полезностью CRR
Предположим, что вы можете перенести риск X утраты доли F своего благосостояния, в обмен на получение безграничного благосостояния в противоположном случае. Для с > 1 даже безграничное благосостояние предлагает только конечную полезность, поэтому вы никогда не сделаете подобную ставку, за исключением случая, когда —Х(1 - > ~1 или,
эквивалентно, X > (1 — Т7)'1-
Оптимизация портфеля с полезностью CRR
Предположим, что рациональный инвестор с полезностью CRR распределяет свой портфель между рисковым индексом и без рискованными векселями. Предположив, что параметры риска и предпочтения остаются стабильными и, проигнорировав транзакционные издержки, он выберет рисковый актив/долю портфеля <z>, чтобы максимизировать свою ожидаемую полезность. Если х обозначает процентную избыточную доходность по рисковому активу, чистая избыточная процентная доходность по портфелю будет сох. Максимизация ожидаемой полезности требует, чтобы:
dco
1 — с
= Е| (1 + <ух) с х I — 0 •
Так что если мы наблюдаем долгосрочную доходность по портфелю сох, то можем оценить с как значение, которое обнуляет ожидаемую маржинальную полезность Е{(1 + сох^х].
На практике сложнее идентифицировать соответствующую долю рискового актива со, чем правильно выбрать временной период. Снижение со повышает расчетное неприятие риска примерно в обратной пропорции. Однако это снижение также способствует ослабеванию вкладов в данный рисковый актив, так что в некоторой степени разности поглощают друг друга.
Упрощение ожидаемой полезности CRR
Ожидаемая полезность CRR не является четкой для нормальной и других безграничных плотностей. Последнее подразумевает положительные шансы получения отрицательного благосостояния, в том случае если CRR представляет отрицательную бесконечность, так что ожидаемая полезность тоже будет равна отрицательной бесконечности.
299
Часть 2. Постижение невежества
Даже плотности, ограниченные положительным благосостоянием, редко дают простые аналитические выражения для ожидаемой полезности CRR. Однако мы можем преуспеть, произведя биномиальное раскрытие:
После подчленного интегрирования и обозначения /-го момента с помощью Mh ожидаемая CRR полезности составляет:
л л Х’’ (—— j + 2)
Л/. + > ----—-----------М •
1 г.
Упрощение ожидаемой полезности CAR
Ожидаемая полезность CAR принимает форму Е[—е к/г]. Если рассматривать ее как функцию — к и проигнорировать знак минус, она очень напоминает три другие похожие функции:
• Преобразование Лапласа, за исключением необходимости интегрировать по отрицательным значениям так же, как по положительным.
• Генерирующую момент функцию, за исключением того, что —к является отрицательной, а не положительной.
• Характеристическую функцию, за исключением того, что —к является реальной, а не воображаемой.
Для большей части обычно, применяемых вероятностных плотностей ожидаемая полезность CAR сокращается до простого выражения. В частности, при заданной нормальной плотности со средним |Л и стандартным отклонением о ожидаемая полезность CAR равняется — ехр(—к/л ч—к2сг2) .
Заманчивая путаница
Время от времени мы встречаем упоминания о полезности в виде компонента —ехр(-кх), где х измеряет процентные доходности. Это выглядит как гибрид полезностей CAR и CRR. На самом деле это даже не является правильной функцией полезности, поскольку единственными сравнениями с ожидаемой полезностью, которые могут быть сокращены до относительных изменений, являются CRR. В свете этого, если вы имеете дело с высокочастотными данными ежедневно или ежечасно, где абсолютные доходности обычно составляют менее 2%, экспоненциальная функция в доходностях может разумно аппроксимировать функцию CRR. Это происходит потому, что, когда х мало:
(1 + = ехр((1 — с) • 1п(1 + х)) = ехр((1 — с)х) .
Последующие главы более подробно рассказывают об этом. На настоящий момент я предлагаю эту информацию вниманию читателя в качестве заманчивой путаницы.
17. Оптимальные наложения
Конвей никому на работе не сказал о своей субботней прогулке. В то время как работники инвестиционной банковской сферы являются признанными трудоголиками, менеджеры активов считают дурным тоном работать по выходным. А если бы они знали, что я общаюсь с сумасшедшими... Нужно дождаться, что придумает Девлин. На этот раз Конвей был рад, что у него имеется много входящих писем. Он посвятил себя тому, чтобы ответить на все, и неделя прошла незаметно.
В следующую субботу, когда Конвей приехал в Club Mad, Девлин и Регретга его уже ждали. «Что так долго?» — спросил Девлин.
«Я сел на первый же паром: они по выходным отправляются не раньше 10 утра».
«Не обращайте внимания, — сказала Регретга. — Это Девлин так говорит, что он рад вас видеть».
«Спасибо, Регретга, — сказал Конвей. — Я это знал. Но я рад, что вы тоже об этом знаете».
Девлин покраснел: «Довольно светских разговоров. Нам пора поработать». Помахав пачкой бумаг, он повел их в холл. «Готов получить ответ, Конвей?»
«Я весь обратился в слух».
«Функции разбиения».
«Разбиение, которое функционирует как что?»
«Да нет. Это название. Функции разбиения. Они представляют собой взвешенные суммы экспонент».
«Я никогда о них не слышал».
«Я тоже, до тех пор пока не прочитал работу Шредингера по статистической термодинамике. Все, что нам нужно сделать, — это реинтерпретировать переменные».
«А что ты делаешь с этими функциями разбиения?»
«Сравниваю их величины с помощью различных весов портфеля. Самое низкое значение максимизирует общий эквивалент надежности».
«И все?»
«Для первого подхода — да», — Девлин сиял.
Конвей онемел. Прежде чем он смог ответить, Регретга вмешалась в разговор. «Извините, Девлин. Теперь, когда вы сказали Конвею ответ, не могли бы Вы озвучить для меня вопрос?»
«Без проблем. Вопрос таков: как соединить полезность CRR с условной
301
Часть 2. Постижение невежества= многомерной нормальностью, чтобы быстро оценивать портфели?»
«Почему вас так привлекает условная многомерная нормальность?»
«Регретга, меня поражает ваш вопрос. Я думал, что четко объяснил это на сеансе групповой терапии в прошлом месяце».
«Но, Девлин, меня, наверное, там не было. Должно быть, это было захватывающе», — ответила Регретта с деланной серьезностью.
«Так и было, по крайней мере для меня. Все началось, когда я работал на Конвея в «Мегабаксе», и нам нужно было оценить риск стоимости по трем бинарным опционам, которые были некоррелированными, но не независимыми...»
О, нет, я просто обязан вернуть их к нашей теме. И Конвей вмешался в разговор: «В двух словах, Регретта, нам с Девлином нравится условная нормальность, поскольку она достаточно гибка для того, чтобы аппроксимировать почти любой тип распределения портфеля, не заставляя оценивать много перекрестных моментов более высоких порядков».
«Спасибо», — поблагодарила Регретга.
«Условная многомерная нормальность, — поправил Девлин. — Позвольте я объясню отличие...»
«Позже, — сказал Конвей. —У вас с Регретгой будет уйма времени после того, как я уеду».
«Да, жду не дождусь, — сказала Регретта. — Итак, Девлин, как функции разбиения могут помочь нам получить ответ?»
«Они не помогают получить ответ. Они и есть ответ. Поскольку ожидаемая полезность в любом заданном режиме является экспонентой, общая ожидаемая полезность будет просто взвешенным средним экспонент, только со знаком минус. Это и есть функции разбиения, за исключением знака».
«Погоди-ка, Девлин, — сказал Конвей. — Мы уже разбирали это в прошлый раз. Ожидаемая полезность CAR является экспонентой при нормальных распределениях. А ожидаемая полезность CRRV нет. Она даже не определена для нормальных распределений».
«Это зависит от того, как измерять портфели».
«Ты слишком сильно углубился в физику, Девлин. Независимо от того, какую валюту или временные рамки ты выберешь, это все равно не даст «отрицательного благосостояния»».
«А нам и не нужно, чтобы благосостояние было отрицательным. Неограниченные доходности сработают почти так же хорошо».
«Отлично, но доходности тоже должны быть ограниченными».
«Нет, если производить измерения в логарифмах».
«Какая разница?»
«Небольшая для изменений — менее 10%. Но различия могут быть огромными. Вот два графика, которые я подготовил в качестве иллюстрации».
Логарифмическое изменение против процентного изменения. Logarithmic change versus percentage change
0-15 -j ......... -........-............ T 0.006
0.10
0.05
0.00
—0.05
-0.10
-0.15
0.005
0.004
0.003
0.002
0.001
0.000
-10% -5% 0% 5% 10%
Percentage change
Percentage change
«Замечательно, Девлин, но я знаком с логарифмами. Что ты хочешь этим сказать?»
«А ты подумай. Если мы сконцентрируемся на логарифмических, а не на процентных доходностях, нам не придется беспокоиться по поводу недопустимых величин. Нормальность снова допустима, что значительно упрощает подсчет ожидаемой полезности».
«Не вижу, каким образом: тебе все равно придется проинтегрировать по отрицательной степенной функции, умноженной на экспоненту. Мне неизвестно никакой сокращенной формы для этого».
303
Часть 2. Постижение невежества
«Я поняла, — сказала Регретта. — В то время как полезность CRR является степенной функцией валовой процентной доходности, она является и экспоненциальной функцией логарифмической доходности».
«Здорово! Так что если мы предположим, что логарифмические доходности являются нормальными, то как будет выглядеть выражение для ожидаемой полезности CRR?»
«Оно выглядит как выражение для ожидаемой полезности CAR, за исключением того, что вы интегрируете по логарифмическим доходностям вместо абсолютного благосостояния. Так что это в основе своей будет генерирующей момент функцией для распределения логарифмических доходносте й ».
«И приводит нас это к чему? Вот ручка и бумага, если нужно».
Регретта взяла ручку с бумагой и провела интегрирование. «Вот экспонента. Это делает общую ожидаемую полезность средним взвешенным этих экспонент с весами, заданными вероятностями различных режимов. Вот ваша функция разбиения».
«Вы все правильно поняли, за исключением того, что экспоненте обычно предшествует знак минус. Теперь позвольте, я задам вам более сложный вопрос. О чем говорит каждый показатель степени в каждой экспоненте?»
Регретта снова обратилась к своим записям и начала экспериментировать с перестановкой членов. «Вот кратное эквивалента надежности в этом режиме, гарантированный доход, который принесет ту же ожидаемую полезность».
«Гарантированный логарифмический доход, — поправил Девлин. — А какое это кратное эквивалента надежности?»
«Степень в степенной функции, которая равняется единице минус CRR».
«Верно. Какая же получается формула для эквивалента надежности в каждом режиме?»
«Условная средняя логарифмическая доходность минус —
умноженная на условную дисперсию».
«А как с экономической точки зрения интерпретируется — (CRR — 1) ?»
«Цена дисперсии в терминах эквивалентного гарантированного логарифмического убытка. Чем сильнее вы не приемлете риск, тем выше будет цена».
«Хорошая работа, Регретта. Отличная. Теперь понимаете, Конвей?»
«Не совсем. Когда мы в первый раз пытались рассчитать ожидаемую полезность CRR в условиях нормальности, ответом стала отрицательная бесконечность. Как перестановка в логарифмических членах помогла нам от этого избавиться?»
«Я не просто произвел перестановку. Я изменил определение вероятностной плотности так, что теперь являются нормальными
логарифмические доходности вместо процентных доходностей».
«Откуда ты знаешь, что так лучше?»
«С большинством ежедневных доходностей определить разницу невозможно. Однако при крупных крахах логарифмическая нормальность не позволит остаться ни с чем, а нормальность — позволит».
«Я утверждаю, что в этом отношении логарифмическая нормальность лучше. Но кто скажет, что логарифмическая нормальность где-то в другом месте не напортачит по-крупному?»
«Существует также теоретическая причина для того, чтобы отдать предпочтение логарифмической нормальности. Это разница между умножением и сложением».
Хотел бы я, чтобы объяснениям Девлина требовалось бы меньше объяснений. «То есть?»
«Совокупная валовая доходность равняется произведению валовой доходности за каждый субпериод, так что логарифмы являются аддитивными. Если доходности субпериода независимы и идентично распределены, долгосрочный логарифм, согласно центральной предельной теореме, должен приблизиться к нормальности, что делает совокупную валовую доходность логарифмически нормальной».
«Понятно. Итак, каковы выводы для диапазонов от нескольких кварталов до нескольких лет?»
«Единственное заметное отличие состоит в том, что логарифмическая нормальность добавляет асимметрии. Вот построенный мной пример, где логарифмические доходности нормально распределены со средним 10% и нормальным отклонением 20%. Толстая линия отмечает их плотность. Закрашенная область представляет из себя логарифмически нормальную плотность для процентных доходностей».
Логарифмическая нормальная против нормальной плотности для р = 10%, <г=20%.
Lognormal versus normal densities for д — 10%, a — 20%
305
Часть 2. Постижения невежества
Конвей задумался над графиком. «Знаешь, это действительно не так уж сложно. Странно, что мы раньше об этом не подумали».
«Это потому, что мы слишком много думали как сторонники стандартной теории портфеля. Если бы мы работали с опционами, мы бы сразу об этом задумались. Они почти всегда предполагают логарифмическую нормальность».
«Почему теоретики портфеля не принимает ее?»
«Потому что с портфелями логарифмически нормальных ценных бумаг иметь дело гораздо сложнее, чем с портфелями многомерно нормальных активов».
«На самом деле? Каким образом?»
«Портфели логарифмически нормальных активов не являются логарифмически нормальными. Правда, они не являются и нормальными».
«Даже если они многомерно логарифмически нормальны?»
«Даже тогда. Они в некотором роде частично нормальные, частично логарифмически нормальные, а насколько они склоняются в ту или иную сторону — зависит от того, сколько у нас активов и насколько велики веса».
«Звучит не очень здорово с точки зрения обработки».
«Так оно и есть. Поэтому когда теоретики опционов имеют дело с портфелями — скажем, валютными корзинами — они обычно ссылаются на различия между логарифмами и процентами. А именно они предполагают, что портфель логарифмически нормален с логарифмическим средним, которое является взвешенным средним логарифмических средних актива и дисперсии, которая является квадратичной формой в ковариационной матрице».
«Насколько хороша эта аппроксимация?»
«Это аппроксимация Тейлора первого порядка: отличная, если изменения довольно малы, но ужасная, если они велики. В качестве примера предположим, что актив, составляющий 1% нашего портфеля, полностью повержен в прах, в то время, как другие 99% удерживают свою стоимость. Какова логарифмическая доходность по портфелю?»
«Минус 1%».
«Конечно. Но стандартная аппроксимация нам об этом не скажет. Логарифмическая доходность по слабеющему активу будет равняться минус бесконечности, так что среднее логарифмов тоже должно будет равняться минус бесконечности, что заставляет весь портфель выглядеть негодным».
«Ясно, почему теория портфеля не может без него жить. Шизофрения, да?»
Конвей кивнул. И вот я — пришел в сумасшедший дом, чтобы это выяснить. «И что ты предлагаешь?»
«В настоящий момент я просто собираюсь проигнорировать и это несоответствие».
«Я правильно расслышал? Ты, Девлин, соглашаешься со стандартной практикой, которая, как сам знаешь, является ошибочной?» Очень непросто заставить тебя следовать стандартной практике, даже когда она верна.
Девлин улыбнулся. «Дай мне время. Я пока не вижу обходного пути. Кроме того, дело обстоит не так, будто я что-то путаю, на что однорежимные модели дают однозначный ответ».
«Кстати, если уж вы заговорили о том, чтобы давать однозначные ответы, — заговорила Регретга. — У меня есть некоторая проблема. Вы не возражаете, если мы быстро проверим ваш многорежимный вариант?»
«Конечно. Оцените условное среднее и дисперсию с помощью логарифмической линейной аппроксимации для портфелей. Вычтите кратное дисперсии из среднего, чтобы сформировать эквивалент надежности для каждого режима. Преобразуйте в условные ожидаемые полезности и рассчитайте общую ожидаемую полезность как их вероятностно-взвешенное среднее. Затем выберите веса портфеля, чтобы максимизировать общую ожидаемую полезность».
«Если разбирать по шагам, то все, кажется, просто. Но...»
«Это просто. Все равно, что испечь пирог. Вот рецепт, который я напечатал. Он поможет вам обоим все запомнить. Я поставил тильды на большинство переменных, чтобы напомнить вам, что мы имеем дело с логарифмическими, а не более широко используемыми процентными доходностями».
Конвей перечитал рецепт. «Спасибо, Девлин. Но все эти разговоры о пирогах и рецептах раззадорили мой аппетит. А как ты?»
307
Часть 2. Постижение новвжоотва
«Я умираю от голода, — сказал Девлин. — Пойдемте обедать».
«Я есть не очень хочу, но составлю вам компанию, — сказала Регретта. И они направились в столовую.
Пока они обедают, давайте разжуем эти функции разбиения. При уже разработанных нами инструментах переварить их будет несложно. Самая большая сложность — сохранить отличие между логарифмами и процентами только частично прямым. Считайте это упражнением в преднамеренной небрежности. Позднее мы все расставим по своим местам.
Терминология
Для Pt, цены актива, или портфеля, за время t без безрисковой ставки (т.е. номинальной цены, разделенной на совокупный безрисковый индекс), пусть xt обозначает избыточную процентную доходность ~ , a xt —
логарифмическую избыточную доходность 1п —!— = ln(l + xt) • Дальше буду
опускать подстрочный индекс времени как подразумеваемый. Я обозначу векторный эквивалент х как X = ln(l + X) и действительно воспользуюсь — (тильдой), чтобы идентифицировать логарифмические эквиваленты более общо. Однако не предполагайте, что логарифмические моменты равняются логарифмам единицы плюс соответствующие процентные моменты. В связи с нелинейностью это вряд ли когда-либо случится.
В качестве стенографического символа я также иногда описываю процентное среднее со'М и дисперсию co'Sco портфеля при помощи символов т и v, не включая веса рискового актива со, от которых зависят т и v. Точнее говоря, т, v и их логарифмические эквиваленты послужат указателями места различных аппроксимаций. Сходным образом, со будет идентифицировать примерно оптимальную смесь портфеля. Большая часть как этой, так и следующей главы посвящены выработке и совершенствованию аппроксимаций.
Различия между логарифмическим и процентным Изменением
Разложение в ряд Тейлора показывает, что: „2 „3 4
4 2 3 4
Когда х близок к нулю, условия более высокого порядка в разложении в ряд Тейлора будут малы по сравнению с первым, так что х будет примерно равен х. Гэп х — х составляет всего 0,0002, или 2 базисных пункта (б.п.) при х -2%, 12 б.п. при 5% и 47 б.п. при 100%. По мере роста х гэп стремительно
расширяется: 600 б.п. при х = 40% и 9000 б.п. при х = 200%. Расширение становится еще более сильным, когда х отрицателен: 1100 б.п. при х — -40% и бесконечным при х = —100%.
Два понятия о среднем изменении
Если средние логарифмические изменения будут равны нулю, конечная
цена
будет равняться стартовой цене,
поскольку
Поскольку
процентные изменения всегда превосходят логарифмические за исключением точки ноль, среднее процентное изменение будет положительным, несмотря на то что цена вернулась к своей исходной величине. В экстремальных случаях средние процентные изменения могут быть положительными даже тогда, когда актив является ничего не стоящим. Это делает процентное изменение обманчивым критерием в финансах.
Однако логарифмические изменения тоже могут быть обманчивыми. Рассмотрим портфель, состоящий из многих равновзвешенных активов. Портфель будет стабильным тогда и только тогда, когда среднее процентное изменение по каждому активу будет равно нулю. Теперь если среднее процентное изменение равно нулю, среднее логарифмическое изменение будет равно нулю, если только каждая цена не является неподвижной. Таким образом логарифмы будут преуменьшать изменения в портфеле. В экстремальном случае, если один из активов становится ничего не стоящим, среднее логарифмическое изменение будет равно --со, несмогря на то что портфель в
целом мог вырасти в цене.
Среднее логарифмическое изменение и относительное неприятие риска
Средние изменения могут быть соотнесены с относительным неприятием риска следующим образом. Инвестор нейтральнее к риску полезности CRR с коэффициентом с, равным 0, если она индифферентна к любой ставке с нулевой ожидаемой процентной доходностью. Ее с равняется 1, если она индифферентна к любой нулевой ожидаемой доходности на ее логарифмическое благосостояние — например, даже к шансам вдвое сократить или удвоить свое благосостояние. Напротив, инвестор, чей с превышает 1, что считается типичным, предпочтет держать деньги при себе, а не ждать, пока средний логарифм ее благосостояния будет дрейфовать вниз. Как уже отмечалось ранее, с < 1 изменит знак функции разбиения.
Логарифмическая нормальность
Нормальное распределение является неограниченным. Иными словами,
309
Часть 2. Постижение невежества
допустимы любые значения, включая экстремально отрицательные. Но это не может быть справедливо в отношении цен. Поэтому аналитики обычно предполагают логарифмическую нормальность. Валовая процентная доходность 1 + х считается логарифмически нормально распределенной, если ее логарифм нормально распределен. Словами, совокупное распределение Т7 задано следующим образом:
,. Яп(1+х)
—~— \ах , 2<т~ 1
—у=-ехр ст д/2тг
обозначают среднее и дисперсию относительно
где /л и
х — 1п(1 + х) . Дифференциация обеих сторон показывает, что
1
= -ехр
7Г
2 ст2
Моменты логарифмически нормального распределения
Как известно, л-ый момент логарифмически нормального распределения может быть рассчитан как:
п
^•ехр
ехр(нх)
— г— -exp
~2
= М(н) = ехр(нД + — и2 ст2),
где М(-) обозначает генерирующую момент функцию для нормального распределения. Отсюда следует, что:
— 1. Разложение в ряд Тейлора указывает, что
L J I 2
среднее процентное изменение превышает среднее логарифмическое изменение на — (Д2 + ст2) плюс члены более высоких порядков.
^2
PW[x] = Иш-[1 + х] = ехр(2// + 2ст2)-ехр(2Д + ст2) = ехр(2Д +<т2) • (exp(cf2)-1) , что сокращается до ст2 + 2 Дет 2 плюс члены более высокого порядка.
Асимметрия Е
составляет — я опущу жуткие подробности
— — (ехр^сг2J + 2j^ехр^сг2 j — 1 , что сокращается до Зет плюс члены более высокого порядка. Таким образом, логарифмически нормальная плотность действительно является положительно ассиметричной, но только в незначительной степени, если & мало.
Эксцесс Е
-3
составляет — и снова я не буду приводить
подробности — ехр(4ст2 ) + 2 ехр(3сг2 ) + 3 ехр(2сг2 ) — 6 , что сокращается до 16ст2 плюс члены более высокого порядка.
Зависимость от временных периодов
Теория финансов обычно предполагает, что базовые законы движения стабильны, а движения цен в различных, неперекрывающихся периодах некоррелированны. В этом случае, как средняя доходность, так и дисперсия будут изменяться линейно с течением времени, в то время как стандартные отклонения будут меняться с квадратным корнем времени. Чтобы в этом удостовериться, разложите заданное изменение на сумму изменений по некоррелированным компонентам и примените формулы для моментов сумм.
В краткосрочных периодах о будет доминировать над ц, несмотря на то что они обе стремятся к нулю. В этом случае логарифмически нормальные и нормальные плотности будут в основном соответствовать при условии сдвига среднего в <5^2. Напротив, по длинным диапазонам логарифмически нормальные плотности будут намного более асимметричными вверх и толстохвостыми, нежели нормальные. На практике решения по распределению активов, как правило, концентрируются на среднесрочных временных периодах, где можно разумно преобразовывать одну форму в другую, но сдвиг среднего о2/2 может быть недостаточным.
Многомерная логарифмическая нормальность
Вектор 1 + X считается логарифмически нормальным, если его логарифм X = ln(l + X) является многомерно нормальным. Я обозначаю среднее и дисперсию последнего символами М и Z соответственно. Многомерная нормальность логарифмов эквивалентна утверждению, что любая линейная комбинация св X является нормальной при среднем й)' М и дисперсии cw'Scw .
311
Пасть 2. Псстижснис невежества
Портфели логарифмически нормальных активов
Давайте рассмотрим разовую игру с портфелем. Распределение ведется между рисковыми активами с процентными весами св и портфель остается ненарушенным в течение одного периода. Чистые избыточные процентные доходности по портфелю тогда принимают простую форму св'Х. К сожалению, соответствующая логарифмическая доходность не равна 69' X . Скорее она равна In (1 + со ’ X ) = ln(l + со ’(ехр(X) — 1)) . Это делает портфель логарифмически нормальных активов более сложным в работе, чем портфели нормальных активов, по крайней мере в разовой игре.
Более того, портфели логарифмически нормальных активов едва ли будут логарифмически нормальными; они не подходят также ни к одному типу стандартных распределений. Однако этот недостаток не является для логарифмической нормальности особенным. Любой портфель, который может быть четко охарактеризован несколькими суммарными параметрами, независимо от количества активов или их весов, должен быть на 100% многомерно нормальным. Чтобы сделать любой другой подход легко поддающимся обработке, нам нужно искать аппроксимации.
Первые аппроксимации к логарифмической нормальности
Когда речь заходит о портфелях логарифмически нормальных активов, финансовая наука обычно страдает некой выборочной амнезией. Одни обращаются с X как с многомерно нормальной величиной, игнорируя нелепые последствия для цен на долгосрочные активы или вероятности отрицательного благосостояния. Другие обращается с логарифмической доходностью портфеля так, будто она составляет со' X , а не ln( 1 + св'А). При использовании первого подхода процентная средняя доходность и дисперсия портфеля равны св'М и св'L св соответственно. При использовании второго подхода логарифмическое среднее и дисперсия портфеля оцениваются как со'М и со'Ъм соответственно.
Мы можем наполовину оправдать любой из этих подходов, взяв очень короткий временной период и проигнорировав возможные скачки. Применение последовательных аппроксимаций ряда Тейлора первого порядка сокращает логарифмическую доходность ln( 1 + св'А} до чистой процентной доходности со' X — су'(ехр(АД — 1) и в свою очередь до средней логарифмической доходности со'X. Я употребляю термин «наполовину оправдать», поскольку временные диапазоны и риски, в которых мы заинтересованы, предостерегают нас от игнорирования членов второго порядка и скачков. Но подход Девлина уже обращается к большей части этого, делая допуск на множественные режимы. Поэтому я последую путем Девлина и приму аппроксимации за стартовую точку.
Ожидаемая полезность CRR при логарифмической нормальности
Полезность CRR может быть записана как signal - с) • (1 + х)'“с = signal - с) ехр((1 - с)х). При заданной
логарифмической нормальности ожидаемая полезность CRR, заданная
. /л х Г ехр((1-с)х) ( (х-/2)2Л|
EU = 5- с) • ---- .--—- * ехр------dx
2 ст )
1 .
= sign(\ -с)*ехр((1-с)/} + — (1
1
= sign(l - с) • ехр((1 -с)со' М ч—(1 — су со'Ъсо)
2^*
Второй шаг —еще одно применение генерирующих момент функций, в то время как третий шаг следует из логарифмическо-линейной аппроксимации.
Эквивалентность надежности при логарифмической нормал ьности
Логарифмическим эквивалентом надежности СЕ рискового портфеля является гарантированная логарифмическая доходность, которая принесет такую же ожидаемую полезность EU. Легко проверить, что СЕ = —-—Применив аппроксимации для логарифмической нормальности, о которых говорилось ранее, получаем, что для портфеля св'Х с логарифмическим средним пг и дисперсией v :
СЕ = пг ~ — (с — l)v = со'М — — (с — .
*2* 2
Множитель — (с — 1) измеряет стоимость дисперсии в терминах эквивалентного определенного убытка. На первый взгляд, это предполагает, что кому-то, у кого с < 1, нравится риск. Например, когда с = 0, что означает ™ ~ 1 ~ нейтральность риска, СЕ равняется m+ — v , так что инвестор может охотно принять ставку с отрицательным т . Однако очевидная ошибка исчезает, когда мы вспоминаем, что т обозначает среднюю логарифмическую доходность, а не логарифмический средний доход. Логарифмическим средним доходом действительно является сама СЕ, как должно быть при нейтральности риска.
313
Пасть 2. Постижение невежества
Ожидаемая CRR полезность при условной логарифмической нормальности
Для каждого возможного режима риска к рассчитайте условный эквивалент надежности СЕ к и преобразуйте в условную ожидаемую полезность EU^ Затем рассчитайте общую ожидаемую полезность EU как ожидание EUk при заданных, воспринимаемых вероятностях рк, что характерно для режима к\
Еи = ^,РкЕик = знак(\-с')-^рк^(к\-с')СЕк') к к
= знак(\ ехр
к
^Мк
-----со'Е.со
2 к
Рецепт Девлина представляет формулу для типичного случая с>1.
Аналогия с термодинамикой
В своих лекциях по статистической термодинамике Шредингер
определил функцию разбиения Z = схр
/
где к
константа
Больцмана, Т — температура, a G i — энергия в состоянии Z. Он заметил, что — K?ln(Z) измеряет свободную энергию. Поэтому если мы истолкуем 1 — с как 1/кД EU как -Z, СЕ к как условную энергию, а СЕ как совокупную свободную энергию, уравнение будет аналогичным. Более высокое неприятие риска соответствует более низкой температуре и более приглушенным энергиям.
Чтобы сгенерировать вероятностную меру р в различных состояниях,
просто позвольте каждому состоянию выполняться множество раз при рк, измеряющем его относительную частоту. В термодинамике также используется эта процедура. На самом деле каждая условная ожидаемая полезность EUk сама по себе является сокращенной формой функции разбиения. Дисперсия представляет случайные столкновения, которые рассеивают энергию, а следовательно, сокращают СЕк , при заданном коэффициенте столкновений относительно более дорогостоящие, когда неприятие риска высоко или
температура низка.
18. Откорректированный совет
«Было очень вкусно, — сказал Конвей после обеда. — Мне всегда было интересно, каковы трюфели на вкус».
«А мне нет, — сказал Девлин. — Мама учила меня не есть никакой пищи, на которой растут поганки. Но мне понравился шоколадный торт с двойной прослойкой. По крайней мере тот кусок, который мне оставила Регретта».
«Не преувеличивайте, Девлин. Я съела всего-то маленький кусочек, — сказала Регретта виновато.
«Если это маленький кусочек, то вы просто капибара, — хихикнул Девлин. Регретта покраснела.
Бедный Девлин, ну кто его тянет за язык Попробую-ка помочь ему выбраться из неловкой ситуации. «Девлин, тебя, наверное, удивит, но не всякой женщине понравится, когда ее сравнивают с огромным водным грызуном. Возможно, ты имел в виду голодную пушистую норку?»
«Я всего лишь хотел сказать... — начал было Девлин, но поймал взгляд Конвея и осекся. Девлин повернулся к Регретте и медленно осмотрел ее сверху донизу. — Да, именно это я и хотел сказать. Извините, Регретта».
«Да ладно, — сказала Регретта, — Но все равно спасибо вам обоим. Давайте вернемся к работе?»
«Согласен, — сказал Конвей. — Вперед, Девлин, пора продемонстрировать нам свое решение».
«Что ты имеешь в виду? Я же дал тебе рецепт».
«Не совсем. Не хватает последней строчки».
«Понял. Ты хочешь получить точную формулу для оптимальной смеси портфеля».
«Конечно».
«А ты считаешь, что я дал тебе рецепт только для того, чтобы разбудить твой аппетит простым ответом?»
«Да, это приходило мне в голову».
«Тогда крепитесь. Четкой закрытой формулы не существует. По крайней мере, для множественных рисковых режимов».
«Ты хочешь сказать, что нам придется решать это для каждого случая в отдельности?»
«Боюсь, что да. Но все не так плохо, как кажется. При всего нескольких активах и сценариях я обнаружил, что табличное решающее устройство оптимизируется в худшем случае за несколько секунд. А экспоненциальные
315
Часть 2. ТТостижонио новожоства
многочлены кажутся достаточно солидными, так что подозреваю, что даже сложные задачи можно решить довольно быстро, хотя и не проверял этого строго».
«Вы можете вывести хоть какие-то количественные подтексты своей модели не перелопатив кучу цифр?» — спросила Регретта.
«Немного. Например, если CRR превышает единицу, рациональным игрокам не понравится направленная вниз асимметрия или толстые хвосты. Они предпочтут толстохвостые распределения, которые наклонены вверх».
«Это обнадеживает. Как вы это проверяе те?»
«Проводя разложение в ряд Тейлора четвертого порядка по эквивалентам надежности и изучая знаки по асимметрии и эксцессу».
«Интересно. А моменты более высоких порядков сильно отличаются?»
«По-разному. Помните ваш график толерантности к риску по максимальной CRR? Я мог бы задрать коэффициенты Шарпа очень высоко по некоторым из этих ставок в стиле «пан или пропал», но инвестор бы их не принял. Напротив, если я достаточно ослаблю риск, любой инвестор будет в состоянии его переварить при условии, конечно, положительной ожидаемой доходности».
«Ну, хватит говорить о классификации портфелей по коэффициенту Шарпа».
«Я бы не стал так говорить. Он действительно ранжирует большинство портфелей правильно при условии, что можно повысить или понизить риск так, как нужно. На самом деле сама оптимизация может быть истолкована как модернизированная максимизация коэффициента Шарпа. Веса оптимального рискового портфеля равны величине, обратной взвешенному среднему ковариационной матрицы, умноженной на соответствующее взвешенное среднее вектора избыточной доходности, разделенное на CRR минус один. Безрисковый актив слабеет».
«А каковы веса? Вероятности каждого режима?»
«Нет, это вероятности, откорректированные с учетом риска. Они пропорциональны реальным вероятностям, умноженным на маржинальную ожидаемую полезность в этом режиме. Чем хуже режим, тем выше ожидаемая маржинальная полезность. Так что корректировки заставляют больше концентрироваться на повышении эффективности в самых худших режимах, чем то, что предлагается только чистыми вероятностями».
«Разве это не дает четкой формулы для весов портфеля? Я думал, что такой формулы нет».
«Ее и нет. Когда модифицируешь портфель, то модифицируешь и корректировки риска. Так что здесь надо будет начать с исходной догадки и произвести итерацию. Или воспользоваться компьютером, чтобы сделать это быстро».
И тут заговорил Конвей: «Хорошо, Девлин, думаю, я понимаю, как
работает твоя модель, и вижу ее теоретические преимущества. А каковы практические преимущества?»
«По большей части — уверенность в большинстве примеров, с которыми я практиковался. Рекомендации по портфелю не сильно улучшаются в рамках аппроксимации одного режима».
«Да ну? Разве они не помогают в работе с неопределенностью?»
«Нет, если неопределенность является всего лишь белым шумом вокруг истинных средних. Тогда однорежимный метод тоже можно использовать при условии, конечно, что безусловная дисперсия включает в себя как риск, так и неопределенность точно так, как ты предположил».
«И что делает эти два подхода разными?»
«Айсберги. Чтобы смягчить катастрофы, моя модель будет придавать особое значение удерживанию на борту низкодоходных спасательных шлюпок — казначейских векселей и им подобных — даже ценой более низких коэффициентов Шарпа. Ты помнишь пример, который ты привел во время первого посещения, — с маленькими шансами обычного 30%-ного краха?»
«И некоррелированный во всем остальном? Да, помню».
«Ну вот, я взял оттуда некоторые параметры — среднюю доходность в 5 и 3% соответственно, за исключением наличных, — и оптимизировал с учетом риска краха в 4,5% и CRR равной 4. Обращение с парой активов, как с двумерно нормальными, как того требует стандартная теория, совету'ет инвестировать примерно в пять раз больше в первый актив, нежели во второй, при практическом отсутствии вкладов в казначейские бумаги. Метод функций разбиения повышает вклады в наличные до 30%. Более того, он берет грубо равные куски из обоих активов, что приводит к тому, что второй актив почти исчезает из портфеля». Девлин выложил гистограмму.
Обычные риски катастроф, различные советы
Common disaster risks, different advice
Unconditional mean/variance
Ш Risky asset 1 Risky asset 2 □ Risk-free asset
CRR utility maximization
317
Часть 2. постижонио новожоства=============^
«Это резкий контраст. Но только как, по-твоему, я смогу убедить кого-то, кто не отличает одну модель от другой, что твоя лучше?»
Девлин пожал плечами. «Сдаюсь. Ты знаешь, какие это люди — финансисты. Они настолько приспосабливаются к вычислению общего мнения, что у них возникают проблемы, когда приходится думать за себя. Первый вопрос, который тебе зададут с ходу, будет таким: кто еще пользуется рекомендуемой вами системой? — гарантирую. Второй вопрос: почему нет. Так что придется тебе выдержать два удара еще до того, как ты начнешь говорить».
Регретта тоже вступила в разговор. «Помимо этого, вряд ли вас будут судить справедливо, сравнивая исходы портфелей с ожиданиями. Чаще всего кризиса не случается, и поэтому ваши рекомендации покажутся не оправдавшими ожиданий. А если кризис все же произойдет, люди будут склонны винить вас в том, что вы заранее не захеджировались в большей степени».
«Я все понимаю. Но разве здесь нет ничего, что делает новый подход более привлекательным?» — спросил Конвей. Девлин с Регреттой непонимающе взглянули на него. «Пожалуйста, помогите мне разобраться».
После минуты молчания Девлин заговорил: «Я не могу сравнивать себя с этими типами. Возможно, именно поэтому я сижу тут взаперти, а они гуляют на свободе. Но я могу сказать тебе, что мне кажется интуитивно привлекательным. Во-первых, распределения не имеют тенденции быть настолько экстремальными, как рекомендует стандартная теория. Вам не нужно столько облигаций, чтобы сгенерировать внутреннее решение или придать рыночному консенсусу столь большой вес. Вам просто нужно признать риски айсберга, которые в любом случае имеются где-то в глубине сознания у большинства инвесторов и инвестиционных менеджеров».
«Я думал, что одной из характерных черт риска айсберга является то, что люди не знают точно, что это такое. Если бы капитан «Титаника» хотя бы думал об айсбергах, он, возможно, предпринял бы больше мер предосторожности».
«Согласен. Никогда нельзя полностью знать о неожиданном. Это ограничивает возможность предупреждать события. Тем не менее, решение, состоящее в поиске возможных неприятностей, как правило, увеличивает нашу осведомленность. А путем подстройки вероятностных прогнозов в модель, можно по достоинству оценить, какие пороги имеют значение и какое. В этом состоит вторая привлекательная сторона модели. Она помогает внедрить управление рисками в распределение активов, вместо того чтобы навязать его как запоздавшую мысль».
«Можешь привести пример?»
«Конечно. Должен только предупредить: он очень яркий. Но хорошо освещает риск айсберга. Более того, он достаточно прост, чтобы производить расчеты без нормальной или логарифмически нормальной аппроксимации».
«Хорошо. Я обеими руками за все простое».
«Представь, что у рискового актива имеются только два возможных
исхода: первый исход падает на х стандартных отклонений ниже среднего...»
«Эй, помню я его. Это распределение, которое ты использовал, чтобы
1 показать, что 5-хвост стандартного отклонения может иметь вероятность —-.
х' +1
Второй исход падает на 1/х стандартных отклонений выше среднего».
«Точно. Теперь предположим, что портфель инвестора состоит из этого актива и безрисковых казначейских векселей. Так что единственный выбор — какую часть портфеля держать и в каком активе. Как, согласно стандартной теории, 5 должно влиять на выбор?»
«Не должно. Среднее, стандартное отклонение и неприятие риска Регретты решают все. Хвостовой риск сам по себе не будет иметь значения».
«Верно. А это интуитивно не очень привлекательно, не так ли?»
«Мы уже это проработали. Почти все считают, что хвостовой риск имеет значение. Иногда довольно большое значение».
«Тогда тебе понравятся функции разбиения. Я проработал несколько примеров с избыточной средней доходностью 5%, стандартным отклонением 10% и CRR равным 3. Когда х = 1, так что хвосты коротки и симметричны, рекомендуемый вес портфеля по рискованному активу составляет почти 2, а это значит, что тебе следует занимать, чтобы удвоиться. При х = 3, т.е. при 10%-ном шансе 25%-ного убытка и при 8,3%-ной прибыли в противном случае, ты совсем не растешь. При х = 10, т.е. при 1%-ном шансе потери 95% и 99%-ном шансе получения 6%, тебе не следует подвергать риску больше половины своего портфеля».
«Удваивать позицию или урезать ее пополам — большая разница. Но мы все знаем, что два портфеля могут выглядеть абсолютно по-разному и, тем не менее, приносить сравнимые откорректированные с учетом риска доходы. Насколько большой смысл имеет тогда выбор стратегии?»
«Ну, мы знаем, что это огромная разница — использование совета, основанного на ограниченной сумме, на которую может упасть актив, или случая, где х = 10. Если ты поднимешь ставку, которая уже подвергает риску потери почти всего, что ты имеешь, тогда твоя ожидаемая полезность будет равна минус бесконечности».
«В теории — да. В реальной жизни вариант банкротства внесет свой вклад, так что это не такой уж ясный пример».
«Справедливо. Но даже когда х = 2, предположение, что х — 1, может сократить ваш откорректированный с учетом риска доход почти вполовину. А если х = 4, ошибка будет стоить больше 15 базовых пунктов в откорректированном с учетом риска доходе, а гэп расширяется экспоненциально по мере роста х. Взгляните на график, который я подготовил в качестве иллюстрации».
Конвея график восхитил. «Здорово. Даже мои типчики будут поражены. Но если ты позволишь внести по дружбе редакторскую правку, то почему не
319
Часть 2. Постижоиио новожоства
сказать «стандартный совет» вместо «совет использования 5 = 1»? Так короче и понятнее».
«Короче, но не понятнее. Стандартный совет подразумевает нормальность, что, как мы знаем, технически несовместимо с полезностью CRR. Я мог бы преобразовать нормальность в логарифмически нормальную аппроксимацию, но это тоже не стандарт, и при этом существует более одного способа проведения преобразования».
Стоимость игнорирования хвостового риска для ц = 5%, о = 10%, CRR — 3.
Costs of ignoring tail risk for « = 5%, tr = 10%, CRR = 3
Регретту это заинтриговало. «Методики множественного хеджирования? Что вы хотите сказать? Разве вы не хотите просто подогнать средние и дисперсии?»
«Это зависит от того, что вы подразумеваете под словом «подогнать». Предположим, я применяю аппроксимацию, которой отдают предпочтение в теории опционов, где логарифмическая и процентная доходности обладают идентичными дисперсиями и средними, которые отличаются только половиной дисперсии. Предположим, что я применяю аппроксимацию по своему рецепту, которая обращается с логарифмической доходностью так же, как с процентной, когда дело доходит до подсчета средних и дисперсий портфеля. Оптимальная доля портфеля для рискового актива тогда составляет 225%, что превышает 199%, рекомендуемые для $ = 1, и приносит в жертву еще более откорректированный с учетом риска доход. Однако для большей точности вы, возможно, захотите отказаться от одной или от обеих аппроксимаций».
«Какое это имеет значение?»
«Если вы откажетесь от первой аппроксимации, но не от второй, оптимальная доля составит 245%. Если откажетесь от второй аппроксимации, а не от первой, то 167%. Если же откажетесь от обеих аппроксимаций, ответ
18. Откоррвктир в ванный свввт
будет 211 %. В любом случае рекомендуемый совет оставляет чрезмерную подверженность риску айсберга для любого 5 больше 2,5».
«Но это все равно крупное расхождение в рекомендациях. Что, на ваш взгляд, его вызывает?»
«Две вещи. Для начала вы делаете аппроксимацию откорректированной по риску доходности, а не оптимального портфеля. Изменение второго порядка в доходности означает изменение первого порядка в ее уклоне, а изменение первого порядка в ее уклоне может легко означать изменение первого порядка в расположении максимума. И более того, наиболее откорректированные с учетом риска доходности имеют склонность характеризоваться в меньшей степени острыми пиками, нежели гребнями, так что два существенно отличающихся друг от друга портфеля могут давать почти оптимальные результаты для данной задачи».
«Но я так полагаю, некоторые почти-решения могут быть намного менее устойчивыми к неправильной спецификации, чем другие».
«Точно. Почти-решение для нормальности с 245%-ной долей рискового актива гораздо более подвержено айсбергам, нежели почти-решение с 167%-ной. Недостаток устойчивости — одна из основных слабостей стандартной оптимизации среднего и дисперсии».
«Но вы не можете предотвратить неправильную спецификацию даже в своей модели. «Мусор на входе — мусор на выходе» — это фундаментальный закон. Вы не можете его отменить».
«Да, не могу. Но моя модель все-таки для того, чтобы усилить даже самые скромные предупреждения о риске. Например, предположим, вы уверены, что одно из двухточечных распределений, которые мы смотрели, применимо и что л-равно 1 или 4, но совершенно не уверены, чему именно. Наивный подход усреднит наилучший портфель для 5 = 1 с наилучшим портфелем для s ~ 4, приносящим долю рискового актива в 142%. Но мой подход предлагает смоделировать вашу неопределенность как два различных равновероятных режима — один, в котором 5 = 1, а второй, в котором 5 — 4. Что, на ваш взгляд, он будет советовать?»
«Менее 142%, полагаю».
«Намного меньше. Ожидаемая полезность максимизируется, когда доля составляет всего 101%, как если бы вы были уверены, что 5 составляет 2,9. Ваш откорректированный с учетом риска доход составит 299 б.п. — почти вполовину больше, чем принесет наивный подход».
Регретта одобрительно кивнула: «Здорово. Действительно здорово. Думаю, Вы получили в моем лице неофита».
«Двух неофитов, — сказал Конвей. — Как насчет того, чтобы построить мне оптимизатор портфеля, который обеспечит выполнение твоего рецепта? У меня в бюджете предусмотрены услуги консультантов, так что я смогу тебе заплатить».
«Не так быстро. Сначала мне. придется улучшить рецепт».
321
Часть 2. Постижонио нвввжоства_________________________________________
Гы, должно быть, ненавидишь, когда с тобой соглашаются, да? «Я думал, ты доволен своим рецептом».
«Не очень. Эти аппроксимации к моментам портфеля меня беспокоят. Меня беспокоит, что они слишком грубые».
«И это все? Только не надо делать лучшее врагом хорошего».
«Оно не всегда хорошее. Например, для CRR меньше единицы мой рецепт сходит с ума и советует отдать предпочтение безграничному риску».
«А, вот почему ты ввел это ограничение. Но, как говорите вы с Регреттой, это в любом случае не самое важное».
«Важно то, что мой рецепт дает сбой, а я не знаю почему».
Экий перфекционист. «Послушайте, Девлин, почему бы сначала не построить простую версию и не подстроить ее потом?»
«Сами строй простую версию, если тебе угодно. Может, Регретта тебе поможет. А я лучше подумаю над проблемой».
«Отличная мысль. Что думаете, Регретта?»
Регретта взглянула на Девлина, прежде чем ответить Конвею. «Ну, мне бы не хотелось подсиживать Девлина...»
«Я не возражаю, — сказал Девлин. — На самом деле».
«Хорошо, тогда я займусь этим. Но, можно задать вам вопрос, Конвей?» «Конечно».
«Сколько вы хотите заплатить?»...
Пока Конвей с Регреттой обсуждают условия, давайте повторим расчеты Девлина и попытаемся разобраться в том, что его беспокоит.
Примерный эквивалент надежности
Хотя формула, синтезирующая условные эквиваленты надежности, в совокупности является простой, она не дает достаточного интуитивного понимания их взаимодействия. Вот способ получения лучшего понимания. Во-первых, применяя разложение в ряд Тейлора четвертого порядка для различных ехр((1 — c)CEi) , оцените функцию разбиения как:
|gLr|sl + (l-c)£'[CE;] + ^1 Е Се}
(1 — cY r>V-'3~| (1 — с)4 Г----------4 "I
4-1-----}—Е СЕ, 4-—----------— Е CEi ,
6 L J 24 L J
что мы можем выразить
Тейлора четвертого
как 1 + Q. Затем воспользуйтесь разложением в ряд
О2 О3 О4 порядка 1п(14- ~ ч---------, чтобы
аппроксимировать ----In (2ГС7). Игнорируя члены пятого порядка и выше,
1—с v 7
некоторые утомительные алгебраические вычисления дают следующий результат:
СЕ = Mean — ~—- Var + ——Var3/2 Skew — ——— Var2Kurt, 2 6 24
где Mean, Var, Skew и Kurt обозначают соответственно среднее, дисперсию, асимметрию и эксцесс CEt .
Отрицательная асимметрия (уклон влево в распределении) штрафует совокупную СЕ в добавление к дисперсии так же, как и положительный эксцесс (толстые хвосты). Риск катастрофы — маленький шанс крупного убытка — почти всегда вычитает из асимметрии и прибавляет к эксцессу. Следовательно, он сокращает откорректированную с учетом риска доходность в большей степени, чем предполагает анализ среднего и дисперсии. Чем более неприемлем риск для инвестора, тем более высокого порядка моменты будут иметь значение.
Оптимизация при заданном единичном режиме
При единичном режиме максимизация ожидаемой полезности сводится к максимизации единственного СЕ выражения. Для совершенно логарифмически нормального актива, как мы помним, это будет равняться средней логарифмической доходности за вычетом — (с —1), умноженной на
дисперсию логарифмической доходности. Для портфеля логарифмически нормальных активов рецепт Девлина аппроксимирует СЕ как cd М — ~(с ~ 1)69^69. Максимизация относительно со дает оптимальные
рисковые доли со* в -Х~1М .
с — 1
Матрица вторых производных, или гессиан, СЕ составляет всего (1 — c)S и является определенно-положительной или определенноотрицательной в зависимости от знака с—1. Следовательно, со действительно максимизирует откорректированные по риску доходности в типичном случае с > 1. Однако при с < 1 со дает минимум вместо максимума, и инвесторам советуют стремиться к безграничным рискам. Мы будем искать способы исправить это.
323
Часть 2. ТТостижонио нооожоства
Отношение к стандартной максимизации коэффициента Шарпа
Вспомним, что числа, кратные Х~'М максимизируют коэффициент Шарпа. Итак, кажется, модель Девлина как особый случай включает в себя стандартную максимизацию коэффициента Шарпа. К сожалению, раньше мы подменили определение среднего и ковариаций, чтобы применить логарифмическую доходность вместо процентной. Это делает соответствие всего лишь примерным.
Некоторое несоответствие отражает ошибки в методе Девлина. Например, в то время как его метод обращается с логарифмической доходностью портфеля как с линейной в весах портфеля, разложение в ряд Тейлора второго порядка также выявляет квадратичный элемент:
£[1п(1 + бу'Х] = £'[бу'Лг]-|-£[((у'Х)2] = бу'М-^-бУ'ММ'бУ-^-бу'ХбУ
Если мы заменим эту квадратичную форму на со'М в аппроксимации Девлина к СЕ, предположив, что Ё = S, оптимальная смесь станет такой: со = (сЕ + ММТ1 М =-------—-—Е"'М =----Ц^Х"’М=——z-E-'M,
v 7 с + M'Z’'M c + S2 c + S2
где 5 обозначает максимальный коэффициент Шарпа, а 5 — реальный коэффициент Шарпа. Первое равенство может быть проверено путем предварительного умножения обеих сторон на сЕ + ММ'. Второе равенство следует из уравнения для максимального коэффициента Шарпа, в то время как последнее равенство следует из со*, максимизирующего коэффициент Шарпа.
Короче говоря, переработанная оптимальная смесь максимизирует коэффициент Шарпа без безграничного риска даже для с < 1. Это важный шаг к согласованию различных мер. Однако не забывайте, что пересмотр применим только к аппроксимации второго порядка для среднего портфеля, но не для дисперсии.
Логарифмически нормальные аппроксимации против баланса моментов
Единственный способ подогнать логарифмически нормальную аппроксимацию к доходности — это баланс первых двух моментов. Вспоминая формулы для логарифмически нормальных моментов из предыдущей главы, мы должны выбрать такие Д и &2, которые удовлетворяли бы следующим критериям:
ехр //+ — гг2 | -1 = у/; ехр(2 // + &2 )(ехр(ст2 ) -1) — ст2 ,
где т и v обозначают целевые процентные средние и дисперсию. Это дает решение:
= 1п( 1 + //) —
То же отношение применимо между статистическими данными портфеля т, v, т и V. Таким образом, мы можем соотнести коэффициент Шарпа, S = т / , основанный на логарифмической доходности, со стандартным
коэффициентом Шарпа S = т / yfv как:
Следовательно, два коэффициента Шарпа дают почти одинаковые табличные данные в районе единицы. Коэффициент Шарпа выше единицы больше вознаграждает за дисперсию, чем стандартный коэффициент Шарпа. Коэффициент Шарпа ниже единицы больше наказывает за дисперсию.
Несколько примеров
Чтобы проиллюстрировать влияние различных аппроксимаций, упомянутых выше, давайте рассмотрим пример Девлина, в котором рисковый актив обладает средним ц = 5% и стандартным отклонением о = 10% для коэффициента Шарпа, точно равного 0,5. Чтобы логарифмически нормальная плотность соответствовала этому среднему и стандартному отклонению, он должен устанавливать {// = 4,428%, сг — 9,502%} для основанного на логарифме коэффициента Шарпа 0,466., Для сравнения: стандартная логарифмически нормальная аппроксимация, используемая в финансах, установила бы {Д — 4,5%, & = 10%} для основанного на логарифме коэффициента Шарпа 0,450. Аппроксимации о(1 — ц) и //— — ^//2 + ст2} , заданные выше, намного совершеннее: они устанавливают
{ Д = 4,424%, сг = 9,500%} для основанного на логарифме коэффициента Шарпа 0,466.
Теперь давайте рассмотрим портфель, который удваивается по рисковому активу. Применяя аппроксимации в рецепте Девлина, чтобы подогнать
325
Часть 2. Псстижвнив нвввжвства_____
логарифмически нормальную плотность к портфелю, мы рассчитаем {ш = 9%,у = 20%} с помощью стандартной эталонной оценки против рц — 8,855%,v = 19,005%| , рассчитанных с помощью лучшего эталона. Однако еще более предпочтительной процедурой будет применение формул преобразования непосредственно к удвоенному портфелю, т.е. к т ~ 10% и v — 20%. Это дает {т = 7,905%,v = 18,039%} для основанного на логарифме коэффициента Шарпа 0,438.
Аппроксимация Девлина достигает лучшего результата, когда рисковый актив ослабляется. Например, если рисковый актив включает в себя только половину портфеля, рецепт Девлина предлагает — 2,214%, у — 4, 750%} с помощью наилучшей логарифмически нормальной аппроксимации, в то время как более прямой расчет по портфелю дает = 2,350%, v — 4,875%} . Тем не менее несоответствия остаются слишком большими, чтобы чувствовать себя комфортно, и это объясняет неудовлетворенность Девлина.
Оптимизация с множественными режимами
При множественных возможных режимах условия первого порядка для оптимизации примерной формулы Девлина EU для ожидаемой полезности становятся такими:
1-с)Мк -(1-с)2£Л<у) = 0.
dco к v
Это подразумевает, что
=\YpkEU^k
^PkEUkMk
ддя оптимального портфеля со*. Гессиан составляет (с~1)2pkEUktk , а поскольку EUk все несут знак 1 — с, он будет отрицательным
полу определенным, что гарантирует, что со максимизирует EU , если с > 1. Если с < 1, метод Девлина не сработает так же, как и в случае с одним режимом: со* минимизирует EU, и инвесторы получат совет принимать на себя безграничные риски.
Зависимость оптимальной смеси от неприятия риска
В классической теории финансов оптимальная смесь пропорциональна обратной ковариационной матрицы, умноженной на вектор среднего, в то время как неприятие риска не оказывает никакого влияния, кроме левереджа. На первый взгляд вышеприведенная формула для со* сохраняет те же свойства. При 326
ближайшем рассмотрении неприятие риска вводит выражения для EU, так, что это невозможно распутать. Не существует общего конечного решения, и состав рискового пакета меняется вместе с неприятием риска инвестора. Оптимизацию следует делать многократно, чтобы повторно откорректировать веса полезности.
Интерпретация коэффициента Шарпа оптимальной смеси
Однако существует ощущение, что максимизация коэффициента Шарпа в некотором роде все равно применима. Сформируйте новый вектор X с
_ pkEUk
элементами Лк — -------. Поскольку в сумме составляют единицу, они
2^PkEUk
к
могут быть интерпретированы как определяющие откорректированные по риску вероятности для различных режимов. При с > 1 «режим катастрофы», в котором ожидаемая полезность является высоко отрицательной, будет иметь больше веса, чем это предполагает его простая вероятность наступления. Чем больше инвесторам не нравится риск, тем больший вес они придадут худшему режиму относительно лучшего.
Затем, используя X* в качестве весов, сформируйте вектор средневзвешенной избыточной доходности М = ^7 Мк и к
откорректированную ковариационную матрицуS = . Говоря
к
экономическим языком, М и S представляют из себя откорректированные с учетом риска среднее и ковариации соответственно. Оптимальный портфель тогда принимает очень простую форму:
а/ =—L-s^m
с — 1
с подразумеваемой безрисковой долей в 1 — со ’1. Оптимальный портфель максимизирует откорректированный по риску коэффициент Шарпа, с тем же множителем, как и в случае одного режима.
Введение нормально распределенной неопределенности
Предположим, вы уверены, что логарифмические доходности являются многомерно нормальными, с правильной ковариационной матрицей Z , и, хотя вы неуверенны относительно среднего логарифмического дохода, ваши представления о среднем могут быть описаны как многомерно нормально распределенные с средним М и ковариационной матрицей Н . С операционной точки зрения, это все равно, что сказать, что ваши представления о логарифмической доходности являются многомерно нормальными со средним М и ковариационной матрицей S + Н.
327
Часть 2. Постижонио новожоства я==
Единственным способом проверить этот результат является моделирование ожидаемой полезности в два этапа. Во-первых, следует рассчитать ожидаемую полезность, обусловленную средним X и долей
1 ~ ,
портфеля со как ехр((1 — с)(а>'Х — — (1 — с)й>^со')) . Затем проинтегрируйте
последнюю согласно вашим убеждениям относительно X :
Это всего лишь ожидаемая полезность при заданном портфеле со рисковых активов, имеющем среднее М и ковариационную матрицу S + Н .
Генерирующая момент функция для многомерно нормальной плотности
В приведенных выше расчетах ЭЯ” обозначает «-мерную область реальных чисел, в то время как Ми — это генерирующая момент функция для «-мерного нормального распределения. Давайте проверим, что действительно ли М„(<о) есть ехр(<г>' М — со) . Одним из способов является перестановка экспонент в интеграле:
М„О) - [ „ ехр((У'^)(2ил-"5)'1/2 ехр(--(^ - м)"ЁХ (Х - M))dX
= ехр(бу' М — — со'Зсо)
= ехр(бо'тИ - — су'^су)
Последний этап следует из необходимости, чтобы вероятностные плотности интегрировались к единице. Еще более простой способ указывает, что рассматриваемый интеграл равен величине характеристической функции М(1) для одномерно нормальной случайной переменной, имеющей среднее а>'М и дисперсию бо’Нсо.
Моменты многомерных логарифмически нормальных переменных
Предшествующая формула облегчает расчет среднего и ковариационной матрицы многомерных логарифмически нормальных переменных. Чтобы рассчитать среднее ц, х. = ехр(х,) — 1, установите со, = 1 и обнулите все другие
компоненты со. Это подтверждает, что J2. = ехр(Д + у ст) — 1.
Чтобы рассчитать ожидание (1 + х,)(1 + Xj) установите со, = со, = 1 и удерживайте остальное на нуле. Вычтите (1 + ц;)(1 + ц,), чтобы сформировать ковариацию:
= ехр(Д + Д +1+ &tj)) - ехр(Д +1 ехр [ Д +1
= ехр(Д +у<т„)ехр(Д +^-ст7/)(ехр(ст,7)-1)
= (! + //, )(1 + fdj )(ехр(<5\ ) -1).
Когда i = у, это сокращает выражение до формулы, выведенной в главе 17 для дисперсии одномерной логарифмически нормальной переменной.
329
19.Уловки высоких порядков
«Я не толстая», — думала Регретга следующим утром, глядя на себя в зеркало. Она поворачивалась к зеркалу то одним боком, то другим, чтобы получше себя рассмотреть. Нет, определенно, она не толстая. Чтобы быть уверенной наверняка, она пропустила завтрак и удвоила время тренировки. Впоследствии, уставшая и голодная, она съела плитку шоколада и отругала себя за то, что позволила Девлину затронуть ее за живое.
Осознав, что она слишком болезненно отреагировала на замечание Девлина, Регретга успокоилась. Ей пришлось признать, что ей приятна компания Конвея и Девлина. Страто. Кто бы мог подумать? Девлин был таким ничтожеством.
Внезапно Регретгу осенило. Девлин, должно быть, втюрился в нее. Вот почему он перестал называть ее Плаксой и так быстро извинился за шутку с капибарой. Бедный Девлин. Должно быть, он одинок. Но из его тщетных надежд ничего путного не выйдет. Я должна положить этому конец.
В понедельник утром на групповой терапии Регретга глянула через плечо несколько раз, чтобы проверить, не смотрит ли на нее Девлин. И несколько раз ловила на себе его взгляд. В таких случаях он быстро отводил глаза, но Регретта-то знала.
И точно, после сеанса Девлин подошел к ней. «Добрый день, Регретга, у вас есть свободное время? Нам нужно поговорить».
«Да, я тоже так считаю. Однако не здесь». Она не хотела смущать его перед всеми.
«Хорошая идея. Как насчет того, чтобы нам погулять в парке?»
Регретга согласилась. На улице стояла отличная погода, было тепло и нежарко. Они пошли к дубовой роще, сели на лавочку и стали наблюдать за тем, как резвятся белки.
Девлин откашлялся. «Позвольте я сразу перейду к делу, Регретта... Полагаю, нам следует перевести все на более высокий уровень».
Регретта смутилась. «Извините, Девлин, но я так не считаю. Меня все устраивает».
«Не может устраивать. Но мы можем сделать так, что всех все будет устраивать. Это можно сделать тремя способами».
Регретта была ошеломлена. «Послушайте, любезный. Уж не знаю, что там происходит в ваших куриных мозгах, но я не такая. Конвей тоже не производит на меня такого впечатления».
Девлин поджал губы и кивнул. «Полагаю, вы правы насчет Конвея. Но я уверен, что Вы с этим справитесь. Давайте сначала все проработаем вдвоем, а его введем в курс дела позже».
«Да как вы смеете, Девлин? Мы друг друга совсем не знаем».
«Верно. Но есть много вещей, о которых вы не знаете. Однако я считаю, что вы быстро учитесь».
Самонадеянный нахал! «Почему вы так уверены, что можете чему-то меня научить?»
«Не обижайтесь, Регретта. У меня просто было больше времени на то, чтобы самостоятельно всему научиться».
«Наверно, это было забавно».
«В большинстве случаев — да. Но, возможно, другие помогут найти какие-то новые ходы».
«Почему бы вам не заняться этим с Конвеем?»
Девлин покачал головой. «Пожалуйста, Регретта. Я знаю Конвея. Он классный парень, но это просто не его сильная сторона. Возможно, нам следует скрывать от него по-настоящему эксцентричные вещи и просто позволить ему сконцентрироваться на результатах; Что думаете?»
«Думаю, вы просто ужасный человек. Я не хочу иметь ничего общего с эксцентрикой».
«Ну, Регретта, я в вас разочарован. Разве так сложно один раз через это пройти? Это поможет мне убедиться в том, что все работает».
«Если вам нужна проверка, обратитесь к врачу».
«Вы, наверное, шутите, Регретта. Что эти врачи знают о наших проблемах? Они просто пытаются перевести разговор на что-то неважное, типа моих взаимоотношений с матерью».
«Возможно, здесь больше связи, чем вы думаете».
«Ха, ха, ха! Очень смешно. Ну ладно, перейдем к делу, хорошо? У меня есть кое-что, что я хочу вам показать». Он сунул руку в карман.
«Нет, Девлин, определенно нет!» — она отвернулась.
«Расслабьтесь. Вас никто не укусит», — Девлин вытащил из кармана сложенный лист бумаги и развернул следующую гистограмму.
331
Часть 2. Постижонио невежества
Общие риски катастроф, усовершенствованный совет.
Common disaster risks, refined advice
Регретга была ошарашена. «Какого...!» — воскликнула она, а затем прикусила язык. Она вскочила на ноги, покраснев чуть ли не до кончиков ушей.
«Все в порядке?»
Регретте было слишком стыдно, чтобы что-то объяснять. Быстро, придумай что-нибудь. «Ой! Я, наверно, села на шип». Она отряхнула брюки, притворившись, что ищет шип. «А, вот он». Регретга смахнула воображаемый шип, затем медленно оправила одежду, отвернувшись от Девлина.
«Хотите пойти домой?»
«Нет, теперь все в порядке». Она села. «Так скажите, что должна показывать эта гистограмма?»
«Помните двухрежимный сценарий Конвея, в котором два актива имеют некоррелированную 5%-ную и 3%-ную доходность соответственно, за исключением кризиса, когда они оба падают на 30%? А вероятность кризиса составляет 4,5%?»
«Да. Первые два прямоугольника представляют из себя смеси портфелей, рекомендуемые классической теорией среднего и дисперсии, и вашим рецептом. Каковы же эти усовершенствования?»
«Это как раз то, о чем я вам говорил. Они представляют собой три различных способа усовершенствования оценки».
«Почему бы не выбрать только один?»
«Потому что я не уверен, какой из них самый лучший. Но они все-таки лучше, чем мой исходный рецепт в той же степени, в которой мой рецепт лучше обычных среднего и дисперсии».
«Откуда вы знаете?»
«Потому что они все основаны на аппроксимациях ряда Гейлора более высоких порядков к оценкам в различных режимах».
«Каким оценкам? Среднего и дисперсии логарифмической доходности?»
«Частично. То есть да. Именно этим занимается третий подход. Он предполагает логарифмическую нормальность».
«А два других?»
«Они концентрируются на процентной доходности».
«Если два других концентрируются на одном и том же, тогда в чем же разница между ними?»
«Первый подход берет аппроксимацию четвертого порядка к условной ожидаемой полезности. Второй подход берет аппроксимацию второго порядка к условной, откорректированной с учетом риска доходности».
«Разве аппроксимация четвертого порядка не должна быть намного лучше аппроксимации второго порядка?»
«Не обязательно. Первый подход концентрируется на исходах, близких к условному среднему распределению, в то время как второй подход интегрирует по полному многомерному нормальному распределению».
«Я думала, что процентная доходность не может быть полностью многомерно нормальной».
«Так оно и есть. Я же вам сказал, что не уверен в том, какая аппроксимация лучше. К счастью, это редко имеет большое значение».
«Почему вы так говорите? В вашем графике третье усовершенствование дает заметно отличную от других смесь».
«Я хотел сказать: небольшое значение в терминах полезности. Независимо от того, какое усовершенствование вы считаете «верным», другие подходят близко к нему в терминах ожидаемой полезности. На самом деле мой исходный рецепт тоже неплох. Но обычная теория «среднего и дисперсии» тащится далеко позади, поскольку она принимает слишком много риска».
Откорректированная с учетом риска доходность, приведенная в качестве примера.
Risk-adjusted returns sacrificed in example
Classical Quick recipe Refinement 1 Refinement 2 Refinement 3
г! #1 is best model
#2 is best model
; #3 is best model
333
Часть 2. Постижвнив новожоства
Регретта изучила гистограмму. «И это все, что усовершенствования добавляют к быстрому рецепту?»
«В этом примере — да. В целом — нет. Чем больше хвосты, тем полезнее усовершенствования».
«И когда вы собираетесь показать мне новые рецепты?»
Девлин улыбнулся: «Я уже начал думать, что вы об этом не спросите. Вот они». Он вытащил из кармана другой лист бумаги.
Усовершенствования рецепта
Усовершенствование №1: Пусть тк = со'Мд обозначает среднюю процентную доходность в режиме к, а ? = yv’SA гг(1 +) 2 — дисперсию доходности относительно ее валового среднего. Рассчитаем ЕUk как:
Усовершенствование №2: С помощью той же системы обозначений рассчитайте EUk как:
signal-с)-рк{Х + тк) (N-(l-c)vJ exp --—
. . ... I 2 14 Г ~cJvk )
Усовершенствование №3: Обозначьте с помощью
Ак 1п(1 + б9’(ехр(Л?А) — 1)) логарифмическую доходность портфеля, когда логарифмические доходности актива соответствуют их средним, с помощью Вк — diag(a>yехр(Л/'' — Ак1) — веса портфеля, откорректированные для
различных относительных ожидаемых логарифмических доходностей, а с помощью у/к I + (с — V)(diag(Bk ) — ВкВ \ - - корректировку на кривизну.
Рассчитайте Е77А. как: ??
,/2схр| .
\ . X J )
«Ого! — сказала Регретта. —- Это так просто не переваришь».
Девлин кивнул: «Согласен. К счастью, для того чтобы ими пользоваться, не обязательно их понимать. Просто вмонтируйте расчеты в таблицу. Но вы уверены, что не хотите, чтобы я провел вас по ним разок?»
«Ну, если вы настаиваете...»
Пока Девлин объясняет все Регретте, позвольте мне попробовать проделать то же самое с вами.
Быстрое повторение
Исходный рецепт Девлина резюмировал процентную доходность портфеля 1+ оо'X как exp(oo'JV), рассуждая следующим образом:
1 + w’X = cxp(ln (1 + w’ АЛ)) = ехр( w’X)
- ехр^а>'(ехр(Х) - Qj exp (69’%)
Это превратило условную ожидаемую полезность в генерирующую момент функцию с простым закрытым выражением. Условный эквивалент надежности был линейным как в средней логарифмической доходности, так и в дисперсии, со штрафом на единицу дисперсии в — (с — 1) .
Эта глава предлагает три способа для дальнейшего усовершенствования аппроксимации. Все они основываются на разложении в ряд Тейлора более высокого порядка. Первый подход создает аппроксимации четвертого порядка к условным эквивалентам надежности. При этом один подход концентрируется на процентной доходности, а второй — на логарифмической доходности.
Еще несколько терминов
Я прошу у читателей снисхождения и терпения принять еще несколько терминов. Хотя я мог бы обойтись без них, однако они сделают приведенные ниже выводы намного проще для понимания. Самым полезным является с , который переводит исходы портфеля в процентное отклонение от их среднего значения. Иными словами, нам задана смесь портфеля
„ w'X-m w’(X-M)
w, е=--------—-----------. Легко проверить, что е имеет среднее 0 и
1 + т 1 + w'M
v
дисперсию ------которую я обозначу другим символом у. Из главы 18
(1 4- т)~
вспомним, что у близко v, параметру логарифмической дисперсии в логарифмически нормальном портфеле, имеющем логарифмическое среднее т , процентное среднее т и процентную дисперсию v.
Другие новые члены — это А^В и С. Они представляют, соответственно, логарифмическую доходность, ее первую производную или градиент, и ее вторую матричную производную, или гессиан, оцененный при средней логарифмической доходности М .
335
Часть 2. Постижение невежества
Усовершенствование №1 Аппроксимация полезности CRR с помощью процентной доходности
Первое усовершенствование начинается с разложения в ряд Тейлора процентной доходности портфеля o'Y вокруг условного среднего тк = w' Мк в режиме к:
где
j + 1)
целое число. Подбор ожиданий по
даже когда п — неположительное
различным возможным режимам
устанавливает, что:
EU = sign(\-cy^pk (1
к
Предупреждение о допустимости
Предыдущие итоги не обязательно должны сходиться, поскольку EU может быть не вполне определенным для рассматриваемого распределения. Например, ни одна из не может быть полностью нормальной, даже условно, поскольку полезность CRR не может управлять убытком более 100%. Давайте в любом случае проведем разложение в ряд Тейлора и посмотрим, что произойдет. Ясно, что нечетные моменты будут равны нулю из-за
симметрии. Каждый четный 2/-ный момент выражается как (vA )7 , умноженное на все положительные целые числа менее 2/: это можно проверить, оценив центральные производные генерирующей момент функции
M(n) — exp — vkn2
. Ожидаемая полезность тогда сокращается до:
EU — sign(\ - с)
18. Уловки высоких порядков
Теперь взгляните на соотношение соседних членов в этом разложении.
_ (с + 2у-3)(с-н2/-2) _ -
Оно равно ---------------:----vA. , или грубо 2 /ту . Независимо от того.
2.7
насколько мало это соотношение сначала, оно в конечном итоге превзойдет единицу, сделав подсчет бесконечным.
Ожидаемая полезность квазинормальных портфелей
Я буду называть портфель квази нормальным, если его асимметрия и
эксцесс близки к нулю. В этом случае
Е ё3 = О,а
Д За; . Обратите
внимание, что портфель может быть квазинормальным, даже если составляющие его активы решительно ненормальны. Действительно, если портфель состоит из достаточного количества независимых, примерно равных взвешенных активов, центральная предельная теорема указывает, что он должен быть квазинормальным.
Теперь наша модель не предполагает квазинормальности для портфеля в целом. Она далеко отстоит от этого. Но мы можем попытаться поделить мир на условно квазипормальные режимы. Оценка разложения в ряд Тейлора до четвертого порядка тогда указывает, что:
= 5 7^/7 (1
t fV f F К
+ -(c-l)c(c + l)(c+2)v;) , где снова тк =w'Mk,a vk =—------------
8 (1 + w Mk у
Максимизация коэффициента Шарпа как аппроксимация второго порядка
Предположим, что все средние и дисперсии ничтожно малы или что мы слишком ленивы, чтобы включить любые члены выше второго порядка. И действительно, мы даже используем аппроксимацию второго порядка к (1 + . Тогда выражение для EU значительно упростится и мы упростим его еще # |£77|-1
больше, выразив его в терминах EU = ------, что подразумевает абсолютно
1 — с
те же предпочтения:
337
Часть 2. Постижение невежества
= т — — сут + ст2 J = wr М — — сд(иЕ Л/) 4-vv'Ew
= v/.W -г;/|А/А/'-Енд
2
где переменные без нижнего индекса являются совокупными безусловными средними и дисперсиями. Аппроксимация ожидаемой полезности будет максимизирована при
*
W
= -(Х + ММ’Г' м =
2v ’
-----------Z~'M = с(1 + М'17'М)
-----— £-'М, с(1 4- ЛГ )
где S обозначает коэффициент Шарпа. Это напоминает аппроксимацию, выведенную в предыдущей главе, за исключением множителя с по члену ММ’. Чтобы проверить второе равенство, предварительно умножьте обе стороны равенства на L + ММ'. Решение, действительное для всех с, всегда достигает максимального коэффициента Шарпа (М' Е-1 AZ)l//2 , что подразумевает последнее равенство. Единственным отличием от предшествовавших основанных на коэффициенте Шарпа решений будет то, что эта формула рекомендует меньший левередж.
Вклады более высоких порядков
Чем более неприем риск для инвестора, тем важнее включать члены более высоких порядков. Для случая с = 3 выражение четвертого порядка сокращается до:
тгг г 1 + 3vk 4-1 5v~
Еи^=------,,----
(1+лиД
Члены более высокого порядка в этом выражении не имеют большого значения для |ш| меньше 10% или v меньше 20%. Для у выше 35% это выражение, вероятно, не является выражением достаточно высокого порядка, но такой высокий потенциальный риск снижения делает квазинормальность сомнительной в любом случае.
Стимул к снижению высоких рисков
Для общего квазинормального случая откорректированная по риску доходность для каждого режима составляет:
338
18. Уловки высоких порядков
CEt = \EUk X -1 == )лк + (1 +1 (с -1) cvk V 2
1 „
= тк-------cv,
2
где последний шаг следует из разложения в ряд Тейлора после выпадения всех членов в vk и выше. Отрицательный знак по vk налагает дополнительный штраф на высокую дисперсию помимо стандартной формулы среднего и дисперсии. Более того, поскольку vk само по себе измеряет дисперсию относительно условно ожидаемой полезности, дисперсия в плохих режимах штрафуется больше, чем дисперсия в хороших режимах.
Усовершенствование № 2
Другая аппроксимация к полезности CRR
Усовершенствование №2 сильнее возвращается к исходному рецепту Девлина. Оно переписывает (1 + се>3¥)'^ как ехр((1 — с) ’ In (1 + w* X)) , аппроксимирует логарифм с легче поддающимся обработке выражением, а затем использует генерирующие момент функции, чтобы оценить ожидание. Однако второй подход не аппроксимирует ln( 1 + со'20 как со'Х Вместо этого он берет разложение в ряд Тейлора второго порядка вокруг среднего:
ln(l + w'%) = In (1 + w’M) +-----
1 + w ’ M
Оценка ожидаемой полезности
1 ( w' X — w' М 2< ] + w'M
2
Чтобы оценить ожидание, второй нормальность процентной доходности квазинормальности. Отсюда следует, что:
подход предполагает условную
&)Х
вместо
простой условной
•(2^va) 1/ ехр
1 G2 1
2 >
d
= sign( \ — с) • (1 + тк )
Г ехр((1 — с) ехр
339
Часть 2. Постижение невежества
= sign(\-с)-Д73-(1 + тк)'
ехр((1 — с) еА. )-(2л77) ' "е.хр
= 5/^(1-с)-——(l + /wA. )‘ с -ехр -(1-е)2 Н
V, ’ <2
Третья сярока — это всего лишь перестановка членов, в то время как четвертая оценивает генерирующую момент функцию. Второй шаг требует, _ 1 1 1 тт v,
чтобы — = 1 — с + или Н =----------------. Следовательно:
// vk 1 + (1 -c)vA
EU = 5/g/7(l — с)
ZT(i+/w*Tо -о ем ' "exp
предостережение
Интеграл не является определенным, если Н отрицательна, как это
происходит, когда с > 1, a vk >-. Однако если только инвестор не является
с — 1
чрезвычайно нетерпящим риск, этот предел попадает намного выше 1раниц, где нормальная аппроксимация имеет смысл. Например, для с = 3 стандартное отклонение должно превосходить 70% условной валовой доходности, что подразумевает под собой серьезные шансы потери большего, чем все ваше состояние.
Откорректированные с учетом риска доходности
В каждом режиме логарифмическая, откорректированная с учетом риска доходность составляет:
Эти результаты выглядят очень знакомыми. Если мы аппроксимируем 1 ,
ln( 1 + по тк Ч—vk , a vk по vk и опустим члены более высоких порядков,
340
19. Уловки высоких порядков
мы вновь получим рецепт Девлина тк +-(1-с)^. Более того, как эта формула, так и формула СЕ из усовершенствования №1 включают в себя член, который является квадратичным как в х>к , так иве. Действительно, когда СЕ преобразуется в СЕ == 1п(1 + СЕ} , оно даст такую же аппроксимацию, что и выше.
Усовершенствование Ns 3
CRR полезность в терминах логарифмической доходности
Усовершенствование №3 ближе всего подходит к исходному рецепту Девлина. Подобно усовершенствованию №2, оно переписывает (1 + со'А)1'1’ как ехр((1 — с) • 1п(1 + w'АД) и берет аппроксимацию ряда Тейлора второго порядка к логарифму в районе своего среднего. Однако оно выполняет аппроксимацию в терминах логарифмической, а не процентной доходности:
ln( 1 + со' X) = 1п(1 -г со'(ехр(X) — 1))
Расчет А
Чтобы определить И, оцепите логарифмическую доходность портфеля при X — XI :
А — In И т- бс/(ехр(л7) — 1)1 In (1 + со' М} ~ ln( 1 + гп) .
Иными словами, А равно логарифмической доходности портфеля, оцененной по средней логарифмической доходности по активам, а нс по средней процентной доходности.
Расчет В
Чтобы определить В , продифференцируйте логарифмическую доходность портфеля относительно логарифмической доходности активов, а затем оцените при X = XI . Давайте будем осторожны и проделаем это поэлементно:
1 + со
Х^-\1
б9,ехр(х,-)
1 4- б9'(ехр(X ) — 1
'(ехр(Д)-1))|
341
Часть 2. Постижение невежества
ехр(Д)
1 + t'j'f ехр^Л? j — 1
— <о. exp(/z. — A),
где нижний индекс z относится к компонентам вектора, а нс к режимам. Следовательно, Ь. представляет вес портфеля пенных бумаг, если все активы достигают своей ожидаемой логарифмической доходности за период. Чтобы выразить совокупный результат в форме матрицы, я использую diag(co), диагональную матрицу со: В — diag(co)' ехр(Л/ — А1) .
Расчет С
Чтобы определить С, продифференцируйте логарифмическую доходность портфеля дважды относительно логарифмической доходности активов, а затем оцените при X = М. И снова давайте сделаем это поэлементно. При условии, что j Ф i:
со, ехр (й.со, ехр ( и.) , ~ х
=---------------—--------— = — со ехр ( /7 — А ) • и- ехр(//. — А)
(1 + су’(ехр(Л/)-1))2 ' 7 ! 7
Помимо этого,
— со, ехр(Д - А) — I coj ехр ( Д
После воспроизведения матрицы С становится очевидно, что:
С — dicig — ВВ'.
С корректирует кривизну, чтобы настроить оптимизацию. В основном оно гласит, что следует применять откорректированные веса bi не только к отклонениям xi — g,, но также к половине Д — Д в квадрате, а затем вычитать половину квадрата отклонения портфеля в целом.
342
18. Уловки высоких порядков
Ожидаемая полезность
После того как мы рассчитали наши АВС, остальные расчеты EU точно предполагают под собой логарифмическую нормальность. Обозначив X — М с помощью знака X и помня о том, что параллельные линии вокруг матрицы обозначают ее определитель, рассчитываем:
EU к — с
. 1 -ехр[ --X't~'X\dX
X’7tn tk V 2 )
• exp
= sigr?(\ — c)
ехрЦ(1-с)25/(Ё;' +(C-1)CJ"' sJ
= 5/^(1-C)-|Tj-'/2exp|
для ^ + (с-1)СД.
Откорректированная с учетом риска доходность
Условная логарифмическая откорректированная с учетом риска доходность составляет:
СЕ = Ак +
2 2 с — 1
Здесь Ак выступает в качестве средней логарифмической доходности,
343
Часть 2. Постижение невежества
Вк — в качестве откорректированных весов портфеля (которые, в отличие от со изменяются в зависимости от режима), a корректирует на кривизну. Чтобы получить несколько более глубокое понимание, мы можем переписать Ч7/ как разложение в матричный ряд:
чу =7 + (1-с)сЛ +((1-с)СЛ)2+...
Это подразумевает, что эффективная ковариация портфеля, опускающая нижний индекс к ради удобства, равняется:
B"¥~'t.B = B'tB + (\-c)B’Ct-B + {\-c'y B’C2tyB + ...
Первый член в разложении — это просто ковариация портфеля с весом В и ковариациями S , но мне не хватает интуиции пояснить роль других членов или корректировки |, что дана выше. К счастью, мы можем
воспользоваться рецептом, даже не понимая его полностью.
Переключение между логарифмической нормальностью и нормальностью
Чтобы избежать расчета С , перейди те с многомерных логарифмически нормальных на многомерные нормальные спецификации и примените усовершенствования №1 или 2. Чтобы осуществить это переключение, примените выведенные ранее формулы:
А = ехр( Д. + у ст.. ) -1,
с,/ = (1 + А)(1 + Д )(ехР(<У ) - 1) •
Если по какой-то причине вы хотите преобразоваться из нормальной спецификации в логарифмически нормальную, рассчитайте:
Д = 1п(1 + х/,)-^ст„..
344
20. Вопрос перенастройки
У Девлина ушло два часа на то, чтобы познакомить Регретту со своими математическими построениями. Все было максимально и понятно, так по крайней мере казалось Девлину. Регретга, пристыженная тем, что она так вольно истолковала его поведение, слушала очень внимательно. Время от времени она повторяла некоторые расчеты Девлина, для того чтобы убедиться, что все правильно поняла.
«Ну, и что вы думаете?» - спросил Девлин, когда они закончили.
«Думаю, это замечательно».
«Интересно, а как это воспримет Конвей?»
«Думаю, на него это тоже произведет большое впечатление».
«Вы действительно так думаете? Спасибо. Я боялся, что вам это не понравится».
«Я не сказала «нам» - я сказала «ему». Ему это понравится. Восхититься и полюбить — это разные вещи».
«Думаете, здесь слишком много формул, да?»
«Слишком много и слишком сумбурно. Финансисты-практики не любят зависеть от ряда Тейлора». В отличие от вас.
Девлин отвел взгляд. «Именно этого я и боялся. Но что я могу сделать, нужно же ввести расчеты в таблицы?»
«Ищите, как это упростить».
«Я сделал все, что мог».
«Уверены? Как насчет того, чтобы попытаться переформулировать проблему?»
«Например?»
«Не знаю. Я подумаю над этим».
«Спасибо, Регретга».
«Не за что. А теперь как насчет того, чтобы пригласить даму пообедать?»
«А уже пора? - Девлин взглянул на часы. - Отлично. Обед уже почти закончился. Лучше я побегу, а то не успею. До встречи, Регретга». И он убежал, оставив ошарашенную Регрету в недоумении.
В ту ночь Девлин спал плохо. Ему снилось, будто он на церковном собрании, куда ребенком брала его мать. Все женщины-прихожанки сложились,
345
Часть 2. Постиженио нооожестоа
чтобы приготовить праздничный стол. Но когда Девлин подошел к ним, женщина, которая раздавала угощения, не стала ему ничего накладывать. Это была Регретга: она что-то шептала на ухо его матери. И мать покачала головой. «Иногда я его просто не понимаю, - сказала она. - Разве ты не голоден, сынок?»
Когда Девлин проснулся, первым делом он решил, что ему следует пригласить Регретту на обед. Она вчера его смутила. Какая он удивительная. Ни одна из знакомых ему женщин-прихожанок и в подметки не годилась Регретте. Она была красивее их всех вместе взятых, но и в два раза вспыльчивее. Плохо, что общего у них с Регреттой — одна лишь математика.
Или нет? Девлин никогда не пытался говорить с Регреттой о чем-то еще. Только математика и теория финансов. Это все, что она в нем видела, и чья в том вина? Ему следовало взять инициативу в свои руки.
Большую часть дня Девлин потратил на то, чтобы продумать, что он скажет Регретте и как. Он долго собирался с силами, но так и не решился ничего ей сказать. Ему была невыносима мысль об отказе.
В четверг они вновь встретились на сеансе групповой терапии. После сеанса Девлин спросил, есть ли у нее время поговорить, и, к его радости, она сказала «да». Пока они шли к дубовой рощице, в которой сидели в прошлый раз, Девлин откашлялся и заговорил. «Послушайте, Регретга. Извините, что я не пригласил вас в понедельник на обед. Я просто не думал...»
«Что я женщина?» - вставила Регретга.
«Нет. То есть да, вы замечательная женщина. Просто не прихожанка. Я смутился».
ТИь/ оба смутились. «Ничего, Девлин. Полагаю, вы иногда чрезмерно увлекаетесь какой-то идеей».
«Возможно, вы правы. Я слишком сконцентрировался на сложных разложениях в ряд Тейлора. Мне следовало бы нацелиться на достижение большего равновесия».
«Теперь понимаете, да? Я поражена, Девлин. Что помогло вам понять, что проблема в этом?»
«Ничего, в общем-то. Я просто начал смотреть на все в перспективе и понял, что кратчайший путь вперед — это внесение поправок».
«И продолжение внесения поправок».
Девлин грустно кивнул. «Вы правы. Полагаю, у меня никогда не получится быть последовательным. Но я хотел...»
«Никто никогда не может быть последовательным до конца, Девлин. Перенастройка — это постоянная борьба. Сложно вычислить, сколько будет достаточно, а сколько - перебор. Я составила небольшую таблицу, чтобы было понятнее».
«Таблицу? Какую? По шансам того, что...»
«По некоторым простым задачам перенастройки. Вот, давайте я вам покажу». Регретга вытащила из сумки гистограмму и вручила Девлину.
346
20. Вопрос поронастройки
«Предположим, ваш целевой вес составляет 5%, в то время как актив падает на 80%. Без перенастройки убыток по портфелю 4%. Если вы перенастройтесь один раз в середине - на полпути вниз, когда падение актива достигнет 40%, -общий убыток составит 5,45%. При достаточно частой перенастройке убыток по портфелю не превысит 7,7%».
Перенастройка с одним рисковым активом при со = 5% ил = 80%.
Rebalancing with one risky asset for — 5% and x 80%
f s
5% 4% 3%
Percent return oji portfolio
Несмотря на совсем другие мысли, Девлин проглотил наживку: «Что вы хотите сказать?»
«Я хочу сказать, что постоянная бесплатная перенастройка делает график доходности портфеля линейным как в логарифмической доходности, так и в целевых весах портфеля. Это серьезно упрощает ваши рецепты. Условная логарифмическая, откорректированная с учетом риска доходность упрощается до логарифмической доходности портфеля за вычетом с/2, умноженной на ее дисперсию. И это точное значение, а не аппроксимация. Удивительно, не так ли?»
«Конечно».
«Мне не терпелось вам это рассказать. Я не поняла, почему вы сами это не вычислили» свелся.
«Ну, я...»
«Но все равно, возможно, я обнаружила кое-что, чего вы не обнаружили. Например, я думала, что столкнулась с парадоксом, когда позволила изменяться периоду пересмотра».
«Периоду пересмотра?»
«Я имею в виду временной интервал наблюдения. Чтобы расчеты легко поддавались обработке, я позволяю режимам и показателям портфелей меняться только при конкретных нересмо грах».
«А в чем заключался парадокс?»
347
Часть 2. Постижение невежества
«В одном случае все рухнуло, так как пересмотр свелся к нулю, несмотря па то, что мы допускаем максимальное переключение режимов. Но оказывается в этом был свой смысл».
«Почему?»
«Ага! Так я же обнаружила то, чего не нашли вы. Видите ли, когда переключение с режима на режим происходит достаточно часто, в силу вступает закон крупных чисел. Активы начинают вести себя так, будто они все время находились в среднем режиме. Чтобы сделать быстрые возвраты интересными, мне пришлось ввести пуассоновские скачки, предполагающие мгновенную вероятность спада. Это дало еще один милый рецептик, результаты которого в целом довольно легко подсчитать. На самом деле пока пуассоновские риски не слишком сильны, оптимальная смесь выглядит как решение задачи максимизации коэффициента Шарпа. Вот, давайте я вам покажу». Регретта вытащила из сумки другой лист:
Упрощенные рецепты
При логарифмически нормальной доходности и непрерывной бесплатной перенастройке условная логарифмическая откорректированная с учетом риска доходность CEk равняется:
со'ln(l + Мк) — ~ссо'Хксо, или эквивалентно
д. -л слу [ Ш’ -“ппк j ~ к •
2. Если пересмотры наблюдаются часто, тогда совокупная СЕ стремится к а>М + ? а> ’ [ Д,.. ± са>' S а>
где М =
к к
3. Если базовый режим О является логарифмически нормальным броуновским и пуассоновским вектором, убытки в 100А% случаются с частотой Z, то СЕ равна
и и л
2 1 —с
4. Если пуассоновские риски являются умеренными, оптимальная смесь портфеля со может быть оценена как
348
20. Вопрос перенастройки
Девлин просмотрел рецепты. «Хорошо. Но в последнем рецепте как мы узнаем, являются ли пуассоновские риски умеренными?»
«Это зависит от риска скачка, квадрата неприятия риска и куба процентного покрытия риска. Чувствительность хорошая причина для того, чтобы сбалансировать риски концентрации и беты в вашем портфеле».
«У меня такое ощущение, что большинство инвестиционных менеджеров стремятся к этому, это больше, чем прелагает стандартная теория портфеля».
«Да, я тоже так считаю. Наш подход — я хочу сказать, ваш подход, — кажется, в большей степени согласуется с практикой. И он дает возможность количественной оценки. Например, вот показывает, как сильно искажается логарифмическая, откорректированная с учетом риска доходность, когда мы игнорируем влияние третьего порядка в пуассоновских скачках, предполагая CRR равным 3».
Преувеличение СЕ с помощью пуассоновской аппроксимации второго порядка.
Overstatement of СЕ by second-order Poisson approximation
Portfolio loss in crash
«Теперь это наш подход. Но на этот раз вам придется поподробнее мне все объяснить. Как насчет того, чтобы пригласить парня пообедать?»
«Какого парня? - спросила Регретга и улыбнулась. — Да, конечно. Буду рада».
Теперь пришла очередь Девлину причесывать свою математику. Поделом ему, раз уж навязывал всем свои громоздкие расчеты. Постараюсь сделать этот раздел проще предыдущего.
349
Часть 2. Постижонио новожоства__________________________________
Подразделение логарифмически нормальных доходностей
Вспомним, что логарифмические доходности, в отличие от процентных, являются аддитивными по времени: например, логарифмический годовой доход равняется сумме логарифмических ежедневных доходов за тот же год. Предположим, что мы делим интервал на /V отдельных подин тер валов и обнаруживаем, что доходы в каждом подинтервалу независимы и идентично распределены. Тогда если логарифмические доходы за весь интервал являются многомерно нормальными со средним М и ковариационной матрицей S , то логарифмические доходы за каждый подинтервал будут многомерно нормальными при логарифмическом среднем М / N и дисперсии Z / /V .
Бесконечно делимые распределения
Предположим, что независимо от того, на сколько частей разделили мы заданный интервал; доходности в каждом непересекающемся, равной длины подинтервале являются независимыми и идентично распределенными. В этом случае распределение доходности считается бесконечно делимым.
Ясно, что логарифмически нормальные доходности могут рассматриваться как бесконечно делимые. Но другие распределения тоже могут быть бесконечно делимыми. Например, если доходности время от времени осуществляют дискретные скачки, их совокупное распределение все равно будет бесконечно делимым при условии, что вероятность любого заданного скачка в следующее мгновение является постоянной, независимо от того, что произошло ранее. Подобный скачок известен как пуассоновский. Теория статистики с помощью методов, слишком сложных для того, чтобы приводить их здесь, доказала, что все бесконечно делимые распределения являются смесями пуассоновских скачков и явления, называемого броуновским движением.
Броуновское движение
Считается, что постоянно движущаяся случайная переменная следует броуновскому движению, если она никогда не совершает дискретных скачков, ее дисперсия является конечной, а ее распределение — бесконечно делимым. Центральная предельная теорема гласит, что сумма многих маленьких независимых, идентично распределенных движений конечной дисперсии должна быть асимптотически нормальной. Следовательно, броуновское движение должно быть нормально распределенным. Более того, основные формулы для сумм независимых переменных указывают, что средние и дисперсии должны изменяться линейно со временем. Действительно, распределение броуновского движения должно всегда быть многомерно нормальным со средним М/ и ковариацией Е/ за любой временной период t для некоего вектора М и положительного полуопределенного Е.
350
20. Вопрос перенастройки
Броуновское движение — самый простой способ моделирования рисковых, пос гоянно движущихся финансовых активов. Оно особенно привлекательно для моделирования логарифмической доходности как броуновской, которую я буду называть для краткости «логарифмически нормальной броуновской». Логарифмически нормальное броуновское движение запрещает отрицательное благосостояние и упрощает расчеты совокупной доходности.
Перенастройка
Веса портфеля всегда изменяются спонтанно, за исключением редкого случая, когда все активы имеют совершенно одинаковые процентные доходности. Перенастройка направлена на то, чтобы сохранять целевое процентное распределение со. Она делает это путем приобретения непропорционально большего количества активов, которые падают и/ил и продаются сильнее, чем растущие активы.
Перенастройка склонна к тому, чтобы делать доходность портфеля линейной в логарифмической доходности А' — 1п(1гА^ активов. Чтобы увидеть это, предположим, что перенастройка возникает в конце каждого из Т равноотстоящих подинтервалов. Логарифмическая доходность будет равна
Т - In 1 4- со ехр — — 1
Г-In
что стремится к w’ X , как Тстремится к бесконечности.
Компромиссы в перенастройке
Небольшое число перенастроек — скорее норма, чем исключение. Если вы не меняете свои прогнозы или убеждения, вам не следует менять и свои цели. Действительно, если вы считаете, что движение ценной бумаги аберрантно и надо ждать отката, то вам следует перекомпенсироваться по-другому. Но никто не перенастраивается постоянно: на это уходит слишком много времени и денег.
Много перенастроек проходит под видом других гранзакций. Менеджер, который получает новые фонды для инвестирования, пользуется случаем, чтобы «дозаправить» активы, которые упали ниже целевых весов. Напротив, активы, которые превосходят целевые веса, проявляют тенденцию к тому, чтобы быть диспропорционально распроданными со скидкой в погашениях. Это осложняет оценку издержек и выгод перенастроек, не говоря уже о разработке оптимальной политики перенастраивания.
Я подозреваю, что большая часть портфелей разумно аппроксимируются постоянной перенастройкой по транзакционным издержкам от нескольких десятков до нескольких сотен базисных пунктов в год. Но я могу ошибаться. Вот почему я привожу инструменты для разных расчетов.
351
Часть 2. Постижение невежества
Ожидаемая полезность с перенастройкой
Давайте переработаем расчеты ожидаемой полезности, предположив, что активы следуют логарифмически нормальному броуновскому движению и что портфель при этом бесплатно перенастраивается. При абсолютной ожидаемой полезности j ZTCZ| , выраженной в форме степенной функции, целого будет равняться произведению |EU\ его частей. При заданных Т равных мелких ---------------------------------------------InlE’Cd
частей логарифмический эквивалент надежности СЕ —-!--- будет равен 7~,
умноженному на СЕ по каждому подинтервалу.
R
Теперь подинтервал СЕ может быть переписан в форме —- г
где каждое R; не зависимо от Т. СЕ интервала в целом будет равно 7?! + что приближается к R} по мере приближения Т к бесконечности.
Итак, давайте сфокусируемся на идентификации R}.
Пусть /77#(б9, Т) и Т) обозначают процентные средние и
дисперсию соответственно по каждому из Т подинтервалов. С помощью усовершенствования №2 легко установить, что:
"ZT — 1п(1 + пС (a>,r))-ycv# (&>, Г); -1
Воспользуемся преобразованием из нормальные, выведенные ранее. В то время как портфель логарифмически нормальным, преобразования среднего основанные на разложениях в ряд Тейлора второго порядка, приблизительно действительными. И снова сфокусировавшись только на членах
1 *
— CV
2
и
777
нормальных в не будет точно и дисперсии, все равно будут
первого порядка, mn (а), Т) = (О'
в то время как
2
V* Т) = О)
w . Нахождение пределов по мере того, как Т стремится к
бесконечности, показывает, что:
СЕ = А} = а)' М .
1 'V
СО----с со Е со .
2
След матрицы
Вы можете легко проверить, что
[ст, j ...crw; ] w равняется сумме
352
2D.Вопрос поронастройки
диагональных элементов диагонали (бэ)'12. Сумма диагональных элементов известна как след и обозначается tr. След имеет некоторые полезные свойства, в том числе и коммутативность. Иными словами, порядок произведения матриц не оказывает влияния на ее след при условии, что как АВ, так и В А являются четкими квадратными матрицами. Это дает возможность иначе записать полученный ранее результат:
СЕ = со' М +-Гг 2
((aVag(ew)
что нам еще понадобится.
Подтверждение
Хотя каждый промежуточный шаг расчета является приблизительным, результат выражает точный асимптотический предел. Чтобы это проверить, произведу пересчет с помощью усовершенствования №3. Во-первых, я аппроксимирую символы как:
А = In 1 + 69 ’ exp
-1
В = diag(&y exp
69 + 0
С = diag(B) — ВВ' = diag(co) — coco ’+ о
где 1 IT) относится к членам, которые кратны 1 !Т и принимают приблизительные матричные размеры. Подставляя в формулы эквивалента надежности и находя пределы, получаем:
СЕ = со'М А-(\-с}со'Еа>
1
2(с-1)
I + (с — \\diag(cd) — 6969*) —
Вспомним, что определитель является суммой и разностью произведений элементов, взятых из каждой строки и каждого столбца. Произведение, содержащее только диагональные элементы, будет кратно 1. Остальные должны содержать по меньшей мере два недиагональных элемента и будут кратны Следовательно, аппроксимация первого порядка к определителю должна оценивать только диагональное произведение. Теперь логарифм произведения равняется сумме отдельных логарифмов, а все элементы, логарифмы которых мы берем, близки к единице. Таким образом, детерминант рушится до следа матрицы, который прибавляется к I. Другими словами,
353
Часть 2. Постижонио новожоства
limr
Т hi I + (с — l)(diag ( cd) - cdcd ') —
— (С) а)'
= — tr 2
Подставьте это выражение в предыдущую формулу и упростите, чтобы подтвердить предшествовавший результат.
Заманчивое упрощение
Чтобы получить более компактную формулу СЕ, вспомним, что многомерно логарифмически нормальное распределение
Л/ + — [ст, j ...ст|7Л ]' = ln(l + М) , где М обозначает соответствующее процентное среднее. Отсюда следует, что:
2
Эта формула проста и интуитивно привлекательна. Логарифмическая, откорректированная с учетом риска доходность равняется логарифму валовой ожидаемой доходности за вычетом уценки на непрерывную дисперсию. Имеет смысл использовать непрерывную дисперсию, поскольку портфель постоянно перенастраивается. Теперь стоимость дисперсии кажется более дорогой, чем
раньше, при с72 вместо
Однако «недостающая» стоимость по
большей части является доходности.
2 4 возмещением за увеличение ожидаемой валовой
И еще одна проверка
Предыдущие результаты могут' быть получены намного проще при помощи моделирования броуновского движения как предела дискретного случайного блуждания, которое в короткое время dt с равной вероятностью перемещается либо на Licit ч- cyyfdt , либо на Lidl — суy[dt . Здесь // обозначает среднюю процентную доходность. Если вы имеете дело с логарифмически нормальным движением, то необходимо определить //=// + —<т". Отсюда
следует:
354
2D. Вонрос норонаетройки
так как это в пределах СЕ = /л -- —- со-- .
Многомерный аналог допускает движения Mdt \!~dt , где J -
случайный вектор с независимыми элементами +1 или —1 и средним О. При логарифмической нормальности М заменяется 1п(1+М). При заданной непрерывной перенастройке портфель продолжает следовать одномерному броуновскому движению. Осуществляя подстановку в моменты портфеля, мы
получаем СЕ = со' 1п(1 + Л/) —— сеСХа), как и ранее.
Оптимальная смесь портфеля при заданном броуновском движении
Выражение СЕ является вогнутым в со для всех с, в отличие от исходного рецепта Девлина, а следовательно, всегда дает внутренний максимум. Оптимальная смесь портфеля равно:
СО 1П(1 + Л/).
С
Максимальная логарифмическая, откорректированная с учетом риска доходность составляет:
СЕ =—1п(1 +Л/)'Ё’‘ 1п(1 + ЛУ) с*
Ожидаемая доходность в оптимуме в два раза выше, но дисперсия отнимает половину.
Внедрение условного броуновского движения
К сожалению, стандартное броуновское моделирование сохраняет самый большой недостаток дискретного нормального эквивалента. Оба считают среднее и дисперсию фиксированными в течение всего времени. Самое простое решение проблемы - сделать допуск на различные броуновские режимы и переключения между ними. Но как мы должны моделировать переключения?
В одноразовых моделях любой режим применим для всего периода в целом, с единственным вероятностным распределением, резюмирующим неопределенность. Непрерывное время открывает намного больше осложнений. Я начну, сделав допуск на изменения режимов в заранее установленное время,
355
Часть 2. Постижонио новожоства
называемое «пересмотрами». Между пересмотрами допускается возможность бесплатной перенастройки.
Если между пересмотрами иет перенастройки, все, что мы имеем — эго последовательность одноразовых моделей. При каждом пересмотре мы просто повторно оптимизируем портфель, соответствующий нашим текущим убеждениям, с помощью рецептов из предшествовавших двух глав. Если возьмем другую крайность - перенастройка идет непрерывно и бесплатная, тогда при заданных вероятностях рк для каждого режима нам следует выбрать г», чтобы максимизировать:
EU = signal -с^Рк ехр
к
1 > 'V
— С CD Х.СО
2
Оптимальная смесь с условным броуновским движением
Условия оптимизации первого порядка требуют, чтобы:
^Рк |£ТЛ|(1п(1 + МД-сЁА<у’) = О к
при оптимальном со*. Условия второго порядка требуют, чтобы:
к к
Второй член всегда является отрицательным для с < 1. По мере того как с стремится к нулю, первый член будет положительным и начнет перевешивать второй, за исключением однорежимного случая, где первый член исчезнет. Но это не является недостатком уравнения; это просто указывает, что при некоторых условиях почти нейтральные в отношении риска инвесторы могут стремиться к безграничным рискам. Если предположить, что условия второго порядка удовлетворены, получаем:
ы =~[^pkEuktJ +
С у к ) к
В особом случае некоррелированных активов это упрощается до:
<4 =-^- + -[^PkEUk&,ik ^PkEUkPik
2 С? С у к J к
И снова со* может быть интерпретировано как модифицированная максимизация коэффициента Шарпа, где наихудшие ожидаемые режимы по весу считаются более крупными, нежели чем лучшие. Делитель с вместо с — 1, как мне кажется, советует придерживаться более осторожного поведения, чем предыдущие аппроксимации, хотя различия в других членах компенсируют час ть промежутка.
356
2D. Вопрос поронастройки
Быстрые пересмотры
Предположим, что мы делаем пересмотры более быстро без каких-либо других изменений в модели. Хотя вышеприведенное уравнение остается таким же, соответствующие моменты рассчитываются в более коротком временном диапазоне. Чтобы сделать эту зависимость явной, я перепишу логарифмические средние и дисперсии как Мkdt и lLkdt , где dt - это интервал между
пересмотрами. Пусть
/ _ ] т 1
обозначает'
процентную среднюю доходность в единицу времени.
При очень быстрых пересмотрам ЕUк для каждого броуновского
режима стремится к единице, что подразумевает:
X X - I
=- ЕрА Еа1п(1+Ч)-
с у к ) к
В этой формулировке, кажется, неприятие риска не имеет значения, разве что для с. На самом деле оптимальная смесь — это именно то, что рекомендуется при единичном логарифмически нормальном режиме, имеющем Ё = 2^ к Рк^к и М = 22 к ркМ к . В конечном итоге нам не нужно будет умножать режимы!
При ближайшем рассмотрении этот результат - артефакт нашей формулировки. Каждый пересмотр, который вы предпринимаете, приводит к случайному выбору режимов. Чем чаще вы проводите эти выборы, тем меньше внимания уделяете исходу любого единичного выбора. В пределе можно с тем же успехом обращаться с доходностями, как если бы они все время находились в одном-единственном среднем режиме. Это подтверждает и математика.
Пуассоновские скачки
Мы можем вернуть все на круги своя при помощи быстрых пересмотров, сделав допуск на случайные дискретные скачки. Пуассоновские скачки характеризуются мгновенным вероятностным показателем / интенсивности. Я имею в виду, что вероятность их возникновения за короткое время dt равняется Idt плюс члены более высокого порядка. Будем считать / средней частотой возникновения.
Чтобы это максимально легко поддавалось обработке, предположу, что скачок при возникновении вызывает мгновенную потерю вектора в 100/.%. Отсюда следует, что ожидаемый процентный убыток во времени dt будет примерно равен ILdt и его дисперсии примерно ILL 'dt.
357
Часть 2. Постижонио новожества
Ожидаемая полезность броуновских-пуассоновских смесей
Предположим, что базовый режим О является логарифмически нормальным броуновским с логарифмическим средним Л/о , ковариационной
матрицей Хо и процентным средним Л/о на единицу времени. Обусловленная
этим режимом ожидаемая полезность за короткий период времени t примерно
равна:
EUq = sign (1 — с) - 1 + (1 — г) со' M^dt
- — (1 - I .
При возникновении пуассоновского скачка доходность по рисковому активу составит L. Я мог бы смоделировать скачок как наложение па броуновское движение, а не как подстановку в него, но результаты в целом не изменились бы. Полезность в режиме скачка составляет х/£/7(1 —с)-(1 — гу’Л)1 ' . Совокупная ожидаемая полезность равна:
| EU | (1 - Idt) | EU01 + ldt( 1 - со1L )'
= 1 + (1 - с) со' M.dt -1( 1 - с)ссо' tncodt -ldt + (\- со'L)'~4dt
-1
dt .
2
Если найти предел, логарифмический эквивалент надежности на единицу времени будет равен точно:
-1
СЕ = бэ' ---ссо' +1 ------------.
° 2 0 1-с
Оптимальная смесь портфеля с умеренными пуассоновскими рисками
Переписывание степенного ряда как разложения в ряд Тейлора дает:
СЕ- со'М0 -Eco’t0co-lco'L-Cl(co’L)2 -%(с + l)/(co'L)3 -
Член ~c(c-i-1) l(co' L)3 часто бывает ничтожно малым. Например, в том случае с = 3, риск скачка составляет 10% в одногодичном диапазоне и портфель потеряет 10% в случае, если произойдет скачок, тогда он составит 2 б.п.
Так что спокойно можно его отбросить, обойтись аппроксимацией второго порядка к степенному ряду и оценить оптимальную смесь портфеля как:
358
20. Вопрос порепостройки
со ==-(S0 + ILL')~' (Мо — IL).
Это выглядит как максимизация коэффициента Шарпа, в которой безусловная дисперсия равняется ожидаемой условной дисперсии плюс дисперсии скачка, а безусловное среднее равняется среднему броуновскому движению за вычетом среднего пуассоновского скачка. Однако есть здесь некие тонкости, относящиеся к отличиям между обычными моментами и логарифмическими моментами. Например, у меня нет хорошего интуитивного объяснения того факта, почему безусловная дисперсия смешивает логарифмическую дисперсию с процентной.
Риск концентрации
Если портфель настаивает па том, чтобы пережить убыток более, чем в одну треть во время пуассоновского скачка, тогда опасно полагаться только на расчеты среднего и дисперсии. Мы можем рассматривать соЪ как подверженность портфеля этому конкретному риску, умноженную па максимально вероятный убыток, связанный только с этим риском. Шансы краха, вероятный масштаб краха, а также бета или риск концентрации относительно краха — все следует принимать во внимание. Из них проще всего понять риск концентрации. Более того, удвоение концентрации вчетверо увеличивает уязвимость, и наоборот. Так что инвестиционным менеджерам имеет смысл придавать особое значение пределам риска концентрации, измеряемым различными способами. Предыдущие уравнения помогают это измерить количественно.
359
21. Взвешивание опционов
Девлину понравилось бы завтракать с Регреттой, даже если в Chib Mad не подавали бы буритто. Она была настолько живым, остроумным, проницательным собеседником! И ей так шел черный цвет. Но что-то в их разговоре стало его беспокоить. «Не усложняйте», -— все время повторяла она. В тот момент он подумал, что она просто хочет, чтобы он сократил свои объяснения. Но теперь понял, что она, возможно, намекала на что-то большее. Не пытается ли она держать дистанцию? Не старается ли мягко осадить меня? Не слишком ли сильно я в нее внепился?
Девлин вздохнул. Так и есть. Слишком сильно. Все так считают. Все, кроме меня, вот в чем вопрос. Почему они все так напрягаются? Если проблема зацепила тебя и держит в заложниках до тех пор, пока ее не решишь, то в этом нет твоей вины. Это вина проблемы. Правда, я, кажется, сталкиваюсь с проблемами чаще, чем остальные. Но это просто невезение.
Невезение? Не выдумывай. У каждого есть выбор. Жизнь не движется по прямой. Она предлагает возможность выбора, и ты легко можешь переключиться с одного пути на другой. Возможно, пора призадуматься о выборе4...
Моем выборе. Выборе Регретты. Наших выборах! Так .много всего накопилось, в чем нужно разобраться. Девлин записал мысли, что пришли ему в голову, и задумался. Первые расчеты они ни к чему не привели. Страницу за страницей он комкал и выбрасывал в корзину для мусора.
Помнишь, что сказала Регретта. Не усложняй. Но как? И тут его осенило. Не совсем просто. Но проще и не бывает. Он не мог дождаться, когда сможет рассказать об этом Регреттой.
Теперь подожди секунду. Зачем бежать прямо сейчас? Это будет выглядеть глупо? Так можно все разрушить. Нет, я не должен этого делать. Я не повторю этой ошибки снова. Не так быстро. И Девлин никому ничего не сказал. Он старался держаться подальше от Регретты и доверял мысли только своим записным книжкам.
Девлин держал себя в руках почти неделю. Но не долго не выдержал. Однажды утром Регретта нашла у себя под дверью конверт, вскрыла его и начала читать:
4 Здесь и далее игра слов: по-английски option — выбор и опцион.
360
21. Взвешивание опционов
Дорогая Регретга!
Извините, я старался не надоедать вам, но больше не могу таиться. Я согласен, мы далеко зашли, и я благодарен вам за это. Но если мы оставим все, как есть -—- это не даст нам того удовлетворения, которое мы можем получить, если перейдем к более высокой ступени наших отношений. Я хочу, чтобы вы продумали о возможности выбора, и делаю вам несколько предложений.
Не сомневаюсь, вы уже поняли, о какой проблеме идет речь. Опционы слишком нелинейны, чтобы поместиться в рамки традиционного анализа портфеля. Лучшее, что можно сделать — это смоделировать их как фиксированную долю «дельта» стандартных активов, что в некотором роде упускает их суть. Какая прямая линия лучше всего приближается к путу или коллу?
Калькуляция кривых для стандартных опционов
Value of ordinary call Value of ordinary put
Но наша структура может с ними справиться. И, думаю, может справиться двумя способами. Первый способ — это позволить дельте варьировать в зависимости от режимов. Пут может иметь дельту почти ноль во время бума и почти единицу во время спада. Второй способ — позволить дельте изменяться даже в пределах одного режима, допуская постоянный темп изменения роста «гамма», который сам по себе может меняться в зависимости от режима.
Все, что нужно для расчета, помимо того, что у нас уже есть, это средняя величина опциона, его дельта и гамма в среднем для каждого из режимов. Общие формулы для риска портфеля остаются такими же; дельты просто меняют эффективную дисперсию. Невозможно представить себе более простого способа внедрения нелинейности. И он, безусловно, намного превосходит альтернативы, поскольку я не помню ничего даже близко стоящего.
Конечно, и этот способ не совершенен. Гамма не является постоянной, даже в пределах одного режима. Действительно, она очень резко может достичь пика в районе страйка, близящегося к окончанию. Чтобы с этим справиться, следует брать дискретные аппроксимации к дельте и гамме, основанные на средних величинах по диапазону. Это не настолько запутанно, как кажется: стоимости опционов при среднем и при одном стандартном отклонении выше и ниже его в целом достаточны для расчета.
361
Часть 2. Псстижонио новожоства
Если вы можете постоянно и бесплатно перенастраиваться, ошибки в аппроксимации в конечном счете исчезнут. Одним из способов это увидеть будет сравнение с советом Блэка- Шоулза. Они идентичны, по крайней мере в диапазоне, где пересекаются два подхода. Действительно, можно использовать наши рамки, чтобы обновить расчеты Блэка-Шоулза. Но наш подход теоретически богаче, поскольку мы допускаем множественные режимы и неправильную оценку.
Вероятнее всего, на практике он тоже богаче. Я не говорю «безусловно», поскольку даже если вы можете получать прибыли на опционах, обычные длинные и короткие сделки, возможно, повысят вашу откорректированную с учетом риска доходность портфеля в той же степени. И тем не-менее иногда это может помочь, либо при идентификации действительно отличной возможности, либо путем развенчания неких ложных требований. Это необходимо банку или хедж-фонду, которые на деле работают с опционами, особенно важно для взаимных фондов, которые тонут в них.
В итоге чего мы на самом деле хотим от опционов — это страхования риска айсберга. Чтобы проиллюстрировать значение, которое это может иметь, представьте, что ваш портфель совершенно логарифмически нормален, за исключением подверженности внезапному краху. Крах — это Пуассон: он возникает при ставке I за единицу времени и вызывает убыток 100Л%, когда это происходит. График, приведенный ниже, показывает, какую надбавку за риск помимо ожидаемой выплаты инвестор с CRR = 3 должен заплатить за абсолютную страховку от краха.
Величина страховки риска айсберга при CRR = 3
0% 4% 8% 12% 1 б% 20% 24% 28% 32 % 36% 40%
Uninsured portfolio loss from disaster
Внедрение опционов, безусловно, выглядит привлекательным, не так ли? Но здесь есть одна загвоздка. Рецепты становятся громоздкими. Но не настолько громоздкими, что с ними невозможно. работать. Не настолько громоздкими, чтобы вы не смогли понять, что они означают: главным образом, для того чтобы адаптировать средние и дисперсии к дельтам и гаммам. Но они достаточно громадные, чтобы многие них отказались.
362
21. Взвешивание епционев
Я знаю, что вы хотите, чтобы я все упростил. Я старался. Правда. Но как только вводишь различия между активами и базовыми ценовыми операторами и допускаешь нелинейные отношения между ними, уже не остается способов избежать дополнительных членов, даже если сократить все, как это я сделал, просуммировав все дельты и гаммы в двух матрицах. На самом деле, для того, чтобы хранить гаммы, мне нужна была трехмерная матрица. Надеюсь, вас это не сильно обеспокоит*
В любом случае вот рецепты:
Внедрение опционов
Пусть К обозначает Л-вектор нелинейных активов, связанных с условно многомерно нормальными операторамм X. При условии, что Jf ' М, обозначим величину Y при помощи П, частные производные Y относительно X при помощи N х п матрицы Л, а вторые частные производные Y относительно X
при помощи трехмерной N х п х п матрицы Г, где и/р = - Тильда
Й=1
отмечает сравнительные оценки, когда X М, крышка — предельные значения с постоянной перенастройкой. Тогда предыдущие совершенствования применимы при условии следующих изменений:
Усовершенствования № 1 и 2: Пересчитайте моменты портфеля как:
Л , v = щ'Д’ £аД4м’ + — Г)
Л у Л J п- J п Л Л* гС \ Л Л J
Усовершенствование № 3: Пересчитайте А, В, С и Я* как:
Ак = 1п( 1 + и’’( ехр(77Л ) —1) I, д
' w
С* = '+с/ш^(ехр(Л/Л - Д 1))(Д w)diag(exp(MkJ) ,
4>k = / + (с-1)ДД.
Постоянная перенастройка: пересчитайте СЕ” как:
СЕ = и'П + м’’р) Еу ~~сгг’ЛЕЛ1 .
Если вы хотите посмотреть расчеты, я к вашим услугам в любое время.
Всегда ваш, Девлин
363
Часть 2. ПВСТИЖ8НИ8 НВВВЖВСТВа
В любое время? Жаль, что Девлин не предложил таких же услуг всем остальным. Пока Регретта перечитывает письмо, ища в нем потаенный смысл, давайте постараемся воспроизвести рецепты.
Опционы
Опцион — это контракт, который предлагает право, но не обязательство, заключить сделку по ценной бумаге по указанной цене. Например, колл — это опцион на покупку по определенной цене; пут — это опцион на продажу. Определенная цена известна как страйк, решение заключить сделку называется исполнением опциона, а последняя возможная дата заключения сделки — это истечение. Опцион — при деньгах, если цена в настоящий момент превосходит страйк; в противном случае он без денег. Европейский опцион может быть осуществлен только в дату истечения, в то время как американский опцион можно осуществить в любое время до истечения срока.
Ключевым математическим свойством опционов является их нелинейность в базовой цене актива. Например, на дату истечения колл обесценен ниже страйка, в то время как выше страйка он равен цене актива за вычетом страйка.
Оценка опционов
Большую часть опционов оценить сложно. Помимо оценки распределения цен активов на дату истечения, часто приходится анализировать вероятную временную траекторию эволюции цены актива и/или оптимальные стратегии исполнения опциона. Чтобы проиллюстрировать сложности, существует незакрытое решение для обычного американского пута. Также стоимость одиночного опциона может зависеть от нескольких активов: например, от колла по наилучшему активу в корзине.
Предпочтительный способ описания опционов — это оценка их ожидаемых стоимостей при каком-то определенном сценарии и их чувствительность к небольшим изменениям в этих сценарии. Наиболее важными отношениями с этой точки зрения являются частная производная относительно базовой цены актива (дельта), вторая частная производная относительно цены (гамма) и частная производная относительно времени (тета).
Условные аппроксимации для опционов
Стандартная теория портфеля не может справиться с нелинейностью. Она может внедрить в себя опционы, только аппроксимируя их как некую постоянную долю базового актива. Многорежимная структура может лучше к ним приспособиться. Например, краткосрочный пут по Nasdaq, достигнувший страйка на 25% ниже текущей рыночной цены, может быть смоделирован как обесцененный в обычное время или как полная или почти полная краткосрочная сделка по Nasdaq в режиме краха.
364
21. Взвешивание опционов
Более удачные аппроксимации используют дельты, гаммы и теты опционов или их дискретные копии. С математической точки зрения это эквивалентно моделированию опционов как квадратичных функций или точнее условно квадратичных функций, поскольку их коэффициенты могут варьироваться от режима к режиму.
Внедрение этих квадратичных функций в анализ портфеля несет в себе два вызова. Первый вызов — подсчет различных ожиданий. Второй — отслеживание всех членов. Второй вызов в некоторых отношениях более устрашающий, чем первый. Перед тем как пойти дальше, давайте определим еще несколько матричных условных обозначений.
Термины для стоимости опционов
Позвольте мне начать, проведя грань между N рисковыми активами, которых инвесторы могут’ удерживать или на понижение которых играть, и п базовыми операторами цен активов. Я обозначаю процентную доходность по первым при помощи Y и зарезервирую X для процентных доходностей по операторам. Хотя %, как правило, относится к обычным цепным бумагам, это не обязательно. Сходным образом, У не обязательно должен включать все ценные бумаги в X, хотя обычно так и получается. Бросающееся в глаза математическое отличие состоит в том, что X моделируется как условно многомерное нормальное, в то время как У моделируется как условно многомерно квадратичное в X.
Как и раньше, Р будет обозначать цену //-вектора X, дисконтированную по безрисковой ставке. Считайте это дисконтирование повторным измерением, которое преобразует безрисковую ставку в ноль. Для ясности я порой буду ставить Р с индексом времени /. Например, Ро будет обозначать цену в начальное время 0. За основной интервал принимается единица, так что /> = A . Рассматривая доходности по другим временным
интервалам, я тоже буду ставить нижний индекс X.
TV-вектор V будет обозначать стоимость опциона при цене Р и времени /, дисконтированную по безрисковой ставке. Ясно, что = diag(l + Y)P0. Я обозначу избыточную процентную доходность с помощью П = К| Г=ЛУ если Х=М, а избыточную логарифмическую доходность с помощью П = Y | ~ = In (1 + Y )| д-.= , если X = М. Поскольку временной период
сокращается, то же самое происходи! и с соответствующими доходностями. П fVln(l + K) 1 dV(Xft,tX
будет обозначать предел -------- - л л =-------------,_п .
dt л=0-'~° Vo dt 1
365
Часть 2. П8СТИЖ8НИ8 Н8Н8Ж8СТ88
Дельты
А будет обозначать TV * z? матрицу с элементами <5/?/
дР<
частную производную ожидаемой цены опциона h относительно цены оператора /. Обычно А должна всего лишь быть одним ненулевым элементом в ряду, поскольку активы обычно зависят только от одного оператора.
На самом деле мне в меньшей степени интересна чувствительность ГкЛ чем чувствительности процентных доходностей Y к X. Однако между ними есть тесная взаимосвязь:
дх-
д
^,0
др,
г hl
АО
h
Мы
д¥
1 /о
можем выразить это в матричной форме как: = diag(PQ )&(diag ( Ко )) '.
BY I «
--- Х-Л7 обозначают первую производную
и
конечного
периода,
оцененную соответственно при среднем X и среднем X
соответственно.
х 7 дР
соответствующие начальные величины периода.
обозначает
Трехмерные матрицы
Я прерву обсуждение производных, чтобы представить вам трехмерную матрицу. Так же, как прямоугольная матрица является вектором векторов, трехмерная матрица Г является вектором прямоугольных матриц Г/?, чьи элементы могут быть обозначены как уЛ/>.Умножение трехмерных матриц потенциально сбивает с толку из-за дополнительного выбора направлений, но для У х /? х и-матриц, которые интересуют меня, есть четыре ситуации, где это (почти) точно выражено:
Для w — скаляра: ыГ = •
/V
Для со — обычного JV-вектора: а)'Г = .
Л=1
Для W—диагональной 2V * Л-матрицы: ИТ— это вектор прямоугольных матриц whhrh .
Для W — диагональной п * /7-матрицы: ИТИ7имеет элементы у/;// .
366
21. Вэвошиванио опционов
Гаммы
Та Г, которая интересует меня, — это 7V * л? * л?-матрицы с элементами
dPidPi
Каждый компонент Г/, является гессианом (второй
производной матрицы) актива h тотносительно цен. И вновь, поскольку мне больше интересны чувствительности У к X, я воспользуюсь отношением
д2У/, = Pj0 дри„)_Р70 д2у„ ЭР, _ PinPi0 dx,.dXj у1М дх, (дР. J у„0' ы>дР; Зх, г„0
чтобы наполнить N х л? х ^-матрицу
. Напротив,
diag(Pu) Pdiag (Ро)( diag(y„)) ' •
Поскольку опционы обычно зависят только от одного актива, у них будет лишь один ненулевой элемент гамма. Обычные «линейные» ценные бумаги не имеют ненулевой гаммы. Так что у этих потенциально огромных трехмерных матриц обычно будет меньше чем У ненулевых элементов. На практике для упрощения сведения в таблицы вам следует постараться сгруппировать активы в зависимости от того, от какой ценной бумаги они зависят.
По аналогии с дельтами,
а2 у ах2
а2 У
будут
X- м
обозначать вторые производные конечного периода, оцененные соответственно при среднем X и среднем X Трехмерная матрица Г с элементами - Pi0P,0 52ГДРо,О)
:-------------обозначает соответствующие исходные стоимости.
Ию дРдР-
Смягчение неполадок
Рассмотрим простой опцион по одной ценной бумаге, который истекает точно в срок и страйк которого очень близок к среднему. Вы рассчитаете его будущий 6 как 0 или 1, в зависимости от того, на какую сторону от среднего упадет страйк, а у — как 0, если только страйк точно не равняется среднему, в
случае чего у будет бесконечной. Установка <5 = — с положительным, но 2
конечным у будет намного более разумной.
Общая проблема уходит корнями в неполадку или почти что неполадку в опционе, вызывающую острый пик в у. Это предполагает под собой следующее практическое решение. Рассчитайте для времени 1 стоимость
367
Часть 2. Постижение нооожоства
опциона V}+ при х = //4-ст и стоимость И, для х — /7 — су вдобавок к при х = // . Затем подгоните квадратичную аппроксимацию к этим фем точкам. В то время как О оценка останется такой же, 8 будет оценена заново, как V8 -V- V.+ -2V + V-
, а у как --—. Если вас больше беспокоит подгонка 2<т---------------------------сг~
хвостов, нежели центра, вы можете оценить опцион в точках, разделенных более чем на одно стандартное отклонение.
Ожидаемая полезность
Как только мы идентифицировали соответствующие параметры активов, мы можем переключить свое внимание на расчеты портфеля. Веса портфеля (<) теперь находятся на TV-векторе. Доходности портфеля могут быть аппроксимированы как разложение в ряд Тейлора второго порядка:
_ х _
гУ Гк — 22 <®hFhk .
Л=1
Как и ранее, А обозначает скаляр, В — /7-вектор, а С — симметричную п х n-матрицу. Если предположить условную многомерную нормальность, это подразумевает под собой моменты портфеля:
vk= В \ ЕкВк +1 tr (1СкЕ, )2 ) = 6У’а;.Еа.А,+ 1/г (((<у' ГДЕ, )') .
V, Тогда мы рассчитываем vk =--------------— и подставляем в
(1 + W,)-
усовершенствование №1 или 2:
EU#\ = 5Zgy(l -с)-
EU#2 = sign(\ - с)-
368
21. Взвешивание опционов
Sa (’
к
т, к
ехр
Средние и дисперсии квадратичных форм
Предыдущие результаты для моментов квадратичных форм, когда X является многомерно нормальным, а С — любой симметричной матрицей (нс обязательно диагональной), используют следующие формулы:
£[(%- Л/)’С(Х- Л/)] = /r(CS),
Var [(X - Л/)' С (X - Л/)] = 2 • tr (( CS)2) .
Чтобы это доказать, сначала определите новый вектор Y == S-1^2 —Л/), который является многомерно нормальным со средним 0 и
ковариационной матрицей I, и новую матрицу Q = ТУ2 Г^У2 . Наблюдаем, что:
Оцените ожидание как:
= 22 Я,7 =fr(s1/2CS1/2) = /r(CZ1/2S,/2) = rr(CS) . /л
Заметим, что для любых нижних индексов ожидание У,У ;-УкУ1 будет равно О, за исключением комбинации у\у2 j, чье ожидание равняется 3, когда / =J, и 1 в противном случае. Отсюда следует, что:
/л/
п п л? п
+SS ЯцЯ;,Е[_у. + SS ЯиЯлЕУ у.,хуГ\
/ = 1 /=1 /=1 _/ = 1 7*'
п ft
369
Часть 2. Постижонио невежества
хj + ?х 11=(tr(q))~+tr(q ) , / — I J /-1 /=1
а следовательно:
= tr^Q-') = tr^ClL')~\
Как справиться с бесплатными опционами
Пакеты опционов могут быть бесплатными. Например, пут без денег может финансироваться продажей коллов без денег. Когда = 0 для некоего актива /?, его процентные доходности являются неопределенными. В этом случае просто опустите все Кю члены из расчета 7Vh, с> и / и переинтерпретируйте со/, как вес, необходимый для достижения валовой доходности И/71. Это все равно, что установить равный некоему ничтожно малому £ , переопределяющему вес по этому опциону h так, чтобы он равнялся ccoh, и позволить £ стремиться к нулю. Короче говоря, все, что нам нужно сделать для того, чтобы задача с бесплатными опционами легко поддавалась обработке — это несколько переопределить соответствующую переменную выбора.
Модификации для логарифмической нормальности
Для того чтобы применить усовершенствование №3 необходимы дополнительные модификации. Разложение в ряд Тейлора второго порядка устанавливаег, что:
In (1 + со' Y) = 1п(1 4- <у'(ехр(У) -1))
= А + В'(Х-М)+Ех~МуС(Х-М), где
А = 1п(1 + <w'(exp(77) — 1)) ,
В = б//^(ехр(Л? — /П))Л ,
С = diag(B) — ВВ'+ dic?g(eKp(M — Al))(ra))diag(cxp(M)) .
Хотя я и опустил индекс к, каждая из этих новых переменных будет в целом варьироваться по режимам. Так что вам периодически придется проводить эти расчеты. Также рассчитайте Ч7* s 1 + (с — . Затем
осуществите обратную подстановку в усовершенствование №3:
EU43 = знак(\ — с)
370
21. Взвешивание опционов
Проверка греческих символов
Формула для Л немедленно проверяется оценкой формулы при А" = А/ . Каждый элемент bf. В может быть рассчитан как:
v-л/
где 69 = <z>. exp(/zz — А) . Недиагональными элементами С являются:
бУ^ехр(х,.) dyh
'7
Ух
v-.w
дх,
С’УХ дх.
й>/, ехр(х,.)
дх1-дх/.
hi
<4 ехР( A,
м
N
N
/j= I
expl/.e+jUj -А),
в то время как диагональные элементы 3 включают эти члены (очевидно, при / = f) плюс дополнительный член:
1 ду d exp (х) I ~
7—77 Е -А —= ехр(-Л)Е ехр(А )^> 1 4- 69 1 OX- ClXj
?v
= ехр(/7, - •
h — 1
Опционы с постоянной перенастройкой
По мере того как опционы приближаются к истечению, их стоимости, дельты и гаммы меняются, даже если не меняются базовые цены. Это увеличивает уязвимость опционов к перенастройке сильнее, чем обычных ценных бумаг. Тем не менее, ради обсуждения, давайте предположим, что бесплатная перенастройка возможна, и выработаем ее аналитические результаты. Если вспомнить предыдущую главу, то если перенастройка возникает в Т равноотстоящих подинтервалах, откорректированная по риску доходность может быть аппроксимирована как:
371
Часть 2. Постижение невежества
СЕ = А +-(1-с)В'ЁВ+-Гг(СЁ) + оГ—\ где
2 7 2 v 7 IТJ
А ~Т • 1п(1 + <у'(ехр(/7 /Т} — 1= соП -к Ol —
В = diag (ехр ( Л7 / Т — А1}} Д' со — А' 69 -к О
С = diag (В) — ВВ ’+ со' Г + О — = diag ( А' со} — А' coco' А '-к со' Г + О
Вспомним, что П^Д и Г отражают пределы при стартовых величинах. Если позволить Т приблизиться к бесконечности, то
СЕ = А +1(1 -с}В'1В + Xr(CS)
2V 7 2 v 7
= со' 77 -к — (1 — с} со' АХА' со -к — tr [^diag^d со} + со' Г — Дсосо' А') X j
= со' П -к — tr {^diag ( А ’ со} -к со' 7") X j - — с со' АХ А ’ со .
Это намного проще, чем усовершенствование №3. И модификации для опционов довольно просто понять. Две дельты корректируют среднее и дисперсию портфеля соответственно для эффективного веса базовых операторов X. Гамма корректирует среднее портфеля с учетом выпуклости активов.
Как и в предыдущей главе, все эго может быть аккуратно проверено с помощью переформулировки портфеля как дискретного случайного блуждания и сокращений интервала между шагами. Однако это не столь ясно показывает связь между различными подходами, а применение члена -\[cd может оттолкнуть некоторых читателей. Вог почему я воспользовался обходным путем.
Одиночный риск, одиночный опцион, одиночный режим
Интересный особый случай включает в себя одиночный базовый оператор риска в одиночном режиме. Предположим, что инвестор может приобрести актив 1, который напрямую включает в себя этот риск, актив 2, который является опционом по активу 1, или безрисковые казначейские векселя. По структуре актив 1 имеет среднее д , дисперсию ст. д - 1 и у = 0 при начальной цене Ро = 1. Применив предыдущие формулы, мы можем рассчитать:
А — cogi 4- со2Х2,
372
21. Вэвешиввние опционов
В — cd} ч- cd282,
С = б<?2/2,
А 1 „ 2 1 - .
т ~ А ч—Сет “ cd. и. ч- CD..7Z. ч—со.у.су ,
2 - - 2 ./.
> 1 Х"г2 4 ( 3 \“ 2 1 2 —2 4
V = В СУ ч— С СУ — ( CD. + CD. <\ СУ ч- — CD. СУ
2 V ' - -) 2 ~ ~
и подставить т и v в усовершенствование №1 или 2. Я опущу громоздкие формулы для усовершенствования №3 за исключением предельного случая с постоянной перенастройкой, где:
А = CD}ju + CD27T 2 ,
В = CD} + CD2 62 ,
С = CD2y2 ,
Рыночное равновесие с одиночным режимом
Одним из отличий деривативов от обычных ценных бумаг является то, что чистое предложение деривативов на рынке должно быть нулевым. Следовательно, если бы все инвесторы были бы похожи друг на друга, деривативы должны были бы оцениваться равновесно, так, чтобы оптимальная длинная или короткая позиция была бы нулевой. Итак, давайте взглянем на условия первого порядка и посмотрим, чего они требуют при со2 = О и оптимальном од*. Фокусируясь на постоянно перенастраиваемом сценарии, получаем:
Тогда второе условие требует, чтобы:
373
Часть 2. Постижение новежоства
= тг2 — 32/л ч— у2ст2 — О .
Мы можем упростить выражение, заметив, что:
1 dV(jUt^t) dP^fot}
V(j dt ,=0~ дТ '"° ~dT
dv(/itd) ~дТ
,=о = Zz<5 + & ’
где О обозначает частичную производную стоимости опциона относительно времени, также известную как «разрушение временем». И снова вспомним, что цены дисконтируются по безрисковой ставке г; стандартная О измеряется в номинальных терминах, так что 0=0 —г. Подстановка в уравнения дает следующий результат:
О. + — у-у&~ = 0 . “ 2 ~
Это справедливо для рыночного равновесия для всех времен и цен. Умножая на стоимость опциона, выписывая частичные производные и опуская нижние индексы, мы получаем:
Интерпретация Блэка—Шоулза
Если ценная бумага следует логарифмически нормальному броуновскому движению, любой опцион по этой ценной бумаге должен удовлетворять дифференциальному уравнению в частных производных, известному как уравнение Блэка—Шоулза. Предыдущее уравнение является в точности уравнением Блэка—Шоулза при заданной безрисковой ставке ноль. Если бы мы повторно измерили V и Р в номинальных терминах, то сгенерировали бы стандартное уравнение Блэка—Шоулза, которое содержит дополнительные дР
члены — rV + гР---. Следовательно, рекомендуемый здесь подход для
дР
внедрения опционов в анализ портфеля включает в себя в качестве особого случая стандартную теорию опционов. Особенное внимание обратите на то, что параметр относительного неприятия риска с выпадает точно так, как это следует из уравнения Блэка—Шоулза. Действительно, нам даже не нужно предполагать, что с является константой.
Бесполезные опционы
Совместимость с теорией Блэка—Шоулза означает, что наличие опционов по существу не меняет оптимальную стратегию портфеля. Очень заманчивой представляется уверенность в том, что сама структура опциона — скажем, то, что пут достигает страйка намного ниже среднего, — делает ее полезной 374
21. Взвпшивание опционов
прибавкой к портфелю. Это не так. При отсутствии ошибочной цены нет необходимости покупать опционы.
Даже когда имеется ошибочная цена, опционы могут не воспользоваться этим наилучшим образом. Возвращаясь к примеру одиночного режима, лежащего в основании фонда, предположим, что вы считаете, что настоящее смещение актива на с выше, чем считает рынок. Тогда вам следует также считать, что 7Д по вашему опциону растет в гл)-, раз быстрее, чем думает рынок. Тем не менее, ваш портфель может быть оптимизирован и без опционов:
~ 1 ~ 2 *~2
. — /л- е + — бт — CW] ст О , us “О
„ - / ~ + е) 4--Ч--------/2^2 “ CW1 <^2бТ2
Д -о' 2, 2
dCE с/ил
dCE
Страхование риска айсберга
Однако опционы могут быть очень полезны, если вы концентрируетесь на режимах, которые рынок опционов игнорирует. Например, предположим, вы считаете, что риск дефолта по ценной бумаге полностью нейтрализует ее привлекательность. Если рынок опционов игнорирует риск дефолта, вам следует купить немного этих ценных бумаг и много дешевых путов без денег.
Давайте уста! ювим, с кол ько стоит страхован и е рис ка а йсберга. Представим себе пуассоновский крах, который происходит с частотностью I и съедает 100Л% благосостояния. Пусть CEq обозначает откорректированный учетом риска уровень доходности при отсутствии краха, в то время как СЕ принимает в расчет крах. Если мы вспомним расчеты в последней главе для пуассоновских скачков, то:
-- ----- -1
СЕ - С£о +М------L.
1 — с
Следовательно, инвесторы, скорее всего, захотят заплатить до 1 -(1 -
/ ——>------- за полное страхование от краха. Из этой величины IL
1 — с
представляет из себя ожидаемый убыток. Остаток — это рисковая премия:
1,1. , ,
I--Ь---------lL=-clL- +-c(c + V)lL3 +
1 — с 7. 6
375
Часть 2. Постижение невежества
(с + 1)...(с + 7) .
3...(2 + 7)
376
22. Закрепление фокуса
Ha следующий день посещений Конвей приехал рано. Девлин с Регреттой по очереди рассказывали ему об усовершенствованиях более высоких порядков, об упрощениях, предоставляемых постоянной перенастройкой и о внедрении опционов.
«Я поражен, как много вам двоим удалось сделать за две недели», — сказал Конвей. Это почти так же удивительно, как и то, насколько хорошо вы поладили. «Но, надеюсь, Вы не рассчитываете на то, что я все это запомню».
«Конечно, нет», —- сказала Регретта. — «Просто запомните самое важное».
«А именно?»
«Что этот подход всеобъемлющий», — заявил Девлин.
«Но гибкий», — добавила Регретта.
«И в нем столько деталей, сколько тебе будет надо».
«Или он может быть аккуратным и экономным. Так что вы можете фокусироваться на чем хотите и вытаскивать тот рецепт, который вам больше всего подходит».
«А еще лучше заставить вас двоих вытащить его для меня, — вставил Конвей, прежде чем они оба чересчур увлеклись.- Как насчет того, чтобы пойти со мной в «Мегабакс»?»
«Только не я, — сказал Девлин. — Я не стремлюсь стучаться в дверь, которая для меня один раз закрылась».
«И не я, — сказала Регретта. — Слишком много дурных воспоминаний о напряженной жизни».
«Поверьте, управление активами -— не такой уж волнующий бизнес. Вполовину менее волнующий, чем вам кажется, — Конвей улыбнулся, но не получил улыбок в ответ. —- Послушайте, я же вас не заставляю. Мне просто нужна помощь, чтобы разобраться со всеми этими активами и режимами. И к кому еще, по-вашему, я могу обратиться?»
«Будь проще», — сказали ему Девлин с Регреттой чуть ли не в один голос и рассмеялись. «Расскажите ему о вашей идее, Регретта».
«Вы можете назвать этот подход моделью оценки финансовых активов», — сказала Регретта.
«Модель оценки финансовых активов? Что общего у нее с переключением режимов?»
«В ее исходной форме — ничего. И я не говорю о равновесной рыночной
377
Часть 2. Постижение невежества _______=в=^_=и=^=====____
цене. Я просто имею в виду идею разложения всех активов на общие делители и независимые остатки».
«И в чем тут смысл?»
«Если вы сможете это сделать, это сэкономит тысячи на информационные нужды».
«Каким образом? Разве для того, чтобы отследить все альфы и беты нужно еще больше параметров?»
«Конечно, но тогда большая часть ковариаций исчезает. Они все становятся нулевыми, за исключением ковариаций между самими рыночными индексами. А все альфы и беты и остаточные дисперсии, как предполагается, не варьируются в зависимости от режимов. Вот гистограмма, иллюстрирующая, насколько меньше параметров необходимо, не считая те, что вам понадобятся, чтобы разобраться с опционами. Контраст был настолько сильным, что мне пришлось перевести его в логарифмы».
Степени свободы в анализе портфеля из 100 активов
Degrees of freedom in portfolio analysis of 100 assets
All -1t.il and Iower moments
All and lower moments
n normal regimes, no restr ictions
5 regmies. 3 common factors
о r egrrrres, 1 common factor
4.598,125 J
100 1 .000 10,000 100,000 1,000,000 10,000.000
Degrees of freedom
«Это действительно огромная экономия. Но разве она не уничтожает риск айсберга?»
«Едва ли. Ведь вы о чем вы в действительности беспокоитесь — о том, что огромная часть вашего портфеля подвержена одновременному краху. Если не допускать сверхконцентрации активов, этого не произойдет, если только один или более ключевых индексов не потерпят крах тоже. Так что вы можете с тем же успехом сфокусировать свое внимание, направленное на риск айсберга, на этих ключевых индексах. Пусть их средние сильно варьируют в зависимости от режимов, как и ковариационные матрицы, но главное, постарайтесь понять шансы этих режимов».
«Что происходит со всеми остальными активами?»
«Ну, части активов, которые отслеживают ключевые индексы,
378
22. Закрепление фокуса
включаются с ключевыми индексами. Что же касается остатков, с ними обращаются как с независимыми нормальными переменными. Вы пытаетесь максимизировать их коэффициент Шарпа с помощью стандартных правил независимо от того, что происходит в остальном портфеле. Удобно, не так ли?»
«Определенно. Но я был свидетелем, как удобство порой приводит к беде. Девлин, а ты что думаешь? Разве ошибки, которые непременно накапливаются в аппроксимациях, тебя не беспокоят?»
«Да, они меня беспокоят. Но увеличение количества расчетных параметров в пятьдесят раз от них не избавит. Я уж лучше сделаю анализ чувствительности по нескольким ключевым параметрам, а еще лучше — смоделирую неопределенность о них напрямую».
«Ты имеешь в виду подход Блэка—Литтермана?»
«Не совсем. Я не разбавляю взгляды рыночным консенсусом, поскольку когда есть множественные режимы, довольно сложно определить, каков консенсус. Вместо этого я моделирую сомнения как дополнительные, создающие шум случайные переменные. Иногда можно точно рассчитать их воздействие; иногда просто его аппроксимировать».
«И пяти режимов достаточно?»
«Возможно, недостаточно. Возможно, более чем достаточно. Это зависит от рисков концентрации».
«Ты имеешь в виду кластеры в одном секторе или на одном рынке?»
«Отчасти. Если говорить в целом, я имею в виду любую общую подверженность. Если корейские фонды, которыми ты владеешь, начинают двигаться точь-в-точь как Nasdaq, то у тебя появляется дополнительный концентрированный риск по Nasdaq, независимо от сектора или рыночного листинга».
«Разве это не это, как предполагается, должны охватывать спекуляции на множественных режимах?»
«Вот именно — «как предполагается». Но довольно просто можно принять айсберг за небольшие льдинки. Я начинаю сомневаться, что следует моделировать больше нескольких штук: скажем, БЫЧИЙ и МЕДВЕЖИЙ или ИДИ, ЛЕТИ и НЫРЯЙ».
«Тогда как ты охватишь множественные подверженности корейских активов специфичным для Кореи потрясениям, колебаниям доллар/иена, рынка Nasdaq и глобального рынка в целом?»
«Множественные общие множители могут уладить это без необходимости введения отдельного режима для каждого риска взрыва. Если твоя абсолютная бета портфеля относительно корейского риска составляет менее 0,05, например, я бы вообще не стал заниматься отдельным его моделированием».
Конвей покачал головой с притворным неодобрением. «Ты меня подвел, старик. Я-то ждал более высоких стандартов. В следующий раз ты станешь
Часть 2. Пестижение невежества_____________________________^^===^^==
пропагандировать абсолютные потолки концентрации по всему, прямо как менеджер рисков старого образца».
«Потолки концентрации примитивны. И мне не нравится слово «абсолютный». Но многое из того, что советует новая теория, выглядит как комбинация максимизации коэффициента Шарпа и потолков концентрации».
«Что в некотором роде и происходит на практике».
Девлин пожал плечами. «Ты уверен?»
Спокойно, Девлин! «Нет, я не уверен. Возможно, они просто стараются не упасть намного ниже исходных данных, независимо оттого, каков он. Полагаю, твоя теория этого не затрагивает».
«Не совсем, — сказала Регретта. — Но существует быстрое решение, которое, я полагаю, сумеет это сделать».
«Правда? И что за решение?»
«Просто повторно измерьте доходности относительно исходных данных, а не относительно безрисковой ставки».
«Допустим, это просто. Но как этот новый оптимум сравнить со старым?»
«Подумайте. Вы станете искать портфель, который будет оптимальным после того как вы вычтите единицу избыточной доходности по исходным данным. Это означает, что вы просто возьмете предыдущий оптимальный портфель и прибавите к нему единицу исходных данных или их заместителя с заемными казначейскими векселями».
«Спасибо, Регретта. Но что если с этим не согласятся инвестиционные менеджеры?»
«Тогда, возможно, вам следует оценивать портфель по его эффективности».
«Разве вы не хотите принять в расчет риск?»
«Под эффективностью я имею в виду полезность доходностей, а не сами доходности. В конце концов, если прогнозы верны, это должно составить среднюю величину ожидаемой полезности».
«Я боюсь, что полезность не будет интуитивно привлекательной. Не все примут эти рамки».
«Тогда преобразуйте среднюю полезность в эквивалент надежности. Это просто откорректированная с учетом риска доходность. Все люди, занятые в этом бизнесе, это понимают».
«Я в этом не уверен».
«Они поймут, если вы начнете включать это в их вознаграждения».
Конвей кивнул: «Справедливое замечание. Но эти меры полезности применимы к портфелю в целом. Как я должен рассчитывать индивидуальную эффективность в фонде, где работает много менеджеров?»
«Совершенного метода, как это сделать, не существует. Но в целом я отдаю предпочтение измерению маржинальных вкладов. Что-то типа
380
22. Закрепление фокуса
откорректированной с учетом риска доходности фонда в целом за вычетом того, какой была бы откорректированная с учетом риска доходность, если бы там не было бы этого менеджера».
«Если бы там не было бы конкретного менеджера, многое было бы по-другому. Например, больше одной меры, чем могло бы быть».
«Что будет означать более одной меры управленческой эффективности. Но в целом, я думаю, вы будете склонять менеджеров к тому, чтобы они прибавляли диверсифицированную альфу, не усиливая при этом риск айсберга в кризисные периоды. Именно это пытаются сделать маржинальные вклады. Вот пример, построенный мной для двумерно нормального мира, в котором остаток портфеля имеет коэффициент Шарпа 0,5. Если бы корреляции нс имели значения, линии равных маржинальных вкладов были бы горизонтальными. Вместо этого они по большей части очень круты».
Маржинальные вклады в откорректированную с учетом риска доходность (СЕ)
Correlation with rest of portfolio
«Я понимаю, — сказал Конвей. — Я пользовался коэффициентами Шарпа для достижения той же цели. Какую роль играют здесь ваши меры?»
«В многомерном нормальном мире коэффициент надежности будет пропорционален совокупному коэффициенту Шарпа, возведенному в квадрат. Но это будет сильнее штрафовать за риск айсберга, чем возведенный в квадрат коэффициент Шарпа».
«Отлично. Я понял, Регретта. Спасибо».
Внезапно заговорил Девлин. «Ну, возможно, вам двоим и все ясно, но обо мне этого не скажешь».
381
Часть 2. Пестижение невежества
«В чем дело? — спросила Регретга. — Я думала, вы согласны с оценкой эффективности. Мы говорили об этом ранее».
«Тогда я действительно согласился. И в принципе я до сих пор согласен. Но пока вы объясняли Конвею, стал сомневаться в надежности».
«Надежности чего?»
«Средних баллов полезности. Насколько сильно они могут отклоняться от ожидаемой полезности?»
Регретга на минуту задумалась. «Полагаю, это зависит оттого, как много шума в портфеле — волатильности и тому подобного — и от того, на сколь длительный период вы рассчитали портфель».
«Тогда почему бы нам не попытаться оценить надежность и не включить ее в оценку?»
«Я не понимаю», — сказал Конвей.
«А я понимаю, — сказала Регретга. — Реальные баллы эффективности могут представляться как случайные величины от настоящего балла ожидаемой эффективности. И считаю, что, в конце концов, средние будут стремиться к ожидаемому значению».
«Как и положено, — сказал Конвей. —Ты с этим не согласен, Девлин?»
«Нет, я не несогласен. В долгосрочном периоде метол Регретты должен отлично сработать. Но в краткосрочном периоде нам следует быть настороже. Вы же не будете увольнять менеджера или проводить крупную перетасовку портфеля на основании одной только торговой сессии, не так ли?»
«Нет, если только она не была чрезвычайно ужасной. Но даже тогда я, скорее всего, буду рассматривать ее как выброс».
«Согласен. Но долгосрочный период — всего лишь цепочка ежедневных результатов. А каждый результат несет некоторое информационное значение, и мне хотелось бы знать какое».
«Понятно. Это хороший вопрос. Но, если вы не возражаете, давайте отложим его до следующего раза. У меня голова пухнет от информации. Я больше не выдержу».
«Что если я запишу вас на spa? — спросила Регретга. — Это одно из многочисленных удобств Club Mad».
«Звучит заманчиво. Знаете, я начинаю вам завидовать».
Пока Конвей принимает ванны, давайте исследуем поглубже сокращения типа модель оценки финансовых активов и оценку эффективности. Но не слишком глубоко: Конвей — не единственный, у кого голова пухнет от обилия информации.
382
22^3акреплвнив факуса
Привлекательность простоты
Как уже отмечалось ранее, модели А многомерных нормальных активов при К режимах могут иметь — АГ(А"-Ь 1)(7V-Ь 2) — 1 степеней свободы: КХ —
среднее, —AT(N + 1) — дисперсии и ковариации, а К — 1 — вероятности режимов. Это намного проще, чем пытаться установить все моменты третьего или четвертого порядков и смешанные моменты. Тем не менее сумма растет линейно с К и квадратически с X. Более того, каждый опцион прибавляет по меньшей мере ЗХ степеней свободы; действительно —K(J + 1)(У + 2) , если он зависит от J ценных бумаг. В то время как компьютеры легко справляются со сложностью, о людях этого не скажешь. Это создает серьезный стимул к дальнейшему упрощению.
Разложение типа «модель оценки финансовых активов»
Модель оценки финансовых активов (САРМ) предполагает, что все риски актива могут быть разделены на два типа. «Рыночный» риск совершенно коррелирован с совокупным рыночным индексом. «Идиосинкратический» риск независим от любых других рисков. В сущности САРМ разлагает каждый актив /? на /3h единиц рыночного индекса плюс независимый остаток, имеющий среднее cch и дисперсию T]h . Единственными дополнениями, необходимыми для того, чтобы характеризовать среднее т и дисперсию v со-взвешенного портфеля, являются среднее /л и дисперсия ст2 рыночного индекса. Описание /V активов подобным образом требует'только ЗА + 2 параметров.
Самый простой способ внедрения нормальных рыночных рисков в САРМ — это позволить // и ст2 меняться в зависимости от режима, но только не cth , j3h или Tjh . Если определить А, В и Н как векторы och , (3h или соответственно, мы можем легко рассчитать:
Mk= А + ркв ,
— diag{H ) + су~ВВ ’
для подстановки в усовершенствование №1 или 2 рецепта оптимизации. Альтернативно мы можем применить разложение САРМ к логарифмическим доходностям, произвести аналогичные расчеты для Мк и ЁА., а затем осуществить подстановку в усовершенствование №3.
Часть 2. Пестижение невежества
Когда рыночный индекс является рыночным
Разложение САРМ становится еще более простым, когда рыночный индекс является свободно рыночным. Замените каждый актив h хеджированным пакетом, состоящим из актива h минус единиц рыночного индекса. Затем прибавьте новый актив, состоящий только из рыночного индекса. Переопределив со так, чтобы она охватывала вес iv по рыночному индексу и веса й> по различным хеджированным пакетам, тогда мы получаем:
V
тк — а)' М - сд' A c У'//к — d)ha/7 + ~ гп + и’//А ,
/7 = 1
V
vk — со ’Zw = со' diag(M)co + ш2сг2 = co^r}h + w2cr2 — v + /2 = 1
в усовершенствованиях №1 или 2. Я резюмировал вклады хеджированных пакетов активов в среднее и дисперсию, как т и у соответственно, чтобы подчеркнуть их инвариантность к режиму или весу по рыночному индексу. Однако они все-таки варьируют с со . При заданном у инвестор всегда предпочитает самую высокую возможную гп и должен выбрать w соответственно. Доведение до конца этой условной максимизации - аи показывает, что cof = —— для некоего общего множителя со0 .
7lh
Другими словами, выбирайте относительные веса по различным некоррелированным хеджированным пакетам, чтобы максимизировать их совокупный коэффициент Шарпа с помощью простых, возведенных в квадрат правил Шарпа. Обозначив отдельные коэффициенты Шарпа как Sh = oth / ,
мы можем переписать совокупные моменты как:
тк — coQS2 + w//A.,
vk - со{) S + iv ,
_ _ V ____
где lV2 = S 'S = Sz2 обозначает коэффициент Шарпа для совокупного /7=1
хеджированного пакета. Теперь наша оптимизация зависит только от двух свободных параметров: соо и w. Это наиболее простой из возможных способов внедрить ненормальный рыночный риск при заданной, менее чем постоянной перенастройке.
Мультииндексное разложение
Стандартная САРМ подразумевает, что единственным общим риском портфеля является совокупный рыночный. Иногда это слишком грубо. Например, глобальный фонд, который по большей части отслеживает MSCI
384
22. Закудяви» »акуаа
World, может, тем не менее, обладать большим совокупным риском Nasdaq. даже если вычесть те риски, которые Nasdaq и MSCI World несут вместе.
Разложение активов на п ключевых индексов плюс остатки, требует о — 2
параметра на актив или N(n + 2) в целом. Помимо этого, — К(/? 4 1)(/7 ~ 2 1 — 1 2
параметров необходимо, чтобы описать первые два момента индексов и вероятности различных режимов. Если п намного меньше /V, это может сократить информационные нужды. Когда имеется 5 возможных режимов, разложение 50 активов на 3 индекса 4 50 идиосинкразических рисков сокращает количество свободных параметров более чем на 95% — с 6629 до 299.
Чтобы получить больше свободных параметров, можно предположить, что условные корреляции идентичны по всем режимам. В этом случае
'InK 4 — I) 4 К — 1 параметров будет достаточно для того, чтобы описать
моменты индексов и вероятности режимов. Если вы идете еще дальше и ограничиваете условные дисперсии, чтобы они были идентичны по всем
режимам, вам необходимо только пК 4 — «(/7 4 1) 4- К — 1 параметров. Однако здесь я не налагал этих ограничений.
Матричное представление
Предположим, мы получили линейное разложение, или «сокращение альфа/бета» N активов на п ключевых индексов плюс А независимых нормальных или квази нормальных остатков. Обозначив активы через У, ключевые индексы — через X, а остатки — через Е, мы можем написать:
Y = ВХ 4 Е, где В = [/?/„ ] является /V >• /7 матрицей бета, при /7Л/., обозначающей чувствительность актива h относительно ключевого индекса /. Давайте обозначим среднее вектора Е через А, а его диагональную п * п ковариационную матрицу —- через diag(H). Среднее и дисперсия портфеля в каждом режиме составляют:
mk = со\А 4 ВМ.) ,
vk = со' ВХ2к В' со + со' diag{H )(о .
Следовательно, усовершенствования №1 и 2 продолжают применяться при условии, что мы заменяем МА на А 4 ВМА, а Е,- — на ВЕ*В'4 diag(H).
Если мы применяем разложение САРМ к логарифмической доходности вместо процентной доходности, то в основном применимы те же уравнения с тильдами над переменными. Иными словами, усовершенствование №3 и рецепт Регретты с постоянной перенастройкой заменят Л4к на А 4ВМк , a Y2k — на BlLkB'+ diag(J~I) .
385
Часть 2. ТТестижение невежества
Матричные повторные представления
Чтобы лучше понять полученные ранее результаты, сформируйте
расширенный X вектор Х+ = Е , который имеет среднее М ' = А и
“S 0
ковариационную матрицу Е+ = .0 diag(H) Также сформируйте
расширенную бета-матрицу Д
/]. Поскольку Y = В Х^ , У должна
быть условно многомерно нормальной с условным средним В' Мк — А + ВМк ,
а условная ковариационная матрица ВХкВ ’ = BYkBX diag(H) . Результаты
для усовершенствований №1 и 2 следуют немедленно. Для усовершенствования
№3 примените соответствующее разложение Y — В'Х' , где В
В Л, а
В качестве альтернативы можно рассмотреть приемлемые для инвестиций
активы в усовершенствованиях №1 или 2 как X’ с весами портфеля В+ ' ш. Однако эта интерпретация не действует для усовершенствования №3, поскольку логарифмическая доходность портфеля равна In (I + со' exp ( В + Х+ П , а не
со'В+Х+
Рыночные индексы — выход на «бис»
Если все ключевые индексы являются свободными рыночными индексами, мы можем упростить подход еще больше, действуя по тем же принципам, что и для одиночного ключевого индекса. Во-первых, заменим активы Y хеджированными пакетами Y—ВХ. Пусть и ’, как и раньше, обозначает веса портфеля по хеджированным пакетам, a w — веса вектора по J индексам. Поскольку хеджированные пакеты повторяют Е, ясно, что
тк — со' А + со' Мк — т + w' Мк ,
vk — IX diag(H )со + = v + w'Spv.
Применима та же логика, что и раньше. Для любого v инвестор предпочитает самое высокое возможное vv, а следовательно, старается максимизировать коэффициент Шарпа S совокупного хеджированного пакета. Таким образом, мы получаем:
со — cd^(dicig(H)yx А ,
тк = оу 5*2 + wMk = A(diag(//))”’ А + wMk,
386
22. Закрвплвнив фокуса
vk = o}qS2 + и/Ek w = 69q A \diag(H)) 1 A + w'w.
И снова, mk и vk следует подставить в усовершенствования № 1 или 2.
Результаты для постоянной перенастройки
Вспомним, что при постоянной бесплатной перенастройке
СЕ = 69* 1п(1 i Л7) — = 69' М + ^tr(^diag (л>) ~ .
Чтобы применить сокращение альфа/бета, замените М на А + Bh4 , a Z — на ВЁВ Ч diag(H) :
— '^ВЕВ Ч diag(H)} со.
Если все индексы X являются свободно рыночными, разместите на них веса w, а веса и; — на хеджированные пакеты Y — ВХ , что дает:
Если все индексы подвержены пуассоновским потрясениям —L, возникающим со средней нормой /, просто вычти тс корректировку 1-(1-и2АГс /-------------, выведенную ранее:
1 -- с
СЕ — vv' ln(l + М)-cw'tw — I-----------—
2 1 — с
+ бУ' Л+ — ZjA—cgj'diag(H^cd . < 2 J 2
Поскольку w и никогда не появляются в одном и том же члене уравнения, они могут быть решены по отдельности. Для со , например:
387
Часть 2. Пестижение невежества
_* а, 1
с элементами 69, — —---1---. В этом случае абсолютное распределение для
7/,с 2с
каждого хеджированного пакета Yh — ВХ h определяется его средним, дисперсией и общим неприятием риска инвестора, независимо от риска и эффективности где-то в другом месте. Напротив, и/ зависит только от общих рисков X.
Внедрение опционов
Сокращения альфа/бета по духу очень похожи на тс сокращения дельта/гамма, которые используются для опционов. Для опционов
<»' Y s а>' Пк + АДХ - Мк) +X - Л/А)'(«,' Гк )( X - М J ,
так что мы можем свернуть Y = В Х+ как опцион путем замены X и М на .V и М+ соответственно и установив Ал = В , Пк — А + ВМ к и Гк = 0 . Все
опционы, привязанные напрямую кУ, могут быть внедрены «как есть».
Единственной остающейся проблемой является выражение опционов, привязанных к Y или к смеси Y и X как разложению второго порядка в X . Обозначив через Z вектор опционов, привязанный к У, получим:
ю'7 = (о'П. + (О' А. (у - В~ ЛГ ) + -(Г - В'МГ\((О' г,. )(у - В 'м:)
А К у к у у л у \ А 7 у А у
s (О’ Пк +(о'ккВ'- (х+ -Мк)
+|(х+ -м^'в^'((о'гк)в^х^-м;).
Следовательно, преобразование основанного на X разложения второго порядка в .V-разложение является прямолинейным. Просто замените Аа.В + на Ал , а В+ '(с?)' Гк }В^ на а>'Гк . Параллельное преобразование применимо для логарифмических доходностей.
Беты «краха»
Чтобы обрести больше гибкости, прибавьте индекс к к А, В и Н везде, где они появляются. Это позволяет оценкам разложения варьировать в зависимости от режима, проводя различие между «обычными» бетами и бетами «краха». Хотя это и кажется привлекательным, меня беспокоит возможный перегиб. Большая часть эффекта, которого вы пытаетесь достичь, воплощена в самом изменении режима, так что это добавляет дополнительные переменные для того, что, скорее всего, приведет к небольшим маржинальным выгодам. Более того, я боюсь, что оценка множественных групп коэффициентов сделает
388
22. Закрепление фокуса
каждую из этих групп намного менее надежной, так что она скорее лишает нас уверенности, чем вселяет надежду. Финансовые аналитики редко имеют достаточно данных, которые, как они считают, имеют отношение к текущим условиям, чтобы чувствовать себя уверенно даже с одним рядом оценок.
Неопределенность параметров
Как отмечалось ранее, для классических моделей оптимизации портфеля, кажется, не слишком важна возможная ошибка измерения. Они просто предполагают, что вводимые вами цифры верны. Огромным достоинством подхода Блэка—Литтсрмана является то, что он позволяет вам сказать, что «эта оценка может оказаться мусорной», и перейти к некоему подразумеваемому рыночному консенсусу. К сожалению, довольно сложно оценить общерыночный консенсус, когда в наличии множественные возможные режимы.
Вместо этого я предлагаю внедрить неопределенность напрямую, дополнив расчеты соответствующими ковариационными матрицами. Один такой пример приведен в главе 14. Если вы уверены, что логарифмические доходности многомерно нормальные с ковариационной матрицей Z , но не уверены относительно среднего и если ваши убеждения относительно среднего многомерно нормально распределены со средним М и ковариационной матрицей S, вы можете с тем же успехом сказать, что логарифмические доходности будут многомерно нормальными со средним М и ковариационной матрицей Z + Н .
Хотя они сокращают ряд свободных параметров, сокращения альфа/бета не сокращают связанную с ними неопределенность. Скорее, они концентрируют ее в сомнения относительно оценок А, В и Н, с эффектами, которые варьируют в зависимости от того, что подвергается сомнению и как.
Сомнения как случайные переменные
Сомнения относительно ряда параметров Ф легче моделировать как скрытые случайные переменные Еф, которые многомерно нормально распределены со средним 0 и ковариационной матрицей . Еф для разных Ф обычно считаются независимыми от всех Ф, что упрощает расчеты. Однако это предположение не всегда оправдано и должно быть исследовано на предмет достоверности.
Например, в то время как сокращение альфа/бета производит разложение Y = B.Y + Е, мы можем представить, что подлинное отношение таково: Y = (В + Ев )Х + Е + Еа = ВХ + (£* + Еа + ХЕН ) . Имеет смысл предположить, что ЕА и Ен независимы от В, X и Е. Не имеет смысла предполагать, что для заданного актива Л, ва11 и различные Ерь будут независимы
389
Пасть 2. Постижение невежества
друг от друга, поскольку это сложно — обнаружить отдельные влияния коррелированных компонентов X.
Как насчет отношения между различными и в разных активах? Зависимость между этими сомнениями, скорее всего, возникает из-за некоего скрытого общего множителя, который нс был включен в X. Если вы считаете, что этот множитель важен для портфеля в целом, внедрите некий его заместитель в X. В противном случае забудьте о нем, чтобы сохранить удобство диагональной ковариационной матрицы по остаткам.
Заместитель по возможности должен быть рыночным активом. Например, предположим, что вы управляете огромным опционным портфелем, который будет подвержен общему сжатию ликвидности, подобному тому, что произошел с Long-Term Capital. Применение индекса кредитных спредов в качестве заместителя этого сжатия могло бы подтолктгуть к игре на понижение кредитных спредов в качестве хеджа. Если ваш заместитель не является рыночным, тогда он просто поощряет диверсификацию или уменьшение размеров опционного портфеля. Конечно, если вы выбрали плохой заместитель или сильно преуменьшили риск, тогда анализ портфеля вам не поможет.
Заполнение Н
Предположим, что ваши единственные сомнения касаются А. В сущности, это заменяет Е на Е + Ел, что все еще независимо от X. Единственным изменением, которое вам нужно внести в расчеты ожидаемой полезности, является замена дисперсии diag(H) на diag(H) + rLA . Более того, если предположить, что X охватил все общие множители, будет диагональным. Просто увеличьте каждый T]h до т]и + £a/lh .
Если ваши сомнения включают и В, тогда остаток Е + ЕЛ -т АТЕф больше не является независимым от X. Однако очень хочется притвориться, что является, поскольку мы можем заполнить Н несколько больше, не производя никаких других изменений. Например, предположим, что ваши сомнения касаются одной конкретной беты в однофазном разложении. При заданном любом конкретном х, соответствующая дисперсия составляет х2^. Следовательно, безусловная дисперсия составляет Е = (//“+ , и мы можем
попытаться просто прибавить ее к T]h .
В целом сомнения относительно каждого В/; будут иметь ковариационную п х /7-матрицу , а также /7-вектор НAl)h ковариации между А и В. Для каждого актива h мы можем рассчитать:
Е Х\к +ЕВ„Х\ХУ\ = Zahh +2^BhMk + Ех\к [X'^BhX]
= £см,+2^лВ1,Мк +мк '^BhMk + vec(Ss„)’vec(Ej
390
22. Закрепление фвкуса
П
+ Е Е ^Bh„- ( A* Bjk + <Ejk ) ’ 7=1 /=]
где vec(-) преобразуег прямоугольную матрицу в вектор путем последовательного образования пучков столбцов. Снова предположив, что X охватил все общие множители, наша аппроксимация просто прибавляет это к
T]h , игнорируя все другие члены.
Правила Шарпа, возведенные в квадрат, притупленные
Предшествовавшие корректировки дисперсии варьируют в зависимости от режима. Это не удивительно: ошибки в бета непременно становятся больше, когда E^xtXj J велика. Однако они притупляют применение возведенных в квадрат правил Шарпа к остаткам или хеджированным пакетам, которые являются их заместителями, поскольку остатки коэффициентов Шарпа больше не будут постоянными в разных режимах. При одиночном режиме мы все равно можем применить возведенные в квадрат правила Шарпа к остаткам, по меньшей мере в этой аппроксимации.
Неопределенность с большей точностью
Более точное обращение рассчитывает ожидаемую полезность для каждой оценки А и В, а затем интегрирует по воспринимаемой вероятностной плотности этих оценок. Этот расчет может быть довольно громоздким, так что я сконцентрируюсь на относительно ясном случае постоянной перенастройки при отсутствии пуассоновских скачков. Если наши предположительно хеджированные пакеты на самом деле имеют совокупные веса Z = EBw по X , то расчеты ожидаемой полезности должны заменить w на гг + Z :
что может быть выражено в форме:
СЕ = А + В'Z + — Z'CZ 2
при условии, что:
Л-С'Х
В — In(1 + М) — cw' Z ,
С = -ct.
391
Часть 2. Постижанив новожоства
Затем преобразуйте СЕ в EU и интегрируйте по вероятностной плотности Z . Величина Z является многомерно нормальной со средним 0 и ковариационной матрицей У = Е Е8(дсд'Ен . (При условии, чтоXохватывает
<\
все общие множители, У имеет элементы vtJ .) Отсюда следует,
что:
|ЕЕ/| = Е
ехр(1 -с) СЕ
/ + (с-1)СУ ,/
= EU
•ехр -^-(1 -с)“ В'^Х 1 + (с -1)С) В
Еще более продвинутое обращение будет включать в себя неопределенность относительно ковариаций и гамм опционов. Это намного сложнее главным образом из-за того, что ошибки в ковариационных оценках проявляют тенденцию следовать распределениям хи-квадрат, а не нормальным распределениям. Анализ я не буду здесь рассматривать.
Совокупные меры эффективности
Если ваши прогнозы верны, полезность доходностей портфеля должна составить среднюю величину ожидаемой полезности. Это делает среднюю полезность очевидным способом измерения эффективности портфеля. Однако коэффициент надежности обеспечит такое же ранжирование эффективности, и его гораздо проще охватить интуитивно, поскольку он измеряет откорректированную с учетом риска доходность.
Различные разработанные нами меры предлагают различные интерпретации оптимальности. Но все согласны с тем, что при отсутствии крупных рисков айсберга коэффициент надежности должен находиться в районе 1/2с, умноженной на квадрат совокупного коэффициента Шарпа S. Так происходит потому, что СЕ для одиночного режима напоминает со'М — — cco'Zco , которое максимизируется при (О У-1 М для
2 с
1 _ S~
максимального значения —MZZ}М —------. Различные отклонения от этой
2с 2с
формулы отражают время до перенастройки и различия между логарифмами и процентами. Хочется сказать, что (логарифмический) коэффициент Шарпа в квадрате является еще более фундаментальной мерой, чем откорректированная с учетом риска доходность, поскольку коэффициент Шарпа не зависит от неприятия риска с. Однако коэффициент Шарпа может споткнуться на рисках айсберга, в то время как коэффициент надежности — нет.
392
22. Закрапление фекуса
Меры маржинальной эффективности
Маржинальный вклад инвестиции в портфель является разностью между ожидаемыми полезностями с и без инвестиции. Обе меры должны подразумевать, что портфель оптимизирован для имеющихся инструментов. Если инвестиция, на которой вы фокусируетесь, является малой частью целого, ее присутствие или отсутствие не должно значительно изменить оптимальную структуру остального портфеля, позволяя нам оценить «что было бы» цугом взгляда на реальную эффективное!ь без повторной оптимизации. Приведенные ниже расчеты предполагают, что аппроксимация оправдана.
Двумя наиболее важными влияниями на маржинальный вклад инвестиции являются ее коэффициент Шарпа S и се корреляция р с остальным портфелем. Чтобы численно это измерить, давайте проигнорируем риски айсберга и сравним возведенные в квадрат коэффициенты Шарпа. Обозначим коэффициент Шарпа остального портфеля через 5'0, тогда маржинальный вклад будет составлять:
S’" 4- - 2pSS„ 2 _ S2 - 2pSS0 + p2S2 _ (5 - PS0 )2
1 2 ^0 i 2 i 2
1 - р 1 - р 1 ” р
Этот вклад растет с квадра том гэиа между S и pS0.
Административное предупреждение
Предыдущая формула показывает, что более низкий Шарп может быть ценнее высокого. Однако это предполагает, что мы играем на понижение инвестиции, у которой S меньше pS0. Это, может быть, будет сложно понять, особенно если маржинальная инвестиция является любимым портфелем инвестиционного менеджера. Но как только менеджер поймет, что вознагражден за свои плохие коллы, он, скорее всего, улучшит их, особенно если осознает, что бумаги, лучшие с его точки зрения, могут ухудшить портфель при игре на понижение. Единственное стабильное равновесие, с которым я когда-либо встречался, получило громкую огласку: в его были вовлечены несколько аналитиков Уолл-стрит, которые «прославились» способом заключения сделок, и их крупные клиенты, хотя продавцы и скрывают это родство.
Если мы нс можем играть на понижение ни маржинального менеджера, ни остатка портфеля, тогда нам нс стоит инвестировать ни в один угол, ни в 1
другой, если только не р <—- <---------. Чем выше р, тем уже будет
5 тах(£>, 0)
диапазон. Секрет успешного управления фондом с множеством менеджеров — в том, что каждое X — /?5() должно быть положительным. В отрасли это известно под названием «поиск диверсифицированной альфы».
393
Часть 2 Пестижение невежества
Определение эффективности
Определение эффективности подразделяет меры эффективности целого на меры эффективности частей. В идеале определение должно как измерять маржинальные вклады частей, так и обеспечивать, чтобы отдельные вклады в сумме давали целое. Когда все компоненты нормально распределены и независимы, а портфель выбран оптимально, числа, кратные возведенному в квадрат' коэффициенту Шарпа, сделают свое дело. В противном случае крайне маловероятно, чтобы маржинальные вклады в сумме дали целое.
Снова рассмотрим портфель с двумя двумерно нормальными компонентами, где два компонента имеют коэффициент Шарпа S и соответственно с ненулевой корреляцией р между ними. И снова предположим, что портфель сформирован оптимально. Маржинальные вклады двух
компонентов в совокупную эффективность будут составлять U______и
1 - р~
12__' 1 соответственно. Их сумма явно меньше, чем совокупная
I ~Р~
1- р2
, если max
---, и больше, чем совокупная,
если max
f—
< ^0 >
Несправедливость и неправильное управление
Одним из методов работы с этой проблемой будет предоставление каждому менеджеру кредита на этот маржинальный вклад, разделенный на сумму всех маржинальных вкладов. Однако несправедливо, если, например, два инвестиционных менеджера Том и Дик будут управлять очень успешными, но высоко коррелированными портфелями. Пока эти два портфеля могут совместно управлять эффективностью фонда в целом, ни Том, ни Дик нс получат за них большого кредита.
Одна из возможных альтернатив позволяет Тому и Дику разделить кредит на маржинальный вклад их совместного портфеля. Но это гоже нс приносит полного удовлетворения. Почему бы не рассмотреть подгруппы из трех или более менеджеров? Если вы эго сделаете, вы разводните долю Тома и Дика.
Вообще, основная проблема здесь явно не в использовании маржинальных определений. Возможно, период измерения слишком короток и охватил только временную корреляцию. Если, однако, высокая корреляция сохраняется, тогда Том и Дик используются чрезмерно. Их портфели должны быть консолидированными, а если две головы не будут лучше одной, тогда, возможно, одного из них следует послать на создание альфы в каком-то другом месте.
394
223акроплонио фокуса
Сравнение эффективности
Исходные данные — это стандарт, используемый для оценки эффективности. Обычно это некий индекс того, что делают все остальные. Нс совсем в духе теории ожидаемой полезности, которая гласит, что ваша полезность должна зависеть от вашего собственного благосостояния и потребления, а нс от благосостояния и потребления других людей. Применение этих двух концепций потребует более глубокого обсуждения административных стимулов и их стоимостей, чем может предложить эта книга. Однако существует одни простой способ внедрить эталон, не перерабатывая теорию.
Вместо того чтобы максимизировать ожидаемую полезность избыточной доходности портфеля ю'У, максимизируйте ожидаемую полезность ui'Y-q, где q — избыточная доходность по исходным данным. Если со является оптимальным портфелем для первой задачи, тогда оптимальный портфель с исходными данными должен выглядеть как «со плюс единица исходных данных». Другими словами, проводите все свои оптимизации гак, как если бы исходных данных не было, а затем в конце приобретите единицу исходных данных (или их заместителя), субсидированную казначейскими векселями. Сходным образом, для того чтобы оцепить эффективность менеджеров, можно измерить ожидаемую полезность не их избыточных доходностей, но их доходностей относительно исходных данных.
Неточность измерения
На протяжении нескольких месяцев или ле г средняя фактическая полезность часто значительно отклоняется от той, что ждали. Гак что если вы слишком концентрируетесь на краткосрочной эффективности, вы будете хорошо вознаграждены, если вам повезет. Это может не только отпугнуть хороших менеджеров, но и приведет к риску превращения стратегии портфеля в тщетную погоню за вчерашними лучшими инвестициями.
Болес разумный подход признает, что все оценки эффективности являются неточными. Это не означает, что вы их будете игнорировать. Лучше вам модернизировать свою информацию в байсовском стиле, взвешивая каждую оценку на предмет ее точности. Это гарантирует большее внимание, по, боюсь, у нас внимание и силы уже заканчиваются.
395
23. Принцип петуха
В течение какого-то Конвей помалкивал о своих поездках в Club Mad. Он был далеко не уверен, что они окажутся продуктивными и не хотел, чтобы его судили по тем людям, с которыми он общается. Но сейчас у него было нечто, чем можно было хвалиться. Девлин с Регреттой нарисовали ему схему анализа портфеля, намного превысившую его ожиданий.
Безусловно, Джим ото оценит. Но когда Конвей обрисовал новый подход, Джим повел себя осторожно. «Интригующе. Очень находчиво, и, возможно, полезно. Но, боюсь, большая часть этих расчетов выше моего понимания».
«Эго выше и моего понимания. К счастью, друзья помогли мне с математикой. Мы можем запрограммировать расчеты, чтобы они проводились машинами».
«Я чувствую себя не в своей тарелке, когда пользуюсь тем, что я не понимаю до конца».
«Вы водите машину и пользуетесь компьютером. Вы полностью понимаете устройство двигателей впуфенпего сгорания и силиконовых чинов?»
«11ет, ноя знаю, как ими пользоваться, поскольку так ими пользовались и до меня. А здесь вы предлагаете мне стать пионером. Не думаю, что я на это способен».
«Кто-то должен начинать. 11очему не мы?»
Джим откинулся на спинку стула и усмехнулся. «Первое, чему я научился в финансах, — это важности того, чтобы быть вторым. Пионер — это парень со сфслой в спине».
Конвей рассмеялся. «Отлично сформулировано. Только это совсем другое. Этот подход разработан для сокращения наших рисков, а нс для их повышения».
«Даже если я вам поверю, могут не поверить другие. Помните, нам следует управлять внешней стороной риска, а не самим риском».
«Да, ваш брат однажды мне это объяснил. Я не забыл. Я просто хочу получить шанс завоевать людей. Некий эксперимент, форум, некий..» Голос Конвея сошел па пет. «Не знаю», — сказал он тихо и опустил глаза.
«Конвей, позвольте я дам вам дружеский совет, - сказал Джим. — Никогда не придерживайтесь сильных убеждений в финансах. Они, возможно, для вас всего лишь обуза».
396
23. —ИВ
«Я никогда этим раньше не страдал. Но это завладело мной».
«Я это вижу. Хорошо, Конвеи, вот что я сделаю. Я —.ч_у инвестиционных менеджеров на собрание по теме: «Риск айсберга и чт w делать». Но не буду заставлять их приходить и не стану заставля ть их ос.дтъг* Но я предоставлю вам возможность осветить этот вопрос, как вы считаете нужным. В зависимости от восприятия ваших идей попробуем верпчться вопросу проведения эксперимента после собрания».
Конвея просиял: «Спасибо, Джим. Я действительно очень ценю эт> возможность. Вы об этом нс пожалеете».
«11адеюсь, вы тоже. В пятницу вечером для вас не слишком рано?»
«Нет, это было бы здорово».
Конвей провел несколько дней в подготовке. Главное было не в том, ч тобы включить в доклад все подробности, а напротив, в том, чтобы выбросить все ненужное. Я должен показать им, как все это просто. Каким-то образом ему это удалось. К утру пятницы Конвей был вполне удовлетворен презен тацией и уверен в успехе.
Джим открыл собрание кратким введением. «Спасибо всем присутствующим. Такая явка предполагает, что нам всем интересен один и тот же вопрос. Но она также показывает, что мы все еще ищем ответы. Конвей утверждает, что у него они есть. Он поделился своими со мной, и они произвели впечатление. Впечатление и тем, что я понял, и чем, что я гак и не понял, — Джим улыбнулся и вызвал у аудитории несколько ответных смешков. Поэтому я попросил его поговорить об этой геме с более умной публикой, а именно с вами, пока я проверяю, не пойму ли я его лучше со второго раза. Л теперь предлагаю вам обратиться в слух, а Конвей постарается поразить вас интересным рассказом».
Конвей подошел к проектору. «Спасибо. Я хочу познакомить вас с новым способом анализа риска портфеля. Он делает все то же самое, что и старый, и даже больше. Эго самый простой вариант расширить старый способ, нс Hoi реши в против теории или здравого смысла. Я постараюсь быть четким, но если что-го непонятно, не стесняйтесь меня прерывать и задавать вопросы».
В воздух поднялась рука: «Этот подход будет включать в себя много расчетов?»
«Нет. Совсем чуть-чуть. Новый способ основан на теории, которая включает в себя большое количество математических расчетов. Она более сложна, чем стандартная теория, и требует применения большого количества расчетов. Но я говорю —- давайте оставим расчеты компьютерам, чтобы смогли сконцентрироваться на том, для чего нужна голова. На самом жж большая часть того, что я хочу сказать, может быть резюхифовава a jbptb. картинках. Вот первая из них».
Часть 2. Пестижанив наважаства
Нормальный риск
Normal risk
0.40 • - - ........ .. -- - ....---- -----------
0.35 -
£ 0.30
35 0.25
А о 20 !
0.15 .
0.10 .
0.05 j '
0.00 - - - ------!------ :----------7------г----- : - ..-.
-4 3-2101 23 4
Standard deviations from the mean
«Вот картина нормального колоколобразного риска: 95% действий происходит в пределах 2 стандартных отклонении от среднего; время от времени ты получаешь до 3 стандартных отклонений, а о 4 или больше стандартных отклонениях вы можете фактически забыть. Конечно, я знаю, что вы с этим знакомы. Но я показываю вам это снова, чтобы напомнить об одном: это единственный риск, который рассматривает стандартный способ. Да. Стандартный способ предполагает, что всякий риск во всяком портфеле выглядит подобным образом. Единственным отличием являются величины для среднего и стандартного отклонения, которые вы рассчитываете с использованием стандартных формул».
«А теперь если вам нужно выбрать один риск для анализа, этот риск будет правильным. Почему? По двум причинам. Первая состоит в том, что если вы вычислите среднее по множеству независимых переменных, риски всегда будут выглядеть нормальными, за исключением, может быть, экстремальных хвостов. Это было доказано сто лет назад в центральной предельной теореме самой знаменитой теоремы статистики. Вторая причина состоит в том, что многие коррелированные риски могуч’ рассматриваться как независимые, если вы просто меняете способ их измерения, так что можно применить центральную предельную теорему к ним тоже».
«Однако часто в крупных блоках активов присутствует общий ведущий фактор. Например, большая часть фондов США в конечном итоге зависит от здоровья экономики страны, так что если последняя дрогнет, они дрогнут тоже.
398
23. Принцип пвтуха
На одних это повлияет в большей степени, на других - в меньшей, поскольку экономический рост затрагивает одни б}'маги больше, чем другие, и ни для кого из них этот фактор не является единственным, оказывающим влияние. Тем не менее, эта группа раздели г общую подверженность».
«Когда доходности актива имеют общий фактор риска, они нс могут рассматриваться как независимые, вне зависимости оттого, как вы пытаетесь их нарезать. В этом случае риски портфеля не будут нормальными, если только общий риск нс является нормальным».
Еще одна рука взметнулась вверх: «Что если общий риск является примерно нормальным или если он мал относительно других общих рисков?» — спросила женщина.
«Хороший вопрос. Да, в этом случае стандартный подход, будет приемлем. Что касается экономического роста США, я, например, склонен обращаться с ним как с примерно нормальным влиянием. Но некоторые движущие факторы не являются даже приблизительно нормальными».
«Например?»
«Например, влияние рынка в целом. Если Nasdaq рухнет; roj да большая часть фондов рухнет вмест е с ним».
«Конечно. Если пег, то Nasdaq не рухнет. Разве это нс порочный круг?»
«Н да, н пег. Думаю, точнее будет сказать, что Nasdaq рухнул, поскольку некая комбинация общего шока и эффектов влияния заставила много фондов в Nasdaq упасть вместе. 'Гак что подлинным общим множителем является шок и.'или влияние которых я просто заменяю индексом Nasdaq. Сказав эго, я не вижу никакого вреда в том, чтобы идентифицировать общий фактор с его заместителем — индексом. На самом деле в некоторых случаях это даже лучше, поскольку мы можем смягчить риски, сыграв на понижение его заместителя, даже если не можем заключить сделку ио самому риску. Это отвечает на ваш вопрос?»
«Да», — кивнула женщина.
«Хороню. Теперь, думаю, мне не придется никого убеждать, что риск Nasdaq не является нормальным. Только не после того, что случилось за последние два гола. Его впечатляющий рост и падения могут быть уподоблены спуск}' и краху «Титаника». Известный риск айсберга. Только он сильнее распространен в финансах, нежели в судоходстве. Как мы можем внести поправки в стандартный анализ риска, чтобы внедрить туда риски айсберга?»
«Это серьезный вызов. Для начала, какие предположения нам следует сделать относительно вероятностного распределения риска айсберга? Означает ли это округлые хвосты или общее утолщение? Является ли это асимметрией вниз и если да, то насколько? И как мы внедряем вероятность, когда мы даже точно не уверены в том, каково распределение? Риски айсберга почти всегда покрыты пеленой неопределенности. На самом деле, чем больше я об этом думаю, тем больше убеждаюсь, что существует только один хороший способ резюмировать риск айсберга. Вот посмотрите картинку».
399
Часть 2. Постижвнив нвввжвства
Риск айсберга
Iceberg risk
Конвей дождался, когда смех утихнет, а затем продолжил, «Как сделать полезную модель из представления, что произойти может все, что угодно? Мой друг боролся с этой идеей долгие месяцы, прежде чем он нашел единственный ответ, который можно отследить. Пусть общий множитель (или множители) определяет общее состояние мира, также называемое «режимом». В пределах каждого режима предположим, что все нормально. Но параметры различных режимов и их вероятности возникновения могут варьироваться так, как вы хотите. Это называется «условной нормальностью». Графически это эквивалентно наложению различных колоколообразных кривых».
«Любые риски, в которых вы заинтересованы, могут быть смоделированы таким образом. Но важно то, что ряда режимов обычно достаточно для того, чтобы охватить все основные концепции».
Тут заговорил Генри: «Конвей, почему вы называете это единственным поддающимся обработке ответом? Существует множество распределений, из которых вы можете выбрать. Некоторые из них охватывают толстые хвосты намного проще, чем это делают нормальные распределения».
«Толстые хвосты отдельных активов, да. Но в анализе портфеля нас нс так беспокоят толстые хвосты отдельных активов, насколько нас беспокоят толстые хвосты портфелей. Между ними нет необходимой связи. Портфель высокопродуктивных векселей, каждый с огромным риском дефолта, может выглядеть нормальным в совокупности, если вы достаточно диверсифицируете и хеджируете рыночные риски. Напротив, активы с фактическим отсутствием хвостов могут все быть подвержены одному и тому же общему риску, что вызывает огромный толстый хвост в портфеле:
«Так моделируйч е и корреляцию тоже».
«Корреляция сама по себе не может охватить всех шансов, когда множество сольется в одно. Это невозможно, если только каждый актив и
400
23. Принцип пвтуха
комбинация активов не являются нормальными. С любым другим распределением вам следует указать моменты более высоких порядков и смешанные моменты. Коасиммстрии и коэксцессы портфеля среднего размера легко насчитывают миллионы. Так что вы можете с тем же успехом моделировать условную зависимость напрямую, а условная нормальность — самый простой способ это сделать».
«Мне нужно над этим подумать», — сказал Генри.
«Когда я впервые услышал об этом, я тоже не поверил. Теперь это кажется очевидным. Приходите после собрания ко мне в кабинет, и я покажу вам свидетельство, которое резко изменило мое отношение. Тем временем, независимо от того, считаете ли вы, что я могу делать это но-друтому или нет, понимаете ли вы, что я имею в виду под условной нормальностью?»
«Конечно, — сказал Генри. — Каждый режим является полностью нормальным, но средние, дисперсии и ковариации подлежат изменению».
«Точно. Режим это что-то типа бычий рынок, или медвежий рынок, или сжатие ликвидности. Это то, что большинство людей считают картиной рынка. На самом деле, если вы удалите математику, это естественный способ размышления о крупном риске. Стандартный анализ среднего и дисперсии в большей степени концентрируется на маленьких рынках. Иногда эго г о достаточно. Иногда он путает айсберг с льдинками».
«11и один подход не можег полностью избежать айсбергов», — сказал Генри. — «Как вы взвешиваете риски относительно упущенных возитраждений?»
«Снова хороший вопрос. Правда состоит в том, что сама по себе условная нормальность ни к чему вас не приведет. Вам нужна система баллов: некий метод сравнения нормальных рисков, рисков айсберга и вознаграждений, так чтобы вы могли судить, какой портфель лучше остальных».
Еще одна рука взметнулась вверх: «Вы имеете в виду что-то типа коэффициентов Шарпа?»
«Да. Но коэффициенты Шарпа игнорируют риск айсберга, поскольку они принимаюг во внимание только среднее и дисперсию. А поскольку коэффициенты Шарпа независимы от левереджа, они не могут сказать, сколько левереджа вам надо. Поэтому нужна более сложная мера».
«Как можно принять решение о чем-то типа левереджа, не зная толерантности инвестора к риску?»
«Нельзя. В то же время мы не хотим, чтобы наши правила подсчета баллов требовали бы слишком много информации о толерантности инвесторов к риску, поскольку у пас на руках обычно бывает мало информации. Например, было бы здорово, если при прочих равных оптимальные процентные распределения портфеля не зависели бы от его абсолютной величины. Давайте предположим, что наши инвесторы не трусы: что они никогда намеренно не вступают в сделки, которые гарантируют им потерю денег. Или, ио крайней мере, не хотят, чтобы «Мегабакс» заключал сделки труса от их имени. Звучит нс очень ограничивающе, не так ли?»
401
Часть 2. Постижение невежества ш
Конвей подождал, не появятся ли возражения, но возражений не последовало, так ч то он продолжил. «Отлично. Кажется, мы все одинаково ого понимаем. И угадайте-ка... При изложенных мной условиях экономисты доказали, что существует фактически только одно правило подсчета баллов, которым можно воспользоваться. Это ожидаемая величина степенной функции благосостояния инвестора со знаком, выбираемым с целью обеспечить, что больше — это лучше, чем меньше. Я покажу вам его на слайде:
При заданном коэффициенте относительного неприятия риска
CRR > О,
максимизируйте ожидаемую полезность
у—> у—* I — С /? Л
Е Благ о с ост оя и и е
1 - CRR
«На самом деле вы можете прибавить любую константу или умножить на любую константу и получить такое же подразумеваемое поведение. А когда CRR равна единице, вам следует заменить степенную функцию на логарифм. Помимо это г'о, она уникальна. Ожидаемая полезность — это просто экономическое название для правил подсчета баллов, которые люди, как кажется, максимизируют, причем, скорее всего, подсознательно. Е’(-) —это просто статистический символ ожидания при заданном соответствующем вероятностном распределении но благосостоянию. Что же касается CRR, то, несмотря на столь длинное название, это обычное число: ноль, если вы не возражаете против риска, или большее ноля — если возражаете».
«В применении этой формулы имеются две сложных части. Первая — это принятие решения об определении благосостояния. Любой игюгоящий экономист скажет, что благосостояние включает в себя не только ликвидные активы, но и недвижимость и человеческий капитал; т.е. дисконтированный будущий ноток доходов от занятости. Для большинства человеческий капитал — эго самая большая часть. Но мы, финансисты, любим упрощать, гак что давайте просто ограничим благосостояние только благосостоянием портфеля. Па самом деле для того, чтобы держать все в порядке, мы часто просто ограниваем это благосостоянием портфеля, которым мы управляем».
«Вторая закавыка в том, чтобы установить CRR, соответствующую определению благосостояния. Если вы предположите, что большинство инвесторов более или менее правильно применяют данный подход, тогда некоторые расчеты, которых я не буду пытаться здесь защитить, предлагают использовать CRR в диапазоне от двух до четырех для фондового рынка в целом. В качестве альтернативы Вы можете напрямую задать инвесторам несколько некорректных вопросов относительно их желания делать крупные славки. Если ставка предлагает равные шансы удвоения вашего общего
402
23. Принцип пвтуха
портфеля или его сокращения вполовину и вы не сделаете такой ставки, тогда CRR составит по меньшей мере 1. Если вы тахотите рискнуть половиной своего портфеля ради 94%-пого шанса крупного выигрыша, CRR будет меньше 5».
«Есть интересная игра — задавать одному и тому же человеку различные некорректные вопросы и проверять ответы. Более того, полезно задавать вопросы друг о друге, со ссылкой, что это не вопрос нашего личного благосостояния, но вопрос о том, как, на наш взгляд, нашим клиентам хотелось бы, чтобы мы управляли их фондами. Давайте посмотрим, придерживаемся ли мы примерно одинаковых мнений и проверим, разделяют ли их наши клиенты».
Люди зашевелились, и в воздух поднялось еще несколько рук. «Это может быть преждевременно, — сказал Джим. — 51 не хочу смущать наших клиентов или подкинуть им мысль, что мы растерялись». Другие пробормотали слова одобрения, и руки снова опустились.
Ого, да они, однако. обидчивы. «Возможно, нам не следует распространяться об этом. Кроме того, нич то не мешает нам экспериментировать с различными величинами CRR н определять, какое влияние это оказывает. Гак что, с вашего разрешения, мне хотелось бы перейти к следующему вопросу, а именно — к тому, как оценивать условно нормальные портфели. Вы со мной?»
«Подождите секундочку, — сказал Генри — Нормальные доходности являются неограниченными. Но ваша ожидаемая полезность определяется только для положительного благосостояния. Так что вы не вправе их смешивать».
Конвей погрозил Генри пальцем, буд то ругая его. «Стыдитесь, Генри. Если бы пс вы, этого бы никто не заметил. Но вы нравы. Ч тобы примирить эти два понятия, вам следует либо переключиться с нормальности на логарифмическую нормальность, либо проигнорировать отрицательные члены. Это делает расчеты намного сложнее и заставляет принимать некоторые аппроксимации. Какую аппроксимацию вы выберете, частично зависит и от того, насколько часто вы перенастраиваете свой портфель, чтобы восстановить целевые веса».
«51 что, единственный, кого это сбивает с толку?» — спросил Джим. Другие отозвались: «Нет», «Меня тоже», «Это выше моего понимания».
>7 их теряю. «Вы правы, Джим, и все остальные тоже. Это сбивает с толку. Воз почему я хочу предоставить детали компьютерам. Что я хочу представить сейчас —- это широкая структура, с формулировкой, которая охватывает главное и игнорирует все остальное. Думаю, она вам все разъяснит».
«Ну, что ж, мне бы хотелось ее увидеть, — сказал Джим. — По нам нет смысла удерживать тех, кто считают, что этого им довольно. Если кто-то из вас хочет уйти — вперед».
Почти половина людей ушла. Конвей сделал вид, что ему все равно. «Я не удивлен, что наши ряды поредели. Давайте взглянем проблеме в лицо: ожидаемая полезность эго не обычный способ понимания доходностей. Он
403
Часть 2. Постижение невежества
действительно привлекателен, хотя ожидаемая полезность целого составляет среднюю величину ожидаемой полезности его частей. Иными словами.
Если в каждом режиме к имеет вероятность рк и условную ожидаемую полезность EU^ то
к
«Теперь давайте преобразуем ожидаемую полезность в нечто более естественное, а именно - в гарантированный доход, который принесет такое же удовлетворение. Экономисты называют эго «эквивалентом надежности». Другими словами;
Определите эквивалент надежности СЕ, такой что |£’ГАР(1 + СД)|-</,/<.
«Скобки вокруг EU обозначают абсолютную величину. Я их ввел для того, чтобы не беспокоиться о знаке. Я также разделил по линии отсчета благосостояние, чтобы преобразовать все в процентные доходности. Причина, но которой я это сделал, состоит в том, что здесь даи очень простой и интуитивный способ оценить СЕ:
(ррр
СЕк = Услов ноеСредн еек------—'хУс.1ОвнаяДиснерсияк .
«Другими словами, откорректированная с учетом риска доходность в каждом режиме примерно равняется среднему в этом режиме минус кратное — СЕЕ дисперсии в этом режиме. Обратите внимание, что штраф на дисперсию растет вместе с вашим неприятием риска, что имеет смысл».
Коивей сделал паузу, подождав реакции. «И эго все?» — спросил Генри.
«В основном да. Вам нужно провести несколько маленьких корректировок, чтобы компенсировать различия между логарифмами и процентами и ожидаемое сокращение в весах портфеля. I Iа самом деле лучше преобразовать все в логарифмы. Помимо прочего, это позволяет вам переинтерпретировать оптимизацию портфеля как род минимизации неопределенности. Это заставляет финансы стать более похожими на физику. Но здесь я стараюсь не усложнять».
«Где формула для оптимальной смеси портфеля?» — спросил Генри.
«Четкой формулы не существует, за исключением особого случая одного режима. Тогда это сокращается до стандартной максимизации коэффициента Шарпг1 плюс правило, которое делает абсолютные веса по рисковым активам инверсными CRR. Оптимальный портфель для общего случая также представляет из себя род максимизации коэффициента Шарпа при условии, что
404
23. Принцип нвтуха
вы заменяете вероятности режима откорректированными с учетом риска вероятностями».
«О каких корректировках вы говорите?»
«Корректировки придают больше веса режимам с более низкими ожидаемыми полезностями и делают вас более чувствительным к риску айсберга».
«Г Гасколько более чувствительным?»
«Это зависит от вашей CRR и специфических альтернатив риска/вознаграждсния. В противном случае вы не захотите делать коррс ктировки ».
«Ваш подход может справиться с опционами?»
«Да, может. Вам просто нужно наполнить его предполагаемыми стоимостями опционов, дельтами и гаммами при средних различных режимов. А стандартный анализ среднего и дисперсии должен притворяться, что дельта опциона фиксирована, игнорируя все нелинейности, которые отличают опционы от обычных ценных бумаг».
«Как* же гак, я об этом не знаю, - сказал Джим. Вы сказали, что старались экономить на информации. Но мне это кажется перегрузкой».
«Это не обязательно должно быть так. Вы можете сократить каждый актив в стиле модели оценки финансовых активов до случайного отклонения вокруг бета-взвешенной суммы некоторых ключевых множителей плюс константа. Предположив, что эти случайные отклонения являются независимыми, вы можете сконцентрироваться на корреляциях и рисках айсберга, которых вы считаете наиболее важными, с минимальными информационными потребностями и отвлечением внимания».
«Я по-прежнему сомневаюсь, что большинство наших менеджеров и аналитиков серьезно воспримут информационные запросы. Мы практики, а не банда теоретиков».
«Тогда, возможно, нам следует отслеживать, сколько каждый из нас привносит в откорректированные с учетом риска доходности и использовать это как часть их оценки. Практичные ребята, как правило, понимают цель деятельности довольно хорошо, когда она связана с деньгами».
«Что вы хотите сказать, Конвей?» — голос Джима приобрел стальной оттенок.
Я что-то не так сказал? «На самом деле — ничего особенного. Я просто хочу указать, что с помощью оценки полезности деятельности и ее преобразования в откорректированные с учетом риска доходности, вы можете измерить не только эффективность целого, но и маржинальные вклады его частей».
«Правда?»
«Да. Например, вы можете измерить маржинальный вклад менеджера как разность между откорректированной с учетом риска доходности всего портфеля
405
Часть 2. Постижяниа нявяжяства _________________
и того, что бы он из себя представлял без менеджера — скажем, заменив реальный субпортфсль неким эталонным индексом. В принципе, мы могли бы объективно измерить эффективность всех, невзирая на ранги и старшинство».
«Я полагал, что это собрание будет посвящено риску айсберга, — произнес седовласый мужчина. — Какое это имеет отношение к измерению эффективности?»
«Я полагаю, они имеют много общего, — начал Конвей. — Например...»
Седой мужчина перебил: «Джим, кажется, мы здесь затеоретизировались. Зачем думать о ремонте того, что еще не сломалось? Конечно. Мы упали по Nasdaq за последние 15 месяцев, но то же самое произошло со многими другими; мы потеряли не намного больше, чем средние показатели по рынку. Меня обижает наговор, что что-то не гак с нашими стимулами».
«Согласен, — сказал кто-то еще.- Если Вы спросите мое мнение, то уже сама мысль о том, чтобы ввести новую систему, чтобы анализировать риск айсберга — это уже большой риск айсберга. Кто знает, какие новые проблемы могут возникнуть?»
«Вот-вот», —добавил сшс кто-то.
Прежде чем Конвей смог произнести хоть слово в свою защиту, Генри згщал вопрос: «Конвей, вы .тел ал и какие-то расчеты по ошибкам, которые могут возникнуть в связи с применением фактической эффективности в качестве заместителя ожидаемой полезности?»
«Да, пег, -— неуклюже ответил Конвей. — Но у меня и в мыслях нс было предлагать, чтобы вознаграждения выплачивались только на этом основании. На это потребуется гораздо больше усилий...»
Тут уже вмешался Джим: «Я полагаю, мы все можем в этом согласиться. Всегда приятно закончить обсуждение достижением согласия. Конвей, от имени всех присутствующих и, уверен, всех ушедших тоже, я бы хотел поблагодарить вас за очень красноречивую презентацию. Неплохо каждые несколько лет или около того получить подобную абстрактную теоретическую перспективу».
Многие в знак одобрения кивнули, и все быстро разошлись, перешептываясь друг е другом. Конвей с Джимом остались наедине. Конвей закрыл лицо руками.
«Разочарованы?» — спросил Джим.
«Потрясен, — Конвей поднял глаза. — Что было не так?»
«Вы нарушили самый важный принцип в практических финансах: принцип петуха».
«Это что еще такое?»
«Петух диктует правила».
«И кто же петух?»
«Хотите сказать, что не знаете? Это еще одно нарушение».
«Так это вы?»
406
23. Принцип петуха
«Я, некоторые из старших менеджеров иди любой известный финансист. Ребята с вершины. Мы диктуем правила. А не какая-то математическая теория».
«Вы не верите в достоинства?»
«Безусловно, я верю в достоинства. Но существует много видов достоинств. Есть достоинство в управлении большим «эго» и тем, чтобы заставить их хорошо взаимодействовать друг с другом. Есть достоинство в том. чтобы привлекать новых клиентов. Есть еще большее достоинство в том, чтоб гл убедить уже имеющихся у тебя клиентов в том, что за свои удачи им следует благодарить ваши умения, а виной большей части их убытков является простое невезение».
«Что же в этом хорошего?»
«Это их успокаивает. Умение и удача слишком тесно сплетены в финансах. Почему наши клиенты должны мучиться, пытаясь во всем разобраться? Вместо этого я помогаю им чувствовать себя спокойнее в отношении их инвестиций и их самих». Джим говорил без тени сарказма.
Конвей был озадачен. «Я не понимаю, Джим. Если вы действительно так считаете, то зачем было слушать мою презентацию? Зачем брать меня на работу?»
«Потому что у принципа петуха есть определитель: сегодня петух, а завтра метелка из перьев».
Конвей рассмеялся. «Возможно, этот принцип глубже, чем я думал. Гак я понимаю, Вы все-гаки хотите о тслеживать риск айсберга».
«Сейчас это не приоритетная задача. Пас по-прежнему трясет от айсберга Nasdaq, с которым мы столкнулись. Тем нс менее из вашей презентации я узнал две очень важные вещи».
«А именно?»
«Во-первых, что более изощренный взгляд па финансовый риск может потенциально добавить стоимость. Во-вторых, что это никогда не будет сильной стороной этой группы».
«Должно быть, вы считаете это очень неприятным».
«Вовсе нет. В наш холдинг входит гигантский финансовый рисковый трейдер. Он берет на работу сотни докторов, чтобы произвести на свет аналитические модели рисков и идентифицировать возможности для арбитража. На этой основе он делает огромные ставки. Раньше я никогда ис покупал крупных позиций, поскольку действительно не понимал, что они делают, а вы знаете, что я думаю по поводу инвестирования в то, чего я не понимаю. Но ваша сегодняшняя презентация изменила мое мнение. Это соединилось с тем фактом, что сделки по фонду идут намного ниже половины от прошлогодних максимумов».
«Вы говорите об End Run?
«Совершенно верно. Я собираюсь сделать его нашей самом крупной одиночной позицией: 10% нашего общего портфеля. Я понимаю, что эго
407
Часть 2. Постижвнив нвввжвства_______________
больше наших установленных ограничений. Но я придумал некую непростую бухгалтерию, которая в течение какого-то времени позволит нам это делать. Достаточно долго для того, чтобы снова встать на ноги».
Конвей еле сдержал волнение. «Ходят слухи, что End Run не может обеспечить клиентам ликвидности, как раньше, а это сбивает цены по многим из их ставок, что, в свою очередь, еще больше ограничивает ликвидность, которую они могут обеспечить».
«Я об этом знаю. Частично из-за этого фонд и упал так сильно. Но Вы заставили меня поверить, что у умных ребят все получится».
«В Long-Term Capital были люди не глупее, но он все равно лопнул».
«Но у End Run есть опыт «Long-Term Capital», которым можно воспользоваться. На самом деле я не удивлюсь, если узнаю, ч то они разрабатываю! модели риска айсберга точно такие же, как ваши. Или еще лучше. Не обижайтесь, Конвей, но сотня голов -—-лучше, чем одна».
«На самом деле их было три. И две из них — весьма необычных».
«Конвей, прекратите. Одна или три — какая разница по сравнению с сочнями. Не завидуйте; я хвалю вас за проработку этой идеи. Кроме того. End Run не может повлечь для нас убытки большие чем в 10%».
«На самом деле, если вы продолжите перенастройку, вы можете потерять намного больше 10%».
«Вас, очевидно, слишком задело за живое, Конвей: 10% эго 10%. Впереди выходные; почему бы вам нс взять отгул в понедельник, чтобы отдохнуть? А теперь извините меня...»
Конвей остался один.
Вечером того же дня Девлин с Регреттой сидели в холле Club Mad. «О чем Вы думаете, Регретта?» — спросил Девлин.
«Мне интересно, чего Конвей добился своей сегодняшней презентацией».
«Уверен, она прошла хороню. Он умеет преподнести информацию. В отличие от меня».
«Не прибедняйтесь, Девлин. Без вас Конвею нечего было бы преподносить».
«Без вас у нас обоих было бы нечего преподносить. Спасибо, что научили нас функциям разбиения».
«Не за что. Но ключевым этапом было соединение CRR полезности с условной нормальностью. Это было гениально».
«Это было примитивно. А мои доработки более высокого порядка были такими накрученными. Мне следовало прямо пойти к постоянной перенастройке, как это сделали вы. Вот это действительно было гениально. И изящно».
«И почти что тривиально по сравнению с вашими деривативами по опционам».
408
23. Принцип петуха
Девлин покраснел. «Должен признать, в этом вопросе я сам себя удивил. Но знаете, какая часть мне понравилась больше всего? Работа с вами нал сокращениями алъфы/беты и правилами оценки».
Регретта улыбнулась. «Мне тоже больше всего понравилась эта часть. И Конвею она, кажется, гоже понравилась».
«Ну, у меня перед ним был должок. В последний раз, когда я подбросил ему идеи для презентации, они завели его в такую беду, что он потерял работу. Я ужасно переживал по этому поводу. Воз* почему и поехал в Chib Mad. Ну. еще и беспокойство по поводу моего невежества. Кто бы ни был тот человек, который сказал, что «неведение — это блаженство», он не знал, о чем говори г».
«Я рада за вас, Девлин. Счастлива и завидую».
«О чем вы говорите, Регретта?»
«Разве вы не видите? Вы выздоровели. Вы возместили ущерб Конвею и преодолели свое невежество. У вас больше нет причин здесь оставаться».
«А как насчет вас?»
Pci ретта вздохнула, и на глазах ее выступили слезы. «Я не могу изменить того, что привело меня сюда».
«Что? Вы никогда мне не рассказывали, и я никогда не слышал, чтобы вы говорили об этом на терапии».
«Некоторые вещи слишком личные, чтобы говорить о них на терапии».
«Вы можете рассказать об этом мне», сказал Девлин мягко.
«Возможно, в другой раз. Вы будете иногда навеща ть меня?»
«А кто сказал, что я уезжаю?»
«Вы вылечились. Мы же пришли к этому выводу».
«Я не соглашался с вами. Я просто нс дошел до объяснения, почему я не вылечился».
«Так почему?»
«Потому что я по-прежнему невежественен. Все, что мы делали до сих пор — эго моделировали риск айсберга, находящегося над поверхностью. А как насчет подводных 90%?»
«Надводных? Подводных? Девлин, о чем вы говорите?»
«Извините, я же говорил вам, что не силен в передаче информации. Я хочу сказать, что модели, которые мы рассматривали, поверхностны. Доходности в различных режимах не зависят от наших убеждений. Если поразмыслить, то это нс имеет смысла. А что происходит на самом деле и что, как ты считаешь, произойдет, должно зависеть друг от друга».
«Я не понимаю. Бычий рынок имеет одно распределение доходностей. Медвежий рынок — другое, обычно с более низким средним и более высокой волатильностью. Какое отношение к этому имеют убеждения?»
«О|ромное. Давайте проведем мысленный эксперимент. Предположим, что в настоящий момент мы находимся на бычьем рынке, который, по нашему
409
Часть 2. Постижение невежества
убеждению, продлится вечно. Внезапно загадочный, но очень влиятельный незнакомед информирует всех нас, инвесторов, что на следующей неделе, скорее всего, начнется медвежий рынок. Что происходите ценами активов сегодня?»
«Они резко падают вниз, поскольку мы должны принять в расчет вероятное сокращение будущих доходностей. О, теперь я понимаю. Шансы различных режимов влияют на будущие ожидаемые вознаграждения, которые должны быть дисконтированы в текущие цены».
«Хорошо. А теперь второй мысленный эксперимент. Мы сейчас на бычьем или на медвежьем рынке?»
«Сложный вопрос. 51 хочу сказать, что мы были на медвежьем рынке некоторое время, но мне кажегся, он идет к концу. Фонды получили разбег несколько недель назад, но он r некотором роде приостановился. Возможно, он снова возобнови гея. Да, возможно, этот разбег был началом бычьего рынка. Но мы были свидетелями такого большого числа ложных донышек, да н недавние данные по занятости разочаровывают. Так что, возможно, мы в конечном итоге все еще на медвежьем pi.гике».
«Другими словами, вы бы предпочли сказать, что с вероятностью АТо мы на бычьем рынке и с вероятностью 100 — Х% мы на медвежьем рынке».
«Определенно. На самом деле, если вы допускаете вероятность раскачивающегося из стороны в сторону рынка, я бы включила и такой шанс тоже».
Девлин улыбнулся и пригрозил ей палы гем. «Это лукавство. Придерживайтесь мысленного эксперимента. Теперь предположим, что вышли новые статистические данные, которые представляют из себя сюрприз с оптимистической стороны. В результате и вы, и все остальные инвесторы решают, что шансы, что мы сейчас на бычьем рынке действительно составляют А”-1- 1%. И что это делает с ценами активов?»
«Конечно, несколько их поднимает».
«Другими словами, текущие ценьг должны зависет ь от ваших убеждений как о природе текущего режима, гак и о вероятности различных будущих режимов. Тем нс мснсс переключающие режимьг модели, которые мьг построили для Конвея, не принимают этого в расчет».
«Боже мой. И как вы предлагаете это уладить?»
«Не знаю, — сказал Девлин печально. — Действительно, нс знаю».
Регретга заглянула ему в глаза. Бедняга Девлин. «Должно быть, чувствуешь себя очень одиноко, когда видишь го, что не можешь заставить замечать других». Она положила свою руку на его.
Девлин ответил благодарной улыбкой: «Вы заметили. Конвей гоже заметил».
«Но будут другие, Девлин. Будьте терпеливы. У нового подхода всегда уходит какое-то время на то, чтобы завоевать сторонников. Тем временем, нс забывайте о том, что вы уже сделали».
410
23. Принцип пвтуха
«Вы хотите сказать о том, что я нашел дыры в теории портфеля, не залатав их?»
«Вы нашли нс просто дыры, Девлин. Вы нашли пропасть. А затем вычислили, как ио ней передвигаться». Регретта увидела, что Девлин собирается возразить. «Хороню, не совершенно. Но то, что вы предложили, намного лучше, чем статус кво».
Девлин сухо рассмеялся. «Только если вас меньше волнуют реальные риски, а не их внешний вид. Так, кажется, думают большинство тех, кто занимается финансами».
«В финансах внешняя сторона всегда будет иметь значение. И вы об этом знасгс. Но реальные риски тоже имеют значение. И рядом с вами появится больше людей, когда они поймут и оценят разницу».
Девлин смотрел на Регретгу и боялся пошевельнуться. В конце концов он дотронулся до ее руки, наклонился и поцеловал ее в щеку. «Спасибо», — сказал он нежно.
«Думаю, мы привлекаем к себе слишком много внимания, — прошептала Регретта, оглядываясь вокруг. — Возможно, нам следует продолжить этот разговор в каком-нибудь другом месте».
«С удовольствием. С огромным удовольствием. Но мне неприятна мысль, что это может впоследствии вызвать у вас сожаления».
Регретта улыбнулась Девлину: «Не будет никаких сожалений».
Они медленно пошли гго коридору, рука об руку. Эго был удивительно ясный вечер, и они остановились, глядя в небо и наблюдая за звездами. Затем знакомый голос разрушил очарование вечера. Ошарашенные, они оглянулись.
«Привет, Девлин. Привет, Регретта, — сказал Конвей. — Приятно снова вас видеть. С нетерпением жду продолжения нашего обсуждения».
Девлин моментально отпустил руку Регретты. «Привет, Конвей, — сказал он несколько смущенно. — Я не знал, что они пускают посетителей по вечерам в пятницу».
«А кто сказал, что я посети гель?»
(продолжение следует)
411
Рекомендую прочитать
Хотя история Девлина, Конвея и Регретты далеко не закончена, вы ее здесь не найдете. Вместо этого я хочу рассказать вам о нескольких книгах и статьях, которые дополняют недостающие куски или предлагают иные подходы. Я сконцентрируюсь на тех, которые мне показались особенно интересными, а не стану давать полный список. Тем не менее, в упомянутых здесь книгах и цитируемых источниках вы найдете много пищи для размышлений. Чтобы облегчить ваш поиск, я распределил рекомендации по темам.
Магия риска
Первобытные люди, как и юристы сфаховых компании в наши дни, были склонны отрицать понятие слепого шанса. И это неудивительно. Всегда хочется понять точный смысл, и сложно доказать, что прорицатель нс прав. Но лаже науке сложно победить риск. Как можно точно определить понятие о чем-то, что нельзя точно определить?
В конце концов, люди загнали риск в аккуратные теории, которые популярные сегодня. К сожалению, отделять риск от окружающего — это все равно, что считать, что львы живут только в клетках. Чтобы воскресить в вас ощущение магии и чуда, я от всего сердца рекомендую бестселлер Питера Бернштейна «Against the Gods: The Remarkable Story of Risk»» (New York: John Wiley & Sons, 1998). Она передает как волнение вековой борьбы за понимание, так и показывает рубежи, которые еще остаются неизведанными.
Одним из этих рубежей является наш собственный мозг. День за днем имея дело с риском в течение миллионов лет, наши предки завещали каждому из нас глубокое интуитивное чувство ощущения риска. В джунглях Африки эта интуиция помогала нашим предкам спасать свою шкуру. К сожалению, в каменных джунглях Уолл-с фиг она от потери шкуры не часто нас защищает. Очень немногие понимают это лучше Нассима Талеба со степенью доктора философии в области статистики. Его книга «Fooled by Randomness» New York: TEX ERE, 2001)^ полны занимательных рассказов об озарениях в этой сфере.
Теория вероятности
Если у вас с математикой настолько плохо, что вы не можете вспомнить, что вы забыли, я рекомендую книги научно-популярной серин Шаума
5 Одураченные случайностью. Нассим Талеб. М: Омега-Л, 2007
412
________________==^===______________Рекомвндую начитать
(например, «Probability and Statistics», 2-е издание (New York: McGraw-Hill, 2000) Мюррея Шпигеля, Джона Шиллера и Элу Сринивасана) для того, чтобы освежить ваши знания. Мне особенно нравится манера Шаума представлять каждую новую идею в отдельном блоке, и я старался ее скопировать.
До того как я начал бриться, мне посчастливилось изучать математику в Принстоне, на родине выдающегося теоретика вероятности, Уильяма Феллера. Десятилетия спустя, разбирая детские подарки, я стряхнул пыль со своего старо io экземпляра его «Ап Introduction to Probability Theory and Ils Appi cations», том I, 3-е издание (New York: John Wiley & Sons, 1968) и попытался вспомнить, о чем гам речь. Несколько месяцев спустя я открыл и том 11, 2-е издание (1971). Если у вас сеть время, рекомендую прочитать и то и другое. Их не назовешь легким чтивом, но эти книги уча i думать... или переучат вас.
Конечно, если вы остановитесь на Феллере, вы не узнаете о многих хичрых уловках. Чтобы получить полный конспект этих приемов и связанных с ними отклонений, взгляните на «Numerical analysis for Statisticians» Кеннета Ланже (New York: Springer, 1998).
Одной из тем, почти не освещаемых в вышеупомянутых книгах, является смешанная многомерная нормальность. Если вы жаждете именно этого, от души рекомендую «Finite Mixture Models» (New York: John Wiley & Sons, 2000) Джеффри Маклахлана и Дэвида Пила.
Теория финансов
Чтобы привести в порядок ваши знания по основной теории финансов, я рекомендую взять типовой учебник школы бизнеса, такой как «Principles of Corporate Finance», 6-е издание (New York: McGraw-Hill, 2000) Ричарда Брили и Стюарта Майерса. Он дает обзор, которого часто не хватает более глубоким иеследова ниям.
«Theory of Financial Decision Making» Джонатана Ингерзолла (Savage, MD: Rowman & Littlefield, 1987) представляет более глубокое исследование. Dio четко выстроенная и хорошо структурированная книга, хотя и ужасно сухо написанная. Я часто пользуюсь ей в качестве справочника.
Когда вы будете готовы взяться за деривативов, возьмите одну из книг Пола У ил мотта. Последней и величайшей из его книг является двухтомник «Paul Wihnott on Quantitative Finance» (Chichester, UK: John Wiley & Sons, 2000). Сложно представить себе более ясное изложение, тем более что автору не чуждо чувство юмора. Также загляните на www.wilmott.com, в настоящее время наиболее популярный сайт по количественным финансам.
Наиболее «продвинутые» финансовые теории склонны рассматривать все через мартингалы (бескомпромиссная концепция честной игры). Я здесь о них нс говорил по той же причине, по которой я не пускаю в ход пушки, сражаясь с воробьями. Но если вы хотите овладеть этим супероружием, то книга Марека Мусилы и Маркета Рутковски «Martingale Methods in Financial Modelling» (Berlin: Springer-Verlag, 1998) дает хорошую тренировку. Для еще более
413
Часть 2. Пестижение невежества
усиленной тренировки предлагаю начать с «Probability with Martingales» Дэвида Уиллиамса (Cambridge, UK; Cambridge University Press, 1991).
Управление риском
В моей книге дан краткий обзор стандартной методологии VAR. Для более полного изучения почитайте очень легкую и содержащую некоторые конструктивные идеи книгу Кевина Доуда «Beyond Value at Risk: The New Science of Risk Management» (Chichester, UK: John Wiley & Sons, 1 998).
Инвестиционным менеджерам, желающим получить хороший практический совет, следует приобрести «Active Portfolio Management» (New York; Mcgraw-Hill, 1993) Ричарда Гринольда и Рональда Канна. Хотя эта книга формально нс включает в себя риск айсберга, она рассказывает о многом, чек.) я даже не касался
Фишер Блэк н Роберт Литтерман отразили свою модель портфеля в работе «Asset Allocation: Combining Investor Views with Market Equilibtium», распространенной в 1990 г. Goldman Sachs. Также советую изучить работу Goldman Sachs издания 1999 г. «The Intuition Behind Black—I ittennan Model Portfolios» Литтермана и Гуанглпанг Хе.
Если после этого вы все еще не потеряете интерес к более продвинутой статистике, возьмите «Theory of Financial Risks: From Statistical Physics to Risk Management» (Cambridge, UK: Cambridge University Press, 2000) Жана-Фили ина Бу шала и Марка Потгерса. Фокусируясь на характеристических функциях вероятностных распределений, она обращается к гораздо более продвинутым темам, нежели я, чипа рисков от хеджирования опционов в дискретное время. Но отрицательной стороной этой книги является то, что режимы изменений освещены очень слабо. Надеюсь, ччо в дальнейшем эти два подхода будут объединены.
Физика
Вам совершенно необязательно знать физику, чтобы понимать теорию финансов, но эго помогает. Мне особенно правятся книги, которые объясняют, как физика охватила неопределенность, поскольку они вселяют надежду, что однажды теория финансов сделает то же самое. Международный колледж LEX издал замечательную книгу — смесь истории с математикой — «What is Quantum Mechanics? A Physics Adventure» (Босчон; Language Research Foundation, 1996), перевод оригинального японского издания 1991 г.
Эрвин Шредингер читал блестящие лекции в Дублине в 1944 г. по функциям разбиения и связанным с ними темам, Я обнаружил их в перепечатке Ду вера 1989 г. Это «Statistical Thermodynamics (Cambridge, UK: Cambridge University Press. 1952). Но для максимального воздействия советую прочитать книги Ричарда Фейнмана или что-нибудь о нем; например, его чрехтомник «Lectures on Physics», написанный в соавторстве с Робертом Лейтоном и Мэттью Сэндсом (Reading, МА: Addison-Wesley, 1963-1965) или Genios
414
Рекомендую начитать
Джеймса Глика (New York: Random House, 1992). Хотя Фейнман не мог быть отцом Девлина, вы поймете, почему я представил, будто так оно и было.
Искусство видеть
Иногда конформистская реальность окружает нас гак крепко, что мы четко видим се только во сне. Но чтобы найти ткачей, плетущих наши мечты и сны, следует обратиться от науки к искусству. Хотите увидеть, как Сталин посещает Москву и приноравливается к ней? Прочитайте «Мастера и Маргариту» Михаила Булгакова. Хотите увидеть историю Латинской Америки, бесконечно повторяющуюся в жизнях одной семьи? Прочитайте «Сто лет одиночества» Габриэля Гарсиа Маркеса, Хотите увидеть тиранию исполненных благих намерений технократов? Прочитайте «О дивный новый мир» Олдоса Хаксли. Я черпал вдохновение из этих источников и вставил в эту книгу несколько аллюзий.
415
Об авторе
Кент Осбанд —• известный ученый, опытный специалист в решении задач государственной политики и эксперт Уолл-стрит. Он с отличием закончил Гарвард, защитил диссертацию по экономике в Калифорнийском университете в Беркли, преподавал в Гарварде и Университете Лос-Анджелеса, опубликовал несколько десятков научных статей. В течение восьми лет Кент Осбанд работал в Rand Corporation, Международном Валютном Фонде и Всемирном банке экспертом по советским и постсоветским экономическим реформам. После того как в 1994 г. Кент Осбанд перешел на работу на Уолл-стрит, он последовательно занимал должности экономиста-международника Goldman Sachs, главного аналитика рынков стран с развивающейся экономикой банка Credit Suisse First Boston, управляющего глобального фонда облигаций с самым высоким рейтингом CI Funds of Toronto. В настоящее время Кент Осбанд возглавляет отдел внедрения количественных методов в торговле финансовыми инструментами и оценки риска в нью-йоркском Drawbridge Global Macro Fund.
416