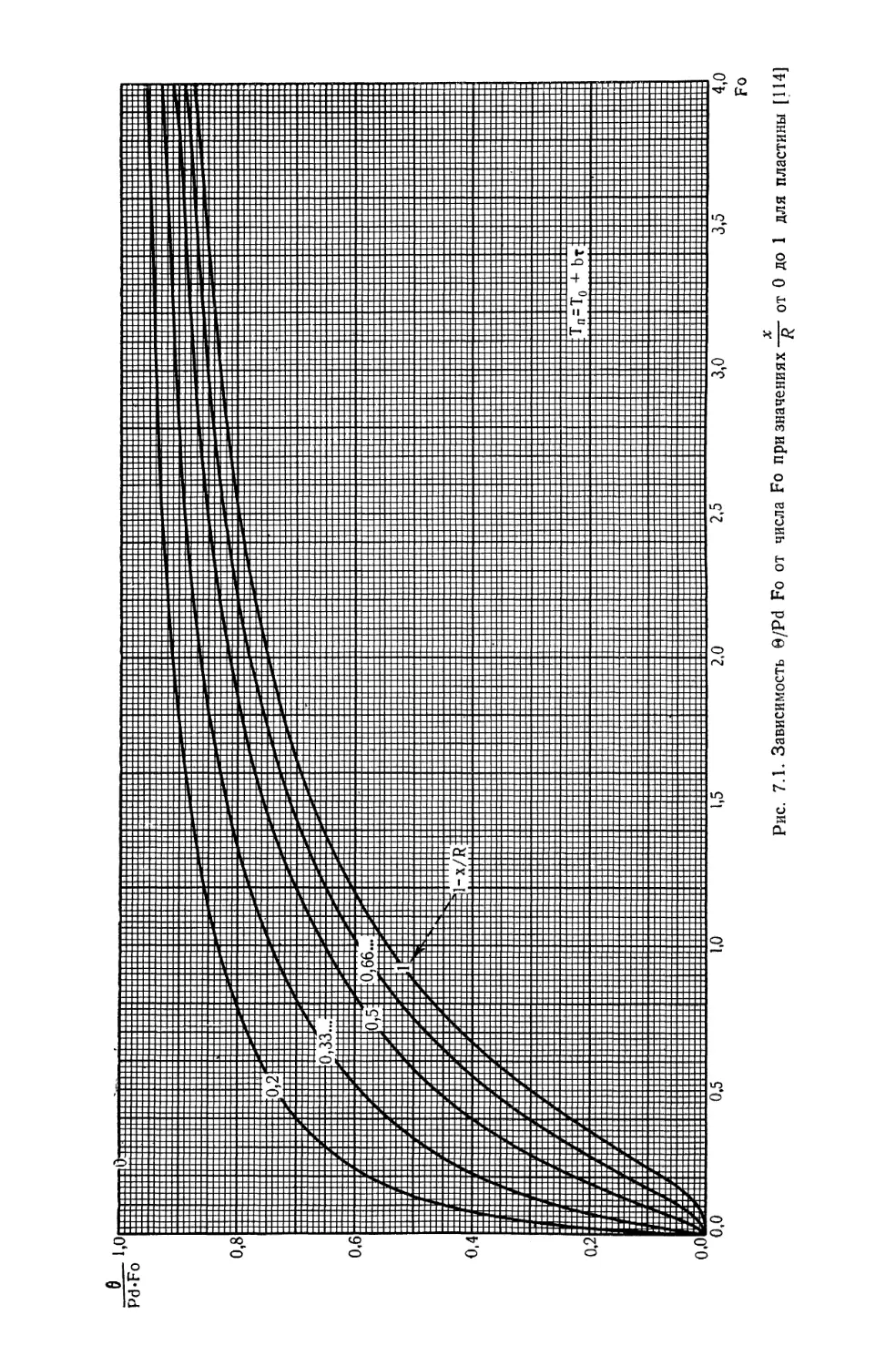
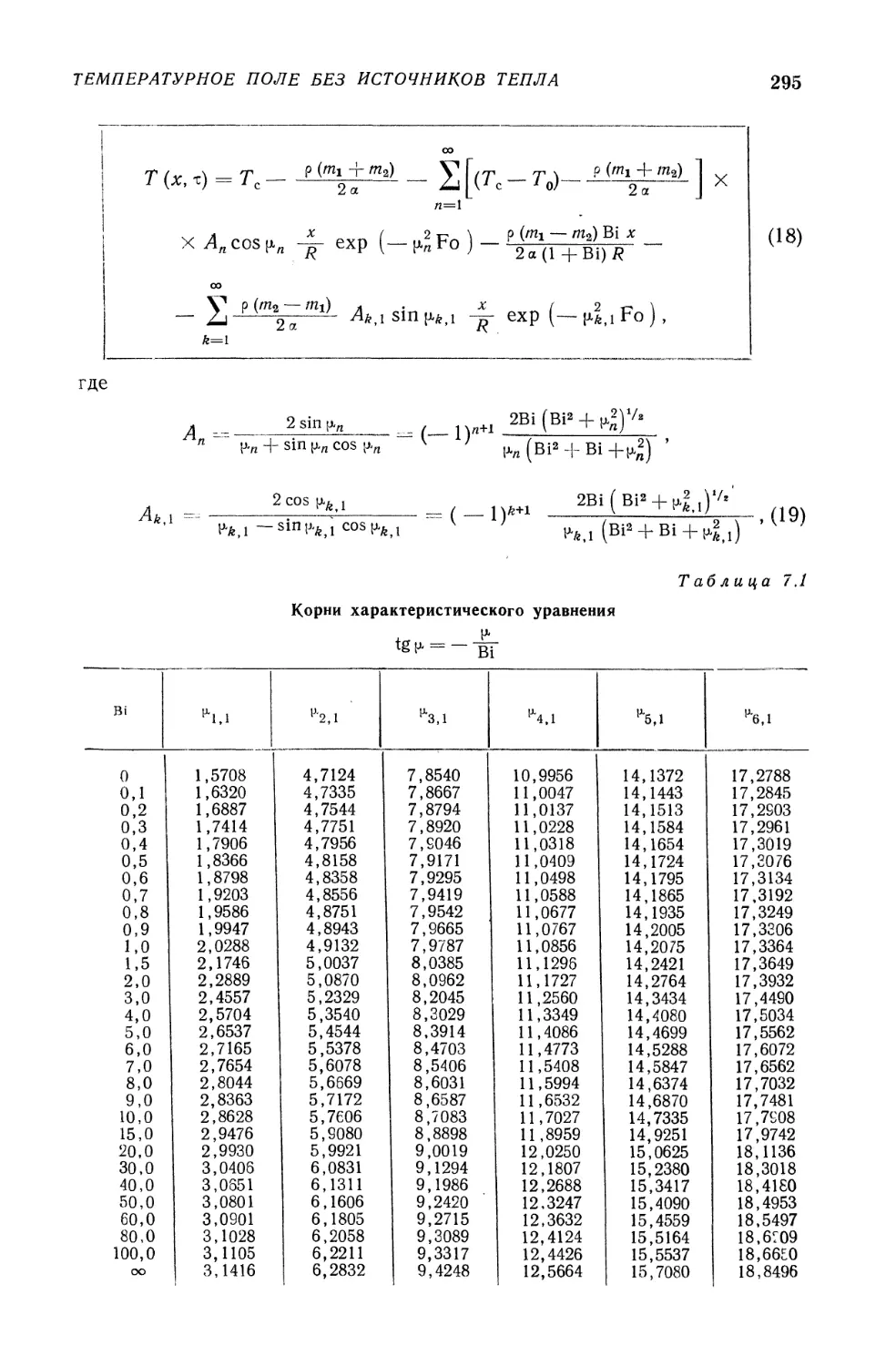
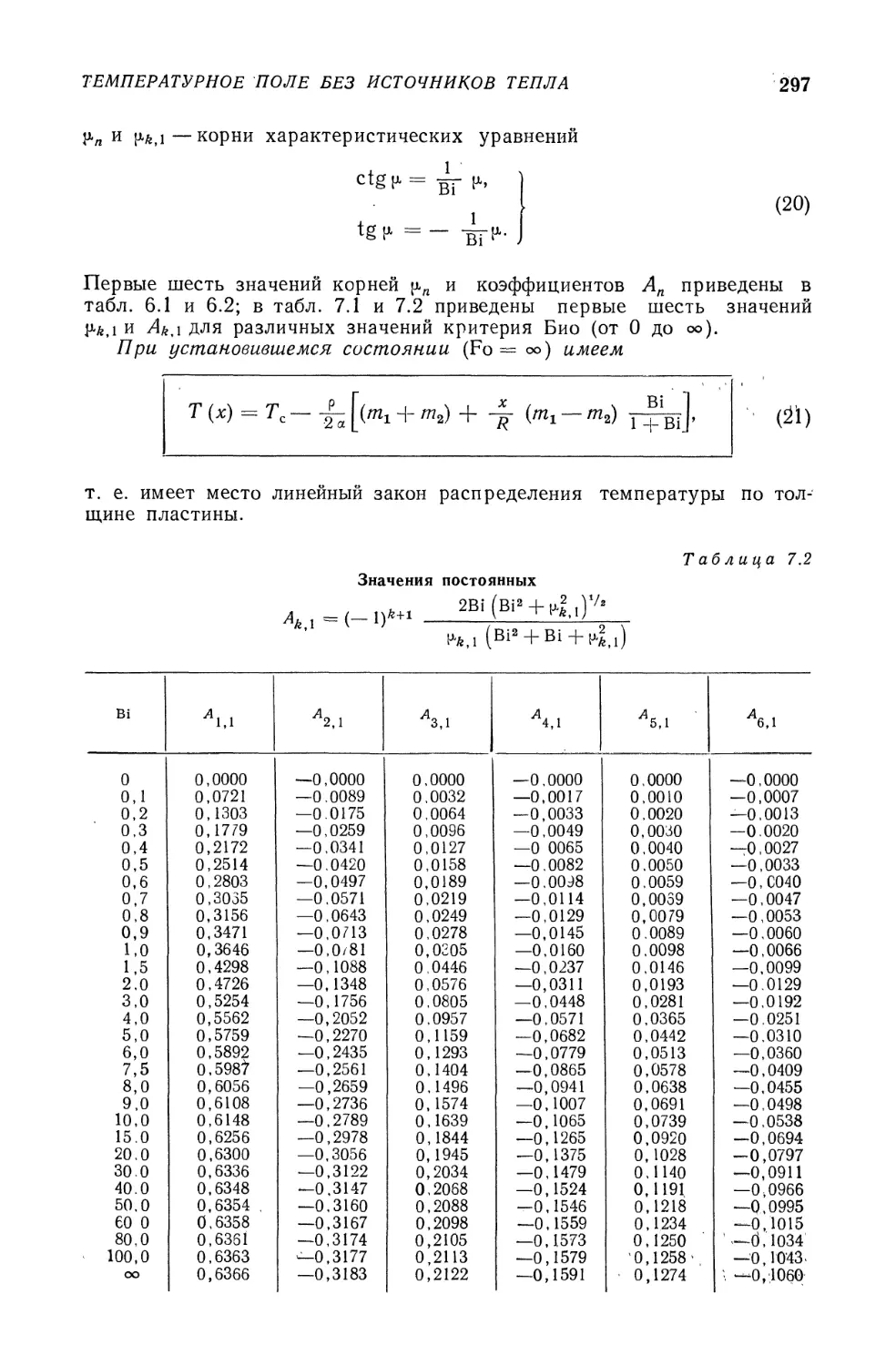
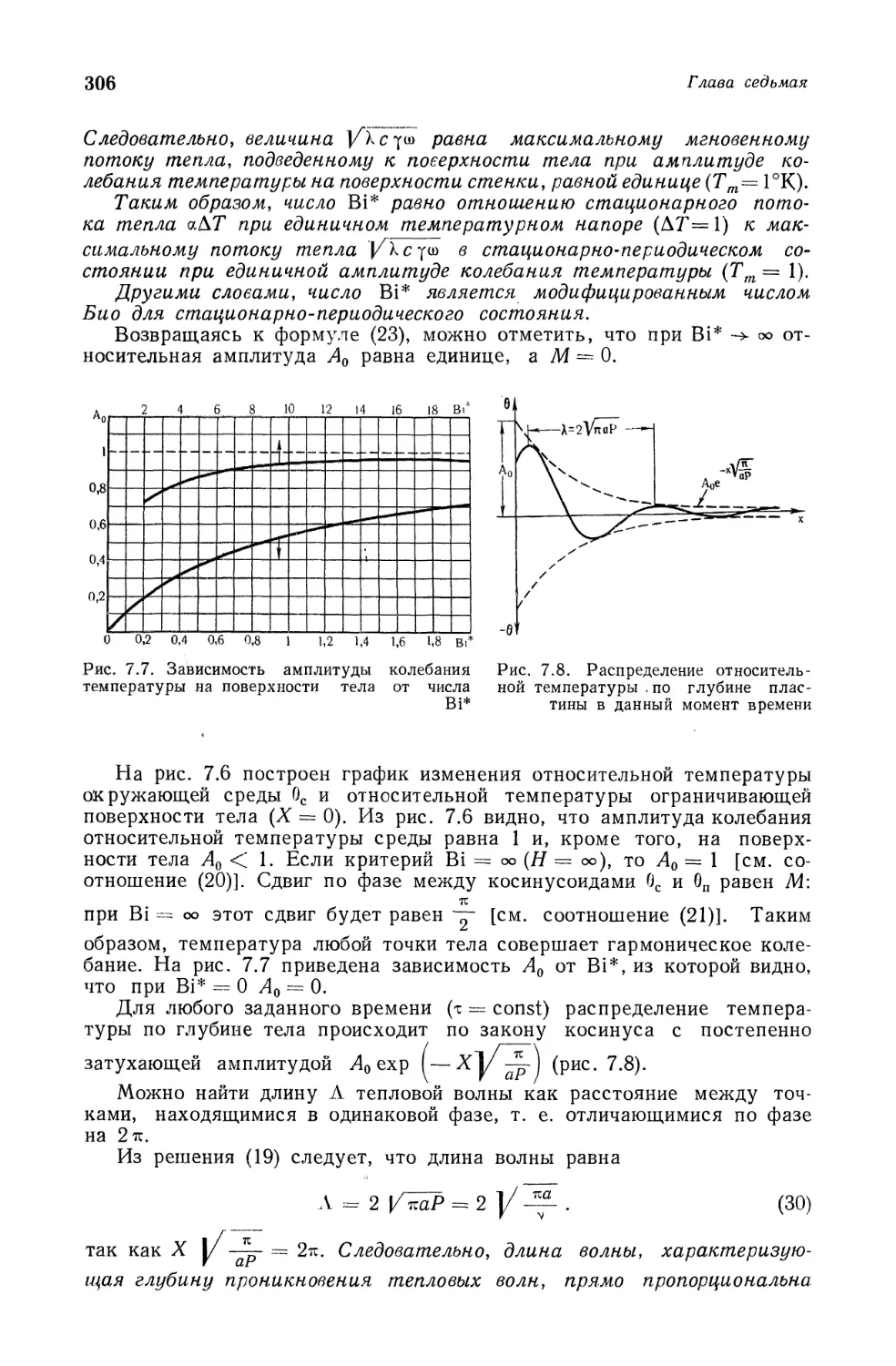
Текст
А. В. ЛЫКОВ
теория теплопроводности
ДОПУЩЕНО
МИНИСТЕРСТВОМ ВЫСШЕГО
И СРЕДНЕГО СПЕЦИАЛЬНОГО
ОБРАЗОВАНИЯ СССР
В КАЧЕСТВЕ
УЧЕБНОГО ПОСОБИЯ
ДЛЯ СТУДЕНТОВ
ТЕПЛОТЕХНИЧЕСКИХ
СПЕЦИАЛЬНОСТЕЙ
ВЫСШИХ
УЧЕБНЫХ
ЗАВЕДЕНИЙ
ИЗДАТЕЛЬСТВО
„ВЫСШАЯ ШКОЛА"
МОСКВА
1967
УДК-536.2
2-3-5
64-65-66
ПРЕДИСЛОВИЕ
Процессы переноса тепла являются одним из основных разделов
современной науки и имеют, большое практическое значение в станционной и
промышленной энергетике, в технологических процессах химической, строительной,
легкой и других отраслей промышленности. Например, расчет тепловых
аппаратов, работающих при нестационарном режиме, расчет ограждающих
конструкций в условиях переменных тепловых воздействий (теплоизоляция
зданий, печей, трубопроводов), нагревание машин, температурные
напряжения в мостах и многие другие вопросы связаны с решением задач
нестационарной теплопроводности. Исследование кинетики процессов сорбции, сушки,
горения и других химико-технологических процессов связано с решением
задач диффузии, которые аналогичны задачам нестационарной теплопроводности.
Особое значение приобретают вопросы нестационарного теплообмена в
реактивной и ракетной технике, где тепловая аппаратура работает в условиях
нестационарного режима.
Таким образом, аналитическая теория теплопроводности находит самое
широкое применение в решении различных технических проблем.
Предлагаемая вниманию читателей книга значительно отличается от
предыдущих монографий автора, последняя из которых была опубликована
в 1952 г.
В данном учебном пособии подробно рассматриваются решения задач
нестационарной теплопроводности основных тел (полуограниченное тело,
неограниченная пластина, сплошной цилиндр, шар, полый цилиндр) несколькими
методами (разделение переменных, операционные, интегральные
преобразования Фурье и Ханкеля). Таким образом, читатель, знакомясь с особенностями
каждого из применяемых методов, может в своей самостоятельной работе для
решения поставленных задач выбрать наиболее простой метод, дающий
наиболее эффективное решение, пригодное для инженерных расчетов.
Решения даны в обобщенных переменных с использованием
метода теории подобия, они иллюстрированы многочисленными графиками и
таблицами. Наличие графиков позволяет быстро производить технические
расчеты, что несомненно будет способствовать внедрению решений в инженерную
практику. Кроме того, решения основных, наиболее важных задач даны в
двух видах, один из которых удобен для расчетов при малых значениях
чисел Фурье, а второй—для больших значений чисел Фурье.
Опыт преподавания автором курса теории теплопроводности в разных
высших учебных заведениях показал, что необходимо приводить подробный
ход решения с основными преобразованиями и расчетами, а задачи располагать
по степени трудности так, чтобы последующие из них были развитием
предыдущих. Поэтому в первых главах (IV—VI) даны подробные решения с
конкретными расчетами, с использованием графиков, а задачи
классифицированы по принципу взаимодействия тела с окружающей средой, а не по
4
принципу геометрических форм рассматриваемых тел, что с методической
точки зрения является более правильным.
Большое внимание уделяется решению задач с граничными условиями
четвертого рода, что связано с актуальными исследованиями в области
нестационарного конвективного теплообмена. Решение задач с переменными
теплофизическими коэффициентами выделено в специальную главу
(гл, XIII).
В гл. XIV дано краткое изложение методов интегрального
преобразования Лапласа, Фурье и Ханке л я применительно к решению задач
нестационарной теплопроводности.
Для читателей, интересующихся более глубокими проблемами теории
теплопроводности (асимптотические приближения и др.), в гл. XV дано
краткое изложение теории аналитических функций и их приложение к
решению задач теплопроводности.
В приложении даны справочные материалы в виде формул и таблиц.
Основной задачей книги является обучение студентов и инженеров,
имеющих математическую подготовку в объеме технических вузов, решению
задач нестационарного теплообмена, встречающихся в многочисленных
инженерно-технических расчетах.
ФИЗИЧЕСКИЕ ОСНОВЫ ПЕРЕДАЧИ ТЕПЛА
1
В данной главе будут рассмотрены основные положения
аналитической теории теплопроводности.
Передачу тепла от одной части тела к другой или от одного тела
к другому, находящемуся в соприкосновении с первым, обычно
называют теплопроводностью. Аналитическая теория теплопроводности
игнорирует молекулярное строение вещества; она рассматривает вещество
не как совокупность отдельных дискретных частиц, а как сплошную
среду-—континуум. Такое модельное представление вещества может
быть принято при решении задач распространения тепла, если размеры
дифференциальных объемов достаточно велики по сравнению с
размерами молекул и расстояниями между ними. Во всех расчетах и
примерах тело предполагается однородным и изотропным.
§ 1. ТЕМПЕРАТУРНОЕ ПОЛЕ
Всякое физическое явление, в том числе и процесс теплопередачи,
происходит в пространстве и времени. Поэтому аналитическое
исследование теплопроводности сводится к изучению
пространственно-временного изменения основной физической величины — температуры,
характерной для данного явления, т. е. к нахождению зависимости
T = f(xt у, г, т), A)
где х, у, г —пространственные координаты в декартовой системе, т —
время.
Совокупность мгновенных значений температуры во всех точках
изучаемого пространства называется температурным полем. Так как
температура есть величина скалярная, то и температурное поле
является скалярным полем.
Различают стационарное и нестационарное температурные поля.
Нестационарным температурным полем называется такое поле,
температура которого изменяется не только в пространстве, но и с
течением времени, или, как образно говорят, «температуру есть функция
пространства и времени» (неустановившееся состояние). Уравнение A)
есть математическая запись нестационарного температурного поля.
Стационарным температурным полем называется такое поле, темпе-
6
Глава первая
"Т+24Т
T-f-dT
ратура которого в любой его точке
не изменяется во времени, т. е.
является функцией только координат
(установившееся состояние):
Т = Ф (х, у, г),
дТ
dz
= 0, B)
т-дт
Рис. 1.1. Изотермы температурного поля
В некоторых задачах
нестационарное температурное поле
переходит асимптотически в
стационарное, когда л ->оо.
Температурное поле,
соответствующее уравнению A) или B),
является пространственным
(трехмерным), так как Т есть функция трех
координат. Если температура есть
функция двух координат, то поле
называется двухмерным:
T = F(xt у, х), -|^=0.
Если же температура есть функция одной координаты, то поле
называется одномерным:
Примером одномерного температурного поля может служить поле
неограниченной пластины (пластина, ширина и длина которой очень
велики по сравнению с толщиной) при распространении тепла
перпендикулярно к ее поверхности. ;
Если точки поля, имеющие одинаковую температуру, соединить, то
получим изотермическую поверхность. Пересечение изотермической
поверхности плоскостью дает на этой плоскости семейство изотерм
(линии, соответствующие одинаковой температуре).
Изотермические поверхности и изотермические линии не
пересекаются между собой и при непрерывном поле не обрываются внутри него.
На рис. 1.1 показаны изотермы, проведенные через точки,
температуры которых отличаются на ДТ.
Вдоль изотермы температура не изменяется, в любом другом
направлении температура изменяется. Наибольший перепад температуры
на единицу длины происходит в направлении нормали к изотермической
поверхности.
Возрастание температуры в направлении нормали к изотермической
поверхности характеризуется градиентом температуры (grad T).
Градиент температуры есть вектор, направленный по нормали к
изотермической поверхности в сторону возрастания температуры, т. е.
gradT = ln-|^, C)
где 1Й — единичный вектор, направленный по нормали в сторону возра-
стания температуры (см. рис. 1.1), -^ производная температуры по
направлению нормали п к изотермической поверхности. Следовательно,
градиент температуры численно равен первой производной температуры
по нормали к изотермической поверхности. Градиент обозначается так-
ФИЗИЧЕСКИЕ ОСНОВЫ ПЕРЕДАЧИ ТЕПЛА
7
же символом у. Составляющие градиента по осям декартовых
координат равны соответствующим частным производным, так что
gradr = Vr = l^+ly-|f + l,-f-, D)
где \х, \у, \z — ортогональные между собой векторы единичной длины,
направленные по координатным осям. Это соотношение обусловлено тем
обстоятельством, что любой вектор можно представить как векторную
сумму трех векторов, направленных по координатным осям.
Можно ввести понятие напряженности температурного поля по
определению
Е = — grad Т. E)
Вектор Е называется вектором напряженности температурного поля.
§ 2. ОСНОВНОЙ ЗАКОН ТЕПЛОПРОВОДНОСТИ ФУРЬЕ
Необходимым условием распространения тепла является наличие
температурного градиента. Опыт показывает, что передача тепла
теплопроводностью происходит по нормали к изотермической поверхности
от мест с большей температурой к местам с меньшей температурой.
Количество тепла, проходящее в единицу времени и отнесенное к
единице площади изотермической поверхности, называется плотностью
теплового потокам соответствующий вектор определяется соотношением
dQ
где -~- — количество тепла, проходящего в единицу времени, или
скорость теплового потока, S — площадь изотермической поверхности,
(—\п) — единичный вектор, направленный по нормали к поверхности S
в сторону уменьшения температуры.
Следовательно, вектор q называется вектором теплового потока,
направление которого противоположно температурному градиенту (оба
вектора направлены по нормали к изотермической поверхности, но в
противоположные стороны).
Проекция вектора q на любое избранное направление / есть также
вектор q[f скалярная величина котогого равна q-cos(n, I).
Линии, касательные к которым совпадают с
направлением вектора q, называются линиями теплового тока. Линии теплового
тока перпендикулярны к изотермическим поверхностям в точках
пересечения с ними. Касательная к линиям теплового тока, взятая в
обратном направлении, указывает направление градиента температуры
(рис. 1.1).
Основной закон теплопроводности может быть сформулирован так:
плотность теплового потока прямо пропорциональна напряженности
температурного поля, или плотность теплового потока прямо про-
порционалъна градиенту температуры, т. е.
q = WB--Xgradr = -Xvr = -Xlll^> B)
где X — коэффициент пропорциональности, называемый коэффициентом
теплопроводности.
Чтобы выяснить физический смысл коэффициента теплопроводности,
напишем основное соотношение B) для стационарного одномерного тем-
8
Глава первая
пературного поля. В этом случае температура зависит только от одной
координаты — нормали к изотермическим поверхностям; скалярная
величина вектора теплового потока будет равна
. dT I дТ дТ дТ Л /оч
<7"Х„Г ^„^„^„^oj. C)
(AT \
~г~- = COnst) ,
что обозначает изменение температуры с увеличением х по линейному
закону, то можно написать:
dT Г2 - Тг
dx х2 — хх
= const. D)
Отсюда следует, что и скорость теплового потока -— будет
величиной постоянной:
JjL=JL= const, E)
где Q — количество тепла, протекающего за время т.
Следовательно, на основании A) — E) можно написать:
Q __ \ t2 — Ti _ ^ Ti — T2 ,g.
St х% — хх х% — хх '
так как Тг > Т2, а х2 > хг.
Таким образом, коэффициент теплопроводности равен количеству
тепла, протекающего в единицу времени через единицу поверхности,
при перепаде температуры на единицу длины нормали, равном одному
градусу. Отсюда следует, что коэффициент теплопроводности
измеряется в em/м-град (ккал/м-ч-град).
Коэффициент теплопроводности является физической
характеристикой тела в отношении его способности к теплопроводности.
Физический смысл коэффициента теплопроводности и его зависимость от
основных параметров тела могут быть вскрыты при рассмотрении механизма
передачи тепла в теле в соответствующем состоянии.
Отношение —'■ = -г— (em/м2-град) называется тепловой прово-
Х<£ X \ 1\Х
димостью данного участка тела, а обратная величина—^— (м2-град!em)—
тепловым, или термическим, сопротивлением участка тела.
Коэффициент теплопроводности разных веществ изменяется в
широких пределах: например, X = 0,0086 ет/м-град @,0074 ккал/м-ч-град)
для четыреххлористого углерода при 100°С и X = 416 ет/м-град
C58 ккал/м-ч-град) для серебра при 273°К @°С). Коэффициент
теплопроводности зависит от химического состава, физического строения и
состояния вещества.
Теплопроводность в газах и парах в значительной мере обусловлена
молекулярным переносом кинетической энергии движения молекул,
поэтому вполне естественно, что коэффициенты X для газов и паров малы.
В жидкостях перенос тепла теплопроводностью происходит по типу
распространения продольных колебаний аналогично распространению
звука. Поэтому коэффициенты теплопроводности жидкостей больше
коэффициентов теплопроводности газов. Молекулярная структура
кристаллических тел способствует переносу тепла.
ФИЗИЧЕСКИЕ ОСНОВЫ ПЕРЕДАЧИ ТЕПЛА
9
В металлах перенос тепла теплопроводностью в значительной мере
определяется переносом энергии свободными электронами. Различия в
коэффициенте теплопроводности разнообразных неоднородных
материалов объясняются эффектом пористости. Для волокнистых материалов
типичным нарушением однородности является анизотропия,
проявляющаяся в неодинаковой теплопроводности в различных направлениях.
Коэффициент теплопроводности зависит от температуры; для многих
металлов он уменьшается с повышением температуры по линейному
закону.
Коэффициент теплопроводности газов увеличивается с повышением
температуры, а от давления практически не зависит, за исключением
очень высоких (больше абсолютного давления 2000 am) и очень низких
(меньше 10 мм рт. ст.) давлений. Для смеси газов коэффициент
теплопроводности X определяется опытным путем и не подчиняется закону
аддитивности. Коэффициент теплопроводности жидкости лежит в
пределах от 0,093 до 0,7 вт/м-град. С повышением температуры для
большинства жидкостей коэффициент теплопроводности уменьшается,
исключение составляют вода и глицерин. Коэффициент теплопроводности
строительных и теплоизоляционных материалов изменяется в пределах
от 0,0233 до 2,8 вт/м-град, с повышением температуры он
увеличивается примерно по линейному закону. Материалы с низким значением
коэффициента теплопроводности (Х^0,23 вт/м-град) обычно называют
теплоизоляционными материалами.
Для практических расчетов можно принять линейный закон
изменения коэффициента теплопроводности газов от температуры:
$т = -£f = const.
Для определенного интервала температуры ДТ = Т2—Тг можно считать
коэффициент теплопроводности постоянным, равным среднему
арифметическому значению коэффициента X при температурах Т2 и 7\.
Закон теплопроводности Фурье B) можно написать в ином виде.
Обозначим объемную концентрацию внутренней энергии тела через uv%
тогда скалярную величину градиента температуры можно написать так:
дп \ duv)v дп ~~ Cv дп ' ^ '
где
Cv~ ~1#~ "" ^Т
дТ ,
(8)
— изохорная объемная теплоемкость тела (дж/м3-град),
cv—удельная изохорная теплоемкость (дж/кг-град),
7 — плотность тела (кг/мд).
Следовательно, уравнение теплопроводности будет иметь вид
дТ
где av ~ коэффициент температуропроводности при постоянном объеме
тела (v = const), равный
«■--^---гг- A0)
Согласно уравнению (9), плотность потока тепла прямо
пропорциональна градиенту объемной концентрации внутренней энергии тела,
Коэффициент пропорциональности равен коэффициенту
температуропроводности при постоянном объеме тела.
10
Глава первая
При стационарном одномерном потоке тепла (q = const, —~- =const)
уравнение (9) можно написать так:
Q uvl — uv2
Sz v x% — хх
(И)
Таким образом, коэффициент av равен количеству тепла,
протекающего в единицу времени через единицу поверхности, при перепаде
объемной концентрации внутренней энергии в 1 дж/м3 на единицу
длины нормали.
Следовательно, коэффициент температуропроводности имеет
размерность
г 1 дж-м* ж2
L vi м2-сек-дж сек
и по своему физическому смыслу характеризует молекулярный перенос
внутренней энергии тела.
При постоянном давлении (р — const) коэффициент
температуропроводности ар(м2/сек) определяется соотношением
a -=__L_ = 2., A2)
где ср и Ср — соответственно удельная и объемная изобарные
теплоемкости тела;
ср = сл = Н£г) • A3>
/р
Ну— объемная концентрация энтальпии (дж/м*).
По своему физическому смыслу коэффициент
температуропроводности ар характеризует перенос энтальпии тела путем молекулярного
движения.
Закон теплопроводности теперь можно написать так:
Ч = -^Щ,^Г = -^"„. 04)
Таким образом, коэффициент температуропроводности является
коэффициентом диффузии внутренней энергии (av) или энтальпии (ар)
в зависимости от условий сопряжения тела с окружающей средой
(v = const или р = const).
Для твердых тел удельная изохорная теплоемкость cv мало
отличается от удельной изобарной теплоемкости ср9 поэтому можно считать
cv = ср = с. В аналитической теории теплопроводности твердых тел
коэффициенты температуропроводности считают одинаковыми независимо
от условий сопряжения тела с окружающей средой, т. е.
a = ap = av=, — . A5)
Вернемся к основному соотношению B). Скалярная величина вектора
теплового потока равна
я — ь-w- <16>
Составляющие вектора q по осям координат х, у, z обозначим через
Ч*> Чу Чг» скалярные величины которых соответственно равны
FIT 7\Т
qx = q cos (п, х) = — I -^- cos (/г, х) = — X -^- , A7)
ФИЗИЧЕСКИЕ ОСНОВЫ ПЕРЕДАЧИ ТЕПЛА
11
Ь
дТ
ду
дТ
dz
Определим количество тепла, проходящее через
элементарную площадку dSlt расположенную
под углом ф к изотермической поверхности
(точнее, к плоскости, касательной к изотермической
поверхности):
qt = q cos ф
dQ l
dz dSi
так как (рис. 1.2)
dQ l
dz dSn
COS^
Рис. 1.2. Поток тепла
через элементарную
поверхность
B0)
dSn = dSt cos ф
является проекцией площадки dSt на изотермическую поверхность.
Из равенства B0) получаем:
dQ = qjdSjd i = q {dSt cos ф) dx = ^dSrtd т. B1)
Равенство B1) допускает двоякое понимание переноса тепла dQ:
1) поток тепла через площадку dSt в направлении нормали / к ней; 2)
поток тепла через проекцию площадки dSt на изотермическую
поверхность в направлении нормали п к последней.
Количество тепла Q, протекающее за время т через поверхность S
конечных размеров, равно
Q = -\fJ4rdSid'
B2)
0(S)
Следовательно, для определения количества тепла, протекщего через
какую-либо поверхность твердого тела, необходимо знать
температурное поле внутри тела. Нахождение температурного поля и составляет
главную задачу аналитической теории теплопроводности.
§ 3. РАСПРОСТРАНЕНИЕ ТЕПЛА ПРИ ВЫСОКОИНТЕНСИВНЫХ
ПРОЦЕССАХ
В феноменологической теории теплопроводности предполагается, что
скорость распространения тепла является бесконечно большой. Это
предположение подтверждается результатами расчета температурных
полей в различных телах при обычных условиях, встречающихся в
практике. Однако в разреженных средах при высокоинтенсивных
нестационарных процессах теплообмена необходимо учитывать, что тепло
распространяется не бесконечно быстро, а с некоторой, хотя и очень
большой, но конечной скоростью wr На это впервые обратил внимание
П. Вернотт [117]. Независимо от него автором книги была предложена
гипотеза о конечных скоростях распространения тепла и.массы для
тепло- и влагопереноса в капиллярно-пористых телах [44].
Скорость распространения тепла равна
12
Глава первая
где *г — постоянная времени или время релаксации. Для азота величина
wr примерно равна 150 м/сек, а ъг ^ 10~9 се/с, для металлов wr еще
больше, например, для алюминия тг ^ Ю-11 сек. Поэтому опытное
измерение хг при современной технике измерений не представляется
возможным. Но для газов в условиях сверхзвукового потока влияние конечной
величины скорости распространения тепла wr на теплообмен становится
заметным. В этом случае закон распространения тепла будет иметь вид
-*vr-',3-
B)
Для стационарного потока тепла (-^Д- = 0) уравнение B) совпадает
с уравнением B) §2. Для высокоинтенсивных нестационарных
процессов второй член уравнения B) становится сравнимым с первым.
Уравнение B) аналогично уравнению вязкого течения для
неньютоновских (вязкоупругих) жидкостей. Остановимся на этом подробно.
Максвеллом сто лет назад было выдвинуто представление об
отсутствии принципиальных различий в механических свойствах жидкостей и
твердых тел на основе представления о релаксации. Релаксация есть
явление постоянного рассасывания упругих напряжений сдвига при
постоянстве заданной деформации, т. е. постоянного рассеивания упругой
энергии, запасенной в деформируемом теле, путем перехода ее в тепло.
Процессы релаксации, как и процессы диффузии, неразрывно
связаны с хаотическим тепловым движением молекул.
Если период релаксации очень велик по сравнению с обычным
временем наблюдения, то жидкость ведет себя, как твердое тело. Если
период релаксации очень мал, то тело ведет себя как вязкая жидкость.
Между предельными состояниями идеально упругих твердых тел и
вязких (ньютоновских) жидкостей имеет место непрерывный ряд
переходов, образующих многообразие реальных тел промежуточного
характера.
Для вязкоупругих (неньютоновских) жидкостей напряжение сдвига
р зависит от меры деформации сдвига е. Вблизи от поверхности тела
это соотношение можно написать так:
de т] dp /оч
где ^-—коэффициент вязкости, G —- модуль упругости на сдвиг,
-1 скорость деформации сдвига.
Величина -4- равна периоду релаксации ^ГЫГ = -4н . Обозначим
скорость деформации через s(s =ds/dx). Тогда будем иметь
p==7]8__T/._^Le D)
Если период релаксации мал (ъг-+0), то из уравнения D) получаем
уравнение Ньютона вязкого течения жидкости для ламинарного
плоскопараллельного потока:
р = 7JS = — Y] -ф , E)
так как
• ds _ d I dlx \ __ dwx ,fi,
B-~dT-~'dT[dy) dy ' K f
ФИЗИЧЕСКИЕ ОСНОВЫ ПЕРЕДАЧИ ТЕПЛА
13
где у —нормаль к направлению движения х, wx — скорость движения
жидкости1).
Если коэффициент вязкости т] очень велик (tj-^оо), то из уравнения
C) получаем классическое уравнение закона Гука
/^ _de 1_ dp
т. е. *■
p = Ge1 = 4W2cs, G)
где wc — скорость распространения деформации сдвига (скорость
распространения поперечных волн), равная
шс=-/Х~. (8)
Аналогичным методом из уравнения B) получим следующие
предельные случаи.
Уравнение B) в скалярной форме можно написать так:
_ JUL — JL 4- * дд
дп ~~ I + стш2 дх • (9)
Если коэффициент теплопроводности мал (X -> 0), а скорость wr велика,
то из уравнения (9) получаем классическое уравнение закона Фурье
я = -^-щ-- 0°)
Если же коэффициент теплопроводности велик (Х-^оо) или объемная
теплоемкость с*[ мала (с^ ->■ 0), то из уравнения (9) после некоторых
преобразований получим
Я-Ч-^ЬТ, A1)
где wT—скорость распространения изотермы, равная
«г = -£. 02)
Поясним понятие скорости распространения изотермы. Пусть имеется
изотермическая поверхность, уравнение которой
Т(х, у, г, т) = const. A3)
Полный дифференциал от уравнения этой поверхности равен
dTdx+^Ldn^0. A4)
дт дп
О Уравнение E) является приближенным, справедливым для частного случая
плоскопараллельного ламинарного потока. В общем случае напряжение трения равно
(dwx dwv
dwv dwr
Для плоскопараллельного потока ■ ■<
дх ду
Рху~—'чёи>х1ду.
14
Глава первая
Это уравнение можно написать так:
дТ . дТ dn дТ . дТ п „ сч
-rr + -^-w--d^ + WT^r-0' A5)
Производная от нормали к изотермической поверхности по времени
есть скорость перемещения или скорость распространения
изотермической поверхности.
Уравнение (И) показывает, что плЬтность потока тепла прямо
пропорциональна температурному смещению 1ST .объемной теплоемкости
тела с\, квадрату скорости распространения w2r тепла и обратно
пропорциональна скорости распространения Wt изотермической
поверхности.
§ 4. УРАВНЕНИЯ РАСПРОСТРАНЕНИЯ ТЕПЛА В ЖИДКИХ
И ГАЗОВЫХ СМЕСЯХ
В газовых смесях и растворах перенос тепла теплопроводностью
связан с переносом массы. При наличии температурного градиента в
таких системах происходит термическая диффузия (эффект Соре), а
диффузия вещества вызывает перенос тепла, который называется
диффузионной теплопроводностью (эффект Дюфо). Например, для бинарной
газовой смеси плотностью р (кг/м3) плотность потока тепла равна
q = -bVr-DpQ*vPio.
A)
где D — коэффициент взаимной диффузии (м2/сек), р10 — относительная
концентрация компонента 1 (р10 = рх/р), рх — объемная концентрация
первого компонента смеси;
Pi + p2 = p; Рю + р2о = 1- B)
Следовательно,
VPlO = — VP20-
Удельная теплота Q* (дж/кг) изотермического переноса, равная
количеству тепла, переносимого единицей массы в изотермических условиях,
может быть выражена через химический потенциал первого компонента
смеси \ьг и термодиффузионный коэффициент kr :
_^_[^_\ . C)
Следовательно, поток тепла q зависит не только от температурного
градиента у7\ но и от градиента концентрации ур10. Плотность потока
массы для первого компонента равна
Ji—A>(vPio+-^V^)
D)
Таким образом, поток массы ]\ зависит от градиента концентрации ур10
и градиента температуры уТ.
Аналогичными уравнениями A) и D) описывается перенос тепла и
растворенного вещества в растворах. В этом случае величина pkr/T
называется коэффициентом Соре о (о = ркт/Т). Поэтому процесс
переноса тепла неразрывно связан с переносом массы и является комлекс-
ным процессом тепло- и массопереноса.
ФИЗИЧЕСКИЕ ОСНОВЫ ПЕРЕДАЧИ ТЕПЛА
15
Перенос тепла во взаимосвязи с переносом массы рассматривается
в термодинамике необратимых процессов. Поток какой-либо субстанции
(энергии, массы, электричества и т. д.) обусловлен действием всех
термодинамических сил Xk (А = 1, 2, 3,...):
h=%L"X* (f = l, 2, 3,..., п). E)
/8=1
Формула E) является системой линейных уравнений Онзагера, она
является основным соотношением термодинамики необратимых
процессов.
Величины Lik называются кинетическими коэффициентами, между
которыми имеет место соотношение взаимности:
Термодинамические силы Xt и потоки j^ должны удовлетворять
основной формуле термодинамики необратимых процессов
G)
где S — энтропия рассматриваемой системы.
Используя уравнение Гиббса
TdS ^du + pdV — ^ рк dMk , (g)
k=i
где &— внутренняя энергия, \ък — химический потенциал, V — объем
М — масса, и дифференциальные уравнения переноса энергии, массы
по формуле G), можно определить термодинамические силы Х^.
Например, в случае переноса внутренней энергии и массы в
газовой смеси термодинамические силы равны:
Хи = -±уТ; Xm, = F,-TV~f-, (9)
где Fk — внешняя сила.
п
С учетом соотношения V j^ == 0 потоки энергии и массы 7-го
£=i
компонента соответственно равны:
п
lmi = ~Liu\vT- J Lift[rV(-^p^-(Fft-F„) ], (И]
k=l
где Laai Luk, Liu, Lik—кинетические коэффициенты Онзагера.
16
Глава первая
Между потоком энергии ]и и потоком тепла ]q существует связь в
виде
j, = Je-2^j*. A2)
где hk— удельная энтальпия ^-го компонента. В этом случае
термодинамические силы переноса тепла Х^ и массы Xmk будут равны:
Х, = ХВ=—-JLvT; Xw/k = -(v^. A3)
Тогда в отсутствии поля внешних сил (F^ = 0) будем иметь
j^-L^-LyT-^L^yi^-^h , A4)
Я—1
imi--Lig±VT-^Lik[V(H~?n))T . A5)
&=i
Кинетические коэффициенты Lqq, L^ Llqj Lik выражаются через
коэффициенты переноса тепла и массы. При постоянном давлении (р = const)
для бинарной газовой смеси (п = 1,2) в соответствии с уравнением
Гиббса — Дюгема
Piodth + РгоФа == ° A6)
V(H — pJt будет равен
Тогда будем иметь
vfr*-^ = ib(^rLVPl0- A7)
h = — LQq -i- v T - Lql -^- у Рю . A8)
L = Llq ~y V T — Lu -—■ vpio. A9)
где через р[ обозначено выражение (-^А
Сравним уравнения A8), A9) с уравнениями A) и D) и, полагая
jq = q, находим
1 — Lqq • тл L^\ • П* LqX - h — Ll<lP™ /om
y p2 ^n Lu^! v '
Аналогичным методом рассматривается молекулярный перенос тепла
во взаимосвязи с переносом других субстанций в более сложных
системах.
§ 5. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ
Для решения задач, связанных с нахождением температурного поля,
необходимо иметь дифференциальное уравнение теплопроводности. Под
дифференциальным уравнением обычно понимают математическую за-
ФИЗИЧЕСКИЕ ОСНОВЫ ПЕРЕДАЧИ ТЕПЛА
17
^ -И
висимость, выражаемую
дифференциальным уравнением, между
физическими величинами,
характеризующими изучаемое явление, причем
эти физические величины являются
функциями пространства и времени.
Такое уравнение характеризует
протекание физического явления в
любой точке тела в любой момент
времени.
Диффер енциальное у р авнение
теплопроводности дает зависимость
между температурой, временем и
координатами элементарного
объема.
Вывод дифференциального
уравнения сделаем упрощенным
методом. Предположим, что имеется
одномерное температурное поле
(тепло распространяется в одном
направлении, например в направлении оси х). Термические коэффициенты
считаем не зависимыми от координат и времени.
Выделим в однородной и изотропной неограниченной пластине
элементарный параллелепипед, объем которого равен dxdydz (рис. 1.3).
Количество тепла, втекающего через левую грань dydz в
параллелепипед в единицу времени, равно qxdydz, а количество тепла,
вытекающего через противоположную грань в единицу времени, равно qx+dxdydz.
Если qx > qx+dx, то элементарный параллелепипед будет нагреваться,
тогда разница между этими потоками тепла по закону сохранения
энергии равна теплу, аккумулированному данным элементарным
параллелепипедом1 >, т. е.
li
\Ai
dx
Рис. 1.3. Поток тепла через
элементарный объем
qxdydz — qx+dxdydz = с^ -^dxdydz
A)
Величина qx+dx есть неизвестная функция х. Если ее разложить в
ряд Тейлора и ограничиться двумя первыми членами ряда, то можно
написать:
Ях+dx ~ Qx +
ддх
дх
•dx,
Тогда из равенства A) будем иметь:
q* dxdydz = cf -^r dxdydz.
дх
дх
дТ
Применяя уравнение теплопроводности qx =—^~тг~•» получим
дТ , д2Т
дх
дх2
1) Аккумулированное тепло вычисляется по элементарному соотношению
AQ = сМД ft = c^VM.
где Д&— приращение температуры в единицу времени в теле, масса которого равна
М, а объем V, с — удельная теплоемкость.
18
Глава первая
ИЛИ
dt ** дх2
дТ. д2Т \ /оч
=== а -^s- • B)
Уравнение B) есть дифференциальное уравнение теплопроводности для
одномерного потока тепла. Если тепло распространяется по нормали
к изотермическим поверхностям, то вектор q можно разложить на три
составляющие по координатным осям. Количество аккумулированного
элементарным объемом тепла будет равно сумме
I $Ях . dqy dqz \
Тогда дифференциальное уравнение примет вид
ет _ i ь2т
дх ~ а[ дх*
д2т , д2т . д2т v й/г /оч
д2 д2 д2
где у2 ^-^т" + -fT" + IT2" оператор Лапласа (выражение оператора
Лапласа в сферических и цилиндрических координатах дано в
приложении).
Иногда внутри тела имеются источники тепла. Источники тепла
могут быть положительными и отрицательными. В качестве примера
отрицательного источника тепла можно считать испарение влаги
внутри материала при нагревании. Пусть удельная мощность (количество
поглощаемого или выделяемого тепла в единицу времени в единице
объема тела) этих источников будет равна w (впг/м3). Тогда количество
тепла, выделяемого в элементарном объеме в единицу времени, будет
равно wdxdydz; это количество тепла надо вычесть из
аккумулированного тепла, чтобы сохранить равенство A). После аналогичных
преобразований дифференциальное уравнение теплопроводности с
источниками тепла будет иметь вид
^=а^Т + -^. D)
Дифференциальное уравнение C) можно вывести более общим
методом, воспользовавшись формулой Остроградского—Гаусса.
Пусть имеется некоторая среда, в которой можно выделить объем У,
ограниченный поверхностью 5. Тепло распространяется в этой
среде путем теплопроводности. Количество тепла, прошедшего через
поверхность S в единицу времени, согласно соотношению B) § 2, будет
равно
J X grad T-dS = J X \n • grad TdS
(S) (S)
(здесь интеграл берется по всей поверхности 5). При отсутствии
источников тепла этот тепловой поток вызовет изменение внутренней
энергии среды в данном объеме в единицу времени на величину
{V) (V)
dv
(здесь интеграл берется по всему объему V).
По закону сохранения энергии изменение внутренней энергии среды
ФИЗИЧЕСКИЕ ОСНОВЫ ПЕРЕДАЧИ ТЕПЛА
19
в объеме V равно потере тепла через поверхность S, ограничивающую
данный объем, т. е.
JCT-^.£fo= j4.XgradT.dS. E)
{V) (S)
Используем преобразование Остроградского — Гаусса
J \п X grad T-dS= j div (X grad Г) do.
(S) (V)
Тогда равенство E) примет вид
Г с Т -|^- dc; = Г div (X grad Г) <fo, F)
(V) (V)
откуда, ввиду произвольности объема, получаем
cT-g- = div(Xgradr). G)
Если коэффициент теплопроводности не зависит от температуры, то
из G) получим дифференциальное уравнение теплопроводности
-|L = aV2r = adiv (gradT). (8)
Для одномерного симметричного температурного поля у2 Г является
функцией одной координаты. Поясним это на примере бесконечного
круглого цилиндра. Если ось такого цилиндра совпадает с
координатой г, то температура в любой точке цилиндра будет зависеть только
от координат х и у. При равномерном охлаждении или нагревании
цилиндра в любой точке, отстоящей на расстоянии г от оси цилиндра,
температура в данный момент времени будет одна и та же.
Следовательно, изотермические поверхности будут представлять собой
цилиндрические поверхности, коаксиально расположенные к поверхности
цилиндра. Между радиальной координатой г (радиус-вектор) и координатами
х и у существует связь
г* = х* + у2. (9)
Тогда дифференциальное уравнение теплопроводности
дТ = a (*L- + *L\ A0)
дх \ дх2 ду'
для бесконечного цилиндра можно преобразовать так:
дТ ___ _дТ__ _дг_ __ JT_ х __ _дТ_ _х_
дх ~~ дг дх ~~ дг у ^ . 2 ~~ дг г
дТ ^ дТ д^ ___ дТ^ j_
ду дг ду дг г
Дифференцируя A1) по х9 а A2) по у, получаем
A1)
A2)
дх2 ~~ дг* г2 + дг г* ' "*^
д2Т _ д2Т у* дТ х2 {Ы.
ду2 ~ дг2 г2 + дг г3 ' ^ '
20
Глава первая
Складывая уравнения A3) и A4) и принимая во внимание (9), получим
для уравнения теплопроводности A0) следующее выражение:
— = а 1 —
дх \ dr2 г дг
A5)
В общем случае, когда температура зависит от всех трех координат
(я, у, г), дифференциальное уравнение теплопроводности конечного
цилиндра имеет вид
дТ _ / а2г , j_ _зт_ j_ &п_ д2т\
дх "" й \ дг2 г дг г2 ае2 dz2 J
A6)
где в — полярный угол (угол между радиусом-вектором г и осью х).
Дифференциальное уравнение теплопроводности в сферических координатах
приведено в приложении III.
В заключение остановимся на физическом смысле коэффициента
температуропроводности. Выше было показано, что коэффициент а
является коэффициентом диффузии внутренней энергии (аа) или энтальпии
(ар) в зависимости от условия сопряжений рассматриваемой системы с
окружающей средой. Однако коэффициенту а можно придать и другой
физический смысл.
Выше было показано, что для изотермической, поверхности
Т (х, у, z, т) = const имеет место соотношение
^.+wtVT = 0. A7)
Тогда из дифференциального уравнения теплопроводности (8) будем
иметь
а = -~wt-^y. A8)
Величина у77у2Т есть отношение первого дифференциального
параметра ко второму; эти параметры инвариантны относительно линейной
группы преобразования. Следовательно, их отношение будет любой
величиной, имеющей размерность [лг1]. Обозначив эту величину через
А = — у Т/у2 7\ будем иметь
A9)
а = AwT,
Следовательно, коэффициент температуропроводности
пропорционален скорости распространения изотермической поверхности.
Величина, обратная коэффициенту температуропроводности, —
характеризует инерционные свойства тела в отношении распространения
температурного поля.
Одним из наиболее теплоинерционных тел является вода,
коэффициент температуропроводности которой при температуре 363° (90°С) и
абсолютном давлении 1 am равен а = 1,39 • 10"8 м2/сек (— = 0,67 X
X 108 сек/м2). Газы обладают малой тепловой инерцией, например для
воздуха при тех же условиях а = 2,58-10-5 м2/сек (— = 0,39-105 сек/м2\
Коэффициент температуропроводности зависит от температуры, а
для пористых тел — от плотности и влажности тела. Поэтому только в
ФИЗИЧЕСКИЕ ОСНОВЫ ПЕРЕДАЧИ ТЕПЛА
21
качестве приближения теплофизические характеристики (коэффициенты
теплопроводности, температуропроводности и теплоемкости) можно
считать постоянными.
§ 6. ГИПЕРБОЛИЧЕСКОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ
В § 3 было показано, что при высокоинтенсивных нестационарных
процессах перенос тепла описывается обобщенным законом Фурье B).
В этом случае дифференциальное уравнение теплопроводности будет,
иметь иной вид. ---
Из уравнения баланса тепла для одномерного температурного поля
имеем
Вместо qx подставим из уравнения B) §3 соответствующее выражение
Ч* = -Ь-%Г-*г-%- B)
Полагая X и тг постоянными, будем иметь
Если продифференцировать A) по т, то будем иметь
дхд х L т д та * w
Следовательно, дифференциальное уравнение C) можно написать так:
E)
дт . а2г а2г
h % —- = д
д% т дч* дх*
Для трехмерного температурного поля дифференциальное уравнение
теплопроводности по аналогии можно записать в виде
-^-4-r-J5-=aV27v> F)
Сделаем анализ уравнения F), которое можно написать так:
ОТ . А д2Т s огр ,~ч
ст^г + ^ "^г = ХуТ- G)
так как, согласно соотношению A) § 3, w2r =a/ir. При малых давлениях
газа величина су мала (су ->■ 0), а средняя длина свободного пробега
молекулы, от которой зависит эта величина, значительно увеличивается.
Поэтому первым членом уравнения G) можно пренебречь. Тогда
получаем дифференциальное уравнение распространения тепла, совпадающее
с гиперболическим волновым уравнением:
^ = ^V2^. (8)
ПВопрос о возможности обобщения уравнения E) на трехмерный случай рассмотрен
в работе [108 а].
22
Глава первая
Поэтому обобщенное уравнение F) распространения тепла называют
гиперболическим уравнением теплопроводности. Для распространения
тепла дополнительный член в уравнении теплопроводности
а а2Г
— -g^r» учитывающий конечную скорость распространения тепла, мал,
так что в обычных практических расчетах им можно пренебречь.
§ 7. СИСТЕМА ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
ТЕПЛО- И МАССООБМЕНА
Система дифференциальных уравнений тепло- и массопереноса в
движущейся газовой смеси выводится на основе законов сохранения
массы и энергии.
Дифференциальное уравнение, отображающее закон сохранения
массы k-vo компонента вещества, можно написать так:
где Рд, — объемная концентрация &-го компонента, w^ — скорость его
движения, которая связана со скоростью w движения центра тяжести
смеси соотношением
w = у £ Р* w* . B)
k
Источник Ik массы &-го компонента обусловлен фазовыми или
химическими превращениями.
Суммируя B) по всем компонентам смеси, из уравнения A) получим
обычное уравнение непрерывности
-§£- = — divpw, C)
так как сумма всех источников и стоков массы в рассматриваемом
объеме смеси равна нулю f Zj /& = 0)«
k
Уравнение C) можно написать в ином виде. Так как
div p w = w у Р + Р div w,
то будем иметь
dp
dz
— р div w, D)
где-—р полная или субстанциональная производная, равная
^ = 4f+wVP. E)
Диффузионный поток массы fe-ro компонента равен
h = Pk(wk — w). F)
ФИЗИЧЕСКИЕ ОСНОВЫ ПЕРЕДАЧИ ТЕПЛА
23
Суммируя F) по всем компонентам с учетом B), получим
£ U = 0. G)
k
Из уравнения F), определив величину pk wk и подставив ее в A),
находим
4^+divP,w = -divjft +/,. (8)
Если обозначить через pk0 относительную концентрацию (pk0 = рЛ/р),
то уравнение (8) можно написать так:
P-^T=-divj* + /ft. (9)
Если вместо }k подставить соответствующее выражение D) § 5 для
бинарной газовой смеси (k = 1,2), то уравнение (9) будет иметь вид
p-^=div[DP(VPl0+>r)]+/,
A0)
Уравнение A0) является дифференциальным уравнением переноса массы.
Дифференциальное уравнение переноса энергии имеет вид
p-37=-divi*- <")
Если вместо jtt подставить выражение A2) § 5, то для бинарной газовой
смеси будем иметь
d
Р "J7 (ftl Рю + Л2 Рао) = — div q — div (hx — h2) jx. A2)
/ dhk \
Обозначим удельную изобарную теплоемкость через cpk \cpk~ -~гг"}> а
изобарную объемную теплоемкость смеси через с0р, то
Ср? = CplPl + Ср2?2- (Щ
Тогда используя A) § 5, получим
dT
срР^Г =div(XvT)+div(DpQ* у 9l0) +(hx—h^Ix—(cpX—c^-yT.
A4)
Левая часть дифференциального уравнения A4) представляет собой из-
менение энтальпии смеси газа с течением времени \срр -*—] и перенос
ее движущейся смесью (ср р w*v T). Первый член правой части
характеризует перенос тепла теплопроводностью, второй член — перенос тепла за
счет диффузионной теплопроводности (эффект Дюфо), третий член
является источником или стоком тепла, обусловленным фазовым или
химическим превращением. Последний член в уравнении A4) отображает
перенос энтальпии за счет диффузии.
24
Глава первая
Обычно разность срг — срг мала, поэтому последним членом можно
пренебречь. Если принять все коэффициенты переноса за постоянные
d д
величины, то для неподвижной газовой смеси I w = 0, -т- = -=тЛ из A0)
и A4) получим следующую систему дифференциальных уравнений:
дТ 2т , DQ* 2 , <**-*«> г
A5)
A6)
Аналогичная система дифференциальных уравнений тепло- и массопере-
носа описывает перенос тепла и массы в растворах.
Если пренебречь термодиффузией (kT = 0, Q* = 0), то из уравнения
A6) получим дифференциальное уравнение теплопроводности Фурье с
источником тепла. Дифференциальное уравнение диффузии массы A5)
аналогично дифференциальному уравнению теплопроводности Фурье.
Поэтому все решения, полученные для нестационарных задач
теплопроводности, можно применять к расчетам нестационарной диффузии
массы.
§ 8. КРАЕВЫЕ УСЛОВИЯ
Дифференциальное уравнение теплопроводности устанавливает связь
между временными и пространственными изменениями температуры
тела; оно математически описывает перенос тепла внутри тела. Для
того чтобы найти температурное поле внутри тела в любой момент
времени, т. е. чтобы решить дифференциальное уравнение, надо знать
распределение температуры внутри тела в начальный момент времени
(начальное условие), геометрическую форму тела и закон
взаимодействия между окружающей средой и поверхностью тела (граничное
условие).
Совокупность начального и граничного условий называется краевыми
условиями; начальное условие называется временным краевым
условием, а граничное условие — пространственным краевым условием.
Начальное условие определяется заданием "закона распределения
температуры внутри тела в начальный момент времени, т. е.
Т (х, у, z, 0) = / (*, 'у, г),
A)
где / (х, у, z) — известная функция.
Во многих задачах принимают равномерное распределение
температуры в начальный момент времени; тогда
Т (х9 у, z, 0) = Т0 = const.
B)
Граничное условие может быть задано различными способами.
1. Граничное условие первого рода состоит в задании
распределения температуры по поверхности тела в любой момент времени,
Тп (х) = / (х), C)
где Тп (т) — температура на поверхности тела.
ФИЗИЧЕСКИЕ ОСНОВЫ ПЕРЕДАЧИ ТЕПЛА
25
В частном случае Tn(i) = Тс = const, т. е. температура на
поверхности постоянна на протяжении всего процесса теплообмена. Это может
быть осуществлено при искусственном поддержании постоянной
температуры или при особых условиях теплообмена между окружающей
средой и поверхностью тела (см. граничное условие третьего рода).
2. Граничное условие второго рода состоит в задании плотности
теплового потока для каждой точки поверхности тела как функции
времени, т. е.
G,W = /W. D)
Простейший случай граничного условия второго рода состоит в
постоянстве плотности теплового потока:
Чп(*) = Яс =. const. E)
Такой случай теплообмена имеет место при нагревании тел в
высокотемпературных печах, где передача тепла в основном происходит при
помощи излучения по закону Стефана — Больцмана, когда температура
тела значительно меньше температуры излучающих поверхностей
(см. гл. V).
3. Обычно граничное условие третьего рода характеризует закон
конвективного теплообмена между поверхностью тела и окружающей
средой при постоянном потоке тепла (стационарное температурное
поле). В этом случае количество тепла, передаваемого в единицу
времени с единицы площади поверхности тела в окружающую среду с
температурой Тс в процессе охлаждения (Тп > Тс), прямо
пропорционально разности температур между поверхностью тела и окружающей
средой, т. е.
<7п = «(Тп-Тс). F)
где а — коэффициент пропорциональности, называемый коэффициентом
теплообмена (вт/м2-град). Для процесса нагревания тела можно
написать аналогичное соотношение, поменяв местами ТП и Тс. Коэффициент
теплообмена численно равен количеству тепла, отдаваемого (или
получаемого) единицей площади поверхности тела в единицу времени при
разности температур между поверхностью и окружающей средой в 1°.
Соотношение F) можно получить из закона теплопроводности Фурье,
полагая, что при обтекании поверхности тела жидкостью или газом
передача тепла от жидкости к телу вблизи его поверхности происходит
по закону Фурье:
я, = -х,(^)Л- *■ "V'"- -.(TV-rj.. G,
где Хж — коэффициент теплопроводности жидкости, Ь — условная
толщина пограничного слоя, а = "kjo.
Следовательно, вектор теплового потока qn направлен по нормали п к
изотермической поверхности, его скалярная величина равна qn.
Условная толщина пограничного слоя S зависит от скорости
движения жидкости и ее физических свойств. Поэтому коэффициент
теплообмена зависит от скорости движения жидкости, ее температуры и
изменяется вдоль поверхности тела в направлении движения, В качестве
приближения можно считать коэффициент теплообмена постоянным, не
зависящим от температуры, и одинаковым для всей поверхности тела.
В нестационарных процессах теплообмена между поверхностью
тела и потоком жидкости условная толщина пограничного слоя будет
26
зависеть не только от скорости жидкости и ее физических свойств,
но и от теплофизических свойств тела, а также будет непрерывно
изменяться с течением времени [Ь = / (т)]. Поэтому при
нестационарном конвективном теплообмене соотношение F), строго говоря, не имеет
места. Однако для некоторых частных задач нестационарного
теплообмена соотношение F) можно принять в качестве граничного условия как
расчетную схему первого приближения.
Однако граничные условия третьего рода могут быть использованы
при рассмотрении нагрезания или охлаждения тел лучеиспусканием.
По закону Стефана — Больцмана лучистый поток тепла между двумя
поверхностями равен
<7пМ = **[ГпМ -71], (8)
где а* ■— приведенный коэффициент лучеиспускания, Та — абсолютная
температура поверхности тепловоспринимающего тела. При малой
разности температур (ТП — Га) соотношение можно приближенно написать
так:
qn (т) = о* {[1* (т) + 71] [Тп (т) + Г.]} [Тп (х) - Тш] =
= « (Т) [Т„ <*) - Га], (9)
где а (Т) — коэффициент лучистого' теплообмена, имеющий ту же
размерность, что и коэффициент конвективного теплообмена, и равный
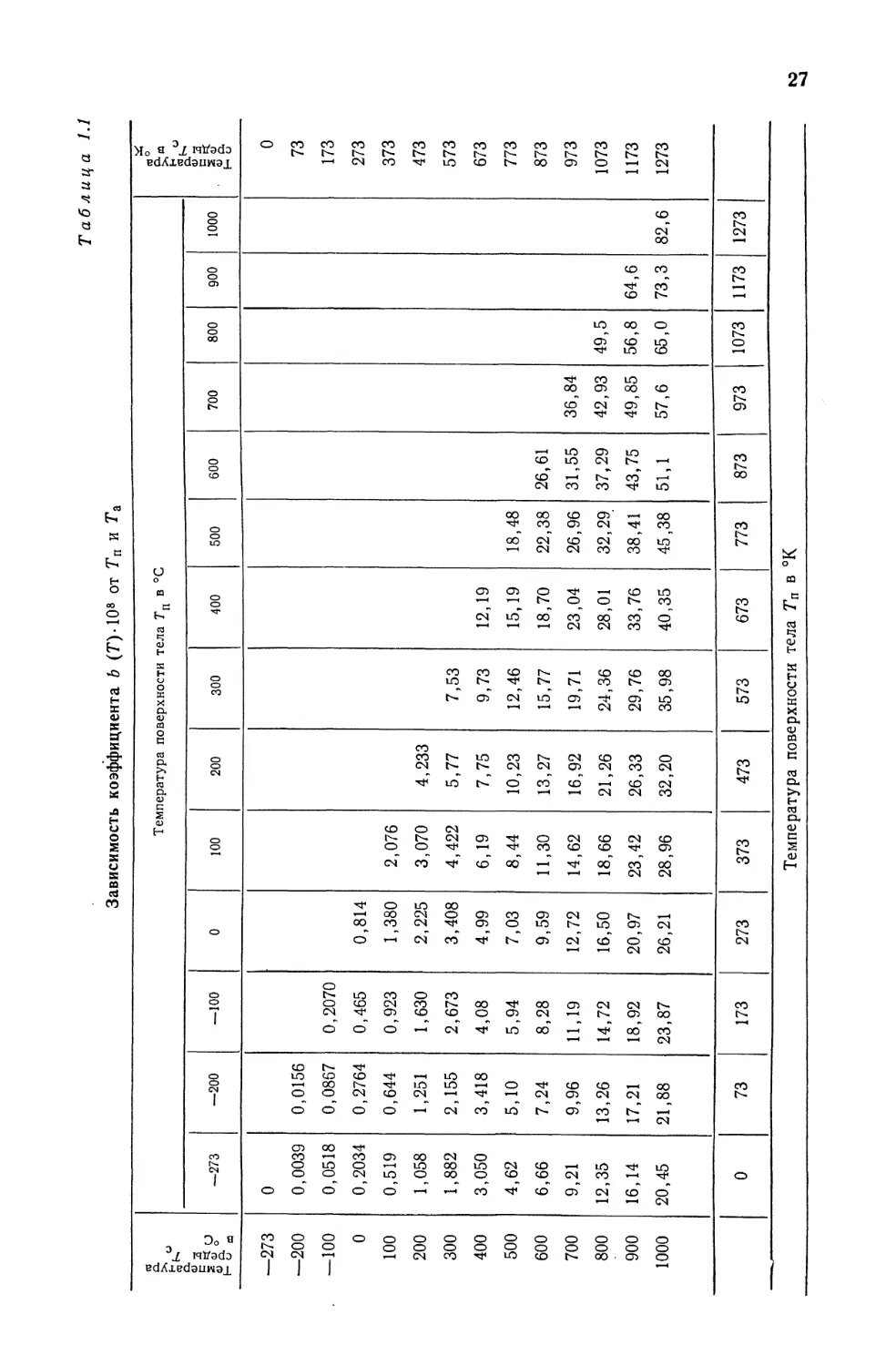
* СО = [Г„(т) + Та] [Т2п(т) + Tl] а* = о* b (Т). (Ю)
Значения коэффициента Ъ (Т) приведены в табл. 1.1.
Соотношение (9) является выражением закона Ньютона охлаждения
или нагревания тела, при этом 7а обозначает температуру
поверхности тела, воспринимающего тепло. Хотя соотношение (9) аналогично
выражению F) для закона конвективного теплообмена при постоянном
потоке тепла, его физический смысл совсем иной. Коэффициент
лучистого теплообмена а (Т) зависит от температуры (см. табл. 1.1), а
также от свойств поверхности тел, участвующих в лучистом
теплообмене. Если температура Тп (т) изменяется незначительно, то
коэффициент а(Т) приближенно можно принять постоянным.
Если температура окружающей среды (воздуха) Тс и температура
тепловоспринимающего тела Та одинаковы, а коэффициент лучепогло-
щения среды очень мал, то в соотношении A0) вместо Та можно
написать Тс. При этом небольшая доля потока тепла, отдаваемого телом
путем конвекции, может быть положена равной ак А 7\ где ак —
коэффициент конвективного теплообмена. В этом случае в соотношении
?пМ = «[ГпМ-тс] (П)
коэффициент а будет суммарным коэффициентом теплообмена:
a = aK + a(T). A2)
Однако при этом надо помнить, что при нестационарном теплообмене
формула A0) отображает закон лучистого теплообмена в первом
приближении, доля конвективного теплообмена должна быть достаточно
мала, чтобы можно было пренебречь изменением коэффициента ак от
времени и его зависимостью от теплофизических свойств тела.
27
a*
<я
С-ч
К
F-,
н
о
00
О
т—'
/—Ч
^
"ч—'
нта
4)
Я"
S
коэф(
л
н
О
о
£
о
я
со
«*
со
Но а 1 миэии |
BdXxedauw9X
О
о
М
1 С
к
4
CD
К
<->
ft
си
со.
о
.га
атур
ипер
0>
Н
1000
о
о
о
00
700
о
СО
500
о
■***
о
со
200
о
о
о
о
о
о
1
СО
t^
1
Эо Я
BdXxe
dauwai
о со
t^
СО
Ю
о
°~
СТ)
со
О
о
о о
со о
о. о
СМ СМ
1 1
СО
г^
о
t*-.
о
см
о
I4*
СО
00
о
о
00
ю
о
о
о
о
г—(
1
СО
ь-
см
TF
00
о
ю
со
т**
о
xf
СО
1^.
см
о
^
СО
о
см
о
о
СО
г^
со
СО
Г--
о
см
о
00
со
СО
см
СТ)
о
тИ
^h
CD
о
СТ)
ю
о
о
о
СО
г-»*
-^
со
со
см
о
t-~
о
со
ю
см
см
см
о
со
CD
г~ч
to
см
—•
00
LO
о
г~Ч
о
о
см
СО
1^
ю
со
ю
г^.
t-
5,7
см
см
^
тр
00
о
Т}4
со
со
IS-
CD
см
ю
ю
см
см
00
00
*~*
о
о
со
со
г-
со
СТ)
см
*—'
со
h-
СТ)
to
7,7
СТ)
»—«
со
СТ)
СТ)
Th
оо
о
чф
00
Тр
со
о
to
о
со
о
о
^
СО
1^
с--
ОО
*ф
оо
»—!
СТ)
ю
,—ц
СО
ЧФ
см
»—1
со
см
о
r-t
-ф
XJH
00
со
о
t^
rt<
СТ)
ю
о
»-ч
to
см
со
ч*
о
о
to
со
!>■
00
t
СО
СО
см
ОО
СО
см
см
о
00
—*
Is-
г-.
ю
»-н
г>-
3,2
_м
о
СО
^
»—«
СТ)
ю
СТ)
оо
см
00
Tf
см
t»-
со
со
СО
о
о
со
со
[•»
СТ)
тн
36,8
to
ю
со
СО
СТ)
СО
см
о
со
см
_ц
г-
СТ)
см
СТ)
со
t—«
см
со
чф
"—•
см
с*-
см
СТ)
-
СО
СТ)
СТ)
см
СТ)
о
о
t-*
со
1^
о
to
стГ
со
42,9
СТ)
см
со
СТ)'
см
см
со
о
оо
см
со
со
-ф
см
со
см
см
СО
CD
оо
о
ю
СО
см
с--
rf
СО
см
СО
U0
со
см
о
о
00
со
Г--
со
64,
оо
со"
ю
ю
49,8
to
t^-
со
г—<
•*«
ОО
со
СО
СО
СО
СО
г~
СТ)
см
со
6,3
см
см
т^
ОО
см
t-»
СТ)
о
см
см
СТ)
00
см
ь-
4f
со
о
о
СТ)
со
t-~
см
82,6
со
со
о
з 1
57,6
'—*
ю
оо
СО
to
Tt«
со
о
Tt<
оо
СТ)
ю
00
о
2,2
со
СО
ст>
00
см
см
СО
см
t>-
оо
со
см
00
00
см
ю
**
о
см
о
о
о
1273
СО
117
со
о
973
СО
оо
со
^
t^
со
ь-
со
со
473
СО
со
со
см
со
1>S"
со
t^
о
28
Глава первая
В дальнейшем нестационарный теплообмен тела, механизм которого
описывается соотношением A1), будем называть теплообменом по
закону Ньютона.
По закону сохранения энергии количество тепла ^п(т), отданного
поверхностью тела, равно количеству тепла, которое подводится изнутри
к поверхности тела в единицу времени к единице площади поверхности
путем теплопроводности, т. е.
<7п (*) = а [ТП (т) - Тс (х)] = -X (^-)п, A3)
где для общности постановки задачи температура Тс считается
переменной, а коэффициент теплообмена а (Г) приближенно принят
постоянным [а (Г) = а = const].
Обычно граничное условие пишут так:
х (-ж-)„ +а [Т" <х> - Тс W1 = °- A4>
Из граничного условия третьего рода, как частный случай, можно
получить граничное условие первого ,рода. Если отношение <х/Х
стремится к бесконечности [коэффициент теплообмена имеет большое
значение (а -^ оо) или коэффициент теплопроводности мал (X -> 0)], то
г„<*)-гс(т)= alim [i (ж)J - °> <15>
откуда
Т„(т)-Тс(т),
т. е. температура поверхности теплоотдающего тела равна
температуре окружающей среды. Аналогично при a «-»- 0 из A4) получаем
частный случай граничного условия второго рода — равенство нулю потока
тепла через поверхность тела.
4. Граничное условие четвертого рода соответствует теплообмену
поверхности тела с окружающей средой {конвективный теплообмен
тела с жидкостью) или теплообмену соприкасающихся твердых тел,
когда температура соприкасающихся поверхностей одинакова. При
обтекании твердого тела потоком жидкости (или газа) передача тепла
от жидкости (газа) к поверхности тела в непосредственной близости к
поверхности тела (ламинарный пограничный слой или ламинарный
подслой) происходит по закону теплопроводности (молекулярный перенос
тепла), т. е. имеет место теплообмен, соответствующий граничному
условию четвертого рода
Гп(т) = [Тс(т)]п. A6)
Помимо равенства температур, имеет место также равенство
потоков тепла
-».(■£).--*(£),
Таким образом, при конвективном теплообмене твердого тела с
/дТ Л
жидкостью в случае стационарного температурного поля 1-^— = 0)
пользуются граничным* условием третьего рода — соотношением A4),
а в случае нестационарного температурного поля (дТ/дъфО)
необходимо при точной формулировке задачи применять граничные условия
четвертого рода [соотношения A6), A7)]. В случае нестационарного
ФИЗИЧЕСКИЕ ОСНОВЫ ПЕРЕДАЧИ ТЕПЛА
29
лучистого теплообмена
необходимо применять
граничные условия
второго рода (соотношение D)).'2П
При малых разницах
температур, когда [Тп (т) —
—Тс (х)] -+ 0, можно ис- Тп
пользовать закон
Ньютона, т. е. граничные
условия третьего рода. При
этом величина а будет
Обозначать Коэффициент a)tg<p = Var;
лучистого теплообмена тп= const
[а = а(Т) == const].
Дадим графическую
интерпретацию четырех
видов граничных условий
(рис. 1.4).
Скалярная величина
вектора теплового
потока пропорциональна
абсолютной величине
градиента температуры,
который численно равен
тангенсу угла наклона
касательной к кривой
распределения температуры
вдоль нормали к
изотермической поверхности, т.е.
IT х IT
б) tg<J>= const
Tn=Var
в) tg<|>-Var;
TJ
V
T
:TC(T)
'/ '
Lj
T
G
,
^Sj "
r)T„=Var
'g*c
= const
Рис. 1.4.
Различные способы задания условий на
поверхности
tg^n«
На рис. 1.4 изображены на поверхности тела четыре элемента
поверхности AS с нормалью к ней п (нормаль считается
положительной, если она направлена наружу). По оси ординат отложена
температура.
Граничное условие первого рода состоит в том, что задана Тп (т);
в простейшем случае Тп (т) = const. Отыскивается наклон касательной
к температурной кривой у поверхности тела, а тем самым и
количество тепла, отдаваемое поверхностью (см. рис. 1.4, а).
Задачи с граничными условиями второго рода имеют обратный
характер; задается тангенс угла наклона касательной к температурной
кривой у поверхности тела (см. рис. 1.4, б); находится температура
поверхности тела.
В задачах с граничными условиями третьего рода температура
поверхности тела и тангенс угла наклона касательной к температурной
кривой—величины переменные,но задается на внешней нормали точка С, через
которую должны проходить все касательные к температурной кривой
(см. рис. 1.4, в). Из граничного условия A4) следует
tg*n = №=^44^. us)
дп
D)
Тангенс угла наклона касательной к температурной кривой у
верхности тела равен отношению противолежащего катета [ТП(х)-
по-
30
Глава первая
к прилежащему катету — соответствующего прямоугольного
треугольника. Прилежащий катет — является величиной постоянной, а
противолежащий катет [Ти (т) — Тс] непрерывно изменяется в процессе
теплообмена прямо пропорционально tg %. Отсюда следует, что
направляющая точка С остается неизменной.
В задачах с граничными условиями четвертого рода задается
отношение тангенсов угла наклона касательных к температурным кривым
в теле и в среде на границах их раздела (см. рис. 1.4, г):
__ = _ ^ const A9)
с учетом совершенного теплового контакта (касательные у
поверхности раздела проходят через одну и ту же точку).
Дифференциальное уравнение совместно с начальным и граничным
условиями полностью определяют задачу, т. е., зная геометрическую
форму тела, начальные и граничные условия, можно
дифференциальное уравнение решить до конца и, следовательно, найти функцию
распределения температуры в любой момент времени. Таким образом, в
результате решения должна быть найдена функция
Т (х, г/, 2, т) = / (х, у, г, т). B0)
Функция / (х, у, 2, тт) должна удовлетворять дифференциальному
уравнению (при подстановке ее вместо Т в дифференциальное
уравнение теплопроводности оно должно обращаться в тождество), а также
начальному и граничному условиям.
По теореме единственности решения (доказательство теоремы дано
в приложении), если некоторая функция Т (х, у, г, х) удовлетворяет
дифференциальному уравнению теплопроводности, начальным и
граничным условиям, то она является единственным решением данной задачи.
§ 9. МЕТОДЫ РАСЧЕТА РАСХОДА ТЕПЛА
В процессе нагревания или охлаждения тело воспринимает или
отдает определенное количество тепла. Существуют три способа
определения расхода тепла в процессе теплообмена.
1. К элементу поверхности dS за время dz подводится тепло,
равное
\ дп )
dSdz. A)
Для нахождения количества тепла AQ, воспринимаемого телом за
промежуток времени Ах = т2 — %v нужно соотношение A)
проинтегрировать по всей поверхности S и интервалу времени Дт:
AQ = -j .Ы-ж)*^- B)
xt (S)
Обычно температура и температурный градиент одинаковы вдоль
поверхности; тогда расчетная формула B) упрощается:
*2
C)
ФИЗИЧЕСКИЕ ОСНОВЫ ПЕРЕДАЧИ ТЕПЛА
31
2. Элемент объема dv = dx dy dz за время Д т = т2 — хх нагревается
от Тг до Т2; он воспринимает количество тепла, равное
CTiTt-TJda. D)
Общее количество тепла A Q, которое пошло на нагревание за
время Ат, найдем, если проинтегрируем по всему объему V, т. е.
AQ=Q2~Qi = cT J "(T%-TJdv=ctV±- j {T%-TJdv. E)
(V) (V)
Обозначим среднюю (интегральную) температуру по всему объему
тела через Т, т. е.
T=^jJTdv,
(V)
тогда можно написать:
b.Q=Qt-Qi = ciV{Tt - Tj, F)
так как в процессе нагревания Т2 > 7\.
Расход тепла (Q — Q0) на нагревание за время т от начала (хг = 0)
процесса будет равен
Q-Qo-cjViT-To), G)
где Т0 — средняя (интегральная) начальная температура. Если
начальная температура одинакова во всех точках тела, т. е. Т0 = Т0 = const,
то удельный расход тепла равен
AQV = C1{T-T0). (8)
Следовательно, основная задача в этом методе расчета сводится к
определению Г(т).
3. Элемент поверхности dS за время dx воспринимает из
окружающей среды количество тепла, равное
a(Tc—Tn)dSd*. (9)
Для нахождения общего количества тепла AQ, воспринимаемого по
всей поверхности тела, нужно проинтегрировать по всей поверхности и
промежутку времени Ат = т2 — %v
Если температура поверхности тела одинакова во всех точках и
коэффициент а не зависит от температуры, то будем иметь:
AQ = Q* - Qi = «s j [Tc - тп (х)} dxy
A0)
Рассмотрим несколько примеров.
1. Дана пластина толщиной 2R. Ширина BЛ) и длина B/) пластины значительно
больше толщины, так что градиент температуры по длине и ширине пластины равен
нулю (случай одномерной задачи). Тогда температура в любой точке пластины будет
зависеть от х и т, т.е. Т (х, %).
32
Если начало координат находится в центре пластины, то средняя интегральная
температура будет равна
-f# -К -\-h +R
T(%)=y-$T(x%%)dv= 2R2l2h J J \т(х,х)йхйу*г=-щ{т(х9%)йх =
(V) ~-R -I -h -R
R
0
2. Пусть температура сферического тела (шара) будет функцией г и т, т. е. Т (г, х)
(сферически-симметричная задача).
Тогда средняя (по объему) температура Т (т) будет равна
R 2к % R
¥(%)=* 4kR3 Г Г ^T(r,x)r*sinededi>dr = 1^ (W(r,x)dr, A2)
О 0=0 ф=0 0
так как элемент объема равен
dv ~ г2 sin ddedfydr.
3. Дан цилиндр радиусом R и длиной /. Длина цилиндра значительно больше
диаметра (/ > 2R), поэтому цилиндр можно считать неограниченным, а температура внутри
него есть функция гит, т. е. Г(г,т). Тогда средняя температура цилиндра будет
равна
R 2% I R
T^)--^^^T{rJx)rdrdMz=^^rT{r^)dri A3)
0 0 0 0
так как dv — rdrdBdz.
В дальнейшем одновременно с нахождением температуры Т тела в задачах будет
определяться и Г. Зная величину Г, можно определить теплосодержание Q тела и
расход тепла на нагревание (Q — Q0) или потерю тепла (Q0 — Q) при охлаждении тела.
В тех случаях, когда определить Т затруднительно, расход тепла может быть
подсчитан по формуле C).
33
ТЕОРИЯ ОБОБЩЕННЫХ ПЕРЕМЕННЫХ
2
В связи с развитием машинной вычислительной техники многие задачи
математической физики решаются в виде конкретных числовых
соотношений. При этом с целью уточнения и приближения задачи к
реальному процессу вводится большое количество переменных. Однако привести
результаты расчетов в определенную систему, найти скрытые связи
между переменными очень трудно. Поэтому весьма ценным является
использование методов теории подобия, которая в настоящее время может
быть названа теорией обобщенных переменных.
В этой теории на основании общих физических соображений
доказывается, что множество связей не является собственным свойством
исследуемых задач, обусловленным их физической природой. В
действительности влияние отдельных факторов, представленных различными
величинами, проявляется не порознь, а совместно. Поэтому надо
рассматривать не эти отдельные величины, а их совокупности или комплексы,
имеющие определенный физический смысл. Методы теории подобия
позволяют на основе анализа дифференциальных уравнений и граничных
условий находить эти комплексы, которые можно назвать обобщенными
переменными.
Для каждой проблемы существует совокупность характерных для
нее переменных, в которой ее надо рассматривать. Переход от обычных
физических величин к величинам комплексного типа, которые
составлены из тех же величин, но в определенных сочетаниях, создает важные
преимущества. Прежде всего происходит уменьшение числа переменных.
В этих величинах более отчетливо выступают внутренние связи,
характеризующие процесс.
Кроме того, новые переменные обладают и другим преимуществом.
Заданное значение комплекса величин может быть получено как
результат бесчисленного множества различных комбинаций величин, входящих
в этот комплекс. Следовательно, фиксированным значениям новых
переменных отвечает не одна определенная совокупность первоначальных
величин, а бесчисленное множество таких совокупностей. Это значит,
что при рассмотрении задачи в новых переменных исследуется не
единичный случай, а бесчисленное множество различных случаев,
объединенных некоторой общностью средств. Таким образом, новые
переменные по своему существу являются обобщенными. Замещение обычных
переменных обобщенными является основной задачей теории подобия
или теории обобщенных переменных.
2 Заказ т 640
34
Глава вторая
Совершенно очевидно, что теория подобия наиболее плодотворно
может быть использована в том случае, когда невозможно
проинтегрировать дифференциальное уравнение и найти зависимость между
переменными в явном виде. Если дифференциальное уравнение может быть решено,
то надобность в теории подобия по существу отпадает. Однако теория
подобия приносит и в этом случае определенную пользу. Если решения
представить в форме связи относительных переменных» то число
переменных существенно сократится. Кроме того, решение в такой форме
позволяет установить внутренние связи между переменными и
параметрами, входящими в безразмерные комплексы, а тем самым более
глубоко вскрыть физический смысл полученных решений.
§ 1. КРИТЕРИИ И ЧИСЛА ПОДОБИЯ
Дифференциальные уравнения, описывающие процесс, отражают
наши представления о физической сущности процесса. Например,
дифференциальное уравнение теплопроводности является частным случаем
закона сохранения энергии и сводится к утверждению, что изменение
внутренней энергии элементарного объема тела равно количеству
теплоты, которым он обменивается с остальной массой тела.
Основные уравнения исследуемой задачи представляют собой
специальную форму общих физических законов. Развитие процесса определяется
соотношениями между отдельными членами уравнений. Такие соотношения
и должны вводиться в качестве переменных, характерных для
рассматриваемой задачи. Однако во многих случаях каждый из членов
уравнения представляет собой сложные дифференциальные выражения, в состав
которых входят основные переменные задачи. Следовательно,
необходимо установить правила перехода от дифференциальных выражений к
выражениям в конечной форме.
Теория подобия дает общий метод непосредственного
преобразования выражений, содержащих дифференциальные onef аторы, к
простейшим алгебраическим выражениям. Суть этого метода состоит в
том, что реальный процесс заменяется простейшей условной схемой,
в которой все диффгренциальныг операторы сохраняют постоянное
значение в прост; анстве и во (ремени.
В качестве примера рассмотрим оператор m-кратного
дифференцирования по независимой переменной х. Тогда результатом действия этого
dmu
оператора на функцию y = f(x) будет функция, z = ~~-. Однако сле-
дует рассмотреть влияние у и х на г. Поэтому полагаем -^-~Г = const.
Очевидно, для удовлетворения этого условия достаточно положить
у s Ахт, откуда А = -^-, где у и х — любые значения переменных,
получаемые из соотношений y = f(x). Пусть какие-либо значения
переменных х и у известны или заданы по условию (х0, у()). Эти заданные
значения х0 и у0 называются параметрическими значениями. Поэтому
А~-Щг. Следовательно, z~-^r.
XQ xo
Таким образом, закон построения z из величин х и у заключается
в том, что z определяется как величина, пропорциональная у0 в первой
степени и обратно' пропорциональная х0 в степени т. Только это
соотношение существенно при решении вопроса о структуре комплекса,
отвечающего оператору z. Параметры х0 и у0 заданы по условию.
ТЕОРИЯ ОБОБЩЕННЫХ ПЕРЕМЕННЫХ
35
Таким образом, переход от производных к простейшим
алгебраическим выражениям совершается без всякого труда. Поясним этот переход
на примере теплоотдачи нагретой пластины в окружающую среду. Если-
теплообмен происходит по закону Ньютона, то в соответствии с
граничными условиями третьего рода имеем
а(Гп-Гс) = -ХDг); 0)
где Тп и Тс — соответственно температуры стенки и средьц
а—коэффициент теплообмена, X—коэффициент теплопроводности материала стенки.
(Индексами «п» отмечены величины, относящиеся к поверхности пластины.)
Положим теперь -^- = const. В данном случае это требование не
является заменой реального процесса условной схемой, так как оно
действительно удовлетворяется при стационарном распределении
температуры. Таким образом, произведем переход от общего случая
стационарного распределения температуры. Соответственно температура Т
становится функцией одной только переменной — координаты х. В этих
условиях имеем
-*L = _-?£- B)
dx I ' W
где ЬТ — перепад температуры на толщине пластины /.
Если ввести еще понятие о температурном напоре AT, определив его
уравнением
АТ = ТП-ТС, C)
то уравнение A) приведется к виду
ьт
или
аД7 = Х- {
AT \ 1л W
Итак, в соответствии со свойствами процесса, которые определены
основным уравнением A), соотношение между температурным перепадом к
температурным напором определяется непосредственно выражением ~ L
В общем случае при переменном градиенте температуры (-^— = var ),
когда распределение температуры имеет вид, отличный от линейного,
этот простой результат теряет силу, так как теперь уже нельзя пред-
/ дТ \ ЬТ
ставить производную -т— в виде т—.
Однако, если положить
дТ\ ът /еч
_ «_8_, E)
то множитель е («степень искажения») будет зависеть только от
конфигурации кривой распределения температуры. Поэтому для всех
температурных распределений, подобных между собой, е имеет одинаковое
значение.
Теперь уравнение D) перепишется в виде
If-TT'* F>
2*
36
Глава вторая
Таким образом, для определения отношения -^- в общем случае
требуется знать е. Поскольку е для подобных распределений имеет одинаковые
значения, поэтому, если для какого-нибудь одного распределения значение s
найдено, то оно автоматически распространяется на все распределения,
ему подобные. Несложные рассуждения, которые здесь приводиться не
будут, показывают, что подобными являются те распределения, которым
отвечают одинаковые значения -^- /. Но это значит, что коэффициент е
есть однозначная функция величины -?-/ и, следовательно, уравнение
F) можно представить в виде
Этот результат важен в том отношении, что решение представлено в
виде функции от одного аргумента, хотя совершенно очевидно, что
распределение температуры обусловлено влиянием трех параметров: а,
/ и X. Подлинный смысл этого замечательного факта заключается в
том, что в соответствии с нашими представлениями о физической
природе процесса (выраженными в основном уравнении) существенное
значение имеет не каждый из этих параметров в отдельности, а
вполне определенная их комбинация -|-/.
Выражение ~1 представляет собой характерный пример
обобщенной переменной или комплекса, заданного по условию задачи. В теории
подобия такие переменные принято называть критериями подобия и
обозначать первыми двумя буквами фамилии ученого, особенно много
сделавшего для развития данной области знаний.
Для выражения —I принято название критерия Био:
-J-/-BL
(8)
Следовательно, уравнение G) можно переписать в виде
-gr=F(Bi). (9)
Вследствие перехода от первоначальных переменных а, /, X к новой
переменной Bi не только уменьшается число аргументов, но и
совершается изменение в самой подстановке всего анализа. Действительно, если
основными величинами взять а, /, X, то для каждой совокупности
заданных значений этих параметров получим некоторый частный случай.
В противоположность этому, заданному значению Bi вовсе не отвечает
какой-либо частный случай, так как это значение может быть
реализовано бесчисленным множеством различных комбинаций величин а, /, X.
Таким образом, фиксируя значение Bi, определяем не одно
конкретное явление, а бесчисленное множество различных явлений.
Следовательно, в новом понимании индивидуальный случай (отвечающий за-
данному значению аргумента) — это щ единственное явление, а
бесконечная по численности группа подобных между собой явлений. В этом
смысле можно сказать, что новые переменные являются обобщенными
и, соответственно, весь анализ приобретает обобщенный характер.
ТЕОРИЯ ОБОБЩЕННЫХ ПЕРЕМЕННЫХ
37
Физический смысл уравнения (9) заключается в том, что заданным
значениям Bi отвечают подобные между собой температурные распре-
ьт
деления, для которых отношение -^=- имеет одно - и то же значение.
Однако решение еще не доведено до конца, так как исследуется
нестационарный процесс. Необходимо выяснить, как определить те моменты
времени, для которых получаются подобные распределения.
Очевидно, что процессы в разных системах не будут развиваться
синхронно, так как темп перестройки температурного поля зависит и
от X, и от /. Следовательно, возникает задача о правилах определения
взаимно соответствующих моментов времени. Для решения этой задачи
обратимся к основному уравнению теплопроводности, которым уста*
навливается связь между темпом перестройки температуры во времени
и распределением температуры в пространстве.
Для одномерной задачи имеем
дТ д*т /1ПЧ
где а — коэффициент температуропроводности материала пластины.
Если и в этом случае принять наш прием перехода к условной схеме
дТ
с постоянными значениями производных, то производную -g— можно
ьтх д*т ътг
заменить через , а производную ~§^г — через *-]а~~ (индексы х и /
означают соответственно изменения температуры за время х и на
протяжении /). Следовательно, для рассматриваемой схемы можно написать
-^- = — A1)
Если в какой-то момент (например, в начале процесса)
распределения подобны, то это подобие может сохраняться только при
условии, что соотношение между пространственными и временными
изменениями всегда остается постоянным. Отсюда следует, что
выражение -—- для всех систем должно иметь одинаковое значение.
При заданном начальном распределении температуры любое
последующее распределение зависит от длительности процесса х,
коэффициента температуропроводности а и размера системы /. Но
существенное значение имеет не каждая из этих величин в отдельности, а вполне
определенная их комбинация -^-. Очевидно, выражение ~
представляет собой обобщенную переменную, которую принято называть
критерием или числом Фурье:
= Fo.
A2)
Отсюда ясно, что число Фурье имеет смысл обобщенного времени.
Поэтому его можно назвать числом гомохронности (гомохронность —
однородность по времени; если для двух систем отношение — имеет
одно и то же значение, то для них, очевидно, гомохронность
переходит в синхронность),
В своей последней работе А. А. Гухман [16] предлагает различать
критерии подобия и числа подобия. Критерии подобия — это такие комплек-
38
Глава вторая
сы, которые целиком состоят из параметров, заданных по условию.
Характерным примером является критерий Bi (Bi = -^-J. Комплекс
~ является не критерием, а обобщенной переменной или числом
Фурье. Однако, если по условию^ задачи задано некоторое характерное
время, например» период колебания температуры окружающей среды
(т0), то аналогичный комплекс ^~ будет называться критерием Фурье
ач*
Fo/= —2~ф В этом случае комплекс -^ можно представить как
произведение] критерия Фурье «^~[на безразмерную переменную т/т0
параметрического типа, т. е.
Fo=J£- = Fo'^). 03)
В этом случае все критерии подобия являются безразмерными
параметрами, а обобщенные переменные комплексного типа — числами.
Вернемся к нашей задаче:
-^ = <p(Bi,Fo). A4)
Заметим, что это решение, определяющее температурные условия
на поверхности пластины, можно перестроить так, чтобы оно было
справедливо для любой точки внутри пластины. Будем фиксировать
местоположение точек внутри пластины с помощью отношения х/1. Тогда,
обозначив через Т текущую температуру, отсчитываемую от
температуры окружающей среды как от нуля, а через Т0 — некоторую заданную
по условию температуру, будем иметь
Т
То
0)(Bi,Fo,-f). 15)
Отсюда видно, что в число аргументов, помимо Bi и Fo, входит
отношение -у-. Это отношение выражает одно из условий задачи «для
точки, расположенной на расстоянии х от поверхности пластины
толщиной /, найти...» и т. д. Такого рода отношения, вводимые
непосредственно на основании условия задачи, называются переменными
параметрического типа. Очевидно, отношение Т/Т0 в левой части уравнения
также представляет собой параметрическую переменную, так как и оно
отвечает определенной части условия задачи «...найти температуру 7\
если начальная температура равна Т0».
Таким образом, в теории обобщенных переменных различают
безразмерные величины: критерии подобия и безразмерные переменные.
Критерии подобия, состоящие из постоянных безразмерных
параметров задачи, могут быть двух видов. Критерии
подобия!параметрического вида представляют собой отношение одноименных параметров,
заданных по условию задачи (отношение длины к высоте или ширины
к высоте, параллелепипеда и т. д.). Критерии комплексного типа
объединяют разнородные параметры (критерии Био, Фурье и т. д.).
Относительные переменные являются отношением переменной
величины к постоянному параметру или к их комбинации. Поэтому
различают два типа относительных переменных. Наиболее простой
тип переменной — это отношение текущей переменной к
одноименному параметру (х/1, Т/Т0 и т. д.).
ТЕОРИЯ ОБОБЩЕННЫХ ПЕРЕМЕННЫХ
39
Если параметр, соответствующий данной переменной, не задан,
то строится комплекс, состоящий из переменной и ряда разнородных
параметров, например, -у- , где /2/а является комплексом разнородных
параметров, имеющим размерность времени. Такие переменные
комплексного типа будем называть числами (число Фурье Fo = -p-j.
В качестве примера можно привести решение задачи о нагревании
пластины в среде при наличии постоянного источника тепла мощностью
№(вт'м3-ч).
Решение этой задачи в наших обозначениях можно написать так
(см. гл. IX, § 2—4):
-£^ = /(Bi.^.Fo,Po), A6)
где Тс — температура среды, 70 —начальная температура тела,
П Wl2 /174
Ро- XGWo) . A7)
Если по условию задачи Тс и Т0 заданы, то комплекс Ро является
параметром и он будет критерием подобия (критерий Померанцева), а
величина i~T~zrf~) является относительной переменной.
Однако, если рассматривается стационарная задача (Fo->oo), то
начальная температура TQ не ехэдит в решение задачи, а температура
среды Тс может служить в качестве начала отсчета температуры тела
(Т — Тс). Тогда критерий Померанцева теряет свой физические смысл.
В этом случае относительной переменной будет являться величина
Wi*/k
-/(BI.-J-). A8)
Комплекс разнородных параметров №72/Х имеет размерность
температуры и служит в качестве заданного температурного параметра.
В качестве второго примера можно привести различие между
критерием Bi и числом Нуссельта Nu. Критерий Bi\ играющий важную роль
в теории температурного поля твердого тела, представляет собой
отношение термического сопротивления стенки A/1) к термическому
сопротивлению передачи тепла на поверхности {— j, причем оба
сопротивления непосредственно заданы по условию задачи. Таким образом, Bi
является параметром, т. е. критерием псд бия.
В противоположность этому при исследовании процессов
теплообмена между твердым телом и окружающей средой коэффициент
теплообмена а является величиной неизвестной и подлежащей определению.
Поэтому вводится новый комплекс, содержащий а. Этот комплекс
получается из рассмотрения процесса теплообмена на основе
предположения, что у поверхности твердого тела образуется жидкая пленка, через
которую тепло передается только теплопроводностью. В таком случае
можно написать уравнение
«(Гп-7с) = -хЩ, A9)
формально совершенно тождественное уравнению A). По существу оба
уравнения, конечно, различаются тем, что сюда входит коэффициент
40
Глава вторая
теплопроводности X жидкости (а не твердого тела) и производная l-~ \
определяется в приближении к поверхности со стороны жидкости.
Обработка этого уравнения методами теории подобия приводит к
уже знакомому выражению -|~/. На первый взгляд представляется, что
полученный результат отличается от критерия Bi только тем, что он
содержит коэффициент теплопроводности жидкости. В
действительности же различие гораздо глубже, так как теперь а является величиной
неизвестной и, следовательно, комплекс должен быть отнесен к
категории относительных переменных или чисел. Поэтому целесообразно
ввести здесь новое обозначение и новое наименование. К настоящему
времени вполне установилось наименование числа Нуссельта и
обозначение Nu. Число Nu всегда выступает в уравнениях теплообмена в
качестве функции.
Приведем наиболее часто встречающиеся числа и критерии подобия:
Критерий Био Bi = HR = ~R
Кирпичева Ki - Х(/сс*ГоГ
» Кондратьева Kn = i?2 -~
» Предводителева Pd = i-jw-j *
» Померанцева Ро = ^, — г )
» Фурье Fo' = —g^
Число Нуссельта Nu = ~у-
» Фурье Fo = ax/R2
Таким образом, решение задачи должно быть представлено в форме
безразмерных величин, которыми искомые относительные переменные
определяются как функции независимых относительных переменных и
критериев подобия, играющих роль постоянных параметров:
ут = / (хр Пг pi)i (i = 1, 2, 3,..., п)9 B0)
где #г — искомая переменная, х®— независимые переменные, IL — кри*
терий комплексного типа, Р. — параметрические критерии.
Если вид функции уравнения B0) найден для какого-либо частного
случая с помощью численного решения уравнений или путем
эксперимента, то полученный результат автоматически распространяется на
бесчисленное множество явлений, которые объединяются вместе с
исходным случаем в одну группу при выполнении следующих требований
(которые необходимо удовлетворить для того, чтобы одинаковым
значениям критериев действительно отвечали подобные явления): 1)
геометрическое подобие систем; 2) подобие их физической структуры; 3)
подобие начальных состояний; 4) подобие условий на поверхности
взаимодействия систем с окружающей средой.
ТЕОРИЯ ОБОБЩЕННЫХ ПЕРЕМЕННЫХ
41
В заключение необходимо отметить, что любая комбинация
критериев подобия есть также критерий подобия. Произведение
относительной переменной на любую комбинацию критериев подобия есть также
относительная переменная.
Возможность комбинировать критерии и относительные переменные
имеет важное значение для рационального построения решений задач
тепло- и массообмена.
§ 2. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ И ТЕОРИЯ ПОДОБИЯ
Критерии подобия получаются из дифференциального уравнения и
граничных условий в результате перехода от дифференциальных
соотношений к алгебраическим. Этот способ перехода имеет связь с
методами операционного исчисления.
Уравнение A1) § 1 является отношением температурных разностей,
преобразованных по времени и по координатам, т. е. число Фурье есть
отношение преобразованных разностей температур.
Отсюда возникает идея нахождения критериев подобия по
отношению не оригиналов функций, а их изображений. Известно, что
оператор Хевисайда р, введенный по отношению к временной переменной
^4дает следующие соотношения:
^. = рГ-:Г0; ^^7_р*-1Г@)- ..-Г-ЧО); [A)
JL -z- Jl.-±-Jl *. JL -*. JUL (9\
р "^%; р3 -*"" 2! Х 1 рт Т. т\ f ^'
где*»» —знак операционного соответствия.
Следовательно, замена производных отношением исследуемой
физической величины к переменной в степени т, по сути говоря, есть
переход от оригинала функций к ее изображению по Карсону — Хевисайду.
Это отвечает сущности самого аналитического преобразования.
Операционные методы есть математические методы, преображающие символы
одной операции в символы другой:
jW^pvT^-ZrmU [если 7@) = Г @) = ... -^(О) = 0.1C)
Метод Карсона — Хевисайда является методом интегрального
преобразования, он позволяет расчленить операции, ввести дробные
d х1г 1
дифференциаторы и интеграторы» например, р = -г-; р ' = —:= . One-
У тех
рация интегрирования заменяется оператором i, в этом случае при
определенных условиях существует взаимосвязь между I и оператором:
Р4 = /Ф^ р~2 = *'==4г и т-Д- Поэтому для получения критериев
подобия можно воспользоваться не только системой дифференциальных
уравнений, но и системами смешанных интегро-дифференцнальных
уравнений. Это обстоятельство дает определенное преимущество
операторным методам.
Обычно метод преобразований Карсона — Хевисайда или метод
Лапласа применяется к нестационарным процессам, т е. преобразование
проводится по временной координате (интегрирование происходит в
пределах от 0 до оо).
42
Глава вторая
К телам конечных размеров применяются конечные интегральные
преобразования Фурье, Ханкеля и др. Однако только в некоторых
частных случаях можно написать соотношение, аналогичное
d"T фр*Т. D)
dx2
Кроме того, косинус- или синус-преобразование Фурье не дает
возможет1 / *
ности исключить производную -т— (и любую нечетную производную),
так как интеграл I °dx2n+i lslnpx\dx не может быть выражен в виде
простого операционного соотношения типа D).
Конечное интегральное преобразование Ханкеля дает возможность
исключить совокупность членов вида
F(T) = —w(r-¥-} ^. E)
При этом имеет место соотношение
Р(Т)Ф-р*Т + <?(р,Та), F)
где ср (р, Тп) — функция, зависящая от граничных условий.
Следовательно, переход от дифференциальных уравнений к
алгебраическим уравнениям состоит не только в замене частной производной
д т выражением ртТ, но и во сведении дополнительных соотношений,
учитывающих граничные условия, т. е. процесс взаимодействия тела с
окружающей средой. Физически это означает переход от актуальных
значений исследуемых величин (дифференциальные уравнения и условия
однозначности) к усредненным значениям, сделанным в соответствии
с условиями конкретной физической задачи методами преобразования
операторов.
Операторный метод Хевисайда имеет некоторое преимущество перед
методами интегральных преобразований в теории операторного
подобия. В процессе эволюции операторного исчисления первоначальная
точка зрения Хевисайда была вытеснена работами Карсона [92], Бром-
вича [90], Дейча [96],. Ван-дер-Поля [6], которые в своих
исследованиях опирались на преобразование Лапласа и интеграл Меллина. Возврат
к первоначальной точке зрения Хевисайда был сделан в 1946 г.
польским математиком И. Микусинским [109]. В операторном исчислении
Хевисайда—Микусинского рассматривается оператор р = -^-, при
помощи которого дифференциальное уравнение сводится к
алгебраическому.
В последнее время В. А. Диткиным [25] введен оператор Бесселя
В = — 1--J—, тесно связанный с уравнением Бесселя, который дает
возможность решить ряд дифференциальных и интегральных уравнений.
Возвращаясь к методу перехода от реального процесса к простей-
dmT T
шей модельной схеме по соотношению -^т ~^п > можно отметить,
что такой метод дает возможность получить критерии подобия целого
класса явлений, так как дифференциальные уравнения описывают класс
dmT —
подобных явлений. Замена -j-^ на ртТ с учетом граничных условий
ТЕОРИЯ ОБОБЩЕННЫХ ПЕРЕМЕННЫХ
43
позволяет не только получить комплекс критериев подобия для
данного закона взаимодействия тела с окружающей средой, но и установить
взаимосвязь между критериями подобия, а значит, найти основные
критерии подобия.
Следовательно, решения для изображения, которые можно получить
в подавляющем большинстве случаев, являются основными исходными
соотношениями для нахождения связи между обобщенными переменными.
Известно, что трудность аналитических исследований состоит в
переходе от изображения к оригиналу, а не в получении решения для
изображения. Кроме того, из решения для изображения можно
получить ряд приближенных расчетных соотношений, на основе таблиц
изображений оригиналов функций и в результате упрощения путем
аппроксимации решения для изображения.
Таким образом, операторные методы при применении их к
дифференциальным уравнениям совместное условиями однозначности дают
возможность получить соотношения между усредненными значениями
основных критериев подобия тепло- и массообмена и, следовательно,
способствуют дальнейшему развитию теории тепло- и массообмена на основе
методов операторного подобия.
ОСНОВНЫЕ МЕТОДЫ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ
3
В гл. I было выведено дифференциальное уравнение
теплопроводности, которое устанавливает зависимость между температурой,
временем и координатами тела для бесконечно малого объема. Это
уравнение является линейным, однородным дифференциальным уравнением
второго порядка с частными производными.
Исследованию и методам решения классического уравнения C) § 5
гл. I в математической физике посвящено большое количество работ.
Здесь не рассматриваются эти работы, а приводятся основные методы
решения и главное внимание уделяется выяснению физической сущности
соответствующих преобразований. Поэтому в наших выводах отсутствует
детальное математическое исследование применяемых приемов, что
сделано с целью приближения методики решения к техническим,
инженерным расчетам.
Читатели, интересующиеся математической стороной вопроса, могут
обращаться к соответствующим работам [14, 74а].
§ 1. АНАЛИЗ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ
ТЕПЛОПРОВОДНОСТИ
Дифференциальное уравнение теплопроводности без источников
тепла можно написать так:
Напомним, что решения этого уравнения обладают свойством
наложения аналогично решениям обыкновенного однородного
дифференциального уравнения, т.е. если Тг и Т2 — два частных решения уравнения,
то выражение СгТг + С2Т2 является также решением этого уравнения
при произвольных значениях постоянных С, и С2. Дифференциальное
уравнение с частными производными типа A) имеет бесчисленное
множество частных решений.
Поясним это» на примере. Имеем однородное дифференциальное
уравнение с постоянными коэффициентами (а, Ь, с, d, e, /) для некоторой
функции Т от двух" переменных ? и т\:
аЖ+Ь1Щ+с1^+аЖ + е^ + ?Т==0- B)
45
Тогда подстановка
Т = CekWn C)
является частным решением этого уравнения, а именно
-щ- — кие , ^ — L^e , ^ — RiK,e
Если подставим эти соотношения в уравнение B), то после
сокращения на Cek^+l7] получим так называемое уравнение коэффициентов
ak2+bkl + cl2 + dk + et + f = 0. D)
Следовательно, выражение C) является частным решением для тех
значений k и /, которые удовлетворяют уравнению коэффициентов D).
Таким образом, можно взять произвольное значение одного из этих
двух коэффициентов, но тогда второй должен находиться из уравнения
D), т. е. получим бесчисленное множество частных решений.
Уравнение коэффициентов является квадратным уравнением,
например, по отношению k (считаем k переменным, а / постоянным), и >в
зависимости от значения его дискриминанта можно получить для k два
корня: 1) неравных действительных, 2) равных действительных и 3)
комплексно-сопряженных.
Получаемый результат для корней k находится в зависимости от
физической сущности изучаемого процесса, описываемого
дифференциальным уравнением B).
Необходимо обратить внимание на то, что решение C) можно
написать как произведение двух функций:
Т^Се^е^ = С&(£)б (</]),
одна из которых Щ) = eki зависит только от £, а другая 6(yj) = е1^
зависит только от у\.
Однако существуют такие решения уравнения B), для которых это
разделение невозможно.
§ 2. НАХОЖДЕНИЕ РЕШЕНИЯ УРАВНЕНИЯ КЛАССИЧЕСКИМИ
МЕТОДАМИ
Метод разделения переменных. Классический метод решения
дифференциального уравнения теплопроводности состоит в том, что
находится совокупность частных решений Тт удовлетворяющих уравнению
и граничному условию, а затем по принципу наложения составляется
ряд этих решений:
Т = С1Г1 + С17, + ... = ЕС|G'Я. A)
П=г\
Коэффициенты Сп находятся из начального условия.
Строго говоря, это свойство наложения для бесконечного ряда
нуждается в специальном обосновании, так как оно безоговорочно
справедливо только для конечной суммы. Такое обоснование состоит в том,
что необходимо доказать равномерную сходимость ряда, полученного
после дифференцирования ряда A), а также законность почленного
интегрирования ряда при определении коэффициентов Сл. Это
обоснование можно найти в монографиях по математической физике.
46
Глава третья
Частное решение Т ищется в виде произведения двух функций,
одна из которых Цх) зависит только от времени т, а другая Цх, у, г)
зависит только от координат, т. е.
Т = СЪ(х)Ъ(х,у,г)9\ B)
где С — произвольная постоянная.
Если подставим решение B) в уравнение A) § 1, то получим
fl'OW*. У. г) = аЦх)у*Ъ(х, у, г);
это равенство можно написать еще так:
6(х) ~а Ъ(х, у, г) " \9)
Левая часть равенства может зависеть только от х или быть
постоянным числом, но она не зависит от координат. Правая часть может
зависеть только от координат или быть постоянным числом, но она не
зависит от времени. Равенство должно иметь место при любых
значениях времени и координат. Это возможно только в том случае, если
правая и левая части равенства равны некоторой постоянной величине
D, т. е.
^ = D = const; D)
*™*'У**1=В = const. E)
Уравнение D) можно проинтегрировать, и тогда получим
6(<с) = eD\ F)
Постоянную интегрирования не пишем, поскольку ее можно отнести к
постоянной С.
Постоянная величина D выбирается из физических соображений. Для
тепловых процессов, стремящихся к температурному равновесию, когда
по истечении длительного промежутка времени (т~>оо) должно
установиться определенное распределение температуры, величина D не может
быть положительной величиной, она будет только отрицательной. Если
D есть величина положительная, то при длительном промежутке
времени температура будет больше любой наперед заданной величины, т. е.
стремиться к бесконечности, что противоречит физической сущности
процесса.
Если температура тела есть периодическая функция времени,
например в случае распространения тепловых волн в теле, то величина D
должна быть мнимой величиной, чтобы вместо простой экспоненты F)
получить периодическую функцию времени. .
Рассмотрим первый случай, когда D<0. Так как величина D пока
произвольная постоянная по числовому значению, то можно положить
D = -ak\ G)
где а — коэффициент температуропроводности (величина положительная),
k — некоторая постоянная, которая определяется из граничных условий.
Подставляя эти значения для D, получим:
6(т) = е-***, (8)
V4(x, у, г) + k4{x, у, г) = 0. (9)
Дифференциальное уравнение (9) часто называют уравнением Покеля;
оно хорошо, изучено в математической физике.
ОСНОВНЫЕ МЕТОДЫ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ
47
Таким образом, применяя метод Фурье, уравнение теплопроводности
сводим к уравнению типа Покеля, решение которого определяется
геометрической формой тела, начальным распределением температуры, а
также условиями теплообмена тела с окружающей средой или с
окружающими телами.
Пусть при соответствующих заданных условиях известно решение
уравнения (9), т. е. нами найдена функция Ь (х, у, г). Тогда частное
решение уравнения теплопроводности можно написать так:
Т = Ce-akH »(*, у, г). A0)
Решение A0) удовлетворяет дифференциальному уравнению
теплопроводности при любых значениях С и k, т. е. является частным решением.
Следовательно, давая постоянным С и k различные значения, получим
бесчисленное множество частных решений.
По принципу наложения общее решение будет равно сумме частных
решений согласно соотношению A). Постоянные k определяются
граничными условиями, а постоянные С — из начальных условий.
В простейших случаях, когда & зависит только от одной координаты \
(одномерные задачи, связанные с нахождением симметричного
температурного поля в неограниченной пластине, цилиндре, шаре), решение
уравнения (9) можно представить как сумму двух частных решений,
ФE) и ф(£), т. е.
»(У = Ф(«) + ф(«). (И)
Это обусловлено тем, что общее решение всякого линейного
однородного дифференциального уравнения второго порядка
Г + рF)&'+ ?(?)» = 0 A2)
можно написать в виде
» = сл + сл. A3)
где Сг и С2 — постоянные, а Ьг и ft2 являются линейно независимыми
интегралами уравнения A2), т. е. такими интегралами, отношение которых
не является постоянной величиной:
~^—Ф const.
Достаточно знать только одно линейное независимое решение,
например bv тогда второе находится по формуле1*:
»2 = &Л»Г2е~^#. A4)
1) Формулу A4) можно получить следующим образом: положим &2 = &*? и
подставим в уравнение A2):
vV" + B&J + p*i)z'+ №l + Ph + qbi)z = &! z" + B*; + р»,)г' = 0
[так как вторая скобка равна нулю, поэтому $i есть решение уравнения A2)].
Перепишем полученное уравнение в виде
z' h
откуда
In г' = —21n&! — J pdt + lnCa.
Интегрируя еще раз, будем иметь
& = с,»! + C2&i J ft e~^Md£ = СА + С„&«.
48
Глава третья
Вернемся теперь к анализу частного решения дифференциального
уравнения теплопроводности. Согласно соотношению (И) частное
решение A0) можно написать так:
Т - Ce~akH ф(«) + De~akH ф(«), A5)
т. е. оно представляет собой сумму или линейную комбинацию двух
собственных функций.
В общем случае величина k определяется из граничных условий, а
постоянные С и D — из начального условия.
Частное решение непригодно для расчета температурного поля, так
как из частного решения нельзя определить постоянные С и D. Напри-
мер, в начальный момент времени (т = 0) температура может быть
постоянной Т= То = const, что не следует из частного решения A5).
Если положить т = 0(e~akH = 1), то получается, что постоянная Т0
должна быть равна переменной С<р(&£) + Dty(k%), чего быть не может.
Поэтому для получения общего решения уравнения теплопроводности,
удовлетворяющего и начальным условиям, берут сумму частных решений, в
которых постоянные С и D имеют свои определенные значения.
Температура в начальный момент времени может быть заданной функцией ?.
Тогда при помощи совокупности таких частных решений можно как
угодно близко подойти к заданному распределению. Это
осуществляется подбором подходящих значений С и D; такой путь подбора
постоянных С и D обычно называют удовлетворением решения начальному
условию.
Таким образом, первое частное решение можно написать так:
Тг = Схг~а^ ф(Ах5) + D^ ф^),
второе частное решение
Т2 - C2e~ak"x Ф(АЯ5) + Dte-*& ф(Л25)
и т. д.
Общее решение будет иметь вид
оо .2 оо 2
Т = Б СМК§е~акпХ + Е Dmi? (kj)e-ak^ . A6)
n—l m=l
При этом необходимо, чтобы функция Т0(£), описывающая начальное
распределение температуры, могла быть разложена в ряд по
собственным функциям:
n=i m==l
Поясним вышерассмотренную методику решения на простейшем
примере. Дифференциальное уравнение теплопроводности для неограниченной
пластины имеет вид
дТ(х, т) __ д2Т(х, т)
* —*^Р- <17>
Ищем частное решение этого уравнения в виде произведения двух
функций:
ОСНОВНЫЕ МЕТОДЫ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ
49
Тогда после подстановки его в дифференциальное уравнение получим:
б'(т) Ь"(х) ,9 /fm
iU^a-wr^^akK A8)
Интегрирование уравнения
ягг = -~ak2 = const
даст значение для функции 6(т), т. е.
Дифференциальное уравнение для функции Цх) имеет вид
>'(*) = —кЩх). A9)
Следовательно, функция Цх) должна быть такова, чтобы ее вторая
производная была равна самой функции, умноженной на некоторую
величину (—А2). Легко показать, что такими функциями могут быть sin kx
или cos kx, а именно
Ц(х) = sin kx, &j(x) = k cos kx, ft|(x) = —A2sin kx = —к%Ьг(х);}
&2(x) = cos kx; %(x) = —k sin kx, $(x) == —^2 cos ^* ^ —А29а(х).,
Таким образом, sin kx и cos Ax являются частными решениями
уравнения A9), причем эти решения линейно независимы, так как
§2(х) cos kx '
Общее решение уравнения A9) будет суммой частных решений:
Цх) = СЬг(х) + Dft2(x) = Csinkx + D cos kx, B0)
где С и D — произвольные постоянные.
Второе частное решение Ь2(х) = cos Ах можно было получить также
по формуле A4), зная первое решение fr^x^sinAx, а именно
»а(*) = ft^x) J ^We^^dJC = ^(х) J &F2W^ = sin Ax X
f A 1 1
X \ . * == r- sin Ax ctg Ax = r- cos Ax
J sin2£x /г ь А
{в этом случае р(х) = 0). Общее решение будет иметь тот же вид:
Цх) = СЦ(х) + D'(b2) = С sin kx —— cos kx = С sin Ax + D cos Ax,
где £) = -r~Df ~ произвольная постоянная.
Частное решение дифференциального уравнения теплопроводности
будет иметь вид
Т(х, т) = С sin kxe~~ak^ + D cos kxe~-akH. B1)
Постоянная А определяется из граничных, а постоянные С и D —
из начальных условий; они принимают вполне определенные
значения в зависимости от условий задачи. Подробно методика расчета бу-
50
Глава третья
дет изложена при рассмотрении отдельных конкретных задач. Общее
решение можно написать так:
00 00
Т = 2 Cnsinkn[xtxp(—aklx)+ У] Dmcoskmxexp(—ак2тч). B2)
л=1 m—1
Метод источников. Физическая сущность метода источников состоит
в том, что любой процесс распространения тепла в теле
теплопроводностью можно представить как совокупность процессов выравнивания
температуры от множества элементарных источников тепла,
распределенных как в пространстве, так и во времени. Решение задач
теплопроводности по этому методу в основном сводится к правильному выбору
источников и их распределению.
Действие элементарного источника в неограниченном теле при
одномерном потоке тепла характеризуется формулой (см. гл. XV)
G(x, l т) =-г== ехр
У 4тшт
(*-iV
4at
B3)
называемой функцией источника на бесконечной прямой. Функция
G(x, £, т) удовлетворяет уравнению теплопроводности, именно
£0
fa V\-mt
П*-^J _ JL1 ехо Г- (*-аJ1
дх2 yAl[
т. е. -=— — а х *
от ох*
Функцию G обычно называют фундаментальным решением
уравнения теплопроводности. Непосредственной проверкой можно
убедиться в том, что функция G представляет температуру в точке х,
если в начальный момент времени в точке % выделяется количество
тепла Q = Ьс^.
Количество тепла на прямой равно
Q. „ £7„Р [--**=*- ]■£= - ^7 -•«« - *.
— 00 —ОО
где
-{-00
и = ^=4 , Г е- dM= "[/IT B4)
2/ах J
— 00
Следовательно, количество тепла Q не меняется с течением времени и
численно равно произведению площади, ограниченной кривой G и осью
абсцисс х, на объемную теплоемкость су. Для малых значений
времени почти все тепло сосредоточено в окрестности точки £.
Функция температурного влияния мгновенного источника тепла для
тела конечных размеров и одномерного потока тепла может быть
представлена так (см. гл. XV):
00
G,(*, 5, *) = —2j sin~T" sin -T"exp( Ках)' B5
Функция Gz показывает распределение температуры в неограниченной
пластине @<#</) в момент временит, если температура в начальный
ОСНОВНЫЕ МЕТОДЫ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ
51
момент времени равна нулю и в этот момент в точке £ мгновенно
выделяется количество тепла Q = Ьс^.
Ниже (см. гл. IV и IX) будет показано применение метода
источников к решению отдельных конкретных задач.
Существует еще ряд классических методов решения уравнений
теплопроводности, но на них мы останавливаться не"будем. Наиболее
распространенным методом является метод разделения переменных.
§ 3. ПРИМЕНЕНИЕ МЕТОДОВ ИНТЕГРАЛЬНОГО
ПРЕОБРАЗОВАНИЯ
Операционные методы. Для многих задач теплопроводности
использование классических методов оказывается неэффективным, например,
применение метода разделения переменных для задач с внутренними
источниками тепла. Решения, получаемые классическими методами, не
всегда удобны для практического использования. Часто требуется
иметь приближенные решения, которые получить из классических
решений трудно. В результате запросов техники за последние
десятилетия инженерами и физиками стали широко применяться операционные
методы решения. Основные правила и теоремы операционного
исчисления были получены проф. М. Ващенко-Захарченко [7] и независимо от
него Хевисайдом [102]. Наибольшее распространение они нашли в
электротехнике, благодаря работам Хевисайда. Этот метод оказался
настолько эффективным, что позволил решить многие задачи, считавшиеся
до него почти неразрешимыми.
В дальнейшем операционные методы нашли применение в
теплофизике при решении разнообразных задач нестационарной
теплопроводности, в химической технологии при решении задач нестационарной
диффузии В последние годы эти методы стали использоваться при
решении задач гидродинамики, переносе нейтронов в поглощающих
средах и т. д.
Строгое математическое обоснование операционного метода
Хевисайда дано в работах Бромвича [90], Джефрейса [104], Эфроса и
Данилевского [85], Дейча [23], Ван-дер-Поля [6], Диткина [25] и др. В
настоящее время он рассматривается как самостоятельный метод
решения уравнений математической физики, по своей стройности
равноценный классическим методам. Операционный метод Хевисайда
равнозначен методу интегрального преобразования Лапласа.
Метод преобразования Лапласа состоит в том, что изучается не
сама функция (оригинал), а ее видоизменение (изображение). Это
преобразование осуществляется при помощи умножения на
экспоненциальную функцию и интегрирования ее в определенных пределах. Поэтому
преобразование Лапласа является интегральным преобразованием.
Интегральное преобразование fL(s) функции /(т) определяется
формулой
к (s) = J /(x)e-«dx = L[f(x)],
о
где Дх) является оригиналом функции, a /L(s) —ее изображением,
которое обозначается в виде L[f(%)]. Здесь s может быть и комплексным
числом, причем предполагается, что вещественная часть его будет
положительной. Для того чтобы изображение существовало, интеграл A)
52
Глава третья
должен сходиться. Это накладывает определенные ограничения на
функцию Дт) (подробно см. гл. XIV).
Если задача решена в изображениях, то нахождение оригинала по
изображению (обратное преобразование) в общем случае выполняется
по формуле обращения
а-{-*оо
/(x) = L-1[/z.(s)] =
2ri
1ш
esxds.
B)
Интегрирование происходит в комплексной плоскости s = £ + Щ вдоль
прямой о = const, параллельной мнимой оси. Действительные числа Е
выбираются так, чтобы все особые точки подынтегрального выражения
в B) лежали в левой полуплоскости комплекснэй плоскости s(Res>-s1>
>о0). Методика такого интегрирования детально изложена в
специальных руководствах по теории функций комплексного переменного. В
подавляющем большинстве случаев обратное преобразование можно
осуществить, не прибегая к контурному интегрированию, а
воспользовавшись таблицами [118]
Нахождение оригинала функции по ее изображению может быть
выполнено особенно быстро, если изображение совпадет с одним из
изображений, содержащемся в таблице (см. приложение V). Вместо
формулы B) для определения оригинала функции по ее изображению
можно воспользоваться следующей формулой обращения:
/w
= Игл ]
П-+со
п \я-Н
f(n)( n
Bа)
Эта формула в принципе дает возможность получить оригинал
функции лишь при помощи операций дифференцирования и перехода к
пределу (подробно см. гл. XIV).
1. Если изображение представляет собой дробную функцию s:
Ms)
<P(s) _ A0 + AiS+AJ+..
<\>(s) B,s + B2s2 + ..
C)
которая является частным случаем двух целых трансцендентных
функций, то по теореме разложения имеем
D)
/1=1
где sn — простые корни функции ф(я); при этом знаменатель имеет
счетное множество простых корней и не содержит свободного члена при
условии, что А0 =£ 0, для этого необходимо, чтобы существовал
интеграл B) от функции /l(s).
2. Если изображение Д ^представляет собой отношение двух
полиномов (дробно-рациональная функция), причем степень полинома cp(s)
меньше степени полинома ^(s) и полином ф(я) имеет корни кратности k
в точках sm, то
dk~l [<?<s)(s-sm)k *т
fM - L-i Г JPW. 1 = V \ lim tJZLW'X*-
Da)
где сумма берется по всем корням /l(s). Если все корни <|>(s) простые
т. е. все k равны единице, то формула Dа) переходит в D).
ОСНОВНЫЕ МЕТОДЫ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ
53
Поскольку в нашей монографии преобразование Лапласа
используется в качестве основного метода решения задач теплопроводности, то
отдельной гл. XIV подробно рассмотрен этот метод.
Для иллюстрации техники применения преобразования Лапласа
приведем следующий пример.
Дифференциальное уравнение теплопроводности для одномерного
потока тепла в пластине имеет вид
«^.„«£4. E)
Применим преобразование Лапласа относительно переменной t:
* [-*£*]-»1 НИ- <«>
откуда получим обыкновенное дифференциальное уравнение второго
порядка с постоянными коэффициентами относительно изображения:
d2T (x s)
а £Н-^- - sTL (*, s) + и(х) = 0, G)
где функция и(х) описывает начальное распределение температуры.
В этом примере рассмотрим более простой случай, когда
Т(х, 0) = и(х) = 0, (8)
т. е. когда в начальный момент времени температура во всех точках
была одинакова и равна нулю.
Тогда уравнение G) примет вид
T'L(x>s)--±-TL(x,s) = 0. (9)
Решение дифференциального уравнения (9) можно написать
непосредственно (см. гл. XIV, пример 1), а именно
TL(x, s) = Achy-^x + Bshy— x = Axe * + Bxe \ A0)
где A, 5, Аг = —~ и Bx = ^ постоянные относительно х,
но зависящие от s величины.
Если заданы граничные условия, то, определив постоянные А и В,
или Аг и Bv при помощи таблицы изображений или теоремы
разложения находим оригинал Т(х, t).
Рассмотрим ту же задачу, но при начальном распределении
температуры как некоторой функции х, т. е.
T(x,0) = u(x). (И)
Пссле применения преобразования Лапласа относительно
переменной т к дифференциальному уравнению F) получим дифференциальное
уравнение для изображения G):
aTnL(x, s) — sTL (x, s) + u(x) = 0. A2)
Решение этого неоднородного уравнения легко получить
стандартными методами, например методами вариации произвольных постоян-
54
Глава третья
ных, изложенных в учебниках по теории обыкновенных
дифференциальных уравнений.
Оно имеет вид
х
TL(x, s) = ^ch]/-~ x + BshY^-x + ]/"Ach]/A x J и$)shY~ Ы1-
0
x
-j/\ish Ytx f U{i)ch VtIUI A3)
о
После определения произвольных постоянных Л и В из граничных ус*
ловий решение задачи сведется к определению оригинала по
изображению Tl(x, s).
Если в начальный момент времени температура во всех точках
одинакова и равна Tq, т. е. и(х) = Т0 = const, то из A3) получаем
TL(x, s) —?f- = A'ch l/jL x + B'shY±-X = Ai eV a* +Вге V a\ A4)
где
A' = TL@,s)-?f=A-l±, A5)
В' = В, A6)
„' А' + Вг г>' Аг — В'
А1= 2 ' Bl = 2 ' A7)
К этому же результату можно было прийти, если в
дифференциальном уравнении A2) при постоянной начальной температуре и(х) = Г0==
т
= const сделать замену переменной TL (x, s) = U(x,s) — ——, в
результате чего уравнение A2) превратилось бы в уравнение (9), а решение
последнего известно.
Так как А', В\ Аь В\ — постоянные относительно л: и определяются
из граничных условий, то верхние индексы можно отбросить и
написать решение дифференциального уравнения A2) при постоянной
начальной температуре в таком виде:
TL(xfs) — -lf- = Ach ]/i_* + £shl/Ax = AxeV aX+B±e V a * ; A8)
постоянные А и В каждый раз определяются из соответствующих
граничных условий.
В заключение отметим, что наибольшая трудность в решении
уравнения теплопроводности для разнообразных краевых условий состоит в
нахождении/оригинала по полученному изображению TL.
Применение интегрального преобразования Лапласа к решению
дифференциальных уравнений теплопроводности имеет ряд преимуществ
перед классическими методами интегрирования дифференциальных
уравнений и перед некоторыми другими методами интегральных
преобразований.
Во-первых, процесс применения интегрального преобразования
Лапласа однотипен для задач самого различного характера и различных
форм тела, способ решения является более прямым, не требующим
особого искусства и подхода к решению каждого нового типа задач.
Во-вторых, интегральные преобразования Лапласа позволяют
одинаково хорошо решать задачи при граничных условиях первого, второго,
ОСНОВНЫЕ МЕТОДЫ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ
55
третьего и четвертого родов, без введения каких-либо новых
допущений или преобразований.
В-третьих, наличие большого числа простых теорем позволяет
получить наиболее подходящие для конкретной обстановки результаты; в
частности, получать решения в форме, удобной для расчета при малых
и больших значениях времени.
В-четвертых, этот метод позволяет особенно легко решать задачи с
простыми начальными условиями; наиболее эффективно использование
преобразования Лапласа по временной координате, а также по
пространственной координате для тел, имеющих неограниченную или
полуограниченную протяженность.
В-пятых, эффективность решения разнообразных задач методом
преобразования Лапласа в значительной мере усиливается наличием весьма
подробных таблиц изображений.
Интегральное преобразование Лапласа имеет свои недостатки. В
частности, известные трудности возникают при решении задач, когда
начальные условия заданы в виде функции пространственных координат,
или при решении некоторых многомерных задач. В этой связи был
предложен ряд методов интегральных преобразований по
пространственным координатам в соответствии с геометрической формой тела.
Если преобразование берется по пространственной координате ху то
интегральное преобразование функции f(x) может быть представлено
так:
\fip)\p.H=lKiP,x)f(x)dx.
A9)
/:
Если ядро преобразования К(р> х) берется в виде!/ A sin px или
— cos px, то это интегральное преобразование соответственно назы-
вается синус- или косинус-преобразованием Фурье. Если же ядром
преобразования выбрана функция Бесселя /С(р, х) = xJ^ (px), то оно носит
название преобразования Ханкеля. В частном случае, если пределы
интегрирования изменяются от —оо до +°°» а ядро имеет вид К(р, х) —
——_ exp (ipx), то получаем комплексное интегральное преобразование
Фурье. Комплексное преобразование Фурье удобно применять для тел
неограниченной протяженности, синус-преобразование Фурье следует
использовать, когда на поверхности тела задано значение функции, т. е.
имеют место граничные условия первого рода, а
косинус-преобразование Фурье— когда решаются дифференциальные уравнения переноса
при граничных условиях второго рода. Преобразование Ханкеля
применяется в том случае, когда тело имеет осевую симметрию.
Практическое применение названных интегральных преобразований после
появления подробных таблиц изображения не вызывает особых
затруднений.
В тех случаях, когда использование преобразований Фурье
оправдано, а значения интересующих нас изображений отсутствуют,
оригиналы изображений можно найти по следующим достаточно простым
формулам обращения для:
комплексного преобразования Фурье
/(*) = у= J [/(PIf exp( -ipx)dp9 B0)
56
Глава третья
синус-преобразования Фурье
09
/(*) = yi J [/8(p)]fs sin px dp, B1)
0
косинус-преобразования Фурье
со
fix) = yi J [/c(p)]Fc cos px dp, B2)
0
преобразования Ханкеля
/W=Jr[A(p)]HA(pr)dp. B3)
о
Особенностью названных преобразований является то, что верхний
предел интегрирования равен бесконечности. Если в преобразовании
Лапласа A), которое в большинстве случаев применяется по отношению
к временной координате, бесконечный предел интегрирования
обусловлен самим ходом нестационарного временного процесса, то в
преобразованиях Фурье и Ханкеля B0—23) по пространственным координатам
наличие бесконечного предела суживает круг применения этих методов.
Другими словами, интегральное преобразование B0)—B3) успешно
можно применять только к задачам для тел полуограниченной
протяженности. Кроме того, следует отметить, что при использовании
преобразований Фурье, особенно синус- и косинус-преобразований, необходимо
обращать большое внимание на сходимость интегралов, так как
условия сходимости здесь становятся более жесткими, чем условия
сходимости соответствующих интегралов для преобразования Лапласа.
Конечные интегральные преобразования. Ограниченность
интегральных преобразований Фурье, Ханкеля и отчасти Лапласа, с одной
стороны, и острая необходимость в решении задач с конечной областью
изменения переменных, с другой, привели к созданию методов
конечных интегральных преобразований. Даже в тех случаях, когда эти
методы позволяют решать круг задач, который решается классическими
методами с помощью рядов Фурье или Фурье—Бесселя, им следует
отдать предпочтение. Простота методики решения — ее «стандартность»—
дает методу конечных интегральных преобразований большие
преимущества перед классическими методами, хотя математически он
эквивалентен методу собственных функций.
Впервые идея метода конечных интегральных преобразований типа
[f(p)]F,H = !JK(p,x)f(x)dx
была предложена Н. С. Кошляковым [37]. Наиболее полно теория
таких интегральных преобразований была разработана Г. А. Гринбергом
[14], который дал обобщение этих методов на случай скачкообразного
изменения свойств среды в направлении той координаты, по которой
производится преобразование. Детальная разработка интегральных
преобразований с конечными пределами была проведена Снеддоном [72],
Трантером [75], Дейчем [23] и др.
Если граница интегрирования заключается между 0 и Л ядра
конечных синус- и косинус-преобразований Фурье, а также
преобразования Ханкеля соответственно имеют вид:
ОСНОВНЫЕ МЕТОДЫ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ
57
К(р, x) = sintf'; B5)
К(р, х) = cos [х л:// B6)
(при граничных условиях первого и второго родов р. = п те, а при
граничных условиях третьего рода р- являются корнями уравнения ц tg ^ =
-а/А);
*(р. *)=r/v((.-f), * B7)
где р — корень уравнения Jv (|л) = 0 (граничные условия
первого рода), при граничных условиях третьего рода ц определяется из
уравнения
/» = -^/>). B8)
Формула обращения обычно находится при помощи разложения
функции в ряды по ортогональным функциям соответствующей задачи
Штурма— Лиувилля. Поэтому решения, получаемые этими методами, имеют
те же принципиальные недостатки, как и решения, получаемые
классическими методами. Так, формулы обращения имеют вид:
для синус-преобразования
f (х) = — 2л fs (n) sin n ъ x\U B9)
для косинус-преобразования
00
/(*) = T/c@) + -f-£/c(n)cosn**/Z C0)
л=1
при граничных условиях второго рода и
£ + (* W2
SV-n ""Г Ка ЧЧ
Г^+ « /А1+-/А /сЫC0S*nХП
C1)
при граничных условиях третьего рода, где суммирование ведется по
всем положительным корням уравнения \х tg у. = а //X;
для преобразования Ханкеля
2 V» «/„ fan ХИ)
f (х) = -я- L /н Ы г^,р" > C2)
Км Г '
где суммирование ведется по всем положительным корням /v (jx) --- 0 ,
или
я=1
где суммирование ведется по положительным корням B8).
Преобразование Ханкеля B7) применяется при решении задач
теплопроводности для сплошного цилиндра. Для полого цилиндра в
преобразовании Ханкеля ядро преобразования К(р> х) берется в ином виде
(см гл. IV и VI).
В целях преодоления упомянутых выше трудностей были
разработаны различные методы приближенных интегральных преобразований, в
58
Глава третья
которых прямое преобразование и обратный переход осуществлялись по
приближенным формулам. Вместе с тем возникла идея разработки
метода так называемых конечных интегральных преобразований Лапласа,
или, правильнее, конечных интегральных преобразований Грина.
Остановимся на последнем вопросе несколько подробнее.
Формулой обращения интегрального преобразования Лапласа в общем
случае является интеграл Римана — Меллина (см. гл. XIV). Эта формула
позволяет получать решения в интересующей нас форме, в том числе
в замкнутой форме. Идея метода состоит в том, чтобы выбор ядра
интегрального преобразования /С(р, х) осуществлялся в соответствии с
дифференциальным уравнением и граничными условиями, т. е. с учетом
геометрической формы тела и законом его взаимодействия с окружающей
средой. Другими словами, ядром преобразования является функция
Грина для данной задачи. Изображение функции f(x) получается с помощью
интегрального преобразования
1/(P)]G=J ^(P> x)f[x)dx%
C3)
а обратное преобразование по формуле B), где вместо [/(s)]L следует
подставить [/(p)]G.
Такой способ интегрального преобразования имеет и свое физическое
обоснование, Дело в том, что любое интегральное преобразование,
взятое по пространственным координатам, является с физической точки
зрения некоторым усреднением исследуемой физической величины. Вполне
естественно, что это усреднение должно быть сделано не только в
соответствии с характером прсц?сса и формой тела (видом
дифференциального уравнения), но и в соответствии с граничными условиями.
В этом случае решение для изображения функции будет представлять
самостоятельный интерес, поскольку такое преобразование в физическом
отношении будет представлять переход от анализа актуальных значений
исследуемых функций (дифференциальное уравнение, условия
однозначности) к усредненным значениям, сделанным в соответствии с
конкретной постановкой той или иной физической задачи. Таким образом,
методы интегрального преобразования приобретают новое весьма
существенное преимущество перед классическими метода ни, так как
они дают возможность получить ряд закономерностей протекания
физических процессов на оснсвг анализа решения для усредненных
значений исследуемой физической величины (анализ решения для
изображения). Это обстоятельство сближает данные аналитические
методы с методами теории подобия.
Особые преимущества интегральных преобразований обнаруживаются
при решении систем дифференциальных уравнений в частных
производных. Методика решения систем уравнений при этом принципиально не
отличается от методики решения отдельных уравнений и
осуществляется рядом последовательных операций. Например, для одномерных задач
теплопроводности, зависящих от координат и времени, необходимо:
1) на основе анализа дифференциального уравнения и краевых
условий выбрать подходящее интегральное преобразование или группу
интегральных преобразований;
2) умножить дифференциальное уравнение и граничные условия на
выбранное ядро преобразования и проинтегрировать полученные
выражения в соответствующих пределах по переменной, подлежащей исклю-
ОСНОВНЫЕ МЕТОДЫ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ
59
чению; в результате вместо системы дифференциальных уравнений в
частных производных относительно оригинала функций получим
систему обыкновенных дифференциальных уравнений для изображений
функций, которые учитывают начальные (при использовании преобразования
Лапласа) или граничные (при использовании преобразования Фурье)
условия;
3) решить обыкновенное дифференциальное уравнение относительно
преобразованных функций. (Если решение полученного уравнения
вызывает известные трудности, то к нему следует еще раз применить
подходящее интегральное преобразование относительно второй независимой
переменной. В результате преобразования получаем алгебраическое
уравнение, решение которого более элементарно. После нахождения
выражений для дважды преобразованных функций применяют к ним об:*
ратное преобразование. Получаемое решение и будет являться решением
искомого дифференциального уравнения);
4) уточнить выражения произвольных постоянных, содержащихся в
решении уравнения, для чего используются краевые условия
рассматриваемой задачи;
5) используя известные соотношения между изображением функции
и ее оригиналом или формулы обратного преобразования, найти оригиналы
преобразованных функций, а следовательно, и окончательное решение
задачи.
§ 4. МЕТОДЫ ЧИСЛЕННЫХ РЕШЕНИЙ ЗАДАЧ
ТЕПЛОПРОВОДНОСТИ И МОДЕЛИРОВАНИЯ
Методы математической физики, в частности методы интегральных
преобразований, позволяют эффективно решать сравнительно узкий круг
задач теории переноса. При рассмотрении систем дифференциальных
уравнений с весьма общими краевыми условиями точные методы
решения наталкиваются на большие трудности, которые становятся
непреодолимыми при рассмотрении нелинейных задач. В этих случаях
приходится обращаться к тем или иным численным методам решения. Важно
отметить, что использование численных методов зачастую позволяет
отказаться от упрощенной трактовки математической модели процесса,
В настоящее время практически наиболее ценным методом
приближенного решения уравнений теплопроводности является метод конечных
разностей, или, как его еще называют, метод сеток.
Метод конечных разностей основан на замене производных их
приближенным значением, выраженным через разности значений функции
в отдельных дискретных точках — узлах сетки. Дифференциальное
уравнение в результате таких преобразований заменяется
эквивалентным соотношением в конечных разностях, решение которого
сводится к выполнению несложных алгебраических операций.
Окончательный результат решения дается выражением, по [которому значение
«будущего» потенциала (температуры) в данной точке (узле) является
функцией времени, ее «настоящего» потенциала и «настоящего»
потенциала смежных узловых точек. Повторяемость одинаковых операций при
расчете полей температуры создает большие удобства для применения
современной вычислительной техники, благодаря чему эффективность
работы во много раз увеличивается.
Приближенную замену первой и второй производных через
разностные отношения можно провести элементарно следующим образом. Пусть
дана функция y=^f{x), график которой представлен на рис. 3.1. Если
60
Глава третья
через (xt обозначить угол,
образованный с положительным
направлением оси абсцисс касательной
к кривой, проведенной в точке
M{xt yt), то производная
функция при х = X} определится по
формуле
#;-tg<v A)
Возьмем на кривой две
соседние точки A (x^v у^) и Р (X; v yul)
так, чтобы разности xt — xhl —
= xt j — xt = h были бы
достаточно малы, и приближенно
заменим о. на р^ или 7/ (или, что
то же самое, рассмотрим вместо касательной МГ одну из секущих MP
или AM). Тогда
Рис. 3.1. К определению производной
функции / (х)
</;~tg^ =
QP
MQ
У1 1 - У1
или
У\ ~ tg Т/ =
вм
лв
Ух " Ум
h
B)
C)
Если же угловой коэффициент касательной МГ приближенно заменить
угловым коэффициентом секущей АР, то
Vi =
Ум — Ух
2h
D)
Правые части формул B)—D) называются соответственно: разностным
отношением вперед, разностным отношением назад и симметричныvi раз-
костным отношением.
Приближенное значение второй производнол у'[ функции y = f(x)
при х =Xi может быть получено элементарно, если заменить кривую на
участке АР ломаной линией AMPf имеющей в точке М два наклона, т. е.
E)
у",-
*/ 1
^w
1
h
(Ум —
\ h
Ж _
_ iL
— У\
h
-А
)
Ух
1 ~ *Ух
К1
+ Ух
-1
Разумеется, приведенные формулы B) — E) для замены производных
разностными отношениями не являются еди ственно возможными. Иногда
бывает целесообразно проводить другие замены, однако при численном
интегрировании уравнений теплопроводности наиболее часто применяют
именно эти формулы.
Рассмотрим, например, одномерное уравнение теплопроводности для
изолированного тонкого стержня длиной L:
9Г(х.ч) ^Wfr.*)., {0<X<L)
• dz дх2
F)
Так как функция Т (х, т) зависит от двух переменных х и т то
используем сетку прямоугольного типа (рис. 3.2). На оси абсцисс
откладываем отрезок длиною L и делим его на п равных частей. Полученный
ОСНОВНЫЕ МЕТОДЫ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ
61
i.k-Ч
i.k-1
i-Ч.к
ряд (к-И)
ряд (к)
ряд (к-1)
x=2h
x=th
k = L
шаг на оси абсцисс обозначим
через h = Lin. Точки деления
(узлы) на оси х имеют
абсциссы х = О, х = h , . . ., х = L. t=kl^
По оси ординат отложим
значения времени т через
равные промежутки /. Проводим »-2i|
через полученные узлы на осях г-1 *-
координат (на рис. 3.2 они от- <^*-
мечен.1 крестиками) прямые,
параллельное координатным Рис" 3*2* Схема Расчета по Тке пРногот^[
осям, которые образуют
прямоугольную сетку. Значения Т
в узлах, лежащих на осях координат и на прямой, параллельной оси
ординат и расположенной от нее на расстоянии L, находятся из
начального и граничных условий.
Задача приближенного численного интегрирования уравнения F) по
методу сеток состоит в нахождении приближенного значения функции
Т в каждом узле сетки.
Обозначим через Т t k истинное значение температуры в точке
стержня х = i h в момент т = к /, т. е. в узле, отмеченном на рис. 3.2,
символом i\ k.
Заменим частные производные -^ и yg- в точке (ih, kl) через
разностные отношения по формулам B)—E), т. е. положим:
дТ.
TL Л+1 ~~Т; k
д%
+ ч\
G)
<з2г,
/, k
дх2
Ti~\,k —2TL k + Ti+l, k
/г2
+ Ч\
(8)
где ег и е2 — остаточные члены, стремящиеся к нулю при стремлении
к нулю / и h Тогда в узле (ift, kl) дифференциальное уравнение F)
заменяется следующим соотношением:
Т1, АН-1 — Ti% k
+ Ч = а
_2 + e2j
или
T = (\ — 2*±\т
/a
/, A
/г2
(Г/-1.* + 71Ч-1.*) + 'Л
(9)
(Ю)
где i? = a s2 — elrf
Отбрасывая в A0) остаточный член /#, получаем разностное
уравнение
<♦ 6-М
= 1-
2/а
/а
'/, k
+ ^~(Vi. *+»*!.*)'
(И)
в котором через &. ^ обозначено приближенное значение величины
Tt k в том же узле (i'A, A/).
Формула A1) позволяет вычислять значения & в узлах
горизонтального ряда (k+l) по значениям &, находящимся только в одном
предшествующем ряду (k). Поэтому с помощью формулы A1) можно найти
62
Глава третья
значения Ь в узлах первого
горизонтального ряда (при т = /) по
известным из краевых условий значениям
температуры в узлах самой оси Ох
(при * = 0). Получив таким образом
значения Ь в первом ряду, по той же
формуле находим значения в узлах
второго горизонтального ряда (т. е.
при % = 21). Этот процесс
построения можно продолжать как угодно
далеко, так как значения
температуры в узлах прямых х = 0 и х = L
будут известны из граничных условий.
Формулу A1) можно вывести,
применяя законы Фурье и Ньютона к
составлению тепловых балансов
элементов, на которые разбито тело. Этот
способ вывода расчетных формул
широко практикуется в настоящее время многими зарубежными
исследователями.
Перепишем, следуя Д. Ю. Панову, формулу A1) в более удобном
виде (см. схему на рис. 3.3):
21а
Рис. 3.3, К выводу формулы A2)
^ = [1-
>0 +
la
(h + h)-
A2)
Выбирая соотношения между шагами / и А различным образом, из A2)
можно получить ряд частных соотношений. Так, например, при
I = Лг/3а
ал = :
при / = Л2/6а
при / = Л2/12а
и вообще при / =
ра
ь =&L+iV+A.
А 12
а h + (Р - 2) »„ + »2
Р
Особенно простой вид формула A2) получает при р = 2:
A3)
A4)
A5)
A6)
A7)
Эта последняя формула, называемая формулой Э. Шмидта, была
впервые получена Д. Ю. Пановым в 1938 г. и имеет большое практическое
преимущество по сравнению с формулой A4) и особенно A5), так как
при том же h величина / самая большая, а следовательно, и объем
вычислительной работы при применении A7) сокращается в 3 раза по
сравнению с A4) и в 6 раз по сравнению с A5). Следует отметить, из-
за своей простоты формула A7) широко используется при графическом
решении нестационарных задач переноса [56].
ОСНОВНЫЕ МЕТОДЫ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ
63
Исследования показывают, что при р=Л получаем уже
расходящуюся вычислительную схему. Вообще следует отметить, что при
решении нестационарных уравнений в частных производных
параболического типа вопросы соотношения между h и /, а также ошибка округления
в численном решении играют первостепенную роль, ибо ими
определяется сходимость и устойчивость получаемых решений. Из строгих
теоретических рассуждений следует:
1) пользоваться формулой A6) можно только при р>>2;
2) самый большой шаг / дает формула A7), т. е. при р = 2;
3) формула A6) тем точней, чем больше р.
Рассмотренная сетка для численного интегрирования уравнения F)
удобна, когда задача решается при граничных условиях первого рода:
i
4
1Т
1
i
—i
, ,
» <
п,кт|
А ,
^В ,
п-И,к
lC
Tn.k T Tn+i.k
> <
h
*2~
>
1
i—»-
Рис. 3.4. Расчетная схема для задачи нестационарной
теплопроводности (граничные условия третьего рода)
в этом случае граничные прямые х = О и x = L принадлежат самой
сетке. Если уравнение решается при граничных условиях третьего рода»
практика вычислений и теоретические исследования показывают, что
для повышения точности определения потенциала на границах следует
вводить дополнительные узловые точки, лежгщие вне изучаемой
области. Например, решая уравнение F) при граничных условиях
Vi =-г1Т(М-Гс]. If-) ~—J- IT(L,,)^TC],
дх/х^о X \ox/x=L a.
A8)
сетку надо строить так, чтобы правая граничная прямая лежала бы
посредине между двумя прямыми х = хп и х = xn+v а левая —
посредине между прямыми х = х0 и х = хг (рис. 3.4) (х = /г/2), т. е. в
рассмотрение вводятся значения &я+кл и &0 ^ — значения функции для то-
— | , входя-
дх Jx^L
щую во второе условие A8), т. е. в точке B(Lfkl), заменяем
симметричным разностным отношением
дх )x=l ~~ Л/2 + /г/2 + В '
A9)
а значение температуры на самой поверхности, т. е. T(L.kl), берем
как среднее арифметическое значение температур в точках А и С:
T(Lkl) =
' n.k
+ Гп + 1,<
Тогда условие A8) запишется так:
7\н_1. k ~~^л, k
+ е'
-х[-
k^~ Тп+\, k
т],
B0)
B1)
64
Глава третья
или, переходя к приближенным значениям Ь, получим после
преобразований
/ h а \ а _
V,.*-1 2 ' И а ■ B2)
1+тт
По этой формуле и находятся приближенные значения функции в узлах
вспомогательной прямой х = L + — .
Значение же температуры на самой граничной прямой х = L
определяется по формуле
Ь (I, kl) = ^i^±bJL , B3)
что после преобразований дает
А а
b{JL, kl) = -— f-^ = Vt+ ' , B4)
1 + '2 X
25+ /i
где
5 = X/2. B5)
Значение температуры в узлах вспомогательной прямой ж=— —
находится по формуле
6 а \ а ...
v 4 =, _Л11^п^^т^_ B6)
1 ^ 2 X
На левой поверхности получим
h
»@, /И) - ___fLJL_ = __ЬА!—1. B7)
1+Т'х
25 + h
Методика решения дифференциального уравнения теплопроводности
с источниками не отличается от изложенной выше. Метод конечных
разностей позволяет успешно решать как одномерные, так и двух- и
трехмерные задачи. Случай, когда на область изменения переменных
х и у наносится квадратная сетка, полностью исследован Ш. Е. Мике-
ладзе [49]. Треугольные и полярные сетки рассмотрены П. П.
Юшковым [86, 87] и некоторыми другими авторами [83]. Необходимо
отметить, что полярные сетки особенно удобны для решения задач с осевой
симметрией. Нахождение температурного поля в пространстве трех
измерений при постоянных теплофизнческих характеристиках дано в
работе [87], а при переменных — в работах [5,89]. Все эти вопросы
достаточно подробно изложены в монографиях [66,87].
Метод конечных разностей, как показал П. П. Юшков, позволяет
эффективно решать также систему дифференциальных уравнений
теплопроводности как при постоянных [86,87], так и при переменных [86]
коэффициентах.
Описанный выше метод носит название явного, поскольку выражает
значение 8- в момент т^+1 через значение в момент ^.
ОСНОВНЫЕ МЕТОДЫ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ
65
Несмотря на простоту вычислительных формул, он имеет
существенный недостаток, связанный с ограничением р%>2п, где п —
размерность пространства.
Поскольку при этом /~А2, требуется произвести очень много
шагов по времени, чтобы проследить поведение решения на протяжении
достаточно продолжительного периода, например до Fo~l.
Детальный анализ этого положения показывает, что при попытке
увеличить шаг по времени начинают быстро возрастать сильно
колеблющиеся по пространственным переменным компоненты решения. В то
же время для медленно меняющихся (и по пространственным
переменным, и по времени) гладких компонент сохраняются условия хорошей
аппроксимации, и здесь не наблюдается каких-либо особенностей.
Поскольку в реальном процессе наступает быстрое сглаживание всех
особенностей, а сильно колеблющиеся компоненты решения быстро
затухают, ограничение на l2/h2 представляется искусственным и связанным
только с особенностями построения вычислительной схемы»
От таких недостатков свободны неявные схемы, в которых
увеличение / достигается за счет того, что на каждом временном шаге
приходится решать систему уравнений. При этом в случае одной
пространственной переменной решение достигается небольшим числом операций
благодаря трехдиагональному виду матрицы этой системы. В качестве
„ an
примера рассмотрим шеститочечную схему, в которой
аппроксимируется по формуле
. . . -4- А \ 4- / А. . 9А. . 4- А. .. Л [
|<28>
в то время как —^ производная по времени аппроксимируется
по прежней формуле G).
Нетрудно убедиться, что для достаточно гладкой функции состав-
ленная из этих выражений приближенная формула для ——- — а •
\дЧ (»*-it |_1-2&А-1
\дх* ~
./ + »*-!
, /+1) + (h, /-1 — 2ht i + h, t+i)
2h?
д% dx%
имеет ошибку О (А2 + l2) для точки х = ih, x = ( k ) /. Поэтому
уравнение является неоднородным, значение правой части следует брать
в этой точке.
Известно, что уравнение
l
__ „ (h-u i-i — 2$k-u i + h-i, /+i ) + (**, /~i — Щ, i + h, i+x) , ft ,0Qv
-a— —^ _ + f i ^y)
устойчиво: и его решение при А-^0, /-^0 сводится к решению
дифференциального уравнения теплопроводности.
Большое многообразие неявных методов и способов решения,
получающихся на каждом шагу систем уравнений, а также методы выбора
ионов й и / приводятся в книгах [66,20].
Здесь покажем только, как в случае одной пространственной
переменной решать систему уравнений на каждом слое. Нетрудно убедиться,
что B9) для неизвестных { $k ^ можно переписать в виде
».i-i-2A + --^)Vf + **.i+i = *i'
C0)
3 Заказ № 640
66
Глава третья
где Вь образованы из fk^x t и значений bk_x v которые известны.
Пусть краевые условия (первого, второго или третьего рода) имеют
вид
,= 4$L
C1)
при этом ос<^1 и 7<Л. Будем искать зависимость вида
h,i=Pih.i-i + 1i< C2)
которой должно удовлетворять решение C0).
Определяя bfc t_x при помощи C2) и используя C0), имеем
»*,i-i - [2 A + -%г)-Рм]А.* = Pi-^i- C3)
Потребуем, чтобы C3) было следствием C1); так как коэффициенты
при одинаковых & и свободные члены должны быть пропорциональны,
будем иметь
Pi =* —г #Ц ; Ц% = Pi {Вi — <7i+1). C4)
По этим формулам можно найти pt(i = N—1, N — 2, . . ., 1), на*
чиная с pN = т- При этом будет \pt\ <
я2
1 + 2-
at
Зная р^, вычисляем ql(i = N—I» . . ., 1; = S).
Взяв C2) при t = 1 и первое из соотношений C1), решим
систему уравнений для ftk 0 и $k {; неравенства а< 1 и \р±\ <
1 + 2——
al
обеспечивают ее разрешимость. По соотношениям C2) находим
последовательно все остальные Ьк .. Ввиду полученных для pt
оценок в этих операциях не будет происходить существенного накопления
и роста погрешностей. Этот метод носит название метода прогонки
[Па].
Численные методы решения имеют большие потенциальные
возможности, однако до последнего времени их широкое применение к решению
уравнений переноса сдерживалось большим объемом вычислительной
работы. Быстрое развитие и распространение счетнорешающей техники
кардинально меняет их роль в исследовании явлений переноса. Если
новые электронно-вычислительные устройства дискретного типа
предназначены для выполнения трудоемких вычислительных операций, то
некоторые устройства непрерывного типа могут также выполнять роль
физических моделей.
Использование моделей для исследования явлений переноса
основывается на формальной одинаковости в аналитическом описании ряда
процессов, которая является следствием далеко идущего соответствия
в поведении сравниваемых систем, их аналогии. «Единство природы, —
писал В. PL Ленин, — обнаруживается в «поразительной аналогичности»
дифференциальных уравнений, относящихся к разным областям
явлений» (В. И. Ленин, Собр. соч., изд. IV, т. XIV, стр. 276). Метод моделирова-
ОСНОВНЫЕ МЕТОДЫ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ
67
ния позволяет исследовать процессы реального объекта с помощью других
процессов, протекающих в модели. Решение, полученное на аналоговой
модели, естественно, не будет носить аналитического характера, но оно
может быть успешно выполнено экспериментальным путем, после чего
выражено в параметрах первоначальной задачи." Наибольшее
распространение в настоящее время имеют модели, построенные на
гидравлической, электрической, механической и акустической аналогии процессов.
Гидродинамическая аналогия, основанная на тождественности в
формально математическом смысле между функцией тока и
потенциалом скорости идеальной жидкости в невихревом потоке и между
функцией теплового потока и температурой в системе без
источников тепла, была использована Муром и другими авторами для
решения двухмерных задач стационарной теплопроводности [83]. В
дальнейшем область применения этой модели была расширена на системы
с распределенными источниками [111]. В 1928 г. Эмануэлем и несколько
позднее Д. В. Будриным были сконструированы и построены модели,
основывающиеся на аналогии математических соотношений,
описывающих распределение температуры в твердом теле и распределение
напоров в воде, движущейся через капиллярные трубки [3]. Установки,
названные гидравлическими интеграторами, позволили решать задачи
нестационарной теплопроводности. В. С Лукьяновым позднее был
разработан ряд интеграторов для решения двух- и трехмерных задач
теплопроводности [39], а Будриным [3] — гидростатические интеграторы
для решения нелинейных уравнений переноса параболического типа.
Подобно методу гидродинамической аналогии М. Б. Койл [34]
разработал метод воздушно-аэродинамической аналогии. Принцип работы
его установки похож на работу гидростатических интеграторов Будрина.
Количество тепла и температура в теплопроводящей системе здесь
соответствуют количеству воздуха и давлению. Были предложены и
другие виды гидродинамической аналогии, например аналогии,
построенные на соответствии, между переносом тепла и переносом жидкости в
пористом теле, т. е. между законами Фурье и Дарси [103].
Ценность гидродинамических моделей снижается из-за громоздкости
установки,, сложности ее эксплуатации и некоторых трудностей при
решении задач с переменными теплофизическими характеристиками.
Наиболее широкое применение для исследования явлений переноса
тепла и вещества находит электрическая аналогия. Необходимое для
этой цели оборудование портативно, дешево, может быть выполнено
достаточно просто и с большой степенью точности. К тому же
электротехника обладает весьма совершенными приборами и методами
измерения электрических величин.
Электрическая аналогия основана на формальном сходстве
дифференциальных уравнений теплопроводности, с одной стороны, и
уравнений электропроводности, с другой. Вместе с тем аналогия между
рассматриваемыми процессами идет дальше идентичности
соответствующих уравнений переноса. Последнее становится ясным из сравнения
электрических и термических величин. Анализ соответствующих
уравнений показывает полную возможность воспроизводить нестационарные
поля потенциала теплопереноса средствами электрической аналогии при
различных граничных условиях, равно как и при различном характере
распределения источников.
Электрическая аналогия реализуется многими экспериментальными
установками. Моделирующие устройства, в которых воспроизводится
геометрия оригинала, а модель изготовляется из материала с
непрерывной проводимостью, называются геометрическими аналогами, или моде-
3*
68
Глава третья
лированием полей методом сплошных сред. Если же модель
представляет собой эквивалентную электрическую цепь с сосредоточенными
постоянными, то устройство называется моделирующей цепью.
Удобной моделью для нахождения поля потенциалов в проводнике
служит электролитическая ванна. Довольно широкое применение
электролитических ванн обеспечило однородность жидкой моделирующей
среды, возможность создания моделей больших размеров и сравнительно
легкий доступ в жидкости к внутренним точкам области при
моделировании объемных полей.
Электрические аналоги с жидкими моделями основаны на
использовании ионной проводимости электролитов. В качестве проводника берется
электролит (слабые растворы солей, кислот и щелочей, растворы
различных купоросов и др.) с постоянным удельным сопротивлением.
Модели бывают объемные и плоские. Их форма должна быть тождественна
форме исследуемого тела — оригинала. Граница ванны должна иметь
потенциал, пропорциональный температуре на границе оригинала, что
осуществляется применением металлического проводника, по которому в
электролит подается электрический ток. На подобной модели, например,
Ленгмюром, было проведено исследование теплопередачи через стенки
оболочки в форме параллелепипеда [47]. В случае моделирования
потенциалов переноса в неоднородном поле применяется электролит с
переменной концентрацией или создается ванна с переменной глубиной [73].
Моделирующим устройством, работающим по принципу
геометрического аналога, являются также модели из твердых электропроводящих
материалов и покрытий.
Для моделирования плоскопараллельных полей известное развитие
получили модели из тонкого листа электропроводящего материала. В
качестве такого листа используется металлическая фольга,
металлизированная бумага или нормальная бумага, на которую наносится слой
электропроводного графита с определенным сопротивлением (например,
теледельтос-бумага). Лист вырезается по форме, тождественной оригиналу.
Электроды приклеиваются или наносятся хорошо проводящей краской.
Соответствующим подбором последних достигается задание граничных
потенциалов. Источники задаются с помощью электродов из фольги,
приклеиваемой проводящим клеем в соответствии с чертежом на обратной
стороне листа. Площади с разными коэффициентами теплопроводности
или массопроводности воспроизводятся путем перфорирования листа
квадратными отверстиями или склеиванием отдельных участков из
нескольких слоев бумаги.
При моделировании объемных задач прибегают к твердым сплошным
средам. Применяются дисперсные среды разной проводимости, например
графитовый порошок в смеси с кварцевым песком, или коллоидные массы
(желатин) [47].
Возможность использования электрических сеток для целей
моделирования впервые была обоснована в 1926 г. русским математиком
С А. Гершгориным. Одним из достоинств сеток является то, что
координаты их точек являются электрическими, а не геометрическими. Это
обстоятельство позволяет решать на прямоугольных сетках задачи в любой
системе координат. Гибкость схемы создает большие удобства при
изготовлении модели и обеспечивает ее надежность в эксплуатации.
Для получения модели исследуемое тело разбивается на ряд
элементарных объемов, как в методе конечных разностей. Значение потенциала
находим для конечного числа выбранных точек, т. е. непрерывное поле
потенциалов в теле заменяется их «эквивалентными» сосредоточенными
значениями. Электрическая сетка, или, как ее еще называют, модели-
ОСНОВНЫЕ МЕТОДЫ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ
69
рующаяцепь, составляется из параллельно включенных электрических
емкостей, сосредоточенных в узловых точках сетки. Источники тока и
вещества воспроизводятся включением источников питания в одну или несколько
узловых точек сетки для случая сосредоточенных-источников или во все
узловые точки для равномерно распределенных источников.
Для моделирования стационарных и нестационарных полей
температуры были разработаны и построены различные типы универсальных
электрических сеточных моделей — электроинтеграторов; например, для
исследования плоских стационарных полей потенциалов при граничных
условиях первого, второго и третьего родов — электроинтеграторы ЭИ-11
и ЭИ-12 системы Л. И. Гутенмахера, для исследования нестационарных
полей с коэффициентами, зависящими от координат, —
электроинтеграторы ЭИ-22, ЭИ-21, ЭИ-31. Эти модели позволили решить многие
важные задачи из различных отраслей науки и техники [8].
Эффективные моделирующие устройства были созданы за границей.
Из них следует отметить установки Бойкена в Голландии, Пашкиса,
Мак-Канна и Либмана в США, Лаусона и Джексона в Англии, Фишера
и Мюллера в Германии и др.
Особый интерес представляет модель Либмана [105] для решения
нестационарных задач с помощью сеток сопротивления. В модели
создавались возможности прерывать решения, т. е. счет в этой модели
осуществляется использованием явной конечно-разностной
пространственной и временной аппроксимации. Последнее, подобно
гидростатическому интегратору Д. В. Будрина, позволяло определять температурные
поля с учетом анизотропии и изменения теплофизических характеристик
вещества в зависимости от температуры.
Недостатком модели Либмана является ее сравнительно малая
универсальность: для каждой новой задачи необходимо менять величину
всех сопротивлений, Этот недостаток устранен в новых статических
(емкостных и омических) интеграторах, созданных в проблемной тепло-
физической лаборатории Казахского государственного университета им.
С. М. Кирова [9]. Подробный обзор применения различных
электрических моделей для решения теплофизических задач можно найти в
работах [32, 34].
Для исследования и расчета процессов тепло- и массопереноса
используются и другие виды аналогий. В частности, за границей
достаточно широкое распространение для решения задач по определению
объемно-напряженного состояния тела и задач стационарной
теплопроводности с источниками тепла получила мембранная аналогия [83].
Методы численного решения и аналогий применяются в тех случаях,
когда решить задачу в замкнутой форме не представляется возможным
или когда полученные решения настолько сложны, что не могут быть
использованы для практического расчета. Выбор между методами
численного решения и аналогий зависит от конкретной задачи, требований,
предъявленных к расчетным данным, и оценки затраты времени для
решения поставленной задачи с заданной степенью точности.
ГРАНИЧНОЕ УСЛОВИЕ ПЕРВОГО РОДА
4
Из большого количества задач, которые могут быть рассмотрены
в данной главе, остановимся только на основных классических задачах.
В граничных условиях первого рода задается температура
поверхности тела как функция времени. Рассмотрим простейшие случаи,
когда температура поверхности тела остается неизменной на протя*
тении всего процесса теплообмена. Это достигается при помощи
специальных приборов, поддерживающих постоянную температуру на
поверхности тела, или путем теплообмена между телом с окружающей
средой, происходящего с постоянной температурой по закону Ньютона
(граничное условие третьего рода), но с бесконечно большим
коэффициентом теплообмена а, точнее, когда Bi-^ со. В этом случае граничное
условие третьего рода превращается в граничное условие первого рода в
простейшем его виде.
Задачи, в которых температура поверхности тела есть заданная
функция времени, будут рассмотрены в гл. VII как частный случай
решений более общих задач.
Все решения задач, которые будут рассмотрены в этой главе, могут
быть получены из соответствующих решений задач гл. VI, если
положить в последних критерий Био равным бесконечности. Такое выделение
данных задач в специальную главу методически целесообразно, так как
показывает читателю постепенное усложнение техники расчета.
Применяя методику расчета вначале к более простым задачам,
читателю легче усвоить технику расчета и установить преимущества и
недостатки того или иного метода, в частности преимущества
операционного метода решения задач по сравнению с классическим.
Прежде чем перейти к решению первой основной задачи (нахождение
температурного поля в полуограниченном теле), рассмотрим
вспомогательную задачу.
§ 1. НЕОГРАНИЧЕННОЕ ТЕЛО
Если имеется -твердое тело, размеры которого очень велики по
сравнению с интересующими нас участками его, то тело можно считать
неограниченным. При этом необходимо, чтобы заметное изменение
температурного поля происходило только на данном участке тела.
71
Вначале рассмотрим задачу, когда температура изменяется только
в одном направлении х; в двух других направлениях у и z температура
/ дт дт, л п
не изменяется = = 0 . Следовательно, изотермические поверх-
\ ду dz J
ности будут представлять плоскости, параллельные плоскости yz.
В начальный момент времени задано распределение температуры по
направлению х в виде некоторой-функции Т(х, 0) = f(x). Требуется найти
распределение температуры в любой момент времени в направлении х.
Наша задача связана с решением дифференциального уравнения
теплопроводности
дТ(х, т) ___ &Т(х,х)
dz
дх2
(т>0; _co<jt<+oo)
A)
при заданном распределении температуры в начальный момент времени:
Г(*,0) = /(*). I B)
Граничные условия отсутствуют, но их можно заменить условием,
учитывающим неограниченность размеров тела
дТ (+OQ, т) __ ОТ (—оо , т) _ ^
дх дх
C)
Решение задачи можно получить по методу Фурье, но при этом на
функцию f(x) накладываются определенные ограничения, связанные с
возможностями представления функции f(x) в виде интеграла Фурье.
Для этого достаточно потребовать, чтобы существовал интеграл
+f\f(x)\*dx.
— 00
Поэтому здесь приводится решение по методу источников, который
не требует этих ограничений для функции f(x). Решение по методу
Фурье будет дано в конце настоящего параграфа.
В § 2 гл. III было показано, что частное решение уравнения (I)
имеет вид
Т =
Уа%с
■ехр
(*-8J
4ат
D)
Рассмотрим это решение. Из анализа выражения D) видно, что при
заданном времени т кривая распределения температуры в направлении
х имеет максимум, который приходится на расстояние х = 6 (рис. 4.1).
Площадь S под кривой, т. е. площадь, образованная кривой и осью
абсцисс, есть величина конечная и равная интегралу от выражения D)
в пределах —°о до +оо (начало координат переносим в точку £):
+ СО
5 =
-CJ
1/4*
-ехр
(*-iJ
4az
\d(x — £) =
Y~ir
J
Л—22
dz = С.
Здесь произведена замена переменной
72
Глава четвертая
так как известно, что
г
л~ -г2
£fe = У" 1С •
Таким образом, площадь под кривой равна постоянной С. Ордината
кривой в точке максимума равна — ■« Следовательно, с увеличением
У~4%а%
времени т ордината уменьшается и кривая становится более пологой
(см. рис. 4.1) и, наоборот, с уменьшением времени т ордината
увеличивается. При уменьшении времени (% -> 0) получается бесконечно узкая
полоска, но площадь ее сохраняется; она равна постоянной С.
Пользуясь этим свойством выражения D), можно заданное начальное
распределение температуры Т (х, 0) = / (х) в неограниченном теле пред-
Рис. 4.1. Распределение температуры в
неограниченной среде в случае действия
мгновенного теплового импульса
Рис. 4.2. Представление начального
распределения температуры как
суммы частных решений
ставить как сумму отдельных частных решений вида D), т. е. кривую
f(x) заменить суммой бесконечного множества кривых вида
hrn —z==r exp — ♦
При этом необходимо отметить, что, несмотря на бесконечно малую
ширину отдельной полоски d\ (рис. 4.2), высота ее будет величиной
конечной и равной /(I). Площадь такой полоски, равная С, будет
бесконечно малой величиной, т. е.
T(S,0)d5 = /(£)#= С.
Полное начальное распределение температуры в неограниченном теле
будет равно
-{-оо
lim T (х, т) = lim ' j / (S) exp [- -^^-]^. E)
<r-*0
t->0 уЧтсат
Это соотношение будет справедливо не только для начального мо-
ГРАНИЧНОЕ УСЛОВИЕ ПЕРВОГО РОДА
73
мента времени (т->0), но и для любого последующего промежутка
времени, т. е. общее решение нашей задачи будет иметь вид
F)
Можно общее решение F) переписать по-иному. Введем новую
переменную и по соотношению I = х + 2 У ахи. Тогда будем иметь
Т (х, т) = -Лг Г / (х+2Уоти) в"" da. G)
Уте J
—оо
Можно показать, что решение G) удовлетворяет дифференциальному
уравнению A) и начальному условию, гласящему, что при т->0
f(x + 2У^ахи) ->/(#). Следовательно, будем^иметь
+ 00 +00
Т(х, 0)=-L- Г f(x)e~u*du^f(x) -J— Г e~utdu = f(x).
Уте J Уте J
Можно сделать обобщение на случаи плоской и пространственной
задач. Именно, по аналогии имеем:
+ 00 +ОЭ
Т (х, у, т) = -JL- J j / (S, -г)) exp [- fr-Q' + fr-^] dW4, (8)
Г(*,
#, z,
■с)-
1
(У4теат
—oo —oo
+ 00
f Pf ftp ~,
— 00
C) exp Г—
i£z
ii)!
4crc
-ЦЯ
"]*
(9)
Решение нашей задачи можно получить и по методу Фурье.
В § 2, гл. III было установлено, что общее решение одномерной
задачи имеет вид
T(xt-z) = 2^Cns'mknxe n +2^Dmzoskmxe
-akmx
Так как граничное условие отсутствует, то можно считать, что
величины k образуют непрерывный ряд чисел и каждое последующее
отличается от предыдущего на бесконечно малую величину dk. Тогда
обе суммы перейдут в определенный интеграл, взятый от 0 до оо.
Кроме того, постоянные Сп и Dm будут некоторыми функциями от k.
Таким образом, имеем
оо
Т (х, т) = Г e~ak2x [fx (k) sin kx + /2 (k) cos kx] dk. A0)
о
Для определения ft(k) и f2(k) воспользуемся начальным условием
00
Т (х, 0) = / (х) = f [/Х (k) sin kx + /, (ft) coskt] dk. A1)
74
Глава четвертая
Т(*,т) =
оо -|-оо
~ Г e~akl4k \ /(?)cos[*(£-
0 ~оо
-*)]#.
Из теории рядов Фурье известно, что если заданная функция f(x)
удовлетворяет определенным условиям, то ее можно разложить в ряд
Фурье, который можно заменить через интеграл Фурье
00 -j-°°
/(*) = — \dk\ /E)[sin«sinfcc + cos«cos&c]rfe. A2)
О —оо
Сравнивая соотношения A1) и A2), приходим к заключению, что
введенные нами функции fx(k) и /2(&) равны, т. е.
-|-00 -f-00
fx(k)^-L f/(S)sin«d5, h{k) = -~ f/E)cos&d5.
— 00 —OO
Окончательное решение в форме Фурье нашей одномерной задачи для
неограниченного тела будет иметь вид
A3)
Решение F) или G) для неограниченного тела имеет для нас
вспомогательное значение. Оба эти решения удовлетворяют условиям
неограниченности C).
В нашем случае Т(х, т) ~* 0 при х~+ ± оо. Тепловой процесс в
таком неограниченном теле состоит из выравнивания температуры,
которое возникло в некоторый момент времени, принимаемый нами за
начальный. Это возникновение неравномерного распределения температуры
возможно в результате кратковременного действия некоторого источника
тепла (мгновенного источника тепла), мощность которого
пропорциональна /(I). Поэтому рассмотренный метод решения задачи часто
называют методом точечных источников. В гл. IX мы вернемся к этому
вопросу, а теперь перейдем к рассмотрению основных задач.
§ 2. ПОЛУОГРАНИЧЕННОЕ ТЕЛО
Имеем тело, с одной стороны ограниченное плоскостью yz, а с
другой стороны простирающееся в бесконечность. Такое тело называют
полуограниченным телом, например, бесконечно длинный стержень,
боковая поверхность которого имеет идеальную изоляцию.
Постановка задачи. Температура полу ограниченного тела во всех
точках имеет определенное значение, заданное некоторой функцией
/(х), т. е. Т(х, 0) = f(x). Будем решать задачу на охлаждение тела,
так как задача на нагревание всегда может быть сведена к задаче на
охлаждение путем замены переменной.
В начальный момент времени конец стержня принимает темпера-
туру Тс, которая поддерживается затем постоянной в течение всего
процесса теплообмена. Найти распределение температуры по длине
стержня в любой момент времени и потери тепла через конец его.
Задачу математически можно сформулировать следующим образом.
Имеем дифференциальное уравнение
1 ЭТ(х,х) =a_^TJ^)_ I (T>0;0<*<oo) A)
dz дх2 I
ГРАНИЧНОЕ УСЛОВИЕ ПЕРВОГО РОДА
75
при краевых условиях
Ti
Т(х,0) =
Т@, т) = Тс
дГ(+оо,т)
= const,
- = о,
B)
C)
-f(x)
-T(x,t)
W///////J///////////////////////t///////////////////i
Рис. 4.3. Распределение температуры
в полуограниченном стержне с тепловой
изоляцией боковой поверхности
причем отсутствует перепад
температуры в бесконечно удаленной
точке (см. рис. 4.3).
Вначале для упрощения расчета
положим Тс = 0.
Требуется найти Т (х, т).
Решение задачи классическим
методом^ Решение этой задачи может
быть получено из предыдущей (для
неограниченного тела). Для этого
продолжим стержень в
отрицательном направлении оси х, т. е. будем считать его неограниченным (рис.
4. 3). Начальная температура в точке х>0 равна f(x), а начальную
температуру в точке —х выбираем равной —f(x), т.е. считаем
функцию f(x) нечетной:
Тогда из соображений симметрии распределение температуры в
последующие моменты времени будет нечетной функцией, а для х = 0 ее
значение всегда будет равно нулю. Следовательно, условие на
поверхности выполняется.
При замене х на £ в кривой начального распределения температуры
общее решение на основании предыдущего имеет вид
{оо
Г /E) ехр Г ^=^-1Л +
J L 4ат J
о
—оо '
Запишем это решение в другом виде:
D)
Выражение D) есть общее решение нашей задачи.
Если начальная температура постоянна и не зависит от х
(температура стержня в начальный момент времени одинакова и равна Г0), т. е.
Т (х, 0) = Т0 = const,
то решение можно упростить. Подставив в первую часть
подынтегральной функции
5 = х +2иУал ,
а во вторую часть
£ = — х + 2u Y~ax ,
76
Глава четвертая
получим
х/2 Yen
ТЦх, т) = Т0 -L- Г е-иг du.
—х/2 Vax
Так как функция е~~и2 является симметричной функцией по
отношению к и, то можно написать
х/2 Vaz
Т(х.,) _ 2 р e—da = erf
\ 2V\k /
где интеграл
и
-^з- ( е~и* du = erf (и)
г о
называется функцией ошибок Гаусса.
Функция erf (г/) изменяется от 0, когда а = 0, до 1, когда и->оо
(практически, когда #>2,7, так как erf B,7) = 0,9999).
Если конец стержня поддерживается не при 0°, а при некоторой
температуре Т @, т) = Тс = const, то путем введения новой переменной
0 = Т—Тс наша задача сведется к вышерассмотренной, так как
0@, т) = Т@, т) — Тс = 0.
Следовательно, решение данной задачи можно написать так:
Т(х,х)-Тс =erf
То-Гс \2^;
F)
Решение задачи операционным методом. Применим преобразование
Лапласа к дифференциальному уравнению A):
L [Г (х, т)] = J Г (х, т) <TSX dT = TL(x, s).
где
В левой части уравнения надо взять преобразование Лапласа от
первой производной. Согласно основной теореме операционного метода,
оно равно произведению изображения на оператор s минус значение
функции в начальный момент времени, т. е.
№ d2Tr (х, s)
sTL(x, s)-f(x) = a-^r [L [T(x, z)]} = a £-- . G)
Таким образом, дифференциальное уравнение A) в частных
производных для оригинала функции Т(х, т) превращается в обыкновенное
дифференциальное уравнение для изображения Tl(x, s), так как TL(x, s)
не зависит от времени т. При этом переходе используется начальное
условие.
Перепишем уравнение G) в виде
T"L{x, s)-—TL(x, 8) + Ш = о. (8)
а а
ГРАНИЧНОЕ УСЛОВИЕ ПЕРВОГО РОДА
77
Рассмотрим более простую задачу, когда температура стержня до
охлаждения всюду одинакова и равна Т0, т. е. f(x) = TQ = const. В этом
случае уравнение (8) примет более простой вид
T"L (*, s)-± ]TL(x, s) ^.J '= 0. (9)
Общее решение данного дифференциального уравнения " для
изображения можно написать так (см. § 2, гл. III):
TL{X, s)--f = АгеУ * + Bxe V * , A0)
где Аг и Вг — постоянные, определяемые из граничных условий.
Применим преобразование Лапласа к граничным условиям:
L[T@,T)] = 0f TL@,s)=0. A1)
ь[дТ(+д"'Х)]==0, Ti(+oofs) = 0. A2)
Из условия A2) следует, что Аг = 0, так как в противном случае
первый член в правой части A0) неограниченно возрастает с ростом xf
а именно
о=т1(+оо,,)=1/-тгЛе^+") - у^Гв*-^*-*
откуда и следует А± = 0.
Воспользуемся условием A1)
0-.1и- = В1(Г*'* =В19 т. е. В1==- ^-,
тогда решение для изображения будет иметь вид
s
TL(x, s) =-A-exp(— Y— х)
Для нахождения оригинала воспользуемся таблицей изображений
функций, из которой известно, что
В нашей задаче k = —^~. Следовательно, решение упрощенной за-
Уа
дачи будет
откуда
erf —Ьг-Ь A3>
т. е. получаем то же решение E) для случая равномерного начального
распределения температуры по длине стержня.
Если температура конца стержня не равна нулю, а равна
Тс = const, то граничное условие A1) напишем так:
L[7@, %)]=L[TC], TL@, s) = Л. A4)
78
Глава четвертая
Следовательно, постоянная Вг = ——- , так как Т0 > Тс. Тогда
S
решение для изображения примет вид
Jjl_t (*, s)= То~~Тс Г*^х . A5)
$ s
Применяя аналогичный прием перевода изображения в оригинал, т. е.
обратное преобразование Лапласа, получим
Г0-Т(х,т) = (Г0-Тс)
где
1 - erf (—~А] - (Т0-Tc)erfc (—?—
erf с (и) = 1 — erf (и).
Это решение можно написать так:
T(x^)-Tc „erf/ ±—\, A6)
То — Тс \ 2"|/ат
т. е. получаем выражение, тождественное F).
Решение A6) непосредственно следует из A3), достаточно только
заменить начало отсчета температуры, но здесь приведены подробные
расчеты, чтобы показать применение преобразования Лапласа к
постоянным граничным условиям, отличным от нуля.
Решение поставленной задачи с заданным начальным
распределением температуры f{x) можно получить аналогичным путем, только
надо исходить из дифференциального уравнения (8) для изображения.
В результате получим то же решение D).
Решение задачи методом преобразования Фурье. В нашей задаче
температура Тс = 0 при х = 0. Начальная температура Т(х,0) =Т0 =
= const. Температура на бесконечно большом расстоянии не
изменяется, т. е. — ■ ■'%) = 0. Для удобства расчета задачу на охлаждение
дх
(Т0>ТС) сведем к задаче на нагревание путем введения функции
Ь(х, т) = Т0 — Т(х, т). Тогда граничные условия будут иметь вид
Ь (х, 0) = 0, & @, т) = Т0 — Тс = const,
>&_(оо,_т) _ Q \ A7)
дх
Так как задана температура на поверхности (х = 0), то воспользуемся
синус-преобразованием Фурье:
оо
Fs[${x, т)] = bF(*z, р) = Г Ъ(х, т)sinpxdx. A8)
о
Применим это преобразование к дифференциальному уравнению A):
Вначале вычислим преобразование от правой части уравнения
ГРАНИЧНОЕ УСЛОВИЕ ПЕРВОГО РОДА
79
DO
I
дЩ (х, х) _ а/ ч
sin рх v ; ах = — pv (x, т) cos px
*=о
+ ^(х> т) sin рх Г °° — р2 Г & (х, т) sin pxdx = р (Г0 — Тс) — p2&F (p, т),
A9)
так как при д; = оо &(оо, х) = 0 и О@, т) = Т0 — Гс; ^(<*W = 0.
Следя
довательно, имеем
^f = ар (Т0 - rj - ap2&F (р, т). B0)
Интегрируя уравнение (£0), с учетом начального условия, получим
&f (Р, т) = (Г°-Гс) [1 - ехр (-р2ат)}. B1)
Р
Воспользуемся формулой обращения
Ъ(х, т)
(П-Гс)
00
= —■ Г [1 — ехр (—р2ат)] sinpx
Р
Известно, что
Тогда получим
Гыпрх_ dp = _*_
О
оо
— f <T^sinpx----erf ,
о ч г
Г.-Г(*,т) =1__erf _
Го — Гс V 2 Vax
B2)
или
Г(х,т) — Тс
erf
2 У ах
т. е. решение A6).
Определение потери тепла. Определим потери тепла на конце
стержня при охлаждении. Потери тепла dQs за время d% через единицу
площади равны
Известно, что
д
дх
дТ
дх Jx=o
erf
_:=-Х(Г0-Гс)
дх
Terff—5_
L \ 2 у™
„=0
2Уа
)/"то2Х
ехр
4ах
При х = О экспоненциальная функция равна единице. Тогда получим
(в вт/м*):
^т . Утсах У™
B3)
80
Таким образом, скорость теплоотдачи с единицы поверхности, или
плотность теплового потока, прямо пропорциональна разнице темпе-
ратур (То — Тс), некоторому термическому коэффициенту ]Acf и
обратно пропорциональна У*. Следовательно, в первые моменты
времени скорость теплоотдачи бесконечно велика, а затем постепенно
уменьшается. Термическую постоянную jAc? называют коэффициентом
тепловой активности тела1), или коэффициентом аккумуляции тепла
е = |Аеу ; он измеряется в единицах дж/м2град-сек1/2.
Соотношение B3) можно было получить операционным методом,
а именно
L ш = - х JL [L [Т (х, х)])^0 д _ х dT^ s> ,
Дифференцируя по х решение A5) для изображения, получим
L[q\ = _ X J^I*. l/"X" е'Гт ° = - ГЩ(Т0-ТС)__!_ .
У а ут
Пользуясь таблицей изображения, находим
Я = -УЩ(То-Тс)-±~, B4)
т. е. получаем то же соотношение для скорости теплоотдачи.
Такой метод для определения теплопотери из решения для
изображения во многих задачах является наиболее простым.
Количество тепла, отдаваемого в течение конечного промежутка
времени т, найдем путем интегрирования в пределах от 0 до т, т. е.
Qs = Qs,o~ fe(T0-Tc)—L-^=QS@--^-(r0-Tc)VT
J У tzz У к
B5)
Таким образом, количество тепла (Qs,o — Qs), отдаваемого единицей
поверхности конца стержня, прямо пропорционально корню
квадратному из времени, разности температур (Т0 — Тс) и коэффициенту
тепловой активности.
Количество тепла, отдаваемого всем концом, площадь которого
равна 5, будет равно
bQ = -J±-{T0-TJSVT. B6)
Анализ решения. Напишем решение A6) в критериальной форме.
Отношение —L-L- является относительной избыточной темпе-
То-Тс
ратурой. Обозначим это отношение через 6, т. е.
а __7^^)-7с # B7)
T0-Tt
с
Отношение -^- является числом гомохронности для процессов чистой
х2
О О физическом смысле коэффициента тепловой активности тела см. в гл. X.
0,бг
III
0,02
0,04
Wfc
0,4t
O^h
0,2b
Clt
0,06
0,08 1—M),l
1 11 1111 m 1111 1 11 H HtffLIM 111111 11 111 1 1 1 1 1 1 1 1 1 1 1 |J
М I 1 J 1 1 J III || I I 1 I 1 I i^^Ll 1 1 1 1 1 1 II 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 \ \ Mil 1 1 Mill III 1 1 1 1 1 1 F^tJ II
Ml V 1 II 1 1 1 1 1 1 1 1 1 1 1 1 1 II 1 1 1 Tru III
I ч I II 1 II 1 II 11 MM 1 r%J. lii II
м i_ lv II Mill 1 1 1 11 1 III 1 МММ i^L т i 1 1 1 1 1 II 1 1 1 1 1
1 11 \ 1 1 1 1 1 1 It II 1 1 M 1 1 II 1 1 1 1 II II TnL 1 II I.I 1 1 II 1 II 1 1
"Hi 1 p T 1 itttt r
H\ iTv
1 ]v] 11 MI M1 II II 1 II II 1 1 1 1 1 II II Гл. 1 II II 1 1 1 1
1 1 ul III 111 11 [ 1 1 1 MM 11 II II M M Г ItlI 1 1 1 1 1 II1
Mil 1 Iwl Ml 11 11 1 1 II II 1 II1 II II 11 Mill 1л. 1 МММ
i v i II i 1 11II1 1 1 II Mill 1 МММ Mil II N. 1 1 1 М 1
1 1 1 1 1 1 1 II ik II 1 II 1 1 М 1 1 II II II II II II II М II 1 xl II 1 1
|1 MY \ г
\\\\\\ М 1 MrJ 1
| 1 J || \ М М 1 1 1 II 1 TL III \1 1
1 1 II 1 1\М 1 1 1 1 1 II 1 1 N. 1 1 II II II II 1 1 II 1 1 1 1 II 1 1 1 1 1 1 II 1 1 v 1
Mill l\ 11 11 I Ml I I I i\i 1 1 1 11 MM Mill 1 M
1 1 1 1 II \ 11 11 1 II 1 1 II 1 nI 111
II1111 M II1 11 1 11 III 1 plI I II Mill MM II Mil 1
МММ l\l 11 1 1 M II 1 1 1 ix II M M 11 1 II 1 II 1 1 1 1 1 M 1 1 II II 1
1 1 II 1 tUI \ll M II [NL 4- ii ill
11111 itI \l 111111111111 Till 11111111111II11111111II1 к
1 1 1 1 1 1 1 1 tilrW 1 1 1 1 1 III 1 1 f II |Sl 1 II 1 1 1 1 II II 1 1 1 1 1 II 1 II 1 1 1 I
i ifl Lii ш i ivl MM II II1 1 [ 11 1 TSk. Ill
llfll! it irJ II 1 II 1 11 1 III Гтк.1 II 1 1 1 1 II 1 II 1 III II 1 II 1
II 1 1 1 1 1 II II IrJ lllllllll IrJ lii ijllf) lllijl ijf III
■ j j j j 1 j j j I j Pvj M j M 1 1 M II II ipJ 1 1 II M II I-1 1 II 1 1 M II 1
II 11 11II 1 11 II ipJ. 11 II1 II 1 1 II 1 1 I^KL III III III 1 Mill
1 1 I 1 II 1 II 1 1 1 II lWk_l 111 1тк_1 II II II 1 1 II II II 1 1 I
1 1 1 III 1 II II Mill TrJ. Ill irJ. II II 1 1 II II II II 1 I
г 1 M II1 11 1 1 M 1 M 1 ГГ>4_ 1 iSL 1 и" Mil
1 1II 1 1 M 1 11 1 II II M II1 Гп4| II II 11 II 1 II 1 1гч1 III
1 1 II II II 1 1 1 1 II II 1 1 1 1 1 II iiPniJ III Гтч| lllllllll
■ 1111111111111111111111 МгЖт-Щ M mpU 111111
■ ■ ГГмМтНтт^^
1 11 1 II 1 M 11 II 1 M II 1 11 II II II II 11 II II 1 II 1 1 1 II 1 IT iTtJ
1 1 1 1 II111 II II 1 II II 1 1 1 1 II II II II 1 II 1 1 II II 11 II II M II П
IШ_11.Ш 11-lJ 1 1 111 lllllllll 1 1.111 1 1 1 I...IJ 1 111 1 1 1 1 II II к
1,0 ll.CK
11
J0,9
J0,8
H0,7 '0,9'
I
L0.9V
0,9t
Ш
0,2
0,4
0,6
0,8
J0r5
J,0
0
4.0
8,0
12,0
16,0
III-
20,0
Fox
Рис. 4.4. Зависимость между относительной избыточной
температурой 6 и числом Фурье Fo^ для полуограниченного стержня (случае
малых значений чисел Фурье
20 '40 60 80 -^^КХ
' 1 М\М 1 II II 1 II II 1 II II 1 II 1 1 М II II М 11 '1 1 М 1 1 II М II II М
11 1 Ii II 1 1 1 1 11 1 1 II 1 1 111 II 1 Mill 11 1 1 Ml 11 1 11 1111 М II 1 1
Hi
Bill
INI
1 M fill M II1 II 1 1 1 II II1 II 1 II1 1 M 11 II II II 1 11 1 II 1 II II 11
1 1 11« 1 1 1 1 11 1 1 1 1 1 1 Ml 1 111 1 11 1 1111 1 1 1 11 111 1 II III II 11
* 1 111 VI 1 Mil II II 1 II II 1 M M 1 M II 1 1 II II II II 1 II II it i Ii
I ||i я I || || 1 II II 1 M M 1 M II 1 II II11IIIIIIII1IIII II 1 1 11
I || i f\| || 1 11 1 1 II 1 1 1 II1 1 1 II II II 11 1 II II 1 1 II1 M 1 1 1 1 II 11
III
1 1 \ 1 \ Mill II II II Mil 1 MM 1 1 II 1 II II II II1 1 1 II II 1 1
1 II 111 \ll II 1 1 II 1 II II 1 1 II II II 1 II 1 1 II 1 II II 1 1 1 11 1 II II 1 1
1 II III l\ II 11 II M 1 M II1 11 II II 1 II1 1 1 II 1 II II1 II II II 1 II 1
11 M11\II1111 M 1 M II1II11IIII11M II II 1II1 II M II 1 1 11
1 II 1 \ 1 \ll 11 M II 1 11 M 1 1 1 II 1 1 II 111 11 1 1 M M 1 II II II 1 II 1
u.uui ' i\i' | \ f | I '["t" I I II II I II I I II II I I I I II II II I l"l II I II M 11
I M ll\ I i\. II II I II I I I 11 Mill M III I II IIII III II I I II I II I
I 111 I \ I \j I II M I M M I 111 l M I M I M M M M 11 M M M II I I
I II II INI II xl I M I II I M I I II I II I I I I II II I I I III I I I I I I I I I I
I||II I\II Pi I IIII I M 11 II II M I III II II I M III II I I II I I M
I || || M TnJ lllllllll 11 I III III III II II III I I II 11 II M
I I II II I Гч. I M^L I M 11 II Mill I 11 I I II I III II I 11 III
III ^J I iNk. I III II II II II II II II ll I II I I I I M II II
л л I II I II II I bJ I I I TSwl I M I II II II I I I I II II I I II I I II ll I II II I
0,04 XJ ГгМ.
I II II I II II l^^-l rWj I I M A II I I I II II II M I I Mill II I I I
I I I I I I I I Ттч1 (III iWJ T II 1 1 1 1 II II 1 i 1 1 1 1 I 1
ГГН4 T MTtIJ
imi ( i 1 1 1 г ill t 1 l*f rW^l 1 1 1 г 1 1 ii^nLJ у 1 1 1 1 1 M II i 1 1
It (ТТтгтЦХ1 ГГП MMTT W--LLLL
,\ /-vol II 1 1 II II 1 1 1 II 1 1 II II 1 1 1 II II II 1 1 1 "i t 1 1 1 II 1 1 1 1 II II 1 1 11
o,uzi f-j-f 1 if"- г 'i"t"l I ITT Г "Г М * i i мм
1 II 11 11 II 1 1 1 II 1 II 1 II 1 11 ll 1 11 1 1 1 II 1 II 1 II 1 1 1 M II ll II 1
0M1II11i 1 IIIlllllllll iiiiiiiiiilllllllll 1 lllllllll
0,25
0,2Г
РДг
0,K
0,0:
200
400
600
800
Fo
■1000
Рис. 4.5. Зависимость между относительной избыточной
температурой в и числом Фурье Fo^ для полуограниченного стержня (слу
чай больших значений чисел Фурье
Глава четвертая
оо \
ем* g
Ць
*^*
см
"--*
о
о
я
ч
ока
ч
о
Г—1
Tji
И
05
я
*
тер
о
ч
о
я
о
ч
я
s
«
я
я*
«
я
н
св.
О,
(D
С
»я
о
ее
СО
я
CU
та
ГРАНИЧНОЕ УСЛОВИЕ ПЕРВОГО РОДА
83
теплопроводности, называемым числом Фурье для координаты х\
обозначим его через Fo^, т. е.
Тогда решение A6) напишем так:
9 = erf /
ч2уТ5Г/'|
B8)
На рис. 4.4 и 4.5 приведены графики, построенные по решению B8).
По оси ординат отложена безразмерная температура б, а по оси
абсцисс—безразмерное время (число Фурье). Приведенные графики могут
служить в качестве расчетных. С этой целью начерчено несколько
кривых для чисел Фурье от 0,02 до 1000.
На рис. 4.6 приведены графики, характеризующие изменения 8,
х и гох в зависимости от числа го„. Из рис. 4.6 видно, что
дх д¥ох
1 1 ае ае
при значении , равном ——., производные и имеют
2V~Fox V~2 дх д¥ох
максимум.
Иллюстрируем изложенное конкретной задачей. Требуется определить температуру
грунта Т (х, т) на глубине л; = 0,5 м, если в результате подогрева поверхность грунта
поддерживается в течение т = 24 ч при температуре Т @, т) = 1273°К A000°С).
Температура грунта до подогрева Т (х, 0) = 293°К B0°С), коэффициент
температуропроводности грунта а = 7-10~7 м2/сек.
Данная задача — на нагревание полуограниченного тела; ее можно свести к
задаче на охлаждение путем замены переменной &(х, т) = 1273 — Т(х, t). Тогда &@, t)=
= 1273 — Т @, т) = 0°; & (л:, 0) = 1273 — Т (*, 0) = 980° = const.
Найдем число Фурье для координаты х — 0,5 м:
7-10-7-24
25-10™2
•3600 = 0,24.
По графику 6 = f(Fox) находим относительную температуру; она равна 6 —0,852,
Откуда температура грунта будет равна
6 = - v ; = 0,85; ft (х, т) = 0,85-980 = 833°,
980 — 0 » . v » /
Т (х, т) == 1273 — % (х, т) = 1273 — 833 = 440°К A67°С).
В данной задаче предполагается, что испарение влаги из грунта отсутствует.
При наличии испарения влаги температура будет меньше. Задачи с отрицательными
источниками тепла рассматриваются в гл. VIIL
§ 3. НЕОГРАНИЧЕННАЯ ПЛАСТИНА
Под неограниченной пластиной обычно понимают такую пластину,
ширина и длина которой бесконечно велики по сравнению с толщиной.
Таким образом, неограниченная пластина представляет собой тело,
ограниченное двумя параллельными плоскостями. Изменение
температуры происходит только в одном направлении х, в двух других на-
(дТ дТ \
= — = 0). Следова-
ду dz J
тельно, задача является одномерной.
Постановка задачи. Дано распределение температуры по толщине
пластины в виде некоторой функции f(x). В начальный момент ере-
мени, ограничивающие поверхности мгновенно охлаждаются до неко-
84
Глава четвертая
торой температуры Тс, которая поддерживается постоянной на
протяжении всего процесса охлаждения. Найти распределение температуры
по толщине пластины и расход тепла в любой момент времени.
Поместим начало координат в середину, толщину пластины
обозначим через 2R, т.е. R— половина толщины пластины.
Условие задачи математически может быть сформулировано
следующим образом. Имеем дифференциальное уравнение
аг(дс,т)
d<z
d2T(x,z)
дх2
(т>0; _Я<*< +R)
при условиях
1 т
T(+R,
\ T(-R,
(х,
т) =
,):
0) =
= ТС
= тс
/«,
= const,
= const.
}
Решение задачи методом разделения переменных,
что функция f(x) четная, т. е. /(#) = /(—я); поэтому (
Для этого случая граничные условия C) можно написать так:
дТ@,ч)
A)
B)
C)
Предположим,
df (*) \ = 0
дх )х=о
дх
= 0.
(За)
Последнее соотношение есть следствие условия симметрии кривой
распределения температуры в любой момент времени; оно будет иметь
место на протяжении всего процесса охлаждения, поскольку
теплообмен с ограничиваемых поверхностей происходит одинаково.
Случай, когда функция f(x) нечетная, будет обсужден ниже.
Частное решение дифференциального уравнения A) можно написать
так [см. § 2, гл. III, решение B0)]:
D)
Т (х9 т) = С sin kxe~ak2x + D cos kxe~akH
Из условия симметрии следует, что
дГ@,т)
дх
lim (kC cos kx — kD sin kx) e
-ak2z
-ak2x
= kCe
r-ak2x
= 0,
откуда С = 0, так как е "~ " на протяжении всего процесса
охлаждения @<т< оо) не равно нулю.
К этому результату можно прийти из анализа условий охлаждения
пластины. Распределение температуры должно быть симметричным
относительно оси ординат, следовательно, должно описываться четной
функцией. Такой функцией является cos&x, a sin&x: есть нечетная
функция х, она должна быть опущена из решения.
Удовлетворим второму граничному условию. Для упрощения
расчета временно положим Тс = 0. Имеем
Отсюда следует
T(R, <z) = DcoskRe~ak2z= 0.
cos kR = 0, kR = — тг;
•тг;
knR = B/1-1)
E)
ГРАНИЧНОЕ УСЛОВИЕ ПЕРВОГО РОДА 85
т. е. k имеет не одно значение, а бесчисленное множество.
Следовательно, общее решение будет суммой всех частных решений,
т. е.
оо I
г- П -1 I
F)
Т(х,
х) =
ОО
Dn
COS
B/г-
-1)
71
~2~
X
ехрГ-
-Bл-
-IJ
4
"я»
I
-]-|
Постоянные Dn в каждом частном решении будут иметь свои
собственные значения, поскольку сумма частных распределений
температуры для любого заданного времени должна описывать действительное
распределение температуры.
Таким образом, наложение косинусоид должно дать действительную
кривую распределения температуры, в том числе и начальное
распределение температуры.
Следовательно, положив т = 0, получим заданную функцию f(x)f
причем она будет представлена в виде ряда Фурье
оо
Т(х,0) = /(*)=£ A* cosknx. G)
Тригонометрические функции cos&a; и sin Лаг образуют
ортогональную систему функций.
Напомним читателю, что система функций
АD М4 /з(*)> •-• ./«W
называется ортогональной в интервале (а, Ь), если интеграл
J/,(*)/y(*)d* = 0 (8)
а
при любых значениях i и /, но не равных друг другу.
Можно, например, показать, что система функций o,o&knx является
ортогональной:
+^ [ =0 при тфп,
/ = cos (kmx) cos (knx) dx \ (9)
' JrR' [ >0 при т = п.
Преобразуем подынтегральную функцию при помощи формулы
cos a cos р = —[cos (а — р) + cos (а + РI-
Тогда интеграл / будет равен
j __ sin (km — kn) R , sin (km + kn)R ^
(km — kn) (km + kn)
Воспользовавшись тригонометрической формулой
sin (a ± p) = sin a cos p ± cos a sin p,
получим
/ ss 2 [^m Sin km R COS fe^ff — kn COS fem ft Sin knR] /jqv
В нашем случае km R=Bm — 1) —; £„ R = Bn — 1) —. Следовательно,
86
Глава четвертая
cos kmR = cos knR = 0. Числитель равен нулю, а знаменатель при m =f=*n
отличен от нуля, следовательно, интеграл равен нулю.
Случай т~п надо рассмотреть отдельно, так как числитель и
знаменатель равны нулю, В этом случае имеем
+R
/= J cos^knxdx^2]^ + ^^], (И)
—R
т. е. интеграл отличен от нуля.
Воспользуемся этими формулами для определения постоянных
коэффициентов Dn.
Умножим обе части равенства G) на cos&mx и проинтегрируем в
пределах от —R до + R, т. е.
+R +R со
Г Т (х, 0) cos kmxdx = Г ]£ ®n cos knx cos kmxdx =
—R -R n=\
oo +R
= 2 1 Dncosknxcoskmxdx. A2)
Все интегралы в правой части равенства равны нулю согласно
соотношению (9), за исключением одного, который равен Im^n = R,
когда m = п.
Следовательно, можно написать:
+R R
Dn = -Q— \ T(x,0)cos&„ #d# = —£- 1 T(x,0)cosknxdx. A3)
-я о
При выводах неявно использовались два предположения: 1)
интеграл A3) имеет конечное и определенное значение, 2) интеграл
бесконечного ряда равен сумме интегралов отдельных членов ряда.
Эти предположения требуют, чтобы функция f(x) удовлетворяла
условиям Дирихле: 1) в определенном интервале она должна быть
однозначной, конечной и интегрируемой, 2) иметь конечное число
максимумов и минимумов, 3) иметь конечное число точек разрыва
непрерывности.
Таким образом, общее решение F) нашей задачи можно написать
так:
| J» 2 ах ~Я |
(И)
\'Цхл)'-
00 2 ах
= 2j cos pn-£-e
л=1
R 1
IJ /(*) cos |*л -~ dx,
где
*n = knR = Bn—\)-^-.
Это решение является одновременно решением задачи нахождения
температурного поля в неограниченной пластине толщиной
I = R@ <x< /), когда одна поверхность ее имеет тепловую изоля-
аг(о,х) \
цию (при х — 0 поток тепла отсутствует, так как ^ =01,
а противоположная поверхность х = I поддерживается при
температуре 0°С. В начальный момент времени задано некоторое распределение
ГРАНИЧНОЕ УСЛОВИЕ ПЕРВОГО РОДА
87
температуры в виде функции f(x)t причем в этом случае функция f(x)
может быть любой, лишь бы удовлетворяла условиям Дирихле.
Если функция f{x) нечетная, то аналогичным путем получим
решение в виде
оо R
Т (x,z) = £ sin {^—-exp (— Pn^rj • -~-J / (x) sin \in ~~ dx,
A40
где (Ал = /гтс.
Решение A4') одновременно является решением задачи охлаждения
неограниченной пластины толщиной / = /?@< х< /), когда поверхности
ее поддерживаются при температуре 0°С (начало координат находится
на одной из поверхностей, пластины). В начальный момент времени
задано распределение температуры в виде произвольной функции f(x),
удовлетворяющей условиям Дирихле.
Если начальное распределение температуры равномерное, т. е.
Т(х90) = Т0 = const, то можно вычислить интеграл A3):
я
^
х 27 х
R_R_ = 2slnft,T 2Г„ , _ j +1
так как sin \ъп = sin Bя— 1) —^- = =fc 1 „т.е. синус последовательно
принимает значение + 1 или — 1 в зависимости от величины аргумента (для
четных п синус равен — 1, для нечетных он равен + 1).
Таким образом, решение нашей задачи можно написать так:
оо
^ = 1-|Г(-1Г1со5,й^-ехр(-^-^). A5)
П = \
Если температура ограничивающих поверхностей не равна нулю, а
равна Гс, как это следует из условий задачи, то можно решение
переписать в виде
%$=^=2 -£-( - D"+1 cos ft, -f exp (-^ Fo).
A6)
Решение задачи операционным методом. Дифференциальное
уравнение теплопроводности после применения преобразования Лапласа будет
иметь такой же вид, как и в предыдущей задаче, т. е.
TL (x,s) - -i- TL (x,s) + *£- = 0. A7)
Начальное условие Т(х,0) = TQ = const нами использовано при
переходе от уравнения в частных производных для оригинала Т(х,х) к
уравнению A7) для изображения TL(x,s), а именно при применении
преобразования Лапласа к производной температуры по времени.
Граничные условия для изображения будут иметь вид
TL(R,s) = £, |
S A8)
T'L @,s) = 0. I
88
Глава четвертая
Решение дифференциального уравнения A7) можно написать так
(см. § 3, гл. III):
TL(x,s) — -£l = Л ch Y~7rx + В sh V4" x> <19)
где А и В — постоянные, определяемые из граничных условий A8). По
условию симметрии В = О, так как
откуда В = 0.
Постоянную А находим из первого граничного условия A8)
TL(R,s) = If- + AchY^R=^-,
откуда
А = -- <Т°-Гс)
s-ch y±.R
Таким образом, решение для изображения будет иметь вид
(T0-rc)ch Y-т*
" TL(*.s) = -Г7= = fw * B0)
Можно показать, что правая часть равенства есть отношение двух
обобщенных полиномов *> относительно s, а именно
ФE) = (Г0-Гс)сп YTX = (То-П)( 1 + -ш s + 4& ** + ...) ,
Обобщенный полином ф (s) не содержит постоянной (первый член равен $),
т. е. все условия теоремы разложения соблюдены, поэтому ее
можно применить при переходе решения для изображения B0) к решению
для оригинала.
Теорему разложения можно написать так:
где sn — корни полинома ^(s). .
Найдем корни функции ф(я) = s-ch 1/ -^-/?, для чего приравняем ее
нулю. Тогда получим: 1) простой корень s = 0, 2) бесчисленное
множество простых корней, определяемых из соотношения
']/"^*=P»=Bn-l)-f, B2)
откуда
_ щ& __ Bя-1)»*»д т.
О Бесконечный сходящийся степенной ряд, показатели степени которого есть
натуральные числа, называют обобщенным полиномом, или полиномом бесконечно
высокой степени. Иногда сокращенно будем называть его просто полиномом.
ГРАНИЧНОЕ УСЛОВИЕ ПЕРВОГО РОДА
89
Затем найдем <]/ (s):
= ~llVlrXsbVlrR + chVlrK- B4)
Имеем
limf(s) = 1,
s-*o
limf(s)=-K- t>/zsh t>„ =
= —2"^sin^ = f(S/1).
Величина sin \in равна + 1 или — 1 в зави- Рис- 4-7- Распределение тем-
симости от значения /г, т. е. пературы в неограниченной
пластине (внутренняя симмет-
sin |хЛ = (— 1)л+1. ричная задача)
Найдем величину 0(sn):
ф@) = 70-7с,
Ф (Sn) = (Т0 - TJ Ch ]Д^-* = (Т0-Тс) Ch /(X, ^ = (T0 - Те) COS ^ -*- .
Окончательно [получим
GY-rc)ch"j/jL *
^[■r1-^^)]^-1
s-ch
Y\
T0-T(x,x) = (Т0-ТС)-(Г0-ГС) 2 -L (_l)»+i cos jx„ -£- exp (- ^-g-) ,
т. е. решение тождественно решению A6):
6 = T(To-TcTc = S К cos (,„ -£- ехр(-ц* Fo), B5)
л=1
2 дх
где Ап = —- (— l)n+1 — начальная тепловая амплитуда, Fo = -^ — чис-
ло Фурье.
Анализ решения. Относительная избыточная температура является
функцией относительной координаты и числа Фурье:
е = ф(х'Ро)
Следовательно, процесс охлаждения состоит из процесса
постепенного выравнивания температуры по толщине пластины (температура
на ограничивающих поверхностях все время одинакова и равна Тс),
90
Глава четвертая
Рис. 4.8. Распределение температуры в
неограниченной пластине при числе Фурье Fo = 0,05.
Косинусоиды построены по формуле
I — для /г=1; II
Л„ехр [
- ДЛЯ /2 = 2, III
-К Fo) :
- для п = 3.
скорость протекания
которого определяется
коэффициентом
температуропроводности. Такой процесс
теплообмена называется
внутренним процессом, а
сама задача — внутренней
задачей.
Распределение
температуры в неограниченной
пластине в различное время
приведено на рис. 4.7.
Из анализа решения B5)
видно, что оно представляет
сходящийся ряд, т. е.
алгебраическую сумму
косинусоид с постепенно
затухающими амплитудами,
определяемыми выражением
2
Апе~^п¥о, т. е. тепловые
амплитуды убывают как с
увеличением \ьп, так и с
течением времени.
Циклическая частота таких
косинусоид увеличивается с
увеличением п, так как она
равна B/z—1)/4.
На рис. 4.8 дано
распределение температуры по
толщине пластины для
числа Fo = 0,05, построенное
по решению B5). Кривая
распределения температуры
с достаточной степенью
точности может быть
представлена как сумма трех
косинусоид:
6 »
Fo
COS
4
Зтс
-Fo
COS
Згсл
2R
4
5*
— 25*2
Fo
Т~ 5
cos
2R'
Из рис. 4.8 видно, что сложение трех косинусоид с различными
амплитудами и частотами дает кривую распределения температуры в
данный момент времени, определяемый равенством Fo = 0,05. При малых
значениях Fo необходимо брать несколько членов ряда, поскольку
амплитуды затухают медленно; при больших значениях Fo все члены
ряда пренебрежимо малы по сравнению с первым, так как
t^< 1*2<Р<3< •• •< Рп= BЯ—1)-у .
Экспоненциальная функция expf—P^Fo) быстро уменьшается с
увеличением |хл; например, при Fo = 0,5 expf — p^Foj^exp ( «~ тс2 j =
ГРАНИЧНОЕ УСЛОВИЕ ПЕРВОГО РОДА
91
= 0,291, а ехр( — p|Fo) = ехр( — 9-g~] < 0,00004. Поэтому, начиная
с определенного значения Fo, можно ограничиться одним первым
членом ряда B5). Такое решение будет удобным для практических
расчетов.
Для малых значений Fo решение B5) мало удобно. Операционный
метод позволяет получить решение задачи в другой форме, наиболее
пригодной для малых значений Fo.
Вернемся к решению B0) для изображения.
Разложим в ряд (см. приложение)
* Vir* _
_■ ^-V*" -.-* "> +.- У* -..
ch V.J-R
оо
2 £ (_ i)»+i exp [_Bя—l)"|/"-J-/?]
П = \
Тогда решение B0) можно написать так:
^_Г1М=(^L(Л-+«-П^х
S
- X
То—Г,
о—* с
со
X 2 2 (— 1 )"+1ехр [- Bл — 1) |/-^- я]
2 (-1Г1 {exp[-(Bn-l)i? -х) |/Х] +
5
/г=1
+ ехр [ - (B/1 - 1O? + х) |/-^-]} . B6)
Для перехода от изображения к оригиналу воспользуемся табличной
формулой
L-if_Le-*v-j] = erfc * #
Тогда решение нашей задачи получим в виде
Т0-Т(х,х) у Г ГB«—1)/?—дс Л ГBв-1)/г+х]1
Го-Гс = 2i(~D-+1 { erfc [ 2/- J + erfc [ 2 ^ J) • B7)
/2=1
Это решение можно переписать так:
Г(*,т)-Ге.. = j _ 2 <_!).* f erfc ^ZT +erfc B»-1)+х/Д
rt= 1 i
B8)
Решение B7) удовлетворяет дифференциальному уравнению,
начальному и граничному условиям. При т -> 0, т. е. при малых значениях
Fo, аргументы функций велики, а сама функция близка к нулю, так
что Т(х,0) = 70; при х = R сумма равна 1, т. е. T(R^) = ТС.
92
Глава четвертая
При малых значениях Fo все члены ряда исчезающе малы, за
исключением первого; так функция erf с и быстро уменьшается с
увеличением аргумента: например, при и = 2,7 erfc и = 0,0001, т. е.
практически равна нулю.
Функция erfc u = 1 —erfи табулирована, и использование решения
B8) для практических расчетов не представляет трудностей.
Для иллюстрации сделаем небольшой расчет. Вычислим
относительную температуру 6 как функцию числа Фурье для центральной
плоскости пластины (лг=0) по следующим приближенным формулам (с
точностью до четвертого знака после запятой), взятым из решений B5)
и B8):
к « 4 {ехр (- -тFo) - 4- ехр (- -т- F°) +
1 / 25т:2 \ 1 / 49тс2
+ — ^р [ - — Fo j - —ехр (^ - _ Fo
eu « 1 — 21 erfc -—7= erfc -=- + erfc — _
ц 1 2]AFo 2|/Fo 2/Fc
rF^ j
B9)
C0)
и по точной формуле B5), которую можно написать так:
00
9u = 4-2-$Sf exV[-Bn-ir~Fo].
Я = 1
Результаты расчета приведены в табл. 4.1.
Таблица 4,1
Температура неограниченной пластины в точке х=0 (середина пластины)
Fo
0,001
0,004
0,010
0,020
0,040
0,050
0,060
0,080
0,100
0,2
0ЦB5)
1,0000
1,0000
1,0000
1,0000
0,9992
0,9969
0,9922
0,9752
0,9493
0,7723
6ЦB9)
0,9332
0,9591
0,9850
0,9978
0,9991
0,9971
0,9923
0,9752
0,9493
0,7723
У 30)
1,0000
1,0000
1,0000
1,0000
0,9992
0,9969
0,9922
0,9752
0,9493
0,7723
Fo
0,4
0,6
0,8
1,0
1,2
1,4
1,6
1,8
2,0
2,5
ец<25)
0,4745
0,2897
0,1769
0,1080
0,0659
0,0402
0,0246
0,0150
0,0092
0,0026
ецB9)
0,4745
0,2897
0,1769
0,1080
0,0659
0,0402
0,0246
0,0150
0,0092
0,0026
6ЦC0)
0,4744
0,2896
0,1768
0,1079
0,0660
0,0402
0,0244
0,0146
0,0082
—0,0007
Из рассмотрения табл. 4.1 видно, что расчет по приближенной
формуле C0) даст полное совпадение с расчетом по точной формуле от
малых значений Fo до Fo < 0,4. Начиная с Fo > 0,4, наблюдается
расхождение только в четвертом знаке до Fo<Cl,8. Для Fo > 2
получаем ошибочный результат. Необходимо заметить, что в пределах Fo от
0,001 до 0,1 приходится пользоваться только одним членом фигурной
скобки формулы C0). Расчет по приближенной формуле B9) дает явно
неверные результаты при малых значениях Fo от 0,001 до 0,08;
начиная с последнего значения, формула B9) дает правильные результаты.
При этом, начиная с Fo > 0,4, можно ограничиться одним первым
членом формулы B9). -Неверные значения, полученные по формуле B9)
для малых значений Fo, объясняются недостаточным количеством
взятых членов ряда B5).
ГРАНИЧНОЕ УСЛОВИЕ ПЕРВОГО РОДА
93
Таким образом, для малых значений Fo необходимо пользоваться
решением B7). На этом конкретном примере видно большое
преимущество операционного метода, который позволяет получить решение
задачи в двух видах: одно удобное для расчетов при малых значениях
Fo, другое—для больших значений Fo.
На рис. 4.9 приведены кривые распределения относительной
температуры по толщине пластины для различных значений критерия Fo
(от 0,005 до 1,5). Из рис. 4.9 видно, что температура в середине плас-
Рис. 4.9. Кривые распределения относительной избыточной
температуры 6 в неограниченной пластине по относительной
координате xIR
тины заметно уменьшается, начиная с Fo > 0,06. Процесс охлаждения
заканчивается примерно, когда Fo>l,5.
На рис. 4.10 приведены графики изменения относительно! темпера-
туры———7р- = A— б) в зависимости от числа Фурье для разных зна-
■* о * с
чений (l—x/R) от 0 до 1.
Приведенные графики могут служить в качестве номограммы для
практических расчетов. В табл. 4.2 даны значения относительной
избыточной температуры в середине пластины для различных значений
числа Фурье
Определение удельного расхода тепла. Количество тепла (в дж)9
теряемого пластиной, равно
A Q = СМ(Т0 - Т) = £?Т V(T0-T).
где Г — средняя по объему температура пластины. Удельный расход
тепла (расход тепла на единицу объема; дж/м3) равен
AQ„ = cTGV--T). C1)
94
Глава четвертая
Щ\\ II ||| 111 1
jjPI|j^^^^4~H"l М М1М ГП М li~H~M~hHT i 11 ж 1111 1 1Щ
\Ш\\л\й^ 11 rrfei%4JJ 111 i 111 " i
ИД! UttlfflW111 №1 ВИД
Fill 1 NPn. RTTll1 TOIkшЩЩШ1 n
U1 \ \ \ \x \ \ IV N Pv Гч ' г «э ■ Nl r>J>J - i
ИТОГУ Ш M ГГОТЦ ШШтffflWU Ш
1 \ \ Их ПЧ iU ^U пч пчiNv1ЧчЬ1
l \ \ \ \ Гч ]\J I'M Tr. M4' * ^ ^ * i4' i^l^ ■ 11
Pj-JFI- 1 А1~1"~ГТ \ ! 1 "l 1 1 ГЧ 1 1 I4i"l IV^^t" 1 1 l\l "[~1~РФ-4Г 1 KJ~tЫ МЧ 1 I
ЯЯЗгН~И 1 1тй 1 1 N 1 1 1\тЧ~ 1~4J i ^^^1 1 l~1\l I I I T4J 1 "l\[ iNJ \ 1SJ-J
Мз^ К f~r 1 \ 1 1 1 1 \~i~t 1 141 1 4~гч;цэ4 ГЧ 1 1 1 1 -pJ г ттч. KJ \ iNlnrH
вэь^ \ ~f4\| 1 1 |\"~ 1 1 1 i4l 1 1 Г^ I | ГЧ 1 1 1 1 1ч1 1 IN 1 W V V \ 1
ННтгт 1 \l 1 1Ч 11111 M 1 1 1 nJ т?"гН iN 1 11 1 1 "KM 1" 1 тЧ 1 lv 1" rdVfti
J4H4b4i м Ч NJ4~г?^ь| l l~wi M NJ —Fx \W 1 v \\\l
Mt441 1 1 l\ 1 1 -+~A 1 IV1 1 1 if\ 1 1 1 P°i\ 1 1 INl 1 1 t xl 1 1 1 1 1 \l 1 1 1\ 1 IN lvfli
111 ' h:\'i 1 ."" \ ' T"f 1 N3 Т1~Т~ТНЛ Г 1 ""lis. l^KJ MM ^- 1 J 1 Nl 1 \ Iffl
Й1111111ИШ11111Ш1[Ц|Ц'111111Я
1 \ ?\1 Ml KJ Г1] 14J 14 N M
1 M\ \ W\ M> N N \\ \
1 \ \ M\ M> TSJ \ N \
Mi mJ ид 11 J |Ч Г> It IrJ\ 1
hi 1 1\ !■ \ Год ■{ 1-1 1 1 1 IN. I-—1—l—l^^-7!-1 1 f~l гчг 1 -l~ РЧ— ■■■■!■■ \ ГЧ YfI
j-^—j-j-ffc^^o зн-^^ гтгч 11111 INu Г1 ГЧГГГт^^
III 1 trTi^ л LINct "t i" 1 xl 1 1 1 1 П 1 r4! 1 1 1 1 N1 1 INHH
llll\lll\lllllll||\ll|||ilillll f\l 1 1 м 1 1 г "fSvi 1 11 'Гч! 1 prm
tt
fl,01
JHzjifciy- РНЧймТыТ^^ M 1 Гч 1 1 1 111 1 \'l 1 1 \-ffl
Prjfl \и4N" м insJГиг MillPNJUГ! 11411\^
—[o-x/r:
\ МЧ ГИ \wn
\ N ПЧ \ 1
\ \ IS \
111 1 II1 M N LLLLLLN IN LLN.. 111.11 J .. U\l 1
ȣ
§
О
P
3
ex
8
О
О
о"
s
ГРАНИЧНОЕ УСЛОВИЕ ПЕРВОГО РОДА
95
Таблица 4.2
Относительная температура в середине неограниченной пластины
BяЬг (-1)Л+1 6ХР
л=1
г.2 1
B/г~1)* — Fo J
Fo
4
0,001
0,002
0,003
0,004
0,005
0,006
0,007
0,008
0,009
0,010
0,011
0,012
0,013
0,014
0,015
0,016
0,017
0,018
0,019
0,020
0,021
0,022
0,023
0,024
0,025
0,026
0,027
0,028
0,029
0,030
0,031
0,032
0,033
0,034
0,035
0,036
0,037
0,038
0,039
0,040
0,041
0,042
0,043
0,044
0,045
0,046
0,047
0,048
0,049
0,050
0,051
0,052
0,053
0,054
0,055
6ц
1,0000
1,0000
1,0000
1,0000
1,0000
1,0000
1,0000
0,9998
0,9996
0,9992
0,9985
0,9975
0,9961
0,9944
0,9922
0,9896
0,9866
0,9832
0,9794
0,9752
0,9706
0,9657
0,9605
0,9550
0,9493
0,9433
0,9372
0,9308
0,9242
0,9175
0,9107
0,9038
0,8967
0,8896
0,8824
0,8752
0,8679
0,8605
0,8532
0,8458
0,8384
0,8310
0,8236
0,8162
0,8088
0,8015
0,7941
0,7868
0,7796
0,7723
0,7651
0,7579
0,7508
0,7437 i
0,7367
Fo
4
0,056
0,057
0,058
0,059
0,060
0,061
0,062
0,063
0,064
0,065
0,066
0,067
0,068
0,069
0,070
0,071
0,072
0,073
0,074
0,075
0,076
0,077
0,078
0,079
0,080
0,081
0,082
0,083
0,084
0,085
0,086
0,087
1 0,088
0,089
0,090
0,091
0,092
0,093
0,094
0,095
0,096
0,097
0,098
0,099
0,100
0,102
0,104
0,106
0,108
0,110
0,112
0,114
0,116
0,118
0,120
8ц
0,7297
0,7227
0,7158
0,7090
0,7022
0,6955
0,6888
0,6821
0,6756
0,6690
0,6626
0,6561
0,6498
0,6435
0,6372
0,6310
0,6249
0,6188
0,6128
0,6088
0,6009
0,5950
0,5892
0,5835
0,5778
0,5721
0,5665
0,5610
0,5555
0,5500
0,5447
0,5393
0,5340
0,5288
0,5236
0,5185
0,5134
0,5084
0,5034
0,4985
0,4936
0,4887
0,4839
0,4792
0,4745
0,4652
0,4561
0,4472
0,4385
0,4299
0,4215
0,4133
0,4052
0,3973
0,3895
Fo
4
0,122
0
0
0
0
0
0
1 °
0
0
0
0
0
1 о
1 °
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1 о
0
0
о
0
i °
0
0
0
0
0
| 0
о
1 о
0
0
0
о
0
0
о
0
0
124
126
128
130
132
134
136
138
140
142
144
146
148
150 "
152
154
156
158
160
162
164
166
168
170
172
174
176
178
180
182
184
186
188
190
192
194
196
198
200
205
210
215
220
225
230
235
240
245
250
255
260
265
270
275
ед
0,3819
0,3745
0,3671
0,3600
0,3529
0,3460
0,3393
0,3326
0,3261
0,3198
0,3135
0,3074
0,3014
0,2955
0,2897
0,2840
0,2785
0,2731
0,2677
0,2625
0,2574
0,2523
0,2474
0,2426
0,2378
0,2332
0,2286
0,2241
0,2198
0,2155
0,2113
0,2071
0,2031
0,1991
0,1952
0,1914
0,1877
0,1840
0,1804
0,1769
0,1684
0,1602
0,1525
0,1452
0,1382
0,1315
0,1252
0,1192
0,1134
0,1080
0,1028
0,0978
0,0931
0,0886
0,0844
96
Глава четвертая
Продолжение табл. 4.2
Fo
4
0,280
0,285
0,290
0,295
0,300
0,31
0,32
0,33
0,34
0,35
0,36
0,37
0,38
0,39
0,40
9«
0,0803
0,0764
0,0728
0,0693
0,0659
0,0597
0,0541
0,0490
0,0444
0,0402
0,0365
0,0330
0,0299
0,0271
0,0246
Fo
4
0,42
0,44
0,46
0,48
0,50
0,52
0,54
1 0,56
| 0,58
' 0,60
0,62
1 0,64
| 0,66
! 0,68
0,70
9д
0,0202
0,0166
0,0136
0,0112
0,0092
0,0075
0,0062
0,0051
0,0042
0,0034 ,
0,0028
0,0023
0,0019
0,0016
0,0013 1
Fo
4
0,72
0,74
0,76
0,78
0,80
0,82
0,84
0,86
0,88
0,90
0,92
0,94
0,96
0,98
1,00
ед
0,0010
0,0009
0,0007
0,0006
0,0005
0,0004
0,0003
0,0003
0,0002
0,0002
0,0001
0,0001
0,0001
0,0001
0,0001
Таким образом» необходимо определить среднюю температуру
пластины. Имеем
R
T(x)=-±-§T(x,x)dx.
Из решения B5) получаем
C2)
где
d == An s*n Учг __ / iy*+l
К*
2 sin \Ln
£ ~ Bл-1)%*
Таким образом, получаем сходящийся ряд; коэффициенты Вп
быстро уменьшаются с увеличением \ьп.
Найдем среднюю температуру, исходя из решения B0) для
изображения. Воспользуемся соотношением
i4
fL (s) = -L.^TL (x,s)dx, If- - TL (s)
(Го-Тс)
th
V-t*-
C3)
Применим теорему разложения для нахождения оригинала.
Решение C3) перепишем так:
sh
Y±
JL_7L(S) =
(То-Тс) г—
s.ch YJ- R
Ф(«)
ГРАНИЧНОЕ УСЛОВИЕ ПЕРВОГО РОДА
97
Аналогичным путем находим корни ф(я) = s-ch |/ —R) в результате
а '
получим s0 = 0, sn = — \ь% /jT . Выражение
sh У ~1ГR R2 . RA
JL«
= 1 + ТГ~ s+ 1ГГ2 s2 + ••• '
1 ■ 3!a 5!a2 '
является обобщенным полиномом, первый член которого равен единице.
Аналогичным путем находим
1 sh«: р-я sin [лЛ
f Eд) = — -J" 1*11 Sin Рп> Ф (SJ = (Т0—Тс) —— = (Г0—Гс) ~^— .
Следовательно,
00
Т0 - Г(т) = Т0-ТС-(Т0 - Гс) S 4- е - ^р0
или
Т(х)-7-с VD ~^.Р°
Г0-Гс
S-|i„bO
В„е ,, C4)
/1=1
т. е. получаем выражение, тождественное выражению C2).
Сделаем анализ решения C3) для изображения. Для малых
значений времени, точнее числа Fo, величина 1/ — R велика, тогда th 1/~Я
можно положить равным единице (th j/ —R « 1 при 1/ — /?>2| и
можно написать
^W = 4-(Z7^. C5)
Согласно таблице изображений оригинал этого изображения равен
7f,, ч ™ 2 (Г0 Тс) -|/\<2Т
или
в = 1
V^ ■ C6)
Приближенное решение C6) дает хорошее совпадение с точным
решением C4) при малых значениях Fo<0,l.
Иллюстрируем результаты на двух численных примерах.
1. Пусть Fo=-^2" ~ 0,1- Тогда из решения C4) имеем
= 4- • 0,7906=0,6408.
8
Из
4
-М-~
1
^ 9
решения C6) получаем
1 =
Совпадение
Заказ № 640
результатов
9
+
= 1 —
полное.
25
2V(~J-
••■•)■
0,6408.
98 Глава четвертая
2
2, Положим Fo = -^2~ж0,2, тогда из решения C4) получим 0 = 0,4926, а из
решения C6) имеем 0 = 0,4921. Совпадение вполне удовлетворительное, если учесть,
что в данном случае Fo^0,2.
Из этого примера видно, что при малых значениях Fo вместо нескольких членов
ряда C4) можно с достаточной степенью точности пользоваться приближенным
решением C6), а при больших значениях Fo можно из всего ряда C4) ограничиться одним
первым членом, т. е. при Fo > 0,1
— 8 / ГС* \
e= ^-exp (-:— Fo). <37>
Метод получения приближенных решений на основе соотношения
для изображения дает большие преимущества при решении сложных
задач по сравнению с классическим методом.
Решение для средней температуры 6 можно получить в другой
форме, если преобразовать решение для изображения и
воспользоваться следующей формулой перехода от изображения к оригиналу
функции:
Разложим th I/ — R в ряд
тогда будем иметь
^~ТФ)= sVTR f~2 S(-l)«+1exp (-2* Y±R)
Следовательно, решение для оригинала функции Т(т) можно написать
так:
Гв - Т(х) = (Г0-Тс) {4"]/"-?- - 2 S(-l)"+i X
п=1
В окончательной форме решение примет вид
У ~1С = 1 - 2l/— + 4/Fo 2 (- l)»+4erfc
п=\
V Fo
C8)
Из решения C8) также следует, что при малых значениях времени,
точнее Fo, оно превращается в приближенное решение C6), так как
/ л2 \ п
при Fo -> 0 ехр I — -р^-1 ->0и erfc : -> 0.
Решение C8) можно было- получить непосредственно из решения B8),
воспользовавшись иным методом расчета. Можно было определить
вначале AQS по формуле
AQ, = -j^g^x, C9)
ГРАНИЧНОЕ УСЛОВИЕ ПЕРВОГО РОДА
0 0,05 0,1 0,15 0,20 0,25 -£2»
:1 1 1 1 1 II 1 Mill III
(ч м
[ 1 1 111111 м
li ^ TlI L M М 1 1 1 М 1 1 1 М
it \ j li j 1 i 1 ММ
1 11 1 1 1 II II II II II
1 1 к 1 1
1 1 и| 1) II 1 II II 1 II 1
1 II Ы 1 1 1 II II II 1 II 1
III \ Vi\ 1 1 1 1 II II М II
* 1 II II 1\ и 1 1 М 1 II III 1 II II М 1
1 II II II iu 1 М 1 1 М II II МММ'
МП
ММ
\ N
\ ГУ
\ \
г \ MNJ
\ N
ni \ Г№
и»о| М II II 1 \ 1 1 II 1 ГчМ М 1 1 1 И 1 1 1 ГМ
1 М\ 1 ГМ
\ ГМ
\ TSJ
м\ mSJ I
li Гтч 1
! II 11 || I j | |\ || II II II 1 1 iMl 1~в!
1 1 II 1 1 1 1 М 1\1 II II 1 1 II 1 | | Рч II
0,2] М\ TSJ
1 II II 1 1 М 1 1 L"l 1 \ 1 II II 1 II М II М 1
1 1 I М М 1 М 1 ill 141 М II 1 III МММ
1 1 II 1| 1 1 II 1 1 II A rs.1 II 1 1 II II II 1 II
■ 11 М II1II1 II у \1 М 1 II II II 1 II
л «1 1 II М 1 II II 1 II I 1 ISI II 1 1 II II II II
о,1 mSJ
1 1 1 II 1 1 II 1 1 II 1 1 II 1 1 1 III II 1 1 1 1 1 1-
111 1 111 111111111 1 111! 1 г
1 II 1 1 1 1 II 1 II M II 1 II II 1 II 1 1 1 1 1 In'
1
! 1 Г II II 1 1 1 1 1 II' 1 II M 1 Г II II 1' II 1 1 r'<
1 II II II II 1 i II II II 1 1 1 1 1 1 1 II II 1 1 lf\
М1Г 1 " 1 1 1 '
J. |...|. 1 ] .M.-nkl-l-Ul-. 1 1 II 1 1 1 1 1 II 1 1 1 1 1 In
J 11111111111111111111 1111111 Hi ГП1+Н41111111111111 НШао,
U 0,5 1,0 i,5 2,0 2,5 -—-*-
Рис. 4.11. Зависимость между средней относительной избыточной
температурой 6 и числом Фурье Fo для неограниченной пластинь:
а затем и среднюю температуру Т ('с) из соотношения C1). Резуло-
таты получаются одинаковыми.
Анализ решения. Зависимость между средней безразмерной темпе
ратурой 8 и безразмерным временем Fo в виде C4) или в виде C8
широко применяется в задачах по диффузии. Роль средней
температуры в этих задачах играет средняя концентрация. Поэтому в табл. 4.с
приведены значения 6 для различных значений числа Fo, а на рис. 4.1
построен соответствующий расчетный график 6 как функции Fo.
Найдем скорость нагревания -тр— * Согласно C4) она равна
D0
Пользуясь приближенными формулами C6)~и C7), можно написать
JL
dFo
YtzFo
iz \i
при Fo < 0,1,
db 0
—rr- = 2 exp
__Fo ) = -^-8 при Fo>0,b
D1
DГ
100
Глава четвертая
ю сп см ю со
"Ф CD СО »-ч 1>-
00 00 н Ю О)
Ь- CD СО Ю -*
сп
J4-
со
СО
сп
см
со
со
см
о
СО
(О ^ Oi N М
СО СО —I CN 1П
^ СМ О 00 СО
CM CM СМ -н i-«
00 СМ СП СО
СО LO СП Г--
СП СП *-• Ю
t-- СО СО Ю
00 СО
О —<
^ со
СМ *-« —I
^f Ю О
О Г- "*
со СМ СМ
СО СП Ю О
LO CO Tt* !>.
СМ О 00 СО
СМ СМ ^ г-ц
сп
CD
О
GO
00
СО
О
о.
t-«
со
СМ
СО
см
со
со
m
CD
Г--
о
LO
CD
СО
Ю
^
О
ю
«^
со о со
г- оо —«
со см см
СО О т*« СО
с-- со со оо
см о оо со
см см t-ч у-*
о
PL,
о ь. t-* ■-« -«
Tf* CM CO СП 00
см —* со со .-ч
оо t- со ю ю
со
СО
СО
^
СМ
СТ>
"Ф
СМ
СП
t»-
со
о
СО
ч-р
СО
Tt«
о
со
ел
о
GO
см
^-(
^fl
ю
см
о
о
со
см
—ч
оо
о
см
см
00
О0
со
о
г-
о*
^ 00 00 - ^ N 'Ф
СП »-« О Ю ОО 00 СО
со см ^ i4- *-* со см
ОО Ь». СО Ю Ю -Ф *5f
СО
со
см
см
со
см
,-н
о
см
см
о
СП
о
см
г>-
«и
со
со
ю
00
см
СО
t>-.
т—»
оо
^f
со
см
оо
ю
t^
со
см
ю
оо
со
оо
СО
СП
СП
тр
со
со
со
со
ю
со
а)
см
СО
ТГ
со
см
см
см
см
о
см
СП
оо
со
1^
'•as
к
5Г
М
Ж
>>
•е-
К
ж
ф
ST*
№
00
со
ю
h-
оо
о
^
с^.
ю
ю
ю
СО
СО
t--
00
Ю
СМ
СП
см
ю
СП СП t^- rf СП
t^ ^н О СО СП
t4- СО СП Ю у-«
rf rf СО СО СО
^
СП
00
СМ
о
00
СО
СМ
о
СП
со
СО
см
о
^
^
1—1
(М
о
о
^
СП
Г-Н
о
ю
ю
г^
"—'
о
^
00
СП
оо
см
ю
(>.
у—*
со
со
СО
со
СО
СП
ю
со
^
со
ю
СО IN.
СО Tt*
со сп
^Р СО
о
со
см
со
ю
*ф
СО
см
со
СП
СО
см
ю
со
см
СП
ю
СП
со
h-
г^
t—«
см оо оо
оо —• о
СМ СО Г"-
СП IS- СО
о см in. оо со t^-
О О IN. О 00 О
О Tf 00 ^Г СП СО
СО Ю "Ф Tf СО СО
со
СО
СМ
СО
см
ю
СП
СМ
h^
^
СМ
Г"-
00
СМ
СП
г^.
СП
_4
СП
h-
OOOIS-COOOCOCMIS.
осмоосоюсмюсм
ot^-^o^cn^fo
ОС>-СОСОЮ-^Г',^,,=Г
со
СП
СМ
СО
СМ
00
СП
см
00
СП
СО
см
,__!
"ф
4f
см
СП
о
см
см
СП
СП
СП
»—<
00
о
00
о о
О «-н
о
со
о о
О -н
о
со
о
ю
ГРАНИЧНОЕ УСЛОВИЕ ПЕРВОГО РОДА
101
о
о
ю
СО
Ю 00
см о
СМ —
о см
со оо
О О
см
h-
СО
о
о
ю
ю
о
*-ч 00
to о
СО
со
о
со
со
СО
о
см см
о о
_н
to
о
ю
см
ю
о
^f
ю
о
СО
ю
LO
о
СО
(^
ю
г-
со
со
о
оо
со
о
^
CD
со
о
ел
о
■ч<
о
.- со
см
Т1
г^
со
см
о
CD
^f
см
о
см
со
см
о
*<*•
t^
см
о
г^
оо
см
ст>
о
СО
о
см
-4F
i~-1
о
со
ю
о
ю
СО
см
о
о
со
см
о
о
со
со
о
о
СО
"*•
о
о
^f
ю
о
со
CD
о
о
СО
см
CD
о
о
ю
СО
(D
о
о
Th
^
ел
о
о
"*•
ю
. ел
о
о
см
оо
о
о
t^
СО
ОО
о
о
СО
^
00
о
о
^н
ю
оо
о
о
СО
СО
00
о
т—4
ю
г-
о
о
00
ю
г-
о
о
ю
со
t^
о
о
со
г-
ь-
о
о
00
г>
о
00
h-
со
о
о
со
00
СО
о
о
см
CD
СО
о
о
о
о
г-
о
о
1^
о
г-
о
!*
СО
о
о
о
см
СО
о
о
IS.
см
со
о
о
со
со
со
о
о
о
^т<
со
о
СО
to
ю
о
о
см
со
ю
о
о
h-
СО
Ю
о
о
СО
h-
ю
о
о
ел
1>-
ю
о
со
о
to
о
о
оо
о
ю
о
о
со
ю
о
о
оо
LO
о
о
т*«
см
ю
о
ю
ю
-vf<
о
о
о
со
F
о
о
^f<
со
4f
о
о
CD
со
^г
о
о
СО
f^
^<
о
см
-Ф
о
о
со
^
о
о
о
см
"ф
о
о
rf
см
■ч^
о
о
CD
см
^н
о
со
t^
со
о
о
со
1^
со
о
о
о
оо
со
о
о
^р
ОС)
со
о
о
h-~
оо
СО
о
со
СО
со
о
о
о
^т1
СО
о
о
Tt<
■"ф
СО
о
о
t^
Tt<
СО
о
о
о
ю
со
о
со
о
со
о
о
00
о
СО
о
о
со
о
о
LO
ф
о
о
оо
СО
о
со
|>-
см
о
о
оо
г-
см
о
о
оо
см
о
о
со
00
см
о
о
!>■
оо
см
о
о
to
см
о
о
см
ю
см
о
о
ю
to
см
о
о
00
ю
см
о
о
о
со
см
о
со
см
см
о
о
оо
см
см
о
о
о
СО
см
о
о
со
со
см
о
о
ю
СО
см
о
ОО
00
ю
о
^
о
со
со
со
rf
о
см
to
*=ф
о
о
со
о
СО
СО
СО
г-
*—1
о
00
00
тр
со
о
о
СО
Г--
о
со
СО
CD
о
о
со
h-
CD
о
v—t
h-
00
о
о
о
ОО
оо
о
CD
00
h-
о
о
h-
CD
h-
о
СО
h-
с^
о
см
h-
о
со
*ф
со
о
о
со
ю
СО
о
тр
00
ю
о
о
о
CD
ю
о
оо
см
ю
о
о
-=*•
СО
ю
о
00
1^-
тр
о
о
СО
со
^
о
со
СО
"Чр
о
о
h-
СО
•ГР
о
см
CD
со
о
о
СО
CD
со
о
п*
to
со
о
о
N
to
СО
о
Т-+
см
со
о
о
гр
см
со
о
CD
00
см
о
о
со
CD
см
о
СО
со
см
о
о
to
со
см
о
h-
со
см
о
о
о
^
см
о
о
см
со
со
СО
^
г-
см
со
О CD CM CD
О 00 00 00
СМ О CD ОО
— — О О
in
о
оо
О
00
см
г~-
о
CD
Ю
СО
О
СО
CD
Ю
О
CD
СО
Ю
О
ОО
00
««f
О
см
^
f
о
о
о
•^г
о
г—1
со
СО
о
|>-
см
СО
о
ю
ел
см
о
00
со
см
о
см
Чф
см
о
СО I—" О СО 1^ СО
СО 00 ^т1 ^—| CD CD
00 ^ ' СО СМ О CD
ОО
(D
00
О
СО
ОО
О
ю
СО
h-
О
ю
со
со
о
см
о
со
о
ю
-^
ю
о
со
CD
^
о
ю
СО
т
о
У-Ч
СО
со
о
см
CD
см
о
у—,
г^.
см
о
ю
-^
см
о
о о
О *-н
о
о о
^ to
^^^^^^^^(^СМС^^^^^^^^^^^^0^^
102
Глава четвертая
Н
0,5-
Так как Fo
az
то скорость
Рис, 4.12, Кривые распределения
температуры в неограниченной пластине
(несимметричная задача)
нагревания-^- будет прямо
fпропорциональна коэффициенту
температуропроводности и обратно
пропорциональна квадрату половины толщины
пластины.
В__табл. 4.4 приведены значения
и Jf~~ для Разных чисел Fo.
Все вышеприведенные решения
справедливы и для случая охлаждения
неограниченной пластины, когда одна
ограничивающая поверхность имеет
идеальную тепловую изоляцию
(отсутствие потока тепла, что характеризует-
дТ @, т)
ся равенством
дх
= 0), а
противоположная поверхность в начальный момент времени мгновенно
охлаждается до постоянной температуры Тс, т. е. Т (R, т) = Тс (начало
координат переносим из центра на поверхность пластины). Начальное
распределение температуры по толщине пластины может быть задано в
Таблица 4,4
S -
Зависимость между -тр— , 6 и числом Fo
Fo
0,005
0,01
0.02
0.04
0,06
0,10
0,2
0,3
—
е
0,91978
0,8849
0,8401
0,7729
0,7236
0,6430
0,4960
0,3859
1 dti
2 d¥o
3,9894
2,9735
1,9941
1,3904
1,1536
0,8917
0,6323
0,4772
Fo
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,1
i e
0,3021
0,2353
0,1844
0,1475
0,1127
0,0900
0,0687
0,0537
l rfe
2 oFo
0,3728
0,2912
0,2275
' 0,1820
0,1389
0,1110
0,0848
0,0663
виде некоторой функции / (x) или быть равномерным, т. е. Т {х, 0) =
= Т0 = const. В этом случае под R надо понимать не половину
толщины, а толщину всей пластины.
Если одна поверхность пластины все время поддерживается при
постоянной температуре Тс = const, а противоположная — при
постоянной, но иной температуре, например при начальной T0=const,
то граничные условия можно записать так (рис. 4.12):
Г@,т) = Гс
Г(#,т)=70
const
const
D3)
Начало координат находится на левой поверхности пластины
@'<*<Я).
ГРАНИЧНОЕ УСЛОВИЕ ПЕРВОГО РОДА
103
Решение для изображения TL(x,s) имеет вид
-^- — TL(x,s) = -^- Тс
sh
V^
D4)
Пользуясь аналогичным приемом, решение задачи получаем в двух
видах. Во-первых, при применении теоремы разложения получим
Т(х, т) — Гс
т0-тс
f + ^(~1Г1^зт,й-^ехр(-^Ро), D5)
/2=1
где [хл = ятс — характеристические числа. В стационарном состоянии
(? = оо) распределение температуры будет происходить по прямой,
проходящей через точки @, Тс) и (R, Т0). Во-вторых, разлагая (sh
в ряд и пользуясь таблицей изображений, находим
v±
R
Т(х, т) — Тс
т0-тс
= erf-
2/о
л=1
erfc
2л/г-
2}Лп
■erfc
2яЯ-
2У^Г
■)■■
D6)
Первый член решения D6) представляет собой решение для
полуограниченного тела, так как из этого решения можно получить решение A6)
§ 2, положив R= оо. Отсюда следует, что при малых значениях
времени, точнее при малых значениях Fo, распространение тепла в пластине
происходит так же, как и в полуограниченном теле. В этом случае
(малые значения Fo) сумма ничтожно мала по сравнению с первым
членом при достаточной толщине пластины. Это следует непосредственно
из решения D6), если его переписать в критериальной форме
D7)
При малых значениях Fo аргументы функций erfc велики, а сами
функции близки к нулю. Поэтому суммой можно пренебречь.
К этому важному физическому положению распространения тепла
в пластине при малых значениях Fo можно было прийти из анализа
решения B8), а именно: если перенести начало координат из середины
пластины на левую поверхность, т. е. сделать замену переменной
xJrR = X и положить 2i?-> ©о, то решение B8) примет вид
= erf-
2 У с
D8)
что является решением для полуограниченного тела.
На рис. 4.13 приведен график изменения температуры 6 от числа
Фурье для разных координат пластины от 0 до 1.
В этом параграфе приведен анализ решений для неограниченной
пластины, чтобы показать читателю большое преимущество операцион-
104
Глава четвертая
(фр
Ц|
пт
II
1 '
1
1
1 1
г^ЕЕ
У ""£
BE
ш
р£
IX
г *
|_< 1
8i
T-f~r
l
I
I
i I
]
1
V
BFi^
Wk
=
1 '
1
1 ..
1
.....
1
I
I
1
рд
шш
A
Ш
EC
p
1
3
s=k
Щ
?ef
g
"H
T.
cT:
1
=.
I
rr£
3
В
Ш
1 с
1
о
э
5=
=
i
1
1
5c
= c
=:
N
s
in
-C
~r
'
h
v.
C-J *
5j
=.
=
iO "_
(V
N
_
*
\
_
~'o:
г CD:
,
Л
ч
e:
^
—
—(-
-0O-
-o:
—If
E<*
—с
^3
D^3
=c
J_°o J
iioli
1 \ 1
\
\
CM 0^7
о
о
о
51
1?
«В
О
e
о
к
вг
о
о
к
со
оо
о"
<D
О
о"
ГРАНИЧНОЕ УСЛОВИЕ ПЕРВОГО РОДА
105
ного метода перед классическим. Решения в
форме Лапласа, представляющие известную
комбинацию функций erf или erf с, удобны для
малых значений числа Фурье. Наоборот,
решение в форме Фурье, состоящее из
произведения двух функций (одна —
экспоненциального вида, учитывающая изменение
температуры во времени, другая — тригонометрического
вида, характеризующая изменение
температуры по толщине пластины), удобно для
больших значений числа Фурье. В этом
случае всегда можно ограничиться одним
(первым) членом ряда, отбросив все остальные.
Операционный метод Лапласа позволяет
получать ряд приближенных решений с любой
степенью точности. Эти решения достаточно
просты и могут быть с большим успехом
использованы при технических расчетах.
Рис. 4.14. Кривые распределения температуры в шаре
(симметричная задача)
T,rconst
To=const
§ 4. ШАР (СИММЕТРИЧНАЯ ЗАДАЧА)
Постановка задачи. Дано сферическое тело (шар) радиуса R с
известным начальным распределением температуры /(г). В частном
случае температура может быть одинакова и равна Т0. В
начальный момент времени поверхность шара мгновенно охлаждается до
некоторой температуры, равной Тс, которая поддерживается
постоянной на протяжении всего процесса .охлаждения. Требуется найти
распределение температуры внутри шара в любой момент времени
и удельный расход тепла. Охлаждение происходит равномерно, так
что изотермы внутри шара представляют собой концентрические
сферы, т. е. температура зависит то-лько от радиуса-вектора г и времени %
(рис. 4.14).
Дифференциальное уравнение теплопроводности при симметричной
задаче имеет следующий вид:
д^(г, ч) / д*Т(гу т) 2 дТ{гух)
при условиях
дг2 г дг
(*>0; 0<r<R)
Г(г,0) = /(r),
Т(Ц,хт) = Тс = const,
T@,T)=f со,
дТ@, z) ^Q
дх
A)
B)
C)
D)
(последнее условие есть условие симметрии).
106
Глава четвертая
Дифференциальное уравнение (I) можно написать так:
д\гТ(г^)} ^а д*{гТ(г, т)] -
Можно показать тождественность уравнений A) и E):
дт ( д г д (гТ)
г
\ дг I дг J J дг \ дг j
1 дг2 дг дг V дг2 дг
сокращая на г, получим
дТ ( д2Т , 2 аг
= а
ат \ ar2 ' аг
Решение задачи методом разделения переменных. Будем вначале
решать задачу методом разделения переменных. Если сделать замену
переменных гТ(г, т) = &, то уравнение E) относительно 9- тождественно
уравнению для неограниченной пластины. Частное решение этого
уравнения нам известно [см. § 3, решение D)]:
» = гТ (г, т) = (С sin kr + D cos kr) e~ak*\ F)
Следовательно,
T (r, x) = (c -^ + D ^Щ e~akt\ G)
Так как распределение изотерм симметрично относительно центра,
а температура в центре шара (г = 0) не может быть бесконечно
большой, то постоянная D равна нулю; последнее необходимо, так как
sin kr * п cos kr ъ
- -~±k при r-^0, a ^оо. Этот вывод непосредственно
вытекает из решения F), потому что при г = 0 &(г, т) должна быть равна
нулю, откуда D = 0.
Таким образом, частное решение будет следующее:
Г (г, т) = С—— е . (8)
Для упрощения расчетов положим Тс = 0; это означает, что отсчет
температуры ведется от Гс. Тогда, удовлетворяя частное уравнение (8)
граничному условию C), будем иметь
T(R^) = C^^-e~ak2x = Tc = 0.
Следовательно, sin&/? = 0, т. е. kR = тс, 2тс, Зтг, ... @<т< оо).
Таким образом, будем иметь бесчисленное множество значений &,
определяемых из равенства
knR = пк = рпУ где п = 1; 2; 3; . . . ; (9)
значения \ъп берутся, начиная с тс, так как при п = 0 соответствующий
член будет равен нулю для всех точек г < R.
Общее решение будет суммой частных решений:
гТ(г,%) = 2 Спsinknre~ak"x . (Ю)
ГРАНИЧНОЕ УСЛОВИЕ ПЕРВОГО РОДА
107
Для определения постоянных Сп воспользуемся начальным условием
00
гТ(г, 0) = rf (г) = 2 С„ sin knr. (И)
Л=1
Если функция г/(г) удовлетворяет условиям Дирихле, то ее можно
разложить в ряд Фурье. Помножим обе части равенства A1) на sinkmr
и проинтегрируем в пределах от 0 до R; тогда
R со R
J rf (г) sinkmrdr = 2 J Cn Sln knr sin kmrdr. A2)
/i=10
Тем же способом, что и в § 3, можно показать, что
R
J(m+;) = §smknrsmkmrdr = kmS'mk»Rcosk"R2-kfink>»Rcosk''R , A3)
О ^п~~^т
^m=n) = jsin4,rdr = |--ii^. A4)
о п
Так как kn = mz, то J{m+n) = 0, а «^т=/г) ==-?г Я» т- е- все интегралы
равны нулю за исключением одного, равного 1/2/?, когда т = п.
Таким образом, для определения коэффициентов Сп получаем
следующее соотношение:
я
Сп= j^-^rf (r) sin knrdr. A5)
Общее решение нашей задачи примет вид
R
— J rfir)sinpn^drexp(^pl~y A6)
При равномерном начальном распределении Т(г, 0) = f(r) = Т0
получим
R
R
так как cosjj^ = cosmr == (-— 1)п.
Окончательно будем иметь
Т(г, т)
2
л=1
(_!)««.
Л sin («•„
^_^„ «т
V-n
A7)
Если температура Гс не равна нулю, то решение задачи можно
написать так:
A8)
где
^л = (-1)п+1-2, ця = я*.
A9)
108
Глава четвертая
Решение задачи операционным методом. Решение A8) получим
методом преобразования Лапласа, применяя его к дифференциальному
уравнению E):
[rTL (r, s) ]" - JL rTL (r, s) + ^ = 0. B0)
Решение уравнения B0) можно написать по аналогии с решением
уравнения A7)
гТь(г, s)--ф^= Ach]/^-r + Ssh]/-^г. B1)
Так как в центре шара (г = 0) температура Т@, т) и ее
изображение 7^@, s) не могут быть величинами бесконечно большими, т. е.
должно быть Mm гТ. (г, s) -> 0, то непосредственно ясно, что следует по-
ложить А = 0.
Таким образом, имеем
/¥
sh
^ s) - -Ь- = Я 4^- . B2)
Граничное условие C) для изображения будет иметь вид
TL(R,s)=^f. B3)
Удовлетворим решение B2) условию B3):
откуда
S ^ £
в = (T„-T^R ^ B4)
,sh-|/JL*
так что решение B2) можно написать так:
(r0-Tc)*sh"|/-^r
-^_TL(r,s)= _ а . B5)
Числитель Фх (s) = (Т0 — Тс) i? sh у ~- г и знаменатель ^ (s) =
= rs sh у — R не являются обобщенными полиномами относительно s,
но их можно привести к ним, умножив или разделив на 1/—, а именно
1 rS
r+-L-L-s + .. •
31 ° . B6)
8{« + Ж.*а1Г+:
ГРАНИЧНОЕ УСЛОВИЕ ПЕРВОГО РОДА 109
Из операционного исчисления известно, что если Ф($) и <J>(s) —
обобщенные полиномы относительно s, где Ф(s) = sk<Px(s), ty(s) = sktyx(s)f
то
Hm A(£L= Hm .^Jl, если s*^=0, B7)
где srt—корни уравнения фхE) = 0.
Поэтому за исключением первого корня s = 0 переход от
изображения к оригиналу может быть сделан по обычной теореме разложения,
так как в нашем случае Ox(s) и ^1(s) удовлетворяют условию B7).
Найдем корни 4>i(s)> Для че1^° необходимо положить <|>i (s) = 0:
^(s) = rs.sh]/-^/? = 0.
Отсюда получим следующие корни: 1) s = 0 (нулевой корень),
2) sh Y~^R = 4- sin i Y~ R = 09 откуда t jAj-Я = *, 2тс, 3<t,... =
= wk или srt = = , так как и*п = mz.
Воспользуемся теоремой разложения:
t;(s,)-Jira [rsh ]/TR +->., j/XRchl/jL«] =, ir|.,co3|i.
Следовательно, будем иметь
со оо
Vft/и ,, VI 2R (Т0-Тс) sin vn— .
jmU ^ (sn) Jmi v ; 'ft, . V у Vn R2 j
П=1 /2=1
B8)
Для нулевого корня воспользуемся отношением B6):
ФE) = (г0-гс)*|у + -1-г^+...],
t(s) = rS^+-^^-^+ .-.]; B9)
тогда
Йт?>-<г--т->' <"»
Окончательно решение задачи можно написать так:
/г—1
110
Глава четвертая
Перепишем в безразмерных величинах:
г
R sin р.л —
Т(r,^)-T0 -2jAn ""~™ * exp (-^Fo), C2)
Г0-Гс *шА " Фя
где Лл = 2 • (— 1 )n+1, \ъп = тс, т. е, получим решение, тождественное
решению A8). Решение C2) представляет быстро сходящийся ряд, так
как с увеличением jxn экспоненциальная функция ехр (—p^Fo) быстро
уменьшается.
Для малых значений Fo необходимо брать несколько членов ряда,
что представляет собой известные неудобства при расчетах. Для
больших значений Fo можно ограничиться одним членом ряда, а всеми
остальными можно пренебречь. Следовательно, решение C2) наиболее
удобно для больших значений Fo.
Для малых значений Fo найдем решение в другом виде. Разложим
в ряд (см. приложение):
sh
= 2[exp(-/-i-R)+exp(-3/i *)+...]
п
sh / Л- R
= 2^ех?[-Bп-\) ]/"-£-/?].
Кроме того, воспользуемся формулой
* V?' - т N (У?0 - е!"> (""/ТО] •
Тогда решение B5) для изображения можно написать так:
00
-LL-TL(r,s)= <T*-JJ* ^(ехр{-[Bя-1)/г-г1 |/^}-
exp{-[Bn-l)i? + r]]/-J-}). C3)
Пользуясь таблицей изображений, получим решения для оригинала в
виде
Т(г, х)-Гс = j R_ V
Тп-Тс г **d
Bп-1)-~ {2п-1) + ~-
erf с erfc ■
"о — Тс г *веЛ \ 2 l^Fo 2 /Fo
л=1 ч
C4)
Это решение пригодно для г>0. Для температуры в центре шара
(г = 0) решение получим так. Из выражения B5) имеем
ГРАНИЧНОЕ УСЛОВИЕ ПЕРВОГО РОДА
111
0,8 1,0
A-r/R)
Рис. 4.15. Кривые распределения относительной избыточной
температуры 6 в шаре по относительному радиусу rjR.
Тогда, применяя соотношение
находим
Лтг^У
Уъ
ехр
k*
4т '
7@, т) — Тс
1-2
/^2>[-^]-
C5)
Уравнения C4) и C5) показывают, что решения для неограниченной
пластины и шара можно представить в одних и тех же функциях.
На рис. 4Л5 приведены кривые распределения температуры по
безразмерной координате -^- для различных значений Fo от 0,005 до 0,4.
Из рис. 4.15 видно, что при Fo = 0,005 температура на глубине-4-<!0,б
мало отличается от начальной; только, начиная с критерия Fo > 0,04
заметно изменение температуры в центре шара. Процесс охлаждения
почти заканчивается при Fo>-0,4.
Расчетные графики изменения относительной температуры A—6)
в зависимости от числа Фурье Fo приведены на рис. 4.16 для
различных относительных координат.
112
Глава четвертая
иллТ \\-
ШЩ\-\
|те#
BS№:f:'|'T"
I^^Se
ШгКг^
п v\nN"iS
| 1 \ V К
rffiw
\ WM1
г tn тк
УфкШ|
ВНр
B4v4w
ГТ" 1ТГ1
□ЕЕгргр
II II с
■ч
Е
~
Е
о
31
\ \ \ \ \ \ У
м
1 1 I 1 1 X \
1 1 1 1 V\ \
\Л \qzA
Mr NT
Ь4=гЬг|-—b::|:u=i:-
Ц-4- 4 1-
aJiiSE
вееЕУШ
tiiijrxdziz
z>
х
1
1
Т.
~
:т
1
\
\
—
щ
J
\
\
It
zr
оо
g
*1г
=рф
Щ
Epik
тго
4-ц
Щ
1
_!__
ТЕП
*F
л
\
\
н~=
_
~ф
_оо
=о
к
\
\]
Щ--
L.
ЗЕ
Ш
—t
ЕЕ
_1
ЕЕ
-0,8
ЕЕ
111
т
щф
-:r.-*Js
4zj
ю
S
If
fe
L-—
Ш
3
-C
E
5:
54
~
—
E
_.
iiO =
—
Ё
^7
E
i
z
CO
/
"V
1
/
/
1
*c
1
-C
0
^
r
E
-c
'
|
-
r
E
^
-
Щ
Щ
\\\
AW
\\\
u
\ 1
\
1
1
1
"МП
HI
У11
a,
о
о
«
я
о
Он
е
S
о
о
о.
о
К
a
о
и
н
о
СП
a
а
ГРАНИЧНОЕ УСЛОВИЕ ПЕРВОГО РОДА
113
Определение потерь тепла. Для определения теплопотерь в
процессе охлаждения найдем среднюю температуру по объему шара; она
определяется формулой (см. гл. 1, § 7)
R
C6)
T{*) = -^$r*T(r,x)dr.
Если подставить в это соотношение вместо Т (г, т) соответствующее
решение C2), то после интегрирования получим
C7)
где Вл = —р
v-n
Можно получить решение для б в иной форме. Найдем TL(s),
пользуясь решением B5) для изображения, а именно
R
Т,
M) = ~l^TL{r,s)dr^
= J\__ 3 (Т0 - Гс) УТ № лГ±_ р , 3 (Г0 - Те) а
s sVJR Y a s2R2
C8)
Разложим cthl/-j-/? в ряд:
cth Y^R = 1 + 2 exp (-2 ]/"-!. R) + 2exp (-4 ]/-?- /?) + ...=
oo
= l+2\]exp(-2n]/^i?). C9)
tl=l
После перехода от изображения к оригиналу получим решение в виде
D0)
Для иллюстрации приведем численный пример. Определить температуру шара в
г
процессе охлаждения в точке -^- = 0,4, а также среднюю температуру его для
безразмерного времени 0,2 (Fo = 0,2), если шар был нагрет до температуры 473° К B00° С)
и в начальный момент времени был помещен в тающий лед Тс — 273° К @°С),
г
Найдем температуру в точке -75-= 0,4 по решению C2):
-ц
sin0,4rc п 1 sin0,4-2rc 1
exp (— 0,2u2) —-^ exp (—0,2. 4гс2) =
0,4 1 ч " ' ' 2 0,4
= 1,591-0,951-0,139 — 0,7960,588-0,0004 ^0,21.
Такой же результат получим из решения C4):
e1 = i.
1
erfc
1—0,4
erfc
1+0,4
т)-
0,4 V"" 2 У 0,2 ~д~ 2/0,
= 1—2,5@,3427—0,0270) = 1—0,79^0,21,
114
ii
0,05
от
0,03
0,02!
0,0!
»0Ю,4
Рис. 4.17. Зависимость между средней относительной избыточной
температурой 6 и числом Фурье Fo в случае шара
Это значение можно получить и по графику рис. 4.15: для -б~ =0,4 и Fo = 0,2
относительная температура равна 0 = 0,21.
Температура шара в этой точке будет равна
Тг = Тс + (Т0 — Тс) 6х = 273 + 200-0,21 = 315° К D2° С).
Средние температуры 6 находим по формуле C7)
<St=B1 exp (—PiFo) + £2ехр (— p|Fo) = ~ exp (-0,2гс2)
4тс2
ехр (—0,8тс2) =
= JL ехр (~-0,2и2) = 0,6070- 0,1389 « 0,084.
Можно также 6 определить по графику рис. 4.17, на котором дана зависимость
0 = / (Fo); из графика находим, что для Fo = 0,2 0 = 0,085.
Следовательно, средняя температура шара
Т (т) = 273 + (Т0 — Тс) Т=* 290° К A7° С).
Если известны радиус шара и его теплофизические коэффициенты, то можно
определить время охлаждения и потери тепла за это время по элементарным формулам.
Для удобства расчетов в табл. 4.5 приведены значения 0Ц @Ц = 0(О,
х)—температура в центре шара) и 0 для разных значений Фурье.
ГРАНИЧНОЕ УСЛОВИЕ ПЕРВОГО РОДА Ш
Таблица 4.5
Значения функций
0Ц= 2 2 (—l)n+1 ехр (— пЧ2¥о) и 6=-^2ехР <~ n27c2Fo)
n—l п=\
*2Fo
0,00
0,02
0,04
0,03
0,08
0,10
0,12
0,14 1
0,16
0,18
0,20
0,22
0,24
0,26
0,28
0,30
0,32
0,34
0,36
0,38
0,40
0,42
0,44
0,46
0,48
0,50
0,52
0,54
0,56
0,58
0,60
0,62
0,64
0,66*
0,68
0,70
0,72
0,74
0,76
0,78
0,80
0,82
0,84
0,86
0,88
0,90
0,92
0,94
К
1,0000
1,0000
1,0000
1.0000
1,0000
1,0000 |
1,0000 !
1,0000
1,0000
1,0000
1,0000
0,9999
0,9998
0,9995
0,9990
0,9983
0,9972
0,9957
0,9938
0,9913
0,9883
0,9846
0,9804
0,9755
0,9700
1 0,9639
0,9573
0,9500
0,9422
0,9339
0,9251
0,9158
0,9062
0,8962
0,8858
0,8752
0,8643
0,8531
0,8418
0,8303
0,8186
0,£068
0,7950
0,7831
0,7711
0,7591
0,7471
0,7351
б
1,0000
0,8537
0,7967
0,7543
0,7195
0,6897
0,6632
0,6394
0,6176
0,5976
0,5789
0,5615
0,5451
0,5296 !
0,5149
0,5010
0,4877
0,4750
0,4629
0,4513
0,4401
0,4294
i 0,4190
, 0,4090
1 0,3994
1 0,3901
0,3810
0,3723
0,3639
0,3557
0,3477
0,3400
0,3325
0,3252
0,3181
0,3113
0,3045
0,2980
0,2916
0,2854
0,2794
0,2735
0,2678
0,2622
0,2567
0,2513
0,2461
0,2410
rc2Fo
0,96
0,98
1,00
1,05
1,10
1,15
1,20
1,25 1
1,30
1,35
1,40
1,45
1,50
1,55
1,60
1,65
1,70
1,75
1,80
1,85
1,90
1,95
2,00
2,10
2,20
2,30
2,40
2,50
2,60
2,70
2,80
2,90
3,00
3,20
3,40
3,60
3,80
4,00
4,50
5,00
5,50
6,00
6,50
7,00
7,50
8,00
8,50
8д
0,7232
0,7112
0,6994
0,6700
0,6413
0,6132 1
0,5860 !
0,5596
0,5340
0,5095
0,4858
0,4631
0,4413
0,4204
0,4005
0,3814
0,3631
0,3457
0,3291
0,3133
0,2981
0,2837
0,2700
0,2445
0,2213
! 0,2003
1 0,1813
0,1641
0,1485
0,1344
0,1216
0,1100
0,0996
0,0815
0,0667
0,0546
0,0447
0,0366
0,0222
0,0135
! 0,0082
0,0050
1 0,0030
0,0018
0,0011
0,0007
0,0004
6
0,2360
0,2312
0,2264
0,2150
0,2042
0,1940
0,1844
0,1752
0,1665
0,1583
0,1505
0,1431
0,1360
0,1293
0,1230
0,1170
0,1112
0,1058
1 0,1006
0,0957
i 0,0910
\ 0,0866
! 0,0823
0,0/45
' 0,0674
t 0,0610
0,0552
0,0499
0,0452
0,0409
0,0370
0,0335
0,0303
0,0248
0,0203
0,0166
0,0136
0,0111
0,0068
.0,0041
0.0025
0,0015
0,0009
0,0006
0,0003
0,0002
0,0001
§ 5. НЕОГРАНИЧЕННЫЙ ЦИЛИНДР
Если длина / цилиндра значительно больше его диаметра 2R (-—> 11,
то его можно уподобить неограниченному цилиндру, у которого длина
бесконечно велика по сравнению с диаметром.
116
Глава четвёртая
Рис 4.18. Кривые распределения
температуры в неограниченном* цилиндре
(симметричная задача)
Если теплообмен между
поверхностью цилиндра и окружающими
телами происходит одинаково по
всей поверхности, то температура
его будет зависеть только от
времени и радиуса (симметричная
задача)
Постановка задачи. Дан
неограниченный цилиндр при некотором
заданном радиальном
распределении температуры, те. в виде
функции f(r). В начальный момент
времени поверхность цилиндра
мгновенно охлаждается до
некоторой температуры Т<., которая
поддерживается постоянной на
протяжении всего процесса
охлаждения. Необходимо найти
распределение температуры внутри
цилиндра в любой момент времени и
удельный расход тепла.
Дифференциальное уравнение теплопроводности в нашем случае
напишется так (см. приложение III):
^_«(*!£^- + -L»£i). „>(,; <><,•<*>.
Краевые условия следующие (рис. 4.18):
Т
аг(о,
1 дг
т
(R,
А
{г, 0)
т) =
= 0,
= /И. 1
Тс = const,
Т@,х)ф со.
A)
B)
C)
D)
Последнее условие означает, что температура, на оси цилиндра на
протяжении всего процесса теплообмена должна быть конечной.
Решение задачи методом разделения переменных. В гл. III, § 2
было показано!, что частное решение уравнения теплопроводности по
методу разделения имеет вид
Т = е~ак2Ч, E)
где & есть решение дифференциального уравнения
В нашем случае &(г) должно быть решением уравнения Бесселя
<' Ъ*'(г)+±Ъ'(г) + кЧ(г)=±0, F)
ГРАНИЧНОЕ УСЛОВИЕ ПЕРВОГО РОДА
117
которое можно написать еще так:
г$« (Г) + »' (Г) + k2rb (г) = 0.
Будем искать решение
уравнения Бесселя
хи" + и' + хи = 0
в виде степенного ряда
и = а0 + агх + а2х2 +
4- a*xs + ... .
(a)
(б)
М403,32; 0,22)
y=j0(x)
y=i»(x)
3 4\ 5 \6 /7 8,' 9 Ю\ И 12 i/ 14 х
\У М4A1,75; -0,23)
-0,1-1
Дифференцируем почленно *0'2-
ряд (б) и подставляем в левую "ол
часть выражения (а) значения и,
и!, и!\ тогда получим
и = а0 + агх + а2х2 + а3х3 +
+ а4*4 + . . . ,
и' = ах + 2а2* + За3х2 +
+ 4а4х3 + 5а5*4 + ... ,
ц" = 2-1-а2+3-2а3х +
+ 4.3а4л:2 + ... •
Умножая первый ряд на х, "°'5j |
второй— на 1, третий — на х, *6»
складывая и собирая члены с
одинаковой степенью X, получим рИс. 4.19. Графики функций Бесселя: а) пер-
Л v Л вого рода; б) второго рода
аг + (а0 + 22а2) х+(а± + 32а3) х* +
+ (а2 + 42а4)л;3 + ... . (в)
Для того чтобы выражение (в) обращалось в нуль при переменном
я, необходимо, чтобы все коэффициенты при х равнялись бы нулю, т. е.
^ = 0, а0 + 22а2 = 0,
а± + 32а3 = 0, а2 + 42а4 = 0, ..., ал_2 + п2ап = 0.
Из этих равенств находим, что все коэффициенты с нечетными индексами
равны нулю (так как аг = 0), а все коэффициенты с четными индексами
выражаются через а0:
_ 1
Ч — — а<»
а4 =
42
• а9 =
1
22-42
<20, й6 —
«4
б3
22.42. б2
Подставляя полученные значения коэффициентов в (б), находим
и =: а0 1 h
22 22-42
22-42,
+ ... •
Если положить а0=1, то частный интеграл уравнения (а) будет
равен функции
^oW = l-ir +
22*42
22.42. б2
(г)
118
Глава четвертая
Эта функция называется функцией Бесселя первого рода нулевого
порядка.
Для нахождения второго частного решения уравнения (а) можно
воспользоваться формулой [см. гл. III § 2, решение A4)]
(Д)
где u1(x)^=J0(x) — первое частное решение, щ(х) — второе частное
решение, линейное, независимое от их(х).
Аналогичным путем находим, что второе частное решение равно
u2(x) = J0(x)lnx + — — (l+—) Н ^— (l+— + —)—....
2V / ow 1 2а 22-42 V 2 / 22-42-62 \ -23/
(е)
Обычно вместо функции и2(х) берут Y0(x), связанную с и2(х)
следующим образом:
К0 (х) = 4u2W+4 Л (х) (С - In 2),
где С = 0,5772 ... — постоянная Эйлера, YQ(x)— функция Бесселя
второго рода нулевого порядка. Такой вид функции Y0(x) взят для того,
чтобы получить простые приближения при больших значениях х.
Частные решения иг(х) = J0(x) и иъ(х) или Y0(x) линейно независимы,
У (х)
так как —iL1^- ф const; общий интеграл уравнения Бесселя (а) равен
J0 (х)
и(х) =: CJQ(x) + DY0(x),
где С и D — произвольные постоянные.
Уравнение F) приводится к уравнению (а), если положить г=—г~,
доказательство предоставляем читателю.
Тогда общий интеграл уравнения F) будет равен
»(г) = С/0(йг)+ DY0(kr). G)
Так как температура на оси цилиндра (г = 0) должна быть
конечной, то решение G) не может содержать бесселеву функцию второго
рода, которая стремится к бесконечности при г->0 (рис. 4.19)
Следовательно, из физических условий задачи постоянная должна быть равна
нулю (D = 0). Тогда частное решение уравнения теплопроводности A)
будет иметь вид
T = CJ0(kr)e-akH. (8)
Функция J0{kr) является четной функцией, а именно
22 22-42 22-42-62
Она удовлетворяет условию D), так как
к ' [ 2 224 22426 ]
и при г->0 J0(kr)-±0.
Найдем постоянные k и С из граничного и начального условий. Для
упрощения расчетов положим Тс = 0; это означает, что отсчет темпе-
ГРАНИЧНОЕ УСЛОВИЕ ПЕРВОГО РОДА
119
ратуры производится от Тс. Тогда, удовлетворяя решение (8)
граничному условию C), будем иметь
Tc = CJ0(kR)e-ak2x = 0.
Отсюда следует, что в процессе охлаждения @<т<оо) должно
иметь место равенство
J0(kR) = 0. (9)
Это равенство называется характеристическим уравнением; из него
определяются характеристические числа kn.
Функция J0(kR) аналогична тригонометрической функции coskR
(рис. 4.19); она имеет бесчисленное множество корней knR = р.л, а
именно: [*! = 2,4048, р.2 = 5,5201, р3 = 8,6537 и т. д. Следует отметить, что
при достаточно большом п разность |хл+1 — [хл близка к тс.
Таким образом, из характеристического уравнения следует
*„£ = {*„, *» = -^-. (Ю)
Значит, имеем бесчисленное множество частных решений:
T = CJ0(knr)e~ak2n\ A1)
и любое из них будет удовлетворять не только дифференциальному
уравнению A), но и граничному условию C).
Такие функции A1) называются фундаментальными функциями; ряд,
составленный из них, будет общим решением
Г(м) = 2С»;о(*/)«°*' A2)
Я=1
Для определения постоянных Сп воспользуемся начальным условием
B), т. е.
7(г,0) = /(/•).= 2 С„/„ for). A3)
/2=1
Соотношение A3) представляет собой разложение функции в ряд по
функциям Бесселя. Для определения постоянных Сп воспользуемся тем
же приемом, что и в предыдущей задаче, но предварительно докажем,
что система функций "\Гх J0 (ax), Ух J0 (bx) является ортогональной.
Введем обозначения
ух = J 0 (ах), у2 = J0 (bx). A4)
Функции J о (ах) и J0 (bx) удовлетворяют соответствующим
дифференциальным уравнениям, и потому ух есть интеграл уравнения
ху" + у' + а2ху = О,
а уъ — интеграл уравнения
ху" + у' 4- Ь2ух = 0.
Эти уравнения можно написать так:
(ху'у = — а2ху, (ху'У = — Ь2ху.
120 Глава четвертая
Следовательно, имеем
[ху'гУ = — a2xyv A5)
\хуг2)' = -Ь*хуг. A6)
Умножим равенство A5) на у2, а равенство A6) на ух и вычтем из
первого второе, тогда получим
Ь2ху±уш — а2ху±у2 = у2 [ху[у — уг [xy'2)f = у'2 [ху[)' — уг [xy'2)f +
+ У% (ху[)' — у\ (ху'2)' = [у*ху\)' — (Угху'ъУ = (у&у[—У1ху'2у.
Перепишем это равенство так:
(Ь2 — а2) хугу2 = [у2ху\ — угху'2у. A7)
Интегрируем обе части равенства от 0 до х:
X
(Ь2 — a2) J xyty2dx =: x*/2#; — лгад. (* 7а)
"о
Переходя к прежним обозначениям, находим
\xJQ(ax) J0(bx)dx =, bxJ«{ax) Jl (*%~ ff °{ЬХ) Jl(aX) > A8)
6
так как у'{ === aJ'Q (ах) = — aJx (ах),
У 2 = bJo (bx) = — bJi (bx)-
Если b = а, то правая часть A8) обращается в неопределенность
типа -jj-, которую можно раскрыть по правилу Лопиталя
(дифференцируя числитель и знаменатель дроби по Ь, считая а постоянным):
xJq (ax) Ji (Ьх) + bx2J0 (ax)Jx bx —ax2J0 (bx) J± (ax)
{ xJ*(ax)dx = lim
J b-±a
26
*= — {xJQ (ax) h (ax) + ax2Jo (ax) p0 (x) — ^~] + ax2J\ (ax) j,
так как
J'Q (ax) == —J1 (ax),
j\ (ax) = J0 (ax) — —. Jt (ax).
Окончательно получим
(хЦ (ax) dx~£-[Jl (ax) + J\ (ax)]. A9)
b
Эта формула справедлива при любых значениях а и Ь и будет нами
использована в дальнейшем.
Умножим обе части равенства A3) на rJ0(kmr), где kmr— корни
функции J0(kmr), и интегрируем в пределах от 0 до R:
J rf (r) J0 (kmr) dr= j J CnrJo (V) 'o (kmr) dr =
0 " 6 n=\
= 2Cn$rJ0(knr)J0{kmr)dr. B0)
n=\ 0
ГРАНИЧНОЕ УСЛОВИЕ ПЕРВОГО РОДА
121
Согласно A8), все интегралы в правой части равенства B0) равны ну
лю за исключением одного, когда т = п. Действительно,
]' rJ0 (knr) J0 (kmr) dr=R k™U (KR) ^ {kmRJ ~У ° <*"*> 7l <*"*> = 0,
m vn
так как J0 (knR) = J0 (kmR) = 0. Для случая т = п согласно формуле
A9) имеем
$rJl(knr)rd=^-J*(knR).
Таким образом,
2 *
д>2- j rf (r) J о (knr) dr
о
Окончательно решение нашей задачи получим в виде
с- = -^7[Ш> <21)
00 ^0 \^п п
Т(г, х)=.
B2)
Предположим, что f(r) = TQ = const. Тогда необходимо
вычислить интеграл
^§T^J0(un-^\dr.
о А '
Предварительно покажем, что
J xJ0 (ах) dx = —xJ± (ax) + const. B3)
Функция ух — J о (ах) есть интеграл уравнения
ху" + у'+ а2ху = 0,
которое можно написать так:
(ху'У + а2ху = 0.
Следовательно, имеем
(ху[)'= — a2xyv
у\ =±= aJ'Q (ах) = — aJx (ax),
[— axJx (ax)Y = — a2xJ,0 (ax).
Интегрируя последнее равенство, получим формулу B3). Итак, имеем
р
, j;]TsJ0(vn^)dr=¥±JM, B4)
122
Глава четвертая
Тогда решение нашей задачи при условии Тс Ф О будет иметь вид
B5)
где
РлЛ (iart)
Таким образом, распределение температуры внутри цилиндра
зависит от критерия Fo и относительной координаты r/R:
Решение задачи операционным методом. Применим преобразование
Лапласа к дифференциальному уравнению теплопроводности. Тогда
получим обыкновенное дифференциальное уравнение Бесселя для
изображения TL(r, s):
Г>, s) + ±T'L(r, s)--f TL(r,s) + ^- = 0.
Перепишем это уравнение так:
rTl (r, s) + fL (г, s)--±rr [TL (г, 8) - -^] = 0. B7)
Если сравнить уравнение B7) с уравнением F), то видно, что
последнее отличается от уравнения B7) знаком перед последним членом.
—
В нашем случае k2' = —, следовательно, k=i у -—•
Решение уравнения типа B7), называемого модифицированным
уравнением Бесселя, состоит из суммы двух частных решений.
Первое решение отображается модифицированной функцией Бесселя
первого рода нулевого порядка или функцией первого рода от чисто
мнимого аргумента нулевого порядка
I (z) = J0(iz) = 1 + — + -^- + —— + ... . B8)
о \ / и \ / ' 22 2242 224262
Функция I0(z) по сравнению с /0(z) играет такую же роль, как
гиперболический косинус chz по сравнению с тригонометрическим cos г.
Второе частное решение отображается функцией Бесселя второго
рода нулевого порядка от чисто мнимого аргумента
(±гУ . 7-1,)'
+ fl+ _L)iA_L+fl + _l + -L)i2_l + ...) B9)
^ V 2 ) B!J \ 2 / Г 3 / (З!J S '
где С = 0,5772... —постоянная Эйлера.
Таким образом, общее решение уравнения B7) можно написать так:
Tl ('• s) -Ь- = Л/0 (-уТ-т )+ВК0( У~^г ), C0)
ГРАНИЧНОЕ УСЛОВИЕ ПЕРВОГО РОДА
123
от
А = {Т° ~^j . C3)
где I0 i у ■—- г ) = J0 ( i у ~ г ), А и В — постоянные, не зависящие
г и определяемые из граничных условий.
Так как по условию D) температура на оси цилиндра (г г= 0) не
может быть равна бесконечности, то постоянная В равна нулю,
поскольку при г -* 0 /С0A/ — г ) ""*" — °°• Следовательно, имеем
^ *)-^ = Л/0(}/^г). C1)
Функция /0(]/— г) четная [см. разложение B8)]; она удовлетворяет
условию симметрии.
Граничное условие C) для изображения напишем так:
TL(R, *)=■%-. C2)
Тогда, удовлетворив решение C1) условию C2), получим
гЖ*) = £ = £+л'.(]/Т*).
откуда
Решение для изображения в окончательной форме будет иметь вид
ь-тм-*'-™-}У\')-т. C4,
Полученное решение C4) представляет собой отношение двух
степенных рядов с натуральными показателями относительно s, причем ряд
знаменателя не содержит постоянной (первый член ряда равен s).
Таким образом, все условия теоремы разложения соблюдены и ее
можно применить для перехода от изображения к оригиналу.
Найдем корни полинома ty(s), для чего приравняем его нулю:
W - sl0 (Y^-R) = sJ0(i V^r) - 0. C5)
Отсюда получим: 1) s = 0 (нулевой корень), 2) i у — /? = |лХэ (л2,..., рп-*г
корни функции Бесселя J0(y<). Таким образом, имеем бесчисленное
множество корней для s; они равны
Найдем ф' (s):
124
Глава четвертая
0,8 1,0
O-r/R)
Рис. 4,20. Кривые распределения относительной избыточной
температуры 0 в неограниченном цилиндре по
относительному радиусу rlR
так как
Следовательно, имеем
,-1Гф<вП - ф@) д- V -£М eV
L Wj ~ Ф'@) ^ 2- «кы
я=1
2(Го~-Гс)
т0 - т (*,„ - (Г. - tj - 2 Jg^jp. '• («*■ т)ехр (" "- f) ■
Окончательно получим
0 = ^^ = iVo(^i)exp(-^Fo),
C6)
где
А =
^л^1 (Нтг)
Решение C6) тождественно решению B5).
На рис. 4.20 приведены кривые распределения температуры по
относительной координате ~ для различных значений Fo (от 0,005 до
0,8). Из рис. 4.20 видно, что процесс охлаждения практически закан-
ГРАНИЧНОЕ УСЛОВИЕ ПЕРВОГО РОДА
125
чивается при Fo>-0,8. Данные кривые могут служить номограммой для
определения 6 при заданных числах Fo и -^-.
Из анализа решения C6) следует, что ряд быстро сходится, так как
Н <[Л2< ^з < • • • < Рп и с увеличением \кп начальная амплитуда Ап
уменьшается, а также резко уменьшается экспоненциальная функция
ехр(—^Fo). Поэтому если исключить из рассмотрения малые значения
Fo, то можно ограничиться одним членом ряда C6), и расчетная
формула C6) приобретет простой вид.
Для малых промежутков времени можно получить приближенное
решение в ином виде. Вернемся к решению C4) для изображения. Для
малых значений времени величина V — R = qRlq = у — 1 велика;
тогда можно воспользоваться следующим асимптотическим
приближением для функции Бесселя при больших значениях аргумента:
/0(z) - —^—ez(l +— + —— + ...). C7)
Применяя это разложение для 10 ( у -^- R ) и
для изображения C4) можно написать так:
+
V±'
решение
Is)//?exp[-|/_i.(/?-r)]
(^о—Tc)i/-p
1 + -
1 / 1
8 V <?'■.
9
+ 128
qzr*
+ ■■
1 +
SqR
T0-Tc
У'1<*[-У±<*-ф+!& +
128<?2/?2
9RZ — 7r2
+ ■
-2/?r
128#2r2
+
...}.
Согласно таблице изображений решение для оригинала будет иметь
вид
Го-Г (г., -с)
То-Те
-V-
2 V
ax
2V
ax
(9g-7r«-2fir)a-c .. . K-r , '
+ i^TTi J erfc ^7= +... ■
Напишем :это решение в безразмерном виде
C8)
Т (г. -с)-Г,
Го-Г,
+
erfc
2 j/Fo
+
4 V г
R
2 l/Fo
+
r
+ il/4H^-7-#)]^^*7^l + :-
2 /Fo
C9)
126
Глава четвертая
Данное решение справедливо не только для малых значений Fo, но
и при условии г > (X При малых значениях Fo, когда аргумент функций
i erfc и i2 erfc велик, а сами функции близки к нулю (см. приложение),
решение C9) становится аналогичным решению для полуограниченного
тела. Следовательно, охлаждение цилиндра в первые моменты времени
происходит аналогично охлаждению полуограниченного тела.
Решение для осевой линии (г = 0) можно получить из решения для
изображения, положив в нем /0( 1/ — г) = 1. Тогда будем иметь
-£• - П (г, S) = (Г. - Т,)У23Г -^srexp (- |/|«) X
Таблица 4.6
^-2:£[заЬН-й*')
Fo
0,005
0,010
0,015
0,020
0,025
0,030
0,035
0,040
0,045
0,050
0,055
0,060
0,065
0,070
0,075
0,080
0,085
0,090
0,095
0,100
0,Ю5
0,110
0,115
0,120
0,125
0,130
0,135
0,140
0,145
0,150
0,155
0,160
0,165
0,170
0,175
0,180
0,185
0,190
0,195
0,200
6ц
1,0000
1,0000
1,0000
1,0000
0,9999
0,9995
0,9985
0,9963
0,9926
0,9871
0,9798
0,9705
0,9596
0,9470
0,9330
0,9177
0,9015
0,8844
0,8666
0,8484
0,8297
0,8109
0,7919
0,7729
0,7540
0,7351
0,7164
0,6980
0,6798
0,6618 i
0,6442
0,6269
0,6100
0,5934
0,5771
0,5613
0,5458
0,5306 •
0,5159
0,5015
Fo
0,205
0,210 i
0,215 !
0,220 !
0,225
0,230
0,235
0,240
0,245
0,250
0,255
0,260
0,265
0,270
0,275
0,280
0,285
0,290.
0,295
0,300
0,305
0,310
0,315
0,320
0,325
0,330
1 0,335
0,340
0,345
0,350
0,355
0,360
0,365
0,370
0,375
0,380
0,385
0,390
0,395
0,400
V
0,4875
0,4738
0,4605
0,4475
0,4349
0t4227
0,4107
0,3991
0,3878
0,3768
0,3662
0,3558
0,3457
0,3359
0,3263
0,3170
0,3080
0,2993
0,2908
0,2825
0,2744
0,2666
0,2590 1
0,2517 j
0,2445
0,2375
0,2308
0,2242
0,2178
0,2116
0,2056
0,1997
0,1940
0,1885
0,1831
0,1779
0,1728
0,1679
| 0,1634
0,1585
Fo
0,41
0,42 1
0,43 1
0,44
0,45 1
0,46
0,47
0,48
0,49
0,50
0,52
0,54
0,56
0,58
0,60
0,62
0,64
0,66
0,68
0,70
0,72
1 0,74
0,76
| 0,78
0,80
0,85
0,90
0,95
1,00
1,05
1,10
1,15
1,20
1,25
1,30
1,35
1,40
1,50
1,60
1,70
0ц
0,1496
0,1412
0,1332
0,1258
0,1187
0,1220
0,1057
0,0998
0,0942
0,0887
0,0792
0,0Ю4
0,0628
0,0560
0,0499
0,0444
0,0396
0,0352
0,0314
0,0280
0,0249
0,0222
0,0198
0,0176
0,0157
0,0117
0,0088
0,0066
0,0049
0,0037
0,0028
0,0021
i 0,0016
1 0,0012
0,0009
0,0007
0.0005
0,0003
0,0002
0,0001
ГРАНИЧНОЕ УСЛОВИЕ ПЕРВОГО РОДА
127
[4-1—
jlj
•ррр
И—1~~
==—===:=:[=: 1= ======!== р=== 1 1 1 ! 1 1 III III lit I--I-1 1 1 1 1 1 1 1 1 1 1
"ci—1 ЕЕ —FE—Щ 1 1 i 1 1 ГТ1
p=====pi===i==j "=Hj 11 щmi jiri 11 и |~H
5|s5|^ J| С T 11
— ^—г*1—гЦ|1^чч^,ч5,*к: !—1—1—1—1—1—1—1—1—1—1—1—i^rr~?sT~l—1—1—1—1—1—1—1—1—1—1—1—r~i
Ч;^1^рч^ЫМ 1 ; 1 1 gr^b?-
=^-фк^ф^^Ы1 И \/[ш\ ШШи\
—^^Frkrsgs H^fflS^bkU \Y \Y / N 1111 li
V \Г r^Pv ilNJ I^4^iItO'jQ>'TxJ /M II 1 1
V Ks ^i IP*!»- f\J |^H^H4lP>J III
\ ;. О sJ TrsL IrsL Tt4C"i4o''sU 1 1 1 1 1 1 1 1 1 1 I
\i II 1 ГЧ r^L 1 1 1 iNw 1 1 T4^ 1 ("isJr^Xi^sL 1 1 1 1 1 1 1 1 1 1
^LL^^omimga>гид^ш \иш
===pppM=^=P=~kJ T "NJts^ i l^ | |~f*-N h^itJN- 1 1 Щ
^1 1 1 1 1 | 1 | ]\| 1 1 1 1 1 1 гч^ 4=1 1 1 pvl 1 1 fnJ I 1 rJ lxi\l\M
Л1 1 1 1 Ti 1 i\] 1 ii "T^J risi4 П nvTl isl IWVI
N Г00г Ггч ГгчГ 1 1 |Ч| 1~^гтт1
\ <pB pJ AJ f"ТнННтН
\M \ T4J |k[ KrVi
\ NN. ГЧ. тч. \ M
\ r^ ТЧ ГЧ \ \
4 - тч
\ Vi PN \W \\\\\
\ TSl fsl ГЧ \ i
4^^М= МИ'"'тЧгт|Н:::т=1 11ч11"Ч~ 1 1 iVPt
~| г | |-^сг^^^ 1111 НИ 1 ТЧ. 11111111 1 1 I I | | ГЧ 1~К1—IA-]
=^Ц=|=Ц=^*=Ы=^^
:——————ii 1 л. гф 1—г~ гт 1 |^Ч«у| | || 1 11 |—г [■■■EiVH
1 j———[и11!—1—1—1—{-—FNr Ч'^г^рТ 1111 n 1 tii Рр^^Ш^Ь^^Ш1
U— 1— \ М Гт HfdlTTi j—j—ffl
N4 \
1 1 1 1 1 1 1 11 1 1 1 1 1 I 1 11 1 1 IkI 11 1 1 1 11 1 1 1 1 Ill I M I
,0 0 |м ~*
U. со "*
ex со
о о,
о кс
* м
a
£3
m
о
tuQC
л
e
о
о «
о
о
о,
н
СО
си
2
«я
о
к
►А
. ч
ф
и
Я
о
о
55
о
о
«
о
и
а
о
к
со
я
Он
128
Глава четвертая
О
III
0,25
0.20|
0,15
0,10]
0,05
A
0,9
0,8
0,7
0,6
0,5
0,1
0,2
0,3
0,4 1-^-0,5
01 0,4
Н i 1Т и м 1 Т N И U
Т М и
м
м
\ И М I
Мм
11И \ !! 1 1 1 Г
I п I Г ' 1 III 1 1 1 1 1 1 In
11 I I 11 1 \ 1 М 1 1 1 1 1 1 М 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 11 1 ! 1 I I 1 1 1 1 I
11 | I 1 ш i 1 1 1 1 1 1 1 1 ! 1 1 1 ! 1 1 1 1 1 1 1 1 1 1 1 11 ! 1 1 1 1 1 1 1 1 1
1 1 1 | 1 1 | Ml 1 1 1 1 1 1 1 М 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 ! 1 1 1
1 i 1 1 11 1 1 \' 1 1 1 1 1 1 1 1 1 11 i 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 ! 1 1 1 1 ! 1 1 1
11111111ч 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 Mi 1 1 1 1 1 1 М 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 I 1 1
1 \ \ 1 1 Г 1 •
11 1 1 1 \1 1 1 11\ 1 11 1 1 1 1 1 1 1 1 1 1 1 1 1 11 1 1 1 1 1 1 1 1 1 11 1 1 1 1 1 1 1 1 1 1
1 f\ Mil \1 11 1 1 1 1 1 1 1 1 1
1 \ 1II \ 1 1 1 1 11111111 1 1 ! 1 1 1 I I I I I I I I I I I I I I I I I I I I
1 IVj ill \ 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
| | | | | | 1 \ ■ | Pv I Mill I 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
j | 1 ! i i ■ |\j I j 1 I VI i 1 1 I 1 1 1 1 1 1 1 1 1 1 I 1 1 1 1 1 1 1 1 1 1 1 I 1 1 1 j 1 1 1 1 f'
I M || I ii I \ I I I M\ 1 1 1 II 1 1 1 1 1 1 1 1 M 1 1 1 II II 1 1 1 1 1 1 1 1 1 1 1 1 1
i 1 1 1 1 Ml 1 l\l 1 1 1 l\l M II 1 II 1 1 II 1 1 1 1 1 1 1 1 1 II I 1 1 1 1 1 II M 1 1 In
\N NM NY
1 M M 1111 1 \| 1111\ 111 11 м и и i j 1111 и 11111 111 и I и I
l\ 1 \ 1 1 II l\l 1 1 ! II II 1 1 1 1 i 1 1 1 1 1 1 M II 1 1 II 1 1 1 1 1 1 1
I | | | | | | 1 1IVM is.) | j | 1 M | I 1 M | 1 1 1 | | | 1 1 1
I Ml III PL Л. Mill
Mil l\ N Mill
Mil [41 Тч1 III
M 1 1 1 1 1 1 i 1 1 1 1 1 xl 1 I 1 1 к 1 1 1 1 1 M II II II II II 1 1 II 1 1- II 1 II 1 I
\4 NY NYJ n
\ | M\ 1 TV 11
| j и | I 1 | ill I | и и i\j III iNs.l f | 1 1 | 1 M | | 1 1 | | | 1 | 1
Mill j 17\| |M! ikJ Mill
vim г-' rv Mil PHiiLj l> III
\M и 1 iSj Ггч! (III
MIX 1111ч1 ^^L III
W МММ I iV iNi^I Ml
IV МММ] II mW. lrJ Ml
l\l ^^L i^L Ml
|||||M \ II M MM i^ МММ r4wl II II 1 II 1 II II M 1 in
1 II 111 \ II 1 1 1 lis. M M 1 mtsI Mill
l \ | || | I | || | || i Pivl МММ mWJ. Ml
1 1 M 1 M i Iv M M 1 M M M 1 i\L 1 Tit**J_ M M M M 1
M 1 1 M 1 II 1 'MIM. II II 1 II 1 M II 1 iSl Pt^W^I 1 II II 1 1
1 1 1 II II 1 i 1 It l4l 1 1 I 1 1 1 1 1 1 1 M 1 1 TrJ 1 1*""T" M M 1
III msI Ml i\L II H
Hi iNL Ml iMsJ Ml
I I I I I I I M || I M 1 мтчМ1 1 |\J Mi
1 1 1 1 1 1 1 1 1 1 II II 1 1 1 Гг'р II 1 1 II 1 1 II 1 1 |4J Ml
II 1 1 1 II 1 I I 1 |.ll_LI.I 1 I | I II II II 111 II 1 1.1. 1 J ItvI | 1 II II 1 I II \U
0
0
0,025
0,050
0,075
0,4
0,8 in-
Fo
1,2
0,1
Рис. 4.22. Зависимость между средней относительной избыточной
температурой 6 и числом Фурье Fo в случае неограниченного
цилиндра
Пользуясь таблицей изображений, получим
« 1
V tiFo
ехр
1
SFoJ^Ufo)
D0)
В табл. 4.6 приведены численные значения относительной
избыточной температуры на оси цилиндра для разных значений числа Фурье.
Расчет был сделан по формулам C9) и C6).
Расчетные графики (Т0 — Т)/(Т0 — Тс) = f (Fo) для разных
относительных координат r/R приведены на рис. 4.21.
Определение потерь тепла. Найдем среднюю температуру цилиндра
по формуле
т(т)=jrirr(r'x)d/'-
Подставляя вместо Т (г, т) соответствующее выражение из C6) и
принимая во внимание равенство B4), после преобразования получим
ГРАНИЧНОЕ УСЛОВИЕ ПЕРВОГО РОДА
129
D1)
I ■■ U * С t I
4
где Вп = —^-, т. е. получим решение, аналогичное решению для плас-
тины и шара. Разница состоит в том, что в решении для пластины
тс 2
(х = Bп — 1)—, Вп = —2~~, для шара соответственно (л = тс, Я =
2 ^
= —5-. Таким образом, уменьшение средней температуры во всех слу-
чаях описывается простым экспоненциальным законом.
Зависимость между б и критерием Fo приведена на рис. 4.22,
который может служить в качестве расчетного графика.
Решим конкретную задачу. Стеклянный длинный стержень, нагретый до
температуры 393° К A20° С), помещен в тающий лед Гс = 273° К @°С). Определить температуру
внутри стержня через 1 мин охлаждения, а также количество отданного тепла единицей
поверхности его, если диаметр стержня равен 2 см.
Считаем стержень за неограниченный цилиндр, термические коэффициенты стекла
следующие: Л = 0,743 впг/м • град, с = 0,668 • 103 дж/кг • град и | = 2500 кг/м3; тогда
а = 4,45 • Ю м2/сек.
Находим число Фурье
4,45 • Ю-7 • 60
Fo= ■' = 0,266 «0,27,
1 • 10~4
так как т = 60 сек, R = 1 см = 0,01 м.
Определим относительную температуру по формуле C6) для г = 0. Так как Fo =
= 0,27, то можно ограничиться первым членом ряда C6), т. е.
„ -a2Fo 2 2 -B,4J-0,27
К = Ахе *1 ———= yz-rrj^z^r e = 1,60 • 0,211 = 0,34;
l*i/i(m) B,4)/iB,4)
здесь учтено, что Jt B,4) = 0,52; ё~~B'4)* ' °'27 = 0,211.
Можно было бы величину А% определить непосредственно по табл. 6.10 для Bi—oo
(см. гл. VI).
Полученное значение 0Ц = О,34 можно проверить по табл. 4.6, из которой видно,
что для Fo = 0,27 0^0,34. Температура на оси цилиндра при Гс = 0 будет равна
Г@, т) = Гс + (Г0 — Гс) 0ц = 273+ 0,34 • 120 = 314° К D1°С).
Для подсчета расхода тепла определим среднюю относительную температуру по
формуле D1)
_ — ^7^"° 4 — B 4^2 • 0 27
в=В1Й = <W ' =0,147^0,15.
Проверяем по графику рис. 4.22. Из графика находим при Fo = 0,27 (Г=0,15,
т. е. расчет верен.
Средняя температура равна
Г (т) = ТС + (Г0 — Tc)f= 273 + 0,15 • 120 = 291°К A8°С),
Удельный расход тепла равен *■
&Qv = сч (Г0 — Г) = 0,668 • 103 • 2500 C93 — 291) = 17 ■ 107 дж/м*.
§ 6. НЕОГРАНИЧЕННЫЙ ПОЛЫЙ ЦИЛИНДР
Постановка задачи. Дан неограниченный полый цилиндр
(цилиндрическая труба). В начальный момент времени температура внешней
и внутренней поверхностей цилиндра поддерживается постоянной на
5 Заказ № 640
130
Глава четвертая
Рис. 4.23. Изотермы Г (г, т) в полом цилиндре (RQ< r < R)
протяжении всего процесса охлаждения. Найти распределение
температуры в любой момент времени.
Следовательно, краевые условия следующие (см. рис. 4.23):
Т
T(R,
T(R0,
@,
X):
*)
r) =
= т2
= тг
f(r), \
— const,
= const,
где R — радиус внешней поверхности, R0 — радиус внутренней
поверхности.
Решение задачи методом разделения переменных. Вначале для
упрощения задачи положим Тг = Т% = 0. В § 5 было показано, что ре-
щецие уравнения Бесселя имеет вид
b(r) = CJ0(kr)+DY0(kr).
Однако здесь нельзя полагать D = 0, так как функция У0 (kr) в
промежутке R0 < г < R, в котором нет особой точки г =. 0, будет величиной
конечной.
Следовательно, решение уравнения теплопроводности будет иметь
вид
Т (г, т) = [СJ0 (kr) + DY0 (kr)) е~акг\ D)
Для нахождения постоянных С и D воспользуемся граничными
условиями B) и C), при этом считаем 7\ = Т2 = 0, тогда
CJo(kR0)+DYo(kRo) = 0, E)
CJo(kR)+DYo(kR) = 0. F)
Коэффициенты С и D не могут быть одновременно равны нулю, так
как в этом случае температура была бы равна нулю (тривиальное ре-
ГРАНИЧНОЕ УСЛОВИЕ ПЕРВОГО РОДА
131
шение). Система двух линейных однородных уравнений E) и F) отнб-
сительно неизвестных С и D будет иметь отличное от нуля решение
в том случае, когда определитель системы равен нулю:
|Л(*Яо). П№) | -
\Jo(kR), Y,(kR) I
или
J0 (kR) Y0 (kR0) - J0 (kR0) Y0 (kR) = 0. G)
Следовательно, собственные числа задачи или характеристические
числа kn получаются из уравнения G). Характеристическое уравнение G)
не имеет комплексных корней, а имеет бесчисленное множество
положительных вещественных корней kn. Следовательно, общее решение
будет иметь вид
Т (г, ,) = 2 l<Vo (V) + DnY0 (V)l e~ < \ (8)
Решение (8) можно написать так: из уравнения E) следует
_p_==z_ Jo(kRp)
С r0 (kRo) '
тогда
Т(Г' Х) ~ 2 1Ж) e"^ ' [^(V)^ (*««о)-/о (*«/?a)^o(V)b (9)
Введем обозначения:
An = CJY0(knR0),
V0 (Кг) = Jo iKr) Y0 (knR0) - J0 (knR0) Y0 (kar).
Тогда решение (9) примет вид
Т(г, т) = 2 Ane~akl*VQ{knr). A1)
/г=1
Для определения постоянной Ап воспользуемся начальным условием
(т = 0):
f(r) = ^AnV0(knr). A2)
/2=1
Если функцию /(г) можно разложить в ряд, членами которого
являются комбинации Бесселевых функций A0), то предполагается, что
можно почленно интегрировать A2). Умножим левую и правую части
A2) на rV0(kmr) и проинтегрируем от R0 до R. Тогда получим
f rf(r) V0 (kmr) dr = Jm„ \ rVQ (knr) V0 (kmr) dr. A3)
Докажем, что все члены ряда A3) равны нулю при всех n=fcm.
Воспользуемся формулой A7а) § 5:
X
(Ь2 — a2) j xyty2dx = ху2у[ — хуху2.
о
5*
A0)
132
Глава четвертая
Полагая
Уг =* AJQ (ах) + BY0 (ах) = V0 (ax),
у2 = AJQ (bx) + BY0 (bx) = VQ (bx),
получим формулу, аналогичную формуле A8) § 5,
J xV0(ax) V0 (bx)dx = Ш« (ax) Уг (»*) - «^о (bx) Vt (ax) + cQn$t {Щ
Если положить а = kn, b = km, x = г, то
]rV0(knr)V0{kmr)dr<= M'M^^WMMK e
1
k2 —к2
[kmRV0 (knR) V, (kmR) - knRV0 (knR) V, (knR) -
-kmR0V0 (knR0) V, (kmR0) + knR0V0 (kmR0) Vx (knR0)], A5)
где F0(^r) определяются формулой A0), a V± (knr) — следующей
формулой:
Ух (V) = h (V) V0 (knRQ) - /0 (knRQ) Yx (knr). A6)
Согласно характеристическому уравнению G) величины VQ(knR) и
V0(kmR) равны нулю. Поэтому первые два слагаемых правой части
A5) равны нулю.
Также третий и четвертый члены A5) равны нулю, так как VQ(knR0)
и F0(£mi?0) равны нулю согласно формуле G), т. е.
V0 (kR0) - /0 (kRQ) Y0 (W0) - /0 (kR0) Y0 (kR0) - 0. A6a)
Следовательно, при n=f=m интеграл A5) равен нулю.
Поэтому интеграл A3) равен нулю при пфт и имеет конечное
значение при я = т, равное
f rf (r) V0 (knr) dr == An j rV2Q (knr) dr. A7)
Аналогичным путем, как это было сделано в § 5, из формулы A4)
можно подучить следующую формулу:
J rV2Q (knr) dr = { JL [ Vl (kn r) + V\ (knr)} }* =
-~ [Vl (knR) +V2 (knR)] - f- [Vo2 (knRo) + V\ (knR0)}. A8)
Так как VQ(knR) = V0(knR0) = 0, то из A8) получим
( rVl (knr) dr = 4" [RW* <***) - *oV? (W\' A9)
Эту формулу можно преобразовать. Из теории функций Бесселя
известно
Тогда
Vi (W = Л (knR0) Y0 (knR,) - h (Mo) Yi (W = %knRo B1)
ГРАНИЧНОЕ УСЛОВИЕ ПЕРВОГО РОДА
133
Для нахождения Vx(knR) воспользуемся характеристическим
уравнением G):
V / Ы? 1 A (kRp) Y0 (kR)
V, (KR) = Л (knR) Y0 (knR0) - /0 (knR0) Y, (knR) =
= 7$Ж[Jl {k"R) Y°{k»R) ~ У°{KR) Yl (k«R)l
Применяя B0) к последнему соотношению, находим
v {kR) = i^L_l^. B2)
Подставляя B1) и B2) в A9), получим
я
2 [4(knR0)~J20(knR)]
<rviMir= ■^(W;--". и
До
Тогда постоянные Ля будут равны
«*nj0(*nK) ttrf(r)V0(knr)dr. B4)
n 2 [^(^o)-4(^)] Йо
Таким образом, решение упрощенной задачи будет иметь вид
п={
™-1%Я£Шг -/и™**-
B5)
Вернемся к нашей задаче. Предположим, что 7\ и Т% не равны
нулю.^ Будем искать решение задачи в виде
7 (г, т) = в(г)+»(г, т). B6)
При этом функция 6 (г) должна удовлетворить дифференциальному
уравнению
d4 +— -^1 = 0 B7)
dr2 г dr
и граничным условиям
в(/?о) = ^ 6(^) = Т2. B8)
Функция ft (г, т) удовлетворяет дифференциальному уравнению A) § 5
и граничным условийм
»(Я0, т) = 0, ft (/?, т) = 0, B9)
а также и начальному условию
8@, г) = /(/•)-6 (г). C0)
Очевидно, функция Т (г, т) будет удовлетворять дифференциальному
уравнению и граничным условиям B) и C); следовательно, имеем
Т (Д0, т) = 6 (R0) + Ъ (R0, *) = Тх + 0 = 7\;
T(R, т) = 6G?) + »(/?, х) = Т2 + 0 = Г2;
Т(г, 0) = 6 (г) + &(/", 0) = 8 (г) + /(г) - в (г) = /(г).
134
Глава четвертая
Для решения уравнения B7) введем новую переменную -т- = z. Тогда
B7) примет вид
JE_ + _Lz=,o. C1)
dr r
Решение уравнения C1) имеет вид
_Б _
г ~~ dr*
— 4-£ C2)
Интегрируя еще раз, получим
6(r)-£lnr +C. C3)
Постоянные В я С определим из граничных условий B8):
7*2 — Тх ^ 7\ In # — Т2 In R0 /Q ,ч
£ = £—, С = ^ . C4)
In —- In —-
Ro Ro
Подставим C4) в C3), тогда получим
Л In—+ Та In p-
8(r) = г—ц ^- C5)
1пя7
Функция 0(г) представляет собой распределение температуры в полом
цилиндре в стационарном состоянии. Решение Ь (г, 'с) можно получить
из B5), заменив f(r) на [/(г) — 6(г)]:
* , , ^ £, ** 'о (*ЛЛ) 1/0 (V) ~ **£ * v
tf (Г, t) = ~о- > —S о £ X
2 ^ «^0 (*л«о) ~4(^)
R
X ( f r/ (r) F0 (*яг) dr - f гб (г) V0 (V) ^ ] . C6)
Второй интеграл в C6) можно вычислить, если вместо G (г) подставить
его значение из C5). Полагая
ы = Гх1п-|- + Г11п-^г;
* = -§-V0 (knr); du = (Г, - 7\) ^; d& = гУ0 (knr) dr,
интегрируем по частям
R
Г r8 (r) V0 (knr) dr = -^ f ГГХ In -f + T2 In £-1 X
АО
R R
x-rVi (knr) | - ^=Ii- f v^r) <Й = —V fa -f v^nR) x
При интегрировании* была использована формула
dr
ГРАНИЧНОЕ УСЛОВИЕ ПЕРВОГО РОДА
135
Используя формулы для V0(knR) и Vx(knR), получим
Г гЬ (Л V (Ь г\ Нг — Т 2R J° ^Ro) _ 2ri^° —
J " (П V°(кп) dr~l2 «k*R 'о (knR) . ^2 Rq "
p. n n
2 [7V0 (knR0) - 7V0 (*««)]
ЧЛМ)
Окончательное решение получим в виде
In — L J л=1
I/0(V)exp(—а^т)
C7)
X
71 l2 t2
x ^ *„ К (KR) \ rf (r) F0 (M ^ - 4> (knR) x
X [Г2/0(^о)-^Л(^)]|-
Введем обозначения [л„ = knR0; R/R0 = m; Fo = ax/RQ,
Тогда решение C8) можно переписать так:
Voft% £Г-)ехр(— f^Fo)
Г (Г) т)=1Гг11п A + r.ln-^l +У \ 0/ ^
/I i
X
X
2ЛЙ
2 / \
■£Г #! УоKm) j *7@ ^о (Си -ЦА dr — *Jo(iV") [ЗД (t*«)—
7У0(т[л„)]
C8)
C9)
Корни [лЛ определяются из характеристического уравнения
/0 И Ко ("¥) — Jo (ти) У о W = 0. D0)
Первые пять значений [х приведены в табл. 4.7 для величины m от
1,2 до 4,0.
Таблица 4,7
Корни (лл характеристического уравнения
J0 (jx) F0 (т[л) — Г0 ((*) /0 (^и) = 0
m
1,2
1,5
2,0
2,5
3,0
3,5
4,0
н
15,7014
6,2702
3,1230
2,0732
1,5485
1,2339
1,0244
Р-2
31,4126
12,5598
6,2734
4,1773
3,1291
2,5002
2,0809
1*8
47,1217
18,8451
9,4182
6,2754
4,7038
3,7608
3,1322
Р<4
62,8304
25,1294
12,5614
8,3717
6,2767
5,0196
4,1816
tH
78,5385
31,4133
15,7040
10,4672
7,8487
6,2776
5,2301
136
Глава четвертая
о
Ч
^ рг
ю
о
НИИ
наче
со
1
X
3
К
со
«3
СЦ
«
ч
к
о
Ьи
<У
А
а,
>>
е
ИСЛОМ
II
ч*
к
ч
о
<У
л
3
>>
СХ,
Н
8S
СКО
су
р»
К
Он
ч;
ч
О
>>
О
со
а:
ГРАНИЧНОЕ УСЛОВИЕ ПЕРВОГО РОДА
137
————L
1—|—| 1 1
[—[—N-o
1 '
1 i 1 ^l 1
| J |0 |
Рпнт
FHTllt5
иви
rm —i—г
Го*
1 1
1 \
\
i< Л
1 \
\
mat
\Ц-
ЦЦ
Шъ
'|-~ф
я
Ч:Щ
So
и
Щ
111
Шр
1
it
-фп
_Х__
и
В
з
о
2£
*
л
/ •
Я
щ
щ
Я
ipl
В
1
и
i
г0,2-
щ
Ш
щ
щ
Ш
щ
=
Ё
о
В
я
щ
Щ
1
В
■ф=
8
ЖозШШ
В
ш
ЕЕЕ
(
И
=р=
8
=3
Ш
§
=^
i
:"_Г-
g
1
Ё
Ц
ш
~:
Ш
|
Hj
щ
щ
ш
щ
щ
ш
rZE
fet
В
РР
в
Я
(И
Фу
Я
2Е±
И
Я
в
ipi
И
щ
=
jir
1
ш
щ
щ
щ
в
Щ
И
щ
я
В
и
Я
S
Ш
я
Ш
ффф|
2 щ
— о =f—1
ц & Щ
— II ±3
1
1
^ q=|
щ
1
ЕЕ
3
1
И
и
я
^РЗ
v\W
\™
\И
V ли
И
I
О*
Си
с
S
ю
о
о
о"
о
К
о
см
о*
к
О,
138
Глава четвертая
Рассмотрим частный случай. Предположим, что начальная
температура всех точек трубы постоянна и равна
T(r, 0) = /(r) = r0 = const.
D1)
Тогда интеграл будет равен
J? r
rf (r) V0 (knr)dr=?f Vt (kn r)\ = 2T; - [JQ (knR0) - JQ(KR)h D2)
При этом были использованы формулы B1) и B2). Тогда решение C8)
примет вид
[
т (г, т) = ' (тгin А + т, in±-) + * У G; (Г"У0/(^" r/J? х
^ ' In от \ 1 г и- 2 ^ / ^ ^ I J0 (fx„) + У0 ((ЛЯ от)
X ехр(-[л2 Fo) \то - TJobJ-TiJofrnm)
D3)
На рис. 4,24 приведены расчетные графики для случая, когда
температура на внутренней поверхности трубы постоянна и равна
начальной температуре Т1 = Г0 = const, а температура на внешней
поверхности трубы в начальный момент времени принимает значение ТС(Т2 =
= Тс) и поддерживается все время постоянной на протяжении всего
Г
процесса нагревания (Тс > Т0). Графики построены для разных значе-
ний относительных координат -^- , равных -^- 1 + -~
На рис. 4.25 приведены аналогичные расчетные графики для случая
равномерного начального распределения температуры: Т (г, 0) =
= Т0 = const и для граничных условий Т1 = ТС = const, Т% = Т0 =
= const. В графиках рис. 4.24 и 4.25 число Фурье определяется по
отношению к внешнему радиусу цилиндра (Fo = ai/R2).
Если Т1 = Т2 = ТС9 то выражение в квадратных скобках под знаком
суммы будет равно Т0 — Тс, а первое слагаемое формулы D3) будет
равно Гс. Тогда получим
Т (г z) - т ^ J°(mfJ7l) V° ( ^ ~^~)
= У01Тее = «± /0у + ;оЫ exp(-^Fo).
/2=1
D4)
В ряде решений вместо функции V0(kr) вводится функция U0(kr). Это
D
происходит потому, что отношение постоянных -^ определяется не из
уравнения E), а из уравнения F).
Между этими функциями существует простая связь
Уо(*Г> = 4о|Йу-адГ)- D5)
Очевидно,
Рассмотрим задачу- на охлаждение цилиндрической трубы, когда
внешняя поверхность теплоизолирована, а внутренняя —
поддерживается при постоянной температуре Тс.
ГРАНИЧНОЕ УСЛОВИЕ ПЕРВОГО РОДА
139
Начальное распределение по толщине стенки трубы принимаем за
равномерное. Задача математически запишется так:
дТ(г, т)
а д
~г~ дг
[r~), (Ro<r<R, x>0)
D7)
T(r, 0) = T0 = const,
|аТ^' т) = О, Т (/?„, т) = 7С = const.
D8)
D9)
Поскольку начальная температура постоянна и не зависит от
координаты, то для решения задачи целесообразно воспользоваться методом
преобразования Ханкеля
TH(p)=]rT(r,*)U0(pkr)dr,
«о
E0)
E1)
E2)
Применим преобразование Ханкеля к ураЕнению D7). При изменении
порядка дифференцирования и интегрирования левая часть уравнения
будет иметь вид
где рк— корни трансцендентных уравнений:
Л (pR) У о (pRo) -Jo (pR0) Yi (PR) = 0,
Uo (РГ) = Jo (P r) Y0 (PR0) - J0 (pR0) Y0 (pr).
fjrVApr^dr
дТн (р)
dx
E3)
Правую часть уравнения D7) интегрируем по частям:
Rq r=R0
R
-aj r^p^V0(pr)dr. E4)
Выражение в квадратных скобках равно нулю, так как при
r= R—L_lIL = o по условию, а при г = R0 функция V0(pRQ) = 0 по
формуле A6а).
Интеграл в E4) интегрируем по частям, он равен
- ар [ rV'0 (pr) T (г, т) J +ар] T{r9x)[ V'0 (pr) + pr VQ (pr) } dr. E5)
r=RQ RQ
Далее
- V'o (pr) = Vt (pr) = J, (pr) Y0 (pR0) - J0 (pR0) Yl (pr). E6)
Из формулы A6) следует V1(pR) = 0. Кроме того,
V:0 (pr) + pr V (pr) = - rPV0 (pr), E7)
140
Глава четвертая
так как у — V0(pr) является решением уравнения Бесееля при рг = х.
Таким образом,
a J V0(pr) А( г ^Ц^-)йг = -apR0V1(pR0)T(R0^)-
E8)
- ар2 J r V0 (pr) T (r,,) dr.
Ко
Согласно B1)
Мр*о) = ^, ' E9)
а по условию T(R0,%) = ТС получим преобразованное по Ханкелю
дифференциальное уравнение
ЛТи(р,ч) _ 2аТс
Общий интеграл этого линейного уравнения имеет вид
Тн(р,х)= exp (-^ap*fc j^-J^-exp (jap»dx)] =
= Лехр(-ар2т)-^. F1)
Постоянную А найдем из начального условия, к которому применим
преобразование Ханкеля
R
«о
\rVb{pr)T{r,0)dr =
F2)
Т0 j rV0 (pr) dr = ?f[ rVx (pr) ]'7 = tf [RV1 (pR) ~R0V1 (pR0)].
r
r=R<
Учитывая, что Vx(pR) — 0, и используя E9), находим
Tn(p,0) = -2^. F3)
Теперь, полагая в F1) т = 0, получаем
„ _ 2(ГС-Г0)
F4)
Тн (Р, т) = 2{Тс~/о) ехр (- ар- х) - |§. F5)
Применяя формулу обращения
оо 2
rr-lrj:/ Ч1 т? V PnJiyPn*<) VoKPnr) ■
н3 1ПР^^2,ирМ_,(РпЮ?(Рп), F6)
я2 у Рп Ji (РпЮ Уо (РпГ)
получаем
P2nJl(pnR)V0(Pnr)
Н3 [Тн (р, ,).] = Т (г,х) _ * ^ ^ [ 4 (рЛ) _ ^^j X
X {[Тс -Г0] ехр (-apl t)~-T0). F7)
ГРАНИЧНОЕ УСЛОВИЕ ПЕРВОГО РОДА
141
Выше было представлено
разложение формулы /(г) в ряд:
г« = /(г) = 2слм
/lei
= -2
«t0j? (*„/?) v0(V)
;£, Jo(knRo)-Ji(knR)
■ F8)
Таким образом, окончательно
получим
Рис, 4.26. К задаче о параллелепипеде
Т(г,
тс - тп
^1 ^о(н-л)— «ffOVH)
ехр(—t^Fo).
F9)
§ 7. ПАРАЛЛЕЛЕПИПЕД
Постановка задачи. Дана пластина конечных размеров URtX2R%X
X2RB, температура которой везде одинакова и равна Т0. В момент
времени т = 0 все поверхности пластины мгновенно охлаждаются
до некоторой температуры Тс< Т0, которая поддерживается
постоянной на протяжении всего процесса охлаждения. Требуется найти
распределение температуры в любой момент времени, а также
среднюю температуру пластины, необходимую для определения тепло-
потерь.
Поместим начало координат в центр параллелепипеда (рис. 4.26);
тогда нашу задачу математически можно сформулировать следующим
образом.
Имеем
дТ(х, у, z, т)
а^
+
д2Т(х, y,z,%) д*Т(х, у, г,-с). ,
дх2 *"*" ду* +
]Т(х, г/, z, т) 1
dz*
(^>0; -Rx<x< +/?!; —/га<у<+/?2;
^R3<z<+Rs);
Т (х, у, г, 0) = Т0 = const,
T(±Rvy,z,x) = Tc,
T(x,±R2,z,x) = Tc,
T(x,y,±R»x) = Tc.:
A)
B)
C)
142
Глава четвертая
Решение задачи. Докажем, что решение этой задачи можно
представить как произведение решений для трех неограниченных пластин,
толщина которых соответственно равна 2RV 2R2 и 2RS, т. е.
Т(х,у,г,*)-Тс T(x,z) — Tc ш Г(у,т)~Гс Т{г,*)-Тс ш
1 о 1 с Л о Л с 2 о ic ■* о — * с
При этом температуры Т (х, т), Т(у, т), Т(г, *) определяются
решением дифференциальных уравнений
дТ(х, т) __ aar(*, т) аг(у, х) _ У Г (у, т) аг(г, х) _
'дт ~~а дх% ' ах ""а ду* ах ""
азгB,т)
E)
а*2
при краевых условиях
Т (х, 0) = Т (у, 0) = 7 (z9 0) = T0 = const; F)
T(±Rvx) = Tc; T(±R2,<z)^Tc; T(±R3^) = TC. G)
Соотношение D) можно написать так:
Т (х, у, г, т) = Гс + (-~ [Г (х, т) - Гс] [Т (у, т) ^ Гс] [Т (г, т) - Гс], (8)
где АГ = Т0 — Тс, Подставим решение (8) в дифференциальное
уравнение A). После преобразования получим
[Т(у, х)-Тс][Г(г, ,)-Тс]{^^-~аЩ^} +
+.[Г(х,х)-ТЛГ(г,,)-Ге1{^а-:в^^} +
+ [T(x,x)-Te\[T(y,i)-Te] {^^-_a^^-j = 0. (9)
Так как Т(х, т), Т(#, т), 7 (г, т) удовлетворяют дифференциальным
уравнениям E), то все величины в фигурных скобках в уравнении (9)
будут равны нулю; следовательно, уравнение (9) обращается в
тождество. Таким образом, решение (8) удовлетворяет дифференциальному
уравнению A).
Подставим решение (8) в начальное условие B):
П = ТС + ^L. [Т (х, 0) - 7С] [Т (у, 0) - Тс] [Т (z, 0) - Гс);
тогда, согласно условию F), получим тождество
T0-T^-^^Tf = T0-Tc.
Следовательно, наше решение (8) удовлетворяет начальному условию.
Подставим решение (8) в граничные условия C):
T(RV у, г, *)=ТС= Тс + ^ [Т (Rv х) - Те] [Т (у, т) - Тс] [T(z, х)- Тс],)
Т (х, Rv 2>; х)=Тс =ТС+^Ь [Т (х, х)- Тс] [Т (Д»т)" - Гс] [Т (г, т)- Тс],
г (ж, у, я,; х)= тс=тс+^т, [Г (х, т) - тс] [т (у, х) - тсцт (я„ х)-тс].
A0)
ГРАНИЧНОЕ УСЛОВИЕ ПЕРВОГО РОДА
143
Так как Т (Rv т) = Т(/?2, %) = Т (R3, т) = Тс, то в каждом равенстве
соотношений A0) одна из величин в квадратных скобках равна нулю
и все три решения дают тождество
Т =Т
Следовательно, решение (8) удовлетворяет и граничным условиям;
таким образом, по теореме единственности это решение является
решением нашей задачи.
Итак, решение нашей задачи можно написать в виде (8) или D):
Т (х, у, z, т) — тс
00 СЮ ОО
22 2 АпАтАк<*&Рп 4гХ
~, 1 «, 1 Ь 1 ^1
П=\ /71=1 &=1
X
т0-тс
cos^^cos^^-exp [— ((х^ + Hm/t2 +
A1)
где
А, - (- D"+' f. А. - <-1)"+' Л Л - <-1)'+'^
^/г ^т г/г
1*я = Bл— 1L-, И-т = B/гг— 1) -^-, \ьк^{2к— 1)
2 '
Fo — число Фурье Fo = -бг)> #—обобщенный размер,
к*
Я.
Ri
Можно воспользоваться соответствующими решениями для
неограниченной пластины в другой форме и получить решение для
параллелепипеда в виде
О (х, у, z, т) = 6 (х, т) Q (у, х) G (г, х).
A2)
Таким же способом находим среднюю относительную
температуру, пользуясь выражением A2):
ОО С» 00
2V
п—1 tn=l k=\
6 = 2 2 2 *A**«P [-(^/Cj + (t^+rf О Fo ] >
A3)
где
Вп-
-«■ и т- Д*
Таким образом, задача о параллелепипеде сводится к задаче о
неограниченной пластине. Поэтому анализ решения и примеры расчета
здесь не приводится.
§ 8. ЦИЛИНДР КОНЕЧНЫХ РАЗМЕРОВ
Постановка задачи. Имеется цилиндр, диаметр которого равен
2#, а длина 21. Температура цилиндра одинакова и равна Т0. В на-
чальный момент времени поверхность цилиндра {боковая и торцевые
144
Глава четвертая
Рис. 4,27. К задаче
о цилиндре
конечных размеров
поверхности) мгновенно
охлаждается до некоторой температуры
ТСУ которая поддерживается
постоянной на протяжении всего
процесса охлаждения. Требуется
найти распределение температуры
внутри цилиндра в любой момент
времени, а также определить
среднюю температуру как функцию
времени.
Нахождение температурного
поля цилиндра конечных размеров,
когда температура его есть
функция только трех переменных
(времени, радиуса и координаты 2),
связано с решением
дифференциального уравнения теплопроводности
дТ(г, z, т)
fd2T(r, z, т) 1 дТ(г,г,%) а2 Г (г, г,
Л)
A)
(т>0; 0<r<R;—t<z<+l)
при начальном условии
Т (г, г, 0) = Т0 = const
и при граничных условиях
T(r, ±l,x) = Tc, T(R,z,x)=Tc
B)
C)
Начало координат находится в центре цилиндра (рис. 4.27).
Решение задачи. Аналогичным методом, что и в предыдущем
параграфе, можно доказать, что решение нашей задачи б (г, z, %) имеет
вид
б (г, z. х) = 6 (г, т) 6 (г, т), D)
где 6 (г, т) — решение для неограниченного цилиндра, а 6 (г,
t)—решение для неограниченной пластины, пересечением которой с
неограниченным цилиндром образован конечный цилиндр. При этом начальные
и граничные условия остаются прежними:
Т (г, 0) = Т (г, 0) = Т0 = const,
Т (R, т) = Т (± /, т) = Тс = const. E)
Таким образом, решение нашей задачи будет иметь вид
G
Г (г, г, т) —гс __
= 224«^;» 1*«Т cosf*m-?-e
п—\ т=1
t« + ^/)Fo
F)
ГРАНИЧНОЕ УСЛОВИЕ ПЕРВОГО РОДА
145
где Ап =—г /\ $ V-n — корни функции Бесселя первого рода нулевого
порядка,
К = (- l)m+1~ , V-m = Bm-l) -f, Kt =-f, Fo = ^ .
Средняя температура цилиндра равна
00 00
п—\ т
ВпВтехр [-({** +j£/C?)Fo]j
где
д -А я - 2
Н* til
G)
Сделаем небольшой расчет. Стальной диск диаметром 20 см и толщиной 12 см
нагрет до температуры 573°К C00°С). В начальный момент он помещен в тающий лед.;
Определить температуру в центре диска через 2 мин после охлаждения.
Считаем температуру поверхности диска в процессе охлаждения постоянной и
равной Тс = 273°К @°С). Коэффициент температуропроводности стали принимаем равным
а =1,25-10-* м2/сек D5.10~3 м*/ч).
Решение задачи можно написать в виде
в (г, г, т) = б(г, тN(г,т),
где 6 (г, т) и 0 (z, т) —соответственно решения задачи для неограниченного цилиндра и
неограниченной пластины.
Воспользуемся таблицами для нахождения 0Ц. Для этого предварительно
вычислим число Фурье для цилиндра и пластины:
FOj =
1,25-10-».120
36-10-4
так как / = 6 см = 0,06 ж, т = 2 мин = 120 сек;
1,25-10-*.120
= 0,416^0,42,
Foc
10-2
= 0,15,
так как R = 10 см — 0,1 м.
По табл. 4.2 находим, что для Fo = 0,42 относительная температура в середине
неограниченной пластины равна 6ЦП = 0,45, а по табл. 4.6 температура всей осевой
линии неограниченного цилиндра для Fo=b=0,15 равна 0ЦЦ = О,67. Следовательно,
безразмерная температура конечного цилиндра равна
откуда
6ц = вцп. 0ЦЦ = 0,45-0,67 = 0,30,
Гц = Тс + 0ц (Т0 — Тс) = 273 + 300 - 0,30 = 363°К (90°С).
§ 9. ЗАДАЧИ НА НАГРЕВАНИЕ
В вышеприведенных задачах рассматривалось охлаждение тела с
некоторой начальной температурой при условии, что поверхность тела
в начальный момент времени принимает некоторую постоянную
температуру, которая поддерживается постоянной на протяжении всего
процесса охлаждения (ТП = ТС = const). Задачу на нагревание тела с
некоторой заданной начальной температурой TQi когда температура
поверхности в начальный момент времени мгновенно становится
постоянной и равной ТС(ТС>Т0), можно свести к задаче на
охлаждение путем простой замены переменной.
146
Имеем задачу на охлаждение
g = aV2T; Т @) = Г0, Тп = Гс (Тп < Г0).
Сделаем замену переменной Ь = Т0—Т. Тогда будем иметь
-g- = aV2<>, »@) = 0, 0п=Т„-Гс = &с.
Получаем задачу на нагревание тела, когда начальная температура
0-@) равна нулю, а температура поверхности тела равна $с@) =
==Го—Тс = const. Следовательно, все выведенные формулы будут
справедливы и для задач на нагревание тела, только под б надо понимать
6' = ■ """ '* при охлаждении (Т0>ТС);
■* о ~~ 1 с
6 - 1)~,Г = 1 — 1~Т° при нагревании (Гс> Г0).
i c -Iq * С "~~ -« О
Таким образом, при переходе к задаче на нагревание в решении
для охлаждения тела безразмерную величину 6 надо заменить на
-^—ттг- или 1 7f\ т£- . Этот прием применялся в расчете за-
' с — ■*« \ ■'с — * о /
дачи § 2.
ГРАНИЧНОЕ УСЛОВИЕ ВТОРОГО РОДА
5
Процесс передачи тепла к нагреваемому телу в печах с высокой
температурой в основном происходит излучением; конвективной
передачей в большинстве случаев можно пренебречь.
Тепловой поток, получаемый поверхностью тела от нагретых стен
и свода печи, прямо пропорционален разности четвертых степеней
абсолютных температур поверхностей, участвующих в теплообмене:
qn = o-C[T* + TAn), A)
где а — постоянная Стефана — Больцмана, С — постоянный
коэффициент, зависящий от способности поверхности тела поглощать лучистую
энергию и от взаимного расположения облучаемого и излучающего
тел. Индекс «п» обозначает, что данная величина соответствует
поверхности тела, а индекс «и» — поверхности излучения.
Теплообмен с нагретыми газами происходит по видоизмененному
закону, в котором величины Т% и Тп имеют множители
соответственно ег и ет, называемые степенями черноты излучающих газов при
температуре газа и при температуре тела. Обычно значения ег и ет
близки между собой, поэтому можно взять среднее значение е и вынести
его за скобку. Тогда получим обычное выражение закона теплообмена
излучением.
Таким образом, поток тепла, подведенный к поверхности тела,
является некоторой функцией времени / (-с), подлежащей определению
<7«. = /ео. B)
В некоторых частных случаях граничное условие B) может быть
упрощено.
В теории теплообмена в печах доказывается, что все источники
излучения могут быть заменены одним, имеющим некоторую среднюю
температуру, называемую температурой печи Тс.
Если температура поверхности тела (Тп) значительно меньше
температуры печи (Гс), то вторым членом в скобках можно пренебречь, и
получим постоянный тепловой поток, воспринимаемый поверхностью
тела:
« а СТ4 = Const.
C)
148
Глава пятая
Данное граничное условие является частным {простейшим) случаем
граничного условия второго рода B), когда тепловой поток является
величиной постоянной. Решение задач с переменным тепловым
потоком qn = f (%) можно получить из соответствующих решений для
постоянного теплового потока при помощи теоремы Дюамеля или
методом интегральных преобразований Фурье и Ханкеля.
§ I. ПОЛУОГРАНИЧЕННОЕ ТЕЛО
Примером полуограниченного тела может служить длинный
стержень, боковая поверхность которого изолирована, при условии, что*
толщина и ширина стержня незначительны по сравнению с длиной.
В предыдущей главе было показано, что распространение тепла при
малых значениях числа Фурье происходит аналогично распространению
тепла в полуограниченном теле.
Постановка задачи. Дано полуограниченное тело при температуре
Т0. Ограничивающая поверхность нагревается постоянным тепловым
потоком qc = const. Изменение температуры происходит в одном
направлении. Найти распределение температуры по данному
направлению в любой момент времени.
Имеем
si— -as^— (t>0>
0<Х< op);
Т (х, 0) = Т0 = const;
дх
7(оо, т) = Т0,
+ <7с = 0;
дТ (оо, т)
дх
= 0.
A>
B)
C)
D)
Решение задачи классическим методом. Данную задачу можно
свести к задаче теплопроводности с граничным условием первого рода,
рассмотренной в гл. IV, § 2.
Вместо переменной Т введем новую переменную q (плотность
теплового потока), определяемую соотношением
^ дТ(х, т)
Х дх
q (x, т)
Продифференцируем уравнение A) по х:
■[■
_д_\дТ{х, т)
дх
дъ I ох | дх2
Тогда дифференциальное уравнение F) можно написать так:
'dT(x,z)
di [
дх
ение F) можно наш
1— д2 [дТ(х,%) 1
J ~~ a дх2 [ дх J '
E)
F)
или
dq {х, т) _ ^ д2ц (х, т)
дх
дх2
G)
ГРАНИЧНОЕ УСЛОВИЕ ВТОРОГО РОДА
149
т. е. получим обычное дифференциальное уравнение для одномерной
задачи, только вместо переменной Т здесь стоит переменная q.
Начальные и граничные условия для новой переменной имеют вид
q(x, 0) = 0 " (8)
(для упрощения расчета полагаем, кроме того, Т0 = 0);
Я @» т) = Qc = const; (9)
<7(oofT) = 0.' A0)
Решение уравнения G) при условиях (8) — A0) нам известно1* (см.
гл. IV, § 2), а именно
^i£L^L = erfc —4=-. (И)
qc 2~]fa%
Чтобы найти Т (х, т), подставим в выражение E) вместо q (x, t)
соответствующее выражение из A1) и проинтегрируем от х до оо:
Т (х, т) = -%- f erfc -4- dx - Ц*У a* ierfc —?— ,
A2)
где
i erfc и = J erfc tt^W = ~Лг е""'— и erfc и. A3)
Решение задачи операционным методом. Решение
дифференциального уравнения A) для изображения TL(xt s) имеет вид (см. § 3, гл. III):
TL(x9s)—?f = А^*** + BYf***. A4)
Граничные условия C) и D) для изображения можно написать так:
lT'L@,s)+^ = 0; A5)
fL (оо, S) = 0. A6)
Из условия A6) следует, что ^ = 0, так как при х -> сю
температурный градиент стремится к нулю, а температура тела не может быть
бесконечно большой [при х -> оо Т(оо, т)-^ Т0].
Постоянную Sx определяем из граничного условия A5). Имеем
]/-^1 + £ = о,
откуда
Вг= qc
Xs
Vi
' 1) В гл. IV, § 2 было дано решение задачи на охлаждение полуограниченного
стержня. Задача на нагревание получается из задачи на охлаждение путем замены О
( Тс-Т
на [ т0-тс
150
Глава пятая
Следовательно, решение A4) примет вид
У?
Ks
A7)
Для нахождения оригинала воспользуемся таблицей изображения,
согласно которой
!
—k Ys
i + -
= D-с) i" erfc _
2 ']Л
Окончательно будем иметь
Г(х, т) —T0=-^|^ierfc
2/£
A8)
A9)
т. е. получаем решение, тождественное A2).
Из приведенного примера видно, что решение операционным
методом быстрее приводит к результату.
Анализ решения и определение расхода тепла. Введем новый крите-
рии
, где Тс — средняя температура нагревательной печи,
X (ТС~Т0)
назовем его критерием Кирпичева:
qcx
Х(Гс-Го)- B0)
Критерий Кирпичева равен отношению плотности потока тепла qc
через конец стержня к максимально возможней плотности теплового
потока в точке х стержня при условии, что градиент температуры в
т f
данной точке максимален и равен — ~.
Решение A9) можно переписать так:
Т(^Т)~Г° = Ki, Fo, i erfc L_
B1)
где Fox = ат/х2 — число Фурье.
На рис. 5. Г приведены расчетные графики. Даны изменения
обобщенной переменной G/Ki* Fo^, относительного температурного
градиента 2х д$/дх/К'\х и относительной скорости нагревания 2 ]/тс Fo* дВ/д Fox
в зависимости от числа 1/2 VFox. По этим графикам можно производить
приближенные расчеты.
Можно дать и другое выражение для критерия Ki^. При малых
перепадах температуры АГ = Тс—Тп соотношение для лучистого
теплообмена можно описать законом охлаждения Ньютона:
<7п = °С [Т\ + Т\ ) (Тс + Тп) (Тс- Тп) = <Х (Г) (Тс- Тп).
B2)
Максимальный тепловой поток для заданной Тс будет при Тп = Т0
Таким образом, в этом случае
aJ7^ = Bi)
B3)
т. е. критерий Кирпичева равен критерию Био.
ГРАНИЧНОЕ УСЛОВИЕ ВТОРОГО РОДА
151
1
:
f" 11111111
4-4- ~Н
Iff || 11 11 Щ
II
' IT' 1 1 1 1 1 1
Н4
111111 ||В
[.[ 1111111111
III
11111111111
Н11111 П111
of
1 "
.1-1 1 1 1 1 1 1 1 1
|" || Г 1 1 1 1 1 1
111111111 г
111111114+
мм
1111111111
■i-j III
11111 м 111
00
1 1 1 1 1 1 1 II 1 1 1
II 1 1 1 1 1
+Ш+1+Н ^
III I i 1 1 Ft *?
11 1 I I 1 11 I '"м
11 | | | | 1 | | | 11 |
II IT I 1111 1 1 1 1 m ^ 11
1 1 11II 1 1 1 1 1 II11II x 1
1 1 11111111 " lllll о П
lit* 1
^ 1
Ml J r*^ 1
И!] |r||| . ' lllll см II
HUM lllll lllll Nil 111 In
1 III lllll [III 1II III 1 1 1 1 1 1
1II111111111111111111111
| ill 111111111| 1111| 11 u^
j | j lllll 11 [ 1111 LiH^TI 1 ^hp
III | LrfT 111111
v 111111111111 JUrf 1 III
1114, ЬШ|| 1111111111111H"
Si? IB
1111.^^ 111111111IIM 11II
Mlllilllllll^fflff
1]^ H
CO rf
lllll Шм 1 lllll
1-1111N 1 j 1111111
JIHIftPI
TTTTTI11111111111111
и
ii h'1 '7
fl
1
in
1 1 II
1 f II
Mr II
' / 11
/II
1 1 / II
Mr II
/II
/II
in/fl
1 J II
1 1 / HI
МЯ Mr 1
/II
M/ 11
II/ I 1
1 1 Мл I 1
Я | fl
МЛ Mr И
1 un Mr II
1 /f / II
Mil / Mil
г L/l #M II
1 J4 Mr II
Мл / II
M/ / 1
/M MrM 11
1 LPT 11/ II
K/ /II
Ja МЛ 11
мл / Л
1 Ыч И ' 111 i 1/111 ii l
Ып 1 Мм 1 1
Jr\ / / 1
Л 1 1 1 11 1/ Mill II
1 / д 1
Л г
г / Mr
/Mil
Мл / 1
'ПУП / И
м/ у П
IТ /1 1 Жтггп
1 Ln 1 1 1 | 1/ 1 111
I \jf\ н-" / 1
иди
1*шШ444444я
4] 1 /
/
М 1 М М 1II11/ II М 1 НИ
11| | | at \\ 111 М 1111
| о ЩЗ
II И'.. Ы.Ж 1"Ш|-Ш
см о
I .*
ч
О
к
33
О
К
ч
о
J1CJU
00
§
В
О
О
О,
О
Ь4
•а
ь
as
feC
о
w
а,
ь
О*
в
о
о
со
Я
152
Глава пятая
Таким образом, критерий Ki^ численно равен отношению
внутренне
него сопротивления у к внешнему термическому сопротивлению
^р=г- при замене лучистого теплового потока приближенным
выражением закона охлаждения Ньютона.
Следовательно, решение A9) можно написать так:
е-г£'т)гг'-к1
То
V
Fo,
ехр
4Fo,
— erfc
2 l/Ftai
B4)
Расход тепла на нагревание стержня нам задан в виде плотности
теплового потока qc, т. е.
dQs
dz
= qc = const.
B5)
Отсюда расход тепла на единицу площади поверхности конца стержня
&Q$ будет прямо пропорционален времени:
&Qs = qcx = C4(Tc-Tn).
B6)
§ 2. НЕОГРАНИЧЕННАЯ ПЛАСТИНА
Постановка задачи. Дана гнеограниченная пластина толщиной 2R
при температуре Т0. Пластина нагревается с обеих сторон
одинаково от источника с постоянным тепловым потоком (нагревается в
печи с достаточно высокой температурой Тс). Найти распределение
температуры по толщине пластины в любой момент времени.
Дифференциальное уравнение будет то же, что и в гл. IV.
Начальные и граничные условия для симметричной задачи имеют вид
Т (*, 0) = Г0 = const,
dT(Ryz)
дх
4- l£_ ^0
1- А v,
дТ @, т)
дх
= 0
A)
B)
C)
Решение задачи классическим методом. Для решения задачи вводим
новую переменную q (x, t) по соотношению E) § 1. Тогда получим
дифференциальное уравнение G) § 1 для новой переменной, аналогичное
дифференциальному уравнению теплопроводности.
Начальные и граничные условия для новой переменной будут
следующие:
q (х, 0) = 0, D)
q (Я, *) = <7с, E)
q @, т) = 0. F)
Последнее условие следует из условия симметрии C).
ГРАНИЧНОЕ УСЛОВИЕ ВТОРОГО РОДА
153
Таким образом, получаем как бы задачу «на нагревание»
неограниченной пластины с нулевой начальной «температурой», когда одна
ограничивающая поверхность поддерживается при «температуре», равной
нулю, а противоположная — при «температуре», равной qz.
Решение почти такой же задачи приведено в гл. IV, § 3. Чтобы
получить решение нашей задачи, надо в решении D5) § 3 разность R — х
заменить на а: и величину б на A—6), т. е. задачу на охлаждение
свести к задаче на нагревание.
После такой замены получим
оо
а(х,х) х V / i\»+i 2 . X — t^Fo
^^-=Х- L (-1Г1— sin^^e « , G)
/1=1
где рп = пти — характеристические числа.
Температурное поле найдем по формуле
Т (х,х) = 4" J <7(*> *) dx + ср (т) + С, (8)
где 9 W — некоторая функция от времени, С — постоянная.
Подставляя решение G) в (8) и интегрируя его, получаем
Чтобы определить <р(т) и С, воспользуемся следующим соотноше*
нием:
qc = C1R^-, A0)
где Т (т) — средняя температура неограниченной 'пластины,
определяемая по формуле
r •
Т (*) = -£- J T (х, т) Же. A1)
о
Выражение A0) можно написать в интегральной форме
T(T)=-^V'c + :ro. A2)
Найдем Т (т) из соотношения (9)
т(т) =_*£-+*(*) +с, A3)
так как интеграл от суммы по л; в пределах от 0 до R равен нулю
(sin |1Я = 0).
Сравнивая A2) и A3), находим
су Я ' " 6Х
154
Глава пятая
Окончательно решение нашей задачи примет вид
| Т (*.
00
1 /г=1
я>-
-?v
-1г+1-4
<7с
COSJJ.
Га т
„хехр
А!
(-
— За:2
6R
-^Fo;
+
']•
A4)
Таким образом, чтобы получить решение основной задачи,
приходится предварительно найти решение вспомогательной задачи для
q (x, %). Кроме того, необходимо пользоваться дополнительным
соотношением A2) для определения постоянных интегрирования. Все это
значительно затрудняет нахождение решения, поэтому в дальнейших
задачах данной главы будут использованы методы интегральных
преобразований.
Решение задачи операционным методом. Решение одномерной
задачи для изображения TL (х, s) в случае неограниченной пластины имеет
вид
TL{x, 5)-^ = ЛсИ Y-T * + £sh Y-^x. A5)
Начальная температура пластины везде одинакова и равна Т0.
Граничные условия B) и C) для изображения будут иметь вид
7l (Я, *) + £- = О,
A6)
A7)
T'L (О, s) = О
Из условия симметрии A7) следует, что В —0 (распределение тем
пературы симметрично относительно центральной линии).
Постоянную А находим из условия A6), т. е.
-V-TMVir *+%-<>•
»*/-> V-т*
Следовательно, решение A5) примет вид
TL(x,s)-ij- =
Ф(з)
A8)
Решение A8) есть отношение двух обобщенных полиномов, так как
ФE) = <7с ( 1 + 14^ 4~4^2 +
2! а
4! а2
♦ «-*«■ I-S- + 1S-.+ -£-£- +
••)-
Xs2cp(s),
где <р (s)— выражение, стоящее в скобках. Степенной ряд ф (s) не
содержит постоянной, т. е. все условия теоремы разложения выполняются.
Найдем корни sn обобщенного полинома ф (s), для чего приравняем
его нулю:
t(S) = xs Yir ^YirR=:Ut * (s> =
0.
A9)
ГРАНИЧНОЕ УСЛОВИЕ ВТОРОГО РОДА
155
Отсюда находим: 1) s0 = 0 (двукратный корень), 2) sn
численное множество корней, так как
бес-
sh Y-L- R = -I" sin * Y-T * = °> l V'lT R = n*^Pn>
где п = 1,2, 3,... .
Воспользуемся теоремой разложения
lim { ' f *W еЧ = lim Г
s-,o U* U<p(s) Ji «-о L
, ST Ф (&■■) . sx Ф' (s) sx Ф (.
X<p(s)
^ + «c
Xy (s)
<7c Я
') ?' («I _
It (»)]* J
x/?
2Atf
6X •
так как
Ф@) = ?с ср@) = 4,Ф'@)=-£-, Т'@) = -£-.
Далее имеем
так
2
/1=1
как
Ф(*л) **
Ф'(*л)
f (s) -
г
X
<7с#
оо
"S~2"^ C0S^ "J" eXP ( ~ Йтзг)'
^ tl£ COS p.„ A . \ Г« /?Я /
/г=1
Следовательно, решение нашей задачи будет иметь вид
Т (x,*)-T0=-f
а х
R2 — Зд:2
+
оо
+ /? S (— 1)"+1 \ cos |»я -£• ехр (— ^ Fo) J
/г=1
B0)
Решение B0) тождественно A4).
Анализ решения и определение расхода тепла.
Введем критерий Кирпичева Ю по формуле
^ Х(ГС-Г0) '
где Тс — средняя температура печи. Тогда наше решение примет вид
|= Ki [Fo—
+('-
„ Г (X, т) - Г„
d= гс-г0 =
СО
л;2 \ V1 п^ 2 х 2 1
-3^-J+2j(— 1) -^cos^ — ехр(—[х„ Fo)|.
B1)
156
Глава пятая
1,50|
А
Ki
1,25|
1,00
1 III L4
i i МММ 1 1 1 1 1 1 1 ill 1 1 1 1 1 1 1 1 11 1 1 1 1 ! 1 1 vfl
I М II i 1 II II М 1 1 11 М II М 1 М 1 II II 1 Ijri 1 1
i МММ ! 1 1 11 1 11 J МММ!! 1 \NLnT I
1 1 1 1 1 1 Ц,\vt| j J
I I И J 1 1 I 1 1 1 1 ] | 1 I 1 I | I 1 1 1 I 1 l^^iVi 1 1>Г|
1 1 1 j 1 I 1 1 1 1 i 1 i и 1 1 1 и 1 и 1 115^гТ j*\\ 1
J | M I 1 1 I 1 I I 1 I 1 1 1 I I 1 1 1 1 Lti LtI 1
МММ Г 1 J^i \^^ni M \a
i~ МММ М МММ МММ! J/^rT 1 u^i i/n
1 Ml! \jt\\ 1 J^l \jt\\ 1
j | 1 1 1 1 I 1 1 | J 1 1 i 1 j 1 MWl Lti ' л LtT 1 I
i M M M M M M M 1 1 _i^ii J*hT cn^J^i 1L-!
1 МММ M M M 1 Ij-ill Lni 1 ljt*T .Wi
1 Mi LaW*! 1 LjWi 1 vn jrfi 1
1 I и i j 1 i jJj*inTMil MWi Lri 'л Jyri 1
1 1 M 1 M II LrWii Mill _W*i J^rT o^^jWi 1 l/l
Ш-Шх| [Ш^гт 4jj>HT ШпТ Uii LinT
b-=^g44ii^H^Tfi ЬШ4тП ШтГмШт1!л]^нмИ
ill i_ni»(T*il1 LI-ill L-!^^ 1 IjirM 1 Ihi
11 1 1 li 11 1 1 ! 11 11 гхттТ! LiWii \jr\\ 1 j/п J^i 1
l —г Ml 1 JjJ^iti l_Wi^l ' LkWi I cS*t4ynT Ln
1 1 1 1 II II II 1 II II M i 1 Jr^rT! Mill 1*т1 ' Х*Г\ 1 Ljf^r L*rl
ПТмТтН 1|..н4тттТмП 1 1 1 144тГ 11 1 1 ИТГ1 1 linP 1 UhiI 1
Hfffffl
н4:Й4тт1 тмим м LUmT LlfiP(Llvfil J
1 j I 1 1 j LJ^*K| 1 rW*> W*i 1 i j^i 1 1 1 _^ч
111 Jr4"T*il 1 1 M LkW'T 1 1 1 1 LtI 1 l/T^l LnT I
Liii-гНп | I I \^r^\ 1 jWl J^l J/f| 1
ц i гтттт г i 1 1 II II 1! 1 i Ij-ktm 1 _W*i Jrf*ri ri^Lri 1 1 1
Ml 1 1 II 1 II 1 II 1 1 1 II _!_1iitTi i-T' M -^^l 1 1 vVn 114
MM -гттГ"Г1 LWii L-гТ T 1 l>Hi Lnl
МММ IL L—1— 'i""i Ml ML^rT*! 1 \-Jr\\ _ип1 i _Wi 1
L.1. 1 i Г' j Л 'ill Li^ftl \Jr\\ M l/тГ M Д Lti 1
Г LLLLJJ LU44tTT \jr\\\ 1 \ln\\ Qvrtl
1"Тг1г]Д-,Ипч iTTl LJ^hMI \Jr\\\ vnl Ы
lj.ijiii'i1 [""rriii 1 LuL'^H^T Millъ^гм LrT х*\л
Г1 M 1 II 1 11 1 II 1 1 11 1 \^r\\\ _L**Wi \-)г\\ II II 11 J^jfjl
[—|~j—1111 j 14^ЬШ4тТт1Т 1111 Шпм 1111 ипм 111 с^1>И>И>гя
Fm^^ Штт^
г"п" Н ММТНТ МД44тмТТ ilM^^^^T^nFn
|| II II 1 II 1 II II 1__L1 " Т 1 Mill М 1 -Ц*Т"*^СгГ*^г5-тТМ vJ,UO I
" 1" птП 1144'1^Цд51дЗТм^ iw^ 1111
Ч4та^^шД||И 1111111111111
0,75Щ±£=Н
0,50
0,25
0,2 0,4 0,6 0,8 ■—*- 1,0
Рис. 5.2. Температурное поле неограниченной пластины при
постоянной плотности теплового потока на поверхности
X
1Г
Таким образом, относительная температура будет функцией Ki, Fo,
т. е.
= /(Ki, Fo,-±-
B2)
С увеличением времени, точнее числа Fo, ряд быстро
уменьшается и при некотором значении Fo^Foj становится ничтожно
малым по сравнению с двумя первыми членами решения B1), так что
всем рядом можно пренебречь. Начиная с этого момента времени,
температура в любой точке пластины будет линейной функцией времени, а
распределение температуры по толщине пластины описывается законом
параболы, т. е. наблюдается квазистационарный режим для поля
градиента температур.
Для координаты х = 0 (середина пластины) квазистационарный
режим наступает с точностью до -у % при Fo > 0,5 (см. § 10 гл. VI).
Можно получить решение нашей задачи в другом виде, удобном для
малых значений Fo.
Пользуясь разложением /— / ) в ряд (см. приложение), ре-
sh
VJ
шение для изображения напишем так:
ГРАНИЧНОЕ УСЛОВИЕ ВТОРОГО РОДА
with Ml ! ГГГГТТITTTTI ! 1 Г( ММ П 1 П 1 1 1 1 II 1 1 1 И Ml 11
^ 111 1 11 1 1 1 1 i 1 II м II 1 II 1 11 1 1 1 1 1 1 1 1 II1111111 1 1 1 1 1 1 1 1 1 II
' 41 г I I I L
id M 1111II Г Г liiii^tl
Mill ум
1 1 1 11 1 1 1 | 11 1 1 1 1 ум
1 1 I 11 1 1 1 1 1 1 1 1 1 1 1 I 1 I 1 1 1 I I 1 1 1 1 1 1 1 1 1 1 М 1 1 ! 1 1 1 i 1 \Jr\
1 °1 I I I I I I I I I I I I I I 1 1 1 1 1 1 1 1 1 1 1 1 1 1 11 1 1 Ml Ln
*' 1 М I ! М 1 I И | II | | j м | | и И ' | | уП | i !
1 1 1 1 L/Г 1
I'll L/r 1
III уг 1 1 1 1 1 1 1 1
III \Jr\ III! I
III Ут1 III
III Ут1 |'|
| I | | I 1 I : I 1 I | I I 1 1 1 I I 1 I I 1 1 1 1 1 I I 1 1 I I l/f] i I 1 I I | I 1 1 1 1 1 1
III' Lfli II
УМ
III 1УМ III
II \Jr\ II
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 \Jr\ II
1 1 1 1 1 1 1 1 \ jf\ II 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 IjtI III
|(|||(( 1 1 1 1 1 1 1 1 I ( 1 \ж\ III
III ПУМ I ' I I I i I I I I I I I I I I I I I I I \A
/Ч Гк 1 I I I I I 1 I I I 1 I I I I I I 1 ! I 1 I I I *J/| 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 Jr\
U,o M \Jn Г \jf\ I
I'll Lrl Ml \Jt\ 1
1 1 1 1 I I 1 1 1 i'l M \jf\ MM L/tI 1
II j/i Ml Lrf 1
II \/\ Ml \jf\ Mill
ill vt III L/m 1 1 1 1 1 1
111 1 \ jt\ 1 1 i 1 1 M 1 M 1 1 \j\\ '
II Jr\ Ml \j\\ 1 1 1 1 1 I
II J^T Ml \Jr\ 1 1 M 1 1 1 1 1
fipllJ^llllMIMMMMMIl \Jf II ■ 1 ■ 1 1 1 1 1 1 1 1
AJ,o г lyr L/M 1 Ml
II iff \ Ml LtI Ml
II L/r Ml 1уг 1 Ml
|| ifj Ml I/m Mill
1 1 1 1 1 1 1 M 1 r\ Ml L/r Ml
1 1 ( I i 1 1 1 i l/i Ml L/r Ml
1 \j\ 1 Ml L/r Ml
II y\ Mill L/r 1 Ml
мм \ж\ Ml pLn I Ml
0,4 / I! U<T 1 111 M
| Lr III 1 1 1 1 1 II 1 1 1 1 1 1 1/T II 1 1 1 1 1 I 1 1 1 1 1 1 1 1 1 II II 1 1
III vT Ml lrf \ Ml
III) /\ 1 1 1 1 M 1 1 1 1 1 1 1 1 1 II 1 \/\\ Ml
1 / Ml Ln Ml
1 / Mil \r\ \ Ml
I \ \§\ I I j I I I 1 1 \J\\ Mill
1 Mr 1 lrf Mill
II /1 1 1 1 1 1 i 1 1 1 1 1 1 II 1 [/i 1 ! 1 1 I 1 I 1 I 1 1 1 1 I 1 i 1 1 1 1 1 1 1 1 M I 1 1
{jn / ~|"" l/n "T1 'I T" IT "Г ГТ г и'
III l/f III
III Jr\ III
II I \)f\ 1 lllf 1 II 1 II
li 1 III Lrl 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 ■ I 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 I
It 1 11/^fi I i i I | f]
If 1 j | 1 I I I 1 vn i I 1 1 1 1 ! 1 1 1 1 1 1 1 1 1 1 1 II i 1 1 1 m 1 1 1 1 1 1 1 1 1 1 ! 1
11 1 1 1 1 1 1 \jr\ 1 1 1 1 1 1 M 1 1 1 ! 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 l 1
II LJ^rT 1 1 M 1 11 Mil 1 1
QI1 1 1 1.KT1 III 1 1 1 1 11 1 11 1 1 M 11 1 1 111 II 1 11 1 Mil 1 1 1 II 1 1 11
0,2
0,8
Fo
-1,0
Рис. 5.3. Зависимости между -jtt и Fo для поверхности A)
и середины B) пластины
TL {x, $) ■
ЯсУ а
со
H{eXp[-|/-f (B/x-l) R~x)] +
+ ехр [-]/"-£- (Bл-1) R+x)
B3)
Тогда при пользовании таблицей изображения и, в частности,
соотношением A8) предыдущего параграфа общее решение нашей задачи
будет иметь вид
B/i — l) Я — х
д=1
+
IV ах \
B4)
158
Глава пятая
Из формулы B4) можно получить решение A9) § 1, если сделать
замену переменной х + R = X и положить 2R = оо. В критериальной
форме решение B4) можно написать так:
Г (*, *) — Т0
2Ki 1/Fo V Г:
Bя-1)+-|
ierfc B-1)^^+
+ i erfc
2 )/Fo
2 /Fo
B5)
При малых значениях Fo все члены ряда ничтожно малы, так что
можно ограничиться одним первым членом ряда. Тогда расчетная
формула приобретает простой вид.
На рис. 5,2 приведены кривые распределения температуры внутри
пластины для различных значений критерия Fo (от 0,05 до 1,1), а на
рис. 5.3 —кривые нагревания поверхности и середины пластины.
Для иллюстрации приведем конкретный пример. В сушильной камере
инфракрасного излучения нагревается керамическая пластинка BR = 4 см) в течение 15 мин.
Найти температуру поверхности и в центре пластины, если средняя температура
камеры 673°К D00°С), а плотность лучистого потока qc — 2Э10 em/м2 B500 ккал/мЧ),
коэффициенты переноса тепла пластины принимаем равными X —0,291 вт/м2-град
@,25 ккал/м-ч-град), а = 13,3-10~"8 м2/сек D,8-10~4 м2/ч). Начальная температура
пластинки равна 293°К B0°С).
Предварительно вычислим критерий Кирпичева и число Фурье:
Ki
2910-0,02
0,291 .F73—293)
13,3-Ю-8-15-60
Fo =
4-10-4
0,53;
= 0,3,
так как R = 2 см = 0,02 м.
Вычисляем по формуле B1) величину -^ для центра (х= 0):
1
-^Fo-.-g- +_,
-tc2Fo
-2,961
Ki
= 0,3 — 0,1667 + 0,2026 е =0,144.
Полученное значение проверяем по графику рис. 5.3: для Fo = 0,3 находим
= 0,14, т. е. расчет сделан верно.
Представляет интерес вычислить это значение по формуле B5)
1 ... 1
^ = 2^Fo
i erfc
+ ierfc 7=~~) =2/0,3.2ierfc @,913) =
2 /Fo п~1"" 2 VF
= 1,095-0,132 = 0,144
Величину ierfc @,913) находим по таблице [ierfc @,913)^0,066].
Таким образом, получаем один и тот же результат. Итак,
Т @, т) = Г0 + 8ц (Тс — Т0) = 293 + 380-0,53.0.144 = 322°К D9°С).
Найдем температуру на поверхности пластинки. По формуле B1) имеем
ft 1 9 —tc2Fo —2,961
|~- = Fo+ -g -53- е =0,3 + 0,3333—0,2026.*? «0,623.
ГРАНИЧНОЕ УСЛОВИЕ ВТОРОГО РОДА
159
По формуле B5) получим
-jjj = 2 VFo' (i erfc 0 + 2 i erfc * ) = 1,0954 @,564 + 0,005) « 0,623, так
как i erfc 0 = 0,5642.
Таким образом, по обеим формулам получаем один и тот же результат. Прове-
е
ряем по графику рис. 5.3: для Fo = 0,3 находим тт-г-=0,62.
Окончательно находим температуру на поверхности пластинки:
Т (R, i)=T0 + (Tc—T0) вп = 293+ 380.0,53-0,623 «418° К A45°С).
Расход тепла на нагревание пластины находится по соотношению B6) §1.
Решение задачи методом интегрального преобразования Фурье.
Рассмотрим более общий случай, когда поток тепла qc является
функцией времени qc = / (т).
Для общности задачи берем неравномерное начальное распределение
температуры
Т (х, 0) = / (х).
Граничные условия можно написать так:
**ЧН + *М = о,
дх
дТ @, t) =()
дх
B6)
B7)
B8)
Воспользуемся интегральным косинус-преобразованием Фурье:
R
Тс (л, t)=J Т (x,t)cos -5^- dx,
B9)
где п = 0,1, 2, 3,...; Тс (п, т) — изображение функции Т (х, т),
удовлетворяющей условиям Дирихле.
Переход от изображения функции к оригиналу осуществляется по
формуле
т (*,т)= 4-Тс (о, -о + 4 £ т* (п9 т)
cos
л=1
R
C0)
Умножим обе части дифференциального уравнения теплопроводности
на cos —^— и проинтегрируем в пределах от 0 до R:
R
R
Г дТ(х,
J ax
т) пи л;
COS
d* = J a^Tdx^Z) cos ^F^" d*' C1^
1
о о
Выражение для частной производной второго порядка будет
д2Т (*, *) п 7z х
дх2
cos 1£L dx = (- 1)« aXg^L _ *?Ж± _ J^L rc („, xj. C2)
160
Глава пятая
Используя граничные условия B7), B8), получим
^#^ + ^ Гс (п, х) = (- 1)« -f g (х). C3)
Решение этого простого уравнения таково:
Тс (п, х) = ехр (- ^^-) [с (я) +
+ (-!)" "Г J ^ (») ехр (-^£- ) d» ] . C4)
о
Для определения постоянной С (л) воспользуемся начальным условием
B6):
R R
Тс (л, 0) = С (л)= J T (х, 0) cos -2^- dx = J / (*) cos -^- djc. C5)
о о
Следовательно, решение для изображения будет иметь вид
•с
Тс(л,т) = (-1)» -f § q (&)ехр[-^-(т-в)] d& +
О
R
. / Art2 ^2 Т \ 'Г г , ч ПТЪХ j /0~ч
+ ехр у ^—j J / (*) cos —g— dx. C6)
о
Для удобства перехода к оригиналу по формуле C0) решение C6)
перепишем так:
Тс (п9 т) = Г @,т) + Гл (Л,т), C7)
где во втором слагаемом л = 1, 2, 3,... .
Тогда имеем
R т
^с (?z,t)=J/(x) ^+-f J 7 (&)<*& +
о о
R
. I an2 тс2 т \ P £ / ч пкх . .
+ exp ^ ф J J f{x) cos —g— d* +
o
+ (-!)" -f J *(&) «P [--^~('e-») ] db- C8)
0
Перейдем от изображения функции к ее оригиналу в соответствии с
формулой C0)
ГРАНИЧНОЕ УСЛОВИЕ ВТОРОГО РОДА
161
1\ ь
Т (х,х) = -L{ j /(*)<** + -f j q(*)db } +
+
4-1
R
nnx
cos —~— exp
л=1
n2 u2 x \
X
X
П Tt X j .
cos —=r— ад: +
. 2a V / i\n nnx С /Ci4 Г an27t2 , Q4
+ -^X 2j (—l)ncos-^— J ?(»)exp |^___(т—»)
n=l 0
d&. C9)
Решение C9) является более общим по сравнению с A4) и B0). Из
него можно получить и решение A4) или B0).
Если распределение температуры в начальный момент времени
равномерное, т. е.
/ (х) = Т0 = const,
то из решения C9) получим
Z
Г(*,т)-Т0= Д| <?(»)£
©
X ехр
со х
г» + Й S(-i)"cos(xn -£-J q(b) x
п—\ 0
Г 2
D0)
где [xrt = ял. ■
При выводе было учтено, что для n=j=0
J T^cos^ -^ dx=0,
т. е. первый ряд в решении C9) обращается в нуль в силу
ограниченности членов
/ а&\ х
ехр {- -ф- ) и cos^ — .
Если тепловой поток у поверхности пластины постоянный, т. е.
q (i) = qc = const,
то из решения D0) получим
+ 2tf 2(-1Г1Лсо8^
/|яя»1
Л=1
л:
fti
ехр
(-I^Fo)],
D1)
6 Заказ
162
Глава пятая
Из теории рядов Фурье известно, что
00
2R 2 (-1)»-^ cos,», 4 =
Л=1
Й
ff2 — 3*2
Тогда окончательно получим
что тождественно выражениям A4) и B0).
D2)
Т (х х\ Т — qc \ax R2~3xZ -и
1 (де, х> J в ST" L "R" ад— +
00
+ R 2 (- 1Г1 Л cos [x„ -f exp (- [x„2 Fo) l,
n=l ^
D3)
§ 3. ШАР (СИММЕТРИЧНАЯ ЗАДАЧА)
Постановка задачи. Эта задача аналогична предыдущей, только
вместо неограниченной пластины имеем шар. Нагревание шара
происходит равномерно по всей поверхности {симметричная задача) при
постоянной плотности теплового потока qn = qc = const. Требуется
найти радиальное распределение температуры в любой момент
времени и удельный расход тепла.
Дифференциальное уравнение приведено в § 4 гл. IV,
Начальное условие следующее:
Т (г,0) = То
A)
Так как решение будет найдено операционным методом, то
граничные условия напишем для оригинала и изображения:
dT(R, т) , Яс
~*~ х.
дг
аг(о, т)
дг
:0, -T'L(R, S) + £ = 0,
= 0, T'L@, s).= 0,
Т (О, т)^=оо, TL@, S)=^oo.
B)
C)
D)
Решение задачи. Решение дифференциального уравнения
теплопроводности для изображения при симметричном расположении изотерм
относительно центра шара, т. е. при учете условий C) и D), имеет вид
[см. решение B2) § 4 гл. IV]
TL<r,s)-lf-B
Постоянную В определяем из граничного условия B), т. е.
E)
ГРАНИЧНОЕ УСЛОВИЕ ВТОРОГО РОДА
163
откуда
В
qcR2
Следовательно, решение для изображения будет иметь вид
F)
П(Г,8)-Ц- =
V+
\s
ch
V^R-
sh
VT
ф(»)
и»)
G)
Оно представляет собой отношение двух обобщенных полиномов
qc Rsh Y-L. г
Ф(8)
QcR
14- —- — s -4- — —- s2
1 ^ 3! а & ^ 5! а2 6
/?
sh
R
/т*
где ср (s) — выражение в квадратных скобках, которое является
обобщенным полиномом относительно s. Таким образом, условия теоремы
разложения соблюдены.
Найдем корни выражения i|>(s), для чего его необходимо приравнять
нулю. Отсюда получаем: 1) s=0 (двукратный корень), 2) sn =
2
= — ^L — бесчисленное множество простых корней, определяемых из
характеристического уравнения
tgp = [*, (8)
которое выводится следующим образом:
ch
V-т.*-
sh
VI-
1
У?*
;in i ]/-i- R = 0;
если обозначить iy-^-R = v, то cosn— — sinji = 0, т. е. имеем
характеристическое уравнение (8).
Для корня s = 0 применим теорему разложения (случай кратных
корней):
Ф@) ,.
-г е —— 1 = hm
_ и Ф(«)т'(«) 1 <7c-R
[<f (,)]■
]■
Зат
<p(s)
^ 2^ 10 J
Ф'(')
>
164
Глава пятая
так как
Ф@)= -*£-, ?@) = ^ *.,Ф'@) = 4-4- *'«» = Ж £ •
Затем используем теорему разложения для простых корней sn .
Предварительно найдем:
V-т*
¥(sn )=4- D- |/^ я sin; j/^я) =-4 ^fi sin^ =
1 2
= ~-2~ V-n COS(i„.
Последнее равенство было написано с учетом характеристического
уравнения (8).
Величина Ф (sn ) равна
sin J l/ lu. r qc R* sin [j.„ -L-
Ф(вл )^- 'с/? Г а R
i
а
'V
Следовательно, решение нашей задачи будет иметь вид
T{r,x)-T0 = -*sg- [
Зат З/?2 — 5г2
R* Юг2
г
Rsin\xn -щ
-I 9 еХР
=1 К cos н-« г Рп
2 ат\ ]
**ф) J.
(9)
Корни характеристического уравнения (8) являются рядом чисел, не
зависящих от критерия Ki, а именно: jj^^ 4,4934, jia = 7,7253, jj-3 =^
= 10,9041, р,4= 17,2208 и т. д. (см. табл. 6.5 для Bi = 0).
Анализ решения и определение удельного расхода тепла. Напишем
решение в обобщенных переменных:
Г(г,т)-Г0 ==к.
ЗРо-^(з-5^
г
2 # sin ^я ~^-
n==l'KC0S^n г^
ехр (— [4 Fo) J ,
(Ю)
где Ki —критерий Кирйичева.
ГРАНИЧНОЕ УСЛОВИЕ ВТОРОГО РОДА
165
' i П~П111'ТТГТ1ТИТТТТ"ГТГ(ТТТ1 1 ГП 1 1 1 1 1 1 1 1 1 ! 1 1 1 1 1 1
ol N J
о 14 LM
ir« 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 MM Jr\
MM i^rfl
1 1 1 II III 1 1 1 1 1 1 1 1 1 1 1 _W"
It 1 1 1 , ! 1 ! 1 1 1 1 1 ! 1 i 1 1 1 WJfT M
ItuUH-r "- г ■■ T" 1 I i I 1 1 1 1 M 1 1 1 1 1 I 1 i 1 1 гсЧЙч It'
Mill l/*Ki 1 1 1 1 1 1 1 1 1 1 1 1 1
M i ! 1 1 II 1 1 1 1 II II 1 1 II 1 1 1 1 1 1 1 1 J^rT 1 1 1 1 1 II 1 I 1 1 1 1 1 1 1
Mi LWn 'И ШИ
I LUtTi n \Jr\\
Li-ИТ LHn
JJJ^tmT \уп\
Hj ! ' J J ieUJв i "T *1 ' II l^it^i 1
"In ^ i\\ i ' II \^\\ II
1 1J Mill! iJrll II 1 1 1 1 1 1 1 1 1 1
II "H 1 1 1 1 M M 1 1_>гпТ 1 1 1 1 1 1 1 1 1 1 1 1 1 i
III MmIII 1 1 1 1 II 1 11 ill! M^rT 1 1 1 1 11 1 1 1 1 J
|| 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 _W*"i 1 1 1 1 1 1 1 M L*rl
1 1 I I! 1 1A 1 1 1 I I 1 I I I 1 \Jr\\\ 1 i I I I I I I I I I 1 I I Wi I
f\f\ 1 1 1 ' 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 I 1 1 rl^TlT 1 III 1 II 1 III! <T\ 1
i,uuj ti|| Jw^Ti II J*h7 Mill
1 M 1 1 II II i i II) J "Г! 1 1 II II 1 II 1 МММ 1 Lri 1 II 1 1 1
1 1 | 1 1 1 1 1 1jJ44tTTm i^ "^Hl 1
1 "" n'TTl 1 И Lwii НИ
1 МММ i II 1 1 II II 1 1 II II 1 1 II 1 II 1 1 II 1 _J*ni 1 1 1 1 1 II II II 1 1
■ I! Ml 1 I J I] 1 IM II II II M M II M 1 LfT Mill
1 1 1 II M II 11 III 1 1 MM 1 II 1 II II 1 1 _L*tM 1 II II 11 II II II IIJ
1 1 1 II II II 11 M I 1 II II 1 1 II II II II 1тП II II II 1 1 II II II II \^i
U'J U-tT 1 1 1 Wn
1 1 1 II 1 1 II 1 1 II II II II 1 1 YAfT\\ II 1 1 1 II II II 1 II 1 II 1 1 Jr\\ 1
1 Щ^'НмТ N laU^HI Щ
M | tTTTl г" г! 1 J>prn ttt'RTm
1 i 1 II M M 11 II II II M M II II 1! 1 M 1 M M _L*^i MMIII j^\\ \
1 1 1 1 II 1 II 1 1 II II II II 1 1 II II 1 i 1 II 1 II \_Jr\\ 1 1 1 1 II L/f Mill
и,Щ 1 ПЪИТ Md IJ^r 1 1 1 II II J
1 i 1 1 1 i I 1 1 1 1 1 i I j | 1 | | I i 1 1 I | | 1 l>^ II IV"^! 1 МММ \Jr\
1 Mill Mill Ml II II III II 1 МигГТ 1 II li 1 M _i**ri 11 Wi 1
III IL-^ni II 1 II II 1 L*r\\ 1 M 1 i 1 LtT 1И
11 1 Ml M 1 1 МММ гтттТ II II 1 JjtTi Mill yn 1 Jr\\
[И] ^44t*M^ttT U rill WJ^tiT J/ИгуИ
мГГ mi "МММ М^ч^тпм М ы^м^^1>т^/ч
л or III [ 1 I 1 1 JJnT | | i 1 ! 1 | | | М^члл ХяТ 1 1 ^J^Hr Un I
Uj^o III LLjL-l"l'n i II II 1 II II 1 L-^ni^ sh^ti I^rT i^> Mi
MM ,1 H4TTTIj ill L rfTT L Ии^ \jr\\Jr\\
ImT'I M-14nMbi4Hi^^ 1
MM |LU4nTL^
щ^ш^^^^^^^^^|
0,?
0,4
0,6
0,8
*- 1,0
Рис. 5.4. Температурное поле шара при qc = const
(симметричная задача)
Ряд в решении A0) быстро сходится и поэтому, начиная с
некоторого значения Fo>Fox, им можно пренебречь по сравнению с двумя
первыми членами выражения в квадратных скобках. Начиная с этого
значения, температура в любой точке шара будет линейной функцией
времени, а распределение температуры — параболическим.
Найдем приближенное решение для малых значений Fo. Вернемся к
решению G), которое можно переписать так:
TL{r,s)-T-f = ^
sh
VT
[/-f«chv4*-sh^-«
A1)
При малых значениях Fo величина |/ — JR велика. Известно, что при
больших начениях
/:
R (больше 6,0) будем иметь с точностью до
166
Глава пятая
2,4
Ki
2,0
1,6
1,2
0,8
0,4j
1 1 1 1 1 1 1 1 1 1 1 1 11 1 1 1 11 1 1 1 1 I 1 1 1 11 1 1 1 1 1 1 1 1 11 1 1 1 1 I 1 1 1 .г!
1 1 1 1 1 1 1 1 1 1 I 1 1 1 1 1 1 1 1 1 1 1 I 1 1 1 1 1 1 ж\ !
1 1 1 1 1 1 1 1 1 1 1 I 1 1 II II II 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 r\ 3
1 1 1 I 1 1 1 1 [/[ [ 1 ( ( i
1 1 1 1 1 1 ! 1 1 ! 1 1 1 I 1 1 1 1 1 1 h 1 1 ! ! I 1 1 1 1 1 1 1 1 1 1 1 1 I r\ 1 1 1 1 1 1
1 I I I I I I I I I III! I I I I I I I I I 11 I \*\ 1 1 1 1 1 1 1
III \r\ 1 1 1 1 1 1 1 1 !
Ill r\ 1 1 1 1 1 1 1 1 I I
III )f\\ 1 1 1 1 1 1 1 1 1 1
III .г* II 1 l/i
I II [III I 1 1 r\ 1 1 1 1 1 1 1 1 1 1 1/Г 1
I 1 I 1 1 1 1 ||] I I 1 I I I I I 1 1 1 1 rf 1 ' ' ' 1 1 1 1 1 1 1 r\\ 1
III r\ 1 1 1 1 1 1 1 1 1 1 (УМ Mil
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 r\ 1 L/l 1
Mill Wi \J\\ II 1 1 1 II i
Г||1|||| 11I1 I j! III ij ill 1 \/\ 1 L/il I
lln \r\ \ 1 1 1 1 1 1 II 1 L/fi 1 II II 1 II 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1*41 1 L/fl II
II r\ II 1 M 1 1 1 II /Г Ml
Mil ж\ 1 II 1 1 1 1 II 1 /i III
II -гГ 1 II 1 II 1 1 M 1/Г 1 II 1 II II II 1 II 1
|| \J% || II 1 II 1 1 1 \S\\ II II 1 II II II 1 M 1
II 1 1 II 1 1 1 1 II 1 1 1 II 1 1 ж\ II 1 1 II II 1 1 l/l 1 II II 1 1 II 1 1 II II 1 1
1II 1 II 1 II 1 II 1 II II 1 J/f 1 II II II II 1 Wi II 1 II 11 M 1 1 1 1 II 1 1
1 1 1 1 II 1 1 1 1 1 1 1 1 1 1 i 1 _rT 1 1 II II 1 1 II 1/Г II
II 1 1 M 1 1 1 1 II 1 1 1 1 y*\ II M 1/ГI II
M III 1 Ж\ III "^TKX II
1 II II 1 1 1 1 1 II 1 1 Jr\ II 1 1 1 II 1 II \S\\ 111
M 1 M I I I I 1 1 M ]/\ II 1 II 1 II Ln 1 II 1 1 1 II 1 1 II 1 II II II II M
1 M II 1 1 11 1 Mjr\ 1 II 1 11 1 II 1 Wi III
1 II 1 1 1 1 1 1 1 1 1 Jr\ II 1 1 1 1 1 1 II w\ III
Ml jtI 1 irf III
j | II II 1 1 II jtT II 1 1 II II 1 1 \r\ III
JTI II II 1 II II 1 Ж\ III
V\ 1 II 1 1 1 1 1 1 1 \r\ III
iMI r\ 1 1 1 1 II 1 1 II r\ III
\уГ | | 1 II II 1 1 1 Wi III
1/Г1 M 1 1 1 1 1 II \r\ 11 1 II 1 II II II 1 1 1 II M II1 1 1 1 II 1 II 1 1
\Jf\ II 1 1 II II 1 1/| 1 11 II II M II 1 II 1 1 II M 1 11 1 1 1 II II 1 1 1
ж\ 1 1 II 1 1 II 1 J/f Mil 1 II II M M 1 Ml III 1 1 II 1 II II 1
1 \f\ 1 1 1 1 II 1 1 1 J/) II II 1 1 II II 1 II 1 1 1 II 1 II II 1 1 II II II II 1 1
1 1 1УГ II II 1 1 1 1 1 ¥\ 1 II II 1 II II II II 1 1 1 1 1 II 1 1 1 1 1 1 1 1 1 II 1 1 1 I
Jr 1 II 1 II II 1 Jr\ II II 1 1 1 1 II II 1 II 1 M 1 1 II 1 1 1 1 1 1 1 1 M II 1 1 1
I / 1 jti II II II 1 1 II II II II 1 II 1 1 II II 1 1 1 1 1 1 i 1 II M 1
1 /M II 1 II LtTII111II11IIII11II111IIIIIIII11111IIII1 1
/j \jf\ M II M II 11 МММ II 1 M M M II 1 II11 11 1 1 !l 1 1 1 1
1/1II II \jr\\ M II 11 M II M I I M M M II II M M 111 11 I M 1 1 II 1
I/ II 1 1 _J^tT III II II II II 11 II 1 II 1 II 1 11 i II II 1 II1 11 1 i 1 1 1 II 1
L.1, iLj-ri 1 MM 1.1 1 J_l_LI II1 II II 1 II M 1 1 II M II II1 1 1 i M 1 1 II 1
0,2
0,4
0,6
0,8
Fo"
-1,0
Рис. 5.5. Зависимости между -ттт и Fo для поверхности A)
и центра B) шара
третьего десятичного знака sh a=chu= -у еа > thw^cthu— 1. Тогда
для значений г, близких к R, можно и sh у — г заменить через
ехр
У^Л, т. е.
TL(r,s)-±*-~
QcR2
\ rs
v4«-'
ехр
/-f'^-o]. A2)
Пользуясь таблицей изображений [см. приложение VI, формула E6)],
находим
т-!^-к<4[«рК^')-.с
R
2 /Fo
■ ]/Fo / — erf с
2 /Fo"
A3)
ГРАНИЧНОЕ УСЛОВИЕ ВТОРОГО РОДА
167
Для центра шара (г = 0) решение A1) можно написать так:
TL@, s)-
т0
qcR
Is
[*V-r
R
-sh
V-т*
V4«]
i yily-.-Vf.
A4)
Тогда согласно формуле E7) таблицы изображений (см. приложение VI)
находим
6 « 2Ki {[ exp (Fo-1)] erfc ( g ^L. - УЩ • A5)
Из точного решения A0) и приближенных решений A3) и A5)
следует, что относительная избыточная температура прямо пропорциональна,
критерию Кирпичева и зависит от числа Fo и относительной координа-
ты -£-.
Таким образом, отношение -j-- есть функция только Fo и -5-:
Ki
A6)
На рис. 5.4 построены кривые распределения величины-^-по
относительной координате для разных значений числа Фурье (от 0,05 до
0,5). Начиная с Fo = 0,5, процесс нагревания становится
квазистационарным; температура любой точки повышается по линейному закону, а
распределение температуры следует закону параболы. На рис. 5.5
построены графики изменения величины ^т- от числа Фурье для
поверхности и центра шара. С помощью этих графиков расчет значительно
упрощается.
Удельный расход тепла находится по формуле
АО = —
.т.
A7)
Решение задачи для случая q (т), Т0 = f (r). Рассмотрим более
общую задачу со следующими граничными условиями:
T(r,0) = f (r),
х?ЩЛ. + A{х) = о,
дг
dT@,i)
дг
0.
A8)
A9)
B0)
Воспользуемся конечным интегральным преобразованием
Ъ(р,х)= |гГ(г,х)-М-^,
B1)
168
Глава пятая
где р— корень характеристического уравнения
sin pR ~~ pR cos pR = 0. B2)
Обратный переход от изображения 7> (р, т) к ее оригиналу Т (г, т)
осуществляется по формуле
со
Г<г,,) = з*.7>@.,) + 42 -jjj^.^iLrp^.x). B3)
Применим преобразование B1) к дифференциальному уравнению
теплопроводности и учтем условие B0), тогда
*> ^ г ^2L dr =
_ . . Р
о
J \ дг% 'г дг
г _«IL^]^ -~р27>(р,т). B4)
аг(г. т)
дг
Из условия A9) следует
J \ дг2 'г дг ) р
о
= ^/?^-р2Гр(р,т). B5)
Если теперь умножить все члены дифференциального уравнения
теплопроводности на г smpr и проинтегрировать по г в пределах от 0 до R,
то на основании B5) получим
ЛТ¥£ Т) + аР- ТР (р, х) = -f R -*L£*- q <*). B6)
Решение уравнения B6) имеет вид
X
7>(р,т) = ехр (-ар2т) {С(р)+ -f Я^ |<7(»)ехр (ap2»)d& }. B7)
о
Для определения С (р) воспользуемся начальным условием A8):
R
С (р)=§ rf{r)^Z-'dr. B8)
о
Тогда решение B7) можно написать так:
R
7>(р,т) = ехр (-ар^) { Jr/(r) sinppr dr +
о
-+- -f tf sin/r [ <? (») exp (ap2 Ь) d» } . B9)
о
ГРАНИЧНОЕ УСЛОВИЕ ВТОРОГО РОДА 169
Для удобства перехода к оригиналу предварительно найдем
R т
7V @, т)= J г2 / (г) dr + -f /? J ^ (&)d ». C0)
о о
Подставим значения 7V @, т) и TF (/?, т) в формулу B3), тогда получим
решение
R %
7'(r,x)=^-Jr»/(r)dr+ *±§ q(b)db +
о о
оо
/г=1
J х оо
х 2 (V/(r)^E^Ldr+4-S ^si2nPno x
« J /w Pn l Pnsm2pnR
0 /2=1
x
2^-exp[-ap2„ т) -|- j q (»)• exp (ap* &) d 0. C1)
X^L
Обозначив \xn = pn R; Fo = a т/#2 и используя характеристическое
уравнение sin ;л = jj, cos jj., получим решение в окончательном виде
Т(г,т)= ^-|'rV(r)dr+ Й.|' <7(»)<*» +
о о
оо
л_ V 2 1*я sin ^ r/R x
R
х sin
exp(-^2Fo)f г/(г) sin^r,R dr+4-S -^— X
О /г=1
х
^^exp (-^Fo) j ?(&) exp (j* ^-) d&. C2)
В частном случае, когда
Т (г,0) = Т0 = const,
9 (т) = Яс = const,
из решения C2) получаем * решение (9).
§ 4. НЕОГРАНИЧЕННЫЙ ЦИЛИНДР
Постановка задачи, Для неограниченного цилиндра с радиусом R
постановка задачи такая же. Нагревание постоянным тепловым
потоком происходит равномерно по всей поверхности цилиндра
(симметричная задача).
170
Глава пятая
Дифференциальное уравнение теплопроводности . для
неограниченного цилиндра при условии, когда температура зависит только от гит,
приведено в § 5 гл. IV.
Начальное и граничное условия тождественны условиям A) — D)
предыдущей задачи.
Решение задачи. Решение дифференциального уравнения при
начальном условии A) и условиях C) и D) можно написать так (см.
решение C1) § 5 гл. IV):
TL{r,s)-?f =AI0[Y^r])t A)
где 10 ( 1/ — г ) — модифицированная функция Бесселя первого
рода нулевого порядка, Л —постоянная [относительно г. Постоянную А
находим из граничного условия
V±rt[V+*)'+ti-b
откуда
А= ■ q*
так как /0 (г) = 1г (г) — модифицированная функция Бесселя первого
рода первого порядка.
Следовательно, решение для изображения можно написать так:
Это решение является отношением двух обобщенных полиномов
относительно s, причем полином ф (s) не содержит постоянной, а полином
O(s) имеет постоянную, равную qcR, а именно
1Ф(в) = ,c*/0( j/jLr) = q'R (l +=£=3 + ^** + ...)], C)
= Xs*cp'(s), D)
где <p(s)— выражение, стоящее в скобках, которое является полиномом
относительно s.
Воспользуемся теоремой разложения. Предварительно найдем корни
выражения ty(s), для чего приравняем его нулю:
Отсюда получаем: 1) s = 0 (двукратный корень), 2) ^i(~J/~5~~#) =
— jj i у — Rj = 09 т. е. бесчисленное множество корней sn =
, где i у — R = р — корни функции J^p) (см. табл. 5.1).
i
ау?п
ГРАНИЧНОЕ УСЛОВИЕ ВТОРОГО РОДА
171
Таблица 5.1
Корни характеристических уравнений J0 (\i) = 0 и /х (^) = О
п
1
2
3
4
5
Корни \х уравнений
Jo(P-)=0 | JxM = 0
2,4048
5,5201
! 8,6537
| 11,7915
1 14,9309
3,8317
7,0156
10,1735
13,3237
16,4706
п
6
8
10
Корни и уравнений
•Л>Ы = о
18,0711
21,2116
24,3525
27,4935
30,6346
Jt (tx) = 0
19,6159
22,7601
25,9037
29,0468
32,1897
Находим значение
Ф@) t. Г d
Y @) s_o L ds
Ф@) .
Ф' @) •
;х ФE)
Acp(s)
]--¥Ч
асЯ / 2ат ' 1 г2
Г
2 R*
так как
Ф@) = <7СЯ, q>@) = -g-, ф'@) = </<:#-£-, Ф'@)
Я4
2а
Далее найдем ty'(sn):
4а
~2а~~
16а2
/-И-
/;(/*-*) =:-4*W'
так как /J B) = J\ (iz). Таким образом, получим
Ф(зя) 6v = ' ^
00
/2=1 П=\
Воспользуемся рекуррентной формулой
Рп J[ (tO = Рп J0 (fti) ^ А (ftt) •
Так как согласно характеристическому уравнению J1(pn) = 0, то б;у«
дем иметь
Следовательно, решение нашей задачи можно написать так:
Гс-Т0
»[!*-4('-*t)-2ii^4>--*H->-,Fo)].
п=1
E)
Анализ решения и определение удельного расхода тепла. Ряд в
решении E) быстро сходится, так как рп — величины большие (см. табл.
5.1). Поэтому, начиная с определенного значения Fo>Fo1? этим рядом
можно пренебречь; тогда температура в любой точке цилиндра будет
линейксй функцией времени, а распределение температуры —
параболическим (квазистационарный режим).
172
Глава пятая
,j/ чТТТТТТ 1ТГГТП' ITIТГГГ П" 1 1 1 1 1 1 ГП 1 II 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
fill
*'т и 1 '
£Г 1 J
М и ШИ
Г 1 Г Mill Г 1 Ml I j/] 1
1 I 1 1 1 1 1 1 1 II 1 1 1 1 1 1 1 1 1 1 1 1 1 1 \j*r\ 1 1
1 II II M 1 M I 1 1 1 11 1 1 1 1 1 1 1 11 1 1 I 1 1 1 11 1 1 1 I 1 1 1 l/j I I
МММ 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 I 1 1 1 1 1 1 \_Jr\ II
1 1 1 1 1 1 1 I 1 III 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 г^Л. 1 Wi 1 1 1 1 1 i 1 I 1
Г M J0^ifT LM
1 Г 1 III ill \jr\\ 1 I 1 1 1 1 1 1 1 .Wi 1
J j J J 1 1 I 1 j J J I J MW| 1 1 | 1 I I \_Jr\\ 1 1 1
II 1 I 11 I l_W"i 1 11 11 III _Wi 1 1 1 1
j 1 Ijl! i Ml 1 1 11 1 1 1 1 1 1 LWi^ 1 1 1 1 1 1 1 1 1 1 \Jri\ II
I I . j i 1 1 1 1 1 1 1 1 1 I JjfW^i 1 1 1 1 1 f 1 ' w L^rT fill
i • c\ .LI.-! M . LLLi Ml LhtT 1 k^yfl
i,zbf \fj\ ! LwnTi LC*rT _И
1J 1 1 ' 1 1 1" T 111 L*rT 1 1 1 1 1 1 1 1 \Jf\ 1
г III' -^гт иТм 1111111111111 ilnf] 11111111 LHi
И гi ггГ"|'"Г~~гН—[ •}• г j гЫп i г 1 М 1 Ц'пТ N
lilil I I I I 11 I I I I I I Lrni I 1 1 1 1 1 1 1 1 I _Wi II
г 1 1 1 1 1 1 1 1 1 1 1 \Jr\\\ 1 M w LtT 1 1 1 1 1 II 1
I 1 Iff *Wii III m'S^ti 1 1 1 1 1 i
II LnWii 1 1 1 1 1 1 1 1 1 1 1 1 L^i\ 1 1 1 1 1 1 1 1 1 1у1
I nnl ! 1 1 1 1 1 1 1 I 1 1 1 1 J—WtT 1 1 1 1 1 1 1 1 1 1 1 I 1 |^ИП 1 1 1 1 1 1 1 1 1 \/\ 1
1 II j J nil" II \Jr\\ 1 Lri 1 !
1 j j 1 j 1 1 1 rl 1 " ГТТ I JirrtT LMi
prj II' И ЬМПМ Ml LHl 1
1 ■ 1 Г 1 1 1 1 1 1 1 1 LW^Ti 1 л. 1 yti Ml
illl JJn] I 1 1 I 1 1 II 1 1 pJvb*rl Ml
Г1 II 1 II II1 I _L*t^i II L+Wi 1 1 1 1 1 W
III jJe-W*!^ 1 1 1 1 M 1 1 1 1 1 1 1 LkTI III \r\\
1 1 M 1 1 II II 1 L 1T| -III Li^rT 1 1 1 II I \jr)\ 1
f\ 71-! j!( 1 ' I | |i'| r [ ]| 1 1 1 (I 1 | 1 [I (I ( 1 1 1 1 ]>rl 1 I 1 1 1 1 1 1 1 1 \Jr\ 1 1 1
и, / xj i—| | II™'' \-~\~ \'\ мм it'M I'l 1 1 1 MMI 1 i \Jr\ 1 II 1 M 1 1 1 II Wr Mil
1 1 M 1 II 1 1 II II II 1 1 1 II «Ш1 II 1 1 1 1 1 1 1 1 Lni III
III \J^r\\\ 1 M II J ^ч 1 jHi 1 M M 1 1
III Lbpl 1 1 1 1 1 1 ! 1 1 1 К iiuJ"f 1 1 1 II II 1 1
III \-л^\\\\ 1 \jr\\ 1 II 1 1 1 II L4
III II i |'"T1 | 1 1 1 | | I 1 | 1 | I I | | J^TI 1 1 II 1 II 1 Vfl
м 1 -M M 1 JrjJ НчмТ 11 Hi LtT
I' T Мм Ml l мним i>Hi
л c/il II II II 1 II 1 II II II II 1 1 1 1! II II _L*Kil II II 1 II 1 1 1 1 ^\ 1 II II 1
U,l>U| 'Мм \\JrT i 1 1 ! J^l III 1
I I 1 I | 1 | 1 Ml II 1 1 1 II M 1 1 l*Wii 11 oi^LtT M II II M 1
II LL*-!!! II hjj"HI II II II 1 1 1 I
I4++4+ JJjphtttm Шпм jJH
144т4т444ФммТ 141111111111111 LUiiT i 111111111 \JruA
LU4tTT LwVhu
1 11 L MM 144*п*п| III LWrM 0$й| [угО^тС
гш| Г Г Г III \\**г\\ ±*rC\ \-JrOr\\
1 МММ I II 1 II 1 II 1 1 1 1 1 II II \\j^r\\ LJ-^WcTv^^TjW'T
„Mi^J:^i^ffi^|^tll 11111111
0,2
0,4
0,6
0,8
-*- 1,0
Ki
Рис. 5.6. Температурное поле неограниченного цилиндра при
qc = const (симметричная задача)
На рис. 5.6 даны кривые распределения безразмерной величины
для разных значений Fo. Из рис. 5.6 видно, что, начиная с Fo =
е
= 0,6, парабола, характеризующая распределение -^г по относительной
координате, равномерно смещается вверх. Зависимость между ~^г и
числом Fo для поверхности и на оси цилиндра приведена на рис. 5.7.
Найдем приближенное решение для малых значений Fo. В решении
B) для изображения разложим функции 10 ( у JL #j и /J j/JL#j в
асимптотический ряд:
У2тш
•е" 1
8и
128аа
15
128а2
ГРАНИЧНОЕ УСЛОВИЕ ВТОРОГО РОДА
2,tii | | 1 1 | | | гт-i | | 1 | | | | | | I | | | | | | | | | 1 | 1 | || |Т| 11 {1/1 1 1 1 I I \
1 1 1 1 1 1 ' III Ml Mill 1 11 1 II I/I II M 1 II
л ji II \л\ 1 1 1 1 1 IJ
v L 1 1 1 II II 1 II 1 1 1 1 1 М 1 1 М 11 II II ММ 1/1 МММ уГ
[\1 ||| 1 1 1 II 1 1 1 1 1 1 1 1 II II II 1 1 1 1 1 1 II II lit 1 ж\
III L/| ьЛ *
1 III 1 1 1 1 1 1 1 1 1 II 1 II 1 1 1 II II 1 МММ* 1/Г МММ 1уГ
о alll l L j МММ 1 MM xl III l/i
» fi™ Гм III IxT III \j\\ MM
II \JK\ МММ Y\ Mill
Mil ж\ 11 1 II 1 1/T МММ
1 1 1 1 1 1 II 1 i 1 1 1 1 M M 1 1 1 Ln МММ \J\
j 1 1 I I | | | 1 1 | | | | | 1 Mill I 1 1 1 1 1 \J\ 1 1 1 II 1 1 m\ II II 1 II
1 1 1 1 1 1 i 1 M 1 1 II 1 1 1 1 1 1 1 1 1 1 II II 1 II ж\ Ml l/T 1 1 1 II II 1
Mill \r\ МММ \J\ 1 II 1 II II 1
III J\ II 1 1 II 1 Jr\ II II II II 1
Mill f\ 1/T II 1 1 II II 1 1
r> aM 1 1 1 1 I I i | | | I I | I | j | | | | | | M 1 l/i Ln 1
j * 1 1 i 1 1 1 1 I 1 II 1 1 1 1 1 ! 1 1 1 1 1 1 1 i 1 \X\ МММ i\ 1 II 1 II II II 1
ill v\ МММ i/т 111 м м м м i
i i | I j I | | | | | 1 1 1 1 1 1 1 1 1 1 1 II 11 1 l/f МММ \ж 1 1 1 1 1 II 1 II 11 1
lljiij IlliiilllilltlSlilIfiji1 1 II II \A 1 II 1 II II II 1 1 1 1
III lil/f МММ \Л\ II 1 1 II 1 II II II 1
III in 0 Jr I | II 1 1 1 II II II 1 1 1
i 1 | 1 1 ' Mill i 1 1 1 1 1 1 1 1 1 1 1 1 1 w\ II l/T 1 II II 1II II II II 1 1
1 /-1 II II 1 II 1 1 1 1 II 1 1 'I II 1 1 II M II M 1 1 1 Jr 1 1 1 1 1 1 1 1 1 1 1 II 1 1 1 1 1
N l/i Шч
Mill \J\ II 1 ■ II 1 I Jm II 1 II 1 II II II 1 II 1 1 1 1
III t\ l/T Mill
II l/T L/r 1 Mill
j ММ' Mill 1 1 1 1 1 1 1 ' уг 1 1 1 I II 1 Jm 1 II II 1 1 II 1 1 II II II II 1 1
III t\ L/l 1 1 II II II II 1 1 II II II II 1 I
II Lri 1 1 1 1 1 1 \jK\ II ' II II II 1 II 1 1 1 II 1 1
Ml \J\\ 1 1 1 1 II jtI III!
II /Г1 1 1 1 1 1 1 Y\ Mill
Ml Jr j МММ l/T 1 M 1 1 1 1 1 II II II II II 11 МММ
II l/i 1 | || 1 1 l/T II II 1 1 1 II 1 M 1 II 1 1 II 11 1 II 1 1 1
II \J\ 1 1 II II 1 )r\ 1 1 1 1 1 1 f II 1 I II II 1 II II 1 1 1 II 1 1
II ir 1 МММ l/T Mill 1 II M 1 II 1 1 II МММ III
III i/l \J\ 111
III \J\ 1 1 1 1 1 1 1 Jr\ III
МММ ж\ i l/T 111
u,o ! / Jn 1 M 1 ! 1 1 1 1 1 1 1
1 MM jf\ v\ 1 1 1 1 II 1 1 1 1 i El M 1 II 1 II 1 II 1 1 II 1 1 1 I
Ml r\ МММ \r\\ 1 ! 1 1 1 II 1 1 1 1 1 1 i 1 II II 1 1 1 1 1 1 1 II II 1 1
i I I 1 I 1 \J\ 1 II 1 1 1 1 ж\ Mi 1 M 1 II 1 II II II II 1 II II 1 1 1 i
MM *\ MM l/i III!
Mil Lri ММ /Г Mill M 1 1 1 1 II 1 1 II II II II 1II II 1 1 1 1 1
1 jr | w\ | | 1 | 1 Ml II 1 1J II II II II 1 II 1 II 1 I 1 II 1 1
Mill w\ MM МгП МММ Ml 1 1 II II II II II II 1 II 1 1 1
MM \A МММ \f\ 1 1 1 1 1 1 1 1 II II II 1 II II II 1 1 II 1 1
11 1 И II 1 I 1 1/1 'ttttIt " Ml 1 1
|| l/f 1 I I I 1 I л 1 * M 1 1 1 1 M 1 1 1 II 1 II II 1 1 Mill '
1 /1 i 1 1 1 1 r\ I l МММ 1 1 1 11 1 1 1 1 1 11 11 11 II 1 II MM 1
11 / I ll lX I 1 1 1 1 1 I 1 II 1 II 1 1 1 1 1 1 ! 1 1 1 II 1 II 1 1 1 II 1 1 i I 1 1 1
1 l/l 1 1 1 1 lyf 1 ! I 1 M 1 1 1 M 1 II 1 1 1 1 1 I 1 1 II II II II 1 1 II II 1 i II I
1 / \jf j IMttMIMIMMIM
l/l \jf\ II! M M MM M [ 1 1 11 II II 1 1 1 II II 1 II 1 1 1
l/l \J\\ 1 M I I Ml i II 1 1 1 1 1 1 1 III M I 1 II 11 M 1 M
0ifl LK1 1 1 1 III 1 II M i II III II 1 11 1 111 11 1 11 II Ml 11 1 i 11 11 1
0,4
0,6
0,8
Fo
.1,0
Рис. 5.7. Зависимости между -jtj и Fo для поверхности A)
и оси B) цилиндра
Ограничиваясь двумя первыми членами, решение B) можно написать
так:
т ( \ Т° Яс
aR
(R + Зг) а
s Yrs 8rs2 YrR
У^Я-r
F)
Пользуясь таблицей изображений, получим приближенное решение
где
i erfс и =
1
у%
е — uerfcu,
i2 erfc и = — [erfc и — 2и i erfc и].
174
Глава пятая
Температура на поверхности цилиндра (г = /?) будет изменяться
с течением времени по следующему соотношению
6n«2Ki ]/"-*£-■+J-KiFo.
Следовательно, в начале процесса нагревания температура
поверхности цилиндра увеличивается по параболическому закону, а затем — по
линейному закону (квакдстационарный режим); таким образом, имеется
некоторая аналогия с изменением средней температуры Т(х) при
нагревании неограниченной; пластины (см. §3).
В последнем случае средняя температура пластины в начале
повышается по параболическому закону, а затем — по экспоненциальному
закону.
Удельный расход тепла &Q.V можно определить по формуле
AQz,^-^-^-
(8)
Решение задачи для случая q (т), Т0 = /(/*). Рассмотрим более
общую задачу с краевыми условиями
Т(г, 0) = /(г),
.Х^|^_+^)=0,
дг
дТ@, т)
дг
(9)
A0)
(П)
Для решения задачи воспользуемся конечным интегральным
преобразованием Ханкеля
- Тн{р, х) = $гТХг,х)Мгр)Aг, A2)
о
где J0(z) — функция Бесселя первого рода нулевого порядка, ар —
корень характеристического уравнения
/о (Р. #) = а
Переход от изображения функции Тн (р, т) к ее оригиналу Т(т, г)
осуществляется по формуле
Т (г, .) = -J" Тн @, *) + -£- ^Тн (р.,,) А^
/г=1
■)_
R)
A3)
Применим преобразование A2) к дифференциальному уравнению
теплопроводности и учтем условия A1) и A0):
]{Щ^ + ~ ЩЙ-) rh (гР) dr = RJ0 (RP) *^> - Р>ТН (р, ,) =
о
= RJ0 (Rp) -U& р*Тн (р, т). A4)
ГРАНИЧНОЕ УСЛОВИЕ ВТОРОГО РОДА
175
Умножая все члены дифференциального уравнения
теплопроводности на rJ0(pr) и интегрируя по г от 0 до R с учетом A4), получим
-^1- + ар*Тн (р, х) = aR^LjoiPR). A5)
Решение этого обыкновенного дифференциального уравнения будет
Тн (р, т) = ехр (- ар2 «с) ГС (р) + Я -f- /0 (pfl) f <7 (») ехр (ар2 ft) dft 1 .A6)
О
Для определения С(р) воспользуемся условиемЗ(9). Из выражения A6)
при т-^0 получим
Тя(р,0) = С(р).
С другой стороны, согласно формуле A2) начальное условие (9)
можно написать так:
R R
Тн(Р, 0) = J T(r, 0)rJ0(pr)dr = $f(r)rJ0(pr)dr. (i7)
0 0
Следовательно,
C{p) = $f(r)rJ0(pr)dr. A8)
0
Подставим A8) в A6), тогда получим
Тя(р,т) = ехр(~ар2т) [ j/(r)r/0(pr)dr + R^rJ0(pR) ^(&) X
о о
X ехр (арЧ) d& 1 . A9)
Затем перейдем от изображения функции Т# (р, ъ) к ее оригиналу Г(г, т)
при помощи формулы A3). Предварительно найдем Тя @, t):
Г„ @,т) = J/(r)rdr + -f R f </(»)<». B0)
о о
Подставим значения Тн @, t) и Тн(р,%) в формулу A3)
R X ОТ
ГС. *) = ^fV)rdr Ч—хй^J* 9(»)d» + 2'7^Й"ехр(~ор»'с)-><
0 0 n=l °
X -j,J/(r)r/.fof)rfr+-f jf] /,°'"/^у) «Р(-<¥>,'*) X
0 л=1 °
4-J?(»)exp(ap»»)d». B1)
х
о
Вводя обозначения рл = р„ /?, Fo = ат//?2, получим решение задачи в
виде
176
Глава пятая
+ ^
2j Z*J exP ( ~ V-l Fo) -| j ? (») • exp ^„ -^-) dft, B2)
где [*„ — корни характеристического уравнения
B3)
Из решения B2) получаем, как частный случай, решение E), для чего
достаточно положить
T(rfO) = /(r) = T0 = const,
<7 (т) = 9с = const,
тогда
r(r,„-r„.^-[2Fo-4-(l-24-)-2-^5x
XJ0^^exp(-^Fo). B4)
Если обозначим Ki = qc /?Л (Тс — Г0), то решение B4) будет
тождественно решению E).
§ 5. НЕОГРАНИЧЕННЫЙ ПОЛЫЙ ЦИЛИНДР
Постановка задачи. Дан неограниченный полый цилиндр с
заданным начальным распределением температуры f(r). На наружной и
внутренней поверхностях заданы тепловые потоки, как функции
времени. Необходимо найти распределение температуры в любой момент
времени.
Дифференциальное уравнение теплопроводности приведено в §5
гл. IV. Начальное и граничные условия следующие:
Т(г, 0) = /(г),
-*-*£%3-+*(*) = о.
A)
B)
C)
ГРАНИЧНОЕ УСЛОВИЕ ВТОРОГО РОДА ffl
Для решения этой задачи воспользуемся конечным интегральным
преобразованием Ханкеля
Н [Т (г, х)] = Тн (р, т) = J V (г, т) М (р, г) rdr, D)
где ядро преобразования М(р, г) имеет вид
М(р,г)
71
^^Щу-^м}' <5)
где Y1(z) и К0(г) — функции Бесселя второго рода первого и нулевого
порядков.
Параметр р определяется из характеристического уравнения
JiipRi)yi{pRi) = Y1{pR1)J1{pRt). F)
Формулой обращения для этого преобразования служит разложение
функции Т(г,х) в ряд по ортогональным функциям ядра преобразования
Т(г,х)=^АрМ(р,г), G)
Р
где
Ар = Тн(р, x)/fM*(p,r)rdr.
Применим преобразование D) к правой части дифференциального
уравнения теплопроводности с учетом условий B) и C):
-£- q% М М (р, R2) —%-qx (т) М (р, Rx) + р2 j' гГ (г, т) М (р, г) dr =
= F(p>*)+pTH{p,*), (8)
где через F (р, т) обозначена сумма двух первых слагаемых.
Согласно формуле (8) дифференциальное уравнение
теплопроводности преобразуется в линейное уравнение первой степени:
dT"iP'Z) = a[F(р, х) + p*TL(р, *)] . (9)
Начальное условие для этого уравнения примет вид
Тн (р, 0) = Н U (г)] = J rf (г) М (р, г) dr. (Ю)
Уравнение (9) имеет решение
Тн(р, т) = ехр(ар*т){а jV(p, »)d» + Я[/(г)]} . (И)
о
Переходим от изображения Тн(р, %) к оригиналу по формуле G)
оо
Т (г, *)=S\ Rz M iP' Г) ехр (ар* х) j Я [/ (г)} +
+ а CF(p, &)exp(— арП)с1&\ A2)
178
Глава пятая
Первый член суммы ряда, соответствующий нулевому корню р = О,
имеет вид
lim Rz М(Р> Г) ехр (ар**)!#[/(г)] +а Г F (р, ») ехр (— ар2 &)d& =
j%M2(p, г) dr ' 5 J
Я2 т
J / (г) ^ + ~T f №<?2 (Щ - Riqi (»)] d&
#1
#2
rdr
A3)
Для всех остальных рфО имеем
IM* br)rdr = - яр-/?о>ад^(РЛ) ' A4)
*^>Ч4Ж-^ЭД- A5)
Таким образом, решение будет иметь вид
j r/ (r) dr + -f f [/?a<7. (*) - RiQi (»)] ^& +
J?! 0 )
^p" /?(ряед-у!(ряад Го(РйГ) АО».*) r°(p"r)J x
Хи/г,М[л^^й^-Г.(Р.0]*-5гЯт«&-
~7f(&]exp(^)dMeXP^"X)' A6)
Найдем частное решение при краевых условиях
T(r,0) = /(r) = r0 = const, A7)
q1(i) = 0; q2 (x) = qc = const. A8)
Условие <7Х (т) = 0 означает теплоизоляцию, т. е.
dT(Rlfz) _ п
дг
При упрощении воспользуемся соотношением
*U PnJiiPnR*) \A(PnRi)~J\{PnR*)] [oyFnJ Ji(PnRi) °^л/]
я=1
[4-(/?»-2r«) + /??(ln^ + ^^.ln^ + 4-)]. A9)
r>2 p2 4
ГРАНИЧНОЕ УСЛОВИЕ ВТОРОГО РОДА 179
Окончательно будем иметь
-f(lni+ I
B0)
где Fo = ax/jR2, pn = pnR2—корни характеристического уравнения F)»
которое можно написать так
Ji(v- -it) У г (V) = П (р -^) Л GO ■ B1)
Решение B0) симметрично относительно граничных условий. При
/?!->0 из формулы B0) получается решение для неограниченного
сплошного цилиндра.
г^-г.-**.!^* [*рь-4{1-*4)
^2 — /?1
R22
lnlt + i
+
+
оо
2
Ri
« ;i ^TariW
X У^ (^" -fr)l ^P (— ^ F0>
ГРАНИЧНОЕ УСЛОВИЕ ТРЕТЬЕГО РОДА
6
Данная глава является некоторым обобщением и развитием гл. IV,
поскольку рассматриваемые здесь задачи является более общими и из
них как частный случай вытекают задачи гл. IV, для чего достаточно
положить Bi = оо.
На отдельных конкретных задачах гл. IV можно было установить,
что операционный метод имеет большие преимущества по сравнению с
классическим методом разделения переменных при условии
равномерного начального распределения. Если в начальный момент времени
температура тела зависит от его координат (неравномерное начальное
распределение), то классический метод или метод интегральных
преобразований Фурье и Ханкеля быстрее приводит к результату, поэтому для
решения таких задач будем пользоваться этими методами.
Операционный метод имеет преимущество в том отношении, что
позволяет получить эффективное решение для малых значений Fo, в
котором часто отсутствуют специальные функции.
Для рационализации расчетов введем единую систему обозначений
для всех задач, дадим значения характеристических чисел, а также
табулируем начальные тепловые амплитуды Ап и коэффициенты Вп,
входящие в соотношение для средней температуры. При наличии таких
таблиц и графиков конкретный расчет может быть сделан быстро и с
достаточной степенью точности.
В данной главе будут рассмотрены задачи на нагревание,
поскольку в следующей главе эти задачи получают свое дальнейшее развитие
(температура среды изменяется от времени). Покажем, что задачи на
нагревание всегда можно свести к задачам на охлаждение.
Пусть имеется тело с заданным начальным распределением
температуры в виде некоторой функции /(х, у, г, P). В начальный момент
времени тело помещается в среду с постоянной температурой
Тс> Т (х, у, г> 0). Теплообмен между поверхностью тела и окружающей
средой происходит по закону Ньютона. Это отображает в первом
приближении сложный лучистый и конвективный теплообмен, в котором
доля лучистого потока тепла является преобладающей. При этом разность
температур AT (AT = Тс — Тп) должна быть достаточно малой. Таким
181
образом, имеем задачу на нагревание тела при наличии граничных
условий третьего рода:
-§- = "ГТ, A)
T(x,y,z,0) = f(x,y,z), B)
-(уГ)п + #(Тс-Гп) = 0 (Тс>Тп), C)
где индекс «п» обозначает поверхность тела.
Сделаем замену переменной
Тс — Г = ».
Тогда имеем
= ау2&, (Г)
» (х, у, z,0) = Tc-T (х, у, г, 0) = Тс - / (х, у, г) = <р (*, у, 2), B0
(у»)п+Я»п = 0, C0
т. е. получаем задачу на охлаждение тела в среде с температурой,
равной нулю (&с = 0), когда начальная температура тела задана в виде
некоторой функции ф (#, у, г).
Если начальная температура тела одинакова во всех его точках, т. е.
f(x, у, г) = Т0 = const, то все полученные решения для нагревания тела
в виде зависимостей относительной температуры 0 от критерия Био,
числа Фурье и относительных координат будут справедливы и для
охлаждения тела, только под величиной 6 надо понимать:
при нагревании
при охлаждении
-£^-=ф(рО. Bi,-!;, -I, -f). E)
Последнюю величину также можно написать в виде
Т°-Г = 1 _ Г-Гс F)
То-Тс Т0™ТС • W
§ 1. ПОЛУОГРАНИЧЕННОЕ ТЕЛО
Постановка задачи. Дан полуограниченный стержень, боковая
поверхность которого имеет тепловую изоляцию. Температура стержня
везде одинакова и равна Т0 (начальная температура). В начальный
момент времени конец его помещен в среду с постоянной
температурой Тс > Т0. Теплообмен между окружающей средой и неизолированным
182
Глава шестая
Рис. 6.1. Кривые распреде- концом стержня происходит по
ления температуры в полу- зак0Ну Ньютона (граничное условие
ограниченном стержне с теп- м ~ л ч v ^ ^
ловой изоляцией боковой третьего рода). Требуется найти
поверхности распределение температуры по
длине стержня в любой момент
времени и удельный тепловой поток
через его конец (рис. 6.1).
Так как потери тепла с боковой
поверхности стержня отсутствуют,
то его можно считать за
полуограниченное тело, распространение
тепла в котором происходит только
в одном направлении. Таким образом,
нахождение температурного поля
связано с решением
дифференциального уравнения
{////У//////////////////////////////////////////
х*шшш;ш/шммшмш»ш»/*
дТ (х, т) д2Т (х, т) . . А п . . ч
дх*
при начальном условии
и граничных условиях
Т (х, 0) = Т0 = const
т / \ т дГ(оо, т) А
0)
B)
C)
D)
Коэффициент теплообмена а считается постоянным.
Решение задачи. Задачу будем решать операционным методом, так
как при равномерном начальном распределении температуры
операционный метод быстрее приведет к результату.
Если применить преобразование Лапласа к дифференциальному
уравнению A), как это неоднократно было сделано, то уравнение для
изображения с учетом начального условия будет иметь вид
rL(x,$)-±-TL{x,s) + -± = 0.
Граничные условия для изображения будут следующие:
T'L@,s) + H[-£—TL@,s)] = 0,
T'l(oo,s) = 0,
Тс .
E)
F)
G)
так как
L[T@,t)] = Tl@,s), L[Tc]= s ,
в условии F) Н = -^ относительный коэффициент теплообмена.
ГРАНИЧНОЕ УСЛОВИЕ ТРЕТЬЕГО РОДА
183
Решение уравнения E) в общем виде можно написать так:
TL (х, s) —£- = Л ехр (уХх j + В± ехр (_ j/jL * ). (8)
Из условия G) протяженности следует Аг = 0; действительно, из
соотношения
0 = У-^ А1ехр(+ оо)_ l/"_i_5lexp(- во)
следует, что Лх = 0. Физически это означает, что температура на
бесконечно большом расстоянии от конца стержня не изменяется за все
время процесса теплообмена, т. е. Т -^ Т0 при л;->- оо.
Постоянную Вх находим из граничного условия F):
откуда
Si = . (ге-г.)
'A + V4
Тогда решение для изображения примет вид
TL(x,s)
Т0
WT)"'<-^'
(9)
A0)
Для нахождения оригинала воспользуемся таблицей изображений,
из которой находим
1
-k Ys
1 r-
Wi + тг/-
= erfc ^= - ехр (Ck + СЧ) erfc (^=r + С V^) .
Следовательно, решение нашей задачи можно написать так:
— erfc —т=-
2]Лгс
fl Г(х,т)-Г0 _
Гс-Го
Нх + Н*ах ( 2 , ,- \
егГс^+Я!^).
A1)
Анализ решения. £сли коэффициент теплообмена а очень велик,
то #-> оо. Тогда из граничного условия C) следует: Г@, т) = Тс =
=const, m. е. температура конца стержня сразу становится равной
температуре окружающей среды. В этом случае наша задача
аналогична задаче §2 гл. IV. Функция erfc г быстро, уменьшается с
увеличением z и при г>-2,8 практически равна нулю. Поэтому при #->оо
второй член решения A1) стремится к нулю (что можно показать,
раскрыв неопределенность по правилу Лопиталя), и решение примет вид
= erfc ^__
2Уа%
A2)
184
Глава шестая
Решение A2) тождественно решению задачи в §2 гл. IV на
охлаждение полуограниченного стержня, только под б в случае охлаждения
надо понимать 6 =
То-
т0-тс
-, где Т0>ТС.
Относительная температура конца стержня
= Г<0^-Г° = 1 _ /"" erfc Н Ум
1 С ' О
A3)
При больших значениях времени пользоваться решением A3)
затруднительно из-за резкого увеличения экспоненциальной функции.
Поэтому найдем эффективное решение для больших значений времени.
В приложении показано, что
еи* erfc и
У~к
2и*
+
4иб
Следовательно, приближенное решение, удобное для больших значений
времени, можно написать так:
1 Л Г , 3
е.
1
Н У пах
1
2H2az
+
4Я4а2 т2
A3а)
Напишем решение в критериальной форме. Число Фурье для
данной точки с координатой х обозначим через Fo^ =
а критерии
Био — через Bi^ (Bi^= Нх).
Таким образом, решение нашей задачи можно написать так:
6 = erfc
2VFox
exp[Bl,+(By2FojX
X erfc
2У¥ол
+ Bi^Fo,
A4)
Произведение Bi^]/Fo^ дает новый обобщенный аргумент, или новое
число гомохронности нестационарного температурного поля
полуограниченных тел _
N = 31,1/4^=*-^- = —УТ,
где s — коэффициент тепловой активности . тела. Число Na,z равно
отношению количества тепла, передаваемого к единице поверхности
тела в единицу времени при разнрсти температур между поверхностью
и окружающей средой в один градус, к коэффициенту тепловой активности
тела.
Для технических расчетов на рис. 6.2 приведены графики
зависимости безразмерной температуры от числа Bi^V^Fo^ для различных
1
значении числа ? .
2 VFox
Вычисление потока тепла. Плотность теплового потока через конец
стержня равна
? = -Х
аг(о,т)
дх
A5)
ГРАНИЧНОЕ УСЛОВИЕ ТРЕТЬЕГО РОДА
185
5 оо t^ h- t>. i>-a><Nuooio2co
э оо t-» id ю tj^ cyl^C4icvi.'~l,~i.ct
-Г" О* O" CD CD CD CD" CD CD~ CD CD CD CD"
[ЦП Н^Ц-lx
1 1 1 |-1Д^
р=Шф
x|/1 |~
UhI 1 |
11 ^4-H-
(Ml 1
1 1 1 1 1 1 """^-
[_|-|-LT^^^^^
^^^Bfe
ПТП п мтт
hi——1 [".'](——i——i
II
^ф^^|В|щ
B4^^s
[_| i^^^^S
^ "ttitiii^
ii i i
11111 i ill
1...J 1 1 1 1 1 L.1..LJ
.Lj I { j I1 1" .U.,~|""|","|~j IIM
l\l 1 1 1 1 \ 1 1 1 1 M 1 1
4 \ M\ \
IV гттХ pbfcj
н 1 \ 1- 1 1 1 1И 1 ГЗ^^^РР
~Г~ \\\\ yF 7 о"Шёе
ll
(:'2
Щ CD |Щ 1 1 |\J 1 1 1 Kj 1 1
H| "j" 1 |4z^]4~W
^mfff^^H
фЖ^^
^^^^^^^^^^^
^^^^^ft^3^B
^^l^^1]^^^^^^
ЕШ-1- mhn4i4f
iiii11111111111
11 iiii 111111
^i^j__j 111111111111
ft 1 Нп~4тт441 111 111! IPB
111|||1||т^[4ЗД||^
л \ I }\ 1 cJT \\\ ~i It^ii 1 H
l\l 1 1 1 \l 1 1 l 1 1^1 1 Zrl V 1 II T1 1 1 1 1
\\\ j" [ J CQ^ 1 | Q [ | Oj 1^1 |1 | 11 |
^cT^^i w[""j-^^^pt^\\\i mill i^и
^фг!^^^^^^^^^^^^^^д
\\a f гл. 1 г~т~Г\1 1~^^мНУт\T\1 1 "И
~i 1 N1 1 W 1 1 Нх^пггмД i\i' \ l\ \ 1
NL Ггч iNl Nhffi К ШттпН
^^^fr^y^^^^^^^^^ffpp
[ 1 ГР^^^^^И
ШШ^^^Д
н-н Н^Ш^\\Шп
i \М\МшШ
\Ч\\\та11
"Л Ml 1 l^^M||^^ffff^^H
Ф4-4-1 ["ffHT^Ir+TГТ ffflmj
"8 2
iPu
Ш
CM
О**
о
CD
186
Глава шестая
Если продифференцировать A1) по х и положить х = О, то получим
^± = -Н(Тс-Т0)е"^ evlcHV^. A6)
Это соотношение можно было получить иным путем.
Дифференцируем решение для изображения A0) по х и, полагая х — 0, имеем
rL@,s) = /'"''• . ,. A7)
Пользуясь таблицей изображения, из A7) получаем то же соотношение
A6). Следовательно, плотность теплового потока равна
q = a(Tc-TQ)eH2azericHV^ .
A8)
Из соотношения A8) следует, что скорость потока тепла в первые
моменты максимальна, а затем постепенно уменьшается, стремясь к
нулю при t~> оо. В начальный момент плотность теплового потока
максимальна и равна
^шах^ а (■* с.— Tq) ,
что непосредственно следует из граничного условия.
Расход тепла на нагревание стержня за данный промежуток тх
времени можно найти, если проинтегрировать выражение A8) по т от 0 до
\ и умножить на площадь поверхности конца стержня.
§ 2. ПОЛУОГРАНИЧЕННЫЙ СТЕРЖЕНЬ БЕЗ ТЕПЛОВОЙ ИЗОЛЯЦИИ
БОКОВОЙ ПОВЕРХНОСТИ
Постановка задачи. Рассмотрим такую же задачу, но при
отсутствии тепловой изоляции боковой поверхности, т. е. между боковой
поверхностью стержня и окружающей средой происходит теплообмен
по закону Ньютона. Температура среды, окружающая боковую
поверхность стержня, принимается постоянной и равной начальной
температуре его.
Если высота и ширина стержня малы по сравнению с длиной, а
коэффициент теплопроводности значителен, то можно считать, что
перепад температуры по высоте и ширине стержня равен нулю, т. е.
__ = __ == 0. Таким образом, поставленная задача сводится к
одномерной задаче, когда перепад температуры происходит только в одном
направлении (рис. 6.3). Теплоотдачу с боковой поверхности стержня в
окружающую среду необходимо учесть в самом дифференциальном
уравнении в качестве отрицательного источника тепла.
Таким образом, дифференциальное уравнение теплопроводности
можно написать так:
сг
«^=Х-*Г^_Ю (,>0;0<*<оо), A)
дт дх2
где w — количество тепла, отдаваемого единицей объема стержня в
единицу времени в окружающую среду.
Если обозначим площадь сечения стержня через S, периметр
сечения через Р, а длину достаточно малого участка стержня через /, то
ГРАНИЧНОЕ УСЛОВИЕ ТРЕТЬЕГО РОДА
187
можно написать
w = -?fl[T(x,>z)-T0].Pl =
= а[Т(х9х)-Т0]±,
где а — коэффициент теплообмена
в вт/м2 • град, А = — — отношение
площади сечения стержня к-
периметру сечения (для
цилиндрического стержня h =~y R, для стержня
квадратного сечения h =■ — а, где
а — сторона квадрата и т. д.) в м.
Таким образом, имеем
дифференциальное уравнение вида
Рис. 6.3. Распределение
температуры в
полуограниченном стержне без тепловой
изоляции боковой
поверхности
1 ГТ
dT(x,z)
д*Т{х, т)
дх*
-^№.,)-rj.
B)
Упростим задачу, положив Н = -^- = оо для конца стержня. Это
означает, что температура конца стержня сразу становится постоянной и
равной температуре Тс, Тогда начальные и граничные условия можно
написать так:
C)
D)
E)
Т(х, 0) = Т0,
Ц0, х) = Гс,
гр/ ч гр ЭТ@0 , Т)
0.
Решение задачи при конечном значении Н для ограниченного
стержня будет дано в § 4.
Решение задачи. Дифференциальное уравнение для изображения
Tl(x, s) имеет вид
T2(*,S)-^rL(x,S)+^-
Xh
TL (x, s)
аТл
Xhs
= 0.
Граничные условия для изображения напишем так:
S '
TL(Q,s) =
T'L(oo, S) = 0.
Уравнение F) можно переписать в виде
а ^ Xh
TL (х, S) ■
-]-"•
TL(x, s) — |
Решение уравнения (9) при условии (8) будет иметь вид
Т,(х.8)-Ь-=В1ехр(-|/Х^г).
F)
G)
(8)
(9)
188
Глава шестая
Постоянную Вх определяем из граничного условия G)
в тс-т0
1 s
Следовательно, решение для изображения имеет вид
TL(x,s)-
т0
Тс-Т<,
ехр
[-V-r+i*
A1)
Для перехода от изображения TL{x,s) к оригиналу Т(х,х)
воспользуемся таблицей изображений. Известно, что
Zr1
WI+ъ ] = JL[ e~kYb erfc (-ф=,- VK) +
+ е kYb erfc (-1=, + у^
Следовательно, решение нашей задачи будет
A2)
Анализ решения. Если теплоотдача с боковой поверхности стержня
отсутствует, т. е. jj- = 05 то из решения A2) получаем решение A2) §1,
а именно
6=erfc-^. A3)
Это — решение для полуограниченного тела, когда температура
ограничивающей поверхности постоянна и равна Тс.
Введем число Фурье и критерий Био в следующей форме:
т^ az . ah
Тогда наше решение можно переписать так:
Г(*.-0-Г. _ ± . ехр
Т, — Т0 ~ 21 6ХР
■VBi-
•erfc
h
\2]AFo
VFo*
+
+ ехр (l/Bi-f) erfc l-^ + l/Fo*
2j/"Fo
A4)
здесь введено обозначение Fo* = BiFo. Произведение критерия Био на
число Фурье дает нам новое число, которое характеризует теплообмен
тела с окружающей средой при малом перепаде температуры внутри
ГРАНИЧНОЕ УСЛОВИЕ ТРЕТЬЕГО РОДА
189
тела (так называемая внешняя задача [см. § 3]), названное числом го-
мохронности.
В нашем случае перепад температуры по высоте и ширине стержня
отсутствует, несмотря на теплообмен его с окружающей средой, так что
число Fo* равно
Fo* = Bi Fo = ^r.
A5)
Таким образом, первый член в аргументе функции erfc
характеризует теплообмен чистой теплопроводностью в направлении х, а второй
член — теплообмен боковой поверхности стержня с окружающей средой
при отсутствии температурного градиента в двух других направлениях.
В стационарном состоянии (т = оо) будем иметь некоторое
распределение температуры по длине стержня. Когда т~>оо, первая функция
erfc zx ш= 1—evtzx будет стремиться к 2, так как erf zx-+—1, а вторая
функция erfz2 ~>0. Следовательно, распределение температуры в
стационарном состоянии будет описываться простой экспоненциальной
функцией
6а> = ехр {- yjL. *) = ехр (- У'вГ-f-). A6)
Если время мало, точнее Fo -> 0, то величиной Fo* можно
пренебречь по сравнению с первым членом аргумента функции erfc. Кроме
того, при малых значениях времени тепло распространится на
незначительное расстояние, следовательно, и x/h тоже мало. В этом случае обе
экспоненциальные функции близки к единице. Тогда решение A4)
будет близко к решению A3), т. е. в первые моменты времени
нагревание стержня происходит так, как будто теплоотдача с боковой
поверхности отсутствует.
^Определение плотности теплового потока. Плотность теплового потока
ъ.вт1м2 (ккал/м2ч) находим по значению температурного градиента у конца
стержня. Расчет будем производить операционным методом.
Из решения A1) для изображения находим
T'L@, s)
-v[
+
Mi
A7)
Переход к оригиналу Т7@, т) производим по таблицам изображений, а
именно
1
V~
е-ь, + у berf У'Ъъ.
Тогда будем иметь
-Т'@,-с) =
Следовательно, плотность потока равна
Т/Г
X
ox h
-i=exp (—Fo*) + KBTerf/Fo*
У tcFo
,
A8)
190
Глава шестая
В состоянии, близком к стационарному (Fo->oo), первый член в
квадратных скобках соотношения A8) стремится к нулю, а второй —к 1/вГ,
так что плотность потока тепла будет равна
^Mzwyyen A9)
Таким образом, удельный поток тепла прямо пропорционален
потоку тепла через стержень длиной Л, когда температуры
ограничивающих плоскостей его соответственно равны Тс и Т0. Чем больше
критерий Bi, тем больше коэффициент пропорциональности, а следовательно,
и расход тепла.
Для иллюстрации сделаем небольшой расчет. Длинный стальной вал диаметром
140 мм нагревается с одного конца в печи с температурой 1073°К(800°С). Температура
вала до нагрева равна температуре окружающей среды Т0 = 293°К B0°С). Найти
температуру на расстоянии 17,5 см от конца стержня через 15 мин нагревания.
Коэффициент теплообмена принимаем равным а — 163 вт'1м%-град. Коэффициенты теплопе-
реноса стали равны А = 46,5 вт[м*-град, а=1,25-10~5 м21сек.
Вначале вычислим необходимые для расчета критерии:
характерный размер
/i = JL#=3,5 сж = 0,035 м;
2
число Фурье
критерий Био
Fo — az = 1,25-Ю» 15-60 _ g 2.
/i2 12,25-10-4 ' '
в ah __ 163-0,035 __п 19р;
X 46,5
модифицированное число Фурье
Fo* = BiFo = 0,125-9,2= 1,15;
относительная координата
JL - 17>5 =5
h 3,5
Определим относительную избыточную температуру по решению A4):
8 = J.
2
Тогда получим
^[ехр(-/0,125.?) erfc (-—=-- Vhl5~) +
+ ехр (/07Т25:5) erfc(^~=2 + VTJ5~ jj =
= ~y @> 170-1,2744>:0,043)> 0,130.
T — T0 = d(Tc —IT0) = 0,130^780 = 101,
T = 101 + 293 = 394°K A21°C).
Итак, температура вала равна 394°КA21°С).
Если пренебречь теплоотдачей е боковой поверхности, то температуру вала для
х
координаты ^-г- = 5 найдем по формуле
х
б = erfc £_ = erfc !>__ = 1 —0,756 = 0,244,
2]/"Fo 2)^9,2
откуда температура вала равна
Т = 293°К + 0,244-780°К = 483°К B10°С).
Таким образом, пренебрегая теплоотдачей, мы получили завышенную температуру
примерно на 90°С.
ГРАНИЧНОЕ УСЛОВИЕ ТРЕТЬЕГО РОДА
191
§ 3. НЕОГРАНИЧЕННАЯ ПЛАСТИНА
Постановка задачи. Дана
неограниченная пластина,
толщина которой равна 2R.
Начальное распределение температуры
задается некоторой функцией
Т(х, 0) = f(x). В начальный
момент времени пластина
помещается в среду с постоянной
температурой Тс > Т(х, 0). Между
ограничивающими
поверхностями пластины и окружающей
средой происходит теплообмен по
закону Ньютона. Требуется
найти распределение температуры
по толщине пластины, а также
удельный тепловой поток.
Имеем
Рис. 6.4. Распределение температуры в
неограниченной пластине (симметричная
задача)
ldT(x,z)
д%
аЩ±± (х>0;
R<x< + R),
дх*
Т(х, 0) = /(*),
-Xar(g;T) +а[Гс-Г(Д,т)]=:0,
+ Xar(-f'T) + а [Т- T(-R, т)] = 0.
A)
B)
C)
D)
Начало координат выбираем в середине пластины (рис. 6. 4).
Решение задачи будем производить двумя методами. При наличии
неравномерного распределения температуры лучше воспользоваться
классическим методом Фурье.
Для упрощения расчетов предположим, что функция f(x) является
четной функцией относительно х, тогда задача становится
симметричной, так как теплообмен между поверхностями и окружающей средой
происходит со всех сторон одинаково. В этом случае вместо условия
D) можно написать
Решение задачи методом разделения переменных. Сведем задачу на
нагревание к задаче на охлаждение путем замены переменной Гс —
— Т(х, т) = Цх, т). Тогда дифференциальное уравнение для %(х, т) будет
тождественно дифференциальному уравнению A).
Частное решение уравнения A) при условии D') имеет вид (см. §2
гл. III):
d(x,z)=.Dcoskxe-k*a\ E)
Удовлетворим решение E) граничному условию C), которое для
новой переменной примет вид
<ЭД(#,т)
дх
+ Hb(R, ч) == 0,
F)
192
Глава шестая
тогда
— k D sin kRe~kZax +
+ HD cos kRe-k*ax = 0.
G)
Можно сократить на De~~k*ax, так как
0<т< оо, тогда получим
тригонометрическое уравнение для определения
постоянной к.
Величина HR =
kR
Bi
(8)
Рис. 6.5. Графический способ
определения корней характеристического
уравнения
-^- /? = Bi есть
критерий Био.
Обозначим kR через \ъ. Из
анализа уравнения (8) видно, что jx имеет
бесчисленное множество значений.
Наиболее просто можно определить
корни уравнения (8) графическим путем.
Если левую часть уравнения ctg |x
обозначить через уг(ух = ctgp), а правую часть — через г/2(#2 =
—-gr-^), to пересечения котангенсоиды уг с прямой у% (рис. 6. 5) дают
нам значения корней \ь характеристического уравнения. Из рис. 6. 5
видно, что имеется бесчисленное множество корней jx, причем каждое
последующее решение больше предыдущего:
Pi < ^2 < 1*з < • • • < Н*я < • • •
Чем больше п, тем ближе \ьп к числу (п—1)тг.
Тангенс угла наклона прямой уг равен -gp Поэтому при Bi-> оо
тангенс наклона будет равен нулю, и прямая совпадает с осью абсцисс.
Тогда ]хп = Bп— 1) ■— , т. е. получаем характеристические числа для
задачи охлаждения с постоянной температурой на ограничивающих
поверхностях (см. §3 гл. IV).
Если критерий Био стремится к нулю, то тангенс угла наклона
прямой уг стремится к бесконечности, что означает, что прямая у2
совпадает с осью ординат. Тогда корни уравнения равны |хл = (п—1)тг, где
п = 19 2,..., т. е. ^ = 0, ^2 = in и т. д.
Таким образом, характеристическое уравнение (8) можно написать
так:
ctg ц = рт Iх-
(9)
Первые шесть корней р,я приведены в табл. 6.1 для разных
значений критерия Bi (от 0 до оо). Значения рп даны с точностью до
четырех знаков после запятой. В большинстве случаев приходится
пользоваться только одним, редко двумя корнями \ьп, так как для малых
значений Fo решение дается в другой форме.
Таким образом, общее решение будет равно сумме всех частных
решений:
оо
Цх, i) = S Dn cosiyj- exp (—\ft |JH .
A0)
ГРАНИЧНОЕ УСЛОВИЕ ТРЕТЬЕГО РОДА 193
Таблица 6.1
Корни характеристического уравнения ctg^=^j-(x.
Bi
0
0,001
0,002
0,004
0,006
0,008
0,01
0,02
0,04
0,06
0,08
0,1
0,2 I
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,5
2,0
3,0
4,0
5,0
6,0
7,0
8,0
9,0
10,0
15,0
20,0
30,0
40,0
50,0
60,0
80,0
100,0
оо
1*1
0,0000
0,0316
0,0447
0,0632
0,0774
0,0893
0,0998
0,1410
0,1987
0,2425
0,2791
0,3111 1
0,4328 !
0,5218
0,5932
0,6533
0,7051
0,7506
0,7910
0,8274
0,8603
0,9882
i 1,0769
1,1925
1,2646
1,3138
1,3496
1,3766
1,3978
1,4149
1,4289
1,4729
1,4961
1,5202
1,5325
1,5400
1,5451
1,5514
1,5552
1,5708
1*2
3,1416
3,1419
3,1422
3,1429
3,1435
3,1441
3,1448
3,1479
3,1543
3,1606
3,1668
3,1731
3,2039 !
3,2341
3,2636
3,2923
3,3204
3,3477
3,3744
3,4003
3,4256
3,5422
3,6436
3,8088
1 3,9352
4,0336
4,1116
4,1746
4,2264
4,2694
4,3058
4,4255
4,4915
4,5615
4,5979
4,6202
4,6353
4,6543
4,6658
4,7124
1*3
6,2832
6,2833
6,2835
6,2838
6,2841
6,2845
6,2848
6,2864
6,2895
6,2927
6,2959
6,2991
6,3148 1
6,3305 l
6,3461
6,3616
6,3770
6,3923
6,4074
6,4224
. 6,4373
6,5097
6,5783
6,7040
| 6,8140
6,9096
6,9924
7,0640
7,1263
7,1806
7,2281
7,3959
7,4954
7,6057
7,6647
7,7012
7,7259
7,7573
7,7764
7,8540
1*4
9,4248
9,4249
9,4250
9,4252
9,4254
9,4256
9,4258
9,4269
9,4290
9,4311
9,4333
9,4354
9,4459 1
9,4565 '
9,4670
9,4775
9,4879
9,4983
9,5087
9,5190
9,5293
9,5801
9,6296
9,7240
1 9,8119
9,8928
9,9667
10,0339
10,0949
10,1502
10,2003
10,3898
10,5117
10,6543
10,7334
10,7832
10,8172
10,8606
10,8871
10,9956
1*5
12,5664
12,5665
12,5665
12,5667
12,5668
12,5670
12,5672
12,5680
12,5696
12,5711
12,5727
12,5743
12,5823
12,5902
12,5981 1
12,6060
12,6139
12,6218
12,6296
12,6375
12,6453
12,6841
; 12,7223
12,7966
12,8678
12,9352
12,9988
13,0584
13,1141
13,1660
13,2142
13,4078
13,5420
13,7085
13,8048 .
13,8666
13,9094
13,9644
13,9981
14,1372
p-e
15,7080
15,7080
15,7081
15,7082
15,7083
15,7085
15,7086
15,7092
15,7105
15,7118
15,7131
15,7143
15,7207
15,7270
15,7334
15,7397
15,7460
15,7524
15,7587
15,7650
15,7713
15,8026
1 15,8336
15,8945
15,9536
16,0107
16,0654
16,1177
16,1675
16,2147
16,2594
16,4474
16,5864
16,7691
16,8794
16,9519
17,0026
17,0686
17,1093
17,2788
Постоянные Dn определим из начального условия B), которое для
переменной & можно написать так:
Цх90) = Тс-Т(х,0) = Тс-Кх) = Мх), A1)
откуда :
/1(x) = SD„ cos^ -|-.
Если функция fx{x) удовлетворяет условиям Дирихле, то ее можно раз*
ложить в ряд Фурье. Умножим обе части равенства на cosja ~ dx и
возьмем интеграл в пределах от —R до +/?:
-fR оо +R ^
§Шсо$рт~Aх = ^оп J cos ^-J-cos iv ^d*. A2)
—R tt=l -R
7 Заказ № 640
194
Глава шестая
В § 3 гл. IV было показано [формула A0)], что интегралы в правой
части соотношения A2) равны
2R[\ims'm $LmCQs pn — p^cos vamsin pn] ,« ~\
гдеЛ/? = 1!..
Так как \ьт и рп — корни характеристического уравнения (9), то
можно написать
gj -^ И-yi $in Рп -Qi^PmSinPm
COS \Ьп COS \Lm
Отсюда находим
Pm S'inV*m C0SPn = Bi COS рп COS |Xm,
[хл sin ця cos pm == Bi cos ^ cos jim.
Следовательно, выражение в квадратных скобках в равенстве A3)
равно нулю при тфп. Поэтому интеграл A3) равен нулю, если тфп. Для
случая m = п интеграл A3) равен
+R
\0S2^ *dx^R(l+^)==R(l+ Sin tM COS ft,
= lT"(l*n + sin(«./,cost*ll) A4)
[см. формулу A1) § 3 гл. IV].
Следовательно, все интегралы в правой части равенства A2) равны
нулю, за исключением одного, когда т = п. Последний интеграл
определяется формулой A4). Таким образом, постоянные коэффициенты Dn
равны
J ft(x)cos [1л -—- dx +R
Dn =~~R_rr> = ;—~ • -б- \ /i(*)cos V*n "ft dx.
n . +* Р-я + sin р.я cos ^Л # J R
J cos2|x„-|-dx -R
Общее решение нашей задачи можно написать в виде
цх,х) = Тс — Т(х, т)=-
R -t*2£I
f%
rt=l О
A5)
Решение A5) есть одновременно решение задачи на нагревание
неограниченной пластины толщиной I ~ R, когда одна поверхность ее
(х = 0) имеет тепловую изоляцию, а противоположная (х = /)
нагревается благодаря теплообмену с окружающей средой.
Если функция fx(x) есть функция нечетная относительно х, то
вместо частного решения E) пришлось бы взять частное решение
Цх, т) = С sin kxe~k*a\
ГРАНИЧНОЕ УСЛОВИЕ ТРЕТЬЕГО РОДА
195
Тогда аналогичные расчеты привели бы к следующему решению:
тс-т(х, т>= 2
со fim sin [xm
R
m=\
\ьт—sm[xmcos jxm
- X
X
#
Г f±(x) Sin JAm -J- e-^mFo d.x„
A5a)
где fx„
корни характеристического уравнения
Решение A5а) является одновременно решением задачи нагревания
неограниченной пластины толщиной I = R, когда одна поверхность ее
(х = 0) поддерживается при постоянной температуре Тс == const, а
противоположная поверхность (х = /) нагревается по закону Ньютона
(функция fx(x) является любой функцией, удовлетворяющей условиям
Дирихле). В общем случае, когда обе поверхности нагреваются, решение
задачи можно написать так:
цх, -о = 2
a ms и —-г- + Bi sin ,u„ —
Л=1
2Bi + ^ + Bi2
■f /1(je)[(*«cosjt„-j- +
Bi sin |xn —
dx I. exp ( — [4~
A6)
где l = 2R — толщина пластины, ^.й — корни характеристического урав*
нения
х p.2—Bi2
ьг 2kaBl
A7)
Начало координат находится на одной из поверхностей пластины
@<л:</).
При равномерном начальном распределении температуры имеем
Т(х, 0) = f(x) == Т0 = const;
/х (л:) = Тс -^ /(*) = ТС — Т0 = const.
Тогда интеграл в решении A5) будет равен
R
(Тс — ^о) -д- Г c°s {*„ 7Г d* = — <Тс — 7\>) sin цп,
а решение примет вид
Tc~-T(x,z) _
Тс-То
S2 sin [Ln x f 2 ах
^ + sm^cos<% C0S ^ "^ eXP _^
n=l
Напишем это решение в обобщенных переменных
= Г(*'1~Г° = 1 - £ 4 cos ця -£- exp (-i4Fo),
Л=Л
A8)
A9)
7*
196
Глава шестая
где
А„ =
2sin^
\><п + sin \хп cos ц.л
B0)
Решение задачи операционным методом. Решение
дифференциального уравнения A) для изображения TL(x, s) можно написать так (см.
§ 3 гл. III): _ _
TL(x1s)~^f = Ach TAi_x + Sshl/^x. B1)
Граничные условия для изображения будут иметь вид
-T'dR, s) + H^f- TdLR, *)] = 0,
Tl@, s) = 0.
B2)
B3)
Из условия симметрии B3) следует, что В = 0 (распределение
температуры симметрично относительно оси ординат).
Подставим решение B1) в граничное условие B2):
s s
-AV~rshVirR-
НА ch уJ_ R = 0;
отсюда определяем постоянную А:
А
Тс ~Т0
Таким образом, решение для изображения будет
(rc-7\,)ch ]/-£-*
TL(x,s)-
,[*у±*+±у±.*у±*]
B4)
= Ш ■ B5)
Решение B5) есть отношение двух обобщенных полиномов:
выражение ch у J-R— полином относительно s, выражение у JLsh уJLR—
тоже полином, а именно
VT*VT*-V±{Yt:R+MV±tf+--:)-
Таким образом, решение B5) удовлетворяет условиям теоремы
разложения, так как полином ty(s) не содержит постоянной.
: Найдем корни функции ty(s), для чего приравняем ее нулю:
m = s[cbyT* + ^yjLsbyiLR] =
= s[cosiyTR + ±y^±smiy^R]=0; B6)
здесь использовано соотношение ch z = cos iz, sh z = -j- sin i z„
ГРАНИЧНОЕ УСЛОВИЕ ТРЕТЬЕГО РОДА
197
Отсюда получаем: 1) s = О (нулевой корень), 2) бесчисленное
множество корней sn, определяемых из уравнения
cos ц + -г^щ sin ix = О,
где 1l/"-±J? = р.; так как i2 = — 1, то получим
ctgi* = -gr-ii.
B7)
Это характеристическое уравнение тождественно уравнению (9); анализ
его был сделан выше.
Найдем i|/(s) и подставим в него вместо s соответствующее значение
корня sn ~
аУ2п
W>-[*VirR + -rV-T*V-T*]
+
при s = sn выражение в квадратных скобках равно нулю на основании
равенства B6). Следовательно,
lim Y(s)= — -j- tvin [Ln —— V*n sin iln —g" ^ ~HR cos ^ ^
s-»sn
= — 4~ ten sin ^ + sin Рл ct§ И-я + fti cos (хл ctg [д,я) =
^ —T ' ^TT" (^ sin2ft, + sin [хя cos |*я + y.n cos2 р,я) -
Sin [Хл
Кроме того, имеем
2 sin ixn
f@) = l, Ф@) = Тс-Г0,
Ф(«л) = (Гс — ^o) COS |1Л -J- .
Окончательно получим
Г(х, т)-~Г0
Гс-Го
1_Y-
1 ^j
2 sin u,„ x / 2 at \
;—r-J-i? cos[x„ -yr- exp — №n-5*\
pn + 81П {l„ COS jjl„ Г/2 /? F l Г Д #2 I
/1=1
B8)
Решение B8) тождественно решению A8).
Анализ решения. Перепишем решение B8) в безразмерных
величинах:
где
Т(х,ч)-Т0
Тс - То
= 1 ~ S An cos (x^ exp(—ji^Fo),
я=1
B9)
-1)'
1+1
2sin^
+ sin \Ln cos [Ад
2Bi]/ Bi2 +
MBi2-pBi +
=
"*'
tf '"
C0)
198
так как sin^ и cos^ можно заменить через |хл и Bi из
характеристического уравнения.
Из решения B9) видно, что относительная избыточная температура
6 есть функция числа Fo, относительной координаты ~ и критерия Bi,
так как начальные тепловые амплитуды Ап являются однозначными
функциями критерия Bi [см. формулу C0)]:
= W-J-. Bi> F°
Численные значения первых шести амплитуд Ап приведены в табл. 6. 2
с точностью до четырех знаков после запятой.
Bi
0
0,001
0,002
0,004
0,006
0,008
0,01
0,02
0,04
0,06
0,08
0,10
0,20
0,30
0,40
0,50
0,60
0,70
0,80
0,90
1,00
1,5
2,0
3,0
4,0
5,0
6,0
7,0
8,0
9,0
10,0
15,0
20,0
30,0
40,0
50,0
60,0
80,0
100,0
оо
2Bil/"
Значения постоянных А» = (—l)n+1——^—-
At
1,0000
1,0002
1,0004
1,0008
1,0012
1,0015
1,0020
1,0030
1,0065
1,0099
1,0130
1,0159
1,0312
1,0450
1,0581
1,0701
1 1,0813
1,0918
1,1016
1,1107
1,1192
1,1537
1,1784
1,2102 |
1,2287
1,2403
1,2478 1
1,2532 1
1,2569
1,2598
1,2612
1,2677
1,2699
1,2717
1,2723
1,2727
1,2728
1,2730
1,2731
1,2732
Л2
—0,0000
—0,0002
—0,0004
—0,0008
—0,0012
—0,0016
—0,0020
—0,0040
—0,0080
—0,0119
—0,0158
—0,0197
—0,0381
—0,0555
—0,0719
—0,0873
—0,1025
—0,1154
—0,1282
—0,1403
—0,1517
—0,2013
—0,2367
—0,2881
—0,3215
—0,3442
—0,3604
—0,3722
—0,3812
—0,3880
—0,3934
—0,4084
—0,4147
—0,4198
—0,4217
—0,4227
—0,4232
" —0,4237
—0,4239
—0,4244
Л3 -
0,0000
0,0000
0,0001
0,0002
0,0003
0,0004
0,0005
0,0010
0,0020
0,0030
0,0040
0,0050
0,0100
0,0148
0,0196
0,0243
1 0,0289
0,0335
0,0379
0,0423
0,0466
0,0667
0,0848
0,1154 |
0,1396
0,1588
0,1740
0,1861
0,1959
0,2039
0,2104
0,2320
0,2394
0,2472
0,2502
0,2517
0,2526
0,2535
0,2539
0,2546
Таблица 6, 2.
"ша+^
MBi2 + Bi + ^)
А*
—0,0000
—0,0000
—0,0000
—0.0001
—0,0001
—0,0002
—0,0002
—0,0004
—0,0009
—0,0013
—0,0018
—0,0022
—0,0045
—0,0067
1 —0,0089
—0,0110
—0,0132
—0,0153
—0,0175
—0,0196
—0,0217
—0,0318
—0,0414
—0,0589
—0,0750
—0,0876 ;
—0,0991
—0,1089
—0,1174
—0,1246
—0,1309
—0,1514
—0,1621
—0,1718
—0,1759
—0,1779
—0,1791
—0,1803
—0,1808
—0,1819
Аь
0,0000
0,0000
0,0000
0,0001
0,0001
0,0001
0,0001
0,0003
0,0005
0,0007
0,0010
0,0013
0,0025
0,0038
0,0050
0,0063
i 0,0075
0,0087
0,0100
0,0112
0,0124
0,0184
0,0241
0,0351
0,0451
0,0543
0,0626 1
0,0701
0,0768
0,0828
0,0881
0,1072
0,1182
0,1291
0,1340
0,1365
0,1379
0,1394
0,1405
0,1415
Ав
—0,0000
—0,0000
—0,0000
—0,0000
—0,0000
—0,0001
—0,0001
—0,0002
—0,0003
—0,0004
—0,0006'
—0,0008
—0,0016
—0,0024
1 —0,0032
—0,0040
—0,0048
—0,0056
—0,0064
—0,0072
—0,0080
—0,0119
—0,0157
—0,0231
—0,0300
—0,0366
—0,0427
—0,0483
—0,0535
—0,0583
—0,0676
—0,0795
—0,0901
—0,1015
—0,1069
—0,1098
—0,1115
—0,1132
—0,1141
—0,1157
Ш-Ц
(pEpf
[IJlJo
1 ii l
1 l\
111 И И
Гс
o=
" " г
—)—[
У
< II
H
и
рф:
^\-j-
i
1
1
jl
=
:ci
1
>=
1
1
У
1
1
1
1
1
1
:СГ
5
Ч^
С
1111|[|||НШШ1!ВШ1111Ш.и.61111
гл
н
/
/JJ
о~5
Щ
щ
Ш
=
щ
ш
щ
ш
щ
шш
-ftJ4"
звииии
НИИВрИ
Щл §^|1|||
^й^^^И
^^^^^Я
^Н^^^И
лм i VNtm
Д^Р^^^
1 I'M 1 \ 1 \111
J 1 1\1 LALJill
о о
О {и
о
ю
рэ^:
«.—1
к
тер
300)
S ,_,
сх
« V
«В
я V
а
си
9S
о
к
8
60
о"
со
о
о"
о"
о
о"
*2
53
К
О,
200
Глава шестая
S О
о) V
S ш
СО v
ей
О
о
*3
ее
СО
6
а
ГРАНИЧНОЕ УСЛОВИЕ ТРЕТЬЕГО РОДА
201
р
в
1
1
i
1
=
]
_
1
1
1
i
и.
=
—
ц
I
1
=i
1
■
~~~
1
g
= С
1. Fo<lllllllllllllllllllllllllllllllllllll
0
|
V-
DQ
1
- (
1°
=
Ё
• -
: x:
;
с
I
|
/
Г
1
1
^r^:
1 *
.
■ ь~ 1
:° i
О _r~i
1
1
1
ж
1
=
I
^
1
SCO ]
:0 j
i
=
j
1
= c
1
с
1
=c
■
g
1
1
|
1
LZ
1
~
I
■ll
e!
^
E
к
r
1
|
1
*CN =
1
—
i
1
i
1
i
i
1
j
ш
I
I
1
=
i
■Щ
1
Z L
i
I
|
I
_^ :
=
1
P
1
H
1
Ё
1
1
1
1
щ
t
—
1
j
|
3
J
._
1
1
!
..„■
si
I
EPPpH
^^^Д
^^prizd
^f^^fl
шдд
\ 1 I r 1
Tilrrti
ill 1
V \ I
\ i 1
\ l i
\ I I
i \ \\\
V A 1
XJllJhi
м|1|щШ
Щ1|§11
Mini
:9!S5ESS!S
MMIlE
tlllllEE
MtlUH
шшл\
Щ "wtiili
Win ill II
Mil №111II
Я1Ш111111
■Ulllllllll
Ш1ШШН11
:^ЭД
1" 1" I III 1
о
g V
(=3 V
fcCCQ
О Pt
о а>
а о*
га
-о
C£?V
Яо
схо
ей О
Ф
Е
Ж
З4
о
н
9»
о
к
о
S
и:
а
ей
О*
и.
CN
О
00
С£5
Я
202
—• о
и.
ю
о
о
Ю
о
о
,01
о
ю
о
о .
о
£5"
«w.*
я
Ло
S<2
та
xQQ
та _^
s^
■r-t
яф
e-
{=CsS
»
« ж
sS o>
к sr
к та
c-r к
У со
та
*S X
и к
~ 3
к л
М ^
Я о
й*>
XJ х
си
О) ,-*-»
B3 -ч
gv
е ■
О
та ги
V
с
со «—*
S
>>о
Н "*-~*
та
пер
s
О)
н
»к
о
о
и
О,
К
О
к
СО
pip
ЩШ
И
1
в
Г~[
=
ч
-с
ё!
"S
=>
1
х!
= С
N.
j
=<
1
1
D
-t
|
o_
|
1
Ё1
1
|
1
\£
Ш
I
il
|
I
i
|
i
i
1
Э
i
.._
1
i
.^
и
|
"
i
E
=
0,2
._.
1
|
о
I
s
I
|
=£
|
^
|
s
a=
1
E
|
I
I
I
1
1
I
^
I
I
1
p=
=d
1
Щ
1
1
1
H
1
1
1
О Э г-,
О [jl -^
О ^
V
s
V
к
BS
a
л
о
о
«
ВС
К
с
о
n
«
к
CO
u
о
204
Глава шестая
JIW
So
S v
ч v
о
К
о*
о
Си
ГРАНИЧНОЕ УСЛОВИЕ ТРЕТЬЕГО РОДА
205
Для практических инженерных расчетов на рис. 6.6—6. 11
приведены номограммы, взятые из работы [114], для определения
температуры на поверхности пластины 0П и в центре пластины 0Ц при
заданных значениях Fo и Bi.
Если критерий Bi стремится к бесконечности, то температура
поверхности пластины сразу становится равной температуре окружающей
среды, так как из граничного условия C) следует:
7С — T(R, -с) = lim
Bi->oo
R аг(/?,т)
Bi
дх
■]-
о,
C1)
а характеристические числа (лл будут равны
р,я==B/г—1)-|-,
т. е. \хп не будут зависеть от толщины пластины. Из формулы C0)
следует, что при Bi -> оо
V-n ~~К } Рп~~К } B/1-1)*
C2)
так как cosBn—1)-^-= 0. Тогда решение B9) примет вид
= 1- £(-!>
.л+1
п=\
Bя —1) те
COS
Bл — 1) 7i х
2R
ехр
Bп — 1Jте2
Fo
C3)
Это решение тождественно решению A6) § 3 гл. IV, только
необходимо положить бохл = 1 — 6наг.
В этом случае интенсивность нагревания -j- будет обратно
пропорциональна второй степени характерного размера пластины и прямо
пропорциональна коэффициенту температуропроводности, так как
d8
= ^2 2 Р2аАп C0S ft* x exp ("~ ^ Fo)*
Л-1
Следовательно, интенсивность нагревания пластины в данной точке
будет определяться теплоинерционными свойствами тела и зависеть
только от скорости перемещения тепла внутри пластины
(внутренняя задача).
Если критерий Био мал (Bi < 0,1), то все члены ряда ничтожно
малы по сравнению с первым, так как при рп -> (п — l)it Ап -»- о
за исключением амплитуды Av которая равна
Аг = lim
Sin [К\
'Pi
1 + COSfXj
sin iii
Pi
= 1.
Для малых значений ^ можно tg |xx заменить через pv тогда из
характеристического уравнения получим:
[a? =Bi.
206
*т
T(x,t)
Рис. 6.12. Распределение температуры в неограниченной пластине
для различных значений критерия Био:
а — внутренняя задача (Bi -*• оо), б — внешняя задача (Bi ~>0), в — краевая
задача @ < Bi < оо)
Следовательно, решение B9) примет вид
= 1 — cos V Bi-p-exp (— BiFo).
C4)
В этом случае интенсивность нагревания
А!
б COS |/ Bl -к-
-Fo*
C5)
прямо пропорциональна коэффициенту теплообмена и обратно
пропорциональна первой степени характерного размера пластины. Таким
образом, скорость нагревания определяется скоростью переноса тепла из
окружающей среды к поверхности пластины (внешняя задача).
Если же критерий Bi больше 0,1 и меньше 100 @,1 < Bi < 100),
то \in есть функция Bi, т. е. зависит от толщины пластины. В этом
случае интенсивность нагревания обратно пропорциональна п-й степени
толщины пластины A < п < 2) и определяется как скоростью
переноса тепла внутри материала, так и скоростью переноса тепла через
пограничный слой (краевая задача).
Все эти три случая изображены на рис. 6.12 в виде кривых
распределения температуры в различные моменты времени.
Из рис. 6.12 видно, что в первом случае температура на
поверхности пластины равна температуре среды, начиная с самого начала
нагревания. Температурный перепад между центральным слоем и
поверхностью пластины наибольший. Во втором случае температура
поверхности близка к температуре центрального слоя, температурный перепад
между ними'наименьший. Последний случай занимает промежуточное
значение между двумя первыми.
Если продолжить кривые распределения температуры за поверхность
пластины по направлению касательных, то они все пересекаются в
одной точке, расположенной на линии Тс = const (см. § 6 гл. I).
Таким образом, если толщину пластины увеличить на 2 у (на
~jjr с обеих сторон) и принять в этом фиктивном слое распределение
0 0,4 0,8 1,2 1,6 -^-*- 2,
Ji MM
.M 1
V, M М
II Ш
f п1 1 1 1 1 N 1 1 I I 14*тГ1 1
и'-Н 11 1 1 ITTI Г Г II II 1 II III LWnT 1 11 til
II11 I Ml 1111 1111 1 1II M II 1_*кгТ1 Mil 1 МММ! II
MiIIIMIIIIIMIIIIt LWi 1 111II II 11 II 1 1 II II1
M>f
H1 Tl ПГГГГГП^ЛМ Ш MM m
Itttlttl 111IKI1111111 IJJ444J^'tttTI 11111111 WWW
f\ el 1 1 1 1 1 1 1 1 1 1 Jr\ 1 1 1 1 1 1 1 L^rn4 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
'1111 1 Jr\ 1 L-кгн M 1 w 11 1 11 11 T Ml Г Ml
1IIIII! \m\ 11 l^ril 111IIII111II1II MM IIII1 1IIII IIII11
n a\ 1 irl 11 Jrl 1 11 ' I 1
/ Им 1
/M / M M 1
mi II Ifl 111N 1! 11II M 111 M 111II11 M 111II1111111111111
n ol 11 | /1 1 1 1 I 11 I И [ j I 1 | 1 1 1 | 1 1 1 1 I 1 J 1 1 1 1 1 I 1 I 1 | | 1 I I I I I I I I
u'^ f f
If Nil M MM M
IN/
Mr
I / 4- 1
M rrff |Щ^^
П711111111111.1 Ш114iffifflTll ТГГи-i-J-11111111 ill
4,0
8,0
12.0
16.0
H,
1,4
1,2
1,0
0,8
Bi
Рис. 6.13. Зависимость между первым корнем jxi
характеристического уравнения и критерием Bi для
неограниченной пластины
1
1
А1
1,2
1,2
1,
0 4,0 8,0
*1 1 1 1 1 II II 1 1 II 1 1 II 1 1 II 1 II
'III
it м М1II1 г
J111111111111111 |JJ44*H11'g
5 М LrTiT M"
1 1 1 II 1 II 1 \J\\ 1 1 II 1 1
1 Г М/м IT
1 1 1 1 I 1 / 1 1 1 I 1 1 II 1 1 1 1 1 II 1 1
1 11 1 1/ 1 11 11 1 1 1 M 11 II i 1 1 M
^1 1 M/M 1 1 1 1 M II 1 1 1 1 1 11 1 1 1!
||l/l11|11| . II11 i T
/
r
пГГП 111" 111111111111 ыпмТ
им \jn
1 Ьм ""'" " "
12,0 16,0 -^*-2Q,0
iii г ■ "i 'I'll
0
0,4
0,fi
1,2
1,6
Bi
-2,0
Рис. 6.14. Зависимость между коэффициентом Аг и
критерием Bi для неограниченной пластины
208
Глава шестая
температуры по закону прямой, то все кривые распределения будут
пересекаться в одной точке, и краевая задача сведется к обобщенной
внутренней задаче.
Вернемся к решению B9) нашей задачи. Благодаря неравенству
H-i < Н < • • • < Pvz
ряд B9) быстро сходится, и, начиная с определенного значения Fo1?
все члены ряда становятся исчезающе малыми по сравнению с первым
членом, так что ими можно пренебречь (ниже будет показано, что с
точностью до 0,25% при
R
0 и Bi = 1 всеми членами ряда можно
пренебречь, начиная с Fo>-0,55).
Следовательно, при Fo >- ¥ог решение B9) значительно упрощается
и имеет вид
6 = 1 - Аг cos |хх ~ е~ ^ Fo . C6)
Для удобства расчетов на рис. 6.13 и 6.14 построены графики
(xx = /(Bi) и ^!==9(Bi) для значений Bi от 0 до 20 [при Bi >0,1
значение |ах можно вычислить по формуле A9) § 10]. Для малых значений Bi
приходится брать несколько членов ряда, что приводит к известным
трудностям в расчетах.
Найдем приближенное решение нашей задачи, пригодное для малых
значений Fo. Решение B5) для изображения можно написать в иной
форме:
X
ехр
х) + ехр
m
«' (/-И+- (- /i«)+l V~ h [Vs.R)
То
»[! +
Wl
ехр
VJ*)}
ехр [- ]/"-£- (R - х)] + ехр [- ]/-^ (R + х)
X
X
1 +
н
1 +
—V—
Н У а
ехр
v±
R
C7)
Если выражение, стоящее в квадратных скобках, разложить в
геометрический ряд и ограничиться первым членом ряда, то получим
TL(x,s) — = —
• 1 +
Н V а
{«р [-/-£(*-*)] +
ГРАНИЧНОЕ УСЛОВИЕ ТРЕТЬЕГО РОДА
209
+ ехр [- Y~ (R + *>]
C8)
Переход к оригиналу производим по соотношению, примененному
в § 1:
Т (х, т) — Г0 „ R—x
к ^ erfc — exp[H(R — x) +
TC — TQ 2 ]/ ai
/ D y \ D I %
+ aH2 %] erfc ---- 4- H Va т + erfc = — ехр [Я (R + x) +
\ 2/ax / 2 У at
I R + x r \
+a#2 x] erfc —^ + HVax . C9)
\ 2 Y a% )
Если перенести начало координат из середины пластины на левую
поверхность, т. е. сделать замену переменной х + R = X и положить
2R -> оо, то решение C9) превращается в решение A1) § 1.
Перепишем решение C9) в критериальной форме
X / X
6 « erfc £- — ехр Гв1 f 1 1.) + Bi2Fol erfc I £- +
2 /Fo" L V Я У J I 2 у- p^-
+ Bi2Fo I erfc I ^ + Bi2 Fo I. D0)
2 /Fo
Решение D0) является приближенным решением, пригодным для
малых значений Fo; оно заменяет несколько членов ряда обычного
решения B9).
Для иллюстрации эффективности решения D0) при малых значениях Fo приведем
численный пример. При малых числах Фурье температура в центре тела практически
не изменяется, и поэтому наибольший интерес представляет изменение температуры
на поверхности пластины (x = R). В 1932 г. Пешль [112] вычислил температуру на
поверхности пластины в процессе охлаждения при малых значениях Fo (от 0,0003
до 0,01) для разных значений Bi (от 0,1 до 2000). Результаты вычислений приведены
в табл. 6.3.
Вычисления были произведены по решению B9), причем, как отмечает Пешль,
при Fo = 0,0003 пришлось брать 36 членов ряда. Громоздкость вычислений поистине
вызывает удивление.
Вычислим A—0П) по нашей приближенной формуле D0). Для поверхности
пластины можно взять только два первых члена решения D0), т. е.
1 _ еп = е (Ш V F° J erfc Bi /То" . D1)
Это приближенное решение D1) удобно для расчетов при малых значениях критерия
Bi Y F°; пРи больших значениях Bi/Fo пользуемся соотношением
' erfc и =
1/1 1.3
+
Y tz \ и 2а3 4 и
1/1 1 \
1 - еп = _____ _ _ + ...). D2)
У и \Bi У Fo 2 (Bi T/FoK /
210
Глава шестая
Вычислим A—6П) Для Fo = 0,0003 и Bi = 1000. Число Bi У~¥о равно
Bi l/~Fo = 1/0,0003-1000=: 17,32.
По формуле D2) имеем
1 / 1 1
0,033.
1
у~т
17,32
2 A7,32K
Таким образом, получаем значение, совпадающее с табличным, которое было
вычислено при использовании большого числа членов ряда.
Для Fo = 0„0100 и Bi = 1000 число Bi ]/To = 100; тогда
i _ еп = ——z=- « о,ооб.
100 У тс
Из табл. 6.3 находим, что при Fo = 0,0100 и Bi= 1000 число A — 6П) = 0,006, т. е.
получается полное совпадение результатов.
Возьмем малые значения критерия Био (Bi = 0,5); тогда при Fo = 0,0010 будем
Bi T/Fo = 0,5- 1/0,0010 = 0,0158.
По формуле D1) находим
1 — 6П = g0'00025 erfc (о,0158) » 0,983,
что также совпадает с табличными данными.
Из приведенных расчетов видно, что приближенное решение D1) дает вполне
удовлетворительные результаты и заменяет колоссальный труд вычисления по
классическому решению B9). В этом состоит большое преимущество операционного метода
перед обычным методом, поскольку он позволяет получать ряд приближенных решений
для разных значений Fo и Bi.
Таблица 6.3
Относительная температура на поверхности пластины
A -6П) = ф (Fo, Bi)
Bi
0,1
0,5
1
4
10
20
50
100
200
500
1000
2000
0,0003
0,999
0,996
0,980
0,927
0,833
0,705
0,468
0,287
0,157
0,066
0,033
0,017
0,0010
0,997
0,983
0,965
0,872
0,726
0,555
0,309
0,171
0,088
0,036
0,018
0,009
Число Фурье Fo
0,0025
0,995
0,975
0,947
0,809
0,615
0,441
0,211
0,111
0,057
0,023
0,011
0,006
0,0050
0,993
0,963'
0,926
0,747
0,522
0,336
0,154
0,079
0,040
0,016
0*008
0,004
0,0100
0,989
0,948
0,897
0,670
0,428
0,256
0,111
0,056
0,028
0,011
0,006
0,003
Определение удельного расхода тепла. Найдем среднюю
температуру пластины, которая необходима для определения расхода тепла на
нагревание, по формуле
R
T(x) = ~^T(x^)dx. D3)
ГРАНИЧНОЕ УСЛОВИЕ ТРЕТЬЕГО РОДА
211
Таблица 6.4
Значения постоянных Вп
2Bi2
£(Bi» + Bi + i$
Bi
оо
50,0
30,0
15,0
10,0
9,0
8,0
7,0
6,0
5,0
4,0
3,0
2,0
1,5
1,0
0,9
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
Bt
0,8106
0,8250
0,8354
0,8565
0,8743
0,8796
0,8859
0,8932
0,9021
0,9130
0,9264
0,9430
0,9635
i 0,9749
0,9862
0,9882
0,9903
0,9920
0,9939
0,9955
0,9973
0,9982
0,9995
1,0000
Вг
0,0901
0,0899
0,0893
0,0885
0,0839
0,0821
0,0797
0,0766
0,0723
! 0,0664
0,0582
! 0,0468
i 0,0313
0,0220
0,0124
0,0105
0,0088
0,0070
0,0054
0,0040
-0,0027
0,0016
0,0007
0,0002
1
в,
0,0324
0,0323
0,0315
0,0279
0,0236
0,0222
0,0205
0,0185
i 0,0162
0,0135
0,0104
0,0070
0,0037
0,0023
0,0011
0,0009
0,0007
0,0006
0,0004
0,0003
0,0002
0,0001
в4
0,0165
0,0161
0,0152
0,0120
0,0090
0,0081
0,0072
0,0062
i 0,0051
0,0040
0,0029
0,0019
0,0009
0,0005
0,0002
0,0002
0,0001
0,0001
0,0001
0,0001
вб
0,0100
0,0095
0,0086
0,0060
0,0040 ■
0,0035
0,0030
0,0025
0,0020
0,0015
0,0010
0,0006
1 0,0003
0,0002
0,0001
0,0001
B«
0,0067
0,0061
0,0053
0,0033
0,0020
0,0017
0,0015
0,0012
0,0009
0,0007
0,0005
0,0003
0,0001
0,0001
Если подставить вместо Т (х, т) соответствующее выражение по
решению B9), то после интегрирования получим
б (т) = у-/0 = 1 - 2 Впехр (- ^Fo),
п=1
D4)
где
вп = -
An sin y.n
V-n
2 Br*
р.2 (Bi« + Bi + p.»;
D5)
Коэффициенты Bn все положительные, причем с увеличением \ьп они
быстро уменьшаются. В табл. 6.4 приведены первые шесть значений
Вп (с точностью до четвертого знака после запятой) в зависимости от
критерия Bi.
При Bi ~> оо коэффициент Вп будет равен
В„
Й
ti2 B/г — IJ
Для удобства расчетов на рис. 6.15 построены графики Вг = /(Bi)
для значений критерия Био от 0 до 20.
212
Глава шестая
Рис. 6.15. Зависимость между коэффициентом В± и
критерием Bi для неограниченной пластины
Удельный расход тепла (в дж/м3) за данное время т находим по
формуле _ _
bQv=,cl[TM-T0]. D6)
Дополнительно рассмотрим задачу охлаждения пластины в среде с
температурой &с = 0, когда задано начальное распределение
температуры по закону параболы: Ъ (х, 0) = &ц — (&ц — 8-п) -^-7 где &ц,&п —
соответственно температуры в центре и на поверхности пластины.
Решение такой задачи широко применяется в теории диффузии, а
также в сушильной технике.
Решение задачи будет иметь вид
ь (х, т) = 2
V-П C0S H-AZ "^"
Р-л + sin И*л cos Н-я
-^F°
X
X
cos Ря ~£Г
d#,
D7)
где Д (x) = & (*, 0) — распределение температуры в начальный момент
времени.
Интеграл в решении D7) может быть взят в явном виде.
Воспользуемся формулой
J и2 cos udu -2м cos и + (и2 — 2) sin и.
ГРАНИЧНОЕ УСЛОВИЕ ТРЕТЬЕГО РОДА
213
Тогда имеем
R
2 С х 2 sin {хл
-£-J &ц cos рп -£- dx = — *- »ц,
о
2 Г /а а ч *2 * л 2 (V-»n)8in рп ( 2 2 \
XJ (&« - d") "F"cos ^ T dx = й tactg^+1 ~7г
Заменим — ctg \ьп через Bi согласно характеристическому уравнению;
тогда после необходимых преобразований решение примет вид
со
О (х, х) = £ [»„ - 2 (»ц - &п) (-1- - -L)l Л„ cos ft, 4" X
/1=1 ^я
X ехр (—. [4 Fo ), D8)
где Ап — постоянные ' коэффициенты, определяемые из
соотношения C0).
В заключение данного параграфа приведем конкретный расчет. Требуется
определить температуру в середине и на поверхности резиновой пластинки толщиной в 6 мм
после нагревания в течение 2 мин в термостате, температура которого равна
423°К A50°С). Начальная температура пластинки 293°К B0°G).
Теплофизические коэффициенты резины принимаем равными Х= 0,245 вт/м-град,
с=1,51-103 дж/кг-град, ^ = 1100 кг/м3, а= 14,7-10"8 м2/сек. Коэффициент
теплообмена принимаем равным а = 33,0 дж/м2-град.
Найдем предварительно расчетные величины. Число Фурье равно
ат 14,7.10-8.2-60
Fo = = — = 1,96,
Я3 9-Ю-6
так как R = 3 мм~ 0,003 м* Критерий Био равен
aR 33,0
Bi = -^ в 0>245 '0.003 = 0,4.
Так как Fo = 1,96, т. е. число Fo больше единицы, то можно ограничиться одним
первым членом ряда решения B9), т. е.
Т (х, -с) — Т0 , х г 9 \
б = т — Т = 1 — -4i cos ^ -п~ ехр ^— \*гх FoJ.
Тогда из табл. 6.1 и 6.2 находим:
8jlx = 0,5932 « 0,593, Аг = 1,0581.
Таким образом, имеем
6П = 1 — 1,058-cos 0,593 е-°'35161'96==: j _ 0,440 = 0,560.
Проверяем полученное значение по номограмме рис. 6.6. Для Fo = 1,96 и Bi=0,4
по номограмме находим 0П = 0,56.
Относительная избыточная температура в середине пластины равна
6Ц=: 1 -1,058 е-0-3516-1'96^ 1 _ о,529 = 0,471.
По номограмме рис. 6.10 находим для Fo=l,96, Bi = 0,4, 0Ц ж 0,47
Таким образом, имеем
Тп = 293 + 130 6П = 293 + 130-0,56 = 365,8 °К (92,8 °С);
Гц = 293 + 130 6ц = 293 + 61,2 = 354,2 °К (81,2 °С) .
214
Глава шестая
Найдем удельный расход тепла. Для этого определим среднюю температуру
пластины Г(т), Имеем
Г(т)
-Ъ^Х-Вге-**0:
1
0,997-е 0>689== 1—0,498 = 0,502 « 0,5.
- Тс - Го
Постоянную В% определяем из табл. 6.4. Следовательно,
f = 293 + 130-0,5 = 358 °К (85 °С).
Удельный расход тепла будет равен
&Qv = n [Т(х) — Т0] = 1,51-Ю3-1100 C58 — 293) = 108-Ю6 дж'м* = 108 дж/см*.
Такое количество тепла было затрачено на нагревание 1 см3 пластины в течение
2 мин»
В заключение этого параграфа рассмотрим несимметричный нагрев
неограниченной пластины при краевых условиях
+
Т (х, 0) = Т0 = const,
дТ @, т)
дх
дТ (R, т)
дх
+ Нх [Тс - Т@, т)] = 0,
•■ + Ht [Тс - Т (R, т)] =0,
D9)
E0)
E1)
где Ях = о^/Х, Я2 = я2/Х. Применим преобразование Лапласа
относительно т. Решение дифференциального уравнения A) для изображения
можно написать так:
S
VT
V^r*-
E2)
TL (x, s)- -^ = A ch [/ -^- х + Bsh
Граничные условия E0), E1) для изображения будут иметь вид
- T'L @,s) + Ht [tl@, s)-~] = 0, E3)
TL (R, s) + Яа [tl (R, s) - -£-] = 0. E4)
Постоянные Л и В в решении E2) определим из граничных условий
E3), E4). Полученные значения Л и В подставим в E2), тогда будем
иметь
То
S
TL (x, s)
(Г, - Го) (ch У^х+Нг ]/Z sh У J x
+(»)
E5)
Решение E5) есть отношение двух обобщенных полиномов,
причем ф (s) не содержит постоянной, т. е. условия теоремы разложения
соблюдены.
Найдем корни функции ф (s), для чего приравняем ее нулю:
+ и.У-J-)-{■*■'/т *]-»•
E6)
ГРАНИЧНОЕ УСЛОВИЕ ТРЕТЬЕГО РОДА
215
216
Глава шестая
Отсюда получаем: 1) 5 = 0, 2) бесчисленное множество корней sn,
определяемых из характеристического уравнения
где i у — R = Ъ Bix = H±R, Bi2 = H2R. Точки пересечения котанген-
соиды уг = ctgp. с гиперболой вида у2 = f-^- --—) / (l + ~в^-)
дают корни p-w уравнения E7), число их бесконечно велико. Они
попарно равны по абсолютному значению, но противоположны по знаку.
Так как sn = R2 , то для определения sn нужно рассмотреть только
положительные значения корней р.Л. Применим теорему разложения для
случая простых корней, находим
Тс-То
X
1 + Bix
i + Bi1+ ш
~вй~\ — 2j An (cos vn — +
+ -^- sin pn -£-) ехр ■(— [4 Fo),
E8)
где An — начальная тепловая амплитуда, равная
Ап = U1 + _В1Ц sin ^ cos ^+^ + _Bix_ sin j-i E9)
IV Bi2 / 2sin^ рп J
Удельный расход тепла находится обычным методом.
Если положить Bix = Bi2, то характеристическое уравнение E7)
превращается в уравнение A7). Тогда из решения A5) получаем решение
E8), если положить fx (х) равной Т0 = const. На рис. 6.16 приведены
графики б = /(Fo) для случая, когда температура на одной
поверхности пластины (х = R) поддерживается постоянной и равной начальной
температуре
Т (R, т) = Т0 = const, F0)
а на противоположной поверхности пластины происходит теплообмен
по закону Ньютона
- dTf; T) +Н[ТС~Т @, *)].= 0.
§ 4. ОГРАНИЧЕННЫЙ СТЕРЖЕНЬ БЕЗ ТЕПЛОВОЙ ИЗОЛЯЦИИ
БОКОВОЙ ПОВЕРХНОСТИ
Постановка задачи. Имеется ограниченный стержень длиной 2 R.
Стержень находится в тепловом равновесии с окружающей средой при
температуре Т0, т. е. температура стержня везде одинакова и
равна температуре окружающей среды. В начальный момент времени
концы стержня приводятся в соприкосновение со средой, температура
которой равна Тс > Т0. С боковой поверхности стержня происходит
ГРАНИЧНОЕ УСЛОВИЕ ТРЕТЬЕГО РОДА
217
теплоотдача в окружающую
среду с температурой Т0
(отсутствие тепловой изоляции
боковой поверхности). Требу-
ется найти распределение
температуры по длине стер-
ОЮНЯ о любой момент
времени у а также расход тепла в
предположении, что перепад
температуры происходит
только в направлении длины
стержня. Теплообмен
стержня с окружающей средой
происходит по закону Ньютона.
Наша задача аналогична
задаче § 2, только стержень имеет
конечную длину.
Поместим начало координат
в центре стержня (рис. 6,17).
Тогда дифференциальное
уравнение теплопроводности на
основании расчетов, аналогичных
расчетам § 2, запишется в
виде
тс
♦ ♦ ( \ t
-U2R-
1 I 1 I Г
Тс
Рис. 6.17. Распределение температуры в
ограниченном стержне без тепловой
изоляции боковой поверхности
О)
его
где h — отношение площади сеченця стержня к периметру
сечения.
Для общности задачи принимаем коэффициент теплообмена ах для
боковой поверхности не равным коэффициенту теплообмена а2 для
концов стержня (ах =f= а2), как это вытекает из физических условий
процесса нагревания.
Краевые условия можно написать так:
B)
C)
Т (х, 0) = Т0 = const;
~ хЁЧг^ + а* FC-T.(R, -с)]
дТ @, т) = Q
дх
= 0,
D)
Решение задачи операционным методом. Если применить
преобразование Лапласа к уравнению A), то будем иметь (см. § 1)
T"L (х, s) - (-1 + -Й") [П (х, *)--£-] = 0. E)
Общее решение уравнения E) следующее:
lh
X.
F)
218
Глава шестая
Граничные условия для изображения:
- T'L (R, s) + Яг [-£- - TL{R, s)] = 0, G)
7^@, s)= 0, (8)
где #, = -£- .
Из условия симметрии (8) следует, что В = 0. Постоянную Л
находим из условия G):
f н-Йг)"'" *(■!- +-Йг)''** + -^-
откуда
л Тс-Г0 1
«.. I «i У/г » л. 1 /■ « . «1 Y/».h/'s a- «iY^
Следовательно, решение для изображения будет иметь вид
(9)
ъ-т**(-т + -ягIи-
Ь (-f + -А-Г * + i (-f + 4тГsh (-J- + -*Г *]
A0)
Прежде чем перейти к оригиналу, рассмотрим более простую
задачу. Положим Я2 = оо; тогда из граничного условия C) следует
T(±R,*) = TC, A1)
т. е. концы стержня с самого начала процесса нагревания принимают
температуру среды Тс.
Решение для изображения при условии Я2 = °° имеет вид
(rc-r0)chl/"-£- + -^-*
tl(x, .)-4- = / а Xh -£$-• (i2)
Здесь Ф (s) и ф (s) -— обобщенные полиномы относительно s, что уже
неоднократно было доказано; применяя теорему разложения, находим
* (*) = sch /-f + xr * = о;
1) s = 0 (нулевой корень), 2) i ]/-J- + -^- # = *п = Bп - 1) -J,
s» — \ R! "•" \h r
Найдем значение ij/(s) при s=sn:
*»- «ь (т + нйгГ * + -£- (-г+-а-Г * (-f+-аГ *.
ГРАНИЧНОЕ УСЛОВИЕ ТРЕТЬЕГО РОДА
219
Следовательно, решение упрощенной задачи имеет вид
6 =
Т (х, т) - Г0
ch У~Ш-
Тс -Г»
ch-TBi4
£-- S(-ir-
2НТ2
л=1
й+в.14
X
X
cos ft, if exP L— ( ^ + Ш~ж) Fo
A3)
ах h
— критерий Био, Fo = -^ число Фурье.
где Bi
Если стержень имеет тепловую изоляцию (отсутствие теплоотдачи
с боковой поверхности), то Bi = 0; тогда
= 1-2 (- l)n+i -JL cos ^ JL ехр {- & Fo)
A4)
Решение A4) есть решение для неограниченной пластины при
постоянной температуре ограничивающих ее поверхностей. Это обусловлено
тем, что распространение тепла в ограниченном стержне, имеющем
теплоизоляцию на боковой поверхности, аналогично распространению
тепла в неограниченной пластине.
Решение A3) можно получить в ином виде, если решение для
изображения A2) преобразовать методом, описанным в § 3 гл. IV.
Тогда будем иметь
оо
TL(x.s)—^ = -^^1 (- 1)"* (ехр {-(jAf+ -JL-) 1Bя -
П=\
- 1) R - х]} + ехр {-{V-T + "Иг) К2л ~ !) * + *]})•
Переходя к оригиналу, получим
A5)
О =
VBi Fo
S(-i)
— n«+i
л=1
rkil^i
erfc
2 УТо
+ e
(—*) ^ * erfc r~lZJ + К Wo" A
2 '/Fo
+
+^<^4-(в-'+-^М^#
л=1
2 1/ Fo Л ' l
+ в
(a>_I+^Irgr-|.
erfc
2/г -1 + -£-
2 /То"
+ УЖРо-^)\. A6)
Если в решении A6) положить Bi = 0, то получим решение B8)
§ 3 гл. IV. Если же начало координат перенести из середины к
левому концу, т. е. сделать замену переменной х + R — Х>- & R — х =
220
Глава шестая
= 2R — X и положить 2/? = оо, то решение A6) будет тождественно
решению A4) § 2.
Вернемся к рассмотрению поставленной задачи.
Можно показать, что решение A0) для изображения удовлетворяет
условиям теоремы разложения, т. е. числитель и знаменатель —
обобщенные полиномы относительно s, причем полином знаменателя не
содержит постоянной благодаря присутствию множителя s.
Применяя теорему разложения и производя аналогичные
преобразования, которые были сделаны в предыдущем параграфе, получим
решение нашей задачи в виде
Т(х, т)-70 Ch ^Bil_T
R
h паи h
£ _J^L__ Д, cos ^ -^ exp [- ( £ + Bix ^) Fo ],
я=1 V-% + Bii ~W
A7)
где Bix — -Ц—, An = -—, ? ^n начальные тепловые амплиту-
л №п \ sin V*n cos рп
ды, приведенные в табл. 6.2; они являются функциями критерия Bi2 =
s= ~ R\ pn — характеристические числа, определяемые из уравнения
Анализ решения. Если Bi2 = оо (это означает, что температура
е =
1
оо
— £ A*cos^„-^- exp (—^Fo) ,
я=1
концов стержня постоянна), то решение A7) становится тождественным
2 тс
решению A3), так как Ап= (— 1\п+г —, где \ьп = Bп — 1) -^-.
Если положить Bix = 0, то получим
A8)
т. е. решение для неограниченной пластины, когда теплообмен между
ограничивающими поверхностями происходит по закону Ньютона. Это
решение тождественно решению B9) § 3.
В стационарном состоянии (Fo = оо) ряд A7) равен нулю и
распределение температуры по длине стержня описывается законом
гиперболического косинуса (законом цепной линии).
Если теплопотери с боковой поверхности отсутствуют, то в
стационарном состоянии будет равномерное распределение температуры,
равное 6 = 1 [Т(х, оо) = Тс = const].
Определение удельного расхода тепла. Для этого найдем среднюю
температуру стержня, применяя известное соотношение. Тогда будем
иметь
ГРАНИЧНОЕ УСЛОВИЕ ТРЕТЬЕГО РОДА
0,25i
221
0,20
0Д5
0,10
0,05
Рис. 6.18. Зависимость между относительной
избыточной температурой в центре стержня и
критерием Био для разных значений числа Фурье,
если Rlh = 10
Г(т)-Г0
ш уШх f
Тс-То
VBh~
-—- —- th /ВЦ -—
Bi2 &2 f h
-s
A
„, -i + *v
■B„exp
- ^ + Bix
j5i
Л3
Fo
]•
A9)
где £„— постоянные коэффициенты, определяемые соотношением D5) § 3.
В качестве примера сделаем следующий расчет. Требуется
определить относительную избыточную температуру в центре стержня, если
концы его поддерживаются при постоянной температуре (бп = 1), а с
боковой поверхности происходит теплоотдача в среду с температурой,
равной начальной температуре стержня, для разных значений Bix и Fo.
Отношение -^— равно 10.
h F
Для расчета используем решение A3). Имеем
fi - T(R^)-T0 _ 1 те
TQ
ch (|/ВЦ . 10)
X
тс2+ ЮОВЦ
X ехр Г-D- + lOOBi^Fol + -g—*= exp Г-(-2-««' +
^2+100Bi!
+ 100Bi1)Fo]
B0)
222
Глава шестая,
Из анализа формулы B0) видно, что при больших значениях Bi (при
—- = 10) 8Ц = 0. Это означает превышение теплоотдачи над
поступлением тепла через концы стержня теплопроводностью, так как стержень
тонкий и длинный. Поэтому берем критерий Bi2 от 0,05 до 1,0.
Вычисляем 6Ц для чисел Fo = 0,l; 0,2; 0,3 и 0,4.
Результаты расчетов представлены в виде графика на рис. 6.18,
где по оси ординат отложено 6Ц, а по оси абсцисс — критерий Bix. Из
рис. 6.18 видно, что, начиная с Шг ^ 0,4, все кривые сливаются в одну,
которая приближается к оси абсцисс. При малых значениях критерия
Био(В11<0,1) кривые резко возрастают с увеличением Fo.
Если критерий Bix = 0, то из решения A3) получаем решение A4),
которое уже было табулировано нами (см. табл. 4.2).
§ 5. ШАР (СИММЕТРИЧНАЯ ЗАДАЧА]
Постановка задачи. Дано сферическое тело (шар) радиуса R с
некоторым заданным начальным распределением температуры в виде
функции /(г). В начальный момент времени шар помещается в среду
с постоянной температурой ТС>Т (г, 0). Требуется найти
распределение температуры внутри шара в любой момент времени и
удельный расход тепла при условии, что температура в любой точке шара
есть функция времени и радиуса г.
Последнее условие соответствует равномерному нагреванию шара
по поверхности его, при котором изотермические поверхности пред-
ставляют собой концентрические сферы (симметричная задача).
Дифференциальное уравнение теплопроводности для шара в этом
случае может быть написано так:
d[rT(r,z)]
д*[гТ(г,х)]
(т>0; 0<r<R).
(О
Начальные и граничные условия следующие:
dT(R,
дг
дТ@,
дг
Т
±
Л.
(г, 0) =
+ Н[Т
■ = о,
= /(').
с-Т
Т@,-
(Я.
*)ф
*)]-
оо .
=0,
B)
C)
D)
При наличии неравномерного начального распределения
температуры решение методом Фурье быстрее приводит к результату.
Решение задачи методом разделения переменных. Сделаем замену
переменной Тс—Т (г, т) = ft (г, т), чтобы свести задачу нагревания к
задаче охлаждения и тем самым воспользоваться частным решением,
полученным в § 4 гл. IV:
ft (г, т) = ТС-Т (г, *) = С -^^- <Г*'в*
E)
ГРАНИЧНОЕ УСЛОВИЕ ТРЕТЬЕГО РОДА
223
Величина k определяется из граничного +у|
условия C), которое для переменной Ь (г, т)
примет вид
дг
+ Я»(/?, т)= 0.
F)
Удовлетворим решение E) граничному
условию F)
sin kR —akzz
R2
+ C
+ C
k cos kR
-ak2i
+
R
0.
G)
Сокращая на
С —ak2
— e
R
получим
Я ) sin kR + &cos kR = 0,
откуда
IgkR^-
kR
Рис. 6,19. Графический
способ определения корней
характеристического
уравнения в случае шара
HR — 1
(8)
Уравнение (8) является тригонометрическим уравнением, которое
имеет бесчисленное множество корней (kR). Обозначим
характеристические корни через р = kR, а критерий Био— через Bi = HR, Тогда
левая часть характеристического уравнения y1 = tgp представляет
тангенсоиду, а правая часть у2 — прямую, тангенс угла наклона которой
равен— I——— J, т. е. при значениях Bi > 1 прямая расположена
в четвертом октанте, а при значениях Bi < 1 — в первом. Точки
пересечения тангенсоиды уг и прямой у2 дают значение корней ^ (рис. 6.19).
На рис. 6.19 видно, что имеется бесчисленное множество корней fi,
причем каждый последующий больше предыдущего:
Pl<>2< ^3< ••♦ < Рп< ••• « (9)
При Bi = оо тангенс угла наклона прямой у2 равен нулю, и прямая
совпадает с осью абсцисс; тогда характеристические числа р будут
пропорциональны тс, т. е.
\in = mr при Bi = оо#
Если критерий Био равен единице (Bi = 1), то прямая у% совпадает
3 5
с осью ординат. В этом случае \it = —,
т. е. [in = Bn— 1)
IV
-тс,
^3 =
•тс и т. д.,
тс
Если Bi ~> 0, то тангенс угла наклона прямой равен единице,
IV
■ у 3Bi , так как из характеристического уравнения следует
Bi — 1 J_^
ctg н = —
Pi
3
tf
Ограничиваясь двумя членами ряда в разложении ctg^, получаем
р?
3Bi.
A0)
224
Глава шестая
Остальные корни (^2, р-3> • • •) определяются из уравнения
tg jx = ji при Bi -* 0. A1)
Таким образом, характеристическое уравнение можно написать так:
tgp "ST1-Г»*- A2)
Таблица 6.5
Bi—1
Корни характеристического уравнения tg ^ = — -7
1
Bi —-1
t*
14
0,0000
0,1224
0,1730
0,2445
0,2991
0,3450
0,3854
0,4217
0,4551
0,4860
0,5150
0,5423
0,6609
0,7593
0,9208
1,0528
1,1656
1,2644
1,3525
1,4320
1,5044
1,5708
1,6320
1,6887
1,7414
1,7906
1,8366
1,8798
1,9203
1,9586
1,9947
2,0288
2,1746
2,2889
2,4557
2,5704
2,6537
2,7165
2,7654
2,8044
2,8363
2,8628
2,9476
2,9930
3,0406
3,0651
3,0801
3,0901
3;1028
3,1105
3,1416
^2
4,4934
4,4945
4,4956
4,4979
4,5001
4,5023
4,5045
4,5068
4,5090
4,5112
4,5134
4,5157
4,5268
4,5379
4,5601
4,5822
4,6042
4.6261
4,6479
4,6696
4,6911
4,7124
4,7335
4,7544
4,7751
4,7956
4,8158
4,8358
4,8556
4,8751
4,8943
4,9132
5,0037
5,0870
5,2329
5,3540
5,4544
5,5378
5,6078
5,6669
5,7172
5,7606
5,9080
5,9921
6,0831
6,1311
6,1606
-. 6,1805
6,2058
1 6,2211
6,2832
Р-з
7,7253 ]
7,7259 !
7,7265 1
7,7278
7,7291
7,7304
7,7317
7,7330 i
7,7343
7,7356
7,7369
7,7382
7,7447
7,7511
7,7641
7,7770
7,7899
7,8028
7,8156
7,8284
7,8412
7,8540
7,8667
7,8794
7,8920
7,9046
7,9171
7,9295
7,9449
7,9542
7,9665
7,9787
8,0385
8,0962
8,2045
8,3029
8,3914
8,4703
8,5406
8,6031
8,6587
8,7083
8,8898
9,0019
9,1294
9,1987
9,2420 .
9,2715
9,3089
9,3317
9,4248
^4
10,9041
10,9046
10,9050
Л0,9060
10,9069
10,9078
10,9087
10,9096
10,9105
10,9115
10,9124
10,9133
10,9179
10,9225
10,9316
10,9408
10,9499
10,9591
10,9682
10,9774
. 10,9865
10,9956
11,0047
11,0137
11,0228
11,0318
11,0409
11,0498
11,0588
11,0677
11,0767
11,0856
11,1296
11,1727
11,2560
11,3349
11,4086
11,4773
11,5408
11,5994
11,6532
11,7027
11,8959
12,0250
12,1807
12,2688
12,3247
12,3632
12,4124
12,4426
12,5664
У-5
14,0662
14,0666
14,0669 *
14,0676
14,0683
14,0690
14,0697
14,0705
14,0712
14,0719
14,0726
14,0733
14,0769
14,0804
14,0875
14,0946
14,1017
14,1088
14,1159
14,1230
14,1301
14,1372
14,1443
14,1513
14,1584
14,1654
14,1724
14,1795
14,1865
14,1935
14,2005
14,2075
14,2421
14,2764
14,3434
14,4080
14,4699
14,5288
14,5847
14,6374
14,6870
14,7335
14,9251
15,0625
15,2380
15,3417
15,4090
15,4559
15,5164
1 15,5537
15,7080
H-e
17,2208
17,2210
17,2213
17,2219
17,2225 *
17,2231
17,2237
17,2242
17,2248
17,2254
17,2260
17,2266
17,2295
17,2324
17,2382
17,2440
17,2498
17,2556
17,2614
17,2672
17,2730
17,2788
17,2845
17,2903
17,2961
17,3019
17,3076
17,3134
17,3192
17,3249
17,3306
17,3364
17,3649
17,3932
17,4490
17,5034
17,5562
17,6072
17,6567
17,7032
17,7481
17,7908
17,9742
18,1136
18,3018
18,4180
18,4953
18,5497
18,6209
1 18,6650
18,8496
ГРАНИЧНОЕ УСЛОВИЕ ТРЕТЬЕГО РОДА
225
Первые шесть корней рп (с точностью до четвертого знака после
запятой) приведены в табл. 6.5 для разных значений критерия Био.
В большинстве случаев приходится ограничиваться одним, редко двумя
значениями рп.
Вернемся к решению E). Так как имеется бесчисленное множество
постоянных kn= -^-, определяемых из характеристического уравне-
R
ния A2), общее решение задачи может быть записано как сумма всех
частных решений:
оо г
Ssina„ 2 ах
сп r -*»~w #
A3)
Постоянные Сп определяем из начального условия
ft (г, 0) = 7С- Г(г, 0) = Тс - f(r) = ft(r). A4)
Имеем
г
00 sin {лЛ —-
С известными оговорками относительно функции fx (r), которые
неоднократно проводились, можно определить Сп по методу Фурье.
Умножим обе части равенства A5) на rsm^m — dr, где pm — m-й
R
корень характеристического уравнения A2), и проинтегрируем от 0 до R:
R R со
Г гД (г) sin pm ~ dr = f J Cn sin jim ~- sin ^ JLdr=
J
0 0 /2—1
= 2C* J sin^m-^-sin^-^dr. A6)
/г=1 О
В гл. IV было показано [формула A3) § 4], что любой интеграл правой
части равенства A6) может быть представлен так:
R
1= С sin^ sina, JL-dr = * ^sin **« C0S *" ~ ^sin^ C0S M =
о
= _^_(ji» tg^ctg^-l). A7)
Из характеристического уравнения A2) можно написать:
Следовательно, интеграл A7) равен нулю при m=f=n. Если т = п, то
интеграл A7) будет равен
R
J sin»^ ^- d^ = /? (-|- — -5[^1-) ^— (I**—sin^cosi*^. A8)
о
8 Заказ № 640
226
Глава шестая
Таким образом, все интегралы в соотношении A6) равны нулю, за
исключением одного, когда m = п. Следовательно, постоянная Сп равна
J rfx(r)sin\Ln-jj-dr
С -JL
2\Ln
Isin2^T
dr
I r/i (r) sinp.^ — dr.
\Ln — sin \Ln cos \Ln R ] R
Общее решение нашей задачи имеет вид
»(*,т) = Тс —Г(*,т) =
2\Ln
sin ft,
-^Fo
л«1
ft, — Sin \ьп COS {i.n
^- r/iW shift,-£-dre я ■. A9)
0
Если температура шара в начальный момент времени не зависит
от г, т. е.
T(r,0) = /1(r)-r0 = constf
то интеграл в решении A9) может быть вычислен до конца:
R
~ J (Тс ~ То) Г Sill ?nj~dr= (Гс"Го)^ (Sin ft, - ft, COS ft,),
так как
J #sin л: dx = sin x —x cos x,
В окончательной форме решение задачи можно написать так:
00
-5
i—J
я=1
Q _ Г(г,г)-Тв
J2 (sin pn — у-п cos txn)
ц„ — sin (i„ cos (i„
- = 1 —
Л sin ,!„-£- ^
*>Л 1
B0)
Решение задачи операционным методом. Решение дифференциального
уравнения A) для изображения 77,(г, s) при условии D) имеет вид [см.
решение B2) § 4 гл. IV]:
TL(r,s)-
То
sh
В-
Vi
Граничное условие C) для изображения будет иметь вид
-T'L(R, s) + Н [-^- - TL{R, s)] - 0.
Находим постоянную В:
B1)
B2)
ГРАНИЧНОЕ УСЛОВИЕ ТРЕТЬЕГО РОДА
227
откуда
Б = Gу-го)я^ ; ^ B3)
Решение B1) примет вид
TL(r,s)-^- =
S
(Tc-T0)H^sbY^r w
r.[m-l)*Yi R+V~a **Vt*]
<M*)
B4)
Числитель Фх (s) и знаменатель ф2 (s) решения B4) не являются обобщенными
полиномами относительно s, но их можно привести к таким полиномам
<D(s) и ф(я), умножив тот и друпой на 1/— . В этом случае можно
воспользоваться соотношением
Y (*п) «К (*п) '
где Ф (s) = sk Фг (s),. ф (s) = sk фх (s) (при условии s^ =£ 0), Ф (s) и ф (s) —
обобщенные полиномы относительно s.
Найдем корни s„, для чего ^x(s) приравняем нулю, т. е.
^(s) = rs [(HR- l)sh|/"-l Я + }/*£ /?ch ]/У #] = 0.
Отсюда будем иметь: 1) s = 0 (нулевой корень), 2) (HR~ 1) sh 1/ — i? +
+ yT"* ch |/T* = (HR- 1) "f sin * /T/J + /Гflees*/!*-
— i? == jx, тогда sn = ^2— , причем -(ля
определяются из характеристического уравнения
(#i? — 1) sin р + р cos (л = 0
или
tgFL = Ji_, B6)
sr Bi — 1
где Bi = HR— критерий Био.
Для первого (нулевого) корня найдем значение ', ■ > для чего пре-
образуем B4) так, чтобы оно представляло собой отношение двух
обобщенных полиномов:
Ф1(8) ___
/ Is Is3 \
T0)BiR[r + — -г8+— — '5 + ...
\ 3! а 5! а2 /
Is \ / Is Is2
R3+ ...+/? + ~#3 + " R5+ .
3! а ^ / ^ \ ^ 2! а ^ 41 а2 ^
••)]
rs Г(В1 - 1) U +
~ Ф («)
228
В результате получаем
lim
Ф(в)
(Тс-Т0)
s-»o У (s)
Для остальных корней находим ф| (s):
где [~] означает выражение, стоящее в квадратных скобках в
знаменателе решения B4); оно равно нулю при s = sn. Таким образом,
2 i
ФИО
[(Bi — 1) cos ця + cos [1Я — [хл sin [хя ] =
2/
[Bicos^ — f^sinpJ =
*>Л
2* sin pn
(sin^cos^ —^),
0>i (О - (П- То) -^А"sin Vn~- (Гс. T°)i? (sin ft,- ft, cos ^) sin ft, J~
г /< шп р-л ы
Итак, решение нашей задачи имеет вид
Г (г,*)-Го
= 1
*>л
ехр(—i^Fo) ,
/г=1
B7)
где
2 (sin {хя — р.я cos pn)
\^п — sin \хп cos )хп
B8)
Таким образом, получаем решение, тождественное решению B0).
Начальные тепловые амплитуды являются однозначными функциями
критерия Био. Поэтому для расчета более удобно пользоваться таким
выражением для ЛЛ, в котором тригонометрические функции заменены
через )ъп и критерий Био согласно характеристическому уравнению.
Так, для Ап можно написать:
B9)
Вычисленные по этой формуле шесть значений Ап с точностью до
четвертого знака после запятой приведены в табл. 6.6.
Для практических расчетов на рис. 6.20 и 6.21 приведены
номограммы для определения бп (относительная избыточная температура
поверхности шара) и 6Ц (относительная избыточная температура в
центре шара) в зависимости от критерия Био и числа Фурье.
Анализ решения. Если Bi->oo, то согласно характеристическому
уравнению B6)
V-n = пщ
C0)
231
а начальные тепловые амплитуды равны
Ап = (—1)"+1-2 = 2(— 1)"п.
C1)
Тогда решение B7) становится тождественным решению C2) § 4 гл. IV,
= 1 — 6
Т-Т0
если в последнем положить бохл = 1 — 6наг, где 60ХЛ = —, (Т0>Т(
охлаждение шара), а 6Н
Если Bi = 1, то
Т0
То-Тс
(Тс> Т0— нагревание шара)»
**"
= Bя —
1)
ТС
Л„
(-
-1)"+1
2
1%
C2)
Тогда скорость нагревания будет зависеть только от теплоинерцион-
ных свойств материала.
При малых значениях Bi(Bi->0) все коэффициенты Ап-±0 за
исключением первого (Аг = 1), а \^\ = 3Bi [см. соотношение A0)]. Тогда
решение B7) для малых значений Bi можно написать так:
6 =
1
—
R
siny3Bi
г УШГ
г
н
~е"
-3BiFo
C3)
Из анализа решения B7) следует, что благодаря неравенству (9) ряд
быстро сходится при не слишком малых значениях Fo, так как
экспоненциальные функции ехр (—f^Fo) быстро уменьшаются с увеличением
|хя. Поэтому если исключить из рассмотрения малые значения Fo, то
можно ограничиться одним членом ряда; тогда решение примет
простой вид
RsmH~ 2Fo
6 = 1 _ А £- е 1 при Fo > Fop C4)
Для удобства практических расчетов на рис. 6.22 и 6.23 построены
графики рг = /(Bi) и A1 = f(Bi) для разных значений критерия Bi (от
0 до 20). При Bi > 0,1 корень ^ можно вычислить по формуле A5) § 11.
Для малых значений Fo в решении B7) приходится брать несколько
членов ряда, что представляет известные трудности для расчета.
Поэтому найдем приближенное решение нашей задачи, пригодное для
малых значений Fo.
Решение для изображения можно написать так:
Т (г *\ — J±= Bi (TC-T0)R
JL^S) s rs m~l) + qR]
0-q(R-r)
~q(R+r)
)x
XI
['
qR — (Bi — l)e-2qR
qR + (Bi - 1)
Bi R (Tc - To)
_(е-«я->_в-«*-к>) t C5)
rsUBi — l)+qR]
где q = l/ — . Выражение, стоящее в квадратных скобках, мы
разложили в ряд и ограничились первым членом, так как для малых значений
Fo величина qR = у ^ R велика.
232
Глава шестая
Таблица 6.6
2Bi j/(Bi-l)a+t*2
Значения постоянных Ап — (— 1)л+1 ъ
^ Н-* + Bi» — Bi
Bi
0,000
0,005
0,01
0,02
0,03
0,04
0,05
0,06
0,07
0,08
0,09
0,10
0,15
0,20
0,30
0,40
0,50
0,60
0,70
0,80
0,90
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
2,5
3,0
4,0 1
5,0
6,0
7,0
8,0
9,0
10
И
16
21
31
41
51
61
81
101
оо
At
1,0000
1,0025
1,0035
1,0055
1,0089
1,0121
1,0147
1,0181
1,0206
1,0239
1,0266
1,0297
1,0443
1,0592
1,0880
1,1164
1,1440
| 1,1713
1,1978
1,2237
1,2488
1,2732
1,2970
1,3200
1,3424
1,3640
1,3848
1.4051
1,4247
1,4436
1,4618
1,4793
1,5579
1,6223
1,7201
1,7870 i
1,8338
1,8673
1,8920
1,9106
1,9249
1,9364
1,9663
1,9801
1,9905
1,9948
1,9964
1,9974
1,9985
1,9993
2,0000
Л,
—0,0000
—0,0023
—0,0046
—0,0091
—0,0137
—0,0182
—0,0227
—0,0273
—0,0318
—0,0363
—0,0409
—0,0454
—0,0679
—0,0894
—0,1345
—0,1781
—0,2216
1 —0,2633
—0,3048
—0,3455
—0,3854
—0,4244
—0,4626
—0,4999
—0,5364
—0,5720
—0,6067
—0,6405
—0,6735
—0,7063
—0,7368
—0,7673
—0,9073
—1,0288
—1,2253
—1,3733
—1,4860
—1,5731 1
—1,6409
—1,6949
—1,7381
— 1,7732
—1,8766
—1,9235
—1,9626
—1,9780
—1,9856
—1,9901
—1,9942
* —1,9962
—2,0000
Лг
0,0000
0,0013
0,0026
0,0052
0,0078
0,0104
0,0130
0,0156
0,0183
0,0209
0,0235
0,0260
0,0390
0,0520
0,0779
0,1036
0,1292
0,1546
0,1799
i 0,2050
0,2299
0,2546
0,2792
0,3035
0,3276
0,3515
0,3752
0,3986
0,4218
0,4447
0,4674
0,4899
0,5980
0,6993
0,8811
1,0363
1,1673
1,2776
1,3703
1,4482
1,5141
1,5698
1,7489
1,8385
1,9186
1,9515
1,9680
1,9773
1,9869
1,9915
2,0000
л4
—0,0000
—0,0009
—0,0018
—0,0037
—0,0055
—0,0074
—0,0092
—0,0110
—0,0129
—0,0147
—0,0166
—0,0184
—0,0276
—0,0368
—0,0551
—0,0734
—0,0916
1 —0,1098
—0,1270
—0,1460
—0,1640
—0,1819
—0,1997
—0,2175
—0,2352
—0,2528
—0,2703
—0,2878
—0,3051
—0,3228
—0,3395
—0,3565
—0,4365
—0,5205
—0,6719 |
—0,8095
—0,9333
—1,0437
— 1,1415
—1,2280
-1,3042
—1,3713
— 1,6058
— 1,7360
—1,8616
—1,9161
—1,9441
— 1,9601
—1,9769
—1,9850
—2,0000
А5
0,0000
0,0007
0,0014
0,0029
0,0043
0,0057
0,0071
0,0085
0,0100
0,0114
0,0128
1 0,0142
| 0,0214
0,0285
0,0427
0,0569
0,0710
0,0852
0,0998
0,1134
0,1275
0,1415
0,1555
0,1694
0,1833
0,1972
0,2110
0,2248
0,2385
0,2522
0,2659
0,2795
0,3449
0,4122 |
0,5384
0,6570
0,7702
0,8695
0,9633
1,0489
1,1269
1,1677
1,4633
1,6256
1,7950
1,8732
1,9145
1,9387
1,9644
1,9767
2,0000
А*
—0,0000
—0,0006
—0,0012
—0,0023
—0,0035
—0,0047
—0,0058
—0,0070
—0,0081
—0,0093
—0,0105
—0,0116
1 —0,0174
1 —0,0232
—0,0349
—0,0465
—0,0580
—0,0696
—0,0812
—0,0927
—0,1042
—0,1157
—0,1272
—0,1387
—0,1501
—0,1616
—0,1730
—0,1843
—0,1957
—0,2078
—0,2183
—0,2296
—0,2855
—0,3405
—0,4476
—0,5501
—0,6428
—0,7398
—0,8264
—0,9073
—0,9827
—1,0527
—1,3305
—1,5149
—1,7225
—1,8263
—1,8802
— 1,9135
— 1,9492
— 1,9667
—2,0000
ГРАНИЧНОЕ УСЛОВИЕ ТРЕТЬЕГО РОДА
233
4,0 8j0 \%0 16,0 -^^20,0
Рис. 6.22. Зависимость между первым корнем jj^
характеристического уравнения и критерием Био для шара
Переход от изображения к оригиналу производим по таблице
изображений (см. приложение):
T(r,z)-T0 ^ (±) BiR
ТС~Т0 r(Bi —1)
iq=
erfc
R
2V"Fo
— exp[(Bi—lJFo +
^ + (Bi -^l)l/Fo) ; C6)
+ (Bi-l)(l + ^)lerfcl
здесь введено условное обозначение
[(±)А(*г)]= +A(-z) — A( + z).
Для Bi = 1 можно найти точное решение. Соотношение C5) можно
написать в таком виде:
TL{r,s)
(Те - То) R
VI
Ш_ £ (-,)•
,/f+l I e-l№-l)R-rl t
R
n=i
— e
~qtBn-l)R + rh
C7)
Глава шестая
Щ
О
А,
1,9!
1,8
U
1,6
1,5
1,4
1,3
Вт
4,0 8,0 1ЗД 16,0 » 20,0
—~'~ 1 I I ITfbrrl I I ! I I I I 1 1 I 1 I 1 I I I 1 1 гтт
ян
1,5
I
г
1,4
1,3
1,2
1,1
0,4
0,8
1,2
1,6
Bi
-2,0
1,0
Рис. 6.23. Зависимость между коэффициентом Аг и
критерием Био для шара
Из таблицы изображений находим
1 _e-kVs
1/1
= 2 ]Л ierfc
2]Ли
Тогда наше решение примет вид
= 2 -£- ]/Fo ][] (—1)*+1 ierfc
л=1
2л — 1 —
2y"Fo
—ierfc
2п— 1+-
2l/Fb~
C8)
C9)
Если в решении C6) положить г = 0, то получим неопределенность.
Найдем приближенное решение для центра шара (г = 0) из решения
ГРАНИЧНОЕ УСЛОВИЕ ТРЕТЬЕГО РОДА
235
для изображения Ть(г, s), которое в этом случае можно написать так:
Г9 __ BiqR(Tc~T0)
S
TL(r,s)
«2Bi(Tc-T0)[l--^i
s[(Bi — 1) shqri?
— 1
q.RchqR]
-J-j-exp(—qR),
D0)
так как при больших значениях qR можно положить sh qR = ch <//?
2
Пользуясь таблицей изображений, находим
6Ц » 2Bi exp [(Bi — lJ Fo + (Bi — 1)] X
1
X erf с
2 У Fo"
+ (Bi-l)KFo
D1)
Полученные приближенные решения C6) и D1) справедливы для
малых значений Fo; при больших значениях надо пользоваться
решением B7).
При малых значениях Fo температура в центре шара почти не
изменяется. Поэтому наибольший интерес представляет изменение
температуры на поверхности, которая при малых значениях Fo, но при
больших Bi изменяется в широких пределах.
В табл. 6.7 приведены значения A — 9П) для чисел Fo от 0,0003
до 0,0050 при изменении Bi от 0,1 до 1000, полученные Пешлем из
решения B7) путем громоздких расчетов (см. § 3), Наши приближенные
решения дают тот же результат при помощи очень простых расчетов.
Таблица 6.7
Относительная температура на поверхности шара 1 —бп — Ф* (Fo, Bi).
Bi
од
0,5
1
4
10
20
50
100
200
1000
0,0003
0,999
0,991
0,981
0,925
0,830
0,701
0,463
0,284
0,154
0,031
0,0005
0,998
0,988
0,975
0,905
0,787
0,638
0,392
0,227
0,131
0,026
Числа Fo
0,0010
0,996
0,982
0,964
0,868
0,717
0,545
0,300
0,164
0,084
0,015
0,0025
0,994
0,971
0,944
0,805
0,603
0,413
0,197
0,103
0,052
0,010
0,0050
0,991
0,959
0,920
0,734
0,502
0,315
0,137
0,071
0,035
0,007
Иллюстрируем изложенное на примерах.
Пусть Bi = 1, a Fo = 0,0003. Тогда, применяя формулу C9), получим
6П = 2 yW ierfc 0 = 2 *|/Fo" — , D2)
так как
ierfc и ■■
у%
е uZ — aerfca,
D3)
а следующие члены формулы C9) ничтожно малы по сравнению с первыми. Далее,
1
1— 6П= 1 — 2]/0,0003 _ =0,981,
что полностью совпадает с данными табл. 6.7.
D4)
236
Глава шестая
1,00
А
0,99;
0,98
0,97
0,96
0,95
4,0, 8j0 VI
0.4
fi 16,0
Ж^
0,8
1,2
П~ I "Г II TU f 1 I I 1 1 I 1 1 I I I I I I 1 I 1 I 1 I I 1 I I I I I I I I I I I 1 I I I 1 1 I I
FF~KFFN Гггк 11 l"i 11111 ThLltI i 1111111111111111 i"l 11H
111111111111II1111111111 у PHJ 111111111111111111 г! 11
1,0
t=,
0,9
0,8
0,7
0,6
1,6 ^ 2,0
Bi
Рис. 6.24. Зависимость между коэффициентом Вг и критерием
Био для шара
так:
Пусть Fo = 0,0025, a Bi = 10,0. Воспользуемся решением C6), которое напишем
1-вп=1-вГ=Г [l-^Bi_1JF°erfc (fii-l)VTb ]
D5)
Остальными членами в решении D5) пренебрегаем, так как они ничтожно малы
по сравнению с взятыми. Имеем
(Bi—l)|/"Fo"=0,45.
Следовательно,
1 __ еп = 1 — ^A — е °,2°25 erfc 0,45) =0,6028.
D6)
Согласно табл. 6.7 разность A—6П) для этого случая равна 0,603, т. е. имеем опять
очень хорошее совпадение^результатов.
Таким образом, приближенные решения дают вполне удовлетвори-
тельные результаты и заменяют громоздкие вычисления по формуле B7).
Определение удельного расхода тепла. Найдем среднюю температуру
шара по формуле
Ч*)= -§rjjr*T (rrtdr. D7)
ГРАНИЧНОЕ УСЛОВИЕ ТРЕТЬЕГО РОДА
237
Если подставить вместо Т (г, т) соответствующее выражение из
решения B7) и воспользоваться формулой
j и sin и du — sin и — и cos и,.
то после интегрирования получим
= Г^-Го = 1 - £s„exp (-^ Fo)„
Го
л=1
где 5„ — постоянные коэффициенты, определяемые из соотношения
*.= 6Ш2
" ^+Bi*-Bi)
D8)
D9)
Первые шесть постоянных коэффициентов Вп приведены в табл. 6.8
для разных значений чисел Фурье.
Таблица 6.8
Значение постоянных В =
6Bi2
К (^ + Bi2-Bi)
Bi
оо
51,0
21,0
10,0
9,0
8,0
7,0
6,0
5,0
4,0
3,0
2,5
2,0
1,9
1,8
1,7
1,6
1,5
1,4
1,3
1,2
1,1
1,0
0,90
0,80
0,70
0,60
0,50
0,40
0,30
0,20
0,15
0,10
0,09
0,08
вх
0,6079
0,6427
0,6886
0,7667
0,7737
0,7889
0,8068
0,8280
0,8533
0,8829
0,9171
0,9353
0,9534
0,9569
0,9605
0,9641
0,9678
0,9707
0,9739
0,9770
0,9800
0,9828
0,9855
0,9881
0,9905
0,9926
0,9944
0,9959
0,9974
0,9985
0,9994
0,9996
I 0,9997
1,0000
1,0000
вг
0,1520
0,1518
0,1510
0,1496
0,1453
0,1396
0,1319
0,1215
0,1075
0,0890
0,0655
0,0520
[ 0,0380
0,0352
0,0325
0,0297
0,0270
0,0243
0,0217
0,0192
0,0167
0,0144
0,0122
0,0101
0,0081
0,0064
0,0048
0,0034
0,0022
0,0013
0,0006
0,0003
0,0001
0,0001
0,0001
В3
0,0675
0,0671
0,0652
0,0485
0,0455
0,0408
0,0360
0,0305
0,0245
0,0180
0,0115
0,0085
0,0057
[ 0,0052
0,0047
0,0043
0,0038
0,0034
0,0030
0,0026
0,0022
0,0019
0,0016
0,ШЗ
0,0010
0,0008
0,0005
0,0004
0,0003
0,0001
0,0001
я4
0,0380
0,0380
0,0363
0,0196
0,0175
0,0152
0,0128
0,0104
0,0079
0,0055
0,0034
| 0,0024
0,0016
0,0014
0,0013
0,0011
0,0010
0,0009
0,0008
0,0007
0,0006
0,0005
0,0004
0,0003
0,0003
0,0002
0,0001
0,0001
0,0001
вь
0,0243
0,0236
0,0180
0,0091
0,0079
0,0067
0,0055
0,0044
0,0032
0,0021
0,0013
0,0009
0,0006
0,0005
0,0005
0,0004
0,0004
0,0003
0,0003
0,0003
0,0002
0,0002
0,0001
0,0001
0,0001
0,0001
в.
0,0169
0,0158
0,0108
0,0047
0,0040
0,0033
0,0027
0,0021
0,0015
0,0010
0,0006
0,0004
0,0003
0,0002
0,0002
0,0002
0,0002
0,0001
0,0001
0,0001
0,0001
0,0001
0,0001
238
Глава шестая
Обычно приходится пользоваться одним первым коэффициентом,
поэтому на рис. 6.24 построены графики B1 = f(Bi) для значений Bi
(от 0 до 20). Для удобства пользования графиком построены две
кривые с разным масштабом по оси абсцисс.
Удельный расход тепла находим по формуле
AQ. = cT[T(t)-70].
E0)
Для малых значений времени удельный расход тепла находим по
соотношению
ас—нИ^-^*
E1)
Вычисление —т~2~^ производится тем же способом, что и в
предыдущих параграфах.
При наличии номограмм и табл. 6.5, 6.6, 6.8, а также
соответствующих графиков для pv Аг и Вг конкретные расчеты выполняются
быстро и легко. Поэтому в дальнейшем эти расчеты производиться не
будут.
§ 6. НЕОГРАНИЧЕННЫЙ ЦИЛИНДР
Постановка задачи. Дан неограниченный цилиндр радиуса R и
задано радиальное распределение температуры в виде некоторой
функции f(r). Предполагается, что изотермы представляют собою
коаксиальные цилиндрические поверхности, т. е. температура цилиндра
зависит только от радиуса и времени. В начальный момент времени
цилиндр помещается в среду с постоянной температурой Тс>Т(г,0).
Требуется найти распределение температуры в цилиндре в любой
момент времени, а также удельный расход тепла.
Дифференциальное уравнение теплопроводности для неограниченного
цилиндра нами было написдно в § 5 гл. IV.
Начальные и граничные условия можно написать так:
Г(г,0) = /(г),
дТ(ЯЛ) +Я[Гс_7(/?,т)]=0,
дг
дТф.ъ)
дг
0, Т@,т)^ос.
О)
B)
C)
Решение задачи методом разделения переменных. Сведем нашу
задачу на нагревание цилиндра к задаче на охлаждение путем замены
переменной, т. е. полагаем $(г,х) = Тс—Т(г, т). Тогда начальные и
граничные условия примут вид
b(r,0) = Tc-f(r) = f1(r),
dHR, х)
дг
Э»@,т)
дг
+ НЬ (Д,т) = 0,
= 0,&@,т)=£оо.
D)
E)
F)
ГРАНИЧНОЕ УСЛОВИЕ ТРЕТЬЕГО РОДА
239
Частное решение
дифференциального уравнения
теплопроводности для неограниченного
цилиндра при коаксиальном
распределении изотерм относительно оси
цилиндра имеет вид
%■ (г,т) = [CJo (kr) + DY0 (kr)] e~k2ax,
G)
где J о (kr) и F0 (kr) — функции -од4
Бесселя соответственно первого -o,2-j
и второго рода нулевого поряд- -о,з-
ка, а С и D — постоянные (см.
§ 5 гл. IV). Из условия F)
следует, что D = О (см. там же);
постоянную С найдем несколько
позже из начального условия. *
Удовлетворим частное
решение G) граничному условию E):
-kCJ±(kR) е~кгах +
+ HCJ0 (kR) ё
так как
dJ0(kr).
dr
-k2ai
= 0,
— ыг(кг).
Сокращая на Се Лт@< т < оо)
получим
J о (kR) _&#_ _&#
J±(kR) HR ~~ Bi
^r- (8)
Рис. 6.25. Графический способ
определения корней характеристического уравнения
в случае цилиндра:
а) графики функций у0 и ух\ б) зависимости у0/ух
и у от величины ^*
Уравнение (8) является
трансцендентным; его можно решить
графическим способом. Обозначим kR через р. (^ = kR). Функция—\
обратим
щается в нуль в тех точках, для которых /0([л) = 0, т. е. в точках vx ,
v2, ,.., ул, где vw—корни функции J0(^)- В тех точках, в которых
функция Jx(v<) обращается в нуль, функция j* ^y претерпевает разрыв
непрерывности и становится равной ± оо. Обозначим корни функции </i(h<)
через хп.
Построим кривые уг =■ / , у которые в точках v„ пересекают ось
абсцисс, а в точках *п имеют асимптоты, расположенные параллельно оси
ординат (рис. 6.25). Кривые уг = Д *t напоминают котангенсоиду, но
период их неодинаков.
Затем строим прямую у% — -gr- p. Точки пересечения прямой у% с
кривыми уг дают нам значения характеристических корней. Из рис. 6.25
видно, что имеется бесчисленное множество корней \ьп, причем все эти
240
Глава шестая
корни заключены в пределах между vn и *п ^я<[ая<хл). Если Bi->oo,
то прямая совпадает с осью абсцисс и корни \in становятся равными
корням vn (jj^ = vj, т. е, не зависят от критерия Bi.
При Bi -> 0 !*! -> ]/*2Bi, что следует из характеристического
уравнения, если функции J0 (р.) и Ух (ji) разложить в ряд и ограничиться
первыми членами ряда. Действительно,
1 — JL ul2 4-
Bi
/i(rt
■{л =
ji —
224
V +
откуда получаем
jif = 2Bi.
Остальные корни определяются из уравнения
Корни характеристического уравнения ° "^.
Таблица 6.9
Bi
Р
Bi
0,0
0,01
0,02
0,04
0,06
0,08
0,10
0,15
0,20
0,30
0,40
0,50
0,60
0,70
0,80
0,90
1,0
1,5
2,0
3,0
4,0
5,0
6,0
7,0
8,0
9,0
10,0
15,0
20,0
30,0
40,0
50,0
60,0
80,0
100,0
оо
р-1
0,0000
0,1412
0,1995
0,2814
0,3438
0,3960
0,4417
0,5376
0,6170
0,7465
0,8516
0,9408
1,0184
1,0873
1,1490
1,2048
1,2558
1,4569
1,5994
1,7887
1,9081
1,9898
2,0490
2,0937
2,1286
2,1566
2,1795
2,2509
2,2880
2,3261
2,3455
2,3572
2,3651
2,3750
1 2,3809
2,4048
Р-а
3,8317
3,8343
3,8369
3,8421
3,8473
3,8525
3,8577
3,8706
3,8835
3,9091
3,9344'
3,9594
3,9841
4,0085
4,0325
4,0562
4,0795 1
4,1902 !
4,2910
4,4634
4,6018
4,7131
4,8033
4,8772
4,9384
4,9897
5,0332
! 5,1773
5,2568
5,3410
5,3846
5,4112
Г 5,4291
5,4516
5,4652
5,5201
Р-з
7,0156
7,0170
7,0184
7,0213
7,0241
7,0270
7,0298
7,0369 !
7,0440
7,0582
7,0723
7,0864 1
7,1004 !
7,1143
7,1282
7,1421
7,1558
7,2233
7,2884
7,4103
7,5201
7,6177
7,7039
7,7797
7,8464
7,9051
7,9569
8,1422
8,2534
8,3771
8,4432
8,4840
8,5116
1 8,5466
8,5678
8,6537
Р-4
10,1735
10,1745
19,1754
10,1774
10,1794
10,1813
10,1833
10,1882
10,1931
10,2029
10,2127
10,2225
10,2322
10,2419
10,2519
10,2613 J
10,2710
10,3188
10,3658
10,4566
10,5423
10,6223
10,6964
10,7646
10,8271
10,8842
1 10,9363
11,1367
11,2677
11,4221
11,5081
11,5621
11,5990
11,6461
11,6747
11,7915
Р-5
13,3237
13,3244
13,3252
13,3267
13,3282
13,3297
13,3312
13,3349
13,3387
13,3462
13,3537
13,3611
13,3686
13,3761
13,3835
13,3910
13,3984 !
13,4353
13,4719
13,5434
13,6125
13,6786
13,7414
13,8008
13,8566
13,9090
1 13,9580
14,1576
14,2983
14,4748
14,5774
14,6433
14,6889
14,7475
14,7834
14,9309
р-в
16,4706
16,4712
16,4718
16,4731
16,4743
16,4755
16,4767
16,4797
16,4828
16,4888
16,4949
16,5010
16,5070
16,5131
16,5191
16,5251
16,5312
16,5612
16,5910
16,6499
16,7073
16,7630
16,8168
16,8684
16,9179
16,9650
1 17,0099
I 17,2008
17,3442
17,5348
17,6508
17,7272
17,7807
17,8502
17,8931
18,0711
ГРАНИЧНОЕ УСЛОВИЕ ТРЕТЬЕГО РОДА
241
и, следовательно, не зависят от радиуса цилиндра. В случае, когда
О < Bi < оо, корни \Ln зависят от Bi, а значит, и от радиуса цилиндра.
Первые шесть корней y.v jj-2, ..., \i6 приведены в табл. 6.9 для разных
значений критерия Bi.
Итак, характеристическое уравнение (8) можно написать так:
Jifa) " Bi r- W
Вернемся к решению G). Общее решение будет суммой всех
решений:
00 / ■ г \ _ „2 ах
b(r^)=Yfnh[^)e n^- (Ю)
Л = 1
Постоянные Сп определяем из начального условия, которые напишем
так:
»(r,0)=fl(r)=fiCnJo(^) . A1)
п=\
С некоторыми допущениями, о которых было сказано в § 5 гл. IV,
функцию fx(r) можно разложить в ряд. Для этого умножим обе части
равенства A1) на г J0l pm-jf) dr и проинтегрируем по г в пределах от О
до R [напомним, что ортогональны не сами функции Бесселя, а
произведение У г JQ (^л~б-)]- Тогда, предполагая возможность
почленного интегрирования ряда, получим
R оо R
j rfx(r) J0 (pm-jA dr=Y± Cn^rJ0^n-^) J0 ^[xm-^j dr. A2)
Л=1 О
Покажем, что все члены ряда A2) при тфп обратятся в нуль.
Согласно соотношению B0) § 5 гл. IV можно написать
K(t*„4Wtw)dr = R[l'mJo(iln)Ji^)-^Ji{l'-m)Ji{lln)]. (i3)
j-
Rl-K^Rr »l~,l
Из характеристического уравнения имеем pnJx (рп) = J0(pn)Bi. Тогда
можно написать
V-mJo fan) Jl fam) = Bi/0 fan) J0 fam)>
V-nJQ fam) Jl fan) = Bi^0 fan) J0 fam)-
Следовательно, интеграл A3) равен нулю.
Если т = пу то воспользуемся формулой A9) § 5 гл. IV, которую
напишем так:
.ИИ
^=^№К) + ЛЫ1. A4)
242
Глава шестая
Таким образом, из равенства A2) при условиях A3) и A4) получаем
_0
R* 14ы + Аы]
X
X
J rfl (Г) J0 hn "Xj dr
Окончательно общее решение нашей задачи примет вид
»(гус) = ГС — Т (/тс) =
2а 14ы + Аьп)] w Jr/l {r)J° (^ -*)dr exp
A5)
Если fx(r) = Tc — Т0 = const, то интеграл в решении A5) равен [см.
формулу B4) § 5 гл. IV]
R
-^ f (Тс — Т0)/70 U^\dr =—^Jx(\lJ. A6)
о
Тогда решение A5) можно написать так:
/1=1
A7)
где
2/i Ы
РтЛ ^0 (^л) + J\^n)\
постоянные коэффициенты (так называемые
начальные тепловые амплитуды), зависящие от критерия Bi.
Решение задачи операционным методом. В § 5 гл. IV было
показано, что в случае симметричной задачи решение для изображения TL(r,s)
имеет вид
Ть(>-,*)-^ = А10(уТгу A8)
где А — постоянная, не зависящая от г; /0( j/_i_r) =«/0( *1/ — г ) -""
модифицированная функция Бесселя первого рода нулевого порядка.
Переход от модифицированных функций к обычным функциям
Бесселя может быть сделан по соотношению
/v(z)=rv/v(fe). A9)
Постоянную А находим из граничного условия B), которое для
изображения TL(r,s) примет вид
- TL (*,s) + Я [-£- TL (#,s)] = 0. B0)
Удовлетворим решение A8) граничному условию B0):
ГРАНИЧНОЕ УСЛОВИЕ ТРЕТЬЕГО РОДА
243
откуда
['•(/т")+тП'.(/^)]'
где 1± (г) = / о (г) = -^ z + -^ц"*:3 + gi^e" 2& + • • • — Функция, нечетная
относительно z[I1(— z) = —I1(z)]\ она играет такую же роль, как sh z.
Следовательно, решение A8) будет иметь вид
TL(r,s)-^f- =
lK a ; -m. BD
['•(К-г^+тУТ'^-г*)]
Решение B1) является однозначной функцией s и представляет
отношение двух обобщенных полиномов, причем полином знаменателя не
содержит постоянной, т. е. условия теоремы разложения соблюдены.
Найдем корни ф($), для чего приравняем его нулю:
*(S)=8 [/„ (j/X *)+4]/^р1 ( У\ R)] = §Ф (S) = 0' B2)
где выражение в квадратных скобках обозначено через ф (s). Из ра-
2
венства B2) находим корни: 1) s0 = 0, 2) ср (s) — 0, откуда sn = "~^бг *
где \ь = i j/_JLi?. Постоянные jx определяем из уравнения
+ -1-уГ-1-А(.'|/л_л) = ЛA.)-1^-|./1(|») = 0. B3)
Трансцендентное уравнение имеет бесчисленное множество корней \хп,
которые могут быть найдены графическим способом (см. выше).
Следовательно, характеристическое уравнение имеет вид
Ш - -БГ.^ . <24>
Находим вспомогательные величины
Ф'(*Л = Ф(*) + 5Ф'(*) =
Ч (s) +
2|/ш>
m)l(V-t«) + -B-V4r'{V-r*)]-
1
п
Ф@)
<|/ @)
— •« с ^ 0»
Ф(«„) st 2(Tc-r^W,Lj
*' («я) [(Я/? + 1O, ([,„) + Mi Ы11*» F V ' " «*
так как
1[(г) = J[(iz).
244
Глава шестая
Таблица 6.10
Значения постоянных А
2Bi
(^+BiVoW
Bi
0,0
0,01
0,02
0,04
0,06
0,08
0,1
0,15
0,20
0,30
0,40
0,50
0,60
0,70
0,80
0,90
1,0
1,5
2,0
3,0
4,0
5,0
6,0
7,0
8,0
9,0
10,0
15,0
20,0
30,0
40,0
50,0
60,0
80,0
100,0
оо
+At
1,0000
1,0031
1,0049
1,0102
1,0150
1,0199
1,0245
1,0366
1,0482
1,0711
1,0931
1,1142
I,1345
1,1539
1,1724
1,1902
1,2071
1,2807
1,3377
1,4192
1,4698
1,5029
1,5253
1,5409
1,5523
1,5611
1,5677
1,5853
1,5918
! 1,5964
1 1,5988
1,5995
1,6009
1,6012
1,6014
1,6021
-A%
0,0000
0,0034
0,0067
0,0135
0,0201
0,0268
0,0333
0,0497
0,0653
0,0972
0,1277
0,1571
0,1857
0,2132 .
0,2398
1 o,2654
1 0,2901
0,4008
i 0,4923
0,6309
0,7278
0,7973
0,8484
0,8869
0,9225
0,9393
0,9575
1,0091
1,0309
1,0488
1,0550
1,0587
1,0589
1,0599
1,0631
1,0648
+A*
0,0000
0,0013
0,0027
0,0052
0,0081
0,0110
0,0135
0,0202
0,0269
0,0401
0,0582
0,0662
0,0790
0,0917 -
0,1043
0,1167
0,1289
0,1877
0,2422
0,3384
0,4184
0,4842
0,5382
1 0,5825
I 0,6189
0,6491
0,6784
0,7519
0,7889
0,8195
0,8335
0,8396
0,8428
0,8463
0,8505
0,8558
-A,
0,0000
0,0008
0,0015
0,0031
0,0046
0,0062
0,0077
0,0116
0,0154
0,0231
0,0307
0,0383
0,0458
0,0533
0,0608
0,0682
0,0756
0,1117
0,1404
0,2114
0,2699
0,3220
0,3679
0,4080
0,4430
0,4735
0,5000
0,5901
0,6382
0,6827
0,7018
i 0,7112
0,7165
0,7212
0,7245
0,7296
1
H-As
0,0000
0,0005
0,0010
0,0021
0,0031
0,0041
0,0051
0,0077
0,0103
0,0155
0,0205
0,0256
0,0307
0,0358
0,0408
0,0459
0,0509
0,0756
0,0998
0,1463
0,1898
0,2301
0,2672
0,3010
0,3316
0,3593
0,3843
0,4760
0,5303
0,5853
0,6133
I 0,6227
0,6301
0,6398
0,6415
0,6485
-A*
0,0000
0,0004
0,0007
0,0015
0,0023
0,0030
0,0037
0,0056
0,0075
0,0112
0,0150
0,0187
0,0224
0,0261
0,0298
0,0335
0,0372
0,0554
0,0732
0,1084
0,1420
0,1735
0,2038
0,2317
0,2579
0,2826
0,3042
0,3913
0,4461
0,5062
0,5390
i 0,5544
0,5642
0,5770
0,5850
0,5896
Следовательно, решение нашей задачи имеет вид
где
\а
00 1
6 = Т(;с170Г° = 1 - Е4Л (ft.Tr) ехр (- *l Fo) .
[ _ 2Bi __ 2/j(^„) I
п [(Bi + l)Jt (л,) + ft, j[ (ft,)] ft, ft, [J20 (ft,) + J\ (ft,)]
B5)
B6)
Последнее преобразование сделано на основании рекуррентной формулы
v-n «f I0*/i) = Р/Л (pj — Л (Iх n)
и характеристического уравнения B4).
ГРАНИЧНОЕ УСЛОВИЕ ТРЕТЬЕГО РОДА
245
Постоянные коэффициенты Ап могут быть вычислены по
соотношению B6), которое может быть преобразовано в следующую формулу:
2Ш . B7)
Ап =
Jo ы К + Bi2 ]
По этой формуле были вычислены первые шесть коэффициентов Ап;
результаты расчетов приведены в табл. 6.10.
Для инженерно-технических расчетов на рис. 6.26 — 6.29 приведены
номограммы для определения бп (температура поверхности цилиндра)
и 6Ц (температура в центре цилиндра) по заданным Fo и Bi.
Анализ решения. Выше было уже отмечено, что при Bi -*- оо корни
Рп определяются из уравнения J0 (|хя) = 0, т. е. являются корнями
функции J0(pn). В этом случае коэффициенты Аю как это следует из
формулы B6), будут равны
А„ =-
Vn Ji (Рп)
Решение B5) становится тождественным решению C6) § 5 гл. IV,
если в последнем величину 6 заменить на A — б), так как при этом
задача на охлаждение заменяется задачей на нагревание цилиндра. Из
граничного условия C) следует, что температура на поверхности
цилиндра Т (R,г) сразу становится равной температуре окружающей
среды Тс и весь процесс нагревания сводится к выравниванию
температуры внутри цилиндра (внутренняя задача). В стационарном
состоянии (Fo — оо) температура в любой точке цилиндра равна
температуре окружающей среды.
При малых значениях Bi(Bi->0) все коэффициенты Ап-ч>0 [см. фор-
J (z)
мулу B6)], так как Jx (рп)-+0, за исключением Аг-> 1, а отношение -^ -^ 1,
когда z-^0, ap2 = 2Bi [см. соотношение (8)]. Тогда для малых
значений Bi решение B5) можно написать так:
0=l-/ofl/2Bl-^U-'2BiF°
B8)
В этом случае перепад температуры внутри цилиндра будет малой
величиной, и процесс нагревания определяется теплообменом между
окружающей средой и поверхностью цилиндра (в н е ш н я я з а д а ч а). Во
всех остальных случаях процесс нагревания зависит как от скорости
переноса тепла внутри цилиндра, так и от скорости теплообмена с
окружающей средой (краевая задача). Постоянные
характеристические числа (лл зависят от Bi, а следовательно, и от радиуса цилиндра.
Поэтому скорость нагревания будет обратно пропорциональна /г-й
степени радиуса цилиндра, где п лежит в пределах 1 < п < 2.
Ряд B5) быстро сходится, так как на основании неравенства
t*l < 1*2 < 1*3 < ••• < Рп< ••••
с увеличением \кп экспоненциальная функция ехр ( — j-^Fo) быстро
уменьшается. Поэтому, если исключить из рассмотрения малые значе-
IJJHii li-lXItttT 1 ITTTl I'tT tT И 1 г Г Hrn И Г
^^^^^щ^^^^^^^Щ
pj^jTpsir 14-MpHJ т М н"ГTTт4т~*""Н~Н1 ТТ1 \ \~Ы
ПгчТ^м^ ТггЦ Т MmnJ mtv '11 Т м
г1г1—h^NirTS-tJ—Р^|ч1г~1—HI—p^^Lj ~l—|—]—I—I—|—| TSsJ 1—1—j—1—1—f~ I'^sl—t—1—1—1—1—h"t1—i—1—i—1
11 v 1 1 1 ^SJ. FisJ Pn^L 1 f^1 li —^ 1 1 ! 1 ! 1 tv. 1 1 1 1 1 1 ! 1 III
I^^^h^^^^^H
^^АЦ^^^^^ЗД^ЗДД ^^Д ^ Цф^-Ш- H"wf '{"PR
IIN \NlH ItsH iг^гмт 1~ш4441Ц^Ф1 In! 11 KhAI-h
1Я#^^
^^^^дивн
ИШ ПЧ \ \ \ PH
Юй^^ 1 ll^^^l^P^Jfcfc^^a
l|L\Jll_|LJ 1 1 К1 1 1 1 1 | s'H^d~H iN~ » 1 FHJ1 |—f\J 1A1 \|\ \|\ ilil
Kl \\M 1 NN 1 nH-^ H t"H\NN \ m
111 niWl Kin inJ \11 ГК1 Гч. М м in 44 N \ \ Ml 11
IS 11\ l \ 1 \ 1 li^ 1 Гч! Pn. ! i^ !lll гч. 1 I\l Xniiili
III IftA | l\| [ -1 1 Й|4'4-4--14^-|ц]4^ l-44^j-4-4-4- \M £У\1АЦЦ[|-1
mfWil^n i Ш^ттг^^^т^ mTnI 11 Mtttttffli
[др^!]^^
[фрр^Щр^^ \ \i\ \|[
^№^^^^^^^^^^^^^^д
1д^^^^^^^иш [ш in m
НФ'^тиК! К1 IipJ 11111 hTSvJ llll mr^NdiNJ 1\11W IWUfl
н—ft".^?-]— лГ\ 1 i\j Г1 "J \. 1 1 1 1 1 1 1 iK] 1 1 1 1 \ 1 1 NJ l\. 1 l\j l\l \ \ \ 1 ffllfl
II 11 IV1 1 \ Nl I\j 1 14. II iSl 1 1 1 1 1 1 1 Pv \l X \ 1 Л liiilu
| 1 111 l\l 1 1 \l\ 1. 1 vLI I iSl 1J LJ l__J 1 1 x 1 1 1 1 1 1 1 1 \ 1 \ 1 l\l 1 A1 1 ill llilllj
О о —-
2 £ 2
О ^н
о
т
К
1=Г
X
О)
и
о
с
,— О)
К
S
о
оо
о
СО
о
см
о"
о
о
S
\\
I
J
4
1
j
J
=
1
—
1
s
i
=
i
Щ
=
_c
1
4*
3
5*1
В
В
s
ill
st^
i
ifcz
o4'
4 о
k;
0
:>
pp
T"^|_~~
p
!C
С
|
1
1
i
I
f-
э:
5-
1
E it
— \
u.
*=]
=
I
I
1
ч
= r
"С
Ц
:0
Шщ
Щ
Щ
и
^и
С
1
1
:*,
->
irS
■^
Э
—
|
|
3
I
~
1
1С
i
!
|
=^.
С
с
;c
с
о--
э :
L
Э,002
:cn
;0
0,00
i
с
:>;
5
c5
|
|
=
§
1
:0
-C->
1
s
1
1
I
1
1
я
и
=^
s
m
m
m
И
И
i
E
I
|
И
э
n
~f' T fi
-|—[—t—1
РРЯ
ИЯ
4ФИ
рш
ЯШ
гИйтН
■
дрд
о о ^
о •—'
о >-
о
о
«=t
о
о
о
о
н
о
S
К
я
ч
К
и
о
с
о
— ч
о
ч
«
00^
о"
со.
о"
с5
см
о"
о
о*
о
о
«к
о*
2
«а
о
в
sr
о
О
ев
с
о
к
ее
К
К
•в*
оо
о
К
а»
250
Глава шестая
4,0
8,0
12,0
1-6,0 -^U- 20,0
2,0
1,5
1,0
0,5
0
и и j M i I M I 1 1 1 ! 1 M t И Г M I M I 1 1 1 1 I 1 ! 1 I 1
и[ LintiTT I ГГГП"ТТ
0,4
0,*
1,2
1,6
Bi
-*- 2,0
Рис. 6.30. Зависимость между первым корнем jjlx
характеристического уравнения и критерием Био для
неограниченного цилиндра
Рис. 6.31. Зависимость между коэффициентом А\ и
критерием Био для неограниченного цилиндра
ГРАНИЧНОЕ УСЛОВИЕ ТРЕТЬЕГО РОДА
251
ния Fo, то можно ограничиться одним членом ряда, а остальными
можно пренебречь. Тогда решение B5) примет вид
6 = 1 — Аг J0 иг -^~\ ехр ( — [х2 Fo) при Fo > Fox
(нахождение предельного значения Fox см. в § 11).
Для удобства практических расчетов на рис. 6.30 и 6.31 построены
графики [ьг = /(Bi) и Аг — /(Bi) для значений Bi от 0 до 20 [при
Bi > 0,1 корень [хх можно вычислить по формуле A9) § 10].
Если число Фурье мало, то приходится брать несколько членов
ряда, и поэтому применение решения B5) для практических расчетов
затруднительно.
Найдем приближенное решение, пригодное для малых значений Fo.
В решении B1) для изображения разложим функции /0A/— R) и
h ( V — Rj B асимптотический ряд (см. приложение), так как для
малых значений Fo величина 1/—/? велика, т. е.
Т (г л Т0_(Тс-Т0)а -К*-г) A+-^Г + ^Щ^+---)УтН _
1 lV> s> a — ,r- e 1 / 3\ 1 / 15\
VS 1+^И-8'+8^^-Тб+'
(Tc — Г0) а е-я(К- r)
\ + ^[^+~-HR) + ...^Y^H,
qR \ 8r
sY .
где q — 1/ ——. Пользуясь таблицей изображений, находим
2Bi V—Fo i erfc — +
+ 4/4
где
■Го r r 2 У7Б
2 l/Fb"
R . з DS\.a *- *"
FoBi (-^ + ^ _ Bi) i2 erfc —e— , B9)
i erfc w = —— £ — & erfc &,
i2 erfc м = — ["A + 2^2) erfc a -
2 —#2~i
we
|/V
При разложении в асимптотический ряд предполагаем, что велика
не только величина 1/-~#» ной величина у —г. Поэтому для
малых значений г такое разложение будет несправедливо. В этом случае
(г-^0) функцию I0(qR) можно разложить в асимптотический ряд, а
^о(Яг)—в степенной, т. е.
/о(^)=1 +-5" ?*/* + ■...
22
252
Глава шестая
Тогда, производя аналогичные преобразования, получим
6Ц == 1 — 4 BiFo exp
4Fo
C0)
Решения B9) и C0) справедливы для небольших значений Bi. При
больших значениях Bi найдем другое приближенное решение для
температуры поверхности цилиндра.
Для поверхности цилиндра (r=R) решение B1) можно написать так:
TL(r, s) — -^ - Тс~Т° - ~ - Тс~~Т° —
[ + HR !0(qR)\
1 +
qR
1
HR 2HR
так как
h(z)
h (z)
1-8T+-
1
1
8z 128г2
Пользуясь таблицей изображения, находим
9n-—EV[l-exp[Fo(Bi--i-J].erfc(Bi-^-)|/Fo]. C1)
Решение C1) аналогично решению D1) §5 для шара, только вместо
(Bi —1) здесь входит множитель (Bi —
Подобно тому, как это было сделано в § 3, 5, можно показать, что
приближенные решения B9), C0), C1) дают вполне
удовлетворительные результаты и заменяют громоздкие вычисления по формуле B5).
В табл. 6.11 приведены значения 1—6П FП — относительная
избыточная температура поверхности цилиндра) для малых значений числа
Фурье при разных значениях Bi. Табл. 6.11 взята из упомянутой
работы Пешля. Приближенные расчеты по формулам B9) и C1) дают
результаты, хорошо согласующиеся с данными таблицы.
Таблица 6.11
Относительная температура на поверхности цилиндра 1—6n = ^(Fo, Bi)
Bi
0,1
0,5
1
4
10
20
50
100
200
500
1000
2000
0,0003
0,999
0,991
0,981
0,926
0,831
0,703
0,465
0,286
-0,156
0,064
0,032
0,016
0,0005
0,998
0,988
0,975
0,905
0,789
0,643
0,394
0,230
0,122
0,050
0,025
0,012
Числа Fo
0,0010
0,996
0,983
0,965
0,868
0,720
0,551
0,305
0,168
0,087
0,034
0,017
0,009
0,0025
0,994
0,972
0,945
0,815
0,611
0,421
0,205
0,107
0,054
0,022
0,011
0,006
0,0050
0,992
0,960
0,923
0,740
0,514
0,325
0,147
0,075
0,038
0,016
0,008
0,004
ГРАНИЧНОЕ УСЛОВИЕ ТРЕТЬЕГО РОДА
253
Bi
; 0,4 0,8 1,2 1,6 ^-2,0
1,lOhi"]4us i и м 1 1 1 1 1 1 | 1 | 1 1 1 1 1 1 1 1 1 1 1 1 | 1 1 I 1 1 I 1 I 1 1 1 1 !
LI *1 J 1 1 1 1 1 1 1 1 1 1 111 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1" 1 Ik I PW_ Ill
1 \ I 1 iN*_l III
■1 1 III 111 TrJ III
j in 111 ipJ. Ill
c\ * a ....... \, „.„. 11,.]...]..L.L iNLI 1
U,JO \ I пТТ |^v ill
\ 1 1 1 1 I 1 1 1 1 1 rNk. 1 rfl 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 л 1 11 1 1 1 1 1 1 rNk.ll II
1 \ 1 I 1 1 1 1 1 1 1 1 1 1 1 iTk. Til
1 1 1 1 1 1 1 l\l II Гтк.1 II 1
j 1 | | | I I | |\l I | I | I | | | | | I | | I | | |\l I ||
1 1 1 1 1 1 1 1 1 \ 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 INl1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
л on 1 1 1 1 1 1 1 1 1 M 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 T\_ II
1 1 1 1 1 1 1 1 1 1 M 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 ^1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 I\J 1 1 1 1 1 1 1 I 1 1 1 1 1 1 1 1 1 1 IV 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
II |\ I | I 1 | | | I 1 1 1 1 1 1 1 I L II Гл. 1 1 1 1 1 1 1 1 1 1 1 1 1 1 I I
1 1 1 INI 1 f III ГЧ. II
II л! II 114.1 1 1 1 1 1 1 1 1 1 1 1 1
n n.r \ 1 Py
U,oJ| 1 I 1 I 1 I I I I I 1 I I 1 |\ 1 1 1 N1 |
III [41 I | | | | 1 I 1 | | | | 1 1 | | | | I | iSl 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 11 1 1 1 il 1 r\_ III ivl
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 l 1 1л. 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 Гл.
Ill TSk. 1 II Tx
III TSkJ II iSj
U,ou TV 1 1 \J 1 1 1 1
1 " 1 1 1 1 1 1 1 i 1 1 1 1 1 1 1 1 1 11 1 1 1 1 1 TrJ III is.
Ill iW~ 11 л.
III I^tJ 1 1 11 1 1 1 1 1 1 1 1 1 1 Pv
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 [\1 1 1 1 1 1 1 1 1 1 1 1 1 14.
Пп^^+лх И
n.75i 11111111И И 11111111111 111 ТжттН г Ш
4,0
8J0
12,0
16,0
1,0
1
в,
0,9.9
0,98
0,97
0,96
Bi
-20,0
10,95
Рис. 6.32. Зависимость между коэффициентом В\ и критерием
Био для неограниченного цилиндра
Определение удельного расхода тепла. Найдем среднюю
температуру цилиндра по формуле
_2_
rw==iHr7>'T)
dr,
C2)
в которую вместо Т(г, т) надо подставить соответствующее
выражение из решения B5). Тогда, принимая во внимание равенство A6),
будем иметь
C3)
где
^ 2^^ или 4BI-
V-n n n t£(^ + Bi»)
C4)
т. е. коэффициенты Вп зависят от критерия Bi. Первые шесть
коэффициентов Вп приведены в табл. 6.12.
Ряд C3) быстро сходится, поэтому для не слишком малых
значений числа Фурье можно ограничиться одним (первым) членом
ряда. Для удобства расчетов первого приближения на рис. 6.32
приведены кривые ^^/(Bi) для значений Bi от 0 до 20.
Удельный расход тепла находится по обычной формуле
AQv = rt\T(x)-T0].
254
Глава шестая
Таблица 6.12
Значения постоянных Вп ■■
4Bi2
Н-дК+В!*)
Bi
оо
50,0
30,0
10,0
9,0
8,0
7,0
6,0
5,0
4,0
3,0
2,0
1,5
1,0
0,90
0,80
0,70
0,60
0,50
0,40
0,30
0,20
0,15
0,10
0,08
Bt
0,6917
0,7170
0,7359
0,8041
0,8133
0,8242
0,8375
0,8532
0,8721
0,8984
0,9225
0,9535
0,9694
0,9843
0,9868
0,9893
0,9916
0,9936
0,9955
0,9970
0,9983
0,9992
0,9995
0,9998
0,9999
в2
0,1313
0,1309
0,1289
0,1260
0,1229
0,1187
0,1132
0,1057
0,0953
0,0813
0,0625
0,0388
0,0240
0,0136
0,0114
0,0093
0,0074
0,0056
0,0040
0,0026
0,0015
0,0007
0,0004
0,0002
0,0001
в3
0,0534
0,0530
0,0529
0,0387
0,0361
0,0331
0,0296
0,0254
0,0207
0,0156
0,0103
0,0053
0,0032
0,0015
0,0012
0,0010
0,0007
0,0006
0,0004
0,0003
0,0001
в4
0,0288
0,0284
0,0268
0,0152
0,0137
0,0120
0,0103
0,0084
0,0064
0,0045
0,0028
0,0013
0,0008
0,0003
0,0003
0,0002
0,0002
0,0001
Вб
0,0179
0,0172
0,0155
0,0070
0,0061
0,0052
0,0043
0,0034
0,0025
0,0017
0,0010
0,0005
0,0003
0,0001
0,0001
0,0001
0,0001
в«
0,0122
0,0113
0,0097
0,0035
0,0030
0,0025
0,0021
0,0016
0,0012
0,0008
0,0005
0,0002
0,0001
0,0001
§ 7. НЕОГРАНИЧЕННЫЙ ПОЛЫЙ ЦИЛИНДР
Постановка задачи. Дан неограниченный полый цилиндр с
радиусами Rx и R2 и задано начальное распределение температуры в виде
некоторой функции /(г). Температура цилиндра зависит от радиуса
и времени. В начальный момент времени цилиндр помещается в среду
с постоянной температурой Тс. Коэффициенты теплообмена
наружной и внутренней поверхностей различны (а±=1=а2). Найти
распределение температуры в цилиндре в любой момент времени.
Дифференциальное уравнение теплопроводности написано в § 5
гл. IV. Начальные и граничные условия можно написать так:
Т(г, 0) = /(г),
О)
B)
C)
Решение задачи методом разделения переменных. Вначале наша
гем
D)
задача на нагревание цилиндра сводится к задаче на охлаждение путем
замены переменной
.(Г> т) = Гс —Г(г, т).
ГРАНИЧНОЕ УСЛОВИЕ ТРЕТЬЕГО РОДА
255
Затем находится частное решение дифференциального уравнения
аналогично решению задачи для полого неограниченного цилиндра при
граничных условиях первого рода.
В результате всех преобразований решение нашей задачи будет
иметь вид
Ь(г,
0
= т -
х с
-Т(г,
х) =
00
2£.
л=1
ехр(-
-ар2п
*)
к
(р«.
г),
где рп являются корнями характеристического уравнения
[-у Л (pRi) + Ph (pRx)] [~ У о (PRJ - рУг (/*»)] -
r-[-YJo(pK2)-pJi(pR*)][~ Y0(pRi) + pyi(pRi)] = o. F)
W0(pn, r) есть линейная комбинация бесселевых функций!
W0 (р„, г) = - [2L Y0 (рМ+р^ (р„^)] J0 (Pnr) +
+ [рЛ Mi) + ~J0 (PnRi)] У о 0>Л G)
Число Еп является коэффициентом разложения в ряд функции
fi(r) = Tc-f(r) (8)
по функциям W0(plt r), W0(p2, r)...:
h(r)-^EnW0(Pn,r). (9)
Расчет показывает, что
J Rt M
x {{pI+Щт- Jo(PnRi)+ PnJAPnRdJ -U + w)x
X [if J0 (ft.**) - Pnh (Pn^Jf1* . A0)
Можно написать решение в иной форме, если обозначить ря/?1=(х
и Fo = от//??. Эту форму записи решения задачи и
характеристического уравнения F) предлагаем сделать читателю. Если в решении E)
положить а± = оо, а а2 = 0, то получим решение рассмотренной в гл. IV
задачи.
Если же принять равномерное начальное распределение
температуры
T(r, 0) = /(r) = ro = constf A1)
то из решения E) получаем решение задачи Г. Карслоу и Е. Егера
[91]. Данная задача может быть решена методом интегрального
преобразования, который будет рассмотрен ниже при решении более общей
задачи, когда температура среды есть функция времени.
256
Глава шестая
о
о"
CD
CD
CD
ОО
о'
О
—ГО
—ю>
г Г frfc
[VI |/-]Ф
it If j^r-
Ш40
И-|\ 1 о
11 1 II 1 /
1Г1 1 " I I
II 1 Г
1 If Iff /
1 Iff ff /
Will и/
и! У
VI 1
11/ 1
5*
5*
1
Р
^
i
1Г
О
1
1
ш
V
1
1
Ш
v
=
1
:ч
= С
«О
zlTV
1
1
^
^о
^
5
: II
Ё
к'
л
:о"
1 с41
1 СсГ
и
И
5°
чгт
fNjb
j и
~1 *■"
\Sk
fcp
So
■И*-
.J L.
.....
31
1Ё1
ЩВ
И
У
V
\/
ZL
Цц|44^
1~вй1
Ц-4 I ]~
■SprF
Lr
смф
\А \ 1 1
г
Г
\\ \, [Tj^j^^1 Н°? ^^
1 L 1 _L[otvJ -1 1
|| | |-|-|-| | ^Ч^.|-| \\
^t+TSJ^UJ^
ЕтйМ^^Т^чЦ.. 1 iJz.l-L-p
1 \\ I l°*ThLI 1 1 1~т
1 1 \Jf* Р\ 1 1 1"SKL I I ~t
\А П^Ц>-Г*1Ч-1Л^М/1
4 mt4JSh3i
=4= i rC{—|—[—1—|—|—1
\ 1 1—i jt\ 1 1 1 1 1 ^^H
и | |^| | | | | =g=|C.
t 4° л*
| 1 jzz-t ---t/\ J—1
JAji M±4flzJ
-4— l**T V ' • • 1 jH i
4 1 ут Г1 "Hfc/rl
- |Ni^(—гЧ—r——xH—1
4ЖТ ppJ И И
arfl \| У/ flit
J^iiv 1 1 \"I.A /И
rxir i—i ]^ i /i \ \m
Р^К%_УЧ%-1 1^1 \ Т1Ч
/1 Нв=ЯвЯ|
—1 1 -j 1 1 1 1 1l \Ш
1 1 1 1 -j—|-0{ЕЕрг|
1 1 1 1 / 1 1 1 1 1
J 1/ LLLL1
Ко
^
r4 K
S
О
4
О
в
CO
о"
CN
о
о,
о'
о
К
о
н
VO
8Я
о
о
и
н
о
«
К
К
CD
ч
О)
CU
CU
с
о
«.
ч
Он
К
ГРАНИЧНОЕ УСЛОВИЕ ТРЕТЬЕГО РОДА
257
о
о"
с*
°9.
с"
1 1 1 1 1^
ГУ '|"i с
|.\у- |—{-={==
[_\ || О
I л[ о
1\1 М 1
\ 1 >L
У N
1 \/1 V4*
Ш 1/
111/1'
S=
0,5
■о ■
-О ■
1
9
/
"О
Щ
~о
4 =
:оч
= L
2j
Id
°*\
W
■c
DC
;6f
■O
~pp
djp
IfCN;
1 D
3 1
CM
1
■sjf-l
Щ=с
Щ
4—. '
7^
n
Zj
I
i
ЕЕ
Щ
1
^^
'o
1
I
|
Ш
=
I
-4
-O.
ц
si
■
Щ
4,
gin I
^s
1
|
s
I
1
-
|
|
5
I
|
=
1
|
^
ГоЁ
■?
2
1
kf
i
loi
EC
:__
1
=4
_j
1
I
—
1
1
I
f
i
g
1
1
о
LO
1/1
f-
H--4-J
411
ЯЗВ
jppg
ши
1 1-M
-го о *c П
2 ^ 4»
c*
to
О
О
О
о
I!
и
к
s
о
§.
с
«
H
u
о
к
a*
CD
ca
о
с
■8
о
Е-
о
к
t?
я
о
о
ад
о
. к
О)
S
р*
G
о
3:
К
м
К
со
О*
9 Заказ № 640
258
Глава шестая
ГРАНИЧНОЕ УСЛОВИЕ ТРЕТЬЕГО РОДА
259
261
Для практических расчетов на рис, 6.33 — 6.37 приведены графики
относительной избыточной температуры на поверхностях полого
цилиндра как функции чисел Fo и критерия Bi при значениях отношения
jRx/jR2 от 0,2 до 0,9. При этом было принято, что начальное
распределение температуры равномерное A1), коэффициенты теплообмена а±
и а2 одинаковы (Bix = Bi2 = Bi).
§ 8. ЦИЛИНДР КОНЕЧНЫХ РАЗМЕРОВ
Постановка задачи. Дан цилиндр радиуса R и длиной 2/,
температура которого равна Т0. В начальный момент времени он
помещается в среду с постоянной температурой Тс>> Т0. Требуется найти
распределение температуры в любой момент времени при условии
симметричной задачи (см. рис., 4.27).
[меем
дТ(г, г, х) __а 1&Т{г, г, т) ±_ дТ(г, г, т) д*Т{г,-г,
дх { дг2 г дг йг2
(т>0; 0< г < Я; —/<'«<+/).
J±)
A)
B)
C)
D)
E)
F)
Начало координат находится в центре цилиндра.
Т f(r z х\
Решение задачи. Докажем, что относительная температура —— v ' ' ;
Т(г
_dT(R, г,
дг
дТ@, г,
дг
дТ(г, 1,
дг
, z, 0) = Т0
±'+И[Тс-
-^- = 0, Т
±+Н[Тс-
дТ(г, 0, т)
dz
= const,
-T(R,z,
,)] =
@, г, т)^=оо,
-Т(г, 1,
= 0.
•*)] =
0,
= 0,
Тс-Тй
G)
в любой точке цилиндра равна
Тс — Т(г, г, т) = Tc — T(rt т) аГс-Т(г, т)
где Т(г, т) и Т(г, т)— температуры в той же точке неограниченного
цилиндра и пластины, пересечением которых образован цилиндр
конечных размеров.
При этом начальные и граничные условия для неограниченного
цилиндра и пластины остаются такими же, как и для цилиндра конечных
размеров, т. е.
T(r, 0) = 7(z, 0) = Г0, (8)
_дт(g, -)+H[Tc_T{R< т)] g Q) (9)
дТA' т) +Я[ТС-Г(/, тI = 0, A0)
дг
дТ@, -с) = дТ@, т) ^q
(И)
262
Глава шестая
Напишем соотношение G) в виде
Т(гш г, x) = Tc~^[Tc-T(rt *)].[ТС-Т{г, т)], A2)
где ДТ = Гс — Т0, и подставим его в дифференциальное уравнение A).
После преобразования получим
[Гс-Г(г,,)]{<^^а<^} +
+ [Гс-Г(г,,)]{^^_а(^^ + Х^^)} = о. A3)
Выражения в фигурных скобках равны нулю, так как T(rt x) и
T(z, т) являются решениями соответствующих уравнений.
Следовательно, соотношение A2) удовлетворяет уравнению A).
Подставим A2) в начальное условие B):
Г (г, г. 0) = Гс--^г[7;с-Г(г,0)].[Тс-Т(г.0I = Гв. A4)
Тогда получим тождество
Т(г, г, 0) = Тс- J-(rc-T0)(rc-T0) = Т0,
так как
ДТ = Тс — Т0.
Таким образом, решение A2) удовлетворяет начальному условию.
Подставим A2) в граничные условия C) и E):
{_«^J> +Н[ТС-ПИ.*)]} T'~lf%) -0. A5)
i-dT{ldzx) +H[TC-T(t, *)]}Тс~~^т{Г' T)-Q> A6)
Выражения в фигурных скобках равны нулю на основании условий
(9) и A0), следовательно, решение A2) удовлетворяет граничным
условиям.
Таким образом, решение G) удовлетворяет дифференциальному
уравнению, начальным и граничным условиям и по теореме
единственности является решением нашей задачи. Итак,
со со
я=1 ш=1
iAn
.гЛ/^я,
1 — 8 =
Tsl
1 -j-A COS pm
~T(>
Тс-
2
■2т
ехр
Л =
[-(%"
/2
-1
от],
A7)
где Ап, и Ат, 2 — постоянные коэффициенты, определяемые по формулам
Д|.1 =
уо (fV
2Bii
:)[d.+Bi1]
4 _, ir+i 2BI,VBI? + ^.,
' Л"- < l) ^..(Bli+BL+rf,.,)'
где (xrt( ь [xmt 2 — корни соответствующих характеристических уравнений.
Необходимо отметить, что коэффициенты теплообмена для боковой
и торцовой поверхностей могут быть отличны друг от друга; такое
ГРАНИЧНОЕ УСЛОВИЕ ТРЕТЬЕГО РОДА
263
же замечание можно сделать в отношении других теплофизических
коэффициентов. Таким образом, решение A7) будет справедливо для
анизотропного тела.
Для малых значений Fo можно взять соответствующие
приближенные соотношения из решений для неограниченной пластины и
неограниченного цилиндра* так как решение нашей задачи состоит из
произведения решений этих более простых задач.
Средняя температура конечного цилиндра находится по формуле
Если подставить вместо Т(г, z, т) соответствующее выражение из
решения A7), то после интегрирования получим
= 1
2 ^Bn,iBm,2exp
п=\ т~\
2 2 \
R2
Р
A8)
где
Вт. 2 =
2Btf
Вп, 1
4Bi?
Удельный расход тепла находится по известным соотношениям.
§ 9. ПЛАСТИНА КОНЕЧНЫХ РАЗМЕРОВ
Постановка задачи. Дана пластина конечных размеров 2RXX2R2X
X2RS (параллелепипед), температура которой равна Т0, В начальный
момент времени пластина помещается в среду с постоянной
температурой ТС>Т0. Требуется найти распределение температуры и
удельный расход тепла в любой момент времени.
Поместим начало координат в центр параллелепипеда (см. рис. 4.26),
так что Rv R2, Rs— соответственно половина размера пластины по
трем направлениям (по осям х, у и г).
Для такой трехмерной задачи имеем
дТ(ху г/, г,т) 9~,
-—1 \у' ' = ау2Т(х, у, z, т)
(т>0; —Rt<x<+Rt{ -R2<y<j-R2; -R3<z<+R3),
Т(х, у, г9 0) = Г0 = const,
4ZdT(±R1 у, z, *) + H[Tc-T{±Rl9 у, г, т)] = 0,
ох
=F EJ^^l^l^L + н [Тс- Т(х, ±Rt, z, т)] = 0,
ду
dz
(i)
B)
C)
D)
E)
Распределение температуры симметрично относительно центра
пластины.
264
Глава шестая
Решение задачи. Аналогичным способом, как и в предыдущей
задаче, можно доказать, что решение поставленной задачи можно
представить в виде произведения решений для трех неограниченных пластин,
пересечением которых образован данный параллелепипед, т. е.
Тс — Т(х, у, 2, т) _ТС — Т(х, т) Tc — T(y,z) Tc — T(z,t)
Т/Т» /XI ГТ1 ГТ% ГТЛ ГГ\ ГГЧ
с — * о * с—■* о * с — *о * с — -'о
F)
где Т(х, т), Т (у, z), T(z> т) — температуры соответствующих трех
неограниченных пластин.
При этом решения для Т{ху т), Т(у, т), T(z, т) удовлетворяют
соответствующим дифференциальным уравнениям A), начальным
условиям B) и граничным условиям, аналогичным C)—E),
Доказательство производится тем же способом, поэтому мы
предоставляем его читателю.
В результате решение нашей задачи можно написать так:
СО ОО 00
Г(*'у'г-т)~Го * 1 - 2 2.2 4,. i4.f 2 Ам, з х
*С ° «1 «,—1 Ь 1
/г=1 т=1 /г=1
X cos [лЛ, 1 ~ cos (xWt 2 -~- cos fi*t з -^- exp
Al Д2 A3
2 2
^m,2 , ^, з
*<9 *<Я
G)
где
,_ 2sinp, _, (я, т, «,) + ! 2Bi V Bi2-j-;ла
(j. -f sin [j. cos [A — ^ ' (x (Bia + Bi + ja2) '
ctgl*—sr1*' (8)
Bi,= -f££ (i= 1,2,3). (9)
Если длина 27?2 и ширина 2R3 велики по сравнению с толщиной
2RtBR2 = 2R3-± oo), то решение G) превратится в обычное решение
B9) § 3 для неограниченной пластины.
Для подсчета удельного расхода тепла необходимо определить
среднюю температуру пластины по формуле
р D р
Т W = pop f f fГ <*' *» Z' X> ^^ (! °>
Подставим вместо Т(х, у, z, 1) соответствующее выражение из
решения G), тогда будем иметь
"ё = !-22 2 Bn.iBm,2Bk,,exp\-(^ +
+^r+^rjoxJ' A1)
ГРАНИЧНОЕ УСЛОВИЕ ТРЕТЬЕГО РОДА
265
где
2Bi2
В = ^— . A2)
{л2 (Bi2 + Bi + р2) v '
Для практических расчетов можно воспользоваться
соответствующими графиками jxlfi = /(Bi^), A\ti = /(Bi^ ц Bi,/ = /(Bij), где i =
= 1, 2, 3. Для более точных расчетов необходимо брать значения {А,
А, В из соответствующих таблиц.
Для малых значений Fo можно взять соответствующие
приближенные решения для неограниченной пластины (см. § 3).
Решение G) справедливо и в том случае, когда по всем трем
направлениям х> у, z термические коэффициенты будут различны, т. е. в
случае анизотропного тела.
§ 10. АНАЛИЗ ОБОБЩЕННОГО РЕШЕНИЯ
Сделаем анализ решений рассмотренных задач. Для тел простейшей
геометрической формы (пластина, шар, цилиндр, параллелепипед)
решение задачи на нагревание в среде с постоянной температурой
(граничное условие третьего рода) можно написать так:
-£=£- =| П/..,ф(^.^)ехр[_^,,|-)ро„], (,)
где Anf i = (An, i4,2 Аг, з) — начальные тепловые амплитуды, зависящие
от начального распределения температуры и геометрической формы тела;
Ф(Рл,/—) — функция, учитывающая изменение температуры по
координатам (х = xv у = xv z = хв); Rt, i?2> Rs — размеры тела; Rv —
обобщенный размер тела, равный отношению объема тела (V) к его
поверхности (S), т. е. Rv = — (для неограниченной пластины Rv =* /?, для
неограниченного цилиндра Rv = — R, для шара Rv = —R); [ая, * —
£ о
корни характеристических уравнений, причем
Pi, i < ^2, * < рз, * < • • • < t4 t < ...; B)
Fo^=—\ число Фурье, в котором в качестве определяющего разме-
pa тела взят обобщенный размер.
В силу неравенства B) каждый последующий член ряда A) с
увеличением Fo^ будет исчезающе малым по сравнению с предыдущим,
а сумма всех корней будет отличаться лишь на малую величину от
величины первого члена. Поэтому, начиная с определенного значения
числа Фурье Fo^ можно ограничиться одним первым членом ряда, т. е.
" ^0 i—\ \ %i
npnFoz;>Fo1. C)
Начиная с этого значения Fo^ зависимость между (Тс — Т) и
временем т будет описываться простой экспонентой.
Логарифмируя C), получим
Тс-Т 3
In
•То
|{1пА,,ф(,,,^)-(,,,^)«^}. D,
266
Глава шестая
ln(Tc-T,)
ln(Tc-T2)
Рис, 6.38. Логарифм температурной разности
как функции времени в процессе нагревания
1п[тс-т(&д)] Таким образом, графическая
^|ста*ия~.~ 1нн^ ли^ зависимость между lnGc— T)
и временем будет иметь вид
прямой. При длительном
нагревании (Fo^-^oo)
температура во всех точках тела
одинакова и равна Тс (стационарное
состояние).
Следовательно у весь процесс
нагревания можно разделить
на три стадии. Первая
стадия неупорядоченного режима
характеризуется тем, что
здесь большую роль играет
начальное распределение
температуры. Всякая
неравномерность в начальном
распределении отражается на
распределении температуры в следующие моменты времени. Зависимость меж-
ду (Тс — Т) и т описывается рядом A). Вторая стадия называется
регулярным режимом. Зависимость между (Тс—Т) и т описывается
простой экспонентой (рис. 6.38). Распределение температуры внутри
тела описывается функцией Ф и не зависит от начального
распределения, так как величины A\j входят в качестве множителя, т. е.
определяют масштаб, а не сущность явления. Третья стадия
соответствует стационарному состоянию (Fow = оо), при котором температура
во всех точках тела равна температуре окружающей среды.
На рис. 6.38 приведены графики величин 1п(Гс — Т) как функции т
для поверхности и центра тела. Из рис. 6.38 видно, что в стадии
регулярного режима эти графики имеют вид прямой. Если в начальный
момент времени температура во всех точках одинакова и равна Т0, то
кривые должны исходить из одной точки.
Так как поверхностные слои нагреваются быстрее, чем центральные,
то кривая 1п(Гс — Т) = f(t) в первой стадии для центрального слоя
обращена выпуклостью к оси ординат, а для поверхностных слоев — к
оси абсцисс (см. рис. 6.38).
Вышеприведенный анализ справедлив для тел любой формы.
А. Г. Темкин показал [74], что задачу на нагревание тела сложной
формы можно свести к задаче на нагревание тела основной формы
(пластина, цилиндр, шар) путем введения критерия приближенного
подобия.
Тангенс угла наклона прямой (стадия регулярного режима) будет
равен
tgA80 — ф) = — tg<|> = 1п(гс-П)--1п(Тс^-72) = m = const E)
Т2 — Tj
Постоянная m есть скорость изменения логарифма избыточной
температуры по времени, т. е.
д[\п(Тс — Т)]
dz
m:
F)
она является одинаковой для всех точек тела, а также для средней по
объему температуры Т и называется темпом нагревания или
охлаждения тела. Из равенства D) имеем
ГРАНИЧНОЕ УСЛОВИЕ ТРЕТЬЕГО РОДА
267
т= - ■•• • ■**
2 К- * £- р)
Следовательно, численное значение т определяется теплофизическими
коэффициентами, размерами и формой тела.
На основании равенства F) и граничного условия третьего рода для
тела любой формы можно написать следующее равенство,
справедливое в стадии регулярного режима нагревания:
C4V ~k = «S (тс- Тп) = ciV (Тс- Т) т.
(8)
Отсюда получим
где
т = _gg- . гс-_Гд = _g£_ig = -i.Kn, (9)
Кп = В1Д = -£ ЯД A0)
7* 71
— критерий Кондратьева1), ЧГ = —9—=-— параметрический крите-
Тс-—Т
рий, характеризующий неравномерность температурного поля, так как
он равен отношению избыточной температуры поверхности тела к
средней по объему тела избыточной температуре. Если распределение
температуры в теле равномерное (Вц-^0), то ЧР" = 1. Чем больше
неравномерность температуры, тем меньше W. При ЧГ=0
неравномерность распределения температуры наибольшая (Вц-х», а ТП~±ТС).
Таким образом, критерий Кондратьева характеризует не только
неравномерность температурного поля, но и интенсивность взаимодействия
поверхности тела с окружающей средой.
Теория регулярного режима Кондратьева исходит из основного
соотношения F), т. е. отношение локальной скорости нагревания к избыточной
температуре есть величина постоянная:
дт I 1 \
-g^ Tc-T j=^-const, A1)
Нашими работами (см. § 5 гл. IX) было показано, что более общим
признаком регулярности нестационарного температурного поля является
постоянство отношения скорости нагревания к средней избыточной
температуре, т. е.
dT ( 1 \
ST[ тс-~т )~m=sconst- a2>
Значения [хх в зависимости от Bi для характеристических уравнений
основных тел приведены в соответствующих таблицах. Можно найти
приближенные формулы для расчета [хх в зависимости от критерия Bi.
Из (9) мы получаем важную зависимость теории регулярного режима
кп - та. _.=£-2(к. .-£■)". 03)
1) Критерий Bi^l1, является основной величиной, определяющей характер
теплообмена тела в стадии регулярного режима, и назван в честь выдающегося теплофизика
Г. М. Кондратьева, впервые изучившего законы охлаждения тела в этой стадии. В
отличие от критерия Коссовича Ко критерий Вц¥ обозначаем через Кп.
268
Глава шестая
Щ
0,8
0,6
0,4
[Кп
Й!
Biv
Рис. 6.39 Универсальная приближенная
зависимость Кп=/(Вц);
1 — для пластины, 2 — для шара, 3 — для цилиндра
Следовательно, критерий Кп
определяется формой тела и
характеристическими числами [*it г,
I*if 2» И-i, з, а значит, и критерием
Био, так как характеристические
числа являются функциями
критериев Био.
Оказалось, что кривые Кп —
= /(Вц,) для геометрически
совершенно различных тел: шара,
параллелепипеда, цилиндра и др.
— настолько близко
располагаются друг к другу, что практически
все семейство их можно заменить
одной осредненной кривой (рис.
6.39).
Аналитическим выражением
этого является соотношение Н. А.
Ярышева
W =
Кп
Y Bi*+1,437 Bi„+1
A4)
Если Bi„-*0 (практически достаточно, чтобы Bi^<0,l), то Тп->Т
(W = 1), Следовательно, критерий Кондратьева будет равен критерию
Био:
(KnH = Bv A5)
В этом случае темп нагревания m равен
m
Я
(КпH^
c^Rv
A6)
Если Bi^, ~> оо (практически Вц> 100), то критерий Кондратьева
будет величиной постоянной
(Кп)» = 2(и-Ь)«
1=1
*?
const.
A7)
В этом случае темп нагревания прямо пропорционален коэффициенту
температуропроводности {первая теорема Кондратьева):
(тH
(Кп)с
A8)
Таким образом, критерий Кп лежит в пределах от нуля до некоторой
постоянной величины (Кп)<», которая определяется формой тела.
Рассмотренный характер кинетики нагрева по предложению
Г. М. Кондратьева назван регулярным режимом первого рода. Его
начало для центра пластины и цилиндра в зависимости от Fo, Bi^,
температурного симплекса центра Т@, Fo) = -~—~к
допустите ' 0
мой погрешности расчета е приведено на рис. 6.40 и 6.41. Из этих
рисунков видно, что при малых значениях критерия Био центральные
точки рассматриваемых тел достаточно быстро вступают в стадию регу-
ГРАНИЧНОЕ УСЛОВИЕ ТРЕТЬЕГО РОДА
269
Оц
0,9
0,7
0,5
(
10°/Г*
3,04
29^5
0,12
0,
0,20
2%^
е=0,
°/0 ^^*
0,28
0,36
Г—, F-]
\#?
p-Ofln
,-0,5-]
ГТо1
3
JO
0,44
Fo
Рис. 6.40 Зависимость начала регулярного теплового
режима от Fo, Bi и допустимой погрешности расчетов
s (%) для середины пластины
0,6
0,4
^0%^
5°^^
2%^
1%^
0,5%
0,2%V
е=
),1%^
VS?
\0
>Ч^
Bi:
4sn£
0,2
Н
*-Д5.
i"
i5
0,04
0,12
0,20
0,28
0,36
0,44
Fo
Рис. 6.41. Зависимость начала регулярного теплового
режима от Fo, Bi и допустимой погрешности расчетов
е (%) для оси неограниченного цилиндра
лярного режима. С увеличением критерия Био относительное время
регуляризации растет, достигает максимума при Bi ^ 2 и при
дальнейшем увеличении Bi снова несколько уменьшается. При одинаковых в и
Bi момент начала стадии регулярного режима наступает раньше по оси
цилиндра, чем в центре пластины.
На рис. 6.42 приведены графики зависимости lg ' -L^
А
1
от lg Bi
для основных тел. Из рис. 6.42 видно, что точки хорошо расположены
на прямой. Следовательно, можно написать
(и?)- 1
л
л
или
«4
(Щттш]'
A9)
B0)
где ((х^оо — значение [лх при Bi = оо [характеристические числа ([%)оо
являются постоянными числами; например, для шара ((л^с = тс, для
цилиндра ((х^ = 2,405 и т. д.].
270
Глава шестая
Н2'
и"
2
igBi
к+1
к-ь2 к+3
к+4
Рис, 6,42. Зависимость между
безразмерной величиной [( ^i)oo / H-f — О и
критерием Био:
/—для шара, 2—для цилиндра, 3—для пластины
Рис. 6.43. Оценки
приближенности решения
Из рис, 6.42 можно определить постоянные Auk. Для
неограниченной пластины А = 2,24, k =1,02; для неограниченного цилиндра
А = 2,45, k = 1,04; для шара А = 2,70, & == 1,07.
Таким образом, пользуясь соотношением B0), можно вычислить
критерий Кондратьева по формулам A0) и A5) для любого тела.
Соотношение регулярного режима
Тс-Т= П Ai, ,Ф
И-1. /^т")ехр(—KnFo„)
B1)
послужило Г. М. Кондратьеву и его ученикам основанием для
разработки новых методов определения теплофизических коэффициентов
различных материалов. Однако применение решения при граничных
условиях третьего рода (Bi=^=oo) для определения коэффициентов
теплопроводности и температуропроводности встречает большие трудности
в реализации граничных условий.
§ 11. ОЦЕНКА ПРИБЛИЖЕНИЯ
Применение полученных решений в § 3—8 для практических
расчетов требует оценки степени точности приближенных соотношений,
когда из решения отбрасывается несколько членов ряда. Особенно это
необходимо при расчете в случае малых значений числа Fo, когда
приходится брать несколько членов ряда. Рассмотрим метод оценки на
конкретном примере.
Возьмем решение B9) § 3 для неограниченной пластины и положим
х = /?, что соответствует температуре на поверхности пластины, т. е.
л=1
где
1 — еп = ^ К cos fx„ exp (— jx^Fo)»
2Bi(Bl»+<fl1/2
fl„ (Bi* + Bi + $ '
4, = (-l)»+i.
A)
B)
ГРАНИЧНОЕ УСЛОВИЕ ТРЕТЬЕГО РОДА
271
|хл—корни характеристического уравнения
tgp = -~. C)
Подставим в решение A) вместо cos^w соответствующее выражение,
используя характеристическое уравнение
IcospJ = A + tg>„)-1/2 = |l 4- -Ц- Г,/2= !*„ (^ 4- Bi»r,/2.
Следовательно, имеем (учитывая, что cos^ =* (•—1)л+11 cos р.л |):
с»
'-"■-2BiI] а + в/р + ц) "Ч-"**» D)
Обозначим остаточные члены ряда D) через
09
*'-M'S ^■'ctiB|"-<B* <5)
Из характеристического уравнения C) видно, что каждое значение \ъп
отличается от предыдущего немного меньше, чем на к (см* рис. 6,43).
При Bi -* О каждое \ъп больше предыдущего точно на я, а при Bi -+ оо
р„=BЛ-1)-|-.
На рис. 6,43 показан ход кривой ф^ в зависимости от \ьп. Из
кривой рис. 6.43 следует
Ф*
<~ 1„.+<,;в1)в,'""'<-'"р°"'- <6»
«4
Так как площадь а больше площади Ь, то можно написать
4" J (~)>4W G)
где срА — член ряда E), или
*Ч
*+т *+т
J (~)= J (~)+ J (-) + •
*+т *+f *+т
Обозначив C = A 4- Bi) Bi, получим
»*<-?" Г^ТТ ехР <-«*"Fo> = ПГ- f 7= ехР <-°Fo + ^F°) dv>
*» И&+Р- (8)
где [j.2 4- p = p.
272
Глава шестая
Окончательно имеем
о-и
k + — J
Fo/н.2 t + р
Значение интеграла в выражении (9) может быть взято из
соответствующих таблиц.
Приведем конкретный расчет. Требуется найти, с- какого значения числа Fo
можно пренебречь всем рядом D), за исключением первого члена, если требуемая
точность составляет 0,25=%.
Пусть Bi = 1,00; тогда ^ = 0,86, ^2 = 3,426 (см. табл. 6.1).
В нашем случае &= 1; следовательно, ^ 3 =2,14 ( ^3 находим как среднее а риф-
Т Т
метическое ^ и f*2), а Р = 2. Имеем
00
0,0025 < l-—expBFo) Г e~U du, A0)
2,14ti J "
6,6Fo
00
0,01685e-2Fo< Г e~U du = — Ei(—6,6Fo), A1)
6,6Fo
где
oo
Ei(—z) = — Г e~U da. A2)
z
Задавая различные значения Fo, вычисляем отдельно правую и левую части
неравенства A1). В результате находим такое значение Fo, при котором левая и правая
части этого неравенства дают одинаковые численные значения.
Для нашего примера находим: Fo > 0,55.
Более точное решение можно получить графически. Таким образом, начиная с
Fo> 0,55, можно ограничиться (с точностью до 0,25%) одним членом из всего ряда A).
В работе Пешля приводится такой пример: чтобы высчитать с
точностью до третьего знака после запятой значение бп для Fo = 0,0003,
необходимо взять 36 членов ряда A).
Аналогичным методом можно показать, что оценка ряда
00
9n=y]-Vexp(-^Fo) A3)
может быть выражена следующим соотношением:
**<тйг-г Г '-£-**• A4)
2 / 2
Неравенство A4) дает возможность получить следующую оценку
ряда: с точностью до 0,25% мфжно пренебречь всеми членами ряда A3),
если Fo>-l,0 (при расчете принимаем: к = 0,\ь1 = —\.
Рассмотрим метод последовательных приближений для вычисления
корней характеристического уравнения. В первом грубом приближении
ГРАНИЧНОЕ УСЛОВИЕ ТРЕТЬЕГО РОДА
273
находят графическим путем корни характеристического уравнения,
например, для цилиндра
ЬШ. = J-a. A5)
Логарифмируем уравнение A5):
ln|/1([x)| + lnlx-lnBi = ln|/0(ix)|. A6)
Пусть значение первого корня равно ^°{. Подставим это значение в
левую часть уравнения A6) и по вычисленной левой части находим \*>[ из
правой по формуле
ln|/1(lxO)|+lnlxO-lnBi-ln|/0(ix;)|.
Затем в левую часть уравнения A6) подставим р.| и из правой части
находим у*J по формуле
in | jx (jij) | + in p.; — in Bi = in | /0 (p.;) |,
Этот процесс продолжается до тех пор, пока из уравнения
in | Jx (^>) | + in р,<"> - In Bi = In | /0 (pf+D) |
в пределах заданной точности получим
р(п+1) = ^(/2) в
Такие же вычисления необходимо выполнить и для остальных корней.
ТЕМПЕРАТУРНОЕ ПОЛЕ БЕЗ ИСТОЧНИКОВ ТЕПЛА С
ПЕРЕМЕННОЙ ТЕМПЕРАТУРОЙ СРЕДЫ
7
В данной главе рассматриваются задачи, когда температура
поверхности тела является заданной функцией времени. Для общности
вначале приводится случай, когда температура среды изменяется по заданному
закону от времени Тс = f(%). Затем, полагая, что критерий Био бесконечно
велик (Bi -> оо), получаем решение задачи при заданной температуре
поверхности тела Тп = /(т). Следовательно, решения задач данной главы
являются некоторым обобщением решений задач главы IV, поскольку
из приводимых здесь решений можно получить как частный случай
решения ранее рассмотренных задач.
Вначале приведены решения задач с наиболее простым законом
изменения температуры Тс (температура среды — линейная функция
времени), а затем с более сложными законами. Сюда относятся и задачи
на температурные волны. В конце главы даны некоторое обобщение
и вывод теоремы Дюамеля операционным методом. В отличие от
принятого в предыдущих главах порядка, вначале рассмотрим задачи на
нагревание неограниченной пластины, шара и цилиндра. Задача на
полуограниченное тело разобрана в § 7.
§ 1. НЕОГРАНИЧЕННАЯ ПЛАСТИНА. ТЕМПЕРАТУРА СРЕДЫ —
ЛИНЕЙНАЯ ФУНКЦИЯ ВРЕМЕНИ;
Постановка задачи. Дана' пластина 2R, которая находится в
тепловом равновесии с окружающей средой, т. е. имеет температуру,
равную температуре окружающей среды Т0. В начальный момент ере-
мени среда нагревается с постоянной скоростью Ъ (град/сек), т. е.
температура среды есть линейная функция времени Тс(т) = Г0 + ^Т~
Теплообмен между поверхностями пластины и окружающей среды
происходит по закону Ньютона. Требуется найти распределение
температуры по толщине пластины в любой момент времени, а также
удельный расход тепла.
ТЕМПЕРАТУРНОЕ ПОЛЕ БЕЗ ИСТОЧНИКОВ ТЕПЛА
275
Начальные и граничные условия можно написать так:
Т(х, 0) = Т0 = const,
дГ@, т)
дх
= 0,
- дТ У; т) ■ + я [(т0 + и - г да, х)] = о.
A)
B)
C)
Решение задачи операционным методом. Решение для изображения
TL(x,s) дифференциального уравнения теплопроводности в случае
неограниченной пластины при условиях A) и B) имеет вид (см. §3 гл. VI)
TL(xts)-~^- = AchY-^x. D)
Постоянную А находим из граничного условия C), которое для
изображения будет иметь вид
-Т;(Я, s) + ^ + -5т - HTL(R, s) = 0,
E)
нъ
Удовлетворим решение D) граничному усло-
нь
так как L [Hbt] = 2
вию E):
-^УТ-^Тя + ^-н-
Определим из равенства F) постоянную А и полученное выражение
подставим в решение D):
НТо
-AHchY~~R = 0. F)
TL (x, s)
V
6ch
/?
• (*утя+±ут.*у±й)
O(s) Ф($)
G)
где ф (s) — выражение, стоящее в скобках в знаменателе.
Как было показано в § 3 гл. VI, Ф (s) и <J> (s) являются
обобщенными полиномами относительно s, причем полином ф (s) не содержит
постоянной, т. е. условия теоремы разложения соблюдены. Приравнивая
функцию ^(s) = s29(s) нулю, находим корни: 1) s0 = 0 (двукратный ко-
рень); 2) s^ = -—- , где i "I/ ~^-R = ^ — простые корни,
определяемые из характеристического уравнения
, 1
Ctg и- = —г Р-
Bi
Таким образом, нахождение оригинала производим тем же путем,
что и в § 3 гл. VI, за исключением нулевого корня.
Так как. нулевой корень—-двукратный, то применяем теорему
разложения для кратных корней (в нашем случае k = 2), имеем
L Ф @) J *-o L ds \
= lim Г-
s—o L
■се" Ф (s)
9 (s)
ф(«)
еэт Ф' (s)
+
9(s)
= li4JL(.me«Y|
s^ol ds V <p(s) /J
276
Глава седьмая
= bx
bx* ___ bR2 _ bR2 bR2 ^fo , b
2a 2a 2a HR 2a HR ~ 2a
так как
bxsh
ф@)=6, <p@) = l, Ф'@) = Ит-
["-«"("■"ИГ)]'
s-*0
r / \ i a . fa .
Ф (S) = r_ 1 ._ h
2 У as
#2
bx2
2a
ch
УЯЙ-
Результат при подстановке остальных корней находим обычным
путем:
ф('я) су
я=1
Ф' (««)
— JU («*« +Sinn-» cos Ы »*» C0SlA» Л еХР(-^ ^J
/1=1
Таким образом, решение нашей задачи получим в следующем виде:
с»
(8)
где Лл — начальные тепловые амплитуды, определяемые соотношением
C0) § 3 гл. VI.
Анализ решения. Введем критерий, характеризующий интенсивность
повышения температуры окружающей среды:
dFo /max
Pd
(9)
и назовем этот критерий критерием Предводите лева (Pd).
В нашем случае скорость нагревания —т^ постоянна на
протяжении всего процесса и равна Ь, так как Тс (т) = Т0 + Ьх.
Следовательно, критерий Предводи те лева равен
Pd =
R2
a dz
ГсМ
о /
bR2
A0)
Относительная температура среды 6С здесь взята по отношению к
начальной температуре; ее можно также взять по отношению к
некоторой средней температуре или к конечной, если последняя известна.
Таким образом, решение нашей задачи будет иметь вид
T(x,z)—T0
[ Ifo — — I
со
/1=1
■w'F-t[(I + -s-)-v] +
An
2-cos|i„ —exp(—|»«Fo)
(H)
ТЕМПЕРАТУРНОЕ ПОЛЕ БЕЗ ИСТОЧНИКОВ ТЕПЛА
277
Из решения A1) видно, что относительная температура в любой
точке пластины прямо пропорциональна критерию Предводителева,
а следовательно, и скорости нагревания среды. При больших значениях
критерия Pd возможны интенсификации процесса нагревания. Безраз-
0 х
мерная величина -^ есть функция Bi, Fo и -^-:
A2)
-^ = WFo, Bi, -iL).
Pd V Rj
Из решения A1) видно, что ряд быстро сходится; с течением
времени он становится все меньше и меньше, и, начиная с определенного
значения Fo>Fo!, им можно пренебречь. Тогда температура в любой
точке пластины будет линейной функцией времени, а распределение
температуры по толщине будет параболическим. Такой режим нагревания
называют квазистационарным, так как поле градиента температуры
будет стационарным (температурный градиент в данной точке не
изменяется от времени).
Положим Bi -> оо, тогда согласно граничному условию C)
температура поверхности пластины мгновенно становится равной
температуре окружающей среды и затем изменяется по линейному закону
T(±R,x) = T0 + tn.
A3)
Следовательно, получаем задачу с граничным условием первого рода
(см. гл. IV). Для решения такой задачи необходимо в A1) положить
Bi = оо, т. е.
A4)
где
ц = B/г — 1) — , Ап = (— l)n+1 -
Г/г v J 2 п \ ) Bл —1) я
Решение A4) можно получить в ином виде. Положим в решении G)
для изображения #=оо, что соответствует случаю Bi=oo. Затем
==— \ разложим в ряд [см. соотношение B6) § 3 гл. IV]. Тогда
будем иметь:
Используя соотношение E6) таблицы изображений, получаем
A5)
Pd
= 4Fo
2
— n«+1
<-!>
Bn-l)--^ {2n~l)+-~
i«erfc ^-+i2erfc- *
2^Fo
2l/Fo"
A6)
Это решение наиболее удобно для малых значений Fo, так как в этом
случае можно ограничиться одним членом ряда A6).
278
На рис. 7.1 приведены графики изменения обобщенной функции
6/PdFo в зависимости от числа Фурье для разных значений
относительной координаты.
Определение удельного расхода тепла. Удельный расход тепла
находим по обычному соотношению
b>Qv = C4[T(T)-Te]. A7)
Интегрируя решение A1) по -^р в пределах от 0 до 1, получаем
- Г(х)-Г„
--г
A8)
где Вп — постоянные коэффициенты, определяемые из соотношения D5)
§ 3 гл. VI.
Удельный расход тепла можно найти другим способом. Количество
тепла, передаваемое в единицу времени единице поверхности
пластины от окружающей среды по закону Ньютона, будет равно
9=^=а[Гс(т)-Т(/?,т)].
Тогда удельный расход тепла будет равен
AQ, = "Т" J trc М - Т (Я, т)] Л, A9)
о
где —: — отношение поверхности к объему для неограниченной
пластины (оно равно —). Температура среды Тс является линейной
функцией времени, т. е.
Тс (т) = Т0 + frc = Т0 A + Pd Fo). B0)
Тогда разность [Гс(т) — Т (R, т)] будет равна
00
■ Pd - r0Pd ^ 7f Л cos ft, exp (-^ Fo). B1)
Bi
ra=l
Подставив это выражение в A9), после интегрирования и необходимых
преобразований получим
AQ„ = сТГ0 Pd Jfo ~2~4"B"[l ~ ехр (_|Л« FoIl>
B2)
где Вп — постоянные коэффициенты, определяемые из соотношения D5)
оо
§ 3 гл. VI. Так как \\—2~ВЯ = 1 , то соотношение B2) стано-
^Д ^ 3 Bi
вится тождественным соотношению A7).
:::::::::::::::::::^-:::::::::::^v:::::^-:^^a:::
3
я
к
и
ft?
с
к
с*
о
X
о,
с
о
К
о
г
S
со
К
О*
280
Глава седьмая
§ 2. ШАР. ТЕМПЕРАТУРА СРЕДЫ — ЛИНЕЙНАЯ ФУНКЦИЯ
ВРЕМЕНИ
Постановка задачи. Постановка задачи одинакова с предыдущей.
При концентрическом распределении изотерм относительно центра шара
краевые условия следующие:
Т (г, 0) = Г0 = const,
аГ(°' Т) =0, Т@,т)^оо,
дг
dT(R9z) + H[T0+trz-T(R9x)] = 0.
дг
О)
B)
C)
Решение задачи. Решение дифференциального уравнения A) § 5
гл. VI для изображения TL(r, $) при условиях A) и B) имеет вид
TAr,s)
То
Г
Г .
L v * -/ s r fa
Граничное условие C) для изображения следующее:
-T'L(R,s)
HTp Hb
г -5-
HTL(R,s) = 0.
S ' S'
Удовлетворим решение D) граничному условию E):
D)
E)
R
-H-^aY^R-O. F)
Из равенства F) находим постоянную В и подставляем в решение D):
TL(r,s)
MWsh I/ -f_ /•
[т-1)*У±* + У-7г**У-1г*]
rs<
G)
Числитель O^s) и знаменатель tyt(s) не являются обобщенными
полиномами относительно s, но они могут быть преобразованы в
обобщенные полиномы путем умножения на s1/2.
Тогда можно воспользоваться соотношением
Ф1 (sn) _ Q(sn)
<h (sn)
V (*л)
Ф1М
(8)
, если корни sn
и применить теорему разложения для отношения
отличны от нуля.
Для нахождения корней sn приравняем ^(s) нулю:
<Ы*) = га»[(я/г- i)sh]/^i? + ]/"^-^ch|/^ /?] = о.
Выражение, стоящее в скобках, даст нам корни sn = d£-u l/ -j# = M>
ТЕМПЕРАТУРНОЕ ПОЛЕ БЕЗ ИСТОЧНИКОВ ТЕПЛА
281
которые определяются из характеристического уравнения
1
tgp =
(подробно см. § 5 гл. VI). Следовательно, имеем
Ф1 fe)
г
'+1 (Sn)
е п =
2bR'<
а
00
Л=1
/? (sin ця — р.я cos tx„)
П** (Р-л ~ sin V-n cos р.Л)
sm ft, — exp^-^—j.
(9)
Для нулевого корня (s = 0) преобразуем решение G), для чего shz
и chz разложим в ряд. Тогда будем иметь
<Ы«)
м"Я1+1г"-1г+1гг4-5-+-
('
(Я/?
-1)[1+i;?2^+---]+[1+ir;?2^+---]
s2<p (s)
A0)
где /(s) — числитель отношения A0), q> (s)—выражение, стоящее в
фигурных скобках знаменателя.
Применяем теорему разложения для кратных корней, т. е.
s-*o L ds \ <р (s) /J s^0 I
/(О , ^f'(s)
= bx
br*
<t(s)
IbR
<P(s)
bR2
rsz f (S) <?' (S)
[? Ml*
6a 6aHR
так как / @) = bHR, <p @) = ЯД, ф' (О)
6a
2Я2
(П)
+
Я#Да
6a ' 6a
Окончательно решение нашей задачи будет иметь вид
Т (г, т) - г0
Го
= Pd
Fo
со
-i[K)-£]+2
Л=1
ti
/? sin р.л —-
ехр(—(iJFo)
A2)
где Bi = HR, Pd :
б/?2
аТ0
■ критерий Предводителева, Ап
начальные
тепловые амплитуды, определяемые соотношением B8) или B9) §5 гл. VI.
Анализ решения. Из решения A2) видно, что относительная
избыточная температура 6 прямо пропорциональна критерию Pd, т. е.
скорость нагревания окружающей среды непосредственно влияет на
повышение температуры тела в любой точке его.
Ряд в решении A2) быстро сходится, и поэтому для
квазистационарного режима, определяемого условием Fo > Folf им можно пренебречь.
Величина ¥ог определяется по методу, изложенному в § 11 гл. VI.
282
При Bi -*■ оо температура поверхности тела будет линейной
функцией времени Т (R, х) = Тс -{- Ьх. Решение A2) превращается в
следующее:
в 1 / * \ V A Rsm^~F
-^-^Fo 41 г—)+ Уj -Щ- — exp(--№2Fo),
A3)
где Л„ = 2(-1)п+1, ft, = яте.
Сделаем оценку ряда A3) для центра шара (г = 0). Напишем
решение A3) так:
J_=Fo--±-[l-<p(T)], A4)
где
СО
Потребуем, чтобы <р (t)< 0,005, что составляет 1/2% от 1. Тогда,
пользуясь методом, изложенным в § 11 гл. VI, находим, что при
Ф(т)<0,005 Fo>0,54.
Для точки с координатой -~ = 0,5 значение ф (т; 0,5),
соответствующее ряду в решении A3) при Fo = 0,5, равно 0,0008, что составляет
0,11% от 0,75.
Для малых значений Fo можно получить решение в другом виде.
Положим в решении G) Bi = HR ~> оо; тогда после некоторых
преобразований будем иметь (см. § 5 гл. VI):
TL(r,s)—pL = ^7^- =
rsPshr/ J-R
00
= bR \^ ( ~V^Wn-\)R-r1 _ -]/^[B/i-l)*+r]|
Используя соотношение E6) таблицы изображений, находим
B/1-1)--£- Bя-1) + ~-
Iserfc — i2erfc -
2 |/Fo 2 /Fo
A6)
На рис. 7.2 приведены графики изменения обобщенной переменной
6/PdFo от числа Фурье для разных* относительных координат rlR.
Для малых значений Fo можно из всего ряда A6) ограничиться одним
первым членом. Значение функции i2erfc берется по графику или из
таблиц.
283
aaaaai <ai ana la i
bbbbbi bi at at tat
aaaaai bibi ai bi
bbbbbi bibb aaai
bbbbbiававвааа
вавава вв aa ta ib
вавваава ia ia.ii
■ввававв шип
ааввав ibi ib i an
вавава ibi «mi
aaaaaatai ваввi
■■ававнмаааа,!
laaaaaiaiBa ibi
вавава iaa ваива
вавава шашн
ввавав iaa aaiaa
aaaaaa ibbibbbb
BBBBBI IBB. IBB 11
BBBBBI «BI IBB II
:.::.:: E.i is.!
■bbbbbi aaabbia
aaaaaai вввaaai
■aaaaai авв аввi
aaaaaai авв iaa. i
aaaaaai aaa taai
■BBBBBIBBB IBBI
■aaaaaa aaa «ai
■aaaaaa bbbi aaa
вававав aaai aai
■■■■III 1Ш ЯЯЯ
aaaaaaaibbiaaa
аввавваibbbaai
■вававаibbbaaa
вававав ibbb ibi
■ававав! шва ibi
■■aaaaai «a anal
■bbbbbbi «aai ibb
■аявавв! «bbi «a
■aaiBHi aaai aa
вававав! вваавв
■aaaaaai вавв «■
ваввваа
BBBBBBI
вававаi
вваввав
■вавава
■вавава
.IBBBBBI
1 IBBBBBI
1 BBBBBI
■вяявяа
вввввав
ВIBBBBI
a ibbbbi
«Н!
...sssi
1 IB. IBBBI
k'BUBBBI
iiinai
aiaibbi
a ia ibbi
внапава
at ataaa
aaaaaaa
BBBB IBI
■aii ibi
ВВПВГВ1
aaiwiaa
■вавава
iaaaa«a
IBBIBltl
вавваава
aaaiaaai
BBBBBBBI
BBBBBBBI
BBBBBBBI
BBBBBBBI
вааавввв
авававав
вваввавв
ввававва
вааавввв
BBBBBBBI
вавваава
вавваава
BBBBBBBI
BBBBBBBI
аявваава
вавваава
авва aaai
::::::::
■■BBBBBI
ввававаа
BBBBBBBI
■BBBBBBI
BBBBBBBI
ввававв)
авваввав
SSSSHSS
■ hi «a BBaaiaaBi
1BBlBBBBBBBBBBI
sss..SiSS5s:ssi
::::.:.:.::;
aiaaiaiввававва
ai aaa «■■Шваaaai
в1вва1В1вавввв1
■bbbbbbiаяяаibbb «вага
вваавава вавв ibbbi ibii a
вваавава авва laaai «bi i
вавааввв aaaai «bbi авв\
ввваааввibbbi bbbiaaa
■ааввавв miai яяяв ibb
■аввввввibbbiавва ibbi
.:...:..'.:::..::.::.
■аввваав ibbhb |ЯЯЯ1ааа
ваавваав laaaa ibbbi ibi
ssssssssissssissss^i
ваавваав! «bbbi aaaai ai
ваавваав! аввваaaaai ва
■анаяаяя! паннами
bbbbbbbbi аввавibbbi■■
■■bbbbbbi ваавв ibbbb ii
bbbbbbbbi аввав. ibbbbi ii
■«■aaaaai aaaaai taaaai i
■■■■■■■■шиш hiii a
вававвавв bbbbbiaaaai■
вавваавав аввава аааааI
■вавваава ааввав вавва
аавввавяа ibbbbb ibbbbi
■вааавввв! iniaai ibbbb ■
вавваавав!ibbbbbi aaaai
аавваввав! ibbbbbiaaaai
■aaaaaaaai ниш явваа
аяваввяяв! ввававваава
■явваавваа вваавв ibbbi
ssssssss
■BBBBBBI
■■BBBBBI
аааваааа
авававав
■BBBBBBI
аавввввв
вваавава
вваввввв
аааввавв
■BBBBBBI
вававваа
вавааввв
■■вавава
■bbbbbbi
■аавввавав! bbbbbbi bbi
ававвавава! bbbbbbiaaa
■ввававвава аавввваibi
■■вававвавваввавва ibi
BBBBBBI
ввввааа
вававав
вваввав
BBBBBBI
авввввв
BBBBBBI
■аввааввавва ia
вавввяааавва ib
■авааваавв bbi ib
ВВВВВВВВВВВВ1 В
■ававвааваbbia
■авввввяаяаяа а
вавааввавввввi
■ввавявввввааi
■ввввввван aaai
аававввваявав!
■■вававваавааа
■■ававвваввавв
ввввввааааваВ!
■аввввввввавв!
■вавваавав вавв
■вввавваавввв!
■вввававвявяав
■ааааавааааяяв
IBBBBBBBBBBBBI
■■■■■■авававав
■аваававаяая||
■■■■■■■аввавва
■■■■■■■ваяаява
■вававававввв!
■вввааааанввв!
■авввававввваа
■■ввававвававв
ававвававававв
вввваввввавввв
аавааввавяаввв
■явввавввяавав
■аваававвваввв
■аввваввввввва
явваавваввввва
..S....SSS.S..
«■■■■■■■■яяяав
аававввваяаям
■■■■■■■вававав
■■■■вваавваяаа
■■■■вваавааавв
■авав авваввавав■■■■!laaaaввв
■ваваааввавааавваааНававааа
■■■■■■■■■■■■■■■■■■■■■■■■■■■я
■вавв ааввананааааввааааавввв
авав. ibi
■ BBBI BI
•■HI II
i «аввава
1BBBBBBI
■■■■bbbi
■.«вваавв
ш«ваява
at вавава
вавваава
::!.::.!
,iS..SS5!
i «aibbbi
■ ва «авва
■ BBIIBBBI
aaai аяяа
Я! «В 1BBI
В1ВВНЯЯ1
■a hi aai
ВВ *BB«5i
bbi aa. «bi
bbi aai «i
BBB IBBBI
bbbi aa.»
авва ibi'i
1BBBIB*f
.шва.шв
I'aiiraa
1 BBBIBBk
В BBBIBBl
в авав ibi
■1 ШВВ1 BI
BI BBBBBI
at aaaaai
aa ibbb ii
яя ibbbi n
BB. IBBBI I
ввв вами
авв ibbbi
II BBBB
аввва
вавва
a. ibbi
sshss
iBBiiaa
«BIBB
bbbi авва чввкч
авав ibbbi aai a
авав ibbbibbbi
ibbbbi «aai ■■■.
■BB81 ■■■■ IBBI
ssss.?sssk'5s.
авввв.1вааа1ав
ВЯВВВ1 ■■■■■■IWIIBIBI
:::::: :;:.:^::::ki
авваваiаввавваaa aaai
■bbbbbiаавваввibbbbi
ааяаввв(ввввяв!ааава
■■■ana шавваввibbbb
вввввя hi <■■■■■■■ швна
BBBBBIBt BBBBBBBI BBBB
■вававав«■■аввва«ваа
IBBBBBBB lllllllinill
паввваав!вавававаая!
i вваавваввааввава mi
■ вввав ввв ta аввав bi «a
a bbbbbbbbi ававававmm
bi ibbbbввва bbbbbbbbi a
■1яввавввв шаванаи
ai авав вавв. шяяяввав \
■■■■■BBBBBI BBBBI BBBI
aa ibbi aaa» ваввавава
aai «вввввав «вваавава
bbiавааааввиаваааавв
■ва ■■■■■■hi вваавава
вввнвааввввавввваав
авв, шаввавав «авввввв
bbbiвваавваввааввава
авва«ввавваввibbbbbi
авванаввваавапваваав
BBBBIBBBBBBBBI■■■■■■
аввва 1ввввавав1
BBBBBI BBBBBBBBI
вавава «■■■■aaai
ввавав в. «аввав:
ввааввaibbbbbbi
вававваа«■■■■■
ввавав sat <ааяяа1
■■ававвваавава!
ввавав ввапвввв!
ввавава
BBBBBBI
■BBBBBI
JcTr
ffloo H HI 11
SSEaCS!
вавава вавваавь i
вавава bbbbbbbbi
■вавва ааввавав!
ввавав вваавава!
вваавв■■■bbbbbi
вввававввввавв!
■вввввавваввав!
аавввв вввввава!
ВВВВВВBBBBBBBBI
ааввав анававвя!
IBBBBI
BBB
BBB
BBB
BBB
IBB
III
•III
BIB
BBI
■a.«
■■I
■ai
BBB
BBB
IBI
IBI
■ IB
a. ia
■i«
вавваава
вваавава
авааавав
ававввав
■ВВВВВВ!
авааавав
вававваа
вваввввв
вававваа
■ваввваа
вваавава
вваввавв
вваввяяя
■аавввва
■BBBBBBI
■BBBBBBI
вваввяяя
яяа ввяяя
■aaaaaaa
вваавава
вваввавв
вавваава
вваавава
■ааввавв
■BBBBBBI
вввaaaai
вваввавв
авававав
■ввавяяа
вававваа
■BBBBBBI
ввавваяв
BBBBBBBI
SSSSSSSS
SSSSSSSS
авваввав
аввввяяа
ввваввав
5SSSSSSS
ввававва
вваавава
■BBBBBBI
вввввяяв
вававваа
вввввава
вваввввв
ваааввя!
вввввава
авааавав
■ввававв
■ввававв
■вввввав
ававввав
вваавава
BBBBBBBI
BBBBBBBI
ввававва
вввввава
■BBBBBBI
авваввав
яявававв
ваяваяна
авваввав
вваввавв
■■■■авва
■■■■■яяа
■вваввав
ававввав
яяаваавв
вваввввв
ввввввяа
■вававав
■BBBBBBI
■ваявяяа
■BBBBBBI
ssssssss
ssssssss
■BBBBBBI
■ввававв
■■■■■■■а
BBBBBBBI
вввввава
вввввава
ввававва
ваавваав
1BBBBBBI
к«аввяя!
1 «IBBBBI
■ «аввава
внаваавв
an вавва
■в<аввва
авк вввав
T * l|\[ 1 1
.НИМИ™
щ
aai
IBI
ваа». aaai
вва в. «ввв
вааbiавв
ваавв «■■
авваваив
■SBHIi'l
esssr
Гг
■Л BBBBBI«
ававвавава
вваапввавв
аваавпвввв
аваавачввв
вваввак-авв
■ваяяяалвв
ввв
BBI
BBI
BBI
авв
ввв
BBI
ввв
■аа
ава
ваа
ввв
ввв
авв
ваа
ввв
ввв
■BI
■аа
ввв
■вв
авв
ввв
ввв
■ва
■BI
IB!
ввв
BBI
IBI
ввв
IBI
■вв
авв
ввв
ава
ава
■BI
BBI
■вв
ава
ввв
ввв
ввв
ввв
ввв
ввв
авв
ввв
ввв
ввв
ввв
ввв
ваа
BBI
■В1
■В!
ава
ввв
ВВ!
ВВ!
■ва
ввв
■ва
вва
ввв
ввв
■В!
BBI
BBI
■■■
ВВ!
■В!
■■■
авв
авв
ввв
яга
'•ли
<■■■
■BI
■вв
авв
ввв
ввв
вва
BBI
III
вал
BBl
ввв
ввв
авв
ввв
ввв
■ai
ьвв
В.1В
aai
BBI
авв
вва
вва
ВВ!
■■■in ввававвава
■BBBwa вававвввв!
■■■aa. ававвавава
аввава ввававвава
ававав а, ававваава
ввавав вь.чввваааа
ввавав bbi.вввввав
аввава вавь/аввааа
вваавв авввк'ввавв
ввввввававвавава
■вавваававваава!
вввава вавваавь-аа
■ явввн ■■■■■■■■_•■
вввввв вавваававь,
авваваавваввавав
ьчаава вавааввавв
■квааа аввваввввв
ввивавввававвава
вавк-яв аввваввввв
ваввк.-а ввававвава
■ввввк. «ававваава
■авввак^аввваяав
■■■■■■■ь-.»на«1
■вваваававвавава
■аввва ввввь^вав!
■ аввав ввввавь.-чвв
■авввавввавввя^ч
■ваавввввавввввь
впав
ВВВ!
вааа
вавв
авав
BBBI
BBBI
вааа
аяяа
вавв
ВВВ!
BBBI
■ава
вавв
аяяа
ВВВ!
BBBI
BBBI
яяяв
sssss
BBBI
SSSi
вавв
SSSi
BBBI
ввва
авва
ваяв
■aaa
SSS!
SSSS
вавв
вавв
вавв
вавв
ВЯВ1
BBBB
■BBI
i-li
BBBI
■■BB
BBBB
ввва
BBBB
BBBB
BBBB
BBBB
■BBI
■BBI
BBBB
SSSS
SSSS
яяяв
BBBB
SSSi
SSSS
SSSi
вавв
BBBB
BBBB
BBBB
BBBB
BBBB
SSSS
■BBI
■BBI
ввва
SSSS
SSSi
SSSS
BBBB
SSSS
BBBB
BBBB
BBBB
вавв
вавв
аава
ввва
вавв
вавв
■ВВ!
авв!
■ЯВ1
■bbi
тттк
ВВ1В
яьяв
^ввв
ВВВ!
BBBI
BBBI
BBBI
BBBB
ввва
авва
авва
ввва
BBBI
вавв
BBBI
яяяв
вавв
ВВВ!
чваа
IBBI
ВВП
ваья
вавь
аава
вавв
ВВВ!
ввва
лввв
ачвв
■4BI
■Вк'1
авв..'
ввва
ввва
."«ВВ
■ .-«В!
■ Ill
ваа.'*
аваа
ввва
ввва
авав
ввва
■ава
■авв
ввва
вавв
чваа
аю!
ваа."
авва
авав
вавв
ввва
авав
■вва
BBBI
вава
авав
■ и
BBBBI
■авав
вввав
■■■■■
■■ввв
вввав
вавва
аввва
аввва
аввва
ааааа
вавва
ваавв
вввав
ваавв
аввав
Bill!
■авва
аввва
лава!
ьчвав
ВкВВВ
■ ■..'ВВ
■ва.ч
■aaai
■яяяв
вввав
Я1ЯВВ
аь-чаа
BBBBI.
вввав
аввва
BBBBI
ВЛВВ1
ва.^ва
■■■."■
авва».
аввва
аввва
аввав
аввва
■■■■а
■ ввва
аввав
■авав
аьчаа
авюя
■вавь.
аввав
■ ■■■■
IBBBI
■ вавв
■ вавв
ааааа
ssssssssssssssssssssssssssssssssissssHi:
ssssisssssisssissssssiisiiissssssssssssi:
в вяяваввввавввававввв■ааававваваааввваввя
яяяяяяяяяяввяяяаяяяяаяяяяяавававваяяяаава
sssssssssssssssssssssssssssssssssssssssss
sssssssssssssssssssssssssssssssssssssssss
■ваввяяяяяяяяяяаяяяяяааааааняяаввяяяяяааа
■ввававваваавввавввввввававвававваввааввв
■ваваавваввававваввавававваввавввававвавв
■ваваавваввавввававвававваввааввввввваввя
авяяяяяяяяаавяяяяяяяяяяяяяавяяаяяяяааяааа
яяявавааваававаавваввваваавваввваваВававя
ававвававвааавввввваяввававваваааававввая
■ваввававвававвававваававвввввавааввваава
■ вввввававв вавааввавв вааввааавааавваямаав
■явваааввввввввваавв!ваваавваввававвавава
авввавввяявавваввяяяаяавввввввававвввавав
ввввввввввававвававвааввваааааававаававав
■вавввввввааввваввввввввввававвавваввавав
аававвававававаавваввваввававваававвавава
вввававвававввввававввввввааваавваваяяааа
вааававввааавввввввваввввваввваввававвава
■аввааввваааавваававааавваанввававааввавв
i авааавааваавввввааав вавД Дшвв ваввававва
■ ававваввав ававв вавва аввНВваввавввваввв
■ ввававвава ваввававва аввВХава авваввавав
111 HI Ml Т llli Mil " о| || И
11 j|l 1 1 iM h-~M
1 1 1 и 111N11H11111II1II ч "НИМИ 14-fH-l
1 [ [ 1 [ 11 [ [ 111 [ | [ | [ | [ 11111 ^ 11 [ 11 [ |; M
■ ававвававв вваааавввяваввваавваввавнввва
вввваявававвввввйвваааааввааввввйаввавввв
ввавававааявваввнявваванвавававаавааваа
■ ввва1ввяааввав1ввамяав11яввв|вам11аап
■явввяамввваавввавввввввввввввавввввваввв
вввввваавваввавамивв ваввававва ваяявяиява
ввввввяяяаяняаяаяяяваваяяааяаяаяяяявяявва
■ ввввааввивввааавввваавваавава ваввввввва
ввввааавваааишнввваавааввавввнвввввавма
■■ввавввввававааввввааввявяяававввваяяаав
ввваяаяяяняявваввяваяяавяаввввввввввяяави
■ввяяяяяяваяввавяняяаяяааивавввяяяяяяявав
вваввввввваававвннваавяавававваввявяаваав
вввавввввавваввввввваввввавввввввваааввня
■вавваяаявавваввваввявиииаававвававввяаив
а ввваяяяяввнавввнвяяя яяявваввввввввяаяввв
ll^zzlii^zUlizl^^ll^z:^
в аававввваввввввввавв ваваявавввввваяааааа
вяяяяяяяяаввввваввавяввввявввввввввяавввв
вяяявваввввааваававвнаввааавааявивваавввв
■ яввавввваааааваааававввввввважвяянвввав
■вааваававввваааяаняваавваввавввяяваавввв
в ■ввваавввввавааамав ■■■■■■■■■■■■■■■■■■■■
вввваавввавааававвваиваваавввааввввВааваа
аааввававваввввавваваанвавваввавввввввяав
вваававвавяааавввааввваваяввавввавваввваа
■вавааввваявавваввввааавввввваввввваавава
■вввяаяяяяяяяявяяаваяваяаяяяяаяяяяяаяввав
вваваавваввавваввававааввяввваавввввавввв
ввавввааввваваавнавваввавяввввваавваввавв
вваавяввваявававваваяваааввввааававвавава
вввввввввввввввваввваавввввввавваввваввая
■ BBBBIBBBBBваввававва ваваявяяяа ввввяввяая
ввааааввмаяяаававваавававвававввввваввааа
вввввяваавнваааававввваванвяяяаввввиняааи
ававаавяяявяввввввввяяяяаяваяааввняаяяяяа
■ввввввввяввввавввввааавввввввввававввваа
аввввЕававввваввваавваааааавваввввввввавв
вввввааввввваавявааввввввавяяяяаавввввавв
■ававвававвввававвававааааввявававвавввая
вввваввваввввввввваввваввввввваааввввввав
■ваавяввввваввавваввввввввввввавававвввав
^ваввввввяяяяяяаяавваввввяяаяявяяяаавяааа
вяввк.'яввваявввиаввввввввва8яяяаавваавявав
чввввавк''яаваавввввввааавввавввняввааняяан
кввавввак «■■■■вваввавв ■■■■■■■ввв вввввававв
■ кчявяяяяья ■■ввававвавваававававввав■■■«■
вв1к1ваавва1.чвввввваваааваавввваввввййваав
аввь.-чвваваак.чвввваввваввааввааяаяяввяяная
в вавь-чавваавк-чвававав ааавввввввавввавввав
■ ■вв*в^вввяавк.^авввва«авяняввввввваввввав
■ ■вваяв^ааввава -«вввав вваааввввавввввввааа
аввавяввкяавяява.^ававааяяаяяявяавваяяявав
к. авваявавь.чавввав.^авваавааавввв вавааввавв
■ кчввввава»^ааввва^ававваввавав ввавввваая
в вк.^ввваавва^аввава^а вавваавав! ■вввяввваа
■■валавввавва^чваваач'вававвяапииввааявввв
ававакчааавввва^вававк.-чввваввайвявавввввв
■аааавя^нвявааиа^чвваакчваваяяввяявввваав
■ ■■ввавв.'-ааваааавкчввввкчаввваииавввввйвн
вввввваввь'чааввавва^ававк.^вавяввввввввяаа
вввававвава^вяваввав^авваи^вваннвввявввав
вввввавваввв>.-чаавааввк.^вааа.'<ваяйввв1ввваа
■ аввв|ввввавак|^аваавввк1.^ааав1.-'аяаввнвввааа
чввванввавввааакяайвавва.'-авввкяввамввввав
а ^вввяяяявввввввк^ввв яявЯк. ававк«вявявввав
■ в.'чааяамивавввввв^«ап«1>ав>.чнаа.'яаа11яяа||в
■ ■■к.'аааввввааваавввк^»ввввк<-чаввк«вяавваа
вввввк,^авввваааавввав^яававак.^аав^ввввавв
ввввввв^чваавваавваввяк'чяявваа.-чяввлввваая
в вавааввавв авваввавав ■■а.'чааааа'чавачвввая
v.|c^
ф
я
о.
р
о
О
Си
i
«У
К
а
со
о
284
Глава седьмая
Для центра шара решение G) в случае Bi = оо можно написать так
(см. § 5 гл. IV):
TL(r,s)
^-^lM-V?«<*—>]•
откуда, пользуясь соотношением E2) таблицы изображений (см.
приложение), получим
A7)
Определение удельного расхода тепла. Для нахождения удельного
расхода тепла найдем среднюю температуру шара
_. Г(т)-гв _
То
= Pd
00
F°-^A+ii)+s?B"exp("''"F0)
A8)
где Вп — постоянные коэффициенты, определяемые соотношением D9)
§ 5 гл. VI. Далее расчет производится, как обычно.
§ 3. НЕОГРАНИЧЕННЫЙ ЦИЛИНДР. ТЕМПЕРАТУРА СРЕДЫ —
ЛИНЕЙНАЯ ФУНКЦИЯ ВРЕМЕНИ
Постановка задачи. Эта задача аналогична предыдущей, только
нагреваемое тело берется в форме неограниченного цилиндра. Для
симметричной задачи дифференциальное уравнение теплопроводности
неограниченного цилиндра не раз приводилось в предыдущих главах.
Краевые условия аналогичны условиям A) — C) предыдущей задачи,
поэтому они здесь не приводятся.
Решение задачи. Решение для изображения TL{r,s) при начальной
постоянной температуре цилиндра Т0 в случае симметричного поля
температур относительно оси цилиндра имеет вид (см. § 6 гл. VI)
TL(r,s)
То
AL
/?-)■
A)
Постоянную А находим из граничного условия, аналогичного условию
E) предыдущей задачи:
Определив из этого равенства постоянную Л, решение A) можно
написать так:
tl ('.*)- -£■ =
«•(/-И
■Ni/?«)+t/-H/-H]
ф(«) _
ТЕМПЕРАТУРНОЕ ПОЛЕ БЕЗ ИСТОЧНИКОВ ТЕПЛА
285
"" s2y (s) • B^
Решение B) является отношением двух обобщенных полиномов <5(s) и
^(s), причем последний не содержит постоянной (см. § 6 гл. VI).
.Приравнивая нулю фE), находим корни полинома <|ф): 1) s = 0 (двукрат-
ау?
ный корень); 2) sn = ™ бесчисленное множество простых корней,
определяемых из характеристического уравнения
^- = JLj,. C)
Это уравнение получается, если приравнять cp(s) нулю. Воспользуемся
теоремой разложения
Шп [JL Г е- ^W.1) = Нш f ^ *W. + ^^L_ е- *МЗЖ) =
s-o ( ds L <Р (s) JJ s-*o I <p (s) cp (s) [<p (s)]2 J
i. i *"  &Я2 6#2 *. Ь Г «Л , 2 \ al
4a 4a 4aHR 4aHR 4a |_ \ HRj J
так как
Ф@) = 6, ф@) = 1,
Ф'@)=11ш 1Ч- 'U^,
' • s-o \ 2Vas J 4a
f w - ^ [A + -Ar)'. (/? «) + ^ /?/; (•? *)
Далее
Ф foi) .st _ <D(s„) v __ &/?
• t> — о _ с —
^--H^il-N?:
так как <|/(s) = 2s<p(s)-f-s2q/(s). Следовательно, решение нашей задачи
будет иметь вид
где Ап — начальные тепловые амплитуды, определяемые соотношением
B7) § 6 гл. VI.
Анализ решения. Если положить Bi-^oo, то температура
поверхности цилиндра будет линейной функцией времени, m. e. T(Rf%)^
= Г0 + Ьх. В этом случае решение задачи будет иметь вид
286
си
д
к
С*
О
«
SJ
«"
&
§г
о
ос
S
S3
ex.
с
о
Си
•о
S'
со
287
E)
где \^п — корни функции JQ(v<), так как /0([л) = 0 при Bi = оо.
На рис. 7.3 приведены графики изменения обобщенной переменной
6/Pd Fo от числа Фурье при разных значениях относительной
координаты rlR.
Для квазистационарного состояния в решении E) рядом можно
пренебречь. Для малых значений Fo можно найти приближенное решение.
Применяя метод разложения функции I0(z) в асимптотический ряд,
после некоторых преобразований получим решение для изображения в
случае Bi = оо в таком виде (подробно см. § 5 гл. IV):
Тс </•,«)—£■«-£ lAf A + *~'\ «Р I" l/~~ <* - г) I. F)
^('^K^-']-
Пользуясь соотношением E4) таблицы изображений (см. приложения),
иаходим
6 ^Pd
/4
4Fo i2erfc Jjr- + -£pl- DFoK/2 i3erfc ^
2 VFo 8r 2 /Fo
• G)
Значения функций i2erfcx и i3erfc д: можно определить по табл. VII
в приложениях.
Определение удельного расхода тепла. Найдем среднюю температуру
цилиндра, необходимую для расчета удельного расхода тепла. Применяя
интегральное соотношение C2) § 6 гл. VI, получим
т (%) -т0
= Pd
00
(8)
где Вп — постоянные, определяемые соотношением C4) § 6 гл. VL
Первые шесть значений Вп приведены в табл. 6.12.
Сравнивая рассмотренные выше задачи с задачами гл. V, можно
увидеть аналогию между ними. В обоих случаях через определенный
промежуток времени, определяемый неравенством Ро>Рох, наступает
dT
квазистационарное состояние, когда -т— становится величиной
постоянной (температура в любой точке тела есть линейная функция времени).
Поэтому при квазистационарном состоянии в одномерных задачах
распределение температуры следует закону параболы. Разница между
указанными задачами состоит в том, что в данных задачах скорость
нагревания --т— (производная средней температуры по времени)
становится величиной постоянной только через определенный промежуток
времени, когда Fo>Fo1, а в задачах гл. V скорость нагревания
является величиной постоянной с самого начала процесса нагревания, что
непосредственно следует из граничного условия.
288
Глава седьмая
Таким образом, удельный расход тепла равен
где Rv =s отношение объема к поверхности тела.
§ 4. НЕОГРАНИЧЕННАЯ ПЛАСТИНА, ШАР И НЕОГРАНИЧЕННЫЙ
ЦИЛИНДР. ТЕМПЕРАТУРА СРЕДЫ — ЭКСПОНЕНЦИАЛЬНАЯ
ФУНКЦИЯ ВРЕМЕНИ
Постановка задачи. Дано изотропное тело (неограниченная
пластина, шар и неограниченный цилиндр), находящееся в тепловом
равновесии с окружающей средой. В начальный момент времени
температура среды повышается по закону Тс(т) = Тт — (Тт — T0)e~kz, где Тт—
максимальная температура среды Тс (оо)=Tm, k—постоянная. Требуется
найти распределение температуры внутри тела и удельный расход
тепла.
Подробно рассмотрим задачу для пластины, а для остальных форм
тела приведем конечные результаты.
Имеем обычное дифференциальное уравнение теплопроводности для
неограниченной пластины толщиной 2R. Начало координат находится в
середине пластины, относительно которой кривые распределения
температуры являются симметричными. Имеем:
начальное условие
Т{х, 0) = Г0-const;
условие симметрии
граничное условие
ЭГ@, *с)
дх
О)
B)
а7ТУ'Т) + Н [Та- GV- Т0) «г* - Т (R, -с)] = 0
дх
Решение задачи операционным методом. Решение
изображения Tl (x, s) при условиях A) и B) имеет вид
Граничное условие C) для изображения напишем так:
НТт Н(Тт-Т0)
C)
уравнения для
-TL(R,s) +
s + k
HTL(R:s) = 09
D)
E)
так как L [e~~kx] =
1
s + k
Удовлетворим решение D) граничному условию E):
- Н^^1А _ ял ch Y-T R = °-
s + k
ТЕМПЕРАТУРНОЕ ПОЛЕ БЕЗ ИСТОЧНИКОВ ТЕПЛА 289
Определив из этого равенства постоянную А и подставки
полученное выражение в решение D), будем иметь
TL{x,s)-lf =
(Tm~T0)ch "J/JL x
[с]/^*+-±->^-»н|/-Н(^ + 1)
ф(8) F)
+ «
Числитель и знаменатель — обобщенные полиномы относительное,
причем полином ty(s) не содержит постоянной (его первый член pa^eHs).
Полином i]>(s) имеет следующие простые корни: 1) s,= 0, 2) s = -—&,
3) sn = р2^~> г#е i у — R = р — бесчисленное множество корней,
определяемых из характеристического уравнения (см. подробнее § 3 гл. VI).
Применяя теорему разложения для случая простых корней, находим:
cos I/ — х
= Т (*» т) ~~ Т° = 1 — . = га ^ ^-Лх
2-т ccs (!.„ -^- ехр ^— {4 |£-
G)
где Ап — постоянные тепловые амплитуды, определяемые из
соотношения C0) § 3 гл. VI.
Анализ решелия. Введенный в § 1 критерий Предводителева Pd в
данном случае будет равен
(8)
так как
(dTc
\ d-\ ^
Максимальная скорость нагревания среды будет соответствовать
начальному моменту времени; с течением времени она уменьшается и при
dTc (т) п ,
т^ оо ). w ->0 (температура среды становится постоянной и
равной Тт).
Решение G) б безразмерных величинах можно написать так:
а
0|'Ыт La(rm-r0).
jmax
Pd4
= 1 — j % ехр (- PdFo) —
COS
2j "i^^
.«=71 Pd
V" cos Pn 4r exp ( — ц* Fo).
(9)
10 Заказ № 640
290
Глава седьмая
Таким образом, относительная температура является функцией Fo, Bi,
Pdn-^:
Ч- Fo, Bi, Pd,
Я '
A0)
Если положить Pd — оо (k-** 00), то температура среды постоянна и
равна Тт (Тс =- Тт). Тогда решение (9) превращается в решение B9)
§ 3 гл. VI.
Если положим Bi = оо, что означает, что температура поверх-
ности пластины есть экспоненциальная функция времени (граничное
условие первого рода):
T(±R,x) = Tm-(Tm-TJ е-*,
то решение (9) превращается в следующее:
cos "J/ Pd —
W~ exp (—PdFo)-
VPd
00
An
Pd
COS
!*« "J- exP (— 1*2 Fo),
(И)
где jj.„ - Bn—1)
Определение удельного расхода тепла. Для нахождения удельного
расхода тепла найдем среднюю температуру:
Т{х)- Г„
I —
-Pd Fo
/Pd
:l^Pd- -gj-VPd]
00
s
вл
у-- exp (—!A„Fq),
Pd
A2)
где Bn —постоянные коэффициенты, определяемые соотношением D5)
§ 3 гл. VI. Далее расчеты производятся обычным способом.
ТЕМПЕРАТУРНОЕ ПОЛЕ БЕЗ ИСТОЧНИКОВ ТЕПЛА 291
Решение для шара записывается в следующем виде:
R Bi sin Y Pd Л
R
1— r[(Bi~l)sin l/Pd+l/Pdcos l/Pd] "eXp ^ PdFo)
00
s
Л„ «!ll4>.-f- j
л=1 Pd
'^Л
exp (— }x„ Fo),
A3)
где An — начальные тепловые амплитуды, определяемые соотношением
B9) § 5 гл. VI;
j 3Bi(fg V Pd — У Pd) -pd Fo
Pd [ (Bi — 1) tg "[/Pd + l/T?d]
oo
- V ^|— exp (-^Fo),
n=i "~"pd~
A4)
где Bn —постоянные коэффициенты, определяемые соотношением D9)
§ 5 гл. VI.
Решение для неограниченного цилиндра:
[ущ -тт)
6 = 1 — i -JL:—_— ехр (_ pd Fo) —
y0(l/Pd)-4- VPdJdVPd)
ы
oo
s
i-.«*
j0( p«4-Wp(—^Fo)'
я=1 Pd
A5)
где Л„ —коэффициенты, определяемые соотношением B7) § 6 гл. VI;
Т = 1 2Л(Т^) __ exp(„PdFo)_
l/Td У0 (V~Pd) — -gj Pd /i (j/ Pd)
«=1 Pd
Bn exp (— |x| Fo),
A6)
где Bn — постоянные коэффициенты, определяемые соотношением C4)
§ 6 гл. VI.
10*
292
Глава седьмая
§ 5. НАГРЕВАНИЕ ВЛАЖНЫХ ТЕЛ (НЕОГРАНИЧЕННАЯ
ПЛАСТИНА, ШАР И НЕОГРАНИЧЕННЫЙ ЦИЛИНДР)
Постановка задачи, К подобного рода задачам относятся задачи
на нагревание влажных тел в среде с постоянной температурой, к,ог-
да испарение влаги происходит на поверхности.
Из теории сушки известно, что интенсивность испарения (количество
испаренной влаги в единицу времени с единицы поверхности тела)
^начале ;(в первом периоде) постоянная, а затем (во втором периоде)
изменяется с течением времени по экспоненциальному закону. Таким
образов, в первом приближении для интенсивности испарения т можно
написать:
т — m0e~kx, A)
где k — коэффициент сушки (l/сек), т0 — максимальная интенсивность
(кг/м2-сек). Если. положить k = 0, то т = т0 — const, т. е. получим
постоянную интенсивность испарения, соответствующую первому
периоду с^шки.
.Рассмотрим задачу на нагревание влажной неограниченной плас-
muntjf в среде с постоянной температурой Тс = const. Начальные и
граничные условия можно написать так:
Т (х, 0) = Го,
аг(о,т)
— р m0 e
0,
дх
-0,
где р;—уделъйа^ теплота испарения (дж/кг).
Граничное условие D) можно переписать так:
dT(R,t)
дх
н[{тс-^-е-к)-Т (*,т)] = 0,
B)
C)
D)
;E)
т. е. ;это гранитное условие аналогично граничному условию C) § 4,
только вместо (Тт — Т0) здесь входит величина ——— .
Решение задачи. Решение для изображения имеет вид
TL(x,s)- -?f =
(Тс
■Го) (« + *)- — pm0
а
]*Ут
При ^помощи теоремы разложения находим решение для оригинала:
eMcos ypd -|-
F)
Гс-Го
1^-
—PdFo
е —
оо
1 —
cos VrPd~-gr-yPdsin]/Pd
■аг)
Pd
G)
ТЕМПЕРАТУРНОЕ ПОЛЕ БЕЗ ИСТОЧНИКОВ ТЕПЛА
293
где Pd = — R2 — критерий Предводителева, бм = — ,_? т° „ ч некото-
а а U с — •« о)
рый критерий, который, как будет показано ниже, равен отношению
психрометрической разности (Тс—Тм) к избыточной температуре
окружающей среды, т. е.
п _ тс-тм (8)
7с-Го '
где Тм — температура мокрого термометра.
Таким образом, температура пластины есть функция ряда
критериев, а именно
8 = Ф (bi, -J-, Fo, Pd, 6M ). i(9)
Если интенсивность испарения есть постоянная величина, т. е.
т = т0 = const (первый период сушки), то критерий Предводителева
равен нулю (коэффициент сушки k = 0). Тогда решение G) примет вид
A0)
В первом приближении можно считать, что в стационарном
состоянии (Fo = оо) температура влажного тела (первый период сушки)
равна температуре мокрого термометра, т. е. 6^ = 1 —бм или
Тгр гр гр р 171
м ' 0 = * с ^ 0 ~ >
откуда
1£ = тс-ты. (П)
Таким образом, получаем новое выражение для критерия 8М, который
приобретает значение параметрического критерия.
Решение A0) можно написать так:
со
e = i-sM-S(i-eM) л„со8[хп
п=\
-£- ехр (— р* Fo).
Т(х, г)—То
Тм — Т0
л=1
1 — S К costs, -J- ехр ( — p.* Fo ).
A2)
Выражение A2) по форме совпадает с решением для нагревания сухой
пластины, только вместо температуры среды Тс входит температура
мокрого термометра Тм. Следовательно, задача на нагревание влажного
тела с постоянной интенсивностью испарения на его поверхности
Может быть сведена к задаче на нагревание сухого тела с заменой Тс на
Тм. Это непосредственно следует из граничного условия, которое
можно написать так:
dT(R
дх
или
1^ + я[(тс-^)-Г(Д,т)]=0, A3)
dT(R *) +н [Tu-T(R,x)] = 0. A3а)
294
Глава седьмая
Аналогичные решения для шара и неограниченного цилиндра будут
соответственно иметь вид:
е-!
00
■2
#0MBisin У Pd-
г [(Bi — 1) sin YPd + yPd cos У Pd]
exp (—PdFo)
1 —
(-tHJ *
Л„ exp [ — |ал FoJ;
'Р-в
A4)
= 1
eM Л (v~Pd -Lj
Jo(VPd)- ~V~PdJi(VP<i)
exp (—PdFo) —
00
л==1
I -
('-»J
Anccspn -^ exp (—|*«Fo).
A5)
Если сравнить решения G), A4) и A5) с решениями (9), A3) и A5)
§ 4, то можно найти большое сходство между ними. Второй член
наших решений отличается от второго члена решений предыдущего
параграфа только множителем 6М. Третий член решения имеет другой
множитель при коэффициенте Ап : вместо / г \ здесь стоит мно-
1~Pd *\
житель
1 —
(-я-")
Поэтому средние температуры для нашей
задачи можно получить непосредственно из решений A2), A4) и A6)
§ 4, произведя указанные замены.
Пусть интенсивность испарения постоянна, но не одинакова на
обеих поверхностях пластины (несимметричная задача). Имеем:
+
dT(+R,z)
дх
дГ(-#,т)
дх
Т (х, 0) = То,
+ н[тс- -^- -Т ( + Д,т)] = 0,
+ я[гс--^- — г(—я,т)] = о,
A6)
A7)
где тг и т2—соответственно интенсивности испарения на
противоположных поверхностях пластины (кг! м?-сек). Решение уравнения имеет
вид
ТЕМПЕРАТУРНОЕ ПОЛЕ БЕЗ ИСТОЧНИКОВ ТЕПЛА
295
Т (х, х)
р (mi + mg)
2а
со
2[G-с
/2=1
^о)-
2а
X
X Ля COS |*я -^- ехр ^— |1Л t4) J — 2a(l+Bi)# —
со
__ ^„d^ZL^iL ^,isiri[x^i -~- ехр (— [4,i Fo),
£=1
A8)
где
2 sin р.я
**,1
* р.л + sin ^ cos ^
2cos^,i
f*f 1 ~~ sin hfe,i cos^,i
-(-1Г+1
2Bi (Bi« + ^)v*
^(Bi^ + Bl+^j '
2Bi (Bi2 + a? ,У/г
( —l)*+i Л ^^w A9)
Таблица 7 J
Корни характеристического уравнения
tgy. = -
Bi
Bi
1,1
2,1
r3,l
4>,l
4i
0,7
0,8
0,9
,0
,5
,0
,0
,0
,0
,0
1
1
2,
3,
4,
5
6.
7,0
8,0
9,0
10,0
15,0
20,0
30,0
40,0
50,0
60,0
80,0
100,0
1,5708
1,6320
1,6887
1,7414
1,7906
1,8366
1,8798
1,9203
1,9586
1,9947
2,0288
1746
2889
4557
5704
6537
2,7165
2,7654
2,8044
2,8363
2,8628
7124
7335
7544
7751
7956
8158
8358
,8556
,8751
,8943
,9132
,0037
,0870
,2329
,3540
,4544
5,5378
5,6078
2,9476
,9930
3,0406
3,0651
3,0801
,0901
,1028
.1105
3,
3,
3,
3,1416
6669
7172
7606
9080
9921
0831
1311
,1606
,1805
,2058
6,2211
6,2832
7,8540
7,8667
7,8794
7,8920
7,9046
7,9171
7,9295
7,9419
7,9542
7,9665
7,9787
8,0385
8,0962
8,2045
8,3029
8,3914
8,4703
8,5406
8,6031
8,6587
8,7083
8,8898
9,0019
9,1294
9,1986
9,2420
9,2715
9,3089
9,3317
9,4248
10,9956
11,0047
11,0137
11,0228
11,0318
11,0409
11,0498
11,0588
11,0677
11,0767
11,0856
11,1296
11,1727
11,2560
11,3349
11,4086
11,4773
11,5408
11,5994
11,6532
11,7027
11,8959
12,0250
12,1807
12,2688
12,3247
12,3632
12,4124
12,4426
12,5664
14,1372
14,1443
14,1513
14,1584
14,1654
14,1724
14,1795
14,1865 !
14,1935
14,2005
14,2075
14,2421
14,2764
14,3434
14,4080
14,4699
14,5288
14,5847
14,6374
14,6870
14,7335
14,9251
15,0625
15,2380
15,3417
15,4090
15,4559
15,5164
15,5537
15,7080
17,2788
17,2845
17,2903
17,2961
17,3019
17,3076
17,3134
17,3192
17,3249
17,3306
17,3364
17,3649
17,3932
17,4490
17,5034
17,5562
17,6072
! 17,6562
17,7032
17,7481
17,7908
17,9742
18,1136
18,3018
18,4180
18,4953
18,5497
18,6Г09
18,66E0
18,8496
296
Глава седьмая
jOJ
\
Т
о
^
О*
°Ч
О
к
Си
м
S
_J
ч
нтом
к
я
К
-6-
•н-
коэ
>^
t=t
й
<р
н
о
*3
со
U*
cd
сЗ
со
W
етрич
s
^
д
3
и
К
03
в
«
fc3
• CO S
ю
t^
о
к
Он
к
И
ТЕМПЕРАТУРНОЕ ПОЛЕ БЕЗ ИСТОЧНИКОВ ТЕПЛА
297
}i„ и |xAjl—корни характеристических уравнений
ctgfX= ВТ ^
tgfX = —
Bi
B0)
Первые шесть значений корней |хл и коэффициентов Ап приведены в
табл. 6.1 и 6.2; в табл. 7.1 и 7.2 приведены первые шесть значений
.jAjfe,! и Л*,1 для различных значений критерия Био (от 0 до <х>).
При установившемся состоянии (Fo = оо) имеем
T(x) = Tc--fa
(mx + ma) + -£- (mx ■
■m
" 1 + BiJ'
(Й)
т. е. имеет место линейный закон распределения температуры по
толщине пластины.
Таблица 7.2
ЧМ
Значения постоянных
2Bl(Bi» + t*f.i)V'
= (— l)ft+1
H-ik.i(Bi* + Bi+H-2.,)
Bi
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,5
2,0
3,0
4,0
5,0
6,0
7,5
8,0
9,0
10,0
15,0
20,0
30.0
40.0
50,0
60 0
80,0
100,0
оо
\l
0,0000
0,0721
0,1303
0,1779
0,2172
0,2514
0,2803
0,3035
0,3156
0,3471
0,3646
0,4298
О;4726
0,5254
0,5562
0,5759
0,5892
0,598t
0,6056
0,6108
0,6148
0,6256
0,6300
0,6336
0,6348
0,6354 ,
0,6358
0,6361
0,6363
0,6366
\i
—0,0000
—0,0089
—0.0175
—0,0259
—0,0341
i —0,0420
—0,0497
—0,0571
—0,0643
—0,0/13
—0,0/81
—0,1088
—0,1348
—0,1756
—0,2052
—0,2270
—0,2435
—0,2561
—0,2659
—0,2736
—0,2789
—0,2978
—0,3056
—0,3122.
—0,3147
—0,3160
—0,3167
—0,3174
M),3177
—0,3183
\l
0,0000
0,0032
0,0064
0,0096
0,0127
0,0158
0,0189
0,0219
0,0249
0,0278
0,0205
0,0446
0,0576
0,0805
0,0957
0,1159
i 0,1293
0,1404
0,1496
0,1574
0,1639
0,1844
0,1945
0,2034
0,2068
0,2088
0,2098
0,2105
0,2113
0,2122
\l
—0,0000
—0,0017
—0,0033
—0,0049
—0.0065
—0,0082
—0,0098
—0,0114
—0,0129
—0,0145
—0,0160
—0,0237
—0,0311
—0,0448
—0,0571
—0,0682
—0,0779
—0,0865
—0,0941
—0,1007
—0,1065
—0,1265
—0,1375
—0,1479
—0,1524
—0,1546
—0,1559
—0,1573
—0,1579
—0,1591
\i
0,0000
0,0010
0,0020
0,0030
0,0040 1
0,0050
0,0059
0,0039
0,0079
0.0089
0,0098
0,0146
0,0193
0,0281
0,0365
0,0442
0,0513
0,0578
0,0638
0,0691
0,0739
0,0920
0,1028
0.1140
0,1191
0,1218
0,1234
0,1250 "
0,1258-
0,1274
\i
—0,0000
-0,0007
—0,0013
—0.0020
—0,0027
—0,0033
—0,0040
—0,0047
—0,0053
—0,0060
—0,0066
—0,0099
—0,0129
—0,0192
—0.0251
i —0,0310
—0,0360
—0,0409
—0,0455
—0,0498
—0,0538
-0,0694
—0,0797
—0,0911
—0,0966
—0,0995.
—0,1015
'-0,1034
—0,1043-
\ —0,1060
298
Глава седьмая
Если тг — m% = т, то из B1) получим
Т(х)-Тс~р-Е = Тм = const
Средняя температура пластины равна
в— ^ — т° =_ 1 _ Р(«i + m-г)
Тс-Т0 ' 2а(Гс-Г„)
-S[l-^^)]B„exP(-^Fo). B2)
На рис. 7.4 и 7,5 приведены графики |xIfl ~/(Bi) и i4iti —/(Bi),
построенные по данным табл. 7.1 и 7.2.
§ 6. ТЕПЛОВЫЕ ВОЛНЫ. НЕОГРАНИЧЕННАЯ ПЛАСТИНА,
ПОЛУОГРАНИЧЕННОЕ ТЕЛО, ШАР И НЕОГРАНИЧЕННЫЙ
ЦИЛИНДР. ТЕМПЕРАТУРА СРЕДЫ — ПРОСТАЯ
ГАРМОНИЧЕСКАЯ ФУНКЦИЯ ВРЕМЕНИ
Во многих тепловых процессах температура среды является
периодической функцией времени. Тогда распределение температуры в
твердом теле, нагреваемом в этой среде, будет аналогично распределению
смещения колеблющихся точек при распространении волнового
процесса в упругой среде. Поэтому такие задачи обычно называют задачами
на распространение тепловых волн, понимая последние в
макроскопическом смысле слова.
Рассмотрим задачи на нагревание тела (неограниченная пластина,
шар и неограниченный цилиндр), когда температура среды изменяется
по закону простого гармонического колебания, т. е. изменяется по
закону косинуса или синуса.
Обычно решения задач на тепловые волны даны для
квазистационарного состояния, т. е. предполагается, что процесс продолжается
столь долго, что первоначальное распределение температуры потеряло
свое влияние на ход процесса (задачи без начальных условий). Здесь
приводятся решения для общего случая с учетом начальных условий,
из которого как частный случай получаются известные решения для
квазистационарного состояния.
Рассмотрим подробно решение задачи для неограниченной пластины.
Постановка задачи. Дана неограниченная пластина толщиной
2R при температуре Т0. В начальный момент времени она
помещается в среду, температура которой изменяется по закону простого
гармонического колебания
Т,{х)-Т0-=Тт cos2tcvt,
A)
где V — частота колебания, Тт — амплитуда колебания температуры
среды. Теплообмен между поверхностями пластины и окружающей
среды происходит по закону Ньютона. Требуется найти
распределение темперлтуры по толщине пластины в любой момент времени и
удельный расход тепла.
ТЕМПЕРАТУРНОЕ ПОЛЕ БЕЗ ИСТОЧНИКОВ ТЕПЛА
299
Имеем
B)
C)
D)
Т (х, 0) = Т0,
дТф.х) п
дх
-дТ(*;х) +Н[Т0 + Тп ccs2tcvt-T[/?,t)] = 0.
Задача — симметричная, начало координат находится в середине
пластины.
Решение задачи. Решение для изображения при условиях B) и C)
будет
TL (х, s)—?j- = A ch Y~ x. E)
Постоянную А определяем из граничного условия D), которое для
изображения будет иметь вид
-T'L(R,s) +н[^ + ^~^r~T(R,s)] = 0, F)
так как
L [ccs 2 тг v т] = 2 , /0—го-.
Подставляя решение E) в условие F), имеем
~А VJsh VJ* + l?T^-HAch VJ* = °- G)
Определив из равенства G) постоянную А и подставив полученное
выражение в решение E), будем иметь
^ JL<fL (8)
Решение (8) представляет собой отношение двух обобщенных
полиномов, которые удовлетворяют условиям теоремы разложения.
Приравнивая полином знаменателя нулю, т. е. <J> (s) = 0, находим корни:
i) sx = /2 тс v, 52 = —t2 7cv; 2) s„ = — -^ бесчисленное множество
корней, которые определяются из обычного характеристического
уравнения.
Воспользуемся теоремой разложения (случай простых корней), тогда
решение нашей задачи получим в виде
300
Глава седьмая
+
ch
V <"т
"I / *° 1 I / ш 1/ М>
К 1-а-« + 1Г V 1!Г*ЬУ 1Т*
i сот
е +
ch
ch
У ~<^Г*
1/ со 1 1 / <*> 1/ <*>
ch
00
2
ti
£ + -**<
cos|j.„ -^- exp ^ — i*« ^i-l»
2 ат
(9)
где ш = 2 тс v — круговая частота (v~-p-, где Р — период колебания), Лл —
коэффициенты, определяемые из известного соотношения для неограни-
чёйной пластины.
Анализ решения. Максимальная скорость изменения температуры
среды ~~jf~ равна 2 тг v Tm. Тогда критерий Предводителева будет
A0)
равен
Pd
dFo
2^D2 ^ JL D2
Следовательно, решение (9) можно переписать так:
= -±- [#, exp (i Pd Fo) + #-/exp (__;pdFo)] —
°° 4
2 (^+м») л«со8^ хехр (-^F°)>
(ii)
где
ch]/i Pd-
iV; -
R
Fchl/TPd
i: Pd + -L- l/i Pd sh
Vi Pdj
Л-, =
ch V—iPd
#
[ch -|Л-
tPd + -^r- V— i Pd sh V— i Pd
Bi
A2)
A3)
Сумма в рещении A1) с течением времени уменьшается и, начиная
с некоторого значения Fo > Fox (квазистационарное состояние), она ста-
нрвцтся ничтожно малой по сравнению с двумя первыми членами, так
что ею можно пренебречь.
ТЕМПЕРАТУРНОЕ ПОЛЕ БЕЗ ИСТОЧНИКОВ ТЕПЛА 301
Тогда для квазистационарного состояния можно написать
6 = -L [(Nt exp (t Pd Fo) + W_£ ехр (— i Pd Fo)] =
= -L [(Ni + N4 ) cos Pd Fo + i (Nt - N4 ) sin Pd Fo] =
= (Nt N4 )V.COs
;pdF—«ct^/js^)].
A4)
Из решения A4) следует, что температура в любой точке пластины
совершает простое гармоническое колебание с той же частотой, что и
температура среды, но фаза колебания отстает от фазы колебания темпе-
Nt-NA _ vntr fi _ Тс~-Т0
ратуры среды на величину arctg i Л/ л. * 1, так как tfc ^
\ ^/ -г ^-1 / * т — 1 о
-=cosPdFo (критерий Предводителева прямо пропорционален частоте).
Амплитуда колебаний температуры в любой точке пластины
уменьшается с глубиной. Поэтому максимальная амплитуда соответствует
поверхности пластины (х — R), но она меньше • амплитуды колебаний
температуры среды на величину (Ni N_t I/г.
Положим критерий Bi — оо; тогда температура поверхности все
время равна температуре среды, которая изменяется по закону
косинуса, т. е.
Т (±R,i) = T0 + Tm cos27tvz = T0 + Tm cosPdFo.
В этом случае
** =
ch Yi Pd -4-
ch "j/TPd"
,N.t
X \
ch У—iPd-^-
A5)
Значение V±i можно найти следующим образом.
= 1 + 2i — 1 = 2i9 откуда
1/7 =± ]/^(l+0-
Имеем A + iJ
Аналогичным путем получим:
у=з = ±/4-о
о-
Знак ± для решений A2), A3) можно опустить, так как chz есть
функция четная, а перед нечетной функцией shz стоит в качестве
множителя z. Поэтому, независимо от знака (±) получится один и тот же
результат.
Пользуясь известными формулами типа
302
Глава седьмая
= ch 1/4 Pd^ccs]/-i~ PdX +
-fish ]/■
-2- Pd -£- sin
/:
Pd
получим решение такого же вида, как и решение A4), но в нем
значение вспомогательных величин будет следующее:
W, #,)«/.=
i- Pd)+/f
'/2
A6)
. N:
arctg
-■ (Vi «) '•( /4-" *)-'•(/4- *) '■ (V\ О
{Vt»H V:
1 X ,
/-i-Pd)/.
/:
т Pdin
A7)
где /c (z) -- = chz ccsz, /s (г) --- shzsinz. Значения гиперболо-тригономет-
ричсских функций можно найти в монографии А. И. Крылова «О
расчете балок, лежащих на упругом основании» (Л., Изд. АН СССР, 1931).
Вычисление коэффициентов Nt и N„t по формулам A6) и A7) менее
удобно, чем вычисление непосредственно по формулам A5).
С целью упрощения расчета в табл. 7.3 приведены значения
коэффициентов Л5, Bs, Ас и 5С, по которым можно вычислить
гиперболические функции в формулах A5), а именно
ch z V~±J = Лс ± i Ba sh z V~±i = Л3 ± i£s.
Решение для полуограниченного тела можно получить из решения
A1). Перенесем начало координат из середины пластины на левую
поверхность, т. е. сделаем замену переменной х на X — R, и положим
2R -»- оо. Рассмотрим выражение
N{
ехр
v
• -£-(*-*>] + ехр [~У i -~-(R+x>]
1 f
w-t
1 +
-irV>j_
+ ttV~1
-2R
V'i-
При R—x ^ 2i?—X, R + x = X величина TV/ будет равна
lim Ni
2R-+cx>
Аналогично найдем
1 +
4/'-f
ехр
-X
/'-г-)-
ТЕМПЕРАТУРНОЕ ПОЛЕ БЕЗ ИСТОЧНИКОВ ТЕПЛА 303
Таблица 7.3
Значения постоянных Ас, Вс, Л8 и Bs.
Z
0,01
0,025
0,05
0,075
о,ю
0,15
0,20
0,25
0,30
0,35
0,40
0,45
0,50 !
0,55 |
0,60
0,65
0,70
0,75
0,80
0,85
0,90
0,95
1,00
1,05
1,10
1,15
1,20
1,25
1,30
1,35
1,40
1,50
1,60
1,70
1,80
1,90
2,0
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3,0
3,2
3,4
3,6
3,8
4,0
4,2
4,4
4,6
4,8
5,0
5,5
лс
1,000
1,000
1,000
1,000
1,030
1,000
1,000
1,000
1,000
0,999
0,999
0,998
0,997
0,996
0,994
0,993
0,990 1
0,987
0,983
0,978
0,973
0,966
0,958
0 £50
0,938
0,927
0,916
0,8£8
0,881
0,862
0,834
0,790
0,727
. 0,654
0,566
! 0,460
1 0,340
0,199
0,038
—0,146
— 0,355
— 0,58/
— 0,851
v~™ 1,105
— 1,468
— 1,821
— 2,206
— 3,086
— 4,129
— 5,304
— 6,629
— 8,0ЭЗ
— 9,628
—11,227
—12,839
—14,437
—15,851
—17,939
Вс
0,0001
0,0003
0,001
0,003
0,005
0,011
0,020
0,031
0,045
0,062
0,080
0,095
0,125
0,151
0,180
0,212
0,245
0,281 1
0,320
0,362
0,404
0,451
0,499
0,549
0,601
0,658
0,705
0,776
0,839
0,906
0,970
1,108
1,258
1,411
1,571
1,741
| 1,911
2,087
2,261
2,440
2,616
2,787
2,953
3,0ЭЗ
3,259
3,389
3,502
3,656
3,695
3,553
3,256
2,589
,1,660
0,353
— 1,393
— 3,715
— 6,568
—16,982
А"
0,0071
0,0177
0,035
0,050
0,070
0,106
0,140
0,175
0,209
0,242
0,275
0,307
0,339
0,369
0,398
0,427
0,454
' 0,479 1
0,505 1
0,526 1
0,547
0,566
0,583
0,599
0,612
0,622
0,629
0,636
0,639
0,639
0,636
0,621
0,5S0
0,546
0,484
0,402
0,302
0,180
0,036
—0,135
— 0,291
— 0,554
— 0,803
— 1,057
— 1,413
— 1,761
—2,143
— 3,021
— 4,057
-г- 5,239
— 6,657
— 8,038
— 9,578
—11,183
—12,800
— 14,404
—15,824
—17,984
bs
0,0071
0,0177
0,035
0,050
0,071
0,106
0,142
0,179
0,215
0,253
0,290
0,329
0,369
0,408
0,449
0,492
0,534
0,578
0,625
0,670
0,718
0,771
0,819
0,871
0,924
0,980
1,026
1,096
1,155
1,216
1,271
1,410
1,550
1,692
1,8?9
1,995
| 2,151
2,312
2,477
2,636
2,798
2,954
3,107
3,234
3,386
3,504
3,604
3,639
3,752
3,602
3,239-
2,607
1,669
0,355
— 1,393
— 3,724
— 6,759
—16,996
304
Главй "седьмая
Продолжение табл 7 3
Z
6,0
6,5
7.0
7,5
8,0
8,5
9,0
. 9,5
10,0
Ас
—15,794
— 5,796
16,616
55,532
115,788
196,188
289,033
375,199
414,391
вс
—30,897
—49,149
—68,601
—83,365
—83,919
—54,969
23,791
175,924
417,288
^s
—15,W
— 5,795
16,614
55,529
115,786
196,186
289,019
375,197
414,525
Bs
—30,911
—49,159
-^68,601
—83,369
—83,921
i—54,970
23,791
175,925
417,289
Рис 7 6 Изменение относительных
температур окружающей среды и
поверхности тела с течением времени
Тогда получим
Г(Х,т)-Г0 1
-4-1-
■т-хA-Н)|Л
2 а
+
11 + -яA+0-|/4--Т
р f z a
A+8)» + !
[(l+8)cos(x/4-T
+
— 8 sin X
У+Т
[A+SJ+S2]
cot + arctg
1/. c
V
1 + S / '
2 a cosix/^-^—
A8)
где 8 = -ft-,]/ -g- -|- = -jfY -£p-. P = — период колебания.
Решение 'A8) уожно переписать так:
в = V^ cos [^-(^ + ")] .
A9)
ТЕМПЕРАТУРНОЕ ПОЛЕ БЕЗ ИСТОЧНИКОВ ТЕПЛА
305
где величина
М' + т/^+тЙрГ <20>
есть амплитуда колебания температуры ограничивающей поверхности,
а величина
M = arctgf—77=т\ B1)
представляет собой смещение по фазе колебания температуры
ограничивающей поверхности по сравнению с колебанием температуры среды
(рис. 7.6).
В обобщенных переменных это решение можно написать так:
6 = А0 ехр ( — jAl-PdJ cos [Fo^/Fo; - (]/-Lpdx+ M
B2)
где
A0 = [l +K2/Bi*+(gLJ] Y\ B3)
M = arctg ( у= ) B4)
Pdx = локальное число Pd для координаты X, Fo^ = —^
clP
обобщенный локальный аргумент (безразмерное время), Fo^ = —тг —
критерий периодичности; отношение Fo^/Fo^ = сот, Bi* — обобщенный
аргумент, характерный для стационарно-периодического состояния и равный
Bi* =
}/ Хс^а
B5)
Выясним физический смысл числа Bi*. Мгновенный поток тепла на
поверхности тела равен
q @,т) = — X (-g^-).^ = — ^ У ■£ (sin сот — cos сот) . B6)
Воспользуемся соотношением
cos (сот + —) = (cos сот — sin сот) (]/" 2 у^1,
тогда получим, что величина мгновенного потока тепла на
поверхности тела равна
q @,т) = УЩ* Тт cos (сот + -pj - qm cos (сот + -J) , B7)
где <7m — максимальный удельный поток тепла (или амплитуда
колебаний удельного потока тепла), равный
gm = TnVU^._ B8)
Отношение амплитуд колебаний потока тепла и температуры
равно
306
Глава седьмая
Следовательно, величина }Аср> равна максимальному мгновенному
потоку тепла, подведенному к поверхности тела при амплитуде
колебания температуры на поверхности стенки, равной единице (Тт= 1°К)*
Таким образом, число Bi* равно отношению стационарного
потока тепла аДТ при единичном температурном напоре (АТ=Г) к
максимальному потоку тепла j/Xcyco в стационарно-периодическом
состоянии при единичной амплитуде колебания температуры (Тт = 1).
Другими словами, число Bi* является модифицированным числом
Био для стационарно-периодического состояния.
Возвращаясь к формуле B3), можно отметить, что при Bi* ~> сю
относительная амплитуда А0 равна единице, а М = 0.
Л
м0
1
0,8
0,6
0,4
0,2
1
/
1
6
8
1
10
X
12
14
16
18
Bt*
0 0,2 0,4 0,6 0,£
1,2 1,4 1,6 1,8 Bi*
Рис, 7.7. Зависимость амплитуды колебания Рис. 7.8. Распределение относитель-
температуры на поверхности тела от числа ной температуры .по глубине плас-
Bi* тины в данный момент времени
На рис. 7.6 построен график изменения относительной температуры
окружающей среды 0С и относительной температуры ограничивающей
поверхности тела (X = 0). Из рис. 7.6 видно, что амплитуда колебания
относительной температуры среды равна 1 и, кроме того, на
поверхности тела Л0 < 1. Если критерий Bi — оо (Я = оо), то А0 = 1 [см.
соотношение B0)]. Сдвиг по фазе между косинусоидами 0С и 0П равен М:
при Bi == оо этот сдвиг будет равен — [см. соотношение B1)]. Таким
образом, температура любой точки тела совершает гармоническое
колебание. На рис. 7.7 приведена зависимость А0 от Bi*, из которой видно,
что при Bi* = 0 А0 = 0.
Для любого заданного времени (т = const) распределение
температуры по глубине тела происходит по закону косинуса с постепенно
затухающей амплитудой Л0ехр (— Xl/^-J (рис. 7.8).
Можно найти длину А тепловой волны как расстояние между
точками, находящимися в одинаковой фазе, т. е. отличающимися по фазе
на 2 тт.
Из решения A9) следует, что длина волны равна
А = 2|/^Р = 2|/-^. C0)
так как X I/ —^- == 2к. Следовательно, длина волны,
характеризующая глубину проникновения тепловых волн, прямо пропорциональна
ТЕМПЕРАТУРНОЕ ПОЛЕ БЕЗ ИСТОЧНИКОВ ТЕПЛА
307
Iя
;Я*
Я«
-<?
•к
О
^Т*
о £
X О
разных [значения
полуограниченног
О- t2
- н
о
о
•вн»
ishjt
>»
н
о
о
н
о
к
41
о
ЕС
н
о
к
к
•в*
са
о,
U
308
Глава седьмая
корню квадратному из произведения коэффициента
''температуропроводности на период колебания.
Из теории колебаний известно, что скорость распространения
волны равна длине волны, деленной на период колебания. В нашем случае
скорость тепловой волны и (скорость, с которой перемещается какая-
либо точка волны) равна
u~^=2Y^p-=2V^9
C1)
т. е. скорость распространения тепловой волны увеличивается с час-
тотой и с повышением коэффициента температуропроводности.
На рис. 7.9 приведена зависимость б от ¥ох1¥о'х для разных
значений обобщенного аргумента 1/2 V^o'x от 0° до 180° при условии
Bi*= оо.
Решения для шара и цилиндра записываются соответственно в
общем виде
-4r(Nt
/PdFo
+ N-i e
—/PdFo
)-
-2-^1
ftt+Pd* "
Am - fLexp(-^Fo),
r\>t
C2)
где
#Bish jA-/Pd-
N: =
N-t =
r [(Bi — 1) sh Yi Pd + j/7Pd ch Y'i Pd ]
R Bi sh Y—i pd—
R
r [(Bi — 1) sh Y ~ '"Pd + Y— *Pd ch У —iPd]
An—постоянные, определяемые соотношением B9) § 5 гл. VI; и
C3)
C4)
b = -L.{Nt e'pdFo +iV_,-e-/pdFo) -
°° 4
n=\
C5)
где
Ni =
/0(l/7Pd"_
JV_,=
[/„ (Vi Pd)+ ^- ViPd h (/.Pd) j'
/0 1Л=7р1
Г/о (l/-/Pd ) + ij- l/-i Pd /,(^=TPd)J
C6)
C7)
An — постоянные, определяемые соотношением B7) § 6 гл. VI.
ТЕМПЕРАТУРНОЕ ПОЛЕ БЕЗ ИСТОЧНИКОВ ТЕПЛА
309
Определение удельного расхода тепла. Удельный расход тепла за
любой промежуток времени Дт = т2 — тх находим по обычной формуле
Средняя температура по объему равна
1 = _L(Jv,VPdFo +AUe-'pdFo)
L 4.^ B„exp(-^Fo)
Л~1
C8)
где B„—постоянные коэффициенты, определяемые соответственно по
соотношениям § 2, 5, 6 гл. VI, а коэффициенты Ni и Л/_,- равны для
неограниченной пластины
1
для шара
Nt =
N-i =
N,=
1/fPd cth Yi Pd + — I Pd
ЛГ-*
V^TPd cth 1/— »Pd—__ Pd
3Bi (j/t'Pd —th VtPd)
tPd [(Bi — 1) th l/Ш + l/7Pd] '
3Bj (V=7Pd —th l/=?Pd)
—tPd [(Bi — 1) th Y—»'Pd + 1^—'Pd]
для неограниченного цилиндра
Nt =
2/i(l/tPd)
#_,- =
Г /о (l/tPd) + i_ 1/lPd /t ( 1/iPd ) jViPd
2/i (l/^lPd)
l^=7Pd Г/о (l/=7Pd)+J_ y^TPd Л A/^lPd) 1
C9)
D0)
D1)
D2)
D3)
D4)
Для периодически стационарного состояния средняя температура
будет периодической функцией времени. Пользуясь аналогичными
преобразованиями, будем иметь
б = {NiN-хУ* cos
2тс
■т—М ,
где
М = arctg i
. W/ — #_/
Отсюда получаем
М + -JV-/
2тгт2 —
COS | R M
-COS
2тсгх
2cTtm {NiN-iY* sin ttv(t2—T^sin [M—^(t^tJ] ,
-Я)]-
D5)
D6)
D7);
310
Глава седьмая
Таким образом, удельный расход тепла изменяется во времени по
закону простого гармонического колебания с тем же периодом, что и
период колебания температуры среды, но со сдвигом по фазе.
Из соотношения D7) следует, что количество тепла,
израсходованное в продолжение периода колебания к2—тх = Р =—)» равно нулю.
Рассмотрим расход тепла за промежуток времени Дх, равный
полупериоду
Для этого промежутка времени sin tcv(t2 —тх) = 1. Начало отсчета ^
выбираем так, чтобы величина sin [М — rcv^-f-Tj)] была равна единице, т.е.
^ = -ткгGй-«). <48)
Тогда расход тепла за полупериод Д т = V2 v будет равен
AQv = 2crTm [N1N-J*. D9)
Величина (A//AL_/I/2 есть функция критереев Pd и Bi, т. е. зависит от
коэффициента теплообмена а, частоты ш и теплофизических
характеристик (а, X, у).
Сделаем анализ формулы D9) для случая неограниченной
пластины (стенки) npnBi-^oo. В этом случае температура поверхностей
стенки изменяется по закону гармонического колебания
Тп(х)-Т0 = Тт cos шт. E0)
Если стенка обладает большой толщиной или изменения температуры
происходят очень быстро, то колебания температуры, которые
распространяются в толщу стены от обеих поверхностей, должны полностью
затухнуть, не дойдя до середины (см. рис. 7.10, а). Тогда каждая из
а) б)
Рис 7 10 Проникновение температурных волн в толщу стены
а — при значительной толщине, б — при средней толщине
обеих половин стенки ведет себя как тело неограниченной толщины
(полупространство). Таким образом, пластина большой толщины
представляет один из предельных случаев.
ТЕМПЕРАТУРНОЕ ПОЛЕ БЕЗ ИСТОЧНИКОВ ТЕПЛА
311
В противоположном случае
(очень тонкой стенки или
чрезвычайно медленных изменений
температуры) Можно считать,
что вся толща стенки
участвует в температурных
колебаниях поверхности без
уменьшения амплитуды и без
отставания во времени. В этих
условиях температура по всей
толще стенки одинакова (не
зависит от х), т. е. Тх = Тп.
Тогда количество
аккумулированного тепла в течение полу-
■Чф
0,7
0,5
0,3
од
10 12 14 16 18 20 Pd
Рис. 7.11. Зависимость коэффициента
аккумуляции тепла от критерия Предводителе-
ва при симметричном нагревании стены
конечной толщины
периода Дт = т2— тх единицей объема стенки будет равно
(AQ„JR_o - ст j (Т0 + Tm cos о х - Т0) dx - 2Тт сТ.
E1)
Это соотношение E1) аналогично элементарной калориметрической
формуле kQv = суДГ при нагревании тела на Д7\ В нашем случае
кТ = 2Тт. Следовательно, формула E1) определяет количество тепла,
воспринимаемого единицей объема стенки, при равномерном нагревании
ее от Т0-Тт до Т0 + Тт.
Между этими предельными случаями — очень толстой и очень
тонкой стенками—лежат все действительные ограждающие конструкции
(стены). Постепенно уменьшая толщину стенки, можно прийти к
такому случаю, когда колебания, распространяющиеся с обеих сторон,
соприкоснутся в середине стенки и начнут проникать друг в друга.
Мгновенное распределение температуры для этого случая приведено
на рис. 7.10, б, а решение задачи рассмотрено выше.
Согласно формуле D9), расход тепла за полупериод будет равен
E2)
AQv^=2c1TmK^
где /Сф — некоторый коэффициент, равный
/Сф - [(l/WcthylPd) (]/"=Ж cth |/ИШ)]/а . E3)
Формула E2) отличается от формулы E1) коэффициентом /Cj,; он
показывает, какая доля тепла аккумулируется стенкой толщиной 2R по
сравнению с бесконечно тонкой стенкой Bi?->0), т. е.
Кф
E4)
Поэтому коэффициент /Сф называется коэффициентом из пользования
тепла. Коэффициент /Сф зависит от Pd (см. табл. 7.4). Из рис.
7.11 видно, что при Pd = 0 коэффициент Кр = 1 (случай
бесконечно тонкой стенки), при Pd~>oo коэффициент К^ = 0.-
Представляет интерес анализ формулы для потери тепла
бесконечно толстой стенкой (полупространство). При больших значениях чисел
PdBjR-*oo) коэффициент использования тепла /Сф стремится к
величине V2 *|/"Pd. Следовательно, формула E2) примет вид
(AQVJR^ = 2су Tm2/VPd = 2cTTffl]/ Д- -L .
E5)
где / толщина стенки (/=2/?).
312
1 Глава седьмая
Таблица 7.4
Зависимость коэффициента использования тепла /С. от числа Pd
[ Pd
0,0
0,5
1
2
3
^ф
1,00
0,96 .
0,92
0,79
| 0,66
Pd
4
5
7
10
■Кф
0,55
0,48
0,40
0,32
;■■■
Pd
15
20
30
40
50
^Ф
0,260
0,225
0,180
0,150
0,135
Pd
60
80
100
оо
-Кф
0,120
0,105
0,0Э6
0,00
Для полупространства в качестве характеристики аккумуляции
тепла рассчитывается количество тепла, поглощаемое единицей
площади поверхности стенки за полупериод, т. е.
&Qs = bQvl = 2ciTmy^-.
E6)
Соотношение E6) имеет следующий физический смысл: kQs равно
количеству тепла, которое воспринимает слой стенки единицей площади
толщиной 1/ ~ (величина 1/ ~ имеет размерность длины) при
равномерном его нагревании по всей толщине от—Тт до Тт.
Следовательно,
— характеризует условную толщину равномерного прогревания
однородного полуограниченного тела в стационарно-периодическом
состоянии. Обозначим величину 1/ -^- через 5. Она является по
своему физическому смыслу коэффициентом теплоусвоения
однородной стенкой. Коэффициент теплоусвоения £ примерно в девять раз
меньше длины температурной волны «Л (£ = 0,11 А), так как
л = y%tz у -£- = 1/8* е.
E7)
Коэффициент теплоусвоения обратно пропорционален ^ы и прямо
пропорционален У а. Поэтому с увеличением частоты колебаний
температуры коэффициент теплоусвоения уменьшается. При больших
частотах теплоусвоение мало. При постоянной частоте (ш = const)
коэффициент теплоусвоения зависит только от коэффициента
температуропроводности. Например, при периоде колебания в 24 ч (ш=тг/12)
коэффициент теплоусвоения пробковых плит (£ = 0,039 ж), примерно,
в 3,5 раза меньше коэффициента теплоусвоения мраморных плит
<? = 0,137 ж).
Если передача тепла через воздушную прослойку происходит
теплопроводностью, то коэффициент теплоусвоения ее очень большой
{% = 0,543, ш = 1г/12, Т = 293°К).
Коэффициент теплоусвоения определяет интенсивность затуханий
температурных колебаний в толще стены.
Глубина Хп, на. которой температурные колебания уменьшаются в п
раз по сравнению с колебаниями на поверхности, составляет
Хп •= уТИп п = Af(n). E8)
ТЕМПЕРАТУРНОЕ ПОЛЕ БЕЗ ИСТОЧНИКОВ ТЕПЛА
313
Таблица 7.5
Значение функции затухания f (п) температурных колебаний
п
№
2
о,по
4
0,221
10
0,367
20
0,477
50
0,623
100
0,733
1000
1,100
Значения функции f(n) приведены в табл. 7.5, из которой видно,
что при п = 2 /(я) = 0,1 Ю. Следовательно, при п = 2 Хп = 0,110Л=£,
т. е. коэффициент I численно равен глубине слоя Хп, в котором
колебания температуры уменьшились в 2 раза по сравнению с колебанием
температуры на поверхности.
Количество тепла, аккумулированное единицей поверхности
полуограниченной стенки за полупериоду при Bi*=^=0 будет
(Qs)l^co = 2c1TmA0 у
E9)
т. е. получаем соотношение, аналогичное E6), поскольку" температура
колебания на поверхности стенки равна ТтА0.
Расход тепла можно подсчитать по иному методу. Скорость
теплового потока равна
dQv
dz
= а^[Тс(т)_Гп0с)].
F0)
где Tn(i) — температура поверхности тела (при х = R или при r=jR),
отношение площади поверхности тела к его объему.
Таким образом, если построить кривую изменения температуры
среды во времени
Tc(*)]-To = Tmcos2™ F1)
и кривую изменения температуры поверхности тела
ТП Ос) - TQ = TJn = Tm (#,.„ #_,.„)* cos B™-Л!„) F2)
(индекс «п» указывает, что соответствующие величины взяты при x = R
или при г = R)> то площадь между этими двумя кривыми и даст
величину, пропорциональную удельному расходу тепла за данный
промежуток времени. Например, на рис 7.6 заштрихованная площадь
дает величину, пропорциональную удельному расходу тепла за полупе-
риод.
Если в уравнение F0) подставить соответствующие выражения для
Тс(х) и Тп(т) из соотношений F1) и F2) и проинтегрировать по тв
пределах от тх до т2, то получим формулу для удельного расхода
тепла, аналогичную формуле D7).
§ 7. ПОЛУОГРАНИЧЕННОЕ ТЕЛО. ТЕМПЕРАТУРА СРЕДЫ —
ФУНКЦИЯ ВРЕМЕНИ
Постановка задачиГВ качестве примера полу ограниченно го тела
может служить тонкий длинный стержень с тепловой изоляцией
боковой поверхности. В начальный момент времени конец стержня
помещается в среду, температура которой есть некоторая заданная
функция времени Тс(ъ) = Дт). Теплообмен между неизолированным кон-
314
Глава седьмая
цом стержня и окружающей средой происходит по закону Ньютона.
Требуется найти распределение температуры по длине стержня.
Дифференциальное уравнение теплопроводности для одномерной
задачи известно. Краевые условия следующие:
A)
B)
C)
Т(х,0)=-~0,
дП1Л) +H[f(r)-T@,*)]=r-Q,
7(оо,т) = 0.
Решение задачи. Решение дифференциального уравнения для
изображения Tl(x,s) при условиях A) и C) будет иметь вид
TL(x,s) — В ехр ( — у ~ х) .
D)
Постоянную В определяем из граничного условия B), которое для
изображения будет иметь вид
rL@,s)+HF(s)-HTL@,s) == О,
где F(s) есть изображение функции /(-с), т. е.
F(s) = L[/(x)].
Решение D) после определения постоянной будет следующим:
1
TL(x,s)=F(s)
1 +
Ш
ехр ( _ y'j-'x ) = F(sH>(s).
E)
F)
G)
Для перехода от изображения к оригиналу воспользуемся
теоремой умножения изображений.
Обратное преобразование изображения <p(s) нам известно (см.
таблицу 4изображений в приложении):
1-ЧФ(з)] - L-1
ехр
фф»
Ф W - И У ~ ехр ( - £) - аН* ехр (Нх +аН*г) *1с(-^+НУЦ.
Тогда по теореме умножения изображений можно написать:
I [<b(s)F{s)] = ]'Ф(д)/(х—»)d»= J ф(х —e)/(»)d»,
о о
где ф (т) есть оригинал изображения Ф (s).
Следовательно у решение нашей задачи имеет вид
Т (х, х) f /(х - »)[ Я ]/1^- ехр ( - -^р) -
о
— аЯ2 ехр (Нх + аНЧ) erfc (—р= + tfj/a» YI db.
(8)
ТЕМПЕРАТУРНОЕ ПОЛЕ БЕЗ ИСТОЧНИКОВ ТЕПЛА
315
Анализ решения. Если /(т) = Тс = const (температура среды —
постоянная величина), то решение (8) превратится в решение A1) § 1 гл. VI:
G = r(f, 'т) = erf с -А= — ехр (Нх+аНЧ) erfс (^—+Н Уа^\ . (9)
'с 2 '[/ ат \ 2 ]/ ах }
Пусть Тс = ТдаУТ; тогда решение (8) примет вид
Т(х,х)
= ]А:ехр —
4ат
л: Т/тс - л:
v erfc
2 /а "w" 2"j/ax
-'^i/T [erfc *fc -ехр(аЯ2х+Нх) erfcGHh* +яv^)
При Я -»■ оо Т @, х) = Тт У~х, из решения A0) получим
Т (х, х) = Tm V^ ехр ( - -^-) - xf
- 2^ еГ1С
\ 2 l/ax/
A0)
A1)
В общем случае, когда Tc=f(i), при #-* оо температура конца
стержня будет изменяться так же, как температура среды, т. е.
Г@,т) = /(т).
A2)
Тогда будем иметь
\т(х,х) =
£ 1 ' (-
X
2 /at
*2 "\ г~Ъ* dft -
4a»2 J С ай _
- * f^-^cW
2/^.1 4V. CXP(
0
"НО**
Если температура поверхности постоянная, то из A3) получим
r(*^> = erfc —*=
^с 2 j/a-с
A3)
A4)
§ 8. ОБОБЩЕННОЕ РЕШЕНИЕ. ТЕОРЕМА ДЮАМЕЛЯ
Сделаем некоторое обобщение задач на нагревание тела в среде,
температура которой есть функция времени. Пользуясь теоремой
умножения изображений, можно доказать известную тесрему Дюамеля.
Для лучшего уяснения начнем с рассмотрения решения задачи для
неограниченной пластины.
Если температура среды постоянна и равна единице (Гс=1), то
решение для изображения при Т0 = 0 будет иметь вид
ch
T(x,s)^^\
У—*
г а
Л/т« + 71/Ч-Н!/Ч«
__ =_!_ФМ, A)
где — есть изображение постоянной Тс = 1.
316
Глава седьмая
Если Гс = /(т), а изображение /(т) равно F (s), т. е. L [/(т)] =-= F(s),
то решение для пластины будет иметь вид
TL(x,s) = F(sH(s).
B)
Если умножить и разделить выражение B) на s, то полученное
решение B) можно представить как произведение двух изображений
sF (s) и Ты (х, s):
TL (x, s) = sF (s)
ФE)
= sF (s) Tu (x, s).
C)
Оригинал второго изображения TL\(x, s) нам известен—это есть
решение задачи для постоянной температуры среды (Тс = 1):
оэ
L-1 [TLl(x, s)] - Тг (х, т) = 1 - 2 Л„ cos ,»„ -£- ехр ( - ц* Fo ) . D)
Оригинал первого изображения s.F(s) может быть найден так:
L[f(*)) = F(s), E)
L[f'(x)]=sF(s)-f@),
sF(s) = L[f'(z)] + f@). F)
Если /@) — 0, то оригинал изображения sF (s) есть /' (т); тогда,
применяя теорему умножения изображений, получим
Т (х, Ч) = j /' (т — ft) 71! (х, ft) d».
G)
Если /@) = const, сделаем следующее предварительное
преобразование:
TL (*, s) = sF(s) TLl(x,s) - L If' (*)]TLi(x, s) + /@) TLi(x,s).
Применяя обратное преобразование Лапласа и теорему умножения
изображений, получим
Т(х, т) = J /' (т - ft) 7\(*, ») d» + / @) 7\ (*, т).
(8)
Соотношение (8) есть формула теоремы Дюамеля для одномерной
задачи.
Для нашего конкретного примера имеем
T(x,z) = m
0
1 — 2j An cos |1.я -J- ехр ( — |i*Fo )
00 ~
1 — 2j ^ncos[i„ -|- exp /_р,а-
+
/!=1
а»
Я3
d&
(9)
Соотношение (9) есть решение для неограниченной пластины, когда
температура среды есть функция времени.
Сделаем обобщение для тела любой геометрической формы.
ТЕМПЕРАТУРНОЕ ПОЛЕ БЕЗ ИСТОЧНИКОВ ТЕПЛА
317
Пусть тело нагревается в среде, температура которой есть
функция времени Тс = /(т). Будем искать температурное поле для
любого момента времени. Имеем
дТ(х, г/, z, т) _ 2
ау2Т (х, у, z, т),
Т(х, у, z, 0) = 0,
_(уТ)п + Я[/(т)-Тп] -0.
Применим преобразование Лапласа, тогда получим
s TL (x, yf z,s) = ay2T (x, у, z, s),
-(yTL)n+HF(s)-HTLn = 0.
A0)
A1)
A2)
A3)
A4)
Пусть u(x,y,z,%) есть решение нашей задачи, когда температура
среды равна единице, т. е. /(х) = 1; тогда
L [и (х, у, г, х)] = UL (x, у, г, s). A5)
Так как изображение 1 равно •—■, то решение задачи при Tz — f(t) для
s
изображения TL(x, y,z,s) будет равно
TL (x, у, z, s) = sF (s) UL (х, у, z, s). A6)
Заменим выражение sF (s):
sF(s) = L[f'W + f@). A7)
Тогда можно написать
TL (х, у, z, s)= [L [/' (т)] + / @)} UL (х, у, z, s) =
== / @) L [и (х, у, z, т)] +1 [/' (х)] L [и (х, у, z, х)].
A8)
Воспользуемся обратным преобразованием Лапласа и теоремой
умножения изображений:
Т(х, у, г, т) - / @) и (х, у, г, т) + J Г (т - Щи (х, у, г, Ь) d ft. A9)
Данное соотношение A9) можно переписать так:
Т(х, у, z, х) = -^— Г /(х -&)и (х, у, z, &)d&,
B0)
т. е. получаем известную теорему Дюамеля: «Если f(%) и производная
/' (х) кусочно-непрерывны при х > 0, то функция Т (х, г/, z, т),
определяемая соотношением B0), является решением краевой задачи A0) с
краевыми условиями A1) и A2)».
На основании свойства теоремы умножения изображений можно
соотношение B0) переписать так:
Т (х, у, z, х) = -L- Г / (») ц (лс, #, 2, х - &) d&.
их J
B1)
Пользуясь теоремой Дюамеля, можно было решить задачи,
рассмотренные в § 1—7, исходя из решений для постоянной температуры среды,
т. е. все задачи, в которых температура среды изменяется с течением
318
Глава седьмая
времени. Но этот классический метод для подобного рода задач имеет
следующие недостатки: 1) необходимо предварительно решить
вспомогательную задачу с постоянными граничными условиями, так что для
решения поставленной задачи требуется много времени; 2) решение
получается в виде рядов, которые нуждаются в дальнейшей доработке;
3) во многих случаях не получаем эффективного решения, так как оно
представляет собой некоторый интеграл, окончательно решить который
затруднительно. Поэтому для решения краевых задач с так называемыми
переменными краевыми условиями пользуются методом преобразования
Лапласа, который обладает рядом преимуществ по сравнению с
классическими методами.
Иллюстрируем на конкретном примере.
В § 1 был рассмотрен случай, когда температура среды есть
линейная функция времени, т. е. Тс (т) = Т0 + Ъ т. Получим вновь решение
данной задачи методом Дюамеля. Для сокращения вывода воспользуемся
соотношением (9) и положим Т0 = 0. Тогда
о L n=i
x l 2 ab
t cos ft,— ехр(-|хя —
&Ъ. B2)
Соотношение B2) есть решение нашей задачи (см. § 1); оно
представляет собой некоторый интеграл, который, однако, еще следует вычислить,
т. е. требуются дальнейшие преобразования. Из B2) получаем
00
Т (X, т) = бх-^- V ^COS^ +
л=1
^^cos^expf™^^), B3)
а *■» р; " R * \ ' п R*
Это решение внешне отличается от решения (8) § 1. Чтобы доказать
их тождественность, нужно показать, что
оо
Общую задачу с заданным сложным начальным условием и
переменной температурой среды можно свести к двум задачам. Действительно,
— = ау2Т, B4)
дх
Т Uo = Ф (*» У> z)> B5)
-{уТ)п + Я[Гс(т)-Гп] = 0. B6)
Положим Т = и + 9-; тогда будем иметь
^- = ау*Ъ, B7)
»Lo = 0' B8>
-(У»)п + Я[7-с(х)--»п] = 0, B9)
^- = ау2"; C0>
01
ТЕМПЕРАТУРНОЕ ПОЛЕ БЕЗ ИСТОЧНИКОВ ТЕПЛА
319
C1)
C2)
Таким образом, получили две задачи. Решение для 9 только что
было приведено; решение и было рассмотрено в гл. IV.
ип = 0.
§ 9. ПОЛЫЙ ЦИЛИНДР
Постановка задачи. Дан неограниченный полый цилиндр с
заданным начальным распределением температуры f(r). Теплообмен с
внешней средой происходит по закону Ньютона. Температура среды —
заданные функции времени Тс1— <Pi(^)> Тс% = <р2(ъ):
а)
+
дТ (R2, x)
дг
dT(Rltx)
дг
T(r,0) = f(r);
-7-[ф.(*)-Т(#,.т)]-0,
B)
C)
Решение задачи. Для решения задачи воспользуемся формулой ко-
D)
вечного интегрального преобразования Ханкеля:
я.
где ядро преобразования
у>п— корни характеристического уравнения
их (к \хп)
"Bi!
«i (k V-n) = [Yo (ft,) + ^ Y1 (ft,) ] А (*ц„) -
Bix == axRJ\, Bia == aa /?2/X — критерии Био, k = /?2/#i-
Формула обращения имеет вид
*2Bi2 ,2. / , \ i--.
E)
. F)
Уг (kv-n)> G)
Г(Г'Х) = ^ГЬ? ^н(^)'"о(^
2R
1
«=1
2
L «1 BiJ
ri+>Bi;j
Bi1
(8)
Для решения задачи необходимо каждый член дифференциального
уравнения теплопроводности умножить на ядро симметричного
преобразования ги0(\ъп—\ и проинтегрировать в пределах от Rt до R^
Собственная функция щ (рп —) является решением уравнения
Бесселя нулевого порядка при однородных граничных условиях первого
рода.
320
Глава- седьмая
1 При интегрировании учитывались граничные условия B) и C),
характеристическое уравнение F), а также соотношения
«о(Ря) = —;■ %Ы = •
Тогда дифференциальное уравнение будет иметь вид
(9)
.dTH(\in, *)
"V-n
2а
+ _^_Гн((хл,т)^аВ!2^0(А1хл)ф2(т) + —Фх(т)- 0.A0)
Изображение функции /(/*) обозначим
*V2
«1
(П)
Решение обыкновенного дифференциального уравнения A0) с учетом
начального условия A1) будет иметь вид
т
Тн (!*„, -О = / (н-я) ехр (— [1П Fd) + a Bi2 и0 (Л цд) J Ф2 (9-) X
х ехр
fi„ а (т — %)
R'
db-
—J 9i(t)exp -г ЫЬ, A2)
71 о L Ri J
где
Fo, = ат/Я' .
Воспользуемся формулой обращения (8), тогда получим
Т(г,х).
00
п=1
!*«"о ( (%^)ехр(—!\iFoi)
-^-fe2"! (Ак-я)
hI+^bi;
- X
rc2Bi
-К+и!)
X { \rf(r)uo Unj-\dr + aE\2u0{k^n) Гф2(&)ехр ^ t^-^W —
Rt 1 0 V i / ■
т
§ 10. ПАРАЛЛЕЛЕПИПЕД. ТЕМПЕРАТУРА CPEДЫ — ЛИНЕЙНАЯ
ФУНКЦИЯ ВРЕМЕНИ
При помощи теоремы Дюамеля можно получить решение для
пластины конечных размеров B/?t X 2R2 X 2R3). Для этого воспользуемся
решением для параллелепипеда при постоянной температуре среды
Тс = const, которое приведено в § 9 гл. VI. Если воспользоваться
соотношением B0) в § 8, то после интегрирования получим
ОЭ ОО 00
Т{х,у,г,х) = Т0 + Ъ*- J 2 2
Ап, 1 ^т, 2^&, 3
X
ТЕМПЕРАТУРНОЕ ПОЛЕ БЕЗ ИСТОЧНИКОВ ТЕПЛА 321
X cosu -^-cosa -£- COS U. „ — X
1 » Л, 1 г> * /7t,2 n к «,3 г> I
I х {1-ехр[-(^,,/с; +^,2к; +rtt>ir.)Po]}, AI
где
К, = А<.--.,2,3),^ = ^ + Х + ^, R,_i. B)
1 2 3
^я i' Дя.2» ^а з — коэффициенты, определяемые по заданному
значению критерия Bi.
Если критерий Bi=oo, то рп г = Bп—1) —, |i.m2 —Bm— 1)—-
и ^ 3=B&—1) —. Решение A) является более общим решением по
сравнению с решением G) § 9 гл. VI.
21 Заказ № 640
ТЕМПЕРАТУРНОЕ ПОЛЕ С НЕПРЕРЫВНО
ДЕЙСТВУЮЩИМИ ИСТОЧНИКАМИ ТЕПЛА
8
Во многих процессах теплообмена внутри тела действуют источники
тепла. Эти источники могут быть положительными (например,
нагревание тела электрическим током, выделение теплоты испарения при
увлажнении тела паром) или отрицательными (испарение влаги во
влажном теле при его нагревании). Поэтому задач теплопроводности при
наличии источников тепла очень много. Рассмотрим только некоторые
из них, наиболее характерные и часто встречающиеся в теплотехнике.
Все задачи можно, разделить на два вида: 1) задачи с постоянными
или переменными источниками, действующими на протяжении всего
процесса теплообмена (непрерывно действующие источники тепла), и
2) задачи с мгновенными источниками, действующими в течение
бесконечно малого промежутка времени (тело получает в начальный момент
времени некоторый тепловой импульс). К последним относятся задачи
на теплообмен проводников, в которых произошло короткое замыкание,
когда внутренний источник тепла действует практически мгновенно.
§ 1. ПОЛУОГРАНИЧЕННОЕ ТЕЛО
Постановка задачи. Имеется тонкий полу ограниченный стержень
с тепловой изоляцией боковой поверхности при температуре Т0. В
начальный момент времени неизолированный конец принимает
температуру Тс > Т0, которая остается постоянной на протяжении всего
процесса теплообмена (граничное условие первого рода). Внутри
стержня действует источник тепла, удельная мощность которого w (вт/м3).
Найти распределение температуры по длине стержня и удельный
расход тепла в любой момент времени. Поставленную задачу
математически можно записать так:
*ШЬ± = а^Е^Л + JL (т>0; 0<*< со);
дт дх2 с-[
Т(*,0) = 70;
дТ (cot z)
&х
0;
T@,i) = Tc = const.
О)
B)
C)
D)
ПОЛЕ С НЕПРЕРЫВНО ДЕЙСТВУЮЩИМИ ИСТОЧНИКАМИ ТЕПЛА 323
Решение задачи при w = const. Применим преобразование Лапласа.
Тогда получим
TL(x,s)--?-TL(x,s) + ^ +
SOCf
= 0.
E)
F)
Уравнение E) можно переписать так:
ТЦх, s) -J-\TL(x,s) - ^ - -^-1 = 0.
а [ s s2Cf J
Общее решение уравнения F) можно написать в двух видах:
Т,(х,8)-?2---£- = АсьУ±х +
Lк ' s s2c у га '
г— V^x -Vix
+ B$hy-±-x = A1e +Bxe
Граничные условия C) и D) для изображения можно написать так:
7i,(oo,s) = 0, (8)
G)
TL@,s)=±.
О)
Из условия (8) следует Ах = 0. Постоянную Bt находим из
граничного условия (9):
S
То
s2c y
= вг.
A0)
Тогда решение G) примет вид
TL (x, s)
S* С\
+
(Тс ~Т0)
■VI-
-VJ
S* С f
(И)
Из выражения A1) видно, что оно состоит из трех слагаемых, каждое
из которых является табличным изображением с соответствующим
оригиналом [см. соотношения B), E0) и E3) таблицы изображений в
приложении].
Окончательно решение нашей задачи будет иметь вид
+
6 =
W
с? (Гс -
Т(х,
Тс-
Т
■То)
*)-Тр =
-То
w
с-1 (Тс -
eric
^тЦ
2~|/ат
4т i2 erfc
X
2l/"S *
A2)
Величина
является безразмерной величиной; она показы-
сч(Тс-Т0)
вает отношение количества тепла, выделяемого источником тепла за
данный промежуток времени в единице объема, к тому количеству тепла,
которое необходимо сообщить единице объема тела при нагревании его
от начальной температуры до температуры среды. Эту величину можно
11*
324
Глава восьмая
представить как произведение числа Фурье и нового критерия,
названного нами критерием Померанцева:
«* = Fo, ^!_=Fo,Po,, A3)
т? а% у^ ~ wx2
гдеРо^ = —— число Фурье для координаты х, Ро ^ =
критерии Померанцева. Физический смысл критерия Померанцева
состоит в том, что он показывает отношение количества тепла,
выделяемого источником в единицу времени в объеме х (объем
параллелепипеда, основание которого 1 ж2, а высота х), к максимально возможному
количеству тепла, передаваемого теплопроводностью через единицу
площади в единицу времени на расстоянии х от конца стержня (при
условии, что температура в данной точке равна начальной, а
распределение температуры происходит по линейному закону).
Если источник тепла отсутствует (Ро^ = 0), то из решения A2)
получаем обычное решение для полуограниченного тела при граничном
условии первого рода.
Плотность теплового потока q через поверхность тела найдем по
соотношению
дх
Из соотношения A1) имеем
L[qb)\= l(Tc~Jo) -
Хш
У as c^s У as
Пользуясь таблицей изображений, находим
Й=(ТС-Т0)У^— 2»/т- <15)
Из соотношения A5) видно, что при малых значениях времени
нагревание происходит в основном путем теплопроводности через
неизолированный конец стержня. Для больших значений времени нагревание
происходит за счет источника тепла, а с открытого конца при этом
наблюдаются теплопотери в окружающую среду (второй член
соотношения A5) становится больше первого).
Решение задачи при w~wQerkx. Источник тепла является
экспоненциальной функцией координаты w0e~kx, где w0 — максимальная удельная
мощность источника, k — постоянная. Начальные и граничные условия
остаются прежними. Для упрощения расчета положим Т0 = 0.
Применяя преобразование Лапласа, получим
Г (х, S) — — TL (x, s) + —^— е-** = 0 . A6)
^ а и sc\a
Это неоднородное уравнение может быть легко решено, так как
известно его общее решение и легко определить одно частное решение вида
Ae~kx. Однако, имея в виду решение более сложных задач и следуя
общему стилю изложения, принятому в пособии и основанному на
возможно более широком использовании метода интегральных
преобразований, применим к уравнению A6) синус-преобразование Фурье.
ПОЛЕ С НЕПРЕРЫВНО ДЕЙСТВУЮЩИМИ ИСТОЧНИКАМИ ТЕПЛА 325
Обозначая
от
TLs(s, р) = Т/ТЕ Г rL(s, ж) sinpxd*
A7)
и используя граничные условия уравнения A6)
7^E,0) = -^; T^(s,oo) = 0,
A8)
получим решение уравнения A6) в виде
^s(s. Р) = У — • (— + 17 ^+F-|
A9)
С помощью таблиц определенных интегралов и выполнения обратного
синус-преобразования Фурье получим
00
TL (s,x)= ]/-§" J Tls (s> P) sin pxdx =
-Kl-
+
a>0 _ e
As '
-Аж .
■n
s
a
B0)
Отсюда, используя таблицы изображений, помещенные в конце книги,
окончательно имеем
6 = r(*'T) ^ erfc * 55!о_
erfc-
2]/ат:
. £-*•* —
1 k2ax—kx
~2~
erfc [ k Y~ax ■
2/~шГ
lj**+kx erfc Л ^— _J^_\
+ 2 ^ 21/^ J
+
B1)
v.*
Решение задачи при ш = ш0т . Удельная мощность источника теп-
%/гП
ла является некоторой функцией времени вида ш0^ , где ш0 —
постоянная, п—показатель степени, равный — 1,0,... или любому
положительному числу, т. е. п > — 2.
Дифференциальное уравнение для изображения напишется так:
T'L(x98) L-rL(*,s) + ^- +
го0Г 1 +
-Ь)
ac^s
I+V2*
= 0,
B2)
1
Г 1 + Tn
где L [т1/**] = — —L_ ? г (m) — гамма-функция.
326
Глава восьмая
Решение уравнения B2) при заданных граничных условиях имеет
вид
TL(x,s) — £l = Гс~Го е
B3)
Пользуясь таблицей изображений, находим
Т (х, -с) - т0
Тс-То
erfc
2ТЛп~
+
Ш0т:
1+7"
ci(Tc~To)\\+ — n
1— Г B+ — nV2"+ai"+2erfc- x
2Уа
B4)
Усложним задачу, заменив граничное условие первого рода
граничными условиями третьего рода:
аг@'т) + Н [Тс — Т (О, т)] = 0.
дх
Тогда решение для изображения будет иметь вид
TL(x,s)-^ =
S
B5)
Те-То ,е ' а
+
s 1 +
8У0ГA+—П
CfS
2+V2«
Я Г а
1 —
-ЛП-
1 К а
■е
J_l/JL
1 +
B6)
Решение для оригинала будет следующим:
i -. erfc ■
Нх-\-Н2ах
+
2 У ах
е
+
erfc/ 1_ + яКат ) +
\ 2 V ах
1/2п л+2
CT(rc-r0)(l+-i-n] ст(Гс-Г0)а1/2П(~Я)Л
erfc [ зз- + Ну с
X
X
ат
2-|/ат
S(_ 2Я K^)m im erfc —
п+2
2"jA
т—0
B7)
ПОЛЕ С НЕПРЕРЫВНО ДЕЙСТВУЮЩИМИ ИСТОЧНИКАМИ ТЕПЛА 327
Если источник тепла отсутствует (w0 = 0), то получаем решение для
полуограниченного стержня в случае теплообмена неизолированного
конца с окружающей средой по закону Ньютона.
§ 2. НЕОГРАНИЧЕННАЯ ПЛАСТИНА
Вначале рассмотрим более простую задачу (w = const) при
граничных условиях третьего рода, а затем более общую задачу (w = var
и q(i)).
Постановка задачи. Дана неограниченная пластина толщиной 2R
при температуре Т0. В начальный момент времени она помещается
в среду с температурой Тс >Т0. Теплообмен с окружающей средой
происходит по закону Ньютона (граничное условие третьего рода).
Внутри пластины действует источник тепла, удельная мощность
которого равна w. Найти распределение температуры по толщине
пластины и удельный расход тепла в любой момент времени.
Имеем
дТ(х, т)
д2Т (*, т) .
а —^ » ; +
дх2 с-{
Т (х, 0) = Т0,
(x>0; — R<x< +R),
дТ@, х)
дх
= 0,
dT(R>^ + Н [Тс —T(R, т)] = 0.
дх
A)
B)
C)
D)
Начало координат находится в середине пластины.
Решение задачи при ш^ const. Решение для изображения Т L (x,s) при
условии B) было приведено в предыдущем параграфе. Для
симметричной задачи это решение можно написать так:
TL (x, s)
То
c^s*
+ ЛсЬ
У?
E)
Постоянную А находим из граничного условия D), которое для
изображения ТL (x, s) будет иметь вид
-TL(R,s)+H
\(*>*)]
= 0.
F)
Удовлетворив решение E) граничному условию F), можно определить
постоянную А. Тогда решение E) примет вид
S S^C{
+
(Тс - Г.) ch
V-т-
СТ
ch
'["/т' + т^/т"]
(?)
328
Глава восьмая
Решение G) состоит из трех слагаемых. Первое слагаемое
ет оригинал
s^cy
имеет
т, второе слагаемое является решением B5) для
изображения задачи § 3 гл! VI (решение задачи без источника тепла) и
третье слагаемое есть решение G) для изображения задачи § 1 гл. VII,
в котором вместо b надо написать —. Поэтому решение нашей задачи
можно получить из решений предыдущих задач, т. е. из решений B9)
§ 3 гл. VI и (8) § 1 гл. VII, а затем прибавить величину —т.
Решение задачи в безразмерных величинах будет иметь вид
Тс-т0 ^ l + ~2~F0 (l — Ж + Ж
(8)
где Po — критерий Померанцева, равный
Po =
Чтс-т9) ■
(9)
Если положить Ро = 0 (отсутствие источника тепла), то решение (8)
превращается в решение B9) § 3 гл. VI.
В стационарном состоянии (Fo = оо) распределение температуры
по толщине пластины следующее:
Т(х, х) = Тс + ж(R* - х* + -вг
Тт(х, *).
A0)
Решения (8) с учетом A0) можно написать так:
п
е„-в = ZV£^Z^)=2(i + ^„cos^exp (-,'Fo) . A0 а)
Средняя температура пластины равна
Г(*) - Т0
1+^-Ро
Гс-Г0 ~ * ' 3 *" V: + Bi / •
(И)
Значения постоянных Ап, Вп> а также характеристических чисел \ьп
приведены в задаче § 3 гл. VI.
Удельный расход тепла находится по обычной формуле, по данным
значениям средней температуры.
Решение при w = w0e~kz. Удельная мощность источника тепла
изменяется по экспоненциальному закону w0e~kz, где w0 — максимальная
удельная мощность источника, соответствующая начальному моменту
ПОЛЕ С НЕПРЕРЫВНО ДЕЙСТВУЮЩИМИ ИСТОЧНИКАМИ ТЕПЛА 329
времени; k—постоянная, численно равная максимальной скорости
изменения относительной удельной мощности, т. е.
L di Am
A2)
Так как изображение L[w] =
будет иметь вид
TL(x,s)-^-
Щ
, то решение для изображения
(rc-r0)ch -j/JL
\*yjL*+±yjL*Y±*]
+
+
w0
s (s-\-k) cf
ch
1 —
Г ch УН R + -L-У— sh У J- r]
L V a H V a fa])
A3)
Для перехода от изображения к оригиналу воспользуемся готовыми
решениями § 3 гл. VI и § 4 гл. VII. Тогда, суммируя эти решения,
получим в окончательном виде следующее решение нашей задачи в
критериальной форме:
6 ^ Т(х,*)-То = j _
Ро
П-Г(
Pd
cos
1 —
, X
■J/Pd — "щ-l/Pd" sin T/PdJ
X
00
Xexp(—PdFo)—2j f 1 p^2 ) К c°s p.-jjf exp (—j*JFo)
A4)
w0R2 k
где Ро = x(rc — r0) — критерий Померанцева, Pd == — R2 — критерий
Предводителева, который определяется как максимальная скорость
изменения относительной удельной мощности источника тепла по
относительному времени, т. е.
ш0
L d?o
= Л- %* =, Pd.
тп й
Решение при w=w0x%n . Решение для изображения при Bi = °©
(граничное условие первого рода) можно написать так:
(Гс-Г0)сИт/Х*
TL(x,s)-T±-= У а +
schl/ — R
У а
330
Глава восьмая
Для перехода от изображения к оригиналу разложим
1
в ряд, как это было сделано в § 3 гл. IV. Тогда, пользуясь
соотношением F4) таблицы изображений (см. приложение VI), получим решение
задачи в следующем виде:
X ■
г
5=1
Bm-l) + *
+ erfc ._ н
2|/Fo
Bm-I)--1-
erfc __ « +
2 l/Fo
, ^'An+l x
а(Гс-Го)(и--^-п)
' 00
1— Г^2 +4-nJ"+25](—1)™+1
m=l
Bm-l)—|-
i"+2 erfc r— 4-
e 1C 2^Fo ^
B/я — 1) + —
+ i"+2 erfc . R
2l/Fo J
I-
A6)
Если источник тепла отсутствует (w0 =0), то из решения A6)
получим решение B7) § 3 гл. IV.
Решения A4) и A6) упрощаются, если положить ТС=Т0; это
соответствует случаю, когда поверхности пластины мгновенно охлаждаются,
а затем поддерживаются при постоянной температуре; нагревание
происходит только за счет источника тепла. ,
Решение задачи для переменного источника тепла w(x, т) с гранич-
ным условием второго рода <7(т). Рассмотрим более общую задачу при
[И Т„
Bа>
источнике тепла, который является функцией координаты х и времени т
Начальное условие принимаем в более общем виде
Т(х, 0) = /(*)•
Граничное условие второго рода принимаем в виде
dT(R, т)
— X
дх
+ <7(т) = 0.
Dа>
Решение найдем методом интегрального преобразования Фурье.
Воспользуемся косинус-преобразованием Фурье
R
Гс(л,т) = J7(*,T)cos^
их
A7)
и формулой перехода от изображения функции Тс(п, х) к ее оригиналу
Т(х, т):
Пх, х) = -L. Тс@, х) + 4-S Те(п х) cos
R
пъх
~R~
A8)
ПОЛЕ С НЕПРЕРЫВНО ДЕЙСТВУЮЩИМИ ИСТОЧНИКАМИ ТЕПЛА 331
Умножая обе части дифференциального уравнения A) на cos —^—и
интегрируя в пределах от 0 до i? с учетом граничных условий C) и Dа),
получим *>
dTc
где
■^Г1- + -Ц2— ТсМ = (—1) —^— + — wc (л, т), A9)
R
wc (п, т) == \ w (х,т) cos n™ dx. B0)
о
Решение этого уравнения будет
Тс(п, х)=ехр ( - ^) [С(п) + (-ly-f j tfft) exp (-»£»-) d» +
О
т
+ -^-J wc(n,b) exp (-£**- ft ) d» ] . B1)
О
Для определения С (п) воспользуемся начальным условием Bа):
R R
Тс (л, 0) = С(п) = j Г(*,0) cos ^ dx = J/(x) cos^- dx. B2)
о о
Тогда
х
Tc(n,x) = (-l)»-f-j^)exp[-^l (,_»)]d» +
о
if Г <m27t2 I / cm2TC2t\
+ —J ^ (л, т) exp [ ^- (т — »)J d» + exp ^ — —^-j X
о
R
§ f(x) cos ^j?-dx. B3)
X
о
Для удобства перехода к оригиналу по соотношению A8)
перепишем решение для изображения B1) в виде
Тс(пл) = Тс@,х) + ТспМ, B4)
причем во втором слагаемом п = 1, 2, 3,...
Имеем
R х х
Тс(л,,) = j' /(х)dx+^q(&)db+±\wc@,%)db +
0 0 0
R
+ Jexpj^ ^-jj f(x)cos-^-dx+(—l)nirX
о
i)ГПодробно см. формулы C1)—C3) § 2 гл. V.
332
Глава восьмая
X J <#) ехр[—^ (х -Ъ) ] db +
6
-с
+ ±j wc(n,b) exp[-^-(T-d)]dft j ,
где
wt
@,т) = ( w(x,t)dx.
B5)
B6)
Переход от изображения Тс(я, т) к оригиналу производим по фор^-
муле A8)
Т (х,х) = "Щ / (х) dx + ^q (9) db + -^rjV@, Ь) d&j 4-
0 0 0
, 2 Глп, Птсх Л^Л/ ап*п*ъ\ Г х/ ч «тех , г
+ X2jc0s-X^exp( ^~JJ f(x)cos—^dx +
я=1 О
/г=1
00 «С
+ -^-2 cosi^-j шс (л, 0) ехр [--^- (х - ф*. B7)
Решение B7) является общим решением поставленной задачи.
Решение в обобщенных переменных можно написать так:
(X'F°)=J f{i)d[-w) + § Ki(Fo*)dFo* +
О О
I со
+ JPo^Jb*)dFo*+2 JcosivJ- x
О п=\
1
X ехр (— р* Fo) J / /-J-) cos ря -|- d*/# +
6
oo Fo
+ 2 2 cos ^ J[ (- 1)" Ki (Fo*) +
/2=1 0
1
+ JPo(-|-)Fo*jcos!An-^d(^-)x
exp( —1*2 (Fo — Fo*I)] d Fo*,
о
X
B8)
где pn = mc, Ki (Fo)=-^ число Кирпичева, Ро = —-1
число Померанцева или обобщенная переменная, Тс — фиксированное зна-
ПОЛЕ С НЕПРЕРЫВНО ДЕЙСТВУЮЩИМИ ИСТОЧНИКАМИ ТЕПЛА 333
чение температуры, например температуры среды, в = Т(х,х)/Тс —
безразмерная температура.
В случае равномерного начального распределения температуры
Т@,х) = Т0 Dа)
и постоянного потока тепла на поверхности пластины
Я (т) = Qc = const D6)
решение B8) примет вид
00
6 (-£. ,Fo) = Ki [ Fo-± (l-3-f2) -2(-l)"-^-cos^exp(-^Fo)] +
Fo 1 oo
+ jdFo* j Po (-%. ,Fo* ) d (-|) +2 J costv^-exp (-^ Fo) X
0 6 /2=1
Fo 1
X J exp (p2 Fo*) dFo* j Ро,(-£- ,Fo* ) cos^-J-d (-J-) . B9)
о о
При этом отсчет температуры производится от начальной температуры
тела (Т0 = 0). Первое слагаемое в решении B9), заключенное в
квадратные скобки, является решением задачи при отсутствии источников
тепла (Ро = 0). Остальные члены характеризуют влияние на
распределение температуры источника тепла.
Из решения B9) можно получить ряд частных решений.
1. Постоянный источник тепла Ро (-~р , Fo ) = Рос = const :
6 (JL ,Fo ) = Рос Fo + Ф (-£ ,Fo ) , C0)
00
- 2 (™" 1)п -4- c°s^4- exp {-\l* Fo) 1 C1)
где
/i=i
является решением задачи при отсутствии источника тепла.
2. Источник тепла — линейная функция от координаты
[Ро (-£,*>) =РРвA-^)]:
8 /JL ,Fo ) = Рос {-1- Fo+^2- cosB^1)^/^
Bn—1L
X
X cosivjil- exp(- |i»Fo)]J + Ф (-J-, Fo ) . C2)
3. Источник тепла — параболическая функция от координаты
[Po(£,Fo) = Poc(l--g-)]:
334
Глава восьмая
0 (JL ,Fo ) = Рос {-|-Fo-2-^- (- 1)» coS(*„ -£-[1 -
- exp (-pa Fo) ] j + ф (JL ,Fo ) . C3)
4. Источник тепла — экспоненциальная функция координаты
[Po(-jj-,Fo) = Pocexp(-6-|-)].:
e(^1Fo) = P0c{A d-^)Fo+ S[l-(-D"^] ^^ X
/2=1
X cosn„ -J [1 -exp (-ji2 Fo) ] } + Ф (-£, Fo ) . C4)
5. Источник тепла — линейная функция времени Ро j-jjp ,Fo ) =
= Poc(l+Pd'Fo) 1:
6 (-*., Fo j = PocFo (l + 4" pd'Fo ) +ф (x ' Fo ) ' C5)
k
где Pd'= — i?2 —критерий Предводителева, равный максимальной
скорости изменения относительной удельной мощности источника
тепла по числу Фурье:
*»,__pg/^f C6)
Pd'=—#2=
k — постоянная, численно равная максимальной относительной
скорости изменения удельной мощности источника тепла, w0 — удельная
мощность источника тепла при -с = 0.
6. Источник тепла — экспоненциальная функция времени
[ Ро (-£• ,Fo) = Рос ехр (- Pd'Fo) ] :
б (JL, Fo ) = -|£-[l - exp (- Pd'Fo)] + Ф (-£-, Fo ) . C7)
7. Источник тепла — периодическая функция времени
Г Ро /-£-, Fo ] = Рос cos Pd' Fol:
G (-JL, Fo ) = -^r sinPd' Fo + Ф (-J- ,Fo ) . C8)
8. Источник тепла зависит от времени в n-й степени
[Po(-^-,Fo) = Poc(Pd'Fo)" l:
•(*•*) = -gq^°+4*'F°)' C9)
ПОЛЕ С НЕПРЕРЫВНО ДЕЙСТВУЮЩИМИ ИСТОЧНИКАМИ ТЕПЛА 335
§ 3. ШАР (СИММЕТРИЧНАЯ ЗАДАЧА)
Постановка задачи при граничных условиях третьего рода. Задача
аналогична предыдущей и математически записывается так:
d[rT(r,z)]
d*[rT(r, z)]
дт
дг2 ' С7
Т(г, 0) = Т0,
Ш1±=о, Т@,т)^=оо,
(т>0; 0<r<R),
дг
- dTfr'x) +H[Tc-T(R,i)} = 0.
A)
B)
C)
D)
Решение задачи при w = const. Решение для изображения TL(r, s)
получаем аналогичным методом. На основании условий B) и C)
решение имеет вид
Bsh|/_i-r
TL(r,s)-
+
E)
Постоянная В определяется из граничного условия D), которое
преобразуется для изображения. Таким образом, решение для изображения
приобретет вид
X
X
Bi R sh "[/"— i
[pi-l)*yj-*+Y-L.R<byj-R]l
+
s*c^
F)
Из рассмотрения решения F) видно, что оно является
алгебраической суммой решений рассмотренных нами задач.
Таким образом, решение нашей задачи может быть получено, если
из решения B7) § 4 гл. VI вычесть решение A2) § 2 гл. VII,
предварительно заменив величину Ъ на—, и добавить величину—т, которая яв-
ляется оригиналом изображения w/s2c^.
Следовательно, решение нашей задачи будет иметь вид
,
= l+-^Po(l + -|I
Г(г, т) - Т0 _
Тс-Т0 ~
-^)-Ё(>+Р^^±ехр(-йРо),
G)
wR*
где Ро = -ут= =-: критерий Померанцева, Ап — начальные тепловые
к\* с * о)
амплитуды, определяемые соответствующими соотношениями (см. § 4 гл.
VI).
В стационарном состоянии будем иметь параболический закон
распределения температуры.
Средняя температура шара, необходимая для расчета удельного
расхода тепла, равна
336
Глава восьмая
6 =
ТЬ)-Т0_ , , 1 р /, , 5 ] —
00
-S^+l^expHp'Fo).
(8)
Решение при а; = w0e-~kz. Применяя аналогичный метод расчета,
решение получим в виде
= 1
Ро
Pd
i? Bi sin l/Pdf-I-
R
.]■
1 - r[(Bi-l)sinl/Pd+l^Pdcos^Pd] I eXP (~PdI?0) ■
# sin \in -ц-
-s«
Po
n=l
Pd-^
2 /'*» />„
exp(—^Fo),
(9)
где Pd — критерий Предводите лева; он равен в данном случае Pd =
е-. ^2у р0 _ критерий Померанцева, Ро =~х7т~^ТгТ"
Решение задачи при w = w0%4*n. Удельная мощность источника
тепла есть некоторая степенная функция времени: w = w0 т1/*", где п =
= —1, О, 1, 2,.... Решаем задачу при граничном условии первого рода
(Bi = оо), т. е. T(R, т) = Тс. Пользуясь вышеописанным методом,
решение получим в виде
гп=\
+ —
Bт-1)--в- Bт-1) + -£-
erfc == erfc
2l/Fo
Шо^+1/г"
CY^c — To) 1+-0-»
2"|/"Fo
ll — ГB+4-»Jп+2 X
+
xS
A
Bm — 1) —^- Bm - 1) + -^T
in+* erfc „ * i"+2 erfc
Я
2-j/Fo
2]/Fo"
A0)
При отсутствии источника тепла (wQ = 0) решение A0) превращается в
соответствующее решение § 4 гл. IV.
Постановка задачи при переменном источнике тепла и граничных ус-
ловиях второго рода. Источник тепла является функцией координаты и
времени w (г, т):
Т(г,0) = /(г),
дг
дТ@, г)
дг
= 0; 7@, i)^fe оо.
(И)
A2)
A3)
ПОЛЕ С НЕПРЕРЫВНО ДЕЙСТВУЮЩИМИ ИСТОЧНИКАМИ ТЕПЛА 337
Решение задачи при w(r, i). Для решения поставленной задачи
воспользуемся конечным синус-преобразованием Фурье:
я
T.{p,*) = $rT{r,t)^dr,- A4)
О
где р— корень характеристического уравнения
sinpR — pRcospR = 0. A5)
Обратный переход от изображения функции Ts(p, т) к ее оригиналу Т(г, х)
осуществляем по формуле
Цг, ,) = А Г.@, г) + А^ -^ -i!SJ2-I. Г.(ря, x). A6)
Л=1
Умножая все члены уравнения A) на rsin pr и интегрируя по г от 0 до
jR, с учетом граничных условий A2) и A3), получим1)
^+«, х) =^**L(* </ (x) + ^ш.^ х), A7)
где
(р, т) = fr5^-o;(r, T)dr
б
есть изображение для оригинала внутреннего источника тепла.
Решение уравнения A7) будет
TJj>, -с) = exp [-ap\]{C(p) + ^R -^_ X
х х
X Г ф)ехр (ap*v)dv + — Гш8(р, i>)exp(ap%)dt>}. A8)
о о
Для определения С(р) используем начальное условие
C{p) = ^rf{r)^dr. A9)
о
Для удобства перехода к оригиналу предварительно найдем Ts@, т):
я
Ts@, T)«JrV(r)dr +
о
х х Я
+ -£- #* Г 9 до ^ + _L Г Г Г2Ш(Г> t,)dt;dr. B0)
0 00
Подставляя значение 7\@, т) и 7\(р, т) в формулу A6) и используя A9)
получим решение нашей задачи:
я х х я
0 0 0 0
!) Подробно см. формулы B4) —B6) § 3 гл. V.
338
Глава восьмая
^=1 0
/z=l 0
. r sin o„r , n v , _,
it.
/2=1 0 0
+ ^i „Ski, 'Г"" е,р<-ч^L.||,(г,Р)^^е,Р(агф»^
B1)
Обозначим [л„ = р„ /?, Fo = -^, Ki(Fo) = -^ , Po = "^{^ . Тогда
решение B1) в обобщенных переменных можно написать так:
1 . — , .
•(тт. *•) =3{1(Я'М^)+Яю<Р<>*,+К-Ро^'Ро,)х
О 0 0
X dfc)]dFo«}+2i; ^^ ехр^Го) X
л=1
О /г=1
Fo l
X f[sin^Ki(Fo*) + j^Po^,Fo*)siniy£-d (-£-)] X
о
X exp[—^(Fo—Fo*)]dFo*.
B2)
Для равномерного начального распределения температуры имеем
Т(г, 0) = Т0 = 0, B3)
когда отсчет температуры производится от начальной температуры тела
и при постоянном значении числа Кирпичева
Ki(Fo) = -§£- = Ki - const. B4)
Решение B2) примет вид
Fo 1
е(^'Ро) = ф(^'Ро)+3|^°*1(ЯРо(^'Ро*)"(^) +
о о
оо
, \i 2R sin pn г/7?
sin2fxrtr
^ехр(-^о)Х
Л=1
Fo
X J exp(^Fo*)d Fo* j (JL) Po (-^ , Fo* ) sin ^ d (-£-), B5)
ПОЛЕ С НЕПРЕРЫВНО ДЕЙСТВУЮЩИМИ ИСТОЧНИКАМИ ТЕПЛА 339
где
Ф (■*-. Fo) - KI 13FO -i ( 3-5 £) - f 2«" «PC-riP°>l <26)
«==1
является решением задачи без внутреннего источника тепла.
Из решения B5) можно получить ряд частных решений.
1. Постоянный источник тепла Ро (•—-, Fo J = Poc = const :
e(y,Fo) = PocFo + Ф (~^ , Fo у B7)
2. Источник тепла — линейная функция координаты [Ро(-^-, Fo] =
6(T.Fo)=Poc{TFo + 2S x
n==l
х gsln^r/g n _exp(_!J.2Fo]} + ф (-1-, Fo j. B8)
3. Источник тепла — параболическая функция координаты
[Po(^-.Fo) = Poc(l--J)]:
00
б(' Fo) = PoJ^-Fo-S-r1— X
x Rsm^rlR {l _ ^p^^po)] j + ф j^_ Fo ) . B9)
4. Источник тепла — экспоненциальная функция координаты
ГРо (-£-, Fo ) = Рос ехр (- Ь rlR )]:
~i 26[2fx„ - е-»B + б2 + 26 + ^)sin ^n]
6(-i-.Fo) =Poc{S
X
x ^sin v-n rIR
[l-expt-^FoJlJ + O^, Fo). C0)
5. Источник тепла — линейная функция времени Ро(-^-, Fo ) —
= РосA + Pd'Fo)]:
e(-J-,Fo) = PocFo(l +4-Pd'Fo)+0^f Fo). C1)
6. Источник тепла— экспоненциальная функция времени
Г Ро (-£-, Fo \ = Рос ехр (— Pd'Fo)]:
6 (^ , Fo ) = ^ [1 - exp(-Pd'Fo)] + Ф (-£■, Fo ). C2)
340
Глава восьмая
Ро
C3)
7, Источник тепла — периодическая функция времени
= PoccosPd'Fo :
6 (^ , Foj = ^ sin PdTo +Ф (-£- , Fo ).
8. Источник тепла зависит от времени в п-й степени Ро(-^-, Fo) =
= Poc(Pd'Fo)" ]:
°(тг-р°)-^р^°+ф(ж.р°)- w
§ 4. НЕОГРАНИЧЕННЫЙ ЦИЛИНДР
Постановка задачи. Аналогичную задачу для неограниченного
цилиндра математически записываем так:
-£%^ = -(^^ + i^rL) + -?r^>0;0<,<i?). A)
Краевые условия те же, что и для шара.
Решение задачи при w = const. Решение для изображения
получается в следующем виде:
TL(r,s)-^-
S2C{
+
+
тс - т.)
W
s*ci
>m
'•(/-нК-АУ-И/т*)
B)
Сравнивая решение B) с соответствующими решениями B1) § 6 гл. VI
и G) § 3 гл. VII, находим
00
0 = 1+4-po(i +ж--^)-2A + 7|-)л«/«'(^х)ехр(-[л«ро)'C)
где Ро
wR2
критерий Померанцева.
ЦТс-То)
Из решения C) видно, что в стационарном состоянии распределение
температуры происходит по закону параболы.
Средняя температура цилиндра равна
6 =1+ i-Po(l + ^)-2(l+^|-)^exp(-^Fo).
/2=1
D)
Постоянные Ап и Вп и корни рп характеристического уравнения
определяются из соответствующих соотношений для неограниченного
цилиндра (см. §6 гл. VI).
Решение задачи при w = w0e~kx. Аналогичным методом находим
решение в виде
= 1-^-
1 Pd
Jo[VPd-]£
jJiVPd)—-щ-ураМУШ)
х
ПОЛЕ С НЕПРЕРЫВНО ДЕЙСТВУЮЩИМИ ИСТОЧНИКАМИ ТЕПЛА 341
00
X exp (-Pd Fo) - 2 (l - й^г~) A"J° ( **« lf)exp {-^n Fo)- E>
Коэффициенты Ап определяются соответствующим соотношением для
цилиндра.
Решение задачи при переменном источнике тепла ш(г, т) и граничных
условиях второго рода. Задача математически записывается так:
Т(г, 0) = /(/-), F)
-*-^И+*т) = 0. G)
ЗГ(а°;т) =°: П0,х)фоо. (8)
Для решения задачи воспользуемся конечным интегральным
преобразованием Ханкеля
R
Тн (р, т) = J rT(r, т) J0(pr) dr, t (9)
о
где р— корень характеристического уравнения
■да?) = 0. (Ю)
Переход от изображения Тн(р,х) к оригиналу T(r, i) осуществляется по
формуле
ЦП т) = АТн@, х) + * £гн(рл, -)-^f ' A1)
72=1
Применяя преобразование (9) к дифференциальному уравнению A)с уче*
том граничных условий G), (8), получим1)
dTH(p,%)
—ж Ь ар2Тн(р, х)^
= aRq-^J0 (PR) + -^wh (р, т), A2)
где
я
wH(p, *) = J w(r9 %) rJ0(pr)dr. A3)
о
Решение обыкновенного дифференциального уравнения A2) имеет вид
Тн(р, *) = [ С(р) + 2*L J0 (pR) j q{b) exp (ap4)db+
0
T
+ -—- Г о>н(р, ») exp (ар2») d& 1 exp (~ap2x), A4)
о
Для определения постоянной C(p) воспользуемся начальным условием
F). Из решения A4) следует, что при т->0
7н(р, 0) = С(р). A5)
х) Подробно см. формулу A4) § 4 гл. V.
342
Глава восьмая
Кроме того, по определению изображения имеем
R R
Тн(р9 0) =§Цг, 0)rJ0(pr)dr = Г f(r)rJ0(pr)dr. A6)
Следовательно,
С(Р) = ] MrJ0(pr)dr
A7)
Если вместо С(р) подставим выражение A7) в решение A4), то получим
решение задачи для изображения Тн(р, ^).
Для перехода к оригиналу Т(г, т) по формуле A1) предварительно
определим 7н@, т) из решения A4):
R х т
Тн@, х) = j /(r)rdr + -^-j ?(») d& + ± ja»H@,»)d», A8)
о о о
где аУн@, t) = ) o>(r, t)ni/\ A9)
о
Подставив значение Гн@, т) и Гн(р> т) в формулу A1), получим
решение
R т т
ГС> х) = A J /(r)rdr + ^j q(b)db + -^ |шн@,&) d& +
0 0 0
oo R
+S if£^- exp (-a^) • i? j ^r)r ^(/v)^+
«=i о
00 X
+ aR £ J.(P,*)/.(/V) exp (_ap,x) . 2 Г ^(ft) exp {ap2^ +
rt=l
00 T Я
+ "^ £ "T^j- exP (~а#) ^ J J да(г' »)r'o(/V) ^Р (ap2&)d&dr. B0)
«==1 ° 00
a&
Обозначим Fo = ax/i?2, \kn = pnR, _ = Fo*, тогда решение B0) в
обобщенных переменных можно написать так:
Fo
Ki(Fo*) +
о о
о
dFo*
ПОЛЕ С НЕПРЕРЫВНО ДЕЙСТВУЮЩИМИ ИСТОЧНИКАМИ ТЕПЛА
343
1 °°
+22
л=1
Х Л ( Рп ~£
Fo
- jpoGOKi (Fo
0
r) <<(-£)] «р[-
0
-^(Fo-
Po /-^- , Fo*] X
-Fo*)]dFo*.
A2)
где
Ki<F.)-!g£. Po(^,Fo) = %S*\ B2)
(хл — корни характеристического уравнения «/о([а) = 0.
Если распределение температуры в начальный момент времени
равномерное
Т(г, 0) = Т0 = const, B3)
а Т0 без потери мощности принято равным нулю, то при постоянном
тепловом потоке на поверхности тела [q (т) = const, Ki(Fo) = const]
решение B1) можно написать так:
9(^°)=^=ф(^°)+
0 0 л=1
Fo
X
о
го 1
j d Fo* exp (^ Fo*) J -£- Po (-£, Fo*) /„({*„ -^-) d (-£-) , B4)
где
£ , Fo) = Ki[2Fo - 4 . Ri
Ф 4-, Fo =Ki[2Fo-4- 1-2-U -
-^^^^(^expC-^Fo)], B5)
Отсчет температуры производится от начальной температуры тела (Г0==
= 0).
Если источник тепла отсутствует (Ро = 0), то решение B4)
б(^)Ро) = ф(-^)Ро)
становится тождественным решению E) § 4 гл. V.
Найдем решения для ряда частных задач при выполнении условия
B3) и постоянном значении критерия Кд.
1. Постоянный источник тепла
Ро (-^-, FoW Рос = const]
6 (-L-, Fo) = PocFo + ф(Jl, Fo). B6)
2. Источник тепла — параболическая функция радиальной координа-
ш [Po(^,Fo) = Poc(l-^)]:
(г „ \ n fir: , V ^^lW-^oW]
(Х- Fo) = Ро< {т Fo +£ ,3 ,,(|1<|) х
n=l
* л(^х)[1-ехр(-^ро)]} + ф(х' Fo): B7)
344
3. Источник тепла — линейная функция времени Г Ро (~ , Fo) =
= РосA+Pd'Fo)]:
6 ^ , Fo) = PocFo f 1 + ±- Pd' Fo )+ Ф f^- , Fo) , B8)
где Pd' = -g критерий Предводителева, равный максимальной
относительной скорости изменения удельной мощности источника тепла, т. е,
РН' —Г d(w?wo) 1
™ ~ dFo
4. Источник тепла—экспоненциальная функция времени Ро(-^-, Fo) =
= Росехр(—Pd'Fo)l:
6 [^, Fo) = f^ [ 1 - exp (-Pd'Fo)] + Ф (-£-, Fo). B9)
5. Источник тепла — периодическая функция времени
Г Ро (-^ , Fo] = Poc cos (Pd'Fo) j :
G (-£ , Fo) = g? sin (Pd'Fo) + Ф ^ , Fo). C0)
6. Источник тепла зависит от времени в п-й степени Po(-^-,Fo ) =
= Poc(Pd'Fo)ral:
•(*.*°)-^**» + *(t-Fo)- m
Расход тепла во всех случаях вычисляется по средней температуре
6(Fo). Среднее значение <P(Fo) определяется соотношением (8) §4 гл. V.
ТЕМПЕРАТУРНОЕ ПОЛЕ С МГНОВЕННЫМИ
ИСТОЧНИКАМИ ТЕПЛА
9
ВВЕДЕНИЕ
В некоторых тепловых процессах нагревание тела происходит в
результате воздействия кратковременного теплового источника постоянной
силы (тепловой импульс). К числу таких задач относится задача на
нагревание кабеля, в котором произошло короткое замыкание, в
результате чего кабелю сообщается некоторый мгновенный тепловой импульс.
Существует ряд методов определения теплофизических
характеристик, основанных на закономерностях нестационарного температурного
поля, создаваемого действием мгновенного теплового импульса.
Прежде чем перейти к рассмотрению конкретных отдельных задач,
остановимся на свойствах решения дифференциального уравнения
теплопроводности неограниченного тела при наличии мгновенного источника
тепла.
Дифференциальное уравнение теплопроводности
*Г(х.У.п.*) ^ as/2T(Xt y> г> т) A)
удовлетворяется при подстановке в него следующего решения:
Пх, У, г, *)=-£_ ехр Г - (x-^ + tt-^ + C*-*)' I, B)
бутсахK |_ 4ат J
Из решения B) видно, что температура тела стремится к нулю, когда
т->0 во всех точках, за исключением одной точки (хг, уг, zt), где она
становится бесконечно большой.
Если решение B) проинтегрировать по всему объему от—оо до +оо,
то получим
-{~оо-|-оо-|-оо
J J J T(x, у, z, i)dxdydz — bv
— 00—OO—OO
так как
= L_Tcxp Г - (z~ZlJ1 dz = 1
2yw J 4 te J
346
Глава девятая
Следовательно, выражение B) является решением задачи распределения
температуры в неограниченном теле в любой момент времени,
вызванного действием мгновенного источника тепла напряжением Ьг в точке
xv Уъ zv B момент времени т =0, так как, если в этой точке
выделяется количество тепла Qx = c^bx (дж), то распределение температуры
будет определяться соотношением B). Следовательно,
Ьг = -^-(град-м3).
Функция
С{х, у, ,Л ,„ й. ,j _ ^ехр [ - "-'- + ^ + '—■'• ]
называется функцией температурного влияния мгновенного источника
тепла. Эта функция обладает свойством симметрии
G(x, у, z, т, xv уъ гх) === G(xl9 уъ zl9 т, х, у, z),
являющимся выражением принципа взаимности: действие в точке х, у, z
источника, находящегося в точке х19 уг, гъ равно действию в точке
xi> Ун zi такого же источника, помещенного в точку х, у, г. Однако
относительно переменной т такая симметрия не имеет места, что
является выражением необратимости тепловых процессов во времени.
Определим вид функции G для других случаев. Выражение
т(*>У>*)=-ШГекР
(x^XlJ+{y^yiJ
4ai
-] О)
удовлетворяет дифференциальному уравнению
дТ(х, у, т) __ (d*T(x,y,<z) д2Т(х, у,т)
di "[ дх2 ' ду2
и является решением задачи распределения температуры в
неограниченном теле при двумерном потоке тепла, вызванного действием
мгновенного источника тепла на прямой xv yly проходящей через точку (xv уг)
параллельно оси z, в момент времени i = 0, так как
-{-00 -\-СО
\ \ Т(х, у у i)dxdy = b2 (град-м2),
где 62 = —, Q2 — сила источника тепла на единицу длины (дж/м). Ре-
ст
шение C) может быть получено из решения B), если считать, что гх
распространено от —оо до +оо, т. е. если заменить точечный
источник линейным.
Формула
Т(х, т) = ^=~ехр Г - ^=^
удовлетворяет уравнению
дТ(х_у т) _ д2Т(ху т)
D)
дъ дх2
и является решением задачи распределения температуры в
неограниченном теле при одномерном потоке тепла, вызванного действием
мгновенного плоского (вдоль плоскости хх) источника тепла силой QB на
единицу площади в момент времени т = 0, так как
-J-00
\Т(Х, z)dx=b3,
ТЕМПЕРАТУРНОЕ ПОЛЕ С МГНОВЕННЫМИ ИСТОЧНИКАМИ ТЕПЛА 347
где Ь3 = — (град-м), Q3 — количество выделенного тепла (дж/м2).
Аналогично можно показать, что формула0
Пг, *) = -т^ехр
bo Г Г + Г
2-1-г? -,
4тсат ^ 4ат
■м-e-i (б)
удовлетворяет уравнению
dT(r,z) __ (д2Т(г, т) ( 1 J7(t,t)
и является решением задачи распределения температуры в
неограниченном теле, вызванного действием мгновенного источника тепла силой
Q2 на поверхности цилиндра г = гх в момент времени % = О на единицу
длины.
Имеем
00
2 тс J rT(r, i)dr = b2 (град-м2)j
о
где Q2 = c^b2 (дж/м), так как
СО _C2_
О
Наконец, формула2)
удовлетворяет дифференциальному уравнению
дТ(г, т) __ / а2Г(г, t) , 2 ЯГ(г, и)
4ат
F)
дт 1 <^2 г дг
и является решением задачи распределения температуры в теле в
любой момент времени под действием источника силой Qt = bxc^ (дою),
мгновенно распределенного на сферической поверхности г = гг в момент
времени т= 0, так как
00
4тг (r2T(r, x)dr = Ьх = I1 (град-ж3).
о
Соотношение B) является аналогом функции Грина, которая находит
широкое применение в теории потенциала. Функция Грина
определяется внутри замкнутой поверхности как некоторый потенциал, который
обращается в нуль на поверхности, а в точке P(xlf yx, zx), находящейся
внутри поверхности, стремится к бесконечности.
!) Решение E) получается из выражения
Ъггйгф л Г ra + rf —2rr!C0sft
11 .exp —
Апах L 4a t J
интегрированием по переменному & в пределах от 0 до 2% и заменой 2%гхЫг{г'ш b%*
2) Решение F) получается из соотношения
1 9 Г г* + г\ — 2п1со$Ь1л
Т = . о ftrf а>х sin ММф1 exp — 1
интегрированием по поверхности сферы радиуса гг и заменой 4%г\Ыгх на fri.
348
Глава девятая
Поэтому соотношение B) надо считать как функцию, определяющую
температуру в точке (х, у> г) в момент времени г, вызванную действием
мгновенного источника тепла, помещенного в точку (xl9 yv zt) в момент
времени т = 0. При этом полагаем, что начальная температура тела
равна нулю, а граничная поверхность поддерживается при нулевой
температуре.
Пользуясь соотношениями B) — F), можно решить ряд конкретных
задач по нахождению температурного поля внутри тела при наличии
мгновенного источника тепла с соответствующими краевыми условиями.
При этом необходимо заданную задачу разбить на две задачи, одна из
которых должна удовлетворять условиям функции Грина, а вторая —
заданным начальным и граничным условиям.
§ 1. ПОЛУОГРАНИЧЕННОЕ ТЕЛО
Постановка задачи. Дан полуограниченный тонкий стержень,
боковая поверхность которого имеет тепловую изоляцию. В начальный
момент времени (т = 0) действует мгновенный источник тепла Q3 {дж1м2)
в сечении стержня на расстоянии хх от конца его. Между
изолированным концом стержня и окружающей средой (Тс = 0) происходит
теплообмен по закону Ньютона. Требуется найти распределение
температуры по длине стержня в любой момент времени. Начальную тем -
пературу стержня принимаем равной нулю.
Имеем:
i^.-aJ^>(,>0;0<*<oo),
Т(х, 0) = 0,
Г(ос,т)=0,
дТ@,
дх
+ НТ@, т) = 0.
A)
B)
C)
D)
Отсчет температуры в теле происходит от температуры окружающей
среды, так как Тс = 0. Таким образом, поставленная задача является
задачей на охлаждение стержня, получившего в начальный момент
времени кратковременный тепловой импульс.
Решение задачи. Для неограниченного тела при одномерном потоке
тепла и наличии мгновенного источника тепла решение
дифференциального уравнения A) имеет вид
Ь _Г (* —*iJ
и(х, т) —
2"|/Wc
ехр
Г (*-*iJ1
L 4ат J
E)
где Ьс*( = Q3 — количество тепла, выделенного мгновенным источником,
на единицу площади сечения стержня (дж/м2). Следовательно,
коэффициент Ь имеет размерность град-м.
Из решения E) видно, что при т~>0 и(х, т) стремится к нулю при
всех х, за исключением х = xv где и (х9 т) стремится к бесконечности.
Разобьем нашу задачу на две задачи, введя новые переменные
Т(х, т) == и(х, *) +v(x, т). F)
ТЕМПЕРАТУРНОЕ ПОЛЕ С МГНОВЕННЫМИ ИСТОЧНИКАМИ ТЕПЛА 349
Переменная v(x, т) удовлетворяет дифференциальному уравнению A),
так как и(х, т) является решением его. Следовательно,
dv(x, t) •__ g d2v(x, т) ,-
дт дх2
Начальное условие для переменной v (х> т) будет
v(x,0) = 0. (8)
Для решения уравнения G) воспользуемся методом преобразования
Лапласа. Имеем
V'Ux,s)-±Vi.(x9s) = 0, (9)
где Vl(x, s) = L[v(х, т)] — изображение функции v(x, *).
Решение уравнения (9) в общем виде можно записать так;
VL(x9 s) = Ach У^- х + Bsh ]/^" x = A<? Т* + ВХ<Г* *** . A0)
Соотношение F) для изображения имеет вид
Ти (х, s) = UL (х, s) + VL (x, s), A1)
где UL (x, s) — изображение функции и (х, т), т. е.
Ul{x,s)=\l\ '_
1 2"|А
e 4ax
2 У as
:r^|4MPtl A2)
[см. соотношение E1) таблицы изображения в приложении].
Необходимым условием для существования изображения функции
J VT
1_е 4V ^J^^kYs
является выполнение неравенства &>.0. Поэтому в изображении A2)
надо брать абсолютное значение разности (х-—хг). Благодаря этому не
нарушается условие симметрии функции и ее изображения
относительно хг.
С этими существенными оговорками вернемся к решению нашей
задачи. Имеем]
TL(x, s) ^-J-e-^*-^ + а/±* + Ble~V^x . A3)
2yas
Из условия C) следует, что Аг =* 0. Постоянную Вх определяем из
граничного условия D), которое для изображения TL (x, s) примет вид
-T'L@,s) +HTL@,s) = 0. A4)
Следовательно, имеем
350
Глава девятая
откуда постоянная Вх будет равна
,y5rU/*+,7
Таким образом, решение для изображения можно написать так:
A5)
TL (x, s) =
2 У as
-*i)
— l/- +1
6 -Vt1*-**1 ,
е +
2 "j/as"
6 -Vt^^
-е
2 l/osT
l/jL№l)
У as A +
i/т)
A6)
Пользуясь таблицей изображений, находим решение для оригинала
Т(х,т):
Т (х, х)
1-\Гъ
ехр
Аах
+ ехр
(х + *i)a
— ЬН ехр [Н (х + xj + aHH]-eric ( х+^_ + ЯУ^ат М
V 2 1/ат /J
A7)
Последний член в решении A7) можно написать в виде
ЪН
У
м
ехр
я. (а: + агх + £J
4а т
л.
A8)
Если Я~>оо, что соответствует постоянной температуре (равной
нулю) конца стержня в процессе охлаждения (граничное условие
первого рода), то соотношение A8) равно нулю. В этом случае из решения
A7) можно получить обычное решение для охлаждения
полуограниченного стержня при заданной начальной температуре в виде некоторой
функции от х, т. е. Т (х ,0) = f(x). Положим
db = f(x1)dxv A9)
Ь = j/(*i№.
Подставляя это соотношение в решение A7), находим
Т(х, т) =
2Ука1
/(*х) ехр
(х — *iJ
Аах
+ ехр
(а: + *iJ
4ат
B0)
► (ХХ\ ,
т. е. получаем решение, тождественное решению* D) § 2 гл. IV.
ТЕМПЕРАТУРНОЕ ПОЛЕ С МГНОВЕННЫМИ ИСТОЧНИКАМИ ТЕПЛА 351
§ 2. НЕОГРАНИЧЕННАЯ ПЛАСТИНА
Постановка задачи. Дана неогра-
температу-
ниченная пластина при
ре Т0 = 0 (отсчет температуры про-
изводим от температуры тела). В
начальный момент времени (т = 0)
действуют мгновенные симметрично
расположенные источники тепла при
х = ± хг (—R < х < -\-R) силой Q3 на
единицу площади (источники тепла
действуют вдоль плоскостей -\-хг и
—хг). Между противоположными
поверхностями пластины (+R и —R) и
окружающей средой происходит
теплообмен по закону Ньютона
(граничное условие третьего рода).
Требуется найти распределение температу- Рис. 9.1. Распределение
температурь/ ПО толщине пластины в любой ры в неограниченной пластине в слу-
момент времени.
Имеем
чае мгновенного источника тепла
Т (х, 0) = 0,
.ОТ @. *) _ 0.
дх
A)
B)
начало координат находится в середине пластины (задача симметричная)
_dT(R, т)
дх
+ HT(R,x) =0.
C)
Для упрощения расчетов температуру окружающей среды принимаем
равной начальной температуре тела (Тс = Т0 = 0).
Решение задачи. Применяем аналогичный прием решения задачи.
Положим
Т (х, т) = и (х, т) + v (х, *с),
где
и (х, т) =
2 j/W
ехр
(х — х-
= *£-] + ехр Г- <*±Щ
4ат J [ 4ах J
D)
является решением задачи охлаждения ^неограниченного тела при
действии мгновенных источников тепла вдоль плоскостей ±хх (рис. 9.1).
Переменная v (x, т) удовлетворяет дифференциальному уравнению
теплопроводности, решение которого для изображения Vl(x, s)
приведено раньше [см. решение A0) § 1].
Выражение для изображения можно написать так:
TL(x, s) = UL(x, s) + VL(x,s) =
[е f a
+ е f «
• (x+xj
J + ЛсЬ|А х +
+ fish
/т*
E)
так как изображение Ul(x, s) = Ь[ы(х, i)] определяется соотношением
A2) § 1.
352
Глава девятая
Согласно соотношению D) функция и (х, т) является четной функцией
относительно xv как и ее изображение. Поэтому из условия B) следует
дх
F)
откуда В = 0.
Постоянную А находим из граничного условия C), которое для
изображения TL(x, s) напишем так:
T'L(R,s)+HTL(R,s) = 0.
Следовательно, имеем
2-J/5T v a L
+ е а
+
+fi**Vi*+^~['-y*
(«-*»)
2 У as
+
+ e~V^^]+HAcbY^ R = 0.
G)
Определив из равенства G) постоянную А и подставив ее значение
в решение E), будем иметь
TL (х, s) = — ^ — — х
+[tYI^ )*fi
У±™+е
(8)
Заменяя экспоненциальные функции через гиперболические по
соотношению e"z = chz — shz, можно показать, что решение (8)
удовлетворяет теореме разложения. Корни характеристического уравнения хорошо
известны [ср. решение B5) § 3 гл. VI]; они определяются из
соответствующего уравнения.
После необходимых преобразований решение для оригинала получим
в виде
г<*.*) = -!-2
/i=i
^ ^costv-^- X
Ря + sin \ъп cos ]xn R
Хсоз[л„— ехр(-^—j
(9)
где рп— корни характеристического уравнения B7) § 3 гл. VI. Если
мгновенный источник тепла находится в середине пластины (хх = 0), то
cos IV—
1.
Из решения (9) можно получить решение A5) § 3 гл. VI задачи на
охлаждение неограниченной пластины в среде с нулевой
температурой при заданном начальном распределении температуры в виде
некоторой функции f(x).
ТЕМПЕРАТУРНОЕ ПОЛЕ С МГНОВЕННЫМИ ИСТОЧНИКАМИ ТЕПЛА 353
Если положить db = f (x^)dxv то можно написать
2Ъ= [ fix^dx,.
-я
Если подставим это выражение в решение (9), то получим
я
Т(х,*У=%
И-л
/2=1
\ъп + sinp^cos^
■п К К. J К
X
X exp (-[**Fo) ,
A0)
т. е. получим решение, тождественное решению A5) § 3 гл. VI.
Решение (9) можно написать в форме, более удобной для расчета,
поскольку постоянные коэффициенты Ап табулированы:
Ая = -
2sin \xn
Рп + sin \ьп cos р,л
(_1)я+1
^(Bi» + Bi + ^) '
а именно
Т(х, г) = J-^-cos^-^cos^^-exp (-^Fo) . A1)
/1=1
Средняя температура Т(т), необходимая для определения
количества тепла, теряемого пластиной в процессе охлаждения, будет равна
хг
Т{
„ fcpviCOStXn R
R sin \><n
-Яяехр(—j^Fo)
/2=1
A2)
Если Bi -> oo, то Лл = (—!)■
(И) упрощается:
n+l
— , а ^л = B#—1) — , и решение
Т (*, *) = -?*- V (_l)»«cos B/г~1)тсХ1 cos Bn^1)ir
/г
R
X
/1=1
X ехр
B/г— 1Jтт2—1.
A3)
Если задача несимметрична @< х </, где t = 2R — толщина
пластины) и имеется один плоский источник при х == xv то решение
аналогичной задачи для случая Bi = оо (граничное условие первого рода)
имеет вид
TL(x,s) =
ch "I/ — (t + x — x{) — ch
a
A-х
-*i)]
2 У as s 1/ — /
Отсюда находим решение для оригинала
со
26
Т (х, т) = — 2j $ш sm exp(—n2it2Fo).
A4)
A5)
п=\
12 Заказ № 640
354
Глава девятая
§ 3. ШАР (СИММЕТРИЧНАЯ ЗАДАЧА)
Постановка задачи. Дано сферическое тело при температуре,
равной нулю. В начальный момент времени действует мгновенный
источник тепла силой Qx (дж), распределенный вдоль сферической
поверхности г = гг. Между поверхностью шара и окружающей средой
происходит теплообмен по закону Ньютона (граничное условие
третьего рода). Требуется найти распределение температуры и среднюю
температуру в любой момент времени.
Имеем
*1гГ(г,-01 =дУ1гГ(г,*I {x>0.0<r<R)> A)
дх дг2
Г(г,0)=0, B)
дТ @' %) = О, Т @,т) ф оо при т > 0, C)
дг
дГ(^>т) + НТ (R, т) = 0; D)
дг
при Bi = оо (Я = оо) Г (/?, х) = 0. E)
Решение задачи. Для сокращения расчетных соотношений решим
задачу вначале при Bi = оо (граничное условие первого рода), а затем
приведем решение поставленной задачи.
Полагаем
T(r,>z) = u(r,%)+v(r,x), F)
где и (г, т) есть решение задачи на охлаждение неограниченного тела,
которое в начальный момент времени получило тепловой импульс Qx ==
= Ьс\ (дж), мгновенно распределенный вдоль сферической поверхности
г = гг.
Согласно соотношению F) «Введения» решение имеет вид
G)
и(г х\ = Ъ {схр Г (г~fl)'1 схрГ <г + г^11
ewriV^Tl L 4от J *Ч 4ат Jj'
Изображением этой функции будет
£/L(r,s) = Il«(r,*)] = ^.Гг^1^1 -Г^'Н (8)
втс/Т! Y as L J
с аналогичными замечаниями относительно разности (г—гг).
Функция у (г, т) удовлетворяет уравнению A), так как Т (г, т) и а (г, т)
являются его решениями. Следовательно, изображение функции и(г,ъ)
должно удовлетворять уравнению
[rVL(r,s)]'-|rVL(r,s) = 0, (9)
где FL(r, s) =L[v(r, %)].
Решение этого уравнения при условии C) имеет вид
Bsh т/"±- /■
VL(/\s) = ?-^ . A0)
ТЕМПЕРАТУРНОЕ ПОЛЕ С МГНОВЕННЫМИ ИСТОЧНИКАМИ ТЕПЛА 355
Тогда решение для изображения ТL (r, s) можно написать так:
TL(r,s)
8тсггх У as *-
е т а — е
У* <'+'.>
Bsh
+
Постоянная В определяется из граничного условия E), которое для
изображения можно написать так: TL (R, s) = О, т. е.
8%rrt J/ as
' а
(R-ri)
■V\
■(R+rt)
+
Bsh 1/ — R
a
-0. A2)
Определим из равенства A2) постоянную В и полученное выражение
подставим в решение A1); тогда после небольших преобразований получим
bsh
TL(r,s)
± rsh-|/-i
а У а
(Л-ri)
4тс rrx V as sh 1/ — R
@<r<r1).
A3)
Если /?>г>гх, то в решении A3) г и гх надо поменять местами.
Решение A3) удовлетворяет всем условиям теоремы разложения,
и поэтому переход от изображения к оригиналу производится обычным
путем:
Г(г,*) =
2tzR *-» rrx
sjn
nicri
sin -^^- exp (—n2it2Fo).
R R FV ;
A4)
Если критерий Био есть конечная величина, то при определении
постоянной В надо воспользоваться граничным условием D). Произведя
аналогичные преобразования, решение в окончательном виде можно
написать так:
Т(г,т)
zR jLJ
\±п
sin \ьп
sin \хп
R
2kR
л=1
t% —sin^cos^
X exp (— [x2Fo)
X
A5)
где \ьп— корни характеристического уравнения A2) § 5 гл. VI.
Поскольку мгновенный источник тепла Q± = сф распределен вдоль
всей сферической поверхности 4тгг|, то величина db будет равна
db = 4^rf / (гг) drv
A6)
где /(гх) — некоторая функция распределения температуры в начальный
момент времени при охлаждении шара в среде, температура которой
равна нулю (см. § 5 гл. VI). Тогда величина b равна
Ь = 4к J r\f{ri)drv A7)
12*
356
Глава девятая
Если подставить это выражение в решение A5), то получим
2^7*
л=1
[% — Sin {ХЛ COS р.л
X
X
sin^~ { R
Y f ^/(^sm^-^-^exp (—jt2F0);
A8)
т. е. получим решение, тождественное решению A9) § 5 гл. VI.
Так как начальные тепловые амплитуды Ап9 определяемые
соотношением B9) § 5 гл. VI, табулированы, то решение A5) перепишем в
другой форме:
п ^- ь Ь [(В1-1J + ^11/2Ли sin^"T sin^T'
Bi
X
n=\
X exp (—p2Fo)
A9)
Если источник тепла находится в центре шара (гг = 0), то решение
A5) примет вид
Т(Г' '> = ТПёГЪ ,л-з1п1соз,„ sin,n^-exp(_^Fo). B0)
Я=1
Средняя температура Т(г, т) равна
Т(г,т) =
.2lV.
Г" S UBi
п=1
4it^nBi
+ ^]V>n-6„exp(—^Fojsini*,, ^
1J +
B1)
где Brt—постоянные коэффициенты, определяемые из соотношения D9)
§ 5 гл. VI.
§ 4. НЕОГРАНИЧЕННЫЙ ЦИЛИНДР
Постановка задачи. Имеется неограниченный цилиндр. В
начальный момент времени действует мгновенный источник тепла силой Q2
(дж/м) на единицу длины цилиндрической поверхности г = гг. Между
поверхностью цилиндра и окружающей средой происходит теплообмен
по закону Ньютона, Требуется найти распределение температуры и
.среднюю температуру в любой момент времени.
Имеем
di \ дг2 г дг J
дТ@, т)
дг
Т(г,0) = 0,
= 0, Г@, т)=^оо при т>0
дТ (R> ^ + НТ (#, т) - 0.
дг v '
B)
C)
D)
ТЕМПЕРАТУРНОЕ ПОЛЕ С МГНОВЕННЫМИ ИСТОЧНИКАМИ ТЕПЛА 357
Для упрощения расчетов начальную температуру цилиндра и
температуру окружающей среды принимаем равной нулю.
Если Bi = ©о, то
Г(Д,т) = 0 E)
(граничное условие первого рода).
Решение задачи. Решим задачу вначале при граничном условии
первого рода (Bi =oo). Полагаем
Г(г,т) = м(г, т) + 1>(г,т), F)
где и {г, т) есть решение уравнения A) при наличии мгновенного
источника тепла Q2 = bc^ (дж/м), действующего на цилиндрической
поверхности г = rv
Согласно соотношению E) «Введения»
и (г, т) =
4тшт
ехр
r2 + rj
4az
л
2ai
G)
Изображение этой функции находим по таблице изображений;
^^^Ч/^МуТО при г>г»
^(r's) = -^-/o(vTr)^(i/Tri) °ри г<г- ^
Функция u(r,s) удовлетворяет дифференциальному уравнению A).
Решение уравнения для изображения Ul(^ s) при условиях B) и C)
можно написать так:
Л_ ' (9)
TL^S) = ^io{YJr1)Ko{}/J'r) +Л/„(/ГГ)„рИГ>Г1. (Ю)
Постоянную А находим из граничного условия E), т. е. из условия
TL(R, s) = 0. Тогда решение A0) будет иметь вид
UL(r,s) = AI0(y ^ г).
Тогда решение для изображения ТL (r, s) имеет вид
TL{r, s)
6ЧУ1
^['•(/т*)*.(/т')-
A1)
{при г < гг в решении A1) г и гг надо поменять местами)*
Применяя теорему разложения, находим решение для оригинала:
00
Л=1
A2)
358
Глава девятая
где (хя~ корни бесселевой функции первого рода нулевого порядка, т. е.
они определяются из характеристического уравнения
Решение A2) справедливо для г>г± и г <С rv так как оно
симметрично относительно г и гг.
Если между боковой поверхностью цилиндра и окружающей средой
(Тс ~ 0) происходит теплообмен по закону Ньютона, то решение будет
иметь вид
1 ; «R* ^ fBi«
■Л
П—l Ч '
где уп— корни соответствующего характеристического уравнения,
являющиеся функциями критерия Био.
Из решения A3) можно получить обычное решение для
неограниченного цилиндра, если в начальный момент времени температура его
есть некоторая функция г, т. е.
Т(г,) =/(г).
Положим
db — 2-nrJ (r1)drv
Тогда
R
b = 2тг f r1f{r^)dr1.
6
Если подставить в решение A3) полученное выражение, то будем
иметь:
00 2
Т(г, *) = У! -John—) х
^ (в1» + ^)/2ы ЧРя*/
2 j г/('Ко (ft, —) drexp (-^Fo) . A4)
R
9
X
R2
. о
Решение A4) тождественно решению A5) § 6 гл. VI, так как
Л 1
Решение A3) можно написать по-иному, введя табулированный
коэффициент Ап [см. соотношение B7) § 6 гл. VI]:
'A5)
ТЕМПЕРАТУРНОЕ ПОЛЕ С МГНОВЕННЫМИ ИСТОЧНИКАМИ ТЕПЛА 359
Средняя температура Т (т) равна
/2=1
где Вп — постоянные коэффициенты, определяемые из соотношения C4)
§ 6 гл. VI.
В заключение этого раздела необходимо отметить, что метод
источников дает возможность решать не только непосредственно задачи с
мгновенными источниками тепла, но и задачи на охлаждение или
нагревание тела, когда в начальный момент времени задано распределение
температуры как функции координат. К такому же результату можно
прийти, если решать эти задачи методом интегрального преобразования
Фурье — Ханкеля.
Задачи с мгновенными источниками тепла можно решать с
использованием дельта-функции Дирака. Подробно с этим методом читатель
может ознакомиться в работе А. И. Мочалина [53].
§ 5. РЕГУЛЯРНЫЙ ТЕПЛОВОЙ РЕЖИМ
Г. М. Кондратьевым впервые было введено понятие регулярного
режима охлаждения или нагревания первого рода, при котором изменение
температуры в любой точке тела с течением времени описывается
простой экспонентой (см. § 10 гл. VI). Производная от логарифма
избыточной температуры по времени будет величиной постоянной и называемой
темпом нагревания или охлаждения тела (т = const):
д[1п(Гс — Т)] 1 дт . /1ч
L_L_ „ ___ _ =, m » const (i)
Г. М. Кондратьев и его ученики различают регулярный режим
второго рода, при котором температура в любой точке тела является
линейной функцией времени
ВТ
= Ь = const, B)
а распределение температуры в теле описывается некоторой функцией
от координат (для одномерных симметричных задач такой функцией
является парабола).
Такой режим нагревания тела имеет место, когда температура
окружающей среды является линейной функцией времени (граничные
условия третьего рода):
ТС = Т0 + Ьх, C)
или когда тепловой поток у поверхности тела
Qn W = <7с = const. D)
Регулярные режимы нагревания тела наступают, спустя определенный
промежуток времени, определяемый неравенством Fo > Fox. Анализ
решений (см. гл. V, VI, VIII) показывает, что регулярные режимы
первого и второго родов имеют общее свойство, которое характеризуется
независимостью от времени отношения удельного потока тепла q
в любой точке тела к потоку тепла на его поверхности qn:
q/q„ - / (х9 у, z). E)
360
Глава девятая
В случае регулярного режима первого рода (Тс
гл. VI):
а) для неограниченной пластины
q (xy т)
б) для шара
Яп
sin piX/R
sin р^
const) имеем (см.
F)
Я (г, 1)
г cos р*! r/R — ein \хг r/R
qn r2 (R cos (xx — sin H)
в) для неограниченного цилиндра
q{r,i) ^ Jii^r/R)
Яп
Для регулярного режима второго рода
= const)
. dz J
ков тепла равно безразмерной координате, т. е.
я (*, *) _ JL- ^(г>т)
G)
(8)
отношение пото-
rlR.
(9)
<7п К Яп
Эти соотношения справедливы и для граничного условия второго рода
в самом общем случае, когда поток тепла задан как некоторая
функция времени [qn = /(x)]. Соотношение E) в одномерных задачах
теплопроводности, как общая характеристика регулярных режимов первого
и второго родов, остается справедливым при наличии постоянно
действующего источника тепла. Следовательно, регуляризация кинетики
нагревания тела происходит не только по температурным полям, на
и по потокам тепла. Поэтому нет надобности различать регулярные
режимы нагревания первого и второго родов.
Развивая этот принцип регуляризации, можно в качестве общего»
свойства теплового регулярного режима принять соотношение
dT
(тс — т) &
= пг = const,
A0)
где Т — средняя по объему тела температура. Следовательно, скорость*
dT .ч
нагревания тела —г~ прямо пропорциональна разности между
температурой среды и средней температурой тела, т. е.
^- = т(Тс-Т),
(И)
где m — коэффициент пропорциональности, называемый темпом
нагревания.
Иллюстрируем конкретными примерами.
1. Температура среды постоянна (Тс = const).
Из решений D4) § 3, D8) § 5, C3) § 6 гл. VI можно написать:
Г dT
(Тс —~Т) dx
И ^exp(-^Fo)
а п=\
R2 °°
2 Вп ехр (-м* Fo)
л=1
A2>
ТЕМПЕРАТУРНОЕ ПОЛЕ С МГНОВЕННЫМИ ИСТОЧНИКАМИ ТЕПЛА 361
Для Fo > Fox можно ограничиться первым членом ряда, тогда
отношение A2) не будет зависеть от времени:
= р.2 = т = const. A3)
(Tc-f-) dz R* ri
Темп нагревания зависит от Bi, коэффициента а и определяющего
размера R тела.
2. Температура среды — линейная функция времени /—— = 6=const) .
Из решений A8) § 1, A8) § 2 и (8) § 3 гл. VII можно написать
dT L n=i j ,щ
а
R2 .
Pd
Pd
-и-
Г " 1
1+ 2j Bnexp (-v.2nFo)
L «-1 J
oo 1
f"S") + S"^"B»exp(-,,,«Fo)
/1=1 J
(rc-r) <**
где Г и П — постоянные, соответственно равные для пластины,
цилиндра и шара
Г = 3, П = 3; Г = 8, П = 4; Г = 15, П = 5.
Если Fo > Fox, то можно пренебречь рядами, т. е.
1 dT а Г
G\.-Т) dz Л2 A+П/В1)
= const. A5)
Следовательно, темп нагревания, определяемый по соотношению A5),
является величиной постоянной, зависящей, как и в первом случае, от
Bi, а и R.
3. Температура среды — периодическая функция времени (Тс = Т0 +
+ Tmcosa)T).
Из решения D5) § 6 гл. VII для периодически стационарного
состояния получаем
-^r- — =Pd— ctgM = const. A6)
(Тс~т) dz R*
Следовательно, темп нагревания тела зависит от критерия Pd,
коэффициента а, характерного размера тела /?, так как величина М является
функцией Pd.
4. Наличие внутренних постоянно действующих источников тепла.
Если при нагревании тел без внутренних источников тепла конечное
распределение температуры равномерное (Тс = const), то при наличии
внутренних источников тепла предельное тепловое состояние тела
является неравновесным, а температурное поле неравномерным.
Обозначим неравновесную температуру стационарного состояния
через Too, т. е.
Tco-liml, A7)
т-*оо
Тогда решения A1) § 2, (8) § 3, D) § 4 гл. VIII можно написать так:
feS = £ [l +jfPo) s«exp (-^Fo)- <18)
362
Аналогичное соотношение получим для темпа нагревания в стадии
регулярного режима
A9)
Следовательно, основной признак регулярности теплового режима
сохраняет тот же вид, только под величиной средней избыточной
температуры надо понимать (Т^ — Т).
5. Наличие мгновенных источников тепла.
Из решений A2) § 2, B1) § 3 и A6) § 4 данной главы для значения
Fo > Fox, когда из всего ряда можно ограничиться первым членом,
можно написать:
— = -5L- и? = m = const. B0)
т. е. справедливо соотношение A0).
Таким образом, в стадии теплового регулярного режима скорость
нагревания тела прямо пропорциональна разности между
температурой среды в стационарном состоянии Т^ и средней объемной
температурой тела Т :
dT
dz
= /и (Г» — T).
B1)
Коэффициент пропорциональности т (темп нагревания) является
функцией характерного размера тела, коэффициента
температуропроводности, критериев Bi, Pd. Признак регулярности кинетики
нагрева тела определяется соотношением B1), справедливым при
наличии источников тепла.
ГРАНИЧНОЕ УСЛОВИЕ ЧЕТВЕРТОГО РОДА
10
В гл. V и VI были рассмотрены задачи нестационарной
теплопроводности, в которых теплообмен между поверхностью тела и окружающей
средой происходил в основном излучением. В практике тепловых
расчетов встречаются задачи, в которых теплообмен между телом и
окружающей средой происходит конвекцией. Если в задачах стационарного
конвективного теплообмена применяются граничные условия третьего
рода, то в задачах нестационарного конвективного теплообмена и в задачах
стационарного теплообмена при точной формулировке проблем необходимо
применять граничные условия четвертого рода. Например, при
обтекании плоской пластины, в соответствии с теорией пограничного слоя,
дифференциальное уравнение переноса тепла для жидкости можно
написать так:
dTl (xLy'т) + - (к х) эт-<'■/■*>
Тг (*, у ,г)
ах
дх
R < у < °°>
0 < х < /,
ду*
A)
где w (у, х) — скорость потока жидкости, /—длина пластины в
направлении х движения жидкости. Гидродинамический пограничный слой
предполагается стационарным.
Дифференциальное уравнение теплопроводности для пластины
будет
дТг (*, у, т) _ / д*Т* (х, у, т) д*Тъ (х, у, т) \
__ _ а2 ^ _ + _ ___ _j B)
0 < х < /,
- R < у < + R,
где 2R — толщина пластины. Индекс «2» относится к пластине
(твердое тело), индекс «1» — к жидкости.
Граничные и начальные условия следующие:
Тг (х, у,0) = Тс — const,
Т2 (х, y,0)=f {х, у); Тх (х, оо, т) = ТС; Тх @, у, х) = Гс; C)
364
Глава десятая
Тг (х, Д, т) = Г2 (л:, R, т), D)
1 ду 2 ду ' ^ '
ЭГ* У *> = 0. F)
Если принять, что теплообмен происходит только через поверхность
у == ± R, то можно написать
дТг (/, у, т) = дТ2 @, у, т) = 0 ,7
дх дх ' ^ *
Решение системы дифференциальных уравнений A) и B)
представляет известные трудности, так как профиль скорости w {у, х)
определяется решением дифференциального уравнения гидродинамики
(уравнение Навье — Стокса). Однако в первом приближении можно считать
второй член уравнения B) в качестве переменного источника тепла
, ч дТг (х, у. т) А ч /оч
w (У *) — дх = w (х> У- т)- (8>
Тогда система уравнений A), B) сводится к дифференциальным
уравнениям теплопроводности с источниками тепла при граничных условиях
четвертого рода и решение этой системы в конечном итоге сводится к
выбору правильного приближения вида источника w*.
Если коэффициент теплопроводности тела значительно больше
коэффициента теплопроводности жидкости и длина пластины мала, то
можно упростить задачу. Обозначим среднюю температуру вдоль х через
т (у> *) = ~т J т (*> у> т) dx- (9>
Тогда получим систему дифференциальных уравнений теплопроводности
dTi (и, т) д2 Тл (и, т) —л , ч /1ПЧ
•—dz = % -—Ч&^— w (y> т)> (l°*
w2(y, т) __ а»та (у, т) пп
ат ~~ ^ %2
где w* (у, т) — источник тепла, усредненный вдоль поверхности
пластины.
Решение системы дифференциальных уравнений A0), (И) при
граничных условиях четвертого рода будет рассмотрено ниже. В данной
главе вначале рассматриваются задачи без источников тепла, а затем
приводится решение этих задач с источником тепла.
К задачам нестационарной теплопроводности относятся задачи
нагревания или охлаждения системы соприкасающихся тел (слоистые
среды), когда теплообмен между ними происходит по закону
теплопроводности.
ГРАНИЧНОЕ УСЛОВИЕ ЧЕТВЕРТОГО РОДА
365
§ 1. СИСТЕМА
ДВУХ ПОЛУОГРАНИЧЕННЫХ ТЕЛ
Постановка задачи. Возьмем
простейшую систему, состоящую
из двух полуограниченных тел (два
полу ограниченных стержня с
теплоизоляцией боковых поверхностей).
Начальные температуры тел раз-~^
ные. В начальный момент времени
тела приведены в соприкосновение.
Найти распределение
температуры в любой момент времени.
Имеем
Рис. 10.1. Температурное поле двух
соприкасающихся' полуогр аниченных
стержней
Л^±=а1Щ^ (т>0, х>0);
<ЭГ3 (х, х)
дх
_ д*Т2(х, х)
- а* дх*
- (т > 0; х < 0).
A)
B)
Начало координат находится в месте соприкосновения (рис. 10. 1).
Краевые условия запишем так:
7\ (х, 0)
= h (*);
дТх (+ со , х)
дх ■
Тг
дТг @,
дх
(+ 0, х)
_!) = _
Т2 (х,
дТг (-
дх
= т2(-
*а дТ2
0)
°°,
-0,
дх
= /.
±.=
*),
■3-.
(*). 1
= 0,
C)
D)
E)
F)
Вначале рассмотрим более простую задачу (см. рис. ЮЛ)
Тх (х, 0) = Т01 - const; Г2 (х, 0) = 0 (За)
(отсчет температуры производится от начальной температуры второго
тела).
Решение задачи. Решения уравнений A) и B) для изображений
Ты (*» s) и TL2 (x, s) при условиях (За) и D) имеют вид
Ты (х9 s) - -^i- = ^exp (- Y~ x) (* > 0), G)
TL2 (x, s) = Вг ехр (~j/™~ \x\J (x < 0).
(8)
Постоянные В± и В2 находим из граничных условий E) и F),
которые для изображения перепишем так:
TLl @, s) = TL2 @, s),
Ты @, s)
L2
@, s).
(9)
366
Глава десятая
Тогда решения G) и (8) можно написать в виде
TL{ (,, s) = -£ _ (П=^у_ ехр (- /Z д) (* > 0), A0)
TL2 (*, s) - (Г^г ехр A /Z \х\) (х < 0), A1)
где
X2 Г а2 Г X2 c3 72 e2 '
к^ *
/<e —критерий, характеризующий тепловую активность первого
стержня по отношению ко второму; он равен отношению коэффициентов
тепловой активности; К\ — критерий, характеризующий относительную
теплопроводность тела \,К\ = -у—); К а — критерий, характеризующий
теплоинерционные свойства второго тела относительно первого тела,
В решения A0) и A1) входят табличные изображения, поэтому
решение для оригинала можно написать непосредственно:
Ti (х, х) К, / X ..
1 + тг erf а , (х > 0),
То 1 + Кш \ К, 2 V «11
Тг (*, т) Кв \х\
= = eric —————— (х < 0).
Го 1 + *, 2 У~^Г
A2)
A3)
Если начальная температура второго тела равна Т02, а первого тела Т01,
то решение будет иметь вид
A2а)
A3а)
к-
Г1(*,,)-Г01 *. / , 1 * \ I
— 1 А 1 y^W. | > |
fi _ ^2 (*, -с) - Т02 _ Кг _^ \х\ 1
^oi — Т02 1 + А"е 2 У а2%
Из анализа решений следует, что при i -> оо (в стационарном
состоянии) относительная температура обоих стержней будет
одинакова и равна
0 (х, оо) = _^—.
V ' 1+А£
Если тепловые активности стержней одинаковы (Кв = /), то
относительная температура в стационарном состоянии будет равна
ГРАНИЧНОЕ УСЛОВИЕ ЧЕТВЕРТОГО РОДА
367
На границе соприкосновения эта температура устанавливается
сразу после соприкосновения тел и остается постоянной на
протяжении всего процесса теплообмена (см. рис. 10.1), так как
6 @, т) = б (д, оо) = ——— = const. A4)
Если тепловая активность одного тела значительно больше другого
(ei ^> ч)> то /Се > 1. В этом случае б @, т) будет максимальна и
равна 6 @, т) = 1. Если же относительная тепловая активность тела мала
(Kz -> 0), то величина б @, %) равна нулю. Следовательно, величина
6 @, т) изменяется от нуля (минимальная тепловая активность тела) до
единицы (максимальная тепловая активность).
Таким образом, величина б @, т) характеризует понижение
относительной температуры полуограниченного тела при его
соприкосновении с другим полуограниченным телом. Поэтому величина
1 - 9 @, х) = -j-L- = X A5)
может быть названа холодящим эффектом. Если б @, т) = 1 (X = 0),
то холодящий эффект равен нулю; наоборот, если б @, т) = 0 (X = 1),
то холодящий эффект максимален.
Приведем решение задачи при более общих начальных условиях C)
[71, 72].
Предположим, что
h^§^ = -h^^ = iu as)
— неизвестная функция потока тепла на границе соприкосновения тел.
Применим к уравнению A) бесконечное косинус-преобразование Фурье:
оо
1Т (Р> 01с = \ \ J Т(х> т) cos pxdx. A7)
6
Тогда с учетом граничных условий E), F) получим
j-z =- р*агТг (р, т)с - -j- у^ ](х). A8)
Решение уравнения A8) с учетом начального условия C),
преобразованного по соотношению A7), будет иметь вид
°
о г
Для определения Т2 (х, т) преобразуем область Q (— оо < х <; 0)
путем замены переменной х = — z в область Q/ @ <J z <J оо). Решение
для Т2 (— г, х) можно получить аналогичным путем
Tt <- г, ,) = -—L^ f/, (- «) {ехр [_Щ +
2Уяв2 т J I L 4а2т J
388
Глава десятая
+ ехр
(г - W
402Х
]) ' V^7~= «P [" 1м^г]<"*- M
Для определения j (х) используем граничное условие A6). Имеем
,) тЛ: _^*
^ (О,
где
F(x) =
хх х2
(?ч V<ч +ЪУ
00
——=: Г-^= f Л F) ехр (—/-) d (■-
ехр —
4a2t
d5
B1)
Уравнение B1) представляет интегральное уравнение Абеля
относительно функции / (т); его решение имеет вид
Дт) =
I
F (т*)
о г
dx*.
B2)
риво-
Г (х=ь£2Л
Отметим, что в решениях A9), B0) наличие ядер ехр 2ПГ п
дит к сходимости несобственных интегралов для широкого класса
функций ft (х) и /2 (х). В частности, можно показать, что
х-»0+ дх
/W
lim
дТъ
1 СО
*1 * /Го" ^ Х2
Если положить
ft (х) = Т01 = const, /2 (*) = ^02 = const,
то после преобразований из B1) получим
(Г01 —Тог) xi ^2 У тс
B3)
F(x) =
- = const.
^1 ]/^2~ + ^2 V «1
Если подставить это значение для F (т) в формулу B2), то получим
е1 Ч (^01 — ^02)
B4)
/00 = ^—
Тогда решения A9), B0) примут вид
е1 =
Тх (*, т) — Г01
^01 — Т 02
Г2 (х, т) — Т02 ___
Г01—Тог
1 f
* (i + к. у 1
v 7 о
ехр
Г
с2 "
ехр
L 4ai(x
а:2
—T*)J
« A + /Св ) J L 4a2(x-T^)J у т
dx*
]/х*(х—х*)
* (х — «с*)
B5)
B6)
B7)
ГРАНИЧНОЕ УСЛОВИЕ ЧЕТВЕРТОГО РОДА
369
В уравнениях B6), B7) интегрирова- т^
ние производится по времени. Если
интегрирование производится по
координате, то решения B6), B7) будут
тождественны решениям A2а), 13а).
Решение при наличии источника
тепла хюг @, т) = q0 = const.
Видоизменим поставленную задачу. Пусть в
начальный момент времени
температура обоих стержней была одинакова
и равна
Тг (х, 0) = Г2 (х, 0) - r0-const. B8)
Начиная с момента соприкосновения, на
границе тел постоянно действует
источник тепла мощностью q0 (дж/м2-сек)
на единицу площади соприкосновения.
Решения в этом случае будут иметь
вид
'№Ш/"«""У""""""""'Ъ
©
\^^^^^^^
Рис. 10.2. Температурное поле
системы двух тел (полуограниченный и
ограниченный стержни)
Введем следующие обозначения:
Fox - -^-, Fo2 = -^-, Kii =
go*
Ki2 =
__ ИР*
^2 Trs
Тогда решения B9) и C0) можно переписать так:
2 Kb Кг
2Ki2
1+^з
Fo2{2 i erfc •
1
FoY i erfc
2 V Fo!
1
2 V Fo2
C1)
C2)
§ 2. СИСТЕМА ОГРАНИЧЕННОГО И ПОЛУОГРАНИЧЕННОГО
ТЕЛ
Постановка задачи. Ограниченный стержень приведен в
соприкосновение с полуограниченным стержнем, имеющим другие
термические коэффициенты. Боковые поверхности стержней имеют тепловую
изоляцию. В начальный момент времени свободный конец стержня
мгновенно нагревается до температуры Тс, которая поддерживается
постоянной на протяжении всего процесса нагревания (граничное
условие первого рода). Найти распределение температуры по длине
стержней.
Рассмотрим два случая: а) начальная температура обоих стержней
одинакова и равна нулю; б) начальные температуры различны.
370
Глава десятая
Имеем (рис. 10.2):
dTt (х,
дх
{Х
дТ2 (х,
i дх
(*
*L =
>0;
*) =
>0;
Тг (х, 0) =
Тг
(Я, ?
h_ dTt (R,
Х2 дх
Тг
@, х
Г,(
= fli -
о<
= а2 -
Ж
= Г2(-
:) = 7-
^L =
) = тс
эо, т)
д2Т! (X, X)
ftt3
дс < R), ;
азг2 (х, т)
a*3 i
* < оо),
*, 0) = 0, I
2 № *),
аг2 (R, т)
5*
— const,
= 0.
A)
. B)
C)
D)
E)
F)
G)
Решение задачи при условии 7\ (х, 0) = Г2 (х, 0) = 0. Решения
уравнений A) и B) при условиях C) и G) для изображений функции
Т (г, т) будут иметь вид
TLl (х, s) «= Аг exp (j/"_L х) +5xexp (- yjL
TL2 (x, s) = d exp (- Yt~ 4
xl
(8)
(9)
Постоянные Av Bx и Сх находим из граничных условий D), E) и F),
которые для изображений можно написать так:
Ты (/?, s) = TL2 (/?, s), Kx T'L1 (R, s) = Ti2 (Я, s), A0)
Тиф, s) = -^-. A1)
После нахождения постоянных решения (8) и (9) будут иметь вид
Ъ, (х, *) = -£- ехр (- /-£ х) - J^- exp (- j/jL *)
X
X
expf/^,) -exp(_]/.JL*)'
exp
/:
«i
# — h exp
V^J
Ti2(x, s) =
s
'-(-^if
X
hTc
exp
(-/.
«l
«p[-V?c-4
A2)
X
A3)
ГРАНИЧНОЕ УСЛОВИЕ ЧЕТВЕРТОГО РОДА
371
где
h =
к = — = \Г х* Ci Ti
£2 Г ^2 с2 Ъ
Так как |А| < 1, то можно воспользоваться следующим преобразованием:
ехр
(- Yi«)
= S Л* ехр Г— Bл — 1) ~|/-^- /?] A4)
/г=1
на основании разложения
1
1
= 1 + х + *2 + . . . , если \х\ < 1.
Величина /G > 0, а Щ < 1; поэтому ряд A4) быстро сходится.
Решения A2) и A3) перепишем так:
tl\ (*• s)
ехр
/-=-*
— 2 Л" {ехр [- B/Л - х) ]/-i] - ехр [- BпЯ + *) |/|]), A5)
а=\
TL2 (*• s>
1 —/г
2 А«-1 ехр {— [(х — Я) +
п=1
Переходя от изображения к оригиналу, получим
A6)
е1 =
= Ш*±*>. = erfc —^ Л У Л-
тс 2 V ajz AJ
_ erfc 2nR + X I
2 У ах т
•г-1
»
r 2/zi? — х
erfc
2 У aiT
Л =
Г2 (л:, т)
fc~~ ~
2Ке
1 + *Е
ОО
- $] й* erfc
я=1
"л: -
~ # + B/г — 1)/С~Vs .R-
2 У а2 т
>
A7)
A8)
где
372
Глава десятая
Если термические свойства стержней одинаковы (/С£ = 1» ft = 0), то
из решений A7) и A8) получим такое же решение, как и для одного
полуограниченного стержня:
б = erfc
2 V <*'
Решение задачи при условии Тг (х, 0) = Т0, Т% (х, 0) = 0.
Рассмотрим второй случай, когда начальные температуры различны. Граничные
условия сохраняются. Применяя тот же способ расчета, получим
аналогичные решения, которые будут отличаться от предыдущих
присутствием добавочных членов, содержащих в качестве множителя величину
1 -l к ^° для ограниченного стержня, и Т0 для полуограниченного'
стержня.
В окончательном виде решения для оригинала будут иметь вид
к =
l\(x,^-T» = erfc х_
тс~т0
2 V ах'
4= h Yi h"~X erfc
2nR hF x
л=1
2 V
ax t
T° -V IJHerfc &-l)R*x
A+tf.) (TC~T0) ^ 2Уа~^
n=\
T2(x, т)
Tc-To
2K
l + K
e— V ft«-i erfc
-R + Bл - 1) /СГ/- /?
^o *£
(Гс-Г0) A +Ke )
erfc
x—R
2]/"а2т
X J] ft" erfc
/2=1
2 ]/~^ A+ *. J(^C-7o)
x - R +2n K~ I R
+
X
2 у а2т
A9>
B0>
здесь введено условное обозначение =f Ф (=f z) = — Ф (—z)'+ Ф ( + г).
Если положить Т0 = 0, то решения A9).и B0) превращаются в
решения A7) и A8).
Данную задачу можно рассматривать как задачу на нагревание
неограниченной пластины, одна поверхность которой соприкасается с
неограниченной твердой средой (граничное условие четвертого рода), а
противоположная поверхность поддерживается при постоянной
температуре.
Решение задачи при переменной температуре поверхности.
Температура свободной поверхности стержня является линейной функцией
времени
Г@, т) = Т0 + Ьт.
B1)
Решения системы уравнений при условиях C) — E) и B1) имеют вид
ГРАНИЧНОЕ УСЛОВИЕ ЧЕТВЕРТОГО РОДА
373
7\ (х, т) = 4 Ь* /i2erfc 5__ + V /^-i i2erfc 2(n-1) ^+*.
' 2 У ах т ^ 2 У ах -с '
2«-* + £ ft*-i i2erfc 2яЯ-*
— /г
i2 erfc
2 1/aiT
ra=2
T2(x, t) = 46x A — h) Perfc
00
+ A — h) J] ft*-42erfc
2 У аг т
/2=2
2 ]/ aXT 2 У а2т
Bл — 1)-/? R — x
+
2 ]/ ai.T 2 У аат
B2)
B3)
Если начальная температура стержней равна Т0 = const, то решение в
обобщенных переменных можно написать так:
6i = Tl (*, ,) -Т0 = pdip0i |.2 erfc _^/Я_
Та
2 Y Foi
+
+ ^ /г" i2 erfc
Bл —1) + */#
п=2
2 У Fgx
i2 erfc 2~X,R +
2 У Foi
+ J] /z* i2 erfc
2/г — */#
/г=2
2 У Fox
Го (я, т) — r0
62 = 2K } L = p^ Fo! A — A) i2 erfc
l
l—x/R
+ A —h) Yi hn~x i2erfc
л=2
2 УТБГ 2 У Fo2
2лг — 1 l—x/R
2 У Foi 2 У Fo2
B4)
+
B5)
Решение задачи при условии Тг (О, т) = Tm sin со т. Решение нашей
задачи будет иметь вид
TjL^r = -ж [ехр (- v4-pdnr)sin (PdiF°i - У4- Pdi *
—/гехр[— У4-р<*1 (г — -^-)] sin [pdx Fox +
+ /4-Pd1B-^
X sin^Fc^ + -|/4-pdi x/RJ + ехр [- У4"рсЦ B-^)]
X sin [Pdx Fo^-y^-Pd, B - -|-)]
X
+
L 0
exp (— Pd* Fox) sin (— у Pd*
R
374 Глава десятая
, —hs\n2V Pd* \ dPd*
arete ■ — i — —
1 -Л cos 2 1ЛР^~ j (Pd*)» + Pdf
~h f exp (— Pd* F0l) sin ( - VPd* — arctg —sin2^Pd* ^ x
J V ^ cos 2 У" Pd* — & /
dPd*
X
(Pd*J + Pd?
T2 (*, x) 1—Л
{exp [- |/^pS - /-f^T D- - l)] X
X sin [Pdx F^ - ]/4~ Pd* - Y~Y Pd* (lT ~ *)] ~~
- Л exp [- 3 Y±- Pdx - Y±. Pd2 (-1 - l)] X
X sin [pd1Fo1 + Y-T Pdi - Y~T Pd* D" _ *)]} +
oo
+ A — A) Pdx -~{ exp (— Pd* F0l) sin 17— _ A x
X УШКа* + arctg *Vpd*
dPd*
(Pd*J + Pdf
B6)
B7)
где М =- 1 — 2/гехр f— 2 Y~T Pdl )cos21^4~ Pd* +
+ A«exp(-4 |/"-L Pdx );
Ot) @*
Pd^ = __ /2. р^* _ /2 — критерии Предводителева.
§ 3. СИСТЕМА ДВУХ НЕОГРАНИЧЕННЫХ ПЛАСТИН
Постановка задачи. Две неограниченные пластины толщиной Яг
и R2 и с разными теплофизическими коэффициентами находятся в
соприкосновении. Начальная температура их одинакова. В начальный
момент времени одна из свободных поверхностей мгновенно
нагревается до температуры Тс, которая поддерживается постоянной на
протяжении всего процесса нагревания. Противоположная поверхность
поддерживается при начальной температуре Т0 = 0 (рис. 10. 3).
Требуется найти распределение температуры по толщине системы
из двух пластин.
Начало координат выберем в плоскости соприкосновения (рис. 10.3).
Тогда краевые условия можно написать так:
• Тг (х, 0) = Т2 (х, 0) - 0, A)
Тг (- Rv *) = Тс; Т2 (R2y т) = 0, B)
ГРАНИЧНОЕ УСЛОВИЕ ЧЕТВЕРТОГО РОДА
375
Тх (О, *) = Тг @, т),
57"! @, т) дТг @, г)
Лс
дх
C)
Решение задачи. Решение для изображений находим обычным
методом, используя граничные условия A) — C). Эти решения будут иметь
вид
ы
(х, s)
L2
(x,s)
где
Кг
Кв ch qx x sh q2 R2 — sh qx x ch q2 R%
s [ Ke ch qx Rx sh q2 R2+ sh qx Rx chq2 R2]
KB sh q2 (R2 — x)
s [Ke ch qx Rx sh #2 i?2 + sh qx Rx ch q2 R2 ] '
D)
E)
S
a2
Воспользуемся теоремой
разложения [решения D) и E)
удовлетворяют всем условиям теоремы].
Приравнивая знаменатели соотношений
D) и E) нулю, получим
характеристическое уравнение
Sin {X COS Ка2 Kr, [А +
+ Ks cos |i sin /Ca/2 KRl [x = 0. F)
Следует отметить, что корни
уравнения F) являются одновременно
корнями уравнения
ctgК1!2 Kr± P + K*ctgp=0 Fа)
и общими корнями (если они
существуют) уравнений
sinjx =0; sin K1J2Kr1 t* = 0. F6)
Система уравнений F6) имеет реше- Рис. 10.3. Температурное поле системы
tvi/2 тг двух тел (неограниченные пластины)
ние тогда, когда Ка2 Kr± — рацио- м J \ r /
нальное число. Тогда решение
нашей задачи можно написать так:
ft Тг (*, т) ДХ ~ R2
01 = =-
*х +
-S
Rz
sin
2 Ыв cos^-^ sin /Сд/я к-я ^ — sin ^ -^ cos./C*/» Hti^J
Ил [(К. + К^2^ ) sin ^ sin K^nKR~
A + *. К/2 KRl ) cos к.л cos ^2 ^ /(^ ]
X exp (— v-l Fox),
X
G)
376
Глава десятая
Т2 (х, т) R,
Я2 + RiK^1
- 2^s sin kV.^-^—LJ^
2j ~ ~
n=l
^ [(^.+ ^/*^R1 ) sin ,iB sin /#» ^ ^ -
' — A +/C. K^ ^ ) cos ^ cos /СУ- tf^ "(i„]
где
exp (- /Ce /Cl, £ Fo2) , (8)
^ -t- ^ =-2-. *. = i- ** = £-. Fo* = -|r> F°2=-|
3
Если коэффициент Ка'Къ представляет собой правильную дробь, т. е.
равен отношенщо двух чисел
то Ка* Kr± \ъп = -4- ^я = ятг. Следовательно, [хл = —^- = Ьтк.
Тогда к решениям G) и (8) надо добавить соответственно следующие
выражения:
оо
2 V1 cos тЪ тс . тЪ п х , 9 ,9 9 ^ ч /лч
sin —5— ехр (—m262^2Fo1), (9)
« (Р #£ + Ь) ^J m Rx
т=\
2 А 8 v-ч cos mb к . 8 т тг л: , ,« о » »^ r^ c v /iA\
^JK-Гьу L т sin Rt exp(-b2tn2K*KaKRlFo2). A0)
Если же коэффициент Ка2 Krx — число иррациональное, ряды (9) и
A0) не появляются в решении, а корни характеристического уравнения
F) по-прежнему существуют1). Пользуясь уравнением F), решения G)
и (8) можно упростить:
Кх R2— х
2/С, sin» K1^ KRiVn^iVn
Кх R2 + Rt
Ri + х
^[Kss^K^KRii,n+K^KRisin^n] 6ХР (~ ^ FOl)' (П)
гс=1
(#2 — *) /С;
£
2 К
л=1
sin [лп sin К^ KRi v-n sin/сУ2 (#л> — -^-) н.„|
X
Кв sin* J^« ^ ^ + /#» tf Ri sin* ц„ ]
X ехр (- ^/Ce K%t Foa). A2)
' Появление дополнительных корней трансцендентного характеристического
уравнения возможно и в других задачах (см. ниже). Эти дополнительные корни находятся
аналогичным путем и мы не будем больше специально оговаривать такие случаи.
ГРАНИЧНОЕ УСЛОВИЕ ЧЕТВЕРТОГО РОДА
377
В стационарном состоянии (Fo = оо) распределение температуры
происходит по линейному закону. Относительная температура на левой
поверхности пластины (х = — R±) равна единице, на противоположной
(х = /?2) равна нулю. На границе соприкосновения (х = 0)
относительная температура равна
6@, оо)
Г
A3)
Если термические коэффициенты пластин одинаковы, К\ = 1 при Rx =
= #2 (KRl = 1), ТО 6 @, оо) = 1/,.
Решение при граничных условиях второго рода. В отличие от выше
рассмотренной задачи одна поверхность системы пластин
теплоизолирована, а ко второй поверхности подводится тепловой поток постоянной
мощности.
Имеем
A4)
A5)
A6)
A7)
A8)
Решения для изображений будут иметь вид:
Тг
(х,
0) =Г2
дТх
Тг@,
дТг @,
дх
дТх (- Ял
дх
(х,
дх
т) =
0)
t)
-Тг
-
= т0 =
= 0;
@, х);
дГ2 @,
1 = °
const;
>
7Yi (x, s)
[*b<bY-kxcbV-k«*-
TL2 {X, S)
Ka sh У±х ch У± R] {[/Cx ch /^ Я2 sh /-£ *1+
У а2
1°
s
s {kx ch l/-L /?2shl/"— #$+
+K**Y-k***Y-kR;\4V-k
B0>
Воспользуемся теоремой разложения. Приравнивая знаменатели
(выражения в фигурных скобках) в формулах A9), B0) нулю, получаем
характеристическое уравнение1 >
/Cxtgt* + /Cetg [*/#■**, = <>. B1 >
^ Здесь также возможно появление доподнительных корней, возникающих из-за
деления знаменателя выражений A9), B0) на cos ^ cos p Kj2 KR . Рассмотрение этого»
специального случая аналогично приведенному в предыдущей задаче.
378
Глава десятая
Решение задачи можно написать так:
о1 = 1ЦМ= 1 + k. + Ik^^ + T [**-**■ +
+ ** (-жJ - 2/^в *«. ж-] - 4- И *« *«. + ^ *<• **.+
00
n=z\
+ -|j- sin ft, -|- sin (,„ /C«/a Кнг ) exp (- ^ FoJ,
Kii /Cx f , / x \2
6^1+ «x+«„««, t^+T^l^-ls) -
oo
+ 2Ю2 S —V c<* ^ iC;/2 ( /f* - ^-) exp (- & Fox),
tel ЧпГп ' '" \ " «i
B2)
B3)
где
«Рл = (l + -^ ^2 *«. ) cos^cos^/сУ2 KRz - (KR2 К£ + ~Ka ) x
X sinpn sin{1ЛKasKR2, B4)
K*2=§, F0l = fllT//& Kix - -^ .
Если теплообмен между поверхностью (л: = — R±) системы пластин
происходит по закону Ньютона q — а [Тс — Т (—/?х, т)], то температура на
этой поверхности (x/R1 ~ — 1) и на границе ее соприкосновения с
поверхностью ~ =0 определяется из графиков, приведенных на рис.
10.4 и 10.5. Графики получены для случая, когда коэффициент
теплопроводности второй пластины бесконечно большой (Х2~> °°)> и для
разных значений р [р = п + (п 4- 1)/Ву, где п = с2 Тг Яъ/сг ух Rv a Bix =
На рис. 10.4 по оси ординат отложена величина
а* _ 1 _ ^Bi* [~i _ T@,z)-t0~\
• ~ (n+1) L Tc~-T0 J'
а по оси абсцисс — число Фурье Fox = atx/R\.
ГРАНИЧНОЕ УСЛОВИЕ ЧЕТВЕРТОГО РОДА
379
«57
и 9S
и Я
я
о
К
с
о
К
о
ас
к
о>
а" -
ю
о
о
>>
о
я
О-
380
Глава десятая
YTl \\\ К
\Ч\\ К rSv
\\\\ \\\ TSJ
IlK N TSJ
\\NX\ ГК1 TSJ
W\H N lis
\\ N N N \\\\
|l\|\|\| 1 к! Ph. 1 Its
SrMNl №кНр^1Г
м
Шх ГхН пчтх
TOrNI\ Н Hh
lu-L4\l 1x114.1 Ттч
In \ \ tv rv rSJ——Н5
HVfd-N-f4H^X[
\\\h \\W\ NL nL tsJ
li\ W ГЧ m\J ТЧ. iK
1\ \ 4 14 MsJ ТЧ
\\\ \ x rSJ гч
\\W\ W Гк ТЧ.nv
i \ \ INi Mv ГЧ.
г \K\ |>J H Is
\4N MfJ IS
INN пЧ 1>
N\n mSJ i
\\iN rri
l\IN 14J I?'
1J1 N rkJ Ш
L—j l^ fc^^+__psL^^ e?jj=
^^Щ^ФрРЩрФ
1—1———J—[- — "
H^1^^!!! oT
i 1 1 1 1 1 1 1 1 1 1 1 x
1 '
11MI IJJJ 1 1 1 1.1
TsJ— [Si Jl
MsJ см
PsJ T lv 1 1
,g(irTq.rs
sj LpsI p
?"tJ""t"l"M
04 ~ \ 1 1
>- и f-M
CN _ J 1
и cq {qzf
i cv":
£+
8p
и—-p4«
* ]S1
гм «Li
=fio:
:^-
^L
of
-£lO
—1—!—1 1 I 1 1 1 1 ! 1 1 1
III 1 ! 1 1 I 1 ! Ill
1 1 1 1 I 1 ! 1 1 "zi 1 1 1
"■ 1" 1 J | | j 1 1 | CQ | 1 1
у L^r I
X | | | | | 1 j 1 ' ,"* '|| |
_" M ' III
i \l 1 1 1 1 Lij^'l 1 1
\ И +
1 1 l\J/H 1 1 с | 1 1
1111 INI I'H
Po M 1 1 1 M 1 1 111
•см 1 \ 11 111
-W\ IT 1 \ 1 1 In
vjl\ \Фт
\ \ Prntl
ЖН fltm
"К Щ \\\\\\
\ \ \ \
4J \ \ \M 1 1
N. \ \ \\ \
TV \ \ X V
N V \M
\ \ \ \ \ 1
4 Мл \\\ I
V MN \ \ \ 1
\ \ \\\\Ml
N N \ К\\\ \\\
к N \\\ Щ \\\
W 4M\\ 1
l\l\ N\\\ i
J NN \\\\
^l-jr-lH-. NX4N1 -1
J^M4^^
Nj f\ \ |\J \\\l 1 1
MsJXlK \l\k\ 1 1
is 14 \ X \\\ 11
\ \ ГЧ] \ [\\\ 11
1 1 1 1 тч. l\l \ 1 \l Villi 1 1
N [V ГЧ| \ \\i 1 j
ГЧ \ \j\\\\il
iNNnW
N N\\ll
I ШШ
Mi
%£
oo
cT
cT
o.
o"
ГРАНИЧНОЕ УСЛОВИЕ ЧЕТВЕРТОГО РОДА
381
На рис. 10.5 по оси ординат
отложена величина
ft _ T(-R1^)-T0
Тс-Т0
а по оси абсцисс — число Фурье
Fox.
§ 4. СИСТЕМА ДВУХ СФЕРИЧЕСКИХ ТЕЛ
Постановка задачи. В
начальный момент времени один шар
при температуре Т0
помещается в полый шар с той же
начальной температурой. Между
ними существует совершенный
тепловой контакт. Внешняя
поверхность наружного шара на
протяжении всего процесса
охлаждения поддерживается при
постоянной температуре,
равной нулю. Найти распределение
температуры в любой момент
времени в такой сложной
системе— шар в шаре (рис. 10.6).
Имеем
д\гТг(г,
дх
д[гТ2(г,
дх
Тг (/?,
2I
м
.•о
д2[т
= «1 ~
д2[г
= а2 -
Тх (г,0) =
= Т, (Rv
Т2 (Я„ х)
■П\г,
дг2
■П(г,
дг2
= Т0,
г), К
= 0;
Ж
ж
т,
(
х -
Тг
- (т>0;
- (t>0;
о<
Ri
(г,0) = Т0,
дг
@, х) ф
- =
00.
г < Яг),
<r<R2),
дТ2(Яг,х)
дг
Рис. 10.6. Температурное поле системы двух
тел (шар в шаре)
а)
B)
C)
D)
E)
Решение задачи. Решение задачи находим операционным методом,
используя условия C) — E). Решения для изображения получим в
следующем виде:
TLl (Г ,8)
1
RXR2 ft sh ft r
Tc s
TL2(r,s) _ 1
rs [фя (R2) sh ft Rt +KX Ф1 (fli) sh ft (R2 - RJ] '
R* №2 W sh ft /?! + iCx фх (/?!) sh ft (r - /gO]
rs [ф2 (#2) sh ft Rt + /Cx фх (/?!) sh ^ (/?a - tfj] '
F)
G)
382
Глава десятая
где
<h (r) = q1R1chq1r — sh 4l r,
Ф« (г) = <7а ^i ch <72 (г — /?х) + sh q2 (r — RJ,
S
в*"
Приравнивая знаменатель нулю, находим корни: 1) s = 0; 2) sn —
бесчисленное множество корней, определяемых из характеристического
уравнения
[*tf>ctg Ka/2 (KR-l)p + l]+Kx [^ctgjJL— I]=0t
(8)
где
К а = "~- > Kr =
#2
Кроме этих корней, будем иметь дополнительные корни,
определяемые из уравнений
sin|* = 0, sin/CaA(#s— 1) ц = 0.
Если Ка* (Kr — 1) — величина иррациональная, то последние
уравнения не имеют корней и решения будут следующие:
е _ Тг (х, т) _ 2R2 у 1 г
п=1
X sin |1Л Каг (Кк — 1) ехр ( — |»2FoJ ;
(9)
е2 =
г
X ехр (—/Cfl /С|[4 Fo2),
йг)^х
A0)
где
«Р ((О == *■ t*„ sin2 /СУ2 i»n (/С* - 1) +К%> (/Сл - 1) X
X^sm2|^ + -£ — sin2[xw sin2 /Ca/f (/Сл — 1)ця,
Fo — * Fo
roi — D2 ' го2
а^х
э2 '
(П)
Если величина Ка2 (Kr— 1) равна отношению целых чисел-|-, то
В * * '
-£- jx = /г тс, или [х — 6m -jr. Тогда дополнительно к первому решению
надо прибавить выражение
ГРАНИЧНОЕ УСЛОВИЕ ЧЕТВЕРТОГО РОДА
383
2#2
Г тс (Р/Се +Ь)
(—1) . — sin-^- exp (—т*Ь* к* FoJ, A2)
т=\
Ri
а ко второму решению — выражение
2R2Ks
S4-
г«(р/С* +Ь) — m
m=l
sin
(**--£)е*'
*«-i
■ exp (— m2 &2*2 Fo2 /Cfl /&)
4
A3)
Tn = const
§ 5. СИСТЕМА ДВУХ ЦИЛИНДРИЧЕСКИХ ТЕЛ
Постановка задачи. Имеем бесконечный
цилиндру окруженный тонкой оболочкой. В
начальный момент времени система двух
цилиндров, имеющих одинаковую начальную
температуру Г0, помещается в среду с
температурой Тс < Т0. Теплообмен между
оболочкой и средой происходит по закону
Ньютона. Найти распределение температуры в
системе двух цилиндрических тел (рис. 10.7).
Тонкую оболочку в первом приближении
можно считать плоской. Тогда задача
формулируется следующим образом:
Рис. 10.7. Температурное
поле системы двух
цилиндрических тел
* = а±
ЪТг
62Tl +-Г§?Ь>0;0<г<*1);
дг*
= я245" (->0;i?1<r<i?2);
di 2 dr2
7\ (г,0) = Г2 (г, 0) = Т0 = const;
т (Р -\-т (f? rv х JUiSBiiJL-x ar»№';) .
11 (Ai, V — 12 (А^, т), Ах д- = h2 д- ,
йг
ал
Гх @, *)<<*>; -Х2 ^.(g.,*) +а[Гс_Гг (£„,)]=().
A)
B)
C)
D)
E)
Решение задачи. Используя преобразование Лапласа, получаем
решение в виде
384
Глава десятая
Г'(:-У =1 - 2 Ап Jo (v-n '■//?!) ехр ( -^ Fo),
Тс-Т0
Г2(;,тOГо = 1- S л (л ы cos ^й /с;л (r/^-i)]-
'с — 'о
п=\
K.JAv-n) sm [(xn /СУ2 (г//?!—1)]} exp(—14 Fo),
F)
G)
где [ля — корни характеристического уравнения
J0 (jx) [Bi cos KlJ* (Kr - 1) (^ - /#**« [x sin /Св/я(/С/г - 1) (*] -
-K* Ji (v) [Bisin^2 (Kr — 1) v. + Ka/2 Кrv-cos K'J2 {KR — 1) ?]=0;
2Bi /C. [/#' (KR -l)y.„ + Bi tg /ff» (JCg - I) y-n]
A,=
Pn Jo (Ы sin К a* (Kr — 1) Рл
lJ^ + Bi2]ctg^/2№- !)(«.„
[/c.2/Ce(^-
2KS K'j4KR - 1)
tB
i24-
sin 2^(^-1)^
.+ Ka (Kr - lJ [4] + [Ka (Kr - lK vl + 2/C« <Л (/Ся - 1) Bi +
+ /Cf Bi2] tg/c;/2 (tf* - 1) (x„ + K, Ka (Kr - lJ 1*2 +
+ 2/Cs2 КУ2 (/С* - 1) ^ Bi - 2Klaf* (Kr-1) ft, Bi - *Ц^ Г'. (8)
г/г ;
jB предельном случае (Bi ->■ оо) второе условие E) заменяется
условием
Тг (Rv т) = 7С. (9)
При этом решение F) остается прежним, а решение G) принимает
вид
тс-т0
2 sin [/СУ» (/Сд - г//?!) ^ ] ехр ( - pg Fo)
я=1
Рп
/С?-1
/Cs
sin2 КУ2 (/Сд - 1).н.Л •
2^
-sin2/C^(K»-l)^
■n+frj
A0)
где b = /СЛ^ — 1) + 1//С. (подробно см. [47]).
§ 6. НЕОГРАНИЧЕННАЯ ПЛАСТИНА
Постановка задачи. Дана неограниченная пластина при
температуре Т0. В начальный момент времени она помещается в среду с
температурой Тс < Т0. Охлаждение пластины происходит путем
теплопроводности. Найти распределение температуры в любой момент
времени.
ГРАНИЧНОЕ УСЛОВИЕ ЧЕТВЕРТОГО РОДА
385
Рис. 10.8. Охлаждение пластины в
неограниченной среде
Имеем (начало координат находится в середине пластины; индекс
«1» относится к пластине, индекс «2» — к среде; рис. 10.8)
d^± = a1^^L <*> <);-*<*<+*),
дх
дТ2 (х, т)
= йо
дх*
<Э2 Тг (х, *)
(т>0;Я<х<оо),
7\ (х, 0) = Г0, Г2 (х,0) = Тс,
±К:
дТг (± Я, -и)
dTA±R, *)
дх дх '
т\ (± /г, х) = г. (±/г,т),
апсо.т) __Q аг2(±оо, т) _Q
дх ' дх
A)
B)
C)
D)
E)
F)
Решение задачи. Решения уравнений A) и B) с учетом условий
C) и F) для изображений можно написать так:
+ ехр (_]/-£-*)],
TL2 (x, s) — Ц- = ^ехр (— у -j- х).
G)
(8)
Постоянные Аг и Бх определяем из граничных условий D) и E); тогда
решения G) и (8) примут вид
TL\ (x,s)
То (Т0-Тс)
1+^s
X
(9)
13 Заказ №> 640
386
Глава десятая
ехр
X
fli
х + ехр
-V-
ах
ехр
V-
ах
R + h ехр
-/i
Я
Т, /v о\ ^с _ (Г0 — Тс)
I L2 {X, S) г - I 1 + Ке
/Се
X
ехр
X
Утг*)—>[-Ут,
R
ехр
/■
fli
Я + ft ехр
-v^-
/?
етр [-/-£<*-*>
A0)
1-Ks
1+/Св
где К в = — —критерий тепловой активности пластины, А =
безразмерная величина, абсолютное значение которой всегда меньше
единицы (|А| < 1).
Сделаем следующее преобразование:
exp(/i*)+*exp {-V-k*
1 + h ехр
->v-
ax
^(-ЙГ1 ехр [_B«-1)У^-Я
Я=1
(П)
Полученный ряд быстро сходится при |Л|< 1.
Таким образом, решения можно переписать так:
Ты (х, s) =
G".
«A +/С ■)
+
л=1
+ е
-^[BЯ-
■!)«+*]
A2)
00 .
-d+A) S (-^Г-1 ехр [-Bm* }/^- + ж-Я ) У^]}.A3)
ГП—1
ГРАНИЧНОЕ УСЛОВИЕ ЧЕТВЕРТОГО РОДА 387
Пользуясь таблицей изображений, получаем решения в виде
Тг (х, т) — Тс _ = j
Ть-Тс
1 V/ t.\/,-i J * Bл — 1) /? — jc ,
+ erfc ^L=p±£l
2 У aii: J'
, T2 (*, x) - Tc K* , x-/? _ Ks A + ft) v
2 Г0-Гс 1+tfs mL2y^ 1+/C.
x 2 (_Л)„-1 erfc x~R+2nRV^^_
„t, 2 У^^
A4)
A5)
Решения A4) и A5) удовлетворяют соответствующим уравнениям»
00
начальным (так как 2j (-—й)л""г= | , h = — ^ £ ) и граничным ус-
/г=1
ЛОВИЯМ.
Предположим /Се -> 0 (тепловая активность пластины бесконечно^
мала по сравнению с тепловой активностью среды); это означает
мгновенное восприятие тепла от нагретой пластины, сопровождающееся
быстрым понижением температуры поверхности пластины до
температуры среды. Действительно, если положить /G = О (А = 1), то 62(х, т)=0,.
а первое решение превратится в следующее:
в1=1- 2(— D-1 Г erfc (fr-lbg.-* + erfc &=*ЩА
л=1
A6)
Решение A6) представляет собой решение задачи охлаждения
неограниченной пластины, когда температура на поверхности ее"
мгновенно понижается до температуры среды, а затем остается постоянной на
протяжении всего процесса охлаждения (граничное условие первого
рода). Это решение нами было получено в § 3 гл. IV.
Температура на границе соприкосновения равна
Таким образом, 6 (/?, т) непрерывно уменьшается, ее максимальное
значение соответствует начальному моменту времени (при т~*0
функция erfc n стремится к нулю), тогда
ь-* = -тткг A8)
13*
388
Глава десятая
—та относительная температура, которая устанавливается на границе
соприкосновения двух полуограниченных тел (см. § 1). Величина
1
Кг
1+Kz
= 1—9(/?,0) = Х
A9)
называется холодящим эффектом. Интенсивность изменения 0П>0
зависит от коэффициента температуропроводности и толщины
пластины. При малых значениях Рог=~-^~- величина 6п,о мало изменяется.
Анализ решения A5) показывает, что температура в любой точке
среды вначале увеличивается, достигает максимума, а потом
уменьшается. Максимум температуры на границе соприкосновения (х = R)
устанавливается мгновенно, а по мере увеличения х (х > R) время,
необходимое для установления максимума, увеличивается.
При малых значениях Fo2 = °^2 можно из всего ряда в решении
A5) ограничиться одним первым членом, и тогда можно написать
приближенное равенство
Кг
1 + К,
erfc
х
2Kb
ае2
erfc
R
-1+2/С
■Vt
2 V Fo;
=Г—• B0)
Если взять производную dp и приравнять ее нулю, то получим
уравнение, из которого можно определить (Fo2)OT —число Фурье,
соответствующее максимальному значению температуры:
(Fo2)„
1 +
1\Кп
Да In l+IU
iH-i-1)
B1)
Из соотношения B1) видно, что относительное время достижения
максимума увеличивается с увеличением относительной координаты; (Fo2)m ==
= 0 для х = R.
Решение задачи с источником тепла w = const. Несколько усложним
задачу введением положительного источника тепла, мощность которого
равна w (вт/м3). Дифференциальное уравнение для среды остается
таким же, а для пластины будет иметь вид
B2)
дТ
i(x,
д-t
А
= а1
д2 74 (х,
дх*
Л.
+
W
*7'
Краевые условия остаются теми же [см. условия C) — F)].
Решения для изображения получим в виде (метод решения
подобного рода задач подробно описан в предыдущей главе):
TLl(xfs) = *f +
w
-(
То~Тс
S2C*{ J 1 -f-iCe
Е(-л)*-
X
»=»l
ГРАНИЧНОЕ УСЛОВИЕ ЧЕТВЕРТОГО РОДА
389
ехр [-(Bл-1) R-x) У^] +
+ ехр[- ]/"-£- (Bn - 1) /? + х) ]},
B3)
Ти (*,.)_If = (-^+ ^
^ ехр [-/£(*-*)]-
s2 с 7 / I 1 + j
оо
*\ 1+шН) £ (- Л)" ехр [ - / J ((х - *)+ 2/*) *-*
/1=1
B4)
Для перехода от изображения к оригиналу пользуемся
соотношениями E5) и E6) таблицы изображений в приложениях:
1
1+К*
9, = Jj^iA=1il = 1 + Ро F0l -
•'о — * с
» ( B4-1) =F-|-
2j (— A)" erf с —^ ^-_. * +
/i=i
2 l/Foi
Bл — 1)
+ 4РоРоЛ2 erf с ==-
1 2 "J/ Fo!
^2 (*, ?) — ^C
Кг
. — 1
1 + /Се
erf с * +
2 1/ Fo2
+ 4PoFo2i'erfc_^=r
B5)
^^£(-/0-|erfc
я=1
+ 4Po Fo2 i2 erf с
2 j/Fo^
2"-K7'/2+-£--!
2 /Fo2
где Ро — критерий Померанцева, равный
w R* wR2
Po
b(T0-Tc) C1(T0-Tc)a
B6)
B7)
Здесь введено условное обозначение — Ф (=f г) = — Ф (—2) — Ф (+ 2).
Решение задачи с мгновенным источником тепла. Задача
формулируется следующим образом. Неограниченная пластина, находящаяся в
неограниченной среде, получает в начальный момент времени тепловой
импульс от мгновенного плоского источника тепла, расположенного в
середине пластины (хг = 0). Сила мгновенного источника тепла равна
390
Глава десятая
Q = bcj {дж/м2). Начальная температура пластины и среды равна
нулю.
Дифференциальные уравнения для пластины и среды, а также
граничные условия остаются прежними [уравнения A), B) и условия
D) — F)]. Начальное условие следующее:
Тх (х, 0) - Г2 (х, 0) = 0.
Задача решается методом, подробно рассмотренным в § 2 гл. IX.
Решения для изображений TL (х, s) получим в следующем виде:
T»(x'* = T=r°*v[-V-k*)-
bh
ехр^-]/^- (R-x) J + exp J~ j/jL (R + x) j
Yaxs
exp
R
Yaxs
oo
x ) — h £ (— hy~l X
exp
s
«1
n=l
X
exp [ - Y~ BnR — x)] + exp [ — Y~- BnR + x)
TL2 (x, s) =
B8)
6A -h)
ехр[-У>(*-*)
HLgL S(_^ exp {-Y^[x-R + Bn-l) YKH
■ B9)
Решения B8) и B9) являются табличными изображениями, и
переход к оригиналу производится непосредственно:
Тг (х, т) =
RVn Foi
оо
exp
л=1
exp
4#2 Foj
\2
2/z-
+ ехр
4Fox
2\ •
2л-
4Foi
C0)
ГРАНИЧНОЕ УСЛОВИЕ ЧЕТВЕРТОГО РОДА
391
Г2 (х, х) -
сю
V РХР 1
JL _1 + Bя_1)К-'^2|
1 4F°2 J
C1)
Анализ решений C0) и C1) показывает, что при малых значениях
Fo можно ограничиться одним членом из всего ряда, и тогда
расчетные формулы приобретают простой вид.
Температура Т2 (х, т) в любой точке неограниченной среды вначале
увеличивается, достигая некоторого максимума, а затем уменьшается.
Если взять производную —**' и приравнять ее нулю, то
получим следующее приближенное решение (в случае, когда из всего ряда
C1) можно ограничиться только одним первым членом, ^то
справедливо для не слишком больших значений Fo):
(Fo2)„
[Х - 1 +ГКа-'/2 ]\
C2)
т. е. графическая зависимость между (Fo2)
п2 и ^-=— представляет пря-
/ш
мую, которая отсекает на оси ординат отрезок, равный BКа)
(x — R
Таким образом, чем меньше относительная координата
меньше время достижения температурного максимума.
R
тем
§ 7. ШАР (СИММЕТРИЧНАЯ ЗАДАЧА)
Постановка задачи. Дано сферическое твердое тело (шар) при
температуре Т0. В начальный момент времени шар помещается в
неограниченную среду с температурой ТС<СТ0. Охлаждение шара
происходит путем теплопроводности. Найти распределение
температуры в любой момент времени.
Имеем (индекс «1» относится к шару, индекс «2»—к среде):
щ^ = а1^г^п (т>0; 0<r<R)t
^l^^=ei^f^.(t>0;/?<r<co),
7\ (г,0)=Го, Г2 (г,0)=Гс,
_ К dTl <R' т> - _ дТг(Я-х)
АХ дг ~~ дг '
Г, (R,x) = T2 (Д,т),
дЩО. х) _ дТ2 (оо.т)
дг
дг
= 0, 7\@,T)=f оо.
О)
B)
C)
D)
E)
F)
392 Глава десятая
Решение задачи. Решения для изображений можно написать так:
ц—тн <#-, s) = 4sh Vltr- <7>
(8)
TuM-Tf.-'b.evl-Y-k
где
^!b=ZUL нр(^Я)_ЛЛ |/^-Лехр {У+К\ (9)
A0)
"-^sSH'+V^-*).
Найдем приближенное решение. С этой целью напишем
приближенные выражения для Тц (г, s) и TL2 (r, s), справедливые для малых
значений Fo или больших значений 1/ — /?. Имеем:
TL2 (r,s) —
а±
Тс
ехр
-V-k
,A2)
Т0~ТС
\ г г
где
R *
А
/£
/г+л".
к4
Л A + К, ) + К, A - Кх )
«Р [-/^(г-*)]. A3)
ехр(-/^)- <14>
Полученные приближенные решения являются табличными
изображениями. Следовательно, решения для оригинала можно написать так:
Т0 — Тх (г, т)
То ~ тс
R
1-Кх
Кг +1
ехр
nfFOi— Пх 1
**)]
X
X erfc
1=F
2Foi
Г» {г, *) - ^с
nil/^ —erf —yif,
1 V 2/ Fox '
4 ег,с *
2 V Fo2
A5)
ГРАНИЧНОЕ УСЛОВИЕ ЧЕТВЕРТОГО РОДА
393
1 , "Ж-1 «X +Кг Гтт2с.
~КГ=Г erfc YVT^ - '(*х-!)(*. + !) 6ХР [П2 F°2
Г
— 1
.n2(-^_l)]erfc^^7f=r-n2l/Fo!
Г
-\+2K?l* K,+Kt
erfc-'ТТГ'- +,/t,^,,x
X exp
+2ДТ
n|Fo2-II2(-L- 1 +
A6)
где
A ZT. _ Л1 Z^ __ £1 TT ___ X
Пх = — , /Cx = -—, /Ce = —, П2
*x + —
и введено условное обозначение Ф (=f z) = Ф (—г) — Ф ( + г).
Полученные выражения справедливы только для малых значений Fo.
На рис. 10.9 приведены графики изменения относительной
избыточной температуры в разных точках среды для случая, когда
температура на границе соприкосновения поддерживается постоянной на
протяжении всего процесса нагревания: Тх (R, т) = Т2 (R, т) = Тс = const при
тс>т0.
§ 8. НЕОГРАНИЧЕННЫЙ ЦИЛИНДР
Постановка задачи. Дан неограниченный цилиндр радиуса R при
температуре Т0. В начальный момент времени он помещается в
неограниченную среду с температурой Тс < Т0. Теплообмен между
поверхностью цилиндра и средой происходит по закону теплопроводности.
Найти распределение температуры внутри цилиндра и в среде в любой
момент времени.
Имеем
Тх (г, 0) = Т0, Тг (г,0) = Тс,
дТ2(оо,г) _п
Т ID ~\ Т ID т^ К dTl ^' ^ — дТ* ^' т>
1 г (К, У — 1ъ (Л. 1), —Ах ■=£ — gp •
A)
B)
C)
D)
E)
F)
394
Глава десятая
аю
Г 1
J
г
р
|_1
р
1
1=
Е
1
ш
-"■-
-
~
-
х=^
—
1
i
|
rrd
ЕЕ
F
з
-7=
l
=Jd
S
==i=
щ^-
щё
В
Р
3=
щ=
S
В
l
§
ш
=
^
I
1§
1
1
—
I
Е=
Щ
d
1
I
Ш
Ш
\~
[
\
\
*
nl
1
Е
j
Я
i
^
s
\
■£
1
1
I
У
щ
1
1
ш
1
ш
ЕС
1
1
Я
1
Я
щ
1
1
V
1
J .
1
1
il/
■э|
н4^
j
э
1
^Е
^ '
^1
===
~i
о^
|
сг>
1
о
ш
щ
1
с
о
^5
>Г1
Цп-J
.о
§
Ш
щ
щ
ф=1
d-*=j:
Ц
В
1
—р-4
«И»
Я
Щщ
1
о о
00_
о
СО
о
сГ
о"
ГРАНИЧНОЕ УСЛОВИЕ ЧЕТВЕРТОГО РОДА 395
Решение задачи. Решения для изображений при условиях C) — E)
получаются в следующем виде:
v-TdK'- /.(/?*) *.(/£')■
Ти (x;s)-lf = ?±=^
TL2 (X,S)- -^
бФ (s)
- G)
(8)
где Ki (z) и Ко (z) — модифицированные функции Бесселя второго рода
соответственно первого и нулевого порядков;
Применяя обратное преобразование Лапласа и переходя от
интеграла в области комплексного переменного к интегралу от вещественной
переменной, получим
A0)
Т,(г -Л-Т 4 Г 'oU-jA'iM -J..FO,
о _ J1 (г, 1) — 1 с __ J^ „ 1 у / ,
0
7 о — * с
00
1 2КХ р Jl M
•^ (</21* -£-) т w - у о (</2т=г) ф w
0
.-i^Fo,,
С- U^>
A1)
где
¥ М = Кх J1 ft*) F0 (/ft* р) ,* - Д-У* У0 ((л) Yx {Ka/2 V- ),
Ф (,») = /Сх A (р) J0 {&'• t*)- К1!2 Л («*) А № {*).
A2)
На рис. 10.10 и 10.11 приведены графики изменения относительной
избыточной температуры среды в разных ее точках в зависимости от числа
Фурье (Fo2 = a2x/R2) для случая, когда температура на границе
соприкосновения поддерживается постоянной на протяжении всего процесса
нагревания, т. е. Тг (R, т) = Т2 (R, х) = Тс = const.
Решение задачи с источником тепла w = const. Усложним задачу
введением положительного источника тепла, мощность которого равна
w (вт/мд).
Дифференциальное уравнение для среды остается прежним, а для
цилиндра уравнение будет иметь вид
дТг (г, т)
dz
! Тх (г, т)
дг2
J_ дТг (г, «с)
г дг
+.-
CiTi
A3)
396
397
398
Глава десятая
граничные условия остаются те же [условия D) — F)]; начальную
температуру среды и цилиндра принимаем равной нулю, т. е.
7\ (г, 0) = Г2 (г,0) = Т0 = Тс = 0.
Тогда решение для изображения получим в виде
&Ш1 7*1
7*2 (r,S)
Х2 S2 ф (s)
(У?
Функция Ф (s) определяется формулой (9).
Решение для оригинала можно написать так:
7\ (г, х)
4«) fl3
Г. (Л т)
2ш)Я!
X? г. j/ а2
=- A
в )
JiM
v-'WM + VM]
х
[Л (Ка* V-Ji) 9(V) - У о (#;Л j*-£-) ф <(*)] rf £*.
где ср([л) и ф((х) определяются формулами A2).
X
A4)
A5)
A6)
A7)
A8)
§ 9. ТЕПЛООБМЕН МЕЖДУ ТЕЛОМ И ОБТЕКАЮЩИМ ЕГО
ПОТОКОМ ЖИДКОСТИ
В заключение этого раздела рассмотрим задачу обтекания
полуограниченного тела потоком жидкости, т. е. задачу нестационарного
конвективного теплообмена.
Постановка задачи. В трубе прямоугольного сеченая движется
несжимаемая жидкость. Движение ламинарное и стационарное. В
нижней стенке трубы имеется отвер-
iy стие, в которое вводится ограниченный
I стержень, открытая поверхность его
является частью поверхности трубы
(рис. 10.12). Все остальные поверхности
стержня теплоизолированы. Стержень
предварительно нагревается до
постоянной температуры Тг @) = Т0 = const. В
начальный момент времени стержень
вводится в гидродинамическую трубу и
охлаждается протекающей жидкостью,
температура которой равна Тс = const.
Требуется найти удельный поток теп-
Ряс. 10.12. Обтекание полуогра- ла в процессе нестационарного тепло-
ниченного тела потоком жидкости обмена.
е,Д2Д,
-w(y)
С9.Т9Д5
у///////////,
ГРАНИЧНОЕ УСЛОВИЕ ЧЕТВЕРТОГО РОДА
399
За начало отсчета температуры возьмем температуру натекающей
жидкости. Длина стержня в направлении х равна /, а толщина его R
(см. рис. 10.12),
Теплообмен между стержнем и потоком жидкости описывается
системой дифференциальных уравнений A), B), приведенной во введении к
гл. X.
Граничные и начальные условия можно написать так:
' а)
B)
C)
D)
Если длина стержня мала, точнее, если — <С —•, то можно
воспользоваться формулой C) § 9 гл. I для усреднения температуры вдоль
направления х. Тогда будем иметь
-^^ + ^(у)^^-а1^^-. E)
дТ,(у,х) _ д* Г2 (у, х) .-
— "а аТя • \°)
Тг
(х
Тг
У>
(х,
-\
0) =
оо, т]
Тг
дТг
К
= тс =
= т(
(х,0,
(*,о,
ду
= 0;
т) =
±
Г2 (х,
0; 7@,
= Тг (х,
у,0) =
У>*) =
0,т);
дТ2 (х, 0
ду
' 02 ~
= Т =
1 с
•-$-.
= const.
= 0;
dz ~2 ду'
Температура Тг (x,y,t) не является монотонно убывающей функцией х,
поэтому величину Тг (/, у, т) можно выразить через 7\ (у, т) при помощи
теоремы о среднем значении:
Т1(у,х)=Т1{1,у,т)A-£-у G)
где /* — некоторый параметр.
Введем некоторое значение эффективной скорости wt:
Wl = w(y)(l iPi (8)
и примем ее за постоянную величину, как это обычно делают при
решении задач теплообмена по методу Кришера. Тогда уравнение E)
можно написать так: ___
дТг (у, т) . Щ тр , х d*Ti (У» т) /кя\
Тогда решение уравнений Eа) и F), усредненных по х, при граничных
условиях A)—D) будет иметь вид
■™4~1С7гЫ-г-&-)Л!%Р-*> <9>
о
где
6= JVL = ^PeFo1, A0)
400
Глава десятая
ре = JUl число Пекле, Fox = а£2 — число Фурье, D —
эквивалентный диаметр трубы, К\ = ^Л2» Ф (?) — безразмерный тепловой поток у
поверхности тела, определяемый по соотношению
-Ъ^^ = --ЩЛ- = №- A2)
Аналогичное соотношение можно написать и для Г2E, v\).
Не приводя промежуточных вычислений, которые можно найти в
работе [106], получим следующее выражение для потока тепла ф(Е):
00
У"^ ехр (— £ и) dw
-Ех
1 1 + а+i^ctg2(W ]Л + а ) ' A3)
о
где \ъп — корни характеристического уравнения
■Htgp# = /Ce Kl-Ji2 . A4)
Численное значение характеристических чисел ^ приведено в табл, 10.1.
При малых значениях ч5 = -у-«1) главным в формуле A3)
является последний член. Тогда ф (I) уменьшается пропорционально
с ростом £. С увеличением 5 функция ф(£) продолжает монотонно
убывать, причем главными становятся члены, входящие в сумму.
Наконец, при больших значениях Е(£>1/[^) из всей суммы остается
лишь первое слагаемое. Тогда получим приближенное соотношение
«1» E) - 2/Сх (j/Т^ЯГ) е~*1' [NKt (l/Т^Г) +
A5)
+ N^ + 1/A - JX2)
Значение \ь0 определяется из табл. 10.1. Для ряда случаев можно
получить простые формулы для расчета \ь0.
При малом Кг 9 точнее при KeN<^l, имеем
vl = NIK* • A6)
Если N мало, а Кг — произвольная величина, то
,2 1 / *,
^о = -2"
Ж/'+Чх-Г-1)- A7>
Найдем удельный поток тепла:
ГРАНИЧНОЕ УСЛОВИЕ ЧЕТВЕРТОГО РОДА
401
V
OjO
О,
X
о,
о
"*
А
«
dL
=L
dL
=L
=L
d£
dL
=L
dL
dL
d!
d!
dL
d.
i<
^
СП
t^
oo
о
СП
CO
oo
о
__
^H
Ю
t^-
o
CO
T—t
СП
CD
о
CD
CD
см
CD
О
00
Ю
CD
Ю
О
о
CO
о
to
о
СМ
О
^
TJH
О
ю
IN.
IN.
' СО
о
00
^
со
о
,
см
ю
см
■о
! СО
СП
оо
о
' см
? IN.
CSJ
о
СП
! Ю
со
о
1 °"
00
СМ
о
| о"
-
1 °
1 °~
f о
( 1°
оо
сп
г^
оо
о
1—(
IN-
00
о
со
Tt<
ю
с^-
о
to
СП
СО
о
оо
00
см
со
о
,_
СО
со
ю
о
со
со
о
ю
о
СО
о
^F
^
о
о
00
in-
со
о
■^
ю
СО
о
СП
см
ю
см
о
со
о
сп
о
ю
00
см
о
ю
ОО
СО
о
о
см
IN.
о
о
см
о
о
о
о
оо
оо
о
см
Г--
00
о
ю
Tf
to
о-
о
оо
О)
СО
о
—«
СП
см
СО
о
"*>
со
со
ю
о
г^
со
о
ю
о
о
"Ф
^
о
ю
а)
IN.
СО
о
ел
to
СО
о
со
со
ю
см
о
СО
СП
о
_<
о
со
о
00
о
г^
о
о
t^
сп
о
о
СО
о
о
о
ОО
00
о
^
h-
ОО
о
IN.
•^
ю
IN.
о
о
см
СП
со
о
СО
СП
см
СО
о
со
СО
СО
ю
о
о
"ф
о
ю
о
ю
^
тн
о
СП
00
IN.
СО
о
со
СО
со
о
«ф
■*f
to
см
о
ю
см
СП
о
ю
СО
о
СП
см
IN.
о
о
ю
см
о
о
■"*
о
о
см
о
00
00
о
ю
о-
00
о
00
^
ю
1^
о
см
см
СП
СО
о
ю
СП
см
со
о
СП
со
со
ю
о
■*
тН
о
ю
о
00
-^1
^
о
^h
СП
1^
СО
о
IN.
1^
со
о
, ,
ю
ю
CN
о
^
со
СП
о
00
см
со
о
со
тр
h-
о
о
1^
см
см
о
о
ю
о
о
о
00
00
о
см
00
00
о
г^
Ю
ю
IN.
о
см
СО
СП
СО
о
оо
о
со
со
о
*ф
00
СО
ю
о
__
СО
о
ю
о
оо
со
■^
•*
о
оо
оо
со
о
СП
СП
т—(
со
о
TF
00
ю
см
о
IN.
in.
СП
о
__
оо
со
о
со
о
ОО
о
о
со
СО
см
о
о
о
о
со
см
-ф
СП
о
_ц
^
СО
00
о
СО
ю
00
1>-
о
г_^
|>-
о
1>-
о
СО
00
см
CD
о
см
о
ю
ю
о
1>-
1>-
^
о
СО
СО
СП
со
о
СП
см
Т-*
со
о
СО
СО
СО
см
о
о
со
ю
о
СО
оо
о
о
СП
"*
о
о
о
о
о
IN-
см
■^
СП
о
см
*чР
СО
00
о
00
ю
00
t>-
о
^
с--
о
о-
о
СП
00
см
со
о
ю
о
ю
ю
о
см
см
|>-
"=t«
о
СП
СО
СП
со
о
см
СО
со
о
IN.
ь-
со
см
о
СО
|>-
ю
о
^
^
00
о
о
оо
ai
о
о
см
о
о
IN-
см
^
05
о
-*
"^
со
00
о
о
СО
а)
IN-
о
СО
г-.
о
t--.
о
^
01
см
СО
о
СП
о
ю
ю
о
1>-
см
1^
^
о
"ф
^
СП
СО
о
СП
СО
со
о
г-.
00
со
см
о
СО
г^
ю
о
00
СО
00
о
о
о
СО
см
о
о
СО
о
о
оо
см
<*•
СП
о
ю
TF
СО
00
о
см
СО
00
t^
о
оо
|>-
о
ь-
о
СО
СП
см
СО
о
со
ю
ю
о
т_н
со
IN-
rt*
о
о
ю
СП
со
о
ю
^
1—4
со
о
INCH
со
см
о
IN.
IN.
ю
о
,
СП
00
о
о
см
ю
см
о
о
кн
о
о
СП
см
Th
СП
о
IN-
^
со
00
о
^
СО
00
IN-
о
т_
ОО
о
IN-
о
СП
СП
см
СО
о
«^
ю
ю
о*
со
со
IN-
rf
о
СО
ю
СП
СО
о
СО
ю
со
о
со
о
^
см
о
СП
IN.
ю
о
о
СП
о
о
СО
со
см
о
о
ю
о
о
^
со
-ф
СП
о
^
ю
со
00
о
СО
с--
оо
IN-
о
СО
СП
о
IN-
о
см
со
СО
о
ю
сг>
ю
ю
о
00
to
IN.
Tt<
о
^и
оо
СП
со
о
СО
см
со
о
о
ю
""*•
см
о
см
о
t--
о
СО
оо
СП
о
о
со
СО
о
о
о
о
СО
см
4f
СП
о
о
00
СО
оо
о
^
со
СО
с^
о
00
00
см
со
о
см
-^
см
ю
о
со
СП
"Ф
о
см
ю
СО
о
о
см
о
о
00
о
о
ю
IN-
о
о
_4
о
о
о
t>-
см
^
СП
о
см
00
со
оо
о
Г"-
со
СО
IN-
о
см
СП
см
СО
о
h-
«ф
OI
ю
о
СО
о
см
■^
о
__,
со
СО
о
ю
см
см
о
СО
о
о
ю
со
см
о
о
см
о
о
СП
см
-ф
СП
о
Tt<
00
СО
оо
о
о
■^
СО
IN-
о
to
СП
см
СО
о
см
ю
см
to
о
о
т—<
см
*ф
о
_
с-.
со
о
о
чф
см
о
со
со
о
СО
IN-
см
о
о
СО
о
о
ел
см
"ф
СП
о
СО
00
со
00
о
СО
**f
со
IN-
о
о
о
СО
со
о
оо
ю
см
to
о
г^
см
^f
о
»-ч
00
СО
о
"*•
ю
см
о
00
ю
о
со
о
со
о
о
4f
о
о
,
со
^
СП
о
СП
оо
со
00
о
СО
«ф
со
IN-
о
^f
о
со
СО
о
СО
СО
см
ю
о
ю
см
см
^
о
о
Oi
СО
о
СП
со
см
о
о
00
о
о
со
СО
о
о
ю
о
о
Is-
СО
""ф
СП
о
СП
СП
со
00
о
*-«
00
СО
IN-
о
^
см
со
со
о
СП
оо
см
ю
• о
СП
to
см
^
о
со
со
см
со
о
Г-Н
со
см
см
о
оо
СО
см
о
г^
СП
СО
о
о
о
^-*
о
402
Глава десятая
о
о
•«
d.
d-
N
£
=L
1 о
=L
d.
d-
=L
dL
d.
rL
d.
=L
d!
d.
^
^
CM
■Ф
CD
о
00
00
b-
О
oo
см
CO
о
CM
CS|
Г».
-^
o~
CO
о
CM
о
CO
r—1
о
CO
CM
о
о
_
о
о
о
см
00
см
"Ф
05
о
СМ
со
00
С4-
о
СО
•ф
СП
о
ю
со
а>
с^
о о
ю
CD
см
со
о
о
со
N.
"*
о
см
С0
о
♦—с
со
СО
»—1
о
см
Оз
см
о
о
см
о
о
см
о
СО
со
о
о
'ф
г-
Tt<
о
00
СО
о
аз
ю
СО
т—Ч
о
см
ю
СО
о
о
со
о
о
СМ
со
*ф
05
о
О)
СО
00
1"-
о
00
о
со
СО
о
Оз
N.
т^
о
о
см
со
о
СО
00
со
'—|
о
со
Оз
со
о
о
"ф
о
о
СО
со
^
аз
о
со
00
1^
о
-^
со
СО
о
00
ю
h-
'ф
о
ю
см
со
о
СМ
ь-
,—|
о
СП
см
*ф
о
о
ю
о
о
см
^
аз
о
со
а>
00
о-
о
со
*ф
со
СО
о
СМ
о
ОО
-ф
о
00
СМ
СО
о
ОО
00
"—*
о
оо
со
ю
о
о
о
о
оо
<м
•ф
ст>
о
СО
а>
см
СО
о
СМ
г^.
*-н
со
о
,
СО
о
о
о
о
о
см
со
Tt*
аз
о
00
о
со
СО
о
»—1
о
см
СО
о
со
со
"ф
о
о
СМ
о
о
ю
со
Tt<
аз
о
о
см
со
со
о
аз
см
см
со
о
см
см
ю
о
о
со
о
о
аз
со
•^
аз
о
см
СО
СО
СО
О
n-
ю
см
со
о
со
аэ
ю
о
о
-ф
о
о
см
Tf
аз
о
-ф
со
СО
о
Tt*
оо
см
со
о
со
ю
СО
о
о
ю
о
о
аз
ю
■ф
а>
о
СО
о
ТР
СО
о
,
Tj<
со
о
о
СО
00
о
о
о
о
00
о
со
СО
о
оо
^f
■^
о
о
о
о
ю
СМ
со
со
СО
о
см
со
СО
о
о
см
о
о
со
ю
со
СО
о
45h
N.
n-
о
о
СО
о
о
аз
n-
СО
СО
о
со
аз
00
О
о
TF
о
о
СО
о
тР
СО
О
ОО
аз
а>
о
о
ю
о
о
ю
ю
СО
о
см
о
со
о
о
о
N.
00
аз
о
о
о
о
-
Т*<
аз
со
—•
о
СМ
о
о
о
см
N-
о
со
о
о
00
со
а>
о
*ф
о
о
ю
аз
см
о
ю
о
о
аз
*м
о
СО
о
о
о
ГРАНИЧНОЕ УСЛОВИЕ ЧЕТВЕРТОГО РОДА
403
Если для fi0 воспользоваться формулой A6), то из соотношения A5)
получим
Я (т) = Кто У ^5Т ехР I — Xi у "Ш"
Dl c^2R J
A9)
Следовательно, удельный поток тепла убывает с течением времени по
закону экспоненты.
Из решений (9) и A3) следует, что в случае нестационарного
конвективного теплообмена число Нуссельта
Nu = чЫ1 B0)
[Г@,т)-Гс]^
будет величиной переменной, зависящей от времени и параметрических
критериев Кх , Ка> Kv а также от числа Пекле. Поэтому для
нестационарного теплообмена целесообразно ввести обобщенную переменную
Nu' (т):
где вместо переменной температуры поверхности тела Т @, х) входит
некоторая постоянная характеристическая температура, равная
начальной температуре тела.
В этом случае число Nu'(т) будет прямо пропорционально ф (?). По
аналогии с числом Стантона можно ввести число, равное отношению
удельного потока тепла между телом и жидкостью, отнесенного к
единичной температурной разнице AT = 1 (Т0 — Гс = 1), к потоку тепла
(энтальпии), приносимого потоком жидкости:
Р (*) = gff T, . B2)
Кроме того, можно ввести интегральную обобщенную переменную,
характеризующую нестационарный конвективный теплообмен:
Q*(*)=-^q^)dx/c^T0Rv,
где Rv = —^ отношение объема тела к площади поверхности, через
которую происходит теплообмен.
Функция Q* (т) изменяется от 0 до 1; она показывает, какая доля
всего тепла уже передана в ходе процесса теплообмена.
§ 10. СИММЕТРИЧНАЯ СИСТЕМА ТЕЛ, СОСТОЯЩАЯ ИЗ ТРЕХ
НЕОГРАНИЧЕННЫХ ПЛАСТИН
Постановка задачи. Дана пластина толщиной 2R BR = 2/х),
соприкасающаяся с двумя пластинами, каждая из которых имеет толщину,
равную /2. Теплофизические свойства крайних пластин тождественны,
но отличны от свойств средней пластины (рис.10.13). Требуется
найти температурное поле системы трех соприкасающихся пластин.
404
Глава десятая
■■»: — " —
|Т0= const
Т2(х,т)
1Т,(х.т)
т ■
1 \г-\
, , _„.... 1 •
Т2(х,т)
Рис. 10.13. Температурное
поле системы трех
соприкасающихся тел
Имеем (см. рис. 10.13)
7\ (х, 0) = Т2 (*, 0) = Т0 = const,
Tx(lv т) = T2(lv т);
^(/ь т)
1 дх
дГ2(/, т)
374@, т)
За:
ara(/i, *)
о,
+ *[Г2(/, т)-Тс] = 0.
A)
B)
C)
D>
Решение задачи. Применяя метЪд преобразования Лапласа, получим
решение в следующем виде:
Т0-Т(х,ъ)
Т0-Тс
= 1 - 2 -^ cos (ix„ Ka~1/2x/lt) ехр (- даС-1 FGl) ,
оо
/2=1
• ^е sin ^ ^=А. sin ^Лв-«/2 ^ j ехр (_ ^-i^ FOi);
Л=1
Т0~Т(х,
Т0-Тс
_2
COS^^COSft,/^*,-
*2
где
Ф„
1 + /С
1 + /Се /СЛГ'Л + -4ГЧ ^П ft, + ft, -4Р- A +
1 + ^г
E>
F>
ГРАНИЧНОЕ УСЛОВИЕ ЧЕТВЕРТОГО РОДА
405
+ К, К(Ка-1/ш )cosft,] cos ^KtK-1'* + [A + КГ1 K,Ka-l/t +
XKeSm^KiKa'1",
G)
Pn — корни характеристического уравнения
К, £ A + К,) tg WtK-4') = 1 - ■£- A + /С,) tg v. -
— /С. tg j* tg (i* /C,/Ce-V-), (8)
Bi=4-; •*, = -£-, Fo1 = -^-; Ka = ailat. (9)
Если Bi = «о, то граничное условие D) примет вид
Т2 (/, т) = Тс = const. Da)
В этом случае общее решение сохраняется, но
Фл = A + /Се КгКГЧш) sin Рп cos ^ /СЛГ7' +
+ К, A + КГ1 /СЛа~1/2) cos ,*„ sin ^ KtKa-1/2 , A0)
Рл определяются из уравнения
KAg^tg^KiKa/a) = l. (И)
Общий случай системы тройной пластины с источниками тепла шДх,т),
где i = 1,2,3, рассмотрен в монографии [47], там же дано общее решение
для системы, состоящей из многослойной пластины.
ДВУХМЕРНОЕ ТЕМПЕРАТУРНОЕ ПОЛЕ. НЕКОТОРЫЕ
ЧАСТНЫЕ ЗАДАЧИ
11
Решение задач нестационарной теплопроводности, когда температура
является функцией времени и двух координат, представляет большие
трудности. Только некоторые задачи могут быть решены методами,
изложенными в данной книге. В частности, в гл. VI были рассмотрены
задачи на нагревание цилиндра конечных размеров и трехмерной
пластины при условии симметрии температурного поля относительно центра
тела (симметричные задачи). Эти решения были получены как
обобщение решений для неограниченного цилиндра и неограниченной пластины.
В данной главе рассмотрены некоторые частные задачи двухмерного
температурного поля, когда решение может быть получено методами
интегрального преобразования.
§ 1. ПОЛУОГРАНИЧЕННАЯ ПЛАСТИНА
Постановка задачи. Дана полу ограниченная пластина толщиной I,
температура которой везде одинакова и равна 0°С. В начальный
момент времени одна из ограничивающих поверхностей мгновенно
принимает температуру Тс окружающей среды, которая остается
постоянной на протяжении всего процесса нагревания. Две остальные
ограничивающие поверхности поддерживаются при начальной температуре
(рис. 11.1). Требуется найти распределение температуры внутри
пластины.
Имеем
дТ (х, y9z)
(х>0; 0<х<1; 0<у< со),
Т(х,у,0)=0; Г @,0,1) =0,1
Т'(х, оо, т) =0; Т (/, у, т) = Тс; Т (х, 0, т) = 0. '
Применим преобразование Лапласа по временной координате и конечное
синус-преобразование Фурье по пространственной координате х.
407
Прямое и обратное
преобразования для конечного
синус-преобразования Фурье записываются
соответственно так:
Fs(n)= J/(S) sin л WS,
о
00
/(£) = —2 sin леЛ(л),
Т@,у,т)=0
■ТA,у,т)=Тс
т. е. переменная I изменяется от 0
до тс. Для удобства вычислений
введем новую переменную S = тс ~т~~
и обозначим безразмерную темпера- Рис> п л граничные условия для по-
туру через 0 в соответствии с соот- луограниченной пластины
ношением
Т(х,0,т)=0
Т
х
Тогда краевая задача A), B) запишется так:
ае __ / тс \2 дч дч
^ - а [ i ) ае2 + а дф •
Начальные и граничные условия примут вид:
тс
Q(x,0,y) = 0; в(т,*,у) = 0; ^Щ^~ - 0 ;
6(х,5,0) = -^-5.
Уравнение D) последовательно подвергаем конечному
синус-преобразованию Фурье и преобразованию Лапласа. Тогда для функции BLs с учетом
краевых условий E)—G) получим уравнение
C)
D)
E)
F)
G)
d2hs (У)
dy*
= [т + (т-»)*К<й-Ь5г
с условиями
6Ls@) =
(-1)"
aeLs(oo)
Ls \ / ns ' ду
Решение уравнения (8) при условиях (9) имеет вид
0.
(8)
(9)
*м
(-1)л
+
(-
■[
1)"(-
,+(-
■К \2
г) ап
1С \2 '
Тп) aJ
X
"[s+(~f я) fl]
X
A0)
408
Глава одиннадцатая
Для перехода по Лапласу от изображения к оригиналу воспользуемся
соотношением
Второй член формулы A0) переводится к оригиналу по формуле
обращения синус-преобразования Фурье.
Имеем
а
р 11
ехр — у
VJ
s ап*к*
Iехр — у
VJ
+
(И)
Далее,
L-1
s +
( 1 /~S ' П2К2
= е
erfc
2/от
-Lexp(-yyr-f + -^-)]
A2)
Теперь остается лишь выполнить обратное синус-преобразование Фурье-
Возвращаясь к первоначальным переменным, решение нашей задачи
окончательно получаем в виде
T(x,y,z) х . 2 vi (—\)n . х .. ..
л=1
А у (-'
К Ami П
(~\)п о.^ jc 1
2
/2 = 1
г^(^ + ^>^) +
+ е l erfc
' ^ [ V 2 у az
2Уах I '
erfc
2/ат
A3)
Таким образом, путем двух последовательных интегральных
преобразований получено решение двухмерной задачи распространения тепла
в полуограниченной пластине.
§ 2. ДВУХМЕРНАЯ ПЛАСТИНА
Постановка задачи. Рассмотрим двухмерную задачу для
прямоугольника, на сторонах которого поддерживается заданным образом
меняющееся во времени распределение температуры.
ДВУХМЕРНОЕ ТЕМПЕРАТУРНОЕ ПОЛЕ
409
Имеем
дТ
д2Т
дх2
+
д2Т
ду2
(т>0; 0<х<Л; 0<*/<d>
при начальных условиях
и граничных условиях
T(x,y,0) = f(x,y)
A)
B)
Т@,у,
Т (х, 0,
= 0;
•0;
Т(/г,г/,
Т (х, d,
х) =
= ) ,
= 0.
C)
D)
Решение задачи. Воспользуемся совместным применением конечного
синус-преобразования Фурье
h d
Тр= TF(m, п, т) = I \ Т (х, у, T)sin m*x sin-^~- dxdy E)
о о
и формулы обращения
СО 00
Г (х, у, х) = -^- V V Гр (т, л, т) sin -^- sin -^ . F)
т=1 /г=1
Применяя преобразование E) к уравнению A) и используя
граничные условия C), D), получим
d
[ tri1 n2 \ armz С nny
при условии
h d
7V
x=0
f (x, y) sin —т— sin dxdy .
о о
Решение последнего уравнения имеет вид
h d
—аох "
Т „ = е
f (х, у) sin ~~jj— sm —jT dxdy +
о о
x d
-\ jj-- \\e ф (у, т ) Sin —^- dy dx'
0 0
Отсюда согласно формуле обращения F) получим окончательно
т(х, у, х)=-Н-.22 -_аэт - •'- *"* -'-шу
~аах . Titnx
е • sm —=— -sm
X
m=l д= 1
X
'О О
h d
0 О
fjVW,xOsin^^' +
sin —r— sin—-f- dx' dyf
G)
410
Глава одиннадцатая
где
п —. тг2
«"(т + т)- <8)
Из решения G), как частные случаи, вытекают решения, данные
И. Снеддоном [72] и Г. Гринбергом [14].
Для полуограниченной пластины d = оо. В этом случае можно
показать, что при условиях
Т(х, у, 0)=0;
T(h,y,^)=Tc; \ (9)
Т @, £/, т) = Т (х, 0, *) - Т {х, d, т) = 0
решение G) запишется так:
Т(х,у,%) х . 2 ^П (™l)w • ттгд:
* . 2 VI (—1)"* • т™ / тЧ \ i
/71=1
со
+ ехр (- т. -f) erfc (-*= - ^]/^) - 2ехр ( - ^>)erfc ^=[
A0)
что совпадает с решением A3) §1.
§ 3. ПОЛУОГРАНИЧЕННЫЙ ЦИЛИНДР
Постановка задачи. Дан полуограниченный цилиндр диаметром 2R
при температуре Т0. В начальный момент времени температура
боковой поверхности цилиндра мгновенно принимает постоянную
температуру Тс, которая поддерживается постоянной на протяжении
всего процесса нагревания. Температура торца остается постоянной
и равной начальной температуре. Требуется найти распределение
температуры внутри цилиндра.
Имеем
д% 1 дг% ' г dr ' dz2 J ^ '
(х>0; 0<г<#; 0<^< оо),
Г (г, г, 0) = 70, Т (г, 0, т) - Г0, Т (/?, г, т) = Гс, B)
Т @, г, х) =£ оо , — д2 = 0. C)
Решение задачи. Решение уравнения A) для изображения при
условиях B), C) имеет вид
Т, (г, г, s)-^- =
ДВУХМЕРНОЕ ТЕМПЕРАТУРНОЕ ПОЛЕ
411
(tc-to)ib(Yj-
оо
2
/ lxnr \
х
х
exp(-z|/4-+4
D)
где \ьп — корни характеристического уравнения J0 (\i) = 0.
Пользуясь таблицей изображений, находим
Т{г.*.*)-Т. У М*"' , ,_ , 2pw
Гс-Го = 1-^У ^,Ы Bexp(-^Fo) X
х erf тЬ + ехр (*п -т?)erfc Ы^ + •*« ^) +
expl — [i„-^- lerfc
2Vai
E)
где Fo = -на число Фурье.
Рассмотрим аналогичную задачу. В начальный момент времени конец
цилиндра мгновенно принимает температуру Тс, которая
поддерживается постоянной. С боковой поверхности происходит теплоотдача по
закону Ньютона в среду с температурой, равной начальной температуреТ0.
Дифференциальное уравнение и начальное условие остаются
прежними. Граничные условия можно написать так:
Г(г,0,т) = Гс, dTl*;*'z) + H[T(R9z,x)-T0] = 09
Т @, Z, т) =f= оо , Ц- L. = 0 .
dz
F)
G)
Решение данной задачи производится аналогичным способом, и
результат имеет вид
Г(г,г,т)-Г0
оо
л==1
Г 2Bi/0 VrTW
J о (^) (Bi* + vZn)
R i i z
_exp( —ря1?
+
j^l B^o( ^л~£Г
2
exP I v-nx)erfc(v-nV¥o
шш*4 /„((.„) (Bi2 + ^)
- exp (- pn ^) erfc ( ,„ KF5 - -^
где jx/j — корни характеристического уравнения
z
J о fa)
1
Br**
(8)
(9)
Тем же методом можно решить трехмерные задачи по нахождению
стационарного температурного поля.
412
Глава одиннадцатая
§ 4. ЦИЛИНДР КОНЕЧНЫХ РАЗМЕРОВ
Дифференциальное уравнение теплопроводности для круглой
трехмерной цилиндрической области в цилиндрических координатах г, ср, z
имеет вид
дТ I д*Т . 1 дТ . д*Т . 1 д2Т \ , 1 , ч /1Ч
Если имеется симметрия относительно оси г, то оператор -^-
тождественно равен нулю, тогда получим
дТ / д2Т . \ дТ , а2Г \ , 1 , ч /оч
"аГ = а (-дРГ +—-зГ + ^г) + 7Г^(г9г9х). B)
Если, кроме того, рассматриваемый цилиндр имеет достаточно большую
длину, а начальные и граничные условия таковы, что параллельные
сечения цилиндра, нормальные к его оси, имеют одинаковое
распределение температуры, то оператор д/дг также тождественно равен нулю.
Осесимметричный цилиндр. Приведем решения уравнения
B) при граничных условиях первого, второго и третьего родов.
Необходимость в решении таких задач возникает при исследовании
самых разнообразных вопросов, например при моделировании тепловых
процессов в активной зоне ядерного реактора, при рассмотрении
теплоотдачи тепловыделяющих элементов реакторов, в вопросах теплообмена
трубопровода с грунтом, массопереноса, сопровождающегося
химическими превращениями, через цилиндрическую пористую среду и т. д.
1. Рассмотрим решение уравнения для конечного цилиндра длиной
I при граничных условиях второго рода на боковой поверхности. Для
определенности положим, что один из торцов (z = 0) изолирован для
переноса, тогда как температура другого является функцией времени
и радиальной координаты, т. е. ищем решение уравнения B) при
следующих краевых условиях:
Т @, г, т) =f= оо ; ^ = —q (z, <с);
дТ (г, 0, т) n rr, t 1 ч / Ч1
yd'z = 0; Т (г, I, т) = Ф (г, т)д;
T{r,z,0) = f(r,z).
C)
Решение этой задачи можно получить различными методами, в
частности используем конечные интегральные преобразования Лапласа
путем совместного применения интегральных преобразований Фурье и
Ханкеля.
Для простоты последующих выкладок запишем уравнение B) и
условия C) в безразмерной форме:
6 (X, Z, 0) = F (X, Z), E)
. а6 Aа/' Fo) = Ki (Z, Fo). F)
d4Xdz' F0) = °; 6 (X' TC' Fo) = ф (Х' Fo)' G)
ДВУХМЕРНОЕ ТЕМПЕРАТУРНОЕ ПОЛЕ
413
где б = (Т — т*)/Т* — безразмерная температура (Г* — некоторое
начальное значение температуры, фиксированной для определенной точки
цилиндра), X = r/R; Z = kz/1 — безразмерные координаты;
F(X,Z) = lf(r,z)-T*]/T*; O(X,F0) = ^^Г^* ; b = ■=*- ,
D2
Po (X, Z, Fo) = -jfjr w (r> z> T) —критерий Померанцева, Кд (Z, Fo) =
R
= -y^- 9 (z, t) — критерий Кирпичева .
Воспользуемся по переменной X конечным интегральным
преобразованием Ханкеля
{Г (X, Z, Fo)}H .= {Г}н = \XJQ(v.X)T(X, Z, Fo)dX (8)
о
и формулой обращения
Т (X, Z, Fo) = 2 ^ ^l^ (r (*.-Z> F°))h • (Q)
где p — положительный корень характеристического уравнения
а по переменной Z — конечным косинус-преобразованием Фурье
тс
{r(X,Z,Fo)}Hc={r)Hc = J>}H cos(n + ±)ZdZ A0)
о
а формулой обращения
оо
{Т(X, Z, Fo)}H = А^] (Пне cos(" + 4")Z- (П>
Согласно приведенным преобразованиям получим решение задачи в
следующем виде:
X ехр ( - [ ^ + Ъ* (ft + 4)] Fo) tF <Х- Z)>hc +
Fo
+ Jexp ( - [ ^ + Ь*(п + 4-J]<Fo - Fo*)) ^ W fKi <Z' Fo*)b +
+ (-1)*6»(л + 4-){Ф(ХРо^ }. A2)
Если положить в A2) / (г, г) = <р (г, т) = Г0 и принять 7* = Т0, то
найдем
414
Глава одиннадцатая
Т-Тп
оо I оо Fo
m=\ v n=0 0
■6»^)(Fo-Fo*)]
/0 Ы j Ki (Z, Fo*) cos ix„ ZdZ +
j" cos |*„ Z j X/0 frmX) Po (X, Z, Fo*) dX
dZ]d¥o*\, A2a)
где |*„ = Bл + 1)/2(л - О, 1,2,...).
2. Рассмотрим теперь решение уравнения D) npw выполнении
граничных условий третьего рода на боковой поверхности цилиндра.
Пусть краевые условия задачи имеют вид
дг ' I
дТ(х,0,х)
дг
= 0; Т (х, I, т) = Тс;
Т(х,г,0) = Т0,
или в безразмерной форме:
ЦХ, Z,0)-60,
a6(l^,Fo) + BiO(l,Z,Fo) = 0;
^°>F°> = 0; б (X,., Fo) = 0.
A3)
A4)
A5)
В уравнении D) и условиях A3)—A5) в отличие от предыдущей
задачи безразмерный потенциал б имеет вид
т—Тс
е (X, z, Fo)
кроме того,
Т0-Тс
То
,Bi =
aR
Применяя к уравнению D) и условиям A3) — A5) последовательно
преобразования (8) и A0), найдем обыкновенное неоднородное
дифференциальное уравнение в изображениях. Решая его и выполняя
обратные интегральные преобразования A1) и (9), после некоторых
упрощений получим окончательное решение:
0(Х„
X
ZFoH^L
X
Fo
Я
0
1С
AJ4(-
00
z*
V'm
h4+b
Ро(Х, Z,Fo*)}Hcexp[-
62
7C
i2
V1 m
-Fo
•>o2(
+ 62
\dZ
mX)
OO
•s-
^)(Fo-
exP ( — ^тр°)
cospi„Z X
-Fo*)]dFo*
- X
1
A6)
ДВУХМЕРНОЕ ТЕМПЕРАТУРНОЕ ПОЛЕ
415
где
Ж 1
iPo (X,Z,Fo))Hc = f 1 {XJ0(ixmX) Po(X, Z, Fo)dX] cos\xnZdZ,
о о
a \i.m — положительные корни характеристического уравнения
tV
2n+ 1
(n = 0, 1, 2, 3, ...)•
В A6) введено разложение для тета-функции %t:
Z
h
2ъ
,t-£-Fo) = 2 2 (—1)" exp [-ft^Fo] sin^Z.
я-=0
Рассмотрим некоторые частные случаи решения A6). Для
некоторых высокоинтенсивных теплообменных процессов источник тепла
(критерий Померанцева) можно аппроксимировать следующим
выражением:
Ро (X, Z, Fo) = Рох [1 — exp (—p Fo)] J0 faX) sinZ, A7)
где [хх — наименьший положительный корень бесселевой функции
нулевого порядка J0 ((xx) = 0 (\1г ж 2,405).
Из соотношения A6) с учетом выражения A7) и формулы
суммирования Пуассона для условия jvL > C получим [57]:
ТС СО
е (X, z, Fo) =-^L e0 j »x (_g_ ,,• _*!_ Fo)dz* £
m==l
X
+2Pol[x1/1((x1M]
exp (-p, ^Fo)
l4 + Bi2
X
m=\
К
Bi2) G4-n$)
«^0 (Pm)
X
X
^m-
62
chJ^L (те —Z)
ch J™_ Bте — 2)
6 6
Pw
Sh-^L те
b
exp(-pFo)
Гт + b2~$
ch
Vs.
sh 2-&2L. те
b
— sinZ
(те-Z)
^
sh
V
\xm-
— 2
ch——^ lL Bте — Z)
b
V
£■
sh2
V a
— sinZ
+ -AJ_exp(-^Fo) X
X
00
exp [ — b\2n Fo] cos pn Z
<tf -1)
U
*« +
62 /J
A8)
416
Глава одиннадцатая
Если |х^ < р, то в A8) следует всюду произвести замену у V2m—?
на f j/F^
Приведем некоторые другие решения для более простых краевых
условий, чем A3) — A5).
Если переносом через торцы цилиндра можно пренебречь по
сравнению с переносом через боковую поверхность, то выражение A5)
принимает вид
дЬ(Х ,Q,Fo) __ a8(X,7u,Fo) _ п {]Q.
и решение, аналогичное A6), можно найти посредством обычного
конечного косинус-преобразования Фурье:
«(х,z,f„) _ж!e„ i -''-I::' Jj^r+4-s ^
m=l m==l
Fo
X
ГО К r» l
X ^^exp (_^Fo)[ jexp(^Fo*) { J (j X/0 (^mX) X
0 m о о
oo
X Po (X, Z, Fo*) dX) dZjdFo* +]T exp ( — b2 n2 Fo) cosnZ X
Fo 7x; 1
x j exp [([£+ 62n2) Fo*]{ j" ( j' XJ0 (fxmX) Po (X, Z, Fo*) dX)X
0 0 0
X cosn ZdZ} dFo*]. B0)
Если температура на торцах равна нулю, т. е. б (X, 0, Fo)=
= 6 (X, тг, Fo) — 0, то решение задачи можно получить, используя
конечное синус-преобразование Фурье:
4Bi Л С а / Fo* ? 462 ,-.. Y,t-_..V< exP ( —K-m F°)
e(x,z, Fo)=^-e0 j4(-^- ,* ^-Fo )dFo*S
H-^+Bi
0 =0
X
oo 2
x U^nXl + AV -^ ^^1 exp (- i^Fo) X
m==l
oo Fo
X Г J] exp (— b2n2 Fo) sin (nZ) Г exp [(^ + b2n2) Fo*] X
/2=1 0
X ( ( ( XJ0 ((xmX) Po (X, Z, Fo*) dX) sinn ZdZ dFo* J- B1)
6 о
Некоторые другие случаи решения рассматриваемой задачи с
источником вида A7) приведены в работе Т. Л. Перельмана. Отдельные
решения уравнения B) или D) при отсутствии источника приведены
в монографиях [30, 46]. Необходимо отметить, что решения без
источника можно получить наложением решений частных задач.
Например, для конечного цилиндра это будет наложением решений для
неограниченных одномерных цилиндра и пластины.
ДВУХМЕРНОЕ ТЕМПЕРАТУРНОЕ ПОЛЕ
417
Методика определения нестационарных полей температуры для
полого осесимметричного цилиндра не отличается от методики
решения сплошного цилиндра. Однако в этом случае вместо
рассмотренного конечного интегрального преобразования Ханкеля (8) следует
использовать другие его формы. Например, если на внутренней и
внешней боковых поверхностях цилиндра заданы граничные условия
третьего рода, то следует использовать преобразование
[Т (r,z, т)}я = j Г (г, г, т) г U0 (\im r/Rx) dr, B2)
где
Ri
U0 ft*m r/Rx) = [J0 (|*m) + -ШГ^ J^")] Y° ([X- r/Rl) -
Гт-корни уравнения %[^> = -^jj-(m = 1, 2, .. .).
UX (\><m /"//?!) - [J0 (ftj + -^- A ({Xm)] Kx (^ Г/^) - B3)
-1П W + -^-^ Yi GO! П (ft»/V*i);
11== 1 > bl2 ~~ ~~
1 +
Формулой обращения для преобразования B2) будет
со
Т (г, г, х) = 2 2 \Т\Н U0 (|*m г//?а) i?r2 { *2^ Dim)
+(^-П-^кг['+(-^)Т- B4>
Приведем здесь только окончательный результат для задачи со
следующими краевыми условиями:
Т {г, z, 0) = Т0, B5)
дП%'гл) -^T(Rvz, -0=0; аг <%■«■*> + _J-T<*„z, x) = 0, B6)
ar(r,o,x) а0..аг(^ + _^ Т(Г) /(т) = 0 B7)
(/?!</•</?„-/<z</);
его можно записать так [60]:
со со
9 = т~-т[ = !- SS А^Ап и* bmr/Ri) cos r*„-7- х
x exp [_(^ + fe«^)Fp1], B8)
14 Заказ № 640
418
Глава одиннадцатая
где
Лт —
2 [BI, ий{ъЫ) + 2/*]
'- <**.) [ £ + (-^-J] —^г [£ + В1?1 '
2 Bii/ Bia H- f 5
А. = (—1)»+! -—г-^— -9 , Bi
al
B9)
C0)
При одинаковых значениях коэффициентов обмена на внешней и
и внутренней поверхностях (аг = а2 = а) коэффициент Лт принимает
вид
2BU
■^т
(^+Bi?)
%UQ (%^m)-
-2—1 '
ti: Bii J
C1)
Бесконечная сумма в решении B8) быстро сходится, так что для
практических расчетов достаточно одного-двух членов ряда. Для
удобства выполнения расчетов Ш. Н. Плят [60] при условии аг = а2
3,5 x=R2/R,
Рис. 11.2. Зависимость корней
характеристического уравнения \i<i и ^2 от % =
= R2IR1 Для разных значений Bli.
3,5 X = R2/R,
Рис. 11. 3. Зависимость коэффициентов
Ai и Л2 от % = Rz/Ri для разных
значений Bii.
дал графики первых двух корней \хт уравнения B3), коэффициентов
Ат, а также функций U0 (щт) для значений критерия Bix =—~, =
= 1-Г-10 и отношения х = R^Ri = 1,5 4-4,0; эти зависимости приведены
ria рис. 11.2—11.4.
Другие решения полного осесимметричного цилиндра как при
постоянной, так и переменной температуре среды можно найти в
работах [60, 61, 17].
Осенесимметричный цилиндр. Рассмотрим общий метод
решения осенесимметричного дифференциального уравнения A).
Следуя А. П. Прудникову и Р. И. Гавриловой [10], для уравнения A)
при весьма общих "краевых условиях
Т (г, ф, г, 0) = / (г, ф, г),
C2)
ДВУХМЕРНОЕ ТЕМПЕРАТУРНОЕ ПОЛЕ
419
дТ(г, ф,0,т) .. .
Г (г, ф, /,х) = X (г, ф, х); C3) U°j>^
х эг~—h
Г (Я, ф,2,х) = 0
C4) о,
будем искать решение в виде ряда \
Фурье: о,2|
r™ + IlT^)sinmcp+
m=l
T2m cosmcp].
3,5 x = R2/R,
/35) Рис- 11.4. Значения функций i/0=({Jbi*)
Представив аналогичным образом
функции w, /, ф и X, сведем
рассматриваемую задачу к решению
дифференциального уравнения
U0= (|л2 х) и Uо \хг
для разных
значений ВЦ и % = #2/#i
дх \ дг2 ' г
д7(/)
~~дГ~
r2 wm ^ dz2 ^
п
w% C6)
при краевых условиях
TW(r,z,0)=/W(r,Z);
flrfffr. о, х)
= €' (г, *); Т@ (Г, /, х) = Х« (г, х);
х arff (*,,,*) Чг£?(^г1,) = 0 {/==1J).
C7)
C8)
C9)
Дальнейшее решение задачи можно вести по-разному: используя
специфические для этой задачи конечные преобразования Ханкеля,
как это делает М. В. Елистратова [26], тогда решение получается в
виде рядов по собственным функциям соответствующей задачи
Штурма— Лиувилля; разлагая входящие в C7) — C9) функции в ряд Ди-
ни — Бесселя
T$=%T£iJMfrllutr/R),
D0)
где
Пй(^)
2
*#2 [Jm (^mn)]2
-§T$Jmfrmnr/R)rdr9 D1)
\ътп — корни уравнения
lxj'm(x) + RJm(x) ^ ^
D2)
14*
420
тогда уравнение C6) и условия C7) — C9) сводятся к новой задаче:
^-[-^-W^J+^-ifc D3)
т!2, <*■ 0) - «. <*
дГ<<> @, -с)
D4)
Решение новой задачи не вызывает особых трудностей. Методика ее
решения аналогична методике решения обычных уравнений переноса
при граничных условиях второго рода и может быть реализована
совместным применением преобразований Фурье и Лапласа. В
результате решения мы получим
где
Тй.<* *)=«р[-а(-^
0
т{i-ir»>[^. °-^]х<?„ и*.- /..[^., tfc^i х
6 о
, х ее*) *•} + -4- / /{•. №- ■^1 +
о о
*а(*,т) = 2^] ехр Г — т:2 f /г +—~\ \ 1 cos тт B/г + 1) х. D6)
я=0
Ряд частных задач для осенесимметричного цилиндра рассмотрен
в известных монографиях Карслоу и Егера; поэтому они здесь
проводиться не будут.
Решение более сложных задач на двухмерное и трехмерное
температурные поля не входило в нашу задачу. Интересующихся
читателей можно отослать к оригинальным работам и специальным
монографиям [30а, 72].
421
ТЕМПЕРАТУРНОЕ ПОЛЕ ПРИ ИЗМЕНЕНИИ
АГРЕГАТНОГО СОСТОЯНИЯ ТЕЛА
12
Многие процессы теплообмена связаны с изменением агрегатного
состояния или физико-химической природы материала. При этом теп-
лофизические коэффициенты тела изменяются скачкообразно, и для
переходов требуется теплота плавления (сорбции, испарения) или
теплота химических реакций. Решение подобного рода задач имеет
большое практическое значение в металлургии, строительной
теплотехнике и в других прикладных дисциплинах.
Из многочисленных задач, относящихся к этому разделу,
остановимся только на задачах по промерзанию влажного грунта и
затвердеванию металла.
§ 1. ПРОМЕРЗАНИЕ ВЛАЖНОГО ГРУНТА
Постановка задачи. Влажный грунт находится в талом состоянии
и имеет некоторое заданное распределение температуры f(x)TB
начальный момент времени на поверхности грунта внезапно
устанавливается некоторая температура Т( 0,т) = ф (%), которая при всех
изменениях всегда ниже температуры замерзания Т3. В результате
образуется промерзший слой переменной толщины % = / (т). Нижняя
подвижная граница его всегда имеет температуру замерзания. На
этой границе происходит переход из одного агрегатного состояния
в другое, на что требуется теплота перехода р (дж/кг). Таким
образом, верхняя граница (х =Е) талой зоны имеет постоянную
температуру замерзания, а нижняя граница (х = /) — некоторую
постоянную температуру грунта на большой глубине его. Часто нижнюю
границу талой зоны принимают лежащей бесконечно глубоко (/ = оо).
Коэффициенты переноса промерзшей и талой зон различны.
Предполагаем, что перенос тепла в грунте происходит только вследствие
теплопроводности.
Таким образом, задачу математически можно формулировать так
(рис. 12. 1; индекс «1» относится к промерзшей зоне, индекс «2» —
к талой):
422
Глава двенадцатая
1 дТг
дТ2
(х,
дх
(X,,
дх
Т
Л. =
_zL =
а (х,0)
тх (£,
д*Тг (х,
а1 §^-
д*Тг {х,
Щг~
_1>
JL
= / (х) [так
П @, *)
<ЭГ2 (оо,
5л;
=
(t>0
(х>0
как 1
фМ.
= г =
= 0.
0 < х < 1),
£<Х<оо),
@) = 0],
const,
На границе раздела
374 (£,. *)
>ч
дл:
dz
дх
О)
B)
C)
D)
E)
F)
G)
где W — влажность грунта (масса влаги в единице массы абсолютно
сухого грунта; кг/кгI\ ^2—плотность грунта (кг/мв). В промерзшем
грунте имеются две зоны (мерзлого и
талого грунта), изменение
температуры в которых описывается
уравнениями теплопроводности A) и B) и
граничными условиями E) и F). Таким
образом, задача о промерзании
грунта может быть сформулирована как
задача о сопряжении двух
температурных полей при наличии особого
граничного условия на движущейся
границе раздела.
Задача несколько упрощается, если
считать, что температура талой зоны
везде одинакова, не изменяется в
процессе теплообмена и равна Т0 = Т2.
Физически это означает, что талая
зона представляет собой жидкость, в
которой благодаря совершенной
конвекции имеет место постоянство
температуры. В этом случае задача промерзания грунта сводится к
задаче образования льда в стоячей воде.
T,@,r)=f(t)
[■
L
о2,А2,с2
f
/
О
\ ® 1
'х
Рис. 12.1. Распределение
температуры при промерзании влажного грунта
Тогда условие G) приобретает вид
дх
=№
dz
(8)
Основная трудность решения задачи состоит в том, что условие
G) или (8) относит ее к классу нелинейных задач, т. е. к задаче с
нелинейными граничными условиями. Решению этой задачи посвящено
более 50 оригинальных работ, опубликованных за последние 100 лет.
Весьма распространено мнение о том, что впервые задача о
промерзании грунта в простейшем виде была решена венским математиком
Стефаном. Впервые такая задача была решена в 1831 г. членами
Российской Академии наук профессорами Ляме и Клапейроном. При реше-
х) Предполагается, что вся влага грунтi замерзает при одной и той же
температуре Г3, т. е. является свободной влагой.
ПОЛЕ ПРИ ИЗМЕНЕНИИ АГРЕГАТНОГО СОСТОЯНИЯ ТЕЛА
423
нии задачи ими было принято Т2 (х, 0) = Т0 = const (начальное
условие) и 7\ @, т) = 0 (отсчет температуры производится от температуры
поверхности).
Решение Ляме и Клапейрона. Ляме и Клапейрон решили
упрощенную задачу [граничное условие (8)], предполагая, что температура
воды равна температуре замерзания, т. е.
ГХ(Е, т) - Т2 (*, 0) = Т0 = Т3 = const. (9)
Если положить Тг(х, т) = % (и), где и = , то после подстанов-
у *
ки в уравнение A) получим
J}
ll du* "Г 2 du
• d4 . и db л /1АЧ
а1-1Ж- + -> 7ПГ-=°- A°)
Обозначим
d$ /11 ч
Тогда уравнение A0) можно написать так:
^- + J-uz = 0. A2)
du 2а± ч 7
Решение уравнения A2) имеет вид
г = Лехр(-1^)' <13>
где А — постоянная интегрирования.
Далее, на основании A1) получаем
x/VT 2
Тг(х,.*) = А J ехр — —W + Б.
Из условия 7\ @, т) = 0 следует, что В = 0.
Итак,
X
Ух -
Тг(х, ^) = л § е du. A4)
Воспользуемся граничным условием (8), при этом положим £ = р ]А,
Тогда получим следующее соотношение:
"£«>(-£)-т>- <15>
Из граничного условия на поверхности раздела (х = Е) следует:
Г3 = Го = Л J ехр (-~) du. A6)
Тогда из соотношений A5) и A6) можно определить постоянные Лир.
424
Глава двенадцатая
Т2<х,т)
т,=о° о
Таким образом, решение задачи
окончательно будет иметь вид
Тг(х, т) =
Го
erf
2 V ахъ
erf
КХТ0 exp
Р2
2 У^~
= РТ2-
A7)
A8)
Рис. 12.2. Распределение температуры
по глубине грунта в процессе
промерзания
У аг erf
Решение Стефана. Задача
решается при краевых условиях C) — G),
причем принимают f(x) = Т0, ф (т) =
= Тс = const (рис. 12.2), т. е.
Т2(х, 0) = f(x) = T0, A9)
Тг @, т)-Гс. B0)
Если величина £ = /(т) будет достаточно большой, то поставленная
задача будет аналогична задаче охлаждения системы тел (составной
полуограниченный стержень), на границе соприкосновения которых
поддерживается постоянная температура и имеется отрицательный
источник тепла. Поэтому решения дифференциальных уравнений A) и B)
ищем в виде
Тг{х, x) = A1 + B1erf
2 У ax-z
Tt(x, *) = Л + £2erf ^=3 .
2 У аат
Постоянные Аг и А2 находим из граничных условий A9) и B0):
Следовательно, имеем
7\ (лг, х) = Тс + Вх erf
B1)
B2)
2 У
fllT
Tt(x9 х)-Г0 — В2A —erf
2 Уа2-
B3)
B4)
Из условия E) следует:
rc + Sierf
2 yfllT
= Гп — В2 erf с
е
const.
2 У а2т
Так как Вх и В2 — постоянные при любом значении т, то очевидно,
что величина —= должна быть постоянной, т. е.
$ = рут,
B5)
где р — коэффициент пропорциональности, характеризующий скорость
углубления зоны промерзания,
ПОЛЕ ПРИ ИЗМЕНЕНИИ АГРЕГАТНОГО СОСТОЯНИЯ ТЕЛА
425
Таким образом, получаем
Т3-Тс
В,=
£*-
То-
erf-
erfc
2 Уах 2 У аг
Следовательно, решение нашей задачи имеет вид:
erf.
Тг{х, ^) = Тс + (Тг-Тс)
2 V агх
erf.
Р
erfc -
2 /d
• erfc
2 l/.
2 1^g2x
«2
B6)
B7)
Коэффициент р определяется из граничного условия G), т. е. из
следующего характеристического уравнения:
МП-Гс)
У ах erf
Р
ехр
4ах
А2 (Го - Г3)
У 02 erfc ■
р
.eXp(-J-).№,
B8)
2 "j/ai 2 |/fljs
Анализ решения. Предположим, что Т0
Т3, что означает
образование льда в стоячей воде. Если функции expz2 и erfz разложить в
ряды и ограничиться первыми членами, то получим
?=V ^<-т*-т<)'
B9)
т. е. коэффициент р не зависит от теплоемкости льда, а зависит от
коэффициента \v плотности ^2, теплоты плавления р и разности
температур (Г3-Тс),
Если взять два члена разложения ехр z2 и ограничиться первым
членом разложения erf z, то получим
р-
L рта
тс)\
11/2
CiTi(r3-Tc) 11/2-
1 +
C0)
2рТ2
Следовательно, в последующем приближении коэффициент р зависит и
от теплоемкости льда.
В общем случае для определения коэффициента р в критериальной
форме характеристическое уравнение B8) можно написать так:
^=Я + X. (*=*■) "Р.(-^? - УЪоК.,
erf/Cft e \T3~TCJ erfcK-i/2K
C1)
где /Ср = •
— — некоторый критерии, характеризующий скорость рас-
2 Vat
пространения зоны промерзания в грунте по отношению к скорости
охлаждения грунта, или относительная способность грунта к промерза-
... If _£2_ ~l/"^2C2T2
j. J\ * — ■—• I/ "т '
нию;
критерии тепловой активности талого грун-
426
Глава двенадцатая
та по отношению к промерзшей зоне его; Ка —
аа
~—— отношение коэффициентов
температуропроводности талого грунта к промерзшему,
--■ — критерий Коссовича. Крите-
Ко
ЧЪ (Тд-Тс)
рай Коссовича показывает отношение
количества тепла, выделенного при замерзании
единицы объема грунта, к количеству тепла, необ-
КР ходимого для охлаждения этой единицы объема
Рис, 12. 3. Графический промерзшего грунта от температуры замерза-
способ определения К из ния до температуры среды.
характеристического ура- Полученное характеристическое уравнение C1)
внения C1) в критериальной форме можно решить
графическим путем относительно критерия Кр (рис. 12.3).
Если обозначить левую часть уравнения C1)
через yv а правую — через у2, то величина /Ср будет определяться
пересечением кривой ух с прямой у2. Тангенс угла наклона прямой у2 равен
"jAc Ко. Следовательно, чем больше критерий Коссовича, тем меньше
критерий /Сэ» чт0 физически обусловливается замедлением углубления
зоны замерзания в связи\ с повышением доли поглощенного тепла по
сравнению с теплом охлаждения промерзшей зоны.
Критерий /С(з зависит от относительной тепловой активности
влажного грунта (/Се), относительной температуропроводности (Ка) и
температурного критерия КТ, равного
КТ
Тр-Тв
Тъ-Тс
C2)
Температурный критерий Кт показывает отношение начальной
температуры грунта к температуре поверхности промерзшего грунта, если
отсчет температуры ведется от температуры замерзания
Решения B6) и B7) в критериальной форме можно написать так:
е1 =
П(х, т) —Г, _
т3 - тс
Т0 — Тъ(х, т) _
Т0-Т3
4- = 2/Ср V
erf \ -
2 V~fox
erf Kp
erfc \
2 У FoxKa
erfctfptf-1/2 '
F°x.
C3)
C4)
C5)
где Fo^ = ~~ — число Фурье для данной координаты х.
Предположим, что £ = const и — = 0 (отсутствие поглощения тепла),
тогда наша задача становится аналогичной задаче § 2 гл. X
(охлаждение системы двух тел: ограниченного стержня длиной £,
соприкасающегося с полуограниченным стержнем).
ПОЛЕ ПРИ ИЗМЕНЕНИИ АГРЕГАТНОГО СОСТОЯНИЯ ТЕЛА
427
Решение такой задачи можно написать так (см. § 2 гл. X):
б т11х.,)-те=,а1__* h у Л„-х/erfc ^b£_.
_erfc^i±^V C6)
2 V aXT
Г0 - Тг (х, х) _ Ж
x-i+Bn-l) j/-^-S
=-г-У Л»-1 erf с —^ , C7)
2 Го-Гс 1 + *е -£ '" \ 2 У5Г
где /С =-~, Л
1-*.
1 + Ке
Из решений C6) и C7) видно, что для больших значений £ или для
малых значений времени можно написать приближенные соотношения
C8)
Следовательно, распространение тепла в стержне конечной длины £ при
малых значениях Fo происходит так же, как в полуограниченном теле.
Можно показать, что исходные решения B1) и B2) нашей задачи
являются приближенными решениями, справедливыми для малых значений
Fo или для больших значений £, т. е. для больших значений
критерия Кр .
В разобранных выше простейших примерах предполагалось, что
температура на поверхности грунта Т @, t) = Тс не изменяется во
времени и всегда остается ниже температуры замерзания воды. Если
температура Г @, т) может стать выше Т3, то может образоваться
несколько переслаивающихся талых и мерзлых зон, и задача в этом
случае усложняется еще более. Даже наиболее простые задачи в этом
случае не могут быть решены аналитически в замкнутой форме, а
решаются лишь приближенно.
Естественно, что более сложные задачи теплопроводности с
изменением агрегатного состояния решались и решаются лишь в результате
развития приближенных методов. Следует указать, как наиболее важные,
разработанные Л. С. Лейбензоном методы приближенного решения,
позволяющие получить простые решения ряда задач, имеющих
практическое значение, и разработанный В. С. Лукьяновым метод
гидравлических аналогий, позволяющий получать решения (посредством
применения гидравлического интегратора) практически важных, но весьма
сложных задач, в том числе и двухмерных.
428
Глава двенадцатая
§ 2. ПРИБЛИЖЕННЫЕ РЕШЕНИЯ ЗАДАЧИ ЗАТВЕРДЕВАНИЯ
ПОЛУОГРАНИЧЕННОГО ТЕЛА, НЕОГРАНИЧЕННОЙ
ПЛАСТИНЫ, ШАРА И НЕОГРАНИЧЕННОГО ЦИЛИНДРА
В 1931 г. Л. С. Лейбензоном [41] был предложен приближенный
метод решения задач промерзания, который обычно называют первым
методом Лейбензона. В 1939 г. им был предложен второй метод
решения такого рода задач [41]. Оба метода нашли широкое применение в
инженерной практике и подвергались экспериментальной проверке.
Рассмотрим подробно первый метод.
Метод приближенного решения заключается в том, что функции
Тг(х, t) й Т%(х, t) подбираются так, чтобы они удовлетворяли
начальным ;и граничным условиям. Подобранные таким образом функции
подставляют в условие сопряжения на границе раздела фаз и решают
полученное дифференциальное уравнение относительно ?.
Затвердевание полуограниченного тела (промерзание грунта).
Рассмотрим вначале задачу о промерзании грунта. Граничные условия
будут теми же, что и в задаче Стефана.
Принимаем линейный закон распределения температуры в
замерзшем грунте:
Т1(х,х) = Те+1^-х, A)
что соответствует стационарному состоянию, и закон Гаусса для талой
части грунта
Т2 (*, ,) = Г3 + (Т0- Г3) erf *~1_ . B)
2 У a%t
Выбранные функции Тг(х, т) и Т2(х, т) удовлетворяют начальным и
граничным условиям, а также дифференциальным уравнениям.
Найдем градиенты температуры на границе раздела фаз:
flTi(£, т) = Т3~ТС дТ2£,х) = Гр-Гз
Id* S ' дх Уш^
Тогда из граничного условия G) § 1 следует:
^i (Т3 — Тс) А2 (Гр — Т3) = \jpjfe_ C)
Решение уравнения C) относительно £ при начальном условии 6@) =
= 0 есть g = р |/" х . Постоянная р определяется из характеристического
уравнения
ЫГ,-Гс) _ ЫГо-Г») = ±_ щ D)
которое в критериальной форме имеет вид
1 1
Щ Т/ъ
Ке Кт = Ко/Ср . E)
Таким образом, критерий /Ср зависит только от критериев Ко, Кг и Кт.
Критерий /Са в уравнение E) не входит, что объясняется линейным
законом распределения температуры в промерзшей зоне грунта,
отвечающим стационарному состоянию.
ПОЛЕ ПРИ ИЗМЕНЕНИИ АГРЕГАТНОГО СОСТОЯНИЯ ТЕЛА
429
Затвердевание цилиндра. Имеется
неограниченный цилиндр с жидкостью при температуре
Т0. В начальный момент времени температура
боковой поверхности мгновенно понижается до*
некоторой температуры Тс < Т3, которая
поддерживается постоянной на протяжении всего
процесса охлаждения. Начиная с поверхности
цилиндра, образуется замерзший слой жидкости
толщиной R — т] = £, где yj — расстояние от оси
цилиндра до границы замерзания (рис. 12.4). Для
упрощения задачи предполагается, что
температура жидкости везде одинакова и равна
температуре замерзания, т. е.
Т2{х9 т)= Т0
Т3 = const.
F)
Рис. 12. 4. Граничные
условия при затвердевании
неограниченного цилиндра
Тогда задача математически формулируется так:
дТг (г, т) __ ^ (РТг (г, т) , 1 дТг (г, т)
дг2
дг
■) (t>0; R>r>% Ч = /(т)),
Т (yj, т) = Т3 = const,
Т (/?, %) = Тс = const,
дг
9Ъ
dz
G)
(8)
О)
A0)
Принимаем распределение температуры в промерзшей зоне (зона
льда) по закону распределения температуры в полом цилиндре в
стационарном состоянии, т. е.
Г (г л- (T3-Tc)\nr + Tclnyi-^T3\nR Л1
1п(т)
Решение A1) удовлетворяет граничным условиям и дифференциальному
уравнению G). Подставим решение A1) в граничное условие A0):
-V
TQ 1П
= РТ2
dt\
d%
A2)
и проинтегрируем его. Тогда получим
Jlln А-_!_(£. _,,«).
2 тг) 4
РТа
A3)
откуда получаем зависимость между щ и временем т.
Время полного промерзания трубопровода (при t = %m iq = 0) будет
равно
РТз#2
4Кг (Т3 - Тс)
= -*-Ко.
4ai
A4)
Затвердевание шара. Задача аналогична предыдущей; она была
решена С. С. Ковнером [28]. Граничные и начальные условия остаются
прежними.
430
Глава двенадцатая
Распределение температуры в полом шаре из льда принимаем по
закону стационарного распределения температуры, т. е.
Tlir, х) = ljL=J±. * (JL _ i) + г,. A5)
Решение A5) удовлетворяет дифференциальному уравнению
теплопроводности для шара (симметричная задача) и краевым условиям.
Подставляя решение A5) в граничное условие A0), получаем после
интегрирования уравнение Для определения т:
т== ?ъ(п-Ю2(^ + Ю {16)
6*i (Г, - Тс) R
Время полного затвердевания шара хт равно
1 хт= ^^~~ = *LKo. 1 A7)
I m Qh(T3-Tc) 6ai J
Полученные соотношения A3) — A6) являются приближенными; как
показали опыты А. А. Померанцева [58], точность их — порядка 15—20%.
С целью лучшего приближения к действительному процессу А. А.
Померанцев ввел поправку в формулы A4) и A7), учитывающую влияние
теплоемкости воды. Величина этой поправки равна
Д = 1+-^(г0-:Гз), A8)
PTi
где Т0 — начальная температура воды (при Т0 = Т3 А = 1).
В формулах для хт надо соответствующее выражение в правой
части умножить на Д, чтобы получить соотношения А. А. Померанцева
для времени полного затвердевания шара или цилиндра.
В технической литературе опубликован ряд работ по
приближенному решению рассмотренных выше задач. В этих работах задача
промерзания грунта значительно упрощена (полагают теплоемкость грунта
равной нулю), а решения ищут для случаев промерзания
полуплоскости, цилиндра и т. п. Такой способ решения представляет собой
применение метода Л. С. Лейбензона, в котором для функций Тг и Т2
принимаются выражения, соответствующие стационарному состоянию.
Затвердевание неограниченной пластины. Во втором методе Л. С.
Лейбензона условие сопряжения заменяется интегральным условием
затвердевания. Это условие непосредственно вытекает из уравнения теплового
баланса.
Составим подобное уравнение для процесса затвердевания.
Подсчитаем теплосодержание всего тела, причем отсчет будем производить от
теплосодержания тела в жидком состоянии при температуре Т3.
Теплосодержание жидкой фазы равно
Qf= \ c^%(T-T3)dv9 A9)
(vf)
где Vf — изменяющийся во времени объем жидкой фазы.
Теплосодержание твердой фазы равно
Qs = 9Wl2Vs+ J clb(T-Ta)dv. B0)
(Vs)
где Vs — переменный объем твердой фазы.
ПОЛЕ ПРИ ИЗМЕНЕНИИ АГРЕГАТНОГО СОСТОЯНИЯ ТЕЛА
431
С помощью равенства
4- (Qs + Q/ + Qm) = o,. B1)
ах
где Qln — тепло, отданное фиксированным объемом V = Vs + Vy = const,
нетрудно получить для малого объема вблизи границы фазового
перехода, используя малость интегральных членов, условие G) § 1, т. е.
обычное условие затвердевания, которое будет иметь вид
h~~Tx—-l*-^--~9W^ir,- B2)
Применяя аналогичный способ расчета, Л. С. Лейбензон получил
следующую формулу для полного затвердевания (т = хт)
неограниченной пластины толщиной 2R, противоположные поверхности которой
охлаждаются и поддерживаются при температуре Тс, меньшей, чем
температура замерзания:
= дчрт, + е) B3)
где
\><-=^-с2Ъ(Т0-Т3) + ±с1Ь(Т3-Тс). B4)
Аналогичные формулы им были получены для цилиндра и шара;
они отличаются от соответствующих формул A4) и A7) добавочными
членами, учитывающими влияние теплосодержания жидкости и льда на
процесс затвердевания1).
Задача о промерзании грунта является задачей о сопряжении двух
температурных полей со специальным условием на границе раздела.
Возможен иной приближенный метод решения этой задачи, когда
рассматривают лишь одно температурное поле в промерзшей части грунта,
а влияние талой зоны учитывается посредством введения теплового
потока внизу фронта промерзания. Этот метод получил применение при
расчете сезонного промерзания грунта. При этсм оказалось, что
влияние нижнего (талого) температурного поля на верхнее (промерзшее)
невелико, и поэтому в расчет может быть введено приближенное
значение величины теплового потока, кроме тсго, еще усредненное за весь
период промерзания. В обстоятельной работе В. С. Лукьянова [39]
предложена расчетная формула для определения глубины промерзания,
по которой были М. Д. Головко [46] составлены номограммы. Формула
достаточно проста и надежна в смысле совпадения результатов
расчета с данными наблюдений.
§ 3. ЗАТВЕРДЕВАНИЕ МЕТАЛЛА ПРИ ЗАВИСИМОСТИ
КОЭФФИЦИЕНТА ТЕПЛОПРОВОДНОСТИ И ТЕПЛОЕМКОСТИ
ОТ ТЕМПЕРАТУРЫ
Расчет скоростей продвижения фронта кристаллизации
металлического слитка или оттаивания промерзшего грунта обычно ведется при
постоянных значениях всех теплофизических характеристик материала
*) Следует заметить, что сильное изменение ^ при фазовом переходе может вызвать
смещение и деформации в обеих фазах. В этом случае задача усложняется, так как
в уравнениях появляются конвективные члены.
432
Глава двенадцатая
Точность получаемых при этом результатов можно оценить лишь на
основе более общих решений. Такое решение для линейной зависимости
коэффициентов переноса температуры было получено Б. Я- Любовым
[48]. Использованная им методика нахождения решения посредством
рядов достаточно проста и может быть использована как для решения
других подобных задач переноса с подвижными границами, так и для
решения задач с более общими граничными условиями или более
сложной зависимостью коэффициентов переноса от температуры.
Предположим, что прогрев зоны материала, претерпевшей фазовое
превращение, отсутствует, а температура материала зависит лишь от
расположения поверхности фазового превращения и от времени. В этом
случае уравнение, описывающее изменение температуры в зоне,
претерпевшей фазовое превращение (например, в затвердевшей корочке
металла), имеет вид
t (x, 0) = tф при х > 0;
t@, z) = t0, B)
где /ф — температура, соответствующая фазовому превращению; в
частности для затвердевания слитка — это температура кристаллизации
металла (°С), t0 — температура поверхности материала (°С).
На фронте фазового превращения х = у(%), где у{ъ) — координата
фронта фазового превращения,
t[y(*)> *] = *Ф. C)
Из уравнения теплового баланса определяется закон изменения
фронта фазового превращения:
ду _ К + ^Ф ( dt\ до
д% Р7 \дх )х=у{т)
где р — теплота фазового превращения.
Если обозначить
^-Х0 + * ——; c==c0+v —; а = —, E)
Z Z Q .у
* (*ф — 'о) . _ . V (*Ф — ^о) . . __ 2Р ,fiv
-т^г('-^)- <7>
то уравнение A) совместно с условиями B) — D) перепишется так:
0+*«>£ = « ж[о+^й ^
6@, ,) = -!; вЦ,(х), х] = 1; ^=^A+в1)(^)я_К1). (9)
Посредством подстановок
ПОЛЕ ПРИ ИЗМЕНЕНИИ АГРЕГАТНОГО СОСТОЯНИЯ ТЕЛА
433
последнее уравнение преобразуется в обыкновенное дифференциальное
уравнение
' [A+^6)^] 4-1A+а26)^- = 0 A1)
с условиями
6@) = -1; в(р) = 1; A2)
е =—(fl • <13>
Если в A1) и A3) положить <*.,_ = <х2 = 0, то задача будет сведена к
задаче с постоянными коэффициентами, когда величины этих
коэффициентов приняты равными среднему арифметическому из их значений
для /ф и t0. Решение ее имеет вид
е = 2 erf(e/V2)_la A4)
erf (p/l/2)
Условие же A3) при ах = а2 = 0 приводит к уравнению
erf (P//2) ехр[ |-]р/= *^-, A5)
определяющему значение р.
Решение уравнения A1) ищем в форме ряда
61
dnd\ (8 — р)я
«•-SSL-4?- <16)
... - «-*
Значения — при I — р и для я > 1 найдем последовательным диффе-
d£n
ренцированием уравнения A1), а при п = 1 из условия A3)
'd^ P /; A7)
£Й Д==? 1 + Ч
^1 =-Р2|Гт\^' + 7ТТ^^1; <18>
<й2 /e=p L (! + <*iJ (I + °iK J
\dS"/W> A + «lJ L A + <*lK d+«lL (l+«lM J''
A9)
(d*b\ = g2 Г 3A+а,)« . 6at + 4at a2 - 2a2 Л __
V л* Л-э L (i+«iK (i + «iL J
_ М ГС+а2J ; , (l+a2)(lla1 + 7a1a2-4a2) 2
p L(i+«iL (i + «iM
1 B5ax + 18aia2 — 7a2) .3 15al -4 /2Q\
(l+«l)8 (l+«lO J
и т. д.
Согласно первому условию A2) запишем
-i = |v-iw^ .£-. BD
434
(dnQ \
1 , после некоторых
преобразований найдем ряд для определения р.-:
/ L3(l+«i) 2A + оцJ J Ll5(l- + ai)a
''+^'1+р*[-
12A + ^K ' 2 (!+«!)* J J k L 105A -botiK
5«1 + 4o£1a2— a2 . _j_ ai ;2~| , _ Q8 [ A + cc2K ^
I A + аг) C1«i + 22aiQc2 — 9a2) • j at A9«! -f 15?ia2 — 4a2) ,2 ,
180 A + aiL ] "^ 30 A -f «0* 7
5;
3]+... . B2)
8A faxN'
Можно показать, что при ax = a2 == 0 ряд B2) переходит в ряд,
который можно получить из A3) [48]. Зная р, по выражению A6) можно
найти значения 8(E) для различных значений £ и определить из графика
этой зависимости изменения температуры во времени для различных
координатных точек. Скорость продвижения фронта фазового
превращения определится по формуле
i£ = p!T. B3)
d-z у 2т
Среди других методов решения аналогичных уравнений в последнее
время получил распространение интегральный метод [15].
ТЕПЛОПРОВОДНОСТЬ ПРИ ПЕРЕМЕННЫХ
КОЭФФИЦИЕНТАХ ПЕРЕНОСА
13
Значения коэффициентов переноса и термодинамических
характеристик материала или среды, вообще говоря, могут быть различными для
разных точек тела. С изменением потенциалов переноса они
претерпевают иногда существенное изменение. Решение большого количества
вопросов в области науки и техники может быть значительно уточнено
путем введения поправок, возникающих в связи с переменным
характером коэффициентов. Необходимость проведения такой работы
особенно остро стала сказываться в связи с широким внедрением в различные
отрасли техники высокоинтенсивных процессов. Отметим также, что
путем соответствующих подстановок многие задачи конвективной
диффузии и теплопроводности, гидродинамики вязкой жидкости и другие
могут быть сведены к дифференциальным уравнениям типа
теплопроводности с переменными коэффициентами. Это указывает на
необходимость накопления и обобщения полученных результатов решения
неоднородных и нелинейных уравнений теплопроводности, а также
дальнейшего развития методов решения этих уравнений.
В ходе процесса материал в той или иной степени изменяет свои
структурные свойства. Когда свойства тела меняются по координате
незначительно или самым беспорядочным образом, допустимо при
исследовании явлений переноса соответствующие коэффициенты и
термодинамические характеристики принимать постоянными и равными
средним эффективным их значениям. Однако в ряде случаев неоднородность
физических свойств оказывается столь значительной, а изменение их
по координате столь закономерным, что пренебрегать ею недопустимо.
Последнее вынуждает нас переходить от решения дифференциальных
уравнений переноса с . постоянными коэффициентами к решению
уравнений, где все или отдельные коэффициенты являются в конечном
счете функцией координат.
Решение дифференциального уравнения теплопроводности с
переменными коэффициентами связано с большими трудностями. Поэтому
точное аналитическое решение удалось получить в настоящее время для
весьма ограниченного круга задач. В этой связи первостепенной
задачей, стоящей перед аналитической теорией теплопроводности, является
разработка методов решения дифференциального уравнения
теплопроводности с переменными коэффициентами.
436
Глава тринадцатая
§ 1. ПОЛУОГРАНИЧЕННОЕ ТЕЛО. ТЕПЛОПРОВОДНОСТЬ
И ТЕПЛОЕМКОСТЬ — СТЕПЕННЫЕ ФУНКЦИИ КООРДИНАТ
Рассмотрим в основном методику решения одномерного
дифференциального уравнения теплопроводности:
Краевые условия следующие
)уюи
сч— = — X — .
Eт дх \ дх J
ще\
Т(х, 0) = 0, @< х< оо),
Г(оо,т) = 0, Т@, т) = Гс.
0)
B)
C)
1. Пусть с\ = const; коэффициент теплопроводности X зависит от
координаты следующим образом:
\ = \х«. D)
Применим к уравнению A) преобразование Лапласа; тогда с учетом
B) и D) получим
xnfL(x, s) + nx"-1 TL(x, s) — —TL(x, s) - 0, E)
где а0 -= \/c^.
Подстановкой I == kxm уравнение E) сводится к уравнению
d2Tr dTr о
тЧ2х2гп+п-2 _£. + m (m + п _ 1) kxm+n~2 -± — -£- TL - 0. F)
В использованной подстановке кит были выбраны произвольно;
потребуем теперь от них выполнения условий
2т + л —2 = 0, А=1.
Тогда F) преобразуется в уравнение типа уравнения Бесселя:
d2TL п 1 dTL
dp i 2 — /г g d£
Частными решениями его являются
B-яJ «о
TL =0.
67, g
>—л К а0]'
г /с, е
2 — п
где /v и i^v—функции Бесселя от мнимого аргумента первого и
второго родов v-ro порядка; v = 0~2~; п — любое число, не равное 2.
2 — п
2 — п
~~2~
Возвращаясь по соотношению 6 = х к первоначальной переменной х,
получим
—V-\
— п у а0 / )
4-A-я) / i-4-n
*2 /Cv * 2
ТЕПЛОПРОВОДНОСТЬ ПРИ ПЕРЕМ. КОЭФФИЦИЕНТАХ ПЕРЕНОСА 437
В большинстве случаев п меньше единицы (/г< 1).
Первое решение не удовлетворяет первому условию C); поэтому
решение уравнения E) берем в виде
где А — постоянная относительно х, определяемая из второго гранич-
т
ного условия C); при х->0 Tl (x, s) ->- —-, а при z-> 0 zv /С (z)->2v~1r(v),
где v>0; Г (v) — гамма-функция. Поэтому постоянная А равна
А = 2Тс ( s Y2
Следовательно, решение для изображения будет иметь вид
тих, s)=tc 2xVAl-n) (^-Y2 к, (sv-iii/z) •
(8)
Пользуясь таблицей изображений, получаем из (8) решение для
оригинала:
Ы/# -.
du
г (у, X)
T(v)
где Г (v, X) — некоторая гамма-функция,
X =
B — nJa0z
Задачи с ненулевыми начальными условиями и для ограниченного
тела (O^x^R) могут быть решены аналогичным путем. Для случая
п == 2 решением уравнения E) будет
x[-l±Vl+*s/a0]/2
2. Если теплоемкость и теплопроводность зависят от
координаты в степени п:
с = с0хп, X = \0хп, ^ = const, (9)
то после применения преобразования Лапласа с учетом начального
условия B) и законов изменения коэффициентов (9) получим
rL(x, s) + -^T'L(x, s)-^TL(*, s) = 0, A0)
где
Решениями этого уравнения являются
x4\Vix)>x*K\Vix)'
где
v = 4-(l-n).
438
Глава тринадцатая
С учетом первого граничного условия C), как и в предыдущей задаче,
получим
TL(x, s) - Ах* К, [Yi-X ) • (п)
Удовлетворяя это выражение второму граничному условию C),
найдем, что
Тс / s \У2
s2v-1r (v) \ а0
А =
Следовательно, решением уравнения A0) является
S V/2
TL (х, s) = Тс
К,
(Vi-)-
Оригиналом этого решения будет
rw
где
X =
Aa0z
3. Если теплоемкость и коэффициент тепло проводности
подчиняются уравнениям
су = с0ч0хт, X = \хпу То = const (m < — 1),
то после применения преобразования Лапласа получим следующее
уравнение в изображениях:
rL(x,s)+^rL(x,s):
S
:яЬ«-Ъ (*, s) = 0.
Решения этого уравнения, аналогичные решениям задачи в первом
случае, имеют вид
х
где
i v
2х :
(т — п+2)
1т-
■п + 2
г а0
х 2 К,
~ (m—л+2)
2* 2
т—п+2
V,
S
«о J
1— л
т—п-\-2
Отметим, что решения для тел цилиндрической и сферической форм
с коэффициентами с, 1 и у, являющимися степенными функциями
координат, включаются как частные случаи в последнюю из
рассмотренных задач. Например, уравнение в изображениях для шара имеет вид
п
п+2
а0
TL=0,
т. е. в этом случае постоянные пят увеличиваются на две единицы.
Физический смысл условия п < 1 заключается в отсутствии
бесконечно большого теплового сопротивления сколь угодно малого^ участка
вблизи х = 0. В цротивном случае было бы невозможно
удовлетворить граничным условиям при х=0. Точно так же при т<^—1 из-за
бесконечной теплоемкости участка вблизи х=--0 невозможно
удовлетворить в этой точке граничным условиям.
ТЕПЛОПРОВОДНОСТЬ ПРИ ПЕРЕМ. КОЭФФИЦИЕНТАХ ПЕРЕНОСА 439
Частным случаем рассмотренных задач являются задачи с линейным
законом изменения коэффициентов от координаты. Путем
соответствующей подстановки их можно свести к частному виду уже
рассмотренных решений. Так, в случае су = const, ^ = Х0 A -f ах) вводится
новая переменная £ = 1+а#. В этом случае получим уравнение
d2Tr 1 dTT s m
d& ^ g dt
которое при n = 1 тождественно уравнению E). Его решениями
поэтому будут
Таким же образом можно показать, что в случае, если с = с0 A+ал;),
^ = \>A + ах)> т = const, решениями уравнения в изображениях
являются
В более общем случае, когда
с = с0A + ах)т и X = Х0 A +ах)п,
введением новых переменных
6 = A+^)(Я|-я+2)/2,
14
-Ц = ~4Г (т—п+2J т,
1-я
С =
m—я+2
уравнение A) преобразуется в уравнение
Дальнейшая методика не отличается от методики решения первой
задачи. Ряд решений конкретных задач такого типа приведен в
монографиях А. Ф. Чудновского [81]. В частности,, в этих задачах, так же
как и в [47], [36] и других работах, приведены решения ряда задач для
тепловых волн.
§ 2. ОГРАНИЧЕННАЯ ПЛАСТИНА, КОЭФФИЦИЕНТ
ТЕПЛОПРОВОДНОСТИ — ЭКСПОНЕНЦИАЛЬНАЯ ФУНКЦИЯ
КООРДИНАТЫ
Рассмотрим решение уравнения A) § 1 при граничных условиях
первого рода, когда
Х = Х0ехр(—*х), су — const @ < л; <;#;*> 0).
о.)
Пусть
Цх, 0) = 0; B)
7@, г) =ф(х); Т(Я, т) = ф (х). C)
440
Глава тринадцатая
Применим к уравнению A) § 1 и условиям A)—C) преобразование
Лапласа; тогда получим
Т^ (х, s) — х T'L (х, s) ехр(—у.х) TL (x, s)=0, D)
TL@,s) = <fL, TL(R,s) = '<|>L. E)
Подстановка i = — y —exp I-у-(преобразует D) в уравнение
rL(l s) — 4- t'l& s) - T**& s) = °>
решением которого является
Уравнение F) в координатном выражении х запишется так:
TL (х, s) = A ±-У± exp (^) /x [4/t-p [Щ +
F)
+в -Vi -р G?) ъ [4i/v«p Ш
G)
Постоянные относительно координат величины Л и В найдем, используя
граничные условия E). После выполнения ряда преобразований
получим
s
а0
%"J/a0
2
+
L *V4)
(-)
4--(-)/t)-^/'(-/?)J-(-).x
X
x/U^-expf-^-
Выражение (8) является решением рассматриваемой задачи в
изображениях.
Оригинал решения (8) можно получить по формуле обратного
преобразования:
a-J-f'oo
т (*• т) = W J Г£ (*' s) ехр (s х) ds' (9)
а—too
где интегрирование ведется вдоль любой прямой, параллельной мнимой
оси плоскости комплексного переменного s, проходящей правее всех
особых значений подынтегрального выражения.
Вычислим контурный интеграл (9) при следующих условиях E):
Ф£ = 0, ^ -
тс
A0)
ТЕПЛОПРОВОДНОСТЬ ПРИ ПЕРЕМ. КОЭФФИЦИЕНТАХ ПЕРЕНОСА 441
что соответствует граничным условиям
Г@,т) = 0, Г(#,т) =7с. (И)
После небольших преобразований выражение (9) -перепишется с учетом
A0) в следующем виде:
a-\-ico
Hh(Vi)'-(^
„, v Г<= \ 6ХР | 2 - -' || -* \ * V «о / - \ * V °о
Т (X, х) = 2^"
*l4-/i)"D-/i^)-
-'.(-ИЛЬМ-!-/-^)
-^PM-ds. A2)
Вычисление этого интеграла дает следующий результат:
Л Т(х, т) exp(xx)—1 Г х , _ч~| ч,
х 5]Т"^ 2г"еХР ТД К [ «*• ехр И Fl <*•> -
^x(l*«)Vi[ !*„ ехр [^-)]} ехр [ - ^- [# ] . A3)
[рактеристического уравнения
фехрЩ _К1[,ехрD)]
где [хя — корни характеристического уравнения
A4)
JiM Y± (fx)
В стационарном состоянии (т-> с») решение A3) принимает вид
~,, ~ ехР (ХЛ:)~— 1
Г (*, оо) = Тс ' , . A5)
v ' с ехр (х#)—1 v ;
Ряд решений других задач с экспоненциальной зависимостью
коэффициентов переноса от координаты, в частности для тепловых волн,
приведен в работах [36, 81].
§ 3. ЛИНЕАРИЗАЦИЯ НЕЛИНЕЙНОГО УРАВНЕНИЯ
ТЕПЛОПРОВОДНОСТИ
В высокоинтенсивных процессах температура претерпевает
значительные изменения за малые промежутки времени, например, при тепловом
взрыве, химических превращениях и других явлениях. Описание
явлений переноса, протекающих в большом интервале изменения
температуры, связано с необходимостью учитывать зависимость коэффициентов
переноса от температуры. В этих условиях поток тепла становится
442
Глава тринадцатая
нелинейным, а для определения поля температуры необходимо решить
дифференциальное уравнение переноса
дТ
с(ТЫТ) -^- = div [X (Г) grad T]. A)
Решение уравнения A) при соответствующих краевых условиях
связано с еще большими трудностями, чем решение задач, в которых
коэффициенты зависят от координат, поэтому здесь широко
используются различные приближенные методы. Весьма полный обзор состояния
проблемы решения нелинейных уравнений переноса дали Н. Фридман
[97] и Дж. Кранк [94], к работам которых мы отсылаем
интересующихся читателей.
Для решения проблемы нелинейного переноса тепла в настоящее
время используется ряд методов. Так, в методе линеаризации,
основанном на аппроксимации нелинейного коэффициента, специально
подбирается новая зависимость коэффициента, при которой уравнение A)
становится линейным [13]; в различных методах подстановок вводятся
новые переменные, которые позволяют преобразовать нелинейное
уравнение в частных производных к обыкновенному нелинейному уравнению
в полных производных (см. [47] и др.), решение которого является
более простой задачей. Существуют и некоторые другие методы решения
нелинейного уравнения переноса, например приведенные в работе [113]
и др Покажем методику применения отдельных методов к решению
вопроса нелинейного переноса тепла.
Обычно коэффициент теплопроводности на графиках выражается ела
бо растущей кривей X = ХG"), которую с достаточно высокой точностью
можно представить линейной или экспоненциальной зависимостью.
И. А. Чарный предложил [79] для этого случая два способа
линеаризации уравнения переноса при условии су = const.
Уравнение (!) можно переписать в следующем виде:
дТ dl Г дТ 1
СТ Ж.-gr = div [X (Г) -я- grad X J . B)
Если в уравнении B) положить
X ~^~ = А= const, -0^- = В = const, C)
то получим линейное уравнение с постоянными коэффициентами.
Первое условие C) соответствует экспоненциальному виду кривой ЦТ):
Л- InVx. '
а второе — ее линейной аппроксимации
В = ^i—^о
Xi—Х0
Легко видеть, что условия C) противоречивы, за исключением
случая X = const. Поэтому можно предполагать, что точно выполняется
лишь одно из них, а в другом величину А или В следует заменить ее
средним значением в рассматриваемом интервале температур. Можно
обе эти величины А и В заменить их средними значениями в данном
интервале температур. ,
ТЕПЛОПРОВОДНОСТЬ ПРИ ПЕРЕМ. КОЭФФИЦИЕНТАХ ПЕРЕНОСА 443
Другой способ линеаризации состоит во введении новой функции
т
G = J X {Г) dT',
То
которая преобразует уравнение A) в уравнение
Если в уравнении D) положить
ОТ ,
~— ~ const,
то также получится линейное уравнение. Эта аппроксимация
предполагает, что некоторый участок кривой G = G(T) заменяется
соответствующим образом проведенной хордой.
Возможность линеаризации одномерного уравнения переноса для
условий, когда скорость переноса тепла через ограничивающую
поверхность (х = 0) является известной функцией времени ср(т), а коэффициент
теплопроводности описывается соотношением
X-v2 = x-v,[l +а(Г-Г0)], E)
была показана М. Штормом [116]. В этом случае соотношение E)
служит аппроксимацией при рассмотрении задач с экспоненциальной
зависимостью коэффициента X от температуры:
Х = Х0ехр[-2а(Г0—Г)],
где а == const, а Х0 соответствует значению Т0. Посредством
подстановок
- J X-Va dxr, i] ■= J УцТ^йГ
одномерное уравнение A) превращается в линейное уравнение
где
1 "
[Q0 О) — — 71.
* Xn/a [
Шторм использовал этот метод для решения задачи о нестационарном
распределении температуры в полуограниченной среде при постоянной
скорости переноса через поверхность х=0.
В заключение следует остановиться еще раз на одном способе
линеаризации нелинейного уравнения теплопроводности, предложенном
О- Видебургом [119]. Рассмотрим одномерное уравнение A) при
условии линейной зависимости коэффициента теплопроводности от
температуры Х = Х0A +<хТ). В этом случае уравнение A) можно переписать
так:
«- = -«-[„(i-M^l. W
444
Глава тринадцатая
или
UL - a *L Л- ^L д2Т2 /А \
ах ~" а°дх* ~г 2 дх* ' v°aJ
где
а = —о_ — const.
Запишем краевые условия в следующем виде:
Т(х, 0) = Т0; @<х< + оо),
При постоянном значении коэффициента температуропроводности
(точнее теплопроводности) а (Г) = а0 (си = 0) решение этого уравнения
известно и определяется соотношением
{Г}а = 0==Г°ег!("^г)- ■ G)
О. Видебург предлагает для линеаризации исходного нелинейного
уравнения F) в слагаемом, содержащем а, положить такое значение
температуры, которое соответствовало бы выражению этой температуры при
а = 0, т. е. решению G). Путем такой замены вместо нелинейного
уравнения F) получаем линейное дифференциальное уравнение с
источником, зависящим от координаты и времени:
дТ _ д2Т , °^о д2
дт ^а° дх* +а° 2 дх*
erf
2|/ а0х
(8)
Аргументом функции Гаусса является I = 7 . Если в толь-
2 "|/а0х
ко что написанное уравнение ввести новую переменную, равную 5,
получим обыкновенное дифференциальное уравнение в полных
производных:
ае2 ' * ds 2 de
с условиями
Г - 0 при I = 0; Т = 7 при £ == + оо. (9)
Решение последнего уравнения будем искать в виде
Г = ф1F) + ф,(Е)ФE),
где в целях сокращения записи обозначим Ф (I) = erfc ($). Легко
убедиться подстановкой, что функции <рх и фа определяются уравнениями
^L-__m^l. d?» ЛФ __ «rg dHl-Ф)* nny
d8 ~ ф d5 ' d£ dS ~ 2 d? ' { }
Решая уравнение A0), получаем
■2-1-Ф _
ф1(|) = Л + *Т% Е«ф + a7g 1=* _ ^ S ехр ( - Е2) -
ТЕПЛОПРОВОДНОСТЬ ПРИ ПЕРЕМ. КОЭФФИЦИЕНТАХ ПЕРЕНОСА 445
-aTg6»0»-aTgi=*! + 2аЦ -£= \ ехр ( - £») + ^ [1 -
-ехр(-2£2)]+-^-Ф2; ■
ф2 (?) = В - аЦ £» + аГ* ^ Ф + аГ2 1=1* - ^ ехр (_5«)_а7^Ф«.
"|/ ТС
Следовательно,
Т = А + ВФ — -^[1—ф] g ехр (—£2) + — [1— ехр (—2£2)]—^ Ф2,
у % те ^
где Л и В — постоянные относительно 8. Удовлетворяя полученное
решение краевым условиям (9), находим
Совершенно аналогичным образом можно получить решение
уравнения F) при условиях
T{x,0) = Tlt 0<x<+ оо,
Т(х, 0) = 72, — оо < дс < 0, (Г, > 7\),
дГ (± оо , т) _ ^
Используя при a = 0 решение
находим
T = A + B<b + aTl (T*~Tl) I ехр (—12)+ а(Г2 "llJ Ф £ ехр (-I2) *
2 |/ it 4 У тс
+ аG\-;Г1J [1 - ехр (-2$2)] - а G\~Г1J A - Ф + Ф») -
где
тТгфг-Тг) A_ф)>
Л_ у1 + _ ___ +—j
д_ Ту-ту a GW4)» ^i (?Wi)
Следует заметить, что, преобразуя только выражение для Г, нельзя
добиться точной линеаризации при a^const. Из рассмотренных здесь
задач только в методе Шторма получена точная линеаризация при a=^const
путем введения преобразования координат, зависящего от Т (через X),
Некоторые другие методы линеаризации приведены в работе Н.
Фридмана [97].
446
Глава тринадцатая
§ 4. ПРЕОБРАЗОВАНИЯ, ИСПОЛЬЗУЕМЫЕ ПРИ РЕШЕНИИ
НЕЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПЕРЕНОСА
Точное или приближенное (в том числе численное) решение
нелинейных дифференциальных уравнений значительно упрощается, если
преобразовать его в обыкновенное нелинейное дифференциальное
уравнение. Эффективность некоторых таких, преобразований была показана
при рассмотрении вопроса о линеаризации нелинейного уравнения.
Остановимся теперь на этом более подробно.
1. Рассмотрим одномерное дифференциальное уравнение
теплопроводности'.
с(тыт)^^4г[нт)^^-]- О)
Для определения некоторых подстановок можно воспользоваться
методом теории обобщенных переменных.
Из соображений размерности величин, входящих в A), следует, что
это уравнение остается неизменным, если масштаб длины изменить в k
раз, а масштаб времени в k2 раз. При таком изменении масштабов
краевые условия
Т (*, 0) = Т0, B)
Г@, т) = Тс C)
также остаются неизменными, т. е.
T(x1z)~T(kxy k4)
при любых значениях х, х и k. Положим k = —— ; тогда получим
где Г* берется при некотором фиксированном значении Т,
Таким образом, Т зависит только от аргумента £.- Поэтому можно
попытаться искать решение задачи от такой комбинации переменных £ и
т, которая оставалась бы неизменной при подобном преобразовании.
Имеем
dT _ xT* df __ г* 8 df
__ j^*
d% 4 jA3 d£ 2т dk '
dx ~~~~ 2 |ЛГ ^ ' dx \ dx ) ~ dx { 2 УТ d4)~~~ Ax ' dt[ dk
Подставляя полученные соотношения в уравнение A), находим для Т
уравнение в полных производных:
-**#--*[ч/>£]. <«
Краевые условия' B) и C) примут следующий вид:
/(оо) = Г„ /@) = ГС.
ТЕПЛОПРОВОДНОСТЬ ПРИ ПЕРЕМ. КОЭФФИЦИЕНТАХ ПЕРЕНОСА 447
Функция / в тех случаях, когда ее не удастся вычислить
аналитически, мсжет быть найдена при помощи численного интегрирования.
Подстановку £ = ——=.' иногда называют преобразованием Больцмана,
2 у т
который использовал ее в 1894 г. [89] для решения уравнения A).
Подстановку D) можно применять к уравнению A), когда явления
переноса происходят в неограниченной и полуограниченной средах. Только
в этом случае удается так разделить переменные, чтсбы граничные
условия зависели только от одной переменной £. В частности,
подстановку D) нельзя использовать для ограниченного тела толщиной R и с
граничными условиями
Г@,.т)=Гс, Г(Я,т)=То
ибо аргумент во втором условии после преобразования D) становится
отличным от нуля и зависит от т.
В качестве примера использования рассмотренной подстановки
решим уравнение A) для полуограниченного тела (т>0, 0<л;<оо) со
следующими краевыми условиями:
Т (х, 0) =.- Го, Т (О, <с) = ТС9 дТ{^ т) = 0. F)
Пусть k — 11у~, в этом случае £ = —— . Тогда будем иметь
S „ дТ д [, дТ\ /7Ч
2 "' д% й! й
. — Т'. тпгп
Обозначим -^f".= Tr\ тогда уравнение G) можно написать так:
Отсюда получим
£_ Jfc_ __ d(\Tf)
2 СТ X ~~ XT' •
1п(ХГ)--ст|-^-+1п'Л,
или
5
XT' - Л ехр [— ctJ-2T~ Ws ] *
о
При дальнейшем интегрировании находим
r = ^Jexp[-qrJ^r-d5]-4-+B.
о о
Постоянные Л и 5 определяются из граничных условий F). Решение в
окончательной форме имеет вид
(8)
Тс—Т(х, т)
~" Тс-Т0
5
jexp[
0
00
Jexp
0
V
С
0
— сТ \
6
1 - £ d^
2Х =й" J
-4-«"
dkf
X
448
Глава тринадцатая
Соотношение (8) не является явным выражением для решения, а
представляет собой нелинейное интегральное уравнение, поскольку в его
правую часть входит Т.
Покажем один из возможных способов расчета нестационарного
поля температуры б методом итерации. Сущность метода итерации
состоит в том, что если известно первое приближенное решение
уравнения
8 = ф(Т),
равное 0О, то, подставляя его в первоначальное уравнение, находим
второе приближение 6Х = <p(Q0)- Подставляя 6Х в уравнение, находим
третье приближение б2 и т. д. Повторяя этот процесс несколько раз,
можно получить решение с любой наперед заданной степенью точности.
Для упрощения положим су = const; тогда (8) можно переписать в
следующем виде:
А — Ус—Г(х,т) __ j) о /Qx
и ~ Т Т„ ~~ со т] » W/
df\
о о
где
\* =-±- = 'к* @). (Ю)
К
Здесь т| = —= , а0 = —— (Х0 соответствует начальному значе-
2уа0ъ с1
нию температуры Т0).
При постоянном значении коэффициента теплопроводности (Х=Х0=
=const) соотношение (9) переходит в решение
6 = erf YJ, A1)
которое является первым приближением для начала расчета.
Используя A1) для равных интервалов изменения yj, найдем
соответствующее им значение 60. Следует при этом иметь в виду, что уже при
71 = 3,0 с точностью до пятого десятичного знака erf irj = 1 и,
следовательно, в материале устанавливается стационарное распределение
температуры. Тем самым определяется целесообразный интервал изменения ч\.
Для каждого из найденных значений 0О оцениваются значения X*
по формуле A0). Подставляя эти значения в (9), по любым формулам
численного интегрирования (если интегрирование нельзя осуществить
непосредственно) определяем для выбранных г\ новые значения 6Х.
После этого процедура расчета повторяется снова для получения
приближений ва, 63,... до тех пор, пока отличие между следующими друг за
другом приближениями не даст результата с интересующей нас
точностью.
Это соответствует приближенному интегрированию методом
прямоугольника. Применение других методов аналогично.
2. Для численных расчетов нелинейного уравнения переноса A) на
электронносчетных машинах или аналоговых моделях желательно
уравнению A) придать другой вид. В этом случае целесообразно
использовать подстановку
I Т I
A2)
ТЕПЛОПРОВОДНОСТЬ ПРИ ПЕРЕМ. КОЭФФИЦИЕНТАХ ПЕРЕНОСА 449
которая преобразовывает уравнение A) в уравнение
0G
дх
= a(G)v2G, A3)
где a(G) = X(G)/c(G)y(G). Отметим здесь, что уравнение A3) имеет
самостоятельное значение в гидро-аэродинамике. Его решение при
соответствующих граничных условиях получается в виде зависимости
функции G от координат и времени. Соответствие между G и
температурой Т устанавливается соотношением A2), которое может быть выра
жено либо в явном виде (когда возможно проинтегрировать выражение),
либо в виде графика (при необходимости численного интегрирования).
Для ряда материалов или сред зависимость интегральной
проводимости и объемной теплоемкости от температуры, получаемая по
формуле A2), хорошо аппроксимируется показательным законом
т т
Щ^£Г' = <х7\ J3&p &T = рр», A4)
о о
f
где Х0, у0, с0, а, п, C и m — постоянные. Например, интегральные
теплопроводности и объемные теплоемкости для чистого алюминия и
железа в широком интервале температур описываются соотношениями
A4) и имеют следующие значения:
алюминий —а = 1,57; п = 0,905; р = 0,871; т = 1,03;
железо — а = 2,04; п = 0,84 ; C = 0,561; /и = 1,125.
Преобразование A2) можно обобщить также на переменный
коэффициент теплоемкости.
Преобразованное уравнение теплопроводности примет тогда вид
о о
Н. Фридман решил [97, 98] это уравнение при условиях
Т(х, 0) = Г(оо, т) = 0, Т @, т) - Тх
и с учетом зависимости A4). Для аппроксимации уравнения второго
порядка решение имеет вид
р7гГ=erfc*~4s (т(Е' -4-) (erfc?J-lyrехр (_|2) х
' х (5 erfc ?— —~ ехр (—S2) 1 + -1- ¥ erfc I + A + erfc %) X
х [-1= ехр (-I2) - I erfc 5 + -УA + 2S2) erfc? - -1= \ ехр ( - S2)Y| -
- (-т +-зг) <** * Ь A5)
ч 4 ' 2тт
где
ho a n
£ = ^ ftmn—\V $ s = I — m/n; k = - —. . _
15 Заказ № 640
450
Глава тринадцатая
Максимальное отклонение результата расчета по формуле A5) от
расчета с учетом последующей аппроксимации не превышает 3% E°С).
Аналогичные решения были получены для линейного характера
изменения коэффициентов \ и с от температуры Т как для
полуограниченной, так и для ограниченной среды [30, 97]. Сравнение полученных
результатов с точными решениями во всех случаях дало хорошее
совпадение.
3. Рассмотрим теперь ряд специальных подстановок, используемых
при решении нелинейных уравнений переноса, когда коэффициенты
проводимости линейно или экспоненциально зависят от температуры.
Если принять су = const, то уравнение A) можно переписать в
следующем виде:
дТ
ах
д Г ™ дТ 1
A6)
где
а(Г) = ^-ХG)
Рассмотрим неограниченную среду. Пусть потенциалы
переноса тепла (температура) удовлетворяют начальным условиям
Т(х,0) = Тг при х<0, A7)
Т(х, 0) = Т2 при х>0, A8)
а коэффициент температуропроводности а(Т) является линейной
функцией температуры:
а
ч
1+4-«G\ + Г2)-а:Г
]■
Здесь а соответствует значению коэффициента а при среднем значении
температуры Т = -к- G\ + Т2). Используя подстановки
ф =
1 + ^-а(Тг + Т2)-аТ
i + Y«(Ti- т*)
2\\+-ja{Tx-
Тг)
]'"<•
У
уравнение A6) можно преобразовать в уравнение
с граничными условиями
где
при
при
1
? = +оо,
£ = —оо,
ь =
1— aGV
2 V X
■Тг)
1 + — а (Г!-Г,)
A9)
ТЕПЛОПРОВОДНОСТЬ ПРИ ПЕРЕМ. КОЭФФИЦИЕНТАХ ПЕРЕНОСА 451
Численное решение уравнения A9) получил Р. Стоке [115].
Тот же случай линейной зависимости коэффициента
температуропроводности
т
а = а0
То
был рассмотрен П. Я. Полубариновой-Кочиной [62].
Действительно, для полуограниченной среды с условиями
Г@, т) = Г0, Т(х,0) = 0
путем подстановки
2(а0т)^
уравнение A6) преобразовывается в уравнение
Здесь 6 = Т/Т0. Дальнейшее упрощение уравнения может быть
достигнуто подстановкой v = б2; тогда B0) принимает вид
d2v . 2S dv = 0
d£2 -J/7 Л
с граничными условиями
v = 1 при 6 = 0,
V = 0 ПрИ £ = оо.
£с./ш в полуограниченной среде, удовлетворяющей условиям
Т(х, 0) = Г0, 7@, т) = Тп, B1)
коэффициент температуропроводности а следует экспоненциальной
зависимости
а = аПехр[ИТ-Тп)]
(индекс «п» характеризует значение параметра на поверхности), то пос*
ле преобразования получим уравнение
, dl \ dt I ds
= 0,
где
2 (On-с)
v.
^ИТ-ТП). B2)
Ввиду условий B1) и B2) интегрирование здесь следует выполнять,
начиная с С = 0 и 5 = 0. Более детальная методика численного
расчета и его результаты, а также и некоторые другие преобразования,
используемые при существовании экспоненциальной зависимости
коэффициента температуропроводности от Т, приведены в монографии [94].
Итерационный метод Ньютона — Канторовича. Имеется много
методов решения общих нелинейных задач. Укажем только итерационный
метод Ньютона — Канторовича [28а], идею которого изложим очень
коротко.
15*
452
Глава тринадцатая
Пусть имеется некоторое приближенное решение нелинейного
уравнения
и (л:, у, ..., т). B3)
Представим следующее приближение в виде и + аЪи. Подставим его в
уравнение (и в краевые, начальные или другие условия) и разложим
в ряд по а, сохранив только линейные члены. Тогда относительно аЬи
получится новое уравнение с коэффициентами, зависящими только от
независимых переменных.
Разрешив это уравнение, возьмем в качестве исходного приближения
(и + аЬи) и повторим процесс. Особенностью метода Ньютона является
чрезвычайно быстрая в отдельных случаях сходимость, так что обычно
применяют не более двух-трех итераций. Оценка погрешности в этом
случае имеет вид ~q2 при некотором |<7|<1 вместо qk при обычных
итерациях. Следовательно, сходимость действительно очень быстрая.
В оценке q при этом участвуют вторые производные от коэффициентов
в уравнении и граничных условиях по неизвестной величине и юценка
для общего решения линейных задач в промежуточных приближениях.
Повышение точности достигается за счет того, что на каждом шаге
ставится новая, уточненная линейная задача (а не учитываются только
неоднородные члены линейного уравнения).
В случае, если вторые производные коэффициентов не существуют
(или очень велики), метод Ньютона теряет свое преимущество.
Следует заметить, что при решении общих линейных задач,
получающихся на каждом шаге метода Ньютона, приходится применять
различные приближенные методы. Поэтому применение метода для
эволюционных, нестационарных задач не всегда рационально, поскольку при
приближенном решении по шагам имеется возможность вносить
поправки на нелинейность на каждом шаге. Наиболее перспективно
использование метода Ньютона для краевых задач, например для задач
стационарного и квазистационарного нелинейного переноса, в том числе и в
многомерных областях, особенно если их решать на ЭЦВМ.
В качестве примера запишем схему метода Ньютона для уравнения
E) при с\ = const. Пусть имеется некоторое (исходное или предыдущее)
приближение fk.t; пусть следующее приближение равно
/* = /*-! + «*/*• B4)
В результате подстановки fk в уравнение и сохранения только
членов со степенями а0 и а в разложении Тейлора для поправки получим
уравнение
= -N%+iM/H©)%]- B5)
при краевых условиях
(«8/*)о = Гс-/^@). } ^
В дальнейшем после решения задачи B5), B6) такую же операцию
следует провести для перехода от fk к fk+1 = fk + а8/Л+1 и т. д.
Подробное описание дано в [28а].
ТЕПЛОПРОВОДНОСТЬ ПРИ ПЕРЕМ. КОЭФФИЦИЕНТАХ ПЕРЕНОСА 453
§ 5. НЕКОТОРЫЕ РЕШЕНИЯ НЕЛИНЕЙНЫХ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ ТЕПЛОПРОВОДНОСТИ
На примере ряда решений нелинейных дифференциальных уравнений
теплопроводности покажем влияние нелинейности коэффициентов
переноса на распределение температуры.
1. Пол у огр аниченная среда. Имеем
а (Т) = —~— (я0 f х — постоянные). A)
Краевые условия имеют вид
•Г(*,0) = 0, Г@,т) = Го. B)
Введем новые переменные
в = Г/Го, А(Ь) = а(Т)/а0; i = ^_, C)
2]/ а0т
тогда уравнение A6) § 4 превратится в обыкновенное
дифференциальное уравнение
dt dk L Л J
а краевые условия
Кроме
Введем
того,
B)-
-C) п
6 =
8 =
Л F) =
новую переменную
В
римут вид
0 при % =
1 при £=
= —L_ (a
1—«0 V
q
]'ЛF')<2в'
_ 0
~~ Г"
00,
0.
= ХТ0).
»
D)
E)
J A @) dd
о
и, подставив ее в D), получим
ы А—*» = * F)
1пA—а) ■ ' W
Новая переменная E) превращает ранее полученное дифференциальное
уравнение и краевые условия в уравнение
с условиями
g = Q при 5=оо, (8)
Я = 1 при N0. (9)
р связан с а соотношением р =—InA —а). В настоящем решении X
и а предполагаются положительными и 0<<х<1. Следовательно, р>0.
Введем далее подстановки, определяемые соотношениями
-§- = -<PI exp(-te)/p = ?. A0)
454
Глава тринадцатая
В этом случае уравнение G) примет вид
d2<p __ 2
dq2 р<р
В результате интегрирования последнего уравнения находим
<?/V7 __
lnq+Ct = — J (С, + -L z* 1 lnzY~Vl <fe, A 1)
о
где Cj и С2 — постоянные интегрирования.
Из (8) и A0) следует, что ф-^0 при q-+—£-. Это условие
позволяет определить Сг в уравнении A1). С учетом выражения для Сх
уравнение A1) примет вид
Щд=- ^C2+±z*~j-\nzyhdz. A2)
о
Из условия (9) далее следует
-^- = 0; </ = ехр(-р)/р.
Подставляя эти условия в уравнение A2) и выполняя небольшие
преобразования, получим
c-fta" -tew-
и уравнение A2) с учетом значения С2 запишется так:
lnr = —Waf —jilna?)*^!, /1Q.
где
r = (#I/2f а = Ф/(е]/7), ii = 8/(pe»)
— новые переменные.
Уравнение A3) используется для нахождения р и, следовательно,
неизвестного параметра е как функции от данного параметра р,
определяемого соотношением
1
р = 2 j (а2 — р In иаГ7" da. A4)
о
Соотношение A4) получается из уравнения A3) с учетом условия, что
ф/]/"<7 =е при q= ехр ^ ^ . Интеграл A4) устанавливает связь
между параметрами р и ^. Для определения ц. по заданному р необходимо
численно решить уравнение A4), например, путем приближенного
интегрирования.
Из уравнения G) и последующих условий определяется выражение
для 5 в зависимости от и и г:
ТЕПЛОПРОВОДНОСТЬ ПРИ ПЕРЕМ. КОЭФФИЦИЕНТАХ ПЕРЕНОСА 455
Исключая из него г с помощью уравнения A3), получаем
" и
% = —Кг К — ^1п и2L2 — и] ехр
B(л.) /» ' г
. A5)
С другой стороны, комбинируя второе соотношение A0), уравнения A3)
и г == ф<7I/в, находим выражение для g:
и
£ = yj(«?-l»ln«?r,/'
du-i
С учетом соотношения F) получаем окончательное выражение для 6:
1
1 —ехр (-
1 — ехр —2 J (u\ - v In u\ )"~1/2 йиг
A6)
0,4
Необходимо заметить, что параметр \i в приведенных уравнениях свя
зан с данным параметром C соотношением A4).
Это решение было получено в
работе [99], где указывается, что в|
решение при постоянном значении
коэффициента (а = C = X = 0) прев- °'8
ращается в хорошо известное реше- о,б|
ние с функцией вероятности. Метод
решения для заданного р состоит в
следующем: о,2|
1) численным интегрированием J
уравнения A4) оценивается значе- -2,о ч,з -to -0,5 6 0,5 1,0 1,5 w 2,5 i»H
ние р и, следовательно, находится а
по соотношению р ===== —In A —а); Рис* 13- L Зависимость между парамет-
2) соответственно численным ин- ром а и ^
тегрированием уравнений A5) и A6)
определяются $ и 6.
Соотношение между а и 1п[а определяется уравнением A4) и
выражением р = — In A—а). Графически оно показано на рис. 13.1; если
найдено значение а, то по этому графику сразу же может быть
определено значение \>>. Результаты расчетов приведены на рис. 13.2.
2. Полуограниченная среда. Имеем
а(Т)
а0
A — ХГJ
Краевые условия остаются прежними. Подставим
Тп
5 =
2/;
Т01.
а0%
Это ""позволяет получить обыкновенное дифференциальное уравнение в
переменных^? и 6:
с краевыми условиями
_ 21JL = JL Г 1 **9 ]
<& di L A—«бJ dt J
8=0 при I = оо,
A7)
A8)
456
Глава тринадцатая
1 при I — 0.
A9)
Решая уравнение A7) при условиях A8) — A9), найдем соотношение
между 6 и I,
Приведем здесь окончательный результат, полученный Фуджита;
детальные выкладки и анализ полученных результатов приведены в
работе [99]. Решение можно представить в следующем виде:
Ф («. Р)
«[i-« + f(«.M
B0)
B1)
I = -1- {[1 - а + ф (и, р)] и - exp [J32 A - и2)]},
1 —а
где <J> (а, Р) находится из соотношения
ф (а, р) - уТр [1 -erf (pa)] exp (p2),
Р — константа, определяемая как функция данного параметра из
уравнения
фA,р)=а @<а<1).
0
и,у
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0
--50
^40
so
--20
--10
6
0,9
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0
^-50
---40
W-30
Ал5
2,0
Рис. 13. 2. Зависимость
относительной температуры 6 от £=
= xl l/4a0'c для значений -J—.
1—a
от 5 до 50
1,0
2,0
РисЛЗ/'ЗДЗависимость между
относительной температурой б и ?=#/ "j/TaoT для
значений 1/A—аJ от 5 до 50
Уравнения B0) и B1) дают решение 6 = 6 (?) с параметром и,
значения которого лежат в интервале 1<^<^оо.
Результаты решения этой задачи отражены на рис. 13.3.
3. Полуограниченная среда. Имеем
а(Т)
^0
1 + 2хГ •+- vT2
(х и v — постоянные).
ТЕПЛОПРОВОДНОСТЬ ПРИ ПЕРЕМ. КОЭФФИЦИЕНТАХ ПЕРЕНОСА 457
Краевые условия прежние.
Рассматриваемая зависимость коэффициента температуропроводности
от температуры включает в себя как частный случай предыдущие задачи.
Вместе с тем эта зависимость позволяет решать задачи для условий,
когда коэффициент температуропроводности (точнее теплопроводности)
при изменении температуры проходит через минимум или максимум.
Решения этой задачи были также получены Фуджита.
Посредством подстановок
6 = 77Г0, £ = х-=г, а = *Г0, p = vT§
уравнение теплопроводности преобразуется в обыкновенное
дифференциальное уравнение
<ft dk L 1+2«8 + рб2 dt J
с краевыми условиями
6 = 0 при 5 = оо,
0 = 1 при 5=0.
Рассмотрим случай, когда а (Т) проходит через максимальное
значение между Т = 0 и Т = Т0. Последнее эквивалентно условию, по
которому функция /F), определяемая выражением
/ F) = 1 + 2а6 + ре2,
имеет минимум между 6 = 0 и 6 = 1. Легко показать, что такое
условие определяется неравенствами
0< JL<1, B2)
г
Р>0, B3)
откуда вытекает, что
а<0. B4)
Физически любой максимум а (Т) в рассматриваемой области изменения
температуры должен оставаться конечным; последнее требует» чтобы
соответствующий минимум/F) был положительным, что равноценно условию
0<у<1. B5)
Соотношения B2) — B5) выражают условия прохождения
коэффициента а через максимум.
Для удобства обозначим а — — f; тогда приведенные неравенства
запишутся так:
0<л/р<1,
0<Т7р<1.
Окончательное решение задачи можно представить в следующем виде:
ре = (р — f)v« tg [F (и, s) - tg-1*] + т, 0< 6 < 6lf B6)
PO = (p - f)t/2 tg [tg-1™ -F(u,s)-F (um, e)] + T. B7)
e1<6<iI
458
Глава тринадцатая
где
Кроме того,
h = (Р - Т2Oя tg [F A,в)- tg-1*] + Т.
где
— k< z< zx,
\ = Г P ]v« Ггы _ (i _ „2 _ e 1п иу/.1
zx < z < m,
tg-1«1 = F(l,e)-tg-1*,
tg-1* = i7 (и, s) — tg-1 k, -k<z<z1
tg-12 = tg-1m — F(u, e) + F(um, s), Zl<2<m.
B8)
B9)
0,6
0,4
0,2
■0,2
0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 Qm
Рис. 13.4. Зависимость относительного
коэффициента диффузии am/am0 от относительной '
концентрации Ц™ = 1/A—2авда + рт«); о
0 0
,1 0
,2 0
/1
,3 0
,4 0
2 1
,5 а
л Рис. 13.5. Графики для определения об-
а=—1,646; р=2,877 Щих решений:
1—уравнения C1);* —уравнения C2)
Вспомогательные переменные в этих уравнениях определяются
соотношениями
к-т5г- —irVO-i)- C0>
где 7 = —а и р — постоянные величины, входящие в выражения для
коэффициентов температуропроводности. Кроме того, е и ит связаны с k
и т выражениями
где
в\пит + (т* + 1)^=1,
tg* + Ч~гт = 2F A, в) - F (ит, в),
и
F (и, е) = J A — и\ — г In «i)-7' ut«!.
C1)
C2)
ТЕПЛОПРОВОДНОСТЬ ПРИ ПЕРЕМ. КОЭФФИЦИЕНТАХ ПЕРЕНОСА 459
Оценивая B6) и B7) в
зависимости от и, можно заметить,
что в соотношении B6) и
меняется от 0 до 1, а в
уравнении B7) ограничено
интервалом ит<Си < 1.
В качестве примера
рассмотрим процесс диффузии.
На рис. 13.4 представлена
графическая зависимость
коэффициента диффузии ат /ат0 от
безразмерной концентрации Ьт. При
этом в выражении для
коэффициента диффузии of = — ^ =
= —1,646; р == 2,877. При
em = 1 ajam0 = 1,710; ajam0
имеет максимальное значение,
равное 17,20, при 8 = 0,572; k
соответственно равны k
0,8
0,6
0,4
0,2
\
1
Рис. 13. 6. Зависимость относительной
концентрации бт от £ для коэффициента
диффузии, изменяющегося в соответствии с
графиком рис. 13.4
и т, рассчитанные по уравнению C0),
4,025; т = 3,010. Значения е, рассчитанные
по уравнениям C1) и C2) для различных ит, приведены на рис. 13.5;
точка пересечения кривых г = е (ит) дает решение этих уравнений.
Окончательный результат в виде соотношения между Вт и I,
рассчитанный по уравнениям B6) —B9), представлен на рис. 13.6.
§ 6. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ
ТЕПЛОПРОВОДНОСТИ С КОЭФФИЦИЕНТАМИ,
ЗАВИСЯЩИМИ ОТ КООРДИНАТЫ
Приведенные выше решения можно обобщить и получить их из более
общего решения. Вначале рассмотрим результаты работ [4а], [46] для
уравнения вида
дт дх \ дх
1. Следуя [4а], введем новую переменную
■)■
Тогда уравнение A) примет вид1)
дТ(г, т)
дх
К(х)
1 д2Г (г, т)
Я (г) дг2
где
д(г) = с{х)т{х)К(х).
A)
B)
C)
D)
*) Заменой переменных dy = yrq(z) dz уравнению C) можно придать форму
уравнения теплопроводности для стержня с переменными значениями теплоемкости и тепло-
проводности, но постоянной температуропроводностью, равной единице. Такой стержень
будем называть «эквивалентным» стержнем [4а].
460
Глава тринадцатая
Предполагается, что функция q{z) удовлетворяет в промежутке
Q^z < оо следующим условиям:
1) не принимает отрицательных значений и может обращаться в нуль
лишь при 2 = 0;
2) имеет непрерывную вторую производную везде, кроме, может быть,
точки z = 0;
3) вблизи начала координат функция q(z) имеет вид
Я(г)^г*A+р(г)),
где р@) = 0, s>0;
4) интеграл
расходится при z ■
5) модуль
IV Я (г)
dz
5 q'2 (г) __ д" (г)
16 ql%(z) 4q3/*(z)
убывает достаточно быстро, так что интеграл
со
J
Я'* (г) <7"(г)
dz
16 qb/z(z) 4q*/2(z)
о
сходится.
2. Для построения решений краевых задач уравнения C) с функцией
q{z), удовлетворяющей условиям 1—5, приведем результаты задачи
на собственные значения для уравнения E)
d2u +x*+2?(z)a = 0, E)
dz2
которое получается из уравнения C), если в последнем положить
Т(г, *) = иB, Х)е-^+2-. F)
Доказательство результатов и подробности, касающиеся задачи
Штурма — Лиувилля для уравнения E) на полубесконечном промежутке,
можно найти в работе [4а], а также в монографиях [75а, 386].
Рассмотрим решение уравнения E), удовлетворяющее условиям
dua @, X)
иа @, X) = sin a, п = cos а G)
(o<«<f).
(8)
Вводя новые зависимые и независимые переменные согласно соотноше
ниям
v(i,l) = rs/iq/t(z)u(zA), }
2
преобразуем уравнение E) к виду
-2£-+\'+iS>v = R®v, (9)
ах*
ТЕПЛОПРОВОДНОСТЬ ПРИ ПЕРЕМ. КОЭФФИЦИЕНТАХ ПЕРЕНОСА 461
где
*© = t(t + 1)if-
6V (г) , 1 Vq» (z)
16 Я3 (*)
(Ю)
4 <f (z)
Считая правую часть уравнения (9) известной и используя условия G)?
методом вариации произвольной постоянной получим
иA1) = аА$)У1и г
s+2
s+2
s + 2
(щ 2 )+bB(t)Vuj 1
s+2>
5+2 ч '
(Щ
A1)
где использованы обозначения
Л (£) = sin a ■
5(Н)=^^ +
JyXTjJ^
5+2
5+2
■s+1
s + 2
fJ^
(Щ2 Я ft) r, ft) A,,
s + 2
A2)
a = ■
s + 2
1
s + 2
l
(s + 2)*+2
£+1
(s + 2)s+2
A3)
3. Приведем асимптотическое выражение для функции v (£, X) из
формулы A1) при z-± оо. Используя 5-е свойство функции q\z) и
известные свойства бесселевых функций, можно показать, что интегралы A2)
в выражениях для А(Ъ) и 5(E) сходятся при S-^ оо, откуда на основании
4-го свойства функции q(z) и асимптотического поведения бесселевых
функций (см. приложения) при £ -»• оо получим
v(l
• ч-/-^
I
(Щ
5/4
X
X M(X)cos X l )Vq(z) dz)+N(k) s'm\ X
где введены обозначения
A4)
М(к) = ai4(oo)sin
8 + 4 -к)+ЬВ(°°)со*( s + 4 ic
4(s + 2)
4 (s + 2)
N(Ц = аА (оо)cos ( s + 4 «) + 65(оо) sin / s + 4 те
A5)
Возвращаясь к исходной функции &a B, X), получим для нее при z -*■ о©
асимптотическое выражение
T)r^q-x^{z)X
X
s±2 ,, .
q(z) dz ) + N (X;sin( X 2 J |Л?(г) dz
A6)
462
Глава тринадцатая
Из формул A1) и A2) весьма просто получить также
асимптотическое поведение для собственной функции иа (г, X) при X -* оо;
результат имеет вид (при a=f=0)
£±? С
/ £±f Г \ / — Г
X P(X)cos X 2 J V~oWdz + Q(X) sin X 4 J VW) dz
A7)
где
P(X) = a sin a-sin
s + 4
4(s + 2)
s 4- 4
Q (X) = a sina • cos —
4(s + 2)
A8)
daa (z, X)
Соответственно для производной ^ при X -> оо имеем (a=f=0)
<Ц» (*> х)
dz
s+4
X
/ £+2 % \ / s+2 %
—P(X)sin X 2 J Yq(z)Ydz +Q(X)cos X 2 J Vq(z) dz
Аналогично при a = 0 и X -> оо имеем
£+4
4
X
A9)
X \К(X)cos X 2 )VJWik + L(X)sin X 2 )Vq
s+2
2
B) dz
B0)
d"°^;X) « |/Ш 9v«(г) х^/4 x
x
—/C(X) sin X 2 J Yq(z) dz +L(X)cos X 2 J Vg(z) dz
В последних формулах использованы обозначения
К (X) = Ь cos s + 4 к;
W 4(s + 2)
L(X) = 6sin S + 4 тс.
W 4 (s + 2)
B1)
B2).
4. Выше были приведены некоторые сведения о свойствах
собственных функций уравнения E). Вопрос о возможности разложения
функций по собственным функциям уравнения E) в полубесконечном
интервале 0<^2<оо можно исследовать, рассматривая задачу Штурма —
ТЕПЛОПРОВОДНОСТЬ ПРИ ПЕРЕМ. КОЭФФИЦИЕНТАХ ПЕРЕНОСА 463
Лиувилля для уравнения E) на конечном интервале 0 <^ z <^ / с краевыми
условиями
и (О, X) cos а — и' (О, X) sin a = О B3)
2
и (/, X) cos p — а' (/, X) sin p = 0 B4)
(»<р<т)-
Рассмотренные выше решения а« B, X) уже удовлетворяют условию B3),
а из условия B4) определяются собственные значения Хл.
Как известно, для любой непрерывной на интервале @, /) функции
f(z) имеет место равенство (равенство Парсеваля):
/ с»
$f*(z)q(z)dz = $F*(l)dPl(l), B5)
где
F (к) = [q{z)-f (г) • иа (г, I) dz, B6)
рг(Х)= У\1——' B7)
о<хл<х о
J 9 (г) w„ (г, Хл) dz
Можно показать [46, 386], что существует монотонно-неубывающая
функция р(Х), являющаяся пределом функции pt (X) при /->оо. В
формулах B5) и B6) можно перейти к пределу 1-><х>, если существует
1
/2 (z) <7 (г) dz. Таким образом, соотношения B5) и B6) сохраняют свою
силу и в случае полубесконечного промежутка (/ = оо).
Из равенства B5) при / = оо легко получить
оо
f(z) = §F(k)ua(z,l)d9(k) B8)
о
при условии, что последний интеграл сходится равномерно в любом
конечном интервале.
Для завершения изложения сведений о задаче Штурма—Лиувилля
в полубесконечном интервале наметим способ построения и приведем
выражение для функции р(Х). Используя асимптотическое выражение
A6) для функции Ua(z, X), нетрудно показать, что при / -> оо
j g(z) u\ (г, X)dz~-^ X-«/* ^> + ^>| УЩ dz, B9)
о о
где М(к) и N(k) определены согласно формулам A5). На основе извест-
464
Глава тринадцатая
ных свойств собственных значений Xft, определения B7) и оценки B9)
при / -> оо получаем, что
Рг (х + Л) _ Рг(Х) = ЖЛ1
S
1
J <7(г)и*(г, \п) UZ
о
x<xrt <x~j- д
Х+Д
/Гоо J M»(X)+JV»(X) ' C°)
где в последнем равенстве (асимптотическом) сумма преобразована в
интеграл.
Отсюда окончательно имеем для функции
х+д
Р(Х + Д)-Р(Х)= J МЦЦ+ЫЩ) ' CD
Приведем также асимптотические оценки для функции р(Х) приХ~><».
В случае, если в условии B3) а=^0, из формул A5) и A4) имеем
М*(\) +N*(k) ^a2sina«,
т. е.
^)--Ййт C3)
или
Р(Ь) ^ / ■ П 2 • 2 ' C4)
rw (s+ 1) а2 sin2 а х '
Аналогично при а = 0 имеем
p^-iSp-- C5)
Из приведенных результатов [в частности, формулы C2)] уже не-
1 d2
посредственно следует, что спектр оператора —рг -гт [см. уравнение
E)] при выполнении условий 1—5, накладываемых на функцию q(z),
непрерывен, т.е. собственные значения X заполняют всю
полубесконечную прямую @, оо). Подчеркнем особое значение 4-го свойства
функции q(z) в вопросе о, непрерывности спектра, так как интеграл
со
•IVq (z) dz играет роль длины «эквивалентного» стержня. Поэтому при
выполнении 4-го условия, когда «эквивалентный» стержень бесконечен,
граничное условие B4) оказывается несущественным. В случае же
оо
сходимости интеграла J]/" q(z)dz мы имели бы аналог задачи на ко-
о
нечном интервале для обычного уравнения теплопроводности, спектр
собственных значений был бы дискретным, а условие B4) было бы
существенно и после перехода / -* оо.
ТЕПЛОПРОВОДНОСТЬ ПРИ ПЕРЕМ. КОЭФФИЦИЕНТАХ ПЕРЕНОСА 465
5. Прежде чем перейти к исследованию краевых задач для
уравнения теплопроводности C), приведем обобщение формулы
(х-х')*
1 Г е 4<г-^>
lim —т= \ Ф (х')—г dxf =
О, если x.лежит вне [а, Ь\\
<p (Ь-0)
, если х=а;
, если л: = b;
ф (х+0) + ср (х—0)
TV 2 ' если * ле"
жит внутри [а, 6].
Эта формула утверждает, что если ф (х) — ограниченная функция,
кусочно-непрерывная по л: и непрерывная по /, то (О^а <b<^ оо)
Ь оо
lim J / (л:', х)9 (*') dx'§ e-*s+V-&) и. (дг, X) и. (*', X) dp(X) =
а О
О, если х лежит вне [а, 6];
-у/(а+0, т) при х=а;
-g-/(fr—0, т) при х=Ь\
I / (* + 0,т) +f(x — 0,т) , ,ч /оСЧ
( 2 ' если х лежит внУтри (а, Ь). C6)
6. Перейдем к основному вопросу настоящего параграфа —
рассмотрению краевых задач для уравнения C).
Пусть
Т @, т) cosa— аГ@'т) sina = 0 C7)
0<а<-
Г(г,0)=/(г).
C8)
Из обобщенной формулы Пуассона C6) непосредственно следует, что
решение этой краевой задачи имеет вид
t+2.
T(z,x) = $f (С) <7(С) Л]e~x T«a (z, X) Ua (С, X)dp (X),
C9)
где иа (z, X)—собственные функции краевой задачи для обыкновенного
дифференциального уравнения E) при условии B3).
Пусть при прежнем начальном условии C8) задано неоднородное
граничное условие первого рода
Г @, т) = Ф(т). D0)
Будем искать T(z, t) в виде суммы T(z, т) = U{z, т) + V (z, x)t где
функции U я V удовлетворяют уравнению C) и условиям
£/@,т) = <р(т), (/B,0) = 0, D1)
У@,т)=0, 1/B,0)=/(г). D2)
466
Глава тринадцатая
Из рассмотрения краевой задачи C7) — C8) следует, что функция
V (z> т) является ее частным случаем, если в условии C7) а = 0. Таким
образом, функция V(z, x) определяется формулой, аналогичной C9)
00 00
V(z,x) = $ f (С) q (С) йХ, \е~^^ u0(z, X) и0 (С, X) dPo (X), D3)
О 6
где и0 (z, X) — собственная функция уравнения E) такая, что и0@, Х)=0,
дг ' = 1, а р0 (X)—соответствующая и0(г, X) функция р(Х) (см. 27).
Остается найти функцию U (г, %). Покажем, что она определяется
формулой
X 00
U (г, т) = J ф (») d Ь jV*s+2 (^ - *> и0 (г, X) dPo (X). D4)
о о
Для доказательства достаточно убедиться, во-первых, что функция U
удовлетворяет уравнению C). Это легко проверяется непосредственной
подстановкой формулы D4) в C). Во-вторых, из D4) очевидно, что
U(z, т)-> 0 при т->0 (z=f=0) и, таким образом, второе из условий D1)
выполняется.
Остается показать, что интеграл, стоящий в правой части формулы
D4), при 2->0 имеет пределом ф (т). Из формул A1) и (8) получаем,
что при z -> О
ъ / s±2\
Щ (г, X) с*о х q-*u (z) р* V Ъ •/ М ^2 ^ * ) + — <45>
где многоточием обозначены члены высшего порядка малости по z.
Из формулы D5) очевидно, что в интеграл в правой части формулы
D4) вносят вклад лишь большие значения X, поэтому для dp0(k) можно
воспользоваться асимптотической формулой C5), т. е. подставить ее в D4):
Фо(^D^- + ". W, D6)
где многоточием в скобке обозначены члены асимптотического
разложения, растущие не быстрее, чем Xs4*1, при Х-> оо.
Итак, подставим в интеграл асимптотические соотношения D5) и
D6), тогда при z -> 0 интеграл D4) примет вид
X СО
_L<?-v^B) e*/4 j q> (») d& . fe-xs+2<*-»>KTT x
b oo
X ' i (j— (Щ^ Xs+1 dk + ... D7)
В работе [46] строго показано, что все последующие члены
асимптотического разложения, обозначенные в формуле D7) многоточием,
исчезают при z -> 0. Поэтому остается показать, что интеграл D7) при
z->0 оказывается равным ф(т). Заметим, что множитель q~xl* (z) £s/4
при z -> 0 стремится к единице, как это следует из 3-го свойства
функции q (z) и второй формулы (8).
ТЕПЛОПРОВОДНОСТЬ ПРИ ПЕРЕМ. КОЭФФИЦИЕНТАХ ПЕРЕНОСА 467
Интегрирование по X в D7) может быть выполнено (см. [7]), в
результате формула D4) примет вид
ехр
g.TW '" + ^-"'*. D8,
Ь (s + 2)s+2 J (t-b)s+2
о
Покажем, что функция
£S+2
F (т, Е) =
-}
a i (s+2J т ,
i+з i+з при т>0, D9)
6(s + 2)s+2 ts+2
О при т<0
имеет при г -> 0 (£ -> 0) пределом 8 (т—0) в смысле обобщенных
функций. Для этого нужно показать [10а], во-первых, что при любых
действительных тх и та (тх < т2) интеграл
L2
j> (х, |> dx
ограничен сверху постоянной, не зависящей от zv т2 и £.
Действительно, так как функция F(t, Е) неотрицательна, то
Es+2
6(s + 2)s+2 J ^s+2
0 0
Во-вторых, при любых х± и т2, отличных от нуля, должно выполняться
0 при хх < т2 < 0
1 при тх < 0 < т2,
т* ( 0 при тх < т2 < 0
lim \ F (т, Е) ch = I или 0 < тх < т2,
е-*0 i К 1 при т, < 0 < т.,
что также легко проверить.
Таким образом, доказано, что формула D4) действительно является
решением уравнения C) при условиях D1).
Рассмотрим краевую задачу с граничным условием второго рода
дТ @, т) , , ч /СЛЧ
—^-^ = Ф (*) E0)
и начальным условием C8). Будем искать Т (z, т) в виде Т (гу т) =
= U (z, т) + V (z, т), где функции U я V удовлетворяют теперь условиям
^± = ф (т), t/ B, 0) = 0, E1)
iK|^L=0, V(z,0) = f(z), E2)
а также уравнению C).
468
Глава тринадцатая
Функция V (г, т) является частным случаем решения D3) при а = -»- и
имеет вид
00 00
V (г, т) = J / (С) q (С) dC J е-^^и^ (z, X) ^(С, X) ф^(Х), E3)
О 0 2 2 2
ди%/2 (О, X)
где и %(z, X) —решение уравнения E) такое, что ^ = 0, р% (X) —
F Т
соответствующая и%/ (z, X) функция р(Х).
Совершенно аналогично можно показать (см. D4)), что функция U
определяется формулой
X О©
С/ (г, т) == J ф (&) d& J *-*8+2(-»>и_* (г, X) dPjL(X), E4)
0 0 2 2
удовлетворяющей уравнению C) и условиям E1).
Перейдем к построению решения уравнения C) при неоднородном
условии
дТ @, т)
Т @, т) cos а — ^ sin а = ф (т) E5)
(a=f=0 или аф—\
и при начальном условии C8). Для этого представим Т (z, %) в виде
суммы Т (z, i) = U (z, т) + V (z, т), где функции U и V удовлетворяют
уравнению C) и условиям
Т Г /Л Ч 017@, Т) . п
С/ @, т) COS a * 7 Sin a = 0;
г/Bг, o) = /(^)f * E6)
V (О, т) cos a * 7 sm a = ф (т),
V(z,0)=o, -*^<L = o. [ E?)
Функция £/(z, *) дается формулой C9). Для определения функции
V (z, т) введем неизвестную функцию
ФМ—^.' E8)
Если бы функция Ф (т) была известна, то функцию V (z, т) можно было
бы определить по формуле E4):
X 00
V (z, т) = J. Ф (&) d& J g-xH-2(T_») ^ Bj X) dp^ (X) E9)
0 0 2 2
Полагая в последней формуле z = 0 и пользуясь тем, что и*_ @,Х) = 1,
~2~
получим
•с оо
V @, х) = J <D(»)d» j е-^+2<—») dPjL(X). F0)
ТЕПЛОПРОВОДНОСТЬ ПРИ ПЕРЕМ. КОЭФФИЦИЕНТАХ ПЕРЕНОСА 469
Подставляя F0) в первое из условий E7), получим для функции Ф(х)
интегральное уравнение Вольтерра второго рода
т
Ф(х) + А J/С Ос—»)Ф(»)*» = х(т), F1)
где
/С (т) = J e-xs+2- dPjL (I),
h = ctga, *(,) = -|£L. F2)
Уравнение F1) может быть решено в явном виде с помощью
преобразования Лапласа для некоторых конкретных видов ядра К (х) или же
методом последовательных приближений. Тогда, как уже упоминалось,
функция V (г, т) определится с помощью формулы E4).
Рассмотрим краевую задачу для уравнения с источником
при краевых условиях C8) и E5).
Представим Т (г, т) в виде
T(z,T) = t/B,T) + V(z,T),
где U удовлетворяет уравнению C) при краевых условиях C8) и E5),
а функция V является решением уравнения F3) при условиях
V@, т) cos ос— dV(%9 т) sin а = 0, |
dz F4)
V B, 0) - 0. )
Функция U (г, т) совпадает с решением задачи F1).
Функция V (г, т) может быть представлена в виде
X 00 00
V (z, т) = J dft f Q (С, ft) dC j g-^V-fr) Me (z, X) ua (C, X) dp (X). F5)
0 0 0
Для доказательства этого утверждения следует показать, что функция
V удовлетворяет уравнению F3) и условиям F4). Вычисляя
производные
0 0 О
х оо оо
X н« (С, X) dp (X) - — j dft j Q (С, ft) dC J Xs+2 e-xs+2<—»> x
0 0 0
X ua (z, X) Ua (C, X) dp (X);
OO OD
4£- = lim J Q (C, ft) dC J e- xe+2<*-*> ^a (z, X) ua (C, X) dp (X) -
®~*% о о
x оо со
■ — J dft J Q (C, ft) dC Jx*+2 e- xs+2<-») ^ (z> X) ^ (C> X) dp (X)
0 0 0
и предполагая, что плотность источника Q (z, т) удовлетворяет
условиям применимости обобщенной формулы Пуассона (т е. Q (г, т)
ограничена, кусочно-непрерывна по -г и непрерывна по т), получим, что пер*
470
вое слагаемое в выражении для производной -^- равно q (z) • Q (z, т).
тл dV d2V T,
Из сравнения производных -^ и -^- получаем, что V действительно
удовлетворяет уравнению F3). Проверка выполнения условий F4) еще
более проста.
Итак, для построения решений краевых задач для уравнения C) или
F3) необходимо знать решение обыкновенного дифференциального
уравнения E).
7. В заключение проиллюстрируем, как с помощью развитой общей
теории для уравнения C) можно получить решения, приведенные в
§ 1—5 (см. также [9]):
q(z)=z\ F6)
Рассмотрим, например, краевую задачу, когда
Т@, т) = Ф(т), Т(г90) = 0. F7)
Собственная функция легко определяется из решения уравнения E)
при q(z) вида F6)
Фо (X, z) = -^yU J _J ^(Xz)^J • F8)
Согласно A5) имеем
M*(k) + N*(k) = 1—-^- Г* (-g-)j_ F9)
откуда по C2) определяем dp0(k). Теперь по формуле D4) имеем
С* г$+
Т{г, х) = -J— Ф(х) е- ^- db. G0)
(*+2)s+2r(_y J (^)S+2
Аналогично можно получить, что при краевых условиях
дТ @,т) = _ ф ^ Т(г,0) = 0 G1)
dz
имеем
- / Н-2
<Pjc_(z, X) = a yXz J { 2 А-л 2
2 -1T2-V *+
УИ2(Х) + JV2 (X) = 5—g- Г2 (i±j.) G3)
s_i_2
(S+2)s+2 X
и согласно E4)
zs+2
(s+2J (x — u)
T (z, x) = / , . \ ф (&) ^ ^p— d&. G4)
(*+2)S+2 <Ш) «1 ' ««H»*"
ОСНОВЫ ИНТЕГРАЛЬНОГО ПРЕОБРАЗОВАНИЯ
ЛАПЛАСА
14
При решении уравнений теплопроводности классическими методами
для некоторых задач (задачи с переменными граничными условиями,
с системой неоднородных тел и т. д.) встречаются большие трудности.
Решения часто получаются в виде интегралов или рядов, которые мало
пригодны для практического использования. В последнее время в
теплофизике с большим успехом применяются операционные методы,
которые позволяют получать не только точное решение, но и ряд
приближенных решений с заданной степенью точности. Операционными
методами можно с таким же успехом решать задачи, в которых
искомая функция терпит разрыв непрерывности, а такие задачи в
теплофизике встречаются довольно часто.
Операционные методы решения некоторых задач применялись очень
давно в качестве подсобного математического аппарата, призванного
облегчить получение уже известных результатов. Дальнейшее развитие
этих методов показало, что они являются самостоятельными
математическими методами, обладающими известными преимуществами перед
классическими при применении их к решению дифференциальных
уравнений в частных производных.
Символическое, или операционное, исчисление как самостоятельный
математический метод было впервые создано профессором Киевского
университета М. Ващенко-Захарченко. В своей монографии
«Символическое .исчисление и его приложение к интегрированию линейных
дифференциальных уравнений», вышедшей в 1862 г., автор дает
систематическое изложение операционного исчисления и выводит основные
соотношения и их применения к решению дифференциальных уравнений с
постоянными и переменными коэффициентами.
В работе Ващенко-Захарченко впервые выведена теорема разложения,
которая обычно приписывалась Хевисайду, и рассмотрен случай
кратных корней.
Теоремы разложения Ващенко-Захарченко формулируются
следующим образом: если /(D) — целая рациональная функция от оператора
дифференцирования D, то имеет место соотношение
Г1 (D) х = -pJLy (D-ax)-i*+ уг^- (D-a2)-*x + ... + j±^ (D-a^x, A)
472
Глава четырнадцатая
где av а2, а3, ... , сап— простые корни уравнения f(x) = 0 (случай
простых корней).
В этой же монографии автор выводит теорему разложения и для
кратных корней. Таким образом, мы с полным правом должны считать
проф. Ващенко-Захарченко создателем операционного исчисления
В конце прошлого столетия Хевисайд применил метод
операционного исчисления к решению некоторых электротехнических задач. Им
был введен оператор р, действие которого по определению следующее:
P»(Ss„^-) = SBnl^=l-. B)
В этом определении оператора р величина, стоящая под знаком
факториала (обозначим ее через т), удовлетворяет функциональному
уравнению
/(m)=m/(m-l), /@) = 1. C)
В случае, если m — дробное число @<т<1),
т! = Г(/п + 1), D)
где Г (m -f 1) — гамма-функция; если m —целое и положительное число, то
Г(т+1)! =ml -=1-2-3....-m.
Например,
Р
2 я 2
Если а — целое число (положительное или отрицательное), оператор
р производит такое же действие, как оператор D. Никакого строго
математического обоснования своего метода Хевисайд не дал.
Необходимо отметить, что идея дробного дифференцирования
принадлежит создателю Московского математического общества А. В. Лет-
никову, который в своей работе «Теория дифференцирования с
произвольным указателем», опубликованной в 1868 г., задолго до Хевисайда
применил метод дробного дифференцирования к решению
дифференциальных уравнений1). Операционный метод решения дифференциальных
уравнений заключается в том, что в уравнении
Zj amn д^тдхП - и (Ъ)
т,п
операция дифференцирования по времени заменяется оператором р, и
уравнение приобретает вид
Sm dnu (х, т) п /сч
«ш • рт —Ln = °; F)
dxn
т,п
это уравнение рассматривается как обыкновенное дифференциальное
уравнение по переменному х с параметром р.
Строгое обоснование операционного исчисления было дано
значительно позже, когда была установлена связь между функциональным пре-
О Дальнейшей разработкой этого вопроса занимались Н. Я. Сонин и П. А. Не-
красЬв (работы опубликованы в журнале «Математический сборник» в 1868—1888 гг.).
ОСНОВЫ ИНТЕГРАЛЬНОГО ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
473
образованием Лапласа J / (т) e~pzdi и операционным исчислением. Ока-
о
залось, что при преобразовании Лапласа оператор дифференцирования
заменяется операцией умножения на некоторую комплексную величину.
Впервые строгое обоснование было дано Эфросом и Данилевским в
монографии «Операционное исчисление и контурные интегралы», вышедшей
в 1937 г. Эфрос и Данилевский установили ряд новых соотношений и
правил операционного исчисления, а предложенная Эфросом теорема
является эффективным способом для нахождения начальных функций
по изображениям.
Большой вклад в развитие операционного исчисления внес В. А. Дит-
кин, который дал обоснование операционного исчисления на основе
современных математических представлений. Таким образом, операционное
исчисление в настоящее время является вполне совершенным
математическим методом.
Успех операционных методов состоит в том, что эти методы в
большинстве случаев являются наиболее прямыми методами; они
значительно сокращают технику вычисления. Во многих случаях, когда решение
классическими методами получить наиболее трудно, операционными
методами оно получается наиболее просто. Пользуясь операционными
методами, многие проблемы, представляющие исключительные трудности,
можно быстро и эффективно решать, что имеет большую ценность для
инженера и физика.
Нахождение температурного поля твердого тела в задачах
теплопроводности связано с решением дифференциальных уравнений с
разнообразными краевыми условиями. Необходимо иметь способы
эффективного решения этих задач с целью практического использования.
Остановимся на наиболее общем и простом по технике вычисления
методе преобразования Лапласа, т. е. применим функциональное
преобразование Лапласа
F(s) = J f(<tNr-d<t. G)
Во многих работах, посвященных решению электротехнических задач
методами операционного исчисления, применяется функциональное
преобразование Лапласа—Карсона:
Ф(Р)=р{/М^Л- (8)
Изображение одних и тех же функций будет иметь различный вид
в зависимости от того, каким интегральным преобразованием
пользоваться. Изображение функции F(s) по Лапласу будет соответствовать
изображению -—— по Лапласу—Карсону, Это надо иметь в виду
при пользовании таблицами изображений, приводимыми в разных
монографиях по операционному исчислению.
Учитывая, что данная монография предназначена в основном для
инженеров и студентов, мы стремились дать изложение метода
функционального преобразования Лапласа наиболее просто, в
доступной форме, опуская некоторые детали, общие исследования и
обобщения.
474
Глава четырнадцатая
§ 1. ОСНОВНЫЕ ПОНЯТИЯ
Метод преобразования Лапласа состоит в том, что изучается не
сама функция (оригинал), а ее видоизменение (изображение). Это
видоизменение — преобразование — производится при помощи умножения на
некоторую экспоненциальную функцию и интегрирования в
определенных пределах.
Пусть изучаемая функция у = f(i) есть кусочно-непрерывная
функция вещественной переменной т. Кусочно-непрерывной функцией
называют однозначную функцию, имеющую в конечном интервале @</т<^6)
конечное число разрывов непрерывности в точках тх, т2, ..., %k. В каждом
интервале (т/_ь т/) функция /(т) непрерывна, причем она стремится к
конечному пределу при приближении к границе.
Функцию у = 1(ч) называют оригиналом функции.
Преобразование Лапласа функции у = f (т) будет состоять в
умножении ее на e~sx и интегрировании в пределах от 0 до оо:
J/(t)e-"dx = F(s), A)
О
где s = £ -\-щ— некоторая комплексная величина. В результате
интегрирования получим некоторую функцию F(s), которая называется
преобразованной функцией по Лапласу, или изображением функции.
Таким образом, преобразование Лапласа является интегральным
преобразованием; это преобразование изображается символом L[f(i)]:
оо
L[/(x)] = F(s) = |/(т)е-*Ж B)
О
причем изображение F (s) существует, если интеграл A) сходится.
Более детальное обоснование преобразования функции / (t) будет
дано в § 9, где будут выяснены необходимые условия существования
функции F(s).
Для упрощения основных соотношений ограничим класс
рассматриваемых функций. Функцию /(т) принимают кусочно-непрерывной и
отличной от нуля только при т > 0. Величина / @) обозначает в
дальнейшем /( +0) = Пт/(т), а /(—0) равна нулю. Далее из класса кусоч-
т-Н-0
но-непрерывных функций выделяем подкласс функций, характеризуемых
тем, что асимптотические значения функции / (т) при т -> оо меньше
асимптотического значения функции еах , где а > 0, т. е. при
достаточно большом т:
|/(т)|<Ме- (а>0, М>0)
или
|е-ет/(т)|< Ме-^-^,
где а — некоторое конечное положительное число.
При указанных ограничениях, накладываемых на функцию /(т),
интеграл A) является регулярной функцией от s в правой полуплоскости
от прямой о (см. § 9), т. е. функция F (s) имеет производные всех
порядков в указанной области и все ее особые точки расположены в
комплексной плоскости слева от прямой а.
Условимся оригинал функции обозначать строчными буквами, а ее
изображение — прописными буквами, например: у(ч) — оригинал
функции, a Y (s) — изображение, тогда:
L[yW = Y(s).
ОСНОВЫ ИНТЕГРАЛЬНОГО ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
475
Приведем несколько примеров.
1. Пусть оригинал есть постоянная величина
/ (т) = Л = const (т>0).
Тогда
+ 00
[А]= Г Ae-Sxdz=—
0
00
s
=
0
(если s>0).
А
s
2. Пусть / (z) == Az. Тогда
о
3. Пусть / (т) = екх (т > 0). Тогда
L [ ekx ] = Г e-ts-Vx dz = _i_ (если 5 > 6).
J s — k
0
Отсюда
4. Пусть f(z) = ,— = z %. Тогда
V z
Положим
тогда
L [ пгИ] = f т/* e-sx dz.
2xdx
sz = х2> ax = —
C)
L [Az] = Г Az e~szdz = -A- . D)
E)
L I ^J = 7T* ' <6>
I [ ,-*] =/-fAf .-* - J/J (так как ^ J ,r**- l). G)
F о о
5. Пусть f(z) = zk, где & может быть не только целым, но и дробным числом
(k > — 1). Тогда
со
L [zk] = f т* e-sx dx.
о
Положим sx = г; тогда
LH-J 2*е- _g_ = ^L, (8)
где П (&) = Г (k + 1) (см. приложение I).
Если Л — целое число (к=п), то П(л) = п!, так что
^Й = 4г. (9)
476
Глава четырнадцатая
Таким образом можно найти изображения и ряда других функций. В приложении
приведена таблица, в которой для некоторых функций / (х) даны соответствующие
изображения.
Необходимо отметить, что не всякая функция F (s) имеет
изображение. Например, не существует оригинала для функции F(s)==;tgs,
так как полюсы этой функции расположены на всей вещественной
оси 5, а не слева от прямой а (см. § 9, 10). Однако можно показать,
что если Ф (s) является изображением, то соответствующий оригинал
будет единственным, который являлся бы кусочно-непрерывной
функцией.
Если функция /(т) растет быстрее, чем eJX, то для нее не
существует изображения. Например, функция f(z) = ex2 не имеет изображений,
так как для нее интеграл Лапласа расходится. Однако, например,
разрывная функция /(т) = —т= (она стремится к бесконечности, когда
0) имеет изображение F(s) =т/-^-, так как интеграл Лапласа
упенчатой; напри
0 при 0 < т < А,
сходится.
Функция /(х) может быть ступенчатой; например,
( 0 при 0 < т <
k^x' = [1 при «с > k.
Изображение ее следующее:
OQ СО СО
= j«k(*)e~w<fc = J er^dx = \-e
—sx
k k
V-- №
§ 2. СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
Свойство линейности. Преобразование Лапласа является
линейным, т. е. если А и В — постоянные, то по определению
преобразования Лапласа можно написать:
L [Af(x) + Bg(x)) = AL [/(т)] + BL [g(x)] = AF(s) + BG(s), A)
где F(s) и G(s) — соответственно изображения функций f(x) и g(x).
Пользуясь этим свойством, можно найти изображения ряда функций.
Примеры.
1. Пусть / (х) = sh&x. Тогда
Г 1 кх 1 Л 1 1 11 k
L [sh kt\ = I e — — e~kx = ~ — 7 = ——- . . B)
1 J |_ 2 .2 J 2s — k 2 s + k s*—k2 x }
2. Пусть / (т) = ch ki. Тогда
L[ch^]=4-{L[^+^]}=4-G^+7^) = s-^F3'
C)
Изображение, производной. Пусть L [f (x)] = F(s). Найдем
M/'WL где f'b) = d-^.
ОСНОВЫ ИНТЕГРАЛЬНОГО ПРЕОБРАЗОВАНИЯ ЛАПЛАСА 477
Имеем
L [/' (*)] = J/' W e~szdx = е~эт /(т) J+ s J /(х) е~етЛ. D)
О 0 0
Если /(т) принадлежит подклассу с указанным выше
асимптотическим свойством, то e~sx f (т) ~> 0, когда т~>оо, и равна /@), когда
^ 'Т' *' I[/'CO] = sF(s)-/@). E)
Таким образом, дифференцирование оригинала функции
соответствует умножению изображения функции на s и последующему вычитанию
постоянной /@), т. е. величина s обладает свойством оператора.
Следовательно, применяя функциональное преобразование Лапласа,
операцию дифференцирования оригинала функции можно заменить
алгебраическим действием над изображением. В этом состоит связь
операционного исчисления с преобразованием Лапласа.
Если /@) = 0, то L [/'(т)] = sF (s), но величина s не тождественна
d A
оператору D = -г-, так как для постоянной А имеем L [А] = — , а
DA = 0.
Найдем изображение производной второго порядка:
L [/" (х)] = sL [/' (х)] - /' @) = s {sL [/ (х)] _ / @)} _ /' @) =
= s*F(s)-s/@)-/''@).
Таким же образом можно найти изображение /'" (т):
L [Г (*)] = s'F (s) - s2/ @) - 5/' @) - Г @).
Вообще
L [fin)(x)] = s»F (s) — 5я/ @) — s"~T @) — ... — fin~~l) @). F)
Таким образом, для функции /(?) с указанным асимптотическим
поведением при условии существования непрерывных ее производных
вплоть до /(л~) (ъ) существует изображение для производной /(л)(т).
Формула F) имеет большое практическое значение для нахождения
изображений. При ее помощи можно найти изображения функций,
рассмотренных в § 1.
Примеры.
3. Пусть / (х) — Лх, /' (х) = Л. Тогда
M/'W] = sMfW]-f@),
т. е.
L [Л] = sL [Лх].
Известно, что L [А] = —, откуда
>[Ж] = 1Г» G)
т. е. получаем то же соотношение D) § 1.
4. Пусть / (х) = sin &х, /' (х) = k cos &x; /" (х) == — k% sin kt, Тогда
MfffW] = sVW-»/@Hf'@),
— /г2/, [sin £х] = s2L [sin £х] — k.
Отсюда
L[sinfo] = s2+A,2 - (8)
478
Глава четырнадцатая
5, Пусть / (т) == cos At, /' (t) == — & sin &т, /" (т) = — k2 cos &т. Тогда
L[/(t)] = F(s),
— &2L [cos &т] = s2L [cos &c] — s;
отсюда
L [cos &?] = s2^_£2
(9)
6. Пусть / (т) = т1/2, /' (z) = -L т 1/2. Тогда
Известно [см. формулу G) § 1], что L Г т~~1/21 = 1/ — . Следовательно,
7. Пусть / (,) = ,"+1/2 , . Г (х) = (« + 1/2) ,"+1/2-!,
A0)
/ (т) = ( п + -у
^•^...../«(х)-(»+4-)...ж
_3_ _1_ -1/2 1-3-5 ■ ■ . Bл+1) -1/2
2 " 2 т _ 2("+1) Т
с1/2
L [ ,<"+"(х) ] = s<"+" L [ /+] _ s« , @) - ... ,
откуда, пользуясь формулой G) § 1, получим
г г л+1/2] _ ЬЗ-5 . . . Bп + 1) те
L1T J ~" «yi+l * 0п4
1/2
2"+1 5л+3/2
(И)
Интегрирование оригинала функции. Найдем изображе-
ние функции g(x) = Г / @) d9, т. е. найдем
L[g(x)] = L
//(в) ^1
Если #(т) удовлетворяет нашим условиям, то
«ТОО = /('),
£ lg' (*)] = £ [/ W3 = sL [g (x)] = sL
J/'(в) del
Так как L [/ (x)] = F (s), то
//(в) del =
■F(s).
A2)
Таким образом,, интегрирование оригинала функции /(т)
соответствует делению изображения F (s) на величину s, т. е. величина s_1
обладает свойством оператора интегрирования.
ОСНОВЫ ИНТЕГРАЛЬНОГО ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
479
Применяя тот же прием, можно показать, что двукратное
интегрирование оригинала функции соответствует делению изображения на $2:
JJ/(g)dWe
Lo о
4rF(s). . A3)
Теоремы подстановки. Рассмотрим два соотношения между
оригиналом функции и ее изображением, известные под названием
теорем подстановки.
Первая теорема. Пусть F ($) есть изображение функции /(х).
Сделаем замену х на ах, где а — постоянная; тогда можно написать:
L[/(ax)]=jO(ax)dT= ±^e~^9 f(B)dQ = JLW-±-), A4)
о о ^ '
где 0 = ах.
Если же сделать замену х на —, то получим
L[f(^=]e-*f(^y, = a]e-astf{t)dt = aF{as), A5)
Т
где t = —, т. е. замена независимой переменной т на ах в оригинале
функции соответствует замене в изображении функции величины 5 на
— и делению изображения на а. Эту теорему часто называют также
теоремой подобия.
Пример.
s
8. Имеем L [cos т] = 2 i p Тогда
s
1
L[cos/h] = ^p / s \2
■4-1+1 s2+k2'
к
т. е. получаем тот же результат, что и в формуле (9).
Вторая теорема. Имеется функция /(х), удовлетворяющая обычным
условиям; ее изображение есть Р (s). Сделаем замену в изображении
функции величины s на 5 — а, где а — постоянная. Тогда
F(s.-fl) = Je-<M)'/<'c)dx = Je"^eeT/(t)dt = L[^/(-c)], A6)
о о
т. е. замена переменной s в изображении функции на {s—a)
соответствует умножению оригинала функции на величину е<1Х. Эту теорему
часто называют теоремой смещения.
Примеры.
т\
9. Известно, что gm+1 = L [%m] (s > О, т = 1, 2, . . . ). Пользуясь второй
теоремой подстановки, получаем
480
Глава четырнадцатая
^^-tM
1 ■ ^ *
^w>
Г1 ~".
Рис. 14.1. Графики функций /(-с) и /#(т)
10. Имеем L [coskz] = sa'_L^2« Тогда
s + a
Ч
>£т].
(s+aJ + A
Применяя обе теоремы одновременно, можно написать
F(as — b)=F\a[s—JL
ML
a V a
A8)
A9)
Теорема запаздывания. Пусть функция /(т), отличная от
нуля только при т > 0, определяет течение некоторого процесса
(рис. 14.1). Рассмотрим функцию /6(т), определяющую течение такого
же процесса, но запаздывающего на время Ь (см. рис. 14.1):
М*) =
о
при 0 <т <6
/ (т — Ь) при % > Ь.
Имеем
о
Найдем изображение функции /6 (т):
B0)
B1)
B2)
Вводя новую переменную Ь = х — 6 и замечая, что пределы
интегрирования будут от 0 до оо, получим
Fb(s) = J/(»)e"*(H*)d»=^*6 f/(*)*"* <»=*"" FE),
т. е.
г-зЬ
L[fbW}^e~S0F(s).
B3)
B4)
Обратное преобразование Лапласа. Символ L[/(t)] =
— F (s) обозначал преобразование функции /(т), т. е. по оригиналу
функции находили ее изображение. Это действие называют прямым пре-
ОСНОВЫ ИНТЕГРАЛЬНОГО ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
481
образованием Лапласа. Во многих задачах необходимо найти оригиналы
функции по ее изображению F(s). Условились символом L~1[/7(s)]
обозначать обратное преобразование Лапласа, которое должно обозначать
искомую функцию, т. е. оригинал функции.
Если прямое преобразование дает изображение функции
L[f(x)] = F(s),
то обратное преобразование должно давать оригинал функции
L-4F («)] = /(*).
Например,
i-[?Tp] = «""»••
Более строгое рассмотрение вопроса приводит к заключению, что
обратное преобразование Лапласа в общем случае не есть оригинал
функции и только при известных условиях дает оригинал функции. Напри-
мер, обратное преобразование функции ——г равно fx (i) = e , так как
S К
прямое преобразование е дает изображение ——г, но можно найти и
другую функцию /2(т):
fM(e*\ когда 0<т<2 и т>2,
НКХ) \ 1, когда т = 2,
которая дает то же изображение. Необходимо отметить, что f% (?) имеет
разрыв непрерывности при т = 2. Найти вторую непрерывную функцию
для заданного изображения нельзя. Поэтому заданное изображение
функции F ($) не может иметь больше одного оригинала функции /(?),
непрерывной для каждого значения т. В большинстве рассматриваемых
задач математической физики обратное преобразование является
однозначным.
Обратное преобразование является линейным, что вытекает
непосредственно из соотношения A), т. е.
L-i [AF (s) + BG (s)) = Af (т) + Bg (т) = Air* [F (s)} + BL^ [G (s)]. B5)
§ 3. МЕТОД РЕШЕНИЯ ПРОСТЕЙШИХ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЯ
Пользуясь основными свойствами преобразования Лапласа, можно
решать простейшие дифференциальные уравнения.
Метод решения состоит из следующих трех этапов.
1. К дифференциальному уравнению применяем преобразование
Лапласа и вместо дифференциального уравнения для оригинала функции
получаем уравнение для изображения функции.
Так как преобразование Лапласа является интегральным
преобразованием и обладает свойствами операторов, то вместо дифференциального
уравнения для оригинала функции получаем алгебраическое уравнение
относительно изображения.
16 Заказ № 640
482
Глава четырнадцатая
2. Полученное алгебраическое уравнение решается относительно изо-
бражения функции, причем s рассматривается как число. Следовательно,
второй этап сводится к нахождению решения для изображения функции.
3. При помощи известных соотношений между изображением
функции F (s) и ее оригиналом /(т) находится решение для оригинала
функции, т. е. оригинал искомой функции.
Таким образом, вначале применяется прямое преобразование, а затем
обратное. Преимущество этого метода состоит в том, что решается не
дифференциальное уравнение для оригинала функции, а алгебраическое
уравнение для изображения.
Приведем несколько примеров.
1. Имеем
d2z
-^Г~^ = 0 A)
Пусть искомая функция z (т) равна А при т = О, т. е. z @) = А = const, а ее произ-
dz(Q)
водная zr @) = —-г-1- = D = const.
Дифференциальное уравнение можно переписать так:
г"(т) — k2z(x) = 0.
Применим прямое преобразование Лапласа:
Z (s) = $e~s%z (z) dx = L[z (т)],
о
L[zff (t)]-/e2L[z(T)] = 0.
Пользуясь формулой F) § 2, получим
s2Z (s)—As — D— k2Z (s) == 0.
Последнее уравнение является простым алгебраическим уравнением относительно
изображения функции Z (s); решаем его, считая s простым числом:
As + D s k
Z{s) = s2 — k2 ~ As2 — k2 + D (s2— k2)k'
В результате получили решение относительно изображения.
Пользуясь соотношениями B) и C) § 2, находим решение относительно оригинала
функции z(t), т. е. применяем обратное преобразование Лапласа:
L-i [Z (S)] = Л1-1 \угЬцг\ + 4 L_1 \w~w] •
откуда
D
z (x) = A ch ki + ~y sh kz = A ch kz + В sh to, B)
D
где В = -т- = const.
dz @)
Если z' @) = —2— = D = 0, то решение дифференциального уравнения примет вид
z(t) = Лепит. C)
2. Имеем
z" (т)— z'(t) — 6z(t) = 2.
Искомая функция удовлетво ряет условиям z @) = 1, z' @) = 0.
ОСНОВЫ ИНТЕГРАЛЬНОГО ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
483
Применяем прямое преобразование Лапласа:
Z \z" (х)] - L [zr (х)] - 6L [z (х)] = L [2],
s2Z (s) — sZ (s) — s + 1 — 6Z (s) = — •
Полученное алгебраическое уравнение с одним неизвестным Z (s) решаем
относительно Z (s):
" s + 2
* (*) = Г^=
-б)
Прежде чем воспользоваться обратным преобразованием Лапласа, перепишем
полученное решение в ином виде
*(*) = ■
В
г — 3
+
J 1_ J^ 1
3 s + 15 7—3
5 s + 2
откуда
*(т) = -
'JL1 8
s J+ 15
L-1
1
■ +
8 зт
15е
s — 3
4
L-i
ы
3. Имеем
z'"(t) — 2z"(x)+5z'(x) = 0,
z @) = z'@) = О, z"@) = l.
Пользуясь тем же способом, что и в примере 2, находим
s3Z (s) — 1 — 2s2Z (s) + 5sZ (s) = 0,
z w -
l
s (s2 — 2s + 5)
±(±
5 5
-2s+ 5
1 1
1
1
5 s 5 (s— IJ+ 4
D)
+ 10 (s — l)a + 4 '
откуда получаем искомое решение
1
1 , 1 т
z (х) = ~ё- —~£~б cos 2t + -Т7Г" ^ sin 2т.
E)
Для усвоения метода решения дифференциальных уравнений и основных
соотношений преобразования Лапласа читателю предлагается решить следующие задачи;
1. y"(z)-&y(x)=0.
kx —- k~
Отв. у (т) — Cte +C2e
2. ^(т)-(а + Ь)^(х)+а^(х) = 0.
Отв. у (т) = С2е + С2е .
3. fW+%W = «.
Отв. «/ (х) — Ci sin &х + Сг cos &г + -р--
4. у" (х) - 2ш/' (х) + (а2 + б2) г/ (х) = 0; г/ @) = 0, у' @) = 1
Отв. у (х) = —г- еах sin 6x.
16*
484
Глава четырнадцатая
5. ymW+y'(*)=e2v; t,@) = r/'@) = t/"@) = 0.
11^1 2
Отв. у (х) = — ~y +-jQ e — -g» sin x + -g- cost.
6. ^(x) + ^W=-^ + 2t; 0@) = 4; t/' @) == — 2.
Ome. 0 (t) = -g- тз + 2<?~T + 2.
7. /V) (t) + #'" (T) _ cos T. y @) = y, @) = y„ @) = 0. ^ @) = const
Ome. r/ (x) = —-1 + x + Cx2 + -y ( e"~T + cos x — sin x) •
у" (x) — 2z'(x)+#(x)<=0; J
Ome. t/(x) =2 — 2г ~x—2xe~~T; z (x) = 2 — 2e~x —- 2x£~x— т.
9. yim (x) + 2#" (x) + у (x) = 0, i/ @) = 0; */' @) = 1; y" @) - 2; y» @) = - 3.
Отв. у (х) = x (sin x + cos x).
§ 4. ОСНОВНЫЕ ПРАВИЛА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
В § 2 было рассмотрено изменение изображения функции при
дифференцировании или интегрировании оригинала функции по переменной t.
Здесь остановимся на обратной задаче: будем производить операции
дифференцирования и интегрирования по параметру 5 изображения
функции и искать, какому действию над оригиналом функции соответствуют
эти операции.
Дифференцирование изображения. Пусть F(s) = L [/(*с)].
Возьмем ряд производных от F (s) no s:
0
/="' (s) = j e" л x2/ (x) dx = L [x2/ (x)].
0
Вообще
F{n)(s)^L[(~z)nf(z)] A)
Таким образом, я-кратное дифференцирование изображения функции
соответствует умножению оригинала на (—ъ)п.
Пример.
1. Известно
k
S2 + A,2 =Msinfex].
Применим полученное правило:
— 2ks
(S2_J_£2J = ^ .[— * Sin ^
откуда
2&s
L [x sin fcx] = (s2 + ft2ja' * B)
ОСНОВЫ ИНТЕГРАЛЬНОГО ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
485
Из формулы B) можно получить новое соотношение между
оригиналом новой функции и ее изображением, если вспомнить, что деление
изображения на s соответствует интегрированию оригинала:
Г 0 sin kQdQ = -ш (sin kx — kx cos kx),
о
Тогда получим
L [sin kx — kx cos kx] = (g2 + k2J - C)
Пользуясь соотношением A), можно получить ряд новых
преобразований.
Интегрирование изображения. Пусть функция f(x)
удовлетворяет обычным нашим условиям и ее изображение будет F(p), т. е.
00
■pz
F(p) = $e P% /(т)Л.
О
Интегрируем F (р) в пределах от 5 до Ь\
]F(p)dp=b^e-pzf(,)d,dp=]f(,)^e-pzdpd,=]l^(e-"-^)d-c.
s s 0 0 5 О
Если функция / (х) такова, что существует предел '-^- при % -> 0, то
интеграл равномерно сходится относительно Ь. Тогда положим Ь-*оо,
откуда будем иметь
]f(p)dP = fl^-^5'd, = L\-^]. D)
so L j
Таким образом, получаем следующую теорему: «Интегрирование
изображения функции по параметру s в пределах от s до оо соответствует
делению оригинала функции на х».
Примеры.
2. Известно
к
L [ sin kx] =* s2 +fe2 .
Тогда будем иметь
J P! + is 2 ft [ т J
E)
/у- -Г /с- л /t 1^1
Если полученный оригинал новой функции проинтегрируем от 0 До т, то изображение
надо разделить на $-.
Положим As= 1; тогда
f sine de^si (т),
откуда
L [Si (т)] = — arctg a.
3. Имеем
т
О
При а = 0 и 6=1 получим
J ^ р + а р + 6 / s + а '
i
486
Глава четырнадцатая
Умножение изображений. Пусть Ft(s) и /^(^ —
изображения соответствующих функций Д (г-) и /2 (т), т. е.
F2(s)==L[/2(t)],
Тогда произведение изображений равно
F^F^s) -L | j/1F)/2(T~e)d0 = L f Д(т — в)/а(в)йв|. G)
Lo J Lo J
Соотношение G) известно под названием теоремы умножения
изображений или теоремы Бореля (доказательство этой теоремы будет дано в
§ 9).
Введем условное обозначение
причем
тогда
/iW/^) = J7i(e)/,(*-e)de,-
О
(8)
(9)
F1(s)Fa(s) = L[f](T)ft(t)],
L-1[F1(s)Fa(s)]=f\(-z)ft('z).
Соотношение (9) иногда формулируют так: «Произведению из
изображений функций соответствует свертывание оригиналов функций»; оно
имеет исключительно большое значение в операционном исчислении.
Теорема Эфроса. Эфрос доказал важную теорему, из которой
как частный случай вытекает теорема Бореля. Если F (s) есть
изображение функции /(х), т. е.
оо
F(s) = J7(t)£T*xdT,
о
то оригинал изображения
оо
F[cp(s)]<D(s) -J /*(») е"*
о
дается формулой
*db
о
где <Ь (т, Ь) является решением интегрального уравнения
оо
A0)
(И)
A2)
A3)
Доказательство этой теоремы будет дано в § 9.
Из этой теоремы Эфроса, как частный случай, получаем следствие:
если /(т) есть оригинал изображения F (s), т. е.
L[f{*)] = F{s)%
то имеет место равенство
FWj) = L I —^г Г е~ Я"/ (х) йт |. A4)
I/ ТГ.Т У
у.
|/л
ОСНОВЫ ИНТЕГРАЛЬНОГО ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
487
Примеры.
4. L-iTl 1
Если
s2 s — k
kz
[=j(T_6)/edfl=J_(^_b-l)
10
5. L--
х Г £! 1
L(s2 + *Tj
[F (s)f = L[f* {z) f (x)},
X
= cos &x* cos ki = f cos & (x — 6) cos ktidd •
2k
Если имеем изображение трех функций: fx (х), f2 (х), /3 (т), то
^i W ^2 (s) ^з W = L [ f\ (х) /; (х) /3 (х) ],
[sin£x-|-&xcos&x].
A5)
При помощи соотношений (9) и A5) можно снова показать, что интегрирование
оригинала соответствует делению изображения на s:
L-i|"iF(s)l=l*/(x)=(/@)
dti,
L'1 ["JL F (s)~| = 1* j / F) dd = j J f (g) Л(Ю,
Ls Jo oo
Te е. получаем соотношения A2) и A3) § 2#
1
где
т/т.
Yn
,e.^-[,-,j^-
=!•
У тс О
2j/6
<?х erf (i),
A6)
erf
(z) = 2_ f e ** d*.
"|/тс о
7. Найдем оригинал изображения F (s) =
i
i
тогда
Vs — 1
L
T/s +1
s — 1
1
1/"
% Прежде всего можно написать:
1
1
ys — i
s —1
1
i^('^)'
j/тсх
У7-
+ eT [1+erf l/x~].
A7)
Изображения некоторых функций, В заключение данного
параграфа рассмотрим прямое изображение некоторых функций, часто
встречающихся при решении задач теплопроводности. Для нахождения
изображения будем пользоваться соотношением (9).
Примеры.
/ fe2' \
8. Пусть оригинал функции есть / (х) = x"~3/2expf— ~4х~). где k > 0. Найдем
изображение этой функции:
со __/^
■3/2
^Т:
-4;-'i-[-+-s-])—4*-Tj-'[-('-fn--
488
Глава четырнадцатая
где 0 =
к V-
У-л
2 Ух
Таким образом,
f 6 — "гГ Vs • Последний интеграл равен —к- , так что
, с, ~2-£ .-"Г
[ft» П
2 У^т* J
-ЛтЛу (&> О, s> 0).
A8)
9. Если оригинал функции в формуле A8) умножим на (—х), то от изображения
необходимо взять производную по s:
£2
1 --
У ni
ут
A9)
Если & = 0, то получим выведенную ранее формулу
10. В соотношении A8) оригинал функции интегрируем, а изображение
разделим на s:
fc2
L-i
s *
2 У тс J0
jr^"e-3/2d8 = -4r J Г*л~
Vti
2 Ух
2 Ут
Уте 0 l/rc
e *" Д = 1 — erf -*-
2 Ух
В результате получаем одно из важнейших для задач теплопроводности соотно-
ше ний: __
-kVsl ' .erf-A- = erfc—k—. B0)
L-i
[-i--?1--
2 Ух
2 l/т
И. В соотношении A9) оригинал функции интегрируем, а изображение
разделим на s:
Г Ч т &2 ft2
[ s )/s J # ]Ax V %
— & erfc
2 Ух
syS
2
__ Г i __JlL ^ £ 1 _ £
T/x —=7- e 4x — — erfc — = 2 "J/x i erfc =
[ У тс 2 J/Ч 2 Ут J 2 Ух
где
i erfc и:
1 —и2
• е
У и
- и2 С
— и erfc и = \
erfcSdS.
, B1)
B2)
Следовательно, функция i erfc и обозначает интеграл от функции erfc и, взятый в
пределах от и до оо.
Аналогичным путем можно показать, что
Ul k2\ e k
-Х- + -5Г erfc
8х
2 Ух
4~— е. > = 4xi*erfc *
2 Ух
B3)
ОСНОВЫ ИНТЕГРАЛЬНОГО ПРЕОБРАЗОВАНИЯ ЛАПЛАСА 489
где
i2 erfc a = f i erfc SdS = -^ ГA + 2a3) erfc и —
9 -i i
— —— ue I = -д- [erfc и — 2 w i erfc a]. B4)
Применяя последовательно такой прием получения новых изображений, найдем
следующее соотношение:
■VT.
\Х,
1 + ЧгП г
S = L
где
DTI/2Verfc-^=: , B5)
2 1/axJ
.Iя erfc u= f i* erfc £d£ B6)
(л = 0, if 2, 3, ...)•
^Следовательно,
i° erfc и — erfc к. B7)
Для \п erfc и существует общая рекуррентная формула
2nin erfc и = irt~2 erfc и — 2шя-1 erfc a, B8)
Можно показать, что z = in erfc и есть решение дифференциального уравнения
d2z dz
—Т+ 2«—— 2/22=0. B9)
dw2 eta
Из формулы B8) следует
i* erfc 0 = —
«(±.+.)- «D-.)' C0>
Соотношения B5) и C0) имеют широкое применение при решении
задач теплопроводности.
Все соотношения между оригиналом функции и ее изображением,
полученные нами в этой главе, приведены в сводной таблице в
приложении.
§ 5. РЕШЕНИЕ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
ОПЕРАЦИОННЫМ МЕТОДОМ
Дано линейное обыкновенное дифференциальное уравнение с
постоянными коэффициентами:
Ап^- + Ап.1^^-^... + А1^-+Айг{,) = ^,), A)
которое можно переписать так:
Апг(п\х) + А^ 2(я~1}(т) + ... + AJ (т) + А0г (т) - <р (т). B)
Для простоты вывода начальные условия примем следующие:
z{n)@) = zin~l) @) = ... = г @) = 0. C)
Такие начальные условия необязательны; можно взять более общие
условия (каждая производная от z при т = 0 равна постоянной), однако
результат получим тот же.
Применим способ решения дифференциального уравнения,
рассмотренный в § 3.
490
Гл'лва четырнадцатая
Применяя прямое преобразование Лапласа, получаем алгебраическое
уравнение первой степени относительно одного неизвестного:
Ans»Z (s) + An.t s"-1 Z (s) + ... + AxsZ (s) + A0Z (s) = Ф (s), D)
где Ф (s) = L [ф (т)]. Решение этого алгебраического уравнения имеет
вид
где ф E) = Лд$я + Л^ я"-1 + Ап_2 sn~2 + ... + Axs + Л0 — полином
степени я относительно s.
Решение заданного дифференциального уравнения получается, если
применим обратное преобразование Лапласа:
'М-КЩ <6>
Нахождение оригинала функции по ее изображению может быть вы*
полнено быстро, если изображение функции совпадает с одним из
рассмотренных выше изображений. В данном случае необходимо знать
соотношение, которое позволяло бы находить оригинал функции, если
изображение ее имеет вид ~гЩ, где ф E) — полином /г-й степени
относительно s. Оригинал функции обычно находится при помощи
интеграла по некоторому контуру в области комплексной переменной (см. §8).
В данной монографии этот способ нахождения оригинала не
используется, поскольку от читателя тогда требовалось бы знание основ
теории функции комплексного переменного.
Для нахождения обратного преобразования вида F) можно
воспользоваться методом Ващенко-Захарченко. Таким образом, основная
трудность при решении дифференциальных уравнений с постоянными
коэффициентами возникает при нахождении обратного преобразования
Лапласа, т. е. при переходе от изображения функции к ее оригиналу.
§ 6. ТЕОРЕМЫ РАЗЛОЖЕНИЯ
Теоремы разложения были впервые выведены Ващенко-Захарченко,
причем в том виде, в котором они получаются при помощи
преобразования Лапласа. Хевисайд значительно позже Ващенко-Захарченко
получил теоремы разложения; последние имеют иной вид, поскольку
преобразование в методе Хевисайда производится по Лапласу — Карсону.
Метод преобразования по Лапласу — Карсону нам кажется менее удоб*
ным по сравнению с методом Лапласа*
Пусть изображение F (s) функции / (т) можно представить как
отношение двух полиномов
F(S) = ^-, A)
ф (S)
где
ф (s) = A0 + AlS + Л252 + ... + Ап& B)
есть полином относительно s степени n,w а
Ф (s) = B0 + BlS + £2s2 + ... + Bms™ C)
есть полином относительно s степени т, причем п > пг. Случай пг > п
не может иметь места, так как оригинал функции, соответствующей
ОСНОВЫ ИНТЕГРАЛЬНОГО ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
491
целой положительной степени st представляет некоторую разрывную
функцию особого рода.
Полином ф (s) степени п имеет п корней sv s2, s3, .. . , sn.
Рассмотрим отдельно два случая.
Полином ^(s) имеет простые корни. Пусть все корни sv's2> ..., s4
различны, т. е.
,ф(з) = (s — SiMs — sa) ... (s —s„). D)
Тогда соотношение A) можно написать так:
ФE) - Cl + С2 + ... + Сп E)
ф (s) s — sx s — s2
Коэффициенты Clf C2, ..., Cn не зависят от s, поэтому, если они будут
найдены, то обратное преобразование ряда E) не вызывает затруднений,
так как известно
L.1r_Q_j =c »лх
L * — s„ J
Найдем коэффициенты Сл. Умножим обе части равенства E)'на (s — Sj):
*(»)(—i)=Ci + E,^).r_^_+.>. +_Ss_]. F)
ф (s) L s — s2 s — s„ J
Пусть s~>sx, тогда все члены правой части равенства F), за
исключением первого, будут равны нулю. Левая часть равенства становится
« о
неопределенной, т. е. равной —, так как числитель и знаменатель
равны нулю. Раскроем неопределенность по правилу Лопиталя:
s-+Sl [ ф (*) J s-Sl L Y (s) J Y (si)
1"аким образом, для нахождения коэффициента Сх надо в функцию Ф (s)
подставить вместо s корень sl9 взять производную по s от ф (s) и
подставить в Y (s) вместо s корень sx и, наконец, Ф (sA) разделить на ф'^х).
Аналогичным путем найдем коэффициент С2; для этого умножим обе
части равенства E) на (s — s2) и положим s-±s2:
Сг =
Ф(,)|('7") = с,+ (д-*)Г-^-+ -£*- + .. + -^4- (в)
ф (s) Ls—sx s —s3 s — sfl J
откуда
Ф(*) Ф'(*2)
Аналогично для коэффициента С3 получим
Г _ ФE3)
im Ф (s) (s — s2) = €>(s2) ^ (щ
Y(sb)
Вообще
Cn = ±&L. A0)
Применим обратное преобразование Лапласа к ряду E):
/ (х) = L [F (s)] = L-i \^Щ = С^ + С^ + ...+ С/*' =
L Ф (s) J
492
Глава четырнадцатая
/г=1
Тогда получаем теорему разложения Ващенко-Захарченко
L ф (s) J ^ ф' (s„)
Соотношение A2) отличается от теоремы разложения Хевисайда тем,
что в последнюю вместо s входит оператор р, а вместо ф' (sn) входит
произведение рпУ (рп). Кроме того, в формуле Хевисайда имеется до-
Ф@)
полнительныи член —^-, что создает определенное неудобство при
Ф (°)
применении его к практическим расчетам.
Обобщение теоремы. Теорема разложения справедлива и для
случая, когда изображение F(s) есть отношение трансцендентных
функций <D(s) и ф(я). В теории функций комплексного переменного
доказывается, что такая функция разлагается в ряд по простейшим дробям
вида E). В результате получим то же соотношение A2):
L-i Г±М_] в у ЛЫ. eV . A3)
я=1
При этом предполагается, что функция ф (s) есть обобщенный полином
и имеет только простые корни s19 s2, ..., sn, причем она не имеет
нулевого корня (все полюсы F (s) лежат слева от прямой а; см. § 8). Если
Фх (s) и tyt (s) не являются обобщенными полиномами, но путем
умножения на sk(\k\<Cl) их можно привести к ним, то также можно
пользоваться теоремой разложения.
Пусть Ф^-д^ <J>(s), Ф1 E)s* = ф(s), где |&|<1, sk=f=0. Тогда
sk Ф1 (s)
1. Ф (s) 1. s*Oi(s) 1
lim —^-^- = lim —u w— = 1
s-S/? ф'(*) s^ l**h(s)]'
skV\(s) +ksk"^1(s)
Если s„ есть корень уравнения ^(s), т.е. tyi(sn) = 0, то получим
1- Ф (S) 1- Ф1 (s) /1 л\
lim —i-i-= hm—?A-L-. A4)
s^s« +' (s) +1 (s)
Если какой-либо корень sk = 0, то необходимо изображение F (s)
представить как отношение двух сходящихся степенных рядов
относительно s, показатели степени которых должны быть натуральными
числами, т. е.
ф (s) = а0 + axs + a2s2 + ... , A5)
<!>(s) = b0 + b1s + b2s*+ .... A6)
Такие степенные ряды Ф (s) и ф (s) можно назвать обобщенными
полиномами или полиномами бесконечно высокой степени.
При этом необходимо, чтобы отношение —— не было равно постоян-
ф (s)
ной или функции sr (где г — любое положительное целое число), так
как для них не существует оригинала.
ОСНОВЫ ИНТЕГРАЛЬНОГО ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
493
Если отношение двух целых трансцендентных функций можно
привести к отношению двух сходящихся степенных рядов с показателями
степени в виде натуральных чисел (обобщенных полиномов), то
последнее условие можно распространить и на них.
Итак, необходимое условие теоремы разложения заключается в том,
чтобы изображение F (s) могло быть представлено в виде отношения
двух сходящихся степенных рядов, показатели степени которых суть
натуральные числа, при этом постоянная а0 должна быть равна нулю
при Ь0фО.
Полином ф (s) имеет кратные корни. Пусть ф(я)— полином п-й
степени (я>т) имеет п корней, из которых некоторые суть кратные
корни (sr = sr+1 = ... = sm), т. е.
^(s) = (s — Si)(s — s2) ... {s — sm)k ... (s — sn),
где k — степень кратности корня sm (k — целое число, &> 1). Как и
раньше, можно написать
Р{8) = Л®- = _*_ + _^_ + .... + _^_ + ... + *. в
ф (S) S — S! S — S2 S — Sn (S— Sm)R
лт5? + ™ A7)
Коэффициенты Cl9 C2,..., Cn находятся обычным путем, т. е. для них
применяют теорему разложения для простых корней. Таким образом,
оригинал изображения W (s) находим по соотношению A2). Остановимся на
изображении . Определим коэффициент D; для этого умножим
обе части равенства A7) на (s — sm)k, т.е.
Ф(8)('-8"*к =D + (s- smY W (s). A8)
Ф (*)
Пусть s-+sm, тогда будем иметь
D==lim •(»)(—■»)*,
*-+*т ф(8)
С другой стороны, можно написать
[Dx*"i es™x ] = l- L -±^- (Df»
(«-««)* (*-!)> L J (*-»)! dsi
4-
"m
так как известно [см. формулу A7) § 2], что
(s — sm)*
Таким образом, получаем
/2 (,) = L-i Г ^-1 = ' lim (-4^ ГФ(я)(—'»>* HI • A9)
2W L (s-*m)* J (*-l)! s^Sm\ ds*"i L +(s) Jj V '
Отметим, что соотношение A9) можно получить совершенно строго из
интегральной формулы для обратного преобразования Лапласа, так как
оно представляет известную формулу Коши для нахождения вычета
полюса s = sm кратности k (см. § 9). Если k = 1 (простой корень), то
соотношение A9) превращается в предыдущее A8).
Применяя формулы A2), A3), A4) и A9) для нахождения оригинала
функции, можно решить любое дифференциальное уравнение с
постоянными коэффициентами.
494
Глава четырнадцатая
< р, то можно
причастный случай теоремы разложения. Ограничим
функцию F (s) дополнительным условием, чтобы она была аналитической
функцией аргумента— при < р. Тогда F (s) можно разложить в
s \s\
сходящийся степенной ряд:
оо
F(s)=°±- + ±-+... =£-fr- B0)
/1=1
Функция F (s) должна быть такова, чтобы ряд не содержал постоянной
D0, так как она не имеет оригинала.
Так как ряд B0) равномерно сходится при —
| S
менить почленное обратное преобразование, в результате которого
получим
со
/(х) = L-*[F(s)]= 2 -^ЗТУГ Х*, B1)
/2=1
Соотношение B1) может быть получено как частный случай теоремы
разложения (для кратных корней), если считать, что ф (s) имеет
бесчисленное множество нулевых коррей различной степени кратности (от
1 до л).
Большинство задач по теплопроводности, рассматриваемых в этой
монографии, может быть решено, если для нахождения оригинала
функции пользоваться только формулами A3) и A9). Поэтому формулы A3)
и A9) являются основными формулами при решении дифференциальных
уравнений теплопроводности.
Приведем для иллюстрации несколько примеров, рассмотренных нами ранее.
1. В примере 1 § 3 изображение функции получено в виде
As + D ФE)
Z (s) = = ;
W s2 — /г2 Ф (s) '
•ф (s) = s2 — k2 = (s — k) (s + k) — полином второй степени; он имеет два простых корня:
si = k,t s2 = —/г, Y (s) = 2s.
Применяя формулу A3), находим
glx)BJk + DL^ + JAkI1D_e_^w_A(hJn+D_aik%
т. е. то же самое соотношение B) § 3.
2. В примере 2 § 3 при решении дифференциального уравнения получено
следующее соотношение для изображения функции:
s2-s + 2 Ф(8)
Z(s) =
s (s2 — s — 6) ф (s)
ф (s) = s (s2 —■ s — 6) — s (s — 3) (s + 2) — полином третьей степени; он имеет три корня:
Sl = 0, s2 = 3, s3=—2; у (s) = 3s2 — 2s— 6.
Тогда
з
Ф (sn) „snx
/(x)=L-i[Z(s)] = 5]
V (Sa)
+ (9-3 + 2) e3x+ D + 2 + 2) e-*__± + ±p + ±e-*
(_6) B7 — 6 — 6) ' A2 + 4 —6) 3 15 5
т. е. получаем тот же результат.
ОСНОВЫ ИНТЕГРАЛЬНОГО ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
495
3. Найти по изображению оригинал функции cos&x.
По формуле A3) имеем
L s2 + k2 J *-» <|/ (sn) ,
где Ф (s) = s, ф (s) = s2 + &2 = (s + ik) (s — Ik), <|/ (s) = 2s; sx — ik, s2 = — ik. Отсюда
имеем
Г С3 1
4. Найдем обратное преобразование L~l •
Ls(s + CKj
/ (т) = L-i Г——1 = L-i Г 1 , Ф (s) = С3,
<\> (s) = s (s + CK — полином четвертой степени; он имеет корни sx = 0, s2 = —- С
(трехкратный корень). Получим
'«-^ + -Л:{^[т-4-'-('+С- + Т-)
е~*
5. Найти функции г/(т) и z(z), которые удовлетворяют следующей системе
дифференциальных уравнений:
у" СО -г" М + *' W - </ W = *т -2,
2#" W - г" <Ч) - 2у' (т) + 2 (т) = - т,
с начальными условиями
у @) = у' @) = г @) = г'Щ = 0.
Решаем обычным способом:
s27 (s) — s2 Z (s) + sZ (s) — Y (s) =
s — 1 s
1
2s2 Y (s) — s2 Z (s) — 2s Y (s) + Z (s) =
Эти уравнения перепишем так:
(s + l)Y{s)-sZ(s)= *~~2
с2
2sF (s) — (s + l)Z(s) = —
s (s — lJ
1
(s-1)
Решая два алгебраических уравнения с двумя неизвестными, получаем
1
Y(s) =
Z(s)
s(s —IJ '
2s — 1
s2(s — lJ ' .
Для нахождения оригинала функции воспользуемся соотношением A9).
Полином ф ($) = s (s — IJ имеет корни sx — 0, s2 = 1 (двухкратный корень). Тогда
•«-^ + i5[-i-D-•")]-+"'-'•
Так же находим
2s— 1
2 (т) = lim {—- — esx\\ + lim {—- —
est
== % e ■— t.
Для усвоения техники вычисления обратного преобразования по формулам A2)
и A9) читателю предлагается решить следующие задачи:
1 • У" W + 30' Ос) + 2^/ (т) = 4; 0 @) = 2; у' @) = 0.
Отв. у (т) = 2.
496
Глава четырнадцатая
2. y"(t)-2y'(z)+y(*) = l.
Отв. t/(x) = (d + C2x)^ + 1.
3. */"(*)+J/W = 3sinx; */@) = 1; *,'@) = --у .
О/яв. # (х) = 11 — — х I • cos т.
4. у" СО + лау (х) = asin (mx + «); m =£ п; у @) = */' @) = 0.
а
Отв. у (х) = — {m cos а sin/г х +/zsin а cos nx -—л sin (/лх + а)Ь
5. l/'7 (т) — т^ (х) = аетх + Ьепх ; у @) = у' @) = 0.
Отв. у (х) = (-М (mxe^ -shmx) + * — . {(т -л) е~тх +
\ 2т2 J 2т (т2 — /г2)
+ (т + л)етг — 2тепх) .
6. #" (т) + у (х) = sin х sin 2x.
Отв. |/ (х) = \у @) —— cosх + ^rcosЗх + у' @) + — х sinx.
Отв. ^(x)-l+^+^^+^e-T~^e^^cosY^3" +
+ T/Tsin-yxyTJ.
3. #" (т) + г/(т) =*xcos2x.
5 1 4
Отв. у (%) = у @) cos х + у' @) sin х ^-~~т- sin х — —- х cos 2х + ~ sin 2x.
§ 7. РЕШЕНИЕ НЕКОТОРЫХ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ С ПЕРЕМЕННЫМИ КОЭФФИЦИЕНТАМИ
Линейное дифференциальное уравнение, коэффициенты которого
являются полиномами относительно т, можно преобразовать в линейное
дифференциальное уравнение для изображения функции, коэффициенты
которого будут постоянны относительно 5. Решение такого
преобразованного уравнения проще, чем решение оригинального уравнения, если
степень полиномов ниже степени исходного уравнения.
Если коэффициенты дифференциального уравнения для оригинала
функции — полиномы первой степени, то дифференциальное уравнение
для изображения функции будет линейным уравнением первого порядка,
которое решается обычными методами. Трудность возникает при
переходе от решения для изображения к решению для оригинала, т. е. при
нахождении оригинала функции по ее изображению.
В качестве примеров рассмотрим два дифференциальных уравнения
Бесселя, решения которых были использованы в задачах по
теплопроводности.
1. Дано дифференциальное уравнение Бесселя первого порядка
■А^ +-L^- *,w = o (i)
dx2 x dx
с начальными условиями г @) = 1, z' @) = 0.
Перепишем уравнение в ином виде:
'^,,W + 2,W-^2^(t) = 0. B)
ОСНОВЫ ИНТЕГРАЛЬНОГО ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
497
Воспользуемся при преобразовании соотношением A) § 4:
L \iz" (т)] = — -4" [s2Z (s) — s] = - 2sZ (s) — s2Z' (s) + 1,
as
l[«(t)] = -^j-z(«) = -z'(«); C)
as
тогда
2sZ (s) + s2Z' (s) — 1 — sZ (s) + 1 — &2Z' (s) = 0,
(s2 — &2) Z' (s) + sZ (s) = 0. D)
Получаем дифференциальное уравнение первого порядка с постоянными
коэффициентами, которое решаем обычным методом:
dZ sds
z
7 /сЛ
Z (s) —
s2 — k2 '
С
, »
Vs2 — k*
где С — постоянная интегрирования.
Для перехода к оригиналу разложим Z (s) в ряд:
С / /г2 \-1/2 С Г 1 / А; \2 1 3 /И* I
у Bп)\ &"
^ Bпп\J s2n+l '
п=0
Воспользуемся известным преобразованием Лапласа; тогда
оо
*и = сЛ-&г^г№- <6>
Постоянная С = 1, так как z @) = 1 по условию.
Полученный ряд для z (т) представляет собой функцию Бесселя первого рода
нулевого порядка от чисто мнимого аргумент (&т), т. е.
2(т) = /0(йх). G)
Таким образом, получаем новое преобразование
1
L-1
J—/г2 J
Ys2
Если положить & = i (k2 — — 1), то I0(iz) = JQ (%), откуда получаем
1
L
т]
= /oW. (9)
*|А2 + ;
2. Дано дифференциальное уравнение Бесселя порядка v:
Т2 z* (т) +U' (т) + (т2 — V2) 2 (^) = 0, A0)
к которому применено преобразование Лапласа (v — положительное целое число).
Применяем тот же способ перевода дифференциального уравнения от оригинала
функции к ее изображению:
(s2 + !) Z" (s) + 3sZ' (s) + A —-v2) Z (s) - 0, A1)
Полученное уравнение является довольно сложным, за исключением частного слу*
чая, когда ч = 1.
Введем новую переменную у (т) = tv z (т); тогда получим
*У" W + A - 2v) у' Ь) + ту (*) - 0. A2)
498
Глава четырнадцатая
откуда
Так как у @) = 0, то имеем
(s* + 1) V (s) + (Г—» sY (s) = 0. A3)
Решение данного дифференциального уравнения имеет вид
Y(e)--£±.f (-D"B« + 2v)! 1
Y()~ Bv)l ^ 2™/z!(v + n)! s2" + 2v+i • u*>
n=0
, (T) = _J>L V (=!>! t2v+2„ . A5)
yw Bv)! *-* 2*nn\ (v + /i)!
/2=0
ч!С 1
Выберем постоянную С так, чтобы =—— , тогда искомая функция z (т)
Bv). 2
равна
S(—1)л / т \Ч-2я
—-— — =/,(i A6)
где Jv (x)— функция Бесселя первого рода порядка -v.
Из данного примера получили новое соотношение для изображения функции у (т);
2v!
2V v! (?~+l)v
м *v, wi = .,.,,,..; Mv+v2 • <17>
§ 8. ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ И ОПЕРАЦИОННЫЕ
МЕТОДЫ
Все операционные методы базируются на интегральном
преобразовании функции и поэтому могут быть названы методами интегрального
преобразования.
В теории аналитических функций доказывается, что любую функцию
и (г) от комплексной переменной z — х + iy, удовлетворяющую
определенным условиям, можно преобразовать в новую функцию v (С) от
комплексной переменной с = I -\- щ с помощью соотношения
u(z) = f /C(z,?)o(?)fc (О
с
причем ядро преобразования К (г, <;) является аналитической функцией
от каждой из комплексных переменных, а путь интегрирования С
следует каждый раз выбрать надлежащим образом.
При ядре
К(г^)=е2' или K(z^) = eiz<
получаем преобразование Лапласа. Остановимся на этом несколько
подробнее.
Пусть дана некоторая функция F (s) от комплексной переменной s =
v°
= ? + Щ> причем F (s) регулярна в полосе а < I < р и \ \F(t + Щ)\Лч\
—с»
сходится в этой полосе. Допустим, что в каждой более узкой полосе
a + S<J£<;p — 8 (8>0 — произвольно малое постоянное положительное
число) функция F (s) равномерно стремится к нулю с возрастанием
абсолютного значения ординаты ч\. Тогда для действительных
положительных значений х имеют место соотношения
ОСНОВЫ ИНТЕГРАЛЬНОГО ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
499
*ы = -Ь
F(s) =
a-f-/oo
Г x-*F(s)ds, B)
(s) = Г х3'1 g (x) dx.
C)
Формулы B) и C) известны
под названием формул
обращения Мелина1*, или формул
преобразования Мелина.
Сделаем замену
действительной переменной х = е~т; тогда
g (х) == / (х) и получим
a-J-/oo
/W = -^- j (TF(s)ds, D)
О + »oo
ч 1
!
-Г"~ о
v -J
0
\
1
Рис. 14. 2. Схема интегрирования
-}-oo
F(s) = j e~s7(x)dx.
E)
Интегральное соотношение E) является преобразованием Лапласа.
Следовательно, если интегральное преобразование E) принять в
качестве прямого преобразования функции / (т) от действительной
переменной, то соотношение D) является обратным преобразованием, т. е.
функция F (s) есть изображение функции /(V).
Соотношения D) и E) непосредственно получаются из формул
обращения Мелина, но они могут быть доказаны упрощенным методом,
который наглядно иллюстрирует представление функции / (т) в виде
интеграла от комплексной переменной. Ниже приводится этот метод
в несколько сокращенном виде2).
Рассмотрим интеграл
c-j-г'оо
2ni
1
ds
F)
Интеграл берется по прямой, параллельной мнимой оси и лежащей
справа от нее на расстоянии о (рис. 14.2). Модуль подынтегрального
выражения при х > 0 быстро стремится к нулю, когда s^ oo в правой
полуплоскости по направлению, непараллельному мнимой оси. Для
т >0 интеграл равен 1, так как слева .от о подынтегральное выражение
имеет одну особую точку — простой полюс s = 0.
Следовательно, имеем
a -J-/ оо
2т J
ds
0 При т < О
1 при т > О
(о>0).
Заменим т на % — 6; тогда
<j-f-/oo
— f
s(x—6) ds
0 при х< б,
1 при -с > 6.
G)
(8)
1) Доказательство приведено в кн. Курант и Гильберт. Методы
математической физики, т. 1. М.—Л., Гостехтеоретиздат, 1933, стр. 95.
2) См. подробнее: Эфрос и Д а н и л ев с к и й. Операционное исчисление и
контурные интегралы. Харьков—Киев, УОНТИ, 1937, стр. 19.
500
Глава четырнадцатая
a-j-гоо
/
= — С
sx e
-sBt
-s62
Заменим 6 на 81 и на 62 @Х < 62) и из первого интеграла вычтем второй.
Тогда получим
[ 0 при т < 01?
•ds = | 1 при 6Х< т<62, (9)
( 0 при т > 62.
Следовательно, интеграл / представляет собой некоторую разрывную
функцию, график которой приведен на рис. 14.3.
Возьмем произвольную функцию /(т) от вещественной переменной т,
определенной в промежутке от хг до т2. График этой функции изображен
на рис. 14.4. Непрерывную кривую /(т) можно заменить ступенчатой
линией ФлСс), значения которой совпадают с /(т) в п точках 60, 9lf
62, ..., вЯв1, причем
хх = е0<ех<е2< ...че^т,.
U
Рис. 14, 3. График единичной фун-
, кции
Рис. 14. 4. К выводу
формулы обращения Мелина
Каждую ступеньку FЛ, б^+1) можно выразить с помощью интеграла /,
а вся ступенчатая линия выразится как сумма интегралов I:
a-f-/oo
**—и я—/о
*« e
-ев.
"k+1
a—too
п-\
2%i
a+i°° (n-
•е,
-s6A
Д9А)дей Us,
CS =
где
Д6.
__--«(в*+1-9*)
h+i-h —^р (вй+1 — е*J s + ...
A0)
(И)
Если неограниченно увеличивать п так, чтобы все разности (bk+l —
— ®k) ~* 0> то срл (т) -> / (т), а Абд, будет отличаться от Fл+1 — 6Л) на
бесконечно малую величину второго порядка. Тогда будем иметь
/со
O-J-IC0
2xi
^limpS1 в ,в*/(в*I F^-6,)^ =
п*в L*=o J
с-}-* со хг
- Г еет f e~sxf(x)dzdi. A2)
ОСНОВЫ ИНТЕГРАЛЬНОГО ПРЕОБРАЗОВАНИЯ ЛАПЛАСА 501
Изменим пределы интегрирования функции / (т) по т от — оо до
+ оо (тх = — оо, т2 = оо). Тогда, обозначив интеграл от /(т) по т через
F (s), получим
а-}-/ оо
/W = -^7" j e"^(s)^ A3)
а—*оо
-|-00
F(s)= j Г"/(^т. A4)
— 00
Поскольку в наших задачах т>-0, то
00
F(s)= j е-т/(х)Л. A5)
О
Карсон в обосновании операционного исчисления воспользовался
видоизмененным интегральным преобразованием A5):
00
W(p)=p J e-P'f(t)dt9 A6)
о
где р — некоторый параметр, равнозначный s. Соотношение A6)
называется интегралом Лапласа — Карсона. Исходя из соотношения A6),
можно показать, что параметр р обладает свойствами оператора Хевисайда
{>-+)■
Преобразование A6) отличается от преобразования Лапласа A5)
только тем, что вместо F (s) входит функция W (р). Функцию W (р) также
можно назвать изображением функции /(т) по Лапласу — Карсону.
Соотношения между W (р) и f (t) могут быть использованы при получении
соотношений между F (s) и / (/), если положить
/@=Ж> F(s) = ^Sl. A6а)
Р
В большинстве работ по операционному исчислению в качестве
интегрального преобразования принимается соотношение Лапласа—Карсона.
Для нахождения обратного преобразования A6) надо в соотношении
A3) функцию F (s) заменить на—— , s — на р и т — на t. Тогда получим
Р
f{t) = -±-XeP<^dp, A7)
о—too
Интегральное соотношение A7) называется формулой Бромвича; оно
применяется для нахождения оригинала функции по ее изображению,
если преобразование функции производится по Лапласу—Карсону.
Таким образом, все операционные методы основаны на интегральном
преобразовании A) и, в частности, на формулах обращения Мелина.
Можно отметить, что из преобразования Лапласа непосредственно
получается преобразование Фурье. Для этого достаточно вместо
комплексной переменной написать соответствующее выражение s = !• + /т), т. е.
оо
FF + *7j)= j" e-^[e-ufW]dr. A8)
502
Глава четырнадцатая
Так как в формуле A3) интегрирование производится по прямой (Res = a),
то, сделав замену переменной s = a -f- ir\, получим
+ 00
— оо
Введем новые обозначения f(x)e~ax = g(*), F(o -f- щ) — G(tj). Тогда
1/2тс
формулы A8) и A9) примут вид
оо
G(yd = -±T[gWe-'*dv, B0)
о
.-{-со
g^) = ^=\G(^d^ B1)
— 00
Таким образом, преобразование Лапласа, связывающее функции / (т) и
F(s), является преобразованием Фурье между функциями g(%) и G(r\)y
где а — произвольное действительное число, большее показателя роста
функции /(х). Область применения преобразования Фурье значительно
уже области применения преобразования Лапласа, так как для
сходимости несобственного интеграла функция #(т) должна удовлетворять
довольно жесткому условию по бесконечности, например условию
абсолютной интегрируемости, т. е* сходимости интеграла
+ 00
J|gCc)|dT.
— 00
Из всех рассмотренных методов интегрального преобразования
остановимся на преобразовании Лапласа
F(s) = L[/(t)] = {Vs7W*, B2)
о
которое является прямым преобразованием оригинала функции /(т) в
изображение F (s).
Обратное преобразование (нахождение оригинала по изображению)
находится по соотношению
а+/оо
/ (х) = L-1 [F (s)] = ^ J e" F (s) ds. B3)
а—/оо
Интеграл Лапласа B2) сходится абсолютно, если рассматриваемые
функции / (т) являются кусочно-непрерывными функциями при т > 0 и
равными нулю при х <0. Кроме того, при т -> оо должно быть
|/(т)|<М/°\
При этих условиях интеграл B2) представляет функцию F (s)
комплексного переменного s, регулярную в полуплоскости Re s ^>s± > о0.
Если s неограниченно возрастает по модулю, оставаясь в этой
полуплоскости, то
lim F (s) = 0.
I si-»-оо
ОСНОВЫ ИНТЕГРАЛЬНОГО ПРЕОБРАЗОВАНИЯ ЛАПЛАСА 503
JB обратном преобразовании интегрирование происходит вдоль
прямой а = const, причем число о может быть произвольным и большим,
чем а0. Интегрирование происходит по прямой а = const в плоскости
s = I + щ, параллельной мнимой оси и расположенной в полуплоскости
Res > sx > а0.
§ 9. НАХОЖДЕНИЕ ОРИГИНАЛА ФУНКЦИИ ПО ЕЕ
ИЗОБРАЖЕНИЮ
Для нахождения оригинала функции по ее изображению были
использованы известные соотношения между оригиналом функции и ее
изображением, получаемым прямым преобразованием Лапласа, или
специально выведенными теоремами разложения, когда F (s) представляет
собой отношение двух сходящихся степенных рядов относительно s,
показатели степени которых суть натуральные числа.
Рис. 14. 5. Система контуров
интегрирования (полюсы
расположены на действительной
оси)
С3
с
V-2
с,
г
(
0
i
i
1
i
>
,
О-Ное
0-Ир3
1
o + if>2
в-Ир,
<j-ips
«-Ф2
о-\ф
Рис. 14. 6. Система построения
контуров интегрирования
(полюсы расположены на мнимой и
действительной осях)
Из предыдущего параграфа следует, что оригинал функции дается
обратным преобразованием Лапласа
/ (х) = L-1 [F (s)] = -gL- j e" F (s) ds. A)
a—-ico
Необходимым условием для существования L^lFis)] должны быть
ограничения относительно F (s), отмеченные выше; главное из них:
функция F (s) должна равномерно стремиться к нулю в отношении аргумента
s, когда |s|-*- ©о. Интегрирование происходит вдоль прямой а, функция
F(s) должна быть такова, чтобы все особые точки находились с левой
стороны пути.
504
Глава четырнадцатая
Так как подынтегральная функция регулярна справа от прямой
а = const, то путь интегрирования (а) можно заменить другим путем
при условии, чтобы он кончался у прямой а ± too.
В большинстве задач функция F (s) такова, что все полюсы лежат
на отрицательной вещественной оси или на мнимой оси; тогда путь
интегрирования может быть в первом случае взят в виде
полуокружности с центром на прямой а = const, a во втором случае — в виде
прямоугольника (рис. 14.5 и 14.6).
Если все особые точки будут внутри контура, а подынтегральная
функция на контуре регулярна и однозначна, то интеграл по
замкнутому контуру С равен сумме вычетов относительно всех особых точек
внутри контура:
-±- j eK F{s)ds^-^r^ e" F (s) ds=^ Res [ е" F (s)] . B)
о—/оо С n=i
Пользуясь формулами A) и B), можно по обратному
преобразованию получить все соотношения, рассмотренные в предыдущих
параграфах.
Примеры
Ф($)
1. Пусть F (s) = -, -; v ■, где ф (s) == (s — si) (s — $г)... (s — $п) — полином степени
п относительно s. Тогда
•.-нп^-^гу-Ш^Н^Ш C»
С 1
Корни полинома sit s2, . . . , sn являются полюсами функции F (s), так как ф (s)
есть полином относительно s. Если кратных корней нет, то все полюсы являются
простыми полюсами. Тогда
т. е. получаем формулу теоремы разложения (случай простых корней).
2. Если полином ф ($) имеет кратные полюсы sr = sr+1 = sr+2 = . . . = sm кратности
kt а все остальные корни простые (k— 1), то будем иметь
С 1
Если все корни простые (k = 1), то из E) получим соотношение D). Если один
корень sm кратности k, то вычет для него будет равен
1 и™ Г<**-1 [®(s)(s-sn)k
lim
И*'1 [Ф(^)('-%Г „]\ = L_! Г Р
\dsft-i [ t (s) J/ L(s - sm)*
F)
т. е. получается соотношение, тождественное формуле A9) § 6 теоремы разложения
(случай кратных корней).
Отсюда вытекают ограничения на теорему разложения. Функция
F (s) должна быть однозначной и иметь в качестве особых точек полюсы,
лежащие слева от прямой а. Если эти условия не выполняются, то при-
ОСНОВЫ ИНТЕГРАЛЬНОГО ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
505
менять теорему разложения нельзя, и в этом случае надо пользоваться
непосредственно соотношением A).
Вместо обычной формулы обращения A) преобразования Лапласа
можно вывести формулу обращения, не содержащую контурного
интегрирования, а содержащую лишь операцию дифференцирования и
перехода к пределу.
Для вывода такой формулы прежде всего определим оператор eaD:
eaDf(x) = f(x + a), G)
где D — оператор дифференцирования независимо от того,
дифференцируема функция1) или нет.
Далее, введем преобразование свертки
оо
^{x) = ^G{x-y)9(jy)dy (8)
— 00
и двустороннее преобразование Лапласа ядра свертки (8)
00
JG(x)e-sxds = -^, (9)
— 00
тогда
ОО 00
^Т(д) = { ^G{y)e-yDdy^(.x) = JG{y)9(x-y)dy =
— 00 —00
00
= JG(x-y)<f(y)dy = y(x), A0)
—оо
т. е. получаем обращение свертки (8) в виде
?W = £(D)tD A1)
Пусть ядро G(x) в формуле (8) имеет вид
G(x)-=ex-e\ A2)
тогда
^ = JV-V «<*-•>*d* = г A-е)
A3)
(Res < 1)
и формула обращения A1) принимает вид
г(Г^ГБ) *(*> = ?(*)• A4)
Целую функцию г . , можно разложить в бесконечное произведение
1 -U™Jnz-4ZTT (л Z \*/k
= lime
ГA—• z) n_^00 k=sl
fi(l--f).-. 05)
ОО
l) Имеем eaD f (x) = ^i~£j"/ (*) = /(* + аЬ т- е» Действие оператора Диффе-
ренцирования D сводится к сдвигу аргумента функции, на которую он действует.
506
Глава четырнадцатая
где f — число Эйлера, а Ъп — последовательность вещественных чисел,
обладающая свойством Нт6л = 0. Последнему условию удовлетворяет
последовательность вида
п
Ьп = \пп — V-
A6)
С учетом последнего равенства, выполнив в формуле (8) замену
переменных [при ядре G (х), определяемом согласно A2)]:
ф (х) = exF (ex)t
<?(y) = f(e-y),
х = In т,
у = —-In»,
получим из соотношения A5)
'«-ш.№(+Г *"(+))
A7)
A8)
A9)
B0)
B1)
где F(s) является изображением функции /(-с)*
Проиллюстрируем полученную вещественную формулу обращения преобразования
Лапласа простым примером. Пусть
тогда
Следовательно,
F(s)
F{n)(s)
s+1 •
{—\)пп\
(s + l)n+1 ■
B2)
B3)
/ (т) = lim
(— \)n (_n_\n+1 (~l)n • n\
= 'lim
n+i
lim
1 +
n )
B4)
В качестве второго примера рассмотрим функцию, имеющую точку ветвления.
Например,
F (.*)-
V-T-
B5)
Следовательно,
1*0,4 1./- <~1)" B/г~1)!! /««X
-. Ы£ . Bя-»)"| _ -I/" lim /Bя-1)ПУя \ _
"yfim.{ г(« + 1) v»}- <27>
ОСНОВЫ ИНТЕГРАЛЬНОГО ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
507
Воспользовавшись известным асимптотическим разложением для гамма-функции
(формула Стирлинга)
Г (г) ^ У^2?-1/2 <г%
получаем
m = -^. • B8)
В заключение данного параграфа выведем теорему умножения
изображений и теорему Эфроса.
Пусть изображения функций /х (т) и /2 (т) будут соответственно Ft (s)
и ^(s), т. е.
F1(s) = L[/1(t)],
Fa(s) = L[/a(<c)]'. B9)
Найдем оригинал А(^), соответствующий произведению изображений
Fiis), F2(s):
h(x) = L-1[F1(s).Ft(s)]. C0)
Воспользуемся интегральным соотношением A):
а+г'оэ'
^W^^T ^ ^F1(s)Ri(s)ds.
а—/оо
Известно, что
00
F2(s)=:^e-sxU^)d^
о
Следовательно,
оо а_[_/оо
AW=-2Srf/«(e)d0 J fi(s)^(T"G)ds. C1)
Однако
a-f-гоо
2я/
a-j-гоо
^-JF1(S)es('-e,ds = /1(T-e), C2)
а—гоо
откуда получим
А(*) = |Мв)М*-в)
dO.
Известно, что /i(t) = 0, когда т:<0. Следовательно, /х(х — G) = 0,
если 0>т, и поэтому верхний предел интегрирования (оо) можно
заменить на t. Тогда
AW = jMe)/i(x-6)do. C3)
о
Можно сделать также замену C2) относительно функции /2 (т — 6).
Тогда будем иметь
A'W = f/i(e)/,(t-e)de. C4)
508
Глава четырнадцатая
Таким образом, получаем теорему Бореля
L-1 [Fi (s) F* (s)] = J h F) hЬ ~ 6) db = j /2 F) /x (x - 6) db =
0 0
=шт*) = /:«/,(.). C5)
Как следствие из этого соотношения вытекает еще одна теорема.
Сравнивая C2) с интегралом
a-f-/°o
А (т) = L-i [F, (s)] = -JL- j en F, (s) ds,
a—i со
получаем
L-i[F1(s)es9]=/1(x-8). C6)
Таким образом, умножение изображения функции на величину esB ,
где 6 >0, соответствует замене в оригинале т на т — 8 (теорема
запаздывания). При этом имеет место следующее равенство:
l/l (т — 6)> * >6
C7)
Теорема Эфроса может быть сформулирована следующим образом.
Если F (s) есть изображение функции /(т):
F(s) = Jf(x)e-s%dzf C8)
о
тогда оригинал /* (т) изображения
00
F [? (s)] Ф (s) = Г /* (ft) <TS* dft C9)
о
дается формулой
/*(») = J7(Wx,&)dT, D0)
О
где ф(т, &) является оригиналом изображения
со
e-^{s)<b(s) = J ф (х, &)^d». D1)
о
Оригинал функции /(х) определяется соотношением
<j-f-/oo
/<x) = i J e^^Wds. D2)
a—/oo
Если в C8) подставить <?(s) вместо s, то из формул C8) и (ЗЭ) получим
F[<?(s)] = Jf(*)e~*9{§)dz9 D3)
о
o-\-i со
f* (*) = -2^Г j ^ F [? (SI Ф (S) dS- D4)
ОСНОВЫ ИНТЕГРАЛЬНОГО ПРЕОБРАЗОВАНИЯ ЛАПЛАСА 509
Подставим соотношение D3) в D4) и переменим порядок
интегрирования:
оо a-\-i со
f*(») = -щ- j/W f Г«"+*Ф(#Л; D5)
О а—/оо
очевидно, при этом требуется, чтобы интеграл
а-\-£со
_i_ j f*-*W ф (s) ds = ф (Т) &) D6)
а—/оо
сходился.
Из соотношения D6) следует, что ф(т, &) есть оригинал изображения
бГтср(s) Ф (s) = J<f~s* ф (т, ft) a. D7)
о
Выражение D5) может быть написано так:
/*(&) = |/(т)ф(т,»)йт, D8)
о
т. е. теорема доказана.
Соотношения D5) и D8) являются весьма важными для нахождения
оригинала по данному изображению и наоборот.
§ 10. ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ ФУРЬЕ И ХАНКЕЛЯ
Формулы обращения интегральных преобразований Фурье и Ханке-
ля могут быть получены из формулы интеграла Фурье.
Предположим, что функция f\x) с периодом 2тгХ представлена
рядом Фурье
00
Постоянные коэффициенты а0, ап, Ьп получаются путем умножения каж-
пх . пх
—, sin^
дого члена ряда A) на единицу, cos~^-, sin ~* и интегрированием по
х в пределах от —кк до + тиХ.
Используя свойство ортогональности тригонометрических функций:
7сХ 7СХ
\ sin -^-dx = 0; ( cos-^- dx = 0, B)
—тсХ —тсХ
С • пх пх j г\ С пх , пх 1 ~ /оч
v sin ~y~ cos ~y~ ^x = > \ cos -x"810-!"** = > №
7ГЛ
I
-яХ —тсХ
па; . mx , f 0, m=h n
sin—^— sin -Y~dx = { '
k l \ tzI, m = n
—nX
rcX
Г пх . mx , f 0, тфп
\ cos-^— sin-^— dx = { ^
J Л л l тгХ, m = /г
cos-y-sin-y-dx = | ^ , D)
510
Глава четырнадцатая
из ряда A) получаем
%к
izla0= \ f(x')dxf; ккап = I f{x') cos-^y- &х'\
—тсХ —itX
ъ\Ъп = i / (У) sin -^~ dx'.
E)
—тсХ
Таким образом, разложение функции f (х) в ряд можно представить так:
тгХ оо 7сХ
f(x)
1
~2тсХ"
j/(xW+J_2 j /(х0созя(х~^^.
F)
/2=1 7tX
Полагая /гД = a, 1/X = da, а также )ч->оо, получим вместо суммы F)
интеграл Фурье
со -J-oo
it/ (х) = f da f /■ (х') cos a (д: — xr) dxr. G)
0 —оо
Приведенный вывод является несколько формальным. Для строгого
обоснования и выяснения условий существования интеграла Фурье читателя
можно отослать к специальным руководствам. Однако необходимо
отметить, что функция / (х) должна удовлетворять условиям Дирихле в
-j-oo
любом конечном интервале и интеграл J f(x)dx должен абсолютно
— со
сходиться.
Формулы обращения можно вывести из интеграла Фурье. Это
оправдано тем обстоятельством, что в рассматриваемых теплофизических
задачах, для решения которых применяются интегральные
преобразования, условия, обеспечивающие справедливость формул обращения,
всегда выполняются.
Перепишем формулу G) в виде
со Г -(-со
cospxdp
sin px dp.
(8)
nf(x)= Г f f{xr) cos px'dx'
0 L—со
со Г -f- со
+ N f f{xr)smpx'dxr
0 L—°o
Если функция f(x) нечетная, то
-f 00
f /(*')cosp*'dA:' = 0.
— CO
CO
f / (*') sinpx' dxf = 2 j* / (*') sin pxr dx' = 2/Fs (p):
-co 6
где /Fs (p) — синус-преобразование Фурье функции /•(*), определяемое
со
f?s(p) = § fix) sin pxdx. A0)
+ O0
(9)
выражением
ОСНОВЫ ИНТЕГРАЛЬНОГО ПРЕОБРАЗОВАНИЯ ЛАПЛАСА 511
Следовательно, формула обращения для синус-преобразования Фурье
имеет вид
00
/w = 4-J fFs(p)>s[nPxdp- (и)
О
Если функция /(х) четная, то,
+ 00
f / (x') sin pxf dx' = О,
—оо
-J-00 00
J f(xf)cospx/dxr = 2 j f(x') cos px'dx' = 2/Fc(p), A2)
—оо О
где /Fc(p)-—косинус-преобразование Фурье, определяемое соотношением
00
/fc(p) = j/(*)cospxdx. A3)
о
Следовательно, формула обращения для косинус-преобразования Фурье
будет иметь вид
00
/ (*) = -~ J /fc (P) cos ^* dP' (!4)
О
Пример. Найти изображение функции / (х) = £-*.
Синус-преобразование Фурье для функции f(x) будет иметь вид
00
/WW = J e~*sin Рх d* = Г+7* • <15)
о
Косинус-преобразование Фурье для функции f(x) будет иметь вид
00
/fc (P) = J е~* C0S PX d* = iqi^ • A6)
0 : *
Наоборот, если известно изображение синус-преобразования Фурье
/Fs(p) == р/(\ + р2), то оригинал функции равен
f W = 4 j ТТ7*sin px dp = <"*• ^ 7>
О
Если же известно изображение косинус-преобразования Фурье /Fc(p) =
, то оригинал функции равен
1 + Р2
оо
/ (х) = 4" J г^ cospxdp = е-*. A8)
о
Интеграл Фурье G) можно написать в виде
-}-00 -J-00
-i- Г da Г / (*') cosa (х — *') dx'. A9)
Известно, что
— 00 —00
512
Глава четырнадцатая
Г da J / (*') sin a (х — *') d*' = 0, B0)
— 00 —ОО
тогда формулу G) с учетом A9) можно написать так:
2тг/ (х) = j>* da J/ (*') *-<«*' dx'. B1)
—oo ~oo
Отметим, что из формулы B1) можно получить формулу обращения
для преобразования Лапласа. Однако воспользуемся соотношением B1)
и получим формулу обращения для комплексного преобразования
Фурье, которая определяется соотношением
+«>
' fFi{p) = ]fix)eP*dx. B2)
—оо
Обозначим а == —-р, тогда из формулы B1) получаем формулу
обращения для комплексного преобразования Фурье:
+ 00
f(*) = -%T$e-ipxfFl(P)dp. B3)
— 00
Пример. Найдем комплексное преобразование Фурье для функции
/(х)-<Ги|.
В соответствии с формулой B2) имеем
оо О
/fi 0°) = J exj) [— A — ip) x] dx + j exp [A + ip) x] dx =
0 —oo
= A - ip)-1 + A + ip)-1 = j^-s. B4)
Наоборот, если дано изображение комплексного преобразования Фурье
/Fi(p) = 2/A +р2), то оригинал функции будет равен
+ О0
/ (*) = JL j {{^p2) exp (— ipx) dp. B5)
— 00
Предположим, х > О, тогда интеграл B5), взятый по окружности с
центром в начале координат, лежащий в плоскости Р ниже
действительной оси, стремится к нулю, когда радиус окружности стремится к
бесконечности. Следовательно, интеграл B5) можно заменить интегралом
по замкнутому контуру» который равен произведению —2ти на вычет
в полюсе р = — i. Отрицательный знак берется потому, что контур
обходится по часовой стрелке.
Имеем
f (x) = -r^ = = «г*. B6)
[-а^+л],-,
Для случая х<;0 путь интегрирования замыкаем полуокружностью,
лежащей выше действительной оси. Интеграл равен произведению 2iu
на вычет в полюсе р = U т. е.
f{x) = e\ B7)
Оба результата объединяются одной формулой f(x)=e-№.
ОСНОВЫ ИНТЕГРАЛЬНОГО ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
513
Из формул обращения B2), B3) получаются ф.орму^льг
обращения Ханкеля. Сделаем обобщение формул B2), B3) на случай двух
независимых переменных х и у.
Введем обозначение
-J-00 -}-00
/F (s, 0 = J § f{x,y)exv[i(sx + ty)}dxdy. B8)
00 —ОО
Тогда получим
-j-00 -J-00
4тг2/ (х, y) = j J /F (s> 0 exP [— * (*s + ^01ds <#. B9)
— 00 ■—CO
Положим x = rcos0, #-=rsin0, s=p cos a, t=psina, тогда формулы
обращения B8), B9) примут вид
оо 2тс
/F (р, а) == f / (г) rdr f / (г, 6) exp [tpr cos(9 — a)] db, C0)
о о
оо 2тс
4тс2/ (г, 0) = j pdp J /F (P> ос) exp [— tpr cos F — a)] da. C1)
о о
Возьмем в качестве функции / (г, 0) функцию e~inB fir). Тогда из
формулы C0) получим
оо 2тс
/F (P. a) = j / W rdr f exp [i [— nO + p/* cos @ — a)]} d0. C2)
о о
Обозначим ф = a — 0 — ти/2, тогда интеграл по 0 можно переписать так:
2%
exp in ( -| ■ a J ( exp [i (лср — pr sin <p)] dcp =
о
- 2n exp [ in (^ - a j j /„ (pr), C3)
так как интеграл по 9 является известным интегралом Бесселя,
Обозначим изображение функции /(г) в преобразовании Ханкеля
через /н(р):
оо
fn(P)*=lrJn{pr)f{r)dr. C4)
О
Тогда вместо формулы C2) можно написать
/F (p, a) = 2тг ехр Г ш (~ — a jl /H (р). C5)
Если подставим e~inbf(r) вместо /(г, 0), а выражение для /f(p, a)
по соотношению C5) в формулу C1), то получим
2тс
2тг/ (г) <Г/Лв = J р/н (р) dp J ex p {i ]^i{~ - a \- pr cos @ - a)]} da. C6)
о о
17 Заказ № 640
514
Глава четырнадцатая
Положим <р = 6 — a -f- -cjri тогда интеграл по а можно представить в
виде
2гс
е~ш f exp [i (п<? — Pr sin ?)l dy.
о
Если снова воспользоваться интегралом Бесселя, то это выражение
можно представить в виде 2ne~~lnB Jn{pr). Следовательно, окончательно
получаем^формулу обращения для преобразования Ханкеля
f(r) = fpJn(pr)fH(p)dp. C7)
о
Пример. Предположим, что функция f(r)=l/r. Тогда
изображение функции в интегральном преобразовании Ханкеля имеет вид
со
fn{p) = [jn(Pr)dr = ±-. C8)
О
Наоборот, если 2 имеем изображение в виде /н(р) = 1/р» то, пользуясь
формулой C7), получим
со
f(r)=§Jn(pr)dp = -j-. C9)
О
В заключение этого параграфа остановимся на области применимости
преобразований Фурье и Ханкеля в задачах теплопроводности.
Преобразованиями Фурье и Ханкеля, рассмотренными в данном
параграфе, можно пользоваться, когда независимая переменная
изменяется в пределах от 0 до оо (теплопроводность полуограниченных тел).
Необходимо следить, чтобы интегралы, входящие в формулы
преобразования, сходились. Выбор синус- или косинус-преобразования Фурье
определяется видом граничных условий (условия теплообмена тела на
границе раздела тело—среда).
Остановимся на этом подробней. В дифференциальное уравнение
теплопроводности для одномерных задач входит вторая производная
температуры по координате -^. Найдем ее изображение при помощи
синус-преобразования Фурье:
smpx-j^-dx = Ujsinp* _ —Р \ cos pxj^-dx. D0)
0 о
Первое слагаемое правой части формулы D0) обращаем в нуль при
х = 0, так.как sinpx = 0. Если -=—>■ 0 при #~>oo, что имеет место
в задачах теплопроводности, то первый член формулы D0) равен нулю
и при #->оо. Интегрируя по частям второе слагаемое формулы D0),
получим
со со
1 -0~t slnPxdx =—р[Ъcospx] _ —р2 \Ь sin pxdx. D1)
о 6
Второе слагаемое правой части формулы равно произведению изображе-
ОСНОВЫ ИНТЕГРАЛЬНОГО ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
515
ния функции & на р2, а первый член равен — рЬх==0 при условии, что
& ->0 ПрИ X -± оо.
Следовательно,
!
^s- sin pxdx = p [b]xss0 — p2 &Fs, D2)
б
где [Ь]х=о — значение функции на границе тела, т. е. температуры на
поверхности тела.
Аналогичным методом найдем изображение -j-^ в интегральном
косинус-преобразовании Фурье
\-^-cospxdx = —[-%-) — р29 , D3)'
6
где 9Fc —косинус-преобразование Фурье, при этом предполагается, что
выполняются следующие условия:
» =т = о.
Величина (-^-) выражает температурный градиент на поверхности
тела, который должен быть задан по условию задачи. Отсюда следует,
что синус-преобразование Фурье целесообразно применять, когда задана
температура на поверхности тела (граничные условия первого роди), а
косинус-преобразование Фурье — когда задан тепловой поток (граничные
условия второго рода).
Заметим, что, в отличие от преобразования Лапласа, производная
-ч- или любая производная нечетного порядка не может быть исключе
на синус- или косинус-преобразованиями Фурье; так, при интегрировании
интегралов
о
по частям получим интегралы
\ -з— sm рх ах, \ у- cos px dx
Г & cos px dx, Г & sin px dx,
которые не выражаются через &Fs и 9Fc.
Однако применение синус- и косинус-преобразований Фурье дает
большие преимущества перед преобразованием Лапласа, когда ^задано»
начальное распределение температуры в виде функций координат.
§ 11. КОНЕЧНЫЕ ПРЕОБРАЗОВАНИЯ ФУРЬЕ И ХАНКЕЛЯ
Интегральные преобразования, рассмотренные выше, обычйо
называются бесконечными преобразованиями Лапласа, Фурье, Ханкеля, по-
скольку исключаемая переменная > изменяется; ot 0 до ©о или от — оо.
до + оо. Если временная переменная в йестационарных процессах теп-
17*
516
Глава четырнадцатая
лопроводности изменяется от 0 до оо и преобразование Лапласа по этой
переменной применимо всегда, то бесконечные преобразования Фурье
и Ханкеля относительно пространственных координат ограничены в -
своем применении областью неограниченных и полуограниченных тел.
Поэтому в последнее время работами Н. С. Кошлякова [37], Г. А.
Гринберга [14], Снеддона [72] и Дейча [23] интегральные преобразования
Фурье и Ханкеля распространены на конечную область исключаемых
переменных.
Конечное синус-преобразование Фурье определяется
формулой ^
Fs[f{x)\^hs(p)=lf (*)sin pxdx,
A)
где р — целое положительное число. Выбор числа тг в качестве
верхнего предела интегрирования не ограничивает общности преобразования
A), так как, путем соответствующей подстановки область
интегрирования всегда можно свести к отрезку @, тг).
Формула обратного перехода выводится из соотношений теории
рядов Фурье. Известно, что функцию / (х) можно разложить в ряд Фурье
по синусам, коэффициенты ар которого определяются формулой
тс
2 Г 2
ар = — J f(x) sin pxdx = — /Fs (p).
B)
Формула B) является формулой преобразования A), следовательно,
формула обращения будет иметь вид
/ (х) =
2
7С
ОО
2j /fs (p) sin px.
C)
Если функция / (х) изменяется в пределах 0 < х < с, то, введя
переменную z = тс х/с, получим
D)
Например, / (х) = х (О < х < с); имеем
Fw [х] = — Fs[—\ = .—к—у- ■» где р = 1, 2, 3. ..
Найдем изображение второй производной от оригинала функции:
% . % тс
J Г (х) si*1 Pxdx = f (x) sin px | —■ p J /' (x) cos pxdx =
E)
= —p cos dxf(x) J =—p2J / (x) sin pxdx.
F)
ОСНОВЫ ИНТЕГРАЛЬНОГО ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
517
Следовательно, получим
^s [f (*)] = - Р2 Fs [/ (*)] + р [/ @) - (- \)р f («)].
Для иллюстрации приведем пример: / (х) = х2. Имеем /" (х) = 2;
Л [2] = -р2 Fs [х2]-р (-1K ^2.
С другой стороны,
G)
(8)
Следовательно,
F. [2] = 2FS [1] = 2 [1-(-1)р]
Fs [x*] = -~(-iy-1-~r [I—(—1П-
Аналогично можно показать, что
F [/* (х)] =р*М (Р)-Р3 [/@)-(-1У /(*)] +
+ р [f @)-(-W И].
(9)
A0)
В табл. 14.1 приведены изображения некоторых функций при
помощи синус-преобразования Фурье.
Косину с-п реобразование Фурье определяется
соотношением
^с [/ (*)] = /fc (р) = j / (*) cos pxdx,
(И)
где р — целое положительное число или нуль.
Если функция■/ (я) = 1, то /fc (р) = 0 (р = 1, 2, 3,..), a /Fc @) = тс.
Если функция / (х) = х, то имеем
- /fc (rt^-^-K-iy-n; /Fc @)= 4'
fFc W> — ^2"LV АГ AJ> /fc W -- "' A2)
Для косинус-преобразования Фурье справедливы соотношения:
Fc [f (х) + Л] = /Рс (p) рфО A3)
^o t/ (x) + A] = fFc@) + «A, A4)
где А — постоянная.
Обратное преобразование или формула обращения
для конечного косинус-преобразования Фурье имеет вид
A5)
/ (х) = F7l [/Fc (/>)] =
оо
4" /fc (°) + "Г ij /fc (^) C0S ?*•
p=l
где
/fc (°) - J / (*) d^"
A6)
518
Глава четырнадцатая
Таблица 14.1
Конечное синус-преобразование Фурье для изображения
h, <р)
It
' Fs ' ^' ~ \ f (x) s in pxdx;
0
P = l, 2, 3, . .
(-l)p+1/Fs (Р)
1
Р
y(-l)^1
~"[l-(-lF]
^Г sin pc; @ <c < те)
— cos pc; @ < с < те)
-^(-i)"+i
•^F [1 - (- 1VJ
-L*. (-iF^-^-li-Hin
M-iy(f—|r^)
-^F-[i-(-i)'«'"l
p
p2 + c*
, f_ . /| U | _j_ П 1 О \
—^2ZZ^T> A Л I =^= U, 1, 2. . .)
/Fs И^ "IP (Я*)
-~2Z7jr [l-(-l)p cos£*]
P м / i\p+/ni. /n_/_m\
-__—^- ^—^„-.J^ J? {р-^Щ
f (x)
/ (*); 0 < X < те
/ (*-*)
те — д:
те
X
1
Г (те — с) х\ х < с,
\ с(те — х); х > с
( — х; х < с,
\ те— х; х > с
1
X
X2
X3
есх
1
she* shc ^~х)
Sin k (те — х)
Sin & те
sin/nx; (m = 1, 2, 3, . . .)
cos£x; (|fc|=#l, 2, 3, . . .)
cos m# (m = 1, 2, 3, . . .)
Для косинус-преобразования Фурье справедливы следующие
соотношения:
^с U" (х)] = - Р3 ^с ■' ( »' - /' @) + (- 1)" /' (*). A7)
При этом
Hm /Fc (P)=A
ОСНОВЫ ИНТЕГРАЛЬНОГО ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
519
Аналогично соотношению A0) имеем
1 Fc
[/4
(*)] =
= р*
/Fc
Г///
(Р) + Р2
@) + ( -
[/'
@)-
_(_
(и).
-1)"
/'
001 - ' 1
A8)
Изображения /Fc (p) для некоторых функций / (х) приведены в табл.
14.2. При конечных интегральных преобразованиях Фурье вторая
производная температуры по координате тела преобразуется в случае
синус-преобразования к виду
тс
J
дх2
sin pxdx = р [&0 — (— I)/7 &тс ] — р2 $Fs ,
A9)
а в случае косинус-преобразования к виду
I
а2 а
д*2
ccspxdx = ( — 1}?
дх
■P2»Fc.
B0)
Таким образом, при синус-преобразовании необходимо знать
температуру на поверхности тела (&0 и 9,), а при косинус-преобразовании — зна-
т
д$
чение температурных градиентов на поверхности тела ,. Л , « i -Л-
При граничных условиях третьего рода задается закон теплообмена меж
ду поверхностью тела и окружающей средой. Например, в случае одно
Таблица 14.2
Конечное косинус-преобразование Фурье для изображения
fFcW
■<*)
/Fc (р) = j / (x) cos pxdx;
о
(р = 0, 1,2,3, ...)
(- 1)р /Fc 0>)
/Fc @)=я, где р= I, 2,3, .
sin pc; f @) = 2с — п
1 - (- \)Р
• /Рс<°)
^1
bi£;/p @)=i,i
'Fc
4г;/в„ №) = о
fFc
(—1)Р + -^[1 _(_1)Р];
>Fc (°> ^ "Г
/ (х) @ < х < ж)
f («-*)
1
Г 1; @ <* <<?)
1 — 1; (с < х < it)
л;
_£?.
2"те
2 те 6
520
Глава четырнадцатая
fFC(p)
p* + c2
1
p3 + c2
-^-i^T [(-l)p coskn-1];
(\к\ф0, 1, 2, 3, . . .)
-уЦ- [(- 1)^^—1]; / (m) -
p2 —m2 Fc
= 0 (m= 1, 2, 3, . . .)
1 • (\k\ + 0 1 2 3 )
n2_&2 » V |"l / u> i, -6, u, . . . ;
0; (n=#m); /pc (m) = -|_; (m =
= 1, 2,3 . . .)
f (*>
JL e^
с
chc (tz~ x)
с she к
— s'mkx
k
—. sin тле
m
cos k (к — x)
k sin Ь
cosmx
мерных симметричных задач теплопроводности граничные условия имеют
вид
0;{д4:\ =0, B1)
(£+"»
X=R \дх )х==0
отсчет температуры 8- производится от температуры среды. Тогда
интегральное косинус-преобразование Фурье определяется соотношением
я
/fc ^ = J f M cos pxdx> B2^
о
где р является не целым положительным числом, а представляет собой
положительный корень трансцендентного уравнения
ptgpR = H. B3)
Можно показать, что если р и q — корни уравнения B3), то1)
Г cos px cos qxdx = 0 (p=hq), B4)
Я(р2 + #2)+#(
j cos2 pxdx = 2(Р2 + я2) ; (р == 9)
B5)
Формулой обращения служит формула для разложения в ряд Фурье
/ (х) = S ap cos рх, B6)
в котором суммирование происходит по всем положительным корням
уравнения B3), а коэффициенты ар определяются соотношением
ар = ^(/'ГяУ+я I ' W'cos Pxdx- <27)
1) Подробно см. § 3 гл. VI.
ОСНОВЫ ИНТЕГРАЛЬНОГО ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
521
Следовательно, формула обращения для косинус-преобразования Фурье
при граничных условиях третьего рода будет иметь вид
2 (Р2 + Я»)
/ (*) = 2 А(Р2+№)+я А* М cos^x-
B8)
Конечное интегральное преобразование Ханкеля
определяется соотношением
/н(р) = J г/ (г) /„ (pr) dr,
где р — положительный корень уравнения
К (р) = 0-
B9)
C0)
Выбор единицы в качестве верхнего предела интегрирования сделан
ради удобства, когда задача решается в обобщенных переменных.
Функция / (г) может быть представлена в интервале @<^><^1) при
помощи ряда Фурье — Бесселя
/ (г) - 2 ар Jn (pr),
C1)
где коэффициенты, определяемые по формуле C2), связаны с
изображением /н(р) простым соотношением
а„ =
4+1 (Р)
Г rf (r) Jn (pr) dr=-^
2/н(р)_
(p)
C2)
Следовательно, формула обращения для конечного
интегрального преобразования Фурье имеет вид
/ (г)=£ 21п(р:\ /н(р),
'я+1
(р)
C3)
где суммирование происходит по всем положительным корням
уравнения C0). Для граничных условий третьего рода конечное
преобразование Ханкеля определяется тем же соотношением B9), где р
определяется из уравнения
pfn(p) + HJn(p) = 0. C4)
В этом случае формула обращения будет иметь вид
/ (г)=2 F2
2р2
+ Р2~ п*
Jn(P)
/н(р),
C5)
где суммирование происходит по всем положительным корням
уравнения C4).
522
Конечное интегральное преобразование Ханкеля
для полого цилиндра, когда переменная г изменяется в
интервале #1<>-<#2> имеет вид
C6}
где
Вп {pr)^Jn (pr) Yn (PR1)-Yn (pr) Jn (pRx),
C7)
Ул (Рг) — функция Бесселя второго рода порядка п, а р —
положительный корень уравнения
Jn №) Yn (pRi) = Yn (рЯа) Jn (pRi)-
Формулой обращения будет служить соотношение
/w = 4Sb»h
Р24 (PR*)
Ja (рЯг) -Jn(pRJ
/н(р).
C8>
C9)
При помощи указанных преобразований можно исключить из
дифференциального уравнения теплопроводности совокупность членов
/ (») =
д
дг
пП
D0)
Конкретное применение конечного интегрального преобразования
Ханкеля дано в задачах теплопроводности.
В данном параграфе показана сущность конечных интегральных
преобразований и их связь с формулами разложения в ряды Фурье и
Бесселя, т. е. связь с классическим методом решения задач
нестационарной теплопроводности. Конечные интегральные преобразования
Фурье и Ханкеля вместе с методом интегрального.'преобразования
Лапласа для исключения временной переменной, которая изменяется от 0 до
оо, дают возможность решить широкий круг задач нестационарной
теплопроводности.
ЭЛЕМЕНТЫ ТЕОРИИ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
И ЕЕ ПРИЛОЖЕНИЯ
15
Настоящая глава содержит минимум сведений, необходимых для
использования мощного аппарата теории аналитических функций
применительно к разделу математической физики, который называется
теорией теплопроводности.
Так как аналитическая функция по. существу полностью
определяется характером и распределением ее особых точек, то можно
высказать суждения о поведении различных функций, имеющих сложные
интегральные представления; например, по особым точкам изображения
по Лапласу можно судить об асимптотическом поведении оригинала,
не прибегая к вычислению соответствующего контурного интеграла.
Теорема Коши и теорема о вычетах дают широкие возможности для
преобразования интегралов и сумм, в частности для вычисления
контурных интегралов при обращении преобразования Лапласа. Но так как
большинство интегралов, встречающихся на практике, не вычисляются
в конечном виде, то особое значение имеют различные методы
асимптотических оценок; некоторые из этих методов также приведены здесь.
Весь материал, содержащийся в главе, излагается возможно более
элементарно и доступно. За дополнительными сведениями и строгими
доказательствами читателю следует обратиться к специальным
руководствам [38а, 25а].
§ 1. АНАЛИТИЧЕСКИЕ ФУНКЦИИ
Рассмотрим функции комплексного переменного z = х + iy. Как
известно, такая переменная может быть изображена двумерным вектором,
имеющим компоненты х и у вдоль соответствующих координатных осей.
Длина этого вектора — модуль комплексного числа — равна ]/Y3 -|- у1 ,
а угол с положительным направлением оси х отсчитывается против
направления вращения часовой стрелки и равняется arctg#/x.
Если известен закон, по которому, задавая значение переменной г,
можно определить одно или совокупность значений другой комплексной
переменной до, то говорят, что задана функция до — / (z), однозначная
или многозначная соответственно. Совокупность значений, которые
принимает независимая переменная 2, называется областью определения
функции. Задание функции комплексного переменного до--/ (г)
равносильно заданию двух функций действительного переменного до — и -\- iv,
где и = и (х, у) и v = v (х, у).
524
Глава пятнадцатая
Приведем несколько простейших примеров функций комплексного
переменного
w
__ ~2 ._
z% = х2 — у2 + 2ixy;
W = ZZ
— v2
^ + у
20.
о> = е* = е* (cos у + t sin у);
ш = ]/!:.
Из всех функций комплексного переменного оказывается
целесообразным выделить довольно узкий класс функций, называемых
аналитическими. Аналитические функции можно определить, если рассмотреть
производную функции / (г) в некоторой точке г0. Производная
определяется как предел отношения
/(го + Az)-/ (г0)
при A z -> О, если этот предел существует. Однако, в отличие от
функции действительного переменного / (х), здесь приращение Az = Ах + ity
представляет собой вектор и может стремиться к нулю самыми
разнообразными способами. Можно, например, положить А у = 0, а потом
переходить к пределу Ах^О вдоль действительной оси и т. д. Если
однозначная функция / (г) = и + iv имеет производную в точке г0 и эта
производная определяется единственным образом, т. е. не зависит от
способа перехода к пределу А г -» 0, то такая функция называется
аналитической в точке г0.
Выведем условия, с помощью которых в каждом отдельном случае
можно установить, является ли функция аналитической в какой-либо
точке. Для этого выпишем подробно определение производной:
' lim
Дл:-*0,
Ду-*0
Г (г)
/ди
lim /•
Д2->0 (
/(г0 + А*)--/(*о))
. дх
+'й4*+
(t+'t'4»
А х + i A i
(i)
Перепишем формулу A) в следующем виде:
/' (z) = Нт
Дх-^0,
Дг/->0
(ди , , до
i + /
Дат
1+i
Дх
до
dw
— i
+ i
ди ~~|]
да 1
^ 1
B)
Зависимость производной f (z) от направления, по которому она
вычисляется, определяется отношением Д*//Дя, которое и обозначает
тангенс угла наклона "вектора А г. Этой зависимости не будет только
тогда, когда знаменатель формулы B) и сомножитель числителя, заклю-
1) Комплексно-сопряженную величину будем обозначать чертой сверху.
ЭЛЕМЕНТЫ ТЕОРИИ АНАЛИТИЧЕСКИХ ФУНКЦИИ И ЕЕ ПРИЛОЖЕНИЯ 525
ди
дх
ди
ду ~
dv
dv
дх
ченный в квадратные скобки, равны между собой, т. е. если
выполняется равенство
dv t ди
ду ~~~ 1 ду
Ж ТскГ = * • C)
дх +1 дх
Приравнивая друг другу в последнем равенстве вещественные
части, а затем мнимые, получаем
D)
Эти условия, необходимые для того, чтобы функция / (z) была
аналитической в некоторой точке, называются условиями Коши —
Рима н а. Эти условия не только необходимы, но и достаточны, если
производные -^-, -—-, ~9 ~^- непрерывны в рассматриваемой точке.
Точки, в которых условие D) не выполняется, называются особыми
точками функции. Например, у функции / (z) = 1/z- не существует
производной в точке z = 0. У функции / (г) == Vz — 1 такой точкой, как
легко проверить, является точка 2 = 1, где соответствующая
производная обращается в бесконечность, а функция / (г) = zz неаналитична
повсюду.
§ 2. КОНТУРНОЕ ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
КОМПЛЕКСНОГО ПЕРЕМЕННОГО
Пусть на некоторой кривой С (рис 15.1) задана функция
комплексного переменного / (г). Разобьем контур С на конечное число участков
с концами [z0, zx],..., [Z£, Zk+1],..., [£„_!, zn] и т. д. Обозначая через
С& произвольную точку на k-ы участке, составим, по аналогии с
теорией интегралов от функций действительного переменного, сумму
£/(Са) (zft+1-zft). A)
Предел этой суммы при п-^оо в предположении, что длины всех
участков стремятся к нулю, называется интегралом от функции / (z) по
контуру С и обозначается символом
J № dz.
B)
Если функция / (z) кусочно-непрерывна, а контур С можно
составить из непрерывно примыкающих друг к другу дуг, имеющих
непрерывно изменяющуюся касательную (кусочно-гладкий контур), то
интеграл B) всегда существует.
Контурный интеграл обладает свойствами обычных вещественных
криволинейных интегралов. В частности, постоянный множитель можно
выносить за знак интеграла; интеграл от суммы функций равен сумме
526
Глава пятнадцатая
Рис. 15. 1. Разбиение Рис. 15. 2. Односвязная (а) и двухсвяз-
контура С на участки ная (б) области
интегралов от слагаемых; при перемене направления обхода контура
интеграл меняет знак.
Если контур С представляет собой замкнутую кривую, то за
положительное направление обхода этого замкнутого контура принимается
то направление, при котором внутренняя область, ограниченная этим
контуром, остается слева.
Область, ограниченная замкнутым контуром, является односвязной,
если граница области состоит из одной связной части (рис. 15.2, а),
или более точно, если любой замкнутый контур, лежащий в этой
области, можно стянуть в точку путем непрерывной деформации, не задевая
границу области. Пример многосвязной области приведен на рис. 15.2, б;
здесь контур С, лежащий внутри области, не может быть подвергнут
описанной деформации без того, чтобы не задеть границу области.
Докажем теперь, что если / (г) — аналитическая функция,
непрерывная внутри замкнутого контура С и на самом контуре, то
j f(z)dz=0.
с
Это важное утверждение называется теоремой Кош и.
Докажем эту теорему для случая, когда контур С ограничивает
звездообразную область, а производная /' (z) (которая существует, так
как функция f (z) аналитична) ограничена внутри контура и на
контуре С.
Область является звездообразной, если в ней существует такая
точка z0, что любой луч, выходящий из этой точки, пересекает границу
области лишь один раз.
Примем точку z0 за начало координат. Рассмотрим интеграл
W(\)=-k J / (\z) dz @<X<1). C)
Нужно доказать, что ЧГ A) = 0. Продифференцируем W (X) по X:
W (к) = j / (kz) dz + X J г? (Xz) dz. D)
с с
ЭЛЕМЕНТЫ ТЕОРИИ АНАЛИТИЧЕСКИХ ФУНКЦИИ И ЕЕ ПРИЛОЖЕНИЯ 527
Воспользовавшись ограниченностью
производной /' (z), интегрируем
второй интеграл в формуле D) по
частям:
W (X)-j / (\г) dz +
с
где для члена
zf(kz)
E)
следует взять
Рис. 15.3. Контур в многосвязной области
разность его значении в конечной
и начальной точках контура. Для
замкнутого контура С, ввиду
однозначности функции zf (Xz), эта
разность обращается в нуль. Отсюда
следует, что и W (К) = 0, т. е.
функция W (X) постоянна; полагая в
формуле C) X = 0, находим, что эта постоянная равна нулю. Таким
образом, и W A) =0, что и требовалось доказать.
Теорема Коши непосредственно неприменима к многосвязкой
области. Однако она легко обобщается и на этот случай, Рассмотрим
двухсвязную область, изображенную на рис. 15.3. Если взять интеграл по
контуру, состоящему из Cv С2 и разрезов С3 и С4, то к такому
контуру теорема Коши уже применима. Направления обхода различных
частей полного контура подчиняются общему правилу и указаны на
рис. 15.3. Интегралы по С3 и С4 взаимно сокращаются, и мы имеем
J f (г) dz + j / B) dz = 0
ИЛИ
J / (z) dz
j / (г) dz = 0,
F)
F0
т. е. интеграл по внешнему контуру равен интегралу по внутреннему
контуру, если они оба обходятся против часовой стрелки.
Из теоремы Коши немедленно следует, что если / (z) — функция,
аналитическая внутри некоторой области, то интеграл J / (z) dzi взятый
вдоль любого контура, соединяющего точки zt и z2 (но целиком
лежащего в области аналитичности функции), зависит только от zt и z2 и
не зависит от пути интегрирования. Для доказательства достаточно
сравнить интегралы по двум различным контурам Сх и С2,
соединяющим точки гх и z% (рис. 15.4). К области, ограниченной контуром С2
и контуром Съ проходимому в обратном направлении от z% к zb
можно применить теорему Коши, откуда немедленно следует, что
J / (Z) dz = j / .B) dz
G)
(здесь Сх уже обходится в направлении, указанном на рис. 15.4).
Отсюда также вытекает, что значение интеграла не меняется при произ-
528
Глава пятнадцатая
вольной деформации контура, если
только при этой деформации контур не
выходит за пределы области аналитичности
*h подынтегральной функции, т. е. не
пересекает ни одной ее особой точки.
Соблюдая это правило, можно непрерывно
деформировать путь интегрирования в
контурных интегралах, выбирая контур, наи-
^ более удобный для их вычисления.
Рис. 15. 4. Независимость J f(z)dz от Заметим также, что может быть до-
пути интегрирования внутри области казана [38а] теорема, обратная теореме
аналитичности Коши: если функция /(г) непрерывна и
однозначна внутри некоторого замкнутого
контура С и J / (z) dz = О для любого замкнутого контура, лежащего
внутри С, то / (z) аналитична внутри С.
Эта теорема дает, таким образом, интегральный признак
аналитичности функции, эквивалентный условиям Коши — Римана.
Перейдем теперь к выводу весьма важной для приложений
интегральной формулы Коши.
Рассмотрим интеграл
F (*)= f !&£-
С
(8)
по некоторому замкнутому контуру С, внутри которого и на котором
функция / (г) аналитична. Точка z — произвольная точка внутри
контура. Как было показано выше, контур С можно деформировать, не
меняя значения интеграла. Заменим С окружностью малого радиуса р
с центром в точке z; тогда, полагая z' = z + p ei(?, получим
2ти
F (z) = i j /(z + Pe'*)d<p,
(9)
и, переходя к пределу (р->0), находим
F (г)=2ш f (г),
т. е.
/ (г)
2тЛ J z'
С
J z' — z
A0)
Формула Коши дает возможность исследовать различные свойства
аналитических функций, в частности, позволяет вычислить значение
функции / (z) в любой точке внутри контура по ее значениям на
контуре. Таким образом, значения аналитической функции в различных
частях комплексной плоскости не произвольны, а тесно связаны между
собой.
С помощью интегрального представления аналитических функций,
даваемого формулой Коши, можно доказать, что производные этой
функции также аналитичны в той же области, что и функция / (z). Дейст-
ЭЛЕМЕНТЫ ТЕОРИИ АНАЛИТИЧЕСКИХ ФУНКЦИЙ И ЕЕ ПРИЛОЖЕНИЯ 529
вительно, при выполнении условий, в которых была выведена формула
Коши, имеем
с
1_1 ^ 1 = _J_ lim Г О?0 &, =
г' — г J J 2 gi / A2_0 J (z' — z) (г' — z — А г)
с
/(г')
7t i J B' — zJ
Возможность предельного перехода под знаком интеграла может быть
доказана из условия аналитичности (и, следовательно, ограниченности)
функции / (г) на контуре С
Вычисляя аналогичным образом высшие производные, получим
формулу для п-й производной, выражающую ее значение в любой точке
внутри контура через значение функции на контуре:
' v ' 2fti 1 (z' —z)n+1
A2)
§ 3. ПРЕДСТАВЛЕНИЕ АНАЛИТИЧЕСКИХ ФУНКЦИЙ РЯДАМИ
Рассмотрим бесконечный ряд, члены которого являются функциями
комплексного переменного z, заданными в некоторой области D.
Область, во всех точках- которой этот ряд
2 uk(z)
A)
&=1
сходится, называется его областью сходимости.
Как и в случае функций вещественного переменного, введем
понятие равномерной сходимости ряда с переменными членами A).
Равномерная сходимость ряда A) в некоторой области означает, что ряд
сходится одинаково «хорошо» во всех точках этой области.
Приведем точное определение равномерной сходимости: ряд A)
называется равномерно сходящимся в некоторой области D, если при
любом заданном положительном е существует положительное число N,
одинаковое для всех z в области D, такое, что
п + т
2 Mz)
*=я + 1
<е
B)
при п > N и произвольном целом положительном т.
Для равномерной сходимости ряда A) достаточно, чтобы для всех z
из области D имело место оценка для модуля членов ряда A);
I ик (z) I < mk
при всех k, где mk — положительные числа, образующие сходящийся
ряд. При этом ряд A) сходится и абсолютно, т. е. сходится ряд из
модулей членов ряда A).
530
Глава пятнадцатая
Для равномерно сходящихся рядов можно доказать несколько
интересных утверждений относительно оперирования с такими рядами к
свойств их суммы.
Во-первых, если члены ряда A) uk(z) (&=1,2,...)— непрерывные
функции в некоторой области D и ряд равномерно сходится в этой об*
ласти, то сумма ряда будет непрерывной функцией.
Во-вторых, если ряд A), состоящий из непрерывных функций,
сходится равномерно на некоторой кривой, то этот ряд можно почленно^
интегрировать вдоль этой кривой.
И, наконец, если члены ряда A) являются аналитическими
функциями в замкнутой области D с контуром С и ряд равномерно сходится
на контуре С, то он сходится равномерно и во всей области D, сумма
его представляет собой аналитическую функцию внутри области D, а
ряд A) можно почленно дифференцировать сколько угодно раз
(теорема Вейерштрасса).
Теперь рассмотрим частный случай рядов A) —ряды вида
со
2 «»(*-*)". C)
' л = 0
которые называются степенными рядами.
Для степенных рядов весьма просто может быть доказана [38а]
теорема Абеля: если ряд C) сходится для некоторого z ~ z0, то он
сходится абсолютно во всякой точке z, удовлетворяющей условию
\г — Ь\< \г0 — Ь\,
т. е. расположенной ближе к точке Ь, чем z0. Кроме того, ряд C)
будет сходиться равномерно во всяком круге с центром в точке b и
радиусом, меньшим расстояния \z0 — b\.
Из теоремы Абеля следует, что если ряд C) расходится в
некоторой точке zv то он расходится и во всякой точке, которая находится
дальше от точки 6, чем zv Следовательно, для всякого степенного
ряда C) существует положительное число R, такое, что ряд сходится
при | z — b | < R и расходится при \z — b | > R. Число R называется
радиусом сходимости степенного ряда, а круг \z — b\<CR— кругом
сходимости этого ряда. Из теоремы Абеля следует, что ряд C) будет
сходиться равномерно внутри своего круга сходимости1*.
Если радиус сходимости R равен бесконечности, то соответствующий
степенной ряд сходится во всей комплексной плоскости.
Наконец, отметим необходимый для дальнейшего факт. Так
как ряд C) сходится равномерно внутри своего круга сходимости,
то к нему применимы теоремы, сформулированные выше для общего
случая рядов с переменными членами, в частности, и теорема
Вейерштрасса. Поэтому сумма степенного ряда C) является аналитической
функцией внутри круга сходимости этого ряда, а ряд можно почленно
интегрировать и дифференцировать сколько угодно раз.
Покажем теперь, что всякая функция /(г), аналитическая в
некотором круге \z — b | < R с центром Ь9 может быть представлена внутри
этого круга степенным рядом C) и что такое разложение единственно.
Представление функции таким степенным рядом называется
разложением в ряд Тейлора.
О Вопрос о сходимости ряда на окружности \z — b\ = R требует специальных
ис следований.
ЭЛЕМЕНТЫ ТЕОРИИ АНАЛИТИЧЕСКИХ ФУНКЦИЙ И ЕЕ ПРИЛОЖЕНИЯ 531
Для доказательства сформулированного утверждения построим
контур С, имеющий форму окружности с центром в точке бис радиусом,
меньшим радиуса круга сходимости R, но содержащим некоторую
фиксированную точку г. Тогда для функции f(z) будут выполнены все
условия применимости формулы Коши A0) § 2, и можно записать:
С
Знаменатель подынтегрального выражения в формуле D) можно
представить в виде то
z'^z zr — b z — b *шЬ B'_мл+1 \°)
1~7^Гь п~°
на основании формулы для суммы бесконечной геометрической
прогрессии, которая, в свою очередь, применима потому, что \z — b\ <
< \zr — Ъ\ (|z' — b\ — радиус окружности С, а точка z по условию
находится внутри этой окружности).
Для модулей членов ряда E) имеем оценку
(z — Ь)п I _
(z' — b)r>
=
=
■к*-
z — Ъ
г' — Ъ
и 0<<7< 1.
F)
Таким об-
где #с — радиус окружности С, a q =
разом, из теорем, сформулированных в начале настоящего параграфа
для рядов с переменными членами, и формулы F) вытекает, что ряд
E) будет сходиться равномерно относительно переменной z' и,
следовательно, его можно почленно интегрировать. Умножая левую и правую
части соотношения E) на 2 / (zf) и интегрируя по контуру С,
получим, воспользовавшись формулой D),
со
/(z)= 2 an(z-bf, G)
п = 0
где
а = _L_f tV) dzr
с
или, согласно формуле A2) § 2 для п-й производной функции f (z)*
имеем
т. е. получаем окончательно, что значение функции f(z) в любой точке
внутри круга \z — b\<R, в котором f(z) аналитична, может быть
представлена рядом Тейлора
со
f(n\b)
—КГ-(г-Ь)*. A0)
/г= 0
Легко показать, что разложение A0) единственно. Для этого
достаточно показать, что коэффициенты ап в формуле G) определяются
532
Глава пятнадцатая
однозначно по формуле (9), Полагая в G) z = b, находим a0 = f(b);
далее, дифференцируя ряд G) и после каждого дифференцирования
полагая z = Ь, получим формулы (9) для коэффициентов ряда.
Из всего изложенного ранее следует, что ряд Тейлора в точке Ъ
функции f(z) сходится внутри круга с центром в точке 6, внутри
которого функция f(z) аналитична. Таким образом, радиус сходимости ряда
Тэйлора совпадает с расстоянием от точки Ь, в которой ищется
разложение, до ближайшей от нее особой точки функции /(г), в которой
1
последняя уже не является аналитической. Например, функция \ ±_z „
которая в точке z = О разлагается в ряд Тейлора вида
1+Z
1— Z+Z* — ... , AJ)
имеет особую точку z = — 1, в которой она и ее производные
бесконечны. Поэтому радиус сходимости ряда A0) равен единице, т. е. он
сходится лишь при |г|< 1. Функцию . в точке г = 4 можно раз-
ложить в ряд Тейлора
Tir = 2w^-4)n' {12)
п = 0
который сходится и представляет функцию 1 в круге с центром в
точке z = 4 радиуса 5, равного расстоянию от точки 2 = 4 до
ближайшей (и в данном случае единственной) особой точки z~ — 1.
Очевидно, что функция не может быть разложена в ряд Тейлора в
окрестности ее особой точки. Однако можно получить некоторое
разложение, справедливое и вблизи некоторых типов особых точек. Для
этого рассмотрим степенной ряд вида
оо
У\аа(г-ЬГ, A3)
П = — оо
содержащий не только положительные, но и отрицательные степени
(z — b). Такой ряд называется рядом Лорана. Определим его область
сходимости. Часть ряда A3), содержащая положительные степени
(z — &), является обычным степенным рядом и, следовательно, имеет
некоторый круг сходимости | z — b | < Rv Для . рассмотрения части ряда
A3) с отрицательными степенями (z — b) введем новую переменную
zf = (z — b)~x. Тогда эта часть ряда превратится в обычный степенной
ряд вида
а_1г'+а_2г'2 + а-з2/3 + .... A4)
Такой ряд имеет некоторый круг сходимости, радиус которого
обозначим */я2 с центром в точке zf = 0. Таким образом, область сходимости
ряда A4) определяется неравенством |z'|< —5~ • Переходя к прежней
переменной z, получим, что ряд A4) сходится при [г — й|>/?2. Поэтому
ряд A3) сходится в области, определенной неравенствами
z — b\<Rv п-.
z-b\>R2. (lb'
ЭЛЕМЕНТЫ ТЕОРИИ АНАЛИТИЧЕСКИХ ФУНКЦИЙ И ЕЕ ПРИЛОЖЕНИЯ 535
Эти неравенства могут выполняться
и, следовательно, определять собой
некоторую область только в том случае,
если Rx > R2. Эта область представляет
собой кольцо, ограниченное
концентрическими окружностями радиусов Rx и R2
с центром в точке Ь. Так как в
предыдущих рассуждениях мы разбили ряд
Лорана A3) на два степенных ряда, то из
свойств степенных рядов следует, что
ряд A3) внутри его кольца сходимости
сходится абсолютно и равномерно, сумма
его является аналитической функцией в
кольце, а ряд можно почленно
дифференцировать.
Докажем теперь, что если функция
f{z) аналитична внутри кольца R2 <|z —
—b |< Rx (внутри окружности \z — b \ = R2 и вне окружности |z —
— b\ = Rl у функции f(z) могут быть особые точки), то она может
быть разложена внутри этого кольца в ряд Лорана.
Несколько сжав внешнюю окружность CR и несколько расширив
внутреннюю окружность CR (рис. 15.5), можно считать, что функция
f(z) является аналитической на обеих окружностях. Тогда к внутренней
части кольца можно применить формулу Коши. Для произвольной
точки г внутри кольца имеем
Рис. 15. 5. Контур,
используемый при выводе разложения в
ряд Лорана в окрестности
точки z=b
№
1
2щ
I
7(z)'
dz' +
l
/(*')
2та
J^
'dz'.
A6)
"Ri
"Rz
Применяя к каждому интегралу в формуле A6) рассуждения,
совершенно аналогичные приведенным в случае ряда Тейлора, получим для
коэффициентов ряда A3) выражения
*Я = -2Д- f "Т^&г^ A7)
(г' - Ъ)
Я-„ = — ■
(/1 = 0, 1, 2,...),
1
2щ
J./(*')(*'■
bf-1 dzf
A70
(/г = 1,2,...).
Направления обхода контуров CR и CR указаны на рис. 15.5. Нетрудно
показать, что и при сформулированных условиях разложение A3)
функции f(z) с коэффициентами, определенными согласно соотношениям A7)
и A7"), будет единственным.
В качестве примера разложения функций в ряд Лорана рассмотрим
функцию е z. Особой точкой этой функции будет точка г = 0. Следо-
вательно, кольцом сходимости ряда Лорана будет вся комплексная
плоскость, за исключением начала координат. Ряд Лорана имеет вид
а все коэффициенты а_п(п = 1,2,...) равны нулю.
/1 = 0
534
Глава пятнадцатая
§ 4. КЛАССИФИКАЦИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
ПО ИХ ОСОБЫМ ТОЧКАМ. ПОНЯТИЕ ОБ АНАЛИТИЧЕСКОМ
ПРОДОЛЖЕНИИ
Представление функций рядами Лорана дает возможность
классифицировать изолированные особые точки аналитической функции, т. е. те
особые точки, которые являются центром некоторого, достаточно
малого круга, в котором нет других особых точек функции. Вблизи такой
точки аналитическая функция может быть разложена в ряд Лорана с
кольцом сходимости, у которого внутренняя окружность вырождается в
точку. Если разложение A3) §3 содержит конечное число членов с
отрицательными степенями (г — Ь)х\ т. е. имеет вид
/B)= 2 an{z-bY, A)
n = -N
то в точке b функция имеет полюс N-vo порядка.
Если же ряд отрицательных степеней в лорановском разложении
бесконечен, то точка Ь называется существенно особой точкой функции.
В качестве примера рассмотрим функцию
i_
2—1
При z~2mn (п = О, ± 1, ±2,...) числитель дроби аналитичен и
отличен от нуля, а знаменатель обращается в нуль. Таким образом, в
точках z = 0, ± 2ш, ± 4ти и т. д. функция имеет полюсы первого порядка
(простые полюсы). Далее, при z; = 1 знаменатель аналитичен, а
числитель имеет изолированную особую точку, в которой он представляется
рядом
1 оо
е " 2а п\ (z-i)»
п = О
поэтому и все разложение функции B) будет содержать бесконечное
число членов с отрицательными степенями (г—1), поэтому функция B)
при z = 1 имеет существенно особую точку.
Аналитические функции с изолированными особыми точками можно
классифицировать по типу и расположению в комплексной плоскости
их особых точек. Прежде всего покажем, что функция, которая не
имеет никаких особенностей (в том числе и в точке z= оо), равна
постоянной величине. Более точно это утверждение, называемое теоремой
Лиувилля, формулируется так: если f (z) — аналитическая функция при
всех значениях z и | / (z) \ <; М для всех z, где М — некоторое
положительное число, то f (z) является постоянной.
Действительно, оценим производную /''(z), определенную согласно
формуле A2) §2 как
1 W 2%i J (zr — zJ a* '
с
1) Если разложение в точке Ъ совсем не содержит членов с отрицат ельными
степенями (z—b), то этот ряд есть ряд Тейлора и функция аналитична в точке Ь.
ЭЛЕМЕНТЫ ТЕОРИИ АНАЛИТИЧЕСКИХ ФУНКЦИЙ И ЕЕ ПРИЛОЖЕНИЯ 535
где контур С выбран в виде окружности радиуса R с центром в точке г.
Имеем оценку
г «I - \Мта*■ I - Ml е~"' U + **'dv
с
2ъ
<
<T^Jk"''/(«+«',,)|*K^«-*—^.
О
таким образом,
Так как функция / (г) аналитична и ограничена во всей плоскости, то
радиус окружности R может быть выбран скоЛь угодно большим.
Устремляя #->оо, получим, что /'B) = 0 при всех z, т. е. /' (г) является
постоянной.
Таким образом, все нетривиальные аналитические функции
обязательно имеют особые точки (возможно, на бесконечности).
Рассуждениями, аналогичными приведенным при доказательстве
теоремы Лиувилля, можно показать, что единственной функцией,
аналитической при всех конечных значениях z и возрастающей не быстрее, чем
\z\m при "z-> оо, является многочлен степени <^т.
Многочлены являются частным случаем целых функций, т. е.
функций, аналитических при всех конечных z. Например, часто
встречающимися целыми функциями являются ez9 sin z, cos z, /v (z)/zv и многие
другие. Все эти функции не имеют особых точек при конечных z, а в
бесконечно удаленной точке имеют существенную особенность (это лег-
1
ко показать, введя новую переменную zr = ~y~ и разлагая упомянутые
функции в ряд Лорана вблизи точки zf = 0).
Далее, функции, единственными особыми точками которых в любой
конечной части комплексной плоскости является конечное число
полюсов, образуют класс мероморфных функций.
Нетрудно показать, что единственной мероморфной функцией, не
имеющей никаких особых точек, кроме конечного числа полюсов,
включая и бесконечно удаленную точку z= оо, является рациональная
функция, т. е. функция, представляющая отношение двух многочленов.
Примерами трансцендентных мероморфных функций являются tgz
[простые полюсы лежат на действительной оси в точках (п + Va) тс, п = 0,
=Ь 1,... ], Г (zI) (простые полюсы в точках г = —п9 п = 0, 1, 2, ...)ивообще
отношение любых двух целых функций (tgz =~~5—~ и т. д., при этом нули
целой функции, стоящей в знаменателе, являются полюсами
соответствующей мероморфной функции J .
Итак, по характеру особых точек и их расположению в комплексной
плоскости однозначные аналитические функции, имеющие
изолированные особые точки, могут быть подразделены на следующие классы:
а) функция не имеет никаких особых точек—это постоянная;
1) Функция Г (г), как известно, может быть определена при Rez>0 интегралом
00
о
536
Глава пятнадцатая
б) функции, единственная особая точка которых расположена в
бесконечности, — это класс целых функций. Частный случай целых функций,
единственная особая точка которых при | z \ -* оо является полюсом я-го
порядка, представляет многочлен /г-й степени относительно г;
в) функции мероморфные, которые при всех конечных \z\ не имеют
никаких особенностей, кроме полюсов. Если бесконечно удаленная
точка не является существенно особой, то в этом частном случае имеем
простейшую мероморфную функцию — рациональную, т. е. отношение
двух полиномов.
Кроме перечисленных классов однозначных функций, имеющих
изолированные особые точки — полюсы и существенно особые, в
приложениях столь же часто встречаются многозначные функции, которые
имеют специфические неизолированные особенности, так называемые
точки ветвления. При обходе по некоторому контуру вокруг такой
точки функция приобретает значение, отличное от исходного.
Рассмотрим, например, функцию У~г . При обходе точки z = 0 вдоль
окружности с центром в этой точке и радиусом г значение функ ции
У z = У г elB/2 изменяется от У г при 6 = 0 до — У г при 6 = 2тг-
Таким образом, точка z = 0 является точкой ветвления функции У z .
Аналогичными рассуждениями легко убедиться, что точка z = оо
также является точкой ветвления функции У z . Вообще, точки
ветвления существуют всегда попарно.
Многозначность функции может быть устранена, если ограничиться
некоторой частичной областью ее определения. Тогда можно сказать,
что в этой области определена ветвь функции. Например, для функции
г— г— "ГЛ
У z совокупность значений, определенная формулой у г е при
— тс < 0 < тс, является ветвью функции в области, которая получается
из всей плоскости разрезом вдоль отрицательной действительной
полуоси от точки z = 0 до z = оо, являющихся точками ветвления этой функ-
ции. Совокупность значений, заданных формулой — У г е , будет
другой ветвью функции в той же области. Рассмотренная функция У z
m
имеет две ветви1*. Аналогично получаем, что функция zn ,где — —
рациональное вещественное число, имеет п ветвей, если дробь — не
сокращается. Из функций, имеющих точки ветвления бесконечного
порядка, наиболее важной является In г. Бесконечное множество его ветвей
определяется формулой
lnr+tF + 2rc/z)
(—7г<е<тс).
Каждое п ~ 0, 1, 2,... дает ветвь In г. Точки ветвления z = 0 и z = оо.
Если определить функцию za, где а — иррационально, как e^ln^ TOj
зная свойства функции In г, нетрудно убедиться, что функция za будет
иметь бесконечно много ветвей.
0 Число ветвей функции не зависит от способа проведения разрезов, соединяющих
точки ветвления.
ЭЛЕМЕНТЫ ТЕОРИИ АНАЛИТИЧЕСКИХ ФУНКЦИИ И ЕЕ ПРИЛОЖЕНИЯ 537
С наличием у функции точек
ветвления связан вопрос о возможности ее
единственного аналитического
продолжения, если первоначальное
определение функции имеет смысл лишь в
ограниченной части комплексной
плоскости. Например, степенной ряд
1 + Z +Z2 + ...
непосредственно определяет функцию
. __ лишь внутри круга |z|< 1, а
интеграл
]e~x{l-z)dx
О
определяет ту же функцию, но уже во всей полуплоскости Re г < L
Возникает вопрос о способах выполнения аналитического продолжения
функции, заданной первоначально в некоторой части комплексной
плоскости, а также об условиях, когда процесс аналитического продолжения
будет давать единственный результат! Если, например функция задана
степенным рядом с конечным радиусом сходимости, то, по крайней
мере, теоретически процесс аналитического продолжения может быть
выполнен с помощью следующего построения. Пусть функция f(z) в
точке z0 задана степенным рядом с радиусом сходимости R0, равным
расстоянию до ближайшей от z0 — особой точки функции/(z). Тогда в
любой точке (обозначим ee2x), лежащей внутри круга сходимости | z — z0 \<R&
и отличной от z0, также можно вычислить все производные и
построить ряд (рис. 15.6)
п = 0
с некоторым радиусом сходимости Rv равным расстоянию от zx до
ближайшей особой точки, которая, вообще говоря, отлична от
упоминавшейся ранее. Строя теперь степенной ряд с центром в некоторой точке
круга \z — z1\<Rl и т. д., можно получить значение функции f{z) во
всей комплексной плоскости. Однако, как видно из приведенных
рассуждений, процесс аналитического продолжения был бы неприменим,
если особые точки плотно заполняют границу первоначальной области
определения. Тогда говорят, что функция непродолжима за пределы
своей естественной области существования. Примером такой функции
является функция, заданная степенным рядом вида
f(z) = l +z2 + z4 + ... ^28л+...,
сходящимся внут]ри круга [z\ < 1. Так как /A) = оо, то z = 1 является
особой точкой, но для f(z) верно соотношение
f(Z)^Z*+f(z%
поэтому и при 22 = 1 (т. е. еще и при z = — 1) у функции f (z) будут
особенности. Так как
/B)-22+Z4 + /(Z4),
то все точки, определяемые уравнением z4=l, также будут особыми.
Рис, 15.6. Схема построения
степенного ряда для
аналитического продолжения функции f(z)
538
Глава пятнадцатая
Повторяя эти рассуждения, получим,
что все точки, определяемые из
уравнений
г*" =\ (/2 = 1,2, ...),
будут особыми. Но на любом сколь
угодно малом участке окружности
корней этих уравнений будет беско-
n ir -? tr нечно много. Поэтому
рассматривавшие. 15. 7, К теореме единственности « j r r
аналитического продолжения мая ФУНКЦИЯ не может быть продол-
жена за пределы сплошной линии
особенностей | z\ = 1.
Аналитическое продолжение не обязательно выполняется путем
построения последовательности степенных рядов. Можно воспользоваться
также функциональными соотношениями, с помощью которых можно
связывать значения функции в исходной области с ее значениями в
области, в которой она первоначально не была определена. Например,
гамма-функция может быть определена в полуплоскости Re 2 > 0
интегралом
о
Однако с помощью известного функционального соотношения
2ГB)-ГB+1)
ее можно продолжить и в полуплоскость Re z < 0.
Наконец, по поводу единственности аналитического продолжения
может быть доказано следующее утверждение: если функция f{(z),
определенная в области Dx (рис. 15.7), и функция /а (z), определенная в
области D2, получены аналитическим продолжением функции f(z),
заданной первоначально в области ' D, и если область D3 (заштрихованная
на рисунке), общая для Dx и D2, перекрывается с D, то f± (z) = /2 (z)
в области Ь3.
Таким образом, получим, что ft(z) в области D3 совпадает с /2(z),
каким бы путем ни была продолжена функция f(z).
Теорема единственности аналитического продолжения будет, однако,
нарушаться, если между двумя различными путями продолжения
функции лежит особая точка функции — ее точка ветвления.
§ 5. ТЕОРИЯ ВЫЧЕТОВ И ЕЕ ПРИМЕНЕНИЕ К ВЫЧИСЛЕНИЮ
ИНТЕГРАЛОВ И СУММИРОВАНИЮ РИДОВ
3 Рассмотрим разложение функции f (z) в ряд Лорана вблизи
изолированной особой точки Ь, разложение это в общем случае имеет вид [см.
A3) §3]-
00
./(*)= 2 ап(г-ЬУ. A)
п = —со
В этом разложении особую роль играет коэффициент при (z — &)"~\ т. е.
а_х. Этот коэффициент а_2 называется вычетом функции / (z) в
рассматриваемой особой точке Ь (в полюсе или в существенно особой точке).
Покажем, что интеграл по некоторому контуру, окружающему точку Ь,
может быть выражен через вычет функции в этой точке. Для этого
проинтегрируем формулу A) по какому-либо небольшому замкнутому
ЭЛЕМЕНТЫ ТЕОРИИ АНАЛИТИЧЕСКИХ ФУНКЦИИ И ЕЕ ПРИЛОЖЕНИЯ 539
контуру С, окружающему точку Ь,
предполагая, что на этом контуре ряд A)
равномерно сходится. Итак,
lf(z)dz = 2 an${z — b)ndz.
B)
Как следует из теоремы Коши, контур
С можно деформировать в окружность
малого радиуса р с центром в точке Ь.
Тогда формула B) перепишется
©<
<а>
2тс
\f(z)dz = i 2a„P-je/(" + I)^?. C)
2тс
Рис. 15. 8. Контур для вывода
теоремы о вычетах
■<я+1)<
Нетрудно убедиться, что все интегралы J e аср равны нулю, за
исключением одного интеграла, соответствующего значению п
торый равен 2тг. Таким образом, имеем
j / (z) dz= 2ni а_г.
1, ко-
D)
Аналогично рассматривается и более общий случай, когда функция
f(z) является аналитической в некоторой области D с контуром С, за
исключением конечного числа точек, являющихся полюсами или
существенно особыми точками функции. Окружим каждую особую точку
bv b2,...9 bk контуром, представляющим собой, например, небольшую
окружность Ck (рис. 15.8). Тогда, согласно теореме Коши [см. F') § 2],
имеем
т.
J f{z)dz= 2 lf(z)dz.
E)
k=l Cu
Но каждый из интегралов в правой части формулы E) по окружностям
Ck, как легко установить, повторяя рассуждения, использованные при
выводе формулы D), равен 2nia№v где а&\ — вычет в точке Ьк. Тогда
т
lf{z)dz = 2vi J a<*\ . F)
С k=*l
Теперь можно окончательно сформулировать теорему выч'етов,
Если функция f{z) аналитична всюду в области, ограниченной
замкнутым контуром С, за исключением конечного числа особых точек,
лежащих внутри контура С, то значение \ f(z) dz равно умноженной на
с
2т сумме вычетов подынтегральной функции f(z) во всех ее особых
точках, находящихся внутри С.
Прежде чем перейти к многочисленным приложениям этой теоремы,
следует указать простые способы определения вычетов. Пусть у
функции f(z) имеется в точке b полюс m-го порядка. Тогда ее лорановское
разложение в этой точке имеет вид
Пг)= 2 an{z-bf.
G)
540
Глава пятнадцатая
•Функция (z— b)mf(z) будет аналитической в точке Ъ и, следовательно,
может быть представлена в этой точке рядом Тейлора. Коэффициент
а[_г для разложения в ряд Тейлора функции (г — b)mf(z) будет
коэффициентом при (г — Ь)т~г, Вспоминая формулу (9) § 3 для коэффициентов
ряда Тейлора, получим
1 ( d™-1 }
Я-1 = (/72-1)! [dz^ Kz — bT КЩг e t
(8)
Укажем еще один часто встречающийся случай формулы (8), когда функ-
<р(г)
ция / (г) имеет вид / (г) = I /zj , где функции ср (z)r ф(г) аналитичны в
точке b и ф (г) имеет в этой точке простой корень. Тогда, если ср (Ь) =^=0,
то функция f(z) имеет простой полюс в точке 6. Используя общую
формулу (8) при т = 1 и учитывая, что Ф (z) = ф' {b) (z—6) + ...,
получим
9F)
a-i = ф' (Ь) • (9)
Теперь перейдем к приложениям, основанным на том, что с помощью
теоремы о вычетах операцию контурного интегрирования можно свести
к определению вычетов, которые в ряде случаев вычисляются просто
дифференцированием.
Начнем с применения теоремы о вычетах к вычислению
определенных интегралов.
Рассмотрим интегралы вида
оо
I f(x)dx, A0)
— оо
где f (z) — функция, аналитическая всюду в верхней полуплоскости
Imz >0, за исключением конечного числа особых точек, которые, однако,
не лежат на действительной оси — оо < х < оо. При | z | -* оо функция
zf{z) должна стремиться к нулю, т. е. \f(z)\ должен стремиться
А
к нулю при | z | -> оо быстрее, чем пл. Для вычисления интеграла
A0) рассмотрим контурный интеграл, состоящий из отрезка
действительной оси и полуокружности большого радиуса R с центром в
начале координат, лежащей над вещественной осью (рис. 15.9). Тогда,
согласно теореме о вычетах, интеграл по этому контуру равен
я
j/ (z) dz = J / (x) dx + J / (г) dz = 2tci ^-v A1)
С - R Г
где символом 2 a-i обозначена сумма вычетов функции f(z)
относительно особых точек, лежащих выше действительной полуоси, а Г —
полуокружность.
Для оценки интеграла по полуокружности имеем ^г = Re J
I тс I тс
j f(z) dz\ = \§ f(Rei<?) Re* id <p < max |/ [Re* )\R$dy = TtR max|/(/?e'*)|f
r I p I о
где max \f(Rei(?)\ обозначает максимум модуля функции f (z) на
полуокружности Г и где принято во внимание, что | iel?\ = 1. Так как
ЭЛЕМЕНТЫ ТЕОРИИ АНАЛИТИЧЕСКИХ ФУНКЦИЙ И ЕЕ ПРИЛОЖЕНИЯ 541
R \f(Rel9)\ -±0 при R -> оо для всех
О^ср-^тс, то рассматриваемый
интеграл по полуокружности
обращается в нуль.
Попутно заметим, что способом,
аналогичным выполненной оценке,
может быть доказано более общее
утверждение, называемое леммой
Жордана: если функция / (г) в
верхней полуплоскости и на
вещественной оси удовлетворяет условию, что
она равномерно стремится к
нулю при z-> оо, а 7 — некоторое
положительное число, то при i?->oo
Рис. 15. 9. Контур для вычисления
интегралов в бесконечных пределах с
помощью теории вычетов
I
I'fZ
f (z) e dz-^Oy
где контур Г — полуокружность в верхней полуплоскости с центром в
начале координат и радиусом R. Эта лемма понадобится нам в
дальнейшем1*, а сейчас, возвращаясь к интегралу A0), получаем
окончательно из формулы A1) при R
сти, что
I f(x)dx = 2tu %
Рассмотрим примеры.
1. Интеграл
оо и оценки интеграла по полуокружно-
Iвычетов f(z) относительно особых}
точек, лежащих в верхней
полуплоскости
dx
(х*+1)*
A2
A3)
принадлежит к типу A0) и удовлетворяет, как легко проверить, всем
условиям, необходимым для применимости формулы A2).
Подынтегральная функция / (г) = ■ ■, g | 1K имеет полюсы третьего порядка в
точках z = i и г = —и Из них только полюс z = i лежит в верхней полу-
з
-jg-t, вычисляемым кпо формуле (8). Согласно
плоскости с вычетом
A2) имеем
j
dx
(х* + IK
=2izi
_з_
16
i =
-тс.
2. Интеграл
cos xdx
(*2 + a2)(x2 + 62)
(Rea > Reft > 0)
A4)
1) Для вычисления контурных интегралов, возникающих при обращении преобразо*
вания Лапласа, необходима модификация леммы Жордана, получающаяся при замене
переменной iz = s, т. е. утверждающая, что для любой функции F(s), стремящейся
равномерно к нулю при R->oo на полуокружности Г' радиуса R, лежащей в левой
полуплоскости, имеем при любом положительном у
lim J F(s)eslds = 0.
R-*<x> Г'
542
Глава пятнадцатая
можно представить в виде
00 00
1 С cosxdx 1 С eixdx
С со
"J (** + а
2 1 (х2 + а2) (х2 + б2) 2 (х2 + а2) (*2 + б2)
— оо
sin л;
так как интеграл от нечетной функции , а , 2w 2 , ,2) по
симметричному промежутку обращается в нуль.
Последний интеграл принадлежит к типу A0). В частности, легко
убедиться, что подынтегральная функция
№ «
(г2 + а2)(г2 + Ь2)
стремится к нулю при возрастании z в верхней полуплоскости (т. е.
когда 1тг>0) быстрее любой степени z. Особые точки этой функции—
четыре полюса первого порядка в точках г= ±ш, z = ±ib. Два из них
2= ш и z = ib лежат над действительной осью. Вычеты в этих точках,
вычисленные по формуле (9), равны соответственно
2Ca(a2 — b2) 2ib(a2~b2)
Отсюда получаем
оо
Г* cosxdx ___ % 1
J Тх2 + а2)(х* + b2) ~~ ТсЧ2
о
Далее рассмотрим новый тип интегралов
J7(cos6, sin6)d6, A5)
6
где функция /(cos 6, sin б) — рациональная функция от своих аргументов
cos 6 и sin 6. Для вычисления интегралов этого типа следует выразить
по формуле Эйлера cos 6 и sin 0 через комплексную переменную z —
= eiB, после чего интеграл A5) преобразуется в контурный интеграл по
окружности единичного радиуса. Этот контурный интеграл по теореме
о вычетах выражается через сумму вычетов относительно особых точек,
лежащих внутри единичного круга.
В качестве примера вычислим интеграл
2гс
6 dB (а>6>0). A6)
С fsins
cos б
Заменяя соответственно sin б = -—2. , cos б = —— и d6 =
dz
=r_t—, получим, что интеграл A6) равен следующему контурному
интегралу по единичной окружности:
ЭЛЕМЕНТЫ ТЕОРИИ АНАЛИТИЧЕСКИХ ФУНКЦИЙ И ЕЕ ПРИЛОЖЕНИЯ 543
Подынтегральное выражение в этом
интеграле имеет особые точки:
полюс второго порядка в точке 2=0,
простой полюс в точке z =
_ уа* — Ь2 — а
~ Ь
и еще один простои
У а* — Ь2+а
полюс в точке z = — ~ ^ .
Внутри единичного круга лежат лишь
первые две из трех особых точек
{так как -у- > 1). Вычет в точке 2 = 0
2а , У а2 — Ь2 —а
равен г- а в точке z— т
равен 2 1/ -—■ —1. Получаем
С sin2 6 ,д __// Г
J a + &bcoSj6 а 26 J
Рис. 15. 10. Контур для вычисления
интегралов типа A8) с точкой
ветвления 0=0
(z2 — 1J
l2lU г2(г2 + 2-Тг+1
dz =
26
2^(^^ + 2/-i-l) = if(a-l/S^).
Перейдем теперь к случаю, когда вычисление вещественного
интеграла приводится к вычислению контурного интеграла от
многозначной функции. Рассмотрим интеграл
J x*~x f(x)dx,
A7)
где f(z)—рациональная функция, не имеющая полюсов на
положительной части вещественной оси, (х — вещественное число и х^ f(x) -^0 при
х-±0 и при х-> оо. Для вычисления интеграла A7) введем контурный
интеграл
J (-2)^1/(*)&, A8)
где С —замкнутый контур, изображенный на рис. 15. 10.
Подынтегральное выражение в A8) представляет собой многозначную функцию из-за
наличия множителя (—z)v-—1, если ^ не является целым числом. Чтобы
сделать функцию однозначной, на рис. 15.10 проведен разрез вдоль
положительной оси, соединяющий точки ветвления г = 0 и 2= оо, В
разрезанной таким образом комплексной плоскости подынтегральная
функция будет уже однозначной и остается лишь зафиксировать выбор
определенной ветви этой функции. Для этого условимся, например, что на
верхнем берегу разреза, на котором z положительно, аргумент
отрицательной величины — z будет — тс. При обходе вокруг начала координат
против часовой стрелки аргумент получает приращение 2тс и,
следовательно, на нижнем берегу разреза, на который мы перешли, совершив
обход точки г = 0, аргумент — z будет —тс + 2тс = тс. Таким образом,
имеем, что —z = ие~ы на верхнем берегу разреза и —z = uet% — на
нижнем берегу, где и — модуль z. Теперь имеем для интеграла A8), запи-
544
Глава пятнадцатая
сывая его соответственно в виде суммы интегралов по верхнему и
нижнему берегам разреза и по малой и большой окружностям:
R R
J (—zy-1 f(z)dz = J e-Mn.-i> и*-1 f(u)du —j e^-i) ^-i f(u)du+
С 9 9
+ J (—zy-1 f(z) dz+ f (—zy-1 f(z)dz =
"вычетов функции (—zy~lf(z) 1
относительно полюсов функции f(z) J
= 2tu ]Г]
„A9)
С помощью простых оценок нетрудно показать, что интеграл
j (—zy-1 f(z)dz обращается в нуль при р-±0, ввиду условия #*- f(z) -^0
С9 V
при 2~>0; интеграл J (—zy~lf(z)dz, в свою очередь, исчезает при /?->оо,
с* >
так как 2*х f(z) -^ 0 при z-*oo. Таким образом, формула A9) примет
вид
оо оо
—e-in^ u^-1 f(u)du + еы^ [ u?-lf(u)du = 2rci S [вычетов...],
6 6
или окончательно (возвращаясь к прежнему обозначению для
переменной интегрирования) имеем
со
j
x!,_i f /- dx = тс у Гвычетов функции (—z)^-1/*»
v ; sinтс{д.^[относительно полюсов /(z)
о
В качестве простого примера вычислим' интеграл
ОО
^-1
B0)
I
о
■d* @<|*<2),
удовлетворяющий всем условиям применимости формулы B0). Подын-
тегральная функция f(z) = 2j_ i , кроме точки ветвления при z = О,
2 -j- 1
имеет простые полюсы в точках z = i и z = —i с вычетами
Г^
/2»
соответственно.
2
По формуле B0) имеем
оо
I
.7С
х[
i^-i . * / .-'¥*
С1П три \ гч '
е !_ е
1 + х2 sin 7TJX \ 2 2
о
7С(Х ТС ТС(Л
= iiH-^r • cos-f- = -т cosecir • <21>
Теперь, ввиду особого значения теории вычетов для задач
теплопроводности, на ряде примеров проиллюстрируем применение ее для
вычисления специального класса контурных интегралов, связанных с
обращением интегрального преобразования Лапласа, т. е. к вычислению
ЭЛЕМЕНТЫ ТЕОРИИ АНАЛИТИЧЕСКИХ ФУНКЦИЙ И ЕЕ ПРИЛОЖЕНИЯ 545
Рис. 15. 11. Контур для
вычисления обратного преобразования
Лапласа от однозначных
функций
Рис. 15. 12. Контур для
вычисления обратного преобразования
Лапласа от функций, имеющих
точки ветвления 2=0 иг=оо
функции /(т), заданной в интервале т>-0, по ее изображению F(s).
Итак, будем вычислять контурный интеграл
a-\-i оо
№=-Щ- J F(s)eSxds>
B2)
a—i oo
где а — действительное число такое, что прямая Res = а лежит правее
особых точек функции F(s).
1. Пусть F(s) = -7^F>0).
Единственная особая точка F(s)—это простой полюс в точке s~
= —Ъ* Для вычисления f(%) рассмотрим интеграл
J F(s)esxds
по контуру С, изображенному на рис. 15.11 и состоящему из отрезка
мнимой оси и левой полуокружности С % радиуса R. Вычет подынтег-
esx
ральной функции . & в точке s = —Ъ равен е~Ъх. Следовательно,
a+iR
J7+Tds= J 7+Fds+J TfFds = 2«ien*.
B3)
a—iR
"R'S
Устремим /?-нюо, тогда интеграл по отрезку мнимой оси перейдет в
искомый интеграл B2), а интеграл по полуокружности обратится в нуль
согласно лемме Жордана. Окончательно, из B3) следует
a-f-ioo
1 С е^
~ о-Ьх
B4)
х/а 19 Заказ № 640
546
Глава пятнадцатая
2. F(s) = —т= . Особые точки: простой полюс при s = b2 и точ-
ка ветвления при s = 0. Рассмотрим интеграл
-«Ar-f ^ rfs B5)
по контуру С, показанному на рис. 15.12. Комплексная плоскость s
разрезана вдоль отрицательной части вещественной оси, чтобы
выделить в подынтегральной функции однозначную ветвь. Внутри контура С,
состоящего из отрезка, параллельного мнимой оси, левой
полуокружности С к, верхнего и нижнего берегов разреза и малой окружности Ср с
центром в точке s = 0, имеется одна особая точка—полюс s = b2 с выче-
том — ш Интеграл B5) представим в виде
a+lR
2ш )cy?(.-») ds~~ ь ~ ^i JiRYs(s-b^)as^
1 С esz do t С esx do
CR«> C9 S
R R
1_ Г e-mdu 1_ С e~uxdu m)
M J 1/77 еы'2(и+Ь*) + 2itf J i/a e~iW2(a + 62) *
p P
где в двух последних интегралах было положено s = иеы — на верхнем
берегу разреза и s = ue~~i% — на нижнем.
При /?~>оо интеграл по С#, согласно лемме Жордана, обращается в
нуль. Оценим интеграл по С9 при р->0, полагая s = pei(?:
lim ' Г ,- g" ds = lim ' Г «^ ^ <«* = 0.
Теперь B6) запишется в виде
00
= / СО + — f r- e~m du. B7)
«***
Последний интеграл может быть выражен через интеграл вероятности.
Введем для этого новую переменную и = z2, имеем
со
е dz.
z2 + b2
о
Функция /(х) удовлетворяет, как нетрудно убедиться непосредственной
проверкой, дифференциальному уравнению
1
№-ь*№-
V"
ЭЛЕМЕНТЫ ТЕОРИИ АНАЛИТИЧЕСКИХ ФУНКЦИИ И ЕЕ ПРИЛОЖЕНИЯ 547
при условии ]\0) = — я Решение этого уравнения имеет вид
ьут
Окончательно формула B7) запишется
№ = -^-е*фУ*). B8)
—ЬУТ
3. F(s) = £ __ . Особая точка — точка ветвления при s = 0. Кон-
V*
тур тот же, что и в предыдущем примере. Так как внутри этого
контура с разрезом функция F(s) не имеет особых точек, то
-ьУГ+
J yi ds = °- <»)
2ш
с
Легко проверить, что интегралы по левой полуокружности при R-±oo
и по малой окружности с центром в точке s = 0 при р->0 исчезают.
Равенство B9) можно переписать теперь в виде суммы интегралов вдоль
мнимой оси, один из которых равен /(т), другие определяются по
берегам разрезов.
Полагая на верхнем берегу разреза s = иеы , а на нижнем s = ие~ы,
имеем
л —ЫУи — их л С Ь1Уи — их
_ lYu 2«f J ,у„
da = 0,
т. e.
/(x) = J_Je-m™££Ldu. C0)
Чтобы вычислить этот интеграл, введем новую переменную
интегрирования z = Ун, тогда
OO -J-00 ~|~°°
/(т) = 4" ] ^"^ cos 6z d2 = 4~ i e~Z2X cos 6z dz = 4" ] ^"~2Sx+^ ^2;
0 —со —oo
полагая здесь z = —— + 4~~ » получим
1 p 4x Г 1 p 4x
/(*)==_£_-* e-^dx-^-^. C1)
4. F(s) = In S'ta - Функция In l~ta имеет точки ветвления при
s = —C и s = —а. Бесконечно удаленная точка не является точкой
ветвления. Действительно, если описать замкнутый контур, обходящий
вокруг обеих точек —р и —а в положительном направлении, то ln(s + р)
и In (s + а) получают одно и то же слагаемое 2ш, а разность ln(s + р)—
—In (s + a) = F(s) не изменится. Таким образом, функция F(s) будет од-
*/а 19*
548
Глава пятнадцатая
Рис. 15. 13. Контур для
вычисления обратного преобразования
Лапласа от функции, имеющей
точки ветвления s=~—оси s=— fJ
нозначна в плоскости с разрезом,
соединяющим точки s = —р и s = —а.
Для вычисления оригинала F(s)
рассмотрим интеграл по контуру, изображенному
на рис. 15.13. В области, ограниченной этим
контуром, функция F(s) однозначна и не
имеет особых точек, следовательно,
интеграл по этому контуру, состоящему из
отрезка мнимой оси, левой полуокружности
и верхнего и нижнего берегов разреза,
соединяющего точки —р и —а, равен нулю.
Полагая s = —р + иеы и s = —р + w~in
соответственно на верхнем и нижнем
берегах разреза и учитывая, что интеграл по
полуокружности при стремлении ее радиуса
к бесконечности обращается в нуль
согласно лемме Жордана, получим
№ + ii\e~^~uxXn
о
-ад- J
ие™
g-p-c-ttx Jn
а—p_|_we/7c
ue~
-du —
а — p -j- ue-
■ du = 0,
или
/(X) = -
2itf
- P + we**
<2m 1/7// —
d« =
p-P*
+ -Ъ-1п(в«)>
e(P-«>* __ !
e-aT-e-pT
C2)
На этом закончим рассмотрение контурных интегралов, которые
могут быть вычислены в конечном виде, т. е. выражены через
элементарные и специальные функции. Однако применение теории вычетов
далеко не исчерпывается вычислением таких интегралов, тем более, что их
сравнительно немного. В частности, большинство таких вычисляемых в
конечном виде контурных интегралов типа B2), обращающих
преобразование Лапласа, приведены в таблицах и справочниках [118] по
операционному исчислению.
Если же решение некоторой задачи получено в виде контурного
интеграла, который не вычисляется в конечном виде, то теория вычетов
дает возможность выразить этот контурный интеграл через обычные
интегралы по действительной переменной. Такое интегральное
представление решения часто делает более обозримым его поведение и облегчает
численные расчеты.
В качестве примера рассмотрим задачу теплопроводности для тела,
занимающего полупространство 0<^х< оо, плотность или теплоемкость
которого возрастает линейно с удалением от поверхности х = 0, на
которой происходит теплообмен по закону Ньютона. Требуется определить
ЭЛЕМЕНТЫ ТЕОРИИ АНАЛИТИЧЕСКИХ ФУНКЦИЙ И ЕЕ ПРИЛОЖЕНИЯ 549
плотность теплового потока через эту
поверхность. Итак, задача
формулируется следующим образом:
а 4 iR
х дТ
а2г
' дх*
дТ@^) =h[Tc_T{Q^)]t
C3)
C4)
Здесь Тс, с, у, X, /, h — постоянные
величины. Можно показать [116а, 57а],
дТ@, т)
дл;
что искомый поток q(x) = —X-
удовлетворяет следующему
интегральному уравнению Вольтерра второго рода с
разностным ядром:
0
Рис. 15. 14. Контур для вычисления
интеграла, определяющего
плотность потока тепла по формуле C6)
M7V
где
Ь = -
i
?м
(•с — г'J/3
V3
-dx',
C5)
*f)
X/
Зет
Так как в правой части интегрального уравнения C5) стоит свертка
функций q(z) и-^, то оно легко решается применением преобразования
Лапласа. Решение имеет вид
c~\~ico
q(x)=XhTc-
Чщ J
ds
SV, (eV. +№A/8))
(c>0).
C6)
Этот контурный интеграл может быть легко преобразован в
вещественный интеграл интегрированием подынтегрального выражения по
контуру, состоящему из отрезка мнимой оси, разреза, соединяющего точки
ветвления s = 0 hs= оо, и левой полуокружности (рис, 15.14). Так как
внутри этого контура подынтегральная функция не имеет особенностей,
то искомый интеграл равен просто интегралам вдоль берегов разреза
(интегралы по полуокружности исчезают.; согласно лемме Жордана, при
стремлении радиуса полуокружности к бесконечности). Имеем
хагс
+
и j ■
'du
V:
__.2тс
+
— Г
2тм J
'« , 3 [и /Зе-^'3+6ГA/3)]
е~ит du
о и 'г е
,' з («V. e l з + бГA/з)]
После простых преобразований получим
= 0.
31/3
2те
L
-Е23
■2+1
dZy
C7)
где
1 8 Заказ № 640
I = [6ГA/3)]"Ч.
550
Глава пятнадцатая
Из решения в форме C7) сразу видно, что q(t) является монотонно
убывающей (от ШГС до 0) функцией т. Интеграл C7) удобно
интегрировать численно, а при больших £ для него в следующем параграфе
будет получена простая асимптотическая оценка.
Методы теории вычетов могут быть использованы и для задач, в
каком-то смысле обратных рассмотренным выше. Часто оказывается
полезным выразить какую-либо функцию через контурный интеграл. При
этом интегральное представление сложной функции может оказаться
удобным для исследования, если подынтегральное выражение в
контурном интеграле имеет простой вид и содержит элементарные функции.
Кроме того, деформируя контур в соответствии с теоремой Коши,
можно получить различные приближенные оценки для интегралов,
например их асимптотические оценки. В частности, если функция задана
рядом, то представление суммы ряда через контурный интеграл
позволяет в некоторых случаях найти сумму ряда в конечном виде.
Пусть f(z) — рациональная функция и, следовательно, имеет
конечное число полюсов в точках гъ..., zp, пусть также степень многочлена,
стоящего в числителе функции f(z), ниже степени многочлена в
знаменателе не меньше, чем на две единицы, так что f(z) убывает при z-±qo
не медленнее, чем ~ —^. Рассмотрим интеграл по окружности
радиуса (п + Va)
J f(z) ctgvzdz (/z = 0, 1,...). C8)
|z|=/*+V,
Мероморфная функция ctg ^ z ограничена повсюду, за исключением
окружностей с целочисленными радиусами. Поэтому для интеграла C8)
имеем оценку
| J f(z) ctg « dz I < J I f{2) Ctg *Z I dz<
<(^P7i)i-^:2"(« + 1/,), C9)
где M — максимум модуля ctgnz в плоскости z с удаленными
окружностями целочисленных радиусов. Из оценки C9) следует, что
интеграл J f(z) ctg 7г z dz -> 0 при п-^оо. Этот же интеграл может быть вы-
числен с помощью теоремы о вычетах. Особыми точками
подынтегральной функции в круге \z\ =/г + 1/2 будут простые полюсы мероморфной
функции ctgirzB точках z = 0, ±1, ±2,..., ±п с вычетами — f(z) и
полюсы рациональной функции /(-г). Предположим, что п достаточно
велико, так что все полюсы zv г2,..., z функции f(z) попали в круг
| z | < п + -н~ • Тогда по теореме о вычетах имеем
п
J/(z) ctgvzdz = 2iri {4-S /(*) +
-f S вычеты [/(z) ctg к z] в полюсах /(z)
ЭЛЕМЕНТЫ ТЕОРИИ АНАЛИТИЧЕСКИХ ФУНКЦИИ h ЕЕ ПРИЛОЖЕНИЯ 551
Переходя к пределу п ~> оо, получим
р ( вычеты [/(z)ctgiczj
в полюсах / {г)
D0)
Совершенно аналогично может быть получена формула для рядов
типа
И (-!)"/("),
где f(z) обладает прежними свойствами Следует лишь в интеграле C8)
ctg 1Г2 заменить на . В результате получим
sin nz
__ - _ _
А I вычеты I—'-1-1—I II
D1)
В качестве примера применения доказанных формул просуммируем ряд
оо
V 1 !
Л=1
п2 + а2
D2)
Прежде всего запишем D2) в виде
v
п=\
п2 + а2
Далее, рациональная функция
1
г2 + а2
имеет два простых полюса в
точках z = ± ш, а вычеты функции
ctg 7i iz
2ia
cth я 2
ctg тег
z2 + a2
в этих полюсах равны
V
2a
каждый. Итак, согласно D0), получим
2а2 2
1 ~ cth тс а
— тс-2
S
п2 4- 0"
2а3
2а
2а
сШтта
1
2а2
D3)
§ 6. НЕКОТОРЫЕ АНАЛИТИЧЕСКИЕ СВОЙСТВА
ПРЕОБРАЗОВАНИЯ ЛАПЛАСА И АСИМПТОТИЧЕСКИЕ
ОЦЕНКИ
В предыдущей главе были изложены основы операционного ^исчисле-
ния и связанные с его использованием свойства преобразования
Лапласа. Эффективность операционного исчисления цесомненна, вэиду его
простоты и возможности пользоваться обширными таблицами
интегральных преобразований. Однако обращение к непосредственному
исследованию контурных интегралов, к которым сводится выполнение
обратного преобразования Лапласа, весьма полезно, тт как' форма решения
552
Глава пятнадцатая
задачи, выраженная в виде контурного интеграла, является наиболее
гибкой и позволяет путем деформации контура интеграла и изучения
поведения подынтегрального выражения в комплексной плоскости
получить представление о ходе решения и различные достаточно простые
приближения для решения, К изучению аналитических свойств
преобразования Лапласа и к простейшим методам получения
асимптотических оценок мы и перейдем, не повторяя содержания гл. XIV.
Напомним лишь, что функции, к которым применяется преобразование Лапласа,
должны быть кусочно-непрерывными, отличными от нуля лишь при
t^O и должны возрастать не быстрее показательной функции.
Последнее означает, что существуют постоянные Л > О и а0>^0 — такие, что
для всех т > О
\f(x)\<Ae"\ A)
Число а0 называется показателем роста функции /(т). При этих
условиях, как уже упоминалось в предыдущей главе, можно показать, что
изображение F (s) будет существовать в полуплоскости Re s>a0 и,
более того, будет в этой полуплоскости аналитической функцией. Отсюда
вытекает, что при Re s = о -> ~|~ °° любое изображение F (s) стремится
к 0. Это немедленно следует из неравенства A) и оценки
\F(s)\ =
f e~sxf(x)fc <Л|<Г(Мв)гЖ==-
Условие F (s) -> 0 при Res-^ + oo является необходимым для того,
чтобы функция F (s) была изображением по Лапласу. Поэтому,
например, функция sa(a>-0) не может быть изображением функции в
обычном смысле1*. Однако условие F (s) -> 0 при Res -> оо не является
достаточным для того, чтобы F (s) было изображением, как это видно на
примере функции e~s.
Заметим, что область, в которой функция F (s) будет аналитической,
как правило, шире полуплоскости Re s > a0, в которой F (s) представле-
00
на интегралом J e~sxf(^)dx. В этом легко убедиться с помощью таб-
. о
лицы изображений в приложении VI. Например, функция F (s) =
= — vj_i > являющаяся изображением функции tv , имеет лишь одну
особую точку при s = 0, которая в случае целого положительного v =
= m (m = 0, 1, ... ) будет полюсом (т + 1)-го порядка. Во всей
плоскости, за исключением этого полюса, функция —— является анали-
^J . sm+i
тической. Если v не является целым числом, то F (s) будет
многозначной функцией с ветвлением при s = 0 и s = оо, а областью
аналитичности ее однозначной ветви, определенной условием — к < б < тс (s =
~ Ы ), будет вся плоскость с разрезом вдоль действительной
отрицательной полуоси. Например, функция F (s) = , являющаяся изоб-
s2 + 1
ражением sinT лишь в полуплоскости Re s > 0, будет аналитической во
зйсей плоскости, за исключением двух простых полюсов в точках s =
= :fc i. Поэтому хотя различные соотношения между изображением по
1) Здесь не рассматривается теория преобразования Лапласа от так называемых
обобщенных функций [25а, 20а], примером которых является известная 5-функция Дирака.
ЭЛЕМЕНТЫ ТЕОРИИ АНАЛИТИЧЕСКИХ ФУНКЦИЙ И ЕЕ ПРИЛОЖЕНИЯ 553
Лапласу и, в частности, все свойства такого рода, выведенные в
предыдущей главе, установлены для соответствующей полуплоскости сходимо-
00
сти интегралов \ e~sx f (т) diy эти соотношения можно путем аналитиче-
о
ского продолжения распространить на всю область аналитичности
соответствующих функций.
Исходя из аналитических свойств преобразования Лапласа в
комплексной плоскости, установим теперь два практически важных
предельных соотношения.
Во-первых, если функция /(т) удовлетворяет неравенству
I/WKAJ
для всех т > 0, где М > 0 — некоторая постоянная, то
lim sF (s) = /(<*>)
s-Ч-О
B)
при условии, что /(oo) = lim /(т) существует.
Во-вторых, если функция /(т) удовлетворяет неравенству
|/(т)|<Ле^
для всех т > О, где А и а0 — положительные величины, то
lim sF(s) = f{0)
S _»._J_ 00
C)
в предположении, что /@) = lim/ (т) существует.
В формулах B) и C) s .стремится к соответствующим предельным
значениям вдоль действительной оси.
Для доказательства предельного соотношения B) рассмотрим разность
sF(s)-f(oo)=s
j e"ST / (т) d% — f (сю) j «f^dx
D)
Так как s согласно условиям теоремы можно считать действительным,
то, вводя в формулу D) новую переменную интегрирования ^=?st,
получим
со , х0
sF(s)-f(oo)= j" [/(-j-)-/(oo)]e-*d*= J [/(-f-)-/(«)]e_xd* +
d о
oo
+ j [/(-j-)-7 («•)]«-*<**. E)
XQ
где x0 > 0 — пока произвольная величина.
Рассмотрим сначала интеграл
л = J°[/(f-)-/(°°)]^^.
о
Так как функция /(х) ограничена (|/(т)|<М для всех т>0), то,
очевидно,
IAI<Ai(l — e~Xo) .
554
Глава пятнадцатая
В последнем неравенстве х0 может быть выбрано настолько малым, что
\JX\< Мх0
станет меньше любой сколь угодно малой наперед заданной величины,
которую обозначим е>0. Зафиксировав такое х0> выберем некоторое
s0>0 настолько малым» чтобы при х > х0 для всех 0<s< s0
/(JLj__/(oo)
<в.
Тогда для интеграла
00
^!(~)~Г(-о)\е-хс1х
/3== f
имеем
со
| Л1 < £ \ е~х dx — ее~~х° < е.
Складывая полученные для \J1\ и |/2| оценки, находим, что
\sF(s) — /(oo)|<2e.
Таким образом, можно выбрать такое достаточно малое s, что
|s^($) —/(оо) | станет меньше заданного сколь угодно малого
положительного числа, что и доказывает соотношение B). На основании
аналогичных рассуждений доказывается и формула C).
Полученные предельные соотношения позволяют по известному
изображению F(s), не вычисляя контурного интеграла, обращающего
преобразования Лапласа, определить значения функции / (т) при т = О и
т = оо, если известно, что /(+0) и /(оо) существуют. В задачах теории
теплопроводности существование этих значений может быть часто
установлено из физических соображений. Например, если из условий задачи
очевидно существование стационарного температурного поля, то оно
может быть определено по изображению решения с помощью
соотношения B).
Рассмотрим несколько примеров.
1. В § 2 гл. IV было получено, что изображение по Лапласу
температуры полупространства х > 0 с начальной температурой Т0, на границе
которого поддерживается нулевая температура, равно
TL(x, s) i __e
-VI-
Прежде всего, отсюда можно проверить, удовлетворяет ли полученное
в результате вычитаний выражение для Tl(x, s) начальному условию.
Имеем
.П*.0) _ 1}m „ TL(x..) (i.-VT*
lim s • — = lim 1 1 — e r a j = 1
Tq s->-t-oo ■* о s->-{-oo
Далее, найдем стационарное значение температуры:
Т(х, оо) = limsTL(*,s) = T0lim 1 — е~* т) = 0.
ЭЛЕМЕНТЫ ТЕОРИИ АНАЛИТИЧЕСКИХ ФУНКЦИЙ И ЕЕ ПРИЛОЖЕНИЯ 555
2. В качестве несколько менее тривиального примера рассмотрим
задачу о температурном поле в двух полупространствах, находящихся
в тепловом контакте (см. § 1 гл. X). Правое полупространство имеет
в начальный момент температуру Г0, а левое — нулевую начальную
температуру. Изображения имеют соответственно вид
-ух.
T2L (*, s) = К;Т\ е^^х (х< 0), F)
A +Ае )S
где
Имеем
«.-V&&
2С2Т2
к.
lim sTiL (x, s) = T0
s->-\-0 1 + As
к.
lim sT2L (x,s) = T0 .
S-++0 1 + Ae
Таким образом, при z -> oo оба полупространства имеют совпадающую
(как и должно быть при существовании равновесного состояния)
температуру Г0—^— .
1 + Ае
Также легко проверить с помощью предельного соотношения C),
что выражения F) удовлетворяют начальным условиям задачи.
3. Пусть F (s) = — , тогда
S2 + 1
lim sF (s) = lim s = 0,
lim sF (s) = lim —-— = 0.
5->+0 s-*+0 S2 + 1
Однако лишь первое из равенств дает значение функции /(т) =-sini;
при т = 0. Но lim sF (s) не дает значения предела /(т) при т->оо,
S-++Q
так как этого предела не существует.
Аналогичная ситуация может встретиться и в некоторых задачах
теплопроводности, например, в задаче о полупространстве #>0, на
границе которого температура изменяется со временем по
гармоническому закону. При простейших краевых условиях можно записать
дТ{Х'Х) =ad2TjX:X) <0<*<со),]
\ G)
Т(х,0) = 0,
Т@, x)=Tmsino)x,
дТ (*, eo) __ q
556
Глава пятнадцатая
Легко вычислить, что
TL(x,s) = Tml^e ^'°х . (8)
Хотя из (8) следует, что
lim sTL(x, s) = О,
s->-fO
но это не означает, что UmT (х, т) = О, так как последнего предела
Т->00
не существует»
Рассмотренные предельные соотношения для преобразования
Лапласа, выражаемые формулами B) и C), являются весьма частным случаем
асимптотических оценок.
Рассмотрим некоторые методы асимптотических оценок, полезные
при исследовании задач теории теплопроводности.
Две функции f (х) и g(x) называются асимптотически равными
при стремлении их аргумента х к некоторому значению х0, если
отношение f{x)lg(x) стремится к единице при х~^х0.
Асимптотическое равенство будем записывать в виде
Например,
f(x)c*g(x) (х-±х0).
Х + 1 с^ X При X -> оо,
§Ъх~-?— при л:-> + °°»
х% + 3* + 2 1 ,
1 ' ~ При X -> + оо,
6X3 + JL.+ 1 Ьх
sinx^x при х-±0
и т. д.
Практический интерес представляет случай, когда функция g (х)
является более простой с точки зрения способа ее вычисления при
х~±х0 по сравнению с функцией f(x). При х-^оо такими простыми
функциями часто могут служить ряды по убывающим степеням х:
оо
(К < h < h <...)•.
Ряд (9) не обязательно сходится, но и для расходящихся
асимптотических рядов, в практически встречающихся случаях, погрешность от
N
замены функции / (х) отрезком ряда (9) ^. ~y~ может быть сделана
/г=0 х
с
меньше последнего члена суммы , т. е.
хХ*
N
Сп
/w-2-x
л х
-> О ПрИ X ->■ оо. A0)
ЭЛЕМЕНТЫ ТЕОРИИ АНАЛИТИЧЕСКИХ ФУНКЦИЙ И ЕЕ ПРИЛОЖЕНИЯ 557
Далее заметим, что асимптотическое разложение функции, если оно
существует, определяется единственным образом. Однако один и тот
же асимптотический ряд может служить асимптотическим разложением
различных функций. Например, две функции f (х) и / (х) + е~х имеют
одинаковые асимптотические разложения при- х -~> + °°» так как
lim х пе~х = О для любого \п .
Асимптотические ряды можно почленно складывать, перемножать и
интегрировать.
Если известно, что производная функции допускает асимптотическое
разложение, то его можно получить, дифференцируя асимптотическое
разложение функции.
Практическая значимость асимптотических оценок чрезвычайно
велика. Это объясняется тем, что решение многих нетривиальных задач
математической физики получается очень громоздким или сложным по
форме. Например, оно может быть задано сложным функциональным
рядом или контурным интегралом. Вместе с тем часто в задачах надо
знать точное решение не при всех значениях параметров и переменных,
а лишь при некоторых предельных значениях. Например, иногда
достаточно знать поведение решения по истечении большого промежутка
времени. В этих случаях о поведении сложного точного решения можно
судить по его асимптотическому разложению. Так как решение
линейных задач теории теплопроводности может быть всегда выражено в виде
контурных интегралов (а в ряде случаев и интегралов по действительной
переменной), то, естественно, в первую очередь надо рассмотреть методы
асимптотических оценок интегралов соответствующих типов.
Начнем с вещественных интегралов вида
ь
F{g) = §y(x)erhWdx, (II)
а
где все величины действительны. Интеграл A1) при больших значениях
положительного параметра а может быть оценен с помощью метода
Лапласа, сущность которого заключается в том, что если функция
h(x) имеет на отрезке (а, Ь) максимум, то при больших о этот
максимум будет выражен очень резко и основной вклад в значение интеграла
даст окрестность точки максимума. Если функция h (x) имеет несколько
максимумов, то промежуток интегрирования в A1) можно разбить на
конечное число интервалов так, чтобы функция h (x) принимала
максимальное значение лишь в одной из концевых точек каждого из
интервалов (например, на левом конце) и не достигала максимального значения
в других точках. Поэтому достаточно ограничиться случаем, когда в
интеграле A1) функция h (х) имеет единственный максимум при х = а,
т. е. h(x)<h(a) при всех а<Сх<^Ь. Пусть функция h (x) имеет
непрерывную производную второго порядка. В точке максимума h! (а) = О
и К' (а) < 0. Существует такое достаточно малое число ^ > 0, что
производная К (х) < 0 при а < х < а + -р При а -^ + °° тогда имеем
F(a)- j <f(x)e*hWdx. A2)
a
Предположим также, что функция ф (х) непрерывна, и введем вместо х
новую переменную интегрирования у согласно соотношению
h (а) — h (х) = уъ.
A3)
558
Глава пятнадцатая
Тогда A2) можно переписать в виде
у
F@)~-2e«*C> j" у -р$Цк е~°«> dy, A4)
О
где
Y = yh(a) — h(a + -fi > 0.
Как уже говорилось выше, существенным в A4) является лишь
значение подынтегральной функции в окрестности точки х = а (т. е.
у = 0). Поэтому в A4) под интегралом можно приближенно заменить
t ч / ч и (х) ,. и (х) t. ~Vh (а) — h (х)
<р (х) на ф(а), а частное у v ; на lim ■ v } = hm -1—— ^-^- =
h'(x) x^a+0 hr (х) х^а+0 hr (х)
= hm
лг^а+о Л" (а) (х— a) Y—2K" (а)
С учетом этих результатов соотношение A4) теперь запишется
у
Р{?)~У -zzww ф {а) е°Ш 1 е~** dy' A5)
1 ' о
При а -> + °° в последний интеграл вносят вклад лишь значения у,
близкие к 0. Поэтому, не внося сколько-нибудь существенной ошибки,
можно заменить верхний предел интегрирования Y на бесконечность.
Окончательно получим асимптотическую оценку интеграла типа A1)
для о -> + °° при условии, что h (х) имеет максимум при х = а:
'ю-Ч^ет^фМ
A6)
Путем аналогичных рассуждений могут быть получены и
последующие члены асимптотического разложения F (а). Приведем полное
асимптотическое разложение лишь для одного важного частного случая
интеграла (И), когда h(x) = —ха (а > 0), а = 0, а 0<6<[оо. Если также
ь
J | ф (х) | е~а<>ха dx сходится для некоторого с0, то интеграл
а
Ь
F (а) = J Ф (х) е-°х* dx A7)
о
имеет асимптотическое разложение
ГЫ^^т(-±Ш.).-^ (,8)
п—0
где р> —1, и коэффициенты Сп определяются из разложения функции
Ф (х) в степенной ряд вида
00
который предполагается сходящимся при | х | < /? > 0.
ЭЛЕМЕНТЫ ТЕОРИИ АНАЛИТИЧЕСКИХ ФУНКЦИЙ И ЕЕ ПРИЛОЖЕНИЯ 559
Непосредственным следствием из оценки A8) для интеграла A7) (при
а = 1, Ъ — оо и замене обозначений х -> т, с-> s) является теорема об
асимптотическом разложении изображения по Лапласу: если интеграл
оо
F(s) = |в-*7(т)Ж:
о
где-либо сходится, а оригинал /(т) может быть разложен вблизи точки
^ = 0в сходящийся ряд вида
оо
(—1 <\><*1<.. .)>
то изображение F(s) имеет при s^+oo асимптотическое разложение
оо
F(s)~^CnT^ . A9)
Более полезной явилась бы теорема, которая по некоторому разложению
изображения давала возможность судить об асимптотическом поведении
оригинала. Такая теорема будет приведена ниже.
Следующим примером полученной асимптотической оценки для
интегралов типа A7) может служить приведенное в § 5 интегральное
представление для плотности потока тепла через поверхность
полупространства, плотность или теплоемкость которого линейно возрастает с
удалением от поверхности [см. C3)—C7) § 5]. Было показано, что
поток тепла пропорционален интегралу
3]/
е
-&»
F{l)=JLJL±[ ' dz. B0)
2тс J z2 + г + 1
о
При ^ —> оо (большие значения времени) из формулы A8) (если р = 0,
а = 3, ф (г) = 2 . < 1 при 0 < х < сю) получим
Z" -\~ Z \ 1
т^У.г(Ч±)-^Г. B.)
где С„ — коэффициенты разложения
V
C„zn
г^ + г+1 ^ »
1 ' » П
/г=0
(С0 = 1, Сг = —-1, С2 = 0, С3 = 1, . . .)• Последний степенной ряд имеет
отличный от нуля радиус сходимости (радиус сходимости этого ряда
равен расстоянию до ближайшей к 2 = 0 особой точки функции 2 , , 1 ,
т. е., как легко убедиться, Rcx= 1). Из оценки B1) следует, что
тепловой поток убывает при т -> оо обратно пропорционально кубическому
корню из времени.
560
Глава пятнадцатая
Рассмотрим хотя бы один пример оценки интегралов типа A1).
Практический интерес представляет асимптотическая оценка очень часто
встречающейся в анализе функции
оо
Г(а + 1)== jV**°d* B2)
о
При а -> -(- °° •
Начнем с преобразования формулы B2) к интегралу типа A1).
Введем новую переменную интегрирования х = az, тогда B2) перепишется
оо оо
Г (о + 1) = °a+l J z° e~QZdz = oH-1 J е-°<*-1пгЫг = 0H-i [/х (a) _|_ j2 @)j?
B3)
где
i
Л(°) = |е-~аB-1пг)й2,
о
00
J2(g) == J е-аB~1пг) ^2.
1
Интеграл /2(a) принадлежит к типу A1). Имеем <р(г)==1, a = 1, h{z)^=
= — (z —lnz), Л'(О =0, ЛA) = — 1 иЛ"A) = —КО. Согласно фор-
муле A6) имеем для /2(а) оценку при а-> + °°'
•М°)~"|/"-£-е-. B4)
Теперь преобразуем интеграл J±(o), вводя новую переменную
интегрирования z = — , тогда J1 (a) примет вид
т / \ Г —a (-77 +ln") du
В такой форме уже очевидно, что и /х(а) является интегралом типа (И),
в котором h (и) = — ( Ь 1пи] , и максимум h (и), как и необходимо,
достигается на нижнем пределе при и = 1 (точка и = оо, в которой
также А'(оо) = 0, не является максимумом). Далее, учитывая, что для
J1(a) ф(и)--^-, ЛA) = —1 и А"A) = —1 <0, получим из A6)
hW^Ylrtr* B5)
При a ~> -f- оо.
Подставляя в соотношение B3) оценки B4) и B5), получим первый
член асимптотического разложения для гамма-функции
Г (а + 1) ~ у1ЙГ о°+". е— , B6)
представляющей собой известную формулу Стирлинга, которая была
использована в предыдущей главе (при выводе формулы вещественного
обращения преобразования Лапласа).
ЭЛЕМЕНТЫ ТЕОРИИ АНАЛИТИЧЕСКИХ ФУНКЦИЙ И ЕЕ ПРИЛОЖЕНИЯ 561
С методом Лапласа, служащим для асимптотической оценки
интегралов по действительной переменной, тесно связан так называемый
метод перевала асимптотических оценок контурных интегралов
вида
/(о)= jV*<2>(p(z)dz. " B7)
с
Контурные интегралы такого вида тесно связаны с преобразованием
Лапласа. При больших значениях параметра (Rea-> + oo)
подынтегральное выражение в B7) будет очень быстро колебаться из-за наличия
в нем множителя enmlahw] y изменяющегося с частотой,
пропорциональной с Эти колебания делают практически невозможным прямое
вычисление интеграла B7). Поэтому естественно попытаться деформировать
контур интегрирования, не пересекая особых точек и, следовательно, не
меняя значения интеграла согласно теореме Коши таким образом, чтобы
свести к минимуму колебания подынтегральной функции, особенно на
тех участках, которые вносят наибольший вклад в интеграл. Значение
интеграла будет, очевидно, определяться тем участком контура
интегрирования С, на котором модуль \eah^\ = e^e^h(^z^ будет принимать
наибольшие из возможных значений.
Чтобы избежать колебаний подынтегрального выражения,
деформируем путь интегрирования так, чтобы
eilm{ah{z)} = const B8)
на участке, где Re [ah (z)] принимает наибольшие значения. В точке z0,
в которой Re[aA(z)] принимает наибольшее значение, будет
А'(*о) = 0. B9)
Эта точка не может быть точкой максимума или минимума функции
Re^(z), так как согласно условиям Коши — Римана [см. D) § 1]
вещественные (и мнимые) части аналитических функций удовлетворяют
уравнению Лапласа (г = х + iy)\
а2 Re h (z) . d*Reh(z) _Q
дх2 ду2
а такие функции (называемые гармоническими), как известно, не могут
иметь максимумов и минимумов. Следовательно, точка z0 будет седловой
точкой (или точкой перевала). Направление пути интегрирования в
точке перевала должно быть выбрано согласно B8) и определяется
уравнением
lm[oh(z)) = lm[oh{z0)]. C0)
Интеграл C0) по контуру, проходящему через точку z0, уже может
быть оценен по методу Лапласа, причем при больших о вклад в
интеграл будет определяться только ближайшей окрестностью точки z0.
Повторяя те же рассуждения, использованные при оценке интеграла A1),
для первого члена асимптотического разложения B7) получим
/ (о) - 1 / —~ е'А<*о> ф (Z ).
V ' V oe'^h" (z0)
C1)
Рассмотрим один пример. Функция е2^ г' в окрестности своей
■Л-±)
562
Глава пятнадцатая
существенно особой точки z = О может быть разложена в ряд Лорана.
e*\z *)= ^ Cn(p)z\ C2)
где Сп (а) — коэффициенты лорановского разложения. Эти коэффициенты
определены формулами A7) и A7') § 3. Меняя в формуле A7')
направление обхода контура на обратное и заменяя индекс — я, где п
пробегает значения 1, 2, . . . , на индекс п, где п принимает значения — 1,,
—2, . . . , а также учитывая, что в качестве С^2 (и Cr±) может быть
выбран любой контур, охватывающий точку 2 = 0, можно записать
единое выражение для коэффициентов Сп(о) в виде
'Сп(а) = —!— f e*v т) -^- . C3)
С
Эти коэффициенты можно непосредственно получить в виде степенного.
ряда по а, для чего достаточно воспользоваться разложениями
2 ' '
я=0
(_1)л / а \л 1
/2=0
отсюда легко находим, что коэффициент при zm (m = О, 1, . . .) равен
оо
с»-2кЛя)и, Ы - C4>
/2=0
1
а при
2"
С_,>) = (-1ГСщ(с) C5>
(т= 1, 2, .. .)•
Однако выражения C4) и C5) совпадают с определением функции
Бесселя первого рода целого порядка (см. приложение II). Таким образом,
формула C3) дает интегральное представление функции Jn(a). В
формуле C3), как уже говорилось, контур С должен лишь содержать внутри
себя точку z — 0. Выберем в качестве С окружность единичного радиуса,
тогда интегральное представление функции Бесселя Jn(o) запишется
в виде
■(--!.)_*.
7 (о) = —— е2^ *}-!?-. C3а)
1*1 = 1
Из этого интегрального представления можно методом перевала опре*
делить асимптотическое поведение функции Jn (а) при а -> + о©. При
этом ф (г) = ; h{z) = — (z ), точками перевала являются
гг = i = e~^ и z2 = —t = е '2 . Путь интегрирования для каждой из то-
ЭЛЕМЕНТЫ ТЕОРИИ АНАЛИТИЧЕСКИХ ФУНКЦИИ И ЕЕ ПРИЛОЖЕНИЯ 563
чек перевала соответственно определяется уравнениями 1т[г ]
= ±2*. Суммируя вклады от обеих точек перевала, получим из C1)
VbTz \ I
-V
A-cOsfa-JL/i ~). C6)
Наиболее ценными для нас были бы теоремы, которые позволили
бы по известному изображению F(s), исходя из его аналитических
свойств, т. е. по положению и характеру особых точек, определить без
вычисления соответствующего контурного интеграла асимптотическое
поведение оригинала /(т) при т-> оо.
Сначала рассмотрим отдельные случаи, когда функция F(s) имеет
точку ветвления, затем полюсы, а потом сформулируем теорему и для
общего случая.
Итак, пусть F (s) имеет точку ветвления при s = 0 и не имеет
других особенностей в конечной части плоскости s. Далее, пусть при
)s|->oo F(s) равномерно стремится к нулю в левой полуплоскости.
Если F (s) может быть разложена в ряд
00
F(s) = JiCns\ C7)
/2=0
(Х0<лх<Х2<. . .),
то
т-2т&^- C8>
/2=0
Для доказательства заметим, что интеграл
—— (VF(s)ds-O, C9)
2rd J
с
где С —контур, изображенный на рис. 15.14 и состоящий из отрезка,
проходящего правее и параллельно мнимой оси от точки а — iR до
а -\- iR (a > 0), из левой полуокружности радиуса R, верхнего и
нижнего берегов разреза и окружности радиуса р вокруг точки s = 0. Из
леммы Жордана непосредственно следует, что интеграл по полуокружности
при R -> оо обращается в нуль. Таким образом, равенство C9) может
быть записано в виде
/W = --^jW(*)<k, D0)
где L — контур, состоящий из верхнего и нижнего берегов разреза вдоль
отрицательной полуоси между точками s — 0 и бесконечно удаленной
точкой, и окружности радиуса р вокруг точки s~0. Направление
обхода указано на рис. 15.14.
Подставляя в D0) разложение C7) и предполагая возможность
перемены порядка, в котором выполняется суммирование и интегрирование
564
Глава пятнадцатая
Ф
©(законность такой перемены можно
обосновать при некоторых
дополнительных условиях, которые на
практике, как правило, выполняются),
~ получим
оо
esz slfl ds.
n=0
Рис. 15. 15. Контур для
интегрального представления гамма-функции
Вводя новую переменную st = s (х >0),
т. е. совершая преобразование
подобия плоскости s (окружность вокруг точки s = О преобразуется в
концентрическую окружность радиуса рт и т. д.), получим
л=0
Рассмотрим интеграл
J (г)
2та
s~zes ds,
D1)
D2)
где контур Z/ совпадает с L, но обходится в противоположном
направлении (рис. 15.15). Пусть z<l, тогда интеграл по окружности
71
стремится к нулю при р-> О, и J {г) выражается через интегралы по
берегам разрезов (на верхнем берегу разреза s = uei% и s~z = x~ze~
на нижнем s = ае~/7С и s~ = x~zei%z):
\r—Zp-~lltZ
J (г)
оо с» оо
е««2 Г е—ъ1г Г* Sin 712 f
\ лгге~-Мл: | x~ze~xdx = \ x~ze~x dx
2ш J 2ш J те J
Sin 712
Г A-2),
D3)
так как
Г (и) = j е-**"-1 dx
при Re и > 0.
Для гамма-функции имеет место известное функциональное
соотношение
Г(г)ГA — г)
sin кг '
D4)
поэтому D3) можно записать в виде
ЭЛЕМЕНТЫ ТЕОРИИ АНАЛИТИЧЕСКИХ ФУНКЦИЙ И ЕЕ ПРИЛОЖЕНИЯ 565
т. е. для функции Г (г) имеет место интегральное представление
■ш - iH^"*1 D5)
V
доказанное для z< 1. Однако его можно аналитически продолжить на
любые г. С помощью интегрального представления D1) получаем
разложение C8).
Заметим также, что, если точка ветвления находится в точке,
отличной от нуля, — в некоторой точке s0, то по теореме смещения,
приведенной в предыдущей главе, соотношение C8) по-прежнему будет
иметь место, если его правую часть умножить на es°x.
Доказанная теорема носит название правила дробных показателей,
так как, если какое-либо из чисел Хл нуль или целое положительное
число, то соответствующий член в разложении C8)
= 0 при п = О, 1, ....
Это немедленно следует из соотношения D4), если его переписать в виде
= — г (г) sin кг
Г A — 2) 7z w
и полагать в нем 2 = 1,2,....
Таким образом, асимптотическое разложение C8) содержит лишь
1
нецелые степени —.
В качестве иллюстрации рассмотрим изображение
F(s) =
е
(Т >Р). D6)
Функция F (s) имеет точку ветвления s = 0 и удовлетворяет всем
условиям, при которых было выведено правило дробных показателей, если
выбрать ветвь, для которой Rel/s ;>0. Разлагая в формуле D6)
экспоненту в ряд, получим
^?(*) = 1]±ЭР1^. D7)
п=0
отсюда, согласно C8),
(-7)* 1 1 _
/w-S-^
Н^Г Ф-Т
сю
=1+2
(-т)" L
Ш 1, П \ тп/2
^г ri-7
В сумме \j все члены с четными п исчезают; полагая поэтому п =
=2т +1, получим
566
Глава пятнадцатая
Из теории гамма-функций известно,
что
r(V,-m) = (-l)«
поэтому
22mm\
Bm)!
|Лг
/(х) = 1
-2
1)л
У% /S
т=0
Bm+l)!m!
2 j/i
v 2m+i
D8)
Рис, 15. 16. Расположение
полюсов функции F(s)
что, как и следовало ожидать,
совпадает с разложением функции
erfcj—L| при малых значениях ^/2 ]/ х .
Перейдем теперь к случаю, когда особыми точками изображения
F ($) будут полюсы в точках slf s^...,sN (рис. 15.16). Очевидно, что,
вычисляя интеграл -к-^- \ е F(s)ds по контуру, указанному на рис. 15.16,
и учитывая, что интеграл по левой полуокружности при R-><x> исчезает
по лемме Жордана, получим (а> Resk; £=1,2,..., N):
1 f* Sz
N
f^=-2^i J ** F(s)ds = ^[ вычеты [e > (s)] bsk }.
D9)
£=1
Если x велико, то, очевидно, в правой части D9) следует оставить
лишь член с наибольшим значением Res^, так как из-за наличия
множителя е kX он будет велик по сравнению с остальными. Если имеется
несколько таких членов, у которых Re 5^ равны (a Ims^, различны), то
надо взять сумму этих членов. Например, функция
F(s)
1
s2 (s — 1)
имеет двукратный полюс при s — О и простой полюс при s=l. При
х ~» оо имеем
тогда как
/(т)«<Г
/(т) =ех — х — 1.
Таким образом, для определения асимптотического поведения функции
при х-> оо, если известно только ее изображение, нет необходимости в
выполнении контурного интегрирования. Это асимптотическое
поведение функции будет определяться самой правой особой точкой (точками)
изображения.
Теперь совершенно очевидна следующая общая теорема. Пусть F(s)
имеет особые точки — полюсы и точки ветвления; функция F (s) при
|$|-> со стремится равномерно к нулю в полуплоскости Res<0; число
особых точек sk с наибольшим значением Resk конечно (k = 1, 2,..., N),
ЭЛЕМЕНТЫ ТЕОРИИ АНАЛИТИЧЕСКИХ ФУНКЦИЙ И ЕЕ ПРИЛОЖЕНИЯ 567
2тп
Зт0
4То
5тп
Рис. 15. 17. Импульсный периодический тепловой
поток q0
и если разложение F (s) в окрестности точки s = sk дается рядом
(xS*»<xi«<...),
тогда асимптотическое разложение f(i) будет иметь вид
E0)
N
Ж
ft=i „=ог (—^й)) t "
E1)
где
г (- л<*>)
0, если Х„
0, 1, 2,..
Проиллюстрируем применение этой важной теоремы на нескольких
примерах.
В предыдущих главах с помощью преобразования Лапласа
получено точное решение большого числа задач. Читателю предлагается в
качестве упражнения получить асимптотическое разложение решения
при т -> оо непосредственно из изображения решения, определив самые
правые особые точки этого изображения, и убедиться, что полученное
асимптотическое разложение решения будет совпадать с найденным
путем перехода woo в окончательном решении.
Рассмотрим задачу о температурном поле в полупространстве #>0,
прогреваемом импульсным периодическим тепловым потоком (рис. 15.17),
равным
1 при 0 < т < т0,
0 при х0 < 1 < 2т0,
Я М = Яо
q(i + 2/гт0) = q (т).
E2)
Формулируем задачу:
дТ(х, t) _ д*Т (х, т) m .
—ж— - а —а?— (и < х
Т (х, 0) = 0,
'),
E3)
ет^Л^о, -,Ш^ = д{,)
дх
дх
568
Глава пятнадцатая
Отсюда легко получить, что
__|/~Zx
TL(x,s) = ±-/^e ° -qL{s). E4)
Вычислим
оо
^(s)= \e~szq{x)dx.
&
Пусть / (т) — произвольная периодическая функция с периодом xit
для которой существует преобразование Лапласа. Имеем:
f(x) = f(x + nxl),
(л=1, 2,...),
F (s) = J /(х) e~sxdx = j / (т) е-л dx + j / (x) <ГЭТ dc +. . . =
0 0 zt
m=0 0 1 — £
Применяя общее соотношение E5) к потоку q(x), имеющему период
2т0, получим
^W « ~2sx0 s -2*V
1 —e 1 —e
Подставляя полученный результат в E4), найдем
i/~ ~~ V ~сГ Х 1 ~го
Закон, по которому изменяется температура полупространства при
т->оо, не является очевидным. Однако с помощью соотношений E0),
E1) его легко определить. Особыми точками TL(x, s) будут точка
ветвления при s = 0 t и бесконечное число простых полюсов, лежащих на
мнимой оси в точках
sm = —r^-w E7)
(т = 0, ±1, ±2,...).
Все особые точки имеют Res = 0. Разложим изображение E6) вблизи
точки ветвления s = 0 в ряд:
TL{x.s)~^.-£- + ... . E8)
Отсюда, согласно E0) и E1), получим, что при т-* оо
Т(х,х)^^--/Т^. E9)
Вклад полюсов E7) в асимптотическое разложение функции Т (х, т) не
нужно учитывать, хотя ResOT = 0, как и для точки ветвления 5 = 0.
ЭЛЕМЕНТЫ ТЕОРИИ АНАЛИТИЧЕСКИХ ФУНКЦИЙ И ЕЕ ПРИЛОЖЕНИЯ 569
Это объясняется тем, что каждый из этих полюсов дает в решении
/Bm-flOc —
член, периодически зависящий от времени, как е и сумма
этих членов, представляющая собой также периодическую и
ограниченную функцию т, будет мала при т ->- оо по сравнению с главным
членом формулы E9). Таким образом, температура полупространства, на
поверхность которого падает тепловой поток, изменяющийся по закону
E2), будет возрастать ~]/т при больших т.
Рассмотрим еще один пример. Найдем закон, по которому
температура на границе х = 0 полуограниченного тела связана с плотностью
теплового потока q (т) через ту же поверхность. Применяя
преобразование Лапласа и теорему о свертке, легко выразить температуру Т (х, т)
через плотность потока <7(т)« Предполагая, что начальная температура
принята равной нулю, имеем
-с Аа (х — с,)
Т (*. *) =l-ir j/1 f e , ф dt E9a)
^ о У*—е
Полагая в последнем уравнении х-±0, найдем связь между
температурой на поверхности х = 0 и плотностью потока тепла через эту
поверхность:
Г oJ l/^1^
где введено обозначение
Г @, т) = в(т).
Если задана плотность потока д(т), то определение температуры
поверхности G (т) сводится к квадратуре. Если же 6(т) известна, a q(i)
неизвестна, то F0) представляет собой интегральное уравнение дляд(т).
Пусть, например, температура поверхности задана и равна
0 (т) = в/'; F1)
тогда, решая интегральное уравнение F0) относительно q (т) с помощью
преобразования Лапласа, получим
q (S) = Q0— • J^-. 62)
Функция __^ - имеет две особые точки: простой полюс при s = 7 и
точку ветвления s = 0. Если нас интересует лишь поведение функции
G (т) при больших т, то его можно получить согласно иллюстрируемой
теореме. Асимптотическое поведение q (т) будет определяться самой
правой особой точкой qL(s). Рассмотрим два случая.
20 Заказ № 640
570
Глава пятнадцатая
Во-первых, если ^ = k2 > 0, то правой особой точкой будет полюс
s = k2, и по формулам E0) — E1) имеем
q(x)*cQ0-±=Lkek'x+...r F3)
У а
т. е, плотность потока экспоненциально возрастает со временем.
Если же ^ = — &2 < 0, то наиболее правой особой точкой F2) будет
точка ветвления s = 0. Разложение F2) при ^ = — к2 в окрестности
точки s — 0 имеет вид
Отсюда согласно E0) — E1) имеем
Легко убедиться, что разложения F3) и F4) совпадают с
асимптотическими разложениями, которые можно определить из точных
обращений функций \Ju2~ и _1_^2 '> приведенных в приложении VI.
В заключение еще раз отметим, что последняя теорема позволяет
по расположению в комплексной плоскости, особых точек изображения
сразу, без вычислений судить о поведении оригинала при больших т.
Действительно, если среди особых точек изображения имеются такие,
для которых Resm>0, то оригинал будет экспоненциально возрастать
при т-ч^сю. Наоборот же, если даже для самой правой особой точки
Res^<0, то соответственно оригинал экспоненциально убывает при
т -^ оо.
Теорема об асимптотическом разложении оригинала по известному
разложению изображения особенно важна в тех случаях, когда
последнее имеет очень сложнцй вид и соответствующий контурный интеграл
не может быть вычислен.
Отметим, однако, что предложенные методы асимптотических оценок
применимы при большом значении некоторой переменной или параметра.
Если такой переменной является время, то было бы интересно, наряду
с изложенными методами определения асимптотического поведения
функции времени при т -> оо по аналитическим свойствам ее
преобразования Лапласа, иметь возможность исследовать поведение решения и при
малых значениях времени.
Рассмотрим здесь один такой способ.
Нетрудно убедиться, что решения одномерных задач
теплопроводности с пространственной координатой, изменяющейся в конечном
интервале, с граничными условиями первого и второго родов на концах
этого интервала могут быть выражены в виде линейных комбинаций
интегралов и производных от следующих рядов, играющих важную роль
в теории теплопроводности и других разделах анализа и имеющих
специальное название тэта-функции:
ЭЛЕМЕНТЫ ТЕОРИИ АНАЛИТИЧЕСКИХ ФУНКЦИИ И ЕЕ ПРИЛОЖЕНИЯ 571
Q±(x, iVj = 2 J] (^ l)"e~TC(w+V2JT • sinBn + 1) ъх,
п=0
ва U txJ = 2 ^ «"*(Л+1/2Jх • cos Bn + 1) тгх,
63 (*, £) = 1 + 2 J£ е~ ™2 г • cos 2отх,
60 (*, it) = 1 + 2 2 (— 1)л *~ ял1 т • cos 2п тгх.
/г=1
(;>о)
F5)
Непосредственным дифференцированием легко проверить, что все эти
ряды удовлетворяют уравнению теплопроводности вида
Щ __ 1
dz
4%
F6)
ах2
(* = 1, 2, 3, 0).
Таким образом, переменные тих играют роль безразмерных времени
и координаты соответственно.
Ряды типа F5) хорошо сходятся при больших значениях т и,
наоборот, являются обычно медленно сходящимися при малых т.
Можно, однако, при малых т указать общий способ преобразования
в быстросходящиеся рядов типа F5) (т. е. этих рядов и рядов, которые
получаются из них при дифференцировании и интегрировании).
Рассмотрим ряд
2/B«п),
F7)
где / (т) — является непрерывной и непрерывно дифференцируемой
функцией, так что ряды
2 /B*л.+ Ф) и 2П2«л + Ф)
сходятся абсолютно и равномерно для всех 0 <; ср < 2тс. Следовательно^
00
ряд 2 / B^п + ф) может быть разложен для указанных значений ф в
сходящийся ряд Фурье.
20*
572
Глава пятнадцатая
Итак, имеем
ОО 00
2/<2«п+ф) = ^ 2 {«""Ч*
2к
2 /B1сл + <о)
= —00
m=— со (/1= —со [_0
со Г со Г2тс (/Z+1)
= i 2 Л 2 j /н
da) i =
m— — со [п~—со I 2тс/г
X е
m=~ со (—со
Положим ф = 0, тогда равенства F8) запишутся
со со со
2 /B«») = -^ 2 |/н^('т<^
F8)
F9)
m=—со —со
Полученное соотношение, называемое формулой суммирования
Пуассона, имеет много важных применений, в частности, для
преобразования рядов и их суммирования, если преобразованный ряд, стоящий в
правой части, оказывается настолько простым, что сумма его известна.
Прежде чем применить формулу Пуассона для преобразования тэта-
функций, запишем ее в несколько иной форме, вводя функцию g (п)
согласно соотношению
fBizn) = g(n).
Тогда F9) примет вид
2*<")= 2 ] в ют**"" **
G0)
G1)
/72=—СО —СО
Применим формулу G1), например, к функции 83(я, it), для чего
преобразуем соответствующий ряд
В3 (*, и) = 1 + 2 J] e~~™2x cos 2пт!Х = j? е~~™^ ' cos 2™x =
п=\
—7с/г2х — 2ninx
- 2'
Согласно формуле суммирования Пуассона отсюда имеем
G2)
со
\х, й)= Jj
со со
-тс/г2 х — 2шпх —
X 1 е-ж^ г - 2тс/а> \ jf-f m j ^Шр G3)
m=— со —со
ЭЛЕМЕНТЫ ТЕОРИИ АНАЛИТИЧЕСКИХ ФУНКЦИИ И ЕЕ ПРИЛОЖЕНИЯ 573
Интеграл, стоящий под знаком суммы, уже вычислялся выше. Он
оказывается равным
/~ \2
~ /~ \ 1 тс \х + т)
е-™*х- 2«/<о \х + т) fa — е - л G4)
Подставляя значение интеграла в формулу G3), получим новое
представление функции 6z[x, ii) в виде ряда, чрезвычайно быстро
сходящегося при малых т (т > 0J:
-кх2 со %т2 2-rtmx
ba[x,ii) = -y^e 7 . \ е 7 7 # G5)
т т=—со
Пользуясь определением G2), равенство G5) можно записать в виде
функционального соотношения
%х*
\х, £х) = —-е х -вз!-^:, —1. G6)
т
Аналогичные соотношения могут быть получены и для остальных тэта-
функций:
QAx, it) = —-—е -с •61| —
Дх, it J = —-е ^ • бЛ
-о —>
к
тис2
1 *"T-e,f * -
lz
Для задач с цилиндрической симметрией асимптотические разложения
соответствующих рядов при малых т получены в работе [96а].
ПРИЛОЖЕНИЯ
I. Некоторые справочные формулы
Приводим некоторые соотношения, которые используются при
решении задач теплопроводности.
1. Разложения тригонометрических функций в ряд:
cosx = 1 — -|г + "з» 1г +• •" |*1<°°;
■v* v** V" V*
sinx = -n---3r + Tr-Tr + ..., I^i< °°;
, , х3 . 2х5 , 17л:7 , , , , тс
2, Разложения гиперболических функций в ряд:
X Х^ X®
chx = l+-2[- + -^-+-gr + ..., |*|<°о;
shx-X + ^ + -|j- + |r + ..., . |*|<oo;
th х = 1 — 2£Г2* + 2е~*х — 2е~6х + ..., | х |< -J-;
• cth * = 1 + 2£Г2* + 2<г4* + 2е~6х + . .., | * | < тг;
1
sh х
- 2 (г* + £Г3дг + е~5х + ...)> I * К *;
1 2 (бГ* — 6Г3* + £* — <Г7* + • • •)>• I * К "и" •
£h л:
3. Соотношения между гиперболическими, три го но-
метрическими и экспоненциальными функциями.
Непосредственно из предыдущих разложений следует:
sh х = ~y (ех — егх),
ch х = -у (е* + *г*),
sin x = -^т- (е'-* — e~ix),
cos x = -^-(^u + e~ix)\
575
eix == cos x + i sin x, e~ix = cos x — i sin x (формулы Эйлера);
sin ix = t sh л:, cos ix = ch x, tg ix = i th x,
sh tx = i sin x, ch ix = cos x, th tx = i tg x,
cos (x + iy) = cosx ch r/ — i sin xsh #,
sin (x + 4/) = sin x ch # + i cos x shy.
Значения sinx, cosx, tgx, shx, thx, ex, e"x, chx от О до 10 через одну
тысячную приведены в книге: Б. И. С era л и К- А. Семендяев.
Пятизначные математические таблицы. Изд. АНСССР, М., 1948.
4. Некоторые интегралы, не сводящиеся к
элементарным функциям. Функция ошибок Гаусса:
х
erfx = ——\егх dx,
V * J
о
erf оо = 1, erf (— х) = —erfx,
erfcx = 1 — erfx = —у=- \ е--*2 dx.
Приведем разложение в ряд функции erfx для малых значений х
X оо оо
erfx - -?=- Г dx V (— 1 f^r- = -2— V, (— 1)я ,/C+lir >
0 л=0 /2=0
откуда
J^lLerfx== _£__^W
^™ ~" ~~ 113 "Г 2!5
и для больших значений х
оо со
J2L erf с ж = Г е-*2 dx = i^l _ _L f -L er** dx,
2 J 2* 2 J *a
Vjlerfcx = JLe-*2(-i Л I I:3. ...( ly-* l ' 3 : ,v (.2/t~3)
откуда
i^-er . , _ , , if
2 2 V * 2x8 ' 2ax5 "*,> ' 2я-1**"-»
+ (-irb3--2f-1)f-^-arfx.
л;
Полученный ряд сходится, так как имеет место неравенство
00 ОО
§1pre-*%dx<er*t^1±irdx.
X X
Следовательно, можно написать
f _ 1 _^2 /J 1_ , 1 - 3 ьз-5 ,
576
Имеют место следующие соотношения:
00
С л sin 2ху , 1 г
\е ~ ^-d^ = ^Tuerf^'
о
оо
( е~л'2 sin 2ху dx = ~y V^e~y2 erf у.
о
В задачах теплопроводности приходится дифференцировать и
интегрировать функции erfx и erfcx. Введем обозначение
Тогда
dn erf x = ~т^ erf x.
d erf x = —— е~*2 ,
d2 erf x = — xe~*2
Производные от erf x обычно [приводятся в тех же таблицах, в
которых даны значения для erf*.
Для интегрирования функции erfcx введем обозначение
оо
\п erf с х = Г i"-1 erf с ЫЬ
X
Тогда
i° erfc x = erfc x\
i erfc x = I erfc WE = -^4=- e~x* — x ег^с *>
JC
00
i2 erfc x = I i erfc Ы1 = -j- A + 2x2) erfc x — xe~-*2 =
= -j- (erfc x — 2x i erfc x),
Общая рекуррентная формула имеет вид
2п\п erfc x = iw~2 erfc x — 2х1п~г erfc x.
Откуда следует
1 1
\n erfc 0
2пЩ~п) 2nl(l+-^-n
Можно показать, что функция y = inericx есть решение
дифференциального уравнения
у" + 2ху' — 2пу = 0.
577
Функция i^erfcx имеет важное значение в задачах теплопроводности,
поэтому она табулирована для п = 1, 2, 3, 4, 5, 6 в приложении VI.
Интеграл Гаусса от комплексного аргумента равен
о
2
= erf а + тт^ ^_а2 \ ey2 (sm %аУ + *cos 2ау) d#.
о
Для чисто мнимого аргумента имеем
У тс J
о
Гамма-функция или Л-функция Гаусса:
00
П (£) - Г (£ + 1) = Г е-* xk dx,
о
TL(k) = kH(k — l).
Если k > 0 и & — целое число (k = т), то П (&) = П (т) — т\ — 1 • 2 • 3 X
X ... X т. Далее,
П( * W;, n(+4-UJ£
2)-' "' "\^-Г)--2
5. Функции Бесселя. Функция Бесселя первого рода порядка v
может быть представлена в виде ряда
(•г) = у —, -л / i —пг -тг z are z < тс,
v ' ^^ m! Г (v + "i + 1) \ 2 /
J. B) =
где v есть вещественное число, а 2 может быть комплексной величиной.
Функция Jv (z) есть частное решение дифференциального уравнения
Бесселя
£+-r2+('~S>-o-
Если v есть целое число (v = n), то существует соотношение
/й(г) = (-1Г^(г).
Функция Бесселя второго рода порядка v (для любых нецелых
значений у) определяется соотношением
v , ч /v B) COS VTC —/_v B)
К B) = г- ; arg z < гс.
578
Если v — целое и положительное число (v = n), то можно написать
.YAz) = 2[ln(±z) + c]jAz)-kl(-iy\^h)
1 \n+2k
n-\-k
2Z
m=l
4- £ m-il V/1 Л-"+» (я-*-1I . .
где С = 0,5772 ... — постоянная Эйлера.
Если п = 0, то будем иметь
hH4
2 ^0(г)=[1пD-2)+с]у0(г) + D-2)а-A+4-)-1BТ)^ +
1 , 1 \ I 2 Z
_/i i М г4 I fi 1 х I М г6
^ ^ 2 / 22-42 ^ у ' 2 ^ 3 j 22-42-62 " • " *
Модифицированное уравнение Бесселя
+4*-('+т)»-«
dz2
имеет частные решения, определяемые соотношениями
00 11^-
КЛ*) = ~Г* iiJ^ >
где /Дг) — модифицированная функция Бесселя первого рода порядка v
и /Cv(z)— модифицированная функция Бесселя второго рода порядка v.
Для частного случая v = 0 имеем
;с„B) = -[1пD-г) + с]/0(г) + (-|-гJ + A + 4-)А12!р
= _[inD-z)+cj/eB)+-j-+(l+4-)^- +
^ { ^ 2 ' 3 J 22-42-62 ^ - " " '
Соотношения между / B), Fv(z) и /v (г), АГB) имеют вид
+ ...=
К (i2k z) = Г»* /С, (г) — w * / (г),'
sin v^n
sin V7t
Kv (t2* z) = Г*** Fv (г) + 2* sin *vtc ctg vie У (г).
579
Разложения функций /v (z) и /Cv (г) в ряд при больших значениях
\г\ имеют вид
, ,,ч _ 1- ., /, 4v» - 1» • Dу« - I2) Dv« - 3*) \
**(*)- к -&« ^ + 1!8г + 2iw + •••;•
Соотношения между функциями и их производными следующие:
j'0(z) = -JAz), Y'0(z) = ~Y1(z), l'0(z) = I1(z), K'0(z) = -Ki(z).
В общем случае имеем
гГч(г) + *Г*(г)=г1,_хB),
z/;(z)-v/^z)=z/,+1(z),
z/C;<Z)-v/C^z) = -Z*,+1(z),
z/;(z) + vyv(z) = z/v-1(z),
ti\ (г) — v/v (z) = — z/ v+1 (z),
/c_,(z) = *,(*)> *v.(*) = Vi^2-
II, Теорема единственности решения
В гл. I было показано, что решение дифференциального уравнения
теплопроводности должно удовлетворять не только самому уравнению,
но и начальным и граничным условиям. Возникает вопрос, могут ли
существовать одновременно два решения, которые удовлетворяют
уравнению и краевым условиям. Ниже будет показано, что таких двух
разных решений быть не может. Эта теорема называется теоремой
единственности решений.
Пусть даны два решения: Т±(х, yf z, т) и Т2(х, у, z, т), которые
удовлетворяют дифференциальному уравнению
~ = аГТ, A)
ах
начальным и граничным условиям
limT = f (х, у, г), B)
Та = Ф (х, у, z, х), C)
где индекс «п» указывает величину, относящуюся к поверхности тела.
580
Положим
Тг-Тл = и: D)
тогда
~^- = ау2и, E)
lim и = 0, ггп = 0. F)
т-И)
Рассмотрим следующий интеграл:
/ = [ -у- *»• ' G)
Интеграл берется по объему тела V (dv = dxdy dz), т. е. является
трехкратным интегралом. Тогда
Воспользуемся формулой Грина
I u -JL dv = а \ иу2 и dv. (8)
<$) (К) (К)
где в первом интеграле интегрирование происходит по поверхности
тела (S). Тогда можно написать
д!
E) ' (V)
— 1Ш+(-£),+(-£-)>
(V)
так как первый интеграл равен нулю согласно граничному условию F),
поскольку интегрирование происходит по поверхности, на которой и = 0.
Следовательно,
-г-<о< <9>
Так как / = 0 при т = 0 (и = 0 при т = 0), то
/<0. A0)
Но из соотношения G) следует, что
/>0. A1)
Отсюда вытекает, что 1 = 0. Следовательно,
и = 0, Г] = Г2.
Итак, если некоторая функция Т (*, у, г, т) удовлетворяет
дифференциальному уравйению, начальному и граничному условиям, то она яв-
581
ляется единственным решением данной задачи (теорема единственности
решения).
Необходимо отметить, что решение задачи может быть выражено в
разных функциональных соотношениях, но это не означает наличия
разных решений задач, а следовательно, не противоречит теореме
единственности решения.
III. Дифференциальное уравнение теплопроводности,
выраженное в различных системах координат
В гл. I дифференциальное уравнение теплопроводности было
выведено в декартовой системе координат:
дТ = 2Т __ / д2Т д2Т д2Т \ ,jv
дъ ~ aV ~~ й \ дх2 ду2 '. дг* ] '
Выразим у2Г в сферических и цилиндрических координатных
системах. Положим
х = г sin 6 cos ф, "I
у — г sin 6 sin ф, \ B)
z = г cos б. J
Тогда получим
V2r=-U—f'2—H — j_(si„eiq+ _i_.*qt C)
v r2 [ dr \ dr J sin 6 dQ \ dQ ) sin3 б аф3 J
или
v dr2 r dr г2 ф L\ / ^J r2{\—^) дф2 W
где [x = cos6. Соотношение D) есть выражение у2Г в сферических
координатах (г, 8 и ф).
Положим
х — rcosG,
г/ = г sin б.
Тогда получим
v2r = JLr^(r JL) + .1A JZL\ + -1/r^l E)
или
v.r = J!IL + J_JI. + J_J!L + i^. F)
v dr2 r dr r2 dO2 dz3 v ;
Соотношение F) есть выражение v27 в цилиндрических координатах
(г, б). При подстановке выражений D) и F) в уравнение A) получим
формы уравнения теплопроводности в сферических и цилиндрических
координатах.
582
IV. Основные правила и теоремы преобразования Лапласа
F(s)==L[f(x)]
o-\~ioo
a \ a /
a \ a
f (x — b), если / (т) = 0, при т < О
X
\ f F) M
b
•с в
j ]' / (ft) dft d8
xf(z)
т« f (x)
J M^-fl)M9)d0 = /i/2
—rf /(ft)expf_l_)da
0
oo
J e~s* f* (Ъ) db,
где /*(&)= J/(тЖт,*)*:,
}(<С,&)
2j 17
/2=1
k=i
Ф' (»«)
ГФ(«). («-,„)*
(случай кратных- корней)
f / (т) e~sx dx = F (s)
о
Л/7 (s) + BG (s)
snF (s) — sn~i f (+0) — s«-2 /' (+0) —...
F (s — a)
F (as)
F (as — 6)
£r65F (s)
F(s)
F(s)
-F> (s)
(— l)nF^ (s)
Fi M ?2 W
1
F(V*~)
Fl9 (*)]*(')
e~T^ Ф (s) - J rsl(^^)
о
, где ф (s) = (s — s2) X
d&
ф (8)
X (s — s2) ... (s — s„)
ф(«)
<ж
, где ф (s) = (s — *i) (s — 52) X
X (s — sm)* (s — sm+i) ... (s — sn)
583
V. Изображения некоторых функций
Изображение функции
F(s) = L[f(z)]
Оригинал функции / (х)
(п = 1, 2, 3, . . .)
s-(«+V2) (n = 1, 2, 3, . . .)
Г(т)
Г(/п+1) П(/я)
s — а
1
s + a
1
tit 1 О 9
(/Z — 1 , Z. о , . .
Т(т)
(s — а)т
1
(s — а) (s — Ь)
s
(s-a)(s-b)
1
(s — a) (s — b) (s — с)
k
s2 + &2
s
s2 + &3
k
s2 ~~ &2
s
•)
s2 — fc2
T
Trt-1
(n-l)l
1
"J/TIT
2« Ti-Vi
[ЬЗ-5 ... Bn — 1)] l/u
Tm-i
1
(n-1)!
r"-b?ax
tm-i „ax
1
a — b
1
(a~b)
ax h%\
(e
(aea*^beb")
,kx
(Ь — с)еах + (с-~а) есх + (а — Ь)ё
(a—'bj(b — c)'(c — a)
sin k%
coskx
ъЬкч
ch&t
Продолжение
Изображение функции
/4s) = L[/(t)]
Оригинал функции f (x)
к
(s + аJ + k2
s + a
(s + аJ + k2
1
S (S2 + ,
1
s2 (s2 + k2)
1
(s2 + /г2J
s
(s2 + /г2J
s2
(s2 + 62J
s2 — k2
(s2 + k2J
(s2 +
a2) (s2 + b2)
1
(а2 ф b2)
(s — aJ + k2
3k2
s3 + &3
4&3
(V<
S4 + 4&4
s
s4 + 4&4
1
s
S4—£4
(s2 + k2)n+i
1 / 5 — 1 \П
s [ s )
s
(s — kK/z
? — a — у s —
1
-b)
Ys +k
e ax sin/гт
1
k2
1
&3
-flTcos^x
A — cos &т)
(k t — sin&T)
2/e3
2k
-(sin &т — ^Tcos/гт)
2k
sin&T
(sln^T + U'C-COS&'c)
t COS k'Z
cos ax —cos 6t
b2 —a2
1
eaxsin&T
-b
2 I cos
&t:-j/3
■VFsln ^3
sin kz ch &т — cos &t sh &т
1
2/г2
. sin k'z sh&x
1
2k3
_1_
2&2
(sh^x — sin&x)
- (ch&T — cos&x)
zn sin&T
2я Ы!
/rt(-)--4-^^-(^-x)
л! din
1
>*,
1
==.е*тA+2£т)
(еЬх-еат)
21Л^з"
1
"j/тп
— /г^2тегк/гТЛ
585
Продолжение
Изображение функции
F(s) = L [f(x)]
Оригинал функции f (х)
53
54
55
ут
s—k2
irr
s+k2
1
Y7(s — k2)
1
l/s"(s3 rh k2)
b2—a2
(s~a2)(b+Vl)
1
yi{yr+ k)
1
(s+k)(VI+~b)
b2~k2
Vs (s—k2)(yj+ b)
e~kVT (k > 0)
JL s-kV7
(k>0)
1
yi
1
e-A/s
(&>0)
sYs
o-kY~
(k>0)
-kY s
sY s'
1
e~2l/^ (Zs > 0)
s" У s
V
— + £е*"х erf ft jA
y;
TIT
1ST "J/
1
/г /x
:« j
ex2dx
— e~k2x erf ^1/t
e~k^ f e*2d*
/г
2
Jfej/ic
и
ea2x [ b —a erf a ]/t ] ~bebH erfc 6 /Г
efe2x erfc k 1/T
ekH\A. erf/г Yf— 1 1 +
-\-ebHerfcb 1/7
k
2 Yl
*4x
1—erf
2 У
fJ e erfc
2 У*
^1
'4x
2 yTierfc
2 V"x
&2
= 2]/ -1- * 4V -
&erfc
2 Ут
4-ri2ferfc
2 У?
, + _Jerfc__^_*
Dt)rt/2i«erfc
2 "jA
If -^ dz
(П — 1)! J V ; У 1X2
0
586
Продолжение
Номер
п. п.
56
57
58
59
60
61
62
63
64
65
Изображение функции *
F(s) = L[f(x)]
s(b+ ys)
e~~k VT
e — (k > 0)
V* (ь+Vs)
1 ~* /7
1 6^ /Г
1 -л vT
1 ^-ь VT
iVs+ bf c
1 j-k VT
1 P~k VT
(s-b) e
n(~n)
\ z ) kVT
s2 + %n e
1 --* VT
s u
Оригинал функции f (т)
erfc -~^r - ebk eb^ X
2 ]Л
e c ak ^ > k + 2 1/7 j
l/jL e-^-be*^S"+*' X
Г тех
4 ' Off/-/. _l 1/ Urr \
Лб1Н2 1/г- + >Йг j
2 |/T -£- 1+6A ft
-r- 1/ — e ■ — —Г5— erfc t= 4-
■ .. ^ Jbk + i*t..-f/- / ft i.i i/r\
-26 j/ -^ e 4x + (l+b^+264) x
Xebk+bHerlc(^~= + bV- )
1 „f- * 2/Т -£
--$r(l~bk- 2b4)ebk+bH X
Ae'rcUyr+ /
it i x ■ n <>n+2 ~
1+-2-П ^ /
Xl"+2elfc2 yT
587
Продолжение
Изображение функции
F (s) = L[f (т)]
Оригинал функции f (%)
JL e-kYs + ь
~Vs~+2h~e-kVs+2b
s Ys+2b
-kVs -f 2b
1
1
Vs2—k*
Vs + 2k _i
Vs
(V^+k)(Vs+b)
Г (m)
(lA
1
(s+k)v* (s+bK/*
Y<T+~2k — У7
Vs+2k + УГ
A—s)^
f J -
1
-к
^У*«*сBТГ-^ +
+ efe/6erfcf-^ +
V*)]
B yr
+ J^[e-^erfcB-^
-l/2^L
Qk V2b
erf с
e ertc U i/.
/0 (At)
-At
1/26x1
fte-*x[/„(H+/i(H]
i/a(ft+fc)
"•(■
/fe-^b
У* (г^Г '"* e"W* + ^ x
&--&
X/
£ — 6
■ y2 (A + 6)тГ7 о
m-V%\ 2
k — b
* +
+ /l
k—b
т
n\
e-kx h (fa)
Bn) \ Y%%
yHBn+l)l 2/z+1
V J, (fa)
yr 1* y~* j m
Продолжение
Изображение функции
F(s) = Lif(x)]
Оригинал фуннкии f (г)
1
(s*~k*)m (т > 0)
1
1
-k!$
-k/s
У
_L_ ek's
s Vs
1
J/s
n
s V s
e~kfs (m > 0)
ek/s (m > 0)
e
b"
~kVs(s+b)
e
У s(s + b)
—kVsz + b2
e
У s2 + b2
— k Vs2 — bz
e
У s2 — b2
k (Vs^fW— s)
(к ^>
У s2 + 62
—kVs*-\-b*
e
M
VltTW(V s* + ь* + s )
1
;(v>~D
-lgs
1
lgs
lg 5
ут
m-y2
Г(т) V 2/в
J0 B T/TS)
hm-Vz) №)
Уъх
cos 2 'У&г
1
—z-ch2 У^т
"J/ttt
1
sin2y&T
_ sh2 У^г
y^
m- 1
y^
1
m—_^
V_i)BVr^)
0, когда 0 < t < &,
e~t/ibxI0 (~y b У<ъ*~№ |, когда т> J
0, когда 0 < т < k,
J0(b y-z2 — k2), когда т > k
0, когда 0 < т < &,
/0 (Ь Ут2 —/г2 ), когда ч> k
J0 (b У t2 + 2 fru)
О @ <<r<£),
> _ Ь\ 1/2 v ,
Г' A) — lg-r; [Г' A) = -0,5772]
*_, (£Ж Л1Л
Т \ [Г(А)]« ~ Г (А) ]
e^lgft —Ei(—ftr)];
dx
Ei
(—)=-J
e — (^ > °)
589
Продолжение
Номер
п.п.
96
97
98
99
100
101
102
103
104
105
106
107
108
109
ПО
111
112
113
114
Изображение функции
F(s) = L[f(t)]
> \gs
s2 + 1
4"lg(l+b) (k>0)
s — k
s2 + £2
Ig J2
, s2 — k?
Ig ^2
k
arctg —
1 k
— arctg —
e s erfc ks (k> 0)
1 k2s2
— e erfc ks (k > 0)
e S erfc Y~k~s (k > 0)
1 f—
erfc |/ks
ys .
1 ks
- e erfc Yks (k>0)
Ys
erfc
Vs
i — t k
e erfc
Ys |/s
K0 (ks)
Ко (A T/F)
4" ек'Кг(УЩ
-J^/Ci (ft 1/7)
1 .kl*rc ( k \
Оригинал функции f (%)
cos т si (t) — sin т ci (т)
-«(-*)
— (е&т - ^)
2
—- A — cos ki)
4"(l-chb)
— sin &t
si (&т)
X2
1 ~4k
e
evfik
Yk
% |/7(т + k)
[ 0 @ < т < &)
J
l (их)-V.' (т > &)
1
тЛс (т + /ef
^ sin Bk 1/7)
1 -2Л VT
~—— e
iAct
f 0 @<ч<&),
1 (т2 — £2)-~V2 (т > fc)
1 _____
yVt(T + 2ft)
&2
1 4x
IT*
-Лг#о B l/2ftT)
590
Продолжение
Номер
п. п.
115
116
117
118
Изображение функции
F{s)
1
k y$ $
= b[f<^>]
— tut* тЛ^Г
tn« \ s
.^/Г, (k 1/7)
V
T
X
0,0
0,01
0,02 |
0,03
0,04
0,05
0,06
0,07
0,08
0,09
0,10
0,11
0,12
0,13
0,14
0,15
0,16
0,17
0,18
0,19
0,20
0,21
0,22
0,23
0,24
0,25
0,26
0,27
0,28
0,29
0,30
0,31
0,32
0,33
0,3
4
i erfc x
0,5642
0,5542
0,5444
0,5350
0,5251
0,5156 !
0,5062
0,4969
0,4878
0,4787
0,4698
0,4610
0,4523
0,4437
0,4352
0,4268
0,4186
0,4104
0,4024
0,3944
0,3866
0,3789
0,3713
0,3638
1 0,3564
0,3491
0,3419
0,3348
0,3278
0,3210
0,3142
0,3075
0,3010
0,2945
0,2882
-1
* v (* V» )
i2 erfc x
0,2500
0,2444
0,2438
0,2335
0,2282
0,2230
0,2179
0,2129 '
0,2080
0,2031
0,1984
0,1937
0,1892
0,1847
0,1803
0,1760
0,1718
0,1676
0,1635
0,1596
0,1557
0,1518
0,1481
0,1444
0,1408
0,1373
0,1338
0,1304
0,1271
0,1239
0,1207
0,1176
0,1145
0,1116
0,1087
); x > x%
', X < Xi
Оригинал функции f (x)
oo
V
i >Л
l^Zt Bn
л=1
Jt2
_ B/t-l)»it«t
— IJ*2 e
+*? , ,
4Aa
1 4^ {ХХЛ
k"
exp (- 4r)
Bx)"+x
2V~1 -n / k* N
)
VI. Значения функций in erfc x
i3 erfc x
0,0940
0,0916
0,0891
0,0868
0,0845
0,0822
0,0800
0,0779
0,0757
0,0737
0,0717
0,0697
0,0678
0,0659
0,0641
0,0623
0,0606
0,0589
0,0572
0,0566
0,0540
0,0525
0,0510
0,0495
0,0481
0,0467
0,0454
0,0441
0,0428
0,0415
0,0403
0,0391
0,0379
0,0368
0,035
7
i4 erfc x
0,0313
0,0303
0,0300
0,0285
0,0277
0,0268
0,0260
0,0252
0,0245
0,0237
0,0230
0,0223
! 0,0216
1 0,0209
0,0203
0,0197
0,0190
0,0184
0,0179
0,0179
0,0167
0,0162
0,0157
0,0152
0,0147
0,0142
0,0138
0,0133
0,0129
0,0125
0,0121
0,0114
0,0113
0,0109
0,0105
i5erfc;e
0,0094
0,0091
0,0088
0,0085
0,0082
0,0079
0,0077
0,0074
0,0072
0,0069
0,0067
0,0065
0,0063
0,0060
0,0058
, 0,0056
0,0055
0,0053
0,0051
0,0049
0,0047
0,0046
! 0,0044
1 0,0043
0,0041
0,0040
0,0038
0,0037
0,0035
0,0034
0,0033
0,0032
0,0031
0,0030
0,0029
ie erfc x
0,0026
0,0025
0,0025
0,0023
0,0023
0,0022
0,0021
0,0020
0,0019
0,0019
0,0018
0,0017
0,0017
0,0016
0,0015
0,0015
0,0014
0,0014
0,0013
[ 0,0013
0,0012
0,0012
0,0011
0,0011
0,0011
0,0010
0,0010
0,0009
0,0009
0,0009
0,0008
0,0008
0,0008
0,0007
0,0007
591
Продолжение
X
0,35
0,36
0,37
0,38
0,39
0,40
0,41
0,42
0,43
0,44
0,45
0,46
0,47
0,48
0,49
0,50
0,52
0,54
0,56
0,58
0,60
0,62
0,64
0,66
0,68
0,70
0,72
0,74
0,76
0,78
0,80
0,82
0,84
0,86
0,88
0,90
0,92
0,94
0,96
0,98
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
i er fс x
0,2819
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
2758
2722
2637
2579
2521
2465
2409
2354
2300
2247
2195
2144
2094
2045
1996
1902
1811
1724
1640
1559
1482
1407
1335
1267
1201
1138
1077
1020
0965
0912
0861
0813
0767
0724
0682
0642
0605
0569
0535
0503
0365
0260
0183
0127
0086
0058
0038
0025
0016
0010
i2 erfc x
0,1058
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1030
0998
0976
0950
0925
0900
0875
0852
0828
0806
0783
0762
0740
0720
0700
0661
0623
0588
0555
0523
0492
0463
0436
0410
0382
0362
0340
0319
0299
0280
0262
0246
0230
0215
0201
0187
0175
0163
0152
0142
0099
0068
0046
0030
0020
0013
0008
0005
0003
0002
i3 erfc x
0,0346
0,0336
0,0330
0,0316
0,0306
0,0297
0,0288
0,0279
0,0270
0,0262
0,0254
0,0246
0,0238
0,0230
0,0223
0,0216
0,0203
0,0190
0,0177
0,0166
0,0155
0,0145
0,0136
0,0127
0,0118
0,0111
0,0103
0,0096
0,0089
0,0083
0,0077
0,0072
0,0067
0,0062
0,0057
0,0053
0,0049
.0,0046
0,0043
0,0039
0,0036
0,0025
0,0016
0,0011
0,0007
0,0004
0,0003
0,0002
0,0001
0,0001
0,0000
i4 erfc x
0,0102
0,0099
0,0094
0,0092
0,0089
0,0086
0,0083
0,0080
0,0077
0,0075
0,0072
0,0070
0,0067
0,0065
0,0063
0,0060
0,0056
0,0052
0,0049
0,0045
0,0042
0,0039
0,0036
0,0033
0,0031
0,0028
0,0027
0,0025
0,0023
0,0021
0,0020
0,0018
0,0017
0,0015
0,0014
0,0013
0,0012
0,0011
0,0010
0,0009
0,0009
0,0006
0,0004
0,0002
0,0001
0,0001
0,0000
0,0000
0,0000
0,0000
0,0000
i5 erfc x
0,0027
0,0027
0,0026
0,0025
0,0024
0,0023
0,0022
0,0021
0,0020
0,0020
0,0019
0,0018
0,0017
0,0017
0,0016
0,0015
0,0014
0,0013
0,0012
0,0011
0,0010
0,0010
0,0009
0,0008
0,0007
0,0007
0,0006
0,0006
0,0005
0,0005
0,0005
0,0004 ,
0,0004
0,0003
0,0003
0,0003
0,0003
0,0003
0,0002
0,0002
0,0002
0,0001
0,0001
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000 1
ie erfc x
0,0007
0,0007
0,0006
0,0006
0,0006
0,0006
0,0005
0,0005
0,0005
0,0005
0,0005
0,0004
0,0004
0,0004
0,0004
0,0004
0,0003
0,0003
0,0003
0,0003
0,0002
0,0002
0,0002
0,0002
0,0002
0,0001
0,0001
0,0001
0,0001
0,0001
0,0001
0,0001
0,0001
0,0001
0,0001
0,0001
0,0001
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
ЛИТЕРАТУРА
1. АксельрудГ. А. Теория диффузионного извлечения веществ из
пористых тел. Львов, Изд. Львовского политехнического института, 1959.
2. Бакалеев В. П. О возможности решения нелинейных задач
теплопроводности. ИФЖ, 1961, т. IV, № Ю, стр. 119—122.
2а. Березин И. С, Жидков Н. П. Методы вычислений, т. II.
М., Физматгиз, 1960.
3. Будрин Д. В. Вопросы теплообмена и горения. «Труды Уральского
индустриального института». М., Металлургиздат, 1941; Гидростатический
интегратор для решения дифференциального уравнения теплопроводности с
учетом зависимости теплофизических свойств (коэффициента теплопроводности
и объемной теплоемкости) от температуры. «Труды Уральского
политехнического института», 1955, сб. 53, стр. 22.
4. Будрин Д. В. и Суханов Е. А. Регуляризация температурных
полей тел простой формы. ИФЖ, 1959, т. II, № 1, стр. 79—83.
4а. Баренблат Г, И. Об одном методе решения уравнения
теплопроводности. ДАН СССР, т. 72, 1950, стр. 667; О решении уравнения
теплопроводности при неоднородном граничном условии. ДАН СССР, т. 74, 1950,
стр. 201.
46. Баренблат Г. И. и Левитан Б. М. Об одном обобщении
формулы Пуассона из теории теплопроводности. ДАН СССР, т. 79, 1951,
стр. 917; О некоторых краевых задачах для уравнения турбулентной
теплопроводности. Изв. АН СССР, серия мат., т. 16, 1952, стр. 253.
5. Ваничев А. П. Приближенный метод решения задач
теплопроводности при переменных константах. Изв. АН СССР, ОТН, № 12, 1946.
6. Ван-дер-Поль. Операционное исчисление на основе двухстороннего
преобразования Лапласа. М., ИЛ, 1953.
7. Ваще нко-3 а х а рченко М. Е. Символическое исчисление и
приложение его к интегрированию нелинейных дифференциальных уравнений.
Киев, 1862.
8. Волынский Б. А. иБухманВ. Е. Модели для решения
краевых задач. Физматгиз, 1960.
9. В у л и с Л. А., Жеребятьев И. Ф., Лукьянов А. Т. Решение
нелинейных уравнений теплопроводности на статических
электроинтеграторах. Совещание по тепло- и массообмену. Минск, 1961. В сб. «Тепло- и мас-
соперенос», т. 5, 1963.
10. Г а в рил о в а Р. И. и Пр у д н и ков А. П. Об одной задаче теории
теплопроводности. ИФЖ- I960, т. III, стр. 136—137.
10а. Гельфанд И. М. и Шилов Г. Е. Обобщенные функции и
действие над ними. М., Физматгиз, 1959.
11. Гольдфарб Э. М. Объединение решений уравнения
теплопроводности для плиты, цилиндра и шара. Научные доклады высшей школы.
«Металлургия», 1958, № 3, стр. 129.
12. Годунове. К., Рябенький В. С. Введение в теорию
разностных схем. Физматгиз, 1962.
13. ГреберГ., ЭркС. иГригулльУ. Основы учения о
теплообмене. М., ИЛ, 1958.
14. Гринберг Г. А. Избранные вопросы математической теории
электрических и магнитных явлений. М., Изд. АН СССР, 1948.
15. Гудмен В. П. Интеграл теплового баланса. В кн. «Труды
Американского о-ва инж. мех.», серия «Теплопередача», № 1, 1961.
16. Г у х м а н А. А. Введение в теорию подобия. Изд-во «Высшая школа»,
1963.
17. Данилова И. Н. Распределение температур в неограниченном полом
цилиндре при теплообмене на границах со средами переменной температуры.
Изд. АН СССР, ОТН, 1958, Ш 12, стр. 148—150; О температурном поле в
конечном полом цилиндре при теплообмене на границах. Изв. АН СССР,
ОТН, Энергетика и автоматика, 1960, № 4, стр. 151 —155.
18. Дацев А. Годишник на Софийский университет. 1946—1947, № 43,
стр. 113—131.
19. Денбинг К- Термодинамика стационарных необратимых процессов.
ИЛ, 1954.
20. Дульнев Г. Н. Теплообмен в радиоэлектронных устройствах. Гос-
энергоиздат, 1963.
21. Де Гроот С. Р. и М а з у р П. Неравновесная термодинамика.
М., Изд. «Мир», 1964.
22. Д е Гроот С. Р. Термодинамика необратимых процессов. Гостех-
издат, 1956.
23. Дейч Г. Руководство к практическому применению преобразования
Лапласа. Физматгиз, 1958.
24. Диткин В. А. и Прудников А. П. Операционное исчисление
по двум переменным и его приложение. М.» Физматгиз, 1958.
25. Диткин В. А. и Прудников А. П. Интегральные
преобразования и операционное исчисление. М., Физматгиз, 1961.
25а. Евграфов М. А. Аналитические функции. Изд. «Наука». 1965.
26. ЕлистратоваМ. В. Об одном конечном интегральном
преобразовании Ханкеля. ИФЖ, I960, т. III, стр. 120—125.
27. Иванцов Г. П. и Любов Б. Я- Прогрев неподвижного слоя
шаров потоком горячего газа. ДАН СССР, 1952, т. 86, № 2, стр. 293—296.
28. Ко в н ер С. С. Условия термического подобия в процессах
промерзания и оттаивания. Изв. АН СССР, серия геогр. и геофиз. 1943, т. 3,
стр. 143.
28а. Канторович А. В., Акимов Г. П. Функциональный
анализ в нормированных пространствах. Физматгиз, 1959.
29. Карслоу X. С. Теория теплопроводности. Гостехиздат, 1947.
30. Карслоу X. С. и Егер Д. К. Операционные методы в
прикладной математике. М., ИЛ, 1948.
30а. Карслоу X. С. и Егер Д. К. Теплопроводность твердых тел.
М., Изд. «Наука», 1964.
31. Кирпиче в М. В. Теория подобия. Изд. АН СССР, .1953.
32. Коздоба Л. А. Электромоделирование температурных полей в
деталях судовых энергетических установок. Изд. «Судостроение», 1964.
33. Кон а ков П. К. Теория подобия. Госэнергоиздат, 1958,
34. Койл М. Б. Решение нестационарных задач теплопроводности
методом воздушной аналогии. В сб. «Вопросы теплообмена». Госэнергоиздат,
1959, стр. 69.
35. Кондратьев Г. М. Регулярный тепловой режим. Гостехиздат,
1954.
36. Коренев В. Г. Некоторые задачи теории упругости и
теплопроводности, решаемые в Бесселевых функциях. М., Физматгиз, 1960.
37. К о ш л я к о в Н. С. Основные дифференциальные уравнения
математической физики. М, Гостехтеоретиздат, 1936.
38. К у т а т е л а д з е С. С. Основы теории теплообмена. М., Машгиз, 1962.
38а. Лаврентьев М. А. и Шабат Б. В. Методы теории функций
комплексного переменного. М., Физматгиз, 1958.
386. Левитан Б. М. Разложение по собственным функциям
дифференциальных уравнений 2-го порядка. М., Гостехтеоретиздат, 1950.
39. Лукьянов В. С. Гидравлические приборы для технических
расчетов. Изв. АН СССР, ОТН, № 2, 1939.
40. Лурье А. И. Операционное исчисление и его применение к
задачам механики, Гостехиздат, 1950.
41. ЛейбензонЛ. С. Руководство по ] нефтепромысловой механике.
М.—Л., ОНТИ НКТП СССР, 1934.
42. Лейбе н зон Л. С. О динамическом температурном условии
образования складчатости на поверхности земного шара и при охлаждении. Изд.
АН СССР, ОТН, серия геогр, и геофиз., № 6, 1939, стр. 625.
43. Лыков А. В, К теории теплового регулярного режима. ДАН БССР,
1957, т. I, № 2, стр. 52—56.
44. Лыков А. В. Теплопроводность и диффузия. М., Гизлегпром, 1941,
45. Лыков А, В. Теплопроводность нестационарных процессов. М.,
Госэнергоиздат, 1948.
46. Лыков А. В. Теория теплопроводности. Гостехиздат, 1952,
47. Лыков А. В. и Михайлов Ю. А. Теория тепло-и массоперено-
са. Госэнергоиздат, 1963,
48. Любов Б. Я- Расчет скорости затвердевания слитка с учетом
температурной зависимости теплофизических параметров металла. ДАН СССР,
1953, т. 22, М> 4.
49. МикеладзеШ. Е. Численные методы интегрирования
дифференциальных уравнений с частными производными. Изд. АН СССР, 1936.
50. Микулин Е. И. Температурное поле двух твердых тел,
разделенных зазором. ИФЖ, 1961, т. IV, № 2.
51. Минятов А. В. Нагревание бесконечного цилиндра, заключенного
в оболочку. ЖТФ, 1960, т. XXX, вып. 6.
52. Михеев М. А. Основы теплопередачи. Госэнергоиздат, 1956.
* 53. Мочалин А. И. Применение 5-функции Дирака к решению
дифференциальных уравнений в частных производных параболического типа.
В кн. «Тепло-и массообмен в процессах испарения». М., Изд. АН СССР, 1958.
54. М ю н ц Г. Интегральные уравнения. Т. I. М., Гостехтеоретиздат,
1934.
55. НикитинА. Т. Распределение температуры в неограниченном полом
цилиндре при теплообмене на границах со средами переменной температуры.
ИФЖ, I960, т. III, № 8.
56. Панов Д. Ю. Справочник по численному решению
Дифференциальных уравнений в частных производных. Изд. 5. Гостехиздат, 1951.
57. П е р е л ь м а н Т. Л. Температурное поле в конечном цилиндре с
внутренними источниками. ИФЖ» 1960, т. III, № 5.
57а. Перельман Т. Л. О теплообмене в ламинарном потоке,
текущем в трубе. ИФЖ, 1961, т. 4, № 4.
58. Померанцев А. А., Чернышев А. Б., Ферберов И. Л.
К теории горения угля в канале прямоугольного сечения. Изв. АН СССР,
ОТН, № 7, 1948, стр. 1067.
59. Плят Ш. Н. Тепло-и влагообмен полых цилиндров при граничных
условиях второго рода. International Journal of Heat and Mass Transfer, vol.
5, 59. 1962/
60. Плят Ш. Н. Распределение температуры в абразивных изделиях
в процессе термической обработки (обжига). ИФЖ, I960, т. III, № 7.
61. Пляцко Г. В. Температурное поле в полом цилиндре при
переменных граничных условиях. ИФЖ, 1959, т. II, № 10.
62. П о л у б а р и н о в а-К о ч и н а П. Я- Об одном нелинейном уравнении
в частных производных, встречающемся в теории фильтрации. ДАН СССР,
1948, т. 13, № 6, стр. 623—626.
63. Пригожий И. Введение в термодинамику необратимых
процессов. ИЛ, 1960.
64. Прудников. А. П. Решение в интегральной форме одной
смешанной задачи для системы дифференциальных уравнений параболического
типа. ДАН СССР, 1957, т. 115, стр. 869—871.
65. Прудников А. П. К исследованию тепло-и массообмена в
дисперсных средах. ИФЖ, 1958, т. I, № 4.
66. Саульев В. К- Интегрирование уравнений параболического типа
методом сеток. Физматгиз, 1960.
67. Смирнов М. С. К исследованию нестационарного теплообмена в
хлебопекарных печах. В сб. «Тепло-и массообмен в пищевых продуктах».
Труды МТИПП, 1956, вып. 6, стр. 78—89.
68. Смирнов М. С. О системе дифференциальных уравнений
высокоинтенсивного тепло-и массообмена. International. Journal of Heat and Mass
Transfer, vol. 5, 521, 1962.
69. Смирнов М. С. Задача теплопроводности при переменных
термических характеристиках материала. Труды МТИПП, 1958, вып. 2,
стр. 250—253.
70. Смирнов М. С. Задача теплопроводности для системы двух тел.
В кн. «Тепло-и массообмен в процессах испарения». М., Изд. АН СССР,
1958, стр. 153—155.
71. Смирнов М. С. Температурное поле в трехслойной стенке при
граничных условиях четвертого рода. В кн. «Тепло-и массообмен в
капиллярно-пористых телах». М—Л., Госэнергоиздат, 1957, стр. 17—20.
72. Снеддон И. Преобразования Фурье. М., ИЛ, 1955.
73. Т е т е л ь б а у м И. М. Электрическое моделирование. М., Физматгиз,
1959.
74. Темкин А. Г. Аналитическая теория нестационарного тепло-и
массообмена в процессе сушки и обратные задачи аналитической теории
сушки. Минск, изд-во «Наука и техника», 1964.
595
74а. Тихонов А. И. и Самарский А. А. Уравнения
математической физики. Гостехиздат, 1951.
75. Трантер К. Дж. Интегральные преобразования в
математической физике. Гостехиздат, 1956.
75а. Титчмарш Е. Разложение по собственным функциям. Т. I.
М., ИЛ, 1960.
76. Трофимов Е. П. Задача о нестационарном поле температур
неограниченного полого цилиндра. ИФЖ, 1960, т. III, Щ 10, стр. 47—53.
77. Цой П. В. Краевая задача для системы дифференциальных
уравнений параболического типа. ИФЖ, 1961, т. IV, № 12, стр. 61—69.
78. Цой П. В. Теплообмен системы тел при нестационарном режиме.
ИФЖ, 1961, т. IV, Я* 1, стр. 120—123.
79. Чарный И. А. О методах линеаризации нелинейных уравнений
теплопроводности. Изв. АН СССР, ОТН, 1951, № 6, стр. 829—843.
80. Чиркин В. С. Теплопроводность промышленных материалов. М.,
Машгиз, 1962.
81. ЧуДновскийА. Ф. Теплофизические характеристики
дисперсных материалов. М., Физматгиз, 1962.
82. Шимко Н. Г. Конечное интегральное преобразование Ханкеля для
полого цилиндра. ИФЖ, I960, т. 3, № 10, стр. 39.
83. ШнейДер П. Инженерные проблемы теплопроводности. М., ИЛ,
1960.
84. Эккерт Э. Р. и Дрейк Р. М. Теория тепло- и массообмена. М.,
Госэнергоиздат, 1961.
85. Эфрос А. М. и Данилевский А. М. Операционное исчисление
и контурные интегралы. Харьков, 1937.
86. Юшков П. П. Приближенное решение задач нестационарной
теплопроводности методом конечных разностей. Труды Института энергетики
АН БССР, 1958, вып. 6.
87. Юшков П. П. О численном интегрировании уравнения
теплопроводности в полярных сетках. Труды Ленинградского технологического
института холодильной промышленности, 1956. т. XIV.
87а. Юшков П. П. Функции Бесселя и их приложения к решению
задач теплопроводности. Изд. АН БССР, 1962.
88. Я н к е Е. и Э м д е Ф. Таблицы функций с формулами и кривыми.
М., ИЛ, 1959.
89. Boltzmann L. Ann. Physik, 1894, Bd. 53, s. 959.
90. Bromwich T. G. Symbolical Methods in Theory of Conduction of
Heat. Proc. Camb. Phil. Soc. 220, 441,1921.
91. Cars law H. S. and Jeager J. C. Conduction of Heat in Solids,
Oxford, 1959.
92. Carson J. R. Electric Circuit Theory and Operational Calculus,
New York, 1926.
93. Charles H. Sur Г equation de la chaleur dans la theorie Theredite,
Bulletin de la Socete des Sciences de Liege, 1946/8.
94. Crank J. The Mathematics of Diffusion, Oxford, Claredon Press,
1956.
95. DoetschG. Theorie und Anwendung der Laplase —
Transformation, Berlin, 1937.
96. Doetsch G. Integration von Differentialgleichnungen vermittels der
endlichen Fourier Transformation, Mathematische Annalen, 1935, Bd. 112,
s. 52—68.
96a. Epstein L. F. Some infinite sums involving zeroes of J0 (x),
Journal of Research Nat. Bureau of Standards, 68 В, 1, 17, 1964.
97. Friedmann N. E. Quasilinear heat flow. Transactions of theASME,
1958, 80, No. 3, 635.
98. F r ie dmann N. E. Analog method for study of transient heat flow
in solids with temperature dependent thermal properties, Jr. Appl, Phys.
26, p. 129—130, 783, 1956.
99. Fujita H. Text, Res. Jr., 22, p. 757, 1952.
100. Grigull U. Temperaturausgleich in einfachen Korpern, Springer-
Verlag, 1964.
101. Hamburger L. Introduces in Teoria Propagarii Caldurii. L Con-
ductia prin Solide, Editure Republicii Populare Romina, 1956.
102. He a vi side O. Electromagnetic Theory, 1893.
103. Hooper F. G., Miller С. Н. and Kefferl. F. A hydraulic
analogy to transient conduction in two—dimensional fields. International De-
596
velopments in Heat Transfer, Pt. 1 A961—1962 International Heat Transfer
Conference), 1961, p. 39.
104. Jeffreys H. Operational Method in Mathematical Physics,
Cambridge, 1931.
105. Liebman G. Trans. ASME, 1956. (русский перевод см. в сб.
«Механика», № 3, 12, М., ИЛ, 1957).
106. Luikov A, V. Heat and mass transfer in capillary—porous bodies,
Advances in Heat Transfer, V. I. Academic Press, 1964.
107. Luikov A. V. and Mikhailov Y. A. Theory of Energy and
Mass Transfer, Prentice — Hall Inc., New York, 1961; Pergamon Press,
London, 1965.
108. Luikov A. V. The application of the Heaviside — Bromwich
operational method to the solution of a problem in heat conduction. Phill. Mag.
7,22, 239, 1936.
108a. Luikov A. V. Application of Irreversible Thermodynamics Methods
to Investigation of Heat and Mass Transfer, International Journal of Heat and
Mass Transfer, 1965.
109. Mikusinski J. Rachunek opera torow, Warszawa, 1953.
110. Mikhailov Y. A. Highly intensive heat and mass transfer in
dispersed media. Int. Jr. Heat Mass Transfer, 1, No. 1, I960.
111. Moore A. D. Soap —Film and Sanded —Mapper Techniques.
J. Appl. Mech., Trans. ASME, 72, p. 291. 1950.
112. Poschl. Berechnung der Oberflachentemperaturen geometrisch einfa-
cher Korper bei Abkuhlung oder Erwarmung der Isolierstoffe.
113. Sawada M. On the general solution of basic expression for heat
transmission. Jr. of Soc. Mech. Engrs. Japan, 35, No. 183, p. 695, 1932.
114. Schneider P. J. Temperature Response Charts, John Wiley and
Sons, New York, 1963.
115. Stokes R. H. Trans. Farady Soc. 48, p. 1229, 1950.
116. Storm M. L. Heat conduction in simple metals, Jr. Appl. Phys,
22, p. 940—951, 1951.
116a. Sutton W. G. Proc. Roy.Soc, 182 A, 48,1943.
117. Vernotton P. La nouvelle equation de la chaleur. Journ. de la
Tranms. de la chaleur, 1961.
118. Tables of Integral Transforms, vol. 1, 2, McGraw-Hill Inc., New
York, 1954.
119. Wie deburg O. Uber dieHydrodiffusion Annalen der Physik and
Chemik, 39, 675,1879.
597
СОДЕРЖАНИЕ
Предисловие . ■„ 3
Глава I. Физические основы передачи тепла
§ 1. Температурное поле 5
§ 2. Основной закон теплопроводности Фурье 7
§ 3. Распространение тепла при высокоинтенсивных процессах 11
§ 4. Уравнения распространения тепла в жидких и газовых смесях .... 14
§ 5. Дифференциальное уравнение теплопроводности 16
§ 6. Гиперболическое уравнение теплопроводности 21
§ 7. Система дифференциальных уравнений тепло- и массообмена 22
§ 8. Краевые условия 24
§ 9. Методы расчета расхода тепла 30
Глава II. Теория обобщенных переменных
§ 1. Критерии и числа подобия 34
§ 2. Операционное исчисление и теория подобия 41
Глава III. Основные методы решения краевых задач
§ 1. Анализ дифференциального уравнения теплопроводности ,„ 44
§ 2. Нахождение решения уравнения классическими методами 45
§ 3. Применение методов интегрального преобразования 51
§ 4. Методы численных решений задач теплопроводности и моделирования . 59
Глава IV, Граничное условие первого рода
§ 1. Неограниченное тело 70
§ 2. Полуограниченное тело 74
§ 3. Неограниченная пластина 83
§ 4. Шар (симметричная задача) 105
§ 5. Неограниченный цилиндр л 115
§ 6. Неограниченный полый цилиндр 129
§ 7. Параллелепипед 141
§ 8. Цилиндр конечных размеров 143
§ 9. Задачи на нагревание „ 145
Глава V, Граничное условие второго рода
§ 1. Полуограниченное тело " . 148
§ 2. Неограниченная пластина 152
§ 3, Шар (симметричная задача) 162
§ 4, Неограниченный цилиндр 169
§ 5. Неограниченный полый цилиндр 176
Глава VI. Граничное условие третьего рода
§ 1. Полуограниченное тело 181
§ 2, Полуограниченный стержень без тепловой изоляции боковой
поверхности 186
§ 3. Неограниченная пластина 191
§ 4. Ограниченный стержень без тепловой изоляции боковой поверхности . 216
§ 5. Шар (симметричная задача) . . 222
§ 6, Неограниченный цилиндр 238
§ 7. Неограниченный полый цилиндр 254
§ 8. Цилиндр конечных размеров 261
§ 9. Пластина конечных размеров 263
§ 10, Анализ обобщенного решения 265
§11. Оценка приближения 270
Глава VII. Температурное поле без источников тепла с переменной
температурой среды
§ 1. Неограниченная пластина. Температура среды—линейная функция
времени 274
§ 2. Шар. Температура среды — линейная функция времени 280
§ 3. Неограниченный цилиндр. Температура среды—линейная функция
времени 284
§ 4. Неограниченная пластина, шар и неограниченный цилиндр.
Температура среды — экспоненциальная функция времени 288
§ 5. Нагревание влажных тел (неограниченная пластина, шар и
неограниченный цилиндр) 292
§ 6. Тепловые волны. Неограниченная пластина, полуограниченное тело,
шар и неограниченный цилиндр. Температура среды — простая
гармоническая функция времени 298
§ 7. Полуограниченное тело. Температура среды — функция времени . . . 313
§ 8. Обобщенное решение. Теорема Дюамеля 315
§ 9. Полый цилиндр 319
§ 10. Параллелепипед. Температура среды — линейная функция времени . . . 320
Глава VIIL Температурное поле с непрерывно действующими источниками
тепла
§ 1. Полуограниченное тело ..." 322
§ 2. Неограниченная пластина . • 327
§ 3. Шар (симметричная задача) . . 335
§ 4. Неограниченный цилиндр 340
Глава IX. Температурное поле с мгновенными источниками тепла
Введение 345
§ 1. Полуограниченное тело * 348
§ 2. Неограниченная пластина 351
§ 3. Шар (симметричная задача) 354
§ 4. Неограниченный цилиндр 356
§ 5. Регулярный тепловой режим 359
Глава X. Граничное условие четвертого рода
§ 1. Система двух полуограниченных тел 365
§ 2. Система ограниченного и полуограниченного тел 369
§ 3. Система двух неограниченных пластин 374
§ 4. Система Двух сферических тел 381
§ 5. Система Двух цилиндрических тел 383
§ 6. Неограниченная пластина 384
§ 7. Шар (симметричная задача) 391
§ 8. Неограниченный цилиндр 393
§ 9. Теплообмен между телом и обтекающим его потоком жидкости . . . 398
§ 10. Симметричная система тел, состоящая из трех неограниченных
пластин 403
Глава XI. Двухмерное температурное поле. Некоторые частные задачи
§ 1. Полуограниченная пластина 406
§ 2. Двухмерная пластина 408
§ 3. Полуограниченный цилиндр 410
§ 4. Цилиндр конечных размеров 412
599
Глава XII. Температурное поле при изменении агрегатного состояния тела
§ 1. Промерзание влажного грунта 421
§ 2. Приближенные решения задачи затвердевания полуограниченного
тела, неограниченной пластины, шара и неограниченного цилиндра . . 428
§ 3. Затвердевание металла при зависимости коэффициента
теплопроводности и теплоемкости от температуры 431
Глава XIII. Теплопроводность при переменных коэффициентах переноса
§ 1. Полуограниченное тело. Теплопроводность и теплоемкость —
степенные функции координат 436
§ 2. Ограниченная пластина. Коэффициент теплопроводности —
экспоненциальная функция координаты 439
§ 3. Линеаризация нелинейного уравнения теплопроводности ....... 441
§ 4. Преобразования, используемые при решении нелинейных
дифференциальных уравнений переноса 446
§ 5. Некоторые решения нелинейных дифференциальных уравнений
теплопроводности 453
§ 6. Краевые задачи для уравнения теплопроводности с коэффициентами,
зависящими от координаты 459
Глава XIV. Основы интегрального преобразования Лапласа
§ 1. Основные понятия 474
§ 2. Свойства преобразования Лапласа 476
§ 3. Метод решения простейших дифференциальных уравнений 481
§ 4. Основные правила преобразования Лапласа 484
§ 5. Решение линейных дифференциальных уравнений с постоянными
коэффициентами операционным методом 489
§ 6. Теоремы разложения 490
§ 7. Решение некоторых дифференциальных уравнений с переменными
коэффициентами 496
§ 8. Интегральные преобразования и операционные методы 498
§ 9. Нахождение оригинала функции по ее изображению 503
§ 10. Интегральные преобразования Фурье и Ханкеля 509
§11. Конечные преобразования Фурье и Ханкеля 515
Глава XV. Элементы теории аналитических функций и ее приложения
§ 1. Аналитические функции 523
§ 2. Контурное интегрирование функций комплексного переменного .... 525
§ 3. Представление аналитических функций рядами 529
§ 4. Классификация аналитических функций по их особым точкам. Понятие
об аналитическом продолжении 534
§ 5. Теория вычетов и ее применение к вычислению интегралов и
суммированию рядов . 538
§ 6. Некоторые аналитические свойства преобразования Лапласа и
асимптотические оценки 551
Приложения
I. Некоторые справочные формулы 574
II. Теорема единственности решения 579
III. Дифференциальное уравнение теплопроводности, выраженное в
различных системах координат ,,,...,.. 581
IV. Основные правила и теоремы преобразования Лапласа 582
V. Изображения некоторых функций 583
VI. Значения функций i^erfc* 590
Литература
592
Лыков Алексей Васильевич
ТЕОРИЯ ТЕПЛОПРОВОДНОСТИ
Редактор Е, С. Гридасова
Художник В. М. Лукьянов
Художественный редактор
Т. Н. Скворцова
Технический редактор
Э, М, Чижевский
Корректор С. К. Марченко
Т-02840. Сдано в набор 24/VI-66 г.
Подписано к печати 17/11-67 г. Формат
70хЮ8/16. Объем 37,5 печ. л.
52,5 усл. п. л. Уч.-изд. л. 45,45.
Изд. № ФМ-274. Тираж 20 000 экз.
Цена 1 руб. 49 к. Зак. 640
Тематический план
издательства «Высшая школа»
(вузы и техникумы) на 1966 г.
Позиция № 64—65„
Москва, К-51, Неглинная ул., д. 29/14.
Издательство «Высшая школа»
Ярославский полиграфкомбинат Глав-
полиграфпрома Комитета по печати
при Совете Министров СССР
Ярославль, ул. Свободы, 97.