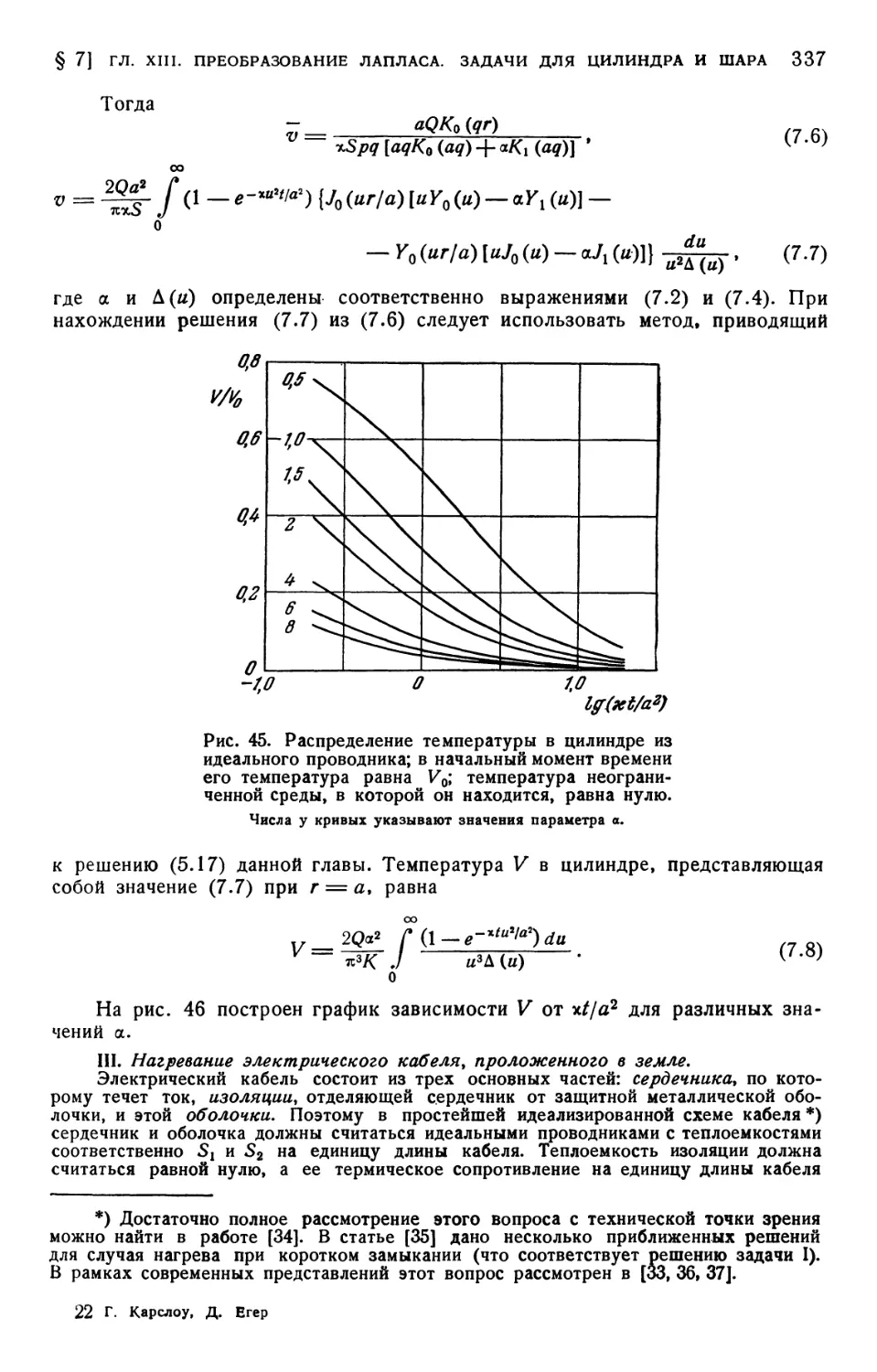
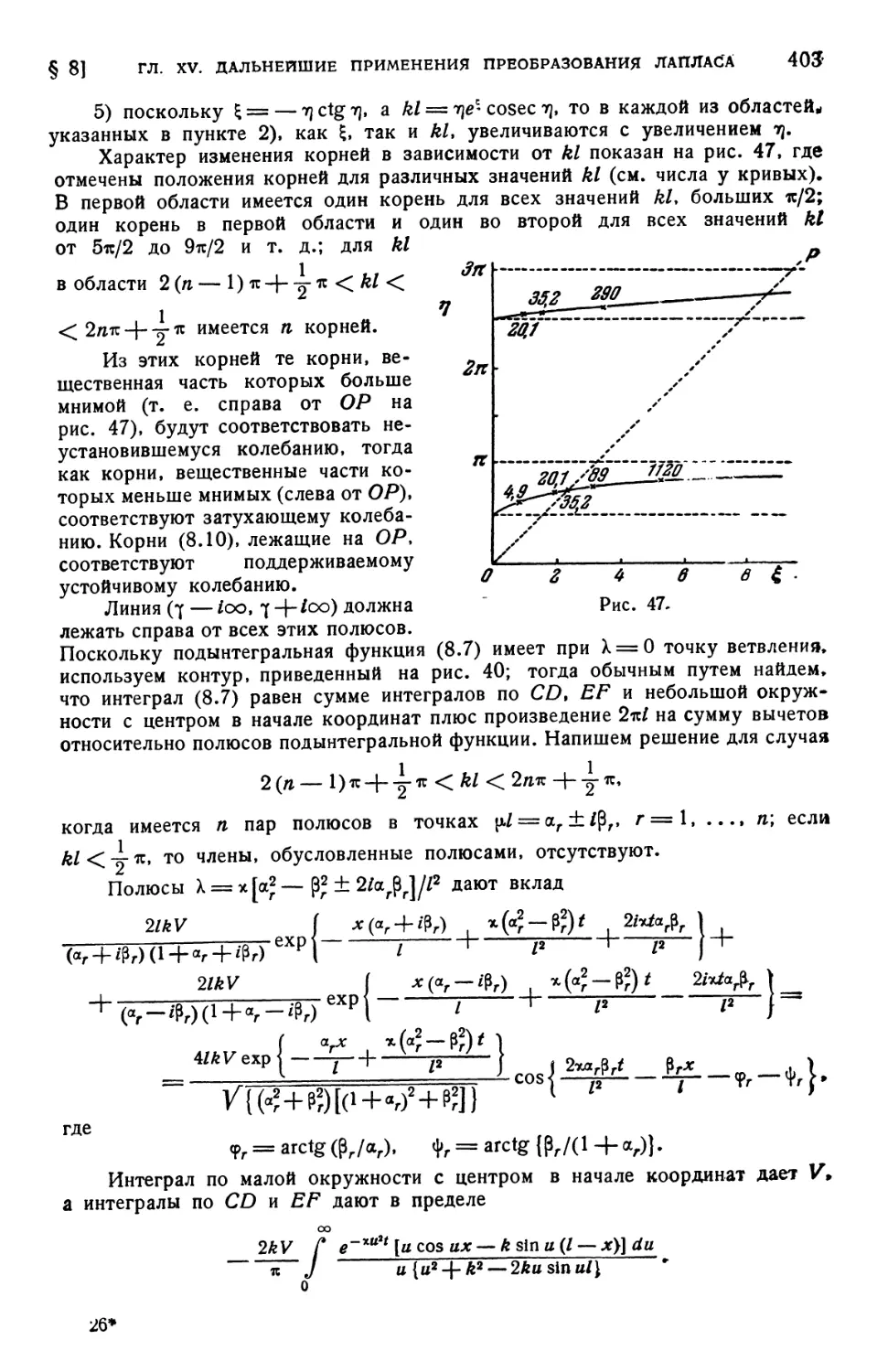
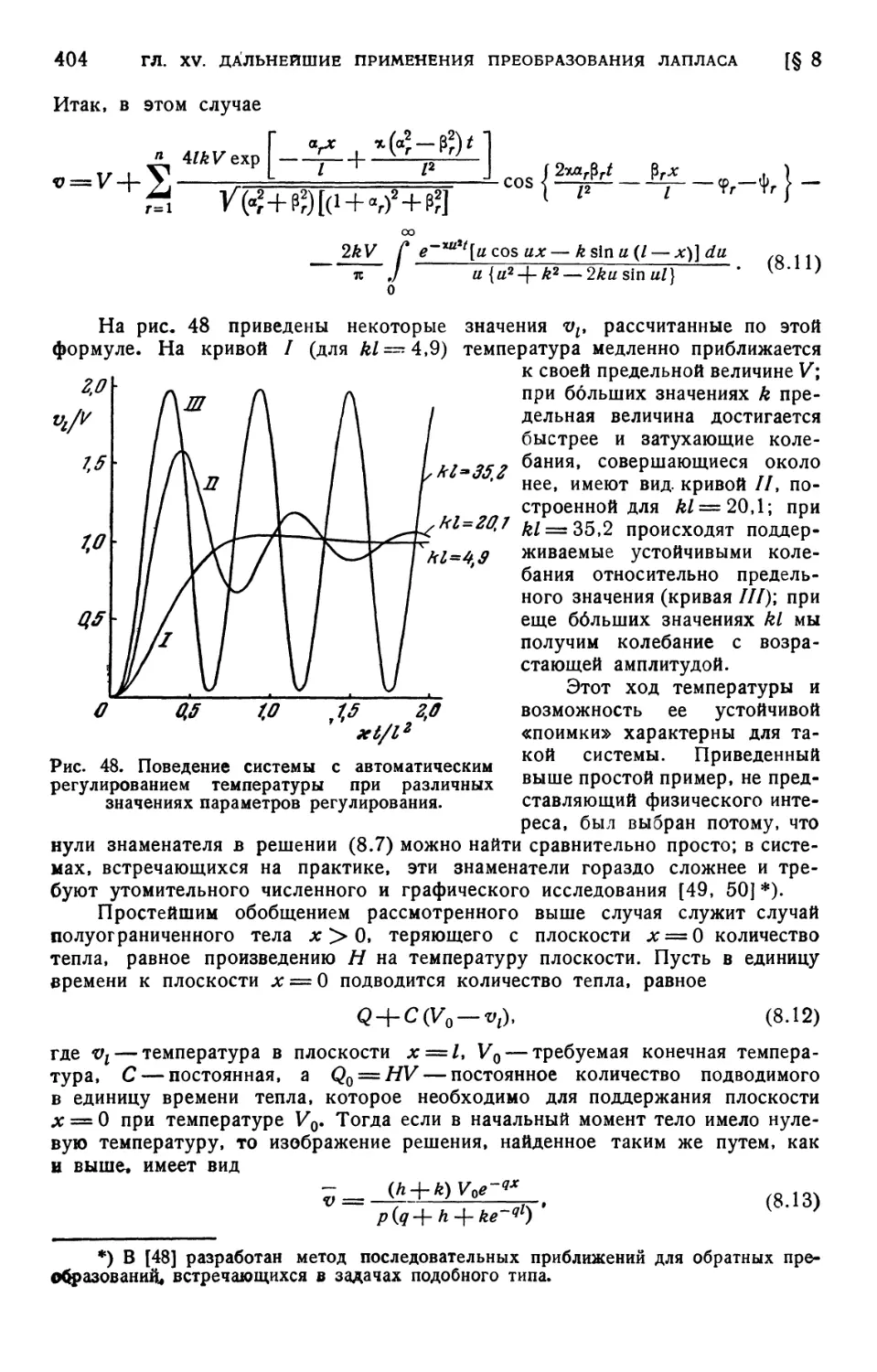
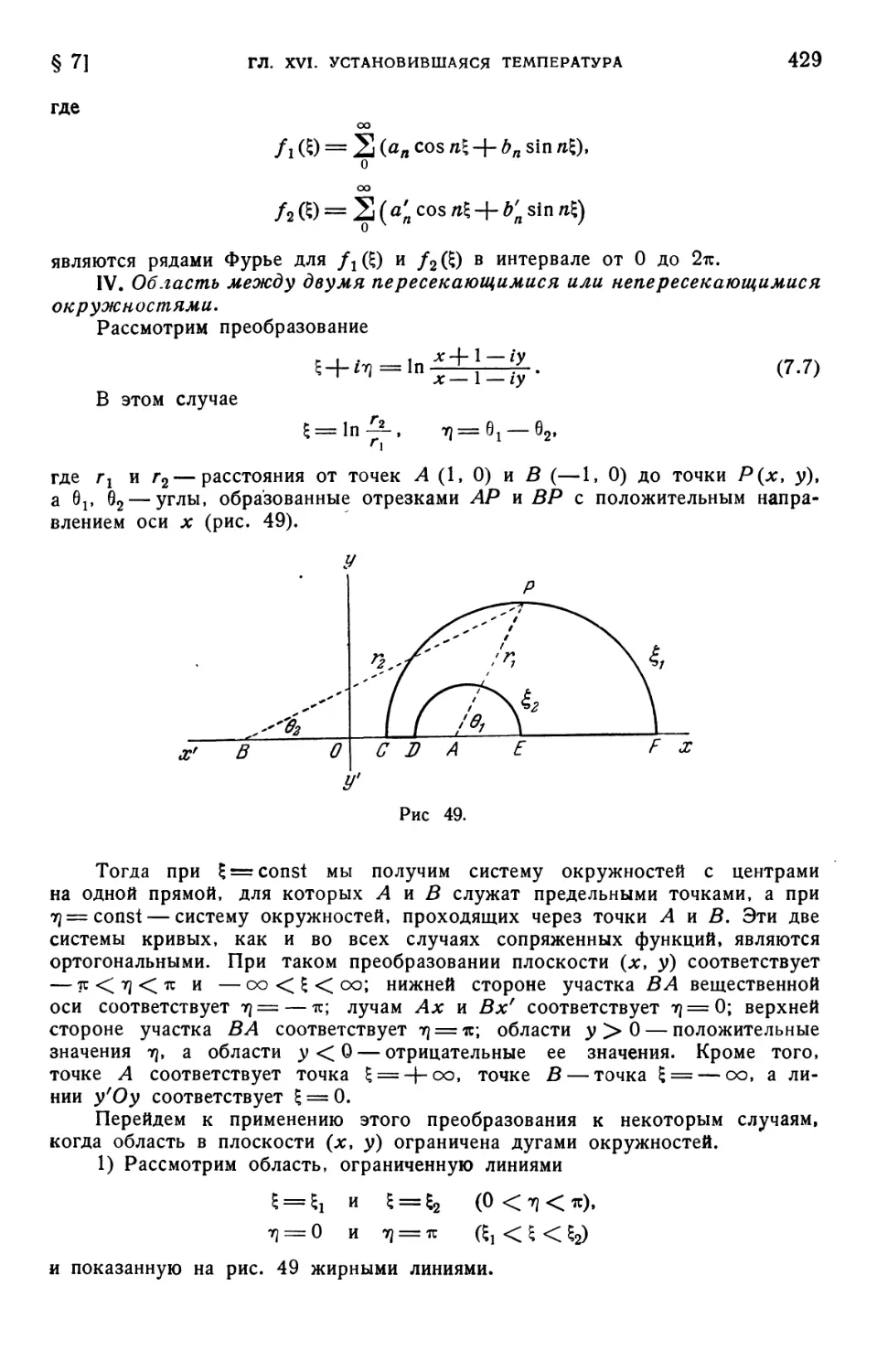
Текст
Г. КАРСЛОУ и Д. ЕГЕР
ТЕПЛОПРОВОДНОСТЬ
ТВЕРДЫХ ТЕЛ
Перевод
со второго английского издания
под редакцией
проф. А. А. ПОМЕРАНЦЕВА
ИЗДАТЕЛЬСТВО «НАУКА»
МОСКВА 1964
536
К 26
УДК 536.21
CONDUCTION
OF HEAT IN SOLIDS
By
H. S. CARSLAW
Emeritus Professor of Mathematics
in the University of Sydney
and
J. C. JAEGER
Professor of Geophysics
in the Australian National University
SECOND EDITION
OXFORD
At the Clarendon Press
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
ОГЛАВЛЕНИЕ
Предисловие редактора русского перевода 7
Из предисловия ко второму изданию 9
Из предисловия к первому изданию 9
Глава I. Общая теория 11
§ 1. Введение (И). § 2. Теплопроводность A1). § 3. Тепловой поток через
произвольную поверхность A3). § 4. Изотермические поверхности A5).
§ 5. Теплопроводность изотропных тел A5). § 6. Дифференциальное уравне-
уравнение теплопроводности для изотропного твердого тела A7). § 7. Дифферен-
Дифференциальное уравнение теплопроводности для движущейся среды B1). § 8. Пре-
Преобразование координат B3). § 9. Начальные и граничные условия B5).
§ 10. Безразмерные параметры C1). § 11. Экспериментальные методы опре-
определения теплопроводности C2). § 12. Математическая интерпретация началь-
начальных и граничных условий C3). § 13. Родственные дифференциальные уравне-
уравнения C4). § 14. Упрощение общей задачи теплопроводности C5). § 15. Задачи,
решения которых можно выразить в виде произведения решений более про-
простых задач C9). § 16. Единственность решения задачи теплопроводности D1).
§ 17. Теплопроводность анизотропных твердых тел D3). § 18. Дифференциаль-
Дифференциальное уравнение теплопроводности для анизотропных твердых тел D6).
§ 19. Теплопроводность тонкой кристаллической пластины D8). § 20. Изме-
Изменение теплопроводности и вектор теплового потока в анизотропных твердых
телах E1).
Глава II. Линейный поток тепла. Неограниченное и полуограниченное
твердое тело 57
§ 1. Введение. Простые решения уравнения для линейного потока тепла E7).
§ 2. Неограниченное твердое тело. Решение Лапласа E9). § 3. Использова-
Использование интегралов Фурье и преобразований Фурье F2). § 4. Полуограниченное
тело с начальной температурой f (х) и нулевой температурой поверх-
поверхности F4). § 5. Полуограниченное твердое тело. Начальная температура
равна нулю. Поверхность находится при температуре <р (t) F7). § 6. Полу-
Полуограниченное твердое тело. Температура поверхности является гармониче-
гармонической функцией времени G0). § 7. Полуограниченное твердое тело. Тепло-
Теплообмен на поверхности в среду с нулевой температурой. Начальная темпе-
температура постоянна G5). § 8. Полуограниченное твердое тело. Теплообмен на
поверхности в среду с температурой / (t). Начальная температура равна
нулю G8). § 9. Полуограниченное тело. Тепловой поток на границе х = 0
является заданной функцией времени. Начальная температура равна
нулю G9). § 10. Применение полученных результатов к определению тепло-
теплопроводности (82). §11. Полуограниченное твердое тело, внутри которого
находится источник тепла (82). § 12. Температура Земли и колебания тем-
температуры на ее поверхности (85). § 13. Геотермический градиент и поток
тепла (87). § 14. Возраст Земли. Анализ Кельвина (89). § 15. Неограниченное
составное твердое тело (91). § 16. Случай зависимости термических харак-
характеристик вещества от температуры (92).
Глава III. Линейный тепловой поток в твердом теле, ограниченном двумя
параллельными плоскостями 97
§ 1. Введение (97). § 2. Установившаяся температура (97). § 3. Область
0 < х < I. Границы поддерживаются при нулевой температуре. Начальная
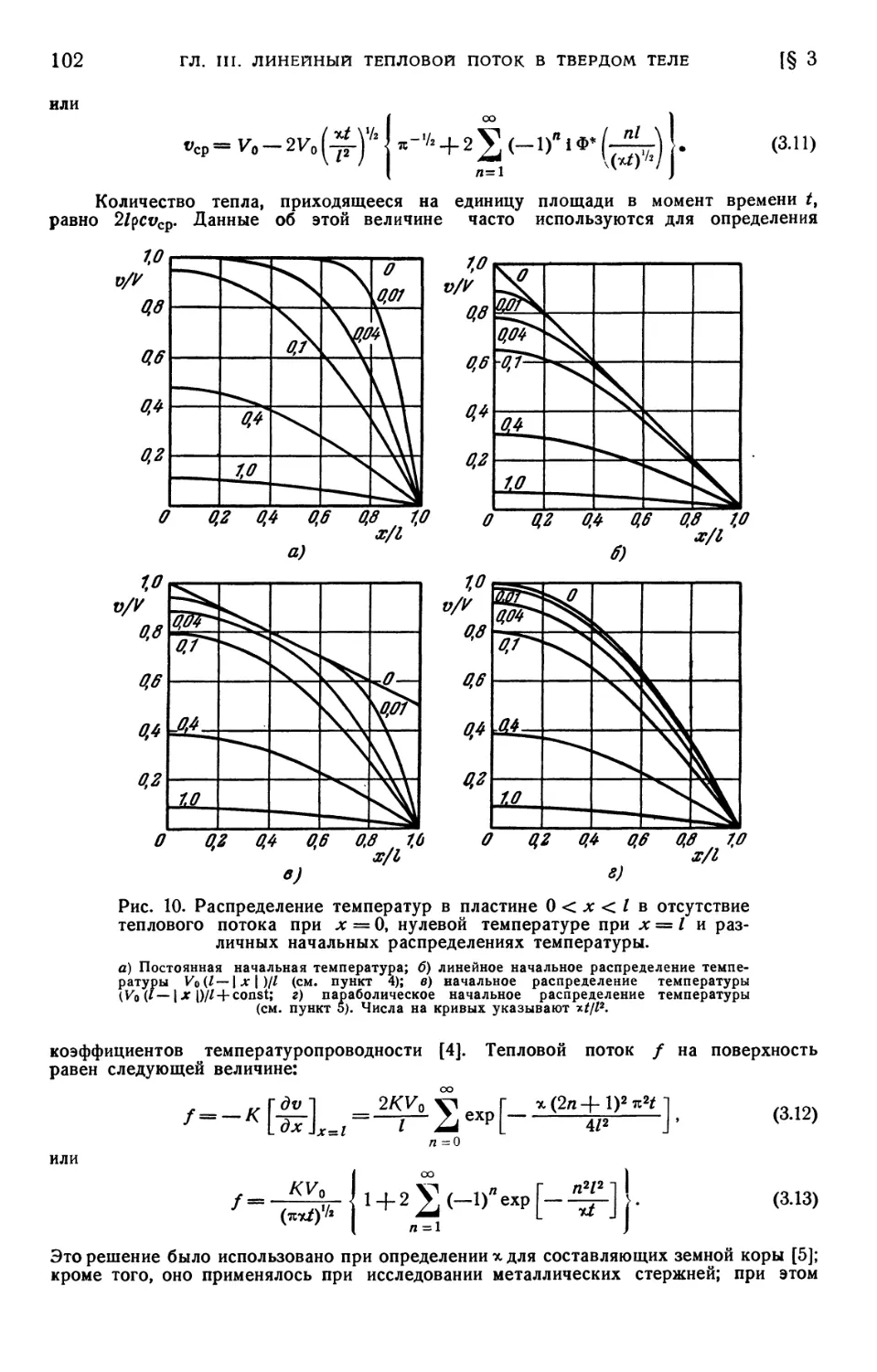
температура f (х) (98). § 4. Область 0 < х < I. Начальная температура /(-*)•
Границы поддерживаются при постоянной температуре или изолированы A03).
§ 5. Область 0 < х < I. Температуры границ равны <fi (t) и <р2 (f). Начальная
температура f (х) A06). § 6. Пластина с периодически изменяющейся
1*
4 ОГЛАВЛЕНИЕ
температурой поверхности A09). § 7. Установившаяся периодически изменяю-
изменяющаяся температура в составных пластинах A13). § 8. Пластина с заданным
тепловым потоком на ее границе A15). § 9. Область 0 < х < /. Теплообмен
на границах в среду с температурой, равной нулю. Начальная температура
равна /(х) A17). § 10. Область —I < х < I. На границах jc= ± / происхо-
происходит теплообмен со средой нулевой температуры. Начальная темпера-
температура f (х) A21). § 11. Частные случаи и численные результаты для пластины
с граничным условием третьего рода A23). § 12. Область —I < х < I с ну-
нулевой начальной температурой и теплообменом на границах со средой, имею-
имеющей температуру <р (t) A27). § 13. Пластина, одна из поверхностей которой
соприкасается со слоем идеального проводника или хорошо перемешиваемой
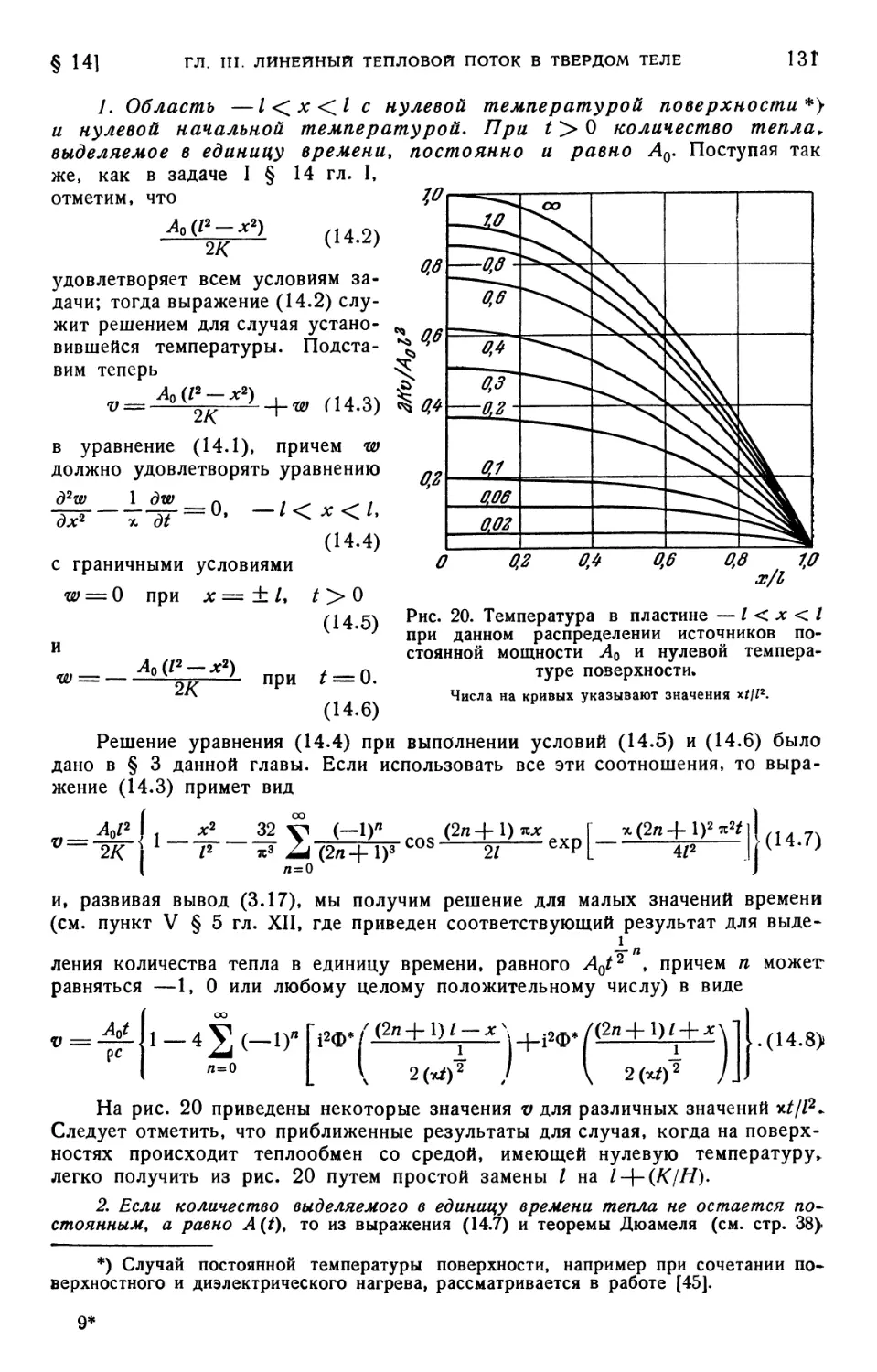
жидкости A28). § 14. Пластина с внутренним источником тепла A30).
Глава IV. Линейный тепловой поток в стержне 134
§ 1. Введение A34). § 2. Дифференциальное уравнение распределения тем-
температуры в тонком стержне A34). § 3. Полуограниченныи стержень. Случай
установившейся температуры. Метод Форбса A36). § 4. Полуограниченный
стержень. Периодически изменяющаяся температура. Метод Ангстрема A37).
§ 5. Ограниченный стержень, концы которого находятся при фиксированных
температурах. Случай установившейся температуры A39). § 6. Стержень
переменного сечения с охлаждающимися ребрами. Случаи установившейся
температуры A41). § 7. Ограниченный стержень при наличии теплообмена
на его поверхности. Случай неустановившейся температуры A44).
§ 8. Ограниченный стержень с периодически изменяющейся температурой
концов. Метод Неймана A47). § 9* Задачи по теплопроводности в движу-
движущемся стержне A48). § 10. Уравнение теплопроводности для тонкой про-
проволоки, нагреваемой постоянным электрическим током A49). § 11. Устано-
Установившаяся температура. Определение коэффициента теплопроводности A51).
§ 12. Сильно нагретая проволока, по которой протекает электрический
ток A54). § 13. Установившийся поток тепла в составной проволоке A56).
§ 14. Неустановившаяся температура в проволоке, по которой течет элек-
электрический ток A57). § 15. Кольцо Фурье A59).
Глава V. Поток тепла в теле с прямоугольным сечением 163
§ 1. Введение A63). § 2. Неограниченное твердое тело прямоугольного сече-
сечения. Установившаяся температура A64). § 3. Установившаяся температура
в неограниченном теле прямоугольного сечения 0 < х < а, 0 < у < b A67).
§ 4. Тонкая пластина с прямоугольным сечением при наличии теплообмена
на ее поверхности A70). § 5. Установившаяся температура в теле прямо-
прямоугольного сечения — а < х < а, — Ь < у <Ь при наличии источника
тепла A71). § 6. Неустановившееся состояние. Решение в виде произведения
решений A72). § 7. Неустановившееся состояние. Произвольные начальные
и граничные условия A75).
Глава VI. Тепловой поток в прямоугольном параллелепипеде 176
§ 1. Введение A76). § 2. Установившаяся температура A77). § 3. Двойные
и кратные ряды Фурье A80). § 4. Неустановившаяся температура. Решение
в виде произведения решений A83). § 5. Определение коэффициента тепло-
теплопроводности и экстраполяция кривых охлаждения A85). § 6. Неустановив-
Неустановившаяся температура. Тройной ряд Фурье A86).
Глава VII. Тепловой поток в неограниченном цилиндре кругового сечения 187
§ 1. Введение A87). § 2. Установившаяся температура. Радиальный по-
поток A88). § 3. Установившаяся, периодически изменяющаяся температура
в круговых цилиндрах A92). § 4. Неограниченный цилиндр. Радиальный по-
а
ток. Неустановившаяся температура A93). §5. Интегралы J rJn(ar)Jn($r)dr
о
а
и Г г [Jn («г)]2 dr A95). § 6. Неограниченный цилиндр с температурой по-
о
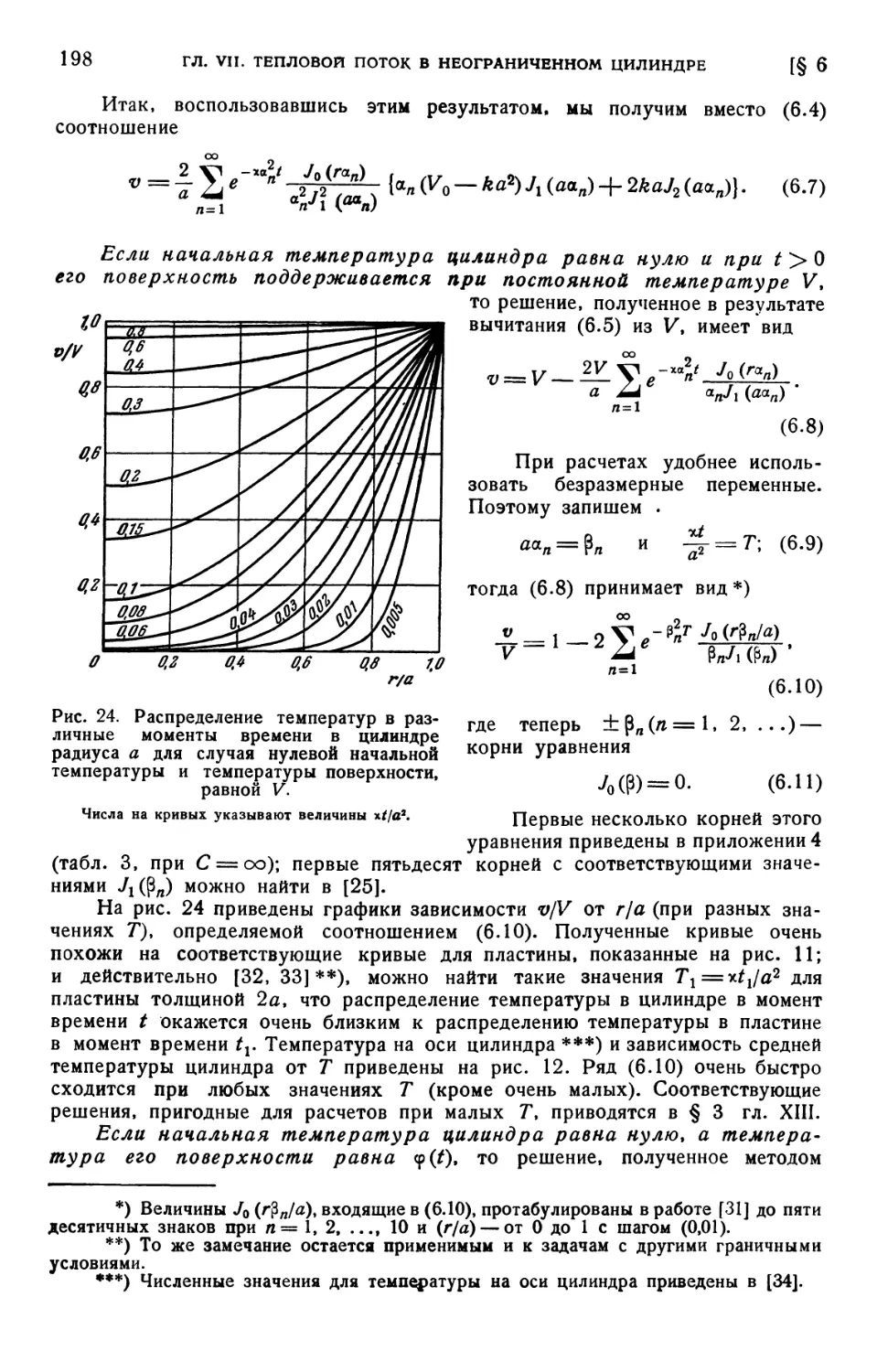
верхности <р (t) и начальной температурой / (г) A97). § 7. Неограниченный
цилиндр с теплообменом на поверхности A99). § 8. Неограниченный цилиндр
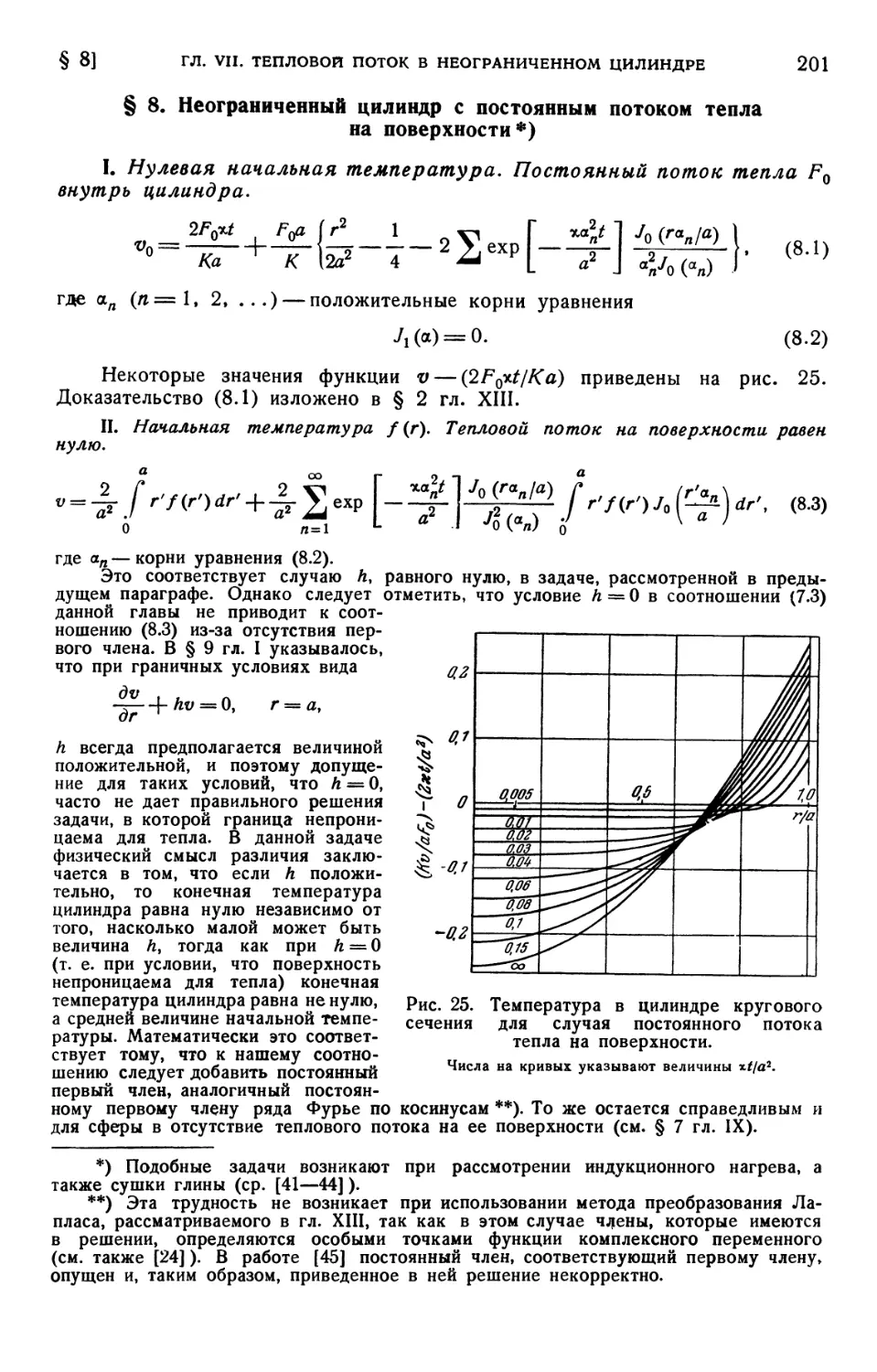
с постоянным потоком тепла на поверхности B01). § 9. Неограниченный
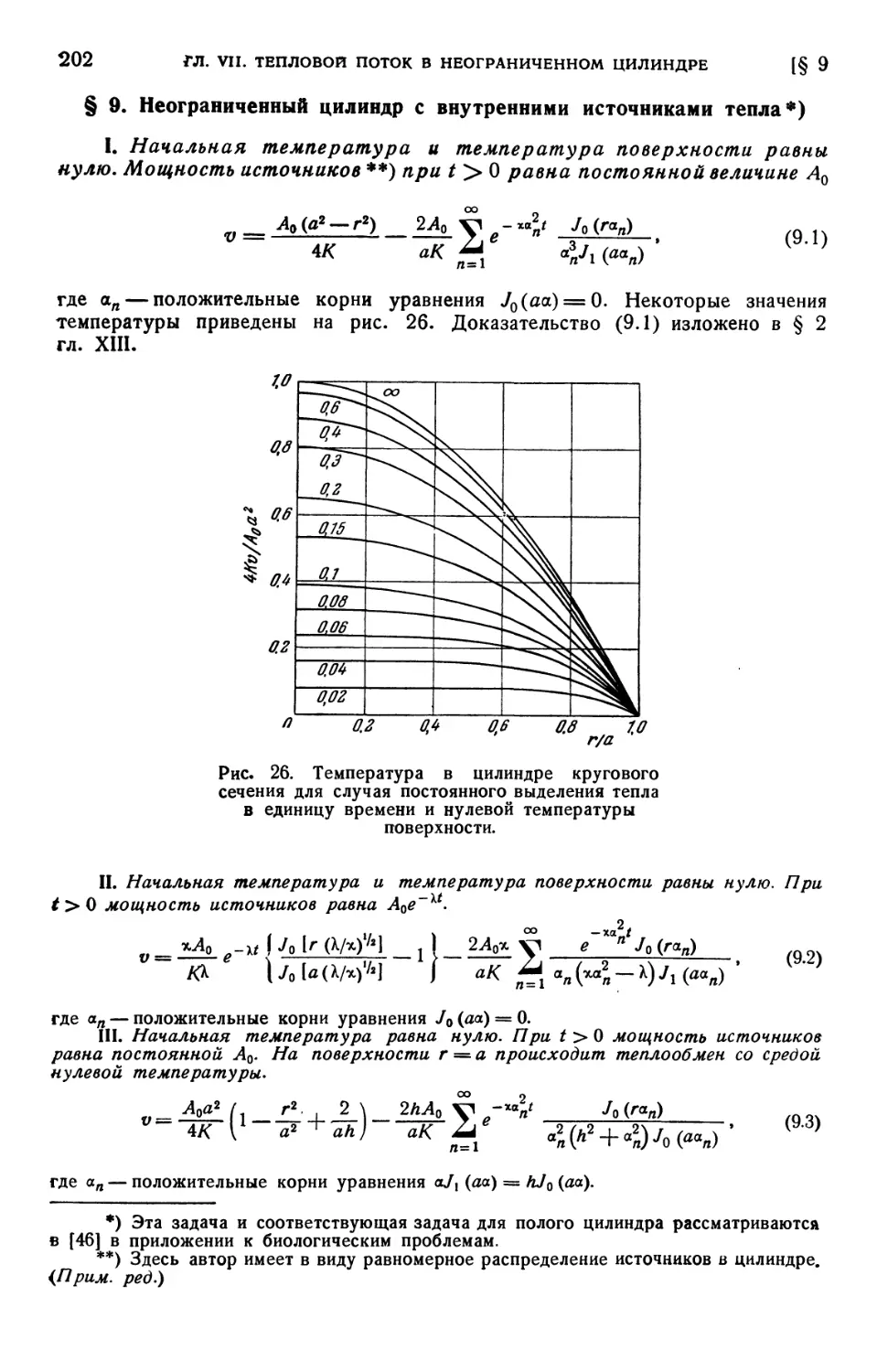
цилиндр с внутренними источниками тепла B02). § 10. Неограниченный полый
ОГЛАВЛЕНИЕ 5
цилиндр. Радиальный поток B03). § 11. Неограниченный цилиндр. Устано-
Установившаяся температура. Общий случай B05). § 12. Неограниченный цилиндр.
Неустановившаяся температура. Общий случай B07).
Глава VIII. Тепловой поток в областях, ограниченных координатными
поверхностями цилиндрической системы координат 212
§ 1. Введение B12). § 2. Установившееся распределение температур в не-
неограниченной и полуограниченной среде, обусловленное подводом тепла
через круг B12). § 3. Установившаяся температура в ограниченном и полу-
полуограниченном цилиндрах B15). § 4. Неустановившееся состояние. Решения
в форме произведений B22). § 5. Определение теплопроводности вещества
в форме цилиндра B24). § 6. Ограниченный цилиндр — / < z < /, 0 <; г < а
с начальной температурой /(г, 0, z) B25). § 7. Полу ограниченный ци-
цилиндр B26).
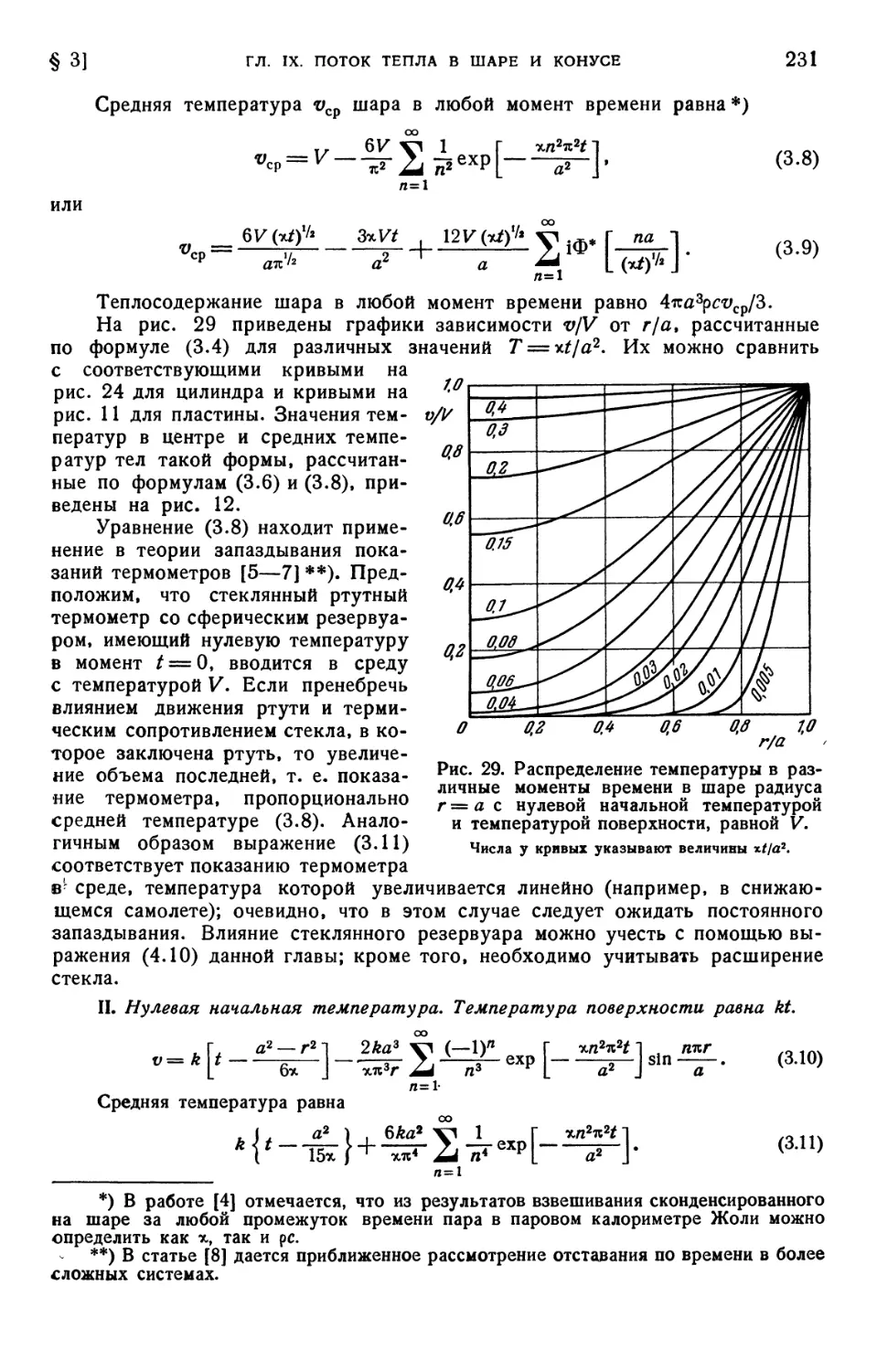
Глава IX. Поток тепла в шаре и конусе 227
§ 1. Введение B27). § 2. Установившаяся температура. Радиальный тепловой
поток B27). § 3. Шар 0 < г < а с начальной температурой / (г) и темпера-
температурой поверхности <р (t) B30). § 4. Шар 0 < г < а. Начальная темпера-
температура / (г). На поверхности сферы происходит теплообмен B33). § 5. Опре-
Определение коэффициентов теплопроводности плохих проводников B35).
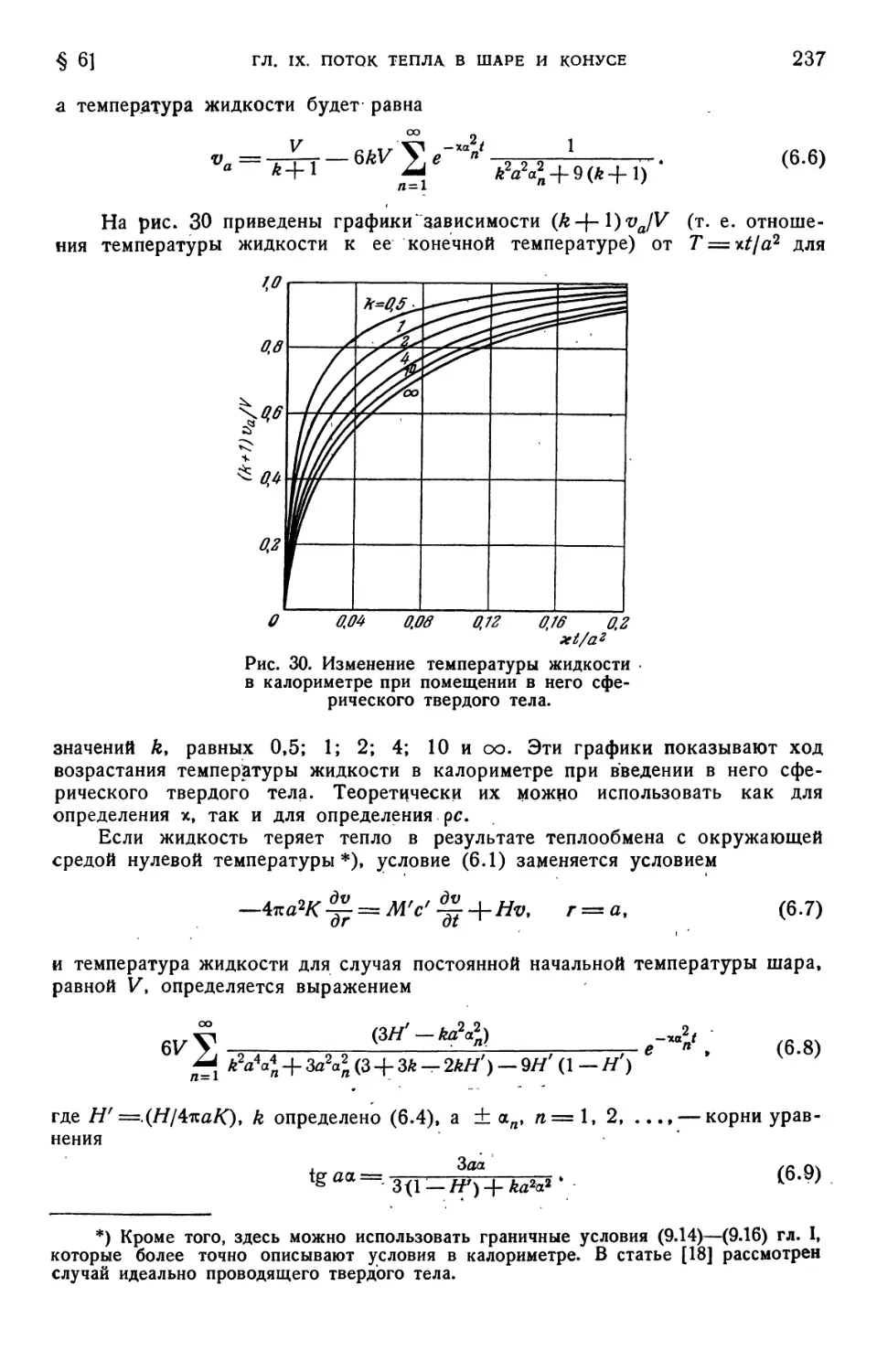
§ 6. Случай шара, находящегося в контакте с хорошо перемешиваемой
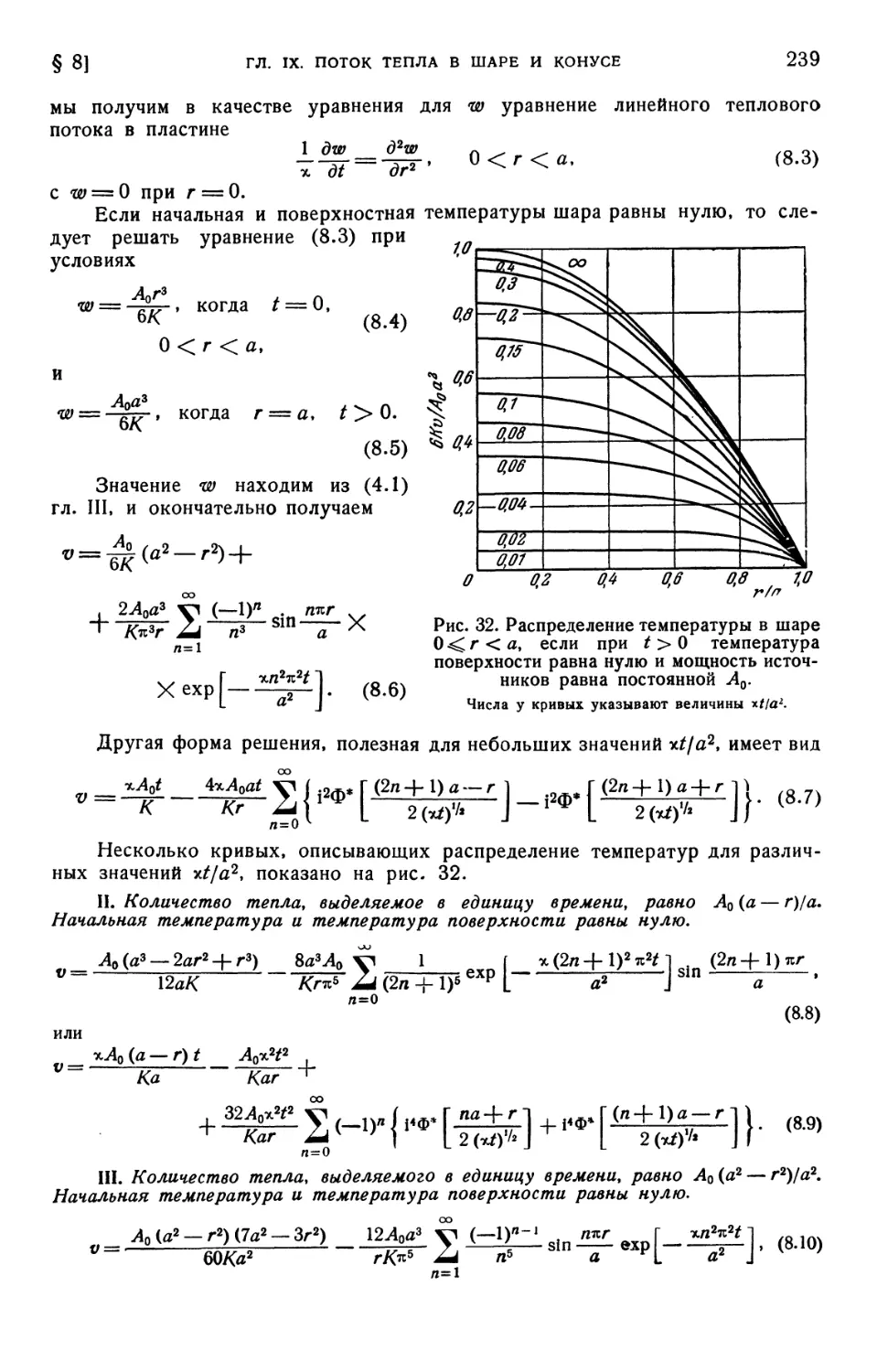
жидкостью B36). § 7. Шар с заданным тепловым потоком на поверх-
поверхности B38). § 8. Шар 0 < г < я, внутри которого выделяется тепло B38).
§ 9. Полый шар а <г <Ь B42). § 10. Область, ограниченная изнутри сфе-
сферической поверхностью г = я B43). § 11. Шар с начальной температурой
/ (л 9, <р). Температура поверхности г = а равна нулю B44). § 12. Поверх-
Поверхность шара г = а поддерживается при температуре F @, <р) B46). § 13. Часть
шара, вырезаемая конусом 0 == 0О. Температура поверхности равна нулю,
начальная температура равна /(г, 0, <р) B46). § 14. Температура внутри
Земли B48).
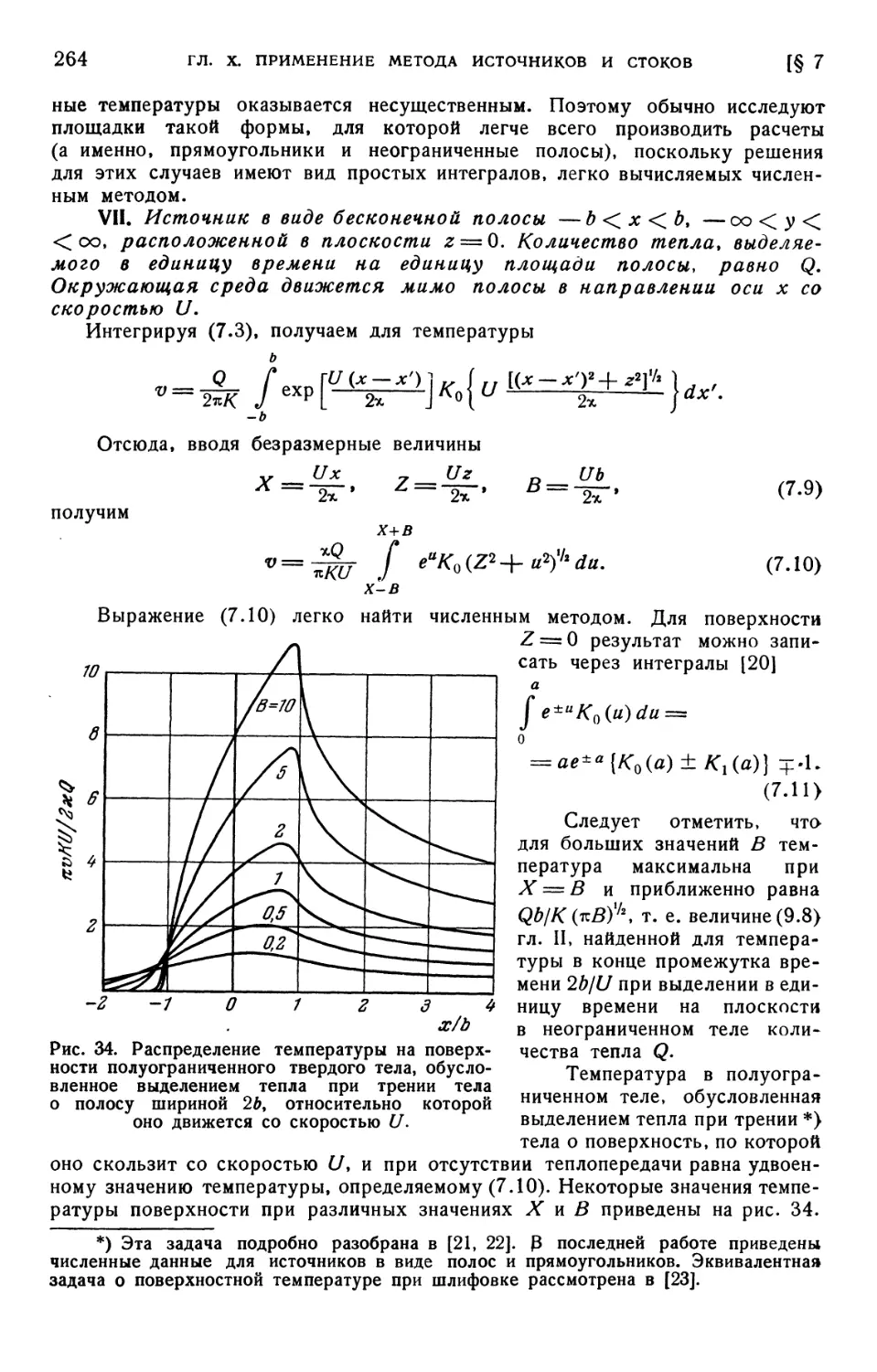
Глава X. Применение метода источников и стоков к задачам с неуста-
неустановившейся температурой 251
§ 1. Введение B51). § 2. Мгновенный точечный источник B51). § 3. Мгно-
Мгновенные источники; линейный, плоский и поверхностные цилиндрический и
сферический источники B54). § 4. Непрерывные и периодические источ-
источники B56). § 5. Поверхностный нагрев полуограниченной области B59).
§ 6. Выделение тепла в неограниченной среде B60). § 7. Движущиеся источ-
источники тепла B61). § 8. Дублеты B65). § 9. Метод последовательных волн B67).
§ 10. Метод изображений. Линейный тепловой поток B67). § 11. Применение
метода изображений к двумерным и трехмерным задачам B71). § 12. Обоб-
Обобщение метода изображений Зоммерфельдом B73).
Глава XI. Изменение физического состояния 276
§ 1. Введение B76). § 2. Одномерные случаи плавления и затвердевания.
Решение Неймана и его обобщение B77). § 3. Область х > 0 при других
граничных условиях B85). § 4. Методы интегрального уравнения. Рассмо-
Рассмотрение задач затвердевания, предложенное Лайтфутом B86). § 5. Решения
в цилиндрических и сферических координатах B88). § 6. Осесимметричные
задачи о замерзании и плавлении B89).
Глава XII. Преобразование Лапласа. Задачи для линейного теплового
потока 292
§ 1. Исторический обзор B92). § 2. Преобразование Лапласа. Основные
свойства B93). § 3. Решение уравнения теплопроводности методом преобра-
преобразования Лапласа B96). § 4. Полуограниченная область х > 0. Решения, по-
получаемые из таблицы изображений B98). § 5. Ограниченная область
0 < х < I. Решения, получаемые из таблицы изображений. Решения для не-
небольших значений времени C03). § 6. Ограниченная область 0 < х < I.
Применение теоремы обращения C06). § 7. Полу ограниченная область х > 0.
Применение теоремы обращения C12). § 8. Составные твердые тела C14).
Глава XIII. Преобразование Лапласа. Задачи для цилиндра и шара .... 322
§ 1. Введение C22). § 2. Цилиндр кругового сечения 0<г < а с различными
граничными условиями C22). § 3. Решения, применимые для малых интер-
6 ОГЛАВЛЕНИЕ
валов времени C25). § 4. Полый цилиндр а < г < b C27). § 5. Область огра-
ограничена изнутри цилиндром кругового сечения г = д C29). § 6. Решения,
применимые при больших значениях времени C34). § 7. Область г > я,
ограниченная изнутри круговым цилиндром из идеального проводника C35).
§ 8. Составная цилиндрическая область C39). § 9. Шар. Радиальный тепло-
тепловой поток C41).
Глава XIV. Применение функций Грина к решению уравнения тепло-
теплопроводности 347
§ 1. Введение C47). § 2. Линейный тепловой поток. Полуограниченное твер-
твердое тело х>0 C51). § 3. Линейный тепловой поток в области 0 < х < а C53).
§ 4. Двумерные задачи. Тела с прямоугольным сечением C54). § 5. Прямо-
Прямоугольный параллелепипед 0 < х < ау 0 < у < Ь, 0 < z < с C55). § 6. Линей-
Линейный тепловой поток. Составные твердые, тела C56). § 7. Шар. Радиальный
поток тепла C59). § 8. Цилиндр. Радиальный тепловой поток C61). § 9. По-
Полуограниченное твердое тело х > 0. Трехмерные задачи C63). § 10. Область,
ограниченная двумя параллельными плоскостями C64). § 11. Полуограничен-
Полуограниченное твердое тело г>0с тонкой пленкой на плоскости z = 0 из материала,
имеющего значительно большую теплопроводность. В точке @, 0, z') распо-
расположен единичный мгновенный источник C67). § 12. Неограниченное состав-
составное твердое тело. В точке @, 0, zr) действует мгновенный единичный источ-
источник C68). § 13. Области, ограниченные цилиндрической поверхностью
г = я C69). § 14. Клин 0 < 0 < б0 C71). § 15. Цилиндрическая область C73).
§ 16. Области, ограниченные сферической поверхностью г = а C74).
§ 17. Конус 0<6 < 0О C76). § 18. Непрерывные источники C78).
Глава XV. Дальнейшие применения преобразования Лапласа 381
§ 1. Введение C81). § 2. Теплопроводность в движущемся теле C81).
§ 3. Тепловые регенераторы и теплообменники C85). § 4. Тепловой поток
в слоистых системах C92). § 5. Установившийся периодический режим C93).
§ 6. Линейная асимптотика и запаздывание C96). § 7. Выделение тепла C98).
§ 8. Система автоматического регулирования температуры D01). § 9. Неодно-
Неоднородные тела D05). § 10. Нагревание «цепочки» пластин, между которыми
происходит теплообмен. Слоистые материалы D07). § 11. Прямое применение
метода преобразования Лапласа к двумерным и трехмерным задачам D09).
Глава XVI. Установившаяся температура 415
§ 1. Введение D15). § 2. Источники и стоки .при установившейся темпера-
температуре D15). § 3. Установившийся поток к почти плоской поверхности. Топо-
Топографические поправки для геотермического потока D18). § 4. Установив-
Установившийся тепловой поток в составном теле D19). § 5. Практические задачи D23).
§ 6. Использование сопряженных гармонических функций в задачах с уста-
установившейся температурой D24). § 7. Приложения этого метода D26).
§ 8. Установившийся тепловой поток в многоугольнике D33). § 9. Тепловой
поток между изотермическими поверхностями* D37).
Глава XVII. Интегральные преобразования 445
§ 1. Введение D45). § 2. Интегральные преобразования и формулы их обра-
обращения D46). § 3. Неустановившийся тепловой поток D48). § 4. Установив-
Установившийся тепловой поток D50). § 5. Конечные преобразования D51). § 6. После-
Последовательные преобразования D53).
Глава XVIII. Численные методы 455
§ 1. Введение D55). § 2. Конечные разности D55). § 3. Линейный тепловой
поток в неограниченном пространстве D58). § 4. Граничные условия D62).
§ 5. Выделение тепла, переменная температуропроводность и скрытая теп-
теплота D64). § 6. Релаксационные методы D64).
ПРИЛОЖЕНИЯ 467
1. Контурные интегралы и проверка решений, полученных при помощи пре-
преобразования Лапласа D67). 2. Функция ошибок и родственные функции D70).
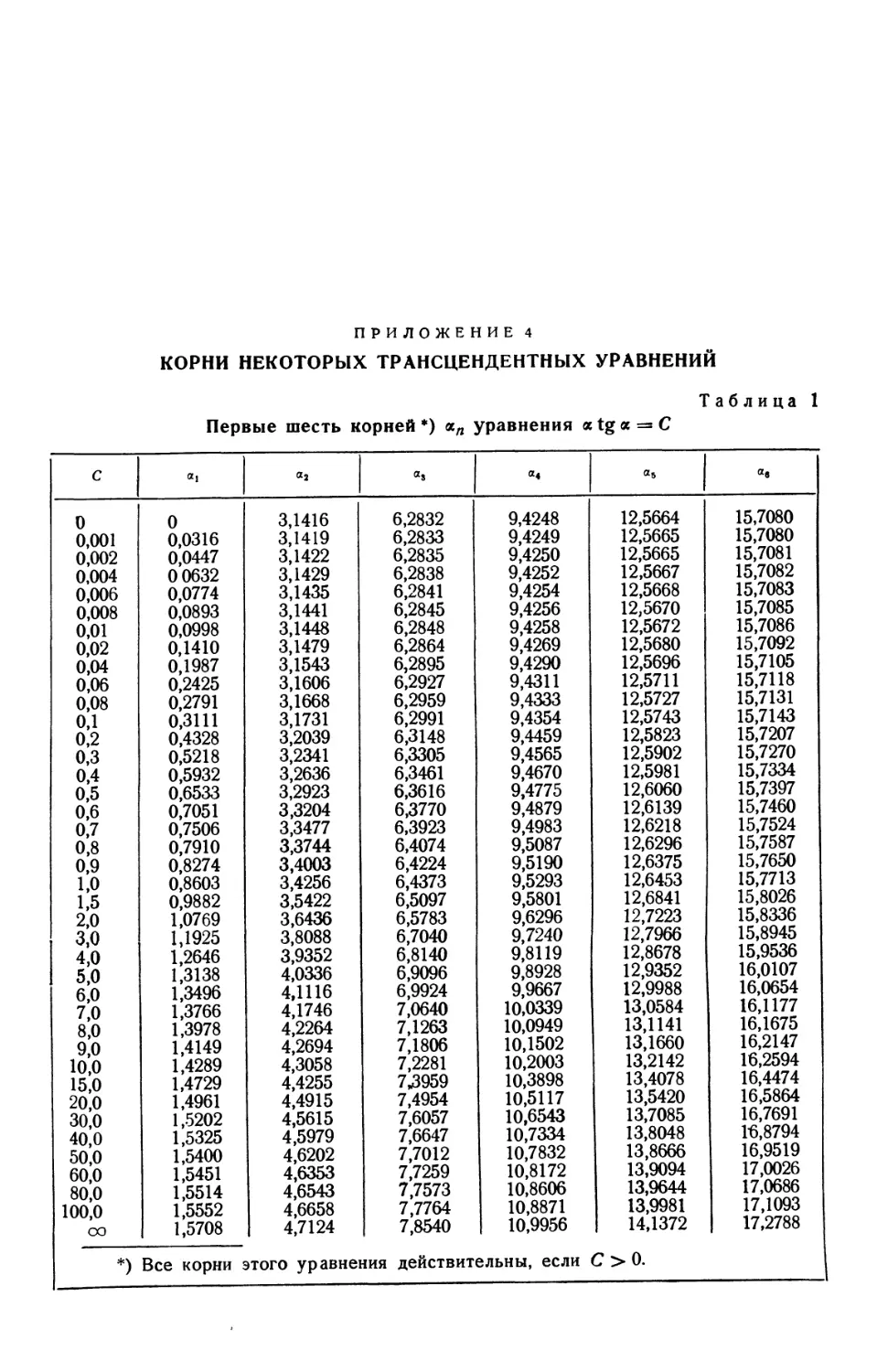
3. О функциях Бесселя D77). 4. Корни некоторых трансцендентных уравне-
ний D80). 5. Таблица преобразований Лапласа v(p) = Г e~ptv(t)dt D83).
о
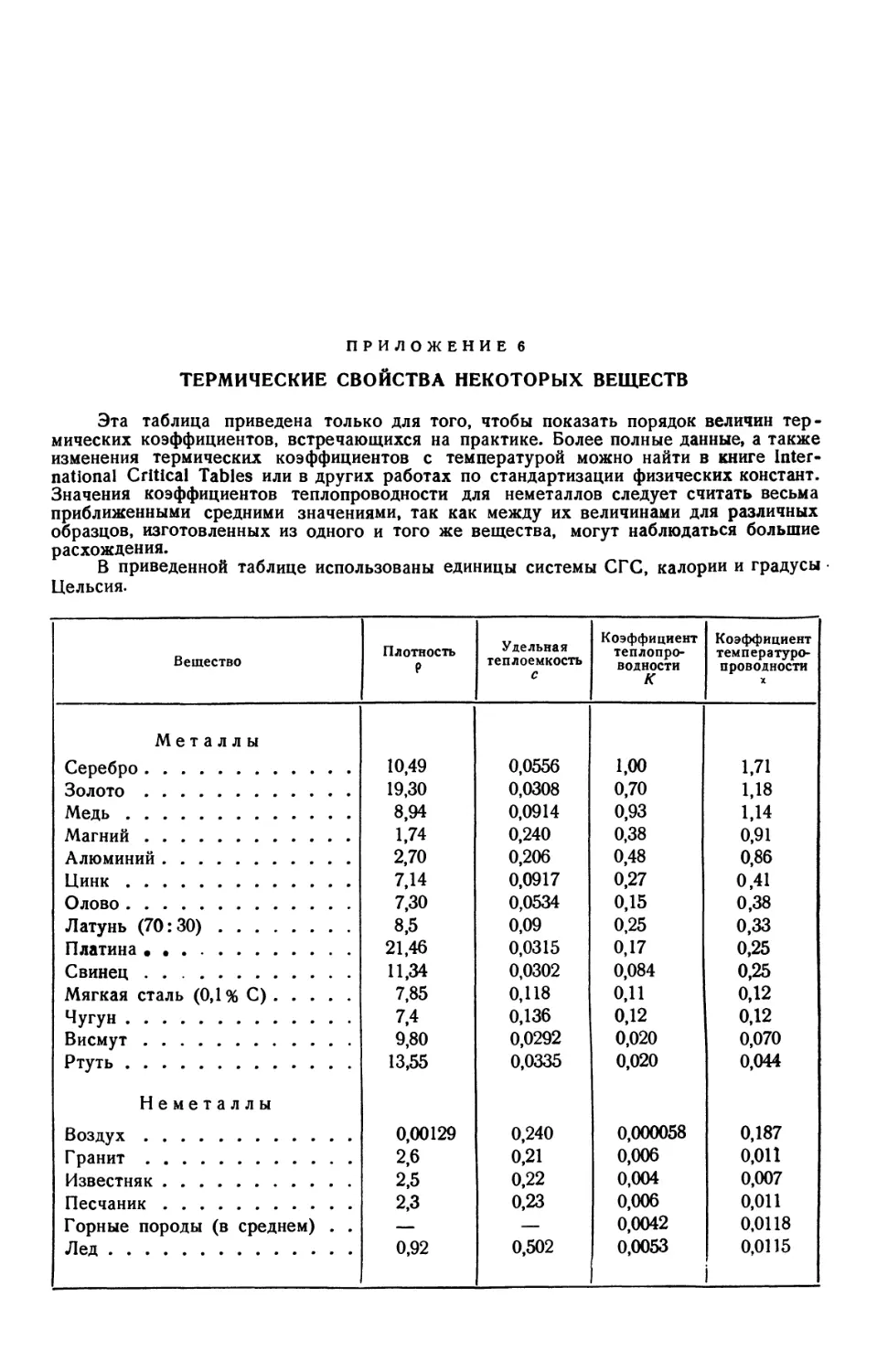
6. Термические свойства некоторых веществ D86).
ПРЕДИСЛОВИЕ РЕДАКТОРА РУССКОГО ПЕРЕВОДА
Книга Карслоу выдержала много изданий. Первоначально — в 1906 г.—
она составляла одно целое с другой книгой Карслоу по теории рядов и инте-
интегралов Фурье *). Это в известной степени предопределило содержание книги—
как первого, так и последующих ее изданий. Настоящая книга пред-
представляет собой как бы вторую часть первоначальной, в которой излагается
применение математических методов, приведенных в первой части, к соответ-
соответствующим задачам теплопроводности. В последующих изданиях A946 и
1959 гг.) число разбираемых задач значительно возросло, но приемы разбора
и глубина рассмотрения изменились незначительно. Как отмечают авторы
в предисловии к изданию 1946 г., материал книги разобран методами Фурье.
В этом и состоит ее главная особенность.
После опубликования первого издания книги наступил период интенсив-
интенсивного развития методов математической физики. Для характеристики их глу-
глубины достаточно упомянуть о ряде фундаментальных трудов, например
о книгах Н. Poincare, Theorie de la propagation de la chaleur, Paris, 1895;
В. А. Стеклова, Основные задачи математической физики, ч. 1 —1922 г.,
ч. 2—1923 г., Петербург; Ф. Франка и Р. Мизеса, Дифференциальные и инте-
интегральные уравнения математической физики, ч. II, ОНТИ, 1937; Р. Куранта
и Д. Гильберта, Методы математической физики, т. I—1933 г., т. II— 1945 г.
В указанных трудах разобраны основные вопросы теории теплопровод-
теплопроводности, а именно: 1) общие свойства решений задач теплопроводности, 2) обос-
обоснование метода разделения переменных, 3) развитие метода источников тепла,
4) теория плавления.
Работы редактора перевода по этим вопросам, задуманные как дополне-
дополнения к настоящей книге, публикуются отдельно от нее.
Следует отметить, что в настоящем издании автор книги существенно
изменил свое отношение к операционным методам решения задач теплопро-
теплопроводности. В первом издании книги Карслоу характеризует операционный ме-
метод Хевисайда следующим образом:
«Операционный метод Хевисайда можно назвать своего рода стенографией.
Его фэрмулы можно получить с помощью контурных интегралов, которыми
мы будем пользоваться на следующих далее страницах. Результаты, которые
здесь получаются, сведены в этой главе. Но за выводами формул Хеви-
Хевисайда трудно следить, и можно смело сказать, что сам он мало заботится
о строгости своих выводов. Действительно строгое обоснование его метода **)
*) Н. S. С а г s I a w, Introduction to the theory of Fourier's series and Integrals,
Lnd., 1921.
.**) Математически строгое обоснование метода Хевисайда дано в работе
G. Doetsch, Theorie und Anvendung der Laplace-Transformation, J. Springer, Berlin, 1937.
С операционными методами можно ознакомиться по следующим книгам: Г. Деч, Руко-
Руководство к практическому применению преобразования Лапласа, Физматгиз, 1960;
8 ПРЕДИСЛОВИЕ РЕДАКТОРА РУССКОГО ПЕРЕВОДА
можно провести, пользуясь контурными интегралами, как показано
ниже» *).
В последнем издании Карслоу пересмотрел свое отношение к опера-
операционным методам. Он их принял в качестве рабочих методов решения задач
теплопроводности и изложил — как сами методы, так и их применение — в гла-
главах XII, XIII и XV. В 1941 г. Карслоу выпустил специальную книгу по опе-
операционному исчислению **).
В главе XI «Изменение физического состояния» дается обзор работ
по теории плавления. Глава написана Егером недостаточно полно и глубоко.
В основном автор изложил в ней работы, вышедшие до 1950 г. После 1950 г.
появились работы принципиального характера, в которых а) исследовались
общие свойства решений задачи плавления—существования и единственности
и б) развивались эффективные методы решения задачи. При этом в общем
случае задача плавления рассматривалась нелинейной—в неоднородном веще-
веществе, плотность и теплопроводность которого изменяются с температурой.
Укажем эти работы:
а) 1. Kyner W. Т. An Existence and Uniqueness Theorem for Nonlinear
Stephan Problem. 2. Friedman A. Free boundary problem for parabolie equa-
equation I. J. of Math. a. Mech., 8, No. 4A959). 3. Sestini G. Rivista Math.
Univ. Parma 3, 3—23, 103—130 A952). 4. Дацев А. ДАН СССР, 87, № 3
A952). 5. Рубинштейн Л. И. Серия работ о единственности решения задачи
Стефана: ДАН СССР, 77, J* 1, 37—40 A951); 79, № 1, 45—47 A951);
117, № 3, 387—390 A957). 6. Олейник О. А. ДАН СССР, 113, № 6 A957).
7. Douglas J. A uniqueness theorem for the solution of a Stephan Problem,
Proc. Am. Math. Soc. 8, 402—408 A957). 8. Evans G. W. II,' Quart. J. AppK
Math. 8, 312—319 A950); 9, 185—193 A951).
б) 1. Landau X. T. Quart. J. Appl. Math. 8, No. 1 A950). 2. Miran-
ker W. L. Quart. J. Appl. Math. 16, 121—130 A958). 3. Citron St. J. Aero-
Aerospace Soc. 27, No. 3 A960). 4. Sounders P. J. Am. Rocket Soc. 30, No. 11,
1030—1032 A960). 5. Померанцев A. A. Tp. I Совещания по тепло- и мас-
сообмену 1961 г., т. Ill, 1963.
Главы I и И и приложения настоящей книги переведены канд. техн.
наук Ю. Н. Петровым, главы III — VIII — канд. техн. наук В. М. Ерошенко>
главы IX — XVIII — канд. техн. наук М. Г. Морозовым.
Редактирование и проверку математического текста перевода книги
выполнили Г. И. Басе и Г. А. Шадрин.
В. А. Диткин и А. П. Прудников, Интегральные преобразования и операционное
исчисление, Фитматгиз, 1961; Б. Ван-дёр-Поль и X. Бреммер, Операционное исчисле-
исчисление на основе двухстороннего преобразования Лапласа, ИЛ, 1952; В. А. Диткин и
А. П. Прудников, Операционное исчисление по двум переменным и его применения,
Физматгиз, 1958; А. В. Лыков, Теория теплопроводности, Гостехиздат, 1952.
*) Г. Карслоу, Теория теплопроводности, Гостехиздат, М., 1947.
**) Г. Карслоу и Д. Е г е р, Операционные методы в прикладной математике,
ИЛ, М., 1948.
А. Л. Померанцев
ИЗ ПРЕДИСЛОВИЯ КО ВТОРОМУ ИЗДАНИЮ
Смерть профессора Карслоу заставила меня самостоятельно готовить
новое издание настоящей книги. При этом я старался — по возможности
сохраняя форму и дух изложения Карслоу — наиболее полно изложить все
точные решения и разрешимые задачи теории теплопроводности. Для этого
пришлось ввести дополнительно очень много новых решений и значительно
расширить изложение ряда вопросов, в частности вопросов генерирования
тепла, поверхностного нагрева, плавления и затвердевания. Более подробно
рассмотрены также применение теории теплопроводности к геофизике, ани-
анизотропные среды, движущиеся среды и вещества с переменными термиче-
термическими коэффициентами.
Добавлены также новые таблицы и рисунки, где приведены численные
данные по наиболее важным проблемам.
При этом оказалось, что число литературных ссылок превысило 700.
Поскольку невозможно перечислить всю литературу, посвященную вопросам
теплопроводности, мне пришлось ограничиться только теми статьями, с кото-
которыми я мог ознакомиться лично; однако при этом я пытался дать правильное
представление о литературе по всем интересующим нас разделам.
В настоящую книгу введены еще две обзорные главы. В одной из них
излагается как введение в метод интегральных преобразований, так и связь
этого метода с классическим методом Фурье. В другой главе приведен обзор
численных методов, получивших в последние годы широкое распространение,
и указана связь полученных результатов с точными решениями, изложенными
выше в тексте.
1959 г. Л. Егер
ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
Книга Карслоу «Введение в теорию рядов Фурье и интегралов Фурье
и математическая теория теплопроводности» (Carslaw, Introduction to the
Theory of Fourier's Series and Integrals and the Mathematical Theory of the
Conduction of Heat) была опубликована в конце 1906 г. В 1920—1921 гг.
она была полностью переработана и разделена на два тома. Второй том
этого труда под названием «Введение в математическую теорию теплопро-
теплопроводности твердых тел» (Carslaw, Introduction to the Mathematical Theory
of the Conduction of Heat in Solids)*) был издан в 1921 г. За последние
25 лет было выполнено столько работ как теоретического, так и приклад-
прикладного характера, содержащих применение полученных результатов, что книгу,
отражающую достижения и успехи в этой области, следует считать новой,
а не переработанным изданием старой. В данной книге, призванной заменить
*) В русском переводе эта книга вышла в 1947 г. под названием «Теория тепло-
теплопроводности» (Гостехиздат, М., 1947). (Прим. ред.)
10 из предисловия к первому изданию
изданную ранее, весь материал трактуется в рамках современных математи-
математических методов. В частности, в нее включено полное изложение метода пре-
преобразования Лапласа и его применение к задачам теплопроводности. Этот
метод заменил собой метод использования контурных интегралов, изложен-
изложенный в гл. X и XI издания 1921 г. Хотя в принципе эти методы родственны
друг другу, первый из них даже проще и глубже. При написании этой книги
мы стремились сделать ее по возможности полезной инженерам и физикам,
не изменяя ее математической сущности. Так, в ней приводятся подробные
решения целого ряда задач практического характера и множество данных
в виде таблиц и графиков. Значительно расширено изложение теории систем,
применяемых в экспериментальных работах; другие вопросы, представляющие
практический интерес, изложены довольно кратко (например, теория авто-
автоматической регулировки температуры; до сих пор в книгах математического
характера такие вопросы не рассматривались).
Можно считать, что первое издание настоящей книги (кроме последних
глав) посвящено в основном изложению методов Фурье, рассматриваемых
классически. В первых десяти главах нового издания мы придерживались
той же схемы. В них точно воспроизведена значительная часть материала,
изложенного в главах I — IX старого издания, но обращено большое внима-
внимание на вопросы, интересующие инженеров и физиков.
В главах XII — XV метод преобразований Лапласа вводится и применяется
к более сложным задачам. Прочитав главу XII, читатель увидит, что приме-
применение этого метода значительно упрощает решение задач, изложенных в пре-
предыдущих главах, и, вероятно, привыкнет пользоваться им.
Много интересных решений напечатано петитом; часто они приводятся
без доказательств и их можно считать примерами. Все главы снабжены биб-
библиографическими ссылками на работы, посвященные как математической тео-
теории теплопроводности, так и физическим применениям теории. Мы надеемся,
что они послужат полезным введением к литературе. Число таких статей вы-
выросло за последнее время настолько, что привести их все невозможно.
Г. Карслоу,
Д. Егер
ГЛАВА I
ОБЩАЯ ТЕОРИЯ
§ 1. Введение
Если различные части тела находятся при различных температурах, то
тепло течет от более горячих частей к более холодным. Следует различать
три механизма распространения тепла: 1) теплопроводность, в результате
которой тепло передается через само вещество; 2) конвекция, в результате
которой тепло передается за счет относительного движения частиц нагретого
тела, и 3) передача тепла излучением, при котором перенос тепла между про-
пространственно разделенными частями тела происходит за счет электромагнит-
электромагнитного излучения.
В жидкостях и газах конвекция и излучение играют первостепенную
роль, тогда как в твердых телах конвекция вообще отсутствует, а излучение
обычно пренебрежимо мало. В настоящей книге мы будем рассматривать
только теплопроводность и, вообще говоря, твердое тело, хотя при опреде-
определенных обстоятельствах полученные результаты остаются справедливыми
и для жидкостей или газов.
В данной главе излагается общая теория теплопроводности; последую-
последующие главы посвящены специальным задачам и методам их решения.
§ 2. Теплопроводность
Можно сказать, что математическая теория теплопроводности основы-
основывается на гипотезе, подсказываемой следующим экспериментом.
Пусть задано некоторое твердое тело в виде пластины, ограниченное
двумя параллельными плоскими поверхностями таких размеров, что при рас-
рассмотрении точек, расположенных в середине плоскостей, эти ограничивающие
поверхности можно считать бесконечными. Обе поверхности пластины под-
поддерживаются при различных температурах, причем разность между ними не
должна достигать таких больших значений, при которых может возникнуть
какое-либо заметное изменение свойств исследуемого твердого тела. Верх-
Верхнюю поверхность пластины можно, например, поддерживать при темпера-
температуре тающего льда, помещая на нее толченый лед, а нижнюю — при неко-
некоторой постоянной температуре, заставляя поток теплой воды непрерывно
обтекать поверхность. Если эти условия сохраняются достаточно долго, то
в каждой данной точке температура пластины достигает определенного зна-
значения, причем в точках, расположенных в какой-либо плоскости, параллель-
параллельной ограничивающим поверхностям пластины, и достаточно удаленных от ее
краев, температура будет оставаться одинаковой.
Рассмотрим часть пластины, ограниченную воображаемым цилиндром
с поперечным сечением S и с осью, перпендикулярной поверхности пластины.
12 ГЛ. I. ОБЩАЯ ТЕОРИЯ [§ 2
Предполагается, что этот цилиндр выделен в середине пластины, и поэтому
тепловой поток через его образующие отсутствует. Пусть температура ниж-
нижней поверхности равна vQ °C, верхней vx °C (v0 > г^), и пусть толщина пластины
равная? см. Результаты экспериментов над различными твердыми телами приво-
приводят к гипотезе, что при достижении установившегося температурного состояния
количество тепла Q, протекающего за t сек через площадку S пластины, равно
где К — константа, зависящая от свойств вещества и называемая коэффи-
коэффициентом теплопроводности данного вещества. Другими словами, тепло-
тепловой поток между двумя поверхностями пропорционален разности температур
между ними.
Нельзя считать, что такой вывод доказывается подобными эксперимен-
экспериментами; они скорее подсказывают этот закон. Более точной проверкой этого
закона служит соответствие экспериментальных данных с расчетными дан-
данными, полученными в математической теории, основанной на предположении
о справедливости указанного закона.
Величина, обратная значению коэффициента теплопроводности, назы-
называется удельным термическим сопротивлением вещества.
Строго говоря, коэффициент теплопроводности К для данного веще-
вещества не остается всегда постоянным, а зависит от температуры. Однако
в ограниченном диапазоне температур этим изменением К можно пренебречь»
и в обычной математической теории предполагается, что коэффициент тепло-
теплопроводности не изменяется с температурой. Более близкое приближение
к действительному положению вещей можно получить, полагая К линейной
функцией температуры vt т. е.
где р мало и для большинства веществ отрицательно.
Из выражения B.1) коэффициент теплопроводности получается в виде
Отсюда следует размерность коэффициента К и природа единиц, в которых
он выражается.
В качестве системы единиц, наиболее часто применяемых в физике,
используется система СГС; в ней температуру измеряют в градусах Цель-
Цельсия (°С), а за единицу тепла принимают калорию, т. е. такое количество
тепла, которое требуется для повышения температуры воды ¦) массой в 1 г
на 1°С. В этой системе К имеет размерность кал/(сек) (см2)(°С/см). В
тех случаях, когда в этой книге даются численные значения, используется
указанная система единиц**).
*) Опыты показывают, что количество тепла, необходимое для повышения тем-
температуры 1 г воды на Г С, не одинаково при различных температурах, и для точного
определения калории должна быть установлена температура воды. Обычно за эту
температуру принимают 15° С, и такая калория определяется как количество тепла»
необходимое для повышения температуры 1 г воды от 14,5 до 15,5° С.
**) В октябре I960 г. XI Генеральная конференция по мерам и весам утвердила
и рекомендовала всем государствам новую Международную систему единиц (систему СИ),
единую для всех областей науки и техники. В СССР она введена в качестве пред-
предпочтительной с 1 января 1963 г.
Новая система единиц основана на шести основных величинах — длине, массе,
времени, температуре, электрическом токе и силе света.
§ 3] ГЛ. I. ОБЩАЯ ТЕОРИЯ 13
В приложении б приведены значения величин (в частности, К), харак-
характеризующих термические свойства некоторых типичных веществ, дающие
представление о порядке этих величин [1].
Из выражения B.2) следует, что в системах, где единицей тепла является
такое его количество, которое вызывает у единицы массы воды увеличение
температуры на одну единицу, К имеет размерность
l B.3)
О
так как отношение —- имеет размерность массы.
с/0 — vx
Если желательно измерять количество тепла работой, необходимой для
получения этого количества, то в качестве единиц используют обычно эрг
или джоуль. Число джоулей У, соответствующее одной калории, называется
механическим эквивалентом тепла. Для определенной выше калории У =4,186.
В основном эксперименте, из которого выведено наше определение
теплопроводности, предполагалось, что исследуемое твердое тело однородно
и что при нагревании какой-либо точки внутри этого тела тепло распро-
распространяется одинаково хорошо во всех направлениях. Такие твердые тела
называются изотропными, в противоположность кристаллическим и другим
анизотропным телам, у которых теплопроводность в одних направлениях
больше, чем в других. Существуют также неоднородные твердые тела,
в которых условия теплопроводности меняются от точки к точке и, кроме
того, в каждой данной точке зависят от направления.
§ 3. Тепловой поток через произвольную поверхность
Количество тепла, передающееся через произвольную поверх-
поверхность S в точке Р и рассчитанное на единицу поверхности в еди-
единицу времени, называется тепловым потоком *) через данную поверх-
поверхность в данной точке и обозначается через /.
Сначала мы покажем, что тепловой поток через плоскость в точке Р
непрерывно изменяется при изменении положения точки Р, если направле-
направление нормали к этой плоскости остается постоянным. Пусть бесконечно малая
площадка а> в плоскости, включающая точку Я, служит основанием цилиндра,
образующие которого равны-и параллельны отрезку РР' длиной е, где е —
бесконечно малая более высокого порядка, чем линейные размеры площадки а>
<рис. 1).
Пусть /jO) и /2а> — величины тепловых потоков через основания цилиндра,
включающие точки Р и Я'. По сравнению с этими потоками тепловой поток
В частности, за единицу температуры в ней принят градус Кельвина (°К).
Из производных единиц в системе СИ отметим следующие:
джоуль (дж)— количество теплоты, эквивалентное работе в 1 дж;
дж/кг • град — удельная теплоемкость вещества, для нагревания 1 кг которого
на 1 град требуется количество теплоты, равное 1 дж;
вт/м • град = дж/м • сек • град — коэффициент теплопроводности вещества,
в котором через 1 м2 сечения при градиенте температуры в 1 град/м в 1 сек прохо-
проходит количество теплоты в 1 дж.
Эти единицы связаны с соответствующими единицами в системе СГС следующим
образом:
количество теплоты'. 1 кал~ 0,239 дж; 1 дж = 4,1868 кал;
удельная теплоемкость: 1 кал/г-град = 2,39-10~4 дж/кг-град; 1 дж/кг-град =
= 4,1868 • 103 кал/г • град;
коэффициент теплопроводности: 1 кал/см - сек - град = 2,39 • 10 вт/м - град;
1 вт/м • град — 418,68 кал/см • сек • град. (Прим. ред.)
*) Численные значения теплового потока обычно даются в кал/см2 • сек.
14
ГЛ. I. ОБЩАЯ ТЕОРИЯ
[§ 3
через криволинейную поверхность цилиндра пренебрежимо мал. Приращение
количества тепла в цилиндре, таким образом, составит m(Ji — /2). Обозна-
Обозначим теперь среднюю температуру вещества в пределах нашего цилиндра
через v, расстояние между основаниями цилиндра — через о, а плотность и
удельную теплоемкость вещества — соот-
соответственно через рис; тогда приращение
fp' ^ количества тепла в цилиндре должно рав-
равняться следующей величине:
'* dv
Приравнивая
получим
обе величины друг другу,
Рис. 1.
Если а—>0, то выражение в правой части стремится к нулю, и следова-
следовательно, /j—>/2.
Важно отметить, что приведенная выше аргументация не требует, чтобы
термические свойства среды изменялись непрерывно; достаточно того, чтобы
они были конечны. Это позволит нам в дальнейшем утверждать, что на
поверхности раздела двух сред тепловой поток непрерывен (см. § 9 данной
главы).
Покажем теперь, что если величины / даны для трех взаимно перпен-
перпендикулярных плоскостей, пересекающихся в некоторой точке, то можно
определить значение / для любой другой плоскости, проходящей через
ту же точку.
Рассмотрим элементарный тетраэдр РАВС, три грани которого РВС,
РСЛ, РАБ параллельны координатным плоскостям, а перпендикуляр, опу-
опущенный из точки Р на грань ЛВС, имеет на-
направляющие косинусы (X, [1, v) и длину р
(рис. 2). Пусть площадь грани ABC равна А;
тогда площади граней РВС, РСЛ и РАВ со-
соответственно равны ХД, [аД, vA.
Если обозначить величины тепловых по-
потоков через элементарные площадки РВС,
PC А, РАВ и ABC через f x% frfzn /. то
приращение количества тепла в тетраэдре
можно записать в виде '
Рис. 2.
С другой стороны, если р и с — соответ-
соответственно плотность и удельная теплоемкость
твердого тела, a v — средняя температура
вещества в пределах нашего тетраэдра, то
это приращение количества тепла должно равняться следующей величине:
1 л dv
Отсюда вытекает, что
C.1)
Далее, если р стремится к нулю, то правая часть соотношения C.1) также
стремится к нулю и /х, /у, /г и / становятся равными потокам тепла,
§ 51 гл. i. общая теория i5
протекающим в точке Р через плоскости, параллельные координатным пло-
плоскостям, и через плоскость, включающую точку Я, нормаль к которой имеет
направляющие косинусы (Х„ jx, v). Таким образом, мы имеем
/ = */* + !*/, + */,• C-2)
Если в точке Р известны значения трех тепловых потоков fx, /y, fz
через плоскости, параллельные координатным плоскостям, то из соотноше-
соотношения C.2) можно определить тепловой поток через любую другую плоскость,
проходящую через точку Р.
Каждой точке Р твердого тела соответствует вектор f, составляющие
которого равны fx, /y, fz. Его модуль равен
/ш = УЩ+Уг+fl)' (з-з)
а направлен он вдоль линии, направляющие косинусы которой равны
А 4- А C 4)
/m /m /m
Такой вектор можно назвать вектором теплового потока в точке Р.
Тепловой поток в точке Р через плоскость, нормаль к которой определяется
отношениями C.4), как раз и равен fm\ поток в точке Р через плоскость,
нормаль к которой образует угол б с направлением, определенным отноше-
отношениями C.4), равен /mcos6.
§ 4. Изотермические поверхности
Рассмотрим твердое тело, в котором распределение температур в момент
времени t задано соотношением
У. г* О-
Выберем теперь в этом твердом теле поверхность таким образом, чтобы
в какой-либо момент времени температура всех ее точек была одинаковой
и равной, скажем, V. Такая поверхность называется изотермической по-
поверхностью температуры V; можно считать, что эта поверхность отделяет
части тела с температурой, большей V, от частей с меньшей температурой.
Мы можем представить себе изотермы, проведенные в данный момент вре-
времени для различных температур, отличающихся друг от друга на целые
градусы и на доли градуса. Эти изотермические поверхности могут распо-
располагаться любым образом, но две такие поверхности не могут пересекаться,
так как никакая часть тела не может иметь две температуры одновременно.
Таким образом, можно считать, что изотермические поверхности раз-
разделяют твердое тело на тонкие слои.
§ 5. Теплопроводность изотропных тел
В дальнейшем, если это не оговорено особо, мы будем рассматривать
только изотропные среды, т. е. такие среды, структура и свойства которых
в непосредственной близости от какой-либо точки одинаковы "во всех напра-
направлениях. Вследствие такой симметрии вектор теплового потока в какой-либо
точке должен быть направлен вдоль нормали к изотермической поверхности,
проходящей через эту точку, в сторону меньшей температуры.
Соотношение между скоростью изменения температуры в направлении
нормали к изотерме и вектором теплового потока, имеющим такое же
16 ГЛ. I. ОБЩАЯ ТЕОРИЯ [§ 5
направление, можно вывести из основного эксперимента, описанного в § 2
данной главы. В этом случае изотермы представляют собой плоскости,
параллельные поверхностям пластины. Предположим, что изотермы темпе-
температур v и v -f- bv распоюжены на расстоянии Ьх друг от друга. Тогда,
согласно соотношению B.1), количество тепла, проходящее в единицу вре-
времени через единичную площадку в положительном направлении х, равно
bv
или при 8лг—>0
/, = -*?• • E.1)
Обобщим этот результат для любой изотермической поверхности и
в качестве основной гипотезы математической теории теплопровод-
теплопроводности примем, что величина теплового потока через любую изотер-
изотермическую поверхность изнутри наружу (т. е. количество тепла,
рассчитанное на единицу площади и единицу времени) равна
где К — коэффициент теплопроводности вещества, а символ -т— озна-
означает дифференцирование вдоль внешней нормали к поверхности.
Приступим теперь к нахождению теплового -потока через любую, не
обязательно изотермическую, поверхность в некоторой ее точке Р. Пусть
изотерма в точке Р касается плоскости XY; тогда тепловые потоки в
точке Р через плоскости, параллельные координатным плоскостям, будут
равны
?
Пусть теперь нормаль в точке Р к заданной поверхности имеет напра-
направляющие косинусы (X, [х, v); тогда, согласно соотношению C.2), тепловой
поток через эту поверхность будет равен
„ dv „ dv
где символ -тгт- означает дифференцирование в направлении (X, ja, v), так как
dv > dv . dv . dv dv dv Л
Таким образом, величина теплового потока в данной точке через любую
поверхность равна
где символ -^j- означает дифференцирование в направлении внешней
нормали.
В частности, тепловые потоки через три плоскости, перпендикулярные
координатным осям, соответственно равны
/,—*&• /,—«?. /.—*?•• <м>
При использовании вектора f* введенного в § 3 настоящей главы, получен-
полученные результаты можно представить в виде
/= — Kgtadv.
§ 6] ГЛ. I. ОБЩАЯ ТЕОРИЯ 17
§ 6. Дифференциальное уравнение теплопроводности
для изотропного твердого тела
Рассмотрим сначала случай, когда тепло течет через твердое тело,
причем внутри тела источники тепла отсутствуют. Температура v в точке
Р(х, у у z) является непрерывной функцией х, yt z и t\ как показано в § 3,
то же утверждение справедливо и для теплового потока.
Выделим в данном твердом теле элемент объема — прямоугольный
параллелепипед с центром в точке Р и ребрами длиной 2dxt 2dy и 2dz>
параллельными осям координат. Пусть ABCD и A'B'C'D'— грани, перпен-
перпендикулярные оси х и отстоящие от центра параллелепипеда соответственно
на расстоянии —dx и -\-dx. Тогда количество тепла, поступающее в парал-
параллелепипед через грань ABCD, записывается в виде
где fx — величина теплового потока в точке Р через плоскость, параллель-
параллельную ABCD. Аналогичным образом количество тепла, вытекающее через
грань A'B'C'D', равно
Тогда приращение количества тепла в параллелепипеде, обусловленное
тепловым потоком через эти две грани, равно
— Sdxdydz-^-.
Точно так же находят аналогичные выражения для приращения коли-
количества тепла, обусловленного потоком тепла через остальные пары граней.
Суммируя эти выражения, мы получим общее приращение количества тепла
в параллелепипеде в виде
F.1)
где /—вектор, определенный соотношением C.4). Вместе с тем это же
увеличение количества тепла в параллелепипеде можно представить в виде
Spc^-dxdydz, F.2)
где р — плотность, а с — удельная теплоемкость *) (при температуре V)
твердого тела.
*) Удельная теплоемкость вещества с при температуре v определяется как bQ/bv,
где bQ — количество тепла, необходимое для повышения температуры единицы массы
вещества в пределах узкой области температур от v до v-\-bv. Теплоемкость зави-
зависит как от температуры, так и от способа нагрева; этот последний мы будем считать
таким, чтобы деформации были постоянными. В данной книге теплоемкость выра-
выражается в единицах #дл/г • г/?дд, причем теплоемкость воды при 15° С равна 1 кал/г*град.
Следует отметить, что в определениях удельной теплоемкости имеются значительные
расхождения. Так, например, некоторые авторы определяют удельную теплоемкость
как отношение количества тепла, повышающего температуру единицы массы вещества
на 1° С, к аналогичному количеству тепла для воды.
Для твердых тел изменением удельной теплоемкости в зависимости от способа
нагрева пренебрегают, и поэтому с можно заменить на ср, т. е. на удельную тепло-
теплоемкость при постоянном давлении. К этому вопросу мы вернемся ниже (см. стр. 21).
2 Г. Карслоу, Д. Егер
18 ГЛ. I. ОБЩАЯ ТЕОРИЯ [§ б
Приравнивая выражения F.1) и F.2), получаем*)
dv (dfx д/у д/2\
Полученное уравнение справедливо для любой точки твердого тела при
условии, что в этой точке отсутствует источник тепла. При использовании
этого уравнения не требуется, чтобы твердое тело было однородным или
изотропным. Уравнение F.3) соответствует уравнению неразрывности в гид-
гидродинамике.
Для однородного изотропного тела, у которого коэффициент теплопро-
теплопроводности не зависит от температуры, fx, fy и fz даются соотношениями E.3)„
и уравнение F.3) приобретает следующий вид:
d2v , d2v . d2v Lj^_o ,* а\
где
Константу у. Кельвин назвал коэффициентом тепловой диффузии, а Мак-
Максвелл— коэффициентом температуропроводности **), так как х харак-
характеризует то изменение температуры, происходящее в единице объема вещества,
которое обусловлено количеством тепла, протекающим в единицу времени
через единичную площадку в слое единичной толщины и при единичной раз-
разности температур на его поверхностях.
Уравнение F.4) известно как уравнение теплопроводности. В случае
установившейся температуры, когда v не изменяется со временем, это урав-
уравнение превращается в уравнение Лапласа
_9 d2v , d2v . d2v л
V2v = -т-т + -3-F+ -5-т = 0. F.6>
ОХ2 ду2 OZ2 х^'^г
Если в точке Р(х, у, z) твердого тела существует источник тепла, выде-
выделяющий в единице объема за единицу времени количество тепла Л(лг, у, z, t)»
то в соотношение F.1) следует ввести дополнительный член SAdx dy dz и
в случае постоянного К соотношение F.4) принимает вид
>. "F.7)
% dt К
Для установившегося режима, т. е при -^- = 0, уравнение F.7) превра-
превращается в уравнение Пуассона.
Почти во всех задачах, имеющих точное решение, а также в задачах*
рассматриваемых в настоящей книге (если нет специальных указаний), терми-
термические характеристики вещества К, р, с считаются постоянными, т. е. не за-
зависящими от положения выбранной точки и от температуры тела. Если это
не так, то соотношение F. 3) все же остается справедливым, причем при
*) В проводниках тепла, например в волокнистых или других материалах с боль-
большой пористостью, перенос тепла вследствие излучения может оказаться значительным,
что приведет к появлению дополнительного члена в соотношении F.3) [3, 4].
**) Значения коэффициентов температуропроводности для различных веществ при-
приведены в приложении 6. Для того чтобы найти размерность этого коэффициента, обо-
обозначим размерность теплового потока и температуры соответственно через [О] и [v]^
Тогда размерности [К] = [Q] [L~l] [T~l] [v~1]; [с] = [Q] [M~l] lv"lY» М = 1^1 U~31 и,
следовательно, [%] = [L2] [Т~1].
§ б] ГЛ. I. ОБЩАЯ ТЕОРИЯ 19
наличии источника тепла к правой его части добавляют член Л(х, у, z, t),
а соотношение F.7) принимает следующий вид:
д („ dv \ , д („ dv \ . д („ dv \ . . /с оч
)+)+)+А F'8)
Если К и Л являются функциями только положения, то при решении
уравнения F.8), в принципе, не приходится сталкиваться с большими труд-
трудностями, и для тел, в которых термические характеристики имеют разрыв
(составные тела), и тел, в которых изменение К с положением подчиняется
простому закону, пригоден целый ряд решений. Если же термические свой-
свойства зависят от температуры, то ситуация значительно усложняется, так как
уравнение становится нелинейным. Таких случаев, связанных с теплопровод-
теплопроводностью, исследовано очень мало, что объясняется относительно слабым изме-
изменением термических свойств с температурой, а имеющиеся данные по этому
вопросу весьма скудны и неточны. Между тем подобные задачи приобре-
приобретают все большее значение в тех случаях, когда приходится рассматривать
значительные изменения температуры, как, например, при застывании отли-
отливок. Кроме того, те же уравнения играют важную роль в теории диффузии,
когда имеет место резкое изменение коэффициентов диффузии в зависимости
от концентрации (см. [71], гл. IX—XI). Для решений в большинстве случаев
были использованы численные методы; несколько общих результатов и слу-
случаи, для которых возможно точное решение, будут изложены ниже.
I. Термические характеристики изменяются с температурой и не зависят
от положения *).
В данном случае соотношение F.8) принимает следующий вид:
V2 i ( dv V2 i / dv \2 ) /я пч
) +(w) +(w) f. F.9)
Как мы видим, это уравнение нелинейно. Соотношению F.8) можно придать более
простую форму [5—7], вводя новую переменную
V
= -^- f Kdv, F.10)
е
где Ко — значение К при v = 0. Ко и нижний предел интегрирования вводят только
для того, чтобы придать величине О размерность температуры и определенное зна-
значение. Из соотношения F.10) следует, что **)
дО К dv G0 К dv v0 К dv v0 К dv
'Ж=='К0"ЬТ'9 17 =~Ко~~дх'у W=='Ko'W'9 ~оЧ ==~Ko"d7*
и соотношение F.8) принимает вид
V20_l^- = _-^L, F.11)
is
где А и х = — выражены через новую переменную 0. Таким образом, при исполь-
использовании этой новой переменной сохраняется форма уравнения теплопроводности F.7),
но коэффициент температуропроводности х становится зависимым от в. В большинстве
случаев изменение х с температурой значительно менее важно, чем аналогичное
изменение К и, таким образом, с достаточным приближением можно считать х по-
постоянным. Например, для металлов, находящихся при температурах, близких к абсо-
абсолютному нулю, как /С, так и с приблизительно пропорциональны абсолютной темпе-
температуре. В таких случаях, если А не зависит от vt то уравнение F.11) принимает
тот же вид, что и F.7). Для случая постоянной теплопроводности можно сразу же
*) Несколько других методов для одномерного случая будет изложено в § 16
гл. II.
**) 0 является по существу потенциалом, градиент которого пропорционален
тепловому потоку [8].
20 ГЛ. L ОБЩАЯ ТЕОРИЯ [§ 6
получить решение, заменив v на 9, но при этом граничные условия должны опреде-
„ dv
ляться только v или л -5—; если они записываются в виде
on
¦%L + hv = 0,
дп '
где h — постоянная, то это замечание не имеет силы.
Случай установившегося теплового потока представляет особый интерес, так как
при А= const уравнение F.11) превращается в уравнение Пуассона, а при Л = 0 —
в уравнение Лапласа. Таким образом, решения задач об установившемся тепловом
потоке при теплопроводности, являющейся произвольной функцией температуры, и
с граничными условиями для температуры или теплового потока, можно непосред-
непосредственно получить из соответствующих решений для случаев постоянной теплопро-
теплопроводности.
Другую удобную форму уравнения легко получить, вводя переменную W — тепло-
теплосодержание единицы массы вещества, измеренное относительно некоторого произ-
произвольного нулевого значения температуры. Подставляя W в уравнение F.8), получим
dW д tKdv\ д („dv\ д (/rdv\ fil9
[K) + K)+K) + A FЛ2)
или, воспользовавшись соотношением F.10),
Ь?« <613>
где W связано с в каким-то определенным образом.
Введение величины W имеет ряд преимуществ при решении задач, в которых
учитывается скрытая теплота.
II. Источник тепла внутри твердого тела.
Случаи, когда внутри твердого тела имеется источник тепла, приобретают все
большее и большее значение в технике. Внутри твердого тела тепло может образо-
образовываться в результате следующих процессов: а) пропускание электрического тока,
б) диэлектрический или индукционный нагрев [9—12]; в) радиоактивный распад
([13, 14]; см. также библиографию к гл. II и IX); г) поглощение излучения *), д) пере-
переход механической энергии в тепловую при вязких или пластических деформациях;
е) химические реакции ([71], гл. VIII; см. также библиографию к гл. XV настоя-
настоящей книги), в том числе ряд самых различных процессов, начиная от гидратации
цемента [15—19] **) и кончая созреванием яблок [20].
Во всех случаях, кроме последнего, количество выделяемого тепла в первом
приближении не зависит от v\ в более точном приближении оно обычно соответствует
формуле
A +b F.14)
где а и b — постоянные, которые могут иметь любой знак ***).
Следует отметить, что уравнение F.7) с величиной А, соответствующей выра-
выражению F.14), можно точно решить многими способами (см. § 14 гл. I и § 7 гл. XV).
Количество тепла, выделяющегося в результате химической реакции нулевого
порядка, обычно рассчитывают по формуле Аррениуса
_А
А = Аое Т> F.15)
*) Например, инфракрасные лучи сильно поглощаются слогм сетчатки глаза
и могут повысить ее температуру до величины, вполне достаточной, чтобы повре-
повредить глаз.
**) В первом приближении количество выделяемого в этом случае тепла можно
записать в виде ke~at, причем количество тепла, выделенного 1 г цемента в тече-
течение 3 дней, примерно равно 50—100 кал\ это позволяет принимать важнейшие техни-
технические решения, в частности при проектировании больших дамб.
***) Как известно, для большинства веществ температурный коэффициент элек-
электрического сопротивления положителен и, следовательно, Ь в соотношении F.14)
положительно; однако для некоторых материалов, в частности для графита и для
расплавленных солей, Ь отрицательно. Значения b оказываются также отрицательными
в задачах о диффузии с одновременно протекающей химической реакцией. Помимо
этого, соотношение F.14) с отрицательной величиной b служит грубым приближе-
приближением для случая тела, отдающего тепло жидкости, циркулирующей в решетчатой
системе трубок [21].
§ 7] ГЛ. I. ОБЩАЯ ТЕОРИЯ 21
где Ао и k—постоянные, а Т — абсолютная температура [22—24]. Для реакций более
высокого порядка следует использовать аналогичное, но более сложное выражение.
В некоторых случаях его находят экспериментально, и оно имеет вид *)
А = AQ exp (bv).
Для всех описанных выше случаев не существует аналитических решений, и поэтому
следует применять численные методы. Выражением F.14) можно пользоваться как
самым грубым приближением, но, по-видимому, точные решения очень сильно отли-
отличаются от перечисленных приближений.
III. Эффекты термического расширения.
Уравнение F.3) выведено в предположении, что в результате деформации
твердого тела работа не совершается, и поэтому с является удельной теплоемкостью
только при постоянной деформации. Если напряжения в твердом теле вызывают
деформацию, т. е. совершается работа, то это надо учесть, соответственно изменив
уравнение F.3). Если возможно неограниченное расширение при постоянном давле-
давлении, то уравнение F.3) все еще имеет силу при условии, что с считают равным ср, т. е.
удельной теплоемкости при постоянном давлении. Если же это расширение ограничено,
то в уравнении появляются дополнительные члены. Так, в случае напряжений, обу-
обусловленных, например, гидростатическим давлением /?, в правую часть уравнения F.3)
следует добавить член
где Т — абсолютная температура, а— термический коэффициент линейного расшире-
расширения, а под с в уравнении F.3) следует понимать ср, т. е. теплоемкость при постоян-
постоянном давлении. Общий случай напряжений разобран в работах [28, 29] **).
§ 7. Дифференциальное уравнение теплопроводности
для движущейся среды
Рассмотрим сначала твердое тело, движущееся со скоростью, компоненты кото-
которой равны иХУ Uy, uz. При вычислении теплового потока через произвольную пло-
плоскость к тепловому потоку в неподвижном теле следует добавить член, обусловлен-
обусловленный конвекцией, с составляющими pcvux, $cvuyy $cvuz. Тогда компоненты вектора
теплового потока можно записать в виде
/г = — К -gj + ?CVUX, fy = — К -jj- + fCVUy, /г=—К-?. + ?CVUZ. G.1)
Подставив эти величины в уравнение F.3), получим для случая постоянного К и
отсутствия источника тепла внутри тела следующее выражение ***):
dv . dv , dv . dv _„ Л ,-n.
dt ' х дх ' у ду ' z dz y '
Уравнение G.2) можно записать в виде
%l—*V*v-0, G.3)
где D/Dt обозначает так называемую субстанциональную, или полную, производ-
производную [37]. Если внутри твердого тела имеется источник, выделяющий в единице
объема в единицу времени количество тепла, равное А, т. е. источник мощностью Д
то к правой части уравнения G.3) нужно добавить член —.
*) Такое соотношение встречается при решении некоторых химических задач [25],
а также в теории теплового пробоя диэлектрика [26—27] (см. также § 7 гл. XV).
**) Эффект увеличения потенциальной энергии вследствие сжатия был впервые
исследован Дюамелем [30].
***) Подобное обсуждение применительно к жидкости было проведено Вильсо-
Вильсоном [31], который решил ряд интересных задач, связанных с установившимися распре-
распределениями температур. Следует также указать на некоторые другие работы [32,33,34].
Известен целый ряд точных решений для случая ламинарного течения вязких жидко-
жидкостей, в частности для течения в трубе при пуазейлевском распределении скоро-
скоростей [35,36].
22 ГЛ. I. ОБЩАЯ ТЕОРИЯ [§ 7
Следует отметить, что уравнение G.2) можно получить путем преобразования
системы координат к системе, движущейся со скоростью {их, иу, uz), в отношении
которой справедливо обычное уравнение теплопроводности F.4).
Вывод уравнений теплопроводности для случая течения сжимаемой жидкости
будет изложен в сокращенном виде, так как эта задача аналогична задаче о тепло-
теплопроводности в деформируемом твердом теле [38, 39]. Ясно, что термодинамические
н гидродинамические величины, встречающиеся в наших исследованиях, должны
быть определены совершенно точно. В дальнейшем мы будем использовать плот-
плотность р, абсолютную температуру Т и внутреннюю энергию единицы массы U. Кроме
того, мы введем подстрочные индексы, например, примем для координат обозначения xit
где / = 1, 2, 3; повторение индексов означает, что нужно производить суммирование;
например, в выражении G.4) Ify означает 1ХЬХ -f- 1?г + h^z- Воспользуемся формулой
Грина*) [37, 40], согласно которой, если функции ^ (/== 1, 2, 3) и их первые произ-
производные внутри замкнутой поверхности «S являются непрерывными функциями jt/, то
//•*«-///¦&*¦
где 1[ (/=1, 2, 3) — направляющие косинусы внешней нормали к поверхности, левая
часть — двойной интеграл по поверхности «S, а правая часть — тройной интеграл
по объему, ограниченному этой поверхностью.
Пусть «S — некоторая малая замкнутая поверхность в жидкости, причем объем,
ограниченный указанной поверхностью, всегда содержит одни и те же частицы
жидкости. Обозначим элемент этой поверхности через dS, а элемент объема, ограни-
ограниченного поверхностью «S, через dz. Сохранение массы р^в произвольном элементе
объема dz означает, что
Dt
Как показал Ламб [37], соотношение G.5) приводит к уравнению неразрывности.
Пусть Xi — сила, отнесенная к единице массы, Ец— тензор напряжений, а щ —
компоненты скорости; тогда уравнение движения для указанного элемента можно
записать в виде
/=1,2,3, G.6)
где поверхностные и объемные интегралы берутся соответственно по всей поверх-
поверхности 5 и по всему ограниченному ею объему.
Используя соотношения G.4) и G.5), уравнение G.6) можно записать в форме
Согласно первому закону термодинамики для указанного элемента получим
IfffXlUldx+f IEijUiljdS~ff fihdS> G'8)
где /(— компоненты вектора теплового потока на поверхности S, т. е.
/ K ' 123
G9)
При использовании соотношений G.4), G.5) и G.7) уравнение G.8) приобретает
следующий вид:
*) В русской литературе эту формулу называют формулой Остроградского.
Прим. ред.)
§ 8] ГЛ. I. ОБЩАЯ ТЕОРИЯ 23
где eij — компоненты тензора скоростей деформации, т. е.
Вц = ~ рЬи + 2{х ( ец - у hjekk) . G.12)
Уравнение вязкости дает связь между Ец и ец, а именно
Вц = ~ рЬи + 2{х ( ец - у hjekk) .
fO при *=?./,
еде р — гидростатическое давление, fx — коэффициент вязкости, а Ъу = < . . —
^ 1 при / = j
символ Кронекера. Используя G.12) и G.9), можно записать уравнение G.10) в виде
?;)- GЛЗ)
совпадающем по форме с уравнением G.3).
Первые двд члена в правой части соответствуют теплу, выделяемому вследствие
процессов сжатия и трения в жидкости, третий член представляет собой обычную div/.
Б левой части G.13) стоит р D , заменяющее величину ?c—jjt b уравнении G.3).
Разумеется, можно выполнить дальнейшие преобразования уравнения G.13), основан-
основанные на термодинамике; в частности, его можно выразить через энтропию.
§ 8. Преобразование координат
Приведенные выше уравнения можно легко преобразовать к другим
системам ортогональных координат *). Наиболее удобными из них являются
сферические координаты, в которых положение точки определяется расстоя-
расстоянием г от начала координат, широтой б и азимутом ср, а также цилиндри-
цилиндрические координаты, в которых положение точки определяется полярными
координатами (г, 6) ее проекции на плоскость (лг, у) и координатой z.
Эти системы координат являются частными случаями общей системы
ортогональных координат, в которой положение точки задается пересечением
трех ортогональных поверхностей
? = const, у\ = const, С = const.
Покажем теперь, как легче всего осуществить это преобразование.
Рассмотрим элемент объема, ограниченный поверхностями k±d?, v\± di\%
С ± rfC, и допустим, что A'B'C'D' и ABCD лежат на поверхностях ? ± d{.
Пусть уравнение
ds2 = X2 d$ -f- [х2 dr? + v rfC2
определяет длину элементарной дуги, соединяющей точки (?, т], С) и
C + Q
^ + Q
Тогда площадь участка поверхности ?, вырезаемого поверхностями
=7] ± d-q и С ± d(> в точке Я(?, у\, С), равна
а количество тепла, протекающее через эту площадку в единицу времени,
равно
где Д — величина теплового потока через поверхность $ в точке Р.
*) В настоящей книге мы не будем рассматривать эллиптические координаты.
Эллиптический цилиндр рассмотрен в работах Мак-Лахлана [41, 42]. Область, огра-
«иченная изнутри эллиптическим цилиндром, рассмотрена в работе Трантера [43].
Вопрос об эллипсоидах изложен в работах [44, 45].
24 ГЛ. I. ОБЩАЯ ТЕОРИЯ [§ 8
Следовательно, количество тепла, втекающее в элемент объема через
поверхность ABCD, окончательно равно
4 {^Д_^(
а количество тепла, вытекающее через поверхность A'B'C'D', равно
Отсюда полный прирост количества тепла в элементе объема, обусло-
обусловленный тепловым потоком через эти две поверхности, равен
Для остальных поверхностей получим соответственно
и — S-
Подставляя вместо Д, / , /с их выражения, а именно:
К dv , _ К dv _ К dv
и приравнивая сумму полученных таким образом выражений величине
8Xp,v dt dri d(,cp -^-,
находим
» /^ dv \ , d ( v\ ,. dv
к
Если К — постоянная и, как обычно, мы можем написать, что х = —, то
это соотношение принимает следующий вид:
Сферические координаты. В этой системе
jc = rsin6 coscp,
у — г sin Gsincp,
z = г cos б
и
ds2 = dr2 H- r2db2 + г2 sin20 df.
Таким образом, уравнение для v принимает следующий вид:
L д (cinfi dv
dt—гПдгУ dr)^ smO
Его можно написать так:
dv _ rd*v , 2 dv , 1 д(п ..2Ч dv \ , 1
' (8-3)
где t* = cos0.
Цилиндрические координаты. В этой системе
х = г cos 6, у = г sin 6
§ 9] ГЛ. I. ОБЩАЯ ТЕОРИЯ 25»
и
Таким образом, уравнение для v принимает следующий вид:
dv х г д ( dv \ , д (I dv \ д ( dv
Его можно записать иначе:
dv \d2v , 1 dv , 1 d2v
§ 9. Начальные и граничные условия
Прежде чем приступить к математическому рассмотрению задач теории
теплопроводности, необходимо сформулировать начальные и граничные усло-
условия, которым должна удовлетворять температура. Эти условия определяются?
частично непосредственными результатами экспериментов, а частично мате-
математической трактовкой гипотез, основанных на этих результатах.
Пусть внутри твердого тела температура v является непрерывной функ-
функцией х, у, z и t\ пусть ее первая производная по t и первые и вторые про-
производные по х, у и z также непрерывны. Указанные предположения не рас-
распространяются на границу твердого тела, а также на некоторый момент
времени, с которого, как предполагается, начинается поступление тепла.
I. Начальные условия.
Предполагается, что в некоторый момент времени, принятый нами за на-
начало отсчета координаты t, температура по всему телу задана произвольно.
Если эта произвольная функция непрерывна, то мы должны найти такое
решение задачи, которое по мере приближения t к нулю стремилось бы к за-
заданной величине. Другими словами, если начальная температура задана в виде
v = f(x, у, z),
то наше решение уравнения
dv
должно быть таким, чтобы для всех точек твердого тела выполнялось условие
\im(v) = f(x, у, г).
Если начальное распределение температуры разрывно в некоторых
точках или на поверхностях, то эти разрывы должны исчезнуть через
очень короткое время, и тогда наше решение должно стремиться к задан-
заданной величине начальной температуры во всех точках, где распределение
непрерывно.
II. Граничные условия, или условия на поверхности.
Перечислим условия на поверхности, обычно встречающиеся в теории
теплопроводности.
А. Задана температура на поверхности. В этом случае темпера-
температура может быть либо постоянной, либо зависеть от времени, либо от поло-
положения, либо, наконец, зависеть и от времени и от положения. Подобный
случай граничных условий наиболее прост и уже достаточно хорошо изучен.
Следует, однако, отметить, что на практике часто очень трудно задать
температуру на поверхности, и поэтому существующие в действительности-
26 ГЛ. I. ОБЩАЯ ТЕОРИЯ [§ 9
условия лучше всего описываются граничными условиями, рассматриваемыми
« пункте Г (см. ниже).
Б. Отсутствует тепловой поток через поверхность исследуемого
тела, т. е. во всех точках поверхности имеет место соотношение
dv -О
где д/дп обозначает дифференцирование вдоль внешней нормали к поверх-
«ости.
В. Задан тепловой поток через поверхность.
Г. Теплопередача на поверхности линейна или происходит теп-
лообмен «излучением» по закону Ньютона,
Если тепловой поток через поверхность пропорционален разности тем-
лератур между поверхностью и окружающей ее средой, то он равен
H(v — v0), (9.1)
где v0 — температура среды, Н — константа; тогда граничные условия запи-
записываются в виде
^ — *0) = 0. или -*! + *(* —*0) = 0. (9.2)
где
*=х- (9-3)
Если h —> 0 *), то указанные условия обращаются в граничные условия типа
Б, если же Л—>оо, то они обращаются в условия типа А.
Величина Н была названа внешней, или поверхностной, теплопровод-
теплопроводностью, но теперь ее обычно называют коэффициентом поверхностной
теплопередачи или теплоотдачи **). Очень часто удобно пользоваться вели-
величиной поверхностного термического сопротивления, отнесенного к еди-
единице площади, т. е. величиной, обратной Н, /? = —.
Если к тому же задан тепловой поток F на поверхности, то выраже-
выражение (9.2) примет следующий вид:
i) O. (9.4)
Соотношение (9.4) совпадает с соотношением (9.2), в котором v0 заменено
77
Это граничное условие называется в классических работах граничным
условием при теплообмене излучением (см. соотношение (9.12)). Однако
в действительности такое название приводит к некоторому заблуждению,
так как, когда речь идет о передаче тепла излучением, тепловой поток про-
пропорционален четвертой степени абсолютной температуры; все же, ради крат-
краткости, в настоящей книге мы обычно будем определять граничное условие
Г как «теплообмен излучением в среду с температурой z;0» вместо громозд-
*) Всегда подразумевается, что h > 0; случай h < 0 соответствует наличию источ-
источника тепла, причем количество поступающего на поверхность тепла пропорционально
^е температуре. Математические решения для случая h > 0 обычно не действительны
для случая h = 0.
**) С нашей точки зрения, наиболее подходящим названием величины Н является
-«коэффициент теплообмена». В дальнейшем мы всюду будем называть величину Н
•коэффициентом теплообмена. (Прим. перев.)
§ 9] ГЛ. I. ОБЩАЯ ТЕОРИЯ 27
кого, но более точного «линейная теплопередача в среду с температурой v0».
Иногда это условие называют законом Ньютона, так как закон Ньютона го-
говорит, что при охлаждении тела обдувом (т. е. в условиях вынужденной кон-
конвекции, см. ниже) количество теряемого тепла выражается соотношением (9.1).
Ниже будет кратко изложено несколько различных физических явлений, при
которых тепловой поток через граничную поверхность выражается соотношением
<9.1). В каждом случае дается несколько численных значений, что позволяет грубо
оценить порядок величины Н для практических задач; точные значения И можно
найти в работах по теплопередаче [35, 36, 46, 47].
/. Вынужденная конвекция. Экспериментально установлено, что если жидкость
{или газ) с температурой v0 быстро движется по поверхности твердого тела, то коли-
количество тепла, теряемого с его поверхности, выражается формулой (9,1), причем коэф-
коэффициент теплообмена Н зависит от скорости движения и природы жидкости, а также
от формы поверхности. Большинство экспериментов было проведено с жидкостью,
движущейся внутри трубок с круговым сечением, и с жидкостью, обтекающей цилин-
цилиндры с круговым сечением в направлении, перпендикулярном оси цилиндра. На осно-
основании полученных результатов были найдены соотношения, приближенно определяемые
-степенными законами следующих типов:
Для случая турбулентного течения воздуха со скоростью и см/сек внутри трубки
диаметром d см находим
И = 5,5.10-6и0'8<*-0'2 кал/см2. сек °С; (9.5)
для воды в аналогичном случае было получено такое же выражение, но большее
в 500—1000 раз.
Для случая турбулентного течения воздуха со скоростью а, направленной пер-
перпендикулярно оси цилиндра с диаметром сечения d см, находим
Н = 8 • 10- 5 i^j) 2 кал/см2 • сек °С; (9.6)
для воды эта величина оказывается примерно в 100 раз больше.
Очевидно, что во всех случаях потеря тепла с единицы поверхности в единицу
времени значительно увеличивается с уменьшением диаметра цилиндра. Для плоской
поверхности величина И имеет тот же порядок, что и для цилиндра очень большого
диаметра.
Зависимость типа (9.1) приближенно справедлива для случая теплопередачи
в результате комбинации вынужденной конвекции и испарения.
2. Случай тонкой оболочки из плохо проводящего материала. Очень часто
оказывается, что на поверхности тела имеется тонкая пленка плохо проводящих
материалов, например окалины (накипи), смазочных масел, окислов. Кроме того, при
охлаждении тела газом или жидкостью, текущей по его поверхности, к последней
обычно прилипает тонкий слой невозмущенной жидкости, а так как этот слой не
движется, то отдаваемое им количество тепла относительно мало.
Если теплопроводность указанной пленки толщиной d равна К' и если в каче-
качестве первого приближения мы пренебрежем ее теплоемкостью *), то количество тепла,
протекающего через эту пленку, отнесенное к единице площади в единицу времени,
равно
~(v-v0), (9.7)
где v и v0 — температуры на внутренней и наружной стороне пленки соответственно.
Это соотношение равносильно граничному условию
*-?+4-(v-v<>)=() (9-8)
для среды с внутренней стороны пленки.
*) Это эквивалентно отбрасыванию члена dv/dt в уравнении теплопроводности;
тогда мы имеем случай установившегося течения, для которого справедливо выра-
выражение B.1). Было показано [48], что во втором приближении, в котором учитывается
теплоемкость пленки, мы получим граничное условие типа (9.14) (см. также § 8
гл. XII).
28
ГЛ. I. ОБЩАЯ ТЕОРИЯ
[§
Ниже приводятся значения*) K'/d в единицах СГС и градусах Цельсия для
слоев различных веществ разной толщины.
Вещество
Воздух . . .
Вазелин . . .
Вода ....
Ртуть1) . . .
Теплопроводность при разной толщине слоя, d
1 см
0,000053
0,00044
0,00144
0,020
0,1 см
0,00053
0,0044
0,0144
0,20
0,01 см
0,0053
0,044
0,144
2,0
0,001 см
0,053
0,44
1,44
20
1) Слой ртути или амальгаму часто используют
для обеспечения хорошего теплового контакта.
Типичная толщина пленки накипи равна 0,1 см.
Если с внешней стороны пленки не поддерживается температура v0 и про-
происходит потеря тепла, величина которой равна произведению Н на разность между
v и температурой окружающей среды vu то граничное условие примет вид
1
(9.9)
Д. Теплопередача нелинейна. В большинстве практических задач тепловой
поток с поверхности не является линейной функцией разности температур между
этой поверхностью и окружающей ее средой. Однако для малых диапазонов темпе-
температур он может быть аппроксимирован зависимостью типа (9.1). Ниже приведены
типичные примеры.
/. Излучение черного тела. Твердое тело с абсолютной температурой Т, окру-
окруженное черным телом с абсолютной температурой TQt будет терять количество тепла,
отнесенное к единице поверхности и в единицу времени, равное
оЕ(Т*-Т§, (9.10)
где а — постоянная Стефана — Больцмана, а ? — относительная излучательная способ-
способность поверхности (степень черноты), т. е. отношение количества тепла, излучаемого
указанной поверхностью, к количеству тепла, излучаемого черным телом при той же
температуре.
Для полированных металлов величина Е меняется от 0,02 до 0,05; для оксидирован-
оксидированных металлов она примерно равна 0,6—0,7, для других веществ, например для кра-
красок, стекла, бумаги, древесины, она равна 0,7 — 0,9, для копоти, ламповой сажи и т. п.
она может достигать 0,98.
Подставляя численное значение величины с в (9.10), получим
1,37. Ю-12 Е (Т4 — Г*) кал/см2 • сек.
(9.11)
Если разность (Т—То) не очень велика, то в первом приближении находим
5,48. Ю-12ЕТ%(Т—Т0), (9.12)
а если 70 = 300°, то указанная величина становится равной 1,48 • 10"~4?G*—То).
Таким образом, применительно к этому случаю выражение (9.1) с константой И
является весьма приближенным, а если Т—То велико, то оно может даже привести
к серьезным ошибкам. Известно лишь несколько точных решений задач теплопро-
теплопроводности с точным граничным условием типа (9.10) **).
*) Обратная величина djK' называется термическим сопротивлением пленки.
Примеры использования этой величины см. в § 2 гл. III.
**) Егер [49] рассмотрел случай полуограниченного твердого тела с граничным
условием (9.11) или (9.13). Манн и Вольф E0] проанализировали общий случай, исполь-
использовав интегральные уравнения.
§ 9] ГЛ. I. ОБЩАЯ ТЕОРИЯ 29
В обычных условиях потеря тепла твердым телом обусловлена как конвекцией,
так и излучением, и поэтому в коэффициенте Н в выражении (9.1) должны быть
учтены оба эти фактора.
2. Естественная конвекция. Когда нагретое твердое тело окружено жидкостью,
то более нагретые части жидкости, находящиеся поблизости от тела, стремятся под-
подняться вверх и таким образом устанавливаются сети конвекционных токов. Такой
процесс называется естественной конвекцией. Экспериментально установлено, что
в данном случае количество тепла, теряемое твердым телом (с единицы площади
в единицу времени), пропорционально разности температур v — v0 между телом и
окружающей жидкостью в степени, приблизительно равной ^ • Например, для поверх-
поверхностей толщиной несколько сантиметров потеря тепла в воздух, отнесенная к еди-
единице площади в единицу времени, приближенно равна
5. Ю-5 (v — Vof4 кал/см2 . сек. (9.13)
Для очень тонких проволок, находящихся в воздухе, эта величина в 20 раз больше.
6 воде те же величины оказываются примерно в 100 раз больше.
Для этого случая, так же как и для случая теплопередачи излучением, нельзя,
пользуясь выражением (9.13), найти точные решения, и поэтому в выражении (9.1)
используется приближенная величина //. Следует отметить, что для тела, находяще-
находящегося в воздухе при нормальной температуре, соотношения (9.12) и (9.13) дают вели-
величины одинакового порядка и поэтому оба они могут быть использованы в расчетах.
Е. Контакт с хорошо перемешиваемой жидкостью или с идеальным
проводником. В калориметрии и в других методах измерения, связанных
с теплопередачей, часто оказывается, что поверхность твердого тела сопри-
соприкасается с жидкостью, перемешиваемой настолько хорошо, что температура
жидкости всюду одинакова. Пусть твердое тело имеет теплопроводность К,
площадь поверхности 5 и температуру поверхности vt причем v сохраняет
постоянное значение на всей поверхности. Пусть, далее, хорошо перемеши-
перемешиваемая жидкость, соприкасающаяся с твердым телом, имеет массу М и удель-
удельную теплоемкость с', и пусть ее температура равна V. Для общности предпо-
предположим, что в жидкость с массой М поступает в единицу времени от внеш-
внешнего источника количество тепла Q и что потеря тепла вследствие излучения
в среду с температурой vQ (отнесенная к единице площади в единицу вре-
времени) составляет Hl(V — vQ). Если bV — увеличение температуры жидкости
с массой М за время bt, то мы можем написать
Qbt —HX(V — v0) bt — Kbt jj^dS = Mc'bV,
т. e.
ff^^ V-v0)-Q = 0. (9.14)
Если предположить, что с некоторого момента времени />0, темпера-
температура поверхности твердого тела равна температуре жидкости (при t — 0 они,
разумеется, могут быть не равны), то в дополнение к соотношению (9.14)
получим
v = V, t>0. (9.15)
Если же вместо этого между твердым телом и жидкостью имеет место
теплопередача по закону типа Г, то условие (9.15) заменяется другим,
а именно
K^ + H(v-V) = 0. (9.16)
Другие физические условия приводят к граничным условиям типа (9.14);
например, для случая, когда поверхность твердого тела соприкасается с хо-
хорошо перемешиваемой жидкостью массы Ж, из которой в единицу времени
30 ГЛ. I. ОБЩАЯ ТЕОРИЯ [§ 9
удаляется масса т и замещается той же массой жидкости с температурой -ро>
находим
МС'ЧГ + К ff^rdS + mc'<y-v0) = 0. (9.17)
Такие же граничные условия (9.14), (9.15) и (9.16) имеют место для
идеально проводящего твердого тела с массой М. Если неметалл соприка-
соприкасается с металлическим проводником со значительно большей теплопровод-
теплопроводностью, то последний с достаточно хорошим приближением можно считать
идеальным проводником. Такая задача решается значительно проще, чем
задача для составной области.
Существенная разница между этими граничными условиями и условиями*
определенными в пунктах А, Б, В и Г, заключается в появлении члена dVjdt,
а в некоторых случаях — члена dv/dt. При использовании классических мето-
методов не всегда можно обойтись без их видоизменения, но преобразование
Лапласа, изложенное в гл. XII, одинаково пригодно для обоих случаев. В
этой главе будут приведены некоторые примеры *).
Ж. Поверхность раздела двух сред с различными коэффициен-
коэффициентами теплопроводности Кх и К2. Пусть vx и v2— температуры двух
сред. В § 3 данной главы было показано, что тепловой поток непрерывен
на поверхности раздела двух сред, т. е. что
*i4? = *.-&" (9.18)
где д/дп означает дифференцирование вдоль нормали к поверхности раздела.
Если предположить, что на поверхности раздела температуры обеих сред
одинаковы, то в добавление к соотношению (9.18) имеем
vx = v2. (9.19)
Это предположение справедливо только для очень тесного контакта, как,
например, в спаях; во всех других случаях, даже в двух оптически плоских
поверхностях, слегка прижатых друг к другу **), теплопередача между двумя
средами осуществляется главным образом согласно механизму, изложенному
в пунктах Г B) и ДA), т. е. тепловой поток между этими двумя поверх-
поверхностями пропорционален разности их температур и, следовательно,
^ -v2). (9.2Q)
Для этого случая граничными условиями служат соотношения (9.18) и (9.20)»
3. Контакт вещества с тонкой оболочкой из значительно лучшего провод-
пика. Подобная задача встречается прл изучении, например, тонкого металлического
листа или проволоки, соприкасающихся с относительно плохим проводником, таким,
как грунт, пищевые продукты или изолирующие материалы. Этот случай рассматри-
*) Задачи с граничными услозиями этих типов рассматривались в ряде работ
[51—61].
Авторы последних четырех работ использовали преобразование Лапласа,
остальные — классические методы. В работе [62] рассмотрен случай линейной зави-
зависимости количества жидкости от времени. Эти задачи имеют большое значение также
и для работ, связанных с диффузией (см. § 4.35 гл. IV книги Крэнка [71] и книгу
Бэррера [63]).
**) Якоб и Стар [64] измерили величину Н для оптически гладких поверхностей,
прижатых друг к другу в вакууме. Когда поверхности просто касаются, величина Н
очень мала, и теплопередача осуществляется только вследствие излучения; по мере
увеличения давления, прижимающего поверхности, растет и величина И. Например»
для серебряных поверхностей при давлении 2 кГ/см2 N = 0,07,
§ 10] ГЛ. I. ОБЩАЯ ТЕОРИЯ 3f
вается также в задачах о поверхностной диффузии или о диффузии по границам зере»
[65, 66] *). Предполагается, что оболочка настолько тонка, что по всей ее толщине,
равной dy температура в любой точке одинакова. Если V — температура в произволь-
произвольной точке оболочки, а К\ и %{— соответственно коэффициенты теплопроводности и
температуропроводности вещества оболочки, то уравнение теплопроводности для обо-
оболочки, выведенное из рассмотрения баланса тепла в элементе ее площади, записы-
записывается в виде
д& + дт? %, dt dKx дп ~~U'
где д/дп — обозначает дифференцирование по направлению внешней нормали к твер-
твердому телу, а д/дг и д/д-ц — соответственно по двум перпендикулярным ей напра-
направлениям.
При идеальном тепловом контакте между оболочкой и твердым телом граничные
условия имеют вид (9.21) и v= V. Если же между оболочкой и внутренней (ил»
внешней) средой происходит теплопередача по линейному закону, эти условия не-
несколько усложняются.
Для случая проволоки с радиусом а, расположенной вдоль оси г в твердом теле-
(г > а), соотношение (9.21) принимает вид
dz* x, dt + aKi dr
f922V
Если оболочка настолько тонка, что ее теплоемкостью можно пренебречь, то»
соотношение (9.21) записывается следующим образом:
JL_^-(> (9 23).
§ 10. Безразмерные параметры
Решение задач теплопроводности всегда можно выразить через безраз-
безразмерные параметры. Например, рассмотрим уравнение, описывающее линей-
линейный тепловой поток,
в области — /<а:</ с граничными условиями типа (9.2), а именно:
-з \-hv = 0, х = I; -5 /w?=0, jc = — L A0.2)
Положение точки х можно определить отношением
а время — величиной т:
которая, как было показано в § 6 данной главы, является безразмерной
величиной. Наконец, вместо h в граничном условии A0.2) тоже можно вос-
воспользоваться безразмерной величиной**)
L = lh. A0.5)
Решения задач, определяемых соотношением A0.Г), с граничными усло-
условиями A0.2) всегда можно выразить через три переменные ?, т, L вместо
*) Егер [65] рассмотрел случай хорошо проводящей проволоки, а Уипл [66] — слу-
случай плоского листа (см. также § И гл. XIV). В работе Уипла» кроме того, приведен
вариант вывода соотношения (9.21).
**) Величину х иногда называют модулем, или числом, Фурье, a Z. — числом Нус-
сельта. При изучении теплопередачи, обусловленной конвекцией, сталкиваются Ил
с другими важными параметрами подобного рода.
32 ГЛ. I. ОБЩАЯ ТЕОРИЯ [§11
исходных величин /, х, х, t, h. Подобную замену всегда желательно проде-
проделать до выполнения численных расчетов. Впоследствии мы покажем, что для
очень многих случаев можно найти специальные формы решений, пригодные
для малых, средних и больших величин т.
Диапазон величин L и т, с которым приходится встречаться на практике,
огромен. При значении х = 0,01 (что соответствует плохому проводнику)
для тонких листов с толщиной, не превышающей 1 мм> т становится боль-
большим после 1 мин, тогда как для тела с размером Земли т остается малым
в течение целых геологических эпох (см. формулу A0.4).—Прим. ред.).
Написанное выше дифференциальное уравнение и граничные условия
можно выразить через безразмерные переменные. Например, подставив соот-
соотношения A0.3), A0.4) и A0.5) в A0.1) и A0.2), получим
d2v dv Л * . „ . * /in e\
^- = 0, —1<с<1, (Ю.б)
S^. + Lv = 0, когда 5=1 и ~--Lv = 0, когда $ = —1. A0.7)
Эта замена переменных привлекательна с чисто математической точки
зрения, так как она приводит к некоторому упрощению математических
выкладок. Однако в настоящей книге мы не будем ею пользоваться, ибо
¦физический смысл формул более ясен, если они выражены через исходные
физические переменные.
§ 11. Экспериментальные методы определения теплопроводности
Для измерения теплопроводности в прошлом использовалось очень много мето-
методов [67—69]. В настоящее время некоторые из них устарели, однако их теория и
сейчас представляет интерес, так как они базируются на решениях уравнений тепло-
теплопроводности для простых систем, которые часто встречаются в практике.
Прежде всего следует отметить, что термические свойства любого материала
проявляются в разнообразных сочетаниях; однако если рассматривать их как харак-
характеристики материала, то их можно определить из различных экспериментов. Пере-
Перечислим основные термические характеристики тел и эксперименты, из которых они
определяются: а) коэффициент теплопроводности /С, измеряемый при стационарном
режиме эксперимента; б) теплоемкость, отнесенная к единице объема, рс, которую
измеряют калориметрическими методами; в) величина (/СрсI/*, измеряемая при перио-
периодическом стационарном режиме экспериментов; г) температуропроводность х, изме-
измеряемая при нестационарном режиме экспериментов. В действительности большинство
экспериментов, проводящихся в нестационарном режиме, в принципе, допускает как
определение /С, так и определение %.
Мы кратко опишем здесь наиболее распространенные методы и укажем разделы,
в которых они рассматриваются. По существу эти методы делятся на те, в которых
измерения ведутся в стационарном режиме (методы стационарного режима), при пе-
периодическом нагреве и в нестационарном режиме (методы нестационарного режима);
далее они подразделяются на методы, применяемые при исследовании плохих про-
проводников и при исследовании металлов.
/. Методы стационарного режима; плохие проводники. В данном методе
следует точно выполнять условия основного эксперимента, изложенного в § 1 на-
настоящей главы, причем исследуемый материал должен иметь форму пластинки [70].
В других вариантах метода можно исследовать материал в виде полого цилиндра
<см. § 2 гл. VII) или полой сферы (см. § 2 гл. IX). Иногда исследуемый материал, по
которому проходит тепло, имеет форму толстого стержня, однако в данном случае
теория оказывается более сложной (см. §§ 1, 2 гл. VI и § 3 гл. VIII).
2. Термические методы стационарного режима; металлы. В этом случае
обычно используется металлический образец в форме стержня, концы которого под-
поддерживают при различных температурах. Полуограниченный стержень рассматри-
рассматривается в § 3 гл. IV, а стержень конечной длины — в § 5 гл. IV.
§ 12] ГЛ. I. ОБЩАЯ ТЕОРИЯ 33
3. Электрические методы стационарного режима; металлы. В этом случае
металлический образец в виде проволоки нагревают, пропуская через него электри-
электрический ток, а его концы поддерживают при заданных температурах (см. § 11 гл. IV
и пример IX § 3 гл. VIII). Можно использовать также случай радиального потока
тепла в проволоке, нагреваемой электрическим током (см. пример V § 2 гл. VII).
4. Методы стационарного режима; движущиеся жидкости. В этом случае
измеряется температура жидкости, движущейся между двумя резервуарами, в кото-
которых поддерживается различная температура (см. § 9, гл. IV).
5. Методы периодического нагрева. В этих случаях условия на концах стержня
или пластинки изменяются с периодом Т\ по достижении установившегося состояния
измеряют температуры в определенных точках образца. Случай полуограниченного
стержня рассматривается в § 4 гл. IV, а стержня конечной длины — в § 8 той
же главы. Подобный метод используется для определения температуропроводности
грунта при температурных колебаниях, вызываемых солнечным нагревом (см,
§ 12 гл. II).
В последнее время эти методы стали играть важную роль в измерениях низких
температур; они обладают также тем преимуществом, что в теории относительно
сложных систем можно пользоваться методами, разработанными для исследования
электрических волноводов (см. § б гл. II).
6. Методы нестационарного режима. В прошлом методы нестационарного
режима использовались несколько меньше, чем методы стационарного режима. Их
недостаток заключается в трудности установления того, насколько действительные
граничные условия в эксперименте согласуются с условиями, постулируемыми тео-
теорией. Учесть подобное расхождение (например, когда речь идет о контактном сопро-
сопротивлении на границе) очень трудно, а это более важно для указанных методов, чем
для методов стационарного режима (см. § 10 гл. II). Вместе с тем методы нестацио-
нестационарного режима сами по себе обладают известными преимуществами. Так, некоторые
из этих методов пригодны для проведения очень быстрых измерений и для учета
малых изменений температуры; кроме того, ряд методов можно использовать «на
месте», без доставки образца в лабораторию, что весьма желательно, особенно при
исследовании таких материалов, как грунты и горные породы. В большинстве старых
методов используется лишь последний участок графика зависимость температуры
от времени; при этом решение соответствующего уравнения выражается одним
экспоненциальным членом. В § 7 гл. IV, § 5 гл. VI, § 5 гл. VIII и § 5 гл. IX рас-
рассматривается случай охлаждения тела простой геометрической формы при линейной
теплопередаче с его поверхности. В § 14 гл. IV рассматривается случай нестацио-
нестационарной температуры в проволоке, нагреваемой электрическим током. В некоторых
случаях используется весь график изменения температуры в точке (см. § 10 гл. II
и § 3 гл. III).
В последние годы все большее внимание уделяют возможности одновременного
определения К и % из одного эксперимента. В одном из таких методов измерялась
некоторая величина, которая в конце концов начинала линейно увеличиваться со
временем (например, количество тепла, проходящее за время t через пластину,
поверхность которой имеет постоянную температуру) и из параметров этой линей-
линейной асимптоты определялись /Сих (см. пример II § б гл. XII и § б гл. XV). В дру-
другом методе использовался нагревающийся зонд, температура которого в конце концов
изменялась линейно относительно \nt (см. § 7 гл. XIII).
§ 12. Математическая интерпретация начальных
и граничных условий
При математическом рассмотрении граничные и начальные условия не следует
рассматривать как условия, которым температура v обязана удовлетворять на самой
поверхности или в момент времени t = 0. Их следует считать предельными условиями.
Граничные условия нужно понимать в том смысле, что для фиксированного t > 0
данная комбинация температуры и ее производных стремится к заданной величине
при приближении точки к поверхности. Начальные условия следует понимать в том
смысле, что для фиксированной точки внутри определенной области температура
должна стремиться к заданной величине по мере того, как t стремится к нулю.
Для примера рассмотрим задачу, которую можно кратко сформулировать сле-
следующим образом. Пусть теплообмен происходит в области 0 < х < I. Темпера-
Температура в точке х = 0 поддерживается на нуле для t > 0, а при х = I происходит
теплообмен со средой нулевой температуры. Начальная температура твер-
твердого тела равна единице. При этом уравнения, которые должны удовлетворяться,
3 Г. Карслоу, Д. Егер
34 ГЛ. I. ОБЩАЯ ТЕОРИЯ [§13
записываются в виде
v->0 при .* -> О для фиксированного t > 0;
-^--|-/ш->0 при jc->/—0 для фиксированного t > 0;
с/ -> 1 при / -> 0 для фиксированного х в области 0 < х < L
§ 13. Родственные дифференциальные уравнения
3 сущности вся эта книга посвящена решению уравнений
div/+Pc-|^ = A A3.1)
/= — Kgradv, A3.2)
или
"-т тг~4 «'•*
для областей различных форм с граничными условиями, обычно выраженными через
v и /. Величины /(, р и с обычно являются константами, а Л может зависеть от поло-
положения или от времени.
Запишем несколько обобщений выражения A3.3), а именно:
где Uy А и В — константы. Эти выражения уже встречались в §§ 6 и 7 данной главьи
Как отмечалось ранее, случаи зависимости термических параметров /С, с и т. п. от v
приобретают все большее значение, хотя эти функции все еще плохо изучены для
достаточно большого диапазона изменения v.
Те же уравнения и те же граничные условия встречаются в целом ряде других,
разделов физики, и поэтому в них часто удается использовать многие из приведен-
ных здесь решений (с изменением обозначений). Вместе с тем имеется много задач,,
имеющих практическое значение, которые мало отличаются от типовых. Некоторые?
основные приложения приведенных соотношений будут кратко изложены ниже.
I. Диффузия.
Это явление подробно рассмотрено в работах Крэнка [71], Бэррера [63] и Джо-
ста [72]*). Если С — концентрация диффундирующего вещества, a F—скорость его
передачи, то соотношения A3.1) и A3.2) принимают вид
divF = — -^ и F = — D grad С. A3.6>
Если D — константа, то уравнения диффузии совпадают с уравнениями тепло-
теплопроводности при # = x=D и, следовательно, задача упрощается. На поверхности
раздела двух сред соотношения (9.18) и (9.19) принимают вид
где k — константа, i Итак, результаты, полученные ниже для составной среды, также-
можно отнести к этому случаю, соответствующим образом изменив обозначения.
Уравнения типов A3.4) и A3.5) используются значительно чаще. Например, они
встречаются в задачах диффузии, происходящей одновременно с химической реакцией
(см. [7Г] гл. VIII, [7 6]), в исследованиях, связанных с диффузией в биологических
тканях [77], в теории консолидации почв [78] и в генетике. Задачи одновременной»
диффузия тепла и водяного пара приводят к системе двух дифференциальных уравне-
уравнений (см. [71], гл. X III, [79]).
*) Много задач, приводящих к уравнению диффузии, рассмотрено в работе Бэб-
бита [73]. Целый ряд приложений этого уравнения к физиологии описан в [74, 75].
§ 14J гл- L ОБЩАЯ ТЕОРИЯ 35
II. Диффузия в силовом поле; седиментация.
В этих задачах мы получаем уравнение типа *)
-i-
где U—постоянный вектор. Указанное уравнение по существу представляет собой
уравнение теплопроводности A3.5) для движущейся среды.
III. Замедление нейтронов.
При некоторых предположениях указанная задача сводится к задаче теплопро^
водности [84, 85]; при ее решении обычно пользуются функцией Грина.
IV. Вязкое движение.
Уравнение теплопроводности встречается в двух родственных, но несколько
отличающихся друг от друга задачах. Во-первых, многие задачи одномерного ламинар-
ламинарного течения приводят непосредственно к уравнению A3.3) с одной переменной [37].
Во вторых, дифференциальные уравнения, описывающие вихревые движения, являются,
уравнениями типа уравнения диффузии [37, 86, 87].
V. Задачи, рассматриваемые в теории электричества.
Дифференциальное уравнение для потенциала в безындуктивной линии пере-
передачи [88] имеет форму A3.4) с одной пространственной переменной при наличии
утечки или форму A3.3) при отсутствии утечки (см. также § 6 гл. II).
VI. Течение жидкостей через пористую среду.
Дифференциальное уравнение, характеризующее течение сжимаемой жидкости че-
через пористую среду [89] **), полностью соответствует уравнению A3.3). Это уравнение »
уравнения A3.4) и A3.5) встречаются во многих других задачах этого типа [90, 91]-
§ 14. Упрощение общей задачи теплопроводности
В данном параграфе будет изложено несколько классических методов,,
которые приводят общие задачи теплопроводности к более простым. Следует
отметить, что при использовании преобразования Лапласа (см. гл. XII—XV)
применять их не нужно, так как все задачи решаются одним и тем же спо-
способом.
I. Условия на поверхности, не зависящие от времена.
Предположим, что требуется удовлетворить уравнению
V2v-±-^- = A(x, у, г) A4.1)
внутри твердого тела при v = f(x. z) в начальный момент и v = <p(x, у, z}
на поверхности. Пусть
v = u + w% A4.2)
где и является функцией только х, у, z и удовлетворяет уравнению
V2u = А(х, у, z) внутри твердого тела A4.3)
и
м=ср(л:, у, z) на его поверхности, A4.4)
a w есть некоторая функция х, yf z, t, которая удовлетворяет уравнениям
V2w -^- = 0 внутри твердого тела, A4.5)
w = f(x, у, z) — и в начальный момент A4.6)
и
«о> = 0 на поверхности. A4.7)
*) В работах [80] — [83] приведено уравнение диффузии ионов в ионосфере»
**) В гл. X цитируемой книги [89] приведено множество-решений задач такого
типа, в том числе задач для линейного источника и цилиндрических поверхностей
раздела.
36 ГЛ. I. ОБЩАЯ ТЕОРИЯ [§ 14
Ясно, что v, заданная выражением A4.2), удовлетворяет всем условиям
задачи и, таким образом, решение последней сводится к решению двух задач.
Одна соответствует случаю установившейся температуры, а другая—случаю не-
неустановившейся температуры при заданной начальной температуре и нулевой
температуре на поверхности. Случай линейной теплопередачи с поверхности
в среду при постоянной температуре можно упростить подобным же образом.
II. Условия на поверхности являются заданными функциями вре-
времени. Источники тепла отсутствуют.
В данном случае решение можно вывести из решения задачи для по-
постоянных условий на поверхности, используя для этой цели теорему Дюа-
меля [92], которая формулируется следующим образом.
Если v — F(xt у, z, X, t) соответствует температуре в момент
времени t в точке {х, у, г) твердого тела, начальная температура ко-
торого равна нулю, а температура на поверхности равна ср(лг, у, z, X),
то решение задачи в случае начальной температуры, равной нулю,
и температуры на поверхности, равной ср(лг, у, z, t), записывается
в виде
, у, zt X, t — \)d\.
Приведем доказательство этой теоремы.
Если температура на поверхности равна нулю в промежуток времени
от ? = — оо до * — 0 и равна ср (л:, у, z, X) в промежуток от t == 0 до t = t,
то можно сказать, что начальная температура равна нулю, а температура
на поверхности равна ср(л:, у, z, X) и, следовательно, в момент времени t
температура тела v равна следующей величине:
v = F(x, у, z, X, t) для t > 0.
Таким образом, если температура на поверхности равна нулю в проме-
промежуток времени от * =— оо до *=Х и равна ср(лг, у, z, X) в промежуток
от ? = Х до t — t, то для ?>Х можем написать
v = F(xt у, г. X, t— X).
Кроме того, если температура на поверхности равна нулю в промежуток
времени от t = — оо до t = l~\-d\ и равна ср(лг, у, z, X) в промежуток
от ? = Х-|-Л до t = t, то для ?>Х—(~rfX получим
v = F(x, у, z, X, t — 1 — dl).
Отсюда следует, что если температура на поверхности равна нулю
в промежуток времени от t = — оо до t = Х, равна ср (л:, у, z, X) в проме-
промежуток от ?=Х до ? = X-|-dX и равна нулю в промежуток от ?=X-|-dX
до t = t, то мы получим
v — F(x, у, z, X, t — X) — ^(л:, у, z, X, t — X — rfX),
или окончательно
д
Таким путем, разбивая интервал от ? = 0 до t = t на малые интервалы
и затем суммируя полученные результаты, мы находим решение задачи для
случая температуры на поверхности, равной ср(х, у, z, t), в виде
v =
о
§ 14] гл. i. общая теория 37
Соответствующая теорема для случая теплообмена с поверхности по ли-
линейному закону формулируется следующим образом.
Если v = F(x, у, z, X, t) соответствует температуре в момент
времени t в точке (х, у, z) твердого тела, начальная температура
которого равна нулю, а на поверхности происходит теплообмен со
средой, имеющей температуру ср(лг, у, z, X), то решение задачи в случае
начальной температуры, равной нулю, и температуре среди, равной
ср (л:, у, z, t), записывается в виде
v-= f-^-F(x, у, z, X, t — l)dl. A4.9)
о
Если температура на поверхности или температура среды, с которой
происходит теплообмен, не изменяется от точки к точке, а зависит только
от времени, то получаемые результаты можно сформулировать в следующей
несколько более простой форме.
Если v = F(x, у, z, t) соответствует температуре в момент вре-
времени t в точке (х, у, z) твердого тела, начальная температура ко-
торого равна нулю, а поверхность поддерживается при температуре,
равной единице (или в случае теплообмена поверхности с окружающей
средой последняя имеет температуру, равную единице), то решение
задачи при условии, что поверхность поддерживается при темпера-
температуре <p(t) (или что происходит теплообмен со средой, имеющей тем-
температуру ср(?)), записывается в виде
v= f9(X)-LF(x, у, z, t — \)d\. A4.10)
Это соотношение сразу же получается из приведенного выше, так как
F(x, у, z, X, t) принимает более простую форму
F(x, у, z, 0?(Х).
Возвращаясь снова к общей задаче с переменной температурой на по-
поверхности, попытаемся решить уравнение A4.1) при v = f(x, у, z) в на-
начальный момент и v = y(x, у, z, t) на поверхности. Ему удовлетворяет
функция v = u-\-w, где
V'«—1^=Л(х. у, z), A4.11)
u = f(x, у, z) в начальный момент, A4.12)
и = 0 на поверхности A4.13)
<и; = 0 в начальный момент, A4.15)
«а; = ср (лг, у, z, t) на поверхности. A4.16)
Уравнения для w мы только что разобрали, а уравнение для и мы рас-
рассмотрели в примере I. Задачи с другими граничными условиями можно разо-
разобрать аналогичным способом.
38 ГЛ. I. ОБЩАЯ ТЕОРИЯ [§ 14
В самом деле, уравнение A4.8) справедливо и в более общих случаях, чем ука-
указано выше. Например, рассмотрим дифференциальное уравнение
<* >¦ * <>-"?• <Ш7>
причем К\У К2у Кг> К4 и рс могут быть функциями х> у, z. Согласно §§ 6 и 17 дан-
данной главы это уравнение является уравнением теплопроводности *) для неоднородного
анизотропного .твердого тела, в котором в единице объема в единицу времени вы-
выделяется количество тепла, равное А (ху у, г, t). Предположим, что граничные условия
записываются в виде
dv , , dv , , dv , , , ,ч /1il1OY
+k+ks-^ + ktV^glx, yt z,t)t A4.18)
где ku ..., kA — функции только х, у и z. Предположим также, что начальное усло-
условие имеет вид
v -><p (jc, у, z) при *->0. A4.19)
Теперь пусть F (jc, yy z, X, f) служит решением той же задачи, но при условии,
ято A (jc, у, z, t) и g (х, у, z, t) заменены А (ху у, z, \) и g (jc, yt z, X), т. е. зна-
значениями этих функций при t = X. Тогда решение **) уравнений A4.17), A4.18) и A4.19)
записывается в виде
t
х/(лг, у, z, 0 = -^-У F(*. У> *, К t-\)d\ =
fF{x9y,z,l,t — \)dkt A4.20)
т. е. в такой же форме, как и уравнение A4.8) при <р (xt yt z) = 0. Следует добавить,
что полученный результат справедлив ив тех случаях, когда термические характе-
характеристики среды имеют разрывы.
III. Случай, когда справедливо уравнение
V2V _ bv _ 1 ^L = а {Ху у, 2)у
где b — постоянная, которая может иметь любой знак. При подстановке выражения
v=ue-xbt A4.22)
уравнение A4.21) принимает вид
V2h — JL J^L = exbtA (jc, у, г), A4.23)
« его можно рассматривать описанными выше методами.
Другим важным случаем, который можно проанализировать даже более простым
способом ***), является случай, описываемый уравнением
V2t,— fo,__ JLj^.= o, A4.24)
где b — постоянная (которая может иметь любой знак), начальная температура равна
нулю, а граничные условия соответствуют либо постоянной температуре, либо тепло-
*) Член /С4 добавлен для большей общности. Он появляется в тех случаях, когда
каждый элемент объема твердого тела теряет в единицу времени количество тепла,
пропорциональное его температуре, как, например, в 31 дачах, разобранных в гл. IV,
а также в других физических задачах.
**) Доказательство, использующее преобразование Лгпласа, приведено в [93]. Его
можно распространить на более общие граничные условия (см., например, пункт Д
$ 9 данной главы).
***) В работе [94] приведены подробные формулы для плиты, сферы, цилиндра
и полуограниченного твердого гела.
$ 15] ГЛ. I. ОБЩАЯ ТЕОРИЯ 39
обмену на поверхности. Тогда, если и является решением для случая Ь = О при тех же
граничных условиях, то дифференцированием можно проверить, что
t
v = *b I е~ш'и (Г) dt' + ue~xbt A4.25)
о
удовлетворяет уравнению A4.24) и принятым в данной задаче граничным условиям.
Таким образом, решения для этого случая можно получить простым интегрированием
-полученных выше решений.
¦§ 15. Задачи, решения которых можно выразить в виде произведения
решений более простых задач
Рассмотрим уравнение теплопроводности
для прямоугольного параллелепипеда
01<*1<*1. я2<*2<^2' az<xz<bz. A5.2)
Для некоторых важных типов начальных и граничных условий его ре-
решением является произведение решений трех задач с одной переменной;
таким образом, если последние известны, то можно сразу же написать и ре-
решение нашей задачи.
Предположим, что vr(xr, t), г=1, 2, 3, служит решением уравнения
с граничными условиями
arl?;-ter = 0- *r = <*r '>0. A5.4)
где аг и рг и т. п. — постоянные, каждая из которых может быть равна
«улю (таким образом, включены случаи нулевой начальной температуры и
•отсутствия теплового потока на поверхности); пусть начальные условия имеют
«вид
vr(xr, t) = Vr(xr), t = 0, ar<xr<br A5.6)
Тогда решением уравнения A5.1) в области A5.2) при
v = Vx (х,) V2 (x2) V3 (*g), когда t = О, A5.7)
« при граничных условиях
аг-г-^ ^ = 0, хг = аг, />0, г=1, 2, 3, A5.8)
= 0, хт = Ьг, />0, г = 1. 2, 3, A5.9)
служит
v t). A5.10)
40 ГЛ. I. ОБЩАЯ ТЕОРИЯ [§ 15
При подстановке выражения A5.10) в уравнение A5.1) и при исполь-
использовании A5.3) получим
vo
При этом очевидно, что удовлетворяются начальные и граничные условия
A5.7), A5.8) и A5.9).
Аналогичный результат остается справедливым и для случая комбиниро-
комбинированного радиального и осевого потока тепла в сплошном или полом цилиндре*
Дифференциальное уравнение (8.5) настоящей главы принимает вид
1 д ( dv \ , d2v I dv /1к 1 iY
Vn <15Л1>
поскольку мы полагаем, что все величины не зависят от 0.
Предположим, что его нужно решить в области
a<r<bt zl<z<z2. A5.12)
Пусть vl(r, t) служит решением уравнения
1 д ( dvx \ 1 dvx . . л . . .
при граничных условиях
1TF — P^i = 0, r = a, t>0.
И
vl = Vl(r) при ^ = 0.
Пусть также v2(z, t) служит решением уравнения
t>0' zi<z<z
d2v2 I dv2
при граничных условиях
«2-^г — feeb = O, z =
¦о = К2 (z) при г = 0.
Тогда v = vv(r, t)v2(z, t) является решением уравнения A5.11) в об-
области A5.12) при граничных условиях
*i-jtr — $iV = 0, r = a, zl<z<z2, t>0,
lHi^0' r = d. zx<z<z2, t>0,
= 0, z = zv a<r<b, t>0.
$ 16] ГЛ. I. ОБЩАЯ ТЕОРИЯ 4Ъ
и при начальном условии
v = Vx (г) V2 (z) при t = 0.
Такой же прием может быть использован и для других областей, напри-
например в случае неограниченного прямого двугранного угла х > 0, у > 0, полу-
полуограниченного цилиндра и т. п. Соответствующие примеры будут приведены
в § 6 гл. V, § 4 гл. VI и в § 4 гл. VIII. В случае анизотропного твердого*
тела с осями, выбранными таким образом, что дифференциальное уравнение
имеет форму A8.4) (см. стр. 46), указанный метод остается применимым,
если ограничивающие поверхности перпендикулярны осям.
Эти результаты имеют практическое значение, так как они позволяют
очень легко получать численные значения температур в упомянутых выше
твердых телах, если их начальная температура постоянна, а с поверхности,
происходит теплообмен в среду с постоянной температурой [95, 96].
§ 16. Единственность решения задачи теплопроводности
Рассмотрим задачу теплопроводности в конечной замкнутой области при.
заданных начальной температуре и температуре на поверхности.
Допустим, что имеется два независимых решения vl и v2 уравнений
-r^- = xV2<y внутри твердого тела,
v = f(x, у, z) внутри твердого тела при ? = П ' Aо.1>
v = y(x, у, z, t) на поверхности.
Пусть V = vx — v2. Тогда V удовлетворяет уравнениям
dV
-—- = xV2K внутри твердого тела,
V = 0 внутри твердого тела при ? = 0,
V = 0 на поверхности.
Если уравнения A6.1) имеют единственное решение, то vx^v2, т. е. V^O»
Рассмотрим объемный интеграл
где интегрирование производится по всему объему твердого тела.
Тогда
A6.4)-
Приняв в формуле Грина (см. соотношение G.4))
дх ' ду dz
и полагая, что V удовлетворяет условиям, достаточным для того, чтобы тео-
теорема Грина была справедлива (например, непрерывность V и ее первой
и второй производных), получим
-//'/
42 ГЛ. I. ОБЩАЯ ТЕОРИЯ [§ 16
<где интегрирование производится по всей поверхности и по всему объему
твердого тела. Тогда
Поскольку на поверхности V равно нулю, первый интеграл обращается
.ъ нуль при условии, что dV/дп ограничена на поверхности, и мы получаем
-&-=-* J J J 1Ы +Ы +Ы
'Поэтому
Если мы можем утверждать, что
У=0 при * = 0. A6.7)
то из соотношения A6.6) следует, что У<]0 при t > 0. При этом, согласно
;<16.3), мы имеем У=0, и поскольку V непрерывно, то, следовательно, V = 0.
Это классическое доказательство единственности решения приводится во
многих работах.
Было отмечено [97—99], что для выполнения соотношения A6.7) необхо-
необходимы дальнейшие допущения, касающиеся V. В самом деле, из условия
!/(х, yt z, t)->0 при t—>0 для любых фиксированных х, у, z в иссле-
исследуемом объеме не вытекает, что У->0 при ?->0. В качестве простейшей
иллюстраци-и этого положения рассмотрим случай одномерной полуограничен-
«ой области х > 0. .
Рассмотрим функцию
_2 *2
V(x, t) = xt 2e ш. A6.8)
Она удовлетворяет одномерному уравнению теплопроводности
d2V
дх2 ""
при
dV
" dt
x =
Кроме того,
V(x, t) = 0 при а: = 0 и
сИ
V(x, t)—>0 при t—>0 для любого фиксированного х > 0.
Таким образом, функция A6.8) удовлетворяет уравнению теплопровод-
теплопроводности и обращается в нуль при t = 0 и на границе области, однако она не
обращается в нуль тождественно. Физически эту функцию можно предста-
представить себе как температуру, обусловленную дублетным источником тепла
<см. ниже § 8 гл. X). Она не стремится к нулю равномерно по х при ?-*()
>и не ограничена в окрестности л: = 0, ? = 0, например при x==t^2.
Интеграл, соответствующий A6.3), записывается в виде
оо 2
— — f хЧ"^ dx — ( гс*3 У
о
>«, следовательно, У->оо, если t—>0. Таким образом, условие A6.7) не
выполняется, и в этом случае приведенное выше доказательство единствен-
единственности решения теряет силу.
§ 17] ГЛ. I. ОБЩАЯ ТЕОРИЯ 43
Для выполнения условия A6.7) должны быть сделаны дополнительные
предположения относительно функции V, исключающие функции, подобные
приведенной выше. Очевидно, что условие A6.7) оказывается справедливым,
если мы примем, что V равномерно стремится к нулю при t->0 для лг, у, z
dV dV dV
no всему объему или что каждая из производных -^—, —х—, -->— меньше
постоянной Ж, которая не зависит от х, у, z по всему объему и от t
в интервале 0 < t ^ t0.
Следует отметить, что было все же сделано несколько попыток устано-
установления более общих условий, при которых решение единственно; кроме того,
доказывалась единственность полученного решения в каждой специальной
задаче. Аналогичное рассуждение*) можно применить и к иным граничным
условиям, к анизотропной среде **) и к случаю установившейся температуры.
Доказать существование решения приведенных выше уравнений еще
Труднее, чем доказать единственность решения. Физическая интерпретация
этих уравнений требует, чтобы решение существовало. Вопросы математи-
математического доказательства таких теорем существования относятся к области
чистого анализа.
§ 17. Теплопроводность анизотропных твердых тел
Анизотропные среды ***) представляют значительный интерес для практики.
Типичными примерами анизотропного вещества служат кристаллы, встречающиеся
в природе некристаллические вещества (например, осадочные горные породы или
древесина), а также слоистые материалы (например, используемые в технике транс-
трансформаторные сердечники).
Для указанных веществ результаты, приведенные в §§ 3 и 4 данной главы, не
изменяются, но оказывается недействительным общепринятое положение о том, что
направление вектора теплового потока в какой-либо точке нормально к изотерме,
проходящей через эту точку. Простейшее основное предположение, обобщающее
допущение E.3) для изотропного тела, заключается в том, что каждая компонента
вектора теплового потока в точке является линейной функцией компонент темпера-
температурного градиента в этой точке, т. е. что
dv , „ dv_ , „ dv
ду dz
dv . _, dv
A7.1)
dv
Величины Krs называют коэффициентами теплопроводности; они являются
компонентами тензора второго ранга. Уравнения A7.1) можно решить относительно
*) Более подробно этот вопрос обсуждается в ряде книг и статей [40, 100—112].
**) При этом использовались формула Грина G.4) данной главы для ? = Vfx и
т. п., и соотношения F.3) и A7.1) той же главы. Кроме того, мы пользовались тем,
что 2Ф, определенное выражением B0.3), всегда положительно.
***) Математическая теория теплопроводности кристаллов была впервые разрабо-
разработана Дюамелем [113, 114] и Ламе [115] на основе гипотезы о механизме молекуляр-
молекулярного излучения. Современной разработкой теории в форме, излагаемой в настоящей
книге, мы, по существу, обязаны Стоксу [116]. Более полная аналитическая трактовка
теории дана Буссинеском [117]. Вопросы, связанные с физикой кристаллов, подробно
излагаются в работе [118]; более краткое, но зато и более современное их рассмотре-
рассмотрение можно найти в книге Вустера [119]. Вследствие трудности точного измерения
теплопроводности (в частности, теплопроводности кристаллов) даже в настоящее время
мы располагаем лишь очень малым количеством достаточно надежных эксперимен-
экспериментальных данных, и поэтому до сих пор решено лишь весьма ограниченное число спе-
специальных задач.
44
ГЛ. I. ОБЩАЯ ТЕОРИЯ
[§
dv n
-- - и т. п. В этом случае мы получим
— — = R f
— — =R
dv
A7.2)
где /?Г5 — коэффициенты сопротивления. Они могут быть записаны в виде определи-
определителей, элементами которых служат величины /Сг5. Например,
К 2 3^V32
где
К31К23 — Къ\Кз
/См
42 =
К12К,
12А, 33
К2
К,
Кзз
A7.3)
A7.4)
A7.5)
Аналогичным образом величины Krs можно выразить через Rrs. Следует отметить,
что для некоторых задач наиболее употребительна запись через Krs* а Для ДРУГИХ —
через Rrs. Если уравнения A7.2) считать основными, то их можно решить относи-
относительно fXf /у, /2, выразив последние через -г—, -т—, -^—; получающийся опреде-
определитель
*\\\ ^<12 ^13
/?21 ^22 ^23 A7.6)
#31 #32 #33
равен произведению A/А3) на присоединенный для А (или взаимный) определитель»
Согласно общей теореме [120]
Д'=4- A7.7)
и миноры Д' равны произведению 1/Д на алгебраические дополнения соответствующих
миноров А, например
^11^22 ^12^21=—д—•
В первую очередь следует отметить, что в выражениях A7.1) знаки fx, fy и /г
изменяются, если все компоненты температурного градиента изменяют свои знаки.
Иными словами, теплопроводность вещества во взаимно противоположных направ-
направлениях одинакова. Для кристаллов с центральной симметрией последнее полО/кение
вытекает из соображений симметрии. К этому классу относятся 21 из 32 классов
кристаллов. Кристаллы остальных И классов не имеют центра симметрии, и следует
считать, что для них уравнение в форме A7.1) подтверждается экспериментами *),
которые показали примерное равенство теплопроводности во взаимно противопо-
противоположных направлениях.
Соотношение в форме A7.1) часто применяют для описания связи между двумя
векторами в анизотропной среде. Вследствие симметрии кристаллов его легко упро-
упростить, выбрав оси в соответствующих кристаллографических направлениях. Резуль-
Результаты, полученные для различных кристаллических систем, приведены ниже; подробное
изложение этих вопросов можно найти в § 4 гл. I книги Вустера [119].
*) Эксперименты проводились с двоякопреломляющими кристаллами, например
с турмалином. Сначала предполагалось, что результаты экспериментов указывают на
существенную разницу в теплопроводности, но впоследствии было установлено, что
эта разница очень невелика или вообще отсутствует [121, 122].
§ 17] ГЛ. I. ОБЩАЯ ТЕОРИЯ 45
Триклинная система кристаллов. Упрощение невозможно.
Моноклинная система кристаллов. Все классы этой системы имеют
либо ось симметрии (такую, что при повороте вокруг нее на 180° кристалл принимает
положение, конгруэнтное первоначальному), либо плоскость зеркальной симметрии.
Если ось z является осью симметрии или нормальна плоскости зеркальной симмет-
симметрии, то коэффициенты теплопроводности образуют следующую схему:
Кп Kit 0
Ktx K22 0 A7.9)
0 0 /Сзз
Ниже будет показано, что, по-видимому, справедливо также равенство К2\ = /С12»
но это не вытекает из соображений симметрии.
Ромбическая система. Кристаллы всех классов этой системы имеют
либо две перпендикулярные оси симметрии, либо ось симметрии и плоскость сим-
симметрии. Если одна из осей координат выбирается вдоль оси симметрии, а другая —
вдоль второй оси симметрии или в плоскости симметрии, то схема коэффициентов
теплопроводности запишется в виде
Кп 0 0
0 К22 0 A7Л0>
0 0 /Сзз
Кубическая система. В этом случае возможен циклический обмен осей
ромбической системы, и схема коэффициентов теплопроводности примет вид
Кп 0 0
0 Кп 0 A7.11)
0 0 Кп
Тетрагональная, тригональная и гексагональная системы.
Если ось z является осью симметрии третьего, четвертого или шестого порядка,
т. е. соответствует поворотам на 90°, 120° или 60°, то мы получим следующую схему
коэффициентов теплопроводности:
Кп Kit 0
A7.12)
Кроме того, в кристаллах некоторых классов этих систем имеется ось симмет-
симметрии, перпендикулярная оси zt или соответствующая плоскость симметрии; если ось х
выбрана так, что она совпадает с этой осью или лежит в этой плоскости, то в выра-
выражении A7.12) /С12 = 0. Существует несколько классов, принадлежащих к таким
системам, для которых равенство К\2 нулю вытекает не только из соображений
симметрии; однако, как будзт показано ниже, это соотношение, по-видимому, оказы-
оказывается справедливым.
Все приведенные выше результаты можно вывести из соображений макроско-
макроскопической симметрии. Но в действительности, вероятно, можно считать, что Krs
в выражениях A7.1) симметричны, т. е. Krss=Ksr для всех г и s. Отсюда следует,
что /<12=0 в выражении A7.12) и К2\ = К\2 в выражении A7.9).
Во многих разделах физики кристаллов, в которых встречается закон типа A7.1),
классическая термодинамика позволяет сделать вывод о симметричности коэффициен-
коэффициентов теплопроводности, т. е. о том, что Kr$== KSr В данном случае общее доказа-
доказательство такого положения невозможно, и поэтому, чтобы показать симметричность
коэффициентов теплопроводности, следует обратиться к эксперименту. По этой при-
причине математическая теория обычно развивается без использования предположения
о симметрии; рассчитав эффекты асимметрии, их сравнивают с экспериментом (см.
§ 19 данной главы). Недавно было опубликовано доказательство закона симметрии,
основанное на принципе Онзагера о микроскопической обратимости [123—126] *).
Кп
— К\2
0
Ki2
Кп
0
0
0
/Сзз
*) Необходимо отметить, что уравнение теплопроводности (см. A8.1)), которое,
по существу, является выражением первого закона термодинамики, содержит вели-
величины Krs только в виде (Krs-\-KSr)> и поэтому симметрия последних или отсутствие
ее не влияют на выводы из этого уравнения. Эффекты антисимметрии выявляются
только при определении направления вектора теплового потока.
46 ГЛ. I. ОБЩАЯ ТЕОРИЯ [§ 1&
Часто приходится пользоваться формулами преобразования координат. Предпо-
Предположим, что мы хотим перейти к новой системе прямоугольных осей х', у', zr, на-
направляющие косинусы которых, отнесенные к старой системе, соответственно равны
(Сц, с21, c3i), (с12, с22, с32), (с13» с23, Сзз)- Тогда коэффициенты теплопроводности K\k%
отнесенные к системе (х'у у', zr), запишутся в виде
з з
^*=2 liWskKrs* A7ЛЗ>
Г=1 5=1
тогда как Krs будут выражаться через K'ik следующим образом:
3 3
2 «г а**»- A7Л4>
Эти выражения являются законами преобразования для тензора второго ранга
(доказательство и приложение изложены в книге Вустера [119]). Те же законы пре-
преобразования применимы и для Rrs.
Наиболее важным примером некристаллического анизотропного тела является
ортотропное твердое тело, которое имеет различные коэффициенты теплопро-
теплопроводности К\у К2> Къ в трех взаимно перпендикулярных направлениях. Приняв их за
оси Ху у и 2У получим
'*—*•&• '»--*•?. '•--*•&• A7Л5>
С другой стороны, для таких веществ, как древесина, коэффициенты теплопро-
теплопроводности которой Ки Кг и Къ в направлениях г, 0, z системы цилиндрических коор-
координат [70] (т. е. в направлении по лучам, кольцам и по оси дерева) неодинаковы,
тепловые потоки в указанных направлениях соответственно равны
§ 18. Дифференциальное уравнение теплопроводности
для анизотропных твердых тел
Теперь приступим к разработке теории, основанной на общем допущении A7.1).
В данном случае остается справедливым уравнение F.3), и, подставляя в него выра-
выражения A7.1), мы получим следующее уравнение теплопроводности при условии, что
среда однородна и что в ней отсутствуют источники тепла:
dv .. d2v . j. d2v , j, d2v . ... , ^ d2v .
^. A8.1)
Распространение указанного уравнения на другие случаи производится так же, как
и в § б настоящей главы.
Рассмотрим теперь квадратичную форму *)
Кпх2 + К22У2 + Кзз*2 + («23 + К32) У2 + (Ksi + Kis) zx + (К12 + К21) ху = const. A8.2)
Известно, что соотношение A8.2) можно преобразовать к новой системе прямо-
прямоугольных координат 6, т), С таким образом, чтобы его левая часть превратилась
в сумму квадратов
К^2 + К2 + К^ A8.3)
Пользуясь теми же переменными, приведем уравнение A8.1) к виду
dv .. d2v , .. d2v , .. d2v l1OiK
*c-dr = Kl-W + K2-W+K3-dV" <1&4)
Эти новые оси называют главными осями теплопроводности, а коэффициенты
Ки %2* Къ — главными коэффициентами теплопроводности. Из соотношений
*) Ниже будет показано, что /Сц^-0, /С22>-0>
§ 18] ГЛ. I. ОБЩАЯ ТЕОРИЯ АЪ
A7.9) — A7.12) следует, что если кристалл обладает осями симметрии, то-они служат
также главными осями теплопроводности.
Если мы проведем дополнительное преобразование системы координат, а именно
положим
К у/2 / К \1/2 г г( К\1/2
где К можно выбрать произвольно, то уравнение A8.4) запишется следующим образом:
dv К ( d2v d2v d2v\
+ + )
т. е. примет тот же вид, что и уравнение F.4) для случая изотропного твердого
тела. Итак, это преобразование позволяет свести решение задач для анизотропных
твердых тел к решению соответствующих задач для изотропных твердых тел в сле-
следующих случаях: когда тело не ограничено, когда оно ограничено плоскостями,
перпендикулярными главным осям теплопроводности, и (в случае /B = /Сз) когда тело
ограничено плоскостями, перпендикулярными оси 5 и круговыми цилиндрами, ось
которых совпадает с осью 6. В большинстве других случаев ограничивающие поверх-
поверхности искажаются; например, сечение кругового цилиндра с осью, направленной вдоль
одной из главных осей, становится эллиптическим.
Для однородных ортотропных твердых тел, для которых справедливо соотно-
соотношение A7.15), уравнение теплопроводности имеет вид
pc'dr=0' A8J)
тогда как для твердых тел с цилиндрической симметрией, т. е. когда справедлива-
выражение A7.16), уравнение теплопроводности примет вид
dv\ K2 d2v d*v dv
J+ + /fpe0
Ниже будет описан ряд важных специальных случаев, для которых дифферен-
дифференциальное уравнение сохраняет только одну или две пространственные переменные.
I. Температура зависит только от х.
Вследствие симметрии этот случай можно свести к случаю потока тепла в по-
полуограниченном твердом теле или в пластине с поверхностями, перпендикулярными
_, dv dv Л
оси ху и с граничными условиями, не зависящими от) и z. Тогда -^— = -^— = 0 и-
соотношения A7.1) примут следующий вид:
— /"г = ^i 1 3с" * —^y=z^2l'djci —^г ==^31 ~5лГ# A8.9)'
Кроме того, дифференциальное уравнение A8.1) преобразуется к виду
Таким образом, вся теория, излагаемая в гл. II и III, оказывается правильной
для анизотропного твердого тела при условии, что
Если для оси х направляющие косинусы относительно главных осей-теплопро-
осей-теплопроводности равны /, /и, п, то из выражения A7.13) следует, что
Кп = l2Ki + т2К2 + п*Кг. A8.12).
После того как найдено v, из A8.9) определяются тепловые потоки /г, /у, /г и
тогда оказывается, что вектор теплового потока направлен не по нормали к изотер-
изотермам. Эти результаты следуют из общей теории, приводящей к. соотношению B0.15).
данной главы.
48 ГЛ. I. ОБЩАЯ ТЕОРИЯ [§ 19
II. Тепло течет только в направлении х.
Это имеет место в тонком стержне, ось которого совпадает с осью х. Тогда
/y = /2 = 0 и из соотношения A7.2) получим
Л/ 0Л«/х. —^-=Л31/Ж. A8.13)
Воспользовавшись соотношением F.3), можно записать теперь дифференциаль-
дифференциальное уравнение A8.1) в виде
1 d2V dv л ,лолл\
*сж=°- (Ш4)
Тогда мы получим уравнение линейного потока тепла, где
1 A8.15)
Следует отметить, что /?п не равно -тт—, а определяется соотношением A7.3).
Если для оси х направляющие косинусы относительно главных осей равны /, т, п,
то из A7.13) мы получим для Rrs выражение
Rrs = -— -\~-7r—г"~77~ ПРИ f = $ и ^г5 = 0 при г Ф s. A8.16)
Это выражение выводится в общем виде (см. B0.25)).
Таким образом, теорией о распространении тепла в стержне, изложенной в гл. IV,
можно пользоваться для кристаллических стержней при условии, что величина х
определяется соотношением A8.15).
III. Температура зависит только от х и у.
Это имеет место в случае распространения тепла в неограниченном цилиндре
с осью, параллельной оси z, и при граничных условиях, не зависящих от z. Так как
dv
—т— = 0, то уравнение A8.1) принимает вид
и тепловые потоки определяются соотношениями A7.1) при -^— == 0. Следует отме-
отметить, что /гфО. Этот случай менее важен, чем случай двумерного течения тепла
в тонкой пластине (/2 = 0), который подробно рассматривается в следующем
параграфе.
§ 19. Теплопроводность тонкой кристаллической пластины
Двумерный случай проводимости интересен тем, что он иллюстрирует основные
черты общего случая; кроме того, в нескольких важных методах определения тепло-
теплопроводности используются тонкие кристаллические пластины. В данном параграфе
будет рассмотрена общая теория распространения тепла в такой пластине без каких-
либо предположений о ее симметрии.
Выберем оси хну так, чтобы они лежали в плоскости пластины, т. е. предпо-
предположим, что поток тепла в направлении z отсутствует (/2 = 0); тогда выражения A7.2)
принимают вид
Решая их относительно /х и /у и используя соотношения A7.3), A7.4) и A7.8),
получим
где
#31^13 is' КпКгЪ — ^13^32 /iq о\
' *12= КГ ' ( }
/iq a\
§ 19] ГЛ. I. ОБЩАЯ ТЕОРИЯ 49
Эти четыре величины Кп и т. д. можно назвать коэффициентами теплопровод-
теплопроводности для тонкой пластины в плоскости ху\ они сводятся к /Сц и т. д. только тогда,
когда одна из величин Кп и Кг\> а также одна из величин /С2з и Кы превращаются
в нуль.
Подставляя соотношения A9.2) в F.3), мы получаем уравнение теплопроводности
при установившемся состоянии
Можно записать его и в другом виде, а именно в виде
гJ <rt д2ч) rJff
Я221?-№2 +Д21)-^ + Ям-|J=0. A9.6)
Относя уравнение A9.5) к главным осям ?, г\ (как и в § 18), получим
где ATj и /Сз можно назвать главными коэффициентами теплопроводности в пло-
плоскости (здесь штрих используется для того, чтобы отличать эти коэффициенты от
главных коэффициентов теплопроводности в трехмерном случае (см. § 18), с кото-
которыми они могут совпадать в специальных задачах). Компоненты теплового потока,
отнесенные к тем же главным осям, должны принять вид
так как уравнение теплопроводности A9.7) в этих координатах не содержит члена
¦ g d э сравнивая полученные уравнения с уравнением A9.5), мы видим, что для их
удовлетворения сумма коэффициентов при ду/д-ц в соотношении A9.8) и при dv/dt
в соотношении A9.9) должна быть равной нулю. К[, К% и А могут быть, в принципе,
определены из коэффициентов в соотношениях A9.1) и A9.2).
В качестве примера, имеющего большое практическое значение, определим
изотермы и линии тока тепла для случая постоянного притока тепла к пластине
в начале координат.
Напишем соотношения, аналогичные A8.5):
() ' (
Тогда уравнение A9.7) примет вид
при радиальной симметрии его решение запишется в виде
+ 714 mln(X + XY 09.12)
где т — константа. Подставляя это выражение в соотношения A9.8) и A9.9), получим
Общее количество тепла, проходящее через круг радиусом а с центром в начале
координат и рассчитанное на единицу толщины пластины, равно
Q = f (Д cos 0 + /^ sin 6j a rfO.
о
4 Г. Карслоу, Д. Егер
50
ГЛ. I. ОБЩАЯ ТЕОРИЯ
[§
Используя выражения A9.13) и считая € = a cos 0, т\ = a sin О, получим
A9.14)
т. е. находим, что Q не зависит ни от а, ни от А. Подставляя в выражение A9.12)
величину /и, определяемую соотношением A9.14), мы получаем установившуюся тем-
температуру, обусловленную наличием в начале координат источника тепла мощностью Q.
Изотермы образуют семейство эллипсов
-Ц- + -V = const.
К[ ^ К'2
Направление вектора теплового потока определяется соотношением
A9.15)
A9.16)
Если Л = 0, то он направлен радиально от источника (но не перпендикулярна
эквипотенциальным линиям). На рис. 3, а показаны эквипотенциальные линии, а также
а)
б)
Рис. 3.
линии тока тепла, т. е. кривые, направление которых в каждой точке совпадает
с направлением вектора теплового потока.
Если А ф 0, то дифференциальное уравнение линий тока тепла имеет вид
A9.17)
Решение его записывается следующим образом:
-^ A In
const.
A9.18)
Кривые, соответствующие соотношению A9.18), образуют семейство спиралей,
которые показаны на рис. 3, б. В плоскости (glt t\x) при К[ = К^ спирали изогональны
к окружностям. Следовательно, если так называемый «вращательный> член А не
равен нулю, то направление течения тепла от точечного источника в неограниченной
пластине будет таким, как показано на рис. 3, б. Если в пластине имеется радиаль-
радиальная трещина, то тепло не сможет течь по этим спиралям и, следовательно, между
двумя сторонами трещины должна возникать разница температур. Тот факт, что
в экспериментах подобного типа не было обнаружено никакого различия температур,
указывает, что А мало. Другие методы показали [127], что А составляет менее одной
тысячной К\ или АГ2.
Эллиптическая форма изотерм (см. соотношение A9.15)) была использована
для определения отношения главных коэффициентов теплопроводности —;¦» причем
§ 20] ГЛ. I. ОБЩАЯ ТЕОРИЯ 51
для демонстрации изотерм на поверхность кристаллической пластинки наносилась
тонкая пленка воска [128—130].
Для случая линейной теплопередачи между поверхностью пластины и внешней
средой при нулевой температуре и теплового потока, равного Hv, уравнение для
стационарного режима (которое находят так же, как в § 4 гл. V), написанное относи-
относительно главных осей в плоскости, имеет вид
где D — толщина пластины. Решением этого уравнения, соответствующим установив-
установившемуся потоку тепла от точечного источника, служит
A9.20)
где /Со — функция Бесселя, определенная в приложении 3. И в этом случае изотермы
имеют вид эллипса (см. соотношение A9.15)), и проведенное выше рассуждение
остается справедливым.
§ 20. Изменение теплопроводности и вектор теплового потока
в анизотропных твердых телах
В анизотропной среде направление вектора теплового потока /т в какой-либо
точке, вообще говоря, не совпадает с направлением нормали к изотерме, проходящей
„ dv dv
через эту точку. Пусть -т— и -^ скорости изменения температуры вдоль нормали
к изотерме, проходящей через точку Р и вдоль направления вектора теплового
потока в точке Р соответственно.
Рассмотрим сначала направление вектора теплового потока в точке Я. Его на-
направляющие косинусы имеют вид
-й-, -г-- т1 B01>
/да J да J тп
и, следовательно, используя A7.1), можно написать
dv fx dv fy dv fz dv 2Ф
~dm ~~ 7даГ + 7да~ 7 + 7да~ ~5F ~~ ~~ Тда"
я
§^ ^г^. B0.3)
Однородная квадратичная форма B0.3) равна — fm(dv/dm), и из физических сообра-
соображений ее величина не зависит от выбора осей. Далее, поскольку производная dv/dm
должна быть отрицательной, если /т положительно, форма B0.3) будет положи-
положительно определенной. Для этого необходимо, чтобы
/<22>0, /Сзз>0. B0.4)
Из соотношения B0.2) следует, что
. „ dv „ 2Ф /ОЛСЧ
/да = —^да^—» где Km = / л ч» * B0.5)
dm /Jv\*
\dm)
Km можно назвать коэффициентом теплопроводности в направлении вектора
теплового потока в точке Р.
Теперь рассмотрим нормаль к изотерме, проходящей через точку Р. Напра-
Направляющие косинусы X, fx, v задаются соотношениями
, 1 dv I dv I dv B06)
52 ГЛ. I. ОБЩАЯ ТЕОРИЯ [§ 20
{(?)(?)№)}•
Отсюда следует, что
dv . dv . dv . dv A /ПЛО.
Кроме того, из соотношения C.2) следует, что тепловой поток /л в направлении,
перпендикулярном к изотерме в точке Р, записывается в виде
fn =* Wx + M-/y + v/2 = — — B0.9)
или в виде
/„ = —/С„^~, где /<я = __. B0.10)
Коэффициент /С/1 можно назвать коэффициентом теплопроводности по нормали
к изотерме в точке Р. Величины Кт и Кп, определяемые соотношениями B0.5)
и B0.10), не зависят от выбора осей.
Теперь посмотрим, каким образом Кп меняется в зависимости от направляющих
косинусов (X, fx, v) нормали к изотермической поверхности. Подставляя их величины,
определяемые B0.6), в соотношения B0.3) и B0.10), получим
Кп = /С, ,Х2 + /<22(х2 -f /<33v2 + (/C23 + Кг2) ^ + (Кы + Кп) vX -f (Kl2 + K2i) X{x. B0.11)
Если отложить отрезки kK^2 (где k — константа) в направлении (X, p., v), то
геометрическое место их концевых точек Q с координатами
х = k\K~ Ч у = kiiK~ Ч * = Ь/С"Vz B0.12)
имеет вид эллипсоида
+ Кгз) *¦* + (*11 + *2i> *У = ^2, B0.13Г
с которым мы уже встречались в § 18 (см. соотношение A8.2)). Как можно видеть,
в таком эллипсоиде квадрат радиуса-вектора, проведенного в точку эллипсоида,
в которой направление нормали к эллипсоиду совпадает с направлением радиуса-
вектора, обратно пропорционален коэффициенту теплопроводности по нормали.
Так же как и в § 18, можно найти систему прямоугольных координат ?, т), С,
относительно которой соотношение B0.13) примет вид
К?2 + К2у\2 + /С3С2 = *2, B0.14)
где /Сь Къ Кз — главные коэффициенты теплопроводности. Тогда коэффициенты
теплопроводности по нормали к изотермам (направляющие косинусы нормали относи-
относительно главных осей теплопроводности равны (/, т> п)) окажутся равными ?2/г2,
где г — радиус-вектор в направлении (/, /и, п). Другим способом это можно записать
следующим образом:
Кя = l2Ki + т*К2 + пЩ* B0.15)
Обычно при проведении основного эксперимента (см. § 2 настоящей главы)
на плоской тонкой пластине кристалла (вырезанной таким образом, что нормаль
к нему имеет направляющие косинусы относительно главных осей теплопроводности
кристалла, равные /, /и, п) измеряется именно этот коэффициент Кп-
Для очень важного специального случая, когда К\ = К2 и п = cos 6 (т. е. для
любого направления, образующего угол в с осью симметрии эллипсоида), соотноше-
соотношение B0.15) принимает вид
Кп = Кх + (Кг — Кх) cos2 в. B0.16)
Обратимся теперь к тепловым потокам через плоскости, перпендикулярные глав-
главным осям теплопроводности. Если переход из системы jc, у, z (см. соотношение B0.13))
в систему ?, т), С (см. B0.14)) записывается в явном виде, то величины тепловых
потоков Д, / , /с через новые координатные плоскости можно получить из соотно-
соотношений A7.1) и C.2). Однако и без этого ясно, что новые соотношения для тепловых
§ 20] ГЛ. I. ОБЩАЯ ТЕОРИЯ 53
потоков должны иметь вид
dv rdv dv
B0.17)
так как, повторяя вывод соотношения B0.13) из A7.1), приходим к выражению B0.14),
которое состоит из суммы квадратов. Таким образом, при переходе к главным осям
теплопроводности в линейной зависимости между тепловыми потоками и производ-
производными температуры появляется самое большее шесть независимых коэффициентов.
Далее, так же как и в двумерном случае, рассмотренном в § 19 настоящей главы,
есть все основания полагать, что так называемые «вращательные» члены А В, С
стремятся к нулю, и следовательно, соотношения B0.17) принимают вид
Из формулы для перехода к новым осям легко показать, что равенство
А = В = С = 0 означает симметрию коэффициентов теплопроводности, т. е. для
любой системы прямоугольных осей в формуле A7.1) мы должны считать, что
Kl2 = K2i, К2з=К*2, АГз! = Ki3. B0.19)
Наконец, определим направление вектора теплового потока и выясним, каким
образом изменяется в этом направлении теплопроводность Кт\ ПРИ этом мы пред-
предполагаем, что справедливо соотношение B0.19) и, следовательно, тепловой поток
определяется соотношениями B0.18).
В соотношении B0.14) точка (?, т), С) была выбрана на радиусе-векторе, перпен-
перпендикулярном изотерме, проходящей через точку Я, т. е.
с г dv dv dv
S:i):C==-g!-:i^:ir-
Используя этот результат, а также B0.18), получим
dv dv dv
6 т) С Kfi /V27) АГзС v
Квадрат каждого отношения в соотношении B0.20) равен
dv . х dv . , dv
+Ч+Л А+А+Л B021)
Используя B0.2) и B0.14), получим
где OR — радиус-вектор точки с координатами (Х= К& К = АГа^, Z= АГзС). Согласно
соотношениям B0.20) направление OR совпадает с направлением вектора теплового
потока. Следовательно, теплопроводность Кт в этом направлении равна
B0.23)
Итак, из соотношения B0.14) следует, что (Х> К, Z) лежит на эллипсоиде
? + ?.+ ** B0.24)
Ал *\2 Аз
Таким образом, если направление вектора теплового потока относительно глав-
главных осей теплопроводности задается направляющими косинусами /, т> л, то тепло-
теплопроводность Кт в этом направлении определяется соотношением
4 -1Г + ТГ + 1Г- B025)
Km Ai Аг Аз
54 ГЛ. I. ОБЩАЯ ТЕОРИЯ [§ 20
Это и есть теплопроводность, которая обычно измеряется в экспериментах с длин-
длинным тонким стержнем, вырезанным в направлении (/, /и, п). Если /С, = /С2, а п = cos 0,
то соотношение B0.25) принимает следующий вид *):
B026>
Эллипсоид, описываемый B0.24), был назван Ламе главным эллипсоидом;
иногда его называют термическим эллипсоидом. Он дает геометрическое предста-
представление об изменении теплопроводности.
Из рассмотрения эллипсоидов, описываемых соотношениями B0.14) и B0.24),
можно сделать множество геометрических выводов о свойствах теплопроводности,
направлениях вектора теплового потока и нормалей к изотермам. Например, из по-
последних трех уравнений B0.20) следует, что если нормаль к изотерме в некоторой
точке имеет направление (?, tj, С), то направление вектора теплового потока в ука-
указанной точке перпендикулярно плоскости, касательной к эллипсоиду B0.14) в точке
(?, •»!, С). С другой стороны, если в некоторой точке известно направление вектора
теплового потока (X, К, 2), то нормаль к изотерме, проходящей через указанную
точку, перпендикулярна плоскости, касательной к эллипсоиду B0.24) в точке (Х> К, Z).
ЛИТЕРАТУРА
1. International Critical Tables, vol. V, McGraw-Hill, 1929. /
2. Birch, Schainer, Spicer, Handbook of Physical Constants, Geol. Soc. of
America, Special papers, No. 36 A942).
3. Van derHeld, Appl. Sci. Res. A3, 237—249 A953).
4. Van der Held, Appl. Sci. Res. A4, 77—99 A954).
5. Van Dusen, J. Res. Nat. Bur. Standards 4, 753—756 A930).
6. Eyres, Hartree, Ingham, Jackson, Sarjaut, Wagstaff, Phil.
Trans. Roy. Soc A240, 1—58 A946).
7. Kirchhoff, Vorlesungen fiber die Theorie der Warme, 1849.
8. Vernotte, С R. Acad. Sci. 218, 39—41 A944).
9. Curtis, High Frequency Induction Heating, McGraw-Hill, 1944.
10. Brown, Proc. IRE 31, 537—548 A943).
11. M a d dock, J. Sci. Instr. 23, 165—173 A946).
12. Brown, Hoyler, Bierwirth, Radio Frequency Heating, van Nostrand, 1947.
13. Jeffreys, The Earth, Cambridge, ed. 3, p. 276, 1952.
14. Low an, Phys. Rev. 44, 769—775 A933).
15. Proc. Am. Concr. Inst. 31, 113 A934).
16. Proc. Am. Concr. Inst. 34, 89, 105, 117, 477, 497 A937).
17. Temperature, its Measurement and Control in Science and Industry, Am. Inst.
Phys., 1941.
18. Davey, Fox, Building Research Technical Paper, No. 15, London, H. M. S. O^
1933.
19. Ra whouser, J. Am. Concr. Inst. 16, 305 A945).
20. A wbery, Phil. Mag. 4, 629—638 A927).
21. Jaeger, Brit. J. Appl. Phys. 3, 221—222 A952).
22. С г a n k, Nicholson, Proc. Camb. Phil. Soc. 43, 50—67 A947).
23. Nichols, P г e s s о n, J. Appl Phys. 25, 1469—1472 A954).
24. Goheen, J. Math. Phys. 28, 107—116 A949).
25. Rice, J. Chem. Phys. 8, 727 A940).
26. G о о d 1 e t, E d w а г d s, P e г г у, J. Instn. Elect. Engrs 69, 695 A931).
27. Hartree, Mem. Manchr. Lit. Phil. Soc. 80, 85 A935).
28. J e f f г е у s, Proc. Camb. Phil. Soc. 26, 101—106 A930).
29. Lap wood, Month. Not. R. Astr. Soc, Geophys. Suppl. 6, 402—407 A952).
30. D u h a m e 1, J. Ec. polyt., Paris, 15, Can. 25, 1—57 A837).
31. Wilson, Proc. Camb. Phil. Soc. 12, 406—423 A904).
32. В о u s s i n e s q, Theorie analytique de la chaleur, т. II, Gauthier-Villars, 1903.
33. Jef f reys, Phil. Mag., 35, 270—280 A918).
34. Goldstein, Modern Developments in Fluid Dynamics, Oxford, 1938, v. II.
(С. Гольдштейн, Современное состояние гидроаэродинамики вязкой жид-
жидкости, М., 1948, т. II).
35. G г б b е г, Е г k, G г i g u 1 1, Warmeubertragung, Springer, ed. 3, 1955, p. 179.
*) Это соотношение было экспериментально подтверждено Бриджменом [131, 132].
ГЛ. I. ОБЩАЯ ТЕОРИЯ 55
36. Jakob, Heat Transfer, Wiley, 1949, p. 451. (M. Якоб, Вопросы теплопередачи,
ИЛ, 1960, перев. с изд. 1957 г.)
37. Lamb, Hydrodynamics, Cambridge, ed. 4, 1916. (Г. Л а м б, Гидродинамика, Гос-
техиздат, 1947, перев. с 6-го изд.)
38. S у n g e, Quart. Appl. Math. 13, 271—278 A955).
39. Е с к а г t, Phys. Rev. 58t 267—269 A940).
40. Gours at, Gnirs d'Analyse, Gauthpier-Villars, ed. 3, 1917. (Э. Гурса, Курс
математического анализа, ГТТИ, 1933, перев. с 5-го изд.)
41.McLachlan, Phil. Mag. 36, 600 A945).
42. М с L а с h 1 a n, Phil. Mag. 37, 216 A946).
43. Tranter, Quart J. Mech. Appl. Math. 4, 461—465 A951).
44. M a t h i e n, Cours de Physique Mathematique, Paris, 1873, Chap. 8, 9.
45. N i v e n, Phil. Trans. Roy. Soc. 171, 117 A879).
46. Fishenden, Saunders, Heat Transfer (Oxford, 1950).
47. M с A d a m s, Heat Transmission, McGraw-Hill, ed. 2, 1942. (В. Мак-Адаме,
Теплопередача, ОНТИ, 1936, перев. с 1-го изд.)
48. Fox, Phil. Mag. 18, 209—227 A934).
49. J a e g е г, Ргос. Camb. Phil. Soc. 46, 634—641 A950).
50. М a n n, W о 1 f, Quart. Appl. Math. 9, 163—184 A951).
51. P e d d i e, Proc. Edin, Math. Soc. 19, 34—35 A901).
52. M а г с h, W e a v e r, Phys. Rev. 31, 1072—1082 A928).
53. Schumann, Phys. Rev. 37, 1508—1515 A931).
54. Peek, Ann. Math. Princeton B) 30, 265 A929).
55. L anger, Tohoku Math. J. 35, 260—275 A932).
56. Low a n, Phil. Mag. 17, 849—854 A934).
57. J a e g e r, J. Proc. Roy. Soc N. S. W. 74, 342—352 A940).
58. J ae g e r, J. Proc. Roy. Soc. N. S. W. 75, 130—139 A941).
59. J a e g e r, Aust. J. Phys. 9, 167—179 A956).
60. В 1 а с k w e 1 1, J. Appl. Phys. 25, 137—144 A954).
61. G a s k e 1 1, Am. J. Math. 64, 447—455 A942).
62. Chao.Weiner, Quart. Appl. Math. 14, 214—217 A956).
63. Barrer, Diffusion in and through Solids, Cambridge, 1941. (P. Бэр pep, Диффу*
зия в твердых телах, ИЛ, М., 1948.)
64. J а с о b s, S t а г г, Rev. Sci. Instr. 10, 140 A941).
65. Jaeger, Quart. J. Mech. Appl. Math. 8, 101—106 A955).
66. W h i p p 1 e, Phil. Mag. 45, 1225—1236 A954).
67. I n g e г s о 11, J. Opt Soc. Am. a. Rev. Sci. Instr. 9, 495 A924).
68. Griff it hs, Proc. Phys. Soc. 41, 151 A928).
69. Dictionary of Applied Physics.
70. G г i f f i t h s, К а у e, Proc Roy. Soc. A104, 71 A923).
71. Crank, The Mathematics of Diffusion, Oxford, 1956.
72. Jos t, Diffusion, Academie Press, 1952.
73. Babbitt, Canad. J.» Res. A28, 449—474 A950).
74. Hill, Proc. Roy. Soc. В104, 39—96 A929).
75. Thews, Acta Biotheoretica A10, 105—138 A953).
76. Danckwerts, Trans. Faraday Soc. 47, 1014—1023 A951).
77. Keynes, Proc. Roy. Soc. B142, 359—382 A954).
78. G i b s о n, H e n k e 1, Geotehcnique 4, 6—15 A954).
79. Henry, Proc. Roy. Soc. A171, 215 A939).
•80. Riemann-Weber, Die Differential und Integralgleichungen der Mechanik und
Physik, ed. Frank, Vieweg, 1927, Bd. 2. (Ф. Франк и Р. Мизес, Дифферен-
Дифференциальные и интегральные уравнения математической физики, ч. II, ОНТИ, 1937.)
81. Furth, Geofis. Рига ё Appl. 31, 80—89 A955).
82. D a v i e s, Proc. Roy. Soc. A200, 100—113 A949).
83. Hulburt, Phys. Rev. B) 31, 1018 A928).
84. M а г s h a k, Rev. Mod. Phys. 19, 185—238 A947).
85. S n e d d о n, Fourier Transforms, McGraw-Hill, 1951. (Снеддон, Преобразова-
Преобразование Фурье, ИЛ, М., 1955.)
вб. Goldstein, Proc Lond. Math. Soc. 34, 51 A932).
87. М с Е w e n, J. Marine Res. 7, 188—216 П948).
88. С а г s 1 a w, Jaeger, Operational Methods in Applied Mathematics Oxford, ed. 2,
1947, Chap. 9. (Г. К а р с л о у и Д. Е г е р, Операционные методы в прикладной
математике, ИЛ, М., 1948, перев. с 1-го изд. 1941 г.)
89. Musk at, The Flow of Homogeneous Fluids through Porous Media, McGraw-Hill,
1937, Chap. 10
90. Rosenhead, Miller, Proc Roy. Soc. A163, 298—317 A937).
56 ГЛ. I. ОБЩАЯ ТЕОРИЯ
91. Hantush, Jacob, Trans. Am. Geophys. Union. 36, 95—112 A955).
92. Memoire sur la methode generate relative au mouvement de la chaleur dans les
corps solides plonges dans les mileux dont la temperature varie avec le temps, J.
Ec. polyt. Paris 14, Cah. 22, 20 A833).
93. Bartels, Churchill, Bull. Am. Math. Soc. 48, 276 A942).
94. Danckwerts, Trans. Faraday Soc. 47, 1014—1023 A951).
95. Newman, Ind. Eng. Chem. 28, 545 A936).
96. О 1 s о n, S с h u 11 z, Ind. Eng. Chem. 34, 874 A942).
97. Doetsch, Math. Z. 22, 293 A925).
98. Doetsch, Math. Z. 25, 608 A926).
99. Doetsch, Enseign. math. 35, 43 A936).
100. Titchmarsh, Fourier Integrals, Oxford, 1937, pp. 281—283. (Э. Титчмарш,
Введение в теорию интегралов Фурье, Гостехиздат, 1948, перев. с 1-го изд.)
101. Тихонов, Математический сборник 42, 199—216 A935).
102. Churchill, Am. J. Math. 61, 651 A939).
103. Mersman, Bull. Am. Math. Soc. 47, 956 A941).
104. Widder, Trans. Am. Math. Soc. 55, 85—95 A944).
105. Widder, Trans. Am. Math. Soc. 75, 510—525 A953).
106. Coop e r, J. Lond. Math. Soc. 25, 173—180 A950).
107. В i г k h о f f, К о t i k, Proc Am. Math. Soc. 5, 162—168 A954).
108. К a m p ё de F ё г i e t, С R. Acad. Sci. 236, 1527—1529 A953).
109. Fulks, Pacific J. Math. 2, 141—145 A952).
110. Fulks, Pacific J. Math. 3, 387—391, 567—583 A953).
111. H а г t m a n, W i n t n e r, Am. J. Math. 72, 367—395 A950).
112. Rayner, Quart. J. Mech. Appl. Math. 6, 385—390 A953).
113. Duhamel, J. Ec. polyt. Paris 13, Cah. 21, 356 A832).
114. Duhamel, J. Ec. polyt. Paris 19, Cah. 32, 155 A848).
115. Lame, Lecons sur la theorie de la chaleur, Paris, 1861.
116. Stokes, Camb. and Dublin Math. J. 6, 215—238 A851).
117. В о u s s i n e s q, Theorie analytique de la chaleur, Paris, 1901.
118. Voigt, Lehrbuch der Krystallphysik, Leipzig, 1910.
119. Wooster, Text-book on Crystal Physics, Cambridge, 1949.
120. В б с h e r, Higher Algebra, Macmillan, 1924.
121. Thomson, Lodge, Phil. Mag. E) 8, 18 A879).
122. Stenger, Wied. An. 22, 522 A884).
123. С г a n d a 11, Physica 21, 251—252 A955).
124. Casimir, Rev. Mod. Phys. 17, 343—350 A945).
125. Onsager, Phys. Rev. 37, 405 A931).
126. Onsager, Phys. Rev. 38, 2265 A931).
127. Voigt, Gott. Nach. 223 A896).
128. S e n а г m о n t, С R. Acad. Sci. 21, 459, 707, 829 A847).
129. Von L a n g, Pogg. Ann. 135, 29 A868).
130. Roentgen, Pogg. Ann. 151, 603 A874).
131 В r i d g m a n, Proc. Am. Acad. Arts. Sci. 61, 101 A925).
132. H u m e - R о t h e г у, The Metalic State, Oxford, 1931, Chap. IV*
ГЛАВА И
ЛИНЕЙНЫЙ ПОТОК ТЕПЛА.
НЕОГРАНИЧЕННОЕ И ПОЛУОГРАНИЧЕННОЕ ТВЕРДОЕ ТЕЛ©
§ 1. Введение. Простые решения уравнения
для линейного потока тепла
В этой главе мы рассмотрим различные задачи, в которых изотерми-
изотермические поверхности представляют собой плоскости, параллельные плоско-
сти л; = 0, поток тепла линеен и линии тока параллельны оси х. Получаю-
Получающиеся результаты применимы и к задаче о потоке тепла вдоль прямолиней-
прямолинейного стержня малого поперечного сечения в отсутствие теплообмена на его
боковой поверхности. Задачи, в которых это условие не выполняется, рас-
рассматриваются в гл. IV.
После того как мы найдем решение для неограниченного тела, мы при-
приступим к детальному изучению многих важных задач о линейном тепловом
потоке в полуограниченном твердом теле, т. е. в твердом теле, которое
ограничено плоскостью х = О и простирается до бесконечности в положи-
положительном направлении оси л:. Во всех случаях предполагается, что терми-
термические характеристики тела во всех его точках одинаковы и не зависят от
температуры. Распространение этой задачи на переменные термические харак-
характеристики рассматривается в § 16 настоящей главы.
Уравнение для линейного потока тепла записывается в виде
Сначала укажем ряд простых решений этого уравнения *). В дальнейшем
все они будут встречаться во многих местах настоящей книги одновременно
с истолкованием их физического смысла.
I. Истокообразное решение.
Рассмотрим выражение
u=f2e"Axt. A.2)
Поскольку
dt
_ * с
ш
i!fi= * e-& | - c
dx2 2^V, ^ 4x3t4,
*) Связь между различными решениями уравнения A.1) дается в работе^!]*
58 ГЛ. II. ЛИНЕЙНЫЙ ПОТОК ТЕПЛА [§ 1
выражение A.2) является частным решением уравнения A.1). Для этого
решения справедливы следующие соотношения:
а—*0 при t—>0 для фиксированного хфО,
#—>оо при t—>0 для л; = 0
и
оо
Г и dx = 2 (icx)Vl при всех t > 0.
—оо
Таким образом, его можно считать решением, соответствующим случаю
выделения количества тепла 2pc(icxI/l с единицы площади в плоскости х = 0
в момент времени / = 0.
Ясно, что ряд других решений уравнения A.1) получается дифферен-
дифференцированием (или в некоторых случаях интегрированием) выражения A.2)
по х или по t.
II. Решение в виде функции ошибок.
Как мы видим, уравнению A.1) удовлетворяет также
х
X 1 Х2 i 2(rt)xlt
0 0
Введем обозначение *)
X
Ф(х) = -ф=- f e-z2db A.3)
6
которым мы в дальнейшем всегда будем пользоваться, и покажем, что
дфГ х
где А — произвольная постоянная, является решением уравнения A.1).
Для «функции ошибок», определенной A.3), справедливы следующие
соотношения:
ф@) = 0, Ф(оо)=1, Ф(—х) = — Ф(х). A.5)
В приложении 2 приведены еще некоторые данные, а также таблицы
числовых значений. Мы будем часто пользоваться, кроме того, следующими
обозначениями:
ф* (jc) = 1 — Ф (а:), A.6)
оо
i<&*(x) = №*(x) = f <&*$)dt% A.7)
X
оо
i«O*(jc)= J i"-i<$*(l)dl n = 2, 3, 4, ... A.8)
X
III. .Решения вида tmf\ x .. 1.
LD^I/2J
Можно доказать, что выражение такого типа удовлетворяет уравне-
уравнению A.1), если /(г),служит решением дифференциального уравнения
*) Эту функцию иногда обозначают также символом erf. (Прим. ред.)
§ 2] гл. :т. линейный поток тепла 59
Это уравнение совпадает с уравнением A6) приложения 2, и поэтому,
если п — целое число, то выражение
п\Л\ A.10)
служит решением*) уравнения A.1).
IV. Решение в виде экспонент.
Простое дифференцирование сразу же показывает, что выражение
Рехр(хЛ2* ± Ах) A.11)
(где Р и А — постоянные), как действительное, так и комплексное, удовле-
удовлетворяет уравнению A.1).
V. Решение для установившегося состояния.
Для случая, когда v не зависит от времени, решение уравнения A.1)
записывается в виде
Ах-{-В, A.12)
где А и В — постоянные.
Было показано [6], что выражения A.4), A.11) и A.12) служат (если
не считать тривиальных их модификаций, например при замене х на х + а)
единственными решениями уравнения A.1), имеющими вид 0
VI. Решение в виде двойного степенного ряда.
Легко проверить путем подстановки, что выражение
12х2*2) + а5 (х5 + 20хл;3*
+ а6 (х6 Н- ЗОха:4^ + 180х2л:^2 + 120x3^3) + .. ., A.13)
где а0, av ...—постоянные, удовлетворяет уравнению A.1).
VH. Решение, содержащее две произвольные функции времени.
Выражение
^ Й " •- AЛ4)
где ср и ф — произвольные функции времени, а точки означают дифференци-
дифференцирование по t, удовлетворяет уравнению A.1). Для этого решения характерно
следующее: если л: = 0, то t/ = cp(?), а -г^- = ф (t).
§ 2. Неограниченное твердое тело. Решение Лапласа
Требуется найти решение уравнения линейного теплового потока A.1)
в бесконечной области — сю < х < оо с начальным условием
v = f(x) при ? = 0.
Обычное формальное рассмотрение этой задачи заключается в следую-
следующем: согласно A.2) данной главы
1
1
2 (тс*)
является частным интегралом уравнения A.1).
*) Рибо [2] и Нордон [3] отмечали, что для всех значений п решениями уравне-
уравнения A.9) служат функции Вебера. Эти вопросы, а также ряд других вопросов анало-
аналогичного типа рассматриваются Аппелем [4] и Гурса [5].
60
ГЛ. II. ЛИНЕЙНЫЙ ПОТОК ТЕПЛА
[§2
Далее, так как уравнение является
линейным, то сумма любого числа ча-
частных интегралов также является инте-
интегралом. Следовательно, функция
Рис. 4. Распределение температур в не-
неограниченной области, одна часть кото-
которой в начальный момент времени имеет
постоянную температуру V, а другая
часть — нулевую температуру.
а) Область | х | < а с начальной температурой,
равной V', б) внутренность цилиндра радиусом
г=а при начальной температуре v; в) внутрен-
внутренность сферы радиусом г*=а при начальной тем-
температуре V. Во всех случаях числа на кривых
указывают величины xt/a2.
(X-XrO
v—*ksffW~ ~Ш dx'
также удовлетворяет указанному урав-
уравнению при условии, что этот интеграл
сходится *).
Пусть
Тогда
сю
у tz •'
оо
В пределе, когда ^->0,
/ \х + 2 Y%t l) = f (x), если эта функ-
функция непрерывна; предполагается, что
предельное значение этого интеграла
дается выражением
оо
Л=. ff(x)e-Pdl.
которое равно f(x).
Итак, в момент времени t тем-
температура неограниченного твердого
тела, имевшего начальную температуру
v = f(x), записывается в виде
оо
Мы можем написать [11]
fe-*-
*2*2 cos 2bx dx =
—
«2
и, следовательно,
оо
cos a (Х' x)dd =
ехР
г
*) Для того чтобы функция v служила решением A.1), необходимо, чтобы этот
интеграл, а также интеграл от ее производных сходились равномерно. {Прим. ред.}
§ 2] ГЛ. II. ЛИНЕЙНЫЙ ПОТОК ТЕПЛА 61
Отсюда выражение для v можно записать в форме
со оо
¦I I dxr I f{x')cosa(xf — x)e~xaitdat B.2)
-оо О
которая напоминает форму интеграла Фурье C.2) для f (х).
Проведенное выше рассуждение было формальным, и поэтому необходимо рас-
рассмотреть условия для f(x), при которых оно справедливо. Было показано [10J, что
если функция f (х) ограничена и интегрируема в любом заданном интервале, а инте-
оо
грал I \f(x')\dx' сходится, то при t->0 функция с/, заданная выражением B.1),
— оо
имеет предел f(x), если эта функция непрерывна в точке х> или предел
¦о" [/ (х "г" Ф ~г" / (х — ^)], если она имеет в точке х разрыв первого рода. Кроме
того, если / (х) непрерывна в интервале [a, fj], то в этом интервале v равномерно
стремится к / (х) при t -> 0.
На самом деле полученные результаты справедливы и при менее строгих усло-
условиях для / (х)У например, если / (х) — любой полином или экспоненциальная функция,
т. е. если
где К и с — постоянные *).
Ниже приводятся некоторые практически важные результаты, полученные на
основе уравнения B.1).
1. Если в начальный момент времени область —а < х < а имеет постоянную
температуру, равную К, а область | х | > а — нулевую температуру **), то
На рис. А, а приведены некоторые численные значения величины v/V, получен-
полученные из выражения B.3) при различных значениях параметра rf/a2. Аналогичные
результаты, найденные для цилиндра с радиусом поперечного сечения а и сферы
радиусом а, находящихся прл постоянной начальной температуре, приведены соот-
соответственно на рис. 4, б и 4, в.
2. Если в начальный момент времени область — а < х < а имеет нулевую тем-
температуру, а область \х\ > а — температуру, равную V, то
-oo<x<oo. B.4)
3. Если в начальный момент времени область \х\ > а имеет нулевую температуру,
область а > х > 0 — температуру v = V (а — х)/а и область — а < х < 0 — темпера-
температуру v = V (а + хIа> то
*) Более общее обсуждение этих вопросов приведено в работах [5] и [7].
**) В работе [8] функция B.3) использована в качестве приближения для тем-
температуры в случае, когда плоский слой расплавленной горной породы вторгается
в другую породу при нулевой температуре. В этой работе приводятся графики функ-
функции B.3) в форме, пригодной для практического применения. Кроме того, в ней
используются функции B.9) и B.10) для случая цилиндрических и массивных интру-
интрузивных пород, а также выражение D.14) для случая течения лавы по поверхности
других пород (см. также [9]). О влиянии теплоты застывания горных пород
см. § 2 гл. XI.
62 ГЛ. II. ЛИНЕЙНЫЙ ПОТОК ТЕПЛА J§ 3
4. Если плоскость х = О непроницаема для тепла, то решение принимает форму
оо оо
~ I dx' If (xf) cos ax' cos axe'™*' da. B.6)
6 6
6 6
5. Для двумерного и трехмерного случаев решения уравнения B.1) прини-
принимают вид
оо оо
v = -^ f f / (*', У') ехр [- (" "^^^ УJ] djc' rfy'. B.7)
—oo —oo
oo oo oo
v== III f (xf\ у'\ z') ex
— ОО — ОО —ОО
B.8)
6. Если в начальный момент неограниченный цилиндр | х ] < а, | у | < 6 имеет
постоянную температуру V» а окружающая его неограниченная область — нулевую
температуру, то
f/^L*) /?±*)Jff^) /J±y)l B.9)
7. Если в начальный момент параллелепипед \ х\ < а, \ у\ < b, \ z\ < с имеет
постоянную температуру V, а окружающая его неограниченная область — нулевую
температуру, то
( ) + ( a+x)\U( *-у
(e + *)]. B.10)
§ 3. Использование интегралов Фурье и преобразований Фурье
В § 2 настоящей главы отмечалось, что решение Лапласа может принять
форму B.2), которая связывалась с интегралом Фурье для f (х). Указанное решение
можно вывести также из интегральной теоремы Фурье. Для этого удобнее всего,
по-видимому, использовать преобразование Фурье. Мы приведем здесь краткое изло-
изложение данного метода и покажем, как он приводит к решению Лапласа.
Согласно интегральной теореме Фурье (см. [11], § 119), если f (х) определена
для всех jc, удовлетворяет условиям Дирихле *) в любом конечном интервале и если
существует интеграл **)
оо
f\/(x)\dx, C.1)
— ОО
оо оо
/ (х) = 1 f d4 f f(x') cos g (x — x') dx', C.2)
TO
*) Об условиях Дирихле см. § 93 в книге Карслоу [11]. Они удовлетворяются
функцией с конечным числом максимумов, минимумов и разрывов первого рода.
**) Это чрезвычайно жесткое условие сильно затрудняет использование инте-
интегральной теоремы Фурье в этой форме для практических приложений. Результаты
для более широкого класса функций можно получить при использовании обобщенных
интегралов Фурье [7] или преобразования Лапласа, причем последнее удобнее всего
применять в целом ряде задач, связанных с теплопроводностью.
§ 3] ГЛ. II. ЛИНЕЙНЫЙ ПОТОК ТЕПЛА 6 3
ИЛИ
оо оо
1 Г Г
/(*) = _ / drz I f(x')tost(x — xf)dx' C.3)
— OO —OO
во всех точках, в которых f (x) непрерывна, а в точке разрыва первого рода
1 г..
Так как
оо оо
— оо —оо
>) sln г (х - х>) dx' -0> C-4>
то из выражений C.3) и C.4) следует, что
оо оо
f (x)=i f e~iUcd* If (x>)ei%x'dx'- C5)
—oo —oo
Указанное соотношение является математическим выражением комплексной
формы интеграла Фурье. Ее можно записать следующим образом: если
оо
F (S) = -~ f elwf (x') dx', C.6)
— ОО
ТО
C.7)
Здесь функции F(t) и / (х) являются преобразованиями Фурье друг для друга; если
одна из них известна, то другая следует из соответствующей формулы C.6) или C.7).
Большое практическое значение имеют следующие два случая. Если / (х) —
нечетная функция х, то соотношение C.2) принимает вид
со оо
f(x)=^-j sin Чх ft I f (x') sin х'Ч dx'. C.8)
6 6
Иными словами, выполнение любого из соотношений:
оо
Fs (?) = |/"|- [ f С*') sin jc'S dx', C.9)
6
оо
»]/"^ /* ^,F) sin Ьс Л, C.10)
6
6
подразумевает справедливость другого. Функции Fs(?) и f (х) называются синус-
преобразованиями Фурье друг для друга.
Если же f (х) — четная функция jc, то выражение C.2) принимает вид
оо оо
= |- I coslxdt J f(x')<:osx'Zdx. C.11)
о о
64 ГЛ. II. ЛИНЕЙНЫЙ ПОТОК ТЕПЛА [§ 4
Иными словами, выполнение любого из соотношений:
с»
F* (О = |/~ / / (*') c°s x'l dx\ C.12)
6
/ <Э cos g* rfg, C.13)
о
подразумевает справедливость другого. Функции Fc(?) и f(x) называют косинус-
преобразованиями Фурье друг для друга.
Теперь мы покажем, как соотношения C.6) и C.7) можно формально применить
к задаче, поставленной в § 2 настоящей главы, т. е. для решения уравнения
d2v I dv
1х1[="Ч~Ж' —<х><х<со, *>0, C.14)
при
t/ = /(jc), —oo<jc<oo, * = 0. C.15)
Отметим, что функция
ехр(—&* — rJzH) C.16)
удовлетворяет уравнению C.14) при любых значениях g. Примем, что общее решение
C.14) и C.15) записывается в виде
оо
1 Г
v (jc, t) = —— I exp (— ibc — %S20 cp (g) dg. C.17)
— CO
При * = 0 получим
оо
/ (x) = -|=- У exp (- Их) <t E) d5.
— оо
Поэтому, согласно выражению C.6),
оо
<Р(?) = -Т=- [exp{iix')f(x')dx'.
Подставляя его *в C.17), получим
v(JC> f) = ^г /ехр("хе2'~/U)rfe /(expiixt)f {х)dx'
—
оо
2^ [/(x')dx'
Конечно, для обеспечения строгости нашего анализа необходимо провести даль-
дальнейшие рассуждения. В книге Титчмарша [7] рассматривается случай, когда f (х)
является экспоненциальной функцией.
§ 4. Полуограниченное тело с начальной температурой f(x)
и нулевой температурой поверхности
Пусть твердое тело ограничено плоскостью х = 0 и простирается до бес-
бесконечности в положительном направлении оси х, причем его начальная тем-
температура задана соотношением v = f(x), а плоскость х = 0 поддерживается
при нулевой температуре. Решение такой задачи можно получить из решения,
найденного для неограниченного твердого тела.
§ 4] ГЛ. II. ЛИНЕЙНЫЙ ПОТОК ТЕПЛА 65
Пусть исследуемое тело продолжено в отрицательном направлении оси х
и пусть его начальная температура в точке —л:/(х/>0) равна —/С*')»
а начальная температура в точке xf равна / (х'). При таком распределении
температур температура плоскости х = О остается равной нулю. Тогда
из соотношения B.1) получим
v=—Д=г| ff(x')exp\—
2/™/ F *•
о
fi-f (-
Ясно, что эта величина г; удовлетворяет всем условиям задачи о полу-
полуограниченном твердом теле, ограничивающая плоскость которого поддержи-
поддерживается при нулевой температуре.
Выражение D.1) для температуры можно преобразовать, как и в § 2, следую-
следующим образом:
оо оо
v = y I dx' j f(x')[cosa(x' — x) — cos а (х'-\-х)]е-хаЧ da =
0 6
OO OO
= — / dx' I f (x') sin ax'sin axe-xaV da, D.2)
о о
т. е. в форму, подсказываемую соотношением C.8). Так же как и в § 3 (неограни-
(неограниченное тело), этот результат легко получить и в данном случае, используя синус-
преобразования Фурье C.9) и C.10).
Если начальная температура постоянна и равна V, то соотношение D.1)
можно упростить, подставляя xr = x -\- 21 y*t в первую его часть,
—во вторую. Тогда мы получим
Vxt 2Vxt
V I"
V-
V
f
2Vxt
Этот интеграл совпадает с A.3) данной главы, и поэтому решение
задачи о полуограниченном твердом теле, поверхность которого поддержи-
поддерживается при нулевой температуре, а начальная температура равна V, имеет вид
D.3)
Полученный результат можно вывести непосредственно из выражения A.3),
так как из свойств функции ошибок следует, что она удовлетворяет нашему
дифференциальному уравнению, а также начальным и граничным условиям.
Важно отметить, что в этом случае, т. е. в случае постоянной начальной
температуры и нулевой температуры поверхности, полученный результат D.3)
5 Г. Карслоу, Д. Егер
66 ГЛ. II. ЛИНЕЙНЫЙ ПОТОК ТЕПЛА
зависит только от одного безразмерного параметра
X
[§4
D.4)
Это позволяет легко сравнивать температуры в различные моменты вре-
времени и в различных точках твердых тел, обладающих различной темпера-
температуропроводностью. Аналогичные результаты справедливы и для часто ветре-
чающихся величин скорости охла-
охлаждения и градиента температуры
в любой точке.
Скорость охлаждения в любой
точке записывается в виде
0,6
0,2
J
/
г
/
X
^—
ч
—
dv
dt
Vx -4т
D.5>
Температурный градиент в лю-
любой точке — в виде
V --J-7
= г е
dv
дх
Переходя к параметру
получим
D.6)
V
dv
dv
Рис. 5. Графики функции Ф [х/2 У~тЗ] (кри-
(кривая /) и функции [х/2 У^уп] ехр [— x2/4tt]
(кривая //).
dt
2V дх
ir^ —^——- 0
X'
' 4%t
D.7>
D.8>
Численные значения этих величин приведены в приложении 2; кроме того*
они показаны в виде кривых / и // на рис. 5. Кривая // имеет максимум*
равный
V*
=0,4288
V2 '
D.9>
Из соотношения D.7) следует, что для любого вещества время, необ-
необходимое для достижения заданной температуры в какой-либо точке тела*
пропорционально квадрату расстояния этой точки от поверхности тела.
Кроме того, время, необходимое для достижения в данной точке заданной
температуры, обратно пропорционально температуропроводности.
Например, из рис. 5 или из таблицы приложения 2 следует, что
._!„
при
iy*t
В серебре, для которого х=1,72, температура достигает указанной
величины на глубине 1 см через 0,64 сек\ в висмуте, для которого х = 0,07,
это произойдет через 15,7 сек, а в грунте, для которого х== 0,0047, — через^
234 сек. Для глубины 10 см соответствующие промежутки времени окажутся
в 100 раз больше.
§ 5) ГЛ. II. ЛИНЕЙНЫЙ ПОТОК ТЕПЛА 67
Наконец, мы приведем некоторые результаты, имеющие большое значение для
практики. Их легко получить из соотношения D.1).
1. Если на границе jc = O поддерживается постоянная температура V, а началь-
начальная температура равна нулю, то
- ф Т77=- ) = Уф* -7^7=Г • DЛ°)
Это легко получить, вычтя из v = V прет х > 0, t > 0, которое является решением
дифференциального уравнения теплопроводности, решение D.3) для начальной тем-
температуры V и нулевой ^температуры поверхности. ' '
Тепловой поток на поверхности равен
*' D.11,
причем при t->0 это выражение стремится к бесконечности.
2. Если в начальный момент времени область х > 0 имеет постоянную темпе-
температуру V, а область х < 0— нулевую температуру, то
— V {
2 1
1 + Ф^=Ч, -со<л:<аэ. D.12)
3. Если в начальный момент времени область х > О имеет температуру V-\-kx,
а плоскость х = 0 поддерживается при нулевой температуре, то
_
D.13)
4. Если в начальный момент времени область 0 < х < d имеет постоянную тем-
температуру V, а область х > d — нулевую температуру, причем для t > 0 поверхность
х = 0 сохраняет нулевую температуру, то
1/ = — Ю 2Ф л Ф л Ф -J—— I. D.14)
2 1 2(*)V* 2@/2 2@/2 )
Ф -J—— I
2(*0/2 )
5. Если в начальный момент времени область а< х < b имеет постоянную тем-
температуру V, а области 0<jc<a и х > Ь — нулевую температуру, причем для t > 0
поверхность х — 0 сохраняет нулевую температуру, то
— KJ Ф — 4-Ф !— Ф Ф L_— I D.15)
2 I 2 (*)V* 2 (ОV» 2 (х*I/* 2 (iI^ J
§ 5. Полуограниченное твердое тело. Начальная температура
равна нулю. Поверхность находится при температуре ср(О
Выше мы видели (см. § 14 гл. I), что из решения для случая постоян-
постоянной температуры поверхности можно, пользуясь теоремой Дюамеля, получить
решение и для случая переменной температуры поверхности.
Для полуограниченного твердого тела, когда v должно удовлетворять
уравнениям
dv d2v
dt — х дх* '
v = 0 при * = 0
и
v= 1 при х = 0
решение D.10) принимает вид
2Vxt
68 ГЛ. II. ЛИНЕЙНЫЙ ПОТОК ТЕПЛА [§ 5
Если же
dv _ d2v
dt ~ * дх2 f
v = О при t = О
при * = 0,
то из соотношения A4.10) гл. I следует, что решение имеет вид
t
д
о
оо
где
В этом случае
— г (а:, г — К) = —. ехр —
dt V* V 4х(^ —X) J ^
(^ — X)»
Следовательно, решение нашей задачи записывается следующим образом:
Положив
получим
со
1^^ ./ У\
2Vxt
Отсюда ясно, что наше решение удовлетворяет дифференциальному
уравнению, а также начальным и граничным условиям.
Ниже приводятся некоторые специальные случаи, представляющие практический
интерес *).
1. <р (t) = Vo (постоянная) при 0 < t < 7\ <р (t) = Vx (постоянная) при t > Т,
^) . 0 < t < Т. E.2)
*) Эти результаты проще всего получить при помощи преобразования Лапласа
(см. § 4 гл. XII).
§ 5] гл. и. линейный поток тепла 69
2. <р (t) = ktt где k — постоянная *)
H(i?MwOir} E-4>
т. е.
() E-5)
Обозначения, используемые в соотношениях E.5), E.7) и E.8), см. в прило-
приложении 2.
3. <р (t) = к№, где k — постоянная.
{^ }} E.6)
т. е.
Как будет показано в § 9 настоящей главы, приведенное выражение соответ-
соответствует температуре поверхности при постоянном тепловом потоке с этой поверхности.
7 п
4. y{t) = kt , где п — любое положительное целое число (четное или не-
нечетное).
При использовании выражения E.8) температуру на любой глубине для случая, когда
температура поверхности является полиномом от t или от *1уЧ можно записать в виде
табулированных функций. Следует отметить, что полиномом от fl* можно пользо-
пользоваться при эмпирическом представлении наблюдаемой температуры поверхности,
так как член, содержащий ^2, соответствует постоянному тепловому потоку с по-
поверхности (см. § 9 данной главы).
5. ср (t) = ext, где X — постоянная (положительная или отрицательная).
е'Х ^ Ф* \-4= -УП] +/^Ф* Г—^ + yjt] 1. E.9)
L2^ J^ L2^^r JJ v
jt] 1.
JJ
Функции ошибок с комплексным аргументом, используемым в очень важном
случае отрицательной X, были совсем недавно затабулированы (см. приложение 2).
Решение для положительных значений X используется в гл. IV.
Мы можем решить задачу о полуограниченном твердом теле с начальной тем-
температурой / (х) и температурой поверхности <р (t)t положив
v = u-\-w.
Здесь и удовлетворяет уравнению
при условии
a w — уравнению
да
dt
а
и
д2и
дх2
= 0в начальный
: = <р (t) при х =
dw d2w
F~"X дх2
момент,
= 0,
*) Линейное увеличение температуры поверхности представляет большой инте-
интерес для некоторых практических приложений (см. [12, 13]).
70 ГЛ. II. ЛИНЕЙНЫЙ ПОТОК ТЕПЛА [§ б
при условии
w = / (х) в начальный момент,
w = 0 при л: = 0.
Иными словами, а служит решением задачи, рассмотренной выше, a w — решением
задачи, приведенной в § 4 данной главы.
§ 6. Полуограниченное твердое тело. Температура поверхности
является гармонической функцией времени
Задачи о теплопроводности твердого тела с периодически.изменяющейся
температурой на поверхности представляют весьма большой практический
интерес. Подобные задачи встречаются в следующих случаях: а) при иссле-
исследовании колебаний температуры коры Земли, периодически нагреваемой
Солнцем (см. § 12 настоящей главы); б) при работе на различных экспери-
экспериментальных установках для определения температуропроводности (см. § 12
настоящей главы, а также §§ 4 и 8 гл. IV); в) при вычислении периодически
изменяющихся температур (а следовательно, и соответствующих термических
напряжений) в стенках цилиндров паровых машин [14, 15] и двигателей
внутреннего сгорания и, наконец, г) в теории автоматических систем регу-
регулировки температуры.
Если температура на поверхности полуограниченного тела х > 0 задается
выражением v = A cos (о>/ — е), а начальная температура равна нулю, то
из E.1) следует, что наше решение запишется в виде
оо
Как мы знаем,
и поэтому F.1) можно записать в следующей форме:
l
-jl
<6-2'
Второй член в правой части соотношения F.2) соответствует нестацио-
нестационарному возмущению *), обусловленному началом колебаний температуры
поверхности в момент времени /^0; при достаточно большом t этот член
*) В § 7 гл. XII приведена другая форма. Если начальная температура твердого
тела равна не нулю, a f (х), то в соотношение F.1) нужно добавить член, соответ-
соответствующий решению задачи о полуограниченном твердом теле при заданной начальной
температуре и нулевой температуре на поверхности (см. § 4 данной главы); при до-
достаточно больших t этот член также должен становиться пренебрежимо малым.
§ 6] ГЛ. II. ЛИНЕЙНЫЙ ПОТОК ТЕПЛА 7\
исчезает. Оставшийся первый член соответствует установившимся колебаниям
с периодом —. Прежде чем приступить к дальнейшему обсуждению, при-
приведем другой вывод [16, 17], в котором мы будем исходить из дифферен-
дифференциального уравнения
d2v I dv n /R ~
Будем искать решение уравнения F.3) в виде
v = uel «°'-шК F.4)
где и — функция только х. Это решение должно иметь период, равный 2тс/о).
Подставляя F.4) в F.3), мы находим, что и должно удовлетворять урав-
уравнению
d2u /<о /с Сч
-I—* = — «• F.5)
dx2 х v J
Уравнение F.5) имеет следующее решение, ограниченное при х—>оо:
и = Аехр [-х |/^Г ] = Лехр [-*A +/) ]/"-? ] .
Таким образом, решения уравнения F.4) с периодом 2тс/со запишутся
в виде
v = Ae~k*x cos (Ы — е — k*x) F.6)
или
v = Ae~k*x sin (o>/ — е — /г*д;),
где
*=(?)*- F-7)
решение, которое при л:==0 соответствует величине Acos(wt — е), имеет вид
v = Ae~k*x cos (Ы — Л*д; — е). F.8)
Соотношение F.8) представляет температурную волну с волновым
числом k* и длиной волны X, которая определяется выражением
где п — частота, равная — .
Для типичных горных пород, для которых х = 0,01, длина волны при-
приблизительно равна 2,7 см при частоте 1 колебание в 1 мин, 1 м при 1 ко-
колебании в 1 день и 20 м при 1 колебании в 1 год. Для металлических
проводников, для которых х=1, длина волны равна 3,5 см при 1 колеба-
колебании в 1 сек и 27 см при 1 колебании в 1 мин, а для металлов при темпе-
температуре, близкой к абсолютному нулю, для которых х равно по порядку
величины 104, длина волны равна II см при 1000 колебаниях в 1 сек. Эти
данные очень важны для измерений методами, основанными на периодическом
нагреве. Обычно наблюдения проводят на расстоянии порядка длины волны,
что и определяет требуемую частоту. Использование области звуковых частот
для металлов при очень низких температурах привело в последнее время
к значительному развитию этих методов [18].
Перечислим важнейшие свойства периодической функции температуры
е установившемся режиме.
72 ГЛ. II. ЛИНЕЙНЫЙ ПОТОК ТЕПЛА
1. Амплитуда колебаний температуры уменьшается по закону
-ххле: jul
л — k*X — о * 2х о ^
[§6
F.10)
и, следовательно, падает тем быстрее, чем больше со. Если на поверхности
тела задать температуру в виде ряда Фурье (см. F.17)), то по мере пере-
перемещения внутрь тела более высокие гармоники исчезают чрезвычайно быстро.
На расстоянии одной длины волны амплитуда уменьшается в ехр[—2тс] =
= 0,0019 раз и, значит, волны очень быстро затухают. Отсюда следует, что
для полуограниченного тела
10
данное решение можно исполь-
использовать для проводника, тол-
толщина которого составляет одну
или две длины волны.
2. Фаза температурной
волны запаздывает по закону
1
О
-as
-го
Рис. 6. Изменение температур на различных глу-
глубинах тела при температуре поверхности, являю-
являющейся гармонической функцией времени.
k*x = x \~
F.11)
Это запаздывание увеличи-
увеличивается с возрастанием со.
3. Температурные колеба-
колебания (например, положение ма-
максимума и минимума темпера-
температуры) распространяются внутри
твердого тела со скоростью
BхсоJ
F.12)
Из выражений F.10), F.11) и F.12) следует, что для определения тем-
температуропроводности х достаточно измерить амплитуды или ф^зы волны на
расстоянии х или скорость распространения волны.
Тепловой поток F на поверхности исследуемого тела равен следующей
величине:
FЛЗ)
Таким образом, в установившемся режиме температура в полуограни-
полуограниченном твердом теле, которое нагревается в результате поступления на
его поверхность х = 0 периодически изменяющегося теплового потока
Fo cos (Ы — е), выражается в виде
v =
cos Lt — k*x — e — -
[ 4
F.14)
Амплитуда данной функции содержит термические параметры в комби-
комбинации /Срс, что позволяет измерить эту величину.
В соотношение F.8) входят безразмерные параметры
х = ш/.
F.15)
§ 6]
ГЛ. II. ЛИНЕЙНЫЙ ПОТОК ТЕПЛА
73
Следовательно, если мы выберем начальный момени времени так, чтобы
8 = 0, то соотношение F.8) можно записать в виде
/($, t) = ?-ScOS(t $). F.16)
На рис. 6 приведен график зависимости /(?, т) от т для величин ?,
равных 0, -?-, .... -д-. По мере возрастания ? увеличивается как отставание
по фазе, так и затухание
амплитуды, что отмечалось
уже выше.
На рис. 7 представлен
график зависимости /E, т)
от ? для величин х, равных 0,
4г,..., тс- Эти кривые по-
о
казывают распределение
температур по глубине тела
в различные моменты вре-
времени. Семейства кривых,
аналогичных указанным на
рис. 6 и 7, часто полу-
получаются как результаты
экспериментов (см. ссылки
в § 12 настоящей главы).
Если температура по-
поверхности является перио-
периодической функцией вре-
времени ср (t) с периодом —, то мы можем получить решение нашего уравне-
уравнения, разлагая эту функцию в ряд Фурье:
Рис. 7. Распределение температур по глубине тела
в различные моменты при температуре поверхности,
являющейся гармонической функцией времени.
ср(t) =AQ-\-Al cos (at — Sj)-f- A2 cosBotf — e2) + ...
Используя формулу F.8), получим решение в виде
F.17)
F.18.
при условии, что, как и раньше,
мало.
В качестве примера рассмотрим случай, когда температура поверхности
задается следующим образом:
2гТ
= 0, 1, 2, ...
3.19)
Тогда
я=0
74
ГЛ. II. ЛИНЕЙНЫЙ ПОТОК ТЕПЛА
Отсюда следует, что при установившемся состоянии периодически изме-
изменяющуюся температуру можно записать в виде
4V \Г\
1
ехр —
л=0
X
ГBя
L
+1)«*
F.20)
Г . ~\ 2*7-
На рис. 8 представлен график зависимости v/V от ? для величин
V x7" ' Равных ^; О»^; *'0; ^.0. На графике ясно видно, как по мере
О
продвижения в глубь твердого
тела более высокие гармоники
исчезают и «прямоугольная» волна
постепенно становится синусои-
синусоидальной.
Наконец, можно указать на ана-
аналогию с теорией передающих ли-
линий. Для общности мы рассмотрим
стержень с сечением Q при отсутст-
отсутствии потерь тепла с боковой поверх-
поверхности *). В этом случае темпера-
температура v и тепловой поток в стержне/
должны удовлетворять уравнениям
^ dv д/ . .,_ dv
Рис. 8. Изменение температур на различных
глубинах тела при температуре поверхности,
описываемой «прямоугольной» волной.
F.21)
Эти уравнения совершенно иден-
идентичны уравнениям, которым удовле-
удовлетворяют потенциал v и ток / в пере-
передающей линии с последовательным
1
сопротивлением -т~г и параллельным
емкостным сопротивлением Qpc на единицу длины, а также в линии с нулевой индук-
индуктивностью и неидеальной изоляцией («подводный кабель»).
Теория такой линии в установившемся периодическом режиме хорошо известна
и ею можно сразу же воспользоваться. Это означает, что усложненную термическую
схему можно описать методами теории электрических цепей. При выбранных нами
обозначениях **) последовательный импеданс на единицу длины линии запишется
в виде Z= -QJ7-> а шунтирующий адмиттанс — в виде К = /со2рс. Характеристический
импеданс линии Zo задается соотношением
ZQ=\ — \' =
1
1
F.22)
а постоянная распространения 7 — соотношением
Величины / и v в любой точке полуограниченной линии получаются из выра-
выражений
F.23)
выра-
F.24)
*) Случай, когда имеет место теплопередача с поверхности, пропорциональная
температуре, аналогичен случаю утечки в подводном кабеле.
**) См. любую работу по теории электрических цепей, например книгу Слей-
тера [19].
§ 7] ГЛ. II. ЛИНЕЙНЫЙ ПОТОК ТЕПЛА 75
Эти результаты совпадают с полученными нами ранее (см. F.8) и F.13)). Дан-
Данный метод был очень подробно разработан Маркусом [20], который использовал ме-
методы, развитые в теории волноводов, для исследования влияния изменения попереч-
поперечного сечения проводника на температурную волну.
§ 7. Полуограниченное твердое тело. Теплообмен на поверхности
в среду с нулевой температурой. Начальная температура постоянна *)
Когда начальная температура постоянна и равна V, уравнения для v
имеют вид
dv_ d2v
dt ~~- * dx2 '
v = V при ? = 0,
' = 0 при л; = 0.
Пусть
1 dv
T h дх
Тогда
cp = V при ? = 0,
ср = 0 при л: = 0.
Поэтому на основании соотношения D.3)
мы замечаем, что при х—>оо функция ср (л:, t) имеет предел V.
Для определения v мы имеем уравнение
их
Отсюда, интегрируя это уравнение обычным путем, находим
х
v = Cehx — hehx fcp(?, t)e~Kdt
оо
Положив ? = лг + т}, получаем
оо
v = Cehx + h Г ср(л:-)-7), t)e-h4d*r\.
о
Однако при л;->оо, ср(лг, t) имеет пределом V и, кроме того, v должно
оставаться конечным; поэтому С должно равняться нулю. Следовательно,
*) Случай, когда начальная температура является функцией /U). разобран
$ 2 гл. XIV.
в §
76 ГЛ. II. ЛИНЕЙНЫЙ ПОТОК ТЕПЛА
решение нашей задачи запишется в виде
[§ 7
= 1™ fe->
лГъ J
2V%T
>,-u* du
Отсюда
.„о
2V
2V7F
— e-hri j e-a2
J dt\
f e-u2du
2Vxt
CO
o4. , V Г Г /и] — (лг + т)I .
— a?)da-\— / exp ¦—~т-^—— \dy\ =
от/ /* i/
= 4= / exp(-flVg+ /•—
1 0
Положим во втором интеграле
тогда
X
2V
= 2
v = -===- / exp (— a2) da -f- тт^ exp (Aa: + h4t) / exp (— w2) da =
1/ ТС е/ Г Я ']
2V Г
6
Поэтому
X+2fixt
2Vxl
ут
2VxT
j e~u*da— f e-u2da
) GЛ)
где Ф(л:) и Ф*(^) — интегралы, определенные в приложении 2.
Температура на поверхности твердого тела vn, которую можно получить»
положив ^ = 0 в соотношении G.1), записывается в виде
_^п = еыф* (Д Y^f). G.2)
В приложении 2 приведена краткая таблица значений этой функции. Для
больших значений времен величина vJV определяется, согласно выражению E)
приложения 2, по приближенной формуле
рп _ 1 f 1 ^. 1 | 3 1 п
V hV™* \ 2кЫ "^ 4hHH2 '")
Таким образом, по истечении значительного времени после начала охла-
охлаждения температуру поверхности можно считать равной
V G.4)
с ошибкой, меньшей, чем V/2A3 (rcx3/3)!/l.
§7]
ГЛ. II. ЛИНЕЙНЫЙ ПОТОК ТЕПЛА
77
Для задачи о полуограниченном твердом теле с нулевой начальной
температурой, которое нагревается вследствие теплообмена на гра-
границе х = 0 со средой, имеющей температуру V, решение записывается
в виде
Это решение можно выразить в виде функции любых двух из следую-
следующих безразмерных параметров:
fix.
G.6)
Любая из выбранных пар обладает своими преимуществами. На рис. 9
представлен график зависимости отношения v/V от lg[*(*O)l/f] для величин
x/2Y%t , равных 0; 0,1; ...; 1,5.
В § 9 гл. I отмечалось, что граничные условия третьего рода, харак-
характеризующиеся теплообменом на границе, имеют место в различных случаях,
а именно при теплоотдаче вслед-
вследствие вынужденной конвекции или г-°
излучения, а также при теплопе- v/v
редаче через тонкую поверхно-
поверхностную пленку. В первых двух 41
случаях величины h можно полу-
получить из формул, аналогичных при-
приведенным в § 9 гл. I, и тогда 4t
температуру полуограниченного
твердого тела в любой его точке
и в любой момент времени можно ^
найти из соотношения G.5).
Представляет интерес оценить
эффект тонкой поверхностной пленки
из плохого проводника и сравнить
результаты, полученные из соотно-
соотношения G.5) для этого случая, с ре-
результатами, найденными в предполо-
предположении, что поверхность je = O под-
поддерживается при температуре V при
всех t > 0 (см. § 4 настоящей главы).
Граничное условие, требующее по-
постоянной температуры на поверхно-
поверхности исследуемого тела, использова-
0,2
к
///////
у
-
^-—1
1
*-—
=====
0.7
0.2
О.Э
ОА
0,6
0.7
О,д
0,9
7.0
1. 1
S"
Рис. 9. Распределение температур в полу-
полуограниченном твердом теле при теплообмене
на его поверхности.
лось в теории теплопроводности значительно чаще, чем любое другое граничног
условие. Однако на практике оно обычно не выполняется, так как, вообще говоря,
при х = 0 контакт не идеален, и поэтому температура V на этой поверхности устана-
устанавливается не мгновенно. Желательно знать, с какими ошибками нам приходится иметь
дело в таком случае.
Рассмотрим на твердом теле поверхностные пленки воздуха, вазелина, воды и
ртути толщиной 0,001 см\ величины коэффициента теплообмена Н указаны в таблице,
приведенной на стр. 28. В качестве твердых тел рассмотрим хороший проводник,
серебро (К =1,001, %= 1,716), плохой металлический проводник, висмут (/(= 0,020,
ос = 0,0699) и плохой неметаллический проводник, стекло (К =0,0028, % = 0,0058).
Пусть х = 1 см во всех трех случаях, а время t выберем равным 0,64 сек, 15,7 сек
и 189 сек соответственно; тогда для всех трех твердых тел величина —?=г равна 0 477
2V*t
а величина v/V для постоянной температуры поверхности равна 0,5. Ниже приведены
величины v/V, найденные по формуле G.5) для различных поверхностных пленок.
78
ГЛ. II. ЛИНЕЙНЫЙ ПОТОК ТЕПЛА
[§ 8
Вещество
Серебро . . .
Висмут . . .
Стекло . . .
Величины vIV
постоянная
температура,
#»оо
0,5
0,5
0,5
*) См. примечание на
воздух,
Я = 0,053
РРР
стр. 28.
контакт под не-
небольшим давле
нием *),
#=0,07
0,029
0,394
0,483
вазе-
вазелин,
#=0,44
0,145
0,481
0,497
вода,
#-1,44
0.295
0.494
0,499
та
0,479
0.500
0,500
Из этой таблички видно, что в случае хорошего проводника с поверхностной
пленкой из плохо проводящего материала влияние пленки оказывается весьма замет-
заметным; в случае же плохо проводящего твердого тела влияние поверхностной пленки
на результаты становится значительно меньше.
§ 8. Полуограниченное твердое тело. Теплообмен на поверхности
в среду с температурой f(t). Начальная температура равна нулю
В этом случае температура v должна удовлетворять уравнениям
dv_ d2^
dt * dx2 *
-т— -+- hv = hf (t) при х = О,
v = 0 при ? = 0.
Поступая так же, как и в предыдущем параграфе, положим
1 dv
Тогда получим следующие уравнения для определения ср:
дер д2ср
при х = 0,
ср = 0 при t = 0.
Эти уравнения уже рассматривались в § 5 настоящей главы, и мы ви-
' дели, что
Отсюда, так же как и в § 7, имеем
(8Л)
Представляют интерес следующие специальные случаи.
1. / (t) = А (постоянная), 0 < / < Т, f(t) = B (постоянная), t > Т.
§ 9] гл. и. линейный поток тепла 79
Здесь
{^^[^ }. 0<t<T, (8.2)
v=A<b*[ *-) + (В — А)Ф*(— X ) —
- A exp (hx + h**t) Ф»( —?=- + h V^f ) -
] <>Г. (8.3)
2.
Здесь
k «-"''•rsin (mt + t — ы'х — Ь) +
22
2х/г /* (q> cos s — %tf2 sin s) (ц cos tfjc -{- h sin
"Т~./ (х2а4 + С02)(
0
где .' - /? , a » [i^T]
Первый член в соотношении (8.4) представляет собой установившееся периоди-
периодическое решение и обладает теми же свойствами, что и решение F.6).
§ 9. Полуограниченное тело. Тепловой поток на границе х = 0
является заданной функцией времени. Начальная температура равна нулю
7. Тепловой поток Fo (в единицу времени через единицу площади)
постоянен. Функция
& <9Л)
удовлетворяет дифференциальному уравнению, аналогичному уравнению для V,
т. е.
Воспользовавшись соотношением D.10), мы получим решение уравне-
уравнения (9.2) при условии
f = F0 (постоянная), х = 0, t > 0, (9.3)
в виде
Таким образом, используя соотношения (9) и A1) из приложения 2,
получим из выражения (9.1) /
или
(9.6)
80 ГЛ. II. ЛИНЕЙНЫЙ ПОТОК ТЕПЛА [§ 9
или, наконец,
Таблица значений функций i<P*(jc) приведена в приложении 2. Темпера-
Температура при х = О оказывается равной
'"'%\ (9.8)
Граничное условие, характеризуемое постоянным тепловым потоком,
представляет значительный практический интерес. Оно встречается при гене-
генерировании тепла в результате пропускания электрического тока через плоский
нагревательный элемент, при выделении тепла вследствие трения; кроме того,
оно приближенно выполняется в ранних фазах процесса нагрева печи или
помещения. Это граничное условие имеет также большое значение в задачах
диффузии. Процесс охлаждения поверхности Земли после захода Солнца
в ясную безветренную ночь [21] весьма похож на процесс отдачи тепла при
постоянном потоке тепла (в единицу времени через единицу площади), и,
следовательно, выражение (9.8) показывает изменение температуры поверх-
поверхности Земли после захода Солнца.
Приведенные выше результаты применимы также к области —оо < х < оо,
когда в плоскости х = 0 тепловой поток равен 2/70. Соответствующие
результаты для случая, когда области х > 0 и х < 0 состоят из различных
материалов, будут приведены в § 15 данной главы.
2. Начальная температура в области х > 0 равна нулю. На плоскости
х = 0 тепловой поток равен f (t). В данном случае
Это следует из соотношения (9.5) и из теоремы Дюамеля (см. § 14 гл. I).
3. Начальная температура в области х > 0 равна нулю. В течение некото-
некоторого времени Т на плоскости х = 0 тепловой поток поддерживается постоянным
и равным Fo. По истечении этого времени поступление тепла прекращается, и
граница х = 0 термически изолируется. Если 0 < t < 7\ то температура в момент
времени t определяется по формулам (9.6) или (9.7); если же t > 7\ то она равна
следующей величине:
_ {f - Т)Ч> \Ф* l—rj—^ и-) }. (9.10)
Указанная температура будет наблюдаться в опыте, в котором в неограничен-
неограниченную среду погружен плоский электронагревательный элемент, выделяющий в единицу
времени через единицу площади количество тепла, равное 2F0, и включенный в те-
течение времени 7\ а затем выключенный.
4. Начальная температура в области х > 0 равна нулю. В течение некото-
некоторого времени Т на плоскости х = 0 тепловой поток *) поддерживается рав-
равным Kfrntyt*. По истечении этого времени поступление тепла прекращается
и ограничивающая поверхность изолируется. В момент времени t температура
*) Это соответствует количеству тепла, которое должно поступать в единицу
времени через единицу площади для того, чтобы поддерживать температуру на по-
поверхности, равной единице (см. D.11)). Интеграл (9.12) затабулирован в работе [22].
Вопрос о минимальном количестве тепла, которое необходимо для заданного повы-
повышения температуры в расчетной точке применительно к методам нагрева, рассмотрен-
рассмотренным в пунктах 3 и 4, разобран в [23].
§ 9] ГЛ. П. ЛИНЕЙНЫЙ ПОТОК ТЕПЛА 81
на границе х = 0 будет равна
t/=l, 0<t<Tt \
2 (Т \Т <9Л1>
v = — arcsin -—I » *>Г.
Эта температура совпадает с температурой поверхности полуограниченного
твердого тела для случая, когда его граница х = 0 в течение некоторого времени Т
поддерживается при температуре, равной единице, а затем изолируется.
Температуру v для любого х при t > Т можно получить из выражения (9.9)
в виде определенного интеграла:
1 Г Г х2 1 dx 2 Г
v~j expr"i^^"J^(^,)Va=^ /
—У
t-T)
х2 A + и2) 1 da
— \Т
j /
(9.12)
5. Начальная температура в области х > 0 равна нулю. Тепловой поток
на плоскости х = 0 для * > 0 равен sin (о>* -f~ e). В данном случае
си
х.^2 sin ? — о) cos s) cos ц^ ^_хи2/ du
Как и прежде, первый член в правой части (9.13) представляет собой устано-
установившееся периодическое решение, а второй — неустановившееся.
6. Тепловой поток на плоскости х = 0 записывается в виде
~(±) при
= — sino)^ — I— при
Тогда периодическая компонента температуры для любого jc в момент времени t
равна следующей величине:
пК* пDя1)
/1= 1
Полученный результат можно рассматривать как некоторое приближение [21] *),
описывающее нагревание Солнцем поверхности Земли в равноденствие; первая строка
в соотношениях (9.14) соответствует условиям в ночное время, вторая — условиям
в дневное время.
7. Начальная температура в области х > 0 равна нулю. При t > 0 тепловой
поток внутрь твердого тела равен Fot , где п может равняться —1, 0 или
какому-нибудь положительному целому числу. В этом случае
1п+1Ф* Х-ТГ. (9.16)
2 (*O*
/С
*) В работе [24] получены результаты для любых высот и любых времен года.
Егер рассмотрел случай, когда поверхность излучает тепло как абсолютно черное
тело [25, 26].
6 Г. Карслоу, Д. Егер
82 ГЛ. II. ЛИНЕЙНЫЙ ПОТОК ТЕПЛА [§ 1 1
Функция 1пФпх определяется в приложении 2. Температура на поверхности равна
<9Л7>
§ 10. Применение полученных результатов к определению
теплопроводности
В математической задаче о полуограниченном теле с начальной температурой,
равной нулю, и границей х = 0, поддерживаемой при единичной температуре, темпе-
температура в момент времени t, согласно D.10), записывается в виде
Таким образом, из наблюдения температуры в любой точке хх в момент вре-
времени tx можно по таблице функции ошибок (см. приложение 2, табл. 1) определить
величину — * , а следовательно, и величину %. Трудность использования этого
метода заключается в следующем: обычно конец стержня х = 0 нагревают, омывая
его потоком жидкости постоянной температуры; однако эксперименты показали, что
он при этом не сразу принимает температуру жидкости. Таким образом, математи-
математическое выражение условий эксперимента следует рассматривать только как некоторое
приближение [27, 28]. Учитывая приведенные выше соображения (см. стр. 77), можно,
по-видимому, считать, что указанное приближение оказывается вполне приемлемым
для плохих проводников, но для хороших проводников оно может привести к значи-
значительным ошибкам, и в этом случае при организации эксперимента следует принимать
специальные меры предосторожности, например значительно увеличивать скорость,
с которой жидкость обтекает твердое тело [29].
Было сделано множество попыток избежать подобных трудностей. Кирхгоф
и Ганземанн [30, 31] предположили, что температуру при х = 0 можно представить
в виде суммы С + <р(О, где С —константа, а <р@ — функция времени, которой
можно пренебречь во всех случаях, за исключением случая малых t. Величину С
следовало определять из данных о температуре в непосредственной близости от на-
нагреваемой границы, не считая ее равной температуре нагревающей жидкости. В одной
из модификаций этого метода предполагалось, что температуру поверхности можно
представить в виде С A — eat), причем а должно быть велико.
В другом методе рассмотрения той же задачи [32—34] исследовалось изменение
во времени температуры в двух точках. Действительные условия на границе х = 0
использовались только для получения решения в удобной математической форме.
Целый ряд математических решений, приведенных в предыдущих разделах,
можно использовать в качестве основы для экспериментальных методов измерения
температуропроводности. Так, например, если твердое тело нагревается плоской на-
нагревательной спиралью с пренебрежимо малой теплоемкостью или излучением источ-
источника с очень высокой температурой, то с некоторым приближением реализуется
граничное условие, характеризуемое постоянным тепловым потоком на поверхности.
Поэтому можно соответственно преобразовать соотношение (9.6) и найти величину *
из двух результатов измерения температуры. Кроме того, можно преобразовать соот-
соотношение G.5) так, чтобы по двум наблюдаемым температурам определить как /г,
так и х.
§11. Полуограниченное твердое тело, внутри которого
находится источник тепла
Для линейного теплового потока дифференциальное уравнение F.7)»
приведенное в гл. I, принимает вид
d*v I dv _ А П1 п
Здесь А — количество тепла, выделяющееся в единице объема в единицу
времени, которое, вообще говоря, зависит от х> t и v. Пока мы рассмотрим
§11] ГЛ. II. ЛИНЕЙНЫЙ ПОТОК ТЕПЛА 83
только случай, когда А не зависит от v. В этом случае *) для решения
уравнения A1.1) пригодны следующие три способа: 1) интегрирование исто-
истокообразных решений (см. гл. X и XIV); 2) использование преобразования
Лапласа (см. гл. XII); 3) приведение уравнения A1.1) к однородной форме
путем замены переменной. Первые два способа являются наиболее сильными.
Здесь мы просто кратко проиллюстрируем третий способ и приведем ряд
результатов, представляющих интерес в связи с тепловыделением в коре
Земли, обусловленным радиоактивным распадом (см. §§ 13 и 14 данной
главы). Некоторые дополнительные сведения изложены в § 4 гл. XII и в § 7
гл. XV. Следует отметить, что случаи, когда количество выделяющегося
в единицу времени тепла является линейной функцией температуры, можно
исследовать методами, приведенными в § 14 гл. I и в § 7 гл. XV.
Решение для случая зависимости количества выделяющегося в единицу
времени тепла от времени можно получить, воспользовавшись теоремой
Дюамеля (см. § 14 гл. I) для случая, когда это количество не зависит
от времени; поэтому вполне достаточно рассмотреть последнее, хотя не так
трудно найти точные решения для простых типов зависимости от времени **).
1. В области #>0 начальная температура равна а-\-Ьх. При
?>0 в единице объема за единицу времени выделяется постоянное
количество тепла Ао. Плоскость х = 0 поддерживается при нулевой
температуре. Здесь мы должны решить уравнение
дх2 х dt ~ К
при условиях
v= a-\-bx при ? = 0
и
v = 0 при jc = O, t > 0.
Положив
¦An п
« «?*«
получим эти уравнения в виде
д2и 1 да А . л
¦Ш--Ж-0' х>0'
и
u = 0 при jc = O,
Из соотношения D.1) следует, что
^ К 2К ! 1.2/-W К
и, следовательно,
+ ^) + y e + bx
x-^^. A1.2)
2К
*) Многочисленные результаты, полученные для полуограниченного твердого
тела, пластины, сферы и цилиндра при постоянной скорости выделения тепла и при
различных граничных условиях, можно найти в литературе [35—37].
**) Некоторые результаты для случая, когда количество выделяющегося в единицу
времени тепла пропорционально t2 , где п = — 1; 0; 1; 2; ..., приведены в § 4 гл. XIL
См. также [38].
84 ГЛ. II. ЛИНЕЙНЫЙ ПОТОК ТЕПЛА [§ 11
2. Условия те оке, что и в задаче 1, но количество тепла, выделяющегося
* единицу времени на единицу объема, равно А^е'**. В данном случае
- ± exp <*«* +«О ^[«»^+—?=¦]}. (И.З)
3. Условия те же, кто и в задаче 1, но тепло выделяется только в слое *)
О < х < I. В данном случае
при 0<х<1 A1.4)
tjc±t\ _ 412ф, 1_х\ |
VJ \2V-dl)
j
\2VxtJ
^±А при х>1. A1.5)
Температурный градиент на поверхности х = 0 равен следующей величине:
При определении температуры в коре Земли нужно помнить, что тепло вы-
выделяется только в поверхностном слое толщиной, меньшей чем 50 км, и следова-
следовательно, в A1.5) / мало по сравнению с 2|/^. Поэтому, воспользовавшись теоремой
Тейлора, мы можем разложить выражение A1.5) по степеням /. Тогда для темпера-
температуры в слоях, расположенных ниже радиоактивного слоя [39], получим **)
2/C
Температурный градиент на поверхности приближенно равен
— ('/
A1.7)
К \ 2\Г* ^ ] '
4. В области х > 0 начальная температура равна нулю. В области 0 < х < I
при t > 0 в единице объема за единицу времени выделяется постоянное количе-
количество тепла Ао. На поверхности х = 0 тепловой поток отсутствует. В данном
случае
*Л* Г / 1±) / 1 + *\ }0 < х < /, A1.9)
A^)^) X>L (НЛО)
Это также является решением для случая неограниченного твердого тела, в котором
тепло выделяется в полосе толщиной 21.
5. В области х > 0 начальная температура и температура на поверхности
равны нулю. В области а < х < b при t > 0 количество тепла, выделяющегося
*) Случай, когда области 0<jc</ и х > I имеют различные термические кон-
константы, рассмотрен в § 8 гл. XII.
**) Распространение полученных результатов для случая, когда термические кон-
константы изменяются с глубиной, проведено в работах [40, 41].
§ 12] гл. и. линейный поток тепла 85
в единице объема за единицу времени, равно постоянной величине Ло. Темпера-
Температурный градиент *) на поверхности равен
\ /» Ч | п
6. В области х > О начальная температура равна нулю, а количество тепла,
выделяющегося в единицу времени в единице объема, равно Аое~и. При t > О гра-
граница х = О поддерживается при нулевой температуре. В данном случае
ф /_?_) - А. ,- " ( 1 - Re *"<* КХ77 Ф* Г ^Ц 1 <А*)*1 ) , A1.12)
Ф* Г ^Ц 1 <А*)*1 )
1.2 <**)''« Jj
где символ Re означает, что берется действительная часть соответствующей функции7.
Вопрос о функции ошибок комплексного аргумента рассматривается в приложении 2.
7. В области х > 0 начальная температура равна а -}- Ьх. При t > 0 в еди-
единицу времени выделяется количество тепла, равное Аое~ах. На поверхности *=O
тепловой поток отсутствует **) [43, 44]. В данном случае
V К*
i Ф*
+ ^А- ехр (а2х^ — ад:) Ф* Га
+ —^- ехр (A* + <ut) Ф* Га Gi)V« -j ?—I. A1.13)
§ 12. Температура Земли и колебания температуры на ее поверхности
Измерения температуры Земли вблизи ее поверхности производились
в течение многих лет на многочисленных метеорологических станциях, рас-
расположенных в различных частях света. Полученные результаты показали, что
колебания температуры поверхности, вызываемые нагреванием в течение дня
и охлаждением в течение ночи, не влияют на температуру Земли на глубине,
превышающей 0,9—1,2 м, тогда как годовые изменения, обусловленные
охлаждением зимой и нагреванием летом, можно наблюдать на глубине,
достигающей 18—21 м. На ббльших глубинах температура остается практи-
практически постоянной и не зависит от перемен, происходящих на поверхности
Земли. Другими словами, тепловые волны, вызываемые изменением темпера-
температуры поверхности, затухают на глубине 18—21 м, и колебания температуры
наблюдаются только в самом верхнем слое земной коры.
Ряд ученых, начиная с Фурье и Пуассона, использовал периодические
колебания температуры Земли вблизи поверхности для определения тепло-
теплопроводности горных пород. Приняв поверхность Земли за плоскость х = О
с периодически изменяющейся температурой
2n(En), A2.1)
получим, воспользовавшись F.18), что температура на глубине х имеет вид
оо
v = Vo + ^] Vпе-*хУ~*co*{fl,ut — еп— k хпы\ A2.2)
*) В работе [42] рассмотрен случай области малой толщины.
**) Эта задача возникла в связи с рассмотрением нагрева тела сантиметровыми
волнами. См. также [44].
86 ГЛ. II. ЛИНЕЙНЫЙ ПОТОК ТЕПЛА [§ 12
где
*•=(?)*• <12-3>
Как отмечалось в § б настоящей главы, теория показывает, что каждая
отдельная волна распространяется внутрь Земли с неизменным периодом и
что амплитуды волн с меньшими периодами уменьшаются значительно быстрее,
чем амплитуды волн с ббльшими периодами. Следовательно, периодическое
изменение температуры принимает все более и более простую форму по мере
продвижения в глубь Земли, причем основная волна с наибольшим периодом
достигает наибольшей глубины. Глубина, на которой амплитуда годовых изме-
изменений температуры уменьшается в 10 раз, приблизительно в |/ 365= 19 раз
больше глубины, на которой во столько же раз уменьшается амплитуда
суточных изменений температуры. Этот результат согласуется с приведенным
выше положением о том, что годовые и суточные изменения температуры
заметны лишь до глубин, равных соответственно 18—21 и 0,9—1,2 м.
Классическая работа по использованию этих наблюдений принадлежит
Кельвину [45], обработавшему данные Форбса, который в течение 18 лет вел
в Эдинбурге измерения. По этим данным была составлена средняя годовая
температурная кривая и были определены ее гармонические составляющие.
Так, для глубин х1 и х2 были найдены температуры vl и v2 в виде
оо оо
vi = Vo-+- 21 v'n cos(пЫ — en)9 v2 = Vq + 2 Vn cos (nut — e?). A2.4)
/2=1 - /2=1
Сравнивая коэффициенты в соотношениях A2.2) и A2.4), получим
^о = ^о = Vo, Vn = Vne * *» K «, Vn = Vne ">Гя,
sn = k X\tin -f- ?/2» en = k x2n + ел.
Отсюда
Из выражения A2.5) следует, что для оценки х можно воспользоваться
как амплитудой, так и фазой любой гармоники. Кельвин нашел, что имеется
почти полное соответствие между величинами х, полученными из данных
об амплитуде или фазе первой гармоники и, как и следовало ожидать, менее
удовлетворительное соответствие при использовании высших гармоник.
Эти методы интересны тем, что они позволяют получить среднюю вели-
величину температуропроводности почвенного слоя; однако было установлено,
что передача тепла в почве является очень сложным процессом, на который
сильно влияет присутствие воды *). Добавление воды к сухому грунту вызы-
вызывает значительное увеличение теплопроводности; так температуропровод-
температуропроводность обычно достигает своей максимальной величины (в 2—3 раза пре-
превышающую величину, соответствующую сухому грунту) при влажности 5—10%.
В дальнейшем, когда почва периодически прогревается, возникают периоди-
периодические колебания ее влажности и температуры. По этой причине теория,
основанная на предположении о постоянстве температуропроводности, может
дать лишь приближенные результаты.
*) Этот вопрос хорошо освещен в [46]. Большое количество результатов, полу-
полученных для различных почв, приведено в [47]. Вопрос о влиянии перемещения воды
в почве рассмотрен в [48].
§ 13] ГЛ. II. ЛИНЕЙНЫЙ ПОТОК ТЕПЛА 87
Теория, изложенная выше, позволяет получить не абсолютные величины,
а лишь колебания температуры на различных глубинах в зависимости от изме-
изменений температуры на поверхности. Для нахождения абсолютных величин
необходимо знать тепловой поток, поступающий от Солнца, и тепловые
потери с поверхности Земли; нужно знать также, каким образом происходит
поглощение тепла атмосферой. Последнее особенно трудно оценить из-за
наличия в атмосфере водяных паров, которые играют доминирующую роль
в этом процессе. Однако Бранту [21, 49] удалось получить кривые для
безоблачных дней, хорошо согласующиеся с наблюдениями, предположив,
что тепловые потери Земли вследствие излучения днем и ночью одинаковы.
Следует указать, что количество тепла, получаемого от Солнца в дневное
время, пропорционально косинусу зенитного расстояния Солнца. Средняя
температура поверхности Земли определяется только солнечным излучением,
причем в данном случае поток тепла, поступающий изнутри Земли (см. сле-
следующий параграф), можно считать пренебрежимо малым.
§ 13. Геотермический градиент и поток тепла
Уже на ранних этапах развития горной промышленности было известно,
что температура Земли повышается с глубиной, причем расстояние по вер-
вертикали между точками, в которых температура отличается на 1°С (иногда
это расстояние называют геотермической ступенью), примерно равно 24 м.
Иногда в глубоких шахтах температура достигает относительно высоких
значений, что приводит к дополнительным трудностям при работе в них.
Множество измерений температур, проведенных в глубоких скважинах,
показало, что на суше скорость возрастания температуры с глубиной (так
называемый геотермический градиент) варьирует в пределах 10—50° С
на 1 км. Несколько измерений, проведенных на дне океана, показали, что
эта величина примерно равна 40° С на 1 км. Величины, приведенные выше,
а также все указываемые ниже данные относятся к областям, удаленным
от зон активной вулканической деятельности. В термически активных зонах
и вблизи действующих вулканов наблюдаемые температуры значительно выше.
Из приводимых ниже расчетов следует, что эти расхождения обусловлены
главным образом разницей в теплопроводности горных пород, и если учи-
учитывать ее, то результаты наблюдений *) во всех точках Земли (в том числе
на дне океана) совместимы с величиной теплового потока, варьирующей
в различных областях от 0,6 • 10~6 до 2 • 10~6 кал/'см2 • сек, причем средняя
его величина примерно равна 1,2- 10~6 кал/см2 • сек. До сих пор не удава-
удавалось обнаружить никакого систематического изменения теплового потока
с положением.
Для определения теоретической зависимости изменения температуры с глубиной
предположим, что теплопроводность К и количество выделяющегося в единицу вре-
времени тепла А являются функциями только глубины х. Уравнение установившегося
теплового потока записывается в виде
4^-A A3.1)
*) Имеющаяся в настоящее время обширная литература по этому вопросу сум-
суммируется в работах [50, 51]. Множество ранних данных о температуре, но не о тепло-
теплопроводности горных пород приведено в работах [52, 53]. Статьи [54, 55] отражают
начало современной практики систематического измерения в буровых скважинах как
температур, так и теплопроводностей. В работе [56] приводятся данные об измерениях
температур в тоннелях. Эффекты, наблюдаемые в областях вечной мерзлоты, описаны
в статьях [57, 58].
88 ГЛ. П. ЛИНЕЙНЫЙ ПОТОК ТЕПЛА [§ 13
Это уравнение примет более простую форму, если мы введем новую переменную
?-. A3.2)
о
Так как R = — — удельное термическое сопротивление исследуемого твердого тела,
то величина S является общим термическим сопротивлением твердого тела, ограни-
ограниченного наружной поверхностью и плоскостью, расположенной на глубине х. Из выра-
выражения A3.2) следует, что
dv „ dv
и, таким образом, —рг служит мерой теплового потока. Подставляя A3.3) в выраже-
ние A3.1), получим
¦% = -АК. A3.4)
/. Случай, когда тепло не выделяется, Л = 0. Интегрируя выражение A3.4),
получим
где Vo и F — постоянные, которые можно считать температурой поверхности и тепло-
тепловым потоком. Таким образом, при отсутствии источника тепла график зависимости v
от ? имеет вид прямой; поэтому, если наблюдаемые величины температур предста-
представляют в таком виде в соответствии с измеренными коэффициентами теплопроводности,
то многие кажущиеся аномалии исчезают. Предполагается, что величина Vo, найден-
найденная таким же образом, должна совпадать со средним годовым значением температуры
воздуха, однако обычно она выше, что приписывают влиянию испарения.
2. В единицу времени через единицу площади в плоскости 6i поступает
количество тепла, равное Q. В данном случае
0<6<6lf |
Отсюда следует, что внезапное изменение формы графика зависимости v от 6
обусловлено притоком или оттоком тепла на данной глубине (например, при тече-
течении воды).
3. Количество выделяющегося в некоторой области тепла постоянно. Эта
может происходить в трех случаях: а) при переносе тепла грунтовыми водами; б) при
радиоактивном распаде; в) при химической реакции вблизи рудного тела. В качестве
примера рассмотрим случаи трех слоев, для которых К = Ки А = 0 при 0 < х < х{;
К=К2, А = А2 при хх < х < х2 и /С= /Сз» А = 0 при х > хъ где К\% /G. Kz*
А2 — константы. Тогда
Fxx . Fix — х{) А2(х — ххJ
j^-\ *-р 1L 2-±——У-, хх<х<х29
Ai Л2 ^Л2
Fx\ 1 ^(*2 —*i) A2{x2 — XjJ ,
A3.6)
, [F — А2 (х2 — х{)] (х — х2)
+ Кз • *>**
Из соотношений A3.4) и A3.6) следует, что график зависимости v от ? вогнут
вниз в области, где выделяется тепло. Соотношения типа A3.6), в которых исполь-
используется известная величина теплового потока на поверхности F и предполагаемое рас-
распределение радиоактивности, часто применяются для оценки температур в земной коре.
Это простое рассмотрение значительно изменяется при учете геологических усло-
условий, например при наличии эффектов противодавления и денудации (см. § 2 гл. XV),
эффектов отклонения от горизонтальной поверхности (см. § 3 гл. XVI), эффектов
изменения теплопроводности в поперечном направлении и эффектов изменения темпе-
§ 14] ГЛ. ТТ. ЛИНЕЙНЫЙ ПОТОК ТЕПЛА 89
ратуры на поверхности. В частности, очень заметно выражено влияние последних
ледниковых периодов, которое в настоящее время уже тщательно изучено [60]. Про-
Простейший случай, из которого вытекает много других, связан с ледниковым периодом,
продолжавшимся в течение времени Т, причем в этот период поверхность Земли под-
поддерживалась при нулевой температуре, а до и после него температура поверхности
была равна Vo. Считая, что ледниковый период закончился в момент времени t = 0,
мы предполагаем, что в момент времени t = — Т температура равнялась у = Vo -f- Gx,
что соответствовало постоянному геотермическому градиенту G. Отсюда, используя
выражения D.10), мы получим для температуры в момент времени t > 0 величину
v = Vo + Gx + У0Ф (
— У0Ф I 2-я-) . A3.7)
§ 14. Возраст Земли. Анализ Кельвина
Еще Фурье [60, 61] показал, что, пользуясь измеренной величиной гео-
геотермического градиента, можно грубо оценить время, прошедшее с начала
остывания Земли, находившейся в расплавленном состоянии. При математиче-
математическом анализе этой задачи он, ради упрощения, пренебрегал кривизной земной
поверхности и считал коэффициент температуропроводности % постоянной
величиной. Поверхность Земли он принимал за плоскость л; = 0 и предпо-
предполагал, что на этой поверхности происходит теплообмен со средой, темпера-
температура которой равнялась нулю. В начале охлаждения, т. е. в момент вре-
времени ? = 0, он считал температуру постоянной и равной v0. Фурье нашел,
что для больших значений t температурный градиент вблизи поверхности
приблизительно равен vo(Tzxt)~^2, т. е. получил результат, приведенный в § 7
настоящей главы.
Кельвин *) решал более простую задачу, считая Землю полуограничен-
полуограниченным телом, граница л; = 0 которого поддерживается при нулевой темпера-
температуре, а начальная температура везде одинакова и равна vQ. Из соотноше-
соотношения D.3) следует, что температура v на глубине х в момент времени t будет
равна
С! = И0Ф ^Цт-. (ИЛ)
и
дУ Ур
дх ~
Отсюда вытекает, что величина dv/dx при л; = 0, т. е. геотермический
градиент G, выражается так же, как и в задаче Фурье, а именно:
Q = vo(mt)-\ A4.2)
Положив г;0=3900оС (так как эту температуру можно считать температурой
плавления горных пород), б = -27бо"' а * = 0,018 (как наиболее приемлемую
среднюю величину), Кельвин нашел из выражения A4.2) величину, равную
94-106 лет, для времени, по истечении которого геотермический градиент
упадет до своего теперешнего значения, т. е. «возраст» Земли**). Кельвин
*) См. [62]. В этой работе Кельвин полностью исключал возможность выделения
тепла за счет химической реакции.
**) В настоящее время широко распространена другая теория, в которой предпо-
предполагается, что Земля образовалась в результате агрегации пылевых частиц, а затем
ее температура начала повышаться вследствие давления и радиоактивного распада
содержащихся в ней радиоактивных веществ. (Прим. ред.)
90 ГЛ. II. ЛИНЕЙНЫЙ ПОТОК ТЕПЛА [§ 14
признавал, что принятая им начальная температура 3900° С слишком высока,
и из более поздних исследований свойств горных пород при высоких темпе-
температурах он заключил, что начальную температуру следует считать равной
1200° С [63, 64]. При этом его оценка возраста Земли снижается до значе-
значения, немного меньшего чем 107 лет, что мало отличается от величины, най-
найденной Кингом [65], который полагал, что у нас нет данных считать возраст
Земли большим, чем 24 000 000 лет.
Предельные значения возраста Земли, которые Кельвин получил в 1864 г.,
вызвали большой интерес, поскольку в те годы, так же как и сейчас, геологи
считали, что для остывания Земли из расплавленного состояния необходим
значительно больший период времени. Они основывали свои аргументы на
данных о наблюдаемых процессах и об эффектах стратификации. Вывод
Кельвина вызвал обширную дискуссию между физиками и геологами [66, 67],
причем полемика закончилась лишь в начале XX века, когда была открыта
радиоактивность. Следует, однако, отметить, что задача Кельвина по существу
сводится к задаче об охлаждении тонкого поверхностного слоя, поскольку
ф B) = 0,995, мы получим, используя приведенные выше численные значе-
значения, что по истечении 108 лет температура на глубине 250 км изменится
лишь на 0,5% и, следовательно, огромные количества тепла внутри Земли
окажутся совершенно незатронутыми. Было отмечено, что если бы физиче-
физические условия внутри Земли позволяли использовать ббльшие количества
тепла, то для возраста Земли мы получили бы значительно ббльшие вели-
величины [68, 69] (см. также § 8 гл. XII).
Теперь известно, что в горных породах земной коры тепло выделяется
вследствие распада содержащихся в них [50—52, 70—74] радиоактивных
веществ. Однако интенсивность выделения тепла при этом оценить довольно
трудно ввиду большого расхождения в содержании радиоактивных веществ
в образцах горных пород одного и того же типа, а также вследствие разли-
различий между горными породами разных типов. Последние из полученных резуль-
результатов составляют 6,3 • 10~6; 1,7 • 10~6; 0,04 • 10~6 кал/г в год для гранитных,
основных и ультраосновных горных пород соответственно. Данные для оса-
осадочных пород сильно варьируют, но величину 2 • 10~6 кал/г в год можно
считать наиболее правдоподобной. Распределение радиоактивных материалов
по глубине неизвестно, однако можно предположить, что количество их,
равное по порядку величины количеству, наблюдаемому на поверхности
Земли, должно сосредоточиваться в относительно тонком слое толщиной
несколько десятков километров; в противном случае количество выделяюще-
выделяющегося тепла было бы больше того, которое можно объяснить наблюдаемой
потерей тепла с поверхности Земли. Таким образом, для решения нашей
задачи можно прибегнуть к физическим моделям, описанным выше (см.
стр. 84, 88). Эти модели часто использовались при обсуждении вопросов
о температуре в земной коре и о возможных значениях возраста Земли.
В связи с тем, что период полураспада некоторых радиоактивных веществ
(в частности, для калия он равен 1,3 • 109 лет) значительно меньше 4 • 109 лет
(что считается вероятным значением возраста Земли), возникают дополнитель-
дополнительные осложнения, так что при определении интенсивности выделения тепла
следует учитывать экспоненциальный характер распада.
Уже в 1893 г. было признано, что предположение Кельвина о постоян-
постоянной начальной температуре должно быть заменено другим, учитывающим
повышение точки плавления с давлением [65, 75]. При этом обычно прини-
принимается линейная зависимость (vo-{-bx), где v0 примерно равно 1400°С,
a b приблизительно равно Ъ°1км. Данная задача по-прежнему сводится к за-
§ 15] гл. и. линейный поток тепла 91
даче 3 § 11, и, идя этим путем, Джеффриз получил величину возраста Земли,
равную 1,6 • 109 лет.
В последние годы на смену попыткам вычислить возраст Земли тер-
термическими методами пришли попытки вычислить температуры внутри Земли,
исходя из ее предполагаемого возраста. Это потребовало рассмотрения задачи
о сфере, обсуждение которой приведено в § 14 гл. IX.
§ 15. Неограниченное составное твердое тело
Пусть область х > О состоит из одного вещества (Кг, рх, -*.{), а область
х < 0 из другого (/С2. р2. *з). причем граничные условия в плоскости раздела
х = 0 совпадают с (9.18) и (9.19) гл. I, т. е.
vx = v2, x = 0, t>0 A5.1)
и
к*ъг=к*тг- х==0't>Ot A5-2)
где vx — температура в области х > 0, a v2— температура в области х < 0.
Многие задачи подобного типа можно решить, используя решения для
полуограниченного твердого тела, приведенные в § 4 данной главы.
1. Начальная температура постоянна и равна в области *>0
величине V, а в области х < 0 она равна нулю. Ищем решения типа
x>0, A5.3)
1=у х<0. A5.4)
Из § 4 данной главы известно, что эти решения удовлетворяют диф-
дифференциальным уравнениям теплопроводности в соответствующих областях.
Находим постоянные Av Bv Л2, В2, удовлетворяющие начальным и гранич-
граничным условиям. Начальные условия дают
а граничные —
Ах = А2 и ^1/С1ос1 2 = — В2К2%2 2.
Решая эти уравнения и подставляя в A5.3) и A5.4), окончательно
получим *)
4 /
2. Начальная температура равна нулю. В плоскости х = 0 при t > 0 через
единицу площади в единицу времени поступает количество тепла, равное Fo.
В данном случае, исходя из соотношения (9.6) настоящей главы, примем, что
*) Другие методы решения см. в [76—78].
92 ГЛ. II. ЛИНЕЙНЫЙ ПОТОК ТЕПЛА [§ 16«
Здесь неизвестные постоянные Ft и F2 следует находить из граничных условий при
х = 0; тогда мы получим
/С, ~ /С2
Отсюда
«>,= .:,:. Г.л i** h^W • A5-ю)
Случай контактного сопротивления между поверхностями раздела был рассмотрен
Шафом [79]. Он различал два случая: а) когда тепло подводится к одной или обеим
поверхностям — случай, соответствующий «сухому» трению, и б) когда тепло подво-
подводится между поверхностями — случай, соответствующий жидкостному трению или
наличию тонкого плоского нагревательного элемента.
3. Условия задачи те же, что и в пункте 1, но в плоскости х = 0 имеется
контактное сопротивление, и поэтому вместо соотношения A5.1) ми должны
написать
/С, .^L+ //<»,--»!) = 0, A5.11)
тогда как соотношение A5.2) по-прежнему остается справедливым (см. пункт Ж
§ 9 гл. I).
Поступая точно так же, как и в пункте 1, и учитывая, что при х = 0 мы имеем
граничное условие третьего рода, будем искать для данной задачи решения вида:
*»» L х_
0(^J /)]}' <15Л2>
(/ \x\ \
- exp (h2x + hW) Ф* y^ + h2 уЦ j , A5.13)
где
77
Эти задачи, а также более сложные задачи легче всего решать при помощи пре-
преобразования Лапласа (см. гл. XII).
§ 16. Случай зависимости термических характеристик вещества
от температуры
В § б гл. I было показано, что если /Сие зависят от температуры, то уравнение
линейного потока тепла
d
дх
или
d2v d{\x\K) ( dv \2 __ J_ dv_
дх2 dv \ дх) х dt
§ 16] ГЛ. II. ЛИНЕЙНЫЙ ПОТОК ТЕПЛА 93
приводится в результате замены переменной
V
е
f-^-dv A6.3)
*1 До
О
к виду
д2в 1 ае
где % =—¦ — функция 0. Здесь можно использовать любое из уравнений A6.1), A6.2)
и A6:4).
Исторически сложилось так, что в первых статьях рассматривались задачи
с переменными термическими характеристиками; однако впоследствии, частично из-за
возникавших трудностей, частично из-за недостатка данных об изменении термических
характеристик с температурой, таким задачам посвящалось очень мало работ.
В последнее время благодаря накоплению сведений о термических характеристиках
веществ, а также ввиду важности подобных задач в теории диффузии эти проблемы
привлекли очень большое внимание. Для их решения обычно следует применять
численные методы, но имеются также некоторые чрезвычайно интересные теоретиче-
теоретические подходы. Здесь мы подробно рассмотрим лишь те из них, которые важны для
задач теплопроводности. Полный разбор остальных методов можно найти в гл. IX
книги Крэнка [80].
I. Преооразование Больцмана [81].
Решения ряда важных задач, в которых температуропроводность постоянна,
представляют собой функции только от
б=.*ГТ. A6.5)
Отсюда следует, что необходимо рассмотреть возможность нахождения в такой
форме решений уравнения A6.1). Если предположить, что v является функцией только б,
то уравнение A6.1) приводится к обычному дифференциальному уравнению
а уравнение A6.4) принимает вид
*-S-+y?4r=a A6-7)
Пригодность выражения A6.5) лимитируется тем, что граничные и начальные
условия также должны выражаться только через б. Например, поскольку б->оо при
t->0 и jc>0, а 6 = 0 при t > 0 и х = 0, очевидно, что это соотношение применимо
в области х > 0 для постоянной начальной температуры и в плоскости х = 0 для
постоянной температуры при t > 0.
Следует отметить, что употребление термина «преобразование» применительно
к соотношению A6.5) нельзя считать правильным, так как при этом предполагается,
что при замене переменных в уравнении A6.1), скажем, на б и t, уравнение
в частных производных приводится к обычному дифференциальному уравнению A6.6),
тогда как на самом деле оно просто преобразуется в уравнение по ?. Смысл данного
метода заключается в том, что если начальные и граничные условия, которым удовле-
удовлетворяет уравнение A6.1), можно выразить только через б, то решение A6.6), которое
удовлетворяет этим условиям, дает решение A6.1) с граничными условиями; при этом
полученное решение представляет собой функцию только xt~4* и можно полагать,
что оно является единственным.
Если х — постоянная величина, то для A6.7) непосредственно получается обыч-
обычное решение
в = АФ (-5—) = АФ / ^-гг). A6.8)
\ 2% I* ] \ 2 (**) /
Имеются различные интегралы уравнений A6.6) и A6.7), например
¦-2»-^. A6.9)
94 ГЛ. II. ЛИНЕЙНЫЙ ПОТОК ТЕПЛА [§ 16
для случая, когда с — постоянная величина. Этот интеграл является исходным для
численного метода Филипа [82] *). Приближенные решения уравнения A6.6) легко
получаются для случаев, при которых К изменяется медленно.
Кирхгоф и Ганземан [30] разобрали случай с == со-\-сху и /( = Ko-\-K\V. При
этом они искали решение в виде v = i/ (?) и считали, что с{ и К\ малы.
II. Преобразование Пика **).
Предположим, что ф является функцией х и t, которая удовлетворяет уравнению
^ - Ш A6.10)
где fx (ф) и /2 (ф) — функции только ф. Тогда, если v — функция только ф, то урав-
уравнение A6.2) принимает вид
dv ( dv\2 d(\nK) ,п\а2у /1А11Ч
Необходимо также преобразовать граничные условия. Так, если граничными
условиями для v служат v = vx = const при Fx (jc, t) = 0 и v = t/2 при /^ (jc, ?) = 0,
то граничные условия для ф имеют вид ф=Кь при Fx(x,t) = 0 и ф = V2
при F2 (-^» 0 = 0.
Например, для области х > 0, в которой граничными условиями служат v = vx
при jc>0, ? = 0 и v= v2 при jc = 0, * > 0, получим, что ф = ехр(— xt~^2) удовле-
удовлетворяет уравнению A6.10), а уравнение A6.11) принимает вид
и решается с граничными условиями v = с/, при ф = 0 и i/ = t;2 при ф = 1.
III. Точные решения для частных случаев.
Задачи, в которых термические характеристики являются ступенчатыми функ-
функциями температуры [80, 85], можно точно решить методами, изложенными в § 2 гл. XI.
Разобраны также задачи, в которых теплопроводности выражаются в виде
/Со/A — Щ, /Со/A — Щ2 и /Со/A + 2av + bv2) [80, 86].
IV. Другие методы.
Были рассмотрены различные приближенные методы для решения задач, в кото-
которых теплопроводности выражаются в виде а -\- bv и ехр (av) [80]. Следует отметить,
что самый важный закон в теории диффузии, а именно закон
где Т—абсолютная температура, a Do, ?, R — постоянные, еще полностью не про-
проанализирован.
Был предложен метод последовательных приближений, причем в качестве нуле-
нулевого приближения используется случай постоянных термических характеристик, а для
получения первого приближения применяется функция Грина [87].
V. Установившееся состояние.
В данном случае уравнение A6.1) сводится к обыкновенному уравнению
К —г- = const,
dx
которое можно сразу же проинтегрировать для целого ряда важных специальных
случаев. В задачах, в которых К зависит только от v, результаты непосредственно
следуют из результатов для постоянного /С, найденных в ряде важных специальных
задач как одномерных, так и двух- и трехмерных (см. § 6 гл. I). Были получены
графики распределений температур при линейном и радиальном потоке тепла для
величин К, выражающихся в виде /<о[1 + /(*О] и ^о [! + /(-*)] [88].
*) О его применении к уравнению A6.1) с дополнительным членом A (v) -p-
см. [83].
**) В работе [84] Пик распространил этот метод на трехмерный случай.
ГЛ. II. ЛИНЕЙНЫЙ ПОТОК ТЕПЛА 95
ЛИТЕРАТУРА
1. Gray, Ргос. Roy. Soc. Edin. 45, 230—244 A924—1925).
2. R i b a u d, С. R. Acad. Sci. 226, 140—142, 204—206, 449—451 A948).
3. N or d о n, С R. Acad. Sci. 228, 167—168 A949).
4. A p p e 1 1, J. Math. Pure Appl. 8, 187—216 A892).
5. Goursat, Cours d'Analyse, Gauthier-Villars, ed. 5, vol. 3. (Э. Г у р с а, Курс
математического анализа, ОНТИ, ч. III, 1934, перев. с 5-го изд.)
6. Р a t e r s о п, Ргос. Glasgow Math. Ass. 1, 48—52 A952—1953).
7. Titchmarsh, Theory of Fourier Integrals, Oxford, 1937. (Э. Титчмарш, Вве-
Введение в теорию интегралов Фурье, Гостехиздат, 1948, перев. с 1-го изд.)
8. L о v e r i n g, Bull. Geol. Soc. Am. 46, 69—93 A935).
9. Lovering, Econ. Geol. Fiftieth Anniv vol., p. 249, 1955.
10. Cars law, Introduction to the Mathematical Theory of the Heat Conduction, Mac-
Millan, ed. 2, 1921. (Г. Карслоу, Теория теплопроводности, Гостехиздат, М.,
1947.)
11. Cars law, Fourier's Series and Integrals, MacMillan, ed. 3, 1930.
12. W i 11 i a m s о n, A d a m s, Phys. Rev. 14, 99 A919).
13. Taylor, Phil. Trans. Roy. Soc. A215, 1 A915).
14. К i r s с h, Die Bewegung der Warme in den Cylinderwandungen der Dampfmaschine,
Leipzig, 1886.
15. Dahl, Trans. ASME 46, 161 A924).
16. Stokes, Scientific Papers, iii, 1.
17. Lam b, Hydrodynamics, ed. 4, § 345. (Г. Лам б, Гидродинамика, Гостехиздат,
1947, перев. с 6-го изд.)
18. Howling, Mendoza, Zimmerman, Ргос. Roy. Soc. A229, 86—109 A955).
19. Slater, Microwave Transmission, McGraw-Hill, 1942.
20. Marcus, Carnegie Institute of Technology, Report, 1953.
21. Brunt, Quart. J. R. Met. Soc. 58, 389 A932).
22. Smith, Aust. J. Phys. 6, 127—130 A953).
23. L a u w e r i e r, Appl. Sci. Res. A4, 142—152 A954).
24. Jaeger, Johnson, Geofis. Рига ё Appl. 24, 104 A953).
25. J a e g e r, Proc. Camb. Phil. Soc. 49, 355—359 A953).
26. Jaeger, Aust. J. Phys. 6, 10—21 A953).
27. Schu 1 z e, Ann. Phys. (N. F.) 66, 207 A898).
28. Schaufelberger, Ann. Phys. D) 7, 589 A902).
29. Fraz.ier, Phys. Rev. 39, 515 A932).
30. Kirchhoff, Hansemann, Ann. Phys. (N. F.) 9, 1 A880).
31. Kirchhoff, Hansemann, Ann. Phys. (N. F.) 13, 406 A881).
32. Gruneisen, Ann. Phys. D), 3, 43 A900).
33. G i e b e, Verh. dtsch. phys. Ges. 60, 1903.
34. Hobson, Diesselhorst, Warmeleitung, Enc. der Math. Wiss., Bd. V, Tl. I,
224—227, 1905.
35. Fox, Phil. Trans. Roy. Soc. A232, 431 A934).
36. P a t e r s о n, Phil. Mag. 32, 384 A941).
37. Pater son, Proc. Glasgow Math. Ass. 1, 164—169 A953).
38. Jaeger, Quart. Appl. Math. 4, 100—103 A946).
39. Jeffreys, Beitr. Geophys. 18, 1 A927).
40. Bui lard, Mon. Not. R. Astr. Soc, Geophys. Suppl. 4, 534 A939).
41. Jeffreys, The Earth, Cambridge, ed. 3, 1952, Chap. X.
42. V a n О r s t r a n d, J. Wash. Acad. Sci. 22, 529 A932).
43. Cook, Brit. J. Appl. Phys. 3, 1—6 A952).
44. Jaeger, Brit. J. Appl. Phys. 3, 221—222 A952).
45. Kelvin, The Reduction of Observations of Underground Temperature. Trans. Roy.
Soc. Edin. 22, 405 A861).
46. К е е n, The Physical Properties of the Soil, Rothamsted Monographs on Agricultural
Science, 1931, Chap. IX.
47. Patten, Bull. U. S. Dir. Soils No. 59 A909).
48. D e V r i e s, Trans. Int. Congr. Soil. Sci. vol. II, 1950.
49. Lett аи, Trans. Am. Geophys. Union 32, 189—200 A951).
50. Bui lard, The Earth as a Planet, Ed. Kuiper, University of Chicago Press, 1953.
51. Jacobs, Encyclopaedia of Physics, Springer, vol. 47, 1956.
52. Internal Constitution of the Earth, Ed. Gutenberg, Dover, 1951.
53. Temperature, its Measurement anx Control in Science and Industry, Am. Inst. Phys.
1941.
54. Benf iel d, Proc. Roy. Soc. A173, 428—450 A939),
96 ГЛ. ТТ. ЛИНЕЙНЫЙ ПОТОК ТЕПЛА
55. В и 1 1 а г d, Ргос. Roy. Soc. A173, 474—502 A939).
56. Birch, Bull. Geol. Soc. Am. 61, 567—630 A950).
57. Ter z a g h i, J. Boston Soc. Civil Engrs 39, 1—50 A952).
58. M i s e n e r, Trans. Am. Geophys. Union 36, 1055—1060 A955).
59. Birch, Am. J. Sci. 246, 729—760 A948).
€0. Fourier, Extrait (Tun Memoire sur le refroidissement du globe terrestre. Bull.
Sci. par la Societe philomatique de Paris 1820.
31. Fourier, Oeuvres complete, Paris, 1888, T. II, p. 284.
€2. Kelvin, The secular cooling of the Earth, Trans. Roy. Soc. Edin. 23, 157 A864).
63. Kelvin, Nature 59, 438 A895).
64. Ke 1 v i n, Phil. Mag. 47f 66 A899).
65. К i n g, Am. J. ScL 145, 1 A893).
66. Woodward, The mathematical theories of the Earth, Am. Ass. Adv. Sci., Toronto,
1889.
67. Woodward, The century's progress in applied mathematics, Bull. Am. Math. Soc.
6, 147 A900).
68. Perry, Nature 51f 224, 341, 582 A895).
69. H e a v i s i d e, Electromagnetic Theory, 1899, vol. II.
70. Rutherford, Chadwick, Ellis, Radiation from Radioactive Substances,
Cambridge, 1930.
71. Holmes, The Age of the Earth, Harper's, 1913.
72. J e f f г е у s, Mon. Not. R. Astr. Soc. Geophys. Supp. 5, 37 A942).
73. Bullard, Mon. Not. R. Astr. Soc. Geophys. Supp. 5, 41 A942).
74. Birch, Nuclear Geology, Ed. Faul, Wiley, 1954, Chap. 5.
75. В а г u s, Phil. Mag. 35, 173 A893).
76. Tranter, Phil. Mag. 28, 579 A939).
77. С a r s 1 a w, Phil. Mag. 30, 414 A940).
78. Churchill, PhiL Mag. 31, 81 A941).
79. S с h a a f, Quart. Appl. Math. 5, 107—111 A947).
80. Crank, The Mathematics of Diffusion, Oxford, 1956.
81. В о 11 z m a n n, Ann. Phys. 53, 959 A894).
82. Philip, Trans. Faraday Soc. 51, 885—892 A955).
83. Philip, Aust. J. Phys. 10, 29—42 A957).
84. Peek, Phys. Rev. 35, 554—561 A930).
85. Crank, Trans. Faraday Soc. 47, 450—461 A951).
86. F u j i t a, Text. Res. J. 22, 757, 823 A952).
87. Hopkins, Proc. Phys. Soc. 50, 703 A938).
88. В ar r e r, Proa Phys. Soc. 58, 321—331 A946).
ГЛАВА III
ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В ТВЕРДОМ ТЕЛЕ, ОГРАНИЧЕННОМ
ДВУМЯ ПАРАЛЛЕЛЬНЫМИ ПЛОСКОСТЯМИ
§ 1. Введение
В настоящей главе мы рассмотрим различные задачи о линейном тепло-
тепловом потоке в твердом теле, ограниченном двумя параллельными плоскостями
(обычно х = 0 и х — 1). Эту область мы будем называть для краткости
«пластина 0 < х < fa. Полученные нами результаты применимы также
к стержню длиной / с теми же условиями на концах при отсутствии тепло-
теплообмена с его поверхности.
§ 2. Установившаяся температура
В случае установившегося потока тепла в пластине толщиной / с коэф-
коэффициентом теплопроводности /С. поверхность которой поддерживается при
температурах vx и vv дифференциальное уравнение принимает вид
d2v 0
1F2 = 0'
Отсюда
"• = const = V2~~vi #
dx
Таким образом, тепловой поток в любой точке равен
. „ dv К (v2 — v{) Vi — v2
где
Л = ?. B.2)
Соотношение B.1) по форме полностью совпадает с законом Ома для
установившегося электрического тока: тепловой поток / соответствует
электрическому току, а разность температур vx — v2 — падению напряжения.
Таким образом, R можно назвать термическим сопротивлением пластины.
Теперь предположим, что мы имеем составную пластину, состоящую
из п пластинок с толщинами 1Х /л и коэффициентами теплопроводно-
теплопроводности Кх Кп соответственно. Если пластинки находятся в идеальном
тепловом контакте по поверхностям раздела, то изменение температуры
между противоположными поверхностями всей составной пластины равно
сумме изменений температур в отдельных пластинках, и, так как тепловой
поток одинаков в любой точке, эта сумма равна следующей величине:
^ /. B-3)
7 Г. Карслоу, Д. Егер
98 ГЛ. III. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В ТВЕРДОМ ТЕЛЕ [§ &
Это равносильно утверждению, что при идеальном тепловом контакте
между отдельными слоями составной пластины ее термическое сопротивле-
сопротивление равно сумме термических сопротивлений отдельных слоев.
Рассмотрим теперь составную пластину с такими контактными сопроти-
сопротивлениями, что тепловой поток между поверхностями последовательных слоев
равен произведению Н на разность температур этих поверхностей (см. соот-
соотношение (9.20) гл. 1). Здесь 1/Н можно считать термическим сопротивле-
сопротивлением контакта, и тогда полное термическое сопротивление составной пла-
пластины равно сумме термических сопротивлений отдельных слоев плюс тер-
термическое сопротивление контактов между ними.
Если коэффициент теплопроводности К является функцией температуры»
то наше дифференциальное уравнение принимает вид
и, следовательно, остается справедливым соотношение
Интегрируя его от vx до v2, т. е. в пределах поверхностных темпера-
температур пластины толщиной /, получим
_ f Kdv = lf,
V\
и, следовательно,
(ух — v2) /Сер
/= i > B-4)
где
^f B.5)
представляет собой средний коэффициент теплопроводности для всего диа-
диапазона температур в пластине. Таким образом, если коэффициент теплопро-
теплопроводности зависит от температуры, то предыдущие результаты остаются
справедливыми при замене К на /Сср.
§ 3. Область 0 < х < U Границы поддерживаются при
нулевой температуре. Начальная температура f(x)
Задача сводится к решению дифференциального уравнения
dt ~ дх2' ^ ^ ' v '
при условиях
с = 0 и х=*1 C.2)
при * = 0. C.3)
Если начальное распределение представляется в виде
. . ппх
v = Ans\n—j-,
§ 3] ГЛ. III. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В ТВЕРДОМ ТЕЛЕ 99
то ясно, что выражение
v = An sin—y-expl -я—1
будет удовлетворять всем условиям C.1), C.2), C.3) нашей задачи.
Предположим, что начальная температура f(x) представляет собой огра-
ограниченную функцию, удовлетворяющую условиям Дирихле*) [1] в интер-
интервале @, /) и, следовательно, ее можно разложить в ряд
ппх
где
)sin
= т f
о
о
Рассмотрим теперь функцию V, определяемую бесконечным рядом
ansm —j- exp [^ ^г—J • C.5)
п = 1
« Г ъп2п4
Благодаря присутствию множителя ехр ^— этот ряд равномерно
сходится **) в любом интервале х при t > 0. Если рассматривать его как
функцию /, то мы увидим, что он равномерно сходится при /^>^0>0, где
?0 — некоторое положительное число.
Таким образом, в указанных интервалах функция V, определяемая рядом
C.5), является непрерывной функцией как от х, так и от t ***).
Легко показать, что ряды, полученные почленным дифференцированием
ряда C.5) по х и t, также равномерно сходятся в указанных интервалах
х и t. Таким образом, они равны производным от v.
Следовательно,
ъх Г ъп2ъ4 Л
Г-еХР[ J2- J
dl/ VI ХЛ2^2 flTCJC
d2t/ v^ хп2^2 . rnzx Г %/г2я:2П
x^ = -^-7^-a»SInnrexPL /Н
1
при ^>0 и 0<л;</.
*) Это требование снимается [2], так как было показано, что приводимые ниже
результаты справедливы, если функция / (х) является ограниченной и интегрируемой
в интервале 0<!jc<; /.
**) Так как / (х) является ограниченной функцией, то имеется такое положитель-
положительное число М, что | / (х) | < М в интервале 0 < х < I. Отсюда следует, что \ап \ < 2М
для всех значений п. Поэтому
В таком случае ряд
сходится: его члены не зависят от х и t> и мы получаем соответствующие решения.
***) Если считать v функцией двух переменных jc, ty то она является непрерыв-
непрерывной функцией от (х, t) в области 0<jc</, *>*a>0 [1].
7*
<2Л1ехр[ —-2^!L]. где
100 ГЛ. III. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В ТВЕРДОМ ТЕЛЕ [§ 3
Итак, уравнение
dv d*v
удовлетворяется во всех точках стержня при / > 0 функцией, определяемой
рядом C.5).
Посмотрим теперь, удовлетворяет ли данная функция граничным и началь-
начальным условиям.
Рассматриваемый нами ряд равномерно сходится относительно х в интер-
интервале 0 ^ х ^ / при t > 0, и поэтому он служит непрерывной функцией х
в данном интервале.
Таким образом,
limz;=0 (т. е. величине суммы ряда при л: = 0)
limz;=0 (т. е. величине суммы ряда при лг = /).
1
Следовательно, граничные условия удовлетворены.
Что же касается начальных условий, то мы можем воспользоваться
обобщением теоремы Абеля [1].
Пусть функция f (х) ограничена и удовлетворяет условиям Дирихле в ин-
интервале @, /). Тогда ряд синусов для f(x)
tzx I . 2пх .
a1sin—-.—\- a2sin— |-
сходится и его сумма равна / (л:) в каждой точке между 0 и /, где / (л:) непре-
непрерывна; во всех остальных точках эта сумма равна *) -^\f {х -\- 0) -f- / (х — 0I.
Из обобщения теоремы Абеля следует, что если v определено рядом C.5),
то
lim v = lim У. ап sin ^~-ехр Г— —р—1 = / (х)
в точках, где функция непрерывна; во всех остальных точках
1 tx/ — I Л\ I х / ,, А\1
Таким образом, мы доказали, что если начальная температура удовлет-
удовлетворяет условиям Дирихле, непрерывна в интервале 0 >. х ;> /, а /@) = /(/) = 0,
то функция, определяемая C.5)**), удовлетворяет всем условиям нашей задачи.
Если начальная температура имеет разрывы непрерывности, то в точках
разрыва функция, определяемая C.5), стремится к -g [f(x-\-0)-{-f(x — 0)}
при *->0. При сколь угодно малом, но не равном нулю t функция v уже
*) Если функция f(x) ограничена и удовлетворяет условиям Дирихле, то она
может иметь только разрыв первого рода [1],
**) Выражение C.5) можно записать в виде
V3fc Т
о 1
поскольку ряд под интегралом равномерно сходится (см. [1], § 70).
§ 3] ГЛ. III. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В ТВЕРДОМ ТЕЛЕ 101
не будет иметь разрыва в указанной точке и кривая температуры будет
проходить вблизи точки -к {/С* + 0) + / (jc—0)}.
Следует помнить, что физическая задача в том виде, в каком мы сфор-
сформулировали ее для разрывного распределения температур на концах стержня
или в самом стержне, представляет собой идеализированный случай. В дей-
действительности же в начальный момент в стержне не может быть прерывного
распределения температуры. Решая физическую задачу, мы должны предпо-
предположить, что происходит мгновенное изменение температуры в стержне
в момент, когда мы начинаем измерения в непосредственной близости от
точки разрыва или от концов стержня (если они являются точками разрыва).
Разрыв температур, таким образом, сглаживается. Наше решение поставлен-
поставленной математической задачи удовлетворяет приведенным выше условиям и
можно считать, что оно соответствует и измененной нами физической задаче.
Представляют интерес следующие частные случаи *).
/. Пластина 0 < х < I с постоянной начальной температурой, т. е. f (х) =
= Vo = const. Тогда
2. Линейное начальное распределение в пластине 0 < х < /, т. е. f (х) = kx.
Тогда
2lk v (—О" Г хл2я*П , ппх
v=—2d ^—k—exp [—zHsin—• <3-7>
Обычно выгоднее использовать результаты, полученные для пластины
— I <х <1 (симметричный случай), так как тогда можно непосредственно сравни-
сравнивать их с аналогичными результатами для сферы и цилиндра. Кроме того, обычно
it х?
для малых значений г^% например для -^ < 0,01, такие ряды, как C.6) и C.7), схо-
сходятся медленно, но ниже будет показано (см. § 5 гл. XV), что для подобных значе-
значений аналогичные ряды с функциями ошибок или их интегралами сходятся быстро.
Для удобства упомянутые ряды будут рассмотрены здесь (см. C.9) и C.11)), а их
производные мы рассмотрим в § 5 гл. XII. Все результаты, приводимые ниже, спра-
справедливы также и для пластины 0 < х < /, если при х = 0 тепловой поток отсутствует,
а плоскость х = / поддерживается при температуре, равной нулю.
3. Пластина —I <х <1 с постоянной начальной температурой, равной Vo.
Перенося начало координат в выражении C.6) в среднюю точку пластины и заме-
заменяя -<?-/ на /, получим
или
<,= К0- К. V (_d-j?«./<*+Ц'-*) + ф. (&Ltm±±\ I. C.9)
Некоторые численные результаты, найденные при решении этой задачи, приведе-
приведены на рис. 10, а и 11. Средняя температура с/ср в пластине в момент времени t равна
»ср - -gr ^ Bл+1J ехР [~ * 41* % ]' (ЗЛ0)
п=0
*) Ряд C.6) можно также выразить через тэта-функции [3].
102
или
ГЛ. III. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В ТВЕРДОМ ТЕЛЕ
[§ з
C.11)
Количество тепла, приходящееся на единицу площади в момент времени t,
равно 2/рС1/ср. Данные об этой величине часто используются для определения
v/V
0.6
о,г
—-^
—
^—
0,4
_J,6
—
\
--——.
А
\\
1,0
V/V
ав
0,6
0,4
0,2
О 0,2 0,4 0,6 0.8 1,0
х/1
а)
"доТ^
ОА _
1.0
ч
—.
>
^—,
¦' т
\
— —
Ц2 0,4 Q6 0,6 1tO
х/1
б)
О 02 6,4 0,6 0,6 1,6
х/1
)
Ц2 6,4 6,6 6,6 1,6
х/1
8)
Рис. 10. Распределение температур в пластине 0 < х < I в отсутствие
теплового потока при х = 0, нулевой температуре при х = / и раз-
различных начальных распределениях температуры.
а) Постоянная начальная температура; 6) линейное начальное распределение темпе-
температуры V0(l— \x\)/l (см. пункт 4); в) начальное распределение температуры
{Vo (/— \х l)//-f const; г) параболическое начальное распределение температуры
(см. пункт 5). Числа на кривых указывают xt/l2.
коэффициентов температуропроводности [4]. Тепловой поток / на поверхность
равен следующей величине:
или
f к\дУЛ -
KV0
/1=0
пЧ21 I
C.12)
C.13)
Это решение было использовано при определении % для составляющих земной коры [5];
кроме того, оно применялось при исследовании металлических стержней; при этом
$ 4] ГЛ. III. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В ТВЕРДОМ ТЕЛЕ 103
определяли разность температур в стержне между точками х = а и х = Ъ [6]. Точки
•а и b были выбраны таким образом, что
cos C%a/2l) = cos Cnb/2l).
В этом случае второй член ряда, полученный из C.8) для разности температур,
обращается в нуль, а третий член ряда, содержащий множитель ехр [—25x7cV/4/2],
очень быстро исчезает.
4. Область —I < х < I с начальной температурой Vo(/ — \x\)/l и темпера-
температурой поверхности, равной нулю. В этом случае
(ИЛИ
\х\\ ,Bя
C.15)
5. Область — I < х < I с начальной температурой Vo (/2 — х2)/12 и темпера-
температурой поверхности, равной нулю . В этом случае
_ 32К0 у (-1)" Г *Bп+\упЧЛ {<2п+\)ъх
v ^~Zl Bя+1)« еХр[ 4Р JC0S S • (ЗЛ6)
«ЛИ
( /Bя+1)/-^\ /Bя+1\ )
1 V 2^I/2 / V2(^rjje
j
C.17)
^. Область — I < х < I с начальной температурой Vo cos (tcjc/2/) и темпера-
температурой поверхности, равной нулю. В этом случае
v=V0 cos -|^ exp |^— ^j-J. C.18)
Приведенные выше решения представляют значительный интерес, так как они
дают качественное представление о том, как отводится тепло из пластины при задан-
заданном начальном распределении температуры. Из соотношения C.5) следует, что
в первую очередь исчезают более высокие гармоники в ряде Фурье для / (jc), оста-
оставляя основную гармонику, амплитуда которой уменьшается по экспоненциальному
закону. Это фактически подтверждается и соотношением C.18). На рис. 10 показано
уменьшение температуры для четырех различных начальных распределений темпе-
температур, а именно: для постоянного, линейного, «линейное + постоянное» и параболи-
параболического распределения. Как мы видим, тепло отводится таким образом, что распре-
распределение температур приблизительно косинусоидально. Для случая постоянной на-
начальной температуры тепло сначала отводится из области вблизи поверхности; при
линейном распределении температур — из области вблизи центра; при «линейном+
-f- постоянном» — как из центра, так и с поверхности.
§ 4. Область 0 < х < /. Начальная температура f(x).
Границы поддерживаются при постоянной температуре
или изолированы
Если границы поддерживаются при постоянных температурах vx и v2»
то мы можем написать
v — vx при Jt = O,
v = v2 при х = I,
104 гл. ш. линейный тепловой поток в твердом теле [§ 4
и
v = f(x) при / = 0.
Как и в § 14 гл. I, сведем эту задачу к задаче об установившейся тем-
температуре и к задаче, в которой границы поддерживаются при температуре»
равной нулю.
Пусть
где и и w удовлетворяют следующим уравнениям:
¦0 = 0 @ <*</).
u = vx при л: = 0,
u — v2 при х = /
тг—й- «><*«>•
w = 0 при х = 0 и х = tp
w = f(x) — и при * = 0.
Отсюда сразу находим, что
и,
где
как следует из § 3
1
и
Таким образом,
настоящей главы,
оо
1
1
оо
1
к** Г
-\vx + {v2-v
1 ХР [ /2
%*п*кЧ
l) — }JS
/
0
D.1)
Наиболее прост и наиболее важен случай области —/ < х < / с у
вой начальной температурой и постоянной температурой V на
плоскостях х= ± I при t > 0. Решение, которое непосредственно сле-
следует из D.1) или C.8), имеет вид
/2 = 0
Вводя безразмерные параметры
7 = ^-, 4==^. D.3)
§ 4] ГЛ. III. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В ТВЕРДОМ ТЕЛЕ
можно записать D.2) следующим образом:
105
V тс Zd Bn+l) expL
C0S
и решение для всех значений х, /, t и х легко получить из семейства
кривых в двух измерениях. На рис. 11 изображен ряд графиков зависимости?
v/V от (• для различных значений Т.
Рис. 11. Распределение температур в различные
моменты времени в пластине — / < х < I при нуле-
нулевой начальной температуре и температуре поверх-
поверхности, равной V.
Числа на кривых указывают значения xt/P.
На рис. 12 приведены графики для температур в центре*) (jc = O) w
средних температур для пластины, цилиндра и сферы. Для случая, когда
конец х = 0 изолирован, конец х = 1 поддерживается при темпера-
температуре V, а начальная температура равна f(x)f решение получается таким
же, как и в §§ 3 и 4 данной главы, но теперь f(x) будет уже выражаться рядом
косинусов. Это решение записывается в виде
л =0
X
2/(—\)*+*\
Bл+1)*
D.5>
*) В работе [7] приводятся обширные таблицы численных значений температу»-
в центре пластин и сфер.
106
ГЛ. III. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В ТВЕРДОМ ТЕЛЕ
[§5
Некоторые результаты для этого случая были приведены выше (см.
стр. 101 — 103).
го
44
/
VIШ/
\ И
Ы
и/
W /IV
//
/
/
0.3 0.4 0.6 О.д 1,0
xt/l2
Рис. 12. Распределения средней температуры
и температуры в центре для пластины толщи-
толщиной 21 (/, //), неограниченного кругового
цилиндра диаметром 21 (Illy IV) и сферы диа-
диаметром 21 (V, VI).
Начальная температура равна нулю, температура по-
поверхности равна V.
Если начальная температура равна f(x) и оба конца д:
1 изолированы, то решение имеет вид
= 0 и
§ б. Область 0 < х < I. Температуры границ равны ^ (f) и ?2 СО-
Начальная температура f(x)
В этом случае уравнение имеет следующий вид:
при л: = 0,
при х = I,
v = f(x) при ^ = 0.
Следуя общему методу, приведенному в § 14 гл. I, положим
где
и = 0 при лг = О и х =
и = /(х) при ^ = 0
ГЛ. III. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В ТВЕРДОМ ТЕЛЕ 107
w = yl(t) при л; = 0,
w = cp2 (t) при х = /,
<и; = 0 при ? = 0.
Решение для и (см. § 3 данной главы) записывается в виде
-x.n2n2t . ппх Г ., /ч . ппх
Jsiny f{xf)sxn
Для определения w мы должны использовать теорему Дюамеля *)
(§14 гл. I), при помощи которой решение для случая, когда температуры
на поверхности равны <?1(t) и ср2(О» получается из решения, найденного для
случая температур на поверхности, равных vx и v2.
Если температура всей пластины в момент t = \ равна нулю, а ее концы
поддерживаются при температурах cpj (X) и ср2 (X) в интервале от t = X до t = tv
то тогда температура в момент времени t определяется соотношением
Следовательно, при температурах поверхности концов, равных <?x(t)
и ср2(^), получим
о
где
Отсюда
J x
X / exp ^^ [cp, (X) - (-1)" <p2 (X)] Л. E.1)
*) Другой метод изложен в [8].
108 ГЛ. III. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В ТВЕРДОМ ТЕЛЕ [§ 5
Наконец, окончательно получаем i
ъп2п4
E.2)
Для области 0 < х < / с начальной температурой f(x), когда
на границе л: = 0 отсутствует поток тепла, а на границе х — 1
поддерживается температура ср2(О» решение, получаемое тем же спо-
способом, будет иметь вид
2VPvnT * Bв + IJ «* 1 ,-. <2я + 1) *х (Bв + 1) ™ (-1)"
Т 2jеХр L 47^ Jcos 2/ j 2/ Х
о I
л-о
/ *Р»+^^ tp2(X)</X + //(,0cos <2n + ;)^ dx>\. E.3)
о J
Приведем ряд решений, представляющих определенную практическую
ценность. Они даются для области —/ < х < /, поскольку в таких сим-
симметричных случаях легче проводить сравнение с соответствующими резуль-
результатами для цилиндра и сферы.
1. Область —/ < х < / с начальной температурой, равной нулю*
При />0 границы х=±1 поддерживаются при температуре
kt [9, 10]*). В данном случае
E.4)
2. Область — / < х < / с начальной температурой, равной нулю.
При t > 0 границы х=±1 поддерживаются при температуре V A—е~$*).
В данном случае
cos / (P/%)Vl
(+)[р (+)] 2/
/г=0
при условии, что р не равно ни одному из значений xB/i-f- lJic2/4/2. Реше-
Решение C.5) полезно для случая, когда температура границы изменяется быстро»
но не мгновенно [И].
3. Область —/ < х < / с начальной температурой, равной нулю.
При />0 границы х=±1 поддерживаются при температуре Ve*'*
*) В этих работах приводятся также некоторые численные результаты.
§ 6] гл. ш. линейный тепловой поток в твердом теле
В данном случае
109
ch
со (
( 1
4/2
4v/«
C0S
2/
§ 6. Пластина с периодически изменяющейся температурой
поверхности
Рассмотрим вначале задачу для пластины — / < х < / с начальной
температурой, равной нулю, и температурой поверхности, изменяю-
изменяющейся по закону sin(otf + e) при t > 0. Решение, получаемое из E.2) дан-
данной главы или из § 6 гл. XII, имеет вид
v = A sin (atf -f- s + cp) -f-
4
' 4
F.1)
где
ch Л*/ A +
*l-f
ch 2k*l + cos
'*Х )Ч2
Первый член соотношения F.1) представляет собой решение для уста-
установившегося периодического состояния, второй член — для неустановившегося
состояния. Первый член можно найти из первых основных уравнений при
помощи рассуждений, используемых в § 6 гл. II (см. соотношения F.4) —
F.6)) для полуограниченного твердого тела.
Величины А и ср, представляющие собой амплитуду и фазу установив-
установившегося колебания температуры в точке х, являются функциями двух безраз-
безразмерных величин х/1 и k*L
Характер изменения Л и ср по поперечному сечению пластины для значений
k*L равных 0,5, 1,0, 1,5, 2,0, 3,0, 5,0, 10,0 ft/, показан на рис. 13 и 14.
Для пластины 0 < х < I с начальной температурой, равной нулю, и грани-
границами х = 0 и jc = /, на которых поддерживаются температуры, равные соот-
соответственно нулю и sin (cof-f- e), можно написать
п (—!
s — о/2 cos е)
^
xn2n2t
F.5)
где
sh k*x A + i)
sh?*/(l-H)
ch 2k*x — cos 2k*x
k* определяется соотношением F.4).
ПО ГЛ. III. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В ТВЕРДОМ ТЕЛЕ [§ 6
Если температуру поверхности можно представить рядом Фурье
то решение для установившегося периодического состояния имеет вид
2
m=l
em +-cpm),
F.8)
где А
10
О,в
0,6
0,4
0,2
т и срт определяются из соотношений F.2) и F.3) или—при рас-
смотрении второй задачи — из^
соответствующих соотношений*
в которых со заменено на дао.
Так как в соотношении
F.8) амплитуды и фазы Ат и
срт определяются при помощи
довольно сложных выражений*
приведенный выше метод, хотя
он остается всегда пригодным,
часто неудобен. Приведем те-
теперь другой изящный метод
([12], см. также § 8 гл. IV
и § 5 гл. XV), где решение
выражается в виде тригоно-
тригонометрического ряда по л: с ко-
коэффициентами, которые яв -
ляются функциями., времени.
Этот метод, в частности, по-
лезен при ""рассмотрении ряда
—
—
—
_—. ¦
-^
^
———
0,5
У
Зу/
У/
ш
/II
1
0,2
0,4
0,6 0,8
1.0
Рис. 13. Изменение амплитуды установившегося
колебания температуры в пластине, вызываемое
гармоническим изменением температуры поверх-
поверхности.
простых колебаний темпера-
температуры поверхности, которые
часто возникают на практике
(например, «прямоугольные» и
«пилообразные» колебания).
В качестве первого примера мы рассмотрим случай установившей-
установившейся периодически изменяющейся температуры в пластине 0 < х < /^
когда граница х = 0 поддерэюивается при температуре, равной нулюУ
а граница х = I — при температуре
ft@ = 0.
rT<t<rT+T1, r =
rT+Tx<t< (г+1O.
2,
F.9>
Иными словами, температура V «включена» на время Тх и «выключена» на
время (Т — 7\), причем эти циклы повторяются неограниченное число раз.
Предположим, что такое колебание температуры поверхности продол-
продолжается так долго, что наступает установившееся периодическое состояние и
исчезает влияние начальной температуры. Приступим к нахождению темпера-
температуры в момент f после начала периода «включения».
В соотношении E.2) мы полагаем, что /(*)=== 0, cpj(X) = O и
F.10>
§ 6] гл. ш. линейный тепловой поток в твердом теле
где 0 < ? < Тг и г — большая величина. Если мы положим
то из E.2) данной главы следует, что решение принимает вид
-600
-400
-200
-100
\
\
—N^
2
Тг^
—??_
/_
0.5
\
\
\
\
\
0,0 0t8 1tO
0,2
Рис. 14. Изменение фазы установившегося коле-
колебания температуры в пластине, вызываемое гар-
гармоническим изменением температуры поверх-
поверхности.
Вводя-величины, определяемые условиями F.9) и F.10), получим
t ( Г, Г+Г, [(г-1O+74] (rT+f)
\f / /
rT
X e-«
Для больших значений г F.13) принимает вид
т\ 1 —-?—-—-^г }•
111?
F.11).
F.12),
F.14),
112 гл. ш. линейный тепловой поток в твердом теле [§ 6
Таким образом, для больших значений времени наше решение запишется
-следующим образом:
Так как
п II
л=1
то уравнения F.15) можно представить также в виде
2V V* (—1)л . ппх е*п х —е*" . t
~^"sln— 1— а*г * F17)
Аналогичным образом, положив t = rT-\-T^ -\-t", где г — большая ве-
величина, найдем
Ve'*"* I ?a/|Xcp2(X)dX->V— -.—-—^Y\ • F.18)
о ап \* е )
Следовательно, через время t" после начала интервала «выключения»
температура равна
:sln^, (,19)
Эти решения обычно более удобны для численных расчетов, чем ряд
Фурье F.8). Кроме того, данный метод оказывается достаточно общим и
формулы F.14) <и F.18) непосредственно пригодны для любой задачи, в ко-
которой решение для постоянных внешних условий выражается в виде суммы
ряда экспонент с показателями (—ant), а решение для внешних условий,
задаваемых F.9), можно получить при помощи теоремы Дюамеля. Таким
образом, используя результаты §§ 8 и 12 настоящей главы с соответствую-
соответствующими значениями ап% легко записать решения задач по теплообмену стержня
со средой, имеющей температуру ср2(/), или с подводом тепла, задаваемым
функцией <р2(?), и т. д., где ср2(?) определяется из условий F.9).
Используя F.14) и F.18) в E.3) данной главы, мы получим следующие решения
задачи для случая установившейся, периодически изменяющейся температуры
в стержне 0 < х < /, когда на плоскости л: = 0 отсутствует тепловой поток%
а на плоскости х = / поддерживается температура <Рг @» определяемая усло-
условиями F.9): для интервалов «включения»
л=0
-}
F.20)
и для интервалов «выключения»
cos
л=0 1 е
F.22)
§ 7] ГЛ. III. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В ТВЕРДОМ ТЕЛЕ ИЗ
§ 7. Установившаяся периодически изменяющаяся температура
в составных пластинах
Такие задачи лучше всего решать матричным методом, который обычно
используется в теории электрических цепей [13—17]. Сначала рассмотрим
периодически изменяющуюся температуру в пластине в обозначениях, принятых
в этой теории. Предполагается, что все величины умножены на временнбй
множитель ехр (/о)/); мы опускаем его повсюду, и он появляется лишь в конце
вычисления, если необходимо выбирать действительные или мнимые части.
В каждой точке нас всегда будут интересовать две величины—температура v
и тепловой поток /. В этом случае, как и в § 6 гл. II, общее решение,
соответствующее установившимся периодически изменяющимся состояниям
(как указывалось выше, мы опускаем временной множитель), имеет вид
vx = P sh k*x A + /) + Q ch k*x A + /), G.1)
fx= — Kk*(\ + /) ch k*x A + 0 — Kk*Q(\ + /) sh k*x A + /), G.2)
где
*•=(?)*• <7-з>
P и Q — (комплексные) константы, a vx и /х — температура и тепловой по-
поток в точке х.
Пусть v и / — температура и тепловой поток на плоскости лг = О
пластины, a vr и /' — соответствующие величины на плоскости х = /. Тогда,
если заданы любые две из этих четырех величин, то можно определить Р
и Q и, следовательно, оставшиеся две величины из vt v't /, /' легко вы-
выразить через первые две. В частности,
_ . G.4)
где
-О '
C = — Kk*(\-\-i)shk*l(l-+-l)t D = chft4(l+/). G.6)
Из уравнений G.5) и G.6) следует, что
AD — BC=\. G.7)
Решая уравнения G.4), получаем
v = Dv' — Bf't
f = —Cv'+Af. ) G'8)
Существенно ново здесь то, что уравнение F.4) можно рассматривать
как матричное уравнение
G.9)
связывающее две матрицы (v\ /') и (vt f) (каждая из двух строк и одного
столбца) при помощи следующего простого правила умножения матриц: если
ars — элемент г-й строки и 5-го столбца в матрице (ars)t состоящей из
т строк и п столбцов, a brs — элемент в матрице (brs), состоящей из п строк
и t столбцов, то произведение матриц (ars) и (ЬГ5) представляет собой ма-
матрицу (crs) из т строк и t столбцов, причем элемент crs в ряду г и столбце s
$ Г. Карслоу, Д. ?гер
114 ГЛ. III. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В ТВЕРДОМ ТЕЛЕ [§ 7
имеет вид*)
crs= IiOrjbjs- G.10)
Например,
(Ах ВЛ(А2 В2\_(АХА2 + ВХС2 AXB2 + BXD2\
\сх dx)[c2 d2) — [cx )
xa2 + dxc2 cxb2 + dxd2)
Предположим теперь, что мы имеем составную пластину, состоящую
из п слоев, г-й слой которой характеризуется толщиной /г, коэффициентом
теплопроводности Кг, коэффициентом температуропроводности хг и величи-
величинами vr, fr и v'r, f'r на его левой и правой поверхностях соответственно. Тогда
в случае идеального теплового контакта между плоскостями слоев повторное
применение уравнения G.9) дает
Сг Dx
G.12)
где Ar Br и т. д. определяются из формул G.5) и G.6) для отдельных слоев.
Умножение матриц в соотношении G.12) можно производить последовательно
при помощи формулы G.11). Таким способом можно записать точные фор-
формулы для пластины, состоящей из п слоев, но они оказываются исключи-
исключительно сложными. Ценность данного метода заключается в том, что он
позволяет очень легко получить числовые величины для частных случаев,
подставляя численные значения Лг, Вг ..., в G.12) и умножая числовые
матрицы.
Если между слоями пластины или на поверхностях имеются контактные
сопротивления, то их также можно представить в виде матриц и включить
в произведения G.12). Например, если контактное сопротивление между пер-
первым и вторым слоем равно Rv то
или
'v2
J = \0 lA/i
Отсюда, например,
(M АЛЛ -ЯЛ/А,
GЛ5)
Конечный результат этих вычислений представляет собой два линейных
соотношения, связывающих температуры и тепловые потоки v[t v'n> fv f'n на
двух поверхностях составной пластины. Граничные условия дадут еще два
соотношения, и поэтому мы сможем найти четыре величины. В случае не-
необходимости температуру в пределах любого слоя можно определить из фор-
формулы G.1).
В качестве простого примера рассмотрим пластину 0 < х < /, в которой
на границе лг = О теплообмен отсутствует, а на границе л; = / с термическим
сопротивлением R происходит теплообмен со средой, температура которой
меняется по закону Vcoswt. Тогда, если vx и /^=0) — температура и
тепловой поток при л: = 0, а V и /2 — температура и тепловой поток во
*) Следует отметить, что произведение матриц не коммутативно.
§ 8] ГЛ. III. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В ТВЕРДОМ ТЕЛЕ 115
внешней среде, то из G.14) и G.9) следует, что
(v\ — (l -R\(A B\(vl\_(Avl-RCvl
\fi)~\0 l)\C D)\0 ) — { Cvx
Отсюда
Вводя временной множитель ехр(Ш) и беря действительную часть, по-
получим решение, которое согласуется с решением A2.7) данной главы.
§ 8. Пластина с заданным тепловым потоком на ее границе
Задачи подобного типа приобретают в технике все большее и большее
значение. Они делятся на два типа. В задачах первого типа тепло поступает
от плоского подогревателя, погруженного в твердое тело. В этом случае
потери тепла на границе отсутствуют и граничное условие точно удовле-
удовлетворяется, если теплоемкость подогревателя пренебрежимо мала; в противном
случае его можно считать идеальным проводником, как и в § 13 данной
главы. В задачах второго типа, которые возникают при индукционном на-
нагреве поверхности металла, эта поверхность может выделять тепло, и если
постулируется линейный перенос тепла с коэффициентом теплообмена в среду
с нулевой температурой, равным Я, то из соотношения (9.4) гл. I следует,
что граничное условие запишется в виде
— K^ = — F + Hv. (8.1)
или
+ h(v — V) = 0. (8.2)
где F — тепловой поток, поступающий через поверхность в твердое тело,
a V = F/H. Таким образом, для постоянного Н эта задача сводится к за-
задаче о нагревании в результате теплообмена со средой, имеющей темпера-
температуру V (см. § 11 данной главы).
Ниже приводятся некоторые решения для случая, когда потери тепла
с поверхности отсутствуют. Эти решения легче всего получить при помощи
методов, изложенных в гл. XII.
/. Область О < х < / с начальной температурой, равной нулю.
Через плоскости х = 1 тепловой поток внутрь твердого тела по-
стоянен и равен Fo. Через плоскость х = 0 тепловой поток отсут-
отсутствует [18—23]. В данном случае
+
3*2 - /2 2 V (-1>л
, (8.3)
/2=1
ИЛИ
[_«?*]co.*«.
v =-
/c
,, ,Bn+l)l-x\ |ф. /BB+l)f + x\ |
Распределение температуры в (8.3) есть сумма линейной функции вре-
времени FQt/pcl и корректирующего фактора, который является функцией вре-
времени и положения. График этого корректирующего члена приведен на рис. 15.
116
ГЛ. III. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В ТВЕРДОМ ТЕЛЕ
[§8
2. Область О < х < I с начальной температурой, равной нулю. Через пло-
плоскость х*=-1 тепловой поток постоянен и равен Fo. Плоскость х^Ъ поддержи-
поддерживается при температуре, равной нулю. В данном случае
п-0
>я+1J«ф[
sin"
21
(8.5)
иди
л=0
5. Тепловой поток задан функцией времени. В этом случае для нахождения
решения можно воспользоваться теоремой Дюамеля. Отметим два простых решения
Рис. 15. Распределение значений (Kv/Fol) —
— (till2) в пластине толщиной / в отсутствие
теплового потока при х = 0 и при постоянном
тепловом потоке при х = /.
Числа на кривых указывают величины х//Я
для теплового потока Fot , где /и =— 1, 0, 1,
соответственно к следующим:
1 ^-(m+l)
..; уравнения (8.4) и (8.6) сводятся
я=0
(8J)
I
n=0
Bn+lO — .
8)»
*) Для случая т — 2 см. [24].
§ 91 ГЛ. III. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В ТВЕРДОМ ТЕЛЕ 117
§ 9. Область 0 < х < /. Теплообмен на границах в среду
с температурой, равной нулю. Начальная температура равна f(x)
В этом случае наши уравнения имеют следующий вид:
4r = *S @<*<0. (9Л)
—-g- + /k; = 0 при д: = 0, (9.2)
J*Ljrhv = Q при х = 1 (9.3)
и
v = f(x) при / = 0. (9.4)
Выражение e~XCLtt(Acosax-{-Bsinax) удовлетворяет уравнению (9.1).
Оно удовлетворяет также уравнениям (9.2) и (9.3) при условии, что
и
а (В cos а/ — A sin а/) + h (В sin а/ + A cos а/) = 0.
Отсюда A/B = a/h и
*g«' = ^F- (9-5)
Следовательно, выражение
A (cosout-)- — sin out) ?-***'
удовлетворяет уравнениям (9.1), (9.2) и (9.3), где А — произвольная кон-
константа и a — некоторый, отличный от нуля корень уравнения
2ha
Чтобы составить себе представление о совокупности действительных
корней*) уравнения (9.5), необходимо лишь отметить, что они соответствуют
абсциссам общих точек кривых
и n = -jj — -j-t
где мы положили а/ = ?.
Вторая из этих кривых представляет собой ги-перболу с центром в начале
координат и асимптотами
Если начертить эту гиперболу и котангенсоиду (рис. 16), то мы увидим, что
в каждом из интервалов @, ic), (тс, 2тс), ... лежит положительный корень
уравнения, а отрицательные корни по абсолютным величинам равны положи-
положительным. Ясно также, что кратных корней нет.
Кроме того, очевидно, что уравнение (9.5) не может иметь чисто мнимого
корня ibt так как мы должны были бы в этом случае написать
что невозможно, поскольку оба члена имеют одинаковый знак.
*) Об этих корнях см. § 10 данной главы. Там же приведены и их численные
значения.
118
ГЛ. III. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В ТВЕРДОМ ТЕЛЕ
[§9
В конце данного параграфа мы покажем также, что уравнение (9.5)
не может иметь комплексных корней вида а ± ib\ следовательно, все его
корни действительны.
Предположим, что f(x) можно разложить в ряд
где
Хп = cos апх + — sin апх,
а ап — л-й положительный корень уравнения (9.5).
Тогда решение нашей задачи будет иметь вид
(9.6)
(9.7)
(9.8)
К вопросу о возможности разложения (9.6) и справедливости решения
(9.8) мы еще вернемся в § 1 гл. XIV. Если предположить, что такое разло-
разложение существует и что этот ряд можно интегрировать почленно, то значения
-2п
2п
Рис. 16.
коэффициентов нетрудно получить тем же способом, каким при аналогичных
предположениях находят коэффициенты ряда Фурье.
Для этого нам нужно доказать, что
J XmXn dx = 0 (тф
п)
(9.9)
Это мы сейчас и сделаем.
Так как
d2Xm i 3-
то
/ 2
-*l)fxmxnax = f(.
= U И
(9.10)
r)jdx — \X4i
X
§ 9] ГЛ. III. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В ТВЕРДОМ ТЕЛЕ 119
Но
k + AAV = 0 при * =
и
JL + hXr = 0 при х =
где г — любое целое положительное число.
Тогда
о
и, если т не равно я, то
— *l) f XmXndx = O
о
i
fxmXndx=O.
0
I
Чтобы получить величину Г X\dx, напомним, что
о
Следовательно,
i i
-1 + / l^-J dx.
Jo ./ V dx )
и о
Но
апХп = ап cos апх + h sin anx
и
--^~ = — ап sin апл: -f Л cos аядг.
Поэтому
2 . . 2
lf X
О
Но мы видели, что
о
Следовательно,
i
24 / Х\ dx = /D + А2) — [Хп -g
6
Но
= 0 при х = (
= 0 при x =
120 ГЛ. III. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В ТВЕРДОМ ТЕЛЕ [§ 9
Следовательно,
при х = 1
при л; = 0.
Но
а2 х2 4- ( dXn У = а2 -4- Л2*
Следовательно,
^2 =: 1 при х = 0 и jc = /.
Таким образом,
^ л1 = — 2h
Итак, если мы предположим, что разложение в ряд возможно и что ряд
можно интегрировать почленно, то
J
Таким образом *),
Если на границах х = 0 и л: = / происходит теплообмен со средо»
с температурами vx и v2 соответственно, то данную задачу можно свеет»
к разобранной выше, воспользовавшись заменой
v== u-\-w.
Здесь и — функция только от х, удовлетворяющая уравнениям
¦0 = 0 @ <*</),
— -j^ + h{u — vx)= 0 при х = 0
dx
так что
—z \-h(u — v2) = 0 при x = L
Th + 2
*) Во всех рассуждениях предполагается, что h > 0. Если h = 0, т. е. поток тепла
через плоскости х = 0 и jc = / отсутствует, то решение (9.12) остается справедливым
I
1 Г
(см. соотношение D.6) гл. III), если мы добавим к нему член -г / / {х) dx.
§ 10] ГЛ. III. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В ТВЕРДОМ ТЕЛЕ 121
a w — функция от х и /, удовлетворяющая уравнениям
= 0 при * = 0,
= 0 при х = 1
и
w = f(x) — и при / = 0.
Задачи, в которых один конец стержня поддерживается при постоянной
температуре, а на втором происходит теплообмен с окружающей средой,,
либо задачи, в которых один конец совершенно изолирован, можно рассма-
рассматривать тем же способом. Некоторые результаты приводятся в §§ 10 и II
настоящей главы.
Мы отмечали выше, что уравнение
не может иметь комплексных корней вида а ± ib.
Если бы это было возможно, то мы получили бы два сопряженных корня а ± ib*.
и они дали бы два выражения
X = cos ах А sin ах, X' = cos а'х 4- —;- sin a'x,
а а
где
а = а + ib и а' = а — ib.
Теперь мы видим, что для любых двух неравных корней уравнения (9.5)
о
Но это применимо также к X и X', и следовательно,
f XX'
о
Отделяя в X действительную и мнимую части
мы должны были бы получить
о
что невозможно.
Итак, мы убедились в том, что уравнение (9.5) имеет только действительные корни-
§ 10. Область —*< jc </. На границах х= ±1 происходит
теплообмен со средой нулевой температуры.
Начальная температура f(x)
Часто начало координат удобно выбирать в центре исследуемой области,
так как тогда яснее выявляется любая симметрия решения. Часто полезно
также считать толщину пластины равной 2/, так как тогда. результаты легче
сравнивать с результатами для цилиндров и сфер диаметром 2а. По этим.
122 ГЛ. III. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В ТВЕРДОМ ТЕЛЕ [§ 10
причинам перепишем соответствующим образом выражение (9.12). Оно будет
иметь вид
Cn COS OLnx-^-dn Sin а„х Г -, ч r IJ* tj у^л^ч
J fMlcncosanx + dnsinanx]dx, A0.1)
f + tfi + h J
где
cn = hsinanl + ancosanlt A0.2)
dn = h cos anl — an sin осл/, A0.3)
a ал — положительные корни уравнения
^ A0.4)
Так как уравнение A0.4) эквивалентно
(h sin a/ + a cos a/) (/г cos a/ — a sin a/) = 0, A0.5)
то его положительные корни ап находят из следующих двух уравнений:
atga/ — /г = 0, A0.6)
(Ю.7)
Из результатов, полученных в § 9 данной главы, следует, что все корни*)
уравнений A0.6) и A0.7) являются действительными и простыми. Это, конечно,
легко доказать. Некоторые численные их значения приведены в приложении 4.
Если ап — корень уравнения A0.6), то dn = 0 и c2n = h2-\-a2n\ если же
ап — корень уравнения A0.7), то сп = 0 и d2n = h2-{-a2n.
Если f(x)— четная функция от х, то выражение A0.1) принимает вид
о V4 -*«2' (Л2 4-«!) cos <
где ал — положительные корни уравнения A0.6). Оно является также реше-
решением задачи о теплопроводности в области 0 < х < / в отсутствие
теплообмена на границе л: = 0, при наличии теплообмена на границе
х = 1 со средой, имеющей нулевую температуру, и при начальной тем-
температуре, равной f (х)\ это решение легко получить непосредственно при
помощи метода, изложенного в § 9 настоящей главы. В данном случае раз-
разложение (9.6), приведенное в предыдущем параграфе, принимает вид
xdx, A0.9)
где ап — положительные корни уравнения A0.6). В частном случае, когда
f(x)=l, из A0.9) следует, что
*) Все корни уравнения A0.6) действительны, если h > 0; все корни уравнения
A0.7) действительны, если lh > — 1 (см. § 4 гл. IX).
§ 11] ГЛ. III. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В ТВЕРДОМ ТЕЛЕ 123
Аналогичным образом, если f (х)— нечетная функция от х% то выра-
выражение A0.1) принимает вид
где ап — положительные корни уравнения A0.7). Это выражение является
также решением задачи о теплопроводности в области 0 < х < / в том
случае, когда при ?>0 на границе х = 0 поддерживается нулевая
температура, на границе х = 1 происходит теплообмен со средой,
имеющей нулевую температуру, и начальная температура равна f(x).
Если f(x) не является ни четной, ни нечетной функцией, то решение
имеет вид A0.1) и содержит корни как уравнения A0.6), так и уравнения
A0.7). В данном случае подход оказывается аналогичным подходу при исполь-
использовании ряда Фурье для представления произвольной функции f(x) в интер-
интервале (— /, /) с дальнейшим его выражением в виде ряда косинусов или
синусов с учетом четности или нечетности функции f (х).
§ 11. Частные случаи и численные результаты для пластины
с граничным условием третьего рода
Это граничное условие характерно для многих задач, имеющих важное
практическое значение. Для их решения мы располагаем множеством числовых
данных в форме таблиц и графиков. Приведем здесь некоторые из имеющихся
результатов, причем для упрощения выразим числовые величины через без-
безразмерные параметры
L = lh, Г = -^-, -у-. A1.1)
Обычно при рассмотрении ограничиваются такими важными величинами,
как температура в центре, на поверхности или средняя температура, которые
содержат только два параметра L и Т и, следовательно, могут быть выра-
выражены в виде семейства кривых. В самом деле, имеется восемь функций *)
от L и Т, при помощи которых можно выразить многие результаты подоб-
подобного рода.
Первые четыре из этих функций имеют вид
(„.4>
4L2sec<zrt -а„т ,ЛЛ -ч
^ ]e - . A1.5)
*) Графики этих функций (их аргументом служит arctg L) для определенных
значений 7\ а также некоторые их применения приведены в работе [25]; графики
функций 1—/ь 1—/2> 1—/3 показаны на рис. 17—19.
124
ГЛ. III. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В ТВЕРДОМ ТЕЛЕ
[§ U
где ал (при я=1, 2, ...) — положительные корни уравнения
atgcc = Z,, A1.6)
которое в принятых нами обозначениях представляет собой уравнение A0.6),
приведенное в предыдущем пара-
параграфе.
Другие четыре функции, соот-
соответствующие корням уравнения
A0.7), имеют вид
-•-2
-'+2
cp3(Z,, Т) =
A1.8)
Рис. 17. Функция [1—/,(L, 71)], где
fi(Lt T) определяется из A1.2).
Показано изменение температуры поверхности пла-
пластины толщиной 2/, имеющей начальную темпера-
температуру V и охлаждаемой в результате теплообмена
со средой нулевой температуры. Числа на кривых
указывают значения L=lh.
=1+2
12/. (Z, + 1)г Sec Pn
„-1
A1.9)
A1.10)
где р„ (при я=1, 2, ...) — положительные корни уравнения
= 0. A1.11)
Некоторые значения корней уравнений A1.6) и A1.11) приведены в при-
приложении 4. Следует отметить, что при больших значениях Т важны только
первые члены приведенных выше рядов. Во многих случаях это оказывается
справедливым, если Т > 0,5.
При малых значениях Т (скажем, Т < 0,01) ряды сходятся медленно и,
пользуясь методом, изложенным ниже (см. § 5 гл. XII), можно вывести другие
выражения. Они не приводят к таким простым и точным формулам, как
это было в некоторых случаях, рассмотренных ранее.
Рассмотрим теперь ряд важных частных задач.
/. Область —/ < х < / с постоянной начальной температурой V
и теплообменом на ее границах со средой нулевой температуры.
Используя здесь A1.1), A1.6), а также соотношение A0.8), получим
A1.12)
1A+
Температура поверхности vn = V[\—/i(?. T)], температура в центре
vn =. [1 —/2(?» Т)], где /г и /2 определяются из выражений A1.2) и A1.3)*
И]
ГЛ. III. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В ТВЕРДОМ ТЕЛЕ
125
ffo
Средняя температура в пластине vcp=V[l—fz(L, 7)]. Количество тепла,
отдаваемое пластиной (с обеих поверхностей) за время t, равно
Q = 219с [V — *ср] = 2lV9cfz (L, Т).
На рис. 17, 18 и 19 изображены графики зависимости vn/V, vJV и
(l—Q/2Vlpc) от \gT для различных значений L @,05; 0,1; 0,2; 0,5; 1; 2;
5; 10; оо).
Ввиду важности рассматриваемых задач был составлен ряд таблиц
и диаграмм с численными значениями этих величин. Были построены графики
зависимости \g (v/V) от Т для фикси-
фиксированных значений L и х/1 [26, 27].
Эти графики, как правило, предста-
представляют собой прямые, что соответ-
соответствует случаю, в котором важен
только первый член A1.12). Дру-
Другие авторы не пытались изучать
эти функции для всех значений
параметров, а исследовали вели-
величины vn, ^ц и Q или vcpt которые
определены выше. Грёбер [28; 29]
приводит краткие таблицы и гра-
графики зависимости этих величин от
\g L при определенных значениях Т,
или от \gT при определенных зна-
значениях L. Шак *) [30] обобщил ре-
результаты Грёбера и построил гра-
графики зависимости от L в линей-
линейном масштабе, придавая L значения
/,= 10* (при /t = l, 2, 3, ...)• Были
составлены также графики зависимо-
0,8
0.6
0,4
0.2
—^
1
1
\
\\
Рис. 18. Функция [1 — /2(?, Т)], где
/2(L, T) определяется из A1.3).
Показано изменение температуры в центре пла-
пластины толщиной 2/, имеющей начальную темпера-
температуру V и охлаждаемой за счет теплообмена со сре-
средой нулевой температуры. Числа на кривых указы-
указывают значения L = lh.
сти In (Г) от \n(L/K) для определен-
определенных значений г;ц, vn и vc? и дана
числовая таблица для построения
таких графиков [34]. Было приве-
приведено множество таблиц с критиче-
критическим введением к ним [35] **). Ней-
Нейман [33, 37] дает таблицы значений
для постоянного и параболического начального распределения температуры.
Кроме того, были опубликованы численные результаты, а также решения,
пригодные для расчетов [38—42].
2. Область — I < х < I при наличии на плоскостях х = ± / теплообмена
со средой нулевой температуры. Начальная температура а — Ьх2. В данном
случае
^ [2La<x2 — 2Ы2 fa2 (L -|- 2) — 2Z.11 cos (anx/l) - a2 r
V=Zi ~ 9 Г V, ,9 , ,1 ~ * П • AU3)
+L]
cosan
где ап — корни уравнения A1.6).
5. Область — I < х < I с нулевой начальной температурой нагревается
за счет теплообмена со средой с температурой V. Как отмечалось в § 8 данной
главы, эта задача сводится к задаче о нагревании пластины постоянным потоком
*) Его кривые воспроизведены в работах [31—33].
*) Некоторые из результатов данной работы воспроизводятся в книге Якоба [36].
126
гл. ш. линейный тепловой поток в твердом теле
г§
тепла, подводимым к его поверхности, при наличии теплообмена со средой, имеющей
нулевую температуру. Искомая температура равна разности между V и температурой,
полученной в примере 1.
4. Область О < х < / с нулевой начальной температурой. Через плоскость
х = О тепловой поток внутрь твердого тела постоянен и равен Fo; на пло-
плоскости х = / происходит теплообмен со средой нулевой температуры *).
В данном случае
I л=1
— положительные корни уравнения
A1.14)
A1.6). На плоскости jc = O температура
равна (IFo/KL) [/, (L, Т) + Lf3 (L, 71)]; на
плоскости х = / она равна (IFO/KL) X
X /2 (?» ^)- Количество тепла, прохо-
проходящее через единицу площади плоско-
плоскости х = / за промежуток времени от
* = 0 до t = t, равно (F0l2/%){T —
__ [(/. _|_ 2)/2Z.] /4 (L, Т)}.
5. Область 0 < х < I с начальной
нулевой температурой. При t > 0 на
плоскости х = 0 поддерживается ну-
нулевая температура. На плоскости
х = / происходит теплообмен со сре-
средой, имеющей постоянную темпера-
температуру V. В данном случае
Рис. 19. Функция [1 — /3(Z., T)], где
/3(?, Т) определяется из A1.4).
Показано изменение количества тепла Q\, теряе-
теряемого единицей поверхности пластины толщиной 2/,
имеющей начальную температуру V и охлаждаемой
за счет теплообмена со средой нулевой темпера-
температуры. Числа на кривых указывают значения ?=/Л.
происходит теплообмен со средой нулевой
v \-\-L{\—xll) ~
A1.15)
где ря (при л= 1, 2, ...) — положи-
положительные корни уравнения A1.11). Тем-
Температура на плоскости х = / равна
[L V/(L + 1)] <Pi (L, ?), а в выражение
для количества тепла, поступающего
через единицу площади плоскостей
х = 0 и х = I за время t, входит соот-
соответственно ср4 (L, Т) и срз (^» Т).
6. Область 0 < х < I с нулевой
начальной температурой. При t > О
температура границы je = O поддер-
поддерживается равной V. На границе х=*1
температуры. В данном случае
X+L
sin фпх/1) -?пт
A1.16)
где ^ — положительные корни уравнения A1.11). Температура на границе * = / равна
7. Область 0 < х < I с начальной температурой vox/l. При t>0 темпера-
температура на границе х =* 0 поддерживается равной нулю; на границе х = / проис-
происходит теплообмен со средой, имеющей температуру Vx. В данном случае
A1.17)
*) Некоторые численные результаты приведены в [43].
§ 12] ГЛ. III. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В ТВЕРДОМ ТЕЛЕ 127
где ря — положительные корни уравнения A1.11). Это выражение показывает измене»
ние температуры на внешней стороне составной пластины при установившихся
условиях. Анализируя соответствующее дифференциальное уравнение, легко показать,
что изменение температуры выражается формулой A1.15), в которой V заменено на
8. Область — I < х < I с нулевой начальной температурой. При х = / проис-
происходит теплообмен со средой с температурой V, а при х = — / — со средой нуле-
нулевой температуры. Коэффициенты теплообмена на обеих границах одинаковы.
Решение этой задачи получается комбинированием A1.12) и A1.15)
пТ +
е~"пГ, A1.19)
где ап и Ря— положительные корни уравнений A1.6) и A1.11).
9. Область О < х < I с начальной температурой f (x). Граничные условия
записываются в виде
Z
k2 -gj + k2V = О, X = / ,
где ?i!>0, hi^O, причем они не должны одновременно обращаться в нуль;
k2 и h2 также должны удовлетворять этим условиям. Записанные нами гранич-
граничные условия включают девять возможных комбинаций нулевой температуры, нулевого
теплового потока или теплообмена со средой, имеющей нулевую температуру на
любой поверхности. В данном случае
§ Zn(x')f(x')dx\ A1.21)
я=1 О
где
_ ,..... [2(*2й+*Э]'*(*iP«cosM+ftisin$n
п{) {(^Й+*^[/да+Ч)+*л]+*1*,(Ф5
Здесь ря (при п= 1, 2, ...) — положительные корни уравнения
(М2Р2 — hxh? sin p/ = р (.kxh2+k2hx) cos p/;
если /г1 = /г2==0, то в соотношение A1.21) следует ввести дополнительный член
у I f{x')dx'. A1.24)
6
Это является обобщением результата, полученного в § 9 данной главы, на слу-
случай различных коэффициентов теплообмена для двух поверхностей. Распространение
результатов на случай теплообмена со средой, имеющей различные температуры,
производится так же, как и в конце § 9 данной главы.
§ 12. Область — /<jc</ с нулевой начальной температурой
и теплообменом на границах со средой, имеющей температуру ср (/)
• Из теоремы Дюамеля (см. § 14 гл. I) следует, что
2. /
v = 2y.h У т ^-9 577^ / * я ?(*)<**. A2Л)
^ Л + Ча» + « ) \COSaJ J
128 гл. ш. линейный тепловой поток в твердом теле [§13
где а-п — корни уравнения
atgal=h. A2.2)
Если температура среды равна Vo при О < t < Т и Vx при t > Т, то искомое
решение имеет вид
-т-г-в— .к lJr Ь 0 < t < Т A2.3)
n=1 [(h2+ *?„) I+ h] cos lan j
f
, - Г, - У Г* 2Н ^ + < V K°> f ^ C°S '"* , />Г. A2.4)
Если температура среди равна V sin (©? -f- e), то решение имеет вид
где
Мое*ъ = ch co'jc cos <o'jc + / sh a>'jc sin со' х, A2.6)
^ == со' sh (o7 cos o>7 — o/ ch a>7 sin o>7 + Л ch «7 cos ©7 +
-f i [со' sh co7 cos co7 + o)' ch ©7 sin ©7 + h sh ©7 sin ©7] A2.7)
. A2-8)
?с./ш температура среды равна kt, то решение имеет вид
-/'*--20 , 2АА V -»S' cos а„.*
где ап — положительные корни уравнения A2.2).
§ 13. Пластина, одна из поверхностей которой соприкасается со слоем
идеального проводника или хорошо перемешиваемой жидкости
Если граница х = / пластины находится в идеальном тепловом контакте с мас-
массой М' (на единицу площади) хорошо перемешиваемой жидкости (или идеального
проводника) с удельной теплоемкостью с', то граничное условие при х = /, как и
в (9.14) гл. I, имеет вид
g -g-=Q. A3-1)
где Q/M' — скорость подвода тепла извне (если он вообще имеет место) на единицу
массы жидкости. Предполагается, что тепло из жидкости передается только пластине.
При решении таких задач встретятся безразмерные параметры трех типов -*t/l2, lh и
xjU В разбираемых ниже примерах 1—6 мы запишем
Л = рс/Л*'с'. A3.2)
Для ряда простых задач приведем решения, которые можно выразить через
корни уравнений
F JF atgal = h A3.3)
р ctg p/ = — h. A3.4)
§ 13] ГЛ. III. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В ТВЕРДОМ ТЕЛЕ 129
Численные значения этих решений можно выразить через численные значений
функций / и % определенных в § 11 данной главы. В более сложных задачах, в кото-
которых рассматривается теплообмен при х*»0 или отвод тепла от жидкости, или кон-
контактное сопротивление между твердым телом и жидкостью, появляются дополнитель-
дополнительные параметры (см. примеры 7—9).
/. Область О < х < I с нулевой начальной температурой. Граница х = 1
твердого тела соприкасается с массой Мг (на единицу площади) хорошо пере-
перемешиваемой жидкости с удельной теплоемкостью с' и нулевой начальной тем-
температурой. На границе х = 0 тепловой поток отсутствует. Постоянный подвод
тепла Q к жидкости. В этом случае решение имеет вид
м ** /2C + **)] 2Qh у
2 6A + /A)J М''А
] у
2* 6*A + /A)J М'с'ъА ft cos fy[/(p2 + A2)+A]'
где рл — корни уравнения A3.4).
2. Задача, аналогичная 1, но Q = О и начальная температура жидкости
равна V. В данном случае
2пУе~%*п'cos
3. Задача, аналогичная 1, но на границе х = 0 поддерживается нулевая тем-
температура, a Q — постоянная величина. В данном случае
, lan COS aj
где а—корни уравнения A3.3).
4. Задача, аналогичная 1, но Q = 0, начальная температура жидкости
равна V, а граница х = 0 поддерживается при нулевой температуре. В этом
случае
2hVe
где ап — корни уравнения A3.3).
5. Задача, аналогичная 1, но Q = 0, начальная температура жидкости равна
нулю, а граница х = 0 при t > 0 поддерживается при температуре V. В данном
случае
2 .
2(«2„
sin «n-^
где /г определяется из выражения A3.2) и ая — корни уравнения A3.3).
6. Задача, аналогичная 1, но Q = 0, начальная температура жидкости равна
нулю, а к границе х = 0 в единицу времени на единицу площади подводится по-
постоянное количество тепла Q'.
Q'l I hti 1-х h(l — xJ lh
V \ + +
21
\ A3.10)
я=1
где h определяется из выражения A3.2) и ря — корни уравнения A3.4).
7. Область 0 < х < I с начальной температурой V. На границе х = 0 потери
тепла отсутствуют, граница х = 1 соприкасается с массой М' (на единицу пло-
площади) хорошо перемешиваемой жидкости с удельной теплоемкостью с'. Коли-
Количество тепла, отдаваемого этой жидкостью (в единицу времени) в результате
теплообмена, равно произведению величины Н на температуру V. Начальная
9 Г. Карслоу. Д. Егер
130 ГЛ. ITT. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В ТВЕРДОМ ТЕЛЕ [§ 14
температура жидкости равна нулю. В данном случае
-ха2*
е п (h — ka2n) cos anx
V п/ п ^ A3.11)
COS anl
где h = Н/К, k = Af'c'/pc, a an — корни уравнения
atgal=h— №. A3.12)
8. Задача, аналогичная 7, но начальные температуры как твердого тела,
так и жидкости равны нулю. Количество тепла, подводимого на единицу массы
жидкости в единицу времени, равно f(t)/M'. В данном случае
2% ^ alcosanxe п Г «&
где an — корни уравнения A3.12).
9. Область 0 < x < /; «а границе х = / тепловой поток отсутствует, а гра-
граница х = 0 соприкасается с массой М' (на единицу площади) хорошо перемеши-
перемешиваемой жидкости с удельной теплоемкостью с'\ к жидкости в единицу времена
на единицу массы подводится постоянное количество тепла Q/M'. Предполагает-
Предполагается, что температура поверхности твердого тела не равна температуре жидко-
жидкости, а между ними происходит теплообмен, величина которого равна произведе-
произведению Н на разность температур твердого тела и жидкости *) (см. (9.16) гл. I).
В этом случае
Kv
oi
где
h = H/K, L =
п — п • п ч~ п^ "
а ал — корни уравнения
<4-*i
l«»(l-4-) • О3-14)
§ 14. Пластина с внутренним источником тепла
Если в единицу времени на единицу объема выделяется количество
тепла, равное Л, то дифференциальное уравнение имеет вид
d2v 1 dv А (Н л^
дх2 % dt ~ К'
Наиболее важен случай ^=.40 = const при t > 0, который наблюдается
при диэлектрическом нагреве. Распространение на случай зависимости А от
места или времени легко выполнить тем же методом, как и в § 14 гл. I
и § б гл. XII. Как отмечалось в § б гл. I, в общем случае, когда А является
функцией от V, аналитическое решение найти нельзя. В § 7 гл. XV рассмат-
рассматривается случай линейной зависимости между А и V. Здесь мы воспользуемся
методом, изложенным в § 14 гл. I; можно также применить преобразование
Лапласа.
*) Другие задачи подобного типа и некоторые численные результаты приведены
в работе Егера [44].
§ hi
ГЛ. III. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В ТВЕРДОМ ТЕЛЕ
131
/. Область —/ < х < / с нулевой температурой поверхности*}
и нулевой начальной температурой. При t > 0 количество теплаУ
выделяемое в единицу времени,
же, как в задаче I § 14 гл. I,
отметим, что
постоянно и равно Ло. Поступая так
Ж
A4.2)
удовлетворяет всем условиям за-
задачи; тогда выражение A4.2) слу-
служит решением для случая устано-
установившейся температуры. Подста-
Подставим теперь
v = -
Ж
в уравнение A4.1), причем w
должно удовлетворять уравнению
дх2 %
с граничными условиями
х2> = 0 при лг= ± /,
и
2/С
при
A4.4)
A4.5)
* = 0.
A4.6)
П4.3) ^ Ц4
Рис. 20. Температура в пластине — I < х < I
при данном распределении источников по-
постоянной мощности Ао и нулевой темпера-
температуре поверхности.
Числа на кривых указывают значения xtjl2.
Решение уравнения A4.4) при выполнении условий A4.5) и A4.6) было
дано в § 3 данной главы. Если использовать все эти соотношения, то выра-
выражение A4.3) примет вид
v =
А012
Ж
1 _?l__32 у (—I)"
I2 ъг Za Bл+1K
cos
- ехр —
4/2
A4.7)
и, развивая вывод C.17), мы получим решение для малых значений времени
(см. пункт V § 5 гл. XII, где приведен соответствующий результат для выде-
—- п
ления количества тепла в единицу времени, равного Aotz , причем п может
равняться —1, 0 или любому целому положительному числу) в виде
v =
Apt
я=0
A4.8)
На рис. 20 приведены некоторые значения v для различных значений %t/P*
Следует отметить, что приближенные результаты для случая, когда на поверх-
поверхностях происходит теплообмен со средой, имеющей нулевую температуру*
легко получить из рис. 20 путем простой замены / на / + (/С/Я).
2. Если количество выделяемого в единицу времени тепла не остается по-
стоянным, а равно A(t), то из выражения A4.7) и теоремы Дюамеля (см. стр. 38).
*) Случай постоянной температуры поверхности, например при сочетании по-
поверхностного и диэлектрического нагрева, рассматривается в работе [45].
9*
132 ГЛ. III. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В ТВЕРДОМ ТЕЛЕ [§ 14
следует, что
4 V* (—1)я Bл+1Iсх Г,/ч Г *Bn+lJn2(t — x) |
1АСО8 УЛМ«Ф[^ '>d,\. A4.9)
АТ7 2/
5. Если количество выделяемого в единицу времени тепла является функ-
функцией положения А(х)> то
i
4/ V Mi Г ъп2п4
HrVl4PJ}^r J w'. A4.10)
л=1
Другая форма для случая установившейся температуры имеет вид
I 71 X 1)
*| f A{t)dl + (x-l) fdti f
f I I
( f f f
x -f -I -I
Задачу о нагревании при помощи вихревых токов можно рассматривать анало-
аналогичным образом. В этом случае количество выделяемого в единицу времени тепла
пропорционально (ch2px— cos2/ur); здесь р = 2п (fA/aL fi и а — проницаемость и
электропроводность вещества соответственно, а /—частота [46]. При очень высоких
частотах тепло почти все сосредоточивается близ поверхности и в этом случае можно
использовать результаты § 8 данной главы.
4. Область — I < x <1 с нулевой начальной температурой. На границах
х = ± / происходит теплообмен со средой, имеющей нулевую температуру. При
t > 0 количество выделяемого тепла постоянно и равно Ао. Здесь вместо подста-
подстановки A4.3) используем подстановку
А° B1 + hi2 — hx2) + wt A4.11)
где первый член в правой части уравнения представляет собой решение для случая
установившейся температуры. Поступая, как и в пункте 1, и используя соотноше-
соотношение A0.8) данной главы, получим
21 + ы* - hx* - 4А* V l°San*e = , A4.12)
где ап — положительные корни уравнения atg<x/= h. В обозначениях, принятых в § 11
(см. A1.4) и A1.5)), температуры при х=0 и х = 1 равны соответственно
L,T) A0l2f3[L,T]
2KL KL
5. Область 0 < х < I с нулевой начальной температурой. На границе х = 0
при t > 0 поддерживается нулевая температура. На границе х = 1 происходит
теплообмен со средой, имеющей нулевую температуру. При t > 0 количество
выделяемого тепла постоянно и равно Ао. В данном случае
Ао ( B +In) 1х 21
V"^{ l + ih * Г
4А0п у sin апх A — cos «я/)
Т"^ ^-in 2.
где ап — положительные корни уравнения a ctg la -\- h = 0. Температуру на границе
х = 1 можно выразить через <р3 и <р4, определенные в § 11 настоящей главы.
6. Пластина — / < х < I с начальной и поверхностной температурами, рав-
равными нулю. При t > 0 количество тепла *), выделяемое в единицу времени,
*) Этот результат и соответствующие результаты для радиального потока (см.
соотношения (9.2) гл. VII и (8.14) гл. IX) представляют значительный интерес при
рассмотрении диффузии радиоактивных газов в геологических материалах [47].
§ 14] ГЛ. ITT. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В ТВЕРДОМ ТЕЛЕ 133
равно Ае~и* В данном случае
^ xA0 f
cos/(ty%)V*
^ 11 с„и
2-
4кД, X1 v ' *Ч ««
^..-r.,... • (Ш4>
ЛИТЕРАТУРА
1. Carslaw, Fourier's Series and Integrals, Macmillan, ed. 3, 1930.
2. Carslaw, Introduction to the Mathematical Theory of the Conduction of Heat in
Solids, Macmillan, ed. 2, 1921. (Г, Карслоу, Теория теплопроводности, Гостех-
издат, М., 1947.)
3. Whittaker, Watson, Modern Analysis, Cambridge, ed. 3, 1920. (Э. У и т т е-
к е р, Г. В а т с о н, Курс современного анализа, ПТИ, 1933.)
4. Anderson, Saddington, J. Chem. Soc, 381—386 A949).
5. Ingersoll, Koepp, Phys. Rev. 24, 92 A924).
6. Frazier, Phys. Rev. 39, 515 A932).
7. О 1 s о n, S с h u 11 z, Ind. Eng. Chem. 34, 874 A942).
8. M о 11 i s о n, Messeng. Math. 10, 170—174 A881).
9. Williamson, Adams, Phys. Rev. 14, 99 A919).
10. G u г n e y, L u г i e, Ind. Eng. Chem. 15, 1170 A923).
11. Austin, J. Appl. Phys. 3, 179 A932).
12. Weber, Ann. Phys. 146, 257 A872).
13. Electric Circuits, M. I. T. Staff, Wiley, 1943, p. 452.
14. Van Goreum, Appl. Sci. Res. A2, 272—280 A951).
15. V о d i с k a, Appl. Sci. Res. A5, 108—114 A955).
16. С a quot, С R. Acad. Sci. 222, 486—487 A946).
17. Шкловер, ДАН СССР 45, 106—110 A944).
18. Duf ton, Phil. Mag. 34, 376 A943).
19. Smith, J. Appl. Phys. 12, 638 A941).
20. M а с е у, Proc Phys. Soc. 54, 128 A942).
21. Brown, PhiL Mag. 37, 318—322 A946).
22. Clarke, Kingston, Aust J. Appl. Sci. 1, 172—188 A950).
23. Vernotte, С R. Acad. Sci. 204, 563 A937).
24. Newman, Trans. Am. Inst Chem. Engrs 30, 598 A934).
25. Jaeger, Clarke, PhiL Mag. 38, 504—515 A947).
26. Gurney, Lurie, Ind. Eng. Chem. 15, 1170 A923).
27. M с A d a m s, Heat Transmission, McGraw-Hill, ed. 2, 1942. (В. Мак-Адаме, Тепло-
Теплопередача, ОНТИ, 1936; перев. с 1-го изд.)
28. Grober, Z. Ver. dtsch. Ing. 69, 705 A925).
29. Grober, Erk, Grigull, Warmeubertragung, Springer, 1955.
30. Schack, Stahl u. Eisen 50, 1290 A930).
31. Fishenden, Saunders, Heat Transfer, Oxford, 1950.
32. Schack, Goldschmidt, Partridge, Industrial Heat Transfer, Wiley, 1933.
33. Newman, Ind. Eng. Chem. 28, 545 A936).
34. E de, Phil. Mag. 36, 845—891 A945).
35. H e i s 1 e r, Trans. ASME 69, 227—236 A947).
36. Jakob, Heat Transfer, Wiley, 1949, §§ 13—19. (M. Якоб, Вопросы теплопередачи,
ИЛ, 1960, перев. с изд. 1957 г.)
37. Newman, Trans. Am. Inst. Chem. Engrs 27, 202 A931).
38. Go 1 d s t e i n, Z. angew. Math. Mech. 12, 234 A932); 14, 158 A934).
39. Pose hi, Z. angew. Math. Mech. 12, 280 A932).
40. Nistler, Z. angew. Math. Mech. 17, 245 A937).
4L McKay, Proc Phys. Soc. 42, 547 A930).
42. Bachmann, Tafeln uber Abkuhlungsvorgange einfacher Кбгрег, Springer, 1938.
43. Newman,Green, Trans. Electrochem. Soc. 66, 345 A934).
44. J aege r, Proc. Camb. Phil. Soc. 41, 43 A945).
45. Nelson, Brit J. Appl. Phys. 3, 79—86 A952).
46. Russell, Alternating Currents, Cambridge, vol. I, p. 197, 1914.
47. Wasserburgin Nuclear Geology, ed. Faul, Wiley, 1954, § 9*5.
ГЛАВА IV
ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В СТЕРЖНЕ
§ 1. Введение
В настоящей главе мы рассмотрим задачи теплопроводности для стерж-
стержней с малым поперечным сечением. Стержень предполагается настолько тон-
тонким, что температуру во всех точках его поперечного сечения можно считать
одинаковой *). Эта задача сводится, таким образом, к задаче линейного
теплового потока, в которой температура определяется временем и расстоя-
расстоянием х, измеряемым вдоль стержня. Если теплообмен на поверхности стержня
отсутствует, то рассматриваемые здесь задачи становятся идентичными зада-
задачам, рассмотренным в гл. III. Существенно новая особенность задач данной
главы заключается в следующем: мы предполагаем, что каждый элемент
поверхности стержня отдает в результате теплообмена тепло в окружающую
среду. Во многих старых и в некоторых новых методах определения тепло-
теплопроводности используются экспериментальные устройства такого типа.
§ 2. Дифференциальное уравнение распределения температуры
в тонком стержне
Предположим, что стержень имеет постоянную площадь поперечного
сечения со, периметр сечения /?, коэффициент теплопроводности К, плотность
вещества р, удельную теплоемкость с, коэффициент температуропроводности х
и коэффициент теплообмена Н.
Предположим далее, что стержень расположен вдоль оси х, и рассмо-
рассмотрим элемент объема, ограниченный сечениями, проходящими через х и x-]-dx
перпендикулярно оси стержня.
Количество тепла, поступающее в этот элемент в единицу времени через
сечение, проходящее через точку х, равно
7, dv
Аналогичным образом количество тепла, уходящее в единицу времени
через сечение, проходящее через точку x-^-dx, равно
(-*?-*?*>--)-
*) Общий случай преимущественного распространения теплового потока в теле
в одном направлении, т. е. при небольших потерях в плоскостях, перпендикулярных
данному направлению, рассматривается в работе [1]. Оказывается, что среднее зна-
значение температуры вдоль плоскостей, перпендикулярных направлению потока,
с хорошим приближением удовлетворяет уравнению вида B.4) следующего параграфа.
§ 2] гл. iv. линейный тепловой поток в стержне 135
Следовательно, приращение количества тепла в элементе объема в еди-
единицу времени, обусловленное потоком тепла через оба сечения стержня,
равно *)
Количество тепла, теряемое в единицу времени вследствие теплообмена
боковой поверхности элемента объема со средой, равно
H(v — v0) p dx,
где v0 — температура среды.
Полный прирост количества тепла в единицу времени в элементе объема
равен
dv ,
шср -37- dx.
Таким образом,
i!L = -?i!?-_2^(v_v) B 1)
или
где
-??. = v и -? = х. B.3)
Срсо рС v 7
Если на боковой поверхности стержня теплообмен отсутствует, уравне-
уравнение теплопроводности принимает вид
dv d2v
и задачи распределения температур в стержне сводятся к задачам линейного
теплового потока, рассмотренным в гл. II и III.
При наличии теплообмена со средой, имеющей постоянную температуру,
последнюю можно принять за нуль, и тогда наше уравнение запишется сле-
следующим образом:
Используя подстановку**) (см. стр. 38)
v = ue~4t% B.5)
B.4) можно свести к виду
ди д2и /о я \
Таким образом, наша задача сводится к рассмотренной ранее задаче
линейного теплового потока.
/. Полу ограниченный стержень х > 0 с нулевой начальной температурой.
При t > 0 граница х = 0 поддерживается при постоянной температуре Vo.
Здесь функция и должна удовлетворять уравнению B.6), обращаться в нуль при t = О
и иметь значение Voevt при х = 0 и t > 0.
*) Здесь отбрасываются члены более высокого порядка относительно dx.
(Прим. ред.)
**) Здесь можно также использовать метод преобразования Лапласа, изложен-
изложенный в гл. XII.
136 ГЛ. IV. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В СТЕРЖНЕ [§ 3
Решение этой задачи приведено в § 5 гл. II (см. E.9)); оно имеет вид
Отсюда получаем окончательно
^К7] 1^^-[^ К7] B-7)
2. Ограниченный стержень — I < х < I с нулевой начальной температурой.
При t > О плоскости х = О и х = I поддерживаются при постоянной темпера-
температуре Ко. В данном случае функция и должна удовлетворять уравнению B.6), обра-
обращаться в нуль при t = О и иметь значения V^e*1 при х = ± /. Используя решение
этой задачи, приведенное в § 5 гл. III (см. E.6)), получим окончательно
(-ц-ежр ]-у*-*B»+1>2*2П cos <2*+/1>**
• , ¦ B.8)
ch/(v/x)V« те ^ Bп+\){\ + [Ы2/Bп + \JпЧ]}
Первый член представляет собой решение, соответствующее установившемуся
состоянию, которое будет получено непосредственно в § 5 настоящей главы.
Если материал стержня неоднороден или его теплопроводность является
функцией температуры, то ясно, что уравнение B.1) следует заменить урав-
уравнением
1 д (vdv\ Hp ,__ ... dv B9)
Если сечение стержня непостоянно, то со и р зависят от х, и анало-
аналогичным образом мы получим для стержня с постоянным коэффициентом
теплопроводности К соотношение
х \ дх ] рс ш v 0/ dt v '
§ 3. Полуограниченный стержень. Случай установившейся
температуры. Метод Форбса
Если в плоскости х = 0 полуограниченного стержня поддерживается
постоянная температура VQt то решение уравнения для установившегося
теплового потока
d2v л
xzf-w=0
принимает вид
l
Это решение можно использовать для стержня конечной длины / при
условии, что величина /(v/x)!/l велика. Если рассматриваются стержни из раз-
различных металлов с поверхностями, обработанными таким образом, что все
они будут иметь одинаковые значения v, то сравнение температур *) различ-
различных стержней позволит получить отношения их коэффициентов теплопро-
теплопроводности ¦¦). Подобные методы имеют тот недостаток, что они дают только
относительные значения коэффициентов теплопроводности; кроме того, трудно
обеспечить равенство значений v для различных стержней.
*) Если а — коэффициент линейного расширения, то при полном расширении
стержня aV0(x/v)^ мы получим другое уравнение для сравнения температур (см. [2]).
**) На этой идее основаны методы ряда авторов, описанные в книгах [3—5].
§ 4] ГЛ. IV. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В СТЕРЖНЕ 137
Классические опыты Форбса (см. [3], стр. 98, [4], стр. 454, [5], § 301.
[11, 48]) позволили создать интересный метод определения коэффициента
теплопроводности одиночного стержня. Пусть один конец полуограниченного
стержня поддерживается при постоянной температуре до тех пор, пока
тепловой поток в нем не установится. В этом случае количество тепла,
протекающее вдоль стержня в единицу времени через сечение, находящееся
на расстоянии х от нагреваемого конца, равно
—/Со)-^, C.2)
где со — площадь поперечного сечения стержня. Эта величина должна рав-
равняться всему количеству тепла, теряемому в единицу времени находящейся
справа за этим сечением частью стержня, т. е.
>ff(v)dx, C.3)
где р — периметр сечения стержня и f(v) — количество тепла, теряемое в еди-
единицу времени с поверхности стержня, имеющего температуру v. Форбс про-
провел две независимые серии экспериментов: в первой серии он численно
определял величину dv/dx в выражении C.2) из данных о температуре
в ряде точек вдоль стержня; во второй серии экспериментов он определял
величину pf(v) в выражении C.3), нагревая другой стержень, подобный
первому, до постоянной температуры и затем охлаждая его при тех же
условиях; при этом температура стержня измерялась в функции времени;
тогда можно найти численное значение
pf(v) = — copc-^-
как функцию от v. Это позволило оценить численную величину интеграла
в выражении C.3). Приравнивая выражения C.2) и C.3), можно получить
значение К. Следует отметить, что данный метод носит весьма общий
характер и в нем не предполагается, что К или v не зависят от v\ кроме
того, в этом методе не используется никакое частное решение уравнения
теплопроводности. Таким способом Форбс определил коэффициент теплопро-
теплопроводности железа в зависимости от температуры.
§ 4. Полуограниченный стержень. Периодически
изменяющаяся температура. Метод Ангстрема [5—10]
В предыдущем параграфе мы показали, как установившееся распреде-
распределение температур в длинном металлическом стержне малого поперечного
сечения можно использовать для определения коэффициента теплопроводности
вещества. Неустановившееся распределение также можно использовать для
этой цели, если температура одного из концов стержня периодически
меняется, что приводит к распространению по нему тепловых волн. Из на-
наблюдений над прохождением этих волн вычисляется коэффициент теплопро-
теплопроводности. Ангстрем впервые применил данный метод, и его работа исклю-
исключительно интересна как строгостью математических рассуждений, так и
новизной экспериментального метода. Позднее Хагстрем [12] рассмотрел ту же
задачу, предположив, что коэффициенты теплопроводности и теплообмена
зависят от температуры. Нейман и Вебер распространили этот метод на слу-
случай короткого стержня, темпеоатура обоих концов которого периодически
меняется (см. § 8 данной главы;.
138 ГЛ. IV. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В СТЕРЖНЕ [§ 4
Ангстрем проводил эксперименты на длинных стержнях малого попе-
поперечного сечения. Температура конца стержня х = О периодически менялась,
так как через равные промежутки времени его попеременно то нагревали
потоком пара, то охлаждали потоком холодной воды. По истечении доста-
достаточного времени температура в стержне становилась некоторой периодической
функцией от х и t, не зависящей от начального распределения температур.
Это периодическое распределение температур и исследовал Ангстрем. В экспе-
экспериментах Ангстрема учитывается, что стержень отдает тепло в среду с по-
постоянной, принимаемой за нуль температурой *).
Как и раньше, поперечное сечение стержня считается настолько малым,
что температуру по всему сечению можно принять равной температуре
в центре. Длина стержня должна быть достаточной для того, чтобы темпе-
температурные изменения, происходящие на конце л; = 0, полностью затухали,
не достигнув противоположного конца. Таким образом, при математической
трактовке задачи можно считать стержень полуограниченным.
Ищем периодическое решение уравнения B.4) данной главы в виде
v = V(x)ein*'.
После его подстановки в B.4) получим для V следующее уравнение:
d2V у + into v Q
Решение этого уравнения, стремящееся к нулю, когда лг-^оо, имеет вид
V = VQexp(-qnx — iq'nx), D.1)
где
следовательно,
Я» = {[* + (v»+ я»ш»УА]/2*}*, q'n = {[-
Таким образом,
со
2 qx q'x + z\ D.4)
я=0 "
представляет собой общее периодическое решение уравнения A.1) с перио-
периодом 2тс/о>.
В опытах Ангстрема период колебания температуры в стержне 2тс/о)
составлял 24 мин. По истечении достаточно большого промежутка времени
после начала эксперимента измеряли температуры в двух точках х1 и х2 и
полученные данные представляли гармоническими рядами
оо оо
2 &п cos (П(й* + Рл) и *2j Сп COS (nut-\-fn).
п-0 * п-0
Их почленное сравнение с D.4) дает
= е«*К В, — ч =lq D.5)
*) Если используется изолирующее кольцо, то эту поправку можно исключить.
§ 5] ГЛ. IV. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В СТЕРЖНЕ 139
где l = x2— xv Используя эти результаты в последнем из выражений D.3),
получаем
О)/2
D'6)
Таким образом, коэффициент теплопроводности определяется независимо
от коэффициента теплообмена. Изменяя характер поверхности стержня,
т. е. изменяя v, мы будем получать одинаковые значения для х. Ангстрем
производил такие изменения, и полученные им результаты совпали с резуль-
результатами его более ранних экспериментов.
Если х известно, то нетрудно найти v.
Пусть при л; = 0 температура равна 1 при гТ < t < (г Ч-у) Т и НУЛЮ
при [г-\--^\Т <^t <i{r-\-\)Tt где г = 0, 1, 2, ...; тогда установившаяся
температура в точке х в момент времени t определяется выражением
я=0
где qn и qn — величины, определенные выше, а о = 2тс/7\
Если при х = 0 температура определяется выражением
Ао -\- Al cos (Ы -\- е^,
то в D.4) остаются лишь первые два члена, и температурные колебания
распространяются со скоростью
2
Используя величину q'v определяемую D.3), получим
и*
и*
~ 4х Т2и2 '
Если и1 и и2 — скорости для периодов Т1 и Г2, то можно исключить v,
и мы получим
Кинг [13] использовал опыты Ангстрема, причем конец х = 0 прово-
проволоки он нагревал проволочной спиралью, по которой протекал ток, пропор-
пропорциональный sin-^-otf.
§ 5. Ограниченный стержень, концы которого находятся
при фиксированных температурах.
Случай установившейся температуры
Если поверхность тела не изолирована от среды, температура которой
равна нулю, то уравнение теплопроводности, выраженное через величины,
определенные B.3), имеет вид
dv __ К d2v Нр
dt ср дх2 срсо
Наблюдение за установившимся распределением температур в стержне,
концы которого поддерживаются при постоянных температурах Vx и V2,
140 ГЛ. IV. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В СТЕРЖНЕ [§ 5
представляет собой один из наиболее ранних методов получения значений
коэффициентов теплопроводности различных твердых тел.
Положив р,2 = ///7//Ссо, получим уравнения
4j 0 @ <*</).
v = Vx при лг = О,
z; = V2 при л: = /.
Тогда искомое решение запишется в виде
где
Таким образом,
Пусть в точках лгр х2 и лг3 температуры равны vv v2 и г>3 соответ-
соответственно, причем
Х% Х2 ==г *^2 *^1 ~^ ^"
Тогда
Отсюда
т. е. полученный результат не зависит от V1 и V2. Для двух стержней
с одинаковыми периметрами, поперечными сечениями и теплообменом на боко-
боковых поверхностях имеем
E.2)
Это дает метод для сравнения коэффициентов теплопроводности двух
веществ [5, 14].
В абсолютных измерениях коэффициента теплопроводности к одному
из концов стержня обычно подводят известное количество тепла с помощью
нагревательной спирали [15—18].
Из соотношения E.1) следует, что величина теплового потока FQ, посту-
поступающего в стержень через плоскость л; = 0, равна
fq—k* L^u0 апз • E-3)
Величина теплового потока Fv отдаваемого стержням через плоскость
= 1, равна
fil] Wi^M E.4)
]
Потеря тепла через боковую поверхность стержня между плоскостями
= 0 и х = 1 равна
^vd. E.5)
§ 6] ГЛ. IV. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В СТЕРЖНЕ 141
На практике jx обычно мало, и поэтому гиперболические функции в E.3),
E.4), E.5) можно представить в виде ряда и ограничиться первыми членами
этих рядов. В таком случае приближенно можно написать
Fo = «?- <уг - V2) +1 К^Ч BV, + V2) E.6)
Л) - Fi = i W (V, + V2)- E.7)
Подставляя в соотношение E.6) найденные в эксперименте Fo или V2,
получим /Си//. Обобщение уравнения E.6), в котором учитывается линей-
линейное изменение коэффициента теплопроводности с температурой, приводится
в работе [16]. Уравнением E.7) удобно пользоваться для введения поправок
на потерю тепла стержнем, например между нагревательной спиралью и
термопарой. Лис [15] рассчитал ряд таких поправок, необходимых в подоб-
подобных устройствах.
В отсутствие потока тепла через плоскость х = 1 мы получим вместо E.1)
выражение
равУ СПИ/-*)
1 chfx/
Тепловой поток, поступающий в стержень через плоскость х = О, равен
следующей величине:
Fo = — /Со) \4^т] = vJCuVi th [x/.
| их Jo
Таким образом,
Fl
к=- п
Это соотношение было использовано при определении К [19].
§ 6. Стержень переменного сечения с охлаждающимися ребрами.
Случай установившейся температуры
Дифференциальные уравнения, приведенные в § 2 настоящей главы,
имеют практическое применение в теории тонких ребер, прикрепленных
к поверхностям с целью повышения эффективности охлаждения последних
посредством теплообмена или вынужденной конвекции [20—28]. Во всех
случаях, рассматриваемых в данном параграфе, ребра считают настолько
тонкими, что температуру по всей толщине ребра можно принять постоянной;
соответствующие задачи для толстых ребер изложены в § 3 гл. V и в § 3
гл. VIII. Здесь мы рассмотрим только случай установившейся температуры.
Задачи с неустановившейся температурой можно решить либо непосред-
непосредственно, применяя преобразование Лапласа (см. гл. XII), либо используя
описанную выше подстановку (см. B.5) данной главы).
Вначале мы рассмотрим задачу, уже разобранную в предыдущем пара-
параграфе, а затем перейдем к другим случаям.
I. Прямоугольное ребро на плоской поверхности.
Возьмем плоскую поверхность, совпадающую с плоскостью д: = 0.
Рассмотрим ребро, ограниченное областью
— jD<z<±D, —сю<<у<оо, 0<х</.
142 ГЛ. IV. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В СТЕРЖНЕ [§ б
где D — толщина ребра (малая величина). Предположим, что плоскость х = 0
поддерживается при температуре V и имеет место теплообмен между поверх-
поверхностью ребра и средой с нулевой температурой. Тогда, воспользовавшись
обозначениями, принятыми в § 2 данной главы, мы получим, что участок
ребра единичной длины в направлении у имеет периметр*) р = 2 и площадь
o) = D. Таким образом, уравнение B.2) данной главы принимает вид
Jg--^ = O, 0<*</, F.1)
где
<*2=w- (б-2)
Это уравнение нужно решать при следующих граничных условиях:
v = V, x = 0 F.3)
Простое граничное условие F.4) означает, что теплообмен на конце
ребра пренебрежимо мал, что обычно выполняется достаточно строго; если же
это не так [29], то граничное условие F.4) следует заменить выражением
K^ + Hv = 0, x = L F.5)
которое выглядит более громоздким, но не вводит новых особенностей.
Решение уравнения F.1) с граничными условиями F.3) и F.4) имеет вид
ch
F6
С инженерной точки зрения наиболее интересной величиной является
«эффективность» ребра. Эта величина определяется как отношение коли-
количества тепла, теряемого поверхностью ребра в единицу времени, к количе-
количеству тепла, которое должно было бы теряться в единицу времени, если бы
ребро было удалено и площадь под его основанием отдавала тепло тем же
путем. Последняя величина равна HDV на единицу длины и, следовательно,
эффективность ребра можно записать в виде
С HVchy.(l — x)dx 2 . . /R7
J ЗПЙ = jDth ^ FJ)
HDV Пj
о
II. Сужающееся ребро на плоской поверхности.
Пусть стороны ребра сближаются на небольшой угол а, так что площадь участка
ребра единичной длины в направлении оси у при х = 0 равна D, а в точке х равна
D — 2ах. Тогда, пренебрегая членами, содержащими а2, мы получим для периметра
нашего участка /?, равное 2. В этом случае уравнение B.10) настоящей главы при-
принимает вид
- 0<x<l F-8)
и его надо решать с граничными условиями F.3) и F.4). Положив
F.9)
*) На самом деле /? = 2 + 2D, но, поскольку D <^ 1, мы можем считать, что
2. (Прим. ред.)
§ 6] гл. iv. линейный тепловой поток в стержне 143
мы получим уравнение F.8) в виде
'** F.10)
Общее решение уравнения F.10) представляет собой линейную комбинацию
модифицированных функций Бесселя *)
А10 [6 BН/К*2)Ц + Я/Со [S BЯ/*>2)Ч F.11)
Постоянные А и В находят из граничных условий F.3) и F.4):
° > F.12)
Л/, fa) — Я/С! fa) = 0, J 1 '
где
е0 = BHD/K*2L* и g, = [2Я (D — 2а1)/Ка2]Ч*. F.13)
Пешая уравнение F.12), получим окончательное решение F.11) в виде
лт 10[2Н(Р — 2ах)/К«2]1/>*
/о F0) /Ci (Si) + /Co (So) Л F0 ' К '
III. Тонкое кольцевое ребро постоянной толщины на цилиндре радиуса а.
Здесь плоскость ребра перпендикулярна оси цилиндра. Толщина ребра D
в направлении, параллельном оси цилиндра, мала. Пусть его внешний радиус равен Ь,
а тепловой поток с внешней поверхности пренебрежимо мал. Поскольку распростра-
распространение тепла происходит исключительно в радиальном направлении, мы можем исполь-
использовать дифференциальное уравнение B.10) данной главы, считая, что площадь участка
радиусом г равна w = 2nrD и его периметр равен /? = 4тиг. Тогда из B.10) следует
это уравнение нужно решать при граничных условиях
i/=K, г=я, F.16)
-5^ = 0, г = Л. F.17)
Общее решение уравнения F.15) имеет вид
v = Л/о ((хг) + В Ко (^г), F.18)
где
<Нтс5-Г- FЛ9)
Используя условия F.16) и F.17), определим А и В и в результате получим
v= V
/о ДО /С. О**) + /Со ((ia) /,
В этом случае эффективность ребра равна
IV. Тонкое кольцевое ребро переменной толщины на цилиндре радиуса а.
В случае линейно сужающегося ребра, рассмотренном в примере II, не суще-
существует решения, которое можно было бы выразить при помощи табулированных
функций. Простые решения можно найти при двух других законах изменения тол-
толщины по радиусу.
Если толщина z ребра изменяется обратно пропорционально радиусу, т. е.
* = ¦?-. F.22)
*) См. приложение 3. Выражения /q (z) — Ix (z\ Kq {z) = — K\ (z) исполь-
используются ниже.
144 ГЛ. IV. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В СТЕРЖНЕ [§ 7
то о) = 2тсг2г = 2nD и р = 4ъг, тогда уравнение B.10), приведенное в настоящей главе,
принимает вид
igl-^rt^O, a<r<b, F.23)
где р. определяется F.19). Общее решение уравнения F.23) записывается следующим
образом:
v = АгЧчЧш (j uA) + Brl'*Klu (у f"). F.24)
где А и В можно найти, как и прежде, из граничных условий F.16) и F.17).
Если толщина z ребра изменяется обратно пропорционально квадрату радиуса, т. е
*=-?-. F.25)
то o> = 2rcD/r и /?=4яг; тогда уравнение B.10) принимает вид
где fi определяется F.19). Решение уравнения F.26), которое удовлетворяет усло-
условиям F.16) и FЛ7), записывается следующим образом:
F.27)
§ 7. Ограниченный41) стержень при наличии теплообмена
на его поверхности. Случай неустановившейся температуры
Для стержня постоянного поперечного сечения дифференциальное уравнение B.2),
приведенное в данной главе, имеет вид
dv d2v ,_1Ч
-W = %-dxZ-*v' GЛ)
где х = /С/рс, * ss Нр/рсщ а температура среды v0, с которой происходит теплообмен,
равна нулю. Как и в § 2 этой главы, уравнение G.1) можно решить, заменив v на
ие~vt, где и должно удовлетворять уравнению
ди д2и ,7 оч
W-^lW' G'2)
Используя результаты, полученные в гл. III, приведем решения ряда инте-
интересных задач.
I. Ограниченный стержень 0 < х < I с начальной температурой f (x) и тем-
температурами концов 4\(f) и <р2 (t).
В этом случае уравнение G.2) следует решать при следующих условиях:
* = 0; " = *%(*), д: = 0; «»-*«?,(*), х = 1. G.3)
Используя соотношение E.2) гл. III, получим
2 X} Г ъп2ъ4 Л . ппх If-,,., ппх' . ,
v== 7 2л ехр L ?>J ~Г" I J f (x) sin ~Г~
л=1
t
ехр р^- + vl] [Ti (X) - (-1)" <р2 (X)]
G.4)
*) Полуограниченный стержень рассматривается в [30].
§ 7] ГЛ. IV. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В СТЕРЖНЕ 145
II. Ограниченный стержень 0<х<1 с начальной температурой f(х).
На плоскости х = 0 теплообмен отсутствует Температура в плоскости х = /
равна <р2 (О-
Используя соотношение E.3) гл. III и обозначая ря = Bл+1)те/2/, получим
Г
2 VI Г 2 1 Г I/ 9 ч 1
t/ == у ^ ехр [—V/ — f^yt\ cos ря* j *ря (—1)я / ехр [(хр^ + v) X] <Рг (X) <*Х +
я«о I о
f{x')QQs$nxdx'\. G.5)
- f
о
III. Ограниченный стержень 0<х<1 с начальной температурой f(x)
Теплообмен на концах отсутствует.
Из соотношения D.6) гл. III следует, что
v = у ехр (— v*) у / (д:') dx' +
О
оо
2 VI Г ъп2п4 "I ппх Г ., /ч ля*' . ,
Т 2л ехр ["" /*~1cos "Т" / ^ ** *cos ~7— *
1 6
IV. Ограниченный стержень — I < х < I с постоянной начальной темпера-
температурой, равной V. На боковой поверхности стержня и на его концах происходит
теплообмен со средой нулевой температуры.
Из соотношения A1.12) гл. III следует, что
1ки4
где ± ап (при я= 1, 2, ...) служат корнями уравнения
V. Ограниченный стержень 0 < х < I с начальной температурой, равной
f (x). На боковой поверхности стержня и на его концах происходит теплообмен
со средой нулевой температуры.
Используя соотношение (9.12) гл. III, получим
где
Хп ш* cos апх + — sin anx, G.9)
П
У G.10)
и ± ая (при /1=1, 2, •••) служат корнями уравнения
GЛ1)
Нейман [31] *) показал, что это решение можно использовать при определении зна-
значений термических коэффициентов. В его методе необходимо знать температуры v0
и vi при х = 0 и х — /.
*) См. также работу [32], в которой рассматривается соотношение между мето-
методом Ангстрема и двумя методами Неймана. Следует отметить, что методы, изложенные
в этом параграфе, позволяют совершенно не учитывать начальное распределение
температуры в стержне.
10 Г. Карслоу, Д. Егер
146 ГЛ. IV. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В СТЕРЖНЕ [§ 7
Из соотношения G.9) следует, что Хп = 1 при х = 0. Кроме того, в § 9 гл. III
мы показали, что Х2п = 1 при х = /; определим теперь знак Хп.
Используя G.9) и G.11), находим, что при х = 1
но
О < а, / < т. < а2/ < 2% < ...
Следовательно,
Хп = (—l)" при jc = /
Таким образом,
-^(*>o + *>z)=-V~Pl '+А&-*'+ ..., G.12)
1 , v
"P4f+ ..., G.13)
где
Поскольку р„ увеличивается с увеличением л, для достаточно больших зна-
значений t мы получим хорошее приближение, ограничиваясь только первым членом
в каждом из этих рядов. Тогда мы получим
y<*o + vz> = ^i«"Pl' G.14)
и
у (Ро ~ v/) = А2е " М* G-15)
В своих экспериментах Нейман сначала нагревал один конец стержня пламенем,
а затем давал ему охлаждаться за счет теплообмена. Спустя некоторое время он
начинал определять v0 ± vt через равные промежутки времени. Эти наблюдения
показали, когда температуры начинают следовать приведенному выше закону. Таким
способом находят постоянные Pi и р2 и получают два уравнения, из которых можно
определить коэффициенты теплопроводности и теплообмена. Однако так как в вели-
величины а{ и <х2 входит Л, эти расчеты следует производить путем последовательных
приближений и они оказываются довольно сложными.
В более простом методе измеряют температуры в средней точке стержня. Как
отмечалось в § 10 гл. Ill, alf а3, ... являются корнями уравнения
«tg-g-o/^Л, G.16)
а а2, а4, ... — корнями уравнения
«ctgya/ + A = 0. G.17)
Кроме того, при х= -^ I
Хп = sec у 1ап для нечетного п
и
X = 0 для четного п.
Таким образом,
v 1 = A^e~ l sec-тг-а.{1 Л-А$е~™ sec-77 <*з^-4- ... G.18)
?' 2 2
Итак, из соотношений G.14) и G.18) следует, что для больших значений времени
§ 81 гл. iv. линейный тепловой поток в стержне 147
Отсюда мы найдем ах; затем определим из G.16) и G.17) соответственно h и <х2-
Кроме того, из выражений
Pi =*«? + * И p2 = xa2 + v
определим % и v, после чего можно найти значения /Си//.
§ 8. Ограниченный стержень с периодически изменяющейся
температурой концов. Метод Неймана
В своей работе «О теплопроводности железа и нейзильбера» Вебер [33] описал
ряд экспериментов, проведенных им по методу, предложенному Нейманом в его лек-
лекциях. Идея этого метода та же, что и идея метода Ангстрема (см. § 4 настоящей
главы), но в данном случае периодически изменяют температуру обоих концов стержня.
Конец А стержня ЛВ поддерживается при температуре vu а конец В— при темпера-
температуре v2 в течение интервала времени 0 < t < Т. Затем, от момента t = Т до t = 2Tr
конец Л поддерживается при температуре t/2, а конец В — при температуре vx. Этот
процесс повторяется неограниченное число раз. Если такое периодическое изменение
температур продолжается достаточно долго, то влияние начального распределения
температур исчезнет и возникающее установившееся периодическое колебание темпера-
температуры можно исследовать методом, изложенным в § 6 гл. III.
Температура определяется из приведенного в предыдущем параграфе соотно-
соотношения G.4) при / (х) = 0 и условий
ср, (t) = vx при 2rT<t< Br + 1) Т,
<Pi(*) = i/2 при Br+l)T<t<Br + 2)Tt
t;2 при 2rT <t<Br+\)T,
1/, при Br+l)T<t<Br
где г равно нулю или любому положительному числу.
Назовем интервалы 2rT < t < Br -f-1) T четными периодами, а интервалы
Bг + 1) Т < t < Br-\-2) T — нечетными периодами. Затем, как и в § 6 гл. III, мы
покажем, что после достаточно длительных колебаний температуры поверхности темпе-
температура в момент U отсчитываемый от конца одного из четных периодов, равна
оо оо
4хтс VI п 2ппх 2хтс VI 2п-\-1 с. Bп-\-1) ъх
v ~~ /2 Vl 2 Za p2n i "• /2 l 2 Zu
оо
8хтс ,
е П /О t*
л = 1 l e
а в момент t, отсчитываемый от конца одного из нечетных периодов, равна
4*71 .VI л . 2ппх 2хтс ,Т1 2л + 1 ,
I ** P2n l l *~ P2n+l I
oo _ _ t
8 2nnx e 2n /a nv
sin—^ Гп-Г' (8*2>
P2n l \-\-e 2n
где
Эти выражения можно упростить при помощи рядов Фурье
оо
ГТ_ shy A-х) — sh [хл: to
^27 T (8*4)
/г=1
10*
148 ГЛ. IV. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В СТЕРЖНЕ [§ 9
2™ \У Bя+1) ,,_
b Sln
я=0
гДе Рп — величина, определяемая (8.3), a p.2 = v/x.
Таким образом, для четных периодов мы имеем
, " _p<tJ . (8-6)
/isl
и для нечетных периодов
\ i ...... . |Л
л=1
Из соотношений (8.6) и (8.7) следует, что температура vx^ в средней точке
стержня имеет следующее постоянное значение:
(8.8)
Chyfx/
Отсюда можно получить отношение v/%. Чтобы получить второе соотношение
между этими двумя неизвестными, нужно взять разность значений температур
в точках * = -?-/ и х=-^1 в любой момент времени. В этих точках члены ряда
(выражающего разность температур), в которых п кратно 2 или 3, пропадут, а остав-
оставшийся ряд настолько быстро сходится, что можно пренебречь членами, начиная
с п = 5. Таким образом, в принятом приближении разность температур в момент
времени t от начала одного из периодов равна
d = M — Ne-ptt (8.9)
где р = v -f- Dхте2//2), а М и N не зависят от t.
Пусть разности температур между этими точками в моменты tu t2t (tt -f- fJ),
(*2 + P) равны tf j, d2y d'v d'2 соответственно. Тогда
и, следовательно, можно найти р. Используя эту величину, а также значение v/%,
найденное из выражения (8.8), получим неизвестные v и х.
§ 9. Задачи по теплопроводности в движущемся стержне*)
Пусть стержень, имеющий постоянные площадь поперечного сечения о> и пери-
периметр /?, движется в направлении оси х со скоростью U. Предполагается также, что
происходит теплообмен стержня со средой, имеющей температуру v0, причем коэф-
коэффициент теплообмена равен Н.
Искомое дифференциальное уравнение можно получить, как и в § 2 настоящей
главы; однако в данном случае, как и в § 7 гл. I, следует добавить член, учитываю-
учитывающий теплообмен конвекцией, в виде •?—; тогда уравнение B.2) настоящей главы
примет вид
d2v U dv v(v — v0) I dv _ft n
*) Теплопроводность движущегося цилиндра конечного диаметра рассматривается
в § 11 гл. VII.
§ 10] гл. iv. линейный тепловой поток в стержне 149
где
х = А и v--2?. (9.2)
Ряд задач для движущихся тел, в которых встречается уравнение (9.1), будет
рассмотрен в § 2 гл. XV. Здесь мы рассмотрим случай установившейся температуры
и теплообмена со средой, имеющей нулевую температуру. В этом случае уравне-
уравнение (9.1) принимает вид
U Полу ограниченный стержень, движущийся в направлении его продольной
оси со скоростью U. Конец х = 0 поддерживается при постоянной темпера-
температуре vx. Решение, справедливое как для положительных, так и для отрицательных
значений U> имеет вид
t/= vx ехр | y—^- }— xy (9.4)
2. Полу ограниченный стержень, движущийся в направлении его продольной
оси со скоростью U. Плоскости х = 0 и х = 2/ поддерживаются при постоянных
температурах, равных соответственно vx и v2- Искомое решение имеет вид
г U B1 — х) 1 ., , Ux . с/о, ч
v2exp Цт- }- sh Ьс + v{ ехр -=— sh ZBl — x)
v- iir^ . (9.5)
где
2) + (Hp/»K)]l/*. (9.6)
Был проведен ряд экспериментов [34, 35] с ртутью, в которых она двигалась
с постоянной скоростью вдоль трубы, соединяющей два резервуара, поддерживаемые
при различных температурах *). Если vt — температура в средней точке х = / трубы,
то из (9.5) следует, что
2vt ch с/ = v2 ехр | — ~j-J + vx ехр -^. (9.7)
Если vx и v2 подобраны таким образом, что v\ = 0, то соотношение (9.7) принимает вид
%- ,-««*. (9.8)
Это уравнение не содержит ?, и из него можно прямо найти коэффициент темпе-
температуропроводности %.
§ 10. Уравнение теплопроводности для тонкой проволоки,
нагреваемой постоянным электрическим током
Распределение температур в тонкой проволоке, по которой течет постоян-
постоянный электрический ток, выведено Верде в 1872 г. [38]**). В течение неко-
некоторого времени подобный способ нагревания металла применялся мало,
несмотря на его очевидные преимущества. Во-первых, электрические измере-
измерения можно производить с такой точностью, что в эксперименте становится
возможным применять малые разности температур и устранять ошибки, вызы-
вызываемые зависимостью электропроводности и теплопроводности от температуры.
*) В работе [35] с помощью этого метода рассматривается эффект Томсона;
в нее также входит рассмотрение полного уравнения A0.4) данной главы. Неустано-
Неустановившееся состояние разобрано в работе Сомерса [36] и — более подробно — в работе
Оуэна [371; см. также § 2 гл. XV.
**) Для той же цели использовался и переменный ток. Можно назвать несколько
важных статей по этому вопросу [39—41]. Последняя из названных работ содержит
ценный список литературы; кроме того, в ней учитывается также изменение темпера-
температуры по сечению и по длине проволоки (см. также [42]).
150 ГЛ. IV. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В СТЕРЖНЕ [§ 10
Во-вторых, при рассмотрении отношения коэффициентов электро- и тепло-
теплопроводности (отношение Видемана — Франца [43]) очень желательно, чтобы
обе эти величины определялись в одном и том же эксперименте.
Выведем сначала уравнение теплопроводности и покажем, как можно
использовать установившееся и неустановившееся распределение температур
в такой проволоке для определения коэффициентов электропроводности и
теплопроводности металлов.
Предположим, как и в § 2 данной главы, что а> — площадь поперечного
сечения проволоки, р — периметр сечения и Н — коэффициент теплообмена.
Пусть / — ток, измеряемый в амперах*), а о — электропроводность прово-
проволоки. Тогда количество тепла, выделяемое на длине dx током /, будет равно
Где у = 0,239...—число калорий в джоуле. Этот член следует добавить
к правой части уравнения B.2) данной главы, и тогда уравнение теплопро-
теплопроводности примет вид
где
* = -?, v = ^-. A0.2)
Некоторые другие факторы, важные для экспериментальной работы,
можно принять в расчет без значительного усложнения математической теории.
1. Электрическое сопротивление проводника можно считать линейной функцией
температуры—это приближение справедливо для узких температурных интервалов.
Если а—температурный коэффициент изменения сопротивления, то мы должны
только заменить (у/2/рсо>2с) в уравнении A0.1) на
где а0 — электропроводность при нулевой температуре.
2. Тепло выделяется в результате эффекта Томсона, причем количество тепла
пропорционально току и градиенту температур; таким образом, к правой части урав-
уравнения A0.1) следует добавить член
Is dv
рсо> дх '
где s — коэффициент Томсона. Этот член учитывает направление тока и обращается
в нуль, если для нагревания проволоки пользуются переменным током. Коэффициент
Томсона зависит от температуры и может иметь любой знак. Обычно нагрев за счет
эффекта Томсона мал, и основное значение этого члена заключается в том, что раз-
различные методы измерения 5 основаны на дифференциальном уравнении A0.4).
3. Если стержень движется в направлении своей продольной оси со скоростью ?/,
как и в предыдущем параграфе, то к правой части уравнения A0.1) нужно добавить
член
дх
При этих обобщениях уравнение A0.1) принимает вид**)
dv ^ К дг%> (ц I 5/ I dv v(Hp aJP ) I Hpv° I jP . A0.4)
dt pc dx2 \ ' pco>) dx \ pco> pcoJa0 / ~ pco> ' pcaJc0 '
*) Здесь и далее тепловые величины измеряют в калориях и в единицах СГС,
а электрические величины — в практической системе единиц.
**) Применение этого уравнения для установившегося состояния при определении
эффекта Томсона изложено в [35, 44—47].
§ 11] ГЛ. IV. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В СТЕРЖНЕ 151
Это уравнение линейно относительно v и его можно представить в виде
где а, Ьу с, d — постоянные. Уравнения подобного вида встречаются во многих обла-
областях математической физики (ср. § 13 гл. I). Их всегда можно решить при помощи
простого видоизменения классических методов для случая b = с = d = 0 или при
помощи метода преобразования Лапласа, изложенного в гл. XII; преимущество по-
последнего заключается в том, что он позволяет «^рассматривать все случаи единооб-
единообразно. Если а, Ь, с и d — простые функции от х, то иногда можно найти точное
решение.
Рассмотрим, наконец, изменение теплопроводности с температурой. Для ограни-
ограниченной области температур можно считать справедливым линейный закон
/С = /^A + М. (Ю.6)
где р — температурный коэффициент теплопроводности (обычно он отрицателен).
В этом случае уравнение A0.4) принимает вид
Hp
pCQJc0
ю
Уравнение A0.7) не линейно относительно v и его исследовали только для случая
установившегося состояния, т. е. для dvfdt = 0. Если, кроме того, ?/ = 0, то с отсут-
отсутствует, и поэтому нет надобности рассматривать его изменение с температурой.
В следующем параграфе мы рассмотрим ряд способов определения коэффициента
теплопроводности с применением дифференциальных уравнений, приведенных в на-
настоящем параграфе. В § 14 данной главы будет рассмотрен случай неустановившегося
состояния.
§ 11. Установившаяся температура. Определение коэффициента
теплопроводности
I. Определение отношения коэффициентов электро- и теплопро-
теплопроводности методом Колърауша.
Кольрауш показал, как наблюдения над установившимся температурным
состоянием в нагреваемой электрическим током проволоке можно использо-
использовать для нахождения отношения коэффициентов электро- и теплопроводности
[41, 49—54].
Температуры на концах проволоки поддерживаются возможно более
близкими друг к другу. Предполагается, что поверхность непроницаема для
тепла и электрический ток / протекает в течение достаточного времени для
достижения установившейся температуры.
В этом случае уравнение теплопроводности принимает вид
Пусть и — электрический потенциал в сечении х.
Тогда
, du
I = 0H —: ,
dx
но
dv dv du
dx du dx
Следовательно,
d v 1 du
dx охГ du
152 ГЛ. IV. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В СТЕРЖНЕ [§ 11
и
d2v _ I2 d2v
dx2 o>2a2 "du2 #
Отсюда
Таким образом,
иг 1
>. A1.2)
где А и В — константы, определяемые из значений температур на концах.
Пусть (av vt), (а2, v2) и (#3, vz) — значения а и v в некоторых трех
сечениях xv х2, лг3 проволоки. Из соотношения A1.2) следует, что
2К
-у [vx (u2 — Uz) + v2 (аг — аг) + ^з (ui — «2>1 =
= («2 — из) (из —а\) (ui — и2>- С11 -3)
Если на концах проволоки поддерживаются одинаковые температуры,
то распределение температур в проволоке окажется симметричным относи-
относительно ее средней точки. Пусть точки хх и лг3 находятся на равных расстоя-
расстояниях от средней точки х2 по обе стороны от нее.
Тогда
Следовательно, из соотношения A1.3) получим
1С 1
р 2 1 2 * 2
Таким образом, мы получили простой метод определения отношения
коэффициентов теплопроводности и электропроводности (К/о). Для нахожде-
нахождения по этому методу значения К/о необходимо лишь измерить разности тем-
температур и потенциалов в двух точках проволоки, причем ток следует регу-
регулировать так, чтобы в ней сохранялось установившееся распределение
температур.
II. Метод Каллендера и аналогичные ему методы.
Рассмотрим участок проволоки 0 < х < 2/, концы которого поддержи-
поддерживаются при нулевой температуре, а весь участок окружен оболочкой, имею-
имеющей нулевую температуру. Проволока нагревается переменным током, и,
следовательно, в соотношении A0.4) данной главы член, содержащий dv/dx
и обусловленный эффектом Томсона, обращается в нуль. Тогда для случая
установившегося состояния соотношение A0.4) из предыдущего параграфа
принимает вид
= —А. A1.4)
U..-V
где
az = ak -p-. A1-5)
§11] ГЛ. IV. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В СТЕРЖНЕ 155
Уравнение A1.4) следует решать с граничными условиями v = 0 при
х = 0 и х = 21. Искомое решение имеет вид
v=^rkxBl — х), если а2 =
2
ch а1 (I — х) ) 9 /2 ^ п
сЬг1-)' если а* = -а' <0.
A1.6)
Этими методами проще всего точно измерить изменение электрического
сопротивления проволоки, вызываемое нагревом электрическим током. Если
о0 — электропроводность при температуре, равной нулю, то сопротивление
проволоки при этой температуре запишется в виде
Сопротивление проволоки при протекании тока / в установившихся
условиях равно 2/
R = -Lj(\+av)dx. A1.8)
о
Подставляя в это выражение значения v из A1.6), получим ([56, 57];
см. также § 2 гл. VII)
(i^L) если а*>0, A1.9)
A1.10)
A1.11)
В методе Каллендера [58] сила тока такова, что о2 = 0, т. е.
A1.12)
Отсюда следует, что в соотношении A0.4) предыдущего параграфа коэф-
коэффициент при v обращается в нуль, т. е. потери тепла с поверхности про-
проволоки в результате теплообмена в точности компенсируются увеличением
притока тепла, вызванного увеличением сопротивления проволоки с темпера-
температурой. При таких условиях К определяется из соотношения A1.10) по данным
об известных или измеримых величинах. Один из способов создания условий,
соответствующих A1.12), заключается в измерении температуры vt в средней
точке проволоки для случая, когда а2 < 0. В длинной проволоке температура
в разных точках центрального ее участка почти одинакова, т. е. величина
h2 пренебрежимо мала, и уравнение A1.4) можно записать в виде
?W <»л8>
Отсюда нетрудно найти величину Нр, и тогда значение / можно выбрать
таким, чтобы оно удовлетворяло A1.12).
Уравнения A1.9) и A1.11) справедливы для любых значений Я;
однако при использовании этих уравнений следует помнить, что Н и К за-
зависят от температуры. Зависимость Н от температуры описывается сложной
154 ГЛ. IV. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В СТЕРЖНЕ [§ 12
функцией *), и поэтому приведенными соотношениями практически можно поль-
пользоваться лишь тогда, когда температура проволоки мало отличается от темпе-
температуры окружающей среды **).
Изменение коэффициента теплопроводности с температурой можно иссле-
исследовать следующим образом [55]***): если уравнение A0.7) данной главы
используется при условии A1.12), то распределение температур в проволоке
записывается в виде
Решение этого уравнения, для которого v = 0 при л; = 0 и г/= 2/,
имеет вид
#о* A + у Р") = Jp* B/ — *)/2<А. A1.15)
Если vt — температура в средней точке проволоки, а
(ПЛ6)
представляет собой среднее значение коэффициента теплопроводности про-
проволоки для всей области температур от 0 до vv то из A1.15) получим
* = <11Л7>
§ 12. Сильно нагретая проволока, по которой протекает
электрический ток
Предположение о том, что обусловленная излучением потеря тепла проволокой в
окружающую среду пропорциональна разности температур, справедливо лишь для слу-
случая, когда эта разность мала: в противном случае следует считать, что потеря тепла
элементом проволоки длиной dx в результате излучения по закону черного тела равна
H'pi^—Ttydx, A2.1)
где Т — абсолютная температура проволоки, То — абсолютная температура окру-
окружающей среды и Н' — постоянная ****).
*) Потеря тепла за счет излучения в вакуум пропорциональна разности {у4— i/q),
и только приближенно ее можно принять пропорциональной v—v0 (подробнее см.
следующий параграф). Справедливость выражения вида H(v —t/0) для определения
потерь тепла через газовую оболочку, окружающую проволоку, рассмотрена Смо-
луховским (см. § 2 гл. VII).
**) Кнудсен [59] и Вебер [57] вывели формулу для случая существенного умень-
уменьшения Н путем помещения проволоки в высокий вакуум. Здесь можно исходить из
соотношения A1.9) и получить приближенную формулу путем разложения в ряд tgal.
***) Существует и другой метод подбора коэффициентов в этом уравнении,
обеспечивающий простой вид решения.
****) На самом деле, //' представляет собой произведение постоянной Стефана —
Больцмана и множителя, содержащего коэффициенты теплообмена проволоки и окру-
окружающей ее среды (см. (9.10) гл. I и [20]). Величина A2.1) представляет собой теоре-
теоретическую величину для излучения черного тела; лучшее приближение в случае нагре-
нагреваемой проволоки получается при использовании степенного закона того же вида,
(Тп— Г$), где п — постоянная, определяемая из эксперимента (см. [61, 62]). В послед-
последней из приведенных работ рассматривается изменение по степенному закону
электрического сопротивления и коэффициента теплообмена проволоки в зависимости
от температуры; в ней обсуждаются также различные случаи, возникающие на прак-
практике, например случаи длинных или коротких нитей накала. Первый интеграл урав-
уравнения A2.2), соответствующий A2.4), всегда можно найти, если электрическое сопро-
сопротивление и коэффициент теплопроводности проволоки изменяются с температурой по
степенному закону.
§ 121 гл. iv. линейный тепловой поток в стержне 155
Тогда в случае установившегося состояния соотношение A0.1) данной главы
следует заменить соотношением
Рассмотрим распределение температур в проволоке длиной 2/, на концах х = 0
и^ = 2/ которой поддерживается абсолютная температура То. Достаточно рассмотреть
область 0 < х < I при условии, что
Первый интеграл уравнения A2.2) записывается в виде
где С — постоянная,
JI2
2Н'р 2N'pTi 2JI
а=—гг- и Ь = __L + -——. A2.5)
Пусть Tt — температура в плоскости х = I. Тогда из A2.3) и A2.4) следует, что
Если Т = Т0 при лг = О, то из A2.4) получим
х =
J in Гг5_ т^__а^т_тМ1/2 *
Отсюда, положив х = /, находим неизвестную величину Тг
dT
'-/¦
A2.7)
Потеря тепла на концах проволоки равна
^^НП-ТЪ-Ь^-Т^. A2.8)
Оказывается, что решение этой простой задачи нельзя представить элементар-
элементарными функциями *).
Для полуограниченной проволоки х > 0, при jc->oo d2T/dx2->0. При этих усло-
условиях из уравнения A2.2) получаем, что Г->Гт, если
Ясно, что в случае длинной проволоки Тт является хорошим приближением для Г/.
*) Этот вопрос рассмотрен в работах [63, 64]. В работе [65] приведен график
интеграла A2.7). В работе [66] даны некоторые численные результаты, полученные
при помощи дифференциальных анализаторов; кроме того, в ней рассматривается
влияние электронной эмиссии и изменение коэффициента теплопроводности с темпе-
температурой. Этому же вопросу позднее была посвящена серия работ [67], в которых
авторы нашли решения уравнений A2.7) и A2.12) в виде рядов, рассмотрели зависи-
зависимость тепловых и электрических свойств от температуры и провели сравнение теоре-
теоретических данных с экспериментальными.
156 ГЛ. IV. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В СТЕРЖНЕ [§ 1$
При использовании этого приближения A2.8) принимает вид
A2.10)
Если То мало по сравнению с Тт, то приближенно получим
A2.11)
Используя выражение A2.9), можно переписать уравнение A2.2) в виде
i«)-a 02-12)
Приближенное решение для изменения температуры вблизи центра проволоки
может быть получено путем подстановки
Т' = Тт-Т, A2.13)
в результате которой уравнение A2.12) принимает вид
- Г'4}=0. (Ш4)
Если V мало, то членами, содержащими Г'2 и т. д., можно пренебречь, и это
уравнение примет вид
-gl-10*7^,7" = 0. A2.15)
Его решение, в котором используется величина Т\ при х = /, имеет вид *)
Г = Т\ ch {(/ -х) Tm (lOaTjb]. A2.16)
§ 13. Установившийся поток тепла в составной проволоке
Задачи по теплопроводности в составных проволоках представляют известный
интерес в связи с теорией термопар и приборов для измерения тока. Здесь мы рас-
рассмотрим только установившееся состояние; решения для неустановившегося состояния
легко получить, воспользовавшись преобразованием Лапласа (см. гл. XII).
Предположим, что участок проволоки 0 < х < а имеет коэффициент теплопро-
теплопроводности /ft, плотность рь удельную теплоемкость си коэффициент температуро-
температуропроводности %ь температуру vu коэффициент теплообмена Ни площадь поперечного
сечения <olf периметр сечения рь р\ = Н^/К^х и коэффициент электропроводности ale
Если в проволоке течет ток / а, то Pi = у/2/»^/^, где j — число калорий в 1 дж.
Соответствующие величины для участка проволоки а < х < b будут снабжены
индексом 2.
Если проволока имеет различные площади поперечного сечения в двух выбран-
выбранных нами участках, то в месте их соприкосновения мы не будем учитывать концевые
эффекты, и граничные условия запишутся в виде
vi = v2 A3.1)
Йg A3.2)
При наличии теплообмена между проволокой и средой, имеющей температуру vOf
искомые дифференциальные уравнения (как и A0.1) данной главы) имеют вид
d2vx
° < * < а-
*<х<Ь. A3.4)
Рассмотрим несколько типичных примеров.
*) Соотношения такого вида используются в работах [60, 67—70J.
§ 14] ГЛ. IV. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В СТЕРЖНЕ 157
/. Температуры в плоскостях х = 0 и х= b поддерживаются равными соот-
соответственно Vx и V2. Теплообмен со средой нулевой температуры. В проволоке
В р р 0 й 133
x 2 р у рур роке
отсутствует ток. В этом случае при р, = р2 = v0 = 0 решения уравнений A3.3)
и A3.4), которые принимают значения Vx и V2 при х = 0 и х = bt имеют вид
vx = Vx ch \lxx + Л sh fXjjc,
v2 « K2 ch fx2 (? — jc) + В sh fx2 F — at).
Граничные условия A3.1) и A3.2) позволяют определить А и В, и мы получим
окончательно
vx = -j- {^2^2К2 ch fi2 (b — л) sh \lx (a — x) + f*i»i#Ci sh ц2 (^ — a) ch \lx (a — jf)> +
^Ijcf A3.5)
где
A = fi2a>2 /C2 sh fx,a ch fx2 (^ — a) + fx,o>i /Ci ch \*.xa sh ?х2 (г> — а). A3.6)
Для i/2 получится аналогичное выражение. Температура в стыке х = а равна сле-
следующей величине:
4 {V>*i sh D (* — «)+ ^2^2(о2/<:2 sh |i,a}. A3.7)
2. Температура в плоскостях х = 0 и х=Ь поддерживается равной нулю.
Теплообмен со средой нулевой температуры. По проволоке тенет ток I. Темпе-
Температура в стыке х = а равна
sh pxa [ch jx2 (b — a) — 1] + p,#Ci»if*2 sh ?x2 (* — a) [ch ji,a — 1]}, A3.8)
где А — величина, определяемая A3.6).
5. Температура в плоскости х = 0 поддерживается равной V,. Тепловой
поток через плоскость х=Ь отсутствует. Ток в проволоке отсутствует.
Теплообмен со средой нулевой температуры. В данном случае
„ — Kx«>xpxVxchtL2(b — x) Q
V2 = дТ • AЛУ)
где
ch p., a ch fx2 (b — a) -\- /C2(o2 fx2 sh fi,a sh fx2 (b — a). A3.10)
4. Температура в плоскости х = 0 поддерживается равной нулю. Тепловой
поток через плоскость х = b отсутствует. По проволоке течет ток I. Тепло-
Теплообмен со средой нулевой температуры. В данном случае
t;2^^+ l 1{?m ^chM—1^ Ch^(^4 A3.11)
где А' — величина, определяемая A3.10).
§ 14. Неустановившаяся температура в проволоке,
по которой течет электрический ток
Наблюдения над неустановившимся температурным полем в проволоке, по
которой течет постоянный электрический ток, при наличии теплообмена на ее по-
поверхности также использовались для определения тепловых и электрических кон-
констант. Ниже приведено исследование, посвященное этому вопросу [41, 71—73].
Мы нашли уравнение теплопроводности A0.1) в виде
dv d2v .
где
Ср Срсо
158 ГЛ. IV. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В СТЕРЖНЕ [$ 14
Пусть температура среды, в которую происходит теплообмен, равна нулю,
а начальные и граничные условия имеют вид
v = О при t = О @ < х < /)
и
v = 0 при л; = 0 и х = 1.
Чтобы проинтегрировать уравнение теплопроводности, мы, как обычно,
сведем задачу к решению двух задач: задачи для установившейся температуры
и задачи для неустановившейся температуры.
Пусть
v = u-\-wt
где и — функция, не зависящая от времени и удовлетворяющая уравнениям
и = 0 при х—0 и х = /,
a w — функция х и t, удовлетворяющая уравнениям
dw d2w
: X -
^ —Л ад:2
<до = 0 при х = 0 и х = 1,
w = — и при ? = 0.
Выражение для и получается сразу в виде
и —-— и I 1 —"~" ———^^^^——————— I у A4» 1)
L sh {л/ J v 7
где
— и д = — .
Эту функцию можно разложить в ряд по синусам
оо
. Bп—1)пх
При таком значении « сразу же получается решение уравнения для w
в виде
X ехр Г— vt — t П~72 ^ I • A4.2)
Отсюда
sh
2-|
J- A4.3)
Исследуя это решение, мы замечаем, что коэффициенты членов ряда
для w быстро уменьшаются и при х = 1/3 или 2//3 второй член этого ряда
равен нулю. Следовательно, с хорошим приближением значение v в этих
§ 15] ГЛ. IV. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В СТЕРЖНЕ 159
точках определяется соотношением
Г3 -expf-vf —*^]. A4.4)
3 v
Пусть vv v2, v3 — температуры в точке x = -gl в моменты времени tv
t-\-~> t-\-2x. Тогда из A4.4) получим
A4.5)
. A4.6)
Значение установившейся температуры г;4 в средней точке проволоки
равно
() A4.7)
Из соотношения A4.5) определим величину (v -}- kiz2/P). Подставляя эту
величину в A4.6), найдем [л, а затем из A4.7) — величину Ъ. Используя
найденные результаты при определении а, Ъ и jjl, найдем значения х, v и а.
В исходных опытах Странео проволоку вначале нагревали током до тех пор,
пока в ней не достигалось установившееся распределение температур. Если
затем ток выключали в момент t = 0, то температура определялась соот-
соотношением
4* у/V
i sin
Г
ехР[
()[() + V]
n-\
Метод определения ос, v и а, описанный выше и приводивший нас
к соотношениям A4.5), A4.6) и A4.7), остается по-прежнему применимым.
Этими результатами можно пользоваться только в тех случаях, когда темпера-
температура проволоки незначительно превышает температуру окружающей среды. При
высоких температурах проволоки, когда ее тепловые потери определяются излучением
по закону четвертых степеней *), уравнение теплопроводности при неустановившемся
состоянии, соответствующее уравнению A2.12) данной главы, принимает вид
где Т—абсолютная температура проволоки, Тт и а определяются A2.5) и A2.9)
данной главы. Можно отметить следующий простой результат: в центре длинной
и Т
проволоки, где -^—^ пренебрежимо мало, в случае включения тока при t = 0 и при
начальной температуре, равной 7*0, температура Т в момент времени t определяется
соотношением
§ 15. Кольцо Фурье
Одной из наиболее простых и показательных задач теплопроводности, в которых
температура зависит только от одной координаты и от времени, является задача
Фурье для кольца. Эта задача особенно интересна еще и потому, что к ней Фурье
*) Недавно было проведено детальное рассмотрение данного вопроса. Обсуждался
также вопрос о запаздывании наступления установившегося состояния [67, 77]. *
160 ГЛ. TV. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В СТЕРЖНЕ [§ 15
впервые применил свою математическую теорию и для нее результаты математических
исследований были сравнены с данными эксперимента [75].
Кольцо представляет собой тело малого поперечного сечения, согнутое по
окружности (или по другой замкнутой кривой). Используя обозначения и предположе-
предположения, принятые в § 2 настоящей главы, мы видим, что дифференциальное уравнение
температурного поля в кольце имеет вид уравнения B.4), а именно:
dv d*v /1K1
—™- A5Л)
Пусть длина окружности кольца равна 21; тогда, выбрав начало координат
в некоторой подходящей точке, мы можем решать уравнение A5.1) в области
— / -< х •< /. Поскольку кольцо образует замкнутую кривую, мы не имеем граничных
условий при х = ± /, но зато v должно быть периодической функцией х с пери-
периодом 2/, т. е.
v (лг, 0 = v (х + 2л/, *). л = 1, 2,... A5.2)
I. Начальная температура f (х). Теплообмен отсутствует.
Предположим, что / (х) можно разложить в ряд Фурье
^l;^ A5.3)
л=0 я=1
Тогда
Г ъп2п4~\ пъх .V*. Г ъпЧЧ! . mix
n ехр L ~\cos ~—*" 2d n exp L—^~Js ~г
л=0 я=1
удовлетворяет всем условиям задачи. Это можно доказать так же, как и в § 3 гл. III *).
Решение для случая теплообмена легко получить путем подстановки v = ие ~*'
в уравнение A5.1).
II. Установившаяся температура; плоскости х = ± / поддерживаются при
температуре V.
В этом случае распределение температур должно быть четной функцией х,
которая при х = ± / принимает значение V и удовлетворяет уравнению A5.1)
при -? = 0.
Тогда решение имеет следующий вид:
где
f*2 = ^- A5.6)
Это выражение можно использовать для сравнения коэффициентов теплопро-
теплопроводности [75] двух твердых тел при помощи метода, аналогичного методу, приведен-
приведенному в § 5 данной главы.
III. Кольцо с установившейся температурой, определяемой A5.5), охлаждаю-
охлаждающееся в результате теплообмена со средой нулевой температуры.
Положив в уравнении A5.1) v = ue~**, будем искать решение уравнения
в виде периодической функции с периодом 2/ и следующим начальным значением:
*) Можно также доказать, что в этом случае v и dv/dx непрерывны при jc= ±1
для t > 0, поскольку кольцо замкнуто. При t = 0 они могут не быть непрерывными.
ГЛ. IV. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В СТЕРЖНЕ 161
Используя соотношение A5.4), находим решение в виде
t/ =
l n=l
Соотношение A5.9) можно использовать для определения х и v из данных о темпе-
температуре при х = 0 и х = 1 [31, 76].
ЛИТЕРАТУРА
1. Fox, Phil. Mag. 18, 209—227 A934).
2. Todd, J. Sci. Instr. 4, 97 A927).
3. Poynting, Thomson. Text-book of Physics, Heat, ed. 6.
4. Winkelmann, Handbuch der Physik, 2. Aufl., Bd. III.
5. Preston, Theory of Heat, ed. 3.
6. Ann. Physik, Lpz., 114, 513 A861).
7. Ann. Physik, Lpz., 123, 628 A864).
8. PhiL Mag. 25, 130 A863).
9. Phil. Mag. 26, 161 A863).
10. В о s a n q u e t, A r i s, Brit. J. AppL 5, 252—255 A954).
H. Griffiths, Proc. Phys. Soc. 41, 151 A928).
12. Hagstrom, Ofvers. Vetensk. Akad. Forh., Stockh. 48, 45, 289, 381 A891).
13. Ki n g, Phys. Rev. 6, 437 A915).
14. J а к о b, E r k, Z. Phys. 35, 670 A926).
15. Lees, Phil. Trans. Roy. Soc. A208, 381 A908).
16. К a n n u 1 u i k, L a b y, Proc. Roy. Soc. A121, 640 A928).
17. В г i d g m a n, Proc. Am. Acad. Arts. Sci. 57, 80 A922).
18. В a r r a 11, W i n t e r, Phil. Mag. 49, 313 A925).
19. Barratt, Proc. Phys. Soc. 26, 347 A914).
20. McAdams, Heat Transmission, McGraw-Hill, ed. 2. (В. М а к - А д а м с, Тепло-
Теплопередача, ОНТИ, 1936, перев. с 1-го изд.)
21. Jakob, Heat Transfer, Wiley, 1949. (M. Якоб, Вопросы теплопередачи, ИЛ,
1960, перев. с изд. 1957 г.)
22. Н а г р е г, В г о w n, NACA Rep. No. 158 A922).
23. В i n n i e, Phil. Mag. 2, 449 A926).
24. S с h m i d t, Z. Ver. dtsch. Ing. 70, 885, 947 A926).
25. Buec h e, S с h a u, Arch. Warmew. 17, 67 A936).
26. Gardner, Trans. ASME 67, 621 A945).
27. J a k о b, Trans. ASME 67, 629 A945).
28. Miles, J. Appl. Phys. 23, 372 A952).
29. J a k о b, Phil. Mag. 28, 571 A939).
30. Lo w a n, Quart. Appl. Math. 4, 84—87 A946).
31. Neumann, Ann. Chim. Phys. 66, 183 A862).
32. Glage, Ann. Physik D), 18, 904—940 A905).
33. Weber, Ann. Physik 146, 257 A872).
34. N e 111 e t о n, Proc. Phys. Soc. 22, 278 A910).
35. N e 111 e t о n, Proc. Phys. Soc. 25, 44 A912).
36. Somers, Proc. Phys. Soc. 25, 74 A912).
37. Owen, Proc. Lond. Math. Soc. 23, 238 A925).
38. Verdet, Theorie mecanique de la chaleur, T. II, p. 197, 1872.
39. С г a n z, Z. Math. Phys. 34, 92 A889).
40. E b e 1 i n g, Ann. Physik 27, 391 A908).
41. Weinreich, Z. Math. Phys. 63, 1 A915).
42. Fischer, Z. tech. Phys. 19, 25 A938).
43. Ann. Physik 89, 497 A853).
44. Net t let on, Proc. Phys. Soc. 29, 50 A916).
45. К i n g, Proc. Am. Acad. Arts Sci. 33, 353 A898).
46. Laws, Phil. Mag. 7, 560 A904).
47. Berg, Ann. Physik 32, 477 A910).
48. Forbes, Trans. Roy. Soc. Edin. 23, 133 A864).
49. К о h 1 г a u s с h, S. B. preuss. Akad. Wiss. 714 A899).
50. Kohlrausch, Ann. Physik 1, 132 A900).
51. С z e г m a k, S. B. Akad. Wiss. Wien 103, 1107 A894).
11 i, Карсло>, Д. Ьгер
162 ГЛ. IV. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В СТЕРЖНЕ
52. Duncan, Pap. Dep. Phys. McGill Univ., No. 11 A900).
53. Jaeger, Diesselhorst, Wiss. Abh. phys.-tech. Reichsanst. 3, 269 A900).
54. Meissner, Ann. Physik 47, 1001 A915).
55. O'Day, Phys. Rev. 23, 245 A924).
56. Kannuluik, Proc. Roy. Soc. A131, 320 A931).
57. Weber, Ann. Physik 54, 165 A917).
58. Encyclopaedia Britannica, 11th ed.
59. Knudsen, Ann. Physik 34, 593 A911).
60. Worthing, Phys. Rev. 4, 523 A914).
61. Langmuir, Phys. Rev. 7, 151 A916).
62. L a n g m u i г, Т а у 1 о г, Phys. Rev. 50, 68 A936).
63. Cox, Phys. Rev. 64, 241 A943).
64. В а е г w a 1 d, Phil. Mag. 21, 641 A936).
65. Nagai, J. Phys. Soc. Japan 11, 329—330 A956).
66. В u s h, G о u 1 d, Phys. Rev. 29, 337 A927).
67. Jain, Kris hn an, Proc. Roy. Soc. A222, 167—180 A954); A225, 1—32 A954);
A227, 141—154 A955); A229, 439—445 A955).
68. W о г t h i n g, J. Franklin Inst. 194, 597 A922).
69. Stead, J. Instn. Elect Engrs. 58, 107 A920).
70. P г e s с о 11, H i n с k e, Phys. Rev. 31, 130 A928).
71. S t г a neo, R. С Accad. Lincei 7, Sem. ii A898).
72. Schaufelberger, Ann. Physik 7, 589 A902).
73. F i s с h e r, Z. tech. Phys. 19, 105 A938).
74. W i n t e г g e г; s t, Z. angew. Phys. 2, 167 A950).
75. Fourier, Theorie analytique de la chaleur, Chaps. II et IV.
76. Neumann, Phil. Mag. 25, 63 A863).
ГЛАВА V
ПОТОК ТЕПЛА В ТЕЛЕ С ПРЯМОУГОЛЬНЫМ СЕЧЕНИЕМ
§ 1. Введение
В последних трех главах мы изучали различные задачи с линейным теп-
тепловым потоком. В этих случаях температура зависела только от времени и
от одной геометрической координаты. Подобные задачи можно назвать одно-
одномерными. Перейдем теперь к рассмотрению случаев, в которых вектор тепло-
теплового потока в каждой точке *) параллелен плоскости ху\ тогда при устано-
установившейся температуре последняя будет зависеть только от х и у, а в случае
неустановившейся — от х, у и t. Такие задачи мы будем называть дву-
двумерными.
Первой задачей теплопроводности, детально разобранной Фурье, была
задача об установившемся распределении температур в бесконечном твердом
теле, ограниченном плоскостями х = ± -к- те, у = О, и бесконечно прости-
простирающемся в положительном направлении оси у. Граничные поверхности
лг=±-о*тс поддерживаются при температуре, равной нулю, а основание
у = 0 — при температуре, равной единице. При изучении этой задачи Фурье
предложил разложить единицу в интервале —-^ тс < х <утс в РЯД**)
— \ cos х — у cos Зл: + у cos 5л: — ... \,
а затем рассмотрел вопрос о разложении производной функции в тригоно-
тригонометрический ряд и получил выражение, известное теперь как ряд Фурье.
Таким образом, он смог найти распределение температур в твердом теле,
основание которого поддерживается при температуре v = f(x), где /(л:)—про-
/(л:)—произвольная функция дг, а плоскости х= ±-~ те поддерживаются, как и раньше,
при нулевой температуре.
*) Здесь автор рассматривает распространение тепла в телах, неограниченных
в направлении, перпендикулярном плоскости ху. (Прим. ред.)
**) Ряд — I cos х —5" cos &* + "с"cos &х — • • •) Для Функции / (jc) можно полу-
получить обычным путем, как ряд по косинусам, если
!!¦
164 ГЛ. V. ПОТОК ТЕПЛА В ТЕЛЕ С ПРЯМОУГОЛЬНЫМ СЕЧЕНИЕМ [§ 2
§ 2. Неограниченное твердое тело прямоугольного сечения.
Установившаяся температура
Вместо того чтобы брать задачу Фурье в том виде, в каком он ее ре-
решает, рассмотрим твердое тело, ограниченное плоскостями л; = 0 и х = 1,
которые поддерживаются при нулевой температуре, и плоскостью у = 0,
которая поддерживается при температуре v = f(x). Предположим, что
функция f(x) ограничена и удовлетворяет условиям Дирихле в интервале
(О, /Mil-
Уравнения теплопроводности в этом случае имеют вид
U | = 0> 0<*<Z; у>0. B.1)
при л; = 0, х = 1, B.2)
при у = 0, 0<л;</. B.3)
Кроме того,
lim ^ = 0.
у-»оо
Начиная с разложения f(x) в ряд по синусам
B.4)
где
B.5)
рассмотрим функцию v, определяемую уравнением
Так как f(x) — ограниченная функция, интегрируемая в интервале @,/),
то из B.5) следует, что
\ап\ < 2/1, когда |/(*)| < М в интервале @, I).
Кроме того,
[^]||^] при у>уо>О.
где у0—произвольное положительное число.
Ряд
сходится, и его члены не зависят от л: и у.
Таким образом, ряд B.6), рассматриваемый как функция х, равномерно
сходится в любом интервале х, когда у > 0. Если же его рассматривать
как функцию у, то он равномерно сходится при у >. у0 > 0.
В этих интервалах сходятся также ряды, получаемые из ряда B.6) по-
почленным дифференцированием по х и у.
§ 2]
ГЛ. V. ПОТОК ТЕПЛА В ТЕЛЕ С ПРЯМОУГОЛЬНЫМ СЕЧЕНИЕМ
165
Таким образом,
Следовательно,
d2v
дх2
d2v
ду2
тс2 ^
I2 л
п
оо
I2 ^^
d2v
дх2
оо
1 = 1
- +
2апе-™У!1 sin п
d2v Q
ду2
и ряд B.6) удовлетворяет дифференциальному уравнению B.1). Кроме того,
он удовлетворяет граничным условиям на плоскостях х = О и лг = /. Дей-
Действительно, ряд B.6) равномерно сходится в интервале 0 <;.*<;/ и его
сумма равна нулю, когда л; = 0 и х = 1; поэтому при положительном у
предел v при х, стремящемся к этим значениям, равен нулю.
Мы предположили, что функция f(x) ограничена и удовлетворяет усло-
условиям Дирихле в * нтервале @, /). Отсюда следует, что ряд B.4) сходится
и его сумма равна f(x) в каждой точке между 0 и /, в которой f(x) не-
непрерывна, и у {/(jc + 0) + / (jc — 0)} во всех других точках. Из рассуж-
рассуждений, изложенных в § 73 книги Карслоу [1], следует, что если v опреде-
определяется рядом B.6), то lim v = f(x) в тех точках, где функция f (х) непре-
у->0
рывна, и равен 2-{/(a: + 0) + /(jc — 0)} во всех других точках.
Таким образом, ряд B.6) служит решением нашей задачи; его можно
записать в виде
B.7)
поскольку ряд под интегралом равномерно сходится.
Если / (х) равно единице, то решение B.6) принимает вид
2 V
1 — cos /гтс
т. е.
Г Bп+1)тсу-|
sin
ехр |^-
B/г +
1)
/гтсу
/
ъх
-lsin
птсл:
/
4 т | Г тс (у — ix) I , 1 Г
:-Im|exp[- ^? ^j+7exp[-
Зтс (у — /jc)
In
[тс/ (х -4- /у) ]
— I \ .
= - lm{ In
1С
B.8)
B.9)
B.10)
•BЛ1)
1166 ГЛ. V. ПОТОК ТЕПЛА В ТЕЛЕ С ПРЯМОУГОЛЬНЫМ СЕЧЕНИЕМ [§ 2
Сопряженная гармоническая функция *) с B.11), т. е. действительная часть лога-
логарифма в B.10), имеет вид
Ць
, /chm + cos[-=?
-lln(
Отсюда следует, что линии тока определяются уравнением
ch(*;
ch(«;
они ортогональны изотермам [2]
ch (ny/l) +cos (пх/1) __
ch (ny/l) — cos (**//) " consi'
sh
¦ const.
Соответствующая задача, но при наличии теплообмена с одной или с двух поверх-
поверхностей х = 0 и х = / рассматривается, как и в § 3 настоящей главы.
Рассмотрим теперь задачу об установившейся температуре в теле с сечением
ш виде полосы 0 < л: < /, у > 0 и с граничными условиями
v = f(y), x = 0, у>0, B.13)
t/ = 0, jc=/, y>0, B.14)
t/ = 0, 0 < х < U у = 0. B.15)
Здесь мы используем интеграл Фурье C.8), приведенный в гл. II, вместо ряда
по синусам, который был использован выше. Отметим, что при любом 5 функция
(удовлетворяет дифференциальному уравнению B.1) и граничным условиям B.14)
¦ <2Л!>-
Таким образом, интеграл
оо
j sin $y sh 5 (/ — х) F (?) dl, B.16)
о
где F (S) — произвольная функция, также удовлетворяет этим условиям. Если, кроме
того, B.16) удовлетворяет B.13), то мы получим
оо
f(y) = § sin Ъу sh UF (I) dl
о
Отсюда, используя C.9) гл. II, находим
sh «/><?) = |
6
Подставляя это значение F (?) в B.16), получим решение нашей задачи в виде
оо оо
v - I/" sin су *h*?yX) d\ f f (У) sin ly'dy'. B.17)
6 6
*) Определение и свойства сопряженных гармонических функций см. §§ б—9 гл. XVI.
Символ Im принят для обозначения мнимой части соответствующего выражения.
3] ГЛ. V. ПОТОК ТЕПЛА В ТЕЛЕ С ПРЯМОУГОЛЬНЫМ СЕЧЕНИЕМ 167
Если мы предположим, что можно изменить порядок интегрирования, то
(/)dy' f Sh^lyX) SinЬ Sin*y' dl
О 6
1 . пх Г ,
6
т. е.
cos [«(/ - x)/l] + ch [« (y -f y')/l] \ dy'- BЛ8)
Ясно, что задачи при наличии теплообмена на поверхностях у = 0 или х = I
можно рассматривать тем же способом (ср. следующий параграф). Однако приве-
приведенный выше анализ, из которого следует соотношение B.18), нужно считать фор-
формальным и не вполне безупречным; не только изменение порядка интегрирования
© B.17), но и применение C.8) гл. II налагает жесткие ограничения на функцию /(у).
На самом деле они не необходимы, и более детальное рассмотрение [3] показывает,
что B.18) справедливо при условии, что / (у) является функцией экспоненциального
вида, т. е. | / (у) \ < Кес' у ', где Кис — положительные постоянные.
Два других важных результата можно формально вывести аналогичным образом,
«спользуя интеграл Фурье.
Рассмотрим тело с сечением в виде неограниченной полосы О < х < /,
— оо < у < оо; граничные поверхности х = 0 и х = / поддерживаются при тем-
температурах f (x) и нуль соответственно. Тогда установившаяся температура равна
2/ sln I J
cos[*(l-x)/l]+cb[n(y-y')/l}
Для случая, когда сечение тела имеет вид полуплоскости *) х > О,
— оо < у < оо, а граничная поверхность х = 0 поддерживается при темпера-
температуре f (у), установившаяся температура равна
^^ B-2°)
§ 3. Установившаяся температура в неограниченном теле
прямоугольного сечения 0<JC<a,
Здесь требуется найти решение следующего дифференциального урав-
уравнения:
-^+-^ = 0, 0<*<а, 0<у<*, C.1)
причем граничные условия зависят от рассматриваемой задачи.
I. Граничная поверхность у = 0 поддерживается при темпера-
температуре f(x), другие поверхности — при нулевой температуре.
В данном случае граничные условия запишутся следующим образом:
v = f(x), y = 0. 0<*<а, C.2)
v = 0, x = a, 0<y<b. C.5)
*) Установившаяся температура в полуплоскости ;с>0, — оо<<у<оо ив чет-
четверть плоскости х > 0, у > 0 рассматривается в [4].
168 ГЛ. V. ПОТОК ТЕПЛА В ТЕЛЕ С ПРЯМОУГОЛЬНЫМ СЕЧЕНИЕМ [§ 3
Как и в предыдущем параграфе, запишем f(x) в виде ряда по синусам
C.6>
оо
/1=1
где
а
j f{x')sxn^fdx'. C.7)
О
Теперь для любого п член вида
h (»->>** C.8)
удовлетворяет соотношениям C.1), C.3), C.4) и C.5). Таким образом, нам
нужно рассмотреть выражение
Sl" (^^/Д) sh К* У) **/*] /о ov
sh
я=1
где ал определяется C.7). Доказательство того, что C.9) удовлетворяет
v3.1)—C.5), можно провести точно так же, как и в предыдущем параграфе*)»
Если f(x) равно постоянной величине V, то C.9) примет вид
sin lBn + 1) пх/а] sh [(b - у) Bя + 1) ж/а] п ш
^ тс
Если некоторые другие граничные поверхности тела прямоугольного се-
сечения также поддерживаются при заданной температуре, то решение можно
получить путем комбинации решений вида C.9).
II. Граничная поверхность у = 0 поддерживается при темпера-
температуре f(x). Тепловой поток через поверхности у = Ь и лг = О отсут-
отсутствует. На поверхности х = а происходит теплообмен со средой ну-
нулевой температуры.
В данном случае граничные условия имеют вид
v = f(x), y = 0. 0<x<a, C.11)
^-=0, y = b. 0<*<a, C.12)
»J = 0. jc = O, 0<y<^, C.13)
|^-f/w=0, x = a9 0<y<b. C.14>
Выражение
cos ax ch a (b — у)
удовлетворяет C.1), C.13) и C.12) при любом а. Оно также удовлетво-
удовлетворяет C.14), если а служит корнем уравнения
h. C.15>
*) Требуется, чтобы —Ц_-р—,, , было меньше 2e~nnyfat если п больше не-
J sh [nnb/a]
которого фиксированного п0. Тогда ход доказательства окажется точно таким же, как
и в предыдущем параграфе.
§ 3] ГЛ. V. ПОТОК ТЕПЛА В ТЕЛЕ С ПРЯМОУГОЛЬНЫМ СЕЧЕНИЕМ 169>
Корни ап этого уравнения при п= 1, 2, ... рассматривались в § 10 гл. III.
Если теперь мы предположим, что / (х) можно представить в форме, анало-
аналогичной уравнению A0.9) гл. III, то решение нашей задачи примет вид
где ал — положительные корни C.15).
Если f(x) = V= const, то оно запишется в виде
cos « *. ch К F - У)] ^ л
Из соображений симметрии следует, что это выражение служит также
решением для тела с сечением — a<Jt<a, 0 < у < 2?, когда граничные
поверхности у = 0 и у = 2Ь поддерживаются при температуре V, а на
поверхностях х = — а и х = а происходит теплообмен.
III. Граничная поверхность у = (X поддерживается при температуре f (х).
Тепловой поток через поверхность х = 0 отсутствует. На поверхностях х = а
и у = Ь происходит теплообмен со средой нулевой температуры.
В данном случае граничными условиями служат C.11), C.13), C.14) и
-1^ + ^ = 0, y = bt o<x<a. C.18>
Выражение cos а х {a ch [а (Ь — у)] -f- h sh [a (b — у)]} удовлетворяет C.1), C.13>
и C.18) для всех значений а. Поступая так же, как и в примере II, находим решение
в виде
где (хп — положительные корни C.15).
Если / (х) = V = const, то C.19) принимает вид
= 2ДК V
COS апХ {ап Ch ап (Ь — у) + h sh ал (^ — у)}
Это выражение представляет собой решение для тела с сечением — а < х < а>.
0 < у < by когда плоскость у = 0 поддерживается при постоянной температуре V
и имеет место теплообмен на других поверхностях со средой нулевой температуры.
Это решение использовалось при изучении распределения температур в охлаждаю-
охлаждающих ребрах конечной толщины [5, о]. Соответствующая задача для тонкого ребра*
рассмотрена в § 6 гл. IV, а для ребра, имеющего форму прямоугольного парал-
параллелепипеда, — в § 2 гл. VI.
IV. Граничная поверхность у = 0 поддерживается при температуре / (х%
поверхность у = b — при нулевой температуре. Тепловой поток через х = 0 отсут-
отсутствует. На поверхности х = а имеет место теплообмен со средой нулевой тем-
температуры.
В данном случае решение имеет вид
— у)
1
где ап — положительные корни уравнения C.15).
Если / (х) = V = const, то наше решение примет вид
v = 2hV
anb
170 ГЛ. V. ПОТОК ТЕПЛА В ТЕЛЕ С ПРЯМОУГОЛЬНЫМ СЕЧЕНИЕМ [§ 4
Это выражение представляет собой решение для тела с сечением — а < х < а,
'О < у < Ь, когда граничная поверхность у = 0 поддерживается при температуре У,
у = 6— при нулевой температуре и на поверхностях х=±а имеет место тепло-
теплообмен.
Если поверхность у = 0 поддерживается при температуре К, у = b — при темпе-
температуре У2, а на двух других поверхностях происходит теплообмен со средой нулевой
температуры, то решение принимает вид
по
'Ух sh ап (Ь — у) -f- V2 sh апу] cos ап х
[(ал + ^2) я + /г] cos ana sh anb
V. Случай различной теплопроводности в направлениях х и у.
Этот случай, который часто встречается в инженерной практике, можно рас-
рассматривать путем простого распространения метода, изложенного выше. Предполо-
Предположим, что теплопроводность в направлении х в k2 раз больше, чем в направлении у,
где k2 — постоянная. Тогда уравнение C.1) заменяется уравнением
-й
Как и в разобранном выше примере I, член вида
sin sh — C.25)
а а
удовлетворяет C.24) и заменяет C.8), Тогда решение этой задачи, соответствующее
C.9), примет вид
оо
sin(mc*:/a) sh [k (b — у) пп/а] ,3 2g\
пп sh (knnb/a)
§ 4. Тонкая пластина с прямоугольным сечением
при наличии теплообмена на ее поверхности
Предположим, что исследуемая пластина лежит в плоскости лгу, причем ее тол-
толщина D в направлении оси z настолько мала, что температуру по толщине пластины
можно считать постоянной. Пусть Н—коэффициент теплообмена материала пластины,
К—его коэффициент теплопроводности, р — плотность и с — удельная теплоемкость.
Тогда, как и в § 2 предыдущей главы, дифференциальное уравнение температурного
поля в пластине имеет вид
d2v d2v pc dv 2H
где v0 — температура окружающей среды.
В случае установившегося состояния это уравнение для пластины прямоуголь-
прямоугольного сечения можно решить методами, изложенными в двух предыдущих параграфах.
Например *), рассмотрим установившуюся температуру в пластине с сечением
0<лг<я, 0 < у <Ь при теплообмене на поверхности со средой нулевой темпе-
температуры в случае, когда кромка у = 0 поддерживается при температуре f (лг),
а другие кромки — при нулевой температуре.
Пусть
*2=w- D-2)
Тогда уравнение D.1) примет вид
-г-^- + —\ — k2v = 0, 0 < х < а, 0 < у < b D.3)
лри условиях
v==f(x), у = 0, 0<х<а, D.4)
v = 0, у = bt 0 < х < а, D.5)
v = 0, х = 0, 0 < у < Ь, D.6)
t/ = 0, x = a, 0<y<h. D.7)
*) Другие задачи и методы рассмотрены в статье талкина [7].
§ 5] ГЛ. V. ПОТОК ТЕПЛА В ТЕЛЕ С ПРЯМОУГОЛЬНЫМ СЕЧЕНИЕМ 171
Выражение
, пкх и tu Jl2 i л2*2l'/2 л с
sin-^-.shF —у)[*2Н—^2—J . "=1,2, ... D.8)
удовлетворяет D.3), D.5), D.6) и D.7). Если предположить, как и в предыдущем пара-
параграфе, что f (х) можно разложить в ряд
JLTS^x, D.9)
л = 1 О
то решение примет вид
2 у sin (пкх/а) sh (b - у) (k* + вУ/д«)'А с шх
п — 1 О
§ 5. Установившаяся температура в теле прямоугольного
сечения —а <лг<а, — Ь <у < 6 при наличии источника тепла
Задачи данного типа имеют важное практическое значение *), так как многие
виды электрических обмоток можно приближенно рассматривать как цилиндры с пря-
прямоугольным сечением [8]. Здесь мы проиллюстрируем применение методов, изложен-
изложенных в § 3 настоящей главы. Можно также использовать функцию Грина, как и в § 2
гл. XVI. Во многих задачах подобного вида коэффициенты теплопроводности в напра-
направлениях х и у различны и в данном случае мы будем считать их равными К и (K/k2),
где k — постоянная.
I. Мощность источников тепла в теле прямоугольного сечения равна постоян-
постоянной величине Ао\ теплоотдача в среду нулевой температуры через граничные
поверхности jc= ±a с поверхностным сопротивлением R на единицу площади
и через поверхности у = ±Ь с поверхностным сопротивлением R' на единицу
площади.
Дифференциальное уравнение имеет вид
d*v 1 дЧ Ао - п
Ix^ + W W = ~~~K" ( }
Выражение
ап cos an x ch kyan E.2)
удовлетворяет E.1) и граничным условиям при х = ±а, если ая(лз=1,2, ...) являются
положительными корнями уравнения
Граничные условия при у = ±Ь требуют, чтобы
с»
ап cos ап х [k~l KR'an sh kban + ch kban] = - aRA0 - A° {а^~ ^ . E.4)
*) В работе [9] рассматривается более общая задача о теплопередаче в случае
различных поверхностных сопротивлений всех четырех поверхностей и различных
температур сред, в которые происходит теплообмен. На практике рост температуры
достаточно велик, чтобы изменения теплопроводности и мощности источников с темпера-
температурой оказались значительными. Данный метод применим в случае линейной зависи-
зависимости мощности от температуры типа Ао A-J-at/). Изменение теплопроводности
с температурой можно учесть, вводя вместо v переменную 8 из уравнения F.10),
приведенного в гл. I (см. также [10]). В работе [11] рассматривается более сложное
граничное условие. Вопрос о • тороидальных катушках с прямоугольным сечением
разобран в [12].
172
ГЛ. V. ПОТОК ТЕПЛА В ТЕЛЕ С ПРЯМОУГОЛЬНЫМ СЕЧЕНИЕМ
da
v = aRA
Тогда ап находят из соотношения A0.9) гл. III, и мы получим окончательно
А0(а*-х*)
4А
Sin aan cos xan ch kyan
sh
kbaa] '
' '
II. Мощность источников тепла в теле прямоугольного сечения равна
постоянной величине Ао. На граничных поверхностях х = ±я, у = ±Ь поддер-
поддерживается нулевая температура
_ Ао (а2 — х2) 16Л0л2
V 2/С /С^3
[B/г
ch [Bn
Bn+\ych[Bn-\-\)nkb/2a]
§ 6. Неустановившееся состояние. Решение в виде
произведения решений
В § 15 гл. I отмечалось, что для начальных и граничных условий опре-
определенного типа решение задач с несколькими переменными можно записать
в виде произведения решений одномерных задач. В двумерном случае началь-
начальная температура должна выражаться как произведение f(x)f(y), а гранич-
граничными условиями должны служить условия нулевой температуры, нулевого
потока или теплообмена со сре-
2.0 \- , дой нулевой температуры.
Здесь мы рассмотрим только
случай постоянной начальной тем-
температуры, являющийся практиче-
практически наиболее важным. Решения
для случаев нулевой начальной
температуры и температуры, рав-
равной единице на граничных поверх-
поверхностях тела (или теплообмена со
средой, имеющей на этих поверх-
поверхностях температуру, равную еди-
единице), всегда можно получить пу-
путем вычитания решений, приво-
приводимых ниже, из единицы.
I. Прямой угол с сечением
в виде квадранта х > 0, у > Q
и с начальной температурой*
равной единице.
Решение для полуограничен-
полуограниченного тела х > 0 с начальной тем-
температурой, равной единице, и ну-
Рис. 21. Изотермы с/= 0,1, 0,2 0,9 для
тела с сечением в виде квадранта, с началь-
начальной температурой, равной единице, и нулевой
температурой поверхности.
левой температурой поверхности л; = 0 (см. D.3) гл. II) имеет вид
F.1)
Следовательно, решение для тела с сечением в виде квадранта х > 0,
у > 0, с начальной температурой, равной единице, и нулевой температурой
граничной поверхности записывается следующим образом:
F.2)
§ 6] ГЛ. V. ПОТОК ТЕПЛА В ТЕЛЕ С ПРЯМОУГОЛЬНЫМ СЕЧЕНИЕМ 173
На рис. 21 показаны изотермы, соответствующие значениям v, равным О,
0.1. 0,2 0,9.
Для тела, ограниченного плоскостями, пересекающимися под прямыми
углами, решение F.2) приближенно справедливо вблизи любого внешнего угла.
Тепловой поток в точке @, у) граничной поверхности равен
К ф*
УЧШ
он меньше теплового потока для полуограниченного твердого тела х > 0 на
величину
2 Y ti I'
Таким образом, величина потери тепла телом в единицу времени на
единицу длины перпендикуляра к ограничивающим плоскостям меньше коли-
количества тепла, теряемого полуограниченным твердым телом, на величину
F.3)
при вычислении интеграла использовалась формула A5) приложения 2.
Если тело с сечением х > 0, у > 0 имеет начальную темпера-
температуру, равную единице, и на его граничных поверхностях происходит
теплообмен со средой нулевой температуры, то температура будет равна
. у), F.4)
где ср(/г, л:)—величина, определяемая G.1) гл. II, а именно
У^у F.5)
II. Полуограниченное тело прямоугольного сечения — / < х < /,
))>0 с начальной температурой, равной единице.
Если граничные поверхности х = ± I поддерживаются при нулевой тем-
температуре, то соответствующее одномерное решение имеет такой же вид, как
и C.8) гл. III, т. е.
О2 ъЧ 1
^—J
cos V • <6-6>
Если же на этих поверхностях происходит теплообмен, то соответ-
соответствующее решение имеет такой же вид, как и A1.12) гл. III, т. е.
<*. U h) = У .., 2*C0Sa"f Г""', F.7)
где ап — положительные корни уравнения
a tg а/ = Л.
Если на всех граничных поверхностях поддерживается нулевая темпе-
температура, то решение имеет вид
174
ГЛ. V. ПОТОК ТЕПЛА В ТЕЛЕ С ПРЯМОУГОЛЬНЫМ СЕЧЕНИЕМ
1§б
Если на всех поверхностях происходит теплообмен со средой нулевой
температуры, то
(xt /, h). F.9)
Если на поверхности у = 0 происходит теплообмен со средой нулевой
температуры, а поверхности х = ± / поддерживаются при нулевой темпера-
температуре, то
г; = ср(/г, y)ty(x, I) F.10)
и т. д.
III. Неограниченное тело прямоугольного сечения —/<#</,
— ^<У<^ с начальной температурой, равной единице.
В этом случае решения соответствующих одномерных задач определяются
из F.6) и F.7).
Если все граничные поверхности тела поддерживаются при нулевой тем-
температуре, то решение имеет вид
v = ty(x, /)ф(у, Ь). F.11)
Значения функций ф(х, /) можно найти из рис. 11; тогда легко построить
изотермы для любого момента времени. На рис. 22 и 23 изображены изотермы
0.9
Рис. 22. Изотермы v = ОД, 0,2 0,9
для тела с сечением в виде квадрата
со стороной 2/, с начальной темпера-
температурой, равной единице, и нулевой
температурой поверхности:
**//* = 0,08.
Рис. 23. Изотермы v = 0,1, 0,2 0,9
для тела с сечением в виде прямо-
прямоугольника со сторонами 2/, 4/, на-
начальной температурой, равной еди-
единице, и нулевой температурой по-
поверхности: -till2 = 0,08.
г; = 0,1, 0,2 0,9 при х///2 = 0,08 для тел с квадратным и прямо-
прямоугольным сечением, у которых b = 2L
Аналогичным образом, если на граничных поверхностях тела происходит
теплообмен со средой нулевой температуры, то решение имеет вид
% К).
F.12)
Как отмечалось в § 15 гл. I, для твердого тела с различными коэф-
коэффициентами температуропроводности в направлениях х и у и различными коэф-
коэффициентами теплообмена на различных граничных поверхностях, решения
по-прежнему можно записать таким же образом.
§ 7] ГЛ. V. ПОТОК ТЕПЛА В ТЕЛЕ С ПРЯМОУГОЛЬНЫМ СЕЧЕНИЕМ 175
§ 7. Неустановившееся состояние. Произвольные
начальные и граничные условия
Как и в § 14 гл. I, общую задачу можно свести к задаче установив-.
шейся температуры, какой-то заданной начальной температуры и нулевой,
температуры граничной поверхности (или теплообмена со средой нулевой
температуры). Если начальная температура представляет собой произведение
функций х и у, то, как и выше, решение можно записать в виде произве-
произведения; в противном случае следует использовать теорию двойных рядов Фурье
и решение примет вид двойного ряда. Этот метод будет детально рассмотрен,
для прямоугольного параллелепипеда в §§ 3 и 6 следующей главы. Кроме
того, в §§ 4 и 5 гл. XIV мы покажем, что для той же цели можно приме-
применить функцию Грина *). Общий обзор применяемых методов приведен в § 1
следующей главы.
ЛИТЕРАТУРА
1. Carslaw, Fourier's Series and Integrals Macmillan, ed. 3, 1930.
2. Fourier, Theorie analytique de la chaleur, § 205.
3. Titchmarsh, Fourier Integrals, Oxford, 1937, §10.11. (Э. Т и тч м а р ш, Введе-
Введение в теорию интегралов Фурье, Гостехиздат, 1948, перев. с 1-го изд.)
4. К а г u s h, J. Appl. Phys. 23, 492—494 A952).
5. Н а г р е г, В г о w n, NACA Rep. No. 158 A923).
6. A v r a m i, L i 11 1 e, J. Appl. Phys. 13, 255 A942).
7. M a 1 k i n, J. Franklin Inst. 232, 129 A941).
8. Cock r of t, Proc. Camb. Phil. Soc. 22, 759—772 A925).
9. H i g g i n s, Elect. Engng 64, 190—194 A945).
10. J a k о b, Trans. ASME 65, 593—602 A943).
11. Buchholz, Z. angew. Math. Mech. 14, 285—294 A934).
12. Higgins,J. Franklin Inst. 240, 97—112 A945).
13. Low an, Phil. Mag. 24, 410 A937).
*) В работе [13] приводится ряд решений, полученных при помощи преобразовав
ния Лапласа.
ГЛАВА VI
ТЕПЛОВОЙ ПОТОК В ПРЯМОУГОЛЬНОМ ПАРАЛЛЕЛЕПИПЕДЕ
§ 1. Введение
Лучше всего исследованы трехмерные задачи теплопроводности для
областей, ограниченных координатными поверхностями прямоугольной, цилин-
цилиндрической и сферической систем. В случае радиального потока тепла
б цилиндрах и сферах решение содержит лишь одну пространственную пере-
переменную и время; такие задачи рассматриваются в гл. VII и IX. В настоящей
главе и в гл. VIII мы обсудим задачи для прямоугольного параллелепипеда
« ограниченного цилиндра, т. е. задачи, в которых приходится рассматривать
две или большее число пространственных переменных. Поскольку решения
можно найти несколькими различными путями, на данном этапе желательно
рассмотреть различные методы и соотношение между ними.
1. Наиболее просты и в то же время наиболее важны для нас задачи,
решения которых можно выразить, как и в § 15 гл. I, в виде произведения
решений одномерных задач.
Основным является случай, когда начальная температура равна единице
и температура поверхности равна нулю (или происходит теплообмен со сре-
средой нулевой температуры); решив эту задачу, легко найти решение для
случая нулевой начальной температуры и температу>ы поверхности, равной
единице, а использовав теорему Дюамеля, —pi ш ние для температуры
ловерхности, равной ср(О-
2. Используя кратные ряды Фурье или их обобщения, можно исследо-
исследовать случай произвольных начальных и поверхностных температур.
3. Использование функции Грина (см. гл. XIV) также позволяет найти
полное решение общей задачи для произвольной начальной и поверхностной
температур. Для простых случаев, указанных в пункте 1, после некоторого
упрощения получается такое же решение. Кроме того, применяя функцию
Грина, легко найти решения для случая, когда количество тепла, выделяю-
выделяющееся в твердом теле в единицу времени, является заданной функцией поло-
положения и времени.
4. Непосредственное применение метода преобразования Лапласа (см. § 11
гл. XV) особенно полезно тогда, когда некоторые из граничных поверхностей
поддерживаются при температурах, являющихся простыми функциями времени,
const, kt, sin (at и т. д. В таких случаях результаты, найденные методами 2
и 3 (и методом 1, если температура поверхности непостоянна) в виде инте-
интегралов, можно получить суммированием частных решений.
В настоящей главе мы применим первые два из приведенных выше мето-
методов к задачам для прямоугольного параллелепипеда. Кроме того, в § 5
гл. XIV и § 11 гл. XV мы рассмотрим аналогичные задачи другими методами.
§ 2] ГЛ. VI. ТЕПЛОВОЙ ПОТОК В ПРЯМОУГОЛЬНОМ ПАРАЛЛЕЛЕПИПЕДЕ 177
Теплопроводность в твердых телах простой геометрической формы,
например тел в виде прямоугольного параллелепипеда и ограниченного
цилиндра, представляет большой интерес, поскольку такие твердые тела часто
встречаются на практике (мясные консервы, ящики с фруктами). В более
старых методах определения теплопроводности плохих проводников также
использовались образцы в виде куба, сферы и ограниченных цилиндров;
описанный выше метод для стержня непригоден, поскольку количество тепла,
теряемое в результате теплообмена с поверхности плохо проводящего стержня,
может оказаться больше потери тепла вдоль стержня.
§ 2. Установившаяся температура
В настоящем параграфе мы рассмотрим задачи, в которых одни гранич-
граничные плоскости твердого тела поддерживаются при постоянной температуре,
тогда как на других плоскостях температура равна нулю или же происходит
теплообмен со средой нулевой температуры. В более сложных случаях,
в которых температуры граничных поверхностей являются заданными функ-
функциями положения, можно воспользоваться, как и в § 4 данной главы, теорией
двойных рядов Фурье.
I. Твердое тело 0 < л; < я, 0 < у < ?, 0 < z < с. Температуры
плоскостей х = 0 и х = а постоянны и равны соответственно v1 и v2\
другие плоскости поддерживаются при нулевой температуре.
В этом случае дифференциальное уравнение для температуры тела имеет
вид
Ясно, что выражение
vx sh / (а — х) + v2 sh lx mizy nizz
ЙГЙ sin-j-sin— B.2)
удовлетворяет B.1) при условии, что
?)». B-3)
Кроме того, если т и п — целые числа, то B.2) обращается в нуль
при у — 0иу = Ьк при z = 0 и z = c. Выражение
оо оо
\^ V1 л V]Shl(a — xL-v2shlx . mizy . nnz o .ч
v=2u lAn.n-J sh/a sin-^s.n— B.4)
m =1 /i = l
имеет те же свойства; кроме того, оно равно vl при л; = 0 к v2 при х = а,
если *)
E4-..^ln^L=l. B-5)
т — \ л=1
*) Для строгости рассуждений необходимо доказать возможность почленного
дифференцирования двойного ряда для v. Это же замечание относится и к другим
задачам, разбираемым в данной главе. См. выше, § 3 гл. III и работы [1, 2].
12 Г. Карслоу, Д. Егер
178 ГЛ. VI. ТЕПЛОВОЙ ПОТОК В ПРЯМОУГОЛЬНОМ ПАРАЛЛЕЛЕПИПЕДЕ [§ 2
Далее, разлагая единицу в ряд по синусам в интервале (О, Ь), получим *)
1 — ± V sin[B/7+lOuy/6]
1— «^ 2/7+1 • ^-°'
Аналогично
1 _4у sln[By+l)«/c]
2q+l К }
Перемножая B.6) и B.7), получим
1-iiV V sin [B/7 + 1) *у/Ь] sin [{2q + 1) nz/e] 9
1 - ъ* Zd Lk B/7+1) B?+1) ' {Z'b)
Сравнивая B.8) и B.5), мы видим, что величина Лтп должна равняться
нулю, если и /71 и л не являются оба нечетными; в этом' случае величина А
должна равняться \6/к2тп. Таким образом, мы можем окончательно запи-
записать B.4) в виде
„ _ 16 V V К sh / (а - х) + v2 sh lx] sin [B/7 + 1) %y/b] sin [Bq + 1) nz/c]
V—~^2uZu Bp+\)Bq+\)shla ' K^}
где
/2=Bp+l)^ + Bg-M)^ B10)
II. Установившаяся температура в твердом теле 0 < х < ау — b < у < Ь,
— с < z < с. Температуры плоскостей х = 0 а л: = а поддерживаются при vx и v2
соответственно, а на других происходит теплообмен со средой нулевой тем-
температуры.
В этом случае граничные условия имеют вид
д%)
•——^— —— /tt/ —~ Q
Выражение
г
при
при
при
х — и;
У = -Ь;
г — х) + v2
д%)
~ду~+ V =
~+hv = 0
sh /jc o
cos ary cos Э,
при
при
при
x — a;
y = b;
z=c.
B.12)
B.13)
B.14)
удовлетворяет уравнению теплопроводности при условии, что
? = 4 + & B-15)
Оно удовлетворяет также граничным условиям B.12) и B.13), если аг является
корнем уравнения
atgab = h, B.16)
a $s—корнем уравнения
р tg Рс = Л. B.17)
Таким образом, решение нашей задачи записывается в виде
со оо
л »ish/(a — x)-\-v2shlx D ._ 1Ov
rs sh la C0S "гУ C0S P^; BЛ8)
Г=1 5=1
*) Этот прием в данном случае позволяет избежать использования двойных
рядов Фурье. Последние следует применять в тех случаях, когда температуры поверх-
поверхности являются произвольными функциями у и z (см. § 3 данной главы). Известно,
что ряд B.8) сходится [3].
§ 2] ГЛ. VI. ТЕПЛОВОЙ ПОТОК В ПРЯМОУГОЛЬНОМ ПАРАЛЛЕЛЕПИПЕДЕ 179
при этом постоянные Ars должны быть выбраны так, чтобы
оо оо
2 2 Ars cos атУ cos $sz = 1. B.19)
Далее, если аг и Р5 — положительные корни соответственно B.16) и B.17), то,
используя соотношение A0.10) гл. III, получим
cos агУ ,
у cos
Перемножая эти выражения, получим
V V 4/г2 cos ary cos
T T 2
Как и прежде, Л^ в B 18) находят путем сравнения B.19) и B.22). Тогда B.18)
окончательно записывается в виде
4ft2 [t>i sh / (д — х) + р2 sh lx\ cos afy cos $sz
2
где / определяется из B.15).
Это решение не очень удобно для численного расчета или для определения
теплопроводности [4].
III. Установившаяся температура в твердом теле 0 < х < а, — Ь < у < b
— с < z < с; плоскость х = 0 поддерживается при постоянной температуре V,
а на других плоскостях происходит теплообмен со средой нулевой температуры.
В данном случае граничные условия имеют вид B.12) и B.13) и
v = V, х == 0; B.24)
-jg- + /it/ = O, x = a. B.25)
Выражение, соответствующее B.14), имеет вид
т. hshl(a — xL-lchl(a — х) о /оос,
V hsbal + lchal ~ COS а'У C0S ^ B'26)
где / определяется из B.15), а аг и р5 — положительные корни B.16) и B.17). Поступая
так же, как и в пункте II, мы получим окончательно
4h2V[hshl(a — x) + lchl(a — x)] cos ary cos Рддг
Это выражение является обобщением решения двумерной задачи о коротком охла-
охлаждающем ребре (см. C.20) гл. V).
IV. Задачи для неограниченного твердого тела прямоугольного сечения рассма-
рассматриваются тем же способом (ср. также § 2 гл. V). Например, рассмотрим твердое
тело л:>0, — Ь < у <Ь, — с < z < с, причем его плоскость х = 0 поддерживаете^
при температуре V, а на других плоскостях происходит теплообмен со средой
нулевой температуры.
12*
180 ГЛ. VI. ТЕПЛОВОЙ ПОТОК В ПРЯМОУГОЛЬНОМ ПАРАЛЛЕЛЕПИПЕДЕ [§ 3
В данном случае выражение, соответствующее B.14), имеет вид
Ve~lx cos ary cos p^, B.28)
и окончательно получим
оо оо
v=4H*vY У *-" cos ary cos
Г = 1 5=1
где ог, $s и / определяются соответственно из B.16), B.17) и B.15).
§ 3. Двойные и кратные ряды Фурье
При обычном формальном рассмотрении (см. [5], § 90) ряда Фурье функции
одной переменной / (л:), определенной в интервале (— /, /), предполагается, что / (х)
можно разложить в ряд
[ап cos -^ + Ьп sin^). C.1)
При этом коэффициенты а0, ап, Ьп получаются в результате умножения C.1), соот-
соответственно, на единицу, cos (ппх/l) и sin (ппх/1) и почленного интегрирования полу-
полученных рядов *).
Таким образом, используя выражения
i
/тпх а ппх , л F тпх ппх , л
sin—у— sin—y-dx = 0, / cos—-—cos —j— dx = 0, т ф п, C.2)
i
/sin m*X cos -^^- dx = 0, C.3)
sin—j—\ dx= cos~7— dx = l, m=l, 2, ..., C.4)
находим, что
bn=-f J f (*') sin irij— d*'- C.5)
Эту формальную теорию нетрудно превратить в строгую путем тщательного
исследования ряда в правой части уравнения C.1) с коэффициентами, определяе-
определяемыми C.5). При этом оказывается, что если f (х) удовлетворяет определенным усло-
условиям, например условиям Дирихле (см. [5], § 93), то этот ряд сходится и его сумма
равна f (х) в каждой точке интервала, в котором функция /(х) непрерывна,
и -j < /C* + O)-{-/(je — 0) > во всех других точках.
Формальную теорию двойных и кратных рядов Фурье развивают точно таким же
образом. Предположим, что мы имеем функцию / (х, у), определенную в прямоуголь-
*) Здесь следует допустить, что ряд C.1) сходится равномерно. (Прим. ред)
§ 3] ГЛ. VI. ТЕПЛОВОЙ ПОТОК В ПРЯМОУГОЛЬНОМ ПАРАЛЛЕЛЕПИПЕДЕ 181
нике — а < х < а, — Ь < у < Ь. В этом двумерном случае функции
sin sin—т^-; /и=1, 2, ...; л =1,2,...
а о
, тъх ппу л о л ,
sin cos ,J ; т= 1, 2, ...; л = 0, 1, ...
а 6
cos sin ' ; /и = 0,1,...; л=1, 2, ...
а 0
0 4 rf"V
C.6)
составляют ортогональную систему; они обладают свойствами, аналогичными C.2), C.3)
и C.4), т. е. интеграл по прямоугольнику от произведения любых двух различных
функций равен нулю, а интегралы от их квадратов равны
а ft aft
/ sin sin —г*- dx dy = / / :
-e -ft -a -
aft
C.7)
/• Г Г /илл: . ятеу I2 . . Г Г Г ^^ Л7СУ I2 ^ ^
/ / cos sin , dx dy = / / cos cos , dxdy =¦ ab
—e —ft -a -ft
для m > 1, л > 1. Если л = 0 во втором, /и = 0в третьем или либо /и = 0, либо л = 0
в последнем из этих интегралов, то искомый результат оказывается вдвое больше;
если т = л = 0 в последнем интеграле, то его величина равна 4ab.
Разложение функции f(x, у), аналогичное C.1), имеет вид
оо оо оо оо
/(-^. У)== 2а 2а Ат>п*1п—— sin-^-+ 2a 2а
ОО ОО ОО ОО
VI VI _ тпх ппу ov
2а 2а Вт>п cos ~Гcos ~Т-' C*8)
т=0 л=1 т«0 л=0
Чтобы найти коэффициенты ряда, умножим обе части C.8) на одну из функ-
функций C.6) и проинтегрируем в пределах от — а до а по л: и от — b до b по у, В этом
случае, используя C.7) и учитывая, что все другие двойные интегралы от произведе-
произведений функций C.6) обращаются в нуль, находим
а ь
Am, п = -?ь J J f(x> У) sin —— sin —Z- dx dy;
-a -ft
a ft
./ 1 Г С ,, ч . тпх
Am n — —Г / / / (X* У) Sin COS
"'» n ab J J a
-a -ft
a ft
m,n = -ab J J
C0S ~^" Sin
-a -ft
a ft
1 /' Г jt , Ч тПХ П%У J J /O nv
>n = ~ri J J f(x* y) cos "~^~cos ь dx dy' C*9)
-a -ft
Коэффициенты Лт> 0, B^ n, BOf л, Bm 0 равны половине, а 5о,о — одной четвер-
четвертой от приведенных выше величин.
В основном мы будем рассматривать случай, в котором f(x, у) является нечет-
нечетной функцией как х, так и у; тогда все коэффициенты Ат д, В'т п и Втя
182 ГЛ. VI. ТЕПЛОВОЙ ПОТОК В ПРЯМОУГОЛЬНОМ ПАРАЛЛЕЛЕПИПЕДЕ [§ 3
обращаются в нуль. Отсюда следует, что
*' y) = Zi 1 Am>nsin^Tsin ь~• (ЗЛ0)
m=l л=1
где
a b
Am'n==!ibJ I f(x'>y')sin—a—s\n—^-dxfdy'y C.11)
о 6
что аналогично ряду Фурье по синусам.
Точно так же, если / (х, у, г) определена в интервалах — а < х < а, —b < у < Ь,
— c<z<c и является нечетной функцией х, у и г, то мы получим тройной ряд по
синусам
оо оо оо
А г 1%Х • ^^У , П%2 /О 1ОЧ
и т> п тsin ~тг sin "г* * ( J
/=rl m=l л=1
где
а Ъ с
Аи т, п = ? f f f /(.', /, г') sin ^1 sin «yl sin «Hi ^ rf/ rf,'. C.13)
0 0 0
Если / (л:, у, г) — четная функция х, у и г, то тем же способом мы получим ряд по
косинусам.
Задачи, в которых встречаются кратные ряды Фурье, можно рассматривать и
другим способом; мы воспользуемся им в гл. VIII, где нам придется иметь дело
с комбинацией рядов Фурье и рядов Фурье — Бесселя. Рассмотрим, например, слу-
случай, в котором / (jc, у) является нечетной функцией х и у в интервалах — а < х < а,
— Ь < у < Ь. Для любого фиксированного у в интервале — b < у < b, f (x, у) является
нечетной функцией х и, следовательно, ее можно разложить в ряд по синусам
оо
/ (*. у) = 2 ««• (у) sin "^ • <ЗЛ4>
т = 1
где коэффициенты
а
ат (у) = 1 //(*', у) sin ^l rf*' C.15)
6
зависят теперь от у. Они являются нечетными функциями у в интервале — b < у < Ь,
и следовательно, их можно разложить в ряд
^т,пв\п^, C.16)
где
6 0 0
C.17)
Таким образом, окончательно находим
f . ппу
, sin sin —г-
где Лш, л — коэффициент, определяемый C.17), что находится в соответствии с C.10)
и C.11). Все другие случаи можно рассматривать аналогичным образом. Так же можно
поступать и при разложении функции нескольких переменных в ряд по функциям,
приведенным в §§ 9, 10 гл. III.
Теперь мы можем записать решения задач, приведенных в § 2 данной главы,
в которых температуры поверхности являются функциями положения на поверхности.
§ 4] ГЛ. VI. ТЕПЛОВОЙ ПОТОК В ПРЯМОУГОЛЬНОМ ПАРАЛЛЕЛЕПИПЕДЕ 183
Возьмем задачу I предыдущего параграфа. Рассмотрим установившуюся тем-
температуру в твердом теле О < х < а, 0 < у < Ь, О < z < с, граничная поверхность
которого х = 0 поддерживается при температуре f (у, г), а другие поверхности—
при нулевой температуре.
В этом случае выражение
sh / (а — х) . тпу . пт ,« ,ftv
X ai sin~irsin— <ЗЛ8>
удовлетворяет дифференциальному уравнению нашей задачи, если
w+J^)%t-- (ЗЛ9)
кроме того, C.18) должно обращаться в нуль на всех поверхностях твердого тела,
за исключением х = 0.
Далее, если / (у, z) можно представить в виде ряда по синусам (ЗЛО), то реше-
решение задачи будет иметь вид
C.20)
Oil U.I UK,
m=l /i = l
где
b с
Amtn=-j— / / / (y't zf) sin m%J sin -^- rf/ dzf. C.21)
о о
§ 4. Неустановившаяся температура. Решение в виде
произведения решений
Решения ряда важных задач можно записать, как и в § 6 предыдущей
главы, используя метод, изложенный в § 15 гл. I, и известные решения одно-
одномерных задач. Здесь мы приведем решения для случая начальной темпера-
температуры, равной единице, и нулевой температуры поверхности (или теплообмена
со средой нулевой температуры). Решения для случая нулевой начальной
температуры и температуры поверхности, равной единице (или теплообмена
со средой, имеющей температуру, равную единице), получаются путем вычи-
вычитания приводимых ниже результатов из единицы. Тогда решения для произ-
произвольных температур поверхности следуют из теорем Дюамеля (см. § 14
гл. I). Для анизотропного твердого тела с главными осями теплопроводности,
параллельными координатным плоскостям, и различными коэффициентами
теплообмена на поверхностях, данный метод по-прежнему остается справед-
справедливым.
I. Область л:>0, у > 0, 2 > 0 с начальной температурой, рав-
равной единице, и нулевой температурой поверхности.
* = Ф(^)Ф(^Ы^1 DЛ)
Н. Та же область с начальной температурой, равной единице,
и теплообменом на поверхности со средой нулевой гпемпературы.
Jc)cp(/z, у) ? (Л. *). ' D-2)
где ср(/г, х) определяется соотношением F.5) гл. V.
III. Область — а < л; < а, — ft<y<ft» 2>0 с начальной темпе-
температурой, равной единице, и нулевой температурой поверхности.
I X \ \
г> = Ф(лг, а)<Ь(у, ^)Ф(—т^*)» D.3J
184 ГЛ. VI ТЕПЛОВОЙ ПОТОК В ПРЯМОУГОЛЬНОМ ПАРАЛЛЕЛЕПИПЕДЕ [§,4
где
ii*?Wifi!?i:sbJ&?is-- D-4)
л=0
IV. Область —а < л; < а, —b<y<b, —с < z < с с начальной
температурой, равной единице, и нулевой температурой поверх-
поверхности.
i> = <!>(*. a)ty(y, b)^(z, с), D.5)
или
2l2 +1) C0S 2а C0S 26 Х
;(-«,.»,<), D.6)
где
+1
Bт +1J
. B/г + 1J1
' С J"
V. Область — а<л:<а, — b <y <b, — c<z<cc начальной тем-
температурой, равной единице, и теплообменом на поверхности со сре-
средой нулевой температуры [6].
v = ty(x, a, h)ty(y, b, й)фОг. с, /г), D.8)
где
оо 2
ф(лг, а, /0=У г/ о 2Ч—-f| ^ я D.9)
и ал — положительные корни уравнения
/z. D.10)
VI. Область —а < л; < а, —b<y<b, —с < 2 < с с начальной
температурой, равной нулю, и температурой поверхности ср(/).
Если ср(?) = К = const, то решение, которое следует из D.6) и D.7),
имеет вид
°° °° ^ (_-1)'+»я+л B/+1)тслг Bт+\)пу
^ B/ + 1)B/и+1)B/г+1) cos 2a COS 26 А
/=0 т-0 л=0
al)m>nO. D.11)
В случае температуры поверхности, равной ср(^), мы получим, используя
теорему Дюамеля
оо оо оо
64у V У «1, ш> п (-1/+т^я B/ + 1) ** Bт
v~ тез jU Zu Zu B/ + 1) B/и + 1) Bл f 1) LOS 2а S
B/ + 1) B/и + 1) Bл -f- 1) LOS 2а S 2b X
t
X cos B/1+с1)яг exp [- a,. m> „f ] J exp Jo,, m, „X] <p (X) rfX. D.12)
§ 5] ГЛ. VI. ТЕПЛОВОЙ ПОТОК В ПРЯМОУГОЛЬНОМ ПАРАЛЛЕЛЕПИПЕДЕ 185
Если y(t) = kt, мы получим*)
/=0 m=0 л=0
Xcos <2/ + ^ cos P" + ')^ cos V*+l>« . D.13)
При выводе D.12) и D.13) из D.11) мы получаем один ряд, так как началь-
начальная температура равна нулю. Выражение для случая периодического измене-
изменения температуры поверхности можно найти из D.12), но конечный его вид
не очень удобен для использования. Эти задачи будут еще раз рассмотрены
в § 11 гл. XV.
§ б. Определение коэффициента теплопроводности
и экстраполяция кривых охлаждения
Решения D.6) и D.8) предыдущего параграфа для прямоугольного парал-
параллелепипеда с начальной температурой, равной единице, и температурой по-
поверхности, равной нулю (или теплообменом со средой нулевой температуры)
позволяют получить исключительно простой метод определения коэффициента
температуропроводности плохих проводников.
При больших значениях времени ряд D.6) очень быстро сходится и
искомая температура с достаточно хорошим приближением определяется пер-
первым его членом. Таким образом, если построить график зависимости лога-
логарифма температуры в любой точке твердого тела от времени, то в конечном
итоге кривая обратится в прямую с наклоном
Если измеряется температура в точке (-т#, *з"*' 1FC)' то в соотноше-
соотношении D.6) данной главы все члены с /, т и п обращаются в нуль, и в дан-
данном случае первый член этого соотношения будет служить достаточно хоро-
хорошим приближением.
Если твердое тело теряет тепло в результате теплообмена со средой
нулевой температуры, то следует определить величины ос и Л. Рассмотрим
для простоты куб а = Ь = с; температура в любой его точке при больших
значениях времени, т. е. когда кривая \nv = f(t) превращается в прямую,
определяется соотношением
8/г2 cos а{ х cos at у COS ахг -Зхоф - 9
V~ [(t + D + f s3е ' (° }
f cos3ага ( }
Отношение температуры в центре к температуре в любой другой под-
подходящей точке определяет аг. Величину h находят из D.10) данной главы,
а ш\ — из угла наклона кривой \nv = f(t). Если начальная температура
твердого тела постоянна, то знать ее не нужно: ее можно вычислить по зна-
значениям а1§ /г, х и данным измерения температуры (или путем нахождения
точки пересечения оси t с асимптотой кривой Inv = f(t)). Это является
проверкой полученных результатов в тех случаях, когда известна начальная
температура; кроме того, появляется возможность вычисления начальной тем-
температуры твердого тела, охлаждавшегося в течение некоторого времени
в результате теплообмена.
*) В работе [7] приводится ряд решений этого вида.
186 ГЛ. VI. ТЕПЛОВОЙ ПОТОК В ПРЯМОУГОЛЬНОМ ПАРАЛЛЕЛЕПИПЕДЕ [§ 6
Тот же метод можно использовать и для других тел простой геометри-
геометрической формы, например для ограниченных цилиндров (см. § 5 гл. VIII) или
сфер (см. § 5 гл. IX). Другой метод обработки наблюдений обсуждается при
рассмотрении сферы.
§ 6. Неустановившаяся температура. Тройной ряд Фурье
Если начальную температуру в параллелепипеде нельзя представить в виде
произведения функций х, у и z или если граничные условия отличны от условий,
рассмотренных в § 15 гл. I, то метод, изложенный в § 4 данной главы, становится
непригодным. Поскольку задачу о твердом теле с заданными начальной и поверхно-
поверхностной температурами можно свести (см. § 14 гл. I) к задаче об установившейся тем-
температуре, рассмотренной в § 2 данной главы, и к задаче с нулевой температурой
поверхности, то в этом случае необходимо рассмотреть только область 0 < х < я,
0<y<b,0<z<cc нулевой температурой поверхности и начальной темпера-
температурой /(х, у, z).
Пусть /(jc, у, z) можно разложить в тройной ряд по синусам (см. C.12) дан-
данной главы)
f(x, у, z)=2j 2d 2d l'm'nS
/=1 m-\ л = 1
где
a b с
AU«. - = -йг / / / / <¦*'• У.г>)sin *г-sin ^sin ^f dx> dy'dz'- <6-2>
и и о
Тогда выражение
2
где
•U.—^T-r+-?¦+-?). <6-4>
удовлетворяет дифференциальному уравнению и обращается в нуль на граничных
поверхностях.
Таким образом, мы получили соотношение
с» с» с»
[о л , . 1ъх тпу mzz /с гч
— ха/ т пЦ -^U т, п sin sin —h sin » (^)
служащее решением нашей задачи.
Это решение и соответствующее решение в случае теплообмена на границе *)
можно получить, используя функцию Грина (см. § 5 гл. XIV, где рассматривается
также задача о прямоугольном параллелепипеде при наличии в нем источника тепла).
ЛИТЕРАТУРА
I.Moore, On convergence factors in double series and the double Fourier's series,
Trans. Am. Math. Soc. 14, 73 A913).
2. Moore, Bull. Am. Math. Soc. 25, 274 A919).
3. Hardy, Proc. Lond. Math. Soc. 6, 410 A908).
4. С h i v e г s, Phil. Mag. 6, 305 A928).
5. Carslaw, Fourier's Series and Integrals, Macmillan, ed. 3, 1930.
6. Berger, Z. angew. Math. Mech.8, 479 A928).
7. Williamson, Adams, Phys. Rev. 14, 99 A919).
*) Здесь можно пользоваться также конечным преобразованием Фурье (см. § 5
гл. XVII).
ГЛАВА VII
ТЕПЛОВОЙ ПОТОК В НЕОГРАНИЧЕННОМ ЦИЛИНДРЕ
КРУГОВОГО СЕЧЕНИЯ
§ 1. Введение
В § 8 гл. I мы видели, что в цилиндрических координатах уравнение
теплопроводности имеет вид
JL—( dv\ | * d*v д2%) — * dv
или
dv^ ld2v , 1 dv . 1 d2v . d2v\
dt~%\dr2^~ r dr "Г" r2 d№ "•" dz2)' A '^
Если ось нагреваемого кругового цилиндра совпадает с осью z, а на-
начальные и граничные условия не зависят от координат б и zt то температура
цилиндра зависит только от г и t, и уравнение теплопроводности сводится
к уравнению
dv
В этом случае тепловой поток перпендикулярен оси цилиндра, а линии
тока радиальны.
Если начальные и граничные условия не зависят от координаты z, то
тепло распространяется в плоскостях, перпендикулярных оси цилиндра, и
уравнение теплопроводности принимает вид
dv {d2v I dv 1 d2v\
Если начальные и граничные условия не зависят от угла 6, то тепло
распространяется в плоскостях, проходящих через ось цилиндра, и уравнение
теплопроводности имеет вид
dv (d2v I dv 02v
В данной главе приводятся решения задач для сплошного и полого
цилиндров с различными граничными условиями. Эти решения всегда имеют
вид рядов Фурье — Бесселя; решения, пригодные для малых значений %t/a2t
находить значительно труднее; мы их будем рассматривать в гл. ХШ еще
и потому, что эти решения нельзя представить в простой конечной форме.
Задачи для составных цилиндрических областей и для областей, ограниченных
изнутри круговым цилиндром, также рассматриваются в гл. ХШ.
188 ГЛ. VII. ТЕПЛОВОЙ ПОТОК В НЕОГРАНИЧЕННОМ ЦИЛИНДРЕ [§ 2
§ 2. Установившаяся температура. Радиальный поток
Если твердое тело представляет собой полый цилиндр, внутренний и
внешний радиусы которого равны соответственно а и Ь, то уравнение A.1)
предыдущего параграфа для распределения температур в теле примет вид
Общее решение этого уравнения имеет вид
v=A + B\nrt B.2)
где А и В — постоянные, определяемые из граничных условий при г = а
и г = Ь.
I. Поверхность г = а поддерживается при температуре vv по-
поверхность г = Ь—при температуре vv
В этом случае
Величина теплового потока на единицу длины равна
dv
II. Поверхность г = а поддерживается при температуре vv На
поверхности г^Ь происходит теплообмен со средой* имеющей тем-
пературу v2, и поэтому граничное условие на ней имеет вид
В данном случае
_ у] [1 + hb In (b/r)] + hbv2 In (r/a) (C) -
V~ \ + hb\n(bla) * (Z'°'
Величина теплового потока на внешней поверхности цилиндра на еди-
единицу его длины равна
Если а/г>1, то величина B.6) непрерывно уменьшается с увеличе-
увеличением Ь. Если же ah < 1, то B.6) имеет максимум при Ь^-г. Это озна-
означает, что при определенных условиях можно увеличить тепловые потери
трубы, окружив ее изолирующим материалом [1].
III. Количество тепла, подводимого в единицу времени внутрь
цилиндра на единицу его длины, равно постоянной величине Fo.
В данном случае тепловой поток через любой цилиндр не зависит от
радиуса цилиндра, так как из B.1) следует, что r(dv/dr) постоянно, и мы
можем написать
F0 = -2*r/C-g-, a<r<b. B.7)
Если vl и v2 — температуры при г, равном гг и г2 соответственно, то,
интегрируя B.7), получим
vx — v2) = FQ In ^J. B.8)
§ 2] ГЛ. VII. ТЕПЛОВОЙ ПОТОК В НЕОГРАНИЧЕННОМ ЦИЛИНДРЕ 189
Справедливость этого соотношения не зависит от способа подвода тгпла
и от граничных условий на цилиндрических поверхностях *). Если тепло
подводится с помощью проволоки, расположенной вдоль оси цилиндра,
с сопротивлением R ом на единицу длины, а сила протекающего по ней
тока равна /а, то мы получим
где у — число калорий в джоуле.
Если коэффициент теплопроводности К зависит от температуры, то соот-
соотношение вида B.8) по-прежнему остается справедливым. Соотношение B.7)
тоже оказывается справедливым; введем теперь
т. е. средний коэффициент теплопроводности для всей области температур
от vx до v2\ тогда, интегрируя B.7), получим
2ъКт(V, - v2) = FoIn (^). B.10)
IV. Составной полый цилиндр, состоящий из п областей (av а2),
(а2, а3), .... (ая, ап+1) с коэффициентами теплопроводности Kv .. .* Кп.
Если vv v2 Vn+i — температуры на поверхностях av a2, ..., an+v
то многократное использование B.4) показывает, что величина теплового
потока, приходящегося на единицу длины системы F, равна
— —
Г— \n(a2lax) — ••• — \п(ап+1/ап)
Следовательно,
F
к;
г=1
Если, кроме того, имеются контактные сопротивления Rv R2 Rn*
Rn+i на единицу площади поверхностей av а2, .. ., ап, ап+1, аиои vn+2 —
температуры внутри и вне составного цилиндра, то мы получим следующее
соотношение:
In п+\
г=1 г=1 )
Приведенное выше выражение B.6) представляет собой простой частный
случай B.13).
V. Выделение тепла в цилиндре.
Если количество выделяемого в единицу времени тепла равно постоян-
постоянной Ло, то для установившегося радиального потока соотношение F.7) гл. I
примет вид
Общее решение B.14) имеет вид
v=A-\-Blnr — D?). B-15)
*) Это соотношение часто использовалось при определении теплопроводности
[2-5].
190 ГЛ. VII. ТЕПЛОВОЙ ПОТОК В НЕОГРАНИЧЕННОМ ЦИЛИНДРЕ [§ 2
Для сплошного цилиндра*) член, содержащий In г, выпадает**),
и B.15) примет вид
где v0 — температура на оси цилиндра. Если поверхность цилиндра г = а
поддерживается при нулевой температуре, то
если же на поверхности г = а происходит теплообмен со средой нулевой
температуры и коэффициентом теплообмена И, то
Для полой цилиндрической проволоки, внутренний и внешний радиусы
которой соответственно равны а и Ь, а температуры внутренней и внешней
поверхностей равны vx и v2, мы получим из B.15)
vl — v2 = В In {alb) — (а* -?> А° . B.19)
Постоянная В определяется из граничных условий. Если, как это обычно
бывает, тепловой поток на внутренней поверхности отсутствует, то можно
написать
Из B.19) и B.20) следует, что
К = 4 (
Соотношения B.16) и B.21) использовались для определения коэффи-
коэффициента теплопроводности [9—12].
Рассмотрим изолированную проволоку, в которой изолирующий мате-
материал с коэффициентом теплопроводности Кх заполняет область а < г < Ь,
окружающую участок проволоки 0 < г < а с коэффициентом теплопровод-
теплопроводности /С, причем в этом участке количество тепла, выделяющегося в единицу
времени на единицу объема, равно Ао. Если при г = Ь происходит тепло-
теплообмен, т. е.
*L + hv = 0, г = Ь.
то решение, полученное из B.2) и B.16), примет вид
<2-231
*) Простейшим является случай нагревания проволоки путем пропускания
по ней электрического тока плотностью / а/см2; в данном случае Ло = у/2/а» где
а — электропроводность проволоки, ay — число калорий в джоуле. Случай устано-
установившейся температуры в проволоке, нагреваемой либо в результате пропускания
переменного тока (здесь AQ является функцией г вследствие скин-эффекта), либо
за счет индукции, рассматривается в работе [6]. Данная задача совпадает с задачей
о нагревании длинной цилиндрической магнитной катушки [7]. Случай индукционного
нагрева цилиндра рассматривается в работе [8].
**) В = 0, так как температура любой точки тела конечна. (Прим. ред.)
§ 2] ГЛ. VII. ТЕПЛОВОЙ ПОТОК В НЕОГРАНИЧЕННОМ ЦИЛИНДРЕ 191
Если изменение сопротивления проволоки линейно зависит от
температуры, то B.14) заменяется уравнением
где
р2=а^, B.25)
а ос— температурный коэффициент сопротивления.
Решение уравнения B.24), которое является конечным при г = 0,
имеет вид
/1 \
B.26)
Если поверхность г = а поддерживается при нулевой температуре, то
температура тела в зависимости от г выражается следующим образом *):
где J0(z) определяется в приложении 3.
Для полого цилиндра а < г < Ь, поверхность которого r = b поддер-
поддерживается при нулевой температуре, при отсутствии теплового потока через
поверхность г = а температурное поле записывается в виде
1 j 70 (рг) К, (pfl) - Ко (рг) 7, (рд) 1 ] 99R
а \ Уо @*) Г, (Ра) — Го (рб) yt (Pa) f * ^°'
VI. Методы с использованием горячей проволоки [13].
Для измерения коэффициента теплопроводности газов и плохих провод-
проводников **) были использованы различные комбинации B.4) и результатов, полу-
полученных методом Каллендера [14, 15]. Как и в пункте II § 11 гл. IV, про-
проволоку радиусом а и длиной 2/ нагревают электрическим током и измеряют
ее электрическое сопротивление. Кольцевую область а < г < Ь, О < х < 2/,
окружающую проволоку, заполняют веществом, коэффициент теплопровод-
теплопроводности которого Кх нужно измерить; при этом температуру внешних поверх-
поверхностей r — b, а также z = 0 и z = 2l поддерживают равной нулю.
Пусть v — температура проволоки в точке х (предполагается, что она
постоянна по всему поперечному сечению, как и в § 10 гл. IV), а поток
в области 0 < г < b радиален ***); если предположить, кроме того, что на
поверхности раздела г — а между проволокой и окружающей средой изме-
изменение температуры происходит непрерывно ****), то из B.4) мы находим
*) Если а — отрицательная величина (как, например, для графита), то /0
в B.27) следует заменить на /0 [г (—aAJK)^2]- Числовые значения B.27) даны Якобом
в работе [56], где а — величина положительная, и в работе [57], где а — величина
отрицательная.
**) Неустановившееся состояние рассматривается в работе [16] (см. также § 4
гл. XIII).
***) Полная задача с двумя переменными, в которой это предположение не де-
делается, рассматривается в § 3 гл. VIII (см. [14]).
****) Как отмечалось в пункте Ж § 9 гл. I, на поверхности раздела двух твердых
тел (если только между ними нет очень хорошего контакта), всегда может быть ска-
скачок температуры. Как показал Смолуховский [17], при наличии контакта между твер-
твердым телом и газом на поверхности имеется скачок температуры, величина которого
зависит от температурного градиента (см. также [18]). В случае скачка температуры
на поверхности для его учета необходимо изменить B.29).
192 ГЛ. VII. ТЕПЛОВОЙ ПОТОК В НЕОГРАНИЧЕННОМ ЦИЛИНДРЕ [§ 3
потерю тепла проволокой в точке х в виде
¦тш"- <2-29>
Тогда дифференциальное уравнение, описывающее распространение тепла
в проволоке, будет иметь вид A0.4) гл. IV, но вместо члена Hpv будет
стоять B.29). Оно исследуется таким же образом, как и в § 11 гл. IV.
§ 3. Установившаяся, периодически изменяющаяся температура
в круговых цилиндрах [19—22]
Как и в § 7 гл. III, ищем решения с периодом 2гс/со, содержащие временной
множитель eimt (напомним, что на этот множитель нужно умножить все выражения
для температур и потоков и что мы условились всюду пропускать его). Тогда соот-
соотношение A.3) данной главы принимает вид
Общее его решение записывается следующим образом (ср. соотношение F) при-
приложения 3):
v = PI0 (*r/V.) + QK0 (kriH C.2)
где
.-(¦?)*• «"»
Поток / определяется уравнением
/ = - К jp = -/ШV/, (Лг/*) + Kk'ibQKx (knt>). C.4)
Функции Бесселя мнимого аргумента в соотношениях C.2) и C.4) выражаются
при помощи табулированных функций ber, bei, ker и kei, которые определяются соот-
соотношениями (ср. [23])
inln Ыъ) = Ьегя г + ? Ье1я «г, C.5)
ГпКп Ы1%) = кегя z +1 keirt г, C.6)
причем их числовые значения для любых значений г и k можно считать известными.
Предположим теперь, что vx и Fx — величины температуры и теплового потока
на поверхности г = аи a v[ и f[ — соответствующие величины на поверхности г = а%.
Решая затем C.2) и C.4) при г=аь получим зависимость Р и Q от величин vx и /j.
Подставляя найденные значения Р и Q в C.2) и C.4) при г — а2, получим зависи-
зависимость v\ и /[ от величин vx и fx в виде _^
(;;)(с:)(;;)
где
А = ах ki^ [/0 (W/f) Ki (kaxil*) + Ко (WA) /i (kaxi^)l C.8)
B = (^\ [/о (Ла,/У«) Ко (W/f) - Ко (&MJ/f) /о (W/2)l. C.9)
С = A:^! [/! (WO ATi (*ai/!/0 ~ A^i (W70 /i (Ла,^01. (ЗЛО)
D = axkixl* [/0 (Ла^'А) /Ci (WO + Ко (W«) Л (WAI. C.11)
^D — BC = -^. C.12)
#2
Для упрощения выкладок используется соотношение B2) приложения 3. Приве-
Приведенная выше запись в виде матриц была рассмотрена в § 7 гл. III. Из соотношения
§ 4] ГЛ. VII. ТЕПЛОВОЙ ПОТОК В НЕОГРАНИЧЕННОМ ЦИЛИНДРЕ 193
C.12) следует, что vx и /х можно выразить через v[ и f[ в виде
Так же, как и в § 7 гл. III, искомые решения для составных цилиндрических
областей можно непосредственно получить, перемножая соответствующие матрицы.
Например, если область ах < г < а2 состоит из вещества, характеризуемого величи-
величинами Av Bv Сх, DXy определяемыми из C.8) — C.12), а область а2 < г < аг — из другого
вещества, характеризуемого величинами Аъ В2, С2, D2, и если между этими двумя
веществами вдоль поверхности а2 термическое сопротивление на единицу площади
равно R, то
U)[ ^ C14)
Как отмечалось в § 7 гл. III, общие выражения быстро становятся слишком
сложными, но для любых заданных условий можно найти из таблиц численные зна-
значения Л, By Су D п выполнить умножение квадратных матриц в соотношении C.14)
или эквивалентных им матриц. Граничные условия на внутренней и внешней поверх-
поверхностях исследуемого тела позволяют получить два дополнительных соотношения для
температур и тепловых потоков на этих поверхностях и, следовательно, мы можем
определить все четыре величины.
Для области 0<г<я мы должны иметь Q = 0 в C.2), так как КО (?пл/2)->оо
при г -> 0. Отсюда следует, что при г = а
У» C-15)
I0
Для неограниченной области г > Ь в соотношении C.2) Р должно равняться нулю,
так как /0 (krl^2)-^co при г->оо. Следовательно, в данном случае при г=6мы можем
написать
к^к(шЦу
§ 4. Неограниченный цилиндр. Радиальный поток.
Неустановившаяся температура
Пусть начальное распределение температур задано в виде v = f(r),
и пусть поверхность г = а поддерживается при постоянной температуре, ко-
которую можно принять равной нулю *).
Уравнения температурного поля записываются в виде
v = 0 при г = а
и
v = f(r) при ? = 0.
Если положить v = e-x%HUy где и — функция только г, то мы получим
для и уравнение
d2u . 1 du
которое представляет собой уравнение Бесселя нулевого порядка.
*) Если температура поверхности постоянна и равна t/0, то, положив v = v0 -\- w,
мы можем свести этот случай к случаю нулевой температуры.
13 Г. Карслоу, Д. Егер
194 ГЛ VII. ТЕПЛОВОЙ ПОТОК В НЕОГРАНИЧЕННОМ ЦИЛИНДРЕ [§ 4
Так как его решение второго рода К0(аг) неограничено при г = 0, то
частное решение уравнения теплопроводности, удовлетворяющее нашей задаче,
имеет вид
v= AJ0(ar) e-xa2t,
где J0(x) — функция Бесселя первого рода нулевого порядка*). Чтобы удо-
удовлетворить граничному условию, а должно служить корнем уравнения
Известно, что это уравнение не имеет комплексных или кратных корней,
а имеет бесчисленное множество действительных положительных корней [24)
Каждому положительному корню а соответствует отрицательный ко-
корень— а. Первые несколько корней приводятся в приложении 4 (см. табл. 3>
С = оо).
Если функцию /(г) можно разложить в ряд**)
••' D.1)
то решением задачи служит ряд
¦то О
,*,-"& D-2)
Допустим, что можно произвести такое разложение в ряд и что сам ряд
можно интегрировать почленно ***). Тогда, воспользовавшись определенными
интегралами, которые мы рассмотрим в следующем параграфе, можно найти
коэффициенты этого ряда.
Ряд Фурье — Бесселя D.1), представляющий собой разложение функ-
функции /(г), можно применить для решения задачи о цилиндре с нулевой тем-
температурой поверхности. Если же на его поверхности происходит теплообмен
со средой нулевой температуры, то граничное условие должно иметь вид
а для того чтобы У0(аг) удовлетворяло заданному условию, а должно служить
корнем уравнения
У0 (аа) = 0. D.3)
В этом случае мы предполагаем, что функцию /(г) можно разложить
в ряд D.1), где ап теперь являются корнями D.3). Разложение в такой ряд
(ряд Дини) и соответствующие разложения в ряд по функциям Бесселя я-го
порядка рассматриваются в книге Ватсона [24].
*) О функциях Бесселя см. приложение 3; см. также [24, 25].
**) Для этого достаточно потребовать, чтобы функция- /(г) была кусочно
гладкой. (Прим. ред.)
***) Исследование возможности разложения произвольной функции в ряд по функ-
функциям Бесселя можно найти в [24, 26—-30].
Если функцию /(г) можно разложить в ряд D.1), то еще необходимо показать,
что D.2) удовлетворяет дифференциальному уравнению и начальным и граничным
условиям; иными словами, этот случай полностью аналогичен случаю линейного потока
тепла, изложенному в § 3 гл. III [27]. Те же замечания применимы ко всем случаям
разложения в ряд по бесселевым функциям, рассмотренным в настоящей и в следую-
следующей главах. Процесс доказательства можно провести также на основе метода пре-
преобразования Лапласа (см. приложение 1).
§5]
ГЛ. VII. ТЕПЛОВОЙ ПОТОК В НЕОГРАНИЧЕННОМ ЦИЛИНДРЕ
195
В следующем параграфе мы найдем основные определенные интегралы,
позволяющие нам оценить коэффициенты во всех рядах, которые предста-
представляют для нас интерес. Там же будут решены различные задачи по тепло-
теплопроводности цилиндра; при этом мы будем исходить из предположения о воз-
возможности разложения в ряд и допустимости почленного интегрирования. Все
решения можно получить при помощи преобразования Лапласа, как это сде-
сделано в гл. XIII, XIV.
а а
§ б. Интегралы *) f rJn («r) Jn @r) dr и J r [Jn (<zr)]* dr
о о
Пусть u=:Jn(ar) и v = Jn($r). Тогда из уравнения Бесселя получим
Тогда
du
Последнее обращается в нуль при
aJn (pa) J'n (ос) — рп (aa) /„ (pa) = О,
где
Таким образом, если аир являются двумя различными положительными
корнями уравнений
1)
или 2)
или 3)
мы получим
j'n (аса) + hJn (aa) = О,
frJn(*r)Jn$r)dr = O.
E.1)
Кроме того, поскольку
da
*) Для сходимости этих интегралов при г = 0 необходимо, чтобы действительная
часть л была больше чем —1. В дальнейшем эти интегралы будут применяться в тех
случаях, когда л действительно и не меньше нуля. •.-.,.
13*
196 ГЛ. VII. ТЕПЛОВОЙ ПОТОК В НЕОГРАНИЧЕННОМ ЦИЛИНДРЕ [§ 5
можно написать
Таким образом,
d ( du\2 i о о du2 9 du2
Интегрируя по частям, получим следующее выражение:
а
2ос2 У г я2 tfr = [r2 {^J + (а2г2 — /г2) я2]*.
Используя соотношение A) приложения 3 при нижнем пределе, находим,
что
а
fr{Jn (ar)P dr = ^^ [aV {J'n (aa)}2 + (aV - я2) {У„ (ая)}2] =
О \
= -f- [{J'n (aa)}2 + A - ~) [Ja (aa)}*).
В результате получим:
1) если а является корнем*) уравнения Jn(aa) = 0, то
а
f r [Jn (ar)}2rfr = ?• {/п (aa)}2; E.2)
о
2) если а является корнем уравнения j'n(<xa) = 0, то
f r {Jn (аг)}Чг = -? A - ^-) {Уя (aa)J; E.3)
О
3) если а является корнем уравнения аУя(аа) + /гУя(аа) = О, то
/ r {Jn (ar)}2 tfr = -^т {^2+ (^2 - /г2)} {Уя (аа)}2. E.4)
Наконец, отметим, что из рекуррентной формулы (см. A7) приложения 3)
следует
Отсюда непосредственно вытекает, что для любого а и п > — 1
г
r«+1J.(ar)rfr =1 r«+Ve+1(ar). E.5)
О
*) Известно, что все корни этого и других уравнений (см. B) и C)) являются
действительными и среди них нет кратных [24].
§ 6] ГЛ. VII. ТЕПЛОВОЙ ПОТОК В НЕОГРАНИЧЕННОМ ЦИЛИНДРЕ 197
§ 6. Неограниченный цилиндр с температурой поверхности y(f)
и начальной температурой /(г)
Рассматривая вначале случай начальной температуры, равной /(/*),
и температуры поверхности, равной нулю, получим
где alt a2, ...—положительные корни уравнения
J0(aa) = 0. F.2)
Умножим обе части уравнения F.1) на rJQ(anr) и проинтегрируем от 0>
до а; тогда, используя соотношения E.1) и E.2) предыдущего параграфа,
а именно
а
/ rJ0 (amr) Jo (anr) dr = Ot тфп,
о
a
f r Vo Kr)]2 dr = \ а2 [Л (aan)\2 = ~ a2j\ (<*<*„).
6
где учитывается, что Jq(z) = —Jt(z), находим
a
An= 2 22 frf(r)J0(r*n)dr. F.3)
a Jx (aan) J
Следовательно,
oo a '
« " 2-''— p F#4)
' = 71 e~<{ TfS Irf (
В случае постоянной начальной температуры, f(r) = V, интеграл
в F.4) вычисляется с помощью E.5). В результате имеем
Используя еще раз E.5), находим среднюю температуру цилиндра;
она равна
a оо
_j rvdr = _^e *. F.6)
1 л
Пусть мы имеем параболическое начальное распределение темпе-
температуры, например
f(r) = V0 — kr*\
тогда, интегрируя по частям и используя E.5), находим
r*J0(ar) dr = ^-Jx (aa) — Ц-
0
198
ГЛ. VII. ТЕПЛОВОЙ ПОТОК В НЕОГРАНИЧЕННОМ ЦИЛИНДРЕ
[§б
Итак, воспользовавшись этим результатом, мы получим вместо F.4)
соотношение
F.7)
Если начальная температура цилиндра равна нулю и при t > О
его поверхность поддерживается при постоянной температуре V,
то решение, полученное в результате
вычитания F.5) из V, имеет вид
F.8)
При расчетах удобнее исполь-
использовать безразмерные переменные.
Поэтому запишем .
аося = ря и -^-=Г; F.9)
тогда F.8) принимает вид *)
v
-у
= 1 —z У,е
г/а
Рис. 24. Распределение температур в раз-
различные моменты времени в цилиндре
радиуса а для случая нулевой начальной
температуры и температуры поверхности,
равной V.
Числа на кривых указывают величины xt/a2.
где теперь ±р„(я=1, 2,
корни уравнения
F.10)
..) —
F.11)
Первые несколько корней этого
уравнения приведены в приложении 4
(табл. 3, при С = оо); первые пятьдесят корней с соответствующими значе-
значениями Ji($n) можно найти в [25].
На рис. 24 приведены графики зависимости v/V от г/а (при разных зна-
значениях Г), определяемой соотношением F.10). Полученные кривые очень
похожи на соответствующие кривые для пластины, показанные на рис. 11;
и действительно [32, 33]**), можно найти такие значения T1=x?1/a2 для
пластины толщиной 2а, что распределение температуры в цилиндре в момент
времени t окажется очень близким к распределению температуры в пластине
в момент времени tv Температура на оси цилиндра ***) и зависимость средней
температуры цилиндра от Т приведены на рис. 12. Ряд F.10) очень быстро
сходится при любых значениях Т (кроме очень малых). Соответствующие
решения, пригодные для расчетов при малых Г, приводятся в § 3 гл. XIII.
Если начальная температура цилиндра равна нулю, а темпера-
температура его поверхности равна ср(/), то решение, полученное методом
*) Величины Jo (r$n/a), входящие в F.10), протабулированы в работе [31] до пяти
десятичных знаков при п= 1, 2, ..., 10 и (г/а) — от 0 до 1 с шагом @,01).
**) То же замечание остается применимым и к задачам с другими граничными
условиями.
***) Численные значения для температуры на оси цилиндра приведены в [34].
§ 7] ГЛ. VII. ТЕПЛОВОЙ ПОТОК В НЕОГРАНИЧЕННОМ ЦИЛИНДРЕ 199
Дюамеля (см. § 14 гл. I) из F.8), имеет вид
— тгЁ'-*5^/'4"*"»*- F12>
/2=1 6
Если начальная температура равна нулю и температура поверхности
равна kt, то
Если начальная температура равна нулю и температура поверхности равна
V sin Ш +е). то
+ ~~ Zj eXP (—"**&) /24 ^ '—^— ' F-54)
Здесь первый член можно считать решением задачи для установившегося перио-
периодического состояния, второй — для неустановившегося состояния. Напишем *)
I ±\
/0\ zi2 ) = ber z + i bei z = Мо (z) ei% {z) ' F.15)
и со' = (й>/%)!/*; тогда первый член решения F.14) примет вид
, sin {о>^ -f- e -f- 0q (w'r) —• 6q (й/а)}. F.16)
§ 7. Неограниченный цилиндр с теплообменом на поверхности
В настоящем параграфе мы рассмотрим круговой цилиндр с начальной
температурой /(г) и теплообменом на его поверхности со средой. Пусть
/ (г) = iVo («iO + iVo (а2г) + •... G.1)
где ±ccj, ±a2, ...—корни уравнения
О. G.2)
Все эти корни действительны и просты [24]. Тогда, используя соотно-
соотношение E.4) данной главы
о
получим
а
fr[J0(*nr)]>dr = J
*) Объяснение символов М0(г) и Ь0(гг) и их численные значения приведены
в книге Мак-Лахлана [23].
200 ГЛ. YII. ТЕПЛОВОЙ ПОТОК В НЕОГРАНИЧЕННОМ ЦИЛИНДРЕ [§ 7
Для случая / (г) = V = const находим, используя соотношение E.5) дан-
данной главы
а к
ап) У,
Для перехода к безразмерным величинам введем следующие обозначения:
Тогда можно написать
оо
где ±р (л=1, 2, ...) — корни уравнения
рУ1ф)=ЛУоф). G.7)
Таблица значений этих корней приведена в приложении 4.
Если начальная температура цилиндра равна нулю и на его поверхности
происходит теплообмен со средой, имеющей температуру V, то
? <л 2 ov2ril/ 7 . G.8)
Численные значения G.6) и G.8) приведены в ряде работ [35—38] *).
Средняя температура цилиндра t/cp определяется соотношением
G.9)
а теплосодержание, приходящееся на единицу длины цилиндра, равно гся2рС1/ср. Если
начальная температура цилиндра равна нулю и на его поверхности происходит
теплообмен со средой, имеющей температуру kty то
" о2-г
где А, Т, рл определяются из G.5) и G.7).
Если начальная температура цилиндра равна нулю и на его поверхности
происходит теплообмен со средой, имеющей температуру V sin (co*-f-?)> то
\ i {(A./*)* /, [a (to./*)'/*] + А/о [а (шМЧ\ )
- 92Т $2„ (а2а> cos е — %.f sin е) Уо (гр_/в)
Используя F.15), можно записать первый член G.11) в виде
где е0 и "По — сложные выражения, содержащие функции ber и bei **)•
*) Приложение к определению поправки на излучение в калориметрии изло-
изложено в [39].
**) Численные значения е0 и y]0 приведены в [40].
§8]
ГЛ. VII. ТЕПЛОВОЙ ПОТОК В НЕОГРАНИЧЕННОМ ЦИЛИНДРЕ
201
§ 8. Неограниченный цилиндр с постоянным потоком тепла
на поверхности*)
I. Нулевая начальная температура. Постоянный поток тепла Fo
внутрь цилиндра.
0
2F0%t
Ка
(8.2)
где ап (#=1, 2, ...) — положительные корни уравнения
^(^ = 0.
Некоторые значения функции v — BF0xt/Ka) приведены на рис. 25.
Доказательство (8.1) изложено в § 2 гл. XIII.
И. Начальная температура f (r). Тепловой поток на поверхности равен
нулю.
где ап — корни уравнения (8.2).
Это соответствует случаю /г, равного нулю, в задаче, рассмотренной в преды-
предыдущем параграфе. Однако следует отметить, что условие h = 0 в соотношении G.3)
данной главы не приводит к соот-
соотношению (8.3) из-за отсутствия пер-
первого члена. В § 9 гл. I указывалось,
что при граничных условиях вида ц%
V4
OJ
h всегда предполагается величиной
положительной, и поэтому допуще-
допущение для таких условий, что h = 0,
часто не дает правильного решения
задачи, в которой граница непрони-
непроницаема для тепла. В данной задаче
физический смысл различия заклю-
заключается в том, что если h положи-
положительно, то конечная температура
цилиндра равна нулю независимо от
того, насколько малой может быть
величина &, тогда как при h = 0
(т. е. при условии, что поверхность
непроницаема для тепла) конечная
температура цилиндра равна не нулю,
а средней величине начальной темпе-
температуры. Математически это соответ-
соответствует тому, что к нашему соотно-
соотношению следует добавить постоянный
первый член, аналогичный постоян-
постоянному первому члену ряда Фурье по косинусам **). То же остается справедливым и
для сферы в отсутствие теплового потока на ее поверхности (см. § 7 гл. IX).
& -о. г
-0.2
Рис. 25. Температура в цилиндре кругового
сечения для случая постоянного потока
тепла на поверхности.
Числа на кривых указывают величины xt/a2.
*) Подобные задачи возникают при рассмотрении индукционного нагрева, а
также сушки глины (ср. [41—44]).
**) Эта трудность не возникает при использовании метода преобразования Ла-
Лапласа, рассматриваемого в гл. XIII, так как в этом случае члены, которые имеются
в решении, определяются особыми точками функции комплексного переменного
(см. также [24]). В работе [45] постоянный член, соответствующий первому члену»
опущен и, таким образом, приведенное в ней решение некорректно.
202 ГЛ. VII. ТЕПЛОВОЙ ПОТОК В НЕОГРАНИЧЕННОМ ЦИЛИНДРЕ [§ 9
§ 9. Неограниченный цилиндр с внутренними источниками тепла*)
I. Начальная температура и температура поверхности равны
нулю. Мощность источников **) при t > 0 равна постоянной величине Ао
АК
аК
J0(ran)
4/, (аап)
где <хп — положительные корни уравнения У0(аа) = 0. Некоторые значения
температуры приведены на рис. 26. Доказательство (9.1) изложено в § 2
гл. XIII.
ав го
г/а
Рис. 26. Температура в цилиндре кругового
сечения для случая постоянного выделения тепла
в единицу времени и нулевой температуры
поверхности.
II. Начальная температура и температура поверхности равны нулю. При
t>0 мощность источников равна Aoe~lt.
2
1г
(г<хп)
92
где ап — положительные корни уравнения Уо (я°0 = 0.
III. Начальная температура равна нулю. При t>0 мощность источников
равна постоянной Ао. На поверхности г = а происходит теплообмен со средой
нулевой температуры.
г*.
2hA0
Уо (гая)
(аап)
(9.3)
где ая — положительные корни уравнения а/, (яа) = hJ0 (aa).
•) Эта задача и соответствующая задача для полого цилиндра рассматриваются
в [46] в приложении к биологическим проблемам.
**) Здесь автор имеет в виду равномерное распределение источников в цилиндре.
{Прим. ред.)
§ 10] ГЛ. VII. ТЕПЛОВОЙ ПОТОК В НЕОГРАНИЧЕННОМ ЦИЛИНДРЕ 203
§ 10. Неограниченный полый цилиндр. Радиальный поток
I. Неограниченный полый цилиндр. Поверхности г = а и r = b
поддерживаются при нулевой температуре. Начальная темпера-
температура /(г).
В этом случае мы имеем
Положим v = ue~%aH% где и зависит только от г; тогда для и получим
уравнение
d2u . 1 du . о п
т, е. уравнение Бесселя нулевого порядка.
Если область изменения г не включает г = 0, то могут встретиться
функции Бесселя второго рода. Рассмотрим функцию
Uo(*r) = Jo(*r)Vo(*b) — Jo(*t>)YQ(*r). A0.2)
Эта функция обращается в нуль при г = ft. Кроме того, она обращается
в нуль и при /* = а, если а служит корнем уравнения
J0(aa) K0(aft) —70(oft) К0(аа) = 0. A0.3)
Известно, что все корни уравнения A0.3) действительны и просты и
что каждому положительному корню а соответствует отрицательный корень
— а [25]*). Некоторые значения этих корней приведены в табл. 4 приложе-
приложения 4. Сначала найдем интегралы от функций U0(ar), аналогичные соответ-
соответствующим интегралам, рассмотренным в § 5 данной главы. Повторяя при-
приведенный там анализ для значений u = U0(ar) и v = U0($r), получим
ъ
= 0, A0.4)
f
где а и C — два различных корня уравнения A0.3).
Кроме того,
а
Теперь, используя соотношение B0) приложения 3, получим
igil = ab [j'o{ab) Y0(ab)— Y'0(ab)M*t>)] = — |. A0.6)
= *а [j'o (аа) Ко (aft) — Ко (aa) Jo (aft)]. A0.7)
лт-Ь
Помимо этого,
\ 4^
L ar Jr-a
Однако если a служит корнем A0.3), то, например,
J0(aa) Y0(aa)
Jo(ba) Y0(ba) P-
*) В цитируемой работе приводится также формула для вычисления больших
корней этого уравнения. Значения корней для Ь/а=\2, 1,5, 2,0 указаны в [47, 48].
См. также [49]."
204 ГЛ. VII. ТЕПЛОВОЙ ПОТОК В НЕОГРАНИЧЕННОМ ЦИЛИНДРЕ [§ 10
Таким образом, A0.7) принимает вид
S]=-^-. A0.8)
Следовательно, A0.5) можно записать в виде
Два других интеграла можно найти почти тем же способом из нашего
дифференциального уравнения, используя A0.6) и A0.8). Эти интегралы
имеют вид
/
а
b
CI0.ll>
где a — корень уравнения A0.3).
Предположим теперь, что начальную температуру /(/•) можно разло-
разложить в ряд
/ (г) = Аги0 (агг) + A2U0 (а2г) + ...,
который можно проинтегрировать почленно; тогда из A0.4) и A0.9) имеем
А(аая)
AJ А()
Т АЫ-АЫ
Таким образом, мы приходим к решению нашей задачи в виде
У§КЬ1(К) ^"оЫ/гти.Ы*. A0.12)
причем суммирование ведется по всем положительным корням уравне-
уравнения A0.3).
Для случая постоянной начальной температуры f(r) = V мы по-
получим, используя A0.8),
II. Начальная температура равна /(г), a /i/?# ^>0 поверхности
г = а а г = Ь поддерживаются при постоянных температурах vx a v2.
В этом случае, имеющем большое практическое значение, мы можем на-
написать, как и в § 14 гл. I,
где
vl\n(b/r)Jt-v2\n(r/a) И0 14v
— йвд • (ШЛ4>
согласно соотношению B.3) данной главы, представляет собой температуру
при установившемся потоке между поверхностями г = а при vx и г = Ь
§ 11] ГЛ. VII. ТЕПЛОВОЙ ПОТОК В НЕОГРАНИЧЕННОМ ЦИЛИНДРЕ 205
при v2, a w определяется A0.12), в котором /(г) заменено на /(г) — и.
Используя A0.11), получим искомое решение в виде
я = 1
оо
{v2Jq (aan) — V\Jq(b*n)} Jo (aan) UQ (ran) ^-xaznt , yx In(b/r) + v2\n (r/a)
\n(b/a)
A0.15)
Ряд других решений для полого цилиндра, выведенных рассмотрен-
рассмотренными выше методами, приводится в [50, 51]. При наличии теплообмена или
других граничных условий на поверхностях подобные задачи можно рас-
рассматривать аналогичным образом, используя соответствующие обобщения
цилиндрической функции U0(ar)\ однако эти задачи, вероятно, лучше рас-
рассматривать методом преобразований Лапласа, что и будет сделано в § 4
гл. XIII.
§ 11. Неограниченный цилиндр. Установившаяся температура.
Общий случай
I. Установившаяся температура в цилиндре 0<;г < а. Температура поверх-
поверхности F @, z).
Разложим F F, z) в ряд Фурье
21 {?я(*)СО8Лб + фяBГ)81Плв}. (Ц.1)
/1 = 0
Запишем теперь интегралы Фурье для уп (г) и фя (г):
О
= -¦¦- /
6
(И.2)
da УЧя(Р)С08а(Р-*)<*р.
6 -оо J
Тогда, поскольку выражения
In (ar) cos а (Р — z) COS лб и In (ar) COS а (? — z) sin лв
<где In (z) определено в приложении 3) представляют собой решения уравнения Лап-
Лапласа в цилиндрических координатах, конечные при г = 0, решение нашей задачи
имеет вид
оо °° +°°
оо
V=4^ f J$^a\da f
я=0 0
ИЛИ
/ У^^ A1.3)
Я=0 -оо
Здесь предполагается, что порядок интегрирования можно изменить.
Чтобы оценить второй интеграл в A1.3), рассмотрим интеграл
A1.4)
206 ГЛ. VII. ТЕПЛОВОЙ ПОТОК В НЕОГРАНИЧЕННОМ ЦИЛИНДРЕ [§ 11
взятый по контуру, содержащему при р > z мнимую ось и большую полуокружность
в правой полуплоскости. Подынтегральное выражение имеет полюсы в точках
as(s = 1, 2, ...), служащих положительными корнями уравнения
Определяя вычеты в этих полюсах, мы получим окончательно
f со"а^-^-тШаа—^11е'^~г1уШ' (Ш5>
Таким образом, из C) следует
оо оо °°
?. A1.6)
л s Jn\aas) J
Если температура поверхности является функцией только zy например имеет
вид f (z), то решение принимает вид
"=тХттЭт / *" "Ч/<*+«> + /<*-«> W«. A1.7)
5 = 1 0
где а5 служат положительными корнями уравнения
у0 (да) = 0.
Например, если
/(I 0
то из A1.7) следует, что
«=1
(П.8)
Л(ras)
" a jj, asjx (да,) ' • * ^" _
где мы использовали соотношение
оо
!2_*jg?._lt ой)
5=1
которое можно получить, положив / = 0в соотношении F.5) данной главы.
Соотношение A1.8) можно также получить непосредственно при помощи ме-
метода, используемого ниже.
II. Установившаяся температура в цилиндре 0<; г < л, движущемся со ско-
скоростью U в направлении своей оси. При z < 0 температура поверхности равна
единице; при z > 0 она равна нулю.
В этом случае, как и в § 7 гл. I, дифференциальное уравнение имеет вид
Если мы ищем решение A1.10) вида
J0(«r)u(z),
то и должно удовлетворять уравнению
d2u U du
§ 12] ГЛ. VII. ТЕПЛОВОЙ ПОТОК В НЕОГРАНИЧЕННОМ ЦИЛИНДРЕ 207
Таким образом, если ± as — корни уравнения
Jo (аа) = 0,
то
*<0,
(k - Vk2 + 4)]t z<0
A1.11)
(где k обозначает ?//2%) удовлетворяют нашему дифференциальному уравнению и
граничным условиям. Для нахождения значений as и bs следует воспользоваться ус-
условием, требующим непрерывности v и -^— при z=0. Используя A1.9), мы нахо-
находим, что из условия непрерывности следует
2
b
Следовательно, окончательно имеем
При рассмотрении ряда задач этого типа [52, 53] был использован метод, опи-
описанный выше, а также метод движущихся источников тепла (ср. гл. X).
§ 12. Неограниченный цилиндр. Неустановившаяся температура.
Общий случай
В данном параграфе рассматривается ряд задач для неограниченного цилиндра,
в котором поток не радиален. При этом используются разобранные выше методы,
а также интегралы, приведенные в § 5 настоящей главы.
I. Температура поверхности г = а равна нулю. Начальная температура
v = f(r, 0).
В данном случае уравнение теплопроводности принимает вид
dv / d2v I dv 1 d2v
а выражение e~xa2tJn(ar) (An cos nb-±-Bnsln лб) удовлетворяет этому уравнению.
Здесь п принимает целые значения, так как температура является периодической
функцией от 0 с периодом 2я.
Разложим функцию /(г, 0) в ряд Фурье
оо
/ (г, 0) = 2 ^п cos л6 + bn sin л0),
п-0
где
r, 0) cos л0
?„ = — Г/(г, 6) sin /гб
208 ГЛ. VII. ТЕПЛОВОЙ ПОТОК В НЕОГРАНИЧЕННОМ ЦИЛИНДРЕ [§ 12
Коэффициенты ат Ьп и а0 являются функциями от г. Разложим каждый из них
в ряд функций Бесселя л-го порядка
оо
«яв ^An.sJnbsr),
5=1
где alt а2, ..., as, ... —положительные корни уравнения
Эти корни представлены в виде таблиц для п от 0 до 5 в книге [24].
Тогда мы можем написать
а тс
,,l ц8 /* [fir, 6) Уо (V) r dr M,
а тс
.М) V
2 f Л М2 / / / <Г' 9> C0S
а
Bn, s = 2ТТ7 v»T / / f (r> 0) sin nQJn (<V) r dr dQ-
tzu \J (а п\\ J *J
Таким образом, мы получим наше решение в виде
оо оо 2
v = 21 21 Dь 5 cos п^ + Вя> 5 Sin Л0) Ул (а5г) ^">**5 . A2:1)
5=1 л = 0
II. Теплообмен на поверхности г=а со средой нулевой температуры. На-
Начальная температура v = / (г, 0).
Разложим в ряд Фурье функцию /(г, 0), как и в задаче I,
/ (г» 0) = 21 (ап cos пЬ + bn sin пЪ).
я=0
Коэффициенты ая и Ьп являются функциями г. Разложим каждый из них в ряд
функций Бесселя л-го порядка
где olf a2. ... —положительные корни уравнения
Тогда получим
А,,=-
2 a *
Ап, s = 2/2 а °д, 2U , v18 /" /*/(г, в)cos пв/„(ct,r)гrfrd6,
Bn,s = 2B. о "', 2U . . иа /" /* / (Л 9) sin лвУ„ (a,r) г dr db
r.a2 (aj + A2 - луа2) {У„ (a,a)}2 ^ j/
§ 12] ГЛ. VII. ТЕПЛОВОЙ ПОТОК В НЕОГРАНИЧЕННОМ ЦИЛИНДРЕ 209
и
оо оо _ 2.
v = 2 2 (Л*' s cos nb + Bnt s sin nb) Jn (asr) e "* . A2.2)
III. Температура поверхности г = а равна нулю. Начальная температура
v = / (г, 0, г).
В данном случае имеем
dv / ^2t; I dv . 1 d2t; . d2v \
dt \ dr2 ' r ^r r2 <^02 d-г2 J
и выражение
является частным интегралом.
Разложим теперь функцию / (г, 6, г) в ряд Фурье
оо
2 (tf/i cos nb + Ьп sin л0).
л = 0
Коэффициенты ал и ^л являются функциями гиг. Обозначим эти функции че-
через Fn (r, z) и G„ (г, г) и разложим их в ряд функций Бесселя, определяемых поло-
положительными корнями уравнения
Пусть, кроме того,
Наконец, выразим функции <рл (г) и фл (г) чеР^з интегралы Фурье
0 -оо
оо оо
j„ ф) cos atf —
0 —ОО
Тогда мы получим наше решение в виде
оо оо
+ фл (р) sin л0] cos а (^ — z) da d$, A2.3)
где суммирование по ?х производится по положительным корням уравнения
Изменяя порядок интегрирования в A2.3), окончательно получим
оо оо
" °° +ф(Р)81пяв}^. A2.4)
IV. Температура поверхности г=а равна t/ = /7@, гг). Начальная темпера-
температура с/ = / (г, 0, г).
Как показано в § 14 гл. I и в § 11 гл. VII, этот случай приводится соответ-
соответственно к примерам III и I, если положить v=u-\-w.
V. Неограниченный цилиндр. Поверхность г=а и плоскости 0 = 0 и 0 = 0О
поддерживаются при нулевой температуре. Начальная температура f (г, 0).
14 Г. Карслоу, Д. Егер
210 ГЛ. VII. ТЕПЛОВОЙ ПОТОК В НЕОГРАНИЧЕННОМ ЦИЛИНДРЕ [§ 12
В данном случае можно написать
ду___ (д2у I dv I д2у\
dt ~~*{дг2 ^~ г дг ~*~ г2 дЬ2 )'
Выражение
является частным интегралом этого уравнения.
Условия при г=а, 0 = 0 и 0=6О удовлетворяются в том случае, если т — по-
положительное целое число, а а — корень уравнения
Разложим функцию /(г, 0) в ряд по синусам
т Sin-
1
где коэффициенты ат являются функциями г, например Fm (r).
Теперь разложим Fm (r) в ряд функций Бесселя, определяемых положитель-
положительными корнями уравнения
Таким образом, мы получим решение нашей задачи в виде
A2.5)
а т — \
где, используя соотношение E.2) данной главы,
а 0О
At, т — 2n f r'
здесь суммирование по а производится по положительным корням уравнения
Решение для клина со щеками 0 = 0 и 0 = 0О можно получить из написанного
выше при я->оо. Если начальная температура равна постоянной*), то A2.5) при-
принимает вид
sins6mf'^ psK^ /ГЛ(^МГ- A2'6)
где
5 = B/г+1)тс/0о и ±ат, да=1, 2, ...
служат корнями уравнения
Js(aa) = 0. A2.7)
ЛИТЕРАТУРА
1. Porter, Martin, Phil. Mag. 20,511 A910).
2. L a m b, W i 1 s о n, Proc. Roy. Soc. A65, 285 A899).
3. Niven, Proc. Roy. Soc. A76, 34 A905).
4. Poo 1 e, Phil. Mag. 24, 45 A912); 27, 58 A914).
5. В г i d g m a n, Proc. Am. Acad. Arts Sci. 57, 80 A922).
*) Некоторые численные результаты для данного случая приведены в [54]. За-
Задача о полуограниченном цилиндре с этим поперечным сечением рассматривается
в [55].
ГЛ. VII. ТЕПЛОВОЙ ПОТОК В НЕОГРАНИЧЕННОМ ЦИЛИНДРЕ 211
6. Strut t, Phil. Mag. 5, 904—914 A928).
7. E m m e r i с h, J. Appl. Phys. 21, 75—80 A950).
8. T h о r n, S i m p s о n, J. Appl. Phys. 24, 297—299 A953).
9. Angel 1, Phys. Rev. 33, 421 A911).
10. Worthing, Phys. Rev. 4, 536 A914).
11. Langmuir, Phys. Rev. 7, 151 A916).
12. Powell, Schofield, Proc. Phys. Soc. 51, 153 A939).
13. Schleiermacher, Wied. Ann. 34, 623 A888); 36, 346 A899).
14. Kannuluik, Martin, Proc. Roy. Soc. A141, 144 A933); 144, 496 A934).
15. Gregory, Archer, Proc. Roy. Soc. A110, 91 A926); Phil. Mag. 3, 931 A927);
15, 301 A933).
16. Fischer, Ann. Physik 34, 669 A939).
17. Smoluchowski, Ann. Physik 64, 101 A898); 35, 983 A911).
18. Gregory, Proc. Roy. Soc. A149, 35 A935).
19. Dahl, Trans. ASME 46, 161—208 A924).
20. Awbery, Phil. Mag. 28, 447 A939).
21. V a n G о г с u m, Appl. ScL Res. A2, 272—280 A951).
22. Vodicka, Appl. Sci. Res. A5, 115—120, 268—272, 327—337 A955).
23. McLachlan, Bessel Functions for Engineers, Oxford, 1934.
24. Watson, Theory of Bessel Functions, Cambridge, ed. 2, 1944 (Г. Ватсон, Тео-
Теория бесселевых функций, ИЛ, М., 1949.)
25. Gray, M a t h e w s, Treatise on Bessel Functions, Macmillan, ed. 2, 1922.
(Э. Гр э й, Г. Мэттьюз, Функции Бесселя и их применение в физике и механике,
ИЛ, М., 1953.)
26. Hob son, Proc. Lond. Math. Soc. 7, 359—388 A909).
27. Moore, Trans. Am. Math. Soc. 10, 391—435 A909); 12, 181—206 A911); 21, 107—156
A920).
28. Young, Proc. Lond. Math. Soc. 18, 163—200 A920).
29. Din i, Serie di Fourier, 1880, pp. 246—269.
30. Ford, Studies in Divergent Series and Summability, 1916, Chap. V.
31. Goodwin, Staton, Quart J. Mech. Appl. Math. 1, 220—224 A948).
32. Jaeger, Proc. Phys. Soc. 56, 197 A944).
33. M а с е у, Proc. Phys. Soc. 54, 128 A942).
34. О 1 s о n, S с h u 11 z, Ing. Eng. Chem. 34, 874—877 A942).
35. G u r n e y, L u r i e, Ind. Eng. Chem. 15, 1170 A923).
36. Schack, Stahl u. Eisen 50, 1290 A930).
37. Newman, Trans. Am. Inst. Chem. Engrs 27, 203 A931), Ind. Eng. Chem. 28,
545—548 A936).
38. H e i s 1 e r, Trans. ASME 69, 227—237 A947).
39. V a s i 1 e f f, J. Appl. Phys. 23, 979—983 A952).
40. Grober, Z. Ven dtsch. Ing. 70, 1266 A926).
41. Mace y, Proc. Phys. Soc. 52, 625 A940); 54, 128 A942).
42. Awbery, Proc. Phys. Soc. 55, 202 A943).
43. Jaeger, Proc. Phys. Soc. 56, 197 A944).
44. Newman, Church, J. Appl. Mech. 2, A — 96 A935).
45. С a r s 1 a w, Introduction to the Mathematical Theory of the Conduction of Heat in
Solids, Macmillan, ed. 2, 1921. (Г. Карслоу, Теория теплопроводности, Гостех-
издат, М., 1947.)
46. Thews, Acta Biotheoretica A10, 105—138 A953).
47. К а 1 a h n e, Z. Math. Phys. 54, 55 A907).
48. Jahnke — Emde, Funktionen Tafeln, Teubner, ed. 3, 1933. (E. Янке, Ф. Эмде, Таб-
Таблицы функций с формулами и кривыми, изд. 3-е, Физматгиз, 1959.)
49. L о w a n, H i 1 1 m a n, J. Math. Phys. 22, 208 A943).
50. М u s k a t, Flow of Homogeneous Fluids, McGraw-Hill, 1937.
51. Musk at, J. Appl. Phys. 5, 71 A934).
52. Wilson, Proc. Camb. Phil. Soc. 12, 406 A904).
53. Owen, Proc. Lond. Math. Soc. 23, 238 A925).
54. J a e ge r, Phil. Mag. 33, 527 A942).
55. С г a g g s, Phil. Mag. 36, 220 A945).
56. J a k о b, Trans. ASME 65, 593—605 A943).
57. Jakob, Trans. ASME 70, 25—30 A948).
14*
ГЛАВА VIII
ТЕПЛОВОЙ ПОТОК В ОБЛАСТЯХ, ОГРАНИЧЕННЫХ КООРДИНАТНЫМИ
ПОВЕРХНОСТЯМИ ЦИЛИНДРИЧЕСКОЙ СИСТЕМЫ КООРДИНАТ
§ 1. Введение
В настоящей главе мы исследуем ряд задач по теплопроводности для
областей, ограниченных координатными поверхностями цилиндрической системы
координат, например ограниченный и полуограниченный цилиндры, ограни-
ограниченные полые цилиндры и т. д. Для этого используем методы, изложенные
в предыдущих главах. Задачи этого типа для областей, ограниченных изнутри
цилиндром кругового сечения, можно рассматривать тем же способом, исполь-
используя решения, приведенные в § 5 гл. XIII.
Кроме того, задачи по теплопроводности цилиндрических областей
решаются в §§ 10—15 гл. XIV при помощи функций Грина, а в § 11 гл. XV—
при помощи преобразования Лапласа.
§ 2. Установившееся распределение температур в неограниченной
и полуограниченной среде, обусловленное подводом тепла через круг
Предположим, что через круг радиуса г (где 0<><а), расположен-
расположенный в плоскости 2 = 0, подводится тепло, количество которого в единицу
времени зависит только от г.
Дифференциальное уравнение теплопроводности
^1?iS- = 0 B.1)
z2
дг2 ' гдг
удовлетворяется
для любого X. Таким образом,
B.2)
служит решением нашей задачи, если функцию /(X) можно выбрать так, чтобы
она удовлетворяла заданным условиям в плоскости z = 0. Для этой цели
можно применить интегральную теорему Неймана (см. [1] гл. XIV); однако
два наиболее интересных случая описываются хорошо известными интегралами,
§ 2] гл. viii. тепловой поток в ограниченных областях 213
содержащими функции Бесселя [см. [1], § 13.42 и [2]):
arc sin —, г > а,
Г B.3)
О, г>а,
1/Bа)' Г = а' B*4)
! 1/а, г < а.
Рассмотрим теперь задачу, в которой круговой диск 0^г<а, лежа-
лежащий в плоскости 2 = 0, поддерживается при температуре, равной V.
Здесь мы выбираем /{X) в B.2) равной [BV7TC)sinXa]/A. Тогда
B.5)
представляет собой решение нашей задачи. Согласно B.3) это выражение
равно V для z — 0 и г^.а. Оно служит решением задачи и для области
z > 0, когда круг 0^г<а, расположенный в плоскости ? = 0, поддержи-
поддерживается при температуре V, а тепловой поток через остальную часть пло-
плоскости z = 0 отсутствует.
Если количество тепла, подводимое к неограниченному твердому
телу в единицу времени через единицу площади круга радиуса а,
лежащего в плоскости z = 0 (например, плоского круглого нагревательного
элемента), равно постоянной величине Q, то условие, которое должно удо-
удовлетворяться в плоскости z = 0, имеет вид
Таким образом, используя B.2) и B.4), мы получим решение в виде
Ха)т^- B-7)
Его можно применить к важной задаче полуограниченного твердого тела
z > 0 при различных условиях на поверхности последнего *). Задачи анало-
аналогичного типа в случае неустановившегося состояния разобраны в § 5 гл. X.
I. Температура области z > 0 постоянна и равна V при 0<г<а,
z = 0; вне этого круга тепловой поток отсутствует.
Из B.5) имеем
оо
г> = — f e-}*J0(\r)sin\a—, B.8)
ТС »/ А.
или
2V . i 2a \
B.9)
2V . ( 2а
= — arcsmj [(re)f +
*) Для других задач подобного типа см. [3, 4J.
214 ГЛ. VIII. ТЕПЛОВОЙ ПОТОК В ОГРАНИЧЕННЫХ ОБЛАСТЯХ [§ 2
Тепловой поток F через круг 0 < г < а равен
оо оо
F = — 2Ж ГГ-ёг! rdr = 4KVa f Jx(ka)sm\a^ = 4KVa. B.10)
0 lOZJ*=0 6
При этом для вычисления интеграла используется цитированная выше
работа (см. [1]). Величину R = V/F можно считать термическим сопротивле-
сопротивлением в случае установившегося потока через круг радиуса а в полупростран-
полупространство. Из B.10) следует, что
*=¦?—аЬ" BЛ1)
II. Области z>0 и z <0 с коэффициентами теплопроводности,
равными соответственно Кх и К2* и температурами на больших
расстояниях от начала координат, равными соответственно 0 и V.
Установившийся тепловой поток проходит через круг радиуса а,
расположенный в плоскости z = 0. Остальная часть плоскости
непроницаема для тепла.
Температуры vx и v2 в областях z > 0 и z < 0 находят, как и в при-
примере I; они равны соответственно
B.13)
Эти выражения можно упростить, как и B.8) и (B.9). Термическое
сопротивление равно (Л\ + К2I4аКхК2.
III. Область z > 0 с постоянным тепловым потоком Q через круг
r<a, z = 0 и нулевым потоком через г>а.
Воспользовавшись B.7), получим следующее выражение для искомой
температуры:
оо
v = — f e-XzJ^r)Jx{\a)^-. B.14)
6
Средняя температура vcp области 0 < г < а равна [1]
v =^
о
Так как величина теплового потока через круг радиуса а равна F=na2Q,
то из B.15) следует, что
^ 8 B.16)
Неустановившееся состояние и соответствующая задача для случая нагрева
полосы рассматриваются в § 5 гл. X.
§ 3] ГЛ. VIII. ТЕПЛОВОЙ ПОТОК В ОГРАНИЧЕННЫХ ОБЛАСТЯХ 215
IV. Область z > О с постоянным тепловым потоком Q через круг
0<г<а, z = 0 и нулевой температурой [5]*) в области г>а.
оо
6
B.17)
V. Термическое сопротивление при переходе в полупространство.
Когда тепло или электричество течет через круг радиуса а в полу-
полупространство, часто важно знать установившееся термическое (поверхностное)
или электрическое сопротивление в полупространстве **). Простейшее прибли-
приближение, которое часто используется для малых кругов, заключается в замене
круга полусферой радиуса а (иными словами, вещество считается идеальным
проводником); при этом поток оказывается радиальным. Тогда, учитывая B.14)
гл. IX, мы находим, что термическое сопротивление /?, определяемое как V/F
(где V — температура контакта и F — поток через него), равно
* <2Л8>
Точное значение R в B.11) в случае, когда круг поддерживается при
постоянной температуре, в -^ тс раз больше значения R в уравнении B.18), что
указывает на важность учета области, находящейся вблизи начала координат.
В задачах, представляющих практический интерес, тепло или электри-
электричество обычно подводится в полупространство через провод, и в этом случае
граничное условие постоянства температуры, предполагаемое в примере I,
оказывается недостаточно точным; действительно, можно считать, что постоян-
постоянство потока, как в примере II, является допустимой идеализацией, поэтому,
сравнивая коэффициент 0,25 в уравнении B.11) и коэффициент 8/3it2=0,27
в уравнении B.16), мы можем получить представление о том, как велика
ошибка в найденных нами величинах сопротивления.
§ 3. Установившаяся температура в ограниченном
и полуограниченном цилиндрах
В настоящем параграфе мы приведем ряд простых решений для случая
установившегося потока тепла в ограниченном и полуограниченном цилиндрах.
Путем комбинации решений приведенных выше задач можно получить реше-
решения ряда многих других задач. Например, используя решения задач, приве-
приведенные в примерах III и IV предыдущего параграфа, можно решить задачу
для ограниченного цилиндра с заданным распределением температур на всех
его поверхностях; приняв /г = 0 в решениях задач с граничными условиями,
учитывающими теплообмен, можно решить различные задачи, в которых
отсутствует тепловой поток через некоторые границы; считая, что в приме-
примерах IV и V функция f(z) симметрична относительно ]/2 /, можно решить
две другие задачи для цилиндра при отсутствии потока через одну из пло-
плоских поверхностей; наконец, считая, что в примере V f (z) антисимметрична
относительно l/2 L получим решение для цилиндра с нулевой температурой
*) Следует отметить, что граничные условия в плоскости z = 0 являются «сме-
«смешанными», т. е. задан тепловой поток через часть этой плоскости и задана темпера-
температура для остальной ее части. Для таких задач применима теория двойных интеграль-
интегральных уравнений (ср. [6]). Соответствующая задача для неограниченной полосы \х\<а
вместо круга рассматривается в работе [7].
**) Для случая потока в ограниченной области см. [2], гл. XII.
216 ГЛ. VIII. ТЕПЛОВОЙ ПОТОК В ОГРАНИЧЕННЫХ ОБЛАСТЯХ [§ 3
на одной плоской поверхности и теплообменом на другой. Рассматривая
совокупность всех этих решений, мы получим все возможные комбинации
граничных условий для ограниченного круглого цилиндра. Аналогичным
образом из найденных данных можно получить много других решений для
конечного полого цилиндра. Столь же легко найти решения задач для важных
случаев неодинаковых коэффициентов теплопроводности в направлениях г и z>
а также для различных коэффициентов теплопроводности на разных поверх-
поверхностях. Однако полученные результаты оказываются несколько сложнее.
Наконец, следует отметить, что во многих частных задачах, в которых рас-
рассматривается теплообмен, решения часто удается представить в более простом
виде через корни A0.6) и A0.7) гл. III, чем через корни (9.5) этой главы,
как было сделано здесь.
I. Конечный цилиндр 0<^><а, 0 < z < Z. Поверхность z = 0
поддерживается при заданной температуре /(/*), поверхность z = l—
при нулевой температуре. Теплообмен происходит при г = а со средой
нулевой температуры.
В этом случае v должно удовлетворять уравнению
при условиях
v = 0, z = L 0<r<a. C.2)
v = f(r)t z = 0, 0<r<a, C.3)
-p-f-/zz; = 0, 0<z</, r = a. C.4)
Функция *)
/0(ar)shoc(Z — z) C.5)
удовлетворяет C.1) и C.2) при всех значениях а. Она удовлетворяет также
C.4), если а служит корнем уравнения
оУо (aa)-r- hJQ (aa) = 0. C.6)
Как и в § 7 гл. VII, мы предполагаем, что /(г) можно разложить в ряд
/(/•)= 2 AnJ0(r*n)t C.7)
1
где ап — положительные корни C.6), а
Таким образом, решение нашей задачи имеет вид
л = 1
*) Уравнению C.1) удовлетворяют либо произведения функций Бесселя на экспо-
экспоненциальные функции, Либо произведения функций Бесселя от мнимого аргумента
на тригонометрические функции. Мы выберем первое из упомянутых решений, когда
температура задана как произвольная функция на плоской границе, и второе реше-
решение, когда она задана на окружности.
§ 3] ГЛ. VIII. ТЕПЛОВОЙ ПОТОК В ОГРАНИЧЕННЫХ ОБЛАСТЯХ 217
Если /(/*) равно постоянной величине V, то, используя соотношение E.5)
предыдущей главы, находим
JL — V 2hJ0(ran)sh(l-z)an
Установившаяся температура используется в этом случае для измерения
коэффициента теплопроводности [8].
Из C.10) находим тепловой поток, поступающий в цилиндр через по-
зерхность z = 0, в виде
C.11)
Аналогичным образом, тепловой поток, «вытекающий» из цилиндра
через поверхность .г = /, равен
со*е? Ы C.12)
Эти решения представляют собой обобщение решений для случая тонкой
проволоки, рассмотренного в § 5 гл. IV. Их можно использовать при рас-
рассмотрении влияния проволоки конечной толщины.
II. Конечный цилиндр 0 < г < а, 0 < z < I. Поверхность z = 0 поддержи-
поддерживается при заданной температуре /(г). На других поверхностях происходит
теплообмен со средой нулевой температуры.
ГЛп)ancha
где ап и А определяются из C.6) и C.8). В работе [8] приводятся некоторые числен-
численные результаты.
III. Конечный цилиндр 0<г<а, 0 < z < I. Поверхность z = 0 поддержи-
поддерживается при заданной температуре /(г), другие поверхности — при нулевой тем-
температуре.
i
) уо df
°п i
где ап — положительные корни уравнения
Jo(aan) = O. C.15)
IV. Конечный цилиндр 0<г<я, 0 < z < /. Поверхность г = а поддержи-
поддерживается при заданной температуре f (-г), другие поверхности — при нулевой тем-
температуре.
v e 2 у Мпхт/0 Sin
/ ^J I(nna/l)
I0(nna/l)
я=1
я« Г f (O Sin ^ ^. C.16)
о
V. Конечный цилиндров г < а, 0 < z < I. Поверхность г= а поддерживается
при заданной температуре f (z), на других поверхностях происходит теплооб-
теплообмен со средой нулевой температуры.
I
} /V<^> {«я сое «• +Л sin «•><!*', C.17)
218 ГЛ. VIII. ТЕПЛОВОЙ ПОТОК В ОГРАНИЧЕННЫХ ОБЛАСТЯХ [§ 3
где ап — положительные корни (ср. § 9 гл. III) уравнения
^«1=^Т*- C-18)
VI, Конечный цилиндр 0<; г < я, — I < z < L На поверхностях z = ± I теп-
тепловой поток отсутствует. Количество тепла (в единицу времени), равное Q,
подводится к одному основанию боковой поверхности с помощью тонкого кольца
шириной Ь и отводится тем же способом от другого основания. Тепловой по-
поток через остальную часть криволинейной поверхности отсутствует *).
В данном случае граничное условие при г= а имеет вид
-/С |? = /<*>, r = a, -/<*</,
где
/ (z) = 0, / — Ь > z > — I + Ь,
Здесь / (z) — нечетная функция, которую можно разложить в ряд
(-1)" в|я B/1+1) «* л|я Bл + 1) *г
2л+1) 2/
Следовательно,
8Q/ у (-1)" /0[B/1+1)*г/2/] (- , ., .
Bn + IJ /, [Bя + 1) «a/2/] sln 27 S1" 27 ' (A19)
л = 0
VII. Конечный полый цилиндр а < г < b, 0 < z < I. Поверхность г = а под-
поддерживается при f (г), другие поверхности — при нулевой температуре.
v e 2 V ^о(^/;; ^/0 sin™ [f {z') sin ^ ^, C.20)
I АА Fx (nna/l; nnb/l) I J I
п=\ о
где
Л> (*; У) = /о W Ко (У) - /Со <*) /о (У)- C-21)
VIII. Конечный полый цилиндр а < г < Ъ, 0 < z < I. На поверхности г = а
тепловой поток внутрь твердого тела является заданной функцией f (z). Дру-
Другие поверхности поддерживаются при нулевой температуре.
k
v = - 2 V F°{r'unnbl?n sin^- ff (У) sin Tf-dz\ C.22)
К* *Л nFx (nna/l; nnb/l) I J I
л = 1 О
где Fq определяется соотношением C.21), а
„ ААЧ Л (^ У) = Л <*) /Со (У) + ^ W /о (У). C-23>
Если **)
f(z) = Q при L<z<l — L
f (z) = 0 при 0<г<1 и l — L<z<l,
то правая часть C.22) принимает вид
4Q/ V ^о [Bт + 1) «г//; Bт + 1) «*/*! ros Bifi+l)L .
Z I
Bm+lJFl[Brn+\)na/l; Bm + l)nb/l] I I
C.24)
*) Эта задача совпадает с задачей о конечном стержне, часть поверхности кото-
которого шириной b нагревается на одном конце нагревательной катушкой и охлаждается
с противоположного конца [9].
**) Эти условия служат грубым приближением к условиям, характерным для
трубчатой печи.
§ 3] ГЛ. VIII. ТЕПЛОВОЙ ПОТОК В ОГРАНИЧЕННЫХ ОБЛАСТЯХ 219
IX. В области — / < г < /, а < г < Ь {полый цилиндр) находится среда
с коэффициентом теплопроводности Кх. Поверхности г = Ь и z = ± I поддер-
поддерживаются при нулевой температуре. Область г < а занята проволокой с коэф-
коэффициентом теплопроводности /С, которая нагревается электрическим током *).
Предположим, что температура проволоки постоянна по всему ее поперечному
сечению и при г = а между проволокой и окружающей ее средой нет разрыва в тем-
температуре.
Если v — температура среды в полом цилиндре, то мы должны решить уравне-
уравнение C.1) для области при v = 0 на поверхности r=b и на поверхностях г= ± /.
В данном случае решение будет иметь вид
v- У а сое &п+1)™ F ГBя+1)»г.
у-2лапсов Т[ /^ -
F
Т[ /^ - , - J,
л = 0
где Fo определяется C.21) и ап — постоянные, определяемые из граничного условия
при г=я. Наше решение получено из уравнения A0.4) гл. IV для температуры про-
проволоки при ?/=5 = 0, причем величина Нр (v —1/0), которая в этом уравнении пред-
представляла потерю тепла проволокой в окружающую среду, заменена величиной
Отсюда мы получим для граничного условия при г = а соотношение
„d*v . 2/Ci dv
Подставляя C.25) в C.26), находим
с»
2 a»cos {2п+21)пг {[^~ К{2п^21) п Yo[{2n+2i)na"; BAZt/1)u6]-
л=0
/С, Bп+1) 1С rB^+l)«g . Baz+1)x^1 I _ jP __
"*" а/ Ч 2/ J 27 ]( "^Ч~
оо
4у72
cos
C0S
где Fq и Fx определяются из C.21) и C.23). Из уравнения C.27) получаем ап для
всех п. Решение C.25) является полным.
X. Конечный полый цилиндр а < г < Ъ, 0 < z < I. Поверхность z = 0 поддер-
поддерживается при f (r), другие поверхности — при нулевой температуре.
2 Г
(а28)
где ио(аг) определяется A0.2) гл. VII, а ал — положительные корни уравнения
Uo (аа) = 0.
XI. Конечный полый цилиндр а < г < Ьу 0 < z < I. Поверхность г = а под-
поддерживается при температуре f (г). На других поверхностях происходит тепло-
теплообмен со средой нулевой температуры **).
nn) ffi2){
*) /
anCOsan2+nsinan2)d2y (з.29)
*) Ниже приводится законченная теория экспериментального метода, рассмот-
рассмотренного приближенно в примере VI $ 2 предыдущей главы.
**) Эта задача совпадает с задачей об установившемся потоке тепла в цилин-
цилиндрическом охлаждающем ребре (ср. § 6 гл. IV).
220 ГЛ. VIII. ТЕПЛОВОЙ ПОТОК В ОГРАНИЧЕННЫХ ОБЛАСТЯХ [§ 3
где ап — положительные корни C.18), а
<Р (Г*, П) = /о (гап) [апКх (К) - Wo (Ю1 + Ко (r«n) [anlx (b*n) + hf0 (ban)]. C.30)
XII. Полу ограниченны и цилиндр 0 <; г < я, z > 0. Поверхность z — 0 поддер-
поддерживается при заданной температуре f (г), а поверхность г = а — при нулевой
температуре
TfSy // () °(л) dr-
где а„— положительные корни C.15).
XIII. Полу ограниченный цилиндр 0< г < a, z > 0. Поверхность г = а поддер-
поддерживается при заданной температуре f (г), а поверхность z = 0 — /г/?и нулевой
температуре.
1
где ап — положительные корни C.15).
XIV. Полуограниченный цилиндр 0<г<я, z > 0. Поверхность z = 0 под-
поддерживается при заданной температуре f (г), а на поверхности г== а происхо-
аит теплообмен со средой нулевой температуры.
^liy •-V Д/ (г) /. (г.л) rfr. C.33)
где ап — положительные корни C.6).
Когда а мало, то корни аи а2, ... быстро возрастают, и поэтому в выражении
для v мы можем ограничиться первым членом разложения. Далее, если величи-
величиной aja2 можно пренебречь, то /0 (аах) = 1 и •/o(aai)== — ll2aa\-
Тогда из C.6) получим
,/2/г
Необходимо отметить, что для справедливости наших рассуждений ah должно
быть мало, и в этом приближении
где V — среднее значение температуры на поверхности г = а. Этот результат совпа-
совпадает с решением, приведенным в § 3 гл. IV.
XV. Полу ограниченный цилиндр 0 <; г < a, z > 0. Поверхность г = я поддер-
поддерживается при заданной температуре /(-г), а на поверхности г = 0 происходит
теплообмен со средой нулевой температуры.
f {
(а34)
где ап — положительные корни C.15).
XVI. Ограниченный цилиндр 0<;г<?, 0 < z < /. Потоки тепла через круг
0<г<д, -г = 0 и через круг 0<!r<a, z = l одинаковы и равны постоянной ве-
величине F. Поток тепла через остальные поверхности отсутствует.
Разность между средними температурами двух областей, через которые подво-
подводится и отводится тепло, равна следующей величине:
FI \ 16 у Ix (niza/l) Г (nnb\K ( пъа \ ( nnb \ ( ппа Щ
где суммирование проводят по нечетным значениям п.
XVII. Ограниченный цилиндр 0 < z < I, 0 <; г < а. Количество тепла, выде-
выделяемое *) в единицу времени единицей объема, постоянно и равно Ао. Темпера-
Температура поверхности равна нулю.
*) Задачи, в которых имеет место выделение тепла, встречаются при рассмотре-
рассмотрении вопросов, связанных с нагреванием обмоток электромагнитных катушек [10, 11],
а также в некоторых биологических проблемах [12].
§ 3] гл. vtii. тепловой поток в ограниченных областях 221
В данном случае следует решить уравнение
Частный интеграл этого уравнения, который обращается в нуль при г = 0и
г = /, имеет вид
Аог (I — z)/2K. C.37)
Полное решение получается путем добавления к этому выражению решения
уравнения C.1), величина которого равна ——° ^ * при г = а и нулю при z = О
иг=/. Последняя задача решена в примере IV, и окончательно получаем
_ Aoz (I - z) 4/М0 у /0 [B/г + 1) кг/1] B/г + 1) ъг
V~ 2К ~Къ^ 2и Bn+\y/0[Bn+l)na/l] Sln T *
л = 0
XVIII. Ограниченный полый цилиндр О < z < /, а < г < Ь. Тепловой поток
через поверхность г = а отсутствует. Поверхности z = 0 и z = / имеют
нулевую температуру. На поверхности r=b температура равна f (z).
г^п ^in ^ f^ C.39)
Fx (пка/l; nnb/l) I J I
/1=1 0
где Fx (jc, у) определяется C.23).
XIX. Ограниченный полый цилиндр 0 < z < /, а < г < b. Количество тепла,
выделяемое в единицу времени единицей объема, постоянно и равно Ао. Тепловой
поток через поверхность г = а отсутствует. На других поверхностях темпе-
температура равна нулю.
Используя C.37) и C.39), получим
Apz(/ — z) 4/Mp у Ft [B/г + 1) па/Ь &п + 1) nr/l] sin B/г + 1/ -/- n4m
* ~ 2/C K*3 <4J Л [B/г + 1) na/l; B/г -f-1) nb/l] B/г + IK * l w'
/2=0
XX. Ограниченный полый цилиндр 0 < z < I, a < r < b. Количество тепла,
выделяемое в единицу времени на единицу объема, постоянно и равно Ао. Поверх-
Поверхности z — 0, z = I и г = b имеют нулевую температуру, поверхность г = а
охлаждается водой.
Подобные задачи можно рассматривать следующим образом. Предположим, что
поверхность г= а обтекается жидкостью, характеризуемой удельной теплоемкостью с'
и температурой V, и что количество М этой жидкости, уходящей в единицу вре-
времени, заменяется тем же количеством жидкости с нулевой температурой, причем сама
жидкость все время хорошо перемешивается. Тогда количество тепла, уносимое
жидкостью, составляет Mc'V, что должно равняться /а, т. е. величине теплового
потока через поверхность г=а, 0 < z < I. Учитывая это и используя C.37) и C.20),
получим решение для v.
XXI. Ограниченный цилиндр 0<r<a, 0<z<l с нулевой температурой
поверхности-, количество выделяемого тепла равно -40A + ^)-
В данном случае следует решить уравнение
d2v , 1 dv . d2v , Ао$ Ао
Частный интеграл, который обращается в нуль при z = 0 и z = /, имеет вид
1
т
cosTl-cf^ — *J
cos ^7'
где
222 ГЛ. VIII. ТЕПЛОВОЙ ПОТОК В ОГРАНИЧЕННЫХ ОБЛАСТЯХ [§ 4
Поступая как в примере XVII, найдем полное решение в виде
1
cos i -n- / — '
W2 у /„(ry,//) sin Bя+!)«*//
„=o ^Jl)Bn+lUl ' C-41)
где
V=T
Здесь на [J налагаются ограничения, аналогичные рассматриваемым в § 7 гл. XV.
XXII. Другие задачи.
Вебер дал ряд решений задач для случая установившегося потока электричества
(или тепла) в областях, ограниченных цилиндрами и плоскостями, перпендикулярными
их оси [13] *). Во многих из этих задач рассматривается электрический ток как
«втекающий» внутрь поверхности, так и «вытекающий» из нее через небольшие элек-
электроды. Задачи подобного типа не представляют большого интереса при обсуждении
вопросов теплопроводности; полное описание их дается в книге [2].
§ 4. Неустановившееся состояние. Решения в форме произведений
Как и в гл. V и VI, решения многих важных задач можно записать
(см. § 15 гл. I) в виде произведения решений простых задач. Они имеют
вид функций ср(лг) и ср(л:, Л), определяемых F.1) и F.5) гл. V, что соответ-
соответствует случаю полуограниченного твердого тела с заданной температурой
поверхности и теплообменом соответственно, а также функций ф(л;, /) и
ф(л;, /, Л), определяемых F.6) и F.7) гл. V, что соответствует случаю пла-
пластины — / < х < / с заданной температурой поверхности и теплообменом
соответственно. К этим решениям необходимо теперь добавить функции
Где ап — положительные корни уравнения
У0(аос) = 0 D.2)
где ап — положительные корни уравнения
аУо (аа) + М> (аа) = 0. D.4)
В § 6 и 7 гл. VII было показано, что выражения D.1) и D.3), анало-
аналогичные F.5) и G.4) гл. VII соответственно, служат решениями задач дль
случаев неограниченного цилиндра с начальной температурой, равной еди-
единице, и либо с поверхностью, поддерживаемой при нулевой температуре,
либо с теплообменом со средой нулевой температуры.
I. Ограниченный цилиндр —/<z</, 0-<г<а с начальной тем-
температурой, равной единице, и нулевой температурой поверхности.
, a). D.5)
Численные значения функций ф и % были приведены в § 4 гл. III и
в § 6 гл. VII. На рис. 27 и 28 приведены изотермы v = 0,1; 0,2; 0,3; ...
*) Большая часть материала первой цитируемой статьи приводится в гл. XII
книги [2]. См. также [14].
§4]
ГЛ. VIII. ТЕПЛОВОЙ ПОТОК В ОГРАНИЧЕННЫХ ОБЛАСТЯХ
223
при -*.t/a2 = 0,08 для осевых плоскостей в цилиндрах, для которых 1=а
и 1 = 2а. Эти значения указывают на важную роль краевых эффектов.
Если теплопроводности цилиндра в радиальном и осевом направлениях
различны (как, например, в бревне), то решение по-прежнему будет иметь
вид произведения D.5) тех же функций, каждой с соответствующим значе-
значением х.
II. Ограниченный цилиндр —Z < z < /, 0<г<сс нулевой началь-
начальной температурой.
Если температура поверхности цилиндра равна единице, то решение
имеет вид
*=1—ф(*. /)х(г, а),
или
„_1 8 V V (-ly-
/1=0 т—\
Bn+\)amJl(aam)
21
X ехр[
D.6)
где ат — положительные корни D.2). Решение для случая температуры по-
поверхности, равной ср(^), легко получить, воспользовавшись теоремой Дюамеля.
Рис. 27. Изотермы v = 0,1; 0,2; ..., 0,8
для цилиндра, длина и диаметр кото-
которого равны 2а, с начальной темпе-
температурой, равной единице, и нулевой
температурой поверхности;
it/a2 = 0,08.
/ г Ось
J2JL
Рис. 28. Изотермы v = 0,1; 0,2; ...,0,9
для цилиндра длиной 4а и диаметром
2а с начальной температурой, равной
единице, и нулевой температурой
поверхности; -d/a2 = 0,08.
III. Ограниченный цилиндр —/<z</, 0<;г<а с начальной
температурой, равной единице. На поверхности цилиндра происхо-
происходит теплообмен со средой нулевой температуры.
а, /г).
D.7)
Численные значения фи/ приведены в литературе (см. ссылки к гл. III
и гл. VII). Некоторые численные значения приведены в [15].
IV. Ограниченный цилиндр —/<z</, 0<г<а с начальной
температурой, равной единице. На поверхностях z= ±/ происходит
теплообмен со средой нулевой температуры. При t > 0 поверхность
224 ГЛ. VIII. ТЕПЛОВОЙ ПОТОК В ОГРАНИЧЕННЫХ ОБЛАСТЯХ [§ 5
г = а поддерживается при нулевой температуре.
г. а). D.8)
V. Полуограниченный цилиндр z > О, 0<г<а с начальной тем-
температурой, равной единице,
Если на всех поверхностях происходит теплообмен со средой нулевой
температуры, то
v = <f(z, h)x(r, а, К). D.9)
Если все поверхности поддерживаются при нулевой температуре, то
<*)• D.10)
Для х?/а2 = 0,08 изотермы вблизи поверхности z = 0 в этом случае
не отличаются от изотерм, изображенных на рис. 28.
Если поверхность z = 0 поддерживается при нулевой температуре, а на
поверхности г= а происходит теплообмен со средой нулевой темпера-
температуры, то
, а, А). D.11)
Если поверхность г = а поддерживается при нулевой температуре, а на
поверхности z = 0 происходит теплообмен со средой нулевой темпера-
температуры, то
v = <?(z, h)x(r, a). D.12)
Ясно, что легко записать решения многих других задач такого же типа,
в частности задач с полыми цилиндрами.
В гл. XIII будут приведены соотношения, определяющие температуры
в областях, ограниченных изнутри цилиндрами; после этого можно написать
аналогичные решения для областей типа г > a, z > 0 или г > а, —I < z < /.
§ б. Определение теплопроводности вещества в форме цилиндра
Для определения теплопроводности вещества, имеющего форму ограниченного
цилиндра, был использован ряд методов, аналогичных методам, изложенным в § 5
гл. VI.
Для ограниченного цилиндра 0<г<я, —Kz<l с начальной температурой,
равной единице [16], при наличии на его поверхности теплообмена со средой нулевой
температуры первый член решения D.7) предыдущего параграфа имеет вид
8ft sin У cos МЛ, (а, г) fxt (xi+ ai)
a (ft2 + а2) [Ш\ + sin 2/Xj Уо (аах) * ' ( ' }
где а. — наименьший корень уравнения
а/, (да) = А/о (аа), E.2)
а X, — наименьший корень уравнения
XtgX/=ft. E.3)
Если боковая поверхность цилиндра, начальная температура которого равна
единице, поддерживается при нулевой температуре и на его основаниях происходит
теплообмен со средой нулевой температуры [17], то первый член решения D.8) пре-
предыдущего параграфа будет иметь вид
8 sin A,/cos M-MtvO -X4x?+|tl)
WiA <<ЧЧ> РЛ, + sin21,1] '
где A.j — наименьший корень уравнения D.3) и ^ — наименьший корень уравнения
0. E.5)
§ 6] ГЛ. VIII. ТЕПЛОВОЙ ПОТОК В ОГРАНИЧЕННЫХ ОБЛАСТЯХ 225
Если начальная температура цилиндра равна единице и при t > О поверхность
z =— / поддерживается при нулевой температуре, а на других поверхностях про-
происходит теплообмен со средой нулевой температуры [18, 19], то первый член нашего
решения будет иметь вид
8/г A - cos 2XtQ sin X, (z +1) Jo (axr) -»' (*?+ $
a (h2 + a?) [4y - sin 4VJ Уо (aal}
где ax — наименьший корень C.2) и А, — наименьший корень уравнения
O. E.7)
Зная любые из решений E.1), E.4), E.6), а также из других решений аналогич-
аналогичного вида, можно, использовав какой-либо метод, изложенный в § 5 гл. VI или
в § 5 гл. IX, получить значения Л, % и, в случае надобности, начальную температуру
цилиндра.
§ 6. Ограниченный цилиндр — /<?</, 0<r<a
с начальной температурой /(г, 0, z)
Если начальная температура или граничные условия таковы, что метод, изложен-
изложенный в § 15 гл. I, оказывается непригодным, то используется комбинация рядов Фурье
и рядов Фурье — Бесселя. Наряду с этим можно применить функцию Грина (см.
гл. XIV) или непосредственно использовать, как в гл. XV, преобразование Лапласа *).
I. Поверхность при нулевой температуре.
В данном случае уравнения теплопроводности имеют следующий вид:
Выражение
, — /<*</), F.1)
v = / (г, 0, г) при t = О F.2)
v = 0 при г=а и 2= ±1. F.3)
ехр [-
удовлетворяет F.1) и F.3), если /и — любое целое число, а fx — корень уравнения
Разложим теперь / (г, 0, г) в ряд Фурье
оо
2 (я* cos nb + 6Л sin л0),
/2 = 0
где коэффициенты % и Ьп являются функциями гиг. Обозначим их через Fn (r, z)
и С?л (г, г) и затем разложим в ряды по функциям Бесселя, определяемым положи-
положительными корнями уравнения Jn (pa) = 0. Коэффициенты этих рядов разложим в ряды
по синусам углов, кратных —^-^т—--
Тогда мы получим искомое решение в виде
X Jn №) sin '""ул (A^ ^ n cos nb _^ B^ ^ n sin л0)
где
• /" г/я (fir) rfr У sin т№^ут*/ <fe / cos /г0/ (r, 0,
*) Неустановившееся состояние для случаев, описанных в примерах I, II, XIII
и XIV § 3 данной главы, рассматривается таким методом в § 11 гл. XV.
15 Г. Карслоу, Д. Егер
226 ГЛ. VIII. ТЕПЛОВОЙ ПОТОК В ОГРАНИЧЕННЫХ ОБЛАСТЯХ [§ 7
Для B^t т, п получаются аналогичные выражения [20] *).
II. Другие случаи.
Решения других задач для ограниченного цилиндра можно вывести с помощью
описанного выше метода, а также метода, изложенного в § 12 гл. VII. Случай, когда
задана температура поверхности, рассматривается в § 60 книги Карслоу [21]; случай
теплообмена на поверхности — в § 61 той же книги, а также в работе [20]. Случай
области, ограниченной плоскостями z = ± /, плоскостями 0 = 0 иб = бои поверх-
поверхностью г = а, обсуждается в § 62 книги Карслоу [21].
§ 7. Полуограниченный цилиндр
Задачи для случая полуограниченного цилиндра с произвольной начальной или
поверхностной температурами могут рассматриваться аналогично тому, как это
делается в § 12 гл. VII и в предыдущем параграфе. Решение для произвольной на-
начальной температуры и нулевой температуры поверхности приведено в § 59 книги
Карслоу [21]. Некоторые решения для полуограниченного полого цилиндра даются
в [22, 23].
ЛИТЕРАТУРА
1. Watson, A Treatise on the Theory of Bessel Functions, Cambridge, ed. 2, 1944.
(Г. В а т с о н, Теория бесселевых функций, ИЛ, М, 1949.)
2. G г а у, М a t h e w s, Treatise on Bessel Functions, Macmillan, ed. 2, 1922. (Э. Г р э й,
Г. М э т ь ю з, Функции Бесселя и их применение в физике и механике, ИЛ, М.,
1953.)
3. Low an, Phil. Mag. 29, 93 A940).
4. Thomas, Quart. J. Mech. Appl. Math. 10, 482 A957).
5. К a rush, Young, J. AppL Phys. 23, 1191—1193 A952).
6. Titchmarsh, Theory of Fourier Integrals, Oxford, 1937. (Э. Титчмарш, Вве-
Введение в теорию интегралов Фурье, Гостехиздат, М., 1948.)
7. Т г a n t е г, J. Appl. Phys. 24, 369 A953).
8. N а п с а г г о w, Proc. Phys. Soc. 45, 447 A933).
9. Lees, Phil. Trans. Roy. Soc. A208, 381 A908).
10. E m m e г i с h, J. AppL Phys. 21, 75—80 A950).
11. S z a 1 a y, Prequenz 7, 81—84 A953).
12. Thews, Acta Biotheoretica A10, 105—138 A953).
13. Weber, Crelle 75 A873); 76 A873).
14. Wei nb e г g, Bull. Math. Biophysics 3, 39 A941).
15. Berger.Z. angew. Math. Mech. 11, 45 A931).
16. Weber, Ann. Physik (N. F.) 10, 103 A880).
17. Weber, S. B. preuss. Akad. Wiss. 457 A880).
18. Beglinger, Verh. Ver. Gew-Fleiss., Berl. 75 A896).
19. Hall, Phys. Rev. 10, 277 A900).
20. Heine, Handbuch der Kugelfunctionen, 2. Aufl., Bd. II.
21. Cars law, Introduction to the Mathematical Theory of the Conduction of Heat in
Solids, Macmillan, ed. 2, 1921. (Г. Карслоу, Теория теплопроводности, Гостех-
Гостехиздат, М., 1947.)
22. Tranter, Phil. Mag. 35, 102 A944).
23. Lowan, Quart. AppL Math. 2, 348 A945).
*) Если n = 0, выражения для коэффициентов следует разделить на 2.
ГЛАВА IX
ПОТОК ТЕПЛА В ШАРЕ И КОНУСЕ
§ 1. Введение
Мы уже видели (см. § 8 гл. I), что уравнение теплопроводности в сфе-
сферических координатах имеет вид
_^j д I^ dv\ , 1 д (_._л dv\ , 1 d2v
Ж
Если рассматривается поток тепла в шаре с такими начальными и гра-
граничными условиями, что изотермические поверхности являются концентриче-
концентрическими сферами и, следовательно, температура зависит только от г и t, та
это уравнение приводится к виду
dv (d2v . 2 dv\
Полагая u = vr, получим
ди д2и
х
В настоящей главе при помощи классического метода разделения пере-
переменных (см. A.3)) будет решен ряд важных задач для шара, полого шара
и области, ограниченной изнутри сферической поверхностью. Для полноты
изложения мы приведем без доказательства ряд решений, которые легче полу-
получить методами, изложенными в гл. ХШ и XIV; Задачи о составных шарах,
сферических или неограниченных областях со сферическим сердечником из
идеального проводника и задачи о выделении тепла в неограниченной среде
будут изложены в § 9 гл. XIII.
§ 2. Установившаяся температура. Радиальный тепловой поток
В данном случае дифференциальное уравнение имеет вид
Общим решением уравнения B.1) служит
^ B.2)
где А и В — постоянные, которые следует определить из граничных условий;
I. Полый шар а < г < #. Поверхность г == а имеет температуру v^
а поверхность г = Ь — температуру vv
15*
228 гл. ix. поток тепла в шаре и конусе [§ 2
В данном случае
т, _ Witt — r) + bv2(r — a)
II. Полый шар а < г < Ь. Поверхность г = а имеет темпера-
температуру vv На поверхности г = Ь происходит теплообмен со средой
температуры v2-
В этом случае
n_avi № + г A - hb)] + hb*v2 (r - а)
r[hb2 + a(\ — hb)] # {*•*'
III. Полый шагр u<r<J. На поверхности г = а теплообмен со
средой температуры vv а на поверхности r — b — со средой темпе-
температуры vv
Если граничные условия имеют вид
то искомым решением служит
— а2Л! (bh2 — 1)] ' ^'и;
IV. Постоянный тепловой поток QJAiza2 через внутреннюю поверх-
поверхность г = а полого шара а < г < Ь.
Так как тепловой поток «через, любую сферическую поверхность радиуса г
равен
dv
и, в соответствии с B.1), постоянен, то
^r. a<r<b. B.6)
Если vx и v2 — температуры поверхностей г = а и г = ? соответственно,
то, интегрируя, получим
Устройства, в которых тепло»выделяется внутри полого шара, исполь-
используются для определения теплопроводности [1—3]. Применение шара обеспе-
обеспечивает устранение краевых эффектов, но вносит другие трудности.
Если теплопроводность К является функцией температуры, то соотно-
соотношение B.6) остается справедливым и интегрирование дает
Qo Q—j) = 4* f Kdv = 4*Km (v, — v2), B.8)
где Кт — средняя теплопроводность для интервала температур» равного раз-
разности между температурами в точках г = а и r = b. Таким образом, соот-
соотношение B.7) остается справедливым, если К заменяется на Кт.
§ 2] гл. ix. поток тепла в шаре и конусе 229
V. Составной полый шар из п областей (av а2), (а2, аг) (ап, ап+1)
с теплопроводностями ,Ki Кп-
Если температуры на поверхностях г = ах, а2 ап+1 равны соот-
соответственно vx, v2, .... vn+v то последовательное использование соотноше-
соотношения B.7) дает
Отсюда
Если, кроме того, на поверхностях г = av a2, .... ап+1 имеются кон-
контактные сопротивления, равные на единицу поверхности Rv R2 Rn+v
а температуры внутри и снаружи составного шара соответственно равны v0
и vn+2t то
VI. Шар аз твердого материала 0 ^ г < а, в котором в единицу
времени на единицу объема выделяется постоянное количество
тепла Ао.
Тогда дифференциальное уравнение F.7) гл. I принимает вид
1 d ( 2 dv\_ Ао
7^47\г 47)- ТС'
Требуется найти решение, имеющее конечное значение при г = (L Если
температура поверхности равна нулю, то оно имеет вид
г; = А.(д2_г2). B12)
Если на поверхности г = а происходит теплообмен со средой нулевой
температуры, то это решение примет вид
BЛЗ)
VII. Область г > а. Поверхность г = а имеет температуру Vo.
v = aVJr, — 4тиа2АГ Г-^-1 = 4nKaV0. B.14)
L or j
VIII. В области 0 ^ г < а с теплопроводностью Ко в единицу вре-
времени на единицу объема выделяется постоянное количество тепла,
равное Ао. В области г > а с теплопроводностью К тепло не выде-
выделяется. На поверхности г — а имеется контактное сопротивление,
равное на единицу площади R.
Q+Q)}/0 0<r < а,
v = A0a*/3Kr, r>a.
230 ГЛ. IX. ПОТОК ТЕПЛА В ШАРЕ И КОНУСЕ [§ 3
§ 3. Шар О < г < а с начальной температурой /(г)
и температурой поверхности <?(/)
Как и в § 1 данной главы, сделаем подстановку
u=vr. C.1)
Тогда уравнения для и записываются следующим образом:
•& = «¦?. 0<Г<а, C.2)
и = 0, когда г= 0,
я = аср (/), когда г = а,
u = rf (г), когда * = 0.
Эти уравнения сходны с уравнениями теплопроводности для плиты тол-
толщиной а, поверхности которой г = 0 и г = а поддерживаются при темпе-
температурах 0 и аср(^) соответственно, а начальная температура равна rf(r).
Решение этой задачи приведено в § 5 гл. III (см. E.2) гл. III). Используя
его, окончательно получим
f *
Н sin - ./ r f <r >sin -Г" dr ~
10
- пы (-1)я / ехр р*5*1 ср (X) Л |. C.3)
Ниже приводятся результаты для некоторых важных частных случаев.
Для большинства этих случаев приводятся также решения, применимые при
малых значениях параметра xt/a2.
I. Нулевая начальная температура. Температура поверхности
постоянна и равна V.
ЛГ , 2aV
или
^1у ГГ^+1)Д-ПГB^+1)Д+П) C.5)
Температура г»ц в центре, получающаяся из соотношений C.4) и C.5)
при переходе к пределу при г->0, равна
2 (-1)" ехр[-^], C.6)
aV ^ Г
п = \
ИЛИ
аУ ]?—Г B/1+1J^2
я=0
§ 3] ГЛ. IX. ПОТОК ТЕПЛА В ШАРЕ И КОНУСЕ 231
Средняя температура vcp шара в любой момент времени равна*)
оо
1
или
_
ср~
I
?*•[¦
па
C.8)
C.9)
Теплосодержание шара в любой момент времени равно 4тса3рсуср/3.
На рис. 29 приведены графики зависимости v/V от г/а, рассчитанные
по формуле C.4) для различных значений Г —otf/a2. Их можно сравнить
с соответствующими кривыми на
рис. 24 для цилиндра и кривыми на
рис. И для пластины. Значения тем-
ператур в центре и средних темпе-
температур тел такой формы, рассчитан-
рассчитанные по формулам C.6) и C.8), при-
приведены на рис. 12.
Уравнение C.8) находит приме-
применение в теории запаздывания пока-
показаний термометров [5—7] **). Пред-
Предположим, что стеклянный ртутный
термометр со сферическим резервуа-
резервуаром, имеющий нулевую температуру
в момент / = 0, вводится в среду
с температурой V. Если пренебречь
влиянием движения ртути и терми-
термическим сопротивлением стекла, в ко-
которое заключена ртуть, то увеличе-
увеличение объема последней, т. е. показа-
показание термометра, пропорционально
о,б го
г/а
Рис. 29. Распределение температуры в раз-
различные моменты времени в шаре радиуса
г= а с нулевой начальной температурой
и температурой поверхности, равной V.
Числа у кривых указывают величины xt/a2.
средней температуре C.8). Анало-
Аналогичным образом выражение C.11)
соответствует показанию термометра
в- среде, температура которой увеличивается линейно (например, в снижаю-
снижающемся самолете); очевидно, что в этом случае следует ожидать постоянного
запаздывания. Влияние стеклянного резервуара можно учесть с помощью вы-
выражения D.10) данной главы; кроме того, необходимо учитывать расширение
стекла.
И. Нулевая начальная температура. Температура поверхности равна kt.
2ka3 Vl (—\)п Г
— •—г~ 71 5— ехР —
хтс3г ^ п3 r L
ппг
Средняя температура равна
/т2
п-\-
1 Г ъп2п41
(ЗЛО)
C.11)
*) В работе [4] отмечается, что из результатов взвешивания сконденсированного
на шаре за любой промежуток времени пара в паровом калориметре Жоли можно
определить как х, так и рс.
**) В статье [8] дается приближенное рассмотрение отставания по времени в более
сложных системах.
232 гл: ix. поток' тепла в шаре и конусе [§ 3
III. Нулевая начальная температура. Температура поверхности меняется
по закону sin (a>t -f- е).
аЛ
V = - sin (со* + е + <р)-)-
(—1)я /г (хп2тс2 sin s — сод2 cos е) Г ъп2п4 ] . итог '
%*л4те* + а>2*4 6XPL ^ J Sm~O~"' ( 2)
где
1
Ch2q>/r--COs2a>/r )Т
сп2а>'я —
Искомое решение получается из соотношения F.5) гл. III.
IV. Начальная температура постоянна и равна V. Температура поверх-
поверхности равна нулю.
Искомые решения получаются вычитанием из V соотношений C.4), C.5), C.6),
C.7), C.8) и C.9).
V. Начальная температура V (а — г)/а. Температура поверхности равна
нулю.
sin v ' x/ C.13)
ИЛИ
°Ч--1)»( !»Ф* ГМ+^1 +12ф* [W)^ |
1 I 1-2(%0М L 2(yi)/2 JJ
а аг ^ аг
VI. Начальная температура V (а2 — г2)/а2. Температура поверхности равна
нулю.
Н' (ЗЛ5)
п=1
или
24У^ у | ГBВ + 1)д-г-| _ 2ф, ГBп
VII. Начальная температура (V/r) sin (nr/a). Температура поверхности равна
нулю.
iep[\ (ЗЛ7>
VIII. Начальная температура V ехр [а (г — а)].
оо
2 2 f2 2 2Ч2 ехр | — ™ гс 1 sin -^- {(—1)л+1 [а2л2 —
пгъг-\-а1а1у L аг \ а
}. C.18)
IX. Начальная температура в области 0 < г < b постоянна и равна
а в области b < г < а равна нулю. Температура поверхности равна нулю.
2V \Л i а г nnb b nnb ) . mzr Г %л2я2П /о 1ПЧ
= 7. < ¦ 9 9 sin cos > sn ехр ъ— . C.19)
г AU \ п2п2 а пп а у a F L a2 J v '
§ 4] ГЛ. IX. ПОТОК ТЕПЛА В ШАРЕ И КОНУСЕ 233
Для области 0 < г < b можно также написать
ф*
2г " '
* J Ф[ 2(^)'А ] + Ф[ 2Ы)'<> Г
L
а для области b < г < а
гBп + 2)а-
J+№L 21^ \
Г
+ L
— ф* I I I у J |ф* I — I — }ф* I ZL.—Л__ I —
L 2(x*)V* JJ г ***\ L 2(**)V* -J I 2Ш)Ч* I
__ гB;г
L
¦«ГУ ^:\\,и^"-\\. C-20)
Решение для случая, когда в области 0 < г < Ь начальная температура равна
нулю, а в области b < г < а постоянна, получается объединением полученного реше-
решения с решением для случая постоянной начальной температуры V в области 0 < г < а.
Из этих решений в свою очередь вытекает решение для случая, когда начальная
температура в области b < г < с постоянна, а в областях 0 < г < b и с < г < а
равна нулю.
X. Начальная температура /(г). Температура поверхности равна нулю.
Решение методом Фурье дается формулой C.3). Решение, используемое при
небольших значениях х*/я2, имеет вид
и
I
л=-оо 0
XI. Температура поверхности равна нулю. Начальное распределение тем-
температур описывается функцией
.. C.22)
sin ^ { -St «-^! + W[^2 - 2> (-1>Л+1 - 21 +
[24 - (nW - 12/22^2 + 24) (-1)»] + ... } exp [- ^Ц. C.23)
§ 4. Шар 0 < г < а. Начальная температура /(г). На поверхности
сферы происходит теплообмен
Если на поверхности шара происходит теплообмен со средой нулевой
температуры, то уравнения для v имеют следующий вид:
dv (d2v . 2 dv \ n . . .. 1Ч
= О, когда г = а, D.2)
234 ГЛ. IX. ПОТОК ТЕПЛА В ШАРЕ И КОНУСЕ [§ 4
и
v-f(r), когда / = 0. D.3)
Пусть u = vr\ тогда
! = «¦?. 0<л<а, D.4)
# = 0, когда г = 0, D.5)
+ (*—"j)a = 0' когда ' = 0, D.6)
u = rf(r), когда / = 0. D.7)
Таким образом, наша задача сводится к задаче о линейном тепловом
потоке в пластине, одна поверхность которой поддерживается при нулевой
температуре, а на другой поверхности происходит теплообмен со средой
нулевой температуры. Решение этой задачи уже давалось ранее (см. A0.11)
гл. III) и нам остается только заменить в нем / на а, х на г и h на
{ah— 1)/а. Следовательно, решение уравнения D.1) при условиях D.2) и D.3)
будет иметь вид*)
где ± ая, л=1, 2, ..., — корни уравнения
аа ctg aa. -f- ah — 1=0. D.9)
Уравнение D.9) аналогично уже рассмотренному выше уравнению A0.7)
гл. III, корни которого представлены в таблице приложения 4; единственное
различие между ними заключается в том, что параметр ah, который в § 11
гл. III всегда был положительным, заменяется параметром ah—1, который
может быть отрицательным. Если /г>0, т. е. ah—1 > — 1, то замечания
в §§ 10 и 11 гл. III справедливы и все корни уравнения D.9) оказываются
действительными **).
Если начальная температура /(г) постоянна и равна V, решение D.8)
принимает вид***)
V «& a2a2 + (ah-lJ
D.10)
s~9 sinao^sinroc,..
22 i дАГдА-Ш п п
*) Это решение легко получается непосредственным путем [10]. См. также при-
пример II в § 7 гл. XIV.
**) Если h < 0, то уравнение D.9) имеет два мнимых корня. Однако этот случай,
как и всегда, исключается по физическим соображениям. Если & = 0, т. е. тепловой
поток через поверхность отсутствует, то уравнение D.9) имеет корень, равный нулю,
и при h = 0 к значению с/, определяемому D.8), следует прибавить член
JLfr*f(r)dr.
(См. также соотношения D.6) гл. III и (8.3) гл. VII.)
***) Графики зависимости температуры поверхности и температуры в центре
от ah при различных значениях -Ufa2 приводятся в работе [11]; см. также [12].
§ 5] ГЛ. IX. ПОТОК ТЕПЛА В ШАРЕ И КОНУСЕ 235
Если шар имеет нулевую начальную температуру и нагревается в результате
теплообмена со средой, температура которой меняется по закону ktt то искомое
решение запишется в виде
по
Sin Гап ~хап*
п
fnah f xr ^ а2п [а2а2п + ah (ah — 1)} sin aan
D.11)
где ап — положительные корни уравнения D.9).
Если шар имеет нулевую начальную температуру и нагревается в результате
теплообмена со средой, температура которой меняется по закону V sin (со* -f- О» то
искомую температуру можно записать следующим образом:
2ahrV ^ ап (ха^ sin ? — со cos e) (ah — 1) sin ran -*a2nt
где
Axel<9x = sh o>'r cos co'r-J- / ch co'r sin w'r,
>' A + 0 ch яа/ A + 0 + (ah — 1) sh a<»' A + /),
a an — положительные корни уравнения D.9).
§ 5. Определение коэффициентов теплопроводности плохих проводников
Полученный выше ряд, сумма которого определяет температуру шара,
охлаждающегося вследствие теплообмена на границе, настолько быстро схо-
сходится, что если после начала процесса прошло достаточно много времени,
то можно пренебречь всеми членами кроме первого. Это дает удобное для
вычислений выражение, используемое в различных экспериментах, в которых
начальная температура шара постоянна.
Пусть, например, шар из исследуемого материала погружают в ванну
с постоянной температурой V на время, достаточное для того, чтобы весь
шар приобрел температуру ванны. Затем его вынимают из ванны и он охла-
охлаждается вследствие теплообмена со средой постоянной температуры. После
такого охлаждения в течение некоторого промежутка времени определяют
его температуру. В одной серии опытов измеряют температуру в центре шара
и на его поверхности. В другой серии опытов измеряют лишь температуру
в центре шара.
Используя обозначения § 4 гл. IX, получим в принятом нами прибли-
приближении
2hV [а2а\ + (ah - IJ sinааг _хЛ .
v== о—о-о * 2 sin га,. E.1)
Следовательно, если va — температура на поверхности г = а в момент
a v0 — температура в точке г = 0 в момент t, то
Отсюда, учитывая, что 0 < а^ < тс, можно найти аг. Кроме того, ш2
можно найти из уравнения
(va)t=tl — *«! (^2"^l) /к Q\
236 ГЛ. IX. ПОТОК ТЕПЛА В ШАРЕ И КОНУСЕ [§ б
Таким образом, значение х оказывается известным [13J, и тогда h нахо-
Дят из' уравнения D.9) предыдущего параграфа.
Для определения теплопроводности камня был использован другой
метод [14]. .
Воспользовавшись уравнением D.9) данной главы можно записать темпе-
температуру в центре, полученную из E.1), в виде
2у sin аа, - аа, cos да, -«# _ N t
aal-^ sin aa{ cos aax e -r-i\e . E.4)
Для определения значения п достаточно двух измерений температуры,
а зная п, можно найти величину N. Таким образом, по таблице значений
sin х — х cos x
х — sin .r cos x
и по значению* N легко найти <ху Отсюда, учитывая, что п = ш2у можно
определить коэффициент теплопроводности х.
§ 6. Случай шара, находящегося в контакте
с хорошо перемешиваемой жидкостью
Пусть поверхность г=а шара, имеющего начальную температуру/(г),
находится в контакте с массой М' хорошо перемешиваемой жидкости
с удельной теплоемкостью с', и пусть в начальный момент времени эта
жидкость имеет нулевую температуру. Если жидкость не теряет тепло,
то, предполагая, что при t > 0 температура жидкости равна температуре
поверхности шара, получим следующее граничное условие при г = а:
М'с'-^, r = a, t > 0. F.1)
Искомое решение имеет вид [15, 161*)
V =
«*"./'/№•,,*. F.2)
1^ Mt + W + iyJ*
где ± ал, я=1, 2, ... служат корнями уравнения
tgfl*=3+w' F-3)
а
является отношением теплоемкостей жидкости и шара.
Если начальная температура шара постоянна и равна.V, то решение F.2)
примет вид
V
/1=1
*) Для получения этого решения в работе [15] был использован видоизмененный
метод Фурье (функции sin ran не являются ортогональными) и контурное интегриро-
интегрирование [16]. Решение легко получить при помощи преобразования Лапласа. В статье
[17] указаны более полные численные данные, чем данные, приведенные на рис. 30.
§ 6] ГЛ. IX. ПОТОК ТЕПЛА В ШАРЕ И КОНУСЕ
а температура жидкости будет равна
л=1
237
F.6)
На рис. 30 приведены графики'зависимости (A-f-Ot^V (т. е. отноше-
отношения температуры жидкости к ее конечной температуре) от T = xt/a2 для
',0
о.в
>
//
ж
ш
[
0,2
О 404 О.Ов 0J2 OJO 0.2
xt/a*
Рис. 30. Изменение температуры жидкости
в калориметре при помещении в него сфе-
сферического твердого тела.
значений k, равных 0,5; 1; 2; 4; 10 и оо. Эти графики показывают ход
возрастания температуры жидкости в калориметре при введении в него сфе-
сферического твердого тела. Теоретически их можно использовать как для
определения х, так и для определения рс.
Если жидкость теряет тепло в результате теплообмена с окружающей
средой нулевой температуры*), условие F.1) заменяется условием
—±ъа>К -^ = Mfcf ^
F.7)
и температура жидкости для случая постоянной начальной температуры шара,
равной V, определяется выражением
F.8)
jU ?V4 + Sa2a2n C + 3k — 2kHf) — 9#' A — H )
где Н'=.(Н1±ъаК), k определено F.4), а ± ая, п= 1, 2, ..., —корни урав-
уравнения
*) Кроме того, здесь можно использовать граничные условия (9.14)—(9.16) гл. I,
которые более точно описывают условия в калориметре. В статье [18] рассмотрен
случай идеально проводящего твердого тела.
238 ГЛ. IX. ПОТОК ТЕПЛА В ШАРЕ И КОНУСЕ [§ 7
§ 7. Шар с заданным тепловым потоком на поверхности
В случае нулевой начальной температуры и постоянного теплового потока Fo
к шар температура v равна
l/==.
3/V F0Er2 — 3a2) 2Foa2 ^ sin (ranja)
pea
л=1
• G.1)
где am /i=l, 2, ..., — положительные корни уравнения
tga = «. G.2)
На рис. 31 приведены графики функций (K/aF0) [v — C/у/рся)] при различных
значениях 74 = it/a2.
Рис. 31. Распределение температуры в шаре
О -< г < а, обусловленное постоянным тепло-
тепловым потоком Fo на поверхности.
Числа у кривых указывают величины xtfa2.
§ 8. Шар 0 < г < а, внутри которого выделяется тепло
Если в единицу времени на единицу объема количество выделяемого
тепла постоянно и равно Ло, то дифференциальное уравнение F.7) гл. I при-
принимает вид
1 dv
1 д
dv
Обычная подстановка и = vr дает
1 ди д2и
Аог
Т
(8.1)
(8.2)
Рассмотрим теперь ряд частных случаев.
I. Количество тепла, выделяемое в единицу времени на единицу
объема, равно постоянной величине Aq. Начальная температура и
температура поверхности равны нулю.
Полагая
§8]
ГЛ. IX. ПОТОК ТЕПЛА В ШАРЕ И КОНУСЕ
239
мы получим в качестве уравнения для w уравнение линейного теплового
потока в пластине
1 *»=*«!., 0<г<а, (8.3)
с w = О при г = 0.
Если начальная и поверхностная температуры шара равны нулю, то сле-
следует решать уравнение (8.3) при
условиях
w= j? , когда / =
0<г<а,
од
(8.4)
(8.5)
Значение w находим из D.1)
гл. III, и окончательно получаем
Г/ГТ
Рис. 32. Распределение температуры в шаре
0<><я, если при ?>0 температура
поверхности равна нулю и мощность источ-
ников равна постоянной Ао.
Числа у кривых указывают величины xt/a2.
w ех Г -*.n2n2t I g
L а л
Другая форма решения, полезная для небольших значений xt/a2, имеет вид
Wi^ t+l)a + ril
2 (**)'* J/
Несколько кривых, описывающих распределение температур для различ-
различных значений х^/a2, показано на рис. 32.
II. Количество тепла, выделяемое в единицу времени, равно Ао (а — г)/а.
Начальная температура и температура поверхности равны нулю.
1
\2аК
;ехР
Л=0
[-ХBл+1IЛ]
sin
Bп+\)пг
(8.8)
или
I
s<->
1/» J
Г
[
V« J I
III. Количество тепла, выделяемого в единицу времени, равно Ао (а2 — г2)/а2.
Начальная температура и температура поверхности равны нулю.
. «ело,
240 ГЛ. IX. ПОТОК ТЕПЛА В ШАРЕ И КОНУСЕ [§ 8
или
Ао (a2 — r*)xt ЗА0г.Ф ,
^ /Car ^<1Ф
IV. Количество тепла, выделяемого в единицу времени, равно (A0/r) sin (ъг/а).
Начальная температура и температура поверхности равны нулю *).
п-^. (8.12)
V. Количество тепла, выделяемого в единицу времени, равно Аоеа^г~аК На-
Начальная температура и температура поверхности равны нулю **).
га) ааг
X [(—1)я Bад — п2п2 — а*а2) — 2аае —*]. (8.13)
VI. Количество тепла, выделяемого в единицу времени, равно Aoe~xt. Началь-
Начальная температура и температура поверхности равны нулю.
\ • \ i "/ г
оо
9/тЗ Л. усг^ i Л\П rttrt- Г vri2w2^-
#._ч _,(v ui^f № l ш J. (8.14)
ИЛИ
a-r) /I
Ф
(8.15)
VII. Количество тепла, выделяемого в единицу времени в области b < г < а,
равно Aoe~xt [22]; в области 0 < г < b тепло не выделяется. Начальная темпе-
температура и температура поверхности равны нулю.
*) В статье [19] приведены значения простых результатов этого типа для слу-
случая, когда изменение интенсивности выделения тепла в зависимости от г известно
недостаточно хорошо. Там же рассмотрены случаи выделения тепла с постоянной
интенсивностью и выделения тепла в слое, вне которого тепло не выделяется.
**) Эта задача рассмотрена в статье [20], где получена отличная от этой форма
решения. Численньде значения приведены в статье [9]. Полученный результат был
распространен на случай учета усадки [21].
§ 8] гл. ix. поток тепла в шаре и конусе 241
Если Ь < г < я, то
ъАоа -Kt f sin r (X/%I/2 г]
V |sina<A/*)l/f * Г
у.Аоа и sin (а — г) (Х/%I/* f Ь cos 6 (Х/%I/» sin Ъ (\/4l2 ) ',
+ Ю* е sina(X/x)!/« ( a e(V*)l/f I
sln а вяС08 а Г
X sin -^- exp | — ^jjr-\ • (8Л6)
Соотношение типа (8.15) можно также вывести и обычным путем.
VIII. В области 0 < г < а выделение тепла определяется функцией f (r).
Начальная температура и температура поверхности равны нулю.
2а
о
а
¦^rfr'2/(г') dr' + f r'f (r') dr'-±f r'2 f (r') dr'
. (8.17)
ИЛИ
2d J r'f (r/) dr' {{ф* [ 2 (*o1/2 J 1Ф L"
I 2<%Q'A
IX. Нулевая начальная температура. Количество тепла, выделяемого
в единицу времени, равно постоянной Ао. Теплообмен на поверхности со средой
нулевой температуры.
-™Ъ
. (8.19)
bnJ\ гд J^ a* \a an -f- ah (ah — 1I sin aa
где ±ani n=l, 2, ..., — корни уравнения
aa ctg aa = 1 — д/г. (8.20)
X. Если начальная температура [23] равна
Ао (а*-г*)
6К
(т. е. равна установившейся температуре в случае нулевой температуры поверхности)
и при г = а для t > 0 происходит теплообмен со средой температуры V, то
(а*—г2) Ао , („ , дЛ0 \[\ 2д2/г у sin гад
где а„ — положительные корни уравнения (8.20).
16 Г. Карслоу, Д. Егер
242 гл. ix. поток тепла в шаре и конусе [§ 9
§ 9. Полый шар*) a<r<b
Если начальная температура шара равна /(/•) и при t>0 поверхности
г= а и г = Ь поддерживаются при постоянных температурах vx и v2, то
решение**), получаемое из D.1) гл. III, имеет следующий вид:
— avx)(r — a) ,
r(b —
л=1 а
Если температуры поверхностей равны yx(t) и ср2(?) соответственно, то
решение получается из E.2) гл. III совершенно аналогичным образом.
Если на поверхностях г = а и r=b происходит теплообмен со средой ну-
нулевой температуры и граничные условия имеют вид
k — — h v = 0 r = a
и
Ко —л Г Ло^ = U, Г = О,
дг
то решение запишется следующим образом:
я=1
где
G = ahx
2 + b2k\a?f
(И2 + Л^а2)/2 {G sin (r — a)an-\- akxan cos (r — а) ап]
{(Ь — a) (a2k2a2n + G2) F2^a2 + Я2) + (Яд^ + G^2) (GH + л^^2а2)}7з
и ± ал, /1=1, 2, ..., — корни уравнения
(G// — abkxk2a2) sin F — a) a + a (akxH+ bk2G) cos F — a) a = 0.
Везде выше ku k2i hx и h2 должны равняться положительным величинам или
нулю. Поэтому соотношение (9.2) служит решением для различных случаев, в которых
поверхность либо имеет нулевую температуру, либо на ней происходит теплообмен,
либо тепловой поток через поверхность равен нулю. Если пх = п2 = 0, т. е. тепло-
теплоотдачи на поверхности нет, то к (9.2) следует добавить член
Распространение решения на случай теплообмена на поверхностях r = a n r= b
со средами с различными температурами, производится так же, как это было сделано
в конце § 9 гл. III.
*) Ряд результатов, а также некоторые их практические приложения приведены
в статье [24].
**) Эти решения, конечно, применимы также и для радиального потока в кони-
конической области. В статье [25] рассмотрен случай слегка суживающейся трубки.
§ 10] ГЛ. IX. ПОТОК ТЕПЛА В ШАРЕ И КОНУСЕ 243
Если область а < г < b находится вначале при нулевой температуре, а при
t > 0 на поверхности г = а тепловой поток равен постоянной величине FOt
а поверхность r=b поддерживается при нулевой температуре, то
a4b-r)FQ 2a% ^ (l + *4f sinа„ (Ь- г) _
где ат л = 1, 2, .... — положительные корни уравнения
tg F — а) а + аа = 0.
§ 10. Область, ограниченная изнутри сферической поверхностью г = а
Пусть начальная температура описывается функцией /(г), а температура
поверхности — функцией ср(^).
Произведем, как обычно, подстановку u = vr; тогда нам нужно решить
уравнение C.2) в области г>а с u = ay(t) на поверхности г = а и
u — rf (г) для начального момента времени. Решение, вытекающее из соот-
соотношений D.1) и E.1) гл. II имеет вид
(r-a)ft Vxt
В частностпу при нулевой начальной температуре а постоянной
температуре поверхности V решение имеет следующий вид:
Если начальная температура равна нулю и на поверхности
происходит теплообмен со средой температуры V, то граничное условие
для v имеет вид
L
а граничное условие для и = rv
+±)HV r = a.
Отсюда, записывая /г/=Л + A/а), находим из G.5) гл. II
A0.3)
Решение для области г > а с начальной температурой V, охлаждающейся
в результате теплообмена на поверхности г = а со средой нулевой темпе-
температуры, получается путем вычитания соотношения A0.3) из V. Решение для
произвольной начальной температуры вытекает из G.15) гл. XIV.
Если начальная температура равна нулю и на поверхности г = а
тепловой поток имеет постоянную величину Fo [26—28], то решение
имеет вид
Кг
16*
244 ГЛ. IX. ПОТОК ТЕПЛА В ШАРЕ И КОНУСЕ [§ 11
§11. Шар с начальной температурой /(г, б, ф).
Температура поверхности г = а равна нулю
В этом случае дифференциальные уравнения для v имеют вид
dv л J д*у , 2 dv , 1 d/ ft 0р \ , 1 d*v
v — f(r, 0, <р) ПРИ * = 0, A1.2)
v = 0 при г = а. (П.З)
Положим v = e-xa2tu, где #— функция только г, б и <р, и положим
= cos0. Тогда из A1.1) получим
+ ^l^^ + + A=0> AL4)
Полином Лежандра степени п, Ял(|а), где Аг — целое и положительное
число, служит коэффициентом при hn в разложении A—2[А/г + А2)~1^1 и
удовлетворяет уравнению Лежандра
Таким же образом присоединенная функция Лежандра [29—33]
Рп ((*) = A - V?fm ?e Р„ (р) A1.5)
удовлетворяет уравнению
Отсюда следует, что выражение *)
Rn(r)PZ(p.)™mv A1.7)
удовлетворяет уравнению A1.4) при условии, что Rn(r) зависит только
от г и что
^ ^ [^±]n = 0. A1.8)
Это приводит нас к выражению **)
причем решение /_(/I+,/4(ar) неприемлемо, поскольку при г->0 Rn стре-
стремится к бесконечности.
Таким образом, мы приходим к следующему решению уравнения A1.1):
*-"" (агГ'1' У(я+1/1) (от) Я? (р) ^°ns якр. A1.9)
где /7t и п — целые положительные числа.
Условия на границе удовлетворяются выражением A1.9), если а служит
корнем уравнения
W<>0 11°
*) При 6 = тс второе решение уравнения A1.6) обращается в бесконечность и
поэтому неприемлемо.
**) Эти функции можно выразить через тригонометрические [34]. В цитируемой
книге приведены некоторые численные результаты.
§ 11] ГЛ. IX. ПОТОК ТЕПЛА В ШАРЕ И КОНУСЕ 245
Если, как и выше, принять, что функцию /(г, 0, ср) можно разложить
в ряд, члены которого имеют вид
и что этот ряд можно почленно интегрировать, то легко найти коэффициенты
разложения.
Пусть, например,
оо оо
/(Г, fi,?)=2 2 2 (<и-)-1АУ(я+.А,(аГ) -Pn(V-){An,m,a
/1 = 0 а m=0
и суммирование по а происходит по положительным корням уравнения A1.10).
Тогда
2* оо
J/(r, 0, <p)cosmcprfcp = iu 2S(ar) ~l/iJ(n+42)(*r)PZ (|0-4,.«.«-
0 Я=0 a
Кроме того, мы знаем, что [29, 30, 32]
1
^ЛГ (И.П)
O. пфп'. A1.12)
-1
Отсюда
2ic
fZ(V.)d?ff(r, 6, ср)cosmcprfcp = {2„1%~\пт-т)?Ап>т,а(агГЧ,+,/а)(аг).
-10 а
Наконец, из E.2) гл. VII получаем
а 1 2тс
f rkJin+4t)(*r)dr fp?(p)dpff(r, 0,
о -i 6
— Bn-\-\)(n—m)\
Если /71 = 0, то в этих формулах тс следует заменить на 2тс.
Коэффициент Bnt m a можно найти аналогичным путем.
Итак, мы получаем решение нашей задачи в виде
222
/7=0 а т = 0
Здесь коэффициенты Anmta и Вп,та определены выше, а суммирование
по а происходит по положительным корням уравнения У(я+1/2)(аа) = 0. При
наличии теплообмена на поверхности или при отсутствии через нее теплового
потока задачи решают тем же путем, используя соответствующим образом
измененное уравнение A1.10).
246 ГЛ. IX. ПОТОК ТЕПЛА В ШАРЕ И КОНУСЕ [§ 13
§ 12. Поверхность шара г = а поддерживается
при температуре F(b, <p)
Как и в предыдущем параграфе, разлагаем F @, <р) в ряд вида
f (». ?) = 2 S /»" (rt {Л, « cos /и9 + В„, m sin my}, A2.1)
/1 = 0 m = 0
где
1 2*
Лп, « = ^±^ g^[ / С W ^ / F (в. т) cos «т d% A2.2)
-1 6
1 2*
/ /? W ^ / ' (в. Г) sin m, a% A2.3)
6
-1 6
и при т = 0 те, как и выше, следует заменить на 2те.
При установившейся температуре мы ищем решение уравнения
V2i/ = 0,
которое при г=я принимает вид A2.1). Такое решение имеет вид*)
оо п
4Л> т cos гщ -\- BHi m sin ;
Если температура поверхности является функцией только 6, например
S АпРпМ. A2.5)
то установившаяся температура определяется суммой
Рп (fx). A2.6)
я=0
Такую форму будет иметь выражение для распределения температур земной коры,
обусловленное уменьшением средней температуры от тропиков к полюсам.
Для шара с начальной температурой / (г, 6, <р) и температурой поверхности F F, <р)
мы примем, как в § 14 гл. I,
v = а + w,
где и — решение приведенной выше задачи для случая установившейся температуры,
a w — решение задачи, разобранной в предыдущем параграфе для случая начальной
температуры / (г, 6, <р) — и.
§ 13. Часть шара, вырезаемая конусом 6 = 00.
Температура поверхности равна нулю, начальная
температура равна /(г, в, ?)
В данном случае дифференциальное уравнение для v имеет следующий вид:
1 dv _ d2v 2 dv 1 д j n dv } , 1 d2v
где fx = cos 0. Его следует решать при условиях
i/ = 0 при r = a, A3.2)
t; = 0 при 6 = е0 A3.3)
*) При а = 0 член, содержащий г, должен удовлетворять уравнению A1.8) пре-
предыдущего параграфа. Следовательно, он должен иметь вид гп или r~n~lt причем
член г~п~х неприемлем в области, содержащей начало координат.
§ 13] ГЛ. IX. ПОТОК ТЕПЛА В ШАРЕ И КОНУСЕ 247
и
v = f (г, 6, 9) при t = 0.
Поступая так же, как и в § 11 данной главы, находим, что уравнение A3.1)
удовлетворяется функцией
,—" <«-)"* /n+I/j <«•) Р"» fci) Cs°nS my, A3.4)
где />^'m(fx) — обобщенная функция Лежандра (см. [29] или [35]), определяемая
формулой
Здесь F — гипергеометрическая функция Гаусса. В функции A3.4) т должно рав-
равняться нулю или целому положительному числу, а п должно быть больше *) чем —72»
но не должно быть целым числом. Функция A3.5) при нецелом п имеет особую
точку при fx = — 1. Таким образом, она не была бы приемлемой в задаче для сплош-
сплошного шара, разобранной в § 11 данной главы.
Если мы положим jx0 = cose0, то из условия A3.3) найдем
О. A3.6)
и следовательно, п должно быть корнем этого уравнения **), превышающим —1/2.
Наконец, условие A3.2) требует, чтобы а было положительным корнем урав-
уравнения
а A3.7)
При таком выборе п и а выражение A3.4) удовлетворяет граничным условиям
и не обращается в бесконечность внутри исследуемого тела.
Если, как и выше, предположить, что функцию / (г, 6, ср) можно разложить
в ряд
/ (г. «. ?> = 2 2 2 <аг>~ Ъ J(n+W <аг> Рпт <Ю {Аи, а, п cos mcp + Bmt а> п sin mcp}
m = 0 а п
A3.8)
и что этот ряд можно почленно интегрировать, то, как и в § 11 данной главы, можно
найти коэффициенты ряда. Единственное отличие здесь заключается в том, что в дан-
данном случае вместо соотношений A1.11) и A1.12) этой главы нужно использовать
следующий результат: если т — любое положительное число или нуль, а п и п' — два
различных, больших —1/2 корня уравнения Р~т(р,0) = 0, то
1
Рпт (К-) рп'т (К-) ^ = 0 A3.9)
Г?Т Ж р-т <*>) ^ рпт (Ы- "зло)
И-о
Это доказывается в конце настоящего параграфа. Тогда найдем, как и в § 11
данной главы,
naVVl —1$ d m d . , 12
1 2тс
hyz)(ar)dr I P~m(v-)d\L I /(r, 6, cp) cos mcp rfcp. A3.11)
P-0 6
*) Поскольку из A3.5) следует, что Р_™_\ (f^) = Рп т (^), эта функция симме-
симметрична относительно п = — 7г-
**) Численные значения приведены в [36].
248 гл. ix. поток тепла в шаре и конусе [§ 14
Если т = 0, то в этих формулах я следует заменить на 2я. Коэффициенты Вт, а> п
можно найти аналогичным путем. Таким образом, мы получим решение задачи в сле-
следующем виде:
V = 2 2 2 ^^ (""•)"%+./,> ^ РПП <*> {4* а, Я C0S «Т + Вт, а, п 81П «Tj. A3Л2)
т = 0 а л
где коэффициенты определяются так же, как и выше.
Если твердое тело является частью шара радиуса г = а, вырезанной кону-
конусом 0 = 0О и плоскостями <р = 0 и <р = <р0, а температура его поверхностей равна
нулю, то так же, как это делалось выше, следует разложить функцию / (г, 0, <р) в ряд
22 %>{аг) р»тк1" мsin ^
m=l а л
Аналогичный метод применим к телам, ограниченным другими поверхностями, запи-
записанными в полярных координатах.
Решение для конуса в = 80 можно получить путем перехода к пределу реше-
решения A3.12) при а->оо. Это будет сделано в § 17 гл. XIV.
Остается еще доказать справедливость использованных выше соотношений
A3.9) и A3.10).
Пусть
и = р-тМ и и =/>-/" fcx).
Тогда
Следовательно,
1
(п' — п)(п' + п+\) fии'
Г/1 9ч I / da du' \ "]!
Отсюда следует, что если п и п'—два различных, больших чем —1/2 корня
уравнения ^т(Н-о)==о» Т0
Точно так же, когда Р~т (fx0) = 0, то
шя -^[/.(,0) -±-я
§ 14. Температура внутри Земли
Знание температуры внутри Земли существенно для понимания многих
геофизических явлений, например для понимания природы магнитного поля
Земли, пластических свойств вещества Земли, а также для выяснения про-
происхождения и причин вулканизма и тектонических движений. Однако если
§ 14] ГЛ. IX. ПОТОК ТЕПЛА В ШАРЕ И КОНУСЕ 249
другие величины, такие, как давление, плотность и упругие свойства,
известны настолько хорошо, что спор может идти лишь о различиях в их
оценке, составляющих несколько процентов, оценки температур сильно отли-
отличаются друг от друга. До сих пор нет достаточно надежного метода опре-
определения температуры на основании наблюдений, и поэтому в настоящее
время для оценки внутренней температуры приходится прибегать к теоре-
теоретическим расчетам, основанным на известной величине теплового потока
у поверхности, принятом распределении радиоактивных материалов и приня-
принятом начальном распределении температур. Такие расчеты произведены в пред-
предположении постоянства температуропроводности *), хотя решения для «двух-
«двухслойной» Земли были получены еще Хевисайдом (см. § 8 гл. XII).
В настоящее время придерживаются двух предположений относительно
начальной температуры Земли: 1) вначале холодная Земля образовалась
в результате слипания твердых частиц и 2) вначале горячая Земля находи-
находилась в газообразном состоянии и, постепенно охлаждаясь, перешла в жидкое
состояние. «Холодная» Земля должна была бы иметь равномерно распреде-
распределенную радиоактивность и постоянную начальную температуру и должна
была бы разогреться, вероятно, до температуры плавления [39, 40]. При
плавлении происходило бы перераспределение радиоактивных материалов, и
последующие условия оказались бы очень похожими на условия в перво-
первоначально «горячей» Земле. В случае первоначально «горячей» Земли рас-
рассмотрение начинается с момента, когда вся она стала жидкой и быстро
охлаждалась в результате излучения с поверхности, теплообмен в жидкой
внутренней области осуществлялся бы конвекцией и градиент температуры
равнялся бы адиабатическому градиенту **), примерно равному 0,2° С/км.
В этом случае затвердевание началось бы в точке, в которой температура
раньше упала до температуры плавления. Поскольку повышение температуры
плавления с глубиной (обусловленное повышением давления) примерно
равно 2° С/км, температура плавления будет сперва достигаться в некоторой
точке внутренней области, вероятно, на границе между ядром Земли и ее
оболочкой [42]. Далее затвердевание будет распространяться по направлению
к поверхности. Таким образом, в данной задаче начальная температура Земли
определяется кривой зависимости точки плавления от глубины; для описания
этой кривой были предложены различные теоретические формулы [37, 41] ***).
После оценки начальной температуры и распределения радиоактивности
расчет последующих температур по существу сводится к интегрированию
соотношения G.7) гл. XIV для случая сферического поверхностного источ-
источника. Тот факт, что значительная часть некоторых радиоактивных элементов
успела уже распасться, вносит дополнительное усложнение, не учитывавшееся
первыми исследователями. В ряде работ приведены численные расчеты, осно-
основанные на различных представлениях о внутреннем строении Земли [38, 43].
Следует отметить, что, принимая х = 0,007, радиус Земли а = 6,4 • 108сл*
и ?=1,26- 1017 сек D- 109 лет), получим, что параметр %t/a2 равен 0,0022.
Данный случай является, таким образом, идеальным для использования
*) Хотя известно, что (в принципе) К может сильно меняться с глубиной, есть
основания предполагать, ,что % может оказаться достаточно постоянной величиной,
равной в коре примерно 0,007 (см. [37]).
**) Общее изложение этого вопроса можно найти в [37, 40, 41].
***) В работе [43] отмечается, что кривые зависимости точки плавления от глу-
глубины могут быть такими, что затвердевание должно начинаться в центре Земли,
переходить на внутреннюю часть ядра, а затем на границу между ядром и оболоч-
оболочкой, оставляя ядро жидким. Следует отметить, что расчеты указывают на весьма
малое падение температуры в ядре за 109 лет.
250 ГЛ. IX. ПОТОК ТЕПЛА В ШАРЕ И КОНУСЕ [§ 14
решения, приведенного в § 5 гл. XII, для «малых промежутков времени», что
установили еще Хевисайд и Джеффриз. Несмотря на это, многие авторы
работали с обычным медленно сходящимся рядом, в котором зачастую необ-
необходимо использовать большое число членов. Ряд результатов приведен
в §§ 3 и 8 гл. IX.
ЛИТЕРАТУРА
1. Laws, Bishop, McJunkin, Proc. Am. Acad. Arts Sci. 41, 457 A906).
2. Muller, Ann. Phys. und Chem. 60, 82 A897).
3. Green, Proc. Phys. Soc. 44, 295 A932).
4. Evans, Phil. Mag, 22, 833—837 A936).
5. В г о m w i с h, Phil. Mag. 37, 407—419 A919).
6. McLeod, Phil. Mag. 37, 134—144 A919).
7. Jeffreys, Operational Methods in Mathematical Physics, ed. 2, 1931, § 6,4.
8. Evans, Proc. Phys. Soc. 50, 242—256 A947).
9. VanOrstrand, Geophysics 5, 57—79 A940).
10. Cars law, Introduction to the Mathematical Theory of the Conduction of Heat in
Solids, Macmillan, ed. 2, 1921. (Г. Карслоу, Теория теплопроводности, Гостех-
издат, М., 1947.)
11. Schack, Stahl u. Eisen 50, 1290 A930).
12. H e i s 1 e r, Trans. ASME 69, 227—236 A947).
13. Weber, Vjschr. naturf. Ges. Zurich 23, 209 A878).
14. Ayrt о n, P er r y, Phil. Mag. 5, 241 A878).
15. Peddie, Proc. Edin. Math. Soc. 19, 34 A901).
16. D о fi g a 1 1, Proc. Edin. Math. Soc. 19, 50 A901).
17. P a t e r s о n, Proc. Phys. Soc. 59, 50—58 A947).
18. H о а г e, Phil. Mag. 29, 52 A940).
19. S 1 i с h t e r, Bull. Geol. Soc. Am. 52, 561—600 A941).
20. Low a n, Phys. Rev. 44, 769—775 A933).
21. Low an, Am. J. Math. 57, 174—182 A935).
22. Allen, Am. Math. Monthly 63, 315—323 A956).
23. A w b e r y, Phil. Mag. 4, 629 A927).
24. В а г г е r, Phil. Mag. 35, 802 A944).
25. T a 1 b о t, К i t с h e n e r, Brit. J. Appl. Phys. 7, 96—97 A956).
26. Holm, J. Appl. Phys. 19, 361—366 A948).
27. Ingersoll, Adler, Plass, Ingersoll, Heat. Pip. Air Condit. 22, 113—122
A950).
28. Von В e r t e 1 e, Brit. J. Appl. Phys. 3, 127—132 A952).
29. В a t e m a n, Partial Differential Equations of Mathematical Physics, Cambridge,
1932.
30. W h i 11 a k e r, Watson, Modern Analysis, Cambridge, ed. 3, 1920, Ch. XV.
(Э. Уиттекер и Г. Ватсон, Курс современного анализа, ГТТИ, М., 1933.)
31. MacRobert, Spherical Harmonics, Methuen, 1927.
32. В у е г 1 у, Fourier's Series and Spherical Cylindrical and Ellipsoidal Harmonics,
Boston, 1893.
33. Hobson, Spherical and Ellipsoidal Harmonics, Cambridge, 1931, Ch. III.
34. Watson, A Treatise on the theory of Bessel Functions, Cambridge, ed. 2, 1944.
(Г. Ватсон, Теория бесселевых функций, ИЛ, М., 1949.)
35. Barnes, Quart. J. Math. 39, 97 A908).
36. Pal, Bull. Calcutta Math. Soc. 9, 85 A917); 10, 187 A918).
37. Jacobs, Encycl. of Phys., Vol. 47 (Geophysics), p. 391.
38. Urr y, Trans. Am. Geophys. Union 30, 171 A949).
39. Birch, J. Geophys. Res. 56, 107 A951).
40. J e f f г е у s, The Earth, Cambridge, ed. 3, 1952.
41. В u 1 1 a r d, см. сб. The Earth as a Planet, Ed. Kuiper, Univ. of Chicago Press,
1954.
42. A d a m s, J. Wash. Acad. Sci. 14, 459—472 A924).
43. Jacobs, Trans. Am. Geophys. Union 35, 161—163 A954).
ГЛАВА X
ПРИМЕНЕНИЕ МЕТОДА ИСТОЧНИКОВ И СТОКОВ К ЗАДАЧАМ
С НЕУСТАНОВИВШЕЙСЯ ТЕМПЕРАТУРОЙ
§ 1. Введение
Представление о мгновенном точечном источнике тепла, т. е.
о конечном количестве тепла, мгновенно выделяемом в определенный момент
времени в заданной точке неограниченного тела, оказалось в теории тепло-
теплопроводности чрезвычайно плодотворным [1]. Одно из больших преиму-
преимуществ этого метода заключается в том, что он основан на очень простом
физическом представлении, что дает возможность получить решение большого
числа важных задач, исходя непосредственно из ряда фундаментальных
положений. С теоретической точки зрения всегда признавалось, что в случае
точечного источника получается фундаментальное решение A/г), встречаю-
встречающееся в теории потенциала, и что полная разработка теории теплопровод-
теплопроводности для ограниченных областей может быть достигнута путем построения
функций Грина, аналогичных этим функциям в теории потенциала *).
Будем называть решение для случая мгновенного точечного источника
фундаментальным. Интегрируя по времени, мы получим решение для непре-
непрерывного точечного источника, что соответствует случаю выделения задан-
заданного количества тепла в данной точке в единицу времени, равного ср(^).
Если ср(^) равно постоянной величине Q и выделение тепла продолжается
достаточно долго, то в пределе решение совпадает с решением для стацио-
стационарного точечного источника и соответствует хорошо известным фунда-
фундаментальным решениям гидродинамики. Задачи со стационарными источниками
рассматриваются в гл. XVI.
Интегрируя решения для точечных источников по соответствующим
координатам, мы получим решения для мгновенных и непрерывных линейных,
плоских, сферических и цилиндрических поверхностных источников, причем
каждое имеет свою собственную простую физическую интерпретацию.
Применяя для конечных областей эти решения или соответствующие реше-
решения гл. XIX, можно сразу же получить решения многих задач в виде опре-
определенных интегралов.
§ 2. Мгновенный точечный источник
Дифференциальное уравнение теплопроводности
дх2 "^ ду2 "•" dz2 ~ % dt }
*) Среди основных работ, посвященных этому вопросу, укажем статьи [27—30,
33, 39]. См. также литературу к § 1 гл. XIV-
252 ГЛ. X. ПРИМЕНЕНИЕ МЕТОДА ИСТОЧНИКОВ И СТОКОВ [§ 2
удовлетворяется функцией
((**'>г + (УУТ + (*-*'П B.2)
Если ?->0, это выражение стремится к нулю везде, кроме точки
(х', у', zr), где оно обращается в бесконечность.
Общее количество тепла в неограниченной области равно
оо оо оо
j pcvdx dydz =
—оо —оо —оо
X fexP[-B-?J]dz = QPc. B.3)
Таким образом, решение B.2) можно интерпретировать как распределе-
распределение температур в неограниченном теле, обусловленное мгновенным выделе-
выделением в момент времени / = 0 в точке (л:, у, z) количества тепла Qpc. Это
фундаментальное решение, соответствующее мгновенному точечному источ-
источнику мощностью Q в момент / = 0 в точке (л/, у', z') *).
Следует отметить, что температура в точке, находящейся на расстоянии г
от источника, достигает максимальной величины в момент времени / = г2/6х.
Точно так же квадрат расстояния точек максимума температуры от источ-
источника в момент / равен 6х/.
Так как температуру в неограниченном теле с начальной температурой
/(л:, у, z) можно рассматривать как результат выделения в объеме тела при
/ = 0 количества тепла, равного
pcf(x', /, z')dx' dy' dz' B.4)
в элементарном объеме dx1dyf dz'', имеющем координаты (л/, у, zr), то темпе-
температуру в любой момент времени / можно определить интегрированием по
объему тела; она равна
8 (*%*)/?
—оо —оо —оо
X ехр \ л / — \ dx' dy' dz' B.5)
I 4%r j
(см. также B.8) гл. II).
Интересно получить решение B.2) как предел действительного случая, когда
в бесконечно малом объеме выделяется конечное количество тепла. Предположим,
что мы берем этот объем в виде шара радиуса а и рассмотрим неограниченную среду
для случая, когда начальная температура шара 0< г < а равна V, а в области г > а
она равна нулю. Если, как и в § I гл. IX, положить и = i/r, то уравнение для и
*) Мощность источника численно равна, таким образом, температуре, на которую
выделяемое количество тепла повышало бы температуру единицы объема материала.
Это определение обладает тем преимуществом, что начальное распределение темпера-
температуры / (х, у, z) можно считать вызванным действием распределенных мгновенных
источников мощностью f (х\ у', zf) dx' dy' dz' в элементе объема dx' dy' dz' в точке
(jc\ у', z'), как и в выражении B.4). Однако при рассмотрении количества выделяе-
выделяемого источником тепла, всегда следует помнить, что оно равно рс, умноженному на
мощность источника.
§ 2] ГЛ. X. ПРИМЕНЕНИЕ МЕТОДА ИСТОЧНИКОВ И СТОКОВ 253
примет вид
ди д2и
-ЗГ = *-йТ' г>0'
при условиях
и = Vr при t = О, 0 < г < а,
и = О при * = 0, г > я,
и = О при г = 0.
В этом случае решение вытекает из соотношения D.1) гл. II и имеет вид *)
а
rf ехр I —
1 L 4^ F L Ш J |
B6)
J |
B.6)
Разлагая подынтегральную функцию в ряд по степеням г и предполагая, что а
мало, получим приближенное решение
р, 3 expL^Li/l-f/^-G)-^), B.7)
8 (тих/)8/' L 4i J 1 Ы / 4Q^ J V '
где (? 43К/3
/
Пусть теперь радиус шара стремится к нулю, но Q остается постоянным. Тогда
решение B.7) примет вид
Q
с/ = ,. ехр
8 (Ш)8/*
Г г2 1
L 4/i J
Это решение для случая выделения тепла в начале координат совпадает с реше-
решением B.2).
Наконец, приведем результаты некоторых обобщений метода мгновенного точеч-
точечного источника на более сложные системы.
I. Для анизотропного материала с главными коэффициентами теплопровод-
теплопроводности Кь %2> Кз в направлении осей ху у и z, решение B.2) следует заменить на
-Л Г <*-*'>2 + <У-У>2 + С-'ТЦ. B.8)
4*1 К, ^2 /Сз JJ
Гу?"ехР
II. Мгновенный тепловой источник в тонком стержне.
Предположим, что на поверхности стержня с площадью поперечного сечения <о
и периметром сечения р происходит теплообмен со средой нулевой температуры.
Пусть коэффициент теплоотдачи равен Н. Тогда функция
v = —9L— ехр Г— it — с*—*'J]9 B9)
2о>рс (uTci)'* |_ Avi J
где v = Я/?/рсо), удовлетворяет дифференциальному уравнению B.2) гл. IV и соответ-
соответствует количеству тепла Q', выделяемому в момент / = 0в точке х = х'.
III. Мгновенный тепловой источник в тонкой пластине.
Пусть пластина толщиной D располагается в плоскости 2= 0 и на обеих ее
сторонах происходит теплообмен со средой нулевой температуры, причем коэффи-
коэффициент теплоотдачи равен Н. Дифференциальным уравнением для этой задачи служит
уравнение D.1) гл. V. Тогда функция
(где k2 = 2H/KD) удовлетворяет дифференциальному уравнению и соответствует
количеству тепла Q , выделяемому в момент t = 0 в начале координат.
*) Решение B.6) было использовано в работе [2] при изучении охлаждения
больших сферических масс горных пород (лакколит). Численные результаты для этого
случая приведены на рис. 4, в.
254 ГЛ. X. ПРИМЕНЕНИЕ МЕТОДА ИСТОЧНИКОВ И СТОКОВ [§ $
§ 3. Мгновенные источники; линейный, плоский и поверхностные
цилиндрический и сферический источники
Температуры в этих случаях проще всего получить интегрированием
фундаментального решения B.2) данной главы; их можно найти также не-
непосредственно, воспользовавшись любым из способов, рассмотренных в пре-
предыдущем параграфе.
I. Мгновенный линейный источник мощностью Q, действующий
в момент времени t = 0 и расположенный на прямой, параллельной
оси z и проходящей через точку (х', у').
Рассмотрим распределение мгновенных точечных источников мощностью
Qdz' в точках z' вдоль прямой. Температура, получающаяся интегрирова-
интегрированием соотношения B.2) предыдущего параграфа, равна
ш
' J' "П C-1)
В данном случае количество тепла, выделяемое на единице длины этой
прямой, равно Qpc.
Если (г, б) и (г', 00 — полярные координаты соответственно точек (л:, у)
и (л/, У), то расстояние между ними определяется выражением
R2 = (х — х'J + (У — У'J = г2 -+- г'2 — 2гг' cos @ — 0'). C.2)
В таких обозначениях решение C.1) принимает вид
=-?« в~тш=¦?• / Xe~xX'tJ°(XR) dk C>3)
оно вытекает из первого интеграла Вебера [3].
II. Мгновенный плоский источник мощностью Q, действующий
в момент времени ^ = 0, расположенный в плоскости, параллельной
плоскости х = 0 и проходящей через точку хг.
В данном случае распределим линейные источники мощностью Qdyf
вдоль прямой х = х/. Интегрируя C.1), получим
4%xt J У V\ 4-х/ J 2}Tmi HL 4^ J
OO
C.4)
Количество тепла, выделяемое на единице площади этой плоскости,
равно Qpc.
III. Мгновенный цилиндрический поверхностный источник мощ-
мощностью Qr и радиусом г\ действующий в момент времени t = 0. Ось
источника совпадает с осью z.
Здесь распредедим линейные источники мощностью Qr' dbr по окруж-
окружности радиуса г'. В таком случае температура в точке (г, 6) будет равна
§ 3] ГЛ. X. ПРИМЕНЕНИЕ МЕТОДА ИСТОЧНИКОВ И СТОКОВ 255
следующей величине:
т.! Н —
— 2rr'cosG'
2тс
rr' cos 6'
C.5)
где Q' = 2тсг/С?. Решение получается из соотношения (9), приведенного
в § 3, 71 книги [3]. Количество тепла, выделяемое на единицу длины цилиндра,
равно pcQ'.
IV. Мгновенный сферический поверхностный источник мощ-
мощностью Q' и радиусом г', действующий в момент времени t = 0.
В данном случае, используя сферические координаты, мы рассмотрим
точечный источник мощностью Qr' sin б7 db' dy't действующий в точке
шара (г', 0', ср).
Тогда температура в точке (г, 0, 0) равна следующей величине:
8 (u
exp
Г r2 + r'2— 2rr'cos8'~l . G/ ,G/
HI sin0/rf0/ =
Q'*'2 Г r2 + r/2l f Г rr7 cos 6'I .
= —гг г" ехР — / exP si
4пЦг*У* F L 4x* J / L 2yi J
C.6)
где Qf = Anr' Q. Количество тепла, выделяемое на поверхности шара,
равно Q'pc.
V. Мгновенный источник мощностью Q' в виде окружности радиуса г',
действующий в плоскости z' = 0 в момент времени t = 0.
Если мгновенные точечные источники мощностью Qr' db' расположены на окруж-
окружности г = г' в плоскости z' = 0, то температура в момент времени t = 0 в точке
с координатами (г, 6, z') равна
2*
-^-У C.7)
2iy V ^
где Q' = 27cr'Q, а полное количество выделяемого тепла равно pcQ\
VI. Мгновенный источник в виде диска радиуса а, действующий в плоскости
2 = 0 в момент времени t = 0.
Положим в выражении C.7) Q' = 2nr'q dr' и проинтегрируем по г1 от 0 до а\
тогда, если на диске радиуса а мгновенно выделяется количество тепла na2q$c, то
256 ГЛ. X. ПРИМЕНЕНИЕ МЕТОДА ИСТОЧНИКОВ И СТОКОВ [§ 4
мы получим для температуры выражение
оо
2(™*)
,-*!*« J «-**•/, (V) У, (Ка) Л. C.9)
За исключением случая, когда г = я, этот интеграл нельзя выразить через табличные
функции. При г = а мы получаем
L [l—e-a2!4xt]e-z2'4xt. C.10)
VII. Неограниченная область с начальной температурой, заданной функ-
функцией f (г) в цилиндрических координатах.
Из соотношения C.5) следует, что температура v в момент времени t записы-
записывается в виде
оо
[if}{?t) (зл1)
о
Если
/ (г) = V = const, 0 < г < а,
/(г)=0, г>0,
то выражение C.11) принимает вид
а
'r'l4xt I e~r'2'4xt 7» Шr'dr>- <зл2>
Этот интеграл следует определять численным методом *), за исключением случая
г = 0, когда он равен
V(l — e-a2/4xt). C.13)
Некоторые значения v/V, рассчитанные по уравнению C.12), приведены на
рис. 4, б.
§ 4. Непрерывные и периодические источники**)
I. Непрерывный точенный источник.
Если в точке (х\ у', z') в интервале времени от ? = 0 до t = t выде-
выделяется в единицу времени количество тепла ср (t) pc, то температура в точке
(х, yt z) в момент времени tt полученная интегрированием соотношения B.2)
данной главы, будет равна
t
^/f^^]^,. D.1)
где
Г2 = (х — хУ + (у — у'? + (z — z'f.
Говорят, что такое распределение температур обусловливается действием
с момента времени t = 0 постоянного точечного источника мощностью ср (t).
*) Этот интеграл называется Р-функцией. Таблица его значений приведена
в статье [4].
**) Под непрерывным или периодическим источником автор понимает источник,
мощность которого описывается непрерывной или периодической функцией соответ-
соответственно. (Прим. ред.)
§ 4] ГЛ. X. ПРИМЕНЕНИЕ МЕТОДА ИСТОЧНИКОВ И СТОКОВ 257
Если мощность источника ср(^) постоянна и равна q, то мы получим,
положив т = (? —1')~"*,
* = -*-*- /"ехрГ—^1Л=-^Ф*Г^4^1. .4.2)
При t — oo это выражение сводится к г; = #/4тсхг, т. е. дает устано-
установившееся распределение температуры для случая распространения тепла
в неограниченном теле от точки (xf, yf, z'), в которой осуществляется
постоянный подвод тепла.
II. Непрерывный линейный источник.
Предположим, что на единицу длины линии, параллельной оси z и про-
проходящей через точку (х', у'), в единицу времени выделяется количество тепла,
равное рсср(^). Если подвод тепла начинается в момент времени ? = 0, когда
тело имеет нулевую температуру, то, согласно C.1) данной главы, темпера-
температура в момент ? = 0 будет равна
t
L. / ср (f) ехр [- 1^7у] у^. D.3)
О
где г*=(х — х'
Если ср (?) = # = const, мы получим
q Г
2
e~udu
J —и—
r2/4xt
где *)
:—du
является интегральной показательной функцией. Численные значения этой
функции можно найти в работе [5].
Для малых значений х
Ei (— х) = 7 -+- In х — х + iлг2+ О(лг3),
где 7 = 0,5772 ...—постоянная Эйлера. Таким образом, для больших зна-
значений t приближенно имеем
Часть выражения D.6), содержащая г, т. е. (^/2техIпA/г), дает темпе-
температуру, обусловленную постоянным подводом тепла, количество которого
в единицу времени на единицу длины равно qpc. Это решение имеет очень
*) —Ei (—x) = 7-|-1пл:-{- V - j— см. СМБ, Операционное исчисление,
Физматгиз, 1961. (Прим. ред.)
17 Г. Карслоу, Д. Егер
258 ГЛ. X. ПРИМЕНЕНИЕ МЕТОДА ИСТОЧНИКОВ И СТОКОВ [§ 4
большое значение. Оно определяет распределение температур в неограничен-
неограниченном теле, нагреваемом вдоль какой-либо линии (например, нагрев бесконечно
тонкой проволокой, по которой пропускается электрический ток), и следо-
следовательно, является приближенным решением для случая нагревания неогра-
неограниченного тела проволокой, по которой идет ток *).
Влияние конечного диаметра проволоки будет рассмотрено в § 7 гл. XIIL
Если полуограниченное тело, поверхность которого поддерживается при
нулевой температуре, нагревается линейным источником, расположенным парал-
параллельно поверхности тела на расстоянии а от нее, то искомое решение можно
получить методом изображений, описанным в § 10 данной главы. Это решение
имеет вид
где г и гг — расстояния точки до линейного источника и до его зеркального
изображения относительно поверхности соответственно.
III. Непрерывный цилиндрический поверхностный источник.
Искомое решение получается из соотношения C.5) предыдущего пара-
параграфа. Его нельзя выразить через табличные функции **).
IV. Непрерывный плоский источник.
Предположим, что, начиная с момента t = 0, в плоскости х' начинает выделяться
количество тепла, равное в единицу времени на единицу площади pc<f (t). Тогда,
согласно C.4), температура в момент времени t будет равна
t
1 Г г (х — хУ 1 y(t')dt'
<4-8>
Если ср (t) = q = const, решение принимает вид
/ t Vh Г (л: — х'JЛ q\x — x'\ г\х — х'\ 1
V. Непрерывный сферический поверхностный источник.
Если на шаровой поверхности радиуса г', начиная с момента * = 0, выделяется
количество тепла, равное в единицу времени на единицу площади рс^ @» то темпе-
температура в точке г в момент времени t запишется в виде
Если <р (t) = q = const, то решение принимает вид
Я
DЛ1>
VI. Периодический ***) точечный источник.
Если, начиная с момента времени t = — оодо t =t, в единицу времени выде-
выделяется количество тепла pcei<ot, т. е. имеют место установившиеся периодические
Этим решением часто пользуются для определения теплопроводности [6,7].
В работе [40] это решение используется как приближенное решение при
исследовании нагревания грунта проложенным в нем электрическим кабелем.
***) Движущиеся периодические источники рассматривались в [8, 9].
ц
/e
§ 5] ГЛ. X. ПРИМЕНЕНИЕ МЕТОДА ИСТОЧНИКОВ И СТОКОВ 259
условия, то, как и в случае I, получим
[г2 1 dt' 1
/сог j- —q- = ехр [— k*r-J- i (ео/—k*r)], D:12)
— оо
где
k* = (со/2%I/з.
Таким же образом можно рассматривать и периодический плоский источник.
Соответствующие решения приведены в § 6 гл. И.
VII. Периодический линейный источник.
Если, начиная с момента времени t = — со до t = t, в единицу времени на еди-
единицу длины выделяется количество тепла рс?/ш/, то
t
v = _* Г ехр \мГ — г^_ 1 d^_ = --J— ешК0 Г("^"I/2 Г1» DЛЗ)
— оо
где г — расстояние до линейного источника.
§ 5. Поверхностный нагрев полуограниченной области
Задачи, в которых область z > 0 нагревается постоянным тепловым потоком,
поступающим через участок ее поверхности, имеют большое значение, например, при
рассмотрении высокочастотного индукционного нагрева. Их можно достаточно просто
решить интегрированием решений, приведенных в предыдущем параграфе для непре-
непрерывных источников. Во всех исследуемых ниже случаях мы будем считать, что
область z > 0 имеет нулевую начальную температуру и что тепловой поток через
другие участки поверхности равен нулю.
I. При t > 0 тепловой поток q подводится к телу через полуплоскость
х <0, — оо<у<оо, г = 0.
Температура v в точке х поверхности в момент времени t равна
о t
? Г dz Г Г (х — х'JЛ , _ qx1* f dz
wJ t-z JeXP[ 4x(^-x)J * ~2K*XI*J V-zI'*
или
2q (rt \!/2 Г 1 Г x . x t?s [ %
Сравнивая соотношение E.1) с (9.8) гл. И, легко увидеть, что первое из них
состоит из множителя 2q(xt)^2/K^l/2i представляющего нагревание тела через неогра-
неограниченную плоскость, и множителя, содержащего х.
Можно показать, что количество тепла, прошедшее через полуограниченную
полосу z > 0 единичной ширины в плоскости х = 0 от нулевого момента времени
до ty равно
2?xV/2/3*'/2. E.2)
Эта величина дает количество тепла, которое теряется областью, расположенной
ниже нагреваемого участка поверхности.
II. При t > 0 тепловой поток q подводится к телу через беско-
бесконечную полосу — а<л:<а, — оо<у< сю, z = 0.
Температура v в точке х поверхности *) в момент t равна
(а+х)*
*> Некоторые численные результаты приведены в статье [10].
17*
260
ГЛ. X. ПРИМЕНЕНИЕ МЕТОДА ИСТОЧНИКОВ И СТОКОВ
[§ 6
где T = *t/a2. Несколько графиков распределения K^l/iv/2qaT 2, т. е. отно-
отношения температуры поверхности к температуре полуограниченного тела
с потоком через поверхность, равным q, показано на рис. 33.
О
0,0/
0,026
0,0625
Рис. 33. Распределение температур на поверхности
аолуограниченного твердого тела, обусловленное
нагреванием полосы шириной 2а.
Числа у кривых указывают значения it/a7.
III. При t>0 тепловой поток q подводится через круг х2-\~у2 < я2, 2 = 0
Температура в точке с цилиндрическими координатами (г, 6, z) записывается
следующим образом:
Это выражение служит обобщением решения B.7) гл. VIII. Температура в точке
@, 0, z) равняется
*^U\}\^ + t 1} E.5)
+ at 1}.
(*01/2 JJ
IV. При t > 0 установившийся тепловой поток q подводится через прямо-
прямоугольный участок — I < х < I, —а<у<а поверхности z = 0 *).
Максимальная 1/макс и средняя с/ср температуры в прямоугольном участке равны
еичинам **):
макс
следующим величинам **):
«'макс = -jr- \ a Arsh \- I Arsh y
E.6)
2?
| la2 Arsh i- -f al2 Arsh -? + -I [a* + /3 — (/2 + a2I'»] |. E.7)
§ 6. Выделение тепла в неограниченной среде
Задачи о выделении известного количества тепла в неограниченной среде можно
решить соответствующим интегрированием решений, приведенных в §§ 2 и 3 настоя-
настоящей главы. Таким путем, например, можно получить решения, найденные в § 11 гл. II.
В качестве следующего примера, определим температуру в начале координат
*) Решения задач такого типа часто используются при изучении температур
в режущих инструментах и ползунах [41, 42].
**) Arsh х = In (x + Vx2 -j- 1 = -т- arcsin (ix); см. СМБ, Операционое исчисле-
исчисление, гл. VI, Физматгиз, 1961. (Прим. ред.)
§ 7\ ГЛ. X. ПРИМЕНЕНИЕ МЕТОДА ИСТОЧНИКОВ И СТОКОВ 261
в неограниченном теле с нулевой начальной температурой при условии, что
при t > О в цилиндрической области этого тела О < г < а, — b < г < b коли-
количество тепла, выделяемого на единицу объема в единицу времени, равно постоян-
постоянной величине А.
Согласно B.2) данной главы температура в начале координат в момент времени U
обусловленная выделением в точке (г', 0', г') в момент f количества тепла, равного
At dtrdb'rdz''dt'', записывается в виде
Ar' dr' dV dz' dt'
-exp
Г r'2 + *'2 1
[ 4* (*-*') J
Интегрируя по t' от 0 до t и по области 0 < г' < a, —b<z'<b, получим
решение
t
= A [ [1 -e-aV^u] ф Г_*Л da. F.1)
Этот интеграл легко вычислить численным методом. Если b = оо, т. е. тепло
выделяется в неограниченном цилиндре радиуса а, то из соотношения F.1) получаем
для температуры на его оси выражение
F.2)
§ 7. Движущиеся источники тепла
Интегрированием решений для мгновенный источников решается ряд
задач, которые можно рассматривать либо как задачи о движении источников
в неподвижной среде, либо как случаи выделения тепла в фиксированной
точке, мимо которой равномерно движется среда*). В данном параграфе мы
рассмотрим в основном неограниченную среду. Аналогичным образом можно
применить и функцию Грина (см. гл. XIV) при решении соответствующих
задач для случая ограниченной среды **) (см. ниже пример VI).
I. Движущийся точечный источник.
Предположим, что при t > 0 в начале координат начинает выделяться
в единицу времени количество тепла, равное q, и что неограниченная среда
равномерно движется относительно начала координат в направлении оси х со
скоростью U. Рассчитаем температуру в фиксированной точке (л:, у, z)
в момент времени t.
В начале координат за элементарный промежуток времени dt' в момент f
выделяется количество тепла qdt'\ кроме того, точка среды, имеющая в мо-
момент времени t координаты (л:, yt z), в момент времени f имела координаты
{x — U(t—t% у. г).
*) Кроме того, можно решить дифференциальное уравнение теплопроводности
в движущейся среде G.2) гл. I с соответствующими граничными условиями. В ра-
работе [13] даны примеры использования обоих методов; один такой пример приведен
в § 11 гл. VII. Если в соотношении G.2) гл. I положить dv/dt = O, то мы получим
установившееся состояние, при котором приводимые ниже решения G-2) и G.3) отве-
отвечают соответственно непрерывному точечному и линейному источникам. См. также
работу [14], где дается много приложений этих решений, и статью [15].
**) Задачу о линейном источнике, движущемся на поверхности цилиндра, а также
различные технические ее приложения см. [16, 17]. Задача об источнике, движущемся
вдоль оси цилиндра, разобрана в статье [18].
262 ГЛ. X. ПРИМЕНЕНИЕ МЕТОДА ИСТОЧНИКОВ И СТОКОВ [§ 7
Таким образом, из соотношения B.2) данной главы следует, что темпе-
температура в точке (л:, у, z) в момент Л обусловленная выделением в момент tr
количества тепла qdt', равна
— *')]8/2 FL 4%(* — Г) \
Температура в момент времени t, обусловленная выделением того же
количества тепла в начале координат за время от 0 до tt равна
д Г Р I 4*(t-t') ]df,_
= q , exp-^- f ежрГ-Р—ffg-lrf;. G.1)
/?/2 Kx*
где /?2 =
Полученное соотношение служит решением для случая выделения тепла
в течение конечного промежутка времени t. Если ?->оо, то устанавливается
стационарный тепловой режим, и температура в точке (л:, у, z) будет равна
ехр - %7 ' ¦ G-2)
II. Движущийся линейный источник; стационарные условия.
Если вдоль оси у количество тепла, выделяемого в единицу времени на
единицу длины, равно q', то температуру в точке (л:, у, z) при установив-
установившемся состоянии находят интегрированием выражения G.2)
Г
L
)V21
J
где /Со (л:) — бесселева функция второго рода ¦) нулевого порядка от мнимого
аргумента.
Соотношение G.3) определяет температуру в неограниченной среде,
которая протекает со скоростью U мимо нагретой проволоки. В работе [43]
решения G.2) и G.3) использованы в качестве приближенных выражений
для распределения дыма в среде, текущей мимо точечного или линейного
источника дыма.
III. Движущийся плоский источник; стационарные условия.
Если в плоскости х = О количество тепла, выделяемого в единицу времени на
единицу поверхности, равно q" и в направлении оси х через эту плоскость движется
среда со скоростью U> то установившаяся температура в точке х записывается сле-
следующим образом:
q"l?cU, если х > Q, )
> G 4)
(q"l?cU) eUxl%, если х < 0. j
IV. Движущийся точечный источник в стержне, охлаждающемся в резуль-
результате теплообмена.
*) См. приложение 3. Если положить у' = (х2 -f- 22)ъ sh щ то интеграл в соот-
соотношении G.3) превратится в интеграл C4) (см. [19]) или в G) § б, 22 (см. [3]).
§ 7] ГЛ. X. ПРИМЕНЕНИЕ МЕТОДА ИСТОЧНИКОВ И СТОКОВ 263
Если в начале координат в единицу времени выделяется количество тепла, рав-
равное q, а стержень движется вдоль оси х со скоростью (J, то, используя соотноше-
соотношение B.9) данной главы и принятые в нем обозначения, найдем для установившейся
температуры в точке х выражение
V. Движущийся точечный источник в тонкой пластине, охлаждающейся
в результате теплообмена.
Пусть пластина расположена в плоскости х, у и движется со скоростью U в на-
направлении оси х. Тогда используя выражение B.10) и обозначения, принятые в § 2
данной главы, найдем, что установившаяся температура в точке х, у, обусловленная
выделением в начале координат количества тепла, равного в единицу времени q\ за-
записывается в виде
Я' eW*KQ { Л (У+ 4*»*»)* )
* Ло1 2% Г
где R2 = + y
VI. Точечный источник, движущийся на поверхности пластины.
Рассмотрим пластину 0 < z < /, движущуюся со скоростью U параллельно оси х.
Пусть в начале координат имеется точечный тепловой источник, выделяющий в еди-
единицу времени количество тепла, равное q, и пусть потери тепла с поверхности пла-
пластины отсутствуют. Данная задача аналогична задаче I, за исключением того, что
здесь толщина пластины конечна^ поэтому единственное изменение заключается в том,
что вместо решения B.2) настоящей главы следует использовать соответствующее
решение A0.18) гл. XIV для источника в области 0 < z < I. Тогда вместо G.1) мы
получим
я
0
r.n2n2(t —1')-\ nnz
Ь—LJcos—
\ 4x(*-O Г
Отсюда, при *->оо, когда превалируют стационарные условия, найдем, исполь-
используя соотношение C0) приложения 3,
Q ts I Ur\ , n V // \Ur Л , 4х2П27С2 XVal nnz I Uxflx ,*^
Ш\КЛ-ЪГ)+2ЪКОЫA + -GЧ^) \cos—\e^, G.7)
где г2 = + у
Соответствующее решение *) для линейного источника, расположенного вдоль
оси х и выделяющего на единицу длины в единицу времени количество тепла q\
имеет вид
^ J у 2сов(|.«/0 е^^Г^Л+^^У/л!
рС/^Г | ^^J [1+4x2/i2W2/^2/2]'/i F 2* L V U2l2 / Jj
Эти решения являются фундаментальными для расчета температур во
многих практических случаях (нагревание трением, шлифовка, механическая
обработка, поверхностный нагрев движущихся объектов, автогенная резка
и сварка и т. д.). Тепло всегда подводится не к точке, а к ограниченной
площадке, для которой решения G.1) и G.3) неприменимы, поскольку при
приближении точки к этой площадке они стремятся к бесконечности; отсюда
вытекает, что следует пользоваться интегральными решениями для источни-
источников, соответствующими подводу тепла к небольшой площадке. Во многих
случаях форма площадки неизвестна; однако влияние формы на максималь-
*) Применение этих решений, а также ряд других можно найти в статье [14]#
264
ГЛ. X. ПРИМЕНЕНИЕ МЕТОДА ИСТОЧНИКОВ И СТОКОВ
[§7
ные температуры оказывается несущественным. Поэтому обычно исследуют
площадки такой формы, для которой легче всего производить расчеты
(а именно, прямоугольники и неограниченные полосы), поскольку решения
для этих случаев имеют вид простых интегралов, легко вычисляемых числен-
численным методом.
VII. Источник в виде бесконечной полосы —b<x<bt —оо < у <
< со, расположенной в плоскости z = 0. Количество тепла, выделяе-
выделяемого в единицу времени на единицу площади полосы, равно Q.
Окружающая среда движется мимо полосы в направлении оси х со
скоростью U.
Интегрируя G.3), получаем для температуры
-ъ
2,
Цх - х
dxf.
Отсюда, вводя безразмерные величины
Y_Ux 7_?L
Л — 2ъ ' ~ 2% ¦
получим
иъ
х+в
xQ Г
v= tsrr /
G.9)
G.10)
х- в
Выражение G.10) легко найти численным методом. Для поверхности
Z = 0 результат можно запи-
записать через интегралы [20]
а
-7
;
= а屫{К0(а)±К1(а)) +-1-
G.11)
Следует отметить, что
для больших значений В тем-
температура максимальна при
Х = В и приближенно равна
Qb/K(KB)l/\ т. е. величине (9.8)
гл. II, найденной для темпера-
температуры в конце промежутка вре-
времени 2b/U при выделении в еди-
единицу времени на плоскости
в неограниченном теле коли-
количества тепла Q.
Температура в полуогра-
полуограниченном теле, обусловленная
выделением тепла при трении *)
тела о поверхность, по которой
оно скользит со скоростью U, и при отсутствии теплопередачи равна удвоен-
удвоенному значению температуры, определяемому G.10). Некоторые значения темпе-
температуры поверхности при различных значениях X к В приведены на рис. 34.
*) Эта задача подробно разобрана в [21, 22]. 3 последней работе приведены
численные данные для источников в виде полос и прямоугольников. Эквивалентна»
задача о поверхностной температуре при шлифовке рассмотрена в [23].
х/Ъ
Рис. 34. Распределение температуры на поверх-
поверхности полуограниченного твердого тела, обусло-
обусловленное выделением тепла при трении тела
о полосу шириной 2Ь9 относительно которой
оно движется со скоростью U.
§ 8] ГЛ. X. ПРИМЕНЕНИЕ МЕТОДА ИСТОЧНИКОВ И СТОКОВ 265
VIII. Источник в виде бесконечной полосы, как и в предыдущей задаче, но
ее плоскость образует с осью х угол 6 *).
Температура в точке полосы, .находящейся на расстоянии а от ее оси, равна
следующей величине:
А + В
f
f G.12)
А-В
где A = Ua/2x.
IX. Источник прямоугольного сечения — Ь < х < 6, — / < у < /, лежащий
в плоскости z = 0. Количество тепла% выделяемого в единицу времени на единицу
площади* равно Q.
4KU B*I/-
чл*ч^]-*[*1^]}?- G13)
где
/ X — Ux/2%, Y=(Jy/2vL, Z = Uz/2yLt ? = Ш/2х, B = (Jb/2i. G.14)
§ 8. Дублеты
В § 2 настоящей главы мы видели, что выражение
Q
ехр
8(icxO/2
где
Г—-^-1, (8.1)
= (х — х'J + (у — y'J + (z — г:'J. (8.2)
Г- ^-1 (8.3)
служит решением уравнения теплопроводности.
Отсюда следует, что
_ *L. или Щ=^ ехр
также будет его решением.
Это решение можно получить, комбинируя источник мощностью Q'
в точке (x'-\-dx\ у', z') и сток**) мощностью —Q' в точке (л/, у', z')
и переходя к пределу при dxr ->0. При этом надо положить, что
Y\m(Q'dx') = Q при dx'->0.
Если воспользоваться соотношением (8.2), то температура в точке
(х, у, z), обусловленная совместным действием источника и стока, запи-
запишется в виде
Q' г 2 (jc — х') dx' — (dx'J tl Г /?21
= —-^—jj- ехр— * '- 1 ехр =
8 (го*)'/» L Ш J L 4x* J
= ^-*——ехР —-^- +члены с более высокими степенями dxr.
FL 4y*J^
*) Эта задача возникает при расчете температур в плоскости среза при обра-
обработке металла резанием. Ее решение, а также несколько численных значений инте-
интегралов G.12) приведены в статье [24].
**) Если мощность источника, определенная в § 2 данной главы, отрицательна,
источник называют стоком.
266 ГЛ. X. ПРИМЕНЕНИЕ МЕТОДА ИСТОЧНИКОВ И СТОКОВ [§ 8
Переходя к пределу, получим решение (8.3). Такое распределение тем-
температуры называют распределением, обусловленным действием мгновенного
точечного дублета мощности Q, помещенного в точке (х\ у', z'), ось
которого параллельна оси х. Аналогичным образом, дифференцируя (8.1)
по у или z, мы приходим к точечным дублетам с осями, параллельными
этим направлениям; частные производные более высоких порядков дают
также решения уравнения теплопроводности.
Точно так же, исходя из мгновенного линейного источника (см. C.1)
данной главы), мы получаем для температуры, обусловленной действием
мгновенного линейного дублета, находящегося в точке (х\ у') с осью, па-
параллельной оси лг, соотношение
V— 8**2*2 exPj
Согласно C.4) данной главы, в случае линейного теплового потока
температура, обусловленная действием мгновенного дублета, помещенного
в точке х', записывается в виде
Q(x-x')
ехр
г (х — х'J-\ /О сч
—- — . (8.5)
L 4x/ J У J
Теперь легко перейти к рассмотрению непрерывного дублета пере-
переменной или постоянной мощности. Например, в случае линейного теплового
потока температура, обусловленная действием непрерывного дублета мощ-
мощностью ср(/), находящегося в точке х', определяется формулой
(8.6)
Вводя подстановку х — х' = 2х'/г (t —1'L2 а, получим
оо
v = —^=г f e-a2y(t—{x~~x'J)da при х > хг
у. У тс J \ 4ха2 /
_
(x-x')/2Vi*t)
9) при х<х'.
J \ 4уя2 /
(x-x')/2V(xt)
Таким образом,
Отсюда следует, что в точке хг имеет место разрыв температуры вели-
величиной <р@/х- Поэтому в случае линейного потока в полуограниченном твер-
твердом теле х > 0 температуру плоскости л; = 0 при ?>0 можно поддер-
поддерживать равной ср(?), помещая на эту плоскость непрерывный дублет мощ-
мощностью 2хср(?) (см. соотношение E.1) гл. I).
Решение двумерной задачи, когда плоскость х = 0 находится при тем-
температуре f(yt t)t можно получить, поместив непрерывный дублет с осью,
§ 10] гл- х ПРИМЕНЕНИЕ МЕТОДА ИСТОЧНИКОВ И СТОКОВ 267
параллельной оси х, и мощностью 2х/(у, t)dy' в точку (у', 0) и интегри-
интегрируя вдоль оси у. Соответствующий результат легко получить и для трех-
трехмерной задачи, когда температура плоскости х = 0 поддерживается равной
f(y', z\ t) (см. соотношение (9.3) гл. XIV).
§ 9. Метод последовательных волн
Согласно F.6) гл. II, функция
e-xwtk cos ^_х ^ул +, | (9 Л)
служит решением уравнения теплопроводности для линейного теплового потока. Это
решение можно рассматривать как волну, движущуюся вправо. Тогда интеграл
оо
f f («) е-' <•/*)* cos | •/ - х (.?.)* -f- г j. da> (9.2)
служит общим решением уравнения теплопроводности, которое можно рассматривать
как комбинацию таких последовательных волн. При изменении знака при х мы по-
подучим последовательные волны, движущиеся влево.
Легко показать, что при х > 0
оо
_1 Г е-х«o/2x)V, cos (t_x/ м«/._IJ^ = —1 е-хщи (9#3)
оо
_ /* ,-,(o,/2x)V2 CQS Г ^_ x /J^V/. | rf<o =
Следовательно, (9.3) и (9.4) представляют соответственно разложения единичного
мгновенного точечного источника и единичного мгновенного точечного дублета в на-
начале координат на плоские волны.
Грин [25], а затем Робертсон [26], использовав (9.2), разработали метод реше-
решения широкого круга задач с линейным потоком и затем распространили его на задачи
в сферических и цилиндрических координатах. Главная особенность этого метода за-
заключается в принятии в качестве частного решения для ограниченной области такой
комбинации волн типа (9.1), которая удовлетворяла бы условиям непрерывности на
границах. Подобный метод хорошо известен в учении о волновом движении. Источ-
Источники и дублеты вводят, используя комбинации частных решений (9.3) и (9.4). Таким
методом можно получить многие решения, приведенные в гл. XIV.
§ 10. Метод изображений. Линейный тепловой поток
Метод изображений, играющий столь важную роль в математической
теории электричества, целиком применим и к решению задач теплопровод-
теплопроводности, если твердое тело ограничено плоскостями, находящимися при нуле-
нулевой температуре *). Мысленно продолжим твердое тело неограниченно во все
стороны и методом изображений найдем распределение источников и стоков,
обеспечивающее нулевую температуру на границах тела. Аналогичный метод
применим и тогда, когда тепловой поток через граничные плоскости отсут-
отсутствует.
В гл. XIV мы увидим, что особую важность при решении общей задачи
теплопроводности для такого твердого тела имеет функция Грина, т. е.
*) Теоретическая электростатика была впервые изложена в книге Максвелла [27J.
В работе [28] исследовалась теплопроводность прямоугольного параллелепипеда,
правильной, треугольной призмы и различных тетраэдров. Решения основных задач
для областей с плоскими границами (в том числе задач с учетом теплообмена на
границах) приведены в [29].
268 ГЛ. X. ПРИМЕНЕНИЕ МЕТОДА ИСТОЧНИКОВ И СТОКОВ [§ 1 О
функция, описывающая распределение температуры, вызванное единственным
источником, в теле с заданными граничными условиями. Для некоторых задач
метод изображений служит одним из методов определения функции Грина»
Положение изображений не зависит от того, рассматриваются ли точеч-
точечные, линейные или плоские источники, параллельные отображающей гранич-
граничной плоскости. В данном параграфе будут рассмотрены плоские источники; ана-
аналогичные формулы для точечных источников будут приведены в § 10 гл. XIV.
I. Полуограниченное тело х > 0. Начальная температура равна
f(x). Температура на границе л: = 0 равна нулю.
Рассмотрим на плоскости х' источник мощностью / (xf) dx'. Будем
считать, что начальная температура тела обусловлена распределением таких
источников вдоль положительной части оси х.
К источнику мощностью f(x')dx' на плоскости хг мы присоединяем
сток мощностью —f{xr)dxr, помещенный в —х'. Тогда оба они дадут на
плоскости лг = О нулевую температуру. Следовательно,
II. Твердое тело ограничено плоскостями л: = 0 и х = а. Началь-
Начальная температура f(x). Граничные плоскости поддерживаются при
нулевой температуре.
Рассматривая на плоскости хг источник мощностью f(x')dx\ мы должньь
взять его изображения от плоскости х = 0 и х = а и комбинировать источ-
источники и стоки так, чтобы граничные плоскости находились при нулевой тем-
температуре. Таким образом, мы получим источники в точках х'-\-2na и стоки
в точках —х'-\-2па, где п — любое положительное или отрицательное целое
число или нуль. Тогда окончательно получим
а ( °°
1 У'/-, /ч Ч^ Г (х — х' — 2ndJ
л=-оо )
В § 3 (см. C.5) гл. Ill) в подобном же случае мы получили для v
другое выражение, а именно
оо а
*—~ / I sin ~~~~~^ e it \Х ) sin ——— clx •
a jmJ a J J v J a
л=1 О
При t > 0 это последнее можно записать в виде
(См. подстрочное примечание на стр. 99.)
Тождественность этих решений может быть доказана несколькими путями:
1) использованием свойств тэта-функций [30, 31]; 2) с помощью преобразо-
преобразования Лапласа; в этом случае решения типа A0.3) получаются в результате
применения теоремы обращения, а решения типа A0.2) — в результате раз-
разложения изображения в ряд по отрицательным степеням показательных функ-
§ 10]
ГЛ. X. ПРИМЕНЕНИЕ МЕТОДА ИСТОЧНИКОВ И СТОКОВ
269
ций (см. § 10, гл. XIV, где этот результат получен при рассмотрении точечного
источника между параллельными плоскостями); 3) с помощью следующей
теоремы:
Если f(x)— четная функция х, которую можно разложить
так же, как и функцию'f {x ±2/ш), в ряд Фурье по косинусам углов,
кратных углу ъх/а, то
л=-оо О Я=1 О
при условии, что интегралы и ряд сходятся.
Так как
а т а
= lf f(x')dx'+
0 Я=1
a
= ± f f(
о я=1 о
Bя+1)а
Чпа п-1 2яа
2па
-ff(x') cos ^fdx'
6
a
™ f f (x' + 2na) cos -2?-'лс' =
Bя+1
_2»в) = 1 / /(*')<**' + ¦§ 2 cosiir f f(x') cos-??fdx'.
2 21
/
Bn-l)a
n-\
f
Bя-1)а
TO
Я=1
[X2 1
—4*7 ' тогда *)
« 2^2 1 F Г jc'2 1
Л=-оо О
— /. cos / ехр Г7 cos ах'=
Отсюда **)
оо
2 «р[—
2 2^cos
Г
L
^~ J
A0.4)
*) Искомые интегралы приведены в § 2 гл. И; см. также 132].
**) Это — формула Пуассона.
270 ГЛ. X. ПРИМЕНЕНИЕ МЕТОДА ИСТОЧНИКОВ И СТОКОВ [§ 1 О
и
? M-U+
^{ |;^bO[^]}. A0.5)
J
Принимая во внимание A0.4) и A0.5), получим решение уравнения A0.2)
в виде
а со
2 С * t /ч V Г ъп2ъ4 Л . ппх . пъх' . г
f(*> 2 ехР LJsin Sln —г dx*
j
6 я=1
Г ъп2ъ4 Л . ппх
L ^~Jsin ~
III. Го же тело. Начальная температура равна нулю. Граница х = 0 под-
держивается при температуре <pj (х), граница х = а — при температуре, рав-
равной нулю.
Поместим в плоскости х = 0 непрерывный дублет мощностью 2хср2 (t) (см. (8.6)
данной главы). Если бы тело было неограниченным, то при наличии такого дублета
плоскость х = 0 поддерживалась бы при температуре ^ (t). Для того чтобы плос-
плоскость х = а находилась при нулевой температуре, необходимо поместить дублет
той же мощности в плоскости х = 2а, и т. д.
Таким образом, в точках 2па располагаются дублеты мощностью 2xcpt (t), где
п — нуль или любое положительное или отрицательное целое число.
Следовательно,
Соответствующий результат можно получить и для случая, когда граница х = 0
находится при нулевой температуре, а граница х = а — при температуре ср2 (t). Скла-
Складывая эти решения, приходим к иной форме решения задачи, приведенной в § 5 гл. III.
IV. Полу ограниченное твердое тело х > 0. Начальная температура f (x). На
границе х = 0 тепловой поток отсутствует.
Поступим здесь, как и в примере I, но, принимая во внимание отсутствие теплового
потока при х = 0, рассмотрим совместно источник мощностью / (xf) dx' в точке — х'
и источник той же мощности в точке х\
Тогда
V. Твердое тело, ограниченное плоскостями х = 0 и х = а. Начальная темпе-
температура равна f (х). На границе х = 0 тепловой поток равен нулю. Плоскость
х = а поддерживается при нулевой температуре.
Поступая здесь так же, как и в примере II, рассмотрим источники в плоско-
плоскостях ± Ana ± х' и стоки в плоскостях
В результате получим
'. (Ю.8)
§11] ГЛ. X. ПРИМЕНЕНИЕ МЕТОДА ИСТОЧНИКОВ И СТОКОВ 27!
§ 11. Применение метода изображений к двумерным
и трехмерным задачам
I. Полуограниченное твердое тело х > 0. Начальная темпера-
температура /(л:, у). Граница х = 0 поддерживается при нулевой темпе-
температуре.
Помещая линейный источник мощностью f(xrt y')dx'dy' в точку (х', у%
мы должны взять равный ему по мощности сток в точке (—х', у'), что
позволит удовлетворить условиям на границе. Тогда
II. Полуограниченное твердое тело х > 0. Начальная темпера-
температура /(jc, у, z). Граница х==0 поддерживается при нулевой темпе-
температуре.
Помещаем точечный источник мощностью /(*', у', zf) dxr dy' dz' в точку
(х', у', zr) и равный ему по мощности сток в точку (—х\ у', z')\ это
обеспечивает на границе х = 0 температуру, равную нулю. Тогда мы получим
v = ) [ [ [ /(*', у', z') {е-**'**' - е-*-Чы) dx' dy' dz\
где
и
R'2 ={x + x'J + {У — УУ + (z — z'f.
III. Клин с углом раствора п/т, где т — любое положительное
целое число.
Двумерные и трехмерные задачи, рассмотренные в примерах I и II,
являются частными случаями общей задачи для клина с углом раствора п/т>
где т — любое целое положительное число. Рассматривая эту задачу, мы
ограничимся случаем двух измерений, т. е. рассмотрением линейного источ-
источника в точке (л;', у'), причем ребро клина совпадает с осью z. Решение
трехмерной задачи с точечным источником в точке (x't y't z') и распро-
распространение полученного решения на более общий случай любой начальной
температуры не представляют трудностей.
Возьмем цилиндрические координаты. Границами клина служат пло-
плоскости 0 = 0 и д = п/т, температуры которых должны равняться нулю.
Внутри клина 0 < 0 < тс/т.
Пусть источник находится в точке Ро с координатами (а, а).
Пусть окружность, проходящая через точку Ро и имеющая центром
начало координат, пересекает плоскости 0 = 0 и 0 = ir/m в точках Л и В
(рис. 35).
Тогда углы АОР0, Р0ОВ и ЛОВ будут равны а, р и 7. где р = -п/т — а,
а ч = п/т.
Поместим источник единичной мощности в точке Яо.
Чтобы получить нулевую температуру на линии ОЛ, поместим сток
единичной мощности в точку Pv которая является изображением *) точки Ра
относительно О Л. Это значит, что угол АОРХ равен —а.
*) Иными словами, Рх симметрична Ро относительно прямой ОА. (Прим. ред.)
272
ГЛ. X. ПРИМЕНЕНИЕ МЕТОДА ИСТОЧНИКОВ И СТОКОВ
[§
Чтобы уравновесить сток, находящийся в точке Pv поместим источник
в точку Р2» которая является изображением точки Рх относительно ОВ. Это
значит, что угол АОР2 равен (a-f-2-f).
Чтобы уравновесить источник, находящийся в точке Р2 на линии ОА,
поместим сток в точку Р3» которая является изображением Р2 относительно О А
Это значит, что угол AOPZ равен — (<х-\-2*()
и т. д.
Таким путем мы получим ряд изображе-
изображений Pv Я2» •••» причем
,= ... =2Т.
. ... Zf.
Следовательно, угол АОР2т_х равен
— [а-\-2(т-\- 1)т}-
Тогда
= 2а + 2 (т — 1) 7 + 2р = 2ir.
Рис. 35. Таким образом, точка Р2т-Х совпадает
с изображением точки Яо относительно ОВ\
поэтому ряд изображений конечен, и последней точкой будет P<im-v
Следовательно, все такие источники и стоки вместе с источником Ро
дадут нулевую температуру на плоскостях 6 = 0 и 6 = ir/m.
Температура в точке (г, 6), полученная в результате действия этой
системы источников и стоков, записывается в виде
2m-l
«= 2
s=0
A1.1)
где vs — температура, полученная в результате действия источника единичной
мощности, помещенного в точке Ps неограниченного твердого тела.
Однако выше (см. C.3) данной главы) мы видели, что температура
в точке (/*, 0), обусловленная источником единичной мощности, помещенным
в точке (г', 6х), равна
где #2=г2_^.г/2_ 2/v'cosF — 60-
Пользуясь разложением Неймана [3, 19]
Уо (KR) = Уо (кг) Уо (ХгО
получим для температуры
0 c°s n F — в').
или
~ 2 cos п F — 60 / ke-*Vn (Xr) Jn (XrO d\.
§ 12] ГЛ. X. ПРИМЕНЕНИЕ МЕТОДА ИСТОЧНИКОВ И СТОКОВ 273
Тогда из соотношения A1.1) следует, что
оо т — 1
1 VI VI
v = -о— У, V [cos/г F — а — 2sf) —
П——оо 5=0
оо
— cos п F -f-а + 2$т)] / \e-xX2tJn(\r)Jn(ka)d\. A1.2)
о
Когда /г не кратно т, сумма по 5 равна нулю. Когда же п кратно т,
сумма по 5 равна
2т sin /10 sin na.
Таким образом, из соотношения A1.2) получаем решение нашей задачи
о температуре в клине 6 = 0, 6 = тс/m, обусловленной источником единичной
мощности, помещенным в точке (а, а), в виде
где, как и выше, мы писали f вместо %/т.
Решая трехмерную задачу, мы исходим из выражения
1 ртп Г г» + г'2 - 2rr' cos F - 6') + (г - z'
ехР[ ш
соответствующего источнику единичной мощности, находящемуся в точке (г\ 0', г').
Поступая так же, как и выше, получаем решение нашей задачи в виде
pel 6 Т 7
§ 12. Обобщение метода изображений Зоммерфельдом
Метод изображений, примененный выше к клину с углом раствора тс/m, где
т — положительное целое число, неприменим к клину с углом раствора пп/т, где т
и п положительные взаимно простые целые числа.
Например, пусть угол раствора равен прямому углу и в точке Ро(г',Ь')
находится заданный источник, причем 0 < в' < -^ те; тогда мы получим следующие
изображения:
сток в точке Р\(г\ —в'), источник в точке Р2(г'> я + в')
и
сток в точке Р3 (г', — те — в').
В этом случае при решении задачи трудности не возникают (рис. 36).
Если же угол равен 2те/3 и заданный источник находится в точке Ро (г', в'),
причем 0 < 0' < 2те/3, то мы получим следующие изображения (рис. 37):
сток в точке Р\(г\ —в'), источник в точке Р2у* "з""^/'
сток в точке рЛг', к в'), источник в точке Р4 (г', -х- + б 'J;
и
сток в точке Рь\г\ q ^'\.
\Ь Г. Карслоу, Д. hi ер
274
ГЛ. X. ПРИМЕНЕНИЕ МЕТОДА ИСТОЧНИКОВ И СТОКОВ
[§ 12
Так как выражение для температуры, обусловленной действием источника, имеет
периодический характер с периодом 2я, а сток в точке Р3 дает особую точку, соот-
соответствующую стоку в точке (г', 2я/3 — в'), т. е. в точке, расположенной между гра-
граничными плоскостями, данный метод оказывается непригодным.
Рис. 36.
Рис. 37.
Однако для полного представления нам нужна только область 0 < в < — п, зани-
занимаемая твердым телом, и если мы можем найти решение уравнения теплопро-
теплопроводности, имеющее период 4п и только одну особую точку при г = О и * = О в ука-
указанной области, причем функция близ этой точки имеет простой вид
или
то мы можем использовать его так же, как и обыкновенное выражение для тем-
температуры, обусловленной источником, и взять изображения в точках, указанных
выше.
Этот метод, впервые разработанный Зоммерфельдом, позволяет непосредственно
исследовать решение уравнения теплопроводности на соответствующей римано-
вой поверхности (или в римановом пространстве). При угле раствора пъ/т риманова
поверхность {или пространство) оказывается л-листной, и решение будет иметь
период 2/гтс. Этот метод интересен в историческом отношении, так как после его
применения к задаче распространения тепла от источника в теле, ограниченном пло-
плоскостями в = 0 и в = 2гс, Зоммерфельду удалось с его помощью дать первое точное
решение задачи дифракции волн на полуограниченной плоскости (например, на пло-
плоскости 6 = 0). В настоящее время развит более простой метод решения этих задач,
пригодный как для уравнений теплопроводности, так и для других дифференциальных
уравнений математической физики в частных производных. Поэтому здесь достаточно
только упомянуть о работах Зоммерфельда, а также о других работах, в которых
используется идея римановой поверхности [33—36].
Мы возвратимся к задаче с клином в § 14, гл. XIV и покажем, что решение A1.3)
предыдущего параграфа для угла п/т справедливо для клина с любым углом раствора *).
ЛИТЕРАТУРА
1. Kelvin, Compendium of the Fourier mathematics for the conduction of heat in
solids and the mathematically allied physical subjects of diffusion of fluids and
transmission of electric signals through submarine cables, статья «Heat» в Encycl.
Britt. A880) или Math, and Phys. Papers, 2, p. 41.
2. L о v e г i n g, Bull. Geol. Soc. Am. 46, 69—93 A935).
3. Watson, A Treatise on the Theory of Bessel Functions, Cambridge, ed. 2, 1944.
(Г. В а т с о н, Теория бесселевых функций, ИЛ, М., 1949.)
*) Другое решение, полученное с помощью контурного интеграла, приведено
в [37]; см. также [38]. *
ГЛ. X. ПРИМЕНЕНИЕ МЕТОДА ИСТОЧНИКОВ И СТОКОВ 275
4. Masters, J. Chem. Phys. 23, 1865—1874 A955).
5. Jahnke —Emde, Tables of Functions, Teubner, ed. 3, i933, p. 83. (E. Янке,
Ф. Эмде, Таблицы функций с формулами и кривыми, Гостехиздат, 1948).
6. Fischer, Ann. Physik 34, 669 A939).
7. А 1 b г е с h t, Met. Z. 49, 294 A932).
8. Podolsk у, J. Appl. Phys. 22, 581 A951).
9. R i t с h i e, J. Appl. Phys. 22, 1389 A951).
10. Jaeger, Aust. J. Sci. Res. A5, 1—9 A952).
11. Oosterkamp, Philips Res. Rep. 3, 49 A948).
12. О о s t e r k a m p, J. Appl. Phys. 19, 1180 A948).
13. Wilson, Proc. Camb. Phil. Soc. 12, 406 A904).
14. R о s e n t h a 1, Trans. ASME 68, 849—866 A946).
15. Grosh, Trabant, Hawkins, Quart. Appl. Math. 13, 161—167 A955).
16. J a e g e r, Phil. Mag. 35, 169 A944).
17. M u 11 e r, Proc. Roy. Soc. A125, 507 A929).
18. Rosenthal, Cameron, Trans. ASME 69, 961 A947).
19. Gray, M a t h e w s, Treatise on Bessel Functions, Macmillan, ed. 2, 1922. (Э. Г p e и,
Г. М э т т ь ю з, Функции Бесселя и их применение в физике и механике, ИЛ, М.,
1953.)
20. Lu ke, J. Math. Phys. 29, 27—30 A950).
21. Blok, Inst. Mech. Engrs, General Discussion on Lubrication 2, 222 A937).
22. J a e g e r, J. Proc. Roy. Soc, N. S. W. 76, 203—224 A943).
23. О u t w a t e r, S h a w, Trans. ASME 74, 73—86 A952).
24. С h a o, T r i g g e r, Trans. ASME 75, 109—120 A953).
25. Green, Phil. Mag. 3, 784 A927); 5, 701—720 A928); 9, 241—260 A930); 12,
233—255 A931); 18, 625—640 A934); 38, 97—115 A947).
26. Robertson, Phil. Mag. 15, 937—957 A933); 18, 165—176 A934); 18, 1009—1022
A934).
27. Maxwell, Electricity and Magnetism, ed. 1, 1873.
28. Lame, Lemons sur la theorie de la chaleur, Paris, 1861.
29. Hobson, Proc. Lond. Math. Soc. 19, 279 A887).
30. Poincare, Theorie de la propagation de la chaleur, p. 91.
31. W h i 11 a k e r, Watson, Modern Analysis, Cambridge, ed. 3. (Э. Уиттекер
и Г. Ватсон, Курс современного анализа, ГТТИ, М., 1933).
32. С а г s I a w, Fourier's Series and Integrals Macmillan, ed. 3, 1930.
33. Sommerfeld, Math. Ann. 45, 263 A894); 47, 317 A896); Proc. Lond. Math.
Soc. 28, 395 A897).
34. S с h w а г z s с h i 1 d, Math. Ann. 55, 177 A902).
35. Cars 1 aw, Proc. Lond. Math. Soc. 30, 121 A899); Rep. Brit. Ass. 644 A900).
36. Hobson, Trans. Camb. Phil. Soc. 18, 277 A900).
37. С a r s 1 a w, Introduction to the Mathematical Theory of the Conduction of Heat
in Slides, Macmillan, ed. 2, 1921. (Г. Карслоу, Теория теплопроводности, Гостех-
Гостехиздат, М., 1947.)
38. Cars law, Proc. Lond. Math. Soc. 8, 365 A910), 18, 291 A920).
39. R а у 1 e i g h, Phil. Mag. 22, 381—396 A911).
40. W h i t e h e a d, Electrician 99, 225 A927).
41. Lo e w e n, S h a w, Trans. ASME 76, 217—231 A954).
42. T г i g g e r, S h a w, Trans. ASME 73, 57—68 A951).
43. Roberts, Proc. Roy. Soc. A104, 640 A923).
18*
ГЛАВА XI
ИЗМЕНЕНИЕ ФИЗИЧЕСКОГО СОСТОЯНИЯ
§ 1. Введение
Особый интерес представляет весьма важный класс задач, в которых
исследуемое вещество претерпевает превращения, в результате чего оно
переходит из одной фазы в другую с выделением или поглощением тепла.
Такого рода задачи возникают во многих случаях, из которых важнейшими
и наиболее распространенными являются случаи плавления и затвердевания.
Поэтому для определенности большинство рассматриваемых здесь задач будет
формулироваться именно в такой форме. Первой опубликованной работой,
в которой рассматривались подобные задачи, является, по-видимому, работа
Стефана [1], посвященная изучению толщины полярных льдов*). Поэтому
задачу о промерзании часто называют «задачей Стефана».
Существенно новой чертой таких задач является наличие движущейся
поверхности раздела между двумя фазами, причем приходится определять
закон движения этой поверхности. На ней происходит поглощение или выде-
выделение тепла; в данном случае термические свойства фаз по обеим сторонам
движущейся поверхности могут оказаться различными, и поэтому такая
задача весьма трудна. Ниже будет показано, что она нелинейна, и, следова-
следовательно, необходимо определять специальные решения, не обладающие к тому же
свойством наложения (т. е. их комбинации не будут служить решениями).
Прежде чем перейти к рассмотрению конкретных решений, желательно
показать, какие точные решения уже получены и какими методами мы сей-
сейчас располагаем. Наиболее важно точное решение Неймана для случая полу-
полуограниченной области х > О, находящейся в начальный момент времени
при постоянной температуре V, превышающей температуру плавления,
с поверхностью х = 0, температура которой во все последующие моменты
времени поддерживается равной нулю. Для других важных граничных усло-
условий при х = 0 (например, постоянство теплового потока или граничные
условия третьего рода), замкнутых решений**) нет, хотя для различных
заданных значений температуры поверхности существует несколько решений,
не представляющих, однако, сколько-нибудь существенного физического
интереса. Часто применяемое приближение заключается в пренебрежении
теплоемкостью исследуемого материала между поверхностью л; = 0 и поверх-
поверхностью раздела, т. е. в предположении, что тепловой поток через эту область
является установившимся.
*) Стефан получил формулы B.18) и B.21) данной главы, которые приводятся
ниже. Более общий результат, известный как решение Неймана, был дан Францем
НейманОхМ в его лекциях 1860 г. (см. [2]).
**) То есть решений в виде интегралов от элементарных или специальных функ-
функций. (Прим. ред.)
§ 2] гл. xi. изменение физического состояния 277
Можно указать также точные решения ряда задач для неограниченной
области, в которой в начальный момент времени при х < О вещество нахо-
находится в твердом состоянии и имеет постоянную температуру, а при х > О
вещество находится в жидком состоянии и также имеет постоянную темпе-
температуру. Эти решения легко обобщить на случай нескольких критических
температур и на случай, когда вместо фиксированной точки плавления мы
имеем интервал температур плавления.
Для других областей, таких, как пластина [3] — а < х < а с поверх-
ностыб, поддерживаемой при нулевой температуре, или для области, в кото-
которой в начальный момент времени участок — а < х < а представляет собой
жидкость, а участок |jc|>a—твердое тело, точные решения отсутствуют.
Что касается задач о радиальном потоке тепла в цилиндрических или
сферических координатах, то здесь положение оказывается еще худшим.
Простое точное решение в цилиндрических координатах известно только
для задачи о выделении или поглощении тепла непрерывным линейным источ-
источником. Для области, ограниченной изнутри или снаружи круговым цилиндром
с постоянной температурой поверхности, имеется только приближенное ре-
решение.
Не считая нескольких задач, имеющих точные решения, все остальные
задачи приходится решать численными методами. Для этой цели используются
цифровые методы, а также дифференциальный анализатор и устройство,
основанное на методе электрической аналогии и названное термическим ана-
анализатором. В таких случаях (ср. § 5 гл. XVIII) упомянутые выше точные
решения часто полезны как нулевые приближения к решениям. Системати-
Систематическое использование численных методов [4, 5] имеет то преимущество, что
с их помощью можно учесть изменение термических свойств материала
с температурой, которое в интервалах температур, встречающихся в задачах
о плавлении и затвердевании, часто оказывается значительным.
Применение полученных результатов представляет значительный практи-
практический интерес. Задача об образовании льда [6, 7] имеет чрезвычайно большое
значение как в геофизике, так и при производстве льда. В последнее время
большое внимание уделяется вопросу затвердевания отливок [8]. Изучение
охлаждения больших масс изверженных горных пород имеет большое значе-
значение в геологии [9]. Часто приходится встречаться также с задачами о диффу-
диффузии, в результате которой появляются аналогичные уравнения и граничные
условия [10—12].
§ 2. Одномерные случаи плавления и затвердевания.
Решение Неймана и его обобщение
Термические коэффициенты материала в твердой фазе мы будем обо-
обозначать в данной главе через р, cv Kv %v а его температуру через vx\ соот-
соответствующие величины в жидкой фазе мы будем обозначать через р, с2» ^2»
х2 и v2- Изменением объема при затвердевании мы везде (кроме примера VIII
данного параграфа) будем пренебрегать, и следовательно, плотность р как
твердой, так и жидкой фаз окажется одинаковой.
Пусть скрытая теплота плавления исследуемого вещества (кал/г) равна Z,,
а температура плавления — Tv Тогда, если поверхность раздела между твер-
твердой и жидкой фазами определяется координатой X (/), одно из граничных
условий, которое должно удовлетворяться на этой поверхности, запишется
в виде
vx = v2 — Tv когда x = X(t). B.1)
278 ГЛ. XI. ИЗМЕНЕНИЕ ФИЗИЧЕСКОГО СОСТОЯНИЯ [§ 2
Второе граничное условие касается поглощения или выделения скрытой
теплоты на этой поверхности. Для определенности предположим, что в области
x>X(t) находится жидкость при температуре v2(x, t), а в области
х < X (t) — твердое вещество при температуре ^(л:, t). В таком случае,
если поверхность раздела перемещается на расстояние dX, то в элементе
вещества выделяется и должно быть отведено в результате теплопроводно-
теплопроводности количество тепла, равное в пересчете на единицу поверхности LpdX.
Иными словами,
j. dvx „ dv2 _ . dX @ 9
Условия B.1) и B.2) являются граничными условиями, которые в данном
случае должны удовлетворяться на поверхности раздела. Легко видеть, что
если в области х < X будет находится жидкость с температурой v2(x, t),
а в области х > X — твердое вещество с температурой гцОс, t), то усло-
условие B.2) также будет выполняться.
Условие B.2) можно записать и в другой форме; для этого рассмотрим
в плоскости (х, t) две кривые постоянной температуры vx(x, t) = Tl =
= v2(xt t) (см. B.1)). В таком случае получаем
отсюда условие B.2) можно записать в следующем виде:
dvi dv2
К\-^—АГо-^ = —?р^— = —?р-з—• B.3)
1 дх * дх dvx r dv2
!п Их"
В этой форме нелинейность задачи становится очевидной. В трехмерном
случае граничное условие B.3) принимает вид
dv\ dv2
=-г. С2.4)
где знаки должны быть выбраны так, чтобы они соответствовали рассмат-
рассматриваемой задаче.
В случае линейного теплового потока температуры vx и v2 в твердой
и жидкой областях должны удовлетворять уравнениям
= 0, B.5)
Помимо условий B.1), B.2), B.5) и B.6), должны выполняться еще
условия на неподвижных границах рассматриваемой области. Ниже приво-
приводятся решения нескольких важных задач в случае линейного теплового
потока [13, 14].
I. Решение Неймана для полуограниченной области х > 0, пред-
представляющей собой в начальный момент времени жидкость с постоян-
постоянной температурой V. При ?>0 поверхность х = 0 поддерживается
при нулевой температуре.
§ 2] ГЛ. XI. ИЗМЕНЕНИЕ ФИЗИЧЕСКОГО СОСТОЯНИЯ 279
В данном случае должны удовлетворяться условия B.1), B.2), B.5) и
B.6), а также дополнительные граничные условия
v2->V при лг-^оо, B.7)
г>! = 0 при лг = О. B.8)
Из A.4) гл. II следует, что
v, = AФ ^—77-. B.9)
О /„ /|/2
где А — постоянная, удовлетворяющая B.5) и B.8). Кроме того, если Б —
постоянная величина, то
Vn = V — ВФ* B 10^
2 2(х201/2 '
удовлетворяет условиям B.6) и B.7). Тогда из условия BЛ) следует, что
Поскольку соотношение B.11) должно оставаться справедливым во все
моменты времени, X должно быть пропорциональным №\ например, должно
быть справедливым соотношение
0Vl. B-12)
где X — численный множитель, который следует определять из остающегося
условия B.2). Воспользовавшись B.9), B.10) и B.12), получим
Klа,-» - К2В (-Ь-f ехр Г—^] = Ш1Р*'\ B.13)
или, используя B.11) и B.12),
...
' }
После того как из B.14) мы найдем X, из B.9) — B.12) можно опре-
определить vx и v2. Выражения для них записываются в виде
B.15)
V~Tl Иттт^!- B.16)
Полученное выше решение является частным решением дифференциаль-
дифференциального уравнения B.6) с граничным условием B.7); оно удовлетворяет начальным
условиям, вытекающим из B.12) и B.16). Они имеют вид
^ = 0, v2 = V при * = 0, B.17)
т. е. вся область х > 0 занята жидкостью с температурой V.
Численно решение уравнения B.14) легко найти при помощи таблиц
функции ошибок. Несколько значений его корней для воды (/С2 = х2 = 0,00144)
2S0
ГЛ. XI. ИЗМЕНЕНИЕ ФИЗИЧЕСКОГО СОСТОЯНИЯ
[§2
и льда (Ki = 0,0053, х1 = 0,0115, /,р = 73,6) при различных значениях
начальной температуры (V — Тг) воды, а также температуры G\) при л; = 0
указаны ниже.
1
2
3
4
5
Значения X, удовлетворяющие
0
0,056
0,079
0,097
0,111
0,124
1
0,054
0,077
0,095
0,110
0,123
2
0,053
0,076
0,093
0,108
0,121
3
0,051
0,074
0,091
0,106
0,119
B.14)
4
0,050
0,073
0,090
0,104
0,117
5
0,049
0,071
0,088
0,103
0,115
В очень важном частном случае, когда в начальный момент времени
температура жидкости равна температуре плавления, т. е. V = TV уравне-
уравнение B.14) принимает вид
= -?%-• BЛ8)
Корн
(рис. 38,
1 этого уравнения можно найти из графика функции \еХ2Ф(к)
кривая /). Отметим, что для ряда материалов, например для горных
пород или металлов с высокой темпера-
температурой плавления, поверхности которых
поддерживаются приблизительно при ком-
комнатной температуре, величина cJ^JLiz1!*
примерно равна единице. Вместе с тем.
в случае замерзания воды при Отводе тепла
в область с температурой на несколько
градусов ниже нуля величина c^i/Ln1!*
мала. В данном случае подстановка в урав-
уравнение B.18) первого члена соотношения D)
из приложения 2 приближенно дает
1
\)
"
//
У
-
с, Г,
2L
B.19)
О
Этот результат можно получить
л также при помощи интересного физиче-
Рис. 38. Графики функций Х/2Ф(Х)(/), ского приближения, а именно предполо-
1 ЛХ2 /ft* /Л \ / Г Г\ 1 ЛХ2 П I гЬ/1\1 / Г Г Г\ .. У/МП 111>Гк ПОЛППОПОПОиНО ТОХЯТИЛПОТЛТП О
(///) и жив, что распределение температур в
твердой фазе примерно совпадает с рас-
распределением, соответствующим устано-
установившемуся тепловому потоку, причем поверхность х = X имеет темпера-
температуру Tv т, е. что
v1 = ^~. B.20)
Подстановка в условие B.2) дает
Отсюда
что эквивалентно B.19J.
B.21)
§ 2] ГЛ. XI. ИЗМЕНЕНИЕ ФИЗИЧЕСКОГО СОСТОЯНИЯ 281
II. Случай переохлажденной жидкости.
Пусть температура плавления твердого тела равна 7\, область х > О в началь-
начальный момент времени представляет собой жидкость с температурой V <ТЪ а ее
затвердевание начинается на плоскости х = 0 и распространяется вправо. Тепло
от затвердевающего материала не отводится, и поэтому его температура будет иметь
везде постоянное значение Тх.
Если x — X(t) — поверхность раздела между твердой и жидкой фазами, то мы
ищем решение в виде
X = 2\{r.2t)xl\ B.22)
t/j = Tl9 х < X,
АФ*Х
Тогда граничные условия при х = X дают.
У+АФ*(К)=ТХ,
Ae-X2=\Ln4c2.
Отсюда следует, что X служит корнем уравнения
\еХ2Ф* (X) = (Тх — V) c2/Liz\ B.23)
который можно найти по кривой // рис. 38.
III. Плавление в области х > 0.
Рассмотрим теперь задачу, в которой в начальный момент времени область х > 0
является твердым телом с нулевой температурой, а при t > 0 плоскость х = 0 под-
поддерживается при постоянной температуре V > Тх. В этом случае, использовав, как
и прежде, для твердой фазы обозначения К\% *i, р» с,, #,, а для жидкой фазы — /С2,
*2> Р. С2» Щу мы получим для положения плоскости плавления выражение
B), B.24)
где X — корень уравнения *)
Тогда температуры твердой и жидкой фаз равны соответственно
V ^ФХ
тг B.26)
Ф(Х) 2(VI/2
Уравнения B.25) и B.14) отличаются друг от друга только тем, что здесь пере-
переставлены местами термические коэффициенты твердой и жидкой фаз и величины Тх
и (V— Тх).
IV. В начальный момент времени область х > 0 представляет собой
жидкость, а область х < 0 — твердое тело.
Предположим, что в начальный момент времени область х < 0 является твердым
телом с термическими коэффициентами /Со, ро> со> *о и нулевой температурой,
а область х > 0 — жидкостью с термическими коэффициентами /Сг, р, с2, %2 и п0"
стоянной температурой V. Термические коэффициенты /flf p, с,, %, затвердевшей
жидкости могут отличаться от термических коэффициентов твердого тела в об-
области х < 0.
Применяемый здесь метод является тривиальным обобщением использованного
выше метода. Обозначая через v0, vx и v2 температуры в областях х < 0, 0 < х < X
*) Такое решение с 7^i = 0, а также другие решения, не имеющие аналогии
в задачах теплопроводности, появляются при изучении диффузии кислорода в мышцу,
в каждой точке которой должно произойти восстановление до того, как кислород
сможет проникнуть дальше [12].
282 ГЛ. XI. ИЗМЕНЕНИЕ ФИЗИЧЕСКОГО СОСТОЯНИЯ [§ 2
и х > X соответственно, где X—координата, определяющая положение поверхности
раздела между твердой и жидкой фазами, примем
В этом случае при х -> оо t/0 -> 0. А, В к С связаны условиями непрерывности
при х = 0, которые дают
Л=Я и /С0^1/2 = /С1Сх^. B.31)
Поступая здесь так же, как и выше, найдем
* = 2А (*,*), B.32)
где X теперь служит корнем уравнения
После нахождения X мы получим для t/0, vx и t;2 соотношения
B-36)
Это решение было введено Шварцом [15, 16] в качестве лучшего, чем B.14) —
B.16), приближения для задачи о затвердевании металла, залитого в форму, поскольку
термические свойства затвердевшего металла и материала формы сильно отличаются
друг от друга. Такое решение может также рассматриваться как фундаментальное
решение задачи об охлаждении интрузивных изверженных пород, но в этом случае,
поскольку термические свойства горных пород мало отличаются друг от друга, обычно
можно считать, что /Со = ^Сь *о = *i и использовать несколько упрощенные
результаты.
Если в начальный момент времени температура жидкости совпадает с темпера-
температурой ее плавления, т. е. V= Tlt уравнение B.33) принимает вид
Как отмечалось выше, для горных пород отношение (K^q2/К0^{2) приблизи-
приблизительно равно единице, тогда как для чугуна в песке оно примерно достигает 25.
Некоторые значения функции, записанной в левой части B.37), показаны на рис. 38
(кривые /// и IV). Если
^ B.38)
то корень уравнения B.33) становится отрицательным, что соответствует плавлению
твердого тела в области х < 0 горячей жидкостью. Если в этой области и в области
х > 0 материалы одинаковы, то полученное выше решение правильно; если же они
§ 2] гл. хт. изменение физического состояния 283
различны, то решение должно быть переписано, с тем, чтобы соответствовать рас-
рассматриваемому случаю.
V. Плавление *) в области х > О, обусловленное контактом с горячим твер-
твердым телом в области х < 0.
В этом случае область х < 0 в начальный момент представляет собой твердое
тело с термическими коэффициентами /Со, ро» с0, %0 и температурой V > Тх\ область
х > 0— твердое тело с термическими коэффициентами К\* Р» ci» %i и температурой,
равной нулю. Термические коэффициенты этого материала в жидком состоянии
равны /С2, р» с2, %2-
Если Х=2\ (x2Ol/f — координата, определяющая положение поверхности раздела,
то X служит корнем уравнения
-» «<#*! е*Р [~ ffi _ М«*
2
VI. Случай интервала температур плавления.
Горные породы и сплавы не имеют фиксированных точек плавления, а плавятся
в некотором интервале температур, например в интервале от Т2 до Ть в котором
выделяется скрытая теплота затвердевания L. Если эта теплота выделяется в интер-
интервале Т2 — Л равномерно, то ее влияние можно выразить, добавив к собственно
теплоемкости жидкости в этом интервале с2 величину L/(T2—Tl). Иными словами,
влияние скрытой теплоты затвердевания в интервале (Г2, Тх) можно приближенно
учесть, используя в этом интервале выражение для удельной теплоемкости в виде
7=ТГ' Bв40)
Таким образом, наша задача сводится к задаче, в которой не нужно^ рассматри-
рассматривать скрытую теплоту, но удельная теплоемкость оказывается переменной.
Подобные задачи, вообще говоря, можно решать так же, как и пример VII,
однако результаты для наиболее важного частного случая, а именно для случая
точного совпадения **) начальной температуры жидкости и температуры Т2 (т. е. наи-
наибольшей температуры интервала температур плавления), можно написать непосред-
непосредственно, положив в соотношениях B.14) и B.33) L = 0. При этом подразумевается,
что с2 есть величина, определяемая B.40).
Таким образом, для области х > 0, представляющей собой в начальный момент
жидкость с температурой Тъ с поверхностью х = 0, поддерживаемой при t > 0 при
нулевой температуре, уравнение B.14) дает
ехР[(*1-х2)Х7х2]Ф*[Х(х1/«2I/'] ^ (Tt-TQK^f
Ф(Х) ТК42
Если в начальный момент область х > 0 представляет собой жидкость с темпе-
температурой Г2, а область х < 0 — твердое тело, как в случае IV, то уравнение B.33)
принимает вид
^ехр^-^ХУчИЧЧУ^ (Тъ-TQKA2 B42)
VII. Многофазные случаи.
Проведенный выше анализ легко обобщить на случай вещества с несколькими
температурами превращений или с несколькими интервалами температур, в которых
выделяется скрытая теплота превращения. В качестве иллюстрации рассмотрим обоб-
обобщение примера I на случай двух температур превращений.
Пусть в начальный момент времени в области х > 0 температура постоянна
и равна V и при t > 0 поверхность х = 0 поддерживается при нулевой температуре.
*) Например, случай плавления припоя нагретым железом. Система твердое
тело — пар — вода рассмотрена в [17] в свяаи с проблемами закалки.
**) По-видимому, это имеет место для большинства магматических. интрузий
(включений). Численные результаты для охлаждения интрузивной оболочки приведены
в работе Егера [18].
284 ГЛ. XI. ИЗМЕНЕНИЕ ФИЗИЧЕСКОГО СОСТОЯНИЯ [§ 2
Предположим также, что исследуемый материал имеет две температуры превра-
превращения Т2 и Тх (V > Т2 > Тх > 0), при которых выделяются скрытые теплоты пре-
превращений L2 и Lx. Пренебрегая изменением объема при фазовом переходе будем
считать, что все фазы #меют одинаковую плотность р. При описании фаз в темпе-
температурных интервалах @, Т{), (Ти Т2) и (Г2, V) мы будем пользоваться соответственно
индексами 1, 2 и 3.
Между фазами 1 и 2 будет существовать поверхность раздела x — Xx(t)y
а между фазами 2 и 3 — поверхность раздела х = Х2 (t). Анализ, совершенно анало-
аналогичный анализу, проведенному в примере I, показывает, что
Хх @ = 2 X, (х,01А. Х2 @ = 2Х2 (%20'/2, B.43)
где
г
—— =-^—•
L ^2 J «1
B.45)
Когда совместные уравнения B.44) и B.45) разрешены относительно X, и 12,
температуры в рассматриваемых трех областях находят из соотношений
= | (Г, - Г,) Ф | Т7ГЖ | + Т,Ф (Х2) - Т2Ф [X, (*,/*,)'/*] | {Ф (Х2)-Ф [X, I
B.47)
B48)
В случае вещества, состоящего из п фаз, мы будем иметь (п—1) границ фазо-
фазового перехода, определяемых соотношениями типа B.43), и (л — 1) уравнений типа
B.44) и B.45) для X,, ..., ХЛ_,. Было показано, что их решение практически воз-
возможно [19].
VIII. Влияние изменения объема при затвердевании.
Если плотности твердой и жидкой фаз неодинаковы, то жидкость будет пере-
перемещаться. Для иллюстрации этого рассмотрим пример I, предположив для опреде-
определенности, что плотность р! твердой фазы больше плотности жидкой р2.
Как и выше (см. B.12)), будем искать такое решение*), чтобы поверхность
раздела находилась при Л" =2Х(%!*)'/*, а температура твердого тела равнялась
B.49)
Далее, при перемещении поверхности раздела на расстояние dX количество
образовавшегося при этом затвердевшего материала, отнесенное к единице поверх-
поверхности р, dX, эквивалентно количеству жидкости, находящемуся в слое толщиной
р! dX/?2- Иными словами, жидкость движется вдоль оси х со скоростью их, опре-
определяемой соотношением
(t)^- <2-50>
Следовательно, уравнение теплопроводности G.2) гл. I для движущейся жидкости
принимает вид
d2v2 , (Pi — Ра> dX dv2 I dv2
*) Несколько иное изложение, а также многочисленные примеры приложения
к задачам диффузии даны в [10, 11].
§ 3] ГЛ. XI. ИЗМЕНЕНИЕ ФИЗИЧЕСКОГО СОСТОЯНИЯ 285
Легко показать, что при приведенном выше значении X уравнение B.51) удовле-
удовлетворяется функцией
f х ^ (Pi — ?о) *'/2 \
\^\ B-52)
значение которой при х -> оо стремится к пределу, равному V. В соответствии с усло-
условием B.1) на границе х = X должно выполняться условие
АФ (X) = V - ВФ* [\н4шМ] = Tv B.53)
Подстановка этих результатов *) в B.2) дает уравнение для X
с, г,
B.54)
При р! = р2 это уравнение сводится к B.14).
Для льда р! = 0,917, для воды р2 = 1, и из уравнения B.54) при V — 7*, = Г, = 5°
получаем X = 0,116. Это значение сравнимо с величиной А = 0,115, найденной из урав-
уравнения B.14).
§ 3. Область х > 0 при других граничных условиях
Метод, изложенный в предыдущем параграфе, заключается в использовании реше-
решения уравнения для линейного потока тепла, являющегося функцией только xt~4*. Как
отмечалось в § 1 гл. II, функция Ф [х D%t)~^2] служит единственным решением такого
Типа, и поскольку нельзя удовлетворить граничным условиям третьего рода или гра-
граничным условиям с постоянным тепловым потоком, точных решений, подобных реше-
решениям предыдущего параграфа, не имеется. Тем не менее мы рассмотрим несколько
задач этого типа.
I. Затвердевание в области х > 0, когда в начальный момент времени жидкость
находится при температуре плавления. При х = 0 тепловой поток F из твер-
твердого тела постоянен.
В данном случае решение можно записать в виде ряда [20]. Для этого X (t)
представляют в виде степенного ряда по t, a vx — в виде двойного степенного ряда A.13)
гл. II. Подставив их в условия B.1) и B.2) предыдущего параграфа и воспользовав-
воспользовавшись граничным условием при х = 0, т. е.
/С,|^- = /7, C.1)
получим искомое решение в виде
Ft FH2 5F5t3
X(t) = -j-- ^/з з + faTJ s - •••' (a2>
Fx F2 (x2 + 2V) F* (x< + \2^x2t + 12%?*2)
V\ = T\ -| 1 g g-g ... C.3)
II. Пример /, но с граничным условием третьего рода
4^- = /ш, * = 0. C.4)
*) Тот факт, что условие B.2) остается справедливым и при замене р на плот-
плотность фазы, остающейся в этой области, можно проверить путем составления тепло-
теплового баланса для области (Л", X -\- dX).
286 ГЛ. XI. ИЗМЕНЕНИЕ ФИЗИЧЕСКОГО СОСТОЯНИЯ [§ 4
В данном случае
Ц C-5)
Некоторые значения температуры поверхности и положений поверхности раз-
раздела в этих случаях, полученные с помощью термического анализатора, приводятся
в статье [21]*).
III. Поверхность, на которой происходит затвердевание, движется с по-
постоянной скоростью.
Простое точное решение для этого случая получено Стефаном [1]. Очевидно, что
t/, = Г, -f А [1 — ехр {у~хт4 — тх)\, х < r.xmt, C.7)
v2=Tu x>r.xmt, C.8)
где постоянные А и т удовлетворяют условиям B.1), B.5) и B.6) предыдущего пара-
параграфа. Это решение удовлетворяет также условию B.2) данной главы, если
A = L/cx. C.9)
Таким образом, оно представляет собой решение задачи о промерзании
в области х > О, в которой в начальный момент времени жидкость имеет тем-
температуру плавления, а поверхность, на которой происходит затвердевание, движется
с постоянной скоростью ъхт. Однако поскольку на плоскости лг = О температура
Тх— (L/cx) (е*1™2*— 1) принимает отрицательные, экспоненциально увеличивающиеся
во времени (по абсолютной величине) значения, найденное решение не представляет
большого физического интереса.
IV. Плавление с непрерывным удалением расплавленного материала.
Пусть твердое тело нагревается благодаря поступлению на его поверхность
постоянного теплового потока F, причем весь расплавленный материал непрерывно
удаляется, например, путем сдувания. Сюда же можно отнести и случай сублимации.
Он имеет важное практическое приложение и именно таким, по-видимому, можно себе
представить механизм разогревания метеоритов в земной атмосфере. Здесь мы при-
приведем только простое решение для случая стационарного распределения темпера-
температур [22, 23].
Примем плоскость, на которой происходит плавление, за плоскость х = 0и будем
считать, что твердое тело в области х > 0 движется относительно этой плоскости
со скоростью U (последнюю и нужно определить). Тогда, если Тх — температура пла-
плавления, температура v в области х > 0 служит решением уравнения G.2) гл. I при
их =— U; при х->0 эта температура v стремится к Ти а при jc->oo она стремится
к нулю. Иными словами,
v=Txe-Uxlx\ C.10)
Если использовать это значение с/, то из G.1) гл. I следует, что тепловой поток
в твердое тело равен нулю и, следовательно, количество тепла, подводимого извне
в единицу времени /\ должно равняться количеству тепла, отводимого в единицу
времени с расплавленным материалом, т. е.
C.11)
а температура v при этом значении U определяется формулой C.10).
§ 4. Методы интегрального уравнения.
Рассмотрение задач затвердевания, предложенное Лайтфутом
Если допустить, что термические свойства твердой и жидкой фаз одинаковы, то
можно применить другой очень мощный метод. Пусть в момент времени t поверх-
поверхность затвердевания будет х = X (t)\ эта поверхность движется со скоростью X (t),
*) Там же рассмотрены пример III и соответствующие задачи для цилиндра
и шара.
§ 4] ГЛ. XI. ИЗМЕНЕНИЕ ФИЗИЧЕСКОГО СОСТОЯНИЯ 287
а количество выделяемой на ней в единицу времени теплоты затвердевания равно
L9X(t). D.1)
Следовательно, выделение теплоты затвердевания соответствует движению источ-
источника тепла на поверхности х = X (t), мощность которого определяется D.1). Темпе-
Температуру в любой точке можно найти путем введения членов, описывающих влияния
этого движущегося источника, а также начального и граничных условий. Тот факт,
что на поверхности х = X (t) температура всегда должна совпадать с температурой
плавления Ти приводит к интегральному уравнению для X(t)*).
Для пояснения данного метода рассмотрим пример I, приведенный в § 2 данной
главы, а именно, случай затвердевания в области х > 0 с начальной температурой
К>7'1 ис поверхностью х = 0, поддерживаемой при t > 0 при нулевой температуре.
Как и в § 3 гл. X, температура w (jc, f) в плоскости х в момент времени t, обусло-
обусловленная движущимся источником D.1), определяется соотношением
к— f ШЖ (ехр Г
2c(
Температура и (лг, t) в плоскости х в момент времени t, обусловленная постоян-
постоянной начальной температурой V, равна
D3)
Температура в плоскости х в момент времени t равна сумме D.2) и D.3). Тогда
условие, согласно которому температура в плоскости x = X(t) совпадает с темпера-
температурой плавления Ти запишется в виде
w {X @, t} + и [X (О, t} = Tl9 D.4)
т. е. будет интегральным уравнением относительно @-
Лайтфут [3] **) решил эту задачу, исходя из сделанного ранее предположения, что
D.5)
При таком значении X(t) интеграл D.2) можно выразить через функции ошибок
После замены переменных
соотношение D.2) принимает вид
*<* ') ^ — V D.7)
= \ «*W ** (S) 11 + Ф {ЩЪ У < 1, D.8)
/, = 1Я/2Ф* (Ху) [A + Ф (X)], у > 1, D.9)
ехР { - Т [^т^" +(у ~!) гГ } = Т ™12ф*(Ху> ** W- DЛ0)
*\
*) Более полно методы, использующие интегральные уравнения, изложены в [20].
**) Он вывел соотношения D.8) —D.10), воспользовавшись разложением в ряд,
но их можно получить и другими методами.
288 ГЛ. XI. ИЗМЕНЕНИЕ ФИЗИЧЕСКОГО СОСТОЯНИЯ [§ 5
Согласно D.6) области у ^ 1 соответствуют жидкой и твердой зонам, а у = 1 —
плоскости затвердевания. Если использовать D.3), D.8) и D.10) при у = 1, то усло-
условие D.4) примет вид
-^~ еХ2Ф* (X) Ф (X) + УФ (А) = Ть D.11)
что согласуется с соотношением B.14) данной главы для случая К\ = Кг и^= х2.
Другие задачи, приведенные в § 2 этой главы, можно рассматривать аналогич-
аналогичным образом. Лайтфут [3] провел приближенное исследование задачи о затвердевании
в области, ограниченной параллельными плоскостями, рассматривая не два изображе-
изображения, как это было сделано выше, а бесконечный их ряд. В другой работе [24] описан-
описанный выше метод использовался иначе.
§ 5. Решения в цилиндрических и сферических координатах
Существование решений для линейного теплового потока, найденных
в § 2 данной главы, зависит в основном от существования решений уравне-
уравнения теплопроводности, являющихся функциями только xt~ . Это позволяет
предположить, что решения в цилиндрических или сферических координатах,
являющиеся функциями только г • t~~ , могут дать полезные результаты.
Легко доказать, что
1) в цилиндрических координатах функция
<5Л>
служит решением уравнения теплопроводности и что
2) в сферических координатах функция
j _ jL] _ 1 тс,/2ф* / ' ) E.2)
служит решением уравнения теплопроводности. Кроме того, было показано,
что они являются единственными решениями такого типа [25]. Эти решения
использованы Франком [26] для изучения радиально-симметричного увеличе-
увеличения объема фазы, регулируемого диффузией, или, придерживаясь принятой
терминологии, радиального увеличения объема сферического или цилиндри-
цилиндрического твердого тела, образующегося из расплавленного материала (одно-
(одномерный случай уже рассматривался выше; см. пример II § 2 данной главы).
Здесь мы допустим, что плотности твердой и жидкой фаз одинаковы. В про-
противном случае будет иметь место движение жидкости [27].
Излагаемые ниже результаты можно получить таким же путем, как и в § 2
данной главы (см. пример II).
I. Область г < R в цилиндрических координатах состоит из твер-
твердого тела, находящегося при температуре плавления Tv а область
г > R — из переохлажденной жидкости, температура которой v2 при
г->оо стремится к V < Tv
Положение поверхности раздела определяется соотношением
где X — корень уравнения
XV-2 EI (- Х2) + с2 (Тг — V)/L = 0, E.3)
а температура v2 жидкости — уравнением
§ 6] ГЛ. XI. ИЗМЕНЕНИЕ ФИЗИЧЕСКОГО СОСТОЯНИЯ 289
II. Для соответствующей задачи в сферических координатах ми
будем иметь R = 2\(%2t)l2t где X — корень уравнения
= *- с2 (Тг — V)/L. E.5)
Температура жидкости v2 равна следующей величине:
§ 6. Осесимметричные задачи о замерзании и плавлении
Несмотря на важность подобных задач в ряде случаев (например, намер-
намерзание льда на цилиндрические трубы), общие данные по этому вопросу очень
скудны.
Мы рассмотрим здесь только случай, когда поверхностью раздела между
твердой и жидкой фазами служит поверхность r = R (t), причем область г > R
содержит жидкость с термическими коэффициентами р, с2, АГ2» *2» а область
г < R — твердое тело с термическими коэффициентами р, cv Kv *j. Тогда,
если v2 и vx — температуры в этих двух областях, а Тг — температура пла-
плавления, то граничные условия при г = R запишутся в виде
v1 = v2 = Tv F.1)
„ dVi „ dv2 . dR 9
I. Решение для случая непрерывного линейного источника, рас-
расположенного вдоль оси г = 0.
Используя фундаментальное решение E.1) предыдущего параграфа, можно
точно показать (как и в примере I § 2 данной главы), что дифференциаль-
дифференциальные уравнения и граничные условия F.1) и F.2) удовлетворяются функциями
*<r<R. F.3)
где
а X — корень уравнения
= X2x1Lp. F.6)
При ? = 0, R = 0 и v2 = V к, следовательно, вначале вся область г > 0
заполнена жидкостью с температурой V. При t > 0
л—
= Q. F.7)
Таким образом, это решение совпадает с решением для случая замерзания
при непрерывно действующем линейном стоке, расположенном вдоль оси,
который при t > 0 отбирает в единицу времени количество тепла, равное Q.
19 Г. Карслоу, Д. Егер
290 ГЛ. XI. ИЗМЕНЕНИЕ ФИЗИЧЕСКОГО СОСТОЯНИЯ [§ 6
Оно является единственным простым точным решением, имеющимся для
цилиндрической области [25, 28]*).
II. Область г > а в начальный момент представляет собой
жидкость, находящуюся при температуре плавленая Tv a nput>0
поверхность г = а поддерживается при нулевой температуре.
Для данного случая точного решения нет. Важное приближенное реше-
решение можно получить, как и в § 2 данной главы (см. соотношение B.20)),
предположив, что распределение температур в твердом теле совпадает
с распределением стационарного типа, т. е. что
Подстановка этого соотношения в F.2) дает
Интегрируя, получаем
F.10)
Уравнение F.10) действительно служит достаточно хорошим приближен-
приближенным выражением для положения поверхности раздела при L^>c, например
в случае замерзания воды. Второе приближение найдено Пекерисом и Слих-
тером [29], которые воспользовались методом разложения в ряд. Они пока-
показали, что ряд
{-.... F.11)
где А и В являются функциями только t, удовлетворяет дифференциальному
уравнению для радиального потока тепла. Затем этот ряд подставляют в гра-
граничные условия и определяют А к В метолом последовательных приближе-
приближений. Случай затвердевания в области внутри цилиндра г = а можно рассмо-
рассмотреть аналогичным образом. Были найдены также решения в виде рядов для
случая, когда поверхность раздела движется с постоянной скоростью [21].
ЛИТЕРАТУРА
1. Stefan, Ann. Phys. u. Chem. (Wiedemann) (N. F.) 42, 269—286 A891).
2. Riemann-Weber, Die partiellen Differentialgleichungen der mathematischen
Physik, ed. 5, 1912, v. 2, p. 121. (Ф. Франк, Р. Мизес, Дифференциальные и
интегральные уравнения математической физики, ОНТИ, 1937.)
3. Light foot, Proc. Lond. Math. Soc. 31, 97—116 A930).
4. Eyres, Hartree, Ingham, Jackson, Sarjant, Wagstaff, Phil. Trans.
Roy. Soc. A240, 1—57 A948).
5. Crank, Quart. J. Mech. Appl. Math. 10, 220 A957).
6. Plank, Z. Ges. Kalte-Ind. Beih., Reihe 3, H. 10 A941); 20, 109 A913).
7. London, Seban, Trans. ASME 65, 771 A943).
8. Ruddle, The Solidification of Castings, The Institute of Metals, 1950.
9. Larsen, Am. J. Sci. 243A, 399 A945).
10. Crank, J. The Mathematics of Diffusion, Oxford, 1956.
11. Danckwerts, Trans. Faraday Soc. 46, 701—712 A950).
12. Hill, Proc. Roy. Soc B104, 39—96 A928).
*) Аналогичным образом из соотношения E.2) предыдущего параграфа можно
найти решение в сферических координатах, но поскольку это решение соответствует
затвердеванию при наличии непрерывного точечного стока, мощность которого линейно
увеличивается со временем, большого физического значения оно не имеет.
ГЛ. XI. ИЗМЕНЕНИЕ ФИЗИЧЕСКОГО СОСТОЯНИЯ 291
13. Lachma п n, Z. angew. Math. Mech. 15, 345 A935); 17, 379 A937).
14. Hube r, Z. angew. Math. Mech. 19, 1 A939).
15. Schwarz, Arch. Eisenhuttenw. 5, 139, 177 A931).
16. S ch w a r z, Z. angew. Math. Mech. 13, 202 A933).
17. H e i n d 1 h о f e r, Phys. Rev. 20, 221—242 A922).
18. J a e g e r, Am. J. Sci. 255, 306 A957).
19. We in er, Brit. J. Appl. Phys. 6, 361—364 A955).
20. Evans II. Isaacson, MacDonald, Quart. Appl. Math. 8, 312—319 A950).
21. К r e i t h, R о m i e, Proc. Phys. Soc. B68, 277—291 A955).
22. Landau, Quart. Appl. Math. 8, 81—94 A950).
23. M a s t e r s, J. Appl. Phys. 27, 477—485 A956).
24. В 1 e v i n, Aust. J. Phys. 6, 203—208 A953).
25. Pater so n, Proc. Glasgow Math. Ass. 1, 42—47 A952—1953).
26. Frank, Proc. Roy. Soc. A201, 586—599 A950).
27. Chambre, Quart. J. Mech. Appl. Math. 9, 224—233 A956).
28. Ingersoll, Adler, Plass, Ingersoll, Heat. Pip. Air Condit. 22, 113—122
A950).
29. P e к e r i s, S П с h t e r, J. Appl. Phys. 10, 135—137 A939).
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
30. А. В. Лыков, Кинетика и динамика процессов сушки и увлажнения, Гос. изд,
легкой пром-ти; 1938.
31. А. В. Лыков, Теплопроводность нестационарных процессов, Госэнергоиздат, 1948*
32. А. В. Лыко в, Теория сушки, Госэнергоиздат^ 1950.
33. А. В. Лыков, Теория теплопроводности, Гостехиздат, 1952.
34. А. В. Лыко в, Тепло- и массообмен в процессах сушки, Госэнергоиздат, 1956.
35. А. В. Л ы к о в, Ю. А. М и х а й л о в, Теория переноса энергии и вещества, Минск,
1959.
36. А. А. Померанцев, Курс лекций по теории тепло- и массообмена, Изд. «Выс-
«Высшая школа», 1964.
37. А. А. По м ер а нцев, К теории оплавления и обгорания тела (задача Стефана)„
Труды 1-го Совещания по тепло- и массообмену, 1961, т. III, 1963,
19*
ГЛАВА XII
ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЗАДАЧИ ДЛЯ ЛИНЕЙНОГО
ТЕПЛОВОГО ПОТОКА
§ 1. Исторический обзор
Можно сказать, что использованные в предыдущих главах методы слу-
служат непосредственным следствием и обобщением классической работы Фурье.
Сравнительно недавно был разработан другой метод исследования дифферен-
дифференциальных уравнений прикладной математики, особенно хорошо приспособ-
приспособленный для решения задач теплопроводности. Этот метод в значительной
степени основан на работе Хевисайда. Все полученные выше решения задач
теплопроводности в случае нестационарного режима можно найти при помощи
нового метода. Однако, поскольку преимущества этого метода практически
возрастают вместе со сложностью задачи, по-видимому, лучше всего при-
приложить его для иллюстрации к нескольким уже рассмотренным задачам, а
затем использовать его в более сложных случаях, исследовать которые дру-
другими методами очень трудно.
В 1890 г. Хевисайд разработал ставший знаменитым операционный ме-
метод для решения систем обыкновенных линейных дифференциальных уравне-
уравнений с постоянными коэффициентами, встречающихся в теории электрических
цепей. Для этого случая Хевисайд дал элементарное обоснование своего ме-
метода. Затем он обобщил *) его на дифференциальные уравнения в частных
производных электромагнитного поля и теплопроводности и получил целый
ряд новых решений, причем этим методом не только удалось найти решения
еще нерешенных задач, но и получить решения новых типов, например реше-
решения, специально соответствующие большим или малым промежуткам времени.
Математическая строгость этих решений оставалась довольно сомнительной,
и поэтому появилась настоятельная потребность математически строго обос-
обосновать всю теорию. Первый шаг в этом направлении был сделан Бромви-
чем **) [2], который в своей классической статье получил контурный интег-
интеграл с операционным выражением Хевисайда в качестве подынтегральной функ-
функции. Далее он доказал, что этот интеграл удовлетворяет дифференциальному
уравнению и начальным условиям, а позже оценил интеграл обычными мето-
методами контурного интегрирования. Его идеи были в дальнейшем развиты
в книге [4] и нашли широкое использование в теории теплопроводности.
Подобный метод, в котором также применяется контурный интеграл, был
разработан Карслоу [5] (см. также приложение 1), но в его методе подын-
*) Краткое описание обобщенного метода Хевисайда дано в историческом вве-
введении в книге Карслоу и Егера [1].
**) Независимо от Бромвича аналогичные идеи были развиты Вагнером [3].
§ 2] ГЛ. XII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЛИНЕЙНЫЙ ПОТОК 293
тегральная функция определялась не по методу Хевисайда, а независимым
образом *).
Другой метод, подтверждающий правильность работы Хевисайда, был
разработан Карсоном и Ван-дер-Полем, которые показали, что искомое
решение можно найти из операционного выражения Хевисайда, решая интег-
интегральное уравнение. Это интегральное уравнение представляет собой просто
интеграл, который появляется в уравнении B.1) данной главы как определение
преобразования Лапласа; отметим здесь же, что упоминавшийся выше кон-
контурный интеграл Бромвича представляет собой просто контурный интеграл*
который появится в соотношении C.8) в теореме обращения преобразования
Лапласа.
Таким образом, излагаемый ниже метод преобразования Лапласа объ-
объединяет теории Хевисайда, Бромвича и Карсона. Важность этого метода под-
подчеркивается в ряде статей, большинство которых посвящено рассмотрению
задач теплопроводности [7].
Ниже мы кратко изложим метод преобразования Лапласа, приводя фор-
формулировку теорем и схемы их доказательств, отвечающие поставленным здесь
задачам; более полное изложение можно найти в работах, специально по-
посвященных этому предмету [1,8—10]. Как отмечалось выше, решения, полу-
полученные методом Бромвича — Джефриза, часто встречаются в литературе, по-
посвященной теплопроводности; операционные выражения, используемые ими
для v, всегда отличаются множителем р от полученных нами выражений
для v, записанных в принятых ниже обозначениях. Метод вывода решений
с помощью теории контурного интегрирования одинаков в обоих случаях, и
поэтому статьи, в которых использованы одни обозначения, легко читать
лицам, привыкшим к другим обозначениям.
§ 2. Преобразование Лапласа. Основные свойства
Ниже везде будет рассматриваться температура v, являющаяся функцией
t и любых координат (например, х, у, z), встречающихся в задаче. Запишем
оо
L [v(x, у, 2, 0} =v= f e-P*v(x9 у, z> t)dt, B.1)
о
где р — величина, действительная часть которой положительна и достаточно
велика, чтобы интеграл B.1) сходился**).
Интеграл B.1) называют преобразованием Лапласа функции z; и он
является функцией р и пространственных переменных х, у, z. Из двух при-
приведенных обозначений символ L [v] удобен при формулировке теорем, тогда
как символ v достаточно компактен и удобен при проведении алгебраических,
выкладок, связанных с нахождением решения.
Аппарат описываемого метода состоит из нескольких элементарных тео-
теорем и таблицы преобразованных по Лапласу функций, т. е. интегралов B.1).,
*) Интересное сравнение обоих методов приведено в статье [6].
**) Бромвич и др. вместо B.1) пользуются следующим преобразованием:
оо
L{v(x, у, г, Ц} = у = р[е-р'*>(х, у, г, t)dt.
о
(Прим. ped.)
294 ГЛ. XII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЛИНЕЙНЫЙ ПОТОК [§ 2
Например,
оо
если v(t)=l, то v(p) = / е~Р*dt = —,
6
или
если
оо
= s\tnot, то v(p)— / е~Р*sm^tdt =
6
2_? 2 ,
6
и т. д.
В приложении 5 приведено большинство преобразованных по Лапласу
функций, которыми пользуются *) при решении задач теплопроводности.
Необходимые нам для дальнейшего теоремы приведены ниже. В боль-
большинстве случаев мы дадим только краткие доказательства без точной фор-
формулировки условий. Точные условия нам здесь не нужны, поскольку, как
отмечено в следующем параграфе, на этой стадии проводится только фор-
формальный анализ, а полученные результаты обязательно подлежат проверке.
Теорема I.
Теорема II.
L{?.} = pL[v)-v0. B.2)
где v0 — значение lim v. В общем случае v0 будет функцией пространст-
венных переменных х, у, z. Формула B.2) непосредственно получается при
интегрировании по частям; действительно
оо
f e-P'vdt^ —
о 6
Теорема III.
d"v ) дпЪ
B*3)
При других пространственных переменных мы получаем аналогичные
результаты. Найденный результат эквивалентен соотношению
Мы считаем функцию v такой, что указанным способом можно менять по-
последовательность операций интегрирования и дифференцирования.
Приведенные выше три теоремы имеют очень большое значение. В до-
дополнение к ним мы укажем ряд полезных результатов, на которые мы также
будем изредка ссылаться.
Теорема IV.
t
B.4)
*) Более полные таблицы этих функций можно найти в уже упоминавшихся ра-
работах, а также в [11—13].
§ 2] ГЛ. XII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЛИНЕЙНЫЙ ПОТОК 295
ибо интегрирование по частям дает
ОО t р t -1ОО ОО
f e-P'dt fv(t')dt= — \-e-P* fv(t')dt' + — f e~P(v dt = -v.
0 0 L б JO 0
Теорема V. Если к является величиной постоянной и положи*
тельной, а
L[v(t)}=v(p). то L{v(kt)}=\v(^< B.5)
ОО
Г 1 /• 1 _ / р *
./ k J k \ k I
ибо
f
6 6
Теорема VI. Если а является величиной постоянной (даже ком-
комплексной), a L{v}=v(p), то
L {e~atv} = v(p + a), B.6)
ибо
= J e-
Теорема VII. Если f (t) = H(t — to)y(t — to)9 где H(t — tQ) —еди-
—единичная функция Хевисайда, определяемая следующим образом:
H(t-to)=U t>to,j B-7)
то
L \f(t)} = e-P^L {<p@ }. B-8)
Теорема VIII. Если f (t) является периодической функцией с пе-
периодом Т, то
т
L{f(t)}= l_pTfe-P<f(t)dtt B.9)
ибо
оо оо (/1+1O- оо Т
L{f(t))=fe-Ptf(t)dt= У f f(t)e-P*dt= У\е-»РТ f e-P''f(t')dt'=
п=0пТ п=0
Г
Теорема IX. Теорема Лерха, или теорема единственности*).
Пусть для всех р L {fx (t))= L {/2 (t)}, тогда fx(t) = f2(t) для всех
0, при которых они непрерывны. Если же функции имеют только
*) Доказательства теорем IX и X можно найти в обычных работах по преобра-
преобразованию Лапласа. Теорема XI и другие, подобные ей теоремы приведены в работе [14].
[См. также М. А. Л а в р е н т ь е в, Б. В. Ш а б а т, Методы теории функций комп-
комплексного переменного. Гостехиздат, 1951. СМБ, Интегральные преобразования, Физ-
матгиз, 1961. (Прим. ред.)]
296 ГЛ. XII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЛИНЕЙНЫЙ ПОТОК [§ 3
разрывы первого рода, то в этих точках они могут отличаться
друг от друга.
Теорема X.
\fx\ = L{f1(t)}L{f2(t)}. B.10)
U ? J
Эта теорема известна как теорема о свертке, а также как теорема Дюа-
меля. Она представляет собой другую форму записи теоремы Дюамеля, при-
приведенной в § 14, гл. I с использованием принятых в данной главе обозна-
обозначений.
Теорема XI. Если
то
( оо
"'^ B.11)
§ 3. Решение уравнения теплопроводности методом
преобразования Лапласа
Предположим, что нам надо решить следующее уравнение для линейного
потока тепла:
d2v I dv л . . , /о 1 \
¦ш-^-ж = 0' а<х<*< (зл>
при условиях
v = vo(x), t = 0, a<x<b, C.2)
v = vl(t), x = a, t>0, C.3)
v = v2(t). x = b, t>0. C.4)
Применим к уравнению C.1) преобразование Лапласа, т. е. умножим
обе его части на е~Р* и проинтегрируем по t в пределах от 0 до оо. Это
дает
оо оо
J дх2 х ,/ dt
о о
Используя соотношения B.2) и B.3) предыдущего параграфа, получим
^ i ^4 а < х < Ь. C.5)
Таким образом, преобразование Лапласа свело дифференциальное урав-
уравнение с частными производными к обыкновенному дифференциальному урав-
уравнению C.5). Полученное этим путем уравнение для v мы всегда будем на-
называть вспомогательным уравнением. Преобразуя аналогичным образом
граничные условия C.3) и C.4), получим
v = v{, x = a, C.6)
v = v2f x = b. C.7)
Изображение v (т. е. преобразование Лапласа v) решения задачи из-
известно, если решено вспомогательное уравнение C.5) при граничных уело-
§ 3] ГЛ. XII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЛИНЕЙНЫЙ ПОТОК 297
виях C.6) и C.7). Перед тем как перейти к методам нахождения v из z/, сле-
следует отметить, что более общие дифференциальные уравнения (например,
уравнение A0.5) гл. IV) и более общие граничные условия (например (9.14)
гл. I) приводят точно таким же путем к обыкновенному дифференциальному
уравнению с граничными условиями при а и b и, следовательно, к вели-
величине V.
Если мы имеем более одной пространственной переменной, например
если дифференциальное уравнение
% dt
нужно решать в некоторой области с начальным условием vo(x, у, z) =
— v(xt у, z, 0) и заданными граничными условиями, то найденное описан-
описанным выше путем вспомогательное уравнение имеет вид
т. е. остается дифференциальным уравнением в частных производных, но
с тремя переменными вместо четырех.
Предположим теперь, что вспомогательное уравнение решено при соот-
соответствующих граничных условиях и, следовательно, известна зависимость v
от р (и пространственных переменных). Тогда требуется по v найти v как
функцию времени, что и будет служить решением исходной задачи.
Проще всего найти v (/?) по таблице изображений и подобрать соответ-
соответствующую функцию *) от t. Таким путем очень просто можно решить целый
ряд задач с линейным потоком. Соответствующие примеры приведены в двух
следующих параграфах.
Если изображения v в таблице нет, то v определяется из v при помощи
теоремы обращения преобразования Лапласа. Согласно этой теореме
f+too
= 4ц f el'v(l)dk, C.8)
у— loo
где 7 должна быть настолько большой величиной, чтобы все особые точки
v(k) лежали слева от линии (? — ioo, y-{-ioo). В соотношении C.8) мы
заменили р на X для того, чтобы подчеркнуть, что в этом соотношении мы
рассматриваем поведение функции v, считая ее функцией комплексного пере-
переменного, тогда как ранее р вообще не должно было быть комплексной ве-
величиной.
Соотношение C.8) будет справедливым только в том случае, если функции
v(k) или v(t) удовлетворяют определенным условиям; однако здесь нет необ-
необходимости рассматривать ни эти условия, ни доказательство самой теоремы,
поскольку в ходе изложения были сделаны другие предположения, например,
что v имеет изображение, что последовательность операций дифференциро-
дифференцирования и интегрирования в соотношении B.3) предыдущего параграфа можно
изменить и т. д. ¦¦). Таким образом, с точки зрения чистой математики необ-
необходимо проверить, удовлетворяет ли полученное решение дифференциальному
уравнению и начальному и граничному условиям данной задачи. Эту проверку
*) Из теоремы IX предыдущего параграфа следует, что найденная таким путем
функция является единственной.
**) Доказательство этих положений можно найти в [1, 15].
298
ГЛ. XII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЛИНЕЙНЫЙ ПОТОК
[§ 4
проще всего выполнить при помощи контурного интеграла C.8). Метод про-
проверки рассматривается в приложении 1. Все полученные здесь решения
можно проверить приведенным там способом.
После нахождения решения в виде контурного интеграла C.8), его
обычно можно привести к вещественному виду одним из двух стандартных
методов.
1). Если z/(X) является однозначной функцией X с рядом полюсов, ле-
лежащих вдоль отрицательной вещественной оси (возможны и другие полюсы),
мы замыкаем контур большой окружностью Г с радиусом /?, не проходящей
ни через один полюс подынтегральной функции (рис. 39).
Во всех рассматриваемых здесь задачах можно показать, что интеграл по
большой окружности Г при R~>oo в пределе равен нулю (дальнейшее из-
изложение этого вопроса дано в при-
д
ложении 1). Таким образом, согла-
согласно теореме Коши, интеграл C.8)
равен в пределе произведению 2tzi
на сумму вычетов относительно по-
полюсов его подынтегральной функ-
функции *). Этот случай обычно встре-
встречается в задачах теплопроводности
в ограниченных областях.
2) В задачах теплопроводности
для полуограниченных областей v (X)
обычно имеет точку ветвления при
X = 0. В таких случаях используется
контур, показанный на рис. 40
_ с «разрезом» вдоль отрицательной
вещественной оси, так что v(X) является однозначной функцией X на контуре и
внутри него. Можно показать, что в пределе, по мере стремления радиуса боль-
большой окружности к бесконечности, интеграл по контуру стремится к нулю, и ин-
интеграл C.8) заменяется двумя несобственными интегралами по отрицательной
вещественной полуоси, полученными из интегралов вдоль CD и EF; воз-
возможно, что к ним добавляется вклад от интеграла по малой окружности
с центром в начале координат, а также вклады от любых полюсов подын-
подынтегральной функции.
Если функция v(h) не принадлежит ни к одному из указанных выше
типов, то для ее рассмотрения должны быть разработаны специальные ме-
методы.
§ 4. Полуограниченная область х > 0. Решения, получаемые
из таблицы изображений
В данном случае вспомогательное уравнение C.5) предыдущего пара-
параграфа имеет вид _
d2v о— 1
— q2v= ^(а:), х > 0, D.1)
где vo(x) — начальная температура. Для краткости запишем
<Г = —
D.2)
*) В данном случае это дает ряд, который можно получить также при помощи
теоремы разложения Хевисайда.
§ 4] ГЛ. XII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЛИНЕЙНЫЙ ПОТОК 299
В настоящей главе мы будем рассматривать главным образом задачи,
в которых vo(x) равно нулю; тогда D.1) будет иметь вид
S-^ = 0, *>0. D.3)
Если vo(x) постоянно, то легко найти решение D.1); если vo(x)— про-
простая функция*) х, то легко получить решение уравнения D.1) в явном виде;
если она является произвольной функцией, то уравнение D.1) следует решать
методом вариации произвольных постоянных или каким-либо иным анало-
аналогичным методом; в конце концов получаются результаты, эквивалентные ре-
результатам, найденным в гл. II. Однако в настоящее время полагают, что
лучше всего искать решения при помощи функций Грина, применению ко-
которых посвящена гл. XIV; в ней и будут рассматриваться эти решения.
Во всех случаях при х —> со функция v, а значит, и функция v должны
быть ограничены. Таким образом, из двух решений уравнения D.1) или
D.3), Ве+чх и Ae~qx, следует использовать только второе.
Рассмотрим теперь различные граничные условия при х = 0.
I. Температура поверхности задана. Начальная температура
равна нулю.
Предположим, что задана функция
и, следовательно,
x = 0.
Решение уравнения D.3), конечное при л:->оо и принимающее при
х = 0 значение v = ср (/?), будет иметь вид
-«x. D.4)
1) Если ср (^) = Vo, где Vo — величина постоянная, то 4 = VqIp* и реше-
решение D.4) принимает вид
v — — е
Из соотношения (8) приложения 5 следует, что
D.5)
— п
2) Если ср(?) = 1Л/2 , где п — любое положительное целое число, то,
согласно B) приложения 5,
¦(¦+*»)
<р=-
1
1+Тп
2
р
В данном случае, в соответствии с A1) приложения 5, получим
^у) D.6)
(см. соотношения E.5), E.7) и E.8) гл. II).
*) Например, vQ (х) может быть комбинацией многочлена от xt ekx и sin lx9
cos lx. {Прим. ред.)
300 ГЛ. XII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЛИНЕЙНЫЙ ПОТОК [§ 4
3) Если ср(О — произвольная функция, то из B.10) данной главы и F)
приложения 5 следует, что
V=W^J ^ —(*-*>* dx' D'7)
Этот результат был уже получен ранее (см. E.1) гл. II).
Таким же путем, воспользовавшись A9) приложения 5, можно найти
решение для случая температуры поверхности, меняющейся по закону еи
(соотношение E.9) гл. II). Случай гармонического изменения температуры
поверхности рассматривается в § 7 данной главы, а случай периодического
изменения температуры поверхности — в § 5 гл. XV.
II. Граничное условие третьего рода *).
Пусть начальная температура твердого тела равна нулю, а при л: = 0
оно нагревается вследствие теплообмена со средой, имеющей постоянную
температуру V. Тогда граничное условие при х = 0 запишется в виде
L=h(v — V), x = 0, t>0.
Граничное условие для вспомогательного уравнения имеет вид
а решение уравнения D.3), удовлетворяющее условию D.8), записывается
следующим образом:
- НУе-*х
Тогда из соотношения A4) приложения 5 следует, что
) V СХР (kX + h4t) Ф* (
III. Контакт с хорошо перемешиваемой жидкостью (или идеальным про-
проводником).
Соответствующие граничные условия рассмотрены в примере Е § 9 гл. I, однако
решение задач подобного типа отнесено к данной главе, поскольку излагаемые здесь
методы особенно удобны для этого. Обозначим через с' удельную теплоемкость
жидкости, через и — ее температуру, а через М — массу жидкости, соприкасающейся
с единицей поверхности х= 0 твердого тела. '
/. Начальная температура твердого тела равна нулю, а начальная темпе-
температура жидкости постоянна и равна V [16]. При t > 0 температура поверх-
поверхности твердого тела равна температуре жидкости. В данном случае для t > О
граничное условие при х = 0 имеет вид и = v и
4jL^ 0, jc = O, *>0. D.9)
Отсюда соответствующее граничное условие для вспомогательного уравнения
запишется в виде
Mc'pv — K^ = Mc'V.
*) Оно соответствует теплообмену на поверхности по закону Ньютона.
{Прим. ред.)
§ 4] ГЛ. XII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЛИНЕЙНЫЙ ПОТОК 30!
Тогда
где
Отсюда из выражения A3) приложения 5 получим
v = V exp {h'x -f ti 2xt) Ф* (—%=¦ + h' УЧ). D.11)
\2yxt j
2. Та же задача, но начальная температура жидкости равна нулю и коли-
количество тепла, сообщаемое жидкости в единицу времени на единицу массы, равно
постоянной величине Q/M. В данном случае граничные условия при х = 0 имеют
вид и = v и
Отсюда получаем _
Mc'jw — K-j? = —,
Следовательно,
где А' определяется равенством D.10). Из выражения A5) приложения 5 следует, что
» = —— (— ехр ——¦ Ф* I —-==
К U / L 4^ J Kh' \У
. exp {h'x + h'\t) Ф* [^=, + Л' V^?J. D.12)
+
3. Та же задача, но между жидкостью и поверхностью твердого тела про-
происходит теплообмен, причем в единицу времени жидкость отдает твердому
телу количество тепла, равное произведению Н на разность температур между
ними. Обозначая температуру жидкости через и, получим граничные условия при
х = 0 в виде
Mc'-^r + H(u-v) = 0, x = 0, t>0, D.13)
— K^ = H(u — v), x = 0, t>0. D.14)
ox
Дифференциальное уравнение для v надо решить при этих граничных условиях,
причем начальная температура и равна V, а начальное значение v равно нулю. Для
вспомогательного уравнения граничные условия, полученные из D.13) и D.14),
имеют вид _
(Afc'p -f Н) п— Hv= Me' V,
Отсюда обычным путем находим
D.15)
D.16)
где А' определяется D.10), а Л = И/К- Если написать
D.17)
302 ГЛ. XII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЛИНЕЙНЫЙ ПОТОК [§ 4
то соотношение D.16) принимает вид
hVe [ J
v
и, согласно A3) приложения 5,
v=-l?— Гехр (ax + *ta*) Ф* {
- ехр фх + х/»р») Ф* j —^ + р ^"г 11. D.18)
IV. Полу ограниченное твердое тело, внутри которого выделяется тепло.
Для таких задач и, в частности, для весьма сложных случаев излагаемый метод
особенно удобен. Этим путем можно получить все результаты, приведенные в § И
гл. II. Для пояснения описанного метода мы приведем здесь несколько дополнитель-
дополнительных результатов.
/. Область х > О имеет нулевую начальную температуру. При х = 0 про-
происходит теплообмен со средой нулевой температуры. При t > О в твердом теле
т п
в единицу времени на единицу объема выделяется количество тепла, равное kt ,
где п может равняться —1, 0, или любому положительному целому числу.
В данном случае дифференциальное уравнение имеет вид
при граничном условии
4 /ш = 0, jc = O, *>0. D.20)
Используя изображение B) приложения 5, получим соответствующее вспомога-
вспомогательное уравнение
Г- х>0'
Кр
при граничном условии
D.22)
как всегда, при х->оо v имеет конечное значение. Решение уравнения D.21) при
условии D.22) имеет вид
1/ = -
Таким образом, используя A6) приложения 5, получим
1-
л+2
{ ^}г ^ |D.23)
Частный случай /г = — 1, соответствующий выделению в единицу времени коли-
количества тепла, пропорционального t~xh, дает грубое приближение, полезное в задачах,
в которых велико выделение тепла в начальный момент (например, при гидратации
цемента).
§ 5] ГЛ. XII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЛИНЕЙНЫЙ ПОТОК 303
2, Область х > 0. При t > 0 поверхность х = 0 поддерживается при нулевой
температуре. В области а < х < b при t > 0 в единицу времени выделяется по-
постоянное количество тепла, равное k [17]. В данном случае вспомогательные урав-
уравнения имеют вид
d2v —
_— — q2v = o в области 0 < х < а и х > b D.24)
и _
d2v — k
-т—2 — q2v = -jt— в области а < х < Ь. D.25)
Они должны быть решены при следующих условиях:
v = 0, х = 0 D.26)
и _
— tft/
v и -^— непрерывны при х = а и jc = b. D.27)
Решения уравнений D.24), D.25) и D.26) имеют вид
Be-***, 0<x<a,
СеЯХ + De-«x, a<x<b,
у = Ее-чх, х>Ь.
Здесь четыре постоянные В, С, D и ? находят из четырех условий непрерыв-
непрерывности D.27). После вычисления этих постоянных можно записать решение* Например,
градиент температуры на поверхности [dv/dx]x=0 имеет изображение
и, следовательно, используя (И) приложения 5, получим
2k Ы)Ч2 [ . ( а \ ( Ь \ \
—-— \ 1Ф | —- J — i Ф* I — J I # D.28)
§ 5. Ограниченная область 0 < х < /. Решения, получаемые
из таблицы изображений. Решения для небольших значений времени
I. Рассмотрим сначала область 0 < х < I с нулевой начальной тем-
температурой при отсутствии потока тепла через поверхность х = 0.
При t > 0 поверхность х = I поддерживается при постоянной тем-
температуре V,
В этом случае вспомогательное уравнение имеет вид
при граничных условиях
и
Его решение имеет вид
fc EЛ)
Так как в таблице изображений величина т/, определяемая E.1), отсут-
отсутствует, мы получим решение v, воспользовавшись теоремой обращения (см.
304 ГЛ. XII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЛИНЕЙНЫЙ ПОТОК [§ 5
C.8) данной главы) *). Это будет сделано в следующем параграфе и при-
приведет к обычному результату D.2) гл. III. В данном параграфе используется
метод, позволяющий при помощи таблицы изображений получить решение
в другой форме. Эта форма часто оказывается удобнее приведенной ранее,
особенно для небольших значений времени.
Выразим гиперболические функции в решении E.1) через показательные
функции и разложим их в ряд по степеням e~2(*nl. Тогда вместо E.1) мы
получим
V{«* + ***) ^V_ t_x _q{l y^ _2nql =
Р л=0
оо оо
______ у ( \\п ?—q[Bn+l)l—jr] [ __ \ ( \\n g — [Bn + l)l+x) /g 2)
Таким образом, воспользовавшись (8) приложения 5, получаем результат,
совпадающий с C.9) гл. III,
Этот ряд **) всегда сходится довольно быстро, за исключением случая
больших значений х?//2. Таким образом, он является дополнением к реше-
решению D.2) гл. III, которое лучше всего сходится при больших значениях
времени. В диапазоне средних значений х?//2, при которых пригодными ока-
оказываются как E.3), так и D.2) гл. III, первым, вероятно, несколько удобнее
пользоваться. Например, если х?//2=1, то из E.3) получим для л; = 0
... =0,4795 — 0,0339 + 0,0004— ... =0,4460.
Если средняя температура пластины равна и, то, используя A1) прило-
приложения 5, получим
E.4)
II. Область 0 < х < / с нулевой начальной температурой. Пло-
Плоскость х = 0 поддерживается при нулевой температуре, а плоскость
х = 1 (при t > 0) — при постоянной температуре V.
*) Выражение E.1) есть изображение функции, которую можно выразить через
тета-функции. Некоторые примеры можно найти в работе [9].
**) Последовательные члены данного ряда указывают температуры на глубинах
1-х, I + jc, 3/ — jc, 3/ + х, ... в полуограниченном теле. Таким образом, этот
результат аналогичен решениям задач о колебании струн, стержней и линий передач,
выраженным в терминах многократно отраженных волн.
Следует отметить, что эти решения для малых значений времени можно также
считать решениями для случаев небольших изменений средней температуры (см., на-
например, [18]).
§ 5] ГЛ. XII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЛИНЕЙНЫЙ ПОТОК 305
В данном случае
? E-5)
Общее количество тепла, проходящее через плоскость л; = 0 за проме-
промежуток времени от t = 0 до t = t, равно
E.7)
III. Область 0 < х < I с нулевой начальной температурой. При х = 0 тепло-
вой поток отсутствует. При х=1 поток тепла Q в твердое тело [19] постоянен.
В данном случае
- Qchqx
Kpqshql f
L 2\Tt \]'
IV. Область 0 < л: < / с постоянной начальной температурой Vo.
На поверхности х = 0 тепловой поток отсутствует. На поверхности
х = 1 происходит теплообмен со средой нулевой температуры.
В данном случае вспомогательное уравнение C.5) данной главы имеет
вид
при граничных условиях
-*--¦?. •<*<«.
-?=<>• *=»•
_
~dx~+hv =
Его решение записывается в виде
h v*ch Я*
р p(qshql+hch ql) '
или
hV°
Последовательные экспоненциальные члены ряда E.10) имеют коэффициенты,
являющиеся сложными функциями q, и поэтому для г; простой ряд написать нельзя.
Однако для этого ряда можно сразу же записать несколько первых членов и, таким
образом, получить решение [20], пригодное для малых значений времени. Итак, вос-
воспользовавшись A4) приложения 5, получим
(!+ ... E.11)
20 Г. К«рслоу, Д. Егер
306 ГЛ. XII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЛИНЕЙНЫЙ ПОТОК [§ б
Аналогичным методом можно воспользоваться при решении задач, приведенных
в §§ И и 13 гл. III.
V. Область 0 < х < / с нулевой начальной температурой. При t > 0 пло-
плоскости лг = 0 и х = I поддерживаются при температуре, равной нулю. При t > О
в твердом теле в единицу времени на единицу объема выделяется количество
Т п
тепла [21], равное at , где п = — 1, 0, 1, 2, ...
В данном случае дифференциальное уравнение A4.1) гл. III записывается в виде
Вспомогательное уравнение имеет вид
d2v o- '
Кр^"
Это последнее должно быть решено при условии, что при х = 0 и jc = / v-
Искомое решение записывается в виде-
v =
,
1 X' ( 1\т\р-д(х+т1)_^р-д[(т + 1I-л
• кр +"Л
:(.+*¦)
- EЛ2>
§ 6. Ограниченная область 0 < x < /. Применение теоремы обращения
I. Рассматривая снова задачу I предыдущего параграфа, перейдем теперь
к определению функции v по ее изображению E.1), т. е. по
Согласно теореме обращения (см. C.8) данной главы)
J
1-i со
где величина f должна быть настолько большой, чтобы все особые точки v (k)
лежали слева от линии G—/oo, f-j-foo). Здесь и везде далее будем по-
полагать
где берется главное *) значение квадратного корня.
*) Известно, что Wn = Y2 =-V\z\e n » причем ^ = 0, 1, ...» /г—1; при
k = 0 значение корня считается главным. (Прим. ред.)
6] ГЛ. XII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЛИНЕЙНЫЙ ПОТОК 307
Функция v(X) имеет простые полюсы при Х = 0 и при тех значениях X,
при которых chjx/ обращается в нуль. Эти значения X определяются соот-
соотношениями
р= B*+1Н* t л = 0. 1, 2, ... F.4)
Иными словами,
х_ *B/г+1J*2 л_0 1 о q /65\
Напомним, что
сЬ[хд:=1 + -^Г+D1)^2-+ ...
является однозначной функцией X; отсюда следует, что tf(X) тоже является
однозначной функцией*) X, и мы можем использовать контур, показанный
на рис. 39, большая окружность которого не должна проходить ни через
один из полюсов F.5) подынтегральной функции. Например, можно взять
радиус этой окружности равным х//Ас2//2, где т — любое большое целое
число.
Из теоремы Коши следует, что интеграл по замкнутому контуру равен
произведению 2тс/ на сумму вычетов относительно полюсов подынтегральной
функции внутри контура.
Легко показать (см. приложение 1), что по мере стремления радиуса
большой окружности к бесконечности интеграл по дуге АСВ этой окруж-
окружности стремится к нулю. Таким образом, в пределе интеграл F.2) равен
произведению 2тс/ на сумму вычетов его подынтегральной функции относи-
относительно полюсов Х = 0 и функции F.5). Вычет относительно Х = 0 равен
единице. Вычет относительно полюса Х = —хBя+ 1Jтс2/4/2 равен следую-
следующей величине:
ехрГ--Bл+1J^]ск[--<2л+1>-]
4(—\)п+1 Г %Bп+\)пЧ1
— тсB/г+1) 6ХР L 472 J ^» 27"
Подставляя эти выражения в F.2), мы, наконец, получаем
* Bя + IJ ^ 1 CQC B/1 + 1) *x
/2 = 0
Если при лг = / температура является функцией времени ср(?), то вместо
F.1) получим
— — ch qx
т ch ql
В данном случае мы находим функцию f(t), изображение которой
имеет вид
chqx
ch ql '
*) Представляя таким способом гиперболические функции в виде рядов, можно
показать, что все изображения, встречающиеся в данном параграфе, являются одно-
однозначными функциями X.
20*
"808 ГЛ. XII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЛИНЕЙНЫЙ ПОТОК [§ 6
и используем равенство B.10) данной главы. Применив, как и выше, контур,
доказанный на рис. 39, получим
fit) =f-| (-
[ ]cos .
п = 0
Таким образом, как и в E.3) гл. III, получим из B.10) данной главы
соотношение
я0
х cos Щ^ f ехр[ *е-ИУ"]?(,0^. (б.7)
о
При линейном увеличении температуры поверхности или ее гармоническом
изменении v лучше всего находить непосредственно по v.
II. Задача, совпадающая с задачей II предыдущего параграфа, а именно:
область 0 < х < / имеет нулевую начальную температуру. При t > 0
плоскость лг = О поддерживается при нулевой температуре, а пло-
плоскость х = 1— при температуре V. Здесь v определяется выражением
E.5) данной главы; воспользовавшись теоремой обращения, получаем
V Г°° ektsh iixdl Q4
Полюсы подынтегральной функции F.8) находятся при Х = 0 с выче-
вычетом х/1, а также при
p = nnt/l, n=l, 2,
т. е.
X = — xnW/P, п = 1, 2, .... F.9)
с вычетом
2 (-1)" ехр [- ^-^] sin (Л«//)
/гтс
Таким образом, используя, как и раньше, рис. 39, находим
F.10)
и L L~ J *
/1 = 1
Пусть Q — общее количество тепла на единицу поверхности, проходящее
через плоскость л: = 0 за промежуток времени от ? = 0 до t=t, равное
t
о
Тогда из соотношений E.5) и B.4) данной главы получим
§ 6] ГЛ. XII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЛИНЕЙНЫЙ ПОТОК
Отсюда
KV
' FЛ2)
В последнем соотношении подынтегральная функция имеет полюс вто-
второго порядка при Х = 0 с вычетом
й FЛЗ>
Другие полюсы определяются выражением F.9), и, действуя, как и прежде,
мы найдем
При больших значениях времени члены в этом выражении, содержащие
показательные функции, пренебрежимо малы и Q имеет значение, соответ-
соответствующее стационарному потоку для времени [t — (Р/бх)]. Путем измере-
измерения /2/6х, т. е. запаздывания наступления стационарного состояния, можно
экспериментально определить величину х [22, 23]. Если мы хотим найти только
эту величину, нужно знать лишь вычет F,13) относительно полюса Х = 0.
Дальнейшее обсуждение этого метода изложено в § 6 гл. XV.
III. Область О < х < I с нулевой начальной температурой. При
/>0 плоскости лг = О и х = 1 поддерживаются при нулевой темпе-
температуре. При />0 в единице объема за единицу времени выделяется
количество тепла, равное ae~at.
В данном случае дифференциальное уравнение имеет вид
0-T&--X'-"' °<*<'« <>О- FЛ5>
Поэтому вспомогательное уравнение записывается следующим образом:
^^ «. F.16)
Его следует решать при условии, что v = 0, когда х = 0 и x = L
Решение имеет вид
— ах
Таким образом,
^^
Полюсы подынтегральной функции находятся в следующих точках:
Х = 0, вычет равен 1/а,
a/cos(y/ —л:] (а/т.I/*
— а, вычет равен
a COS ^
310 ГЛ. XII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЛИНЕЙНЫЙ ПОТОК [§ б
Х== — [хBя+ 1Jтг2//2], я = 0, 1, 2, .... вычет равен
41» sin [Bл + 1) «//] ехр [- »<2"+*>'"*]
Bл + 1) [% Bл + IJ *2 ~ <
F.19)
Если окажется, что а имеет нулевое аначение или одно из значений
х Bп +1 J1С2//2, то при Х = — а имеется полюс второго порядка и необхо-
необходимо произвести отдельный расчет. Если это не имеет места, то мы окон-
окончательно получим
B11+1)« (б20ч
Подобным же образом можно рассмотреть случай с выделением постоян-
постоянного количества тепла в единицу времени. Решение для случая выделения
в единицу времени количества тепла, являющегося какой-либо произвольной
функцией времени, получается так же, как и F.7) из соотношения B.10)
данной главы.
IV. Граничное условие третьего рода.
В качестве примера рассмотрим задачу IV предыдущего параграфа.
По значению v из E.9) данной главы находим при помощи теоремы обраще-
обращения решение в виде
f— / ОО
Здесь полюсы подынтегральной функции находятся при Х = 0 с выче-
вычетом A//0, и при
Х=^ —ха2 |* = /ал. /г=1, 2, 3 F.22)
где ± ая, п = 1, 2, ..., — корни (все простые и вещественные, см. § 10 гл. III)
уравнения
a sin а/ = h cos а/
или
aigai=:h. F.23)
Чтобы найти вычеты относительно этих полюсов, необходимо выполнить
следующие вычисления:
= - у a» {A + /*) sin /а„ + Zan cos /an} = -1 {/ (A2 + 4) + h) cos /an.
Воспользовавшись этим результатом в F.21), окончательно получим
v = 2А1/0 V . /f"c°SY • F-24)
§ 6]
ГЛ. XII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЛИНЕЙНЫЙ ПОТОК
311
Это решение было уже найдено в § 11 (см. соотношение A1.12) гл. III).
Подобным же образом можно получить все результаты §§ 11—13 гл. III.
V. Другие граничные условия. Контакт с хорошо перемешивае-
перемешиваемой жидкостью.
В примере Е § 9 гл. I было отмечено, что задачи, в которых поверх-
поверхность твердого тела соприкасается с хорошо перемешиваемой жидкостью,
имеют определенное практическое значение. Задачи этого типа для пластины
проще всего решать обычным методом с использованием преобразования
Лапласа. Классические методы не всегда можно использовать в неизменной
форме. В § 13 гл. III уже было дано несколько решений без доказательства.
В качестве примера, поясняющего новые особенности таких задач, рас-
рассмотрим следующую задачу:
Область О < х < /; тепловой поток на плоскости х = 1 отсут-
отсутствует. Плоскость х = 0 соприкасается с хорошо перемешиваемой
жидкостью с удельной теплоемкостью с', причем на единицу поверх-
поверхности этой плоскости приходится масса жидкости, равная М'.
Между жидкостью и поверхностью твердого тела происходит те-
теплообмен, и количество тепла, которое отдает жидкость твердому
телу в единицу времени, равно произведению Н на разность темпе-
температур между ними. Начальная температура жидкости равна Vo,
а твердого тела — нулю.
Обозначим температуру жидкости через и, з. температуру твердого тела
через v\ тогда граничные условия (9.14) и (9.16) гл. I при х = 0 запишутся
в виде
dt
dv
F.25)
Функция v удовлетворяет дифференциальному уравнению
и граничное условие при х = I имеет вид ->— = 0, х = /, t > 0,
Начальные условия записываются в виде
u = V0, t = 0
Составляя обычным путем вспомогательные уравнения, соответствующие
дифференциальному уравнению и начальным и граничным условиям, получим
d2v
dx2
— q^v = 0,
0 < x < /,
dv
dx
dv
= 0,
M'c'pu-K^ =
dx
x =
x = 0,
dv
dx
F.26)
312 ГЛ. XII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЛИНЕЙНЫЙ ПОТОК [§ 7
Поскольку в граничное условие F.25) входит член с du/dt, в правой части
F.26) появляется член M'c'VQ, содержащий начальное значение и.
Решая приведенные выше уравнения обычным путем, получим
hVochq(l-x)
V hp ch ql + [p+ (hKlM'c')] qshql9
- V0(hch
U ~
hp ch ql+ [p + (hK/M'c')]qsh qC ^'Zb)
где h = H/K. v и и находят теперь обычным путем при помощи теоремы
обращения. Так
v = -^ - 2LVQ 2 pss~sk«s е~ & cos а, A - х/1), F.29)
jj- е~ а-Г, F.30)
5=1
где L = lh, k = lpc/M'c\ T = xt/P, as — положительные корни уравнения
La
§ 7. Полуограниченная область х> 0. Применение теоремы обращения
В качестве примера задачи, в которой, пользуясь таблицей изображений,
нельзя получить непосредственно ответа, рассмотрим случай полуограни-
полуограниченного твердого тела х > 0 с нулевой начальной температурой.
При ?>0 температура поверхности л; = 0 этого тела меняется
по закону Vosin(a)/-f-s).
В данном случае вспомогательное уравнение имеет вид
-q2v = 0, x>0. G.П
При лг = О мы должны иметь
v = Vo (sin Ы cos e -f- cos mt sin e),
и, следовательно,
v= 0(<»cos^+psin?)e G2)
Решение уравнения G.1) при условии G.2), имеющее конечное значение
при лг—>оо, записывается в виде
Так как в таблице изображений такого выражения нет, применим тео-
теорему обращения и получим
2%i J
t
7— too
Подынтегральная функция G.4) имеет при Х = 0 точку ветвления и обла-
обладает простыми полюсами при Х=±/а). Рассмотрим интеграл по контуру»
§ 7] ГЛ. XII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЛИНЕЙНЫЙ ПОТОК 313
показанному на рис. 40, т. е. интеграл
+ Ume)^^^ G5)
На этом контуре и внутри него подынтегральная функция является одно-
однозначной функцией X. Аргументом X на EF служит тс, а на CD этим аргу-
аргументом служит —тс.
По теореме Коши интеграл по такому замкнутому контуру равен произ-
произведению 2тс/ ria сумму вычетов относительно полюсов внутри контура. Эти
полюсы находятся в точках X = ± /ю. Вычет относительно полюса X = /ц>
равен
-^ ехр {Ш + U — х
Отсюда сумма вычетов относительно полюсов Х = /<й и Х = — /о> равна
— Аг(о)/2хI/2}, G.6)
Рассмотрим теперь интеграл по контуру ABFEDCA при переходе к пре-
пределу, когда радиус большой окружности R стремится к бесконечности, а ра-
радиус малой окружности — к нулю- При /?->оо интеграл по дугам BF и CD
стремится к нулю *). По мере того как радиус малой окружности с центром
в начале координат приближается к нулю, интеграл по этой окружности
также стремится к нулю. При /?—>оо интеграл по АВ становится равным
интегралу в соотношении G.4). В интегралах по EF и CD мы полагаем
Х = р?/я и \ = pe~ix соответственно и получаем
/
» + r.We-""sin(ux)uda. G.7)
о
U
oo
-. Г о) cos e—%u2 sin e
о
где p = %#2.
Итак, используя G.4), G.6) и G.7), окончательно получим
v = VQe~x Y1^Tx sin {ы + e — x (а>/2х)'/2} +
+-пг*- /мсо:::У •--'sin ^ * **• G-8>
6
Первый член соотношения G.8), полученный из вычетов G.6) относи-
относительно полюсов ± /о», представляет собой часть решения, соответствующую
стационарному состоянию, и, если необходима только она, рассматривать
интеграл G.7) нет необходимости (ср. § 5 гл. XV). Результаты (8.4) и (9.13)
гл. И можно получить таким же путем.
Все решения, приведенные в § 4 данной главы, которые были получены
при помощи таблицы изображений, можно, конечно, найти, как и в настоящем
параграфе, воспользовавшись теоремой обращения.
*) Дальнейшее рассмотрение этого вопроса см. в приложении 1. Во всех слу-
случаях, когда используется теорема обращения, справедлив тот же результат и приме-
применимо аналогичное доказательство.
314 ГЛ. XII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЛИНЕЙНЫЙ ПОТОК [§ 8
§ 8. Составные твердые тела
Задачи теплопроводности в составных твердых телах *) обычно лучше
всего решаются методом преобразования Лапласа. Как изображения, так и
решения могут оказаться достаточно сложными, однако при этом не появляется
никаких новых правил. В § 15 гл. II изучалось несколько задач, в которых
рассматривается составное твердое тело. Их можно также решать данным
методом. Здесь будут рассмотрены полуограниченные и конечные составные
области.
Рассмотрим сначала полуограниченную область —/ < х < оо, в которой
при —/ < х < 0 находится одно вещество, а при х > 0 — другое. Обозначим
теплопроводность, плотность, удельную теплоемкость, коэффициент темпера-
температуропроводности и температуру в области —/ < х < 0 через Kv pv cv xA
иг/j, а соответствующие величины в области х > 0 — через К2> р2» сч* *2 и V2*
Требуется найти решения следующих дифференциальных уравнений:
дх2 х2 М * ^ * "^
Если допустить, что на поверхности раздела х = 0 контактное тепловое
сопротивление отсутствует (ср. пример Ж § 9 гл. I), то граничные условия
запишутся в виде
dtJi dt/o
v1 = v2, x = 0, t>0. (8.2)
I. Для описанного выше твердого тела с нулевой начальной тем-
температурой и плоскостью лг = — /, поддерживаемой при t^>0 при
постоянной температуре, вспомогательные уравнения имеют вид
-^г — ф = 0, *>0, (8.4)
где
Эти уравнения должны быть решены при условиях
(8.7)
при л:->схэ. (8.8)
*) Составные пластины рассмотрены в [24—26]. Составные шары — в рабо-
работах [27—30]. Составные цилиндры рассмотрены в [31]. Дополнительные ссылки* на
работы, в которых рассматриваются составные цилиндры и шары, приводятся в сле-
следующей главе. Полуограниченное составное твердое тело с постоянным тепловым
потоком на поверхности рассматривается в статьях [32, 33]. В работе [34] рассмотрена
пластина, состоящая из п слоев, как с постоянной температурой поверхностей, так
и с граничными условиями третьего рода: там же приведены формулы в явном виде
<см. также [35, 36]).
§ 8] ГЛ. XII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЛИНЕЙНЫЙ ПОТОК 315
Решение уравнения (8.3), удовлетворяющее условию (8.7), имеет вид
Ъх = (У/р) ch qx (/ + х) + A sh qx (I + x)\
решение уравнения (8.4), удовлетворяющее условию (8.8), имеет вид
Неизвестные А и В находят из (8.6), и окончательно мы получим
- _ Vjchq.x — oshq.x) g g>
тао^ (8Л0)
здесь используются следующие обозначения:
Л1 a -j- 1
Для оценки v1 и г/2 можно использовать либо теорему обращения, либо
метод разложения в ряд, описанный в § 5 данной главы. Согласно теореме
обращения можно написать
v+i
V С
V<1 = ~bu J
i
J
у— ico
где jxj =: У \/хх. Подынтегральная функция в соотношении (8.12) имеет
при Х = 0 точку ветвления; поэтому, как и в предыдущем параграфе, мы
используем контур, изображенный на рис. 40; тогда интеграл в (8.12) ока-
окажется равным сумме интегралов по малой окружности с центром в начале
координат и по прямым CD и EF.
Интегрируя по малой окружности, получаем V.
Полагая, что на EF \ = хги2еы, а на CD X = x1#2?-/rc, получим, что вклад
со стороны CD и EF равен
V
оо
e-XxU4'ikxu du Г e-*x*t+ihxu du
л e-xxu4-ikxu du /»
./ и [cos a/ -f- iq «in a/] ,/ i~ [cos a/ — /a sin ul] I
о о I
oo
2V Г _XiU*t <J cos kux sin ul -f- sin ^ал: cos a/ .
~ ^TJ в l a [cos2 a/ + a2 sin2 tt/]
Таким образом,
oo
jr 2V Г -%,ti4 a cos kux sin ul-\~ sin kux cos ul , /o 1O4
2 n J tt[cos2tt/ + a2sin2a/] ч '
0
Аналогичным образом получим
oo
Vl~V n Je и [COS2 ul + a2 sin2 ul]' №Л*'
0
Изложенный в § 5 данной главы метод дает решение в форме, которая зача-
зачастую оказывается более удобной. Используя обозначения (8.11), можно из (8.10)
316
получить
ГЛ. XII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЛИНЕЙНЫЙ ПОТОК
[§ 8
Из (8) приложения 5 следует, что
Подобным же образом
<816>
(8,7)
Используя G) приложения 5, таким же путем находим градиент темпе-
температуры на поверхности в виде
n-\
8.18)
Для очень больших значений времени все показательные функции в (8.18)
можно заменить единицей, и мы приближенно получим
' (8Л9)
Если поверхность поддерживается при нулевой температуре, а начальная темпе-
температура всего твердого тела равна V, то, очевидно, что градиент температуры при
х = — / будет равен написанному выше выражению с обратным знаком. Этот резуль-
результат был использован Перри и Хевисайдом при определении возраста Земли ¦). Кель-
Кельвин в своей классической работе (см. § 14 гл. II) установил, что градиент температуры
равен У/Упх^. Теперь известно, что плотность и физические свойства ядра Земли
значительно отличаются от соответствующих величин для наружной оболочки. Приняв
это, мы увидим, что время, необходимое для уменьшения температурного градиента
до существующего в настоящее время уровня, в (/Gc2P2)/(^(iciPi) раз больше времени,
получающегося из теории Кельвина. По данным, принятым Перри и Хевисайдом, эта
отношение примерно равно 450, и оценку Кельвина, равную 108 лет, следует увели-
увеличить до 4,5 • 1010 лет.
Представляет некоторый интерес случай малого /, т. е. случай тонкой
пленки иного материала, находящейся на поверхности полуограниченного
твердого тела. Разлагая гиперболические функции в знаменателе решения (8.10)
по возрастающим степеням /, найдем
v2 =
(8.20)
Учитывая только первую степень I, получим
где h = Кг/К21- Это равно значению v2* полученному с учетом приближен-
приближенного граничного условия (9.7) гл. I, в котором мы полностью пренебрегали
теплоемкостью пленки. Во втором приближении, учитывающем также член с /2,
*) См. ссылки на литературу к гл. II и IX.
§ 8] ГЛ. XII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЛИНЕЙНЫЙ ПОТОК 317
получим
где hr = Kil/2x1K2- Изображения такого типа появлялись в примере III § 4
данной главы. Выражение (8.21) является изображением решения задачи
о полуограниченном твердом теле с нулевой начальной температурой и гра-
граничным условием в виде
Таким образом, это условие можно считать приближенным граничным усло-
условием, учитывающим теплоемкость пленки *).
II. Описанное выше составное твердое тело с нулевой начальной темпера-
температурой* При t > 0 в области — / < х < О в единицу времени на единицу объема
выделяется постоянное количество тепла Ао, В области х > О тепло не выде-
выделяется. Плоскость х = — / поддерживается при нулевой температуре.
В данном случае, используя обозначения (8.11), получим следующие решения:
со
_ 4. (*' — *') 2Ло° С .-„,« A - cos ul) sin и (l + x)
"' Щ ЖГ J «3[c0S2u/ + a2Sin2M/]
(8-23)
«ли
»*] ¦< *o" * «i ¦* *y ^k ' и I 2 9ЛЧ* I \^'^ I II t I Л I о-a I \jLTt ' I Alt "~~ иГ I *
" /(, ^ I L 2 Kv J L 2 Km I
. (8.24)
— ^o^2 2-A0 Г _х,м2г A — cos ul) (a sin и/ cos kux -f- cos и/ sin
или
III. Пластина конечных размеров. Область пластины — / < х < 0 содержит
материал с параметрами К\, Pi, сь %ь vit а область 0<х<а — другой мате-
материал, с параметрами К2, Рг. С2. ^2. V2- Начальная температура равна нулю. При
t > 0 плоскость х = — / поддерживается при постоянной температуре V, а пло-
плоскость х = 0 — при нулевой температуре.
Вспомогательными уравнениями здесь служат уравнения (8.3) — (8.7), но усло-
условие (8.8) заменяется на условие
v2 = 0, х = а.
Решая эти уравнения, находим
— V {ch q\X sh q2a — з sh q^x ch q2u}
1 ~~ p {ch qxl sh q2a + c sh qxl ch gy*}
- Vshg2(a — ^)
*) Случай многослойной оболочки рассматривался в [37].
318 ГЛ. XII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЛИНЕЙНЫЙ ПОТОК [§ 8
Разложение этих выражений в ряды типа (8.15) довольно сложно, и поэтому мы
рассмотрим только решения, получаемые при помощи теоремы обращения. В данном
случае подынтегральные функции являются однозначными функциями X с простыми
полюсами при Х=0 и Х= — ж$2т, где ± Рт, /га=1, 2, 3,...,— корни *) уравнения
cos p/ sin k$a + a sin p/ cos k$a = 0. (8.29)
Применяя обычным образом теорему обращения, найдем
cos $mx sin кфт — о sin §mx cos ka§m - »j &< _ ,.
i sin fJm/ sin ka$m — (a/ -j- ka) cos $ml cos
V2 — —j7
nl sin ka$m — (a/ -j- ka) cos $ml cos ka^m
Ряды в решениях (8.30) и (8.31) можно немного упростить, используя снова (8.29),
Следует отметить, что корни уравнения (8.29) служат корнями уравнения
(8.32)
и общими корнями (если вообще они имеются) уравнений
sin р/ == 0 и sin?pa = 0. (8.33)
Последние уравнения имеют общие корни тогда и только тогда, когда отноше-
отношение kail есть рациональная величина. Таким образом, если
kail = rIs (8.34)
есть несократимая рациональная дробь, то общие положительные корни (8.33)
равны rins/l, /i= 1, 2, 3, ..., и эти корни уравнения (8.29) дадут для vx и v2 соот-
соответственно ряды
сю
l sinep[Lj (8.з5>
2V vi cos /zstc . nnzx г y.{n2s2n41
2—7T-"Sin-^exP[ "-p—J- <8'36>
Если дробь ka/l иррациональна, эти ряды не появятся.
Во всех случаях существует ряд членов, соответствующих положительным кор-
корням **) рл, л= 1, 2, 3, ..., уравнения (8.32).
Воспользовавшись уравнением (8.32), можно представить члены рядов (8.30)
и (8.31), соответствующие этим корням, в виде
sin2 ka$n sin (Зл
, (/ sin2 ka$n + oka sin2 l$n)
*) Ниже в примере IV будет показано, что все эти корни действительны и
просты.
**) В их число входят простые корни уравнений cos р/ = 0 и cos ka$ = 0, кото-
которые могут появиться, если ka/l является рациональной величиной. В этом частном
случае справедливы рассуждения, приводящие к выражениям (8.37) и (8.38).
§ 8] ГЛ. XII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЛИНЕЙНЫЙ ПОТОК 319
И
лт^^ГЧ sin /рл sin ka$n sin k (я — x) рл ~xi°
^^ Рл (/ sin2 kci$n -4- g?# sin2 /P/»)
соответственно для t^ и v2.
IV. Характер корней уравнения (8.32) а уравнений, появляющихся в анало-
аналогичных задачах.
При получении решений в виде бесконечных рядов с помощью теоремы обра-
обращения мы обычно еще должны доказать, что все корни определенного трансцендент-
трансцендентного уравнения действительны и просты. В примере III таким уравнением была
уравнение (8.32); в задаче о твердом теле в виде составного шара им является урав-
уравнение (9.35) гл. XIII; в случае более общих граничных условий появляются другие
типы уравнений, например уравнение (9.25) гл. XIII и т. п.
В § 9 гл. III было исследовано очень простое уравнение. Обобщение применен-
примененного там метода [27, 38] можно использовать во всех случаях. Здесь же в качестве
примера мы рассмотрим уравнение (8.32).
Очевидно, что оно не может иметь чисто мнимого корня р = nj, так как
cth TjZ + o cth kt\l > 0.
Покажем теперь, что оно не может иметь комплексного корня вида 5 ± ii\. Рассмот-
Рассмотрим функцию U, определяемую следующим образом:
IUX = sin р (/ + ¦*)> — / < jc < 0, (8.39)
U =-
где Р — корень уравнения (8.32).
В таком случае получим
= 0, 0 < х < а. (8.41)
Кроме того,
Ui = 0 при х = — /; U2 = 0 при х = a; UX = U2 при х = 0 (8.42)
и
=0, (8.43)
так как р — корень уравнения (8.32).
Пусть теперь Р и а — два различных корня уравнения (8.32), и пусть Vx и V2 —
величины, соответствующие величинам Ux и U2 при замене р на а.
Тогда из соотношений (8.41) и соответствующих уравнений для Vx и V2 получим
о о
(Р2 - «2) J Ux Vx dx + j {Uf[vx - У';иг) dx = 0,
a a
?2 (p2 __ a2) С (J2V2dx+ J (U2 V2 — V'zU2) dx = 0.
0 0
Отсюда, используя соотношения (8.42) и (8.43), находим
0 а
Кх J Ux Vx dx + &K2 j U2V2 dx
-i о
о
= *i / {РУх - uWi)d*+K2 f (U2V'2' - V2U'2) dx =
-/ о
= *i [UiV[ - VtU[f^ + K2 [U2V2 - V2U2f0 = 0. (8.44)
320 ГЛ. XII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЛИНЕЙНЫЙ ПОТОК [§ 8
Из последнего соотношения следует, что а и р не могут иметь вид ? ± и|, поскольку
Uu Vx и U2t V2 были- бы тогда сопряженными комплексными величинами и величина
о а
UiVldx+k*K2
-i о
была бы положительной.
Таким образом, мы доказали, что все корни уравнения (8.32) являются веще-
вещественными. Их симметричное расположение относительно начала координат и то
обстоятельство, что они не повторяются, следует в данном случае из рассмотрения
кривых у = ctg х и у = ctg (kax/l). Другие случаи можно рассмотреть путем обоб-
обобщения описанного выше метода (см. [38]).
V. Составная пластина из произвольного числа слоев.
При написании изображения любой требуемой функции для общего случая п слоев
трудностей не встречается. Легче всего это сделать при помощи описываемого ниже
метода матриц. Вследствие сложности получаемых решений рассмотрение корней зна-
знаменателя в изображении решения и численная оценка температур требуют проведе-
проведения очень сложных вычислений. Следует отметить, что, когда изображение найдено,
оно непосредственно дает стационарное периодическое решение; кроме того, в тех слу-
случаях, когда рассматриваемая величина имеет прямолинейную асимптоту в виде (a-\-bt),
ее легко найти простым хорошо известным численным методом (ср. § б гл. XV).
Для определения изображения рассмотрим сначала пластину 0 < х < I. Тогда,
если ~vx и Yx — изображения температуры и теплового потока в точке х, то из вспомо-
вспомогательных уравнений сразу же получим
vx = щ ch qx — Yo (MKq) sh qx, (8.45)
7x = — v0Kq sh qx -f /o ch qx, (8.46)
или в матричном обозначении, определенном в § 7 гл. III,
/**\_/ chV* —(l/Kq)shqx\(vo\
[fx)-[-Kqshqx chqx ){/)'
Рассмотрим теперь пластину, состоящую из п слоев, (/,, /2), (/2, /3), ..., Aп,
Пусть Кг и *т — теплопроводность и температуропроводность r-го слоя, vr тк Yr —
изображения температуры и теплового потока на границе этого слоя х = /г, a ~vr
и 7г~их значения на границе слоя x = lr+l. Тогда из (8.47) получим
где
Ar= ch(lr+l — lr)qr> Br = — (l/Krqr)sh (/г+1—lr) qn ^
Cr = — КгЯг sh (/r+i -lr) qr, Dr = ch (/r+I - lr)qr ) (849)
и
ArDr — BrCr=l.
Если между пластинами имеется идеальный тепловой контакт, то повторное при-
применение (8.49) дает
А в1
Если теплопередача происходит по линейному закону, контактные сопротивления
равны /?ь ..,, /?я+1 при 1и 12> .... /щ-ь область х<1х имеет температуру v0,
а область х > /я+, —температуру vn+l9 то
^iU/1 —Лв+Л/41 ВлП —Rn\ (At ВЛ/1 —/?Л/^\
Jn+l) [о 1 ){сп dJ[o ir-Чс, dJlo iA7o/
§ 8] ГЛ. XII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЛИНЕЙНЫЙ ПОТОК 321
Таким способом определяются изображения для температуры или тепловых по-
потоков при любом из 1{ ln-u a значения для промежуточных точек можно найти
затем из уравнений (8.45) и (8.46). Этим способом можно, например, вывести соотно-
соотношения (8.27) и (8.28).
VI. Область 0 < х < I состоит из одного материала, а область х > / — из
другого. Тепловой поток при х = 0 отсутствует. Начальная температура
в области О < х < I постоянна, а в области х > I равна нулю.
Решение этой задачи и численные значения температур при х = О приведены
в статье [39].
ЛИТЕРАТУРА
1. Carslaw, Jaeger, Operational Methods in Applied Mathematics, Oxford, 1948.
(Г. Карслоу и Д. Егер, Операционные методы в прикладной математике, ИЛ,
Мм 1948, перев. с 1-го изд. 1941 г.)
2. В г от wi ch, Proc. Lond. Math. Soc. 15, 401 A916).
3. Wagner, Arch. Elektrotech. 4, 159 A916).
4. Jeffreys, Operational Methods in Mathematical Physics, Cambridge, ed. 2, 1931.
5. Carslaw, Introduction to the Mathematical Theory of the Conduction of Heat in
Solids, Macmillan, ed. 2, 1921. (Г. Карслоу, Теория теплопроводности, Гостех-
издат, М., 1947.)
6. С а г s I a w, J e f f r e у s, Math. Gaz. 14, 216, 225 A928).
7. Doetsch, Math. Z. 22, 285, 293 A925); 25, 608 A926); 26, 89 A927); 28, 567
A928).
8. Churchill, Modern operational Mathematics in Engineering McGraw-Hill, 1944.
9. Doetsch, Theorie und Anwendung der Laplace-Transformation, Springer, 1937.
10. Gardner, Barnes, Transients in Linear Systems, vol. 1, Willey, 1942.
11. Campbell, Foster, Fourier Integrals for Practical Applications, Bell System
Techn. Monographs, No B-584.
12. McLachlan, Humbert, Formulaire pour le calcul symbolique, Gauthier-Vil-
lars, 1941.
13. Er d ё 1 у i, Tables of Integral Transforms, McGraw-Hill, 1954.
14. Humbert, Le calcul symbolique, Actualites scientifiques et industrielles, No 147,
1934.
15. С h u г с h i 11, Math. Z. 42, 567 A937).
16. T r a n k 1 e, Frequenz 8, 334—338 A954).
17. V a n О r s t r a n d, J. Wash. Acad. Sci. 22, 529 A932).
18. Lochs, Z. angew. Math. Mech. 34, 79—80 A954).
19. Mace y, Proc. Phys. Soc. 52, 625 A940).
20. G о 1 d s t e i n, Z. angew. Math. Mech. 12, 234 A932).
21. Hartree, Mem. Manchr. Lit. Phil. Soc. 80, 85 A935).
22. Barrer, Trans. Faraday Soc. 35, 628 A939); 36, 1235 A940).
23. Barrer, Phil. Mag. 28, 148 A939); 35, 802 A944).
24. L о w a n, Duke Math. J. 1, 94 A935).
25. Churchill, Duke Math. J. 2, 405 A936).
26. С h u г с h i 11, Am. J. Math. 61, 651 A939).
27. Bromwich, Proc. Camb. Phil. Soc. 20, 411 A921).
28. Carslaw, Proc. Camb. Phil. Soc. 20, 399 A921).
29. С a r s 1 a w, J a e g e r, Proc. Camb. Phil. Soc. 35, 394 A939).
30. Bell, Proc. Phys. Soc. 57, 45 A945).
31. Jaeger, Phil. Mag. 32, 324 A941).
32. M a t r i с о n, J. Phys. Radium 12, 15 A951).
33. G r i f f i t h, H о r t о n, Proc. Phys. Soc. 58, 481—487 A946).
34. S aka i, Sci. Rep. Tohoku Univ. 11, 351—378 A922).
35. Jaeger, Quart. Appl. Math. 8, 187—198 A950).
36. Levy, Trans. ASME 78, 1627—1635 A956).
37. Fox, Phil. Mag. 18, 209 A934).
38. Ince, Ordinary Differential Equations, Longmans, 1927.
39. Lovering, Bull. Geol. Soc. America 47, 87 A936).
21 Г. Карслоу, Д. Егер
ГЛАВА XIII
ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЗАДАЧИ ДЛЯ ЦИЛИНДРА И ШАРА
§ 1. Введение
В настоящей главе мы рассмотрим несколько задач для шара и беско-
бесконечного цилиндра кругового сечения, которые гораздо легче решаются не
классическими методами, а методом преобразования Лапласа. Мы займемся
здесь задачами [1, 2] с усложненными граничными условиями, задачами для
полого и составного цилиндров, а также решениями, применимыми для малых
интервалов времени, решениями для областей, ограниченных изнутри цилин-
цилиндрическими поверхностями, и, наконец, соответствующими задачами для шара.
§ 2. Цилиндр кругового сечения 0 < г < а
с различными граничными условиями
В настоящем параграфе в качестве примера применения преобразования
Лапласа при решении задач для цилиндрической области приведено сокра-
сокращенное решение нескольких задач, уже рассмотренных в §§ 6—9 гл. VII.
Используемые здесь выражения для изображений потребуются также в § 3
гл. XIII, где находят решения, применимые при малых значениях v.t/a2.
I. Нулевая начальная температура. Температура поверхности
постоянна.
В данном случае нужно решить уравнение
при условии, что v = V при г = а, t > 0.
Вспомогательное уравнение имеет вид
^ + 7#-^=0' °<г<а. B.2)
где q2 = /?/x. Его следует решать при
B.3)
и при г/, имеющем конечное значение при г = 0. Из двух решений уравне-
уравнения B.2), I0(qr) и K0(qr), последнее при г—>0 стремится к бесконечности,
и поэтому его следует исключить. Таким образом, решение уравнения B.2)
при условии B.3) имеет вид
§ 2] ГЛ. XIII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЗАДАЧИ ДЛЯ ЦИЛИНДРА И ШАРА 323
Отсюда, используя теорему обращения, получим
—я- /*•"
у— i оо
где, как обычно, (д. обозначает |ЛХ/х.
Подынтегральная функция в соотношении B.5) является однозначной
функцией X (см. [3] или ряд, в который разлагается функция I0(z))t и
поэтому мы воспользуемся контуром, изображенным на рис. 39. Нули функ-
функции 10(\ъа) располагаются в точках Х = — ха^, где ± ал, /г=1, 2, ..., слу-
служат корнями уравнения
У0(аа) = 0.
Тогда обычным путем получаем, что интеграл в соотношении B.5) равен
произведению 2ni на сумму вычетов относительно полюсов подынтегральной
функции. Вычеты оцениваются по следующей формуле (ср. B6) приложе-
приложения 3):
[к ± /0(t*«)]x=xa2 = [у Р«А О"»)] = - j аа„У, (aan). B.6)
Для полюса при Х = 0 вычет равен 1, поскольку I0(z)=\ при z = Q.
Таким образом, окончательно получим
*-К « ij6 «„У, (аая) • ^7>
/1 = 1
Мы получили решение, совпадающее с решением F.8) гл. VII, но здесь
мы не принимаем допущения F.1) той же главы, и можно, как в приложе-
приложении 1, показать, что соотношение B.7) удовлетворяет условиям нашей за-
задачи. Аналогичное замечание применимо ко всем решениям, приведенным
в данной главе.
II. Нахальная температура равна нулю. Температура поверхности равна kt.
Аналогичным путем находим, что
* f
i
-ioo
Единственным отличием служит существование в данном случае полюса второго по-
порядка при Х = 0.
III. Нулевая начальная температура. Тепловой поток на поверхности по-
постоянен и равен Fo.
Вспомогательное уравнение B.2) следует здесь решать при граничном условии
-*#-т- B-9>
Таким образом,
Воспользовавшись теоремой обращения, получим решение в виде
Рр \ 2*4 г2 1
21s1
324 ГЛ. XIII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЗАДАЧИ ДЛЯ ЦИЛИНДРА И ШАРА [§ 2
где as — положительные корни уравнения
J\ («) = 0. B.12)
IV. Нулевая начальная температура. Граничное условие тре-
третьего рода.
Вспомогательным уравнением остается уравнение B.2), и если на гра-
границе цилиндра происходит теплообмен со средой, имеющей постоянную тем-
температуру 1/, то граничное условие имеет вид
dv , - hV
—-±-hv — .— 9 когда r = a. B.13)
Следовательно, решение запишется следующим образом:
-= hVIQ(gr)
p{qli(qa)-\~hlo(qa)}
Воспользовавшись теоремой обращения, находим решение в виде
к «(*ч<икг BЛ5)
где ап — положительные корни уравнения
aJx (аа) = hJ0 (аса). B.16)
V. Контакт с хорошо перемешиваемой жидкостью *) или идеальным про-
проводником тепла.
В качестве примера рассмотрим следующий случай: цилиндр 0 < г < я, имев-
имевший в начальный момент t = 0 постоянную температуру V, помещают в хорошо
перемешиваемую жидкость с удельной теплоемкостью с' и температурой, рав-
равной в начальный момент времени нулю. Пусть на единицу длины цилиндра при-
приходится масса жидкости, с которой он соприкасается, равная М. Пусть, далее,
температура жидкости при t > 0 равна температуре поверхности твердого
тела и тепло, теряемое жидкостью в окружающую среду, равно произведе-
произведению Н на температуру жидкости.
В этом случае вспомогательное уравнение записывается следующим образом:
Граничное условие при г = а имеет вид (ср. (9.14), (в.15) гл. I)
^ ^ г = а, B.18)
где и — температура жидкости, причем и = v при t > 0.
Отсюда получим следующее граничное условие для вспомогательного уравне-
уравнения B.17): _
^ ^О, г = а. B.19)
Следовательно,
c'p + H)I0(qr)
XJ
р \ 2%aKqIx (qa) + (MC p + H) /0 (qa)
}
f *
2V{H'-ka^n)JQ{ran) .„it
_ о О ОчОТ 1
*) Решения ряда таких задач для областей, ограниченных изнутри и снаружи
цилиндрическими поверхностями, и для малых цилиндров приведены в статьях [4, 5].
Подобные задачи возникают, например, при рассмотрении нестационарного нагрева
одножильных кабелей [6].
§ 3] ГЛ. XIII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЗАДАЧИ ДЛЯ ЦИЛИНДРА И ШАРА 325
где ± ant /i=l, 2, ..., — корни уравнения
aaj, (aa) = (Hf — kaW) Jo (aa), B.21)
H' = Я/2тс/С, ? = Мс'12ка*?с.
VI. Выделение тепла при t > 0 в цилиндре О <^ г < а. Начальная темпера-
температура равна нулю.
Если начальная температура цилиндра равна нулю и если при />0 в цилиндре
выделяется в единицу времени на единицу объема постоянное количество тепла Ло,
а поверхность г = а поддерживается при нулевой температуре, то вспомогательное
уравнение имеет вид F.7) гл. I
Решение этого уравнения с величиной v, равной при г = а нулю и имеющей
при г = О конечное значение, записывается в виде
Отсюда, пользуясь B.8), получим
Ао (а2 — г2)
где oin — положительные корни уравнения JQ (aa) = 0.
§ 3. Решения, применимые для малых интервалов времени
I. Постоянная температура поверхности.
Рассмотрим сначала задачу / предыдущего параграфа, в которой темпе-
температура поверхности постоянна. Ранее, в § 6 гл. VII, уже отмечалось, что
решением B.7) предыдущего параграфа неудобно пользоваться при малых
значениях х?/а2, например при значениях, меньших 0,02. Аналогичное затруд-
затруднение встречалось и в задачах для пластины и шара. В этих случаях дру-
другие решения можно найти, как и в § 5 гл. XII, разлагая v в ряд по экспо-
экспоненциальным функциям с отрицательным показателем. В задачах для цилиндра
метод решения еще сложнее; он заключается в использовании асимптотиче-
асимптотического разложения функций Бесселя, вводимого с тем, чтобы получить фор-
формулу с показательными функциями, коэффициенты которых служат членами
рядов по 1/? [1,7].
Таким образом, используя решение B.4) предыдущего параграфа и соот-
соотношение A2) приложения 3, получим для случая, когда (г/а) не мало, соот-
соотношение
рг1г [l + (l/8qa)-{-(9/l28q2a2) + ...]-f О [е~2да] ' '
или
-д(а-г), (з.2)
pr'* \ Sqar
причем членами, содержащими ехр[—q(ba — г)] и т. д., которые соответствуют
многократному отражению (см. E.2) гл. XII), пренебрегают. Используя (i 1)
326 ГЛ. XIII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЗАДАЧИ ДЛЯ ЦИЛИНДРА И ШАРА [§
приложения 5, получим из C.2)
Поскольку мы пренебрегаем последними членами, ряд C.3) неприменим
в таком широком диапазоне значений (xt/a2), как в § 5 предыдущей главы,
но он вполне годится для xt/a2 < 0,02 при условии, что г/а не слишком
мало.
Для температуры в центре, т. е. при г = 0, в соотношении B.4) дан-
данной главы /0(дт)=1, и, применяя, как и раньше, асимптотическое разло-
разложение IQ(qa), найдем
"*)*е-Ча =
}
//«*'/< {1 + (l/8qa) + (9/128^2) + .
Пользуясь выражением B0) приложения 5, найдем, что первый член
в разложении v имеет вид*)
Ч?] (?)
II. Постоянный тепловой поток на поверхности.
Рассмотрим тем же способом решение B.10) данной главы при условии,
что, как и ранее, отношение г/а не мало. Тогда
III. Теплообмен на поверхности.
Принимая, как и раньше, что г/а не мало, и подставляя в соотношение
B.14) данной главы асимптотические разложения /0 и Iv получим
=
pqrll* 1 + [ah - C/8)]/aq + [ah — A5/16)]/8aV + ...
дг I 8/" 8д J i
pqr
Следовательно,
Если отношение г/а мало, то следует использовать метод, приводящий
к соотношению C.4).
*) Этот случай и его обобщение на малые значения г подробно рассмотрены
в статье [8]. Там же приведена таблица функций Бесселя К\^ Кь/4> К*цА и Кг^ необ-
необходимых при решении наших задач.
§ 4] ГЛ. XIII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЗАДАЧИ ДЛЯ ЦИЛИНДРА И ШАРА 327
§ 4. Полый цилиндр a<r <b
Рассмотрим эту область при нулевой начальной температуре*) и при
следующих граничных условиях:
D.1)
где kv kv k'v k'2— постоянные коэффициенты, которые потуг быть поло-
положительными величинами или равняться нулю (при условии, что kx и k2 или
k\ и k'2 равны нулю не одновременно), a kz и k'z — любые постоянные вели-
величины. При соответствующем выборе этих постоянных мы получим в общем
решении задачи решения для случаев постоянной температуры, постоянного
теплового потока, нулевого потока и теплообмена на любой из поверхностей.
Вспомогательное уравнение имеет вид
-^. + ^ — -4^ = 0, а<г<д.
а решение получается в форме
D.2)
где А к В выбираются так, чтобы v удовлетворяло изображениям функ-
функций D.1), а именно:
*;-3f+*?=t- r=b-
Подставляя в них решение D.2) и решая получающиеся уравнения отно-
относительно А и В, окончательно получим
k'2K0 (qb)\ /Q (qr) + [k[qlx (qb) + ftj/o (qb)] Ko (qr)) -
- К [[Wi (Я*) + b2K0 (qa)] IQ (qr) + [k.ql, (qa) - Vo (?«)] * о (?')}. D-3)
где
A (p) = [kxqlx (qa) — fe/0 (Я*)] [k[qKx (qb) — k'2K0 (qb)] —
- [kxqKx (qa) + k2K0 (qa)] [k[qlx (qb) + Щ, (qb)]. D.4)
Теперь v определяется при помощи теоремы обращения. Подынтег-
Подынтегральная функция является однозначной функцией X с простым **) полю-
полюсом при Х = 0 и простыми полюсами при Х = — ха?п, где ±ап — корни (все
*) Случай произвольной начальной температуры рассмотрен в § 8 гл. XIV.
**) Если /fg = ^ = 0, то при X = 0 имеется двойной полюс. Мы опускаем этот
случай, который легко исследовать таким же образом*
328 ГЛ. XIII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЗАДАЧИ ДЛЯ ЦИЛИНДРА И ШАРА [§ 4
действительные и простые) уравнения [7] *)
— [k1aY1 (аа) + k2YQ (аа)] [к[а^ (fat) — ^ (йа)] = 0. D.5)
Используем обычным образом контур, показанный на рис. 39. Вычет
относительно полюса Х = 0 равен
/b)}+b^{kl+ak2\n(r/a)\
Чтобы найти вычет относительно полюса Х = — ха^, нужно, чтобы
dA I Г 1 dA
1№
= т/а Л а [Wo (t*fl) - Vi
- b [ftlP
- b [klV.K, (jxa) ] [ ]}?-|e
Здесь мы использовали соотношение D.4) и рекуррентные формулы (см. A3)
и A5) приложения 3). Чтобы упростить это выражение, отметим, что, на-
например, при (х = /а„
__ Аг^п/, (дап) -f- АгУ0 (aan) _ kxanYx (gan) + k2V0 (mn)
Используя этот результат и соотношение B2) приложения 3, найдем
Х = ~хап Р
Р (г* \
г- D-8)
где
F (а„) = (k JVn + k*) [kpA {aa
n
Таким образом, окончательно получаем
— akz \k[ — bk2 In (r/b)] + ^ [^i + cik2\xi (r/a)]
ak2k[ + bkxk^ + abk2k2 In (b/a)
Ъ -x»2' 1 , ,
*) Отметим, что мы неоднократно используем формулы /0 (ix) = /0 W и т. д.>
приведенные в приложении 3 (см. B5) и B6)).
§ 5] ГЛ. XIII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЗАДАЧИ ДЛЯ ЦИЛИНДРА И ШАРА 329
где ап— корни уравнения D.5), функция F(ап) определена D.9), а
(г. ап) = Уо ('«я) [к^пУх (а*п) + k2Y0 (аап)] —
nJl{aan) + k2J0(aan)]. D.11)
Из этого общего решения можно получить целый ряд решений для част-
частных случаев [9, 10). Последние можно также получить непосредственным
использованием изложенного метода. Предположим, например, что приг = а
мы имеем постоянный тепловой поток FQ, а при г = Ъ — нулевую температуру.
В таком случае в граничных условиях D.1) имеем /&2 =/&| =/&? = 0; kx=\\
&3 = — FqIK\ *2=1. и решение D.10) принимает вид*)
'**2*' j2°(Ч) ^° (г*п) Yl (а"п) ~~ Y°{ran) Jl (да^
к г * ? п[А(пL{п)\
D.12)
где ап — положительные корни уравнения
Jx (аа) Ко фа) — Уг (аа) Jo фа) = 0. D.13)
Более сложные задачи, например задачи, приведенные в § 9 гл. I с гра-
граничными условиями, соответствующими контакту с хорошо перемешиваемой
жидкостью или идеальным проводником на одной или обеих поверхностях **),
могут рассматриваться точно таким же образом. Случай периодического
изменения температуры поверхности рассмотрен в [13]. Задача о выделении
тепла в изолированной проволоке, по которой протекает электрический
ток [14], по существу представляет собой задачу для цилиндра с конечными
размерами, но, кроме того, при ее рассмотрении можно пользоваться различ-
различными приближенными решениями, полученными из анализа теплового потока
в полом цилиндре.
Несколько значений корней уравнения D.5) для случая k — k[ = O при-
приведено в приложении 4. Корни этого уравнения для случая &2 = &j = 0, т. е.
корни уравнения D.13), приведены в [15]. Задача при k2 = 0 также была
решена численным методом ***).
§ 5. Область ограничена изнутри цилиндром кругового сечения r= a
Несмотря на несомненную важность этого случая в связи с задачами
о распространении тепла от проложенных в земле кабелей и труб, об охла-
охлаждении шахт и т. д., области такой формы изучаются сравнительно недавно.
Николсон [18] первым предложил решение E.6), однако его аргумента-
аргументацию нельзя считать безупречной. Титчмарш использовал интеграл Фурье;
Смит [19] применил метод контурных интегралов, изложенный в книге [20].
Ряд решений, для получения которых использовались операционный метод и
метод преобразования Лапласа, можно найти в работах Гольдштейна [1] и
Карслоу и Егера [7]. Некоторые численные результаты опубликованы Еге-
ром [21, 22].
I. Начальная температура равна нулю. Поверхность г = а нахо-
находится при постоянной температуре V.
*) Фишер [11] использовал это решение для определения теплопроводности.
**) Решение для этого случая приведено в [5]. В некоторых экспериментальных
установках возникают случаи аналогичного типа (см., например, [12]).
***) Корни уравнения D.5) для этого случая сведены в таблицу в [16]. Несколько
численных значений температуры дано в [17].
330 ГЛ. XIII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЗАДАЧИ ДЛЯ ЦИЛИНДРА И ШАРА [§ 5
Для такого случая вспомогательное уравнение имеет вид
d2v , 1 dv 9— ~ . /р (.
-dPr+T-jr-№ = 0' r>a- <5Л)
Его нужно решить при условиях, что v имеет конечное значение при г—>оо
и, кроме того,
v = V/p, r = a. E.2)
Решение имеет вид
Далее, используя теорему обращения, получим
Y—too
где {х = ух/х. Подынтегральная функция в соотношении E.4) имеет при
Х = 0 точку ветвления, и поэтому следует воспользоваться контуром, пока-
показанным на рис. 40; известно (см. § 15,7 книги [3]), что в этом контуре
нулей функции К0(ра) нет, и поэтому интеграл в соотношении E.4) можно
заменить суммой интегралов по CD, EF и по небольшой окружности с цен-
центром в начале координат.
Интеграл по небольшой окружности дает в пределе (при стремлении ее
радиуса к нулю) 2тс/.
На линии EF мы принимаем \ = %и2еы; тогда
Г -к» Ко\гие2* ) da _ 2 Г ч J0(ur)-iY0(ur) da
J I 1ж1\ и —*J J0(ua)-iY0(ua) и '
о
так как
Интеграл по CD дает выражение, сопряженное с E.5), с отрицательным
знаком. Объединяя эти результаты, окончательно получим
v = V-±— f с-™1* У°{иг) Уо{иа)~Уо{ar)h{aa) da E 6)
* 'J 4(аи)+У20(аи)
При небольших значениях времени мы поступаем так же, как и в § 3
данной главы, используя асимптотические разложения функций Бесселя в ре-
решении E.3), и получаем
¦ ¦ ¦ }¦
Тогда из A1) приложения 5 находим
Уа* / г-а \ ¦ У(г-а)ЫУ' №«
V(9*-2ar-.7r*)*t /_r-^N
32a' »/¦'/• \2// /^
§ 51 ГЛ. XIII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЗАДАЧИ ДЛЯ ЦИЛИНДРА И ШАРА 331
На рис. 41 показаны графики зависимости температуры от г для раз-
различных значений времени *).
Наибольший практический интерес имеет величина теплового потока на
поверхности, т. е.
an*
J e B[y2((
du
au)+Y20{au)] '
E.8)
Вводя обозначение 7 = xf/a2, получим, что тепловой поток /напове х-
ности определяется также соотно-
шением
v/V
E-9)
для небольших значений Т и соот-
соотношением
1
—2?
J ~
для больших значений Т. В соотно-
соотношении E.10) 7 = 0,57722 ...—по-
...—постоянная Эйлера.
Численные значения интеграла
E.8) сведены Егером и Кларком [22]
в таблицу Графически он предста-
влен рис. 4z.
II. Начальная темпера-
тура V ПОСтОЯННа. На ПО-
верхности г==0 происходит
теплообмен со средой, имеющей нулевую
Вспомогательное уравнение имеет вид
Рис. 41. Распределение температуры
в области, ограниченной изнутри цилиндром
г = а\ начальная температура равна нулю,
а температура поверхности равна постоян-
постоянной V.
Числа у кривых указывают значения xtja2.
температуру.
d2v
1 dv
а граничное условие записывается следующим образом:
dv
dv .
— = hv при r = a.
—
E.11)
E.12)
*) Наиболее полные сведения опубликованы Егером [23], который приводит ре-
результаты с точностью до трех десятичных ^накоз для (г/а)= I, @,1), 2, A), 10, A0),
100 и %*/а2 = 0,001, @,001), 0,01, @,01), 0,1 @,1), 1, A), 10, A0), 100, A00), 1000. Более
точная таблица с точностью до 5 десятичных знаков для (г/а)= 1, A), 10их*/а2 = 0,1,
@,1), 1, A), 10 приведена в [24]. Перри и Бергрен [25] провели широкое исследование
теплопроводности в цилиндрических областях. В процессе анализа они использовали
некоторое количество численных величин, полученных по методу Шмидта. Гольден-
берг [26] привел результаты для (г/а) = 2, 10, 100 и данные о суммарном тепловом
потоке.
332 ГЛ. XIII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЗАДАЧИ ДЛЯ ЦИЛИНДРА И ШАРА [§ 5
Тогда
и
Т+/оо
E.13)
1
Подынтегральная функция имеет при Х = 0 точку ветвления, и поэтому
мы используем контур, показанный на рис. 40. На этом контуре или внутри
1.0
f
1
1
ц-2 -7
Рис. 42. Тепловой поток / на по-
поверхности области, ограниченной
изнутри цилиндром г = а\ началь-
начальная температура равна нулю,
а температура поверхности равна
постоянной V.
\
7,0
0,6
0,6
0,4
0,2
0
\~
V
у \
'—¦—
*—
4
J15
5
т 7д "
6
— —
-
д
>¦ 1-
70
xt/a*
Рис. 43. Распределение температуры
поверхности vn в области, ограни-
ограниченной изнутри цилиндром г — а\
начальная температура равна по-
постоянной V, а на поверхности про-
происходит теплообмен со средой, имею-
имеющей нулевую температуру.
Числа у кривых указывают значения ah.
него полюсов нет [7,27]. Поступая далее так же, как и в предыдущем при-
примере, получим
(иа)]<1и
\
—_ 2?L Г #-
тс J
E.15)
Графики температуры поверхности для величин ah = 0,2, 0,5, 1, 2,5, 5 и 10
показаны на рис. 43.
III. Нулевая начальная температура. Тепловой поток на поверх-
поверхности г = а постоянен и равен Q.
В данном случае решение имеет вид *)
QKo(qr)
V =
KpqKx (qa)
E.16)
*) Здесь можно применить контур, изображенный на рис. 40, однако искомый
интеграл C.8) гл. XII есть интеграл по разрезу (см. F.2) и F.6) данной главы). Фор-
Формула E.17) получена применением к выражению для pv обычного метода с дальней-
дальнейшим использованием теоремы B.4) гл. XII.
§ 5] ГЛ. XIII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЗАДАЧИ ДЛЯ ЦИЛИНДРА И ШАРА 333
И
V=-§- f A-е-*') Jo(ur)YAua)-Yo(ur)Jx(ua)
*KJ u*\j\(ua)+Y\{ua)\ У }
Решение, пригодное для небольших значений xt/a2, имеет вид
(Зг + д) («*)'/' р
Г г-а 1
L I/2 J "
4ar L 2 (vi)v*
E.18)
Отсюда, привлекая метод, излагаемый
в следующем параграфе, находим, что при
больших значениях времени можно напи-
написать
Qa
f V" jn ^" I Q ^
0,5
/
(
E.19)
^
<9 ^
xt/a*
где 1пС=7» а 7=0,57722 . . . —постоян-
—постоянная Эйлера. Соотношение E.19) анало-
аналогично также соотношению D.6) гл. X для
линейного источника, выделяющего на
единицу длины в единицу времени коли-
количество тепла, равное 2izaQ.
Некоторые значения температуры поверхности приведены на рис. 44 *).
IV. Нулевая начальная температура. Температура поверхности меняется
по закону sin (o)^-f-е).
Рис. 44. Распределение температур
поверхности t/n в области, ограни-
ограниченной изнутри цилиндром г = а;
начальная температура равна нулю,
тепловой поток на поверхности равен
постоянной величине Q.
oo
2% Г
-шЧ [Jo (ur) Ko (иа) — Vp (ua) Yo (ur)] [o> cos ? — ъи2 sin e) и du
E 20)
где о)' =
у а Ко (геЫ1А) = ker г + / kei г = Л^о
V. Области z > 0, г>а иО<г</,г>ас начальной температурой, равной
единице. Решения в виде произведения **).
Очевидно, что решения для этих областей можно получить так же, как и в § 4
гл. VIII, воспользовавшись методом, описанным в § 15 гл. 1. Таким образом, для об-
области z > 0, г > а с начальной температурой, равной единице, и нулевой температу-
температурой поверхности решение будет иметь вид
t;= <
(иг) Ко (иа) — Ко (иг) Уо (цд)
E.21)
Численные значения искомой температуры можно найти из рис. 41.
*) Другие значения температуры, а также некоторые результаты при г/а = 2;
5 и 10 приведены в [28]. Там проводится также тщательное сравнение решений
этого типа с решениями, полученными для непрерывного линейного источника в не-
неограниченной области.
**) Другие задачи для области г > 0, в которых рассматривается нерадиальный
тепловой поток, обсуждаются в [29].
334 ГЛ. XIII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЗАДАЧИ ДЛЯ ЦИЛИНДРА И ШАРА [§ 6
§ 6. Решения, применимые при больших значениях времени
В задачах для ограниченных областей решения обычно получаются в виде рядов,
которые сходятся тем быстрее, чем больше величина t. Вместе с тем решения задач
для неограниченных областей обычно принимают следующую форму:
>
е"иЧ f(u)du, F.1)
где Т — параметр (например, **/я2), и при больших значениях Т такие решения, по-
пожалуй, еще труднее для оценки. Обычно оказывается важным знать приближенные
решения при больших значениях Т. Эти решения можно получить, воспользовавшись
интегралом F.1), но_для многих практических задач проще применить метод, излагае-
излагаемый ниже *). Если г7(/?) есть изображение решения v, то это решение можно найти,
воспользовавшись теоремой обращения
t,(*) = -L. / ekt'v(X)dX. F.2)
2iti J
у—/оо
В задачах рассматриваемого класса v (X) имеет точку ветвления в начале коор-
координат и первый шаг при оценке величины v состоит в преобразовании контура
G — /оо, 7 + *'°°)» по которому интегрируют в F.2), в контур CDEF, изображенный
на рис. 40; последний начинается в — оо на нижней полуплоскости, один раз огибает
в положительном направлении точку ветвления в начале координат и заканчивается
в —оо на верхней полуплоскости. Поэтому такой контур можно обозначить символом
(—оо, 0+). Тогда F.2) запишется в виде
@+)
?Xtv(X)dX. F.3)
Во всех рассмотренных задачах это преобразование оказывается вполне закон-
законным; иными словами, можно показать, что интегралы по дугам АА'С и FB'B боль-
большой окружности на рис. 40 стремятся к нулю, когда радиус этой окружности стре-
стремится к бесконечности. При записи в явном виде выражения для v (X) вдоль пути CDEF
контурный интеграл F.3) сводится к действительному интегралу с бесконечным пре-
пределом F.1). Чтобы найти решения, применимые при больших значениях времени, мы
исходим из соотношения F.3), разлагаем v (X) по возрастающим степеням X и инте-
интегрируем этот ряд почленно, предполагая, что последний процесс может быть обосно-
обоснован. Типичные интегралы, которые нам потребуются в дальнейшем, записываются
следующим образом:
@+) @+)
L. f Л-*" еи dX = —J- • _L fxnextdX = O, л = 0, 1, 2,...; F.4)
ш J ГA -j- v) ' 2ш J
— оо
1 Г 1
_ / J_ e l In (kX) dX = — In (Ct/k); F.5)
ni J К
— oo
@+)
i- / eKt [\n(kX)fdX = 2-\n(Ct/ky, F.6)
ш J t
-oo
@+)
j eu [In (kl)? d\ = -g. _ .3 [in (Ct/k)f. F.7)
*) Здесь мы имеем в виду один из основных методов операционного исчисления
Хевисайда (см. [30]); контуры интегралов F.2) и F.3) являются в обозначениях Мак-
Лахлана Вгх и Вг2 контурами. Гольдштейн [1] применил этот метод для решения
целого ряда задач в цилиндрических координатах.
§ 7] ГЛ. XIII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЗАДАЧИ ДЛЯ ЦИЛИНДРА И ШАРА 335
Здесь In C = 7 = 0,5772 ...—постоянная Эйлера, k предполагается действительной и
положительной величиной, a v — любая комплексная величина, причем v Ф — п.
В написанных выше соотношениях F.4) вытекает из определения гамма-функции,
F.5) — из изображения In t, a F.6) и F.7) можно получить обычным методом, исполь-
используя путь интегрирования CDEF. Другие необходимые формулы получаются путем
дифференцирования по t, как по параметру. Тогда из F.5) получим
@+)
-L f eKt\n(k\)d\ = — \/tt F.8)
— oo
@+)
oo
и т. д.
В качестве примера рассмотрим область г > а, в которой тепловой поток
постоянен и равен Q.
Воспользовавшись соотношением E.16) предыдущего параграфа, соотношениями
(9), A0) приложения 3 и положив fx == (X/%I/2, получим
@+)
Q Г еиК0 (fir) dk __
@+)
/
@+)
где, как и выше, inC = 7 = 0,5772 ... —постоянная Эйлера.
Пользуясь F.4) — F.6) и F.8), получим
Таким же путем можно получить решение G.18) и аналогичные решения для
всех задач, рассмотренных в § 7 данной главы. Дополнительные теоретические сообра-
соображения, необходимые для получения соотношений E.3) и E.13) данной главы, развиты
в статье [31].
§ 7. Область г > а, ограниченная изнутри круговым цилиндром
из идеального проводника
Во многих задачах, имеющих практическое значение, например в задачах
о нагреве подземных электрических кабелей, а также при измерении тепло-
теплопроводности методом «зонда» металлический цилиндр окружен неограниченной
средой (такой, как почва или горная порода) со значительно меньшей тепло-
теплопроводностью. С хорошим приближением металл может рассматриваться как
336 ГЛ. XIII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЗАДАЧИ ДЛЯ ЦИЛИНДРА И ШАРА [§ 7
идеальный проводник тепла — влияние конечности коэффициента теплопро-
теплопроводности можно оценить из более сложных результатов, приведенных в § 8 дан-
данной главы. В большинстве задач наиболее интересным оказывается вопрос о
температуре материала внутри цилиндра. Последний либо имеет вначале темпе-
температуру, равную единице (область вне цилиндра имеет температуру, равную
нулю), либо в единицу времени к нему подводится постоянное количество
тепла. Аналогичные задачи возникают в тех случаях, когда область г < а
содержит хорошо перемешиваемую жидкость.
Во многих практических задачах между цилиндром и окружающей средой
имеется контактное сопротивление. Такие задачи будут рассмотрены ниже
(см. примеры III и IV данного параграфа). Однако в первую очередь мы
обсудим более простой случай, когда контактное сопрстивление отсутствует.
1. Область г > а имеет в начальный момент времени темпера-
температуру, равную нулю. На границе г = а эта область соприкасается
с идеальным проводником в виде цилиндра, обладающим тепло-
емкостью S {на единицу длины цилиндра). Начальная температура
проводника равна VQ. На границе г = а контактное сопротивление
отсутствует *).
Обозначая температуру в области г > а через V, получим, как и в при-
примере V § 2 данной главы,
-_ аУрКо(дг) -
*q[aqKoW + "Ki(aq)\ ' к'' }
где
0L = 2na2pc/S G.2)
является параметром, равным удвоенному отношению теплоемкости эквива-
эквивалентного объема среды к теплоемкости идеального проводника. Отсюда сле-
следует, что
«*l* [J0(ru/a) [uYQ(u) — аК, (и)] —
- Ко (иг/a) [uJ0(и) - аУ, (в)]} ~-, G.3)
где
u) — aLYl(u)]*. G.4)
Температура V в области г < а* равная значению G.3) при г = а, за-
записывается в виде
со
у - 4aVQ fe-xtu>la> du G.5)
о
График зависимости V от xt/a2 для различных значений а изображен
на рис. 45.
II. Та же задача, но цилиндр имеет нулевую начальную темпе-
температуру и при t > 0 в него поступает количество тепла, равное
в единицу времени на единицу длины величине Q.
*) Небольшая таблица интегралов G.3) приведена в [32, 33].
§ 7] ГЛ. XIII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЗАДАЧИ ДЛЯ ЦИЛИНДРА И ШАРА 337
Тогда
G.6)
V =
aQKojqr)
v =
iSpq [aqKo (aq) + olKx (aq)] '
- «-XB2'/a2) M>(«'/«) luY0(a) — aK, («)]
- Ko(ar/a) [ujo (a) - a
G.7)
где a и Д(и) определены соответственно выражениями G.2) и G.4). При
нахождении решения G.7) из G.6) следует использовать метод, приводящий
0,6
0,6
ОА
0,2
О
4,0
Рис. 45. Распределение температуры в цилиндре из
идеального проводника; в начальный момент времени
его температура равна Vo; температура неограни-
неограниченной среды, в которой он находится, равна нулю.
Числа у кривых указывают значения параметра а.
к решению E.17) данной главы. Температура V в цилиндре, представляющая
собой значение G'.7) при г = а, равна
-1,0-
2
6
\
\
\
\
1,0
V
_2Qa2 Г
(\ —
du
(и)
G.8)
На рис. 46 построен график зависимости V от xt/a2 для различных зна-
значений а.
III. Нагревание электрического кабеля, проложенного в земле.
Электрический кабель состоит из трех основных частей: сердечника* по кото-
которому течет ток, изоляции, отделяющей сердечник от защитной металлической обо-
оболочки, и этой оболочки. Поэтому в простейшей идеализированной схеме кабеля*)
сердечник и оболочка должны считаться идеальными проводниками с теплоемкостями
соответственно Sx и S2 на единицу длины кабеля. Теплоемкость изоляции должна
считаться равной нулю, а ее термическое сопротивление на единицу длины кабеля
*) Достаточно полное рассмотрение этого вопроса с технической точки зрения
можно найти в работе [34]. В статье [35] дано несколько приближенных решений
для случая нагрева при коротком замыкании (что соответствует решению задачи I).
В рамках современных представлений этот вопрос рассмотрен в [33, 36, 37].
22 Г. Карслоу, Д. Егер
338 ГЛ. XIII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЗАДАЧИ ДЛЯ ЦИЛИНДРА И ШАРА [§ 7
равным R. Пусть внешний радиус оболочки равен а, причем кабель проложен в почве,
с термическими коэффициентами /С, %, р и с. Кроме того, мы пренебрегаем контактным
сопротивлением между оболочкой и почвой.
Практический интерес имеют две задачи: 1) нагревание установившимся током,
проходящим по сердечнику, и 2) нагревание током короткого замыкания, при котором
температура сердечника внезапно возрастает на конечную величину; в последнем случае
требуется исследовать, каким
путем это тепло рассеивается.
Н
0,4
0.2
-у
-1,0 О 1,0
Рис. 46. Распределение температуры V в цилиндре
из идеального проводника, окруженном неограни-
неограниченной средой, при наличии поверхностных источ-
источников постоянной мощности.
Числа у кривых указывают значения параметра а.
Нагревание током ко-
короткого замыкания. Если в на-
начальный момент времени тем-
температура сердечника равна Vo,
а соответствующая начальная
температура оболочки и окру-
окружающей среды равна нулю, то
температура V в сердечнике
в момент времени t будет равна
V=z VQF(h, alt a2, x), G.9)
где
сс2 = 2%a2?c/S2, х = -xi/я2, G.10)
и
ехр (— u2z) da
аД,(и) "
G.11)
Д, (tf)=[«(«i + «2—hu2) Jo (и)—
— M«i — л**2)/, (и)]2+
. G.12)
Нагревание обычным током. Если в начальный момент времени вся система
находится при нулевой температуре и количество тепла, выделяемого в сердечнике
на единицу длины в единицу времени, равно Q, то температура в сердечнике в момент
времени t будет равна
где
О (Л, <zlf a2, х) :
2а\а\ р[\-
-W-J —
а2» т)»
¦ ехр (— и2
du
(и)
G.13)
G.14)
определение остальных символов приведено в G.10) и G.12).
Мы не располагаем таблицами интегралов G.11) и G.14), но Егер [33] приводит
графики F A, а, со, х), ^B, а, оо, х), G A, а, оо, х) и G B, а, оо, х), которые соответ-
соответствуют кабелю без оболочки.
Если кабель окружен не бесконечной средой, а погружен на глубину а, считая
от поверхности земли, то на равном расстоянии над землей должно быть помещено
его «изображение». Этому изображению будет соответствовать непрерывный постоян-
постоянный линейный источник (см. соотношение D.7) гл. X).
IV. Определение теплопроводности методом «зонда».
Пусть цилиндр из идеального проводника радиуса а окружен неограниченной
средой и при t > 0 в нем выделяется количество тепла, равное на единицу длины
в единицу времени Q, причем начальная температура всей системы равна нулю; тогда
температура V идеального проводника в момент времени t при наличии контактного
сопротивления R (на единицу длины) между цилиндром и окружающей средой, будет,
в соответствии с G.13), равна
G.15)
§ 8] ГЛ. XIII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЗАДАЧИ ДЛЯ ЦИЛИНДРА И ШАРА 339
Отсюда, как и в § 3 данной главы, следует, что для небольших значений %
: — ^Г+°№}> если Л=?°' GЛ6>
или
Для больших значений времени т (как и в предыдущем параграфе) можем на-
написать
где С = 1,7811 = ехр 7 (Т = 0,5772 ... — постоянная Эйлера).
Из соотношения G.18) следует, что во всех случаях кривая зависимости V
от \nt имеет прямолинейную асимптоту с угловым коэффициентом, равным Q//C
Поэтому, если известно Q, то можно сразу же определить /С Если %=0,01 и а = 0,1,
то к концу промежутка времени 10 мин ъ = ti/a2 будет равняться 600, и следова-
следовательно, в этом случае быстро получается асимптота. Вместе с тем, если д=1, та
х = %t/a2 равно 6 и время, необходимое для достижения асимптотического значения,
оказывается существенно большим.
Методы зонда [38—41] *) очень удобны при измерении теплопроводности грану-
гранулированных материалов, почв и горных пород. В последнем случае зонд следует по-
помещать в отверстие, просверленное в горной породе, и поэтому можно ожидать, что
его радиус должен иметь порядок 1 см, и ввиду наличия воздушного зазора между
зондом и породой термическое сопротивление окажется довольно значительным. Блэ-
куэлл [29, 42] подробно рассмотрел этот случай и указал на то, что, воспользовавшись
соотношениями G.16) и G.18), можно из экспериментальных данных определить все
три параметра /?, % и К>
§ 8. Составная цилиндрическая область
Задачи теплопроводности в случае составных или пустотелых цилиндров
кругового сечения легко решаются при помощи преобразования Лапласа,
но получаемые решения оказываются довольно сложными [43—48] **). Здесь
мы рассмотрим два случая неограниченных составных областей.
I. Область 0 < г < а (в цилиндрических координатах) содержит
материал с термическими коэффициентами Kv *2 и т. д., а область
г > а — материал с термическими коэффициентами К2, *? и т. д. На-
Начальная температура V в области 0 ^ г < а постоянна, а в области
г>а — равна нулю.
Обозначим через vx и v2 температуры в обеих областях и запишем вспо-
вспомогательные уравнения
# + 7#-«& = 0. г>а, (8.2)
где qx = YJj*l и q2 = Ypfo •
Если принять, что на поверхности г = 0 контактное сопротивление от-
отсутствует (ср. пример Ж § 9 гл. I), то граничные условия запишутся в виде
vt = v2 и Kvrsj~= ^2~&г~ * К0ГДа г = а. (8.3)
*) Влияние конечной длины нагреваемого зонда рассмотрено в [29] и [42]; в них
был сделан вывод, что длина зонда должна составлять по крайней мере 25-—30 его
диаметров.
**) В статье [49] приведены функции Грина для неограниченных составных
областей.
22*
340 ГЛ. XIII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЗАДАЧИ ДЛЯ ЦИЛИНДРА И ШАРА [§ 8
Решения следует находить из условий, что при г = 0 vx имеет конечное
значение, а при г—>оо величина v2 ограничена. Искомые решения имеют вид
V VKod*
^f<I (8.4)
где
A = K2*ixlo (qxa) Kx (q2a) + K\*<?h (qxa) Ko (q2a)- (8.6)
Тогда, используя теорему обращения и контур, показанный на рис. 40,
окончательно получим
/-
_ 2У/С^ f _хиЧ Jx (аа) [/р (*цг)
_%т /р (иг) Л 4иа) du
„2 Гса2/,Л-1_.Ь2/,Л1 * ^О/;
( )
где х = Y%\l%2 и
ф («) = KiifrJi (аи) Jo (хаи) — K**{'J0 (аи) J, (хаи), J
ср («) = /dx^Vi (ав) Ко (хае) — /fot'M (а«) Уг (ми) \
J
II. 7"а же область, что и в задаче /. В обеих областях начальная
температура равна нулю. При ?>0 в области 0 <; г < а в единицу
времени на единицу объема выделяется постоянное количество тепла Ао.
В этом случае уравнение (8.1) заменяется уравнением
Остальные уравнения не изменяются. Уравнения (8.4) и (8.5) заменяются
на уравнения
^^^КЛЯ2аIо(д1Г)' (8Л1)
Решения будут иметь вид *)
о
У, (ид) [Уо (хаг) у (а) - К„ (хат) ф (ц)] du
о
A - с-ж-«'О У, (ид) [Уо (хаг) у (а) - К„ (хат) ф (ц)] du
1
о
где ср(#) и ф(а) определены соотношениями (8.9).
*) Искомые решения получаются из (8.7) и (8.8) при помощи B.4) гл. XII. Если
к (8.11) и (8.12) применить теорему обращения, то мы получим только интеграл по
(— оо, 0-|-) (ср. примечание на стр. 333).
§ 9] ГЛ. XIII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЗАДАЧИ ДЛЯ ЦИЛИНДРА И ШАРА 341
Полученные выражения являются точными решениями задач, приближен-
приближенные решения которых приведены в предыдущем параграфе (см. стр. 337),
и поэтому они позволяют проверить в частных случаях пригодность при-
приближений, использованных в этом параграфе.
Нетрудно записать и изображения для температур в составных цилин-
цилиндрических областях, воспользовавшись для этой цели методом матриц, раз-
разработанным в § 8 гл. XII для пластин. Проводимый в данном случае анализ
аналогичен анализу, выполненному в § 3 гл. VII, для установившихся тем-
температур в составных цилиндрах, причем величина kt'* заменяется величиной q>
Решения, пригодные для больших или малых значений времени, можно по-
получить при помощи метода, использованного в §§ 3 и б данной главы.
§ 9. Шар. Радиальный тепловой поток
Напомним, что задачи с радиальным тепловым потоком в шаре сводятся
подстановкой a = vr к задачам с линейным потоком в стержне, а последние
исследованы достаточно полно; поэтому повторять здесь необходимые расчеты
нецелесообразно. Однако если требуется получить решения для шара, а соот-
соответствующие решения для стержня отсутствуют, то лучше применить пре-
преобразование Лапласа непосредственно к задаче для шара. Ниже приводятся не-
несколько примеров.
I. Шар 0О<а (в сферических координатах) с постоянной на-
начальной температурой V и нулевой температурой поверхности.
В данном случае вспомогательное уравнение имеет вид
ИЛИ
^0L-q4rv) = -rY-, 0<r<«. (9.2)
Его следует решать при условии
v = 0, когда г = а (9.3)
и v при г = 0 имеет конечное значение.
Общее решение уравнения (9.2) имеет вид
rv = A sh qr + В ch qr +^y-; (9.4)
для того чтобы получить конечное значение v при г->0, следует принять В
равным нулю. Тогда
-=:V__aVskqr
р rpshqa к '
Использование теоремы обращения дает решение примера IV § 3 гл. IX.
Кроме того, поступая так же, как и в § 5 гл. XII, можно найти решение,
пригодное для малых значений времени* Из соотношения (9.5) получаем
V =-К JLL V le-q[B/2+1)a-r\ e-q[B/2+1)a+rjl
p rp AA l '
/2=0
и поэтому
}
342 ГЛ. XIII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЗАДАЧИ ДЛЯ ЦИЛИНДРА И ШАРА [§ 9
При г = 0 оно принимает вид
II. При t>0 в области 0<;г<д, находящейся в неограниченной среде
с нулевой начальной температурой, в единицу времени на единицу объема вы-
выделяется постоянное количество тепла Ло [50] *).
В данном случае, как и выше (см. (9.2)), вспомогательные уравнения записы-
записываются следующим образом:
—*{nii — r*Lt 0<r<a, (9.7)
0, r>a. (9.8)
Решение уравнения (9.7), конечное при г->0, имеет вид
rv = ljj$-+Asbqr. (9.9)
Решение уравнения (9.8), конечное при г->оо, записывается в виде
rtT= Be~qr. (9.10)
А и В следует находить из условия непрерывности v и diT/dr при г = 0. Отсюда
Температуру при г=0 находим из соотношений (9.9) и (9.11):
и, следовательно,
Кроме того, при 0 < г < л имеем
а при г > i
v =
*) В работе [51] рассмотрен случай, когда среда в областях г > а и г < а имеет
различные теплопроводности. Там же приведены некоторые численные результаты.
§ 9] ГЛ. XIII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЗАДАЧИ ДЛЯ ЦИЛИНДРА И ШАРА 343
Таким же путем можно получить решения для случая, когда количество тепла,
выделяющегося в единицу времени, равно Aotn, где п может принимать значения
-72;0; v2; I; ...
III. В области 0 < г < а находится идеальный проводник с массой М и
удельной теплоемкостью сх. Он окружен неограниченной областью с теплопро-
теплопроводностью К и температуропроводностью %. На поверхности г = а контактное
сопротивление на единицу площади равно 1/Н. Начальная температура равна
нулю. Внутри области г = а в единицу времени выделяется количество тепла Q.
Обозначая температуру идеального проводника через vit а температуру в области
г > а через и, находим
r*.Mlclp[a*q* + a2q2(l+ah) + ka2hq+kah] 9
где
и h = H/K. (9.17)
Если известны численные значения k и ah, то знаменатели в решениях (9.15)
и (9.16) можно разложить на множители, a vx и v выразить через сумму простых
дробей со знаменателями типа p(q-{-b)\ vx и v можно затем найти из A2) и A4)
приложения 5.
Кроме того, можно воспользоваться теоремой обращения; тогда мы получим
l+ah 2a*k2h2 f е-™*« da I
ah ъ J \a2(\ + ah) — kah]2 + [u3 —kahu]2 Г ^Лб)
) —- kah]2 + [и3 — kahu]2
о )
При малых значениях времени отсюда, как и в § 5 гл. XII, следует, что
_ Q
Щ ~ А1,с,
{,_.**?.+...}. (9.19)
тогда как при больших значениях времени метод, изложенный в § б данной главы,
дает
Q [ \-\- ah a
~ali
Эта задача соответствует задаче, приведенной в § 7 данной главы, в которой
цилиндр заменен шаром. Аналогичным образом можно поступить и при определении
теплопроводности.
IV. Та же задача, что и III *), но Q = 0 и начальная температура шара
равна Vq.
Температура шара vx в момент времени t равна
f
f «-"Wg'rfg
J [u2(l-\-ah) — kahY-\-[u* — kahuY% y }
_ 0
о
Для малых значений времени получим
- **f+...}; (9.22)
для больших значений времени найдем
V. В области 0 < г < а находится идеальный проводник с массой Mi и удель-
удельной теплоемкостью с,. В области а < г < b находится твердое тело с тепло-
*) В работе [52] рассмотрен случай выделения тепла в области г > а.
344 ГЛ. XIII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЗАДАЧИ ДЛЯ ЦИЛИНДРА И ШАРА [§ 9
проводностью К и температуропроводностью %. На границе г — а контактное
сопротивление отсутствует. Начальная температура всей системы постоянна и
равна Vo, а при t > О поверхность r=b поддерживается при нулевой температуре.
Если обозначить температуру в области a^r^b через v, то
ШУ0 у sin*п(Ъ- г)
^ «л sin2 <*„(? — л)— ksiu2(b — а) ап
где ап (/г=1, 2, ...) — положительные корни уравнения
kaa cos a (b — а) = (я2а2 — Л) sin a(b — a) (9.25)
(9.26)
VI. Га ле? задача, что и V, яо начальная температура равна нулю, а в шар
а поступает в единицу времени количество тепла, равное Q.
В данном случае
М
v ' '
„ sin2 ал F — а) — ? sin 2а„ (Ь — а)]
где ал — положительные корни уравнения F.25).
VII. Составные сферические твердые тела.
Рассмотрим задачу для шара радиуса b из твердого материала, в котором цен-
центральная часть, 0<;г < а, имеет теплопроводность, температуропроводность и темпера-
температуру Ки xi» vu в наружной оболочке, а < г < 6, соответствующие величины равны /С2»
Х2 и v2- Примем, что при г = а контактное сопротивление отсутствует.
Пусть в начальный момент времени температура твердого тела равна постоян-
постоянной величине V, а при t > 0 наружная поверхность г = b поддерживается при ну-
нулевой температуре.
Введем, как обычно, обозначения ul = rvl, u2 = rv2\ тогда подлежащие решению
уравнения принимают вид
** *? r<a, t>Oi *<L _*,**-. a<r<*, * > 0, (9.28)
(9.29)
при условиях
дах их\ /1 ди
и2 = 0, г = b, t > О,
ttl = rV, u2=rV, t = О
и #! имеет при г = О конечное значение.
Необходимо отметить, что вследствие формы граничного условия (9.30) решения
для составных шаров не вытекают непосредственно из соответствующих решений
для составных пластин.
Вводя обозначения q\ — р/ъг и q\ = pfo* получим вспомогательные уравнения
в виде
-1277 - rV Л d2u~2 о- rV .
и граничные условия
Jj = и2 при г = л, а2 = 0 при г =
в^-^) при г
а 1?! при г = 0 имеет конечное значение.
§ 9] ГЛ. XIII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЗАДАЧИ ДЛЯ ЦИЛИНДРА И ШАРА 345
Решая эти уравнения, получим
abVK2q2shrqi
l~~ P r
-¦ V ЬУ {К2Ыг) sh Яха + КМ (*)sh q2 (г-а)}
2~ Р rp{K2*<2(b)sbqxa + KAx(a)s\iq2{b-a)}
где
ф, (г) = aqx chqxr — sh qxry (9.33)
ф2 (г) = aq2 ch q2 (r — a) + sh ?2 (г — я). (9.34)
Далее рассуждения очень похожи на рассуждения для случая составной плас-
пластины, рассмотренной в § 8 гл. XII. Ко вторым членам соотношений (9.31) и (9.32)
применяется теорема обращения, в результате чего мы получим интегралы, подынте-
подынтегральные функции которых имеют простые полюсы при X = О (дающие вклады — V)
и простые полюсы при Х = — *iam> где ±ат (^=12, ...) — корни уравнения
K2{kaacos k(b — а) а-\-sin k(b — a) a] sin aa-\- К\ {aacos aa — sin да} sin k (b — a)a=0,
(9.35)
k = УТ&^ъ * = Ki/kK2. (9.36)
Корни уравнения (9.35) служат корнями уравнения
К2 {kaa ctg k (b — a) a + 1} -f Kx {aa ctg aa — 1} = 0 (9.37)
и общими корнями уравнений
sin aa = 0, sin k (b — a) a = 0. (9.38)
Если k(b — a)/a — величина иррациональная, то последние уравнения общих
корней не имеют, и из (9.31) и (9.32) получим
sin Га« йп дая sin Л (* - а) апе Va* t (9.39)
оо 2
v2 = ^~ 2 —^ sin2 лал sin k(b — r) <*ne~Xl*n , (9.40)
л=1
где ±ап (я = 1, 2, ...) —корни уравнения (9.37) и
<р (ал) = ааап Sin2 ^ал (^ — a) -f- ^ (^ — а) ап sin2 аал -J ^ Sin2 aan sin2 ^ F — а) ап.
(9.41)
Если ^ (^ — а)/а — рациональная величина, то можно предположить, что она
является несократимой дробью, равной 1/т. В таком случае уравнения (9.38) имеют
общие положительные корни
a = J^H, Л=1, 2, 3, ... (9.42)
а
Эти корни уравнения (9.35) приводят к появлению в выражениях для vx и v2
дополнительных членов
2bV V (-l)(/*m)* sin rnnnr e-x
a
) ЛЛ n
l
гтс(/а+/и) jU п Ь — а
соответственно.
Ы (b — Г) g_ xx
346 ГЛ. XIII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЗАДАЧИ ДЛЯ ЦИЛИНДРА И ШАРА [§ 9
ЛИТЕРАТУРА
1. G о 1 d s t e i n, Proc. Lond. Math. Soc. 34, 51 A932).
2. Carslaw, Jaeger, Proc. Lond. Math. Soc. 46, 361 A940).
3. Watson, A Treatise on the Theory of Bessel Functions, Cambridge, ed. 2, 1944
(Г. Ватсон, Теория бесселевых функций, ИЛ, М„ 1949.)
4. Low a n, Phil. Mag. 17, 849 A934).
5. J aeger, Proc. Roy. Soc N. S. W. 74, 342 A940); 75, 130 A941).
6. Goldenberg, Engineer 197, 779—780 A954).
7. Carslaw, Jaeger, Operational Methods in Applied Mathematics, Oxford, ed. 2,
1948. (Г. Карслоу и Д. Егер, Операционные методы в прикладной математике,
ИЛ, 1948, перев. с 1-го изд. 1941 г.)
8. Carsten, McKerrow, Phil. Mag. 35, 812 A944).
9. W a 11 e г s, PhiL Mag- 38, 70—78 A947).
10. Comenetz, Quart. Appl. Math. 5, 503—510 A947).
11. Fisch.er, Ann. Physik 34, 669 A939).
12.Stephens, Phil. Mag. 15, 857 A933).
13. Awbery, Phil. Mag. 28, 447 A939).
14. Bu ch h о 1 z, Z. angew. Math. Mech. 9, 280 A929).
15: Bogert, J. Math. Phys. 30, 102 A951).
16. L i p о w, Z w i<: k, J. Math. Phys. 34, 308—315 A955).
17. Geckler, Jet Propulsion 25, 31—35 A955).
18. Nicholson, Proc. Roy. Soc A100, 226 A921).
19. Smith, J. AppL Phys. 8, 441 A937).
20. Carslaw, Introduction to the Mathematical Theory of Conduction of Heat in So«
lids, Macmillan, ed. 2, 192L (Г. Карслоу, Теория теплопроводности, Гостехиздат,
М., 1947.)
21. Jaeger, Proc. Roy. Soc. Edin. A61, 223 A942).
22. Jaeger, Clarke, Proc. Roy. Soc. Edin. A61, 229 A942).
23. J a e g e r, J. Math. Phys. 34, 316—321 A956).
24. Computation Laboratory oi Harvard University, Problem Report No. 76, 1954.
25. Perry, Berggren Univ. California Publ. in Engng 5, 59 A944).
26. Goldenberg, Proc. Phys. Soc. B69, 256—260 A956).
27. E г d ё 1 у i, К е г m а с k, Proc. Cambr. Phil. Soc. 41, 74 A945).
28. Ingersoll, Adler, Plass, Ingersol, Heat Pip. Air. Condit. 22, 113—122
A950).
29. В 1 а с k w e 11, Canad. J. Phys. 31, 472—479 A953).
30. McLachlan, Complex Variable and Operational Calculus, Cambridge, 1939.
31. R i t с h i e, S a k a k u г a, J. AppL Phys. 27, 1453 A956).
32. В u 11 a r d, Proc Roy. Soc. A222, 408—429 A954).
33. Jaeger, Aust. J. Phys. 9, 167—179 A956).
34. W h i t e h e a d, H u t с h i n g s, J. Instn. Elect. Engrs 83, 517 A938).
35. W h i t e h e a d, Proc. Phys. Soc. 56, 358—366 A944).
36. Jaeger, Newstead, Instn. Elect. Engrs Monograph No. 253S, 1957.
37. S ch u b e г t, Z. angew. Phys. 2, 174—179 A950).
38. D e V г i e s, Soil Sci. 73, 83—89 {1952).
39. Van der Held, Hardeboi, Kalshoven, Physica 19, 208—216 A953).
40. Buettner, Trans. Am. Geophys. Union 36, 831—837 A955).
41. В lack well, J. AppL Phys. 25, 137—144 A954).
42. В 1 а с k we 11, Canad. J. Phys. 34, 412—417 A956).
43. Jaeger, Phil. Mag. 32, 324 A941).
44. Penner, Sherman, J. Chem. Phys. 15, 569—574 A947).
45. S с h a a f, Quart. Appl. Math. 3, 356—360 A945).
46. Tranter, Phil. Mag. 38, 131—134 A947).
47. Thiruvenkatachar, R a m a k г i s h n a, Quart. Appl. Math. 10,255—262 A952).
48. Levy, Trans. ASME 78, 1627—1635 A956).
49. J a e g e r, Phil. Mag. 35» 169 A944).
50. Goldenberg, Brit. J. Appl. Phys. 2, 233 A951).
51. G о 1 d e n b e г g, T г a n t e r, Brit. J. Appl. Phys. 3, 296—298 A952).
52. Paters on, Proc Glasgow Math. Ass. 1, 164—169 A953).
ГЛАВА XIV
ПРИМЕНЕНИЕ ФУНКЦИЙ ГРИНА К РЕШЕНИЮ УРАВНЕНИЯ
ТЕПЛОПРОВОДНОСТИ
§ 1. Введение
Применение функций Грина в теории потенциала известно очень хорошо.
Удобнее всего определить эту функцию внутри замкнутой поверхности S как
потенциал, который обращается в нуль на данной поверхности, а в точке
Р(х*\ у', zf)t находящейся внутри нее, стремится к бесконечности как 1/г,
когда г->0. Обозначим такое решение уравнения V2# = 0 через G(P); тогда
решение этого уравнения, не обращающееся в бесконечность внутри данной
поверхности и принимающее на ней произвольное значение V, запишется
в виде
где д/дп означает дифференцирование по внешней нормали [1—4].
Мы покажем, что подобную функцию можно с успехом применить и
в теории теплопроводности. Мы определяем в этом случае функцию Грина
как температуру в точке (х, у, г) в момент времени t, обусловлен-
обусловленную действием мгновенного точечного источника единичной мощности,
помещенного в точку P(xf, y\ z') в момент т, полагая, что начальная
температура тела равна нулю и его поверхность поддерживается
при нулевой температуре.
Такое решение можно написать следующим образом:
u = F(x, у, z х', /, z\ t — z) (t>%).
Оно удовлетворяет уравнению
Однако поскольку t входит только в форме (t — т), то мы получим
также
Кроме того, \imu = G во всех точках внутри 5, за исключением точки
Р(х\ у, zf). Внутри 5 решение имеет вид
1 ехо Г— (•*-*'
8 [тех (t -т))
Наконец, на поверхности 5 и = 0 (х < t).
348 ГЛ. XIV. ПРИМЕНЕНИЕ ФУНКЦИЙ ГРИНА [§ 1
Пусть v — распределение температуры в твердом теле в момент времени t,
обусловленное температурой поверхности <р(лг, у, z, t) и начальной темпе-
температурой f(x, у, г).
Тогда v удовлетворяет уравнению
и условиям
v = f(x, у, z) в начальный момент внутри S,
v = y(x, у, z, t) на поверхности S при t > 0.
Кроме того, поскольку время т в приведенных формулах лежит внутри,
интересующего нас интервала времени, мы можем написать
t; = ср (л:, у, 2, т) на поверхности.
Отсюда
д / dv . ди г _9 _9 _
-fc(uv) = и -^ -{- v-^ = y.[uV2v — vV2u]
^-8 t-9
f [f f f 7^ (uv>}dx dy dz\ dz = % f [fff W2<v—vV2u)dxdydz\ di
6 6
Тройной интеграл берется по всему твердому телу, а е — некоторая поло-
положительная, сколь угодно малая величина, меньшая чем t.
Меняя порядок интегрирования в левой части равенства и применяя фор-
формулу Грина к правой части, получим
j j j (uv)*=t-*dxdydz — j j j (uv)x=odxdydz —
где d/dnt означает дифференцирование по внутренней нормали; мы восполь-
воспользовались здесь тем, что и = 0 на поверхности.
Перейдем теперь к пределу при е—>0. Левая часть равенства прини-
принимает вид
[vp\t [/ / / Ит=*-о dx dydz^ — J J J (и)х=о (v)x=0 dx dy dz.
Первый интеграл берется по элементу объема, внутри которого находится
точка Р(х\ у', zf). В этой точке функция и в момент времени t = z ста-
становится бесконечной. Второй интеграл берется по всему объему тела.
[Vp]t является значением v в точке Р(х', у', z') в момент времени t.
Напомним, что и — это температура в момент времени t, обусловленная
действием единичного источника в момент т в точке Р(х', yf% z')\ тогда
(#)x=f_o dx dy dz — 1,
§ 1] ГЛ. XIV. ПРИМЕНЕНИЕ ФУНКЦИЙ ГРИНА 349
и мы получим
о
t
,x)-^ds]dT. A.1)
Этой формулой выражается температура в точке (х\ у', zf) в момент
времени t при начальном распределении температур /(*, у, z) и при темпе-
температуре на поверхности*) <р(лг, у, z, t).
Если на поверхности происходит теплообмен, то мы определяем функцию
Грина и как температуру в точке (лг, у, z) в момент tt обусловлен-
обусловленную действием в момент х мгновенного точечного источника еди-
единичной мощности, помещенного в точке Р(х', yfY z') тела, на поверх-
поверхности которого происходит теплообмен со средой нулевой темпе-
температуры.
Температура в точке Р(х\ у', z') в момент t, обусловленная начальным
распределением температур f (х, у, z) и теплообменом со средой, имеющей
температуру у(х, у, z, t), определяется из рассуждений, аналогичных при-
приведенным. В конце концов, поскольку на выбранной поверхности du/dnt = hu,
получим
t==jjj ^x=0 f (*'y* ^ dx dydz+h% f [j j i
6
= j J j (и)т=о/(*> У» z)dxdydz +
t
+ * flf'f Ы^)/ ? (^- У- ^»T) rf5lrfT- (] -2)
Таким образом, найденный нами результат имеет такой же вид, как и A.1).
Итак, решение общей задачи теории теплопроводности сводится к опре-
определению функции Грина для тела, температуру которого требуется найти.
Для случая линейного или двумерного теплового потока можно сразу же
получить результаты, аналогичные A.1) и A.2). Вместо бесконечности
порядка
1 г R21
expL~ W
мы получим соответственно
*) Этот вывод принадлежит Минигероду и был опубликован в его диссертации [5]
(см. также [6—14]). О применении вывода к уравнению (V2-J-%2)h = 0 cm. [15, 16].
350 ГЛ. XIV. ПРИМЕНЕНИЕ ФУНКЦИЙ ГРИНА [§ 1
В связи с этими изменениями формулы, соответствующие A.1) и A.2), будут
иметь вид
t
\vp\t = f («).=o / (*) dx + x f <p (x) -g- dx A.3)
6
l*p]t = ff(u)x=of(x. y)dxdy + %f[f9(x.y.x)-§^ds\dx. A.4)
6
где интегрирование поп A.4) производится вдоль границы области.
Физическая интерпретация полученных решений очень проста и вместе
с тем очень важна. Так, например, из соотношения A.1) следует, что тем-
температура в момент времени t в теле с начальной температурой /(л:, у, z)
и температурой поверхности, равной нулю, совпадает с температурой, обу-
обусловленной действием в момент ? = 0 распределенных по объему тела мгно-
мгновенных источников, причем в элементе объема dx dy dz в точке (х, yt z)
выделяется количество тепла, равное pcf(x, yt z)dxdydz. С физической
точки зрения это можно считать очевидным. Аналогичным образом, если
в теле выделяется тепло, то температуру можно найти из распределения не-
непрерывных источников по всему объему этого тела. Кроме того, из соот-
соотношения A.1) следует, что температура в момент времени t в теле с нулевой
начальной температурой и заданной температурой поверхности равна темпе-
температуре, обусловленной распределением по поверхности непрерывных дублетов
с осями, нормальными к поверхности (см. § 8 гл. X).
В настоящей главе мы определим функции Грина для ряда важных
областей и граничных условий. В нескольких случаях эти функции можно
написать сразу. Но обычно мы будем пользоваться преобразованием Лапласа.
Как отмечено в приложении 1, можно показать, что найденные таким путем
функции Грина удовлетворяют требуемым условиям.
Если функция Грина известна, то решение задачи теплопроводности для
заданной области, при заданных граничных условиях и начальной темпера-
температуре, являющейся произвольной функцией пространственных координат, можно
сразу же записать при помощи формул данного раздела. Некоторые из этих
решений были уже получены другими методами, но при этом мы каждый раз
допускали, что возможно такое разложение произвольной функции, которое
требуется задачей. В излагаемом сейчас методе нет необходимости в подобном
допущении *).
Полученные таким путем решения справедливы при t > 0. Когда tf->0,
они стремятся к заданному начальному значению. Полагая в них ? = 0, мы
получаем формальные разложения произвольных функций. Например, приняв
в выражении (8.6) данной главы ? = 0, получим
0<г<а, A.5)
*) Ученый, занимающийся чистой математикой, в первую очередь исследовал бы
форму разложения и условия, при которых оно возможно. В прикладной математике
как форма разложения, так и ее применимость зачастую просто принимаются. Однако
не всегда ясно, какова эта форма, и поэтому легко принять неправильную форму
(ср., например, стр. 131 книги Карслоу [17], где опущен постоянный член; см. также
соотношение (8.3) гл. VII и пример II § 8 данной главы). Одно из преимуществ ме-
метода преобразования Лапласа заключается в исключении ошибок такого типа.
§ 2] ГЛ. XIV. ПРИМЕНЕНИЕ ФУНКЦИИ ГРИНА 351
где ап — положительные корни уравнения У0(аа) = 0. Мы получили разло-
разложение Фурье — Бесселя, которое использовалось в § 6 гл. VII. Функция
Грина для каждой задачи дает, .таким образом, соответствующую теорему
разложения (или интегральную теорему); многие из них еще не исследо-
исследованы *).
§ 2. Линейный тепловой поток. Полуограниченное твердое тело х > О
I. Начальное распределение температур f (х). Температура на
границе поддерживается равной ср(^).
В данном случае функция Грина описывает температуру в момент вре-
времени t в плоскости лг, обусловленную распределением единичных плоских
мгновенных источников, расположенных в плоскости хг в момент т; она имеет
вид (ср. пример I § 10 гл. X)
W^J[i4^Jb BЛ)
В таком случае, делая небольшие изменения в формуле A.3) предыду-
предыдущего параграфа, получим температуру в плоскости х в момент t в виде
о
что согласуется с решением, приведенным в § 5 гл. II.
II. Единичный плоский мгновенный источник**) в плоскости хг
в момент времени t = 0. Теплообмен на плоскости х==0 со средой
нулевой температуры.
Будем исходить из решения для единичного мгновенного источника
в плоскости хг = 0 в момент времени t = 0 в неограниченной среде. Оно
имеет вид
^Г^ЯЧ B.3)
Решение v нашей задачи будем искать в форме
v = u-\-w,
где w удовлетворяет уравнению теплопроводности при х > 0, и обращается
в нуль при t = 0. Решение будет таким, что
-|j = to, когда х = 0, t>0. B.4)
Применим преобразование Лапласа. Из G) приложения 5 следует, что
*) Чтобы сделать строгой формулу A.5), необходимо доказать допустимость из-
изменения порядков интегрирования и суммирования, произведенных при выводе ре-
решения (8.6) данной главы из (8.5), а также допустимость того, что в решении (8.6)
t считают равным нулю.
**) Здесь и далее под единичным плоским источником автор понимает распреде-
распределение источников единичной мощности в некоторой плоскости. (Прим. ред.)
352 ГЛ. XIV. ПРИМЕНЕНИЕ ФУНКЦИИ ГРИНА [§ 2
где, как обычно, q=Yp/x- Вспомогательное уравнение для w имеет вид
q2w _ о.
dx*
Его решение, ограниченное при х—>оо, имеет вид Ае~^х, и следова-
следовательно,
v =
где Л — постоянная, подлежащая определению из условия
--г-= hv при лг = О.
Таким образом, мы получим
V —-l—e-q\x-x'\ _J (Я — К) e-q{x+x') =
= _L e-q \Х-Х' | + _L e-q (X+X') h e
Воспользовавшись G) и A3) приложения 5, находим
— h exp [*th* + h (x + *')] Ф* | ±±?. + Л \Л? j • B-6)
Последний член в этом соотношении можно переписать в виде
оо
h
Он дает распределение температур *), обусловленное действием стоков, рас-
распределенных вдоль прямой от —х' до —оо.
III. Область х > 0 с начальным распределением температур f (x).
Теплообмен на поверхности со средой с температурой y(t).
Из решения B.6) и из соотношения A.3) предыдущего параграфа сле-
следует, что
Ф* [|j^ + А
\ vvx)
- h exp [*A2 (f - О + А*] Ф* [2|/х*_т) + h /*(' — ')] [ Т СО Л- B-7)
*) Первым это решение получил Бриан [18]. См. также [12, 19, 20].
§ 3] гл- XIV- применение функций грина 353
§ 3. Линейный тепловой поток в области 0 < х < а
I. Единичный мгновенный плоский источник в плоскости хг в мо-
момент времени t = 0. Границы х = 0 и х = а поддерживаются при
температуре, равной нулю.
Как и раньше, положим v= u-\-w, где
\ г (х х'у
•ехр — Л '
служит решением для единичного плоского мгновенного источника в пло-
плоскости х' при t = 0 в неограниченном твердом теле, a w — решение урав-
уравнения теплопроводности, обращающееся в нуль при t = 0 и выбранное таким
образом, что на обеих границах v обращается в нуль. Вспомогательное
уравнение для w имеет вид
d2w
Тогда, используя значение и из соотношения B.5) предыдущего пара-
параграфа, получим
v = -—- е-« (х'х>) + ^sh qx + ?ch qx.
Здесь А и Б должны быть выбраны таким образом, чтобы v = 0 при
х = 0 и х = а, т. е. чтобы выполнялись соотношения
_L_ e-qx' _j_ в _ о, JL ?-? (в-*') -}- ЛэЬ ?а + 5ch ^a = 0.
Решая уравнение для v и производя подстановку, найдем
— chq(a-\-x — xf) — chqia — х — х') ^ , /п 4,
v = —ч v ~ ^—г—^ '-, когда х < *'. C.1)
Когда х' < х < а, решение имеет тот же вид, только х и х' меняются
местами.
Определяя v обычным путем при помощи теоремы обращения, получим *)
оо
2 VI Г — xn2n2t I . ппх . ппх' ,п лч
v = — У. ехр 5— sin sin . C.2)
a ?d * i a2 j a a v/
п=1
Распределение температур в момент времени t при начальном распреде-
распределении температур / (х) и температурах поверхностей х = 0 и х = а, поддер-
поддерживаемых при <pj(f) и ср2(?), получается из соотношения A.3) данной главы
в виде решения E.2) гл. III.
II. Единичный мгновенный плоский источник в плоскости хг при
/ = 0. Граничные условия имеют вид
1 = 0, х = а, C.3)
где kv hv hv k2 — постоянные коэффициенты, равные нулю или положи-
положительным величинам (пары коэффициентов kx и hx или k2 и h2 не должны
одновременно равняться нулю). Выбирая соответствующим образом эти коэф-
коэффициенты, можно охватить все случаи, т. е. случаи нулевой температуры,
*) Этот результат можно получить при помощи метода изображений, как и
в § 10 гл. X.
23 Г. Карслоу, Д. Егер
354 ГЛ. XIV. ПРИМЕНЕНИЕ ФУНКЦИЙ ГРИНА [§ 4
теплообмена или отсутствия теплового потока на той или иной поверхности.
Решение, получаемое так же, как и в примере I, имеет вид
v=%Zn(x)Zn(x')e-x*2»t . C.4)
л=1
где
[2D?+^)Nv*cosan*+Minv0 ~_
а ± ал, л=1, 2, ..., —корни уравнения
Если h{ = h2 = 0, то в выражение C.5) надо ввести член A/а). Это
решение в явном виде написано ниже (см. C.7)). Из решений C.4) и A.3)
данной главы получается целый ряд решений, приведенных в §§ 10 и
12 гл. III.
III. Единичный мгновенный плоский источник в плоскости хг при
t = 0. Тепловой поток на границах лг = О их = а равен нулю.
В данном случае решение имеет вид
( оо |
1 ' 1 I
§ 4. Двумерные задачи. Тела с прямоугольным сечением
В таких случаях функция Грина описывает температуру в сечении
z = const в момент времени t в точке (х, у), обусловленную распределением
единичных мгновенных линейных источников, расположенных вдоль прямой,
параллельной оси z, проходящей через точку (л/, у'), в момент времени х.
Иными словами, нам нужно получить решение v уравнения теплопроводности,
удовлетворяющее заданным граничным условиям и ведущее себя при /—>т
как
4%% (t -
г и
Поскольку функцию и можно представить в виде произведения D.1),
из рассуждений § 15 гл. I следует, что для любого из граничных условий C.3)
предыдущего параграфа решение v для двумерной области можно выразить
через произведение соответствующих одномерных решений.
I. Тело с сечением в виде квадранта х > 0, у > 0; температура
граничной поверхности равна нулю,
В соответствии с выражением B.1) данной главы распределение тем-
температур, обусловленное действием мгновенного единичного линейного *)
*) Здесь под единичным линейным источником автор понимает распределение
источников единичной мощности вдоль некоторой прямой, параллельной оси z.
(Прим. ред.)
§ 5] ГЛ. XIV. ПРИМЕНЕНИЕ ФУНКЦИЙ ГРИНА 355
источника в точке (xf, yf) в момент времени т, записывается в виде
1 [ схр Г {х ~ хУ 1 схр [ (* + хУ 1 И схр Г (у - уУ 1
leXPL 4*tf-x)J eXPL 4*(*_t) Jn PL 4*(*-t) J
cxp[
exP|_
Решение для этой области с заданными начальной температурой и
температурами граничных поверхностей можно тогда написать, воспользо-
воспользовавшись соотношением A.4) данной главы.
Аналогичным образом, если на граничной поверхности происходит
теплообмен со средой нулевой температуры, то функция Грина равна произ-
произведению двух выражений типа B.6) данной главы.
II. Тело с сечением в виде прямоугольника 0<лг<а, 0 < у < ft;
температура граничной поверхности равна нулю.
Найденная из решения C.2) предыдущего параграфа функция Грина для
нулевой температуры граничной поверхности равна
4 VI VI ( о/* J/й2 , я2!) . тпх . тпх . ппу . ппу А оч
7И=1 /1=1
III. Тело с сечением в виде прямоугольника 0<л;<а, 0<
теплообмен на граничной поверхности отсутствует.
Функция Грина (см. C.7) данной главы) в этом случае имеет вид
1 1 i г» V Г
-ь 1 + 2^ехр|
I i
ъп2п4 "I mty /гтсу'
\ cosb C0S~T
n=i
§ б. Прямоугольный параллелепипед 0<х<а,
Как и в предыдущем параграфе, при любых граничных условиях
(см. C.3) данной главы) функцию Грина можно записать в виде произведе-
произведения трех решений для одномерных случаев. Таким же путем можно полу-
получить решения для области л;>0, у>0, z>0 и различных других полу-
полуограниченных областей. Здесь мы рассмотрим только конечную область.
В соответствии с условиями C.3) данной главы функция Грина при
температуре поверхности, равной нулю, имеет вид
8
abc
1=1 i
2^ 2^sin"
Inx
a
- sin-
Ых'
a
sin-
mizy .
b ~!
mny'
П b *
с
- sin-
TVRZ'
с
-xrf(/-T)[^ + ^ + ^]}. E.1)
Тогда решение для начальной температуры / (х, у, z) и температуры поверх-
поверхности, равной нулю, можно записать следующим образом:
/__ 1 4 1
— x /7|ssi /1^1
a ^ с
X I J J f (x',y',zf) sin -^- sin -^- sin ^f-dx' dy'dz'. E.2)
0 0 0
23*
356 ГЛ. XIV. ПРИМЕНЕНИЕ ФУНКЦИЙ ГРИНА [§ б
Если при начальной температуре, равной нулю, поверхность х = 0 поддер-
поддерживается при температуре ср (у, г, t), а другие поверхности — при температуре,
равной нулю, то мы получим решение в виде
оо оо оо t Ь с
хл VI Y1 V ; . 1жх i ткУ
/=1 m=l /i=l 6 6 6
J dz J J
6 6 6
X exp { - ™* {f - x) [-J- + Л*- + -g-] J rf^' rfy'. E.3)
/гра t > 0 в твердом теле в единицу времени на единицу объема выде-
выделяется количество тепла А (х, у, г, t), а поверхность поддерживается при нуле-
нулевой температуре, то искомая температура будет равна следующей величине:
abcK
оо
Ы\
оо
X
оо
2
/а
у
0
sin -
а
/
0 0
/я*
/ i
0
sin
/)
г
cin
/W7cy
Ых1
а
sin X
mny'
sin
X ехр < — %п2 (t — х) —j- -f- -rg- H—г~ [ ^' ^У' ^<2'/ ^T- (^'^)
Если А (лс, у, <г, t) равно постоянной величине Ао, то мы получим
64хЛ0 yi VI VI sin {B/+1) пх/а} sin {Bm+l) тсу/^} sin {B/г+1) пг/с] (l—g"g/>m> я» Q
К** 2и 2d 2л B/+1)Bт+1)B/1+1)а/,т,я
/=0 m = 0 /1=0
E.5)
§ 6. Линейный тепловой поток. Составные твердые тела
Функции Грина для составных областей можно найти уже использо-
использовавшимися выше методами.
I. В области х > 0 находится материал с термическими коэф-
коэффициентами Kv *!, рр cv vv а в области х < 0 — материал, для
которого эти коэффициенты равны К2* *2» Р2» С2* V2 соответственно.
Контактное сопротивление на граничных поверхностях отсутствует.
В области х > 0 в плоскости xf в момент времени ? = 0 действует
единичный мгновенный плоский источник [21].
Распределение температур, обусловленное действием в плоскости xf
неограниченного тела с термическими коэффициентами Kv v>\ единичного
мгновенного плоского источника в момент t = 0, равно следующей величине:
иг = —±= ехр Г— (х~х'J) , F.1)
так что
*-ъ\х-х'\. F.2)
Здесь qx = У р/*г; в дальнейшем мы введем также q2 = )//?/х2.
Примем, что в области х > 0
§ 6] ГЛ. XIV. ПРИМЕНЕНИЕ ФУНКЦИИ ГРИНА 357
где w1 — решение уравнения для линейного теплового потока, обращающееся
при t = 0 к х—>оо в нуль; иными словами,
^ = 2^Ьг е~Ях {Х~Х'' + Ae~Ql*> ^ > 0. F.3)
Для х < 0 будем искать решение уравнения линейного теплового
потока, которое должно обращаться в нуль при л;->оо. Оно будет иметь вид
v2 = BeQ2X, x<0. F.4)
А и В должны быть здесь выбраны так, чтобы
llT ^T F.5)
Таким образом, находим
F.6)
v2 = —, n пт—e . F.7)
Следовательно,
1 Г (x _«x'f 1
, = , exp +
,Д ! - - exp \ > F.8)
VK2*t)y™xt FL 4x^ J
Ч
Стало быть, решение в области л: > 0 является решением, обусловлен-
обусловленным совместным действием первоначального источника и источника мощ-
мощностью
в положении «изображения» —х' в неограниченной среде с термическими
коэффициентами К\, «j.
Решение в области х < 0 служит решением для источника мощностью
действующего в плоскости х' j/"x2/xi B неограниченном твердом теле с терми-
термическими коэффициентами /С2. ^2-
II. Задача, аналогичная задаче /, но на поверхности х = 0 имеется контакт-
ное сопротивление *), а следовательно, граничное условие имеет вид
^ ^ у2), х = 0. F.10)
*) В статьях [22, 23] рассмотрен источник в плоскости х = 0; в этом случае
существует несколько возможностей, поскольку тепло может выделяться либо в одной
или другой среде, либо между ними.
358 ГЛ. XIV. ПРИМЕНЕНИЕ ФУНКЦИЙ ГРИНА [§ 6
Решения записываются следующим образом:
. F.11)
v — ехр [/ф^ -f- h2 (kx — jc)] Ф* J + h2 У^ \, F.12)
где
III. В области — / < x < О находится материал с термическими коэффи-
коэффициентами Ки Pi> ci» *i> t/i» я в области 0<х<а — материал с коэффициен-
коэффициентами К?, рг» С2> Х2» V2- Контактное сопротивление на границе отсутствует.
В области О < х < а в плоскости х' в момент времени t = O действует мгно-
мгновенный единичный плоский источник. При t > О поверхности х = а и х = — /
поддерживаются при нулевой температуре.
nsnx
/2=1
_ЧЪт ~ sin k (a — х') ря sin2 l$n sin k (a — х) ря -¦*¦&
•
~-V—J1 F13>
Л=1
оо
. 2ks VI . /гтегд:' , п~гх Г v.xn2s2n2t "I /с1„ч
+ 7 i Г / 1 sin sin ехР То » W'14)
1 /(г +05) -Л a a v \_ I2 \
где k = У Xi/x2> а = ЬКг1К\у а ± рл (/г = 1, 2, ...) — корни уравнения
Ctg р/ + a Ctg k$a = 0.
Вторые ряды в формулах F.13) и F.14) присутствуют только в тех случаях, когда
ka/l = rfs — несократимая рациональная дробь (см. § 8 гл. XII).
IV. В области — / < х < 0 содержится материал с термическими коэффи-
коэффициентами К\, pi, clt х, и vlt а в области х > 0 — мапеоиал с коэффициентами
К2> рг» *2 и V2- контактное сопротивление на границе отсутствует. В области
х > 0 в плоскости х' в момент времени t = 0 действует единичный плоский
мгновенный источник. При t > 0 поверхность х = — / поддерживается при нуле-
нулевой температуре.
Как и в § 8 гл. XII, решения можно представить либо в виде интегралов с бес-
бесконечными пределами, либо в виде бесконечных рядов, соответствующих бесконечному
ряду изображений.
Так, например,
оо
2а? С {sin kux' cos ul-\-z cos kux' sin ul] sin и (/-(- x) _ХИ2/ /«т-\
%)i ~~r ~~~~ I —-—j —— e CLUy (D«1D)
или
/2 = 0
4xr
где а = (а — 1)/(а -f- !)•
, F.16)
§ 7] ГЛ. XIV. ПРИМЕНЕНИЕ ФУНКЦИЙ ГРИНА 359
§ 7. Шар. Радиальный поток тепла
Фундаментальными решениями для радиального теплового потока в сфе-
сферических областях *) служат решения для единичного мгновенного шарового
поверхностного источника радиусом г', действующего в момент времени t = 0.
Решение для источника, действующего в неограниченной среде, имеет вид
(см. C.6) гл. X)
а=
и, следовательно,
-q\r + r'\). G.2)
Как и ранее, мы ищем решение в виде
v= u-\-w,
где w — решение уравнения теплопроводности
д2 (rw) 1 д (rw) п
~~dF2 Т—Ш—= ' ('"*'
кроме того, w должно обращаться в нуль при / = 0 и должно иметь такое
значение, чтобы v удовлетворяло граничным условиям.
I. Шар 0<><а с температурой поверхности, равной нулю.
В момент t = 0 на поверхности r = rf действует единичный поверх-
ностнйй сферический мгновенный источник**).
Здесь w должно удовлетворять вспомогательному уравнению
= 0, 0<г<а, G.4)
и иметь при г = 0 конечное значение. Таким образом, мы должны иметь
— Ashgr ,_ -ч
w=—-~—, G.5)
где А определяется из условия, что при r = a, v = 0, т. е. что
1 г —~<a-r') _ c-g(a+r')\ | Ash qa = Q
Используя это значение Л, получим
-=8ЬУ8М(а-О 0<г<г'. G.6)
\пгг'щ sh да ^ ^ х '
Если а> г > г', то г и г' в этом соотношении следует поменять местами.
*) Функция Грина для шара, определенная в § 1 данной главы, служит реше-
решением для единичного мгновенного точечного источника в шаре (см. § 16 этой главы).
Решение, которое приводится здесь для мгновенного шарового поверхностного источ-
источника, можно получить путем интегрирования A6.8) настоящей главы по источникам,
равномерно распределенным по сфере. Однако задачи, в которых рассматривается
радиальный тепловой поток, настолько важны, что нам представляется целесообраз-
целесообразным вывести решение непосредственно, в частности при помощи метода, соответ-
соответствующего методу, изложенному в § 2 для мгновенного плоского источника. Анало-
Аналогичное замечание справедливо и для решений, приведенных в § 8 этой главы.
**) Здесь и далее автор имеет в виду равномерное распределение единичных
источников на сферической поверхности. (Прим. ред.)
виду
. (Пр
360 ГЛ. XIV. ПРИМЕНЕНИЕ ФУНКЦИЙ ГРИНА [§ 7
Используя обычным путем теорему обращения, найдем
^-JSIn—Sln—
Принимая, что на сфере г = г' действует источник мощностью
4icr'2f (r') drf', и интегрируя по г' от 0 до а, получим для температуры
в шаре с начальной температурой /(г) и нулевой температурой поверхности
величину, равную
оо «
— 2^ ехр [ JJ—J sin -j- J r'f (r') sin -j- rfr'.
1 0
G.8)
Решение для случая, когда температура поверхности равна ср(?), получается
таким же путем, как и в § 1 данной главы.
Вместе с тем, разлагая выражение G.6) в ряд по отрицательным сте-
степеням показательных функций, находим решение
Г Bпа-г + г')П г
L 4^ J eXPL
приводящее к решению C.21) гл. IX для температуры в шаре с начальной
температурой /(г).
II. Шар 0 ^ г < а, #а поверхности которого происходит тепло-
теплообмен*) со средой нулевой температуры. В момент времени ? = 0
на поверхности r = rr действует единичный мгновенный поверхност-
поверхностный сферический источник,
В данном случае
где аЛ — положительные корни уравнения
—1) = 0. G.11)
III. Шаровая оболочка a<r<b. В момент времени ? = 0 на
поверхности r = rf действует единичный мгновенный поверхностный
сферический источник. Граничные условия имеют вид
G.12)
где kv hv k2 и h2 — положительные величины или нули.
В данном случае
G.13)
*) Если h = 0, т. е. тепловой поток на поверхности отсутствует, к правой части
G.10) надо добавить член 3/Dтся3).
§ 8] ГЛ. XIV. ПРИМЕНЕНИЕ ФУНКЦИИ ГРИНА 361
где
^ ^'Д an cos (f - a) «,]
}1А '
и ал — положительные корни уравнения
(GH — abkfaa2) sin (b — а) а-{-a (akxH+bk2G) cos (b — a)<x = 0. G.15)
Если /г1 = /г2 = 0, то к правой части решения G.13) следует добавить член
3
IV. Область ограничена изнутри шаровой поверхностью г = а.
В момент t = 0 на поверхности г = г' действует единичный мгновен-
мгновенный поверхностный сферический источник. Граничное условие на по-
поверхности г = а имеет вид
где &>0, /г>0.
В данном случае
1 г г (г— гул , Г (r-f-r'—2яJ
v = jt-J ехр —-* '—\ +ехр —^—L- —
Ыгг' (тех^
ahA-k /Л ,.у2 Г . / ah A- k
SF- Dтех<) exP [xf (—5
г (г— гул , Г (r-f-r'—2яJ 1
ехр —-* '—\ +ехр —^—L- —\ —
exP [xf (—5* ) + (r + r' - 2a) —^f-J X
§ 8. Цилиндр. Радиальный тепловой поток
В этом случае мы исходим из решения C.5) гл. X для единичного
мгновенного цилиндрического поверхностного источника, действующего в мо-
момент времени t = 0 на поверхности г = rf в неограниченной среде, т. е. из
соотношения
rr'
Отсюда, используя B2) приложения 5 при v = О, получим *)
г ,__х „ ,__/ч корда Г<г/#
Как обычно, мы ищем решение в виде v = u-{-w, где w удовлетворяет
уравнению
d2w , 1 dw 9— л /Q оЧ
-^ + 7-^-^ = ° (8-3)
и должно быть таким, чтобы v удовлетворяло граничным условиям.
I. Область 0 ^ г < а с температурой поверхности, равной нулю.
В момент времени t = 0 на поверхности г = г' действует единичный
мгновенный поверхностный цилиндрический источник.
*) Эквивалентные решения приведены в [3, 24].
362 ГЛ. XIV. ПРИМЕНЕНИЕ ФУНКЦИЙ ГРИНА [§ 8
Решение уравнения (8.3), имеющее конечное значение в начале коорди-
координат, записывается в виде AI0(qr), где А должно быть определено из усло-
условия, что v = 0 при г=а, т. е. что
\
Л/о (да) + 2^- /0 (qr') Ко (да) = 0.
Используя это значение А, получим
г>г'; (8.4)
значение v для 0 < г < г' получается, если поменять местами г и г' в соот-
соотношении (8.4). Используя обычным способом теорему обращения, найдем
^г^ (8вВ)
где ± аЛ (л=1, 2, ...) — корни уравнения
Предполагая, что на поверхности гг действует источник мощностью
2Tzr'f(r')dr', интегрируя от 0 до а по г' и предполагая, что функция /(г)
такова, что можно поменять порядок интегрирования и суммирования, полу-
получим решение для цилиндра с температурой поверхности, равной нулю, и
начальной температурой, равной /(г), в виде
7%
r'f (r° J°(r4) dr'- (8-6)
0
Таким же путем, воспользовавшись результатами § 1 данной главы, можно
решать задачи с произвольными начальными температурами и произвольными
температурами поверхности для рассматриваемых ниже областей.
II. Цилиндр 0<;г<а. В момент t = 0 на поверхности г —г'
действует единичный мгновенный поверхностный цилиндрический
источник. Граничное условие при г = а имеет вид
где &>0, Л>0.
Этот случай включает в себя пример I, а также случай теплообмена
на поверхности и случай равенства нулю теплового потока на поверхности.
где ап — положительные корни уравнения
kaJx (аа) — hJ0 (aa) = 0.
Если /г = 0, то к правой части решения (8.7) надо прибавить член 1/iza2.
III. Та же задача, что и II, но граничное условие *) при г = а имеет вид
_Л, *?+ *,!?+*,* = 0. (8#8)
*) Граничные условия этого типа рассмотрены в примере Е § 9 гл. I. Легко
произвести подобное обобщение и в приведенных ниже примерах IV и V.
§ 9] ГЛ. XIV. ПРИМЕНЕНИЕ ФУНКЦИЙ ГРИНА I t> J
где #1, k2i къ — положительные коэффициенты.
у-
7±х V? (аап)+(*2
где ап — положительные корни уравнения
о. (8.10)
IV. Полый цилиндр а < г < Ь. В момент времени t = 0 на поверхности
г —г' действует единичный мгновенный поверхностный цилиндрический источ-
источник. Граничные условия имеют вид
В данном случае
2
^ f^ ^ 12 с°(г> *п) с° (г'*а^ f™nt *(8Л1)
где ал — положительные корни уравнения D.5) гл. XIII, a F (ап) и С0(г,ап) опреде-
определены соотношениями D.9) и D.11) той же главы; kv k2> К* ^2 Д°лжны быть здесь
больше или равны нулю. Если k2 = k2 = 0, то к правой части решения (8.11) следует
1
прибавить член ¦ .. 2 2. .
V. Область, ограниченная изнутри цилиндрической поверхностью г = а.
В момент времени t = 0 на поверхности г=г' действует мгновенный цилиндри-
цилиндрический поверхностный источник. Граничное условие при г=а имеет вид
^ Л>0.
В данном случае
оо
v = -^ f e~xu2tC (a, r) С (а, г') и du, (8.12)
6
где
С(и г) _ Jo (иг) [kuYx (аи) + пГ0 (аи)] - Го (иг) [kujx (аи) + hjo (аи)]
{[kuJ1(au)+hJ0(au)]2+[kuYl(au)+hY0(au)Y}^
§ 9. Полуограниченное твердое тело х > 0. Трехмерные задачи
Для этого случая функция Грина, представляющая температуру в момент
времени t в точке (jc, у, z), обусловленную действием мгновенного единич-
единичного точечного источника в точке (x't у', z) в момент времени т, когда
граница х = 0 поддерживается при температуре, равной нулю (как и в при-
примере II § И гл. X), имеет вид
? __(
ехрГ-
— x)
Кроме того, в обозначениях, принятых в § 1 данной главы, получим
ди\_(ди\
дх )х=0 8.'V/, {t _ t)'/, 6XP [ 4х « —г)
364 ГЛ. XIV. ПРИМЕНЕНИЕ ФУНКЦИЙ ГРИНА [§ 10
Таким образом, если начальная температура тела равна f(x, у, z),
а при t > 0 температура на плоскости х = 0 поддерживается равной F (у, z, t),
то в соответствии с A.1) данной главы решение имеет вид
* ' 0 -оо -оо
X ехр [— {У~~У) Zt*~* ' \ f(jc'* y'' z'}dx'dy'l
t oo oo
H ^—rr / / / — ' z ' exp j— x ~т~{<У~~У ' \{z~~z ) \dzdyrdzf. (9.3)
8 (tix) '* J J J (t — t) /2 I 4% (t — t) J
0 —oo —oo
Для двумерной задачи, когда все величины не зависят от z, решение
получается либо путем численной оценки в (9.3) интеграла по zf, либо
путем использования вместо (9.1) и (9.2) соответствующих решений для
мгновенного линейного источника. Решение (9.3) подтверждает утверждение,
сделанное в конце § 8 гл. X относительно непрерывных дублетов.
При наличии на границе х = 0 теплообмена со средой нулевой температуры
функция Грина принимает вид
1 ( г (х — х'у
з7 \ ехр —
. Г
+ ехр —
Хехр|Л(.* + -
Чтобы подтвердить правильность этого решения, следует только отметить, что
функция (9.4) удовлетворяет дифференциальному уравнению теплопроводности. Кроме
того, в точке (х', у', z') оно стремится требуемым образом к бесконечности, а во всех
остальных точках при t -> 0 оно равно нулю. При х = 0 оно удовлетворяет нашему
граничному условию, поскольку этими свойствами обладает решение B.6) настоящей
главы. Иным способом решение можно найти методом, изложенным в следующем
параграфе. Решение для области х > 0 при начальной температуре / (jc, у, г) и
теплообмене со средой, имеющей температуру <р (у, <г, t), можно получить, восполь-
воспользовавшись соотношением A.2) данной главы.
§ 10. Область, ограниченная двумя параллельными плоскостями
Приведем сначала несколько изображений для температуры, обусловлен-
обусловленной действием мгновенного точечного источника, которые являются основ-
основными при рассмотрении задач в цилиндрических областях.
Распределение температуры в неограниченной среде, обусловленное
действием единичного источника в точке (х'> у', z')> записывается следую-
следующим образом:
и = г
где
#2 = (JC _ х'J+ (У — у'J = г/2 + г2 — 2rr' cos (б — б'), (Ю.2)
а (г, б) и (г', 6') — координаты точек (л;, у) и (х\ у7) в полярной системе.
Используя F) приложения 5, получим
§ 10] ГЛ. XIV. ПРИМЕНЕНИЕ ФУНКЦИЙ ГРИНА 365
или
[f A0.4)
о
или
где
rl=Y(? + <I2)- (Ю.6)
При решении различных задач в цилиндрических областях изображения *) и
A0.4) и A0.5) оказываются весьма полезными. Здесь нам потребуется только
лоследнее.
I. Плоскости имеют температуру, равную нулю.
Рассмотрим плоскости z = 0 и z = 1. Определим температуру в точке
(х, у, z), обусловленную действием в момент времени ? = 0 единичного
мгновенного точечного источника в точке (*', у', z').
Ищем, как обычно, решение в виде v = u-{-w, где w должно удовле-
удовлетворять дифференциальному уравнению теплопроводности и обращаться
при ? = 0 в нуль. Кроме того, оно должно быть таким, чтобы v удовле-
удовлетворяло граничным условиям. Вспомогательное уравнение для w имеет вид
1 d2w . d2w . 1 dw , d2w 2— л /1Л7Ч
Ему удовлетворяет функция
оо
" = -?; f \МУ*)[А*Ъ Ч*+ 8 3114A —z)} Я. A0.8)
6
где А и В — произвольные функции ?. Они должны быть выбраны таким
образом, чтобы г/, равное сумме выражений A0.5) и A0.8), обращалось
при z = 0 и z = l в нуль. Следовательно,
?sh7}/ = — *-V и ^sh7]/ = — *-ч С-*').
Используя эти значения и выражение B5) приложения 3, мы получим
для 0 < z < zr соотношение
- 1 fjWsM^ln,
2тсх J ц sh у\1 v }
J
о
Если z' < z < /, то решение имеет тот же вид, но z и zr меняются местами.
Для того чтобы по v найти v, можно идти двумя путями. В первом случае
мы представляем интеграл A0.9) в виде
J
sh (/ - z') (q* - Е2)!/* sh z(g* -
J
—•oot
и вычисляем его путем замыкания контура интегрирования дугой большой
окружности в правой полуплоскости. Подынтегральная функция имеет полюсы
при % = qm, где дт = (д2 + тЧ/РI/\ щ=1, 2, ...
*) Эти изображения соответствуют случаям р. = — l/2i v = 0 и р. = 0, v = 1/2 [24].
366 ГЛ. XIV. ПРИМЕНЕНИЕ ФУНКПИЙ ГРИНА [§ 10
Находя вычеты относительно них, окончательно получим
т = \
Используя B3) приложения 5 и соотношение B.6) гл. XII, находим
R2
еХР I 2U/ I «-| Г ^2^1 mizz тЛ4С
sin-т— sin—-.—. A0.12)
/2 J /
Отыскивая решение другим путем, можно написать функцию, изображе-
изображение которой имеет вид
sh (/ - z') (q2 + е2)'/' sh z(q2 + P)* ^ lQ {
(^2 „|_ ^2)V2 gh / (^2 _J_ ^y/2
в любой из двух следующих форм:
оо
-г- V sin —j—-sin —т—exp —%фг -я— , A0.14)
или
л оо
A0.15)
Допуская, что порядок интегрирования и обращения изображения в со-
соотношении A0.9) можно изменить, и используя для интегрирования по ?
форму A0.14) и соотношение B9) приложения 3, снова получим решение
A0.12). С другой стороны, аналогичное использование формы A0.15) дает
следующее выражение:
которое можно получить непосредственно в виде бесконечного ряда изобра-
изображений в плоскостях z = 0 и z = L Равнозначность форм A0.14) и A0.15)
дает другое доказательство справедливости этого решения, которое уже
упоминалось в § 10 гл. X.
II. Теплообмен на плоскостях <г = 0 и z= l со средой, температура кото-
которой равна нулю.
Этот случай можно рассматривать аналогичным образом. Решение для случая
единичного мгновенного источника в точке (х\ у', z)t действующего в момент вре-
времени t = 0, имеет вид
RWt ^ (а„ cos anz+ h sin anz) (an cos *nzf + h sin anz') -™п* lft m
ТЩЩ? ' (ШЛ7)
где ап — положительные корни уравнения
§ 11]
ГЛ. XIV. ПРИМЕНЕНИЕ ФУНКЦИЙ ГРИНА
367
III. Тепловые потока через плоскости z = 0 и z = / равны нулю.
Решение для случая единичного мгновенного источника в точке (х\ у'', z')t
действующего в момент времени t = О, имеет вид
rnzz'
A0.18)
nl + г'— гJ
1 . Г
J + expL
A0.19)
Последнее соотношение можно получить из рассмотрения бесконечного ряда
изображений. Следует отметить, что решение A0.18) нельзя получить, положив
в формуле A0.17) Л = 0.
IV. Совокупность источников, образующих в неограниченной среде прямо-
прямоугольную решетку.
Если в решении A0.18) принять г1 = 1/2 Л то мы получим температуру в точке
(х, У* z)> обусловленную действием в точках г1 = l/21 ± nl ряда мгновенных точечных
источников. Аналогичным образом температура, обусловленная действием бесконечной
прямоугольной решетки мгновенных источников, расположенных в точках х' =
1/' lll ± l де *)
пру р
= 1/га ± па, z' = ll2l ± nl, записывается в виде *)
L /2 J / 1
X
A0.20)
Соответствующие решения для расположения источников в трехмерном про-
пространстве можно получить аналогичным путем. Для случая прямоугольной решетки
линейных источников, параллельных оси у, интегрирование выражения A0.20) дает
1 + 2 2, (-1Уехр [
4х/г2тс2П
X
cos
2nnz
X
A0.21)
§ И. Полуограниченное твердое тело 2>0с тонкой пленкой
на плоскости г = 0 из материала, имеющего значительно большую
теплопроводность **). В точке @, 0, zr) расположен единичный
мгновенный источник
Следует решить уравнение
d2v 1 dv .
d2v
dv
при граничном условии (см. (9.21) гл. I)
*) Решение A0.20) проще всего вывести, записав выражение для ряда изображе-
изображений в направлении х и использовав общее решение, которое получается из формул
A0.18) и A0.19).
**) Здесь мы имеем дело с функцией Грина для полубесконечного твердого тела
при диффузии на его поверхности. Другие задачи подобного типа рассмотрены в [29,30].
368 гл. xiv. применение функций грина [§12
ГДе h = KldK. Если из уравнения A1.1) при z = 0 вычесть (Н.2), то наше граничное
условие примет вид
_
Как и в предыдущем параграфе, ищем решение в виде v = и + w, где и опре-
определяется соотношением A0.5) данной главы, а
w
1 /*
47СХ «/
Здесь Л следует найти из условия A1.3). Действуя далее так же, как и в предыду-
предыдущем параграфе, окончательно получим для z' > z > 0
оо
1 Г Но
Для простоты определим v только для плоскости z = 0. Тогда соотношение
A1.5) принимает вид
]}*. A1.6)
Применим теперь к этому соотношению теорему обращения, помня, что
tq = [(/>/*) + ^2]!/а» и допуская здесь и далее, что порядки интегрирования можно
изменять. Используя теоремы VI и VII, приведенные в § 2 гл. XII, и выражение F)
приложения 5, получим
Используя при взятии интеграла по 5 выражение B9) приложения 3, оконча-
окончательно получим
/
8 (k — I)'2 (™i)'
X ^ » A1-7)
где k = %x/x.
§ 12. Неограниченное составное твердое тело.
В точке *) @, 0, z') действует мгновенный единичный источник
Предположим, что в области z > О находится вещество с термическими коэффи-
коэффициентами К\, pii си хь а в области z < 0 — вещество с коэффициентами /С2, рг. ^2. Х2
и что на границе z = 0 контактное сопротивление отсутствует. Обозначим темпера-
температуру в области z > U через i/lf а в области г<0—через v2- Тогда, если в точке
*) Эта задача имеет большое практическое значение, поскольку с ней довольно
часто сталкиваются на практике, например при нагревании трением или при «охла-
«охлаждении» нейтронов. Изложение этой задачи приведено в [25].
§ 13] ГЛ. XIV. ПРИМЕНЕНИЕ ФУНКЦИИ ГРИНА 369
(О, О, z') в области z > 0 находится единичный источник, то, используя метод, изло-
изложенный в § 10 данной главы, получим изображения для температуре этих двух
§
областях в виде
где
Чтобы определить v2\ исключим из знаменателя формулы A2.2) величину
+ ^2^2» воспользовавшись равенством
Допуская, что порядки интегрирования можно менять, получим (см. B.10) г л» XII
и F) приложения 5)
Интеграл по ? можно взять при помощи соотношения B9) приложения 3,
а интеграл по С хотя и сложен, но элементарен. Окончательное решение, выражен-
выраженное через безразмерные величины,
будет иметь вид
v2 = ^ „ / eiphW/4(ft+l-?)] . ^ e.
82 @•/» / (*2а + 1 — и) в1* A — aI/* V '
где
—u)
l — и + с2иу/* 1 2A — « + а2а) J
jexpf (аУ-^zy у 12
)V2 J F\ 4A— u + a*u) f
Аналогичным путем можно найти и выражение для vu имеющее такой же вид.
§ 13. Области, ограниченные цилиндрической поверхностью г = а
I. Рассмотрим сперва температуру в точке (г, б, г) внутри
цилиндра г^а, обусловленную действием в момент времени t = 0
единичного мгновенного источника в точке (г', 6', 0). Температура
поверхности г = а поддерживается равной нулю.
24 Г. Карслоу, Д. Егер
370 ГЛ. XIV. ПРИМЕНЕНИЕ ФУНКЦИЙ ГРИНА [§ 13
В данном случае мы исходим из формулы A0.4) этой главы для и
и используем для входящей в нее функции Бесселя K0(riR) теорему сложе-
сложения [3,24].
i= S cos л F — ео/я(ч'0*я(ч'"). /•</-',
r>rf.
—оо
A3.1)
Ищем, как и ранее, решение в виде v = u-{-w, где w должно удовле-
удовлетворять A0.7) данной главы, должно быть ограниченным при г = 0 и должно
быть таким, чтобы и-±-т = 0 при г = а. Тогда
/
=-2ЙГ Ё cos »F - 60 / cos \z '» ^ ygg *¦ ^ g. A3.2)
—с»
где 17 определяется соотношением A0.6) этой главы. Отсюда следует, что
для г > г'
5-вг Ё
где
Л, (Jf. У) = /« (х) Кп (у) - Кп (х) 1п (у).
Если г <гг, то в соотношении A3.3) следует поменять местами г и г'.
Интегралы в соотношении A3.3) берут, рассматривая интеграл
J
по контуру, состоящему из вещественной оси и большой полуокружности
в верхней полуплоскости (для z > 0), не проходящей ни через один из
полюсов подынтегральной функции. Эти полюсы находятся в точках
? = / |/V2 ¦+- а2, где а — положительные корни уравнения
0. A3.4)
Обозначая символом 2 суммирование по таким корням и находя вы-
а
четы относительно этих полюсов, окончательно получим
Отсюда, используя выражение G) приложения 5, находим
r2'\ A3.6)
Решение для линейного источника, параллельного оси z, получается
путем интегрирования соотношения A3.6) по z\ его можно получить и непо-
непосредственно методом, аналогичным описанному выше. Решение (8.5) данной
главы для цилиндрического поверхностного источника получается путем
интегрирования по 8'.
§ 14] ГЛ. XIV. ПРИМЕНЕНИЕ ФУНКЦИЙ ГРИНА 371
Н. Задача, аналогичная задаче 1, но на поверхности г-=а происходит
теплообмен со средой, температура которой равна нулю.
# I
Л=— со о
где суммирование производят по положительным корням уравнения aJn (ad) ¦+•
-{- hJn(aa) = 0. Если h = 0, то к соотношению A3.7) необходимо прибавить дополни-
дополнительный член
Г *2 Л
ехр r^-r-1
III. В момент времени / = 0 в области, ограниченной изнутри поверхностью*
г = а,в точке (г', 6 , 0) действует единичный мгновенный точечный источник.
Поверхность г = а поддерживается при температуре, равной нулю.
ехр —
j<I V сов п(>-У) [а*жр1-«*] Un^)Un(^)
где
tf л («О - Jn (*r) Уп (ад) - Л* (ад) кя («¦). A3.9>
IV. Задача, аналогичная задаче III, но на поверхности г = а происходит:
теплообмен со средой, температура которой равна нулю.
ехр —
У cos Л F-6') f Cn(ur)Cn (ur') u*-«*du.
где
с _
§ 14. Клин 0 < в < в0
I. Температура поверхности равна нулю.
Рассмотрим случай, когда в момент * = 0 в точке (г', 0', 0) действует
единичный мгновенный источник. Используя формулу A0.4) данной главы
для а, а также тот факт *), что при действительных и положительных г,
г1 и \ 0 < 0 — 0' < 2те и г > г\ получим
cosv(*
f
-ooi
где P. V. означает, что при v = 0 берется главное значение**). Таким об-
образом, при 0О>0>0' и г>г', можем написать
coi
coi -i
-V- f C0SV(;i~I4/)/v^/)/C,W^v L;.A4.
*) Это легко доказать, замкнув контур большой полуокружностью на правой
полуплоскости и использовав теорему Коши [3].
ь j —в ь \
**) Р. V. |/(v)rfv= lim \ Г /(v)dh-f- Г/W^v 1 — это главное значение
a \a i J
интеграла при v = 0 в смысле Коши. (Прим. ред.)
24*
S72 гл. xiv, применение функций грина [§ 14
Тогда
х [p.v. /
L -oof
поскольку это выражение удовлетворяет уравнению для w и при 0 = 0 и
0 = 0О ~v, равное u-{-w, обращается в нуль. Кроме того, поскольку путь
интегрирования может проходить через v = 0,
J
0
, Г sin v»' sin м(в0 — в) ,. Л„. ,. .. „.^
H J sin А Ч(тО*,(у)*> \dl A4.3)
Если 0 < ft < 0', то 0 и 0' в соотношении A4.3) следует поменять местами,
а если 0 < г < г', то следует поменять местами г и г'.
Интеграл в скобках берут, замыкая контур (—оо/, со/) большой полу-
полуокружностью в правой полуплоскости и вычисляя вычеты относительно по-
полюсов пп/Ь0 подынтегральной функции. Положим, что
s = 17' A4-4)
а суммирование по значениям $ от п = 1 до оо обозначим символом 2-
Тогда для г > г' и О<0<0О получим
о
A4-5)
Далее, из B2) приложения 5 и соотношения B.6) гл. XII следует, что
если r>r't то 1$(т\г')К$(т\г) есть изображение функции
A4.6)
Из формулы A4.5) вытекает, что для всех значений гиб
sin sb sin s67* (•&) exp [— f8tT] /cos ** exP (-
0
или
exp [~ ^] ?exp [~ ^^Ё1]7- Шsin ^6 sin s6/-
И. Тепловой поток на поверхности равен нулю.
Аналогичные рассуждения показывают, что решение для единичного мгновенного
точечного источника, находящегося в (г', 6', 0) в момент * = 0, имеет вид
§ 15] ГЛ. XIV. ПРИМЕНЕНИЕ ФУНКЦИЙ ГРИНА 373
III. Клан с углом раствора ф
В этом частном случае [26] *), когда граничная поверхность представляет собой
полуплоскость у = 0, х > О, для функции Грина существует простое явное выраже-
выражение, а именно:
где
R2 = г2 + г'2 — 2rr' cos F — 6'), R'2 = г2 + г/2 — 2rr' cos F + в'). A4.10>
Отрицательный знак берется в тех случаях, когда полуплоскость имеет нулевую тем*
пературу, а положительный — когда тепловой поток через нее равен нулю.
§ 15. Цилиндрическая область
Функции Грина для любой области, ограниченной координатными поверхностям»
цилиндрической системы координат, можно получить с помощью методов, изложен-
изложенных в нескольких предыдущих параграфах [27].
Например, для изображения температуры в точке (г, 0, z)t обусловленной дей-
действием в момент времени * = 0 в точке (г', Ь\ г') области 0 < z < I, 0<г < д еди-
единичного мгновенного точечного источника, когда поверхность поддерживается при
нулевой температуре, имеем »•
?sin^sin*? ? IArqm)tiZ'r4n) cosn<e-
где
При Г2/1' получим
со
2
sin -у- sin
где a — положительные корни уравнения Ул (aa) = 0.
С другой стороны» если поверхность области а < г <bt 0<r</, 0<6<6a
подерживается при нулевой температуре, а в точке (г', в', z1) в момент времени /=sO
действует единичны^ мгновенный точечный источник, то температура в точке (г, б, z)
в момент времени / записывается в виде
-jg- V ехр ^—I sin —j— sin —j— ^ sin «в sin s6'X
^ а2 ехр (- «А) У| (aft) V, (or) Ua (or')
A5'3>
где s и Us (ar) определены соответственно выражениями A4.4) и A3.9) данной главы
а a — положительные корни уравнения Us (лЬ) = 0.
*) Это решение легко получить методом изображений в римановом пространстве
(см. § 12 гл. X).
374 ГЛ. XIV. ПРИМЕНЕНИЕ ФУНКЦИЙ ГРИНА [§ 16
§ 16. Области, ограниченные сферической поверхностью г = а
Требуется найти температуру в точке со сферическими координатами
(г, б, ср), обусловленную действием единичного мгновенного точечного источ-
источника, расположенного в начальный момент времени в точке (г', 0, 0).
Температура и в точке (г, 0, ср)» обусловленная действием такого источ-
источника в неограниченной среде, равна
где
/?2 _ Г2 + г'2 _ 2rr' cos 8. A6.2)
Тогда из выражения F) приложения 5 получим
Применяя одну из теорем сложения для функций Бесселя (см. [24])
можно выразить и в форме, удобной для использования в сферической
системе координат, а именно в форме
CD
п = Ljp. S Bя + 1) ATn+i for') In+1_ for) Р„ (j»), когда г < r'.
oo
-^^УсгиН-!)^ !(9г)/ iforOPeQi). когда r>r\
A6.4)
где |х = cos 9.
I. В шаре 0 <; г < а действует источник. Поверхность г = а
имеет температуру, равную нулю.
Пусть, как обычно, v = u-\-wt где функция w должна удовлетворять
уравнению теплопроводности, обращаться в нуль при t = 0 и быть такой,
чтобы v (равное u-\-w) при г = а обращалось в нуль.
Функция w должна удовлетворять вспомогательному уравнению
Его решение, имеющее конечное значение в начале координат, имеет вид
оо
•= 2 <V-4i+i/a for)/>„(!»). A6.6)
где коэффициенты Ап следует определять из условия, что u-\-w при г = а
обращается в нуль. Тогда, используя соотношение A6.4), получим
§ 16] ГЛ. XIV. ПРИМЕНЕНИЕ ФУНКЦИЙ ГРИНА 375
Таким образом, когда 0 < г < г',
1/2 (да) — /„+1/2 (Я^) Kn+if2 (да)
+l2tb). A6.7)
Если же г' < г < я, то г и г' в соотношении A6.7) следует поменять
местами.
Функцию v находят, применяя обычным образом теорему обращения
к членам соотношения A6.7). Это дает
A6.8)
где а — положительные корни уравнения
Чтобы найти температуру в точке Р(г, в, ср), обусловленную действием
в точке Р'{г\ 6', ср') единичного мгновенного источника, используем реше-
решение A6.8), в котором [х заменено на cos 7» где -\ — угол POP'. Кроме того,
известно, что
п
m=l
где p = cos8, a ^'tzsrcosO'. При помощи этих результатов можно найти
температуру в шаре 0 ^ г < а с произвольной начальной температурой и
произвольной температурой поверхности.
II. Задача, аналогичная задаче I, но на поверхности г = а происходит
теплообмен со средой, температура которой равна нулю
* = 7= Zi <2n + !> P«W Zj 77 П2 , iTii , -f16-11)
2'c'/rr' t?0 T [(ah-T) +a2a2-(n + ^)Jy'+i/2(ea)
где а — положительные корни уравнения
= 0. A6.12)
Если тепловой поток равен нулю (Л = 0), то к правой части A6.11) следует добавить
член C/4гсл3).
III. Область ограничена изнутри сферой г = а. В момент времени t = 0
s точке (г', 0, 0) действует единичный мгновенный точечный источник. Поверх-
ность г = а поддерживается при температуре, равной нулю.
376 ГЛ. XIV. ПРИМЕНЕНИЕ ФУНКЦИИ ГРИНА [§17
где
C/I+1/2 <*) = Л+1/2 (*) Yn + ll2 (иа) — Yn+l/2 (*) Л* + 1/2 (»*>•
IV. Задача, аналогичная задаче III, но на поверхности г = а происходит
теплообмен со средой, температура которой равна нулю.
!==• V Bл +1) Рп ((х) / e-xa''Fn+v2 (иг) Fn+lft (иг') и du, A6.
14)
где
^ Bah+\) [/v (кг) К, (шг)-К, (иг) 7, {иа)]-2аи [7V (кг) Г,' (шх)-Г, (кг) 7V'
{ [Bап + 1) J4 (иа) — 2«л/; (aa)J2 + [Bah + 1) Kv (йд) — 2uaY[ (ua)}2
A6.15)
§ 17. Конус 0<0<0о
Предположим, что в момент времени ^ = 0 в точке (г', 0, 0) действует
единичный мгновенный источник. Как и раньше, будем исходить из значе-
значений а т а, определяемых уравнениями A6.1) и A6.3) предыдущего пара-
параграфа. Будем искать выражение для и, пригодное в случае конической гра-
граничной поверхности. Это достигается путем использования интеграла для e^p/R
или Bq/TcR)i/tKifi (q /?), аналогичного интегралу A4.1) данной главы для /Со (qR)>
полученному для соответствующей задачи с клином.
Требуемое решение*) [28] для случая, когда г > г' и Re(#)>0, имеет
вид
Bv+l)/v+1/2(^)^v+1/2(^r)Pv(^)^v _
sin vie
С
оо
= 2/J] Bn+\)Kn+iB{qr)In+ii2(qr')Pu{}>), A7.1)
где С — контур, начинающийся на бесконечности в первом квадранте, про-
проходящий через точку (—V2) и заканчивающийся на бесконечности в четвер-
четвертом квадранте.
Чтобы найти температуру в точке (г, 0, ср), обусловленную дей-
действием источника в случае, когда поверхность конуса 0 = 0О поддер-
поддерживается при температуре, равной нулю, будем исходить из величины»
определяемой соотношениями A7.1) и A6.4) данной главы, а именно
- 1 Г С* + 1) Л+1/2(?О K4+lf2(qr) Л (-f*) tfv
U SicixirFF" J sinvic ^
при /:>/•'¦ Есди г</-7, то в этом соотношении гиг' следует поменять
местами. Функция 5 должна удовлетворять уравнению A6.5) предыдущего
•) Решение 1юЛучается замыканйем\ контура в правой полуплоскости дугой
большой1 окружности и применением теоремы Копти. В статье [281 получены и дру-
другие решения, которые потребуются irate ниже, например решение A7.5) данной главы.
§ 17] ГЛ. XIV. ПРИМЕНЕНИЕ ФУНКЦИИ ГРИНА 377
параграфа, и поэтому мы можем написать
5Г= L_ Г^+У'^ПК^ОР^)
8тс/х Yrr' J sin vtc
где функцию /(v) следует выбрать так, чтобы u-\-w = 0 при [а = {х0 = cos 0o.
Это условие требует, чтобы /(v) = —Pv(—(*0)/Л, (l*o)' и, следовательно,
при /¦>/"' мы получим
/(
/Bv+ OW (?/>') *,+i/2»/0 X
Если г < г', то в этом соотношении г и г' нужно поменять местами.
Интеграл в A7.3) берут, замыкая контур дугой большой окружности
в правой полуплоскости и применяя теорему Коши. Подынтегральная функ-
функция имеет полюсы в нулях*) функции Pv(p0), рассматриваемой как функ-
функция v; она не имеет полюсов при целых значениях v, поскольку для них
Рл(|д) = (—\)пРп{—р). Определяя вычеты относительно полюсов, оконча-
окончательно получим
Г? Sin VTC (rf/rfv) [Pv (fl0)]
Суммирование по v проводится по корням, большим —1/2, уравнения
Я?Ы = 0. A7.4)
Однако для этих значений v
Поэтому
v = — 2Ljp 2 Bv + J) A+i/8 С?'"') ^'+i/2 (*r)я» О») X
И окончательно, используя B2) приложения 5, получим для г^г9
причем суммирование проводится по корням уравнения A7.4).
*) Известно, что все нули функций Рч (\х) и Р~т'{р) различны и действительны [31].
Кроме того, поскольку Р~т (р) = Р2™-\(р)> они расположены симметрично относи-
относительно точки v == — V2» через которую проходит контур С.
378 ГЛ. XJV ПРИМЕНЕНИЕ ФУНКЦИЙ ГРИНА [§ 18
Если источникjtaxodumcx не на оси, а в точке (г7, 6', ср'), то функцию Рп (р.)
в соотношении для и следует заменить на Я„ (cos Т)» гДе Т — Угол между радиусами-
векторами от начала координат до точек (г, 6, у) и (г', 6', <р').
Если ввести обозначения fx = cos б и fx' = cos 6', то при 0 > 0' теорема сложе-
сложения для сферических гармонических функций дает
m=0
A7.8)
где
em==l при 0 |
|
при «=1,2,3,... J
Если в < 6', то в соотношении A7.8) 6 и 0' следует поменять местами.
Подставляя величину Pv (— cos 7) из выражения A7.8) в A7.2) и производя та-
такие же операции, как и выше, за исключением того, что вместо соотношения A7.5)
используется его обобщенная форма [28], т. е.
-A -
(-Ы5^Р7т(Ы = r(w+v+12)r(;w_v) . A7.10)
окончательно получим
2 2-
X cos m (9 - ?') P~m ((/) [A - ц0J -~ P~m ((i0) A P~m (|xo)]~ , A7.1
где суммирование по v проводится по корням, большим —'/г> уравнения
При помощи соотношения A7.11) можно найти температуру в любой точке ко-
конуса при произвольной начальной температуре и произвольной температуре поверх-
поверхности. Аналогичным образом можно рассматривать и задачи для твердых тел, огра-
ограниченных другими поверхностями в полярной системе координат.
§ 18. Непрерывные источники
Решения для непрерывных точечных или линейных источников в областях, рас-
рассмотренных в настоящей главе, можно получить путем интегрирования соответствую-
соответствующих функций Грина. Однако эти решения очень просто получаются и непосредственно.
В качестве примера рассмотрим непрерывный линейный источник, выделяющий
при t > 0 в единицу времени на единицу длины количество тепла, равное Q.
Источник располагается параллельно оси z цилиндра r-^а и проходит через
точку (г', 0). Начальная температура цилиндра равна нулю. Теплообмен на его
границе отсутствует.
Требуется найти решение вспомогательного уравнения
при условиях __
J^0, r = a, A8.2)
Urn /?4^-=
где
R = Y(r2 -f r'2 — 2/r' cos 6). A8.4)
§ 181 гл. xiv. применение функций грина
Решение уравнения A8.1) с условием A8.3) имеет вид
379
Согласно теореме сложения (см. пример I § 13 данной главы) его можно запи-
записать в виде
1п igr) Kn {qft) C0S пЬ* К0ГДа Г < Г''
(] 8*5)
п-0
где гп = 1, если п = О, и гп = 2, если /г = 1, 2, ... Если г > г', то в выражении A8.5)
/•иг' нужно поменять местами. Таким образом, для решения уравнения A8.1) при
условиях A8.2) —A8.4) мы получим
ел Vh (ЯП Kn (ЯГ') + anln (qr)} cos /16, 0 < r < r\
?n {*п (Qr') Kn (Яг) + arJn (Qr)} cos /гв, а> r> r\
п=0
A8.6)
где ап следует выбрать так, чтобы функции A8.6) удовлетворяли условию A8.2). Для
этого нужно, чтобы
ln(qr')K'n(qa)
а
Поэтому, если 0 < г < г\ то
оо
- Q
Если же а > г > г', то в соотношении A8.7) гиг' следует поменять местами.
Из теоремы обращения получим
й=0 т-/оо
Если /г = 0, то в начале координат имеется полюс второго порядка с вычетом
ЪЛ , г2 + г'2 а 3
+ +1П
Если л > 0, то в начале координат имеются простые полюсы с вычеточ
Тогда полюсы при X = 0 дают
Q
2%К
380 ГЛ. XIV ПРИМЕНЕНИЕ ФУНКЦИЙ ГРИНА [§ 18
Другие нули знаменателей A8.8) дают
гДе ая, т — положительные корни уравнения
п
Общее решение нашей задачи равно сумме соотношений A8.11) и A8.12).
ЛИТЕРАТУРА
1. Maxwell, Electricity and Magnetism, v. I, § 97 (b).
2. Webster, Electricity and Magnetism, p. 290.
3. Gray, Mathews, Treatise on Bessel Functions, Macmillan, ed. 2, 1922.
(Э. Грэй, Г. Мэтьюз, Функции Бесселя и их применение к физике и механике,
ИЛ. М., 1953.)
4. Sommerfeld, Partial Differential Equations in Physics, New York, 1949.
(А. Зоммерфельд, Дифференциальные уравнения в частных производных,
ИЛ, М., 1950.)
5. Minnigerode, Ober die Warmeleitung in Krystallen, Gottingen, 1862.
6. В е 11 i, Ann. Univ. tosc. Pisa 10, 143 A868).
7. Betti, Ann. Mat. pura appl., Milano I, 373 A868).
8. Betti, Mem. Soc. Ital. Sci. Firenze 1, 373 A868).
9. Betti, Collectanea Mathematica inedita in Memoriam Domenici Chelini, Milano, 238
1881.
10. Sommerfeld, Math. Ami. 45, 274 A894).
11. Weber — Riemann, Die partiellen Differentialgleichungen der mathematischen
Physik, 1912. (Ф. Франк, Р. Мизес, Дифференциальные и интегральные урав-
уравнения математической физики, ОНТИ, 1937.)
12. С а г s I a w, Phil. Mag. 4, 162 A902).
13. С а г s 1 a w, Proc. Edin. Math. Soc. 21, 40 A903).
14. С а г s 1 a w, Proc. Lond. Math. Soc. 8, 365 A910); 13, 236 A914).
15. Pock els, Ober die Partielle-Differentialgleichung (V2 + x2)" = 0, Leipzig, 189 L
16. Schwarzschild, Math. Ann. 55, 177 A902).
17. Carslaw, Introduction to the Mathematical Theory of the Conduction of Heat in
Solids, Macmillan, ed. 2, 1921. (Г. Карслоу, Теория теплопроводности, Гостех-
издат, 1947.)
18. В г у a n, Proc. Camb. PhiL Soc. 7, 246 A891).
19. Bryan, Proc. Lond. Math. Soc. 22, 424 A891).
20. Hobs on, Proc. Lond. Math. Soc. 19, 279 A887).
21. Sommerfeld, Math. Ann. 45, 263 A894).
22. M e г s m a n, Trans. Am. Math. Soc. 53, 14 A943).
23. Schaaf, Quart. Appl. Math. 5, 107—111 A947).
24. Watson, A treatise on the theory of Bessel functions, Cambridge, ed. 2, 1944*
(Г. Вате он, Теория бесселевых функций, ИЛ, М., 1949.)
25. В е 11 m a n, М а г s h a k, W i n g, Phil. Mag. 40, 297 A949).
26. С а г s 1 a w, Proc. Lond. Math. Soc. A) 30, 121—163 A899).
27. С а г s 1 a w, J a e g e г, J. Lond. Math. Soc. 15, 273 A940).
28. Carslaw, Math. Ann. 75, 133 A914).
29. J a e g e r, Quart. J. Mech. Appl. Math. 8, 101—106 A955).
30. Whipple, Phil. Mag. 45, 1225—1236 A954).
31. M а с D о n a 1 d, Proc. Lond. Math. Soc. 31, 265 A900).
ГЛАВА XV
ДАЛЬНЕЙШИЕ ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
§ 1. Введение
В настоящей главе мы рассмотрим различные задачи, которые нельзя
отнести ни к одной из изученных ранее; они объединены лишь тем, что для
их исследования хорошо подходит метод преобразования Лапласа, который
в большинстве случаев приводит к изображениям более сложным, чем рас-
рассматривавшиеся ранее. Мы вкратце покажем применение этого метода к за-
задачам теплопроводности в движущихся твердых телах, к теории теплообмен-
теплообменников, при наличии в твердых телах источников тепла, при расчете устано-
установившихся периодических температур, к задачам о тепловом потоке в неодно-
неоднородных материалах и к ряду других задач. В дополнение к уже использовав-
использовавшимся методам мы рассмотрим также прямое применение преобразования
Лапласа к задачам с несколькими пространственными переменными.
§ 2. Теплопроводность в движущемся теле*
Задач подобного типа решено сравнительно мало. В своем большинстве
это задачи для полуограниченного твердого тела, которое движется со ско-
скоростью их вдоль оси х и имеет на плоскости лг = О различные граничные
условия. Положительные значения их соответствуют увеличению объема
среды (например, снежный покров, толщина которого непрерывно увеличи-
увеличивается вследствие выпадения осадков [1, 2]). Отрицательные значения их со-
соответствуют удалению вещества с плоскости jc = O из-за эрозии [3, 4] *), плав-
плавления, сублимации, при горных разработках [5] или аналогичных процессах.
Было рассмотрено также несколько задач о протекании жидкости по
трубам [7, 9]; при этом предполагалось, что по всему поперечному сечению
трубы скорость жидкости одинакова. При помощи излагаемого здесь метода
можно также решить задачи с движущимися тепловыми источниками, но не-
непосредственное интегрирование, проведенное в § 7 гл. X, здесь более эф-
эффективно и его легче выполнить. Перейдем к решению типичных задач.
I. Область**) х > О движется со скоростью U. Начальная темпе-
температура равна V0-\-ax, а плоскость л; = 0 при ?>0 поддерживается
при температуре Vx-\-bt. В теле равномерно распределены ис-
источники мощностью Ао.
*) Вопрос о теплопроводности в движущихся и деформируемых телах
рассмотрен в [б. 1, б. 3, б. 5], приведенных в предисловии редактора. (Прим. ред.).
**) В этих работах рассматривается также влияние выделения тепла в движу-
движущейся среде.
***) То есть полуограниченное твердое тело. (Прим. ред.)
382 ГЛ. XV. ДАЛЬНЕЙШИЕ ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА [§ ?
При различных значениях постоянных Vo, Vv a, b и Ао этот случай
охватывает множество упомянутых выше задач. Найденные решения остаются
справедливыми при обоих знаках U. Искомое дифференциальное уравнение
(см. G.2) гл. I) имеет вид
дх2 х дх % dt ~ К ( '
с граничными условиями
v = V0-\-ax, л;>0, / = 0, B.2)
v = Vx~\-bt, л: = 0, t > 0. B.3)
Вспомогательное уравнение
dx* * dx %V~ Kp * ( }
должно быть решено при условии
ю—у*+ь * —О (оъ
V= — -)r--?9 X— U. B.Ъ)
Решение B.4), B.5) имеет вид
\+ . B.6)
P P
Используя формулы A9) и B9) приложения 5, а также теорему VI § 2
гл. XII, получим
К )\ L(^
ЛШ\Х B-7)
II. Область х> 0 с начальной температурой Vo движется со скоростью U*
Граничное условие на плоскости х = 0 имеет вид
J*L-hv = 0. B.8>
В этом случае нужно решить дифференциальное уравнение B.1) при AQ — О
с граничным условием B.8). Решение вспомогательного уравнения записывается сле-
следующим образом:
Ux (U2 , р\Чх
Используя формулу C1) приложения 5, получим искомое решение в виде
0= Vo Vo \ Ф* \ п- -\ еи*1хф* ! _L
2 °1 l2(*tL* У xh-(J L 2 <^)"л J
~60 L 2(^ J
Это решение справедливо при обоих знаках U и 2хЛ — ?/. Оно встречается при-
решении задач о диффузии примесей в расплавленном металле [6, 8].
§ 2] ГЛ. XV. ДАЛЬНЕЙШИЕ ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА 383
III. Установившееся периодическое изменение температуры в области х > О,
движущейся со скоростью U и имеющей при * = 0 температуру Vo cos (<o* -j- 0).
Ищем решение в виде
v=Re{V(x)eiio>t+B)}; B.11)
тогда функция V (х) должна удовлетворять уравнению
Решение уравнения B.12), ограниченное при *->оо, имеет вид
Ux ( U2 . /о) \yf
\-ьГ-хЫг + —)
Используя показательную форму комплексного числа
получим искомое решение в виде
v = Vo ехр | ^- — xab cos ~ ср | cos (о>* — ха^ sin ij <р) + 6\. B.14)
IV. Радиальное течение с диффузией в двух измерениях.
Предположим, что при установившемся радиальном течении несжимаемой
жидкости через каждую окружность в 1 сек проходит масса жидкости т. Тогда ра-
радиальная скорость жидкости иТ равна
т-Б^- <2Л5>
Тогда в цилиндрической системе дифференциальное уравнение теплопровод-
теплопроводности принимает вид
дг* "*" г дг х дг ""ТГ"~ ' BЛЬ)
где аг — определяется равенством B.15). Вспомогательное уравнение для B.16) при
нулевой начальной температуре запишется следующим образом:
где v = /п/4тсхр. Решение этого уравнения, ограниченное при г -> оо, имеет вид
B.18)
В качестве одного из примеров применения решения B.18) укажем, что, согласно
формуле C3) приложения 5, функция с изображением
1 ~KAqr) BЛ9)
имеет вид
г2 \--rV4x/ B20)
Решение B.20) обладает тем свойством, что полное количество тепла в области
г > 0 постоянно и равно Q. Таким образом, оно аналогично решению для линейно-
го источника (см. § 3 гл. X) применительно к данному случаю радиального движе-
движения среды.
Приведем еще один пример: из B.18) (как и в § 5 гл. XIII) следует, что реше-
решение уравнения B.16) для области г > 0 при нулевой начальной температуре и по-
постоянной температуре Vo в плоскости г = а имеет вид
a) J
384 ГЛ. XV. ДАЛЬНЕЙШИЕ ПРИМЕНЕНИЯ ПРЕОБРАЗЬВАНИЯ ЛАПЛАСА [§ 2
у V. Неограниченное твердое тело с постоянной начальной температурой Vo
движется вдоль оси х со скоростью —U. При *>0 поверхность цилиндра
х2 + У2 = а* поддерживается при нулевой температуре ¦).
В этом случае дифференциальное уравнение имеет вид
Полагая
v= ue-Uxl2x+V0i B.23)
получим
д2и . д2ы ?/2 - 1 да л /оо,ч
Переходя к полярным координатам в плоскости ху, получим следующее вспо-
вспомогательное уравнение:
д*и , 1. ди , 1 д2и . ,- л
-5^ + Т^ + Т2-^-^^0' B.25)
где
^а х+1^* B.26)
Граничное условие для B.25) имеет вид
и = -±- exp [Ur cos 6/2x] при
или
где
ео=1, а е„ = 2 при /г>1. B.28)
Уравнение B.25) имеет решение
оо
"=2fl« cos пЬ*п (ЯГ), B.29)
л = 0
где коэффициенты лЛ находят, подставляя B.29) при г = а в B.27).
Окончательно получим
Отсюда следует, что
а ° —I Kn(Ua/2%)
л=0
2 *Л> V Г ^2* 1 а / ( i^ Г ****** Wn {ur) Yn (ua) — Yn (ur) Jn (ua)] i
AJ еХР I ?л C^S п\ 2х / / 2 2 12—Г~2 2" Г
°' п п ^^
VI. Тонкий стера/сень 0 < х < I с нулевой начальной температурой движется
со скоростью U. При t >0 его конец х = / поддерживается при постоянной
температуре V, а конец х = 0 — при нулевой температуре. На поверхности
стержня происходит теплообмен со средой с нулевой температурой **).
*) В качестве примера Консер приводит случай, когда цилиндрическое отвер-
отверстие поддерживается при нулевой температуре; материал, удаляемый с одной сто-
стороны отверстия, помещается на другую.
**) Ряд задач подобного типа рассмотрен в [9].
§ 3] ГЛ. XV. ДАЛЬНЕЙШИЕ ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА 385
В этом случае дифференциальное уравнение (9.1) гл. IV принимает вид
его нужно решать при граничных условиях v = V при х = /, v = 0 при ^ = 0 и ну-
нулевой начальной температуре. Вспомогательное уравнение имеет вид
d2v U dv
dx2 у. dx % ' ~-~-"
а граничными условиями служат v = V/p при х = I и v = 0 при .* = 0. Тогда
Г U (х — /) 1
Используя теорему обращения, получим
7"
Подынтегральная функция в соотношении B.34) имеет простые полюсы при
К = 0, а также в корнях уравнений
Т. е. при
л = —v ^ ^—» /1 = 1. А... B.60)
Находя вычеты относительно этих полюсов, окончательно получим
sh U (fj* + Ьф1Ь\ Г ^/ (^ - /)
t/K 6XPL
2х J^[(v/x) + (^2/4x2) + (^2^//2)] Pl L 4х ^ /2 J J
Л=1 B.36)
§ 3. Тепловые регенераторы и теплообменники
Передача тепла от движущейся горячей жидкости к холодной имеет
очень большое практическое значение. Имеются системы двух основных
типов, при помощи которых передается тепло: теплообменники и регене-
регенераторы.
В теплообменнике горячая и холодная жидкости текут по обеим сторо-
сторонам тонкой перегородки, которая предназначена просто для их разделения;
тепло передается от одной жидкости к другой через эту перегородку, кото-
которая в идеальном случае настолько тонка, что ее теплоемкостью можно пре-
пренебречь, а сама она ведет себя при теплопередаче просто как контактное
сопротивление (см. пример Г § 9 гл. I). Жидкости могут течь либо в одном
направлении (параллельное течение, или прямоток), либо в противоположных
направлениях (встречное течение, или противоток); установившееся состояние
достигается очень быстро, и решения для него приводятся во всех работах
по теплообмену (см., например, [10]).
В регенераторах горячая и холодная жидкости попеременно проходят
по твердой стенке; когда по ней протекает горячая жидкость, она погло-
поглощает тепло, а затем отдает его холодной жидкости, причем этот процесс
циклически повторяется. Здесь наиболее важно сохранение тепла стенкой,
и поэтому следует тщательно изучить поток тепла в ней. Следует отметить,
25 Г. Карелоу, Д. Егер
386 ГЛ. XV. ДАЛЬНЕЙШИЕ ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА [§ 3
что данная задача оказывается достаточно сложной. Для практики основной
интерес представляет окончательный установившийся периодический режим.
Изложим несколько приложений метода преобразования Лапласа к не-
неустановившимся режимам в идеализированных системах обоих описанных
типов.
Пусть поверхность стенки*) представляет собой плоскость z = О,
и пусть в области z < 0 в направлении оси х течет равномерный поток
жидкости со скоростью U. Предполагается, что жидкость хорошо переме-
перемешивается и, следовательно, ее температура в любой плоскости, перпендику-
перпендикулярной направлению потока, одинакова; однако при этом предполагается
также, что тепло не распространяется в направлении течения жидкости.
Пусть М — масса жидкости, соприкасающейся с единицей поверхности
стенки, с'—удельная теплоемкость жидкости, и — ее температура в момент
времени t в точке х (т. е. во всей полуплоскости х = const, z < 0),
v^—температура поверхности стенки в точке х (т. е. во всех точках пря-
прямой х = const, 2 = 0) в момент t, a. H — коэффициент теплоотдачи стенки.
Как и в § 9 гл. IV, температура жидкости должна удовлетворять урав-
уравнению
-|f + иЪ7 + b'{u—vs) = 0, C.1)
где
Уравнения C.1) и
? и). z = 0, C.3)
служат граничными условиями для уравнения теплопроводности в теле
d2v .d2v I dv п
Совершенно очевидно, что решение этих уравнений связано со значительными
трудностями **), и поэтому на практике принимают различные упрощающие
предположения. Обычно полагают, что коэффициент теплопроводности тела
в направлении течения жидкости равен нулю и конечен [12] или бесконечен
в перпендикулярном ему направлении.
I. Твердое тело с бесконечно большим коэффициентом теплопро-
теплопроводности в направлении, перпендикулярном направлению течения, и
нулевым коэффициентом в направлении течения ***).
Пусть М — масса твердого тела, приходящаяся на единицу поверхности
стенки, с — его удельная теплоемкость; пусть, далее, температура тела на его
поверхности равна vs(x, t)\ эта функция удовлетворяет дифференциальному
уравнению
^ —«) = 0. C.4)
где
ь
*) Под стенкой автор понимает здесь полуограниченное твердое тело z > 0.
(Прим. ред.)
**) В статье [11] рассматривается установившийся периодический режим в ре-
регенераторах.
***) На практике это приближенно реализуется в случае, когда жидкость течет
сквозь гранулированную набивку, частицы которой настолько малы, что температуру
по всему их объему можно считать постоянной.
§ 3] ГЛ. XV. ДАЛЬНЕЙШИЕ ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА 387
В нашей задаче мы должны рассматривать дифференциальные уравне-
уравнения C.1) и C.4). Рассмотрим*) область х > О, причем начальная темпера-
температура как твердого тела, так и жидкости**) равна нулю и при ?>0 темпе-
температура жидкости в плоскости jc = O поддерживается равной единице.
Вспомогательные уравнения, соответствующие C.1) и C.4), имеют вид
^ C.6)
(p-\-b)vs — bu = O, х>0. C.7)
Их следует решать при условии, что при д: = 0, и=1/р. Отсюда
получим
Чтобы найти vs и и отметим, что, согласно формуле B4) приложения 5,
1 gaxip = l {/0[2 (axtL2]}. (ЗЛО)
Тогда из B.6) гл. XII находим
= /. {e-»I0[2(axtj% C.11)
В таком случае, в соответствии с теоремой IV (см. § 2 гл. XII), получим
1 г 1 1"| ( ах \ 1 ( ах \
т[т~ТТхр+)~ (+ь)ехр\+ь) —
г
— I \ I p~bx/ Г 9 (ахт^Л dr > C\ \9\
(o j
из равенств C.11) и C.12) следует, что
1 ехр у^) = L е-»<10 [2 (axt?>] + Ь f е~Ч0 [2 (axj'*] dx
, C.13)
или
) = L \\+(ax)l/* f e^friax^T-Kdz , C.14)
*) Это задача о начальном разогреве идеального регенератора. Она рассматри-
рассматривалась в [13—16]. Общий обзор и библиографию можно найти в [17]. В работах [18, 19]
получено решение для случая установившегося лериодического режима в виде инте-
интегрального уравнения и рассмотрено его решение. В работе [20] приведено другое
рассмотрение случая установившегося периодического режима. Опубликованы также
приближенные решения для этого случая [21]. Применение численных методов рас*
смотрено в [22].
**) Область х > 0 состоит из двух частей: твердого тела х > 0, z > 0 и жидко*
сти х > 0, z < 0. (Прим. ред.)
25*
388 ГЛ. XV. ДАЛЬНЕЙШИЕ ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА [§ 3
«ЛИ
ах \
±ехр(
ехр (*}-) -1 ехр [**. _ «] / ехр (- ?*1) /0 [2 <«,',)*]
C.15)
где C.14) получается из C.13) путем интегрирования по частям, а другая
важная форма C.15) легко получается умножением обеих частей C.11)
«а ехр( ^у\ и интегрированием по л: от 0 до х.
Используя выражения C.12) и C.14), а также теорему VII § 2 гл. XII,
получим из C.8) и C.9), что если t < x/U\ то и и vs равны нулю, а если
/ > x/U, то
l
« J е-*^2(ахтI/2]т-'/2</т1, C.16)
]
= e-b>xiu\ i+(aJC) J
I о ]
t-X/CJ
J e-40[2(axx)l/2]dT, C.17)
о
где а = bb'jU. Решения для других значений температуры подводимой жидко-
жидкости можно получить, воспользовавшись теоремой Дюамеля.
Уравнения, аналогичные приведенным выше, появляются в теории ионо-
ионообменных колонн; недавно они привлекли к себе большое внимание [23, 24]*).
Поскольку такие уравнения встречаются очень часто, функцию
X
J(x. y)=l— е-* /е-/0[2(гуI/2]</т, C.18)
о
которая появляется в выражениях C.12), C.13) и C.15), называют фунда-
фундаментальной; равенство двух последних выражений дает следующий важный
результат:
. х)=1+е-*-У/0[2(хуL*]. C.19)
Свойства этой функции были достаточно полно рассмотрены Гольдштей-
ном [23].
II. Случай выделения тепла в твердом теле **).
Пусть при t > 0 в твердом теле выделяется в единицу времени на единицу массы
постоянное количество тепла, равное Q. Начальные температуры как тела, так и
жидкости равны нулю. При i > 0 температура жидкости в плоскости х = 0 поддер-
поддерживается равной нулю.
В этом случае уравнение C.4) заменяется уравнением
. + *<*,-„) = .?. C.20)
*) Следует отметить, что Томас [24] вместо функции C.18) использовал функцию
? (-*• У) = [1 — J (х, у)] ехр {х + у)
и что некоторые авторы последовали его примеру. Другие источники указаны
в списке литературы к работе [23].
**) Выделение тепла в шаре, погруженном в движущуюся жидкость, рассмот-
рассмотрено в [25].
§ 3] ГЛ. XV. ДАЛЬНЕЙШИЕ ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА 3891
Решая уравнения C.1) и C.20) с а = vs = 0 при * = 0, л: > 0 и а = 0 при х = 0,
t > 0, получаем для вспомогательного уравнения
b'x px , ax
где
a=^f" C.22>
Чтобы найти й", нам необходимы выражения
ах \ /1 . b \ 1 / ах \ _
) \ Р Р2 ) Р~^г b V Р~\" b /
• i 4- bt — bz] e~bzI0 [2 {axzy2] dz \. C.23>
1 / ax \ Г1 ?' 1 / ал: *
f / |
L \ /0 [2 (ал:О1Л — ?'*"* ' / ^ Vo [2 (axz)ll* ] dz \, C.24)
которые вытекают из C.11) и теоремы X § 2 гл. XII. Используя их и теоремы VI
и VII того же параграфа, получим
Qb' {(b + b')t-l + ezp[-(b + b')t]} t x
а- с(Ь + Ь'У ' есЛ *<!/'
Если t > x/Ut то
Qb'
t-x/U
_ *'exp [—(* + *') ^-(-?.JJ + ^t]|/0 ^(arcI/»]^. C.26)
Если вплоть до момента ^ = x/U количество тепла, выделяемого в единицу вре-
времени, равно нулю *), а при t > xjU оно равно постоянной величине Q (т. е. после
того, как частицы жидкости, находившиеся в момент времени t = 0 в плоскости х = О
достигнут плоскости л:), то C.21) примет вид
Ь'Х I ^'^ 1 I (I O7V
Используя C.23) и теорему VII (см. § 2 гл. XII), получим, что при t < xjU
и равно нулю, а при t > x/U
t-xfU
Q
и
-__ехр(-— / j^^^J-xj+l # /о[2(-^)
о
J
C.28)
Это решение можно выразить также через функцию / (л:, у), определяемую
соотношением C.19).
¦) Этот случай рассмотрен в [26]. Он имеет место, когда тепло выделяется
в результате химической реакции. Аналогичным путем легко рассмотреть и случай,
когда количество выделяющегося тепла является линейной функцией vs, т. е. когда
Q Q(l + P)
390 ГЛ. XV. ДАЛЬНЕЙШИЕ ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА [§ 3
III. Коэффициент теплопроводности твердого тела К в направлении, пер-
перпендикулярном движению жидкости, конечен, а в направлении движения жидкости
равен нулю.
В качестве примера, в котором получается простое решение, рассмотрим полу-
полуограниченное твердое тело z > 0, предположив, что в любой точке температура его
поверхности равна температуре жидкости (например, случай очень большой вели-
величины Н в уравнении C.1)).
В твердом теле температура v должна удовлетворять уравнению
-Й--т4г=0> 2>0- х>0' t>0 C-29>
при условии на поверхности
v = и, х > 0, t > 0, z = 0, C.30)
К^г~=М'с' i^+U-^L , лг>0, />0, г = 0, C.31)
dz \ dt l дх) v '
где а — температура жидкости в плоскости х, а условие C.31) вытекает из C.1)
и C.3). Как и раньше, рассмотрим случай нулевой начальной температуры в области
<гг > О, л: > О и и = 1 при t > 0 на плоскости х = 0. Здесь вспомогательные уравне-
уравнения имеют вид
2^ = 0, г>0, х>0, C.32)
v= и, z = 0, .* > 0, C.33)
t/ -?- + ри — k -^- = 0, х > 0, г = 0, C.34)
где
C.35)
Их нужно решить при_условии, что и= 1/р, когда х = 0; кроме того, v при z->co
ограничено, а при х -> оо и и v ограничены. Искомые решения имеют вид
Й1. C.36)
1 ( рх I kx . \ рЧ* \
р \ U \U^ ) Л* \
Таким образом, из формулы (8) приложения 5 и из теоремы VII § 2 гл. XII
следует, что и и v при t < х/и равны нулю, а при t > x/U
C.38)
L
t; = Ф* Г kx + zU "I C 3g)
Решение вспомогательных уравнений в случае более общих граничных условий
C.1) и C.3), или для тела в форме пластины или цилиндра, не наталкивается на труд-
трудности, хотя изображения получаются значительно более сложными.
IV. Задача, аналогичная задаче III, но с конечной величиной Н.
Положив h = HI К и k = K/M'c\ получим
и решение
и— 1 —-
о
§ 3] ГЛ. XV. ДАЛЬНЕЙШИЕ ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА 391
которое при /z->oo сводится к C.38). Выражение для небольших значений времени
можно получить, разлагая показательные функции в C.40) по степеням (q-\-h)~l
и используя формулы типа A4) и A8) приложения 5.
V. Задача, аналогичная задаче III, но при t > 0 в плоскости (на единицу
массы за единицу времени) выделяется постоянное количество тепла Q. При
t > 0 в плоскости х = 0 температура жидкости равна нулю. Начальные темпе-
температуры жидкости и тела равны нулю.
Температура жидкости и записывается следующим образом:
с'*'*и = 2*' [^ - 1 + **'*' V [*' (**)'*] -
]1/2 г
Un
kk'x-{-U I kx \
U \2[iU{Ut — x)\4*r
> / 111 /Q >1O\
~u~\ \y ( }
где k определяется равенством C.35), a k' = k/i= pc/M'c'.
VI. Неустановившийся режим теплообменников.
В качестве примера условий, имеющих место в теплообменнике до наступления
установившегося состояния, рассмотрим случай противотока в области х > 0.
Пусть по одну сторону тонкой перегородки (с нулевой теплоемкостью) в плоско-
плоскости z = 0 жидкость течет со скоростью U в направлении оси х; пусть, далее,
М' — масса жидкости на единицу поверхности, с' — удельная теплоемкость этой
жидкости, а — температура в плоскости х в момент времени t. Пусть по другую
сторону перегородки на единицу поверхности приходится масса жидкости Мх с удель-
удельной теплоемкостью сх\ пусть, далее, их — температура жидкости в плоскости х
в момент времени t, а — Ux — ее скорость в направлении х. Пусть, наконец, Н общий
коэффициент теплопередачи *), так что тепловой поток в единицу времени через
стенку в точках х = const, z = 0 равен
C.43)
Дифференциальным уравнением для и служит C.1), т. е.
¦|jr+tf-g!+*'<«-«•)-0, х>0, C.44)
для их мы получим аналогичное уравнение, в котором U заменено на — Ux, т. е.
где
Предположим, что начальная температура обеих жидкостей равна нулю и что
яри t > 0 в плоскости х = 0 и = 1. Соответствующие вспомогательные уравнения
лмеют вид
u F + {р + У)"~~ Ь'"х = Oj x> °J C'47)
^M = 0, л:>0. C.48)
Их следует решать при условии, что при_^ = 0, и=\/р, а при х->со их стре-
стремится к нулю. Решая уравнение относительно и, получим
| C.49)
•) Для однослойной стенки Н = K/d, где К — теплопроводность стенки, a d —ее
толщина (см. § 9 гл. I).
392 ГЛ. XV. ДАЛЬНЕЙШИЕ ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА [§ 4
где
АЦЦХЬ'ЬХ , U+Ux
(tf+tfJ' *~ 2?Д/
р~~ U+Ux
Величину и находят при помощи формулы B5) приложения 5, применяя анализ
использованного выше типа (см. C.11) — C.16)).
Искомое решение имеет вид
и = О, если t < -jj ,
txlU
-b'*lc/ f *-*Vi (aK[x(x + 2h)]) ^ -, C.51)
если *>-[/'
Функция их определяется аналогичным образом: если t < x/U, она равна нулк>>
а если t > xfl/, то
.vw,// [MaNT + 2^1 ¦ а^/2 {а [x(x + 2to)]^} j
J # I [( + 2*)]* + + 2^ (
Встречное течение в ограниченной области 0 < х < I рассматривается аналогич-
аналогичным путем: и будет иметь заданное значение при х = 0, а щ — при х = /. При прямо-
прямотоке в области х > 0 как и, так и их точно определяются в плоскости х = 0.
§ 4. Тепловой поток в слоистых системах
Выше неоднократно отмечалось, что в составных системах, в которых имеются
как хорошие, так и плохие проводники тепла, простое и адекватное приближение
получается в том случае, если хороший проводник считать идеальным проводником
с конечной теплоемкостью. То же решение получается и тогда, когда п относительно-
плохих проводников с температурами vx, ..., vn и площадями поверхностей Ш| ©„
прилегают к одному общему идеальному проводнику с массой М, температурой v
и удельной теплоемкостью с .
В этом случае граничные условия на поверхности идеального проводника запи-
записываются в виде
+ /л f г\ /л ov
u^ ("n/n — v» {*•*)
где /i, ..., /л — тепловые потоки, втекающие в проводники, a Q — количество тепла
выделяющееся в идеальном проводнике в единицу времени.
Условия D.1) и D.2), вместе с граничными условиями на других поверхностях
проводников, дают достаточное число уравнений для определения i>i, ..., vn. Ниже
приводится несколько примеров.
I. В областях *) О < х < а и х > а находится одинаковый материал с тер-
термическими коэффициентами /С, р, с, %. При х = 0 тепловой поток равен нулю.
При х = а обе области соприкасаются с массой М (на единицу поверхности)
идеального проводника с удельной теплоемкостью &'. Начальная температура
идеального проводника равна VQ, а окружающих областей — нулю.
В данном случае температура идеального проводника равна
оо
cos2иdu Г ™№Л .
l + 2ku sin 2u + 4fc2a2 cos2 и еХр [ a2 J f
*) В данной задаче рассматривается полуограниченное тело с плоскостью
являющейся идеальным проводником. (Прим. ред.)
§ 5] ГЛ. XV. ДАЛЬНЕЙШИЕ ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА 393
где
'-¦?••
II. В области О <; г < а находится материал с термическими коэффициен-
коэффициентами К\, pi, C\9 "*.{, vlt в области а < г < Ь — идеальный проводник с коэффициен-
коэффициентами р, с, v, в области г > Ь — материал с коэффициентами /B, Рг. С2. Х2> *>2-
В начальный момент область а < г < b находится при температуре Vo, другие
области — при нулевой температуре *).
Температура vx в области 0 < г < а определяется формулой
*к, ,/щ$• D-5)
о
где
k \ k'Ц *" D.6)
и
А (и) = [У, (а) Л (*«) - ЛVo (и) /, (ku) + Л-^и/о (а) /0 (to)]* +
+ [/i (и) ^о (to) — *V0 (и) Ki (to) + *4 (u) Vo (te)]«. D.7)
Если начальная температура всей системы равна нулю, а в область а < г < b
в единицу времени поступает количество тепла Q, то
D.8)
§ 5. Установившийся периодический режим
Во многих практических задачах тело подвергается воздействию перио-
периодического изменения температуры или тепловых потоков; тогда желательно
найти установившийся периодический режим, наступающий после затухания
переходных процессов, на которые влияют начальные условия. Это можно
сделать путем разложения заданной температуры по компонентам Фурье и их
последующего раздельного рассмотрения, как в § 6 гл. III. Однако на прак-
практике получающийся ряд Фурье медленно сходится вблизи наиболее интересных
значений времени, и для нахождения более удобных форм решения долгое
время использовались такие же приемы, как и в § б гл. III и § 8 гл. IV.
Один из удобных методов нахождения таких решений заключается в при-
применении преобразования Лапласа. Излагаемый ниже метод почти точно со-
совпадает с методом операционного исчисления [29—31] для установившихся
состояний, но не предполагает предварительного знакомства с ним.
Для определенности рассмотрим только наиболее важный случай, а именно
волны прямоугольной формы; аналогичным путем можно исследовать и другие
случаи. При расчете мы предполагаем, что при t > 0 температура или тепло-
тепловой поток меняется по периодическому закону, а начальная температура
твердого тела равна нулю. Таким образом, температуру или тепловой поток,
*) Такую систему предлагали в качестве приближенной модели кабеля с ма-
маслом [27, 28]. В тех же статьях приведено несколько приближенных решений для
небольших значений времени.
394 ГЛ. XV. ДАЛЬНЕЙШИЕ ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА [§ 5
воздействующий на тело, можно представить в виде функции
= 1, nT<t <nT-{-Tv n = 0, 1,
= 0, nT+Tx<t<{n+\)T, n = 0, U
E.1)
Например, пусть РоуA) — поток, равный FQ в течение времени Г, и нулю
в течение Т — ^ и т. д., т. е. период функции Foy(t) равен Т. Из теоре-
теоремы VIII § 2 гл. XII следует, что
- 1 —*-*г«
*-,о--*г E-2)
Для пояснения метода рассмотрим задачу, которую мы уже обсуждали
в § б гл. III, именно: при х = 0 область О < х < / имеет температуру
v = 0, а при х = 1 — температуру v = y(t).
Как и выше (см. § 6 гл. XIIj, используя E.2), получим
-_¦ A—
V
или
v = (l— е-РТ>-\-е~РТ — е-Р(г+г-)+ ...) sh.?*. . E.4)
р sn ^/
Вначале нужно найти значения v в первый период после t = 0. Из фор-
формулы E.4) данной главы, F.10) гл. XII и теоремы VII § 2 той же главы
следует, что
л1
E.6)
Эти решения, конечно, можно было получить и в гл. XII, и пока мы
еще не видим их очевидной связи с решением для установившегося перио-
периодического режима.
Для его нахождения применим к выражению E.3) теорему обращения
x(i-,-"¦) eh ,* ' E'7)
f-ioo
где, как обычно, jx = (Х//гI/в. Подынтегральная функция в E.7) имеет простой
полюс в точке Х = 0, который дает член (хТг/1Т), и простые полюсы при
х=2пр19 m=±lt ±2 E.8)
которые в свою очередь дают ряд членов, описывающих колебания с перио-
периодами 7, <jT, ... Они составляют ряд Фурье для установившейся периоди-
периодической части решения (температуры); ее мы сейчас не определяем; обозначив
через vs ее величину, мы затем будем искать ее в более удобной форме.
Наконец, подынтегральная функция имеет еще ряд полюсов при
л=1. 2, ... E.9)
§ 5] ГЛ. XV. ДАЛЬНЕЙШИЕ ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА 395
Определяя вычеты относительно этих полюсов и комбинируя найденные ре-
результаты, мы получим решение, содержащее члены, дающие установившуюся
периодическую его часть, и члены, дающие переходную часть
/ 1 ч/г Г ( *<П2%Ч\ ( m2**(t—Tx)X\
(-D" ехр — -ехр - \2
^sin^-. E.10)
nil
n-l
Итак, E.10) служит общим решением, справедливым для всех значений
времени; поэтому оно должно совпадать с решением E.5), если 0 < t < Tv
и с решением E.6), если Тг < t < 7\ Таким образом, приравнивая E.10) и
E.5), мы получаем при 0 < t < Т соотношение
- EЛ1)
nil —
Поскольку левая часть в формуле E.11) является периодической функ-
функцией с периодом 7, отсюда следует, что правая часть представляет собой ее
значение а в момент времени rT-\-t, где г — любое целое число. Анало-
Аналогичным образом, используя E.6), получим, что установившаяся температура
в момент rT-\-t, где Т1 < t < Г, равна следующей величине:
л=1 л 1 —ехр
Эти решения согласуются с решениями F.17), F.19) гл. III, полученны-
полученными при помощи теоремы Дюамеля. Ниже мы приведем другие решения того
же типа.
I. Полу ограниченное твердое тело х > 0, поверхность х = 0 нагревается
пульсирующим *) тепловым потоком Foy (t).
В этом случае температура поверхности в конце концов становится равной
E13>
Она складывается из периодической части vp9 накладывающейся на возрастающую
температуру, обусловленную средним потоком на поверхности, равным F0Ti/T. Вели-
Величина vp через промежуток времени ЬТ после начала периода нагрева имеет следую-
следующее значение:
г—Н—«г ) 1A — #)#'* — тс '*/(a, b)\, v < b < а, E.14)
а * ~^ '
vp=^ж~(irf(A ~а)ь''г~{Ь~а)'1г~*~'А'{а'Ь)]' a<b<h EЛ5)
где а = Ti/T, a
*) Эта задача появляется в качестве приближения для многих практических задач,
например для задачи о нагреваний пулеметов и для задачи о нагревании цилиндра
трением на участке его поверхности. Нагревание вращающегося анода рентгеновской
трубки рассматривается в статье [32]. Пульсирующий тепловой поток через круглую
площадку на поверхности полуограниченного тела рассмотрен в работе Егера [оЗ].
396 ГЛ. XV. ДАЛЬНЕЙШИЕ ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА [§ 6
Интегралы E.16) взять сравнительно легко. Некоторые их значения приве-
приведены в [33].
II. Пульсирующий точечный источник в неограниченной среде.
Пусть в начале координат находится источник мощностью (на единицу длины) Qcp (О-
Тогда при достижении установившегося режима температура на расстоянии г от начала
координат через время ЬТ после начала периода нагрева равна (Qa/4nKr) + vpj где
периодическая часть vp имеет вид
fp = —-тг- 1*'1^ттг| — <М / — ^ az(, 0<b<a, E.17)
i u /
где
я=^-, С = г(хГ)-^- E.18)
III. Пульсирующий линейный источник в неограниченной среде.
Предположим, что вдоль некоторой прямой расположен линейный источник тепла
мощностью (на единицу длины) Qcp (t). Тогда при больших значениях времени темпе-
температура на расстоянии г от этой прямой равна
где периодическая часть vp при 0 < b < а в свою очередь равна
С*\ Q
E.20)
Величины a, b n С определены выше в примере II.
§ 6. Линейная асимптотика и запаздывание
Если изображение у" какой-нибудь величины имеет вид
F.1)
где дробь f(p)/k(p) при /> = 0 не имеет особенности, то у определяется соотно-
соотношением *)
где
7WM0)
Таким образом, при больших значениях времени у представляет собой в пределе
прямую с наклоном / @)/Д @), отсекающую на оси t отрезок, или «запаздывание», L.
В теории теплопроводности встречается много величин, обладающих аналогичными
свойствами, например: 1) суммарный тепловой поток через стенку, поверхности ко-
которой поддерживаются при постоянных температурах; 2) температура в теле при
линейном росте температуры поверхности и 3) температура в замкнутой, термически
изолированной системе, к которой в единицу времени подводится постоянное коли-
количество тепла.
Эта асимптотика имеет большое значение по двум причинам: 1) она дает при-
приближенные значения температуры, что во многих случаях является достаточным;
2) измерение наклона и отсеченного отрезка служит методом одновременного опре-
*) В соотношении F.2) все члены, кроме первого, содержат отрицательные сте-
степени t, т. е. затухают с увеличением t. {Прим. ред.)
§ 6]
ГЛ. XV. ДАЛЬНЕЙШИЕ ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
397
деления *) К и х. Кроме того, запаздывание служит удобной мерой возможных ошибок
измерительных приборов, подвергающихся воздействию переменных температур.
Выше уже приводилось много примеров для простых случаев, но описываемый
здесь метод применим также для таких сложных систем, что получение для них пол-
полного решения в явном виде становится практически невозможным. Например, для
расчета запаздываний в случае сложных стенок с произвольным числом слоев был
дан обычный простой метод **).
Ниже мы приводим решение для запаздывания температуры в замкнутых си-
системах. Во всех случаях /С, р, с и % — термические коэффициенты твердого тела.
I. Пластана 0 < х < а. В плоскости х = 0 тепловой поток отсутствует.
Плоскость х = а соприкасается с хорошо перемешиваемой жидкостью или
идеальным проводником с массой М (на единицу поверхности) и удельной тепло-
теплоемкостью с', к которой при t > 0 в единицу времени подводится постоянное ко-
личество тепла. На поверхности х = а контактное сопротивление равно 1/hK-
р = Мс'/арс.
Запаздывания Lx в твердом теле и Lf в жидкости равны соответственно
\
ah
2*
J+7h>- <6'4>
II. Цилиндр 0 <; г < а находится в контакте с хорошо перемешиваемой
жидкостью с массой М (на единицу длины). Подвод тепла и контактное сопро-
сопротивление такие же, как и в примере I. р. = Мс'/па2рс.
В данном случае
a2 f ц. 1 . ti ) r*_ L = а2 /11
III. Шар 0 < г < а находится в контакте с хорошо перемешиваемой
жидкостью с массой М. Подвод тепла и контактное сопротивление такие же,
как и в примере I. р. = ЗМс'/4па3рс.
В данном случае
L - п2 I * 1 1 1 ** ] Г\ L - д2 { l I l \ F6)
Следует отметить, что хотя эти запаздывания заметно зависят от h (особенно
если его величина мала), значения (Lc-\-\*.Lf), где Lc — запаздывание в центре (х = 0
или г = 0), не зависят от Л; они равны а2/6ъ, а2/8ъ и а2/10ъ для пластины, цилиндра
и шара соответственно. Численным расчетом можно показать, что этот результат
приближенно справедлив также для ограниченного цилиндра, рассматриваемого ниже.
IV. Цилиндр радиуса а и длиной I всей своей поверхностью соприкасается
с хорошо перемешиваемой жидкостью с массой М и удельной теплоемкостью с',
к которой при t > 0 подводится постоянное количество тепла (в единицу вре-
времени). Контактное сопротивление отсутствует. \*. = Me'/na2lpc, X = 1/A -f- fx).
Ниже приводятся данные***) о запаздывании в жидкости Lf ив центре цилиндра Lc.
На
1,0
1,5
2,0
2,5
3,0
4,0
6,0
оо
0,102—0,040Х
0,162—0,06U
0,201—0,075Х
0,223—0,084Х
0,235—0,09U
0,246—0,099Х
0,248—0Д08Х
0,250—0Д25Х
0,040Х
0,06U
0,075Х
0,084Х
0,09U
0,099Х
0,108Х
0Д25Х
0,062
0,101
0,126
0,139
0,144
0,147
0,140
0,125
*) В статье [34] приведены формулы для определения количества тепла, прохо-
проходящего через пластину, поверхности которой имеют постоянную температуру. Соот-
Соответствующие формулы для шара приведены в [35], а для цилиндра — в [36]. Последний
случай рассмотрен также в [37].
**) Случай цилиндра рассматривается в [38, 39].
***) Решение данной задачи можно найти в [31]. Аналогичным образом можно рас-
рассмотреть отмеченный выше случай наличия на поверхности контактного сопротивления.
398 ГЛ. XV. ДАЛЬНЕЙШИЕ ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА [§ 7
§ 7. Выделение тепла
Выше уже был решен ряд задач, в которых выделение количества тепла в еди-
единицу времени в единице объема либо постоянно, либо является простой функцией
положения или времени. Все эти задачи можно решить непосредственным примене-
применением метода преобразования Лапласа. Здесь мы покажем применение этого метода
к более сложным задачам, в частности к нескольким задачам, в которых количество
выделяемого тепла является линейной функцией температуры, и к задачам, в кото-
которых оно определяется решением уравнения диффузии.
I. Пластана О < х < /. Тепловой поток на плоскости х = О равен нулю. Тем-
Температура плоскости х = / и начальная температура равны нулю. При t > О
в единицу времени выделяется количество тепла, равное K(A-\-Bv).
В данном случае следует решить уравнение
d2v I dv , D .
+ Bt; A <7Л>
Вспомогательное уравнение имеет вид
где
? = {-в- G.3)
Решать это уравнение следует при условиях
' ' dx * г
Искомое решение имеет вид
G.5)
A f cos хВ1!* 11
В \ cos IB1!* j ~r
(— 1)л ехР И—
[4В/2 —
/1=0
( '
Это решение справедливо при любом знаке В. Если В отрицательно (например,
при нагревании электрическим током таких веществ, как графит с отрицательным
температурным коэффициентом сопротивления, или в случае отвода тепла от стержня
излучением или конвекцией), то решение для установившегося периодического режима
содержит гиперболические функции. При положительном В (что обычно имеет место
при нагревании электрическим током) все показательные функции в решении G.6)
при ?->оо стремятся к нулю, если
В<-?г- <7-7>
Если это неравенство справедливо, то существует установившееся распределение
температуры, определяемое выражением*)
&Л G.8)
А1-
В \ cos IB1**
При В > п2/41 количество выделяющегося в единицу времени тепла слишком
велико, чтобы его можно было удалить, и установившееся распределение не наступает.
II. Та же задача, что а в примере I, но граничные условия имеют вид
-gj + *tr = Q. x = l. G.9)
*) Численные значения установившейся температуры для пластины, цилиндра и
шара приведены (для случая В > 0) в статье [40] и (для случая В < 0) в статье [41].
§ 7] ГЛ. XV. ДАЛЬНЕЙШИЕ ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА 399
В данном случае
hA cos хВ1/г А
В {h cos IB1'* — В1'* sin IB1!*} В
\ cos (xa fl\ exo \(Bl2 — а?Л *tt?\
G.10)
где an, /i=l, 2, ... —положительные корни уравнения
atga = lh. G.11)
В этом случае условие существования установившегося состояния имеет вид
В<ф. G.12)
III. Цилиндр 0 < г < а с нулевой начальной температурой; при t > 0 гра-
граничная поверхность г = а поддерживается при нулевой температуре. При t > О
в единицу времени выделяется количество тепла, равное К (А -\- Bv).
В данном случае
^2 J "
где аЛ, /1=1, 2, ... —положительные корни уравнения
/о(«)=О. G.14)
Если В положительно, то решение для установившегося состояния существует
только в том случае, когда В < aj/a2.
IV. Установившаяся температура в пластине, когда количество выде-
выделяющегося в единицу времени тепла является экспоненциальной функцией темпе-
температуры.
Решение такой задачи с установившейся температурой *) представляет интерес
в связи с существованием верхнего предела количества выделяющегося в единицу
времени тепла, что видно из соотношений G.7) и G.12).
Простым изменением переменных подлежащее решению уравнение можно при-
привести к виду
0 = 0, 0<*<1, G.15)
с условиями
-JL = о, х = 0, G.16)
и
i, = 0, х = 1. G.17)
Предположим, что i>0 есть значение v при .* = 0. Вначале решим уравнение
G.15), учитывая G.16) и зная, что при х = 0 v = v0. Первый интеграл G.15), удовле-
удовлетворяющий этим условиям, имеет вид
-^- = — {2Р(**° — е°))Ч%. и G.18)
Повторное интегрирование дает
v = v0 — 2 In ch \x (^ P^°Y/21. G.19)
Так как это решение должно удовлетворять уравнению G.17), то v0 определяется
соотношением
*) Неустановившееся состояние рассматривается в [42], где для расчетов исполь-
использовался дифференциальный анализатор.
400 ГЛ. XV. ДАЛЬНЕЙШИЕ ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА [§ 7
или, полагая
о-г-
z. G.20)
Если 0 < р < 0,88 ..., то это уравнение имеет два корня, соответствующие двум
возможным значениям t/0 и тем самым двум возможным решениям для установивше-
установившегося состояния. Если р > 0,88 ..., то это уравнение не имеет действительных корней
и решение отсутствует.
V. Тепло выделяется в результате необратимой реакции первого порядка.
В этом случае, допуская, что скорость реакции не зависит от температуры,
можно считать, что количество тепла, выделяющегося в единицу времени, равно КАС,
где А — постоянная, а С — концентрация диффундирующего вещества. Последняя
определяется дифференциальным уравнением
где D — коэффициент диффузии, а & — постоянная [43]. Уравнение G.21) имеет форму,
уже рассмотренную в настоящем параграфе; его можно решить при помощи методов
данного параграфа или соотношения A4.25) гл. I. Когда С найдено, искомая темпе-
температура определяется уравнением
Вспомогательное уравнение для G.22) при нулевой начальной температуре имеет
вид
?_?;__*. ,7.23,
Таким образом, если С известно, то его можно подставить в уравнение G.23), и
тогда величину С определять не нужно.
В качестве примера рассмотрим пластину 0 < х < / с нулевой начальной тем-
температурой, нулевой концентрацией и с граничными условиями
? = 0, ? = 0. ,=0, G.24)
C = COt v = 0, х = 1. G.25)
Тогда при этих граничных условиях из G.21) получим
g^ Cochx[(p+k)/D]lb
pchlUp+k)/D]1'* '
Использование этого значения С при решении уравнения G.23) дает
= АСоъР | ch х (/7/*I/2 __ chx[(p+k)/D]4*
V2 ch
i — D) p [p + ?*/(* — D)] ( ch / (p/x)
,4C0D ^___
ch / (k/DL> j ^
oo
/2=0
°° cos B/г + 1) nx/2l
X
[B/г + lJ тс2 (у. _ D) — 46/2]
/2=1
При помощи изложенного метода можно сравнительно легко решить ряд задач
подобного типа [44].
§ 8] ГЛ. XV. ДАЛЬНЕЙШИЕ ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА 401
§ 8. Система автоматического регулирования температуры
На практике часто оказывается желательным поддерживать постоянную
температуру*) в некоторой области, например в печи, которая теряет тепло
как посредством установившегося теплового потока через ее стенки, так и
в результате искусственных возмущений (например, при открывании ее
дверцы). Для этого поступление тепла в печь регулируется по термометру
в печи. Наиболее распространенные методы регулировки температуры заклю-
заключаются в следующем: 1) регулировка «включение — выключение», при
котором нагревающий ток (или часть его) включается при падении до опре-
определенного уровня температуры, показываемой термометром, и выключается
при ее повышении до другого заданного уровня; 2) пропорциональная
регулировка, при которой количество тепла, подводимого в единицу вре-
времени, пропорционально отклонению показания термометра от заданной
величины.
В обоих случаях возникают значительные трудности, связанные с тем,
что между температурой рассматриваемой области и соответствующими изме-
изменениями тока нагрева всегда имеется запаздывание; помимо других причин,
оно объясняется следующим: изменение температуры сначала проникает сквозь
оболочку термометра и лишь затем через какой-то промежуток времени до-
достигает материала самого термометра. Таким образом, самой простой идеа-
идеализированной схемой реальной печи должна быть следующая: масса М
хорошо перемешиваемой жидкости (нагревательный элемент, содержимое
печи и т. д.), в которую в единицу времени подается заданное количество
тепла Q(t) и которая теряет в единицу времени количество тепла, пропор-
пропорциональное ее температуре (в результате передачи тепла сквозь стенки печи),
находится на границе х = 0 в контакте с пластиной 0 < х < / (оболочка
термометра и т. п.), причем на границе х = 1 потери тепла отсутствуют.
Поступление тепла Q(t) определяется температурой vl на плоскости х = 1.
Такая идеализированная схема уже изучалась в примерах 7 и 8 § 13 гл. III.
Аналогичным способом можно рассмотреть и другие случаи. Таким образом,
в случае систем «включение — выключение», в которых Q всегда имеет одно
из двух постоянных значений, поведение vl легко изучить для любой кон-
конкретной системы (общие решения слишком сложны, чтобы приводить их
здесь); в частности, пользуясь приведенными в § б гл. III и § 5 гл. XV
методами, можно изучить поведение vt в случае периодических изменений Q,
имеющих форму прямоугольной волны.
В случае пропорциональной регулировки мы получаем для описанной
системы соотношение Q(t) = C[V — vt], где С и V — постоянные, и предла-
предлагаемая теория открывает нам новые интересные особенности. Чтобы разо-
разобраться в них при помощи простейших расчетов, подробно рассмотрим сле-
следующую систему.
Неограниченное твердое тело — оо < х < оо нагревается в резуль-
результате подвода тепла к плоскости х = 0. Начальная температура
тела равна нулю, количество тепла, подводимого в единицу времена
на единицу поверхности, определяется формулой
vl), (8.1)
где С и V — постоянные, a vt — температура на плоскости х = 1.
*) О системах, применяемых на практике, см. [45, 46]. Теория этих систем
является частью общей теории сервомеханизмов (см. [47]).
26 Г. Карслоу, Д. Егер
402 ГЛ. XV. ДАЛЬНЕЙШИЕ ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА [§ $
Тогда граничное условие для полуограниченного тела х > 0 (в которое
поступает половина общего количества тепла) будет иметь вид
Следовательно, граничное условие для вспомогательного уравнения запи-
запишется следующим образом:
Решение вспомогательного уравнения, ограниченное при лг->оо, имеет
вид v=Ae-4x, так что vt = Ae^1. Подстановка в условие (8.3) дает Л, и
мы окончательно получаем
— Vke~qx
—=»>- <8-4>
где k = C/K — положительная постоянная величина.
Для определения v можно разложить функцию (8.4) в ряд (см. § 5-
гл. XII); тогда мы получим
2^(8.5>
Следовательно,
v = V | (-1)" [2k у5Г+11-+1Ф' (^±f) . (8.6>
Этот ряд полезен только при небольших значениях к и t. При других
их значениях по нему нельзя судить о поведении V. В этом отношении тео-
теорема обращения более полезна. Она дает
у+/оо
kV Г
*в-2=Г J
у— loo
Подынтегральная функция (8.7) имеет при Х = 0 точку ветвления. Ее:
полюсы находятся в точках, определяемых корнями уравнения z-\-kle~z = 0»
для которого Re (z) ^ 0 и где мы принимаем z = y.L Обозначая z = 5 ± i*r\»
-ц > 0, мы получаем в этих точках
14- kle-t cos т] = 0, (8.8>
(8.9>
Отсюда непосредственно выявляются следующие свойства корней:
1) вещественных корней нет, т] = 0;
2) так как в соотношении (8.8) cost] должен быть отрицательным,
а в соотношении (8.9) sin rj должен быть положительным, т\ может лежать-
только в областях Bл + 11^)ъ < ?}<; Bд-(- 1) тс, я = 0, 1, ...;
3) если Ы = {Ап-\- 1)тс/2, д = 0, 1, 2, ..., то имеется чисто мнимый
корень, 7] = Dя-{- 1)тс/2;
4) если &/ = (8д + 3)тг2-8/2ехр |" (8/г + 3) тс ~[, л = 0. 1. 2. .... то суще-
ствует корень
§ 8]
ГЛ. XV. ДАЛЬНЕЙШИЕ ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
403
5) поскольку Ч = — т] ctg т], а /г/ = т)е* cosec т], то в каждой из областей*
указанных в пункте 2), как ?, так и kl, увеличиваются с увеличением tj.
Характер изменения корней в зависимости от kl показан на рис. 47, где
отмечены положения корней для различных значений kl (см. числа у кривых).
В первой области имеется один корень для всех значений kl, больших ic/2;
один корень в первой области и один во второй для всех значений kl
от 5те/2 до 9тс/2 и т. д.; для kl
в области 2(п— 1)ч
1
1
2п
Рис. 47.
• 1?ъ имеется п корней.
Из этих корней те корни, ве-
вещественная часть которых больше
мнимой (т. е. справа от ОР на
рис. 47), будут соответствовать не-
неустановившемуся колебанию, тогда
как корни, вещественные части ко-
которых меньше мнимых (слева от ОР),
соответствуют затухающему колеба-
колебанию. Корни (8.10), лежащие на ОР,
соответствуют поддерживаемому
устойчивому колебанию.
Линия G — loo, 7 + /оо) должна
лежать справа от всех этих полюсов.
Поскольку подынтегральная функция (8.7) имеет при X = 0 точку ветвления,
используем контур, приведенный на рис. 40; тогда обычным путем найдем,
что интеграл (8.7) равен сумме интегралов по CD, EF и небольшой окруж-
окружности с центром в начале координат плюс произведение 2ic/ на сумму вычетов
относительно полюсов подынтегральной функции. Напишем решение для случая
когда имеется п пар полюсов в точках (д./==аг ±/р,, г=\, .... п\ если
?/< * тс, то члены, обусловленные полюсами, отсутствуют.
Полюсы X = х [а2 — pj ± 2/агрг]//2 дают вклад
21 kV
~ехр{- *<?' + ** + X(g' /2 *'>' + gg^gl| +
2lkV \ х(«г — Фг) х(аг — $)* 2Ы«А )
^-/^(l+o.-ipj ехР\ / 1 Т* F~~J
/2 } « 2vjxr$rt $rx .
«л2 i R21V C0St Р Г" ?г ^г
4/Ajl/expj —
где
срг = arctg (Рг/аг), фг = arctg {рг/A + аг)}.
Интеграл по малой окружности с центром в начале координат дает VP
2l интегралы по CD и EF дают в пределе
?"*"*' [и cos их — k sin и (I — х}] du
26*
404 ГЛ. XV. ДАЛЬНЕЙШИЕ ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
Итак, в этом случае
[§8
I I2 J Г2хагрг/ prjc . )
— COS < тР~ ^ Фг —Фг \
2k V Г
*[а cos ах — k sin a (I — х)] da
a {a2-\-k2 — Zkusinul]
(8.11)
15
1,0
5
xt/l2
На рис* 48 приведены некоторые значения vv рассчитанные по этой
формуле. На кривой / (для &/=т4,9) температура медленно приближается
к своей предельной величине V;
%О\ /\ _ а л при ббльших значениях k пре-
предельная величина достигается
быстрее и затухающие коле-
к1=35 2 бания» совершающиеся около
нее, имеют вид. кривой //, по-
построенной для &/ = 20,1; при
к1=2О,7 &/ = 35,2 происходят поддер-
/cl=4 Э живаемые устойчивыми коле-
колебания относительно предель-
предельного значения (кривая ///); при
еще ббльших значениях kl мы
получим колебание с возра-
возрастающей амплитудой.
Этот ход температуры и
возможность ее устойчивой
«поимки» характерны для та-
такой системы. Приведенный
выше простой пример, не пред-
представляющий физического инте-
интереса, был выбран потому, что
нули знаменателя в решении (8.7) можно найти сравнительно просто; в систе-
системах, встречающихся на практике, эти знаменатели гораздо сложнее и тре-
требуют утомительного численного и графического исследования [49, 50]*).
Простейшим обобщением рассмотренного выше случая служит случай
полуограниченного тела х > 0, теряющего с плоскости х = 0 количество
тепла, равное произведению Н на температуру плоскости. Пусть в единицу
времени к плоскости л: = 0 подводится количество тепла, равное
q^_C(V'o — vt)t (8.12)
где vx — температура в плоскости x = l, VQ — требуемая конечная темпера-
температура, С — постоянная, a QQ = HV — постоянное количество подводимого
в единицу времени тепла, которое необходимо для поддержания плоскости
х = 0 при температуре Vo. Тогда если в начальный момент тело имело нуле-
нулевую температуру, то изображение решения, найденное таким же путем, как
и выше, имеет вид
(8.13)
Рис. 48. Поведение системы с автоматическим
регулированием температуры при различных
значениях параметров регулирования.
*) В [48] разработан метод последовательных приближений для обратных пре-
преобразований* встречающихся в задачах подобного типа.
§ 9] ' ГЛ. XV. ДАЛЬНЕЙШИЕ ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА 405
где h = Н/К и k = C//C. Соответствующую задачу для пластины 0 < х < /
в отсутствие тепловых потерь при х = / можно решить аналогичным образом.
Решения для установившегося периодического режима для этого случая были
исследованы в [51, 52].
§ 9. Неоднородные тела
Если термические свойства твердого тела меняются от точки к точке,
то точные решения можно найти только для ограниченного числа частных
случаев. Для задачи с линейным тепловым потоком дифференциальное урав-
уравнение имеет вид*)
а соответствующее вспомогательное уравнение для нулевой начальной темпе-
температуры записывается в виде
ИЛИ __ _
Простейшими являются случаи, когда уравнение (9.2) можно преобра-
преобразовать в уравнение Бесселя; тогда часто используется результат (см. [66]),
согласно которому общее решение уравнения
d'u 2a-2Pv+l du |
dz2 ~ z dz
имеет вид
где Cv(jc) — цилиндрическая функция AJ4(x)-\-BYH(x).
Рассмотрим теперь ряд типичных случаев, поддающихся решению.
I. K = Koxn, pc = const. (9.5)
В этом случае решение уравнения (9.2) имеет вид
(l-л) I «— 2
.-*=*"/ » *' M^H' (9-6)
где
и пф2. Если л = 2, то решения запишутся следующим образом:
у[-1±КA + 4<72)]/2 (О 84
В качестве конкретного примера рассмотрим область х > 0 с нулевой
начальной температурой. В момент времени / = 0 температура
плоскости лг = О становится равной единице.
*) Задачи с уравнениями этого типа впервые исследовались в [53, 54]. В по-
последнее время ими заинтересовались в связи с переносом тепла турбулентным пото-
потоком [55—57]. Решения в явном виде, связанные с рассматриваемыми ниже решениями
i * гго ел, лг ad2(vx) d[(bx-\-c)v] dv л
примера I, были приведены в [58—64]. Уравнение — 2 ——~—-—i—Ж =
встречающееся в некоторых биологических задачах, рассмотрено в [65].
406 ГЛ. XV. ДАЛЬНЕЙШИЕ ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА [§ 9
Для определенности примем также 0<;#<;1; этот случай будет пред-
представлять наибольший практический интерес. Тогда решение уравнения (9.2),
ограниченное на бесконечности, примет вид
??1) (9.9)
где v определяется (9.7), а А должно быть выбрано так, чтобы при л;->0,
v->l/p. Тогда, если 2->0, то
*V/CV (z) -> 2V~ *Г (v). (9.10)
Используя этот результат, мы найдем А и, следовательно, окончательно
получим
v ¦
Итак, используя формулу B6) приложения 5, находим *)
оо
v=TTyT J'e~Ua"~Xdu- (9Л2)
л
где
*==B-^' (9ЛЗ>
Задачи, в которых начальная температура произвольна, и задачи для
ограниченной области 0 < х < Ь можно рассматривать обычным способом.
II. Если
то решения вспомогательного уравнения (9.2) имеют вид
и, следовательно, решения задач, в которых теплопроводность имеет такую форму,
можно получить из решений задач для областей, ограниченных цилиндрическими по-
поверхностями. Таким образом, например, для полуограниченной области х > 0 с тепло-
теплопроводностью, определяемой (9.14), с нулевой начальной температурой и плоскостью
х = 0, поддерживаемой, начиная с момента t = 0, при постоянной температуре Vy тем-
температура в плоскости х в момент t совпадает с температурой на поверхности г =
= а(\ -\-ахI'г в момент времени а2аЧ/4 (см. пример I § 5 гл. XIII) и определяется
уравнением E.6) гл. XIII; кроме того, ее можно найти по графику, изображенному
на рис. 41.
Если в (9.14) а отрицательно, например а< —{J, что соответствует линейному
уменьшению коэффициента теплопроводности с расстоянием до нуля при х = 1/р,
то искомая температура совпадает с полученной выше (см. F.8) гл. VII) при
г = а A — р.*I/* в момент $2аЧ/4 и ее можно найти по рис. 24.
III. Если
К = Кохп, с = сохп, (9.16)
то вспомогательное уравнение (9.2) примет вид
*) См. уравнения A5) и B4) работы [67]. Там же показано, что функция, изо-
изображение которой имеет вид рп /Cv {zpl*) , является функцией Уиттекера. Помимо этого,
можно использовать теорему обращения с контуром рис. 40.
$ 10] ГЛ. XV. ДАЛЬНЕЙШИЕ ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА 407
где q2 = /?/xq» a хо = #о/рсо- Решения уравнения (9.17) имеют вид
*VlA~")J4 О-«><«*> и x>h<1~n)rw-n)^ix). (9.18)
Решения можно получить так же, как и в примере I.
IV. Если
(9.19)
то уравнение (9.2) принимает вид
¦?г + -ТТЪ1ПГ-4*-Ь <9-20>
оде q2 = /?/хо, а %о = Ко/9со- Решениями уравнения (9.20) служат
Л> [— О + ах)] и А"о Г— A + а^I. (9.21)
L а л L a J
Для области jc > 0, имеющей в начальный момент нулевую температуру, с пло-
плоскостью jc = O, поддерживаемой, начиная с момента * = 0, при температуре V,
температура в плоскости х в момент t совпадает с температурой на поверхности
,/• = a(\-j-ax) в момент времени а2а4.
V. Если
К = Кохп, с = cQxmt (9.22)
то уравнение (9.2) принимает вид
еде #2 = /Со/рсо. Воспользовавшись (9.3), (9.4), получим решения (9.23)
1 —л
решение можно получить так же, как и ранее.
VI. Цилиндрические и сферические области.
В этих случаях вспомогательные уравнения принимают вид
M^FH (9-25)
М^)^о' (9-2б)
« поэтому теория для случая степенного закона зависимости /Сие входит в теорию,
изложенную в примере V.
§ 10. Нагревание «цепочки» пластин, между которыми
происходит теплообмен. Слоистые материалы
Данная задача, которую исследовал еще Фурье, представляет интерес
в связи с изучением теплопроводности слоистых материалов [68]; кроме того,
она имеет ряд других практических приложений.
Рассмотрим ряд бесконечных параллельных плоских листков, настолько
тонких, что температуру по их сечению можно считать постоянной. Пусть
Мг — масса единицы поверхности r-го листа, сг — его удельная теплоемкость,
vT — его температура, а количество тепла, передаваемого единицей поверхности
408 ГЛ. XV. ДАЛЬНЕЙШИЕ ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА [§ 10
в единицу времени к (г+1)-му листу, определяется выражением
Hr(vr-vr+1). A0.1)
Тогда температура vr удовлетворяет уравнению
Если начальная температура равна нулю, то вспомогательное уравнение,
соответствующее уравнению A0.2), имеет вид
Система уравнений A0.3) составляет совокупность дифференциальных
уравнений, связывающих изображения температур последовательных листов.
Мы рассмотрим только случай, когда все значения Яг, Мг и ст одинаковы
при всех значениях г; тогда система уравнений A0.3) принимает вид
vr+1 — B + 2&/?)г>г+г/г_1 =0, A0.4)
где
* = -§. (Ю.5>
Решение системы A0.4) имеет вид
vr = АегЬ + Be-*, A0.6)
где А и В — постоянные, подлежащие определению из условий в начале и
в конце «цепи», а 0 дается уравнением
ch 6==1+ kp. (Ю.7)
Если мы имеем п пластин, имеющих в начальный момент нулевую тем-
температуру, причем первая получает тепло от среды с температурой V, а по-
последняя отдает тепло в среду нулевой температуры, то мы получим
— V —
и решение A0.6) принимает вид
т /?sh(/i+lH * V*/
Используя теорему обращения для г=1, ..., п, окончательно получим.
п
„. _У(п-
I — cos {5тс/(/г+1)} ] ^
Хехр[— 4"A— cos7TFt)]' A0'9>
Если число пластин бесконечно, г=1, 2, ..., начальная температура
равна нулю, причем первая пластина получает тепло от среды температуры V,
то аналогичным путем находим
V _й Vkr [( , 1\ г/_ . 1\2 t ТМг (Ю Ю>
A0.11)
Отсюда, используя формулу B7) приложения 5, получим
§ 11] ГЛ. XV. ДАЛЬНЕЙШИЕ ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА 409*
§ 11. Прямое применение метода преобразования Лапласа
к двумерным и трехмерным задачам
Выше отмечалось (см. § 1 гл. VI), что из всех существующих методов
метод преобразования Лапласа обеспечивает наиболее прямое решение задачи
с нулевой начальной температурой *) и заданной температурой поверхнос-
поверхности. В данном параграфе таким путем решается несколько важных задач-
этого типа.
I. Прямоугольный параллелепипед 0 < л; < а, 0 < у < ?, 0 < z < с.
Нулевая начальная температура. Температура поверхности * = O
равна постоянной величине vv температура других граничных поверх-
поверхностей равна нулю.
В данном случае вспомогательное уравнение имеет вид
Его следует решать при условиях
v=y* * = 0' °<У<*. 0<z<c, (П.2>
и при v, равном нулю на других граничных поверхностях.
Чтобы при этих условиях получить решение уравнения (ИЛ), мы посту-
поступаем точно так же, как и в § 2 гл. VI. Единственное отступление заклю-
заключается в том, что к правой части выражения B.3) этой главы должен быть
добавлен член (/?/*). При этом видоизменении (и v2 = 0) мы можем оценить
решение B.9) гл. VI и, следовательно, после некоторых изменений в обо-
обозначениях получим
m = 0 /1=0
где
sin [Bm + *> *У/*1 sin №n + *> **/*) sh <*' (д - *>
l)Bn+l)pshq'a
A1.4>
Тогда, используя теорему обращения, найдем
16^ у yi sin №m +!)TC^]s!n
2m J
Bm+
m=0 я=0
где
,2_Bm+lJrc2 B/г +1J тс2 X
Подынтегральная функция в A1.5) имеет простой полюс при Х = 0 и-
простые полюсы при значениях X, соответствующих
*) Если начальная температура не равна нулю, то этот метод, конечно, тоже
можно применить, но он тогда не имеет преимуществ перед методом, в котором
используются функции Грина.
-410 ГЛ. XV. ДАЛЬНЕЙШИЕ ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА [§ 11
Находя соответствующие вычеты, окончательно получим
у sin [Bm + 1) ny/b] sin [B/г +1) m/c] sh (a — x) V^T0
^L V V V l ^п [Bm + 1) ny/b] sin [B/г+1) nz/c] sin [Ых/а] ^xta
m=0 д=0 Ы\
IW , Bm + lJic2 , Bn+\f^
am,«,/ = -^2-H ^ 1 ^ • A1-7)
Первый член в решении A1.6), который получается из A1.5) при
^полюсе Х = 0, представляет собой уже известное нам решение для стацио-
стационарного состояния (см. B.9) гл. VI).
II. Та же задача, что и в I, но поверхность х = 0 поддерживается при
температуре щ sin {&t -f- e).
Единственное изменение здесь заключается в том, что подынтегральную функ-
функцию в A1.5) следует умножить на
X (со cos e -j- X sin e)
В таком случае она имеет полюсы при Х= ± /а>, что дает решение для устано-
установившегося периодического режима в виде
Л'1 / Л / Л (*)** _L_ I Л /*Jn _L_ 1 Л ---/in» \ II I iTlt tlj* \А**°7
m = 0 л=0
где
**т п sh(a —лг)[Bт+1Jт1:2/^2 + Bп+1J^
Помимо этого, имеются полюсы при — -*лт, Пу h которые дают переходную часть
решения
оо оо оо
kz/c] Sin [Inxfa] (<o cose — xa .sine) „xta
^ m' n*l L e m, n, /.
Если все поверхности поддерживаются при температуре sin (a>^ -\- е), то решение
^получается наложением шести выражений полученного выше типа. Очевидно, что
эти решения настолько сложны, что практически неприменимы для расчета.
III. Прямоугольный параллелепипед 0 < х < а, — Ь < у < Ь, — с < z < с.
Нулевая начальная температура. Температура поверхности х = 0 равна постоян-
постоянной величине vu температура поверхности х = а равна постоянной величине v2.
На других поверхностях происходит теплообмен со средой нулевой темпе-
температуры.
Здесь, используя решение B.23) гл. VI, находим, как и в задаче I,
4/i2 [Pi sh q' (a — х) + Щ sh g'x] cos ary cos $sz A1 10)
где ar и рг — положительные корни уравнений B.16), B.17) гл. VI и
* a*+ {? + </»/*>•
§11] ГЛ. XV. ДАЛЬНЕЙШИЕ ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА 411
Решение v представляет собой сумму установившейся части решения (см. B.23) гл. VI)
и переходной его части
у^ л {(~1)Я v> - Vl]"»а'у cos ?*2 sln Иг]
где
IV. Ограниченный цилиндр 0 ^ г < ay О < z < /. Нулевая начальная темпера-
температура. Поверхность z = О поддерживается при постоянной температуре V, а
z = l — /г/?а нулевой температуре. На поверхности г = а происходит тепло-
теплообмен со средой нулевой температуры.
Здесь, используя, как и выше, задачу I § 3 гл. VIII, получим
=z у У 2hJQ(ran)sh(l-z)zn
A1.13)
еде ап — положительные корни уравнения
аУ, (аа) — АУ0 (да) = 0.
V. Ограниченный цилиндр 0<.г<а, 0 < z < L Нулевая начальная темпера-
температура. При t > 0 поверхность z = 0 поддерживается при постоянной темпера-
температуре V. На остальных поверхностях происходит теплообмен со средой нулевой
температуры.
В данном случае
v^ 2hV yJ0(ran)[anchan(l-z)+hsban(l-z)}
тде ал — положительные корни уравнения
о/, (да) = hJ0 (аа), A1.15)
a pm — положительные корни уравнения
= O. AЫ6)
VI. Полу ограниченны и цилиндр z > 0, 0 <; г < а. Нулевая начальная темпе-
температура. При t > 0 поверхность z = 0 поддерживается при постоянной темпера-
температуре V. На поверхности г = а происходит теплообмен со средой нулевой тем-
температуры.
В данном случае
-У,
A1.17)
Здесь для нахождения v из v мы пользовались обычным решением C.33) гл. VIII,
фрулой A9) при 5 B6) XII
уравнения A1.15).
Здесь для нахождения v из v мы пользовались обычным решением C.33) гл. VIII,
формулой A9) приложения 5 и соотношением B.6) гл. XII. ап — положительные корни
A1.15)
412 ГЛ. XV. ДАЛЬНЕЙШИЕ ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА [§ 11
VII. Полу ограниченный цилиндр z > 0, 0<!г<а. Нулевая начальная темпе-
температура. При t > 0 поверхность г = а поддерживается при постоянной темпе-
температуре V, а поверхность г = 0 — при нулевой температуре.
Как и выше, мы можем использовать пример XIII § 3 гл. VIII, но излагаемый
ниже метод более прост. Легко проверить, что функция
где q = V(PM* а ат — корни уравнения Jo (аа) = 0, удовлетворяет вспомогательному
уравнению и граничным условиям.
Если использовать формулу A9) приложения 5, то отсюда следует, что
Первый член решения A1.18) представляет собой значение v для неограничен-
неограниченного цилиндра с температурой поверхности V, и следовательно, ряд в этом соотноше-
соотношении можно рассматривать как поправку на влияние торца *). Такая схема решения
полезна, когда поверхность, уходящая в бесконечность, поддерживается при постоян-
постоянной температуре, и поэтому интегральная теорема Фурье становится неприменимой,
хотя получаемые с ее помощью решения на самом деле обычно правильны.
VIII. Клин **) г > 0, 0 < 6 < 80. Нулевая начальная температура. При t > О
поверхность 6=0 поддерживается при температуре V, а поверхность 6 = 80 —
при нулевой температуре.
В этом случае вспомогательное уравнение имеет вид
Ищем решение этого уравнения в виде
оо »
tJ sin 5б ffn {u) Js {ar) dr> AL21)
n-\ 0
где s = mz/b0. Оно состоит из члена, соответствующего решению для стационгрнога
состояния, и ряда членов, обращающихся в нуль на обеих граничных полуплоскостях
6 = 0 и 6 = 0О. Неизвестная функция fn (и) должна быть выбрана таким образом,
чтобы решение A1.21) удовлетворяло уравнению A1.20). Подставляя A1.21) в A1.20)
и используя соотношение, приведенное в книге Ватсона [66],
С Js(ur)du _ 1
J и - s '
найдем
. ч _ 2 (—1)" V
Таким образом, окончательно получим
*) Решения для области г>0, г > а п г > а, 0 < г < I, а также для полуог-
полуограниченного цилиндра с постоянной температурой поверхности приведены в [69].
**) Некоторые численные решения этой задачи, а также решения для цилиндра,
сечение которого представляет собой сектор круга, даны в [70, 71]. Аналогичная
задача для полуограниченного цилиндра рассмотрена в [72].
§11] ГЛ. XV. ДАЛЬНЕЙШИЕ ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА 413
A1.23)
Интегралы в решении A1.23) можно выразить в виде вырожденных гипергео-
гипергеометрических функций [66].
Если при t > О обе граничные полуплоскости поддерживают при температуре,
равной единице, а начальная температура равна нулю, то мы получим
-42
2 *»{2nV)%d /V» '«<¦>" A1.24)
/1=0
где
0, а
IX. Конус 0 < 0 < 60. Нулевая начальная температура. При t > 0 поверх-
поверхность имеет температуру, равную единице.
Применяя метод, использованный в предыдущем примере, находим
/.г
где п — положительные корни уравнения Рп (fx0) = 0.
ЛИТЕРАТУРА
1. Benfield, Mon. Not. R. Astr. Soc. Geophys. SuppL 6, 139—147 A951).
2. В e n f i e 1 d, J. Glaciol. 2, 250—254 A952).
3. В e n f i e 1 d, J. Appl. Phys. 20, 66—70 A949).
4. Benfield, Quart. Appl. Math. 7, 436—439 A949); 6, 439—443 A948).
5. W i 1 e s, S. Afr. J. Sci. 39, 95—97 A943).
6. Hulme, Proc. Phys. Soc. B68, 393—400 A955).
7. Sommers, Proc. Phys. Soc. 25, 74—76 A912).
8. Smith, Tiller, Rutter, Canad. J. Phys. 33, 723—745 A955).
9. Owen, Proc. Lond. Math. Soc. 23, 238 A925).
10. Schack, Goldschmidt, Partridge, Industrial Heat Transfer, Wiley, 1933.
11. Schmeidler, Z. angew. Math. Mech. 8, 385 A928).
12. А с k e г m a n n, Z. angew. Math. Mech. 11, 192 A931).
13. A n z e 1 i u s, Z. angew. Math. Mech. 6, 291—294 A926).
14. S с h u m a n n, J. Franklin Inst 208, 405—416 A929).
15. N u s s e 11, Z. Ver. dtsch. Ing. 71, 85 A927).
16. Kronig, van Gi j n, Physica 12, 118—128 A946).
17. T h i e 1 e, Ind. Eng. Chem. 38, 646—650 A946).
18. Nusselt, Z. Ver. dtsch. Ing. 72, 1052 A928).
19. Hausen, Z. angew. Math. Mech. 11, 105 A931).
20. Hausen, Z. angew. Math. Mech. 9, 173 A929).
21. S с h u 1 t z, Appl. Sci. Res. A3, 165—173 A953).
22. Allen, Quart. J. Mech. Appl. Math. 5, 455—461 A952).
23. Goldstein, Proc. Roy. Soc. A219, 151—185 A953).
24 Thomas, J. Am. Chem. Soc. 66, 1664—1666 A944).
25. M о n г о, A m u n d s о n, Ind. Eng. Chem. 42, 1481 A950).
26. В г i n k 1 e y, J. Appl. Phys. 18, 582—585 A947).
27. Grunberg, J. Phys. USSR 4, 463 A941).
28. Grunberg, S о n t z, J. Phys. USSR 4,97 A941).
29. W a i d e 1 i с h, J. Appl. Phys. 13, 706—712 A942).
30. W a i d e 1 i с h, Proc. Inst. Radio Engrs 34, 78P A946).
31. Carslaw, Jaeger, Operational Method in Applied Mathematics, Oxford, ed. 2,
1948. (Г. Карслоу, Д. Егер, Операционные методы в прикладной математике,
М., ИЛ, 1948.)
414 ГЛ. XV. ДАЛЬНЕЙШИЕ ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
32. Oosterkamp, Philips Res. Rep. 3, 161 A948).
33. J a e g e г, Quart. Appl. Math. 11, 132—137 A953).
34. Barrer, Trans. Faraday Soc. 35, 628 A939).
35. Barrer, Phil. Mag. 35, 802 A944).
36. Barrer, Trans. Faraday Soc. 36, 1235 A940).
37. Jaeger, Trans. Faraday Soc. 42, 615 A946).
38. Jaeger, Quart. Appl. Math. 8, 187—198 A950).
39. Levy. Trans. ASME 78, 1627—1635 A956).
40. Jakob, Trans. ASME 65, 593 A943).
41. J а к о b, Trans. ASME 70, 25—30 A948).
42. Cop pie, Наг tree, Porter, Tyson, J. Inst. Elect. Engrs S5t 56—66 A939).
43. Crank, The Mathematics of Diffusion, Oxford, 1956.
44. Danckwerts, Appl. Sci. Res. A3, 385 A953).
45. Griffiths, Thermostats, Griffin, ed. 2, 1943.
46. Rhodes, Industrial Instruments for Measurements and Control, McGraw-Hill,
1941.
47. Thaler, Brown, Servomechanism Analysis, McGraw-Hill, 1953.
48. H u 1 1, W о 1 f, Canad. J. Phys. 32, 72—80 A954).
49. Callender, Наг tree, Porter, Trans. Roy. Soc. A235, 415 A936).
50. Наг tree, Porter, Callender, Stevenson, Proc. Roy. Soc. A161, 460
A937).
51. Turner, Proc. Camb. Phil. Soc. 32, 663 A936).
52. Hopper, Proc. Phys. Soc. 54, 55 A942).
53. К е р i n s к i, Math. Ann. 61, 397 A905).
54. Gevrey, J. Math, pures appl. 10, 105 A914).
55. S u 11 о n, Proc. Roy. Soc. A146, 701 A934).
56. Brunt, Physical and Dynamical Meteorology, Cambridge, 1939.
57. S u 11 о n, Atmospheric Turbulence, Methuen, 1949.
58. Huber, Z. angew. Math. Mech. 7, 469 A927).
59. Sutton, Proc. Roy. Soc. A182, 48 A943).
60. Jaeger, Quart. Appl. Math. 3, 210 A945).
61. С a 1 d e r, Quart, J. Mech. Appl. Math. 2, 153—176 A949).
62. Knighting, Quart. J. Mech. Appl. Meth. 5, 423—431 A952).
63. D a v i e s, Quart. J. Mech. Appl. Math. 7, 462—471 A954).
64. D a v i e s, В о u г n e, Quart. J. Mech. Appl. Math. 9, 457—468 A956).
65. Feller, Ann. Math. Princeton 54, 173—182 A951).
66. Watson, A treatise on the Theory of Bessel Functions, Cambridge, ed. 2, 1944.
(Г. В а т с о н. Теория бесселевых функций, ИЛ, 1949.)
67. Goldstein, Proc. Lond. Math. Soc. 34, 104 A932).
68. Stormer, Wiss. Verott. Siemens-Werken 17, 90 A938).
69. J a e g e r, Bull. Am. Math. Soc. 47t 734 A941).
70. В о с k, J. Phys. Rad. 10, 241 A939).
71. Jaeger, Phil. Mag. 33, 527 A942).
72. С г a g g s, Phil. Mag. 36, 220 A945).
ГЛАВА XVI
УСТАНОВИВШАЯСЯ ТЕМПЕРАТУРА
§ 1. Введение
Задачи с установившейся температурой имеют большое практическое-
значение. Так, установившееся состояние используется в большинстве мето-
методов измерения коэффициента теплопроводности. В промышленности стацио-
стационарные тепловые потоки представляют наибольший интерес. К сожалению,
области, в которых нас интересует тепловой поток, редко имеют простые,
рассмотренные выше формы. В настоящей главе рассматриваются другие-
методы, позволяющие получить некоторые сведения о температурах и тепло-
тепловых потоках в более сложных системах.
Как указывалось в § б гл. I, в области, в которой тепло не выделяется,
установившаяся температура v удовлетворяет уравнению Лапласа
Если на единицу объема исследуемой области в единицу времени выделяется
количество тепла А(х, у, z), то установившаяся температура v должна,
удовлетворять уравнению Пуассона
V2v = — ±А{х, у, z) A.2>
при условии, конечно, что среда однородна и изотропна.
Таким образом, решения задач со стационарным тепловым потоком,
можно получить из известных решений задач теории потенциала, электро-
электростатики, гидродинамики, электродинамики и других разделов науки, в кото-
которых встречаются эти уравнения.
§ 2. Источники и стоки при установившейся температуре
Предположим, что тепловой поток в неограниченном твердом теле вы-
вызван постоянным подводом тепла в одних точках и его удалением в других.
Эти точки можно назвать источниками и стоками тепла.
Опишем небольшую шаровую поверхность радиуса г вокруг точки,.
в которой выделяется тепло; тогда при г->0 количество тепла, проходящее
в единицу времени через шаровую поверхность, должно равняться мощности
источника. Следовательно, решение уравнения
должно иметь вид
416 Гл- XVL УСТАНОВИВШАЯСЯ ТЕМПЕРАТУРА [§ 2
«где ср — решение уравнения A.1) данной главы, ограниченное в точке, в ко-
которой расположен источник, a Q — мощность источника.
Аналогичным образом для линейного источника мощностью Q часть
выражения для v, стремящаяся к бесконечности, когда расстояние гг до ли-
«ейного источника приближается к нулю, имеет вид
Если тепло непрерывно выделяется в ограниченной области неограни-
неограниченного твердого тела, температуру в любой его точке находят интегриро-
интегрированием функций B.1) или B.2).
Если тепло выделяется в ограниченной области, поверхность которой
поддерживается при нулевой температуре (или термически изолирована), то
можно применить метод изображений или, в более общем случае, восполь-
воспользоваться функцией Грина для уравнения Лапласа.
Для точечного источника, находящегося в точке (х'9 у', z') за-
заданной области с заданными граничными условиями, эта функция Грина
определяется как решение уравнения Лапласа и (х, у, z; x', у', zr), которое
удовлетворяет граничным условиям и ограничено везде внутри области,
за исключением точки (л/, у', z'), где оно стремится к бесконечности таким
образом, что
« LI
r I
ограничен. Здесь г2 = (лг — *'J + (У — У'J-Н* — *02.
Итак, если и — определенная выше функция Грина, то температура,
вызванная действием в точке (л/, у', z') источника мощностью Q, будет
равна
»¦
Эти функции Грина хорошо известны *) и их теория изложена в работах
по теории потенциала. Здесь мы только отметим, что для областей, рас-
рассмотренных в гл. XIV, их можно получить из результатов этой главы.
Обращаясь, например, к § 10 гл. XIV, найдем, что если положить # = 0,
то v, определенное в этом параграфе, удовлетворяет уравнению Лапласа и
граничным условиям, а вблизи точки (л/, у', zr) ведет себя как
Тем самым определенная выше функция Грина и равна
где [v]q=0 — значение изображения решения, приведенного в гл. XIV, при
^ = 0 для единичного мгновенного точечного источника в той же области
и при тех же граничных условиях.
Поэтому, например, если плоскости z = 0 и z = l поддерживаются при
нулевой температуре, а в точке с цилиндрическими координатами (г', б', z')
выделяется в секунду количество тепла, равное Q, то температура в точке
*) Полное рассмотрение для поверхностей в цилиндрической системе координат,
включающее различные формы решений, приведено в гл. IX книги Грэя и Мэтьюза [1].
§ 2] гл XVI- установившаяся температура 417
(г, б, z), согласно A0.11) гл. XIV, будет равна
со
Ж Zism-T-sin-i-Ko(-r-)' B-5)
m-\
где
/?2 = r2 + r/2 _ 2rr' cos F — 00. B.6)
Аналогичным образом, если цилиндрическая поверхность г = а поддер-
поддерживается при нулевой температуре, а в точке (г', б', 0) внутри цилиндра
в секунду выделяется Q единиц тепла, то, используя A3.5) гл. XIV, получим,
что температура в точке (г, б, z) запишется в виде
B-7)
где суммирование по а проводится по положительным корням уравнения
Согласно A5.1) гл. XIV соответствующее решение для источника
в точке (г', б', z') ограниченного цилиндра 0 < z < /, 0 < г < а с нулевой
температурой поверхности равно
cos п (б — 6'),
О < г < г', B.8)
где
Fn(x, у) = /п (х) Кп (у)— Кп(х)/п(у), B.9)
и
вп = 1 при я = 0 и еп = 2 при п = 1, 2, 3, ...
Если г' < г < а, то в соотношении B.8) мы меняем местами г и г'.
В качестве примера использования этих решений определим температуру
в цилиндре О^г < а, 0 < z < /, поверхность которого поддерживается при
нулевой температуре и в котором вдоль линии, параллельной оси цилиндра
и проходящей между точками (г', б', Ь) и (г', б', / — #), расположен ли-
линейный источник мощностью Q. Эта температура равна
udz',
ь
где и определено выражением B.8). Следовательно, при 0 < г < г' она равна
2Q
Bт-1)
/Я=1
B/и-1Iс6 Bт-1)«
C0S / Sin I X
Итак, мы получили температуру в цилиндре, нагреваемом проволокой,
параллельной его оси [2].
27 Г. Карслоу, Д. Егер
418 ГЛ- XVL УСТАНОВИВШАЯСЯ ТЕМПЕРАТУРА [§ 3
§ 3. Установившийся поток к почти плоской поверхности.
Топографические поправки для геотермического потока
Как отмечалось в § 13 гл. И., при движении в глубь Земли имеет место при-
приблизительно линейное увеличение температуры с расстоянием от земной поверхности,
нарушаемое локальными неровностями этой поверхности. Определение влияния таких
неровностей и внесение поправки на них в наблюдаемый градиент температуры пред-
представляет большой интерес для геофизиков *).
Для решения этой задачи пользуются двумя методами. В первом из них [4, 5]
рассматривается поверхность Земли на уровне моря, причем ее температура в каждой
точке принимается равной h (g — g')t где h — высота над уровнем моря в данной
точке, g — геотермический градиент, a gf — адиабатический вертикальный градиент
в атмосфере, так что средняя температура поверхности на высоте h над уровнем
моря меньше ее значения на уровне моря примерно на hg'.
Такая задача становится задачей об установившейся температуре в полуогра-
ничейном теле z > О с температурой поверхности, равной F (х, у); решается
она так же, как и ранее.
Если в соотношении (9.3) гл. XIV *->оо, то для температуры v в точке @, 0, z)
получим **)
J
^ ' <ЗЛ>
— oo —oo
где
R2 = *2 4. г'2 и r'2 = x'2 + y'2. C.2)
В данном случае нужно узнать величину dv/dz; она равна
— oo —oo
Если записать F (х\ у') в полярных координатах (г', 0') и среднее значение
F(*ri Уг) по окружности радиуса г' с центром в начале координат в виде
оо
V = JL / F (r1 cos 0', г' sin в') db\ C.4)
о
то уравнение C.3) примет вид
оо оо
-^- = I R-5 (Я2 — Зг*) Vr' dr' = I Я (Я* — 3*2) V dR =
г
** 1 \Г» /V 1 г» 1 dV f r'2 dV Fr'2 dV
Z 2 0
Z 2
Когда 2 = 0 и, следовательно, R=r', мы получаем
оо
dV dr'
ir-p-' C-6)
которое легко найти для любого грунта. Чтобы получить правильное значение гео-
геотермического градиента, эту величину следует вычесть из измеренного значения g.
Были проведены точные расчеты изотерм и градиента температур для различных
почти плоских поверхностей, форма которых приближается к форме обычного рельефа
*) Полное изложение этого вопроса, включая исторический обзор, можно
найти в [3].
**) Эта задача была обобщена на случай линейного изменения температуры по-
поверхности, вызываемого эрозией [3J.
§ 4] ГЛ. XVI. УСТАНОВИВШАЯСЯ ТЕМПЕРАТУРА 419
поверхности *). Если рассматривать только двумерный случай и принять, что ось z
направлена вертикально вниз, то следует искать такое решение уравнения Лапласа
ЧТОбЫ ПрИ 2->СО V->gZ И ЧТобы
v = Vo -f- g'z на поверхности z = / (л:). C.8)
Здесь, как и ранее, g — геотермический градиент, a g/ — адиабатический вертикальный
градиент. Наиболее интересен расчет Лиса [9] **), который отметил, что функция
C.9)
удовлетворяет уравнению C.7), ведет себе требуемым образом при 2->оои удовле-
удовлетворяет условию C.8), если поверхностью исследуемого тела служит
Функция C.10) имеет минимум при х = 0, а при л:->оо монотонно приближается
к нулю. Она дает достаточно правильное представление одиночной горной цепи.
Если Н—высота горы, а 2Ь — ее ширина на половине высоты, так что поверхность,
описываемая C.10), проходит через точки @, —Я) и (б, —о"^Ч» то паРаметРы ^
и а определяются соотношениями
V\ (!)'*. C.11)
Тогда изотермы определяются C.9) при различных значениях v и в этом случае
легко найти градиент температуры.
§ 4. Установившийся тепловой поток в составном теле
Задача о нарушении установившегося линейного теплового потока
в однородной среде погруженным в нее объектом с другой теплопровод-
теплопроводностью очень важна в технике. Математически она точно соответствует
задаче о наведенном магнетизме тела такой же формы, помещенного в одно-
однородное внешнее поле, и ее решения можно найти в учебниках по электричеству
и магнетизму. Однако основные решения вследствие их важности кратко
излагаются ниже. Решения для шаров и эллипсоидов можно использовать
для оценки изменений геотермического градиента, вызываемых погружением
массы с теплопроводностью, отличной от теплопроводности всей среды, и
они представляют очень большой интерес для термических методов разведки.
Кроме того, точное решение для одиночного шара или эллипсоида используется
статистически при расчетах теплопроводности гранулированных материалов.
Последние рассматриваются как ряд частиц одного материала, вкрапленных
в основную породу из другого материала. Ниже, в примере IV, приведен
простой пример использования этого метода.
Изучение поведения теплового потока и температуры вблизи поверхности
соприкосновения двух материалов представляется важным в связи с изуче-
*) В ряде работ [6—8] рассматривается система сменяющих друг друга холмов
и долин.
**) Последний член формулы C.9) дает температуру, облусловленную действием
линейного дублета. Можно также использовать ряд типа 2 An(d/dz)n\n \х2 +
+ (z-\-anJ]; помимо этого, для описания гористой области с параллельными хреб-
хребтами следует прибавить дополнительный ряд, в котором х заменяется на х-\- с.
27*
420 ГЛ. XVI. УСТАНОВИВШАЯСЯ ТЕМПЕРАТУРА [§ 4
нием геотермического потока тепла. Идеализированные задачи для тел, огра-
ограниченных плоскостями, пересекающимися под прямым углом, можно рас-
рассматривать методами, изложенными в гл. V (см. ниже пример V). Кроме
того, использованы простые решения уравнения Лапласа в виде многочленов
(см. пример VI).
I. Область внутри шара 0 О < а имеет коэффициент тепло-
теплопроводности К'> а область вне его — коэффициент К, На больших
расстояниях температура стремится к величине Vz.
Пусть температуры v' и v, внутри и вне шара г = а, описываются
функциями
v = Vr cos 0 + -^- cos 6, D.1)
*/ = i4rcos6, D.2)
где А и В — неизвестные коэффициенты, а г, 0 — сферические координаты.
Функции D.1) и D.2) удовлетворяют уравнению Лапласа, vf при г->0
ограничено, a v—>Vz при г->оо, как и требуется. Граничные условия
при г->а, т. е.
, tJr, dv' r, dv r\ ^ r\ ^
дают
Разрешая эти уравнения относительно А и В и подставляя их значения
в D.1) и D.2), окончательно получим
\ D.3)
_3KVrcosb_ ЖУг
v — 2К + К' ~~ 2К+К' ' { }
Градиент температуры в шаре равен 3KV/BK -\-К').
II. Цилиндр 0 <; г < а с коэффициентом теплопроводности К'\ ось этого
цилиндра перпендикулярна оси z. Область вне цилиндра имеет коэффициент
теплопроводности /С, а ее температура на больших расстояниях равна Vz.
Температуры v' и v внутри и вне цилиндра равны следующим величинам:
D.5)
III. Эллипсоид с коэффициентом теплопроводности К' находится в среде
с коэффициентом теплопроводности К.
Рассмотрим эллипсоид
2 v2 z2
i 1 D7)
и предположим, что температура среды на больших расстояниях от него стремится
к величине
Vxx+V2y + Vzz. D.8)
Пусть для любой точки (л:, у, z) X служит положительным корнем уравнения
х2 у2 z2
+ + 1
§4]
Тогда как хА\,
, так
1
2
ГЛ. XVI.
и уВх и z
оо
аЬс / ¦
./ (л2 -
X
А (и)
УСТАНОВИВШАЯСЯ ТЕМПЕРАТУРА
Съ где
— ^ ас/
= [(аЧ
ОО
с f
CJ (с-
X
-а)(^2-
du
г + «)А(
fa)(c2H
ао
X
¦ v »
h ц)]%
421
D.10)
D.11)
удовлетворяют уравнению Лапласа *).
Путем рассуждений, аналогичных рассуждениям, приведенным в примере I, на-
находим, что температуры vi внутри и v0 вне эллипсоида имеют вид
где
г = К'/К, D.14)
а Ло, Во, Со — интегралы Аъ В^, Сх при Х = 0. Следует отметить, что
Ао + Во + Со = 1. D.15)
Для различных эллипсоидов вращения, в которых две оси равны, интегралы D.10)
можно выразить через элементарные функции. Ниже приводятся полученные резуль-
результаты (расчеты см. в книге [13]).
Вытянутый эллипсоид вращения, Ь = с < а, е' = [(а2 — Ь2)/(а2 + X)]1/2 —
эксцентриситет софокусного эллипса, проходящего через рассматриваемую внешнюю
точку, и е' при X = 0 равно е, т. е. эксцентриситету образующего эллипса
(ln. DЛ7)
2<?3 \1— е'2 2 1 — *'J v '
Сплющенный, эллипсоид вращения, а= Ь> с.
Ах - Дх = ° ^Р* { arcctg v - ^-Ly |, D.18)
D.19)
где
(а2 _ С2)
В качестве простого примера рассмотрим длинный вытянутый эллипсоид вра-
вращения а ^> Ь (которым может служить зонд для измерения теплопроводности или
часть кожуха) с коэффициентом теплопроводности К'\ его ось совпадает с направле-
направлением градиента температуры в материале с коэффициентом теплопроводности К-
В соответствии с формулой D.12) градиент температуры в эллипсоиде вращения
равен V\l\\ -f- Ао (дг—К)/К]. Кроме того, поскольку отношение Ь/а мало, из D.16)
приближенно получим
*) Эти интегралы рассматриваются во многих трудах по гидродинамике и элек-
электричеству [10]. Впервые они рассматривались еще в 1837 г. [11, 12].
422 гл. xvi. установившаяся температура [§ 4
Таким образом, градиент температуры внутри эллипсоида вращения приблизи-
приблизительно равен
IV. Теплопроводность простой гранулированной среды.
Предположим, что в маточной породе с коэффициентом теплопроводности К
размещаются шары с коэффициентом теплопроводности /С', занимающие в ней часть
объема а. Предполагается, что шары находятся настолько далеко друг от друга, что
их взаимное влияние исключается. Допустив, что эти шары имеют радиус а, рас-
рассмотрим больший шар с радиусом Ъ, в котором находится п маленьких шаров так,
что па3 = ab3. Согласно соотношению D.3) температура на большом расстоянии, обу-
обусловленная наличием п шаров, при линейном градиенте температуры будет равна
z
r*BK+K') '
если /Сср — средний коэффициент теплопроводности материала шара радиусом Ь, то
эта температура должна также равняться
Приравнивая эти выражения, получаем *)
V. Установившийся поток в составной неограниченной области О < у < /,
— оо < jc < оо, — оо<2г<оо; в области х > О коэффициент теплопроводности
равен Ki, а в области х < О он равен К2- Граничные условия имеют вид
и = О, у = О, — оо < л: < оо,
v=Vl9 y = l, лг>0,
v = V2, у => Л jc < О.
Если V] и v2 — температуры в областях х > О и х < О соответственно, то от-
отсюда, как и в § 2 гл. V, следует, что
/.. _ ,.т/ _ 2l(V2— Vi)#2 Y (—IO1 . /ггсу (
л=з
—Н-
л=1
Если Vx и И2 таковы, что К\ Vx = /С2 К2 = — Z7/, т. е. при |jc|->oo тепловой
поток в обеих областях стремится к /\ то тепловой поток через плоскость у = О
равен
D.24)
причем положительный знак берется, если х < 0, а отрицательный — если х> 0. Это
указывает на наличие разрыва теплового потока на границе двух материалов.
VI. Решения в виде многочленов.
Известно, что многочлены ах -f- by, ax-\- by -\- cxy -\-d(y2 — jc2), ... первой,
второй и т. д. степени удовлетворяют уравнению Лапласа. Они могут оказаться по-
полезными в простых задачах о составных областях. Например, многочлены
г». = у (х + л), v2 = у {(К,х/К2) + а) D.25)
*) Этот простой вывод получен из [12]. Более точные выводы приводились мно-
многими авторами, в частности Рэлеем [14], который рассматривал решетку из шаров
кубической симметрии. Обзор и список литературы можно найти в [15].
§ 5] ГЛ. XVI. УСТАНОВИВШАЯСЯ ТЕМПЕРАТУРА 423
удовлетворяют уравнению Лапласа и следующим условиям:
Vi — v2 = 0 при у — О
Таким образом, они служат элементарным решением для составной области,
в которой материал справа от плоскости х = О, у > О имеет коэффициент теплопро-
теплопроводности Къ а материал слева от нее — коэффициент К2. Изотермы имеют вид дуг
равнобочных гипербол *).
§ 5. Практические задачи
Как отмечалось в § 1 данной главы, в технических и лабораторных за-
задачах области с установившимся тепловым потоком значительно сложнее
областей, рассмотренных до сих пор.
Перечислим простые задачи, имеющие практическое значение и не
исследованные в настоящей книге.
1. Тепловой поток между цилиндром и плоскостью, например между
проложенной в земле трубой или кабелем и поверхностью земли.
2. Поток между двумя концентрическими цилиндрами.
3. Поток от решетки труб.
4. Поток между двумя полосами, находящимися в неограниченной среде.
5. Поток через стенки печи.
Из этих примеров в первых трех рассматриваются геометрически про-
простые границы, так что для них можно надеяться найти полные теоретические
решения. Два последних примера сложнее.
В последнее время большое внимание уделяется разработке численных
методов решения таких задач (см. гл. XVIII).
Вначале отметим, что в случае изотермических поверхностей тепловой
поток между ними можно найти из теоретического или экспериментального
определения их электрической емкости ¦*). Предположим, что тепло пере-
передается от поверхности Sx с температурой vx к поверхности 52 с темпера-
температурой v2 через среду с коэффициентом теплопроводности /С. Тогда, опре-
определяя термическое сопротивление R исследуемой системы как отношение
разности температур поверхностей к количеству тепла, проходящему между
«ими в единицу времени, находим
R= «>-*» , E.1)
К J I (du/dn)dS2
где символ д/дп обозначает дифференцирование по нормали к 52, направлен-
направленной внутрь среды.
В этом случае температура v, служащая решением уравнения Лапласа,
принимающим на границах значения v1 и vv численно равна электростати-
электростатическому потенциалу, возникающему между поверхностями S2 и S2, разделен-
разделенными материалом с диэлектрической проницаемостью, равной единице, и
заряженными до потенциалов г/, и г/2. Емкость такого конденсатора равна
г
—v2)
s9
E.2)
*) Этот метод был разработан для изучения изотерм вблизи поверхности
Земли [16].
**) Рассмотрение некоторых простых систем приведено в [17].
424 ГЛ. XVI. УСТАНОВИВШАЯСЯ ТЕМПЕРАТУРА [§ 6
Отсюда, сравнивая E.1) и E.2), получим
* E3>
Аналогично, если пространство между двумя поверхностями заполнено
электролитом и при известной разности потенциалов измерен электрический
ток между ними, то можно определить термическое сопротивление между
поверхностями. Этот метод был использован для получения эмпирической
формулы термического сопротивления стенки печи толщиной /, окружающей
прямоугольный параллелепипед со сторонами 2а, 2Ь, 2с, в случае, предста-
представляющем значительный интерес, а именно при /, имеющем тот же порядок
величины, что и а, Ь и с [18] *).
Трехмерные задачи подобного типа довольно сложны. Если их можно
упростить и привести к двумерным, то становится полезным метод конформ-
конформного отображения, оказавшийся весьма плодотворным в других областях
науки. В наших исследованиях этот метод применим к трем типам задач.
Во-первых, он позволяет получить точные решения простых задач, например
задач, изложенных в пунктах 1 и 2; во-вторых, он дает приближенные
решения некоторых задач типа 3 в том смысле, что он дает точные значе-
значения для решеток овальных кривых, которые имеют почти (но не совсем)
круглую форму; наконец, его можно использовать для исследования некото-
некоторых областей простого типа, которые очень часто встречаются на практике»
например стенки, изогнутой под прямым углом, стенки переменной толщины,
изолирующего кольца и т. д.
Этот метод подробно рассматривается в учебниках по электричеству и
гидродинамике. Здесь же мы дадим только краткое введение к приложению
этого метода, сначала к задачам для установившегося теплового потока, когда
температура поверхности является произвольной функцией положения, а затем
к более простому случаю теплового потока между изотермическими поверх-
поверхностями.
§ 6. Использование сопряженных гармонических функций
в задачах с установившейся температурой **)
Пусть ?, т\ — действительные функции х и у, причем такие, что ***)
В этом случае !¦ и г\ называют сопряженными гармоническими функциями х
и у. Тогда мы имеем
дх ^' дх
Следовательно,
<62)
*) Краткое изложение этого метода можно найти в книге Мак-Адамса [19].
**) В этом и в следующих параграфах настоящей главы задачи с установив-
установившейся температурой рассматриваются для пространственных тел; при этом везде
предполагается, что распределение температуры не зависит от одной из координат.
Иными словами, задачи формулируются не для самого тела, а для его сечения*
(Прим. ред.)
***) Здесь, конечно, f (z) является аналитической функцией. (Прим, ред.)
§ 6] ГЛ. XVI. УСТАНОВИВШАЯСЯ ТЕМПЕРАТУРА 425
Отсюда вытекает, что кривые !¦== const и т] = const ортогональны.
Кроме того, поскольку
d2t д2
дх2 дх ду
и
дЧ _ д*у\
ду2 ~ дхду*
ТО
S+fr = 0 F.3,
и аналогично
?+?-•• <">
Далее, если v является такой функцией ? и 7], что
то можно показать, что
d2v , d2v _ п
д.*2 ' ду* ~
Так,
~дх ~~ Ж~дх^г"Ц дх
и
_^_^Ч^/_ае_\2 a2t; dg ^т) a2tr / ду\ \2 . ^t; ^2e . ^t/ a2^
^д:2 ~~ д& [дх ) "•" ае dij d;c дл: "*" dija \ ^л: / "+" д? дх2 "+" dij (?jc2 *
Аналогично,
. a2t; / ^7) \2 ^t; d2S . ^t/ d2t\
~т~ дт\2[ду ) ^ dt ду2 "+" ^т) ^у2 ч
ду2 ~ ae2 l ду ) "^ ae ^7] ду ду
Складывая эти два выражения и используя соотношения FЛ)—:F.5),
получим
d2v . d2v _ п
д*2 "•" ay2 ~
Итак, если мы можем получить решение уравнения
д2у . ^2t; _ п
ai2 "•" ^тJ ~Ui
удовлетворяющее некоторым граничным условиям на кривых
то это решение на плоскости (Е, т\) можно преобразовать в решение на пло-
плоскости (х, у), причем границами служат кривые в плоскости (л:, у), которые
при преобразовании
будут срответствовать кривым1 ? = $1э и т. д.; температуры на этих границах
будут соответствовать температурам на границах в плоскости (?, т]).
Рассмотрим прямоугольник в плоскости (?, т]), определяемый следующим
образом:
7] = 7]!, 7] = 7]2,
426 ГЛ. XVI. УСТАНОВИВШАЯСЯ ТЕМПЕРАТУРА [§ 7
причем
v = fi(n) при ? = hiC*h < У < тJ)'
^ = Л С7!) ПРИ 5 =
1^ = ^@ при 7] =
* = />а© при i7 =
Решение этой задачи получается разбиением ее на четыре случая,
в каждом из которых три границы поддерживаются при нулевой темпера-
температуре. Таким образом, как и в задаче I § 3 гл. V, найдем
F —6l)
1L
и
D72 —
I F,-6.)
где а , а\ Ь и У — коэффициенты в рядах синусов
Находя ? и т] из соотношения
получаем температуру в области, ограниченной кривыми, которые соответ-
соответствуют $ = $!, и т. д., причем на этих кривых температуры соответствуют
/г(г1) и т. д.
§ 7. Приложения этого метода [20, 21]
I. Сектор круга *).
Рассмотрим преобразование
25iL±fi G.1)
В этом случае, обозначая z = reiB, получим
а сектор радиуса а с углом а соответствует области в плоскости (?, г\)
0 < т], 0 < 5 < те.
Тем самым уравнение
*) См. примечание к § 6. (Прим. ред.)
§ 7] ГЛ. XVI. УСТАНОВИВШАЯСЯ ТЕМПЕРАТУРА 427
при условиях
v = 0, когда ? = 0 и 5 = те,
и
v= 1, когда ?] = 0,
приводится к виду
v = 0, когда 6 = 0 и 0=а,
и
<о = 1, когда г = а.
Это уравнение в плоскости (?, tj) уже встречалось при рассмотрении
неограниченного тела с прямоугольным сечением, и его решение, согласно
формуле B.11) гл. V, имеет вид
2
Поэтому температура в рассматриваемом нами секторе дается выра.
жением
sin (гсб/а)
2_ \ sin (гсб/а) )
V ~ 1Г аГС g I sh [(it/a) In (a/r)] f '
Если граница г = а поддерживается при температуре г/= /(9), то за-
задача сводится к решению уравнений
; = 0 при Е = 0 и Е =
v = f — при т] = U.
\ тс у
Это решение уже рассматривалось в § 2 гл. V.
Подобным же образом, если граница 0 = 0 поддерживается при задан-
заданной температуре /(г), а другие границы имеют нулевую температуру, то
решение вытекает из соотношения B.18) гл. V.
Если мы аналогичным путем воспользуемся формулой G.1), то угол
0 < 0 < а, г>0 преобразуется в неограниченную полосу —со < т] < 0,
0 < 5 < ъ и, следовательно, решение для установившейся температуры в клине
с произвольной температурой границы непосредственно вытекает из соотно-
соотношения B.19) гл. V.
И. Круг.
Рассмотрим преобразование
7j = —Пп V • G.3)
В этом случае
а круг г < а соответствует области
0 < ч. 0 < 6
ПЛОСКОСТИ (i, TQ).
428 ГЛ. XVI. УСТАНОВИВШАЯСЯ ТЕМПЕРАТУРА [§ 7
Тем самым решением */(?, т]) уравнения
G.4)
l) = v Bтс, 7j), когда 7] > О,
служит решение уравнения
^ = /(?)• когда 17 = 0,
v@, 7|) = t;Bic, 7j), когда 7j > 0,
дх*^ду* • G.5)
г/= /F), когда r = a. J
Решение уравнения G.4) имеет вид
?Л sin л5).
оо
2 Л
о
где
2*
SO cos я^ */?',
о
2тс
6
Таким образом, получаем
О
2*
1 /» 1 ^-21)
А 1 А g
2тс ./ \ 2е~^ cos (i ?')~f~?~^
о
Отсюда температура в круге запишется в виде
2тс
Интеграл G.6) есть интеграл Пуассона (см. [22]).
III. Область между двумя концентрическими окружностями.
Решение в этом случае можно получить при помощи того же преобразо-
преобразования в виде
§7]
где
ГЛ. XVI. УСТАНОВИВШАЯСЯ ТЕМПЕРАТУРА
Л (9 = 2 («„ cos п\ + bn sin «?),
о
429
являются рядами Фурье для /г(%) и /2(?) в интервале от 0 до 2тс.
IV. Область между двумя пересекающимися или непересекающимися
окружностями.
Рассмотрим преобразование
G.7)
В этом случае
где гх и г2 — расстояния от точек А A, 0) и В (—1, 0) до точки Р(х, у),
а бр 82 — углы, образованные отрезками АР и ВР с положительным напра-
направлением оси х (рис. 49).
F х
Рис 49.
Тогда при Е = const мы получим систему окружностей с центрами
на одной прямой, для которых А и В служат предельными точками, а при
7] = const — систему окружностей, проходящих через точки А и В. Эти две
системы кривых, как и во всех случаях сопряженных функций, являются
ортогональными. При таком преобразовании плоскости (л;, у) соответствует
— :гс<т7<тс и — оо<$< оо; нижней стороне участка В А вещественной
оси соответствует ч\ = — тс; лучам Ах и Вх' соответствует т}=0; верхней
стороне участка В А соответствует т} = те; области у > 0 — положительные
значения т], а области у < Q — отрицательные ее значения. Кроме того,
точке А соответствует точка ? = + °о, точке В — точка 5 = — оо, а ли-
линии у'Оу соответствует 5 = 0.
Перейдем к применению этого преобразования к некоторым случаям,
когда область в плоскости (х, у) ограничена дугами окружностей.
1) Рассмотрим область, ограниченную линиями
? = ?! И ? = ?2 @<7}<ТС),
7] = 0 И 7} = ТС (?, < 5 < У
и показанную на рис. 49 жирными линиями.
при 5 =
430 ГЛ XVI. УСТАНОВИВШАЯСЯ ТЕМПЕРАТУРА
Пусть г> = 0 при $ = 52. ^ = 0ит] = 1си
v = f(
Тогда мы получим
оо
Ssh n (?2 —
i а»8ЬяF,-6
где
[§ 7
Легко распространить это решение на случай:
*=/>!© при т]=о ai<s<y-
tF = ^ (g) ПРИ 7] = 7U (Цг < g < у.
2) Рассмотрим область, ограниченную двумя окружностями 5 = ^ и $ = $2,
охватывающими предельную точку А.
Пусть v = fx(rj) при ? = ?! и г; = 0 при ? = ?2- Тогда решение,
очевидно, запишется в виде
р
где
'*
тс
** = -i f f
Рис. 50.
Подобным же образом, если v = f2(ri) при ? = ;2 и,г> = 0 при ? = $!, то
где а^ и &^ — коэффициенты ряда Фурье для /2 (?]) в интервале — те 1- те.
Складывая эти два выражения, получим решение для случая, когда гра-
граничные окружности i-j и $2 поддерживаются при температурах соответственно
/iOq) и /2(т]).
Ясно, что если /^(т}) и /2(т7) постоянны и равны соответственно vx и v2t
то следует только решить уравнения
v=Vi при 5 =
t; = v2 при 5 ав
§ 7] ГЛ. XVI. УСТАНОВИВШАЯСЯ ТЕМПЕРАТУРА 431
Искомое решение имеет вид
Стационарный тепловой поток в области между двумя заданными окруж-
окружностями будет, кроме того, рассматриваться в § 9 данной главы.
3) Рассмотрим область с границами:
т) = тI @<? <оо),
7] = ТJ @ < g < СО),
? = 0 (т), < т) < тJ),
показанную на рис. 50.
Предположим, что
l/=/l(Y)) ПРИ ? = 0 (YJi < Y) < Y]2),
г/ = 0 при т) = y)i @ < $ < со),
г/ = 0 при т) = тJ @ < ? < со).
Тогда, как и в § 2 гл. V, решение имеет вид
Г nnz
— Г"
G) Y),)
^Г
где
Предположим далее, что
^ = /2 (^) при т) == 7]i @ < е < оо),
V = 0 ПрИ 7) = 7J @ < ? < СО),
г/ = 0 при ? = 0 (т^ < y) < тJ).
Из соотношения B.18) гл. V следует, что
х1 '
COS [ТС GJ - Т))/^ - 7),)] + СП [ТС (g - ?')/(Ч2 -
1
cos [тс (тJ — 7])/(тJ — т),)] + ch [те (? + ?)/{ъ — i
;, когда все тр
:одят сложением
4) Рассмотрим'область с границами
G.11)
Решение для случая, когда все три границы (см. рис. 50) поддерживают при
заданной температуре, находят сложением решения G.10) и двух решений типа G.11).
*)=7I (—со<?<со),
71=7J ( СО<?<СО).
Пусть
*/ = /(?) ПрИ 7]= 7],
и
V = 0 ПрИ 7) = 7J.
Тогда, используя, как и выше, соотношение B.19) гл. V, найдем
2D,-4.) ЯП <Ъ—4i)
— ОО
G.12)
432 ГЛ. XVI. УСТАНОВИВШАЯСЯ ТЕМПЕРАТУРА [§ 7
V. Софокусные эллипсы или гиперболы.
Рассмотрим преобразование
или
Тогда
х = с ch ? cos т), у = с sh 5 sin tj
и
ch2e n
v2 V2
COS2 7) Sin2 7)
Следовательно, кривые е = const и т) = const образуют ряд софокусных эллип-
эллипсов и гипербол, а плоскость (jc, у) соответствует — тс < т) < тс и 0 < ? < оо, причем
для нижней части этой плоскости г\ < 0, а для верхней ее части г\ > 0.
1) Два софокусных эллипса. Рассмотрим область с границами 5 = ?i и ? = ?2-
Пусть
v = /iG)) при 5 = Si,
/2A) ПРИ ? = ^2-
Тогда, как и выше,
оо оо
sh n (?2— ?) . it, ч I V1 sh п (с—?i) / /
(й C°S Щ + К Si" П1)) + 2 hBfeg) (а« C0S
где ап, Ьп, а'п и b'n — коэффициенты рядов Фурье для f1 (т)) и /2 (т)) в интервале
от —те до -f-те.
2) Дед полуэллипса и отрезок большой оси между ними. В этом случае
область имеет границы
6 = 5i и Б = с2 @ < т) < тс),
7) = 0 И Y) = 7C (^<?< ?2)-
Пусть
1/ = /!(тг)) при S=glf
v -= /2 С7)) при 5 = ?2»
и
V = 0 ПрИ 7) = 0 И 7) ¦= ТС.
Очевидно, что в данном случае решение имеет вид
;fi) ^
где дл и д^ — коэффициенты рядов по синусам для /j (тг)) и /2 (тг]).
3) Полуэллипс. В этом случае область имеет границы
Пусть 1/ = /(к]) при c=Si, и пусть на большой оси температура равна нулю.
Тогда
оо
Ssh n\
ап sin пъ —г—г—,
п ' sh /г§,
l
где ап — коэффициент ряда по синусам для / (т)).
4) Полный эллипс. В этом случае решение должно удовлетворять уравнению
d2v d2v
при б = Si (— те < т] < тс).
§ 8] ГЛ. XVI. УСТАНОВИВШАЯСЯ ТЕМПЕРАТУРА 433
Кроме того, при переходе через большую ось или при движении вдоль нее не
должно возникать разрыва непрерывности температуры или теплового потока.
Всем этим условиям удовлетворяет выражение
п = 0
где ап и Ьп — коэффициенты ряда Фурье для /0?) в интервале от —тс до л.
5) Четырехугольник, ограниченный дугами двух софокусных эллипсов и
гипербол. Он приводится к прямоугольнику в плоскости ($?]). Отсюда и получается
соответствующее решение.
§ 8. Установившийся тепловой поток в многоугольнике
Решения, приведенные в предыдущем параграфе, найдены путем исполь-
использования хорошо известных преобразований, соответствующих рассматривае-
рассматриваемым областям. Общий метод нахождения преобразования различных областей
отсутствует. Для двумерного установившегося потока в области, ограничен-
ограниченной многоугольником, теоретически возможно найти соответствующее преоб-
преобразование путем использования приведенной ниже теоремы.
Теорема Шварца — Кристоффёля [23, 24] гласит, что любой много-
многоугольник, ограниченный в плоскости z(z — x-{-ly) прямыми, можно преоб-
преобразовать в ось ? плоскости t(t = b-\-if[) и что точки внутри многоугольника
на плоскости z преобразуются в точки на полуплоскости t. Преобразование,
с помощью которого это достигается, получается из соотношения
4L = C(t-W''-1(t-W*''-1 ¦ ¦ ¦ (t-%nfnl«-\ (8.1)
где alf a2, ..., ап — внутренние углы многоугольника, $lt ..., ?л— точки
на вещественной оси, в которые преобразуются вершины углов, С — посто-
постоянная; кроме того, если одна из вершин углов соответствует бесконеч-
бесконечному значению ?, то соответствующий множитель в соотношении (8.1)
опускается *).
Какими бы ни были значения %v ..., ?л> преобразование (8.1) отобра-
отображает ось ? в многоугольник с внутренними углами аг, ..., ал; если он
должен быть подобным заданному многоугольнику, то можно произвольно
выбрать только три значения из ?v ..., ?л; остальные должны определяться
размерами заданного многоугольника.
Если преобразование известно, то температуру в любой точке можно
вывести из известного решения для температуры в полуплоскости г\ > О,
обусловленной температурой /(?) на границе т] = 0. По аналогии с соотно-
соотношением B.20) гл. V получаем для этой температуры
1 Г /(*')
тс J E-?')
*) Доказательства этой теоремы приводятся в большинстве курсов электри-
электричества и гидродинамики (см. также [25—27]). В последней работе содержится много
примеров, представляющих интерес для рассматриваемых здесь случаев.
Доказательство основано на том, что, согласно соотношению (8.1), аргумент
функции dz/dt постоянен, если t лежит между двумя произвольными точками
?i» ?г» •••» и» следовательно, отрезки [?/, ?/+1] плоскости t соответствуют прямым
линиям на плоскости г. Кроме того, когда t переходит из ?г — е в ?г-+"е по полу-
полуокружности с бесконечно малым радиусом е, аргумент функции dz/dt увеличивается
на я — ап что соответствует внутреннему углу <хг многоугольника. (См. также, напри-
например, М. А. Лаврентьев и Б. В. Шабат, Методы теории функций комплекс-
комплексного переменного, Физматгиз, 1958. Прим. ред.)
28 Г. Карслоу, Д. Егер
434 ГЛ. XVI. УСТАНОВИВШАЯСЯ ТЕМПЕРАТУРА [§ 8
Если при $>0 /(?) = V1 = const, а при % <о /(?) = 0, то это выра-
выражение принимает вид
y{\ + ^rctg\). (8.2)
Приведенное выше преобразование можно использовать для изучения
тепловых потоков в прямоугольнике, а также в области, находящейся между
квадратами с параллельными сторонами и общим центром [28, 29]. В общем
случае решения будут содержать эллиптические или другие специальные
функции. Наиболее простые и вместе с тем наиболее важные результаты
получаются при использовании этого метода в случае вырожденных много-
многоугольников с несколькими углами на бесконечности; в ряде таких случаев
решение содержит только элементарные функции и делает возможным изуче-
изучение двумерных задач, которые являются идеализацией таких широко рас-
распространенных систем, как изогнутая стенка, стенка переменной толщины,
впадина в стенке, изолирующее кольцо и т. п. Рассмотрим несколько при-
примеров такого типа *).
I. Тепловой поток между неограниченной плоскостью АВ и полу-
полуограниченной плоскостью CD (рис. 51).
Рассмотрим многоугольник в плоскости 2, обозначенный ABCDEA.
Он имеет угол, равный нулю при ВС на бесконечности, внутренний угол 2тс
при D; если принять, что точки, соответствующие А и Е, находятся на
бесконечности в плоскости Л то углы В А и DE здесь рассматривать не надо.
ВС
t=-oo t=O t = 1 t=oo
А в
Рис. 51. Рис. 52.
Поскольку в плоскости t три точки можно выбирать произвольным образом,
примем, что точки А и Е располагаются в бесконечности, В и С — в точке
? = 0, a D — в точке t=l. Фигура, полу-
]^ чающаяся в плоскости Л показана на рис. 52.
Тогда соотношение (8.1) принимает вид
— = C-j—. (8.3)
Сокращенный метод с использованием
внутренних углов 0 и 2тс, примененный выше
для получения соотношения (8.3), оказы-
оказывается наиболее удобным. Если угодно, мно-
Рис. 53. гоугольник, показанный на рис. 51, можно
рассматривать как предельный случай много-
многоугольника ABCDD'EFGA (рис. 53) при D'->D и вершинах Л, В, С, Е. F и О,
удаляющихся на бесконечность. Записывая соотношение (8.1) для многоуголь-
многоугольника, показанного на рис. 53, и переходя к пределу, мы снова получим (8.3).
Интегрирование соотношения (8.3) дает
' (8.4)
*) Другие примеры использования этого метода можно найти в [26, 27, 29—32].
Задачи аналогичного типа с закруглением некоторых углов рассмотрены в [33]. Дру-
Другие задачи с закругленными углами изложены в [34]. Метод Шварца был также
обобщен на многоугольники с криволинейными сторонами [35].
§ 8]
ГЛ. XVI. УСТАНОВИВШАЯСЯ ТЕМПЕРАТУРА
435
Произвольные постоянные С и k находят путем точного задания много-
многоугольника в плоскости z. Постоянную С всегда можно считать действитель-
действительной; придание ей комплексного значения просто поворачивает многоугольник.
Если отрезок АВ служит участком оси л;, то величина z при действитель-
действительном и отрицательном t должна быть действительной. Это требует, чтобы
к = ЫС, и тогда (8.4) принимает вид
= C{t — \nt-\-in}.
(8.5)
Теперь в точке D t=\, и, следовательно, z = CA +/ти). Отсюда
следует, что расстояние между данными плоскостями равно тиС.
II. Тепловой поток между неограниченной плоскостью и прямым
двугранным углом.
Здесь рассматриваемым многоугольником служит ABCDE (рис. 54),
и мы преобразуем точки А, В, точку CD и точку Е в точки —оо, —1, О
и -f со на оси ?. Внутренние углы при
точке В и точке CD равны соответственно
Зти/2 и 0; тогда соотношение (8.1) прини-
принимает вид
что дает
-оо
°°
(8.6) Рис* 54*
Чтобы определить произвольные постоянные С и &, воспользуемся тем,
что при переходе t через нуль z уменьшается на НС. Кроме того, при
t > 0 z действительно, т. е. DE является
действительной осью в плоскости z. Таким
образом, если расстояние между ВС и DE
равно Л, то nC = h. Далее, при t = —1,
z = tCTz-{-k. При выборе & = 0 начало ко-
координат фиксируется на пересечении DE и
продолжения АВ.
Hi. Изолирующее кольцо.
Многоугольник, показанный на рис. 55,
можно использовать для исследование влия-
влияния изолирующего кольца на изотермы между
параллельными плоскостями. Пусть А переходит в 6 = — оо, а В переходит
в \ = —1. точка CD — в ? = — а, где а будет определено позднее, EF —
в? = а, О-1—в $=1 и Н — в ? = -f-oO' Внутренние углы в вершинах CD
и EF равны нулю; в вершинах В и О они равны Зтс/2. Тогда
.7?
О-
Е
Рис. 55.
Интегрируя, найдем
dz
dt
+ .С1^Е?1, ,8.7)
где постоянную интегрирования следует выбрать так, чтобы при ? = 0 z = 0.
DE служит отрезком оси у, а ось х располагается посередине между АВ
28*
436
ГЛ. XVI. УСТАНОВИВШАЯСЯ ТЕМПЕРАТУРА
§ 8]
и HG. Чтобы найти а и С, мы предполагаем, что 2k есть расстояние между
плоскостями ЛВ и HG и что h есть расстояние между плоскостями GF
и DE\ тогда точка О имеет координату z = h — Ik. Полагая в соотноше-
соотношении (8.7) /=1. z = h — Ik, найдем
—2
Отсюда
= — >
тс
о
IV, Стенка, согнутая под прямым углом.
Схематическое изображение такой стенки показано на рис. 56. Точки А,
В, CD, E, F отображаются в —оо, —а, 0, 1, ~\-оо в плоскости /. Исполь-
Используемое преобразование определяется уравнением
3 А
dz _
dt -
Чтобы проинтегрировать его, положим
t —
-а
7
О
?
D
А
к
оо
Г
тогда
Рис. 56.
(8.8)
(8.9)
где постоянная интегрирования обращается в нуль в результате выбора z = 0
при t = 1, т. е. выбора в качестве начала координат в плоскости z точки Е.
Соотношение (8.9) можно написать в другом виде
(8.10)
Ца+1)
Полагая в соотношении (8.10) t = — а, найдем значение z для точки В\
оно будет равно — ъСа-Ч*^{-1ъС. Теперь, если расстояние между верти-
вертикальными границами стенки (рис. 56) равно h, а расстояние между ее гори-
горизонтальными границами равно k, то для точки В получаем z = — h-\-ik
при t = — а. Поэтому из (8.10) находим
«Г
-a
-7
Рис. 57.
k = tzCt h = nCa~'*, a = -j~2. (8.11)
V, Скачкообразное изменение тол-
толщины стенки [36, 37, 41].
Схематическое изображение такой стен-
стенки показано на рис. 57, причем значения ?
в плоскости t отмечены у вершин углов. Используемое преобразование опре-
определяется выражением
dz _
dt "
Полагая
находим
= C\n
I
(8.12)
§ 9]
ГЛ. XVI. УСТАНОВИВШАЯСЯ ТЕМПЕРАТУРА
437
Произвольные постоянные интегрирования выбираются таким образом, чтобы
при t = — a z = IkC. Кроме того, полагая в соотношении (8.12) * = —1,
находим z = iKCa-xl*.
Наконец, при t > 0 z действительно. Поэтому EF является отрезком
действительной оси в плоскости z, а начало координат лежит на пересече-
пересечении ВС и EF. Если толщины стенки слева и справа от начала координат
равны h и &, то мы получим
(8.13)
— оо оо
k2
VI. Перегородка в стенке [38] *).
Значения 5, соответствующие вершинам углов, указаны на рис. 58.
Используемое преобразование определяется
соотношением
dz
dt
Ct
(t2—l)(t2 — a2)l/* '
-1
2V \—a>
In
V.T=tf
-a
h
i
l_02_l/*2_
(8.14)
Рис. 58.
где постоянная интегрирования выбрана так, что z = 0, когда t= ± а, т. е.
начало координат в плоскости z находится у основания перегородки. Далее»
из соотношения (8.14) получим
при
при
± оо z-> —
z — —
¦ arctg ¦
Таким образом, если расстояние между стенками равно А, а высота
перегородки k, мы должны получить
= Л, a = sinj±. (8.15)
тсС
§ 9. Тепловой поток между изотермическими поверхностями
Метод, изложенный в §§ 6—8 данной главы, весьма общий, и он при-
емлем для изучения задач, в которых температура поверхности является
произвольной функцией положения. Из теории конформного отображения
здесь используется только преобразование заданной области в плоскости z
в простую область в плоскости t, для которой может быть написано решение.
Из наиболее важных практических задач легче всего решаются задачи,
в которых границы области в плоскости z поддерживаются при постоянной, а не
при произвольной температуре, и решение в плоскости t принимает простую
форму (например, имеет вид G,9) и (8,2) данной главы). Вместо такого
метода получения решения этих задач здесь мы рассмотрим несколько отлич-
отличный метод, точно соответствующий методу, используемому в теории электри-
электричества [43] или гидродинамике. Сама температура v берется в виде одной
из пары сопряженных гармонических функций; затем путем исследования
*) В работе [39] приведено множество решений задач подобного типа. Тепло-
Теплообмен на плоской границе рассматривался в [40]. Выступ на плоскости рассмотрен
в [41, 42].
438
ГЛ. XVI. УСТАНОВИВШАЯСЯ ТЕМПЕРАТУРА
[§9
функции и, сопряженной с v, мы можем найти тепловой поток через любой
участок одной из граничных поверхностей и, следовательно, выражение
для термического сопротивления (см. E.1) настоящей главы) в установив-
установившемся потоке между границами с постоянными температурами.
Пусть, как и выше (см. стр. 426),
w = u + lv = f(x + ly) = f(z).
Тогда все решения § 6 имеют силу при замене ? и т\ на и и v. В частности,
дх2 ~ ду2 к }
Отсюда следует, что мнимая часть (или аналогичным образом действи-
действительная часть) любой функции f (z) служит решением уравнения для уста-
установившейся температуры и, в частности, определяет температуру в области
между кривыми v = vx и v = v2 (где vx и v2 — постоянные) в плоскости z.
Например, если
1 1 ;й
(9.2)
i • ] 1 l I i ft
и-\- iv =— In z = — In г Н ,
тс к к
то мы получим v = b/n, что определяет установившуюся температуру в обла-
области между плоскостью 6 = 0, поддерживаемой при нулевой температуре,
и плоскостью 6 = тс, поддерживаемой при единичной температуре (ср. (8.2)
данной главы).
Отметим далее, что кривые и = const и v = const в плоскости z орто-
ортогональны (согласно F.1) и F.2)). Поэтому, так как линии v = const являются
изотермами, кривые и = const являются ли-
линиями тока. Кроме того, мы можем написать
а
дп Поэтому модуль вектора потока (ср. § 3
гл. I) в любой точке равен
- <9-4)
Рис. 59.
Так же просто можно получить вели-
чину теплового потока через любой участок
изотермической поверхности. Обозначим че-
через д/дп дифференцирование по нормали к поверхности, а через d/ds — диф-
дифференцирование по касательной к ней (рис. 59).
Тепловой поток через поверхность в любой точке записывается в виде
Таким образом, тепловой поток через участок поверхности от sx до s2
равен
К f ^-ds = K(u7~-ux),
(9.5)
где их и и2 — значения и при sx и s2 соответственно.
§9]
ГЛ. XVI. УСТАНОВИВШАЯСЯ ТЕМПЕРАТУРА
439
Как мы видим, введение функции и, сопряженной с v, значительно упро-
упрощает расчет теплового потока через изотермическую поверхность и, следо-
следовательно, расчет теплового сопротивления между изотермическими поверх-
поверхностями.
С этой точки зрения плоскость t = Z-\-iri (см. § 7) можно рассматри-
рассматривать как плоскость w настоящего параграфа. В более сложных задачах пре-
предыдущего параграфа мы отображаем плоскость z в плоскость t, как и раньше.
В простом случае двух изотермических границ записываем решение для пло-
плоскости t при помощи соотношения (9.2), т. е.
W-— In t,
(9.6)
или соответствующей его модификации и получаем из него решение в пло-
плоскости г. Для нахождения модуля вектора потока в любой точке восполь-
воспользуемся соотношением
dw
~Jz~
=
dw
~df
X
dt
dz
=
dw
~df
dz
dt
(9.7)
Перейдем теперь к изучению термического сопротивления между неко-
некоторыми рассмотренными ранее границами.
F. Установившийся тепловой поток между цилиндрами кругового
сечения.
Соответствующее преобразование уже приводилось в § 7 настоящей
главы. Для практических расчетов решение можно записать в самой про-
простой форме. Используя соотношение G.7) данной главы и вводя некоторые
изменения в обозначения, полу-
получим
u-\-iv — i In
, (9.8)
так что
In
rf
и и =
6, (9.9)
с
у
0
[
л
/
/г'
/в'
А
\
)
а,
F
рис 60.
где г кг' — расстояния точки
Р(х, у) до точек (т- с, 0), а 0 и
6х — углы PCX и PDX (рис. 60).
Предположим теперь, что мы хотим найти термическое сопротивление
между двумя цилиндрами с радиусами ах и а2, центры которых находятся
на расстоянии d друг от друга. Подробно рассмотрим случай, когда цилиндр
радиуса аг окружает цилиндр радиуса а2. Обозначим на рис. 60 ли-
линию, проходящую через центры, через ОХ. Следует выразить значение с и
отношение (r/rf) для каждой из окружностей через заданные значения
av a2 и d.
Предположим, что центр А окружности радиуса а расположен на рас-
расстоянии dx от точки О. Обозначим через kx постоянное значение отношения
(г/г') для такой окружности. Тогда, записывая значение этого отношения
соответственно для точек Е и /\ получим
Отсюда следует, что
(9.10)
(9.11)
440 гл. xvi. установившаяся температура [§ 9
Аналогичным образом, для окружности радиуса а2 с центром, располо-
расположенным на расстоянии d2 от О, получим
</2_а2 = А (9.12)
Вычитая (9.12) из (9.11), находим
d\ — d\=a\ — a\. (9.13)
Кроме того, поскольку расстояние между центрами окружностей равно d,
dl — d2 = d. (9.14)
Отсюда следует, что
al-4-d2
^^й(9Л5>
Кроме того, подстановка (9.11) в (9.10) дает
lL. (9.16)
t—а, ах
Таким образом, учитытая (9.9), получим для этого цилиндра
P1 = lnfe,=Arch-^- = Arch{ 2д27 }. (9.17)
а для цилиндра с радиусом а2
{2 9 1 \
ul~~2a27d Г (9Л8)
Помимо этого, из соотношения (9.9) следует, что при полном обходе
любого из цилиндров и увеличивается на 2я. Поэтому, согласно (9.5), теп-
тепловой поток между цилиндрами (на единицу длины) равен 2я/С. Разность
температур между ними, равная v2 — vv определяется (9.17) и (9.18), и, еле-
довательно, термическое сопротивление между цилиндрами на единицу длины
записывается в виде
(v2 — vx)
-2^Г--2^[АГСНД1 2М d Arch^ 2М+" } =
(9.19)
Для цилиндра радиусом ах с осью, расположенной на расстоянии
dx от плоскости* причем и цилиндр и плоскость представляют собой
изотермические поверхности *), как и раньше, справедливо соотношение
(9.17), и для термического сопротивления (на единицу длины) между цилин-
цилиндром и плоскостью получим
(9-20>
Если цилиндры находятся снаружи друг от друга, то мы пред-
предполагаем, что цилиндр с радиусом ах окружает предельную точку D*
*) Это решение находит применение при нахождении постоянных тепловых
потерь кабелями, проложенными в земле [44]. Случай теплообмена на плоской по-
поверхности обсуждается в [40, 45]. Другие задачи с граничными условиями, третьего
рода рассматриваются в [46].
§ 9] ГЛ. XVI. УСТАНОВИВШАЯСЯ ТЕМПЕРАТУРА 441
а цилиндр с радиусом а2 содержит точку С. Будем действовать так же, как
и выше, но в данном случае выражение (9.14) следует заменить на dl-\-d2 = d.
Тогда у1 определяется (9.17), a v2— из соотношений
—-* --i iiM г (9-21)
Таким образом, термическое сопротивление (на единицу длины) между
двумя цилиндрами равно
II. Другие задачи с круговыми границами.
Следующими по трудности и весьма важными для практики системами
являются цилиндр между параллельными плоскостями и решетка, образо-
образованная регулярно расположенными цилиндрами *). Точные решения задач
с помощью конформного отображения получить не удалось, однако известны
решения для овальных кривых; соответствующим выбором параметров можно
получить хорошее приближение к окружностям **).
III. Тепловой поток под непроводящей полосой.
Пусть область —оо < х <—с поддерживается при постоянной темпе-
температуре тс, область х > с — при нулевой температуре, и при этом тепловой
поток через полосу —с < х < с отсутствует. Положим, что
и -f iv = Arch (x + ty)/ct
так что
x = cch ucosv,
у — с sh г/ sin г/.
Эквипотенциальными линиями служат гиперболы
=1
У2
с2 sin2 v
а линиями тока — эллипсы. Эквипотенциальной линией v = 0 служит линия
x = cch и> с, у = 0; —оо<я<0 соответствует нижней стороне луча
?<х<оо, а 0<#< оо —верхней его стороне. Аналогичным образом,
эквипотенциальной линией v = k служит линия х = — cchu< — с, у = 0;
— оо < и < 0 соответствует нижней стороне луча — оо < х < с,
а О < и < оо— верхней его стороне. Согласно (9.5) тепловой поток Q
из участка —X < х <—с нижней стороны оси х равен
K[u\xxZZex=K кхсЪ^-.
IV. Тепловой поток между пластинами АВ и CD (см. рис. 51).
Температура АВ равна единице, температура CD — нулю.
Здесь, как и в (9.2) или (9.6), полагаем
w = — Int.
*) То есть цилиндрами с параллельными осями. Сечение этой системы имеет
вид решетки из окружностей. (Прим, ред.)
**) Цилиндр между параллельными плоскостями рассмотрен в [47], а решетки —
в [48]. Цилиндр между параллельными плоскостями рассмотрен другим методом в [49],
ряд таких цилиндров — в [50]; другие задачи с цилиндрами между параллельными
плоскостями обсуждаются в [51].
442 ГЛ. XVI. УСТАНОВИВШАЯСЯ ТЕМПЕРАТУРА [§ 9
Кроме того, используя соотношения (8.5) данной главы, получим
^ ^ , (9.23)
где d — расстояние между пластинами.
Модуль вектора потока в любой точке равен следующей величине:
К
dw
~dz
„ dw | /| dz
= К
dt \l dt
К
d(t-\) •
При ?—>0, т. е. близ точек на ВС, он стремится к величине K/d,
которая равна установившемуся потоку между двумя параллельными пло-
плоскостями. В точке D, t=\, поток бесконечно велик.
На линии CD (поскольку здесь г> = 0), имеем
Далее, поскольку D является точкой d(\ —f-/ir)/ic, величина и в точке D
равна нулю. Ее значения в точках на CD и DE, удаленных от D на рас-
расстояние /, служат корнями уравнения
^—f 1=^«_ ки. (9.24)
Отрицательный корень этого уравнения соответствует точке на нижней
стороне CD (так как здесь 0 < t < Z, см. рис. 52), а положительный
корень — точке на верхней стороне DE.
Если / велико, отрицательный корень (9.24) приближенно равен
, 1\
- + 1TJ'
и поэтому величина теплового потока (рассчитанная на длину /) через
нижнюю сторону DC полосы запишется в виде
Эта величина на АТ/тс больше соответствующей величины потока между
неограниченными плоскостями.
Для больших значений / положительный корень (9.24) приблизительно равен
Таким образом, тепловой поток на расстоянии / от точки D через
верхнюю сторону DE равен
?(^-+l). (9.26)
V. Тепловой поток в стенке, изогнутой под прямым углом
(см. рис. 56).
Пусть температура поверхности DEF равна нулю, а температура поверх-
поверхности ABC равна единице. Тогда, как и ранее, положим, что
w = ~\nt. (9.27)
При вершине Е, t = 1, мы имеем и = 0. Будем искать тепловой поток
(на единицу длины вдоль угла) на длине х стороны EF, отмеряемой
§ 9] ГЛ. XVI УСТАНОВИВШАЯСЯ ТЕМПЕРАТУРА 443
от угла ?\ принимая, что длина х велика. Для этого, воспользовавшись (8,8),
(8.9) и (8.11) данной главы, получим значение t, соответствующее х, т. е.
^^ ^p2)f (9.28)
где
Теперь, если х велико, то t также велико, а р примерно равно еди-
единице. Полагая C=1 в первых двух членах правой части соотноше-
соотношения (9.28) (напомним, что они малы сравнительно с х и 1пA —Р2))и исполь-
используя (9.29), получим в качестве первого приближения
Так как ? велико, мы можем заменить In (^ —j— а) на \nt (допуская при
этом ошибку порядка a/t); тогда соотношение (9.30) приближенно дает
2h . k , , k2+h2 /n oi4
TarcigT + ln 4h2 ' (9*31)
Поскольку на Z;/7 v = 0, то, согласно соотношению (9.27), tzu== In t и,
следовательно, тепловой поток на длине х, отмеряемой от Е через сторону EF,
равен
Первый член соответствует установившемуся потоку между плоскостями,
находящимися на расстоянии к друг от друга. Прибавляя соответствующий
член, для DE найдем, что влияние прямоугольного изгиба заключается
в увеличении теплового потока вдоль угла на величину
k , 2k . h . 2 , k2+h2 \ /ft ООЛ
Если стенки имеют одинаковые толщины (т. е. k = Л), то это выра-
выражение сводится к
J I _lin2[ = 0,559A:. (9.34)
ЛИТЕРАТУРА
1. Gray, Ma thews, Treatise on Bessel Functions, Macmillan, ed. 2, 1922. (Э. Грэй,
Г. Мэтьюз, Функции Бесселя и их приложения к физике и механике, ИЛ, М.,
1953.)
• 2. L e e s, Phil. Trans. Roy. Soc. A204, 433 A905).
3. Birch, Bull. Geol. Soc. Am. 61, 567—630 A950).
4. Jeffreys, Mon. Not. R. Astr. Soc. Geophys. Suppl. 4, 309—312 A940).
5. В u 11 a r d, Mon. Not. R. Astr. Soc. Geophys. Suppl. 4, 360—362 A940).
6. Volterr a, Nuovo Cim. 4, 111—126 A912).
7. Thoma, Diss. Karlsruhe, 1906.
8. A n d г е a e; Ann. Ponts et Chaussees 128, 37 A958).
9. Lees, Proc. Roy. Soc. A83, 339—346 A910).
10. Livens, Theory of Electricity, ed. 1, 1918.
11. Lame, Liouvilles J. 2 A837).
12. Maxwell, Electricity and Magnetism, ed. 2.
13. В e s a n t, R a m s e y, Hydrodynamics, ed. 2, 1920.
14. R а у 1 e i g h, Phil. Mag. 34, 481—502 A892).
15. De V r i e s, The thermal conductivit> of granular materials, insi. international du
Froid, Paris.
444 ГЛ. XVI. УСТАНОВИВШАЯСЯ ТЕМПЕРАТУРА
16. Sbrana, Bossalasco, Geofis. Рига ё Appl. 23, 3—8 A952).
17. R и d е п b е г g, Elektrotech. Z. 46, 1342 A925).
18. Langmuir, Adams, Meikle, Trans. Am. Electrochem. Soc. 24, 53 A913).
19. M с A d a m s, Heat Transmission, ed. 2, 1942. (В. Мак-Адам с, Теплопередача,
ОНТИ, перев. с 1-го изд.)
20. М a t h i e u, Cours de physique mathematique.
21. Kober, Dictionary of Conformal Representations, Dover, 1952.
22. С а г s 1 a w, Fourier's Series and Integrals, Macmillan, ecL 3, 1930.
23. С h r i s t о f f e 1, Sul problema delle temperature stazionarie, Ann. Mat. Рига ё Appl.
1, 89 A867).
24. S с h w а г z, Crelle 70, 105 A869).
25. В a t e m a n, Partial Differential Equations of Mathematical Physics, § 4.62.
26. Carter, J. Inst. Elect. Engrs 64, 1115 A926).
27. Thomson, Recent Researches in Electricity and Magnetism, Chap. III.
28. M о и 1 t о n, Proc. Lond. Math. Soc. 3, 104 A905).
29. Bowman, Proc. Lond. Math. Soc. 39, 211 A935); 41, 271 A936),
30. Love. Proc. Lond. Math. Soc. 22, 337 A924).
31. Davy, Phil. Mag. 35, 819 A944); 36, 153 A945).
32. Bowman, Introduction to Elliptic Functions, London, 1953.
33. С о с k г о f t, J. Inst. Elect. Engrs 66, 385 A928).
34. Page, Proc. Lond. Math. Soc. 11, 314 A912).
35. Richmond, Proc. Lond. Math. Soc. 22, 483 A924).
36. Lees, Phil. Mag. 16, 734 A908).
37. С a s t о 1 d i, Geofis. Рига ё Appl. 23, 27 A952).
38. Lees, Proc. Phys. Soc. 23, 361 A911).
39. S с h о f i e 1 d, Phil. Mag. 6, 567 A928).
40. Awbery, Phil. Mag. 7, 1143 A929).
41. Lee s, Proc Roy. Soc. A91, 440 A915).
42. L a n g t о n, Davy, Brit. J. Appl. Phys. 5, 405 A954).
43. Jeans, Electricity and Magnetism, Cambridge, ed. 5, 1925.
44. M e 1 s о m, В о о t h, J. Inst. Elect. Engrs 52, 779 A915).
45. Ч а р н ы й, ДАН 48, 27 A945).
46. S с h о f i e 1 d, Phil. Mag. 31, 471 A941).
47. S с h о f i e 1 d, Phil. Mag. 12, 329 A931).
48. Richmond, Proc. Lond. Math. Soc. 22, 389 A924).
49. Knight, Proc. Lond. Math. Soc. 39, 272 A935).
50. К n i g h t, M с Ми 11 e n, Phil. Mag. 24, 35 A937).
51. Howland, McMullen, Proc Cambr. Phil. Soc 32, 402 A936).
ГЛАВА XVII
ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ
§ 1. Введение
Классический метод решения задач теплопроводности заключается в нахо-
нахождении решения в виде ряда частных решений дифференциального уравнения
и некоторых граничных условий, причем коэффициенты ряда определяются
из теории рядов Фурье или аналогичных им рядов. Этот метод вполне при-
пригоден для задач с ограниченными областями. Однако при рассмотрении
неограниченных областей соответствующий метод с использованием инте-
интегралов Фурье следует считать чисто формальным вследствие трудностей,
связанных со сходимостью. (Весьма важные функции, например единица,
не имеют преобразования Фурье.) Тем не менее эта формальная теория дей-
действительно дает правильные результаты, которые могут быть проверены
a posteriori; ее можно сделать строгой путем обобщения [1] теории преобра-
преобразования Фурье на комплексную плоскость. Кроме того, все чаще исполь-
используется не интеграл Фурье, а эквивалентный метод преобразования Фурье
(см. § 3 гл. II).
За последние три десятилетия метод преобразования Лапласа был зна-
значительно усовершенствован. При его применении к одномерным задачам
этот метод обладает следующими преимуществами перед более старыми
методами Фурье: 1) он дает стандартную методику, применяемую ко всем
задачам одинаковым образом; 2) он применим ко всем граничным условиям
и не зависит от последних, что устраняет необходимость разработки новой
теории для каждого типа граничных условий; 3) он позволяет доказать очень
много простых теорем, например теоремы, приведенные в § 2 гл. XII,
которые можно использовать для получения новых результатов и новых
преобразований, и 4) в большинстве случаев трудности, связанные со схо-
сходимостью, не возникают, и решение простых частных задач (например, задачи
с постоянной начальной температурой и постоянной температурой поверх-
поверхности) обычно можно считать совершенно строгим. В случае двумерных и
трехмерных задач положение не столь удовлетворительно, и в методе, исполь-
используемом в данной книге, после исключения времени с помощью преобразо-
преобразования Лапласа мы всегда вынуждены применять классические методы Фурье.
За последнее время для решения таких задач разработана теория неко-
некоторых других интегральных преобразований *), позволяющая рассматривать
все переменные с единой точки зрения. Подобный подход в значительной
степени обладает упомянутым выше преимуществом A) преобразования Лап-
Лапласа, т. е. тем, что использование стандартной методики, применимой
ко всем случаям, позволяет избежать необходимости отыскивать частные
*) Этот вопрос кратко и достаточно хорошо изложен в [2].
446 ГЛ. XVII. ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ [§ 2
решения, что облегчает проведение конкретных расчетов. С другой стороны,
эти преобразования не обладают изложенными выше преимуществами B)—D).
С их помощью нельзя рассмотреть все граничные условия с единой точки
зрения, и каждая область и граничное условие требуют разработки нового
преобразования и новой теории. Обычно для них нет таких хороших таблиц,
какие имеются для преобразования Лапласа, а их теория оказывается очень
сложной. Что касается интегральных теорем, то здесь обычно возникают
серьезные трудности, связанные со сходимостью, и большая часть вычислений
является чисто формальной. Наконец, следует подчеркнуть, что в настоящее
время теория интегральных преобразований применима лишь в некоторых
частных случаях, и поэтому она оказывается не более эффективной, чем
преобразование Лапласа.
Итак, если можно решить задачи теплопроводности с одной координатой
путем преобразования по этой координате, то наиболее мощным и наиболее
подходящим методом следует считать преобразование Лапласа по времени.
Вместе с тем при решении задач с установившимся тепловым потоком нас
привлекает стройность методов интегральных преобразований. Они, по-види-
по-видимому, должны стать весьма важными и для задач с несколькими коорди-
координатами, причем последовательные преобразования (в том числе, вероятно,
преобразования Лапласа) можно провести очень изящно.
Ниже приводится краткое описание некоторых простейших интегральных
преобразований с тем, чтобы указать, какого типа анализ при этом исполь-
используется, и дать возможность провести сравнение с классическими методами
Фурье, применявшимися в настоящей книге.
§ 2. Интегральные преобразования и формулы их обращения
В данном параграфе и в следующих v является функцией х или г, ее
преобразование обозначается прописной буквой V, а вид преобразования —
либо индексом, либо новой переменной w, s или о. Во всех случаях мы
примем (без объяснения), что рассматриваемые интегралы существуют; кроме
того, если потребуется, мы допустим, что функции и их производные стре-
стремятся к нулю при стремлении переменного к бесконечности.
I. Преобразование Фурье в комплексной форме*).
Обозначим через F[v(x)] операцию преобразования функции по Фурье
в комплексной форме, которое определяется соотношением
оо
)] = V(m)=-^ fe''"v(x)dx. B.1)
— оЭ
Согласно выражению C.7) гл. II формула обращения имеет вид
сю
-lmxV{«>)du. B.2)
*) Большая таблица преобразований по Фурье приведена в [3]. Точная матема-
математическая теория, а также многочисленные приложения изложены в [1]. Много практи-
практических приложений можно найти в [4] (гл. V посвящена задачам теплопроводности).
У Титчмарша и Снеддона [1, 4] рассматриваются и другие интегральные преобразо-
преобразования, изложенные в этом параграфе. Следует отметить, что не существует таблиц
этих преобразований, которые по своей полезности равнялись бы таблице Кзмпбелла
и Фостера [3] или каким-либо опубликованным таблицам преобразования Лапласа.
Наиболее полной из вышедших в последнее время таблиц интегральных преобразо-
преобразований служит таблица, приведенная в [5].
§ 2] ГЛ. XVII. ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ 447
Интегрируя по частям, получим
F B-3>
<2-4>
при условии, что v(x) и -^- стремятся к нулю при х->±оо.
II. Преобразование Фурье по синусам.
Обозначим через Fs[v(x)] операцию преобразования функции по сину-
синусам, а через К5(о>) — ее значения; это преобразование определяется сле-
следующим образом:
] = V,((fi) = (^\l2 f v(x)sinu>xdx; B.5)
формула обращения, согласно соотношению C.10) гл. II, имеет вид
оо
= (^\k I ^(^sincoxflfa). B.6)
Кроме того, если при х—>оо как v(x), так и -^— стремятся к нулю,
то, интегрируя по частям, получаем
—°^(««). B-7)
где Vc(co) определяется ниже (см. соотношение B.9) данной главы).
III. Преобразование Фурье по косинусам.
Обозначим через Fc[v(x)] операцию преобразования функции по коси-
косинусам, а через Vc(a>) — ее значения; тогда
оо
Fc [v (х)] = Vc (со) = {^!2 I v (x) cos сод: dx> B.9)
6
и, согласно соотношению C.13) гл. II, формула обращения имеет вид
сю
v(x) = {^\k f Vc(u>)cosv>xdu>. B.10)
6
Помимо этого, если при х-> ~ю как v(x), так и -^— стремятся к нулю,
то
448 ГЛ. XVII. ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ [§ 3
IV. Преобразование Ганкеля.
Преобразование Ганкеля порядка v > — г/2 от функции V (г) обозначается
через Hs[v(r)\ или Vy(o); оно определяется соотношением
оо
Нч [v (г)] = Kv (о) = J гУ, (or) v (г) dг; B.13)
о
формула обращения *) для него имеет вид
v(r) = f оУ? (or) Уы (о) do. , B.14)
о
Далее, двойное интегрирование по частям и использование формулы B)
(см. приложение 3) дает
при условии, что rvj[(or) и г^(аг)\~хр-) стремятся к нулю, когда г—>0
и г—>оо.
V. Преобразование Меллина.
Преобразование Меллина от функции v(r) обозначается через M[v(r)]
или Vm(s); оно определяется выражением
оо
M[v(r)] = Vm(s) = f r*-*v(r)dr; B.16)
о
формула обращения для него имеет вид [1]**)
/ B.17)
у — / оо
Интегрируя по частям, получим
при условии, что rsv и rs+1 \-jf-) стремятся к нулю, когда г->0 и г->оо.
§ 3. Неустановившийся тепловой поток
Этот случай можно проиллюстрировать рядом типичных задач.
I. Область***) — оо < х < оо с начальной температурой f (х).
Ищем решения уравнения
в области —оо < х < оо, ? > 0. Согласно B.4) данной главы для уравне-
уравнения C.1) преобразование Фурье в комплексной форме имеет вид
*) Это и есть интегральная теорема Ганкеля [6, 7].
**) Этот результат связан с формулами обращения для преобразований Фурье
и Лапласа; его часто называют «теоремой Фурье — Меллина».
***) То есть неограниченное пространственное тело; распределение температуры
зависит от одной координаты х. (Прим. ред.)
§ 3] ГЛ. XVII. ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ 449
где Vr(a)) = /7(o)), когда ? = 0. Отсюда следует, что
V (и) = F (и) е-ха*
и, воспользовавшись формулой обращения B.2) данной главы, получим
—ij- / exp (— шх — tisfit) F (о
что точно соответствует решению C.17) гл. II.
II. Область х > 0 с нулевой начальной температурой. При t > 0
плоскость х = 0 имеет температуру v = vQ.
Здесь следует решать дифференциальное уравнение C.1) в области х > 0.
Отметим, что из преобразованных по синусам и косинусам функций (обе они
пригодны для области х > 0) первая вводит в соотношение B.8) предыду-
^ г dv 1
щего параграфа температуру vQ, а вторая — неизвестное значение г^Н
в соотношение B.12). Поэтому мы воспользуемся преобразованием по сину-
синусам; применив его к уравнению C.1), получим
dVs , 9Т7 /2\'/2
Это уравнение нужно решать при условии Vs = 0 при t = 0. Отсюда сле-
следует, что
Воспользовавшись формулой обращения (см. B.6) данной главы), получим
решение
оо
V = 21T f (l ~е'%ш'OsincoA C.2)
о
после некоторых вычислений это соотношение приводится к обычному резуль-
результату г/0Ф* [*/2 (*0'/2]-
Рассмотренная выше задача очень хорошо иллюстрирует сходство между
методами преобразований Фурье и Лапласа в одномерных задачах подобного
типа. Во-первых, если в нашем распоряжении имеются соответствующие
таблицы преобразованных функций, то работа, которую необходимо проде-
проделать при расчетах по одному и другому методу, одинакова. Во-вторых, если
таблиц преобразованных функций нет, то в любом случае необходимо про-
провести определенное количество расчетов с интегралами, полученными из фор-
формулы обращения. Существенное преимущество преобразования Лапласа для
задач этого типа проявляется в связи с граничными условиями, поскольку
в нем рассматриваются одинаковым образом все граничные условия. Однако
ранее было необходимо использовать преобразование по синусам, так как
при лг = О была задана температура тела v\ если бы был задан тепловой
поток на граничной поверхности, следовало бы использовать преобразование
по косинусам; в случае граничного условия третьего ряда ни одно из этих
преобразований не подходит и следует разработать преобразование нового
типа; в случае граничного условия типа Е, приведенного в § 9 гл. I, потре-
потребуется уже другое преобразование и т. л.
III. Неограниченная область г > 0, — оо < z < оо, 0 < 6 < 2тс.
Начальная температура f(r) зависит только от г.
29 Г. Карслоу, Д. Егер
450 ГЛ. XVII. ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ [§ 4
В этом случае следует решить уравнение
d2v . 1 dv 1 dv л /о о
при условии, что v = f(r), когда ? = 0. Согласно B.15) данной главы для урав-
уравнения C.3) преобразование Ганкеля нулевого порядка имеет вид
C.4)
его следует решать при условии, что V0(o) = F0(a), когда ? = 0. Отсюда
находим
V0(o) = e-<F0(o).
Воспользовавшись формулой обращения B.14), получим
-^F0 (о) оУ0 (or) do;
о
вычислив этот интеграл, получим решение C.11) гл. X.
§ 4. Установившийся тепловой поток
Вероятно, самое важное свойство перечисленных в § 2 преобразований
заключается в том, что во многих важных частных случаях они сводят
уравнение Лапласа с двумя переменными к обыкновенному дифференциаль-
дифференциальному уравнению. Поэтому, если мы имеем уравнение
d2v d2v л А л
то применение комплексного преобразования Фурье по х дает
d2V
= 0. D.2)
То же уравнение получается в результате применения к D.1) преобразований
по синусам и косинусам.
Используя преобразования Ганкеля нулевого порядка к уравнению
1 d ( dv \ , d2v Л ,А оч
получаем
d ° —a2Vл = 0. D.4)
Применение преобразования Meллина к уравнению
LJ-(r*L\ + L^L = 0 D5)
г dr \ dr / ' г2 db2 \^'^J
дает
™ _|- s2Vm = 0. D.6)
В качестве примеров рассмотрим следующие задачи.
I. Область z > 0, 0 < г < оо, ? постоянным потоком Q через
поверхность 0^г<а, 2 = 0 и нулевым потоком при г>а, 2 = 0.
§ 51 ГЛ. XVII. ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ 451
Следует решить уравнение D.3) с граничными условиями
-*Ыг=о=\о, г>а)' D'7)
Применим к уравнению D.3) преобразование Ганкеля нулевого порядка.
При этом Vo должо удовлетворять уравнению D.4) и стремиться к нулю
при 2—>оо; граничным условием для этого уравнения при z = О служит
преобразование Ганкеля условия D.7), т. е. соотношение
Отсюда следует, что
Теперь, воспользовавшись формулой обращения B.14) данной главы,
получим
со
cf "ZJ°(аг) Jl (аа) "Г"' D-8>
6
что соответствует решению B.7) гл. VIII.
Решения, приведенные в § 2 гл. VIII, были получены при помощи инте-
интегралов B.3) и B.4) той же главы с тем, чтобы привлечь внимание к про-
простому, но важному методу; если же воспользоваться интегральной формулой
Ганкеля в классическом виде, то требуемый анализ оказался бы аналогичным
изложенному выше.
II. Клан — а<6<а, г > 0 при условии, что v = 1 в области 0 < г < а
и v = 0 в области г > 0 при 6 = ± а.
Следует решить уравнение D.5) при заданных граничных условиях. Если
воспользоваться преобразованием Меллина, то Vm должно удовлетворять
а
уравнению D.6) при условии, что Vm= J rs~l dr = as/s, когда б=±а.
о
Отсюда следует, что
», as cos sb
т'
s cos sa
Тогда применение формулы обращения B.17) данной главы дает
т+* °° оо Г / а4
1_ Г asr~s cos s6 ds _1 . 1 Г sin[cln\7r
V ~ 2tc/ ,/ $ cos set 2 ' тс ,/ С ch
1-i со О
§ 5. Конечные преобразования
Аналогичным методом можно воспользоваться для представления *) рядов Фурье
и аналогичных им рядов через преобразованные функции. Для согласования с преды-
предыдущими результатами возьмем промежуток 0 < х < /, хотя чаще применяется проме-
промежуток 0 < х < те.
Обозначим через fs[v(x)] операцию конечного преобразовения функции по
синусам, а через V5(/i), л=1, 2, 3,..., —значение преобразованной функции; тогда
*) О конечных преобразованиях по Фурье см. [8—14]. О конечном преобразова-
преобразовании Ганкеля см. [15].
29*
[§ 5
E.1)
sin
452 ГЛ. XVII. ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ
по определению
fs [v (х)] ^ Vs (n) = I v (*)sln ^f- dx.
о
Формула обращения, которая является рядом Фурье по синусам, имеет вид
оо
Ъ — — V V
п=\
Интегрируя по частям, получим
^-lf@)-(-
I
Аналогичным образом обозначим операцию конечного преобразования функции
по косинусам через fc[v(x)]t а через Vc(n), /г=1, 2, ..., —значение преобразован-
преобразованной функции; тогда
E.4)
fc [v (х)] = Vc(n) = fv (x) cos ~ dx,
а формула обращения принимает вид
v(x) = l-
Кроме того,
E.5)
Из соотношения E.3) следует, что преобразование по синусам оказывается
полезным для решения задач с заданной граничной температурой, а из соотноше-
соотношения E.6) вытекает, что преобразование по косинусам пригодно для решения задач
с заданным тепловым потоком. Для граничного условия третьего рода следует при-
применять новый тип преобразования, основанный на разложении, приведенном в § 9
гл. III. Аналогичным образом для радиального теплового потока в областях 0 < г < а
и а < г < b могут быть определены конечные преобразования по Ганкелю, однако
для граничного условия третьего рода необходимо применять другое преобразование.
I. Пластина 0 < х < I с нулевой начальной температурой; при t > 0 поверх-
поверхности х = 0 и х = / поддерживаются при температуре, равной единице.
Поскольку в данной задаче рассматривается температура граничных поверхно-
поверхностей, применим преобразование по синусам к уравнению
которое, согласно E.3), примет вид
его следует решать при условии, что Vs = 0, когда t = 0. Искомое решение имеет вид
/[1_(_1уп
Следовательно, воспользовавшись E.2), получим решение
4 V [l-exp(-^i±i>i^
v = —
m=0
Bm 4-1)
Sin
Bт
которое сводится к соотношению D.1) гл. III. (Для получения этого соотношения
нужно воспользоваться разложением единицы в ряд по синусам.)
§ 61 ГЛ. XVII. ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ 453
II. Установившийся поток в теле прямоугольного сечения 0 < х < а, 0 < у < Ь.
Граничная поверхность у = 0 поддерживается при температуре и (х), другие
поверхности—при нулевой температуре.
Применяя синус-преобразование Фурье по переменной х, получим уравнение
= 0,
которое следует решать при условии, что Vs = Us, когда у = 0 и 1/^ = 0, когда
у = Ь. Искомое решение имеет вид
у _ г т sh n7Z iP — УIа
s~ s sh nnb/a '
В таком случае, воспользовавшись E.2), получим
оо
2 V4 тт / ч sh пп(Ь — у)/а ппх
v = — >. Us(n) т~—гг^— sin =
a jL± sh ппЬ/а а
п=\
со а
2 VI sh пп (Ь — у)/а , пкх Г . /ч ппх' , ,
a ^J sh /гтс^/a a J y ' a
л = 1 о
что соответствует решению C.9) гл. V.
§ 6. Последовательные преобразования
В задачах с несколькими переменными можно достичь большой экономии
в используемых обозначениях путем последовательного применения интегральных
преобразований относительно этих переменных. Можно либо сначала использовать
преобразование Лапласа по времени с последующим применением других интеграль-
интегральных преобразований относительно координат, либо использовать последовательные
интегральные преобразования относительно координат *).
Чтобы проиллюстрировать этот метод, рассмотрим уже решенную задачу VIII
§ И гл. XV, которая использована в качестве примера в работе [18], а именно
задачу о теплопроводности в клине г>0, 0<8<80с начальной температурой,
равной нулю, и температурой поверхности, равной единице.
Здесь следует решить уравнение
d*v I dv I d^v 1 dv
при условиях
v = o, г = о, r>o, o<e<eo, F.2)
v = 1, е = о и е = е0, t > о. (б.З)
Обозначим через Vs конечное синус-преобразование функции v относительно 0;
тогда, согласно соотношению E.3) данной главы, Vs удовлетворяет уравнению
#v,_ , 1*У, и 1 ?У* v[I-(-I)"] ^ F4)
где
v = пк/%. F.5)
Обозначим через VSt v преобразование Ганкеля порядка v функции Vs; тогда,
согласно B.15) этой главы, VSf v удовлетворяет уравнению
Х^~Г°5, vvl J / .. К ) b
*) Несколько примеров использования последовательных преобразований приве-
приведено в статьях [16, 17].
30 Г. Карслоу, Д. Егер
454 ГЛ. XVII. ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ [§ 6
поскольку 16]
оо
/ Aifl dz = —. F.7)
J z v v '
0
Решение уравнения F.6) при условии VSy v = О, когда t = О, имеет вид
VSt v = ^""^Г1^ {1 — ^"Х<т2/Ь F8)
Обращая с помощью B.14) преобразованную по Ганкелю функцию и используя
F.5) и F.7), находим
оо
Vs e Ml—(—1)Л1 _ [1 __ (_!)«] I I ^-^2VV (or) da. F.9)
О
Наконец, производя с помощью E.2) обращение конечного синус-преобразования»
получим
/1=1 л=1
V f T^^ F.10)
0
Мы пришли к решению A1.24) гл. XV. Интересно сравнить оба метода. В обоих
случаях время, затрачиваемое на вычисления, примерно одинаково. Оба метода тре-
требуют знания интеграла F.7). Однако если в методе, изложенном в § 11 гл. XV, пред-
предполагается, что для v решение имеет вид A1.21) той же главы, то изложенный здесь
метод применяется непосредственно без каких-либо предположений.
ЛИТЕРАТУРА
1. Titchmarsh, Theory of Fourier Integrals, Oxford, 1937. (Э. Титчмарш, Вве-
Введение в теорию интегралов Фурье, Гостехиздат, М., 1948.)
2. Tranter, Integral Transforms in Mathematical Physics, Methuen, 1951. (К. Т р а н-
т е р, Интегральные преобразования в математической физике, Гостехиздат, М.,
1956.)
3. Campbell, Foster, Fourier Integrals for Practical Applications, Bell Telephone
System Monograph B-584, 1931.
4. S n e d d о n, Fourier Transforms, McGraw-Hill, 1951. (И. Снеддон, Преобразо-
Преобразования Фурье, ИЛ, М., 1955.)
5. Erdelyi, Magnus, Oberhettinger, Iricomi, Tables of integral Trans-
Transforms, McGraw-Hill, 1954. ,
6. W a t s о n, A Treatise on the Theory of Bessel Functions. (Г. Ватсон, Теория
бесселевых функций, ИЛ, М., 1949.)
7. Gray, Mathews, Treatise on Bessel Functions, Macmillan, ed. 2, 1922 (Э. Г р э й,
Г. М э т ь ю з, Функции Бесселя и их применение в физике и механике, ИЛ, М.,
1953.)
8. К п i e s s, Math. Z. 44, 266—291 A939).
9. В го wn, Bull. Am. Math. Soc. 48, 522 A942); 50, 376 A944).
10. Brown, J. Appl. Phys. 14, 609 A943).
11. Koschmieder, Dtsch. Math. 5, 521—545 A945).
12 Roettinger, Quart. Appl. Math. 5, 298—319 A947).
13. Jacobson, Bull. Am. Math. Soc. 55, 804—809 A949).
14. Jacobson, Quart. Appl. Math. 7, 293—302 A949).
15. S n e d d о n, Phil. Mag. 37, 17—25 A946).
16 D e 1 a v a u 1t, С R. Acad. Sci. 236, 2484—2486 A953); 237, 1067—1068 A953).
17. S n e d d о n, Proc. Glasgow Math. Ass. 1, 21—27 A952).
18. Cooke, Am. Math. Mon. 62, 331—334 A955).
ГЛАВА XVIII
ЧИСЛЕННЫЕ МЕТОДЫ
§ 1. Введение
В последние годы много внимания уделялось разработке численных ме-
методов решения задач теплопроводности. Это обусловлено отчасти растущим
интересом к численному анализу, а отчасти — возможностью решения важных
практических задач при помощи электронных и других вычислительных машин.
Из предыдущих глав следует, что точные решения практически имеются
лишь для линейных задач, в которых рассматриваются области простейшей
формы. Для исследования тел сложной формы или нелинейных граничных
условий приходится обращаться к численным методам *). Здесь, конечно,
нельзя дать что-либо, похожее на полное изложение, однако желательно
привести обзор состояния вопроса и указать удобные методы решения встре-
встречающихся задач. Ученые, использующие точные решения, часто достигают
в своей работе стадии, на которой желательно проверить пригодность сде-
сделанных допущений (например, линеаризации) или решить простые задачи,
для которых точные решения отсутствуют. В самом деле, использование
простых численных методов (например, методов, описанных в § 3 данной
главы) представляется очень простым делом, поскольку они не требуют
изучения численного анализа. Поэтому наибольшее место в настоящей главе
отведено простейшим методам последовательных приближений. Поскольку
такие методы применяются при расчетах на машине, именно они лучше
всего изучены теоретически. Наконец, следует указать, что, хотя в теории
конечных разностей описанные в настоящей главе методы оказываются наи-
наиболее очевидными, их никак нельзя считать единственными**).
§ 2. Конечные разности***)
Предположим, что нам известны значения vm функции v(x) при значе-
значениях аргумента х — те, т= ..., —2, —1, 0, 1, 2, ... В таком случае
первая, вторая, третья, ... последующие (forward) разности kvm, A2^,
*) Полное изложение этого вопроса, произведенное с практических позиций,
дано в [1]. Более краткие изложения можно найти в большинстве работ по теплопе-
теплопередаче, а также в [2]. Методы, используемые при решении задач с переменной тем-
температуропроводностью, описаны в [3].
**) Например, в работе Кинга [4] используются методы Монте-Карло. Интерес-
Интересный метод, в котором применяются ступенчатые значения i/, разработан Филипом [5].
В книге Кранка [3] описаны другие методы, используемые при переменной темпера-
температуропроводности.
***) Теория конечных разностей изложена в [6, 7]. Классическими работами
по применению разностей к решению уравнений в частных производных считаются
работы Ричардсона [8]. Следует отметить, что, хотя знание основ теории конечных
разностей очень желательно, в данном случае оно не обязательно, поскольку необ-
необходимые результаты (например, C.4) данной главы) можно получить непосредственно
из теоремы Тейлора. (См. также А. О. Г е л ь ф о н д, Исчисление конечных разностей,.
Физматгиз, 1959.)
456 ГЛ. XVIII. ЧИСЛЕННЫЕ МЕТОДЫ [§ 2
Д3<ут, ... функции vm определяются соотношениями
B.1)
vm, B.2)
vm B.3)
и т. д. Они называются «последующими» разностями потому, что содержат
значения vm, vm+v ... с возрастающими индексами т. Аналогичным обра-
образом можно определить и предыдущие (backward) разности (т. е. разности
с убывающими индексами т), но здесь они нам не потребуются. Однако
ясно, что иногда удобно пользоваться системой обозначений, содержащей
точки, симметричные относительно т. Для этого вводится система обозначе-
обозначений центральных разностей. Первая, вторая, ... центральные разности
определяются следующим образом:
81vm4.»=Avm = "« + l— «*• B-4)
VvM = Vvm+± — ^m_i = bvm — Lvm_x = vm+l — 2vm + vm_l B.5)
и т. д. Можно видеть, что в разности нечетного порядка, как и в B.4),
входят точки, распределенные симметрично относительно /и-{--о-, а не отно-
относительно т. Для получения формулы, симметричной относительно т, вво-
вводятся так называемые средние разности, определяемые соотношениями
J^ +^ l{("v.I B-6)
i+ г B.7)
\ m+T mi
где {л укрывает на операцию усреднения величин для m ± -^.
Вся теория теперь основывается на предположении, что известны вели-
величины ..., г»_2, v_v v0, vv vv ... и что составлена «таблица разностей»
этих величин и их последовательных разностей B.1), B.2), ... В принципе
в данном случае можно найти такой полином, например Р(х), что P(n) = vn
в любом заданном числе точек (его коэффициенты можно выразить через vm
или их разности), и над этим полиномом выполняют любые операции, напри-
например интерполяцию, дифференцирование или интегрирование. Поэтому первая
производная [dv/dx]m означает первую -производную интерполируемого поли-
полинома в точке те. В этом смысле, если известны значения функции в точ-
точках те, то можно указать много формул, позволяющих выразить ее произ-
производные в любой точке или через ее табличные значения, или через их раз-
разности. Например,
или
]_
3
или
§ 2] ГЛ. XVIII. ЧИСЛЕННЫЕ МЕТОДЫ 457
или
¦+-•••. B.12)
или
или
Доказательства этих результатов, а также ряда других можно найти
в трудах, посвященных конечным разностям. В данном же случае, когда е
считается малой величиной, разности #-го порядка имеют порядок ел. Таким
образом, пренебрежение #-й разностью дает ошибку порядка О(ел). В при-
приводимых ниже упрощенных расчетах разности более высоких порядков счи-
считаются пренебрежимо малыми и используются только первые члены в пра-
правых частях соотношений B.8) — B.14). Вносимая при этом погрешность
будет зависеть от порядка первого пренебрегаемого члена; так, формулу B.11),
в которой опускают разности третьего и более высоких порядков и ошибка
в определении dvldx имеет порядок О(е2), следует предпочесть формуле B.8),
в которой мы пренебрегаем уже разностью второго порядка, и поэтому
ошибка в определении dvjdx имеет порядок О (е). При очень важных числен-
численных расчетах всегда сохраняют и используют разности более высоких поряд-
порядков. При этом можно уменьшить время, требуемое для решения задачи,
и повысить точность результатов, но это достигается за счет усложнения
применяемого математического метода.
Приведем еще два результата, которые понадобятся нам при вычисле-
вычислениях в цилиндрических или сферических координатах. Пренебрежем разно-
разностями третьего и четвертого порядков; тогда из B.11) и B.14) следует, что
при т Ф О
^ B.15)
Если (dv/dx) = 0 при д: = 0, то
Подобным же образом, если т Ф 0, то
если (dv/dx) = 0 при д: = 0, то
При рассмотрении функций двух или большего числа переменных можно
совершенно аналогичным образом определить частные разности. Например,
если v(x, у) является функцией х и у и мы выбираем одинаковые интер-
интервалы е по х и у, т. е. vmtn = v(me, пг), то из соотношения B.14)
458 ГЛ. XVIII. ЧИСЛЕННЫЕ МЕТОДЫ [§ 3
следует, что
[S] . ' B.19)
Отсюда мы получаем
+0] =e2(^-i,n +
B.21)
что потребуется нам при изучении уравнения Лапласа в плоской задаче.
§ 3. Линейный тепловой поток в неограниченном пространстве
Следует решить уравнение
при условии, что при ? = 0 температура v задана. Здесь х может быть
функцией v. В § 6 гл. 1 было показано, что в общем случае, когда К
является функцией v, соответствующее уравнение можно привести к фор-
формуле C.1) путем замены переменной.
Выберем теперь на оси х интервал е и обозначим через vm(t) значения
v(x, t) в точке х = те, т = .. ., —2, —1, 0, 1, 2, ... Заменим *) в урав-
уравнении C.1) dhf/dx2 на конечную разность, используем B.14) предыдущего
параграфа и пренебрежем разностями высших порядков; тогда мы получим
систему уравнений
(О - 2f т (О + *ж_, (t) - ~ ^fP~ = 0, C.2)
которые следует решать при условии, что известны значения vm@). Эта
система в точности соответствует системе уравнений A0.2) гл. XV при
Мгсг = рсг, Нг = К/е, и (при постоянном х) ее можно решить при помощи
методов, изложенных в § 10 гл. XV.. Итак, теперь мы видим физический
смысл сделанных приближений. Система C.2) соответствует разделению твер-
твердого тела на пластины толщиной е и замене их пластинами из идеального
проводника той же теплоемкости. Термическое сопротивление **) между этими
пластинами равно е/К> т. е. совпадает с термическим сопротивлением пла-
пластины из исходного материала толщиной е.
Если х постоянно, то сравнение решений C.2), получаемых методами,
приведенными в § 10 гл. XV, с точными решениями позволяет изучить ре-
результаты приближения. В случае переменного х, а также нелинейных гра-
граничных условий система C.2) решается при помощи дифференциального ана-
анализатора [13]***). Проведенные исследования показали, что в ряде случаев
хорошие результаты можно получить не только для малых значений е; так,
для пластины толщиной а хорошие результаты получаются при е = а/6.
*) Производную по времени в уравнении C.1) можно заменить конечной раз-
разностью. Тогда мы получим систему дифференциальных уравнений по лг, которые можно
решать последовательно [9].
**) То же допущение делается при изучении тепловых потоков на ряде вычи-
вычислительных машин непрерывного действия- Наиболее совершенна резистивно-емкостная
система, известная под названием «анализатора тепло- и массообмена» [10], при по-
помощи которой к настоящему времени уже выполнено много работ (см. также [11, 12]).
***) В этой статье приведен обзор важнейших задач и методов их решения-
§ 3] ГЛ. XVIII. ЧИСЛЕННЫЕ МЕТОДЫ 459
Для того чтобы описанный выше метод стал чисто численным, необхо-
необходимо в системе C.2) заменить производную по времени разностью. Для этого
мы выбираем промежуток времени х и обозначаем v(me, nz) через vmtn.
Ни е, ни х пока не определены, и к их выбору мы вернемся позднее.
Здесь можно воспользоваться различными формулами для dv/dt; наиболее
проста формула B.8) данной главы, которая, если пренебречь разностью
второго порядка, имеет вид
\^i] = vm>n+\—Vm,n ^ ъз
L dt ]t=nx x
Подставляя ее в систему C.2), получим
где величину
М = ~ C.5)
иногда называют модулем *). Следует отметить, что в соотношении C.4) зна-
значения v в момент времени (n-f-l)i выражены через его значения в момент #х,
что позволяет использовать это соотношение для дальнейших расчетов, исходя
из известного значения при ? = 0. Поскольку в соотношении C.3) мы пре-
пренебрегаем разностью третьего порядка, можно ожидать, что этот метод
не очень точен. Однако он оказывается достаточно точным; практически он
является самым простым из всех существующих методов, и мы здесь будем
рассматривать только его.
Теперь следует рассмотреть величины е и х и оценить устойчивость
метода. Конечно, е до некоторой степени определяется уже самой за-
задачей. Как отмечалось выше, в случае системы C.2) для пластины тол-
толщиной а величина е=-^-а дает вполне хорошие результаты. В любом
случае е не слишком мало по сравнению с а. В формулах C.4) и C.5) е и х
вместе входят в М\ поэтому, чтобы получить решение через разумное число
операций, желательно выбрать х настолько большим, насколько это допу-
допустимо. Необходимость некоторого ограничения значения х вытекает из сле-
следующих рассуждений**). Пусть при t = nz максимальная ошибка для любого
значения vmt n равна ?]; тогда, согласно C.4), если dvmtn+l — малое измене-
изменение tomn+v вызванное малым изменением dvmn величины vmi п, и если М
постоянно, то
или
Далее, если здесь применим описанный выше метод, то ошибка не должна
возрастать ***), т. е. должно быть справедливым соотношение \dvm% л+1| < ч\\
тогда, согласно C.6), нужно, чтобы было справедливым соотношение
*) Часто рассматривают случай х = 1; величину т/е2 называют характеристи-
характеристикой сети.
**) Этот вопрос обсуждается в статье [14], где рассматривается также влияние
граничных условий на устойчивость метода.
***) Помимо случайных ошибок, в последние цифры используемых десятичных
дробей входят ошибки округления.
460 ГЛ. XVIII. ЧИСЛЕННЫЕ МЕТОДЫ [§ 3
Это и есть требуемое ограничение для т, называемое обычно условием
устойчивости. Ясно, что это условие достаточно, но отнюдь не необходимо.
В настоящее время имеется много работ, основанных на решениях разностных
уравнений, в которых очень тщательно разбирается вопрос об устойчивости *).
Другой простой метод исследования устойчивости и точности численных
решений заключается в изучении случая г>0>0=1, г>т>0 = 0, тФО. При этом
мы либо исследуем распространение по системе единичной ошибки, либо рас-
рассматриваем функцию Грина, соответствующую выделению при t = 0 в начале
координат количества тепла ере. Согласно C.4) гл. X точное решение для
этого случая имеет вид
( }
Для иллюстрации этого метода приведем часть таблички значений vmt n>
получающихся при рассмотрении указанного выше случая; величины М по-
полагают равными 0,25, 0,5 и 0,6; во всех случаях приводят только числа,
соответствующие 0 ^ т < 5. Результаты, конечно, симметричны относи-
относительно т = 0 **).
М = 0,25
1
0,5
0,375
0,312
0,273
0,246
0,226
0,209
0,196
0,185
0,176
1
0
0,5
0
0,375
0
0
0,25
0,25
0,234
0,219
0,205
0,193
0,183
0,175
0,167
0,160
0
0,5
0
0,375
0
0,312
0
0
0,062
0,094
0,109
0,117
0,121
0,122
0,122
0,121
0,120
0
0
0,25
0
0,25
0
0
0
0
0,016
0,031
0.044
0,054
0,061
0,067
0,071
0,074
0
0
0
0,125
0
0,156
0
0
0
0
0,004
0,010
0,016
0,022
0,028
0,033
0,037
0
0
0
0
0,062
0
0
0
0
0
0
0,001
0,003
0,006
0,009
0,012
0,015
0
0
0
0
0
0,031
*) Этой проблеме посвящено много точных аналитических работ, причем иссле-
исследовалось главным образом уравнение C.4) с линейными граничными условиями.
Следует подчеркнуть, что имеется несколько различных, но взаимосвязанных вопро-
вопросов, в частности вопрос о сходимости, т. е. о том, стремятся ли решения разностных
уравнений к решению нашего уравнения в частных производных, когда е и т->0„
и вопрос об устойчивости, т. е. вопрос о той, уменьшаются ли численные ошибки
и ошибки округления с увеличением времени или увеличиваются. Фаулер [15] рас-
рассматривает вопрос о сходимости, изучая точные решения разностного уравнения C.4).
В работе [16] устойчивость уравнения C.4) изучается методом, разработанным Ней-
Нейманом; в ней отмечено характерное превосходство «неявных» соотношений типа C.11).
В статьях Лойтерта [17] указывается, что сходимость возможна в некоторых случаях*
в которых условие устойчивости не выполняется. Соотношения между сходимостью и
устойчивостью рассматриваются также в работах [18, 19]. Последняя статья содержит
довольно полное обсуждение этого вопроса с интересными численными примерами.
В большинстве перечисленных выше работ подчеркивается, что сходимость и устой-
устойчивость зависят от формы начального и граничных условий. В них отмечаются труд-
трудности, с которыми приходится сталкиваться при исследовании линейных задач.
В случае нелинейных задач эти вопросы пока еще практически не затрагивались.
**) В столбцах фиксирован первый индекс т; в строках — второй индекс л-
(Прим. ред.)
§ 31 гл. xviii. численные методы 461
1
—0,2
0,76
—0,44
0,952
—0,836
0
0,6
—0,24
0,72
—0,538
1,042
0
0
0,36
—0,216
0,605
—0,548
0
0
0
0,216
—0,173
0,476
0
0
0
0
0,130
—0,130
0
0
0
0
0
0,078
, , , ,
1,418 —1,039 1,020 —0,502 0,358 —0,093
Рассматривая случай Л1 = 0,6, находим, что ошибка в одной цифре
на единицу в конце концов приводит к большим ошибкам с чередующимися
знаками. При практических расчетах такой эффект быстро становится явным.
Согласно критерию C.7) этот случай является неустойчивым.
В случаях Л1 = 0,25 и Л1 = 0,5, которые, в соответствии с C.7), должны
быть устойчивыми, из соотношения C.8) следует, что величины, стоящие
в одиннадцатом ряду таблицы для первого случая и в шестом ряду для вто-
второго, должны равняться A0тс)-!/:2ехр(—/я2/10), т. е.
0,178 0,161 0,120 0,073 0,036 0,015
Как мы видим, интересующие нас величины при Ж = 0,25 очень хорошо
с ними совпадают (имеются лишь небольшие расхождения в последних зна-
значащих цифрах). При М = 0,5 в таблице чередуются нули и величины, вдвое
превосходящие точные значения (можно считать, что это обусловлено таким же
общим количеством тепла, сконцентрированным в чередующихся через одну
пластинах). Действительно, кривая, проведенная через точки с координатами,
равными половине этих величин, служит по мере увеличения п все лучшим
и лучшим приближением к точному результату. Если vmtQ — точки на непре-
непрерывной кривой, то наблюдаемые колебания сглаживаются.
В данном случае (т. е. при М = 0,5) уравнение C.4) принимает осо-
особенно простой вид
«т. я + 1 = \&т-\. я + ^т+Ья)- C'9)
и, следовательно, значение v при те, (п-\-\)х точно равно среднему ариф-
арифметическому от значений v при (т ± 1)е, /гт. Этот процесс определения сред-
среднего арифметического можно выполнить либо численным, либо графическим
методом; последний, называемый методом Шмидта [20, 21]*), применяется
уже довольно давно при исследовании теплообмена.
В большинстве практических случаев, когда достаточна точность порядка
нескольких процентов, уравнения C.4) и C.9) оказываются одинаково при-
пригодными. Их преимущества заключаются в повторяемости очень простых
операций, и поэтому эти уравнения очень удобны при использовании как
простых, так и сложных электронных вычислительных машин.
Рассматривая далее возможность отыскания разностных уравнений, ко-
которые более точно представляли бы дифференциальное уравнение, естественно
заменить неточное выражение B.8) данной главы выражением B.18) этой же
главы, в котором опущены только третьи разности. Подстановка B.11) пре-
предыдущего параграфа в C.2) дает
. (ЗЛО)
где, как и раньше, Л1 = хх/е2. Это соотношение, так же как и C.4), опре-
определяет vmt n+1 непосредственно через известные величины, хотя последние
*) В работах [22, 23] этот метод распространен на тела цилиндрической и сфе-
сферической формы.
462 ГЛ. XVTTT. ЧИСЛЕННЫЕ МЕТОДЫ [§ 4
теперь находятся в двух предшествующих рядах. К сожалению, эта система
оказывается неустойчивой. Поэтому, если, как и раньше, мы рассчитаем рас-
распространение единичной ошибки, то для М = !/г получим
1
—2
7
0
1
—4
0
0
1
0
0
0
0
0
0
Выражение B.11) используется в весьма удачном методе, разработан-
разработанном в [24] (см. также [3]). В этом методе дифференциальное уравнение для
+у)! заменяется разностным уравнением. Используя соотношение B.11)
для представления (dv/dt) при (/г+у)х и среднее значение величин B.14)
при nz и (tt-f-l)T для представления (d2v/dx2) при t = i n -\- ур» получим
я + 1
Приведенный метод обладает тем преимуществом, что в случаях пере-
переменной температуропроводности, источника тепла переменной мощности или
переменных граничных условий эти изменения можно учесть физически удо-
удовлетворительным образом, а именно, считая, например, х равным не величине,
соответствующей vmtn, а среднему значению по области. Однако уравнение
C.11) не так легко использовать, как C.4), так как оно не дает непосред-
непосредственного выражения vmtn+l через vmn, а позволяет только написать ряд
алгебраических уравнений, которые должны быть решены. Их решение можно
получить при помощи обычных приемов, основанных на методе релаксации
или аналогичных методах. Этот вопрос достаточно полно изложен в лите-
литературе [3]. Дальнейшее уточнение метода с использованием разностей более
высоких порядков выполнено Дугласом [25, 26].
Наконец, следует отметить, что случаи радиального потока в шарах
или цилиндрах можно рассматривать почти таким же способом при помощи
соотношения B.17) или B.15) настоящей главы.
§ 4. Граничные условия
Мы будем рассматривать здесь только левую граничную поверхность;
тогда нас будет интересовать область д;>0и значения v^ n при т = 0, 1,2,...
Аналогичным образом можно рассматривать и только правую граничную
поверхность.
В случае заданной температуры задается и вводится в систему раз-
разностных уравнений функция vOtn. Как отмечалось в § 3 настоящей главы,
характер этой функции может влиять на устойчивость уравнений.
Во все другие граничные условия входит тепловой поток
— K^ = F(v,t) при х = 0. D.1)
Если в задаче с твердым телом используется разностное уравнение C.4)
и для любого п нам известны vmtn, m = 0, I, 2, . .., то из этого уравнения
можно найти значения vmtn+v m=\, 2, ..., и остается найти vOtn+l из
условия D.1) на граничной поверхности. Это можно сделать несколькими
способами.
§ 4] ГЛ. XVIII. ЧИСЛЕННЫЕ МЕТОДЫ 463
I. Подставляя выражение B.8) данной главы в условие D.1) и прене-
пренебрегая вторыми разностями, получим
Это уравнение можно решить относительно t/Ofrt+1.
II. Более точный результат аналогичного типа можно получить, используя
соотношение B.9) вместо B.8). Это дает
ы = т/Кя+1' (л+1)т}. D.3)
Ни один из этих методов нельзя считать достаточно удовлетворительным,
поскольку они требуют экстраполяции функции в область, в которой она
может быстро меняться.
III. Этот метод проще всего изложить, воспользовавшись схемой, раз-
разработанной Шмидтом. Ее особенность заключается в задании совокупности
температур v_hn в фиктивной точке х = — е. Если для т^>—1 известно
vm%n, то из C.4) можно найти vOt n+v Для нахождения г/_ь„ соотношение
B.11) подставляют в условие D.1). Пренебрегая третьими разностями, получим
/ (* . пх). D.4)
В этом случае v_Un, а следовательно, и vOtn+1 определяются непосред-
непосредственно, без решения таких уравнений, как D.2; или D.3).
При отсутствии теплового потока на границе уравнение D.4) при-
принимает вид
IV, Следует отметить, что в методах I и II рассматриваются величины
теплового потока при (п-\- 1)х, тогда как в методе III — его величина при пх.
Если тепловой поток быстро меняется с изменением температуры или во вре-
времени, то можно ожидать, что указанные методы дадут различные результаты,
что можно учесть, вводя в D.4) значения потока при (# + "9")г» тогда при-
приближенно получим выражение
«-1. п = «i. „ + х { / К •• пх ) + y («ь я+1 - «ft „) [-|f]o> n } • D.6)
Объединяя его с C.4), снова получаем для vOi л+1 линейное уравнение.
Приведенные выше формулы, а также ряд других рассматриваются
в работе [14], где исследовались их устойчивость и точность для случая тепло-
теплообмена по линейному закону.
Далее следует остановиться еще на одном, довольно интересном прак-
практическом моменте, а именно на использовании начального решения. Пусть,
например, на тело с постоянной температурой внезапно накладываются гра-
граничные условия; тогда тепловой поток вблизи поверхности окажется боль-
большим и величины dvjdXy рассчитанные на первых нескольких шагах по вре-
времени, будут очень неточными. Поэтому желательно начинать не с постоянных
значений при ? = 0, а с вычисленного решения, например при t = x или 2т,
даже если это решение найдено с учетом приближенного (линеаризованного)
граничного условия. Такие решения легко получить из точных решений,
приведенных ранее. Для важных граничных условий можно, вероятно,
найти новые решения. Например, для случая, когда тепловой поток через
464 ГЛ. XVIII. ЧИСЛЕННЫЕ МЕТОДЫ [§ б
поверхность является степенной функцией ее температуры, известно решение,
пригодное для небольших значений времени [27] *).
Ряд сравнений точных решений при различных методах рассмотрения
граничного условия был сделан в статье [14] для случая теплообмена по
линейному закону.
§ 5. Выделение тепла, переменная температуропроводность
и скрытая теплота
В случае выделения тепла к левой части уравнения C.1) настоящей главы сле-
следует добавить член A (i/, x, f)/K- При использовании метода конечных разностей
к правой части уравнения C.4) нужно прибавить член wA (t/m> n, те, лх)//С, или, для
получения лучшего приближения, член
у (vm, n+l — Vm, n) \-^\m }• EЛ)
В формуле Кранка — Никольсона C.11) к правой части следует прибавить член
тщ{А(ът, п, те, /гх)-f- A (vm, n+lt me, (n-f-l)*)}. E.2)
Над задачами этого типа до настоящего времени работали еще мало. В статье [24]
обсуждался случай выделения тепла при химической реакции. В статье [28] рассмат-
рассматривались вопросы устойчивости и был дан ряд численных примеров.
Случай переменной температуропроводности кратко упоминался в § 3 настоящей
главы. Чтобы учесть ее изменение, в соотношении C.5) % следует приписать величину,
соответствующую vm, n, тогда как в C.11) ей следует приписать величину, соответ-
соответствующую v т, л+Л. Этот случай, имеющий большое значение при рассмотрении
диффузии, достаточно полно изложен в книге [3].
Перечислим теперь наиболее важные задачи этого типа в теории теплопровод-
теплопроводности: 1) задачи, в которых температуропроводность является ступенчатой функцией
температуры (это соответствует также выделению скрытой теплоты в диапазоне тем-
температур плавления), и 2) родственная им задача выделения скрытой теплоты в точке
плавления. Эти задачи имеют большое техническое значение. Кроме того, хотя из-
известны точные решения задач такого рода для полуограниченного тела, для пластины
и для цилиндра они отсутствуют. Для последних случаев решения должны полу-
получаться при помощи численных методов, однако в качестве «начальных решений>
чрезвычайно полезными оказываются точные решения, приведенные в гл. XI [29].
Влияние скрытой теплоты изучалось в [30, 31]. В работе [30] указывается, что
в задачах этого типа удобнее производить расчеты с О, теплосодержанием единицы
массы тела, которое удовлетворяет дифференциальному уравнению
Соответствующая формула в конечных разностях, полученная с помощью C.4), имеет
вид
От, л+1 = От. л + -р" (»т+ь л+ »т-ь я —2»т.л)- E-4)
Расчет проводится так же, как и ранее, причем в точке плавления имеется
разрыв непрерывности О. или на конце интервала температур плавления — разрыв
непрерывности с.
§ 6. Релаксационные методы
В предыдущих параграфах рассматривались методы последовательных прибли-
приближений для решения уравнений в бесконечной области t > 0. Релаксационные ме-
методы [32] применимы к установившимся процессам, заданным в конечной области
с известными условиями во всех точках границы. В течение многих лет эти методы
*) В этой работе, в частности, рассматриваются излучение черного тела и естест-
естественная конвекция.
§ 6] ГЛ. XVIII. ЧИСЛЕННЫЕ МЕТОДЫ 465
использовались для решения уравнений Лапласа и Пуассона; они особенно полезны
для решения таких задач теплопроводности, как задача об установившемся потоке
через стенку, изогнутую под прямым углом, или через область, находящуюся между
кубами с параллельными гранями и общим центром симметрии; подобные задачи
трудно (или вообще невозможно) решить аналитическими методами. Этот метод
слишком хорошо известен, чтобы его нужно было здесь излагать. В литературе
можно найти много достаточно полных его описаний (см., например, [6]) *).
При двумерном установившемся тепловом потоке необходимо решить уравнение
d2v d2v
1F- + I^ = 0' <61>
в данной области при заданных условиях на ее граничной поверхности. Используя
соотношение B.21) настоящей главы и пренебрегая разностями более высоких по-
порядков [37], заменим уравнение F.1) разностным уравнением
fm, n + i + vm, n-\ + Vm-u n + ^m+u n — 4^m, n = 0, F.2)
которое должно быть решено при заданных условиях в точках сети на самой гра-
границе или близ нее. Именно для таких задач и были первоначально разработаны
релаксационные методы; только недавно были сделаны попытки использовать их для
рассмотрения неустановившихся процессов (например, для задач с переменным теп-
тепловым потоком).
Чтобы применить релаксационные методы к дифференциальному уравнению
рассмотрим область 0 < х < I при 0 < t < Т при заданных условиях на линиях **)
х = 0, х = /, t = 0, t = Т.
Один из методов, которым можно воспользоваться, заключается в введении [39]
новой функции w, определяемой соотношением
ю = -ЗГ+*!Р- F4>
при условии w = О, когда х = 0, w = О, когда х = / и dw/dt = 0, когда t= Т. Эти
условия не являются несовместимыми и не накладывают никаких ограничений на v.
Подставляя соотношение F.4) в F.3), получим
с рядом граничных условий, к которым применимы релаксационные методы.
Помимо этого, используется ряд методов, которые считаются релаксационными;
однако на самом деле они являются методами последовательных приближений и в них
релаксационные методы используются для решения системы уравнений для значений v
в любой заданный момент времени. Таким образом, релаксационные методы исполь-
использовались для решения системы уравнений C.11) данной главы, что позволило выра-
выразить vm,n+i через vm> n в методе Кранка — Никольсона ***). Важный метод подобного
типа был предложен Либманом [41] ****), который подставлял в соотношение C.2)
вместо C.3) равноценное выражение
=i{Vmtn~~Vmt n~l)i F*6)
*) В большинстве работ по теплопередаче дается краткое изложение этого
метода с точки зрения теории теплопроводности. Подробно он рассмотрен в< ра-
работе [1]. Хорошее краткое введение в метод дано в [33]. В работе [34] рассматривается
решение уравнения Пуассона для трехмерного случая. Совместное использование
релаксационных методов и интегральных преобразований излагается в [35]. Приме-
Применение релаксационных методов к задачам со скрытой теплотой рассмотрено в [36].
**) В работе [38] отмечается, что здесь можно использовать конечное устано-
установившееся состояние, если оно существует.
***) Этот вопрос изложен в статье [40]; там же рассматривается член А (х, t),
соответствующий выделению тепла.
****) Данный метод [41] легко применить к двумерным задачам.
466 ГЛ. XVIII. ЧИСЛЕННЫЕ МЕТОДЫ [§ 6
и, таким образом, получал разностное уравнение
Mvm_Un-BM+\)vmtn+Mvm+Un + vmtn_l = 0, F.7)
где Л! = хт/е2. Эту систему уравнений для значений vm, n, выражаемых через vm%n-U
затем решают релаксационными методами. Эти методы обладают тем преимуществом,
что они устойчивы при всех значениях М.
ЛИТЕРАТУРА
1. Dusinberre, Numerical Analysis of Heat Flow, McGraw-Hill, 1949.
2. Ingersoll, Zobel, Ingersoll, Heat Conduction, University of Wisconsin
Press, 1954.
3. С г a n k, The Mathematic of Diffusion, Oxford, 1956.
4. King, Ind. Eng. Chem. 43, 2475 A951).
5. Philip, Trans. Faraday Soc. 51, 885 A955).
6. H a r t r e e, Numerical Analysis, Oxford, 1952.
7. Milne, Numerical Calculus, Princeton, 1949.
8. Richardson, Phil. Trans. Roy. Soc. A210, 307 A910); A226, 299 A927).
9. Hartree, Womersley, Proc. Roy. Soc. A161, 353 A937).
10. Paschkis, Baker, Trans. ASME 64, 105—112 A942).
11. Paschkis, Heisler, Elect. Engng 63, 165 A944); J. Appl. Phys. 17, 246—254
A946).
12. Moore, Ind. Eng. Chem. 28, 704 A936).
13. Eyres, Hartree et al., The Calculation of Variable Heat Flow in Solids, PhiL
Trans. Roy. Soc. A240, 1—57 A946).
14. P r i с e, S 1 а с k, Brit. J. Appl. Phys. 3, 379—384 A952).
15. Fowler, Quart. Appl. Math. 3, 361—376 A946).
16. O'Brien, Hyman, Kaplan, J. Math. Phys. 29, 223—251 A950).
17. Leutert, Proc. Am. Math. Soc. 2, 433—439 A951); J. Math. Phys. 30, 245—251
A951).
18. H i 1 d e b г a n d, J. Math. Phys. 31, 35—41 A952).
19. Evans, Brousseau, К e i r s t e a d, J. Math. Phys. 34, 267—285 A955)
20. Schmidt, Foppl's Festschrift, Springer, 1924.
21. Nussbaum, Z. angew. Math. Mech. 8, 133—142 A928).
22. N e s s i, N i s о 1 1 e, Chal. et Industr. 9, 193 A928J.
23. P a 11 о n, Ind. Eng. Chem. 36, 990—996 A944).
24. С г a n k, N i с h о 1 s о n, Proc. Cambr. Phil. Soc. 43, 50—67 A947).
25. D о u g 1 a s, J. Math. Phys. 35, 145—151 A956).
26. С r a n d a 1 1, Quart. Appl. Math. 13, 318—320 A955).
27. Jaeger, Proc. Camb. Phil. Soc. 46, 634—641 A950).
28. В 1 a nch, J. Res. Nat. Bur. Stand. 50, 343—356 A953).
29. Jaeger, Am. J. Sci. 255, 306 A957).
30. P г i с e, S 1 а с k, Brit. J. Appl. Phys. 5, 285—287 A954).
31. Crank, Quart. J. Appl. Math. 10, 220 A957).
32. Southwell, Relaxation Methods in Engineering Science, Oxford, 1940; Relaxa-
Relaxation Methods in Theoretical Physics, Oxford, 1946.
33. E m m о n s, Trans. ASME 65, 607—615 A943).
34. A 1 1 e n, D e n n i s, Quart. J. Mech. Appl. Math. 4, 199—208 A951).
35. Tranter, Quart. J. Mech. Appl. Math. 1, 125—130 A948).
36. A 11 e n, S e v e r n, Quart. J. Mech. Appl. Math. 5, 447—454 A952).
37. Fox, Proc. Roy. Soc. A190, 31—59 A947).
38. Gilmor, Brit. J. Appl. Phys. 2, 199—204 A951).
39. A 11 e n, S e v e r n, Quart. J. Mech. Appl. Math. 4, 209—222 A951).
40. Mitchell, Appl. Sci. Res. A4, 109—119 A954).
41. Lib ma n n, Brit. J. Appl. Phys. 6, 129—135 A955).
ПРИЛ0ЖЕНИЕ1
КОНТУРНЫЕ ИНТЕГРАЛЫ И ПРОВЕРКА РЕШЕНИЙ, ПОЛУЧЕННЫХ
ПРИ ПОМОЩИ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
В § 3 гл. XII отмечалось, что с точки зрения чистой математики решения, по-
полученные методом преобразования Лапласа *), являются по существу формальными;
иными словами, различные операции, например перемена порядка дифференцирования
и интегрирования, производятся без достаточного обоснования. Там же указывалась
необходимость проверки того, что все полученные решения
(для линейного потока) удовлетворяют дифференциальным
уравнениям, а также начальным и граничным условиям.
Метод обоснования заключается в следующем. Во
всех случаях **) мы ищем v, a v находим при помощи
формулы обращения (см. C.8) гл. XII)
2те/ j
A)
т— ico
y+ioo
y-ioo
где 7 так велико, что все особые точки v (к) лежат слева
от линии G — /со, 7 + /оо).
В рассмотренных в настоящей книге задачах этими
особыми точками служило конечное число полюсов и точек
ветвления, а также, быть может, бесконечное число полю-
полюсов в изолированных точках на отрицательной вещест-
вещественной полуоси. Таким образом, мы можем всегда вы-
выбрать новый путь интегрирования L' (рис. 61), который
начинается в бесконечности в направлении arg А = — (^
0 1 \ ' Рис. 61.
> р > — тс I, проходит справа от начала координат и
уходит в бесконечность в направлении arg \ = р, причем все особые точки подынте-
подынтегральной функции остаются слева.
Для функций v(k), с которыми мы встречались ранее, можно всегда показать,
что
Т-Ыоо
B)
Г eKt v (\) d\ = Г еи v (К) d\.
U i
*) То же замечание применимо почти ко всем общим решениям, полученным
при использовании более ранних методов. В самом деле, их значительно легче рас-
раскритиковать, так как при их использовании обычно предполагают, что произвольную
функцию можно разложить в ряд по некоторой системе функций, но не проверяют
эту систему на полноту; таким образом, возникает опасность исключения части ре-
решения (см. сноску к стр. 201). В настоящее время строго проанализировано лишь
очень мало даже сравнительно простых задач, в которые входят произвольные функ-
функции. (Вопрос о радиальном тепловом потоке в цилиндре кругового сечения рассма-
рассматривается в заметке Мура [1].)
**) С этой точки зрения использование таблицы преобразований является во-
вопросом удобства. Так, все приведенные в ней результаты можно получить, применяя
формулу обращения.
468
ПРИЛОЖЕНИЕ I
в'
Для этого рассмотрим замкнутый контур ABB"А"А на рис. 62, который состоит
из отрезка АВ линии Re (X) = 7, из отрезка А"В" контура U и из дуг ВВ'В" и А"А'А
большой окружности с радиусом R и с центром в начале координат. Внутри этого
контура особые точки отсутствуют. Формула B) следует из теоремы Коши, если
в пределе, по мере того как /?->оо, интегралы вдоль
дуг А АА"^ и ВВ'В" стремятся к нулю. Рассмотрение подын-
подынтегральной функции показывает, что это справедливо в лю-
любом из специальных разобранных в данной книге случаев *).
Таким образом, в этих случаях мы получаем
C)
Далее можно показать, что интеграл C) сходится равно-
равномерно по пространственной переменной в заданной области
при фиксированном t\ он сходится также равномерно по t
для t :> О при фиксированной пространственной переменной.
Дифференцирование под знаком интеграла является закон-
законным и, таким образом, легко показать, что данное дифферен-
дифференциальное уравнение удовлетворяется. Аналогичным путем на-
находят, что удовлетворяются начальные и граничные условия.
Преимущество пути U перед путем по прямой (f— /оо,
7 + /оо) заключается в том, что в первом случае мы полу-
получаем множитель типа
Рис. 62.
1
ехр
{ —
где тс>р>-^тс, а ? — положительная величина, содержащая пространственную пере-
переменную. Этот множитель обеспечивает требуемую равномерную сходимость. Если
в соотношении C) произвести замену переменной , а = Х1/г еы/2, то мы должны будем
производить интегрирование по пути Р (рис. 63), который начинается в бесконеч-
бесконечности в направлении arg a = в, где
О < 6 < -? тс, и уходит в бесконеч- \ /
ность в направлении arg а = тс — 8.
Очевидно, что интегралы вдоль ука-
указанного пути можно рассматривать
таким же образом, как и интегралы
вдоль пути L't и мы получим
тег ./
D)
О
Рис. 63.
В книге Карслоу [7] контурные интегралы этого типа считаются фундаменталь-
фундаментальными, и их использование позволило решить целый ряд задач. Следует отметить, что
при этом применялся такой же метод, как и используемый здесь, но производилась
указанная выше замена переменной.
Для обоснования метода с использованием функций Грина (см. гл. XIV) мы по-
поступим таким же образом; правда, здесь мы должны лишь доказать, что w удовлет-
*) Здесь, а также в других случаях необходимо исследовать порядок величины
подынтегральной функции на окружности с большим радиусом R. Теоретически это
следует делать для каждой специальной задачи, однако на самом деле можно сов-
совместно рассматривать обширные классы задач. Подробности для задачи I, приведен-
приведенной в § 6 гл. XII, изложены в §§ 41 и 58 книги Карслоу и Егера [2]; для задачи
§ 7 гл. XII — в § 47 той же книги; для задачи о составном сферическом твердом
теле — в работе [3]; для некоторых задач о круглых цилиндрах — в работе [4]; по-
подробные решения достаточно полного набора задач о цилиндрических областях
0<г<а, а < г < b и г > а с граничными условиями, приведенными в § 9 гл. I, из-
изложены в [5]. Использование параболического контура интегрирования имеет некоторые
преимущества по сравнению с применением кругового контура [6].
КОНТУРНЫЕ ИНТЕГРАЛЫ 469
воряет нашему дифференциальному уравнению и стремится к нулю при ?=0 и чго у
удовлетворяет граничным условиям.
Окончательные формы решений, которые мы обычно давали, были представлены
в виде рядов или интегралов путем использования контуров, изображенных на
рис. 39 и рис. 40 соответственно. Проведенной вышэ проверкой мы установили, что
соотношение A) удовлетворяет всем условиям задачи, и для того чтобы окончатель-
окончательные решения оказались вполне строгими, необходимо тщательное обоснование при-
приведения A) к его конечной форме. Это требует доказательства того, что в пределе
по мере стремления радиусов больших окружностей контуров к бесконечности (в слу-
случае необходимости набор значений радиусов может оказаться дискретным, так что
окружности не проходят через полюсы подынтегральной функции) интегралы вдоль
этих окружностей стремятся к нулю. Последнее положение можно доказать для всех
приведенных здесь решений, используя изложенный выше анализ; дальнейшие под-
подробности можно найти в приведенной литературе.
ЛИТЕРАТУРА
1. Moore, Bull. Amer. Math. Soc. 51, 650 A945).
2. Carslaw, Jaeger, Operational Methods in Applied Mathematics. (Г. К а р с л о у,
Д. Е г е р, Операционные методы в прикладной математике, ИЛ, М., 1948.)
3. Carslaw, Jaeger, Proc. Camb. Phil. Soc 35, 394 A939).
4. Carslaw, Jaeger, Proc. Lond. Math. Soc. 46, 361 A940).
5. Carslaw, Jaeger, Proc. Roy. Soc. N. S. W. 75, 130 A942).
6. Churchill, Math. Z. 43, 743 A938).
7. Carslaw, Introduction to the Mathematical Theory of the Conduction of Heat in
Solids Macmillan, 1921. (Г, Карслоу, Теория теплопроводности, Гостехиздат,
1947.)
ПРИЛОЖЕНИЕ 2
ФУНКЦИЯ ОШИБОК И РОДСТВЕННЫЕ ФУНКЦИИ
Введем обозначение *)
х
Ф(Х)=^=Г /«"*<«, О)
так что
Ф(сх>)=1, B)
а
Ф (_ х) = — Ф (*).
Кроме того, мы можем написать
оо
Ф* (х) = 1 — Ф (х) = -4=r / e-^dl. C)
|/ тс •/
тс
Будем теперь искать приближения для Ф (х) при малых и больших значениях х.
Для малых значений х используем разложение в ряд е~^ в выражении A); тогда
Так как этот ряд равномерно сходится, то его можно почленно проинтегриро-
проинтегрировать, и следовательно,
Для больших значений х мы поступим следующим образом. Простое интегриро-
интегрирование по частям дает
-AJ VM
*) Первая таблица этих интегралов была приведена в [1], где указываются зна-
значения Ф(*), вычисленные до седьмого знака после запятой, для х с шагом 0,01
в интервале от jc = 0 до х = 2. В работе [2] эти значения вычислены до х = 3. В ста-
статье [3] приведены новые пятизначные таблицы для интервала от *=0до.* = 3
с шагом 0,0001. Самые новые таблицы можно найти в [4, 5]. В работах [6] и [7] при-
приведены более краткие таблицы значений функций Ф(*), причем в последней указаны
также значения ее производных. Для функции A) применяется множество различных
обозначений [8].
функция ошибок и родственные функции 471
Повторяя этот процесс п раз, получим
X
2 U 2^з ^ 2V
Этот ряд не сходится, так как отношение л-го члена к (л — 1)-му при увеличе-
увеличении п не остается меньшим единицы. Однако если мы возьмем п членов этого ряда,
то остаток, т. е.
будет меньше п-го члена, так как
оо оо
<>
!§¦
Таким образом, мы можем остановиться на любом члене ряда; тогда сумма всех
членов до него служит приближением для нашей функции, причем допускаемая
ошибка меньше абсолютной величины последнего еще не отброшенного нами члена.
С такой точностью значения Ф* (х) для больших х можно вычислить по формуле
Функция ех7Ф*(х) часто встречается в задачах теплопроводности.
Укажем некоторые другие важные интегралы, также сводящиеся к функции
ошибок [9] *):
оо
е б g-i- dg =-5- *Ф (у), F)
б
у*Ф (у). G)
Производные и интегралы функций ошибок.
Последовательные производные функции ошибок обозначаются следующим
образом:
Ф Iх\ *"~ —~—^^ Ф Tjc^ f8)
и, следовательно,
к™
*) О других интегралах смотри [10].
472 ПРИЛОЖЕНИЕ 2
и т. п. Их значения затабулированы и приведены в [7]. В задачах теплопроводности
интегралы функции ошибок играют очень большую роль *). Введем обозначения
оо
1«Ф* (х) = J i«- 1Ф*? tf?, /г = 1,2,... (9)
х
причем
РФ* (х) = Ф* (х). A0)
Для краткости мы часто будем писать вместо 11Ф*(лг) тоже 1Ф*(х). Тогда, интегри-
интегрируя по частям, получим
1Ф* (*) = -L. е~х2 — хФ* (х\ A1)
У п
2х2) Ф* (х) ?=г хе~Л , A2)
4 L V* J
или
12Ф* (х) = ^ [Ф* (jc) — 2*1Ф* (х)]. A3)
Общая рекуррентная формула имеет вид
2п1пФ* (х) = 1«-2ф* (jc) — 2дг1л" 1Ф* (*), A4)
причем A3) для случая, когда п = 2, легко получить методом индукции.
Из соотношения A4) следует, что
2пГ
(!¦+•)'
A5)
Кроме того, из A4) следует, что у = 1ЛФ* (х) удовлетворяет дифференциальному
уравнению
pL+2xJlL-2ny = 0. A6)
dx2 ' dx J K '
Функция ошибок при комплексном аргументе.
Эта функция, имеющая огромное значение для задач теплопроводности, лишь
недавно затабулирована Фадеевой и Терентьевым [13] **). Они определили ее следую-
следующим образом:
Z
¦+?/•4
A7)
где
так что
®(/2Г)
Некоторые значения функций и (х, у) и v(x, у) приведены в табл. 2 и 3 на-
настоящего приложения.
Соотношения D) и E), полученные выше для действительного г, справедливы
также и для комплексного z.
*) Они изучены и затабулированы Хартри [11]. Значения, приведенные в табл. 1
данного приложения, заимствованы из его статьи. В работе [12] указаны значения
для п от 1 до 11, для х от 0 до 0,2 (шаг 0,01), от 0,2 до 1 (шаг 0,05) и от 1 до 3
(шаг 0,1).
**) В этой работе приведены значения с 6 десятичными знаками и с шагом аргу-
аргумента, равным 0,02. В книге Карпова [14] приведена аналогичная таблица с аргумен-
аргументами в полярных координатах. В работах [15] и [16] приведены затабулированные
значения функции w (z) для действительного z. Если х = у, то интересующий
нас интеграл можно выразить через интегралы Френеля; таблица его значений при-
приведена в [17].
ФУНКЦИЯ ОШИБОК И РОДСТВЕННЫЕ ФУНКЦИИ 473
ЛИТЕРАТУРА
L Encke, Method of Least Squares, Astronomisches Jahrbuch, 1834.
2. De M о г g a n, Essay on Probabilites, 1838.
3. Burgess, Trans. Roy. Soc. Edin. 39, 257 A899).
4. Sheppard, The Probability Integral, Brit. Ass. Adv. Science, Math. Tables.
Vol. VII, 1939.
5. Sheppard, Tables of the Probability Function, Works Projekt Administration,
New York, 1941.
6. Milne — Thomson, Comrie, Standard Four-Figure Mathematical Tables, Mac-
millan, 1931. (Милн — Томсон и Комри, Четырехзначные математические
таблицы, Физматгиз, 1961.)
7. Jahnke—Emde, Tables of Functions, Teubner, ed. 2, 1933. (E. Янке, Ф. Эмде,
Таблицы функций с формулами и кривыми, Гостехиздат, 1948.)
8. Jeffreys, Operational Methods in Mathematical Physics, Cambridge, ed. 2, 1931,
p. 110.
9. С a f s 1 a w, Fourier's Series and Integrals, Macmillan, ed. 3, 1930.
10. H о r e n s t e i n, Quart. Appl. Math. 3, 183 A945).
11. Hartree, Mem. Manchr. Lit. Phil. Soc. 80, 85 A935).
12. К а у e, J. Math. Phys. 34, 119—125 A955).
13. Фадеева, Терентьев, Таблицы значений функции w(z) для комплексного
аргумента, Гостехиздат, 1954.
14. Карпов, Таблицы функций w(z) в комплексной области, Изд-во АН СССР, 1954.
15. Dawson, Proc. Lond. Math. Soc. 29, 519 A897—1898).
16. М i 1 1 е г, G о г d о n, J. Phys. Chem. 35, 2785 A931).
17. С 1 e m m о w, M u n f о r d, Phil. Trans. Roy. Soc. A245, 189—211 A952).
31 Г. Карслоу, Д. Егер
474
ПРИЛОЖЕНИЕ 2
К
в;
2
ев
I
CO
о
a.
о
о
s
о
ОС
5
а:
-<e-»^NO»«iO^«NN«-0000000
«в^СЧ—-<-<-<ОООООООООООООООООО
ооооооооо © о^о^о о о^о о о о о о^о о^о о
*" о^сГсГо* ©* о4 о" сГсГсГ сГсГсГо* о" ©* о' сГ
ОЮ-«^'¦^•«О — Ю00О}<О00и'5<©©Г"»<ОГ"»©'*'О}СЧГ»'*'С*ЭЯ«
©©©©©©©©©©©©©©©©©©©©©©с
© © © © © с
* 00 Ю СО — Oi С
^«C4—« — ©©©©©©
- - -
©©©©©©<
¦^«©¦^¦ч*»© — г»оос^05©сооо«ою«ооосч?о — •^•oito^'CJ — — ©©о©
СО ^У^ 00 f^ O'J 00 ^ij* ^^ I4* 1^5 ^^ ^*^ ^?^ Х~^ ^О ^^5 ^}* СО 00 ^^ ^^ ^"^ ^^ ^^ ^^ ^^ ^^ ^^ ^^ ^^ ^^ ^^
O^^fM«M(MN —_— --ООО © ©^© © ©,© Я°.О.О-О.°.О.С!^° Z
•-htrtN-
сГ ©"©" ©~
1 сГ сГ©4 ©"сГ ©^ © сГ с
. . _ -_3©«*5COt--*S4
5С»«СО»00 — «ОчгСЧ — ©©©
-. Jr^-^еч—.—.©©о©©©©
?««;-eoeo|oopocop
Го'о'о'сГо""
5*
— — м ei
©"сГ ©"©*©* ©'
»lOr»«»f О- Ж — —
С^С^ — ©OOCOC^OS^CJIrOOOC
—. — —. -^© ©_© 0^05 О 00^00 t- l
i^j-Oi^©^ — С*5«О©Ю — Q
Ч— ©©©©
©©©©©
»00»Г^ООМ00>ЛМСЧ ©©©©
©Ю — QOtO^COCJ—.©©©О©©©©©
"^ — — ©© © © ©^© © © © © © © О © ©_
¦о.
О O> 00 00 00 Г
>©©©©©©©©c
Г©"©*©"©**©4
© P^""!.-"!.6* сч w w ^< чв^ю
сГсГ©*4©"*©"©©"'©"*©"'©"'
ФУНКЦИЯ ОШИБОК И РОДСТВЕННЫЕ ФУНКЦИИ
475
ost-ooeNoo^e*—«•-*с*эоо»лю©оосче*г-С1Г'*с*«о©»©*^о»оо«>еоо»<о<мооюсчв»
- _. » _^. ^ _ л _.» «. -^ __ - - .^^. .^fc .^^. ч .^fc. .^^. .^». .^^ .^^. ^а^ fT^ ^Ji ?tf^
о о о ©
г^юоог- — el — г- — ^ЗЙиэ^с^ог-^ечлЗдаго^ — «0)*»-#0«- оо^> —
г-©С1'*«ог^оооо<ло»о>о>о>а>о><7>осоооог'Г-<о«оиэиэ^«Лс1С1С1 — ^-©о©
S
S
S
ф
ВТ
.ФЮб>
OOOOOOOOOOOOOOOOOO
Z* ?^ ^ Jf ^ Х^ ^ ^4Г* Г^^T^SI* ^*^*Т* ?*
>ооооооооооо
©©©©©©о©
jiO ©
ГсГ© ©*© ©~сГ
»Ф«ОМП«<0«Ф10«)ФМ><0Ф@ФОФ1Л1С««ППМММ<^<^ОООФ
>оооооооос
о* о о4 о* о" о" о" о~о" о* сГо" сГ
©** ©сГ©4©©""©* сГ ©* ©"©*©"*©""©** ©**сч©ло"ч©"чсГ ©"с
r0>rC5<*>«000000
aOMi/H)^o)tco@
^^пмсч-•—• — о
5oo«'*'Ci'-NCsr-o^esi — O00r^»o^«rt- ©оог^«>«0 1Л^в«;«<мс» — — ©
Г©©"©*"©"©" сГ ©* ©"©"©" сГсГ о*©*©*©* ©* о4 сГ ©"©*
>©©©©©©с
5МООООО
NOtfl
««в»оо5
— «ОЙ- ОО-Ч'С
) ^^> ^^ ^^
E?°,S
— ©©©©©©©© сГ© © © © <
с» ^ о ао о в^ н»
31*
476
ПРИЛОЖЕНИЕ 2
ее
СГ
К
•9-
0>
В"
се
со
>оооооооооооос
4 о" сГ сГ сГо* о*сГ сГсГ сГсГсГсГ сГ сГсГ сГ о* <
со со oi *^ ^^! ^^^ ^^ о^ ^^^ ^^* ^^ ^^^ ^4) »*^ oi ^т* оо с^ ^о i^^ оо
гсч©05г^Ю'^"сч-^©с:оог*сою'^?ссч«^©!Г>оог-г^«с
©о©©©©©©©©©©©
>oooooooooo<
©"©**©*о©о**©©"©"©*¦© с
J- CSI © Г-
. . _ . .j-^^соЛсососч
> © © ©^о^© ©^© о^о © © ©
> © ©~ ©~©~ ©* о4 ©" о*©*4©* сГ © о4 © ©*
>сос-10«ечсосоеч"ч*«
Ir^COOtOC^OOOCO'*
__. -^^^«СОСОСОСЧСЧСЧ
*-«©©©©©©©©©©©©©©©
о'сГо'сГсГсГсГо'сГсГсГо'сГсГсГо сГсГо сГо о" о" о4 о4 о4 сГ о* с
>ооооооооо
0ic0^«c*?
©'*d>»o«-*OicOi^«c*?i—•©о>оог>»сосою>01^'1^'1*1<Лсовчсч<м«^«^ — — т-«^«^©©©
•ч*«СОСЧСЧСЧ-<-<-<^-<^©0©©©©©©©©©©©©©©©©©©©©©©©
©©©©©©©©<
>©©©©©©©©
ПРИЛОЖЕНИЕ 3
О ФУНКЦИЯХ БЕССЕЛЯ
Здесь мы отметим некоторые свойства функций Бесселя, используемые в настоя-
настоящей книге *).
Функция Бесселя /v (z) определяется соотношением
r=0
где v — действительное число, а 2 может быть комплексным; из различных возмож-
возможных значений комплексной функции /v (г) выбирают главное значение. Функция
Л С2') удовлетворяет уравнению Бесселя порядка v
Если v не равно целому числу, то функции /v (z) и /_v(^) служат линейно неза-
независимыми решениями уравнения B), но когда v — целое число, равное п, то
В качестве второго решения уравнения B), пригодного для всех значений v,
выбирают функцию **)
YB)= JA*) cos ™-J-Л*) C)
функцию Yn (z) (когда п — целое число) определяют как lim Kv (z). При таком опре-
делении
где 7 = 0,5772 — постоянная Эйлера.
*) Более полные данные по этому вопросу можно найти в книгах: В а т с о н,
Теория функций Бесселя (ИЛ, 1949) или Грэйи Мэтью з, Функции Бесселя и их
применение в физике и механике (ИЛ, 1953), а также в книге Мак-Лахлана (М с L а с h 1 а п,
Bessel Functions for Engineers, Oxford, 1934).
**) Эта функция называется функцией Неймана порядка v; ее обозначают также
N4(z). (Прим. ред.)
478 ПРИЛОЖЕНИЕ 3
Итак, если л— любое положительное целое число, то
\П+2г
/ 1 \
оо I * I
|«) + T}^(«)-]g(-y г|(||
П+Г
л-1
г=0
I 2Л1~1"'Л1) следУет заменить суммой V/n-i
\m=l msl / m=l
где при г = 0 сумму
Уравнение Бесселя вида
удовлетворяется функцией *)
1 \v4
00
(-4'
г=0
Если v не равно целому числу, то /_v (г) служит независимым решением урав-
уравнения F); в качестве второго решения, пригодного для всех значений v, выбираем
функцию
функцию Кп (z) (когда п — целое число) определяют как lim /Cv (г). При таком опре-
делении
если л — любое целое положительное число, то
I/i+r r
л-1
г=0
(л+г г \ л
S т~! + S ml ) следУет заменить суммой 2j m~l-
т =1 mel / m=sl
*) Эту функцию называют функцией Бесселя от мнимого аргумента. (Прим. ред.)
О ФУНКЦИЯХ БЕССЕЛЯ 479
Для больших значений z
1
I 1^2 12 Г4м2 1 2\ D.^2 Я2\ / 1 \ *
A1)
ехр — г± (V + -S- \т\
L V ^/ J i 1 . ^/_L) I A2)
положительный знак берется тогда, когда — "о"те < аг? * < "о" те' а отрицательный —
3 1
когда — y n < arg z < -~ я.
Ниже приводятся наиболее часто используемые соотношения между функциями
Бесселя:
<B')-v/v(^)=2'/v4.1(^), A4)
^< (^) + **, (^) = - ^v-1 (^). A5)
г< (г) - v/Cv (г) = - гК,+1 (г), A6)
*/; (г)+ v/v (*) = */,_!(*), A7)
^ (г) - v/v (г) = - */v+1 (г). A8)
Функция Ку(г) удовлетворяет тем же соотношениям A7) и A8), что и функция
/v (г). В случае v = 0 эти соотношения принимают вид
*> = -7- <21>
/v (г) Kv+1 (г) + К, {г) /,+, (*) = !, B2)
Z
(zemKi) ^e™1 У, (г), B3)
(^m«) = e - тш1 у^ ^ _|_ 2/ sin mv^. ctg v^y^ (^^ B4)
l
7 '* [— y,(*)±'y.(^)]. B5)
:2" |_л 2W Л(г) B6)
B7)
'«-г, B8)
У ?/„ (ri) «"«"Л = -^е-''»" , B9)
) > 0. C0)
ПРИЛОЖЕНИЕ 4
КОРНИ НЕКОТОРЫХ ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ
Первые шесть корней *) лп уравнения
Таблица 1
с
0
0,001
0,002
0,004
0,006
0,008
0,01
0,02
0,04
0,06
0,08
од
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,5
2,0
3,0
4,0
5,0
6,0
7,0
8,0
9,0
10,0
15,0
20,0
30,0
40,0
50,0
60,0
80,0
100,0
оо
*)
0
0,0316
0,0447
0 0632
0,0774
0,0893
0,0998
0,1410
0,1987
0,2425
0,2791
0,3111
0,4328
0,5218
0,5932
0,6533
0,7051
0,7506
0,7910
0,8274
0,8603
0,9882
1,0769
1,1925
1,2646
1,3138
1,3496
1,3766
1,3978
1,4149
1,4289
1,4729
1,4961
1,5202
1,5325
1,5400
1,5451
1,5514
1,5552
1,5708
3,1416
3,1419
3,1422
3,1429
3,1435
3,1441
3,1448
3,1479
3,1543
3,1606
3,1668
3,1731
3,2039
3,2341
3,2636
3,2923
3,3204
3,3477
3,3744
3,4003
3,4256
3,5422
3,6436
3,8088
3,9352
4,0336
4,1116
4,1746
4,2264
4,2694
4,3058
4,4255
4,4915
4,5615
4,5979
4,6202
4,6353
4,6543
4,6658
4,7124
6,2832
6,2833
6,2835
6,2838
6,2841
6,2845
6,2848
6,2864
6,2895
6,2927
6,2959
6,2991
6,3148
6,3305
6,3461
6,3616
6,3770
6,3923
6,4074
6,4224
6,4373
6,5097
6,5783
6,7040
6,8140
6,9096
6,9924
7,0640
7,1263
7,1806
7,2281
7,3959
7,4954
7,6057
7,6647
7,7012
7,7259
7,7573
7,7764
7,8540
9,4248
9,4249
9,4250
9,4252
9,4254
9,4256
9,4258
9,4269
9,4290
9,4311
9,4333
9,4354
9,4459
9,4565
9,4670
9,4775
9,4879
9,4983
9,5087
9,5190
9,5293
9,5801
9,6296
9,7240
9,8119
9,8928
9,9667
10,0339
10,0949
10,1502
10,2003
10,3898
10,5117
10,6543
10,7334
10,7832
10,8172
10,8606
10,8871
10,9956
12,5664
12,5665
12,5665
12,5667
12,5668
12,5670
12,5672
12,5680
12,5696
12,5711
12,5727
12,5743
12,5823
12,5902
12,5981
12,6060
12,6139
12,6218
12,6296
12,6375
12,6453
12,6841
12,7223
12,7966
12,8678
12,9352
12,9988
13,0584
13,1141
13,1660
13,2142
13,4078
13,5420
13,7085
13,8048
13,8666
13,9094
13,9644
13,9981
14,1372
Все корни этого уравнения действительны, если С > 0.
15,7080
15,7080
15,7081
15,7082
15,7083
15,7085
15,7086
15,7092
15,7105
15,7118
15,7131
15,7143
15,7207
15,7270
15,7334
15,7397
15,7460
15,7524
15,7587
15,7650
15,7713
15,8026
15,8336
15,8945
15,9536
16,0107
16,0654
16,1177
16,1675
16,2147
16,2594
16,4474
16,5864
16,7691
1^6,8794
16,9519
17,0026
17,0686
17,1093
17,2788
КОРНИ НЕКОТОРЫХ ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ 481
Таблица 2
Первые шесть корней*) а„ уравнения actga
с
—1,0
—0,995
—0,99
—0,98
—0,97
—0,96
—0,95
—0,94
—0,93
—0,92
—0,91
—0,90
—0,85
—0,8
—0,7
—0,6
—0,5
-0,4
—0,3
—0,2
—од
0
ОД
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,5
2,0
3,0
4,0
5,0
6,0
7,0
8,0
9,0
10,0
15,0
20,0
30,0 -
40,0
50,0
60,0
80,0
100,0
оо
*) Все
0
0,1224
0,1730
0,2445
0,2991
0,3450
0,3854
0,4217
0,4551
0,4860
0,5150
0,5423
0,6609
0,7593
0,9208
1,0528
1,1656
1,2644
1,3525
1,4320
1,5044
1,5708
1,6320
1,6887
1,7414
1,7906
1,8366
1,8798
1,9203
1,9586
1,9947
2,0288
2,1746
2,2889
2,4557
2,5704
2,6537
2,7165
2,7654
2,8044
2,8363
2,8628
2,9476
2,9930
3,0406
3,0651
3,0801
3,0901
3,1028
3,1105
3,1416
КОрНИ ?
4,4934
4,4945
4,4956
4,4979
4,5001
4,5023
4,5045
4,5068
4,5090
4,5112
4,5134
4,5157
4,5268
4,5379
4,5601
4,5822
4,6042
4,6261
4,6479
4,6696
4,6911
4,7124
4,7335
4,7544
4,7751
4,7956
4,8158
4,8358
4,8556
4,8751
4,8943
4,9132
5,0037
5,0870
5,2329
5,3540
5,4544
5,5378
5,6078
5,6669
5,7172
5,7606
5,9080
5,9921
6,0331
6,1311
Ь,1606
6,1805
6,2058
6,2211
6,2832
>того уравнения
ные значения С встречаются при
7,7253
7,7259
7,7265
7,7278
7,7291
7,7304
7,7317
7,7330
7,7343
7,7356
7,7369
7,7382
7,7447
7,7511
7,7641
7,7770
7,7899
7,8028
7,8156
7,8284
7,8412
7,8540
7,8667
7,8794
7,8920
7,9046
7,9171
7,9295
7,9419
7,9542
7,9665
7,9787
8,0385
8,0962
8,2045
8,3029
8,3914
8,4703
8,5406
8,6031
8,6587
8,7083
8,8898
9,0019
9,1294
9,1987
9,2420
9,2715
9,3089
9,3317
9,4248
10,9041
10,9046
10,9050
10,9060
10,9069
10,9078
10,9087
10,9096
10,9105
10,9115
10,9124
10,9133
10,9179
10,9225
10,9316
10,9408
10,9499
10,9591
10,9682
10,9774
10,9865
10,9956
11,0047
11,0137
11,0228
11,0318
11,0409
11,0498
11,0588
11,0677
11,0767
11,0856
11,1296
11,1727
11,2560
11,3349
11,4086
11,4773
11,5408
11,5994
11,6532
11,7027
11,8959
12,0250
12,1807
12,2688
12,3247
12,3632
12,4124
12,4426
12,5664
действительны, если С
рассмотрении сферы (см.
14,0662
14,0666
14,0669
14,0676
14,0683
14,0690
14,0697
14,0705
14,0712
14,0719
14,0726
14,0733
14,0769
14,0804
14,0875
14,0946
14,1017
14,1088
14,1159
14,1230
14,1301
14,1372
14,1443
14,1513
14,1584
14,1654
14,1724
14,1795
14,1865
14,1935
14,2005
14,2075
14,2421
14,2764
14,3434
14,4080
14,4699
14,5288
14,5847
14,6374
14,6870
14,7335
14,9251
15,0625
15,2380
15,3417
15,4090
15,4559
15,5164
15,5537
15,7080
>—1.
§ 4 гл.
17,2208
17,2210
17,2213
17,2219
17,2225
17,2231
17,2237
17,2242
17,2248
17,2254
17,2260
17,2266
17,2295
17,2324
17,2382
17,2440
17,2498
17,2556
17,2614
17,2672
17,2730
17,2788
17,2845
17,2903
17,2961
17,3019
17,3076
17,3134
17,3192
17,3249
17,3306
17,3364
17,3649
17,3932
17,4490
17,5034
17,5562
17,6072
17,6562
17,7032
17,7481
17,7908
17,9742
18,1136
18,3018
18,4180
18,4953
18,5497
18,6209
18,6650
18,8496
Отрицатель-
IX).
482
ПРИЛОЖЕНИЕ 4
Таблица 3
Первые шесть корней лп уравнения ajt (а) — CJ0 (а) = О
С
0
0,01
0,02
0,04
0,06
0,08
0,1
0,15
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,5
2,0
3,0
4,0
5,0
6,0
7,0
8,0
9,0
10,0
15,0
20,0
30,0
40,0
50,0
60,0
80,0
100,0
оо
0
0,1412
0,1995
0,2814
0,3438
0,3960
0,4417
0,5376
0,6170
0,7465
0,8516
0,9408
1,0184
1,0873
1,1490
1,2048
1,2558
1,4569
1,5994
1,7887
1,9081
1,9898
2,0490
2,0937
2,1286
2,1566
2,1795
2,2509
2,2680
2,3261
2,3455
2,3572
2,3651
2,3750
2,3809
2,4048
3,8317
3,8343
3,8369
3,8421
3,8473
3,8525
3,8577
3,8706
3,8835
3,9091
3,9344
3,9594
3,9841
4,0085
4,0325
4,0562
4,0795
4,1902
4,2910
4,4634
4,6018
4,7131
4,8033
4,8772
4,9384
4,9897
5,0332
5,1773
5,2568
5,3410
5,3846
5,4112
5,4291
5,4516
5,4652
5,5201
а8
7,0156
7,0170
7,0184
7,0213
7,0241
7,0270
7,0298
7,0369
7,0440
7,0582
7,0723
7,0864
7,1004
7,1143
7,1282
7,1421
7,1558
7,2233
7,2884
7,4103
7,5201
7,6177
7,7039
7,7797
7,8464
7,9051
7,9569
8,1422
8,2534
8,3771
8,4432
8,4840
8,5116
8,5466
8,5678
8,6537
«4
10,1735
10,1745
10,1754
10,1774
10,1794
10,1813
10,1833
10,1882
10,1931
10,2029
10,2127
10,2225
10,2322
10,2419
10,2516
10,2613
10,2710
10,3188
10,3658
10,4566
10,5423
10,6223
10,6964
10,7646
10,8271
10,8842
10,9363
11,1367
11,2677
11,4221
11,5081
11,5621
11,5990
11,6461
11,6747
11,7915
а5
13,3237
13,3244
13,3252
13,3267
13,3282
13,3297
13,3312
13,3349
13,3387
13,3462
13,3537
13,3611
13,3686
13,3761
13,3835
13,3910
13,3984
13,4353
13,4719
13,5434
13,6125
13,6786
13,7414
13,8008
13,8566
13,9090
13,9580
14,1576
14,2983
14,4748
14,5774
14,6433
14,6889
14,7475
14,7834
14,9309
«в
16,4706
16,4712
16,4718
16,4731
16,4743
16,4755
16,4767
16,4797
16,4828
16,4888
16,4949
16,5010
16,5070
16,5131
16,5191
16,5251
16,5312
16,5612
16,5910
16,6499
16,7073
16,7630
16,8168
16,8684
16,9179
16,9650
17,0099
17,2008
17,3442
17,5348
17,6508
17,7272
17,7807
17,8502
17,8931
18,0711
Таблица 4
Первые пять корней ая уравнения Jo (a) Yo (ka) — Yo (a) Jo (ka) — 0
ft
1,2
1,5
2,0
2,5
3,0
3,5
4,0
15,7014
6,2702
3,1230
2,0732
1,5485
1,2339
1,0244
а2
31,4126
12,5598
6,2734
4,1773
3,1291
2,5002
2,0809
47,1217
18,8451
9,4182
6,2754
4,7038
3,7608
3,1322
62,8302
25,1294
12,5614
8,3717
6,2767
50196
4,1816
а5
78,5385
31,4133
15,7040
10,4672
7,8487
6,2776
5,2301
ПРИЛОЖЕНИЕ 5
ТАБЛИЦА ПРЕОБРАЗОВАНИЙ ЛАПЛАСА v(p) = f e~ptv(t)dt
о
Обозначим q = У р/х. хил; всегда действительны и положительны.
а и h — любые
v(p)
1.
о
3-
1
5-
6.
7.
9.
I
р
«-«*
e-QX
11.
7
г , /г—0, 1,2,..
1 * V
1
sin с
COS
2*/
* j X
484
ПРИЛОЖЕНИЕ 5
Продолжение
v(p)
v(t)
13.
14.
15.
16.
17.
18.
19.
20.
21.
e~qx
pq(q+h)
*-**
p{q+hy
p — a
pi*
22. I,(qx')KAqx)>*
23. /
24.
< x' J
%ехр(/иг + х*/12)Ф*
1 /^_V/j в-**« -
h \ « /
(-Л)"
exp {hx + %*Л2) Ф*
I 2 Vtt )
n-l
— V [- 2
_ 2Л (^-V/J e-*m%t + % A + hx + 2h\t) X
1 ^ % 2 /'
A2 2]/*^ Л \
X
ТАБЛИЦА ПРЕОБРАЗОВАНИИ ЛАПЛАСА 485
Продолжение
v(p)
v{t)
25 ехр \хр — х[(р + а) (р + Ь)]1**
1( + )(+Ь)]1'
26.
27.
28.
29.
30.
31.
32.
33.
2* l
KA*V7)
ехр {х \(р + аIг -
(р-а)
q(p —
Г—«)(*+*)
oo
l Ce-«u>
X>j4t
(xt)/t
>е*р[4
(e —ft
•A»
Bt)'
,-,+1
ПРИЛОЖЕНИЕ 6
ТЕРМИЧЕСКИЕ СВОЙСТВА НЕКОТОРЫХ ВЕЩЕСТВ
Эта таблица приведена только для того, чтобы показать порядок величин тер-
термических коэффициентов, встречающихся на практике. Более полные данные, а также
изменения термических коэффициентов с температурой можно найти в книге Inter-
International Critical Tables или в других работах по стандартизации физических констант.
Значения коэффициентов теплопроводности для неметаллов следует считать весьма
приближенными средними значениями, так как между их величинами для различных
образцов, изготовленных из одного и того же вещества, могут наблюдаться большие
расхождения.
В приведенной таблице использованы единицы системы СГС, калории и градусы
Цельсия.
Вещество
Плотность
Р
Удельная
теплоемкость
с
Коэффициент
теплопро-
теплопроводности
К
Коэффициент
температуро-
температуропроводности
Металлы
Серебро
Золото
Медь
Магний
Алюминий
Цинк
Олово
Латунь G0:30)
Платина
Свинец
Мягкая сталь @,1% С) . . .
Чугун
Висмут
Ртуть
Неметаллы
Воздух
Гранит
Известняк
Песчаник
Горные породы (в среднем)
Лед
10,49
19,30
8,94
1,74
2,70
7,14
7,30
8,5
21,46
11,34
7,85
7,4
9,80
13,55
0,00129
2,6
2,5
2,3
0,92
0,0556
0,0308
0,0914
0,240
0,206
0,0917
0,0534
0,09
0,0315
0,0302
0,118
0,136
0,0292
0,0335
0,240
0,21
0,22
0,23
0,502
1,00
0,70
0,93
0,38
0,48
0,27
0,15
0,25
0,17
0,084
0,11
0,12
0,020
0,020
0,000058
0,006
0,004
0,006
0,0042
0,0053
1,71
1,18
1,14
0,91
0,86
0,41
0,38
0,33
0,25
0,25
0,12
0,12
0,070
0,044
0,187
0,011
0,007
0,011
0,0118
0,0115
ТЕРМИЧЕСКИЕ СВОЙСТВА НЕКОТОРЫХ ВЕЩЕСТВ
487
Продолжение
Вещество
Плотность
Р
Удельная
теплоемкость
с
Коэффициент
теплопро-
теплопроводности
К
Коэффициент
температуро-
температуропроводности
Стекло (кронглас)
Бетон A:2:4)
Кирпич (строительный) . . . .
Снег (свежий)
Грунт (в среднем)
Грунт (песчаный, сухой) . . . .
Грунт (песчаный, влаж-
влажность 8%)
Древесина (еловая, вдоль во-
волокна)
Древесина (еловая, поперек во-
волокна)
Вода
Земная кора
2,4
2,3
2,6
0,1
2,5
1,65
1,75
0,41
0,41
1,0
0,15
0,20
0,23
0,20
0,5
0,2
0,19
0,24
0,30
0,30
1,0
0,48
0,0028
0,0022
0,0020
0,00025
0,0023
0,00063
0,0014
0,00055
0,00030
0,00144
0,0001
0,0058
0,0042
0,0038
0,0050
0,0046
0,0020
0,0033
0,0045
0,0024
0,00144
0,0014
Г. Карслоу, Д. Егер
Теплопроводность твердых тел
М., 1964 г., 488 стр. с илл.
Редактор И. Л. Райская
Техн. редактор И. Ш. Аксельрод
Корректор О. А. Сигал
Сдано в набор 13/IV 1964 г. Подписано к печати 21/IX 1964 г.
Бумага 70xl08Vie- Физ. печ. л. 30,5. Условн. печ. л. 41,79.
Уч.-изд. л. 38,11. Тираж 6500 экз. Цена книги 2 р. 11 к.
Заказ № 344.
Издательство «Наука».
Главная редакция
физико-математической литературы.
Москва, В-71, Ленинский проспект, 15.
Ленинградская типография № 2 имени
Евгении Соколовой «Главполиграфпрома»
Государственного комитета Совета Министров СССР
по печати. Измайловский проспект, 29.