Н. Я. Виленкин,
Е. С. Куницкая,
А. Г. Мордкович
МАТЕМАТИЧЕСКИЙ
АНАЛИЗ
ДИФФЕРЕНЦИАЛЬНОЕ
ИСЧИСЛЕНИЕ

МИНИСТЕРСТВО ПРОСВЕЩЕНИЯ РСФСР
Московский государственный заочный
педагогический институт
Н. Я. Виленкин,
Е. С. Куницкая,
А. Г. Мордкович
МАТЕМАТИЧЕСКИЙ
АНАЛИЗ
ДИФФЕРЕНЦИАЛЬНОЕ
ИСЧИСЛЕНИЕ
Учебное пособие для студентов-заочников
I курса физико-математических факультетов
педагогических институтов
J МОСКВА «ПРОСВЕЩЕНИЕ» 1978

Рекомендовано к печати Главным управлением высших и средних
педагогических учебных заведений Министерства просвещения
РСФСР
Рецензенты: кандидат физико-математических наук В. /С. Егерев,
кандидат физико-математических наук В. Ф. Молчанов,
кандидат физико-математических наук Л. С. Симонов
Редактор МГЗПИ О. Л, Павлович
ИБ № 1977
Наум Яковлевич ВИЛЕНКИН
Елена Сергеевна КУНИЦКАЯ
Александр Григорьевич МОРДКОВИЧ
МАТЕМАТИЧЕСКИЙ АНАЛИЗ
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Редактор Л. В. Привезенцева
Художественный редактор Е. Н. Карасик
Технический редактор Т. В. Самсонова
Корректор Л. П. Михеева
Сдано в набор 16. 12. 77. Подписано к печати 14. 06. 78 60x90Vi6.
Бумага № 3. Гарнитура литерат. Печать высокая. Условн. печ л. 10,0 Уч -изд.
л. 9,51. Тираж 25 000 экз. Заказ 467. Цена 35 коп.
Ордена Трудового Красного Знамени издательство «Просвещение*
Государственного комитета Совета Министров РСФСР по делам издательств,
полиграфии и книжной торговли.
Москва, 3-й проезд Марьиной рощи, 41
Саратовский ордена Трудового Красного Знамени полиграфический комбинат
Росглавполиграфпрома Государственного комитета Совета Министров РСФСР
по делам издательств, полиграфии и книжной торговли.
Саратов, ул. Чернышевского, 59.
(g) Московский государственный заочный педагогический
институт (МГЗПИ), 1978 г.

ПРЕДИСЛОВИЕ
Настоящее пособие является непосредственным продолжением
книги Н. Я. Виленкина и Е. С. Куницкой «Математический анализ.
Введение в анализ»1*. Оно содержит изложение курса
дифференциального исчисления и его приложений к исследованию функций.
Значение этого материала для будущего учителя определяется
в первую очередь тем, что соответствующие вопросы по новой
программе изучаются в средней школе. Одна из задач пособия —
выяснение основных понятий дифференциального исчисления,
необходимых для школьного преподавания, строгое доказательство
утверждений, которые в школе лишь поясняются. В связи с этим
большое внимание в пособии уделяется естественнонаучным и
геометрическим истокам вводимых понятий; вопросы техники
дифференцирования играют подчиненную роль.
В отличие от большинства учебников, в которых на первый
план выступает понятие производной, авторы сочли основным
понятием понятие дифференцируемой функции, т. е. функции, из
приращения которой можно выделить главную линейную часть
(такой подход становится необходимым в теории функций
нескольких переменных, а поэтому нецелесообразно иначе трактовать
функции одной переменной). Производная при этом выступает как
коэффициент при приращении аргумента в главной линейной
части, а выводу формул дифференцирования предпосылаются
доказательства дифференцируемости соответствующих выражений.
При изложении темы «Исследование функций» основное
внимание уделено глобальному исследованию (убывание и возрастание
функции на отрезке, выпуклость и вогнутость на отрезке и т. д.).
Локальное исследование проводится для точек экстремума и точек
перегиба, в которых происходит смена одного глобального
поведения другим. Это объясняется тем, что понятия «возрастания
функции в точке», «выпуклости в точке» и т. д. не дают полной
информации о поведении функции в окрестности этой точки: в сколь
угодно малой окрестности точки, в которой функция «возрастает»,
х) М., «Просвещение», 1973. Ниже цитируется как «Введение в анализ».
3

она может иметь бесконечно много промежутков убывания. Поэтому
вместо введения таких терминов авторы предпочитают говорить о
знаке приращения функции и т. д.
При изучении выпуклости функций дается несколько
определений этого понятия, имеющих различную общность (применимых
соответственно для непрерывных, дифференцируемых и дважды
дифференцируемых функций). Понятия монотонности и выпуклости
используются для доказательства неравенств. Значительное
внимание уделено построению графиков функций и кривых, заданных
параметрическими и полярными уравнениями.
Книга состоит из двух глав, разбитых на параграфы, которые
в свою очередь делятся на пункты. Каждый пункт содержит
изложение теоретического материала и ряд разобранных типовых
примеров и задач. В конце каждого параграфа предлагаются вопросы
для самопроверки и упражнения, которые могут быть использованы
при проведении аудиторных занятий, при составлении контрольных
работ и межсессионных заданий для студентов-заочников.
Нумерация формул сохраняется в пределах одного параграфа, нумерация
упражнений сквозная.
В основу пособия легли лекции по дифференциальному
исчислению, которые авторы читали на протяжении многих лет на физико-
математическом факультете МГЗПИ. Ротапринтный вариант книги
был составлен Н. Я. Виленкиным и Е. С. Куницкой («Конспект
лекций по дифференциальному исчислению», МГЗПИ, 1973).
Переработка книги для настоящего издания выполнена Н. Я.
Виленкиным и А. Г. Мордковичем.

ГЛАВА
1
ДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ.
ДИФФЕРЕНЦИАЛ. ПРОИЗВОДНАЯ
§ 1. ПРИРАЩЕНИЕ ФУНКЦИИ
1. Приращение функции. Рассмотрим
квадрат, длина стороны которого равна х. Его
площадь равна х2. Если длину стороны увеличить
на h, то площадь квадрата увеличится на
величину, называемую приращением площади
квадрата и равную (х + hJ— х2 = 2xh + h2 (рис. 1).
В математике приращение переменной х
обозначают Ал:1. Обозначив приращение
площади через AS, получим:
AS= (х + АхJ — х2 = 2хАх + (АхJ.
Аналогично определяется понятие приращения для любой функции.
Определение. Пусть функция у = f(x) задана на
множестве X и пусть х € X, х + Ах € X. Разность между значениями
функции в точках х + Ах и х называется приращением функции
при переходе от точки х к точке х + Ах и обозначается Ау:
Ay = f(x+ Ax)-f(x).
Заметим, что термин «приращение» не следует отождествлять
со словом «увеличение»: приращение как аргумента, так и
функции может быть как положительным, так и отрицательным.
Пример 1. Найдем приращение функции у = С при
переходе от точки х к точке х + Ах.
Решение. Имеем:
/ (х + Ах) = С, / (х) = С,
значит,
Ду = / (х + Ах) — f (х) = С — С = 0.
Итак, функция у = С обладает следующим свойством:
(V*) (VAx) Ay = 0.
Читается: «дэльта икс», А — греческая буква.
5

У>
с
0
i
f
1
I
1
X
у-с
]лу-о
1
1
1 ,.
Х+4Х ~Х
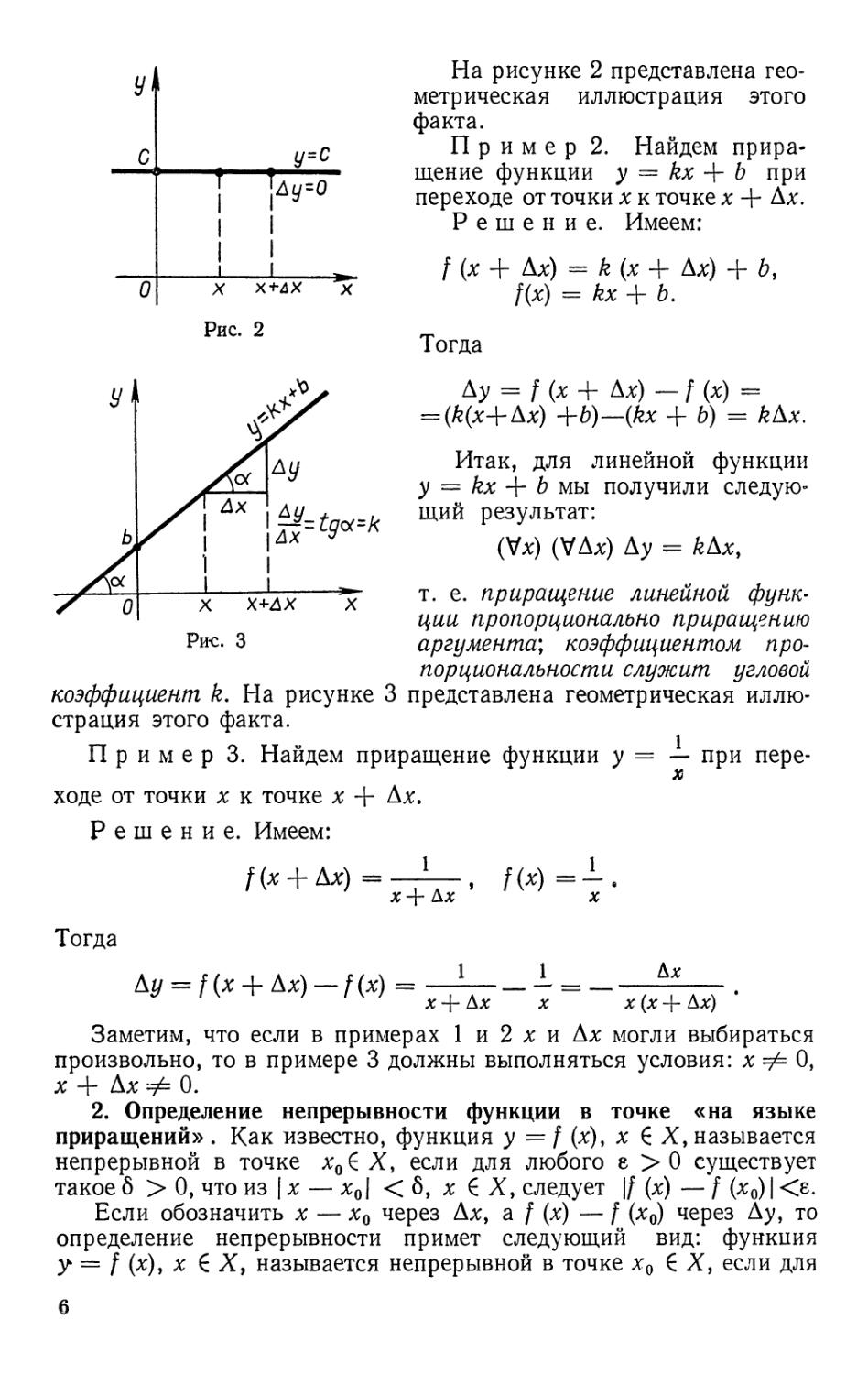
На рисунке 2 представлена
геометрическая иллюстрация этого
факта.
Пример 2. Найдем
приращение функции у = kx + b при
переходе от точки х к точке х + Дл;.
Решение. Имеем:
Рис. 2
/ (х + ах)
Тогда
•¦ k (х + Ах) + Ь,
kx + b.
Ay = f (x + Ax) - / (x) =
= (k(x+Ax) +b)—(kx + b) = kAx.
Итак, для линейной функции
у = kx + b мы получили следую-
|Д</_? . щий результат:
iAx (Vx) (VAx) Ду = Ш,
т. е. приращение линейной
функции пропорционально приращению
аргумента; коэффициентом
пропорциональности служит угловой
коэффициент k. На рисунке 3 представлена геометрическая
иллюстрация этого факта.
Пример 3. Найдем приращение функции у = — при
передо
ходе от точки х к точке х + Ах.
Решение. Имеем:
</<
ь
j^*
S 0
1
<
/У*
j/\ Ax
/ 1
щ
ft*
1 i
i i
X Х+
АХ
Рис. 3
f(x + Ax) =
1
# + &Х
Тогда
Ay = f(x + Ax)-f(x) =
1
X
1
д*
* + Ах х х (х + Да:)
Заметим, что если в примерах 1 и 2 я и Ах могли выбираться
произвольно, то в примере 3 должны выполняться условия: х Ф О,
х + Дл: ^= 0.
2. Определение непрерывности функции в точке «на языке
приращений». Как известно, функция у =f (х), х € X, называется
непрерывной в точке х0? X, если для любого г >0 существует
такое 8 > 0, что из | х — х0\ < 8, х € X, следует |/ (х) — f (х0) \ <е.
Если обозначить х — х0 через Ах, а / (х) — / (х0) через Ду, то
определение непрерывности примет следующий вид: функция
у = f (л:), х ? X, называется непрерывной в точке х0 ? X, если для

любого е > 0 существует б > 0 такое, что из | Дх| < б следует
| Ду| < е. Короче:
(Ve > 0) C б > 0) (VAx, |Д*| < б) |Ду| < е.
Полученная запись означает, что lim Ду = 0, т. е. предел
Дх-*0
приращения функции равен нулю при условии, что приращение
аргумента стремится к нулю. Это и есть определение непрерывности
функции в точке «на языке приращений».
" Определение. Функция у = / (х), х € X, называется
непрерывной в точке х0 € X, если lim Ду = 0.
Пример 4. Докажем непрерывность функции у = sin x в
произвольной точке х, пользуясь определением непрерывности «на
языке приращений».
Решение. Имеем:
Ал; / Дя\
Ду = sin (х + Да:) — sin х = 2 sin — cos lx H .
Так как
sin —
2
<
Д*
Т
, a cos he +
<1, то
|Ду|<2|^|.1 = |Дх|(
Итак, |Ду| ^ [Ал:]. Отсюда следует, что lim Ду = 0, а это и
д*-*о
означает непрерывность функции в точке.
Вопросы для самопроверки
1. Что называется приращением аргумента, приращением функции?
2. Может ли приращение функции быть положительным, отрицательным,
равным нулю? Приведите пример, когда Дх^О, а Ду = 0; Д* > 0, а Ду < 0.
3. Чему равно приращение функции, если Да: = 0?
4. Сформулируйте определение непрерывности функции в точке «на языке
е — б».
5. Сформулируйте определение непрерывности функции в точке «на языке
приращений».
Упражнения
1. Для функции у = х2 найдите Ду, если даны значения х и Д*:
1) х = 1, Дх= 0,1; 2) х= 1, Дх= —0,02; 3) х = —2, Дх = ОД
Найдите приращение функции при переходе от точки х к точке х + Д#:
2. у = 2х2 — х — 3. 3. у ==» г>. 4. у = 2г> — 3*. 5. у = уТ. 6. у = cos 2x.
Пользуясь определением непрерывности «на языке приращений», докажите
непрерывность следующих функций:
7. у = х2 — За: + 1 для любого х ? ]—оо; оо[#
8. у = а? для любого х ?]—оо; оо[.
*) См. «Введение в анализ», с. 142.

9. у = — для любого х Ф 0.
X
10. у == }Гх для любого х > 0.
11. у = cos х для любого х ? ]—оо; оо[.
§ 2. ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИИ В ТОЧКЕ
1. Определение дифференцируемости функции в точке. Одной
из основных задач математического анализа является изучение
свойств функций. Различают локальные и глобальные свойства
функций. Локальными1 называют свойства функций, зависящие от
их значений в произвольно малой окрестности рассматриваемой
точки, а глобальными2 — свойства функции на заданном множестве
(например, в области определения функции). Например,
непрерывность функции в данной точке — локальное свойство, а ее
непрерывность на отрезке — глобальное.
В изучении локальных свойств функции большую роль играет
приращение функции. Например, в предыдущем параграфе мы
видели, что непрерывность функции у = f (х), х € X, в точке х0 € X
равносильна требованию lim Ду = 0. Для многих функций спра-
Дх-*0
ведливо более сильное утверждение о Ах и Ду.
Рассмотрим примеры:
1) если у = kx + fr, то Ду = kAx (см. § 1);
2) если у = х2, то Ду = 2хАх + (АхJ (см. § 1);
3) если у = х3, то Ду = За:2 Да: + (ЗхАх + -(АхJ) Ах.
В самом деле, Ау = (х + АхK — х3 = За:2 Да: + Зх (АхJ +
+ (АхK = За:2 Да; + (ЗхАх + (АхJ) Ах.
В примере 1 приращение функции пропорционально приращению
аргумента, в остальных примерах такой пропорциональности нет.
Однако в примерах 2 и 3 приращение функции при малых значениях
|Да:| «почти пропорционально» вызвавшему его приращению
аргумента. Чтобы получилась «настоящая» пропорциональность, нужно
в примере 2 отбросить слагаемое (ДхJ, а в примере 3 — слагаемое
(ЗхДх + (АхJ) Ах. Эти слагаемые при Да: -^ 0 являются
бесконечно малыми более высокого порядка, чем Ах\ они имеют вид а Ах, где
а -> 0 при Ах ->¦ 0. В самом деле, в примере 2 имеем (Да:J =
= Да: • Да:, здесь а = Ах. В примере 3 имеем а = За: Д х + (АхJ.
Теперь уже ясен математический смысл, который надо вложить
в термин «почти пропорционально»: приращение функции у = f(x),
х ? X, в точке xQ€ X «почти пропорционально» приращению
аргумента, если Ду = Л Да: + а Да:, где А —число, а а-^0 при Дх->- 0.
Оказывается для большинства изучаемых в математическом
анализе функций имеет место «почти пропорциональность» приращения
функции приращению аргумента.
1 От латинского слова localis — местный.
2 От французского слова global — всеобщий.
8

</'
0
у
i
| *о
?
X
Дело в том, что графики большинства
элементарных функций представляют собой гладкие
кривые1, одна из которых изображена на рисунке 4.
Если смотреть на эту кривую через сильное
увеличительное стекло, то можно заметить, что, чем
ближе увеличительное стекло к нашей кривой, т. е.
чем меньше окрестность точки М, тем теснее кривая
сливается с некоторой прямой у = kx + Ъ
(происходит как бы «выпрямление» кривой). Прямая
у — kx-j- b называется касательной к графику
функции в точке х0. Если для прямой А у
пропорционально Ал;, то для графика функции Ау «почти Рис. 4
пропорционально» Ах. Позднее дадим точное
определение касательной и увидим, что ее угловой коэффициент k равен числу А
в выражении для приращения функции Ау = Ла*+ аАлг.
Определение. Пусть функция у == f (х)9 х ? X,
определена в некоторой окрестности точки х0 € X. Эта функция называется
дифференцируемой в точке xQf если ее приращение в точке х0
может быть представлено в виде
Ау = ААх + аДл:, A)
где А — число, а а -> 0 при Ах ->- 0.
Рассмотренные выше функции у = kx + b, у = х2, у = х3
дифференцируемы в любой точке х.
Число А зависит от х09 его называют производным числом и
обозначают f'(x0). Ясно, что если функция у = f (x) дифференцируема
на всем множестве X (т. е. в каждой точке этого множества), то,
сопоставив каждому х € X число /' (х)9 получим функцию у =
= /'(#), х ? X. Ее называют производной от функции у = f (х),
х (: X, и обозначают у'.
Отметим, что множитель а в равенстве A) зависит и от числа
х, и от Ах : а = а (х, Ах). Считают, что а = 0 при Ах = 0.
Произведение А Ах, т. е. /' (я) Ад;, называют дифференциалом
функции у = / (х) в точке х и обозначают dy. Таким образом,
dy = f'(x) Ax.
Это произведение пропорционально Ах (поскольку х —
фиксированная точка, то f (х) —постоянный множитель). Таким образом,
дифференциал функции пропорционален приращению аргумента.
Значение коэффициента А в равенстве A) можно вычислить
следующим образом: разделим обе части равенства A) на Ах и
перейдем к пределу при Ад; -»- 0.
lim ^= lim (A + а).
Дл;^о Ад: д*-*о
1 Определение понятия гладкой кривой дадим позднее, пока будем считать,
что гладкая кривая — это кривая без разрывов и заострений.
9

Так как lim a = 0, то получим:
Дх-*0
А= lim ^, B)
Из единственности предела следует, что Л, а значит и а, в
равенстве A) определены однозначно.
Мы показали, что из дифференцируемости функции в точке
вытекает существование предела lim —. Верно и обратное: из
существования предела lim — вытекает дифференцируемость
функции в точке.
В самом деле, пусть lim — = А. Тогда — =* А + ос, где а -> О
Ах-^о А* Ая
при Ах-> 0. Значит, Ду = А Ах + а Ах, т. е. функция
дифференцируема.
Тем самым доказана следующая теорема.
Теорема 1. Для того чтобы функция у = f (х), х ? X, была
дифференцируема в точке х0 ? X, необходимо и достаточно, чтобы
в этой точке существовал предел lim —. Этот предел равен
Ах-О А*
значению производной в точке х0:
/'(*„) = lim ^.
2. Связь между непрерывностью и дифференцируемостью
функции в точке. Заметим, что рассмотренные в предыдущем пункте
функции у = kx + by у = х2, у = х3 были во всех точках
одновременно и непрерывны, и дифференцируемы. Не следует, однако,
думать, что всякая непрерывная функция дифференцируема.
Пример 1. Покажем, что функция у = | х\ не является
дифференцируемой в точке х = 0.
Решение. Имеем:
Ду = | х + А*| — | х\.
Если jc = 0, то Ду = \Ах\. Предположим, что функция у = \х\
дифференцируема в точке х = 0, т. е. что ее приращение в этой
точке можно представить в виде A). Тогда будем иметь:
|Дх| = ААх + ссДя, C)
где А — число, аа-^0 при Да: -* 0. Если Д*> 0, то из
равенства C) получаем:
Ах = А Ах + а Да: D)
и потому А + а = 1. Если Дл:< 0, то из равенства C) получаем:
—Дл: = А Ах + а Ах E)
?9

и потому А -т а = —1. Так как сс->0 при
Д*->- 0, то из D) получаем А = 1, а из E)
получаем А = —1. Полученное
противоречие показывает, что функция у = |а:|
не является дифференцируемой в точке
х = 0.
Дадим геометрическое истолкование
этого результата. На рисунке 5
представлен график функции у = \х\. Ясно, что
«выпрямить» его в точке х = 0 (т. е.
заменить его в достаточно малой
окрестности точки х = 0 некоторой прямой)
невозможно— он имеет излом. А дифференци-
руемость функции в точке, как мы отметили
выше, геометрически означает возможность
«выпрямления» графика в достаточно
малой окрестности рассматриваемой точки.
Пример 2. Покажем, что функция
з,—
у= у л: не является дифференцируемой в
точке х = 0.
Решение. Имеем:
&у = f (х + кх) —f (х) = ¦у/'х + Да: — ^х.
з ——
В точке х = 0 получаем Ду = у Да:. Предположим, что функция
з —
у = ух дифференцируема в точке х = 0. Тогда
Рис. 6
3/-—
у^Ах
где А — число, а а ¦
А Да: + аД#,
0 при Ах -> 0. Далее имеем:
А +а =
]ГКх_
т. е.
А + а =
7(Д*J
F)
Если Да: -> 0, то левая часть равенства F) имеет своим пределом
число Л, тогда как правая часть стремится к сю. Полученное проти-
Зу
воречие показывает, что функция у = у х не дифференцируема в
точке х = 0.
з —-
На рисунке 6 представлен график функции у = ух. Хотя здесь
а происходит «выпрямление» кривой в точке х = 0, но получаемая
прямая не является графиком линейной функции у = kx + 6,
как это имеет место в случае дифференцируемой функции; она
перпендикулярна к оси абсцисс. Уравнение этой прямой а:=0.
Итак, существуют функции, непрерывные, но не дифференцируе-
11

мые в данной точке. С другой стороны, почти очевидна следующая
теорема.
Теорема 2. Если функция у = f (х), х ? X, дифференцируема
в точке х0 6 X, то она непрерывна в этой точке.
В самом деле, из равенства Ay = f'(xQ)Ax + аДл; следует, что
lim Ау= О, а это и означает непрерывность функции в точке х0.
Таким образом, если D (X) — множество функций,
дифференцируемых в каждой точке множества X, а С (X) — множество функций,
непрерывных на X, то D (X) с: С (X), причем D (X) Ф С (X).
Иными словами, множество дифференцируемых функций
представляет собой собственное подмножество множества непрерывных
функций.
3. Производная и дифференциал. Пусть функция у = / (х),
х (: X, дифференцируема в точке л: € X и ее приращение
представлено в виде
Ду = А Ах + а Ах,
т. е. Ay = f'(x)Ax + а Ал:, где lim а = 0. Выше мы назвали СЛа-
Дя-». О
гаемое f(x) Ах дифференциалом функции у = / (х) в точке х и
обозначили dy. Таким образом,
dy = f'(x) Ax,
или
dy = у'Ал:. G)
Возьмем для примера линейную функцию у = kx + b. Для
нее имеем: Ay = kAx. Значит,
dy = kAx. (8)
Определим теперь понятие дифференциала независимой
переменной. Из формулы (8) видно, что для функции у = х выполняется
равенство dy = Ах. Так как для этой функции значение функции
совпадает со значением независимой переменной, то естественно
положить dx = Ах, т. е. считать дифференциал независимой
переменной равным ее приращению.
Поэтому для любой дифференцируемой функции
dy = y'dx. (9)
Ниже мы увидим, что формула (9) охватывает и случаи, в которых
формула G) теряет силу. Из этой формулы следует, что
dx
Запись — часто используется для обозначения производной
dx
функции у по независимой переменной х (читается: «дэ игрек по дэ
икс»).
Заметим, что если /' (х) = 0, то при Ал: -> 0 Ау есть бесконечно
12

малая более высокого порядка, чем Д*. В самом деле, в этом случав
имеем:
Нт ±1 = Иш П*)А* + «Д* = lim ^? = цт а=0.
Ax-*0A# A*-vO А* Д*-*0 А* Д*-»>0
Если же f'(x) Ф О, то при Да: -> 0 Ду и Да: — бесконечно малые
одного порядка, а Ду и dy — эквивалентные бесконечно малые. В
самом деле, имеем:
Нт ДУ = ит Г(х)Ах + аАх=ш Ш±«. = \.
Av^ocfy дл'-о f'(x)Ax д*-*о f'(x)
Итак, Ду ~ dy. Поэтому говорят, что дифференциал функции—
главная линейная часть ее приращения.
Найдем производную и дифференциал для рассмотренных выше
функций у = х2 и у = а:3. Для функции у = х2 имеем: Ду =
= 2а:Да: + (Да:J. Значит, dy = 2хкх или, в соответствии со
сказанным выше, dy = 2xdx, а у' = 2х.
Для функции у = л? имеем: Ду = 3*2Да: + (За:Да: + (Да:J)Да:.
Значит, dy = За:2 Да: = 3x2dx, a j/'= За:2.
Следует отметить, что, делая выводы о формулах для
дифференциала и производной в рассмотренных случаях, мы
фактически опираемся на замечание о единственности представления Ду в
виде A).
Пример 3. Найдем дифференциал и производную функции
у = С.
Р е ш е н и е. В § 1 мы видели, что постоянная функция обладает
следующим свойством: для любых а: и Да: имеет место равенство
Ду = 0, т. е. Ду = ОДа: + 0Да\ Приращение функции представлено
в виде A): здесь А = 0, а = 0. Значит, dy = 0, у' = 0.
Пример 4. Найдем производную функции у = х2 — 4х +3
в точке х = 1 и дифференциал функции в этой точке при Да: = 0,1.
Решение. Сначала решим задачу в общем виде. Имеем:
Ду = ((х + АхJ — 4 (х + Ах) + 3) — (а;2 — 4х + 3) =
= Bх — А) Да; + (АхJ.
Значит,
dy = Bх — 4) Ах,
или dy = Bх — 4) dx, а у' = 2х — 4.
Имеем /'A) = —2. Вычислим значение дифференциала при
х = 1, Да: = 0,1:
dy = Bх — 4)Да: = — 2 • 0,1 = —0,2.
Итак, найдены производные следующих элементарных
функций:
(kx + Ь)' = k, A0)
(х2)' = 2х, A1)
(**)' = з*2, A2)
(СУ = 0. A3)
13

Из равенства A0), в частности, получается:
(*)' = 1. A4)
Для вычисления производной удобно пользоваться полученным
в п. 1 равенством у' = lim—, которое означает, что производная
д*-о Ах
функции у = / (х), х € X, в точке х ? X есть предел отношения
приращения функции к приращению аргумента, когда приращение
аргумента стремится к нулю (если указанный предел существует).
Пример 5. Найдем производную функции у = ха, х > 0
(а — действительное число).
Решение. Приращение функции у = ха в точке х имеет
вид:
Ду = (х + Ах)а — X*.
Преобразуя это выражение, получаем:
= '"((' +7T-1
Итак,
Ay = xa((l+^)a-l). A5)
Разделим обе части равенства A5) на Ал: и перейдем к пределу
при Ах ->- 0. Получим:
lim — = lim
'(О+тГ-'
Дл'-*0Дх Д*-*0 АХ
Множитель ха не зависит от Дл; и его можно вынести за знак предела,
а бесконечно малая величина A + —) —1 эквивалентна беско-
нечно малой а • — . Значит,
X
Ах
lim А? = х« lim !HjL = х«. « = а^.
Д*->оДх дл--*0 Ах х
Но lim — =y'f значит,
Д*-*оАх
(*«)' = ах*-1. A6)
При а = 1, 2, 3 получаем из формулы A6) уже знакомые нам
формулы A1), A2), A4).
Мы вывели формулу A6) при положительных значениях х. Если
*) См. «Введение в анализ», с.212 и 144.
14

а — целое число, то этой формулой можно пользоваться и при
х <0.
Пример 6. Найдем производные следующих функций:
1) у = х18; 2) у = хп\ 3) у = х-5; 4) у =jr"; 5) у =y^j? ;
6) у - ij^.
Решение.
1) у' = (х™у = 18л;18 = 18а;1'; 2) /=(**)' = /г*";
3) / « (л;)' = —5л;-8-1 = —5л;; 4) у' = (г*)' = — п*"";
9 --
= --* 10.
10
4. Односторонние и бесконечные производные. Мы видели,
что функция у = 1*1 не является дифференцируемой в точке х = 0,
так как lim —У при х = 0 не существует. Однако в этой точке
Ах-*.оДл:
существуют односторонние пределы lim— =—1 ц lim — = 1.
д*-+— оД# д*_.+оДл:
Предел lim (*° Х)—\\Ч) на3ывают производной слева
Д*-»—0 А*
функции у = / (х) в точке #0 и обозначают /' (х0 — 0), а предел
lim "*° x> — i(xo) называют производной той же функции
д*->4-0 Да;
справа в точке х0 и обозначают f'(x0 + 0). Эти производные называют
односторонними производными.
Если в некоторой точке х0 существуют односторонние
производные для функции у = / (х), причем эти производные различны,
то это означает, что график функции в данной точке имеет излом.
Если производные слева и справа в точке х0 равны, то существует
и предел lim '*0+ х)~~~"х\ а потому функция у = / (х) диффе-
д*г-0 Да:
ренцируема в этой точке и ее производная равна общему значению
односторонних производных.
Пример 7. Найдем односторонние производные в точке
х = 1 функции
' Зх + 1, х ^ 1,
^ + 3 , х > 1.
Решение. Так как Зх + 1 и х + 3 при х = 1 принимают
значение, равное 4, то функция непрерывна в точке х = 1. Далее,
находим, что (Зх + 1)' = 3, а (х + 3) =1, поэтому /' A — 0)=3,
а Г (\ + 0) = 1.
15

Не исключена возможность, что в некоторой точке
односторонний предел lim — или lim — есть бесконечность. Если
Да:-». +0 Д* Ал:-*.—0 Д*
lim 'х° + х)~~'х°) =^-00^0 говорят, что функция у = / (х) имеет
Длг-*-}-0 Ах
в точке х0 одностороннюю производную /' (х0 + 0), равную +оо,
и пишут /' (х0 + 0) = +оо.
Аналогичный смысл имеют записи f'(xQ + 0) = —оо, /' (х0 — 0) =
=+оо, /'(*0 - 0) = -оо.
Пример 8. Рассмотрим функцию у = }/~х, т. е.
з
х , х > О,
j
— И3, х<0
и найдем ее производную в точке х = 0.
Решение. Воспользуемся не формулой A6) п. 3 (она
доказана лишь при х > 0), а определением производной. Так как при
2
х = 0 имеем у = 0, то при Ах > О имеем: Ду = @ + ДхK — 0 =
= (Дхр, а при Ах; < О имеем:
Ду =_|ДЛ:| Зв
Поэтому
/' (+0) = lim (M2= lim _L_= +оэ
ДХ-+0 Д* Дх--{-0 J '
(ДхЯ
/'(—0) = limni^JL = lim 1А*13 = lim * = +оэ
Д*-_О Д* Д*—О I Дд;| Д*--0 1 '
I Д*13
Итак, рассматриваемая функция в точке х = 0 не имеет
производной ни слева, ни справа (напомним, что производная в данной
точке — это число, а бесконечность не является числом). Но
поскольку и /' (—0) и /' (+0) равны +оо, условно считают, что в точке
з,—
х == 0 производная функции у = у х равна +оо.
Вообще будем говорить, что функция у = / (х) имеет в точке
х0 производную +оо, если
1}т /(*о + А*)— /(*о) = jim f(x0 + kx)— f(x0) ^ ^
д*-*_о Дя Длг-v+o Да:
Пишут/' (д:0) = +оо. Точно так же определяется равенство/' (х0) =
= —оо.
16

Может случиться, что /' (х0 — 0) =
=—оо, а /' (л:0+ 0) = +оо. В этом случае
считают, что в точке х0 функция не имеет
производной (даже бесконечной). В таких
точках график функции имеет пикообраз-
ные заострения (рис. 7). Аналогично
обстоит дело в случае, когда /' (х0 —0) = -}- °°,
а /' (*0 + 0) = -оо (рис. 8).
Так, функция у = ¦/!?, —оо <х < оо,
не имеет производной в точке х = 0. В
самом деле,
/'(+0)= lim
(А*)'
Д*
+ °°,
/'(-
-0) = lim
|Д*
Дл:
- lim i
А*|
Д*|
Рис. 7
Рис. 8
Вопросы для самопроверки
1. Сформулируйте определение дифференцируемости функции в точке.
2. Всякая ли непрерывная в точке функция дифференцируема в этой точке?
3. Всякая ли дифференцируемая в точке функция непрерывна в этой точке?
4. В чем состоит необходимое и достаточное условие дифференцируемости
функции в точке?
5. Что такое производная?
6. Как вычисляется производная?
7. Что такое дифференциал?
8. Каким равенством связаны дифференциал и производная?
9. Чему равен дифференциал независимой переменной?
10. Разъясните смысл высказывания «дифференциал есть главная линейная
часть приращения функции».
11. Что такое односторонняя производная?
12. Как определяется бесконечная производная?
Упражнения
Докажите, что функция у = / (х) дифференцируема в точке х, найдите
производную и дифференциал:
12. у = х2 — 4. 13. у = 2х2 + х. 14. у = 3 — 5л; — х\ 15. у = 2*3.
16. у = х — х3.
Воспользовавшись определением производной «на языке пределов», найдите
производные следующих функций»
17. у = Зх + 5. 18» у = х2 — 2х + 8. 19. у = х8 + х. 20. у = х*.
21. у = — (х Ф 0). 22. у = /7(х > 0). 23. у = "ТТ^-
X X —J- /,
А. Воспользовавшись формулой производной степенной функции, найдите
производные следующих функций:
17

1) у = дЮ; 2) у = -; 3) у = /Г; 4) у = lA5;
5) у = ; 6) у = ; 7) у ==]
8) У = а:2 •
1 1
25. Найдите дифференциал функции!
1) у = х8 при я = 1, Ла: =0,1*
2) у = — при х — 2, А* = —0,1;
х
л— 2
3) у = j/x8 при х = 42,25, Дх = —.
1о
26. Докажите, что функция
{л;, если л; < 0,
0, если 0 ^ х ^ 1,
х — 1, если х > 1
непрерывна на всей числовой прямой, но не дифференцируема в точках 0 и 1.
27. Приведите пример функции, которая определена и непрерывна на всей
числовой прямой, но не дифференцируема в заданных точках:
1) х = 2; 2) х = 0, х = —1; 3) х = —3, д; =• 0, л: = 3.
28*. Докажите, что функция
_ ( х3, если л; — рациональное число,
^ \—х3, если л; — иррациональное число
разрывна во всех точках, кроме точки х = 0, а в точке а: = 0 непрерывна и
дифференцируема.
29*. Докажите, что функция
0, если х = 0,
1 1 1
—, если —— < х <—,
п п-\-1 /г
1 1 1
— —, если — — < х <
«/ =
Л Д И + I
дифференцируема в точке х = 0.
30. Дана функция
Г л;3, если * < 1,
у \ ах + 6, если я > 1.
Какими должны быть коэффициенты а и Ь, чтобы функция была непрерывна и
дифференцируема на всей числовой прямой?
§ 3. ПРИМЕНЕНИЯ ПРОИЗВОДНОЙ И ДИФФЕРЕНЦИАЛА
ДЛЯ РЕШЕНИЯ ГЕОМЕТРИЧЕСКИХ И ФИЗИЧЕСКИХ ЗАДАЧ
1. Задача о проведении касательной к графику функции.
Геометрический смысл производной и дифференциала. Мы уже упоминали
выше о связи понятий производной и касательной к графику
функции. Уточним, в чем заключается эта связь. Для этого дадим сначала
точное определение понятия касательной к произвольной плоской
линии. Касательную нельзя определять как прямую, имеющую лишь
ы

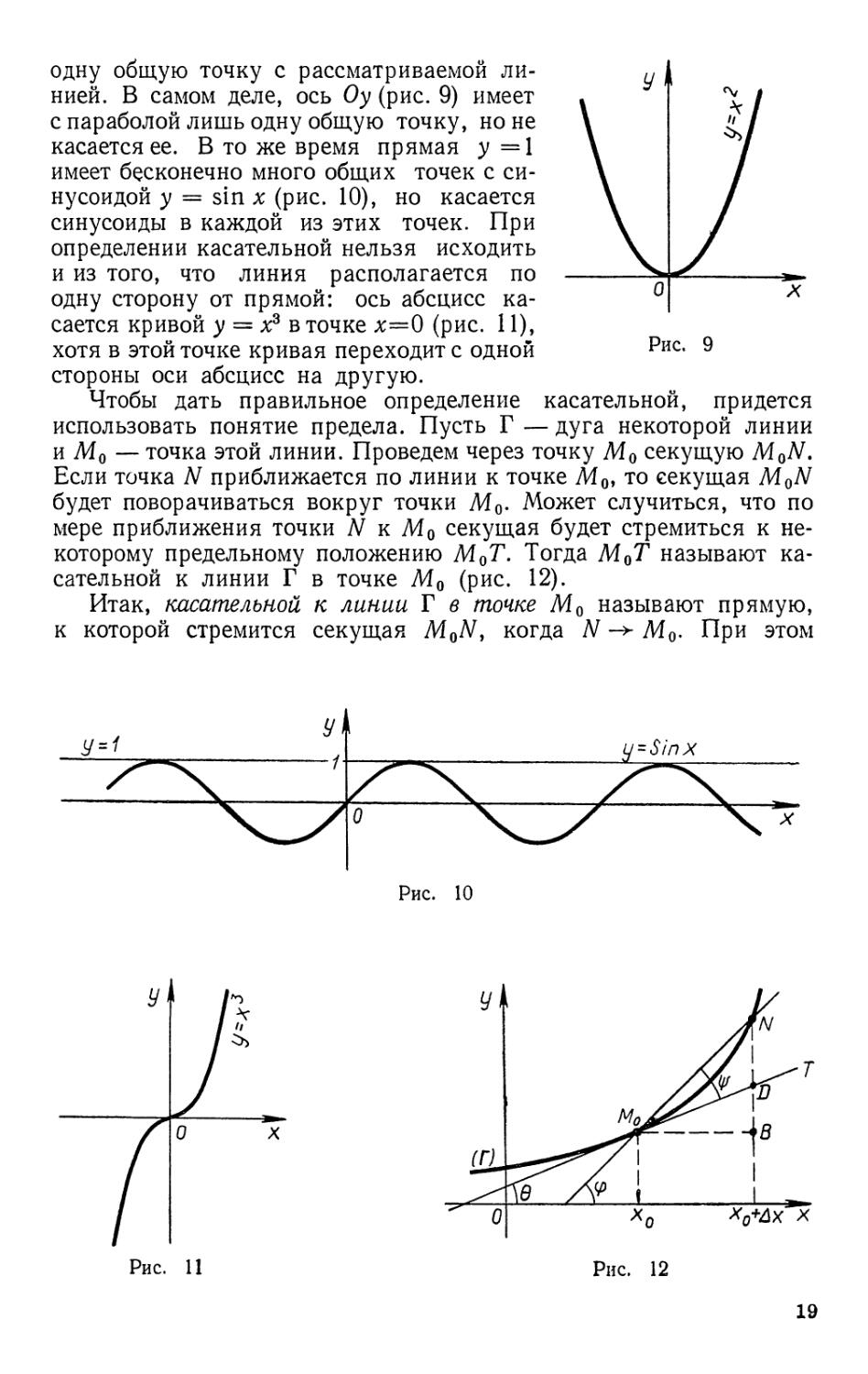
одну общую точку с рассматриваемой
линией. В самом деле, ось Оу (рис. 9) имеет
с параболой лишь одну общую точку, ноне
касается ее. В то же время прямая у = 1
имеет бесконечно много общих точек с
синусоидой у = sin х (рис. 10), но касается
синусоиды в каждой из этих точек. При
определении касательной нельзя исходить
и из того, что линия располагается по
одну сторону от прямой: ось абсцисс
касается кривой у = Xs в точке #=0 (рис. 11),
хотя в этой точке кривая переходите одной
стороны оси абсцисс на другую.
Чтобы дать правильное определение касательной, придется
использовать понятие предела. Пусть Г — дуга некоторой линии
и м0 — точка этой линии. Проведем через точку М0 секущую M0N.
Если точка N приближается по линии к точке М0, то секущая M0N
будет поворачиваться вокруг точки М0. Может случиться, что по
мере приближения точки N к М0 секущая будет стремиться к
некоторому предельному положению М0Т. Тогда М0Т называют
касательной к линии Г в точке М0 (рис. 12).
Итак, касательной к линии Г в точке М0 называют прямую,
к которой стремится секущая M0N, когда N ->- М0. При этом
Рис. 9
Рис. 10
y = Sinx
У\
Рис. 11
II
у\
(ГЦ
^~0
lL
Мо?
^/\
Л !
*0
УУ%^
-ч
*0
VV
>Я
+Дк*х
Рис. 12
19

предельное положение не зависит от того,
с какой стороны точка N приближается к
М0. Утверждение «секущая M0N
стремится к прямой М0Т, когда N-> М0» означает
следующее: прямая М0Т проходит через
точку М0 и lim ty = 0, где т|) — угол между
прямыми М0Т и M0N', а % — расстояние
между точками М0 и N.
Может случиться, что предельного по-
Рис- 13 ложения секущей не существует. В этом
случае говорят, что в точке М0 нельзя провести
касательную к линии Г. Чаще всего это связано с тем, что точка М0
является точкой заострения, излома, самопересечения и т. д. (рис.
7, 8, 13). Такие точки называют особыми. Для большинства
встречающихся на практике линий касательную можно провести почти
во всех точках линии. Однако существуют линии, к которым ни в
одной точке нельзя провести касательную. Иными словами, для
таких линий все точки особые.
Приведем пример линии, ни в одной точке которой нельзя провести
касательную. Для этого построим равносторонний треугольник, разделим каждую
из его сторон на три конгруэнтных отрезка и на среднем отрезке каждой стороны
построим равносторонний треугольник. После этого разделим на три
конгруэнтных отрезка каждое звено получившейся ломаной и на каждом среднем
отрезке снова построим равносторонний треугольник (рис 14). Продолжая этот
процесс до бесконечности, получим в пределе линию, ни в одной точке которой
нельзя провести касательную.
Чтобы написать уравнение касательной, достаточно знать
координаты точки касания и угловой коэффициент касательной. Для
случая, когда линия Г является графиком некоторой функции,
отыскание углового коэффициента сводится к вычислению
производной.
Возьмем на графике Г функции у = f (x) точку М0 с абсциссой
х0 и ординатой у0 = / (х0). Пусть существует касательная к графику
Г в точке М0. Возьмем другую точку N (х0 + Ах\ у0 + Ду) 6 Г
(см. рис. 12) и проведем через точки М0 и N прямую. (Не ограничивая
общности рассуждений, будем считать,
что Ах > 0 и Ду > 0.) Обозначим через
Ф угол наклона секущей к
положительному направлению оси абсцисс. Тогда
, 1ВЛМ Л у
tg ф = J L = —.
Угол наклона касательной к оси
абсцисс обозначим 0. Тогда
tg 0 =• lim tg Ф.
РИС 14 N-*M0
20

Если 9 Ф —, то в силу непрерывности функции tg ф получим:
6Kac = tge= limtgcp
Дх-*0
= lim^.
д*-*о Ах
Таким образом, для того чтобы к графику функции у — f (x)
можно было провести невертикальную касательную в точке с
абсциссой х0, необходимо,чтобы при х=х0 существовал предел lim—,
Д*-+0 Да:
причем этот предел равен угловому коэффициенту касательной. Но
указанный предел есть не что иное, как значение производной в
точке х0 для функции у = f (x). Дифференцируемость не только
необходима, но и достаточна для существования касательной.
Итак, мы доказали следующее утверждение: для того чтобы
существовала невертикальная касательная к графику функции
у = f (х) в точке с абсциссой х0, необходимо и достаточно, чтобы
функция у = f (х) была дифференцируемой в точке х0. Угловой
коэффициент касательной равен значению производной в точке
касания. В этом состоит геометрический смысл производной.
Обратимся еще раз к рисунку 12. Мы дали абсциссе приращение
Ах. Тогда ордината графика функции получила приращение Ду =
= \NB\, а ордината касательной получила приращение \DB\.
Но из треугольника DM0B находим:
| DB | = | М0В\ • tg 0 = /Ах = dy.
Таким образом, если Ду — приращение ординаты кривой, то
дифференциал dy есть приращение ординаты касательной. В этом
состоит геометрический смысл дифференциала»
Пусть функция у = / (х) непрерывна в точке х0, причем
lim
д*-*о
/(*о + Ал)—/(*0)
Ад;
+ с°,
т. е. функция имеет в точке х0 бесконечную производную. В этом
случае линия имеет вертикальную касательную и располагается
относительно нее так, как показано на рисунке 6, где изображен
график функции у = j/"x~, для которого ось ординат является
касательной в точке О @; 0).
Если
ит /t*0+A*)— /(*o) __
lim
д*-о
Ал:
то линия также имеет вертикальную
касательную и располагается относительно
нее так, как показано на рисунке 15.
Сложнее обстоит дело, если
И*ь + А*)-/(*о)
lim
Ах
+ °°,
i/l
0
' \'
\y*fM
1 \ X
Х0 \ X
Рис. 15
21

а предел
lim /(*о+А*)-/(*0) = _ со<
дх->—о Ал;
В этом случае график функции в окрестности точки х0 выглядит
так, как показано на рисунке 7.
Если же
lim /(* + **)-/(*«> =_COt
lim Пъ + ^-Нь) = + ^
дх->-о А*
то график функции у = / (х) в окрестности точки х0 располагается
так, как изображено на рисунке 8. Считают, что в таких точках
не существует касательной к графику функции.
2. Геометрические приложения производной. Пусть функция
у = / (х) дифференцируема в точке х0 и М0 (х0\ у0) — точка
графика этой функции. Составим уравнение касательной к кривой
у = / (х) в точке М0 (х0; у0), где у0 = / (х0}.
Из аналитической геометрии известно уравнение прямой,
проходящей через точку М0 (х0\ у0) и имеющей угловой коэффициент k:
У — Уо = k (x — x0).
Так как угловой коэффициент касательной в точке М0 (х0\ у0)
равен f (х0), то уравнение касательной к графику функции у = f (x)
в данной точке имеет вид:
У — Уо = /' (*о) (х — *о). (!)
где у о =» / (*0)«
Прямая, проходящая через точку М0 (х0\ у0) и
перпендикулярная касательной, называется нормалью к линии в данной точке.
Так как угловые коэффициенты kx и k2 двух взаимно
перпендикулярных прямых связаны соотношением kxk2 = —1, то угловой
коэффициент нормали равен —; . Следовательно, уравнение
/' (хо)
нормали таково:
У — Уо = — 7ГГТ (х — хо)- B)
Углом между линиями у = fi (х) и у = /2 (х) в точке их
пересечения М0 (х0\ у0) называется угол между касательными к этим
линиям в данной точке.
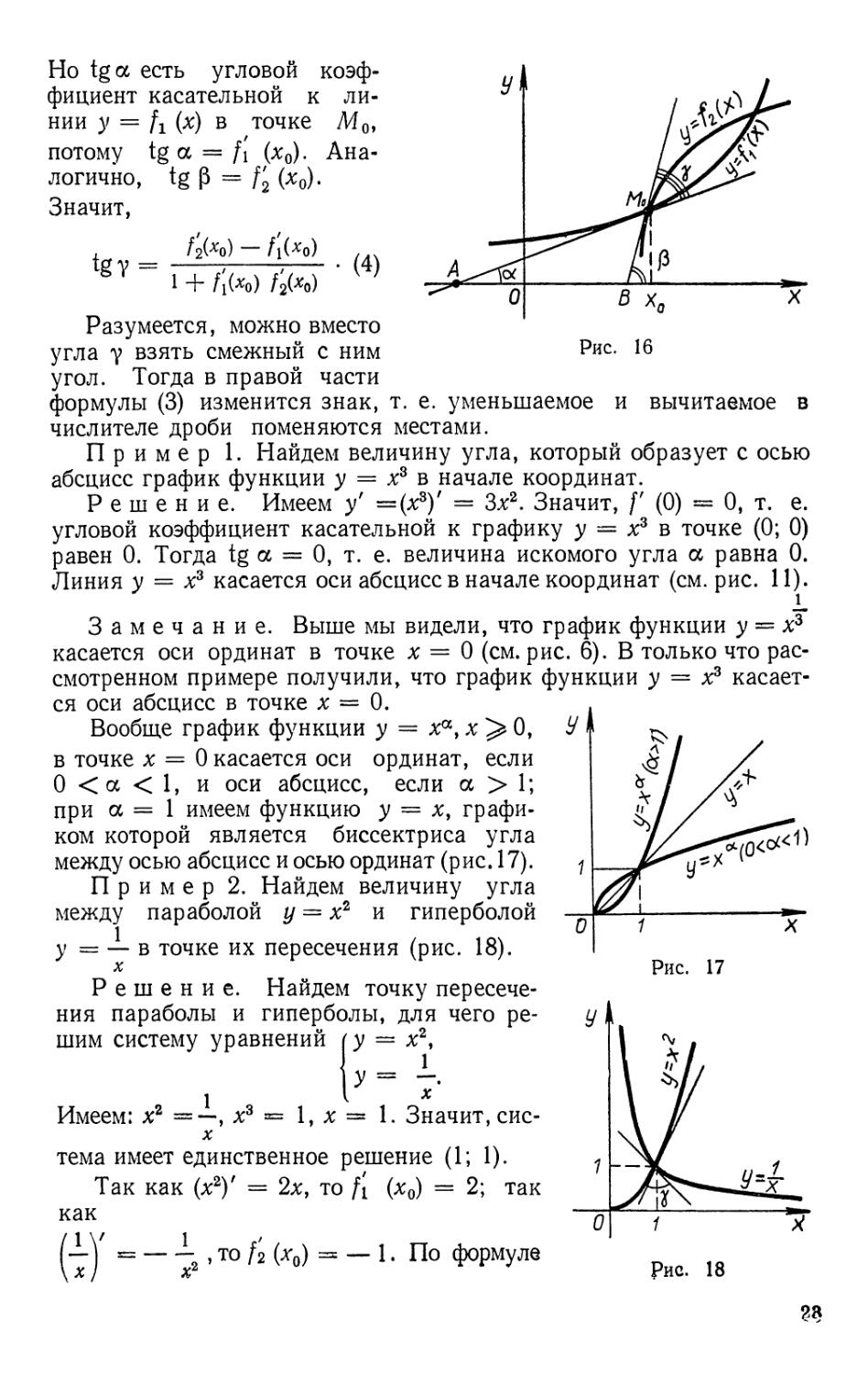
Выведем формулу для тангенса угла между двумя линиями.
Пусть линии у = f± (х) и у = /2 (х) пересекаются в точке М0 (х0\ у0),
касательная к линии у = f± (x) в точке М0 образует с осью абсцисс
угол а, а касательная к линии у = f2 (х) — угол C (рис. 16).
Если у — угол между касательными, то у = р — а (внешний
угол р треугольника АМ0В равен сумме двух внутренних, не
смежных с ним). Тогда
*Y &W ) 1+tgPtga W
22

Ho tga есть угловой
коэффициент касательной к
линии у = /i (x) в точке Л!о,
потому tg a = f[ (x0).
Аналогично, tg р = f2 (xQ).
Значит,
tgv =
/2(*о) — /i(*o)
1 + f[(xo) /0(^0)
D)
Рис. 16
Разумеется, можно вместо
угла у взять смежный с ним
угол. Тогда в правой части
формулы C) изменится знак, т. е. уменьшаемое и вычитаемое в
числителе дроби поменяются местами.
Пример 1. Найдем величину угла, который образует с осью
абсцисс график функции у = Xs в начале координат.
Решение. Имеем у' = (#8)' = Зх2. Значит, /' @) = 0, т. е.
угловой коэффициент касательной к графику у = х3 в точке @; 0)
равен 0. Тогда tg а = 0, т. е. величина искомого угла а равна 0.
Линия у = х3 касается оси абсцисс в начале координат (см. рис. 11).
Замечание. Выше мы видели, что график функции у = хъ
касается оси ординат в точке х = 0 (см. рис. 6). В только что
рассмотренном примере получили, что график функции у
ся оси абсцисс в точке х = 0.
Вообще график функции у = ха, х ^ 0,
в точке х = 0 касается оси ординат, если
0 < a < 1, и оси абсцисс, если a > 1;
при a = 1 имеем функцию у = х,
графиком которой является биссектриса угла
между осью абсцисс и осью ординат (рис. 17).
Пример 2. Найдем величину угла
между параболой у = х2 и гиперболой
у = — в точке их пересечения (рис. 18).
х3 касает-
Решение. Найдем точку
пересечения параболы и гиперболы, для чего ре-
Рис,
шим систему уравнении
(У = х >
1
у = -.
х
Имеем: х2 ==—, х3 = 1, х = 1. Значит, сис-
X
тема имеет единственное решение A; 1).
Так как (г*)' = 2х, то f[ (x0) = 2; так
как
- , то /2 (*0) = — 1. По формуле
Ш'-
У*
1
0
[
\ ч/
^иг\"
1
^?
.1
"Я
Рис. 18

D) находим:
BY l + 2.(-l)
Значит, величина искомого угла у = arctg 3.
Пример 3. На параболе у = х2 найдем точку, в которой
нормаль к параболе параллельна прямой у = — х — 5. Составим
уравнение нормали в этой точке.
Решение. Имеем у' =(х2)' = 2х. Угловой коэффициент
нормали вычисляется по формуле:
k -_1=_±
Норм "" / 2*
Так как нормаль должна быть параллельна прямой у = —х — 5,
то &норм = —. Значит, ¦ = —, х = — 1. Поскольку у = х2,
то у = 1. Итак, искомая точка имеет координаты (—1; 1).
Для составления уравнения нормали воспользуемся формулой
B):
у_1=1(*+1).
Уравнение нормали имеет вид: у = —х -\—.
3. Применения производной в физических задачах. Механический
смысл производной. Пусть точка движется вдоль некоторой
прямой. Выберем на этой прямой начало отсчета, положительное
направление и единицу измерения. Тогда положение точки на прямой
будет определяться ее координатой. Зависимость х = f (t)
называется законом движения точки. Средней скоростью движения
в физике называют отношение перемещения к промежутку
времени, в течение которого это перемещение произошло. Если, скажем,
точка за промежуток времени от tx до t2 прошла путь от Л до В и
вернулась обратно в Л, то перемещение равно 0 и средняя скорость
vcp равна 0. В общем случае имеем:
х2 — хг
ср / — t •
ИЛИ
12 — h
Если положить t± = t, t2 = t + А/, то средняя скорость за
промежуток времени [f; t + Л/] окажется равной:
<>ср =
А/
Мгновенной скоростью в момент времени t называют предел
24

средней скорости движения за промежуток [t\ t + ДО, когда
At-^О. Значит,
,мгн = Нт ,ср = Нш MJ + A0-/H вНт?
Д*-»0 А/-*.О А? Д/-*0 А*
Так как Нт —= x(t), to мгновенная скорость прямолинейно
движущейся точки есть производная координаты (пути) х по
времени L В этом состоит механический смысл производной.
Дифференциал координаты равен х' (t) At, т. е. vMrH • АЛ
Это путь, который прошло бы тело за промежуток времени [/; ? +
-f ДО, если бы его скорость была постоянной и равнялась
мгновенной скорости в момент времени t.
Пример 4. Найдем мгновенную скорость при свободном
падении.
at2
Решение. Закон свободного падения имеет вид s = —.
Согласно сказанному выше, vurH = —. Значит, нужно найти
dt
производную функции s = — .
Дадим аргументу приращение At. Тогда
Главная линейная часть приращения As имеет вид gt At, а потому
s'= g*. Итак, умгн = gt.
Пример 5. Пусть q = q (t) — количество электричества,
протекающее через поперечное сечение проводника за время t.
Найдем силу тока в данный момент времени t.
Решение. Если At — промежуток времени, a Aq —
количество электричества, протекшее через поперечное сечение
проводника за время At, то — — сила тока за промежуток
времени At:
г — ^1
Уср ~ А/ '
За силу тока / в момент времени t принимается lim /cp. Таким
образом,
У~~ dt'
т. е. сила тока есть производная от количества электричества по
времени.
Пример 6. Пусть дан неоднородный стержень длины /,
т = т (х) — масса части стержня длины х (один из концов
стержня принимается за начало отсчета). Найдем линейную плотность
стержня в данной точке х.
25

Решение. Если Am — масса части стержня между
точками, расположенными, соответственно, на расстоянии х и х + Ах
от фиксированного конца, то — — средняя линейная плотность
,. Дт
стержня на рассматриваемом участке, a lim искомая ли-
Д*-0 Д*
нейная плотность р. Таким образом,
dm
р = тх>
т. е. линейная плотность стержня в данной точке есть
производная массы стержня по его длине.
Рассмотренные примеры показывают, как используется
производная для изучения скорости протекания неравномерных
процессов. При этом само понятие скорости понимается в широком
смысле. Например, плотность стержня есть скорость изменения массы
части стержня как функция ее длины.
В общем случае можно сказать так: если у = f (x) —
дифференцируемая в точке х функция, то — есть средняя скорость измене-
д*
ния у относительно изменения х на отрезке \_х\ х+Ах], а — есть
dx
скорость изменения у относительно х в данной точке.
Вопросы для самопроверки
1. Что называют касательной к линии?
2. Всегда ли можно провести касательную к линии в данной точке?
3. Сформулируйте необходимое и достаточное условие существования
невертикальной касательной к графику функции у = f (х) в точке х = х0.
4. Как вычисляется угловой коэффициент касательной к графику функции
у = f (х) в точке х = х0?
б. В чем состоит геометрический смысл производной?
6. В чем состоит геометрический смысл дифференциала?
7. В кашгх случаях график функции у — f (x) в точке х0 имеет вертикальную
касательную?
8. Что называется нормалью к линии?
9. Напишите уравнения касательной и нормали к графику функции у = / (х)
в точке х = х0.
10. Как определяется угол между двумя линиями?
11. Как вычислить величину угла между двумя линиями?
12. Как определяется мгновенная скорость прямолинейного движения?
13. В чем состоит механический смысл производной, дифференциала?
14. Приведите примеры физических понятий, определяемых с помощью
производной .
Упражнения
31. Напишите уравнения касательной и нормали к графику функции у — х?
в точке х = 2.
32. Напишите уравнения касательной и нормали к графику функции у = —
1
в точке х = -—%
2
26

33. Напишите уравнения касательной и нормали к параболе у = х2 + 2х — 1
в точке ее пересечения с параболой у = 2х2.
34. В какой точке касательная к параболе у = х2'. 1) параллельна прямой
у = Ах — 5; 2) перпендикулярна прямой 2х — 6у + 5 = 0; 3) образует с
прямой Зх — у -г 1 = 0 угол 45°?
35. На параболе у = х2 взяты две точки с абсциссами хг= 1, л:2 = 3.
Через эти точки проведена секущая. В какой точке параболы касательная к ней
будет параллельна проведенной секущей?
36. Составьте уравнение нормали, перпендикулярной к прямой,
соединяющей начало координат с вершиной параболы у = х2 + 4х + 1.
37. Через фокус параболы у = х2 проведена хорда, перпендикулярная оси
параоолы. Через точки пересечения этой хорды с параболой проведены
касательные. Докажите, что эти касательные пересекаются под прямым углом.
38. Докажите, что отрезок касательной к гиперболе у = —, заключенный
х
между осями координат, делится в точке касания пополам.
39. Под какими углами парабола у — х2 пересекается с прямой 3* — у —
— 2=0?
40. Под какими углами пересекаются параболы у = х2 и у2 = х?
41. Под каким углом гипербола у = — пересекается с полупараболой у =
= ут?
42. Канат висячего моста имеет вид параболы и прикреплен к
вертикальным опорам, отстоящим одна от другой на 200 м. Самая нижняя точка каната
находится на 40 м ниже точек подвеса. Найдите величину угла между канатом
и вертикальной опорой.
43. Точка движется прямолинейно по закону s= P. Найдите мгновенную
скорость точки в момент времени t= I.
44. Найдите мгновенную угловую скорость вращающегося тела, если в
момент времени t угол поворота равен <р = 2t3 — 3t + 1?
45. Колесо вращается так, что угол поворота пропорционален квадрату
времени. Первый оборот был сделан колесом за 8 с. Определите угловую скорость
через 32 с после начала движения.
46. Колесо вращается так, что величина угла поворота пропорциональна
кубу времени. Первые два оборота были сделаны колесом за 4 с. Найдите
угловую скорость через 16 с после начала движения.
47. Имеется тонкий неоднородный стержень А В длиной 20 м, и пусть для
любой точки С стержня, отстоящей от А на расстоянии / см, масса куска стержня
АС определяется по формуле т = З/2 + 5/. Найдите линейную плотность
стержня: 1) в точке, отстоящей от точки А на расстоянии / = 5 см; 2) в самой точке Л;
3) в конце стержня.
48. Количество электричества, протекшее через проводник, начиная с
момента времени t = 0, указывается формулой q = 2t2 + 3t + 1 (кулонов).
Определите силу тока в конце пятой секунды.
49. Если опустить кристалл вещества в насыщенный раствор этого
вещества, то кристалл начнет увеличиваться. Обозначим его массу в момент времени t
через т (t). Дайте определения следующих понятий: средняя скорость изменения
массы кристалла за промежуток времени [t; t+ Af], скорость изменения массы
кристалла в момент времени t
§ 4. ДИФФЕРЕНЦИРОВАНИЕ ОПЕРАЦИЙ
Мы видели, что понятие производной находит приложения в
разнообразных задачах по геометрии и физике. Однако класс
функций, которые мы йока умеем дифференцировать, крайне узок.
Чтобы расширить его, выведем правила дифференцирования суммы,
произведения, частного.
27

Прежде чем переходить к формулировке и доказательству
соответствующих теорем, сделаем следующее замечание. Пусть дана
функция у = f (х), х € X. Приращение функции в точке х ? X
имеет, как мы знаем, вид:
ду == / (х + Ах) — / (х) = f (х + Ах) — у.
Отсюда находим: / (х + Ах) = у + Ду.
Полученное равенство будем использовать при доказательстве
теорем настоящего параграфа. Условимся выбирать приращение
Да: таким, чтобы х + Ах ? X.
1. Дифференцирование линейной комбинации конечного числа
дифференцируемых функций.
Теорема 1. Пусть функции и = / (х), х € X, и v = g (х),
х € X, дифференцируемы в точке х0€ X. Тогда функция у = f (х) +
+ g (x) дифференцируема в точке х0, причем
Короче: сумма двух дифференцируемых функций
дифференцируема, причем производная суммы равна сумме производных.
Доказательство. Дадим х0 приращение Ах. Тогда
функции и и v получат соответственно приращения Аи и Av, a
для функции у будем иметь:
Ду = ((" + Ди) + (v + Av)) — (и + v) = Аи + Av.
Итак, Ду = Аи + Av. A)
Разделим обе части равенства A) на Да;:
Ду Аи Av
Дл; Дл: Дл;'
Пусть Да: стремится к 0. Так как по условию и и v —
дифференцируемые функции, то существуют lim — и lim —. В таком
дх_о Д* Дх->.оДя
случае существует и lim —, причем
Дяч.0 АХ
,. Ду ,. Аи ,. Ду
lim — = lim —о- 'im —•
д>;->0 Ах д*-оДл; д^_о Дл:
Но существование lim — означает дифференцируемость функции
Дх-*0Д*
у = u+v в точке х0. Так как lim — = у' lim — = и', lim — = х/,
Дх->0 Дл: д*-о Дл: д*_*о Ах
то у' = и' + i/, т. е.
(и + v)' = и' + v'.
Теорема доказана.
Получим выражение для дифференциала суммы:
dy = d (и + v) = (и + v)'dx =
= (и + v) dx = и' dx + v' dx = du + do.
28

Тем самым получено следующее правило.
Правило 1. Производная суммы двух дифференцируемых
функций равна сумме производных этих функций, а дифференциал сум-
мы равен сумме дифференциалов.
Теорема 2. Если функция и = f (x)f x € X, дифференцируема
в точке х0 ? X, то функция у = kf (х), где k — действительное
число, также дифференцируема в точке х0, причем
(kf (х)Ух==Хо = kf (х,).
Доказательство. Дадим х0 приращение Д#. Тогда
функция и получит приращение Дм, а для функции у будем иметь:
Ду = k (и + Д^) — ku = k&u.
Итак,
Ду = kku. B)
Разделим обе части равенства B) на Ах:
Ду Да
\х кх
Пусть Дх стремится к 0. Так как по условию и —
дифференцируемая функция, то существует lim — . Тогда существует и lim —,
дх-*о Д* д*-*о Дя
причем
lim — = k lim —.
д*_*о Д* д^-»о Дя
Дифференцируемость функции у = ku в точке х0 доказана.
Так как lim — = /, a lim —= и',
Ax-»Q Да; д*-*о Д*
то
у = (Ы)' = ku'.
Теорема доказана^
Отметим, что
dy = d (ku) = (kti)' dx = k (uf dx) = kdu.
Тем самым получено следующее правило.
Правило 2. Постоянный множитель можно вынести за знак
производной и за знак дифференциала.
Непосредственным следствием (и обобщением) первых двух
правил является правило 3.
Правило 3- Производная (дифференциал) линейной комбинации
конечного числа дифференцируемых функций равна (равен) такой же
линейной комбинации производных (дифференциалов) этих функций:
(k±U± + k2U2 + ... + knUnY = kxu\ + k2U2 + ... + knu'n.
d (&!«! + k2u2 + ... + knun) s= kxdu± + k2du2 + ••• + kndun-
29

Мы установили дифференцируемость линейной комбинации
конечного числа дифференцируемых функций. Это позволяет
сделать следующий вывод: класс D (X) функций, дифференцируемых
на множестве X (т. е. дифференцируемых в каждой точке
множества X), образует линейное пространство.
Рассмотрим несколько примеров вычисления производных с
помощью полученных правил и выведенной ранее формулы (ха)' =
= ах*'1.
Пример 1. Найдем производную функции
у = Зх3 — 5х2 + 1.
Решение. По правилу 3 имеем: у' = (Зх3 — 5х2 + 1)' =
= 3 (Xs)' — 5 (х2У + A)'. Так как (х3)' = Зх\ (х2)' = 2х, а A)' =
= 0, то окончательно получаем:
/ = 3 • Зх2 — 5 • 2х + О = 9л;2 — 10*.
Пример 2. Найдем производную функции
3*+1 2
У = -
2 ьУх
Решение. Имеем у' = (*?±1__* Y = 1C* + \)'—Цх 2"
\2 Ьу х ] 2 5 \ j
Так как C* + 1)' = 3, а (х А'=—х 2,
то получаем:
/-•i-8-4. (-^-4 +
2 5 \ 2' / 2 5х]/*х *
Пример 3. Объем шара есть функция радиуса. Докажем,
что производная объема шара по радиусу равна площади шаровой
поверхности.
4
Решение. Имеем: V = —яг3. Тогда
3
"=(т
яг»У = -я-И' = -п-3гг = 4яг2.
J О «J
Но площадь поверхности шара радиуса г вычисляется по формуле
S = 4дг2. Итак,
dr
Из последней формулы получаем dV = S<ir. Это равенство имеет простой
геометрический смысл: если радиус шара увеличить на dr, то объем шара
увеличится на Д V, причем приращение объема примерно равно дифференциалу объема.
Его можно вычислить, умножив площадь шаровой поверхности на величину
приращения радиуса, т. е. на толщину добавленного слоя.
30

2. Дифференцирование произведения.
Теорема 3. Если функции и = / (л;), х € X, и v = g (а:), л; € Л",
дифференцируемы в точке х0€ X, то функция у= f (х) g (х) также
дифференцируема в точке x0i причем
if (х) g (x))'x=Xo = /' (*„) • 8 (*о) + f (Хо) ¦ 8' (*о).
Короче: произведение двух дифференцируемых функций и и v
дифференцируемо, причем (uv)' = u'v + uv''.
Доказательство. Дадим х0 приращение Да:. Тогда
функции и и v получат приращения, соответственно Аи и Avf а
для фун кции у будем иметь:
Ду = (и + Аи) (v + Av) — uv =»
= у Ди + и Av + Д^Ду.
Итак,
Ду = аДи + «Ду + AuAv.
Разделим обе части полученного равенства на Да::
Ду Ды , До . А Да /оч
Д* Дд: Дл: Д*
Пусть Да: стремится к 0. Так как по условию и и v —
дифференцируемые функции, то существуют lim — и lim—, причем
д*-*оД* Дх-оД*
первый предел равен и' > а второй равен v'.
Под и и v в равенстве C) понимаются значения функций и = f (х)
и v = g (х) в фиксированной точке а:0, поэтому а и v — постоянные
множители, и их можно вынести за знак предела. Кроме того,
воспользовавшись непрерывностью дифференцируемой функции v =
= g (х) (теорема 2 § 2), приходим к выводу, что lim Ли = 0.
Таким образом,
lim( v — + и — + Да — ) = v lim— -\-u lim— +lim — НтДс; =?
Ах-+о\ Ах Ах Ах] /±х->о&х &х->оАх Дя-*о Д* д*-*о
s=UfV + UV*.
Значит, предел правой части равенства C) при Да: -^ 0 существует
и равен uv + uv'. В таком случае существует и lim — , причем
д*-*о Д*
этот предел равен u'v + uv'. Значит, у = uv в точке х0
дифференцируема, причем (uv)' = u'v + uv'. Теорема доказана.
Выведем формулу для вычисления дифференциала произведения,
Имеем:
dy = d (uv) = (uv)'dx — (u'v + uv') dx =*
= v (udx) + и (v'dx) = vdu + udv*
Тем самым получено следующее правило.
31

Ir
Правило 4. Производная произведения двух
дифференцируемых функций вычисляется по
формуле:
(uv)' = u'v + uv'.
Дифференциал произведения вычисляется
по формуле:
d (uv) = vdu + udv.
На рисунке 19 представлена геометрическая
иллюстрация правила вычисления дифференциала
произведения. Рассмотрим прямоугольник, длины сторон
которого равны и и vf и найдем дифференциал площади d (uv). Он равен
площади udv + vdu заштрихованной фигуры, которая представляет собой объединение
двух прямоугольников, причем длины сторон одного равны v и du, а другого —
и и dv.
В
dv
В
If
А
и DduD1
Рис. 19
Пример 4. Найдем производную функции у = B + Ух) х
х (х2 — Зх) в точке х = 1 и дифференциал функции в этой точке
при Ал: = —0,1.
Решение. Имеем:
у' = B + У7)' {х2 — Зх) + B + ]/х) (х2 — Зх)' =
2
Тогда
B)' + U" i } (*2 - Зх) + B + Vx) ((х2)' - 3 (х)') =
= --^= (х2 — Зх) + B + ]/"х) B* — 3).
ГО)
A - 3) + B + 1) B - 3) = -4,
dy = /' A) Ах = — 4 • (—0,1) = 0,4.
Правило 4 распространяется на произведение любого конечного числа
дифференцируемых функций. Пусть функции uf v, w дифференцируемы в точке х.
Найдем производную функции у = uvw.
Имеем:
/ = (uvw)' = ((uv) • w)' = (uv) w + (uv)w = (u'v + иг/)ад + (fw)i0 =
= u'vw + ai/o> + идоЛ
Итак,
(ищу)' = u'vw + ыу'о; + иш)'.
Методом математической индукции можно доказать что
Заметим, что правило 2, непосредственно следует из правила
4. В самом деле,
(си)' = (с)'и + си' = 0 • и + си' = ш'.
32

3. Дифференцирование частного.
Теорема 4. Если функции и = f (х), х € X, и v = g (х), х ? X,
дифференцируемы в точке х0 ? X, причем g (х0) Ф О, /по функция
f (х)
у = i-^-i также дифференцируема в точке х0> причем:
8(*)
±Щ = Г (*о)?(*о)-/(*о)^(*о)
?(*)/*=*„ (g(^o)J
Короче: частное от деления двух дифференцируемых функций
дифференцируемо, причем \~) = uv~~~u ? ^^^ у =5^=0.
\ у/ о2
Доказательство. Дадим аргументу приращение Дл; так,
чтобы #0 + Ах ? X и g (#0 + Л*) =т^ 0. Тогда будем иметь:
Л — / (*о + A*) f(xo) ___ и + Аи ^ __ аДц — цДо
#(л:0 + Да:) g(*0) u + Ду и у(у + Ду) #
Далее получаем:
Ди Да
и —— и —
Ду Да; Дл:
Да: v (v + Дя)
Пусть Да: стремится к 0. Тогда
1а Да , ,. Ди ,
hm — = и, lim — = у',
д*-*оД* д*-»оДа:
значит,
!• / Ли ДгЛ , /
hm о и —) = и v — ии
Лх-^О \ Да: Да:/
(здесь, как и выше, под и и v понимаются значения функций и = / (л:)
и у = g (x) в точке х0, а потому он — постоянные множители).
Так как по условию v = g (x) — дифференцируемая в точке
х0 функция, то она непрерывна в этой точке, а тогда lim Ду = 0.
Значит, lim v (v + Ли) = v2 Ф 0. В итоге получаем:
д*->о
/ Да Ао\
lim \v— — и —
г ^У — д*-»°\ Да: Да:/ __ и'v — uv'
Дх-^оДа lim и (и-|-Да) а2
Дх->0
Из существования lim — следует дифференцируемость рас-
Ах-+0 Да:
сматриваемой функции. Кроме того, мы получили, что
(f у- -
Теорема доказана.
Правило 5. Производная частного в точках, еде знаменатель
отличен от 0, вычисляется по формуле:
'v — ш/
(i)'--

Дифференциал частного вычисляется по формуле:
* I иЛ __ vdu — udv
v<
Если и = С, то из правила 5 получим:
С v Cv — Cxf о . v — Си'
ш
—с?.
7.2
Если у = С, то, воспользовавшись правилом 2, получим:
С) \С J С С
Пример 5. Найдем производную функции
За;2 — 2* + 1
' 7х+1
Решение.
_ (Зх2 — 2* + 1 у (Зх2 — 2х + 1)' G* + 1) — (З*2 — 2* + 1) Gх + 1)'
7*+1 / G* + 1J
_ Fjc — 2) Gл: + 1) — C*2 — 2х + 1) 7 21л2 +6* — 9
""" Gл; + IJ ~~ Gл+1J
Пример 6. Составим уравнения касательной и нормали к
кривой у = в точке с абсциссой, равной 2.
^ J \ + х2 *
Решение. По заданному значению х0 = 2 находим у0 =
— _!_ — JL
"" 1 + 22 ~~ 5'
Значит, касательная и нормаль проходят через точку М0 B; —
Найдем угловые коэффициенты касательной и нормали.
Имеем:
A + х2)' ___ 2х
к1 + х2) A + х2J A + х2J
Тогда
кас ' 1 ' "" 25' норм~ feKac~ 4'
1 4
Уравнение касательной: у = (л: — 2), или Ах + 25у —
о 2d
— 13 = 0.
1 25
Уравнение нормали: у = — (л:—2), или 125а:—20у—246=0.
34

Вопросы для самопроверки
1. Сформулируйте теорему о дифференцируемости суммы.
2. Как вычисляется производная суммы?
3. Как вычисляется дифференциал суммы?
4. Как вычисляются производная и дифференциал от линейной комбинации
конечного числа дифференцируемых функций?
5. Является ли множество дифференцируемых на отрезке функций
линейным пространством? Поясните свой ответ.
6. Может ли сумма двух недифференцируемых функций быть
дифференцируемой?
7. Может ли сумма дифференцируемой и недифференцируемой функций быть
дифференцируемой?
8. Сформулируйте теорему о дифференцируемости произведения.
9. Как вычисляется производная произведения двух функций? трех
функций?
10. Как вычисляется дифференциал произведения двух функций?
11. Верно ли равенство (/(*0) + g (х0))' = /' (xQ) + g' (x0)?
12. Дайте геометрическое истолкование правилу вычисления дифференциала
произведения трех функций.
13. Может ли произведение двух недифференцируемых функций быть
дифференцируемой функцией?
14. Сформулируйте теорему о дифференцируемости частного.
15. Как вычисляется производная частного?
16. Как вычисляется дифференциал частного?
17. Покажите, что множество функций, дифференцируемых на данном
промежутке, образует кольцо.
Упражнения
Найдите производные следующих функций:
50. 1) y=ll*3 + 3x2-*-0,7; 2) у = — ** + ^- - 2,7*+ 1;
2 5
1 i ¦*-
3) у = — 9лг-з + 5*-2 + — х-и 4) у = х4 —8л:4;
6) у = 6* 3 - Зх 3 + 1.
Зх2 — 6* + 7
4) y = -6V7+~
л- X
5) у = 5 Ух~ + Зх уТ — у/~х\
6) у=24/х~+ —=----- +2хУх~.
ух xd
52, 1) у = (Ъх — 2)Gх + 4); 2D у = (х2 + 3* + 2) (х3 — 3);
3) у={Ух-+1) (|+54 *> ув-^(з«^4).^.
х Зд: —5
5)
3)
51.
У =
3
X —
1)У
бх4-
JL _L
•2*3 + 3*3;
2 4 5
X X2 Хъ
- 7*3 +х2 — 2х +
6
**;
1
53. 1) у = ——; 2) у
*+Г ' У 2х + 7'
д^ + х+2 1-х3
3) у= Т , ; 4 у=- -;
х2 — 4 1 — я5
35

54. 1 У = ^= "• 2> ^=7= !
f/T+2 |/T+1
8 — 3 f/T3 + 2* 2
3)y = V : 4) у
1+&C/7-3X» (l-*2)(l+*4)
55. Покажите, что если S — площадь круга, а г — радиус круга, то —
равняется длине окружности. Дайте геометрическое истолкование этому
результату.
56. Покажите, что если V — объем прямого кругового цилиндра, h — высо-
dV
та, а г — радиус основания, то при постоянном г производная — равна площа-
dh
dV
ди основания цилиндра, а при постоянном п производная — равна площади бо-
dr
ковой поверхности цилиндра.
57. Дана функция у = 5*2 — 16 j/7+ 7. Найдите: 1) f A); 2) f D);
3)Г
(i)
3/--7Г
58. Дана функция у — -/я2 — х. Найдите f A) — f (—1).
59. Дана функция у = х3 + Зх2 — 9. Найдите корни производной.
60 64
60. Дана функция у = Зя + Ь 5. Найдите корни производной.
61. Докажите, что функция у = 3+ — удовлетворяет дифференциальному
X
равнению1) ху + у = 3.
х3
62. Докажите, что функция у = — —2х2 удовлетворяет дифференциальному
о
уравнению ху' — 2х2 = Зу.
63. Найдите дифференциалы заданных функций:
1) y = 2*2-8* + 5; 2) у = A + 3/7J;
о 5/-- 3 *2__3л: —4
*>У-*Ух+Т. 4)У- ъу- .
64. Найдите значение дифференциала функции у = f (х) в заданной точке
при заданном значении приращения аргумента:
3
l)y = *3+-3 — 1, х = 8, dx = —0,1;
65. В каких точках графика функции у = 2 + х — х3 касательная к нему:
1) параллельна прямой llx+ у+ 1 = 0; 2) перпендикулярна биссектрисе
второго и четвертого координатных углов?
66. Составьте уравнения касательных и нормалей к графику функции
у = (х — 1) (а: — 2) (х — 3) в точках его пересечения с осью абсцисс.
дг + 9
67. Составьте уравнение касательной к графику функции у = —— так,
х-\- о
чтобы касательная проходила через начало координат.
г) Дифференциальным называется уравнение, связывающее аргумент,
функцию и производную искомой функции по аргументу.
36

68. При каком значении а парабола у = пересекает ось абсцисс в
начале координат под углом 45°?
69. Докажите, что графики функций у — х2 и у = 2 — я3 в пересечении
образуют угол, величина которого равна 45°.
(&
70. Тело движется прямолинейно по закону х = 2t2 + Ы. Определите
о
скорость в момент времени /= 1,5 с.
71. Точка движется прямолинейно по закону х = .
В какой момент времени точка остановится?
72. Количество электричества, протекшее через поперечное сечение
проводника, начиная с момента времени t = 0, задается формулой q = f — 9t2 +
+ 15? + 1. В какие моменты ток в проводнике будет равен 0?
§ 5. ДИФФЕРЕНЦИРОВАНИЕ СЛОЖНОЙ ФУНКЦИИ
1. Дифференцируемость сложной функции. Напомним
определение сложной функции.
Пусть у = ф (f) и t = / (х) — числовые функции, такие, что:
1) функция t = f (х) определена на множестве X. 2) если х0€ X,
то U = / (хо) принадлежит области определения функции у=ф (t).
Тогда на множестве X определена функция у = ф (fix)), которая
называется сложной функцией, составленной из у = ф (/) и t =
= f (x)\ х называют независимым аргументом (независимой
переменной), a t — промежуточным аргументом (промежуточной
переменной). Сложную функцию называют также композицией1*
данных функций.
Теорема 1. Пусть у = ф (t), t = f (x) и пусть существует
окрестность точки х0, в которой определена сложная функция
У = Ф if (*))• Если функция t = / (х) дифференцируема в точке
х0, а функция у = ф (t) дифференцируема в точке tQ = f (x0), то
сложная функция у = <р (/ (х)) дифференцируема в точке х0.
Короче: композиция двух дифференцируемых функций есть
дифференцируемая функция.
Доказательство. Дадим переменной х0 приращение Ах
так, чтобы точка х0 + Ах принадлежала указанной в
формулировке теоремы окрестности точки х0. Тогда функция t = f (x)
получит приращение At> которое, в свою очередь, вызовет
приращение Ау функции у = ф (t).
Так как функция t = / (х) дифференцируема в точке х0, то
имеем:
At = ААх + аАх, A)
где А — число, аа->0 при Да: -*- 0.
х) В книге «Введение в анализ» вместо «композиция» говорилось
«суперпозиция». Сейчас в школе принят термин «композиция».
37

Так как, далее, функция у = ф (t) дифференцируема в точке
t0} то имеем:
Ду = В At + рд/, B)
где В — число, а Р -> 0 при At -> 0.
Подставив в равенство B) выражение для А/, получим:
Ду = В (ААх + а&х) + р (ААх + аДх) =
= АВАх + (аВ + М + оф) Дх.
Если Да: -> 0, то а -»- 0. Кроме того, из непрерывности
дифференцируемой функции t = f (х) следует, что при Ах ->- 0 будет Д? -»- 0,
а тогда и C -^ 0. Таким образом, аВ + М + оф -* 0 при Ах -> 0.
Если обозначить аВ + (ЗЛ + оф через у, получим:
Ду = АВАх + yA*, C)
где А В — число, а у -> 0 при Дя -> 0. Но это и означает дифферен-
цируемость сложной функции в рассматриваемой точке х0.
Теорема доказана.
Из равенства A) следует, что А = tx , а из равенства B)
следует, что В = yv Тогда из равенства C) получаем:
У'Х = ЛВ = у'/х.
Теперь мы можем сформулировать следующее правило
дифференцирования сложной функции.
Правило 6. Производная композиции двух функций по
независимой переменной равна произведению производной по
промежуточному аргументу на производную промежуточного аргумента по
независимой переменной:
у* = у; • *;•
Правилу б можно дать наглядное физическое истолкование: yt есть скорость
изменения у относительно t, t'x есть скорость изменения / относительно х.
Иными словами, в данной точке у изменяется в yt раз быстрее, чем U a t — в t'x
раз быстрее, чем я. Ясно, что тогда у изменяется в yt • t'x раз быстрее, чем ху
т. е. Ух=у; . ?
Это правило распространяется и на случай композиции трех и большего
числа дифференцируемых функций. Если, например, у = у (t), t= t (и), и= и (х),
то можно рассуждать так: рассмотрим у как композицию двух функций. Тогда
у' = y't • t'x. Теперь будем считать и промежуточным аргументом. Тогда t'x =
= tu • их. В итоге получаем:
Пример 1. Найдем производную функции
38

Решение. Положим t = х2 Ь 5. Тогда данную функ-
х
цию можно рассматривать как композицию двух функций: у = Р
и t = х2 [-5, а значит,
X
у; - у; • с - п (*2 - 7+*]х - ^ Bх+?).
Осталось вместо < подставить его выражение. Получим в итоге:
>' = 3(*'-т+5)>+г)-
Пример 2. Докажем теорему: касательная к окружности
перпендикулярна к радиусу, проведенному в точку касания.
Решение. Возьмем точку М0 (х0\ у0) на дуге окружности,
лежащей в первом квадранте (рис. 20). Из уравнения окружности
имеем у = ]/~# — х2. Найдем производную этой функции:
-А—1
у' = (Y R2 — x2)' = \{R2 — x2J ) =-L(R2-x2)* '(R2 — x2)' =
±(F>2_X2) 2 .(_2x)=_
VR2-'
--. Таким образом, у' =
= , значит, kK
У Уо
Угловой коэффициент радиуса ОМ0 та-
1.
ков: &рад = ^. Так как kK
«рад
то касательная и радиус взаимно
перпендикулярны, что и требовалось доказать.
Пример 3. Плот подтягивается к
берегу при помощи каната, который
наматывается на ворот со скоростью 3 м/мин.
Определим скорость движения плота в
тот момент, когда его расстояние от
берега будет равно 25 м, если известно, что
ворот расположен на берегу выше
поверхности воды на 4 м.
Решение. Пусть (рис. 21) длина
каната между воротом и плотом | PN\ = s,
расстояние плота от берега | РВ\ = х,
тогда, так как | NB\ = 4, s = Ух2 + 16.
Поскольку х зависит от времени t, то
продифференцируем это соотношение по
Мо(х0;Уо)
Рис. 20
39

времени t. Получим:
_JL
{V^TT%)yt = ± (** + 16) 2 2xx't =
X , X ,
~~ yx2 + \6 l ~ r
' — ?. c'
Xu —= S,.
f л: f
3, x = 25 и, следовательно, s = У^б2 + 42 =
*; =1^1.3 «3,03.
Итак, искомая скорость примерно равна 3,03 м/с.
2. Инвариантность формы записи дифференциала. Мы
первоначально определили дифференциал функции формулой
dy = у'х Ах, D)
а затем, положив по определению dx = Ах, получили следующую
запись:
dy = ух dx. E)
Переход ко второму виду записи дифференциала делается потому,
что формула E) остается верной и в случае, когда х —
промежуточная переменная, в то время как формула D) в этом случае
становится неверной.
Докажем, что если у = ф (t) — композиция двух
дифференцируемых функций у = f (х) и х = g (t), то dy = y'x dx.
Так как t — независимая переменная, то dy = y't dt.
Воспользовавшись формулой производной композиции функций,
получим:
dy = y'x x't dt.
Но х\ dt = dx, значит, dy = yx dx.
Таким образом, форма дифференциала сохранилась:
дифференциал функции имеет один и тот же вид как в том случае, когда
х — независимая переменная, так и тогда,, когда х —
промежуточная переменная, а именно, он равен произведению производной на
дифференциал того аргумента, по которому взята производная.
Следует, однако, иметь в виду принципиальное различие между
двумя рассмотренными случаями: если х — независимая
переменная, то dx = Ах и потому не зависит от х\ если х — промежуточный
аргумент (х = ф (t)), то dx = cp'(?) At и зависит от t. Только в
случае, когда х = ф (f) = kt + b — линейная функция, dx = kdt,
т. е. dx не зависит от t.
st — sxxtz
откуда
По условию s'(
= |/^641. Тогда
40

Доказанное свойство называют инвариантностью формы dy =
= у'х dx дифференциала.
Запись dy = ух Ал: свойством инвариантности не обладает. Если х —
промежуточная переменная, то Ах = xtkt + [5А? и потому У^Ах = ух (xt A^+
+ РАО = y'JtM + $у'хМ = y'tM + Ру>.
Получившееся выражение отличается от ytkt слагаемым C УХЫ.
Пример 4. Найдем дифференциал функции у = у х : 1) в
случае, когда х — независимая переменная; 2) в случае, когда х =
= fi + t2 - 3.
Решение. 1) Имеем:
3 3^?
dy =—х ъ dx — -g
2) Воспользовавшись инвариантностью формы дифференциала,
получим:
Далее имеем: dy = 3 1 . d {tb +t2 - 3) = j^0—•
з / (*5 +t2 — зJ з |/ (tb+t2—3J
Вопросы для самопроверки
1. Как определяется композиция функций?
2. Сформулируйте теорему о дифференцируемости сложной функции.
3. Как вычисляется производная сложной функции?
4. Что означает фраза «инвариантность формы дифференциала»?
5. Обладает ли свойством инвариантности формула dy = f'(x) Ax?
6. Для функций у = х3, х= t2 вычислите y^tf, y'^dt, yxdx, у'х&х*
y'jPfit, если /= 2, А? = 0,1.
Упражнения
Найдите производные следующих функций:
73. у = (Зх3 — 4л; + IM. 74. у = V^+i-
2 \ 3
3 3 2
75. у = \а — а: / . 76. у -
10
37 Bх2 + IK
Тг+W ""' ' *+^*+4/^
77. у = , * . 78. у = т/ _д/- _ 4Т~
41

79. у
-V<*
1
(х2 + lJ (x — 2) 3 .
*A + *2)
80. У = ?^+Я5,
82. Составьте уравнение касательной к графику функции у=(х + 1) |/ — л:
в точке х = — 1. з_
2~
83. Составьте уравнения касательных к графику функции у = (х + 4)
в точках его пересечения с осями координат?
84. Под каким углом пересекается с осью Оу график функции у = -у=?
85. Из пункта О по двум прямым, образующим между собой угол, величина
которого равна 60°, движутся два тела. Первое тело движется равномерно со
скоростью 5 км/ч, второе — по закону s = 2t2 + t (путь s выражен в километрах,
время t — в часах). С какой скоростью они удаляются друг от друга в момент,
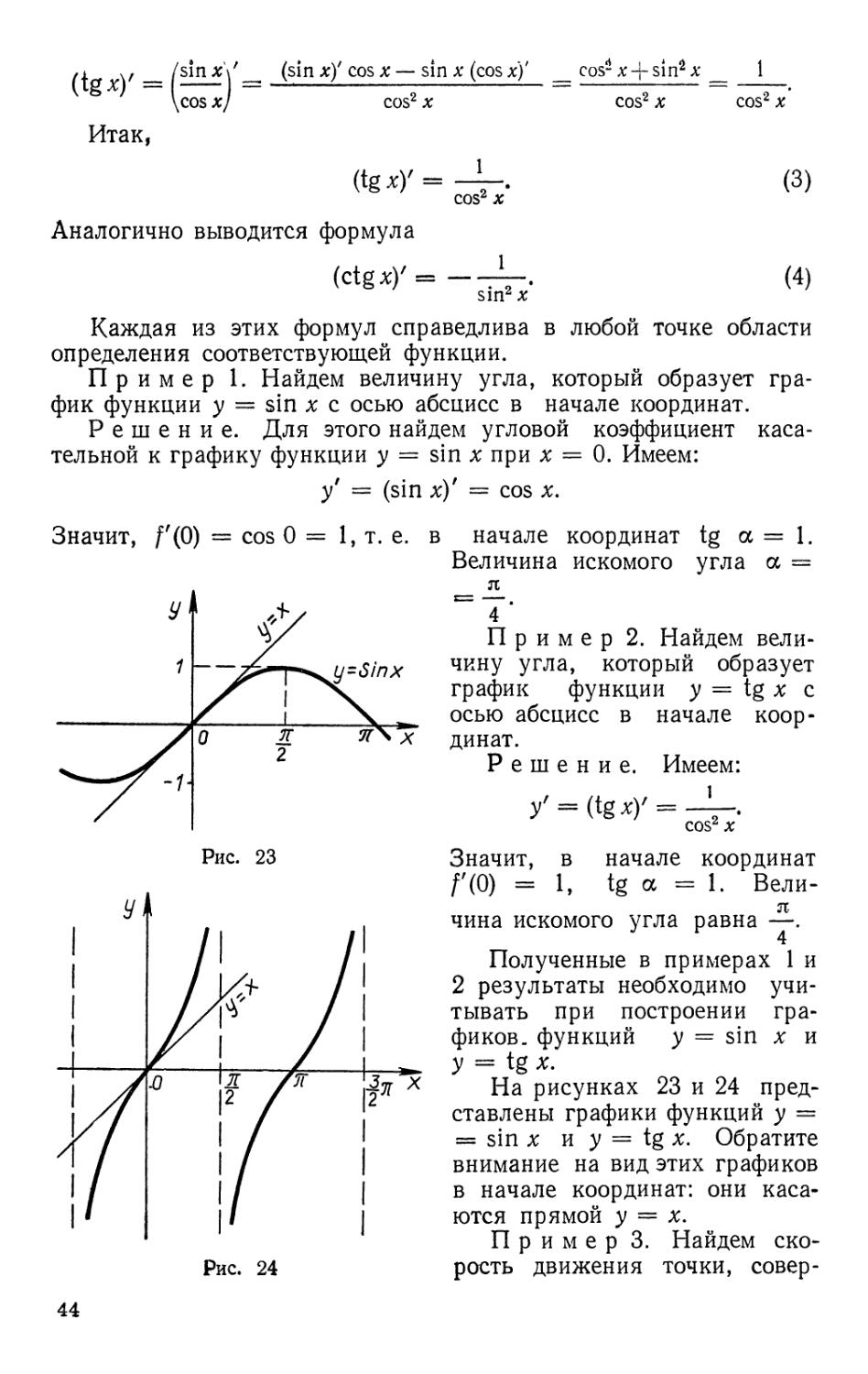
когда первое тело находится от пункта О на расстоянии 10 км?
86. Тяжелую балку длиной в 13 м опускают на землю так, что нижний ее
конец прикреплен к вагонетке, а верхний удерживается канатом, намотанным на
ворот. Канат сматывается со скоростью 2 м/мин. С какой скоростью откатывается
вагонетка в момент, когда она находится на расстоянии 5 м от стены?
§ 6. ДИФФЕРЕНЦИРОВАНИЕ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
До настоящего времени мы располагаем шестью правилами и
только одной формулой дифференцирования: (ха)' = аха~~\ В
этом параграфе получим формулы дифференцирования других
элементарных функций.
1. Дифференцирование тригонометрических функцийс Найдем
производную функции у = sin х. Дадим х приращение Ад;. Тогда
Ay = sin (х + Ах) — sin x.
Воспользовавшись формулой преобразования разности синусов
в произведение, получим:
Ду = 2 sin — cos (x + —).
Разделим обе части этого равенства на Да: и перейдем к пределу
при Ах -> 0. Получим:
2 sin — cos a: +"
lim^-lim 2 V 2
Ля
Заменим бесконечно малую величину sin —- эквивалентной бес-
„ Д*
конечно малой — и воспользуемся тем, что в силу непрерывности
косинуса
д*
42
lim cos [x + ^] = cos x.

Будем иметь:
Лу
)А.
Таким образом,
2-Ч &*
lim — = lim lim cos [ x + —
= cos x.
(sin x)' = cos x.
Аналогично выводится формула
(cos x)' = —sin x.
Вывод этой формулы мы оставляем читателю1*.
A)
B)
Формулы A) и B) можно получить, руководствуясь физическими
соображениями. Пусть по окружности единичного радиуса с угловой скоростью со =
= 1 рад/с движется точка и пусть в начальный момент времени она находится
в положении Л0, а в момент времени / — в положении А (рис. 22). Дуга А0А
имеет длину t и величина центрального угла А0ОА равна t радиан. По
определениям синуса и косинуса имеем: ордината точки А есть sin t, абсцисса точки А
есть cos t. Значит, проекция В точки А на ось абсцисс движется по закону x=cos t,
а проекция С точки А на ось ординат движется по закону у = sin t. Найдем
скорости этих движений.
Заметим, что линейная скорость v точки А выражается формулой v = &R.
Так как в нашем случае со= 1, R — 1, то и с/ = 1. Разложим линейную скорость
на две составляющие — горизонтальную и вертикальную Вектор v скорости
-»•
точки Л, где \v\= 1, направлен по касательной к окружности, проведенной в
зх
точке Л, и потому образует с осью Ох угол t Н , а с осью Оу—угол t.
Следовательно, его проекция на ось Ох (т. е. скорость движения точки В) равна
^ = cosf/+yJ== —sin^,
а его проекция на ось Оу (т. е. скорость движения точки С) равна
vy = cos /.
Так как скорость есть производная пути по
времени, то, учитывая, что х = cos t — закон
движения точки В, а скорость vx = — sin t,
заключаем, что
(cos 0' = —sin t.
Аналогично учитывая, что у = sin t — закон
движения точки С, а скорость vy = cos tt
заключаем, что
(sin f)' = cos t
Рассмотрим теперь функцию у — tg x.
Для вычисления производной этой
функции воспользуемся правилом
дифференцирования частного. Имеем:
Рис. 22
1) Формулу B) можно получить и другим способом:
(cos*)' = (sin(x+ YJJ = cosf*+ y)(* + y)= —:
sin x • 1 =
-sin x.
43

,i w /sin*/ (sin *)'cos л: — sin я (cos л;)' cos- x + sin2 x
(tg*) = — = -— -—— =
\cos xj
Итак,
1
COS* X
COS2 X
(tgx)' =
Аналогично выводится формула
(ctgx)' =
1
cos2 x
sin*5*
C)
D)
Каждая из этих формул справедлива в любой точке области
определения соответствующей функции.
Пример 1. Найдем величину угла, который образует
график функции у = sin х с осью абсцисс в начале координат.
Решение. Для этого найдем угловой коэффициент
касательной к графику функции у = sin х при х = 0. Имеем:
у = (sin x)'
Значит, f'@) = cos 0 = 1, т. е.
У
1
v—*у -ь
\
0
<У
I
I
г
Ku=Sinx
?TN X
COS X.
в начале координат tg a = 1.
Величина искомого угла а =
Пример 2. Найдем
величину угла, который образует
график функции у = tg x с
осью абсцисс в начале
координат.
Решение. Имеем:
y' = (tgxy '
cos**
Рис. 23
Значит, в
ПО) = 1,
начале
tg a =
координат
1. Вели-
Рис. 24
чина искомого угла равна —.
Полученные в примерах 1 и
2 результаты необходимо
учитывать при построении
графиков, функций у = sin х и
У = tg х.
На рисунках 23 и 24
представлены графики функций у =
= sin х и у = tg х. Обратите
внимание на вид этих графиков
в начале координат: они
касаются прямой у = х.
Пример 3. Найдем
скорость движения точки, совер-
44

3*—1
Шающей гармоническое колебание по закону s = A sin (at + a).
Решение. Имеем:
v = - = (A sin (cot + а))' = A (sin @/ + а))' =
dt
= Л cos (со? + а) • (со/ + а)' = Лео cos (со/ + а).
Пример 4. Найдем производную и дифференциал функции
у = cos2 (ctg :
Решение. Имеем:
t = —=—, г = ctg /, и = cos z, у == гг2.
Воспользовавшись правилом дифференцирования сложной
функции, получим:
1 \ 3
уг = 2и (— sin г) (-
sin21 / 5
. 3* —1\ . / , Зх—1\ 1 3
2 cos ctg sin ctg
5 / 03*— 1 5
sin2 —-—
dy =2
3x -
3 . sin B ctg —-
5 sin2 —-—
5
/ Зл:— 1\
3 sin 2 ctg —-—)dx
5 sin2 —
2. Дифференцирование обратной функции. Мы знаем, что если
функция у = f (x) непрерывна на отрезке [а; 6] и строго монотонна
на этом отрезке, то для нее существует обратная функция х = Ф (у),
непрерывная и строго монотонная на отрезке [f(a);f F)]. Докажем,
что если функция у = / (х), кроме того, дифференцируема в какой-
нибудь внутренней точке х0 € [а; 6], причем в этой точке f'(x0) Ф О,
то функция х = ф (у) дифференцируема в точке у0 = / (#0), причем
Рассмотрим функцию х = ср (у) в точке у0 и дадим у
приращение Ду =т^= 0. Тогда х получит приращение Да:, где
Дл: = ф (у0 + Ду) — ф (у0).
45

При этом в силу строгой монотонности обратной функции Дх Ф 0.
Так как по условию функция у = f (х) дифференцируема в точке
х09 то
Ay = f'(x0) Ах + а Ах, E)
где а ->- 0 при Ал: ->¦ 0. Из равенства E) получаем:
^ = —!—. F)
ьу Г (*0) + а
Перейдем в равенстве F) к пределу при Ду -> 0. В силу
непрерывности обратной функции из Ду ->¦ 0 следует Да: -> 0, а из
Ах ->- 0 следует а ->- 0. Так как по условию /'(*<>) =^= 0, то в итоге
получаем:
lim^ = -J-. G)
ду_о Ay f (*0)
Да:
Но существование lim— и означает дифференцируемость
Ду-0 Ду
обратной функции х = ср (у) в точке у0.
Таким образом, доказана следующая теорема.
Теорема 1. Пусть функция у = / (х) непрерывна и строго
монотонна на отрезке [а; Ь] а дифференцируема во внутренней
точке х0 этого отрезка, причем f'(x0) Ф 0. Тогда обратная
функция х = ф (у) дифференцируема в точке у0 = f (x0), причем
ф'(Уо) = ^
Эта теорема позволяет сформулировать следующее правило
вычисления производной обратной функции: производная обратной
функции есть величина, обратная производной заданной функции:
ху = —> если Ух^°-
Ух
Ниже (см. п. 2 § 3 главы 2) будет доказано, что для строгого возрастания
непрерывной функции у =/ (х), х ? [а; 6], достаточно, чтобы она была
дифференцируема во всех внутренних точках отрезка [а; Ь] и ее производная была
положительной в этих точках. Отсюда следует, что если функция у = f (x), x ? [а\ 6],
непрерывна на отрезке [а; &] и имеет положительную производную во всех
внутренних точках этого отрезка, то для нее существует обратная функция х= Ф (у),
заданная на отрезке [/ (a); f F)], непрерывная, строго возрастающая и
дифференцируемая на этом отрезке. Аналогично обстоит дело, если производная функции
у — f (х) отрицательна внутри отрезка [а; Ь] (в этом случае функция у = f (x)
строго убывает).
3. Дифференцирование обратных тригонометрических функций.
Найдем производную функции у = arcsin x, воспользовавшись
правилом дифференцирования обратной функции. Обратной к
функции у = arcsin х, —1^**^1, является функция х = sin у,
^ у ^ — Эта функция непрерывна, монотонна и дифферен-
46

цируема на отрезке -——; — , причем производная х = cos у
существует и отлична от нуля в любой внутренней точке отрезка.
Имеем:
1 1 1
х cos у cos (arcsin х)
Но cos (arcsin л:) = ]/l —x*l\ Таким образом,
(arcsin x)'
Аналогично выводится формула
(arcsin х)' = г (8)
(arccos*)'= -^J_. (9)
Обе полученные формулы справедливы при условии —1 <х < 1.
Найдем производную функции у = arctg x. Обратной к
функции у = arctg х, —со < х < со, является функция х = tg у,
—— < у < —. Имеем: ху = .
2^2 У cos2 у
Условия теоремы 1 о дифференцируемости обратной функции
выполнены, значит,
у'х = — = cos2 у = cos2 (arctg x).
х'у
Но cos (arctg x) = . Таким образом,
у 1 + х2
(arctg*)'=¦——2 ¦ A0)
1 -f- X
Аналогично выводится формула
(arcctgx)'=-—Ц (И)
1 + X2
Замечание. Формулы (9) и A1) могут быть выведены иначе. Известно,
я
что arccos х = — — arcsin я3). Значит,
2
, / л V /я V
(arccos #) = I — — arcsin д: = — — (arcsin x)'
У г
Аналогично из соотношения arcctg х = — — arctg л; может быть
получена формула A1).
Пример 5. Найдем производную функции
у = arcsin х • arccos x.
х) См. «Введение в анализ», с. 218.
2) Там же с. 219
3> Там же, с. 220.
47

Решение. Воспользовавшись правилом
дифференцирования произведения и формулами (8) и (9), получим:
у' = (arcsin х • arccos x)' = (arcsin x)f • arccos x +
l
+ arcsin x (arccos x)! =
\ У 1 — x2
arccos x + arcsin x X
x
/1 —r
arccos x — arcsin x
V\—x2
Пример 6. Найдем дифференциал функции у = arctg3 Y x
в точке х = 1 при Ал: = 0,08.
Решение. Имеем: / = У~х, и = arctg t, у = и3.
Воспользовавшись правилом дифференцирования сложной функции,
получим:
у>у;>;-';=зи«
1
= 3 arctg2 Ух
1
Значит,
Тогда
У U =
l + (/TJ
3 arctg2 1
1 + t2 2 J/7
1 _ 3 arctg2 /7
2"j/7 2}/7A + *)'
2. 1.A + 1)
4
Зя2
64 '
dy - y'd* = — . 0,08 = —.
J J 64 800
Пример 7. Найдем производную функции
у = arcsin (sin х).
Решение. Имеем:
1 ... cos х cos л:
У =
COS X :
1/1 —sin2 л: l^cos2^ | cos x f
Замечаем, что если cos x > 0, то у' = 1; если cos я < 0, то
у' = —1, если cos х = 0, то у' не существует. Полученный
результат хорошо иллюстрируется на графике функции у= arcsin (sin x)l\
изображенном на рисунке 25. В
точках х = (- лп график
имеет излом.
4. Дифференцирование
показательной и логарифмической
функций. Найдем производную
функции у = ех. Дадим аргумен-
Рис. 25
1) Эта функция рассматривалась
во «Введении в анализ», с. 219
48

ту приращение Ал:. Получим:
Ау=ех+Ах-ех = ех(еАх-1)
и далее:
1« А у 1- еХ (е
Дя-оАя Дд;-*о
Ах
-1)
Ах
Постоянный множитель ех вынесем за знак предела, а бесконеч-
1 заменим эквивалентной бесконечно малой
ЛД*
но малую е
кхг). Получим:
Итак,
д^_о А*
оХ lim — = ех
Д*-оА*
(е*)' = е*. A2)
Мы видим, что функция у = ех обладает замечательным
свойством — она остается неизменной при дифференцировании. Этим и
объясняется большое значение, которое имеет функция у = ех
в математическом анализе.
Пример 8. Вычислим величину угла, который образует
график функции у = ех с осью ординат в точке пересечения с этой
осью.
Решение. Имеем у' = е*.
График функции у = е* пересекает ось ординат в точке @; 1).
Так как у' \х=0 = е° = 1, то тангенс угла наклона касательной
к графику функции у = ех в точке х = 0 равен 1, а потому
касательная образует с осью абсцисс угол, величина которого равна —.
4
Тогда и с осью ординат касательная образует угол, величина
которого равна —.
На рисунке 26 изображен график функции у = ех
внимание на поведение графика в точке х = 0).
Полученный в примере 8
результат позволяет дать новое
определение числу е: числом «е»
называется основание
показательной функции, график
которой пересекает ось ординат под
л;
углом —.
Найдем производную
функции у = In х, х > 0. Эта
функция является обратной по
отношению к функции х = еУ.
(обратите
1) См. «Введение в анализ», с. 212.

Функция х = еУ непрерывна, строго монотонна на ]—оо; оо[ и
имеет производную х'у = еу, нигде не обращающуюся в 0. Значит,
все условия теоремы о дифференцируемости обратной функции
выполнены и мы получаем:
1 1
Но еу = х, значит:
Aп*)'=-. A3)
Формула A3) справедлива при х > 0.
Заметим, что формула A3) может быть получена аналогично
тому, как была получена формула A2).
Отметим одно важное обстоятельство. Из формулы A3) следует:
lim (In х)' = Нт — = 0.
х-*--\-оэ х-*-+°° X
Но (In x)' геометрически выражает тангенс угла наклона
касательной к графику функции у = In x в точке х. Таким образом,
lim tg a == 0,
т. е. lim а = 0. Это означает, что при достаточно больших х каса-
x-*-foo
тельная становится «почти параллельной» оси абсцисс. Указанное
обстоятельство необходимо учитывать при построении графика
функции у = In х.
Пусть теперь дана функция у = ах, где а >0 и а Ф 1. Так как
а = е{па, то
у = ах = (е1п а)х = ек 1п а.
Значит, функцию у = ах можно рассматривать как композицию
функций у = е*, t = х In а. Тогда
(ах у = (ех 1п ау '= (е% - (х In а)'х = е? • In a = ex In a In a = ax In a.
Итак,
(аху = я*1па. A4)
Равенство A4) можно записать в виде:
(ekxy = kekx,
где fe = In а. Оно показывает, что функция у = ekx является одним
из решений уравнения у' = ky. Легко проверить, что при любом С
функция у = Cekx также является решением этого уравнения.
Таким образом, уравнение у' = ky имеет бесконечно много решений,
зависящих от одного параметра С. Уравнения, содержащие
функции и их производные, называет дифференциальными
уравнениями.
60

Дифференциальное уравнение у' = ky показывает, что скорость изменения
величины у пропорциональна значению этой величины. Такой закон изменения
называется законом натурального роста. По такому закону возрастают вклады
в сберегательной кассе (чем больше вклад, тем большую сумму начисляют в
виде процентов), популяция животных, имеющая неограниченный запас корма
(чем больше особей, тем больше потомства), и т. д. При k < 0 мы имеем дело с
убывающей величиной, скорость убывания которой пропорциональна ее
значению. Примером такой величины может служить масса радиоактивного вещества
(чем больше вещества, тем большее число атомов распадается за данный
промежуток времени).
Найдем, наконец, производную функции у = loga x. Имеем:
У' = flog. хУ = (!!!?.)' = -J- • (In х)' = -L-.
\ In a J та xln a
Итак,
2х
Пример 9. Найдем производную функции у = .
In л:
Решение. Воспользовавшись правилом
дифференцирования частного и формулами A4) и A3), получим:
2х у __ BХУ -In* — 2х • (In jc/ __
\пх) ~ (In л:J ~~
2х- In 2 • lnx — 2х • —
= П ?=-^1-(х1п2. 1п*-1).
In2 a: xln2 x
Пример 10. Найдем производную функции у = e*rctg3x.
Решение. Воспользовавшись правилом дифференцирования
сложной функции и формулами A2) и A0), получим:
у = (earctg зху == garctg з* . (arctg 3^/ = ^arctg sjt x
х—L-.C^=3earctg3\
1 + C*J ' 1+9jc2
Пример И. Докажем, что функция у = log^. а
удовлетворяет дифференциальному уравнению xy'ln д; + у = 0.
Решение. Найдем у' для данной функции, перейдя в
выражении log* а к натуральным логарифмам:
1 kia
log* я
Имеем:
In*
lna V — In/» <1П*)' _ 1пД
\ In х / (In *J a: In2 л;
Тогда
что и требовалось доказать.
/ 1м . i^ —In а . , w In a , In а Л
ху lnx + y =xlnx - __- + log^a = — 1- = 0,
х In2 x In x In x
51

Пример 12. Докажем, что множество L функций вида
у = ekxPn (*),
где k фиксировано и Рп (*) — многочлен, степень которого не превышает п,
является линейным пространством, причем дифференцирование — линейный
оператор в этом пространстве.
Решение. Так как сумма многочленов, степень которых не
превышает п, является многочленом того же вида, равно как и произведение такого
многочлена на число, получаем, что как сумма екл Рп (х) + ekxQn (x), так и функция
aekxPn (х) принадлежат L. Значит, множество L — линейное пространство*
Далее имеем:
(ekxPn (*))' = Ье**Рп (*) + е**Р'п (*) = ekx (kPn (х) + Р'п (х)).
Ясно, что kPn (x) + Р'п(х) многочлен, степень которого не превышает я,
и потому (ekxPn (х))' ? L. Значит, дифференцирование —оператор в L. Так как
(аУ1 + Р Уг)' = аУ{ + Р Уг» то этот опеРатор линеен.
5. Дифференцирование гиперболических функций1). Напомним, что
гиперболическим синусом sh х называется выражение , а гиперболическим
вх -\- в~~х
косинусом ch х — выражение . Найдем производные функций
у = sh х и у = ch х.
Имеем:
/ ех __ р-х \'1 1 рх _}_ е~х
<**>'-(—j—) -?М'-Т<«-')' ^—-*«•
Итак,
(sh x)' = ch х, A6)
(ch x)' = sh *. A7)
Найдем производные гиперболического тангенса и гиперболического
котангенса.
Имеем:
Sn* Y (sh *)'ch * — sh * (ch *)' ch2* — sh2*
(th*) : -
A8)
СП" *
Аналогично выводится формула
(cth*y=-—L-. A9)
sh2*
Обратите внимание на то, что формулы для вычисления производных
гиперболических функций аналогичны формулам для вычисления производных
тригонометрических функций.
ит,
(th*)'
(ch x2)
1
ch2*'
ch* / (ch*2) ch2*
Ho ch2 * — sh2 * = l2). Значит,
1) См. «Введение в анализ», с. 200—202.
2) Там же, с. 202.
52

6. Сводка правил и формул дифференцирований.
1) Правила вычисления производных:
(см + с2и2 + ... + спипУ = аи\ + с2и'2 + ... + спи'п\
(uv)' = u'v + uv';
I и У u'v — uv'
\v
, в частности,
xf
Vй \ V t
Если у = у @, t = t (х), то у'х = у\- fx.
2) Правила вычисления дифференциалов:
d (см + с2и2 + ... + спип) = cxdu± + c2du2 +
d (uv) = vdu + udv\
и \ vdu — udv
+ cndan\
\ V J V*
3) Формулы вычисления производных:
(СУ = 0;
(kx + Ь)' = k\
(sin я)' = cos x\
(cos a:)' = —sin x\
1
(tg*)' =
(ctg*)' =
1
snr jc
(*<*)' = a%a_1, в частности:
(lnx)' = l;
(a*)' = a*lnfl;
(log^)'= !
1
1
(arcsin х)' =
(arccosx)' = _
(arctgx)' = -^;
(arcctg x)f =
л; In a
(shx)' = chx;
(ch л;)' = sh x\
1
(thx)' =
ch2*'
1 + *'
¦2'
(cth x)'
я дифф<
d(tg*) =
l
sh2*
4) Формулы для вычисления дифференциалов:
dC = 0; J '*- - ^
d (fee + b) = Adx;
d (xa) = owe»-1 dx;
d(ctgx) = ¦
d (arcsin x)
d*
sirr х
dx
vr.
d (sin x) = cosxdx;
d (cos я) = —sinxdx;
d (arccos x) =
- г
. '
У 1-х2
53

d (arctg x) = -^--; d (logfl x) = -^-;
1 + я2 * In a
d (arcctg x) = ; d (ch x) = sh xdx:
d(ex) = e* d#; d (sh *) = ch xdx
d(ln*)=-; d(th*) =_^-_
л: ch2*
d(a*) = a4nadr, d(cthx) = — dx
sh2 x
При вычислении производной данной функции сначала
выясняют, каким правилом следует руководствоваться, а после
применения правила используют необходимые формулы. Именно так мы
и поступали при решении примеров этого параграфа.
7. Логарифмическое дифференцирование. Пусть нужно найти производную
функции
У-1ПК5Г=П" >B* + 3K
х— 1
Упростим выражение, пользуясь свойствами логарифмов. Получим:
у = — In C* — 1) + 3 In Bx + 3) — In (x — 1).
Теперь искомая производная может быть легко найдена последовательным
применением правила дифференцирования линейной комбинации и композиции
функций (это будет сделано ниже).
Во многих случаях при нахождении производных частного двух функций,
произведения нескольких функций, показательно-степенных функций
пользуются формулой логарифмического дифференцирования. Так называется формула
для производной логарифма данной функции. Пользуясь свойствами логарифма,
сначала находят производную логарифма данной функции, а по ней легко
получают искомую производную самой функции. Покажем, как это делается.
Пусть нужно найти производную функции у= f (х), х ? X, в такой точке
х0 ? X, где f (а:0) > 0. Введем в рассмотрение функцию и— In (/ (x)) и найдем
ее производную (как мы отметили выше, во многих случаях и' находится проще,
чем f (а:)). Но и — In у, а и' = (In у)' = —у'. Значит,
У
Aпу)' = -. B0)
Это и есть формула логарифмического дифференцирования. Из нее следует, что
/ = У (In у)'. B1)
Пример 13. Найдем производную функции
/З^Л .B* + 3K
у х—\
Решение. Воспользуемся методом логарифмического
дифференцирования. Рассмотрим функцию
х — 1
54

и = — In (Зл: — 1) + 3 In B* +3) — In (x — 1).
Имеем:
и' = j (In C* - 1))' + 3 (In Bx + 3))' - (In (x - 1))' =
11 11 30л;2 — 59*+ 9
3 + 3- -• 2-
2 Зл:— 1 2л:+3 x—l Fл: — $) Bx + 3) (x — 1)'
Тогда по формуле B1) получим:
, _ УЪх — 1 • Bx + ЗK _ 30л:2 — 59л: + 9
* — 1 F* — 2) Bл- + 3) (х — 1)
Bх + ЗJ C0л:2 — 59л: + 9)
~ 2 (х — IJ Bл: + 3) /3* — 1 '
Пример 14. Найдем производную функции
у = (sin x)cos * , 0 < х < я.
Решение. Рассмотрим функцию и = In у и вычислим ее производную:
ы' = (In у)' = (In (sin л:)С055 *)' = (cos л: • In sin x)' = (cos x)' • In sin л: +
, 1 cos2 x
+ cos x • (In sin л:) = —sin л: In sin x + cos x • cos x = —:— —
sin л: sin л:
— sin x In sin л:.
Тогда
(cos2 x \
— sin x In sin x}.
sin* /
У рассмотренной в примере 14 функции и основание, и показатель степени
были переменными. Такие функции называются показательно-степенными
Выведем правило дифференцирования показательно-степенной функции.
Пусть у = uv, где и и v — дифференцируемые в точке х функции, причем
и (х) > 0. Тогда / = uv • (In uv)' = uv -(v In u)' = uv ( iHn a + у —и'J.
Отсюда получаем:
(Uvy = uv\nu • v + vu*-1 • и'. B2)
Воспользуемся этой формулой для вычисления производной функции у = хх.
Получим у' = Xх In х + л: • л:*-1 = л:* (In л: + 1).
Вопросы для самопроверки
1. Где при выводе формулы (sin x)' = cos x была использована
непрерывность функции у = cos х?
2. Эквивалентность каких бесконечно малых мы использовали при выводе
формулы (sin х)' = cos х?
3. В чем состоит физический смысл формул (sin х)' = cos xt (cos x)' ==»
= —sin x?
4» Для каких значений х справедлива формула (tg х)' = —— ?
55

1
5. Для каких значений х справедлива формула (ctg х) = — , ?
sin2 х
6. Сформулируйте теорему о дифференцируемости обратной функции.
7. В чем заключается правило вычисления производной обратной функции?
Дайте геометрическое истолкование этому правилу.
8. Эквивалентность каких бесконечно малых мы использовали при выводе
формулы (ех)' = ех?
9. Какой угол образует с осью ординат график показательной функции
у = ех7
10. В чем состоит метод логарифмического дифференцирования?
Упражнения
Найдите производные следующих функций.
1 ЯГРРЛ^ У
87. 1) у =s х2 + ех + sin х\ 2) у = — 2х — In х\ 3) у =3arcsin х— .
3 5
88. 1) y-^tg,; 2) „-.!„,.8*; 3) , , ^; 4) у = 4l?±SLfL.
1 + #3 sin л; — cos jc
89. 1) у = sin 3*; 2) у = cos -~ 3) у = In2 *; 4) у = е5*"; 5) у =Уtg*;
6) у = arcsin Зд;; 7) у = arccos3 х\ 8) у == 21-*.
5
90. у = sin (*2 — 5л:+ 1) + tg—.
з. 1
91. у = у sin2 л: 4
cos2 х
92. у = /2е* + 2*+1.
93. у = arctg In ^ + In (arctg л:).
х
94. у => In cos2 *—. 95. у = In "j/ cos л; + }/~2\
96. у = In (л; — 1) /(* + IJ (л: — 2).
97. у = In sin (*л). 98. у = sin (nV7).
99. у = In5 tg Зх. 100. у = In tg2 f-|- + — |.
101. у = In (arccos 77=Ч'
X 1
102. у = In tg — + cos x + — cos3 л:.
^ о
103. у = In l/ S,m2* ¦ Ю4. у = sin 2*sin2 *.
Г 2A+a;N
l(\+xy
105. у = 2 " * . 106, у = In tg
tg— e2sin*
107,
56
. у = 1/ arcsin ~. 108. у = sin3 arctg Ъ/\ — 2х,

109.
111.
И 2.
113.
114.
116
118.
119.
120.
121.
122.
123.
125.
У =
У =
У =
У =
У =
У =
У =
у =
У =
У =
У =
У =
У =
. arccos Yхь—4
sin л: 1, ,
:^^r-7lntg
— sin д: A + In cos x).
— tg2 (sin x) + In cos
1— X2
arcsin ——-.
1 + x2
5a:+1
= arcctg ]/Щ.
дг arcsin x ,
1 In 1/1
: , -j- 1П У 1 •
У 1 — A:2
= a- (arcsin a-J + 2 ]/T
1 * •
T g x
-e «cos a:.
= x arcctg V cos e
2
= bg2tg-.
= bgx22-f 2^.
<(t-
(sin x).
~».
~^72a
T
no.
•!)•
115.
117.
У =
У
У
resin a: —
124.
У =
1 А*
In +rt
- 2btg2~
2a:4
= arctg -.
1 —X8
X
= ^утТ.
•2x.
5X
= bg3ctg-.
COS A*
2 sin2 a:
P~*
Найдите частные значения производных для следующих функций.
126. у=4 arcsin — — V16 — а:2 при х — 2.
127. у = 2 /3 arctg -=. + In Yx2 + 3 при х = 3.
У з
A: COS At ЗТ
128. у = 15 lntg -- + -7-7- (8cos4 a; — 25 cos2 x + 15) при а: = —.
129. Покажите, что функция у = Аге1""^, где С — произвольная постоян-
/ У У
ная, является решением дифференциального уравнения у = — In —.
130. Покажите, что функция у = 2а- arctg Сх является решением дифферен-
у
циального уравнения ху' = х sin by.
X
131. Покажите, что функция у — Се~х -\ (cos x + sin x) является
решением дифференциального уравнения у' + у — cos x.
132. Составьте уравнения касательных к кривой у = е{"~*2 в точках ее
пересечения с прямой у = 1.
57

I x
133. Составьте уравнение касательной к линии у = arctg — в точке ее
пересечения с прямой х — 2 = 0.
134. Составьте уравнение касательной к графику функции у=е^^Ш{^ 3)
4
в точке его пересечения с прямой у = е .
135. Составьте уравнение той нормали к кривой у = In Bл; + 1), которая
перпендикулярна прямой у = х.
136. Зависимость пути от времени при прямолинейном движении точки зада-
1 2 jt
на уравнением s = — г5 ~\ sin -—-1 (время в секундах, путь в метрах).
Определите скорость движения в конце второй секунды.
137. Тело массой 8 г движется прямолинейно по закону s=— 1 +
_|_ in(^_|_i)_j_(f + 1K (путь в метрах, время в секундах). Вычислите кинетическую
(mv2\
энергию — через одну секунду после начала движения.
Найдите производные следующих функций.
138. у = sh3 4х +_ ch3 V~x~.
139. у = th6 BeVx— l):
140. у = sh (In (x + Yx* + 1)).
141. Дана функция f (x) = cth2 x. Найдите f A).
В следующих примерах вычислите производную, применив метод
логарифмического дифференцирования.
142. у = (ctg xf\ 143. у = (х* + 3)/Г.
144. у = (cos *)arctg * . 145. у = (j/Tg^)^1.
1 л:
. ,xsinx <Л^ In2 х
146. у = (*+1) . 147. у = х
у гх
148. у = (*-!). 1 (* + *J(*-2) 5-
149. у = (* + IJ • V (*- ЗL • D - х) 3
150*. Покажите, что функция у = / (х) не имеет производной в точке л; = 0:
f . 1 л ( ^Т> *=^0,
1WM== „in-. ^0, 2)/w= -
I 0 , * = 0; [О , х = 0;
если л: рационально,
если х иррационально,
0 , х = 0.
151*. Докажите, что функция
( sin x,
'= 1 *,
дифференцируема в точке х = 0.
58

152*. Какие условия нужно наложить на показатель h, чтобы функция
1
*ftsin —, хфО,
X
О , * = 0,
а) была непрерывна при х = 0; б) была дифференцируема при х = 0; в) имела
непрерывную производную при х = 0?
§ 7. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
1. Понятие производной /г-го порядка. Пусть на некотором
множестве X определена дифференцируемая функция у = f (x).
Производная /' (х) этой функции, рассматриваемая на
множестве X, является функцией от х. Следовательно, можно говорить о
производной полученной функции, т. е. о производной от первой
производной. Если она существует, то ее называют производной
второго порядка функции у = f (х) или, короче, второй
производной и обозначают у" или /" (х). Значит, по определению у" = (у')\
Аналогично, если существует производная от второй
производной, то она называется третьей производной и обозначается у"'
или /'" (х). Значит, по определению у'" = (у")'.
Вообще, производной п-го порядка называют производную от
производной (п — 1)-го порядка. Производную n-го порядка
обозначают у(п) или f{n) (х). Значит, по определению
у (П) = (у(й-1))'#
Мы видели выше, что, обозначая первую производную, иногда
указывают переменную, по которой берется производная, например,
пишут у'х, y't, s't и т. д. Необходимость в указании переменной
может возникнуть и при повторном дифференцировании. В таком
случае вместо у" пишут у"х2. Такая запись означает, что первая
производная по х еще раз дифференцируется по этой же переменной:
у* = (уТ.
Аналогично третья производная обозначается у"^ и вообще
производная п-то порядка обозначается у^п.
Заметим, что понятие л-й производной определено нами индуктивно: от
первой производной перешли ко второй, от второй к третьей и т. д.
Соотношение у№ ~ (У^*-1))' называют рекуррентным («возвратным»), поскольку оно от
п-й производной «возвращает» нас к (л — 1)-й производной.
Пример 1. Найдем /"' A) для функции у = хъ.
Решение.
у' = Ъх\
у" = E*4)' = 20х3,
у'" = B0Х3)' = 60*2.
Значит, /"' A) = 60 • I2 = 60.
У =
59

Пример 2. Найдем у(п) для функции у = ха, я > 0.
Решение. Имеем:
у' = ах*-\ у" = а (а - 1) ха~\
у'" = а (а — 1) (а - 2) ха~3.
Отсюда можно сделать индуктивное предположение, что
(ха)(п) = сс(а - 1)(а — 2)... (а - п + 1) ха~п.
Эта формула уже доказана при п = 1. Предположим, что она верна
при п = kt т. е. что
(хУ* =а(а— 1)...(а —ft+l)*06-*.
Тогда имеем:
(*af + l)^{(xa){k)y^{a(a-l)t..(a-k+l)xa^ky=a(a^l).t.
...(a-ft)*"-*.
Следовательно, формула верна и при п = k -\- 1. По принципу
математической индукции выводим, что она справедлива для любого
натурального /г. Отметим, что если а — натуральное число и а=т,
то
(*m)(m) = m!
При /г > m имеем:
(хт )(rt> = 0.
Пример 3. Найдем у{п) для функции у = sin x.
Решение. Имеем:
у = cos х,
у" = —sin xf
у'" = —cos х,
D)
У ' = sin x,
E)
)Г = COS X,
Чтобы установить закон последовательного составления
производных, воспользуемся формулами приведения:
cos х = sin (х + —) , — sin x = sin (x + n),
— cos л; = sin (a: 4— я ], sin я s=s sin (x + 2n).
Тогда получим:
/ = sin (*+!),
у" =sin (* + 2|),
60

/" = sin(* + 3f),
у =cosxlx + 4—\.
Возникает естественное предположение:
yn) = sin^ + «|). A)
Докажем его справедливость методом математической индукции.
При п = 1 формула A) верна. Предположим, что
У = sintx + k— , и докажем, что тогда
В самом деле,
/ + » = (/у e (sin (х + k f ))' = cos (* + А|) =
- sin(f + (* + *|)) - sin ((* + (*+ l) |).
По принципу математической индукции заключаем, что формула
A) верна для любого натурального п.
Например,
(sin*) 115) = sin (x+ 115 • —] = sinuc + — J = —cosx.
Точно так же доказывается, что
(cosx)(n) = cos (л: + пА).
Пример 4. Докажем, что
хп
Решение. Так как (In х)' = —, то (см. пример 2)
х
Aпа-)("> = (x-if1^ (- 1)(- 2)... (-п + \)х'п = (~1)П"^~1)!.
Пример 5. Докажем, что функция у = e*cos *
удовлетворяет дифференциальному уравнению у<4> + 4у = 0.
Решение.
у'- = (e^cos л:)' = (ех)' cos я + ех (cos л:)' =
= ех cos л; — е* sin л; = е* (cos x — sin x);
у" = е* (cos я — sin я) + б* (—sin я — cos х) = —2е* sin л;;
61

у'" = — 2ех (sin x + cos x);
у( ' = — 4е* cos х .
Значит,
уD)+ 4у = — 4е* cos* + 4e*cos# = 0,
что и требовалось доказать.
2. Механический смысл второй производной. Выше было
установлено, что первая производная пути s по временность
мгновенная скорость:
V = St .
Рассматривая производную скорости по времени tf получим
производную второго порядка, выражающую скорость изменения
скорости, т. е. ускорение:
а = (st )'t = st2.
Пример 6. Тело движется прямолинейно по закону s =
= I0t2 + 3t — 1 (s в метрах, t в секундах). Докажем, что тело
движется под действием постоянной силы.
Решение. Имеем:
s' = A(М* + 3* — 1)' = 20* + 3,
s" = B0* + 3)' = 20.
Так как s" = а, то ускорение постоянно и равно 20 м/с2. Но по
закону Ньютона сила пропорциональна ускорению. Значит, сила
постоянна.
Пример 7. Гармоническое колебание описывается законом
s = A cos (со* + а), где * — время, s — смещение колеблющейся
точки от оси, Л, со, а — постоянные величины (амплитуда, угловая
частота и начальная фаза колебаний). Докажем, что закон
гармонических колебаний удовлетворяет дифференциальному уравнению
s" + co2s = 0.
Решение. Имеем:
s = —Л со sin (ш* + a),
s" = —А со2 cos (со* + а).
Тогда
s" + co2s == —Л со2 cos (со* + а) + a2 A cos (со* + а) = 0,
что и требовалось доказать.
Пример 8. Длина вертикально стоящей лестницы равна 5 м.
Нижний конец лестницы начинает отодвигаться от стены с
постоянной скоростью 2 м/с. С какой скоростью опускается в момент
времени * = 2 с верхний конец лестницы? Чему равно его ускорение
в этот момент времени?
62

Решение. За/с нижний конец лестницы Т]\6=5-[/25-И2
пройдет расстояние 2 t м. По теореме Пифагора * и ~
(рис. 27) находим, что верхний конец
находится в этот момент на высоте К25 — 4Г2, а значит,
он прошел путь s = 5 —j/25 — 4/2. Это закон ^J
движения.
Имеем:
г
s' = —1 B5 — 4/2) 2 (— 80 = . 4/
2 V ' ' V 25 - 4/2 '
S =
4/
.У 25-
1-/25 — 4/2 + *•
4/
= 4--
У 25 —4*2
2t
Рис. 27
100
4? / 25 —4/2 УB5 — 4/2K'
Тогда искомая скорость находится следующим образом:
и =s' B) =
а искомое ускорение
a=s"B) =
4-2
/25 —4-22
100
8 ,
7 м/с>
100
м/с2
У B5 —4-22K 27
3. Натуральная степень бинома (формула Ньютона). Пусть дана
целая рациональная функция
/ (х) = а0 + агх + а2х2 + ... + апхп.
При х = 0 получим: а0 = f @).
Покажем, что остальные коэффициенты этого многочлена
выражаются через производные от / (х) в точке х = 0.
В самом деле, имеем:
р (х) = аг + 2а2х + 3asx2 + \atf? + ... + папхп"\ B)
Положив в этом равенстве х = 0, получим: аг = /' @).
Продифференцировав обе части равенства B), будем иметь:
/" (х) = 2а2 + 3 ¦ 2а3х + 4 • 3a4x2 + ... + п (п — 1) аЛл;Л-2.
Положив в этом равенстве х = 0, получим:
_/"@) НО)
Аналогично находим:
„ _ ГЖ а - /D)@) a
3! ' * 4!
Итак, если / (я) — многочлен я-й степени, то
/(п)@)
п!
/w-/(o) + Mx+m^.
?®,*+.л+е±т*
3!
л!
C)
6?

Точно так же выводится более общее равенство:
/(Л) = /(а)+021(^_а)+...+^)(^-аГ,
называемое формулой Тейлора для многочлена f(x).
Применим формулу C) к целой рациональной функции / (*) =
= A + х)".
Имеем:
Г(х) = пA+х)я-\
!"{х) = п{п-\){\+х)п-\
Г (х) = п (п — 1) (п — 2) A + х)п-\
Тогда
р*-*\х) = п (п — 1) (п - 2) ... 2 A + х),
/<«> (х) = п (п — 1) (п — 2) ... 2 • 1.
а0 = f @) = 1,
Gl = /' @) = п,
_ f" @) _ n(tt-l)
2 2! 2!
_ f"@) _ n(«-l)(n-2)
Uq ' .
8 3! 3!
/ (n-\) (Q) * л (я— 1) (/г —*2)!. .2
йй_1 =
Л~1 (/г-1)! (л-1)!
_ /(*) @) /г (/г — 1)(/г —2). . .2»! _ .
п п\ п\
Таким образом, по формуле C) получаем:
(l + Xy = l+nx + SLULzRх' + »("-')fr»-g) *з +...
21 3!
...i - * -t-...+ я в D)
Обычно обозначают
П(П — 1)(П_2) = Сз /г (п — 1) (п — 2).,.(/t — fe+1) ^ с*
3! П ' "' /г!
Тогда формула D) перепишется в виде
A+х)п =1 +Clnx + CU*+...+Cknxk +...+СГ1 ^-] + ^.E)
Полученное равенство называется формулой Ньютона, а
коэффициенты 1, С1п, Сп9 ..., C«,..., Сп ~1, 1 — биномиальными,
64

Отметим некоторые свойства биномиальных коэффициентов.
Прежде всего получим более компактное выражение для С*. Имеем:
ck__ n(n- \)(n — 2). .(n — k+\) n(n—\)...{n — k+\)(n—k). . .3-2-1 __
П~~ k\ ~ Щп — Щ...Ъ-2Л ~~~
"" k\(n — k)\ #
Итак,
Гк — п]'
п~~~ k\(n — ky #
Так как
рп — k _ П\
П ~ (n — k)\k\ *
то
С к рп — k
Полученное равенство показывает, что биномиальные
коэффициенты, равноудаленные от концов разложения A + х)п по
степеням х, равны между собой.
Положив в равенстве E) х = 1, получим:
2* = 1 + С\ + С2п + . .. + СГ2 + Спп~1 + 1,
т. е. сумма биномиальных коэффициентов в разложении A + х)п
равна 2п.
Отметим еще одно свойство биномиальных коэффициентов.
Для этого умножим обе части равенства E) на 1 + х. Получим:
A + х) п + Х = A + *)A + х)п =A + х)(\ +С\х + С\х* + ... +
+ С* # + С* +V+1 + ... + ОТ1 хГ~1 + *") = 1 +0+Ci ) х +
+ (Cln +C2n)x*+... + (Ckn + Ckn + l)xk + l + ...+*"+1. F)
С другой стороны, применив к A + х)п + 1 формулу Ньютона,
получим:
A + Х)» + 1 = 1 +Cln + lx + C2n + l х* +-..+ Ckn%\ xk + l + ... +
+ *n + l. G)
Сравнивая в равенствах F) и G) коэффициенты при одинаковых
степенях х, получаем:
Ckn + Ckn+l^ Ckni\. (8)
Пример 9. Напишем разложение по степеням х для A + л:N.
Решение. Имеем:
A + x)Q = 1 + Cl х + CgV + Cl xs + Ct л-4 + Cl x5 + x6.
65

Вычислим биномиальные коэффициенты:
Ci = C8 = 6, Cl =Ci =6-' = 15, Cl =|^=20.
В итоге получаем:
A + xf = 1 + 6x + 15a:2 + 20х3 + 15x4 + 6хъ + x\
4. Свойства производной п-то порядка.
а) Производная п-го порядка от суммы конечного числа п раз
дифференцируемых функций равна сумме производных порядка п,
взятых от каждой слагаемой функции.
Доказательство (для случая суммы двух функций). Пусть дана
функция у = и + v\ последовательно дифференцируя ее, будем
иметь:
у' = и + v',
у" = (/)' = (и' + Г/)' = (и')' + (V'Y = U" + v".
Используем метод математической индукции. Предположим, что
производная порядка п = k будет
у<*> = а<*> + !><*>,
и покажем справедливость нашего предположения для п = k + 1,
т. е. покажем, что
у(/г+1) __ и(А+1) _|_ 0(ft+l)e
В самом деле, имеем:
y(*+i) = (и<*> + г/*>)' = (и<*>)' + (*;<*>)'= a<*+1> + г/*+1>.
По принципу математической индукции заключаем, что наше
утверждение верно для любого натурального п.
б) Постоянный множитель можно вынести за знак
производной п-го порядка (Си){п) = Си{п).
Доказательство предоставляем читателю.
в) Если и и v — две функции, имеющие производные до п-го
порядка включительно, то
(uv)W = и№ + Clu'ifi»-» + C%u"zfin-v + ...+¦
+ &rj№vi»-b + ... + С!Гхи&-Ъх/ + u^v. (9)
Эта формула носит название формулы Лейбница.
Доказательство формулы Лейбница проведем методом математической
индукции. Для п = 1 формула верна
(uv)f = uv + и'v.
Предположим, что она верна для п= р, т. е. предположим, что
(ио)М = w№ + Clpu'v{p-l) + су^Ъ-Ъ + ... + Ckp u^k) o<P-*) +

Докажем, что тогда формула верна и для п = р + 1, т. е. что
(ati^+D = ш><Р+1) + CpJrXu'v{p) + C$+iu"v<P-l) +
+ ... + Ckp%\ u<k+l) J"-*> + ... + и<*+1>0.
В самом деле, имеем: (uv){p+l) = ((w»)°,))/ = (uv(p) + СриЪ(р~1) +
+ C^V^2* + ... + Ckp u& v<p-k> + CjH «<*+!> 0(p-*-1>+ .. +Cp~l u<p-%'+
+ Л)' = t/vW + uv{p+l) + C* (u"v&-V + 1/0»)) + C^'V* + u"v<P-l)) +
+ ... +Ckp(u{k+l)v(p-k) +u<k) v(p~k+l)) + Ck+\u{k+2) 0(P-*-D+M(*+iHC^-*))+
+ ... + и^+^о + uip)v' = ио»+1> + A + Cp) u'v{p) + (Clp + C2p) u"v(p~V +
+ ... + (Cj + CJ+1) «<*+« o<^> + ... + ^V
Так как С\ + С2 = C2+1, Ckp + C^1 = Ckp+\ (см. равенство (8))
и 1 + Cp = 1 + p = С^+1. то получаем:
(ao)(^+1> = uv{p+l) + ^+1^(^ + С2+1и "t^-1* +
+ ... + Ckp%\ а^1) 0<"-*> + ... + u<p+%.
По принципу математической индукции заключаем, что формула (9)
справедлива для любого натурального п.
Для запоминания формулы Лейбница рекомендуем обратить
внимание на аналогию формул (9) и E). Например, для п = 6
имеем:
(ии)Ю = uv™ + 6и'о<в> + 15aV4> + 20uf"x/" + IbuPW + 6a<5V+
+ ti^h (см. пример 9).
Пример 10. Найдем выражение для /г-й производной
функции
2* + 3
У = ! .
' х2 — Ъх + б
Решение. Имеем:
2* + 3 _ 2х + 3
х2 — 5* + 6 (* — 2) (* — 3)
Подберем коэффициенты А и В так, чтобы выполнялось равенство
2*+3 =-^- + -g-. A0)
(л;__2)(х —3) х —2 х —3 v ;
Тогда по свойствам а) и б) будем иметь:
2* + 3 Г = а . (-1-Г + в (JLY*.
*2__5* + 6/ U —2у U —з/
Чтобы найти коэффициенты А и В, освободимся от
знаменателей в равенстве A0). Получим:
2х + 3 = А (х — 3) + В (х — 2)
67

и далее:
2х + 3 = (А + В) х + (—ЗА — 2В).
Но два многочлена тождественно равны тогда и только тогда,
когда равны их коэффициенты при одинаковых степенях
переменной. Это замечание приводит к системе уравнений
Г А + В = 2,
{-ЗА — 2В = 3,
решив которую находим:
(А = -7,
15 = 9.
Итак,
Осталось вычислить п-е производные функций и .
Пусть
и = = (х + а).
Тогда
и = — (х + а),
и" = 2 (х + а)",
и'" = —3! (х + а).
Методом математической индукции можно доказать, что
№ = (_1)я . п\ (х _j_ a)-"'1. A2)
Таким образом, из равенств A1) и A2) получаем:
у(я) = —7 . (—1)п . п\ (х — 2Р + 9 (—\)п -п\(х — Зр-1 =
= (-!)«. nlf—1
Пример 11. Найдем уC0) для функции у = xsex.
Решение. По формуле Лейбница имеем:
},C0) = (Х3е* )C0) = Х3 {ех )C0) + С10 {х3у {ех )B9) + ^ ^у {&X )B8) +
+ Cio (х3Г (в* р> + С|о (*3)D) (е* )B6) + ... + (x*f°>ex.
Заметим, что
(Xs)' = Зх\ (х3)'" = 6,
(*3)'' = 6х? (Х3)D) = О
и все последующие производные функции х2 равны 0. Таким образом,
уC0) ^ Х3{ех )C0) + С10 . 3^2 (^ )B9) + C2Q . fo (g* )B8) + Q^ . 6 . (^ )B7>в
68

Далее имеем:
(е*)' = {ех)" = ... = (ех)М = ех.
Значит,
у(зо) ==ех(х3 + ЗС\0х2 + QCiox + 6С|0).
Осталось вычислить коэффициенты. Имеем:
С'0 = 30, Сз2о=^ = 435, С8» = 3° • * • 28 ¦= 4060.
Окончательно получим:
у(зо) = (jc8^)(80) = е*(хв + дох2 + 2610* + 24360).
5. Дифференциалы высшего порядка. Пусть функция у = / (х)
задана на некотором множестве X. Дифференциал dy данной
функции, представляющий собой главную линейную часть приращения
функции, вычисляется, как мы знаем, следующим образом:
dy = /' (х) dx.
Он является функцией независимой переменной х, и,
следовательно, от этой функции можно взять дифференциал, считая
значение dx дифференциала независимой переменной, тем же самым:
d (dy) = d (f (x) dx).
Такой дифференциал называют дифференциалом второго
порядка и обозначают d2y. Таким образом,
d2y = d(dy) = d(f (x)dx).
Так как dx = Ах не зависит от х, то dx — постоянный множитель
и его можно вынести за знак дифференциала:
d (f (х) • dx) = dx • d (f (x)) = dx - f" (x) dx = f" (x) dx2.
Таким образом, дифференциал второго порядка равен
произведению производной второго порядка на квадрат дифференциала
независимой переменной:
d2y = /" (х) dx2.
Полученную формулу можно переписать в виде
d2y = y"dx2, A3)
откуда получаем:
J dx2
Выражение — используется для обозначения второй производной
dx2
(читается: «дэ два игрек по дэ икс квадрат»).
Дифференциалом третьего порядка называют дифференциал от
дифференциала второго порядка (при том же значении dx):
d?y = d (d2y).
69

Имеем:
d*y = d (y"dx2) = dx2 • d (y") - dx2 • (/" • dx) = /"d*8.
Итак,
d3y = y"'dx\
Отсюда получаем:
(это выражение используется для обозначения третьей производной).
Вообще дифференциалом п-го порядка называют дифференциал
от дифференциала (п — 1)-го порядка:
d<*>y = d (dP-Vy) A4)
при том же значении dx.
Таким образом, понятие дифференциала п-то порядка, как и
понятие производной п-то порядка, определено нами индуктивно с
помощью рекуррентного соотношения A4).
Выше мы видели, что dy = y'dx, d2y = y"dx2, d3y = y'"dxz.
Предположим, что d^y = yWdxk, и докажем, что тогда
ctk+1)y = y(k+1)dxk+\
Имеем:
d{k+l)y = d (d(k)y) = d (y{k)dxk) = dxk-d (y(k)) =
= dxk • (y(/°)' dx = dxk y(*+1> dx = /*+1> dxk+\
По принципу математической индукции заключаем, что для
любого натурального п верна формула
d(n)y = y{n)(ixnm A5)
Замечание. Записанная формула дифференциала п- го
порядка верна, если х является независимой переменной. В случае,
когда х — промежуточный аргумент, эта формула, как правило,
неверна. Если у = f (х), х = ф (f), то dx = ф' (t)dt и dx не является
постоянной. Тогда по правилу вычисления дифференциала
произведения (см. правило 4 § 3) имеем:
d2y = d (dy) = d (/' (x) dx) = d (/' (x)) dx + f (x) d (dx) =
= (/" (x) dx) dx + f (x) d2x = f" (x) dx2 + f (x) d2x.
Лишь при условии, что d2x = О, получаем d2y = f" (x) dx2,
т. е. формулу A3). Это будет иметь место, если х—линейная функция
от t: х = kt + b.
Таким образом, форма записи f{n)(x) dxn для дифференциалов вые -
ших порядков неинвариантна.
Пример 12. Найдем d5y для функции у = е2Х при х = О,
dx = 0,1.
70

Решение. По формуле A5) имеем:
d* у = y^dx\
Найдем у<5>: у' = 2е2\ у" = 4е2Х, уг" = 8е2*, у^ = 16^, У5> =32е2*.
Таким образом,
d5y - 32e2W.
При л; = 0, dx =0,1 получаем:
йъу = 32 • е° - @,1M = 0,00032.
Пример 13. Найдем d2y для функции у = я3 + Зл:2 — Зл: + 1
в случае, когда: 1) # — независимая переменная; 2) х — функция
от другой переменной.
Решение. 1) Имеем:
у' = Зх2 + 6х — 3, у" = 6* + 6.
Значит,
d2y = (fa + 6) dx2.
2) Так как для дифференциалов второго и более высоких
порядков свойство инвариантности нарушается, формулой A5)
пользоваться нельзя. Имеем:
d2y = d (dy) = d ((x3 + Зх2 — Зх + 1)' dx) = d (Cx2-{-Qx—3)dx) =
= d Cx2 + 6x — 3) • dx + Cx2 + 6x — 3)-d (dx) =
= Cx2 + 6x — 3)' dx • dx+ Cx2 + 6x — 3) • d2x =
= F* + 6) dx2 + Cx2 + 6% — 3) d2x.
Вопросы для самопроверки
1. Как определяется производная ai-го порядка? Как она обозначается?
2. В чем состоит механический смысл второй производной?
3. Как вычисляется производная га-го порядка от суммы конечного числа
функций?
4. Сформулируйте правило вычисления производной га го порядка от
линейной комбинации конечного числа га раз дифференцируемых функций.
5. Как вычисляется производная га-го порядка от произведения двух
функций (формула Лейбница)?
6. Напишите частные случаи формулы Ньютона для га = 3, 4, 5
7. Как определяется дифференциал 2-го порядка? 3-го порядка? га-го
порядка?
8. Как вычисляется дифференциал га-го порядка?
9. Инвариантна ли форма записи y^dxn для дифференциалов высших
порядков?
10. Напишите формулу для d3y в случае, когда х — промежуточный
аргумент.
Упражнения
Найдите производные второго порядка для следующих функций.
153. у = х У\ + х2. 154. у = е"**-
155. у = arcsin —у- 156. у = arccos -.
у 1 + х2 1 + х2
71

157. Докажите, что функция у = Л cos х + В sin x удовлетворяет
уравнению у" + у = 0.
158. Докажите, что функция у = У*2 — 2 удовлетворяет уравнению
у*у" +2=0.
Найдите производные указанного порядка для заданных функций.
159. у = jc6 -I- е2х, уD) = ? 160. у= х sin2 *, уD) = ?
л:2
161. у= х\пх, у(о) = ? 162. у = , у(8) = ?
1 — X
163. у = х2е2х, уA0)=? 164. у = х2 sin 2х, уE0) = ?
165. у = JL±^, у<100>=?
V 1 — *
166. у = D*3 + За: - II1 (х4 + 4I2 (х7 - 5)в, у<123) = ?, у<124) = ?
Найдите у(/7) для следующих функций.
х2 1 1
167. у = 1п— . 168. у-.
х2 — 4х + 4 х2 (х—1)
х+ 1
169. у = L—-. 170. у = (З*2 + 2х + 1) In (ж + 1).
х (х — 1)
Вычислите дифференциал второго порядка для следующих функций.
Зл-в
171. у = /а:2. 172. у =|/In2 ^ — 4.
1 —л:2
173. Дана функция у = In . Найдите <22у при условии, что: 1) х—
1 + *2
независимая переменная; 2) х — промежуточный аргумент.
174. Покажите, что если тело движется по закону s = ael + be~K то его
ускорение численно равно пройденному пути.
175. Докажите, что ускорение гармонического колебания х = A sin (со/ + а)
пропорционально отклонению х от положения равновесия.
176. Точка движется так, что ее скорость пропорциональна квадратному
корню из пройденного пути. Покажите, что движение происходит под действием
постоянной силы.

ГЛАВА
2
ПРИМЕНЕНИЯ
ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
1. СВЯЗЬ МЕЖДУ ХОДОМ ИЗМЕНЕНИЯ ФУНКЦИИ
И ЕЕ ПРОИЗВОДНОЙ
До сих пор мы занимались исследованием функций, не
пользуясь производной. Производная помогает детальнее изучить
свойства функций: установить, в каких интервалах функция возрастает,
а в каких убывает, в каких точках функция достигает наибольшего
значения, а в каких — наименьшего, где график функции
представляет собой выпуклую кривую, а где — вогнутую и т. д. Изучение
этих (и других) вопросов составляет содержание главы 2. Цель
настоящего параграфа — ввести читателя в указанный круг
вопросов, дать наглядное истолкование ряда результатов, которые в
дальнейших параграфах получат строгое доказательство.
1. Возрастание и убывание функций. Как известно1*, функция
у = f(x), х (: X, называется возрастающей на множестве X, если
для любых х19 х2 € X, таких, что х±< х2, имеем / (х)г ^ f(x2):
(V*x, *2? X) хг<х2=^ [fa) < f(x2).
Если
(V*!, Х2 ? X) Хх < Х2 => f(x±) < f(X2),
то функцию у = f (x) называют строго возрастающей на
множестве X.
Аналогично определяются понятия убывающей и строго
убывающей функций.
Оказывается, характер монотонности функции связан со
знаком производной. Геометрически очевидно, что если
дифференцируемая функция у = f (х), х б X, возрастает, то касательная
к графику функции в любой точке л: (X либо составляет с
положительным направлением оси абсцисс острый угол ср, либо
параллельна оси абсцисс (рис. 28). А так как tg ср = у', то получаем, что
у' ^ 0. Если же дифференцируемая функция у = f (х), х ? X,
убывает, то касательная к графику функции в любой точке х € X
либо составляет с положительным направлением оси абсцисс тупой-
х) См. «Введение в анализ», с. 72.
73

У
0
1
xl \
\р
X
Рис. 29
угол ф, либо параллельна оси абсцисс
(рис. 29). В этом случае tgcp ^ 0, и,
значит, у' ^ 0.
Сделанные выводы подтверждаются
конкретными примерами. Так, функция
у = Xs возрастает на всей числовой
прямой, а ее производная у' = Зх2 всюду
неотрицательна (см. рис. 11). Функция у = х2
убывает на луче]—оо; 0] и возрастает на
луче[0; оо[ (см. рис. 9), а ее производная
у' = 2х неположительна на первом и
неотрицательна на втором из указанных
промежутков.
Итак, если дифференцируемая функция
у = f(x), х ? X, возрастает (убывает) на X,
то ее производная на этом промежутке
неотрицательна (неположительна).
Обратно, по знаку производной
можно установить характер монотонности
функции. Имеет место следующее утверждение.
Если функция у = f(x) непрерывна на
промежутке X и имеет в каждой
внутренней точке этого промежутка положи-
тельную производную, то эта функция строго возрастает на X.
Остановимся на физических соображениях, поясняющих это
утверждение. Пусть точка М движется по прямой и х = f (t) —
закон движения. Тогда f (t) является мгновенной скоростью
движущейся точки в момент времени /. Из физических соображений
ясно, что если на [а; Ь] выполняется неравенство f (t) > 0, т. е.
в течение промежутка времени от а до Ь скорость точки была
положительной, то точка все время движется слева направо и ее
координата х возрастает.
Аналогичные соображения позволяют сформулировать
следующее утверждение.
Если функция у = / (х) непрерывна на промежутке X и имеет
в каждой внутренней точке этого промежутка отрицательную
производную, то эта функция строго убывает на X.
2. Экстремумы функции. На рисунке 30 изображен график
непрерывной функции у = / (х), я€[а;Ь]. Значение функции в
точке хг не является наибольшим на отрезке [а; 6], но если
ограничиться сравнением / (л^) со значениями функции в точках, «близких»
к хъ то окажется, что / (хг) больше всех этих значений. Иными
словами, существует такая окрестность U точки х1у что для любого
х € U выполняется неравенство f(x) <J / (хг). Говорят, что функция
у = f (x) имеет в точке хг (локальный) максимум.
В точке х2 функция у = / (х) принимает значение, меньшее
значений функции в точках, «близких» к х2. В таких случаях
говорят, что функция в точке х2 имеет (локальный) минимум. Значит,
74

4у<0[С
I I
i lAx,
й*у>°
Рис. 30
функция у = f (x) имеет минимум в точке л:4 и максимум в точке х3.
Терминам «максимум», «минимум» мы придаем лишь локальный
смысл. Свойство быть точкой максимума или точкой минимума
функции зависит лишь от поведения функции в некоторой
достаточно малой окрестности точки.
Теперь дадим точное определение этих понятий.
Определение. Пусть функция у = f (х), х € X,
определена в некоторой окрестности точки х0(Хи непрерывна в этой
точке. Тогда х0 называется точкой максимума функции, если
существует ее окрестность, в которой выполняется неравенство
/ (х) <; / (х0) (причем знак равенства имеет место лишь в случае
X = Xq).
Аналогично определяется точка минимума функции.
Точки максимума и минимума функции называются точками
экстремума1).
Определение точек максимума и минимума можно дать иначе,
используя понятие «приращение функции». Из рисунка 30 видно,
что в точке максимума при достаточно близких к нулю значениях
Ах имеем Ду <; 0 (как в случае, когда Ах > 0, так и в случае,
когда Дл: < 0), а в точке минимума при достаточно близких к нулю
значениях Ах имеем Ду ^ 0, причем Ду = 0 лишь в случае, когда
Д* = 0.
Обратимся снова к рисунку 30. Замечаем, что в точках
экстремума хи х2, *4 касательная к графику функции параллельна оси
абсцисс, т. е. в каждой из этих точек у' = 0. В точке же х3
касательную провести нельзя, значит, в этой точке производная не
существует. Это наблюдение позволяет предположить, что если функция
1) От латинского слова extremum — крайний.
75

у = f (x), x ? X, имеет экстремум в точке
х0€ X, то в этой точке производная
данной функции либо не существует, либо
равна нулю.
Геометрически это означает, что в точке
экстремума касательная к графику
функции либо горизонтальна (рис. 31), либо не
существует (рис. 32).
Точки, в которых производная равна
рис 31 нулю или не существует, называют
критическими, а точки, где производная
равна нулю, — стационарными.
У * Следует иметь в виду, что не всякая
стационарная точка является точкой
экстремума. Например, функция)/ = х3 монотонна,
но имеет стационарную точку л;=0(см.
рис. 11). Точно так же не всякая точка, где
] не существует производной, является точкой
3< *х экстремума (см. рис. 13).
0 Таким образом, множество точек
экстру 32 ремума функции—подмножество
множества ее критических точек , вообще говоря,
не совпадающее с ним.
Вопросы для самопроверки
1. Сформулируйте определения возрастающей и убывающей функций.
2. Как связан характер монотонности функции со знаком производной?
Сделайте геометрическое и физическое обоснование этой связи.
3. Как определяется точка максимума функции?
4. Можно ли утверждать, что в точке максимума функция имеет наибольшее
значение? Приведите примеры.
5. Как определяется точка минимума?
6. Можно ли утверждать, что в точке минимума функция имеет наименьшее
значение? Приведите примеры.
7. Что такое стационарная точка? Что такое критическая точка?
8. Можно ли утверждать, что всякая критическая точка является точкой
экстремума? Поясните свой ответ примерами.
Упражнения
Для данной функции у — / (х) выполните следующее: 1) постройте график
функции; 2) найдите участки монотонности, установите характер монотонности;
3) найдите точки экстремума функции; 4) найдите (если возможно) наибольшее
и наименьшее значения функции, сравните их со значениями функции в точках
максимума и минимума; 5) найдите производную; 6) определите знак
производной на участках монотонности функции; 7) найдите критические точки; 8)
сопоставьте критические точки с точками экстремума.
177. у = Зх2 — 2х, — 4 < х < 1. 178. у = хъ — 1, —2 < х < 2.
179. у = A — х)\ — 2 < х < 2.
180. у = sin х, —оо < х < оо.
76

T too л, _ /COSX, X < О,
181. у = (х2) , —оо < х < оо. 1Ъ<3' > " [х2 + 1, л: > 0.
182.
х2, —1 <*< 1,
*, 1 < л; < 2,
4
—, 2<х<4.
л:
§ 2. ТЕОРЕМА ЛАГРАНЖА И ЕЕ СЛЕДСТВИЯ
Производная позволяет характеризовать поведение функции
лишь вблизи от данной точки. При необходимости делать выводы
о поведении функции на всей области ее задания, используется
теорема, называемая теоремой Лагранжа, которую рассмотрим в
настоящем параграфе. Докажем сначала следующие леммы.
1. Леммы о знаке приращения.
Лемма 1. Пусть в некоторой точке х0 производная функции
у = f (х) положительна, f (лг0) > 0. Тогда у этой точки есть
окрестность, в которой знак приращения функции совпадает со
знаком приращения ее аргумента, т. е. в этой окрестности
Ду = / (*о + д*) — f (*о) > 0>
если Ах > 0, и Ау < 0, если Ах < 0.
Доказательство. Так как в точке х0 функция у = / (х)
дифференцируема, то ее приращение в этой точке можно
представить в виде
Ау = /' (*0) Ах + оЛх = (/' (*0) + а) Ах,
где а ->- 0 при Ах -> 0. При этом по условию /' (х0) > 0.
Так как а ->¦ 0 при Ах ->¦ 0, то у точки х0 найдется такая
окрестность, в каждой точке которой выполняется неравенство
1*1 <fW,
т. е.
-fW <<* <fD
Тогда /' (х0) + а > 0 и, следовательно,
^ = П*а) + «>0,
А*
а потому знаки Ах и Ду совпадают, что и требовалось доказать.
Лемма 2. Пусть в некоторой точке х0 производная функции
у =z f (х) отрицательна, \г (х0) < 0. Тогда у этой точки есть
окрестность, в которой знак приращения функции противопаложен
знаку приращения аргумента.
Доказательство этой леммы аналогично доказательству леммы 1.
Из лемм 1 и 2 вытекает следующая теорема, дающая
необходимое условие того, что х0 — точка экстремума функции.
77

Теорема 1. Пусть функция у = f (х), х € X, непрерывна в
некоторой окрестности точки х0 и имеет экстремум в этой точке.
Тогда производная функции в точке х0 либо равна нулю, либо не
существует.
Доказательство. Возможны четыре случая: 1) f (x0) >0,
2) F (х0) < 0, 3) /' (х0) = О, 4) производная в точке х0 не существует
(функция не дифференцируема в этой точке).
Если /' (х0) > 0, то по лемме 1 у точки х0 есть окрестность, в
которой знаки Ах и А у совпадают. Поэтому Ду может принимать
в этой окрестности и положительные, и отрицательные значения.
В то же время мы видели в п. 2 § 1, что если х0 — точка экстремума,
то у нее есть окрестность, в которой Ду имеет один и тот же знак
(положительный в точке минимума и отрицательный в точке
максимума). Полученное противоречие показывает, что точка, в
которой /' (х0) > 0, не может быть точкой экстремума.
Аналогично доказывается, что отпадает и второй случай,
следовательно, остаются лишь третий и четвертый случаи, т. е. в
точке экстремума производная либо равна 0, либо не существует.
2. Теорема 2 (теорема Ролля). Пусть функция у = f (x)
удовлетворяет следующим условиям: 1) непрерывна на отрезке [а; Ь]\ 2)
дифференцируема в интервале ]а; ?>[; 3) на концах отрезка [а; 6]
принимает равные значения: f (a) = f (b). Тогда в интервале ~]а; Ь[
существует, по крайней мере, одна точка с, производная в которой
равна нулю.
Доказательство. По условию данная функция
непрерывна на отрезке [а; 6], следовательно, на этом отрезке она
принимает свое наименьшее значение т и свое наибольшее значение М.
Возможны два случая: 1) значения т и М данная функция
принимает на концах отрезка; 2) хотя бы одно из значений т или М
данная функция принимает во внутренней точке отрезка.
Рассмотрим первый случай. Пусть f (a) =m,f(b) = М. Так как
по условию f (а) = f (b), то получаем:
m=±f(a) = f(b) = M.
Это значит, что наибольшее значение функции у = f (x) на отрезке
\_а\ 6] совпадает с ее наименьшим значением, и потому данная
функция на этом отрезке постоянна. Но тогда всюду на этом отрезке ее
производная равна нулю, и в качестве
точки с можно выбрать любую точку интервала
]а; 6[ (рис. 33).
Рассмотрим второй случай, когда хотя
бы одно из значений т или М достигается
во внутренней точке отрезка; пусть для
определенности f (с) = М, где а < с <Ь.
Это значит, что с является точкой
максимума функции, а тогда в силу необходи-
Рис 33 мого условия экстремума (по теореме 1) в
</'
0
1
1
/77|
1
а
f(x)=0
i t
i i"
1 i »
с b х
78

Г | I
II 1 ^
0
a b х
Рис. 34
И
_J 1 1—э*.
о] а ьх
Рис. 36
этой точке производная либо не существует, либо равна нулю По
условию данная функция дифференцируема в любой внутренней
точке отрезка, значит, она дифференцируема и в точке с. В таком
случае возможно только, что /' (с) = 0. Теорема доказана.
Покажем, что все три условия теоремы необходимы.
1) Непрерывность функции на отрезке [а; Ь~\. Функция, график которой
изображен на рисунке 34, дифференцируема в интервале ]а; Ь{_ и f (a) = f (b).
Тем не менее производная этой функции не обращается в 0 ни в одной точке
интервала ]я; Ь\_. Причина в том, что нарушено первое условие теоремы Ролля
(функция имеет разрыв в точке Ь).
2) Дифференцируемость функции в интервале ]а; Ь\_. Для функции, график
которой изображен на рисунке 35, в точке с не существует производной. На ]а; Ь\_
нет ни одной точки, в которой производная была бы равна нулю, хотя первое и
третье условия теоремы Ролля выполнены.
3) Равенство значений функции на концах отрезка. На рисунке 36 изображен
график функции, непрерывной на [а; Ь~\ и дифференцируемой на ]а; 6[, но у
которой / (а) Ф f (b). На ]а; Ь\_ нет ни одной точки, в которой производная была бы
равна нулю.
Пример 1. Проверим, применима ли теорема Ролля к
функции у = sin х на отрезке [0; 2я]. Если окажется, что теорема
применима, то найдем точку с, в которой производная данной функции
равна нулю.
Решение. Функция у = sin x непрерывна на отрезке
[0; 2я], ее производная у' = cos x определена всюду на ]0; 2я[,
наконец, sin 0 = sin 2я = 0. Значит, все три условия теоремы
Ролля выполнены. В качестве точки с можно выбрать х = —, так
^ 2
как f'(— ] = cos — = 0.
\2) 2
_ Зя
~ 2 '
Заметим, что можно было положить
0
Пример 2. Покажем, что уравнение хъ + Зх3 + х — Е
имеет только один действительный корень.
Решение. Рассмотрим функцию / (х) = хь + Зг3 + х — 5.
Она непрерывна и дифференцируема на всей числовой прямой,
причем f'(x) = 5л:4 + 9х2 + 1. Легко видеть, что при любом зна-
79

f/i
0
\
л
1
a
Я5
i
с
ъ
1
1 »
Ь х
чении л: имеем f'(x) ф 0. Но тогда
уравнение может иметь не более одного
действительного корня. В самом деле, если бы
оно имело два корня хг и х2 (х± <х2),
то, применив к функции у = f (x) на
отрезке \_хх\ х2~\ теорему Ролля все
условия теоремы Ролля здесь выполнены:
f (x) непрерывна на [_хх\ я2>]
дифференцируема на }хг\ х2[ и / (x1)=f (х2) =
Рис. 37 =0), мы получили бы, что между*! и х2
существует точка с такая, что f'(c) = 0.
Последнее невозможно, значит, уравнение
имеет не более одного действительного корня. Существование
действительного корня следует из того, что f(x) — многочлен
нечетной степени (корень х=1 в данном случае легко найти подбором).
3. Теорема Лагранжа. Проведем хорду АВ графика функции
у = f (х), изображенного на рисунке 37. Из чертежа видно, что на
дуге А В найдется точка М, касательная в которой к данной кривой
параллельна хорде АВ. Угловые коэффициенты этой касательной и
прямой АВ равны. Но
k =f<(c) k f(b)-f(a)
Значит, внутри отрезка нашлась точка с, в которой выполняется
равенство
Г (с) = №=№.
Ь — а
Это утверждение и составляет суть теоремы Лагранжа. Дадим
строгое доказательство этой теоремы, не опирающееся на
наглядность.
Теорема 3 (теорема Лагранжа). Пусть функция у = f (x)
непрерывна на отрезке [а; 6] и дифференцируема во всех внутренних точках
отрезка. Тогда в интервале ]а; Ь\_ найдется точка с (а <с < 6),
в которой выполняется равенство
о — а
Доказательство. Пусть у = kx + I — уравнение
хорды, проходящей через точки (а; / (а)) и ф\ f (b)). Угловой
коэффициент k этой прямой равен, как известно,
f(b)-f(a)
Рассмотрим функцию F (х) = укровой — ухорды = /(*)— (kx+l).
Функция F (х) является разностью двух непрерывных функций, а
80

потому непрерывна на отрезке [а; 6]. Аналогично доказывается,
что она дифференцируема в каждой внутренней точке отрезка.
Наконец, при х = а и при х = Ъ значения укрив0й и уХ0Рды
совпадают, а потому функция F (х) обращается в 0:
F (а) = 0, F (Ь) = 0.
Итак, вспомогательная функция F (х) удовлетворяет всем
условиям теоремы Ролля, и, следовательно, в интервале ]а; Ь{_ найдется,
по крайней мере, одна точка с, производная в которой будет равна
нулю. Так как F' (х) = f (х) — k
Ь — а
то
PW-fW-/(>H(fl).
При х = с получаем:
0 = /'(с)
f(b)-f(a)
откуда
Теорема доказана.
Г(с) =
_ f(b)-f(a)
Ь — а
Заметим, что если f (а) = f F), то из равенства A) следует
/' (с) = 0. Это значит, что теорема Ролля есть частный случай
теоремы Лагранжа. Геометрическая иллюстрация представлена на
рисунке 38.
Неудобно, что в формуле A) фигурирует неизвестное число с.
Тем не менее, как увидим позднее, это не является препятствием
для многочисленных применений этой формулы в математическом
анализе.
Пример 3. Проверим, применима ли теорема Лагранжа к
функции у = Ах3 — 5х2 + ^ — 2 на отрезке [0; 2]. Если окажется,
что теорема применима, то найдем точку с, в которой выполняется
равенство A).
Решение. Функция у = 4л:3 — 5х2+
+ х — 2 непрерывна на отрезке [0; 2] и
дифференцируема в интервале ]0; 2[.
Значит, условия теоремы Лагранжа
выполнены. Из формулы A) получаем:
f(b)-f(a) = f (с)(Ь-а). B)
В данном случае
f(b)=f B) = 12, / (а) = f @) = -2,
/' (х) = 12*2 - 10* + 1, /' (с) = 12с2 —
— Юс + 1. Рис. 38
81

Подставим полученные значения в формулу B) Лагранжа:
14 = 2 A2с2 — 10с + 1).
Из этого уравнения находим с = 5+}^ (второй корень уравнения
с _ 5 —у 97 не Г0ДИТСЯ) так как это число не принадлежит отрезку
[0; 2]).
Пример 4. Докажем неравенство In х2 — In хх <х2 — хъ
где 1 < хг < х2.
Решение. Функция у = In x на отрезке [X; х2~\
удовлетворяет всем условиям теоремы Лагранжа. Так как (In х)' = —, то,
применив к функции у = In x на отрезке [хг\ х2~] формулу B),
получим:
In х2 — In хх = — (х2 — хг).
с
Так как с > 1, то — < 1. Значит, — (х2 — хг) <х2 — хъ откуда
с с
получаем:
In х2 — In #! <х2 — х±.
4. Условие постоянства функции.
Теорема 4. Если функция у = f (x) непрерывна на отрезке
[а; 6] и во всех внутренних точках отрезка ее производная равна
нулю, то функция у = / (х) постоянна на этом отрезке.
Доказательство. Пусть х — точка из промежутка
\а\ 6]. Тогда по теореме Лагранжа
f(*)-/(a) =m
х — а
где а <с <х. Но по условию f (с) = 0, следовательно,
f(x)-f(a) =Q>
д; — а
откуда f (x) = f (а). Это и означает, что рассматриваемая функция
постоянна на данном отрезке. Теорема доказана.
Доказанное утверждение имеет простой физический смысл: если
скорость точки все время равна нулю, то точка покоится и ее
координата не меняется (постоянна).
Из теоремы 4 вытекает следующая теорема.
Теорема 5. Если функции у = f (x) и у = ср (х) непрерывны на
отрезке [а; 6] и имеют равные производные во всех внутренних
точках отрезка, то разность этих функций постоянна:
f (х) - ср (х) = С.
Доказательство. Введем вспомогательную функцию
У = ё(х)у равную разности данных функций:
g(x) =/(*) — ф (х).
82

Найдем производную функции у = g (x)i
У' = g' (x) = Г (х) - <р' (х) = 0.
Так как gf (х) = 0 на ]а; Ь[, то на отрезке [а; Ь] функция у = g (x)
постоянна, т. е.
/ (х) - Ф (х) = С,
что и требовалось доказать.
Пример 5. Докажем, что arcsin х = — — arccos x.
Решение. Обозначим функцию, стоящую в левой части
равенства, через / (х), а функцию, стоящую в правой части равенства,
через ф (х):
f (х) = arcsin х, ф (х) = arccos х.
Обе функции определены и непрерывны на отрезке [—1; 1].
Найдем производные этих функций:
f (х) = (arcsin x)f = , ф' (х) = (— arccos х ) = ¦
v2
у\ —х^ ^ w \ 2 / у\ — х
Эти производные определены во всех внутренних точках отрезка
[—1; 1]. Так как производные /' (х) и ф' (х) равны, то по теореме 5
сами функции могут отличаться лишь на произвольную постоянную,
а значит, можно записать
/ (х) - Ф (х) = С
или
arcsin х — (— arccos x ) = С.
Полученное равенство справедливо при любом значении
х € [—1; 1]. Найдем значение постоянной С, для чего в полученное
равенство подставим какое-либо значение из отрезка [—1; 1],
например, х = 0:
arcsin 0 — | — arccos 0 ) = С,
т. е. 0 — (— —) = С, следовательно, С = 0, а значит,
arcsin х = arccos x,
2
что и требовалось доказать.
Пример 6. Докажем, что
arccos l = f arctg х, если х > 0,
У\ + х2 1 — arctg х, если х < 0.
83

Решение. Положим
/ (х) = arccos
1
Имеем:
/1 +а;2'
ixt х^О
arctg х, х < 0.
1
'(*)==( arctS*> *>°>
/' (х) = (arccos у
1А
Значит,
1 + х2
fw
-j]0+*2)
1
2х =
1*10+Я8)
-, если х > 0,
1 + х2 '
, если х < 0.
1 + х2
Вычислим теперь g' (x). Имеем:
_1
1 + Х2
1
1 + г
, если х > О,
, если я < 0.
Итак, при х > О имеем: /' (х) = g' (я), при х < 0 также имеем:
/' (*) = g' (х).
Заметим, далее, что обе функции непрерывны при всех
значениях х (при х = 0 имеем g (—0) = g (+0) = 0). Поэтому из
^ (л;) == g' (x) следует, что для любого х имеем:
f(x)-g(x) = C.
Если х = 0, то f @) = 0, g @) = 0, значит, / @) — g @) = О,
т. е. С = 0. Таким образом, / (х) = g (x), что и требовалось
доказать.
Вопросы для самопроверки
1. Сформулируйте теорему о необходимом условии экстремума.
2. Сформулируйте теорему Ролля.
3. Поясните на примерах необходимость каждого из трех условий теоремы
Ролля.
4. Сформулируйте теорему Лагранжа. В чем состоит ее геометрический смысл?
5. Поясните на примерах необходимость каждого из условий теоремы
Лагранжа.
6. Покажите, что теорема Ролля — частный случай теоремы Лагранжа.
7. Сформулируйте условие постоянства функции, непрерывной на отрезке.
В чем состоит физический смысл этой теоремы?
84

Упражнения
Для функции у = f (х) на заданном отрезке [а; &] проверьте возможность
применения теоремы Рол л я и найдите с.
184. / (х) = х3 + 5х2 — 6а:, 0 < х < 1.
185. / (х) = cos2 х, — — <*< —.
4 4
186. / (*) = sin2 jc, 0 < л: < я.
187. / (лг) = (* — 1) (* — 2) (.v — 3), 2 < х <3.
188. / (х) = Ъ/х2 — Зх + 2, 1 < л; < 2.
я 5я
189. / (х) = In sin х, — < jc < —-.
6 6
190. Покажите, что между корнями функции / (х) = х2 — 4х — 5 находится
один корень ее производной, и найдите с (/' (с) = 0). Приведите графическую
иллюстрацию.
191. Покажите, что уравнение х3 + Зх + q = 0 имеет только один
действительный корень.
192. Докажите с помощью теоремы Ролля, что уравнение л:4 — 4х — 1 = 0
не может иметь более двух действительных корней. Установите с помощью
теоремы Больцано — Коши, что два указанных корня существуют.
Для функции у = f (х) на заданном отрезке [а; Ь~\ проверьте возможность
применения теоремы Лагранжа; найдите с в формуле Лагранжа.
193. у = In х, 1 < х < е. 194. у = }/"? 0 < х < 4.
j_
195. у = х2, а < х < 6. 196. у=*3, а < х < Ь.
197. В какой точке М кривой у = 4 — х2 касательная параллельна хорде,
проходящей через точки А (—2; 0), В A; 3)?
Г 2я1
198. Почему к функции у = | cos х\ на отрезке 0; — нельзя применить
теорему Лагранжа? Сделайте чертеж.
199. Почему к функции у = х +| sin л; | на отрезке [—1; 1] нельзя применить
теорему Лагранжа? Сделайте чертеж.
200. Используя формулу Лагранжа, докажите справедливость следующих
неравенств:
1) | sin х2 — sin хг\ < | х2 — хх\\
2) arctg х2 — arctg хх < х2 — хъ где х2 > xv
Докажите тождества.
arcsin х, 0 ^ х ^ 1,
; |Л — *2 = ( '
I —<
201. arccos", _
- arcsin x, —1 < х < 0.
2х [ я — 2 arctg х, х > 1,
202. arcsin = | 2 arctg x, — 1 < х < 1,
1 + х2 { _ л _ 2 arctg х, * < —1.
203. arctg x + arctg 1
204. Покажите, что функция у = cos2 х + cos2 \- х I — cos a: cosl —¦ + х 1
есть постоянная. Найдите значение этой постоянной.
85

205. Покажите, что функция у = 2 arctg х + arcsin : является постоян*
1 + х2
ной при х ^ 1. Найдите значение этой постоянной.
§ 3. ИССЛЕДОВАНИЕ ФУНКЦИЙ
1. Возрастание и убывание функций. В § 1, исходя из
геометрических и физических соображений, мы установили связь между
знаком производной и характером монотонности функции на
промежутке. Теперь соответствующие утверждения будут доказаны.
Теорема 1. Если функция у = / (х) непрерывна на отрезке [а; 6]
и если ее производная положительна всюду в интервале ]а; 6[, то
у = / (х) строго возрастает на [а; Ь].
Доказательство. Рассмотрим две любые точки
х1у х2 6[а; 6], связанные неравенством хг < х2. Так как для функции
у = f (x) на отрезке \_хг\ х2] выполняются условия теоремы Лагран-
жа, то имеет место равенство
f(x2)-f(x1) = r (c)(x2-Xl), A)
где точка с лежит между хх и х2.
Так как оба множителя правой части равенства A)
положительны (/' (с) > 0 по условию, х2 — х± > 0 в силу выбора точек), то
Г (с) (х2 - хг) > 0,
а значит, и
f(x2)-f(Xl) >0.
В таком случае / (хг) < / (х2) и, следовательно, функция у = f (x)
строго возрастает на [а; 6], что и требовалось доказать.
Аналогично доказывается следующая теорема.
Теорема 2. Если функция у = f (х) непрерывна на отрезке [а; Ь]
и если ее производная отрицательна всюду в ]а; й[, то у = f (x)
строго убывает на [а; 6].
Доказательство этой теоремы предоставляем провести читателю.
Заметим, что в формулировке обеих теорем можно было вместо
отрезка [а; Ь~\ взять произвольный промежуток X и потребовать
непрерывности функции на X и дифференцируемое™ ее в любой
внутренней точке промежутка X.
Теорема 1 (теорема 2) остается справедливой и в случае, когда
f (х) ^ 0 (/' (х) ^ 0), причем производная не обращается
тождественно в нуль на каком-либо отрезке из рассматриваемого промежутка
X. В самом деле, пусть х±, х2 ? X и хг < х2. Если /' (х) > 0 всюду
в X, то из равенства A) следует f (хг) ^ / (х2). Предположим, что
/ (xi) — f (х*)' Так как при хг < х < х2 выполняются неравенства
f (xi) ^ / (х) и / (х) <;/ (х2), то на основании равенства / (хг) = f(x2)
получим f (х) = f (х^. Тогда функция у = f (x) постоянна на
86

[л*; а:2], и потому ее производная вопреки условию обращается в
нуль на целом отрезке. Значит, / (хг) ф f (х2), т. е. / (х±) < f (я2),
и потому функция / (х) строго возрастает на промежутке X.
До сих пор, говоря о возрастании или убывании функции, мы придавали этим
понятиям глобальный смысл, т. е. рассматривали возрастание или убывание
функции на промежутке. Иногда полезно локальное рассмотрение этих понятий.
Сформулируем соответствующие определения.
Функция y—f(x) называется возрастающей в точке х0, если существует
окрестность ]х0— 6; *о+ ^ [точки х0 такая, что функция определена в этой
окрестности и знак приращения функции Лу = f (х) — f (x0) в этой окрестности сов-
падает со знаком приращения аргумента.
Функция у = f (x) называется убывающей в точке х0, если существует
окрестность точки х0 такая, что функция определена в этой окрестности и знак
приращения функции в этой окрестности противоположен знаку приращения
аргумента.
Мы знаем (см. лемму о знаке приращения функции), что если f (х0) > 0, то
в некоторой окрестности точки х0 знаки Ал: и Ду совпадают.
Таким образом, если функция у = f (х) определена в некоторой окрестности
точки х0 и имеет в этой точке положительную производную f (х0) > 0, то
функция у =±= f (x) возрастает в точке х0.
Аналогичные рассуждения приводят к условию убывания функции в точке:
если функция у = f (х) определена в некоторой окрестности точки х0 и f (x0) < О,
то у = f (х) убывает в точке х0.
В точках, где производная обращается в нуль, локальное поведение функции
может быть любым. Например, функция у = х3 возрастает на всей числовой
прямой (глобально), значит, она возрастает и в точке х = 0 (локально), но / = О
при х = 0. Функция у = —Xs убывает на всей числовой прямой, значит, и в
точке х = 0, но х = 0 — стационарная точка. Наконец, для функции у = х2
стационарной является точка х — 0, но в этой точке нет ни возрастания, ни
убывания функции (это — точка экстремума).
Не следует отождествлять понятия возрастания (убывания) функции в
точке с понятиями возрастания (убывания) функции в окрестности точки.
Рассмотрим для примера функцию
4, __ \ х + х2 sin —, х Ф 0,
У — \ х
10, х = 0.
Вычислим производную этой функции в точке х — 0. Имеем:
A* + (A*Jsin^-0 ,
HmTZ = lim — = lim 1 +Ах sin— .
Ах^о Ал: Дх-о Ах Дх-сД Дя/
Так как sin —
Да:
^ 1, а Ал: -> 0, то
я
Нш Да: -sin — = 0.
Дх-о Да:
Ду
Таким образом, lim— = 1. Значит, f{0) =1. Отсюда следует, что рассматри-
Дх-о ^x
ваемая функция возрастает в точке х = 0. Покажем теперь, что эта функция не
возрастает ни в какой окрестности точки х = 0.
87

График функции у— х + х2 sin—
изображен на рисунке 39. Видно, что она по мере
приближения к точке х=0 бесконечно много
раз переходит от возрастания к убыванию и
обратно. В этом можно убедиться, вычислив
производную функции в точке х Ф 0:
/ о Л у t , _ . я
у' = \х + х- sin — = 1 + 2 х sin — —
Рис. 39
— я cos —.
X
В точках, где х достаточно близко к
нулю, a cos — ^ 1, имеем /< 0 — в этих точ-
X
ках функция убывает. В точках же, где
cos — ~ — 1, имеем / > 0 и функция в них
X
возрастает. Поскольку в любой окрестности
точки х = 0 есть точки и того и другого вида, то нельзя говорить о
направлении изменения функции в окрестности точки х = 0, а можно говорить лишь о ее
возрастании в самой этой точке.
Если потребовать не только существования производной в точке х0, но и ее
непрерывности в этой точке, то из неравенства /' (х0) > 0 будет следовать
существование окрестности точки х0> в которой f (х) > 0. Тогда в этой окрестности
функция будет строго возрастать. В рассмотренном примере производная в
точке х = 0 разрывна, так как lim f (x) не существует.
Пример 1. Исследуем на монотонность функцию у = х3 —
— Зл: и построим ее график.
Решение. Имеем:
/ = (*s __ з*)' = Зх2 — 3 = 3 (х — 1) (х + 1).
На луче ]—со; —1[ / > 0,
на
Рис 40
интервале ]—1; 1[ у' < 0, а на
луче ]1; оо[ у' > 0. Значит,
наша функция возрастает на
лучах ]—со; —1[ и ]1; оо[ и
убывает на интервале ]—1; 1[.
Для построения графика
найдем несколько контрольных
точек. Прежде всего отметим,
что если х = —1, то у = 2, а
если х = 1, то у = —2 (это
точки, в которых происходит
изменение характера
монотонности функции). Кроме того,
из уравнения хъ — Зх = 0
находим точки пересечения
графика с осью абсцисс: xL = 0,
х2 = —УН, х3 = ]/~3. График
изображен на рисунке 40.
88

Пример 2. Докажем, что функция у
на всей числовой прямой.
Решение. Имеем:
у' = (arctgx — х)' = ——2 — 1
1 + X2
X2
Так как при любом л; выполняется неравенство - ^Ои так
как, кроме того, равенство у' = 0 выполняется только в одной
точке х = О, то на всей числовой прямой у' ^ 0, причем у' = О в одной
точке. Значит, по теореме 2 функция убывает на всей числовой
прямой.
Пример 3. Покажем, что уравнение Зхъ — 25л:3 + 6(к +
+ 15 = 0 имеет только один действительный корень.
Решение. Рассмотрим функцию/ (х) = Зхъ — 25х3 + 60х +
4-15 и найдем ее интервалы монотонности. Имеем:
f (Х) = 15х4 — 75х2 + 60 = 15 (х + 2) (х + 1) (х — 1) (х — 2).
Производная /' (х) обращается в 0 в четырех точках: —2, —1, 1, 2.
Эти точки разбивают числовую прямую на 5 промежутков: ]—оо;—2[,
]—2; —1[, ]—1; 1[, ]1; 2[, ]2; оо[. На каждом из указанных
промежутков производная сохраняет постоянный знак. Отсюда
заключаем, что на каждом из этих промежутков функция у = f (x)
монотонна, т. е. или строго возрастает, или строго убывает. Тогда
график функции на каждом из указанных промежутков пересекает
ось абсцисс не более, чем один раз. Это значит, что функция
у = f (x) на каждом из рассматриваемых промежутков может иметь
не более одного корня, причем корень функции может быть в том
и только в том промежутке, на концах которого функция имеет
разные по знаку значения.
Имеем:
Нт / (Х) = _оо, / (-2) < 0, / (-1) < 0, / A) > 0, / B) > 0,
х-*—оо
Нт / (х) = +оо.
х -*•-[- оо
Так как f (x) имеет различные знаки только на концах интервала
]—1; 1[, то заданное уравнение имеет только один действительный
корень, лежащий внутри этого интервала.
2. Исследование функций на экстремум с помощью первой
производной. Рассмотрим такой пример. Прочность балки, которая
является основным элементом любой строительной конструкции,
зависит от того, какую форму имеет ее поперечное сечение.
Инженерные расчеты показывают, что прочность балки с прямоугольным
сечением пропорциональна ширине балки а и квадрату ее высоты /г.
Иными словами, прочность такой балки равна kah2, где k —
коэффициент, зависящий от длины балки, материала, из которого она
сделана, и т. д. Деревянные балки приходится обычно вытесывать
из круглых бревен. В связи с этим возникает задача, как из бревна,
имеющего радиус /?, сделать балку наибольшей прочности.
89
arctg х — х убывает
X2
1 + *2'

Решение этой задачи, как и многих других задач, имеющих
большое практическое значение, сводится к отысканию наибольшего
(или наименьшего) значения некоторой функции. Эти задачи можно
решать с помощью дифференциального исчисления.
В § 1 были введены понятия максимума и минимума функции,
там же было сформулировано необходимое условие экстремума,
согласно которому функция может иметь экстремум только в
точках, где производная равна 0 или где производная не существует.
Такие точки объединяются иногда общим названием — точки,
«подозрительные» на экстремум.
Однако необходимое условие не является достаточным для
существования экстремума. Рассмотрим одно из достаточных условий
экстремума.
Теорема 3. Пусть функция у = f (x) определена в точке х0
и пусть существует б > 0 такое, что функция у = f (x) непрерывна
на отрезке [х0 — 6; х0 + б], дифференцируема на интервалах
2х0 — 6; х0[ и~]х0\ х0 + б[ и производная данной функции сохраняет
знак на каждом из этих интервалов.
Если на ]х0 — б; х0\_ и ]х0; х0 + б[ знаки производной различны,
то х0 — точка экстремума, а если совпадают, то х0 не является
точкой экстремума. При этом если при переходе через точку х0
производная меняет знак с «+» на «—», то х0 — точка максимума,
если же производная меняет знак с «—» на «-)-», то х0 — точка ми-
нимума.
Доказательство. Пусть производная /' (х)
положительна на интервале ]#0 — б; х0\_ и отрицательна на ]х0; х0 + б[.
Докажем, что х0 — точка максимума функции.
По условию функция у = f (х) непрерывна на отрезке [л:0 —
—б; Xq], дифференцируема в интервале ]х0 — б; х0[ и всюду в этом
интервале имеем /' (х) > 0. Значит, по теореме 1 из п. 1 функция
у = f (х) строго возрастает на отрезке [х0 — б; *0]. Поэтому из
неравенства х < х^, где х €[х0 — б; х0\_, следует f (x) <f (x0).
Аналогично устанавливаем, что функция у = / (х) строго убывает на
отрезке [х0; х0 + б], а потому из неравенства х0 < х, где х (: ]л;0;
х0 + б], следует f (х0) > f (x).
Таким образом, в б — окрестности точки х0 для точек х,
отличных от х0, выполняется неравенство
/(*) </(*о).
Это и означает, что х0 —точка максимума функции у = f (x).
Рассмотрим случай, когда производная не меняет знака при
переходе через точку х0] пусть она отрицательна как слева, так и
справа от х0. Тогда функция строго убывает как на отрезке [х0—б; х0~],
так и на отрезке [х0; х0 + б]. В таком случае х0 не является точкой
экстремума (это точка убывания функции).
Остальные два случая рассматриваются аналогично. Теорема
доказана.
90

Условие и утверждение
теоремы можно записать в виде
таблицы (рис. 41).
Таким образом, чтобы
исследовать функцию у = f (х) на
экстремум, нужно: 1) найти ее
производную; 2) найти
критические («подозрительные»)
точки; 3) рассмотреть окрестность
каждой из «подозрительных»
точек, не содержащую других
«подозрительных» точек, и
исследовать знак производной
слева и справа от рассматриваемой
точки; 4) опираясь на теорему
3, сделать соответствующие
выводы.
Заметим, что условия,
сформулированные в теореме 3, являются
достаточными, но не являются
необходимыми для существования
экстремума в «подозрительной» точке.
Рассмотрим для примера функцию
„_ 2а:2 + л:2 sin—, х Ф О,
У — 1 х
О, х = 0.
\f(x)
\f(x)
\f'(x)
\fM
]*o5;xo[
+
—
+
—
]х0'Л+Ы
—
+
+
—
Геом
иллюст
7Т\
\Ls
s
s~
^
Вывод]
max
min
нет
экстр.
нет
экстр
Рис. 41
Найдем производную этой функции в
точке х = 0. Имеем:
Рис. 42
2 (Ад:J + (Лд:2) sin-- — 0
lim -— = lim = lim BАд: + ^x sin —
Ax-+o A* Ax-+o Ал: д*-*о Да:
Значит, f @) = 0, т. е. х = 0 — стационарная точка. Построим график функции.
Так как —1 ^ sin — <[ 1, то график будет заключен между параболами у = а:2
и у = За:2, причем в любой окрестности точки х= 0 имеется как бесконечное
множество точек графика, лежащих на параболе у = х2, так и бесконечное
множество точек графика, лежащих на параболе у = За:2 (рис. 42). Ясно, что х = 0 —
точка экстремума (минимума), но как слева от точки х = 0, так и справа от
нее производная бесконечное множество раз меняет знак.
Пример 4. Исследуем на экстремум функцию у = хд
+ 24;с.
Решение. Имеем:
у' = Зх2 — 18* + 24 = 3 (х — 2) (х — 4).
— 9х2+
91

х
/
! У
У
Вывод
2
+ о-
/i\
max
4- 1
-0 +
М/!
min
Рис. 43
Рис. 44
х
1 У'
У
Вывод
0
+ 0 +
у
S
возраст.
3
+ 0-
А
max
Приравняв производную нулю,
находим хх = 2, х2 = 4.
Результаты исследования сведем в
таблицу (рис. 43). При переходе
через точку х = 2 производная
меняет знак с «+» н-а «—»,
значит, в этой точке функция
имеет максимум. При переходе
через точку х = 4 производная
меняет знак с «—» на «+»,
значит, в этой точке функция имеет
минимум.
Итак, утах = у B) = 20,
Утт = У D) = 16. На
рисунке 44 представлен эскиз
графика этой функции.
Пример 5. Исследуем на
экстремум функцию у = х3е~х.
Решение. Найдем
производную данной функции:
у'=3х2е-х + х3е~х(-1) =
= х2 C — х) е~х.
Приравняв производную
нулю, находим стационарные
точки: хг = 0, х2 = 3. При
переходе через точку х = 0
производная знака не меняет, значит,
в точке х = 0 экстремума нет,
при переходе через точку х = 3
производная меняет знак с «+»
на «—», значит, это точка
максимума, утах = Ц-. Результаты ис-
е3
следования сведены в таблицу
(рис. 45).
На рисунке 46 представлен
эскиз графика функции у=х3е~х.
Пример 6. Исследуем на
экстремум функцию
Рис. 45
у =уг(*-1)а + 1/Ъ+1)8.
Решение. Найдем
производную:
/ = !(*—1)" +
3
92

+ f(*+ 1) 3 =
11-
Решив уравнение
2_( 1
*3
+
1
Vx+l
+
1
= 0,
?x—i V* +1
получим я = 0.
Кроме того, в данном случае
имеются две точки, в которых
производная не существует:
х = 1, л; = —1.
Итак, мы нашли три
«подозрительные» точки: хг= —1,
х2= 0, х3 = 1. Дальнейшее
исследование представлено
таблицей на рисунке 47. Наша
функция имеет три точки
экстремума:
Ушах = У @) = 2,
Ут1п = УA)=1^4-
На рисунке 48 представлен эскиз
графика рассматриваемой
функции.
3. Использование второй
производной для исследования
функций на экстремум.
Теорема 4. Пусть f (х0) = 0
и в точке х0 существует вторая
производная. Тогда если f" (x0) >
> 0, то х0 — точка минимума
функции, а если f" (x0) < 0, то
х0 — точка максимума функции.
Доказательство.
Пусть /" (х0) > 0. Так как f"(x)
есть производная функция у' =
= /' (х), то по лемме о знаке
приращения функции (с. 77) у
точки х0 есть окрестность ]л'0 — б;
#о+б[» в которой знак Ду'
совпадает со знаком Да:. Но Ду' =
= Г(х)-Г(Хо). a fW = 0,
значит, /' (х)<0 в ]х0— б; х0[,
Рис. 46
X
/
У
У
Вывод
-1
-нет +-
У
mm
0
+ 0-
л
max
1
-нет +
у!
/771П ¦
Рис. 47
Рис. 48
93

и /' (х) > 0 в ]х0; х0 + б[. Так как
оказалось, что при переходе через точку х0
производная /' (х) меняет знак с «—» на
«+», то в этой точке имеем минимум.
Доказательство случая, когда /" (г0) < О,
проводится аналогично.
Пример 7. Исследуем на
экстремум функцию у
Решение.
г
— 12*.
Рис. 49
Найдем производную:
= Ъх2 — 12.
Из уравнения З*2 — 12 = 0 находим
Xl = 2, х2 = —2. Далее найдем вторую
производную:
у" = (Зх2 — 12)' = 6х.
Определим знак второй производной в
каждой из найденных точек.
Имеем:
/" (-2) < О, Г B) > 0;
= —2 есть точка мак-
- точка минимума функ-
следовательно, х
Рис. 50 симума, а х = 2
ции.
4. Нахождение наибольшего и наименьшего значений функции
на данном отрезке. Пусть функция у = f(x) непрерывна на отрезке
[а; Ь]. Тогда по теореме Вейерштрасса (см. «Введение в анализ»,
с. 'l 78) на этом отрезке данная функция принимает и свое наибольшее,
и свое наименьшее значения. Однако в теореме Вейерштрасса ничего
не говорится о том, как искать эти значения. Здесь возможны два
случая:
а) наибольшее (соответственно, наименьшее) значение достигается
во внутренней точке отрезка [а; Ь] (рис. 49);
б) наибольшее (соответственно, наименьшее) значение
достигается в одной из концевых точек отрезка (рис. 50).
Если наибольшее значение функция принимает во внутренней
точке х0 отрезка, то х0 будет точкой максимума функции, если же
во внутренней точке х0 данная функция принимает наименьшее
значение, то х0 будет точкой минимума (рис. 49).
Итак, для того чтобы найти наибольшее (наименьшее) значение
функции у = f (x) на отрезке [а; &], нужно:
1) найти производную данной функции;
2) найти критические точки;
3) вычислить значения функции в найденных точках и на концах
отрезка;
4) из всех найденных значений функции выбрать наибольшее
(наименьшее). Здесь мы предполагаем, что таких значений конечное
94

множество, а во всяком конечном числовом множестве есть
наибольший и наименьший элементы.
Иногда оказываются полезными следующие замечания,
позволяющие упростить вид исследуемой функции и ее производной.
а) Если выражение функции содержит постоянное слагаемое, то
его можно отбросить, не изменив точек, в которых достигаются
наибольшие и наименьшие значения (сами эти значения изменяются
на это постоянное).
б) Если выражение функции содержит положительный множитель,
то его можно отбросить, не изменяя точек, в которых достигаются
наибольшие и наименьшие значения (сами эти значения изменяются
в соответствующее число раз). При изменении знака функции эти
точки не изменяются, но наибольшие значения становятся
наименьшими и наоборот.
в) Если у = f (ф (х)), а <; х ^ Ь, причем у = f (и) строго
возрастает, то значения аргумента, при которых у принимает
наибольшие и наименьшие значения, совпадают со значениями
аргумента, в которых наибольшее и наименьшее значения принимает
и = (р (х).
Пример 8. Найдем наибольшие и наименьшие значения
функции у = 2arctg Bх — х2) + — на отрезке [0; 3].
4
Решение. Так как постоянное слагаемое, а функция
4
у = 2arctg& строго возрастает, то достаточно найти точки, где
принимает наименьшее и наибольшее значения функция и = 2х — х2.
Так как и' = 2 — 2х, то и = 0 лишь при х = 1. Поэтому нам
надо сравнить значения функции и = 2х — х2 в точках хг = 0,
«^2 = *у %з = О.
Мы имеем и @) = 0, и A) = 1, и C) = —3. Заданная функция
принимает наименьшее значение при х = 3, а наибольшее при х = 1:
yC) = JL-2arctg3, у A) = ^-.
4 4
Поэтому наибольшее, а 2 arctg 3 — наименьшее значе-
4 4
ние функции на заданном отрезке.
П р и м е р 9. Из всех прямоугольников с данной площадью S
найдем прямоугольник с наименьшим периметром.
Решение. Пусть х — длина одной из сторон прямоугольника,
5
тогда длина другой стороны, а периметр р, т. е. исследуемая
функция, будет иметь вид:
р-2х+ —,
X
где х > 0.
95

Рис. 51
Нам надо найти наименьшее значение
этой функции при х > 0. Имеем:
р> = 2 — — = 2 (*2 ~ s).
х2 х°
Производная не существует в точке х = 0,
но в данном случае она нас не интересует,
ибо по смыслу задачи х > 0. Решая
уравнение
2(x*-S) __
х2 ~U'
получаем х = 1^5 (отрицательный корень
уравнения не учитываем). Поскольку
limy = 4-°° и limy = +oo, то х =
х-*-\-0 х_>-|_оо
=]/S—точка минимума функции, причем в
этой точке функция принимает наименьшее
д значение (рис. 51). При х = ]AS получаем:
p = 2K5 + ^| = 4j/S.
Заметим, что если длина одной
стороны прямоугольника равна j/S, то и длина
другой будет равна VS, т. е. из всех
прямоугольников с данной площадью S
наименьший периметр имеет квадрат.
Данная задача часто формулируется следующим образом:
доказать, что если произведение двух положительных чисел постоянно,
то их сумма наименьшая, когда числа равны. В такой формулировке
задача полезна в алгебре.
П р и м е р 10. Из круглого бревна радиуса R требуется
вытесать балку прямоугольного сечения. Каковы должны быть
ширина и высота этого сечения (ширина меньше высоты), чтобы балка
имела наибольшую прочность (прочность балки пропорциональна
произведению ширины полученного сечения на квадрат его высоты).
Решение. На рисунке 52 изображено поперечное сечение
бревна. Выразим прочность балки как функцию ее ширины х. Из
треугольника ABC, изображенного на рисунке 52, видно, что
высота балки равна ]/4#2— х2. Значит, прочность р балки будет
равна
р = kx DЯ2 — х2)
(k — коэффициент пропорциональности). Найдем производную
функции
р = 4kR2x — kx3.
Рис. 52
96

Рис. 53
Имеем:
р' = AkR2 — 3kx2.
Приравняв производную нулю,
находим:
х ==2RY"S
3
Итак, самая прочная балка
будет, если ее ширина х =
_ 2RY3
~ 3
Высота балки определится по
формуле
h = YAR2 — х2 = 2Rfb .
Пример 11. Населенные пункты А и В находятся по одну
сторону от полотна железной дороги на расстояниях а и Ь
соответственно. Где нужно построить станцию С, чтобы расстояние \АС\ +
+ \СВ\ было наименьшим?
Решение. Обозначим через х расстояние от D до С (рис. 53),
\DE\ = / (заданное число). Тогда \СЕ\ = 1-х. Так как
\АС\ = КоЧ7?, \СВ\ = Vb2 + (I - хJ,
то
s = \АС\ + \СВ\ = Va2+ х2 + Vb2 + (/ - хJ
Здесь 0 < х < /. Найдем наименьшее значение функции s на
отрезке [0; /]. Имеем:
Уравнение s'
т. е.
Но
/ х
Va2+ х2
0 имеет вид
X
Ya2+ х2
\пс\
1-х
Vp + u-
[:
1-х
Vb2 + {l—xJ
\СЕ\
XJ
9
АС\
\СВ\
\DC\
\АС\
I CF \
= sin a, -J - = sin 6. Значит, а = C.
|СЯ|
Таким образом, станцию надо построить в таком пункте С,
чтобы отрезки АС и СВ образовывали конгруэнтные углы с
перпендикуляром, восставленным из точки С (угол падения
конгруэнтен углу отражения). Величину этого угла можно найти так:
\DC\ = atga, \CE\ = b tg a,
97

тогда
a tg a + b tg а = /, tg а = , а = arctg
а + Ъ а-\- b
Вопросы для самопроверки
1. Сформулируйте условия строгого возрастания функции на отрезке.
2. Сформулируйте условия строгого убывания функции на отрезке.
3. Может ли производная строго монотонной на отрезке [а; Ь~\ функции
обратиться в нуль в конечном множестве точек из отрезка [a; bj?
4. Сформулируйте необходимое условие экстремума функции; сделайте
геометрическую иллюстрацию.
5. Как отыскивается экстремум функции с помощью первой производной?
6. Как исследуется экстремум функции с помощью второй производной?
7. Как отыскивается наибольшее и наименьшее значения непрерывной на
отрезке функции?
8. В каком случае можно утверждать, что минимум функции является и ее
наименьшим значением на данном отрезке?
9. В каком случае можно утверждать, что максимум функции является и
ее наибольшим значением на данном отрезке?
Упражнения
206. Докажите, что функция у = f (x) возрастает на всей числовой прямой:
1) у = х3 + 6х -— 7; 2) у = х + cos x\
3) у = In (х + уТ+^?).
1 — х-
207. Докажите, что функция у = убывает на лучах ]—оо; 0[ и ]0;оо[.
х
Найдите интервалы монотонности следующих функций.
208. у = 2х? — 15л:2 + 36* — 6.
209. у = х4 — 2х2 — 8. 210. у = 2х2 — In x.
211. При каких значениях коэффициента b функция у — х2 — Ьх убывает
на отрезке 0—1; 1]?
212. При каких значениях р функция у = cos х — рх + q возрастает на
всей числовой прямой?
213. Известно уравнение Кеплера для определения положения планеты на
эллиптической орбите х = е sin х + Ь, где 0 <е < 1 — эксцентриситет орбиты,
b > 0 — данное число. Докажите, что уравнение Кеплера имеет единственное
решение.
214. Докажите теорему: пусть функция у = f (х) дифференцируема на
интервале ]а; Ь[ и возрастает на этом интервале, тогда производная функции в любой
точке интервала ]а; 6[ неотрицательна.
215. Докажите теорему: пусть функция у = f (х) дифференцируема на
интервале ]а; Ь\_ и убывает на этом интервале, тогда производная f {x) в любой
точке интервала неположительна.
Исследуйте функции на экстремум:
216. у = 6х — х3. 217. у = х3 + Зх2 — 9х + 6.
218. у = хъ — 5л-4 + 5х3 — 1. 219. у = (* — IJ (х— 2)\
х
1~х2
(jc'+1K D — xf
220. у = ——j. 221. у = (х — 2M B* + IL.
222. у = -——г~• 223. у = ft
' (х — 2)* ' 2—л:

224. у--
10
4л;3 — 9л:2 + 6х
226. y = 3yrx2(x — 1).
228. у = sin х + cos л:.
230. у= х2 е~х.
232. у = sin4 х + cos4 *.
234. у = In (л:2 + 2* — 3).
225. у = ]Ал: — л:2.
227. у = sin 2л: — х.
2х
229. у = —.
х
231. у — sin3 л: + cos3 x.
233. у = In sin x.
235. у = е* — 2л: — е-*.
Найдите наибольшее и наименьшее значения функции на указанном отрезке.
236. у =
238. у =
х2_2х—\
х* + 2л:2
*-2 '
-, [4; 6].
[-1; 1].
240. у = х +3/7, [—10; 1].
241. у = л:2^(л: + IJ, [—2; 1].
242. у = ^(л:+ IJ — 2у^(л: — 1),
243. y^arctg^-;, [-1; 2].
In х
X2— 1
х2+ Г
244. у = ~^—, [1; 4].
л;
245. у
246. у
247. у=егх • х3
249. у = е2х~х2
х— 1пA + х), [—0,5; 2].
л: in л:, |—г; 1
ln*> [l)r;
237. у =
2х3
9*
[4; 6].
239. у = (*+1)^*2, [-1; 3].
[-2; 4].
[-1; 4].
[-2; 2].
248. у = ¦
[1; 3].
250. у = C — х)ег
[0; 5].
251. Найдите длины сторон прямоугольника наибольшего периметра,
вписанного в полуокружность радиуса R.
252. Покажите, что из всех равнобедренных треугольников, вписанных в
данную окружность, наибольший периметр имеет равносторонний треугольник.
253. Из всех треугольников с данным основанием и данным углом при
вершине найдите тот, который имеет наибольшую площадь.
254. Из всех круговых секторов, имеющих данный периметр Р, найдите тот,
который имеет наибольшую площадь. Каков его радиус?
255. На окружности радиуса R дана точка А. Требуется провести хорду ВС
параллельно касательной к окружности в точке А так, чтобы площадь
треугольника ABC была наибольшей.
256. Определите длины сторон параллелограмма наибольшей площади,
вписанного в равнобедренный треугольник с основанием а и углом а при
основании (одна сторона параллелограмма лежит на основании треугольника, другая —
на боковой стороне треугольника).
257. Сечение тоннеля имеет форму прямоугольника, завершенного
полукругом, периметр сечения 18 м. При каком радиусе полукруга площадь сечения
будет наибольшей?
258. Дана точка М A; 2). Проведите через эту точку прямую так, чтобы
она отсекала в первом квадранте: а) треугольник наименьшей площади; 2)
отрезок наименьшей длины.
99

259. Даны две точки А @; 3) и В D; 5). Найдите на положительной полуоси
Ох такую точку С, чтобы \АС\ + \СВ\ было наименьшим.
260. Впишите в эллипс
Г
— + ——= 1 прямоугольник наибольшей площади.
а? Ь2
261. Статуя высотой 4 м стоит на колонне, высота которой 5,6 м. На каком
расстоянии от статуи должен стать человек, если расстояние от земли до уровня
глаз равно 1,6 м, чтобы видеть статую под наибольшим углом?
262. Открытый бак с квадратным основанием должен вмещать V литров.
При каких размерах на его изготовление пойдет наименьшее количество жести?
263. Консервная банка цилиндрической формы должна иметь объем V.
Каковы должны быть высота цилиндра и диаметр его основания, чтобы на
изготовление банки пошло наименьшее количество жести?
264. Найдите наибольший объем коробки (без крышки), которую можно
изготовить из куска картона 30 х 14 см2, вырезав по углам равные квадраты.
265. Цилиндр завершен сверху полушаром. Объем тела V. При каком радиусе
полная поверхность тела будет наименьшей?
266. В данный конус впишите цилиндр наибольшего объема. Радиус
основания конуса R, высота конуса Н.
267. Определите, при какой высоте конуса, вписанного в данный шар
радиуса R, объем конуса будет наибольшим.
268. Найдите высоту цилиндра наибольшего объема, который можно вписать
в шар радиуса R.
269. Найдите высоту конуса наименьшего объема, описанного около шара
радиуса R.
270. В полушар радиуса R вписан прямоугольный параллелепипед с
квадратным основанием. Каковы должны быть его размеры, чтобы объем был
наибольшим?
271. Периметр равнобедренного треугольника равен 2р. Какими должны
быть его стороны, чтобы объем тела, полученного от вращения этого
треугольника вокруг его основания, был наибольшим?
272. Два водных канала шириной 27 м и 64 м пересекаются под прямым
углом. Какова наибольшая длина бревна, которое при сплаве перейдет из
одного канала в другой?
273. Пункт В находится на расстоянии 60 км от железной дороги.
Расстояние по железной дороге от пункта А до ближайшей к пункту В точки С
составляет 285 км. На каком расстоянии от точки С надо построить станцию, чтобы
затрачивать наименьшее время на путь от Л до Б, если скорость движения по
железной дороге 52 км/ч, а скорость движения по шоссе 20 км/ч?
§ 4. ВЫПУКЛЫЕ ФУНКЦИИ
1. Определение выпуклости. Рассмотрим графики функций,
изображенные на рисунках 54, 55 и 56. Первый график обращен
выпуклостью вниз, второй — выпуклостью вверх, а третий имеет
В
Рис. 54
Рис. 55
Рйс. 56
100

у-
Уг
У
У1
0
I
с
i
i
I
—Ts
~~А\
*i
*г
ЛМ(х;у)\
I I
I I
1 • »
х х2 х
Рис. 57
участки, где график обращен
выпуклостью вверх, и участки, где обращен
выпуклостью вниз. Чтобы уточнить
соответствующие понятия, заметим, что какую
бы хорду дуги Л В на рисунке 54 мы ни
провели, она окажется выше
соответствующего участка кривой; какую бы хорду
дуги CD на рисунке 55 мы ни провели, она
окажется ниже соответствующего участка
кривой; наконец, на рисунке 56 хорды
могут оказаться и выше, и ниже
соответствующих участков кривой.
Введем следующее определение.
Определение 1. График функции у = / (х), непрерывной
на отрезке [а; 6], обращен выпуклостью вниз на этом отрезке, если
хорда, соединяющая любые две точки Аг (хг\ уг) и А2(х2\ у2) этого
графика, расположена на отрезке [_хг\ x2l не ниже графика. В этом
случае и саму функцию у = / (х) называют выпуклой вниз на отрезке
[а] Ы
Аналогично определяется график выпуклый вверх на отрезке
[а\ Ь]. Соответствующие понятия можно рассматривать для любого
промежутка.
Дадим аналитическую запись определения выпуклости вниз.
Возьмем произвольную точку М (х; у) хорды АХА2 (рис. 54). По-
х~~ Xl = t, получим х = *1+ *2, где t > 0.
х2 — х 1 + t
Из геометрических соображений (рис. 57) заключаем, что
ложив
Уг
-*1
у2 — у
L
Отсюда получаем, что ордината точки М хорды АгА2 вычисляется
по формуле
У1 + *Уь
У =
1 + *
Значение функции у = f (x) в выбранной точке х равно
*1 + tX2
f
l + t
Поэтому условие, что хорда лежит не ниже дуги, означает, что для
любых хъ х2 (: [а; 6], где хг < x2t и любого t > 0 выполняется
неравенство
*i + tx2 \ ^ f (xj + if (x2)
f(xi + txz
'[ l + t
<
1 + *
A)
Это неравенство является аналитическим определением понятия
выпуклости вниз.
101

Аналогично функцию у = f (х)9
непрерывную на отрезке [a; ft], называют
выпуклой вверх на этом отрезке, если для любых
х1у х2 € [я; ft], где х± < х2, выполняется
неравенство
/
Ч + tx2
>
/fa)+*/(*«)
B)
Рис. 58
1+t )~ \+t
Определениям выпуклости вниз и
вверх можно придать иной вид. Из
рисунка 58 видно, что если кривая обращена
выпуклостью вниз, то угол наклона хорды
АгС к положительному направлению оси абсцисс не больше угла
наклона хорды СА2 к положительному направлению оси абсцисс.
Но
мхс
f(x)-f(*i) и _ fjx2)-fjx)
> кг А — '
X —Хг 2 Х2 — X
Значит, для выпуклой вниз функции при хх ^ к <! х2 получаем:
fix)
•/(*i) < /(*,) — /(*)
C)
Неравенства A) и C) эквивалентны.
Докажем эквивалентность неравенств A) и C). Если в неравенстве A)
полола -f- tx2
жить -7——— = х, то получим:
1 + *
•хг
Х% — X
Тогда неравенство A) примет следующий вид:
•Хг
т. е.
откуда
/(*)<¦
/(*)<
f(xi)-
Xt
¦Xt
Xq ~~~ X X -
——/(*l) + —
x2 — X\ x2
/(*i) .
¦Хг
¦Xi
f(*i
f(x)-f(x1) <f(x2)~f(x)
X — X, Xn ~—~ X
Мы доказали, что неравенство C) следует из неравенства A). Выполнив те
же преобразования в обратном порядке, получим, что и неравенство A) следует
из неравенства C).
Аналогично определение выпуклой вверх функции можно
записать в виде следующего неравенства:
f(x)-fix,) > f(x2)-f(x)
х — хх
D)
102

Неравенства B) и D) эквивалентны.
Неравенство D) имеет простой геометрический
смысл: для выпуклой вверх функции имеем
kAlc^cA2 (рис. 59).
Теорема 1. Пусть функция у = f (x)
определена и непрерывна на отрезке [а; Ь~\
и дифференцируема в интервале~\а\ Ь\_. Для
того чтобы функция у = f (x) была
выпукла вниз на отрезке [а; 6], необходимо и
достаточно, чтобы на этом отрезке ее
график лежал не ниже касательной,
проведенной к графику в любой точке отрезка[а\ Ь~\.
у\
0
л
1
1
с
1
1
1
1
А2
1
1
1
1
1 ^
X
Рис 59
Доказательство необходимости. Пусть функция у =
= f (х) выпукла вниз на отрезке [а; Ь~] и пусть х0 ? ]а; Ь\_. Составим уравнение
касательной к графику функции у = f (x) в точке х0:
Укас = / (*о) + /' (*о) (х — хоУ
Нужно доказать, что для любой точки из отрезка [а; Ь] будет выполняться
неравенство Укривой > Укас Т. е.
/ М > I (*о) + Г Ы (х - х0). E)
Если х > х0, то неравенство E) можно переписать в виде
/(*)-/(*о)
fw<-
F)
если же х < х0, то неравенство E) можно переписать в виде
G)
Итак, нам надо доказать, что при х > х0 выполняется неравенство F), а
при х < х0 — неравенство G).
Пусть х > х0. Дадим аргументу х0 положительное приращение Дх так, что
х0 < х0-\- &х < х. По условию функция у = f (х) выпукла вниз на отрезке
[я; Ь]\ тогда, применив к точкам х0, х0 + Лх, х неравенство C), получим:
f(x0 + Hx)-f(x0) ^ f(x)-f(x0 + bx)
(о)
Ах
<
* — (*о + A*)
Перейдем в этом неравенстве к пределу при Дл; •
ция у = f (х) дифференцируема в точке х0, то
/(*о + А*)-/(*0)
?±х
¦О. Так как по условию функ-
lim
Д*-0
Г(*о,
так как функция у = / (х) непрерывна в точке Л'0, то
.. f(x)-f(x0+bx) /(,).
lim =
Дд^О X — (Х0 + Д*) X -
Значит, из неравенства (8) получаем:
/(*) — Г(х0)
-f(x0)
Г кх0) ^
что и требовалось доказать.
103

Аналогично доказывается, что при х < х0 выполняется неравенство G).
Если х = х0, то неравенство E) обращается в верное числовое неравенство / (х0)^
> f (*о).
Итак, для любой точки х € [а\ Ь] справедливо неравенство E). Необходимость
доказана.
Доказательство достаточности. Пусть график функции
y=f (x) на отрезке [а; 6] лежит не ниже касательной, проведенной к графику в
любой точке отрезка [а\ Ц. Докажем, что функция у = / (х) выпукла вниз на
отрезке [а; Ь].
Возьмем две точки *lf х2 € [а; 6] так, что х1 < х2. Пусть х0 — произвольная
точка интервала ]*i; х2[, т. е. Хх < х0 < х2. Проведем касательную к графику
у = / (х) в точке х0:
По условию укр > укас, т. е.
В частности,
/ (*i) > f (*о) + Г (х0) (хх - *о). (9)
f(*2)>f(Xo) + r (*o)(*i-*o). A0)
Из неравенства (9), учитывая, что хг — х0 < 0, получаем:
Х1 Х0
Из неравенства A0), учитывая, что х2 — х0 > 0, получаем:
ха — д^о
Значит,
fM-fixp) < tJxJ-fMe
Х\ — Xq Х2 Xq
Поскольку х0 — произвольная точка из ]хх; х2[, то, положив *0= х, получим
_____ ^ в
Но это (см. выше неравенство C)) и означает выпуклость вниз функции
у = / (х) на отрезке [а; Ь] Теорема доказана.
Обозначим D* [а; 6] класс функций, непрерывных на отрезке
[а; 6] и дифференцируемых в интервале ]а; 6[. Теорема 1 позволяет
дать для функции из D* [а; Ь] другое определение выпуклости вниз,
эквивалентное данному выше.
Определение 2. Пусть у = / (*) — функция на отрезке
[а; Ь], принадлежащая классу D* [а; 6]. Она называется выпуклой
вниз на [а; 6], если на этом отрезке ее график лежит не ниже
касательной, проведенной к графику в любой точке отрезка [а; 6].
Аналогично можно определить понятие выпуклости вверх.
Определение 3. Пусть у = f (x) — функция на отрезке
[а; Ь], принадлежащая классу D* [а; 6]. Она называется выпуклой
вверх на [а; 6], если на этом отрезке ее график лежит не выше
касательной, проведенной к графику в любой точке отрезка [а; 6].
104

Замечание. Ясно, что определение 1 применимо к более
широкому классу функций, чем определения 2 и 3: оно применимо
к классу С[а\ 6] функций, непрерывных на [а; 6], тогда как
определения 2 и 3 применимы к классу D* [а; 6] функций, непрерывных
на [а; 6] и дифференцируемых в ]а; 6[. Значит, для функций из
D*[a; Ь] можно пользоваться как определением 1, так и
определением 2 или 3.
2. Достаточные условия выпуклости.
Теорема 2. Пусть у = / (х) — функция из класса D* [а; Ь] и
пусть в любой внутренней точке х отрезка [а; 6] существует f"(x).
Если всюду в интервале ]а; 6[ выполняется неравенство f" (х) ^ О,
то функция у = f (x) выпукла вниз на [а; &]; если всюду в ]а; 6[ #&?-
полняется неравенство f"{x) ^ 0, то функция у = f (x) выпукла
вверх на отрезке [а; Ь].
Доказательство. Рассмотрим случай, когда f"(x) ^ 0.
Возьмем произвольную точку х0 ? ]а; Ь[_ и запишем уравнение
касательной к графику функции у = / (х) в точке х0:
Укас - /'(*о) (* — *о) + / (*о)-
Тогда
Укр — Укас = / (*) — /'(*о) (* — *о) — f (Xo).
Применив к разности / (х) — / (х0) формулу Лагранжа (теорема
Лагранжа применима, так как по условию функция у = / (х)
непрерывна на [а; 6] и дифференцируема в ]а; fe[), получим;
Укр — Укас = /'fcl) (X — Х0) — f (*0) (* — *0) -
= №-/'(*о))(*-*о),
где сх — точка, лежащая между точками х и х0.
Теперь, применив формулу Лагранжа к разности /'(q) —f'(x0),
получим:
ffe)-fW = rWte-4
где точка с лежит между точками сг и х0. Значит,
Укр — Укас = Г (С) fa — *о) (X — *о)- A1)
Точки сг и х лежат по одну сторону от точки х0 и потому fa —х0) х
Х(х — х0) >0. Кроме того, по условию f"(c) ^ 0. В итоге получаем
Укр ^ Укас» а это означает, что на отрезке [а; 6] график обращен
выпуклостью вниз.
Аналогично доказывается, что в случае f"(x) ^ 0 функция
выпукла вверх.
С соответствующими изменениями теорема верна для любого
промежутка X.
Пример 1. Покажем, что функция у = ех, выпукла вниз
на всей числовой прямой.
Решение. Имеем у" = ех. Так как ех > 0 при любом х9
то по теореме 2 функция у = е* выпукла вниз на ]—оо; оо[.
105

У\
У *
Рис. 60
Рис. 61
Хп
Рис. 62
Пример 2. Покажем, что функция у = lg х выпукла вверх
на луче ]0; оо[.
Решение. Имеем:
, п ., / \п х V 1 „ 1
У = (lg*) = 7777 = 7ТГ7^ У =
In 10
х\п Ю'
*2 In 10
Если л: Ф 0, то у"< 0. Значит, функция у = lg х выпукла вверх
на луче ]0; оо[.
ПримерЗ. Исследуем на выпуклость функцию у = ха, а > О,
х>0.
Решение. Имеем:
/ = а (а — 1) ха-2.
При а = 1 получаем у" = 0, при а > 1 у" > 0, а при а < 1 у" < 0.
Значит, график степенной функции у = ха представляет собой
выпуклую вниз кривую при а > 1 и выпуклую вверх кривую при
а< 1; если а = 1, то имеем линейную функцию у = х, которая
может считаться как выпуклой вверх, так и выпуклой вниз (см. рис. 17).
3. Точки перегиба. До сих пор, говоря о направлении выпуклости
непрерывной и дифференцируемой функции у = / (х), х?\_а; 6],
мы исследовали расположение графика функции относительно
касательной к графику глобально, на всем отрезке [а; 6]. Теперь
мы изучим взаимное расположение графика и касательной в
некоторой окрестности точки касания (локально).
В большинстве случаев график локально располагается по одну
сторону от касательной; так на рисунке 60 он в достаточно малой
окрестности точки касания лежит выше касательной, а на
рисунке 61 —ниже касательной. Однако могут существовать точки, слева
от которых (в достаточно малой окрестности) график лежит по
одну сторону от касательной, а справа — по другую (рис. 62).
Такие точки называются точками перегиба.
Определение 4. Точка М линии Г называется точкой
перегиба, если существует дуга АВ этой линии, содержащая точку
М, такая, что дуги AM и MB расположены по разные стороны от
касательной, проведенной в точке М к линии Г.
Обычно точка перегиба отделяет участок, где функция выпукла
вниз, от участка, где функция выпукла вверх.
106

f(x)-f(x0)
y\
0
<^ \
1
Xo
/ Укр-Укас
X
Рис. 63
Рис. 64
Для отыскания точек перегиба полезна лемма, аналогичная
лемме о знаке приращения функции (с. 77). В лемме о знаке приращения
функции речь шла о знаке разности f(x) — f(x0), т. е. о знаке разности
между ординатой кривой и ординатой горизонтальной прямой
у = f (х0) (рис. 63). В лемме, которая формулируется ниже^речь
идет о знаке разности между ординатой графика и ординатой
касательной (рис. 64).
Лемма. Пусть функция определена на промежутке X и имеет
вторую производную в некоторой внутренней точке х0€ X. Если
}"(х0) > 0, то график функции в некоторой окрестности
точки х0 располагается выше касательной к графику в точке х0; если
Г(*о)< °> то график в некоторой окрестности точки х0
располагается ниже касательной.
Доказательство. Пусть /" (х0) > 0. Как и при
доказательстве теоремы 2, введем вспомогательную функцию:
Ф (*) = Укр — Укас,
ф(х) =f (х) — f'(x0) (х — x0)—f (х0).
Ясно, что Ф (х0) = 0. Имеем, далее, Ф'(х) = /'(*) — /'(*о)>
ф"(х) = Г(х). Значит,
Ф' (х0) = 0, Ф"(х0) = Г(х0).
Так как по условию f(x0) > 0, то Ф" (х0) > 0. Тогда по теореме 4
из § 3 заключаем, что х0 —точка минимума функции Ф (х). В
таком случае в некоторой окрестности точки х0 выполняется неравенство
Ф (х) > Ф (*о)> т- е- ф W > ° (напомним, что Ф (х0) = 0). Так
как Ф (х) = >'кр — Укас, то получаем укр > укас- Это и означает,
что в указанной окрестности график располагается выше
касательной. Вторая часть леммы доказывается аналогично.
Теорема 3 (необходимое условие точки перегиба). Для того
чтобы график функции у = f (x) имел перегиб в точке х0,
необходимо, чтобы функция была дифференцируема в точке х0 и чтобы
в этой точке вторая производная либо не существовала, либо была
равна нулю.
Доказательство. Могут представиться лишь четыре
случая: а) /" (х0) > 0; б) f (*0)< 0; в) f"(x0) = 0; г) f"(x0) не
107

существует. Но в случаях а) и б), по лемме, график располагается
по одну сторону от касательной, т. е. в этих случаях точка х0 не
может быть точкой перегиба. Значит, возможны лишь случаи
в) и г), что и требовалось доказать.
Подчеркнем, что эта теорема дает необходимое, но недостаточное
условие точки перегиба. Например, для функции у — х4 имеем
у" = 12л:2. Вторая производная обращается в нуль в точке х = О,
но это — точка минимума функции, а не точка перегиба.
Теорема 4 (первое достаточное условие точки перегиба).
Пусть функция у = f (x) дифференцируема в точке х0 и пусть у
этой точки есть окрестность ]*0 — б; х0 + б[ такая, что в
интервалах ]*0 — б; *0[ и ]*0; х0 + б[ существует вторая производная
f" (х), причем она сохраняет знак на каждом из этих интервалов.
Тогда если на ]*0 — б; *0[ и ]*0; х0 + б[ знаки второй производной
различны, то х0 является точкой перегиба, если знаки одинаковы,
то перегиба нет.
Доказательство. Воспользуемся равенством A1),
полученным при доказательстве теоремы 2:
Ф (X) = Укр — Укас = Г (С) (С± — Х0) (X — Х0).
Так как точки х и с± лежат по одну сторону от точки х0, то
(х — х0) (сг — х0) > 0. Отсюда следует, что если знаки второй
производной слева и справа от точки х0 различны, то и знаки
Ф (х) = укр — Укас различны, а это означает, что график переходит
с одной стороны касательной на другую, т. е. х0 — точка перегиба.
Если же по обе стороны от х0 имеем /" (х0) > 0, то и слева, и справа
будет укр > укас, а это значит, что график лежит выше
касательной и перегиба нет. Случай, когда f"(x) < 0, рассматривается
аналогично.
Доказанные теоремы приводят к следующему правилу
нахождения точек перегиба графика функции у = f (x):
1) находим точки, в которых f"(x) не существует или обращается
в нуль;
2) пусть х0 — одна из найденных точек. Исследуем знак f"(x)
слева и справа от точки х0 (разумеется, в достаточно малой
окрестности точки *0). На основании теоремы 4 делаем соответствующие
выводы (см. таблицу на рисунке 65).
Пример 4. Найдем точки экстремума и точки перегиба
функции у = Зх4 — 8а:3 + 6#2 + 12 и построим график.
Решение. Имеем:
у' = 12х3 — 24jc2 + 12* = 12* (х — IJ,
у' = 0 при хг — 0 и х% = 1. Производная при переходе через точку
* = 0 меняет знак с «—» на «+», а при переходе через точку * = 1
не меняет знака. Значит, * = 0 — точка минимума, ymin = 12.
а в точке х = 1 экстремума нет.
у" = 36а;2 — 48* + 12 = 36 (* — 1) (х —-).
108

f'(x)
\f"(x)
J1
\f(x)
ft*)
Jx0-5;xQ[
+
—
+
—
1
]Xo\*o+8[
—
+
+
—
Геометр,
иллюстр.
i
*o
г
*0
1
*0
1
1
i Xo
Вывод
Перегиб с
выпуклости
вниз на
выпуклость
вверх 1
Перегиб с
выпуклости
вверх на
выпуклость
вниз
Выпуклость
вниз
Выпуклость
вверх
Рис. 65
Вторая производная- обращается в нуль в +
точках х2 = 1 и х3 = —. Знаки второй
о
производной распределены следующим
образом (рис. 66): на луче
3
имеем
имеем
у">0, на интервале
у" < 0, на луче ]1; оо[ имеем у" > 0.
Значит, х = точка перегиба
(переход с выпуклости вниз на выпуклость
вверх) и х = 1 — точка перегиба (переход
с выпуклости вверх на выпуклость вниз).
При х = — имеем у = 12—, при х = 1
имеем у = 13.
Используя найденные контрольные
точки @; 12), [-; 12-] и A; 13), строим
график функции (рис. 67).
+ У"
Рис. 66
Рис.
109

ции у = х4
Теорема 5 (второе достаточное
условие точки перегиба). Если
f"(x0) = 0, f'"(x0) ф 0, то х0—
точка перегиба графика функции
У = / (х).
Доказательство.
Положим для определенности
f'"(x0) > 0. Так как f"'(x) —
производная функции /" (х), то из
условия /'" (х0) > 0 следует
возрастание функции /" (х) в точке х0.
Но /" (х0) = 0, значит, при х < х0
имеем /" (х) < 0, а при х > х0
имеем /" (х) > 0. Так как
вторая производная меняет знак при
переходе через точку х0, то по
теореме 4 х0 — точка перегиба.
Теорема доказана.
Пример 5. Найдем точки экстремума и точки перегиба функ-
6х2 + 5 и построим ее график.
Решение. Прежде всего заметим, что функция является
четной, а потому достаточно провести исследование для х ^ 0.
Имеем:
у = 4х3 — 12* = 4х(х2 — 3).
Решая уравнение у' = 0, находим х± = 0 и х2 = |/ (точку х=—]/~3
не берем, так как условились рассмотреть случай х ^ 0). Далее,
у" = \2х2 — 12 = 12 (х2 — 1), /"@) = —12 < 0, f" (|/3) = 24>0.
Значит, л; = 0 — точка максимума, а х = ]/3 — точка минимума.
Из уравнения 12 (х2 — 1) = 0 находим х = 1. В этой точке
возможен перегиб графика. Чтобы выяснить это, найдем третью
производную:
?" (х) = 24*.
Так как /'" A) = 24 Ф 0, то х = 1 — точка перегиба.
Для построения графика используем найденные точки: @; 5) —
точка максимума, (]/;—4)—точка минимума, A; 0)—точка
перегиба. Кроме того, найдем точки пересечения графика с осью
абсцисс. Решив уравнение х4 — 6х2 + 5 = 0, получим: xlj2 = ±1,
#з,4 = ±1/. График изображен на рисунке 68.
Вопросы для самопроверки
1. Как располагается график выпуклой вниз функции по отношению к
хорде? по отношению к касательной?
2. Как располагается график выпуклой вверх функции по отношению к
хорде? по отношению к касательной?
НО

3. Сформулируйте аналитическое определение выпуклой вниз функции.
4. Сформулируйте аналитическое определение выпуклой вверх функции.
5. В чем состоят достаточные условия выпуклости функции вниз на отрезке?
6. В чем состоят достаточные условия выпуклости функции вверх на отрезке?
7. Что такое точка перегиба кривой?
8. В чем состоит необходимое условие точки перегиба?
9. В чем состоит первое достаточное условие точки перегиба?
10. В чем состоит второе достаточное условие точки перегиба?
11. Опишите правило нахождения точек перегиба данной функции.
Упражнения
Исследуйте данные функции на направление выпуклости; найдите интервалы
выпуклости вверх и вниз и точки перегиба.
274. у = л:4 + х2. 21Ъ. у = л:4 — 12л;3 + 48л;2 — 50.
276. у = х3 — Зх2 — 9* + 9. 277. у = In (х2 — 1).
278. у = ех + (х + IL. 279. у = хе~х.
280. у = 2 + (л: — 4) 3 . 281. у = х* A2 In x — 7).
3
282. При каких значениях а кривая у = л;4 + ах3 -\ л;2 + 1 будет
выпукла вниз на всей числовой прямой?
283. При каких значениях а и Ь точка А A; 3) является точкой перегиба
кривой у = ах3 + Ьх2?
х+ 1
284. Покажите, что кривая у = имеет три точки перегиба, лежащие
х2 + 1
на одной прямой.
285. Докажите, что график всякого многочлена, содержащего переменную
только в четных степенях с положительными коэффициентами обращен
выпуклостью вниз.
286. Докажите, что график всякого многочлена нечетной степени, большей 1,
имеет хотя бы одну точку перегиба.
287. Докажите, что точка О @; 0) является точкой перегиба для графика
функции у= W*4*inA ХФ0,
[ 0, х = 0.
288. Постройте график функции в окрестности заданной точки, если
известно, что в этой окрестности функция непрерывна и имеет непрерывную первую
производную:
1) х = 3, у = 2, у' = —2, у" < 0; 2) х = — 1, у = 1, у' = 1, у" < 0;
3) х = — 1, у = 2, / = 0, у" < 0; 4) х = 1, у = 0, у' = 0, у" > 0; 5) х = 2,
у = 2, / = 2, у" > 0; 6) х = 1, у = —1, / = —1, у" > 0; 7) х = 0, у = 1,
у' = 1, у" = 0, у"' > 0; 8) х = — 1, у = 3, / = —1, у" = 0, у'" < 0;
9) х = 0, у = 0, у' = 0, у" = 0, у'" > 0; 10) х = 2, у = 1, / = 0, у" = 0,
у'"< 0.
§ 5. ПРИМЕНЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
К ДОКАЗАТЕЛЬСТВУ НЕРАВЕНСТВ И РЕШЕНИЮ УРАВНЕНИЙ
1. Доказательство неравенств. В настоящем пункте покажем,
как используются при доказательстве неравенств такие свойства
функций, как строгое возрастание, строгое убывание, выпуклость
вверх, выпуклость вниз.
Ш

Пример 1. Докажем, что для всех х ^ 0 справедливо
неравенство
е* > 1 + х. A)
Решение. Составим вспомогательную функцию g (x) =
=ех — A + х) и найдем ее производную:
g' (х) = ех -1.
Так как при х ^ О выполняется неравенство ех — 1^0, причем
равенство возможно лишь в случае х = 0, то функция g (x) строго
возрастает на луче [0; оо[ (с. 86). В частности, выполняется
неравенство g (x) ^ g @). Но
g @) = е« - A + 0) = 0.
Значит, g (х) ^ 0, т. е.
ех - A + х) > 0.
Таким образом, ех ^ 1 + х, что и требовалось доказать.
Пример 2. Докажем, что при х ^ 0 выполняется
неравенство
е*р\+х + ?. B)
Решение. Составим вспомогательную функцию
g{x) = e*-(l+x + jL}
и найдем ее производную:
g' (x) = ех-(\+ х).
Из неравенства A) следует, что g'(x) ^ 0, значит, функция g (x)
возрастает на луче [0; оо[. Но тогда из неравенства х ^ 0 вытекает
неравенство g(x) ^ g"@), а так как g @) = 0, то получаем g(x)^ 0,
т. е.
и, следовательно,
ех>1+х + ^9
что и требовалось доказать.
Неравенства A) и B) являются частными случаями неравенства
^>l+x + - + |r + ... + ir, C)
справедливого при х ^ 0 для любого натурального числа п.
Для доказательства неравенства C) воспользуемся методом математической
индукции. При п = 1 неравенство справедливо, так как оно обращается в этом
112

случае в доказанное выше неравенство A). Предположим, что неравенство верно
при п = k, т. е. что
X2 Х^
**>!+*+-+...+Т. D)
и докажем, что тогда верно и при п = k + 1, т. е. что оно
•*>1 + *+-я+-+^+1ГПГ E)
Иными словами, докажем, что из неравенства D) следует неравенство E).
Для доказательства рассмотрим функцию
Х2 yk+l
W=e*_ 1+*+-- +...+
2! ^ "' ] (k+l)\ ]'
Производная этой функции имеет вид:
,и_*_(, + ,+_+й±!?)_,_(,+,+... + ?).
Из неравенства D) следует, что g' (х) ^ 0. Значит, функция g (x) возрастает при
х ^ 0, и, следовательно, при х ^ 0 имеем!
g(*)>g @) = 0.
Тем самым доказано выполнение неравенства E). Отсюда по принципу
математической индукции заключаем, что неравенство C) верно для любого натурального п
Пример 3. Докажем, что при х ^ 0 выполняется
неравенство
ех ^ 1 + хех.
Решение. Составим вспомогательную функцию g (х) =
= ех — A + хех). Ее производная имеет вид:
g' (х) = ех — ех — хех = —хех.
Поэтому при х ^ 0 имеем g' (х) ^ 0 и функция у = g (x) убывает
на луче [0; оо[. Значит, при х ^ 0 имеем g (x) ^ g @). Hog@) = 0
и, следовательно, g (х) ^ 0, т. е. ех — 1 — хех ^ 0 при х ^ 0.
Это и означает, что ех ^ 1 + хех, если х ^ 0, что и требовалось
доказать.
Пользуясь методом математической индукции, можно доказать,
что при х ^ 0 для любого натурального п справедливо неравенство
у2 уП уП+1
ех < 1 + х + ^- + ... + — + — е*. F)
^2! п! (л+1)! V '
Неравенство, доказанное в примере 3, является частным случаем
неравенства F) при п = 0.
Доказанное выше неравенство C) дает оценку для ех по
недостатку, а неравенство F) дает оценку для ех по избытку. Откло-
хп+\
нение этих оценок друг от друга равно ех . Можно доказать,
что при п -> со это выражение стремится к нулю при любом поло-
пз

жительном значении х. Поэтому,
чем больше /г, тем сильнее график
многочлена у = Рп (х), где
У2 УП
P.W-1 +х+- + ... + -
^ /^ «прилипает» к графику функции
\х у = бх (рис. 69). Значит,
ех « 1 4- х +— + .-.+ —• G)
2! /г! '
Таким образом, чтобы найти
приближенное значение функции ех, нужно
найти значение Рп (х) при достаточно
большом п. Но вычисление Рп (х)
сводится к операциям сложения, умножения и
деления, а эти операции может выполнять
электронно-вычислительная машина.
Поэтому с помощью равенства G) можно
осуществить вычисление ех на ЭЗМ.
Вычислим для примера значение е с точностью 0,001. Воспользовавшись
равенством G), получим:
1 1 1
^ ^ 2! ^ 3! ' /г!
Рис 69
Как мы отмечали выше, погрешность не будет превышать
(п+1)
¦ех, т. е. посколfa-
Для достижения точности
ку х= 1, погрешность не будет превышать
0,001 достаточно взять п = 6. В самом деле, так как е < 3, то
е 3 3
< — = < 0,001.
F + 1)! 7! 5040
Итак, с точностью 0,001 имеем:
, , 11111
Г Т 21 Т 31 f 41 Г 51 ' 6!
Пример 4. Докажем, что если 0 < а < C < —, то -^- > —.
2 tga a
Решение. Исследуем на монотонность функцию у = -^.
х
Имеем:
1
' — /tgx У__ cos2 х'
• tgx
¦ sin х cos x
Если 0 < х < —, то, как известно, sin х < х и тем более sin x cos x <
<х. Значит, в интервале 0; — выполняется неравенство у' >0,
114

а потому функция у = -^- строго возрастает на этом интервале.
Тогда из а < 6 следует -^ < -|А т. е. -^- > —, что и требо-
а р tga a
валось доказать.
Пример 5. Докажем, что при п ^ 2 выполняется
неравенство
ап + ьп *>(<* + Ь\п
где а > О, Ь > 0.
Решение. Если a = 6, то неравенство очевидно. Пусть
афЬ, положим для определенности а <Ь. Рассмотрим функцию
у = хп на отрезке [а\ Ь]. Имеем:
/"(*) =/г(/г— 1) **-*>().
Значит, функция у = хл выпукла вниз на отрезке [а; 6]. Но если
функция у = f (х) выпукла вниз на отрезке [а; 6], то для любых
точек ^ и #2 этого отрезка выполняется неравенство
с /хг + tx2\ ^ / (*i) + */ (*2)
'\ i + * j^ 1+*
где t > 0 (с. 101). В частности, если х± = а, х2 = b, t = I,
получаем:
/(a + b\ < /(<») + /№) , (8)
Применив неравенство (8) к функции у = хл, получим:
a + b\n an + bn
что и требовалось доказать.
2. Приближенное решение уравнений. При отыскании точек
экстремума и точек перегиба возникает необходимость в решении
уравнений. Часто эти уравнения не могут быть решены по
известным формулам, и потому надо найти приближенные значения их
корней. В этом пункте изложим некоторые методы приближенного
решения уравнений.
Мы знаем, что если функция у = / (х) непрерывна на отрезке
[а; Ь], причем / (а) и f (b) имеют разные знаки, то уравнение f (х) = 0
имеет хотя бы один корень, расположенный на этом отрезке. Если
при этом функция у = f (x) строго монотонна на [a; b] (например,
если она имеет внутри этого отрезка производную постоянного
знака), то уравнение / (х) = 0 имеет лишь один корень,
расположенный на этом отрезке.
Чтобы найти приближенное значение этого корня, применяет
методы хорд и касательных. При использовании метода хорд заме-
115

няют график функции на отрезке [я; 6]
хордой, соединяющей точки А (а; / (а)) и
В F; / (Ь)). Уравнение этой хорды имеет
вид:
f(a)
f(b)-f(a)
(9)
Рис 70
Она пересекает ось абсцисс в такой
точке, где у = 0. Полагая в равенстве (9)
у = 0, находим, что
Ъ — а
х1=а — f (а)
(Ю)
f{b)-f(a)
Это число является абсциссой точки пересечения хорды с осью Ох.
Его можно принять за приближенное значение корня уравнения
/ (х) = 0. Чтобы получить более точное значение корня, надо
вычислить значение функции в найденной точке и провести хорду,
соединяющую соответствующую точку графика с тем концом
графика, в котором функция имеет знак, противоположный
полученному. Например, если / (а) < 0, / (Ь) > 0, а / (хх) < 0, то надо
провести хорду, соединяющую точки Мг (х±\ f (х±)) и В ф\ f (b)) (рис. 70).
Она пересекает ось абсцисс в точке
2 * Vi;/(*)-f(*i)
Далее находим следующее приближение к корню:
Х3 — %2 / \%2/
Ь — Х9
f (*)-/(*«)
В общем случае можно записать:
b — xn
vrt+l
f(b)-f(xn)
Мы получили последовательность чисел х1у х2> ..., хп, ... Можно
доказать, что она сходится к корню I уравнения / (х) = 0. Вычисления
прекращают, когда в пределах заданной точности совпадают
значения хп и хп+1.
Второй способ приближенного решения уравнений, называемый
методом касательных, основан на замене графика функции не
хордой, а касательной. Предположим, что на отрезке [а; 6] не только
первая, но и вторая производная сохраняет один и тот же знак.
Тогда график функции у = f (x) на всем отрезке обращен
выпуклостью в одну и ту же сторону. Рисунки 71 и 72 показывают, что
касательную надо проводить в точке, в которой знак функции
совпадает со знаком второй производной: в точке, где функция
положительна, если /" (х) > 0 (т. е. график обращен выпуклостью вниз),
и в точке, где функция отрицательна, в противном случае. Такая
116

Рис. 71
Рис. 72
точка обозначается обычно через х0 и называется начальным при
ближением.
Предположим для определенности, что / (а) < О, f ф) > 0 и
/" (х) > 0. Тогда касательную надо проводить в точке В ф\ f (й)),
т. е. начальное приближение х0 = Ь. Уравнение этой касательной
имеет вид:
y-f(b)=f'(b)(x-b).
Чтобы найти точку пересечения касательной и оси абсцисс,
положим у = 0. Мы получим, что —f Ф) = f ф) (х± — &), откуда
находим абсциссу точки пересечения:
xi = хо 77—\9 ( ==z хм'
Г \хо)
Это число можно принять за приближенное значение корня
уравнения / (х) = 0 (рис. 72). Чтобы получить более точное значение
корня, проведем касательную в точке с абсциссой хъ и найдем
точку ее пересечения с осью Ох. Продолжая этот процесс, получим
последовательность чисел хъ х2, ..., хп, ..., вычисляемую по формуле
Она сходится к корню I уравнения / {х) = 0. Вычисления
прекращают, когда с заданной степенью точности совпадают аначения хп и
Xn+i.
Пример 6. Найдем действительный корень уравнения
г3 — 2л:2 + За: — 5 = 0 с точностью до 10~4: а) методом хорд;
б) методом касательных.
Решение. Имеем:
/ (х) = х3 — 2х2 + Зх — 5, /' (*) = Зх2 — \х + 3.
Так как дискриминант квадратного трехчлена Зг2 — Ах + 3
отрицателен, то знак трехчлена при любых х совпадает со знаком
старшего коэффициента. Таким образом, при любом х имеем /' (х) > 0,
т. е. функция у = f (х) строго возрастает на всей числовой прямой.
В таком случае заданное уравнение может иметь не более одного
действительного корня.
117

Далее, заметим, что / A) = —3 < 0, а / B) = 1 > 0. Значит,
наше уравнение имеет единственный корень ?, лежащий в интервале
]1; 2[: 1 <| <2.
а) По методу хорд, воспользовавшись формулой A0), получим
первое приближение:
*1==1—— • 1 = 1,75.
1 4
Так как / A,75) = —0,5156 < 0, a f B) = 1 > 0, то 1,75 < I < 2.
Воспользовавшись формулой (И), находим второе
приближение:
х2 = 1,75 + ^? ' °>25 = U75 + 0,0850 = 1,8350.
1,5156
Так как / A,835) = —0,05059 < 0, то 1,835 < ? < 2.
Процесс сходится весьма медленно. Попробуем сузить
интервал, учитывая, что значение функции f (х) в точке х2 = 1,835
значительно меньше по абсолютной величине, чем / B). Имеем / A,9) =
= 0,339 > 0. Следовательно, 1,835 < I < 1,9.
Применяя к интервалу ] 1,835; 1,9[ метод хорд, получим новое
приближение:
х = 1,835— ~0'05059 .0,065= 1,8434.
3 0,339 + 0,05059
Дальнейшие вычисления по методу хорд дают л;4 = 1,8437,
хъ = 1,8438. Так как / A,8437) < 0, a f A,8438) > 0, то с требуемой
точностью 10~4 можно считать, что ? « 1,8438.
б) Для метода касательных в качестве начального приближения
выбираем х0 = 2, так как / B) = 1 > 0 и /" (х) = €>х — 4 > 0 в
интервале ]1; 2[, первая производная ? (х) = Зх2 — 4х + 3 > 0
также сохраняет знак в интервале ]1; 2[, так что метод касательных
применить можно.
Первое приближение:
xi = x0 —f-^ =2 — — = 1,857.
Второе приближение:
X2 = ^_L^= 1,857-°-^^= 1,8439.
2 1 !'(хг) 5,9275
Третье приближение:
х« = 1,8439 —/A>8439) = 1,8438.
3 /' A,8439)
Нужная точность достигнута уже на третьем шаге. Здесь
сходимость процесса более быстрая, чем по методу хорд.
118

Вопросы для самопроверки
1. Опишите процесс решения уравнения / (х) = 0 методом хорд. Дайте
геометрическое истолкование.
2. Опишите процесс решения уравнения / (х) = 0 методом касательных.
Дайте геометрическое истолкование. Каким условиям должна удовлетворять
функция у = f (x), чтобь( можно было применить метод касательных?
Упражнения
Докажите неравенства.
х^ х3
289. cos х > 1 — —. 290. sin x > х — -— (х > 0).
1 д;3
291. 2V х >3 — — (х> 1). 292. tgx > х + — (х > 0).
х 3
293. arcsin х > х @ < х < 1).
J? X Х^
294. jc — — < arctg х < л: — — + — (л: > 0).
3 3 5
х2
295. л: — —- < In A + х)< х (х>0).
а + Ь cos a + cos b I я я \
mix»—> ? -7<а<6<Т:
2)tg^T< ? (°<а<&<у1-
а+2Ь
"Г" ^ еа + 2е*
297. е <¦
3
298. VlE^4^3^
/"
Найдите приближенно действительные корни уравнений.
299. х3 — х — 1 = 0 с точностью до 0,0001.
300. х3 — 5л: + 1 = 0 с точностью до 0,001.
301. я3 — 2х — 5=0 с точностью до 0,001.
302. х3 — 9х + 6 = 0 с точностью до 0,0001.
§ 6. ПРИМЕНЕНИЕ ПРОИЗВОДНЫХ ДЛЯ ВЫЧИСЛЕНИЯ ПРЕДЕЛОВ
ФУНКЦИЙ
Пусть нужно вычислить lim/(x), где а — число или один из
символов со, +оо, —со. Часто этот предел не удается вычислить
непосредственным применением теорем о пределах — их формальное
применение приводит к «неопределенному выражению» одного из
следующих видов:
?t ~э оо — оо, 0 • оо, 0°, со0, О00 ИЛИ 1°°.
0 оо
119

В таких случаях приходится, как говорят, «раскрывать
неопределенность». О различных приемах раскрытия
неопределенностей говорилось в разделе «Введение в анализ». Существуют
способы отыскания пределов, связанные с дифференциальным
исчислением; некоторые из них изложим в настоящем параграфе.
1. Теорема Коши. В этом пункте рассмотрим теорему, которая
наряду с теоремами Ролля и Лагранжа, относится к основным
теоремам дифференциального исчисления и является обобщением
теоремы Лагранжа.
Теорема Коши. Пусть на отрезке [а; U] заданы две функции
у = f (х) и у = g (x), причем: 1) обе функции непрерывны на отрез-
ке\_а\ Ь]\ 2) обе функции дифференцируемы в интервале~\а\ 6[; 3) g\x)
ни в одной точке интервала~]а\ Ь\_ не обращается в нуль.
Тогда в ]а; 6[ найдется точка с такая, что
f(b)-f(a) = г (с)
g(b)-g(a) g'(c)'
Доказательство. Составим вспомогательную функцию
F(x) = f(x)-Xg(x),
где X — число. Так как функции f (x) и g (x) по условию
непрерывны на [а; 6] и дифференцируемы в ]а; Ь[, то и функция F (х)
непрерывна на [a; b] и дифференцируема в ]#; ?>[. Значит, функция
F (х) удовлетворяет первым двум условиям теоремы Ролля (с. 78).
Подберем постоянный множитель X так, чтобы функция F (х)
удовлетворяла и третьему условию теоремы Ролля:
F(a) = F ф).
Для этого должно выполняться равенство
f(a)-Xg(a) = f(b)-Xg(b),
т. е.
b(g(b)-g(a)) = f(b)-f(a). A)
Заметим, что g (b) — g (а) Ф 0. В самом деле, если бы было g (b) —
— S (а) = 0> то> применив к функции g (х) на отрезке \_а\ Ь~]
теорему Ролля, мы заключили бы, что существует точка сг (а <сг < Ь)
такая, что g' (сг) = 0, а это противоречит условию доказываемой
теоремы: g' (х) Ф 0 всюду в ]а; Ь[. Поэтому обе части равенства A)
можно разделить на коэффициент при X, в результате чего получим:
х= f(b)-f(a)
g(b)-g(a)'
При найденном значении X вспомогательная функция F (х)
удовлетворяет всем условиям теоремы Ролля. Но тогда по теореме
Ролля в ]а; Ь[ найдется, по крайней мере, одна точка с такая, что
F' (с) = 0. Так как F' (х) = f (х) — Xg' (x), то, учитывая, что
F' (с) = 0, получим:
/' (с) - Ч' (с) = 0,
120

откуда
% = ш
ё'(с)
т. е.
f(b)-f(a) f (с)
g(b) — g (a) g' (с)
B)
что и требовалось доказать.
Замечание. Теорема Лагранжа является частным
случаем теоремы Коши. Если в формуле B) положить g (х) = х, то
получим формулу Лагранжа
f(b)-f(a)
Ь—а
Г {С).
Пример 1. Пусть f (х) = х4, g (х) = л:8, а = 1, Ъ = 2.
Составим формулу Коши и найдем значение с.
Решение. Функции f (х) и g (x) непрерывны на отрезке
[1; 2], дифференцируемы в интервале ]1; 2[ и g' (х) = Зх2 Ф 0 в
интервале ]1; 2[. Следовательно, условия теоремы Коши выполнены
и, значит, существует точка с такая, что
/B)-/A) = Г(с)
*B)-g(l) i(c)m
Найдем эту точку. Имеем:
/B) = 24= 16, /A)= 1* = 1,
gr B) = 23 = 8, g(l)= 13 = 1,
f'(x) = 4х3, /' (с) = 4с3, g' (х) = Зх2, g' (с) = ЗА
Значит,
16—1 __4c*
8 — 1 ~~ Зс2#
Из этого уравнения находим с = —.
28
2. Правило Лопиталя.
Теорема 1. Пусть функции у = f (х) и у = g (x) непрерывны
в точке а, дифференцируемы в некоторой проколотой окрестности
точки а (т. е. дифференцируемы во всех точках окрестности, за
исключением, быть может, самой точки а) и обращаются в нуль
в точке a (f (a) = g (а) = 0). Пусть, кроме того, g' (x) не
обращается в нуль ни в какой точке проколотой окрестности точки а.
Г (х) f (х)
Тогда если существует lim , то существует и Urn *-^,
х->а g* (х) х-+а g (X)
причем эти пределы равны:
x-*ag(x) x-ag(x)
121

Доказательство. Используем теорему Коши. Заметим
прежде всего, что функции f (х) и g (x) удовлетворяют условиям
теоремы Коши на каждом из промежутков [а — б; а[, ]а; а + б],
лежащих в проколотой окрестности точки а. Рассмотрим
отношение '-^- и преобразуем его так, чтобы можно было использовать
формулу B) Коши.
Рассмотрим случай, когда х > а. Вычтем из числителя и зна-
f (х)
менателя дроби L^-Li соответственно, / (а) = 0 и g (а) =* 0:
/(*) = f(x)-f{a) ^
g (*) g(x) — g {a) *
Так как по теореме Коши
f(x)-f(o) = Г (с) ^
g(x) — g(a) g'(c)'
где а < с < х, то
/(*) = Г (с)
g(x) gip)
При х -> а имеем с -> а, и так как по условию существует
lim ' , то существует и предел hm ---s причем эти пределы
с-а g* (С) х^а g(x)
равны. Заменив в первом пределе с на х, получим:
х-+а g (X) х-+а g' (X)
что и требовалось доказать.
Аналогично рассматривается случай, когда х < а.
Теорема 2. Пусть функции у = f (х) и у = g (x)
дифференцируемы на луче ]а; +оо[, причем g' (х) Ф 0, и пусть lim / (х) =
Х-*- 00
f (x)
= lim g (х) = 0. Если существует lim V"A mo существует и
Х-+СО Х-* СО g (X)
lim ^^-, причем эти пределы равны:
x-cog(x)
hm ^-^- = hm ' v '
х-+аэ g(x) х-*оэ g' (X)
Доказательство. Положим х = —. Тогда
11 ' \t
1 \V r, / 1 \ / 1 \ / / 1 W , / 1 \ / 1
c(})i^(i)KH«(i));
/ *2
Имеем: lim -i-^- = lim ^
x-+oo g{X) t-+0
7)
122

Для вычисления предела lim
лучим:
/т
hm -L±J- = hm
g(x)
/-*o
um
g'
воспользуемся теоремой 1. По-
= lim
nj
g'T
. lim №..
Х-+ОЭ g' (X)
Теорема доказана.
В этих теоремах мы рассмотрели случаи раскрытия
неопределенности вида —, когда х ->¦ а и когда х -> оо. Аналогично обстоит
дело и в случае, когда х-+ ±оо. Заметим, что проведенные дока-
зательства сохраняют свою силу и в том случае, когда lim равен
*-*e g(x)
+оо или —оо, где а — число или один из символов +оо или —оо.
Теперь мы рассмотрим вопрос о раскрытии неопределенности
вида —. Начнем со случая, когда #->- +оо.
оо
Теорема 3. Пусть функции у = / (х) и у = g (x)
дифференцируемы на луче ]а; оо], причем g' (х) Ф 0, и пусть lim / (х) =
*-*-оо
F (х)
= оо, lim g (х) = оо. Тогда если существует lim 't , то суще-
х-юо х-*оо g (х)
ствует и hm -L^-L , причем lim -^-^- = hm -*-*-?-.
^оо gW х->оо g(*) *-*оо g' (*)
Доказательство. Возьмем произвольное положительное число
f (*) Г (*)
8 > 0. По условию существует lim ; положим lim = А. Тогда по оп-
x-oog (X) x-oog' (X)
ределению предела найдется такое число N, что для x^N выполняется неравенство
А-^<-^-<А + ^. C)
2 g' (*) 2
Не ограничивая общности рассуждений, мы можем считать, что N > а. Тогда
из х > N следует х ? ]а; оо[, а на луче ]а; оо[ по условию функции f (л:)
и g (х) дифференцируемы
Пусть х > N. Применив к отрезку [N; я] теорему Коши, получим:
~Г^ 7^7 = 377' где W < с < *.
? М — g (W) g7 (с)
Так как с > N, то, воспользовавшись неравенством C), получим:
8 Г W я е
A--2<TV)<A + r
откуда
2 gW-g№ ^ ' 2"
D)
123

Так как f {N) и g (N)—числа, а по условию f (x)->oo и g(x)-+oo, то для достаточно
. . , f(x)-f(N)
больших значении х дробь сколь угодно мало отличается от дроби
g(x)-g(N)
f (х) f (х)
. Но тогда существует такое число М, что для х > М дробь заключена
g(x) g(x)
между А —г и А + е:
А-г<Ц^<А + г. E)
g(x)
Итак, для любого 8 > 0 существует число М такое, что для х ^ М
выполняется неравенство E), а это и означает, что
х-*оо g (X)
Замечание 1. Теорема сохраняет свою силу и в случае, ког-
1 • /' (Х) Т-» 1 • g! (Х) А
да hm —— = со. В этом случае lim 6 v ' = О, а тогда и
х-оо g' (X) х-оо Г (л;)
lim ^-^- = 0. Отсюда следует, что lim -^- = со, т. е.
х-*оо f{x) х+оэ g{x)
lim iW. = Hm Ш.
x-oo g(*) *->oo g'W
Замечание 2. Теорема справедлива и в случае х -> я, где
а — число. Для доказательства достаточно положить t = < .
х — a
Если х -> а, то ?->¦ оо и теорема сводится к уже доказанной.
Теоремы 1, 2, 3 называют правилом Лопиталя.
Рассмотрим примеры применения правила Лопиталя для
вычисления пределов функций.
Пример 2. Вычислим
lim .
х-+2 X — 2
Решение. Здесь имеем неопределенность вида —.
Воспользовавшись правилом Лопиталя, можем записать:
lim е*~~е% =lim (eX~e2y = lim- = e2.
х->2 Х—2 Х-+2 (Х — 2)' х-»2 1
Разумеется, используя здесь и в дальнейшем подобную краткую
запись, мы предполагаем, что все условия соответствующей
данному случаю теоремы выполнены и, в частности, что предел
отношения производных существует.
Пример 3. Вычислим
Hm ?+**».
Х-++ОЭ 2х + sin x
Решение. Здесь имеем неопределенность вида —.
оо
124

Применив правило Лопиталя, получим:
,. ех + sin х ,. (ех + sin #)' i. ех + cos д;
hm — = lim -—— — = hm —— .
jt^+oo 2x + sin x x^+оэ Bx + sin x)' x-*+oo 2 + cos x
Так как —1 ^ cos x ^ 1, то 1^2 + cos x <[ 3 и потому дробь
ограничена: она не превосходит число 1.
2 -р cos х
С другой стороны, при х-> +оо е* -f cos х стремится к +°°,
как сумма бесконечно большой функции у = ех и ограниченной
функции у = cos х. Поэтому
л. е* + sin х .
hm —! = +оо.
x-»+cn2x+smx
Иногда при вычислении пределов с помощью правила Лопиталя
получается, что lim ' ' снова представляет собой
Неопределенна g (X)
О оо 0
ность вида — или —. В таком случае, если выполняются условия
О оо
соответствующих теорем, можно еще раз применить правило
Лопиталя, заменив отношение функций /' (х) и g' (x) отношением
Г (х)
их производных, т. е. выражением „ .
Пример 4. Вычислим
lim * + **..
х—j_oo еъх
Решение. Имеем неопределенность вида —. Восполь-
оо
зуемся правилом Лопиталя:
,. х2 + 6х ,. (х2 + 6*)' 1. 2*+ 6
hm ——— = hm ———— = hm —-1—.
,+00 #* *->+со (е*х)' Х-++ОЭ Ъе™
оо
оо
Снова получилась неопределенность вида —. Условия теоремы 3
оо
выполняются. Применим к полученному выражению еще раз
правило Лопиталя:
lim ^= lim B' + 6)' - lim -J-= 0.
Х-++ОЭ Зе3* *-+оо (№*)' х->+оо 9е™
Итак,
lim il±6? = 0.
Х-+00 €8*
Заметим, что раскрывая неопределенности по правилу
Лопиталя, следует помнить и те способы раскрытия неопределенностей,
с которыми мы знакомились в разделе «Введение в анализ».
Например, во многих случаях дифференцирование, которое мы
применяем по правилу Лопиталя, приводит к более простым
выражениям, если предварительно заменить бесконечно малую
эквивалентной бесконечно малой или выполнить необходимые упрощения.
125

Пример 5. Вычислим
1. sin л: — tg*
lim —.
*-*o sin3 л:
Решение. Так как sin х ~ х при х ->• 0, то sin3 x ~ хъ и,
следовательно,
limsin*-tg*:=limsin*-tg*.
х-+о sin3* x-*o *3
Имеем неопределенность вида —. Применив правило Лопиталя,
получим:
1
cos * —
1. sin* — tg* i. (sin* — tg*)' ,. cos2 л: r cos3* —1
lim — = lim- 2-^- = lim = lim .
x-*0 X3 x-»0 (*3)' x-+0 3*2 *-*0 3*2C0S2*
Снова имеем неопределенность вида — и вновь применим правило
Лопиталя. Но прежде чем перейти к повторному
дифференцированию, воспользуемся тем, что lim 3 cos2 x = 3. Получим:
у COS3*— 1 1 у COS3*— 1 1 у (COS3*— 1)' __
х-,0 3*2COS2* ~~ 3 х->0 *2 "" *-0 (*2)' ~~
1 г 3 cos2 * (—sin *) 1 / 3 \ i. sin * 1
= — lim —* - = н I lim = .
Зы 2* 3\ 2/х-о * 2
-f-А) и
>\ 2/,.
Пример 6. Вычислим
У * + sin*
Решение. Данный предел представляет собой
неопределенность вида —. Однако правило Лопиталя не может быть к нему
,. 1 + cos *
применимо, так как предел отношения производных, т.е. lim — ,
не существует. Для вычисления предела разделим числитель
почленно на знаменатель:
lim ?±^И* = lim A + ^
a;->oo * де-»-оо \ *
Так как lim -^^- = 0, то
х-*оо *
Hm(l + i]?? =1.
Итак,
lim ?+!!!!? = 1.
126

Неопределенности вида 0 • оо или оо — оо легко приводятся
О оо ^
к виду — или —, обычно это достигается с помощью элементарных
преобразований заданного выражения.
Пример 7. Вычислим
х-*о \ х ел —
Решение. Здесь мы имеем неопределенность вида оо — оо.
Сведем ее к виду—, для чего достаточно привести выражение
к одному знаменателю. Получим
х ех — 1
1 1 ех __ 1 _ х
х ех — 1 х (ех — 1)
Для вычисления lim е ~~ ~~— воспользуемся тем, что ех—1~х
х-+о х(ех — 1)
при х ->- 0. Значит,
lim «*-*-* ^Hm^-1-^
х-+о х(ех — \) х-+о х2
К последнему пределу применим правило Лопиталя. Получим:
lim^-1-;c=lim(eAf-1-A:)/=lime-l^i = lim-l=l.
х-+о х2 х->о (х2)' х-+о 2х х-+о 2* 2
Пример 8. Вычислим lim (я — 2 arctg x) In x.
#->-{-00
Решение. Здесь имеем неопределенность вида 0 • оо. Чтобы
о , 1
свести ее к виду —, воспользуемся тем, что In х = , после
О (In x)~l
этого применим правило Лопиталя.
Имеем:
lim "-2arctg*= lim (jt~2arctgA;)' = lim X + *
x^-j-оэ (In*) x-*+co ((In*)-1)' x-*+oo _2'x J_
X
v 2* In2*
lim
Полечили неопределенность вида — . Снова применим правило
Х-+ + ОЭ 1 + X2
оо
оо
Лопиталя:
,. 2х In2 х о ,. (х In2 x)f 0 ,. In2 x + 2 In x
lim = 2 lim — = 2 lim !
*->-H» 1 + *2 *-+oo A -f X2)' *-*+oo 2*
,. In2 л:+ 2 In л:
= lim — .
я->4-оо X
127

Так как опять получилась неопределенность вида —, в третий
раз применим правило Лопиталя:
lim ln2' + 21n':= ton (ln^ + 21n^ = lim 21П" x + x =
0 ,. 1 + In x 0 t. A + In x)' 0 1; 1 л
= 2 lim — = 2 lim v—— - = 2 lim — = 0.
^->-j-oo a: x_*_j_oo x1 x-*-\-cq x
Итак,
lim (я — 2 arctg х) In x = 0.
Рассмотрим примеры раскрытия неопределенностей видов:
Iе0, 0°, оо<\
Пример 9. Вычислим
lim B-х) 2.
л:->1
Решение. Этот предел представляет собой
неопределенность вида 1°°. Для вычисления заданного предела поступим так:
найдем сначала предел логарифма данной функции, а затем
воспользуемся тем, что для непрерывной и принимающей только
положительные значения функции / (х) справедливо равенство
In lim / (х) lim In / (x)
lim/(*) =e *-+a = e*"a
x-t-a
Итак, найдем предел логарифма данной функции:
лх
lim In B — xfT = lim tg - In B - x) = lim ln<2-*) =
x-\ x-*\ 2 x-*\ , ш
«И —
' (-.)
r (In B-х))' г 2 — x ' 2 ,.
= lim -— — = hm = — lim
2 _ _2_
*.*i / лх \' x-*\ 1 я я х-и 2-х л
ctg-
Значит,
2 / 0 лх 2
sin2 —
limB-x)g2 = e\
JC-l
Пример 10. Вычислим
lim (IVg*
128

Решение. Имеем неопределенность <х>°. Найдем сначала
предел логарифма данной функции:
,. 1 /l\tg* 1- J. 1 1 Т — 1П* i. (In*)'
limln — = limtg*ln—= lim =— hm —
X++Q \x] яч-1-о x x-++o ctg* x-*+o(ctg x)'
\_
,. x i. sin2* i. sin* . r,
== — lim = lim = hm sinx = 0.
*-*-f0 1 X--J-0 * x-»+Q *
sin2 x
Значит,
lim (IVх = «• = !.
3. Сравнение быстроты роста функций. Пусть при * -> + оо функции у =
= / (*) и у = g (x) неограниченно возрастают, стремясь к бесконечности.
Говорят, что функция у =f (х) быстрее стремится к бесконечности (или имеет боль-
f (х) f (х)
ший порядок роста), чем функция у = g (*), если lim = оо. Если же lim =
Ж-+00 g (X) *^+00 g (X)
= 0, то говорят, что функция / (*) медленнее стремится к бесконечности, чем
функция g (х). Аналогично можно сравнивать быстроту роста функций при х -»» а
и при х -*¦ —оо.
Пример 11. Сравним рост показательной функции у = ех и степенной
функции у = *100.
Решение. Сто раз воспользовавшись правилом Лопиталя, получим:
рХ pX pX рХ
lim -ттт-= lim = lim = . . . = lim = + оо.
*-*+оо *100 X-.+QO 100*" *-+оо 100 • 99*98 *->-}-оо 100!
Этот результат говорит о том, что показательная функция растет быстрее
степенной функции у = *100. Аналогично можно показать, что показательная
функция при х -*- + оо растет быстрее любой степенной функции у = *а, где
а >0.
Пример 12. Сравним рост логарифмической функции у = In * и
степенной функции у = *а , где а > 0.
Решение. Имеем;
1_
In* (In л:У * 1 1 _0
lim —— = lim a t = lim —^If = — lim —— = и.
*-*-j-oo * *-»-+oo (* ) x-*-foo&* 0& лг-^-foo х
Полученный результат говорит о том, что логарифмическая функция при х -*- -j- оо
растет медленнее любой степенной функции.
Вопросы для самопроверки
1. Сформулируйте теорему Коши.
2. Поясните, почему теорема Лагранжа является частным случаем теоремы
Коши.
3. К раскрытию неопределенностей какого вида применимо правило
Лопиталя?
4. Поясните смысл выражения «при * -*• -f- оо функция у = / (*) стремится
к бесконечности быстрее (медленнее), чем функция у = g (*)».
5. Даны три функции: показательная у = е*, логарифмическая у = In *
и степенная у = *« (а > 0). Какая из них при * -^ + оо имеет наибольший
порядок роста, а какая — наименьший?
129

Упражнения
303. Определите значение с в формуле Коши для функций f(x) = х? и g (x) =
= х2 + 1 на отрезке [ 1; 2].
304. Определите значение с в_ формуле Коши для функций / (х) = sin a
и gf W = 1 + cos д: на отрезке
305. Поясните, почему теорема~Коши не применима для функций / (х) = х2
и S (х) == & на отрезке [—1; 1].
Вычислите пределы.
3*3 —5*2 + 2х— 1
я 1
306. lim
308. lim
^^оо 2х* + 3
sin 2x — cos 2x — 1
я sin a; — cos х
х — sin a:
310. lim .
Х-+0 Sin? X
ех + в-х_2
312. lim — .
*_0 х — sin л:
sin2 x — — tg x
314. lim
n 1 + cos 4a:
316- lim
318. lim
x-+o x — sin a;
arcsin B — x)
x-+2 У*2--За: + 2
/ 1 *
320. lim - —~
x+i \x—l mx
322. lim i
324. lim .
x-*o \x(\+x) x2,
,. f nx — 1 n
326. lim(-^— + -—Ш
-+2\x — 2 ln(*—1)
1 ln(l + a:)
¦h>o\ 2a:2 ' *(e^*-l)
328. lim B — *)tg—.
x->2 4
x—-3
Э30. lim arcsin • ctg (я — 3).
*-*з 3
307.
309.
311.
313.
315.
317.
319.
Q91
lim
lim
lim •
lim
*-*0
lim
x-*3
lim
x-*0
lim
*->i
a:2— 16
x2 —• 6a: + 8 '
In sin a:
я— 2a; "
1 —tgjg
cos 2a:
sin4 a:
In (a:2 — 8)
^2 + 2a:—15
sin a: — x cos x
sin3 x
У2х — х* —j/x
i-i^
л„... ? \
323.
325.
327.
329
x-*t
lim 1
lim
x-0
lim
л
*-—
lim
^2
/ я
\4*
A-
fc
*-*+0
-ctg«A
я
2*(ея*+ 1)
tg ^) tg 2л:.
In3 x.
130

331. lim xx.
333. lim(l+x)T.
X->-}-00
1
335. lim (ctgI™.
332.
334.
336.
X
lim xx
х-И
lim
я
lim (
¦-*+oo\
(tg
' 2
-1^
*)tg 4
arctg л:
337. lim (¦?---arctg дЛ*- 338- lim f—У •
*-*+oo\ 2 / ^0 \ X J
339. lim (cos ax)cosecZbx. 340. lim я111*6*-1).
341 < Покажите, что lim существует и равен 1, но не может быть
Х^оэХ + COSX
вычислен с помощью правила Лопиталя.
342. Применимо ли правило Лопиталя для вычисления следующего
предела:
lim : ?
Х-*оэ X— Sin*
Найдите этот предел, не пользуясь правилом Лопиталя.
343. Сравните порядок роста при х -> + оо следующих функций!
1) у = In2 х и у = х-, 2) у = In3 х и у = УИ\ 3) у = Irr6 x и у = ха, где
а > О, Р > 0.
344. Сравните порядок роста при х -> + °° многочлена Рп (х) = а^хп -jr
+ аххп~1 + ••• + ##-1* + «/г и показательной функции у = Л
§ 7. ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ
В предыдущих параграфах мы не раз строили графики функций,
учитывая те или иные свойства функций. Но в общем случае,
ставя перед собой задачу исследовать свойства функций и построить
ее график, мы должны иметь план решения такой задачи, схему
исследования функции и построения ее графика. Рекомендуем
придерживаться следующей схемы:
1. Найдите область определения функции.
2. Исследуйте функцию на периодичность.
3. Исследуйте функцию на четность.
4. Исследуйте поведение функции на границах области
определения; найдите точки разрыва и установите характер разрыва,
найдите асимптоты.
5. Найдите точки пересечения графика с осями координат и
определите интервалы знакопостоянства функции.
6. Исследуйте функцию на экстремум.
7. Исследуйте направление выпуклости графика функции,
найдите точки перегиба.
131

8. Составьте таблицу значений функции для некоторых
значений ее аргумента.
9. Используя все полученные результаты, постройте график
функции.
Прежде чем переходить к рассмотрению примеров, напомним,
как отыскиваются асимптоты х) графика функции.
Прямая х = а является вертикальной асимптотой графика
функции у = / (х), если выполняется одно из следующих условий:
1) lim / (л:) = +оо; 2) lim/ (х) = —оо; 3) lim/ (x) = +<х>;
х-*а—О х-+а— 0 х-*а-\-0
4) lim/ (х) = —оо.
X-+CL+Q
Прямая у = b является горизонтальной асимптотой графика
функции у = / (х), если выполняется одно из следующих условий:
1) \\mf(x) = Ъ\ 2) Пш/(х) = Ь.
*->4-оо я-*—со
Наконец, для существования наклонной асимптоты графика
функции у = f (х) необходимо и достаточно, чтобы
существовали два предела:
lim li*L = k и lim(/(x) — kx) = b.
я«*±со X я-^оо
Тогда прямая у = kx + Ъ является наклонной асимптотой.
Рассмотрим примеры.
х? + 9х
х2 —4
график.
Решение. 1) Область определения функции: D (/)=
= ]-oo;~2[U]-2; 2[U]2; oo[.
2) Функция не является периодической.
3) Функция нечетная, так как определена на симметричном
множестве и / (—х) = —f (x). В самом деле,
f (_дЛ = (~*K + 9 (-*) ^ -х*-9х = & + 9х = f , .
М ' (-хJ — 4 х2-4 х2--4 М '*
Значит, для построения графика функции достаточно
исследовать функцию при х ^ 0, построить ее график при х ^ 0 и
отобразить его симметрично относительно начала координат.
Таким образом, для дальнейшего исследования
ограничиваемся промежутками [0; 2[ и ]2; оо[.
4) Имеем:
/@) = 0, lim ^±^.=_оо,
1. %3 4- 9х
lim —-— = +оо.
*-*2+о #2—-4
Пример 1. Исследуем функцию у = J1" и построим ее
*> 'См. «Введение в анализ», с. 105.
132

Значит, график рассматриваемой функции
имеет при х ^ О вертикальную
асимптоту х = 2.
Далее имеем:
lim
х3 + 9х
*-ЮО Х2—4:
оо.
Так как числитель данной
дробно-рациональной функции имеет степень, большую
степени знаменателя на 1, то существует
наклонная асимптота у — kx + b. Найдем Рис 73
коэффициенты k и Ь:
и 1- fix) I- х3 + 9х <
k = lim*-^- = lim —— = 1,
Х-+ОЭ X X -ОО X (%2 — 4)
6= \imlf(x) — kx) = \\m (х^±^—х) = lim-^L
*-*оо х-юэ \ л;2 — 4
= 0.
Значит, уравнение наклонной асимптоты таково: у = х.
5) График пересекает оси в начале координат, поскольку / @) =
= 0. Других точек пересечения с осью ординат не может быть, а
с осью абсцисс в данном случае нет, так как уравнение —— =
= 0 не имеет других решений, кроме х = 0.
Отметим интервалы знакопостоянства функции: ]0; 2[ — здесь
функция принимает только отрицательные значения, и ]2; оо[ —
здесь функция принимает только положительные значения.
На рисунке 73 представлена геометрическая иллюстрация тех
сведений о графике, которыми мы располагаем к настоящему
моменту. Показаны асимптоты, заштрихованы те участки
координатной плоскости, где графика нет, отмечена известная точка
графика О @; 0). Это — заготовка для будущего графика.
6) Найдем точки экстремума функции на промежутках [0; 2[
и ]2; оо[. Имеем:
/
х3 + 9х
х* „ 21л? — 36
(л;2 — 4J
На рассматриваемых промежутках у' не существует лишь в
точке х = 2, но в этой точке функция не определена. Приравняв
производную нулю, находим точку х « 4,8. Это — точка минимума
(такой вывод можно сделать из геометрических соображений,
воспользовавшись рисунком 73). В этой точке имеем у « 8,1.
7) Исследуем функцию на выпуклость. Для этого найдем
вторую производную данной функции. Имеем:
x4_21*2 —36 \'^ 2х A3л:2 + 156)
(*2 —4)а J ~" (х2 —4)з
У =
133

Замечаем, что у" = 0 лишь при
х = 0. Значит, внутри
промежутков [0; 2[ и ]2; оо[ точек
перегиба нет. Так как в интервале
]0; 2[ имеем у" < 0, то на этом
интервале функция выпукла
вверх; так как в интервале
]2; оо[ имеем у" > 0, то на этом
интервале функция выпукла
вниз.
8) Составим таблицу
значений функции для некоторых
значений аргумента:
X
У
0
0
1
1
—3—
3
3
4
107
4,8
8,1
6
7
8 —
16
9) Воспользовавшись
полученными результатами,
построим график функции (рис. 74).
С помощью построенного
графика отметим дополнительно
Рис. 74 некоторые свойства заданной
функции: 1) х = —4,8 — точка
максимума; 2) х = 0 — точка перегиба; 3) на луче ]—оо; —2[
функция отрицательна, на интервале ]—2; 0[ положительна; 4) область
изменения функции: Е (/) = R.
Пример 2. Исследуем функцию у = sin х ——sin 2x и
построим ее график.
Решение. 1) Область определения функции: D (/) = R.
2) Функция является периодической, ее основной период
равен 2п.
3) Функция нечетная, так как
/ (—х) = sin (—x) sin 2 (—а:)
-sin;cH—sin 2л: = —f(x).
Поскольку период функции равен 2я, то достаточно провести
исследование только от —я до я, построить график функции на
отрезке [—я; я] и продолжить его, пользуясь периодичностью. Но
так как функция является нечетной, то достаточно исследовать
функцию и построить ее график на отрезке [0; я], затем
отобразить его на отрезок [—я; 0] симметрично относительно начала
координат, а далее уже воспользоваться периодичностью.
Итак, дальнейшие исследования проведем для отрезка [0; я].
134

4) Функция непрерывная и периодическая, следовательно,
асимптот график функции не имеет. Найдем значения функции на
концах рассматриваемого отрезка [0; я]. Имеем / @) = 0, f (я) = 0.
5) Найдем точки пересечения графика с осью Ох. Для этого
решим уравнение sin x sin 2x = 0. Имеем:
sin х — sin л: cos x = 0, sin x A — cos x) = 0.
На отрезке [0; я] последнее уравнение имеет два корня: хг = 0 и
х2 = я. Значит, график функции не пересекает ось абсцисс ни в
какой внутренней точке отрезка [0; я]. В интервале ]0; я[ функция
принимает только положительные значения.
6) Найдем точки экстремума. Имеем:
у' = cos х — cos 2х.
Приравняв производную нулю, получим:
cos х — cos 2x = 0.
Далее имеем:
cos х — A + cos 2x) + 1 = 0, 2 cos2 х — cos x — 1 = 0,
! 1
cos х = 1; cos x = .
2
Из первого уравнения находим хг = 0, из второго получаем
__ 2я
2 з
Таким образом, внутри отрезка [0; я] имеется только одна ста-
2я
ционарная точка х = —, которая является точкой максимума,
о
так как на концах отрезка [0; я] функция обращается в нуль, а
всюду внутри отрезка — положительна. Найдем значение функции
в найденной точке:
'(
2л \ . 2я 1 . 4я УЗ , V3 3/3
— = sin sin = •*¦ Ь -— = —-—.
3 ) 3 2 3 2 4 4
7) Исследуем функцию на выпуклость. Имеем:
у" = —sin х + 2 sin 2x.
Приравняв у" нулю и решив полученное уравнение, находим, что
1
х = arccos —.
4
При переходе через точку х = arccos— вторая производная
меняет знак с «+» на «—», следовательно, эта точка является
точкой перегиба графика функции (с выпуклости вниз на выпуклость
вверх).
135

Рис. 75
8) Составим таблицу значений функции для некоторых
значений ее аргумента:
X
У
0
0
1
arccos—
4
_ 3
~ 4
2я
Т
з/з"
4
2
1
я
0
9) Пользуясь полученными результатами, построим график
функции сначала на отрезке [0; я], а затем на всей числовой
прямой (рис. 75). Отметим, что при х = 0 как у', так и у"
обращаются в нуль. Эта точка является точкой перегиба, причем в ней
кривая касается оси абсцисс.
Пример 3. Исследуем функцию у = у 2х2 —л:3 и
построим ее график.
Решение. 1) Область определения функции: D (/) = R.
2) Функция не является периодической.
3) Функция не является ни четной, ни нечетной.
4) Функция непрерывна на всей числовой прямой.
Имеем:
lim у2х2 — х3 = + оо, Нт у 2х2 — х3 = — оо.
Х-*—00 X-+-TCQ
Выясним, имеются ли наклонные асимптоты. Имеем:
3/
lim
#-*оо X
= lim •
Х-+ 00
*&.*= italic
* = lim f 2±
-1; ft = -l.
lim (f(x) — fee) = lim (i/x2 — x3 + x) =
X-t-OO X-+CO
(?2x* - x3 + x )((Y2x2 - x*J - xYW=x*
C/2x2— x3 J— x \r2x2 — x3 + *2
*2)
136

= lim
2л:2 — л? + л? j^ h—jL
(|/2л:2 — х3J — х V2x2 — х3 + х2 ~ 3' ~~ 3 '
Значит, наклонная асимптота есть, ее уравнение таково: у =
. 2
= ~х+т
5) Если jc = 0, то у = 0, т. е. график пересекает ось Оу в
начале координат. Для отыскания точек пересечения графика с осью
з,
абсцисс решим уравнение у 2х2 —х3 = 0.
Имеем последовательно:
2х2 — Xs = 0, х2 B — х) = 0, хг = 0, л;2 = 2.
Отметим интервалы знакопостоянства функции: на ]—оо; 0[
и на ]0; 2[ — функция положительна; на ]2; оо[ — отрицательна.
На рисунке 76 представлена геометрическая иллюстрация тех
сведений о графике, которыми мы располагаем к настоящему
моменту. Заштрихованы те участки координатной плоскости, где
графика нет, выделены две известные точки графика, проведена
наклонная асимптота.
6) Найдем точки экстремума. Имеем:
1
3 у Bх2 — jc3J
Dл:— Зх2) -
•3*
ЪУ х{2 — хJ
Находим две точки: хг = 0, х2 = 2, где у' не существует, и одну
стационарную точку х3 = —. Поскольку на интервалах ]—оо; 0[
о
и ]0; 2[ функция положительна, а в точке х = 0 обращается в нуль,
то х = 0 — точка минимума функции. Поскольку, далее, на
концах отрезка [0; 2] функция обращается в нуль, а всюду внутри
4
отрезка принимает положительные значения, то х= точка
максимума, причем fl—) = 2v 4.. Наконец, х = 2 не является
точкой экстремума, так как слева от
точки х = 2 функция положительна,
справа отрицательна, а в самой точке
х = 2 обращается в нуль.
7) Исследуем функцию на
выпуклость. Найдем вторую производную.
Имеем:
у = ( 4-3' V =
— 16
~~ 9 |/V(a: — 2M
\^чч
137

Замечаем, что вторая
производная нигде не обращается в
нуль и не существует в
точках хг = О и х2 = 2. Эти точки
разбивают числовую прямую
на три интервала знакопос-
тоянства /" (х): на ]—оо; 0[
имеем у" < 0 — значит, на этом
луче функция выпукла вверх;
на ]0; 2[ имеем у" < О — значит,
на этом интервале функция
выпукла вверх; на ]2; оо[ имеем
у" > 0 — значит, на этом луче
функция выпукла вниз.
8) Составим таблицу
значений функции для некоторых
значений ее аргумента:
X
У
0
0
2
0
4
7
2J/T
3
—1
'^з
3
|-^1
9) Используя все
полученные результаты, строим график
функции (рис. 77).
Пример 4. На рисунке
78 изображен график
функции у = / (х). Изобразим
схематически график ее
производной.
Решение. На отрезке
[0; а] функция возрастает,
значит, ее производная на этом
участке положительна. При
этом, так как график функции
обращен на интервале [0; а\_
выпуклостью вверх, производная
убывает от значения /' @) до 0
(производная обращается в нуль
в точке х = а). Так как
касательная к графику функции при
х = 0 образует с осью абсцисс
угол а « —, то
/'@)~tg^ = j/.
о

На интервале ]а; Ь[ функция убывает, а потому ее производная
отрицательна. В точке х = Ъ производная не существует, причем
lim/' (х) = —оо. Значит, при х = Ъ график функции / = f'(x)
x->b—Q
имеет вертикальную асимптоту. При #-> Ъ + 0 имеем у' -> +оо.
На интервале ]6; с[ производная убывает от оо до нуля. Она на этом
интервале положительна, так как функция у = / (х) возрастает.
На интервале ]с; fe[ функция у = f (x) убывает, значит,
производная отрицательна. Точкой минимума производной является точка
х = d, соответствующая точке перегиба графика функции у =
= / (х).
Используя полученные выводы, изобразим график
производной (рис. 79).
Упражнения
Исследуйте функции и постройте графики.
345. у = (х — IJ (х + 2). 346. у = х3 — 4х2 + 7х — 4.
347. у = х{х— IK. 348. у = —
х2 — 1 1 — х-
349. у = . 350. у =
х2 +4* ' 4-х2'
(х+1J х2 — 2х + 2
Зх4 +1 (х + IK
353. У = -^-. 854. у--j^,
355.y=]/Lz* 356^=Y!=i-
357* У = у^~Т' 358, У==УГ*+ V^*-
359. у = /8 + * — У"8 —*. 360. у = /х2 + 1 — /х2"
361. у=уЧ — х3. 362. у = х + ^(х2— IK.
363. у = (х — 3) |/Т. 364. у = х /х+Т*.
365. у = х У А — х2. 366. у = х |/4х — х2 .
367. y = l^l_±JL. 368. у = sin2 х + cos х.
X
369. у = sin x + sin 2x. 370. у = cos Зх — 3cos x.
371. у = . 372. у = sin3 х + cos3 х.
sin x + cos x
373. у = cos x — cos2 x. 374. у = cos x • cos 2x.
375. y = ex. 376. у = e x* .
377. у = ex2~2x. 378. у = е8*-*2"4.
379. у = xerx. 380. у = A + x2) ex.
381. y = x + e~x. 382. y=x3e-\
139

а а1 аг а3 ak a5 а6 Ъ х
Рис 80
Рис. 81
383. у = B + х2)<Г
385. у =
lnx
387. у = х — In (х + 1).
389. у = х (In х + 1).
391. у= In D — х2).
393. у = (х + 1) In2 (х + 1).
395. у = х — arctg У*.
х2— 1
397. у = arctj
х2 + Г
384. у =
386. у =
16-
1п %
lnx
388. у =
390. у = х In A + х2).
392. у = гЧп2 х.
394. у = я + arctg х.
х —3
396. у = arctg—--.
х2 + 4
х
398. у = arcsin
х2- 1
399. По графику функции изобразите схематически график производной:
1) функция изображена на рисунке 80; 2) функция изображена на рисунке 81;
3) функция изображена на рисунке 82.
400. Выясните вид графика функции по данному графику ее производной
(рис. 83).
I К
а\ а\ / ь *х
Рис. 83
140

§ 8. КРИВЫЕ НА ПЛОСКОСТИ
1. Примеры параметрического задания кривых. График
непрерывной на [а; 6] функции у = f (x) представляет собой линию на
плоскости. Однако не все линии являются графиками функций —
для этого необходимо, чтобы на каждой прямой, параллельной оси
ординат, лежало не более одной точки этой линии. Так, например,
окружность радиуса R с центром в начале координат не является
графиком какой-либо функции. Для любой точки М (х\ у) такой
окружности выполняется соотношение х2 + У2 = R2- Из него
следует, что для точек верхней полуокружности имеем у =
= У R2— х2, а для точек нижней полуокружности у = —YR2—х2.
Таким образом, эта окружность является объединением
графиков двух различных функций. Многие другие линии тоже могут
быть заданы уравнениями вида F (х\ у) = 0 (например, уравнение
эллипса имеет вид ~г +-~—1 = 0). Такие уравнения линий
а2 №
будут рассмотрены в разделе функций нескольких переменных.
В этом параграфе мы рассмотрим способ задания линий на
плоскости, при котором обе координаты точки кривой выражаются
через третью переменную, называемую параметром. Такое
задание линии имеет наглядный механический смысл. Представим себе
точку М, движущуюся по плоскости. Чтобы задать закон
движения этой точки, достаточно указать в каждый момент времени t
значения координат этой точки. Мы получим тогда две функции:
х = Ф (О и У = *Ф @- Если движение происходит в течение
промежутка времени а ^ t <; 6, то эти функции заданы на отрезке
[а; Ы
Задание функций
Ь = Ф @, ^
однозначно определяет движение точки и тем самым ее
траекторию, т. е. линию Г, по которой движется точка. Поэтому эти
функции можно рассматривать как уравнения линии Г. Такие
уравнения называют параметрическими уравнениями линии Г. Очевидно,
что если обе функции х = <р (t) и у = г|) (f) непрерывны на отрезке
[а; Ь], то и движение точки происходит непрерывно. Это значит,
что для любого значения t 6 [а; Ь] имеем:
lim \M{t+ АО, М (t)\ = 0,
т. е. что расстояние между точками М (t + At) и М (f) стремится
к нулю, когда Д? стремится к нулю.-
В некоторых случаях t имеет иной смысл, например может быть
углом и т. д. Рассмотрим некоторые примеры.
Пример 1. Выведем параметрические уравнения
окружности радиуса R с центром в начале координат.
141

Рис. 84
М(х; у)
Решение. Мы знаем, что
координаты каждой точки М окружности
радиуса R с центром в начале
координат удовлетворяют уравнению х2+ у2=
= R2. Обозначим через t угол между
осью абсцисс и радиусом [ОМ] (рис. 84).
Тогда имеем:
'x = *°?st> 0<*<2я.
^у = R sin t, ^ ^
Это и есть параметрические уравнения
окружности. Заметим, что эллипс
получается из окружности сжатием к оси
абсцисс. Поэтому параметрические
уравнения эллипса с полуосями а и Ъ имеют
вид:
(х = a cos U п ^ , ^ 9тг
\у = Ъ sin U ° < ' < 2я'
Геометрический смысл Параметра t
виден из рисунка 85.
Пример 2. Выведем
параметрические уравнения кривой,
описываемой точкой окружности радиуса R,
которая катится без скольжения по
прямой. Эту кривую называют циклоидой.
Она изображена на рисунке 86.
Решение. Будем считать, что в начальный момент времени
точка, описывающая циклоиду, находилась в начале координат,
и примем за параметр t угол, на который поворачивается радиус
[OiA] (рис. 87), т. е. угол В02М. При этом, поскольку окружность
катится без скольжения, длина дуги ВМ равна длине отрезка [ЛВ].
Но длина дуги ВМ равна Rt, и потому \АВ\ = Rt. Так как \BN\ =
= R sin t, а абсцисса точки М равна \АВ\ — \NB\, то получаем,
что
х = Rt — R sin t = R (t — sin f).
Точно так же определяем, что
у = \MN\ =R + R sin (t——)=R(l —cost).
Рис. 85
Рис. 86
142

Таким образом,
параметрические уравнения циклоиды
имеют вид:
fх = R (^ — sin О,
у = R A —cos f).
В этих уравнениях параметр
вменяется от—оо до оо.
Циклоида состоит из бесконечного
множества арок. Чтобы
получить уравнения одной арки, соединяющей точки 0 и Л, следует
ограничить изменение параметра t отрезком [0; 2я]:
(x = R(t-smt) 0<г<2я.
\у = R A — cos f), ^ ^
2. Жордановы кривые. Пара функций
определяет отображение t-+ М (ф @, ^ @) = М @ отрезка [а; Ь] в множество
точек плоскости. Обозначим через Г образ этого отрезка. В примерах, которые мы
рассмотрели выше, образами [а; Ь"] были окружность, эллипс, дуга циклоиды
и т. д. Если функции х = ф (t) и у = г|з @ непрерывны на отрезке [а; 6], то
задаваемое ими отображение называют путем на плоскости. Поскольку при отобра-
t — а
жении q = отрезок [а; 6] переходит в отрезок [0; 1], то, не теряя общности,
Ь — а
можно считать, что путь является отображением отрезка [0; 1]. Например,
окружность является образом отрезка [0; 1] при отображении
jx—R cos 2nt,
\у = R sin 2itt, 0 < t < 1. D)
Одно и то же множество Г на плоскости может быть различными способами
получено как образ отрезка [0; 1]. Например, поскольку функция q — г3
отображает отрезок [0; 1] на себя, то уравнения
R cos 2я?3,
\у= Rsin2nt?t 0< *< 1,
B)
задают ту же окружность, что и уравнения A). Разница между этими
уравнениями лишь в том, что при движении по формулам A) точка пробегает окружность
равномерно, а при движении по формулам B) — неравномерно.
Назовем два пути:
: Ф1 @,
!*i@.
0< /< 1,
C)
D)
геометрически эквивалентными, если существует такая непрерывная строго
монотонная функция q = / @, 0 < t < 1, что / @) = 0, f A) — 1 (или / @) = 1,
f A) = 0) и фх (/ (t)) = ф2 @, i|>! (/ @) = ^2 V) Для всех t на отрезке [0; 1].
Очевидно, что образ отрезка [0; 1] для двух геометрически эквивалентных путей
является одним и тем же, т. е. они задают одну и ту же кривую. Легко показать,
что отношение «пути Гх и Г2 геометрически эквивалентны» обладает свойствами
рефлексивности, симметричности, транзитивности. Поэтому множество всех пу-
ИЗ

тей разбивается на классы
геометрически эквивалентных путей. Каждый
такой класс путей назовем жордано-
вой кривой1).
Рис. 88 Условие строгой монотонности
функции q = / (t) в определении
геометрической эквивалентности —
условие того, что кривая пробегается в одном и том же направлении, без
поворотов назад. Отметим, что условие «пути Гх и Г2 геометрически эквивалентны»
не совпадает с условием «образы отрезка [0; 1] при двух отображениях
одинаковы». Например, на рисунке 88 показаны два геометрически неэквивалентных
способа пробегания «восьмерки».
Если кривая Г задана инъективным отображением t -> М (t) отрезка [0; 1]
(т. е. таким отображением, при котором различным значениям t соответствуют
различные точки кривой), то ее называют простой дугой. Например, простая дуга
изображена на рисунке 86. В частности, простой дугой является график функции
У — f (х)> а^ х ^b, непрерывной на отрезке [а; Ь]. Его можно задать
параметрическими уравнениями
/ *= U
Если ф @) = ф A) иг|? @) = я|) A), то жорданова кривая называется
замкнутой — пробегая эту кривую, точка возвращается в исходное положение.
Примерами замкнутых жордановых кривых могут служить окружность, эллипс,
астроида (рис. 92) и т. д.
Если существуют такие значения /t и t2l что хотя бы одно из чисел tlt t2
отлично от 0 и 1, причем ф (t±) = ф (t2), 'ф Ьг) = гр (t2), то М (tt) = M (t2) и в
соответствующую точку кривой путь попадает дважды. Такую точку кривой
называют точкой самопересечения (рис. 89). Может случиться, что через одну и
ту же точку кривой путь проходит более двух раз (рис. 90).
Доказано, что если Г — замкнутая жорданова кривая, не имеющая точек
самопересечения (такая кривая состоит из двух простых дуг, имеющих общие
концы), то она делит плоскость на две части (внутреннюю и внешнюю). При этом
любые две точки, лежащие в одной и той же части, можно соединить путем, не
пересекающим эту кривую, а точки, лежащие в различных частях, таким путем
соединить невозможно. Несмотря на геометрическую очевидность этой теоремы,
ее строгое доказательство весьма сложно. Геометрическая иллюстрация дана
на рисунке 91.
3. Связь между различными видами уравнений линий. Мы
видели, что окружность можно задать и уравнением вида х2 + у2 =
= R2, и параметрическими уравнениями х = R cos t, у = R sin t,
Рис. 89 Рис. 90 Рис. 91
1) К. Жордан A838—1922) — французский математик.
СЮ QO
144

О <; t ^ 2я. Рассмотрим в общем виде переход от одного вида
задания кривых к другому. Пусть кривая задана параметрическими
уравнениями
'х = Ф (О,
y=^(t), а<?<&.
Если на отрезке [а; 6] функция х = ср (t) не только непрерывна,
но и строго монотонна (в частности, если эта функция имеет
положительную производную во всех внутренних точках данного
отрезка), то уравнение х = ср (f) можно решить относительно t:
t = ф-i (х). Подставляя это значение t в уравнение у = г|) (t),
получаем явное задание функции
у =я|) (ф-1 (л;)).
В этом случае кривая Г является графиком функции у =i|) (qT1 (x)).
Точно так же если у =ty(f)—строго монотонная функция, то
кривая Г является графиком функции вида
х = ф (я);-1 (у)).
Чаще всего отрезок [а; 6] можно разбить на конечное число
отрезков, на каждом из которых функция х = <р (f) или функция у =
= яр (?) строго монотонна. Тем самым кривая Г разбивается на
конечное число простых дуг.
Обратно, если задано уравнение кривой вида у = f (x), то,
полагая х = ср @, получаем параметрические уравнения
[х = ф (О,
Ь = /(ф@)=*@
этой кривой. Переход к параметрическим уравнениям позволяет
упростить выражение функции у = / (я) (например, избавиться
от иррациональностей).
Пример 3. Найдем параметрические уравнения кривой
у = j/IF, положив х = f.
Решение. Имеем:
у =¦/" (*3J = t2.
Значит, искомые параметрические уравнения имеют вид:
х= fy
у = t2y —оо < t < оо.
Пример 4. Исключим параметр t из параметрических
уравнений кривой:
3at
—оо< t <оо.
_ Sat2
145

Решение. Имеем:
Тогда х =¦
За-—
х
>+<#
или
х3 + у* — Заху = 0.
Пример 5. Кривая задана параметрическими уравнениями
х = а cos* t о < t < 2я.
у = a sin3 ?,
E)
Построим эту кривую и найдем ее задание в виде уравнения с
двумя переменными: х и у.
Решение. Давая ? различные значения, получим
соответствующие им значения декартовых координат хиу:
*
X
У
0
а
0
п
т
ai/2"
4
4
0
а
я
—а
0
График изображен на рисунке 92.
Чтобы исключить параметр t9 выполним следующие
преобразования уравнений E):
гз
откуда
У х = -j/а cos tf,
[у^у = i/a~sin/f
у^ + ^ = у^.
Кривая, изображенная на рисунке 92, называется
астроидой (от латинского слова «астра» —
звезда).
4. Дифференцирование
параметрически заданных функций.
Теорема 1. Пусть функция задана
параметр ически:
(х = Ф (О, а
\У = * (О,
<'<&,
F)
Рис 92
м пусть выполнены следующие условия:
1) Функция х = ф (/) непрерывна на
[а; 6], дифференцируема в ]а; Ь[, я/ш-
«*&и ф'@ > 0 для всея ? 6 ]а; 6[.
не

2) Функция у = i|) (t) непрерывна на [а; Ь] и дифференцируема
в ]Д; 6[.
Тогда уравнения F) определяют функцию у = Ф(х), непрерывную па
отрезке [<р (а); ф F)] и дифференцируемую внутри этого отрезка,
причем при ф (а) < х< ф F) имеем:
Уг
Ух =* Ф'(*) = —
Ф'(9
Доказательство. Из условия 1) следует, что функция
# = ф (?) непрерывна и строго возрастает на [а; 6]. Поэтому для
нее существует обратная функция * = g (x), непрерывная и строго
возрастающая на отрезке [ф (а); ф F)]. Но тогда у = -ф (Q =» г|? (g (x)) =
= Ф (х), и эта функция непрерывна на отрезке с концами ф (а)
и ф (ft).
Пользуясь формулой для производной сложной функции,
найдем:
У'х = У\ ¦ Ь
но так как производная обратной функции вычисляется по формуле
t'x = ~ (напомним, что по условию xt Ф 0), то окончательно
получим:
%
ф'@ < 0 для всех
У* = У< •  = -,
что и требовалось доказать.
Аналогичная теорема справедлива, если
t € ]а; &[.
Пример 6. Найдем у'х для функции, заданной
параметрическими уравнениями
(х = sin3/,
ty =cos%
0 < t < —.
Решение. Имеем: #J = 3sin2 /cos /, х* >0 на 0; — •
На данном отрезке 0; — выполнены все условия теоремы 1.
Найдем производную ух, пользуясь
формулой производной параметрически заданной
функции:
ух
yj —3 cos21 sin t
3 sin2 t cos t
-ctg/.
5. Полярное уравнение кривой.
Равенство г = / (ф), выражающее длину г радиус-
Рис. 93
147

вектора через полярный угол ср (рис. 93), задает линию Г на
плоскости. Равенство г = f (ф) называют полярным уравнением
линии Г. Оно является частным случаем параметрического задания
линии. В самом деле, возьмем соотношения между декартовыми и
полярными координатами:
(х = г cos ф,
[у = г sin ф
и подставим в них вместо г его значение / (ф). Мы получим
параметрические уравнения кривой, где параметром является ф:
/ х = / (ф) cos ф,
IУ = / (ф) sin ф, а < ф <Ь.
Например, полярное уравнение кардиоиды (рис. 94) имеет вид:
г = а A + cos ф).
Значит, ее параметрические уравнения таковы:
(х = а A + cos ф) cos ф,
[у = а A + cos ф) sin ф, 0 ^ ф ^ 2я.
6. Производная второго порядка для параметрически заданной
функции.
Пусть функция задана параметрическими уравнениями:
(х = ф (t), < t < ь
Тогда, как мы знаем, ух = —- —
У( ъ'Ц)
Ф'@ *
Таким образом, у'х — функция от t. Равенства
(х = Ф@,
а<*<
выражают ух как параметрически заданную
функцию от х. Поэтому
¦GO' =
(у-%
G)
Рис. 94
Таким образом, для нахождения
производной второго порядка функции,
заданной параметрическими уравнениями, нужно
продифференцировать по параметру /первую
производную и результат разделить на хи
Пример 7. Докажем, что арка
циклоиды (см. рис. 86)
148

х = R (t — sin f),
у = Я A —cos 0, 0 < ^<2я,
выпукла вверх.
Решение. Имеем:
x't = /?(! — cos 0. yt = R sin f.
Значит,
/?sin/ *
= ctg
Замечаем, что у* определена для любого t € ]0; 2я[.
Далее, по формуле G) имеем:
1
. (#; 2sin2l ,_.
Для любого t € ]0; 2я[ и, следовательно, для любого х € ]0;
2л/?[ имеем у^ < 0. Но тогда кривая является выпуклой
вверх.
7. Построение кривых, заданных параметрическими
уравнениями. Пусть кривая Г задана параметрическими уравнениями
Предположим, что, за исключением конечного числа точек tu /2,...
..., tn, функции ф @ и г|) (t) дифференцируемы и их производные
непрерывны и отличны от нуля (этот случай чаще всего
встречается на практике). В интервалах ~]tm\ tm+i[9 1 <J tn <; n — 1
производные q/ (t) и г|/ (t) сохраняют знак (так как они непрерывны
и не равны нулю) и, следовательно, функции ср (t) и гр (t) строго
монотонны. Доказанное соображение позволяет усмотреть ход
кривой на этих участках. Дальнейшее исследование сводится к,
изучению кривых вблизи точек
М (tm) = М (Ф (ta); я|) (*J), 1 < т < Д.
Например, если q/ (tk) = 0, а *ф' (tk) Ф0, то в точке Л1 (?А)
касательная вертикальна и т. д.
Остановимся на отыскании асимптот параметрически заданной
кривой. Сначала находим бесконечные ветви кривой Г. Для этого
отыскиваем значения tly t2, ..., tn параметра t такие, что при
приближении t к tm слева или справа ф (t) или г|з (t) стремится к
бесконечности (такими значениями могут быть, в частности, t = -f °°-
или t = —оо).
Если lim ф (f) = оо, limi|) (i) = b, то прямая у = Ъ является
tn tn
149

горизонтальной асимптотой для кривой Г. Если lim ф (t) = a
/->* _о
тп
и Птг|) @ = оо, то прямая х = а — вертикальная асимптота
тп
для Г. Наконец, если lim ф @ = оо, lim г|з (t) = оо, причем суще-
/-/ —о *-*'„,—о
тп тп
ствуют пределы
lim ?Ф = ?, lim (ф (Л — kw (ft) = 6,
^/ _оф@ '-^„-о
/7г ' v ' тп
то прямая у = kx + 6 является наклонной асимптотой для Г.
Аналогично разбираются случаи, когда t-> tm + 0.
Пример 8. Проведем исследование и построим
параметрически заданную кривую
Sat
3at2
1+Р
, (а>0) — оо <*< + со.
Решение. 1) Функции q> (t) и ip (t) существуют на
промежутках ]—оо; —1[ и ]—1; оо[.
2) Определим точки, в которых ф'; (t) и я|/ (t) обращаются в
нуль или бесконечность:
*.A-У) 3rfB-f)
Y w A+/3J A+^3J
Отсюда ф' (t) = 0 при 1 — 2t3 = 0, т. е. при t = ^3-; ф' (t) ->- 00
/2
при /->- —1.
3 —
Аналогично i|/ (?) = 0 при t = 0 и ? = у 2; о)/ (t) ->- оо при
*->—1.
Таким образом, если всю числовую прямую разбить на
промежутки
]-оо; -1[, ]-1; 0[,
0; —
, ^2; + оо[,
то внутри каждого из них производные ф' (t) и гр' (t) будут конечны
и постоянного знака, и потому сами функции ср (t) и ф @
монотонны в указанных промежутках, а именно:
Ф'@>0, Ч>'@<0 при —оо</<0, *=??—1,
Ф' @ > 0, г|/ @ > 0 при 0 < t < -i-,
Ф' (i) < 0, ф' @ > 0 при -!- < < < у^
ф' (/) < 0, г|/ (/) < 0 при /I < / < оо.
150

3) Вычислим на концах промежутков значения ср (t) и г|) (t)
или, если таковые отсутствуют, их предельные значения:
lim ср (/) = 0, lim ср (t) = + 00,
*-*+оо t-+—1—О
lim ф(/)=—оо, ф@) = 0, ф[ ] = aj/~4,
ф (у^2) = а у^ lim ф @ =0, ф @) = О,
V2
3^^- ,з
а /2, ф(у2) =ауТ
Пункты 2)
и
*
]-оо; -1[
]-1; 0[
1
0; 1—
w3/?
\П\ <*>
3) иллюстрируются следующей таблицей:
X
возрастает от 0 до +оо
возрастает от —оо до 0
возрастает от 0 до
убывает от ау/Т до ау/~2
убывает от ауГ2 до 0
У
убывает от 0 до —оо
убывает от +оо до 0
возрастает от 0 до ct^~2
3 3 1
возрастает от ау/г2 до а^/'А
убывает от ау 4 до 0
4) Так как хну обращаются в нуль при t = 0 и t = 00 (т. е.
lim ф (f) = Нтг|) (t) = 0), то кривая имеет точку самопересечения
*-*СО /-ЮО
в начале координат.
5) Выясним, наконец, вопрос об асимптотах кривой. Как
легко видеть, кривая уходит в бесконечность лишь при tf->—1.
При этом
HmiW=_l, т. е. А = —1.
/_>_! ф (t)
lim (ф @ — &ф @) = lim 3fl'2 + 3a/ = —а, т. е. Ъ = —а.
t-+-\ *-*-i 1 + /3
Следовательно, прямая у = —х — а является единственной
асимптотой для данной кривой.
Во второй и третьей колонках таблицы показано, как
изменяется абсцисса х и ордината у точек заданной кривой в зависимости
от изменения t. Учитывая эту связь и пункт 4, можно построить
график данной функции (рис. 95).
3 —- ^ /——
В точке А (а у 2; a j/4) касательная параллельна оси абсцисс,
а в точке В (a-j/Ч; a -j/Y) — оси ординат.
151

Рис. 95
8. Построение кривых,
заданных полярными уравнениями.
Построение линий, заданных
полярным уравнением г = f (ф),
сводится к построению линии,
заданной параметрическими
уравнениями
(х = f (ф) cos ф,
\у = f (Ф) sin ф.
Но во многих случаях проще
непосредственно исследовать
уравнение г = f (ф) и строить
линию на основании этого
исследования. При этом надо иметь
в виду следующие замечания:
1) Если / (ф) = / (—ф), то
кривая симметрична
относительно полярной оси (т. е. вместе с каждой точкой М (г; ф) она содержит
точку N (г; —ф)).
2) Если / (я + ф) = / (ф), то кривая симметрична
относительно полюса.
3) Если / (а — ф) = / (а + ф), то кривая симметрична
относительно прямой ф = а, проходящей через полюс.
4) Если / (ф) = / (ф + 2я), то кривая замкнута.
5) Если для некоторого натурального п f (ф) = f (ф -\ ),
то кривая состоит из п частей, получаемых друг из друга поворота-
ми на углы вида . В этом случае достаточно построить кривую
п
Л ^ ^ 2л:
для угла 0 ^ ф ^ —.
п
6) Если / (а) = / ф) = 0, причем в промежутке ]а; C[ функция
/ (ф) всюду определена и не обращается в нуль, то кривая для угла
а ^ ф ^ р имеет вид лепестка.
Пример 9. Построим кривую г = а | sin 2ф|.
Решение. Так как
а | sin 2 (тс + фI = a I sin 2ф|,
а | sin 2 (я — ф) | = а | sin 2ф|,
то кривая симметрична относительно полюса и полярной оси. Поэ-
тому достаточно построить кривую для угла 0 ^ ф ^ —. Так как
при ф = 0 и ф = — имеем г = 0, то кривая для данного угла
имеет вид лепестка. Так как a sin 2 ( ф] = ?шп2ф,
то этот лепесток симметричен относительно прямой ф = —.
152

Наконец, г принимает наибольшее значение, если sin 2cp = 1,
т. е. ф = —. По этим данным строим кривую — четырехлепестко-
вую розу (см. рис. 90).
Вопросы для самопроверки
1. Что означает выражение «кривая задана параметрическими уравнениями»?
2. Напишите параметрические уравнения окружности, эллипса.
3. Что такое циклоида?
4. Что такое путь? Что такое точка самопересечения пути?
5. Какие два пути называются геометрически эквивалентными?
6. Что такое жорданова кривая?
7. Какая жорданова кривая называется замкнутой?
8. Как перейти от параметрического задания кривой к явному заданию?
Как от уравнения у = / (х) перейти к параметрическим уравнениям?
9. Как вычисляется первая производная параметрически заданной функции?
Как вычисляется вторая производная?
Упражнения
Преобразуйте к параметрической форме уравнения следующих линий,
положив у = tx.
401. (х + уJ = а (х — у). 402. (х + уK = аху.
403. (х + уL = а2 (х2 + у2).
404. Преобразуйте к параметрической форме уравнение
хз +уз = з^
Исключите параметр t из уравнений:
405. (х = 1 + *», 406. (х = a cos4 t, п ^ п
\y=t2+t+\. \y=asin4*, a>u*
407. (х = a cost,
J a sin3 ? л ^j ^ я
1 2 +sin * 2
Преобразуйте к полярным координатам уравнения линий и постройте эти
линии:
4*у.
408. (х2 + у2J = 2ху. 409. (х2 + у2K =
410. хъ + у3 = х2 + у2.
411. Найдите точку самопересечения кривой
н - dy
Найдите производную —:
dx
6at*
У = 1 + tQ'
412. (х= In A — t),
\у = sin2 2t.
413. (х = е~? sin ?,
1у = el cos ?.
153

414.
t 415.
cos-,
t
x = V 1—Yt,
y = ^r
cost' b = log8ctg2/.
(X = <
416. ( 1 417. /д; = е-2/
Jx == ,
i cost
b=logatg*.
418. (* = arcsin 2t, 419. f* = arccos 2t%
1 1
^ sin2 *' I rn«ilfW
(,? = ?3^ С
у = e3' sin31 J ' 1
sin21 [ cos 10'
420. (x = e3/cos4 421. (x = e~2t
/In tg t '
У
Найдите —- для следующих функции:
dx2
422. jx = In t> 423. (x = arctg /,
Ь = *3. Ь = 1пA+^2).
424. (x = arcsin ?, 425. (# = a cos3 ^
Vy = yi — Л [у = a sin8*.
426. f* = sin? —*cos?, 427. (х^е'аК
\y == cos t + t sin t. \y = ea/.
Постройте графики функций, заданных параметрически:
428. (х = *2 — 2*, 429. Г* = cos3 *,
\у = *2 + 2*. \у = sin t
430. рк = tef, 431. /* = * + *-',
\у = &""'• \у = Ы + e~2t

ОТВЕТЫ
1. 1) 0,21; 2) —0,0396; 3) —1,11. 2. (Ах — 1)Ах+2(АхJ. 3. Зх2Дх +
+ Зх (Ал:J + (АхK. 4. Fх2 — 3) Ах + 6х (АхJ. 5. Ух + Ах — /х!
6. —2 sin Bх + Ах) sin Ах. 12. у' = 2х, dy = 2x<ix. 13. у' = 4х + 1, dy = Dх+
+ 1) d*. 14. у' = — 5 — 2х, dy = (—5 — 2х) dx. 15. у' = 6х2, dy = 6x2dx.
16. / = 1 — Зх2, dy = A — Зх2) dx 17. у' = 3. 18. у' = 2х — 2. 19. у' = Зх2 +
1 1 2х
+ 1. 20. /=4x3. 21. /==__ 22. у>=^у=. 23. / = -("^Г^2- 24' Ч 10*9'
3 15 2 7 1 4 — 44
2) _—; 3) ; 4) ; 5) — —~ ; 6) — ; 7) — ; 8) —х 15.
* ЬУ? 9^? 3^3? 2/?' 2]Л?' 15
25. 1) 0,8; 2) —; 3) 1,5; 30. а = 3, 6 = —2. 31. у = 12х — 16; 12у + х = 98.
40
32. у = —4х — 4; 2х — 8у — 15 = 0. 33. у = 4х — 2; х + 4у = 9. 34. 1) х =
= 2; 2) х = —1,5; 3) хх = —, х2 = —1. 35. х = 2. 36. 32х + 48у + 157 = 0.
4
1 1 я 3
39. arctg —, arctg —. 40. —, arctg—. 41. arctg 3. 42. arctg 0,8.43. 3. 44. 6*2 — 3.
45. 2я. 46. 48я. 47. 1) 35; 2) 5; 3) 125. 48. 23. 57. 1) 2; 2) 36; 3) —13,5. 58. —.
о
31 2
59. 0; —2. 60. 2, —2, 4, —4. 64. 1) —19 —; 2) — —. 65. 1) —2; 2; 2) 0.
160 150
66. у = 2х — 2, 2у + х — 1 = 0; у = —х + 2, у — х + 2 = 0; у = 2х — 6,
2у + х — 3 = 0. 67. у = —х в точке (—3; 3); у = —0,04 х в точке (—15; — J.
68. а= 4. 70. —0,75. 71. *= 3. 72. ^ = 1 с, t2 = 5 с. 82* у= ^/Т(х+ 1).
83. В точке (—4; 0) х = —4; в точке @; 8) у = Зх + 8; в точке @; —8) у = —Зх —
— 8. 84. —. 85. 7 км/ч. 86. 0,4 м/мин. 126. /з! 127. 0,75. 128. 0. 132. v +
6
Л Л
+ 2х = 3; у — 2х = 3. 133. 4у — х = я — 2. 134- у = хе 4 — е 4. 135. 2у +
гм2 8е2 (е2 4- \)
+ 2х= 1+2 In 2. 136. 16 м/с. 137. 625 — 141. * ,, . 152. a) /i>0;
с2 A — e2f
155

б) Л>1; в) h>2. 153. *C + 2*2> . 154. 2e~x' Bх*- 1). 155. - 2*
"о A+*2J
A + х»)
4# 6
158. — /л , 9Ч9 . 159. 360х2 + 16е2*. 160. —16 sin 2х — 8л: cos 2x. 161. — —
A + х2J д4
162. — • 163. 220е2*(л:2+20л:+95). 164. 249(sin 2х . (-2x2+1225)-H00a:cos24
(х—I)9
1 . 3 • 5 • 7 • ... • 197 399 —л:
165. — yjy=^»r 166.4.123!;0. 167.(-l)--i.(n-l)lX
1 ¦ —х— -*^ 168. (-i)-m (^±! + Д-
(x—1)я (*+1)л (х — 2)п) ' \ xn+2 ' jcw+i
1 \ . ... . / 2 1
/(„-1)(„-2) 5(/г-2) 6 v _1,-T
(* — l)ln2x — 4x — x\nx(\n2x — 4) j9 , 4C*4-fl)
172. V l 37^ ~dx\ 173. 1) —Ух> ^2.
x3(ln2x —4J
2) -4(i±^ w,2+_^_d2A 184. J^l 185. 0. 186. A 187. 6-±l^~.
*' \A—A^J Ч —Я4 / 3 2 3
/ 2_ 1_ ]_ 2_\ 3_
188. 1,5. 189. —. 190.2. 193. e-1. 194. 1. 195. ^^. 196. U3 +a3 Ъъ +ЬЪ j2 ,
2 2 V 3 /
197. —0,5. 204. 0,75. 205. я. 208. ]—oo; 2[, ]2; 3[, ]3; oo[. 209. ]—00; —1[.
]-l;0[, ]0; 1[, ]l;oo[. 210.
0; —Г, 1—; ooj. 211. b > 2. 212. p < —1. 216. x •-
= — У~2 — точка минимума, х = Y2 — точка максимума. 217. x = —3 —
точка максимума, х = 1 — точка минимума. 218. х = 1 — точка максимума,
х = 3 — точка минимума. 219. *= 1—точка максимума, х— 1,4 — точка
минимума. 220. х = —1 — точка минимума, х = 1 — точка максимума.
—1 11
221. х = точка максимума, # = — — точка минимума. 222. х = 8 —
2 18
точка минимума. 223. л; = 1 — точка минимума. 224. х~ точка
минимума, х = 1 —точка максимума. 225. х = 2 —точка максимума. 226. х = 0 —
2 я ,
точка максимума, х = точка минимума. 227. х = Ь я/г — точка
3 6
я , я ,
минимума, х = h я/г — точка максимума. 228. х— \- 2я/г — точка мак-
6 4
5я , 1
симума, *=--- + 2я/г — точка минимума. 229. х = — — точка минимума.
230. х = 0 — точка минимума, х = 2 — точка максимума. 231. л: = 2я/г —
точка максимума, л: = \- 2я/г — точка максимума, л-=—+2я/г—точка
2 4
156

максимума, х = \-2лп — точка минимума, х = л + 2лп — точка миниму-
4
л , ллл я/г
ма, # == — \- 2лп — точка минимума. 232. х = — —точка максимума, х =
2 ^
= — -| — точка минимума. 233. х = — + 2шг — точка максимума.
4 2 2
234. Экстремумов нет. 235. Экстремумов нет. 236. 9—; 9—. 237. 9J/ 3; 18—.
/ Zo 7
!
238. —3; — —. 239. 0; 4 /9. 240. 0; 4. 241. 0; 4. 242. 0;1 + 2 уз. 243. — —;
3 4 '
arctg 0,6. 244. 0; —. 245. 0;2 — In 3. 246. — —; 0. 247. — е: —. 248. —.
е е еъ Зе3 '
1 1 R AR
—. 249. е'*\ е. 250. — --; 3. 251. -=; -=. 253. Равнобедренный. 254. /? =
е е у о у о
=— . 255. Расстояние хорды [ВС] от точки А равно 1,5/?. 256. —; —-—
4 2 ' 4 cos a '
257. Д=
18
jt+4
. 258. 1) у + 2х = 4; 2) у + * /2 = 2 + уТ. 259. х=2. 260. aj/T;
72V"
D="-ff-
bV~2. 261. 2)^26 м. 262. у^У, у^2У, JL±L. 263.
2
264. 576 см3. 265. Л/ —. 266. Высота цилиндра равна —. 267. —. 268. ?^1-Д
У Ъл 3 3 3
269. 4/?. 270.
R У 3 . Я/3 . R V_3_u 271. ^; ??. *Е
272. 125 м.
3 ' 3 ' 3 3' 3' 3'
273. 25 км. 274. Выпукла вниз. 275. х = 2, х = 4 — точки перегиба. 276. х =
= 1 — точка перегиба. 277. Выпукла вверх. 278. Выпукла вниз. 279. х =
= 1 — точка перегиба. 280. х — 4 — точка перегиба. 281. х = 1 — точка
перегиба. 282. —2<а<2. 283. а =—1,5; 6=4,5. 299.1,3247. 300.-2,330;
0,202; 2,157. 301. 2,094. 302. —3,2900; 0,7057; 2,5842. 303. Д 304. —. 306. —.
9 4 2
— 1 13
307. 4. 308. V2. 309. 0. 310. —. 311. —1. 312. оо. 313.2. 314. — —. 315. —.
г 6 8 4
1 7 1 12 1
316. 1. 317. —. 318. 0. 319. 1—. 320. . 321. оо. 322. —. 323. —. 324. — —.
3 9 2 2 3 2
325. —. 326. —. 327. 1. 328. —. 329. 0. 330. —. 331. 1. 332. е. 333. 1. 334. —.
8 2 Л 3 е
2 1 _ А2
335. —. 336. е~~ п- 337. 1. 338. е3. 339. е 2Ь\ 340. е. 342. Нет; оо.
е
401. [ а A-0 402- [ at m- (
х =
A + t? '
at(l-t)
A + tf
A + *K
at2
V~ 0 + 'K
at V 1 + t2
A + 02
157

404. f*_2sin»*. 0<{<2я 405> y = ^(jZTi)f+^7Zn + i. 406. у^+
[ у = 2 cos3 /,
__ (fl2 д,2\ у д2 x2
+ Y у =У a. 407. у = 408. г = / sin 2q>.
409. r = fshT4^. 410. r = coS39 + sin39'41b@;0)- «2. / = 2(/-l)sin4/.
413. /=A 414. /=
415./=.
417.
2e2'
In 3 • sin 4/
418.
У 1 — 4/2 . cos t
sin3/
sin/
419. /
*2*
_ln 10/1-4/2. sin 10^ cos/+sin/ 421 y'= "
2 • 10'cos2 10-' ' 'У 5 cos/—sin/' 2 sin 2/./in3 tg /'
422. 9/3. 423. 2 A + /2). 424. —У1 — /2. 425.
427. 2e3e<,
1
3a sin / cos4 /
. 426.
1
6 sin3 i

ОГЛАВЛЕНИЕ
Предисловие 3
Глава 1
ДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ. ДИФФЕРЕНЦИАЛ.
ПРОИЗВОДНАЯ E)
§ 1. Приращение функции 5
1. Приращение функции E).
2. Определение непрерывности функции в точке «на языке
приращений» F).
§ 2. Дифференцируемость функции в точке 8
1. Определение дифференцируемости функции в точке (8).
2. Связь между непрерывностью и дифференцируемостью
функции в точке A0)
3. Производная и дифференциал A2).
4. Односторонние и бесконечные производные A5).
§ 3. Применения производной и дифференциала для решения
геометрических и физических задач 18
1. Задача» о проведении касательной к графику функции.
Геометрический смысл производной и дифференциала A8).
2. Геометрические приложения производной B2).
3. Применения производной в физических задачах.
Механический смысл производной B4).
§ 4. Дифференцирование операций 27
1. Дифференцирование линейной комбинации конечного
числа дифференцируемых функций B8).
2. Дифференцирование произведения C1).
3. Дифференцирование частного C3).
§ 5. Дифференцирование сложной функции 37
1. Дифференцируемость сложной функции C7).
2. Инвариантность формы записи дифференциала D0).
§ 6. Дифференцирование элементарных функций 42
1. Дифференцирование тригонометрических функций D2).
2. Дифференцирование обратной функции D5).
3. Дифференцирование обратных тригонометрических
функций D6).
4. Дифференцирование показательной и логарифмической
функций D8).
5. Дифференцирование гиперболических функций E2).
6. Сводка правил и формул дифференцирования E3).
7. Логарифмическое дифференцирование E4).
159

§ 7. Производные и дифференциалы высших порядков 59
1. Понятие производной п-то порядка E9).
2. Механический смысл второй производной F2).
3. Натуральная степень бинома (формула Ньютона) F3).
4. Свойства производной п-то порядка F6).
5. Дифференциалы высшего порядка F9).
Глава 2
ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ G3)
§ 1. Связь между ходом изменения функции и ее производной 73
1. Возрастание и убывание функций G3).
2. Экстремумы функции G4).
§ 2. Теорема Лагранжа и ее следствия 77
1. Леммы о знаке приращения G7).
2. Теорема Ролля G8).
3. Теорема Лагранжа (80).
4. Условие постоянства функции (82).
§ 3. Исследование функций 86
1. Возрастание и убывание функций (86).
2. Исследование функций на экстремум с помощью первой
производной (89).
3. Использование второй производной для исследования
функций на экстремум (93).
4. Нахождение наибольшего и наименьшего значений
функции на данном отрезке (94).
§ 4. Выпуклые функции 100
1. Определение выпуклости A00).
2. Достаточные условия выпуклости A05).
3. Точки перегиба A06).
§ 5. Применение дифференциального исчисления к
доказательству неравенств и решению уравнений
1. Доказательство неравенств A11).
2. Приближенное решение уравнений A15).
§ 6. Применение производных для вычисления пределов функций 111
1. Теорема Коши A20).
2. Правило Лопиталя A21).
3. Сравнение быстроты роста функций A29).
§ 7. Построение графиков функций 131
§ 8. Кривые на плоскости 141
1. Примеры параметрического задания кривых A41).
2. Жордановы кривые A43).
3. Связь между различными видами уравнений линий A44).
4* Дифференцирование параметрически заданных функций A46).
5. Полярное уравнение кривой A47).
6. Производная второго порядка для параметрически
заданной функции A48).
7. Построение кривых, заданных параметрическими
уравнениями A49).
8. Построение кривых, заданных полярными
уравнениями A52).