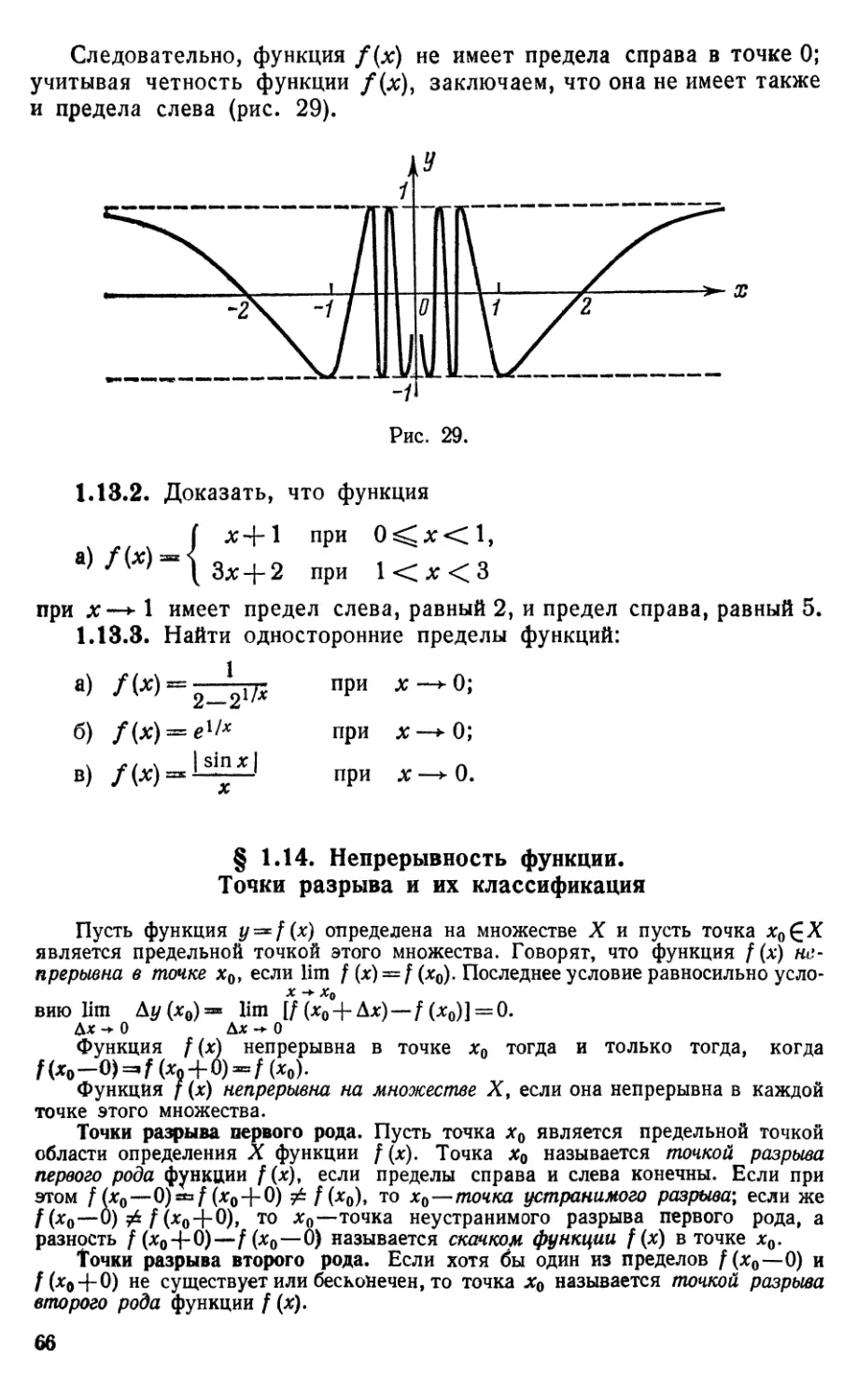
Текст
И. А. МАРОН
Дифференциальное
и интегральное
исчисление
в примерах и задачах
Функции одной переменной
Допущено Министерством
высшего и среднего специального образования СССР
в качестве учебного пособия
для студентов высших технических учебных заведений
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕР А!
МОСКВ А 1 9 7 О
517.2
M 28
УДК 517
АННОТАЦИЯ
Книга представляет собой пособие по решению
задач математического анализа (функции одной пере-
переменной). Большинство параграфов книги содержит
краткие теоретические введения, решения типовых
примеров и задачи для самостоятельного решения.
Кроме задач алгоритмически-вычислительного харак-
характера, в ней содержится много задач, иллюстрирую-
иллюстрирующих теорию и способствующих более глубокому
ее усвоению, развивающих самостоятельное математи-
математическое мышление учащихся.
Цель книги—научить студентов самостоятельно
решать задачи по курсу математического анализа
(изучение теории должно производиться по какому-
либо из существующих учебников).
Книга предназначена для студентов технических,
экономических вузов и нематематических факультетов
университетов. Она может оказаться полезной лицам,
желающим повторить и углубить втузовский курс
математического анализа, начинающим преподавате-
преподавателям, а также учителям средней школы, ведущим фа-
факультативные курсы в старших классах.
2-2-3
182-69
ОГЛАВЛЕНИЕ
Предисловие * • 5
Глава I. Введение в математический анализ 7
§ 1.1. Действительные числа. Абсолютная величина действительного числа 7
§ 1.2. Понятие функции. Область определения • • 11
§ 1.3. Элементарное исследование функций 17
§ 1.4. Обратные функции 22
§ 1.5. Построение графиков функций .... 24
§ 1.6. Числовые последовательности. Предел последовательности .... 34
§ 1.7. Вычисление пределов последовательностей 40
§ 1.8. Признаки существования предела последовательности 42
§ 1.9. Предел функции 47
МО. Техника вычисления пределов 51
.11. Бесконечно малые и бесконечно большие функции. Сравнение их 58
.12. Эквивалентные бесконечно малые. Применением отысканию пределов 61
.13. Односторонние пределы 64
.14. Непрерывность функции. Точки разрыва и их классификация . , 66
.15. Арифметические действия над непрерывными функциями. Непрерыв-
Непрерывность сложной функции 72
§ 1.16. Свойства функции, непрерывной на отрезке. Непрерывность обратной
функции 74
§ 1.17. Дополнительные задачи 78
Глава П. Дифференцирование функций 84
§ 2.1. Понятие производной 84
§ 2.2. Дифференцирование явно заданных функций 86
§ 2.3. Повторное дифференцирование явно заданных функций. Формула
Лейбница 92
§ 2.4. Дифференцирование обратных функций и функций, заданных неявно
или параметрически 96
§ 2.5. Приложения производной ¦¦«.... 100
§ 2.6. Дифференциал функции. Приложение к приближенным вычислениям 106
§ 2.7. Дополнительные задачи , .... ПО
Глава III. Применение дифференциального исчисления к исследованию
функций « * ...... 113
§ 3.1. Основные теоремы о дифференцируемых функциях 113
§ 3.2. Раскрытие неопределенностей. Правило Лопиталя 119
§ 3.3. Формула Тейлора. Приложение к приближенным вычислениям . . 124
§ 3.4. Локальная формула Тейлора. Применение к вычислению пределов 128
§ 3.5. Признаки монотонности функции «*»*•• 129
§ 3.6. Максимумы и минимумы функции 132
§ 3.7. Отыскание наибольших и наименьших значений функции » . • . 138
§ 3.8. Решение задач геометрического и физического содержания .... 141
§ 3.9. Выпуклость и вогнутость кривых. Точки перегиба 145
§ 3.10. Асимптоты 148
§ &.11. Общее исследование функции * • • • • 152
§ 3.12. Приближенное решение алгебраических и трансцендентных урав-
уравнений 160
§ 3.13. Дополнительные задачи 167
Глава IV. Неопределенный интеграл. Основные методы интегрирования 171
§ 4.1. Непосредственное интегрирование и метод разложения 171
§ 4.2. Метод подстановки 175
§ 4.3. Интегрирование по частям 178
§ 4.4. Рекуррентные формулы 187
Глава V. Основные классы интегрируемых функций 190
§ 5.1. Интегрирование рациональных функций 190
§ 5.2. Интегрирование некоторых иррациональных выражений 195
§ 5.3. Подстановки Эйлера 198
§ 5.4. Другие методы интегрирования иррациональных выражений . . . 200
§ 5.5. Интегрирование биномиального дифференциала 203
§ 5.6. Интегрирование тригонометрических и гиперболических функций . 205
§ 5.7. Интегрирование некоторых иррациональных функций с помощью
тригонометрических или гиперболических подстановок 212
§ 5.8. Интегрирование других трансцендентных функций 214
§ 5.9. Обзор методов интегрирования (основных видов интегралов) . . . 216
Глава VI. Определенный интеграл , . 221
§ 6.1. Понятие определенного интеграла 221
§ 6.2. Вычисление определенных интегралов по формуле Ньютона — Лейб-
Лейбница 229
§ 6.3. Оценки интеграла. Определенный интеграл как функция своих пре-
пределов 233
§ 6.4. Замена переменной в определенном интеграле 246
§ 6.5. Упрощение интегралов, основанное на свойствах симметрии подын-
подынтегральных функций 257
§ 6.6. Интегрирование по частям. Вывод рекуррентных формул .... 262
§ 6.7. Приближенное вычисление определенных интегралов 269
§ 6.8. Дополнительные задачи 273
Глава VII. Приложения определенного интеграла 276
§ 7.1. Вычисление пределов сумм с помощью определенных интегралов 276
§ 7.2. Вычисление средних значений функции 278
§ 7.3. Вычисление площадей в декартовых координатах 282
§ 7.4. Вычисление площадей фигур при параметрическом задании границы
(контура) 291
§ 7.5. Площадь в полярных координатах 294
§ 7.6. Вычисление объемов тел 298
§ 7.7. Вычисление длин дуг плоских кривых, заданных в декартовых
координатах 306
§ 7.8. Вычисление длин дуг кривых, заданных параметрически 308
§ 7.9. Вычисление длин дуг кривых, заданных в полярных координатах 311
§ 7.10. Вычисление площади поверхности вращения » 314
§ 7.11. Смешанные задачи на геометрические приложения определенного
интеграла 319
§ 7.12. Вычисление давления, работы и других физических величин . . . 326
§ 7.13. Вычисление статических моментов и моментов инерции. Определение
координат центра тяжести 330
§ 7.14. Дополнительные задачи 339
Главз VIII. Несобственные интегралы 343
§ 8.1. Несобственные интегралы с бесконечными пределами 343
§ 8.2. Несобственные интегралы от неограниченных функций 353
§ 8.3. Геометрические и физические приложения несобственных интегралов 364
§ 8.4. Дополнительные задачи 369
Ответы и указания 371
Светлой памяти
родителей моих
ту книгу посвящаю.
Автор
ПРЕДИСЛОВИЕ
Настоящее учебное пособие написано на основе многолетнего
опыта преподавания курса математического анализа во втузе.
Цель пособия — содействовать активизации упражнений по мате-
математике, придать этим упражнениям, в некотором смысле, характер
семинарских занятий.
Большое внимание обращено на задачи, углубляющие теорети-
теоретический материал. Это определило и содержание книги: наряду с ти-
типовыми задачами вычислительного характера помещены примеры и
задачи, поясняющие теорию, способствующие более глубокому ее
пониманию, развивающие навыки точного математического мышления
обучающихся. В книге приведено также некоторое количество контр-
контрпримеров, позволяющих выяснить необходимость тех или иных
условий в формулировках основных теорем математического анализа.
Структура книги такова. В начале каждого параграфа дается
сжатое теоретическое введение, содержащее основные определения,
формулировки важнейших теорем и главнейшие формулы. Затем при-
приводится полное решение одной или нескольких характерных задач.
Далее помещены задачи без решения в тексте, аналогичные рас-
рассмотренным, но часто содержащие некоторые особенности. Часть
из них снабжена указаниями.
Каждая глава (кроме глав IV и V) завершается отдельным па-
параграфом «Дополнительные задачи». В таких итоговых параграфах
помещены вопросы и задачи для повторения и углубления материала
соответствующей главы. Эти параграфы окажутся полезными любо-
любознательным студентам; возможно, что итоговые параграфы будут не
бесполезными и преподавателям при подборе материала для упраж-
упражнений и для работы математического кружка. В конце книги к боль-
большинству задач указанных параграфов даны указания.
Как было выше отмечено, в тексте книги дано полное решение
ряда примеров и задач. Это оправдано следующими мотивами: имея
учебное пособие с образцами решенных задач, преподаватель полу-
получит возможность уделить меньше времени стандартным задачам вы-
вычислительного характера, отослав студентов к книге, а значительную
часть своего внимания сосредоточит на решении задач более прин-
принципиального характера. Таким образом, будет достигнута некоторая
экономия времени для более содержательной работы. Кроме того,
нада учитывать огромное число лиц, занимающихся самостоятельно —
заочно или самообразованием. Им эти решенные задачи заменят
в известной мере устные указания преподавателя, получаемые сту-
студентами очных факультетов на занятиях. Обучающийся получит
ббльшую пользу, если он будет работать над книгой активно. Это
значит, что прежде чем приступить к решению задач, следует осно-
основательно изучить теоретический материал, относящийся к соответ-
соответствующему параграфу; затем надо подробно разобрать приведенные
задачи с решениями и обязательно закрепить знания решением за-
задач, предназначенных для самостоятельной работы. Еще лучше, если
обучающийся, усвоив теорию, сразу приступит к самостоятельному
решению задач, обращаясь к решениям в тексте лишь в случае за-
затруднений.
Считаю своим приятным долгом поблагодарить Б. П. Демидовича,
М. Ш. Цаленко, Б. В. Шабата, прочитавших рукопись. Их советы
и замечания оказались очень ценными.
Я хочу особенно отметить весьма компетентную работу редак-
редактора книги Л. S. Румшиского, чья работа во многом способство-
способствовала улучшению книги.
Автор с благодарностью воспримет советы и критические
замечания читателей, которые следует направлять по адресу: Москва,
В-71, Ленинский проспект, дом 15, Главная редакция физико-мате-
физико-математической литературы издательства «Наука».
И, Марон
Глава I
Введение в математический анализ
§1.1. Действительные числа.
Абсолютная величина действительного числа
Действительным числом называется любая десятичная дробь, конечная
или бесконечная.
Периодические десятичные дроби называются рациональными числами.
Всякое рациональное число можно записать в виде отношения p/q целых
чисел р и q, и обратно.
Непериодические десятичные дроби называются иррациональными числами.
Если X — некоторое множество действительных чисел, то запись х?Х
означает, что число х принадлежит X, а запись x(fcX означает, что число х
не принадлежит X.
Множество действительных чисел х, удовлетворяющих неравенствам
а < х < Ь, где а, Ъ — фиксированные числа, называется интервалом (а, ^.Мно-
^.Множество действительных чисел х} удовлетворяющих неравенствам a*^x^bt
называется отрезком [а, Ь]. Множество действительных чисел х, удовлетво-
удовлетворяющих неравенствам а^х<Ь или а < х*^Ь, называется полуинтервалом
[а, Ь) или (а, Ь]. Интервал, отрезок, полуинтервал объединяются общим назва-
названием промежуток.
Каждое действительное число изображается определенной точкой коорди-
координатной оси, называемой собственной точкой. Иногда удобно считать, что
имеются еще две несобственные точки, + оо и — оо, бесконечно удаленные
от начала координат в положительном и отрицательном направлениях. Для
всякого действительного числа х по определению считают, что — оо < х < + °°-
Интервал (а—8, а+е) называется z-окрестностью числа а.
Множество действительных чисел х > М называется М-окрестностью не-
несобственной точки +оо.
Множество действительных чисел х < М называется М-окрестностью не-
несобственной точки —оо.
Абсолютной величиной числа х называется число | х |, определяемое усло-
условиями:
\x\-i ~Х>
1 \ х>
Свойства абсолютных ве-
1)
2)
3)
¦4)
5)
6)
неравенство | д
неравенство | х
х±у\<,
х±у\^
ху
X
7
=1*1
_ 1*1
~171
1*1-
(t
если х < 0,
если x^ssO.
ч и ч и н:
; | ^а означает, что —a^jc^a;
|^a означает, что х^а или х^—ос;
Ну к,
-\y\\i
1.1.1. Доказать, что число
0,1010010001...1000...01...
П
иррационально.
Решение. Для доказательства нужно установить, что данная
десятичная дробь не является периодической. Действительно, между
#-й единицей и (л-{-1)-й стоит п нулей, чего не может быть в перио-
периодической дроби.
1.1.2. Доказать, что всякое число, в котором нули стоят на
всех местах с номером 10я после запятой и только на этих местах,
является иррациональным.
1.1.3. Доказать, что сумма или разность рационального числа
а и иррационального числа р есть число иррациональное.
Решение. Рассмотрим случай суммы чисел аир. Предполо-
Предположим, что а + Р = У есть число рациональное. Тогда р = у—<* есть
число рациональное, как разность двух рациональных чисел, что
противоречит условию. Значит, сделанное предположение неверно и
число a + Р—иррационально.
1.1.4. Доказать, что произведение ар и частное a/р рациональ-
рационального числа a 7*= 0 и иррационального числа р есть число ирра-
иррациональное.
1.1.5. а) Найти все рациональные значения х, при которых
у = j/jc2 -J- х -f* 3 есть рациональное число.
Решение, а) Предположим, что х и у^Ух2-\-х-\-3— рацио-
рациональные числа. Тогда их разность у — x = q есть так же рацио-
рациональное число. Выразим х через q
Непосредственной проверкой легко убедиться, что q Ф Vg.
Докажем теперь обратное, а именно: число у = Ух2-\-х-{- 3
a2—3
является рациональным числом, если *=? д-» где q — любое ра-
рациональное число, не равное 1/2.
Действительно,
/
V
A— 2qf ~ V (l—2q)t ~~ \l—2q\
Последнее выражение рационально при любом рациональном q.
б) Доказать, что |/ есть иррациональное число.
1.1.6. Доказать, что число J/3 + K 2 иррационально.
Решение, Предположим противное, т. е. допустим, что число
рационально. Тогда число
1
также является рациональным, как частное двух рациональных чисел.
Поэтому число
V2 = | Щ/3 + V2)-{V* -УЩ
является рациональным, что противоречит иррациональности числа
У2 (задача 1.1.5). Следовательно, наше предположение неверно, и
число Уз + V% иррационально.
1.1.7. Доказать, что каково бы ни было положительное раци-
рациональное число г, удовлетворяющее условию г2 < 2, всегда найдется
бблынее рациональное число г + А (h > 0), для которого (г-[-/г)а<2.
Решение. Можно считать h < 1. Тогда /г2 < h и (г + /гJ <
<г2 + 2гй + /г. Поэтому достаточно положить г2 + 2г/г +/г = 2, т.е.
Л = B-г2)/Bг+1).
1.1.8. Доказать, что каково бы ни было положительное рацио-
рациональное число s, удовлетворяющее условию s2 > 2, всегда найдется
меньшее рациональное число s—k (к > 0), для которого (s — &J > 2.
1.1.9. Решить неравенства:
а) |2*-3|<1; б) (х-2J>4;
в) х2 + 2х—8<0; г) \х2 — 7х+ 12| > л:2 — 7х+ 12.
Решение, а) Неравенство 12л: — 3|<1 равносильно неравен-
неравенствам
—1 <2х—3< 1,
откуда
2<2лг<4 и 1<*<2.
г) Данное неравенство справедливо для тех значений #, при
которых хг — 7jc+ 12 < 0, откуда 3 < х < 4.
1.1.10. Имеют ли решения следующие уравнения:
а) |*|=* + 5; б) \х\=х — 5?
Решение, а) При х^О имеем х = х + 5. Следовательно,
решений нет. При х < 0 имеем —х = х + 5, откуда лг=—5/2. Это
значение удовлетворяет исходному уравнению.
б) При х^О имеем х = х — 5. Следовательно, решений нет.
При лг<0 имеем —х = х—5, откуда # = 5/2, что противоречит
нашему предположению (х < 0). Таким образом, уравнение не имеет
решений.
9
1.1.11. Определить, для каких значений х будут справедливы
равенства
1Х i х 1
х-\-1 х~\~ 1 '
1.1.12. Определить, для каких значений х имеют место равенства
а) I (х* + 4# + 9) + Bх—3) | = | jc
Решение, а) Равенство |# + #| = |#| + |?| имеет место тогда
и только тогда, когда оба слагаемых одного знака. Так как
при любых значениях х, то равенство имеет место для значений х,
при которых 2х — 3^0, т. е. для х^З/2.
б) Равенство \а — &| = |а| — \Ь\ имеет место тогда и только
тогда, когда а и Ь одного знака и |а|^]?|.
В нашем случае равенство будет выполнено для тех значений х,
для которых
*4 — 4>
Отсюда
1.1.13. Решить неравенства:
а) 13л:—5| — |2jc + 3|>0; б) \х*—
1.1.14. Найти корни уравнений
a) J sin jc| = sin jc+ 1; б) х2 — 2 \х\—-3 = 0.
Решение, а) Это уравнение может быть удовлетворено только
при тех значениях х, для которых sin x < 0, поэтому мы можем
переписать его так:
— sinx= sin #+1» или sinx=—1/2;
отсюда x = nk — (—l)kn/6 (& = 0, ± 1, ±2, . ..).
б) Можно решить это уравнение стандартным способом, рассмот-
рассмотрев случаи х^О и л:^0, но проще, пожалуй, решать так: запи-
запишем уравнение в виде
Заменяя |л:| на у, получим
у2 — 2у — 3 = 0,
откуда уг = 3, у2 = — 1. Так как ^ = 1*1^0, то у2 = — 1 не под-
подходит. Остается
т. е. хг= —3, х2 = 3.
10
§ 1.2. Понятие функции. Область определения
Независимая переменная х определяется заданием множества X своих
значений.
Переменная у называется функцией независимой переменной х с областью
определения X, если каждому значению х?Х однозначно соответствует зна-
значение у. Символическая запись: у = у(х) или y = f(x) или у = ц>(х) и т. д.
Множество значений функции у(х) называется областью изменения данной
функции.
В частности, функции, определенные на множестве натуральных чисел
1, 2, 3, ..., называются числовыми последовательностями. Они записываются
следующим образом: хъ х2, ,.., хю ... или {хп\.
1.2.1. Дана функция f(x) = (х + \)!(х — 1). Найти fBx), 2/{х)г
Я*2), [/W]2.
Решение.
l/W-(?{)•.
1.2.2. а) Дана функция
Показать, что при л:^, х2?(—1, 1) имеет место тождество
Решение. При
этому
(—1, 1) имеем A—л;)/A+л:)>0 и по-
поС другой стороны,
1 -f- XtX2 __ i 1 -f" -У 1^2 — xl — Х2 ==3
(\-хг)(\-х2)
что совпадает с правой частью выражения A).
б) Дана функция f(x) — (ax + a"x)/2 (a > 0). Показать, что
1.2.3. Дана функция f(x) = (х+ \)/(х* — 1). Найти /(—1);
+ 1); /(а) + 1.
1.2.4. Дана функция /(д;)==д:3 — 1. Найти
f(b)-f(a)
{b?=a) и
u
1.2.5. Дана функция
-*—I, —1<*<0,
/(*) = { tg(x/2), 0<л:<л,
Найти /(-1), /(я/2), /Bя/3), /D), /F).
Решение. Точка л; =—1 лежит в промежутке [—1, 0). По-
Поэтому
/(—\) = 3-(-D —1=2.
Точки лг = я/2, л; = 2я/3 лежат в промежутке [0, я). Поэтому
/(я/2) = tg (я/4) = 1; /Bя/3) = tg (я/3) = j/3.
Точки л: = 4, л; = 6 лежат в промежутке [я, 6]. Поэтому
6_2 — у» У vu;
у \*/ —
У vu;
— 2~ 17 e
1.2.6, Функция f(x) задана на всей числовой оси следующим
, законом:
( 2л:3 +1, если л:<2,
1/(х — 2), если 2<л:<3,
г \ 2х — 5, если х > 3.
\ Найти: /A/2), /(/8), f(V\og21024).
1.2.7. В квадрате ABCD со сторо-
стороной АВ = 2 проведена прямая MN_[_AC.
Принимая за х расстояние от верши-
вершины А до прямой MN, выразить через
х площадь *S фигуры AMN, отсекае-
~Д мой от квадрата прямой MN. Найти
Рис. 1. эту площадь при л: = 1/2/2 и при
х = 2 (pHC.J).
Решение. Заметим, что АС =21/2; поэтому
Если л:<1/2, то
Если л:>К2, то
S (х) = 4 —
Таким образом,
—л:J = —л:2 + 4л: ]/2 — 4.
— 4,
Так как l/*2/2 < 1/2, то 5(]/2/2) = A/2/2J= 1/2. Так как
2>1/2, то
5B) = —4 +8|/2 —4 = 8A/2—1).
12
1.2.8. Поставим в соответствие каждому натуральному числу п
число а„, равное я-му десятичному знаку в разложении \/~2 в деся-
десятичную дробь. Это задает некоторую функцию ай = <р(#). Вычис-
Вычислить фA), <рB), ФC), фD).
Решение. Извлекая квадратный корень, находим j/*2 =1,4142...
Таким образом,
ФA) = 4; ФB) = 1; ФC) = 4;
1.2.9. Вычислить /(л;) = 49/л;2-{-л;2 в точках, для которых
Решение. /(х) = 49/х2 + х2 = G/х + х)% —14, но
поэтому f(x) = 9—14==—5.
1.2.10. Найти функцию вида /(х) = ах2 + Ьх + с, если известно,
что/@) = 5; /(—1)= 10; 0
Решение.
Из полученной системы определяем коэффициенты ау Ьу с. Имеем
я = 3; Ь=—2; с = 5; следовательно, /(а:)==Злг2—
1.2.11. Найти функцию вида
если /@) = 15; /B)-30; /D) = 90.
1.2.12. Найти ф[я|)(х)] и 1})[ф(л:)], если
Ф()=:л:2 и
Решение.
1.2.13. Дана функция
" 2—jc •
Найти fCx); /(*»); 3f{x); [f(x)]\
1.2.14. Пусть
при —1 < x < О,
f(x) = \ 4 при 0<лг<1,
Зл:—1 при 1^д;^3.
Найти /B), /@), /@,5), /(—0,5), /C).
1.2.15. Доказать, что если для показательной функции у— а*
{а > 0; аф\) значения аргумента х = хп (л=1, 2, ...) образуют
арифметическую прогрессию, то соответствующие значения функ-
функции уп = ахп(п = 1, 2, ...) образуют геометрическую прогрессию.
13
1.2.16. f(x) = x* + 6, (p(x) = 5x. Решить уравнение f(x) =
1.2.17. Найти /(*), если
1.2.18. Вычислить значения функций
в тех точках, в которых \/х + х = 5.
1.2.19. f(x) = x-\-1; ср(х) = л:—2; решить уравнение
1.2.20. В треугольник ABC с основанием b и высотой h вписан
прямоугольник, высота которого х. Выразить периметр Р и площадь
*S прямоугольника как функции от х.
1.2.21. Найти области определения функций:
1
— х\ 6) f(x) = Vx2 — х—
в)
Д)
з)
к)
Решение, а) Область определения заданной функции состоит
из тех значений х, при которых оба слагаемых принимают дейст-
действительные значения. Для этого должны выполняться два условия:
х—1 ^ 0,
6 —
Решая неравенства, получим
Таким образом, областью определения функции является отре-
отрезок [1, 6].
д) Функция определена при тех значениях х, для которых
Это неравенство будет выполнено, если
5?=?>1, или х2 —
Решая последнее неравенство, находим ^^
Таким образом, область определения функции—отрезок [1, 4].
е) Функция определена для всех положительных х, отличнпх от 1.
Значит, область определения функции состоит из промежутков
@, 1) и A, +оо).
14
л) Функция определена при тех х, для которых
sinx
Так как 4 4-2sin;t>0 при любых х, то задача сводится к реше-
решению неравенства
^1
Отсюда
т. е. sin.x;> —1/2.
Решая последнее неравенство, получим
—J + 2?tt<*<~ + 2/m (A = 0, ±1, ±2,...).
м) Функция определена при тех х> для которых | jc | — л;>0,
откуда | х | > х. Это неравенство выполняется при х < 0. Следова-
Следовательно, функция определена в интервале (—оо, 0).
1.2.22. Найти области определения функций:
a) f{x) = j/arcsin(log2j*:);
б)
I
д) /(^) = ]/cos(sinjc) + arcsin ¦¦ g
Найти области изменения функций:
Решение, а) Чтобы функция f(x) была определена, должно
выполняться неравенство
arcsin (log2 х) ^ 0,
откуда 0<!log2x<;i и
б) Функция log2logglog4;c определена при log3log4A; > 0, откуда
log4x>l и д:>4. Следовательно, область определения есть про-
промежуток 4 < х < + оо.
в) Заданная функция определена, если одновременно выполняются
следующие неравенства:
х>2,
но неравенства—l^x^l и х > 2 несовместны, поэтому функция
не определена ни при каком значении х.
д) Должны одновременно выполняться следующие неравенства:
cos (sinx)^О и —Tfir- ^Ь
15
Первое неравенство выполняется при всех значениях х, второе —
при | jc | = 1. Следовательно, область определения заданной функции
состоит лишь из двух точек х = ± 1 ¦
е) Имеем
Так как
—1^cos3a:j<1, to —1
откуда, учитывая, что у > О, получим
—У^%У — 1 ^.у ил
ж) Разрешив относительно х, получим
или 4
Область изменения функции у определится из соотношения
Отсюда
1.2.23. Решить уравнение
arctg]/х(х+1) + arcsin У х2 + х+\ = л/2.
Решение. Изучим область определения функции, стоящей
в левой части уравнения. Эта функция будет определена при
откуда
Таким образом, левая часть уравнения принимает действительные
значения лишь при xL = 0 и х2 = — 1.
Непосредственной проверкой убеждаемся, что они являются кор-
корнями заданного уравнения.
Этот пример показывает, что изучение областей определения
функций иногда облегчает решение уравнений, неравенств и т. п.
1.2.24. Найти области определения функций:
16
1.2.25. Функция f{x) определена на отрезке [0, 1]. Каковы об-
области определения функций
а) /(Зх2); б) f(x-5); в) /(tgx)?
Решение. Заданные функции являются функциями от функций,
или суперпозициями функций, т. е. сложными функциями.
а) Введем промежуточный аргумент и=3х2. Тогда функция
fCx2)=f(u) определена, если 0^#^1, т. е. 0^3#2^1, откуда
в) Аналогично: O^tgx-^l, откуда
(А = 0, ±1, ±2,...).
1.2.26. Функция/(лг) задана на отрезке [0, 1]. Каковы области
определения функций
a) /(sin*); б)/B* + 3)?
§ 1.3. Элементарное исследование функций
Функция f (x), определенная на множестве X, называется неубывающей
на этом множестве (соответственно, возрастающей, невозрастающей, убывающей),
если для любых чисел хъ хг?Х, хх < х2> выполняется неравенство / (л^) <;/(х2)
(соответственно, f(xt) < f (x2)y f(xi)^f(x2), /(%) > f(x2)). Функция f (x) назы-
называется монотонной на множестве X, если она обладает одним из указанных
четырех свойств. Функция / (х) называется ограниченной сверху (или снизу) на
множестве X, если существует такое число М (или т), что / (х) «^ М для всех
х?Х (или m*^f(x) для всех я?Х). Функция f (х) называется ограниченной
на множестве X, если она ограничена сверху и снизу.
Функция fix) называется периодической, если существует такое число
Т > О, что f (x-\-T) = f (х) для всех х, принадлежащих области определения
функции (вместе со всякой точкой х точка х-\-Т должна принадлежать области
определения). Наименьшее число Т, обладающее указанным свойством, если
оно существует, называется периодом функции / (х). Функция / (х) принимает
в точке хо?Х наибольшее значение, если / (xo)^f (x) для всех х?Х, и наи-
наименьшее значение, если f(xo)^f(x) для всех х?Х. Функция f(x), определен-
определенная на симметричном относительно начала координат множестве X, называется
четной, если /(—x) — f(x), и называется нечетной, если /(—х) — —/ (х).
Чтобы составить представление о поведении функции, полезно ответить
на следующие вопросы:
1. Какова область определения функции?
2. Является ли функция четной, нечетной, периодической?
3. В каких точках функция принимает значение, равное нулю? (Найти
нули функции.)
4. Каков знак функции на промежутках между нулями?
5. Является ли функция ограниченной и каковы ее наименьшее и наи-
наибольшее значения?
Конечно, указанный перечень вопросов не исчерпывает задачи полного
исследования функции. В дальнейшем этот круг вопросов будет расширяться.
1.3.1. Найти промежутки возрастания и убывания функции
f(x)~ ax2 + bx-{-ci а также наименьшее и наибольшее ее значения.
Решение. Выделяя из квадратного трехчлена полный квадрат,
имеем
4а в
17
Если а > о> то функция f(x) будет возрастать при тех значениях х,
при которых x-\-bf{2d) > 0, т. е. при л:>—Ь/Bа), и убывать, когда
x-\-bjBa) < 0, т. е. при х <—Ь/Bа). Таким образом, если а > О,
то функция f(x) убывает в промежутке (—оо, —Ь/Bа)) и возрастает
в промежутке (—b/BaI -f-oo). Очевидно, при х = — Ь/{2а) функция
f(x) принимает наименьшее значение
/min J[ 2a)~~
[ ) 4а '
Наибольшего значения функции здесь нет.
Аналогично, при а < О функция f(x) будет возрастающей в про-
промежутке (—оо, —Ь/Bа)) и убывающей в промежутке (—Ь/Bа)} оо);
при х = — Ь/Bа) функция f(x) принимает наибольшее значение
/max —./Д 2а)'—
2а)'— 4а '
тогда как наименьшего значения у нее нет.
1.3.2* а) Найти наименьшее значение функции
б) Из всех прямоугольников данного периметра найти прямоугольник
с наибольшей площадью.
Решение, а) Применим результаты задачи 1.3.1: я = 3>0,
& = 5, с = — 1. Наименьшее значение функция принимает в точке
д;=,_5/6 и
__4ас—Ь* 37
.У min— 4a ~~ 12'
б) Обозначим через 2р длину периметра искомого прямоуголь-
прямоугольника, а через х—длину одной из его сторон; тогда площадь S
прямоугольника выразится так:
S = x(p—х) или S—px—х2*
Задача свелась к отысканию наибольшего значения функции S(x)=s
= —х2 +рх. Применим результаты задачи 1.3,1: а==—1 <0, Ь=р,
с = 0. Наибольшее значение функция S (х) принимает в точке
х = —Ь/Bа)—р/2. Таким образом, одна сторона искомого прямо-
прямоугольника равна р/2, а другая сторона р—х=р/2, т. е. искомый
прямоугольник—квадрат.
1.3.3. Показать, что
а) функция /(лг) = д^ + Здг + 5 возрастает во всей области ее
определения;
б) функция g(x) = x/(lJrX2) убывает в промежутке A, +оо).
Решение, а) Функция определена для всех точек числовой оси.
Выберем на числовой оси произвольные точки хх и д;2, хх <С x%> и
составим разность:
/ (*,) -/ (*i) = iA + 3*а + 5) - {х\ + Зх, + 5) =
= (х,—*i) (х\ + хххг + х\ + 3) «=
[( ) |
18
Поскольку х2—#!> О, а выражение, стоящее в квадратных скобках,
положительно при всех хг и л:2, то f(x2)—/(хг) > 0, т. е.
f(x2)>f(xi)> а 9Т0 значит, что функция f(x) возрастает для всех
значений х.
1.3.4. Найти промежутки возрастания и убывания функции
а) /(л:) = sin дг + cos д:;
б) tg(x + n/3).
Решение, а) Пользуясь известными формулами тригонометрии,
находим
Известно, что функция cos* убывает на отрезках
и возрастает на отрезках
Bя —1)я<л;<2/ш (# = 0, ±1, ±2, ...).
Следовательно, промежутки убывания функции f(x):
я/4-f 2/ш<лг<я;/4 + B/г-И)л; (л = 0, ± 1, ...),
а промежутки возрастания f(x):
эт/4 + Bя — 1)я<л:<я/4 + 2/гя (л = 0, ±1, ...)•
1.3.5. Найти наименьшее и наибольшее значения функции
/ (х) = a cos х + b sin x (a2 + b2 > 0).
Решение. Данную функцию можно представить так:
f(x) = Va2 + b2 cos (x—a),
где cosct = a/]/a2 + #\ sin а = ^/Ка2 + Л Так как | cos (х — а) [< 1,
то наибольшее значение f(x) равно -\-Уа2-\-Ь2 (при cos(a: — а)=1),
а наименьшее значение f(x) равно —\/ а2 ~\-Ь2 (при cos (х — а) = — 1).
1.3.6. Найти наименьшее значение функции
Решение. Обозначим показатель степени через <р (л:), т. е.
Функция f(x) = 3v(x) принимает наименьшее значение там же,
где функция ц>(х).
Имеем
Отсюда видно, что функция <р(л;) принимает наименьшее значение
{равное 0) при х = 0. Поэтому рассматриваемая функция /(л:) имеет
наименьшее значение, равное 3°=1»
19
1.3.7. Исследовать функцию
x, где 0<х<п/2,
на возрастание и убывание.
1.3.8. Даны п чисел av а21 ...}ап. Определить, при каком зна-
значении х функция
f{x) = {x-al)* + (x-a%)* + ... +(х-ая)*
принимает наименьшее значение.
Решение. Перепишем функцию f(x) следующим образом:
Отсюда видно, что f(x) есть квадратный трехчлен ахг-{-Ьх-\-с,
у которого а = /г>0. Воспользовавшись результатами задачи 1.3.1,
получаем, что функция достигает наименьшего значения при
х = — Ь/Bа), т. е. при * = (а1 + а1+...+ай)/л.
Таким образом, сумма квадратов отклонений величины х от п
заданных чисел достигает наименьшего значения тогда, когда х есть
среднее арифметическое значение для этих чисел.
1.3.9. Определить, какая из данных функций является четной,
нечетной и какая из них не является ни четной, ни нечетной
функцией.
a) f(x) = lg(x + VT+tf); б)
в) f(x) = 2**-x+U г)
Решение, а) Можно заметить, что /(+ #)+/(—х) = 0. Дей-
Действительно,
= lg(l+*2—л;2) = 0,
следовательно, /(лг) =—/(—х) для всех х. Значит, функция не-
нечетная.
Таким образом, /(—#) =—f(x) для всех х из области опреде-
определения (—1, 1). Значит, функция нечетная.
1.3.10. Установить четность или нечетность функций:
а) /(*) = 4—2x4 + sin2Ar; б) /(*) = Vl +х + х*-~|Л — х + х2;
в) / (х) - \^~ ; г) / (х) = sin х + cos х\ д) / (х) - const.
1 aRX
—aR
1.3.11. Доказать, что если f(x)—периодическая функция с перио-
периодом Г, то функция f(ax + bO где а > 0, является периодической
с периодом Т/а.
20
Решение. Во-первых,
так как Т—период функции f(x). Во-вторых, пусть Тг — такое по-
положительное число, что
Возьмем произвольную точку х из области определения функции
f(x) и положим х'*=(х—Ь)/а. Тогда
Отсюда следует, что период Т^.аТх, т. е. Тх^ Т/а, и значит, Т/а—
период функции f(ax-\-b).
Замечание. Периодическая функция f (x) = A sin (юя+ср), где Л, со, ф —
постоянные, называется гармоникой с амплитудой | А |, частотой со и начальной
фазой ф. Так как функция sin л: имеет период 2я, то функция A sin (ojt-f-ф)
имеет период Т — 2я/(д.
1.3.12. Указать амплитуду |Л[, частоту со, начальную фазу ср
и период Т следующих гармоник:
a) f(x) = 5 sin 4х; б) f(x) = 4 sin (Зя + я/4);
в) f(x) = 3 sin (дг/2) + 4 cos (дг/2).
1.3.13. Найти период функций:
a) /(x) = tg2x; б) /(x) = dg(*/2); в) /U) = sin2ax
Решение, а) Так как функция tg x имеет период я, то функция
tg2x имеет период я/2.
1.3.14. Найти период функций:
а) / (х) = sin4 х + cos4 х; б) f(x) = | cos л: |.
Решение, a) sin4#+ cos4x = (sin2JC + cos2A:J—2 sin2#cos2#=s
:=l—1A— cos4jc) = ~-
отсюда T = 2я/о> = 2я/4 = я/2.
б) /(#) = | cos д:[== Vrcosax = "|/A +cos2x)/2; но функция cos2x
имеет период Т = я, поэтому и заданная функция имеет тот же
период.
1.3.15. Доказать, что функция f(x) = cos x2 не является перио-
периодической.
Решение. Будем доказывать от противного. Предположим, что
функция имеет период Т\ тогда должно выполняться тождество
COS(#+TJEEECOS.K2.
В силу условий равенства косинусов при некотором целом k имеем
Но это тождество невозможно, так как k может принимать только
21
целочисленные значения, а слева стоит линейная или квадратичная
функция непрерывного аргумента х.
1.3.16. Найти наибольшее значение функции
1.3.17. Установить, какие из следующих функций являются чет-
четными, а какие нечетными:
б)
У)У) ) f \\
в) f(x) = х sin2 х—х3; г) f(x) = (\+2x)V2x.
1.3.18. Найти период функций:
a) f(x) = arctg (tg х); б) f(x) = 2 cos ^p.
1.3.19. Доказать, что функции:
а) / (я) = х + sin х; б) / (х) = cos j/x,
не являются периодическими.
§ 1.4. Обратные функции
Пусть функция y — f(x) определена на множестве X и имеет область
значений Y. Если для каждого y?Y существует единственное значение х
такое, что / (х) = у, то это соответствие определяет некоторую функцию
x—g(y), называемую обратной по отношению к данной функции у = / (х).
Достаточным условием существования обратной функции является строгая
монотонность функции y — f(x). При этом если функция возрастает (убывает),
то и обратная функция возрастает (убывает).
График обратной функции x=g(y) совпадает с графиком функции y = f(x),
если независимое переменное откладывать по оси Оу. Если же независимое
переменное откладывать по оси Ох, т. е. если записать обратную функцию
в виде y=g(x), то график обратной функции будет симметричен графику
функции y — f(x) относительно биссектрисы первого и третьего координатных
угдов.
1.4.1. Найти функцию, обратную функции у = Ъх-\-Ь.
Решение. Функция у = Зх-\-5 определена и возрастает на всей
числовой оси. Следовательно, обратная функция существует и воз-
возрастает. Разрешая уравнение у = Зл; + 5 относительно х, получим
х = 0>—5)/3.
1.4.2. Показать, что функция y — kjx AгфО) обратна сама себе.
Решение. Функция определена и монотонна на всей числовой
оси, кроме точки х — 0. Следовательно, обратная функция сущест-
существует. Область значений функции—вся числовая ось, кроме точки у = 0.
Разрешая уравнение у = k/x относительно х% получим х = k/y*
1.4.3. Найти функцию, обратную функции
y = loga(x + Vx2 + l), (a>0, аф\).
Решение. Функция у — loga(x + j/д:2 + 1) определена для
всех х, так как j^.*2-{-1 > |х|, и является нечетной (задача 1.3.9, а)).
22
Для положительных х она возрастает, следовательно, она всюду
возрастает и имеет обратную. Разрешая уравнение
относительно х, находим
откуда
х=*±(сР — а'У) = sh (у \п а).
1.4.4. Показать, что функции
—3/4
взаимно обратны, и решить уравнение
х2 —
Решение. Функция j/ = x2— х+1 = (^—1/2J + 3/4 возрастает
в промежутке 1/2^х<оо, причем при изменении х в указанном
промежутке имеем 3/4 ^^у <оо. Следовательно, в промежутке
3/4^^ <оо определена обратная функция x = g(y), х^ 1/2, которая
находится из уравнения
Решая уравнение относительно х, получим
Решим теперь уравнение
х2—х + 1 = 1/2 +
Так как графики прямой и обратной функций могут пересекаться
только на прямой у = х, то, решая уравнение х2—jc+1=jc, находим
х=1.
1.4.5, Найти функции, обратные функции jj = sin x.
Решение. Область определения функции у = sinx—вся число-
числовая ось, область значений функции — отрезок [—1, 1]. Однако усло-
условие существования обратной функции не выполнено.
Разобьем ось Ох на отрезки пп—я/2^ х^^я + я/2. Если п
четно, то на отрезках пп—я/2^х^ля + я/2 функция возрастает,
если же п нечетно, то на отрезках пп—я/2 ^ х ^ ля + я/2 функция
убывает. Следовательно, на каждом из указанных отрезков
существует обратная функция, определенная на [—1, 1]. В част-
частности, для отрезка —я/2^х^я/2 существует обратная функция
Функция, обратная функции у = sinх на отрезке пп—
ля + я/2, выражается через arcsinj/ следующим образом:
х = {— \)пгхсыпу-\-пп (/2 = 0, ±1, ±2, ...)•
23
1.4.6. Найти функции, обратные данным:
а) y = sinCx— 1) при —(я/6+1/3)<х< (я/6+ 1/3);
б) y=rarcsin(#/3) при
в) у = 1
г) у =
1.4.7. Доказать, что функция у = A—х)Ц\ +х) обратна сама себе.
§ 1.5. Построение графиков функций
1.5,1. Исследовать функцию и построить ее график:
а)/(*) = х*-2*2 + 3; б) f(x) = ^;
в) f(x) = sin2 x—2 sin х; г) f(x) = arc cos (cos x);
д) /(x) = }/"sinx\ e) /(x) = x1*1*x.
Решение, а) Область определения функции/(л:)—вся числовая
ось. Функция f(x) четная, поэтому ее график симметричен относи-
относительно оси ординат и можно ограни-
ограничиться исследованием функции только
при х^О.
Выделим полный квадрат f(x) =
= (х2—1J + 2. Так как первое слагаемое
(х*—1J^0, то наименьшее значение
функции, равное 2, достигается в точках
х=±\ (рис. 2).
На отрезке O^jc^I функция f(x)
убывает от 3 до 2; на интервале 1 <х<оо
функция f(x) неограниченно возрастает,
б) Область определения функции
f(x)—вся числовая ось. Функция f(x)
нечетная, поэтому ее график симметричен относительно начала ко-
координат и можно ограничиться исследованием функции только
при
Рис. 2.
*- X
Рис. 3.
Так как /@) = 0, то график проходит через начало координат.
Очевидно, что других точек пересечения с осями координат нет.
Заметим, что |/(х)|<1. В самом деле, A— [#|J>0 или 1+2>
24
откуда
¦I/(*)!¦
Так как f(x)^0 при x^O и /A)«1, то в промежутке [0, оо)
наибольшее значение функции f(x) равно 1, наименьшее равно О
(рис. 3).
Докажем, что на отрезке 0^д;^1 функция возрастает. Пусть
*1 < #в^1. Тогда имеем
Аналогично показывается, что на интервале A, оо) функция
убывает. Наконец,
f{x) = 2х/A + л:2)
откуда видно, что f(x) стремится к нулю с ростом х.
в) Область определения функции f(x) — вся числовая ось. Функция
имеет период 2я, поэтому достаточно изучить ее на отрезке [0, 2я].
На этом отрезке она обращается
в нуль в точках х = 0; х = п;
х = 2тс.
Записав заданную функцию в
виде
/(*) = (!—sin*I —1,
,*/*
Рис. 4.
замечаем, что она возрастает при
убывании функции sin x и убывает
при возрастании sin л:. Поэтому
функция f(x) на отрезках [0, я/2]
и [Зя/2, 2я] убывает, а на от-
отрезке [я/2, Зя/2] возрастает. Так
как /(я/2) = —1, а /(Зя/2) = 3, то область изменения функции:
—1^/(д:)^3 (рис. 4).
г) Область определения функции — вся числовая ось, Действи-
Действительно, | cos х | ^ 1 при любом х и поэтому arccos (cos л;) имеет смысл.
Функция f(x) — периодическая с периодом 2я, следовательно, доста-
достаточно построить график этой функции на отрезке [0, 2я]. Но на
этом отрезке имеет место следующее равенство:
f
х,
2я—
Действительно, первое утверждение следует из определения функции
arccos л:, а второе можно доказать следующим образом: положив
лг'=г=2я—х, я^лг^2я; тогда О^лг'^я и
f(x) — arccos [cos Bя—л:')] = arc cos (cos л;') = x1 = 2я—x.
Учитывая все сказанное, строим график (рис. 5).
J
Рис. 5.
д) Функция у = ]/sin л: периодическая с периодом 2я, поэтому мы
можем ограничиться промежутком [0, 2я]. Однако функция не опре-
определена во всем промежутке [0, 2л], а только лишь в промежутке
„Ж
Рис. 6.
10
[О, я], так как на промежутке (я, 2я) подкоренное выражение отри-
отрицательно. График симметричен относительно прямой # = я/2, так же
как график y==sinx (рис. 6). Мы имеем пример периодической
функции, не существующей в бесконечном
множестве промежутков.
е) Область определения функции!
0<д;< 1 и 1 <л;<оо.
Преобразуем формулу к виду
„х Следовательно, графиком данной функции
служит полупрямая j; = 10, в правой полу-
полуплоскости с выключенной точкой х = 1
(рис. 7).
1.5.2. Построить графики функций, задаваемых разными форму-
формулами на разных промежутках (и сводящихся к ним):
sin X при -
2 при
0
1
Рис. 7.
a) jr = .
б)у = .
в) у = х
\/{х— 1) при
—2 при
1/2 при
—х9
при х < 0;
r)y = 2J(x + V>
Решение, а) Область определения функции—отрезок [—я, 4].
График функции состоит из части синусоиды у = sinх на отрезке
—я^лг^О, прямой у = 2 на промежутке @, 1] и части ветви ги-
гиперболы у = \[(х—1) на промежутке A, 4] (рис. 8).
Рис. 9.
б) График функции состоит из части кубической параболы, одной
изолированной точки и полупрямой (рис. 9).
в) Функцию можно задать двумя формулами:
2л:, если лг^О,
О, если х < 0.
Таким
(рис. 10).
образом
у
2
1
0
Рис.
, графиком нашей
кУ /
Г
1 > х
ю.
функции
У,
1
0
I
/
Рис.
служит ломаная
п.
г) Из пункта в) следует, что функция определена только на про-
промежутке @, +°°)> причем у = \\х(х > 0). Таким образом, графиком
нашей функции служит правая часть равнобочной гиперболы (рис. 11).
1.5.3. Построить графики функций:
а) у = cos х +1 cos х |; б) у = | х + 2 | х.
21
\ 2cos х при cos х ^ 0,
Решение, a) cosх + cosх = <
7 \ 0 при cos л: <0.
Удваивая неотрицательные ординаты графика функции у = cos х
(на рис. 12— пунктир) и принимая j/ = 0 в точках, где cosjt<0,
построим искомый график (на рис. 12— сплошная линия).
б) Функцию Jлг-f-21л: можно задать двумя формулами:
У =
при х~^ — 2,
при д:^—2.
Построив отдельно обе параболы у — (дг + 2) х=(х+ IJ—1,
у = —[(#+1J—1]> сохраняем только те их участки, которые
г x—
Рис. 12.
Jjifx
2
соответствуют указанным промежуткам. На рис. 13 сплошной линией
дан график заданной функции, а пунктиром — отброшенные части по-
построенных парабол.
г 1
к
I
! '
-У ff
с
У
1 /
&/
\\г/' >
\\/д *
t
Рис. 13.
Рис. 14.
1.6.4. Построить график функции у~2\х—2| —
Решение. При
При — 1<х<2
Наконец, при д:^—1
2В
Следовательно, заданную функцию можно записать следующим об-
образом:
5, х<— 1,
2л:—5,
л;>2.
Поэтому график представляется ломаной (рис. 14).
1.5.5. Построить график функции
Решение. Построив графики функций yt = 2х и уг?= — 2~х
(на рис. 15—пунктирные линии), складываем графически их ординаты.
При сложении полезно иметь в виду, что
у2<у <-у1 и что у2 стремится к нулю срос-
сростом х, а ух стремится к нулю с убыванием
х (на рис. 15 — сплошная линия).
1.5.6. Построить график функции
у = х sin x.
Решение. Функция у, как произведение
двух нечетных функций уг = х и ^2 = sin л:,
четна, поэтому анализ будем проводить для
- х
Строим графики функций: уг = х и у2= Рис. 15.
= sinA; (на рис. 16 — пунктирные линии).
В точках, где y2~slnx = 0, У~У\-Уъ~ 0, а в точках, где
уг = sin х = ± 1, у = ± ух = ± х. Последнее равенство показывает
/
-/
/
к
/
\ -
Рис. 16.
целесообразность построения графика вспомогательной функции
Отмечая указанные точки и соединяя их плавной кривой, получим
искомый график (на рис. 16 — сплошная линия).
29
1.5.7. Построить график функции у = х (х2—1) путем умножения
ординат графиков yL = x и у2 — х2—1.
1.5.8. Построить графики функций
а) у = х/(х2—4), б) у = 1 /arc cos x.
Решение, а) Так как функция нечетная, то достаточно иссле-
исследовать ее для х ^ 0.
Будем рассматривать ее как частное двух функций:
уг = х и у2 = дг2—4.
Так как при х — 2 знаменатель у2 = 0, то функция не определена
в точке 2. В промежутке [0, 2) функция уг возрастает от 0 до 2,
функция у2 отрицательна и |^2| = 4—х2 убывает от 4 до 0, по-
поэтому частное f(x)=y1/y2 отрицательно и возрастает по абсолют-
абсолютной величине, т. е. f(x) убывает в промежутке [0, 2) от 0
до —оо.
В промежутке B, оо) обе функции у1 и у2 положительны и
возрастают. Их частное убывает, так как из 2^х1<л;2 следует
-оо, так как
При этом указанное частное стремится к нулю при х-
У = 1 __ а / 2—* 0* Общий вид графика представлен на рис. 17 (сплош-
(сплошная линия).
3
тс
!\
\
Ч
Рис. 17.
Рис. 18.
б) Обозначим j;1 = arccosx Область определения этой функции
|*|^1. При дг= 1 имеем j;1 = 0, следовательно, #у = 1/>у1~>оо при
х—И, т. е. д;=1 является вертикальной асимптотой. Функция yt
на всем промежутке определения [—1, 1) убывает, следовательно,
у = \/уг возрастает. Наибольшее значение уг = л имеет при х =—1.
Соответственно, наименьшее значение функции у=* 1 /я. Общий вид
графика — сплошная линия на рис. 18.
30
Простейшие преобразования графиков
I. График функции y=f(x-\-a) получается из графика функции y=f(x)
параллельным сдвигом его вдоль оси Ох на [а\ единиц масштаба в направле-
направлении, противоположном знаку а (рис. 19).
?0
Рис. 19.
Рис. 20.
II. График функции y = f(x)-{~b получается из графика функции y = f(x)
параллельным сдвигом его вдоль оси Оу на | b | единиц масштаба в направле-
направлении, совпадающем со знаком 6 (рис. 20).
III. График функции y—f(kx) (k > 0) получается из графика функции
y=zf(x) «сжатием» к оси Оу в k раз при k > 1 и «растяжением» от оси Оу
в l/k раз при k < 1 (рис. 21).
IV. График функции y = kf(x)(k>0) получается из графика функции
y=zf(x) «растяжением» от оси Ох в k раз при k > 1 и «сжатием» к оси Ох
в l/k раз при k < 1 (рис. 21).
у
Рис. 21.
Рис. 22.
V. График функции у = —f (х) симметричен графику функции y=f()
относительно оси Ох, а график функции y = f(—x) симметричен графику
ф / () О
, рф фу
функции # =* / (х) относительно оси Оу.
VI. График функции yf(\\)
б
у
рф фу yf(\x\) получается из графика функции y = f(x)
следующим образом: для х^О сохраняется график функции y=af(x), затем
эта оставленная часть графика отображается симметрично относительно оси Оу,
определяя график функции для лг«^О (рис. 22),
VII. График функции j/=|,/(*)| получается из графика #=/(*) следую-
следующим образом: часть графика функции y — f(x), лежащая над осью Ох, остается
без изменения; часть графика, лежащая под осью
, и Ох, симметрично отображается относительно оси
^ Ох (рис. 23).
VIII. Графики функций более сложного вида
у\
получаются из графика у — f(x) последовательным
применением преобразований I—V.
1.5.9. Построить график функции
Рис. 23.
2,5)-0,8
с помощью преобразования графика у = УШ.
Решение. Строим график функции
у = Ух (это верхняя ветвь параболы у2 = х)
(рис. 24, а) и последовательно преобразуем
его следующим образом.
Увеличивая в 3/2 раза ординаты точек графика функции
у = Ух и сохраняя неизменными их абсциссы, строим график функ-
функции у = 3 У2х (рис. 24, б).
Зеркальным отображением относительно оси Оу строим график
функции у = 3 У— 2х (рис. 24, в).
Рис. 24.
Теперь остается перенести полученный график на 2,5 единицы
масштаба влево и на 0,8 единицы вниз и построить искомый график
функции у = 3 V—2 {х + 2,5) — 0,8 (рис. 24, г).
1.5.10. Построить график функции y — 3cosx—]/3sin;t с по-
помощью преобразования косинусоиды.
Решение. Преобразуем заданную функцию
:2 J/3
cos *-¦
¦2/3 cos (* + ?).
32
Таким образом, нам нужно построить график функции
Это —график функции jy = 2]/~3 cos x, смещенный на я/6 влево.
Функция имеет период 2л; поэтому достаточно начертить ее график
для —л^х^л (рис. 25).
>-a?
-/
Рис. 25.
Рис. 26.
Подобным образом строится график любой функции вида
acosjc + bsinA;, где а и ft —постоянные.
1.6.11. Построить графики функций:
в)У=-
г)
е)
з)
sin2 х,
, если —
если
(х— 1)/(х+1), если я
д) j,^*2--*3;
ж) у =
—4); и) у = 2]/—
1 |||
к) у = |л:2—2л:—11; л)'у = \\х\ — 1 |; м) ^ = cos (sin ^);
н) j^ = j sin л: j + sin л: на отрезке [0, Зя];
о) ^ = A:2
где
1 при
;=<( 0 При Х = 0,
—1 при х < 0.
1.6.12. Функция y~f(x) задана графически (рис. 26). Построить
графики функций:
a) y=f(x+l); б) у=/(х/2); в) у = \/(х)\;
г) у = (|/(jc)J ±f(x))/2; д) у = |/(лг) |//(х).
83
§ 1.6. Числовые последовательности.
Предел последовательности
Число а называется пределом последовательности хъ х2, ..., хп% ... при
п—> оо, а= lim хп, если для всякого е > 0 существует такое число N (г) > О,
л-> да
что для всех п > N (е) справедливо неравенство \хп—а\ < е.
Последовательность, имеющая предел, называется сходящейся.
Последовательность {хп} называется бесконечно малой, если lim#rt = O, и
бесконечно большой, если lim xn = oo.
1.6.1. Дан общий член последовательности {хп\:
sin (пп/2)
Написать пять первых членов этой последовательности.
Решение. Положив последовательно п = 1, 2, 3, 4, 5 в общем
члене хт получим
sin0V2)_
— 1 *
_sinBre/2)__n.
sinCjt/2)^ ^#
~ 3 "" 3 f
1.6.2. Зная несколько первых членов последовательности, написать
одно из возможных выражений для общего члена:
2_ 5_ 10 17 26,
aJ 3 ' 8 ' 13' 18» 23'
б) 1, ", 2, -д-, 3, -^-, 4, -g-.
Замечание. Знание нескольких первых членов последовательности еще
не определяет эту последовательность. Поэтому поставленную задачу надо
воспринимать как задачу отыскания некоторой простой индуктивной законо-
закономерности, согласующейся с заданными членами.
Решение, а) Заметим, что числитель каждого из заданных
членов последовательности равен квадрату номера этого члена плюс
единица, т. е. пг-\-\. Знаменатели же образуют арифметическую
прогрессию 3, 8, 13, 18, .•. с первым членом в^Зи разностью
d = 5. Следовательно,
ап = аг+ d (п— 1) = 3+5 (/г — 1) = 5л — 2,
поэтому
34
б) В этом примере общий член последовательности можно запи-
записать с помощью двух формул: одной — для членов, стоящих на не-
нечетных, другой — для членов, стоящих на четных местах;
k при n = 2k — 1,
1/(& + 1) при n — 2k.
Можно написать и одну формулу, но более сложную, например,
1.6.3. Найти несколько первых членов последовательности, если
общий член задается формулой
б) хп = 2~п cos /ш;
в) хп=(\ + \/п)п.
1.6.4. Пользуясь определением предела последовательности, до-
доказать, что
а) Нт*я=1, если хп = {2п—1)/Bл+1),
б) Нтл:„ = 3/5, если хп = C#2 + 1)/E#2 — 1). Начиная с какого п
выполняется неравенство \хп—3/51 < 0,01?
Решение, а) Для любого г > 0 попробуем найти такое нату-
натуральное число N(e), чтобы для всякого натурального л> N (е) вы-
выполнялось неравенство
Для этого найдем абсолютную величину разности
—2
2п+1
Значит, неравенство \хп—1|<8 выполняется, если 2/B#+1)<8,
откуда /г> 1/е —1/2. Поэтому в качестве N (г) можно взять целую
часть числа 1/8 — 1/2, т. е. N = ?"A/8 —1/2).
Итак; для каждого 8 > 0 можно найти такое N, что из нера-
неравенства л> N будет следовать \хп— 1|<е, а это значит, что
б) Найдем абсолютную величину разности \хп—3/51:
8
|5/*2— 1 5 ~E/г2—1)'
Пусть 8 > 0 задано. Выберем п так, чтобы выполнялось нера-
неравенство
8
35
Решая это неравенство, находим
л2> —+— •
Положив
мы заключаем, что при /г > N
|*и —3/5|<е,
ч. т. д. (что требовалось доказать).
Если е = 0,01, то
и все члены последовательности, начиная с 6-го, содержатся в ин-
интервале C/5 — 0,01; 3/5 + 0,01).
1.6.5. Дана последовательность с общим членом лг„ =
= (Зл — 5)/(9я+4). Известно, что lim хя=1/3. Найти число то-
чек лг„, лежащих вне интервала
V з юоо * з "*"
\ \
з юоо * з "*" юооу •
Решение. Расстояние от точки хп до точки 1/3 равно
•*» о
19
3(9я +4)
19
Вне интервала L окажутся те члены последовательности, для кото-
которых это расстояние больше 0,001, т. е.
19
откуда
Ю001
*, ^ 18 988 7ЛО 7
п < 27 = 703 27 •
Значит, вне интервала L находятся 703 точки хх, х2, ..., д:703.
1.6.6. Доказать, что число 1=0 не является пределом последо-
последовательности с общим членом хп = (п2 — 2)/Bя2 — 9).
Решение. Оценим снизу абсолютную величину разности
пг 2
— 0
я—9| #
2я2—9
Абсолютная величина разности при /z^3 остается больше постоян-
постоянного числа 1/2; следовательно, существует такое е>0г например,
е = 1/2, что для любого /г^З справедливо неравенство
I Ф—2
|
2/i2-9
—0
Полученное неравенство доказывает, что /==0 не является пределом
данной последовательности.
1.6.7. Доказать, что последовательность
1 1 1 JL 1 L L 1
' 2 ' 3' 3 ' 5' 4' 7 ' 5""
с общим членом
если n — 2k—1,
если п = 2k,
предела не имеет.
Решение. Легко установить, что точки хп с нечетными номе-
номерами «стягиваются» к точке 0, а точки хп с четными номерами —
к точке 1. Следовательно, любая окрестность точки 0, а также
любая окрестность точки 1 содержат бесконечное множество точек хп.
Пусть а есть произвольное действительное число. Всегда можно
выбрать настолько малое 8 > 0, чтобы 8-окрестность точки а не
содержала по крайней мере некоторую окрестность одной из точек О
или 1. Тогда вне этой окрестности будет находиться бесконечное
множество чисел хп и поэтому нельзя утверждать, что все числа xnf
начиная с некоторого, попадут в е-окрестность числа а. А это зна-
значит, по определению, что число а не является пределом данной
последовательности. Но число а — произвольное, поэтому никакое
число не является пределом этой последовательности.
1.6.8. Доказать, что \\тхп=\, если хп — (Зп+ 1)/Зп.
1.6.9. Доказать, что Нтд:л = 2, если лгя = B/г + 3)/(/г + 1). Найти
номер члена, начиная с которого выполняется неравенство
|Bл + 3)/(л-М) —2|<е, где 8 = 0,1; 0,01; 0,001.
1.6.10. Доказать, что последовательность
JL JL A JL L JL
2 > 2 • 4 ' 4 ' 8 ' 8 ' '••'
с общим членом
2(„Л)/2 . если п нечетное,
, если п четное,
2п/2
не имеет предела.
1.6.11. Доказать, что при любом как угодно большом а > 0
хп = 0, если хп=ап/п\
Решение. Пусть натуральное число k > 2а. Тогда при п > k
аП а SL HL—flL SL а\( а а !L\
^I^T* 2maun~~\l * 2тшш k) \k+l ' k+2'-17j
Так как lim(l/2Ol = 0 (доказать!), то при достаточно большом п
имеем: A/2)* < г/Bа)к и, следовательно, ап\п\ < е, а это значит,
что lira(aw//i!) = 0.
37
1.6.12. Какие из последовательностей имеют предел и какие его
не имеют:
\ 1 для четного л,
а) *я=1/Bя); б) л:Л = ^
^ 1/я для нечетного /г;
в) *n = !cosf; г) хя = п[1-(-1)»].
1.6.13, Доказать, что последовательность с общим членом
есть бесконечно малая последовательность.
Решение. Доказать, что последовательность хп бесконечно
малая — эта значит доказать, что lim jcw = O.
п -> со
Возьмем произвольное 8 > 0. Так как \хп\ = \/пк, то необходимо
решить неравенство
откуда #> |/ 1/е, Следовательно, в качестве N можно взять целую
часть j/^T/e, т. е. N=E(y 1/е).
1.Ф.14. Доказать, что последовательности с о&щими членами
а) хп = "^ , б) хп = — зп
— бесконечно малые при п—юо.
1.6.15. Показать, что последовательность с общим членом хп —
= (—1 )п 2/E l/'n + 1) — бесконечно малая при п —> оо. Найти какой-
нибудь номер W, начиная с которого точки хп принадлежат интер-
интервалу (—1/10, 1/10).
Решение. Возьмем произвольное е > 0. Оценим |хя|:
Поэтому |#Л|<в, как только л> 1/е3. Следовательно, lim ^„ = 0,
т. е. посяедовательность бесконечно малая.
Теперь возьмем е = 1 /10. Так как \хп\ < l/pfn, то заведомо
I^K1/^, если \/У"п<\/\0 или я>1000. Поэтому в каче-
качестве N можно взять 1000. Однако можно получить более точный
результат, решив неравенство
Оно справедливо при п > A9/5K = 3,83 = 54,672. Значит, в каче-
качестве 7V можно взять значительно меньшее число 54.
38
1.6.16. Известно, что если хп = а-\-ап, где ап — бесконечно ма-
малая при п—*оо, то lim xn — a. Пользуясь этим, найти пределы:
П -> 00
. .. 2" + (-1)"
' ' п 2п '
sin (ля/4) о . sin(rtJi/4)
Решение, а) хп =
бесконечно малая при п—> оо, а значит, lim л:Л = 3.
/г -> с»
1.6.17. Доказать, что lim (J//z=l.
rt -> со
Решение. Докажем, что переменную у п можно представить
в виде суммы 1 +сел, где ап — бесконечно малая величина при п—> оо.
Положим \/п=\-\-ап. Возводя в п-ю степень, получим
Из последнего равенства заключаем, что для любого л>1 спра-
справедливо неравенство
(так как все члены справа неотрицательны). Перенося влево еди-
единицу и сокращая на п—1, получим
!>¦?«&.
Отсюда следует, что 2/п > а\ или V2fn > ап > 0. Так как
lim |/^2//г = 0, то и lim art = 0, т. е. ап — бесконечно малая вели-
П -> оо П -> оо
чина. Отсюда следует, что
lim у/п = 1.
П -*¦ 00
1.6.18. Доказать, что последовательность с общим членом
есть бесконечно большая при /г —> оо.
Решение. Возьмем произвольное положительное число Ж и
решим неравенство
Прологарифмировав, получим
Vn> bg3 M, n> (log, Mf.
Если теперь взять N = E(\og3 MK, то для всех /z > N будет выпол-
выполняться неравенство |л;„|>/И, а это значит, что последовательность
бесконечно большая.
1.6.19. Доказать, что
lim Уа=\ (а>0).
§ 1.7. Вычисление пределов последовательностей
Если последовательности {хп\ и {уп\ сходящиеся, то:
1) Ит (хп ± уп)«lim хп ± lim (/„;
2) lim (ХяУя) = lim xn lim уи;
3> 11гаЙ=
Если лгя < (/„, то lim ^л < lim yn.
1.7.1. Найти lim xn, если
4лг2 — 4n-f-3
Решение, а) ^ =
lim C + 5/П + 4/П2)
lim л:Л = ^^ = 3.
п-*ф lim
-*¦ 00
г) Вспомним, что
12 + 22 + 32+...-Ь /г2 = /z (лг + 1) B/г -Ь 1 )/6.
Поэтому
lim д:я=1/15.
1.7.2. Найти lim xn1 если:
у.
г) х„={^л«;
40
Решение, а)
2п +7
,. 3+ \/п — 2/п*\* _ ( 3
m U
п*\* _ ( 3 у _ 27
rt-V ~U; ~64
в) При решении этого примера, а также всех остальных приме-
примеров задачи 1.7.2 надо иметь в виду следующие равенства (см. за-
задачи 1.6.17, 1.6.19):
lim у'п=^\ и Urn ifa^X. A)
Имеем
lim д:я= lim {/б/г= lim у/Ъ lim ^/^
но из A) следует, что lim ^5 = 1 и lim?/#=l, поэтому limдгп =
==¦ Ы = 1.
1.7.3. Найти
Решение. Сложив дроби, получим
Отсюда
„mn, *n=niim ra-_?_I5-F5_T
Замечание. Если положить
то предел их суммы lim («/л+гп)= 1/5, хотя каждое слагаемое в отдельности —
бесконечно большая величина. Таким образом, из существования предела
суммы последовательностей не следует, вообще говоря, существование преде-
пределов слагаемых.
1.7.4. Найти lim xnf если:
a) xn = V2n+3 — Vn—\; б) хп= yn*
в) хп = п*(п-Vn2+\); г) хп5= Уп*
1—2 + 3—4 + 5—6+...— 2л
ж) Хп~~ y ;
_ 1 , 1 , 1 I t 1
41
Решение. а) хп = Уп ()/~2 + 3//г—-}Л — 1//г)—>+ оо при
п—> оо, так как второй множитель имеет положительный предел.
_
= —n —> — оо при п—> оо.
1 + 1^1 + 1/п2
г) Хп = п2
Значит, хп—> 1/3.
д) Вынося старшие степени числителя и знаменателя за скобки,
имеем
1.7.5. Найти lim л:Л, если:
/г -> со
-w - ^
=У\ — п3-\-п; г) хп = к- cos/z;
6п+Г
2n n+1 n n(—l)n
COS;
1 + 1/3+1/9+... + 1/3" "
§ 1.8. Признаки существования
предела последовательности
Теорема Больцано—Вейерштрасса. Монотонная ограниченная
последовательность имеет предел.
Теорема о «зажатой» последовательности. Если хп^уп^ zn
и lim xn— lim г„=с, то и lim yn — c.
Л->00 Л->0О tt->00
1.8.1. Доказать, что последовательность с общим членом хп =
= B/г — 1 ICп + 1) — возрастающая.
Решение. Надо доказать, что хп+1 > хп для любого я, т. е.
ладо доказать, что
42
Последнее неравенство равносильно очевидному неравенству
> 6/г2 + 5/г — 4.
Значит, хп+1 > хп, ч.т.д.
1.8.2. Дана последовательность с общим членом
хп=\0п/п1
Доказать, что эта последовательность убывает при
Решение.
10" 10 10
rt+1 (я+l)! n\ rt+1 Ля+Г
Так как 10/(л + 1)<1 при #^10, то с этого номера хп+1 < хп%
а это значит, что последовательность при л ^10 убывает.
1.8.3. Даны последовательности:
5/г2 ^ 2п
в) zn — n cos я/г.
Указать, какие из этих последовательностей ограничены и какие
из них не ограничены.
Решение, а) Последовательность {хп\ ограничена, так как
очевидно, что 0 < 5я2/(я2 + 3) < 5 при всех /г.
б) Последовательность {уп\ ограничена:
в) Последовательность {zn\ не ограничена, так как
) zn | = | п cos пп | = п.
1.8.4. Доказать, что последовательность
(а > 1, х0 > 0) сходится.
Решение. Докажем, что данная последовательность монотонна
и ограничена. Во-первых, хп < хПтт1, так как
Следовательно, данная последовательность убывающая. Во-вторых,
все ее члены положительны (по условию а > 0 и х0 > 0), поэтому
последовательность ограничена снизу. Итак, данная последователь-
последовательность монотонна и ограничена, значит, имеет предел.
1.8.5. Доказать, что последовательность с общим членом
е х -
. е. *i —
сходится.
Решение. Последовательность хп возрастает, так как #п+1=
~^хп-\-1/E"+1 +1) и, следовательно, хп+1 > хп. Кроме того, она
ограничена сверху, поскольку 1/E"-|-1)< 1/5" при любом п и
Следовательно, предел последовательности существует.
1.8.6. Пользуясь теоремой о существовании предела монотонной
ограниченной последовательности, доказать сходимость следующих
последовательностей:
1.8.7. Доказать, что следующие последовательности сходятся, и
найти их пределы:
а) хг =
п радикалов
2" . nW _Е(пу).
г) последовательность десятичных приближений по недостатку
1; 1,4; 1,41; 1,414; ... иррационального числа |/*2;
)я
Решение, а) Очевидно, что л^ < х2 < дг3 < ... < хп <
< д;п+1 < ..., т. е. наша последовательность возрастающая. Оста-
Остается доказать, что эта последовательность ограничена.
Имеем хп = У2 + хп_г, л = 2, 3, .. . Так как х1 = У~2<21 то
*1 = Уг2 + *1<1'/2 + 2 = 2, Л;з==|/'2 + х2<|/ + 2^2, ... Пусть
доказано, что дгя.1 < 2. Тогда хп = ]/г2 + хп_1 < 1/2 + 2 = 2. Таким
образом, с помощью математической индукции мы доказали, что
хп < 2, т. е. последовательность ограничена. Следовательно, она
имеет конечный предел. Найдем его. Обозначим
lim xn=y.
п -*¦ со
Далее, xn~V2 + xtt_1; возводя в квадрат, получим
x*
Перейдя в этом равенстве к пределу, получим
lim x%= lim B + хп_г), или ^2 =
п -* со л -¦ со
44
Корни полученного квадратного уравнения таковы:
Отрицательный корень посторонний, так как хп > 0. Следовательно,
lim хп=ух = 2.
П -*• 00
в) Имеем пу— \<^Е(пу)^пу или ^ —
П
. Но по-
последовательности {у — l//z} и {у) сходятся к пределу .у, поэтому и
lim xn=y.
П -*¦ со
г) Эта последовательность неубывающая, так как каждый после-
последующий ее член д:л+1 получается из предыдущего приписыванием
в десятичной записи хп на конце еще одного десятичного знака.
Последовательность ограничена сверху — например, числом 1,5. Зна-
Значит, последовательность сходится. Ее предел есть 1/^2.
д) Последовательность монотонно убывает. Действительно,
— (и+ 1I __ n! _ _ftj_ nn __ пп
Так как пп/(п+ \)п < 1, то хп+1 < хп.
Далее, так как хп > 0, то последовательность ограничена снизу,
значит, Игл хп существует. Обозначим его через /. Очевидно, что
,хп.
= lim
. Покажем, что / = 0. Действительно,
\
пп i \
Следовательно, /п+1\я<" и хп+\ < ~2хп- Переходя к пределу,
получим
что вместе с / ^ 0 приводит к выводу:
1 = 0.
1.8.8. Найти пределы последовательностей с общими членами:
ft п
#« = ¦
п* + п
2„ =
" i ¦¦ г а ¦ ~т; Г* • • • i _/•¦¦¦
Решение. Докажем, что lim лг„ = 1. В самом деле,
— 1
п
п—У пг-\-п
45
Аналогично доказывается, что
Далее,
Уп ^У"^+
С другой стороны,
Уп > лг-^г
У п* +
Таким образом,
1 }
п \
<Уп
1
1
<z
lim
П -> 00
+-1
п
-п
п
• • +
im х
1.
1
Уп2Ц
п
«2+1
П
п -*¦ со л -> со
и по теореме о «зажатой» последовательности
П -> 00
1.8.9. Доказать, что
lim ^a=l (а>0),
с помощью теоремы о «зажатой» последовательности.
1.8.10. Доказать существование предела последовательности уп =
= а1/2"(а> 1) и вычислить его.
1.8.11. Пользуясь теоремой о пределе монотонной последователь-
последовательности, доказать существование конечного предела у последователь-
последовательности
1.8.12. Пользуясь теоремой о пределе «зажатой» пбследователь-
ности, доказать, что
lim хп=\, если xn = 2n(]fn2-\-l—п).
П-+ 00
1.8.13. Доказать, что последовательность
(a>0)
n радикалов
имеет своим пределом число 6 = (j/4a+ I +1)/2.
1.8.14* Доказать, что последовательность с общим членом
1.1 1
имеет конечный предел.
46
1.8.15. Доказать, что последовательность длин периметров пра-
правильных вписанных в окружность 2"-угольников стремится к пределу
(называемому длиной окружности).
§ 1.9. Предел функции
Точка а действительной оси называется предельной точкой множества X,
если во всякой окрестности точки а содержатся точки из X, отличные от а
(а может быть как собственной, так и несобственной точкой).
Пусть точка а является предельной точкой области определения X функ-
функции f(x). Число А называется пределом функции f (х) при х -> а, Л = lim f (x)t
если для всякой окрестности V числа А существует такая окрестность и числа а,
что для всех х?Х, лежащих в и, f(x)?V (определение предела функции по
Коши). Число А может быть как конечным, так и бесконечным. В частности,
если числа А и а конечны, получаем следующее определение.
Число А называется пределом функции f (х) при х->а, Л= lira / (а:), если
х-+а
для всякого 8 > 0 существует такое число б (е) > 0, что для всех х, удовлет-
удовлетворяющих неравенству 0 < | х—а | < 6 и входящих в область определения
функции /(*), справедливо неравенство \f(x)—A\<e («е—6-определение»).
Если 0= + °°» то получаем следующее определение.
Число А называется пределом функции f(x) при х ->-{- оо, Д= lim f (x),
Х-++ да
если для всякого е > 0 существует такое число М (е) > 0, что для всех х%
удовлетворяющих неравенству х > М (е) и входящих в область определения
функции /(*), справедливо неравенство
\f(x) — ^ I < е («8—М-определение»),
Запись lim f(x) = oo означает, что lira |/(я) | =-foo. Остальные случаи раз-
х-+а х-+а
бираются аналогично»
Определение предела функции по Гейне. Запись Umf(x)= A
х-*а
означает, что для любой сходящейся к числу а последовательности значений х
хг, х2, ..., хт ...
(входящих в область определения функции и отличных от а), соответствующая
последовательность значений у
имеет пределом число А.
1.9.1. Пользуясь определением предела по Гейне (т. е. на языке
последовательностей) и теоремами о пределах последовательностей,
доказать, что
Решение. Рассмотрим любую последовательность хг, х2% ...
значений дг, удовлетворяющую двум условиям: 1) числа х1У хг> ...
принадлежат области существования функции f(x) = Cx-{- 1)/Eд: + 4)
(г. е. хпФ—4/5); 2) последовательность {хп\ сходится к числу 2,
1. е. lim xn = 2.
47
Этой последовательности \хп\ соответствует последовательность
значений функции
3*1+1 . 3*2+1 л
причем на основании теорем о пределах (§ 1.7)
Таким образом, независимо от выбора последовательности \хп\,
сходящейся к числу 2 (хп Ф — 4/5), соответствующие последователь-
последовательности значений функции f(xn) сходятся к числу 1/2. А это на осно-
основании определения предела функции значит, что
.. 3*+1 1
lim ¦=—р-- = -—.
Замечание. Определением предела по Гейне удобно пользоваться тогда,
когда доказывается, что функция f (х) не имеет предела. Для этого достаточно
показать, что существуют две последовательности {х'п} и {х"п} такие, что
lim x'n = lim x"n = а, но соответствующие последовательности {/(х'п)} и
п -> со п -»¦ се
^(*w)} не имеют одинаковых пределов.
1.9.2. Доказать, что следующие пределы не существуют:
a) lim sin-^rJ б) lim %l/x> B) nm sin x.
Решение, а) Выберем две последовательности
/ 2
Хп== 1+Dл+1)я (л=1, 2, ...),
для которых
lim хп = lim д:^ =
П-+ СС «-»- 00
Соответствующие последовательности значений функции таковы:
=sin i+i/(Ui= sin ля=°
+2/[D/;+1)jibl^n = sin
Следовательно,
Иш/(дгя) = О и Пт/(дг;) = 1,
т. е. последовательности {/(хп)} и {/(х'п)} имеют различные пределы.
Отсюда следует, что lim sin г не существует,
43
в) Выберем две последовательности, хп^пп и х'п = 2nn-\-nj2
(я=1, 2, ...), для которых lim хп = lim хп = оо. Так как
lim sin л:п = lim sin nn = О,
п -> со /г -» оо
а
lim sinx^= lim sin Bjc/2 + зх/2) = 1,
П -+ CO П -* CO
то lim sin д: не существует.
*-> оо
Замечание. Приведенные примеры показывают, что вывод о наличии
предела функции нельзя делать, исходя из последовательности значений х
частного вида (например, исходя из хп—\-\-2/(Dп-{-\)п) в пункте а) по-
последней задачи), а нужно рассматривать произвольную последовательность
#!, х2, ..., хП1 ..., имеющую заданный предел.
1.9.3. Исходя из определения предела функции по Коши (т. е.
пользуясь определением на языке «8 — б»; «8—Му> и др.)> доказать,
что:
а) lim C*-8) = — 5; б) lim
в) Jim r—-5= + оо; г) lim logax= оо (а > 1);
д) lim arctg.x: = л/2; е) lim sin* = 1/2.
X -*¦ 00 X -+ Д/6
Решение, а) Согласно «8 — б»-определению нам надо доказать,
что для всякого 8 > 0 существует такое б > 0, что из неравенства
|*_1|<6 следует |/(*) —(—5)| = |/(*) + 5|<в.
Другими словами, необходимо решить неравенство
|3д:—8 +5| = 3|лг—1 |< е.
Последнее неравенство показывает, что как только \х—1 | <e/3 = S,
выполняется требуемое неравенство |/(д;) + 5(<8. Следовательно,
lim (Злг—8) = —5.
х^\
б) Согласно «8—Ж»-определению предела надо показать, что для
любого е > 0 можно найти число Ж> 0 такое, что для всех jc> M
будет выполняться неравенство
5
3*+9 3
Преобразуя это неравенство, получим
5*+1 5
14
3*+9 3
Так как х > 0, то остается решить неравенство
14
Зх+9 <8>
49
откуда
38
таким образом, М=A4— 9е)/3е.
Итак, для е>0 мы нашли Л/= A4 — 9е)/3е такое, что для всех
значений х > М выполняется неравенство (#). Это и означает, что
14 0 09 2
Пусть, например, 8 = 0,01; тогда Ж = —тг-щ—=463-^-.
в) Нужно доказать, что для всякого /С> 0 существует такое
5 > 0, что из неравенства
всегда следует неравенство
1
A-х)*
A-хУ
Выберем произвольное число /С> 0 и решим неравенство
Отсюда
Таким образом, есяи положить б = 1 /V К, то как только | х— 1 | <6,
будет справедливо неравенство (*#). А это означает, что lim ^ = -f- оо.
г) Надо доказать, что для всякого К>0 существует такое М > О,
что из неравенства х>М всегда следует неравенство \ogax>K.
Выберем произвольное число К>0 и рассмотрим неравенство \oga x>K.
Если положить аК = М, то при х> М справедливо неравенство
loga#>/(. Следовательно,
lim \ogax= -f cx>.
X -*¦ +О>
1.9.4. Доказать, что lim cosa; не существует.
Х-+ 00
1.9.6. Используя последовательности корней уравнений sin (l/x) = l
и sin A/jc) = —1, показать, что функция /(аг)= sin A/jc) не имеет
предела при х—> 0.
1.9.6. Исходя из определения предела функции по Коши, дока-
доказать, что:
а) Ига (За:—2) = 1; б) lim y^— = 2;
в) lim sin x = 0; г) lim cos x = 1;
50
д) iim
е) lim а*=+оо (а>1);
*-> + со
v ,. sin ^ л
ж) lim = 0.
7 „ _ х
Х-*- СП
§ 1.10. Техника вычисления пределов
I. Если существуют lim u(x) и lim v(x), то существуют пределы:
х->а х-+а
1) lim [«(*) ± t>(*)J = lim и (*) ± lim о <jc);
2) lim [а(*)-и(*)] = lim u(x)- lim о (*);
ffifi
]imu(x)
3) lim ffifi =?12 { lim у (*) ^ 0).
II. Для всех основных элементарных функций в любой точке их области
определения имеет место равенство
lim /(х) = /(Ишх
III. Если для всех значений # в некоторой окрестности точки а (кроме,
быть может, х = а) функции / (х) и <р(л;) равны и одна из них имеет предел
при х -+а, то и вторая имеет тот же предел.
IV. Частое применение находят следующие пределы:
) i;
х->0 X
2) lim A + 1/*)*= lim A +a)Va = e = 2,71828... ;
х-* со a-*Q
3) lim kgg^+^lo&g (a > 0; а ф 1);
5)lim ^Hi = ina (a > 0).
1.10.1. Вычислить пределы функций:
ч t. 4jc5 + 9*+7 -ч v д;3 + Зх2—9jc—2
a) Jim з^фф • б) ^ х>-х-6 '
fe г) iS^T ^ и
ж) lim //-b'-af/gZlg.; з) lim Flog. x~3 -
51
^5
Решение, а) Так как пределы числителя и знаменателя суще-
существуют и предел знаменателя отличен от нуля, то можно пользо-
пользоваться теоремой о пределе частного:
lim
lim *B + 9 + 7
,
Hm (зх6 + ^+1) 3+1
б) Непосредственно теорему о пределе частного применять здесь
нельзя, так как предел знаменателя при х —*2 равен нулю. Здесь
и предел числителя при х —* 2 также равен нулю. Имеем неопреде-
неопределенность вида -Q-. Для л; =т^ 2 имеем
—9*—2 (*—
х3—jc —6 "~ (х — 2)
Таким образом, во всякой области, не содержащей точки д: = 2,
функции
2—9л; —2
равны; следовательно, равны и их пределы. Но предел функции <р (л:)
находится непосредственно:
15
следовательно, и
2—9jc—2 15
в) Так же как и в п. б), устраняем неопределенность вида -тг-
преобразованием:
lim ^±1 = lim (^+
V62 3
= lim r Q/, —г— = 1.
x —l 3A—*)
1.10.2. Вычислить пределы:
в) lim -— ' ; г) lim
*-+«> УЪх—2+/2jc—3 *->-«>
д) lira xiVx^+l—x);
52
e) lim 4x+2 и lim AvX9 » ж) lim
Решение, a) lir
Здесь имеем неопределенность вида оо — сю; произведем вычитание
дробей
2 + 4/л: _ 2
—12/лс«—8/х»— 9 '
Замечание. Мы видим, что в подобных примерах предел равен отно-
отношению коэффициентов при старшей степени х (если только степени многочленов
одинаковы).
б) li
в) В подобных примерах полезно иметь в виду, что функция
~^/рп{х), где рп(х) — многочлен степени п, стремится к бес-
бесконечности так же, как и функция ^/хп. Это позволяет выделить
высшую степень х, входящую в данное выражение, и разделить
числитель и знаменатель на эту степень х. В данном примере надо
делить на Ух; тогда получим
—2+ 1/2х—3 *-, + «> V3 — 2/х+*/4/х— \
г) Так как сумма двух положительных бесконечно больших есть
также бесконечно большая, то
lim (У2х2 — 3— 5х)= lim
е) При х > 0 имеем J/V5 = х, поэтому
lim
V2
хD-\-2/х) 4 '
При х < 0 имеем Ух2 = — л: и, следовательно,
V2H lim
,11™. ^D + 2/^) -,"_. хD+2/х) - 4 '
Замечание. Отсюда, между прочим, следует, что lim JL ' .
4лJ
не существует.
Hm
ж) lim 5M/<*+») =5*-*" =52 = 25.
63
1.10.3. Вычислить пределы:
*>И«' б) lim
';:; yw+i-з • ',;.i ут+п-2'
в) hm гт^"' г) 'Im '*—целое положитель-
х-,0 х ное ЧИСЛо);
cos*
;
ч ,. sin (я—я/6) ч ,.
д) hm -р^ ^-; е) hm ;
х-,л/в J^3—2cos* jf^ji/a f/(l— sin *>«
. У 2sin2^+stnA:—1
*-!!i?/e2sin2*—3siruc+r
Решение {метод подстановки), а) Положим 26 + x = zs. Тогда
= 2i8—26 иг-^3 при х—*1; отсюда
2х—2 t. 2z3—54 ,. 2 (г—3) (г2-(-Зг+9)
26+3 23 23
hm
г) Положим 1+л: = гй; тогда x = zk—1 и z-+l при л:->0.
Следовательно,
lim /1+*! ^ !im 2р±.=:.^(см. 1.10.1. г).
*-0 ^ 2-^1 2*—1 Й
д) Положим х—я/6 = z; отсюда х = z + ft/6 и z-+Q при д:-—>я/б.
Подставив, получим
Utn sm(x-^a/6) _ Цт _^ smz =
ж->я/в /—2cosa; гн.о ^3—2 cos (г + я/6)
1Jm 2 sin (г/2) cos (г/2)
= иш — =
= иш .—
z-+o 2 у 3sina(z/2)+2sinB/2)cosB/2)
= lim -_ СО8(г/2)
г -у о УЗ sin (г/2) + cos
1.10.4. Вычислить пределы:
v t. 1—cosa; ^ч ,. tgx—s\nx
a iim —-ъ— ; 6) ltm -?-_ ;
-^ 0
л ч ,. 1—cosa: ,. 2sin2(>;/2)
Решение, a) hm —^—= ltm J ; ==
1 f. / sin(x/2)\a 1
- 2 ,"° V r/2 J 2 '
r 1 sin a: 1—cosx 1
54
в) положим 1—x = z. Тогда х=\—z и z—>® при х—> 1.
Следовательно,
JX f П П \ .Я
COS -тг X COS -gz =- Z Sin -zr-Z
,. 2 ,. V 2 2 у ,. 2 я
lim — = lim — = lim = -=-.
Замечание. Более простой метод решения подобных примеров
см. в § 1.12.
1.10.5. Найти пределы:
a) lim (l + l/#O*; б) lim(l-)
Х-+ 00 Х-* О
в) lim (тт~ J J г) lim A
. f. In (l-f-х) ч .. e*x— 1
д) hm * од:__1 5 e) lim —f 5
In x—1
ч ,. 1п(а + х) — \па ч г е—е* ч ,.
ж) lim —v ; з) lim —: ; и) hm
х-+о х х-+о sln х
Решение, a) lim A + \/хIх = lim [A +
х-> оо л:-*- оо
= Г lira (l +
ч
д)
и) Положим xje—\=^z; отсюда x=e(z+\); 2r —^0 при х
Подставив, получим
= i- lim
e
1.10.6. Найти
Нш
Нш A+1)*.
-+ CD V Л /
Решение, lim {\ + \/x2)x= Hm [A + \/х*
X -+ 00 Jf -*¦ 00
1.10.7. Найти
a) lim (l+fyx-™-*); 6) Hm
Решение, а) Обозначим:
en ( y\ (Л 1/ v\//1 v
/. / . 14-х 2
lim /(л:) = lim =т;
\ — Yx~ 1
lim ф (x) = lim = -.
55
Но при конечных пределах limf(x)=A > 0, Шпф(л;)— В имеет
х-+а к -+а
место соотношение
Ига <р(л:Iп/Ч*)
lim [f(x)]w
jc-> a
Следовательно,
Замечание. Если при решении примеров вида lim [f (x)]?u> окажется,
что lim / (х) = 1, a lim ф (л:) = оо, то можно рекомендовать следующее пре-
х-+а х-+а
образование:
lim [f (*)]?<*> = lim
lim Ф(*)[/(*)-i
= lim 1/а())()[/(>]
1.10.8. Найти следующие пределы:
в) lim (l+sinnx)ct?^; г) Нш f^V/U"e> (о#Ая, где ft —
целое число).
Решение, а) Обозначим:
\[m f(x)= lim
lim <p(x)= lim
л:-*- оо дс-* a>
Воспользуемся формулой (*):
f IXй -f- a \ x -* oo
V ) *
lim q>(x)[f(x) — 1]=—lim
Поэтому
50
1.10.9. Функция f(x) задана с помощью предела
Исследовать эту функцию и построить ее график.
Решение. Рассмотрим три случая:
1) |jc|> 1. Так как в этом случае lim #2Л=оо, то
2)
1. В этом случае lim х2п = 0; поэтому f(x)-
ft 00
ft 00
3) х = ± 1 • В этом случае х2п= 1 при любом я, и поэтому f(x) = 0.
Таким образом, рассмотренная функция может быть записана
следующим образом:
A, если \х\ > 1,
— 1, если \х\ < 1,
О, если л:
или, короче, f(x) =
(см. A.5.11.0)).
График этой функции представ-
представлен на рис. 27.
1.10.10. Население страны воз-
возрастает на 2% в год. Во сколько раз Рис. 27.
оно увеличится за 100 лет?
Решение. Если через Л обозначить первоначальное число
жителей в данной стране, то через год количество жителей будет
равно
Л + (Л/100) • 2 = A + 1/50) Л.
Через два года количество жителей будет равно А A -f-1/50J.
Через 100 лет оно будет равно Л A +1/50I00, т. е. увеличится
в [A +1/50M0]2 раз. Учитывая, что lim (I -f- \/n)n — et мы можем
п -*¦ оо
приближенно считать, что A -f-1/50M0 ^ е.
Следовательно, население страны за 100 лет увеличится при-
примерно в еа « 7,39 раза.
Конечно, эта оценка является весьма приближенной, но она дает
представление о порядке величины роста населения (с точностью до
0,001 величина A + 1/50I00 = 7,245).
1.10.11. Вычислить пределы функций
a) lim
cos # + 4 igx t
2 — x — 2x* ;
—7
в) lim
I к ^
Г)
Б7
д) lim
Х-+ СЛ
— ух2 — 1); е) lim
1.10.12. Вычислить пределы функций:
1—2*
+ 2-А
sin а
r) lim tg2xtg(я/4-х);
1.10.13. Вычислить пределы функций:
a) lim
в) lim
/72* 1
д) lim (sin2*)*'«;
Х-^П/4,
ж) lim (tgx)**2*;
6) lim
i'x~l
г) Пт A + 3 tg 2.x;)ct22*;
X-+Q
e) lim
з) lim
Х-+П/2
л) lim
1.10.14. Вычислить пределы функций:
arccos A—х)
a) lim
б) lim -л f—
в) lim -г— In A+ a sin x).
ътх
§ 1.11» Бесконечно малые и бесконечно
большие функции. Сравнение их
Функция а(х) называется бесконечно малой при х—>а, если lima(#) = 0.
х-*а
Аналогично определяется бесконечно малая а(х) г^и х—у со.
Функция / (х) называется бесконечно большой при х —> а, если lim / (х)= оо.
х-*а
Аналогично определяется бесконечно большая f (х) при х—> оо. Величина,
обратная бесконечно большой, является бесконечно малой.
Бесконечно малые функции обладают следующими свойствами.
1) Сумма и произведение любого конечного числа бесконечно малых функ-
функций при х—у а также являются бесконечно малыми при х—>а.
2) Произведение бесконечно малой функции на ограниченную функцию
есть бесконечно малая.
53
Сравнение бесконечно малых. Пусть функции а (х) и E (х) являются беско-
бесконечно малыми при х —> а. Если
lim Ш=С)
х ¦+ а Р W
где с —некоторое конечное число, отличное от нуля, то функции а(х) и $ (х)
называются бесконечно малыми одного порядка. Если с=1, то функции
а(х) и р (#) называются эквивалентными; запись: а(х) ~ Р (х).
Если с = 0, то функция а(х) называется бесконечно малой высшего порядка
по сравнению с Р (х), что записывается так: а(х) = о ф (х)), а р (х)—бесконечно
малой низшего порядка по отношению к а(х).
Если lim zq-j-~r- = с, где 0<|с|< + оо, то функция а(х) называется
х-* а 1р (^)J
бесконечно малой п-го порядка по сравнению с функцией р (х). Аналогично
вводится понятие бесконечно больших различных порядков.
1.11.1. Доказать, что функции:
a)/(x) = B*-4)/(*2 + 5) при х-+2,
б) f(x) = (x—lJsin3-—г при х—> 1 являются бесконечно малыми.
Решение, а) Достаточно вычислить предел
2х 4
Hm/(x)= lim -orc = 0.
Х-+2 X -*• 2Л ~Т~ °
б) Во-первых, функция ф(д:) = (д:—IJ есть бесконечно малая
при х—+\; действительно, lim(A:—1J = 0. Во-вторых, функция
ограничена:
sin3
х — 1
Следовательно, заданная функция f(x) представляет собой произве-
произведение ограниченной функции -ф (д:) на бесконечно малую ср (х). Значят,
f(x)—бесконечно малая при х—*1.
1.11.2. Доказать, что функция
являются бесконечно малыми.
1.11.3. Найти
Ншаг81пA7дг).
х+Ъ
Решение. Так как х—бесконечно малая при х—>О, а функция
sln(\/x) ограничена, те произведение лг81пA/лг) есть бесконечно-
малая, а это значит, что \mxski{)l%) = Q,
1.11.4. Сравнить с бесконечно малой ц>(х) = х следующие беско-
бесконечно малые при х—>0 функции:
а) Л(х)-tgх"; б) /2(х) = УШх; в) /,(х) =
Решение, а) Имеем
[] = lim ^
х-*- 0 * x->oL* J л; -* о
Следовательно, tgje3 является бесконечно малой высшего порядка
по сравнению с х,
б) Имеем
Значит, \/ sin2 jc есть бесконечно малая низшего порядка по срав*
нению с х.
в) Имеем
lim 1—-L = lim = 4
Следовательно, бесконечно малые V9~{-x — 3 и х одного порядка
малости.
1.11.5. Определить порядок малости величины р относительно
бесконечно малой величины а.
a) p = cosa—cos 2a; б) p = tga—sin a.
Решение, а) P = cosa—cos 2a ==2 sin -=¦ a sin -^-.
Отсюда
P __ 2sinCa/2)sin(a/2)_ 3
a->oa a->o a z
Следовательно, р бесконечно малая того же порядка, что и а2, т. е.
второго порядка относительно а.
1.11.6. Считая х—>«>, сравнить следующие бесконечно большие
величины:
а) /(х) = Зл:2 + 2л; + 5 и <р (х) =
б) /(х) = 2*2 + Зл: и ф (х) = (лг+2J;
В) f(x) = ^/^М и Ф (д:) = У7.
Решение, а) Бесконечно большая Зд:2 + 2л: + 5 имеет низший
порядок по сравнению с бесконечно большой 2хъ-\-2х—1, так как
3*+2*+5
ИГО о о , п г= 11Ш
2*3 + 2* 1
1.11.7. Доказать, что бесконечно малые а = х и P = a;c
(при д:—>0) несравнимы между собой, т. е. что предел их отношения
не существует.
60
Решение. В самом деле, lim LL.^ \\т cos A/л:)несущест-
0 Х О
х ->0 Х х-у О
О
вует (докажите !). Значит, эти бесконечно малые функции несравнимы.
1.11.8. Если х—> (), то какие из нижеследующих бесконечно ма-
малых имеют порядок выше, чем х; ниже, чем х; тот же, что х?
а) ЮОх; б) х2; в) 6sinjc; г) sin3jc; д) \/\%Г~х.
1.11.9. Пусть х-^0. Определить порядки следующих бесконечно
малых функций относительно х:
а) 2 sin4 л:—х&; б) }/ sin2
в) |А +л:3 — 1; г) sin2x — 2sinx;
д) 1— 2 cos (х + я/3); е) 2 'u
ж) xl(x — 1); з) tgx-\-x2;
и) cos л: — y^cosx; к) ех — cos л;.
1.11.10. Принимая сторону куба за бесконечно малую, определить
порядок малости диагонали куба (d); площади поверхности куба (S),
объема куба (V).
§ 1.12. Эквивалентные бесконечно малые.
Применение к отысканию пределов
Если функции ol(x) и Р (х) являются бесконечно малыми при х—у а и если
a(*)~YM. Р(*)~6(х), то
Игл -~~ = lim ~-т (принцип замены эквивалентных),
jr.ePW x + a&M
Если
) = k, 0 < |fe| <oo,
ТО
f(x)a(x)~ka(x).
Если
то
а(х)~Р(*).
Для того чтобы две бесконечно малые функции были эквивалентными,
необходимо и достаточно, чтобы их разность была бесконечно малой более вы-
высокого порядка по сравнению с каждой из них.
Таблица эквивалентных бесконечно малых функций
(а (л:) — бесконечно малая при х—*0)
1) sina(x)~a(x); 2) tga(x)~a(x); 3) 1 — cosa(;t)~[a{x)]2/2;
4) arcsina(x)^a(x); 5) arctga(;c)~a(.x:); 6) In [1 +a(x)]~a(x);
7) aa(x) — 1^а(д:Iпа (a > 0), в частности, e*ix}—l^a(jc);
8) [1+а(л:)]р— l~Pa{x), в частности, у/\ +а(л:) — 1^ 2^3.
61
1.12.1. Доказать, что при х-
1 1
а) 1--
в) sin ]/х У"х ~-\/~х2 + У~хъ.
Решение, а) По формуле 8) при Р=1/2 имеем
в) По формуле 1) имеем
sin ух V~x ~ ух У~х =
откуда sin у х V х ~у х2 + У х3 .
1.12.2. Заменить каждую из следующих бесконечно малых экви-
эквивалентной:
а) 3sina — 5a3; б) A — cosaJ+ I6a3 + 5a4 + 6a5.
Решение, а) Заметим, что сумма двух бесконечно малых аир
разных порядков эквивалентна слагаемому низшего порядка, так как
переход от бесконечно малой к ей эквивалентной равносилен отбра-
отбрасыванию бесконечно малой высшего порядка.
В нашем примере величина 3sina имеет порядок малости 1,
(—5а3) — порядок малости 3, значит,
3 sin a -f (—5a3) ~3 sin a~3a.
б) A — cos aJ + 16a3 + 5a4 + 6a5 = 4sin4 -- +16a3 + 5a4 + 6a5.
Низший порядок имеет слагаемое 16a3, поэтому
A—
1.12.3. С помощью принципа замены эквивалентных вычислить
пределы:
ч .. sin Ъх ^ч .. 1 — cos*
а)lim ьт; б)lim
In cos*
v ,. sin2jc+arcsinJt:—arctg2 j
д) hm «- ^—
X-+0 ОЛ
ж)
62
—cos *-f 2 sin je—sin3 x—
—6sin2x+x—
3)lim
Решение, а) Имеем sin5#~5A;; InA + 4л;)~4л; (см. таблицу
эквивалентных бесконечно малых функций на стр. 61). Поэтому
f. sin 5* ,. 5х 5
lim z—(л ч = lim -r- = -г- •
1пA+4д) ^04х 4
2^ = — 2.
л: -* 0 * ^
г) Из таблицы эквивалентных бесконечно малых функций уста-
устанавливаем:
У 1 + х + х2 — 1 — (х + x2)l2~x/2, sin4jc~4#.
Поэтому
цш )СЕ?Е±*Ь±= lim ^.-1
j" sin4x 4л: ~~ 8
^.1
j 0 sin4x л:->о 4л: ~~ 8 '
д) Воспользовавшись таблицей эквивалентных бесконечно малых
функций на стр. 61, получим
sin 2x + arcsin* х—arctg2 x~sin 2лг^2дг.
Следовательно,
t. sin2x+arcsin2x—arctg2* ,. 2х 2
hm J 3^ ^-^ lim ^^T-
з) sin ?~х~У~х\ 1п A + Ъх)~Ъх;
arctg V~x~V~x\ ehV X—\
?(+)
lim "¦ 7 qT^—г == Hm
-«(arctg Г{ШУХ)
1.12.4. Вычислить приближенно значения корней}^ 1,02 и |/г0,994.
Оценить абсолютную погрешность.
Решение. Пользуемся приближенной формулой
(для д;, достаточно близких к 0). В нашем случае
0,006
1 — 0,006 -1 — ^р = 0,997.
63
Для оценки погрешности заметим, что
Следовательно, абсолютная погрешность приближенной формулы (*)
оценивается величиной х2/8.
Пользуясь этой оценкой, находим, что абсолютная погрешность
корня }Л,02^ 1,01 составляет ^@,02J/8== 0,00005, абсолютная
погрешность ]/~0,994^0,997 составляет ^@,006J/8ss0,000005.
1.12.5. Доказать, что при х—>0:
« , ] о
а) yl+x—l^j^l б) arctgmx~mx; в) 1—cos3#~ -H-sin2*.
1.12.6. Определить при х—+0 порядок малости по отношению
к бесконечно малой $(х) — х следующих бесконечно малых:
a) Vsm*x + x*; б) *aA3t- .
*~г у' х
1.12.7. Определить при х—»2 порядок малости по отношению
к бесконечно малой $(х)=х—2 следующих бесконечно малых:
а) 3(л;—2J + 2(л;2 — 4); б) У sin nx.
1.12.8. Пользуясь методом замены бесконечно малых эквивалент-
эквивалентными, вычислить пределы:
«„* ^ у \n(l+sm4x)
а) I™ E(i+55' б) i'f
B)
InB — cos2jc)
1.12.9. Вычислить приближенное значение корня j/lO42.
§ 1.13. Односторонние пределы
Число А называется пределом справа функции f(x) при 0,
А =* lim / (^)=/ (л:0 + 0), если для всякого е > 0 существует такое б (е) > 0, что
0
дс*хо+0
для всех х, удовлетворяющих неравенству 0 < х—х0 < о (г) и входящих в область
определения функции / (х), справедливо неравенство | / (х)—А \ < е. Аналогично
определяется предел слева /(хо—О) при х-+х0—0. Если дго = 0, то пишут
просто х-+-\-0 или *->—0 и соответственно f(+Q) и /(—0).
1.13.1. Найти односторонние пределы функций:
Г — 2дг+3, если
¦)/W-( ЗЛ_5, если
G4
1
при х—¦> 1;
при х —> 0;
при л; —> 1;
при лг—э-0;
при лг —> 2.
Решение, а) Пусть л; ^ 1. Тогда f(x) = — 2х + 3. Следо-
Следовательно, /A— 0)= lim /(д;) = 1—предел
х-» 1-0
слева.
Если л;>1, то /(лг) = Зл;—5; сле-
следовательно, /A+0)= lim f(x)=—2
х-+ 1 + 0
— предел справа (рис. 28).
в)
г)
д) f(x) = cos(n/x)
е) f(x) = 5/(x—2K
в)
\ — cos 2*
sin лг |
но
( sin л;,
| sin х | = \ .
если
если
0 < х < я/2,
-я/2 <лг<0.
\
.1
-1
\
1
0
¦У
\
_ ч
/
. /
/'
Следовательно, Рис. 28.
/(—0)= lim /(#)= lim (— V~2 ^^) =-
/( + 0)= lim /(*)= lim fj/*2^=l/.
г) Выражение 1/A—д:) стремится к +оо, когда х стремится
к единице, оставаясь меньше единицы, поэтому
1 ^ = 0, /A-0) = 3.
Далее, прилг—> 1+0имеем 1/A—л;)—> — оо. Поэтому lim 71/A~л>=0,
х-+ 1+0
д) Выберем две последовательности, {*„} и {л:^}, с общими чле-
членами
1 , 2
*Л==2я И Хп==
соответственно.
Тогда lim xn = lim xn = 0 и
2я+1
=1. 2,
п оо
lim /(д;й) = lim cos 2ял = 1;
lim
п -*• со
;)= lim cosB/x+l)~
65
Следовательно, функция f(x) не имеет предела справа в точке 0;
учитывая четность функции /(я), заключаем, что она не имеет также
и предела слева (рис. 29).
¦>- х
-1
Рис. 29.
¦)/(*):
1.13.2. Доказать, что функция
х+1 при
Зх + 2 при 1<лг<3
при лг —•-1 имеет предел слева, равный 2, и предел справа, равный 5.
1.13.3. Найти односторонние пределы функций:
а) /(*)= 1
б) /(*) =
в) /(ж)-
при
при
при
X —>
Х—+
х-^>~
0;
0;
0.
§ 1.14. Непрерывность функция.
Точки разрыва и их классификация
Пусть функция y=*f(x) определена на множестве X и пусть точка о?
является предельной точкой этого множества. Говорят, что функция f (х) не-
непрерывна в точке х0, если lim f(x) = f(x0). Последнее условие равносильно усло-
условию lim Ау(х9)*ш lim [/Г*о + А*) —/(*0)J==0.
Дх -* 0 Ах -*• 0
Функция f(x) непрерывна в точке х0 тогда и только тогда, когда
OHf( + 0)/()
e-OHf(*b + 0)-/(*o).
Функция f (x) непрерывна на множестве X, если она непрерывна в каждой
точке этого множества.
Точки разрыва первого рода. Пусть точка х0 является предельной точкой
области определения л функции / (х). Точка х0 называется точкой разрыва
первого рода функции /(*), если пределы справа и слева конечны. Если при
этом f (х0—0) »з/(#0 + 0) ф f(x0), то х0—точка устранимого разрыва; если же
f(xQ—0) ф /(^0+0), то х0—точка неустранимого разрыва первого рода, а
разность f(xo+Q)—f(xQ—O) называется скачком функции f(x) в точке х0.
Точки разрыва второго рода. Если хотя бы один из пределов f(xQ—0) и
/(*0 + 0) не существует или бесконечен, то точка х0 называется точкой разрыва
второго рода функции / (х).
66
1.14.1. Используя лишь определение, доказать непрерывность
функции /(х) = Зд:4 + 5х* + 2д;2 + Зл: + 4 при любом значении х.
Решение. Пусть х0—произвольная точка числовой оси. Сначала
вычисляем lim f(x):
lim
х -* х9 х-+х0
Затем вычисляем значение функции в точке л:0:
Сравнивая полученные результаты, видим, что
х-+хе
Следовательно, функция f(x) непрерывна в точке дгв в силу опреде-
определения непрерывности. Поскольку точка х0—произвольная точка чи-
числовой оси, доказана непрерывность функции для всех значений х.
1.14.2. Даны функции:
^ при -оо<*<1,
а) /(*) = < 6—Ъх при 1<дг<а,
\ х—Ъ при 3<#<оо;
—2х2 при х<3,
б) '{Х)~\ Зх при х>3;
2а:—3 '
Найти точки разрыва, если они существуют. Определить скачки
функций в точках, где имеются разрывы первого рода.
Решение, а) Область определения функции—вся числовая ось
(—сю, сю). На интервалах (—сю, 1), A, 3), C, оо) функция непре-
непрерывна. Поэтому разрывы возможны лишь в точках jc=l, jc = 3,
в которых изменяется аналитическое задание функции.
Найдем односторонние пределы функции в точке д: = 1:
/A-0)= lim 1B
х» 1-0 5
/A+0)= lim F —5дг) = 1.
х-*- 1 + 0
Значение функции в точке х = 1 определяется первым аналити-
аналитическим выражением, т. е. /A) = B + 3)/5 = 1. Так как
то в точке х=\ функция непрерывна.
Рассмотрим точку # = 3:
/C — 0)= lim F — 5*) = — 9;
/C -f 0) = lim (x—3) = 0.
67
Мы видим, что правый и левый пределы, хотя и конечны, но не
равны между собой, поэтому в точке лг = 3 функция имеет разрыв
первого рода.
Скачок функции в точке разрыва / C + 0) —/ C — 0) = 0 — (—9) = 9.
в) Функция определена и непрерывна на всей числовой оси, кроме
точки л;=3/2. Так как 2# — 3>0 при д:>3/2 и 2х — 3<0 при
*<3/2, то
1 при х > 3/2,
— 1 при х < 3/2.
Следовательно,
/C/2 + 0) = 1, /C/2-0) = —1.
Поэтому в точке л: = 3/2 функция имеет конечный разрыв первого
рода. Скачок функции в этой точке /C/2 + 0)— /C/2 — 0) равен
1.14.3. Исследовать непрерывность функций:
!^ для х ф 0,
1 для х = 0;
б) /(*)«= sin A/х);
xsin(\/x) для х Ф 0,
{xsin
0
0 для * =
4-3* для
для
Д) /(*) = arctg(l/*); e)
Решение, а) Функция непрерывна во всех точках х Ф 0. В точ-
точке # = 0 имеем
-. sin* ,. sin* i
lim = hm = 1.
Следовательно, и в этой точке функция также непрерывна. Значит,
она непрерывна для всех значений х.
6) Функция определена и непрерывна для всех х Ф0. В точке
дг = О не существуют односторонние пределы (ср. 1.13.1 д)). Поэтому
в точке л; = 0 функция терпит разрыв второго рода (рис. 30).
г) /(—0) = 4, а /( + 0) = 2а; равенство /( — 0)=/( + 0)=/@)
будет выполнено, т. е. функция f(x) будет непрерывной в точке
л; = 0, если положим 2а = 4, а = 2.
е)/( — 1 —0)=/( — 1 +0)= lim (*2 —х+1) = 3, т. е. оба одно-
сторонних предела конечны и совпадают. Однако в точке х = — 1
функция не определена и потому не является непрерывной. График
функции представляет собой параболу у = х2—х-{-\ с «выколотой»
68
точкой М(—1, 8). Если доопределить функцию, положив/(—1) = 3,
то функция станет непрерывной. Таким образом, при х = — 1 функ-
функция имеет устранимый разрыв.
2
%
1
-Ч
1С]
J
1 !
2
3it
1
1
2
Зтс
1 j
2%\
j I
V
/
//
lie
2
%
-я
Рис. 30.
1.14.4. Исследовать непрерывность функций:
а) f(x) = E(x). Напомним, что функция Е(х) определяется как
наибольшее целое число п, содержащееся в числе л:, т. е. удовлет-
удовлетворяющее неравенству п^.х.
( 1, если х рациональное,
б) X (х) = \ Л
I 0, если х иррациональное.
Функция X (х) называется функцией Дирихле. Так, например, X @) = 1;
Я (—1/2) = 1; X(V~2) = Q; Х(п)==0 и т. п.
Решение, а) Функция Е(х) определена на всей числовой оси
и принимает только целочисленные значения. Эта функция разрывна
при каждом целочисленном значении п независимого переменного,
так как Е(п — 0) = #—1; Е(п-\-0) = п (рис. 31).
б) Выберем произвольную точку х0 на оси Ох; могут предста-
представиться два случая: 1) число х0 рационально; 2) число х0 иррацио-
иррационально.
В первом случае X (х0) = 1. В любой близости от рациональной
точки существуют иррациональные точки, а в них X (х) =* 0. Следо-
Следовательно, в любой близости от х0 есть точки х, для которых
Во втором случав к(хо)***О. В любой близости от иррациональ-
иррациональной точки имеются рациональные точки, а в них Я(л;) = 1. Следо-
Следовательно, опять-таки можно найти значения jc, для которых
Таким образом, в обоих случаях разность Ау не стремится к нулю
при Д#—> (). Поэтому х0 — точка разрыва, а так как точка х0 про-
произвольна, то функция Дирихле К (х) разрывна вкаждой точке.
График функции Дирихле X (л:) состоит из множества точек с ирра-
иррациональными абсциссами на оси Ох и из множества точек с рациональ-
рациональными абсциссами на прямой у = \.
Его изобразить невозможно.
1.14.5. Используя определение
непрерывности функции на языке
«е — б», исследовать на непрерыв-
непрерывность следующие функции:
(x2f если
нально,
—х2
х рацио-
рацио(
Рис. 31.
если х ирраци-
иррационально.
Решение.
а) Выберем произвольную точ-
точку #0. Согласно «е — б»-определению
нужно показать, что для любого наперед заданного сколь угодно
малого числа е > 0 можно найти число 6 > 0 такое, что при | х—х0 \ <б
справедливо неравенство \f(x)—/(#0)|<8.
Рассмотрим абсолютную величину разности
— | ax + b—ах0—Ъ \ = | а \ \ д: — х01.
Потребуем, чтобы было \f(x)—f(xo)\ < e. Это требование будет
выполнено для тех х, для которых имеет место неравенство
Iя 11*--#о| < 8 или |х—х0\<в/\а\ (аф0).
Следовательно, если взять б^е/|а|, то при \х—^о!^^ выпол-
выполняется неравенство
Непрерывность, таким образом, доказана для любой точки л: = дг0.
б) Выберем произвольную точку #<>. Если \хп} — последователь-
последовательность рациональных чисел, стремящаяся к xOi то lim f(xn) = xl.
хп-+х0
Если {х'п} — последовательность иррациональных чисел, стремящаяся
к #0, то lim /(*4) #а При #^0 указанные пределы различны
то lim /(*4)=s — #а При #0^0 указанные пределы различны
хп-*х0
и, следовательно, функция разрывна во всех точках
70
С другой стороны, пусть теперь л; = 0. Найдем абсолютную ве-
величину разности \f(x)—/@)|:
Очевидно, что #a<e при jx^j/'e. Если е>0 задано, то, поло-
положив 6<]Лв и [х- 01 == | лг | <6, получим | Д/@)[ = л;а < в. Следо-
Следовательно, в точке х = 0 функция непрерывна. Итак, точка х = 0 яв-
является единственной точкой, в которой функция непрерывна. Заметим,
что рассматриваемую функцию f(x) можно выразить через функцию
Дирихле (задача 1Л4.4 б)): f(x) = x*[2X(x)~I].
1.14.6. Установить, какого рода разрыв в точке х = х0 имеют
функции:
х + 2 для х<2,
б) ^
д) /(*) = !/"*—/?(!/*х); л:0 = л2, где л—натуральное число.
Решение, а) Вычислим односторонние пределы в точке лс0 = 2:
— 0)= Urn
lim
Здесь пределы справа и слева существуют, конечны, но не сов-
совпадают, поэтому функция имеет в точке хо = 2 разрыв первого рода.
д) Функция Е(]/Гх) имеет разрывы первого рода в каждой точке
д^ = /г2, где п—натуральное число (см. 1.14.4 а)). Функция же У^х
непрерывна при всех лг^О. Поэтому функция f(x) = yrx—Etyx)
имеет разрывы первого рода в точках 1, 4, 9, ..., л2, ...
1.14.7. Исследовать на непрерывность следующие функции:
а) П*)
при хфЪ, (ех>х при
) /() "
( р ф,
3 при х = 0; 1° при л-
г) f(x) - lim (sin *)*»; д) /(«) =
е)
1.14.8. Для каждой из следующих функций найти точки разрыва
и определить скачки функции в этих точках:
71
—х при
1.14.9, Следующие функции требуется доопределить в точке
= 0 так, чтобы они стали непрерывными:
я\ ft \_*&*. *\ ft \— 5х%—3*
§ 1.15. Арифметические действия
над непрерывными функциями.
Непрерывность сложной функции
Если функции f (х) и g(x) непрерывны в точке х=х0, то функции
1) / М ± * М; 2) f(x)-g (*); 3) -Ц1 (g (*0) ф 0)
также непрерывны в этой точке.
Если функция и = у(х) непрерывна в точке х = х0, а функция y~f(u)
непрерывна в точке мо = ф(*о)> то сложная функция y = f[<p(x)] непрерывна
в точке х — Хц.
1.15Л. Исследовать на непрерывность следующие функции:
f(
D) /W- 4 cos x-2
sin x
C0S(l/sinA;)
Решение, а) Функция, представляющая собой отношение двух
непрерывных функций (в нашем случае—двух многочленов), раз-
разрывна только в тех точках, в которых знаменатель обращается
в нуль. Но в нашем случае
а:4 + 4*3 + 8*2 + 8* + 4 = (а:2 + 2* + 2J,
и так как х2 + 2х + 2 = (х+ 1J+ 1 >0 при любом х, то знамена-
знаменатель нигде не обращается в нуль. Следовательно, функция f(x)
непрерывна на всей числовой оси.
б) Функция f(x) терпит разрывы только в точках, в которых
знаменатель равен нулю, т. е. в точках, являющихся корнями уравнения
4 cos л:—2 = 0 или cos *= 1/2,
откуда
S (я = 0, ±1, ±2, ...)•
Таким образом, функция f(x) непрерывна везде, кроме точек хп.
72
в) Как и в примере б), числитель непрерывен на всей числовой
оси. Знаменатель же по теореме о непрерывности сложной функции
непрерывен в тех точках, где непрерывна функция u=\/sm х, так
как функция cos и непрерывна везде. Значит, знаменатель непреры-
непрерывен всюду, кроме точек x = kn (k—целое). Кроме того, надо исклю-
исключить точки, в которых cos (I/sin л;) = 0, т. е. те точки, в которых
1 /sin л: = Bр + 1) jx/2 (р—целое число), или sin x = 2/[Bp + 1) я].
Таким образом, функция f(x) непрерывна всюду, исключая точки
x = kn и х =»(— 1 )пarcsin 2р { я + т (*, р, /2 = 0, ±1, ±2, ...).
1.15.2. Исследовать на непрерывность следующие сложные
функции:
а) y = cosxn, где п—натуральное число;
б) у = cos log х\ в) у = j/"l /2 — cos2 х.
Решение, а) Имеем сложную функцию у = cos и, где и = хп.
Функция у = cos и непрерывна в лдобой точке и, а функция и — хп не-
непрерывна при любом значении х. Поэтому функция у = cos xn непре-
непрерывна на всей числовой оси.
в) Здесь у==У\/2—и2, где u = cosx. Функция у 1/2—и2 опре-
определена и непрерывна на отрезке [—1^2/2, j/*2/2], функция # = cosa;
непрерывна на всей числовой оси. Поэтому функция^ =1/^1/2—cos2л;
непрерывна при всех значениях л;, для которых
( я/4 + 2яя<#<Зя/4 + 2ял,
| cos л; К |/2/2, т. е. | 5п/4 + 2ш2< х<7яц + 2т.
1.15.3. Для следующих функций найти точки разрыва и опреде-
определить их характер:
( х—1 при х^ О,
б) v = #2, где и =< , л . _
1 * \ jc-f-1 при х < 0;
в) y^-jr^y гДе ti = tgx.
Решение, а) Функция
терпит разрыв в точке х=1. Функция
терпит разрыв в точках, где и2-\-и — 2 = 0, т. е. йх=—2 и м2==1-
По этим значениям и находим соответствующие значения #, решая
П
уравнения:
—2 = —L-, 1= ! ;
отсюда #==1/2 и # = 2.
Следовательно, сложная функция терпит разрыв в трех точках:
^ = 1/2, X2 = lf лг3 = 2. Выясним характер разрывов в этих точках.
lim у = lim у = О,
*-* 1 И-»- СО
поэтому л:2=1—точка устранимого разрыва.
lim y= lim j;==oo; Hm ^y == lim ^y ===== с»;
следовательно, точки ^=1/2, л:а = 2—точки разрыва второго рода.
1.15.4. Дана функция /(*)== 1/A—х). Найти точки разрыва
сложной функции
у =/{/[/(*)]}¦
Решение. Точка х=\ есть точка разрыва функции
Если х Ф 1, то
Следовательно, точка д;==0 есть точка разрыва функции #
Если х Ф 0, х Ф 1, то
непрерывна везде.
Таким образом, для этой сложной функции точки разрыва суть
д: = 0, х=1, причем эти разрывы—устранимые.
§ 1.16. Свойства функции, непрерывной на отрезке.
Непрерывность обратной функции
I. Функция /(#), непрерывная на отрезке [а, 6], обладает следующими
свойствами:
\) f (х) ограничена на [а, Ь\\
2) /(*) имеет на [а, Ь] наименьшее и наибольшее значения;
3) Если т= min f(x), M— max f(x), то для всякого Л, удовлетво-
ряющего неравенствам т^А^М, существует точка хй?[а> Ь], для которой
f(xo) = A.
В частности, если f(a)-f (b) < 0, то найдется такая точка с (а < с < Ъ), что
= 0.
II. Непрерывность обратной функции. Если функция y — f(x) определена,
непрерывна и монотонна в строгом смысле на промежутке X, то сущест-
существует однозначная обратная функция х = у(у), определенная, непрерывная и
строго монотонная (в том же смысле) на промежутке изменения функции i/ = / (x).
74
1.16.1. Имеет ли корень уравнение
sin х—*+1=0?
Решение. Функция
f(x) = sin x—
непрерывна на всей числовой оси. Кроме того, эта функция меняет
знак, так как/@) = 1, а/(Зя/2) = —Зя/2. Следовательно, по свой-
свойству 3) внутри отрезка [0, Зя/2] имеется по крайней мере один
корень данного уравнения.
1.16.2. Имеет ли уравнение хь — 18л; + 2 = 0 корни, принадле-
принадлежащие отрезку [—1, 1]?
1.16.3. Доказать, что всякое алгебраическое уравнение нечетной
степени с действительными коэффициентами
п + ... + а2пх + а2п+1 = 0 (*)
имеет по крайней мере один действительный корень.
Решение. Рассмотрим функцию
f{x) = a
которая непрерывна на всей числовой оси.
Пусть, для определенности, а0 > 0. Тогда
lim /(дг)==+оо, a lim f(x)=—оо.
Следовательно, найдутся числа а, Ь, а<?, такие, что /(#)<0;
f(b) > 0. По свойству 3) между а и Ь существует такое число с,
что /(с) = 0. Тем самым доказано, что уравнение (*) имеет по край-
крайней мере один действительный корень.
1.16.4. Пусть функция f(x) непрерывна на [а, Ь] и пусть урав-
уравнение /(д:) = 0 имеет на отрезке [а, Ь] конечное число корней.
Расположим их в порядке возрастания
а < хг < х2 < х3 <... < хп < Ь.
Доказать, что в каждом из промежутков
(а, хг), (х19 х2), (х2У хв), ... 9 (xni b)
функция f(x) сохраняет постоянный знак.
Решение. Если бы на каком-нибудь промежутке функция ме-
меняла знак, то внутри него нашелся бы еще один корень функции,
что противоречит условию. Для определения знака функции на
любом из указанных промежутков достаточно вычислить значение
функции в какой-либо одной точке соответствующего интервала.
1Л6.5. Дана функция на отрезке [—2, +2]:
если —2<дг<0,
Существует ли на этом отрезке точка, в которой /(jc) = O?
75
Решение. На концах отрезка [—2, +2] заданная функция
имеет различные знаки:
/(_2)= +6; /( + 2)=~6.
Однако легко заметить, что она не обращается в нуль ни в одной
точке отрезка [—2, +2]. Действительно, дг2 + 2>0 и —(л:2 + 2)<0
при любом х\ это объясняется тем, что f(x) терпит разрыв в точ-
точке х = 0.
1.16.6* Принимает ли функция
f(x)~=xd14— sin ял;-h 8
значение 24- внутри отрезка [ — 2, 2]?
Решение. Функция f(x)=*x*/4—sin юс+ 3 непрерывна на от-
отрезке [—2, 2]. Кроме того, на концах этого отрезка она принимает
значения
/(-2)=1; /B)-5.
Так как 1-<2-х-<<5, то по свойству 3) внутри отрезка [ — 2, 2]
существует хотя бы одна точка х такая, что /(лг) 2
1.16.7. Показать, что функция
определенная и ограниченная на отрезке [—1, 1], не имеет ни
наибольшего, ни наименьшего значений.
Решение. На промежутке [ — 1, 0) функция возрастает от 3/2
до 2, на промежутке @, 1] функция возрастает от 0 до 1; при этом
функция не принимает ни значения 2, ни значения 0. Поэтому
функция ограничена, но не достигает своих верхней и нижней граней.
Причина кроется в наличии разрыва в точке х = 0.
1.16.8. Показать, что функция f{x) = x—Е(х) на любом отрез-
отрезке [а, Ь] длины ббльшей, чем 1, достигает своего наименьшего
значения, но не достигает наи-
большего значения.
Решение. Заданная функ-
функция f(x) на любом промежутке
[я,л+1), где п—целое число,
^ [
? ? г. * "f i • **~ ® возрастает от 0 до 1, не принимая
значения 1. Следовательно, 0^
Рис.32. :С/М<1 Для любых х. По*
скольку на отрезке [а, Ь] най-
найдется хотя бы одна внутренняя целочисленная точка п, то f(n) = Q
и Ит /(#) = 1, однако /(х)*уЫ для любого х. Значит, функция до-
Х-+П-0
стигает своего наименьшего значения и не достигает своего
76
наибольшего значения. Причина кроется в наличии разрыва в точке
х = п (рис. 32).
1.16.9, Доказать, что функция у = 2п+1/х (п—натуральное
число) непрерывна на всей числовой оси, рассматривая ее, как функ-
функцию, обратную к y — x2n+l.
Решение. Функция у = х2п+1 непрерывна и возрастает от — оо
до оо на всей числовой оси. Следовательно, для всех у определена,
непрерывна и возрастает обратная функция х=2п+у/Гу. Обозначая
независимую переменную снова через х, получим, что функция
у = 2п+ух обладает требуемыми свойствами.
1.16.10. Доказать, что для всякой функции вида
у =
+
1 + а2х2»-3 + ... + апх + а
я+1,
(*)
где а0У а±1 a2t ..., аю ап+1 — положительные числа, существует
обратная функция, возрастающая и непрерывная на всей числовой оси,
И +1
Решение. Известно, что функции д:, л:3, л:6,
х2п+1
возрастают на всей числовой оси. Далее, так как коэффициенты
ai(i = Oi 1, ..., п + 1) положительны, то и f(x) = aox2n+1 + a1x2n+
+ ... -\-апх-\-ап+1 также возрастает. Кроме того, она непрерывна.
Поэтому для функции вида (*) существует обратная функция, воз-
возрастающая и непрерывная на всей числовой оси.
Замечание. В последнем примере устанавливается лишь существование
обратной функции x=g(y), но ее аналитическое выражение не дается и это
не всегда возможно осуществить в радикалах. Вопросы о существовании об-
обратной функции и о нахождении ее аналитического выражения не равно-
равнозначны.
1.16.11. Доказать, что существует единственная непрерывная
функция х = х{у) (— оо<#у<оо), удовлетворяющая уравнению
Кеплера:
x—esinx = y @ <е<1).
Решение. Покажем, что у {х) — возрастающая функция. Пусть
хг<Схг—произвольные точки числовой оси. Тогда
У (*г) —У (*i) = (*а — 8 sin **) — (*i — 8 sin *i) =
== (х2—xt) — е (sin #2—sin хг).
Оценим абсолютную величину разности | sin дг2—sin jcx |:
cin v cit-i у I — О cfn
Olll Л» "—""Olll •A'j I ^ oil!
cos
sm
1 X2
Так как 0<е < 1, то
ej
откуда
^ixz—xx)y
—*i) — * (sin ^a—sin хг) =y (xj—y (xt) > 0.
77
Рис. 33.
Так как у (х)—непрерывная функция в промежутке (—оо, оо), то об-
обратная функция х является однозначной и непрерывной функцией от у.
1.16.12. Показать, что уравнение
л:3 — Злг-Ь 1 =0
имеет на отрезке [1, 2] один корень.
Вычислить приближенно этот корень с
точностью до 0,01.
1.16.13. Функция f(x) определена на
отрезке [а, Ь] и на концах этого отрезка
имеет значения одного знака. Можно ли
утверждать, что на [а, Ь] нет такой точ-
точки, в которой функция обращается в нуль?
1.16.14. Доказать, что функция
х+\ при —1<#<0,
—х при 0<*^1
разрывна в точке х=0 и тем не менее имеет на [ — 1, 1] как наи-
наибольшее, так и наименьшее значения (рис. 33).
§ 1.17. Дополнительные задачи
1.17.1. Доказать неравенства:
а) л 1 < [ —$— ) для натурального п > 1;
б) 1 . JL. А 2п—1 < 1
"" 4 * 6 * *' 2я 1^2/1 + 1 *
1.17.2. Доказать неравенства:
а) 202*03 > 303202;
б) 200! < 100200.
1.17.3. Решить неравенства:
а)||*|—2|<1; б) ||2—Зл:| —1| > 2; в) (х—2) ]/*2+1 >х*+2.
1.17.4. Может ли сумма, разность, произведение и частное иррациональ-
иррациональных чисел быть числом рациональным?
1.17.5. Существуют ли корни уравнений
a) |sin# | = sin*+3, б) | tg *| = tg я+З?
1.17.6. Доказать тождество [ " '^"' } +{ ^" ' } =х*.
i = l, 2, ... , л).
1.17.7. Доказать неравенство Бернулли
где хъ хъ ... , хп—числа одного знака, причем 1+Х( > 0
1.17.8. Найти области определения функций:
а) / (*) == V&—x*\ б) / (х) = ]/sinj/*j
в) / (х) = У—sin2 nx;
78
'V*-\x\'
1
д)/(x) = arcsin(|*|—3); e) f (*) = arccos-
olli Л
1.17.9. Тождественны ли функции
а)/(*) = ? и <р(х)-1;
б) /(*) = lg*2 и <p(x) = 2lgx;
в) /(*)=* и 9(x) = (j/**J;
г)/(^)а1 и ф(*) = sin2х+cos2#;
a)f(*) = lg(*-l) + lg(*-2) и q>(*) = lg(*-l)(*-2)?
1.17.10. В каком промежутке тождественны функции:
а) /(*)«* и Ф(*)=10!^;
б) f(x) = Vx Vx^l и ф(*)=]/*(*— 1)?
1.17.11. Равнобедренный треугольник данного периметра 2р= 12 вращает-
вращается вокруг основания. Составить функцию, выражающую зависимость объема V
тела вращения от боковой стороны х треугольника.
1.17.12. Исследуя область определения функций,
а) решить неравенство
б) доказать, что неравенство
Iog2-x (*-3);з*-5
не имеет решений.
1.17.13. Функция ^=signA: была определена в задаче 1.5.11, о).
Показать, что
а) | # | = # sign x\ б) х = | х | sign x\
в) sign (sign ^) = sign x.
1.17.14. Доказать, что если для линейной функции
f(x)=ax+b
значения аргумента х = хп (л = 1, 2,...) образуют арифметическую прогрессию,
то соответствующие значения функции
&» = /(*») (л = Ь 2» -О
образуют также арифметическую прогрессию.
1.17.15. Доказать, что произведение двух четных функций или двух не-
нечетных функций есть функция четная, а произведение четной функции на
нечетную есть функция нечетная.
1.17.16. Доказать, что если область определения функции f (x) симмет-
симметрична относительно # = 0, то f (*)+/(—х) — четная функция, a f(x)—f(—х) —
нечетная функция.
1.17.17. Доказать, что всякую функцию f (x), определенную в симметрич-
симметричном промежутке ( — /, /), можно представить в виде суммы четной и нечетной
функций. Представить в виде суммы четной и нечетной функций следующие
функции:
1.17.18. Функцию f(x)~x2-{-x, заданную на отрезке [0, 3], продолжить
четным и нечетным образом на отрезок [—3, 3].
79
1Л7.19. Функция {х}=*х—Е(х)—дробная часть числа я. Доказать, что
эта функция —периодическая с периодом 1.
1.17.20. Построить график периодической функции с периодом Т—\, ко-
которая на полуоткрытом интервале @, 1] задана формулой у = х2.
1.17.21. Пусть имеем две периодические функции f (x) и ф(#), определен-
определенные на общем множестве. Доказать, что если периоды этих функций соизме-
соизмеримы, то их сумма и произведение также являются периодическими функциями.
1.17.22. Доказать, что функция Дирихле Ц*) (см. 1.14.4, б) периодическая, но
периода не имеет.
1.17.23. Доказать, что если функция
периодическая, то а—рациональное число.
1.17.24. Исследовать на монотонность следующие функции:
1.17.25. Доказать, что сумма двух функций, возрастающих в некотором
интервале, есть функция монотонно возрастающая в этом интервале. Будет ли
разность возрастающих функций монотонной функцией?
1.17.26. Привести пример немонотонной функции, имеющей обратную
функцию.
1.17.27. Определить обратную функцию x=*g(y) и ее область определе-
определения, если:
/ х, если —оо < х < 1,
a) |/ = thjc; б) у=\ х2, если 1^*^4,
I 2*, если 4 < х < оо.
1.17.28. Показать, что уравнение *2 + 2я+1=* — 1+ у х не имеет дейст-
действительных корней.
1.17.29. Построить график функции
где
f(r\-l *A-I*l/O ПРИ |*|</,
' W~~ \ 0 при |*| >/.
1.17.30. Зная график функции y*=f(x), построить графики функций:
а) У=Щх); 6)y = VJJx); в) */ =
1.17.31. Доказать, что графики функций y = \oga x и y=\og n x получаются
а
один из другого изменением всех ординат в отношении 1:1/я.
1.17.32. Доказать, что если график функции y = f(x), определенной на
всей числовой оси, симметричен относительно двух вертикальных осей х = а
и х*=Ь(а < Ъ), то эта функция периодическая.
1.17.33. Пусть последовательность хп сходится, а последовательность уп
расходится. Что можно утверждать о сходимости последовательностей:
а) хп+Уп> б) ЧУ г?
1.17.34. Пусть последовательности хп и уп расходятся. Можно ли утвер-
утверждать, что последовательности хп-\-уш хпуп также расходятся?
1.17.35. Пусть <хп есть внутренний угол правильного л-угольника
(я = 3, 4, ...). Написать несколько первых членов последовательности ап.
Доказать, что Нтад=я;.
1.17.36. Доказать, что из lim xn = a следует lim \xn\=*\a\. Верно ли
П -*• оо п -> оо
обратное утверждение?
1.17.37. Если последовательность имеет бесконечный предел, значит ли,
что эта последовательность неограниченная? А если последовательность не-
неограниченная, значит ли, что она имеет бесконечный предел? Доказать, что
хп = п(~1^п неограничена, но не является бесконечно большой.
80
1.17.38. Доказать, что последовательность {ап\, где ап есть д-я цифра
произвольно выбранного иррационального числа, не может быть монотонной.
1.17.39. Доказать, что если последовательность {an/bn} (bn > 0) монотон-
монотонна, то монотонной будет также последовательность
1.17.40. Доказать существование предела последовательности и найти его.
a) j/2 , 1/2 /2 , у 2^2/ ...; б) д:л=с"/|/«! (с > 0, /г > 0);
в) хп = ап/п, где ал есть л-я цифра числа я.
1.17.41. Доказать, что при произвольно выбранном х последовательность
fE(nx)\
J—i—L\ ограничена.
1.17.42. Доказать, что последовательность
f Е (х)+Е Bх)+... + ? (пх) \
X *2 I
имеет предел х/2.
1.17.43. Доказать, что
Ан-0 "~
1.17.44. Дана функция
f(x)= I 1+х для Х9&0*
1 ^ ' \ 0 для х = 0.
Доказать, что
lim f(x)=*l.
х-*0
1.17.45. Пусть
Доказать, что
/ оо, если п > т,
lim P(*) = -j ^o/^o» если л=в/п,
JC">0° 10, если л < т.
1.17.46. Найти постоянные а и Ь из условия:
a) lim (^±1_-а*-_*Л=0; б) lim (yV—*+1 -а*-*) = 0.
1.17.47. Построить графики функций:
а) /(*)=*lim УТ+хВ (х^0); б) /(*)= lim sin2»^.
Л->О0 К Я-* 00
1.17.48. Доказать, что
lim [A+*)<1+*аH+*«)...0 + *")] = Д- A*|<1).
1.17.49. Можно ли при вычислении предела заменять бесконечно малые
слагаемые эквивалентными бесконечно малыми?
81
1.17.50. Определить порядок малости хорды бесконечно малой дуги окруж-
окружности относительно стрелки той же дуги.
1.17.51. Определить порядок малости разности периметров вписанного и
описанного правильных я-угольников относительно бесконечно малой стороны
вписанного многоугольника.
1.17.52. Коэффициент объемного расширения тела принимается прибли-
приближенно равным утроенному коэффициенту линейного расширения. На эквива-
эквивалентности каких бесконечно малых это основано?
1.17.53. Верно ли соотношение
lg(l+x)~x при *—>()?
1.17.54. Обязательно ли будет разрывна в данной точке х0 сумма двух
функций f(x)+g(x), если:
а) функция f (х) непрерывна, а функция g(x) разрывна при х = х0,
б) обе функции f (х) и g{x) разрывны при х = х$? Привести соответствую-
соответствующие примеры.
1.17.55. Обязательно ли произведение двух функций f (x)g(x) терпит раз-
разрыв непрерывности в данной точке #0, если;
а) функция f (х) непрерывна, а функция g(x) разрывна в этой точке;
б) обе функции f (х) и g(x) разрывны при х = х0?
Привести соответствующие примеры.
1.17.56. Можно ли утверждать, что квадрат разрывной функции есть
также разрывная функция? Привести пример всюду разрывной функции,
квадрат которой есть функция непрерывная.
1.17.57. Определить точки разрыва функций и исследовать характер этих
точек, если:
в) ф (дг) = д: [1 —2Л, (л:)], где X (х)—функция Дирихле (см. 1.14.4, б)).
1.17.58. Исследовать на непрерывность и нарисовать графики следующих
функций:
а) у = х—Е (х); б) у = х2 + Е (*2);
в) (/ = (—1)?(*2); г) у= lim t , *.—^-.
' * ч ; ; * n-^oo l+BsniA;Jrt
1.17.59. Исследовать на непрерывность функции f[g(x)] и g[f(x)]t если
= sign;c и g(x)=x(\— х2).
1.17.60. Доказать, что функция
2х при —1 а^*<:0,
при 0 < х*^\
разрывна в точке х = 0 и тем не менее имеет на [—1, 1] как наибольшее, так
и наименьшее значения.
1.17.61. Дана функция
• если * *°'
0, если # = 0.
Убедиться в том, что на отрезке [—2, 2] она принимает все промежуточ-
промежуточные значения от / (—2) до f B), хотя она и разрывна (в какой Точке?).
1.17.62. Доказать, что если функция f (x): 1) определена и монотонна на
отрезке [а, Ь]; 2) пробегает все промежуточные значения между f(a) и / F),
то она непрерывна на отрезке [а, Ь].
1.17.63. Пусть функция y = f(x) непрерывна на отрезке [а, Ь], причем ее
область изменения—тот же отрезок а^у^Ь. Доказать, что на этом отрезке
существует, по крайней мере, одна такая точка х9 для которой /(*)=*.
Пояснить геометрически.
82
1.17.64, Доказать, что если функция f (х) непрерывна на интервале (а, Ь)
и хъ х2у ..., хп—любые значения из этого интервала, то между ними най-
найдется число ? такое, что
/ (&>«•?¦ V (*i)+/ («i)+• • • +/ <*»)]•
1.17.65. Доказать, что уравнение *2*=1 имеет по меньшей мере один
положительный корень, меньший 1.
1Л7.66. Доказать, что если многочлен четной степени принимает хотя бы
одно значение, противоположное по знаку коэффициенту при его старшем
члене, то он имеет по меньшей мере два действительных корня.
1.17.67. Доказать, что функция, обратная разрывной функции t/=(l+*2)sign#,
есть функция непрерывная.
Глава II
Дифференцирование функций
§ 2.1. Понятие производной
Производная /' (х) функции y = f(x) в данной точке х определяется ра-
равенством
Если этот предел конечный, то функция f(x) называется дифференцируемой
в точке х; при этом она обязательно непрерывна в этой точке.
Геометрически величина производной f (x) представляет собой угловой
коэффициент касательной к графику функции y = f(x) в точке х.
Число
называется правосторонней производной в точке х.
Число
называется левосторонней производной в точке х.
Необходимым и достаточным условием существования производной f (x)
является равенство fL(x) = f+(x).
Если 1'(х)=оо, то говорят, что функция f (х) имеет в точке х бесконеч-
бесконечную производную. В этом случае касательная к графику функции у = ? (х)
в точке х перпендикулярна к оси Ох.
2.1.1. Найти приращение &у и отношение ¦— для функций:
а) у = Ух при х = 0 и А* = 0,0001;
б) У = х2+\-б ПРИ ЛГ==1 и Д* = 0,2.
Решение, a) ky =
Д* ~~ 0,0001
2.1.2. Пользуясь определением производной, найти производные
следующих функций:
а) у = cos ах\ б) у = 5#2—2дг.
84
Решение, а) Ду = со8а(л: + Дл:) — cos ал: =
/ CL \ CL
= —2sin( ax + ^Ax j sfriy Ал:;
Ах
Ах
у — lim » —~" тттт ? nm
lim
sin— Д*
Ax
= —а sin ал:.
В частности, если а = 1, то j; = cosa: и у' =—sinx
2.1.3. Показать, что следующие функции не имеют конечных
производных в указанных точках:
а) у=Ухг в точке л: = 0; б) у= \/х—1 в точке х=\;
в) у = 3\х\-\-\ в точке х = 0.
Решение, a) Aj; = У(х+ АхK — Ух*. В точке л: = 0
имеем Ау = УА&, ^? = Х^!. = .^^
у' @) = lim
Длг-»О
1
следовательно,
= сх>, т. е. конечная производная не существует.
в) При Дл: > 0 приращение функции Ау в точке х = 0 выразится
так: Ау = 3 @ + Ал:) +1 — 1 = ЗДл:. Поэтому
lim ^ = 3.
При Ал: < 0 приращение функции Ау выразится
так:
Ау = —3 @ + Ддг) + 1 — 1 = —ЗДл:,
значит,
lim И"8'
Так как односторонние пределы различны, О
то в точке х = 0 не существует производной Рис 34
(рис. 34).
2.1.4. Исследовать дифференцируемость функции >; = |1пл:( в
точке х = 1.
Решение. При л:=1
Ду»=|1пA+Д*)| — |1Ш| = |1пA + Дл:)|,
т. е.
'" -^ Ах) при Ал:^0,
+ Ал:) при Ал: < 0.
83
Поэтому
откуда
> О,
< О,
lim |f=-l.
Поскольку односторонние пределы различны, не существует произ-
производной. Следовательно, функция ^у = j In jc j в точке х = 1 не
дифференцируема (рис. 35).
2.1.5. Определить среднюю ско-
скорость движения, заданного формулой
от tx = 5
до t2 = 15 се/с.
0\ 1
Рис. 35.
2.1.6. Пользуясь определением
производной, найти производные сле-
следующих функций:
2.1.7. Исследовать дифференцируемость функции у = | cos x\
в точках х = п!2-\-пп (п—целое).
§ 2.2. Дифференцирование явно заданных функций
I. Основные правила дифференцирования
1) с' = 0; 2) (и ± и)' = и' ± и'; 3) (си)г=сиг;
4) (uv)' = u'( ' ' ^ ' " х u'v—uo'
'; 5) ^~
Здесь с = const, а и и v—функции от х, имеющие-производные в соот-
соответствующей точке.
6) Если функция u = tp(x) дифференцируема в точке х0, функция y = f(u)
дифференцируема в точке «о==ф(*о)> то сложная функция у = / (<p(*)} диф-
дифференцируема в точке #0 и Ух(хо) —
Н, Дифференцирование основных элементарных функций
1) {ип)' = пип-1и'\ 2) (sin и)'= cos а-и'; 3) (cos «)'=— sintt-ы';
4) (tg иУ
7) (аи)' =
10)
; 5) (ctg и)' = —r
х v & ; si
^; 5) (cg и) r4
cos2 м х v & ; sin
ак In а-и'; 8) (еи)' = ейм'; 9)
'; 11)
; 6) (In и)' = ~;
= — (arccos «)';
a
12) (arctg «/«-^«-(arcctg u/.
86
2.2.1. Найти /, если:
а) у
б) у= - г-т= (й> ^—постоянные).
у х% х у х
Решение, а) / = 5 -jX2'3~l — З-^
J0
2.2.2. Найти /, если:
в) у = (я2 -{-1) arctg лс; г) дг = xz arcsin дг.
Решение, a) jf'==3(cosA:)/ + 2(sinA:)' = —3sinx + 2cosx;
6\ ' — (sin лс+cos ху (sin x—cos л:)—(sin x—cos x)r (sin jc+ cos x)
' ^ (sin*—cos*J
_ (cos x—sin x) (sin л:—cos x) — (cos лг+sin д:) (sin jc+cos x) _
2
(sin*—cos*J •
г) у' == (*3)' arcsinx+ (arcsinx)'jcz = 3x2arcsin x-\—r x
у 1-х2
2.2.3. Найти производную данной функции и затем вычислить
частное значение производной при указанном значении аргумента:
а) / (х) = 1 — У"х* + 1 6/jc при х = — 8;
б) f(x) = (\—]/lcJ/x при # = 0,01;
в) f(t) = (cos /)/(! —sin /) при ^
2 * /о
Решение, а) / (х) = —-^ д:"/3 -
о
Полагая х=—8, найдем
„, m 2 16
„\ <*/^_-sinf(l-8_
В' Т КЦ <1—sin 0* 1-sinr
Отсюда /'(я/6) = 2.
2.2.4. Пользуясь формулами дифференцирования, найти произ-
производные следующих функции:
a) jr = 2*» + 3*-5; б) у =
-±
87
ж) y = ex(cosx + sinx); з)
2.2.5. Пользуясь правилом дифференцирования сложной функ-
функции, найти производные следующих функций:
a) y = sin3Ar; б) y = lntgx; в) y = 5C0S*;
г) дг = In sin (л:3 + 1); д) у =arcsin У 1 —х2;
е) y = ln5(tg3.x:); ж) y = s\n2 V\/(\ — х).
Решение, а) Внешней функцией здесь служит степенная
функция: sin д: возводится в третью степень. Дифференцируя эту
•степенную функцию по промежуточному аргументу (sin*), получим
(sin3 х)'&ш x = 3 sin2 x;
но промежуточный аргумент sin л: — функция независимой перемен-
переменной х; поэтому надо полученный результат помножить на производ-
производную от sin л: по независимой переменной х. Таким образом, получим
у'х = (sin3 xYsin x (sin x)'x = 3 sin2 х cos x;
б) ^«(l^^
в) ух = EСО8 ХУСО5 х (cos х)'х = 5C0S * In 5 (— sin x) = — 5C0S * sin x In 5;
д) yx = (arcsin У 1 - x%j^ A/1=^I -^ A - x% =
1 ! ^(x^O).
1*1 у l-*"
Замечание. Разумеется, нет никакой необходимости в таких излишне
подробных записях. Результат следует писать сразу, представляя последова-
последовательно в уме промежуточные аргументы.
2.2.6. Найти производные следующих функций:
а) у = (\ +3д: + 5д:2L; б) у = C—sin*K;
в) y = ysh^~x+\lcos2x; г) у = ?/2е* + 2*+ 1 + 1пбл:;
д) y = sin3* + cos(x/5) + tg}/T; e) j/== sin (л;2—5х+ l) + tg{a/x);
ж) у = arccos V~x\ з) у = arctg (In x) -fin (arctg #);
и) у = In2arctg(лг/3); к) ^= У х+у х
Решение, а) у' = 4A +3* + 5л;2K A + Зд: + 5л:2)
:2)'
83
ж) "' - -
2.2.7. Найти производную функции
Имеем
1 2A+а;2)—4л;2 2A— х2)
У =
2х у U+*2J
)
_ 2A—л:2)
~~|1— х'
т. е.
у' =
При | х | = 1 производной не существует.
2.2.8. Найти производные следующих функций:
а) у = sh 5л: ch (дг/3); б) j/ = cth (tg x)—th (ctg л:);
в) д; = arccos (th л:) + sh (sin 6л:);
esh ax
Решение.
в) у' = — (ihX)'2 + ch (sin 6л:) (sin 6л:)' =
1/ch2*
cos 6л: ch (sin 6л:) =
¦= —^ + 6 cos 6л: ch (sin 6л:).
2.2.9. Найти производные функций:
а) у - Yx\fA2; б)у = [и {х)]° <*> {и (х) > 0);
г /5—х
sin3 л: cos2 л:; г) у = \
89
Решение, а) Применим метод логарифмического дифференци-
дифференцирования. Вместо у рассмотрим функцию
= 1п
Учитывая, что (In|tt|)' = a7tt> будем иметь
2*
х + 3(*а+1) + 15E—я)""" 15л:(л:2+1) (б—х)
Но ?' = (ln|j/|)';=//j/, откуда
„'-„,'_ З/*3 (*2+l) —24x3 + 125^—14ЛГ+75
У ~~У У у^1Гх 15*(*+1)E-*) •
б) Предположим, что функции и (х) и v (x) имеют в данной обла-
области определения производные. Тогда функция
z = \ny = vlnu
также имеет в этой области производную, причем
и'
z' = (v In u)r = v' In и + v~.
Следовательно, и функция
у = eln 9 = е*
имеет производную в указанной области, причем
y' = e?z'=yz'.
Таким образом,
y' = uv (v' In и + v^\ ==vuv~1u' + uv \п u-v'.
2.2.10. Показать, что функция у = хе~х*/2 удовлетворяет урав-
уравнению
ху' = A—х*)у.
Решение.
у' = е-***2 —x*e~x*/2 = е-х*'2 A — х2);
Ху'=хе-х*/2 (\—х2).
Следовательно,
ху' =j; A —л;2).
2.2.11. Показать, что функция у — хе~х удовлетворяет уравне-
уравнению ху' = A —х)у.
2.2.12. Исследовать дифференцируемость функций:
а) у = arcsin (cos х); б) у = у 1 —}/l —л:2.
90
Решение, а) /- (соахУ_ = —
sin*
/ —cos2* ]Лш12* I sin x I
Следовательно, j;' =—1 в точках, где sinA:> 0; у'=* 1 в точ-
точках, где з!пх<0. В тех точках, где sin# = 0, т. е. в точках
x^kn (& = &, ±1» ±2, ...) функция не дифференцируема, хотя
она в этих точках непрерывна.
б) Область определения этой функции—отрезок —l
(—2х) при
При х—*1—0 или а: —>—1+0 имеем у'—+ + оо. Выясним сущест-
существование производной^' в точке х = 0, т. е. существование предела
У\— Да:2 —1^—-i- Да:2,
*—0.
Таким образом, у'_ @) ^^ @), значит, рассматриваемая функция не
имеет производной в точке а: = 0, хотя она в этой точке и непре-
непрерывна.
Замечание. Можно указать примеры, когда функция в данной точке
не имеет ни производной в обычном смысле, ни односторонних производных,
•г. е. когда график функции в данной точке не имеет ни правосторонней, ни
левосторонней касательной. Например, функция
*sin(l/*) при х Ф 0,
о при * = 0
в точке х*=*0 непрерывна, но не имеет даже односторонних производных*
Д/ (х) . 1
так как ' = sin -r~.
Д# Ах
2.2.13. Найти производные следующих функций:
б) /(а:) = 1п[сЬа:]; в) /(х) = 2У chx— 1;
г) f(x) «= arcsin [th х]; д) f(x) = У1 + sh2 4a:;
е) /(а:) = eax (ch to + sh to).
2.2.14. Пользуясь логарифмическим дифференцированием, найти
производные функции:
2.2.16.
показать, что
/(я/4) —3/'(я/4) = 3.
2.2.16. Показать, что функция
х е~х*
удовлетворяет дифференциальному уравнению
ху' + 2у = е~х\
2.2.17. Найти производные следующих функций:
а) у = In cos j/*arcsin3~2* (x > 0);
б) у = i/arctg ^/cosln3*.
§ 2.3. Повторное дифференцирование
явно заданных функций. Формула Лейбница
Если производная (п—1)-го порядка функции y = f(x) уже определена,
то производная п-го порядка определяется равенством
В частности, у" (х) = [у'(х))', у1" (х) = [уп {х)]' и т. д.
Если и и v суть п раз дифференцируемые функции, то для их линейной
комбинации cxu-\-c2v (cly с2—постоянные) имеет место формула
а для их произведения uv—формула Лейбница
п
где и«» = и,1>«»=1> и с^ = -^ 1.2-3 ^
ные коэффициенты. Имеют место следующие формулы:
1) (xm)W = m(m— 1) ... (m—л + 1)х*-я.
2) (ал)(») = а^1п»а (а > 0). В частности, (в*)<»> =
3)
= (~l)^~
4) (sin^)W = sin(x+/iJt/2).
б) (cos x)W = cos (л:+ля/2).
92
2.3.1. Найти производные л-го порядка от следующих функций:
а) у = \пх; б) y = ekx;
в) у = sin х; г) у = sin 5л; cos 2x;
д) у = sin х cos х; е) у = sin Зл; cos2 x;
ж) у = \п(х2 + х—2).
Решение.
в) у a cos х = sin (a: + я/2);
/' = cos (д; + я/2) = sin (л: + 2я/2).
Вообще, если допустить, что для данного n =
j/<*>= sin
то окажется, что
>= cos [x + k^ = sin
-*-+*] .
Отсюда в силу принципа математической индукции заключаем, что
при любом натуральном п
г) у= sin 5A:cos2A: = Y[sin 7л; + sin Зл;].
Поэтому
^ [Л sin ^ + я-у) +3" sin
Для упрощения вычислений преобразуем полученную функцию:
2*+1 _(*+2
Отсюда
2.3.2. у=Щ1; найти /«>.
93
Решение. Преобразуем выражение следующим образом:
Отсюда
= (_ 1)« л!
2.3.3. у = х/(х2 — 1); найти /в\
Решение. Преобразуем выражение
поэтому (см. 2.3.2):
L Г ! I 1 1
2 [+Х^х— lj »
2.3.4. Применяя формулу Лейбница, найти производные указан-
указанных порядков для функций:
а) у = х2 sin x\ найти ут\
б) у = ех (х2 — 1); найти /24);
в) j> = e*x sin Рд:; найти jf^.
Решение, a) ym> = (sinx-x2)my=*
= (sin *)B5)x2 + 25 (sin х)ш) (x2)'+ ?~ (sin x)m) M"»
так как следующие слагаемые равны нулю. Поэтому
у25)==х2 sin ^х + 25 ЛЛ + 50* sin
+ 600 sin Гд: + 23 —^ = (д:2 — 600) cos x + 50x sin л:.
2.3.5. Вычислить значение n-Pt производной функции ^ = -2—Т &
в точке х = 0.
Решение. По условию имеем у{х)(х2 — 2л;4-5) = Зл; + 2. Про-
Продифференцируем это тождество п раз, применяя формулу Лейбни-
Лейбница; тогда (для п ^2) получим
94
Положив х = 0, получим
5/*> @) — 2nyin) @) + п (п — 1) у{п'2) @) = 0.
Отсюда
ум @) = |-пу*»-» @) —/1(Аг5~1)<У("~2) @).
Мы получили рекуррентную формулу для определения п-й производ-
производной в точке х**0 (п^2). Значения j? @) и у'@) найдем непосред-
непосредственно: у {0) = 2/5;
Затем, последовательно полагая я = 2, 3, 4, ..., с помощью рекур-
рекуррентной формулы получим значения производных высших порядков.
Например,
„ 2 19 2-1 2_56
^ (°) = У2'25 Г'Т"-125'
«"'/m 2 q 56 3-2 19 234
2.3.6. Найти производные второго порядка следующих функций:
2.3.7. Дана функция
у = Cjg2^ -f c2xe2Jf -f" ex.
Показать, что эта функция удовлетворяет уравнению
2.3.8. Применяя формулу Лейбница, найти производные указан-
указанных порядков для функций:
а) у = xz sin x\ найти у20*;
б) у = г""* sin jc; найти j;"';
в) у = ех (Зд;2 — 4); найти у{п);
г) у = A —д;2) cos л:; найти j;B72>#
2.3.9. Применяя разложение в линейную комбинацию более прос-
простых функций, найти производные 100-го порядка от функций
2.3.10. Показать, что функция
у^хп [ct cos (In x) -f- ca sin (In x)]
(где cv c2t n—постоянные) удовлетворяет уравнению
I-2я) */ + (!+л2) j/ = 0.
95
2.3.11. Доказать, что если f(x) имеет производную п-го
порядка, то
[/ (ах + Ь)](и) = anfn) (ах + Ь).
§ 2.4. Дифференцирование обратных функций
и функций, заданных неявно или параметрически
1. Производная обратной функции. Если дифференцируемая функция
y=f(x), a<x<b имеет однозначную непрерывную обратную функцию
x=g(y) и у'хф0, то х' также существует и
* L
Для производной второго порядка имеем
**—
У'хх
2. Производная неявной функции. Если дифференцируемая функция
у=у(х) удовлетворяет уравнению F (х, у) = 0, то надо продифференцировать
его по х9 рассматривая у как функцию от х, и решить полученное уравнение
-*- F (х, у) = О относительно у'х . Чтобы найти у"хх, надо уравнение дважды
продифференцировать по х, и т. д.
3. Производная функции, заданной параметрически. Если система урав-
уравнений
где <p(tf) и ty(t)—дифференцируемые функции и ф'(/)^0, определяет у как
однозначную непрерывную функцию от х, то производная ух существует и
% (О У\
Производные высших порядков вычисляют последовательно:
В частности, для производной второго порядка справедлива формула
., _Wtt-x"tty't
Ухх {x>tK
2.4.1. Найти указанные производные:
а) у = 2л:3 + 3#5 + *) найти ху\
б) у = 3х—(cosa:)/2; найти хуу\
в) у = х + е*; найти л;^.
Решение, л) Имеем у^ = 6л:2 + 15а:4 + 1, следовательно,
1
%и — 7" —
96
*"~ у'х ~~6*2+15^+1 •
в) Ух = 1 + ?*» У** = ^*» следовательно,
1 м- е*
2.4.2. Пользуясь правилом дифференцирования обратной функции,
найти производную у'х для следующих функций:
а) У = ^*»" б) ^ = arcsin ]/"*; в) j; = In УI +x2.
Решение, а) Обратная функция х=уд имеет производную
х'у = Зу2. Следовательно,
в) При х>0 обратная функция х = |/^2^ — 1 имеет производную
= ?2J'/}/"?aJ' — 1. Следовательно,
2.4.3. Для следующих функций, заданных параметрически, найти
производные первого порядка от у по х:
а) x=a(t— sinf), >> = а A —cos t)\
б) -л: — /г sin ^ — sin kt, у =k cos t + cos /г^;
в) x = 2lnctgtf, ^ = tg^ + ctg/;
r) jf = ^, у = e"ct.
Решение, a) Находим производные от х и у по параметру t:
х\ = а A — cos tf); yt = a sin /.
Отсюда
В) ЙТ-
— 2cosec2/
Л ctg / sin 2/ •
dv „ . 9 » 4 cos 2/
JL = sec2 / — cosec21 = —
ф 4 cos 2/ sin !
31 4 sin2 2/
2.4.4. Функции заданы параметрически:
a) ( * = acos3/, 6)
j * = acos3/, 6) J x = /3 + 3/+l,
\ y = bsin*t; \ y = t3 — 3/ + 1;
в) | x = a(cos^ + /sin/)» r) j Ar^e^cos/,
у у = a (sin / — / cos /); \ у = ^f sin /.
Определить для них производную второго порядка от у по л:.
97
Решение, а) Найдем сначала^:
у\ = ЪЬ sin21 cos t\ x't = — За cos21 sin t\
, 36sin2/ cos t b , ,
Далее будем искать yxx по формуле
где
' V — b
CL
Отсюда
a cos21 (—3a cos2 t sin t) 3a2 cos4 t sin t'
r) a:J = e* cos ^ — я* sin t = ?* (cos t — sin /);
y\ = ef sin t + el cos ^ = ^ (cos t + sin /);
, cos^ + sin^
cos / — sin t '
fcost + slntV
^ )
t + slntV
ts\nt )t
^^ ^ e* (cos t—sin 0 e^ (cos /—sin /K
2.4.5. В следующих примерах найти у"х'хх\
а) x = e~f; y = t3; б) x = sect; y — tgt.
Решение, а) Сначала найдем
отсюда
ух~— 3/2/^-
Затем найдем вторую производную
И наконец, найдем третью производную
^ —в"
2.4.6. Найти производную ^ от следующих функций у (х), за-
заданных неявно:
а) *3 + *2у+,у2 = (); б) lnx + e-vt* = c\
В) х2+уг — 4х—\Оу + 4 = О; г) ^/з+<у2/з = а^.
Решение, а) Дифференцируем по х, считая у функцией от х\
получим
Ъх% + 2ху + хУ + 2уу' = 0.
98
Решая это уравнение относительно у\ найдем
у
2.4.7. Найти yXXi если:
a) arctg.y — у+х = 0; б)
в) х+у-^е*-У.
Решение, а) Дифференцируем по х, считая у функцией от х9
и определяем у':
_/ + 1=0) откуда у'=1±?=у-г+1.
Дифференцируем еще раз по х:
у" = —2у-у.
Подставив найденное значение у', окончательно получим
«• - 2A+*/2)
Ухх — уъ
2.4.8. Найти значение у" в точке *=1, если
л;3 — 2х2у2 + 5х+у — 5 = 0 и y\Xssl = \.
Решение. Продифференцировав по х, найдем, что
3*2 — 4ху2 — 4х2уу' + 5 +/ = 0.
Полагая л:=1 пу=\, получим значение у' при х=1:
3~4 — 4у' + 5+^/ = 0; у1 = 4/3.
Еще раз дифференцируем по х\
вх—4у2 — Ъхуу' — Ъхуу' — 4х2у'2 — 4х2уу" +/ = 0.
Полагая х=\; у=\ и у' = 4/3, найдем значение /' при дг=1:
2.4.9. Найти ух для следующих функций, заданных неявно:
a) x + Vxy+y = a; б) axctg(y/x) = \nVx2+y2;
в) e^sinj; — ?~^cosa; = 0;
г) еУ + ху = е; найти у^ в точке @, 1).
2.4.10. Найти у"хх от следующих функций, заданных неявно:
а) y = x + atctgy;
б) х2 + 5ху+у2—2х+у — 6 = 0; найти у9 в точке A, 1).
2.4.11. Для следующих функций, заданных параметрически,
найти указанные производные:
99
a) x
б) X
в) х
г) х
д) х
е) л;
ж) х
a sin ? с cos /
V #
1+bcostf1 * 1+6 cos/'
= ln A -\~t2), y~t — arctgt;
= /2 + 2, y=zt*/3 — t;
= е-*\ у = arctg B/ +1);
= 4 tg2 (t/2)y у = a sin t -f- b cos ^;
= arc sin (t2 — 1), j; —arccos2/;
= arc sin t, y = Kl—^2;
найти у'х;
найти ^;
найти ^j
найти ух\
; найти ^;
найти ух;
найти v^,
2.4.12. Показать, что функция y = f(x), заданная параметриче-
параметрическими уравнениями х = е1 sin t, у = е* cos t, удовлетворяет соотно-
соотношению у" (х-\-уJ = 2{ху' — у).
§ 2.5. Приложения производной
Уравнение касательной к графику дифференцируемой функции
() в точке М(х0, у0), где t/o = «/(^o)» имеет ВИД
Уравнение нормали в той же точке имеет вид
Отрезки ATf AN называются соответственно подкасательной и поднормалью,
а длины отрезков МТ и MN—длинами касательной и нормали (рис. 36).
Длины указанных отрезков выра-
выражаются следующими формулами:
= Д- ; AN=*\w'\.
А
Рис. 36.
N
: 2.5.1. Составить уравнения
касательной и нормали:
а) к кривой у = х3 — Зл; + 2
в точке B, 4);
б) к параболе j; = 2a:2 — #+5 при х = — 0,5;
в) к кривой у = х*-\-Зх2 —16 в точках ее пересечения с пара-
параболой >^=3л:2.
Решение, а) Найдем производную в точке х = 2:
/ = Зл;2-- 3, /B) = 9.
Уравнение касательной имеет такой вид:
<у — 4 = 9(л; —2) или 9л;— j;—-14 = 0.
Уравнение нормали имеет вид
— 4= —-i- (лг — 2)
или
+ 9у—38 = 0.
100
в) Решив систему уравнений
2 —16,
( у =
\ У =
найдем точки пересечения кривых xl = — 2, д:а = 2, у1=у2 =
Найдем теперь производную в точках х =— 2 и х = 2:
у' = 4л:3 + 6*. / (— 2) = — 44, у' B) = 44.
Поэтому уравнения касательных имеют вид
у —12 = — 44(л: + 2), у— 12 = 44 (* — 2).
Уравнения нормалей имеют вид
2.5.2. На кривой у=хъ— Зх-\-5 найти точки, в которых каса-
касательная:
а) параллельна прямой у — — 2х;
б) перпендикулярна к прямой у =— х/9;
в) составляет с положительным направлением оси Ох угол 45°.
Решение. Для отыскания требуемых точек принимаем во вни-
внимание тот факт, что в точке касания угловой коэффициент каса-
касательной равняется производной у'=3х2— 3, вычисленной в этой
точке.
а) Из условия параллельности
Зл:2 —3 = —2,
откуда xx = —1/1^3, х2=^\/У. Искомые точки:
AU-1/K3, 5 + 81/3/9), Л^О/КЗ, 5-8/3/9).
б) Из условия перпендикулярности
Зл:2 —3 = 9,
откуда хг = — 2, х2 = 2. Искомые точки Мг (—2, 3), М2B, 7).
2.5.3. Найти углы, под которыми пересекаются следующие линии:
а) прямая у =4—х и парабола у = 4—л;2/2;
б) синусоида у = sin х и косинусоида у = cos x.
Решение, а) Напомним, что углом между двумя кривыми
в точке их пересечения называется угол между касательными к этим
кривым, проведенными в этой точке. Найдем точки пересечения
кривых, решив систему уравнений
I ^ = 4— *2/2.
Отсюда
ЛМО, 4); М2B, 2).
101
Далее определяем угловые коэффициенты касательных к параболе
в точках Mi и М2:
У@)-0, /B) = -2.
Угловой коэффициент прямой во всех точках один и тот же и равен
в нашем случае —1. Теперь определяем угол между двумя прямыми:
2.6.4. Доказать, что отрезок касательной к гиперболе^ =*с/х, заклю-
заключенный между координатными осями, делится в точке касания пополам.
Решение. Имеем у'ш* — с/#а, следовательно, для касательной
в точке М(х01 у0) величина подкаса-
j У тельной
К
т. е. Ох0 = х0Т (рис. 37), что и тре-
требовалось доказать.
Отсюда вытекает простой способ
дГ j **~х построения касательной к гиперболе
у = с/х: надо отложить на оси Ох от-
Рис. 37. резок ОТ=2х0. Тогда МТ будет ис-
искомой касательной.
2.5.5. Доказать, что у цепной линии у = a ch (х/а) ордината есть
среднее геометрическое между длиной нормали и величиной а.
Решение. Вычислим длину нормали. Так как
то длина нормали
= \у ||Л +у'2 =*у V\+sh*(xla)=y ch (х/а)
откуда y2 = a-MN, y^Va-MN, что и требовалось доказать.
2.5.6. Найти угловой коэффициент касательной к кривой
Г x = t* + 3t—8,
\ y=z2t2—2t—5
в тдчке МB9 —I).
Решение. Прежде всего нужно определить значение t, соот-
соответствующее данным значениям х и у. Это значение должно одно-
одновременно удовлетворять двум уравнениям:
— 8 = 2,
\ 2^а—2t— 5 = — 1.
Корни первого уравнения: ^»2; /2 = — 5, корни второго уравнения:
* 2 ^ 1
К»
Следовательно, данной точке соответствует значение t — 2.
Теперь определим значение производной в точке М:
Итак, угловой коэффициент касательной в точке М B, — 1) равен 6/7.
2.5.7. Доказать, что касательная к лемнискате p = a/
в точке, соответствующей значению Эо = я/6, параллельна оси Ох.
Решение. Напишем уравнение лемнискаты в параметрическом
виде. Имеем
х = р cos 0 = a У cos 20 cos 0,
у = р sin 0 = a j/"cos20 sin 0.
Отсюда
' a cos 6 sin 20 лг ттк . Л
лге = г а у cos 20 sin 0.
/cos 20 '
a sin 0 sin 29 . -, / тгк л
ve = г + а К cos20 cos 0,
у cos 20
(я/6) = — a V% Уе (я/6) = 0.
ув (я/б)
Таким образом, угловой коэффициент k==— = 0. Следова-
xQ (я/6)
тельно, касательная к лемнискате в точке с 0О = я/6 и р0 =
= a j/cos 20О = а/У2 параллельна оси Ох,
2.5.8. Найти уравнения касательной и нормали к кривой
а) 4л:3 — 3*уа + 6*а — Ъху — 8j;2 + 9a:+14 = 0 в точке (—2, 3);
б) хъ+уъ—2ху = 0 в точке A, 1).
Решение, а) Дифференцируем функцию, заданную неявно:
12л:2—Зу2—6хуу' + \2х—5у—Ъху' —
Подставим координаты точки М{—2, 3):
48—27+36/—24 —15 +lQy' —48/+9 = 0;
отсюда
у' = — 9/2.
д
Следовательно, уравнение касательной: у—3=—^(х-{-2). Уравне-
2
ние нормали: у — 3 = -д-(д; + 2).
2.5.9. Через точку B, 0), не лежащую на кривой у = х*, про-
провести касательные к ней.
Решение. Пусть (л;0, х%) — точка касания; тогда уравнение
касательной запишется так:
или
у— х* = 4х](х—xQ).
103
По условию искомая касательная проходит через точку B, 0),
значит, координаты этой точки удовлетворяют уравнению касательной:
—*J = 4*5B—*0); 3*J —8*5 = 0.
Отсюда л:0 = 0; *0 = 8/3. Таким образом, точек касания две: ^@, 0),
Л*,(8/3, 4096/81).
Соответственно уравнения касательных будут
у-0 v_19^ —?048/ ^\
У-v, у 8i-27 v ъу
2.5.10. /(х) = 3хъ— 15*3 + 5д;—7. Выяснить, в какой из точек х
скорость изменения функции наименьшая?
Решение. Скорость изменения функции в некоторой точке равна
производной функции в этой точке:
/(*) = 15** — 45*2 + 5 = 15 [(я2 —1/2J +1/12].
Наименьшее значение /'(*) достигается при * = ±1/уг2. Сле-
Следовательно, наименьшая скорость изменения функции f(x) достига-
достигается в точках *=±1/]/*2 и равна 5/4.
2.5.11. Точка движется по кубической параболе 12у=х3. Какая
из ее координат изменяется быстрее?
Решение. Дифференцируя обе части данного уравнения по
времени tt получим соотношение между скоростями изменения коор-
координат:
12.у; = з*я-*;
или
x't 4
Следовательно,
1) при —2<*<2 отношение у\\х\ меньше единицы, т. е. ско-
скорость изменения ординаты меньше скорости изменения абсциссы;
2) при * = ±2 отношение у\\х\ равно единице, т. е. в этих
точках скорости изменения координат равны;
3) при х <—2 или д:>2 отношение у\\х\ больше единицы,
т. е. скорость изменения ординаты больше скорости изменения
абсциссы.
2.5.12. Тело массой 6 г движется прямолинейно по закону
$=—1 -)- In (^ + l) + (^+lK (s выражено в сантиметрах, t—в се-
секундах). Требуется вычислить кинетическую энергию (rnv2/2) через
1 сек после начала движения.
Решение. Скорость движения равна производной пути по вре-
времени:
Поэтому
104
2.5.13. Скорость прямолинейного деижения тела пропорциональна
квадратному корню из пройденного пути 5 (как, например, при сво-
свободном падении тела). Доказать, что тело движется под действием
постоянной силы.
Решение. По условию имеем
v = s't = a Ys (a = const);
отсюда
s'/ v a sJ aV2
Но по закону Ньютона сила
F—ks"u (k — const).
Следовательно,
F= ко?'/2 = const.
2.5.14. Плот подтягивается к берегу при помощи каната, кото-
который наматывается на ворот со скоростью 3 м/мин. Определить ско-
скорость движения плота в тот момент, когда его расстояние от берега
будет равно 25 л«, если ворот расположен на берегу выше поверх-
поверхности воды на 4 м.
Решение. Обозначим через 5 длину каната между воротом и
плотом и через х—расстояние от плотгГ до берега. По условию
Дифференцируя это соотношение по времени t, найдем зависи-
зависимость между их скоростями:
2ss't = 2хх'и
откуда
Учитывая, что
s't==3; # = 25; s = |/*252 + 42^25,3,
получаем
1^252 4- 42
Xt = -—2Г" 3 ^ 3>03 (М1мин)-
2.5.15. а) Найти угол наклона касательной к кубической пара-
параболе y = xz в точке х = Уз/3.
б) Написать уравнения касательных к кривой >> = 1/A+#2) в
точках ее пересечения с гиперболой у — l/(#+ 1).
в) Написать уравнение нормали к параболе у = х2-{-4х +1, пер-
перпендикулярной к прямой, соединяющей начало координат с верши-
вершиной параболы.
г) Под каким углом кривая у = ех пересекает ось Оу?
2.5.16. Скорость тела, движущегося прямолинейно, определяется
формулой г^ = 3/ + /2.
105
Какое ускорение будет иметь тело через 4 секунды после на-
начала движения?
2.5.17. Тело массой 100 кг движется прямолинейно по закону
s = 2t2-\-3t-\-\. Определить кинетическую энергию (mv2/2) тела
через 5 секунд после начала движения.
2.5.18. Показать, что если тело движется по закону s — ае1 -\-Ье~г,
то его ускорение численно равно пройденному пути.
2.5.19. Тело брошено вертикально вверх с начальной скоростью
а м/сек. На какой высоте будет оно через t секунд? Определить
скорость движения тела. Через сколько секунд тело достигнет
наивысшей точки и на каком расстоянии от земли?
2.5.20. Искусственные спутники Земли движутся вокруг Земли
по эллиптическим орбитам. Расстояние г спутника от центра Земли
может быть приближенно выражено в зависимости от времени t
следующим уравнением:
BM1I где M = ^(t—tn).
= я \\ — ecosAf—y(cos2M—1I,
Здесь а, е, Р и tn—постоянные: а — большая полуось орбиты,
8 — ее эксцентриситет, Р—период обращения искусственного спут-
спутника Земли (ИСЗ), a tn — время прохождения ИСЗ через перигей
(перигей ИСЗ — кратчайшее расстояние ИСЗ от центра Земли). Найти
скорость изменения расстояния г ИСЗ от центра Земли (т. е. найти
так называемую радиальную скорость ИСЗ).
§ 2.6. Дифференциал функции.
Приложение к приближенным вычислениям
Если приращение Ау функции y = f(x) может быть представлено так:
Ах+а(х, Ах) Ах,
где
lim а (я, Дл;)=0,
то такая функция называется дифференцируемой в точке х. Главная линейная
часть этого приращения А (х) Ах называется дифференциалом функции и обоз-
обозначается df (x) или dy. По определению, dx — AJx.
Для существования дифференциала функции y = f (х) необходимо и доста-
достаточно, чтобы существовала конечная производная у' = А(х). Дифференциал
функции можно записать следующим образом:
Для сложной функции y = f(u), u = tp(x) форма дифференциала сохраня-
сохраняется в виде
dy=f'(u)du
(инвариантность формы дифференциала).
Если Д# достаточно мало по абсолютной величине, то с точностью до
малых более высокого порядка, чем Д#, имеет место приближенная форму-
формула Ау та dy. Только для линейной функции у = ах+Ь имеем Ay—dy.
106
Дифференциалы высших порядков функции y = f(x) последовательно опре-
определяются так:
Если y = f(x) и я—независимая переменная, то
d*y = y'" (dx)*t ..., dny =
Если же y = f(u)t где ц = ф(х), то d2y — fn (u)du2-\-f (u)d?u и т. д.
2.6.1. Найти дифференциал функции
у = In A + el»x) + arctg еьх.
Вычислить dy при л; = 0; dx = 0,2.
Решение.
(e*xY I dr -
1-\-е1»х]их~~
Подставив л: = 0 и dx = 0}2, получим
dy\x=0; ^=o,2=4'Oj2==0'5-
2.6.2, Найти приращение и дифференциал функции
в точке х = \ при Ал: = 0,1.
Найти абсолютную и относительную погрешности, которые до-
допускаются при замене приращения функции ее дифференциалом.
Решение.
= 9д;2 Ал: + 9д:Аа;2 + 3 Алг3 + Ал:,
dy = (9x* + l)Ax.
Отсюда
При ^=1 и Ал; = 0,1 получаем
by—dy = 0,09 + 0,003 = 0,093,
Абсолютная погрешность [Ay — tfy| = 0,093, относительная погреш-
0,093
ность равна
или 8,5%.
2.6.3. Вычислить приближенно приращение функции
у = х*—7л:2
при изменении х от значения 5 к значению 5,01.
2.6.4. Пользуясь понятием дифференциала, найти приближенное
значение функции
при л* = 0,15.
107
Решение. Заметим, что из Ау ==у (х + Дл;) —у (х) получаем
у(х+Ах)=у(х) + Ау,
или, полагая Ay « dy,
В нашей задаче положим х = 0 и Ад: = 0,15. Тогда
5 V \2-х)
1
у'@)= -1, rfy = -1. 0,15= -0,03.
Следовательно,
у @,15) «у @) + dy = 1 —0,03 = 0,97.
Истинное значение у @,15) = 0,9702 с точностью до 10~4.
2.6.5. Найти приближенное значение:
a) cos 31°; б) lg 10,21; в) р/33; г) ctg45°10'.
Решение, а) При решении мы будем пользоваться формулой
(*) (задача 2.6.4). Полагаем х = п/6, Ах = я/180 и вычисляем:
«о. 81е - со. E-+ ^)« 1^-1 ^ = 0,861.
в) Полагаем #=32; Длг=1. По формуле (*) получим
?/33« У32+ (Ух)$хяяп. 1=2 + -^= = 2+^ = 2,
5]/324 °
2.6.6. Медный кубик, ребро которого равно 5 ел*, подвергся
равномерной шлифовке со всех сторон. Зная, что вес его умень-
уменьшился на 0,96 г и считая удельный вес меди равным 8, определить,
на сколько уменьшились размеры куба, т. е. на сколько укороти-
укоротилось его ребро.
Решение. Объем куба v = x3, где х—ребро куба. Объем
равен весу, деленному на удельный вес: v=p/d; изменение объема
куба равно Av = 0,96/8 = 0,12 (см3). Считая приближенно Av ж dv
и учитывая, что dv = 3x2dx, будем иметь 0,12 = 3-52-Ах, откуда
Ах = °~^ = 0,0016 см.
Ребро куба укоротилось на 0,0016 см.
2.6.7. Получить выражения для определения абсолютных погреш-
погрешностей функций через абсолютные погрешности их аргументов:
108
a)y=lnx; 6)y
в) y=slnx @<л;<я/2); r) y=tgx @<x<n/2);
Д) У = Iff (sin л:) @ < л; < я/2); e) jr = lg (tg x) @ < * < я/2).
Решение. Если функция f(x) дифференцируема в точке х и
абсолютная погрешность аргумента Дх достаточно мала, то в каче-
качестве абсолютной погрешности функции у можно принять число
а) Ау = | (In л;)' \х Дх = —, т. е. абсолютная погрешность нату-
натурального логарифма равна относительной погрешности аргумента.
м
б) Ду = Aв*)'Дж = ^Дя, где M = lge = 0,43429;
д) A, = |
е) Ay = |
Из д) и е) следует, что абсолютная погрешность lg tg лг всегда
больше, чем абсолютная погрешность lg sin x (для тех же х и AJ.
2.6.8. Найти дифференциалы dy, d2y от функции
у===4хь — 7л:2+ 3,
считая, что:
1) х—независимая переменная;
2) х—функция от другой независимой переменной.
Решение. Дифференциал первого порядка dy в силу свойства
инвариантности его формы записывается в обоих случаях одинаково:
dy =y' dx = B0x* — \4x) dx.
Однако в первом случае под dx понимается приращение незави-
независимой переменной Ax(dx=hx); во втором случае—дифференциал
от х, как от функции (может быть, что dx=?Ax).
Так как дифференциалы высших порядков не обладают свойст-
свойством инвариантности, то при отыскании d2y нам придется рассмат-
рассматривать два случая.
1) Пусть х—независимая переменная; тогда
d*y =y" dx2 = (80л;3 — 14) dx2.
2) Пусть х является функцией от некоторой другой переменной.
В этом случае
d2у = (80л;3 — 14) dx2 + B0л;4 — 14л;) d2x.
2.6.9. Найти дифференциалы высших порядков (л;—независимая
переменная):
а) з> = 4~*2; найти d2y; б) у = j/bi2*—4; найти d2y;
в) у = sin2 x; найти d*y.
109
2.6.10. у — In т-г--2? найти d2y при условии, что: а) х — незави-
симая переменная, б) х—функция от другой переменной. Рассмот-
Рассмотреть частный случай, когда x = tgt.
4
2.6.11. Объем V шара радиуса г равен -g- яг3. Найти прираще-
приращение и дифференциал объема и дать им геометрическую интерпретацию.
2.6.12. Свободное падение материальной точки определяется зако-
законом s = gt2/2. Найти приращение и дифференциал пути в момент t
и выяснить их механический смысл.
§ 2.7. Дополнительные задачи
2.7.1. Даны функции: а) / (л:) = [ л: | и б) ф(*) = |*3|. Существуют ли про-
производные этих функций в точке х = 07
2.7.2. Показать, что кривая y~e]xi в точке х = 0 не имеет касательной.
Каков угол между односторонними касательными к этой кривой в указанной
точке?
2.7.3. Показать, что функция
где ф(#) — непрерывная функция и ф(а)^0, не имеет производной в точке
х = а. Чему равны односторонние производные /1 (а) и /+ (а)?
2.7А. Дана функция
при х^О,
0 при х = 0.
На примере этой функции показать, что производная от непрерывной функ-
функции не обязательно сама является непрерывной функцией.
2.7.5. Пусть
Л *2' если *<*о>
ах-\-Ь, если х > х0.
Чему должны равняться коэффициенты а и Ь, чтобы функция была непрерыв-
непрерывной и имела производную в точке х0?
2.7.6. Из формулы cos3x=cos3* — 3cos*sin2л: дифференцированием вы-
вывести формулу sin Зх = 3 cos2xsinx—sin3*.
2.7.7. Из формулы для суммы геометрической прогрессии
1 .vrt + l
1+*+**+¦¦¦+*"= хх (х^\)
вывести формулы для следующих сумм:
а) \ + 2x+2>x*+...+nxn-i\
б) 12+22х+32х2+...4-п2л;»-1.
2.7.8. Доказать тождество
cos *+cos 3*+ ... +cos Bл— l)*=
и отсюда прлучить формулу для суммы
sin * + 3 sin 3*+ ... + B/z— 1) sin Bn— 1) x.
2.7.9. Найти у\ если:
a) #=/(sin2A;)+/(cos2*); б) у = f (e*) e* {*>;
в) У = logy UL> (x) (ф (x) > 0; у (x) > 0).
110
2.7.10. Можно ли утверждать, что произведение F (х)=f (x) g (х) не имеет
производной в точке x = xQ, если:
а) функция f (x) имеет производную в точке xOf а функция ф (х) не имеет
производной в этой точке;
б) обе функции f (х) и g (x) не имеют производной в точке х0.
Рассмотреть примеры: 1) f(x)~x; g(*) = |*|; 2) f(x) = \x\, g(x) = \x\.
Можно ли утверждать, что сумма F(x) — f(x)+g(x) не имеет производ-
производной в точке х = х0, если:
в) функция f (х) имеет производную в точке х0, а функция g(x) не имеет
производной в этой точке.
г) Обе функции f(x) и g(x) не имеют производной в точке #0?
2.7.11. Доказать, что производная четной дифференцируемой функции
есть нечетная функция, а производная нечетной функции есть четная функ-
функция. Дать геометрическое объяснение этим фактам.
2.7.12. Доказать, что производная периодической функции с периодом Т
есть периодическая функция с периодом Т.
2.7.13. Найти F' (х)9 если
X X2 X9
F(x) =
1 2х З*2
0 2 6*
2.7.14. Найти производную функции у = х\х\. Построить графики функ-
функции и ее производной.
2.7.15. Пусть имеем сложную функцию y — f (и), где и—(р(х). Среди каких
точек нужно искать точки, в которых сложная функция может не иметь про-
производной ? Обязательно ли в этих точках сложная функция не имеет1 произ-
производной? Рассмотреть функцию у = и2, и=\х\.
2.7.16. Найти у" для следующих функций:
Существует ли у" @)?
2,7.17. a) f (х) = хп\ показать, что
F (I) /B) (П f{nU\\
f(l) I¦*- [ 1 ... -[- '_2".
б) / (х) = хп~1е1/х; показать, что
[/(*)](я) = (-1)яз
2.7.18. у — хЧ~х1а\ показать, что
2.7.19. Показать, что функция # = arcsinx удовлетворяет соотношению
(\—х2)у" — ху\ Применяя к обеим частям этого тождества формулу Лейб-
Лейбница, найти у{п)@) (n^s2).
2.7.20. Доказать, что полиномы Чебышева
Тп (*)= 2^=1cos (n arccos *) (я = 1, 2, •. 0
удовлетворяют уравнению
A -х2) Гп (х)-хТ'п (х) + пЧп (х) = 0.
2.7.21. Производная я-го порядка от функции е~х* имеет вид
где Нп(х) — многочлен степени я, называемый многочленом Чебышева—Эрмитпа.
Ш
Доказать справедливость следующего рекуррентного соотношения:
Нп+1(х)-2хН„(х) + 2пНп-1(х) = 0 (п=1, 2, ...)•
2.7.22. Показать, что существует однозначная функция у = у(х), опреде-
определяемая уравнением t/3 + 3*/= *,¦ и найти ее производную у'х.
2.7.23. Выделить однозначные непрерывные ветви обратной функции
х — х(у) и найти их производные, если у = 2х2 —х*<
л п пл 1 1 1+у dudv ,
2.7.24. ц = — In ; проверить соотношение t"j-= *•
2.7.25. Обратные тригонометрические функции непрерывны во всех точках
области существования. Во всех ли точках этой области обратные тригоно-
тригонометрические функции имеют конечную производную? Указать точки, в кото-
которых следующие функции не имеют конечной производной:
a) t/=arccos—~- , б) */ =
2.7.26. Показать, что функция у — у(х), определяемая параметрически
x = 2t — 111, y = t2-\-t\t\, дифференцируема при / = 0, однако ее производная
не может быть найдена по обычной формуле.
2.7.27. В уравнении параболы у = ах2-\-Ьх-\-с определить параметры а,
Ь, с так, чтобы она касалась прямой у = х в точке х=\ и проходила через
точку (—1, 0).
2.7.28. Доказать, что кривые yx = f(x) (f (x) > 0) и y2 = f (x) sin ax, где
fix)—дифференцируемая функция, касаются друг друга в общих точках.
2.7.29. Показать, что для любой точки М (х0, у0) равнобочной гиперболы
х2—у2 = а2 отрезок нормали от точки М до точки пересечения с осью абсцисс
равен радиусу-вектору точки М.
2.7.30. Показать, что при любом положении производящего круга каса-
касательная и нормаль к циклоиде
x=^a(t—sin/), y = a(l — cost)
проходят соответственно через высшую (at, 2a) и низшую (at, 0) точки окруж-
окружности.
2.7.31. Показать, что две кардиоиды p = a(l+cosq>) и p = a(l — coscp)
пересекаются под прямым углом.
2.7.32. Пусть y=f(u), где и = у(х). Доказать справедливость равенства
<Ру = Г (и) du* + ЗГ (и) du d*u + /' (и) d^u.
2.7.33. Пусть y=f(x), где x = q>(t); функции f (x) и ф (t) дважды диффе-
дифференцируемы и dx Ф 0. Доказать, что
d2ydx—dyd2x
Ухх~ № '
где дифференциалы, фигурирующие справа, являются дифференциалами по
переменной /.
2.7.34. Как преобразуется выражение
v ; dx2 dx ' v
где у—дважды дифференцируемая функция от х, если ввести новую незави-
независимую переменную t, положив x=cos/?
2.7.35. При определении силы тока посредством тангенс-гальванометра
пользуются формулой
Где /—сила тока, к—коэффициент пропорциональности (зависящий от при-
прибора), ф—угол отклонения стрелки. Определить относительную ошибку ре-
результата, зависящую от неточности в отсчете угла ф. При каком положении
стрелки результаты получаются наиболее надежными?
113
Глава III
Применение дифференциального исчисления
к исследованию функций
§ 3.1. Основные теоремы
о дифференцируемых функциях
Теорема Ферма. Пусть функция y = f(х) определена на некотором
промежутке и во внутренней точке xQ этого промежутка имеет наибольшее или
наименьшее значение.
Если в точке х0 существует производная /' (xQ), то f (xQ) = Q.
Теорема Ролл я. Если функция / (х) непрерывна на отрезке [at b],
имеет конечную производную в каждой внутренней точке этого отрезка и
f(a) — f(b), то существует такая точка ??(а, Ь), что /'(?) = 0.
Теорема Лагранжа. Если функция / (х) непрерывна на отрезке
[а, Ь] и имеет конечную производную в каждой внутренней точке этого отрезка,
то существует такая точка ??(а, b)t что
/ F)-/(а) = F-а)/'(?).
Признак постоянства функции. Если во всех точках некото-
некоторого промежутка /'(х) = 0, то функция / (х) в этом промежутке сохраняет
постоянное значение.
Теорема Коши. Пусть функции фМ и i|) (х) непрерывны на отрезке
[а, Ь] и имеют конечные производные в каждой внутренней точке этого отрезка.
Если эти производные не обращаются в нуль одновременно и ф (а) ф <р F), то
существует такая точка ??(а, Ь), что
3.1.1. Удовлетворяет ли функция f(x) = 3x2— 1 условиям теоремы
Ферма на отрезке [1, 2]?
Решение. Заданная функция не удовлетворяет условию теоремы
Ферма, так как она монотонно возрастает на отрезке [1, 2] и, сле-
следовательно, принимает наименьшее значение при х=1 и наибольшее
значение при х — 2, т.е. не во внутренних точках отрезка [1, 2].
Поэтому теорема Ферма неприменима; другими словами, нельзя утвер-
утверждать, что /'A)=/'B) = 0. В самом деле, //A) = 6, /'B) = 12.
3.1.2. Удовлетворяют ли условиям теоремы Ролля: а) функция
/(д:)=1 — ?/** на отрезке [ —1, 1]? б) функция f(x) = In sin x на
отрезке [jt/6, 5я/6]? в) /(#) = 1 — |х\ на отрезке [—1, 1J? Если
нет, то почему?
Решение, а) Функция непрерывна на отрезке [—1, 1], кроме
того, /(—1)=/A) = 0. Значит, два условия теоремы Ролля выпол-
выполнены. Производная f'(x) = —2/C Y х) существует во всех точках,
па
кроме точки # = 0. Так как эта точка внутренняя, то третье условие
теоремы Ролля не выполнено. Поэтому теорема Ролля к данной
функции неприменима. И действительно, /'(х)Ф0 на [ — 1, 1].
3.1.3. Доказать, что уравнение
3^+15*—8 = 0
имеет только один действительный корень.
Решение. Существование хотя бы одного действительного
корня следует из того, что многочлен /(х) = Зхъ-\-\5х—8—нечет-
Зхъ-\-\5х—8—нечетной степени. Единственность такого корня докажем от противного.
Предположим, что существуют два корня дг1<л:2. Тогда на отрезке
[xv х2] функция f(x) = 3xb+\5x—8 удовлетворяет всем условиям
теоремы Ролля: она непрерывна, обращается на концах в нуль и в
каждой точке имеет производную. Следовательно, в некоторой точке ?,
хх < I < х>, /' (I) = 0. Однако /' (х) = 15 (х4 + 1) > 0. Полученное
противоречие доказывает, что заданное уравнение имеет лишь один
действительный корень.
3.1.4. Удовлетворяет ли функция f(x) = 3xz— 5 условиям теоремы
Лагранжа на отрезке [—2, 0]? Если да, то найти фигурирующую
в формуле Лагранжа f(b)—f(a)=f'(E>)(b—а) точку |.
Решение. Функция удовлетворяет условиям теоремы Лагранжа,
так как она непрерывна на отрезке [ — 2, 0] и имеет конечную про-
производную в каждой внутренней точке отрезка. Точку ? найдем из
формулы Лагранжа:
г (В 6 6
откуда 5= —1-
3.1.5. Применить формулу Лагранжа к функции f(x) = lnx на
отрезке [1, е] и найти соответствующее значение ?.
3.U6. Проверить, что функции f(x) = x2 — 2х + 3 и g-(jc) = ;t3—
— 7jc2 + 20x—5 удовлетворяют условиям теоремы Коши на отрезке
[1, 4] и найти соответствующее значение ?•
Решение. Данные функции f(x) и g(x) непрерывны везде, а
следовательно, и на отрезке [1, 4]; их производные /' (х) = 2х—2
и g'(x) = 'dx% — 14х + 20 конечны везде; кроме того, g' (x) не обра-
обращается в нуль ни при одном действительном значении х.
Таким образом, формула Коши к заданным функциям применима;
т. е.
27—9~3g2—14| + 20 К ^ 5 ^ '•
Решая последнее уравнение, находим два значения |: ?х = 2 и
5, = 4.
Из этих двух значений только |х = 2 является внутренней точкой.
114
3.1.7. Удовлетворяют ли функции
= ex и
условиям теоремы Коши на отрезке [ — 3, 3]?
3.1.8. На кривой у = х3 найти точку, в которой касательная
параллельна хорде, соединяющей точки А(—1, —1) и ВB, 8).
Решение. Функция у = л:3 на отрезке [—1, 2], концами кото-
которого являются абсциссы точек Л и Б, непрерывна и имеет конечную
производную, поэтому к ней применима теорема Лагранжа. Согласно
этой теореме на дуге АВ найдется по меньшей мере одна точка М,
в которой касательная параллельна хорде АВ. Напишем формулу
Лагранжа применительно к заданной функции:
или
8 + 1 = З^2 • 3;
отсюда
Найденные значения g и являются абсциссами искомых точек (их
оказалось две). Подставляя |х и ?2 в уравнение кривой, найдем соот-
соответствующие ординаты:
Таким образом, искомыми точками являются Afx A, 1); М2( — 1, —1).
Из них только точка ^A, 1) является внутренней точкой дуги АВ.
Замечание. Эту задачу можно решить и не прибегая к теореме Ла-
Лагранжа; нужно составить уравнение хорды как прямой, проходящей через две
заданные точки, а затем найти на кривой точку, в которой касательная
параллельна хорде.
3.1.9. Пользуясь признаком постоянства функции, вывести сле-
следующие формулы, известные из элементарной математики:
a) arcsinx + arccosх = п/2; б) sin2;x;=(l — cos2#)/2;
в) arccos-rp^ = 2arctg# при
fn—2arctgA:
2arctgx при —
— jt—2ardgx при jc< — 1.
Решение, а) Введем в рассмотрение функцию
f(x) = arc sin л: + arccos xf
определенную на отрезке [—1, 1]. Производная указанной функции
внутри этого отрезка равна нулю:
ш
На основании признака постоянства функции f(x) = const, т. е.
arcsin л; + arccos л; = С (— 1 < х < 1).
Чтобы определить постоянную С, положим, например, х = 0,
получим я/2 = С. Отсюда
arcsin х + arccos л; = я/2 (—1 <д:<1).
Справедливость этого равенства в точках д; = ± 1 проверяется непо-
непосредственно.
б) Введем в рассмотрение функцию
/ (л;) = sin2 х + -j cos 2x,
определенную на всей числовой прямой: —оо<д;<оо. Производная
этой функции всюду равна нулю:
/' (х) =а 2 sin х cos x—sin 2x s= 0.
На основании признака постоянства функции
sin2 х + ~ cos 2лг = С.
Для определения С положим, например, х = 0; тогда получим 1/2 = С.
Отсюда
cos2;c
или
. «, 1 — cos 2дс
smj х = о •
в) Введем в рассмотрение функцию
/(л:) = arccos j^W~ 2 arctS *»
II Х2
1 , 2
Производная функции f(x) равна нулю при всех л;>0:
На основании признака постоянства функции
arccos ух^г"—2 arctg л: = С при дг > 0.
Для определения С положим, например, дг=*1, что дает С=
= arccos 0—2 arctg 1 = 0.
Справедливость доказанной формулы при #*=(} проверяется непо-
непосредственно.
116
J x*
Замечание. При #=0 производная функции arc cos ¦ ¦ 2 не суще-
существует. При х < 0 производная от нее равна
» - — 1 ^
что позволяет получить формулу
1 х%
arc cos a = — 2 arctg я (л: < 0).
Последнюю формулу можно также получить на том основании! что
\ х%
arc cos t 2—четная функция, а 2 arctg x — нечетная функция.
3.1.10. Известно, что (ех)'-=ех для всех х. Существуют ли еще
какие-нибудь функции, совпадающие со своими производными всюду?
Решение. Пусть функция f(x) такова, что /' (х)=/(х) всюду.
Введем в рассмотрение функцию
Ф(*) = 7Г=
Производная этой функции равна нулю всюду:
ф' (х) =/' (х) e-*—e-xf{x) = 0.
На основании признака постоянства функции f(x)/ex = C. Отсюда
)
Итак, мы доказали, что класс функций, для которых f {x)=f(x)f
исчерпывается формулой f(x) = Cex.
3.1.11. Доказать неравенство
arctg x2—arctg х1 < x2—xlt
где х2 > хг.
Решение. К функции /(х) = arctgx на отрезке [х19 х2] при-
применим формулу Лагранжа:
arctg x2—arctg xx = j^ (x2—хг),
где хг < I < х2.
Так как
°<jqr|2-<1 и Х2—*i>0t
то
arctg х2 — arctg хх < х2—x1#
В частности, положив ^ = 0 и х2 = х} получим
arctg x<x (х>0).
3.1.12. Показать, что корни квадратные из двух последователь-
последовательных натуральных чисел, больших N2, отличаются между собой
менее, чем на l/BiV).
Д17
Решение. К функций f(x)==]/rx на отрезке [л, я+1] при-
применим формулу Лагранжа:
где
Если n>N\ то и ? > iV2, следовательно, 1/B }/" g) < l/BiV),
откуда
3.1.13. Используя теорему Ролля, доказать, что производная /' (х)
функции
xsin j при х>0,
О при лг = О,
обращается в нуль на бесконечном множестве точек промежутка
(О, 1).
Решение. Функция f(x) обращается в нуль в точках, где
sin(я/х) = 0, n/x = kn, x=\/k, ft=l, 2, 3, ...
Так как функция f(x) во всякой внутренней точке отрезка [0, 1]
имеет производную, то к любому из отрезков [1/2, 1], [1/3, 1/2], ...
. . ., [1/(&+ 1), 1/А], ... можно при-
применить теорему Ролля. Следова-
Следовательно, внутри каждого из отрезков
последовательности имеется точка ?Л,
l/(&-f-l)<C?fc<Cl/&, в которой произ-
производная f (?у = 0. Тем самым мы по-
показали, что производная обращается
в нуль на бесконечном множестве
точек (рис. 38).
3.1.14. Полиномом Лежандра на-
называется полином, который опреде*
ляется следующей формулой (фор-
(формулой Родрига):
Рис. 38.
(я = 0, 1,2, ...).
Пользуясь теоремой Ролля, доказать, что полином Лежандра
Рп (х) имеет п различных действительных корней, которые все содер-
содержатся между —1 и +1.
Решение. Рассмотрим функцию
Эта функция и ее п—1 последовательных производных обращаются
в нуль в точках х = ± 1 (применить формулу Лейбница для высших
производных от произведения двух функций).
118
Из того, что/A)=/(—lJ^O, следует, что найдется внутри
отрезка [ — 1, 1] точка |г, в которой /' (?х) = 0, т.е. х — ^ будет
корнем первой производной. Теперь к функции /' {х) снова применяем
теорему Ролля на отрезках [ — 1, ?х], [|г, 1]. Получим, что функция
f" (х), помимо +1 и —1, на отрезке [ — 1, 1] имеет еще два корня.
Повторяя только что проведенные рассуждения, установим, что
(п—1)-я производная, помимо +1 и —1, имеет на отрезке [ — 1, 1]
еще п—1 корень, т. е. всего у функции /ш~1) (х) на отрезке [—1, 1]
имеется п-\-\ корней, которые разбивают этот отрезок на п частей.
Применяя еще раз теорему Ролля, убеждаемся в том, что функция
f{n)(x), а, значит, и функция Pn(x) = -^-jf^n) (x)t имеет п различ-
различных корней на отрезке [ — 1, 1].
3.1.15. Проверить, применима ли формула Лагранжа к функциям:
а) /(х) = х2 на отрезке [3, 4];
б) f\x) = \nx на отрезке [1, 3];
в) f(x) = 4*8 — 5х2 + *—2 на отрезке [0, 1];
г) f(x)=l/x*(x—\) на отрезке [ — 1/2, 1/2].
В случае применимости найти значения 1-, фигурирующие в этой
формуле.
3.1.16. Пользуясь теоремой Лагранжа, оценить значение In A +?)•
3.1.17. Пользуясь формулой Лагранжа, доказать неравенство
х
т—,— <1пA -\-х) <* при х > 0.
§ 3.2. Раскрытие неопределенностей*
Правило Лопиталя
0 00
I. Неопределенности вида -д-, — . Если функции / (#) и g (x) дифферен-
дифференцируемы в некоторой окрестности точки а, за исключением, быть может, самой
точки а, причем g' (х) Ф 0, и если
limf{x)= limg(#)=0 или lim f (x)=\img(x)~co9
х-* а х-+а х-*а х -*¦ a
TO
f (x)
при условии, что предел lim —гг{ существует {правило Лопиталя). Точка а
х -+ a g \X)
может быть как конечной, так и несобственной точкой +оо или —оо.
II. Неопределенности вида О-оо или оо — оо приводятся к неопределен-
ностям вида тг или — алгебраическими преобразованиями.
U оо
III. Неопределенности вида Iе0, оо° или 0° сводятся к неопределенности
вида 0 • оо с помощью предварительного логарифмирования или преобразования
119
3.2.1. Применяя правило Лопиталя, найти пределы функций:
a) lim
0
еах__е-ъах
ех__е-х_2х
х—sin x *
sin За:2
In cos Bл;2—x) *
б)
e)
lim
lim
* a
cos3*—e-*'
2arctgx*—n'
x-*0
Решение, а) Здесь обе функции f(x) = eax — e~2ax и g{x) =
= ln(l+jc)—бесконечно малые в окрестности нуля, так как
lim / (х) = 1 — 1 = 0; lim g (x) = In 1 = 0.
х-+ 0 х-+ 0
Далее f (x) и g' (x) существуют во всякой окрестности точки
л: = 0, не содержащей точки х=—1, причем
Наконец, существует предел отношения производных:
Поэтому применимо правило Лопиталя:
Замеч ание. Вычисление предела отношения по правилу Лопиталя
обычно записывают сразу так, как это сделано в (#). В существовании
нужных производных и пределов убеждаются в самом ходе вычислений. Если
при этом отношение производных ' снова представляет собой неопределен-
ность, то правило Лопиталя применяют повторно, пока не устранится неопре-
неопределенность или обнаружится, что нужные пределы не существуют. Поэтому в
дальнейшем приводится только запись необходимых преобразований (а про-
проверка выполнения условий их применимости предоставляется читателю).
уТ+2х+\
б) lim v = lim
Y2 + x + x
sin Зл;2 _ •—6л; cos Зл;2 cos Bл;2—л;) __
!л;2—х) ~~ x™Q Dл; — 1) sin B*2—х) ""
— fir cos Зл;2 cos Bл;2—л:) -.
х-*о ^х ^ х + {
Предел первого сомножителя вычисляется непосредственно, а предел
второго сомножителя, представляющего собой неопределенность вида
120
—, находим с помощью правила Лопиталя:
lim
4*—1 ^0 sin B** —x)
e_6 .L} Hm (^d
3.2.2. Известно, что при х—> + °° функции xk{k>0)\ logax;
а*(а>1) являются бесконечно большими величинами. Пользуясь
правилом Лопиталя, сравнить эти величины между собой.
1
Решение, a) hm -^-== lim , fe_x =logflg lim zp"=0;
б) lim -7- = lim —^— = .. . = lim —^n\—r^ = 0.
Следовательно, степенная функция хк (k > 0) растет быстрее, чем
логарифмическая функция logax(a > 1), а показательная функция а*
с основанием, большим единицы, растет быстрее, чем степенная
функция хт.
3.2.3. Найти пределы:
Решение, а) Имеем неопределенность вида оо—оо. Приведем
О
эту неопределенность к неопределенности вида -^-, а затем приме-
применим правило Лопиталя:
x—1
- —;*in*+*--i-;"" in^+2~2 •
3.2.4. Найти пределы:
a) lim*nln* (n>0); 6) lim [In A +sin2x) ctgln2 A +x)].
Решение, а) Имеем неопределенность вида 0«oo.
Преобразуем к неопределенности вида —, после чего применим
правило Лопиталя:
limxn In х = lim —n = Hm —„ * _х = lim xn = 0, так как п >0.
X-+Q X-+Q* х-+0—ПХ п х->0
т
б) Имеем неопределенность вида 0-оо:
lim [In (I -J-sin2 x) ctg In2 <
T-.—r-z— sin 2x
,. 1+sin2* t. sin x t. cosa: -
= hm ——-—= hm ,—yj—.—~ hm,, yi ,— = 1#
3.2.5. Найти пределы:
a) lim (l/#)sin*; 6) Hm ^i/in(e*-i)#
Jt-> + 0 x-+ + 0
Решение, а) Имеем неопределенность вида оо°. Пусть у =
= A/A;)shlj:; тогда
= sin д: In
lim \ny = limslnx\n(\/x) (неопределенность вида 0-оо).
0
Преобразуем к неопределенности вида — и применим правило Лопи-
таля:
.. , -. —In a; t. —\/х f. sin2^ л
hm In v = hm тг-.— = hm —; —-=hm =0.
Следовательно, lim у = e° = 1.
X-+ + 0
3.2.6. Найти пределы:
a) lim (sin *)***; 6) Hm x*.
Х-+П/2 x-+Q
3.2.7. Вычислить
Hm (tgx)ctz*.
О
Решение. Воспользуемся тождеством
но
lim ctgA;lntgA:= lim Ц*?*= lim _1Л?==
Отсюда
lim
3.2.8. Установить, существуют ли нижеследующие пределы, при-
применимо ли к их вычислению правило Лопиталя и приводит ли к
правильному ответу его формальное применение:
^М1/*К б 2+2s+sin2s . . н tg?
122
Решение, а) Предел существует и равен 0. В самом деле,
m xsinl- L0-0.
Предел же отношения производных не существует. Действительно,
Ит 0lim
Х-+0 C0SX X-+0
но Urn cosA/jc) не существует, следовательно, правило Лопиталя
Х-+0
здесь неприменимо.
б) Предел отношения функций не существует:
lim 2 + 2* + sin2* д11ш (л . 2 ^ «,-sfn*
?™ B*+sin2*)*sin* "j™ ^ + 2* + sm2*J *
но lim e~sinx не существует, так как функция e~sinx при х—* оо
пробегает бесчисленное множество раз значения от \/е до е.
Покажем, что предел отношения производных существует!
f. 2+2 cos 2*
lim
[2 + 2 cos2* + B* + sin2*) cos*]
4 cos2 *
4 cos2 * + B* + sin 2*) cos *
cQ
cos ^ + sin2jc в ~ Uj
4 cos x
так как функция в-^*-ограничена, а
Здесь мы сократили числитель и знаменатель на cos*, который
обращается в нуль для бесконечного множества значений х. Именно
наличие этого множителя, обращающего одновременно в нуль про-
производные сравниваемых функций, приводит к неприменимости в этом
случае правила Лопиталя.
ч ,, tgat ,. sec2* f. sec* ,. iex
в) lim -=— = lim -—г—= lim т— = lim -в— = .. .
Здесь применение правила Лопиталя не приводит к цели, хотя
предел существует:
,. tgх n sin* cos* ,.
hm ШИ:Ж lim Cos* ^ Нш
а:->Я/2
3.2.9. Применяя правило Лопиталя, найти пределы функций;
аХпх— х
а llm jrfj-чг 1Q In*
123
в) Hm ^^ ; г) lim
д) lim arcsin ^=^ ctg (a:—a); e) lim (n—2 arctg *) In
ж) lim DУ8*»' 3) lim(al^_i)je (a > 0);
и) lim (cos я»)»/"; к) Hm B—i)**"",
л) lim (Д--Д-) ; м) lim я"'" <**-i>;
н) lim (*_ ctg»*V оI1шГх—*» In f 1+4I;
n) Hm *• fdi ? -11; p) lim (
; т) Ш
'"П *
§ 3.3. Формула Тейлора.
Приложение к приближенным вычислениям
Если функция f (x) непрерывна и имеет на отрезке [a, b] непрерывные
производные до (п—1)-го порядка включительно, а в каждой внутренней
точке отрезка имеет конечную производную n-го порядка, то при х?[а, Ь]
справедлива следующая формула Тейлора:
где g = a+e(jc—а) и 0 < 9 < 1.
Если положить в этой формуле я = 0, то получим формулу Маклорена:
где g=e^, о < е < 1.
Последний член в формуле Тейлора называется остаточным членом фор»
мулы Тейлора в форме Лаеранжа и обозначается Rn {x):
соответственно остаточный член в формуле Маклорена имеет вид
3.3.1. Разложить многочлен Р(х) = хь—2л:4-\-х*—х2-\-2х—1 по
степеням двучлена х—1, пользуясь формулой Тейлора.
124
Решение. Для решения задачи необходимо найти значение
многочлена и его производных в точке ^=1. Проводим соответ-
соответствующие вычисления:
) , () ,
) = 72, РE>A>= 120,
.О (л>6)
при любом х.
Подставив найденные значения в формулу Тейлора, получим
P(x) = gl(x-l)* + '%(x-l)* + ^ (х- IN;
р (х) = 3 (х— 1 K + 3 (х— 1 L + (х — 1 M.
3.3.2. С помощью формулы Маклорена разложить по степеням
х функцию
A
заданную на отрезке [0, 1]. Оценить погрешность, допускаемую
при сохранении только десяти первых членов.
Решение.
/@) = In 1=0.
Производные любого порядка от данной функции (см. § 2.3):
/(-> @) = (_ 1)« -1 (/г — 1)! (/1 = 1,2,3,...).
Подставив в формулу Маклорена, получим
\п(\ +х) = х-^+?- .. . +^- + R10(x),
где остаточный член R1Q (x) в форме Лагранжа запишется так:
Оценим абсолютную величину остаточного члена Rl0 (x); учиты-
учитывая, что 0^#^1 и |>0, получим
— X1
3.3.3. Сколько нужно взять членов в формуле Маклорена для
функции f(x)~ex, чтобы получить многочлен, представляющий эту
функцию на отрезке [—1, 1], с точностью до 0,001?
Решение. Функция f(x) = e* имеет производную любого по-
порядка
125
Поэтому к этой функции можно применить формулу Маклорена.
Вычислим значения функции ех и ее п—1 первых производных в
точке д: = 0, а значение я-й производной —в точке | = 9д; @ <8 < 1).
Будем иметь
Отсюда
где
Так как, по условию, |#|^1 и 0<6<1, то
Следовательно, если выполняется неравенство
А < 0,001, (*)
то заведомо будет выполняться неравенство
Для этого достаточно взять я^7 G! = 5040). Таким образом, в фор-
формуле Маклорена достаточно взять 7 членов.
3.3.4. При каких значениях х приближенная формула
имеет погрешность меньше 0,00005?
Решение. Правая часть приближенного равенства представляет
собой шесть первых членов в формуле Маклорена для функции cosa:
(второй, четвертый и шестой члены равны нулю; проверьте!). Оце-
Оценим Re(x). Так как (cosa:)F) = — cosa;, to
Чтобы погрешность была меньше 0,00005, надо выбрать значения х,
удовлетворяющие неравенству
'¦|j? < 0,00005.
Решая это неравенство, получим |дг|< 0,575.
3.3.5. Вычислить с точностью до 10"* приближенные значения:
a) cos 5°; б) sin 20°.
Решение, а) В формулу Маклорена
подставляем # —я/36; так как
v2 jt2 у4 1 /v2\2
iL^^JL^ 0,003808, ? = !(^) =2,4-10-,
то ограничимся только следующими членами:
1—х2/2.
При этом погрешность оценивается величиной
cos Qx
I*
Итак, с требуемой точностью,
cos 5° = cos ig = 1—0,00381 - 0,99619.
3.3.6. Вычислить с точностью до 10 ~6 приближенное значение
3.3.7. Доказать неравенства:
а) х—х2/2 < In A + х)< х при х > 0;
б) *g * > х + #3/3 при 0<л:<я/2;
в) 1 + y х—~ <|/ч1+л:<1+-уд: при 0 < х < оо.
Решение, а) По формуле Маклорена с остаточным членом
R2(x) имеем
где 0 < 5 < х.
По той же формуле с остаточным членом R3 (x) имеем
InA+*) *+
Так как 2 ^ > а- > 0 и 3п-|-Е )э > 0 при л: > 0, то отсюда следует,
что
х—х2/2
3.3.8. Показать, что sin (а + Щ отличается от sin a + h cos а не
более, чем на А2/2.
Решение. По формуле Тейлора
sin (a -f h) == sin а -f- A cos а —^-sin |;
отсюда
) — (sina-f Acosa) [= ~-|sin?l<^,
327
§ 3.4. Локальная формула Тейлора.
Применение к вычислению пределов
Локальной формулой Тейлора называется формула
где запись y(x) = o[ip (х)] означает, что функция ф (х) имеет при х—>а более
высокий порядок малости, чем функция о|? (х), т. е. lim У *х' = О,
х -+ a ty\x)
В частности, при а = 0 имеем
Локальная формула Тейлора показывает, что, заменив f (х) в окрестно-
окрестности точки а ее многочленом Тейлора п-й степени, мы совершим ошибку,
представляющую собой при х—> а бесконечно малую более высокого
порядка, чем (х—а)п.
Для практических задач наиболее важны следующие пять основных раз-
разложений:
ех= 1 +х +|1+ ... +^ + о (х«);
^^
In A+*) = *—+y+... + (-l)»-1^
3.4.1. Написать разложение функции /(A*) = sin2A:—д:2^"^ по це-
целым положительным степеням х, ограничиваясь членами до четвер-
четвертого порядка малости относительно х.
Решение. Имеем
? + о(х)-х + х~
3.4.2. Написать разложение функций:
а) /(х) = х ]/г\ —x2 — cos х In (I + х);
б) /(x) = ln(l +sinjc)
128
по целым положительным степеням х, ограничиваясь членами до
пятого порядка малости относительно х.
3.4.3. С помощью локальной формулы Тейлора вычислить пределы:
a) hm —rSrx ; б) lim
х-+о 1ь ¦* х-+0
ч ,. cos х—е~х212 ч 1# e*sin
в) 1пп -j ; г) hm уз
д) шп?!±5^.
*-+ о *
Решение, а) Сохраняя в знаменателе и числителе члены до
четвертого порядка относительно х, получим
11Ш
l — yT+^cos* .. 1-A4-^2I/2cosjc
j—Я == 11ПП -г =
- hm
X-+Q
= hm T
X-+Q I6
3.4.4. Написать разложения следующих функций по целым поло-
положительным степеням переменной х до членов указанного порядка
включительно:
а) f(x) = e2x-*2 до члена с хь;
б) In cos x до члена с д:6;
в) х до члена с д;4.
§ 3.5. Признаки монотонности функции
Пусть на отрезке [а, Ь] определена непрерывная функция f (х), имеющая
внутри отрезка конечную производную. Тогда:
1. Для того чтобы / {х) была неубывающей (невозрастающей) на [а, 6],
необходимо и достаточно, чтобы /' (х) ^ 0 (/' (х) ^ 0) для всех х из (а, 6)»
2. Для того чтобы f (х) была возрастающей (убывающей) на [а, Ь], доста-
достаточно выполнения условия /' (х) > 0 (/' (х) < 0) для всех х из (а, Ь).
3.5.1. Определить промежутки монотонности функций:
a) f(x) = 2x2 — In*; б) f(x) = 2x3 — 9x2 — 24л:+ 7;
в) /(*) = *2в-*. г)/ (*) = 1п}х|;
д) /(х) = 4*3 — 2 1л:2 + 18*+ 20; е) /(*)=***+5*.
Решение. Решение задачи сводится к нахождению для каждой
из данных функций промежутков, где производная сохраняет знак.
129
Если функция f(x) в интервале (a, b) обладает непрерывной произ-
производной и имеет в нем конечное число стационарных точек хХ1 х2, ,.. , хп
(a<xt<x2< ... <xn<bI где f{xk)**0 (*«1, 2, ... , л),
то /' (х) сохраняет знак в каждом из интервалов (а, д^), (xv х2), ...
а) Функция определена при х > 0.
Найдем производную
f (х)=**4х—1/л;.
Функция возрастает, если 4л;—1/л;>0, т. е. л;> 1/2.
Функция убывает, если 4л;—1/л;<0, т. е. л;<1/2.
Итак, в интервале 0<#<l/2 функция убывает, в интервале
1/2 <# < + оо возрастает.
б) Вычисляем производную
/' (х) — 6л;2 — 18л;—24 = 6 (л;2 — Зл;— 4).
Производная обращается в нуль в точках х*=*—1 и л; = 4. Так как
/' (л;) есть квадратный трехчлен со старшим коэффициентом 6 > 0,
то /' (л;) > 0 в интервалах
хУ (— оо, —1), D, оо) и /'(*)< О
в интервале (—1, 4). Следова-
Следовательно, в первых двух интерва-
интервалах f(x) возрастает, а в интерва-
интервале (— 1, 4) убывает.
в) В этом случае производная
f (х) *= Bх—л;2) е~х обращается
в нуль в точках л;«=0 и х ^ 2.
Рис. 39. В интервалах (— оо, 0) и B, оо)
производная f (л;) < 0 и функция
убывает, в интервале @, 2) производная /' (л;) > 0 и функция воз-
возрастает (рис. 39).
3.5.2. Найти интервалы убывания и возрастания функций:
a) /(a;) = cos (я/л;); б) /(л;) = sin л; + cos л; на отрезке [0, 2я].
Решение, а) Функция у » cos (я/л;) определена и дифференци-
дифференцируема на всей числовой оси, за исключением точки x***Q;
Очевидно, что знак у' совпадает со знаком множителя sin
1) sin (n/x) > 0 при условии
2&я < п/х < Bk-\- 1) я (& = 0, ±1| ±2, ...);
g) sin {п/х) < 0 при условии
Bk+ 1) я < п/х < 2 (к+ 1) я.
Следовательно, функция возрастает в интервалах
1
1 2k)
130
и убывает в интервалах
3.5.3. Изучить ход изменения функции
f (х) = 2 smx-\-igx—Ъх в интервале (—я/2, я/2).
Решение. Производная
/'(*) = 2 cos ЛГ + -4 3=(l-cos*Hl+cos*-2cos**) =
J v ' ' cos2 a; cos2*
^ 4 sin3 (x/2) sin C*/2)
385 cos2 x
положительна в интервалах (—я/2, 0) и @, я/2), обращаясь в нуль
только при #=0. Следовательно, в интервале (—я/2, я/2) функция
f(x) возрастает.
3.5.4. Доказать, что при 0<л:^1 выполняются неравенства
Решение. Мы докажем только правое из этих неравенств (ле-
(левое доказывается аналогично).
Производная функции
равна
Функция f(x) непрерывна на всей числовой оси; в частности, она
непрерывна на отрезке [0, 1], а внутри этого отрезка /'(•*)<().
Поэтому f(x) убывает на отрезке [0, 1] и, следовательно, для лю-
любой точки ху 0<д:^1, выполняется неравенство /(#)</@) = 0
или
arctg*—л;+л;3/6<0,
откуда
arctgx < х—х3/6.
3.3.5. Доказать неравенства
л;—-л:3/6 <sinA:<x при д?>0.
3.5.6. Доказать, что при O^p^l и любых положительных а
и b справедливо неравенство (а-\-Ъ)р^а?-\-Ър.
Решение. Если разделить обе части неравенства на Ьр1 то око
примет вид
или
A+*)'<!+**, (*)
где х=а[Ь.
131
Покажем, что неравенство (*) имеет место при любом положи-
положительном х.
Введем функцию
Производная этой функции
всюду положительна, так как, по условию, 1—р^О и jc>0.
Следовательно, функция возрастает в промежутке [0, оо), т. е.
f(x)=l+xP — A+*)*>/@) = 0, откуда \+хр>(\+х)р, что и
требовалось доказать. Если положить р=1/#, то получим
З.Б.7. Доказать, что функция у =*= хь + 2л;3 + х везде возрастает,
а функция^ — 1—Xs везде убывает.
3.5.8. Определить интервалы возрастания и убывания функций:
а) /(*) = х» + 2*-5; б) /(*) = 1пA -х*
в) /(*) = cos*-*j г) I1
3.5.9. Доказать неравенства:
a) tg*>* + *8/3, если @<х<п/2);
б) ех^\-\-х для всех значений х\
в) е^ > ех при л: > 1.
3.5.10. При каких значениях коэффициента а функция f(x) =
= л:3—ах возрастает на всей числовой оси?
3.5.11. При каком значении Ь функция
f (х) = sin х—Ьх-\- с
убывает на всей числовой оси?
§ 3.6. Максимумы и минимумы функции
Если функция y = f(x) определена на промежутке X, то внутренняя
точка х0 этого промежутка называется точкой максимума функции f (х) [точ-
[точкой минимума функции / (я)], если существует такая окрестность V ? X точки хо>
в которой для всех x?U выполняется неравенство f (х)^/(#0) lf(x)^f(x0)].
Точки максимума и точки минимума называются точками экстремума.
Необходимое условие точки экстремума. В точках экстре-
экстремума производная /' (х) рарна нулю или не существует.
Точки, в которых производная f (x) равна нулю или не существует, назы-
называются критическими точками.
Достаточные условия экстремума.
I. Пусть функция f (x) непрерывна в некоторой окрестности точки х0.
1. Если /' (х) > 0 при х < х0 и /' (х) < 0 при х > xQ (т. е. при переходе
132
через точку х0 производная меняет знак + на —), то в точке х0 функция
достигает максимума.
2. Если /' (х) < О при х < xQ и /' (х) > 0 при х > х0 (т. е. при перехода
через точку х0 производная меняет знак — на -f), то в точке х0 функция
достигает минимума.
3. Если производная не меняет знака при переходе через х0, то экстре-
экстремума нет.
II. Пусть в критической точке х0 функция f (х) дважды дифференцируема
(значит, f (хо) = О). Если при этом f№ (xQ) < 0, то в точке х0 функция дости-
достигает максимума, если /" (х0) > 0, то в точке х0 функция достигает минимума,
если же /"(л:0} = 0, то вопрос о наличии экстремума в этой точке остается
открытым.
III. Пусть /' (*о) = Г (*о)= ... =р-1) (*0) = 0. но /(я) (*а) Ф 0- Если число п
четное, то при р>(х0) < 0 в точке х0 — максимум, при fin)(x0) > 0—минимум.
Если же число п нечетное, то экстремума в точке х0 нет.
IV. Пусть некоторая функция y = f(x) задана параметрически,
где функции ф (/) и t|? (t) в некотором промежутке изменения аргумента t имеют
производные как первого, так и второго порядка, причем ф' (t) Ф 0. Пусть,
далее, при t = t0
Тогда:
а) если фда(/0) < 0, то функция y — f(x) при x = xo = <p(to) имеет максимум;
б) если ф"(/0) > 0, то функция y = f(x) при д; = л:0 = ф(*0) имеет минимум;
в) если фда(/0)=0, то вопрос о наличии экстремума остается открытым.
Точки, в которых ф' (t) обращается в нуль, требуют специального исследо-
исследования.
3.6.1. Пользуясь первой производной, найти экстремумы функций:
О ж п
а) /(*) = —
б) /(лг) = *4--8л;3 + 22л;2 — 24л:+12;
в) /(х) = х(х+\)Цх-3)*; г)
Решение, а) Функция определена и дифференцируема на всей
числовой оси. Поэтому критическими точками являются только дей-
действительные корни производной
/ (х) = Зл:3 — Зх2 — 1 8л: = Зд: (х + 2) (х — 3).
Приравняв последнее выражение нулю, найдем критические точки:
#! = — 2, л;2 = 0, лг3 = 3 (их всегда следует располагать в порядке
возрастания). Теперь исследуем знак производной в окрестности каж-
каждой из этих точек. Так как левее тдчки х = —2 критических точек
нет, то производная во всех точках х <—2 имеет один и тот же
знак: она отрицательна. Аналогично на интервале (—2, 0) производ-
производная положительна, на интервале @, 3) отрицательна, при х > 3
положительна. Следовательно, в точках х± = —2 и лг8 = 3 минимумы
/(_2) = —9 и /C) = — 40 -—, а в точке *2*=0 максимум /@) = 7.
в) Как и в примере а), критические точки — это корни производ-
производной /' (х), так как функция определена и дифференцируема на всей
133
числовой оси. Найдем f (x):
= 3 (x+ lJ (дг —З) Bл:2 — Злг— 1).
Приравняв последнее выражение нулю, найдем критические точки:
Составим таблицу знаков производной на интервалах между кри-
критическими точками:
Интервалы
Знак /'(*)
X < Xi
*i < х < х2
х2 < х < х3
+
xz < х < #4
х4 < а:
+
Из этой таблицы видно, что в точке хх = —1 нет экстремума,
в точке х2 —-минимум, в точке дг3 — максимум, в точке л:4—минимум.
3.6.2. Пользуясь первой производной, найти экстремумы функций:
*-**; б) /(х)=У&^Л)*+ ^^?
Решение, а) Функция определена и непрерывна на всей чис-
числовой оси. Найдем производную:
лут~х)'
Из уравнения f'(x) — 0 найдем корни производной: х*=±\.
Кроме того, производная обращается в бесконечность в точке
х=0. Таким образом, критическими точками являются хх = —1,
#2 = 0, д;3=1. Результаты исследования знака производной в ок-
окрестности этих точек приведены на рис. 40. Это исследование по-
показывает, что функция име-
^> ' «^
44
ет два максимума: /(—1) =
_ .*>.— ~^ /A) = 2 и минимум
3.6.3. Пользуясь второй
Рис. 40. производной, выяснить ха-
характер экстремума функций:
а) у = 2 sin х-f- cos 2л:; б) /(л:) = 2л:3 15л:2 84л: + 8.
Решение, а) Поскольку функция периодическая, мы можем
ограничиться отрезком [0, 2п]. Найдем первую и вторую производ-
производные:
у9 = 2 cos х — 2 sin 2л: = 2 cos x A — 2 sin дг);
у ж _2 sin л:—4 cos 2л:.
Из уравнения 2 cos x A—2 sin л:) = 0 определяем критические точки
на отрезке [0, 2я]:
Теперь находим знак второй производной в каждой критической
точке:
у" (я/6) = —3 < 0, следовательно, в точке хх = я/6 имеем мак-
максимум у(л/6) = 3/2;
у" (я/2) — 2 > 0, следовательно, в точке х2 = я/2 имеем минимум
У(п/2)=\;
у" Eя/6) = —3 < 0, следовательно, в точке х3 — 5я/6 имеем мак-
максимум у Eя/6) == 3/2;
у" (Зя/2) = 6 > 0, следовательно, в точке л:4=Зя/2 имеем мини-
минимум у (Зя/2) = —3 (рис. 41).
Рис. 41.
3.6.4. Исследовать на экстремум функции:
б) /м-
Решение, а) Хотя производная
)
Зх + 5 (х>0);
/'(*)={
—2 (д:<0),
3 (х > 0)
существует во всех точках, кроме точки я —О, и меняет знак С«—»
на « + » при переходе через точку л;=0, минимума здесь нет1
Объясняется это нарушением непрерывности функции в точке #«яО.
б) Здесь производная /' {х) = 4х (хф 0) тоже существует во
всех точках, кроме д: = 0, и меняет знак с —- на + при пе-
переходе через точку х — 0. Тем не менее здесь мы имеем не мини-
минимум, а максимум, что легко проверить непосредственно.
Объясняется это нарушением непрерывности функции в точке
3.6.5. Найти экстремумы функций:
а>
135
Решение, а) Здесь проще найти экстремумы функции Д
. Так как
f[ (х) = 12л;3 + 24л:2 — Збх = 12х (х2 + 2х—3),
Г1(х) = \2C* + 4х-3),
то критическими точками будут:
Х± = О, #2 == *м "^з == м
а вид экстремума легко определить по знаку второй производной
/i'(~-3) > 0, Следовательно, в точке хг = —3 функция fx (x) имеет
минимум, а заданная функция f(x), очевидно, имеет максимум
/(—3)«*«^2/3; fl@) < 0, следовательно, в точке х2~0 функция
f±(x) имеет максимум, а функция f(x) — минимум /@) = 5/6;
/Jr(l)>0y следовательно, в точке х3 = \ функция fx(x) имеет мини-
минимум, а функция f(x) — максимум /A) = 50/53.
б) Здесь проще найти точки экстремума подкоренного выражения
которые совпадают с точками экстремума функции f{x). Находим
критические точки /г(х):
/i {х) ** 2хех*; /гг(х)^0 в точке х — 0. Определяем знак вто-
второй производной в точке aj = O:
ft(x) * 2е*2 A -f 2л;2), ft @)«- 2 > 0.
Поэтому точка х = 0 есть точка минимума функции ^(х); она же
будет также точкой минимума и для заданной функции f(x): /@) = 0.
3.6.6. Исследовать вид экстремума функции j/^chx-fcosjc
в точке #«»0.
Решение. Функция у четная и, очевидно, имеет экстремум
в точке x*=0. Для определения вида экстремума вычислим произ-
производные этой функции в точке х~0:
у' » shх—-sin ху у' @) = 0;
у" = ch х — cos Xj у" @)« 0;
jy(*> @) «• 2 > 0.
Так как первой отличной от нуля производной в точке х = 0 ока-
оказалась производная четного порядка, принимающая положительное
значение, to в этой точке минимум у @)*» 2.
3.6.7. Исследовать на экстремум в точке л; = 0 следующие
функции:
a) ^cos*— 1+fy—f^' б) y = cosx—l+^.
X2
Решение» а) у = — sinx + д:—-=-; у @) = 0;
у" = — cos jc-{- 1 — х; у" @) = 0;
/" = sin ;;— 1; /" @) = — 1 ф 0,
136
Итак, первая отличная от нуля производная в точке х — 0 есть
производная третьего порядка, т. е. нечетного порядка. Значит,
в точке х = 0 экстремума нет.
3.6.8. Исследовать на экстремум функции:
а) /(х) = х*е-*г; б) f(x) = sin3x — 3slnx.
Решение, а) Функция f(x) = x*e~x* всюду непрерывно диффе-
дифференцируема. Приравняв нулю производную
/' (х) = 4х*е-*2 — 2хъе-*2 = x4~x* D—2х%
находим критические точки:
*! = — /2; xt = 0; xB
Вычислим значение второй производной в критических точках:
Г@) = 0; f(-V2)<0;
Следовательно, в точках хх = —У2 и хъ= +V~2 функция дости-
достигает максимума /(±1^2) — 4е~2 = 4/е2. Что же касается критической
точки х2 = 0, то ничего пока сказать нельзя, надо находить произ-
производные f(x) высших порядков (до четвертого порядка!). Это гро-
громоздко, поэтому обратимся к первому достаточному признаку экстре-
экстремума: найдем знаки первой производной в окрестности критической
точки х2 = 0:
/'(—1)<0; f{\)>0.
Зничит, в точке х — 0 функция достигает минимума /@) = 0.
3.6.9. Функция у = /(х) задана параметрически:
Найти экстремумы этой функции.
Решение. Имеем
ф'(^) = 5/4— Ш2—20.
На интервале (—2, 2) ф'(*)=^0.
Найдем -ф' (t) и приравняем нулю:
<ф'(/) = Ш2 — 6/—18 = 0.
Отсюда tx — —1 и /а = 3/2.
Эти корни являются внутренними точками рассматриваемого про-
промежутка изменения параметра t.
Далее:
^@ = 24/ —6; г|5"(—1) = —30 < 0, ф* C/2) = 30 >0.
Следовательно, функция^ =f(x) имеет при t = —1 (т. е. при л; = 31)
137
максимум j/ = 14, а при t = 3/2 (т. е. при х ——1033/32) минимум
^ = —17,25.
3.6.10. Найти максимумы и минимумы функций:
a) f(x) = x*e~*; б) ^
в) /(х)=-х*У(^2У; г)
д)
е) /(л;) = л;21пл;; ж) f(x) = х In2 x.
3.6.11. Исследовать на экстремум в точке х = 0 следующие
функции:
a) f(x) = sinx—х\ б) f(x) = sinx—
в) f(x) = sinx—* + fy—47;
*/*, если хфО,
, если я — О.
§ 3.7. Отыскание наибольших
и наименьших значений функции
Наибольшее (наименьшее) значение непрерывной функции / (х) на отрезке
\а, Ъ\ достигается или в критических точках функции, или на концах отрезка.
Для определения наибольшего (наименьшего) значения функции надо вычис-
вычислить значения функции во всех критических точках на отрезке [а, Ь], значе-
значения /(a), f (b) функции на концах отрезка и взять наибольшее (наименьшее)
из полученных чисел.
Если функция задана и непрерывна в некотором промежутке и если этот
промежуток не является отрезком, то среди значений функции / (х) может и
не быть ни наибольшего, ни наименьшего.
3.7.1. Найти наибольшее и наименьшее значения функций на
указанных промежутках:
а) f(x) = 2x3—З*2 —12*+1 на отрезке [—2, 5/2];
б) f(x)^=x2\nx на отрезке [1, е];
в) f(x) = xe~x на промежутке [0, +оо);
г) /(*)= У(\—х*)(\+2х*) на отрезке [—1, 1].
Решение, а) Найдем производную f (x):
Она обращается в нуль в двух точках: хг — —1 и х2 = 2. Обе эти
точки лежат внутри заданного отрезка; следовательно, обе должны
приниматься во внимание. Для отыскания экстремальных значений
функции необходимо вычислить значения функции в точках хг и х27
а также на концах отрезка:
/(-2) = -3, /(-1) = 8; /B) = -19, /(-^)=-16^.
138
Следовательно, наибольшее значение равно /(—1) = 8, наименьшее
значение равно /B) = —19.
б) Ищем критические точки: /' (х) = х(\ +2 In jc). Производная
f'(x) не обращается в нуль внутри заданного отрезка [1, е].
Поэтому внутри заданного отрезка нет критических точек, остается
вычислить значения функции на концах отрезка
Таким образом, /A) = 0 есть наименьшее значение функции; f(e) = е2—
наибольшее значение.
3,7.2. Найти наибольшее и наименьшее значения функций в ука-
указанных промежутках:
а) у = sinхsin 2х в промежутке (—сю, сю);
б) у = arccos х2 на отрезке [—V2/29 VV2\\
в) у~х-\~Ух на отрезке [0, 4].
Решение, а) Представим функцию у = sinxsin2x в виде
_ cos л:— cos Зх
У 2 '
Отсюда видно, что функция четная и имеет период 2я. Следова-
Следовательно, наибольшее и наименьшее значения достаточно искать среди
экстремумов на отрезке [0, я]. Найдем производную у':
у' — у C sin 3 х — sin x).
На отрезке [0, я] производная обращается в нуль в точках
Подсчитаем значения функции в этих точках:
= arccos—rr= , A;3 = arccos( — тт^
Следовательно, наименьшее значение функции в промежутке (—оо, оо)
равно —4/C У^З), а наибольшее равно 4/C У 3).
3.7.3. Функция
± (a, b, х>0)
состоит из двух слагаемых: одно слагаемое пропорционально неза-
независимой переменной дг, а другое—обратно пропорционально ей.
Доказать, что такая функция достигает наименьшего значения при
х ^Vb/cT.
Решение. Найдем корни производной f [х) в @, оо);
139
при х = Vb\a (x > 0). Так как f (х) = 2bjx* > 0 для любого х > 0,
то в этой критической точке функция f(x) достигает минимума.
Этот экстремум (минимум) единственный в промежутке @, оо).
Значит, при x=yb/a функция f(x) достигает наименьшего значения.
3.7.4. При п измерениях неизвестной величины х получены чис-
числа х1У лг2, ..., хп.
Требуется найти, при каком значении х сумма квадратов по-
погрешностей
f(x) = (х-хгу
будет наименьшей?
Решение. Вычислим производную
f(x) = 2(x-x1) + 2(x—x2)+...+2(x-xn).
Единственный корень производной
Далее для всех х имеем f (х) = 2/г > 0. Поэтому функция /(х)
достигает минимума в точке
Этот минимум—единственный и совпадает с наименьшим значением
функции (ср. 1.3.8).
Итак, наилучшим в смысле «принципа наименьших квадратов» прибли-
приближенным значением неизвестной величины х является среднее арифметическое
значений хъ х2, ..., хп.
3.7.6. Найти наибольший член последовательности
"л-лз+200*
Решение. Рассмотрим функцию f(x) = x2l(xz-\-200) в проме-
промежутке [1, оо). Так как производная
, *Н00-*!)
J { }~ (*3+200J
положительна при 0 < х < J5/400 и отрицательна при х > ^/400,
то функция f(x) возрастает при 0<д:< ^/400 и убывает при
л:>?/400. Из неравенства 7<j/^400<8 следует, что наибольшим
б б
членом последовательности может быть либо член а1% либо член аь.
Так как а* = 49/543 > а8 = 8/89, то наибольшим членом последова-
последовательности является член
^-
49
543'
14t>
3.7.6. Найти наибольшее и наименьшее значения функций на
указанных отрезках:
а) /(х)==1д4_^&_^хъ + 2 на отрезке [—2, 4];
б) /(*) = УЧ—х2 на отрезке [—2, 2];
в) / (х) = arctg д: —у In л: на отрезке -y=z , КЗ ;
г) / (х) = 2 sin л; + sin 2л: на отрезке 0, у я ;
д) f(x) = x—2 In л: на отрезке [1, е];
е)/(х)={2х* + & Для~2<л:<0| 0<х<2,
( 1 для х = 0.
§ 3.8. Решение задач геометрического
и физического содержания
3.8.1. Сила действия кругового электрического тока на неболь-
небольшой магнит, ось которого расположена на перпендикуляре к плос-
плоскости круга, проходящем через его центр, выражается формулой
F =
где а — радиус круга; х—расстояние от центра круга до магнита
< х < оо); С — постоянная.
При каком х величина F будет наибольшей?
Решение. Производная
имеет единственный положительный корень х = #/^2. Он и дает
решение задачи.
Замечание. Часто соображения чисто физического или геометрического
характера освобождают от необходимости прибегать к дифференциальным мето-
методам исследования вопроса о наличии наибольшего или наименьшего значения
функции в исследуемой точке.
3.8.2. Определить размеры открытого бассейна с квадратным
дном объемом 32 м3 так, чтобы на облицовку его стен и дна пошло
наименьшее количество материала.
Решение. Обозначим сторону основания через х, а высоту
через у. Тогда объем V бассейна будет равен
а облицовываемая поверхность S бассейна равна
141
Выразив у через х из соотношения (*), получим
~ = x* + ™.
Исследуем полученную функцию на минимум в промежутке @, оо):
128 _
х2 ' ~~~ #
S = 2х—jg-; 2х-
Найденная единственная точка, очевидно, дает наименьшее зна-
значение функции S, так как наибольшего значения у нее нет (она
неограниченно возрастает при х —> 0 и
*-*oo).
Итак, искомые размеры бассейна х = 4м,
у = 2 м.
3.8.3. В данный шар вписать цилиндр,
имеющий наибольшую боковую поверхность.
3.8.4. Чтобы огородить клумбу, которая
должна иметь форму кругового сектора, име-
имеется кусок проволоки длиной 20 м. Какой
следует взять радиус круга, чтобы площадь
клумбы была наибольшей?
Решение. Обозначим радиус круга через х, а длину дуги
сектора через у (рис. 42). Тогда
откуда
= 2(\0—х).
Площадь кругового сектора равна 5 = yjcy=jcA0—лг)(О^#<! 10).
Производная S' (л:) =10 — 2х имеет
корень л: = 5.
Так как наименьшее значение S — 0
достигается на концах отрезка [0, 10],
то полученное значение х=5 дает
наибольшую площадь S,
3.8.6. Требуется построить от-
открытый цилиндрический резервуар вме-
вместимостью Vo. Материал имеет тол-
толщину d. Каковы должны быть размеры
резервуара (радиус основания и высота),
чтобы расход материала был наимень-
наименьшим?
Решение. На рис.43 изображен
разрез резервуара.
Радиус основания внутреннего ци-
цилиндра обозначен через л:, высота внут-
внутреннего цилиндра—через А. Объем дна и стенки резервуара равен
Рис. 43.
142
С другой стороны, по условию должно быть
откуда
Подставляя в (*), получим
Полученную функцию V(x) нам нужно исследовать на экстремум
при х > 0.
Имеем
Единственный положительный корень производной—это точка
x—l/VJn. Она и дает решение задачи. При этом
3.8.6. Завод D нужно соединить шоссейной дорогой а прямо-
прямолинейной железной дорогой, на которой расположен город Л. Рас-
Расстояние DB до железной дороги
равно а, расстояние АВ по желез- В
ной дороге равно /. Стоимость пе- /\
ревозок по шоссе в т раз дороже /
стоимости перевозок по железной /
дороге (т> 1). /'
Как провести шоссе DP к же- /
лезной дороге, чтобы стоимость / ^
перевозок от завода к городу была & х Р В
наименьшей?
Решение. Сделаем чертеж Рис. 44.
(рис. 44). Прежде всего ясно, что
шоссе тоже должно быть прямолинейным (прямая короче любой кри-
кривой, соединяющей данные две точки!). Кроме того, пункт Р не может
лежать левее точки А и правее точки В, Если расстояние АР обо-
обозначить через х, то это значит, что О^д:^/.
Пусть стоимость провоза по железной дороге (стоимость тонно-
километра) k; тогда стоимость провоза по шоссе будет km. Общая
стоимость N провоза из D в А равна
Af= kx + km Уа2 + A — х)*.
Следовательно, нужно найти наименьшее значение функции
ИЗ
Возьмем производную
Она обращается в нуль только в одной точке,
2—1
Если эта точка лежит на отрезке [0, /], т. е. если
то найденная точка дает наименьшую стоимость перевозок (что легко
проверить). Если же указанное неравенство не соблюдается, то f(x)
возрастает в [0, /] и поэтому наименьшая стоимость перевозок
достигается при # = 0.
3.8.7. При конструировании трансформатора переменного тока
важно заполнить внутренность катушки железным крестообразным
сердечником возможно большей площади. Каковы должны быть соот-
соответствующие размеры х, у сечения сер-
сердечника, если радиус катушки равен а
(рис. 45).
3.8.8. Если источником тока служит
электрический элемент, то эффект Я(вт),
получающийся при включении в цепь со-
сопротивления W(om), выражается формулой
E2W
P
рис 45.
где Е (в) — электродвижущая сила,
W-t (ом)—внутреннее сопротивление.
Найти наибольший эффект, который
можно получить при данных Е и Wt.
3.8.9. Банка данного объема V имеет форму цилиндра. Каково
должно быть соотношение ее размеров (высота h и диаметр 2/?),
чтобы на изготовление пошло минимальное количество жести?
3.8.10. Вписать в данный конус цилиндр с наибольшей боковой
поверхностью, если плоскости и центры круговых оснований цилиндра
и конуса совпадают.
3.8.11. В прямоугольной системе координат дана точка A, 2).
Провести через эту точку прямую линию так, чтобы она образовала
вместе с положительными полуосями координат треугольник наи-
наименьшей площади.
3.8.12. На оси параболы у2 = 2рх дана точка М на расстоянии а
от вершины. Найти абсциссу ближайшей к ней точки кривой.
3.8.13. Стоимость плавания судна в течение часа выражается
в рублях эмпирической формулой вида a-{-bvB7 где аи b—постоян-
144
ные для данного судна, a v—скорость судна в узлах (узел ра*
вен 1,85 км/час). В этой формуле постоянная часть расхода а от-
относится к амортизации и к содержанию команды, а второй член, bv3,—
к стоимости топлива. При какой скорости судно покроет любое
требуемое расстояние с наименьшими затратами?
3.8.14. Из трех досок одинаковой ширины сколачивается желоб.
При каком угле наклона боковых стенок площадь поперечного сече-
сечения желоба будет наибольшей?
3.8.15. Сосуд с вертикальной стенкой высоты h стоит на гори-
горизонтальной плоскости. Определить положение отверстия, при котором
дальность струи будет наибольшая, если скорость вытекающей
жидкости по закону Торричелли равна |/ 2gx, где х — глубина рас-
расположения отверстия.
3.8.16. Два самолета летят в одной плоскости и прямолинейно
под углом 120° с одинаковой скоростью v км\час. В некоторый
момент один самолет пришел в точку пересечения линий движения,
а второй не дошел до нее а км. Через сколько времени расстояние
между самолетами будет наименьшим и чему равно это расстояние?
§ 3.9. Выпуклость и вогнутость кривых.
Точки перегиба
Если /" (х) < 0 (> 0) в интервале (а, 6), то в этом интервале кривая
y=zf(x) выпукла (вогнута), т. е. лежит ниже (выше) любой своей касательной.
Если /"(*о) = О или не существует, но /'(*0) существует и вторая произ-
производная /" (х) меняет знак при переходе через точку х0, то точка (дг0, / (xQ))
является точкой перегиба кривой yz=f(x).
3.9.1. Найти интервалы вогнутости и выпуклости и точки пере-
перегиба графиков следующих функций:
а) у = х* + х* —18*2 + 24*—12; б) у = Зх* — 8л:3 + б*2 + 12;
в) у = */A + х2); г) у = х + *5/3 ;
Д) у = 4 V(x—\? + 20 J/>-lK(x> 1); е) у = (In2x)jx (x>0);
ж) y = xsln(\nx) (х>0); з) у-=2 — |хь — 1 |.
Решение, а) Находим производные:
у > = 4л;3 + З*2 — 36* + 24,
f = 12л:2 + 6л:—36 = 12 (л:2 + х/2 — 3),
откуда у = 0 при x1 = — 2J л:2 = 3/2.
Следовательно, у" > 0 на интервалах (— сю, —2) и C/2, сю);
у" < 0 на интервале (—2, 3/2). Знак второй производной определяет,
выпукла или вогнута кривая в данном интервале.
145
Это позволяет составить следующую таблицу:
X
Знак у?
Вывод
х<--2
+
Вогну-
Вогнутость
—
Выпуклость
+
Вогну-
Вогнутость
Поскольку при переходе через точки дгх = — 2 и х2 = 3/2 вторая
( 3 \
производная меняет знак, точки (—2, —124) и
ляются точками перегиба.
Н
1 \
Ш/ яв~
10
р
Т) Найдем производные:
Вторая производная нигде не равна нулю и теряет смысл в точке
д:==0. При х < 0 имеем .у"<0 и кривая выпукла, при х > 0 имеем
у* > 01 и кривая вогнута.
В точке л; = 0 первая производная У = 1, вторая производная
меняет знак при переходе через точку # = 0. Поэтому точка @, 0) —
точка перегиба.
ж) Найдем производные:
у' = sin (In x) + cos (In x),
у" = 1 [cos (In x) — sin (In*)H—^ sin (-J— In*).
Вторая производная обращается в нуль в точках
** = **/*+** ft = 0, ±1, ±2,...
Функция sin (я/4 — In x) при переходе через каждую точку хк меняет
знак, а вместе с ней меняет знак у". Следовательно, точки хн яв"
ляются абсциссами точек перегиба. В интервалах
кривая вогнута, в интервалах
кривая выпукла.
з) Заданную функцию можно записать следующим образом:
Поэтому
146
В точке #=1 производная не существует. Далее,
— 20 л;3, *>1,
20 л;3, х<\;
у" = 0 в точке # = 0. Следовательно, исследованию подлежат три
интервала (— оо, 0), @, 1), A, оо).
Составим таблицу знаков у":
.1
X
Знак у"
Вывод
х<0
Выпук-
Выпуклость
0 <х< 1
+
Вогнутость
х> 1
Выпук-
Выпуклость
Точка @, 1) является точкой перегиба, точка A, 2) является
угловой точкой (точкой излома).
3.9.2. Каким условиям должны удовлетворять коэффициенты
я, Ь, с, чтобы кривая у = ax*-]-bx3-\-cx2-]-dx-\-e имела точки
перегиба?
Решение. Найдем вторую производную:
Кривая имеет точки перегиба тогда и только тогда, когда
уравнение
имеет различные действительные корни, т. е. когда дискриминант
9?>2 — 24яс>0 или
З*2 — 8ас>0.
3.9.3. При каких значениях а кривая
будет вогнутой на всей числовой оси?
Решение. Найдем у"\
Кривая будет вогнута на всей числовой оси, если У'^0 для всех
значений х, т. е. когда
4х2 + 2ал;+1^0 при всех х.
Для этого необходимо и достаточно, чтобы выполнялось неравенство
4а2—16^0; отсюда
Д47
3.9.4. Показать, что кривая у = (л:+ 1)/(д;2
перегиба, лежащие на одной прямой.
Решение. Найдем производные:
имеет три точки
-6*-2
Вторая производная обращается в нуль в трех точках, которые
являются корнями уравнения
дз + зл;2 — Зх—1=0,
откуда
Составим таблицу знаков д>"
X
Знак #"
Вывод
— 00 <Х <
—
Выпуклость
—2— Уз<х<
<-2+/3
+
Вогнутость
-2+]/*3<
< а: < 1
—
Выпуклость
1 < л: < оо
+
Вогнутость
Следовательно, (—2-1^3, -(/3—1)М), (—2 + ^3,A+КЗ)/4),
A, 1) являются точками перегиба. Легко проверить, что все они
лежат на одной прямой. Действительно, координаты этих точек
—2—1^3—1 A —
удовлетворяют соотношению -р= =
—2+^3—1 A
3*9.5. Исследовать на выпуклость, вогнутость и точки перегиба
кривые, заданные следующими уравнениями:
а) у = *— У(х — ЗJ; б) jf = ^sinx(—
я/2).
3.9.6. Показать, что точки перегиба кривой y = xsinx лежат
на кривой
§ 3.10. Асимптоты
Прямая линия называется асимптотой для кривой y=xf(x), если расстоя-
расстояние от точки М, лежащей на кривой, до этой прямой стремится к нулю при
движении точки М вдоль какой-нибудь ветви кривой в бесконечность.
Различают три вида асимптот: вертикальные, горизонтальные и наклонные.
Вертикальные асимптоты. Если хотя бы один из пределов функции f (х)
в точке а справа или слева равен бесконечности, то прямая х = а — верти-
вертикальная асимптота.
14в
Горизонтальные асимптоты. Если lim /(х) = Л, то прямая у=А—гори-
х-> ± оо
зонтальная асимптота (правая при х—> -f00 и левая при х—> — оо).
Наклонные асимптоты. Если существуют пределы
lim tS&=klt lira \f (x)-klX} = blt
X -*¦ + 00 * Х-+-\-<К>
то прямая y^kiX+bi—наклонная (правая) асимптота.
Если существуют пределы
lim ?^ = Л2 и lim [f (x) — k2x] = b2.
х-*- -оо х х-+ —оо
то прямая y^k2x-\-b2—наклонная (левая) асимптота. Горизонтальную асимп-
асимптоту можно рассматривать как частный случай наклонной асимптоты при ?=0.
3.10.1. Найти асимптоты кривых:
ОХ _^v <оХ
)
~+4х*; д) У^***'* е) У^Ч^^—
ж) у= |
Решение, а) Кривая имеет вертикальную асимптоту х = 3,
так как
lim у •= lim ^, == q= оо
(точка х = 3 есть точка разрыва второго рода).
Найдем горизонтальную асимптоту:
Бх
lim у— lim —Из~ = 5.
Итак, кривая имеет вертикальную асимптоту х — 3 и горизон-
горизонтальную асимптоту ^ = 5.
б) Кривая имеет вертикальную асимптоту х=\, так как
Mm y= lim f—ЗТ"+^А:):= — °°>
lim j;= hm (——г- -{-ox \ — -{- оо.
Ищем наклонные асимптоты:
k= lim — = lim f --~-r + 3 J = 3;
-ЗлЛ=3.
149
Итак, прямая у = Зх + 3 является наклонной асимптотой
(рис. 46).
д) Кривая имеет вертикальную асимптоту # = 0, так как
et
lim y= lim
= lim — = -|-oo
~~ X
(см. 3.2.2).
Ищем наклонные асимптоты:
k = lim — = lim
lim
-+ ± a>
—#)= lim
x-> ± 00
-= hm =1.
Таким образом, прямая у = х +1 будет наклонной асимптотой
кривой (рис, 47). Заметим, что
lim у= lim хе{/* =0.
е) Функция определена и непрерывна при е — 1/(Заг) > 0, т. е. при
х<0 и х> 1/C«).
\1
Рис. 46.
Рис. 47.
Поскольку функция непрерывна в каждой точке области опреде-
определения, вертикальные асимптоты могут существовать только на ко-
конечных границах области определения.
При х—*-—0 имеем
\\т у= hm -.1п(« —я-)»—^ lim
л
= 0
(cm. 3.2.2), т. е. прямая ^ = 0 не есть вертикальная асимптота.
150
При х—»l/Ce)
lim
имеем
3
т. е. прямая х—\/(Зе) есть вертикальная асимптота.
Найдем теперь наклонные асимптоты:
& = lim -j = -j lira ln( e — ~J = y5
&= lim [y—kx] = ^ lim x In f ^ — 5J/""
^2 lim In A—l/Cjgg)) == 3 / 1^\ L
ДГ-> ± CO L V /
Следовательно, прямая у = Зх/2 — 1/{2е) является наклонной асимп-
асимптотой (рис. 48).
ж) Вертикальных асимптот кривая не имеет, так как функция
непрерывна всюду. Будем искать наклонные асимптоты. Пределы
Рж. 48.
при х—>-4"°° и х—*—оо будут различными, поэтому надо рас-
рассмотреть отдельно два случая.
Найдем правую асимптоту (при х—»¦+ оо):
= lim
Х-> +СО
1
— д:]= lim 1+*2-*2 =n
X-> + <» V \ + X*+X
Итак, при x—^+oo кривая имеет асимптоту у = Зл:.
Найдем левую асимптоту (при х—>¦—оо):
: = lim ¦
*-»¦ -со
= lim
X «*••*• 06
— x] = lim
1
*н>~« У 1 + Х2-Х
= 0,
161
так как в знаменателе оба слагаемых j/^-j-*2 и (—х) положитель-
положительны при х < 0.
Итак, при х—> — об кривая имеет асимптоту у = х.
з) Кривая вертикальных асимптот не имеет, поскольку она не-
непрерывна при хфО, а в окрестности точки * = 0 функция ограничена.
Найдем наклонные асимптоты. Имеем
k— lim ~— lira — _
x-+± ao x х-»±ж х
Далее,
a i- / *. v i. i j ^ /~~i i~ .1 ( 1 при *—> +oo,
6?= lim (у— kx)= lim * I/ 14 rsin— — < <
*_*±00"^ ^^ioo11^ дс4 ^ I—1 при x—9-—оо.
Итак, кривая имеет две горизонтальные асимптоты, ji=-f-l и у = —1
(рис. 49). Этот же результат можно получить из соображений симмет-
симметрии относительно начала координат, заметив, что функция у нечетная.
3.10.2. Найти наклонную асимптоту графика функции у=х2/(\ +*)
при *—юо и показать, что в интервале A00, оо) эту функцию
с погрешностью, не превосходящей 0,01, можно заменить линейной
функцией у = * — 1.
Решение. Найдем наклонную асимптоту:
х2
к = lim -—г-. : -т = 11
Итак, уравнение асимптоты у — х—1.
Составим разность:
Следовательно, приняв
у
мы для всех л:> 100 сделаем ошибку, не превосходящую 0,01.
3.10.3* Найти асимптоты кривых:
а) ^*2~^3+3; б) j, =
в) у = х+ (sin*)/*; г) ^ = 111D--д:2);
д) у = 2х — arccos(l/*).
§ 3.11. Общее исследование функции
Об исследовании функций и построении графиков элементарными приемами
говорилось выше (гл. I, §§ 1.3, 1.5). Теперь, пользуясь средствами дифферен-
дифференциального исчисления, мы можем провести более глубокое и разностороннее
изучение свойств функции и обосновать характерные качественные ее особен-
особенности (возрастание, убывание, выпуклость и т. д.)-
152
Общее исследование функций и построение их графиков удобно выполнять
по следующей схеме.
1. Найти область определения функции.
2. Выяснить, не является ли функция четной, нечетной или периоди-
периодической.
3. Исследовать функцию на непрерывность, найти точки разрыва и выяс-
выяснить характер разрывов.
4. Найти асимптоты графика функции.
5. Найти точки экстремума функции, вычислить значения функции в этих
точках. Установить интервалы монотонности функции.
6. Найти точки перегиба графика функции, вычислить значения функции
и значения производной в этих точках.
Установить интервалы выпуклости графика функции.
7. Используя результаты исследования, построить график функции. При
необходимости уточнить отдельные участки кривой, можно вычислить коорди-
координаты нескольких дополнительных точек (в частности, координаты точек пере-
пересечения с осями координат).
Указанную схему следует рассматривать как сугубо примерную. В част-
частности, эскиз графика рекомендуется набрасывать уже после нахождения
асимптот (если они имеются) и во всяком случае до нахождения точек пере-
перегиба. Однако следует помнить, что основными ориентирами при построении
графика функции являются точки кривой, соответствующие экстремальным
значениям функции, точки перегиба, асимптоты.
3.11.1. Провести полное исследование функций и построить их
графики:
—5; б) у = Ух
__ 1-х3
ч У — ~~tf
е) у = у sin 2х + cos x;
з) у = arcsin
Решение, а) Функция определена и непрерывна на всей чис-
числовой оси. Поэтому вертикальных асимптот кривая не имеет. Функ-
Функция четная, так как /(— x)=f(x). Следовательно, ее график
симметричен относительно оси Оу, поэтому достаточно исследовать
функцию только в промежутке [0, сю).
Наклонных асимптот нет, так как при х—*оо величина у является
бесконечно большой величиной шестого порядка относительно х.
Исследуем первую производную:
2ха + 1) = 6д:(л:2—IJ;
критические точки:
xl=*—\, *2 = 0, xs=l.
Так как в промежутке [0, оо) производная у'^0, то функция
возрастает.
Исследуем вторую производную:
У = 30*4 — Збдг2 + 6-6 E*4--6*2 + 1).
153
Положительные корни второй производной
Для удобства и наглядности исследования составим следующую
таблицу, в которой все интересующие нас точки л: расположены
в порядке возрастания:
X
у'
У"
У
0
0
6
(••
Vb)
1
96
25/5 ^
0
у
1,7
( 1 Л
Us-'1;
1
0
0
A.
00)
+
2
23
Справа подсчитано еще одно дополнительное значение функции
для уточнения графика после точки перегиба.
Используя результаты исследования и эту таблицу и учитывая
симметрию, строим график функции (рис. 50). Из графика видно,
что функция имеет корни л; —±#, где а «1,6.
Рис. 50.
Рис. 51.
б) Функция определена и непрерывна на всей числовой оси и
всюду отрицательна, так как ух <j/#+l .
Вертикальных асимптот нет. Наклонных асимптот нет, так как
при х—> оо порядок величины у меньше единицы. Ищем горизонталь-
154
ную асимптоту:
lim y^ lim (Ух-
->±00 X-f±<X>
« lim ъ-7=-
""
¦ = 0.
Следовательно, прямая j/ = 0 является горизонтальной асимптотой
графика.
Первая производная
у з у& з
(х+1J
обращается в нуль в точке д:2«=—>1/2 и обращается в бесконеч-
бесконечность в точках д:1 = —1, л;3 = 0.
Вторая производная
з\ з; з/F з v з
в нуль, не обращается, бесконечна в тех же точках хг = —1, лг3 = 0.
Составляем таблицу:
л:
—1
— 00
00
(-¦ -i)
¦1
1
2
0
16
93/2
(ч.«)
0
X
X
@, оо)
1
—0,26
С помощью этой таблицы и асимптоты у = 0 строим график
(рис. 51).
в) Функция определена и непрерывна на всей оси, кроме точек
лгяв-4-2. Функция нечетна, ее график симметричен относительно на-
начала координат, поэтому достаточно исследовать функцию в проме-
промежутке [0,оо).
Прямая х «= 2 является вертикальной асимптотой:
lim
- = — оо;
lim
155
Ищем наклонную асимптоту:
k— lim ~== lim
y y2 Л
Х-*> +<Х> * * -¦¦ +00 л ^
= 2,
и»
> = lim (у— 2х)= lim 2 = 0.
ДС -»¦ + СО .? -> + 00
Кривая имеет наклонную асимптоту j; = 2л:, причем
> 0 при л: > 2,
Первая производная
у' =
2-4 \ <0 при л:<2.
-4) — 4л:* 2jc2 (jc2—12)
в промежутке [0, оо) обращается в нуль в точках
3,46
и обращается в бесконечность в точке х = 2.
Вторая производная
^ ~ (л:2 -4K
обращается в нуль в точке # = 0 и в бесконечность при
Составляем таблицу:
= 2.
у1
у11
У
0
—0
+ 0
@, 2)
—
2
00
00
О —-
B, 2^3)
—
+
1
2/3
0
з/з
2
Используя результаты исследования, строим график (рис. 52).
д) Функция определена и непрерывна при всех значениях х, для
которых х2 — 1 > 0 или |#| > 1, т. е. на двух интервалах (—оо, —1),
A, +оо).
156
Ищем вертикальные асимптоты:
lim у = lim [я + ^М*2—1)]=—°oj
lim y = lim [x + \n (x2 — 1)] = — сю.
x -»-l + 0 x-+ 1 + 0
Таким образом, кривая имеет две вертикальные асимптоты:
х= —1 и х= +1.
Ищем наклонные асимптоты
~ ¦= lim
ft= lim \y—x}=- lim In (д:2 — 1)= +oo.
X->± оо x-»±oo
Следовательно, ни наклонных, ни горизонтальных асимптот нет.
-/
ш\
\г
¦X
Рис. 52.
Поскольку производная
Рис. 53.
2х
существует и конечна во всех точках области определения функции,
то критическими точками могут быть лишь нули производной:
В точке х = 1+1^2 функция не определена; следовательно,
имеется одна критическая точка х1=—1—К2, принадлежащая
интервалу ( —оо, —1). В интервале A, оо) производная у' > 0 и
функция возрастает.
Вторая производная
157
следовательно, кривая везде выпукла и в точке
#!= — 1— V2 «— 2,41
функция имеет максимум
у(—1— У2)=— 1— j/*2 + In B+ 2^2)^ — 0,84.
Для уточнения графика в интервале A, оо), где нет никаких
характерных точек, выбраны дополнительные точки:
х = 2; j>«2+ln3«3,10 и л; = 1,2; у= 1,2 + 1п 0,44 « 0,38.
График функции показан на рис. 53.
е) Функция определена и непрерывна на всей числовой оси и
имеет период 2я. Поэтому при исследовании можно ограничиться
отрезком [0, 2я]. Асимптот нет в силу непрерывности и периодич-
периодичности.
Находим первую производную:
У = cos 2л;—sin*.
На отрезке [0, 2я] она имеет три корня:
Вычислим вторую производную:
/' =« —2 sin 2х —cos х.
На отрезке [0, 2я] она имеет четыре корня:
хх = я/2, д;2 = я + arcsin A/4), xz = Зя/2, д:4 «« 2я — arcsin A /4).
Составим таблицу исследования всех критических точек первой
и второй производных (в таблицу включаем и концы отрезка [0, 2я]).
X
у'
У"
У
•1 f
1
0
I ЗУТ
1 2
я
— 2
0
ш.
5л
т
0
з Уз
2
1
0
/ Зл\
Зл
~2"
0
0
/
+
0
0 ^/ М
(*4> 2л)
г/"
2л
1
Ввиду того, что в интервале @, Зя/2) корни первой и второй
производных перемежаются, знаки второй производной в интервалах
между ее критическими точками указаны только в трех последних
интервалах,
158
Результаты исследования позволяют построить график функции
(рис. 54).
Рис. 54.
ж) Функция определена, положительна и непрерывна на каждом
из интервалов (— оо, 0) и @, оо). Точка л; = 0 есть точка разрыва.
Так как (см. 3.2.2)
lim у = lim
== lim ~ =
то прямая х = 0 является вертикальной асимптотой. Но
lim y= lim x2
Наклонных асимптот нет, так как при х—* ±оо функция у = .
имеет второй порядок малости относительно х. Найдем экстремумы
функции. Для этого вычислим производную:
Отсюда находим единственную критическую
точку л; =1/2. Так как при
у" (x) = 2eVx—
то на каждом из промежутков области оп-
определения график функции вогнут, и в точке
л; =«1/2 функция имеет минимум
с ±-е*& 1,87.
-/ 0
1/21
-*~«27
Рис. 55.
По результатам исследования строим график (рис. 55).
Для уточнения графика в интервалах (— оо, 0) и A/2, оо) ис-
использованы дополнительные точки
з) Функция определена и непрерывна на всей числовой оси, так
Как при любом х
159
Учитывая четность функции, мы можем ограничиться исследова-
исследованием функции при х^О.
Вертикальных асимптот нет в силу непрерывности. Горизонталь-
Горизонтальная асимптота есть:
lim у = arcsin (— 1) — — к/2.
Первая производная
, 1__ — 2х(\+х2) —2х(\— х2) __ 1 4х
A+**)»
2\х\ A+*2J
при #>0 отрицательна, поэтому функция убывает.
В точке л; = 0 производная не существует. В силу симметрии
графика относительно оси Оу в точке дг = О будет максимум
у@) = п/2. Заметим, что в точке
х = 0 правая производная равна—1,
а левая равна +1.
Вторая производная положи-
положительна:
у (х) =
2(\+х2Jх
= 2———— _-
8х
A+*2L
с- 56.
для всех х > 0.
Следовательно, график функции
в промежутке @, оо) вогнут.
Дополнительно заметим, что кри-
Вая пересекает ось Ох в точках
* ±1.
Учитывая все сказанное, строим график функции (рис. 56).
3.11.2. Провести полное исследование функций и построить их
графики:
г) у = \+х2—хА/2; б) у = х*/(\+х)*;
в) у = 1 /х + 4*2; г) у = х*/(х2 — 1);
е) у = х2 In (* + 2); ж) у = х*е~Ах;
{ х arctg 1 /х при х Ф О,
3) У~\ 0 при д:=-0.
§ 3.12. Приближенное решение алгебраических
и трансцендентных уравнений
Приближенное нахождение изолированных действительных корней урав-
уравнения /(л;) = 0 обычно складывается из двух этапов:
1. Отделение корней, т. е. установление промежутков [а, р], в которых
содержится один и только один корень уравнения.
2. Уточнение корней, т. е. вычисление их с заданной степенью точностиг
Процесс отделения корней начинается с установления знаков функции
f(х) в ряде точек x = av a2, ..., выбор которых учитывает особенности
функции / (л:).
16.0
Если окажется, что f (ak) f(ak+l) < 0, то в силу свойства непрерывной
функции в интервале (ak, ak+l) имеется корень уравнения /(я) —0.
Действительные корни уравнения можно также определить графически,
как абсциссы точек пересечения графика функции y — f(x) с осью Ох, Если
уравнение не имеет близких между собой корней, то этим способом его корни
легко отделяются. На практике часто бывает выгодно заменить данное урав-
уравнение равносильным ему уравнением
ih(*) = iM*),
где функции г]?! (х) и *ф2 (х) более простые, чем функция / (х). Построив гра-
графики функций y = ty1(x) и t/ = i|>2(*), найдем искомые корни, как абсциссы
точек пересечения этих графиков.
Методы уточнения корня. 1. Метод хорд. Если на отрезке [а, Ь] нахо-
находится единственный действительный корень ? уравнения /(*) = 0 и на этом
отрезке f (x) непрерывна, то первое приближение хг находится по формуле
f(b)-f(a)
Для получения второго приближения х2 аналогичную формулу применяют
к тому из отрезков [а, хг] или [xv b], на концах которого / (х) имеет значения
противоположных знаков. Процесс этот продолжают до получения требуемой
точности, о чем судят по длине последнего полученного отрезка.
2. Метод касательных (метод Ньютона). Если / (a) f (b) < О, причем /' (х)
и f (х) отличны от нуля и сохраняют определенные знаки при а^х^Ь, то,
исходя из начального приближения х0 (хо?[а, Ь]), для которого / (х0) \п (х0) > О,
получают все последующие приближения к корню ? по формулам
у -у
2— !
f'(Xl) /(*„-!)
Для оценки абсолютной погрешности п-го приближения можно восполь-
воспользоваться общей формулой
i/()i
где
ш1= min \f'(x)\.
<<6
При указанных выше условиях метод хорд и метод касательных дают
приближение к корню с разных сторон. Поэтому обычно бывает выгодно комби*
нировать их, т. е. применять оба метода одновременно, благодаря чему уточ-
уточнение корня может быть получено быстрее и создается возможность контроли-
контролировать вычисления. Вычисление приближений хъ х2, ... , хт вообще говоря,
следует производить до тех пор, пока перестанут изменяться сохраняемые
нами в ответе десятичные знаки (в соответствии с заданной степенью точности!).
Для промежуточных выкладок надлежит брать один-два запасных знака,
3. Метод итерации. Уравнение f (х) — 0 сначала приводят к виду х=ц>(х)9
где f<p'(x)|<:<7 < 1 (q = const) при a^x^b. Исходя из любого начального
значения хо?[а, Ь], вычисляют последовательные приближения к корню I по
формулам х1 = у(х0), *2 = q>(*i)> ,.. , *и = Ф(*Л-.1). Для оценки абсолютной
погрешности л-го приближения хп можно воспользоваться формулами
1Ь Л
если приближения хп~г и хп лежат по одну сторону от корня, и
v \ ^г Ч | у у I
п • ^* 1 + J • »~1—хп I»
ееди приближения хЛ-1 и хЛ лежат но разные стороны от корня.
Ш
3.12.1. Отделить кор«и уравнения
Решение. Составляем таблицу знаков f(x) в некоторых выб-
выбранных точках:
X
— 00
—3
0
f(x)
X
1
3
fix)
i
Из этой таблицы заключаем, что уравнение имеет три действи-
действительных корня, лежащих в интервалах (—3, —1), (О, 1) и A, 3).
3.12.2. Определить число действительных корней уравнения
Решение. Так как/ (*)« 1 +e*>0; /(—oo) = — oo; /(+oo) =
«= + cx>, то данное уравнение имеет только один действительный
корень.
3.12.3. Приближенным значением корня уравнения /(д:)==2
езл;4—х—1=0 является д:= 1,22. Оценить абсолютную погреш-
погрешность этого корня.
Решение. Имеем /G) = 2,2153 —1,22 —1 = — 0,0047.
Так как при л:= 1,23 получаем
/(*) = 2,2888 — 1,23 — 1 = 0,0588,
то корень I содержится в интервале A,22; 1,23). Производная
*— 1 монотонно возрастает. Поэтому ее наименьшим зна-
значением в данном интервале является
/^ = 4.1,223—1 = 4-1,816— 1 = 6,264.
Отсюда получим оценку погреш-
погрешности
|5-6 |<Ц^ = ^« 0,00076 <
< 0,001.
3.12.4, Решить графически уравне-
уравнение
x\gx—\=0.
Решение. Запишем уравнение в
Рис. 57. виде
Здесь г|I (х) = lg х, г|)а (х) = 1 jx. Для этих функций имеются таблицы
значений, что упрощает построение их графиков.
162
Построив графики y = lgx и у=\/х (рис. 57), приближенно
найдем единственный корень | « 2,5.
3.12.5. Найти действительный корень уравнения
с точностью до 10~4:
а) по методу хорд,
б) по методу касательных.
Решение. Убедимся сначала, что данное уравнение имеет
только один действительный корень. Это следует из того, что про-
производная
Далее, из /A)=—3<0, /B) = 1>0 следует, что у заданного
многочлена имеется единственный положительный корень, лежащий
в интервале A, 2).
а) По методу хорд получим первое приближение:
Так как
/A,75)=-0,5156 < О,
а /B) = 1>0, то 1,75 < 6 <2.
Второе приближение:
х2 = 1,75 + ?4п| • 0,25 = 1,75 + 0,0850 = 1,8350.
Так как/A,835)=—0,05059 < 0, то 1,835 <|< 2.
Процесс сходится весьма медленно. Попробуем сузить интервал,
учитывая, что значение функции f(x) в точке хг= 1,835 значительно
меньше по абсолютной величине, чем /B). Имеем
/A,9) = 0,339 >0.
Следовательно, 1,835 < ? < 1,9.
Применяя к интервалу A,835; 1,9) метод хорд получим новое
приближение:
Дальнейшие вычисления по методу хорд дают
#4= 1,8437, хв = 1,8438,
и так как /A,8437) < 0, а /A,8438) > 0, то с требуемой точностью
10~4 можно считать
1& 1,8438.
163
б) Для метода касательных в качестве начального приближения
выбираем х0 = 2, так как /B) = 1 > 0 и /" (х) = 6л:—4 > 0 в интер-
интервале A, 2). Первая производная /' (х) = Зх2—4х + 3 тоже сохраняет
знак в интервале A, 2), так что метод касательных применим.
Первое приближение
^ = 2—1/7 = 1,857.
Второе приближение:
fA'85?)
х.» 1,867- fA'85?) - 1,857-Ж= 1,8489.
2 /'A,857) 5>927»
Третье приближение,
/A,8439)
х3 = 1,8439— - = 1,8438,
3 Г 0.8439)
дает уже нужную точность. Здесь сходимость процесса значительно
более быстрая, чем в методе хорд, и в третьем приближении можно
было получить точность до 10~6.
3.12.6. Найти наименьший положительный корень уравнения
= ;t с точностью до 0,0001 по методу Ньютона.
3.12.7. Найти действительный корень уравнения 2—х — lg# = 0,
комбинируя метод хорд с методом касательных.
Решение. Перепишем левую часть уравнения следующим
образом:
Отсюда видно, что функция f(x) есть сумма двух монотонно убы-
убывающих функций и поэтому она сама убывает. Значит, заданное
уравнение имеет единственный корень g.
Непосредственная проверка показывает, что этот корень лежит
в интервале A, 2). Этот интервал можно еще более сузить:
1,6 < Б < 1,8,
так как
/A,6) = 0,1959 >0; /A,8)=—0,0553 <0.
Далее
/' (х) = -1 —I lg e; /" (х) = -L lg е,
причем f (x) < 0; f"(x)>0 на всем отрезке [1,6; 1,8].
Применяя к этому отрезку метод хорд, с одной стороны, и при-
применяя метод касательных с начальной точкой л;0=1,6,— с другой
стороны, получим первые приближения:
^-1,6- A'8-1'6)/A'6) „ 1,6+0,1559= 1,7559;
1 ' fA8)/(l6) ' Т
F?l|) 0,1540= 1,7540.
164
Применяя f e же методы к отрезку [1,7540; 1,7559], получим вторые
приближения:
A,7540—1,7559)/A,7559)
х2 = 1,7559 — : -—¦ - = 1,75558,
/A,7540)—/A,7559) '
/A,75540)
х2 = 1,7540— —^ =1,75557.
2 /'A,7540)
Так как хг—х^ = 0,00001, то корень \ вычислен с точностью
до 0,00001.
3.12.8. Найти комбинированным способом все корни уравнения
f(x) = x3—5д:+1 = 0 с точностью до 0,001.
3.12.9. Найти методом итерации действительные корни уравне-
уравнения х — sin л: = 0,25 с точностью до 0,001.
Решение. Представим данное уравнение в виде
х—0,25 = sin л:.
Графическим способом устанавливаем, что уравнение имеет один
действительный корень ?, приближенно равный лго=1,2 (рис. 58).
Так как
sin 1,1 = 0,8912 > 1,1—0,25,
sin 1,3 = 0,9636 < 1,3 — 0,25,
то корень | лежит в интервале A,1; 1,3).
Запишем уравнение в виде
х = ц(х) = sin х + 0,25.
Так как производная ф' (х) — cos x
в интервале A,1; 1,3) по абсолютной ве- Рис. 58.
личине не превосходит cos 1,1 < 0,46 <
<1, то метод итерации применим. Строим последовательные при-
приближения
ха*=Апхп_г + 0,25 (я=1,2, ...),
принимая за начальное приближение д:0=1,2:
^ = 8^1,2 +0,25 = 0,932 +0,25=1,182;
*2 = sin 1,182 +0,25 = 0,925 +0,25 = 1,175;
AT3 = sin 1,175 +0,25 = 0,923 +0,25=1,173;
jc4 = sin 1,173 +0,25 = 0,9219 + 0,25=1,1719;
^ = sin 1,1719+ 0,25 = 0,9215+ 0,25 =1,1715;
хв = sin 1,1715 + 0,25 = 0,9211 + 0,25 =1,1711.
Так как # = 0,46 и, значит, ql{\—q) < 1, то с требуемой точностью
имеем ?= 1,171.
165
i
0
-0,25
//
//
/
4
<
л
1
/ 1,2
y~Sinx
3.12.10. Найти методом итерации наибольший положительный
корень уравнения
с точностью до 10~4.
Решение. Грубой прикидкой получаем приближенное значение
корня д:0= 10.
Заданное уравнение можно переписать в виде
#=1000—*3,
или в виде
д:«=1000/л;2 — 1/#,
или в виде
*== J/1000—х,
и т. п. Наиболее выгодным среди указанных способов оказывается
последний, так как, взяв за основной промежуток [9, 10] и положив
ф (л:) = УШО—ху
найдем, что производная
Y ' 3J/(i000—*J
по абсолютной величине не превосходит 1/300:
Вычисляем последовательные приближения хп с одним запасным
знаком по формуле
(л«0, 1, 2, ...),
^=$/1000 — 10 = 9,96655,
х2 = ^1000—9,96655 = 9,96666,
дг3 = ^/1000 — 9,96666 =± 9,96667.
С точностью до 10"*4 можно положить ^ = 9,9667.
Замечание. Относительно быстрая сходимость процесса итерации вы-
вызвана здесь малостью величины q. Вообще, чем меньше q, тем быстрее
сходится процесс итерации.
3.12.11. Найти по методу хорд положительный корень уравнения
^xz+ 1, 1л:2 + 0,9* —1,4 = 0
с точностью до 0,0005.
3.12.12. Найти методом хорд приближенные значения действи-
действительных корней уравнения с точностью до 0,01:
а) (х— IJ — 2sin* = 0; б) ех—2 A — *J = 0.
166
3.12.13. Найти по способу Ньютона с точностью до 0,01 поло-
положительный корень уравнений:
а) д:3 + 50* — 60 = 0; б) х* + х—32 = 0.
3.12.14. Комбинированным методом найти значения корня уравнения
на отрезке [1, 2] с точностью до 0,005.
3.12.15. Найти методом итерации все корни уравнения
4х—5 In д: = 5
с точностью до 10~4.
§ 3.13. Дополнительные задачи
3.13.1. Удовлетворяет ли функция
х, если х < 1,
/х, если х^\
условиям теоремы Лагранжа на отрезке [0, 2]?
3.13.2* Доказать, что для функции */ = a#2-J-P*+Y числ© ? в формуле
Лагранжа, примененной на произвольном отрезке [a, b], является средним
арифметическим чисел а и b: ? = (a+&)/2.
3.13.3. Доказать, что если уравнение
имеет положительный корень xQt то уравнение
имеет положительный корень, меньший, чем х0.
3.13.4. Доказать, что уравнение х* — 4х—1 = 0 имеет два различных
действительных корня.
3.13.5. Доказать, что функция / (*) = #|| + Р*+4| не может иметь более
двух действительных корней при четном п и более трех при нечетном п.
3.13.6. Доказать, что все корни производной от заданного многочлена
) = (*+1) (л:— 1) (л:—2) (х—3) действительны.
3.13.7. Обнаружить ошибку в следующих рассуждениях. Функция
f/v\_ J**8111*1^ при
/W~t 0 при *=0
дифференцируема при любом х. По теореме Лагранжа
1 / г . 1 1 \
х2 sin —=х ( 2| sin -z— cos -г- ,
откуда
cos -z-=2ssin -г—х sin — @ < | < x).
При стремлении д: к нулю будет стремиться к нулю и g. Переходя к пределу,
получим lim cos (l/g)=^=0, а между тем известно, что lim cos A/я) не существует.
3.13,8. Обнаружить ошибку в следующем выводе формулы Коши* Пусть
функции / (х) и ф (х) на отрезке [a, b] удовлетворяют всем условиям теоремы
167
Коши. Тогда каждая из них будет удовлетворять и условиям теоремы Лагранжа,
Следовательно, для каждой функции можно записать формулу Лагранжа:
)-ф (а)-ф' (I) (Ъ-а), а<\<Ь.
Разделив первое выражение на второе, получим
3.13.9. Доказать неравенства:
ft .,.,.,.., f% ft ft ' '¦ h
a) < \n-r- < —г— , если 0<:Ь<а,
a bo
б) РУр~1(х—у)^хР — уР^рхР-1(х—у), если 0<у<х и р>1.
3.13.10. Доказать, что у многочлена Чебышева — Лагерра
все корни положительные.
3.13.11. Доказать, что если функция f(x) удовлетворяет следующим условиям:
1) она определена и имеет непрерывную производную (п — 1)-го порядка
/(я-1)(*) на отрезке [*0, хп\\
2) она имеет производную л-го порядка /(и) (х) в интервале (xOi xn);
3) f (xo) = f(xl)= • • • =f (хп) (xo<xt< ... <хп),
то внутри отрезка [д:0, хп] найдется по крайней мере одна точка 5 такая, что
3.13.12. Предел отношения функций
]im .-ficnx+ian* l+iig»
Х-к» е~* (COSAT + SIIIX) х-+ оо 1 + tg ЛГ
1+2 tg л;
не существует, так как выражение ' в точках хп^пп + я/2 (п = 0,1, ...)
1 -f~ tg х
терпит разрывы, но в то же время предел отношения производных существует:
.. [e-2x{cosx+2sinx)]f v ~be-2xsmx 5 .. v .
[e-^tcosjc+sinjc)]' 2e-*sm* 2 ^ e
Объяснить это кажущееся противоречие.
3.13.13. Доказать, что число 9 в остаточном члене формулы Тейлора первого
порядка
стремится к 1/3 при h —> 0, если Г' (х) непрерывна при х = а и /"'(а) ф 0.
3.13.14. Доказать, что число г—иррациональное число.
3.13.15. Доказать, что при 0<*^jt/2 функция / (я) = (sin x)jx убывает.
Отсюда получить неравенство 2x/tt<smx<x при 0<д:<д/2 и дать его геомет-
геометрическую интерпретацию.
3.13.16. Показать, что функция /(*) = *-f cos x—й возрастает. Вывести
отсюда, что уравнение х-\~ cos x — а не имеет положительных кбрней при а<1
и имеет один положительный корень при д>1.
3.13.17. Показать, что уравнение хех = 2 имеет только один положительный
корень, заключенный в интервале @, I).
168
3.13.18. Доказать, что функция
[
\ О при х — 0
не является монотонной ни в каком промежутке, содержащем начало координат.
Наметить эскиз графика / (jc).
3.13.19. Доказать теорему, если: 1) f (jc) и <р(я) непрерывны в промежутке
[а, Ь) и дифференцируемы внутри него; 2) /(а) = ф(а) и 3) /' (х)Хр' (х) (а<х<Ь),
то f(x)><p(x) (a<x<b).
3.13.20. Показать, что функция /(*)=—i~j не имеет ни максимумов, ни
минимумов, каковы бы ни были значения а, Ь, с, d.
3.13.21. В трехчлене x*-{-px-\-q подобрать коэффициенты р и q так, чтобы
трехчлен имел минимум при х = 3 и чтобы, этот минимум был равен 5.
3.13.22. Исследовать на экстремум в точке х=х0 функцию f (х)~(х—хь)п ф(х),
где п—натуральное число, функция ф(х) непрерывна при х — х0 и ф(*0) Ф 0.
3.13.23. Дана непрерывная функция
1! при
У 0 при х=0.
Показать, что f (х) в точке * = 0 имеет минимум, но ни слева, ни справа от
я = 0 не является монотонной.
3.13.24. Найти наибольшие и наименьшие значения на указанных проме-
промежутках следующих функций:
а) y = \x\ при —
б) у = Е(х) при — 2<х<1.
3.13.25» Существуют ли наибольшие и наименьшие значения на указанных
промежутках у следующих функций:
а) f (x) = cos х при —:
б) / (x) = arcsin х при —1
3.13.26. Доказать, что между двумя максимумами (минимумами) непрерыв-
непрерывной функции имеется минимум (максимум) этой функции.
3.13.27. Доказать, что функция
8sin2(l/x) для хфО,
О для х=0
имеет в точке хо = О минимум, причем этот минимум нестрогий.
3.13.28. Доказать, что если в точке минимума существует правая произ-
производная, то она неотрицательна, а если существует левая производная, то она
неположительна.
3.13.29. Показать, что функция
\
(*<0)
имеет минимум в точке * = 0, хотя ее первая производная не меняет знака при
переходе через эту точку.
3.13.30. Пусть Xq—абсцисса точки перегиба кривой y=f(x). Будет ля
точка х0 точкой экстремума для функции |/ = /' (х)?
3.13.31. Нарисовать примерный график функции y — f(x) э окрестности
точки д:=—1, если:
/(—1)=2, /#С—1)=-—1. f(-i)=o, г'(*)>о.
169
3.13.32. При каком выборе параметра h «кривая вероятностей»
Уп
имеет точки перегиба JC=i о?
3.13.33. Показать, что у любой дважды непрерывно дифференцируемой
функции между двумя точками экстремума лежит по крайней мере одна абсцисса
точки перегиба графика функции.
3.13.34. На примере функции
проверить, что между абсциссами точек перегиба графика функции может и не
быть точек экстремума.
3.13.35. Доказать, что всякий многочлен с положительными коэффициен-
коэффициентами, являющийся четной функцией, всюду вогнут и имеет только одну точку
минимума.
3.13.36. Доказать, что всякий многочлен нечетной степени rf^3 имеет
по крайней мере одну точку перегиба.
3.13.37. Исходя непосредственно из определения, проверить, что прямая
у = 2х-\-\ есть асимптота кривой
Глава IV
Неопределенный интеграл.
Основные методы интегрирования
§ 4.1. Непосредственное интегрирование
и метод разложения
Непосредственное интегрирование заключается в прямом использовании
таблицы интегралов:
3) С a* du = -~aa+С; Г ett du = ett+C;
4) \ cos udu = sin u + C; \ sin«dw = —cosa + C;
5) \ chudu = shu + C; \ sh и du =
7)
С du и и
8) I —=arcsin \-С=—arccos \-Ct (я>0);
9) \ 2 ^ =ln
10) С du 9=?-\n
1 J w2—a2 2a
u+a ^ '
Во всех этих формулах переменная и является или независимой переменной
или дифференцируемой функцией некоторой переменной. Если
то
J ^
Метод разложения заключается в разложении подынтегральной функции
линейную комбинацию более простых функций и применении свойства ли-
личности интеграла:
в линейную комби
нейности интеграла
171
4.1.1. Найти интеграл /= i —-у=
1 ,
dx.
Решение.
J V x J
= С x3/* dx + 5 Гx1/.rfx—f x-V. rfx =
Замечание. Ставить произвольную постоянную после вычисления каж-
каждого интеграла (как сделано в разобранном примере; не следует: обычно все
произвольные постоянные суммируются и результат, обозначенный одной бук-
буквой С, записывается сразу в окончательный ответ.
sin2* cos2*
Решение. Преобразуем подынтегральную функцию так:
1 _ sin2* +cos2* __ 1 1
sin2* cos2* sin2* cos2* cos2* ' sin2* "
Следовательно,
sin2 *
4.1.4. I=i\tg2xdx.
Решение. Так как tg2x = sec2x— 1, то
4.1.5. /=
Решение. Разлагая по формуле бинома, находим
75х2-Ц25) dx^= — + —- +—+\25x-h С.
4.1.6. / = j
Решение. Здесь возводить двучлен в 17-ю степень нецелесо-
нецелесообразно, так как « = 3*4-5 — линейная функция.
Исходя из табличного интеграла
172
получаем
3 18
dx
4.1.8. /= Г cos (ял:+1)^.
Решение. Исходя из табличного интеграла
\ cos udu = sin и -f С,
получаем
4.1.9. /= \ cos 4x cos 7л: dx.
Решение. При вычислении подобных интегралов целесообразно
пользоваться тригонометрическими формулами разложения произве-
произведения в сумму. Здесь
cos 4x cos 7х = y (cos Зл: + cos 11 х)
и поэтому
-! С cos3a: dx + Y С cos Их d# = ^- sin
Замечание. При решении подобных задач полезно иметь следующие
формулы разложения:
sin mx
sin mx sin
cosmx
= Y sin (m—n)x+sin (m + n)x ;
sin nx = -^ cos (m—л)дс—cosfm + л)^ ;
os/ix = y cos (m—n)a: + cos (m + n)x .
4.1.10. /= \ cos x cos 2jc cos 5л: dx.
Решение. Имеем
J
2
(cos x cos 2x) cos bx *= -^- (cos .c + cos Зл: ) <:os 5x =«
=»-j- cos Ax + cos 6л: 1 +~-(cos 2л: + cos 8л:).
Таким образом,
= ._- f cos 2л: dx-\- V cos 4x dx -{- Г cos 6л: </л:+ V cos 8л:dx 1 =
i-sm2x+ ^ Sin4x+i sin6x
4.1.11. /=f sln*3xdx.
173
Решение. Так как sin2 Ъх = A — cos 6л:)/2, то
/=iJ(l-cos6x)dx = Y* — ±
4.1.12. /=.f
Решение. Так как ch2« = (ch2a+l)/2, то
/=="У [1+chA6*+10)] Лс=т*+§2811
4.1.18. /-^^^-^pg.
С dx Г dx
Решение. /= J J
4.1.16. /=
4—9x2
ние. /= f —^—^1 f _g_- д 1 arcsin-%¦ + С
J /4-9x2 3 J /4/9—*2 3 2 ^
Реше
4.1.17.
Решение. /=i—— x =s \
J Vr5-xa-4x J ^9-
4.1.18. /= f
J
4-1.19./=
Решение.
x
iL
/"~J 4—x2—4x J 8-
4.1.20. /-J^
2J/T + J
2 / — (x + 2)
4.1.21. Найти интегралы:
ч Г dx Г
P3-2ctgix ¦ . f
J cos2* dJC> Г) J
4.1.22. Найти интегралы:
a) f
B) \
j (sin 5x—sin 5a) dx.
;dx;
174
§ 4.2. Метод подстановки
Метод подстановки (или замены переменной интегрирования) заключается
в том, что заменяют х на ср (/), где ср (/) — непрерывно дифференцируемая
функция, и получают
причем после интегрирования возвращаются к старой переменной обратной
подстановкой t = ф ~х (х).
Указанную формулу применяют также и в обратном направлении:
$ / [ф @1Ф' @ dt = J / (х) dx, где *=ф @.
4.2.1. /=$ лг^я^ВйГл;.
Решение. Применим подстановку
Отсюда
х—5 = t*, xe^+5, dx = 2tdt.
Подставив в интеграл, получим
/= J (
Возвратимся к прежней переменной л::
2(л:-5N/2 10 (х-Б)*^
Решение. Применим подстановку \-\-ex=^t% Отсюда
e* = *_l, jc = In (if — 1), dx
Подставив в интеграл, получим
/— Г dx = Г dt
Jl+e* J ^(< —l)
Но
1 1
поэтому
175
Возвращаясь к переменной дг, получим
Замечание. Можно вычислить этот интеграл проще, умножив числи-
числитель и знаменатель на е~*. Получим
Г* р
\ -
х . 1
e*
Г* «,2 ! Q
4.2.3. /=
'-!¦
4 24 /-1 (^-i)dx
x2 4-1 *
+ 1) arctg ^-±J
Решение. Преобразуем подынтегральное выражение
4i
Применим подстановку x-\-\/x=t; продифференцировав, получим
A — \/x2)dx = dt.
Отсюда
2+1) arctg/'
Применим еще одну подстановку arctg t — u. Тогда
dt
Возвращаясь сначала к переменной t, а затем к переменной л:,
будем иметь
/= In | arctg t\ + С= In | arctg (x + 1 /x) | + C.
4.2.5. / =
Решение. Применим подстановку:
— -!. // _ ^
Следовательно,
176
Применим еще одну подстановку: УаЧ* — \—z. Тогда2a2tdt =
= 2z dz и
Возвращаясь к переменной t, а затем и к переменной х, по-
получим
(а2__х2K/2
dx
Решение.
Г dx I r 1
J а2 sin2 jc + 62 cos2 x b2 \ а2
Применим подстановку у tg х = /; ^=у—^-. Тогда
f 1 р Л 1
Возвращаясь к переменной д:, получим
4.2.7. /=
Решение. Применим подстановку 1 + 3 sin x = t, 3 cos jc djc = Л.
Тогда
4.2.8. / =
4.2.9. / =
J у cos х
Г dx
r
Решен и е. Применим подстановку: arc cos x = t; —dx/\^T^—x2 =
= dt. Тогда
J 4 » 4arccos4A;
4.2.10. /= Г . . x2 + \ =dx.
Д77
f sin2*
Решение. Применим подстановку:
1 + sin2 л; = t; 2 sin л: cos * </* = sin 2x dx = dt.
Тогда
/= С -у- = In t + C = in A + sma x) + C.
4.2.12. f=
Решение. Применим подстановку
и получим
/=Г ^-=ini ^ 1 + с== in | з+at in jc j + е.
4.2.13. Найти интегралы:
4.2.14. Найти интегралы:
cos6 х У sin х dx; г) I
§ 4.3. Интегрирование по частям
Формулой интегрирования по частям называется формула
\ и dv = uv — V у ^м,
где и и и—дифференцируемые функции от х.
Для применения этой формулы подынтегральное выражение следует пред-
представить в виде произведения одной функции на дифференциал другой функ-
функции. Если под интегралом стоит произведение логарифмической или обратной
тригонометрической функции на алгебраическую, то за и обычно принимают
не алгебраическую функцию. Если же под интегралом стоит произведение
тригонометрической или показательной функции на алгебраическую, то за а
обычно принимают алгебраическую функцию.
4.3.1. /= [ bKtgxdX.
178
Решение. Положим здесь
и = arctg jc, dv = dx,
откуда
/ = V arctg x dx = x arctg x— \
xdx
*= x arctg л; — у In A +л:2) -f С.
4.3.2. /= f arc sin x dx.
4.3.3. /= V x cos л: ^д;.
Решение. Положим
и = a:; d^ = cos а; (/л;,
откуда
du = dx; v^sinx,
/= V д: cos л: dx = ^ sinA:—\ sin xdx = x sin л: -f cos x + С
Посмотрим на этом примере, к каким результатам приводит не-
неудачный выбор множителей и и dv,
В интеграле f x cos x dx положим
откуда
В этом случае
—sin л: dx\ v = у а:2.
/= -1 х2 cos * + ~ Ja:2 sin x dx.
Интеграл не упростился, а усложнился.
4.3.4. /=$л;31пл;<*л;.
Решение. Положим
и = In x; dv — хд dx,
откуда
= 1 л:4 In х—\ J Д^ Ц = j л4 In x—\ J х3
4 Id
4.3.5. I=^(x2 —
Д79
Решение. Положим
и = х2 — 2*+ 5; dv = e~xdx,
откуда
du = Bx— 2)dx; v = —e"x;
~xdx=z— е~х(х2 — 2х + 5) + 2 ^ (х — \)е~хdx.
Последний интеграл опять проинтегрируем по частям. Положим
х—l~u; dv~e~x dx,
откуда
du = dx; v = — e~v.
Ix = 2 J (x — 1) e~*dx = — 2e~* (*_ 1) + 2 J *"*tfx = — 2xe~* + C.
Окончательно получим
/=— e~*{x* —
Замечание. В результате вычисления интегралов вида \ Р (х) еах dx
мы получаем функцию вида Q(x)eaxt где Q (х)—многочлен той же степени,
что и многочлен Р (х).
Это обстоятельство позволяет применить для вычисления интегралов ука-
указанного типа метод неопределенных коэффициентов, сущность которого поясним
на следующем примере.
4.3.6. Найти методом неопределенных коэффициентов
/=
Решение. J (З*3 —17) е2х dx = (Ах3 + Вх* + Dx + Е) е2х + С.
Продифференцировав правую и левую части, получим
(З*3 — 17) е%х = 2 (Ахг + Вх2 + Dx + E) е2х + е2х (ЗАх2 + 2Вх + D).
Сократив на е2х% получим
Зл*-_ 17 = 2Лд;3 + BВ+ ЗА) х2 + BD + 28) х + BE + D).
Приравнивая коэффициенты при одинаковых степенях х в левой
и правой частях этого тождества, будем иметь
Решив систему, получим
1. я-_1. п-1- е--1!
Следовательно,
180
4.3.7. Найти интеграл:
/= \^(Х* -f \)cosxdx.
Решение. Положим
и = jc3 -f-1; dv = cos x dx,
откуда
du = Зх2 dx; v = sin x.
I=(xb + \)s\nx—3 ^x2 sinxdx = (x* + l) sinx —3/1?
где Ix = С x% sin x dx.
Интегрируя снова по частям, получим
Iv = — х2 cos x + 2/2,
где /а» Г д: cos x dx.
Опять интегрируя по частям, получим
I2 — x sin x + cosx+C.
Окончательно будем иметь:
/= ^(x*+\)cosxdx =
= (x3-f-1) sin x + Зх2 cos x — бд: $in x—6cosa:+C =
= (л:3 — 6л: + 1) sin x+ (Зх2 — 6) cos x + С.
Замечание. К интегралам вида
V Р (х) sin ах dx, \ Р (х) cos ax dx
можно также применять метод неопределенных коэффициентов.
4.3.8. / = $ (х2 + Зх + 5) cos 2x dx.
Решение. Положим
(х2 + Зх + 5) cos 2x dx =
= (А0х2 + Ахх + А2) cos 2х + (В0х2 + Вхх + В2) sin 2x + С.
Дифференцируем обе части тождества:
(х2 + Зх + 5) cos 2х = — 2 (Лод:а + Лхх + Л2) sin 2д: +
+ BАох + Ах) cos 2х + 2 (^0x2 + ^д: + jB2) cos 2x +
+ BB0x + Bx) sin 2x = [2^ox2 + BБХ + 2Л0) jc -f (Ax + 2Ba)j cos 2x +
+ [— 2Л0дг2 + BB0 - 2Лx) x + (B, - 2A2)] sin 2x.
Приравнивая коэффициенты при одинаковых степенях х у множителей
cos 2x и sin 2xy получим систему уравнений
38J
Решая систему, находим
А, = 0; В, =4, Л1 = 1, В,--^ Л2 = -|; В, = -|.
Таким образом,
4.3.9. /=
Решение. Положим
и = arctg x; dv = (Зл:2 + 6л: -f 5) Лг,
откуда
Следовательно,
Из подынтегральной функции последнего интеграла выделим це-
целую часть, разделив числитель на знаменатель:
:—3 .
Подставив значение /1? окончательно получим
/«(*» + Зл;2 + 5л: + 3) arctg л; — л:2/2 — 3* — 2 In (л;2 + 1) + С.
4.3.10. Найти интеграл
/= J e5:v cos 4л: ^л:.
Решение. Положим
^5:v — щ cos 4л: rf^ — dv%
откуда
5^6Jf djc = du; v = -j sin 4jc.
Следовательно^
1 ц г*
/== — еЪх sin 4л:—-г \ e&Jf sin 4л: dx.
Снова интегрируя по частям, получим
1Х = Г е5х sin 4л: ^л: = — -^ ебх cos 4л: + ^ ^ ^54С cos
182
Таким образом,
т. е.
/ = le**(sin4* + -|-cos4*) — ~/.
Отсюда
/ = — еъ* (sin 4x + -j cos 4x ) + С.
4.3.11. /=$ cos (In #)<*#.
Решение. Положим
и = cos (In jc); dv = Ле,
откуда
d# = — sin (In я) ~; v = #.
Следовательно,
/ ==; J <;os (In jc) ^/д: = x cos (In я) + ^ sin (In jc) ^д:.
Интегрируем еще раз по частям:
и = sin (In х); dv =* dx,
откуда
du = cos (In дс) ~; ^ = д;.
Следовательно,
/А = J sin (In x)dx — x sin (In л;)— J cos (In x) dx.
Таким образом,
/= \ cos (In#)^л; = л;cos (In#)-{-#sin (Inx)—/#
Отсюда
/ = ~ [cos (In A:) + sin (In x)] + C.
4.3.12. / =
Решение. Преобразуем подынтегральную функцию
1п^1+~) = 1п^ = 1п(л:+1)— In*.
Отсюда
/ = j х In (x + 1) ^Глг— ^ # In х dx =* /!—/2.
J83
Проинтегрируем 1г и /2 по частям. Положим
# = 1п(х+1); dv — xdx,
откуда
* dX 1 / 2 1 \
^==rR; * = _(*_!).
Следовательно,
l+x
У2 1 I
: 2 _Г
Аналогично,
J
Окончательно будем иметь
4.3.13. /^
Решение. Сделаем сначала подстановку:
Тогда
2djc dx I
/// ___ _____ Ы ттif ^__ ——I . ___ /У/
X3 X3 2
Следовательно,
р . _. ] р
Полученный интеграл легко берется по частям. Положим
Тогда
t *
Отсюда
184
Возвращаясь к переменной х, получим
/- —i
2
4.3.14. /=
4.3.15. I^
Решение. Положим
и = 1 n (|/"l —
откуда
f »
Следовательно,
Замечание. При вычислении последних интегралов нам приходилось
применять метод интегрирования по частям последовательно несколько раз.
Результат может быть получен быстрее и компактнее, если пользоваться так
называемой обобщенной формулой интегрирования по частям (или формулой
кратного интегрирования по частям)
.<.+(- I)»-1 !*<«-« (X) Vn (*) — (— 1)«-1 \ «!<»> (X) »„ (X) dx,
где
t/j (*) = \ v (x) dx\ v% (x)= \ vx (x) dx; ...; vn (x)= V vn-t (x) dx.
При этом, конечно, предполагается, что все входящие сюда производные и ин-
интегралы существуют.
Применение обобщенной формулы интегрирования по частям особенно вы-
выгодно при вычислении интеграла \ Р„(х)q>(x)d*, где Рп(х)—целый многочлен
степени л, а множитель ф(х) таков, что его легко интегрировать последова-
последовательно л+1 Раз« Например,
J35
4.3.16. С помощью обобщенной формулы интегрирования по ча-
тям найти интегралы
а) \(х3 —2х* + Ъх— \)cos2xdx,
б) <\)B
Решение.
a) j(#3 — 2jc2 + 3jc— \)cos2xdx=(x* —
3-5-7-9
Bд; -j- 6) GOjc3—45л2 — 396* + 897) + С.
Найти
4.3.17.
4.3.18.
4.3.19.
4.3.21.
4.3.22.
4.3.23.
4.3.24.
4.3.25.
4.3.26.
4.3.27.
4.3.28.
интегралы:
\ln(x + VT+?)dx.
\ у/х (In xY dx.
С arcsin х dx
J 3* cos x dx.
^(x9 — 2x* + 5)e3*dx.
l(\+xrcosxdx.
](x* + 2x-\)sin3xdx.
l / v*2 О v* , I,. Q \ 1 n v* /1 v
\ l Д» ™~^ ^*v | " c/1 111 Л 1*Л.
\ д:3 arctg д: йд;.
\ л:2 arccos x dx.
С помощью формулы кратного интегрирования по частям
вычислить следующие интегралы:
dx; б)
J
№
§ 4.4. Рекуррентные формулы
Рекуррентные формулы дают возможность свести интеграл, зависящий от
индекса п > 0, к интегралу того же типа с меньшим индексом.
4.4.1. С помощью интегрирования по частям вывести рекуррент-
рекуррентные формулы для вычисления интегралов:
» т Г* dx ^ , С sin" x -
а) /«~-J(*2 + a2)«; 0) y».-*~J cos»* *
в) /tt==J(a2 — x*)ndx.
Решение, а) Будем интегрировать по частям. Положим
u=whr' dv=dx>
откуда
2п х dx
-n + 2nln -
2)"
Полученная формула сводит вычисление интеграла 1п+1 к вычис-
вычислению интеграла 1п с меньшим на единицу индексом и, следовательно,
позволяет полностью вычислить интеграл с натуральным индексом,
так как
dx 1 , х . ^
——-=* — arctg —\-C.
1 -|~ Qr Q, п
Например, полагая л=1, получим
(jc2 + a2J
полагая /г = 2, получим
Г*
J
1
dx 1 л: 3 ,
4а2 # (д:2+а2J~^4а2 2 *~
б) Применим метод интегрирования по частям, положи»
187
откуда
(m—
Следовательно,
/ sin71-1*
/
n—\ Ps
^ m—1 J
n— 1 .
в) Интегрируем по частям, положив
и = (а2—х2)"; d
откуда
du = — 2пх (а2—х2)"*1 d
Следовательно,
/п = х (а2 — х2)п + 2/г J x2 (a8 —jc
= л:(я2 — л:2)" —
Отсюда, приведя подобные члены, получим
Следовательно,
Например, заметив, что
мы можем последовательно найти
Ч% = j ]/^=^ ах = I (а» - *«) v
*—xT'rfJf-jle^^r' + l-e1/./,, и т. д.
4.4.2. Применяя интегрирование по частям, получить следующие
рекуррентные формулы:
а) Ia=l{\nx)"dx = x(\nx)n — nln_x;
б) /„ = j л- (In хГ их =
в) /„ = J xnex dx = д;"еЛ—/*/„_,;
188
г) In= J e*x sinnxdx =
4.4.3. Вывести рекуррентную формулу для вычисления интеграла
Г* dx
In == \ . я- и воспользоваться ею для вычисления интеграла /3 =
= Г dx
J sin3 x '
4.4.4* Вывести рекуррентные формулы для вычисления инте-
интегралов:
a) In=ltg"xdx; б) /„=$ctg»*rf*; в) /„=
Глава V
Основные классы
интегрируемых функций
§ 5.1. Интегрирование рациональных функций
Р (х)
Если знаменатель Q (х) правильной рациональной дроби -тггт может быть
представлен следующим образом;
причем фигурирующие здесь двучлены и трехчлены различны и, кроме того,
трехчлены не имеют действительных корней, то
Р(х)_ А, А*
где Лх, Л2, ..., Bj, B2» •••» ^fi» #!, Af2. ^2» •••» #1» ^i» ^2» ^2» ... —•
некоторые действительные постоянные, подлежащие определению. Для их опре-
определения обе части последнего тождества приводят к целому виду, а затем при-
приравнивают коэффициенты при одинаковых степенях переменной х> что дает
систему линейных уравнений относительно коэффициентов. (Этот метод назы-
называется методом сравнения коэффициентов.) Можно также получать систему
уравнений для коэффициентов, подставляя в обе части тождества подходящим
образом подобранные числовые значения х. (Этот метод называется методом
частных значений.) При некоторых навыках удачная комбинация указанных
приемов часто позволяет упростить процесс отыскания коэффициентов.
Р (х)
В случае, когда рациональная дробь а) { неправильная, следует предва-
предварительно выделить целую часть.
1/ 1Л *-
5.1.1.
Решение. Подынтегральная функция — правильная рациональ-
рациональная дробь. Все корни знаменателя действительные и простые, поэтому
подынтегральная функция представится в виде суммы трех простейших
190
дробей вида
2__4x-8i
(*-3)
где Л, В$ D—коэффициенты, подлежащие определению. Приводя
к общему знаменателю и отбрасывая его, получим тождество
15л:2—4л;—81 = Л(л; + 4) (л; — \) + В(х—3)(х— 1) +
Сравнивая коэффициенты при одинаковых степенях л: в левой и пра-
правой частях тождества, получим систему уравнений для определения
коэффициентов
= — 4; — 4Л + ЗЯ— 12D = — 81.
Решая систему уравнений, найдем Л = 3, 5 = 5, D = 7.
Следовательно,
= 31п | л:—| + |
= In | (л:—ЗK (л: + 4M (лг— IO1
Замечание. Покажем на этом же примере применение метода частных
значений.
Тождество (#) справедливо при любом значении х. Поэтому, задав три
каких-нибудь частных значения, получим три уравнения для определения трех
неопределенных коэффициентов. Удобнее всего в качестве значений х выбирать
корни знаменателя, так как они обращают в нуль часть сомножителей. Полагая
в тождестве (#) # = 3, получим Л = 3; полагая я=—4, получим В = 5'г полагая
дс=1, получим D=*7.
CIO У- Г
Решение. Так как степень числителя выше степени знамена-
знаменателя, т. е. дробь неправильная, то нужно выделить целую часть.
Разделив числитель на знаменатель, получим
лг+2
Следовательно,
3—л;2 — 2л: J ' J
л;3—л;2 — 2л: J ' J х(х—2) (jc+
Разлагаем оставшуюся правильную дробь на простейшие:
х+2 _А В D
191
Отсюда
Подставив поочередно в правой и левой частях равенства значения
хх — О, л;2 = 2, х3 — — 1 (корни знаменателя), получим
Л = —1; ? = 2/3; D-1/3.
Итак,
г « а т С2х2—Зх + 3 ,
бл-4- '= )*-**+* **•
Решение. Здесь под знаком интеграла стоит правильная ра-
рациональная дробь, у которой корни знаменателя действительные, но
среди них есть кратные:
х3 — 2х2 + х = х (х—1J.
Следовательно, разложение на простейшие дроби имеет вид
А , В , D
Отсюда получаем тождество:
==A(x— \J + Bx + Dx(x—1) =
2 + ( — 2A—
Приравнивая коэффициенты при одинаковых степенях х, получим
систему уравнений для определения коэффициентов Л, В, D:
Отсюда А = 3; В =
Таким образом,
Замечание. Некоторое упрощение при определении коэффициентов по-
получается, если в тождестве (*) положить хх = 0; х2==1 (корни знаменателя),
а *3—равным любому значению.
При Jt = O получим 3=Л; при л: = 1 получим 2 = В\ при * = 2 получим
A + 2B + 2D 5 3 + 4 + 2D отсюда D= — I,
Решение. Так как х3+ 1 =(х+ 1) (л:2—х+\), причем второй
сомножитель не разлагается на действительные множители первой
192
степени, то разложение данной дроби будет иметь вид
Отсюда
х __ A Bx + D
Приравнивая коэффициенты при одинаковых степенях ху получим
А = —1/3; Я =1/3; ?>=1/3.
Таким образом,
Для вычисления интеграла
a:2 — x-f-1
выделим в знаменателе полный квадрат:
и сделаем подстановку .к—1/2 = /. Тогда
р tdt , з f л
Возвращаясь к переменной д;, получим
Таким образом,
-J-In (*•-
Решение. Знаменатель дроби имеет две пары различных ком-
комплексных сопряженных корней, поэтому
Рх+Е
193
отсюда
Здесь удобно применить метод частных значений для определения
коэффициентов, так как комплексные корни знаменателя достаточно
простые {x=*±:i и х = ±2/).
Полагая #=*/, получим
откуда Л = 0, В=*1/3. Полагая # = 2/, получим —ЗЕ—6D/=1,
откуда D = 0, E=*—1/3. Таким образом,
у arctg х —g- arctg-J + С.
U.8. /-J-
Решение. Здесь мы имеем уже кратные комплексные корни.
Разлагаем дробь на простейшие дроби:
Находим коэффициенты:
Л—1; В» —
Следовательно,
Вычислим Л
Так как л;2 + 2л;+ 3==(л:+1J + 2, то сделаем подстановку
1г=/. Тогда получим
1 J(<2 + 2Jar J (<2 + 2)а J(
~ 2(/2+2) ~zli-
dt
194
Интеграл
вычислим по рекуррентной формуле (см. 4.4.1)!
Г l JJL
Таким образом
1 /
Возвращаясь к переменной х> получим
] ^ , 1 ?+1 ! arctg^+1 [ С
'* 2(л;2+2л:+3) 2(^ + 2дс + 3) 2 J/T ё }^2 ^
Окончательно получим
Найти интегралы:
5.1.11. J
5.1.12. j
:2 — 4* + 4)(x2 —
5.1.13.
5.1.14. j *+*
§ 5.2. Интегрирование некоторых
иррациональных выражений
Некоторые типы интегралов от алгебраических иррациональностей надое-
жащей заменой переменной могут быть сведены к интегралам О? рациональных
функций; такое преобразование интеграла принято называть его рационали-
рационализацией.
I. Если под знаком интеграла стоит рациональная функция от дробных
степеней независимой переменной х, т. е. функция R (х, лЛ^1, ... , xPk'qk)t
то рационализация интеграла осуществляется при помощи подстановки # = /OT,
где пг есть наименьшее общее кратное чисел qlt q%> .,. , qk,
II. Если под знаком интеграла стоит рациональная функция от х и дроб-
дробных степеней дробно-линейной функции вида т~4~Г» то рационализация ин-
193
теграла осуществляется подстановкой —ij = /m, где т имеет тот же смысл,
что и выше.
5.2,1, /-
- f
J
Решение. Наименьшее общее кратное чисел 3, 6 равно числу 6,
поэтому делаем подстановку:
откуда
Возвращаясь к переменной дг, получим
/ = A *2/3 4- 6 arctg У х + С.
г »/•:
5.2.2. /
5(Ъ О Т 1 ^лЛ~~~*Оу ОДР
• Z.O. / "» I -— .
Решение. Подынтегральное выражение есть рациональная функ-
функция от УUx—^3, поэтому положим 2х—3 = /6, откуда
Следовательно,
«Зу—3-~+Зу — 3/ + 3 arctg/-f С.
Возвращаясь к переменной х, получим
Bх
/=3
— Bдг—3I/в +arctg Bx—3I/61 + С.
5.2.4.
198
I./-J dx
Решение. Подынтегральное выражение есть рациональная функ-
з /~2—х
ция от переменной х и от выражения 1/ ^-р-, поэтому введем под-
подстановку:
2+х~~ '
откуда
2—2/» о 4*3 , —12/2
Следовательно,
, _ f2(l + rf»)»M2f» 3 Pitf __ 3 r
J 16^A + /3J 2 j *з—4/2 r^.
Возвращаясь к переменной х, получим
'=4
Решение. Так как
то подынтегральное выражение есть рациональная функция от х и
vm __
гх + 2_ х + 2
; поэтому введем подстановку:
откуда
Следовательно,
, f(f*—l)(f*--lI2rf»<tt 4 (* d< 4
J 3-3/4a^4—IK 3 J /a 3/
Возвращаясь к переменной дс, получим
5.2.7,
197
5.2.8. ' dx
.8. f —=
J V (x
5.2.9. J(*-
§ б.З. Подстановки Эйлера
Интегралы типа V R (xt У ах2 + far+c) d* вычисляются с помощью одной
из трех подстановок Эйлера:
1) y~ax*-\-bx + c = t ± х V^a, если а > 0;
2) /a*2+fo + cW* ± Vci если
т, е. если а—действительный корень трехчлена ax2-\-bx-{-c.
dx
5.3.1. / =
Решение. Здесь а = 1 > 0, поэтому применим подстановку
=/—х.
Возведя в квадрат обе части этого равенства и сделав приве-
приведение подобных членов, получим
= t2 — 2,
откуда
2—2 . t + 2t+2,.
2A + 0а
Подставив в интеграл, получим
л 2A + 0(^ + 2^ + 2) ., Г
J (/2+4/ + 4J(l + 02 J
Полученную правильную рациональную дробь разлагаем на простей-
простейшие дроби:
d4J?D
d-4
(t +2J ^ + i"
Методом неопределенных коэффициентов находим А = 1, Б =
= — 2.
Следовательно,
198
Возвращаясь к переменной х, получим
/= In (х+ 1 + ух* + 2х+2)-] 2 + С.
5.3.2. /-Г/х
J
Решение. Так как здесь с = 1 > 0, то можно применить вто-
вторую подстановку Эйлера:
откуда
-х + \=~.
Подставив в /, получим интеграл от рациональной дроби:
dx
Г —2t*
J t{t-
—2 A В
t(t—1)(/ + 1J ~ / ~т t— l
По методу неопределенных коэффициентов находим
А = 2; В = —\/2; D=, — 3; ?" = — 3/2.
Отсюда
1 °J(/ + 1J 2J/ + 1~
где t = -
dx
ч
5.3.4. I=[——JL
5.3.3. / .
A+*)
xdx
10—x2K
Решение. В данном случае а < 0 и с < 0, поэтому ни первая,
ни вторая подстановки Эйлера неприменимы. Но квадратный трехчлен
7х—10—х2 имеет действительные корни а = 2, C = 5, поэтому при-
применим третью подстановку Эйлера:
— Ю — я2 = K(*--2) E — *) = (х — 2) /.
Отсюда
5 — х = (х — 2)t2-
dx 6tdt -
199
Следовательно,
6
где t~У•"-"->
—2
Вычислить следующие интегралы с помощью одной из подстано-
подстановок Эйлера:
J x—
5.3.8. f <*+»?+?> V
§ 5.4. Другие методы интегрирования
иррациональных выражений
Подстановки Эйлера часто приводят к весьма громоздким выкладкам, по-
поэтому их следует применять лишь тогда, когда трудно подыскать другой спэ-
соб для вычисления данного интеграла. Для вычисления многих интегралов,
принадлежащих к виду
существуют более простые приемы,
I. Интегралы вида
Mx+N
'-!¦
dx
с помощью подстановки x-\-b/Ba) = t приводятся к виду
Г Id/ Г dt
~~ l) Y'at* + K г) УаР+R*
где Mv Nv К — новые коэффициенты.
Первый интеграл сводится к интегралу от степенной функции, а второй —
табличный, и сводится к логарифму (при а > 0) или к арксинусу (при а < 0,
II. Интегралы вида
где Рт(х) — многочлен степени т, вычисляются по формуле приведения:
Г 1/:!*^1 -P-tW Va* + bx + e + K Г лГ /\ A)
J у ахг + Ьх+с J yax* + bx\c
где Pw-i (л) — многочлен степени т—1, а К—некоторое постоянное число.
200
Коэффициенты многочлена Рт-.х(х) и постоянное число К находятся ме-
методом неопределенных коэффициентов.
III. Интегралы вида
J (х—а1)"Уах* +
l + bx-\-c
сводятся к предыдущему типу подстановкой
IV. Тригонометрические и гиперболические подстановки—см. дальше § 5.7.
5.4.1. /» Г <*+*>**
J у4х2+4х—3
Решение. Сделаем подстановку 2х-\~\ ~t, откуда
Следовательно,
^t2 4 4 4
Возвращаясь к переменной х, получим
5.4.2. /=
5.4.3. /=
Решение. Здесь Рот(дг)==л:3 — х—1. Следовательно,
Pm-i(x) = A
Будем искать интеграл в виде
Дифференцируя последнее равенство, получим
:BАх
201
Приводим к общему знаменателю и приравниваем числители
Приравнивая коэффициенты при одинаковых степенях х, получим
систему уравнений:
Решая систему, получим
Таким образом,
где
6.4.4. /=
Решение. Преобразуем интеграл к виду
Г 4*»
J ^4jt
Методом неопределенных коэффициентов получим
. ( 1 1 \ л/79
1= ~х—- у 4х2 —
\2 4^
р 9^_Зх2 + 2 ,
5.4.5. г 1= dx.
J V^22 + \
5.4.6.
5.4.7. /= Г <*+4)f
Решение. Представим интеграл так:
(x+4)dx Г *-Н dx
Г (x+4)dx Г
J (A;_i) (x + 2J Yx* + x + I ~" j (
202
Разложим дробь -—*, 2 на простейшие дроби
х+4 __ Л В D
(x-l)(x+2J x-
Найдем коэффициенты
А— б/. П— 2/. П— 5/
Л — /9» D — /3» U— /9«
Следовательно,
2
г= ГГ Ё
J \Ъ(х— 1)
9 J (х—
Первый интеграл вычисляется подстановкой х—1»1/^ второй
и третий — подстановкой x + 2 = \/t. Предоставляем читателю само*
стоятельно решить этот пример.
5.4.8. ' *--»*-г"*-6
f
6.4.9. Г
J
6.4.10.
J I*"
5.4.1
J xVT-
* — 4х-
5.4.12.
5.4.13.
§ 5.5. Интегрирование биномиального дифференциала
Интеграл \ xm (a-\-bxn)? dx, где m, ai, p — рациональные числа, выражается
через элементарные функции только в следующих трех случаях.
Случай I. р—целое. Тогда, если р > 0, подынтегральное выражение раз-
развертывается по формуле бинома Ньютона; если же р < 0, то полагаем x=tk,
где к—общий знаменатель дробей тип.
Случай II. —i целое. Полагаем a-{-bxn = t*t где а — знаменатель
дроби р.
Случай III. —-t~+P—целое. Полагаем a-\-bxn = t*xn, где а—знамена-
тель дроби р,
203
5.5Л. /=J yxB+VxJdx.
Решение. /= [ х1/3 {2-\-xxl*)* dx. Здесь p = 2—целое число,
значит, имеем случай I.
f Г
J J
3 ^4
= -—jc7/$ + ~ д;11/6 +3jc*/8 +C.
8.5.2. /=^д;-2/з|
Г/'
|/л:2
Решение. 1=
Здесь /и=— 2/3; я= 1/3;р= 1/2; (/w + l)//z = (—2/3 + 1)/A/3)=
1 —целое число.
Имеем случай II. Применим подстановку
Следовательно,
/= 6 J /3 dt = 2/3 + С = 2 A + х1/3 )*/* + С.
Б.5.4. /=
6.5.5. 7=
5.5.6. /=
Решение. Здесь р=—1/2—дробное число, )
= ( — 11+ 1)/4=—5/2 —дробное число, но (/я+1)/л+р= — 5/2 —
—1/2=—3—целое число. Имеем случай III. Полагаем 1 +лс4«=л;4/2.
Отсюда
1 , tdt
х 1 dx
Подставив эти выражения в интеграл, получим
-
Возвращаясь к переменной х, получим
204
5.5.7. \ >—±J-LdX.
5.5.8. J dx
xil + УхГ
5.5.9. J ж» A+*•)*/« d*.
5.5.10. f—dx
1 x*V\ +x2
5.5.11.
5.5.12. n dx
§ 5.6. Интегрирование тригонометрических
и гиперболических функций
I. Интегралы вида
I=\sinmxcosnxdx,
где т, л —рациональные числа, приводятся к интегралу от биномиального
дифференциала
-t2) 2 dtt t — sinx
и поэтому интегрируются в элементарных функциях только в трех случаях
1) п — нечетное ((я—1)/2—целое),
2) т—нечетное ((т+1)/2—целое),
3) m + n —четное ((т+1)/2 + (я —1)/2—целое).
Если число п нечетное, применяется подстановка
sin x — t.
Если число т нечетное, применяется подстановка
Если сумма чисел m + л —четная, применяется подстановка
tgx = t (или ctgx — t).
В частности, такая подстановка удобна для интегралов
\tgnxdx Гили \ctgrt#djM,
где л —целое положительное число. Но последняя подстановка неудобна, если
оба числа тип положительны. Если т и п—неотрицательные четцые чис-
числа, то удобнее метод понижения степени с помощью тригонометрических
преобразований:
cos2a;=~A + cos2*)' sin2*=---(l — cos 2л:)
или sin x cos # = —sin 2*.
205
cos2 л:
Решение. Здесь m—S — нечетное число. Полагаем cos^ = i
sinxdx——dt, что дает
Cos2x—A + C.
5.6.3. /= ^ sin4 jc cos6
Решение. Здесь оба числа т, п—четные положительные.
Применяем метод понижения степени:
— \ B sin х cos л;L cos2 xdx =
Второй из полученных интегралов вычисляется подстановкой
sin 2x *=* t, cos 2xdx=*Y dt>
^t ^ + C
К первому интегралу снова применяем метод понижения степени:
А = 52 jsin4 2x dx = щ j(l -cos 4xJ^ =
= А х ~2§6 sin 4х + 2Ш8 sin
Итак, окончательно,
Решение. Здесь оба числа т, п — четные, но одно из них
отрицательно. Поэтому полагаем
COS'5 X
206
Следовательно,
Решение. Здесь можно положить ctgx — t. Но проще интегри-
интегрировать разложением:
Зл
б.в.6. /.
5.6.7. /*
sin11 x cos л;
Решение. Здесь оба показателя —11/8 и
тельные числа и их сумма —11/3—1/3 = — 4 есть
поэтому полагаем
¦у-
¦J'
**
cos4 х ?/1?П"* J
9.6.8. Найти интегралы от tgx и
Решение.
^ctgxdx
5.6.9. /
Решение. Полагаем
807
Получаем
8.6.10. a) /=JctgeA;^; 6) /= J tg3
5.6.11.7=
Решение. Здесь sin*—в нечетной степени. Положим
cos x = /, —sin xdx = dt.
Получим интеграл от рациональной функции.
cos4 х sin x j С t* ,.
ахLи
Здесь проще интегрировать по частям, чем применять общие методы
интегрирования рациональных функций (ср. 4.4.1,6)).
Положим
ut*; dv
Тогда
Отсюда
г_ /3.3 Г t4t
- 2(l-/«)+2j I-
/» 3 . 3 .
A-/2) 2 Т~^ 4 1П
2sin2^-irCOS* + Tln
I+ COS X
I — COS X
c.
II. Интегралы вида \/?(sin*, cos*)d*, где R — рациональная функция
от sinx и cos*, преобразуются в интегралы от рациональной функции
становкой
tg(x/2) = / (—п < х < л).
©та подстановка называется универсальной. При этой подстановке
81пх—1 + /2, cos*~
2dt
=Г+Т2*
208
выгоднее сделать подстановку
Иногда вместо подстановки tg(x/2)
ctg(x/2) = / @<x<2n).
Универсальная подстановка часто ведет к слишком громоздким выкладкам.
Ниже указаны случаи, когда цель может быть достигнута с помощью
более простых подстановок:
а) если выполняется равенство
или
R (—sin х, cos x) ss—R (sin xt cos x)
Я (sin*, —cos*)?s=—R (sin xt cosx),
в первом случае и sin* = /—во
то выгоднее применять подстановку cosx
втором;
б) если выполняется равенство
R (—sin х, —- cos x) ss R (sin x, cos x),
то выгоднее применять подстановку igx = t или ctg*=/.
Последний случай встречается, в частности, в интегралах \ R(igx)dx>
5.6.13. /= С
sin л: B+ cos x—2 sin x) *
Решение. Положим tg-^ = t; тогда будем иметь
2dt
\+t2
4/ \ ~ J t(t2-4t
Разлагаем на простейшие дроби
L
/ (/—3)(/—1> t +/—
Находим коэффициенты
Л=1/3; В = 5/3; D
Следовательно,
У~" 3 J / + 3 J /—3 J ^ —1""
5_
tg-
|ln
tg|-3
— In
dx
5+sin
cos x *
5.6.14. / =
5.6.15. '=
Решение. Если в выражение
1
c.
подставить
sinjcB Cos2jc— 1)
вместо sinA:, то дробь переменит знак на противоположный.
Значит, выгодно применить подстановку t = cos х; dt = — sin x dx,
что дает
dt
Так как
то
— 1)*
B—2^2) —(
r=^—3 iz
t* Y2
^ln
l + <^2
In
V~2
6.6.16. ,
1 + 1^2
COS*
1 — yT cos x
1 + У 2 cos л:
+ 4- In
I — COS X
1+cosa:
4..
f*J|+«-
+ C =
1 — 1^2 cos д:
+ ln
tgT
+c.
Г &in**C0SXdx.
J sin.x;+ cosx
Решение. Так как при изменении знаков у sin л; и cosaj под-
интегрально@ выражение не меняет знака, выгодна подстановка
dx
dt.
COS2 X '
у2 х- cos4 a: dx
Следовательно,
Разлагаем на простейшие дроби
t2 A > Bt+D
t4t
Et + F
Находим коэффициенты
A =1/4; ? = —1/4; D=l/4; ?=1/2; /7
Следовательно,
/_1 C_i^ 1 f JzzLrf/4.1 f JuJ-dt,
—1/2.
: -у In I sin a: + cos x |—-j- cos д: (sin x + cos #) + С
5.6.17. / =
J sinajc4-2cosaA: "*
210
Решение. Разделив числитель и знаменатель на cos2* и заме-
заменив tgx = t; dxjcos2x = dt, получим
Г
J
2tg*+3 ,
sin2 * + 2 cos2 x ^ J tg2 x+2
In (tg2 x+ 2) + -^L- arctg
5.6.18. /= С
J
J 1 + sin x
Решение. Этот интеграл можно, конечно, вычислить е помощью
универсальной подстановки tg(#/2) = /, но проще сделать это, при-
прибегая к следующему преобразованию подынтегральной функции!
sin л: A —sin л:) ^ sin *(l*»*sin *)
' A + sin*) (I—sin*) ~~ cos2*
sin* sin2* _^ sin * , 2
3=3 cos2* cos2* =я cos2* ®
Отсюда
COS*
5.6.19. /= ^
-tgx + x + C.
Решение. Здесь можно подставить tgx = t, но проще преоб-
преобразовать подынтегральную функцию. Вводя в числитель тригоно-
тригонометрическую единицу во второй степени, получим
J cos4 * sin2 * ax""
Г* sin4 * + 2 sin2 *cos2 *+ cos4* .
j cos4 * sin2 * ~"
Sin'* dx 1 2 Г dx I С dx
С sin2 x . . o С
J COS4* J
III. Интегрирование гиперболических функций. Функции, рационально
зависящие от гиперболических функций, интегрируются так же, как и в слу-
случае тригонометрических функций.
Следует иметь в виду следующие основные формулы:
ch2 *—sh2 *-= 1; sh2 x = -~ (ch 2*— 1);
ch2 * = ~ (ch 2*+ l)j sh x ch*=*y sh 2x,
Если th~ = /, то sh*=sr—p; ch* = ._,a;
5.6.20. /=
Решение.
5.6.21. /=Jch3 jc dx.
Решение. Так как chx входит в нечетной степени, то пола-
полагаем sh х = t\ ohxdx — dt. Получаем
/ = Г ch2 x ch x dx = Г A +f2)dt = t + ~ + С = shx + jsh* x + C.
5.6.22. Вычислить интегралы:
§ 5.7. Интегрирование некоторых
иррациональных функций с помощью тригонометрических
или гиперболических подстановок
Интегрирование функций, рационально зависящих от х и
можно свести к нахождению интегралов одного из следующих типов:
II.
III.
где ^ = x-f-^/Ba); ax2-{-bx-\-с — ± рЧг ± q2 (выделение полного квадрата).
Интегралы вида I — III могут быть сведены к интегралам от выражений,
рациональных относительно синуса и косинуса (обычных или гиперболических),
с помощью следующих подстановок:
I. t = ^-tgz или t=±shz.
Р Р
П. t—lLsecz или t=z-Lch 0,
Р Р
III. /=~sin2 или ^ =-?- th г.
Р Р
б
212
.,,. ,_j.
Решение.
Мы получили интеграл типа I. Сделаем подстановку
'-J-
J. Положим лг+1=*. Тогда
cos г
Мы получим
/ = -j \ cos ,г dz
4
5.7.2. /
J
Решение.
Положим
= (x+ 1J + 1.
; тогда
Мы опять получили интеграл типа I. Применим подстановку
Тогда
dt=chzdz; Vt*~+l = "|/*1 + sh2 ^ = ch г.
Следовательно,
J+l
6.7.3. /= J x2 V^ — \ dx.
6.7.4. / =
6.7.5. /= J V(x2-\?dx.
Решение. Применим подстановку:
213
Следовательно,
Возвратимся к переменной я:
/ = Arch x = In (л: + К*2— 1);
sh 2/ = 2 sh f ch f = 2x V хг — 1;
sh 4* = 2 sh 2/ ch 2^ = 4* ]/> — 1 Bjc2 — t).
Следовательно,
dx
5.7.6. /
= f
x) Ух—x2'
Решение. Применяем подстановку:
х = sin21; dx — 2 sin t cos i
и получаем
г С 2 sin t cos tdt _ С 2dt __ g С 1—sin ^
~~ J A +sin /) Vs'in^t—sin4 — J 1 +sin ^ ~" J cos2 / ~"
5.7.7. I=\V$ — 2x —
5.7.8. /
— f
"~J (л:2 — 2
-2*+5K/2 '
§ 5.8. Интегрирование других трансцендентных функций
5.8.1. I-ffi**-
Решение. Будем интегрировать по частям, полагая
\пх; dv ^;
*' —7'
dx Inx J
214
5.8.2. /=
J V\-x
Решение. Положим: ex — t; exdx = dt. Получим
, Г dt
/ —J (l + 'V
Пользуемся рекуррентной формулой (см. 4.4.1)!
l
2 J +
5.8.4. / =
Решение. Интегрируем по частям:
е* .
= — e~x In A + ex) + *—In A + ex) + C.
f g
5.8.5. /= \- —.dx.
J (l+2K'2
5.8.6. /==r
J
Решение. Интегрируя по частям, получим
х dx
u-aictgxi dv =
arctgx— \ ]Л -\-х2
= У\ + х2 arctg х—\п{х + Ух2 -J-1) + С.
215
§ 5.9. Обзор методов интегрирования
(основных видов интегралов)
с
%
1
2
3
4
5
Вид интеграла
$F[<p(*)]<p'(*)d*
$/(Ж)ф'(ж)*С
^f(x)y™(x)dx
J е«* р„ (ж) их,
где р„ (дс) — многочлен сте-
степени п.
Р2__ 4^ < 0
Метод интегрирования
Подстановка ф (д:) == /
Интегрирование по частям
$/(*)ф' (*)<** =
=/(*)ф(*)-?ф(*)П*)«ь-
Метод интегрирования по частям приме-
применяется, например, к интегралам вида
\ р (x)f (x) dx, где р (х) — многочлен, а / (х)
одна из следующих функций:
е*х\ cos ax; sin ax; In лг, arctg x\
arcsin хит. п.,
а также к интегралам от произведений по-
показательной функции на косинус или синус.
Сводится к интегрированию произведе-
произведения f{n) (x) ф (х) с помощью формулы крат-
кратного интегрирования по частям:
$/ЮФ00 (*)** =
..,+нг1/(«-1)(х)фм+
+ (-1)я5/(я)Мф(*)^
Применяя формулу кратного интегриро-
интегрирования по частям (см. п. 3), получим
Подстановка
ИИ
216
S3
с
<
6
7
8
9
10
Вид интеграла
" J(*2-M)"
Г Р (х) . Р {х)
Ь(*Лгде QW пра-
вильная рациональная
дробь,
Q(x) = (x-xiy(x-xir...
...(x*-\-px + q)k...
J Я (х, xmM , ..., *r/s) to,
где R — рациональная функ-
функция своих аргументов.
Г о Г (ах + Ьу/пЛ
где R — рациональная функ-
функция своих аргументов.
J Уах*+Ьх + с
Метод интегрирования
Применение рекуррентной формулы
х 2п-3
п B/1 — 2)(*2+1)"-1 1 2/г — 2 "~L
Подынтегральную дробь представляют
в виде суммы простейших дробей
Р(х) Л± Л2 , Л, j
. Яя М^ + ЛГ,.
•••^(д —х2)* 1 •'• ' Д;2 + рл: + ^'Г
Af2A:-|-/V2 , 1 Л1Лх+Л^Л j_
(x2 + pj: + G)a ' ••' ^2 4-px + ^)*
Приводится к интегралу от рациональ-
рациональной дроби подстановкой x—tk% где к — об-
общий знаменатель дробей
т г
Сводится к интегралу от рациональной
дроби подстановкой
ах+ь tn
cx+d
Подстановкой х-\-^~ — t интеграл приво-
приводится к сумме двух интегралов:
Г »*+» л, мЛ , ш +
J уах* + Ьх + с J У at* + m
Первый интеграл сводится к интегралу
от степенной функции, а второй интеграл —
табличный.
217
Вид интеграла
Метод интегрирования
11
x+c)dx,
Я (*, У
где R — рациональная функ-
функция от х и Уах2+Ьх+с
Приводится к интегралу от рациональ-
рациональной дроби подстановками Эйлера:
Vax*+bx+c=t ± х У~а {а > 0),
У *х ±V"c (c> 0),
t(x—х±) Dac—b2 < 0),
где хх—корень трехчлена
Для вычисления указанного интеграла
применяются также тригонометрические под-
подстановки:
(a<0,
4ac —62 < 0)
(a>0,
b*
(a>0,
c — 62 > 0)
12
где Рп(х) — многочлен сте-
степени л*
1-
Записываем равенство
¦=Qn-Ax)
где Qn«x (д;) —многочлен степени п — 1.
Дифференцируя обе части этого равенства и
умножая на У ах2-\-Ьх-\-с, получим тож-
тождество
Рп (х) - Q'n_x (х)
которое дает систему п-\-\ линейных урав-
уравнений для определения коэффициентов мно-
многочлена Q/2-i (х) и множителя k.
Интеграл же
dx
= 0;
Уах2-\-Ьх + с
берется методом, указанным в п. 10
N=1).
218
с
с
%
13
14
15
Вид интеграла
[ xm(a+bxn)Pdxt
где т, л, р—рациональ
ные числа (интеграл от би
номиального дифференци
ала).
V R (sin xt cos x) dx
Метод интегрирования
Этот интеграл приводится подстановкой
х—xl — \/t к интегралу, рассмотренному
выше.
Интеграл от биномиального дифферен-
дифференциала выражается через элементарные функ-
функции только при выполнении одного из сле-
следующих условий;
1) если р—целое число,
т+1
2) если —! целое число,
п
3) если —¦ Ьр—целое число.
1-й случай
а) если р — целое положительное число,
то нужно раскрыть скобки (а-\-Ьхп)Р по
биному Ньютона и вычислить интегралы от
степеней;
б) если р—целое отрицательное число,
то подстановка x—tkt где к — общий знаме-
знаменатель дробей тип, приводит к интегралу
от рациональной дроби;
2-й случай
т+1
если —¦ целое число, то применяется
подстановка a-\-bxn = tk, где к—знаменатель
дроби р;
3-й случай
т+1 ,
если —¦ \-р—целое число, то приме-
применяется подстановка a-\-bxn — xntk, где к —
знаменатель дроби р.
Универсальная подстановка tg-K- = t.
Если R (—sin х, cos x) = —R (sin x, cos x)y
то подстановка cos x = t.
Если
R (sin х, —cos x) = —R (sin x, cos x),
то подстановка s'mx — t.
Если
R (—sin х, — cos x) = R (sin x, cos x),
то подстановка tgx = t.
219
с
с
16
17
18
19
20
Вид интеграла
\ R vsh xt ch x) dx
\ sin ax sin bx dx
V sin ax cos bx dx
\ cos ax cos bx d*
V sinw л; cos" л; ах, где /п и
/г — целые числа
\ sinP хсоъч xdx
@ < х < л/2),
р и # — рациональные числа.
С R (еах dx
Метод интегрирования
X
Применяется подстановка th ir:=t-
При этом
2/ 1 + /2 2d/
Необходимо преобразовать произведение
тригонометрических функций в сумму или
разность, пользуясь одной из следующих
формул:
sin ax sin bx =
==у [cos (a—b) x— cos (a+b) x]
cos ax cos bx =
= -2"!cos (a —b) jc + cos (a + &)*]
sin ax cosbx =
=— [sin (a—b) Jt-f-si" (a + 6) *]
Если m—нечетное положительное, то
подстановка cos* = /.
Если п — нечетное положительное, то
подстановка sin# = /.
Если т-\-п — четное отрицательное, то
подстановка tg х = t.
Если т и п — четные неотрицательные,
то применяют формулы:
. 9 1—-cos 2л: 9 1+ cos2x
sin2* — ^ ; cos2jc L-2
Подстановкой sin^ = ^ приводится к
интегралу от биномиального дифференциала
С sinPxcos4xdx=\ tP(\ — t*)<l-idt
(см. п. 14).
Подстановкой eax = t преобразуется в
интеграл от рациональной функции
220
Глава VI
Определенный интеграл
§ 6,1. Понятие определенного интеграла
Пусть на отрезке [а, Ь] определена функция / (х). Интегральной суммой
называется
Л» =2 /ffi/)A*/.
i=o
где а = х0 < хг < х2 < ... < хп-г < хп = Ь,
Axi = xi+1—xi\ li€[xh xi+1] (« = 0, 1, ..., я—1).
Верхней (нижней) суммой называется
t=o \ i
где M/ = sup/(A:) [m/ = inf / (x)] для а:^[а:^ j:/+1].
Определенным интегралом от функции /(*) на отрезке [а, Ь] называется
предел интегральных сумм:
\ f(x)dx = l\m 2 f E/) А*/ ПРИ тах I Ах/1 —* О-
а ^=°
Если этот предел существует, функция называется интегрируемой на
отрезке [а, Ь]. Всякая непрерывная функция интегрируема.
6ЛЛ. Для интеграла
я
^ sin х dx
о
найти верхние и нижние интегральные суммы, соответствующие раз-
разбиению отрезка [0, я] на 3 и на 6 равных частей.
Решение. Разобьем отрезок [0, я] на 3 равные части точками
На отрезке [0, я/3] функция sin л; монотонно возрастает и поэтому
для этого отрезка имеем /wo = sinO = O, jW0 = sin (я/3) = \'3/2. На
отрезке [я/3, 2я/3] наименьшим значением функции является тх =
«= sin (я/3) = V3/2, а наибольшим Жх = sin (я/2) = 1. На отрезке
221
[2я/3, я] функция sin л; монотонно убывает и потому
т2 = sin я = О, М2 = sin Bя/3) = У 3/2.
Так как все Axk равны я/3, то
п
При разбиении отрезка [0, я] на 6 равных частей точками
О 6 3 2 23 56
таким же путем находим
т0 = О, Мо = sin (я/6) = 1 /2,
тх = sin (я/б) =1/2, Мгг=г sin (я/3) = ]//2,
т2 = sin (я/3) «=1//2, Ж, = sin (я/2) = 1,
т3 = sin Bя/3) = ]//2, Ж3 = sin (я/2) = 1,
ю4 = sin Eя/6) = 1/2, Ж4 = sin Bя/3) = ]/"Ъ/29
ть = sin я ¦= О, Ж6 = sin Eя/6) = 1 /2.
Для этого разбиения получаем
Как и должно быть, выполняются неравенства
(точное значение интеграла равно 2).
6.1.2. При каком б > 0 из неравенства max &xt < б вытекает
соотношение
\ sinxdx— 2 sin
У 3 — Л
г = 0
< 0,001.
Решение, Так как sn < In < *SW, то для выполнения требуемого
неравенства достаточно, чтобы верхняя и нижняя интегральные суммы
отличались меньше, чем на 0,001:
222
Но
где Mi и mi — наибольшее и наименьшее значения функции slnx на
отрезке [xh х{+1] (/«=0, 1, ..., п — 1). Считая для простоты, что
в качестве одной из точек разбиения выбрана точка я/2 и пользуясь
монотонностью функции sin л: на отрезках [0, я/2] и [я/2, я],
получим
я-1
({,) f-J—sino)=»2.
*=о \ l J
Следовательно, требуемое неравенство удовлетворяется, если
26 < 0,001, т. е. б < 0,0005.
6.1.3. Показать, что функция Дирихле (см. 1.14.4.6) не интегри-
интегрируема в промежутке [0, 1].
Решение. При фиксированном разбиении отрезка [0, 1] мы
должны учитывать, в частности, две возможности: 1) все точки \{
рациональны; 2) все точки \-t иррациональны. В первом случае интег-
интегральная сумма равна единице, во втором случае — нулю. Следова-
Следовательно, как бы мы ни уменьшали максимальную длину частичных
отрезков разбиения, мы всегда получим интегральные суммы, равные
единице, и интегральные суммы, равные нулю. Поэтому не существует
предела интегральных сумм, а это значит, что функция Дирихле
не интегрируема в промежутке [0, 1].
6.1.4. Вычислить путь, проходимый свободно падающим телом
за промежуток времени от t^a сек до t = b сек.
Решение. Свободно падающее тело движется с постоянным
ускорением g и начальной скоростью v0 = 0. Следовательно, скорость
движения в момент времени t равна приращению скорости за период
времени от 0 до t} т.е. v(t) = Av. За малый период времени А/
приращение скорости приближенно равняется ускорению в момент
времени t, умноженному на At. Но в нашем случае ускорение посто-
постоянно. Поэтому Av = gK( и, значит, v{t)=*gt, так как &t*=*t—0 = ^.
Разобьем промежуток времени от t — a до i*=*b на л равных
частей; тогда длительность Д^ каждого промежутка будет равна
At**z(b — аIп. Будем считать, что в течение каждого промежутка
времени тело движется равномерно со скоростью, равной его скоро-
скорости в начале этого промежутка, т. е.
Ъ—а
223
Отсюда находим путь, пройденный телом за /-й промежуток вре-
времени: vt{b — a)jn. Весь путь s, пройденный телом, приближенно
равен
b—a
,[»+,i=S+»i=!+...+„_„!=•]_
п ** l
^—a n(n—
При увеличении числа п величина пройденного пути будет вычи-
вычисляться более точно. Точное значение пути 5 отыскивается как
предел sn при п—> оо:
Так как сумма sn является интегральной суммой
то путь 5 есть интеграл:
ь ь
6.1.5. Вычислить, исходя из определения, интеграл
\xdx.
о
Решение. По определению,
2 /Ajc/ при max Ал:/ —> О,
где
1. Разобьем отрезок [0, 1] на п равных частей точками деления
Xi=i\n (/-0, 1, 2, ..., п).
Длина каждого частичного отрезка равна Axt;= \/п9 причем
1//г—>0 при n—t-oo.
В качестве точек \г возьмем правые концы частичных отрезков:
li = xi+l = (l + l)ln (/ = 0, 1, ..., п—\).
224
Составим интегральную сумму
я-1
Предел этой интегральной суммы при п —> оо равен
Я -> СО ^'* *
Следовательно,
2. Покажем на этом примере, что при другом выборе точек \t
предел интегральной суммы будет тот же.
Возьмем, например, в качестве \t середины частичных отрезков
h (i+\2) (i 0 1 1)
Составим интегральную сумму
л-1
Отсюда
lim /Л=-о-.
6.1.6. Вычислить, исходя из определения, интеграл
ь
\xmdx (тф — \, 0<а<Ь).
Решение. В этом примере оказывается удобным в качестве
точек деления х( выбрать точки
b\i/n /b\n/n
которые образуют геометрическую прогрессию со знаменателем
Длина /-го частичного отрезка равна
дкХ( = а^+1 — aql=^aq({q—1).
Поэтому максимальная длина частичных отрезков равна max Дл\.=
= aqn *(#—1)==a("^"J I ( — ) —1 и стремится к нулю с
ростом /г, так как lim#=l.
Л -*• со
225
В качестве точек |^ выберем правые точки частичных отрезков;
Составим интегральную сумму:
Вычислим предел интегральной суммы при max Лаг^—*0, т.е.
При #—-М:
Таким образом,
6.1.7. Вычислить, исходя из определения, интеграл
Cdx
1
Решение. Разобьем отрезок [1, 2] на п частей так, чтобы
точки деления xf(/ = 0, 1, 2, ..., п) составляли геометрическую
прогрессию:
откуда }и^2,
Длина /-го частичного отрезка равна
так что m&xAxi*=qn~1(q—1)—>0 при /z—^oo, т.е. при q—^1.
В качестве точек ^ выберем правые концы частичных отрезков,
т.е. 11 = Хш^д1*г.
Составим интегральную сумму:
Остается найти предел интегральной суммы:
Hm/.-Um п{
п
так как 2{/п—1 ^—' — In 2 при /г
226
6.1.8. Найти величину интеграла
опираясь на его геометрический смысл,
Решение, Линия у « У 25— х2 есть верхняя половина окруж-
окружности х2-\-у2^25. Та часть линии, которая получается при измене-
изменении л; от 0 до 5, лежит в первой координатной четверти. Отсюда
заключаем, что криволинейная трапеция, ограниченная линиями л: «и 0;
х = 5\ У^О; у = ]/г25—л;2, есть чет-
четверть круга #2+j>2 = 25; ее площадь
равна 25я/4.
Следовательно,
У\
м
6.1.9. Исходя из геометрического
смысла интеграла, вычислить интеграл
/= J Dл:— \)dx.
6.1.10. Доказать, что
х
1
о
Решение. Интеграл
Рис. 59.
V _ Х2 + « arcsin Л @ < л: < а).
выражает площадь S0AMx части круга радиуса а, лежащей в первом
квадранте (рис. 59), Эта площадь равна сумме площадей треуголь-
треугольника ОМх и сектора ОАМ.
Но площадь треугольника
^0Жх — у— " ^ '
Площадь сектора
где
Следовательно,
227
а значит,
а2 —х2 + ~y arcsin — .
6.1.11. Исходя из геометрического значения интеграла, показать,
что
2я 1 1
a) J sin3 х dx = 0; б) J e~x* dx = 2
о -1
Решение, а) График функции у = sin8x изображен на рис. 60.
Покажем, что площадь, лежащая над осью Ох, равна площади,
лежащей под осью Ох. В самом деле, пусть п^.х^,2л> тогда
где 0^хх^тс и
sin8 x = sin8 (n -f- xx) = —sin8 хг.
p Поэтому вторая половина графика
получена из первой сдвигом впра-
вправо на л и симметрией относитель-
относительно оси Ох. Следовательно,
2л
Рис. 60. г .
sin8 д; dx = 0.
о
6.1.12. Дана функция f(x) = x9 на промежутке [—2, 3]. Найти
нижнюю (sn) и верхнюю (Sn) интегральные суммы на заданном про-
меж^ке, деля его на п равных частей.
6.1.13. Исходя из геометрического значения определенного ин-
интеграла, доказать, что:
а)
0
2
sin
2х dx =
0;
б)
2я
j cos8 лг с?лг = 0;
0
3
в) $B*+l)djt = 6; r) J |/9—x*dx = ^.
6.1.14. С помощью предельного перехода от интегральных сумм
вычислить интеграл
1
разбивая отрезок [1, 4]
а) на равные части,
б) точками, образующими геометрическую прогрессию,
причем в каждом из указанных разбиений в качестве |/ выбирать
1) левые концы отрезков,
2) правые концы отрезков,
3) середины отрезков [xh xi+i].
228
§ 6.2. Вычисление определенных интегралов
по формуле Ньютона — Лейбница
Формулой Ньютона—Лейбница называется формула
ь
ХЪ =F(b)-F(a),
где F (х) — одна из первообразных для функции f(x), т. е.
Ff(x)^f(x) (а<*<&).
6.2.1. Вычислить интеграл
VT
/— f ***
1
Решение. Так как одной из первообразных для функции
/{х) = 1/A +х2) является функция F (х) = arctg x, то, применяя фор-
формулу Ньютона — Лейбница, получим
6.2.2. Вычислить интегралы:
я/2
а) Г sin 2x
J
0
6.2.3. Дана
Вычислить
dx; б)
функция
/(*) =
2
\f(x)dx.
Я/2
С cos:
я/6
Iх2
\Vx
'-dx;
при
при
2
D) Г Л
0
0<*<1,
Решение. По свойству аддитивности интеграла
2 1 2
о i
1 2
229
6.2.4. Вычислить интеграл
2
I=^\\—x\dx.
о
Решение. Так как
1—д; при О^лс^1,
л:— 1 при 1^л:^2,
то, применяя свойство аддитивности интеграла, получим
2 1 2
l\l—x\dx=*l(l—x)dx + ^(x—l)dx=*
О 0 1
2 1,1
1 ¦ (*-1J
-t о
i 2
6.2.6. Вычислить интеграл
a
где a<b.
Решение. Если 0 ^ a < b, то /(д:) = | x \/x = 1, поэтому
b b
dx=:b—a. Если a<6<0, то /(*) = —1 и
a a
= — b—(—а) = л—6. Наконец, если a < 0 < b, то разбиваем ин-
ь
теграл ]f(x)dx на два интеграла:
J
Все три случая можно объединить одной формулой:
X iiii
а
Замечание. Вычисляя интегралы с помощью формулы Ньютона—Лейб-
Ньютона—Лейбница, следует обратить внимание на условия законности ее применения. Эта
формула применяется для вычисления определенного интеграла от непрерывной
на отрезке [а, Ь] функции f (х) лишь тогда, когда равенство F1 (x) — f (x) вы-
выполняется на всем отрезке [a, b] (F (х) — первообразная функции /(*)). В част-
частности, первообразная обязана быть непрерывной функцией на всем отрезке
[а, Ь]. Использование в качестве первообразной разрывной функции может
привести к неверному результату.
230
6.2.6. Найти ошибку при следующем зычислении интеграла.
т.
где ^arctg-j-^J —^ (хф\).
Решение. Результат заведомо неверный: интеграл от всюду
положительной функции оказался отрицательным. Ошибка произошла
I 2х
из-за того, что функция -^r- arctg -j ^ в точке х = 1 терпит разрыв
первого рода:
«. 1 , 2х п л. 1 , 2х п
hm -arctgy—2- = tj hm yarctg
io z l~~x 4 i o z
Правильное значение рассматриваемого интеграла равно
VJ
arctg j/~3 — arctg 0«
Здесь формула Ньютона — Лейбница применима, так как функция
F(x) = arctg х непрерывна в [0, я/3] и равенство F' (x)=f(x) выпол-
выполняется на всем этом отрезке.
6.2.7. Найти ошибку, допущенную при следующем вычислении
интеграла:
С *** — Г *** — rw/c°s2^_
J 1+2 sin2 * J cos2 x + 3 sin2 д; ~" J 1 +3 tg* л """
= ^L- arc
(Интеграл от всюду положительной функции оказался равным
нулю!)
Решение. Применение формулы Ньютона — Лейбница незаконно,
так как первообразная F(x)=^—y=r arctg (K3tg x) терпит разрыв
V 3
V
в точке х = п/2. Действительно,
lim F (х) = lim --U- arctg (К 3 tg x )
Х-+Я12-0 лг-^я/2-0 УЗ
= -4=-arctg(+ оо) = ", ,
lim F (х) = lim -i=- arctg {V 3 tg д:)
/2 0 д:->Я/2 + 0 К «
231
Правильный результат можно получить так:
я
С
J
dx
cos2 x+3 sin2x
я
Г
J
1
dx
ctg2*+3 sin2*
Но правильный результат можно найти также и при помощи функции
F(x) =-jr=-avctg(\/r3tgx). Для этого следует отрезок интегрирова-
ния [0, я] разбить на два отрезка, [0, я/2] и [я/2, я], и учесть
указанные выше предельные значения функции F(x) при х —> я/2 + 0.
Тогда на каждом из отрезков первообразная становится непрерывной
функцией и будет законно применение формулы Ньютона — Лейбница:
Л
Г
J
О
Я/2
Г
J
0
J
Я/2
6.2.8. Вычислить интеграл
я
W
Решение.
Поэтому
= у •
2 cos2 *
= cos х \ =
я
I
Я/2
2
COSJC,
— cos х, я/2
(— cos л:) dx ¦
Я/2
О
Я/2
Я/2
= A — 0) + @ —(— 1)) = 2.
Замечание. Если не обратить внимание на то, что cosx отрицателен
в промежутке [я/2, л] и положить
232
то получим заведомо неверный результат:
я
\ cos х dx = sin x
о
6.2.9. Вычислить интеграл
ЮОя
/ =
б
Решение. Имеем
= 0.
Так как | sin л: { имеет период я, то
ЮОЯ ЮОя
| sin л: | tfjc =
о о
= 100 V2 \ sin х dx = 200 К*2.
6.2.10. Вычислить интегралы:
-I
-2 -3
я я/4
в) /= \ sitf^dx; г) /= -^гу dx;
^ i +
е» 2,'я
д) /=\ тьгг; е) /==
J ^2
е 1/я
1 1
ч . С ех . ^ г С x*dx
Я/2
^Я/2
§ 6.3. Оценки интеграла. Определенный интеграл
как функция своих пределов
1. Если /(х)<ФЙ при а^х*^Ь, то
Ь Ь
Ф (х) dx.
а
233
В частности,
Ь
15/м«**|< 51
a
Ь
2. m(b—a)^
где m—наименьшее значение, а М — наибольшее значение функции / (х) на
отрезке [а, Ь] (оценка интеграла).
3. Если функция / (х) непрерывна на отрезке [а, Ь], то
a<l<b
(теорема о среднем значении).
4. Если функции f (я), <р (х) непрерывны на отрезке [а, 6], a cp (х), кроме
того, сохраняет 8нак на этом отрезке, то
(обобщенная теорема о среднем).
х а
б. JJ 1/(*) # = /(*)» jj\/(O^ = —/W в каждой точке * непрерыв-
йости функции / (х).
6.3.1. Оценить интегралы:
dx;
a)
в)
3
i — \ V O~\->
1
* \ x2 12
0
t ил, O| / -
Л/3
|^ sin jc
j a;
л/4
Решение, а) Так как функция f(x)=y 3 + л:2 монотонно воз-
возрастает на отрезке [1, 3], то /я = 2, М = ]/г30, Ь—а = 2.
Следовательно, оценка интеграла имеет вид
з
т. е.
23-1
б) Подынтегральная функция f(x) = (slnx)/x убывает на отрезке
[л/4, я/3], так как ее производная
м / v ^_л cos*—sin* (х—tgх) cos х ^
Следовательно, наименьшее значение функции —
_ 3/"з"
~ 2л '
а наибольшее значение функции —
Поэтому
я л\ Г s'mx
з"~т; ^ J "ir
/4
J
Я/4
т. в.
0,22 «!^<|2!Е?л<!ф1« 0,24.
я/4
6.3.2. Оценить абсолютную величину интеграла
19
I
sin х .
dx.
1 + *8
о
Решение. Так как Jsinxj^l, то при х^\0 выполняется
неравенство
I sin*| <10"8.
Поэтому
19
sin х
С si
J Г
10
dx
A9 —10) 10"8<
(истинное значение интеграла «—10 п).
6.3.3. Установить, какой из двух интегралов
о
больше?
Решение. Известно, что У~х > хг при 0 < х < 1. Поэтому
235
6.3.4. Доказать неравенства:
Решение, а) Так как 0 < ¦
1 1
<х'1 при 0<л;<П, то
г, ^ С х7 dx , С 7 , х8
о к о
8 '
б) Так как при О < х < 1 имеет место неравенство 1 < ?**< *>, то
1 1 1
* \ dx.
Отсюда вытекает справедливость доказываемого неравенства.
6.3.5. Доказать неравенство
Я/2
Решение. Так как функция /(х) = (sin x)/x в интервале @, я/2)
убывает (см. 6.3.1. б)), то при 0<л:<я/2
2
Следовательно, в этом интервале sin x > — х, поэтому
_2Я
^ — i? sin лс ^ g rt
—й е " Jo =ЙО—-*>•
6.3.6. Доказать, что для любых интегрируемых на интервале
{а, Ь) функций f(x) и g(x) имеет место неравенство Шварца—Буня-
ковского:
ь / "Ъ Ъ
\f(x)g(x)dx <]/ \f*(x)dx\g*(x)dx.
а а а
Решение. Рассмотрим функцию
23G
где К—любое действительное число. Так как F(x)^0, то
ъ
или
Выражение, стоящее в левой части последнего неравенства, яв-
является квадратным трехчленом относительно X. Из неравенства сле-
следует, что при любом X этот трехчлен неотрицателен. Следовательно,
его дискриминант неположителен, т. е.
( Ъ \2 Ь Ь
Отсюда
\\
Ь Г~Ъ
\f{x)g{x)dx <]/ l
что и требовалось доказать.
6.3.7. Оценить сверху интеграл
1
_ Г
J
о
sin*
dx
Решение. По обобщенной теореме о среднем значении опреде-
определенного интеграла имеем
Так как на отрезке [0, 1] функция sinx возрастает, то sin? < sin 1.
Отсюда получаем оценку интеграла сверху:
Можно получить лучшую оценку, если ту же теорему применить
в виде
1
1
237
6.3.8. Доказать, исходя из геометрических соображений, что:
а) если функция f(x) в промежутке [а, Ь] возрастает и имеет
вогнутый график, то
ь
(b-a)f(a)<§f(x)dx<(b-a)f(a)+f{b)i
б) если функция f(x) в промежутке [а, Ь] возрастает и имеет
выпуклый график, то
f(b)
f(a)
\C <§f(x)dx<(b-a)f{b).
I
.— ' b
. -——.—.——i k
I I a
—' ^—>*-& Решение, а) Без ограничения
a о общности можно считать /(#)>0.
р fi| Вогнутость графика функции, в
частности, означает, что график
расположен ниже хорды, соединяю-
соединяющей точку A {a, f{a)) с точкой B(b,f(b)) (рис. 61). Поэтому пло-
площадь трапеции аАВЪ больше площади криволинейной трапеции, ог-
ограниченной сверху графиком функции, т. е.
а
Неравенство
ь
(b-a)f(a)<lf(x)dx
а
очевидно.
1
6.3.9. Оценить интеграл j j/l ~\-x*dx, пользуясь
о
а) теоремой о среднем значении определенного интеграла,
б) результатом предыдущей задачи,
в) неравенством |/l +#4 < 1 -\-х*/2,
г) неравенством Шварца — Буняковского (см. 6.3.6).
Решение, а) По теореме о среднем значении
1
/ = J Y\ -f х" dx = ]/ 1 + Ъ\ где 0<|<1.
о
Но
откуда
1 </<]/*2"^ 1,414.
238
б) Функция /(*) = У\+х* вогнута на отрезке [0, 1], так как
^ Q
На основании предыдущей задачи получаем
1
1,207.
в)
г) Положим f(x) = yr\-\-x^% g(x) = l и используем неравенство
Шварца—Буняковского
= /<]/ JA+*V*'J
0 0
1,095.
6.3.10. Найти производную по х от функций:
а)
А*
Jin
б)
cos
Решение, а) Запишем заданный интеграл следующим образом:
С X9 Xs X2
F (х) = J In t dt + J In t dt = \ In t dt — J In t dt,
Xя С С С
где с — произвольная постоянная, с > 0.
Найдем теперь производную F' {х)у пользуясь правилом диффе-
дифференцирования сложной функции и теоремой о производной интеграла
по верхнему пределу:
= In л:3 Зл:2 —In x2 2x = (9a;2 — 4*) In л:.
239
с VI
б) F(x)= J cos (t2) dt+ J cos (f*
\/x с
l/x VH
= — \ cos (/2) dt-\- \ cos
ПА
с
(тУ + f «и(/«)Л (]Л?)
6.3.11. Найти производную по х от следующих функций:
2х О
a) F(x) = j ^ Л; б) У (ж) = j J/T+^ Л.
X
6.3.12. Найти точки экстремума функции F(x)=[^-j~ dt в об-
о
ласти х > 0.
Решение. Найдем производную
рч \__ Г f ?HL*//Л _ sln х
I J ^ I x
Критическими точками являются точки
х = пп (п= 1, 2, ...), где sinAr=O.
Найдем вторую производную в этих точках:
рп /v х, cos х—sin х #
F" (пп) = — cos (ля) = — (— 1 )п Ф 0.
Так как в точках х — пп (п = 1, 2, ...) вторая производная отлична
от нуля, то эти точки являются точками экстремума функции,
а именно: максимумами, если п—нечетное, и минимумами, если п —
четное.
6.3.13. Найти производную от у по х функции, заданной пара-
параметрически:
t* з
х=\ l/lzlnzdz; y= J z*\nzdz.
1 VI
Решение. Известно, что^ = -^-.
240
Найдем х\ и y't:
' )i = /ln<».3<1 = 9<»ln/;
Vt jvi
тсюда
6.3.14. Найти пределы:
f sin l/"i"dx \ (arctgxJdx
a) lim ±_-3 ; 6) lim ° -
в) lim
Решение, а) При х = 0 интеграл j sin \f xdx равен нулю; легко
о
роверить выполнение остальных условий, обеспечивающих закон-
ость применения правила Лопиталя. Поэтому
х*
Гх*
\ si
1Jm Lo
sin Ух dx \\ sin Yx dx (x2)x
lim ^ = lim 1=5 o , -**' = lim
3*2
в) Имеем неопределенность вида—.Применим правило Лопиталя:
/ X v 2
lim Ц L
= lim 2—— = 0.
241
6.3.15. Найти производную -4- функций, заданных неявно:
-4-
У X
о о
о о
б) \e*t
о о
х у
в) 5 j/—2sin2*<te + J cos< d/ = О.
Л/2 О
Решение, а) Продифференцируем левую часть уравнения по х,
считая у =у (х):
V Гх* У
J*~'
J4 SN4 §
Отсюда, решая уравнение относительно -4-, получим
в) Продифференцируем левую часть уравнения по х> считая
у=у(х):
X т г У -V
f ]/r3—2sinizdz +J
Lrt/a Jx Lo
Отсюда
6.3.16. Найти: а) точки экстремума и точки перегиба графика
функции
О
б) кривизну линии, заданной параметрическими уравнениями:
if
*^J-
(спираль Корню).
Решение, а) Функция определена и непрерывно дифференциру-
дифференцируема на всей числовой оси. Ее производная
242
равна нулю в точках х1=^\, хг~2, причем при переходе через
точку хг она меняет знак с — на + , а в окрестности точки х2 знака
не меняет. Следовательно, в точке xL = 1 минимум, а в точке х2 = 2
экстремума нет.
Вторая производная
обращается в нуль в точках х1 = 4г/3, х%*=*2 и меняет знак при
переходе через эти точки. Значит, эти точки являются абсциссами
точек перегиба,
б) Имеем
xt = а у л cos ~y , j^ = а к л sin -^ >
следовательно,
a cos3 -jr-
отсюда кривизна
6.3.17. Доказать, что функция L (х), определенная в проме-
промежутке @, сю) интегралом
1
является обратной для функции ех.
Решение. Возьмем производную
L'(x)=\/x (x>0).
Так как производная положительна, то функция у = L (х) возрастает и,
значит, имеет обратную функцию
x = L-1(y).
Производная этой обратной функции равна
dx__ 1
dy-L'{x)-x'
откуда следует (см. 3.1.10), что
х=СеУ.
Чтобы найти С, подставим х=1. Так как
1A) = 0, т. е. у\х=1 = 0,
ТО
1 = Се° == С,
243
что и доказывает наше утверждение:
f(x), данному на рис. 62, выяс-
Рис. 62.
6.3.18. По графику функции y
нить вид графика первообразной
о
Решение. На отрезке [0, а] заданная функция положительна,
следовательно, первообразная возрастает. На отрезке [0, а/2] произ-
производная заданной функции положитель-
положительна, следовательно, кривая 1 = 1 (х)
вогнута. На отрезке [а/2, а] производ-
производная заданной функции отрицательна и,
следовательно, кривая 1 — 1(х) вы-
выпукла. Точка x = aj2 есть точка пе-
перегиба. Аналогично рассматривается
отрезок [а, 2а]. Точка хг = 0 есть
точка минимума, так как знак произ-
производной Г {х)=/{х) меняется с — на + ; точка х2 = а есть точка
максимума, так как знак производной меняется с + на —.
Первообразная f(x) есть функция периодическая с периодом 2а,
так как площади, лежащие над осью Ох и под осью Ох, взаимно
погашаются на отрезках длины 2а. Учитывая все сказанное, можно
качественно нарисовать график пер-
первообразной (рис. 63).
6.3.19. Найти многочлен Р(х)
наименьшей степени, имеющий мак-
максимум, равный 6, при #=1, и ми-
минимум, равный 2, при х — 3.
Решение. Многочлен есть
всюду дифференцируемая функция.
Поэтому точки экстремума могут быть только корнями производной.
Кроме того, производная многочлена есть многочлен. Многочлен
наименьшей степени с корнями хг — \ и л;2 = 3 имеет вид
а (х—1) (х—3). Следовательно,
Р' (х) = а (х—\) (* —3) = а (х* — 4х + 3).
Так как в точке #=1 должно быть РA) = 6, то
О А
г
Рис.
За.
г
63.
Р (х) = J Р' (х) dx + 6 = а
1
Коэффициент а определяем из условия РC) = 2, откуда
Следовательно,
244
6.3.20. Найти многочлен Р(х) наименьшей степени, график кото-
которого имеет три точки перегиба: (—1,—1), A, 1) и точку с абсцис-
абсциссой 0, в которой кривая наклонена к оси абсцисс под углом 60°.
Решение. Поскольку искомая функция есть многочлен, то абс-
абсциссы точек перегиба могут быть только среди корней второй произ-
производной. Многочлен наименьшей степени с корнями —1, 0, 1 имеет
вид ах(х2 — 1). Следовательно,
= а(х* —х).
Так как в точке х ~ 0 производная Р' @) = tg 60° = Уз , то
Р' (х) = j Р"
0
Далее, так как РA)=1> то
Коэффициент а определяем из последнего оставшегося условия
Р(—1)==—1, откуда а = — ^ "~ . Следовательно,
р (х) = ^А~ (Sx* — 1 О*3) + х УЗ.
6.3.21. Пользуясь теоремой о среднем значении определенного
интеграла, доказать, что
231
В) 13 <J
dx 2я
10 + 3 cos x ^ 7 *
о
6.3.22. Пользуясь неравенством Шварца — Буняковского, доказать,
1
что \ У\ + х3 dx<i У1Г/2. Убедиться, что применение теоремы
о
о среднем дает более грубую оценку.
245
6.3.23. Найти производные следующих функций:
X
a) F(x) = §\ntdt(x>0); б)
t •
Их
6.3.24. Найти производную ~ от функций, заданных параметри-
параметрически:
t in/
v С In z t
a) x = \ — dzt у =
2 5
sin t VT
б) * = J arcsinzdz, ey= f
e
ft
6.3.25. Найти точки экстремума функций:
a)
§ 6.4. Замена переменной в определенном интеграле
Если функция # = <p(f) удовлетворяет следующим условиям:
1) ф(?) — непрерывная однозначная функция, заданная на отрезке [а, Р]
и имеющая в нем непрерывную производную q/ (t);
2) значения функции x=*ip(t) при изменении t на отрезке [а, Р] не выхо-
выходят за пределы отрезка [а, Ь];
3) ф(а) = а и (р) 6
то для любой непрерывной на отрезке [а, Ь] функции / (х) справедлива
формула замены переменной (или подстановки) в определенном интеграле
Часто вместо подстановки x = y(t) применяют обратную подстановку
t = '^(x). В этом случае пределы аир определяются непосредственно из ра-
равенств а = г|)(а) и p = ifF). Ha практике замену переменной обычно произ-
производят с помощью монотонных непрерывно дифференцируемых функций. При
этом замену пределов интегрирования удобно записывать в виде таблицы
X
а
b
t
а
р
6.4.1. Вычислить интеграл \ У4—х2 dx.
246
Решение. Применим подстановку х *=2sin/, считая, что
— я/3^/^я/3. Функция д: = ф(/) = 2sin/ на отрезке [—я/3, п/3]
удовлетворяет всем условиям теоремы о замене переменной в опре-
определенном интеграле, так как она непрерывно дифференцируема, моно-
монотонна и
ф(— т)= — V% <
Итак,
х = 2 sin /; dx = 2 cos / с?/; У 4-х2 = 2 | cos /1 = 2 cos /,
так как cos/>0 в промежутке [—я/3, я/3].
Таким образом,
Я/З Я/8
= 4 J cos2 tdt = 2 J A+cos2/)d/~
..Уз" -я/з -я/з
"j3
2
Решение. Применим подстановку
о
я/3
На отрезке [0, я/3] функция 2sec/ монотонна, что обеспечивает
законность подстановки.
Следовательно,
4 Я/З
J ** dX== J '
' COS2 /
я/з
1
: 4- \ sin2 / cos / dt = j2 sin3
32 •
6.4.3. Вычислить интегралы:
а Уз~
a) §x2Va2—x2dx; б) С
6.4.4. Вычислить интегралы:
Я/2 Я/2
а) J 6-5sinA:+sin2A: ; °' J
2 + cos ^ *
247
Решение, а) Применим подстановку
x\t
cos x dx = dt;
0
я/2
0
Обратная функция x = arcsin^ (О^х^.тс/2 при 0^/^1) удовле-
удовлетворяет всем условиям теоремы о замене переменной. Следовательно,
Я/2
/== J 6-5 si
cos x dx
sin * +sin2* J 6—bi + t
dt i * —3
-= In-—-
3
б) Применим подстановку ^ = tg(je/2),
2dt
0
я/2
законность которой обеспечивается монотонностью функции tg(#/2)
на отрезке [0, я/2].
Л/2 1
Г dx — г 1
2dt
dt
_ 2 t
2 / 1 \ я
= —7г=: I arctg -р^ — arctg 0 = —у=,
V 3 \ /3 / 3 /3
6.4.5. Вычислить интеграл
ЭТ/4
(a>0,
Решение. Применим подстановку
COS2 Jf "
Следовательно,
Я/4 %
я/4
1
dx
a2 cos2 ^+Ь2 sin2 л
о о
=j_^_=^j_
1 Ь
bt
248
Если a — b=it то -г arctg— = arctg 1 =~j~» что> конечно, совпадает
do a 4
с результатом подстановки а = Ь=\ в исходный интеграл
Я/4 Я/4
С dx
J a2 cos2 x+b2 sin2 x =
6.4.6, Вычислить интегралы:
а) С ¦j" **d*; 6) ^ -
J x J x
dx
; в)
л
6.4.7. Вычислить интеграл /= \ 1 о§2^^л:.
Решение. Представим этот интеграл в виде суммы двух инте-
интегралов:
Я/2 Я
J 1 + COS2 JC * J
J
я/2
1 + COS2 X
К интегралу
J
я/2
cos2a:
dx
2~ JLi+c
применим подстановку
x— я—t,
Тогда
О я/2
. С (я—0 sin (n—t) . __ Г (n—f)sint
2~" J l + cos2(^—t) J 1 + cos2^
X
д/2
я
t
я/2
0
Я/2
я/2
я/2 я/2
— С sin t л С
-"J i + cos2/af J
Следовательно,
я/2
-'i-Wt- J 1 + со82^ + Л; J
t sin /
Я/2
sin/rf/
Я/2
0 0 0
Так как первый и третий интегралы отличаются только обозна-
обозначением переменной интегрирования, то
Я/2
249
К этому интегралу применим подстановку
и = cos t,
du — —sin t dt,
du
t
0
я/2
и
1
0
du
я»
Замечание. Неопределенный интеграл \ у-р — ^* не выражается
в элементарных функциях. Однако данный определенный интеграл, как мы
показали, вычисляется, если прибегнуть к искусственному приему.
6.4.8. Вычислить интеграл
Решение. Применим подстановку
dt
cos2 Г
Следовательно,
Я/4
X
0
1
t
0
л/4
j
Преобразуем сумму
Подставив в интеграл, получим
Я/4
Я/4
\ In sin
о
Я/4
Я/4
О
Я/4
Я/4
In sin
-г dt— \ lncos/d/ =
4У J
In sin ('+-J
я/4
—J Incos
0
250
Я/4
Теперь покажем, что It = I%. Для этого к интегралу /2= \ In cos t dt
о
применим подстановку
dt=—dz,
Тогда
/,= -j Incos
Jt/4
Я/4
\ Insia (^
Поэтому
t
0
я/4
z
я/4
0
Я/4
0
Этот пример, как и предыдущий, интересен тем, что неопреде-
неопределенный интеграл
да*
не выражается в элементарных функциях.
6.4.9. Доказать, что всегда можно подобрать линейную подста-
подстановку x=pt-\-q (p, q постоянны) так, чтобы любой данный интеграл
с конечными пределами а и b преобразовать в интеграл с преде-
пределами 0 и 1.
Решение. Прежде всего отметим, что подстановка x=pt-{-q
очевидным образом удовлетворяет условиям теоремы о замене пере-
переменной. Так как при х = а должно быть ^ = 0 и при х=*Ь должно
быть t=ly то для определения величин р и q имеем систему урав-
уравнений
откуда p = b—a, q — a. Следовательно,
— a)t + a]dt.
6.4.10. Вычислить сумму интегралов
-5 2/3
-4
1/3
251
Решение. Преобразуем каждый из интегралов в интеграл
с пределами 0 и 1 (см. предыдущую задачу).
Для этого к первому интегралу применим подстановку х = —t—4.
Тогда dx = —dt и
-5
-4
— J е('~lJ dt.
о
Ко второму интегралу применим подстановку д: =
= (dt)/3 и
2/3
J
Тогда
/
= 3 J
1/3
J
1/3
1 1
Отсюда
Заметим, что каждый из интегралов \ eix+5J dx и Г
в отдельности не берется в элементарных функциях.
6.4.11. Доказать, что интеграл
J sin х
о
при целом k равен нулю.
Решение. Сделаем подстановку
X
0
я
я
0
Тогда при целом k получим
л о л
f*sin2&*, С sin 2k (я—/) ,, Csir\2kt ..
J sin x J sin (я—t) "~ j sin t '
о л о
Так как определенный интеграл не зависит от обозначения перемен-
переменной интегрирования, то
/=—У, откуда /=()¦
6.4.12, Вычислить интеграл
V1/2
252
Решение. Применим подстановку х = sin / (данная функция
не монотонная), dx = cos / dt. Новые пределы tt и /2 находим из
уравнений 1/2= sin/; Y 3/2= sin/; можно принять /^я/6 и /2 =
= я/3, но можно также выбрать и другие значения, например,
/х =х 5я/6 и /2 = 2я/3.
В обоих случаях переменная j*r = sin/ пробегает весь отре-
отрезок [1/2, |//2] (рис. 64), причем функция sin / монотонна и на отрезке
[я/6, я/3] и на отрезке [2я/3, 5я/6].
Покажем, что результаты интегрирования совпадут. В самом
деле,
V1/2
я/з
cos / dt
Рис. 64
С другой стороны, учитывая, что на отрезке [2я/3; 5я/6] cos/
отрицателен, получим
2я/3
У djc _ Г cos tdt =
J xy\Z^e~~ J sin/( — cos О
1/2 5Я/6
5Я/6
5я/б
sin
г = 1п
J
2Я/3
5я/6
2я/3
3
Замечание. Полезно подчеркнуть, что нельзя брать /1==5я/6, /8 = л/3,
так как при изменении f на отрезке [я/3, 5я/6] значения функции x = sin/
выходят за пределы отрезка [l/2, У 3/2].
6.4.13. Доказать, что функция L (х), задаваемая в промежутке
(О, оо) интегралом
обладает следующими свойствами:
253
Решение. По свойству аддитивности
dt Г dt "ft dt
i "J / + J T'
1 1
Во втором интеграле произведем замену переменной
Тогда
t
х,х2
Z
1
х.,
^) + L
1 1
Полагая здесь хгх2 = х9; х2=^х9/х17 получим
L (х8) = I Ю + L (xslxx), т.е. I (лтд/^
Легко также получить и другое следствие L (xmln) = — L (х) для
любых целых тип.
Действительно, для положительных тип это следует из соот-
соотношений
А (*) = /г!
а для отрицательного показателя из
1A) = 0, L{x-*) =
Теперь, пользуясь непрерывностью интеграла как функции верхнего
предела, можно получить общее свойство L (ха) = aL (x).
Замечание. Как известно, L(х)«= Injc. Мы здесь получили основные
свойства логарифма, исходя лишь из его определения с помощью интеграла.
з
6.4.14. Преобразовать интеграл j (х—2Jdx с помощью подста-
о
новки [х — 2J = t.
Решение. Формальное применение подстановки на всем отрезке
[О, 3] приведет к неверному результату, так как обратная функция
лг = ф(/) двузначна: * = 2±У/, т.е. функция х имеет две ветви,
х1 = 2—Уt; x2 = 2-\~yrt. Первая не может принимать значений
х > 2, а вторая—значений х < 2. Чтобы получить верный резуль-
результат, надо разбить данный интеграл следующим образом:
3 2 3
J (х—2)а dx = J (х—2J dx+l (х— 2J их,
254
и в первом интеграле положить х = 2— Уt, а во втором x = 2-\-\/r t.
Тогда получим
Следовательно, / = 8/3 -f-1/3 = 3. Этот результат — верный, в чем
можно легко убедиться, вычислив исходный интеграл непосред-
непосредственна:
6.4.15. Вычислить интегралы:
о о
Л/3 I
Л/4
Л/4
Г
Д)
ж)
J Й + sin 2а:
о
—x*dx\ з) /=
О -1
6.4.16. Применяя подходящую замену переменной, найти сле-
следующие определенные интегралы:
2 а
a) j * , б)[ d*
о о
2
в)
J
6.4.17. Рассмотрим интеграл \ . 2. Легко заключить, что он
-2
равен зхУ4. Действительно,
2
с.
-2
255
С другой стороны, применив подстановку дг=1//, будем иметь
X
2
2
t
-1/2
1/2
-2
1/2
__ Г
" J
l/2
dt
1/2
- f * - 1
1/2
-1/2
1/2
-1/2
Этот результат явно неверный, так как подынтегральная функция
1/D + #2)>0, а следовательно, определенный интеграл от такой
функции не может равняться отрицательному числу —л/4. В чем
ошибка?
2л
Г dx
6.4.18. Рассмотрим интеграл /= \ =—^ . Применив подста-
подстановку tg(x/2) = tf будем иметь
2я О
Г
J
—L_
5 — 2cosjc
2dt
Результат явно неверный, так как подынтегральная функция поло-
положительная, а следовательно, интеграл от этой функции не может
быть равен нулю. В чем ошибка?
6.4.19. Убедиться в том, что формальная замена переменной
2
/ = #2/5 приводит к неверному результату в интеграле \ i/x2dx, и
-2
объяснить, в чем ошибка?
6.4.20. Можно ли в интеграле /=
новку x = sec/?
6.4.21. Пусть имеем интеграл
dx сделать подста-
—x2dx. Применим подста-
новку x = slnt. Можно ли в качестве пределов для t взять числа
я и я/2?
6.4.22. Доказать равенство
а а
I f(x)dx=\[f(x)+f{-x)]dx
-а О
для любой непрерывной функции f(x).
2я
6.4.23. Преобразовать определенный интеграл J /(x) cos x dx
о
с помощью подстановки sinx — t.
256
§ 6.5. Упрощение интегралов, основанное на свойствах
симметрии подынтегральных функций
1. Если функция f (х) четная на отрезке [—а, а], то
-fl О
2. Если функция f (х) нечетная на отрезке [—а, а], то
-a
3. Если функция f (x) периодическая с периодом Т, то
ь ь+пт
w (х) dx = \ / (х) dxt
а а+пТ
где п—целое число.,
1
6.5.1. Вычислить интеграл j J дг | ^/лг.
Решение. Так как подынтегральная функция f(x) — \x\ — чет-
четная функция, то
1 1 1
I
= 1.
-16 О
6.5.2. Вычислить интеграл
7
Г x*s\nx ,
-7
Решение. Так как подынтегральная функция нечетна, то
сразу заключаем, что интеграл равен нулю.
6.5.3. Чему равны интегралы:
я
а) ) f(x) cos nxdx;
-л
я
б) }f(x) sin nxdx,
-я
если: 1) f(x) — четная функция; 2) f(x) — нечетная функция.
5
С хъ sin2 х
6.5.4. Вычислить интеграл \ 4 , 2 2, т^.
— 5
25?
бя/4
6.5.6. Вычислить интеграл \
sin 2x
cos4 я-|-sin4 х
dx.
Решение. Подынтегральная функция является периодической
функцией с периодом я, так как
sin 2x f(x\
Cos4
cos4 * + sin4 x
Поэтому можно от верхнего и нижнего пределов интегрирования
отнять число зх:
5Л/4 Я/4
f sin 2х dx _ Г* si
J cos4 лт+sin4* ~" J cos4
sin 2x dx
я О
Применим подстановку
x J
0
Jt/4
f tgxdx
dx
COS2 X '
0
n/4
t
0
1
n/4
Г tgxdx _C2tdt_
J COS**(l+tg4*)-J l+^-
о о
6.5.6. Доказать равенство
a a
^ cos л/ (#2) dx = 2 J cos л:/ (jc2) rfjc.
-fl 0
Решение. Для доказательства достаточно установить чет-
четность подынтегральной функции:
cos (—*)/[(—хJ] = cos xf(x*).
6.5.7. Вычислить интеграл
VT
J
Р еш ени е.
K2~
J
2x7— 10a;6 —
^V2
— 4) + l
T
?53
VJ
= 0 + 2 J [3(^-
-_ Y2 1 П
VJ
о
При вычислении мы разложили интеграл в сумму двух интегра-
интегралов таким образом, чтобы под знаком первого интеграла стояла
нечетная функция, а под знаком второго интеграла — четная функция.
6.5.8. Вычислить интеграл
1/2
\ cos х In ~— dx.
Л/2
Решение. Функция f(x)= cosx четна. Докажем, что функ-
функция ф(д:)= ln-pi-^ нечетна:
Таким образом, подынтегральная функция представляет собой про-
произведение четной и нечетной функций, т. е. является нечетной
функцией, поэтому
Г
-1/2
1— х
6.5.9. Доказать справедливость следующих равенств:
я/8 1/2 1/2
а) С х8 sin9 xdx = 0; б) f ecosx dx = 2 f ecos X dx;
-Я./8 -1/2 0
л
в) \ sin mx cos nx dx = 0 (/», л—натуральные числа);
г) j sin xf (cos x) dx = 0.
—а
6.5.10. Доказать равенство
ь ь
а а
Решение. В правом интеграле сделаем подстановку
— t, dx=—dt,
X
а
b
t
b
a
259
Тогда получим
Замечание. Соотношению, установленному между интегралами, можно
дать наглядную геометрическую интерпретацию.
График функции / (х), рассматриваемой на отрезке [a, b], симметричен
графику функции / (а-\-Ь—х), рассматриваемой на том же отрезке, относи-
относительно прямой х—(а-{-Ь)/2. Действительно, если точка А лежит на оси Ох и
имеет абсциссу х, то симметричная ей относительно указанной прямой точка
А1 имеет абсциссу х'—а-\-Ь—х. Поэтому f (а-\-Ь—x') = f[a-\-b—(a-\-b—*)]=
= / (х). Но симметричные фигуры имеют равные площади, которые выража-
выражаются определенными интегралами. Итак, доказанное равенство есть равенство
площадей двух симметричных криволинейнььх трапеций.
6.5.11. Доказать равенство
t t
\f{x)g{t-x)dx=\g{x)f(t-x)dx.
о о
Решение. В правом интеграле применим подстановку t — x — z\
тогда будем иметь
о t
-\g{t-z)f(z)dz=[f(z)g(t-z)dz.
t о
Я/2 Я/2
6.5.12. Доказать равенство ^ s\nmxdx— J cosmxdx и приме-
о о
нить полученный результат к вычислению интегралов
Я/2 я/2
\ cos2 х dx и \ sin2 х dx.
о о
Решение. На основании 6,5.10 будем иметь
Я/2 Я/2 Я/2
\sinmxdx= xsitW^r—x\dx— \
о о о
Следовательно, в частности,
Я/2 Я/2
/ = \ sin2 х dx = \ cos2 x dx;
S о
сложим эти интегралы:
я/2 я/2
2/= Г
О
отсюда / = я/4.
260
6.5.13. Доказать равенство
Я Я/2
\jf(sinx)dx = 2 \^f(s\nx)dx.
о о
Решение. Так как
Я Я/2 я
x)dx= \ f(s\nx)dx-\- \ f(slnx)dx,
О
я/2
то достаточно доказать, что
Я Я/2
j / (sin x)dx— J / (sin x) dx.
я/2 О
К левому интегралу применим подстановку
X
я/2
я
я/2
0
Тогда
Я/2
Л/2
Я/2 Я/2
= \ f(sint)dt =
6.5.14. Доказать равенство
С xf (sin л;) d* = ~ \ / (sin л:) dx.
Решение. К левому интегралу применим подстановку
= —dt,
X
0
я
я
0
Тогда получим
x/(sin *) Ле = — J (я — /)/[sin (я — /)] Л
л я
^ я/(sin t)dt— ^ //(sin i
о о
261
Отсюда
л п
2 J xf (sin л;) dx = я $ /(sin л;) </#,
о о
что равносильно доказываемому равенству.
6.5.15. Используя равенство
доказать, что
sin
б
6.5.16. Доказать, что если ц> (х)=-^ a0-\-alcos
аг cos 2х + Ьг sin 2х -f- ... + ап cos пх + Ъп sin nx, то:
2я 2я
а) ] <p(x)dx = na0; б) ] ф(л:)<
о о
2я
в) \ ф (л:) sin kx dx = nbk (k = 1, 2,..., n).
§ 6.6. Интегрирование по частям.
Вывод рекуррентных формул
Если и и v—функции от х, обладающие непрерывными производными, то
Ь ъ
[и (х) v' (х) dx=u(x)v(x)
— ^v (x) и' (х)dx
a a
или, в более короткой записи,
ь ь
\ и dv = tw — \ t/ d«.
а а
1
6.6.1. Вычислить интеграл } хех dx.
о
Решение. Положим
х = и, ех dx — dv;
du = dx; v = ex,
что законно, так как функции и — х и v — ex непрерывны и имеют
непрерывные производные на отрезке [О, I].
Пользуясь формулой интегрирования по частям, получим
262
i i
1
хех
о
о
С
— J ex dx = е — ех
= 1.
nfb
6.6.2. Вычислить интеграл /= \ еах sin bx dx.
о
Решение. Положим
и = sin bx, dv = еах dx;
du — b cos bx dx, v = — eax.
Так как функции u = sinbx, v = — eaxнепрерывны вместе со своими
производными на отрезке [0, п], то применима формула интегриро-
интегрирования по частям:
я/ b
=r. — еах sinbx
щъ
я J
я/Ь Ь
-АС
a J
еах cos bx dx =3
о
Применим теперь интегрирование по частям к интегралу /1# По-
Положим
и = cos bx, dv = еах dx,
1
du = —b sin bx dx, v = — eax.
Тогда
nib
"a \ е<1ХыпЬх4х)
Отсюда
__Ъ_( ea7t'b \\ b* r_b(ean/b +1) b*
~ a\ a a) a* l ~~ ^ Ф ^
b(ean/b +1) f__b{eiMfb
* />2 > * Л2_1_
В частности, при а = Ь=\ получаем
п
\ ех sin х dx = -~ (еп + 1).
о
е
6.6.3. Вычислить интеграл
i
6.6.4. Вычислить интеграл ^ 81п]/д:(/д;.
о
263
Решение. Сначала применим подстановку
X
0
я2/4
t
0
я/2
Отсюда
dx = 2t dty
Я*/4 Я/2
\ sinV^xdx — 2 J t sin tdt.
о о
Последний интеграл будем интегрировать по частям. Положим
* = #; sin f dtf = tft>;
Тогда
/
2 j
о
я/2
j
о
Г
L
я/2
t =
J
^ + $ cos / dt = 2 sin / Jq/2 = 2.
о J
1
farcsin x
6.6.6. Вычислить интеграл /= \ ^-т-г— dx.
\
о
Я/2
6.6.6. Вычислить интеграл \ x2sinxdx.
о
6.6.7. Вычислить интеграл /л=5(а2—х*)п dx, где п~натураль-
о
ное число.
Решение. Интеграл можно вычислить, разлагая подынтеграль-
подынтегральную функцию (а2—х2)п по формуле бинома Ньютона, но это при-
приводит к громоздким выкладкам. Проще вывести рекуррентную фор-
формулу, сводящую интеграл 1п к интегралу /я-1. С этой целью разложим
интеграл 1п та»:
а а
[п== j (а*—л*)""* (а2 —л:2) dx^a4n_x — \x (a2—xt)n~1xdx
о о
и проинтегрируем последний интеграл по частям:
и = х; (а2 — я2)*"" xdx = dv,
da = dx; v = — -^-(a2—x2)n (пф 0).
Мы получим
264
Отсюда
— 2
1п~а
Эта рекуррентная формула справедлива при любых действитель-
действительных /2, отличных от 0 и —1/2.
В частности, при натуральном пу учитывая, что
получим
где Bл)!! = 2-4-6... Bл),
)!! = Ь3.5...Bл+1).
2яBя-2)Bя-4).>.6-4-2 2д+1 BяI1
6.6.8. Пользуясь результатом предыдущей задачи, получить сле-
следующую формулу суммирования;
где С„—биномиальные коэффициенты.
Решение. Рассмотрим интеграл
r*\nd*- {2n)l{
' B/1-4-1)!! '
о
Разлагая степень двучлена по формуле бинома Ньютона и интегри-
интегрируя в пределах от 0 до I, получим
/я =$A-*•)*?/*-
О
1
= J A— Опх* + С%х* — С*пх6+ ... +(—\
¦ I. i ... - I ¦ ¦ I ¦ i ] :
5 7 -г .. .-г 2л-И Jo
Г»3 ( 1 \П
что и требовалось доказать.
6.6.9. Вычислить интеграл
Я/2 Я/2
Ял= J sin/wA:rfA:= U cosw л; А*
о о
(т—натуральное число).
565
Решение. Подстановка
sin x = t,
cos xdx = dtj
сводит второй интеграл к интегралу
Я/2
X
0
я/2
t
0
1
рассмотренному в 6*6.7. сс = 1 и п={т —1)/2. Поэтому здесь спра-
справедлива рекуррентная формула
так как
т—\
т
2.(т
Если w—нечетное число, то полученная рекуррентная формула
сводит Нт к
Я/2
Нх — j cos л: Лс == 1,
поэтому
ml! '
Если /w—четное число, то рекуррентная формула сводит Нт к.
Я/2
поэтому
н (т—1I1 п
т т\\ 2 #
6.6.10. Вычислить интеграл
/= ^ xsmmxdx
о
(т—натуральное число).
Решение. Воспользуемся результатами 6.5.14 и 6.5.13. Мы
получим
Я Я Я/2
= Г xsi
о
= ~ \ sinmxdx
/
о
266
что с учетом результата 6.6.9 дает
-ji— при т четном,
J 2 • mil
Л (/и—1I!
! я —j^y|— при т нечетном.
1
6.6.11. Вычислить интеграл In=^xm(\nx)ndx;m'>09 п—нату-
о
ральное число.
Решение. Прежде всего заметим, что хотя подынтегральная
функция /(х) = хт Aпдг)п при х = 0 смысла не имеет, при любом
/я > G и /2>0 ее можно сделать непрерывной на отрезке [0, 1],
положив /@) = 0. В самом деле,
lim хт(\пх)п = Htn {хт1п\пх)п = 0
Х-+ + 0 Х-+ + 0
в силу 3.2.4.
Отсюда, в частности, следует, что интеграл /„ существует при
т > 0, п > 0. Для его вычисления применим интегрирование по
частям, положив
и = (In #)*, dv = хот б/дг,
Следовательно,
/„ = j х" (In л;)» dx » ??$? |; ^
(Ш до-1 Л =
О
Мы получили рекуррентную формулу, сводящую /„ к /п_1# В част-
частности, при натуральном /2, учитывая, что
получим
/ (- \)п nl
i
6.6.12. Вычислить интеграл /w, я= J л:тA—х)п dx, где /я и л—-
о
целые неотрицательные числа.
Решение. Положим
A —х)п = и; хт dx = dv;
rftt = — n A — л;)*-1 dx; v =
267
Тогда
l
I П
)x { ] ax+
О
Полученная рекуррентная формула справедлива для всех п > О
и т> — 1. Если п—целое положительное число, то, применяя по-
последовательно эту формулу п раз, получим
/ — п Г п(п—\) f
)...(«П + Я)
Но
1
п ..г» л.
'"¦¦•"*
Следовательно,
т* п (т+1) (т+2).. .(т-\-п) (т + я + 1) *
Если т—тоже целое неотрицательное число, то полученный ре-
результат можно записать в виде
т\ п\
6.6.13. Вычислить интегралы:
1 1
а) \ arctg ]/"x dx; б) J (х— 1) <
о е
я/з
я/4 О
1 Я/4
д) Ixln(\+x2)dx; e) J \п(\ + igx)dx;
о о
я/2 16
ж) j sin 2x arctg (sin x) dx\ з) j arctg у V х— 1 dx.
о 1
6.6.14. Доказать, что
1 1
\ (arccosх)пdx = п \-к) —п(п—1) \ (arccosA:)""*2^ (л> 1).
J \г J J
о о
6.6.15. Доказать, что если ff(x) непрерывна на отрезке [а, Ь],
то справедлива формула
ь
\ xf (х) dx= [bf (b)-f(b))-[af (a)-f(a)].
a
2G8
§ 6.7. Приближенное вычисление определенных интегралов
1. Формула трапеций. Отрезок [а, Ь] разбивают на п равных частей точками
кН, где h = (b—а)/п, k = Q, 1, ..., п, и применяют формулу
Ь
Погрешность R этой формулы оценивается так:
(в предположении ограниченности второй производной).
2. Формула Симпсона. Отрезок [а, Ь] разбивают на 2п равных частей точ-
точками Хь = а + kh, где h = (b—a)/2nt и применяют формулу
В предположении существования и ограниченности /IV (x) для погрешности этой
формулы справедлива оценка
\R\<M]UbZf. где М4= sup |/iv(x)|.
180 (Inг s<jc<6
1
6.7.1. Вычислить приближенно интеграл /= \ у—- по формуле
о
трапеций при п =10.
Решение. Составим таблицу значений подынтегральной функ-
функции, причем будем вычислять ординаты у/==/(д:/) (/ = 0, 1, ... , 10)
с четырьмя знаками после запятой.
0,0000
0,1000
0,2000
0,3000
0,4000
0,5000
l+x{
1,0000
1,1000
1,2000
1,3000
1,4000
1,5000
1
У* 1+*/
1,0000
0,9091
0,8333
0,7692
0,7143
0,6667
*
0,6000
0,7000
0,8000
0,9000
1,0000
1,6000
1,7000
1,8000
1,9000
2,0000
1
Уг * + */
0,6250
0,5882
0,5556
0,5263
0,5000
По формуле трапеций получим
1
+ 0,7143 + 0,6667 + 0,6250 + 0,5882 + 0,5556 + 0,5263 J =
= ^ • 6,9377 = 0,69377»0,6938.
269
Произведем оценку погрешности полученного результата. Имеем
/" (Х) = 2/A + л:K. Так как 0 < х < 1, то | /" (л:) | < 2. Следовательно,
в качестве М2 можно взять число 2. Отсюда находим оценку по-
погрешности:
Мы вычисляли ординаты с четырьмя знаками после запятой, при
этом погрешность от округления ординат не превосходит величины
°в5 A+9-1) = 0,00005 (а точнее, ^^ • 9 == 0,000045, так как
ординаты у0 и у10 — точные числа). Таким образом, общая погреш-
погрешность, возникшая от применения формулы трапеций и от округления
ординат, не превосходит величины 0,0018.
Заметим, что вычисляя заданный интеграл по формуле Ньютона —
Лейбница, получим
1
1= С ^L = in (i + X)\l = in 2 « 0,69315.
Таким образом, погрешность полученного результата составляет
лишь 0,0007, т. е. мы получили результат с тремя верными знаками.
1.5
р еолх
6.7.2. Вычислить по формуле Симпсона интеграл \ ^ясточ-
0,5
ностью до 0,0001.
Решение. Чтобы подобрать необходимое для обеспечения за-
заданной точности число 2/2, найдем /1V (л:). Последовательно диффе-
дифференцируя f(x) = eoaxlx, получим
/iv (Х) = ?^! @,0001л:4—0,004д:3 + 0,12л:2 — 2,4л: + 24) = ^ е°>1х,
где Р(х) — многочлен, заключенный в круглых скобках. Функция
<р(х) = е0Лх возрастает на отрезке [0,5; 1,5] и поэтому достигает
своего наибольшего значения при д;=1,5: фA,5) = е0>15 < 1,2. Аб-
Абсолютная величина многочлена Р(х), деленного на хь, оценивается
сверху как сумма модулей отдельных членов. При этом наибольшее
значение каждого слагаемого достигается при #=0,5, поэтому
0,0001 0,004 0,12 2,4 24
Р(х)
Таким образом, |/1V (л:) | < 1,2-808 < 1000. Следовательно, в каче-
качестве МА можно взять число 1000.
Нам требуется вычислить интеграл с точностью до 0,0001. Для
обеспечения такой точности необходимо, чтобы сумма ошибок ме-
метода, действий и окончательного округления не превосходила 0,0001.
Для этого подберем число 2/2 (тем самым определится «шаг» h
270
интегрирования) так, чтобы удовлетворялось неравенство
|/?| <-i--0,0001= 5-10~б.
Решая неравенство
16.1000 ^ ,Л_К
180 BлL
получим
2п> 19.
Возьмем 2п = 20; тогда шаг h интегрирования будет равным
При более точном подсчете получается, что при 2я =
Если мы будем подсчитывать у{ с пятью знаками после запятой, т. е.
с погрешностью не более 10 ~б, то ошибка окончательного округле-
округления будет тоже не больше 10~5, Таким образом, общая ошибка
будет меньше, чем 4,5- 10~б < 0,0001.
Составим таблицу значений функции у~еО}1х/х для значений х
от 0,5 до 1,5 с шагом ft = 0,05.
Вычисления будем вести с пятью знаками после запятой.
i
0
i
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
ч
0,50
0,55
0,60
0,65
0,70
0,75
0,80
0,85
0,90
0,95
1,00
1,05
1,10
1,15
1,20
,25
,30
,35
,40
,45
,5а
0,lxi
0,050
0,055
0,060
0,065
0,070
0,075
0,080
0,085
0,090
0,095
0,100
0,105
0,110
0,115
0,120
0,125
0,130
0,135
0,140
0,145
0,150
eo,\xi
1,05127
1,05654
1,06184
1,06716
1,1O251
1,07788
1,08329
1,08872
1,09417
1,09966
1,10517
1,11071
1,11628
1,12187
1,12750
1,13315
1,13883
1,14454
1,15027
1,15604
1,16183
т
2,10254
1,92098
1,76973
1,64178
1,53216
1,43717
1,35411
1,28085
1,21574
1,15754
1,10517
1,05782
1,01480
0,97554
0,93958
0,90652
0,87602
0,84781
0,82162
0,79727
0,77455
271
Сведем табличные данные для наглядности в следующий расчет-
расчетный бланк:
1
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
ч
0,50
0,55
0,60
0,65
0,70
0,75
0,80
0,85
0,90
0.95
1,00
1,05
1,10
1,15
,20
1,25
1,30
1,35
,40
1,45
,50
Суммы
при t = 0 и i = 20
2,10254
0,77455
2,87709
при i нечетном
1,92098
1,64178
1,43717
1,28085
1,15754
1,05782
0,97554
0,90652
0,84781
0,79727
12,02328
при i четном
1,76973
1,53216
1,35411
1,21574
1,10517
1,01480
0,93958
0,87602
0,82162
10,62893
Применяя формулу Симпсона, получим
1.5
f t^L dx « щ B,87709 + 4.12,02328 + 2 А0,62893) =
0,5
= ^•72,22807=1,2038.
6.7.3. Ширина реки 26 м; промеры глубины в поперечном сечении
реки через каждые 2 м дали следующие результаты:
к
У
0
0,3
2
0,9
4
1,7
6
2,1
8
2,8
10
3,4
12
3,3
14
3,0
16
3,5
18
2,9
20
1,7
22
1,2
24
0,8
26
0,6
где х означает расстояние от одного берега, а у — соответствую-
соответствующую глубину (в метрах). Зная, что средняя скорость течения 1,3 м/сек,
определить секундный расход Q воды в реке.
272
Решение. По формуле трапеций площадь 5 поперечного сечения
26
S = ^ydxtt 2 [у@,3 + 0,6) + 0,9+ 1,7 + 2,1 +2,8 + 3,4 + 3,3 +
+ 3,0 + 3,5 + 2,9 + 1,7 +1,2 + 0,8] = 55,5 (ж2).
Отсюда секундный расход
Оценить погрешность точно здесь нельзя. Некоторые косвенные методы
оценок, приводимые в руководствах по численным методам, позволяют указать
приближенно порядок погрешности. Погрешность S составляет примерно 3 ж2,
значит, погрешность Q составляет примерно 4 м3/сек.
6.7А, Вычислить интегралы:
П/2
а) \ dx с точностью до 0,001 по формуле Симпсона;
Я/4
1
б) [e~*2dx с точностью до 0,001 по формуле трапеций,
о
6.7.5. Пе формуле Симпсона вычислить приближенное значение
интеграла
1,36
/= J f{x)dx,
1,05
если подынтегральная функция задана следующей таблицей:
X
1,05
2,36
1,10
2,50
1,15
2,74
1,20
3,04
1,25
3,46
1,30
3,98
1,35
4,6
§ 6.8. Дополнительные задачи
6.8.1. Дана функция
A-— х при 0<ж1,
0 при 1 <*<2,
B—л:J при 2 < 3
Проверить непосредственно, что функция
X
непрерывна в промежутке [0, 3] и что ее производная в каждой внутренней
точке этого промежутка существует и равняется / (х).
273
6.8.2. Показать, что функция
х\пх
/м-1 1~х
при 0 < х < 1,
О при *=0,
—1 при л: = 1
интегрируема на отрезке [0, 1].
6.8.3. Можно ли утверждать, что если функция абсолютно интегрируема
на отрезке [а, Ь], то она интегрируема на этом отрезке?
6.8.4. Касательная к графику функции y = f(x) в точке с абсциссой х = а
составляет с осью абсцисс угол я/3 и в точке с абсциссой х = Ь угол гс/4.
b
Вычислить \ f"(x)dx, если /"(*) —непрерывная функция.
а
6.8.5. Доказать, что
2
л
С dx
6.8.6. Дан интеграл \ —г-ц % • Убедиться, что функции
п / ч 1 j^STcOS* _ , . 1 tgX
Fi № = TF= arccos J. ¦ о ¦=- и ^2 (x) = тт^г arctg •
У2 |Al + Cos^ 2V/ /2 б V*
являются первообразными для подынтегральной функции. Можно ли восполь-
воспользоваться обеими первообразными для вычисления определенного интеграла по
формуле Ньютона—Лейбница? Если нет, то указать, какой можно.
6.8.7. Найти такую первообразную для f (х), которая при значении х = х0
принимает заданную величину у = у0 (задача Коши).
6.8.8. При каком значении g выполняется равенство
Показать, что
2 #
6.8.9. Исследовать функцию F (х), заданную определенным интегралом
X
о
6.8.10. Показать, что имеют место следующие неравенства:
1
0,692 < С xxdx<\.
о
2
6.8.11. С помощью неравенства jr^sin х^ — х @^х^п/2) показать, что
Я/2
sin х , зх
о
274
6.8.12. Используя неравенство sinjt^sjt—#3/6(#^0) и неравенство
Шварца — Буняковского, показать, что
Я/ 2
1,096 < J Vxsinxdx < 1,111.
о
6.8.13. Пусть на отрезке [а, Ь] заданы интегрируемые функции рг (*),
Ра М> Рз^)> Р*{х)> причем функция рг (х) неотрицательна, а функции р2 (х),
Рз (х), Ра (х) удовлетворяют леравенству
Доказать, что
ь ь ь
Рз (х) Pi (x) dx < ^ р2 W рг (>:) d>: <
а а а
6.8.14. Пусть функция / (х) положительна на отрезке la, Ь]. Доказать,
что выражение
ь ь
а а
достигает наименьшего значения лишь в случае постоянства / (х) на этом от-
отрезке.
6.8.15. Доказать, что
1
Г
J
с "— 2
о
6.8.16. Доказать, что одна из первообразных четной функции есть функция
нечетная, а всякая первообразная нечетной функции есть функция четная.
6.8.17. Доказать, что если f (х) — непрерывная периодическая функция
с периодом Ту то интеграл
/= J f(x)dx
а
не зависит от а.
6.8.18. Доказать, что если и = и(х), v=v(x) непрерывны вместе со своими
производными до п-то порядка на отрезке [a, b], то
ь ь
+(—1)" [
Глава VII
Приложения определенного интеграла
§ 7.1. Вычисление пределов сумм с помощью
определенных интегралов
Часто возникает необходимость вычислить предел суммы, когда число
слагаемых неограниченно возрастает. Такие пределы в некоторых случаях
можно найти с помощью определенного интеграла, если данную сумму удается
преобразовать так, чтобы она оказалась интегральной суммой.
Например, рассматривая точки 1/я, 2/п, ... , п/п как точки деления
отрезка [0, 1} на п равных частей длиной Ах=1/п, для любой непрерывной
функции f (х) имеем
7.1.1. Вычислить
«• зх Г . зх , . 2зх , , . (л—1)зг1
hm — sin—\-s\n г-...+sin- — .
Решение. Числа, стоящие в скобках, представляют собой
значения функции /(Ar) = sinA: в точках
делящих отрезок [0, я] на п равных частей длиной Ах = п/п.
Поэтому, если к нашей сумме присоединить слагаемое sin (ля//г) = О,
то она будет являться интегральной для функции f(x) — sinx на
отрезке [0, я].
По определению, предел такой интегральной суммы при /г—*-оо
есть определенный интеграл от функции /(^) = sinAr от 0 до я:
hm — ( sin—hsln b"-+sm- г-sin—] =
n
= \ sinxdx— —cos x i =2.
J j о
о
7.1.2. Вычислить предел
+ + +
276
Решение. Преобразуем сумму в круглых скобках следующим
образом:
1 I * 1 О- l
4F /Ч1УТ
Полученная сумма является интегральной суммой для функции f(x) =
—х2 на отрезке [0, 1], разбитом на п равных частей. Предел
такой интегральной суммы при п—*оо равен определенному интегралу
от этой функции в пределах от 0 до 1:
1
—4=г)==
1
С dx . х
= ]]А7Г72="ПТ
7.1.3. Вычислить
3
Решение. Преобразуем данное выражение следующим образом:
яГ[ ^ Т+0+ "К 1 + 3/я + Г 1 + 6/Л+ ••• + ]/ 1 + 3(л
Полученная сумма является интегральной суммой, составленной
для функции f(x) = V\/{\-{-x) на отрезке [0,3]; поэтому, по оп-
определению,
3 t
dx =
= 4 — 2 = 2.
о о
7.1.4. Пользуясь определенным интегралом, вычислить следую-
следующие пределы:
а)Лга„
б) lim -
277
в) lim
П-*-СО
г) l[m ~^r
7.1.5. Вычислить предел А — lim
Решение. Прологарифмируем
In Л = lim In VnX =»m 1 Г1п1 + 1п~+... +ln-l.
Выражение под знаком предела есть интегральная сумма для ин-
интеграла
\ In х dx = (х In x— х)
о
Следовательно, 1пЛ==—1 и lim ~ — е"
§ 7.2. Вычисление средних значений функции
Средним значением fx функции / (х) на отрезке la, b] называется число
Корень квадратный из среднего значения квадрата функции
ь
< т \ [/ MI2 dx > называется средним квадратичным значением функ-
а
ции f (х) на [а, Ь\,
7.2.1. Найти среднее значение \х функции f(x)=l/x на от-
отрезке [0, 1].
Решение. В нашем случае
-[i/xdx =
о
3
г- !_0 JK—- 4 |0~ 4 '
О
7.2.2. Найти среднее значение \i функций:
а) f(x) = s\n*x на отрезке [0, 2л];
б) f(x) = \/(e*+l) на отрезке [0, 2].
27S
7.2.3. Определить среднюю длину всех вертикальных хорд
гиперболы х2/а2—у2/Ь2=\ на отрезке а^х^2а.
Решение. Задача состоит в отыскании среднего значения
функции f(x) = 2у = 2 — Ух2 — а2 на отрезке [а, 2а]:
= ft [2/3 — In
7.2.4. Найти среднюю ординату синусоиды y = sinx на отрез-
отрезке [0, я].
Решение.
31
-1С
о
sin х dx = cos x
= - ^0,637.
Перепишем полученный результат следующим образом;
я
2 С
ц-я — — я — J sin* д:.
о
Используя геометрический смысл определенного интеграла, мы можем
сказать, что площадь прямоугольника с высотой |i —2/я и осно-
основанием я равна площади фигуры, ограниченной полуволной сину-
синусоиды y = sinx, О^дг^я и осью Ох.
7.2.5. Определить среднюю длину всех положительных ординат
окружности х2-\-у2=\.
7.2.6. Показать, что среднее значение функции/(jc), непрерывной
на отрезке [а, Ь], есть предел среднего арифметического значений
этой функции, взятых через равные промежутки аргумента jc.
Решение. Отрезок [а, Ь] разделим на п равных частей точками
Xi==a + i(b—a)In A = 0, 1, 2, ..., п).
Составим среднее арифметическое значений функции f(x) в п
точках деления xQ1 х1У ..., хп_х:
п п i=o
Это среднее можно представить в таком виде;
л-1
5=г
279
где
bxt— —^-.
Последняя сумма есть интегральная сумма для функции f(x),
поэтому
= _!_ пт
что и требовалось доказать.
7.2.7. Найти среднее значение давления рт при изменении р от
2 до 10 атж, если давление р и объем v связаны соотношением
?1/3/2= 160.
Решение. При изменении р от 2 до 10 агл* v пробегает отре-
отрезок [4 j/T, 4 j/Too]; отсюда
4C/100-3/4)
?/7
Г
J
J
320
— v
4C/100-3/4)
-1/2
4 j!/Too_ 40
^4,32 атж.
7.2.8. В гидравлике существует формула Базена, выражающая
скорость v течения воды в широком прямоугольном канале в зави-
зависимости от глубины h рассматриваемой точки под свободной поверх-
поверхностью, v = vQ — 20 \^HL(h/HJt где v0 — скорость на свободной
поверхности, Н—глубина канала, L — его уклон.
Определить среднюю скорость vm течения в поперечном сечении
канала.
Решение. Имеем
7.2.9. Определить среднюю величину электродвижущей силы Ет
за один период, т. е. за время от ^ = 0 до t=T, если электродви;
жущая сила вычисляется по формуле
E Esm
где Т—продолжительность периода в секундах, EQ — амплитуда
(максимальное значение) электродвижущей силы, соответствующая
значению / = 0,25Т. Дробь 2Ш/Т называется фазой.
280
Решение.
Е"-т)sm т^те L-cost-Jo e0-
о
Таким образом, среднее значение электродвижущей силы в течение
одного периода равно нулю.
7.2.10. На двух вертикальных столбах ОЛ и CD укреплены на
высоте h электрические фонари; сила света каждого из них / свечей.
Расстояние между столбами равно d. Найти среднюю освещенность
прямой ОС, соединяющей основания столбов.
7.2.U. Найти среднее значение квадрата электродвижущей силы
(Е?)т в интервале от / = 0 до t = T/2 (см. 7.2.9).
Решение. Так как
ТО
Т/2 Т/2
0
~TL* 4я81П Г Jo ~ 2 *
7.2.12. Если функция f(x) задана на бесконечном интервале
[0, оо), то ее средним значением ц называется
6-* оо w v
если этот предел существует. Найти среднюю потребляемую мощ-
мощность в цепи переменного тока, если сила тока / и напряжение а
выражаются следующими формулами:
/=/0 cos (©* +а);
и = и0 cos (со/ + а+ф)>
где ф — постоянный сдвиг фазы напряжения по сравнению с силой
тока (параметры со и а в среднюю мощность не войдут).
Решение. Средняя потребляемая мощность
т
= lim -=- I
Г-^оо J J
о
cos № + а) wo cos
Г-^оо J J
о
Учитывая, что
cos a cos p = -j [cos (a + p) + cos (a—p)],
281
получим
1
w^ = lim *-$• Г [cos B©^ + 2a + ф) + cos <p] dt =
=Z|o cos ф.
Отсюда понятно, почему в электротехнике придается такое важное
значение величине cos ср.
7.2.13. Найти среднее значение |х функций f(x) на указанных
отрезках:
а) f(x) = 2x2+\ на отрезке [0, 1];
б) f(x) = \/x на отрезке [1, 2];
в) f(x) = 3x—2x + 3 на отрезке [0, 2].
7.2.14. Тело, падающее на землю из состояния покоя, пройдя
вертикальный отрезок s = s^ приобретает скорость v1 = ]/'2gsv Пока-
Показать, что на этом пути средняя скорость vcv равна 2vJ3.
7.2.15. Сечение желоба имеет форму параболического сегмента.
Основание его а, глубина h. Определить среднюю глубину желоба.
7.2.16. Найти среднее значение Im силы переменного тока за
промежуток времени от 0 до я/о (см. 7.2.12).
7.2.17. Доказать, что среднее значение фокального радиуса
эллипса р = р/A—ecoscp), где р = Ьг\а, a, b — полуоси и 8—эксцент-
8—эксцентриситет, равняется Ъ.
7.2.18. На отрезке АВ, имеющем длину а, взята на расстоянии х
от конца А точка Р. Показать, что среднее значение площадей
прямоугольников, построенных на отрезках АР и РВ как на сторонах,
равно #2/6.
7.2.19. Вычислить среднее значение функции
~, » cos2 л:
' W ~~ sin2л;+ 4 cos2*
в промежутке [0, я/2]. Проверить непосредственно, что это среднее
значение, равное 1/6, является значением функции f(x) для некото-
некоторого х = % из этого интервала.
§ 7.3. Вычисление площадей в декартовых координатах
Если плоская фигура ограничена прямыми х = а, x = b{a <b) и кривыми
У = У1(х)> У = Уч(х)> причем ух{х)<у2(х)
о ее площадь вычисляется по формуле
ъ
= $ [ft W-
В отдельных случаях левая граница х = а (или правая граница х — b) может
выродиться в точку пересечения кривых y — yi(x) и у = у<ь(х). В этих случаях
282
величины а и b отыскиваются как абсциссы точек пересечения указанных кри-
кривых (рис. 65, а, б).
<
0
У
i
л*
1
1
1
1
а
!Zw/////?*
У*&(х)
1
1
J
1
1
J
в
>
*~х
в
Рис. 65.
7.3.1. Вычислить площадь фигуры, ограниченной прямыми # = 0f
л; = 2 и кривыми у = 2*, у = 2х—х2 (рис. 66).
Решение. Так как максимум функции у = 2х—х2 достигается
в точке х=\ и равен 1, а функция >> = 2*>1 на отрезке [0, 2], то
2___3 ?
о"п2 3*
7.3.2. Вычислить площадь фигуры, ограниченной параболами
= — 2у2, лг=1—Зу2 (рис. 67).
i
' X
/ 2
Рис. 66.
Решение. Решая систему уравнений
найдем ординаты точек пересечения кривых
1—Зу2^—2у2 при —1<^<1, то
г = — 1, ув=1. Так как
j
283
7.3.3. Найти площадь фигуры, заключенной между параболой
= 4у и локоном Аньези (рис. 68): у = 8/(х2-\-4).
Решение. Найдем абсциссы точек А и С пересечения кривых.
Для этого исключим у из
системы уравнений:
откуда 8/(лг2 + 4) = д:2/4 или
х х* + *х2 — 32 = 0.
Действительными корня-
корнями этого уравнения являются
точки дгх = — 2 и х2 = 2. Из
рисунка видно, что 8/(х2 + 4) ^ л:2/4 на отрезке [—2, 2]. (В этом
можно убедиться и прямым подсчетом значений этих функций в любой
точке внутри отрезка, например, в точке д; = 0.)
Следовательно,
—2
¦-Х2+\
7.3.4. Найти площадь фигуры, ограниченной параболоид
и прямой дг-f-jf == 3.
7.3.5. Вычислить площадь фигуры, лежащей в первой четверти
внутри круга х2 + у2 = 3а2 и ограничен-
ограниченной параболами х2 = 2ау иу2 = 2ах (#>0)
(рис. 69).
Решение. Найдем абсциссу точки
А пересечения параболы у2 = 2ах с ок-
окружностью х2+у2 = 3а2. Исключив^ из
системы уравнений
х2 +у2 = За2,
у2 = 2ах,
получим х2-\-2ах—За2 = 0, откуда на-
находим единственный положительный ко-
корень хл = а. Аналогично находим абсцис-
абсциссу точки D пересечения окружности х2-\-у2 = \
Рис. 69.
и параболы
D
Таким образом, интересующая нас площадь равна
aV2
где
284
2—д:2
при
при
По свойству аддитивности интеграла
а а VI
a2 , За2 f . г -
" 6" + " ( arcsin ^^
"о" <*\
Здесь мы воспользовались известной формулой тригонометрии
arcsin a—arcsin р = arcsin (а]Л —р2—р |Л ~^2) («Р > 0)
для преобразования
arcsin
-| — arcsin ^ = arcsin
= arcsin у.
7.3.6. Вычислить площадь фигуры, лежащей в первом квадранте,
ограниченной кривыми 3^== 4л;, х2~4у
** 5
7.3.7. Вычислить площадь фигу-
фигуры, ограниченной линиями у —х + 1,
y = cosx и осью Ох (рис. 70).
Решение. Функция
У =/(*) =
х+1, если —1
(
cos дг, если
я/2
непрерывна на промежутке [—1, я/2]. Площадь криволинейной тра-
трапеции равна
Я/2
S= \f(x)dx =
-1
о
л/2
Я/2
0
2 *
-1 0
7.3.8. Найти площадь сегмента, отсекаемого от кривой у2 = х3 -
хордой х = 2.
Реш е н ие. Из равенства у2 = х2 (х — 1) следует, чтол;2(л;—1
поэтому или х = 0 или х^\. Другими словами, область определения
неявно заданной функции у2 = х* — х2 состоит из точки лг = О и про-
промежутка [1, сю). Изолированная точка @, 0) при вычислении площади
285
роли не играет, поэтому промежуток интегрирования — это отрезок
[1, 2] (рис. 71).
Переходя к явному заданию у — ±хУх — 1, мы видим, что сег-
сегмент ограничен сверху кривой у — хУх—1 и снизу—кривой у =
= —х Ух — 1. Следовательно,
Сделаем подстановку
dx = 2t dt,
X
1
2
/
0
1
Рис. 71.
Тогда
5 =
7.3.9. Найти площадь фигуры, ограниченной двумя ветвями кривой
{у—хJ = х3 и прямой л:=1.
Решение. Заметим прежде всего, что j> как неявная функция
от х определена лишь при лг^О: левая часть уравнения всегда
неотрицательна. Теперь находим уравнения двух ветвей кривой у =
= х—хУ х, у = х + хУх. Так как х^О, то х + хУх^х—хУх
и поэтому
Ux + хУх—
о
Стоит отметить, что при вычислении площади мы обошлись без ри-
рисунка, хотя при исследовании поведения функции у (х) он был бы
полезен.
7.3.10. Вычислить площадь петли кривой у* = х(х—IJ.
Решение. Область определения неявной функции у есть про-
промежуток 0^д;< + оо. Так как в уравнение кривой^ входит во вто-
второй степени, то кривая симметрична относительно оси Ох. Положи-
Положительная ветвь уг(х) задается уравнением
-*), 0<*<1,
=у х\х — 1 \ = \ г—
f
\Vx(x-\),
286
Общие точки симметричных ветвей ух(х) и у2(х) = —ух (х) должны
лежать на оси Ох. Но V1(x)~Y~ х\х — 1J = 0 лишь при ^ = 0 и
при х2 = 1.
Следовательно, петля кривой образована кривыми у =
= V~x(\—x) к у = —]/"х(\—х),
площадь петли равна
5=2
= Т5- О
1 (рис. 72). Поэтому
У у2-х(х-1)г
Рис. 72.
7.3.11, Найти площадь фигуры, огра-
ограниченной завитком кривой
у2 = (х — 1) (х—2J.
7.3.12. Найти площадь между параболой ^ = —х2— 2д: + 3,
касательной к ней в точке AfB, —5) и осью ординат.
Решение. Уравнение касательной в точке МB, —5) имеет вид
у-\-5 =— 6 (л:—2) или у —7 — бх. Поскольку ветви параболы
направлены вниз, то парабола лежит под каса-
касательной, т. е. 7 — 6х^ —х2 — 2х + 3 на отрез-
отрезке [0, 2] (рис. 73).
Следовательно,
2
= Г[7—блг—(—х2—
О
2
7.3.13. Найти площадь, заключенную меж-
между параболой у — х2 — 2х-{- 2, касательной к
ней в точке МC, 5) и осью ординат.
Рис. 73. 7.3.14. На эллипсе
х2/а2 +у2/Ь2 = 1 (а > Ь)
взята точка М {х,у), лежащая в первой четверти.
Показать, что сектор эллипса, ограниченный его большой
полуосью и фокальным радиусом, проведенным в точку Ж, имеет
площадь
S = y arccos — •
G помощью этого результата получить формулу для площади
всего эллипса.
227
Решение. Имеем (рис. 74):
$ОМАО ~
МАВМ* Ь&омв— 2~~2а:
Так как я/2—arcsin (х/я) = arccos (xfa), то получаем
Smabm = Та [—Х V°?-*% + a2 arccos ±
Отсюда
^ $&омв + $мавм — Y arccos "»
что и требовалось доказать.
При л; = 0 сектор превратится в четверть эллипса, т.е.
об я яб
Эллипса = arcC0S
а следовательно, 5ЭЛлипса = я**- При л = * получим площадь круга
Рис. 74.
7.3.15. Найти площадь фигуры, заключенной между параболами
у = 4л;2, д> = х2/9 и прямой ^==2.
Решение. В данном случае целесообразнее интегрировать по
переменной у и воспользоваться симметрией фигуры (рис. 75). По-
Поэтому уравнения парабол разрешаем относительно х:
В силу симметрии фигуры относительно оси Оу искомая площадь
равна удвоенной площади Soabo'-
28Б
7.3.16. Из произвольной точки М(х, у) кривой у=хт (/и>0)
опущены на оси перпендикуляры MN и ML (х > 0). Какую часть
площади прямоугольника ONML составляет площадь 0NM0 (рис. 76)?
7.3.17. Доказать, что площади SOy 6\, S2, S3, ..., ограниченные
осью Ох и полуволнами кривой у = е~а* sin Рх, х ^ 0, образуют
геометрическую прогрессию со знаменателем q =
Решение. Кривая (рис. 77) пересекает положительную полу-
полуось Ох в точках, в которых sin px = 0, откуда
*Л = -у-, я = 0, 1, 2, ...
Функция j; = e"*a;fsin (be положительна в интервалах (д:2Л, x2k+1) и
отрицательна в интервалах (x2k+1, x2k+2)y т. е. знак функции в интер-
вале (хп, хп+1) совпадает со знаком числа (—\)п. Поэтому
'.- f
яя/3
Но неопределенный интеграл равен
-"*sinp*rf*=— jJ^
Следовательно,
Отсюда
что и требовалось доказать.
289
7.3.18. Найти площади фигур, ограниченных окружностью
-f.y2 — 2х-\-4у —11 =0 и параболой у = — х2 + 2х + 1 — 2
Решение. Перепишем уравнения данных кривых в виде
(х— 1J + (у + 2J=16, у = —(х—1J
Следовательно, центр окружности лежит в точке СA, —2) и радиус
окружности равен 4, а ось парабо-
параболы совпадает с прямой х = 1 и
вершина парабэлы лежит в точке
fi(l, 2 —2]/"~3) (рис. 78).
Площадь Sabdfa меньшей фигу-
ры находим по формуле
= J (Упар—.Уокр) dx%
где д:л и xD определяются из систе-
системы уравнений
( (jc —1
Рис. 78.
Следовательно,
откуда хА = —1, xD = §.
Sabdfa= $ {(~д:а + 2д:+ 1 —2\П) + B + }Лб-(x—\J)]dx =
-i
arcsin
| = ~6 V~l + 2 KT2 + 16 arcsin 1 =
Площадь второй фигуры определить легко.
Замечание. Вычисления интеграла можно упростить сдвигом х—\ — г
и использованием четности подынтегральной функции.
7.3.19. Вычислить площадь фигуры, ограниченной линиями
у==(х—4J, ^ = 16—х2 и осью Ох.
7.3.20. Вычислить площадь фигуры, ограниченной параболами
7.3.21. Вычислить площадь частей эллипса x2 + 4y2 = 8, отсечен-
отсеченных гиперболой х2—Зу* = 1.
7.3.22. Вычислить площадь фигуры, ограниченной замкнутой
кривой у2 = A —х2K.
7.3.23» Вычислить площадь петли кривой 4 {у*—х*)-\-хш = 0.
290
7.3.24. Вычислить площадь фигуры, ограниченной кривой]/^ х-\-
-\-Уу=\ и прямой х-\-у=\.
7.3.25. Вычислить площадь фигуры, ограниченной кривой у2 =
^х2(\—х2).
7.3.26. Вычислить площадь фигуры, ограниченной петлей кривой
х*+х2— у2 = 0.
7.3.27. Вычислить площадь фигуры, ограниченной осью ординат
и кривой х=у2(\—у).
7.3.28. Вычислить площадь фигуры, ограниченной кривой у =
— х* — 2л;3+#2 + 3, осью абсцисс и двумя ординатами, соответ-
соответствующими точкам, в которых функция у (х) имеет минимум.
§ 7.4. Вычисление площадей фигур
при параметрическом задании границы (контура)
Если граница фигуры задана параметрическими уравнениями
*=*<*). 0 = 0@,
то площадь фигуры вычисляется по одной из трех формул:
S = - J У @ *' @ dt; 5= J х @ у' (t) Л; 5 = у J W-y*) dt,
а а а
где а и р—значения параметра t, соответствующие началу и концу обхода
контура в положительном направлении (при котором фигура остается слева).
7.4,1. Вычислить площадь фигуры, ограниченной эллипсом
х = a cos /, у = Ь sin t @ ^ / ^ 2я).
Решение. Здесь удобно вычислить сначала
ху' —ух' =s a cos /• b cost + 6 sin /• a sin / = а#.
Отсюда
7.4.2. Найти площадь астроиды (х/аJ^ + (yjaJ/* = 1.
Решение. Запишем уравнение астроиды в параметрическом
виде л: = a ?os3 /, j; = a sin3 /, 0 ^ t ^ 2я. Здесь тоже удобно вычис-
вычислить сначала
ху' —ух' = a2 (cos3 /• 3 sin2 / cos i + sin3 /. 3 cos21 sin 0 = За2 cos2/ sin2 Л
Отсюда
2 Я 2Jt
5 == -g- J (ду' —yx') dt = -~ a2 { sin2 2t dt = -|- я2я.
о о
7.4.3. Найти площадь фигуры, ограниченной одной аркой циклоиды
x-—a(t—sin/), ^ = дA— cos/) и осью Оа:.
10* 2$1
Решение. Здесь граница фигуры
я) и отрезка оси Ох (
Р
состоит из дуги циклоиды
Применим формулу
Так как на отрезке оси Ох имеем ^ = 0, то остается вычислить
интеграл (с учетом направления обхода границы):
О 2Я
^ = _ J а A — cos t) a A —cos t) dt = a3^ A —cos tJ dt =
2Я 0
2Я
= а% С f"l —2 cos / H—5" A + cos2/)"J dt =
о
x^asint
7.4.4. Вычислить площадь фигуры, ограниченной кривой
х — a sin /, у = b sin 2t.
Решение. Для построения кривой учтем, что она симметрична
относительно осей координат. Действительно, если заменить t на
я—ty то переменная х
не меняется, а у изменя-
изменяет только свой знак; сле-
следовательно, кривая сим-
симметрична относительно
оси Ох. При замене же t
на л + f переменная^ не
меняется, а х изменяет
только свой знак. Это
значит, что кривая сим-
симметрична относительно
оси Оу.
Далее, так как функ-
Рис. 79.
ограничиться следующим
ции х = a sin f; у = b sin 2t
имеют общий период 2я,
отрезком изменения па-
пато достаточно
раметра: 0^.t^L2n.
Из уравнений кривой легко заключить, что переменные х и у
одновременно сохраняют неотрицательные значения только при изме-
изменении параметра t на отрезке [0, я/2], поэтому при О^^^я/2
получается часть кривой, лежащая в первой четверти. Общий вид
кривой изображен на рис.. 79.
Как видно из этого рисунка, достаточно вычислить площадь
одной петли кривой, соответствующей изменению параметра / от 0
до я, и затем удвоить результат
S = 2
я п
с' dt = 2 J b sin 2/- a cos tdt = 4ab J cos21 sin t dt —
о о
. ufcos*t\
292
7.4.5. Найти площадь петли кривой:
Решение. Нас будет интересовать общий вид кривой и точки
ее самопересечения. Обе функции x(t) и y(t) определены на всей
числовой оси — оо < t < оо.
Точка самопересечения характерна тем, что в ней совпадают зна-
значения абсциссы (и ординаты) при разных значениях параметра. Так
как х = 3 — A/3) (* — ЗJ, то абсциссы
совпадают при значениях параметра
t^Szt Я. Чтобы функция^@ принимала
при тех же значениях параметра t одно и
то же значение, должно выполняться
равенство —g— C — Я) = —g— C + Я)
при К Ф 0, откуда А, = ±3.
Таким образом, при ^ = 0 и при
t =6 имеем x(t1) = x(ti) = 0 и y(tx) =
=rj>(f2) = 0, т. е. точка @, 0) является
единственной точкой самопересечения.
Когда / меняется от 0 до 6, точки кри-
кривой лежат в первой четверти. При изме-
изменении /от 0 до 3, точка М(х, у) описы-
описывает нижнюю часть петли, так как в указанном промежутке х (t) и
V(t) = 3tx/S возрастают, а затем функция x{t) начинает убывать, в
то время какуУ) сначала еще возрастает. На рис. 80 указан обход
кривой, соответствующий возрастанию / (фигура остается слева).
Площадь искомой петли удобно считать по формуле
Рис. 80.
Найти площадь
абсцисса
петли кривой: x = t2; y — t-
ТАЛ. Вычислить площадь, содержа-
содержащуюся внутри кардиоиды:
х = a cos t (I + cos t);y = a sin / A + cos t).
Решение. Ввиду периодичности
функций x(t) и y(t) достаточно ограничи-
ограничиться рассмотрением отрезка [— я, я]. Крн-
х вая симметрична относительно оси Оху так
как при замене г на — t переменная х не
меняет своего значения, а у меняет лишь
знак; при этом у^О при изменении / от
0 до я.
81 При изменении г' от 0 до я функция
" u = cost убывает от 1 до—1; при этом
x = au(l+u) = a[— 1/4 + (и+1/2J] сначала убывает от
293
jcjM==1 = 2a до лг[ы__1/2 = —a/4, а затем возрастает до #|м=-1 = 0.
Можно показать, что ордината у возрастает в интервале @^/^п/З)
и убывает в интервале (я/З^/^л).
Вид кривой показан на рис. 81; там же указано направление
обхода ее при возрастании t.
Следовательно,
к п
S = 4- ^ W —Ух') dt = a2 U\+cos tf dt = -^-ла*.
-Jt 0
7.4.8. Вычислить площадь фигуры, ограниченной замкнутой кри-
кривой x = acost, y = bsitvit.
7.4.9. Вычислить площадь петель, образованных кривыми:
7.4.10. Вычислить площадь фигуры, ограниченной кривой
х = a cos t\ y — bsmt cos21.
7.4.11. Вычислить площадь эволюты эллипса
а * Ь *
§ 7.5. Площадь в полярных координатах
В полярных координатах площадь сектора, ограниченного дугой кривой
р=р(ф) и лучами q>! = a и q>2 = Pt выражается интегралом
в
7.5.1. Найти площадь фигуры, лежащей в первой четверти и
ограниченной параболой у* = 4ах и пря-
прямыми у = х—а и х — а.
Решение, Введем полярную систе-
систему координат, поместив полюс в фокус
параболы F и направив полярную ось в
положительном направлении по оси Ох.
Тогда, как известно, уравнение параболы
запишется в виде p = -t— . где р —
г 1—cos ф f ^
X параметр параболы. В нашем случае
/> = 2а, а фокус F имеет координаты
(а, 0). Значит, уравнение параболы при-
2а
мет вид р = ! , а уравнения пря-
• 1 — cos ф г
> = я/4 и ф = я/2 (рис. 82). Поэтому
я/а я/а
Рис. 82.
imx примут вид
Sin*(<p/2) •
894
Заменив
Ctg ¦*- = *, ~ oTT
2sin2((p/2)
Ф
я/4
я/2
ctg(n/8)
1
получим
ctg (я/8)
или, учитывая, что ctg — = -
7.6.2. Вычислить площадь фигуры, ограниченной:
а) кардиоидой р = 1 + cos ф; б) кривой р = a cos ф.
7.5.3. Найти площадь фигуры, лежащей вне круга р = а и огра-
ограниченной кривой р = 2а cos Зф.
Решение. Так как функция р== 2а cos Зф имеет период Т=2я/3,
то при изменении ф от —я до я радиус-вектор описывает три рав-
равных лепестка кривой. При этом до-
допустимыми для ф являются те значе-
значения, при которых созЗф^О, откуда
—я/6 + 2&Я/3 < ф < я/6 + 2?я/3
(ft = 0, ±1, ±2, ...).
Следовательно, один из лепестков опи-
описывается при изменении ф от —я/6
до я/6. Остальные два лепестка полу-
получаются при изменении ф от я/2 до 5я/6
и от 7я/6 до Зя/2 соответственно (рис.
83). Вырезая из лепестков части,
принадлежащие кругу р = а, мы полу-
получим фигуру, площадь которой нужно
определить. Ясно, что искомая площадь
х
рис 83
равна утроенной площади
Найдем полярные координаты точек пересечения | и iV, Для
этого решим уравнение 2а cos Зф = а, т.е. cos Зф = 1 /2. Между
—я/6 и я/6 находятся только корни —я/9 и я/9 (k = Q). Таким
образом, точке N соответствует полярный угол ц>± =—я/9, точке
М — угол ф2 = я/9.
Далее из рисунка заключаем, что
я/9
С
Я/9
~ Г
/9
-Я/9
295
7.5.4. Вычислить площадь фигуры, ограниченной окружностями
р == 3 У 2 a cos ф и р = За sin ф.
Решение. Первая окружность лежит в правой полуплоскости,
проходит через полюс р = 0, касаясь вертикальной прямой. Вторая
окружность лежит в верхней полу-
полуплоскости, проходит через полюс
р = 0, касаясь горизонтальной пря-
прямой. Следовательно, полюс есть
точка пересечения окружностей.
Другая точка пересечения окруж-
окружностей В находится из уравнения
ЗУ 2 a cos ф — За sin ф, откуда
В (arctg У~2, а|/*"б). Из рис. 84
видно, что искомая площадь 5
равна сумме площадей сегментов
ОЛВО и ОСВОу причем сегменты
примыкают друг к другу по лучу ф = arctgУЛ2. При этом дуга В АО
описывается концом полярного радиуса р первой окружности при
arctgV^ 2^ф^я/2, а дуга ОСВ описывается концом полярного
радиуса р второй окружности при 0 ^ф^ arctg У 2. Поэтому
Я/2
arctg V~2
arctg V~2
*2 \ sin2 wd(p = -ra2 I arctg: У 2 —Чг-
J 4 \ 3
Рис. 84.
Socbo = y
Следовательно, SOabo + SOcbo = 2,25a2 (я—arc
7.5.5. Найти площадь фигуры,
вырезаемой окружностью р =
= у 3 sin ф из кардиоиды р = 1 +
+ со5ф (рис. 85).
Решение. Найдем сначала точ-
точки пересечения этих кривых. Для
этого решим систему
— V~2).
\ p = 1 + cos cp,
откуда ф1 = я/3, ф2 — я.
Исйомая площадь равна сумме
двух площадей, одна из которых
представляет круговой сегмент, а Рис. 85.
другая сегмент кардиоиды, причем сегменты примыкают друг к другу
по лучу ф = я/3. Дуга ВАО описывается концом полярного ради-
радиуса р кардиоиды при изменении полярного угла ф от я/3 до я,
296
а дуга ОСВ — концом полярного радиуса р окружности при
0<ф<я/3.
Поэтому
Л/3
я/3
Я/3
Я/3
7.5.6. Найти площадь фигуры, ограниченной кардиоидой р =
= аA— созф) и окружностью р = а.
7.5.7. Найти площадь петли декартова листа х3 +у3 = Заху.
Решение. Перейдем к полярным координатам по обычным фор-
формулам х = рсо5ф, у = psin ф. Тогда заданное уравнение перепишется
в виде
р3 (cos3 ф + sin3 ф) = Зар2 sin ф cos ф,
или
За sin ф cos ф За sin 2ф
Р =
cos3 ф +sin3 ф (&1пф+ cos ф) B—sin 2ф) *
Из этого уравнения вытекает, во-первых, что р = 0 при ф = 0 и при
Ф = я/2 и, во-вторых, р—*оо при ф—>Зя/4 и ф —> — я/4. Последнее
означает, что декартов лист имеет
асимптоту, уравнение которой у =
= —х—а можно найти обычным обра-
образом в декартовых координатах.
Следовательно, петля декартова ли-
листа описывается при изменении ф от О
до я/2 и лежит в первой четверти
(рис. 86).
Таким образом, искомая площадь
равна
я/2
9а2 cos2 ф sin2 ф ,
Soao ="о"
Рис. 86.
Пользуясь симметрией кривой от-
относительно биссектрисы у=лг, т, е,
относительно луча ф = я/4, мы можем вычислить площадь половины
петли (от ф = 0 до ф = я/4) и затем удвоить ее. Это позволит вос-
воспользоваться заменой
dz,
dtp
cos2
ф
0
я/4
г
0
1
297
Л/4
что дает
Новая замена
Sz2 dz = dvy
приводит к интегралу
z2d2
z
0
1
V
1
2
7.5.8. Вычислить площадь фигуры, ограниченной одним лепестком
кривых:
а) р = a cos 2ф; б) р = a sin 2ф.
7.5.9. Вычислить площадь части кардиоиды р=«#A—cos ф),
лежащей внутри окружности р = a cos ф.
7.5.10. Вычислить площадь фигуры, ограниченной замкнутой кри-
кривой р = a sin ф cos2 ф, а>0.
7.5.11. Вычислить площадь фигуры, ограниченной кривой р —
= а со83ф {а > 0).
7.5.12. Вычислить площадь части фигуры, ограниченной лемни-
лемнискатой Бернулли p=a j/cos 2ф, лежащей внутри окружности р=а/|/.
7.5.13. Перейдя к полярным координатам, вычислить площадь
фигуры, ограниченной замкнутой кривой (x®-\-y2)s = 4a2x2y2.
7.5.14. Перейдя к полярным координатам, вычислить площадь
фигуры, ограниченной замкнутой кривой x4+j;4 ~#2 (x2Jry2).
§ 7.6. Вычисление объемов тел
Объем тела выражается интегралом
ъ
где S(x) — площадь сечения тела плоскостью, перпендикулярной к оси Ох
в точке с абсциссой х, а и Ь—левая и правая границы изменения х. Функция
S (х) предполагается известной и непрерывно меняющейся при изменении х от
а до Ь.
Объем Vх тела, образованного вращением вокруг оси Ох криволинейной
трапеции, ограниченной кривой y = f(x)(f (#)^0), осью абсцисс и прямыми
х = а и х = Ь(а < Ь), выражается интегралом
а
Объем тела Vx, образованного вращением вокруг оси Ох фигуры, ограниченной
298
кривыми у = Уг(х) и у = у2(х)
жается интегралом
л:)] и прямыми х = а, х = Ь, выра-
выраЕсли кривая задана параметрически или в полярных координатах, то следует
сделать соответствующую замену переменной в указанных формулах.
7.6.1, Определить объем эллипсоида
Решение. Сечение эллипсоида плоскостью х = const есть
эллипс (рис. 87)
с полуосями bV\—х*/а2; cY\—д:2/аа. Следовательно, площадь
сечения (см. 7.4.1)
S{x) = nb ]Л — х*1а*-с У\ —х*!а* =
Поэтому объем V эллипсоида равен
л:2/я2) (—а
4
Положив, в частности, а — Ь = с% получим объем шара УШара = уяа3.
7.6.2. Вычислить объем шарового слоя, вырезанного из шара
= 16 плоскостями # = 2 и jc = 3.
Рис. 87.
Рис. 88.
7.6.3. Оси двух одинаковых цилиндров с радиусами основания,
равными а, пересекаются под прямым углом. Найти объем тела,
составляющего общую часть этих двух цилиндров.
Решение. Примем оси цилиндров за оси Оу и Oz (рис. 88).
Тело OABCD составляет восьмую часть интересующего нас тела.
299
Пересечем это тело плоскостью, перпендикулярной к оси Ох, на
расстоянии л; от 0. В сечении получим квадрат EFKL со стороной
% 16 ,
EF=Va2—х2, поэтому S(x) = a2 —х2 и V = 8 j (a2—x2) dx = ^a\
о
7.6.4. На всех хордах круга радиуса /?, параллельных одному
направлению, построены симметричные параболические сегменты
постоянной высоты h. Плоскос-
Плоскости сегментов перпендикулярны
к плоскости круга.
Найти объем образованного
таким путем тела (рис. 89).
Решение. Предваритель-
Предварительно вычислим площадь парабо-
параболического сегмента с основа-
основанием а и высотой h. Распо-
Расположим оси координат так, как
указано на рис. 90. В этом
случае уравнение параболы
Определим параметр а. Подставив координаты точки В (а/2, 0),
получим 0 = аа2/4 +/г, отсюда a = — 4h/a2y следовательно, уравнение
Ah
параболы у = ^x2-\-h, a искомая площадь —
а/2
а/2
= 2 J (—
о о
Теперь вычислим объем тела. Если расположить оси координат так,
как показано на рис. 89, то в сечении тела плоскостью, перпенди-
перпендикулярной к оси Ох, в точке с абс-
абсциссой х получится параболический
сегмент, площадь которого, как мы
видели, равна «У =B/3) ah, где a =
= 2у = 2 Y^R2—х2. Следовательно,
S (х) = D/3) ]/>—х2 h и
я
V =
Л
S
JlJ
2 1
i
й
ш
щ
У
с
Ъ
ш
0
4h
\
*- X
>—x*dx = 4;nhR2.
Рис. 90.
7.6.5. Плоскость движущегося треугольника остается перпендику-
перпендикулярной к неподвижному диаметру круга радиуса а; его основание
есть хорда круга, а вершина лежит на прямой, параллельной непод-
неподвижному диаметру, на расстоянии h от плоскости круга. Найти объем
тела, образуемого движением этого треугольника от одного конца
диаметра до другого.
300
7.6.6. Вычислить объем тела, образованного вращением вокруг
оси Ох площади, ограниченной осями координат и параболой
Решение. Найдем точки пересечения кривой с осями коорди-
координат: при л; = 0 у = а, при ^ = 0 х = а. Таким образом, отрезок инте-
интегрирования есть [0, а].
Далее, из уравнения параболы получим y = (a1t*—л;1/*J. Поэтому
= п $ (а1/.—**/.)*</* =
= я J (а2 — 4а3/**1/* + бах — 4аV.jcV, + х2) dx = ^ яа3.
15*
7.6.7. Фигура, ограниченная дугой синусоиды у — sin дг, осью
ординат и прямой у=\, вращается вокруг оси Оу (рис. 91).
Определить объем V получающегося тела вращения.
Решение. Обратная функция A: = arcsin^ рассматривается на
отрезке [0, 1]. Поэтому
Уг 1
V= я J х2 dy = я J (arcsin ^yJ rfy.
Применим подстановку arcsin 3;=^. Отсюда
dy = cos t dt,
Значит, V=n W*cos^d/. Интегрируя по частям, получим
о
У=я(яя —8)/4.
y^slnx
У
0
1
t
0
я/2
ч.
0\
?
I
I
{
i
112
4
в
су
1
1
1
1
1
! >
2
Рис. 91.
Рис. 92.
7.6.8. Вычислить объем тела, образованного вращением вокруг
оси Ох фигуры, ограниченной параболой <у = 0,25д:а + 2 и прямой
у+
Решение. Тело образовано вращением фигуры АВСА (рис. 92)
вокруг оси Ох. Чтобы найти абсциссы точек Ан В, решаем систему
301
уравнений:
Отсюда хА=\/2; хв—2. В нашем случае
и j>a(x) = E/8)*+7/4. Следовательно,
= (\/4г)х2
1/2
7.6.9. Вычислить объем тела, полученного вращением вокруг
оси Оу фигуры, ограниченной параболами у — х2 и 8х=у2.
Решение. Очевидно, что Х2(у) = ]/Гу'^х1 (у)=у2/8 на отрезке
от начала координат До точки пересечения парабол (рис. 93). Найдем
ординаты точек пересечения парабол, исключив х из системы
уравнений:
4
Получим ^ = 0, ^2 = 4. Следовательно, V= я\ (у— ~- j dy — — n.
о
7.6.10. Вычислить объем тора. Тором называется тело, получаю-
получающееся при вращении круга радиуса а вокруг оси, лежащей в
0
-2а
0'
в/
щ
Ш
а
В
X
хг
yjf , . _ и \
0[
Рис. 93. Рис. 94.
его плоскости на расстоянии b от центра (Ь^а). (Форму тора име-
имеет, например, автомобильная шина.)
7.6.11. Вычислить объем тела, образованного вращением вокруг
оси Ох фигуры, ограниченной двумя ветвями кривой (у—хJ = хъ и
прямой л:— 1.
7.6.12. Найти объем тела, образованного вращением вокруг прямой
у = — 2а фигуры, ограниченной параболой у2 = 4ах и прямой х = а
(рис. 94).
302
Решение. Если перенести начало координат в точку О' @, —2а),
сохранив направление осей, то в новой системе координат уравнение
параболы запишется так:
(для
Отсюда Уъ = 2а-{-\/г4:ах (для кривой ОАВ), и
кривой OCD). Искомый объем равен
a
= я J [Ba + 2 Vox? — Ba—2l^ox)a] <** = у "«$-
0
7.6.13. Найти объем тела, полученного вращением вокруг оси Ох
фигуры, ограниченной астроидой: x = acosBt; y = asin9t.
Решение. Искомый объем V
равен удвоенному объему, полу-
полученному вращением фигуры ОАВ
(рис. 95). Поэтому
V=2n
Делаем замену переменной:
х = a cos3 /,
dx = —За cos21 sin t dt,
у— a sin81,
Следовательно,
о
V=2n J a2 sin61 (—3a cos21 sin t) dt =
Я/2
0
a
t
я/2
0
[Я/2 Я/2 -|
J sin7/a7— j sin^flY L
о о J
Используя формулу из 6.6.9 для вычисления фигурирующих здесь
интегралов, получаем
42 8642\ 32 3
7.6.14. Вычислить объем тела, которое образуется при враще-
вращении одной арки циклоиды x = a(t — sin t); y = a(l—costf) вокруг
оси Ох.
7.6.15. Вычислить объем тела, которое получается от вращения
кардиоиды p = a(l+ cos(p), вокруг полярной оси.
303
Решение. Кардиоида изображена на рис. 81, стр. 293. Иско-
Искомый объем представляет собой разность объемов, получаемых от
вращения вокруг оси Ох (она же и полярная ось) фигур MNKLO и
OKLO.
Перейдем, как и в предыдущей задаче, к параметрическому
заданию кривой, приняв за параметр полярный угол ф:
х = р cos ф = a cos ф A + cos ф),
у = р sin ф = a sin ф A + cos ф).
Очевидно, что абсцисса точки М равна 2а (значение х при ф = 0).
Абсцисса же точки К есть значение минимума функции х «=
= а{\ +созф) созф.
Найдем этот минимум:
~ = —a sin ф A + 2 cos ф) = О,
<Pi = 0; <ря = B/3)я.
При фх = 0 получаем хм = 2а, при ф2 = B/3) я получаем хк =
= — а/4.
Следовательно, искомый объем равен
2а О
V=n ^ y\dx—n \ y\dx.
-а/4 -а/4
Делая замену х = a cos ф A + cos ф), получим
у2 = а2 A + cos фJ sin2 ф,
dx = —a sin ф A 4- 2 cos ф) <
Таким образом,
о
У = я $ a*(\+cos4
X
—а/4?
2а
Ф
2я/3
0
X
—а/4
0
Ф
2я/3
л
-2 СО5ф)]*/ф—
я J а2 A + cos фJ sin2 ф [—a sin ф A + 2 cos ф)] dq> =
B/3)я
Я
B/3)я
я
1
= яа3 J(l— u2)(\ + uJ(\+2u)du = ~nas (и = cosy).
-i
7.6.16. Вычислить объем тела, ограниченного:
а) однополостным гиперболоидом x2/a2-\-y2Jb2 — z2/c2 — \ и пло-
плоскостями ? = —1 и z=l;
304
б) параболическим цилиндром z — \—у2, плоскостями координат
и плоскостью лг— а;
в) эллиптическим параболоидом z = x2/a2-\-y2/b2 и плоскостью
z = k (k>0).
7.6.17. От прямого кругового цилиндра радиуса а отсечен клин
плоскостью, проходящей через диаметр основания и наклоненной
к основанию под углом а. Найти объем клина.
7.6.18. Вычислить объем тела, образованного вращением фигуры,
ограниченной линиями:
а) лгу = 4, #=1, х — 4, у — О, вокруг оси Ох;
б) у = 2х—х2у у = 0, вокруг оси Ох;
в) у = xsy у = 0, х = 2, вокруг оси Оу;
г) y=zsinx (одной волной), у = 0, вокруг оси Ох;
д) х2—у2 = 4, у = ±2у вокруг оси Оу;
е) (у — аJ = ах, х = 0, у = 2а, вокруг оси Ох.
7.6.19. Найти объем тела, образованного вращением кривой
у2 = (ах3—хА)/а2 вокруг оси Ох.
7.6.20. Вычислить объем тела, образованного вращением вокруг
оси Ох фигуры, ограниченной линиями y = sinx и у = B/п)х.
7.6.21. Вычислить объем тела, образованного вращением вокруг
оси Ох криволинейной трапеции, ограниченной цепной линией у =
— у (e*/a+e~*/a)==ach-^ и прямыми х1 = —с, х2 = с (с > 0).
7.6.22. Вычислить объем тела, образованного вращением вокруг
оси Ох фигуры, ограниченной косинусоидой у — cos x и параболой
у~2я*х '
7.6.23. Вычислить объем тела, образованного вращением вокруг
оси Ох фигуры, ограниченной окружностью х2-\-у2—\ и параболой
y
7.6.24. На кривой у = х3 взяты две точки: А я В, абсциссы ко-
которых соответственно а=\ и Ь = 2.
Найти объем тела, полученного вращением криволинейной трапе-
трапеции аАВЬ вокруг оси Ох.
7.6.25. Дуга эволюты эллипса х = a cos /; у = b sin t, лежащая
в первом квадранте, вращается вокруг оси Ох.
Чему равен объем получающегося тела вращения?
7.6.26. Вычислить объем тела, полученного вращением вокруг
оси Ох петли кривой x = at2, y = a(t — /3/3).
7.6.27. Вычислить объемы тел, полученных вращением лемни-
лемнискаты (х2-\-у2J==а2(х2—у2) вокруг осей Ох и Оу.
7.6.28. Вычислить объем тела, полученного вращением вокруг
полярной оси кривой р = a cos2 ф.
805
§ 7.7. Вычисление длин дуг плоских кривых,
заданных в декартовых координатах
Если плоская кривая задана уравнением у = у (х) и производная у' (х)
непрерывна, то длина дуги этой кривой выражается интегралом:
Ь
a
где а и b—абсциссы концов данной дуги.
7.7.1. Вычислить длину дуги полукубической параболы
заключенной между точками @, 0) и D, 8) (рис. 96).
Решение. Функция^ (л:) определена для х^О. Поскольку дан-
данные точки лежат в первой четверти,у = х^2. Отсюда
У }М(Л,8)
У = у|/ х и у 1+/' =
Следовательно,
7.7.2. Вычислить длину дуги кривой у% = х3,
отсеченной прямой д:г=4/3.
Рис. 96. 7.7.3, Вычислить длину дуги кривой у = In cos x,
заключенной между точками с абсциссами х = 0, х = я/4.
Решение. Так как у' =* —tg х, то у 1 +ув = |/1 + tg2 а: =
= sec х.
Следовательно,
rt/4
7.7.4. Вычислить длину дуги кривой у = \п х^^ от xL = a до
7.7.5. Вычислить длину дуги кривой x = -j-y2—у In^y, заключен-
заключенной между точками с ординатами у = 1 и у = 2.
Решение. В этой задаче удобнее за независимую переменную
принять jr. тогда х' = -?у~5Ц и )А+*'2= |/ D"-у + "^"J в
Следовательно,
зш
7.7.6. Вычислить длину дуги астроиды х2^3-\-у2^3 =
Решение. Как известно, астроида симметрична относительно
осей координат и биссектрис координатных углов. Поэтому доста-
достаточно вычислить длину дуги астроиды, заключенной между биссект-
биссектрисой у = х и осью Ох, и результат умножить на 8.
В первой четверти у = (а2/3— х2^K^2 и j; = 0 при х = а, у = х
==_дг-1/з (а2/з __
Далее,
+у'2 =
Следовательно,
а/23/2
Замечание. Если бы мы стали вычислять длину дуги астроиды, лежа-
лежащей в первой четверти, то пришли бы к интегралу
а
$а1/3 x-1/3dx,
0.
подынтегральная функция которого возрастает до бесконечности при х
7.7,7. Вычислить длину дуги кривой ОАВСО, состоящей из участков
кривых y2 = 2xs и х2+у2 = 20 (рис. 97).
Решение. Достаточно вычислить дли-
длины дуг /^ и 1^у, так как в силу симмет-
симметрии фигуры относительно оси Ох
OA
Решив систему уравнений
найдем точку А B, 4).
Найдем /^w. Здесь
О А
у = у/Их***, y' = \
Следовательно,
—1).
807
Так как /w есть длина дуги окружности радиуса У 20, соответ-
соответствующей центральному углу arctg 2, то
: = 1/20 arctg 2.
A3
Окончательно имеем
7.7.8. Вычислить длину дуги кривой:
а) у = х2/2— 1, отсеченной осью Ох;
б) у = In B cos x) между соседними точками пересечения с осью Ох;
в) Зу2 = х(х—IJ между точками пересечения с осью Ох (поло-
(половину длины петли).
7.7.9. Вычислить длину дуги кривой
у = .1 [ху х2 —1 — In (л: + У^^Л)]
от х — 1 до х = а + 1.
7.7.10. Найти длину дуги кривой, состоящей из участков кри-
кривых х2 = (у-\-1K и у —4:.
§ 7.8. Вычисление длин дуг кривых,
заданных параметрически
Если кривая задана уравнениями в параметрической форме x — x(i)y
y?=zy(t) и производные х'(t), yf (t) непрерывны на отрезке [tlt t2], то длина
дуги кривой выражается интегралом
где tt и t2 — значения параметра t, соответствующие концам дуги (tx < tz).
7.8.1. Вычислить длину дуги развертки круга х = a (cos t-\-t sin t).
y = a(sint — /cos/) от / = 0 до / = 2я.
Решение. Дифференцируя по /, получим
х\ = at cos /, y\ — at sin t%
откуда т/ х* + y't — а*- Следовательно,
о
7.8.2. Вычислить длину одной арки циклоиды:
х = a (t—sin /), у == а A —cos t).
308
7.8.3. Вычислить длину астроиды: # = acos3/, у = asih8t.
Решение. Дифференцируя по /, получим
Отсюда
х\ = —За cos21 sin t;
y't = За sin2 / cos /.
't -\-y't = j/9a2 sin2 t cos21 = 3a | sin / cos t | =
Так как функция | sin 2^ | имеет период л/2, то
Я/2
/ = 4.у J sin2/Л = 6а.
не-
Замечание. Если бы мы забыли, что нужно брать арифметическое
значение корня, и положили у х\ -\-у\ — За sin /cos/, то получили бы
верный результат, так как
2я
За 2п
di = -2
\
За \ sin/
= 0.
7.8.4. Вычислить длину петли кривой д: = |/*3/2, y = t—/3.
Решение. Найдем пределы интегрирования. Обе функции x(t)
и у (t) определены при всех значениях t. Так как функция
х =]/з/2^0, то кривая лежит в правой полуплоскости. Так как
при изменении знака параметра t
величина x(t) не изменяется, а у (t)
меняет знак, то кривая симметрич-
симметрична относительно оси Ох. Кроме то-
того, функция x(t) принимает одно
и то же значение не более, чем
два раза. Отсюда следует, что
точки самопересечения кривой ле-
лежат на оси Ох, т. е. при у = 0
(рис. 98).
На рисунке стрелками показано то направление, в котором теку-
текущая точка М(х, у) пробегает кривую при изменении t от —со до оо.
Hoj/ = 0 при 1г = 0, /2|3 = ±1. Так как x(t2) = x(tB) = Уз, то
точка (j/З, О) является единственной точкой самопересечения кри*
вой. Следовательно, мы должны интегрировать в пределах от /2 = — 1
до t3=l.
Дифференцируя параметрические уравнения кривой по /, полу-
получим x't = 2V3ty y,' = l—3/2, откуда
Рис. 98.
Следовательно,
-1
/4/
7.8.5. Вычислить длину дуги кривой x = f/6, у~2— /4/4 между
точками пересечения с осями координат.
7.8.6. Вычислить длину дуги эллипса х2/а2 -\-у2/Ь2 = 1.
Решение. Перейдем к параметрическому заданию эллипса
х = a cos ty y = bsint, 0 ^ t ^ 2я.
Дифференцируя по tt получаем
х\ = — a sin t; y't = b cos /,
откуда
= a V\—
где в—эксцентриситет эллипса, е = с/а = |/а2—
Таким образом,
2rt я/2
— е2 cos2 tdt = 4а J j/l — e2cos4dt.
о
Интеграл j |/1 —е2 cos2 / rf^ не берется в элементарных функциях;
о
он называется эллиптическим интегралом второго рода. Полагая
t = nj2 — т, приводим интеграл к стандартному виду:
Я/2 Я/2
J V\— e2 cos2 tdt = J Kl—
о
где ^(е)—обозначение для так называемого полного эллиптического
интеграла второго рода.
Следовательно, для длины дуги эллипса имеет место формула
1=4аЕ (е).
Обычно полагают e = sina и пользуются таблицами функции
Ех (а) = EL (arcsin e) = Е (г).
Например, если а =10 и ? = 6, то
e=y 1V/1O"U =Ot8 = sin530,
По таблице значений эллиптических интегралов второго рода
находим /=40 ^E3°) = 40-1,2776 «51,1.
7.8.7. Вычислить длину дуги кривой
между точками пересечедмя с осью Ох.
3t#
7.8.8. Найти длину дуги кардиоиды:
х = а B cos t — cos 2t),
y = aBs\n t — sin2t).
7.8.9. Найти длину замкнутой кривой
х = 4 К2 a sin /; у = a sin 2t.
7.8.10. Найти длину дуги эволюты эллипса
х = — cos3
r = _?.Sin3/, c2 = a2 — I
7.8.11. Вычислить длину дуги кривой
x=*(t2—2)sin/+ 2/cos/,
.у = B — /2) cos/+ 2/sin/
от /г = 0 до /а —я.
7.8.12. На циклоиде x = a(t — sin/); у = а(\—cos/) найти точку,
которая делит первую арку циклоиды по длине в отношении 1:3.
§ 7.9. Вычисление длин дуг кривых, заданных
в полярных координатах
Если гладкая кривая задана уравнением р = р (ф) в полярных координатах,
то длина дуги / кривой выражается интегралом:
ф2
где фх и ф2—значения полярного угла ф в концах дуги (ф! < ф2).
7.9.1. Найти длину первого витка архимедовой спирали р = шр.
Решение. Первый виток архимедовой спирали образуется при
изменении полярного угла ф от 0 до 2я. Поэтому
2jt 2я
= a
7.9.2. Вычислить длину логарифмической спирали р = ает<? от
некоторой ее точки (р0, ф0) до переменной точки (р, ф).
Решение. В этом случае (независимо от того, какая из величин
р и р0 больше!)
ф
С
Ш1
т. е. длина дуги логарифмической спирали пропорциональна прира-
приращению полярного радиуса дуги.
7.9.3. Найти длину дуги кардиоиды р = а A -J- cos ф) (# > О,
Решение. Здесь рф = — a sin ф,
У Рф* + Р2 =
f
= 2а | cos «р/2)| - |
Следовательно, в силу симметрии,
2Я Я
/ = 2а \ cos -2- ^ф = 4а I cos -2- д?ф = 8а.
о о
7.9.4. Найти длину дуги лемнискаты р2==2а2соз2ф от правой
вершины, отвечающей ф = 0, до любой точки с полярным углом
ф < я/4.
Решение. Если 0 ^ ф < я/4, то cos 2ф > 0. Поэтому
г — /
р = а у 2 cos 2ф; рф =
; ;
У cos 2ф
os 2ф ; у cos 2ф
Следовательно,
Последний интеграл называется эллиптическим интегралом первого
рода и его можно привести к виду, удобному для вычисления с по-
помощью специальных таблиц.
7.9.5. Вычислить длину дуги кривой р = a sin3 (ф/3).
7.9.6. Вычислить длину отрезка прямой линии
p = #sec (ф—я/3)
от точки ф = 0 до точки ф = я/2.
Решение, р^ = a sec (ф—я/3) tg (ф—я/3);
== а sec (Ф —л/3) ^/rГ+tg2(ф—я/3) = a sec2 (q> —
(Знак модуля у функции sec (ф — я/3) опущен, так как на отрезке
[0, я/2] эта функция положительна.)
я/ 2 „
С 4 1^3
== а \ sec2 (ф —я/3) dy = ~- а.
312
7.9.7. Вычислить длину замкнутой кривой р —# sin4((p/4).
Решение. Так как функция p = asin4(<p/4)—четная, то за-
заданная кривая симметрична относительно полярной оси. Так как функ-
Рис. 99.
ция sin4 (ф/4) имеет период 4я, то за половину периода от 0 до 2я
полярный радиус возрастает от 0 до а и опишет половину кривой
в силу ее симметрии (рис. 99).
Далее р'ф = a sin3 (ф/4) cos (ф/4) и
|/"р» -f р^2 = У a2 sin8 (ф/4) + a2 sin6 (ф/4) cos2 (ф/4) = a sin3 (ф/4),
если
Следовательно,
2л
я/2
Г
/
/ = 2а С sin3 (ф/4) Жр = 8а Г sin3/ dt = ™a (ф = 4/).
о о
7.9.8. Вычислить длину дуги кривой ф = A/2) (р+1/р) от р =
до р = 4.
Решение. Дифференциал дуги dl равен
Из уравнения крршой находим jr^-n* A г")- Следовательно,
;-»+?•
7.9.9. Вычислить длину гиперболической спирали рф = 1 от
= 3/4 до ф2-4/3.
313
7.9.10* Вычислить длину замкнутой кривой p = 2a(sin cp-j-coscp).
7.9.11. Вычислить длину дуги кривой р=р[(\ -f-cos ф) от
= — я/2 до ф2 = 2
§ 7.10. Вычисление площади поверхности вращения
Площадь поверхности, образованной вращением вокруг оси Ох дуги L кри-
кривой у = у(х) {a^x^b)t выражается интегралом
ь
который удобно записывать в форме Р = 2л \ ydl, где dl—дифференциал
L
длины дуги.
Если кривая задана параметрически или в полярных координатах, то
достаточно произвести замену переменной в приведенной формуле, выразив
соответствующим образом дифференциал длины дуги (см. § 7.8 и 7.9).
7.10.1. Вычислить площадь поверхности, образованной вращени-
вращением астроиды х2/3 4-J>2/3 = #2/3 вокруг
ху . ОСИ Ох.
\/ Рещение. Дифференцируя урав-
уравнение астроиды, получаем
откуда j/ = —
Далее,
.2/3
Рис. 100.
„1/3
•# Так как астроида симмет-
рична относительно оси Оу, то при вычислении площади поверх-
поверхности можно сначала считать лг^О, а затем результат удвоить.
Другими словами, искомая площадь Р равна
/тг П
Заменим
X
0
а
t
а1/3
0
Тогда Р=\2яа1'3
314
7.10.2. Вычислить площадь поверхности, образованной вращением
вокруг оси Ох замкнутого контура ОАВСО, образованного кривыми
у = х2 и х=у2 (рис. 100).
Решение. Заданные параболы, как легко проверить, пересе-
пересекаются в точках О@, 0) и ВA, 1). Искомая площадь Р = Р1 + Р2,
где площадь Рг образована вращением дуги ОСВ, а Р2 — вращением
дуги ОАВ.
Вычислим площадь Р1% Из уравнения х=у2 получаем у = Ух
и у' = 1/B Ух). Следовательно,
о
Вычислим теперь площадь Р2. Имеем у = х*, у' = 2х и
1
Р2 = 2л;
Замена x = (l/2)sh^, д?лг = A/2) ch tdt
Arsh2
|Arsh2
[О
Таким образом,
7.10.3. Вычислить площадь поверхности, образованной вращением:
а) части кривой у = л:а/2, отсеченной прямой j/ = 3/2, вокруг
оси Оу;
б) части кривой j/2 = 4 + at, отсеченной прямой д;=2, вокруг
оси Ох.
7.10.4. Вычислить площадь поверхности эллипсоида, образован-
образованного вращением эллипса х2/а? +у2/Ь2 = 1 вокруг оси Ох (а > Ь).
Решение. Разрешая уравнение эллипса относительно у} для
получим
ть
Отсюда
Р = 2я
—a
a
где величина s = V(a2—Ь2)/а2 = с/а есть эксцентриситет эллипса.
В частности, при Ь—+а эксцентриситет 8 стремится к нулю и
lim arcsin в = #
е-* о е '
так как при этом эллипс превращается в окружность, то в пределе
получаем площадь поверхности шара (сферы):
7.10.6. Вычислить площадь поверхности, образованной вращением
эллипса 4:Х2-\-у2 = 4 вокруг оси Оу.
7.10.6. Дуга цепной линии
у = * (ех/а + е~х/а) = a ch -,
концы которой имеют абсциссы 0 и х, вращается вокруг оси Ох.
Показать, что площадь поверхности Р и объем V образуемого
при этом тела связаны соотношением P=2V/a.
Решение. Так как у' = sh (х/а)} то V 1 +y'z = ch (х/а). Поэтому
X X X
р = 2я С у V1 + у'2 dx = 2ап Г cha ~ dx = -| я f a2 ch2 ~ </*,
но
значит, P=2V\a, что и требовалось доказать.
7.10.7. Найти площадь поверхности, образованной вращением
вокруг оси Оу петли кривой 9ах2=у (За—уJ.
Решение. Петля описывается текущей точкой при изменении
у от 0 до За. Продифференцируем по у обе части уравнения кривой:
\Ъахх' = (За— уJ — 2у (За—у) = 3 (За— у) [а—у).
Отсюда д;л;' = Cа—у) (а—уI$а. Применяя формулу для вычисле-
вычисления площади поверхности тела вращения вокруг оси Оу, будем иметь
316
Уг r Уг
Р = 2п I х V\ +x'z dy^2n\ V х2 + (xx'f dy =
3fl
3a
9a
36a2
Зла2.
7.10.8. Вычислить площадь поверхности, образованной вращением
вокруг оси Ох кривой 8у2 = д:2—х*.
7.10.9. Вычислить площадь поверхности, образованной вращением
вокруг оси Ох дуги кривой x = t2; y = (t/3)(t% — 3), заключенной
между точками пересечения ее с
осью Ох.
Решение. Полагая ^ = 0, на-
находим ^ = 0 и t2tz = ±F3 и,
следовательно, ^ = 0 и x23 = 3.
Отсюда следует, что кривая пере-
пересекает ось Ох в двух точках, @, 0)
и C, 0). При изменении знака па-
параметра t функция x(t) знака не
меняет, а функция у (t) меняет знак.
Это означает, что кривая симмет-
симметрична относительно оси Ох (рис. 101).
Для нахождения площади поверхности достаточно ограничиться
нижней частью кривой ОпВ, соответствующей изменению параметра
от 0 до +КЗ. Дифференцируя по t, находим
Рис. 101.
и дифференциал длины дуги
dl = Vxt+ytdt = A +12) dt.
Следовательно,
V7
7.10.10. Вычислить площадь поверхности тора, образованного
вращением окружности х* + (у—bJ = r2 @<r<ft) вокруг оси Ох.
Решение. Запишем уравнение окружности в параметрической
форме: х = г cos t; y = b + rsint.
317
Отсюда
х\ — —г sin i\ у\—
Искомая площадь Р равна
Р = 2п\ (b + r sin t) V(— r sin tJ + (г cos О2 dt =
о
2Я
г sin *) Л =
7.10.11. Вычислить площадь поверхности, образованной враще-
вращением лемнискаты р — а]/^ zos2q> вокруг полярной оси.
Решение. Действительные значения для р получаются при
cos2cp^0, т. е. при —я/4^ф^я/4 (правая ветвь лемнискаты)
или при C/4) п <! ф ^ E/4) п (левая ветвь лемнискаты).
Дифференциал длины дуги лемнискаты равен
1/ а2со5 2ф+( . у ) ^=
г Y^\ /cos 2фУ Y
/cos 2фУ Y /cos 2ф
Кроме того, д; = р sin ф = a sin ф j/cos 2ф.
Искомая площадь поверхности Р равна удвоенной площади по-
поверхности, образуемой вращением правой дуги. Поэтому
L О С S ' "
7.10.12. Вычислить площадь поверхности, образованной враще-
вращением четверти окружности х2-\-у2 = а2 от точки А (а, 0) до точки
В@, а) вокруг прямой х-\-у=за.
Решение. Найдем расстояние MN текущей точки М(х, у),
лежащей на окружности х2-\-у2 = а2, до прямой х-\-у=^а;«
V2 V2
так как для точек окружности, лежащих в первой четверти,
Далее,
dl=V \-\-y dx= у 1 +(• r =)
Следовательно,
318
7.10.13. Вычислить площадь поверхности, образованной враще-
вращением одной ветви лемнискаты р = а у cos 2ф вокруг прямой ф = я/4.
Решение. Из треугольника 0MN (рис. 102) находим расстоя-
расстояние MN произвольной точки М пра-
вой ветви от оси вращения ф = я/4:
MN = p sin (я/4—ф) =
cos 2ф sin (я/4—ф);
далее
Рис. 102.
Я/4
Поэтому Р=2я
aV^cos2ф sin f-j—ф]
/4
7.10.14. Вычислить площадь поверхности, образованной враще-
вращением вокруг оси Ох дуги кривой у = х*/3 от х=—2 до л; = 2.
7.10.15. Вычислить площадь поверхности, образованной враще-
вращением одной полуволны кривой у = sin х вокруг оси Ох.
7.10.16. Вычислить площадь поверхности, образованной вращением
вокруг оси Оу дуги параболы ха = 4ау, заключенной между точками
пересечения ее с прямой у = За.
7.10.17. Вычислить площадь поверхности, образованной вращением
дуги кривой х = ef sin t\ y = ef cos t вокруг оси Ох от / = 0 до t = я/2*
7.10.18. Вычислить площадь поверхности, образованной враще-
вращением вокруг оси Ох дуги кривой
х = *»/3; у = 4—/2/2,
заключенной между точками пересечения ее с осями координат.
7.10.19. Вычислить площадь поверхности, образованной вращением
кривой р = 2а sin ф вокруг полярной оси.
7.10.20. Вычислить площадь поверхности, образованной вращением
вокруг оси Ох кардиоиды
х = а B cost — cos 2/),
у = а B sin t— sin 2t).
§ 7.11. Смешанные задачи на геометрические приложения
определенного интеграла
7.11.1. Дана циклоида (рис. 103)
x = a{t— sint); y = a{\—cost);
Вычислить:
а) площади поверхностей, образованных вращением дуги ОБА
вокруг оси Ох и вокруг оси Оу;
б) объемы тел, образованных вращением фигуры ОВАО вокруг
оси Оу и вокруг оси ВС;
319
в) площадь поверхности, образованной вращением дуги ВА во-
вокруг оси ВС;
г) объем тела, образованного вращением фигуры ODBEABO
вокруг касательной DE в вершине В;
В
-л:
с
Рис. 103.
д) площадь поверхности, образуемой при этом дугой циклоиды.
Решение, а) При вращении вокруг оси Ох площадь поверхности
2JT 2Я
Г С t С t
. = 2я \у dl = 2n \ a (I —cos /Ja sin у dt — Sa2n \ sin-'y а/ =
L о о
При вращении вокруг оси Оу площадь поверхности
л
2Я 2Я
+ 4ла2 П^ — sin 0 sin -jdt = 4na2 \ (t— sin /) sin у Л = 16я2а2.
б) При вращении вокруг оси Оу получаем объем
2а 2а 2а
Уу = я\ {х\—x!)dy = nj *Jdy —nj xfrfy,
0 0 0
где jc = хх (у) — уравнение кривой В А, х = х2 {у)—уравнение кривой ОВ.
Производя замену у=- аA— cos/), надо учесть, что для первого
интеграла t меняется от 2я до я, а для второго интеграла / меняется
от 0 до я. Следовательно,
V = п\ a*(t— sin tJ a sin tdt — n^a*{t — sin/J a sintdt**
y in о
2П
[00 0П|
^t2 sin tdt— ^t(l—cos2t)dt+ J sin3/d/ =6я3а3.
2Л 2Я 2Л J
320
Для вычисления объема тела, получающегося при вращении
вокруг оси ВС, удобно сначала перенести начало координат в точку С,
что дает в новых координатах уравнения
х' = a(t — я—sin t); у' = аA —cost).
Учитывая лишь дугу ВА, получим
V=n\ x'2dy'=na* l(t—л—s'm tJ sin t4t.
О 2Я
Полагая t—я = z, получим
о я
V= —па3 ^ (?+ sin zJ sin z dz~na3 ^ B+ sin zJ sin zdz~
я 0
в) Совершая указанный выше перенос начала, получим
dl = 2а sin {tj2) \ dt \ = — 2а sin (t/2) dt.
Поэтому
2а я
Р= Г2лхй?/= — 4ла2 Г(/ — я— sin 0 sin ~ ^/=
О 2Я
Я
= 4яа2 \ (z + sin 2:) cos ~ dz = 4 ( 2я —Ti яа2.
J ^ V d /
о
г) Перенося начало координат а точку В и изменяя направление
оси Оу, получим
Xе = a(t — я—sin/), у' — аA + cos/).
Полагая /—n = z, имеем
у' = а A —cos .г),
причем для дуги 05Л величина z меняется от —я до я. Следо-
Следовательно,
я
-я
я я
д) Р = 2п \ydl=-4na2 \ A — cos2) cos-^- dz^-jna2.
-я -я
7.11.2. Найти объем тела, ограниченного поверхностями z2=
^SB—x) и х2+у2=^2х.
Решение. Первая поверхность есть параболический цилиндр
с образующими, параллельными оси Оу} и с направляющей z2 = 8B—х)
321
в плоскости xOZy а вторая—круговой цилиндр с образующими, парал-
параллельными оси Oz, и с направляющей х2 +у2 = 2х в плоскости хОу.
2
Объем V вычислим по формуле V = Jj 5 (х) dx. S (х) представляет
о
собой площадь прямоугольника, основание которого равно 2у, а вы-
высота 2z:
Следовательно,
2 2
1/= С 4}/* B — х) 8 B —х) dx = 4 УТ (* B — J
7.11.3. Доказать, что если фигура S ограничена простым вы-
выпуклым контуром и заключена между ординатами ух и у% (рис. 104),
то объем тела вращения этой фи-
фигуры вокруг оси Ох можно выра-
выразить формулой
у у \С V=2n)yhdy,
JO где
h==x2(y)—x1(y),
х = х1(у) — уравнение левой части
контура, х = х2(у)—уравнение пра-
правой части контура.
Решение. Пусть вращающая-
вращающаяся фигура 5 ограничена простым
Рис. 104. выпуклым контуром и заключена
между ординатами ух и у2. Отре-
Отрезок [ylt y2] делим на части, через точки деления проводим прямые,
параллельные оси вращения, разбивая фигуру 5 на горизонтальные
полоски. Выделяем одну полоску и заменяем ее прямоугольником ABCD,
у которого нижнее основание равно хорде AD= h, соответствующей
ординате .у, а высота АВ=Ау. Тело, образуемое вращением прямо-
прямоугольника ABCD вокруг оси Ох, есть полый цилиндр, объем которого
приближенно можно принять за элемент объема
АV & я (у + AyJ h—ny2h = 2яу Ну h + nh (AyJ.
Отбрасывая бесконечно малую второго порядка относительно Ау,
получим главную часть или дифференциал объема
322
Зная дифференциал объема, мы получаем сам объем интегрированием:
у*
Таким образом, мы получим еще одну формулу для вычисления
объема тела вращения.
7.11.4. Фигура, ограниченная параболой у = 2х2-\-3, осью Ох
и вертикалями х — 0 и х=\, вращается вокруг оси Оу. Вычислить
объем образованного тела вращения.
Решение. Разобьем площадь фигуры на элементарные полоски
прямыми, параллельными оси Оу, Объем AV элементарного цилинд-
цилиндрика, получающегося при вращении одной полоски, равен
Д V = я (х + АхJу —лх2у = 2пху Ах + пу (Ад:J,
где Ах — ширина полоски.
Пренебрегая бесконечно малой второго порядка относительно Дх,
получим дифференциал искомого объема
dV=2nxy dx.
Отсюда
1 1
V = ^ 2яху dx = 2л J х Bх2 + 3) dx = 4я.
о о
7.11.5. Вычислить площадь той части
поверхности цилиндра
2
ax, iz
которая содержится внутри сферы
Решение. Образующие ци-
цилиндра параллельны оси Oz, a
направляющей служит окруж-
окружность (х—а/2J+у2 = а2/4 (на
рис, 105 изображена четвертая
часть искомой поверхности).
Изображенную на рис. 105
часть окружности разделим на
небольшие дуги Д/.
Образующие, проходящие че- "
рез точки деления, делят по- Рис. 105.
верхность цилиндра на полоски.
Если пренебречь бесконечно малыми высшего порядка, то площадь
полоски ABCD равна CD-AL
Если р и ф — полярные координаты точки D, то р = асовф и
Отсюда находим дифференциал площади поверхности:
dP = a2 sin ф dtp.
323
Значит,
jf/2
Р = 4 \ a2 sin ф <2ф = 4а2.
7.11.6. Вычислить площадь поверхности, отсекаемой от прямого
кругового цилиндра плоскостью, проходящей через диаметр основа-
основания и наклоненной к основанию
под углом 45°.
Решение. Примем ось ци-
цилиндра за ось Oz, а данный диа-
диаметр— за ось Ох. Тогда уравнение
цилиндрической поверхности
у х2-\-у2 = а2, а уравнение плос-
плоскости, составляющей с коорди-
координатной плоскостью хОу угол в
45°, будет у = 2.
Площадь бесконечно узкой
полоски ABCD (рис. 106) с точ-
точностью до бесконечно малых выс-
высшего порядка будет dP=zdl,
где dl — длина элементарной дуги окружности основания.
Вводя полярные координаты, получим
г =у = a sin ф; dl — a dq>.
Отсюда dP=a2slnq>dq) и
Рис. 106.
Р= а2 ^ sinф dcp = а2 [ — совф]^ - 2а2.
о
7.11.7. Оси двух круглых цилиндров с равными основаниями пе-
пересекаются под прямым углом.
Вычислить площадь поверхности тела, составляющего общую
часть обоих цилиндров.
7.11.8. Вычислить объем тела, которое получается при вращении
вокруг оси Оу фигуры, ограниченной параболой х2= у — 1, осью
абсцисс и прямыми х = 0 и х = 1.
7.11.9. Найти площадь 5 эллипса, заданного уравнением
\ (8 = АС—В2>0; С>0).
Решение. Решая уравнение относительно у, получим
.. _-вх-Гс~-
Sx2
С
причем значения х должны удовлетворять неравенству
С—б*2>0.
Решая это неравенство, получим пределы интегрирования:
324
Следовательно, искомая площадь равна
Vcjb УЩ
S= J <y*-y1)dx = ± ^
7.11.10. Найти площади фигур, ограниченных кривыми, заданны-
заданными параметрически:
а) x = 2t — t2; y = 2t2 — t3;
б) x = t*/(\+t*); y = t(\—t*)l{l+t*).
7.11.11. Найти площади фигур, ограниченных кривыми, заданны-
заданными в полярных координатах:
a) p = asin3(p (трилистник); б) р = 1_c0S—[я/4^ф<^л;/2];
в) p = 3sin<p и р = 1/^3 cosф.
7.11.12. Найти длину дуги кривой у2 = ~B—хK} отсеченной
прямой х— —1.
7.11.13. Найти длину дуги О А кривой
_ 1 а2
У ~ а Ш а2-х* '
где О@, 0); А (а/2, a In D/3)).
7.11.14. Вычислить длину дуги кривой у2 = B/3) (х—IK, заклю-
заключенной внутри параболы у2 = х/3.
7.11.15. Доказать, что длина эллипса
х = 1^2 sin t; у = cost
равна длине одной волны синусоиды y = sinx.
7.11.16. Доказать, что дуга параболы у=(\/2р) х2, соответству-
соответствующая интервалу О^Ся^а, имеет ту же длину, что дуга спирали
р = Р(р} соответствующая интервалу 0 ^ р ^ а.
7.11.17. Найти отношение площади, ограниченной петлей кривой
y=z ±A/3—х)Ух, к площади круга, длина окружности которого
равна длине контура этой кривой.
7.11.18. Найти объем сегмента, отсекаемого от эллиптического
* У2 . *2
параболоида ~—\-^- = х плоскостью х = а.
7.11.19. Вычислить объем тела, ограниченного гиперболоидом
x2/a2+y2/b2—z2/c2= —I
и плоскостями z = c и z
7.11.20. Найти объем прямого эллиптического конуса, основание
которого есть эллипс с полуосями а и Ь, а высота равна h.
7.11.21. Найти объем тела, образованного вращением йокруг оси Ох
фигуры, ограниченной прямыми: у — х-\-\;у = 2х-\-\ и # = 2.
7.11.22. Найти объем тела, полученного от вращения вокруг оси Ох
фигуры, ограниченной гиперболой х2\а2 —у2\Ь2 = 1, прямой 2ау—Ъх = О
и осью абсцисс.
325
7.11.23. Найти объем тела, образованного вращением кривой
р — а cos2 ф вокруг полярной оси.
7.11.24. Найти площади поверхностей, образованных вращением
следующих кривых:
a)y = tgx @^#<:я/4) вокруг оси Ох;
б) у = хУх/а @^.х^.а) вокруг оси Ох;
в) х2+у2 — 2гх = 0 вокруг оси Ох в пределах от 0 до h.
§ 7.12. Вычисление давления, работы
и других физических величин
I. Сила давления жидкости Р на площадку 5 с глубиной погружения h
по закону Паскаля равна P = yhS, где у—удельный вес жидкости.
II. Если непрерывная переменная сила X^f(x) действует в направлении
оси Ох, то работа силы на отрезке [xv x2] выражается интегралом
л2
III. Кинетическая энергия К материальной точки массы т, обладающей
скоростью v, выражается формулой /C = /nt>2/2.
IV. Электрические заряды отталкивают друг друга с силой F = e1e2/r2,
где ег и е2—величины зарядов, г — расстояние между ними.
Замечание. При решении прикладных задач мы будем считать все
данные выраженными в одной системе измерений и будем опускать наимено-
наименования соответствующих величин.
7.12.1. Вычислить силу давления воды на вертикальную треуголь-
треугольную пластинку, имеющую основание b и высоту к, погруженную
в воду так, что ее вершина лежит на
" " ^ ц поверхности воды.
" Решение. Введем систему коор-
координат так, как показано на рис. 107,
и рассмотрим горизонтальную полос-
полоску, находящуюся на произвольной
глубине х и имеющую толщину, рав-
равную dx.
Приближенно принимая эту полоо
ку за прямоугольник, находим диффе-
z ренциал площади dS — MNdx. Из
Рис. 107. подобия треугольников BMN и ABC
имеем MN/b = x/h.
Отсюда MN=--bx/h и dS = {bx/h)dx,
Сила давления воды на эту полоску с точностью до бесконечно
малых высшего порядка равна dP = xdS (учитывая, что удельный
вес воды равен 1). Следовательно, сила давления воды на всю пла-
пластинку ЛВС равна
h h
7.12.2. Найти величину давления на полукруг» вертикально погру-
погруженный в жидкость, если его радиус равен /?, а диаметр лежит на
свободной поверхности жидкости
(удельный вес жидкости равен у).
7.12.3. Вертикальная плотина
имеет форму трапеции, верхнее
основание которой равно 70 м, ниж-
нижнее 50 ж, а высота 20 м> Найти
силу давления воды на плотину
(рис. 108),
Решение, Дифференциал пло-
площади (dS) заштрихованной на ри-
рисунке области приближенно равен
dS^MNdx. Учитывая подобие тре-
треугольников 0ML и ОЛЕ, находим ML/20
уд
Рис. 108.
B0— хI20; отсюда
70—х. Таким образом, dS*=*
дифференциал силы давления воды равен
^x G0—x)dx.
Интегрируя по х в пределах от 0 до 20, получим
20
G0л:—x2)dx= 11333 j.
7.12.4. Вычислить работу, которую нужно затратить на выкачи*
вание воды из котла, имеющего форму полушара радиуса R.
7 12.5. Прямоугольный сосуд наполнен водой и маслом в равных
по объему частях, причем масло вдвое легче воды. Показать, что сила
давления смеси на боковую стенку
0 I уменьшится на одну пятую, если воду
|—— Г^^У заменить маслом.
Решение. Пусть h—глубина со-
h суда, /—длина стенки. Введем систему
Y координат так, как показано на рис.
х 109, Так как масло располагается над
h\ I водой и занимает верхнюю половину
сосуда, то сила давления масла на
* верхнюю половину стенки равна
h/2
Рис. 109. 1
Давление на глубине х > h/2 слагается из давления столба масла
высотой А/2 и столба воды высотой х — h/2 и потому
327
Следовательно, сила давления смеси на нижнюю половину стенки
равна
Л/2
Полное давление смеси на стенку равно
4 Мб 16 *
Если бы сосуд был наполнен только маслом, то сила давления Р
на ту же стенку была бы равна
h
Следовательно,
7.12.6. Электрический заряд Е, сосредоточенный в начале коор-
координат, отталкивает заряд е из точки (а, 0) в точку (Ь, 0). Опреде-
Определить работу А силы отталкивания F.
Решение. Дифференциал работы силы на перемещении dx равен
еЕ
Отсюда
При Ь—> оо работа А стремится к величине еЕ/а.
7.12.7. Определить работу, необходимую для запуска ракеты
весом Р с поверхности Земли вертикально вверх на высоту h.
Решение. Обозначим через F величину силы притяжения ракеты
Землей. Пусть тр—масса ракеты, тз—масса Земли. Согласно за-
закону Ньютона
где х — расстояние от ракеты до центра Земли. Полагая кгпрт3 = К,
получим F(x)— К/х2у R^.x^h-{-Ry R — радиус Земли. Прих^/?
сила F(R) будет весом ракеты Р, т. е. F(R) — P=K/R2) откуда
K=PR* и F(x) = PR2/x\
Таким образом, дифференциал работы есть
Интегрируя, получим
R+h R+h
328
Предел
lim A (k) = lim
равен работе, которую должен совершить двигатель, чтобы полностью
освободить ракету от земного притяжения (движение Земли при этм
не учитывается).
7.12.8. Какую работу надо затратить, чтобы остановить железный
шар радиуса /?, вращающийся с угловой скоростью со вокруг своего
диаметра?
Решение. Количество необходимой работы равно кинетической
энергии шара. Для подсчета этой энергии разобьем шар на концент-
концентрические полые цилиндры толщины dx; скорость точек такого ци-
цилиндра радиуса х есть тх.
Дифференциал объема такого цилиндра равен я?К=4ялг|//?а—x2dx%
дифференциал массы dM — ydV, где у — плотность железа, диффе-
дифференциал кинетической энергии dl< = 2яуа>ахь VR*—х2 dx.
Отсюда
R
7.12.9. Вычислить кинетическую энергию диска массы М и ра-
радиуса /?, вращающегося с угловой скоростью ш около оси, прохо-
проходящей через его центр перпендикулярно к его плоскости.
7.12.10. Найти количество тепла, выделяемое переменным сину-
синусоидальным током
/=/osin(^-<
в течение периода Т в проводнике с сопротивлением /?.
Решение. Для постоянного тока количество тепла в едини-
единицу времени определяется законом Джоуля—Ленца
При переменном токе дифференциал количества тепла равен
= 0,24/2 (t)Rdt, откуда
Q = 0,24/?J /*dt.
h
В нашем случае
7
Q=0,24/?/02 fsin2(^--<
329
7.12.11. Вычислить силу давления жидкости на вертикальную
стенку в форме эллипса с осями 2а и 26, центр которого погружен
в жидкость на уровень h(h^b) (удельный вес жидкости d).
7.12.12. Вычислить силу давления жидкости на боковые стенки
кругового цилиндра, высота которого равна /г, а радиус основания г»
Удельный вес жидкости равен d, и жидкость полностью заполняет
цилиндр.
7.12.13. Вычислить работу на преодоление силы тяжести, которую
необходимо затратить, чтобы выкачать воду из резервуара, имеющего
форму конуса, обращенного вершиной вниз. Высота конуса //, радиус
основания R.
7.12.14. Вычислить работу, которую нужно затратить, чтобы
растянуть пружину на 6 см, если сила 1 кг растягивает ее на 1 см.
§ 7.13. Вычисление статических моментов и моментов инерции.
Определение координат центра тяжести
Во всех задачах этого параграфа мы будем считать, что масса равномерно
распределена по телу (линейному, плоскому, пространственному) и что плот-
плотность равна единице.
1. Для плоской кривой L статические моменты Мх и My относительно
координатных осей Ох и Оу выражаются формулами
L L
Момент инерции относительно начала координат
При задании кривой L явным уравнением у = у(х) (а^х^Ь) в этих
формулах надо заменить dl на y\-\-yf2dx.
При задании кривой L параметрическими уравнениями х=*=х (/), у = у (t)
(ti^t^,t2) в этих формулах надо заменить dl на У xf2-\-y'2 dt.
2, Для плоской фигуры, ограниченной кривыми y = yi(x), У — Уъ(х)>
Уг(х)^у2(х) и прямыми х = а, x = b(a^x^b) статические моменты выра-
выражаются формулами
ь ь
3. Центр тяжести плоской кривой L имеет координаты xc — My/l, yc — Mx/lt
где /—длина кривой L. Центр тяжести плоской фигуры имеет координаты
xc = My/S, yc = Mx/S, где 5—площадь фигуры.
7.13.1. Найти статический момент верхней части эллипса
х2/а2
относительно оси Ох.
Решение. Для эллипса
у dl=y
330
так
^2 -х2 и у/ = гх, то
у dl = уЬг —^x2 + ^x2dx = ^ yV —е2х2 dx,
где е — эксцентриситет эллипса, е = }
Интегрируя от —а до а, находим
у а% — е2а2+— arcsinej =b
В случае окружности, т. е. при а — b, будем
иметь Мх = 2а2, так как при этом 8 = 0 и
е
7.13.2. Найти момент инерции прямоуголь-
прямоугольника с основанием Ь и высотой h относительно
его основания.
Решение. Выделим из прямоугольника эле-
элементарную полоску, параллельную основанию, от-
отстоящую от основания на расстоянии у и имею-
имеющую ширину dy. Масса полоски равна ее площа-
площади dS = bdy> а расстояния от всех ее точек до
основания равны у с точностью до dy. Поэтому
dlx = by*dy и
—arcsineY
8 I
7.13.3. Найти момент инерции дуги окружности х2 -j-j;2 = /?2,
лежащей в первом квадранте, относительно оси Оу.
7.13.4. Вычислить момент инерции относительно оси Оу фигуры,
ограниченной параболой у2 = Аах и прямой х = а.
Решение. Имеем dfx = x2 dS, где dS — площадь вертикальной
полоски на расстоянии х от оси Оу (рис. 110):
Отсюда
о
7.13.5. При расчете балочных деревянных мостов часто прихо-
приходится иметь дело с круглыми бревнами, отесанными на два канта
(рис. 111). Определить момент инерции подобного сечения относи-
относительно горизонтальной средней линии.
331
Решение. Расположим систему координат, как показано на ри-
рисунке. Тогда (обозначения см. на рис. Ill) dJx=y2dS, где dS =
= MNdy = 2xdy = 2 VR2—y2 dy.
Отсюда
h h
Ix=2 J y* I//?2 — y2 dy = 4 Jy2 VR2 —У2dy.
-h о
Произведя подстановку y = Rs\nt; dy =/? cos tdt; t1^=0; tf2 =
= arcsin(^/i?), получим
h arcsin (h/R)
Ix = 4 \y2VR2—-y2dy = 4 I R2 sin2/-/? cos tR cos tdt =
arcsin (h/R)
f
A—
= «-arcsin *.+ я.BА»-Я
В частности, при А = 7? получаем момент инерции круга относи-
относительно одного из диаметров: /Л. = п/?4/4.
j
T
Ml
1
Ъ -Л
I2
1
\
\
-<—
/
"/a
У
0
\
У
— I
4 dS
^\
I
У
a >
2
Рис. 111.
Рис. 112.
7.13.6. Определить момент инерции относительно оси Ох фигуры,
ограниченной двумя параболами (рис. 112) с указанными на рисунке
размерами (такую форму иногда придают сечению стержней в кон-
конструкциях блоков самолетов, чтобы они хорошо резали воздух).
Решение. Разместим систему координат так, как показано на
рис. 112, и составим уравнения парабол.
Уравнение левой параболы: У2 = тг (#+ -§¦) > уравнение правой
Ь2 ( а \
параболы: у2 = ^ f у— х) .
Для выделенной полоски момент инерции
dIx=y*dS=y*\MN\dy,
332
где
]MN\ — x —
Следовательно,
fc/2
-b/2
x\ — I 2 b2-* J b2
6/2
.
7.13.7. Найти статические моменты относительно осей Ох и Оу
дуги параболы у2 = 2л: от л; = 0 до х = 2(у>0).
7.13.8. Найти статические моменты относительно осей коорди-
координат отрезка прямой xja-\-yjb=\, заключенного между осями коор-
координат.
7.13.9. Найти статический момент дуги кривой у = cos x от точ-
точки х± = —я/2 до точки д:2 = я/2 относительно оси Ох.
7.13.10. Вычислить статический момент фигуры, ограниченной
линиями у = х2; y — Yx, относительно оси Ох.
7.13.11. Найти момент инерции относительно осей Ох и Оу тре-
треугольника, ограниченного линиями х — 0, у~0 и x/a-\-ylb=\
(а>0, &>0).
7.13.12. Найти момент инерции трапеции ABCD относительно ее
основания AD, если AD = a, BC = b, а высота трапеции равна h.
7.13.13. Найти центр тяжести полуокружности х2 -\-у2 = а2, рас-
расположенной над осью Ох.
Решение. Так как дуга полуокружности симметрична относи-
относительно оси Оу, то центр тяжести дуги лежит на оси Оу, т. е.
хс = 0.
Для нахождения ординаты ус воспользуемся результатом задачи
7.13.1: Мх = 2а2; поэтому ус = 2а2/(яа) = 2а/я. Таким образом, хс = 0,
ус = 2а/п.
7.13.14. Найти координаты центра тяжести дуги цепной линии
от точки Л@, 1) до точки В (a, ch а).
Решение. Имеем
Отсюда находим
Далее,
а
= ) х ch
sh2 л: ^л: = ch л:dx.
I = ^rf/ = ^ ch х dx = sh a.
L 0
х sh л:
а
— j sh jc fifx = a sh а — ch a -f 1.
333
oo
Следовательно,
a sha—(cha — 1) cha—1 ,« a
c ~~ sha sh a 2
Аналогично,
l о
a . sh2a
_a/2 + (sh2a)/4_ a cha
Ус~ sha ~2sha~* 2 *
7.13.15. Найти центр тяжести дуги первой арки циклоиды:
x = a{t—sint), y = a(\—cost) @</<2я).
Решение. Первая арка циклоиды расположена симметрично
относительно прямой х = тсау поэтому центр тяжести дуги циклоиды
лежит на этой прямой и хс = па. Так как длина первой арки цик-
циклоиды / = 8<2, то
7.13.16. Определить координаты центра тяжести той части дуги
астроиды x2/3+J>2/3 = a2/3, которая расположена в первом коорди-
координатном углу.
7.13.17. Найти декартовы координаты центра тяжести дуги кар-
кардиоиды p = a(l+cos9) от ф = 0 до ф —я.
Решение. Запишем уравнение кардиоиды в параметрической
форме:
х = р cos ф = а A + cos ф) cos ф;
у ==¦ р sin ф = а A + cos ф) sin ф.
При изменении параметра ф от 0 до я текущая точка (х, у) опишет
верхнюю часть кривой. Так как длина всей кардиоиды равна 8а, а
то
xc — -r \ у dl ~ -г- \ a sin ф A + cos ф) 2a cos ~ dq> =
/ J 4aJ 2
Л
гл Г ^ф.ф» 4 кФя4
= 2а \ cos4 ¦— s\n~ dtp — =- a cos6 — =-р-а.
J 22^ 5 2оо
о
334
Аналогично,
я я
* = 4аг ^'=4а )acoS(P0 + c°s ф) 2а cos -2- rfcp = a \ cos ф cos3 2
l о о
я
= a J Ы cos6|—cos3 -J) Лр.
Положив ф/2 = ^, получим (см. 6.6.9)
Л/2
/
/, = 2а С B cos6 t — cos31) dt -= 4a ^| — 2а ~ = -i ^
о
Итак, хс=ус = '
Интересно отметить, что центр тяжести рассмотренной половины
дуги кардиоиды лежит на биссектрисе первого координатного угла,
хотя сама дуга и не симметрична отно-
относительно этой биссектрисы.
7.13.18. Найти центр тяжести фигу-
фигуры, ограниченной эллипсом 4л:2 + 9.у2 = 36
и окружностью х2 -\-у2 = 9 и расположен-
расположенной в первом квадранте (рис. ИЗ).
Решение. Вычислим сначала ста-
статические моменты:
з з
х'+у'-Я
Рис. 113.
Площадь четверти круга радиуса 3 равна 9я/4, а площадь чет-
четверти эллипса с полуосями а = 3 и Ь = 2 равна Зя/2, поэтому пло-
площадь рассматриваемой фигуры ? = 9я/4— Зя/2==Зя/4.
Таким образом,
хс = My/S - 4/я; ус = MJS = 20/(Зя).
7.13.19. Найти центр тяжести фигуры, ограниченной параболой
! = #Ч2 и осями координат.
333
7.13.20. Найти декартовы координаты центра тяжести фигуры,
ограниченной кривой
р = a cos3 ф (а > 0).
Решение. Так как всегда р^О, то данная кривая описыва-
описывается при изменении ф от —я/2 до я/2. При этом она симметрична
относительно полярной оси в силу четности функции сояф и про-
проходит через начало координат при ф — ± л/2.
Вычислим площадь $ полученной фигуры:
Я/2 Я/2
\ (* С 1 • 3 • 5 л 5
о о
Выберем теперь оси координат так, как показано на рис. 114.
Тогда параметрическими уравнениями кривой будут
х = р cos ф = a cos4 ф;
у = р sin ф = a sin ф cos3 ф.
Центр тяжести фигуры лежит на оси Ох, т. е. ус = 0, в силу
Рис. 114.
Рис. 115.
отмеченной выше симметрии относительно оси Ох. Остается опре-
определить хс:
а
xydx я/2 я/2
-я = -4-1 cos10 ф sin2 ф ^ф = -|- \ (соз10ф — cos
1-3-5-7-9 ЬЗ.5-7-9-11
21
~"(о/32)ла2 V2-4.6-8.10 2-4-6-8-10-12у 2 ~~ 40 а#
7.13.21. Найти координаты центра тяжести фигуры, ограничен-
ограниченной прямой у = B/я) х и синусоидой j> = sin.x; при xt^Q (рис. 115),
Решение. Прямая у = B/я) л: и синусоида j/ = sin.x: пересека-
пересекаются в точках @, 0) и (я/2, 1). Площадь S фигуры, ограниченной
этими линиями, равна
Я/2
336
Отсюда
D-я)/4
и
_ 2 Г1 sin 2л: 4_ 311Л/2__ л
— п[2Х 4 Зя2*Ло ~~6D—л)'
Я/2
С ( 2 \
\ jf sin х х ) dx я/2 я/2
J V я
..•=- \ xsinxdx т-j г \ x2dx-
4 — я J я D—л) J
D-л)/4
о б
4 л2 12—л2
4 — я 3D —л) 12 — Зл; '
7.13.22. Доказать следующие теоремы (Гульдена):
1) Площадь поверхности, полученной при вращении дуги плоской
кривой вокруг некоторой оси, лежащей в плоскости дуги по одну
сторону от нее, равняется произведению длины вращающейся дуга
на длину пути, описанного ее центром тяжести.
2) Объем тела, полученного при вращении плоской фигуры вокруг
некоторой оси, лежащей в плоскости фигуры и не пересекающей еег
равен произведению площади вращающейся фигуры на длину пути,
описанного ее центром тяжести.
Решение. 1) Сравним формулы для площади поверхности вра-
вращения кривой L вокруг оси Ох (см. § 7.10)
и для ординаты центра тяжести этой кривой
Мх
y f
Отсюда заключаем, что
где / — длина вращающейся дуги, а 2пус — длина окружности ради-
радиуса ус, т. е. длина окружности, описанной центром тяжести при
вращении вокруг оси Ох.
2) Сравним формулы для объема тела вращения плоской фигуры
вокруг оси Ох (см. § 7.6)
337
и для ординаты центра тяжести этой фигуры
ь
У<—Т
м
Отсюда заключаем, что
где 5 — площадь вращающейся фигуры, а 2пус — длина окружности,
описанной центром тяжести при вращении вокруг оси Ох.
7.13.23. Пользуясь первой теоремой Гульдена, найти центр тя-
тяжести полуокружности радиуса а.
Решение. Выберем координатные оси так, как показано на
рис. 116. В силу симметрии хс = 0. Остается найти ус. Если полу-
полуокружность вращать вокруг оси Ох,
то поверхность Р тела вращения равна
4яа2, длина дуги 1 — па. Поэтому по
первой теореме Гульдена
4яа2 = па • 2пус; ус- rt a
.
7.13.24. Пользуясь второй теоре-
теоремой Гульдена, найти координаты цент-
центра тяжести фигуры, ограниченной
осью Ох и одной аркой циклоиды:
x = a(t—sin /); у = а(\ —cos t).
Решение. В силу симметрии фигуры относительно прямой
х = па ее центр тяжести лежит на этой прямой; значит, хс = па.
Объем V, полученный вращением этой фигуры вокруг оси Ох,
равен 5я2а3 (см. задачу 7.6.14), а площадь S фигуры равна Зяа2
(см. задачу 7.4.3). Применяя вторую теорему Гульдена, получим
V 5л2а3 5а
2л-Зла2 6 '
7.13.25. Равносторонний треугольник со стороной а вращается
вокруг оси, параллельной основанию и отстоящей от основания на
расстояние Ь > а.
Найти объем тела вращения.
Решение. Имеются две возможности расположения треугольника
относительно оси вращения, которые показаны на рис. 117, а) и б).
Высота равностороннего треугольника равна h = ay 3/2, пло-
площадь 5 равна S = cfiY 3/4. Центр тяжести О' расположен в точке
пересечения медиан и удален от оси вращения в первом случае на
расстояние Ь — а^З/6, а во втором—на расстояние У
338
По второй теореме Гульдена
т/ _ 2яа2/з (и aVJ\__ (аЧУъ аЛ
vi- 4 V 6~/ П\~2 Г/'
v,=
4
2яа2
7.13.26. Найти центр тяжести дуги окружности радиуса R, стя-
стягивающей центральный угол 2а.
7.13.27. Найти центр тяжести фигуры, ограниченной косинусои*
дой y = cosx от точки х = —я/3 до точки х — п/3 и прямой у = 1/2.
Рис. 117.
7.13.28. Найти координаты центра тяжести фигуры, ограниченной
замкнутой кривой у2 = ахъ — л:4.
7.13.29. Найти декартовы координаты центра тяжести дуги ло-
логарифмической спирали р = aev от ф1 = зх/2 до ф2 = я.
7.13.30. Правильный шестиугольник со стороной а вращается
вокруг одной из сторон. Найти объем полученного тела вращения.
7.13.31. Пользуясь теоремой Гульдена, найти центр тяжести по-
полукруга радиуса R.
§ 7.14. Дополнительные задачи
7.14.1. Найти площадь части фигуры, ограниченной кривыми ут — хп и
уп^.хт (т и я—целые положительные числа), расположенной в первом квад-
квадранте. Рассмотреть вопрос о площади всей фигуры в зависимости от характера
четности чисел тип.
7.14.2. а) Доказать, что площадь криволинейной трапеции, ограниченной
осью Ох, прямыми х — а, х = Ь и параболой у = Ахъ + Вх% + С* + А можно
вычислить по формуле Чебышева
b — a
J a + b 1
У \ о , г
b—a
У 2
+ У
339
б) Доказать, что аналогичную площадь для параболы
y=Axb + Bx*+
можно вычислить по формуле Гаусса
7.14.3. Показать, что площадь фигуры, ограниченной любыми двумя радиус-
векторами логарифмической спирали р — ает'? и ее дугой, пропорциональна
разности квадратов этих радиусов.
7.14.4. Доказать, что если два тела, содержащиеся между параллельными
плоскостями Р и Q, обладают тем свойством, что в сечении их любой пло-
плоскостью R, параллельной этим плоскостям, получаются равновеликие фигуры,
то объемы этих тел равны (принцип Кавальери).
7.14.5. Доказать, что если функция 5 (х) @ s^x^h), выражающая пло-
площадь сечения тела плоскостью, перпендикулярной к оси Ох, есть многочлен
не выше третьей степени, то объем этого тела равен V — (h/6) [S @) + 45 (h/2) +
+ S(/i)]. Пользуясь этой формулой, вывести формулы для объема шара, ша-
шарового слоя, шарового сегмента, конуса, усеченного конуса, эллипсоида, па-
параболоида вращения.
7.14.6. Доказать, что объем тела, образованного вращением вокруг оси Оу
фигуры а<,х^Ь, Ъ<*у <*у (х), где у (х) — однозначная непрерывная функция,
равен
Ь
У = 2л ^ ху (х) dx.
7.14.7. Доказать, что объем тела, образованного вращением вокруг поляр-
полярной оси фигуры
равен
2я Г*
7.14.8. Доказать, что длина дуги кривой, заданной параметрическими урав-
уравнениями
* = П0 cos t + f'(t) sin/,
равна ft
7.14.9. Вычислить длину дуги кривой, заданной в параметрической форме
t t
С cos г , С sin г .
x=\j—r-dz, V = )—<b.
1 1
от начала координат до ближайшей точки с вертикальной касательной.
7.14.10. Вывести формулу для длины дуги в полярных координатах, исхо-
исходя из определения, не прибегая к преобразованию декартовых координат в
полярные.
340
^ 7.14.11. Доказать, что длина дуги 1{х) цепной линии t/ = ch#, отсчитывае-
отсчитываемой от точки @, 1), выражается формулой l(x) — shx, и найти параметрические
уравнения этой линии, приняв за параметр длину дуги.
7.14.12. Гибкая нить подвешена в точках А и В, находящихся на одной
высоте на расстоянии AB — 2bt и имеет стрелу прогиба /. Считая форму нити
параболой, показать, что длина нити
2 j
при достаточно малом f/b.
7.14.13. Найти отношение площади, ограниченной петлей кривой
У=± A/3-х) Vx,
к площади круга, длина окружности которого равна длине контура этой
кривой.
7.14.14. Вычислить длину дуги, образованной пересечением параболиче-
параболического цилиндра
с эллиптическим конусом
от начала координат до точки М (я, у, г).
7.14.15. Доказать, что площадь «S эллипса
Ах2+2Вху+Су*
(AC —
0)
равна
где А =
А
В
D
В
С
Е
D
Е
F
7.14.16. Найти: а) площадь S фигуры, ограниченной гиперболой х2—«/2=1,
положительной частью оси Ох и радиус-вектором, соединяющим начало коор-
координат с точкой М (х, (/), лежащей на этой гиперболе.
б) Площадь кругового сектора Q, ограниченного осью Ох и радиусом, про-
проведенным в точку N (х, у), лежащую на окружности *2-j-r/2=l. Доказать,
что координаты точек М и N выражаются соответственно через площади S и Q
по формулам
7.14.17. Доказать, пользуясь теоремой Гульдена, что центр тяжести тре-
треугольника отстоит от его основания на одну треть высоты.
7.14.18. Пусть ^—абсцисса центра тяжести криволинейной трапеции,
ограниченной непрерывной кривой y = f(x), осью Ох и прямыми х—а и х = Ь.
Доказать справедливость следующего равенства:
(правило Верещагина).
7.14.19. Пусть криволинейный сектор ограничен двумя радиус-векторами
и непрерывной кривой р = /(<р). Доказать, что координаты центра тяжести
311
Гакоге сектора выражаются следующими формулами:
Фг Фг
\ р3 cos ф d<$> \ р3 sin ф б/ф
2
9
Ф1
Ф1
7Л4.20. Доказать, что декартовы координаты центра тяжести дуги кривой
р=а/(ф) выражаются следующими формулами:
Глава VHI
Несобственные интегралы
§ 8Л. Несобственные интегралы
с бесконечными пределами
Пусть функция f (х) определена для всех х^а и интегрируема на любом
А
отрезке [а, Л]. Тогда lim \ / (х) dx называется несобственным интегралом
а
-foo
от / (х) в пределах от а до + оо и обозначается \ / (х) dx» Аналогично
В
определяются интегралы \ / (x)dx и V / (х) dx>
— оо — со
Таким образом,
-foo A
f(x)dx= lim \f(x)dxi
а а
В В
f(x)dx= lim \f(x)dxi
[ f (x) dx= lim [ f (x) dx+ lim [ f (x) dx.
Если приведенные пределы существуют и конечны, то соответствующие
интегралы называются сходящимися. В противном случае интегралы называ*
ются расходящимися.
Признак сравнения. Пусть функции / (х) и g (x) определены для всех
и интегрируемы на каждом отрезке [а, А], А^а. Если 0^/(х)(<;g(x)
для всех х^а, то из сходимости интеграла \g(x)dx вытекает сходимость
а
со со со
интеграла \f(x)dx, причем \ / (х) dx ^ \ g (x) dx\ из расходимости интеграла
а а а
со оо
\ / (х) dx вытекает расходимость интеграла \ g (x) dx.
а
613
Частный признак сравнения. Если при х—> оо функция f(x)^O являет-
является бесконечно малой порядка X, > 0 по сравнению с 1/х, то интеграл
\ f(x)dx сходится при л. > 1 и расходится при А.^1.
а
Признак абсолютной сходимости. Пусть функция f \x) определена для
всех х^а. Если интеграл \|/(х)|4х сходится, то сходится и интеграл
«о
\ / (х) dx,
причем
Если интеграл \ f (x) dx сходится, а \ | f {x) \dx расходится, то интеграл
а а
оо
1 / (х) dx называется условно сходящимся.
а
Замена переменной в несобственном интеграле основывается на следую-
следующей теореме
Теорема. Пусть функция f (x) определена и непрерывна при х^а.
Если функция x~y(t), определенная на промежутке а < / < р (а м р могут
быть и несобственными числами —оо и оо), имеет непрерывную производную
q/ U) ф 0 и lim ф (t) = а, lim
а а
Интегрирование по частям не вызывает затруднений.
8.1.1. Вычислить следующие несобственные интегралы с беско-
бесконечными пределами или установить их расходимость, основываясь
на определении этих интегралов:
со
а) Г-^-.; б) С 2 , 1* . .; в) {xsinxdx.
7 J jc In3 x• ' J x2-\-2x +5 ' J
в8 -» О
Решение, а) По определению,
«> а
С dx С dx ( \ И\
i 1
U~2Tn
б) По определению,
О А
dx J; С dx . v С dx
344
(вместо точки х — 0 в качестве промежуточного предела интегриро-
интегрирования можно взять любую другую конечную точку оси Ох).
Вычислим каждый из пределов, стоящих в правой части напи-
написанного выше равенства:
1
1 А 1 . п.
^ +
A
dx
J
0
Следовательно,
Г dx —я
J jc2+2jc+5~ 2 *
в) По определению,
« л
\ х sin л: ^а: = lim \ х sin д: Jx.
О Л-* + оо 0
Полагая а = лг, rfv = sinA;rfjc и интегрируя по частям под знаком
предела, получим
\
А / А А
\xsinxdx= lim ( —jccosjc -J-\
J A-*** \ ° о
J =
= lim (—A cos A -f- sin A).
Однако последний предел не существует. Следовательно, интеграл
00
\xsinxdx расходится,
о
8.1.2. Вычислить следующие несобственные интегралы с бес-
бесконечными пределами, основываясь на определении этих инте-
интегралов:
Г xdx . }_J±_. п\ Г xdx
2 i 0
к2—6*+ 10*
— 00
;; д) о ^
345
Решение, а) По определению,
во А
Г xdx ^ Ит Г xdx ^ Иш Г 1 (х2—ЗГ1/2
2 2
«— lim Г \ —1 [ = 1,
8.1.3. Доказать, что интегралы вида
+ 00 Ь
f e~P* dx и f e?x dx
п — 00
сходятся при любом постоянном /? > 0 и расходятся при р < 0.
8.1.4. Исследовать сходимость интеграла
!
О
Решение. Подынтегральная функция
положительна и является бесконечно малой порядка ^ = 4 по срав-
сравнению с \/х при х—)>оо, Так как 4> 1, то по частному признаку
сравнения интеграл сходится.
8.1,5. Исследовать сходимость интеграла
I:
dx
Решение. Подынтегральная функция f(x) =e 1 /(# -f- sin2 л:) не-
непрерывна и положительна при #^1.
При х—> со функция f(x) является бесконечно малой порядка
К = \ по сравнению с \/х; по частному признаку сравнения интег-
интеграл расходится.
8.1.6. Исследовать сходимость интегралов;
г)
\-\-xYx
8.1.7. Исследовать сходимость интеграла
~ (x+VT+l)dx
I-
Решение. Подынтегральная функция непрерывна и положи-
положительна при х^\. Определим порядок ее малости X относительно \/х
при х-—> оо; так как
то порядок Я = 1. По частному признаку сравнения интеграл
расходится.
8.1.8. Исследовать сходимость интеграла
. Vx(x—\)(x-2)
Решение. Так как функция
1
" Ух* A — 1/х) A — 2/х) *3/2 У(\ — 1/х) A — 2/х)
является бесконечно малой порядка X==S/2 по сравнению с 1/л;
при х—^ + °°» т0 по частному признаку сравнения интеграл схо-
сходится.
8.1.9. Исследовать сходимость интеграла
Решение. Подынтегральная функция непрерывна и положи-
положительна при х^2. Определим порядок ее малости к относительно
1/х при х—>+ оо:
Так как второй множитель имеет предел \/2 при х—>-\~ооу то
%= 11/35 <1. Следовательно, данный интеграл расходится.
8.1.10. Исследовать сходимость интеграла
2 \
— cos— йГл;.
347
Решение. Подынтегральная функция
f(x) = 1 —cos B/x) = 2 sin2 (\/x)
положительна и непрерывна при х^\. Так как 2 sin2 A /х) ~ 2 A /л:J =
= 2/д:2, то по частному признаку сравнения данный интеграл схо-
сходится.
8.1.11. Исследовать сходимость интеграла
00
\ In -Li L dXy П > 0.
J п
Решение. Преобразуем подынтегральную функцию/(jc):
gi/*+(/i— i) Г в1/л:—1
п In]'
Так как функция (е1^—\)jn является бесконечно малой при х—юо,
то f(x) ~ (ех1х—Т)/л ~ \1(пх). Другими словами, lim -jp-= l/n* По
частному признаку сравнения данный интеграл расходится.
8.1.12. Исследовать сходимость интеграла
С 1—4 sin 2x ,
\ ^у=гйх.
Решение. Функция /(д;) = A —4 sin 2x)/(xz + \/x) меняет знак
вместе с изменением знака числителя. Исследуем сходимость инте-
интеграла
| 1 —4 sin 2л: |
J
о .— п 5 dx
Так как |1—4 sin 2л: |/(д:3 + ух) < 5/д:3, а интеграл \—д~ сходится,
то по
Р 11—4sin2jc| ,
первому признаку сравнения сходится интеграл \ J ^ ^ ад:.
1 ^3+ к *
Таким образом, данный интеграл сходится, и притом абсолютно.
8.1.13. Доказать, что интеграл Дирихле
-dx
О
сходится условно.
348
Решение. Представим интеграл в виде суммы дзух интег-
интегралов:
оо Я/2 »
т Г sin х , f sin дс, . Psin* ,
1= \ dx = \ dx + \ dx.
J * J X * J X
Я/2
Первый интеграл собственный (так как lim ---^=-1 Л Приме-
\ х-*о х )
няя ко второму интегралу метод интегрирования по частям, будем
иметь
x
А
m \
С smx , ,. С slnx ,
\ dx= lim \ dx =
dx~ hm \ dx= lim
ix
cos*
cosxdx
—9—
J
J
Я/2
CO
Но несобственный интеграл ^ —2~ й?л: сходится, и притом абсо-
Я/2
GO
лютно, так как | cosa;|/a;2 <I l/x2, а интеграл \ -^ сходится.
GO
Таким образом, интеграл I —- dx сходится.
J %
о
Аналогичным рассуждением легко доказать, что и интеграл
О» 00
\ dx также сходится. Теперь докажем, что интеграл \ -dx
я/2 Я/2
расходится. Действительно,
I sin х I ^_ sin2 х 1 — cos 2л:
х ^ х ~~ 2х
но интеграл
Г 1 — cos 2л: , _ у J_ Г d? 1 Г cos 2л: . __
я/2 Л~*с° я/2 я/2
1 ,. , - 1 , я 1 С cos2л: ,
. lim In Л In i 1 п?
— "о" in «л — tj-ih-tt ~2 \ х
я/2
со
1. 1 л Г COS 2л:
расходится, так как ltm 1пЛ = оо, а интеграл \ ад; сходится.
Я/2
349
8.1.14. Доказать, что интегралы
00 00 СО
а) С sin (л-2) dx; С cos (х2) dx; б) Г 2х cos (x4) dx
0 0 О
сходятся.
Решение, а) Полагая x = V7, найдем
Как и в предыдущем примере, интеграл, стоящий справа, пред-
представим в виде суммы двух интегралов:
Я/2 со
Первое слагаемое есть собственный интеграл, так как lim —= = 0.
t-*+o У t
Ко второму слагаемому применим интегрирование по частям, полагая
00
s*n t л/ cos
1 С cos t dt 1 Р cos^
f2 i
,.
Последний интеграл сходится абсолютно, так как
00
а интеграл ^ з. сходится. Аналогично доказывается сходимость ин-
я/2 '
00
теграла j cos (д:2) ^д:. Рассмотренные интегралы называются интегра-
о
лами Френеля. Они встречаются в теории дифракции света.
б) Подстановкой x2 = t этот интеграл приводится к интегралу
от
\ cos (t2)dt. Последний интеграл, по доказанному, сходится.
о
Замечание. Интегралы Френеля показывают, что несобственный интег-
интеграл может сходиться и в том случае, когда подынтегральная функция не стре-
стремится к нулю при х—> оо. Последний же сходящийся интеграл, рассмотренный
в пункте б), показывает, что несобственный интеграл может сходиться даже
и тогда, когда подынтегральная функция не ограничена. Действительно, при
х = р/пя (п = 0, 1, 2, ...) подынтегральная функция принимает значения
± ^/пзх, т. е. она неограничена.
350
8.1.15. Вычислить несобственный интеграл
со
С dx
J A + *Т ' я —натуральное число.
о
Решение. Сделаем подстановку A:==tg/, где 0
Тогда х = 0 при ^ = 0, х—> + оо при t-+n/2—0 и x't=
Следовательно, в силу теоремы о замене переменной в несобствен-
несобственном интеграле
<ю я/2 Я/2
J 8ес''Л
После замены переменной получился известный собственный интег-
интеграл, который вычислен в задаче 6.6.9.
Поэтому
*х И2- я=1'
TUY^I 1-3-5--Bп-Э) п
T*' ^ 2-4.6...Bп-2) 2' й>1-
00
8.1.16. Вычислить интеграл /= \ ^ 4 t/x.
о
Решение. Применим подстановку
x=\jt\ dx =— (\jt2)dt; tl=ooi /2 = 0;
/«) dt _ г»
0© 00 00
Если прибавить к правой и левой частям по интегралу /, то
получим
l//2+1 А1
Зггр17ггЛ-
о
Применим подстановку ^ = / — 1//, A + 1 //¦) rf^ = rf^r. Тогда при
2__^-]_0 будет z—>¦ — оо, при t—> + oo будет z—^ + cxd. Следова-
Следовательно,
« ГО Л 1
— оо *- S 0 -*
¦1 .. . В
= 7=r Iim arctg-т^
B51
8Л.17. Вычислить несобственные интегралы:
а)
о о
8.1.18. Вычислить с точностью до 0,01 интеграл
аи
ч-
Решение. Представим данный интеграл в виде суммы двух
интегралов
первый из которых вычислим по формуле Симпсона с нужной точ-
точностью, а второй оценим. Так как при дг^1 имеем
\ГуЗ v2 I 1 ^3/2
У X -Г-1 . JC _ v-7/2
1 <^ Ь -Х
ТО
2 1
При N—7 получаем оценку /2 < -=- • ^г=< 0,0031.
Вычисление интеграла
J
1
по формуле Симпсона с шагом h = 1 дает
^ = 0,2165,
а с шагом /г/2 = 0,5 дает
S0j5 = 0,2079.
Так как разность между этими значениями составляет 0,0076, то
более точное значение So 3 = 0,2079 дает интеграл IL с ошибкой по-
порядка 0,0076/15^0,0005.'
Следовательно, искомый интеграл равен приближенно
/«0,208
с ошибкой не более 0,004, или /==0,21 со всеми верными знаками.
352
§ 8.2. Несобственные интегралы
от неограниченных функций
Если функция /(л:) определена при а<х <Ь, интегрируема на любом от-
отрезке [а, Ь—е], 0 < е < &—а и неограничена слева от точки Ь, то по опреде-
определению полагают
ь 6-е
\f(x)dx= lim С f(x)dx.
Если этот предел существует и конечен, то несобственный интеграл назы-
называется сходящимся. В противном случае интеграл называется расходящимся.
Аналогично, если функция / (х) неограничена справа от точки а, то
б ь
;= lim \ f(x)dx.
а а+8
Наконец, если функция в окрестности внутренней точки с отрезка [а, Ь] неогра-
неограничена, то по определению
Пусть функция f{x) непрерывна на отрезке [а, Ь], за исключением конеч-
конечного числа точек. Если существует функция F (х), непрерывная на [a, b], для
которой F' (х) = / (х), кроме конечного числа точек, то имеет место формула
Ньютона—Лейбница
ь
Функция F (х) иногда называется обобщенной первообразной для функции
f (х) иа отрезке [а, 6].
Для функций, определенных и положительных на промежутке а^х<Ь,
справедливы признаки сходимости (признаки сравнения), аналогичные признакам
сравнения для несобственных интегралов с бесконечными пределами.
Признак сравнения. Пусть функции /(х) и g(x) определены на промежутке
IX < Ь и интегрируемы на каждом отрезке [а, Ь—е], 0 < е < Ь—а. Если
а^х
[
ь
О ^ / (х) <; g (x), то из сходимости интеграла \g(x)d* вытекает сходимость
а
b b b
интеграла \f(x)dx, причем \ f (x) dx^\ g(x)dx; из расходимости интеграла
а а а
b Ь
\ / (х) dx вытекает расходимость интеграла \ g {x) dx.
о
Частный признак сравнения. Если функция f (х)^0 определена и не-
непрерывна на промежутке а^х < Ь и является бесконечно большой порядка X
ь
по сравнению с \ЦЬ—х) при х—*-Ь—0, то интеграл \f(x)dx сходится при
а
X < 1 и расходится при А^г I.
353
В частности, интеграл
ь
dx
P dx
J (b—л
сходится при Я < 1 и расходится при X^s 1.
Признак абсолютной сходимости. Пусть функция f (х) определена на про-
промежутке а<;#<6 и интегрируема на каждом отрезке [a, b—е]; тогда из
Ь ь
сходимости интеграла V \f(x)\dx следует сходимость интеграла \ / (х) dx.
а а
Ь
В этом случае интеграл \ / (х) dx называется абсолютно сходящимся. Если же
а
Ь Ь
интеграл \ / (х) dx сходится, а интеграл \ \f(x)\dx расходится, то интеграл
а а
\ / (jc) dx называется условно сходящимся.
а
Аналогичные признаки справедливы и для несобственных интегралов
V / (х) dxt где / (л:) неограничена справа от точки а.
а
8.2.1. Исходя из определения, вычислить следующие несобствен-
несобственные интегралы (или доказать их расходимость);
l
з
6)
г)
I
0
2
Г
0
1
dx
COS X *
dx
Решение, а) Подынтегральная функция /(#) — ^/y
неограничена в окрестности точки х=\. На любом же отрезке
[1+е, е] она интегрируема, так как является непрерывной функцией.
Поэтому
V ^l У1 v |l+e
= lim Г-|~4
б) Подынтегральная функция f(x) = 1/cos x неограничена в окрест-
окрестности точки х = п12 и интегрируема на любом отрезке [0, я/2—е]
354
как непрерывная функция. Поэтому
Я/2 Я/2-8
J cos л: ?_^ + 0 J cos* 8
1Я/2-8
4; о :
= lim In tg (я/2—8/2) = 00.
0
Следовательно, данный интеграл расходится.
в) Подынтегральная функция неограничена в окрестности точек
х=1 и л: = 3. Поэтому, по определению,
3 2 3
С dx _ С dx , С dx
J }Гах—х1—3 ~~ J V~4x—x2—3 J ]/~4jc—jc2—3
(вместо точки л: = 2 можно взять любую другую внутреннюю точку
отрезка [1, 3]). Вычислим теперь каждое слагаемое в отдельности:
\ ^ , ,* ;=•=; lim
Jt/4*_*2_3 8-. + 0
х
= lim
= lim [0—arcsin(e —1)] =
+ o
—2)
1+8
dX
=
—jc3—3
= Ига
3-е
С A dx ¦= lim
J /4-(*-2J e- +
= lim [arcsin(l—e)—0] = я/2.
8-»- + 0
Следовательно,
3
Г rfx я , я
2)
3-е
2
г) Подынтегральная функция f(x) = 1 /Vх" 11—х21 неограничена
в окрестности точки х=1, являющейся внутренней точкой промежут-
промежутка интегрирования. Поэтому, по определению,
2 1 2
О 0 1
Вычислим каждое слагаемое в отдельности. Если 0^л;<1, то
1 1 1-8
dx = Г. dx = lim Г ¦ ¦ dx l=a
^|1—л;2| J ]Al — х2 8-»+о J |/^1—jc2
= lim arcsinx
1-8
= lim [arcsin(l — 8)-^0]=^
355
Если 1 <л:<2, то
2 2
) y 11— *а1 )
«V Г I * Л I %}
dx
2
I-
1+8
lim In (x + J/V — 1 )
dx
8 -> +0
1+e
- lim
8 -* +0
Следовательно,
д) Представим данный интеграл в виде суммы трех слагаемых,
разделив каждый член числителя на у^х3,
У х — 2 *
Г
J
7=—^dX^\
О
-
J
dx
„3/5 *
О 0 0
Первое слагаемое есть собственный интеграл, вычисляемый по фор-
формуле Ньютона—Лейбница:
1
17
0 17
Второе и третье слагаемые неограничены справа от точки х = 0.
Поэтому
1 1
1 1
0
dx
15
аналогично,
dx
= lim
dx
J
0
Следовательно,
1
f. 5 9/R|l 5
= lim тгх*/*! =it*
8-++02 |e 2
15 2 5- 625
11 2 "" 187*
e) Представим подынтегральную функцию f{x) = 1/A -—л;3) в виде
суммы простых дробей:
„ 1 Г 1
J *
356
8-+0
1-8
In A-
8->+0
1-8
О
oo,
to данный интеграл расходится. Второе слагаемое, представляющее
собой собственный интеграл, вычислять не нужно.
Замечание. Вычисление несобственных интегралов в предыдущих при-
примерах можно значительно упростить, используя обобщенную первообразную
и применяя формулу Ньютона—Лейбница. Например, в задаче 8.2.1 а) функция
^ ———
F(x)=-^- jj/ln2 x непрерывна на отрезке [1, ё] и дифференцируема в каждой
точке промежутка 1 < х<е, причем F' (x) = f (х) на этом промежутке. Поэтому
2 "
J xi/ \пх *
8.2.2. Исходя из определения, вычислить следующие несобствен-
несобственные интегралы (или доказать их расходимость):
За
С 2xdx
2/л
1 dx
в)
-1
dx
Х\Ь?Х *
1
8.2.3. Вычислить несобственные интегралы:
1
1И 1
-3 0
Решение, а) Найдем неопределенный интеграл
Функция Z7^) = y f 9 arcsin ^— а; у 9—х2) является обобщенной
первообразной для f(x) = x2l]/r9—х2 на отрезке [—3, 3], так как
непрерывна на этом отрезке и F' (х)=^/{х) в каждой точке проме-
промежутка (—3, 3). Поэтому, применяя формулу Ньютона—Лейбница,
357
получим
3
x*dx
з
-3
б) Преобразуем подынтегральное выражение
24-* = 2 + х -== 2 _^
2 —л: j/" 4—д;2 ]/" 4—л:2
Неопределенный интеграл равен
= 2 arcsin ~
Функция Т7 (л:) = 2 arcsin (x/2)—|/Ч—лг2 является обобщенной перво-
первообразной для f(x) на отрезке [0, 2], так как она непрерывна на
этом отрезке и F' (x)=f(x) в промежутке [0, 2).
Поэтому, применяя формулу Ньютона — Лейбница, получим
8.2.4. Исследовать сходимость интеграла
Решение. В точке х = 0 подынтегральная функция обращается
о 1
в бесконечность. Оба интеграла I —^-г=г и I —^-— расходятся,
J х у х .) xf/x
-1 У О У
так как Я = 4/3 > 1. Следовательно, данный интеграл расходится.
Если бы, не обратив на это внимания, мы формально применили
формулу Ньютона—Лейбница к этому интегралу, то получили бы
неверный результат:
1 х 3/7 ~"
д/х
==—6.
-1
8.2.5. Исследовать сходимость следующих несобственных ин-
интегралов:
а)
Г е* * е>\ Г sin *+cos я
\ ~ dx; б) \ , , -
J Y\ — cosjc ; J l/l — x*
dx.
358
Решение, а) Подынтегральная функция является бесконечно
большой при х—>-)- 0. Так как при х-
1Л — cos* - V~2 sin ~ ~ i^- я,
то подынтегральная функция имеет порядок А, =* 1 по сравнению
с \jx. По частному признаку сравнения данный интеграл расходится,
б) Запишем подынтегральную функцию следующим образом:
s*n •*+ cos x *
Эта функция является бесконечно большой при х-—*1, причем
ее порядок по сравнению с 1/A—х) равен А, = 1/5, так как первый
множитель стремится к 1 при х —+ 0. Поэтому по частному приз-
признаку сравнения данный интеграл сходится.
8.2,6. Исследовать сходимость следующих несобственных инте-
интегралов:
2 2
Г lnl
-l
cos xdx
Решение, а) Подынтегральная функция f(x)-
положительна в интервале @, 2) и не определена при х = 0. Пока-
Покажем, что lim f(x) — oo. Действительно, поскольку
0
)~У!? при jc-
то
lim ,„ / ~= lim — = lim ¦ й ._ =оо.
*шх1 х у
Одновременно мы показали, что f{x)~ \\У х2 при х—»-0, т. е. что
f(x) является бесконечно большой порядка ^ = 2/5 < 1 по сравне-
сравнению с 1/jc. Следовательно, по частному признаку сравнения задан-
заданный интеграл сходится.
б) Определим порядок бесконечно большой функции f(x) =
= ]/л;2+ l/j!/l6—х4 в окрестности точки х = 2 относительно
1/B—л:). Для этого преобразуем выражение для f(x):
359
Отсюда видно, что функция f(x) при х—*2 является бесконечно
большой порядка Л, == 1 /3 < 1. По частному признаку сравнения
данный интеграл сходится.
в) Подынтегральная функция f(x) = (cosx)/(y/rx—sin*) неогра-
ничена в окрестности точки х = 0. Так как
cos л: cos х 1 .
T— = —— -^~
у X—sin* у x\\—(sinx)/y x) ух
то при х—>+0 функция f(x) является бесконечно большой порядка
Х=1/4<1 по сравнению с \/х и по частному признаку сравнения
интеграл сходится.
8.2.7. Исследовать сходимость следующих несобственных инте-
интегралов:
1
ех dx
j
в)
о
о
1
р dx
8.2.8. Доказать, что интеграл
1
сходится.
Решение. Для 0
V".
sin
1
С dx
Но интеграл I -7= сходится, поэтому по признаку сравнения схо-
J V х
о
дится и интеграл
V
X
dx, а следовательно, сходится, и притом
абсолютно, заданный интеграл.
8.2.9. Установить сходимость интеграла
Я/2
= \
О
и вычислить его.
360
Решение, Интегрируем по частям, полагая и = In (sin x), dx = dv;
получим
я/2 Я/2 Я/2
, COS X . С X .
In sin x dx = л; In sin jc
-1
Так как lim т—= 1, lim -— = 0, то последний интеграл яв-
Х-+ + 0 * х-*¦ п/2 — 0 »
ляется собственным. Следовательно, исходный интеграл сводится.
Сделаем теперь в интеграле / подстановку x = 2t. Тогда dx = 2dt;
x~Q при *г = 0; л: = я/2 при *2=ji/4. После подстановки получим:
я/2 я/4 Я/4
j In sin л; d.fc = 2 ^ Insin2*^==2 ^ (In 2 + In sin * + ln cos*) </* =
ooo
Я/4 Я/4
= 2* In 2 +2 ^ lnsin*d* + 2 jlncos*^* =
0 о о
я/4 я/4
п С С
= -тг-1п2 + 2 \ In sin* dt +2 \lncos*rf*.
о о
В последнем интеграле сделаем подстановку *=л/2—z. Тогда
dt = — dz; * = 0 при zl=n/2; * = я;/4 при яа = я;/4. Следовательно,
я/4 Я/4 я/2
2 \ lncos*d*= — 2 \ lncosf-н-—z)dz = 2 \ In sin z dz.
0 Я/2 Я/4
Таким образом,
я/2 я/4 я/2
С я С Г 1
/= \ \ns\nxdx~-zr 1п2 + 2 \ lnsin*rf* + 2 \ lnsinz^ =
J ^ J J
0 U я/4
я/2
/
С ln
о
о
Отсюда
я/2
/= \ In sin л: ^л: = — ~1
о
8.2.10. Вычислить интеграл
1
Г хпс1х . ч
\ (п — натуральное число).
о
Решение. Подынтегральная функция является бесконечно боль-
большой порядка ^ = 1/2 по сравнению с 1/A—х) при х—> 1—0. По-
Поэтому интеграл сходится.
361
Сделаем в интеграле подстановку х ¦= sin t% Тогда dx = cos t dt,
= 0 при t*=0, x**\ при ^шя/2, После подстановки получим
1 Л/2 Л/2
sin* i dt,
Г xndx ^ Г sin" t> cos tdt С
.1 }7T^^ ^ J cos * ** J
bo о
Последний интеграл вычислен в задаче 6.6.9:
{п—1 п—3 1 п
/i-l п-З 2
. . • .-о- * п—нечетно.
Следовательно, и заданный интеграл вычисляется по той же
формуле.
8.2.11. Вычислить несобственные интегралы (или установить их
расходимость):
1/2 2
1 V In Y * ' \
О 1
dx
J^ln*'
1
1
8.2.12. Вычислить несобственный интеграл
1
1п^=\^ xmlnnxdx (я—натуральное число, т> — 1).
о
Решение. При п = 0 интеграл вычисляется непосредственно;
1
1
о • ° т+Г
При п > О проинтегрируем 1п по частям, полагая
и = \ппх\ dv = xmdx;
Мы
получим
Хт + 1
п~~~ m+l
In
l
0
«-1 dx.
X J
n f
m+l J
0
m+1
m+l я-1'
Это дает рекуррентную формулу, с помощью которой можно приве-
привести 1п к /0 при любом натуральном п:
, п j __]п(п—О г _ _(—1)"Л-г
п~~ m+l п-г "" * (m + lJ »-2~ • • • ~" (m+ i)«V
362
И окончательно,
8.2.13. Вычислить с точностью до 0,03 интеграл
2,0
e-xdx
/2 + х—х*
о,з v т
Р е ш е н и е. Интеграл имеет особенность в точке х — 2, так как
2 + х—х2 = B—х)(\+х). Представим его в виде суммы двух ин-
интегралов:
2-8 2
e~xdx r С e~xdx
Г e~xdx _ С
J г/2 4- х—х* J
первый из которых вычислим с нужной точностью, а второй оценим.
При е^0,1 имеем
2
2,9 1е У 2-
Положив е = 0,1, получим оценку /2 < 0,028.
Вычисление интеграла
1,9
/ = Г e~xdx
по формуле Симпсона с шагом h = 0,8 дает
5в,.== 0,519,
а с шагом Л/2 = 0,4 дает
5
Отсюда видно, что более точное значение 0,513 дает интеграл /х
с ошибкой не более 0,001. Учитывая положительность интеграла/2,
округляем полученное значение в большую сторону и получаем
/^0,52
с ошибкой не более 0,03.
Замечание. Положив е = 0,01, мы получили бы оценку /2 < 0,005, но
вычисление интеграла
03
1 QQ
е~хах
J
0,3
потребовало бы значительно более громоздкого расчета.
8.2.14. Исследовать сходимость следующих интегралов:
б)
е*— cos х
363
1
\ Гcos2 x dx
B) J (\-xf ;
0
6/5
f sin
I—-*2
x*\
§ 8.3. Геометрические и физические приложений
несобственных интегралов
8.3.1. Найти площадь фигуры, ограниченной кривой j> = 1/A
(локон Аньези) и ее асимптотой.
Решение. Функция у = 1/A +х2) непрерывна на всей числовой
оси, причем lim jj = O. Следовательно, ось Ох является асимптотой
X -* 00
заданной кривой, которая изображена на рис. 118. Требуется най-
найти площадь 5 фигуры, прости-
простирающейся неограниченно вдоль
оси Ох. Другими словами, тре-
требуется вычислить несобственный
интеграл
s-
Рис.118.
dx
В силу симметрии фигуры относительно оси Оу имеем
dx
5 =
1+х*
= 2 lim arctg x
А -* оо
8.3.2* Найти площадь поверхности, образованной вращением во-
вокруг оси Ох дуги кривой у — е~х от лг = О до ^= + оо.
Решение. Площадь поверхности равна несобственному инте-
интегралу
Сделав подстановку e~x — l, dt =
х = оо при t = 0; отсюда
е~хdx, получим х = 0 при /= Ь
= я [/2+In A+1/2)].
364
8.3.3. Вычислить площадь петли декартова листа
* — Заху = 0.
Решение. Декартов лист изображен на рис. 86. От неявного
задания кривой перейдем к заданию в полярных координатах
Тогда р3 cos3 ф + Р3 sin3 ф — Зар2 cos ф sin ф = 0, откуда, после
сокращения на р2, получим
За cos ф sin ф
p =
Так как петля кривой отвечает изменению ф от 0 до я/2, то иско-
искомая площадь равна
/
о
Для вычисления полученного собственного интеграла сделаем
подстановку tgф = ^;(dф)/cos2ф —<#; ф = 0 при t==0} ф = я/2 при
t=zoo. Подставив, получим
А
, 9а2 f Pdt 9а2 f. р t* dt
9a2 ,.
A A ->oo
За2 t.
= ^ hm
1
8.3.4. Найти объем тела, образованного
вращением циссоиды у2 = х3/Bа — х) вокруг ее
асимптоты лг = 2а.
Решение. Циссоида изображена на рис.
119. Перенесем начало координат, не изменяя
направление осей, в точку О' Bа, 0). В новых
координатах Х = х—2а; Y—y уравнение циссо-
циссоиды примет следующий вид:
Y2 =
— X
Рис. 119.
Объем тела вращения вокруг оси ЛТ=О, т. е. вокруг асимптоты,
выразится интегралом
СО 00
V=n ] X4Y^2n\X4Y.
- 00 О
Перейдем к переменной X. С этой целью найдем dY= Y'dX. Диф-
Дифференцируя уравнение циссоиды в новых координатах как тождество
по X, получим
vv,_
365
отсюда при Y^> 0 имеем
у, = _ (Х + 2аJ (X - а) _ (X + 2а) (X -
X2 ]/ — (Х + 2а)/Х
Следовательно,
= -2п С <*+
J 1А-
Сделаем подстановку (-Y-f- 2a)/X = — /2; Х= — 2д при /==0,
Х = 0 при t—oo. Далее:
Х 2а . ^у ш Hi- ХЛ9п 2at"
отсюда
т/_9 Г 2
о
Полагая / —tg2, dt=^sec2zdzt получим ? = 0 при ? = 0, / = оо
при 2 = 11/2. Следовательно,
Я/2 Я/2
V = 48яа3 J sin2 z cos4 z dz-\-\ бяа3 ^ cos2 2 sin4 z dz~
о о
Я/2 Я/2
J ~^*
о о
Я/2 Я/2
+ 16я#3 ^ sin4 z dz—16яа3 ^ sinezdz.
о о
Я/2
Используя известные формулы для интегралов \^sinnxdxf
о
Л/2
\cosnxdx (см. 6.6.9), получим
8.3.5. Доказать, что площадь области, заключенной между кри-
кривой у~1/У'\—х2, осью абсцисс, осью ординат и асимптотой х=\9
конечна и равна я/2.
306
8.3.6. Доказать, что площадь области, заключенной между кри-
кривой у—Х/^/х2, осью абсцисс и прямыми # = ±1, конечна и
равна 6, а площадь области, заключенной между кривой у=\/х2,
осью абсцисс и прямыми д:= ± 1, бесконечна.
8.3.7. Найти объемы тел, ограниченных поверхностями, получен-
полученными при вращении линий y=ze~x, л;=0, у = 0 (О s^Jt <-?oo):
а) вокруг оси Ох,
б) вокруг оси Оу.
8.3.8. Вычислить площадь, заключенную между циссоидой
y2=z=x*/Ba—л:) и ее асимптотой.
8.3.9. Вычислить площадь, заключенную между кривой у = е~%х
(при х > 0) и осями координат.
8.3.10. Найти объем тела, образованного вращением вокруг оси Ох
бесконечной ветви кривой у = 2(\/х—1/л:2) при х^\.
8.3.11. Пусть в начале координат О находится масса т, которая
притягивает материальную точку Ж, находящуюся на оси Ох на рас-
расстоянии л: от О и имеющую массу 1, с силой F=m/x2 (по закону
Ньютона). Какую работу А произведет сила F при перемещении
точки М вдоль оси Ох из положения, отвечающего х = г, в беско-
бесконечность?
Решение. Работа, очевидно, будет отрицательной, так как
направление силы противоположно направлению движения; отсюда
о» N
Л С tn . «. Г /я , ш
= \— 1Жйх= llm \— -Z?dXz~ Г*
о * N -+<x>J х г
При обратном перемещении точки М из бесконечности в точку
х = г сила ньютоновского притяжения произведет положительную
работу т/г; эта величина называется потенциалом рассматриваемой
силы в точке х = г и служит мерой накопления в точке потенциаль-
потенциальной энергии.
8.3.12. При исследовании затухающего тока, получающегося при
разряде, иногда применяются «баллистические» приборы, показания
которых пропорциональны не мгновенному значению силы тока / или
0D
ее квадрату /2, а «интегральной силе тока» g=^Idt или «интег-
о
ральному квадрату силы тока» S=^I2dt. Здесь t—время, отсчи-
о
тываемое от начала разряда; /—сила переменного тока, зависящая
от времени. Процесс теоретически продолжается бесконечно, хотя
практически уже через конечный промежуток времени сила тока
становится неощутимой; при расчете промежуток времени считают
бесконечным в целях упрощения формул.
Вычислить g и S для следующих процессов:
a) [=Ioe~kt (простой апериодический процесс); к—постоянный
коэффициент, больший нуля.
367
6) I=Ioe~ktsin(ut (простой колебательный процесс); коэффициенты
k И (О ПОСТОЯННЫ.
Решение.
• А
а) ?=$/ое-**<«= lira $/oe-**<tt = /e lim [—e-kilk]f=I0/k;
р о
00
_ Г /2 p-2&* Л/ ^0
б) ?•= \j Ioe~kt sin at dt= lim J/oe~*f sinco/
A -*¦ со
sin* (otdt= lim
ч*
О
= — ±± lim 1 5-т
cos 2cot + coksin
in 2co/I
8.3.13. Пусть бесконечная (в обе стороны) балка, лежащая на
упругом основании, изгибается сосредоточенной силой Р. Если сов-
совместить ось Ох с первоначальным положением оси балки (до изгиба),
а ось Оу провести через точку О приложения силы и направить
вниз, то после изгиба ось балки будет иметь уравнение
<у = ^^-а|^1 (cos а* + sin а | л; |),
где а и k—некоторые постоянные. Вычислить потенциальную энер-
энергию упругой деформации по формуле
W=Ee J (y"Jdx (E, e — const),
о
Решение. Найдем у":
Ра
к
у* = —г- е~*х [(cos ax -f- sin ад:)—2 (— sin ax -f- cos ax)
(— sin ax—cos ад:)] = -т- е~аХ (sin ад:—cos ax).
Отсюда
P2a6?g
оэ
V е~2аХ A —2 sin а л: cos ад:) dx~
__ Р*а«Ее Г 1 2а 1 __ PWEe
~~ № \2а 4a2+4a2J "~ 4/г2 *
368
8.3.14. Какую работу надо затратить, чтобы тело массы т пере-
перенести в бесконечность с поверхности Земли?
8.3.15. Определить работу, которую необходимо затратить, чтобы
электрический заряд е2= 1 приблизить к заряду ei из бесконечности
на расстояние, равное единице.
§ 8.4. Дополнительные задачи
8.4.1. Доказать, что интеграл
dx
сходится при р > 1 и q < 1.
8.4.2. Доказать, что интеграл
\ xPsmx^dx, q Ф 0
о
сходится абсолютно при —1 < (p+l)/<7 < 0 и сходится условно при
8.4.3. Доказать, что эйлеров интеграл первого рода (бэта-функция)
В (/?, q) --
сходится при р > 0 и q > 0.
8.4.4. Доказать, что
1 Г
Вт — \ sin cxjc • sin Pj^ <1« == О,
Г-*- оо ' J
если |а|^|Р1.
8.4.5. Доказать, что
00
/= \ e-xZ-x*n+1 dx = -7Jr (n—натуральное число),
о
со
8.4.6. Доказать, что если интеграл \ dx сходится при любом положи-
J ¦*
а
тельном значении а и если / (х) стремится к пределу А при х —> 0, то инте-
интеграл
(а>0> р>0)
о
сходится и равен A In (P/a).
8.4.7. Доказать, что
р в-а*_?-р* п cos алг—cos Р* . , 6
о
Я/2
р
p j cos x
8.4.8. При каких значениях т интеграл \ —pj—dx сходится?
о
я
С dx
8.4.9. Доказать, что интеграл \ —:—-г сходится, если k < 1, и расхо-
расходится, если
_ fsinx(l—cos a:)
8.4.10. Доказать, что интеграл \ р с?л; сходится, если
о
О < s < 4, и абсолютно сходится, если 1 < s < 4.
8.4.11. Пусть интеграл
+ 00
$/(*)<** A)
сходится и функция q>(#) ограничена.
Обязательно ли сходится интеграл
B)
Что можно сказать о сходимости интеграла B), если интеграл A) сходится
абсолютно?
8.4.12. Доказать справедливость соотношения
х/2)-2/ (Я/4-Х/2)-* In 2,
де
где, / (х) = — J In cos у dy.
о
Вычислить с помощью найденного соотношения
Я/2
/ (-у)=— Jlncos#d#.
о
8.4.13. Для интеграла
Я/2
/я = \ In cos x-cos2nxdx (n—натуральное)
о
вывести рекуррентнук) формулу и вычислить этот интеграл.
ОТВЕТЫ И УКАЗАНИЯ
К главе I
1.1.5. Указание, Доказывать от противного, полагая 2 — p2/q2, где р,
q—целые положительные числа без общих множителей.
1Л.8. Указание. Можно взять & = (s2—2)/2s.
1,1.9. б) х^4, *<0; в) — 4<*<2.
1.1.11. а) х<—1 или x^s\. Указание. Равенство справедливо для тех
значений х, для которых (х—1)/(#+1)^гО; б) 2<:*<;3. Указание. Равен-
Равенство справедливо для тех значений х, для которых х2 — 5#+6<^0.
1.1.13. а) х < 2/5 или х > 8; б) х < 0 или 0 < х < 5. Указание. Неравен-
Неравенство \а—Ь\ > |я| — \Ь\ имеет место тогда, когда числа а и Ъ разных знаков
или когда \а\ < \Ь\.
1.2.3. 0; (а+2)/[д_(а2 + За+3)]; (а3+я)(а3— 1). 1.2.4. №-\-ab+a*;
(a + hf/8—l. 1.2.6.4/2+1; ()/2+1)/2; 2 /Тб—5. 1.2.11. /(*) = 10+5-2*
1.2.13.
[/МГ „125^ + 75^+15^ + 1
э/М
1.2.14. /B) = 5; /@) = 4; /@,5) = 4; /(-0,5)=//3; /C) = 8.
1.2.15. Указание. Из ^n+i = ^n + ^ следует ^n+1 = aJf»^1 aJ:n
1.2.16. л:=±2; ±3. 1.2.17. / (*) = *2—5jc + 6. 1.2.18.
/ () + /() ; ф()
1.2.19. л:<—1 или х^2. 1.2.20. Р = 26 + 2A—6//г)л:; S = b(\—x/h)x.
1.2.21. б) B, 3);в)(— оо, — 1) и B, а>); г)* = я/2 + 2*я(?==0, ±1, ±2, ...).
Указание. Так как sinjc^l, то функция определена лишь тогда, ког-
когда sin*=l; ж) (—со, 2) и C, со); з) [1, 4); и) (—2, 0) и @, \);
к) — n/2 + 2fm<x <jx/2 + 2fax F = 0, ±1, ±2, ...).
1.2.22. г) Вся числовая ось, кроме точек х— ±2.
1.2.24. а) (—оо, оо); б) C—2д, 3-я) и C, 4); в) [ — 1, 3]; г) ( — 1, 0) и
(О, оо). 1.2.25. б) 5<*<6.
1.2.26. а) 2&К*<B?+1)я F = 0, ±1, ±2, ...); б) [—3/2, —1].
1.3.3. б) Указание. Рассмотреть разность x2l(\-\-x\)—^/(l+jcf).
1.3.4. б) Возрастает при — 5я/6 + 6я < х < я/6 + kn F = 0, ±1, ±2, ...)
и убывает в остальных промежутках.
1.3.7. Функция убывает в промежутке 0 < х^.п/4: от + оо до 2 и воз-
возрастает в промежутке зх/4 <^ х < я/2 от 2 до + оо.
1.3.9. в) Функция не является ни четной, ни нечетной; г) четная.
1.3.10. а) Четная; б) нечетная; в) нечетная; г) не является ни четной, ни
нечетной; д) четная.
1.3.12. а) |Л| = 5, © = 4, ф = 0, Г = я/2; б) |Л| = 4, о>=3, <р = я/4,
Г = 2я/3; в) | А | = 5, со= 1/2, <p = arctg D/3), Г = 4я. Указание. 3 sin (х/2) +
+ 4 cos(je/2)=5sin(je/2 + q>), где cos<p = 3/5, sinq>=4/5. 1.3.13. б) Т = 2я;
в) Г=1.
371
1.3.16. Наибольшее значение /A) = 2. Указание. Функция достигает наи-
наибольшего значения в точке, где квадратный трехчлен 2*2—4*+3 достигает
наименьшего значения.
1.3.17. а) Четная; б) четная; в) нечетная; г) четная.
1.3.18. а) Т^щ б) Г=,6я.
1.3.19. Указания, а) Предположить противное. Тогда
Т
откуда cos (х+772)= — . ,T/Ov , что невозможно ни при каком постоян-
<и Sill у I /Л)
ном 7\ так как левая часть не является постоянной; б) предположить про-
противное. Тогда cosjA*+T=cos Y~x~, откуда либо V^x + Т + V~x~ = 2nk ,
либо T/(Vx+T-\~Vx) = 2nk (fc = 0, ±1, ±2, ...), что невозможно, так как
левые части этих равенств являются функциями непрерывного аргумента х.
1.4.6. a) * = (l + arcsin#)/3; б) *=3sin#; в) x=*yl/l85 (у > 0);
г) *=1зЦ^Щ2) (° < у < 2 или
1.6.3. a) /3/2, /3/2, 0, -/372, ...; б) -1/2, 1/4, -1/8, 1/16, ...;
в) 2; 2,25; 2g; 2^, ...
1.6.9. Указание. Неравенство \ Bп-\-3)/(п-\-1)—2|<е удовлетворяется
при п > N-=E A/е—1). При е = 0,1 неравенство удовлетворяется, начиная
с л=10, при 8 = 0,01, начиная с я = 100, при е = 0,001, начиная с /г = 1000.
1.6.10. Указание. Убедиться, что последовательность х2п^х стремится к 1
при п—>(», а последовательность х2п стремится к 0 при п—^оо.
1.6.12. а) Имеет; б) не имеет; в)" имеет; г) не имеет.
1.6.14. Указание, а) \хп\^2/п; б) \хп\^\/п.
1.6.19. Указание. При а> 1 положить у а — 1+аЛ (ап > 0) и с по-
помощью неравенства а = (\-{-ап)п > пап доказать, что ап—бесконечно малая.
При а< 1 положить у а = 1/A+«„) (oLn > 0) и воспользоваться нера-
неравенством 1/а = A+-а„)/1 > пап.
1.7.1. б) 5/4; в) 0; д) 1/2. 1.7.2. б) 1/16; д) 1; е) 1.
1.7.4. б) 1; е) 0. Указание. Умножить и разделить на неполный квадрат
суммы, а затем разделить на я*/3; ж) —i/З; з) 1. Указание, Представить
каждое слагаемое в хп в виде разности
1 J_ __L__L__JL. • 1 __ 1 1__
Ь2~ 2 ' 2-3~ 3 ; "*; n(n+l)~ n п+Г
что приведет хп к виду хп= 1 — 1/(п+ \).
1.7.5. а) 1/2; б) 1; в) 0; г) —1/2. Указание. Величина 1/Bл)—бесконечно
малая, a cos пъ—ограниченная; д) 0; е) 4/3.
1.8.6. б) Указание. Ограниченность последовательности вытекает из того,
чти п! = 1-2-3- • •п^2/1~1 и поэтому
хп< 2+1/2+1/22+ ... +1/2»-1 = 3—1/2*-1 < 3.
1,8.7. б) 0. Указание. Воспользоваться тем, что хп+1/хп*=2/(п-{'Ъ) < 1.
1.8.9. Указание. Для всех л, начиная с некоторого, выполняются
неравенства \/п< а < п. Поэтому ij \/ п < у а < у п, причем lim у п =
/v
1.8.10. Указание. Последовательность {уЛ убывает, так как
Я=в1/B».2, Г- A)
S72
Ограниченность последовательности снизу следует из а > 1. Обозначить
lim уп — Ь и из соотношения уп+1= Vvn найти 6=1.
л->оо
1.8Л1. Указание. Убедиться, что последовательность возрастает. Ограни-
Ограниченность установить из неравенств
1.8.12. Указание. Преобразовать хп к виду хп = 2п/(У^п? + 1 + л) и вос-
воспользоваться неравенствами
2л/Bл+1) <
1.8.13. Указание. См. задачу 1.8.7а).
1.8.14. Указание. Ограниченность последовательности установить путем
сравнения хп с суммой некоторой геометрической прогрессии.
1.9.2. б) Указание. Выбрать последовательности
*я=1/л и *;= —1/л (л = 1, 2, ...)
и убедиться в том, что последовательности соответствующих значений функ-
функции имеют разные пределы:
lim 2l/Xn = + оо,
1.9.3. д) Указание. Воспользоваться неравенством
я/2—arctg* < \g(nj2—arctg *) = !/* (х > 0),
е) Указание. Преобразовать разность
sin х—1/2 = sin x—sin (я/6)
в произведение и воспользоваться неравенством | sin a | ^ | а |.
1.10.1. г) p/q; д) 5/6; е) —1/12. Указание. Умножить числитель и знаме-
знаменатель на неполный квадрат суммы \у 10—*+2); ж) 34/23j з) loga6.
и) 2/3; к) 7/12.
1.10.2. д) 1/2. Указание. После перенесения иррациональности в знамена-
знаменатель разделить числитель и знаменатель на х.
1.10.3. б) 32; в) 5/3. Указание. Положить х~г1Ь; е) оо. Указание. Поло-
Положить я/2—х = г\ * = я/2—г; г—*0 при х—*я/2; ж) —3. Указание, Поло-
Положить sin#=#.
1.10.5. б) <?1/3; в) е-1; г) е»к; е) 4; ж) \/а; з) 2.
1.10.7. б) 1/4. 1.10.8. б) 1; в) \/е; г) ectga.
1.10.11. а) 1/2; б) —3/4; в) 1/2; г) 2/5; д) 0; е) —1.
U0.12, а) 1/20; б) —2; в) я/2; г) 1/2; д) —24.
1.10.13. а) ««; б) —1; в) 2 In а; г) &\ д) е"^2; е) е~\ ж) 1; з) 1; и) 9;
к) 1; л) а—р. Указание.
раХ рЪх pia — Q)x 1
lim €. f-^ lim *3* 5—1 -=а-р.
0 х 0 X
1.10.14. a) ^2. Указание. Заменить arccos A—x)=?arcsin }/ 2x—x2; б) Ц
в) a.
373
1.11.5. б) Третьего порядка малости. Указание.
, tga—- sin a I
lim — 5 = -?r«
1.11.6. б) Одного порядка; в) эквивалентны.
1.11.8. а) 100* есть бесконечно малая того же порядка, что х\ б) х2 есть
бесконечно малая высшего порядка по сравнению с х; в) 6 sin x есть беско-
бесконечно малая того же порядка, что х; г) sin3* есть бесконечно малая высше-
высшего порядка по сравнению с х\ д) у tg2 x есть бесконечно малая низшего по-
порядка малости по сравнению с х.
1.11.9. а) 4-го порядка малости; б) 1-го порядка малости; в) 3-го порядка
малости; г) 3-го порядка малости; д) 1-го порядка малости; е) порядка мало-
малости 1/2; ж) 1-го порядка малости; з) 1-го порядка малости; и) 2-го порядка
малости. Указание. Умножить и разделить разность cos х— у cos x на
неполный квадр?ат суммы; к) 1-го порядка малости.
1.11.10. Диагональ d первого порядка малости; площадь S второго по-
порядка малости; объем V третьего порядка малости.
1.12.3. б) 4; е) 3; ж) 1/2; и) 2. 1.12.6. а) 1; б) 2. 1.12.7. а) 1; б) 1/3.
1.12.8. а) 3/5; б) 4/5; в) 3/2; г) 3/2; д) 2/9; е) 3/4; ж) —2; з) 1.
1.12.9. 10,14. Указание. 1042= 103-0+0,042).
1.13.1. б) /A—0)=— 2, /A+0) = 2, е) /B—0)= —оо; /B + 0)= + оо.
1.13.3. а) /(—0)=1/2; /( + 0) = 0; б) /(-0) = 0, /( + 0)= + оо; в) /(-0) =
1 /( + 0) 1
1.14.2. б) Функция терпит разрыв первого рода в точке х = 3. Скачок
равен 27.
1.14.3. в) Функция непрерывна всюду; д) функция терпит разрыв пер-
первого рода в точке л: = 0; скачок равен я. Указание. arctg( — оо)=—(Я/2,
arctg( + oo) = +я/2.
1.14.6. б) В точке *0 = 5 разрыв первого рода: /E—0)=—я/2, /E + 0) =
= я/2; в) в точке *0 = 0 разрыв первого рода: /(—0) = 1, /( + 0)=0; г) в точ-
точке *0 = я/2 бесконечный разрыв второго рода:
/(я/2-0)= + оо, /(я/2+0) =-оо.
1.14.7. а) В точке # = 0 устранимый разрыв. Для устранения разрыва
достаточно доопределить функцию, положив /@) = 1; б) в точке * = 0 устра-
устранимый разрыв. Для устранения разрыва достаточно переопределить функцию,
положив /@)=1; в) в точке * = 0 разрыв второго рода: /(—0) = 0, /( + 0) =
= + оо; г) в точках x = Bk-\-l) к/2 (& = 0, ±1, ±2, .««) устранимые разры-
разрывы, так как
Г 0, если |sin*| < 1,
/(*)=¦ lim <sinjc)a» = ^ ' ' '
r?^<» (I, если | sin x | = 1;
д) в точках x~kn (k=0, ±1, ±2, ...) разрывы первого рода, так как
*/«ч_ |sin*| Г 1, если
; sin л: ) _1э если sin*<0;
е) в точках jc = n = O, ? 1, ±2, ... устранимые разрывы, так как
— 1, если х = п,
0, если х Ф п.
1.14.8. а) В точке л:=1 бесконечный разрыв второго рода; б) в точке
*=—2 разрыв первого рода, скачок равен 2; в) в точке *-=0 бесконечный
разрыв второго рода, в точке х—\ разрыв первого рода, скачок равен —4;
г) в точке * = 1 бесконечный разрыв второго рода.
S74
1.14.9, a) /@) = l; б) /@)=-3/2; в) /@)*= 1/2; г) /@)»2.
1.15.2* б) Функция непрерывна в промежутке @, +оо),
1.15.3. б) Функция непрерывна всюду. В единственной возможной точка
разрыва * = 0 имеем
lim y=* lim ма=1; lim #= lim u2=l; у \х=0=у |й=-1= 1;
х->-0 м->1 X-+ + Q w-*-l
в) в точках х = я/2-{-пп (л = 0, ± 1, ±2, ...) устранимые разрывы»
так как lim у = lim y= — 1. 1.16.2. Да. 1.16.12. 1,53.
*->rt/2 ы-*±со
1.16.13. Нет. Например, функция у = х2 на отрезке [—1, 1].
1.17.1. а) Указание. Перемножить очевидные неравенства:
V~n<{n+\)I2\
V(n-\)-2<(n+l)/2i
//Л <(л+1)/2.
б) Указание. Пусть Л = у ' "' "б"* • * 2п *
.11 JL 2/1
3 5 7 '" 2/г+Г
Тогда Л < 5, так как Bп—\)/2п < 2п/Bп+\) и Л2 < АВ/( + )
1.17.2. а) Указание. Извлечь из обеих частей неравенства корень 101-й
степени и сократить обе части на 1012.
б) Перемножить очевидные неравенства:
99-101 < 1002,
98-102 < 1002,
2198 < 1002,
Ы00 199-200 < 1004.
1.17.3. а) —3 < х < —1 или 1 < х < 3; б) х <—1/3 или х > 5/3; в) нера«
венство не имеет решений, так как равносильно противоречивой системе
х—2 > 0, л: Dа:2—х+4) < 0. 1.17.4. Да. 1.17.5. а) Нет; б) да.
1.17.7. Указание. Воспользоваться методом математической индукции.
При п = 1 соотношение очевидно. Предполагая, что справедливо неравенство
(l+Xi)(l+x2)"-(l+xn-1)^z:\+x1+X2+*^+xn-1, умножить обе части его
на \+хп и учесть условия \+хп > 0, хгхп > 0 (* = 1, 2, ..., л —1).
1.17.8. а) [1, +оо); б) BшгJ<*<B/г+1Jя2 (л = 0, 1, 2, ...); в)*=0,
±1, ±2, ...; г) (—оо, 0) для f(x), g(x) не определена нигде; д) [—4, —2J
или [2, 4]; е) х = Bп+\)п/2 (п = 0, ±1, ±2,...).
1.17.9. а) Нет: ср@)=1, а /@) не определена; б) нет: fix) определена
для всех *#0, а ф(я)—лишь при х > 0; в) нет: f (х) определена для всех х,
а ф(я) — лишь для я^0; г) да; д) нет: f (х) определена только при х > 2, а
ф (х) — при х > 2 и при х < 1.
1.17.10. а) @, оо); б) [1, оо). 1.17.11. У = 8я (*—3) F—*), 3 < х < 6.
1.17.12. а) я = 5. Указание. Область определения задается неравенствами
jc+2^0, х—5^0, 5—x^zO, которым удовлетворяет лишь одна точка х=5.
Проверить, что число х = Б удовлетворяет заданному неравенству, б) Указание.
Область определения задается несовместными неравенствами х—3 > 0, 2—х >0.
1.17.17. a) /(*) = 2/(l+*2) + */(l+*2); б) ax={ax+a-x)j2 + (ax—a-*)/2
(см. задачу 1.17.16).
375
1.17.18. Четное продолжение определяет функцшо
/ (х) = х2-\-х при
/(—х)~х2-гх при —3<*<0,
Нечетное продолжение определяет функцию
f(x) = *2 + ж при 0^*<3,
х при —-3 ^ х < 0.
рд фуц
I —f(—x) = —x* +
1.17.21. Указание. Если функция / (х) имеет период Ти а функция
имеет период Т2, причем 7l1 = n1flf, Тг~п%& (nlt n2—целые положительные
числа), то периодом суммы и произведения этих функций будет T = /id, где
я—наименьшее общее кратное чисел пх и я2.
1.17.22. Указание. При любом рациональном числе г будет
1 при х рациональном,
0 при х иррациональном.
чисел нет наименьшего числа,
функции f (x) через 7\ то из
Но во множестве положительных рациональных
1.17.23. Указание. Если обозначить период
/(Г) = /@) = /(—Т) получаем
sin T+ cos aT=l=sin( —Т)-Ь cos (—аГ),
откуда sin T = 0, cos aT= 1,и,значит, Т = &л,яТ = 2шг, а =2n/k—рационально.
1.17.25. Разность двух возрастающих функций может и не быть монотон-
монотонной функцией. Например, функции f(x) — x и g(x)=x2 возрастают при х^гО,
а их разность f(x)—g(x) = x—х2 не мо-
монотонна при х^О: она возрастаете
[0, 1/2] и убывает в [1/2, оо).
1.17.26. Пример:
-{-:
1.17.27. а
б)
если лс рационально,
если jc иррационально.
у при —оо < (/ < 1,
Рис. 120.
при
при 16<t/ < оо.
1.17.28. Указание. Функции у = х2 + 2х +1 (х^~-1) и (/ =—1+ }/"лГ ()
являются взаимно обратными, но уравнение у~х, т. е. х2-\-2х-\-1=х не имеет
действительных корней (ср. задачу 1.4.4).
1.17.30. в) Указание. Если Е—область определения функции f(x), то функ-
функция y = f[f(x)] определена только для тех х??, для которых f(x)?E. Построе-
Построение точек искомого графика показано на рис. 120.
1.17.32. Указание. Величина Г = 2F—а) есть период: из условий симмет-
симметрии / (я+*) = / (а—х) и f (b-\-x) = f (b—х) следует, что
1.17.33. а) Расходится; б) может сходиться, может и расходиться. Примеры:
Km
fl-к»
376
1.17.34. а) Нельзя. Пример: хп — п\ уп = —л + 1; б) нельзя. 1.17.35. ап =
= я(/г—2)/п (п = 34 4, ...). 1.17.36. Указание. Учесть, что ||х,,| —|а|К
<*\хп— а\. Обратное утверждение неверно. Пример: хп — (—\)п+1.
1.17.38. Указание. Последовательность а„ может принимать лишь значения
О, 1, ..., 9. Если бы эта последовательность оказалась монотонной, то ирра-
иррациональное число было бы представлено периодической десятичной дробью.
1.17.39. Указание. Если последовательность ап/Ьп возрастает, то
<*ilbi < «я+i/^n+i. т- е- bn+iai < «я + А (* = 1. 2> •••» п).
Отсюда следует неравенство
bn+l (al + a2+ ... +ап) < an + l (bl + bt+ ... +bn),
а значит, и неравенство
... +bn+1 bt + bt+... +bn
... +bn)—bn+1 (fli + fl2+ ¦»> +fln) ft
1.17.40. a) 2; 6) 0; в) 0. 1.17.41. Указание. Из неравенств пх— 1 < ? (пх) <; пх
следует х— 1 < я—1/я < (Е{пх))/п^х.
1.17.42. Указание. Из неравенств
следует
п
1.17.43. Указание. Воспользоваться тем, что lim altn = \im ya = \ (см.
1.6.19), lim a~lfn = —— =1» и при а > 1, \h\< \/n имеют место нера-
n~*ao lim у а
П-+СР
венства a-1/" —i < аЛ—1 < а1/"—1.
1.17.45. Указание. Разделить числитель и знаменатель на хт.
1.17.46. а) а = 1; 6 ——1; б) д=1; 6=1/2. Указание. Для отыскания коэф-
коэффициента а разделить выражение на х и перейти к пределу.
1.17.47. а)
/ 1 при
б)
Г 0 при хф я/2 + пя, _
4 I 1 при х = я/2 + ля
1.17.48. Указание. Воспользоваться тождеством
1.17.49. Вообще говоряг нельзя. Например,
|. In (I +xL-ln(l—х) j-m In A—х2)
377
а если заменить ln(l+#) на х и In A—х) на *—я, то получится неверный
результат: lim ?Z_^=o.
*->о х2
1.17.50. 1/2. Указание. Если а—центральный угол, одирающийся на рас-
рассматриваемую дугу, то хорда равна 2R sin (a/2)—Ra, & стрелка равна
R(l — cosa)~#a2/2.
1.17.51. 2. Указание. Разность периметров описанного и вписанного пра-
правильных n-угольников равна
2Rn (tg^-sin-^)=
где а = л/я, а сторона вписанного я-угольника равна
2/? sin (я/л)=с2/? sin a~2/?a.
1.17.52. На эквивалентности A+аK — 1~3а при а
1.17.53. Нет,
1.17.54. а) Да. Указание. Если функция ф (*)=*/(*)+#(#) непрерывна в
точке * = л:0, то в этой точке непрерывна и функция g(x)*=q)(x)—f(x); б)нет.
Пример: f(x)=*—g(x)=ssignx (см. 1.5.11, о)); обе функции терпят разрыв в
точке # = 0, а их сумма тождественно равна нулю, и значит, непрерывна.
1.17.55. а) Нет. Пример: f(x) — x непрерывна всюду, а g{x) = sin (я/х) при
хфЪ, причем g@) = 0 терпит разрыв в точке # = 0; произведение же этих
функций есть функция непрерывная при х = 0, так как lim я sin (п/х)** 0;
б) нет. Пример: f(x) = — g(x)= < ""*" ' обе функции разрывны в
\ —1 при х < 0;
точке д; = 0, а их произведение f(x)g(x)=z=—1 непрерывно всюду.
е ч / 1, если х рационально,
1.17.56. Нет. Пример: /(*)=< Можно запи-
( —1, если х иррационально,
сать / (л:) = 2Л, (л:)— 1, где Х(х)—функция Дирихле (см. 1.14.4 6)).
1.17.57. а) # = 0—точка разрыва второго рода, #=1 точка разрыва пер-
первого рода; б) *=1 точка разрыва первого рода: f(l—0) = 0, /A+0)=1;
в) ф(я) разрывна во всех точках, кроме * = 0.
1.17.58. а) я = п = 0, ±1, ±2, ...—точки разрыва первого рода: lim t/=l,
_ х-+п-о
lim у = у\х=п = 0. Функция имеет период 1; б) х^±Уп (п=*±1, ±2,...)—
х-+п+о
точки разрыва первого рода:
lim_ у = 2п— 1; lim_ y = y\ x=zy- = 2n.
x-*Vn-0 V
Функция четная; в) х—± V^n (n=±l, ±2, ...)—точки разрыва пер-
первого рода; в этих точках функция переходит от значения 1 к значению —1 и
обратно. Функция четная;
г)
< 1/2, т. е. —я/6 + яя < х < я/
=1/2, т. е. х= ±п/6+пп,
> 1/2, т е. л/6 + пп < х < 5л/6+шг.
х=±л/6-\-пп — точки разрыва первого рода.
1.17.59. Функция f[g(x)] имеет разрывы первого рода в точках л: = — 1;
0; +1. Функция g[f(x)] непрерывна всюду. Указание. Функция f (и) терпит
378
разрыв при « = 0, а функция g(x) меняет знак в точках # = 0, ±1. Функция
" [ ]s==0, так как f(x) принимает только значения 0, ±1.
1.17.61. Указание. Записать функцию в виде
х+1 при <—2<*<0,
0 при х = 0,
"*/* при О
Убедиться, что функция возрастает на промежутке [ — 2, 0) от —1 до 1 и на
промежутке [0, 2] от 0 до 3/2. Применить теорему о промежуточном значении
к отрезкам [ — 2, —1] и [0, 2]. Функция разрывна в точке * = 0: /(—0) = 1,
/( + 0) 0
)
1.17.62. Указание. Пусть задано 8 > 0 и выбрана точка xQ?[a, b\. Можно
считать
е<гшп[/(л:0)-/(а), f(b)-f(x0)).
Выбрать точки хх и х2, хг < х0 < х2, так, чтобы
и положить 6 = min(x0—xv x2—х0).
1.17.63. Указание. Применить теорему о промежуточном значении к функ-
функции g(x) = f(x)—x.
1.17.64. Указание. Применить теорему о промежуточном значении к функ-
функции f (х) на отрезке [xv хп], заметив, что
[/(
[/(
1.17.65. Указание. Применить теорему о промежуточном значении к функ-
функции g(x) = 2x — l/x на отрезке [1/4, 1].
1.17.66. Указание. Значения многочлена четной степени при достаточно
больших значениях независимой переменной имеют тот же знак, что и коэф-
коэффициент при старшем члене; поэтому многочлен меняет знак по крайней мере
два раза.
1.17.67. Указание. Обратная функция
— К —i/ —! ПРИ У<— 1»
О при у=0,
к Vу— 1 при у > 1
непрерывна в интервалах (—оо, —1) и A, оо) и имеет одну изолированную
точку # = 0.
К главе II
2.1.1. б) —20/21. 2.1.2. б) у'^=\0х—2. 2.1.5. иср = 25 м/сек. 2.1.6. а) у'=
=3*2; б) #'=—2/х3. 2.1.7. Функция недифференцируема в указанных точ-
точках. 2.2.1. б) у' = —%ах*-ъ1ъ + ~Ьх~71ъ. 2.2.2. в) у'= 2хarctgх+1.
о о
2.2.3. б) —9000. 2.2.4. а) #' = 6л:2 + 3; б) t/' = —7^=- yr^+х9; в) t/'=
; _ ^_^л: 2jc}^jc
3 У^лг+в У~х + 2 У~\/х , cos9—Б1ПФ—1
ч / ov, 1/ ч t о v ч / л: (cos л:—sin л:)—sin л:—ех
е) у' = 2е*+1/дс; ж) у'=2е* cos л;; з) у' = -± -ф .
2.2.5. е) 30 in4 (tg3 x) -J-r- ; Ж) sin 2
-х 2{\—xf/2
379
2.2.6. 6) y' = -3C-sin*)«cos*; в) у'' = - . 2со**
Зб
Збшл: j/sin2;e
5 In4 л: . , _ о 1 . л: , I
е) j,' = B*-5) со8(х*-Б*+1)—J-sec1 т' з) »'= -.А, ' . , =+
¦* * х у 1 -j-ln3 jc
2'2А б) ^=~
; Д) у' =
2.2.9. B)y'=^j
2.2.13. a) /'M==l^ch|- + shy); б) /'W = thx; в) /'(др) =/
г) /' (х) = 1 /ch л:; д) /' (л:) = 4 sh 4л:; е) f' (х) = (а+Ь) е«^ (ch Ьл: + sh Ьх)
2.2.14. a) у' = (cosx)smx (cos л: In cos л:—tg x sin x);
к—24
— sin Ex)* ; 3 (*—1I/2 (л; + 2M/3 (л:+3M/2
2.2.17. a) ,.-—!°3_.*8.
v_i у arcsin3-2*
sin In3 л:-In2 л:
б) *' = -7-в
2.3.1. 6) *»***; Д) 2"-1 sin Bл: + ля/2); e) ~ sin (x+n^ J
^ sin f3x+/iyj + -^ sin ^
2.3.4. 6) e*(*2 + 48jt + 551); в) ee* /sin
oQft 2л;2+ 3^ A+2л:2)агс8тх
2'3-6' а) (\+*)УТ+*; } A*•)»'•
в) 2^-^2Bлг2 —1).
2.3.8. а) л:3 sin л:—60л:2 cos л:— 1140 х sin л: + 8640 cos x\ б) 2е~* (sin x+
+ cos*); В)^[3л:2 + 6лл:+3л(/г— 1)—4]; г) (-1)" [Dп2 + 2л + 1—*2) cosx—
•—4/ixsinx].
2.3.9. а) 100 ! 1Щх-2)™-Щх-1)ш]; б)
Указание. ^=2 A—дг)~1/2^-A
380
2.4.1. б) хУу=— 4
2.4.3. б) yx=-ctg^~t; г) у'х=—2е-*с*.
2.4.4. б) ?, = _«_; в) у'хх=-±-.
2.4.5. б) у'х'хх= — 3sin
2.4.6. б) ^ = у/* + *-"*; в) yi = B—х)/(у—5); г) yx^-
2.4.7.6) ^х = (е*—^)A—в*+Л/A+^K; в) ^ =
= 4(* + #)/(*+ 0+1K. 2.4.9. а) Bа-2*-#)/(* + 2</-2а); б)
в) -&^й^^; г) ~1/в" 2'4Л0'а) -Bу2+2)/^5; б) 111/256-
2.4.11. а) — с sin t/[a (b+ cos *)]; 6) tf/2; в) (*2+1)/4*з; г) —
2.5Л. 6) 6a:4-2y—9 = 0; 2x—
2.5.2. в) Mi (—2/^3, 5+10/C ^)), M2B//*3, 5-10/C /"з)).
2.5.3. 6) 9 = arctg2 V~2. 2.5.8. 6) x + y—2 = 0; y = jc. 2.5.15. а) я/4;
6) y=l, * + 2y—2 = 0; в) (/ + 39/16=— B/3) (* + 5/4); г) я/4. 2.5.16.11.
2.5.17. 26450. 2.5.19. s = at-gfi/2; v = a-gt; \VB
2.5.20. y = r/ = ?^sinM(l+2ecosM). 2.6.3. Ay
2.6.5. 6) lg 10,21 « 1,009; r) ctg45°10' « 0,9942.
2.6.7. в) A;; = |cosa:|Aa;; г) A^ = (l+ tg2 а:) Л^.
41плг—4 — In3 л:
2.6.9. а) Л, = 4-*2 2 In 4 B*2 In4^ 1) cte»; б) сРу =
в) dsy=— 4 sin 2d3
частности,
cos22/ "
4
2.6.11. АУ = 4яг2Аг + 4л;г Аг2 + -^-яА/8—объем, содержащийся между дву-
двумя шаровыми поверхностями радиусов г и r + Ar; dV = 4nr2Ar—объем пло-
плоского слоя с основанием, равным поверхности шара 4лг2 и высотой Аг.
2.6.12. As — qtAt-\--jr-g At2—путь, пройденный телом за время At; ds =
— gt At = vdt — путь, пройденный телом, которое в течение всего промежутка
времени двигалось бы со скоростью v = gt.
2.7".1. а) Не существует; б) существует и равна нулю*
2.7.2. Прямой. Указание. Так как
ех, х^О
е-*, х<0,
2.7,4. Указание. При х Ф 0 производная
? (х)= — cos (l/#) + 2* sin (l/x).
331
При я = 0 производная равна нулю:
Таким образом, производная /' (х) существует для всех х, но терпит
разрыв второго рода в точке * = 0. 2.7.5. а = 2*0, Ь——х%. 2.7.7. Указание.
Формула для суммы геометрической прогрессии представляет собой тождество
по х. Приравнивая производные от обеих частей тождества, получим
умножив обе части последнего равенства на а: и опять продифференцировав,
получим
2.7.8. sin * + 3sin 3*+ ... + Bя —1) sin Bn—l)* =
B/1+1) sin B/1—1) jc — B/1—1) sin Bn+ 1) *
4 sin2 a;
Указание. Для доказательства тождества умножить левую часть его на
2 sin * и применить к каждому слагаемому формулу 2 sin a sin P=CQs(a-r-ft) —
— cos(a+P). Для рывода искомой формулы продифференцировать обе части
тождества и приравнять производные.
2.7.9. а) sin 2x [/'(sin2 x)—f (cos2 x)\[
б) e'M[e*
У (х) _1 <р'(*) In f (х)
В' # ln<p(*) #
2.7.10. а) Нельзя; б) нельзя; в) можно; г) нельзя.
2.7.И. Указание. Продифференцировать тождества / (—х) = f (x) или
f(—x) = —f(x) соответственно. Этот факт легко иллюстрируется геометрически,
если учесть, что график четной функции симметричен относительно оси Оу,
а график нечетной функции—относительно начала координат.
2.7.12. Указание. Продифференцировать тождество f (x-\-T)=*f (x).
2J.13. F'(*) = 6*2. 2.7.I4. / = 2|jcJ. 2.7.15. Сложная функция /[ф(д:)] может
быть недифференцируема только в тех точках, где ф' (х) не существует и где
ФМ принимает такие значения ф (*) = «, в которых /' (и) не существует. Но
функция f/=«2 = |*|2 в точке х = 0 имеет^ производную «/' = 0, хотя в этой
точке функция и = | х \ не имеет производной.
2.7.16. а) */" = 6|х|; б) ^ = 2sin ^ —-|-cos ——^sin — при х ^0, / @)
не существует, так как у' (х) разрывна при х = 0.
2.7.17. Указание, а) Проверить, что /<*> A)//в1=Сй (ft = 0, 1, ..., п) и
воспользоваться свойством биномиальных коэффициентов, б) Обозначить
un; показать, что
и воспользоваться методом математической индукции.
2.7.18. Указание. Применить формулу Лейбница для я*й производной от
произведения функций и = е~х1а и и=х2.
2.7.19. у<»>@)={ {1.3...B^-1)]2 при Л-2Л+1 (Л—1. 2,
S82
Указание. Продифференцировать тождество п^2 раза и, положив # =
получить «/<"> @) = (п—2J */<"-2> @) (п^ 2).
2.7.21. Указание. Воспользоваться определением
и формулой Лейбница для гс-й производной от произведения u — e~x<i и v =
в. — 2х, 2.7.22. у'
2.7.23. *!- =
= 1, 2, 3, 4) при *, ^0, ± 1.
Указание. Решить биквадратное уравнение *4 — 2*2 + #=0 и найти области
определения полученных функций Х{(у).
2.7.25. а) *! = —3; *2=1; б) х=± 1.
) ! 2
2.7.26. Указание. Заметить, что функция x = 2t — \t |= < J> ?^2' не имеет
{v v ^=* О
л:/3 ^Г<0 П0ЭТ0МУ можно выразить
о, ^ < через ^ ^= { оГ i < 0. ПослеДняя Функция диф^
2727 1/4 612 27 У
( о, < { оГ i < 0.
фереицируема всюду. 2,7.27. а = с=1/4; 6=1/2. 2.7.28. Указание. Кривые
пересекаются в тех точках, где sin ах= 1. Так как в этих точках cos ax=Q, то
Уг =/' W sin a*+/ (*) a cos ax = f' (x) = ylt
т. е. кривые касаются.
2.7.30. Указание. При t ф пп уравнения касательной и нормали приво-
приводятся соответственно к виду
«/ = ctg — (х—at) + 2at y = ~ tg -^(x—at).
При t — nBk— 1) (Л = 1, 2, ...) касательная (у = 2а) касается круга в верх-
верхней точке, а нормаль (x = at) проходит через верхнюю и нижнюю точки; при
t = 2kn (& = 0, 1, ...) касательная (х — at) проходит через обе точки, а нор-
нормаль (f/ = 0) касается круга в нижней точке. 2.7.34. -р + f/. 2.7.35. Относи-
Относительная погрешность 6 = А/// « 2d9/sin 2ф. Наиболее надежный результат,
т. е. результат с наименьшей относительной погрешностью, соответствует
значению ф=45°.
К главе III
3.1.2. б) Да; в) нет, так как производная в точке 0 не существует
3.1.5. Ъ = е-+-1. 3.1.7. Нет, так как g (—3)=?C). ЗЛ.9. г) Указание. Рас-
Рассмотреть функции
2х
/() i ¦ 2 + 2arctg;t при |*| > 1,
2х
2rtg при | лг |
3.1.15. а) 5 = 7/2; б) ? = ?/1пЗ; в) ? = A0± УЩ/24; г) неприменима, так
как функция не имеет производной в точке х^=0.
383
3.1.16. 1,26 < In A+e) < 1,37. Указание. Написать формулу Лагранжа
для функции f(x) = \nx на отрезке [е, е+1] и в полученном соотношении
In A+^) = 1 + 1/5 (^ < ? < 6+1) оценить правую часть.
3.1.17. Указание. Применить формулу Лагранжа к функции /(#) = 1п*
на отрезке [1, 1+#], х > 0 и в полученном соотношении In A+*) = */?
A < I < 1+*) оценить правую часть. 3,2.1. в) 2; г) 0; е) —1/2. 3.2.3. б) 0.
Указание. Представить ctgx—\/х = (х—tg x)/(xtg х); в) 1/2. 3.2.5. б) ёг = е.
3.2.6. а) 1; б) 1. 3.2.9. а) 4/7; б) 1п а—1; в) 2; г) я уТ/б; д) 1/а; е) 0; ж) 1;
з) Inа\ и) е~т2п<2\ к) 2/я; л)—1; м) е; н)_2/3; о) 1/2; п) а2/2; р) е/30;
с) 1; т)—1/2. 3.3.5. б) 0,34201. 3.3.6. ?/83 « 3,018350. Указание. у/Ш =
= ?/81+2 = 3A+2/81I/4. Применить биномиальную формулу и удержать
четыре члена.
3.3.7. Указания, б) Написать формулу Маклорена для функции f(x)~tgx
с остаточным членом Я4 (х); в) написать формулу Маклорена для функции
f{) = (l+x)ll2 с остаточными членами R2 (х) и Я3М»
3.4.2. а) f(x)=-Lx*~*-j
б) f(x) = *^ *g g
3.4.3. б) —1/2; в) —1/12; г) 1/3; д) 1.
3.4.4. а) 1 + 2*+*2 —1-*3—1*4--]15*5; б)—х2/2—
В) 1—*/2+*2/12—^/720.
3.5.1. г) Функция убывает в промежутке (— оо, 0), возрастает в проме-
промежутке @, оо); д) функция возрастает в промежутках (—oot 1/2) и C, +°°),
убывает в промежутке A/2, 3); е) функция возрастает на всей оси.
3.5.2 б) В промежутках @, я/4) и Eя/4, 2я) функция возрастает, а в
промежутке (я/4, 5я/4) убывает.
3.5.8. а) Функция возрастает на всей числовой оси; б) функция возрастает
в промежутке (— 1, 0), убывает в промежутке @, 1); в) функция убывает на
всей числовой оси; г) функция возрастает в обоих промежутках (— оо, 0) и
@, оо), где она определена; д) функция убывает в промежутках @, 1) и A, е),
возрастаете промежутке (е, +°°)i е) функция убывает в промежутках (— оо, 1)
и (Ц оо), возрастает в промежутке (—1, 1). 3.5.10. а^0. 3.5.1Ь 6^1.
3.6.1.6) /A) = /C) = 3 — минимум, /B) = 4—максимум; г) /G/5)=— 1/24 —
минимум. 3.6.2. б) f(± 1)=}/~3—минимумы; /@) = 2—максимум.
3.6.3. б) f(— 2) = 160—максимум; f @) = 2—минимум.
3.6.7. б) /i@)=0— минимум.
3.6.8. б) На отрезке [0, 2я]: / (я/2) = —4—минимум, /(Зя/2) = 4 —
максимум;
3.6.10. а) /@) = 0—минимум, / B) = 4е~2—максимум; б) /(—2)=—_1 —
минимум, /B)= 1—максимум; в) /@) = 0—максимум, / (у ] = —-д- у -д- —
минимум; г)/(? 2) = —1—максимум, /@) = 7—минимум; д)/(—• 3) = 3 jJ/3"
— максимум, /B) = —j/44—минимум.
3.6.11. а) Экстремума нет; б) экстремума нет; в) /@) = 0—максимум;
г) /@) = 0—минимум.
3.7.1. в) /A)=1/е—наибольшее значение, /@) = 0—наименьшее значение;
г) /(± I/2) = ЗуV^8 —наибольшее значение, f (± 1) = 0 — наименьшее значение,
3.7.2, б) #@)=я/2—наибольшее значение, у (± Y2 /2 ) = я/3—наимень-
я/3—наименьшее; в) #D) = 6—наибольшее значение, */@) = 0—наименьшее.
3.7.6. а) /(—2)= 16/3—наибольшее значение, /C) = — 37/4—наименьшее;
б) /@) = 2—наибольшее значение, /( i 2) ==0—наименьшее; в)/A/уТ) =
= я/6+0,25 In 3—наибольшее значение, / (j/~3 ) = я/3 — 0,25 In 3—наименьшее*,
334
г) / (я/3) = 3 Y 3/2—наибольшее значение, f (Зя/2) == — 2—на и меньшее;
д) /A) = 1—наибольшее значение, /B) = 2A — In 2)—наименьшее; е) наиболь-
наибольшего значения нет, наименьшее /@)==1.
3.8.3. // = # ^2, где Я—высота цилиндра, ^ — радиус шара. 3.8.7. х=*
= a sin а, у —a cos а, где a = 0,5arctg 2.
Указание. Задача сводится к нахождению наибольшего значения функции
S = 4xy-\-4x{y—*) = 4a2 (sin 2а—sin2a)
в промежутке 0 < а < л/4. 3.8.8. Ртах = ?2/D№/) при W == Wh 3.8.9. /г = 27? =====
= 2 ^/Зу/Bя). 3.8.10. Радиус основания цилиндра r = R/2, где #— радиус
основания конуса. 3.8.11. Уравнение искомой прямой лс/2 + у/4 = 1.
3.8.12. х — а—р или a > р и # = 0 при а^р.
3.8.13. у= jJ/a/B6). Указание. На покрытие одного узла потребуется
1/и часов. Соответствующие затраты выражаются формулой 7* = (a+fa;3)/o =
/+W
/+
3.8.11. ф = я/3. Указание. При ширине доски а площадь поперечного се-
сечения желоба равна a2 (I -j-cos q>)sin q>, где ф—угол наклона боковых стенок
к днищу.
3.8.15. /г/2. Указание. Точка падения струи отстоит от основания сосуда
на v \^~2H/gy где Я = /г—х—высота расположения отверстия, v—скорость
вытекания; поэтому дальность струи определяется выражением
3.8.16. Через a/Bv) часов наименьшее расстояние будет равно а/2 км.
3.9.1. б) Интервалы вогнутости (—оо, 1/3) и A, оо), выпуклости A/3, 1);
точки перегиба (-»-, 12^ |, A, 13); в) интервалы вогнутости (—УЗ, 0) и
()/1Г, оо), выпуклости (—оо, — ]/Т) и @, уТ); точки перегиба
( X T/) (Т Т)
() ) у ) ( ) р
(— J/X — VT/lO), @, 0), (уТ, УТ/Ю); д) кривая везде вогнута; е) интер-
интервалы вогнутости @, #i) и (х2, оо), выпуклости (xi9 х2), где
х2 = е^+ ь>/2; точки перегиба (дгь f/^, (#2, i/2), где
*/l =
3.9.5. а) Точка перегиба C, 3); кривая выпукла при х < 3 и вогнута при
#>3; б) абсцисса точки перегиба * = arcsin-^—j—; кривая вогнута в
Г я . У"—Л / . VT— 1 я\
—..-. f arcsin -—ц— ), выпукла в { arcsin -— » *о" / •
3.10.1. в) у = 0\ г) * = 0; и) у — 2х для х ->> + оо и # = — 2л: для х —> — оо.
3.10.3. a) jc = 3f у = х—3; б) г/ = ± ял:/2 — 1; в) # = *; г) х=±2;
д) у = 2х-л/2.
3.11.2. а) Функция определена всюду, четная. График симметричен отно-
относительно оси Ог/, асимптот не имеет. Минимум у@)=1, максимумы уA) =
= ^(— 1)==3/2. Точки перегиба (± ^3/3, 23/18); б) функция определена в
(__ оо, —1) и (—1, +оо). График имеет вертикальную асимптоту х =—1 и
наклонную асимптоту у~х—3. Минимум у @) = 0, максимум у (— 4) = —256/27.
Точки перегиба (—6, —3296/125) и B, 16/27); в) функция определена
в (—оо, 0) и @, + оо). График имеет вертикальную асимптоту л; = 0. Мини-
Минимум #A/2) = 3. Точка перегиба (— /2/2, 0;; г) функция определена
в (— оо, — 1), (— 1, 1) и A, оо), нечетная. График симметричен относительно
335
начала координат, имеет две вертикальные асимптоты х= ± 1 и наклонную
асимптоту у = х. Минимум у (У^Ъ) = + 3 ^3/2, максимум у(— ^3) =
=—3 ]//2. Точка перегиба @, 0); д) функция определена всюду, четная.
График симметричен относительно оси Оу, имеет горизонтальную асимптоту
# = 0. Минимум у@)—у 4, максимумы у(± ]/^2) =2 у 2. Точки перегиба
(zb 2, у \)\ е) функция определена в (—2, -f-oo). Вертикальная асимптота
х=—2. Минимум */@) = 0, максимум у(—0,73) «0,12. Точка перегиба
(—0,37; 0,075); ж) функция определена всюду. Горизонтальная асимптота
г/ = 0 для х—>-+оо. Максимум #C/4) = C/4еK. Точки перегиба @, 0),
з-/з /з-/з у уз-з^ /Э+/3 /з+/з~у ,-8-п
з) функция определена и непрерывна всюду. Горизонтальная асимптота у~\.
Минимум (/@) = 0, причем точка @,0)—точка излома графика: у'_ @) = — я/2,
3.12.6. 4,4934. 3.12.8. xt = — 2,330; х2 = 0,202; дг3 = 2,128. 3.12.11. 0,6705.
3.12.12. а) 0,27; 2,25; б) 0,21. 3.12.13. а) 1,17; б) 3,07. 3.12.14. 1,325.
3.12.15. 0,5896 и 2,2805. Указание. Для уточнения меньшего корня записать
уравнение в виде х = eo'&x"lt для уточнения большего корня—в виде х =
= 1,25 A +In х).
3.13.1. Нет. Указание. Показать, что в точке х — \ производная не суще-
существует: /1A)= 1; /'+A) = -1.
3.13.2. Указание. Проверить равенство f {b) — f (a) — (b—a) f ((а-\-ЬI2).
3.13.3. Указание. К функции / (х) = аохп-\-... +а„_1 (х) применить теорему
Ролл я на отрезке [0, х0].
3.13.4. Указание. Убедиться, что производная f (х) = 4(хг—\) имеет лишь
один действительный корень х=1 и применить теорему Ролля.
3.13.5. Указание. Производная /' (x) — nxn~1Jrp имеет только один дей-
действительный корень при п четном, и не более двух действительных корней
при п нечетном.
3.13.6. Указание. Производная есть многочлен третьей степени и имеет три
корня. Воспользоваться тем, что между корнями многочлена лежит корень его
производной.
3.13.7. Указание. Из верного равенства lim cos(l/?) = 0 @ < ? < х), где ?
определяется из теоремы о среднем, не следует равенство lim cos(l/*) = 0, так
как нельзя утверждать, что переменная \ при стремлении х к нулю пробегает
все промежуточные значения в окрестности нуля. Более того, \ принимает
только такую последовательность значений Я, для которых lim cos A/5) = 0
3.13.8. Указание. Ошибка заключается в том, что в формуле Лагранжа
для f (х) и ф (х) берется одна и та же точка ?.
3.13.9. Указание, а) К функции \пх на отрезке [Ь, а] применить формулу
Лагранжа; б) применить формулу Лагранжа к функции zP на отрезке [у, х].
3.13.10. Указание. Убедиться с помощью формулы Лейбница, что коэффи-
коэффициенты многочлена Чебышева—Лагерра чередуются по знаку, причем при
нечетных степенях х стоят отрицательные коэффициенты. Вывести отсюда, что
Ln (х) > 0 при х < 0.
3.13.11. Указание. Используя теорему Ролля, показать, что внутри от-
отрезка [х0, хп] имеется по крайней мере п корней первой производной, /2 — 1
корней второй производной и т. д.
3.13.12. Указание. Правило Лопиталя здесь неприменимо, так как произ-
производные и числителя и знаменателя обращаются в нуль во всех точках, где
обращается в нуль множитель sin xt на который мы сократили при вычисле-
вычислении предела отношения производных.
386
3.13.13. Указание, Написать формулу Тейлора с остаточным членом R2:
f (a+h) = f(a) +hf (а)+У№ (а)+~ Г" ("+Ш
сравнивая ее с разложением, приведенным в тексте задачи, получить равен-
равенство LJ?±—JllLJ2L — -_./"'(а + 9^) и перейти к пределу при h—>0.
3.13.14. Указание. Доказательство вести от противного. Предположить,
что e — plq, где р, ^ — натуральные числа, р > q > 1, и по формуле Тейлора
получить при п > р
умножить обе части этого равенства на п\ и, отметив, что — /г! и
f 1+-ГГ+.-.Н—j-j n\—целые положительные числа, а ¦ ( — ) <
< —т-г • — < 1, получить противоречие.
3.13.15. Указание. Убедиться, что функция
/ (sin*)/*» 0<*<я/2,
jr (jc) = < непрерывна на отрезке [0, jt/2].
Проверить, что производная f (х) < 0 внутри отрезка.
3.13.16. Указание. Показать, что /' (х)^0. Проверить, что
< 0 при а> 1,
и воспользоваться возрастанием функции.
3.13.17. Указание. Показать, что функция f(x) = xex—2 возрастает и на
концах промежутка @, 1) имеет разные знаки.
3.13.18. Указание. Показать, что производная
Р (*) = 1/2 + 2* sin (I/*)— cos (I/*) (* ф 0)
в точках х=1/[Bп+1)я] (п = 0, ±1, ±2, ...) равна 3/2, а в точках
*=1/Bшг) равна —1/2, т. е. в любой близости от начала координат производ-
производная меняет знак.
3.13.19. Указание. Убедиться, что вспомогательная функция ty(x) = f(x)—
— ф (*) возрастает.
3.13.20. Указание. Убедиться, что производная во всех точках области
определения функции сохраняет знак, если ad—ЬсфЪ. Если же ad—fo = 0,
т. е. ajc = bld, то функция является постоянной. 3.13.21. р — —6, </=14.
3.13.22. Минимум f(*0) = 0, если ф (*0) > 0 и п — четное; максимум
f(xo) = O, если ф(*0) < 0 и п — четное; точка х0 не является точкой экстре-
экстремума, если п — нечетное. Указание. При п четном функция в некоторой окрест-
окрестности точки х0 сохраняет знак и либо строго больше нуля, либо строго
меньше нуля, в зависимости от знака ф(*0)« При п нечетном функция в неко*
торой окрестности точки х0 меняет знак.
3.13.23. Указание. При * ф 0 / (*) > 0, следовательно, / @)—минимум.
При х> 0 производная /' (х) = 2 — sin 1 cos— положительна в точках
XX X
х=\/Bпп) и отрицательна в точках *= 1/[B/г+1) я]. Аналогично исследуется
случай х < 0. 3.13.24. а) 1 и 0; б) 1 и —2.
3.13.25. а) Наименьшее не существует, наибольшее равно 1; б) функция
не имеет ни наибольшего, ни наименьшего значения.
387
3.13.30. Да. Указание, Так как f (х) меняет знак при переходе через xOt
то xQ—точка экстремума для функции /' (х).
3.13.31. График проходит через точку М(— 1, 2), имеет касательную
у—2=— (*+1) и точка М является точкой перегиба, причем слева от точки М
кривая вогнута вниз, а справа — вверх. Указание. Функция f" (х) возрастает и
меняет знак при переходе через jc =—1. 3.13.32. /г = 1/(ст ]/^2).
3.13.33. Указание. По теореме Ролля между корнями первой производной
лежит хотя бы один корень второй производной. При переходе через один из
этих корней вторая производная должна сменить знак.
3.13.35. Указание. Многочлен имеет вид а0х2п + ахх2п~2 + • • • +an-ix2 + an-
Многочлены такого вида с положительными коэффициентами не имеют дей-
действительных корней.
3.13.36. Указание. Воспользоваться тем, что многочлен нечетной степени
(а значит, и его вторая производная) имеет хотя бы один действительный ко-
корень и хотя бы раз меняет знак.
3.13.37. Указание. Найти предел lim (Bx*+*3+l)/*3—2x— 1).
4.1.2. /=
2
4.1.7. /=-^- (х-\-
3
иальности в знаменателе.
К г л а ве IV
2
-~-*3^2+С Указание. Освободиться от иррацио-
о
4.1.14. /=larctg^
4.1.15. / =
4.1.IS. / =
4.1.20. /=*-
уз
4.1.21. a) i-
2
r) |
x
j/з
+ С.
\/~\0x—V7
; б) -|(*-4
; в) 3 tg x+2cigx + C;
4.1.22. a) In (jt-f j/"l -f-x2)-barcsin x + C\ 6) sin x— cos x+C;
5дгJ
B)
4.2.3. /=4
; г) —0,2 cos 5*—* sin 5a + С
4.2.8. / = — 2^aJ5T+C. 4.2.10. / = y
4.2.13. a) 0,75 У(\+\пх)*-\-С; б) In |1пхЦ-С;
388
в) Гу—?-s
д) —2cosVx + C; е) у ln2x+ln[ lnx| + C.
4.2.14. a) —ig C5-40х+ 14**) A-jcL/3 + C;
б) |-Aпх-5)}Л+1пх
Г) *
10
4.3.2. xarcsinx+J^l—
4.3.14. —cos л: In tg л:+1п | tg(x/2)
4.3.17. (
4.3.18. -|x j/
4.3.19. 2 lO"+~Farcsinx + 4 l^l—x
4.3.20. — 0,5(x/sinax
4.3.27. ^
4.3.28. а)
_
6) l^^^ ^
4.4.2. г) Указание. Применить обобщенную формулу интегрирования по
частям и выразить /„ из получаемого при этом соотношения
/„ = —y sin"-1 x (a sin x—n cosx)-
/„-2— -j /„.
л л о I
4.4.3. /«==
C0SJC
3~~
(n — 1) sin" x n —
cos x , 1 _ cos x .
389
4.4.4. a) /B =
n—1
6> ^^
в) /„ = 4"^
5.1.2. ?L-2x + 4r In1 X
К г л а в е V
16, ,
(*+ iK
5.1.5. 2 In | л:— 1 | — In | д: |—д:/(д: —
5.1.8.
_l_arctg?±._l
5.1.10. 5х+1п*2(лг+2L|д:—2|S+C.
(* + 3)"
5.1.12. — 1/(jc — 2) — arctg(*—2) + C.
^+тarctg*~
TarctgTT
5.2.2. 4 V x +6
5.2.4. г=-ягг
—1 | + C.
(/+2)*
<-v-
x—l.
5.2.9. II—g- x
5.3.3. —2arctg f ¦
l — x2 —-|arcsiiiA:
+ 1
5.3.5. 21n|
—a;— l
- |- In
5.3.6.
5.3.7. (x—
5.4.2. 5
5.3.8. (jc+ l/T+3?
— \п {x + 1 + j/> + 2a: + 5) + C
390
5.4.5.
6.4.6.
5.4.8.
5.4.9. JL C2^-
5-4-10-
5x+7 +
_ In
+ 2
14
5.4.11. -
~2arcsin
—2
5.4.12. -!
15
5.4.13. In
становку х2 =
5.5.2.
5.5.5. ?<
5.5.7. у
5.5.8. 31n
5.5.9.
5.5.11. tl
+ C. Указание. Сначала сделать под-
. 5.5.4. -|-
+С
+
1+Ух 1+Ух
/—2)/15+С.
5.5.10.
' 5-6-6-
5-6-2-
5.6.10. а) —
б) -jtg»*—i.
5.6.12. —sin x—~ sin3 ^ + 4- In
о z
5.6.l4.garctg/1+21^
1—sin^
+C.
5.6.2, a) -*
391
6.7.3. — ~ In (x+ V&— 0 + 4"x Bx2—l
о о
5.7.4. \n
5.7.7. / = arcsin^±J- + C. 5.7.8. / =
2
4
5.8.2. /=4 VT=^ + 21nB—a;—2 |/T=^) —2 (l + fY^c) In * + C.
e о с? / „f a cos/4-sin/ , _ ,
5.8.5. /=ea* j-i-- }-C, где / =
К главе VI
6.1.9. / = 4-C+19)/2 = 44 как площадь трапеции с высотой 5 —1=4 и
основаниями 4-1 —1=3 и 4-5 —1 = 19.
6 112 , -16 l 175 + 125- S ,6 ' ,175 125
6.1.12. stt- 16т__+_, 5„=16т+^-+Т/гЛ,
в.2.2. а) 1; б) 3/2; в) я/6. 6.2.10. а) 7/72; б) 4" 1п 4-; в) "!
г) зх/4 —arctg(n/4); д)^1п2; е) 1; ж) arctgс—я/4; з) я/16; и) 14/15;
к) 4/3; л) \У'Ъ — Y2)I2. 6.3.1. в) 3 < / < 5. Указание. М = /@) = 5/2,
т = /B) = 3/2. 6.3.11. a) (sin 2х)/х\ б) — /"l + лс4. 6.3.14. б) я2/4.
6.3.15. б) j-=— e-^sin*. 6.3.23. a) In х\ б) 3/*. 6.3.24. а) у'* = */1п/;
б) y'x = (tg)!
6.3.25. а) В точке *=1 максимум, в точке х= — 1 минимум; б) в точках
х~—2; 0; 2 минимум, в точках х=±1 максимум.
6.4.3. а) ла4/16 (подстановка x = asin/); б) (^3—Y^)l^ (подстановка
* = tg/).
6.4.6. а) 1^2 --2- + lnl±^L; б) 2A^3—1); в) 8 + -Ц1-Я.
6.4.15. а) 2—2 In 2; б) 0,2 In 112; в) sin (n/24)/(sin (я/8) sin (я/12));
г) /Г—0,5 In B+l/T); д) 0,25 In 3 (подстановка sin x— cos x = t);
е) а3 (я/4 — 2/3) (подстановка * = acos^); ж) ка2/2 (подстановка * = 2asin2/);
з) я/4+1/2.
6.4.16. а) я/6; б) я/4; в) A/4) In C2/17) (подстановка ** = /); г) я/12 (под-
(подстановка хг — а2 cos2^+^2 ^п2 t)-
6.4.17. Подстановка x—l/t не годится, так как эта функция разрывна
при f = 0
6.4.18. Подстановка / = tg(*/2) не годится, так как эта функция разрывна
при * = я.
6.4.19. Указание. Обратная функция x—±Vtb двузначна. Для получения
верного результата надо разбить исходный интервал на два:
2
-2
0
/— Г 5/—
-2
2
0
и применить подстановки: х= — Ytb в —2 <д:<0, х—-\-У~Р в 0 < х < 2.
6.4.20. Нельзя, так как sec/^1, а промежуток интегрирования [0, J].
392
6.4.21. Можно; см. 6.4.12.
а 0 а
6.4.22. Указание. Записав \ / (х) dx = \ / (х) dx + С / (х) dx, в первом
-а -а о
интеграле сделать замену х=—f.
I -I о
6.4.23. С /(arcsinO^+ \ /(я—arcsin t)dt+ \ I Bя +arcsin t)dt.
о l -l
Указание. Представив данный интеграл в виде суммы трех интегралов по
промежуткам @, я/2), (я/2, Зя/2), (Зя/2, 2я), сделать в них замену перемен-
переменной соответственно x — arcs\nt, х = я—arcsin tt x = 2n-\-aicsin t.
6.5.3. 1) Если fix)—четная функция, то
я я я
С f{x)cosnxdx = 2 f f(x) cosnxdx, a V f(x) sinxdx = 0.
-n о -я
я я
2) Если f (x) — нечетная функция, то \ f (x) cos nxdx = Of a \ f(x)$innxdx=
-я -я
я
= 2 С / (х) sin л dx.
о
6.5.4.0. 6.6.3. 6—2е^ 6.6.5. я /2"—4. 6.6.6. я—2. 6.6.13. а) я/2 — 1;
б) — 1/в; в) я/4 —(//9)я + A/2)_1пC/2); г) я/4—1/2; д) In 2—1/2;
е) In B/8); ж) я/2—1; з) 16я/3—2 |/*3 .
6.6.14. Указание. Два раза проинтегрировать по частям, полагая первый
раз u = (arccos*)*, второй раз « = (arccos x)".
6.6.15. Указание. Интегрировать по частям, полагая и = х.
6.7.4. а) 0,601. Указание. Оценить | /IV (х) \ на отрезке [я/4, я/2] и взять
2д = 6; б) 0,7462. 6.7.5. 0,96.
6.8.1.
\
х—*2/2 при 0<х<1,
1/2 при 1 ¦
с—2K/3-f-l/2 при 2 < ,
Непрерывность проверяется непосредственно. Утверждение о производной
требует проверки только в точках х=1, х — %
6.8.2. Указание. Убедиться, что функция f (х) непрерывна как внутри
интервала @, 1), так и на концах / lim f(x) = f(O) и lim /(x) = f (l)\.
yx-* + o x->i-o J
6.8.3. Нет. Указание. Рассмотреть функцию
/ ч_/ Ь если х рационально,
'PW""^ —1, если х иррационально на отрезке [0, 1].
ь
6.8.4. 1 — УТ. Указание. J /" (x)dx = f (b)—f (a).
а
6.8.5. Указание. Положив для определенности х > 0 и
Е(х)
393
воспользоваться аддитивностью интеграла
л: 1 2 п х
V Е (х) dx = \ Е (х) dx+ \ Е (х) dx + ... + \ Е (х) dx+ \ Е (х) dx.
001 п-\ п
6.8.6. Первообразная Ft (x) приведет к верному результату, a F2 (x) —
к неверному, так как эта функция терпит разрыв в промежутке [0, я].
X
6.8.7. F (x) = yo+\f(t)dt. Указание. Любую первообразную F (х) можно
X
представить в виде F (*)= \ / (t)dt-\-C. Полагая x=xQt находим С=у0.
п о о t ! 1 е2&—е2^°
ft Я й /- — — in —————
U.O.О. fe "о" 11J QL О
6.8.9. Функция определена на отрезке [ — 1, 1], нечетна, возрастает; на
отрезке [ — 1, 0] выпукла, на отрезке [0, 1] вогнута; точка [0, 0]—точка
перегиба.
6.8.10. Указание. Функция
хх при 0 < х ^ 1,
1 при * = 0
непрерывна на отрезке, достигает наименьшего значения т = е~1/в « 0,692 при
х—\/е и наибольшего значения М = \ при * = 0 и при х=\.
6.8.11. Указание. Проинтегрировать неравенство 2/jx^(sin x)/x< 1.
6.8.12. Указание. Проинтегрировать неравенство
Vxsinx > Vx*—x*IQ=x V\— х2/6 в
и записать неравенство Шварца—Буняковского
Л/ -$¦ =—?__
F 8 2|A2
6.8.14. Указание. Применить неравенство Шварца—Буняковского в виде
Ь ь -12 ь ъ
Ь ь -12
a J
6.8.15. Указание. Заменить arctg* = ?/2.
X
6.8.16. Указание. Если f (х)—четная функция, то F(x)=\f(t)dt — нечет-
о
ная функция, так как
-X
о
X
Если же f{x) нечетная функция, то F (x)= \ f (t) с(/~четная функция,
так как
394
все остальные первообразные имеют вид F(x)+C и поэтому тоже являются
четными функциями.
6.8.17. Указание. Производная от интеграла / по а равна нулю: -т- =»
К главе VII
7.1.4. a) In 2; б) B/3) B |/~ — 1); в) 3/4; г) 1: д) 1/2. 7.2.2. а) 1/2;
б) 4 + у 1п Лг\ ~ °'283- 7-2-5- я/4- 7-2Л0- 2i^h V&+h2)- 7.2.13. a) jn = 5/3;
б) |д, = 1п2; в) |х=8/AпЗ) + 2. 7.2.15. 2/г/З. 7.2.16. 2/0/я. 7.3.4. 35/6,
7.3.6. A+Aarcsin-!-. 7.3.11. 8/15. 7.3.13. 9. 7.3.16. l/(m+ 1). 7.3.19. €4/3.
6 L О
7.3.20.8/3. 7.3.21. 2я —B j/T)lnB+}^3). 7.3.22. 0,75я. 7.3.23. 128/15.
7.3.24. 1/3. 7.3.25. 4/3. 7.3.26. 8/15. 7.3.27. 1/12. 7.3.28. 91/30. 7.4.6. 8/5,
7.4.8. 0,75яа&. Указание» Кривая симметрична относительно осей координат й
пересекает их в точках х= ± а, у= ± Ъ.
7.4.9. а) 8/15. Указание. Кривая симметрична относительно оси Ох, дважды
пересекая ее в начале координат при t—±\. Петля расположена во второй
и третьей четвертях; б) 8/15. Указание, Точки самопересечения кривой нахо-
находятся следующим образом: y = tx(t), поэтому у (t1) = t1x(t1)~t2x (t2) при
tx ф ?2JH x(tl) = x(t2) только при условии х (^1)==^(^2) = 0, т. е. ^i = 0; t2 = 2;
в) 8 /У/5.
7.4.10. 0,25лаЬ. Указание. Кривая симметрична относительно обеих осей
координат и дважды проходит через начало координат, образуя две петли.
Поэтому достаточно вычислить четвертую часть искомой площади, отвечающей
изменению t от 0 до я/2, и результат умножить на 4,
7.4.11. Зс4я/(8а6) Указание. Кривая напоминает астроиду, вытянутую в
вертикальном направлении.
7.5.2. а) Зя/2; б) яа2/4. Указание. Кривая является окружностью радиуса
а/2, проходящей через полюс и симметричной относительно полярной оси,
— я/2<ф<я/2. __
7.5.6. 2а2 Eя/8—1). 7.5.8. а) яа2/8; б) яа2/8. 7.5.9. а2 Gя/12— \^Ъ ).
7.5.10. яа2/32. Указание. Кривая проходит через полюс, образуя две петли,
симметрично расположенные относительно оси Оу в первой и второй четвер-
четвертях. Достаточно вычислить площадь одной петли, соответствующей изменению ф
от 0 до я/2, и результат удвоить.
7.5.11. E/32) яа2. Указание. Кривая проходит через полюс, симметрична
относительно полярной оси, расположена в I и IV четвертях. Достаточно вы-
вычислить площадь верхней части фигуры, соответствующей изменению ф от 0
до я/2, и результат удвоить. 7.5.12. а2A+я/6—^3/2).
7.5.13. яа2/2. Указание. Кривая симметрична относительно осей координат
и пересекает их только в начале координат, образуя четыре петли, по одной
в каждой четверти (четырехлепестковая роза). Поэтому достаточно найти пло-
площадь одной петли, соответствующей изменению ф от 0 до я/2, и результат
умножить на 4.
7.5.14. /Тяа2. Указание. Кривая симметрична относительно осей координат
и биссектрис координатных углов; отсекает на осях равные отрезки. Начало
координат—изолированная точка. Достаточно вычислить площадь восьмой
части фигуры, соответствующей изменению ф от 0 до я/4, и результат умно-
умножить на 8.
2
7.6.2. 9 у я. Указание. Плоскость, перпендикулярная к оси Ох в точке х,
пересечет шар по кругу радиуса г= 1^16—jc2, поэтому площадь сечения
5(*) = яA6—х2).
395
7.6.5. 0,5яа2Л. Указание. Площадь треугольника, находящегося на рас-
расстоянии х от центра круга, равна h Ya%—*2*
7.6.10. 2я2а2&. 7.6.11. 8/7 (см. 7.3.9). 7.6.14. 5я2а3. 7.6.16. а) 2паЬ A +
+ 1/(Зс2); б) A6/3) а; в) A/2) ab№n. 7.6.17. B/3) а3 tg а. 7.6.18. а) 12я;
б) A6/15) я; в) F4/5) я, г) я2; д) F4/3) я; е) D/3) яа3. 7.6.19. яа3/20.
7.6.20. я2/12. 7.6.21. -1яа3(е2'/я — е~2^) + яа2с = ~^ sh^ + rca2c.
7.6.22. (я/20)(бя + 5 j/*3 ). Указание. Абсциссы точек пересечения хг = —я/3;
*2 = Я/3. 7.6.23. A9/48) я. 7.6.24. A27/7) я. 7.6.25. 16яс6/(Ю5а62). Указание.
Эволюту эллипса представить в параметрическом виде так: x~(c2fa) cos31;
t/ = — (c2/6)_sin3 *, где_с=/а2 —ЬК 7.6.26. D/3) яа3. 7.6.27. я2а3/D |/ );
(яа3/4) [l^2 ln(l + |^2)—2/3], Указание. Перейти к полярным координатам.
7.6.28. D/21) яа3. 7.7.2. 112/27. 7.7.4. 1п*а~*1д. 7.7.8. а) /бГ +
+ In (/2" + J/T); б) 2 In B — |/У). Указание^ *i = — я/2; *2 = я/3;
bJJ/*3/3. 7.7.9. а(а + 2)/2. 7.7.10. 10 F7/27+ Уъ). 7.8.2._8а. 7.8.5. 13/3.
Указание. Кривая пересекается с осями при /г = 0 и t2— J/8 . 7.8.7. 4 У^З".
7.8.8. 16а. 7.8.9. 8яа. Указание. См. рис. 79. 7.8Л0. 4 (а3—Ь*)/(аЬ). 7.8.11. я3/3.
7.8.12. При * = 2я/3 точка М_[а Bя/3—1/~3"/2), За/2]. __7.9.5. 1,5яа.
7.9.9. 5/12 + 1п C/2). 7.9.10. 2 ^яа. Указание^Кривая р = 2 У2а cos (ф —я/4)
есть окружность. 7.9.1J. р [V2 +1п (l + V2 )]. 7.10.3. а) 14я/3^__б) 62я/3.
7.10.5. 2яA+4я/C/"З)). _ 7.10.8. я/2. 7.10.14. C4 /*17—2) я/9.
7.10.15. 2я [^2 +1п (l + Y2 )]. 7.10.16. E6/3) яа2. 7.10.17. B ]/"/5)я (еи—2).
7.10.18. 29,6я. 7.10.19. 4я2а2. 7.10.20. A28/5) яа2. 7.11.7. 16а2, где а—ра-
а—радиус основания цилиндров. 7.11.8. 1,5я. 7.11.10. а) 8/15; б) 7/50 —
— (l/4)_arctg A/2). 7.11.11. а) яа2/4; б) (р2/6) C + 4 VJ); в) A/8) Eя +
+ 6/). _ 7.11.13. (а/2)B1пЗ—_1). 7.11.14. (/2 /3)E |/~5 —2 |^2 )
7.11.17, 2я //15. 7.11.18. яа2 (/>?. 7.11.19. яа6(/^/Зс2 —/ + 2с/3).
7.11.20. nabh/3. 7.11.21. 12я. _ 7.11^2. (D / —6)/_9) яЬ2а.
7.11.23. D/21) яа3. 7.1!.24.__а) я [(/ — ^2 ) + (]/ + 1) (/ —1)/2];
б) ^B1 |Пз + 2 1п1±р?); в)
7.12.2. B/3) уЯ3. 7.12.4. я^4/4. 7.12.9. Л^/?2со2/4. 7.12ALnabhd. 7A2A2._nrdh2.
7.12.13. A/12)_я/?зя. 7.13.3._0,25я^3. 7.13.7. Мх = (\/3){5 fd'— l);
М =(9/8) / +A/16IпB+)/~5). 7.13.8. Мх=(Ь/2) fd' + b2; Му ==
= (а/2) /а2 + 62. 7.13.9. / +ln(l + /'2). 7.13.10. 0,15. 7.13.11. lx = b^/\
/у = а36/12. 7.13.12. (а + 3^)/13/12. 7.13.16. *с = */г = 0,4а. 7.13.19.
7.13.26. xc = /?sina/a; ^ = 0.
7.13.28. jcc = 5a/8; yc = 0. 7.13.29. jcc = — 0,2 B^ — 6^/(^
= 0,2а(в2я—2е«)/(^—е«^). 7.1ЭЛ0. 4,5яа3. 7.13.31. ^ = 0; yc /()
7.14.1 |(л-я)/(«+Я)|; *\ш-п)!ип+п)\> если m и п —оба четны;
2| (/л-л)/(/л+/г) I» ес^и m и л—оба нечетны; | ш~пIш*п) I» если m и п — разной
четности. Указание. Кривые ут~хп и уп = хт имеют в первой четверти две
общие точки @, 0) и A, 1). Площадь фигуры, лежащей в первой четверти,
равна
В зависимости от четности и нечетности т и п эта
о
фигура либо симметрично отображается относительно осей координат (m, n
четны) либо симметрично отображается относительно начала координат (m, n
нечетны). Если тип разной четности, то кривые ограничивают лишь площадь,
лежащую в первой четверти.
7.14.3. Указание. Воспользоваться формулой для вычисления площади
в полярных координатах,
396
7.14.4. Указание. Так как фигуры равновелики, то функция S(x), входя-
ь
щая в формулу объема V=\ S(x)dx, одна и та же, а значит, и значения
а
интегралов также равны.
7.14.5. Указание. Формула непосредственно следует из формулы Симпсона
h
о
для шара S(x) = n(r2—х2); для конуса S(x) — ztr2x2/h2] для параболоида вра-
вращения S(x) — 2npx и т. д.
7.14.6. Указание. Разбить криволинейную трапецию на полоски ширины
Ах и составить выражение для дифференциала объема AV = 2лхуАх.
7.14.8. Указание. Воспользоваться формулой для вычисления длины кривой,
заданной параметрически.
7.14.9. In (я/2). Указание. Ближайшая к началу координат (/=1) точка с
вертикальной касательной соответствует значению параметра t = n/2.
7.14.13. 2л_//15.
7.14.14. У2-г. 7.14.16. а) 0,5 In (* + {/), б) я/4 — 0,5 arcsinx.
К главе VIII
8.1.2. б) A/2) In 2; в) 1; г) 1 — In 2; д) я; е) 1/2.
8.1.6. а) Расходится. Указание. [In (x2 + \)]/x > 1/х при х> Уе—1;
б) сходится; в) расходится. Указание. B+ cos х)/У х > \1Ух\ г) сходится;
д) расходится.
8.1.17. а) 0. Указание. Представить интеграл как сумму двух слагаемых:
С \пх С \пх р \пх
) 1 л.х2^х== 1 1 4-х2 ~^~ ) 1 ~\-х2 ^° ВТОРОМ слагаем(>м сделать подста-
0 0 1
00 1
Г 1пх С \пх
новку x—ijt и показать, что \ | \Х2"Х=— \ \ \ Х2dx\ б) т\/2.
1 0
8.2.2. а) 9а2/з; б) расходится; в) расходится; г) б JJ/2; д) я/3; е) схо-
сходится при р< 1 и расходится при р^=1. 8.2.7. а) Сходится; б) расходится;
в) сходится; г) сходится; д) расходится; е) сходится. 8.2.11. а) Расходится;
б) 2 У\п 2; в) 51/7. 8.2.14. а) Сходится; б) расходится; в) расходится;
г) сходится; д) сходится. 8.3.7. а) я/2; б) 2я. 8.3.8. Зяа2. 8.3.9. 1/2. 8.3.10. 4я/3.
8.3.14. mgR. Указание. Закон притяжения тела Землей определяется
формулой f — mgR2/r2, где т—масса тела, г—расстояние тела до центра Земли.
R — радиус Земли.
8.3.15. ех. Указание. Электрические заряды взаимодействуют с силой 2
где ег и е2 — величины зарядов, г—расстояние между ними.
8.4.1. Указание. Представить интеграл в виде суммы
+ оо
Г
J
а +
dx C dx С dx
хР\пЯх
и применить частные признаки сходимости, учитывая, что в первом интеграле
ln* = ln[l+(*—Щ ~~ х—1 при х—> \, а во втором интеграле при q<0
логарифмическая функция растет медленнее любой степенной функции.
397
8.4.2. Указание. Применив подстановку x^—tf привести заданный интеграл
+ со +оо
к виду ±~ \ t{p+l)ti-1 sin tdt. Представить интеграл \ t{p+l)/q~l sintdt
+со
Г sin f ... f sin t
в виде суммы \-jz~at-\- \ —ju-dt, где a=l — (p-\-\)/q, и показать, что
о i
интеграл сходится абсолютно при 1 < a < 2 и условно при 0 < а<; 1. Заме-
Заметим, что при (p-\-l)/q = Q интеграл приводится к условно сходящемуся инте-
+ СО +00
Г sin t Г sin /
гралу \ —j-dt, а при (p-\-\)lq=—1—к расходящемуся интегралу \ -j>-dt.
о о
8.4.3. Указание. Представить заданный интеграл в виде суммы
1/2 1
V хР-1 (\~-х)Ч-хdx+ \ xP-x(\— xL-ldx и применить частный признак
О 1/2
сравнения.
т
8.4.4. Указание. Если |а| ф | р |, то \ sin ax-sin $xdx ограничен.
о
8.4.5. Указание. Заменой переменной t = x2 интеграл приводится к гамма-
функции Эйлера,
со {3
8.4.6. Указание.
а
Ра
~ + \
{3
= A In ~ + \ dx. Применив обобщенную теорему о среднем, показать,
аа
что последний интеграл стремится к нулю при а—>»0.
8.4.7. Указание. Для первого интеграла взять функцию f(x) = e~x, для
второго—функцию f(x)=cosx и воспользоваться результатами задачи 8.4.6.
8.4.8. Сходится при т < 3, расходится при т^З. Указание. Воспользо-
Воспользоваться эквивалентностью 1 — cos х~х2/2 при х —> 0.
я
8.4.9. Указание. Представить \ — в виде суммы двух интегралов
J (sin *)*
Я/2 Я
С* dx Г* Иг
\ zZ [^ V ; подстановкой х = п — t второй интеграл свести к пер-
J (sinx)fe ^J2 (sin х)Л
вому и воспользоваться эквивалентностью sin а:—л: при х —> 0.
оо Я/2
Г* sin х A —- cos х) Р sin д: A — cos x)
8.4.10. Указание. \ *-р dx= J к-р Чх+
о о
С sin х A — cos л:)
_|_ 1 _ ?Xt Подынтегральная функция первого слагаемого в пра-
Я/2
вой части при х—>0 является бесконечно большой порядка s—3. По частному
признаку сравнения первый интеграл сходится абсолютно при s—3 < 1, т.е.
s < 4, и расходится при s^4. Второе слагаемое в правой части сходится
абсолютно при s > 1, так как функция sin х A—cos x) ограничена. Если
же 0<s<l, то второй интеграл сходится условно как разность двух
3S8
00 CO
Г* sin % С sin х- cos л:
условно сходящихся интегралов \ -jp- ах и \ -р ах (см. зада-
Я/2 Я/2
чу 8.1.13).
8.4.11. Указание. Интеграл B) может расходиться. Например, пусть
1, 2/1Я<*<Bл+1)я,
Интеграл \——dx сходится (см. задачу 8.1.13). Однако \ y(x)dx =
г) % %) X
о о
оо оо
С Isinjcl Г
— \—-—dx расходится (см. ту же задачу). Если же интеграл \f(x)dx
О а
оо
сходится абсолютно, то и интеграл \ / (х) ф (х) dx сходится абсолютно: если
а
| ф (лг) | < С, то | / (х) ф (х) | < С | / (х) |, и остается использовать теорему срав-
сравнения.
8.4.12. Указание. Преобразовать интеграл f (х) подстановкой у —я/2—г
Я/2-х
к виду /(*)= \ lnsinzdz. Учитывая, что sin z = 2 sin (z/2)« cos (г/2), при-
Я/2
вести последний интеграл к сумме трех интегралов.
8.4.13. Указание. Положив и = In cos x, cos2nxdx = dv, проинтегрировать
Я/2
по частям и получить равенство 1п—-^ \ ът2пх cos? dxf пфО. Так как
о
sin 2nx — s\n Bn—2)x- cos 2*+sin 2x- cos Bn—2)xt
то
'~^И
п ч« • i ^ ' cos а:
/2 Я/2 -I
С sinB/z—2)A:-sin2A:dA: + 2 С sin2^-cosB/z—2)xdx .
о о J
Непосредственным вычислением проверяется, что при п^2 второе и третье
слагаемые равны нулю. Поэтому при п ^ 2
я/2
Г
i
о
Я/2
1 Г . ft sinjc . я ? 1 я . 2 1 я
Так как h — -^ \ sin 2х «*.*—-j-, .« «2 2
о
=^—; И ПО ИНДУКЦИИ /п = (—IO1 Я/D/г).
о • 4
Исаак Абрамович Марон
Дифференциальное и интегральное исчисление
в примерах и задачах
(функции одной переменной)
М., 1970 г., 400 стр. с илл.
Редакторы: Л. 3. Румшиский, Н П. Рябенькая
Техн. редактор А. А, Благовещенская
Корректор Г. С. Смоликова
Сдано в набор 1/VI 1970 г. Подписано
к печати 29/1Х 1970 г. Бумага 60x907ie Физ.
печ. л 25. Условн. печ. л. 25. Уч.-изд. л.
25,71. Тираж 110 000 экз Т-15401 Цена
книги 82 коп. Заказ №1128
Издательство «Наука»
Главная редакция
физико-математической литературы
Москва, В-71, Ленинский проспек; "
Ордена Трудового Красного
Первая Образцовая типог]
имени А А. Ждано:
Главполиграфпрома Комитет;
при Совете Министров
Москва, М-54, Валова