Основы математического анализа. Ч.1 - Ильин В.А., Позняк Э.Г.

1 - Предварительные сведения об основных понятиях математического анализ
4 - Понятие функции. Предельное значение функции. Непрерывност
7 - Комплексные числа. Алгебра многочленов. Интегрирование в элементарных функция
8 - Основные теоремы о непрерывных и дифференцируемых функция
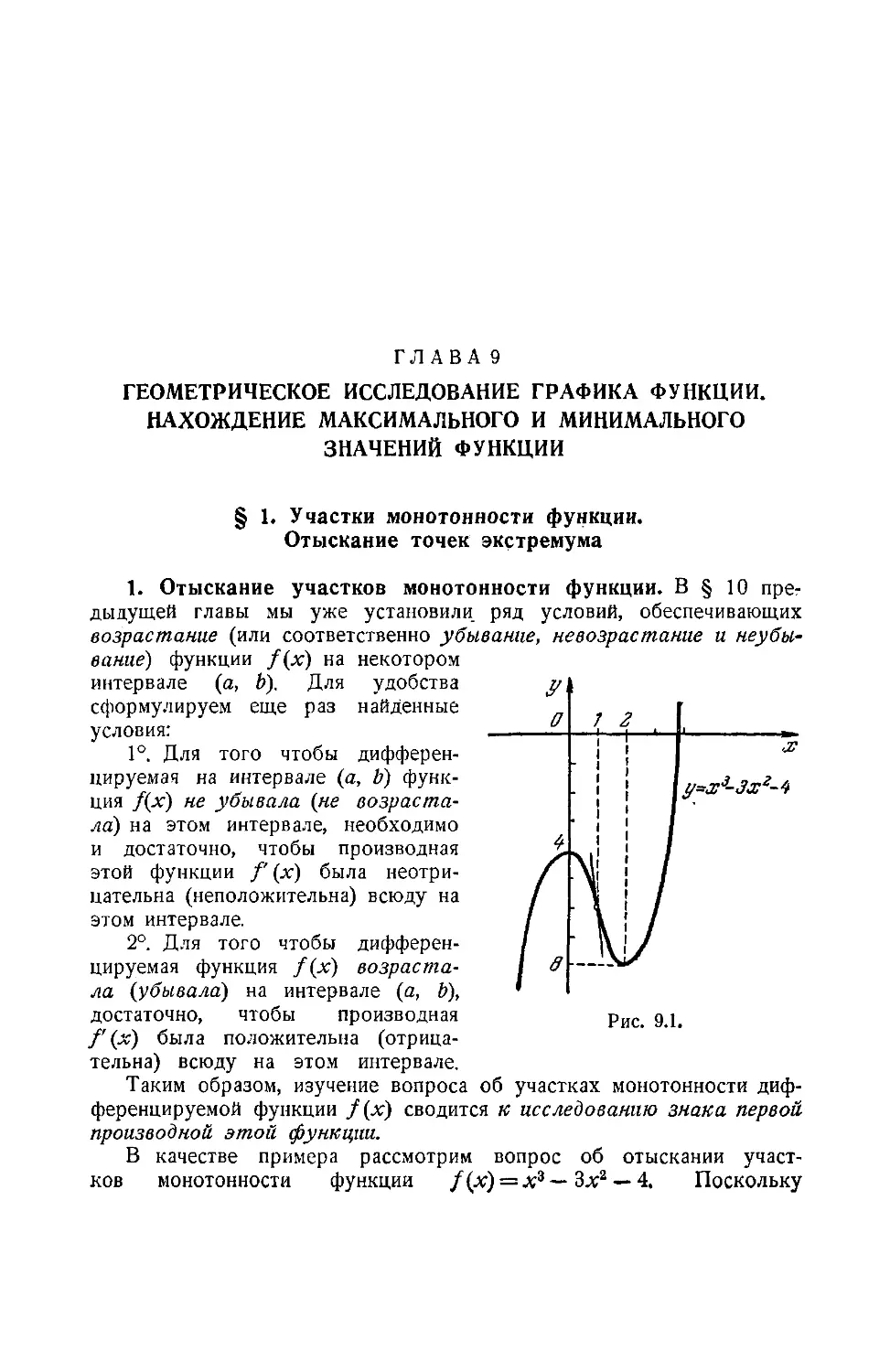
9 - Геометрическое исследование графика функции. Нахождение максимального и минимального значений функци
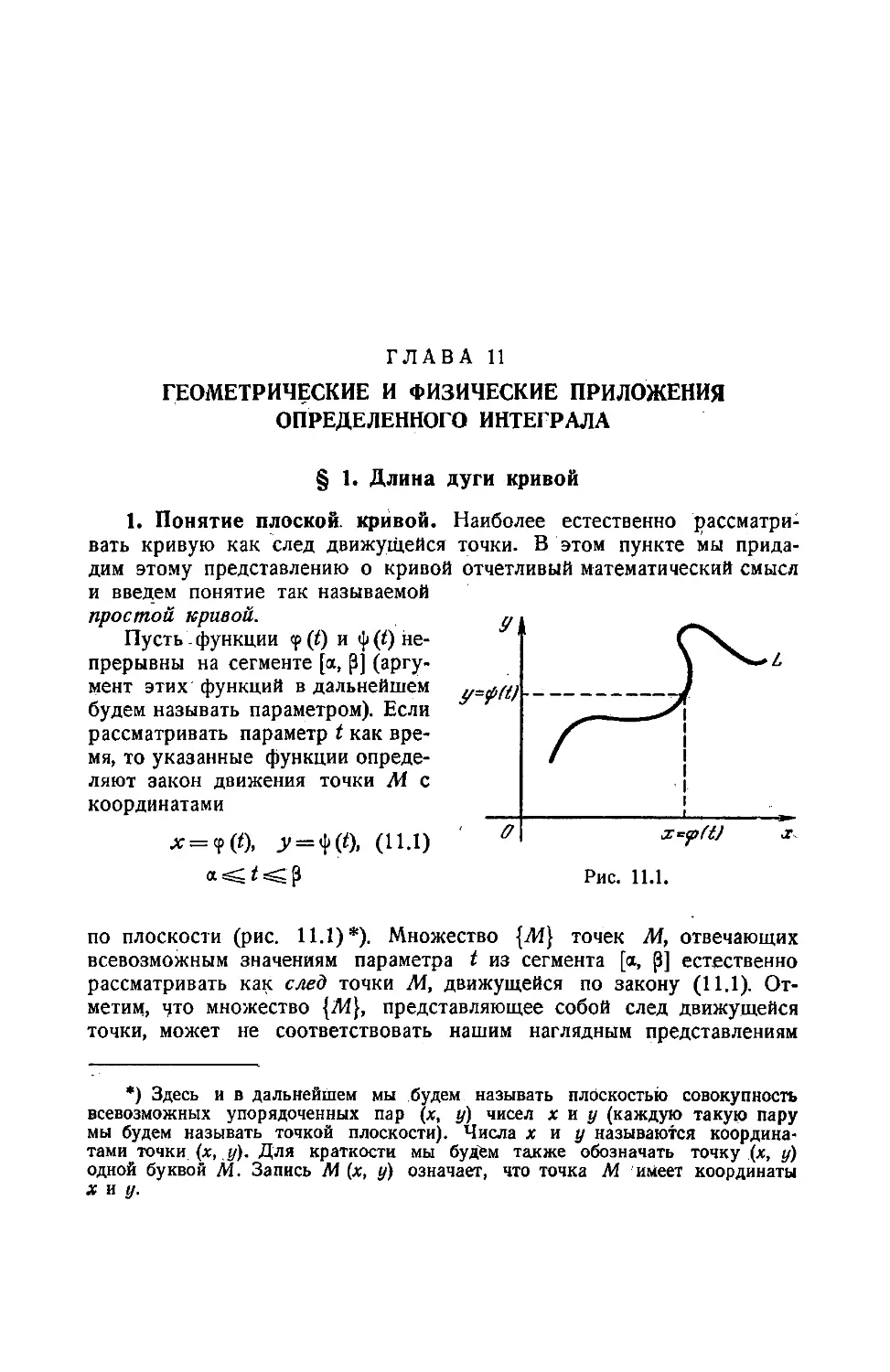
11 - Геометрические и физические приложения определенного интеграл
12 - Приближенные методы вычисления корней уравнений и определенных интеграло
15 - Теория неявных функций и ее приложени
16 - Некоторые геометрические приложения дифференциального исчислени
Приложение - Дальнейшее развитие теории вещественных чисе
Автор: Ильин В.А. Позняк Э.Г.
Теги: математика математический анализ издательство наука главная редакция физико-математической литературы
Год: 1971
Похожие
Основы математического анализа. Ч.2
Основы математического анализа. Том 1
Задачи по математическому анализу, Ч.1
Математический анализ. Конечномерные линейные пространства
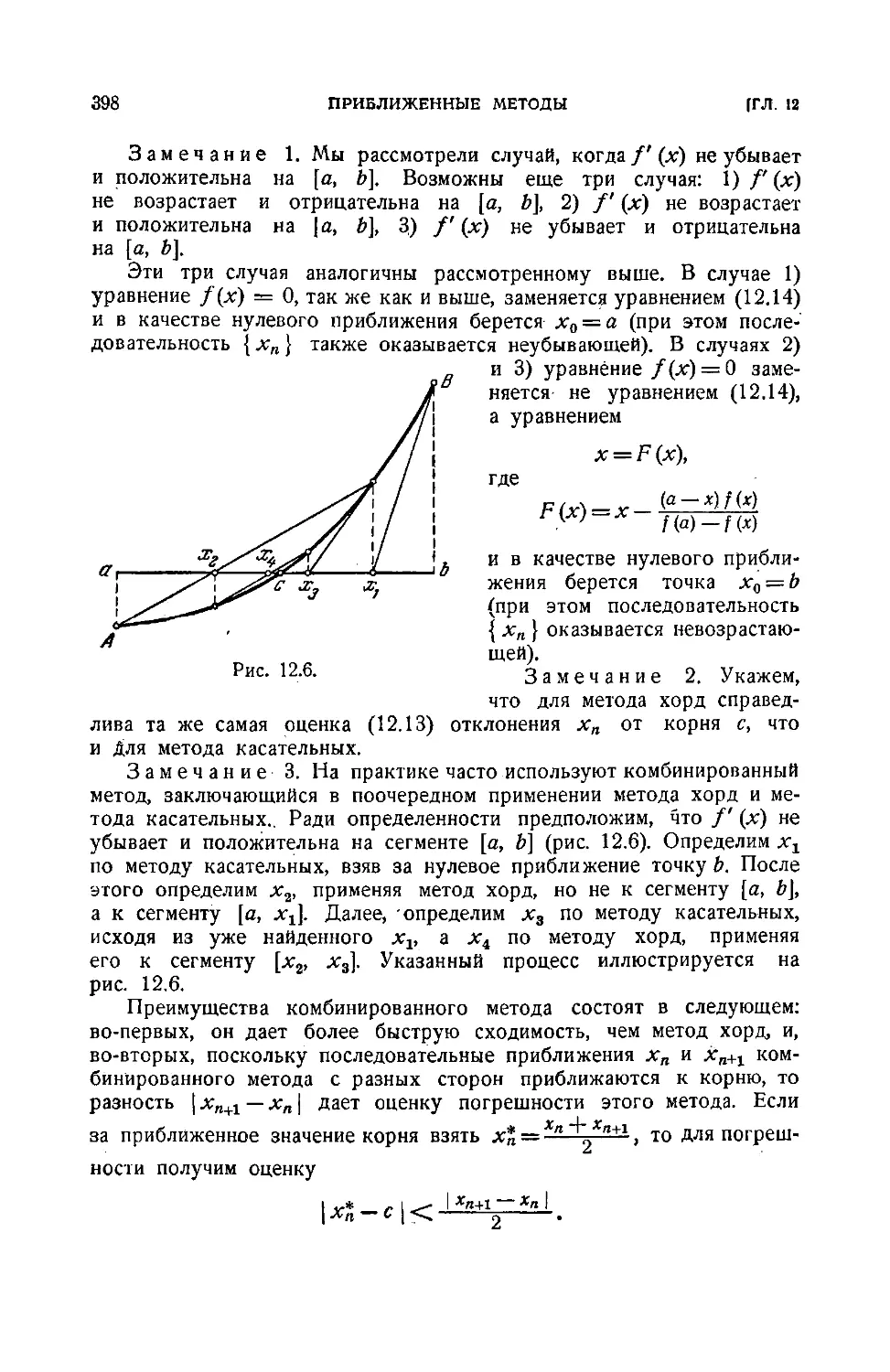
Текст
                    основы
МАТЕМАТИЧЕСКОГО
АНАЛИЗА
В А.ИЛЬИН.Э.Г ПОЗНЯК

КУРС
ВЫСШЕЙ МАТЕМАТИКИ
И МАТЕМАТИЧЕСКОЙ
ФИЗИКИ
Под редакцией
А. Н. ТИХОНОВА, В. А. ИЛЬИНА,
А. Г. СВЕШНИКОВА
ВЫПУСК 1
ОСНОВЫ
МАТЕМАТИЧЕСКОГО
АНАЛИЗА
ЧАСТЬ I
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 10 7 1
В. А. ИЛЬИН, Э. Г. ПОЗНЯК
основы
МАТЕМАТИЧЕСКОГО
АНАЛИЗА
ЧАСТЬ I
ИЗДАНИЕ ТРЕТЬЕ.
ИСПРАВЛЕННОЕ И ДОПОЛНЕННОЕ
Допущено Министерством
высшего и среднего специального образования СССР
в качестве учебника
для студентов физических специальностей
и специальности «Прикладная математика»
университетов
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1 971
ОГЛАВЛЕНИЕ
От редакторов серии................................................. 14
Предисловие к третьему изданию...................................... 13
Предисловие к первому изданию......................................  15
Глава 1. Предварительные сведения об основных понятиях математи-
ческого анализа....................................................  17
§ 1.	Математические’ понятия, возникающие при описании движения 17
§ 2. Мгновенная скорость и связанные с ней новые математические
понятия.......................................................... 20
§ 3.	Задача о восстановлении закона движения по скорости и
связанная	с ней математическая проблематика.................. 27
§ 4.	Проблемы, возникающие при решении задачи о вычислении
пути............................................................   29
§ 5.	Заключительные замечания.................................... 33
Глава 2. Теория	вещественных чисел................................ 35
§ 1.	Вещественные числа ........................................  35
1.	Свойства рациональных чисел (35). 2. Об измерении отрез-
ков числовой оси (37). 3. Вещественные числа и правило их
сравнения (40). 4. Приближение вещественного числа рацио-
нальными числами (43). 5. Множества вещественных чисел, огра-
ниченные сверху или снизу (44).
§ 2.	Арифметические операции над вещественными числами. Основные
свойства вещественных чисел....................................... 47
1.	Определение суммы вещественных чисел (47). 2. Определение
произведения вещественных чисел (50). 3. Свойства веществен-
ных чисел (50). 4. Некоторые часто употребляемые соотноше-
ния (53).
§ 3.	Некоторые конкретные множества вещественных чисел........... 53
Дополнение 1 к главе 2. О переводе чисел из десятичной сис-
темы счисления в двоичную и из двоичной * системы в десятич-
ную ........................................................   54
I.	Перевод чисел из десятичной системы счисления в двоичную
(54). 2. Перевод чисел из двоичной системы счисления в десятич-
ную (56).
Дополнение 2 к главе 2. Об ошибках в округлении чисел в систе-
мах счисления с четным и нечетным основаниями................. 56
Глава 3. Предел последовательности . ..............................  58
§ 1.	Числовые последовательности................................. 58
1.	Числовые последовательности и операции над ними (58).
2.	Ограниченные и неограниченные последовательности (59).
6
ОГЛАВЛЕНИЕ
3.	Бесконечно большие и бесконечно малые последовательно-
сти (60). 4. Основные свойства бесконечно малых последова-
тельностей (62).
§ 2.	Сходящиеся последовательности и их основные свойства ...	64
1.	Понятие сходящейся последовательности (64). 2. Основные
свойства сходящихся последовательностей (66). 3. Предельный
переход в неравенствах (68).
§ 3.	Монотонные последовательности................................... 70
1.	Определение монотонных последовательностей (70). 2. Приз-
нак сходимости монотонной последовательности (71). 3. Некото-
рые примеры сходящихся монотонных последовательностей (72).
4. Число е (75).
§ 4. Некоторые свойства произвольных последовательностей и число-
вых множеств ....................................................... 76
1. Подпоследовательности числовых последовательностей (76).
2. Предельные точки последовательности (78). 3. Существова-
ние предельной точки у ограниченной последовательности (79).
4. О выделении сходящейся подпоследовательности (82). 5. Необ-
ходимое и достаточное условие сходимости последовательности (83).
6. Некоторые свойства произвольных числовых множеств (86).
Дополнение 1 к главе 3. Теорема Штольца.............................. 88
Дополнение 2 к главе 3. О скорости сходимости последовательности,
приближающей У а................................................ 92
Глава 4. Понятие функции. Предельное значение функции. Непрерыв-
ность .............................................................. 95
§ 1. Понятие функции . . ........................................ 95
,	1. Переменная величина и функция (95). 2. О способах задания
функции (97).
§ 2.	Понятие предельного значения функции........................ 98
1.	Определение предельного значения функции (98). 2. Ари-
фметические операции над функциями, имеющими предельное
значение (101). 3. Сравнение бесконечно малых и бесконечно
больших функций (102).
§ 3.	Понятие непрерывности функции............................   104
1.	Определение непрерывности функции (104). 2. Арифмети-
ческие операции над непрерывными функциями (106).
§ 4.	Некоторые свойства монотонных функций . , . ............... 106
1.	Определение и примеры монотонных функций (106). 2. Поня-
тие обратной функции. Монотонные функции, имеющие обрат-
ную (107).
§ 5.	Простейшие элементарные функции............................. ПО
1.	Рациональные степени положительных чисел (110). 2. Пока-
зательная функция (112). 3. Логарифмическая функция (115).
4.	Гиперболические функции (117). 5. Степенная функция
с любым вещественным показателем а (117). 6. Тригонометри-
ческие функции (120). 7. Обратные тригонометрические функ-
ции (124).
§ 6.	Предельные значения некоторых функций...................... 125
1.	Предварительные замечания (125). 2. Предельное значение
функции Sln * в точке х = 0 (первый замечательный предел)
/ 1 \*
(126	). 3. Предельное значение функции (1-|- —1 ПРИ х-*-оо
(второй замечательный предел) (127).
ОГЛАВЛЕНИЕ
7
§ 7.	Понятие сложной функции..................................   130
1.	Определение сложной функции (130). 2. Непрерывность и пре-
дельные значения некоторых сложных функций (131). 3. По-
нятие элементарной функции. Класс элементарных функций
(136).
§ 8.	Классификация точек разрыва функций........................ 136
1.	Точки разрыва функции и их классификация (136). 2. Кусочно
непрерывные функции (139).
Дополнение к главе 4. Доказательство утверждения из п. 6 § 5 . .	139
1.	Доказательство единственности (139). 2. Доказательство суще-
ствования (143).
Глава 5. Основы дифференциального исчисления....................... 149
§ 1. Производная. Ее физическая и геометрическая интерпрета-
ция ......................................................   149
1. Приращение аргумента и функции. Разностная форма усло-
вия непрерывности (149). 2. Определение производной (150).
3. Производная с физической точки зрения (151). 4. Производная
с геометрической точки зрения (152). 5. Правая и левая
производные (153). 6. Понятие производной векторной функ-
ции (153).
§ 2. Понятие дифференцируемости функции......................... 155
1. Понятие дифференцируемости функции в данной точке (155).
2. Связь между понятиями дифференцируемости и непрерывности
функции (156). 3. Понятие дифференциала функции (156).
§ 3. Правила дифференцирования суммы, разности, произведения
и частного.................................................  158
§ 4.	Вычисление производных степенной функции, тригонометри-
ческих функций и логарифмической функции....................  .	161
1.	Производная степенной функции с целочисленным показате-
лем (161). 2. Производная функции y — sinx (162). 3. Про-
изводная функции y = cosx (162). 4. Производные функ-
ций у = tg х и г/= ctg х (163). 5. Производная функции у =
= loga х (0 < а 1) (163).
§ 5.	Теорема о производной обратной функции..................... 164
§ 6.	Вычисление производных показательной функции и обратных
тригонометрических функций..................................'. .	165
1.	Производная показательной функции у=ах (0<ат^1)
(165). 2. Производные обратных тригонометрических функций
(166).
§ 7.	Правило дифференцирования сложной функции.................. 168
§ 8.	Логарифмическая производная. Производная степенной функции
с любым вещественным показателем. Таблица производных про-
стейших элементарных функций............................... 170
1.	Понятие логарифмической производной функции (170). 2. Про-
изводная степенной функции с любым вещественным показате-
лем (170). 3. Таблица производных простейших элементарных
функций (171).
§ 9.	Инвариантность формы первого дифференциала. Некоторые при-
менения дифференциала........................................... 172
1.	Инвариантность формы первого дифференциала (172). 2. Фор-
мулы и правила вычисления дифференциалов (173). 3. Исполь-
зование дифференциала для установления приближенных фор-
мул (174).
§ 10. Производные и дифференциалы высших порядков................. 175
1. Понятие производной n-го порядка (175). 2. n-е производные
некоторых функций (176). 3. Формула Лейбница для п-й произ-
8
ОГЛАВЛЕНИЕ
водной произведения двух функций (177). 4. Дифференциалы
высших порядков (179).
§ 11. Дифференцирование функции, заданной параметрически ....	180
Глава 6. Неопределенный интеграл............................. 182
§ 1, Понятие первообразной функции и неопределенного интег-
рала ..................................................... 182
1. Понятие первообразной функции (182). 2. Неопределенный
интеграл (183). 3. Основные свойства неопределенного интег-
рала (184). 4. Таблица основных неопределенных интегралов
(185).
§ 2. Основные методы интегрирования............................ 187
1. Интегрирование заменой переменной (подстановкой) (187).
2. Интегрирование по частям (190).
Глава 7. Комплексные числа. Алгебра многочленов. Интегрирование
в элементарных функциях........................,......... 195
§ 1.	Краткие сведения о комплексных числах.................... 195
§ 2.	Алгебраические многочлены................................ 199
§ 3.	Кратные корни многочлена. Признак кратности корня.........	202
§ 4.	Принцип выделения кратных корней. Алгоритм Евклида . . .	203
1.	Принцип выделения кратных корней (203). 2. Нахождение
наибольшего общего делителя двух многочленов (алгоритм
Евклида) (204).
§ 5.	Разложение правильной рациональной дроби с комплекс-
ными коэффициентами на сумму простейших дробей................. 206
§ 6.	Разложение алгебраического многочлена с вещественными коэф-
фициентами на произведение неприводимых вещественных мно-
жителей ....................................................  .	208
§ 7.	Разложение правильной рациональной дроби с веществен-
ными коэффициентами на сумму простейших дробей с вещест-
венными коэффициентами.......................................... 211
§ 8.	Проблема интегрирования рациональной дроби................ 216
§ 9.	Метод Остроградского...................................... 219
§ 10.	Интегрирование некоторых иррациональных и трансцендент- '
ных выражений.................................................. 222
1.	Интегрирование некоторых тригонометрических выражений
(223). 2. Интегрирование дробно линейных иррациональностей
(226). 3. Интегрирование биномиальных дифференциалов (226).
4. Интегрирование квадратичных иррациональностей посред-
ством подстановок Эйлера (228). 5. Интегрирование квадра-
тичных иррациональностей другими способами (230).
§11.	Эллиптические интегралы................................... 236
Глава 8. Основные теоремы о непрерывных и дифференцируемых функ-
циях ........................................................ 239
§ 1.	Новое определение предельного значения функции............ 239
.	1. Новое определение предельного значения функции. Его
эквивалентность старому определению (239). 2. Необходимое и
достаточное условие существования предельного значения функ-
ции (критерий Коши) (242).
§ 2.	Локальная ограниченность функции, имеющей предельное зна-
чение ................................................*........ 244
§ 3.	Теорема об устойчивости знака непрерывной функции . . .	246
§ 4.	Прохождение непрерывной функции через любое промежуточное
значение ...................................................... 247
ОГЛАВЛЕНИЕ
9
1. Прохождение непрерывной функции через нуль при смене
знаков (247). 2. Прохождение непрерывной функции через
любое промежуточное значение (248).
§ 5. Ограниченность функции, непрерывной на сегменте ......	248
§ 6. Точные грани функции и их достижение функцией, непрерыв-
ной на сегменте ................................................ 249
1. Понятие точной верхней и точной нижней граней функ-
ции на данном множестве (249). 2. Достижение функцией, не-
прерывной на сегменте, своих точных граней (250).
§ 7. Возрастание (убывание) функции в точке. Локальный макси-
мум (минимум)............................................  252
1.	Возрастание (убывание) функции в точке (252). 2. Локаль-
ный максимум и локальный минимум функции (253).
§ 8.	Теорема о нуле производной............................... 254
§ 9.	Формула конечных приращений (формула Лагранжа)..........	254
§ 10.	Некоторые следствия из формулы Лагранжа.................. 256
1. Постоянство функции, имеющей на интервале равную
нулю производную (256). 2. Условия монотонности функции
на интервале (257). 3. Отсутствие у производной точек разрыва
1-го рода и устранимого разрыва (258). 4. Вывод некоторых
неравенств (260).
§ И. Обобщенная формула конечных приращений (формула Коши) 260
§ 1£. Раскрытие неопределенностей (правило Лопиталя).............. 261
1. Раскрытие неопределенности вида -у (261). 2. Раскрытие
неопределенности вида — (264). 3. Раскрытие неопределен-
ностей других видов (265).
§ 13. Формула Тейлора...........................................  267
§ 14. Различные формы остаточного члена. Формула Маклорена . .	269
1. Остаточный член в форме Лагранжа, Коши и Пеано (269).
2. Другая запись формулы Тейлора (272). 3. Формула Макло-
рена (272).
§ 15. Оценка остаточного члена. Разложение некоторых элементар-
ных функций...........................................    273
1. Оценка остаточного члена для произвольной функции (273).
2. Разложение по формуле Маклорена некоторых элементарных
функций (274). ,
§ 16. Примеры приложений формулы Маклорена.................... 276
1. Алгоритм вычисления числа е (276). 2. Реализация алгоритма
вычисления числа е на электронной машине (277). 3. Использо-
вание формулы Маклорена для асимптотических оценок элемен-
тарных функций и вычисления пределов (278).
Дополнение к главе 8. Вычисление элементарных функций . . .	281
1. Вычисление логарифмической и обратных тригонометри-
ческих функций (281). 2. Вычисление тригонометрических функ-
ций, показательной функции и гиперболических функций (284).
Глава 9. Геометрическое исследование графика функции. Нахождение
максимального и минимального значений функции....................... 291
§ 1.	Участки монотонности функции. Отыскание точек экстремума 291
1. Отыскание участков монотонности функции (291). 2. Отыска-
ние точек возможного экстремума (292). 3. Первое достаточное
условие экстремума (292). 4. Второе достаточное условие экстре-
мума (294). 5. Экстремум функции, недифференцируемой в
данной точке. Общая схема отыскания экстремумов (297).
§ 2.	Направление выпуклости графика функции..................... 299
10
ОГЛАВЛЕНИЕ
§ 3.	Точки перегиба графика функции ................................... 301
1.	Определение точки перегиба. Необходимое условие пере-
гиба (301). 2. Первое достаточное условие перегиба (302).
3. Второе достаточное условие перегиба (303). 4. Некоторые обоб-
щения первого достаточного условия перегиба (303).
§	4.	Третье достаточное	условие экстремума и перегиба. 304
§	5.	Асимптоты графика	функции....................... 306
§	6.	Схема исследования	графика	функции............... 308
§ 7.	Отыскание максимального и минимального значений функции.
Краевой экстремум.................................................. 311
1.	Отыскание максимального и минимального значений функ-
ции (311). 2. Краевой экстремум (313).
Глава 10. Определенный интеграл........................................... 315
§ 1.	Интегральные суммы. Интегрируемость............................... 315
§ 2.	Верхние и нижние суммы............................................ 317
1.	Понятие верхней и нижней сумм (317). 2. Свойства
верхних и нижних сумм (319).
§ 3.	Необходимое и достаточное условие интегрируемости................. 323
§ 4.	Некоторые классы интегрируемых функций............................ 324
1.	Свойство равномерной непрерывности функции (325).
2.	Лемма Гейне—Бореля. Другое доказательство теоремы о
равномерной непрерывности (327). 3. Интегрируемость непре-
рывных функций (329). 4. Интегрируемость некоторых разрыв-
ных функций (329). 5. Интегрируемость монотонных ограничен-
ных функций (331).
§ 5.	Основные свойства определенного интеграла......................... 331
§ 6.	Оценки интегралов. Формулы среднего значения . ................... 334
1.	Оценки интегралов (334). 2. Первая формула среднего значе-
ния (336). 3. Первая формула среднего значения в обобщенной
форме (337). 4. Вторая формула среднего значения (338).
§ 7.	Существование первообразной для непрерывной функции. Основ-
ные правила интегрирования........................................ 338
1.	Существование первообразной для непрерывной функции
(338). 2. Основная формула интегрального исчисления (340).
3. Замена переменной под знаком определенного интеграла
(342). 4. Формула интегрирования по частям (343). 5. Оста-
точный член формулы Тейлора в интегральной форме (344).
Дополнение 1 к главе 10. Некоторые важные неравенства для сумм
и интегралов ..................................................... 346
1. Вывод одного предварительного неравенства (346). 2. Нера-
венство Гёльдера для сумм (346). 3. Неравенство Минковского
для сумм (347). 4. Интегрируемость произвольной положи-
тельной степени модуля интегрируемой функции (348). 5. Нера-
венство Гёльдера для интегралов (349). 6. Неравенство Мин-
ковского для интегралов (350).
Дополнение 2 к главе 10. Доказательство утверждения из п. 4 § 6	351
Глава И. Геометрические и физические приложения определенного
интеграла ........................................................   353
§ 1.	Длина дуги кривой................................................ 353
1.	Понятие плоской кривой (353). 2, Параметрическое задание
кривой (354). 3. Понятие пространственной кривой (357).
4.	Понятие длины дуги кривой (357). 5. Достаточные условия
спрямляемости кривой. Формулы для вычисления длины
дуги кривой (362). 6. Дифференциал дуги (366). 7. Примеры
вычисления длины дуги (367).
ОГЛАВЛЕНИЕ
11
§ 2.	Площадь плоской фигуры...................................  368
1.	Понятие квадрируемости плоской фигуры. Площадь ква-
дрируемой плоской фигуры (368).
2.	Площадь криволинейной трапеции (370). 3. Площадь
криволинейного сектора (371). 4. Примеры вычисления площа-
дей (372).
§ 3.	Объемы тел и площади поверхностей......................... 374
1.	Понятие кубируемости и объема (374). 2. Кубируемость
некоторых классов тел (375). 3. Примеры вычисления объёмов
(376). 4. Площадь поверхности вращения (377).
§ 4.	Некоторые физические приложения определенного интеграла 379
1. Масса и центр тяжести неоднородного стержня (379).
2. Работа переменной силы (381).
Дополнение к главе 11. Пример неквадрируемой фигуры........	381
Глава 12. Приближенные методы вычисления корней уравнений и
определенных интегралов ................................. 387
§ 1. Приближенные методы вычисления корней уравнений........ 387
1. Метод «вилки» (387). 2. Метод касательных (388). 3. Метод
хорд (389). 4. Метод итераций (последовательных приближений)
(390). 5. Обоснование метода касательных (393). 6. Обоснование
метода хорд (396).
§ 2. Приближенные методы вычисления определенных интегра-
лов .............................................. .....	399
1.	Вводные замечания (399). 2. Метод прямоугольников (401).
3. Метод трапеций (403). 4. Метод парабол (405). 5. Заклю-
чительные замечания (409).
Глава 13. Теория числовых рядов.................................. 410
§ 1.	Понятие числового ряда.................................. 410
1.	Ряд и его частичные суммы. Сходящиеся и расходящиеся
ряды (410). 2. Критерий Коши сходимости ряда (413). 3. Два
свойства, связанные со сходимостью ряда (415).
§ 2.	Ряды с положительными членами........................... 415
1. Необходимое и достаточное условие сходимости ряда с поло-
жительными членами (415). 2. Признаки сравнения (416).
3. Признаки Даламбера и Коши (419). 4. Интегральный приз-
нак Коши — Маклорена (423). 5. Признак Раабе (425). 6. Отсут-
ствие универсального ряда сравнения (427).
§ 3.	Абсолютно и условно сходящиеся ряды...................... 428
1.	Понятия абсолютно и условно сходящегося ряда (428).
2.	О перестановке членов условно сходящегося ряда (430).
3.	О перестановке членов абсолютно сходящегося ряда (433).
§ 4.	Арифметические операции над сходящимися рядами ....	435
§ 5.	Признаки сходимости произвольных рядов.................... 437
1.	Признак Лейбница (438). 2. Признак Дирихле—Абеля (439).
§ 6.	Бесконечные произведения . ............................... 442
1.	Основные понятия (442). 21 Связь между сходимостью
бесконечных произведений и рядов (445).
Дополнение 1 к главе 13. Вспомогательная теорема для п. 3
§ 2 ........................................................  .	448
Дополнение 2 к главе 13. Разложение функции sinx в бесконечное
произведение .............................................. 449
Дополнение 3 к главе 13. Обобщенные методы суммирования рас-
ходящихся рядов..........................................   452
1.	Метод Чезаро (или метод средних арифметических) (453).
2. Метод суммирования Пуассона — Абеля (454).
12
ОГЛАВЛЕНИЕ
Глава 14. Функции нескольких переменных.............................  457
§ 1. Понятие функции нескольких переменных.......................  457
1. О функциональных зависимостях между несколькими
переменными величинами (457). 2. Понятия евклидовой пло-
скости и евклидова пространства (457). 3. Понятие функции
двух и трех переменных (459). 4. Понятия m-мёрного коор-
динатного пространства и zn-мерного евклидова пространства
(460). 5. Множества точек m-мерного евклидова пространства
Ет (461). 6. Понятие функции т переменных (464).
§ 2. Предельное* значение функцйи нескольких переменных.......	464
1. Сходящиеся последовательности точек в m-мерном евкли-
довом пространстве Ет. Критерий Коши сходимости последова-
тельности (464). 2. Некоторые свойства ограниченных последова-
тельностей точек в m-мерном евклидовом пространстве (466).
3. Понятие предельного значения функции нескольких перемен-
ных (467). 4. Бесконечно малые функции (468). 5. Необходи-
мое и достаточное условие существования предельного значе-
ния функции (критерий Коши) (469). 6.‘ Повторные пре-
дельные значения (469).
§ 3.	Непрерывные функции нескольких переменных................ 471
1.	Определение непрерывности функции нескольких переменных
(471). 2. Основные свойства непрерывных функций нескольких
переменных (474).
§ 4.	Производные и дифференциалы функции нескольких переменных 477
1. Частные производные функции нескольких переменных
(477). 2. Понятие дифференцируемости функции нескольких
переменных (479). 3. Понятие дифференциала функции несколь-
ких переменных (484). 4. Дифференцирование сложной функ-
ции (484). 5. Инвариантность формы первого дифференциала
(488). 6. Производная по направлению. Градиент (489).
§ 5.	Частные производные и дифференциалы высших порядков . . .	492
1.	Частные производные высших порядков (492). 2. Дифферен-
циалы высших порядков (496). 3. Формула Тейлора для
функции нескольких переменных (500).
§ 6.	Локальный экстремум функции нескольких переменных . .	502
1.	Определение локального экстремума. Необходимые условия
локального экстремума (502). 2. Достаточные условия локаль-
ного экстремума (504). 3. Случай функции двух переменных
(509). 4. Пример исследования функции на экстремум (510).
§ 7.	Градиентный метод поиска экстремума выпуклой функции ....	510
1.	Некоторые сведения о выпуклых множествах в евклидовых
пространствах (511). 2. Понятие выпуклой функции. Некоторые
свойства-выпуклых функций (514). 3. Вспомогательные предло-
жения (519). 4. Поиск минимума сильно выпуклой функции
(521).
Дополнение к главе 14. О выборе оптимального разбиения сегмента
для приближенного вычисления интеграла................... 523
Глава 15. Теория неявных функций и ее приложения................. 526
§ 1. Понятие неявной функции.................................  526
§ 2. Теорема о существовании и дифференцируемости неявной функ-
ции и некоторые ее применения............................ 527
1.	Теорема о существовании и дифференцируемости неявной
функции (527). 2. Вычисление частных производных неявно
заданной функции (533). 3. Особые точки поверхности и плос-
кой кривой (535). 4. Условия, обеспечивающие существование
для функции у = / (х) обратной функции (536). '
ОГЛАВЛЕНИЕ
13
§ 3.	Неявные функции, определяемые системой функциональных
уравнений....................................................  537
1.	Теорема о разрешимости системы функциональных уравне-
ний (Б37). 2. Вычисление частных производных функций,
неявно определяемых посредством системы функциональных
уравнений (541). 3. Взаимно однозначное отображение двух
. множеств m-мерного пространства (542).
§ 4.	Зависимость функций...................................... 543
1.	Понятие зависимости функций. Достаточное условие неза-
висимости (543). 2. Функциональные матрицы и их приложе-
ния (545).
§ 5.	Условный экстремум....................................... 549
1.	Понятие условного экстремума (549). 2. Метод неопределенных
множителей Лагранжа (552). 3. Достаточные условия (553).
4.	Пример (554).
Дополнение к главе 15. Замена переменных...................... 557
Глава 16. Некоторые геометрические приложения дифференциального
- исчисления....................................’................ 560
§ 1.	Огибающая и дискриминантная кривая однопараметрического
семейства плоских кривых...................................... 560
1.	Предварительные замечания (560). 2. Однопараметрические
семейства плоских кривых. Характеристические точки кри-
вых семейства (563). 3. Огибающая и дискриминантная кривая
однопараметрического семейства плоских кривых (564). 4. Оги-
бающая и дискриминантная поверхность однопараметрического
семейства поверхностей (568).
§ 2.	Соприкосновение плоских кривых........................... 569
1.	Понятие порядка соприкосновения плоских кривых (569).
2.	Порядок соприкосновения кривых, являющихся графи-
ками функций (570). 3. Достаточные условия соприкоснове-
ния порядка п (573). 4. Соприкасающаяся окружность (574).
§ 3.	Кривизна плоской, кривой.............................     575
1.	Понятие о кривизне плоской кривой (575). 2. Формула
для вычисления кривизны (577).
§ 4.	Эволюта и эвольвента..................................... 580
1.	Нормаль к плоской кривой (580). 2. Эволюта и эвольвента
плоской кривой (581).
Приложение. Дальнейшее развитие теории вещественных чисел.......	585
1.	Полнота множества вещественных чисел (585). 2. Аксио-
матическое введение множества вещественных чисел (588).
3. Заключительные замечания (593).
Предметный указатель . ...................	..............	595
ОТ РЕДАКТОРОВ СЕРИИ
•Серия «Курс высшей математики и математической физики» воз-
никла как естественный итог многолетнего чтения математических кур-
сов на физическом факультете МГУ.
Выпуски, входящие в эту серию, являются учебниками по соот-
ветствующим математическим курсам. Наряду с основным программным
материалом в них освещено некоторое количество дополнительных
вопросов, которые неизбежно возникают при попытке систематически
и достаточно цельно изложить курс.
В целом серия представляет собой один из возможных вариантов
изложения математических дисциплин на физических и физико-мате-
матических факультетах государственных университетов, но ее не
следует рассматривать как пособие для самообразования.
В 1965 г. выйдут в свет следующие три выпуска серии: выпуск 1 —
«Основы математического анализа» (авторы В. А. Ильин и Э. Г. Поз-
няк), выпуск 2 — «Кратные интегралы и ряды» (авторы Б, М. Будак
и С> В. Фомин), выпуск 3 — «Дифференциальные уравнения и вариа-
ционное исчисление» (автор Л. Э. Эльсгольц).
В последующие годы выйдут еще пять выпусков: «Теория функ-
ций комплексной переменной», «Дифференциальные уравнения мате-
матической физики», «Интегральные уравнения», «Теория вероятнос-
тей» и «Аналитическая геометрия и линейная алгебра».
Естественно, что отдельные выпуски серии, написанные разными
авторами, несколько отличаются друг от друга по стилю и манере
изложения. Они объединяются общей редакцией и едиными методи-
ческими установками.
А. Тихонов, В. Ильин, А. Свешников
Москва
7 января 1965 г.
ПРЕДИСЛОВИЕ К ТРЕТЬЕМУ ИЗДАНИЮ
В третье издание книги внесен целый ряд изменений и дополне»
ний, основная часть которых отражает возросшую роль вычислитель-
ной математики (алгоритмы вычисления элементарных функций, гра-
диентный метод отыскания экстремума функций, оптимальные квадра-
турные формулы и т. д.).
Авторы благодарят Б. М. Будака, В. В. Воеводина, Б. И. Волкова
и С. С. Гайсаряна за предоставление материалов, использованных при
написании этого издания, и редактора третьего издания Ш. А. Али-
мова, работа которого способствовала улучшению этой книги.
Авторы глубоко благодарны Л. Д. Кудрявцеву и А. Г. Свешни-
кову, прочитавшим всю рукопись третьего издания и сделавшим ряд
ценных замечаний.
В третьем издании учтены также некоторые замечания и пожела-
ния, содержащиеся в напечатанной в УМН рецензии П. С. Александрова
и Л. Д. Кудрявцева, которым авторы еще раз приносят глубокую
благодарность.
При подготовке этого издания очень большую помощь оказал
А. Н. Тихонов; авторы приносят ему особую благодарность.
В. Ильин, Э. Позняк
Июль 1970 г.
ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
В основу настоящей книги положены лекции, читавшиеся авторами
на физическом факультете МГУ в течение ряда лет.
При написании книги авторы стремились к систематичности изло-
жения и к выделению важнейших понятий и теорем. Теоремы, играю-
щие особо важную роль, в тексте названы основными. Авторы стре-
мились также не формулировать новых понятий и теорем задолго
до их непосредственного использования.
Порядок расположения материала в книге соответствует устано-
вившемуся на физическом факультете МГУ плану чтения курса лекций.
16
ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
В частности, изложению систематического курса в настоящей книге
предшествует глава 1 — «Предварительные сведения об основных поня-
тиях математического анализа». В этой главе рассматриваются неко-
торые важные физические задачи и обсуждаются математические
средства, необходимые для их решения. Таким путем выясняется тот
круг вопросов и понятий, с которым придется иметь дело в курсе
математического анализа. Опыт чтения лекций показывает, что такое
предварительное выяснение вопросов, которым посвящен курс анализа,
существенно облегчает студентам усвоение абстрактных математиче-
ских понятий.
Возросшая роль вычислительной математики и приближенных ме-
тодов также нашла свое отражение в книге. Именно поэтому авторы
стремились там, где это возможно, к алгоритмичности изложения дока-
зательств теорем и проводимых вычислений. В частности, в главе 12
в первую очередь подчеркнута алгоритмическая сторона приближен-
ных методов вычислений и лишь затем дано обоснование этих методов.
Кроме. основного материала, авторы сочли возможным включить
в книгу некоторые дополнительные вопросы, напечатанные мелким
шрифтом.
При написании этой книги авторы использовали некоторые мето-
дические приемы из курса лекций Н. В. Ефимова и из известных книг
Э. Гурса, Ш. Ж. Валле-Пуссена и Ф. Франклина.
Авторы считают своим приятным долгом выразить глубокую бла-
годарность А. Н. Тихонову за многие ценные идеи и указания и
огромную помощь, оказанную на всех этапах написания этой книги.
Авторы также глубоко благодарны И. А. Шишмарёву, работа ко-
торого по редактированию этой книги способствовала значительному
ее улучшению.
Авторы искренне благодарят Н. В. Ефимова, Л. Д. Кудрявцева и
особенно А. А. Самарского за большое количество методических
предложений, Б. М. Будака и С. В. Фомина за просмотр отдельных
глав и сделанные ими замечания, Б. Химченко, П. Заикина и А. Зо-
лотарева за помощь при подготовке рукописи к печати.
В. Ильин, Э. Позняк
ГЛАВА 1
ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ОСНОВНЫХ ПОНЯТИЯХ
МАТЕМАТИЧЕСКОГО АНАЛИЗА
§ 1. Математические понятия, возникающие при описании
движения
1. Математика имеет своей задачей изучение количественных отно-
шений и пространственных форм окружающего нас мира. Понятия и
объекты математики представляют собой абстракции наблюдаемых
в природе количественных отношений и пространственных форм.
Элементарная математика ограничивается лишь первоначальным
изучением количественных отношений и пространственных форм, ибо
она имеет дело в основном с постоянными величинами и с про-
стейшими геометрическими фигурами (треугольниками, окружностями
и т. п.). Понятий и методов элементарной математики оказывается
недостаточно для описания механического движения и других про-
текающих во времени процессов. Выясним, какие новые математичес-
кие понятия необходимы для этого *).
2. Со всяким процессом связано представление о переменной вели-
чине, т. е. о такой величине, которая в условиях данного процесса
принимает различные значения. Более того, всякий процесс характе-
ризуется по меньшей мере двумя переменными величинами, изменение
которых взаимосвязано.
Рассмотрим, например, механическое движение материальной точки
по прямой линии. Это движение представляет собой процесс измене-
ния положения точки на прямой линии с течением времени. С ука-
занным процессом связаны две переменные величины — время и путь,
пройденный точкой от начала отсчета. Для характеристики рассмат-
риваемого движения нужно знать, на каком расстоянии от начала
отсчета находится точка в каждый данный момент времени, т. е.
*) При этом мы не будем стремиться к точным формулировкам, а поста-
раемся лишь выяснить тот круг вопросов, с которым нам в дальнейшем при-
дется иметь дело.
18
ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
[ГЛ. t
нужно знать зависимость пути, пройденного точкой, от времени.
В механике такую зависимость называют законом движения. Иными
словами, закон движения представляет собой правило, посредством
которого каждому значению времени х ставится в соответствие опре-
деленное значение пути у, пройденного точкой за время х.
Такого рода зависимости между двумя переменными х и у, при
которых каждому значению переменной х ставится в соответствие
определенное значение переменной у, встречаются не только при
рассмотрении механического движения материальной точки, но и при
описании других физических процессов. Абстрагируясь от конкретного
физического содержания переменных х и у, мы приходим к одному
из важнейших математических понятий — понятию функции * **)).
Если известно правило, посредством которого каждому зна-
чению переменной х ставится в соответствие определенное зна-
чение переменной у, то говорят, что переменная у является
функцией переменной х.
При этом переменная х называется аргументом рассматриваемой
функции, а соответствующее данному х значение переменной у назы-
вается частным значением функции в точке х.
Для обозначения функции используются следующие символы:
у=у(х) или j=/(x).
В этом обозначении буква f, называемая характеристикой функции,
символизирует указанное выше правило. Если рассматриваются разные
функции, то для обозначения их характеристик употребляются разные
буквы. Подчеркнем, что для обозначения аргумента и функции вовсе
не обязательно употреблять буквы х и у. Например, запись S—h(t)
означает, что переменная S является функцией аргумента t, причем
характеристика этой функции обозначена буквой h.
Как переменная величина, так и функция обычно характеризуются
различными численными значениями. Поэтому углубление наших
представлений об этих понятиях тесно связано с необходимостью
развития теории вещественных чисел * *).
Рассмотрим несколько примеров функций.
1) Известно, что путь S’, пройденный первоначально неподвижной
материальной точкой при падении под действием силы тяжести
*) Введение в математику понятия функции связывают с именем великого
английского ученого И. Ньютона (1642 — 1727).
**) Следует отметить, что понятие функции и понятие числа относятся
к так называемым начальным понятиям. Каждое из начальных понятий
может быть разъяснено, но всякая попытка дать определение начального
понятия сводится к замене определяемого понятия ему эквивалентным.
С начальными понятиями читатель знаком из элементарного курса. К началь-
ным понятиям относятся, например, понятия прямой линии и плоскости.
§ 1]	ПОНЯТИЯ, ВОЗНИКАЮЩИЕ ПРИ ОПИСАНИИ ДВИЖЕНИЯ
19
за время t, определяется формулой
е g*2
Эта формула и представляет собой правило, посредством которого
каждому значению переменного t ставится в соответствие значение
переменной 5, т. е. определяет 5 как функцию аргумента t.
2) По закону Кулона два разноименных единичных заряда, нахо-
дящихся на расстоянии г друг от друга, притягиваются с силой
F = —
1 —rz >
где с — некоторая константа. Эта формула также представляет собой
правило, посредством которого каждому значению переменной г ста-
вится в соответствие значение переменной F, т. е. определяет F как
функцию аргумента г.
В указанных двух примерах правило сопоставления аргумента и
функции задавалось при помощи формулы. Такой способ задания,
функции называется аналитическим.
Наряду с этим способом существуют и
другие способы задания функции. Отметим
некоторые из них. В практике физических
измерений весьма употребителен табличный
способ задания функции, при котором выпи-
сываются в виде таблицы значения аргумента
и соответствующие им значения функции. Часто
зависимость между аргументом и функцией за-
дается посредством графика, который, напри-
мер, снимается на осциллографе. Такой способ
задания функции называется графическим*).
3. Потребности физики иногда приводят
ния функции y—f(x), аргумент х которой
некоторую функцию х — <р (t) нового аргумента t. В таком
говорят, что у представляет собой сложную функцию аргумента t,
а х называют промежуточным аргументом. Эту сложную функцию
можно задать с помощью одной формулы _у=/[<р(О]- Рассмотрим
следующий пример. Пусть материальная точка М равномерно враща-
ется по окружности радиуса R с угловой скоростью ш. Найдем закон
движения проекции у этой точки на некоторую ось Оу, лежащую
в плоскости окружности и проходящую через ее центр О. При этом
мы будем считать, что в момент времени £ = 0 точка М находится
на оси Оу (рис. 1.1). Обозначим через у координату рассматриваемой
проекции на ось Оу, а через х угол МОу. Очевидно, что
y = Rcosx. С другой стороны, поскольку точка движется по окруж-
ности с угловой скоростью шив момент времени £ = 0 находится
к необходимости
сам представляет
изуче-
собой
случае
Подробнее о способах задания функции см. главу 4.
20
ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
1ГЛ. t
на оси Оу, то x=3 <ot. Таким образом, у представляет собой сложную
функцию аргумента i: y = R cosx, где x = wt, или j = /?coswt
Заметим, что движение по закону .у = 7? cosurf в механике называют
гармоническим колебанием.
§ 2. Мгновенная скорость и связанные
с ней новые математические понятия
1. Пусть функция y=f(x) представляет собой закон движения
материальной точки по оси Оу. Для характеристики движения важ-
ную роль играет понятие средней скорости. Вычислим среднюю ско-
рость движущейся точки за промежуток времени от х до х + Дх,
где х — фиксированный момент времени, Дх —некоторое прираще-
ние времени. Поскольку в момент времени х движущаяся точка нахо-
дится на расстоянии f(x) от начала отсчета, а в момент времени
х + Д-V—на расстоянии f(x4-fac~), то путь Ду, пройденный точкой
за время Дх, равен Ду=/(х-|-Дх) — /(х). Поэтому средняя ско-
рость -иср равна
_ f(x + д*) — f (*)
fa~ fa
Так как момент времени х фиксирован, то из последней формулы
видно, что х>ср является функцией аргумента Дх. Для характеристики
неравномёрного движения, наряду со средней скоростью, большую
роль играет понятие мгновенной скорости в данный момент вре-
мени х.
Мгновенной скоростью ('или просто скоростью) в момент вре-
мени х называется число, к которому приближается значение средней
скорости
_f(X+fa)-f(X)
^ср “ fa
когда промежуток времени Дх стремится к нулю.
Физическое понятие мгновенной скорости является источником
важного математического понятия производной. Абстрагируясь от
конкретного физического смысла функции У=/(х), мы будем назы-
вать производной этой функции в фиксированной точке х предел,
.. Ду f (х + Дх) — f (х) Л
к которому стремится дробь	1—L±-i при Дх, стремящемся
к нулю.
Операцию нахождения производной принято называть дифференци-
рованием. Производная функция _у=/(х) в данной фиксированной
точке обозначается символом у' (х) или /' (х). Используя известный
символ для обозначения предела, мы можем записать
/'(х) = Нш	lim
4 ’ дх-»о Д* Дх-0	д*
§21
МГНОВЕННАЯ СКОРОСТЬ
21
Рассмотрим некоторые примеры.
1)	Вычислим мгновенную скорость материальной точки, падающей
под действием силы тяжести. Поскольку закон движения этой точки
определяется функцией S=^-, то путь AS, пройденный точкой за
промежуток времени от t до £ + равен
AS = g(Z^AZ)2 -	=gt \t + f (А/)».
Поэтому средняя скорость за тот же промежуток времени равна
Следовательно, мгновенная скорость и в фиксированный момент вре-
мени t равна
г>= lim^= lim (^ + gA^=^.
ДМ-0 ш ДМ-0 ' z /
Фактически мы вычислили производную функции 5= так что мы
можем записать S' = gt.
2)	Вычислим производную функции у = хп, где и —целое положи-
тельное число. Фиксируя х и беря произвольное Ах, получим, исполь-
зуя бином Ньютона,
А_у = (х + Ах)" — х” = их'*-1 Ах + п (п~ х"’2 (Ах)2 +... + (Ах)".
Поэтому средняя скорость изменения функции у =f(x) на участке
от х до х + Дх равна
=	+п(п~1)хп~2Дх+ ... +(Дх)«-1 .
Следовательно, производная в данной фиксированной точке х равна
у' = lim Гих"-1 + п— -Ах +... 4- (Ax)"-1] = fix’4.
дх-oL	J
Мы видим, что для вычисления производных фундаментальную
роль играет понятие предела функции. Уточнение этого понятия
в первую очередь связано с необходимостью более детального выяс-
нения самого понятия функции, переменной величины и веществен-
ного числа.
2.	Сейчас мы убедимся, что в процессе вычисления производных
простейших функций возникают новые математические вопросы.
22
ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
(ГЛ. I
Займемся вычислением производной функции у = sin х. Фиксируя л;
и беря произвольное Дх, получим
Отсюда
Ду = sin (х + Дх) — sin х — 2 cos
Дх
= cos
Таким образом, для вычисления производной функции _y = sinx
в точке х нужно найти следующий предел:
lim = lim
дх —д*->о
- (1-1)
Естественно ожидать, что при фиксированном х
lim cos x + -s-) = cosx.	(1.2)
дх-»о \	2 /
Однако не всякая функция у = /(х) обладает свойством
lim /(х + ^=/(х).
Дл-0 \	2 /
Фактически это свойство означает, что когда аргумент функции стре-
мится к числу х, то соответствующее значение этой функции стре-
мится к числу /(х). Функции, обладающие таким свойством, называются
непрерывными (в точке х). Понятие непрерывности функции является
одним из важнейших математических понятий.
Для вычисления предела (1.1), кроме предела (1.2), нужно вычи-
слить еще предел
(1-3)
Этот предел играет важную роль в математическом анализе. Его
часто называют первым замечательным пределом. Доказывается, что
этот предел равен единице, и поэтому предел (1.1) равен cosx.
Итак,
(sin х)' — cos х.
§2)
МГНОВЕННАЯ СКОРОСТЬ
23
В качестве второго примера вычислим производную функции
j/ = logax. Фиксируя х>0 и беря произвольное Дх (такое, что
х + Дх >• 0), получим
Отсюда
= loga (х + Дх) - loga х = loga (1 + y) •
Таким образом, для вычисления производной функции y = logax
в точке х нужно найти предел
lim
Дх-0
Дх
= lim ^logQ +
Дх-*0 х \ х /
(1.4)
Рассмотрим предел при Дх—>0 выражения, стоящего в квадратных
скобках. Он сводится к пределу
lim[(l + h)h ] (при h = —\.
h-О	\	х!
Этот предел также играет важную роль в математическом анализе.
Его часто называют вторым замечательным пределом. Доказывается,
что этот предел существует. Следуя Эйлеру *), число, равное этому
пределу, обозначают буквой е **), т. е.
lim [(1 +h)h] = e.	(1.5)
Л->0
Вернемся к вычислению предела (1.4). Аргументом логарифма вфор-
муле (1.4) служит величина 1(1-)—?•* , стремящаяся, согласно (1.5),
к е при Дх—>0. Если логарифмическая функция непрерывна, то
10ёа [(1 +^х
стремится к logae при Дх->0. Таким образом, для
нахождения предела (1.4) нам нужно обосновать непрерывность лога-
рифмической функции и использовать предел (1.5). Предполагая, что
*) Леонард Эйлер (1707—1783) — великий математик, член Петербург-
ской Академии наук, большую часть жизни провел в России, по происхож-
дению швейцарец.
**) В § 16 главы 8 будет указан способ вычисления числа е с любой сте-
пенью точности. Там же приведен результат вычисления числа е на электронно-
вычислительной машине с точностью до 590 знаков после запятой.
24
ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
(ГЛ. 4
это сделано, мы получим, что предел (1.4) равен у logae. Итак,
(logax)' = ylog0e.
Здесь мы не будем вычислять производных других простейших эле-
ментарных функций: _y = cosx, _y = tgx, j = ctgx, _y = arcsinx,
у = arccosx, _y = arctgx, _y = arcctgx, y = ax и у = хл, где а—любое
число. При вычислении производных этих функций не возникает
никаких новых трудностей, кроме указанных выше. Именно, для
вычисления производных всех простейших элементарных функций по-
требуется лишь их непрерывность и два замечательных предела. .
Приведем таблицу производных простейших элементарных функций:
1°. (ха)' = ах*~1, а — любое число.
2°. (logaх)' = уlogaе, властности, если а = е то (logex)' = y.
3°. (ах)' — ах loge а, в частности, если а = е то (е*)'= е*.
4°. (sin х)’ — cos х.
5°. (cosx)' =— sinx.
6° (tgx)' = —
v 6 ' cos2 x
™	/ X V	1
” • V
9°. (arccos x)' = —	~~ a'
10°. (arctgx/^y^y.
11°. (arcctgx)'= — y-p-j.
3.	Для вычисления производных широкого класса функций следует
присоединить к указанной выше таблице производных правило диф-
ференцирования сложной функции, а также правила дифференци-
рования суммы, разности, произведения и частного функций.
Сформулируем правило дифференцирования сложной функции у —f{x).
где x — <f(t).
Для 'нахождения производной у (f) сложной функции у =
==/[?(0] по аргументу t в данной точке t следует: 1) вычис-
лить производную <p'(t) функции х = ср(О в точке 2) вычислить
производную /'(х) функции у=/(х) в точке х, где х = <р(/);
3) перемножить указанные производные. Таким образом, производ-
ная сложной функции _У=/[?(0] может быть найдена по формуле
у' (f) *=/' (х) tp' (t). Следующие рассуждения разъясняют сформулиро-
ванное правило. Придадим аргументу t в точке t произвольное при-
ращение At 0. Этому приращению соответствует приращение Ах =
= <р (t А/) — (t) функции х = <р(0. Полученному приращению Ах
§2]
МГНОВЕННАЯ СКОРОСТЬ
25
соответствует приращение Ду =/(х 4- Дх)—f (х) функции y—f (х)
в точке х. Опуская случай Дх = 0, рассмотрим отношение >
Ду___Ду Дх
дТ —д7 Др
Поскольку lim = ср' (t), lim т^=/'(х) и из существования пер-
д/-*о“‘	^х-о“х
вого из этих пределов ясно, что при Д£ -> 0 и Дх -> 0 *), то lim 4~
д/~о м
существует и равен /'(х)ср'(0, т. е. yr (f)=f (х)ч' (t).
Приведем теперь правила дифференцирования суммы, разности,
произведения и частного (в предположении, что и(х) и v(x) имеют
производные):
[и (х) ± v (х)]' = и' (х) ± if (х),
[и (х) v (х)]' = и (х) if (х) + и' (х) v (х),
[и (x)l' и' (х) v (х) — и (х) v' (х)
V (X).	’	V2 (х)	’
Покажем, например, как можно вывести вторую из этих формул.
Придадим аргументу х произвольное приращение Дх 0. Этому
приращению Дх соответствует приращение Ду функции у = и (х) v (х)
Ду = и (х 4- Дх) v (х + Дх) — и (х) v (х) =
— и (х 4- Дх) [т> (х + Дх) — v (х)] + v (х) [и (х 4- Дх) — и (х)] =
= и (х 4- Дх) Дк 4- т (х) Д«.
Таким образом,
^ = М(х4-Дх)^ + т)(х)^.
Так как существуют пределы lim ^- = и'(х) и lim ^ = г>'(х) и из
существования первого из этих пределов ясно, что lim и(х4~Д.х)=
•	Дх ->0
=п(х), то lim — существует и равен w (х) ц'(х) 4~ ® (х) к'(х).
Дх->0 ах
Рассмотрим несколько примеров применения указанных правил.
1)	Вычислим производную функции у = си (х), где с —некоторая
постоянная. Легко проверить, что производная постоянной равна нулю.
Поэтому по формуле дифференцирования произведения получим
[си (х)]' = си' (х).
2)	Вычислим производную функции y = tgx. Так как tgx =
то по формуле дифференцирования частного получим
,,	у (sin х)' cos х —sin х (cos х)'  1
° J	COS2 X	cos2x’
*) Если знаменатель дроби, имеющей предел, стремится к нулю, то и
числитель этой дроби стремится к нулю.
26
ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
[ГЛ. 1
3)	Вычислим производную функции, описывающей гармонические
колебания, у = A cos (wt + 8), где А, <о и 8 — постоянные. Будем
рассматривать эту функцию как сложную функцию вида _y = Acosx,
где х = а>< + 8. По правилу дифференцирования сложной функции
получим
У (0 = (A cos х)' (<of + 8)' = — (A sin х) со,
где х = utf-f-8. Поэтому
у' (/) = — Асо sin (<of + 8).
4)	Вычислим производную функции _y = aarct?< Будем рассматри-
вать эту функцию как сложную функцию вида у = ах, где х = arctg t.
По правилу дифференцирования сложной функции получим
У (0 = (ах)' (arctg t)' = (ах loge а) ,
где х = arctg t. Поэтому
(garctg<y = ^Ctg<1°g^
Сформулированные выше правила дифференцирования и таблица про-
изводных представляют собой основной аппарат той части математи-
ческого анализа, которую обычно называют дифференциальным ис-
числением. Таким образом, одной из важных задач дифференциального
исчисления является обоснование всех формул таблицы производных и
правил дифференцирования суммы, разности, произведения, частного
и сложной функции.
4. Выясним геометрический смысл производной. С этой целью
рассмотрим график функции	(рис. 1.2). Пусть точка М
*) Графиком функции y = f(x) называется геометрическое место точек
плоскости, для' каждой из которых ордината есть значение у этой функцииг
соответствующее абсциссе х.
§ 3]	ВОССТАНОВЛЕНИЕ ЗАКОНА ДВИЖЕНИЯ ПО СКОРОСТИ	27
на графике функции соответствует фиксированному значению аргу-
мента х, а точка Р — значению х + Дх, где Дх — некоторое прира-
щение аргумента. Прямую МР будем называть секущей. Обозначим
через <р(Дх) угол, который образует эта секущая с осью Ох (оче-
видно, что этот угол зависит от Дх). Касательной к графику функ-
ции у—f{x) в точке М будем называть предельное положение
секущей МР при стремлении точки Р к точке М по графику
{или, что то же самое, при Дх->0). Из рис. 1.2 ясно, что
tg (Дх) = — =
g т < х> MN Дх	Дх
Так как при Дх—► 0 секущая МР переходит в касательную, то
lim tg ср (Дх) = tg <р0,
4х-0
где <р0 — угол, который образует касательная с осью Ох. С другой
стороны,	ч
lim tg ф (Дх) = lim И* + А*! — f W 
Дх — О	Дх —О
/'
Следовательно, f(x) = tg^0. Тангенс угла наклона прямой к оси Ох
называют угловым коэффициентом этой прямой. Таким образом,
производная f'{x) равна угловому коэффициенту касательной к
графику функции у =f{x) в точке М.
§ 3. Задача о восстановлении закона движения по скорости
и связанная с ней математическая проблематика
Рассмотрим следующую физическую задачу. Пусть для любого
момента времени х задана мгновенная скорость /(х) движущейся по
оси Оу материальной точки и известно положение у0 этой точки в
начальный момент времени х = х0. Требуется найти закон движения
этой точки.
Поскольку мгновенная скорость /(х) является производной функ-
ции y — F{x), определяющей закон движения материальной точки по
оси Оу, то задача сводится к разысканию по данной функции 7(х)
такой функции F (х), производная F' (х) которой равна /(х).
Отвлекаясь от конкретного физического смысла функций /(х) и
F (х), мы придем к математическим понятиям первообразной и не-
определенного интеграла. Первообразной функции /(х) называется
такая функция F (х), производная F' (х) которой равна f{x).
Очевидно, что если функция F {х) является первообразной функ-
ции /(х), то и функция F(x) + C, где С — любая постоянная, также
является первообразной функции f(x) (ибо производная постоянной С
равна нулю).
28
ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
П'Л, i
Можно доказать, что две любые первообразные одной и той же
функции /(х) отличаются на постоянную. Таким образом, если функ-
ция F(x) является одной из первообразных функции f(x), то любая
первообразная функции f(x) имеет вид F(x)-f-C, где С—постоянная.
Совокупность всех первообразных одной и той же функции
f (х) называется неопределенным интегралом от функции f (x)
и обозначается символом ^f(x)dx.
Следовательно, если F (х)— одна из первообразных функции /(х),
то
J f (х) dx — F (х) + С.
Вернемся к решению поставленной выше физической задачи. Инте-
ресующий нас закон движения точки,  имеющей мгновенную скорость
f(x), определяется функцией у = F (х) + С, где F(x) — некоторая перво-
образная функции /(х), а С—некоторая постоянная. Для определения
постоянной С воспользуемся тем, что у=у0 в начальный момент вре-
мени х = х0, т. е. _у0 — ? (хо) + откуда С=у0~ F (х0). Таким обра-
зом, интересующий нас закон движения имеет вид
y = F(x) + y0-F(x0).
Рассмотрим некоторые физические и математические примеры.
1) Пусть мгновенная скорость материальной точки, движущейся
по оси Оу, имеет вид/(х) = cos х. Требуется найти закон движения
этой точки, если в начальный момент времени х = х0 точка занимает
положение у=Уо на оси Оу. Из таблицы производных ясно, что
одной из первообразных функции /(х) = cos х является функция
F(x) = sinx. Следовательно, искомый закон движения имеет вид
у = sin х -|- С.
Из условия у=у0 при х = х0 находим С=уй — sinx0, т. е. окон-
чательно получим закон движения в виде
2) Найти
у = sin х 4- _у0 — sin х0.
-5—j dx. Из таблицы производных ясно,
Г
из первообразных функции /(х) ~ t является функция F (х) =
= arctg х. Следовательно,
что одной
I-p^<Zx = arctg.x4-C.
В предыдущем параграфе мы выписали таблицу производных элемен-
тарных функций. Учитывая, что каждая формула F'(x)=/(x) этой
таблицы приводит к соответствующей формуле j/(x)rfx=F(x)-f-C,
мы получим следующую таблицу неопределенных интегралов:
§4]
ЗАДАЧА О ВЫЧИСЛЕНИИ ПУТИ
29
1°.	=	(а^-1).
2°. J^ = loge|x| + C
3°. ( axdx—^— 4- С.
J	logea
4°. J sin x dx == —cos x + C.
5°. § cos x dx = sin x + C.
6°. ^-^-=tgx + C.
7°. f =—ctgx + C.
J sin2x	&	'
8°. f , d*  = arcsln x + C.
J yT^
96.	= arctgx + C.
J 1 “T” **
Эта таблица вместе с правилами интегрирования (которые здесь
не приводятся) представляет собой важный вычислительный аппарат
той части математического анализа, которую обычно называют инте-
гральным исчислением.
Однако для вычисления многих неопределенных интегралов этого
аппарата оказывается недостаточно. Возникает проблема о существо-
вании первообразной (и неопределенного интеграла) у произвольной
функции f(x), непрерывной в каждой точке х. В следующем параграфе
мы укажем другой подход к задаче об интегрировании функции, ко-
торый позволяет решить эту проблему.
Здесь же мы сразу отметим, что существуют непрерывные (в каж-
дой точке х) функции (например, у — cos ха), первообразные которых
существуют, но не могут быть представлены с помощью конечного
числа операций сложения, вычитания, умножения, деления и образования
сложных функций от простейших элементарных функций, перечислен-
ных нами в п. 2 § 2.
§ 4. Проблемы, возникающие при решении задачи
о вычислении пути
1. Пусть функция f(x) представляет собой скорость движения
материальной точки по оси Оу. Для простоты будем считать, что
все значения функции f(x) неотрицательны. Требуется вычислить
путь, пройденный материальной точкой за промежуток времени от
х — а до х = Ь.
Для решения этой задачи *) разобьем рассматриваемый про-
межуток времени на малые промежутки, ограниченные моментами
*) Связь этой задачи с задачей, рассмотренной в предыдущем параграфе,
будет выяснена ниже.
30
ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
[ГЛ. t
а = х0 < хг <z х2 <. ..<Zxn = b. Естественно считать, что на каждом
промежутке от xk_i до xk скорость f(x~) меняется мало. Поэтому
приближенно эту скорость можно считать на указанном промежутке
постоянной и равной, например, /(х^). В таком случае путь, пройден-
ный материальной точкой за время Дх* = хк — x*_i, приближенно
равен /(х*)Дх*, а путь 5а, пройденный точкой за время от а до Ь,
приближенно равен
5а^/(х1)Дх1+/(х2)Дх2+ ... +f{xn)^xn. (1.6)
Естественно ожидать, что при уменьшении всех промежутков вре-
мени Дх* мы будем получать все более и более точное значение
пути Sa- Точное значение пути 5* мы получим, перейдя в сумме (1.6)
к пределу при стремлении всех Дх* к нулю (при этом, конечно,
число слагаемых в сумме (1.6) будет неограниченно возрастать).
Употребляя символ предела, мы можем записать следующую формулу:
= Um [/'(х1)ДХ1+/(х2)Дх2 + ...+/(х„) Дх„].	(1.7)
При этом вопрос о том, что мы понимаем под пределом написанной
суммы, конечно, требует выяснения. Тем самым мы еще раз убежда-
емся в необходимости углубления и
развития понятия предела. В матема-
тике предел (1.7) называется опре-
деленным интегралом от функции
/(х) в пределах от а до b и обоз-
начается символом
ъ
Sba = \f(x)dx.
а
Сумма (1.6) представляет собой
сумму площадей прямоугольников,
основаниями которых служат отрезки Дх*, а высотами /(х*). Иными
словами, эта сумма равна площади изображенной на рис. 1.3 ступен-
чатой фигуры (эта ступенчатая фигура на чертеже обведена жирной
линией). Естественно ожидать, что при стремлении к нулю длин всех
отрезков Дх* площадь указанной ступенчатой фигуры будет стре-
миться к площади заштрихованной на чертеже криволинейной фигуры,
лежащей под графиком функции _у=/(х) на отрезке от а до Ь.
Эту криволинейную фигуру часто называют криволинейной трапе-
цией. Таким образом, определенный интеграл равен площади указан-
ной криволинейной трапеции.
Конечно, проведенные нами рассуждения носят предварительный
характер. В частности, требует выяснения само понятие площади
криволинейной трапеции и вообще площади плоской фигуры.
2. Мы видим, что с понятием определенного интеграла тесно
связаны две важные задачи; физическая задача о вычислении пути и
§ 4J
ЗАДАЧА О ВЫЧИСЛЕНИИ ПУТИ
31
геометрическая задача о вычислении площади плоской фигуры.
В связи с этим является важным вопрос о способах вычисления опре-
деленного интеграла.
Обозначим через F (х) определенный интеграл от функции f(x)
в пределах от а до х, т. е. положим
F (x') — \f(x)dx.
а
С геометрической точки зрения этот интеграл равен площади
криволинейной трапеции, лежащей под графиком функции у =*f(x)
на отрезке от а до х. На рис. 1.4
эта трапеция обведена жирной чер-
той. Используя наглядные геометри-
ческие соображения, покажем, что
введенная функция F (х) является
одной из первообразных функции
/(х), т. е. убедимся в том, что
F’ (х) = f(x). Пусть Дх — некоторое
приращение аргумента х. Очевидно,
разность F (х -|- Дх) — F (х) равна
площади заштрихованной на рис. 1.4
«узкой» криволинейной трапеций. Площадь этой трапеции при малом
Дх мало отличается от площади /(х)Дх прямоугольника с основа-
нием Дх и высотой /(х). Отсюда ясно, что при малом Дх отношение
F (х + Дх) — F (х)
Дх
(1.8)
мало отличается от высоты /(х) указанного выше прямоугольника.
Так как предел при Дх—>0 дроби (1.8) равен производной Ff(х), то
F' (х)=/(х). Итак, функция F (х) является одной из первообразных
функции /(х). Следовательно, любая первообразная Ф(х) функции
/(х) имеет вид
^{x) = F{x) + C = \f(xy)dx + C.	(1.9)
а
Конечно, приведенные нами рассуждения и вытекающая из них
формула (1.9) справедливы, вообще говоря, не для всякой функции
/(х). Нетрудно убедиться в справедливости формулы (1.9) для любой
непрерывной (в каждой точке х) функции /(х). Тем самым установ-
ление формулы (1.9) решает проблему существования первообразной
(и неопределенного интеграла) у любой непрерывной в каждой
точке х функции /(х).
Установим теперь с помощью той же формулы (1.9) связь между
ь
определенным интегралом ^/(х)Фх и любой первообразной Ф(х)
32
ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
[ГЛ. I
функции f(x). Полагая в формуле (1.9) последовательно х = а и
х = Ь и учитывая очевидное из наглядных геометрических соображе-
ний равенство
^f(x)dx = Q,
а
получим
а	Ь
ф (а) = $ Л*) dx + С = С, Ф (Ь) = 5 /(х) dx + С.
а	а
Поэтому
ь
^f(x)dx = ®(b) — $(a).	(1.10)
а
Формула (1.10) является одной из основных формул интегрального
исчисления и называется формулой. Ньютона—Лейбница*). Эта фор-
мула сводит вопрос о вычислении определенного интеграла к во-
просу о вычислении первообразной
(или неопределённого интеграла).
Обоснование этой формулы явля-
ется одной из важных задач
математического анализа. Для приближенного вычисления определенных
интегралов существует ряд способов, простейший из которых осно-
ван на замене этого интеграла суммой (1.6). Эти способы и соотно-
шение (1.9) дают возможность приближенно вычислять и неопреде-
ленные интегралы, и, в частности, позволяют вычислить первообраз-
ную любой непрерывной (в каждой точке х) функции f(x).
В качестве примера вычислим площадь <$х, заключенную между
графиком функции _y = sinx на отрезке от 0 до я и осью Ох
(рис. 1.5)**). В силу сказанного выше
в
4S'1 = ^sinx(Zx.
о
*) Готфрид Вильгельм Лейбниц — немецкий философ и математик (1646—
1716).
**) Вычисление этой площади средствами элементарной математики при-
водит к большим трудностям.
§ 5]	ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ	33
Так как одной из первообразных функции /(х) = sin х является функ-
ция Ф(х) =—cos х, то по формуле (1.10) получим
Я
<$7 = j sin х dx = (— cos it) (— cos 0) = 2.
0
Вычислим теперь площадь S2 фигуры, отсекаемой от цараболы у = х2
прямой, проходящей через две точки М1(а, а2) и М2(Ь, Ь2) этой па-
раболы (рис. 1.6)*). Йскомая площадь S2 равна разности площадей
прямолинейной трапеции AMjM^B и заштрихованной на чертеже
криволинейной трапеции, т. е.
• &
„	(& + a2)(b-a) С v2. _ (b2 + a?)(b-a)	b2-a*	(b-a)»
o2--------2	jx ax— g	g —	6	.
a
§ 5.	Заключительные замечания
Дифференциальное и интегральное исчисления составляют основу
математического анализа, создание которого является одним из вели-
чайших достижений человеческого разума. Введение в математику
понятий переменной величины и функции позволило перейти от реше-
ния отдельных разрозненных физических и геометрических задач
к созданию общих методов решения этих задач. Развитие дифферен-
циального и интегрального исчислений оказало огромное влияние на
общий прогресс науки и техники.
Дальнейший прогресс науки и техники тесно связан с математи-
зацией наших представлений о природе, с развитием новых направ-
лений в математике. Можно с уверенностью сказать, что математи-
зация наших представлений, точная количественная формулировка
закономерностей, широкое использование вычислительных методов
и электронно-вычислительных машин (ЭВМ) составляют основной стер-
жень современного естествознания.
Внедрение вычислительных методов и использование ЭВМ, как
правило, снимают вопросы трудоемкости и сложности вычислений **).
При этом возникает целая серия математических проблем, к числу
которых относятся вопросы разработки алгоритмов ***) вычислений,
служащих источником составления программ для ЭВМ, разработка
проблем теории управления, теории оптимальных процессов, матема-
тической логики и теоретической кибернетики.
*) Эта задача средствами элементарной математики была решена великим
древнегреческим ученым Архимедом (Ш век до нашей эры).
**) Современные ЭВМ в несколько минут производят вычисления, для
проведения которых человеку потребовалась бы целая жизнь.
***) Алгоритм (или алгорифм) — система вычислений, выполняемых по
строго определенным правилам, приводящая после какого-либо числа шагов
к решению поставленной задачи.
34 '	ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ	[ГЛ. t
Наша дальнейшая задача будет заключаться в построении аппа-
рата математического анализа. Мы рассмотрим также и некоторые
приложения этого аппарата к разработке численных алгоритмов..
Проведенное выше предварительное рассмотрение ставит перед
нами следующие первоочередные вопросы:
1.	Уточнение понятий вещественного числа, переменной величины
и функции.
2.	Определение и развитие понятия предела функции и связанного
с ним понятия непрерывности функции.
3.	Обоснование формул и правил дифференциального и интеграль-
ного исчислений.
4.	Построение теории определённого интеграла как предела сумм
специального вида и развитие методов вычисления определенного
интеграла.
5.	Выяснение некоторых геометрических понятий (площади пло-
ской фигуры, длины дуги и т. д.).
ГЛАВА 2
ТЕОРИЯ ВЕЩЕСТВЕННЫХ ЧИСЕЛ
Из элементарного курса читатель имеет представление о вещест-
венных числах и о том, что они необходимы, например, для измере-
ния отрезков и промежутков времени. Для углубления наших пред-
ставлений о важнейших математических понятиях—понятиях перемен-
ной величины, функции и предела — требуется дальнейшее развитие
теории вещественных чисел.
Рассмотрим, например, физическую переменную величину—время.
Для сравнения между собой различных промежутков времени нам
необходимо уметь сравнивать между собой вещественные числа. Иными
словами, мы должны установить правило, позволяющее выяснить, какое
из двух данных вещественных чисел является большим. Практика
последовательных измерений времени приводит к необходимости опре-
деления операций сложения и умножения вещественных чисел и выяс-
нения свойств этих операций. Отметим также, что выяснение основ-
ных свойств вещественных чисел необходимо для обоснования приме-
нимости к этим числам правил элементарной алгебры.
§ 1. Вещественные числа
1. Свойства рациональных чисел. Напомним, что рациональным
числом называется число, представимое в виде отношения двух целых
чисел *). Из элементарного курса известны определения операций
сложения и умножения рациональных чисел, правило сравнения этих
чисел и их простейшие свойства. Здесь мы перечислим основные
свойства рациональных чисел, вытекающие из соответствующих свойств
целых чисел.
Фундаментальную роль среди свойств играют три правила: пра-
вило сравнения и правила образования суммы
и произведения:
*) Одно и то же рациональное число представимо в виде отношения раз-
12	3
личных целых чисел. Например, = — = — = ...
Зв	ТЕОРИЯ ВЕЩЕСТВЕННЫХ ЧИСЕЛ	ТГЛ 2
\
I.	Любые два рациональных числа а и b связаны одним и только
одним из трех знаков J>, < или = , причем если а > b, mob<.a.
Иными словами, существует правило, позволяющее установить,
каким из указанных трех знаков связаны два данных рациональ-
ных числа. Это правило называется правилом сравнения*).
II.	Существует правило, посредством которого любым двум
рациональным числам а и b ставится в соответствие опреде-
ленное рациональное число с, называемое их суммой и обозначае-
мое символом с = а -\-Ь **).
Операция нахождения суммы называется сложением.
III.	Существует правило, посредством которого любым двум
рациональным числам а и b ставится в соответствие определен-
ное рациональное число с, называемое их произведением и обозна-
чаемое символом c = ab***). Операция нахождения произведения
называется умножением.	-	
Перечислим теперь основные свойства, которым подчинены ука-
занные три правила.
Правило сравнения рациональных чисел обладает следующим свой-
ством:
1° из а~у>Ь и Ь>с вытекает, что а~у>с {свойство тран-
зитивности знака >); из а = Ь и Ь = с вытекает, что а = с
{свойство транзитивности знака =).
' Правило сложения рациональных чисел обладает следующими
свойствами:
2° a-Yb — b + a (переместительное свойство);
3° {а Ь) + с = а + {Ь + с) (сочетательное свойство);
4° существует рациональное число 0 такое, что а-}-0 = а
для любого рационального числа а (особая роль нуля);
5° для каждого рационального числа а существует противо-
положное ему число, а' такое, что а + а' = 0.
Правило умножения рациональных чисел обладает следующими
свойствами:
6° ab — ba (переместительное свойство);
*) Правило сравнения рациональных чисел формулируется так: два неот-
пи , т2
рицательных рациональных числа а = и b = связаны тем же знаком,
что и два целых числа и т^п^, два неположительных рациональных числа
а и b связаны тем же знаком, что и два неотрицательных числа | fc | и | а |;
если а — неотрицательное, а b — отрицательное рациональное число, то а > Ь.
**) Правило образования суммы рациональных чисел а — — и Ь = —
th
, пц , тг
определяется посредством формулы —4--------- = —‘	——-.
Zlj Л 2	^1^2
***) Правило образования произведения рациональных чисел определяется
, пи т- пцпи
посредством формулы —- — = ——-,
Tlj Zig
§ 1]	ВЕЩЕСТВЕННЫЕ ЧИСЛА	37
7° (ab)c-a(bc) (сочетательное свойство);
8° существует рациональное число 1 такое, что а-1—а для
любого рационального числа а (особая роль единицы);
9° для каждого рационального числа а, отличного от нуля,
существует обратное ему число а' такое, что аа'=\.
Правила сложения и умножения связаны следующим свойством:
10° (а + Ь) с = ас 4- Ьс (распределительное свойство умножения
относительно суммы).
Следующие два свойства связывают знак > со знаком сложения
и умножения:
11° из а> b вытекает, что а 4- с > b + с\
12° из а>Ь и с > 0 вытекает, что acZ>bc- '
Особая роль принадлежит последнему свойству:
13° каково бы ни было рациональное число а, можно число 1
повторить слагаемым столько раз, что полученная сумма пре-
взойдет а*).
Перечисленные 13 свойств обычно называют основными свой-
ствами рациональных чисел, ибо все другие алгебраические свой-
ства этих чисел, относящиеся к арифметическим действиям и к соче-
танию равенств и неравенств/ могут быть извлечены как следствие
из указанных основных свойств.
Так, например, из этих свойств вытекает часто используемое
в дальнейшем свойство, позволяющее пбчленно складывать неравен-
ства одного знака:
если а>Ь и с > d, то а 4- с > & 4-
. В самом деле, из неравенств а^>Ь и и из свойств 11°
и 2° вытекает, что а-\-су>Ь-\-с и bс ~у> $d, а из последних
неравенств и из свойства 1° вытекает, что а 4- с > b 4- d.
2. Об измерении отрезков числовой оси. Из элементарного
курса известно, что два отрезка могут быть соизмеримыми (когда
отношение их длин выражается рациональным числом) и несоизме-
римыми (примером несоизмеримых отрезков могут служить диагональ
и сторона квадрата).
Удобно сразу же ввести в рассмотрение числовую ось. Числовой
осью мы будем называть прямую, на которой выбраны определенная
точка О (начало отсчета), масштабный отрезок ОЕ (длину его мы счи-
таем равной единице) и положительное направление (обычно от О к Е).
Естественно, возникает задача о возможности поставить в соот-
ветствие каждой точке М числовой оси некоторое число, выражаю-
щее длину отрезка ОМ. Это число мы будем считать положительным,
если М и Е лежат по одну сторону от О, и отрицательным — в про-
тивном случае.
Прежде всего заметим, что каждому рациональному числу соот-
ветствует на числовой оси определенная точка. В самом деле,
*) Эго свойство часто называют аксиомой Архимеда.
38
ТЕОРИЯ ВЕЩЕСТВЕННЫХ ЧИСЕЛ
[ГЛ. 2
из элементарного курса известно, как построить отрезок, длина кото-
рого составляет — часть длины масштабного отрезка Of (и — любое
целое положительное число). Стало быть, мы можем построить отре-
зок АВ, длина которого относится к длине масштабного отрезка ОЕ,
Мг(-^ О Е М^)
Рис. 2.1.
как —, где т и п — любые целые положительные числа. Считая, что
п ’
точка Е лежит правее О (рис. 2.1) и отложив отрезок АВ вправо
(влево) от точки О, мы получим точку Мг (Л12), соответствующую
. т / т \
рациональному числу + — ( — —).
Вместе с тем существование несоизмеримых отрезков позволяет
утверждать, что не все точки числовой оси соответствуют рацио-
нальным числам.
Естественно, возникает потребность расширить область рациональ-
ных чисел и ввести в рассмотрение такие числа, которые соответст-
вовали бы всем точкам числовой оси и позволяли бы измерить при
помощи масштабного отрезка ОЕ любой отрезок.
Мы опишем специальный процесс измерения отрезка ОМ число-
вой оси и покажем, что этот процесс позволяет поставить в соот-
ветствие любой точке М этой оси некоторую вполне определен-
ную бесконечную десятичную дробь.
О
______________ар.......\
~Е :	Л' ” РМ
Рис. 2.2,
Пусть М — любая точка числовой оси. Ради определенности пред-
положим, что М (как и Е) лежит правее О (рис. 2.2).
Будем измерять отрезок ОМ при помощи масштабного отрезка ОЕ.
Прежде всего выясним, сколько раз целый отрезок ОЕ укладывается
в отрезке ОМ. Могут представиться два случая:
1) Отрезок ОЕ укладываетс^в отрезке ОМ целое число а0 раз
с некоторым остатком NM, меньшим ОЕ (см. рис. 2.2). В- этом слу-
чае целое число а0 представляет собой приближенный результат
измерения по недостатку с точностью до единицы.
2) Отрезок ОЕ укладывается в отрезке ОМ целое число а0 + 1
раз без остатка. В этом случае число а0 также представляет собой
приближенный результат измерения по недостатку с точностью до
ВЕЩЕСТВЕННЫЕ ЧИСЛА
39
§ 1]
единицы, ибо отрезок ОЕ укладывается, в отрезке ОМ а0 раз с остат-
ком NM, равным ОЕ *).
Выясним теперь, сколько раз часть масштабного отрезка ОЕ укла-
дывается в остатке NM. Снова могут представиться два случая:
1) часть отрезка ОЕ укладывается в отрезке NM целое число
аг раз с некоторым остатком РМ, меньшим части отрезка ОЕ (см.
рис. 2.2). В этом случае рациональное число а0, представляет
собой результат измерения по недостатку с точностью до
2) часть отрезка ОЕ укладывается в отрезке NM целое число
Oj + 1 раз без остатка. В этом случае рациональное число а0, aY
также представляет собой результат измерения по недостатку с точ-
ностью до ибо часть ОЕ укладывается в отрезке NM аг раз
с остатком РМ, равным части ОЕ **).
Продолжая неограниченно указанные рассуждения, мы придем
к бесконечной совокупности рациональных чисел:
’ «0> ^1^2 ••• ®Л» ••• >	(2.1)
каждое из которых представляет собой результат измерения отрезка ОМ
по недостатку с соответствующей степенью точности. Вместе с тем
каждое из чисел (2.1) может быть получено посредством обрывания
на соответствующем знаке бесконечной десятичной дроби
а0> ^1^2 • • • ^л • • •	(2-2)
Указанные выше рассуждения применимы и для случая, когда
точка М лежит левее точки О, только в этом случае все числа {2.1) и
бесконечная десятичная дробь (2.2) будут иметь отрицательный знак.
Таким образом, мы установили, что посредством описанного
нами процесса измерения отрезка ОМ любой точке М числовой
оси можно поставить в соответствие вполне определенную бес-
конечную десятичную дробь.
Итак, мы видим, что описанный выше процесс измерения произ-
вольного отрезка ОМ числовой оси при помощи масштабного отрезка
естественным образом приводит нас к рассмотрению чисел, предста-
вимых в виде бесконечных десятичных дробей. Вместе с тем
।
' z
,	*) Конечно, на практике во втором случае процесс измерения считают
законченным и полагают длину отрезка ОМ равной а0+ !• Однако нам удоб-
нее (в целях единообразия) вести измерения строго по недостатку, чтобы
и в этом случае получить остаток NM и иметь возможность продолжать
процесс измерения.
•*) Отсылаем читателя к предыдущей сноске.
40
ТЕОРИЯ ВЕЩЕСТВЕННЫХ ЧИСЕЛ
(ГЛ. 2
каждая бесконечная десятичная дробь (2.2) полностью характеризуется
бесконечной совокупностью (2.1) рациональных чисел, приближающих
эту дробь. Конечно, описанный выше процесс измерения отрезка ОМ
можно видоизменить так, что он будет приводить к рассмотрению бес-
конечных двоичных дробей или к рассмотрению бесконечных дробей
в любой другой системе счисления.
Заметим, что для задания чисел в современных электронных
вычислительных машинах наиболее часто используется двоичная си-
стема счисления, а иногда — троичная система счисления. Это объяс-
няется тем, что входящие в конструкцию электронных машин радио-
лампы и полупроводниковые элементы имеют чаще всего два,
а иногда три устойчивых состояния (например, лампа закрыта, ток
не идет — одно устойчивое состояние; лампа открыта, ток идет —
другое устойчивое состояние; третье устойчивое состояние возникает,
если различать направление, в котором- идет ток).
В связи с отмеченным обстоятельством возникает необходимость
в разработке алгоритмов перевода чисел из десятичной системы
счисления в двоичную систему и обратного перевода чисел из
двоичной системы в десятичную. Примеры таких алгоритмов читатель
найдет в Дополнении 1 к настоящей главе.
3. Вещественные числа и правило их сравнения. Рассмотрим
множество всевозможных бесконечных десятичных дробей. Числа,
представимые этими дробями, будем называть вещественными *).
Данное вещественное число будем называть положительным (отри-
цательным), если оно представимо в виде положительной (отрица-
тельной) бесконечной десятичной дроби.’
В состав множества вещественных чисел входят, конечно, и все
рациональные числа, ибо все они представимы в виде бесконечных
десятичных дробей. Представление данного рационального числа
в виде бесконечной десятичной дроби можно получить, например, из
следующих соображений. Любому рациональному числу соответствует
определенная точка М числовой оси, а этой точке ставится в соответ-
ствие при помощи способа, указанного в пункте 2, определенная бес-
конечная десятичная дробь. Так, рациональному числу ставится
в соответствие бесконечная десятичная дробь 0,4999 ..., рациональ-
4
ному числу -д---бесконечная десятичная дробь 1,333 ...
Вещественные числа, не являющиеся рациональными, принято на-
зывать иррациональными.
Нашей задачей является последовательное перенесение на случай
произвольных вещественных чисел трех правил и всех основных
свойств рациональных чисел, перечисленных в пункте 1. Тем самым
•) Как, уже отмечалось в сноске **) на стр. 18, понятие числа относится
к начальным понятиям.
5 1]	ВЕЩЕСТВЕННЫЕ ЧИСЛА	41
для вещественных чисел будут обоснованы всё правила элементарной
алгебры, относящиеся к арифметическим действиям и к сочетанию
равенств и неравенств.
В этом пункте мы установим правило сравнения вещественных
чисел. Прежде чем перейти к формулировке этого правила, догово-
римся об определенной форме записи тех рациональных чисел, кото-
рые представимы в виде конечной десятичной дроби. Заметим, чтр
указанные рациональные числа допускают двоякую запись в виде
бесконечных десятичных дробей. Например, число у = 0,5 можно
записать: 1) в виде у = 0,4999...; 2) в виде у = 0,5000..,.
И вообще рациональное число а0, аха2 ... ап, где а„ ?£ 0, можно
записать: 1) в виде а0, а^... ап-1(а„— 1) 999...; 2) в виде
а0, а^ ... ап 000 ...
Первая из указанных двух записей может быть получена по спо-
собу, описанному в пункте 2, а вторая — формальным превращением
данной конечной десятичной дроби в бесконечную посредством'допи-
сывания нулей.
Мы договоримся при сравнении вещественных чисел пользо-
ваться для указанных рациональных чисел лишь первой из этих двух
форм записи в виде бесконечной десятичной дроби.
Иными словами, при сравнении вещественных чисел мы не будем
употреблять бесконечные десятичные дроби, все десятичные знаки
которых, начиная с некоторого места, равны нулю (за исключением,
конечно, дроби 0,000 ...)*).
Перейдем теперь к формулировке правила сравнения веществен-
ных чисел. ’ _
Рассмотрим два произвольных вещественных числа а и Ь. Пусть
эти числа представимы следующими бесконечными десятичными
дробями:
а = ±а0, а^ ... ап ...,	(2.3)
& = ±/>0,М2 ... Ьп ...	(2.4)
(где из двух знаков ± берется какой-то один).
Два вещественных числа (2.3) и (2.4) называются равными, если
они имеют одинаковые знаки и если справедливы равенства ай — Ьо,
= bi, ..., ап = bm ...
Пусть даны два неравных вещественных числа а и Ь. Установим
правило, при помощи которого можно заключить, каким знаком, >
или связаны эти два числа:
•) Принятие .такой договоренности вполне соответствует процессу изме-
рения отрезка, описанному в пункте 2, ибо описанный процесс не может
привести к бесконечной десятичной дроби, у которой все десятичные знаки,
начиная с некоторого места, равны нулю.
42
ТЕОРИЯ ВЕЩЕСТВЕННЫХ ЧИСЕЛ
'ЩЛ 2
1)	Пусть сначала а и b оба неотрицательны и имеют следую-
щие представления: а — а0, аха2 ... ап ..b = Ьо, ЬХЬ2 ... Ьп ...
Так как числа" а и & не равны, то нарушается хотя бы одно из
равенств а0 = b0, ах = blt ..., an = bn,... Обозначим через k наимень-
ший из номеров п, для которых нарушается равенство *) ап — Ьп.
Тогда мы будем считать, что а > Ь, если ak Ьк, и а < b, если
а* < Ьк-
2)	Если из двух чисел а и b одно неотрицательно, а другое
отрицательно, то мы, естественно, будем считать, что неотрицатель-
ное число больше отрицательного.
3)	Остается рассмотреть случай, когда оба числа а и b отрица-
тельны. Договоримся называть модулем вещественного числа а
неотрицательное вещественное число, обозначаемое символом | а |
и равное десятичной дроби, представляющей число а, взятой со
знаком 4-.
Если а и b оба отрицательны, то мы будем считать, что aZ>b,
если | b | > | а |, и а<_Ь, если | а | > | b | **).
Убедимся, что правило сравнения вещественных чисел обладает
свойством 1°, сформулированным в пункте 1 для рациональных чисел.
Именно, докажем, что если а, b и с — произвольные вещественные
числа и если а>Ь и ЬУ>с, то а~>с (свойство транзитивности
знака >) ***). Для доказательства этого свойства рассмотрим три воз-
можных случая:
1)	Пусть сначала с^=0. Тогда из правила сравнения веществен-
ных чисел очевидно, что b > 0 и а > 0. Пусть а = а0, а1аг ... ап..:,
b = bQ, ЬД>2 ... Ьп... •, с = с0, с^ ... сп ... Обозначим через k наи-
меньший из номеров п, для которых нарушается равенство ап = Ьп
(т. е. предположим, что а0 = Ьо, а1~Ь1, ..., а^ =	ак>bk),
*) То есть мы считаем, что а0 = b0, ai — bi, ... , ak_i — bk_i, но акДЬк.
**) Легко видеть, что сформулированное правило сравнения веществен-
ных чисел в применении к двум рациональным числам приводит к тому же
самому результату, что и правило сравнения рациональных чисел, указанное
в сноске на стр. 36.
В самом деле, достаточно рассмотреть лишь случай двух неотрицатель-
ных рациональных чисел а и Ь. Пусть а>Ь согласно правилу сравнения
рациональных чисел, и пусть а = а0, ata2 ... ап ...; b = й0,	bn ...
Предположим, что рациональному числу а соответствует на числовой оси
точка Mlt а рациональному числу b — точка М2. Тогда ясно, что точка Мг
лежит правее точки М2. Вместе с тем из пункта 2 вытекает, что целое число
aoai ... ак (bobi ... bk) показывает, сколько раз часть масштабного от-
резка ОЕ укладывается в отрезке OML (ОМ2) с выкинутым правым концом.
Поскольку отрезок OMi больше отрезка ОМ2, то найдется такой номер k,
что ... ak_i = bobi ... bk_i, a aoai ... ak > bobibk, но это и означает,
что а >• b согласно правилу сравнения вещественных чисел.
***) Свойство транзитивности знака =, утверждающее, что из а = Ь и
b = с следует, что а = с, сразу вытекает из правила сравнения веществен-
ных чисел.
ВЕЩЕСТВЕННЫЕ ЧИСЛА
43
§ П
а через р наименьший из номеров п, для которых нарушается равен-
ство Ьп = сп (т. е. предположим, что Ьо = с0, Ьх = сх,..., bp_x — ср_х,
Ьр > ср). Тогда, если обозначить через т наименьший из двух номе-
ров k а р, то будут справедливы соотношения а0 = с0, ах = сх>...
..., аст_1 = Сда-р ат > ст, а это и означает, что а > с.
2)	Пусть с<0, а^О. Тогда равенство а>с будет справедливо
при любом Ь.
3)	Остается рассмотреть случай, когда все три числа а, b и с от-
рицательны. Так как а>£> и Ь> с, то | b | > | а | и|с|>|£|. Но
тогда, в силу уже рассмотренного выше случая трех положительных
чисел, | с | > | а а это и означает, что а > с. Свойство транзитивно-
сти знака > полностью доказано.
4.	Приближение вещественного числа рациональными числами.
В этом пункте мы покажем, что всякое вещественное число можно
приблизить с любой степенью точности рациональными числами. Рас-
смотрим произвольное вещественное число а. Ради определенности
будем считать это число неотрицательным и представим его в виде
бесконечной десятичной дроби а = а0, аха2...ап...
Обрывая указанную дробь на я-м знаке после запятой, получим
V	1
рациональное число а0, аха2... ап. Увеличив это число на по-
лучим другое рациональное число а0, аха2 ... ап +	. Из правила
сравнения вещественных чисел легко установить, что для любого но-
мера п справедливы неравенства
ао> • • • ип a Go, ••• Яд 4"	•	(2.5)
Неравенства (2.5) означают, что' вещественное число а заключено
между двумя рациональными числами, разность между которыми
равна При этом номер п можно взять любой.
Покажем, что для любого наперед взятого положительного ра-
ционального числа в, начиная с некоторого номера п, справедливо
неравенство ~<е. В самом деле, каково бы ни было рациональное
число в > О, найдется лишь конечное число натуральных чисел, не
1 гт
превосходящих числа —. Поэтому лишь для конечного числа номеров
п справедливо неравенство	или	Для всех же осталь-
ных номеров и справедливо обратное неравенство jgs’C6,’ что и
требовалось доказать.
Таким образом, мы приходим к следующему утверждению’, для
любого вещественного числа а и для любого наперед взятого по-
ложительного рационального числа в найдутся два рациональных
числа ах и ag такие, что аа<:а=Саа, причем ag —<^<6.
44
ТЕОРИЯ ВЕЩЕСТВЕННЫХ ЧИСЕЛ
[ГЛ. 2
Неравенства (2.5) позволяют утверждать, что рациональное число
а0, а1а2а3... ап приближает вещественное число а с точностью до
На практике всегда имеют дело с приближенным значением ве-
щественного числа, заменяя его рациональным числом с требуемой
степенью точности.
5.	Множества вещественных чисел, ограниченные сверху или
снизу. В этом пункте мы рассмотрим произвольное множество ве-
щественных чисел, содержащее хотя бы одно число *). Это множество
мы будем обозначать символом {х}. Отдельные числа, входящие в со-
став множества {х}, будем называть элементами этого множества **).
Определение 1. Множество вещественных чисел {х} назы-
вается о гр аниче нн ы м сверху (снизу), если существует
такое вещественное число М (число т), что каждый элемент х
множества {х} удовлетворяет неравенству
х^М (х^т).
При этом число М (число т) называется верхней гранью (нижней
гранью) множества {х}.
Конечно, любое ограниченное сверху множество {х} имеет беско-
нечно много верхних граней. В самом деле, если вещественное число
М — верхняя грань множества {х}, то любое вещественное число
М*, большее числа М, также является верхней гранью множества
{х}. Аналогичное замечание можно сделать в отношении нижних
граней ограниченного снизу множества {х}.
Так, например, множество всех отрицательных вещественных чи-
сел ограничено сверху. В качестве верхней грани М такого множе-
ства можно взять любое неотрицательное вещественное число. Мно-
жество всех целых положительных чисел 1, 2, 3,... ограничено снизу.
В качестве нижней Трани этого множества можно взять любое веще-
ственное число т, удовлетворяющее неравенству zw^l.
Естественно, возникает вопрос о существовании наименьшей из
верхних граней ограниченного сверху множества и наибольшей из
нижних граней ограниченного снизу множества.
Определение 2. Наименьшая из всех верхних граней ограничен-
ного сверху множества {х} называется точной верхней гра-
нью этого множества и обозначается символом Jc = sup {х} ***).
Наибольшая из всех нижних граней ограниченного снизу мно-
жества {х} называется точной нижней гранью этого
множества и обозначается символом x = inf {х} ****).
*) Такое множество обычно называют непустым.
**) Отметим, что понятие множества и его элемента относится к началь-
ным понятиям (см. сноску **) на стр. 18).
***) sup —первые три буквы латинского слова supremum («супремум»),»
которое переводится как «наивысшее».
♦***) inf —первые три буквы латинского слова infimum («инфимум»), ко-
торое переводится как «наинизшее».
ВЕЩЕСТВЕННЫЕ ЧИСЛА
45
§ И
Определение 2 можно сформулировать и по другому, а именно:
Число X (число х) называется точной верхней (точной ниж-
ней) гранью ограниченного сверху (снизу) множества {х}, если
выполнены следующие два требования: 1) каждый элемент х
множества {х} удовлетворяет неравенству х^Х(х^х), 2) ка-
ково бы ни было вещественное число хг, меньшее X (большее х),
найдется хотя бы один элемент х множества {х}, удовлетво-
ряющий неравенству х > х' (х < х').
В этом определении требование 1) означает, что число X (число х)
является одной из верхних (нижних) граней, а требование 2) говорит
о том, что эта грань является наименьшей (наибольшей) и умень-
шена (увеличена) быть не может.
Очевидно, что у множества всех отрицательных вещественных
чисел существует точная верхняя грань—число нуль, причем это
число не принадлежит указанному множеству. Очевидно также,
что у множества всех целых положительных чисел 1, 2, 3, ... суще-
ствует точная нижняя грань х=1, которая принадлежит указан-
ному множеству (т. е. является наименьшим элементом этого
множества). Таким образом, точная верхняя (точная нижняя) грань
множества может как принадлежать, так и не принадлежать этому
множеству.
Существование у любого ограниченного сверху (снизу) множества
точной верхнёй (точной нижней) грани не является очевидным и тре-
бует доказательства.
Докажем следующую основную теорему.
Теорема 2.1. Если множество вещественных чисел содержит
хотя бы один элемент и ограничено сверху (снизу), то сущест-
вует вещественное число X (число х), которое является точной
верхней (точной нижней) гранью этого множества.
Доказательство. Мы остановимся лишь на доказательстве
существования точной верхней грани у любого ограниченного сверху
множества, ибо существование точной нижней грани у любого огра-
ниченного снизу множества доказывается совершенно аналогично.
Итак, пусть множество {х} ограничено сверху, т. е. существует
такое вещественное число М, что каждый элемент х множества {х}
удовлетворяет неравенству
х^М.	(2.6)
Могут представиться два случая: 1°. Среди элементов множества
{х} есть хотя бы одно неотрицательное вещественное число. 2°. Все
элементы множества являются отрицательными вещественными числами.
Эти случаи мы рассмотрим отдельно.
1°. Рассмотрим лишь неотрицательные вещественные числа, вхо-
дящие в состав множества {х}. Каждое из этих чисел представим
в виде бесконечной десятичной дроби и рассмотрим целые части этих
46
ТЕОРИЯ ВЕЩЕСТВЕННЫХ ЧИСЕЛ
[ГЛ. 2
десятичных дробей. В силу (2.6) все целые части не превосходят
числа М, а поэтому найдется наибольшая из целых частей, которую
мы обозначим через х0. Сохраним среди неотрицательных чисел мно-
жества {х} те, у которых целая часть равна Хо, и отбросим все
остальные числа. У сохраненных чисел рассмотрим первые десятич-
ные знаки после запятой. Наибольший из этих знаков обозначим че-
рез Xv Сохраним среди неотрицательных чисел множества {х} те,
у которых целая часть равна Хо, а первый десятичный знак равен хр
и отбросим все. остальные числа. У сохраненных чисел рассмотрим
вторые десятичные знаки после запятой. Наибольший из этих знаков
обозначим через х2. Продолжая аналогичные рассуждения далее, мы
последовательно определим десятичные знаки некоторого веществен-
ного числа X:
X = Х& XiXi ... Хп ...
Докажем, что это вещественное число X и является точной верх-
ней гранью множества {х}. Для этого достаточно доказать два
утверждения: 1) что каждый элемент х множества {х} удовлетво-
ряет неравенству х^Х, 2) что, каково бы ни было вещественное
число х', меньшее X, найдется хотя бы один элемент х множества {х},
удовлетворяющий неравенству х > х'.
Сначала докажем утверждение 1). Так как X неотрицательно,
то любое отрицательное число х из множества {х} заведомо удов-
летворяет неравенству х^~Х. Пусть х = х0, Х\ ... хп ... — любое
неотрицательное число, входящее в состав множества {х}.
Из определения числа X вытекает неравенство х0^х0. Если при
этом хо<хо, то утверждение 1) доказано. Если же хо = Хо, то из
определения числа X вытекает, что Xj Xi. Если при этом Xi < хь
то утверждение 1) доказано. Если же Xi = Xi, то из определения х
вытекает, что х2<ха ... Продолжая аналогичные рассуждения, мы
либо докажем неравенство х < х, либо получим бесконечную цепоч-
ку равенств хо = Хо> Х\=Х\, х2 = х2, ..., х„ = хп, из которой
вытекает, что х — Х. Утверждение 1) доказано.
Докажем теперь утверждение 2). Пусть х' = х'о, xjxj... х'п ...—
произвольное вещественное число*), меньшее X. Тогда в силу пра-
вила сравнения вещественных чисел найдется номер п такой, что
х2 — Хо, Xi = Xi, ...,хл_|=Хл—1, Хпхп.	(2.7)
С другой стороны, число X мы строили так, что среди элементов
множества {х} найдется число х = х0, Xjr2 ... хп ..., целая часть
и первые п десятичных знаков у которого те же, что и у числа X,
т. е.
Х^ — Хо, Хх — Xi,	^л—1 —	%п—Хп-	(2.8)
... ,	,	, ,	’ .ТС',
*) Это число х' мы, не ограничивая общности, будем считать неотрица-
тельным, ибо если бы оно было отрицательным, то неравенству х > х' удов-
летворял бы неотрицательный элемент х множества {х}.
§ 2] АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ НАД ВЕЩЕСТВЕННЫМИ ЧИСЛАМИ 47
Сопоставляя (2.7) и (2.8), в силу правила сравнения вещественных
чисел получим, что х7 <.х. Утверждение 2) доказано. Таким обра-
зом, для случая 1° существование точной верхней грани доказано.
2°. Аналогично доказывается существование точной верхней грани
и во втором случае, когда все элементы множества {х\ являются
отрицательными вещественными числами. В этом случае все эле-
менты множества {х} мы представим в виде отрицательных беско-
нечных десятичных дробей. Обозначим через х0 наименьшую из
целых частей этих дробей; через Хг наименьший из первых деся-
тичных знаков тех из этих дробей, у которых целая часть равна х0;
через х2 наименьший из вторых десятичных знаков тех из этих
дробей, у которых целая часть равна х0, а первый десятичный знак
равен Хх; ... Таким путем мы определим отрицательное вещественное
число
X = — х0, ххх2 • • • Хя • •,
В полной аналогии со случаем 1° доказывается, что число J? является
точной верхней гранью множества {х} (т. е. удовлетворяет двум ут-
верждениям, сформулированным при рассмотрении случая 1°). Теорема
доказана.
Замечание. При доказательстве теоремы 2.1 для случая 2° у
числа х = — -£0, Ххх2 ... хп ... все десятичные знаки, начиная с неко-
торого места, могут оказаться равными нулю, т. е. это число может
оказаться имеющим вид х =— Хо, Х1 ... x^Xh ООО ..., где х* 0.
В этом случае остается в силе приведенное выше доказательство,
но согласно договоренности, принятой в пункте 3, при сравнении с
элементами множества число X следует записывать в виде
х == — Хо, Хг ... Xk l(Xk—V) 999 ...
§ 2. Арифметические операции над вещественными числами.
Основные свойства вещественных чисел
1. Определение суммы вещественных чисел. Одним из важней-
ших вопросов теории вещественных чисел является вопрос об опре-
делении операций сложения и умножения этих чисел и о свойст-
вах этих операций. Прежде всего остановимся на операции сложе-
ния вещественных чисел.
Хорошо известно, как складывают два вещественных числа на
практике. Для того чтобы сложить два вещественных числа а и Ь,
заменяют их с требуемой степенью точности рациональными числами
и за приближенное значение суммы двух данных вещественных чисел
берут сумму указанных рациональных чисел. При этом совершенно
не заботятся о том, с какой стороны (по недостатку или по избытку)
взятые рациональные числа приближают данные вещественные числа
а и Ъ. Фактически указанный практический способ сложения вещест-
венных чисел предполагает, что чем точнее рациональные числа а ц
48
ТЕОРИЯ ВЕЩЕСТВЕННЫХ ЧИСЕЛ
(ГЛ. 2
§ приближают (с любой стороны) вещественные числа а и b соот-
ветственно, тем точнее сумма а + р приближает то вещественное число,
которое должно являться суммой вещественных чисел а и Ь.
Желание оправдать указанный практический способ сложения ве-
щественных чисел, естественно, приводит нас к следующему опреде-
лению суммы двух вещественных чисел.
Дусть ах и а2 —какие угодно рациональные числа, между кото-
рыми заключено вещественное число а (т. е. aj^gasCc^), а {Зх и р2—
какие угодно рациональные числа, между которыми заключено ве-
щественное число b (т. е. [Зх b |32). Тогда суммой вещественных
чисел а и b мы назовем такое вещественное число х, которое'заклю-
чено между всеми рациональными числами (04 + рх) и (а2 4- р2) *).
Иными словами, с у ммой вещественных чисел а и b мы назо-
вем такое вещественное число х, которое для любых рациональ-
ных чисел ах, а2, рх и £2, удовлетворяющих неравенствам
ах < а а2, рх b С р2,	(2.9)
удовлетворяет следующим неравенствам:
а1 + Х а2 + ?2-
(2.Ю)
Существование такого вещественного числа х, и притом. только од-
ного, не вызывает-сомнений. Соответствующее доказательство приво-
дится ниже в петите. Нетрудно убедиться в том, что таким числом х
является точная верхняя грань множества {<xx + W сумм всех ра-
циональных чисел ах ирх, удовлетворяющих левым неравенствам
(2.9) **).
1°. Прежде всего убедимся в том, что указанная верхняя грань сущест-
вует. В самом деле, фиксируем произвольные рациональные числа а2 и р2,
удовлетворяющие правым неравенствам (2.9), и рассмотрим всевозможные
рациональные числа и рх, удовлетворяющие левым неравенствам (2.9).
Из свойства транзитивности знака >, установленного в пункте 3 § 1, за-
ключаем, что	р!^р2, а из этих неравенств следует, что
г^а24-Э2 (см. конец пункта 1 § 1). Таким образом, множество всех рацио-
нальных чисел {®i + Р1} ограничено сверху и число а2.+ ?2 является одной из
верхних граней этого множества. По теореме 2.1 у множества рх + М су-
ществует точная верхняя грань, которую мы обозначим через х. Остается
убедиться в том, что число х является суммой вещественных чисел а и Ь,
т. е. удовлетворяет неравенствам (2.10). В самом деле, по определению точ-
ной верхней грани, справедливо левое неравенство (2.10), а справедливость
правого неравенства (2.10) вытекает из того, что «2 + одна из-верхних гра-
ней, а х — точная верхняя грань множества {“i + Pi}-
2°. Установим теперь, что существует только одно вещественное число х,
удовлетворяющее неравенствам (2.10). Будем опираться на следующую
s *) Заметим, Что в элементарном курсе сумма двух вещественных чисел
определялась аналогичным образом (см. А. П. Киселев, Алгебра II, Уч-
педгиз, 1959, стр. 9).
**) Аналогично, можно было бы убедиться в том, что таким числом яв-
ляется точная нижняя грань множества {«2 + ₽а} сумм всех рациональных
чисел аа и р2, удовлетворяющих правым неравенствам (2.9).
§ 2] АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ НАД ВЕЩЕСТВЕННЫМИ ЧИСЛАМИ 49
лемму (для удобства доказательство этой леммы отнесено в конец настоя-
щего пункта): .
Если для двух данных вещественных чисел хг и хг и для любого наперед
взятого положительного рационального е найдутся два рациональных числа "ц
и т2 таких, что 71 Та> 71 ^*2^ Та и Та — Ti<s> то числа
и хг равны.
Предположим, что существуют два вещественных числа xt и хг, удовлет-
воряющих неравенствам (2.10) (при любых рациональных числах alt a2, рх и р2,
удовлетворяющих неравенствам (2.9)). Возьмем любое положительное рацио-
нальное число е.' Согласно утверждению, доказанному в п. 4 § 1, для вещест-
е
венного числа а и для рационального числа найдутся такие рациональные
числа at и a2, что ax^a^a2, причем я2 — ai< Аналогично для вещест-
венного числа о и для рационального числа -у найдутся такие рациональные
числа и р2, что	причем р2 —
Таким образом, оба вещественных числа xt и х2 будут заключены между
двумя рациональными числами (ах + pj и (<х2 -|- р2), разность между которыми
(по модулю) равна
(«а	₽г) — (ai + Pi) = (а2 — “1) + (Рг — Pi) < е-
Так как е — любое наперед взятое положительное рациональное число, то
xt = ха в силу сформулированной выше леммы.
3°. Установим, наконец, что в применении к двум рациональным числам
сформулированное нами определение суммы вещественных чисел и известное
из элементарного курса определение суммы рациональных чисел приводят
к одному и тому же результату. В самом деле, если а и Ь— два рациональ-
ных числа, удовлетворяющих неравенствам щ sg а sg a2, pi sg &,sgp2, а (а + Ь) —
их сумма, полученная по известному из элементарного курса определению,
то очевидно,
(»i + Pi)*Sa + 6sS(a2 + P2),	(2.11)
причем, согласно только что доказанному утверждению, рациональное число
(а Ь) является единственным вещественным числом, удовлетворяющим нера-
венствам (2.11).
4°. Прежде чем доказывать сформулированную выше лемму, установим
следующее вспомогательное утверждение.
Каковы бы ни были два вещественных числа а и Ь такие, что Ь <.а,
найдется рациональное число а, заключенное между ними, т. е. такое, что
Ь <_а<_а (а следовательно, найдется и бесконечное множество различных
рациональных чисел, заключенных между а и Ь).
Очевидно, достаточно рассмотреть случай, когда оба числа а и b неотри-
цательны, ибо случай, когда а и Ь оба неположительны, сводится к указан-
ному случаю посредством перехода к модулям, а случай, когда одно число
положительно, а другое — отрицательно, тривиален (в качестве а можно
взять нуль).
Итак, пусть Ь^О; Ъ<а\ а — а^а^ ... ап b = bts,blbi ... Ьп ...
Пусть k — наименьший из номеров п, для которых нарушается равенство
ап = Ьп, т. е. а0 = &0, ai = &i, ..., oift-i = &4_i, а^^Ь^.
В силу договоренности, принятой в пункте 3 § 1, можно считать, что все
ап при n>k не могут быть равны нулю. Пусть р — наименьший из номеров п,
превосходящих k, для которых ап > 0, т. е.
а — аа, ах ...	00 ... 0ар ...
50
ТЕОРИЯ ВЕЩЕСТВЕННЫХ ЧИСЕЛ
[ГЛ. 2
Тогда из правила сравнения вещественных чисел непосредственно вытекает,
что рациональное число а — а0, щ ... aft00 ... 0 (ар— 1)999 ... удовлетво-
ряет неравенствам b < а < а. Вспомогательное утверждение доказано.
Обращаясь к доказательству леммы, предположим, что Xi~^x2. Пусть
ради определенности хг < х2. Тогда в' силу вспомогательного утверждения
найдутся два рациональных числа ах и а2 таких, что
%2’	(2*12)
Пусть теперь и ‘(2— какие угодно рациональные числа, удовлетворяющие
неравенствам
Т1 sS Xi	Та. В < *2 < 12-	(2-13)
Из сопоставления (2.12) и (2.13) и из свойства транзитивности знака > по-
лучим < ах < а2 < т2. Но тогда ?2 — 71 > “г — »i, что противоречит тому,
что разность у2 — 7Х может быть сделана меньше любого наперед взятого по-
ложительного рационального числа «. Лемма доказана.
2. Определение произведения вещественных чисел. Поскольку
вопросы, возникающие в связи с определением произведения вещест-
венных чисел, в основном совпадают с вопросами, рассмотренными
при определении суммы вещественных чисел, мы ограничимся лишь
краткой формулировкой результатов.
Определим сначала произведение двух положительных чисел а
и Ь. Обозначим через ар а2, и [32 любые положительные рацио-
нальные числа, удовлетворяющие неравенствам а.у^а^а^,
Произведением положительных вещественных чисел а и b назо-
вем вещественное число х, удовлетворяющее неравенствам
Точно так же, как и для суммы, устанавливается, что такое ве-
щественное число х существует, и притом только одно. Легко убе-
диться в том, что таким числом х является точная верхняя грань
множества {а^} произведений всех рациональных чисел ах и
удовлетворяющих неравенствам 0 < ах а, 0 < рх sC Ь.
Произведение вещественных чисел любого знака определяется
по следующему правилу:
1)	считают, что a-0 = 0-a = 0;
(| а ] • | b |, если а и b одного знака,
2)	считают, что аЬ = \	,
(—| а | • | b |, если а и Ь разных знаков.
В заключение отметим, что точно так же, как и для суммы, можно
доказать, что в применении к двум рациональным числам определе-
ние произведения вещественных чисел и известное из элементарного
курса определение произведения рациональных чисел приводят
к одному и тому же результату.
3.	Свойства вещественных чисел. В этом пункте мы убедимся
в справедливости для произвольных вещественных чисел всех основ-
ных свойств, перечисленных в п. 1 § 1 для рациональных чисел.
Справедливость для вещественных чисел свойства 1° уже уставов-
§ 2] АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ НАД ВЕЩЕСТВЕННЫМИ ЧИСЛАМИ
51
лена выше. Таким образом, нужно выяснить лишь вопрос о спра-
ведливости для вещественных чисел свойств 2°—13°.
Легко убедиться в справедливости для вещественных чисел
свойств 2° — 5° и 11°, связанных с понятием суммы. Справедливость
свойств 2° — 5° непосредственно вытекает из определения суммы
вещественных чисел и из справедливости указанных свойств для
рациональных чисел.
Остановимся на доказательстве свойства 11°, т. е. докажем, что если а,
Ьи с — любые три вещественных числа и а>Ь, то а + с > b + с.
Так как а~>Ь, то в силу вспомогательного утверждения, установленного
при доказательстве леммы (см. конец п. 1 настоящего параграфа), найдутся
рациональные числа ах и р2 такие, что а > ах > р2 > Ь. Для вещественного
числа с и для положительного рационального числа г = ах — р2 найдутся ра-
циональные числа ft и т2 такие, что Ti«JCs£72, причем у2 — 7j<s = ax— р2
(см. утверждение, доказанное в п. 4 § 1).
Пусть далее аг и ?х — любые рациональные числа, удовлетворяющие не-
равенствам а2^а, Ь^рх. Тогда по определению суммы вещественных чисел
“а + 7г а +	?а + 7аЭ=^ + С^Р1 + 71-
Для доказательства того, что а + с > & + с, в силу транзитивности знака >
достаточно доказать, что + 71 > ₽2 + 7а> но это непосредственно вытекает
из неравенства 72 — 7Х < зх — ?2.
Заметим, что вопрос о вычитании вещественных чисел как о дей-
ствии, обратном сложению, полностью исчерпывается на основании
свойств 2° — 5°. Назовем разностью вещественных чисел а и b
вещественное число с такое, что с-[-Ь = а.
Убедимся в том, что такой разностью является число с = а -}- Ь',
где Ь' — число, противоположное Ь.
В самом деле, используя свойства 2° — 5°, можем записать
с	b = (а	Ь') 4“ b = « 4" (!>' 4“ = а -|- 0 = а.
Убедимся в том, что существует только одно вещественное число,
являющееся разностью двух данных вещественных чисел.' Предпо-
ложим' что кроме указанного выше числа с — а-\-Ь' существует
еще одно число d такое, что d-\-b — а. Тогда, с одной стороны,
(d 4- b) 4" = а 4“ Ъ' — с, с другой стороны, (d 4- b) -f- b' = d 4-
4- (b 4~ b') = d 4- 0 = d, т. е. c = d.
Из определения разности и из свойства 5° вытекает, что число а',
противоположное а, равно разности числа 0 и числа а. Это число
обычно записывают в виде — а.
Не вызывает затруднения перенесение на случай вещественных
чисел свойств 6°, 7°, 8°, 9°, 10° и 12°, связанных с понятием произ-
ведения. Отметим лишь в отношении свойства 9°, что если а — поло-
жительное вещественное число, а ах и а2 — какие угодно рациональ-
ные числа, удовлетворяющие неравенствам 0 < Oj а <1 аа, то число а\
52
ТЕОРИЯ ВЕЩЕСТВЕННЫХ ЧИСЕЛ
[ГЛ. 2
вещественное число,
для любых двух ве-
притом только одно,
обратное для а, определяется как единственное
удовлетворяющее неравенствам — гС а — *).
Свойства 6° — 9° позволяют заключить, что
шественных чисел а и Ъ (Ь 0) существует, и
вещественное число с, удовлетворяющее условию cb = a. Это число с
называется частным чисел а и Ь.
Из определения частного и из свойства 9° вытекает, что число а',
обратное числу а, равно частному чисел 1 и а, которое мы обо-
1
значим —.
а
Заметим, наконец, что на случай вещественных чисел переносится
и последнее 13-е свойство рациональных чисел, а именно: каково бы
на было вещественное число а, можно число 1 повторить сла-
гаемым столько раз, что . полученная сумма превзойдет а**).
Докажем это свойство. В случае а < 0 доказательство не требуется,
ибо 1 >> а. Пусть a 0; а = а0, аг ... ап ... В силу того, что опре-
деление суммы вещественных чисел в применении к сумме рациональ-
ных чисел совпадает с определением суммы рациональных чисел,
повторив число 1 слагаемым п раз, получим целое число п. Таким
образом, достаточно доказать, что для числа а найдется целое число п
такое, что л>а. Но это очевидно: достаточно взять п = а0~\-2.
Таким образом, на случай вещественных чисел переносятся все
основные свойства, сформулированные для рациональных чисел
в пункте 1 настоящего параграфа. Следовательно, для вещест-
венных чисел сохраняют свою силу все правила алгебры; относя-
щиеся к арифметическим действиям и к сочетанию равенств
и неравенств.
На этом мы заканчиваем изложение элементов теории вещест-
венных чисел, необходимых для построения курса математического
анализа. Дальнейшее развитие теории вещественных чисел читатель
может найти в приложении в конце настоящей книги.
В заключение заметим, что мы построили теорию вещественных
чисел, апеллируя к их представлению в виде бесконечных десятич-
ных дробей.
Совершенно ясно, что мы могли бы апеллировать и к бесконеч-
ным дробям с любым другим (не обязательно десятичным) основа-
нием. В этом отношении системы счисления с различными основа-
ниями эквивалентны между собой. Однако в некоторых вопросах
приближенных вычислений и, в частности, при округлении чисел до
заданного количества разрядов системы счисления с четными и с не-
♦) В качестве числа а' может быть взята точная верхняя грань множе-
ства всех рациональных чисел
•*) Заметим, что это свойство называют аксиомой Архимеда.
§ 31 НЕКОТОРЫЕ КОНКРЕТНЫЕ МНОЖЕСТВА ВЕЩЕСТВЕННЫХ ЧИСЕЛ 53
четными основаниями ведут себя существенно по-разному (см. по
этому поводу дополнение 2 к настоящей главе).
4.	Некоторые часто употребляемые соотношения. Докажем
справедливость для любых вещественных чисел а и b следующих
двух соотношений:
[ ab | = | а |b |,	(2.14)
> +	(2-15)
Словесная формулировка этих соотношений такова: 1) модуль
произведения двух чисел равен произведению модулей этих чисел,
2) модуль суммы двух чисел не превосходит суммы модулей
этих чисел.
Соотношение (2.14) непосредственно вытекает из определения
произведения двух вещественных чисел. Докажем соотношение (2.15).
На основании определения модуля и правила сравнения для любых
вещественных чисел а и Ъ справедливы неравенства
— ] а |	а «С | а |,	— | b | b -eg | b (.
В силу основных свойств можно почленно складывать неравенства
одного знака (это доказано в конце пункта 1 § 1). Поэтому
-(И + |*|)^а + &<а] + |Н
Используя в случае аЦ-£>;>0 правое, а в случае	левое
из последних неравенств, мы получим неравенство (2.15).
Замечание. Отметим еще два часто употребляемых неравенства:
\а — й|э;|а| —1&|	(2.16)
и
|а-(,|>||а|_р||.	(2.17)
Для получения неравенства (2.16) достаточно учесть, что а = (а — и,
опираясь на (2.15;, записать неравенство | а|sg | а— Ь | 4- | b |. Неравенство
(2.17) является следствием неравенства (2.16) и неравенства | b — а |
:> | Ь | — | а |, которое получается из (2.16), если поменять ролями числа а и Ь.
§ 3. Некоторые конкретные множества вещественных чисел
В дальнейшем нам часто придется иметь дело с различными мно-
жествами вещественных чисел. Будем обозначать произвольное мно-
жество вещественных чисел символом {х}, а числа, входящие в со-
став этого множества, будем называть элементами или точками
этого множества. Мы будем говорить, что точка хг множества {л*}
отлична от точки х2 этого множества, если вещественные
числа хг и х2 не .равны друг другу. Если при этом справедливо не-
равенство хх > х2 (Xj < ха), то будем говорить, что точка xt лежит
правее (левее) точки х2.
Рассмотрим некоторые наиболее употребительные множества
вещественных чисел.
54
ТЕОРИЯ ВЕЩЕСТВЕННЫХ ЧИСЕЛ
[ГЛ. 2
1°. Множество вещественных чисел х, удовлетворяющих неравен-
ствам а^х^Ь, где a<Zb, будем называть сегментом и обозначать
символом [а, &]. При этом числа а и b будем называть граничными
точками или концами сегмента [а, Ь], а любое число х, удов-
летворяющее неравенствам a<Z.x<Zb, будем называть внутренней
точкой сегмента [а, Ь].
2°. Множество всех вещественных чисел х, удовлетворяющих не-
равенствам a^x<Zb {или а<2х^Ь}, будем называть полусегмен-
том и обозначать символом [а, Ь) {или (а, й]}.
3°. Множество всех веществённых чисел х, удовлетворяющих не-
равенствам а < х < Ь, будем называть интервалом и обозначать
символом (а, Ь).
4°. Любой интервал, содержащий точку с, будем называть окрест-
ностью точки с.
5°. Интервал (с— е, c-J-e), где е>0, будем называть г-окрест-
ностью точки с.
6°. Множество всех вещественных чисел будем называть числовой
{бесконечной) прямой и обозначать символом (—оо, -|-оо).
7°. Множество всех вещественных чисел х, удовлетворяющих
неравенству х^а {или х^Ь}, будем называть полупрямой и обо-
значать символом [а, оо) {или (— со, &]}.
8°. Множество всех вещественных чисел х, удовлетворяющих не-
равенству х~у>а {или x<Zb}, будем называть открытой полупря-
мой и обозначать символом (а, со) {или (— оо, £>)}•
Замечание. Отметим, что сегмент иногда называют замкнутым
отрезком или просто отрезком, а интервал — открытым от-
резком.
Произвольное множество {х} будем называть плотным в себе, если в лю-
бой окрестности каждой точки х этого множества содержится хотя бы одна
точка множества, отличная от х. Примером плотного в себе множества
может служить любое из определенных выше множеств 1° — 8°. Другим при-
мером плотного в себе множества может служить множество всех рациональ-
ных чисел, входящих в состав любого из множеств Iе — 8°.
ДОПОЛНЕНИЕ 1 к ГЛАВЕ 2
О ПЕРЕВОДЕ ЧИСЕЛ ИЗ ДЕСЯТИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ
В ДВОИЧНУЮ И ИЗ ДВОИЧНОЙ СИСТЕМЫ В ДЕСЯТИЧНУЮ
В этом дополнении мы остановимся на алгоритмах перевода чисел из
десятичной системы счисления в двоичную и обратного перевода из двоичной
системы в десятичную *).
1. Перевод чисел из десятичной системы счисления в двоичную. Для зада-
ния десятичного числа х10 в разрядной сетке электронной, машины используют
так называемую нормализованную форму записи этого числа
— ?ю • ЮР*’.
(2.18)
*) Излагаемые ниже алгоритмы реализуются, в частности, на электрон-
ной машине БЭСМ-4.
ДОПОЛНЕНИЕ 1 К ГЛАВЕ 2
55
В этой форме записи величина
910 = (1 - 2Sg) (ах • 10-1 + а2. 10-» + ... + а» • Ю"»)	(2.19)
называется десятичной мантиссой данного числа, причем ах 1, Sq берется
равным нулю при q10	0 и равным единице при q10 < 0 *), а показатель
степени
P10 = (l-2Sp)(₽1 + 10W	(2.20)
называется десятичным порядком данного числа, причем Sp берется равным
нулю при р1о ^О и равным единице при р10 < 0 **).
На рис. 2.3 указано, как десятичное число (2.18) — (2.20) задается в раз-
рядной сетке электронной машины^ На изображение каждого из десятичных
			1 Рю 1		1 <710 1			
Л	S9	sp	.А.		а.	а2		а»
								
45	44	43	42 41	40 39 38 37	36 35 34 33	32 31 30 29		4 3 2 1
Рис. 2.3.
чисел рх, ах, а2, ..., ая отводится по четыре двоичных разряда, так что каждое
из указанных чисел может принимать любое целочисленное значение от 0 до 15,
а на изображение числа ₽2 отводится всего два разряда, так что р2 может
принимать значения 0, 1, 2, 3 ***).
Стандартная программа вырабатывает по десятичному числу (2.18) — (2.20)
соответствующее ему двоичное число х2. Эта программа реализуется следующим
образом. Сначала вычисляется величина 7:
7 = (1 - 2Sq) (ах . 10» + а2  10« + ... + а,) • 2»».
Затем указанная величина 7 умножается на величину k = 268  10—10 (последняя
величина задается в машине также в нормализованной форме, причем обычно
с избытком в две единицы младшего разряда мантиссы).
Произведение kf отвечает, очевидно, десятичной мантиссе (2.19). Дальней-
шая процедура заключается в умножении £7 на 10 или в зависимости от
знака р10 (т. е. от Sp), производимом столько раз, какова величина | р101.
В завершение программы в полученном результате обычно очищают три млад-
ших разряда мантиссы.
Указанная программа 1) обеспечивает по крайней мере 30 верных двоич-
ных знаков результата, 2) обеспечивает перевод в двоичное число любого целого
*) Таким образом, множитель (1 —2Sq) в равенстве (2.19) характеризует
знак мантиссы q10.
**) Так что множитель (1—2SP) в равенстве (2.20) характеризует знак
порядка р10.
***) На самом деле, в силу конструкции клавишного устройства, на этом
устройстве нельзя пробить каждое из чисел Р1( аъ а2, ..., а2 большим девяти,
а число р2 нельзя пробить большим единицы. Таким образом, каждое из чисел
Pi, ах, ......а, меняется в диапазоне от 0 до 9, а число ра принимает зна-
чения 0 и 1.
56
ТЕОРИЯ ВЕЩЕСТВЕННЫХ ЧИСЕЛ
(ГЛ. 2
десятичного числа в .диапазоне от 0 до 50 000, 3) обеспечивает перевод деся-
тично нормализованного числа в двоично нормализованное число *).
В заключение заметим, что если при реализации указанной программы
в процессе умножения на 10 двоичный порядок переводимого числа превы-
шает 59, то дальнейшие умножения на 10 прекращаются, даже если они
требуются в соответствии с величиной | р10 |.
2. Перевод чисел из двоичной системы счисления в десятичную- Укажем
стандартную программу, которая вырабатывает по заданному в нормализован-
ной форме двоичному числу х2 = q2 • 2Рг соответствующее ему десятичное
число х10, записанное в нормализованной форме (2.18) — (2.20). В разрядной
сетке машины вырабатываемое число располагается так, как указано на
рис. 2.3.
Программа реализуется следующим образом. Сначала исходное число х2
множится на для того, чтобы при последующем умножении на 10 не полу-
чить машинного переполнения. Затем полученное число множится на 10 или
1 ,
В зависимости от того, больше оно единицы или нет, до тех пор, пока
результат умножений не попадет в интервал от до 1. Количество произве-
денных умножений, очевидно, определяет | р10 |, Что же кдсается знака р1а,
то он положителен, если исходное число превосходит единицу, и отрицателен —
в противном случае.
Далее очевидно, что полученное в результате умножений число и будет
десятичной мантиссой qlB. Цифры alt а2, ..., а, десятичной мантиссы q™
определяются последовательно путем умножения на 10 и выделения целой
части.
ДОПОЛНЕНИЕ 2 К ГЛАВЕ 2
ОБ ОШИБКАХ В ОКРУГЛЕНИИ ЧИСЕЛ В СИСТЕМАХ СЧИСЛЕНИЯ
С ЧЕТНЫМ И НЕЧЕТНЫМ ОСНОВАНИЯМИ
Предположим, что вычислительная машина работает с /-разрядными чис-
лами в системе счисления с основанием РЭ=2. Тогда, не уменьшая общности,
можно считать, что все числа хи>, хранящиеся в памяти машины, имеют вид
ха> = ajp-1 + а2р'2 + ... + а,р~‘,
где коэффициенты а(- (i=l, 2, ..., /) могут принимать значения 0, 1, ...
..., (р—1). Совершенно ясно, что такие операции, как сложение, умножение
или деление, будучи произведены над /-разрядными числами, могут дать
в результате числа, содержащие более чем / разрядов, и поэтому естественно
возникает необходимость в округлении указанных чисел до / разрядов.
Рассмотрим простейшую операцию — округление чисел, содержащих / + г
(где г > 0) разрядов, до чисел, содержащих / разрядов. Каким бы способом
ни производилось округление содержащего (/ + г) разрядов числа х|Г+Г|,
результатом округления должно быть /-разрядное число. Отсюда вытекает,
что ошибка округления числа (обозначим эту ошибку символом е (x,,+''^))
имеет следующий вид:
е (x(t+r>') = — ip-4+” +	р~*.
*) Если исходное десятичное число не являлось нормализованным (т. е.
в (2.19) нарушалось условие ajgil), то и результат его перевода в двоичную
систему может оказаться ненормализованным.
ДОПОЛНЕНИЕ 2 К ГЛАВЕ 2
‘57
Здесь i может принимать значения 0, 1, p'—la зависимости от
значения последних г разрядов числа х|<+п a m(i) — некоторая функция от i,
принимающая целочисленные значения и зависящая от выбранного способа
округления.
Наиболее важной характеристикой.ошибки округления является ее среднее
значение А, которое определяется как дробь *)
па+г> ’
в числителе которой стоит сумма ошибок, соответствующих всем допустимым
значениям чисел х1<+г|, а в знаменателе — количество таких чисел x't+r'.
Предположим, что все рассматриваемые числа х,/+Г| удовлетворяют нера-
венствам Огёх,/+П < 1. Тогда, очевидно, количество л'/+Г| всех чисел x‘t+r>
будет равно pt+r, и мы получим после несложных вычислений, что
Д =	+	= /+Г) Ру1 т  £-1
р‘+г	Ай	2
'г=о „
Сумма S га (О, стоящая под знаком фигурной скобки, зависит от выбранного
нами способа округления, но в любом случае эта сумма будет целочисленной.
pr— 1
Второй член под знаком фигурной скобки —— ,при любом четном р
не будет целым. Таким образом, при любом четном основании р средняя
ошибка А не равна нулю. Это означает, что при любом фиксированном способе
округления, определяемом лишь отбрасываемыми разрядами, ошибка от округ-
ления до меньшего числа разрядов будет иметь систематическое смещение при
любой системе счисления с четным основанием. С другой стороны, легко про-
верить, что обычное «школьное» правило округления в любой системе с нечет-
ным основанием приводит к «несмещенным» ошибкам.
.*) Символ S есть символ суммирования тех слагаемых, которые записаны
вслед за этим символом. Если указанные слагаемые зависят от номера i, то
п
запись У обозначает, что нужно произвести суммирование по всем значе-
i=m
ниям i от т до п.
ГЛАВА 3
ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
Одной из основных операций математического анализа является
операция предельного перехода. Эта операция встречается в анализе
в различных формах. В настоящей главе рассматривается простейшая
форма операции предельного перехода, основанная на понятии предела
так называемой числовой последовательности. Понятие предела число-
вой последовательности позволит нам в дальнейшем определить и
другие формы операции предельного перехода.
§ 1.	Числовые последовательности
1.	Числовые последовательности и операции над ними. Из
элементарного курса читатель имеет представление о числовых после-
довательностях. Примерами числовых последовательностей могут слу-
жить: 1) последовательность всех .элементов арифметической и гео-
метрической прогрессии, 2) последовательность периметров правильных
n-угольников, вписанных в данную окружность, 3) последовательность
хх=1, х2 = 1,4, хэ=1,41 ... приближенных значений числа ]Л2. Этот
пункт мы начнем с уточнения понятия числовой последовательности.
Если каждому числу п натурального ряда чисел 1, 2, ..., п,...
ставится в соответствие по определенному закону некоторое
вещественное число хп, то множество занумерованных вещест-
венных чисел
• • • > %п> • • •	(3-1)
мы и будем называть числовой последовательностью или просто
последовательностью.
Числа хп будем называть элементами или членами последова-
тельности (3.1). Сокращенно последовательность (3.1) будем обозна-
чать символом {%„}. Так, например, символом будем обозначать
последовательность 1, 1/2,..., 1/я, ..., а символом {!-(-(—1)я}
будем обозначать последовательность 0,2,0,2,...
5 11
ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
59
Введем понятие арифметических операций над числовыми последо-
вательностями. Пусть даны произвольные последовательности х1г х2,...
..., Хи,... и yv _у2,..., уп,... Суммой этих последовательностей на-
зовем последовательность хъ -f- ylt х2 -j-y2, ...,хп -)-уп,... (или {хп + уп}),
разностью—последовательность х1—у1, х2 — у2, ...» х„—у„, ...
(или {х„—_у„})> произведением — последовательность	х2-у2,...
..., хп-уп,... (или {хп-^л}), частным — последовательность —, —,...
.	Ух Ух
Замечание. При определении частного нужно требовать,
чтобы все элементы уп последовательности были отличны от
нуля. Однако, если у последовательности	обращается в нуль
лишь конечное число элементов, то частное } можно опреде-
лить с того номера, начиная с которого все элементы уп отличны
от нуля.
2.	Ограниченные и неограниченные последовательности.
Определение 1, Последовательность {хп} называется огра-
ниченной с в е р ху t(c ни зу), если существует такое вещест-
венное число М (число т), что каждый элемент хп последова-
тельности {хп} удовлетворяет неравенству хп^.М (хп^т)*).
При этом число М (число т) называется верхней гранью (ниж-
ней гранью) последовательности {хп}, а неравенство хп^М (хп^т)
называется условием ограниченности последовательности сверху
(снизу).
Отметим, что любая ограниченная сверху последовательность {х„}
имеет бесчисленное множество верхних граней. В самом деле, если
М — верхняя грань, то любое число М*, большее М, также является
верхней гранью. Подчеркнем, что в условии хп^М. ограниченности
последовательности {хга} сверху в качестве М может рассматриваться
любая из верхних граней. Аналогичные замечания можно сделать
в отношении нижних граней ограниченной снизу последователь-
ности {хп}.
Определение 2. Последовательность {х„} называется ограни-
ченной с обеих сторон или просто ограниченной, если она
ограничена и сверху, и снизу, т. е. если существуют числа т и
Ж такие, что любой элемент хп этой последовательности удовле-
творяет неравенствам'. т^хп^М.
Если последовательность {хп} ограничена и М и от —ее верхняя
и нижняя грани, то все элементы хп этой последовательности удов-
летворяют неравенству
|хя|^Л,	(3.2)
*) Это определение полностью аналогично определению ограниченного
сверху (снизу) множества вещественных чисел (см. п. 5 § 1 главы 2).
60
ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
(ГЛ 3
где А — максимальное из двух чисел | Ж | и | т |. Обратно, если все
элементы последовательности {х„} удовлетворяют неравенству (3.2),
то выполняются также неравенства — А ха А, и, следовательно,
последовательность {х„} ограничена. Таким образом, неравенство (3.2)
представляет собой другую форму условия ограниченности последо-
вательности. Уточним понятие неограниченной последовательности.
Последовательность {х„} называется неограниченной, если для
любого положительного числа А найдется элемент хП этой по-
следовательности, удовлетворяющий неравенству . | хп | > А. Рас-
смотрим -несколько примеров:
1)	Последовательность —1, —4, —9,..., —я2, ... ограничена
сверху и не ограничена снизу. Верхней гранью этой последователь-
ности является любое число, не меньшее — 1.
2)	Последовательность 1, у, -у,...,	... ограничена. Дейст-
вительно, верхней гранью этой последовательности является любое
число М 1, а нижней гранью —любое число яг=С9.
3)	Последовательность 1, 2, 1, 3,..., 1, п, 1, (n-f-l),... не огра-
ничена. В самом деле, каково бы ни было положительное число-л,
среди элементов этой последовательности (с четными номерами) най-
дутся элементы, превосходящие А.
3.	Бесконечно большие и бесконечно малые последователь-
ности.
Определение 1. Последовательность {хп} называется бес-
конечно большой, если для любого положительного числа А*)
можно указать номер N такой**), что при п^Ы все элемен-
ты хп этой последовательности удовлетворяют неравенству
|х„|>Л.
Замечание. Очевидно, что любая бесконечно большая после-
довательность является неограниченной, поскольку для любого А > 0
можно указать номер N такой, что при n^N все элементы хп
удовлетворяют неравенству | хп | > А, а следовательно, для любого
А > 0 найдется по крайней мере один такой элемент хл, что | хп | > А.
Однако неограниченная последовательность может и не быть беско-
нечно большой. Например, неограниченная последовательность 1, 2,
1, 3,..., 1, п, ... не является бесконечно большбй, поскольку при
А > 1 неравенство | хп | > А не имеет места для всех хп с нечет-
ными номерами.
Определение 2. Последовательность {а„} ***) называется бес-
конечно малой, если для любого положительного числа е****)
*) Сколь бы большим мы его ни взяли.
**) Так как номер N зависит от числа А, то иногда пишут N =N (А).
***) Элементы бесконечно малых последовательностей мы, как правило,
будем обозначать греческими буквами.
*»**) Сколь бы малым мы его ни взяли.
§ И
ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
61
можно указать номер N такой*), что при n^N все элементы
ап этой последовательности удовлетворяют неравенству | ал | <; е.
Рассмотрим следующие примеры:
1)	Докажем, что последовательность q, q2, q3...... qn,-.. при
|9|>1 является бесконечно большой, а при | q | <; 1 — бесконечно
малой.
Сначала рассмотрим случай | q | > 1. Тогда | q | = 1 + 8, где8>0.
Используя формулу бинома Ньютона, получим | ^=(1-(-8^= 1-]-
-j- 8jV-f- (положительные члены). Отсюда
|?|">8N.
(3.3)
Фиксируем произвольное число А > 0 й выберем номер N столь
большим, чтобы имело место неравенство 8Л/>Д**). Из последнего
неравенства и неравенства (3.3) вытекает неравенство ] q |Л’> А. Так
как при л N и при | q | >• 1 | q |л | q (в силу свойств произве-
дения вещественных чисел), то | q |л> А при n^N. Тем самым до-
казано, что при |у|>1 рассматриваемая последовательность является
бесконечно большой.
Случай | q | < 1 рассматривается совершенно аналогично. В этом
случае = 1-1-8, где 8 > О (мы. опустили случай q = 0). Снова ис-
пользуя формулу бинома Ньютона, мы получим вместо (3.3) следую-
щее неравенство:
^>8М или |?|ЛГ<^.	(3.3*)
Фиксируем произвольное е > 0 и выберем номер из условия
J_ < е***)_ уак как । q । q ПрИ	и ПрИ | |	1, то из по-
лученных неравенств вытекает, что | q |л <е при n^N. Тем самым
доказано, что при | ?|<1 рассматриваемая последовательность является
бесконечно малой.
2)	Докажем, что последовательность 1,-4» ... , —, ... бесконечно
Z	П
малая. В самом деле, если n^N, то — Поэтому по данному в
достаточно выбрать номер N из условия < е. Например, можно
положить Л7= Г-М 4-1.
♦) Так как номер N зависит от числа е, то иногда пишут N = N (е).
(ji.) **) Достаточно положить N = [ v] "Ь 1> где символ [*] обозначает целую
часть числа х. Например, [5,138] = 5, [—172,9] = — 173.
***) Достаточно положить N = [	+ Ь
62
ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
[ГЛ 3
4.	Основные свойства бесконечно малых последовательностей.
Теорема 3.1. Сумма двух бесконечно малых последовательно-
стей есть бесконечно малая последовательность.
Доказательство. Пусть {ая} и {ря} —• бесконечно малые после-
довательности. Докажем, что последовательность {а„ + ря}—бесконечно
малая. Пусть е — произвольное положительное число, номер, начи-
ная с которого | а„ | < , a П2 — номер, начиная с которого | | <
(Такие номера и -N2 найдутся по определению бесконечно
малой последовательности). Так как модуль суммы двух чисел не пре-
восходит суммы йх модулей, т. е. | а„ + ря | «С | а„ | + |f)„[ (см. пункт 4
§ 2 главы 2), то, обозначив через N наибольший из двух номеров
и N2, мы получим, что, начиная с номера N, выполняется нера-
венство К + М<£' Это означает, что последовательность {ая-|-ря}
бесконечно малая. Теорема доказана.
Теорема 3.2. Разность двух бесконечно малых последова-
тельностей есть бесконечно малая последовательность.
Эта теорема доказывается аналогично предыдущей.
Следствие. Алгебраическая сумма любого конечного числа
бесконечно малых последовательностей— бесконечно малая после-
довательность.
Теорема 3.3. Бесконечно малая последовательность огра-
ничена.
Доказательство. Пусть {а„} — бесконечно малая последова-
тельность и е — некоторое положительное число. Пусть, далее, N —
номер, начиная с которого | а„ | < е. Обозначим через А наибольшее
из следующих N чисел: е, |	|, | а2 , | av_j |. Это можно записать
так: А — шах {е, | ах |, | а2 |,..., |	11} *). Очевидно, | ая | А для лю-
бого номера п, что означает ограниченность последовательности. Тео-
рема доказана.
Теорема 3.4. Произведение ограниченной последовательности
на бесконечно малую последовательность представляет собой
бесконечно малую последовательность.
Доказательство. Пусть {хл} — ограниченная, а {ая} — беско-
нечно малая последовательности. Так как последовательность {х„}
ограничена, то существует число А >> 0 такое, что любой элемент хп
удовлетворяет неравенству ] хп | А. Возьмем произвольное положи-
тельное число е. Поскольку последовательность {ая} бесконечно малая,
то для положительного числа 4- можно указать номер N такой, что
при n^N выполняется неравенство |ая|<^. Тогда при п^П
*) Здесь и в дальнейшем символ а = max {aj, а^, ...,ал} означает, что
число а равно максимальному из чисел а1( а2, ... * ап.
«1]
ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
63
| хп • ап | = | хп 1 а„ ] < А = е. Поэтому последовательность {хп  ап}
бесконечно малая. Теорема доказана.
Следствие. Произведение любого конечного числа бесконечно
малых последовательностей представляет собой бесконечно малую
последовательность.
Замечание. Частное двух бесконечно малых последовательно-
стей может быть последовательностью любого типа и даже может не
с	1 а 1
иметь смысла. Если, например, а„ = —, р„ = —, то все элементы после-
довательности равны единице. Если = —, р„ = -^, то последо-
вательность бесконечно большая, и наоборот, если а„ = ^,
а Рп — —, то последовательность бесконечно малая. Если беско-
нечно много элементов последовательности {(Зп} равны нулю, то частное
не имеет смысла.
Теорема 3.5. Если все элементы бесконечно малой последова-
тельности {ал} равны одному и тому же числу с, то с = 0.
Доказательство. Допустим, что с 0. Положим е =	,
е > 0. Начиная с номера N, соответствующего этому е, выполняется
неравенство | а„ | < е. Так как ая = с, а е = -^, то последнее нера-
венство можно переписать следующим образом:	откуда
1
1 < у. Полученное противоречие показывает, что предположение
с Ф 0 не может иметь места. Итак, с = 0. Теорема доказана.
В заключение отметим предложение, устанавливающее связь
между бесконечно большими и бесконечно малыми последователь-
ностями.
Теорема 3.6. Если {хп} — бесконечно большая последователь-
ность, то, начиная с некоторого номера п, определена последова-
тельность которая является бесконечно малой. Если все
элементы бесконечно малой последовательности {а„} не равны
нулю, то последовательность бесконечно большая.
Доказательство. Отметим, во-первых, что у бесконечно боль-
шой последовательности лишь конечное число элементов может быть
равно нулю. В самом деле, из определения бесконечно большой после-
довательности вытекает, что для данного положительного числа А
можно указать такой номер №*, начиная с которого выполняется нера-
венство	Это означает, что при п~з%П* все элементы хп
не равны нулю, а поэтому последовательность У имеет смысл,
64
ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
[ГЛ. 9
если ее элементы рассматривать начиная с номера N*. Докажем теперь,
что — бесконечно малая последовательность. Пусть е —любое
положительное число. Для числа— можно указать номер
такой, что при n^N элементы хп последовательности {хп} удовлет-
воряют неравенству |х„| Поэтому, начиная с указанного номера
N, будет выполняться неравенство | < е. Таким образом, доказано,
что последовательность | бесконечно малая.
Доказательство второй части теоремы проводится аналогично.
§ 2. Сходящиеся последовательности и их основные свойства
1. Понятие сходящейся последовательности.
Определение. Последовательность {хп} называется сходя-
щейся, если существует такое число а, что последователь-
ность {jcn— а} является бесконечно малой. При этом число а
называется пределом последовательности *).
Определение сходящейся последовательности можно, очевидно,
сформулировать также и следующим образом.
Последовательность {хп} называется сходящейся, если суще-
ствует такое число а, что для любого положительного числа е
можно указать номер N такой**), чтоприп^П все элементы
хп этой последовательности удовлетворяют неравенству
|лг„-а]<в.	-	(3.4)
При этом число а называется пределом последовательности.
Если последовательность {.£„} сходится и имеет своим пределом
число а, то символически это записывают так***):
lim хп = а, или хп—?а при п—-оо.
п—>00
*) В соответствии с этим 'определением всякая бесконечно малая после-
довательность является сходящейся и имеет своим пределом число нуль.
**) Так как jV зависит от е, то иногда пишут N = N (е).
***) Отметим, что бесконечно большие последовательности иногда называют
последовательностями, сходящимися к бесконечности. Поэтому, если после-
довательность {хл} бесконечно большая, то символически это записывают так:
lim хп — оо.
П — 00
Если элементы бесконечно большой последовательности, начиная с некоторого
номера, имеют определенный знак, то говорят, что последовательность {хл}
сходится к бесконечности определенного знака. Символически это записывайся
следующим образом:
lim хп — + оо,	lim хя= — оо.
Л->00	Л->00
§21
СХОДЯЩИЕСЯ ПОСЛЕДОВАТЕЛЬНОСТИ
65
Замечание 1. Неравенство (3.4) эквивалентно неравенствам
— е <хл - а <-|~е> или а~~ е<-*:л<а + е- Последние неравенства
означают, что элемент хп находится в е-окрестности числа а (напом^
ним, что e-окрестностью числа а называется интервал (а — е, а -|- г)).
Поэтому определение сходящейся последовательности можно сформу-
лировать также и следующим образом:
Последовательность {хп} называется сходящейся, если суще-
ствует число а такое, что в любой г-окрестности числа а нахо-
дятся все элементы последовательности {хП}, начиная с некото-
рого номера *).
Определение сходящейся последовательности утверждает, что раз-
ность хп — а = а„ является бесконечно малой последовательностью.
Следовательно, любой элемент хп сходящейся последовательности,
имеющей пределом число а, можно представить в виде
хп = а 4- а„,	(3.5)
где а„— элемент бесконечно малой последовательности.
Замечание 2. Из определения предела.последовательности оче-
видно, что конечное число элементов не влияет на сходимость этой
последовательности и на величину ее предела.
Рассмотрим примеры сходящихся последовательностей.
1) Последовательность	сходится; предел этой последова-
D	П	1	1
тельности равен единице. В самом деле, так как । — 1 — — n >
то для доказательства достаточно убедиться, что последовательность
|-----Д бесконечно малая. Если п N, то I--------------г I „-г ,,
I п + If	I « +11 N + 1
и поэтому по данному е>0 достаточно выбрать номер N из условия
jy 1 О или —1. Например, можно положить
+ 1 1,рИ
I 1	при е > 1.
2) Докажем, что последовательность хг = 0,3; х2 — 0,33;...; хп —
= 0, 33 ... 3;... сходится и имеет своим пределом число 1/3. Поскольку
п раз
число 1/3 представимо бесконечной десятичной дробью 0,333..., то
из правила сравнения вещественных чисел (см. п. 3 § 1 главы 2)
вытекают неравенства **)
' °-JL3	3 4 \33 • 3 + ж-
п раз	п раз
*) Зависящего, конечно, от а.
•*) См. также неравенства (2.5) из п. 4 § 1 главы 2.
66
ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
[ГЛ. 3
Из этих неравенств получим, что |хя—g-
то, выбрав по любому е>
< Так как при
О номер N из условия
^<6, получим
1
Хп з
<е при п
Возможность выбора номера N, удовлетворяющего условию | q < г
при любом |g|< 1, была установлена в примере 1 пункта 3 § 1.
2. Основные свойства сходящихся последовательностей.
Теорема 3.7. Сходящаяся последовательность имеет только
один предел.	ч
Доказательство. Пусть а и b — пределы сходящейся после-
довательности {хя}. Тогда, используя специальное представление (3.5)
для элементов хп сходящейся последовательности {хя}, получим хп=^
— а-\-ап, хп = Ь-]-?п, где ая и ря—элементы бесконечно малых после-
довательностей {ая} и {ря}.
. Вычитая написанные соотношения, найдем ая— р„ — Ь — а. Так как
все элементы бесконечно малой последовательности {ая — ря} имеют
одно и то же постоянное значение b — а, то по теореме 3.5 Ь— а = 0,
т. е. Ь — а. Теорема доказана.
Теорема 3.8. Сходящаяся последовательность ограничена.
Доказательство. Пусть {хя} — сходящаяся последовательность
и а — ее предел. Используя формулу (3.5), имеем
хп = а + ая,
где ая — элемент бесконечно малой последовательности. Так как бес-
конечно малая последовательность {ая} ограничена (см. теорему 3.3),
то найдется такое число А, что для всех номеров п справедливо
неравенство |ал|==^А. Поэтому | хп |	| а | + А для всех номеров п,
что и означает ограниченность последовательности {хл}. Теорема
доказана.
Замечание 1. Ограниченная последовательность может и не
быть сходящейся. Например, последовательность 1, —1, 1, —1,...
ограничена, но не является сходящейся. В самом деле, если бы эта
последовательность сходилась к некоторому числу а, то каждая из
последовательностей {хп — а\ и {хл+1 — а\ являлась бы бесконечно
малой. Но тогда, в силу теоремы 3.2, последовательность {(хл — а) —
— (хл+1 — а)} = {хл — хя+1} была бы бесконечно малой, что невоз-
можно, так как |хл —хл+1| = 2 для любого номера п. - -
Докажем следующие основные теоремы.
Теорема 3.9. Сумма сходящихся последовательностей {хл}
и есть сходящаяся последовательность, предел которой
равен сумме пределов последовательностей {хя} и {_ул}.
Доказательство. Пусть а и Ь — соответственно пределы
последовательностей {хп} и Тогда
- хя = а + а„, Уп = Ь + $п,
§2]
СХОДЯЩИЕСЯ ПОСЛЕДОВАТЕЛЬНОСТИ
67
где {а„} и {рл} — бесконечно малые последовательности. Следовательно,
(х„ + уп) - (а + Ь) = а„ + р„.
Таким образом, последовательность {(хл+_уп) —(а + ^)} беско-
нечно малая, и поэтому последовательность	сходится и
имеет своим пределом число а-\-Ь.
Теорема 3.10. Разность сходящихся последовательностей
{х„} и {_уя} есть сходящаяся последовательность, предел которой
равен разности пределов последовательностей {хп\ и {_уп}- Дока-
зательство этой теоремы аналогично доказательству теоремы 3.9.
Теорема 3.11. Произведение сходящихся последовательностей
{х„} и {уп} есть сходящаяся последовательность, предел кото-
рой равен произведению пределов последовательностей {хп| и {_уп}-
Доказательство. Если а и b — пределы последовательностей
{хп} и {>„} соответственно, то хп = а + ап, уп = b + рл и хп-уп =
— а • & + а • рл +	• рп- Следовательно,
хп  уп - а  Ь = а • р „ + b • а„ + а„ • р „.
В силу теоремы 3.4 и следствия из нее, а также теоремы 3.1 после-
довательность {а • р„4- b -а.п-\-ап- р„} бесконечно малая, т. е. и после-
довательность \хп-уп — а'Ь\ бесконечно малая, и поэтому последо-
вательность {хп • .Уп} сходится и имеет своим пределом число а  Ь.
Для доказательства соответствующей теоремы для частного двух
последовательностей нам понадобится следующая лемма.
Лемма 1. Если последовательность {_уп} сходится и имеет
отличный от нуля предел Ь, то, начиная с некоторого номера,
определена последовательность которая является огра-
ниченной.
Доказательство. Пусть е = -1—-L. Так как b # 0, то е>0.
Пусть N— номер, соответствующий этому е, начиная с которого
выполняется неравенство — или |j’„ —	Из этого
неравенства следует, что при n^N выполняется неравенство *) \уп | >
п	„г	I 1 I 2 г-
Поэтому при n^N имеем	Следовательно, начи-
ная с этого номера N, мы можем рассматривать последовательность
{—}, и эта последовательность ограничена. Лемма 1 доказана.
Теорема 3.12. Частное двух сходящихся последовательностей
{х„} и {у„} при условии, что предел {у„} отличен от нуля, есть
*) В самом деле, так как Ь = (6 — уп) + Уп и I b — уп | <	, то | i> | sg
I — Уп I + I Уп I < ^2~ + I Уп |.
68
ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
[ГЛ. 3
сходящаяся последовательность, предел которой равен частному
пределов последовательностей" {хл} и {_уп}.
Доказательство. Из доказанной леммы 1 следует, что, начи-
ная с некоторого номера N, элементы последовательности {_уя} отличны
от нуля и последовательность I ограничена. Начиная с этого номера,
мы и будем рассматривать последовательность 1—1. Пусть а и’ b —
'Уп'
пределы последовательностей {хп\ и {уя}. Докажем, что последо-
вательность 1— — бесконечно малая. В самом деле, так как
* Уп Ь !
хп = а + ат уп = Ь-\- то
Хп  Д  хп-Ь—уп-а 
Уп b уп-Ь уп
Так как последовательность !—} ограничена, а последователь-
ная)
ность — у бесконечно малая, то последовательность
jy-. ьа„—	=	бесконечно малая. Теорема доказана.
Замечание 2. Из сходимости последовательности {хя} сле-
дует сходимость последовательностей {хя + 2>} и {с • хп], и на-
оборот, из сходимости любой из последовательностей {xn + h}
и {с • х„} (с 0) следует сходимость последовательности {хя}.
Справедливость этого утверждения вытекает из только что доказан-
ных теорем. Действительно, пусть {хл} сходится. Полагая уп = Ь, мы
получим сходящуюся последовательность {_уя}. Но тогда из теоремы 3.9
следует, что {х„ + Ь} — сходящаяся последовательность. Если после-
довательность {хя + &} сходится, то, полагая уп = —b и используя
теорему 3.9, мы убеждаемся, что последовательность {хл} сходится.
Аналогично, полагая уп — с или уя =(с 0) и применяя теорему
3.11, убедимся, что из сходимости последовательности \хп} следует
сходимость последовательности {с • хП] и наоборот.
3. Предельный переход в неравенствах. Мы только что выяс-
нили, что арифметические операции над сходящимися последователь-
ностями приводят к таким же арифметическим операциям над их пре-
делами. В этом пункте мы покажем, что неравенства, которым удов-
летворяют элементы сходящихся последовательностей, в пределе
переходят в соответствующие неравенства для пределов этих после-
довательностей.
Теорема 3.13. Если элементы сходящейся последовательно-
сти {xnf, начиная с некоторого номера, удовлетворяют неравен-
ству xn>zb (xn^szb), то и предел а этой последовательности
удовлетворяет неравенству а^Ь (а^Ь).
§ 2]
СХОДЯЩИЕСЯ ПОСЛЕДОВАТЕЛЬНОСТИ
69
Доказательство. Пусть все элементы хп, по крайней мере
начиная с некоторого номера, удовлетворяют неравенству хп^Ь.
Требуется доказать неравенство а^Ь. Предположим, что a<Zb. По-
скольку а — предел последовательности. {хя}, то для положительного
е = b — а можно указать номер N такой, что при N выполняется
неравенство | хп — а | < b — а. Это неравенство эквивалентно следу-
ющим двум неравенствам: — (Ь — а) < хп — а < b — а. Используя
правое из этих неравенств, мы получим хп < Ь, а это противоречит
условию теоремы. Случай хп^Ь рассматривается аналогично. Тео-
рема доказана.
Замечание. Элементы сходящейся последовательности {.v„}
могут удовлетворять строгому неравенству хп > Ь, однако при этом
предел а может оказаться равным о. Например, если хп = —, то
хп > 0, однако lim хп — 0.
п-*оо
Следствие 1. Если элементы. хп и уп сходящихся последова-
тельностей {х„} и {_уя}, начиная с некоторого номера, удовлетво-
ряют неравенству хп^уп, то их пределы удовлетворяют та-
кому же неравенству:
lim хп lim уп.
»-*со	п-*со
В самом деле, элементы последовательности {_у„—хя} неотрица-
тельны, а поэтому неотрицателен и ее предел lim (уп — хп) = limуп—•
rt-^оэ	п-*оо
— lim хп. Отсюда следует, что
Д-* со
lim хп	lim у„.
п-*с&	п-»оз
Следствие 2. Если все элементы сходящейся последователь-
ности {хп} находятся на сегменте [a, ft], то и ее предел с также
находится на этом сегменте.
В самом деле, так как а хп ft, то
Следующая теорема играет важную роль в различных прило-
жениях.
Теорема 3.14. Пусть {хя} и {zn} — сходящиеся последователь-
ности, имеющие общий предел а. Пусть, кроме того, начиная
с некоторого номера, элементы последовательноети	удовлет-
воряют неравенствам хп^уn^zn. Тогда последовательность {_уя}
сходится и имеет предел а.
Доказательство. Нам достаточно доказать, что последова-
тельность {уп — а} является бесконечно малой. Обозначим через N*
номер, начиная с которого, выполняются неравенства, указанные
в условии теоремы. Тогда, начиная с этого же номера, будут выпол-
няться также неравенства хп — а уп — a sS zn — а. Отсюда следует,
70
предел последовательности
[ГЛ. з
что при п N* элементы последовательности {_у„ — а} удовлетво-
ряют неравенству
|_УЯ-а | шах {|хя-а |z„-a|}.
Так как lim хп = а и lim zn — a, то для любого е>0 можно
п—>со	л—* со
указать номера и N2 такие, что при n^Nx \хп— а|<е, а при
n^Nt |гп— а|<е. Пусть Д^=тах{Лг*, Ny лЦ. Начиная с этого
номера, имеет место неравенство \уп — п|<е. Итак, последователь-
ность {уп—а} бесконечно малая. Теорема доказана.
§ 3.	Монотонные последовательности
1.	Определение монотонных последовательностей.
Определение. Последовательность {х„} называется неубы-
вающей (невозрастающей), если каждый последующий
член этой Последовательности не меньше (не больше) предыду-
щего, т. е. если для всех номеров п справедливо неравенство
Хп -^п+1 (,Хп
Неубывающие и невозрастающие последовательности объединяются
общим наименованием монотонные последовательности. Если эле-
менты монотонной последовательности {хл} для всех номеров п удов-
летворяют неравенству хп < хп+1 (хп > хп+^), то последовательность
{х„} называется возрастающей (убывающей). Возрастающие и
убывающие последовательности называются также строго моно-
тонными.
Монотонные последовательности ограничены либо сверху, либо
снизу. Именно: невозрастающие последовательности ограничены
сверху, а неубывающие последовательности ограничены снизу своими
первыми элементами. Поэтому невозрастающая последовательность
будет ограниченной с двух сторон, если она ограничена снизу, а не-
убывающая последовательность будет ограниченной с двух сторон,
если она ограничена сверху.
Рассмотрим примеры монотонных последовательностей.
. гт	. .	1	1	11
1.	Последовательность 1, 1, у, у,	... невозрастаю-
щая. Она ограничена сверху своим первым элементом, равным еди-
нице, а снизу числом нуль.
2.	Последовательность 1, 1,-2, 2, ..., я, и,... неубывающая. Она
ограничена снизу своим первым элементом, равным единице, а сверху
не ограничена.
12 3 п
3.	Последовательность у, у, у, ... — возрастающая. Она
ограничена с обеих сторон: снизу своим первым элементом у,
а сверху, например, числом единица.
§3]
МОНОТОННЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
71
2.	Признак сходимости монотонной последовательности. Имеет
место следующая основная теорема.
Теорема 3.15. Если неубывающая (невозрастающая) последо-
вательность {хп} ограничена сверху (снизу), то она сходится.
Согласно предыдущему пункту последовательность {х„}, удовлет-
воряющая условию теоремы 3.15, является ограниченной. Поэтому
теорему 3.15 можно кратко сформулировать так: если монотонная
последовательность {хп} ограничена с обеих сторон, то она схо-
дится.
Доказательство. Так как последовательность {х„} ограни-
чена, то множество ее элементов имеет точные верхнюю и нижнюю
грани х и х (см. теорему 2.1). Докажем, что если {х„}—неубываю-
щая последовательность, то ее пределом будет указанная точная
верхняя грань х, если же {х„} — невозрастающая последовательность,
то ее пределом будет указанная точная нижняя грань х. Мы ограни-
чимся случаем неубывающей последовательности, поскольку для
невозрастающей последовательности рассуждения аналогичны.
Поскольку Зс — точная верхняя грань множества элементов после-
довательности {х„}, то для любого s > 0 можно указать элемент Ху
такой, что хдг>х —& и х^^х (любой элемент хп не больше точ-
ной верхней грани х, хп^х). Сопоставляя указанные неравенства,
получим неравенства OeCx — xN<3.$. Так как {хп} — неубывающая
последовательность, то при n^N справедливы неравенства
<zxn^x. Отсюда следует, что при n^N выполняются неравенства
О х — xnsxz х — xN. Выше мы отмечали, что х—Хдг<е, поэтому
при n:>N справедливы неравенства 0 х — х„ < е> из которых
вытекает неравенство | х„ — х | < г.' Таким образом, установлено, что
х —предел последовательности {х„}. Теорема доказана.
Замечание 1. Условие ограниченности монотонной последо-
вательности представляет собой необходимое и достаточное
условие ее сходимости.	.. 
В самом деле, если монотонная последовательность ограничена,
то в силу теоремы 3.15 она сходится; если же монотонная последо-
вательность сходится, то в силу теоремы 3.8 она ограничена.
Замечание 2. Сходящаяся последовательность может и не
быть монотонной. Например, последовательность {хя}, для которой
(— 1)"
хп = —-— сходится и имеет пределом число нуль. Так как знаки
элементов этой последовательности чередуются, то она не является
монотонной.
Замечание 3. Если последовательность {хл} неубывающая и
ограниченная и х—ее предел, то для всех номеров п справедливо
неравенство x„sgx. Элементы невозрастающей ограниченной после-
довательности {хп}, сходящейся к х, удовлетворяют неравенству
х^хя. Справедливость этого утверждения была установлена в про-
цессе доказательства теоремы 3.15.
72	ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ	[ГЛ. 3
Следствие из теоремы 3.15. Пусть дана бесконечная система
сегментов [an [а2, Л2], [а3, />3|, ..., [ап, Ьп], каждый после-
дующий из которых содержится в предыдущем *) и пусть раз-
ность Ьп—ап (будем называть ее длиной сегмента [а„, &„]) стре-
мится к нулю при п—>оо (систему сегментов, обладающую этими
свойствами, будем называть стягивающейся). Тогда существует,
и притом единственная, точка с, принадлежащая всем сегмен-
там этой системы.
Доказательство. Прежде всего заметим, что точка с, при-
надлежащая всем сегментам, может быть только одна. В самом деле,
если бы нашлась еще одна точка d, принадлежащая всем сегментам,
то весь сегмент ** ***)) [с, d] принадлежал бы всем сегментам [cz„, йп].
Но тогда для любого номера п выполнялись бы неравенства Ьп — ап
d — с > 0, а это невозможно, ибо Ьп — ап -* 0 при п -> со. Дока-
жем теперь, что существует точка с, принадлежащая всем сегмен-
там [ап, Ьп]. Так как система сегментов является стягивающейся, то
последовательность левых концов {ал} является неубывающей, а по-
следовательность правых концов {/>„} невозрастающей. Поскольку обе
эти последовательности ограничены (все элементы последовательностей
{а„} и {Ьп\ находятся на сегменте [ар Z^]), то по теореме 3.15 обе
они сходятся. Из того, что разность Ьп—ап является бесконечно
малой, вытекает, что указанные последовательности имеют общий
предел. Обозначим этот предел через с. Из замечания 3 вытекает,
что для любого номера п справедливы неравенства ап^с^Ьп, т. е.
точка с принадлежит всем сегментам [ап, 5„].
3.	Некоторые примеры сходящихся монотонных последова-
тельностей. Рассмотрим примеры последовательностей, для нахож-
дения предела которых будет использована теорема 3.15 о пределе
монотонной последовательности. Кроме того, в этом пункте мы поз-
накомимся с одним общим приемом нахождения пределов последова-
тельностей, задаваемых рекуррентными формулами »**).
Пример 1. Рассмотрим последовательность {х„}, элемент хп
которой равен
х„ = |/^ я-|-	а4-]/Га-р...-|-]/ла, а > 0.
Эту же последовательность можно, очевидно, задать следующей
рекуррентной формулой:
Xi = ]/a,	= У a+xn_v
*) Это означает, что ап_г ^ап^Ьп^ Ьп^.
**) Ради определенности мы считаем, что d>c.
***) Рекуррентная формула (от латинского recurrens — возвращающийся) —
формула, позволяющая выразить (п + 1)-й элемент последовательности через
значения ее первых п элементов.
§ 3]
МОНОТОННЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
73
Для того чтобы установить существование предела последователь-
ности {хп}, докажем, что эта последовательность возрастающая и
ограниченная. Первое усматривается непосредственно. Докажем, что
последовательность {хп} ограничена сверху числом А, где А — наи-
большее из двух чисел а и 2. Если хп^1а, то требуемое доказано.
Если же хп > а, то, заменив в правой части неравенства Хп — аА-
4- хп-г sSia-]-xn число а превосходящим его числом хп, мы получим
х„ < 2хя, откуда хп < 2. Итак, мы доказали, что последовательность
\хп\ ограничена сверху. По теореме 3.15 она имеет предел. Обоз-
начим этот предел через с. Очевидно, с >» 0. Из рекуррентной фор-
мулы имеем соотношение
х'п — о, 4~ хп_^,
которое означает, что последовательности {х„} и {а-Ь-х^-т} тождест-
венны. Поэтому их пределы равны. Так как первая из этих последо-
вательностей имеет предел с2, а . вторая а А-с, то сг = а-\-с. Отсюда,
n	1 + /1 4-4а
поскольку с > 0, находим, что с = —	2 — •
П р имер 2. Рассмотрим теперь последовательность {х„}, с помощью
которой обычно вычисляют квадратный корень из положительного
числа а на современных быстродействующих электронных машинах.
Эта последовательность определяется следующей рекуррентной фор-
мулой:
где в качестве хг может быть взято любое положительное число.
Докажем, что эта последовательность сходится и имеет своим
пределом число Прежде всего докажем существование предела
последовательности {хя}. Для этого достаточно установить, что после-
довательность {хя} ограничена снизу и, начиная со второго номера,
является невозрастающей. Сначала докажем, что последователь-
ность {_гл} ограничена снизу. По условию хг > 0. Но тогда из рекур-
рентной формулы, взятой при л=1, вытекает, что х2>0, а отсюда
и из той же формулы, взятой при п =2, вытекает, что х3 > 0. Про-
должая эти рассуждения, мы докажем, что все хп > 0.
Докажем теперь, что при п^2 все хп удовлетворяют неравен-
ству хпА^уа. Переписав рекуррентную формулу в виде хл+1 =
Уа / хп	У а \
= -к-	4-L— , воспользуемся почти очевидным неравенством
2 \У а	хп /
I 4--г^2 *), справедливым для любого />0(мы берем
I	\	1/ п
*) Для доказательства этого неравенства достаточно заметить, что при t >• 0
оно эквивалентно неравенству Z2 — 2Z 4- 1 2= 0.
74
ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
[ГЛ. 3
Получим, что х„+1 при любом и^1, т. е. x^r^jAz, начиная
с номера п = 2.
Докажем, наконец, что последовательность {х„} при п^2 не
возрастает. Из рекуррентной формулы получим ^^ = 471 + -^),
хп	\ хп)
а отсюда, учитывая, что хл^рла, найдем *-+д	1, или xn5=x„ + !
Хп
(при n^s2).
' Так как последовательность {х„} при п^2 невозрастающая и
ограничена снизу числом ]Az, то она имеет предел, не меньший У а
(см. теорему 3.15 и теорему 3.13). Обозначая этот предел через с и
учитывая, что lim хл+1 = с и lim|-^(x„ + —H = -i-(c + —), получим
п —оо	n-»oolJ \ хп1> 1 \ С/
c =	+	*). Следовательно, с — У~й.
Замечание 1. В рассмотренных примерах использовался сле-
дующий часто употребляемый прием разыскания предела последова-
тельностей. Сначала устанавливается существование предела, а затем
находится его числовое значение из уравнения, которое получается
из -рекуррентной формулы путем замены в ней хп и хл+1 искомым
значением с предела последовательности {хл}.
Замечание 2. Рекуррентные формулы часто используются
в современной вычислительной математике, поскольку их применение
приводит к многократному повторению однотипных вычислительных
операций, что особенно удобно при проведении вычислений на быстро-
действующих электронно-вычислительных машинах.
Рассмотренная нами рекуррентная формула определяет, как мы
убедились, алгоритм вычисления (мы доказали, что lim х„ = ]/а).
Я —* СО
В дополнении 2 к настоящей главе изучается вопрос о скорости
сходимости последовательности {хл} к ]/а. Мы доказываем, что для
любого а > 1 при определенном выборе первого приближения xt
уже четвертое приближение х4 дает нам число с ошибкой, не
превышающей 10~10.
Пример 3. Докажем, что последовательность {сл}, для которой
хп + 1
сп= имеет ПРИ Л1<Иб°м фиксированном х предел, равный нулю.
Так как при достаточно большом л
ДрОбь-Д<1,
ТО,
с некоторого номера N, имеем | сп+11 < | ся |, поскольку
|х|п _И__|Г I и
п1 ’п + 1	1 лГп + Г
начиная
I Сп+1 I =
*) Это равенство вытекает из рекуррентной формулы
__ 1 /	। а\
Хп +1 — л \ Хп, “Г v J •
* \ ЛП1
§ 3]
МОНОТОННЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
75
Следовательно, начиная с номера N, последовательность {\сп | }
будет монотонно убывающей и ограниченной снизу (например, нулем).
По теореме 3.15 последовательность {| сп 1} сходится, Пусть с—пре-
'	I X I
дел этой последовательности. Из соотношения | сп+11 = | сп | • 	~
следует, что с = 0, так как предел последовательности {| сп+1 [} равен
I 1*1 1
с, а предел последовательности j । равен нулю;
4. Число е. Применим теорему 3.15 о существовании предела
монотонной последовательности для доказательства существования
предела последовательности {хя}, элемент хп которой определяется
формулой
Хп
Докажем, что эта последовательность возрастает « ограничена
сверху. Применив формулу бинома Ньютона, найдем
V- _ 1 , „ 1 , п(п — 1) 1 , п(п— 1)(л — 2) 1 ,
хл-1+«- + —2|------+----------------3!-+	+
. п(п — 1) (п — 2)... [п — (п — 1)1	1
.	nl	пп ’
Представим это выражение в следующей форме:
Совершенно аналогичным образом запишем элемент хя+1:
Непосредственным сравнением убеждаемся, что *)
Хп <~Z Хп+1>
т. е. последовательность возрастающая.
Для доказательства ограниченности этой последовательности сверху
заметим, что каждое выражение в круглых скобках в соотношении (3.6)
меньше единицы. Учитывая также, что ~ ПРИ ^===2, получим
*п<2 + у + 52 + --- + -2лЧ~=3—2й=г<3-
*) Ибо	——j < U—771^7) для любого	и, кроме того,
хл+1 содержит по сравнению с хп лишний положительный член.
76
ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
[ГЛ. 3
Итак, последовательность возрастает и ограничена сверху. По
теореме 3.15 последовательность {хл} имеет предел. Этот предел
называют числом е. Следовательно, по определению,
е = lim (1 + —
Замечание. В дальнейшем выяснится, что число е играет важ-
ную роль в математике. В настоящем пункте мы даем только опре-
деление числа е, но .не указываем способа вычисления этого числа
с любой степенью точности. Это будет сделано в пп. 1 и 2 § 16
главы 8.
Здесь мы лишь отметим, что поскольку хп < 3 и из (3.6) непо-
средственно очевидно, что 2 < хп, то число е заключено в пределах
2^е=<гЗ
(3-7)
(в силу следствия 2 из теоремы 3.13).
§ 4.	Некоторые свойства произвольных последовательностей
и числовых множеств
1.	Подпоследовательности числовых последовательностей.
Пусть xv х2, ..., хп, ...— некоторая числовая последовательность.
Рассмотрим произвольную возрастающую последовательность целых
положительных чисел kv k2, ., kn, .... Выберем из последователь-
ности элементы с номерами kt, k2,	k„... и расположим их
в таком же порядке, как и числа /гп:
xki, xks, .... хкп, ...
Полученную числовую последовательность будем называть подпо-
следовательностью последовательности {хл}. В частности, сама
последовательность {х„} может рассматриваться как подпоследова-
тельность (в этом случае kn — ri). Отметим следующее свойство под-
последовательностей сходящейся последовательности: если последо-
вательность сходится и имеет своим пределом число а,
то и любая подпоследовательность этой последовательности
сходится и имеет своим пределом число а. В самом деле, так как
{хл} — сходящаяся последовательность и а — ее предел, то для любого
е>0 можно указать номер N такой, что при n^N выполняется
неравенство | хп — а | <; е. Пусть {хк } — некоторая подпоследователь-
ность последовательности {х„}. Так как	то, начиная с но-
мера элементы подпоследовательности удовлетворяют нера-
венству | xk/t — а | << е. Поэтому подпоследовательность {-х^} сходится
и имеет пределом число а. Справедливо и обратное предложение:
§4]
СВОЙСТВА ПРОИЗВОЛЬНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
77
если все подпоследовательности данной последовательности {.гп}
сходятся, то пределы всех этих подпоследовательностей равны
одному и тому же числу а; в частности, к этому же числу
сходится и последовательность {хп}. Действительно, так как по-
следовательность {х„} также является подпоследовательностью, то
она сходится и имеет пределом некоторое число а. Но тогда и лю-
бая другая подпоследовательность также сходится и имеет тот же
предел а.
Подпоследовательности бесконечно больших последовательностей
обладают аналогичным свойством. Именно, каждая подпоследователь-
ность бесконечно большой последовательности также будет
бесконечно большой. Доказательство этого утверждения аналогично
доказательству соответствующего предложения о подпоследователь-
ностях сходящихся последовательностей.
Замечание. Из каждой сходящейся последовательности можно
выделить монотонную сходящуюся подпоследовательность. В самом
деле, если — сходящаяся последовательность и а — ее предел,
то имеет, место по крайней мере один из следующих трех случаев:
1) имеется бесконечно много равных а элементов последовательности,
2) в любой е-окрестности точки а имеется бесконечно много элемен-
тов, удовлетворяющих неравенству хп <Za, 3) в любой е-окресрности
точки а имеется бесконечно много элементов, удовлетворяющих нера-
венству	В первом случае сходящейся монотонной-подпосле-
довательностью является подпоследовательность равных а элементов.
Второй и третий случаи рассматриваются одинаково, поэтому ограни-
чимся рассмотрением второго случая, т. е. будем считать, что в любой
е-окрестности точки а имеется бесконечно много элементов хп, удо-
влетворяющих неравенству xn<za. Иными словами, рассмотрим слу-
чай, когда в любом интервале (а — г, а) содержится бесконечно много
элементов последовательности. Пусть — один из этих элементов,
Xkt < а. Из бесконечного множества элементов последовательности
{.г,,}, находящихся на интервале (х*р а), выберем какой-нибудь эле-
мент Хь2, номер k2 которого больше kr Затем из бесконечного мно-
жества элементов последовательности {хп}, находящихся на интервале
(х*2, а), выберем элемент х*3, для которого k3> k2. Продолжая этот
процесс неограниченно, мы получим монотонно возрастающую подпо-
следовательность	последовательности {хп}, которая, в силу
указанного в этом пункте свойства подпоследовательностей сходя-
щейся последовательности, сходится к а.
Отметим, что из каждой бесконечно большой последовательности
можно выделить монотонную бесконечно большую подпоследователь-
ность.
*) Если бы ни один из этих случаев не имел места, то в некоторой
e-окрестности точки а находилось бы лишь конечное число элементов после-
довательности, т. е. точка а не была бы пределом последовательности.
78
ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
[ГЛ. 3
2.	Предельные точки последовательности.
Определение 1. Точка х бесконечной прямой называется
предельной точкой последовательности {хя}, если в любой
^.-окрестности этой точки имеется бесконечно много элементов
последовательности {хя}.
Справедлива следующая лемма.
Лемма 2. Если х— предельная точка последовательности
{хя}, то из этой последовательности можно выделить подпосле-
довательность {х*л}, сходящуюся к числу х.
Доказательство. Пусть х — предельная точка последова-
тельности {хя}. Рассмотрим систему е-окрестностей точки х, для
,	11	1	D
которых е последовательно равно 1, —, -у,	В первой из
этих окрестностей выберем элемент х^ последовательности {хя}, во
второй окрестности выберем элемент х*2 такой, что А2>АГ В третьей
окрестности выберем элемент х*3 такой, что й3>/г2. Этот процесс
можно продолжать неограниченно, так как в любой \е-окрестности
точки х имеется бесконечно много элементов последовательности {хя}.
В результате мы получим подпоследовательность х^, Хьг< .х*л,...
последовательности {хп}, которая сходится к х, так как (х* — х|<
. Лемма доказана.
Замечание. Справедливо и обратное утверждение: если из по-
следовательности {хя} можно выделить подпоследовательность, сходя-
щуюся к числу х, то число х является предельной точкой последо-
вательности {хя}. В самом деле, в любой е-окрестности точки х
имеется бесконечно много элементов выделенной подпоследователь-
ности, а стало быть, и самой последовательности {х„}.
Таким образом, можно дать другое определение предельной точки
последовательности, эквивалентное определению 1.
Определение 2. Точка х называется предельной точкой после-
довательности {хп}, если из этой последовательности можно
выделить подпоследовательность, сходящуюся к х.
Отметим следующее утверждение.
Лемма 3. Каждая сходящаяся последовательность имеет
только одну предельную точку, совпадающую пределом этой
последовательности.
Доказательство. Отметим, во-первых, что предел а сходя-
щейся последовательности {хя} является предельной точкой этой по-
следовательности, поскольку в любой e-окрестности точки а содер-
жатся все элементы последовательности, начиная с некоторого номера.
Убедимся, что у сходящейся последовательности нет других предельных
точек. Действительно, пусть b предельная точка сходящейся последо-
вательности. В силу леммы 2 из {хя} можно выделить подпоследова-
тельность {х*п}, сходящуюся к Ь, но любая подпоследовательность
§fl
СВОЙСТВА ПРОИЗВОЛЬНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
79
сходящейся последовательности имеет предел а (см. пункт 1 этого па*
раграфа), и поэтому Ь = а.
Приведем пример последовательности, имеющей две предельные
точки. Докажем, что последовательность
1, 2, 1, 2, 1, 2, ..., 1, 2, ...
Z	О	/I
имеет только две предельные точки 0 и 2. Очевидно, что эти точки
являются предельными точками рассматриваемой ' последовательности,
,111
поскольку подпоследовательность 1,	-х-...—, ... этой последова-
£ о . П
тельности имеет предел нуль, а подпоследовательность 2, 2, ..., 2,...
имеет предел 2 *). Других предельных точек у этой последователь-
ности нет. В самом деле, пусть -х — любая точка числовой оси, от-
личная от точек 0 и 2. Рас-
смотрим неперекрывающиеся	,
е-окрестности точек 0, 2 и х	it ее
(рис. 3.1). В е-окрестностях
точек 0 и 2 содержатся, на-	Рис. 3.1.
чиная с некоторого номера,
все элементы последовательности, и поэтому в указанной е-окрест-
ности точки х находится лишь конечное число ее элементов, то есть
х не является предельной точкой.
3.	Существование предельной точки у огранйченной после-
довательности. Справедливо следующее замечательное утверждение.
Теорема 3.16. У всякой ограниченной последовательности
существует хотя бы одна предельная точка.
Доказательство.. Так как последовательность {х„} ограни-
чена, то существуют вещественные числа т и М такие, что все эле-
менты хп последовательности {хп} удовлетворяют неравенствам
т хп М. Рассмотрим множество [х\ вещественных чисел х
таких, что правее **) каждого из этих чисел либо вовсе нет
элементов последовательности {х„}, либо таких элементов лишь
конечное число. Множество {х\ имеет хотя бы один элемент (напри-
мер, число М) и ограничено снизу (любым числом, меньшим т).
В силу теоремы 2.1 у множества {х} существует точная нижняя
грань, которую мы обозначим через х***).
Докажем, что это число х и является предельной точкой после-
довательности {хл}. Пусть е—любое положительное число. Число
х— е заведомо не принадлежит множеству {х}, а поэтому правее
*) См. определение 2 предельной точки.
**) Мы говорим, что число а лежит правее числа Ь, если а~> b (см. § 3
главы 2).
***) Целесообразность обозначения этой ниЖней грани символом X будет
выяснена ниже.
80
ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
[ГЛ: 3
числа X — е лежит бесконечно много элементов последователь-
ности {х„}. По определению точной нижней грани найдется число х'
из множества {х}, удовлетворяющее неравенствам Х^х'
(рис. 3.2). По определению множества {х} правее х' лежит не более
чем конечное число элементов последовательности {х„}. Стало
быть, на полусегменте (х—е, х'], а тем более и в е-окрестности
точки х содержится бесконечно много элементов последовательности,
т. е. х является предельной точкой последовательности {хп}. Теорема
доказана.
Замечание 1. Обратимся еще раз к множеству {х}, введен-
ному при доказательстве теоремы 3.16. Мы доказали, что точная
нижняя грань х этого мно-
х-£ х х' х+е	жества представляет собой
* предельную точку последо-
вательности {х„}. Докажем,
Рис. 3.2.	что ни одно число х, пре-
восходящее X, не является
предельной точкой последовательности {хп}, т. е. X ‘является наи-
большей предельной точкой этой последовательности. Пусть х —лю-
бое число, превосходящее X. Выберем е>0 столь малым, чтобы
число х— е также превосходило число X (рис. 3.3). По определению
точной нижней грани найдется число х' из множества {х}, лежа-
щее левее х—е. По определению множества {х}, правее х',
а стало быть, и в e-окрестности точки х лежит не более чем конеч-
ное число элементов после-
довательности {хп}. Это и	х	х'	х t
доказывает, что число х не	с	°
является предельной точкой.
Определение. Наиболь-	Рис. 3.3.
мая предельная точка X
последовательности {х„} называется верхним пределом
этой последовательности и обозначается символом X = lim х„.
п —* 00
Замечание 1 позволяет утверждать, что у всякой ограниченной
последовательности существует верхний предел.
Совершенно аналогично вводится понятие нижнего предела х
последовательности {х„}, который определяется как наименьшая пре-
дельная точка этой последовательности. Для нижнего предела исполь-
зуется обозначение х= lim хп.
л-+со
Существование нижнего предела у любой ограниченной после-
довательности {хп} доказывается в полной аналогии с рассужде-
ниями теоремы, 3.16 и замечания 1 к этой теореме. Только на этот
раз следует рассмотреть множество {х} вещественных чисел х таких,
что левее каждого из этих чисел лежит не более чем конечное число
элементов этой последовательности.
S 4]
СВОЙСТВА ПРОИЗВОЛЬНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
81
Итак, мы приходим к следующему утверждению.
У всякой ограниченной последовательности существуют верх-
ний и нижний пределы.
Извлечем еще ряд следствий из рассуждений теоремы 3.16 и за-
мечания 1.
Следствие 1. Если (а, Ь) — интервал, вне которого лежит
лишь конечное число элементов ограниченной последователь-
ности {хл}, а х и х — нижний и верхний пределы этой последо-
вательности, то интервал (х, х) содержится в интервале (а, Ь)
и поэтому х— х^Ь— а.
Доказательство. Так как правее точки b находится не более
чем конечное число элементов последовательности, то Ь принадлежит
указанному в доказательстве теоремы 3.16 множеству {х} и поэтому
х^Ь. Рассуждая аналогично, убедимся, что а^х. Это и означает,
что интервал (а, Ь) содержит интервал (х, х).
Следствие 2. Для любого положительного числа s ин-
тервал (х—е, -? + е) содержит все элементы последователь-
ности {х„}, начиная с некоторого номера (зависящего, конеч-
но, от е).
Доказательство. Так как х является точной нижней гранью
множества {х}, указанного при доказательстве теоремы 3.16, то для
любого е > 0 найдется число х', меньшее х + е и принадлежащее {х}.
Но это означает, что направо от х', а стало быть, и направо от
интервала (х—е, х-ре) может лежать лишь конечное число
элементов последовательности {хл}. Аналогично доказывается, что
и налево от интервала (х—е, х + £) может лежать лишь конечное
число элементов последовательности {х„}.
Замечание 2. Выясним вопрос о том, сколько предельных
точек может иметь ограниченная последовательность {хп}.
Обозначим через х и х соответственно нижний и верхний пре-
делы этой/последовательности. Очевидно, что все предельные точки
последовательности {х„} (сколько бы их ни было) лежат на сегмен-
те [х, х].
Если х = х *), то последовательность имеет только одну пре-
дельную точку. Если же х <х, то последовательность имеет по край-
ней мере две предельные точки х и х. Отметим, что последователь-
ность может иметь любое и даже бесконечное число предельных
точек. Последовательность 1, 2, у, 2, ...,	2,..., рассмотренная
в предыдущем пункте, имеет только две предельные точки: нижний
предел х = 0 и верхний предел х = 2. Приведем пример последова-
тельности, имеющей бесконечно много предельных точек. Рассмотрим,
*) Ниже мы докажем, что равенство х = X и условие ограниченности
являются необходимыми и достаточными условиями сходимости последова-
тельности.
82	ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ	[ГЛ. 3
например, последовательность, элементы которой без повторений про-
бегают все рациональные числа сегмента [0, 1] *). Очевидно, любая
точка этого сегмента будет предельной точкой указанной последова-
тельности.
4.	О выделении сходящейся подпоследовательности. Результаты
предыдущего пункта приводят к следующей основной теореме.
Теорема 3.17 (теорема-Больцано — Вейерштрасса**)). Из
любой ограниченной последовательности можно выделить сходя-
щуюся подпоследовательность.
Д о к аз ат е ль с тв о. Так как последовательность ограничена, то
она имеет хотя бы одну предельную точку х. В таком случае из
этой последовательности можно выделить подпоследовательность, схо-
дящуюся к точке х (см. определение 2 предельной точки).
Замечание 1. Из любой ограниченной последовательности
моэкно выделить монотонную подпоследовательность. В самом
деле, в силу теоремы Больцано — Вейерштрасса из любой ограничен-
ной последовательности можно выделить сходящуюся подпоследова-
тельность, а из этой подпоследовательности, в силу замечания пункта
1 этого параграфа, можно выделить монотонную подпоследователь-
ность.
Замечание 2. Пусть {хп} — ограниченная последовательность,
элементы которой находятся на сегменте [а Ь]. Тогда предел
с любой сходящейся подпоследовательности {х fcn} также нахо-
дится на сегменте [а, Ь]. Действительно, так-как a^xkn^b, то
в силу следствия 2 из теоремы 3.13 выполняются неравенства
а с Ь. Это и означает, что с находится на сегменте [а, &].
Отметим, что в отдельных случаях и из неограниченной последо-
вательности также можно выделить сходящуюся подпоследователь-
ность. Например, последовательность 1, у, 2, у,..., в, ~	.
неограниченная, однако Подпоследовательность у, у,..., у,... ее
элементов с четными номерами сходится. Но не из каждой неограни-
ченной последовательности можно выделить сходящуюся подпоследо-
*) Рациональные числа сегмента [0, 1] можно расположить в последова-
тельность без повторений, например, так. Рассмотрим группы рациональных
чисел этого сегмента, причем в первую группу отнесем числа 0 и 1, во
1	Р	п
вторую — число у, в третью — все несократимые числа — со знаменателем 3
и вообще в п-ю группу — все несократимые рациональные дроби из сегмента
[О, 1] со знаменателем п. Очевидно, каждое рациональное число попадает
в одну группу и в каждой группе будет лишь конечное количество рациональ-
ных чисел. Выпишем теперь подряд элементы первой группы, за ними элементы
второй группы, затем третьей и т. д. В результате мы и получим нужную
нам последовательность.
**) Бернгард Больцано — чешский философ и математик (1781—1848),
Карл Вейерштрасс— немецкий математик (1815— 1897).
5 4]	СВОЙСТВА ПРОИЗВОЛЬНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ	83
вательность. Например, любая подпоследовательность неограниченной
последовательности 1, 2........ п,...	расходится. Поэтому теорему
Больцано — Вейерштрасса, вообще говоря, нельзя распространить на
неограниченные последовательности.
Аналогом этой теоремы для неограниченных последовательностей
является следующее предложение.
Лемма 4. Из каждой неограниченной последовательности можно выделить
бесконечно большую подпоследовательность.
Доказательство. Пусть {х„}— неограниченная последовательность.
Тогда найдется элемент этой последовательности, удовлетворяющий усло-
вию |	| > 1, элемент xki этой последовательности, удовлетворяющий усло-
виям |	| >• 2, k2 > klt..., элемент xk этой последовательности, удовлетво-
ряющий условиям | Xhn | > п, kn> kn_r и т. д. Очевидно, подпоследователь-
ность xkt, xks...xkn,... является бесконечно большой.
Из леммы 4 и из теоремы Больцано — Вейерштрасса вытекает следующее
утверждение.
Лемма $. Из совершенно произвольной последовательности можно выделить
либо сходящуюся, либо бесконечно большую подпоследовательность.
Замечание 3. Результаты настоящего пункта позволяют несколько
расширить понятие предельной точки и верхнего и нижнего пределов после-
довательности.
Будем говорить, что -J- со (— оо) является предельной точкой последова-
тельности {хп}, если из этой последовательности можно выделить бесконечно
большую подпоследовательность, состоящую из положительных (отрицатель-
ных) элементов.
При таком расширении понятия предельной точки у последовательности
кроме конечных предельных точек могут существовать еще две предельные
точки + со и — со. В таком случае лемма 5 позволяет утверждать, что
у совершенно произвольной последовательности существует хотя бы одна предель-
ная точка *), а стало быть, и верхний и нижний пределы.
5.	Необходимое и достаточное условие сходимости последо-
вательности. При выяснении вопроса о сходимости последователь-
ности \хп] при помощи определения сходимости нам приходится
оценивать разность элементов хп этой последовательности и ее пред-
полагаемого предела а. Иными словами, приходится предугадывать,
чему равен предел а этой последовательности.
Естественно указать «внутренний» критерий сходимости последо-
вательности, позволяющий выяснить вопрос о ее сходимости лишь по
величине ее элементов. Такой внутренний критерий и будет установ-
лен в настоящем пункте. Для формулировки этого критерия введем
понятие фундаментальной последовательности.
Определение. Последовательность {хп} называется фунда-
ментальной, если для любого положительного е найдется
номер N такой, что для всех номеров п, удовлетворяющих
условию n^N, и для всех натуральных чисел р (р — \, 2,...)
) Либо конечная, либо бесконечная.
84
ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
[ГЛ. 3
справедливо неравенство
I хп+р хп ] е.
Основной задачей настоящего пункта является доказательство
следующего критерия сходимости последовательности (так называемого
критерия Коши *)): для того чтобы последовательность была
сходящейся, необходимо и достаточно, чтобы она была фунда-
ментальной.
Прежде чем перейти к доказательству критерия Коши, мы дока-
жем несколько вспомогательных предложений, имеющих и самостоя-
тельный интерес. >
Теорема 3.18. Для того чтобы последовательность {хп}
была сходящейся, необходимо и достаточно, чтобы она была
ограниченной и чтобы ее верхний и нижний пределы х и х сов-
падали.
Доказательство. 1) Необходимость. Пусть последова-
тельность {*„} сходится. Тогда она ограничена (в силу теоремы 3.8)
и имеет единственную предельную точку (в силу леммы 3 п. 2).
Таким образом, х = х.
2) Достаточность. Следствие 2 из теоремы 3.16 утверждает,
что для любого е>0 интервал (х— е, х-|-е) содержит все элементы
последовательности {хп}, начиная с некоторого номера. Так как
х = х — х, то указанный интервал совпадает с e-окрестиостью точки х,
т. е. число х является пределом последовательности {хп} (см. заме-
чание 1 п. 1 § 2).
Установим теперь важное свойство фундаментальной последова-
тельности, непосредственно вытекающее из ее определения:
Для любого положительного числа г можно указать такой
элемент xN фундаментальной последовательности, в г-окрест-
ности которого находятся все элементы последовательности,
начиная с номера N. Иными словами, вне интервала (х^— г,
xn+s) находится не более чем конечное число элементов после-
довательности **).
В самом деле, из определения фундаментальной последовательности
следует: для любого е > 0 можно указать такой номер N, что
для всех натуральных р(р = \, 2, 3, ...) выполняется неравенство
\ху+р — хЛг|<е, которое и означает, что в e-окрестности элемента х^
находятся все элементы последовательности, начиная с номера N.
Отмеченное свойство позволяет установить ограниченность фунда-
ментальной последовательности. В самом деле, пусть е — некоторое
фиксированное положительное число и Хдг— элемент, в е-окрестности
которого находятся все элементы последовательности, начиная с но-
*) Огюстен Луи Коши — французский математик (1789—1857).
**) Отметим, что указанное свойство эквивалентно определению фунда-
ментальной последовательности.
§ 4]	СВОЙСТВА ПРОИЗВОЛЬНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ	85
мера N. Тогда вне этой e-окрестности могут находиться только эле-
менты хг, х2, ..., Хх^!- Положим А — max{ | хх |, |х2|, ..., IJCjy.xl,
|jQy—е|, Ix^+e |} *). Тогда на сегменте [—А, + А] находятся
числа хг, х2, Xjv_x, Хдг—е, Хдг+е, а следовательно, и все точки
е-окрестности элемента xN. Отсюда вытекает, что все элементы фун-
даментальной последовательности находятся на сегменте [— А, + А],
что и означает ее ограниченность.
Переходим к доказательству основного утверждения этого пункта.
Теорема 3.19 (критерий Коши сходимости последователь-
ности). Для того чтобы последовательность была сходя-
щейся, необходимо и достаточно, чтобы она была фундамен-
тальной.
Доказательство, 1) Необходимость. Пусть последова-
тельность {хл} сходится и х — ее предел. Требуется доказать, что
эта последовательность является фундаментальной. Возьмем любое
положительное число е. Из определения сходящейся последователь-
ности вытекает, что для положительного числа ~ найдется номер N
такой, что п; и n>iN выполняется неравенство	»
I хп х I "ту •
Если р — любое натуральное число, то при n^N выполняется также
и неравенство
I хп+р X I < ~2 •
Так как модуль суммы двух величин не больше суммы их модулей,
то из последних двух неравенств получим, что при n^N и для всех
натуральных чисел р
I Хп+р хп I = I (хп+р х) 4" (X Хп) I -4 I хп+р X I 4" I хп ~ X | < е-
Тем самым фундаментальность последовательности {хл} установлен].
2) Достаточность. Пусть {— фундаментальная последо-
вательность. Требуется доказать, что эта последовательность сходится.
Согласно теореме 3.18 для этого достаточно доказать ограниченность
последовательности {хл} и равенство ее верхнего и нижнего преде-
лов X и х. Ограниченность фундаментальной последовательности уже
установлена нами выше.
Для доказательства равенства верхнего и нижнего пределов X и х
воспользуемся доказанным выше свойством фундаментальной последо-
вательности: для любого положительного числа е можно указать эле-
мент Хдг такой, что вне интервала (xN— е, x^y-J-s) находится не
*) Геометрически это означает, что А равно максимальному из расстояний
от начала отсчета 0 до точек ху, х2, .... xN l, xN—t,
86
ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
[ГЛ. 3
более чем конечное число элементов последовательности. На основа-
нии следствия 1 из теоремы 3.16 интервал (xN — е, x,v +е) содержит
интервал (х, х), и поэтому х —~х^2е, откуда, в силу произволь-
ности е, х — х. Тем самым сходимость последовательности установ-
лена. Теорема полностью доказана.
Пример. Применим критерий Коши для установления сходимо-
сти следующей последовательности {х„}:
хп — а1 + а2 + •  • + ап>
где а-ь (k—\, 2, 3, ..^ — произвольные вещественные числа, удовле-
творяющие условию | ak | гС qk, а # —некоторое число из интервала
0<9<1.
Пусть п— любой номер, р — любое натуральное число. Тогда,
очевидно,
I хп+р ~ Хп I = I ал+1 + ап+2 + • • • + ап-р I I ап+11 +
-Нал+2|Ъ.. + |^|^п+1 + 9я+2 + ---4^+р =
qn+i__qn+1+р qn+i
1— q <1 — q’
Учитывая, что последовательность {<?”} является бесконечно малой
(см. пример 1 из п. 3 § 1), мы можем утверждать, что для любого
е > 0 найдется номер N такой, что
gn+1 < е (1 — q) (при п N).
Стало быть, при n^N и для любого натурального р
ап+1
\xn+p-xn\<Y^<e’
т. е. последовательность {хя} является фундаментальной и сходится
согласно теореме 3.19.
6. Некоторые свойства произвольных числовых множеств. В этом пункте
мы рассмотрим некоторые свойства произвольных числовых множеств. Часть из
этих свойств аналогична свойствам числовых последовательностей.
В п. 5 § 1 главы 2 мы ввели понятие множества, ограниченного сверху
(снизу). Договоримся теперь называть множество {х} ограниченным с обеих
сторон или просто ограниченным, если это множество ограничено и сверху и
снизу, т.' е. если найдутся такие два вещественных числа т и М, что каждый
элемент х множества {х} удовлетворяет неравенствам т х =< М, Множество {х}
будем называть конечным или бесконечным в зависимости от того, является ли
число элементов, входящих в состав этого множества, конечным или бесконечным.
Точку х бесконечной прямой назовем предельной точкой множества (х(,
если в любой ^-окрестности точки х содержится бесконечно много элементов'
этого, множества.
Точку х (точку х) назовем верхней (нижней) предельной точкой множе-
ства {х}, если эта точка является предельной точкой множества {х}, но ни
одна точка, большая X (меньшая х), не является предельной точкой этого
множества.
Дословно повторяя доказательство теоремы 3.16 с заменой термина «по-
следовательность {хл}> на «множество {х}», мы придем к следующему утвер-
§ 4]	СВОЙСТВА ПРОИЗВОЛЬНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ	87
ждению: у всякого ограниченного бесконечного множества существует, хотя бы
одна предельная точка.
Дословно повторяя рассуждения замечания 1 к теореме 3.16, мы полу-
чим, что всякое ограниченное бесконечное множество имеет верхнюю и нижнюю
предельные точки. Следствием указанных утверждений является следующий
факт: из элементов всякого ограниченного бесконечного множества можно выде-
лить сходящуюся последовательность.
Наряду с понятием множества часто пользуются понятием подмножества.
Множество называется подмножеством множества {х}, если все элементы
множества (х'} входят в состав множества {х}. Например, множество всех
четных целых чисел является подмножеством множества всех целых чисел.
Два множества {х} и {</} называют эквивалентными, если между элемен-
тами этих множеств можно установить взаимно однозначное соответствие *).
Заметим, что два конечных множества эквивалентны тогда и только тогда,
когда число элементов у этих множеств одинаковое. Приведем пример двух
эквивалентных бесконечных множеств. Легко видеть, что множество {х},
элементами которого служат четные положительные числа 2, 4, 6.....2п, ....
эквивалентно множеству {р}, элементами которого служат натуральные
числа 1, 2, 3, ..., п, ... В самом деле, мы установим взаимно однозначное
соответствие между элементами этих множеств, поставив й соответствие эле-
менту 2п множества {х} элемент п множества {у}. Обратим внимание на то,
что рассмотренное нами множество {х} является подмножеством множества
{</}• Таким образом, бесконечное множество {р} оказывается эквивалентным
своему подмножеству {х} **).
Из всевозможных множеств выделим следующие два важных типа:
Р. Всякое множество, эквивалентное множеству всех натуральных чисел 1,
2, 3....п, ..., будем называть счетным. Из определения счетного множе-
ства вытекает, что все элементы этого множества можно занумеровать.
2°. Всякое множество, эквивалентное множеству всех вещественных чисел
интервала (0, /), будем называть множеством мощности континуума.
Приведем примеры счетных множеств и множеств мощности континуума.
Первым примером счетного множества может служить рассмотренное выше
множество четных положительных чисел 2, 4, 6, ..., 2п ... Другим примером
счетного множества может служить множество всех рациональных чисел
сегмента [0, 1], ибо, как доказано в сноске на стр. 82, это множество можно
расположить в последовательность без повторений, т. е. занумеровать. При-
мером множества мощности континуума может служить множество всех ве-
щественных чисел (бесконечная прямая). В самом деле, функция p=ctgwx***)
устанавливает взаимно однозначное соответствие между точками интервала
О < х < 1 и точками бесконечной прямой.
В заключение докажем, что множество мощности континуума не эквива-
лентно счетному множеству. Для этого достаточно доказать, что множество
всех вещественных чисел интервала (0, 1) нельзя занумеровать. Допустим
противное, т. е. предположим, что все вещественные числа интервала (0, 1)
*) Взаимно однозначным соответствием между элементами двух множеств
называется такое соответствие, при котором каждому элементу первого мно-
жества отвечает только один элемент второго множества так, что при этом
каждый элемент второго множества отвечает только одному элементу первого
множества.
**) Легко показать, что любое бесконечное множество эквивалентно не-
которому своему подмножеству, не совпадающему со всем множеством. Этот
факт может быть принят за определение бесконечного множества.
***) Читатель имеет представление о функции p = ctgitx из элементар-
ного курса. Вопрос о строгом построении тригонометрических функций вы-
ясняется в главе 4.
88
ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
[ГЛ. 3
можно занумеровать. Тогда, записывая эти числа в виде бесконечных деся-
тичных дробей, мы получим последовательность
Xi = 0, Яц Ди ... ain
= 0, а21 Й22 ... о2л
= 0, ап1 ап2 ... апп ...
Рассмотрим теперь вещественное число х = 0, Ьг b2...bn..., где 6j—
любая цифра, отличная от аи, 0 и 9, Ь2— любая цифра, отличная от а22, О
и 9, и вообще Ьп — любая цифра, отличная от апп, 0 и 9.
Так как число х не содержит после запятой нулей и девяток, то это
число не принадлежит к классу рациональных чисел, представимых двумя
способами в виде бесконечных десятичных дробей *). Но в таком случае
число х заведомо отлично от всех чисел х1( х2, ..., хп, ..., ибо совпадение
числа х с каким-либо хп означало бы совпадение Ьп и апп.
Математиков долгое время занимал вопрос о существовании бесконечного
множества {х}, не эквивалентного ни счетному множеству, ни множеству мощно-
сти континуума, но эквивалентного части множества мощности континуума.
В 1963 году американский математик П. Коэн доказал, что гипотеза о суще-
ствовании такого множества не зависит от остальных аксиом теории множеств.
Это означает, что возможно построить внутренне не противоречивую теорию
множеств, постулирующую как факт существования такого множества, так и
факт его отсутствия (см. книгу П. Дж. Коэна «Теория множеств и контину-
ум-гипотеза», Мир, 1969).
ДОПОЛНЕНИЕ 1 К ГЛАВЕ 3
ТЕОРЕМА ШТОЛЬЦА
Во многих случаях для исследования сходимости частного -I—I после-
\Уп'
довательностей {хя} и {уп} оказывается полезным следующее предложение.
Теорема Штольца. Пусть {у„}—возрастающая бесконечно большая
последовательность, и пасть последовательность !—------сходится и
\Уп~ Уп-il
имеет предел а. Тогда последовательность j—| сходится и имеет предел а.
Таким образом,
lim = lim
п-*а>Уп п->оаУп Уп-1
Доказательство. Поскольку последовательность I—------------------
Уп-1'
сходится и имеет пределом число а, то последовательность {«п}. где
ап = —----—— а, бесконечно малая. Пусть N — любой фиксированный но-
Уп
мер и п > N. Используя выражение для ап, рассмотрим серию равенств:
' ХАГ+ 1 - XN = а (^+ I ~ М +	+ 1 (^+ 1 - yN>
Хй+ 2 ~ ХАГ + 1 = ° (^+ 2 ~ yN+ l) + “аг-1- i (yN+ 2 — %+ 1)’
хп-1 хп-з = а (Уп-1 — Уп-?) 4" ап-1,(Уп-i — Уп-г)>
хп — хп-1 — а (Уп — Уп-1) 4" ^п (Уп — Уп-1)-
*) См. п. 3 § 1 главы 2.
ДОПОЛНЕНИЕ 1 К ГЛАВЕ 3
89
Складывая эти равенства, найдем
Хп - ХЫ = йУп -ayN + aN+X <yN+ 1 - М + aiV + 2 (^+2 ~ Уй+ 1) +
+’••• + ап-1 (Уп-1 — Уп-2> + ап (Уп — Уп-1)‘
Так как {(/„}— возрастающая бесконечно большая последовательность, то,
начиная с_некоторого номера, ее элементы положительны. Будем считать, что
при n^>N уя>0. Тогда из последнего равенства получим
v	Xjn—ay^
^ — а= —--------" +
Уп	Уп
I aN+1 (yiV4-1 ~ У n)	aV + 2 (^V+2 — yN+ t) + • • • + an (У« — (/л-1)
Уп
Поскольку последовательность {//„} возрастающая, то разности
k=^N, N 1, п—1, положительны. Поэтому из последнего соотноше-
ния имеем
хп
Уп
XN~ayN
Уп
| алГ-(-1 | (^+1 УДг) | aN+2 | (^ЛЧ-2	^N+ 1) + ••' ~Ь I g« I (y”	У«-1)
Уп
(3-8)
Докажем теперь, что последовательность | сходится и имеет предел а.
Для этого достаточно доказать, что для любого положительного е можно
указать номер N такой, что при п'^ N выполняется неравенство | —aj_<e.
Во-первых, по данному е > О выберем номер N так, чтобы при п М вы-
полнилось неравенство | ап [ <; — (это возможно, поскольку последователь-
ность {ал} бесконечно малая). Далее, выберем номер N N так, чтобы при
у. Такой выбор номера N
ХН~аУх
Уп
п 5s (V выполнялось неравенство
возможен, поскольку число X—— ау~ фиксировано, а последовательность {у„}
бесконечно большая, и поэтому последовательность | W  —j- бесконечно
малая. Пусть теперь n^zN. Из неравенства (3.8) имеем
е , е (^V+l “ ^jv) (УУ+2~~	Уп-^
2	2 ‘
I Уп
или
Уп
e У"-УК
Уп
Уп — У„
Так как при n^N yn — y-^yn и «/„>0, то —------------^1. Поэтому при
п N из последнего неравенства имеем
— — а I < е.
Уп I
Хп
— —а
Уп
2
Уп
Теорема доказана.
90	ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ	[ГЛ. 3
Замечание. Если {</„}—возрастающая бесконечно большая последова-
тельность. а последовательность 1——также бесконечно большая и
\Уп — Уп-1>
стремится к бесконечности определенного знака, то последовательность
бесконечно большая. В самом деле, пусть
ХП ХП-1 _ д
Уп Уп-i
Последовательность {Д„} бесконечно большая. Имеем при
Xn+i~ xn = Лу+1 (Un+i~ Xv)’
%п ХП-1 — -Ал (Уп   у п-1)’
Складывая эти равенства, найдем
Хп -	= Ллг+к(^+1 - М + • • • + Ап (Уп - ^-1)-
Отсюда
= Л*+ 1 (^+ 1 ~ ^) + '" ~
Уп	Уп	Уп
Из этого соотношения имеем
хп I	ЛАЦ-1 (Ху +1 ~ yjv) + ''' Лп	~ Уn-i)
Уп I	Уп
Будем для определенности считать, что при N элементы последователь-
ностей {(/„} и {Дл} положительны. Выберем, далее, по заданному положи-
тельному А номер N такА чтобы при n^N выполнялось неравенство
Ап>4А, затем такое jVSsA', что при n^N
XN
Уп
(3.9)
Возможность выбора такого N обеспечивается тем, что последовательности
{Ап} и {р„} бесконечно большие и их члены, начиная с некоторого номера,
положительны. Очевидно, при n^N из неравенства (3.9) имеем
или
^|>4Л^У+1 М.
+	+	— Уп-1) хй
Уп	Уп
\
— А > А.
Таким образом, последовательность !—> бесконечно большая.
'Уп'
Рассмотрим несколько примеров.
I9. Докажем, что если последовательность {ал} сходится и имеет пре-
[ а, 4- а» -4- ... + а„ )
дел а, то последовательность	;——=------!) средних арифметических
значений элементов последовательности {ал} сходится. к тому же самому
ДОПОЛНЕНИЕ 1 К ГЛАВЕ 3
91
пределу о *). В самом деле, если положить at + а2 + ••• + ап = хп, a уа — п,
то ——^^Д = ая. Так как lim ——= Нщ Qn существует, то по тео-
Уп Уп-l	п-»соУп Уп-1 л-»со
реме Штольца
..	Qi “I- По “1“ • • ‘"Н- &П 1 •
lim	1—— = lima„ = a.
л—-со	п	п->а>
24. Рассмотрим теперь последовательность {ап}, где
lfe + 2ft + -.- + nfe
°п	пГг+1
и k — целое положительное число.
Обозначим lfe + 2* + ... + п* через хп, a nft+l через уп. Тогда последо-
вательность {а„} приобретает вид 'Исследуем сходимость последователь-
ности	Имеем
УУп — Уп-1 >
Хп—Хп-1	_________________
Уп—Уп-i n*+i-(n-l)*+i (fe + nk  (fe + 1) k nk_± + _	(_])fe+i ’
Поделив числитель и знаменатель последнего выражения на nft, получим
хп ~ Xn-1 _________1_______
Уп Уп-1 ь ,  । 1 r 1 ’
где в знаменателе в квадратных скобках опущено выражение, предел кото-
Г (k +1)	. .
рого при л—-со равен —i—'2~~	послеДнеи формулы находим
л—оо Уп Уп-1 “Ь 1
Следовательно,. по теореме Штольца имеем
lfe + 2* + ... + nft 1
hm -----•----!1.
п — оо nft+1	fe -|- 1
✓	п
3”. Рассмотрим, наконец, последовательность , а > 1. Полагая ап=хп
и п = уп и исследуя последовательность	> находим
УУп Уп~ 1'
lim Хл-1 = lim (an — an-i) = lim ап fl — —) = + co.
п-*-саУп Уп~1 co	n-^co \	O')
Поэтому, в силу замечания к теореме Штольца, имеем
ап
lim — = + оо.
П-+ СО ft
*) Это предложение было доказано Коши.
92
ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
Ц Л. 3
ДОПОЛНЕНИЕ 2 К ГЛАВЕ 3
О СКОРОСТИ СХОДИМОСТИ ПОСЛЕДОВАТЕЛЬНОСТИ,
ПРИБЛИЖАЮЩЕЙ /а
В пункте 3 § 3 этой главы мы доказали, что предел последовательности
{хл}, определяемой рекуррентной формулой
хл+1 = 4- (хп +	, п = 1, 2,	(3.10)
где а>0, а — любое положительное число, равен Уа. В качестве прибли-
женного значения У а мы можем взять любой элемент хл+1 этой последова-
тельности. При этом, естественно, нужно выяснить вопрос о выборе числа п
итераций *), обеспечивающих приближение У а с заданной погрешностью.
Обратимся к последовательности {х„}, определяемой реккурентной формулой
(3.10). Будем называть элемент хп этой Последовательности n-м приближением
числа т = Уа. Величину
=	(3.11)
назовем относительной погрешностью п-ro приближения.
Справедливо следующее утверждение об оценке относительной погрешности
ел+1 через относительную погрешность первого приближения.
Пусть х1 выбрано так, что | е, ] С -%, Тогда при любом п 1 имеют
место неравенства
0^sn+1^ef	(3.12)
Доказательство. Из формулы (3.11) имеем
хя=7(1+ел)-	(3-13)
Обращаясь к формулам (3.10), (3.13) и к равенству у- — 7, получим
1 / . а\ 1 Г /1 , , .	“1 Г, .	1
хл+1- 2	2 [V(l	+2(1+ел)]-
(3-14)
п-
Так как хл+1 = 7 (1	ел+1) то, очевидно,
1
е«+1-2(1 + ел)
По условию hi|<4-. Отсюда следуют неравенства 0 <	-----<1. Но
2	2 (1 -f- sj
тогда из (3.14) при п = 1 вытекает неравенство е25:0. Используя далее со-
отношение (3.14) при п = 2, 3,..., убедимся в неотрицательности ел+1 для
любого п 1.
Из равенства (3.14), из соотношений 0<—-—:—г < 1 и из неотрица-
2 (1 + ej
тельности ел для любого п >• 1 вытекает неравенство en+1sge’ для любого
п>=1. Отсюда сразу же получаем правое из неравенств (3.12). Утверждение
доказано.
*) Итерация (от латинского iteratio — повторение) — результат повтор-
ного применения какой-либо математической операции. В рассматриваемом
случае одной итерацией является вычисление хл+1 по хп с помощью рекуррент-
ной формулы (3.10).
ДОПОЛНЕНИЕ 2 К ГЛАВЕ 3
93
Обращаясь к неравенствам (3.12), мы видим, что относительная погреш-
ность еп+1 вычисления Va после п итераций оценивается через относительную
погрешность первого приближения xt и число п итераций. Ниже мы убедимся,
что при a 1 *) первое приближение можно выбрать так, что ej по абсолют-
ной величине не будет превышать 0,05. Очевидно, что при таком выборе хг
относительная погрешность будет удовлетворять условиям доказанного нами
утверждения. Ясно также, что тем самым будет решен вопрос о выборе числа
п итераций, обеспечивающих приближение к /а с заданной относительной
погрешностью е: это число п может быть найдено из формулы**)
(0,05)2" < г.	(3.15)
Итак, пусть а> 1. Представим число а в следующей форме:
а = 22*+гМ,	(3.16)
где k — целое неотрицательное число, число- i равно либо нулю, либо единице,
а число М удовлетворяет условиям
1<Л4<2.	(3.17)
Отметим, что представление числа а в форме (3.16) единственно.
Выберем Xi следующим образом:
х1 = 2*(12<М + ^).	(3.18)
Убедимся, что для любого М, удовлетворяющего условиям (3.17), первое при-
ближение хх, вычисляемое по формуле (3.18), дает относительную ошибку ех
при вычислении 7 = Va, не превышающую по абсолютной величине числа 0,05.
Для доказательства обратимся к точному выражению относительной ошибки
ех = —----. Так как, согласно (3.16), 4 = 2kV%‘M, то из выражения для sx
и формулы (3.18) получим
'	1 •	17	,----
2>Л1+ yW
Поскольку число i равно либо нулю, либо единице, а М 1, то |/г2/44 ^1.
Отсюда и из (3.19) вытекает неравенство
| ех I < 112‘М + g - Гй’лГ |.	(3.20)
Обозначим V^fM через X. Поскольку 1^M<2 и i равно либо нулю, либо
единице, то все допустимые значения X наверняка находятся на сегменте
II. 2]:
ls=Xsg2.	(3.21)
Используя введенное обозначение X для 1^2’41, перепишем неравенство (3.20)
*) Если a < 1, то а = -7-, где b > 1, и Va равен —т=.
"	V b
**) Справедливость этой формулы непосредственно вытекает из соотноше-
ний (3.12).
94
ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
[ГЛ. 3
в следующей форме:

(3.22)
В силу (3.22) максимальное значение I е, 1 не превышает максимального зна-
I 1	17 I
чения X2 — X -J- jr-j- для значений X, удовлетворяющих условиям (3.21). Для
выяснения вопроса об этом максимальном значении обратимся к графику функ-
1	17
у.	ции f (X) = -g-X2 —Х-J- —. Из курса элемен-
тарной математики известно, что графиком этой
функции является парабола, вершине которой
/	3	_
-------1 —	отвечает точка X = -g- (рис. 3.4)*). Так как
1 li	f(l) = f(2)=^, a = — то ясно, что
’-у-------Д	—г,---J" для значений X, удовлетворяющих условиям
\ ' /	(3.21), значения f (X) заключены между —
-L-------и 1 _ Иными словами,
2ч	24	’
Рис. 3.4.	|/(Х)| = |1х2-Х+^|^1
Из последнего неравенства
неравенство для ej
и неравенства (3.22) вытекает интересующее нас
Ы^й<0’05-
Замечание. Отметим, что если заданная относительная погрешность s
равна 10~10, то для вычисления с такой точностью квадратного корня из любого
числа а>1 после выбора по формуле (3.18) потребуется всего лишь три
итерации (п = 3), поскольку (0,05)г3 < 10~10.
*) На рис. 3.4 масштаб по оси Оу в 20 раз больше масштаба по оси Ох.
ГЛАВА 4
ПОНЯТИЕ ФУНКЦИИ. ПРЕДЕЛЬНОЕ ЗНАЧЕНИЕ ФУНКЦИИ.
НЕПРЕРЫВНОСТЬ.
Эту главу мы начнем с уточнения важнейшего понятия матема-
тического анализа—понятия функции. Опираясь на понятие предела
числовой последовательности, мы введем новую форму операции пре-
дельного перехода, основанную на понятии предельного значения (или
предела) функции. В этой главе вводится также важное математиче-
ское понятие непрерывности функции.
Значительное место в главе отводится выяснению свойства непре-
рывности и других свойств простейших элементарных функций.
Вопрос о приближенном вычислении значений элементарных функ-
ций рассматривается в Дополнении к главе 8.
§ 1.	Понятие функции
1.	Переменная величина и функция. В главе 1 мы уже отме-
тили, что со всяким реальным физическим процессом связаны по меньшей
мере две переменные величины, изменение которых взаимообусловлено.
Рассматривая реальные физические переменные величины, мы при-
ходим к выводу, что эти величины не всегда могут принимать произ-
вольные значения. Так, температура тела не может быть меньше
— 273° С, скорость материальной точки не может быть больше
3-1010 см/сек (т. е. скорости света в пустоте), смещение _у мате-
риальной точки, совершающей гармонические колебания по закону
у = A sin (со/ -j- 8), может изменяться лишь в пределах сегмента [— А,-|- А].
В математике отвлекаются от конкретных физических свойств
наблюдаемых в природе переменных величин и рассматривают аб-
страктную переменную величину*), характеризуемую только числен-
ными значениями, которые она может принимать.
Множество {х} всех значений, которые может принимать данная
переменная величина, называется областью изменения этой переменной
величины. Переменная величина считается заданной, если задана
*) Уместно отметить, что понятие величины относится к числу начальных
математических понятий (см. сноску на стр. 18).
90
ПОНЯТИЕ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ
[ГЛ. 4
область ее изменения. В дальнейшем мы, как правило, будем обозна-
чать переменные величины маленькими латинскими буквами х, у', и,
а области изменения этих переменных символами
{4 {4 {“}>•••
Пусть задана переменная величина х, имеющая
областью изменения некоторое множество {х}.
Если каждому значению переменной х из
множества {х} ставится в соответствие по
известному закону некоторое число у, то го-
ворят, что на множестве {х} задана функ-
ция у—у(х) или y=f(x).
При этом переменная х называется а р гу-
мен т о м, а множество {х} — областью за-
дания функции у—f(х). j
Число у, которое соответствует данному значению аргумента х,
называется частным значением функции в точке х. Сово-
купность всех частных значений функции образует вполне опреде-
ленное множество {у}, называемое множеством всех значе-
ний функции.
В обозначении y=f(x) буква f называется характеристикой
функции. Для обозначения аргумента, функции и ее характеристики
могут употребляться различные буквы.
Приведем примеры функций:
1°. у = х2. Эта функция задана на бесконечной прямой —оо <
<х<-|-оо. Множество всех значений этой функции—полупрямая
0<у<-|-оо (рис. 4.1).
2°. у = У1' — х2. Функция задана на сегменте —1<х<4-1.
Множество всех значений функции — сегмент 0 <_у < 1 (рис. 4.2).
3°. у — п\. Эта функция задана на множестве натуральных чисел
п= 1, 2,... Множество всех значений этой функции — множество
натуральных чисел вида л! (рис. 4.3).
4°. Функция Дирихле *)
( 0, если х — иррациональное число,
у — <
( 1, если х—рациональное число.
*) Петер Густав Лежен-Дирихле — немецкий математик (1805 — 1859).
§ п
ПОНЯТИЕ ФУНКЦИИ
97
Эта функция задана на бесконечной прямой —оо<х< -j-oo,
а множество всех ее значений состоит из двух точек 0 и 1.
5°.
у = sgn Х =
4- 1, если
О, если
— 1, если
х > О,
х = 0,
х < 0.
У
4
(Термин sgn происходит от латинского слова signum — знак.) Эта
функция задана на всей бесконеч-
ной прямой —ОО < X < + оо,
а множество всех ее значений
состоит из трех точек: — 1,
и + 1 (рис. 4.4).
0
г
~з -г -}
—<
/
-Z
-2
Рис. 4.5.
А
Рис. 4.4.
6°. у — [х], где [х] обозначает целую часть вещественного числа х.
Читается: «у равно антье х» (от французского слова entier — целый).
Эта функция задана для всех вещественных значений х, а множество
всех ее значений состоит из
целых чисел (рис. 4.5).
2.	О способах задания
функции. В этом пункте мы
остановимся на некоторых
способах задания функции.
Часто закон, устанавли-
вающий связь между аргу-
ментом и функцией, задается
посредством формул. Такой
способ задания функции на-
зывается аналитическим.
Следует подчеркнуть, что функция может определяться разными фор-
мулами на разных участках области своего задания.
Например, функция
( sin х при xgO,
I х2 при х > 0
задана аналитическим способом на всей бесконечной прямой (рис. 4.6).
98
ПОНЯТИЕ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ
(ГЛ. ♦
Довольно распространенным способом задания функции является
табличный способ, заключающийся в задании таблицы отдельных
значений аргумента и соответствующих им значений функции. При
этом можно приближенно вычислить не содержащиеся в таблице зна-
чения функции, соответствующие промежуточным значениям аргумента.
Для этого используется способ интерполяции, заключающийся в замене
функции между ее табличными значениями какой-либо простой функ-
цией (например, линейной или квадратичной). Примером табличного
задания функции может служить расписание движения поезда. Распи-
сание определяет местоположение поезда в отдельные моменты вре-
мени; Интерполяция позволяет приближенно определить местополо-
жение поезда в любой промежуточный момент времени.
В практике физических измерений используется и еще один спо-
соб задания функции — графический, при котором соответствие между
аргументом и функцией задается посредством графика (снимаемого,
например, на осциллографе).
§ 2.	Понятие предельного значения функции
1.	Определение предельного значения функции., Рассмотрим
функцию у — f (х), определенную на некотором множестве {х},
и точку а, быть может, и не принадлежащую множеству {х}, но обла-
дающую тем свойством, что в любой е-окрестности точки а имеются
точки множества {х}, отличные от а. Например, точка а может быть
граничной точкой интервала, на котором определена функция.
Определение 1. Число Ь называется предельным значе-
нием функции y=f(x) в точке х = а (или пределом
функции при х—► а), если для любой сходящейся к а последо-
вательности Xj, х2,..., хт ... значений аргумента х, элементы х„
которой отличны от а *) (х„	а), соответствующая последо-
вательность /(XJ, /(х2),..., f(xn),... значений функции схо-
дится к Ь.
Для обозначения предельного значения функции используется сле-
дующая символика: lim f(x) = b.
х-+а
Отметим, что функция y—f(x) может иметь в точке а только
одно предельное значение. Это вытекает из того, что последователь-
ность |/(хя)} может иметь только один предел.
Рассмотрим несколько примеров.
1°. Функция /(х) = с имеет предельное значение в каждой точке
а бесконечной прямой. В самом деле, если Хр х2,хт любая
сходящаяся к а последовательность значений аргумента, то соответ-
ствующая последовательность значений функции имеет вид с, с,...
*) Это требование объясняется, в частности, тем, что функция f(x) может
быть не определена в точке а.
§ 21	ПОНЯТИЕ ПРЕДЕЛЬНОГО ЗНАЧЕНИЯ ФУНКЦИИ	99
...,с,... и поэтому сходится к с. Таким образом, предельное значе-
ние этой функции в любой точке х — а равно с.
2°. Предельное значение функции f(x) — x в любой точке а бес-
конечной прямой равно а. Действительно, в этом случае последова-
тельности значений аргумента и функции тождественны, и поэтому,
если последовательность {хп} сходится к а, то и последовательность
{/(х„)} также сходится к а.
3°. Функция Дирихле, значение которой в рациональных точках
равны единице, а в иррациональных—нулю, не имеет предельного
значения ни в одной точке а бесконечной прямой. Действительно,
для сходящейся к а последовательности рациональных значений аргу-
мента предел соответствующей последовательности значений функции
равен единице, а для сходящейся к а последовательности иррацио-
нальных значений аргумента предел соответствующей последователь-
ности значений функции равен нулю.
В дальнейшем мы будем использовать понятия односторонних пре-
дельных значений функции, которые определяются следующим образом.
Определение 2. Число b называется правым (левым)
предельным значением функции f(x) в точке х = а, если
для любой сходящейср к а последовательности хг, х2,..., хт...
значений аргумента х, элементы хп которой больше (меньше) а,
соответствующая последовательность f (Xj), f (х2),.... f(xn),...
значений функции сходится к Ь.
Для правого предельного значения функции используется обозна-
чение
lim f(x) = b или /(а + 0) = А
х-ю+О
Для левого предельного значения употребляется обозначение
lim f(x) — b или f(a~ Q) = b.
О
В качестве примера рассмотрим функцию/(x) = sgnx*). Эта функция
имеет в нуле правое и левое предельные значения, причем sgn (0 -f- 0) =
= 1, a sgn(0—0) = —1. В самом деле, если {х„}—любая сходя-
щаяся к нулю последовательность значений аргумента этой функции,
элементы х„ которой больше нуля (х„>0), то sgnx„=l и поэтому
lim sgn хп = 1. Таким образом, справедливость равенства sgn (0 + 0) =
= 1 установлена. Аналогично доказывается, что sgn(0—0) = —1.
Замечание. Если в точке а правое и левое предельные зна-
чения функции f (х) равны, то в точке а существует предельное
значение этой функции, равное указанным односторонним пре-
дельным значениям. Этот наглядный факт мы снабдим доказатель-
ством.
*) Определение функции p = sgnx дано в n. 1 § 1.
100
ПОНЯТИЕ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ
[ГЛ. 4
Пусть {х„} — любая сходящаяся к а последовательность значений
аргумента функции /(х), элементы которой не равны а. Пусть {х^ } —
подпоследовательность этой последовательности, состоящая из всех
ббльших а элементов последовательности {хя}, а {х/т} — подпосле-
довательность, состоящая из всех • меньших а элементов последова-
тельности {хл} *). Так как в силу п. 1 § 4 главы 3 подпоследова-
тельности {xfem} и сходятся к а, то из существования правого
и левого предельных значений функции f(x) в точке а вытекает,
что последовательности {/(х*т)} и	имеют пределы, которые
по условию равны. Пусть b — предел этих последовательностей. Для лю-
бого е> 0 можно указать номер N такой, что все элементы последова-
тельностей {/(х/гт)} и {/(х<т)}, для которых km^N и lm N, удов-
летворяют неравенствам |/(х*ш) — b | < s и | f(xitn) — b | < в. Следо-
вательно, при n^N выполняется неравенство |/(хя) — b ] < в, т. е.
последовательность’ {/(х„)} сходится к Ь. Тем самым доказано, что
предельное значение функции /(х) в точке а существует и равно Ь.
Сформулируем определения предельного значения функции при
стремлении аргумента х к бесконечности и к бесконечности опреде-
ленного знака.
Определение 3. Число b называется предельным значе-
нием функции f(x) при х—оо (или пределом функции
при х—>оо), если для любой бесконечно большой последователь-
ности значений аргумента соответствующая последовательность
значений функции сходится к Ь.
Для обозначения предельного значения функции при х —со
используется следующая символика:
lim f(x) — b.
л'-»со
Определение 4. Число b называется предельным значением
функции f (х) при стремлении аргумента х к положительной (отри-
цательной) бесконечности, если для любой бесконечно большой
последовательности значений аргумента, элементы которой,
начиная с некоторого номера, положительны (отрицательны),
соответствующая последовательность значений функции схо-
дится к Ь.
Символические обозначения:
lim f(x) — b (lim f(x) = b).
X —♦ CO	x —> — co
В качестве примера рассмотрим функцию f(x) =—. Эта функция
*) Мы исключаем из рассмотрения случай, когда у последовательности
{хд} лишь конечное число элементов лежит правее (левее) точки а. В этом слу-
чае сходимость {/ (ХлД очевидна.
§ 21	ПОНЯТИЕ ПРЕДЕЛЬНОГО ЗНАЧЕНИЯ ФУНКЦИИ	101
имеет равное нулю предельное значение при х—>-оо. Действительно,
если хг х„, хп, ... — бесконечно большая последовательность
значений аргумента, то последовательность —, —, ..., —, ... беско-
Xj Х2	%п
нечно малая и поэтому имеет предел, равный нулю.
2.	Арифметические операции над функциями, имеющими пре-
дельное значение. Убедимся, что арифметические операции над функ-
циями, имеющими предельное значение в точке а, приводит к функ-
циям, также имеющим предельное значение в этой точке. Справедлива
следующая основная теорема.
Теорема. 4.1. Пусть заданные на одном и том же мно-
жестве функции f(x) и g(x) имеют в точке а предельные зна-
чения b и с. Тогда функции f(x)-\- g(x), f(x) — g(x), f(x)-g(x) и
(x)
имеют в точке а предельные значения (частное при условии
с jb Оф равные соответственно Ь-\-с, Ь — с, Ь-с и — .
Доказательство. Пусть хх, х2, ..., хп, ... (хп уЬ а) — про-
извольная сходящаяся к а последовательность значений аргумента
функций f(x) и g(x). Соответствующие последовательности /(х,),
/(х2), .... /(х„), ... и g(x1), g(x2), ..., g(xn),... значений этих функ-
ций имеют пределы Ь и с. Но тогда, в силу теорем 3.9—3.12, по-
следовательности {/(x„) + g(x„)}, {/(x„)-g(x„)}, {/(x„)-g(x„)} и
имеют пределы, соответственно равные b-Ус, Ь — с, b-с и
В силу произвольности последовательности {хя} это означает, что
lira [/(x) + g(x] = & + c, lim t/(x)-g-(x)]=Z>-c, lim [/(x)-g(x)] =
л--» о	x -* a	x a
= b-c, lim	Теорема доказана.
Применим доказанную теорему для отыскания предельных значе-
ний многочленов и несократимых алгебраических дробей *). Имеет
место следующее утверждение.
В каждой точке а бесконечной прямой предельные значения
многочленов и несократимых алгебраических дробей существуют
и равны частным значениям этих функций в указанной точке
(в случае алгебраической дроби а не должно быть корнем знаме-
нателя).
Действительно, в силу теоремы 4.1
lira x2 = lim x-x = lim x-lim x = a2.
x-+a x-+a	x-*a x—*a
Аналогично можно убедиться, что
lim х" = ап.
х^.а
*) Несократимая алгебраическая дробь — частное двух многочленов, не
имеющих отличных от постоянной общих множителей.
102
ПОНЯТИЕ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ
(ГЛ. 4
Следовательно, для многочлена Z>ox“ 4- Ьгхп 14- • - • 4* Ьп-гх 4- Ьп полу-
чим (используя теорему 4.1 для произведения и суммы)
lim (bax" +	4-• • • 4* Ьц-уХ + й„) = Ьоап 4- Ь^а? 1 4-... 4- Ьп-Га 4- Ьп.
х —* а
В случае несократимой алгебраической дроби, когда а не является
корнем знаменателя, получим (применяя теорему 4.1 для частного)
b<jXn 4~ Ь^хп~1 4~ • • 4~ ^n-ix 4~ Ьп_Ьаап 4~	1 4~	4~ Ьп_уа. 4- Ъп
х 4-CiX"*-14- • • • 4-ст_1* + ст-саат 4- с1ат-1 4-... 4- с^а 4- ст'
3.	Сравнение бесконечно малых и бесконечно больших функ-
ций. Функция y=f(x) называется бесконечно малой в точке
х = а (при х-+а), если lim f(x) — 0. Легко убедиться, например,
х~> а
что функция f(x) = (x—a)m, где т — целое положительное число,
является бесконечно малой в точке х — а. В самом деле, в пре-
дыдущем пункте мы установили, что предельное значение много-
члена f(x) = (x — а)т в любой точке бесконечной прямой существу-
ет и равно частному значению многочлена в этой точке. Поэтому
lim (х — а)т = 0.
х -+ а
Отметим, что если функция у = f(x) имеет равное b предельное
значение в точке а, то функция a.(x) — f (х) — b является бес-
конечно малой в точке а. Действительно, предельные значения
каждой из функций f(x) и b в точке а равны Ь, и поэтому в силу
теоремы 4.1
lim а (х) - lim (/(х) — b) = lim f (х) — lim b = 0.
х-*а х -* а	ха
Используя полученный результат, мы получаем специальное представ-
ление для функции, имеющей равное b предельное значение в точке
х = а:
f (х) = b 4- я (х), где lim а(х) = 0.	(4.1)
Представление (4.1) оказывается весьма удобным при дока-
зательстве различных предложений и будет неоднократно исполь-
зовано нами ниже.
Наряду с понятием бесконечно малой функции часто используется
понятие функции, бесконечно большой в точке а справа или беско-
нечно большой в точке а слева. Именно, функция f(x) называется
бесконечно большой в точке а справа (слева), если для любой
сходящейся к а последовательности xv х2, ..., хп ... значений
аргумента х, элементы хп которой больше а (меньше а), соот-
ветствующая последовательность /(xj, /(х2),..., /(хп), ... зна-
5 21
ПОНЯТИЕ ПРЕДЕЛЬНОГО ЗНАЧЕНИЯ ФУНКЦИИ
103
пений функции является бесконечно большой последовательностью
определенного знака.
Для бесконечно больших функций используются следующие обо-
значения:
lim fix)= оо или /(а + 0) = -{- оо,
ж—а+0
lim f(x) =4-оо или /(а — 0) = 4~ °°>
х-*а—О
lim f(x) ——со или /(а 4-0) = — оо,
ж->а4-0
lim /(х) = —оо или /(а —0) =— со.
л-»я —О
Познакомимся с методикой сравнения бесконечно малых функций
и употребляемой терминологией.
Пусть а (х) и р (х) — две заданные на одном и том же множестве
функции, являющиеся бесконечно малыми в точке х — а.
1)	Функция а(х) называется бесконечно малой более высокого
порядка, чем р (х) (имеет более высокий порядок малости), если
.	а (х)
предельное значение функции j^y в точке а равно нулю.
2)	Функции а(х) и Р(х) называются бесконечно малыми одного
порядка (имеют одинаковый порядок малости), если предельное зна-
,	а (х)
чение функции в точке а существует и отлично от нуля.
3)	Функции а(х) и Р(х) называются эквивалентными бесконечно
малыми, если предельное значение функции у^у в точке а равно
единице. .
Часто бесконечно малые функции сравнивают с какими-либо
стандартными бесконечно малыми функциями. Обычно в качестве
функции сравнения берут функцию (х — а)т, где т — целое положи-
тельное число. В этом случае употребляется следующая терминоло-
гия: бесконечно малая в точке а функция а (х) имеет порядок
,	а (х)
малости т, если предельное значение функции	в точке а
отлично от нуля.
При сравнении бесконечно малых функций часто употребляют
символ о (о малое). Именно, если функция а = а(х) представляет
собой бесконечно малую в точке а функцию более высокого порядка,
чем бесконечно малая в этой же точке функция р = р(х), то это
условно записывают так:
а = о(Р)
(читается: а равно о малое от р). Таким образом, символ о(Р) озна-
чает любую бесконечно малую функцию, имеющую в точке а более
высокий порядок малости, чем бесконечно малая в этой точке функ-
ция р = р (х).
104
ПОНЯТИЕ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ
[ГЛ. 4
Отметим следующие очевидные свойства символа о: если^ = о(Р),
то о (В) ± о (у) = о (Р), о (Р) ± о (Р) — о (р).
Заметим также, что если а и р — бесконечно малые в точке а
функции, то функция ар имеет более высокий порядок малости, чем
каждцй из сомножителей, и поэтому
ар = о (а), ар = о (р).
Для бесконечно больших в точке а справа (или слева) функций
используется аналогичная методика сравнения.
Пусть А(х) и В (х) — бесконечно большие в точке а справа
функции, и пусть, например, обе эти бесконечно большие функции
положительного знака, т. е.
lim Л(х)=-]-оо и
х—а-ГО
Мы будем говорить, что функция А (х) имеет в точке а справа
более высокий порядок
А (х)	Л
-~А- является бесконечно
В (х)
lim В (х) — + оо.
л-»а4-0
роста, чем функция В(х), если функция
большой в точке а справа. Если же правое
.	А (х)
предельное значение функции в точке а конечно и отлично от
D (X)
нуля, то в этом случае мы будем говорить, что А (х) и В (х) имеют
в точке а справа одинаковый порядок роста.
Рассмотрим несколько примеров.
1. Функции а(х) = 3х2ф-х3 и р(х) = 2х2 являются бесконечно
малыми функциями одного порядка в точке х = 0. Действительно,
при х 0	+ 4- х. Так как lim4-x = 0, то в силу тевремы 4.1
Р W z х	х-*о 2
lim	& это означает, что а(х) и р (х) — бесконечно малые
одного порядка.
2. Функции а(х) = х2— бх3 и р (х) = х2 — эквивалентные беско-
нечно малые в точке х = 0. В самом деле, ^|=1 —бх. Так как
р \Х)
Нтбх = 0, то в силу теоремы 4.1 lim	Это и означает
х 0	х — 0 Р W
эквивалентность бесконечно малых а (х) и р (х).
j I х	J
3. Функции А (х) = и В(х)=— имеют одинаковый порядок
роста в точке х = 0 справа и слева. Это следует из того, что
lim4r^= lim(l +х)= 1.
§ 3. Понятие непрерывности функции
1. Определение непрерывности функции. Пусть точка а принад-
лежит области задания функции /(х) и любая е-окрестность точки
а содержит отличные от а точки области задания этой функции.
§ 31
.. ПОНЯТИЕ НЕПРЕРЫВНОСТИ ФУНКЦИИ
105
Определение 1. Функция f(х) называется непрерывной
в точке а, если предельное значение этой функции в точке а
существует и равно частному значению f{a).
Таким образом, условие непрерывности функции /(х) в точке а
символически можно выразить следующим образом:
lim/(x)=/(a).
х —*а
Так как a = lim х, то этому равенству можно придать следую-
щую форму: х ""а
lim/(х) =/( lim х).
х^а
Следовательно, для непрерывной функции символ «lim» предельного
перехода и символ «/» характеристики функции можно менять
местами.
Определение 2. Функция f(х) называется непрерывной
справа {слева) в точке а, если правое {левое) предельное зна-
чение этой функции в точке а существует и равно частному
значению f{a).
Символические обозначения непрерывности справа (слева):
lim f{x)=f{a) или f{a + 0) =f{a)
( lim f{x)=f{a) или f {a - 0) = f {a)).
x-*a — 0
Замечание. Если функция f{x) непрерывна в точке а и слева
и справа, то она непрерывна в этой точке. В самом деле, в силу
замечания п. 1 § 2 этой главы в этом случае существует предель-
ное значение функции в точке а, равное частному значению этой
функции в точке а.
Рассмотрим примеры.
1°. Степенная функция f{x) = xn с целочисленным положительным
показателем п непрерывна в каждой точке бесконечной прямой. Дей-
ствительно, в п. 2 § 2 мы .доказали, что предельное значение этой
функции в любой точке бесконечной прямой равно частному значе-
нию а".
2°. Так как многочлены и несократимые алгебраические дроби
имеют в каждой точке области задания предельное значение, равное
частному значению (см. и. 2 § 2), то они являются непрерывными
функциями.
Точки, в которых функция не обладает свойством непрерывности,
называются точками разрыва функции *). Например, функция/(х) =
= sgnx имеет разрыв в точке х = 0 (в п. 1 § 2 мы доказали, что
правое и левое предельные значения этой функции в точке х = 0
*) В § 8 мы дадим классификацию точек разрыва.
106
ПОНЯТИЕ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ
(ГЛ. 4
существуют, но не равны друг другу, и поэтому не существует пре-
дельное значение функции в этой точке). Функция Дирихле разрывна
в каждой точке бесконечной прямой, поскольку она не имеет предель-
ного значения ни в одной точке этой прямой (см. п. 1 § 2).
Мы будем говорить, что функция f(x) непрерывна на множестве
{х}', если она непрерывна в каждой точке этого множества. Если
функция непрерывна >в каждой точке интервала, то говорят, что она
непрерывна на интервале. Если функция непрерывна в каждой внут-
ренней точке сегмента [а, Ь] и, кроме того, непрерывна сйрава в точ-
ке а и слева в точке Ь, то говорят, что она непрерывна на сегмен-
те [а, Ь\.
2. Арифметические операции над непрерывными функциями.
Убедимся, что арифметические операции над непрерывным^ функциями
приводят к непрерывным функциям.
Докажем следующую основную, теорему.	>
Теорема 4.2. Пусть заданные на одном и том же множестве
функции f(x) и g(x) непрерывны в точке а. Тогда функции f(x) +
г (х)
+ g(x), /(х)— g(x)> f(x)'g(.x) н непрерывны в точке а (част-
ное при условии g(a) 0).
Доказательство. Так как непрерывные в точке а функции
f(x) и g(x) имеют в этой точке предельные значения f (а) и g(a),
то в силу теоремы 4.1
f(x)-g(x), f(.x)-g(x)
f(a) + g(a), f(fi)-g(a),
и равны частным значениям перечисленных функций в точке а. Тео-
предельные значения функций f(x)-\-g(x)
7W
и существуют и равны соответственно
f(a)-g(a), Но эти величины как раз
рема доказана.
§ 4. Некоторые свойства монотонных функций
1. Определение и примеры монотонных функций.
Определение. Функция y—f(x) называется неубывающей
(не в о з р а с та ю щ е и) на множестве {х}, если для любых
хх и х2 из этого множества, удовлетворяющих условию х1<х2,
справедливо неравенство /(х1)^/(х2) (/(xj Э=/(х2)).
Неубывающие и невозрастающие функции объединяются общим
наименованием монотонные функции. -
Если для любых хг и х2 из множества {х}, удовлетворяющих
условию х1<х2, справедливо неравенство /(х1)</(х2) (f(x1)>
>/(х2)), то функция y=f(x) называется возрастающей (убываю-
щей) на множестве {х}. Возрастающие и убывающие функции назы-
ваются также строго монотонными.
Приведем примеры монотонных функций.
1. Функция /(х) = х + sgn х возрастает на всей числовой прямой
(рис. 4.7).
5 41	НЕКОТОРЫЕ СВОЙСТВА МОНОТОННЫХ ФУНКЦИИ	107
2. Функция / (х) = sgn х является неубывающей на всей числовой
прямой (см. рис. 4.4).
2. Понятие обратной функции. Монотонные функции, имеющие
обратную. В этом пункте формулируется понятие обратной функции
и устанавливаются условия существова-
пия обратной функции для монотонной	/
функции.	/
Пусть функция y=f (х) задана	/
на сегменте [а, &], и пусть множе-	1 *
ством значений этой функции яв-
ляется сегмент [а, £]. Пусть, да- ___________________,_______
лее, каждому у из сегмента [а, р]	°	х
соответствует только одно значе-
ние х из сегмента [а, Ь], для кото-
рого f(x)=y. Тогда на сегменте	/
[а, р] можно определить функцию	/
х=(у), ставя в соответствие	рис 4
каждому у из [а, р] то значение х из
|о, Ь], для которого f(x)=y. Функция x = f~l(y) называется
обратной для функции y=f(x).
В указанном определении вместо сегментов [а, Ь] и [а, р] можно
было бы рассматривать интервалы (a, b)-u (а, Р). Можно также до-
пускать, что один или оба интервала (а, Ь) и (а, р) превращаются
в бесконечную прямую или в открытую полупрямую.
Отметим, что если x=f~x (у) — обратная функция для у=/(%),
то, очевидно, функция y=f(x) является обратной для функции х =
= /-1(у). Поэтому .функции y = f(x) и х==/-1(у) называют также
взаимно обратными.
Взаимно обратные функции обладают следующими очевидными
свойствами:
Л1(Г(х)) = х.
Рассмотрим примеры взаимно обратных функций.
1°. Пусть на сегменте [0,. 1] задана функция /(х) = 3х. Множе-
ством значений этой функции будет сегмент [0, 3]. Функция (j) =
= у у, определенная на сегменте [0, 3], является обратной для за-
данной функции /(х) = 3х.
2°. Рассмотрим на сегменте [0, 1] функцию, определенную следую-
щим образом:
,	( х, если х — рациональное число,
у = /(х) = {
( 1 — х, если х— иррациональное число.
Функция x = f~1(y), заданная на сегменте [0, 1] и определенная
равенствами
| у, если у — рациональное число,
(у) =! ,
( 1 — .у, если у — иррациональное число,
108
ПОНЯТИЕ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ
(ГЛ 4
будет обратной к данной. В этом нетрудно убедиться непосредствен-
ной проверкой.
Замечание 1. Пусть на сегменте [a, ft] задана строго монотон-
ная функция y—f(x), и пусть множеством' значений этой функции
является сегмент [а, р]. Тогда, в силу строгой монотонности функции
у = /(х), каждому у из [а, р] соответствует только одно значение
х из [a, ft], для которого f(x)=y, и поэтому на сегменте [а, [5]
существует функция х—/~1(у), обратная для функции у =f(x\ Бо-
лее того, если функция у —f (х) является возрастающей на-сегменте
[a, ft], то функция x=f~1(y) также является возрастающей на сег-
менте [а, р], если же y~f(x) — функция, убывающая на [a, ft], то
x=/-1Cv) является убывающей на сегменте [р, а]. Убедимся, напри-
мер, что если у =f(x) — возрастающая функция, то и x=f~1(y) —
также возрастающая функция. Действительно, если У1<^у2, то и
xi <х2 (xi1 (.У1) и х2 — f1 (Уъ))’ ибо из неравенства х}у^х2, и
из возрастания функции у =f(x) следовало бы, что	а это
противоречит неравенству уг <Zy2.
Лемма 1. Для того чтобы строго монотонная на сегменте
[a, ft] функция у =-f(x) являлась непрерывной на этом сегменте,
необходимо и достаточно, чтобы любое число у, заключенное
между числами а=/(а) и	было значением этой функции.
Иными словами, для того чтобы строго монотонная функция у =f(x)
была непрерывна на сегменте [a, ft], необходимо и достаточно, чтобы
множеством значений этой функции был сегмент [а, р] (или [р, а]
при р < а), где а=/(а) и p=/(ft).
Доказательство. 1) Необходимость. Ради определен-
ности рассмотрим возрастающую непрерывную на сегменте [a, ft] функ-
цию y = f(x) (для убывающей функции доказательство аналогично).
Покажем, что если а <; 7 <; р, то существует внутренняя точка с сег-
мента [a, ft], в которой f(c) = 7 (в силу возрастания функции f(x)
на сегменте [a, ft] такая точка с будет единственной). Обозначим
через {х} множество точек сегмента [a, ft], для которых f(x)^i
(этому множеству принадлежит, например, точка а, ибо f(a) = а < 7).
Множество ]х] ограничено сверху и поэтому имеет точную верхнюю
грань с. Докажем, что f(c) = 7. Отметим, что любое число из сегмента
[я, ft], меньшее с, принадлежит множеству {х} *), а любое число,
превосходящее с, не принадлежит этому множеству **). Покажем, что
с — внутренняя точка сегмента [а, Ь]. В самом деле, пусть, например,
с = Ь. Рассмотрим сходящуюся к ft возрастающую последовательность
{х„} значений аргумента функции y=f(x). Так как f(x) непрерывна
в точке ft слева, то lim/(x„) = p. С другой стороны, f (хп)^7 ***),
________________ fl—* 00
*)	Ибо по определению точной верхней грани для любого к, меньшего
с, найдется х' такое, что х<_х' и (Д’) ^7. Но тогда из возрастания f (х)
следует, что и f(*)=S 7. т. е. х принадлежит {х}.
**	) В силу определения точной верхней грани.
**	*) Так как все хп меньше с и, стало быть, принадлежат {х}.
« 41
НЕКОТОРЫЕ СВОЙСТВА МОНОТОННЫХ ФУНКЦИЙ
109
и поэтому в силу теоремы 3.13 lim /(x„)^7. Таким образом,
л—* со
Р7, что противоречит условию 7 < Р- Полученное противо-
речие доказывает, что с<^Ь.- Аналогично можно убедиться, что
a <Z с. Так как с—внутренняя точка сегмента [а, Ь], то найдутся {х„|
н {х„} — сходящиеся к с возрастающая и убывающая последователь-
ности значений аргумента х. Поскольку /(х)4непрерывна в точке с,
io lim/(x'„) = lim/(x£)=/(c). Ho/(x„)<7, а /(х')>7*). По-
л-►со	я-►со
этому lim/(х'п)	7, lim/(х„) 2а 7, откуда следует, что /(<?) = 7.
Л—►СО	л-*оо
2) Достаточность. Проведем доказательство для возрастаю-
щей на сегменте [а, Ь] функции y=f(x) (для убывающей функции
рассуждения аналогичны). Пусть с—-любая точка сегмента [a, и
7 =/(с)—значение функции _у=/(х) в этой точке. Убедимся, что
число 7 является правым и левым предельным значением функции /(х)
и точке с (если с—граничная точка сегмента [а, Ь], то 7 является
соответствующим односторонним
предельным значением в этой гра-
ничной точке). Пусть а<^с^Ь;
докажем, что 7 является левым
предельным значением функции в
точке с. Пусть е — столь малое
положительное число, что а <7 — е
(рис. 4.8). Поскольку по условию
леммы число 7— е является значе-
нием функции /(х), то на сегменте
|«, />] можно указать точку d та-
кую, что f(d) = 7— е. Так как функ-
ция f (х) возрастает, то d <; с. Рассмотрим теперь любую сходящуюся
к с последовательность {хя} значений аргумента X, элементы которой
меньше с. Начиная с некоторого номера N, все элементы хп этой
последовательности удовлетворяют неравенствам d<_xn<Zc (один
такой элемент изображен на рис. 4.8), так что в силу возрастания/(х)
при n^N справедливы неравенства f(d) </(хя) <Zf(c). Так как
/(rf) = 7 —е и f(c) = 7, то из последних неравенств вытекает, что
при n^N справедливы неравенства 0<7 — /(х„)<е. Иными сло-
вами, последовательность {/(хп)} сходится к 7, а поскольку {х„}—
произвольная сходящаяся к с слева последовательность значений аргу-
мента, то тем самым доказано, что левое предельное значение в точке с
существует и равно 7 =/(<?)**). Если а	то, рассуждая ана-
логично, можно доказать, что 7=/(с) является правым предельным
*) В силу того, что х'п < с < х"п для любого номера п.
**) Мы рассмотрели случай столь малого е > 0, что а < 7— е. Если
—е, то достаточно положить d = а и повторить проведенные рассуждения,
используя очевидное неравенство 7 — е f {d).
по
ПОНЯТИЕ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ
[ГЛ. 4
значением функции в точке с. Мы доказали, что правое и левое
предельные значения функции _у—/(х) в любой внутренней точке
с равны частному ее значению f(c), а это, в силу замечания в п. 1 § 2,
означает непрерывность f(x) во внутренних точках сегмента. Непре-
рывность этой функции в граничных точках сегмента следует из того,
что соответствующие односторонние предельные значения f(x) в гра-
ничных точках сегмента равны частным значениям функции. Лемма
полностью доказана.
Следствие. Пусть на сегменте [а, Ь] задана строго монотон-
ная непрерывная функция у = f\х), и пусть a=f(a), $=f(b).
Тогда эта функция имеет на сегменте [а, ЭД (или $, а], если р < а)
строго монотонную и непрерывную обратную функцию x=f~1(y).
Доказательство. В силу только что доказанной леммы мно-
жеством значений функции y=f(x) является сегмент [а, ЭД, а тогда,
согласно замечанию 1 этого пункта, на сегменте [а, ЭД существует
обратная строго монотонная функция x=/-1(j), множеством значе-
ний которой является сегмент [а, Ь] и которая пбэтому, в силу той
же самой леммы, непрерывна на сегменте [а, ЭД.
Замечание 2. Отметим, что монотонные функции имеют пра-
вое и левое предельные значения в каждой внутренней точке области
задания. Доказательство этого предложения предоставляем читателю.
§ 5. Простейшие элементарные функции
Простейшими элементарными функциями обычно называют сле-
дующие функции: у = хх, у = ах, _y = logax, у = sinх, у = cosx,
у = tg х, у = ctg х, у = arc sin х, у — arc cos х, у = arctg х, у — arcctg х.
Йз элементарного курса читатель имеет представление об этих
функциях и об их графиках. Некоторые из этих функций, например
у = ах, без труда определяются для рациональных значений аргумента х.
Мы выясним вопрос об определении простейших элементарных функ-
ций для всевозможных вещественных значений их аргументов. Этот
вопрос не является простым: неясно, например, как возвести произ-
вольное вещественное число х в произвольную вещественную сте-
пень а.
Мы изучим также вопрос о непрерывности простейших элемен-
тарных функций во всех точках области их задания. Нами будет
обосновано то поведение простейших элементарных функций, которое
наглядно вырисовывается из рассмотрения их графиков.
В дополнении к главе 8 приводятся алгоритмы вычисления зна-
чений простейших элементарных функций.
1. Рациональные степени положительных чисел. Возведение
любого вещественного числа х1 в целую положительную степень п
определяется как n-кратное умножение числа х самого на себя. Сле-
.довательно, при целом п мы можем считать определенной степенную
функцию у = хп для всех вещественных значений х. Некоторые
ПРОСТЕЙШИЕ элементарные ФУНКЦИИ
Ill
% 5]
свойства этой функции будут нами использованы для определения
рациональных степеней положительных чисел.
Докажем следующую лемму.
Лемма 2. Степенная функция у = хп при х^О и целом
положительном п возрастает и непрерывна.
Доказательство. Докажем возрастание этой функции. Пусть
О xt < х2. Так как х” — х* = (х2 — хг) (х^1 -ф х^~2х± +... 4- х^1),
.г?"1 + х^~2х1 4-... 4- х"-1 > 0, то х" > х". Непрерывность этой функ-
ции была нами установлена ранее (см. пример 1 пункта 1 § 3).
Следствие. Рассмотрим степенную функцию у — хп на сегменте
|(), N], где Af—любое положительное число. Так как эта функция
непрерывна и возрастает на указанном сегменте, то она имеет в силу
следствия из леммы 1 этой главы на сегменте [О, А/"] возрастающую
и непрерывную обратную функцию, которую мы обозначим через yiln.
Поскольку N можно выбрать как угодно большим, то и Nn также
будет сколь угодно большим. Следовательно, функция x=yiln опре-
делена для всех неотрицательных значений у. Меняя для этой функ-
ции обозначение аргумента jz на х, а обозначение функции х на у,
мы получим степенную функцию y = xi!n, определенную для всех
неотрицательных значений х.
Определим а)/п как число Ь, равное значению функции у = х}/п
и точке а. Мы можем теперь определить любую рациональную сте-
пень г положительного числа а. Именно, если г = -> где тип —
п
целые положительные числа, то мы положим
т / 1 \ т
аг = а п —\ап) .
Договоримся, кроме того, что
а°=1, a_r=f-L\r
\ а ]
Нетрудно убедиться в справедливости следующих свойств рациональ-
ной степени положительных чисел:
(аУ .= ars, arbr = (ab)r, aras = ans.
Убедимся, например, в справедливости последнего свойства, считая,
„	т< т, m	т.п.
что первые два уже доказаны. Пусть г — S = Тогда г =
5 = —^, и поэтому
(1	/ Г \4-т^гц
I \aninsj sz\anin»j
(справедливость последнего равенства следует из того, что т1-п2 и
— целые числа). Итак,
^ТП171g	ЯЦ /Wg
aras — а	= a ni = ar*s.
112
ПОНЯТИЕ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ
[ГЛ. 4
Докажем, что при а > 1 и рациональном г > 0 справедливо нера-
венство аг>1. В самом деле, пусть г = — и ar = amin 1. Пере-
множая почленно п указанных неравенств, получим ат^1. Послед-
нее неравенство противоречит неравенству ат>1, полученному по-
членным перемножением т неравенств вида а>1. Отметим, наконец,
что если рациональная дробь т = имеет нечетный знаменатель п,
то определение рациональной степени можно распространить и на
отрицательные числа, полагая
(— а)г = аг, если т четное,
и
(— а)г = — аг, если т нечетное.
2. Показательная функция. Из рассуждений предыдущего пункта
вытекает, что если а — положительное число, то функция у — ах
определена для всех рациональных х.
Легко убедиться в том, что функция у — ах, а>1, определенная
на множестве {х} всех рациональных чисел, монотонно возрастает
на этом множестве.
В самом деле, пусть хх и х2 — любые два рациональных числа,
удовлетворяющие условию х2> хх. Тогда
ДХ» _ axt — aXt (дХц - X, _ 1)
Так как х2 —л\>0 и а^>1, то aXs~xi>l, т. е. правая часть
последнего равенства положительна, и поэтому аХа > a*i. Возраста-
ние функции ах на множестве рациональных чисел доказано.
Переходим к определению функции ах на множестве всех ве-
щественных чисел.
Фиксируем произвольное вещественное число х и рассмотрим
всевозможные рациональные числа а и р, удовлетворяющие неравен-
ствам
а<х<р.	(4.2)
Определим ах при а > 1 как вещественное число у, удовлетво-
ряющее неравенствам
а“^у^аУ.	(4.3)
Ниже мы докажем, что такое число у существует, и притом только
одно. Мы докажем также, что определенная нами функция у = ах
обладает следующими важными свойствами: 1) возрастает на всей
бесконечной прямой, 2) непрерывна в любой точке х этой прямой.
1°. Прежде всего докажем, что для любого фиксированного х и любых
рациональных чисел аир, удовлетворяющих неравенствам (4.2), существует
вещественное число у, удовлетворяющее неравенствам (4.3).
ПРОСТЕЙШИЕ ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
113
§ 5]
Фиксируем произвольное рациональное число р, удовлетворяющее пра-
вому неравенству (4.2), и рассмотрим всевозможные рациональные числа а,
удовлетворяющие левому неравенству (4.2).
Так как а < р и показательная функция, определенная на множестве
рациональных чисел, возрастает, то аа < а?. Таким образом, множество {а1}
ограничено сверху и число а? является одной из верхних граней этого
множества. Стало быть, это множество имеет точную верхнюю грань, кото-
рую мы обозначим через у. Остается доказать, что у удовлетворяет нера-
венствам (4.3). Из определения точной верхней грани вытекает справедли-
вость левого неравенства (4.3), а справедливость правого неравенства (4.3)
вытекает из того, что а?— одна из верхних граней, а у — точная верхняя
грань множества {а1}.
2°. Установим теперь, что существует только одно вещественное число у,
удовлетворяющее неравенствам (4.3).
Достаточно доказать, что для любого е > 0 найдутся такие рациональ-
ные числа аир, удовлетворяющие неравенствам (4.2), для которых а? — а“ < е.
В самом деле, тогда любые два числа уг и уг, удовлетворяющие неравен-
ствам (4.3), обязаны совпадать, ибо разность между ними по модулю меньше
любого наперед взятого положительного числа е.
Фиксируем произвольное е > 0 и некоторое рациональное р0, удовлетво-
ряющее правому неравенству (4.2). Тогда, так как ах<а|5°, получим
а? — а = а — 1) -< t?’	— 1).
Неравенство цР —будет доказано, если мы установим возможность
выбора таких а и р, что — 1 <
Из главы 2 вытекает, что для любого натурального п можно выбрать
рациональные числа а и р, удовлетворяющие неравенствам (4.2), так, что
разность р — а будет меньше —. Таким образом, достаточно доказать суще-
ствование такого натурального п, для которого
(4.4)
Убедимся в возможности выбора такого натурального п. Пусть
а'/п = 1 + 8„.
Так как а'^л>-1, то 8„ положительно. Используя формулу бинома Нью-
тона, будем иметь а = (а^п)п = (1 -ф 8„)” — 1 -ф пЪп -ф (положительные чле-
ны) > 1 -ф пЪп. Отсюда а — 1 > п8„ и 0 < 8Я <а \ Стало быть, а1/п — 1 =
= 8„ <; — 1, Неравенство (4.4) будет справедливо, если мы выберем п,
,	а—1 с	(а—1)в?“ г,
удовлетворяющим требованию -------< -й- или п^------------, Доказатель-
п дГо	е
ство однозначной определенности числа у, удовлетворяющего неравенствам
(4.3), завершено.
Заметим, что если х— рациональное число и ах— значение в точке х
показательной функции, первоначально определенной лишь на множестве
рациональных чисел, то ах и является тем единственным вещественным чис-
лом у, которое удовлетворяет неравенствам (4.3).
3°. Докажем теперь, что построенная нами функция ах (при а > 1) воз-
растает на всей бесконечной прямой.
114
’ ПОНЯТИЕ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ
[ГЛ. 4
Пусть и х2— любые вещественные-числа, удовлетворяющее нера-
венствам хг < хг. Очевидно, найдутся рациональные числа а и 0, удовлетво-
ряющие неравенствам *!< а < (3 <Сх2 (см. утверждение, доказанное в конце
п. 1 § 2 главы 2). Из определения показательной функции и из возрастания
ее на множестве рациональных чисел вытекают неравенства a*’о1 < t/
^ах*, т. е. ах'<.ах‘. Возрастание функции ах доказано.
4°. Остается доказать непрерывность построенной нами функции ах в лю-
бой точке х бесконечной прямой.
Пусть {хя} — любая сходящаяся к х последовательность вещественных
чисел. Достаточно доказать, что для любого е>-0 найдется номер N такой,
что при n^N справедливо неравенство | ахп — 0х | <в.
Фиксируем произвольное е > 0 и выберем рациональные числа а и р,
удовлетворяющие неравенствам (4.2), так, чтобы было справедливо неравен-
ство а-3— а’-<е (возможность выбора таких а и р доказана в 2°). Так как
последовательность {хя} сходится к х и a<x<jp, то найдется номер М
такой, что при N справедливы неравенства а-<хя<р. Из неравенств
a<z<f.Ha<xn<p и из свойства монртонности показательной функции
вытекает, что аЛ<ахп<:а^ и o' <Zax<.сР (при п>: N '). Так как разность
между числами и меньше г и оба числа ах и ахп заключены между
o’ и а®, то [ахп — ах | <; е (при n^N). Доказательство непрерывности за-
вершено.
Замечание 1. Если 0 < а < 1, то а — ^-, где b >» 1. Поэтому
функцию у = ах при 0 < а < 1 можно определить как функцию
~у = Ь~х, b> 1.
Установим некоторые свойства показательной функции у = ах,
а> 1.
1)	Все значения показательной функции положительны. Действи-
тельно, пусть х~ произвольная точка числовой прямой, а х' — ра-
циональная точка, такая, что х'<Zx. Так как, по определению,
а*' > О и ах' <z ах, то ах > 0.
2)	lini 6х =0, lim ах —<х>.
Л-ч. — ОО
В самом деле, так как а>1, то а=1-}-а, где а>0 и ап~
= (1 +а)л> 1 ф-ла. Следовательно, lim ап= + ех>. В силу моно-
л—00
тонкости функции lim а* =4-00. Так как а-л = -5, то lim а-л = 0,
X—-4"03	°	л—-оо
и поэтому lim ах— Q.
X —►—СО
3)	Из свойств 1) и 2), а также из монотонности и непрерывности
функции у — ах вытекает, в силу леммы 1, что значения у этой
функции заполняют всю положительную полупрямую _у>0.
4)	Для любых вещественных чисел хх и х2 справедливы соотно-
шения
(а*1)*» -= a*1*2, ax'bXi = (а • b)x', fl*!fl*» = а*1+*».
Действительно, мы уже отмечали справедливость этих соотношений
для рациональных показателей. Чтобы. убедиться в справедливости
этих соотношений для любых показателей, достаточно рассмотреть
§5)
ПРОСТЕЙШИЕ элементарные ФУНКЦИИ
115
последовательности {х„} и {Хд} рациональных, чисел, сходящиеся соот-
ветственно к Xj и х2. Тогда, например, аХпаХп = аХп + *п. Переходя
к пределу при и->сои используя свойство непрерывности показа-
тельной функции, мы получим ax4iXt = aXi+Xi. Аналогично можно убе-
диться в справедливости и других из перечисленных выше соотно-
шений.
Замечание 2. Мы установили свойства 1)—4) показательной
функции у — ах, а также непрерывность и монотонное возрастание
этой функции на бесконечной прямой для случая а >1. Отметим,
что при 0<а<;1 функция у = ах, в силу замечания 1, непрерывна
и монотонно убывает на бесконечной прямой. Кроме того, для этой
функции сохраняются свойства 1), 3) и 4), а свойство 2) модифици-
руется следующим образом:
lim ах = + оо, lim  ах = 0.
л*-► — со
На рис. 4.9 и 4.10 изображены графики показательной функции
у — ах для случая а > 1 и 0 < а -< 1.
Замечание 3. Свойство а*» + *> = может быть положено
в основу функционального определения показательной функции у — ах.
Можно доказать, что существует, и притом единственная, функция
/(х), определенная на всей бесконечной прямой и удовлетворяющая
следующим трем требованиям:
1)	для любых вещественных хг и х3 соотношению /(х2 + х2) =
2)	соотношениям /(0)= 1,/(1) = а, где а>0;
3)	непрерывная при х=0.
Такой функцией и является построенная выше функция ах.
3.	Логарифмическая функция. Рассмотрим произвольный сег-
мент [с, d] бесконечной прямой. На этом сегменте функция у=-ах
строго монотонна и непрерывна. Поэтому, в силу следствия из леммы 1,
функция у =/(х) = ах имеет на сегменте [а, р J, где а = ас, р » ad,
обратную функцию х=/'1(>), которую мы будем называть логариф-
мической. Логарифмическая функция обозначается следующим образом:
x=\ogay.
116
ПОНЯТИЕ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ
ГГЛ. 4
Меняя для этой функции обозначение аргумента у на х, а обо-
значение функции х на у, мы получим функцию
У = loga X.
Отметим следующие свойства логарифмической функции, непо-
средственно вытекающие из ее определения:
1°. Логарифмическая функция определена для всех положительных
значений х. Это следует из того, что ее аргумент представляет собой
значения показательной функции, которые, в силу свойств 1) и 3)
этой функции (см. предыдущий пункт), только положительны и за-
полняют всю положительную полупрямую х > 0.
2°. Логарифмическая функция непрерывна и возрастает на всей
открытой полупрямой х^>0 при а>1 (убывает при а<;1), при-
чем при а > 1
lim logax = — со, lim logax=4-co.
х-»0-|-0	x_-|-oo
Справедливость этого свойства вытекает из свойств показательной
функции и из замечания 1 п. 2 § 4.
3°. Для любых положительных хг и х2
loga (*1 • *2) = 10ga X-L + 10ga х2.
Замечание. Следует особо отметить логарифмическую функ-
цию J' = logex, где е — lim (1-|-— V. Мы будем для этой функции
использовать обозначение _у = 1п х. Подчеркнем, что логарифмическая
функция _у = 1пх играет важную роль в математике и ее приложе-
ниях. Логарифмы по основанию е принято называть натуральными.
На рис. 4.11 и 4.12 изображены графики логарифмической функ-
ции у = logoх для случая а > 1 и 0 < а <; 1.
§5)
ПРОСТЕЙШИЕ ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
117
4.	Гиперболические функции. Гиперболическими функциями назы-
ваются следующие функции *):
1°. Гиперболический
синус
ч	рх —— р~- %
shx = g /
2°. Гиперболический
косинус
chx = ^-
3°. Гиперболический
тангенс
,. sh х
th х = -г-
спх
4°. Гиперболический
котангенс
Из определения гиперболических функций следует, что гипербо-
лический синус, гиперболический косинус и гиперболический тангенс
заданы на всей числовой прямой. Гиперболический котангенс опреде-
лен всюду на числовой прямой, за исключением точки х = 0.
Гиперболические функции непрерывны в каждой точке области
задания (это вытекает из непрерывности показательной функции и
теоремы 4.2).
Гиперболические функции обладают рядом свойств, аналогичных
свойствам тригонометрических функций. Например, для гиперболиче-
ских функций имеют место теоремы сложения, аналогичные теоремам
сложения для тригонометрических функций. Именно:
sh (х + j) = sh х ch у -ф ch х sh_y,
ch (x -f-ф) = ch x ch_y -|- sh x shj.
На рис. 4.13—4.16 изображены графики гиперболических Функций-
S.	Степенная функция с любым вещественным показателем а.
Пусть а — произвольное вещественное число. Определим общую сте-
пенную функцию у = хл, х>0, следующим образом:
у = х = [а а ) =а &а (а>1).
Из определения степенной функции следует, что при а>0 она
представляет собой возрастающую, а при а<; 0 убывающую функцию.
*) Наименование «гиперболические функции» объясняется тем, что гео-
метрически функции y = shx и y = chx могут быть определены из рассмот-
рения равнобочной гиперболы по тем же правилам, по которым функции
у — sin х и у = cos х могут быть определены из рассмотрения единичной окруж-
ности.
118
ПОНЯТИЕ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ
[ГЛ. 4
Рис. 4.16.
§ 51
ПРОСТЕЙШИЕ элементарные ФУНКЦИИ
119
Рассмотрим предельное значение степенней функции при х -> 0 + 0.
Докажем, что
{О при а > О,
. 4
+ ОО при а<0.
Действительно, пусть {хл} —любая сходящаяся к нулю справа
последовательности значений аргумента х. Так как lim log0x„ ——оо,
д-*оо
то из свойств показательной функции вытекает, что lim aaloga*« — о
44	л-юо
при а>0 и lim	=-{-оо при а<0. Естественно положить
д—*со
теперь 0а = 0 при а > О и считать это выражение неопределенным
при asgO.
Докажем непрерывность степенной функции в любой точке х
положительной бесконечной полупрямой (х>0). Для этого достаточно
установить, что эта функция непрерывна в каждой точке х указанной
полупрямой слева и справа (см. замечание в п. 1 § 3). Докажем,
например, непрерывность этой функции в точке х слева (непрерыв-
ность справа доказывается аналогично). При этом ради определенности
будем считать а>0. Обратимся к формуле у = № = actlogaJC, а>1.
Пусть {хп}—любая сходящаяся слева к х последовательность значе-
ний аргумента степенной функции, так что xn<Zx. Так как лога-
рифмическая функция непрерывна, то последовательность {«„}, где
ип = a log0 хп, сходится к и = a loga х, причем все элементы ип отличны
от и (в самом деле, поскольку при а > 1 логарифмическая функция
возрастает, то справедливо неравенство ил<^«). В силу непрерывно-
сти показательной функции последовательность {а“л} сходится к а“.
Иными словами, последовательность {alllog<xJC«}, представляющая собой
последовательность [х1^ значений степенной функции, соответствующую
последовательности {х„}, сходится к aalog®*, т. е. к х*. Непрерыв-
ность степенной функции в точке х>0 слева доказана. Аналогично
доказывается непрерывность этой функции в точке х>0 справа.
Но непрерывность функции в точке х слева и справа означает, что
функция Непрерывна в этой точке. Отметим, что если а>0, то сте-
пенная функция у = № непрерывна такЖе и в точке х=0.
Замечание. Отметим, что если показатель а степенной функции
представляет собой рациональное Число где « — нечетное целое
число, то степенную функцию у-х* можно определить на всей чис-
ловой оси, полагая для х<0	'
I la	т
у = | х |, если a — — и т четное,
у — — I х |, если a — — и т нечетное.
120
ПОНЯТИЕ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ
(ГЛ 4
На рис. 4.17—4.20 изображены графики степенной функции у — х*
для различных значений а.
6.	Тригонометрические функции. В курсе элементарной матема-
тики с помощью наглядных геометрических соображений были введены
тригонометрические функции _y = sinx и _y=cosx*).
Перечислим некоторые важные для дальнейшего свойства триго-
нометрических функций:
*) Остальные тригонометрические функции y = tgx, y = ctgx, y = secx
и у = cosec х определяются через указанные:
1 sin х , cos х	1	1
tg х =----, ctgx=-;—, secx =--------, cosec x = ——.
cos x ’	sin x ’	cos x ’	sin x
Подчеркнем, что определение функйий sin х и cos х с помощью нагляд-
ных геометрических соображений не является логически безупречным, ибо
при этом возможность определить эти функции для всех вещественных значе-
ний аргумента х сводится к возможности установления взаимно однозначного
соответствия между всеми точками единичной окружности и всеми веществен-
ными числами из сегмента [0, 2л].
§ 5]	ПРОСТЕЙШИЕ ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ	121
V
1°. При любых вещественных х', х" и х справедливы следующие
соотношения:
sin (х' + x") = sin x'cos х" + cosx' sin х",
cos(x' + х") = cos х' cos х" — sin х' sin х",
sin2x + cos2x= 1.
sin 0 = 0; cos 0=1, A
siny = 1; cos у = 0. J
(4.5)
(4.6)
3°. Если 0 < x < у, то
0 < sin х < х.
Указанные свойства устанавливаются посредством геометрических
рассуждений. Мы не будем давать здесь известные из курса элемен-
тарной математики геометрические выводы
свойств 1° и 2°. Остановимся лишь на гео-
метрическом выводе- неравенств (4.7). Кро-
ме (4.7) мы установим неравенство x<tgx
^при 0<х<уУ
Рассмотрим окружность радиуса 1 с цент-
ром в точке О и точку А на этой окружности
(рис. 4.21). От точки А против часовой
стрелки будем отсчитывать дуги окружности.
Пусть М — точка окружности, находящаяся
в первой четверти, их — длина дуги AM,
(4.7)
0 < х < (х — радианная мера угла АО/И), N — основание перпен-
дикуляра, опущенного из М на О А, 5—точка пересечения пер-
пендикуляра к ОА, восставленного из точки А, с продолжением
отрезка ОМ. Тогда AW=sinx, ON= cos х, AB = tgx. Так
как треугольник ОМА содержится в секторе ОМА, который
в свою очередь содержится в треугольнике ОБА, и площади пере-
численных фигур соответственно равны у sin х, у и у tg х, то имеют
место неравенства sinх<х<tgх, 0<х<у. При указанных зна-
чениях х, sinx>0. Таким образом, справедливость неравенств
0 <sinx<x<; tgx ^при 0<х<|) установлена.
Свойства 1°, 2°, 3° могут быть положены в основу определения
функций sinx и cosx. Можно доказать, что существует, и притом
единственная, пара функций, определенных для всех вещественных
122
ПОНЯТИЕ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ
(ГЛ. 4
значений аргумента, первою из которых мы обозначим sin х,
а вторую cos х, удовлетворяющих требованиям 1°, 2°, 3°.
Доказательство этого утверждения приведено в дополнении к этой
главе.
Подчеркнем, что из свойств 1°, 2° и.3° функций sinx и cosX
можно- вывести все известные из элементарного курса свойства три-
гонометрических функций *).
' Докажем непрерывность тригонометрических функций в каждой
точке области их задания. Установим сначала непрерывность функ-
ции у = sin х в точке х = 0. Пусть {хп} — произвольная сходящаяся
к точке х = 0 справа последовательность значений аргумента х. Из
неравенств (4.7) имеем 0 <sinx„<x„. Отсюда, в силу теоремы 3.14,
вытекает, что последовательность {sinx„} имеет предел, равный нулю.
Такйм образом, lim sinх = sin 0 = 0. Так как при —-к-<х.<;0
х-0+0	2
справедливы неравенства х < sinx<Z 0 **), то рассуждая аналогично,
получим lim sinx = sin0. Мы установили, что в точке х = 0 функ-
х —0 —0
ция _y = sinx непрерывна справа и слева, т: е. является непрерывной
в указанной точке. Для доказательства непрерывности функции у = sin х
в любой точке х бесконечной прямой воспользуемся формулой sinx"—
,— sinx = 2cos—фг- sin——, которая может быть получена из
формул (4.5). Пусть {х„}—произвольная сходящаяся к х последова-
тельность значений аргумента. Полагая в последней формуле х" —хп
и х' = х, получим
lim (sin хп — sin х) = 2 lim cos	—sin	— = 0.
«-►OO	«-*00	*
Справедливость этого заключения вытекает из того, что последователь-
ность {cos ограниченная ***), а последовательность {sin~ ,
в силу доказанного выше, бесконечно малая.
Непрерывность функции y=wsx устанавливается с помощью
аналогичных рассуждений из формулы
,,	 i п • х"-\-х' . х" —,х'
COS X — COS X = — 2 SIH----g-----Sin-g—.
Непрерывность остальных тригонометрических функций (tg х,
ctgx, sec .г, cosec х) в каждой точке области их задания следует из
теоремы 4.2.
*) Например, равенства sin (— х) = — sin х, cos (— х) — cos х.
**) Эти неравенства получаются из неравенств (4.7) путем замены х на
— хи учета формулы sin (— х) — — sin х.
***) Третья из формул (4.5) позволяет заключить, что | cosх| 1 и
| бшх | sg 1. Отсюда очевидна ограниченность последовательности [cos—+у—к
§ S]
ПРОСТЕЙШИЕ ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
123
Рис. 4.23.
124
ПОНЯТИЕ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ
[ГЛ. 4
Область задания каждой тригонометрической функции разделяется
на участки монотонности этой функции *). Функция у = sin х возра-
стает на каждом сегменте рАж —у, 2Лж-|-у^**) и убывает на
каждом сегменте ^(2й + 1) ж — у, (26 Д- 1)	. Функция у = cos х
возрастает на каждом сегменте [(2/е —1)к, 2£ж] и убывает на каждом
сегменте [2/е~, (26 +1)11]- Функция _y = tgx возрастает На каждом
интервале ^Аж—Лж -|- . Функция у = ctg х убывает на каждом
интервале ((А—1)ж, /гж). Для функций _y = secx и _y=cosecx чита-
тель без труда установит области возрастания и убывания.
На рис. 4.22—4.27 изображены графики тригонометрических
'функций.
7.	Обратные тригонометрические функции. Функция j/ = arcsin х
определяется следующим образом. Рассмотрим на сегменте —у, у
функцию _y = sinx. В предыдущем пункте мы отметили, что на этом
сегменте функция у = sinx возрастает, непрерывна и имеет в ка-
честве множества значений сегмент [—1, 1]. В силу следствия из
*) Монотонность функций sinx и cos х на соответствующих сегментах
легко установить из формул
• ,,	 , п Л" + х' . х" — х'
sin х" — sin х' = 2 cos —---sin ——
и
„	, о . х" + х' '. X" — х'
cos х — cos х = — 2 sin —— sin —.
**) Здесь под k мы понимаем любое целое число.
§ 6]
ПРЕДЕЛЬНЫЕ ЗНАЧЕНИЯ НЕКОТОРЫХ ФУНКЦИИ
125
леммы 1 для функции _y = sinx на сегменте [—1, 1] существует непре-
рывная возрастающая обратная функция. Эту функцию мы будем обоз-
начать x=arcsin_y. Меняя для этой функции обозначение аргумента^
на х и обозначение х для функции на у, мы получим функцию
> = arcsinx. На рис. 4.28 изображен график этой функции.
Совершенно аналогично определяется функция у = arccos х. Обла*
стью ее задания служит сегмент [—1, 1], а множеством значений
сегмент [0, тг]. Указанная функция убывает и непрерывна на сег-
менте [—: 1, 1]. На рис. 4.29 изображен график функции _у = arccos х.
Функции у — arctg х и у = arcctg х определяются как обратные
для тангенса и котангенса. Эти функции определены, монотонны и
непрерывны на бесконечной прямой. На рис. 4.30 и 4.31 изображены
графики этих функций.
§ 6.	Предельные значения некоторых функций
. 1. Предварительные замечания. В главе 1 было указано, что
для вычисления производных функций у = sin х и у = loga х нужно
доказать существование предельных значений (или пределов) функ»
. Дх	х
Sin 2	/ Дх\дх
ции при Дх—>-0 и функции (^1+-) при Дх—>0 и фиксиро-
ванном х>0. Этому вопросу и посвящен настоящий параграф. Нам
понадобится предложение о предельном значении функции, заключенной
между двумя функциями, имеющими общее предельное значение в
данной точке. Это предложение представляет собой функциональный
аналог теоремы 3.14.
Лемма 3. Пусть в некоторой Ъ-окрестности точки а (за ис-
ключением, быть может, самой точки а) заданы функции f(x),.
g(x) и h(x), причем функции f(x) и g(x) имеют в точке а оди-
наковое предельное значение, равное Ь. Если в указанной окрест-
ности точки а (за исключением, быть может, самой точки а)
выполняются неравенства f(x)^,h(x)^g(x), то предельное зна-
чение функции h (х) в точке а существует и равно Ь.
Доказательство. Пусть {х„}—произвольная сходящаяся к а
последовательность значений аргумента х, элементы х„ которой
126
ПОНЯТИЕ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ	[ГЛ. 4
лежат в указанной S-окрестности точки а и не равны а, и {/(х„)},
{g(x„)}, {h (хя)} — соответствующие последовательности значений
функций f(x), g(x) и h(x). По условию
lim f(xn) = Hm g (хя) = b и f (x„) h (xn) g (x„).
Д-4-00	n-* *co
Но тогда, в силу теоремы 3.14, limft(xn) = 6. Поскольку {хя} —про-
n-*co	•'
извольная сходящаяся к а последовательность значений аргумента, то
последнее равенство означает, что lim ft (х) = ft. Лемма доказана.
х -* а
2.	Предельное значение функции	в точке х — 0 (пер-
вый замечательный предел). Докажем следующую теорему.
Теорема 4.3. Предельное значение функции в точке х = 0
существует и равно единице'.
lim—=1.	(4.8)
х —О х
Доказательство. Мы уже отмечали, что при 0<х<у
справедливы неравенства 0 <sinx< х< tg х (см. п. 6 предыдущего
параграфа); Деля почленно Эти неравенства на sinx, получим
-i-< —
sinx cos*
sin х
X
Последние неравенства справедливы также и для значений х,
удовлетворяющих условиям — -^-<х<0. Чтобы убедиться в этом,
достаточно заметить, что cosx = cos(—х) и =	Так как
cosх — непрерывная функция, то limcosx=l. Таким образом, для
функций cosx, 1 и ?— в некоторой S-окрестности точки х = 0 вы-
полняются все условия леммы 3 (для того чтобы убедиться в этом,
обозначим /(x) = cosx, g(x)=l и й(х) = ^^и положим 8 = yj.
Следовательно, lim^S2E = limcosx= l. Теорема доказана.
х-. о х х-.О
. Ьх
ЯП у	Дх
*) Выше мы говорили о функции . Если обозначить через х, то
мы и получим функцию —. Условие Дх — 0 при этом обозначении сводится
к условию х-»0.
§6]
ПРЕДЕЛЬНЫЕ ЗНАЧЕНИЯ НЕКОТОРЫХ ФУНКЦИИ
127
3.	Предельное значение функции	ПРИ х->со (второй
замечательный предел)*). Докажем следующую теорему.
/ 1 \*
Теорема 4.4. Предельное значение функции /(х) = 11+ —I
при х -* сю существует и равно е:
lim (14-— 'j = е.	(4.9)
Доказательство. Нужно доказать, что, какова бы ни была
бесконечно большая , последовательность {xk} значений аргумента
функции f(y) = (1 +y I , соответствующая последовательность {/(xft)}
значений этой функции имеет своим пределом число е. Рассмотрим
следующие четыре группы бесконечно больших последовательностей
значений аргумента X'. .
1°. Бесконечно большие последовательности элементами ко-
торых являются целые положительные числа. К указанной группе
относится, например, последовательность
2, 2, 1, 1, 3, 3, 2, 2, 4, 4, ..., иф-1, пф-1, п, п, ....
2°. Бесконечно большие последовательности, элементы которых,
начиная с некоторого номера, состоят из' положительных веществен-
ных чисел.
3°. Бесконечно большие последовательности, элементы которых,
начиная с некоторого номера, состоят из отрицательных веществен-
ных чисел.
4°. Бесконечно большие последовательности, содержащие беско-
нечно много как положительных, так И отрицательных вещественных
чисел **).
*	/ Дх\—
♦) Упомянутая ранее задача о предельном значении функции (1 + —
при Дх, стремящемся к нулю, и фиксированном х > 0, сводится к указанному
вопросу. Действительно, ' если положить ~	, то при Дх —> 0 и —> со и
/1 ,	А , 1
(1 + —Iйх = 11 + ~) , а эта функция только обозначением аргумента отли-
(	1 \х
чается от функции II-)-—1 •
/ 1 \*
*♦) Так как функция (1-|- —I не определена на сегменте [—1, 0] (по-
скольку для значений х из этого сегмента выражение -|- -i-j либо отрицательно,
либо не имеет смысла), то естественно считать, что элементы последователь-
ностей 2”, 3‘ и 4° не принадлежат сегменту [— 1, 0].
128
ПОНЯТИЕ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ
[ГЛ. ♦
Заметим, что совершенно произвольная бесконечно большая после-
довательность значений аргумента относится к одной из групп 2°, 3°
или 4°. Поэтому теорема будет доказана, если мы проведем доказа-
тельство для каждой группы 1°, 2°, 3° и 4°. (При этом последова-
тельности группы 1° имеют вспомогательный характер.) Пусть
-- какая-либо последовательность первой группы. Докажем, что
lim (1-Ь — । к—е. Пусть е— любое положительное число. Так как
й-оо\ «*/
/	1 \п
lim 11 4-= е (см. .пункт 4 § 3 главы 3), то можно указать такой
п -♦ оэ ' П '
номер №*, что при n^N* выполняется неравенство
К'+Я-'И
Поскольку последовательность {пк} бесконечно большая и ее эле-
менты — целые положительные числа, то для положительного числа
N* можно указать такой номер N, что при k^N выполняется усло-
вие nk^N*. Но для таких целых иА, как уже указывалось, выпол-
няется неравенство
1КтГЧ<’-
Следовательно,
lim (1 +— *) к = е.
Перейдем теперь к последовательностям второй группы. Пусть
— любая последовательность второй группы и N—номер, начи-
ная с которого все элементы этой последовательности больше еди-
ницы. Считая k^N, обозначим через пк целую часть хк, пк = [хк].
Тогда
пк^хк <и*+1.	(4.10)
Отметим, что последовательности {«*} и {лй-(-1} представляют собой
последовательности первой группы. Из неравенств (4.10) имеем
«А + 1 хк Пк
ИЛИ
14----^-7 < 1+-=С 1 + —.
«А + 1	' Хк ' Пк
Отсюда, используя еще раз неравенства (4.10), получим
/	1 \пи	!	1	/	1 \л.+1
<П+г) < 1+^-) •	(411)
\	пк Т V	\	xk)	\	пЬ/
§6)
ПРЕДЕЛЬНЫЕ ЗНАЧЕНИЯ НЕКОТОРЫХ ФУНКЦИИ
129
Пределы последовательностей ((1 + i|_ tи' {(1 4~) * | равные.
Действительно, первая из этих последовательностей может быть пред-
ставлена как произведение последовательностей {(* +я j .* } и
{(1 +я" J г|. пределы которых равны соответственно*) е и I.
Вторая последовательность представляет собой произведение последо-
вательностей |(1	и {(1 + пРеделы которых также равны
соответственно е и 1. В силу неравенств (4.11) по теореме 3.14
имеем
lim (l+XVft = e.
^да\ xk)
Рассмотрим последовательности третьей группы. Если {xft}—бес-
конечно большая последовательность, элементы, которой, начиная с
некоторого номера, отрицательны, то последовательность {?*}, где
Zk~—1 — Xk, бесконечно большая и ее элементы, начиная с неко-
торого номера, состоят из положительных вещественных чисел. По-
этому {Zk} представляет собой последовательность второй группы.
Так как
V1
и
* —оо\ Ч! л-от\ zj \ 'zkj
то
lim (1+— P =
Л —со' xki
Для завершения доказательства нам нужно рассмотреть последо-
вательности четвертой группы. Пусть {х*} — такая последовательность.
Обозначим через {х*} подпоследовательность этой последовательности,
состоящую из всех неотрицательных элементов **) последовательности
{хД, а через {х*} — подпоследовательность, состоящую из всех отри-
цательных элементов последовательности {хД ***). Так как по дока-
занному
lim f 1 +	= е и lim (1 + 4W = е.
ft —оо\ xk)	A—co \ Xk)
*) При этом учитывается, что {nfc} принадлежит к первой группе.
**) Эти элементы, начиная с некоторого номера, строго положительны.
***) Здесь мы, в отличие от главы 3, выбранные подпоследовательности
отмечаем знаками ' и ", сохраняя при этом у элемента подпоследовательности
тот номер, который он имел в последовательности
130	- ПОНЯТИЕ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ	(ГЛ. 4
то для любого е > 0 можно указать номер N такой, что при k W
т. е. при k^N
Следовательно,
lim (l+ip = e.
k — ОО \ XkJ
Теорема доказана.
Замечание. ИЗ доказанной теоремы следует, что
lim (1 +х)}1х = е.
jc —О
В самом деле, пусть {хп} — любая сходящаяся к нулю последователь-
ность значений аргумента функции (1 + хУ/х, элементы хп которой
отличны от нуля. Тогда последовательность {zn}, где zn = —, бес-
хп
конечно большая (см. теорему 3.6). Так как’
1
(1+Хл)ж» = (14-1р и lim (l+lV« = e,
\ гп!	а-оо\ г«/
ТО
lim (1 + х^У>хп = е,
П СО
и поэтому
lim (1	=
§ 7. Понятие сложной функции
1. Определение сложной функции. Функции, полученные в ре-
зультате суперпозиции *) двух или нескольких функций, мы будем
называть сложными.
Сложные функций определяются следующим образом. Пусть функ-
ция х = <р (t) задана на множестве {/}, и пусть на множестве {х} зна-
чений этой функции задана функция y = f(x). Тогда на можестве {£}
задана сложная функция
y=f(x), где х = ср(/)^
или
_y = F(f)=/[?(O].
Докажем следующую теорему.
*) То есть последовательного наложения.
ПОНЯТИЕ СЛОЖНОЙ ФУНКЦИИ
131
§ Л
Теорема 4.5. Пусть функция x = y(t) непрерывна в точке а,
а функция y—f(x) непрерывна в точке Ь = <?(а). Тогда сложная
функция y=f(x), где x = <f(t) (у = F(£)=/[<p (ЭД), непрерывна
в точке а.
Доказательство. Нужно доказать, что предельное значение
сложной функции у = F (f) = f [с? (ЭД в точке а равно частному ее
значению F(a) = f [<р(Д)] = f(b) в этой точке. Пусть ЭД	—
произвольная сходящаяся к а последовательность значений аргумента t
сложной функции. Вычисление элементов соответствующей последо-
вательности значений F(t^, F(t2).. F(t„),	... сложной функции
может быть проведено следующим образом. Вначале вычисляются
элементы последовательности {хп} значений функции х = ср(ЭД хп —
— <р (£„), а затем по этой последовательности \хп] вычисляется после-
довательность {/(х„)} значений сложной функции. Эта последователь-
ность {/(хл)} как раз и представляет собой искомую последователь-
ность {Д(ЭД)}. Чтобы убедиться в этом, достаточно заметить, что
f (xn)—f\(p ((„)] —F(t„). В силу непрерывности функции х = <?(£)
в точке а, последовательность {х„} сходится к & = <р(а). Если эта
последовательность содержит только конечное число отличных от
Ъ = 9 (а) элементов, то, начиная с некоторого номера, элементы этой
последовательности равны Ь. Начиная с этого же номера, элементы
последовательности {/(хл)} равны f(b), и поэтому ее предел равен
/(&)=/[ср(а)] = F(a). Если же отличных от b элементов последо-
вательности {хп} бесконечно много, то они образуют сходящуюся к b
подпоследовательность Соответствующая подпоследовательность
{/(хлА)} последовательности |/(хл)}, в силу непрерывности функции
/(х) в точке Ь, сходится к f(p). Но тогда и вся последовательность
{/{*,)} сходится к f(F), так как отличные от /(хл^) ее элементы
равны f(b). Итак, мы доказали, что последовательность значений
сложной функции, соответствующая любой сходящейся к а последо-
вательности значений ее аргумента, сходится к частному значению
этой функции в точке а. Теорема доказана.
2. Непрерывность и предельные значения некоторых сложных
функций. Докажем непрерывность некоторых сложных функций.
1°. Пусть х = <р(0 и у =f(x) — простейшие элементарные функ-
ции (см. § 5), причем множество значений {х} функции х = <р(0
является областью задания функции y—f(x). Из результатов § 5
следует, что простейшие элементарные функции непрерывны в каж-
дой точке- области задания. Поэтому, в силу теоремы 4.5, сложная
функция у =f [ср (ЭД, т. е. суперпозиция двух элементарных функций,
непрерывна. Например, функция у = siny непрерывна, в любой точке
х 0. Чтобы убедиться в этом, достаточно рассмотреть функции
x = t~1 и y = sinx. Сложная функция у = sin V1 только обозначением
аргумента отличается от функции у = sin у и, в силу сказанного выше,
132
ПОНЯТИЕ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ
[ГЛ. 4
непрерывна в любой точке t ф 0. Рассуждая аналогично, легко
убедиться, что. функция _y = lnsinx непрерывна в любой точке каж-
дого интервала (2£л, (2k -|- 1)гс) *).	<
2°. Степенно-показательные .выражения u(x)V(JCX
-Очевидно, имеет смысл лишь случай, когда и (х) > 0. Легко убе-
диться, что если и (х) и т>(х) непрерывны в точке а и zz(x)>0
'в окрестности точки а, то функция и (xf < также непрерывна
в точке а.
В самом деле, и (х)® W = е®,А| 1п “ Поскольку In и (х) представ-
ляет собой непрерывную в точке а функцию, то и функция v (х) In и (х)
также непрерывна в точке а. Но тогда функция ev W 111 “(Х| непрерывна
в точке а. Отметим, что установленное свойство непрерывности по-
зволяет утверждать, что при сделанных предположениях lim и (x)v =
х -» а
= и (a)v <й>.
3°. Предельные значения степени о-показательных вы-
ражений.
Выясним вопрос о предельных значениях степенно-показательных выра-
жений и (х)'и 1X1 при х —<• а. При этом мы будем предполагать, что и (х) > 0
в некоторой окрестности точки а.
Из соотношения и (х)®	= g®(-r>lnuW видно, что предельное значение вы-
ражения и (x)v ,х' при х — а зависит от предельного значения выражения
V (х) In и (х).
1.	Пусть lim v (х) In и (х) = Ь.
X -> а
Убедимся, что в этом случае limu(x)® •*’ = еь.
х а
В самом деле, функция
( o(x)lnu(x) при xzia, ‘
ш (х) = <	.
I	о	при х — а
непрерывна в точке х — а. Поэтому и сложная функция ew tx' непрерывна
в этой точке. Следовательно, lim ew 1Л') = ете ,а’ = е*. Так как lim =
х -» а	х а
= lim a® (JC) 1п ” <х\ то lim и (х)® существует и равен еь.
х—^п	х -» а
Используя полученные в этой главе сведения о-предельных значениях ew
при W-— — оо и to — 4-со, легко убедиться в том, что
II.	Если lim v (х) In и. (х) = — со, то lim и (x)v 1X1 = 0.
х—>а	х-*а
III.	Если lim y (х) In и (х) = -|- со, то lim и (х)® '•*’ = |-со.
х-+а	х-+а
Установленная связь между предельными значениями выражений и (х)™ ’•*’
и v (х) 1п и (х) позволяет в ряде случаев легко найти предельное значение
функции и (х)® 1А|, если известны предельные значения функций и (х> и и (х).
Рассмотрим для примера следующие случаи:
1) Существует lim и (х) > 0 и lim v (х).
2) lim и (х) = b, b> 1,
, 3) lim и (х) = b, b > 1,
х-*а
х-+а
lim v (х) = + оо.
х—* а
lim v (х) — — oj.
*) Там, где sinx>0.
§ 7J
ПОНЯТИЕ СЛОЖНОЙ ФУНКЦИИ
133
lim v (х)
Убедимся, чтов случае 1) lim и (х)°= [lim « (х)]*-*®	. Действитель-
х—*а	х-*а
но, так как lim и (х) > 0, то, в силу непрерывности логарифмической
х^>а
функции, lim In и (х) существует и равен In [lim и (х)]. Поэтому существует
х-*а	х-*а
lim v (х) In и (х) = lim v (х) In [lim и (х)[.
х-*а	' х—>а х-*а
Согласно I отсюда вытекает, что
lim v (х) In u (х) lim v (x) In [lim и (x)[	lira » (X)
lim u (x)® (’v) = e*-”®	=zgx~*a x~*a = [lim u (x)]*-"®
х-»а	x~*a
В случае 2) lim v (x) In и (x) = + co, и Поэтому, согласно III,
lim и (x)® 1X1 — 4- co.
x->a
В случае 3) lim v (x) In и (x) = — co, и поэтому, согласно II,
lim и (x)® l*> = 0.	X~^a'
x-a
В заключение укажем три случая, для которых нахождение предельного
значения и (х)® <X1 требует дополнительных исследований.
1.	Неопределенность типа /°°:
1imw(x) = l, limv(x)=co.
х—а	х—а
2.	Неопределенность типа 0°:
lim и (х) = 0, lim v (х) = 0.
х-*а	х-*а
3.	Неопределенность типа со0:
lim и (х) = 4-оо,-
Нт о(х) =0.
х—>а
Для первого из этих случаев мы приведем формулу, удобную для прак-
тических приложений^
Преобразуем выражение и (х)® ,А’1 следующим образом:
и (x)v •*>
I	। Пи (x) — 1| » (X)
= Ш + («(х)-1)]“1л>-Ч
Положим, далее,
1
U (х) = [1 4- (и (х) — 1)1“ w - 1 и V (х) = [и (х) — 1] v (х),
так что
«(х)® w = 17 (х)и«
Поскольку Hmt/(x)=e (см. замечание к теореме 4.4) и то зна-
х-+а
чеяие lim a (x)v = lim U (х)v зависит от предельного значения функции
х^*а	х^а
k (х) в точке а, т. е. от lim [и (х) — I] v (х). Именно:
х-^а
134
ПОНЯТИЕ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ
[ГЛ. 4
если lim [и (х) — 1] v (х) = lim V (х) = с, то lim и (х)	= lim U (x)V() =
х^а	х-*а	х-*а	х-*а
— ес (см. случай 1));
если lim [и (х) — 1]у (х) =+со, то lim и (х)® '*> = + со (см. случай 2));
х-*а	х->а
если lim [и (х)— 1]и(х) = —со, то lim и (x)v (Xi = 0 (см. случай 3)).
х-*а	х-*а
Таким образом, мы получаем следующую формулу:
lim [« (х) — 1] v (х)
lim и (х)ъ <*> = ех^а
х-*а
Неопределенности типа 2 и 3 приводятся к неопределенности типа 1 еле*
дующим образом.
Положим
U (х) = е® <*>, V (х) = In и (х).
Очевидно, lim U (х) = 1 и lim V (х) = ± со. Кроме того,
х-*а	х-*а
и (х)® (JC) = [е v (JC)]In u (ж) = e,n u (JC) V W = U (x)v
1 '
Пример. Найти lim [cosx]sln‘x. Так как limcosx=l, a lim------------------=
x—o	x-»o	x-»osin2 x
= co, то налицо неопределенность типа 1ет. Используем формулу
„ W limJ“ w - 11 ®
lim«(x) = ех~*'>	, полученную нами выше. Имеем
X -»0	4
lim [и (х) — 1] v (х) = lim [cos х — 1] —1— =
х-»0	х—О	sin2 X
= lim Г—2 sin2 —1--------1-------= —L lim —J—
X— 0 L	2 ] л  x a X 2 X—*0 „ „ x
J 4 sm2 ycos2 -g-	cos2
Поэтому
1
2 ’
lim [cosxjsina x = e 2 =-^=.
x-»o	V e
4°. Предельные значения некоторых сложных
функций. Докажем справедливость следующих равенств:
/1+х_1 1
lim !----— = —
х~о х	п
ех__1
lim^---- = 1,
х^о х
1п (1 + х) .
lim —-—!—- = 1
х—о х
1—COSX
11т„т—
х->0 х
1
~2'
(4.12)
§ 7]
ПОНЯТИЕ СЛОЖНОЙ ФУНКЦИИ
13а
1) Рассмотрим первый из этих пределов. Имеем
^Г+7-l  (1 + х)д -1 _
X	X
Г 1	1[ Д — I	д —2	1
_[(1+а)П_1][(1+х) Д +(1+х) п +...+ (1+х)Д + 1| _
Г п ~'	д—1 I
4(1+хРГ + (1+*)~+-+ (1+х)" +1J
=__________[(1 +х)"| -1 ___=
Ira — 1	га — 2	1	1
(1 4-х)~ + (1 + ^~+...+ (1 +х)’+ 1]
1
'	га — 1	га — 2	1
(1 + х)“ + (1 + х)~ +...+ (1 + xf* + 1
Так как знаменатель последнего выражения при х—>0 имеет пре-
д
дел, равный п (функция (1 -\-х)п непрерывна в точке х = 0 и поэтому
lim (1+х) я= 1), то lim•——х~— = —.
Л->0	х-*0 к	п
2) Перейдем к доказательству второго равенства (4.12). Имеем
-п = In (1 + х) < Доопределим функцию /(х) = (1 + х)х, пола-
= 1п/(0) = In е = 1. Итак, lim
3) Докажем
х= In (1 4-и) и
к нулю. Имеем
гая /(0) = lim/(x) = lim (1 -f-x)x = e. В результате мы получим
х -> О	Л* —* О
непрерывную в точке х — 0 функцию f(x). Тогда и функция 1п/(х)
также будет непрерывна в нулевой точке, и поэтому lim In (1 +х)х =
х-0
In (1 + х)  J
ЛГ—-0 Х
справедливость третьего равенства (4.12). Положим
.заметим, что при х—>0
= In (!+»)-• °ТСЮДа
переменная и стремится
следует, что
1	и
-= lim	—г
и^о1п(1 + «)
4) Докажем справедливость последнего равенства (4.12). Имеем
о . , х	. „ х	• о х
,	2sm3—	sin2—-	sin2 -н-
1—cosx	2	1	2 т,	2	, ,	.. Q4.
----5---—--------=~х~—пг. Так как 1>т -—г- = 1 (см. (4.8)), то
х2 2 (у)	(4)	'
136
ПОНЯТИЕ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ
(ГЛ. 4.
Используя соотношения (4.8), (4.12), равенство (4.1) и символ о (х)
(см. п. 3 § 2), легко убедиться в справедливости следующих формул:
sin х = х + о (х),
+х= 1 + -i- + o(x),
1п(1 +х) = х + о(х),
ех = 1 + х + о (х),
cos х = 1 — у + о (х2).
(4-13)
Докажем, например, справедливость первой формулы. Так как
lim ^2-^=1, то в силу (4.1) ^^=1-|-а(х), где а (х)—бесконечно
ж-о *	z х
малая в точке х = 0 функция. Из последней формулы вытекает, что
sin х = х + ха (х). Поскольку ха (х) = о (х), то sin х = х + о (х).
3. Понятие элементарной функции. Класс элементарных функ-
ций. В приложениях важную роль играет класс функций, получае-
мых посредством конечного числа арифметических операций над про-
стейшими элементарными функциями, а также получаемых путем
суперпозиции этих функций. Например, функции х3 + 3 cos 2х,
1п | sin Зх | — еагс& *, принадлежат этому классу. Мы будем Называть
этот класс функций классом элементарных функций, а каждую
функцию этого класса — элементарной.
Отметим следующее свойство элементарных функций — они непре-
рывны в каждой точке области задания *).
Это свойство непосредственно вытекает из теорем 4.2 и 4.5
и непрерывности простейших элементарных функций в каждой точке
области задания.
§ 8. Классификация точек разрыва функции
1. Точки разрыва функции и их классификация. В п. 1 § 3
мы определили точки разрыва функции как точки, в которых функ-
ция не обладает свойством непрерывности. Мы будем называть также
точками разрыва функции точки, в которых функция не определена,
но в любой е-окрестности которых имеются точки области задания
функции.
Рассмотрим возможные типы точек разрыва функции.
1°. Устранимый разрыв. Точка а называется точкой устра-
нимого разрыва функции у = f(x), если предельное значение функ-
ции в этой точке существует, но в точке а функция f (х) или
*) Если при этом область задания функции окажется состоящей из отдель-
ных изолированных точек, то естественно считать, чТо функция по определе-
нию непрерывна в каждой из этих точек.
§ 8)
КЛАССИФИКАЦИЯ ТОЧЕК РАЗРЫВА ФУНКЦИИ
137
не определена, или ее частное значение f(a) в точке а не равно
предельному значению.
Например, функция
(sin х	,
— при х О,
х
2 при х = 0
имеет в нулевой точке устранимый разрыв, поскольку предельное
значение этой функции в точке х = 0 равно 1, а частное равно 2.
Если функция /(х) имеет в точке а разрыв указанного типа, то этот
разрыв можно устранить, не изменяя при этом значений функции
в точках, отличных от а. Для этого достаточно определить значе-
ние функции в точке а равным ее предельному значению в этой точке.
Так, если в рассмотренном примере положить /(0)= 1, то lim f(x) =
= /(0) и функция будет непре-
рывной в точке х = 0.
Замечание. На практике
точки устранимого разрыва встре-
чаются при сосредоточенных рас-
пределениях физических. величин.
2°. Разрыв 1-го рода. Точка
а называется точкой разрыва
1-го рода, если в этой точке
функция f(x) имеет конечные,
но не равные друг другу правое и левое предельные значения:
lim / (х) 7S lim f(x) (или f(a 4- 0)— 0)).
-» a 4- 0	x —♦ a — 0
1. Для функции /(x)~ sgnx точка x = 0 является точкой раз-
рыва 1-го рода (см. рис. 4.4). Действительно, так как
sgn X —
то'
1 при
0 при
. — 1 при
х> 0,
х = О,
х<0,
lim sgnx=l, lim sgnx = —1.
X — O-I-O	x -> 0 — 0
2.
имеет
Функция f (x)
1
1 + 21/JC
определенная всюду, кроме точки х = 0,
в точке х = 0 разрыв 1-го рода (рис. 4.32). В самом деле,
если {хп} — сходящаяся к нулю последовательность, элементы кото-
рой положительны, то j—} — бесконечно большая последовательность
с положительными членами, и поэтому {1 4~ 21/Л/1} — также бесконечно
138
ПОНЯТИЕ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ
[ГЛ. 4
большая последовательность. Но тогда последовательность. Г-—1
Д1+2Мя/
бесконечно малая, и поэтому lim f(x) = 0. Если же {хп} — сходя-
jc->-0 + 0
щаяся к нулю последовательность, элементы которой отрицательны,
то ]—1 — бесконечно большая последовательность с отрицательными
членами, и поэтому lim 21/JC« = 0. Следовательно, lim/(x) = l.
л->со	х-»0 — 0
3°. Разрыв 2-го рода. Точка а называется точкой разрыва
2-го рода, если в этой точке функция f(x) не имеет по крайней
мере одного из односто-
ронних предельных значе-
ний или если хотя' бы
одно из односторонних
предельных значений бес-
конечно.
Рассмотрим, напри-
мер, функцию /(x) = siny
(рис. 4.33) *). Эта функция
в точке х — 0 не имеет ни
правого, ни левого предель-
ного значения. Действитель-
нулю справа последователь-
К
но, рассмотрим следующие сходящиеся
ности значений аргумента:
2_ 2_ 2_	________
л ’ 5л ’ 9л ’ ' ‘’ (4п — 3) л ’
2
и
_L ± ±	1
л ’ 2л’ Зл ’ ' ’ ’ ’ пл’
Соответствующий последовательности значений функции _y = sin-i
имеют следующий вид:
1, 1,
и
О, 0, 0, ..., 0, ...
Первая из этих последовательностей имеет предел, равный еди-
нице, а вторая имеет предел, равный нулю. Следовательно, функция
/(x) = sini- в точке х = 0 не имеет правого предельного значения.
Так как sin-^ = — sini, т0 эта ФУНКЦИЯ не имеет и левого пре-
дельного значения в этой точке.
*) Рис. 4.33 носит чисто иллюстративный характер.
ДОПОЛНЕНИЕ К ГЛАВЕ 4
139
Другим примером функции, имеющей точки разрыва 2-го рода,
может служить функция у = ctg х (см. рис. 4.25). Эта функция имеет
разрыв 2-го рода в каждой из точек т.п, п = 0, ±1, ±2,...
2. Кусочно непрерывные функции. Функция y=f(x) называется
кусочно непрерывной на сегменте [а, Ь], если она непрерывна во всех
внутренних точках [а, £>], за исключением, быть может, конечного
числа точек, в которых имеет разрыв 1-го рода и, кроме того, имеет
односторонние предельные значения в точках а и Ь. Функция называется
кусочно непрерывной на интервале или бесконечной прямой, если она
кусочно непрерывна на любом принадлежащем им сегменте. Напри-
мер, функция f (х) = [х] *) кусочно непрерывна как на любом сег-
менте, так и на бесконечной прямой.
ДОПОЛНЕНИЕ К ГЛАВЕ 4
ДОКАЗАТЕЛЬСТВО УТВЕРЖДЕНИЯ ИЗ П. 6 § 5
В настоящем дополнении дается доказательство утверждения из п. 6 § 5.
Для удобства сформулируем здесь это-утверждение в следующей форме.
Существует, и притом единственная, пара функций S (х) и С (х), опре-
деленных на всей бесконечной прямой и удовлетворяющих следующим трем
требованиям:
1°. Для любых вещественных чисел х', х” и х выполняются соотношения
2».
S (х' + х") = S (х') С (х") + С (х') S (х"),
С (х' + х") = С (х') С (х") — S (х') S (х"),
S3 (х) + С2 (х) = 1.
<$ (0) = О, С(0) = 1,
3°. При 0 <; х < ~ справедливы неравенства
0<S(x)<x.
(4.5) **)
(4-6)
(4-7)
Доказательство этого утверждения мы разделим на две части. Именно:
сначала мы докажем единственность, а затем существование функций S (х)
и С (х), удовлетворяющих требованиям 1°, 2° и 3°.
1. Доказательство единственности. Для доказательства единственности
достаточно убедиться в справедливости следующих двух утверждений:
1) Функции S (х) и С (х), обладающие перечисленными свойствами, непре-
рывны на всей числовой прямой.
*) Напомним, что символ [х] обозначает целую часть числа х.
**) Нумерацию формул мы оставили такой же, как и в п. 6 § 5. Заметим,
что в этих формулах мы заменили обозначения функций sin х и cos х на 3 (х)
и С (х) соответственно.
140
ПОНЯТИЕ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ
[ГЛ. 4
2) Значения функций S (х) и С (х) определяются единственным образом на
некотором всюду плотном множестве точек бесконечной прямой *).
Действительно, в силу непрерывности функций 3 (х) и С (х) их частные
значения в каждой точке х бесконечной прямой равны их предельным зна-
чениям в этой точке. Если теперь мы рассмотрим сходящуюся к х последова-
тельность значений аргумента, элементы которой принадлежат указанному
выше всюду плотному множеству точек, то соответствующие последователь-
ности значений функций 8 (х) и С (х), в силу сформулированного выше
утверждения 2), определяются единственным образом, а поэтому и пределы
этих последовательностей определяются также единственным образом. Но эти
пределы как раз и являются частными значениями функций 3 (х) и С (х)
в точке х. Следовательно, функции 3 (х) и С (х) определяются единственным
образом на всей бесконечной прямой.
1) Прежде чем перейти к доказательству непрерывности функций S (х)
и С (х), установим некоторые формулы.
Полагая в первых двух из соотношений (4.5) х'= х, х" ——'х и учиты-
вая, что 3(0) = 0, С (0) = 1, получим
0 = S(x)-C(-x) + C(x).S(-x), у
1 = С(х)<С(—х) —3(х)-3(—х). J	' ?
Умножим соотношения (4.14) соответственно на 3 (х) и С (х) и сложим полу-
ченные при этом соотношения. Учитывая, что S2 (х) С2 (х) = 1, получим
С(—х)=С(х).
Совершенно аналогично, умножая соотношения (4.14) соответственно на
С (х) и —3 (х) и складывая их, получим 3(—х) = •—3 (х). Таким образом,
С (х) — четная функция, а 3 (х) — нечетная функция **).
Но тогда, используя первую из формул (4.5), получим
3 (х") = S	=
/х'+х"\ _ /х'' —х'\	_ /х' + х"\ „/х" —х'\
5 \ 2 ;С\	2	2	\ 2 ]
и аналогично

Вычитая почленно последние две формулы, получим
3 (х") - S (х') = 2С	S	•	(4-15)
Докажем теперь непрерывность функций С (х) и 8 (х) в любой точке х
бесконечной прямой. Заметим, что непрерывность функции 3 (х) в точке
х — 0 справа • непосредственно вытекает из соотношения (4.7) и из равенства
8 (0) = 0. В самом деле, если {хга} — произвольная последовательность зна-
чений аргумента, сходящаяся к нулю справа, то из соотношения 0 < S (х„)<
< хп заключаем, что и соответствующая последовательность значений функ-
ции {S (х„)} сходится к нулю, т. е. к частному значению 8 /0).
*) Множество {х} точек бесконечной прямой называется всюду плотным
на бесконечной прямой, если в любой е-окрестности каждой точки этой пря-
мой имеется бесконечно много точек множества {х}.
**) Функция f(x) называется нечетной, если f(—x) — — l (х), и четной,
если f (— х) = f (х).
ДОПОЛНЕНИЕ К ГЛАВЕ 4
141
Из нечетности функции 5 (х) вытекает непрерывность этой функции в
точке х=0 слева. Таким образом, функция S (х) непрерывна в точке х = 0.
Непрерывность S (х) в любой точке х вытекает из соотношения (4.15).
В самом деле, пусть х — любая точка бесконечной прямой, {х„} — произволь-
ная сходящаяся к х последовательность значений аргумента. Положив в (4.15)
х' = х, х" =хд, будем иметь
S (х„) - 5 (х) = 2С S	.	 (4.16)
В силу того, что 5 (х) непрерывна в нуле и 5 (0) = 0, получим, что
о /Хп—х\ п „	(„!х -]- Х„\ 1
lim 5	—j = 0. Поскольку последовательность i—ограничен-
ная*), правая (а стало быть, и левая) -часть (4.16) имеет своим пределом
нуль. Но это означает, что lim 5 (хп) = S (х), т. е. функция S (х) непре-
П—*00
рывна в точке х.
Аналогично доказывается непрерывность функции С (х). Для этого вместо
(4.15) нужно получить формулу
С (х") - С (х') = - 25	S	'
2) Докажем, что значения функций S (х) и С (х) определяются единствеи-
рл
ным образом в точках g- , где р — целое положительное или отрицательное
число, а п — целое положительное число. Отметим, что такие точки обра-
зуют всюду плотное множество точек числовой прямой. Предварительно уста-
новим некоторые свойства функций 5(х) и С(х). Установим, во-первых, что
эти функции периодические и имеют период 2л**). В самом деле, полагая
в (4.15) х" == х -j-2n и х' = х, получим
5 (х 4- 2л) — S (х) = 2С (х 4- л) S (л).
Так как 5 (к) = 5 (у += 25 С = О,
то из последнего соотно-
шения вытекает, что
5 (х + 2л) = S (х),
т. е. функция 5 (х) периодическая и имеет период 2л. Отсюда, в частности,
следует, что S (2л) = 0.
Полагая во второй формуле (4.5) х' = х и х" = 2л и учитывая, что
5 (2л) — 0, найдем
С (х + 2л) = С (х) С (2л).
Так как С (2л) = 1 (в этом легко убедиться, применяя формулы (4.5) сначала
л ' л	,
для х = -£- и х = -g-, а затем для х = п и х = л), то
С (х + 2л) = С (х).
Таким образом, периодичность С (х) также установлена.
Свойство периодичности функций S (х) и С (х) позволяет в наших рас-
суждениях ограничиться сегментом [0, 2л]. Мы установим сейчас, какие знаки
*) Из соотношения S2 (х) + С2 (х) = 1 вытекает, что | С(х) |1 для всех х,
а отсюда вытекает ограниченность последовательности -(С I—g-—Д.
**) Функция f (х) называется периодической с периодом а>0, если для
любого х справедливо соотношение / (х 4- а) = f (х).
142
ПОНЯТИЕ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ
[ГЛ. 4
имеют значения функций S (х) и С (х) в различных точках этого сегмента.
Из (4.6), (4.7) и непрерывности S (х) следует, что на сегменте [о, значе-
ния функции 3 (х) неотрицательны, причем на этом сегменте функция S (х)
обращается в нуль только в точке х=0. Так как 3 (л—х) = 3 (л) С (—х) —
— С (л) 3 (х) *) и 3 (л) = О, С (л) = — 1, то 3(л — х) = 3 (х). Поэтому на сег-
менте л] значения, функции 3 (х) неотрицательны, причем на этом сег-
менте функция 3 (х) обращается в нуль только в точке х = л. Из формулы
3 (2л— х) = — S (х), которая может быть получена аналогично формуле
3 (л — х) = 3 (х), вытекает, что на сегменте [л, 2л] значения функции 3 (х)
неположительны, причем функция S (х) обращается в нуль лишь на концах
этого сегмента. Рассуждая совершенно аналогично, можно убедиться, что
функция С (х) неотрицательна на сегментах |^0, и |^-,2л^ и неположи-
[л Зл-]	л Зл
”2~ ’ "2 И °°Ра1Чается в НУЛЬ только в точках -g- и
Для завершения доказательства единственности функций S (х) и С (х)
нам понадобятся некоторые формулы, к выводу которых мы и переходим.
Во-первых, отметим, что из (4.5) вытекают следующие формулы **)
S2 (Й = ~~2~' ’ С2 (Й =	(Х) -	(4.17)
Полагая в этих формулах х — х'-\-х" и еще раз применяя формулы (4.5),
мы и получим интересующие нас соотношения
/х' + х"\ _ 1 - С (х') С (х”) + S (х') 3 (х")
\ 2	'	2
(х'+х"\ _ 1 + С (х') С (х") — 3 (х') 3 (х")
\ 2	)	2
Эти формулы показывают, что если известны значения функций 3 (х) и С (х)
в точках х' и х", то значения этих функций в точке —-------- определяются
единственным образом, поскольку из приведенных выше рассуждений сле-
дует, что нам известны знаки функций S (х) и С (х) в каждой точке сег-
мента [0, 2л], а следовательно, в силу их периодичности с периодом 2л, и
в любой точке х числовой прямой. Исходя из известных и единственным
71
образом определенных значений 3 (х) и С (х) в точках 0, -g-, л, 2л сегмента
[О, 2п], мы можем, применяя последовательно только что полученные фор-
мулы, вычислить единственным образом значения этих функций во всех точ-
D71
ках вида сегмента [0, 2л] (р и п — целые неотрицательные числа, причем
p=g2n+1). Так как множество точек вида всюду плотно на сегменте
[О, 2л], то, в силу сказанного в начале доказательства единственности, функ-
ции 3 (х) и С (х) единственным образом определены на всей числовой прямой.
*) Эта формула вытекает из первой формулы (4.5) и нечетности функции
3 (х).
**) Достаточно во второй формуле (4.5) взять х' = х" = -i-, а в третьей
а
%
формуле (4.5) взять вместо х.
ДОПОЛНЕНИЕ К ГЛАВЕ 4
143
2. Доказательство существования. Мы докажем более общее утвер-
ждение.
Существуют функции S (х) и С (х), определенные и непрерывные на всей
числовой прямой, удовлетворяющие требованиям:
Is. Для любых вещественных чисел х', х" и х выполняются соотношения
S (х' + х") = S (х') С (х") + С (х') S (х"), '
С (х' + х") = С (х') С (х") — S (х') S(x"),
S2 (х) + С2 (х) = 1.
S(0)=0, С (0) = 1, )
S (О) = 1, С (d) = 0, J
(4.51)
(4.61)
где d — некоторое заданное положительное число.
3°. Существует положительное число L такое, что при 0<х <d спра-
ведливы неравенства
0<S(x)<Lx,	(4.71)
причем, если d — -%, то L = 1.
Доказательство. Определим, во-первых, значения функций S (х) и
С (х) на множестве {s} точек сегмента [0, d], каждая из которых может
быть представлена в виде s = —, где р и п — целые неотрицательные числа,
причем р < 2”. Предварительно мы определим значения этих функций в точ-
ках sn = ^, п — 0, 1, ... Так как sn+1 = ^-’, то, используя формулы (4.17),
можно положить
S (5Л+1) = S	—g (s-n), с м = С fe) = +	1-+£М.
(4.18)
Из соотношения С (d) = С — С (s0) = 0 с помощью рекуррентных
формул (4.1-8) определяются значения S (х) и С (х) во всех точках вп — ^.
Дополнительно к указанным значениям S (х) и С (х) в точках sn мы опре-
делим значения этих функций в точках 0 и d так, как это указано в (4.61).
Перейдем теперь к определению значений S (х) и С (х) во всех точках
множества {s}, s — р и п—целые неотрицательные числа, р <2П. Изве-
стно, что любое целое положительное число может быть единственным обра-
зом представлено в виде суммы целых степеней числа 2 *);
р = У] а#"4 **),
/=1
где а(- равно либо нулю, либо единице. Поэтому
(4.19)
*) В двоичной системе счисления целое число р единственным образом
представляется в виде символа, состоящего из нулей и единиц. Этот символ
и представляет собой краткую запись числа р в виде суммы степеней числа 2.
**) См. сноску на стр. 57.
144
ПОНЯТИЕ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ
[ГЛ. 4
Таким образом, каждое значение s представимо в виде конечной суммы
чисел s,, для каждого из которых значения S (s,) и С (s,-) определены выше.
Мы можем теперь, используя формулы (4.51), определить значения S (х) и
С (х) в точках множества {s}. При этом мы должны убедиться, что после-
довательное применение этих формул приводит к одному и тому же резуль-
тату независимо от способа объединения слагаемых S; в группы в форму-
ле (4.19).	•
' Например, мы можем положить s = x'4-x", где х'— и х"—
п
— 2 aiSi, и затем вычислить S (s) по первой формуле (4.51). Но также
п
можно положить х' = ajSi + a2s2 и х" = У, a,-s;. Для того чтобы убедиться,
<=з
что последовательное применение формул (4.51) будет давать один и тот же
результат независимо от способа объединения слагаемых Si в группы в сумме
(4.19), достаточно, чтобы имели место соотношения
S [(х' 4- х") + х'"] = S [х' + (х" + х"')]
и
С |(х' + х") + х'"] = С [х' 4- (х" 4- х'")].
Справедливость этих соотношений устанавливается непосредственно путем
двукратного Применения формул (4.51).
Убедимся теперь, что функции S(s) и С (s), определенные нами на мно-
жестве {«}, обладают свойством I9 на этом множестве. Пусть s', s" и s' 4- s"
принадлежат указанному множеству. Представим s', s" и s'4-®" в виде
сумм (4.19). Объединяя входящие в s' и s" числа sn с одинаковыми п до тех
пор, пока оставшиеся sn не будут иметь различные индексы, мы придем
к группировке слагаемых sn, дающей представление (4.19) для числа s'4-s"-
Но выше мы показали, что результат вычисления S (s) или С (s) для суммы
нескольких аргументов не зависит от способа группировки слагаемых этой
суммы. Следовательно, если s', s" и s'4-s” принадлежат множеству {s}, то
значения S (s) и С (s), вычисленные в этих точках, удовлетворяют Первым
двум соотношениям (4.51). В справедливости третьего соотношения (4.51) для
указанных значений аргумента убедиться нетрудно. В самом деле, из опре-
деления S (х) и С (х) в точках 0 и d следует, что S2 (0) + С2 (0) = 1 и
S2 (d) 4- С2 (d) = 1. Из рекуррентных формул (4.18) вытекает справедливость
соотношения S2 (sn) 4* С2 (sn) = 1 для всех sn, а из непосредственно прове-
ряемой формулы
S2 (х'-+ х") 4- С2 (х' 4- х") = (S2 (х') + С2 (х')) (S2 (х") 4- С2 (х"))
следует справедливость соотношения S2 (s) 4- С2 (s) — 1 для всех точек мно-
жества {s}.
Покажем теперь, что для всех точек множества {s}, отличных от 0 и d,
справедливы неравенства
0<S(s)<l,	0<C(s)<l*).	(4.20)
Доказательство справедливости неравенств (4.20) проведем по индукции.
Для этого каждому п поставим в соответствие группу элементов множества {«},
"	, ,	pd
относя в эту группу все элементы {s}, которые можно представить в виде ,
где 0 < р < 2” и р — нечетное число. Элементы этой группы будут называться
*) Напомним, что в точках 0 и d значения S (s) и С (s) определены фор-
мулами (4.61).
ДОПОЛНЕНИЕ К ГЛАВЕ 4
145
элементами порядка п. Каждый элемент порядка п 4- 1 лежит между двумя
последовательными элементами, порядок которых не больше п и которые
отличаются друг от друга на т. е. на sa. Первый элемент порядка п + 1
равен sn+1. Все остальные элементы порядка л + 1 могут быть получены
прибавлением к sn+i различных s порядка п. Вычислим значения S (sj и С (sj
(st —единственное значение s порядка единицы). Имеем из (4.18) S (sT) =	-i-
и C(S1) =	Таким образом, для элементов первой группы неравенства
(4.20) имеют место. Допустим теперь, что неравенства (4.20) имеют место для
всех элементов, порядок которых не выше п.
Тогда, в силу первой формулы (4.51), значения S (s) во всех точках,
порядка- п + 1 положительны, а в силу третьей формулы (4.51) эти значения
не больше единицы. Полагая в первой формуле (4.51) к’ = d, х = — з и учиты-
вая четность функции С (s), найдем, что С (з) = 5 (d — з), и поэтому для С (з)
справедливы неравенства (4.20) для значений з порядка «4-1, так как, если s
имеет порядок л 4-1. то и d—s также имеет порядок л 4-1- По индукции
отсюда следует, что для всех точек множества {з}, отличных от 0 и d, спра-
ведливы неравенства (4.20).
Докажем, что функции. S (з) и С (s), определенные нами на множестве {з},
монотонны на этом множестве. Именно, покажем, что S (s) — возрастающая
s' ! ~ s'
функция, а С (s)— убывающая функция. Пусть Osgs' <s" < d. Тогда--------------—
5* __g'
и —2— заключены строго между нулем и d. Из формулы (4.15) и из нера-
венств (4.20) следует, что S (s") > S (s'). Следовательно, S (s) — возрастающая
функция. Из соотношения С (s) = S (d — s) следует, что С (з)— убывающая
на множестве {з} функция.
Докажем теперь, что функции S (s) и С (в), определенные на всюду плотном
множестве {s} точек сегмента [0, d], имеют предельное значение в каждой
точке сегмента [0, d].
Рассмотрим, во-первых, последовательность {з„} и покажем, что limS(s„) =
п -► оо
= 0 и limC(sn) = l (существование этих пределов следует из монотонности
п -* со
и ограниченности S (з) и С (s) на множестве {s}). Для доказательства рассмот-
{t (s ))	S (s )
 —- где t (sn) =	. Из (4.18) имеем
J	L \sn)
•2S C (S/Z4-l) — У" 1 — C2 = S (S-n)
и
C (Sn) — С2 ($7В+1)	(5Л+1) <
Поэтому
fen) __	_ 2S (Sft-iri) C (.sn+i) _ t (%-t-i) Ca (Sim) >
$n SnC (Sn) 2S/I+1 C ($n) sn+l	S/24-1
Итак, >. * fa-и) и £1^2 >, о ПрИ любом n, т. e. последовательность
вп sn+l $п	( $п J
убывающая и ограниченная. По теореме 3.15 она имеет предел, который мы
обозначим L:
lim =	(4.21)
д-*оэ
Так как s„ —0 при л —* оо, то lim ((s„) = 0, и поэтому, в силу ограниченности
л -* со
146
ПОНЯТИЕ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ
[ГЛ. 4
функции С (s) (см. (4.20)),
lim S (s„) = lim (t (s„) C (s„)) = 0.	(4.22)
n->oo	n-*oo
Поскольку C (s) > 0, из (4.22) и соотношения S2 (sn) + C2 (s„) = 1 вытекает,
что
limC(s„)=l.	(4.23)
л-* co
Отметим, что из (4.21) и (4.23) следует, что
lim =	(4.24)
n-»0O Sn
_ S (sn) 2S (sn+1) C (sn+i) S (s«+i)	(S (s„))
Так как —=> л+1< то последовательность {——>
Sn	^л+1	Sn+l	v Sn J
возрастает. Поэтому из (4.21) и (4.24) имеем
или
(sn) < д t (sn)
sn	Sn
S (sn) L • sn (sn)'
(4.25)
Пусть |s*}— любая сходящаяся к нулю последовательность значений s
из множества {$}. Для любого п можно, очевидно, указать такой номер k,
что Q <_s*<sk. Отсюда, в силу монотонности S (s) на множестве {s}, имеем
0 < S (s*) < S (sft). Поэтому из (4.22) следует, что lim S (s*) = 0.
Докажем теперь, что функция S (s), определенная на множестве {s} *),
имеет предельное значение в любой точке х сегмента [0, d]. Пусть —
монотонно возрастающая, сходящаяся к х последовательность элементов мно-
жества {s}. Так как (S(s^)J— возрастающая ограниченная последовательность,
то существует предел lim S (sn), который мы обозначим S (х). Пусть {s’}—
п—* оо
любая сходящаяся к х последовательность элементов множества {s}(s’t^x).
Тогда последовательность
ному lim S
л-» со
sn~sn
2
j- имеет предел нуль. Согласно доказан-
= 0. Из (4.15) и ограниченности функции С (s) имеем
sn~sn
2
= 0.
Иными словами, lim S (s’) = S (х). В силу произвольности последова-
л-*со
тельности }s"| это означает существование предельного значения функции
S (s), определенной на {s}, в каждой точке х сегмента [0, d]:
lim S (s) = S (x).
S-X
Из соотношения S2 (s) + C2 (s) = 1 и неотрицательности функции C (s) на
множестве {s} следует существование предельного значения функции С (s)
*) Напомним, что {$} — всюду плотное множество точек сегмента [0, d].
ДОПОЛНЕНИЕ К ГЛАВЕ 4
147
в каждой точке сегмента [0, d]. Мы будем обозначать предельное значение
этой функции в точке х символом С (х).
Определим теперь значения функций S (х) и С (х) в любой точке х сегмента
[О, d] как предельные значения в точке х функций S (s) и C(s), определенных
на множестве {s}. Докажем, что так определенные функции S (х) и С (х)
обладают свойствами Г и 2° утверждения, сформулированного в начале дока-
зательства существования функций S (х) и С(х). Предварительно установим,
что определенные указанным выше способом на сегменте [0, d] функции S (х)
и С (х) монотонны и непрерывны на этом сегменте. Во-первых, докажем, что
если х — любое число из сегмента [0, d], a s' и s" — любые числа из мно-
жества {s}, удовлетворяющие неравенству s' < х < s', то 3 (s') < 3 (х) < S (s'),
С (s')> C (х)>С (s'). Установим, например, что S(s')<S(x) (неравенства
S (х) < 3 (s') и С (s') >С (х) > С (s') доказываются аналогично). Пусть (s'n) —
сходящаяся к х, возрастающая последовательность чисел множества {s}, все
элементы s'n которой удовлетворяют неравенствам s' <s'n<.x. Так как на
множестве {s} функция S(s) возрастает, то последовательность (S(s„)— S (s’)|
возрастает и имеет положительные элементы. Поэтому предел 3 (х) — 3 (s’) *)
этой последовательности положителен. Таким образом, S (s') < S (х). Докажем
теперь, что функция S (х) возрастает на сегменте „ [0, d] (доказательство
убывания функции С (х) на атом сегменте проводится аналогично). Пусть х' и
х'— любые два числа сегмента [0, d], удовлетворяющие неравенству х'<х'.
Если s'— некоторое число множества {s}, заключенное между х' и х',
x’<s'<x', то по доказанному 3 (х') < 3 (s') и S(s')<S(x'), т. е.
S (х') < S (х'). Монотонность функции S (х) на [0, d] доказана. Прежде чем
перейти к доказательству непрерывности функций S (х) и С (х), устано-
вим, что предельные значения функций S (s) и С (s) в точках множест-
ва {s} совпадают со значениями этих функций в соответствующих точках
множества {s}.
Рассмотрим произвольное число s множества {s} и две сходящиеся к s
последовательности р'я| и |s’J элементов множества {s} таких, что s„<s<s'.
В силу монотонности функции 3 (s) на множестве {s} справедливы неравенства
3 (s„) < 3 (s) < S (s') **). Так как lim S(s„) = lim 3 (s') и указанные пре-
n — co
целы равны предельному значению в точке s функции 3 (s), то только что
сформулированное утверждение доказано. Убедимся теперь, что функции S (х)
и С (х) непрерывны- в каждой точке сегмента [0, d]. Для этого достаточно
установить, что эти функции непрерывны в каждой точке х указанного сег-
мента слева и справа, непрерывны справа в точке 0 и непрерывны слева
в точке d (см. замечание в п. 1 § 3). Докажем ради определенности непре-
рывность функции 3 (х) в точке х сегмента [0, d] слева (непрерывность справа
и непрерывность С (х) доказывается аналогично).
Пусть (s^J — некоторая сходящаяся к х слева последовательность чисел
множества {s}. Так как lim 3 (s^) = 3 (х), то для любого е > О можно указать
fe—>00
элемент s'k этой последовательности, для которого 0 < S (х) — 3 (s^) < е. Рас-
смотрим теперь произвольную сходящуюся к х слева последовательность {хп}.
Пусть N.— номер, начиная с которого выполняются неравенства s'k<Zxn<,x.
В силу возрастания функции при n^:N выполняются неравенства
3 (s^) < S (хп) <_ S (х). Сопоставляя эти неравенства с неравенствами
*) Поскольку . lim 3 (s„) = 3 (х), а 3 (s') — фиксированное число, то
lim Is («к) - $ («')] = S W - S (s').
n —* 00
**) Ради определенности мы доказываем это утверждение для функ-
ции 3(х).
148
ПОНЯТИЕ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ
[ГЛ. 4
О < S (х)— S(s'(i)<e, получим, что при n^N справедливы неравенства
0<S(x)— S(x„)i<e. Иными словами, предельное значение функции S (х)
в точке х слева равно частному ее значению в этой точке. Таким образом,
непрерывность S (х) в точке х слева доказана.
Определим теперь функции S (х) и С (х) на сегменте [d, 2d] с помощью
соотношений S (х + d) — С (х) и С (х + d) = — S (х). Применяя эти формулы
еще раз, распространим эти функции на сегмент [2d, 4d]. Повторяя эти рас-
суждения, мы определим эти функции для всех положительных значений х.
Для отрицательных значений х мы определим эти функции с помощью соот-
ношений S (х) — — S (—х) и С (х) =С(—х). Легко убедиться, что в результате
мы получим функции, непрерывные на всей бесконечной прямой.
Докажем, что функции S (х) и С (х) удовлетворяют требованиям 1°, 2’
и 3° утверждения, сформулированного в начале доказательства существования.
Заметим, что если s', s', s' + s' и s принадлежат множеству {s} сегмента
[О, d], то для этих значений аргумента формулы (4.51) имеют место. Из ука-
занного выше способа продолжения функции S (х) и С (х) следует справед-
ливость этих формул для значений аргумента d + s', s', где s' и s' принадлежат
сегменту [0, d]. Повторяя эти рассуждения, мы докажем, что соотношения (4.51)
справедливы для всех значений аргумента бесконечной прямой вида pd!2n,
где р и п — любые целые числа. Так как эти значения аргумента образуют
всюду плотное множество точек бесконечной прямой *), то в силу непрерыв-
ности функций S (х) и С (х), соотношения (4.51) будут справедливы для всех
значений х.
Поскольку требование 2° выполнено в результате построения функций
S (х) и С (х), остается убедиться в справедливости требования 3°. Отметим,
что если s', s' и s' + s' — элементы множества {s} сегмента [0, d] и справед-
ливы неравенства 0 < S (s') < Ls’ и 0 < S (s') < Ls’, то, в силу первой фор-
мулы (4.51) и неравенств (4.20), выполняются также неравенства 0<S (s' + s")<
< Ls' + Ls’ = L (s' + s'). Используя- это замечание, формулу (4.19) и нера-
венства (4.20) и (4.25),. легко убедиться, что неравенства 0 < S (s) < Ls
справедливы для всех s из множества {s} сегмента [0,d]. Так как это мно-
жество всюду плотно на [0, d], a S (х) — непрерывная функция, то для всех х
из [0, d] имеют место неравенства 0 < S (х) < Lx. Справедливость требования 3’
установлена.
Заметим теперь, что число L зависит от выбора d. Именно, если вместо d
d	s
выбрать число d* = —, то тогда s* = ~, По построению S(s*) = S(sn), и
k	k	' п'
S (s*)	S (s„)	1
поэтому lim—Цт- = lim k--------= kL (см. (4.24)). Выбирая А=— мы опре-
П—уОО	Л-» ОО Sn	L
делим на сегменте [0,' d*] такие функции S (х) и С (х), что будут выполняться
неравенства 0 < S (х) < х.
Геометрические соображения показывают, что если d — -g-, то 2S (sn) —
длина стороны правильного 2п-уголь'ника, вписанного в окружность радиуса
1, 2s„ —длина дуги окружности, стягиваемой хордой длины 2S (sn) и 21 (s„) —
длина стороны правильного 2и-угольника, описанного вокруг этой окружности.
Неравенства (4.25) в этом случае имеют вид S (sn) < srt < t (sn). Поэтому
в указанном случае L= 1. Утверждение полностью доказано.
*) См. сноску на стр. 140.
ГЛАВА 5
ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
В этой главе вводится понятие производной и дифференциала,
устанавливаются правила дифференцирования, вычисляются производ-
ные всех простейших элементарных функций, уже выписанные нами
в главе 1. Далее рассматриваются производные и дифференциалы
высших порядков.
§ 1.	Производная. Ее физическая
и геометрическая интерпретация
1.	Приращение аргумента и функции. Разностная форма усло-
вия непрерывности. Пусть функция y~f(x) определена на некото-
ром интервале *) (а, &). Фиксируем любое значение х из указанного
интервала и зададим аргументу в точке х произвольное приращение
Дх такое, что значение х-|-Дх также принадлежит интервалу (а, Ь\
Приращением функции y=f(x) в точке х, соответствующим
приращению аргумента Дх, назовем число
Ду —/(х ф-Дх) —/(х).	(5.1)
Так, для функции у — sinx приращение в точке х, соответствую-
щее приращению аргумента Дх, равно
Ду = sin (х + Дх) — sin х = 2 cos (х + sin у.	(5.2)
Имеет место следующее утверждение: для того чтобы функция
У—/(х) являлась непрерывной в точке х, необходимо и доста-
точно, чтобы приращение Ду этой функции в точке х, соответ-
ствующее приращению аргумента Дх, являлось бесконечно малым
при Дх -> 0.
*) Вместо интервала (а,Ь) можно рассматривать сегмент [а, &], полупря-
мую, всю бесконечную прямую и вообще любое плотное в себе множество {%}.
Определение плотного в себе множества {х} дано в § 3 главы 2.
150'
ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[ГЛ. 5
В самом деле, по определению, функция у =f(x) непрерывна
в тойке х, если существует предельное значение
lim /(х +Дх)=/(х).	(5.3)
Дх->0
В силу пункта 3 § 2 главы 4 существование предельного значения
(5.3) эквивалентно тому, что функция [/(х + Дх) — /(х)] аргумента Дх
является бесконечно малой при Дх —>- 0.
Доказанное утверждение позволяет выразить условие непрерыв-
ности функции y=f(x) в точке х в новой форме, а именно: функ-
ция y=f(x) непрерывна в точке х, если приращение Ду этой
функции в точке х, соответствующее приращению аргумента &х,
является бесконечно малым при Дх->0, т. е. если
lim Ду = lim [/(х + Дх) — /(х)] = 0.	(5.4)
Дл->0	Дх—>0
Условие (5.4) мы и будем называть разностной формой условия не-
прерывности функции у^—/(х) в точке х. Это условие мы будем
неоднократно использовать в дальнейшем.
С помощью условия (5.4) еще раз убедимся в том, что функция
у = sin х непрерывна в любой точке х бесконечной прямой. В самом
деле, из формулы (5.2), из условия |cos fx-f-^^j 1 и из равенства
lim sin = 0 непосредственно вытекает, что lim Ду = 0.
Ах -* 0	2	А х —>0
2.	Определение производной. Сохраним для функции у = f(x)
предположения и обозначения, сформулированные в начале предыду-
щего пункта.
Считая, что Дх 0, рассмотрим в данной фиксированной точке х
отношение приращения Ду функции в этой точке к соответствующему
приращению аргумента Дх
Ду = f(x + bx)—f(x)	f5
Отношение (5.5) будем называть разностным отношением (в данной
точке х). Поскольку значение х мы считаем фиксированным, раз-
ностное отношение (5.5) представляет собой функцию аргумента Дх.
Эта функция определена для всех значений аргумента Дх, принадле-
жащих некоторой достаточно малой окрестности точки Дх = 0, за
исключением самой точки Дх — 0. Таким образом, мы имеем право
рассматривать вопрос о существовании предела указанной функции
при Дх->0.
Определение. Производной функции y=f(х) в данной
фиксированной точке х называется предел при &х -> 0 разност-
ного отношения (5.5) (при условии, что этот предел существует).
ПРОИЗВОДНАЯ
151
§ 11
Производную функции у — f(x) в точке х будем обозначать
символом у' (х) или f (х). Итак, по определению,
/'(х) = lim lim' /(* + дх)~Ш	(5.6)
Отметим, что если функция _у =/(х) определена и имеет производ-
ную для всех х из интервала (а, Ь), то эта производная будет пред-
ставлять собой некоторую функцию переменной х, также определен-
ную на интервале (а, Ь).
3.	Производная с физической  точки зрения. Понятие произ-
водной мы ввели, исходя из физических соображений, еще в главе 1.
Здесь мы еще раз остановимся на физических приложениях понятия
производной.
Прежде всего, предположим, что функция у = f(x) описывает
закон движения материальной точки по прямой линии *). Тогда,
как известно, разностное отношение (5.5) определяет среднюю ско-
рость точки за промежуток времени от х до х + Дх. В таком случае
производная /' (х), т. е. предел разностного отношения (5.5) при
Дх—► 0, определяет мгновенную скорость точки в момент вре-
мени х. Итак, производная функции, описывающей закон движения,
определяет мгновенную скорость точки.
Чтобы не создалось представление о том, что понятие производ-
ной широко используется только в механике, приведем примеры при-
ложения понятия производной из других разделов физики.
Пусть функция у = /(х) определяет количество электричества у,
протекшего через поперечное сечение проводника за время х. (При
этом момент времени х = 0 берется за начало отсчета.) В таком
случае производная f (х) будет определять силу тока, проходящего
через поперечное сечение проводника в момент времени х.
Рассмотрим, далее, процесс нагревания некоторого тела. Предпо-
ложим, что функция у = f (х) определяет количество тепла **) у,
которое нужно сообщить телу для нагревания этого тела от 0° до х°.
Тогда, как известно из курса элементарной физики, разностное отно-
шение (5.5) определяет среднюю теплоемкость тела при нагревании
его от х° до (х’+ Дх)°. В таком случае производная f (х), т. е. пре-
дельное значение разностного отношения (5.5) при Дх —>- 0, опреде-
ляет теплоемкость тела при данной температуре х. Подчеркнем,
что эта теплоемкость, вообще говоря, меняется с изменением темпе-
ратуры х.	2
Мы рассмотрели примеры приложения понятия производной в трех
разных областях физики. При изучении курса общей физики читатель
*) То есть зависимость пути у, пройденного точкой от начала отсчета,
от времени х.
**) Выраженное, например, в калориях.
152
ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[ГЛ. 5
встретится с другими многочисленными примерами приложения поня-
тия производной.
4. Производная с геометрической точки зрения. В § 2 главы 1
мы рассматривали задачу о нахождении касательной к кривой, явля-
ющейся графиком функции у — f (х) (на некотором интервале (а, &)).
Там мы дали определение касательной к указанной кривой в точке
/И (х, f (х)) этой кривой. (Здесь х — некоторое значение аргумента
из’ интервала (а, Ь). См. рис. 5.1.) Если через Дх обозначить произ-
вольное приращение аргумента, а символом Р обозначить, точку на
кривой с координатами (х-|-Дх, f(x + ^x)), то касательную, прохо-
дящую через точку М
данной кривой, мы опре-
деляем как предельное по-
ложение секущей МР при
Дх->0. Из рис. 5.1 ясно,
что угловой коэффициент
секущей МР (т. е. тангенс
угла наклона этой секущей
к оси Ох) равен разност-
ному отношению (5.5). Из
этого факта и из того, что
в пределе при Дх —> 0 угол
наклона секущей должен
' переходить в угол наклона
касательной, мы в § 2 главы 1 сделали основанный на наглядных
соображениях вывод о том, что производная f (х) равна угло-
вому коэффициенту касательной в точке М к графику функ-
ции у = f(x).
В настоящем пункте мы уточним указанные наглядные соображе-
ния. Предположив, что функция у = f(xj имеет производную в дан-
ной точке х, мы докажем: 1) что график функции у = /(х) имеет
касательную в данной точке М (х, /(х)), 2) что угловой коэффициент
указанной касательной равен f (х).
Будем доказывать утверждения 1) и 2) одновременно. Обозначим
угол наклона секущей МР к оси Ох. символом ср(Дх). Поскольку
угловой коэффициент секущей МР (т. е. tg <р (Дх)) равен отношению
ср (Дх) = arctg
(5-7)
при любом достаточно малом Дх, отличном от нуля. Из существова-
ния производной f (х), т. е. из существования предельного значения
lim ~' = /' (х) и из непрерывности функции и = arctg х для всех
дх -* о
значений аргумента вытекает существование предельного значения
§ 1)	ПРОИЗВОДНАЯ	153
функции (5.7) в точке Дх = 0 и равенство
lim <р(Дх) — lim arctg = arctg f (х).	(5.8)
дл-сО	дх—>о
Равенство (5.8) доказывает существование предельного значения (при
Дх—>0) угла наклона секущей МР, т. е. доказывает существование
касательной в точке М. Кроме того, из равенства (5.8) вытекает, что
если обозначить угол наклона касательной через <р0, то ф0 = arctg f (х),
т. е. tg«0=/'(x).	'	-
5. Правая и левая производные. В полной аналогии с поняти-
ями правого и левого предельных значений функции вводятся понятия
правой и левой производных функции y=f(x) (в данной точке х).
Определение. Правой {левой) производной функции
y=f{x) в данной фиксированной точке х называется правое
(левое) предельное значение разностного отношения (5.5) в точке
Дх=0 (при условии, что это предельное значение существует).
Правую производную функции y—f(x) й точке х обычно обо-
значают символом /' (х + 0), а левую производную в точке х — сим-
волом f (х — 0).
Если функция y—f(x) имеет в точке х производную, то она
имеет в этой точке и правую, и левую производные, совпадаю-
щие между собой. Если функция y=f(x) имеет в точке х и
правую, и левую производные и если указанные производные совпа-
дают между собой, то функция у — f (х) имеет в точке х произ-
водную *). Вместе с тем существуют функции, имеющие в данной
точке х и правую, и левую производные, но не имеющие производ-
ной в этой точке. Примером такой функции может служить функция
,, ч ,	( + х, если х 2s 0,
f(x)= х
( — х, если ,х < 0.
Эта функция имеет в точке х —0 правую производную, равную
lim — = 1, и левую производную, равную lim —.— = —1,
Дх->0-|-0ДХ	Дх-0 —о
но не имеет в точке х = 0 производной.
6. Понятие производной векторной функции. В математическом ана-
лизе и его приложениях часто встречаются понятия векторной функции и
се производной.
Если каждому значению переменной t из некоторого множества {/} ста-
вится в соответствие по известному закону определенный вектор а, то говорят,
что на множестве {/} задана векторная функция а = а (/).
Так как каждый вектор а в заданной декартовой прямоугольной системе
однозначно определяется тремя координатами х, у и г, то задание векторной
функции а = a (t) эквивалентно заданию трех скалярных функций х = х (/),
У = У (0 и г = г (/).
*) Это утверждение следует из соответствующего утверждения для пра-
вого и левого предельных значений функции (см. замечание из п. 1 § 2
главы 4).
154
ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[ГЛ. 5
Понятие векторной функции становится особенно наглядным, если обра-
титься к так называемому годографу этой функции.
Годографом называется геометрическое место концов всех векторов а (/),
приложенных к началу координат О. Кривая L на рис. 5.2 представляет собой
годограф векторной функции а = a (f).
Понятие годографа векторной функции представляет собой обобщение по-
нятия графика скалярной функции.
Введем понятие производной векторной функции а (/) в данной фикси-
рованной точке t. Для этой цели придадим аргументу t произвольное прира-
щение St и рассмотрим вектор Да — a (t + St) — a (t) (на рис. 5.2 указан-
ный вектор совпадает с вектором МР). Умножив указанный вектор на число
1/Д/, мы получим новый вектор
Дд 1
= А 1а(< + ДО-а(/>], (5.5*)
ill ill
коллинеарный прежнему. Вектор (5.5*)
является аналогом разностного отноше-
ния (5.5). Отметим, что вектор (5.5*)
представляет собой среднюю скорость
изменения векторной функции на сег-
менте [<, t + S Z].
Производной. секторной функции
а = a (t) в данной фиксированной точке t
называется предел при St — 0 разност-
ного отношения (5.5*).
Производная векторной функции а (/)
da
обозначается символом a (t) или
Из геометрических соображений очевидно, что производная векторной
функции а = а (/) представляет собой вектор, касательный к годографу этой
функции.
Так как координаты разностного отношения (5.5*) соответственно равны
X(t + st)-x(t) у (tМ) ~ у (t) г(Г + Д[)-г(0
St ’	St ’	St
то ясно, что координаты производной a' (t) равны производным функций х' (t)
у' (t), z’(t). Таким образом, вычисление производной векторной функции сво-
дится к вычислению производных ее координат.
Замечание 1. Так как векторная функция а = a (t) определяет закон
движения материальной точки по кривой L, представляющей собой годограф
этой функции, то производная a' (t) равна скорости движения по указанной
кривой.
Замечание 2. Из курса аналитической геометрии известны различные
типы произведений векторов (скалярное произведение, вектор-ное произведение
и смешанное произведение). Выражение всех этих произведений в координа-
тах дает возможность указать правила, по которым вычисляются производные
соответствующих произведений векторных функций. В качестве примера при-
ведем правило вычисления производной скалярного произведения двух век-
торных функций а (/) = {at (/), ц2 (/), а3 (/)} и b (/) = {Ьх (/), Ьг (t), b3 (О}-
{a (f)b(0}' = a'(W) + a(0b' (t) =
= W (0 bi (0 + a, (t) b, (t) + a, (t) (0} + К (0 Ь\ (/) + а2 (0 Ь' (0 + а3 (0 Ь, (/)}.
Аналогичное правило справедливо и для векторного произведения двух век-
торных функций:
[a (0 b (Of = la' (/)b(01 + la (/)Ь' (0].
§ 2]
ПОНЯТИЕ ДИФФЕРЕНЦИРУЕМОСТИ ФУНКЦИИ
155
§ 2.	Понятие дифференцируемости функции
1.	Понятие дифференцируемости функции в данной точке.
Пусть, как и в п. 1 и 2 предыдущего параграфа, функция y=.f(x)
определена на некотором интервале (а, Ь), символом х обозначено
некоторое фиксированное значение аргумента Из указанного интер-
вала, а символом Дх обозначено любое приращение аргумента, такое,
что значение аргумента х + Дх также принадлежит (а, Ь).
Определение. Функция у, — f(x) называется дифференци-
руемой в данной топке х, если приращение Ду этой функции
в точке jc, соответствующее приращению аргумента йх, может
быть представлено в виде
Ьу==АЬх-\-а Ьх,	(5.9)
где А — некоторое число, не зависящее от Дх, а а, — функция
аргумента Ьх, являющаяся бесконечно малой при Дх->0.
Заметим, что функция а(Дх) может принимать в точке Дх = 0
какое угодно значение (при этом в этой точке остается справедли-
вым представление (5.9)). Ради определенности можно положить
а(0) = 0*).
Так как произведение двух бесконечно малых аДх является бес-
конечно малой более высокого порядка, чем Дх (см. п. 3 § 2 главы 4),
т. е. аДх = о(Дх), то формулу (5.9) можно переписать в виде
Ду = А Дх + о (Дх).
Теорема 5.1. Для того чтобы функция у = /(х) являлась
дифференцируемой в данной точке х, необходимо и достаточно,
чтобы она имела в этой точке конечную производную.
Доказательство. 1) Необходимость. Пусть функция
у = f (х) дифференцируема в данной точке х, т. е. ее приращение Ду
в этой точке представимо в виде (5.9). Предположив, что Дх 0 и
поделив равенство (5.9) на Дх, получим
Й = Л + а-	(5Л°)
Из равенства (5.10) вытекает существование производной, т. е. пре-
дельного значения lim т^- = А.
д.^оДх
2)	Достаточность. Пусть функция y=f(x~) имеет в данной
точке х конечную производную, т. е. существует предельное значение
limg=/(x).	(5.П)
*) При этом частное значение функции а (Дх) в точке Дх = 0 будет сов-
падать с ее предельным значением в .этой точке.
156
ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
(ГЛ. 5
В силу определения предельного значения функция а = ^— f'(x)
аргумента Дх является бесконечно малой при Дх—>0, т. е.
Д^=/'(х)Дх + аДх,	(5.12)
где lim а = 0. Представление (5.12) совпадаете представлением (5.9),
Дх —0
если обозначить через А не зависящее от Дх число f (х). Тем са-
мым доказано, что функция* _у=/(х) дифференцируема в точке х.
Теорема 5.1 доказана.
Доказанная теорема позволяет нам в дальнейшем отождествлять
понятие дифференцируемости функции в данной точке с поня-
тием существования у функции в данной точке производной.
Операцию нахождения производной в дальнейшем договоримся
называть дифференцированием.
2.	Связь между понятиями дифференцируемости и непрерыв-
ности функции. Имеет место следующее элементарное утверждение.
Теорема 5.2. Если функция у =f(x) дифференцируема в дан-
ной точке х, то она и непрерывна в этой точке.
Доказательство. Так как функция y=f(x) дифференцируема
в точке х, то ее приращение 5.у в этой точке может быть представ-
лено в виде (5.9). Но из формулы (5.9) вытекает, что lim Aj = 0,
Ах —0
т. е. функция у— f(x) непрерывна в точке х в силу разностной
формы условия непрерывности (см. п. 1 § I). Теорема доказана.
Естественно, возникает вопрос о том, справедливо ли утвержде-
ние, обратное теореме 5.2, т. е. вытекает ли из непрерывности функ-
ции в данной точке ее дифференцируемость в этой точке. На этот
вопрос следует дать отрицательный ответ, ибо существуют функции,
непрерывные в некоторой точке, но не являющиеся в этой точке диф-
ференцируемыми. Примером такой функции может служить функция
у = | х |. Очевидно, что эта функция непрерывна в точке х = 0,- но
она (как показано в конце п. 5 § 1) не является дифференцируемой
в этой точке. Отметим, что существуют непрерывные на некотором
сегменте функции, не имеющие производной ни в одной точке этого
сегмента *).
3.	Понятие дифференциала функции. Пусть функция y—f(x)
дифференцируема в точке х, т. е. приращение Ьу этой функции
в точке х может быть записано в виде (5.9). Анализируя формулу
(5.9), мы приходим к выводу, что приращение Д_у дифференцируемой
функции представляет собой сумму двух слагаемых: первое из этих
слагаемых А Ьх при А 0 представляет собой функцию приращения.
*) Первый опубликованный пример такой функции принадлежит Вейер-
штрассу. Ранее независимо от него аналогичный пример был построен чеш-
ским математиком Больцано, но этот пример не был опубликован. В Дополне-
нии к главе 11 будет указан пример такой функции.
§ 2J
ПОНЯТИЕ ДИФФЕРЕНЦИРУЕМОСТИ ФУНКЦИИ
157
аргумента Дх, линейную и однородную *) относительно Дх; это
слагаемое представляет собой при Дх -> 0 бесконечно малую та-
кого же порядка, что и Дх; второе слагаемое аДх представляет
собой при Дх -> О бесконечно малую более высокого порядка, чем
Дх, так как отношение = а стремится к нулю при Дх—>0. Таким
образом, при А0 первое слагаемое ЛДх является главной частью
приращения дифференцируемой функции. Эту главную часть прира-
щения называют дифференциалом функции в точке х, соответствую-
щим приращению аргумейта Дх.
Итак, в случае А 0 дифференциалом функции у = /(х) в дан
ной 'точке х, соответствующим приращению аргумента
называют главную линейную от-
носительно &х часть прираще-
ния этой функции в точке х.
Принято обозначать дифферен-
циал функции у = f (x) символом
dy. Если для приращения функции
Ду/ справедливо представление
(5.9), то дифференциал этой функ-
ции по определению, равен
dy = А • Дх. (5.13)
х	л
В случае Л = 0 слагаемое А • Дх	Рис. 5.3.
перестает быть главной частью
приращения Ду дифференцируемой функции (ибо это слагаемое равно
нулю в то время, как слагаемое а-Дх, вообще говоря, отлично от
нуля). Однако договариваются и в случае А — 0 определять диффе-
ренциал функции формулой (6.13), т. е. считают, что он равен нулю
в этом случае.
Если учесть теорему 5.1, т. е. учесть, что A—f' (х), то формулу
(5.13) можно переписать в виде
dy=f (х) Дх.
(5.14)
Формула (5.14) дает выражение дифференциала функции в точке х,
соответствующего приращению аргумента Дх. Следует подчеркнуть,
что дифференциал функции dy в данной точке х, вообще говоря, не
равен приращению функции Ду в этой точке. Это особенно легко
уяснить из рассмотрения графика функции y=f(x) (рис. 5.3). Пусть
точка М на кривой y=f(x) соответствует значению аргумента х,
точка Р на той же кривой соответствует значению аргумента х-ф-Дх,
AIS' — касательная к кривой у— f(x) в точке М. Пусть далее Л'Ш || Ох,
♦) Напомним, что линейной функцией аргумента х называется функция
вида у = Ах + В, где Л и В — некоторые постоянные. В случае В = 0 линей-
ная функция называется однородной.
158	ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ	[ГЛ. 5
PN || Оу, Q — точка пересечения касательной A1S с прямой PN. Тогда
приращение функции Ду равно величине отрезка NP. В то же время
из прямоугольного треугольника MQN и из формулы (5.14) ясно,
что дифференциал функции dy равен величине отрезка NQ, ибо вели-
чина отрезка MN равна Дх, а тангенс угла / QMN равен /' (х).
Очевидно, что величины отрезков NP и NQ, вообще говоря, различны.
В заключение этого пункта мы установим выражение для диффе-
ренциала функции _У=/(х), аргумент х которой является независи-
мой переменной *).
Введем понятие дифференциала dx независимой переменной х.
Под дифференциалом dx независимой переменной х можно понимать
любое (не зависящее от х) число. Договоримся в дальнейшем брать это
число равным приращению Дх независимой переменной **). Это дого-
воренность позволяет нам переписать формулу (5.14) в виде-
dy = f (х) dx.	(5.15)
Подчеркнем, что формула (5.15) пока что установлена нами лишь для
случая, когда аргумент х является независимой переменной. Однако
ниже, в § 9, мы докажем, что формула (5.15) остается справедливой
и для случая, когда аргумент х не является независимой переменной,
а сам представляет собой дифференцируемую функцию некоторой
новой переменной.
Пока что мы можем сделать следующий вывод из формулы (5.15):
для случая, когда аргумент х. функции y=f(x) является независи-
мой переменной, производная f (х) этой функции равна отношению
дифференциала функции dy к дифференциалу аргумента dx, т. е.
В § 9 будет доказано, что это соотношение справедливо и в случае,
когда аргумент х сам является дифференцируемой функцией некото-
рой новой переменной.
§ 3.	Правила дифференцирования суммы, разности,
произведения и частного
Теорема 5.3. Если каждая из функций и(х) и v(x) дифферен-
цируема в данной точке х, то сумма, разность, произведение и
частное этих функций (частное при условии, что v (х) 0)
также дифференцируемы в этой точке, причем имеют место
*) Подчеркнем, что аргумент х функции у = f (х), вообще говоря, сам
может являться функцией некоторой переменной.
**) Эта договоренность оправдывается рассмотрением независимой пере-
менной х как функции вида у = х, для которой dy = dx = Дх.
§ 3]
ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ
159
формулы
[и (х) ± V (х)]' = и' (х) ± ъ’ (X),
[и (х) V (х)]' = и’ (х) V (х) + и (х) v’ (х),	(5.16)
Гм (х) V_и' (х) у (х) — и (х) и' (X)
Ь (х) J	О2 (X)
Доказательство. Рассмотрим отдельно случаи суммы (разно-
сти), произведения и частного.
1°. Пусть у (х) = и (х) ± v (х). Обозначим символами Ди, Дд
и Ду приращения функций и(х), д(х) и у(х) в данной точке х,
соответствующие приращению аргумента Дх. Тогда, очевидно,
Ду = у (х 4- Дх) - у (х) =
= [и (х + Дх) zh v (х + Дх)] — [и (х) ± v (х)] =
[н (х + Дх) — и (х)] ± [Д (X ф- Дх) — д (х)] = Ди ± Дд.
Таким образом, при Дх О
Ду=Д«±Дд	(517)
Дх Дх Дх	'
Пусть теперь Дх—>0. Тогда в силу существования производных функ-
ций и(х) и д(х) в точке х существует предельное значение правой
части (5.17), равное и' (х) ± д' (х). Стало быть, существует предель-
ное значение (при Дх—>0) и левой части (5.17). По определению
производной указанное предельное значение равно у' (х), и мы при-
ходим к требуемому равенству
у'(х) = п' (х)±д'(х).
2°. Пусть далее у (х) = и (х) д (х). Сохраняя за Ди, Дд и Ду тот
же смысл, что и выше, будем иметь
Ду = у (х + Дх) —у (х) =
= и (х + Дх) д (х + Дх) — и (х) д (х) =
= [и (х + Дх) д (х + Дх) — и (г 4- Дх) д (х)] 4-
4- [и (х 4- Дх) д (х) — и (х) д (х)]
(мы прибавили и вычли слагаемое и (х 4- Дх) д (х)). Далее можем
записать:
Ду = и (х 4- Дх) [д (х 4- Дх) — д (х)] 4- f (х) [и (х 4- Дх) — и (х)] =
= и (х 4- Дх) Дд 4- д (х) Дм.
Таким образом, при Дх 0
Е = »<* + 4*)п + ’«Е-	<5Л8>
Пусть теперь Дх —- 0. Тогда в силу дифференцируемости функций
160
ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
(ГЛ. 5
и(х) и v(x) в точке х существуют предельные значения отношений
Ьи \у	, . .	, . . „	, ,
Дл и Д? ’ соответс'гвенно равные и (х) и v (х). Далее из дифферен-
цируемости и(х) в точке х, в силу теоремы 5.2, следует непрерыв-
ность и(х) в этой точке. Стало быть, существует предельное значе-
ние lim /т(х4-Дх), равное и(х). Таким образом, существует пре-
Дх—0
дельное значение правой части (5.18) при Дх —0, равное w(x)©'(x)-|-
-\-v(x)u'(х). Стало быть, существует предельное значение (при
Дх —0) и левой части (5.18). По определению производной указанное
предельное значение равно у' (х), и мы приходим к требуемой формуле
у' (х) = и' (х)v (х) + и (х) ъ' (х)-
3°. Пусть, наконец, у (х) =	. Тогда*)
Д^=>(х + Дх)-у(х)^5^±^-^ =
s 4	1	'	4 ' V (х + Дх) V (х)
и (х У Дх) у (х) — а (х &х) » (х)
~~ у (х) у (х + Дх)
Добавляя и вычитая в числителе слагаемое и(х)и(х), будем иметь:
д __ (u (х 4- Дх) v(x) — u (х),у (х)] — (о (х + Дх) и (х) — и(х)у (х)] _
х	у (х) у (х + Дх)
. у (х) [и (х 4- Дх) — и (х)] — и (х) [у (х + Дх) — у (х)] _
у (х) у (х 4- Дх)
у (х) Ди — и (х) Ду
у (х) у (х 4- Дх) ‘
Таким образом, при Дх 0
. .Ди . . До
Ди’<х>ГГй(х)1й -	(5.19)
Дх у (х) у (х 4- Дх)
Пусть теперь Дх—> 0. В силу дифференцируемости (и вытекающей
из нее непрерывности) функций и(х) и Т'(х) в точке х существуют
предельные значения
lim Хх =
дх—о
lim т— — v' (х), lim v (х 4- ^х) = v (х).
Дд—0ах	Дх —0
*) Так как в дальнейшем в знаменателе фигурирует значение о(х4-Дх),
то следует доказать, что это значение отлично от нуля для всех достаточно
малых Дх. В самом деле, если бы это было не так, то нашлась бы бесконечно
малая последовательность значений Дхп такая, что о (х 4- Дхп) = 0. Но поскольку
функция у (х) непрерывна для значения аргумента х, то мы получили бы из
условия о (х 4-Дхя) = 0, что у (х) = 0, а это противоречит условию теоремы.
'§ 4J	ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ	161
~ *
Таким образом, поскольку v (х) # 0, существует предельное значение
при Дх—►О правой части (5.19), равное
v (х) и' (х) — у’ (х) и (х)
Стало быть, существует предельное значение (при Дх—-0) и левой
части (5.19). По определению производной указанное предельное зна-
чение равно у' (х), и мы получим требуемую формулу
z ч _ и' (х) у (х) — у' (х) и (х)
У	у2 (х)	' '
Теорема .5.3 полностью доказана.
§ 4.	Вычисление производных степенной функции,
тригонометрических функций и логарифмической функции
В этом параграфе мы приступим к вычислению производных про-
стейших элементарных функций.
1.	Производная степенной функции с целочисленным пока-
зателем. Начнем с вычисления производной степенной функции у. — Xя,
показатель п которой является целым положительным числом *). Слу-
чай степенной функции, показатель которой является любым вещест-
венным (не обязательно целым) числом, отложим до § 8.
Используя формулу бинома Ньютона, можем записать
Ду = (х + Дх)" — х" =
— [х" 4- лх"-1Дх + ” ^п~ х"~2 (Дх)2 +... + (Дх)" J — х" =
= дх"-1 Дх +	х"“2 (Дх)2 4-... + (Дх)".
Таким образом, при Дх^ДО
= лх"-1 +	х"-2 Дх +... + (Дх)"’1.	(5.20)
Поскольку все слагаемые в правой части (5.20), начиная со второго,
содержат в качестве множителя Дх в положительных степенях, суще-
ствует предельное значение указанных слагаемых при Дх—-0, рав-
ное нулю. Первое слагаемое в правой части (5.20) от Дх не зави-
сит. Стало быть, существует предельное значение (при Дх —0) пра-
вой части (5.20), равное их"-1. По определению производной указанное
предельное значение равно производной функции у = х", т. е.
(х")' = пхя~1.
*) Эта производная уже рассматривалась в главе 1 с помощью интуитив-
ного представления о пределе.
162	ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ	[ГЛ 5
Проведенные рассуждения справедливы для любой точки х беско-
нечной прямой.
2.	Производная функции y = sinx. Пользуясь формулой приве-
дения разности синусов к виду, удобному для логарифмирования,
можем записать:
Ду = sin (х + Дх) — sin х — 2 cos ^х + у-) sin у-.
Таким образом, при Дх О
Ду	/ . Дх\£'п\1г)	„
t^=cos х + т,- —~	(5.21)
Дх	\ 1 2 ] /Дх\	k	'
Ы
Так как функция у = cosx является непрерывной в любой точке х
бесконечной прямой *), то существует предельное значение
/ Дх \
lim cos |^x + -2j = cosx.	(5.22)
Далее, в силу основного результата п. 2 § 6 главы 4, существует
предельное значение
Иш	(5.2.3)
“-° Т
Таким образом, существует предельное значение (при Дх—>0) правой
части (5.21), равное произведению предельных значений (5,22) и (5.23),
т. е. равное cosx. По определению производной указанное предель-
ное значение равно производной функции y = sinx, т. е.
(sinx)' = cosx.
Проведенные рассуждения справедливы для любой точки х беско-
нечной прямой.
3.	Производная функция у = cosx. Пользуясь формулой при-
ведения разности косинусов к виду, удобному для логарифмирования,
можем записать:
Ду = cos (х + Дх) — cosx= — 2 sin ^х + sin
Таким образом, при Дх 0
Ду . / Дх\sin \ 2 /	_ о.
f- = — sin х + -s-1—(5.24)
Дх \	2 / 1^х\	'	’
*) Это доказано в п. 6 § 5 главы 4. Впрочем, непрерывность функции
у = cos х легко доказать, используя разностную форму условия непрерывности.
ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ
163
§ fl
Так как функция _y = sinx является непрерывной в любой точке х
бесконечной прямой, то существует предельное значение
/ Дх \
lim sin (х +	) = sin X.	(5.25)
Из существования предельных значений (5.23) и (5;25) вытекает
существование предельного значения (при Дх—>0) правой части (5.24),
равного (—sinx). По определению производной последнее предель-
ное значение равно производной функции у — cosx, т. е. .
(cos х)' = — sin х.
Проведенные рассуждения справедливы для любой точки х бесконеч-
ной прямой.
4.	Производные функций y = tgx и _y = ctgx. Так как нами
уже вычислены производные функций у = sinx и у = cosx и так
как
, sin х . cos х
tg х =---, ctg х = -—,
b cosx’	sinx ’
то для вычисления производных функций у — tg х и у = ctg х можно
воспользоваться теоремой 5.3 (точнее формулой, выражающей произ-
водную частного, т. е. третьей из формул. (5.16)).
Мы получим, что всюду, кроме тех точек, в которых cosx = 0,
,4.„	 (sin х)' cosx—(cosx)' sin х 1
' ®	cos2x	cos2x'
Итак,
^для всех значений х, кроме х =-|-+ ттг, где п = 0, ±1, Ана-
логично всюду, кроме тех точек, в которых sinx = 0,
__________(cos ХУ sin х — (sin х)'cos х 1
(Ctgx) -__-- --	— Ип^х*
Итак,
(ctg х)' = —	= — (1 + ctg2 х)
(для всех значений х, кроме х = г.п, где п=0, ±1,...).
5.	Производная функции у = loga X (0 < а =#:!). Взяв в каче-
стве х любую точку полупрямой х>0 и считая, что |Дх|<^х, мо-
жем записать:
Ду = loga (X + Дх) - loga х = log„ —= loga (1 + v) •
Л	Л J
164
ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[ГЛ. 6
Таким образом, при Дх =4 О
Д{/	1 	/, , Дх \ ,	/. , Дх\4/А-»
Дх- Дх	Oga\1+T) —
1 ,	[7, . Дх\*/Д*| /К
= V10go U+v •	(5-26)
Л	\	Л ] J
В силу основного результата п. 3 § 6 главы 4 выражение в квад-
ратных скобках имеет при Дх—>0 (и при любом фиксированном
значении х) предельное значение, равное е. Тогда на основании непре-
рывности функции _у= 10gox в точке х = е существует предельное
значение (при Дх—> 0) правой части (5.26), равное у loga е. По опре-
делению производной указанное предельное значение равно произ-
водной функции у == loga х, т. е.
OOga X)'=Y 10ge 6
(для всех значений х, принадлежащих полупрямой х>0). В частном
случае а~е получим
(1пх)' = у.
§ 5. Теорема о производной обратной функции
Теорема 5.4. Пусть функция y=f(x) в некоторой окрестно-
сти точки х0 возрастает (или убывает) и является непрерыв-
ной. Пусть, кроме того, функция у=/(х) дифференцируема
в точке х0 и производная f (х0) отлична от нуля. Тогда суще-
ствует обратная функция х—/~Л(у), которая определена в неко-
торой окрестности соответствующей точки y0—f(x0), диффе-
ренцируема в этой точке и имеет в этой точке производную,
1
раеную Ш'
Доказательство. Прежде всего заметим, что для _ функции
y—f(x) выполнены в окрестности точки х0 все условия следствия
из леммы 1 § 4 главы 4. Согласно этому следствию существует
обратная функция х=/-1(_у), определенная в некоторой окрестности
точки х0=/,(х0) и непрерывная в этой окрестности. Придадим аргу-
менту у этой обратной функции в точке у0 произвольное отличное
от нуля приращение Ду. Этому приращению отвечает приращение Дх
обратной функции, причем в силу возрастания (или убывания) функ-
ции Дх уЬ 0. Таким образом, мы имеем право написать следующее
тождестве:
Дх _ 1
(5.27)
Дх
§61
ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ
165
Пусть теперь в тождестве (5.27) Ду->0. Тогда, в силу непрерывности
обратной функции х = У"1 (у) в точке _у0 и согласно разностной форме
условия непрерывности, и Дх—>0.
Но при Дх — 0 знаменатель дроби, стоящей в правой части (5.27),
по определению производной, имеет предельное значение, равное
f (х0)	0. Стало
дельное значение,
быть, правая часть (5.27)
1 U
равное Но тогда и
/ (*о/
имеет при Ду — 0 пре-
левая часть (5.27) имеет
при Д_у — 0 предельное значение. По опреде-
лению производной указанное предельное
значение равно *) {У"1 (_Уо)Г- Таким образом,
мы доказали дифференцируемость обратной
функции в точке у0 и получили для ее про-
изводной соотношение
(3.28>
Теорема 5.4 доказана.
Доказанная теорема имеет простой гео-
метрический смысл. Рассмотрим в окрестности
точки х0 график функции у — У(х) (или обрат-
ной функции). Предположим, что точке х0 на этом графике соответ-
ствует точка М (рис. 5.4). Тогда, очевидно, производная f (х0) равна
тангенсу угла наклона а касательной, проходящей через точку М,
к оси Ох. Производная обратной функции {f 1 (у0) у равна тангенсу
угла наклона р той же касательной к оси Оу. Поскольку углы аир
в сумме составляют.тс/2, то формула (5.28) выражает очевидный факт:

§ 6. Вычисление производных показательной функции
и обратных тригонометрических функций
В этом параграфе, опираясь на доказанную выше теорему 5.4,
мы продолжим вычисление производных простейших элементарных
функций.
1. Производная показательной функции у = ах (0<а	1).
Показательная функция у — ах, будучи определена на бесконечной
прямой, служит обратной для логарифмической функции x = logay,
определенной на полупрямой _у>0. Поскольку для логарифмической
функции в окрестности любой точки у полупрямой у > 0 выполнены
все условия теоремы 5.4, то, согласно этой теореме, функция у = ах
дифференцируема в любой точке x = logey и для ее производной
*) Символом {/ 1 (1/0)}' мы обозначаем производную обратной функции а
точке уа.
166
ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[ГЛ. 5
справедлива формула
(0х}' —___1___=_____!____— у .
doga[/)' |]ogae logee*
Из этой формулы, воспользовавшись известным из элементарного курса
соотношением loga& = |^-^ и учитывая, что у = ах, окончательно
получим
(а*)' = ах In а.
Полученная формула справедлива для всех точек х бесконечной пря-
мой. В частном случае а — е эта формула принимает вид
(ех)' = ех.
2. Производные обратных тригонометрических функций. Нач-
нем с вычисления производной функции у = arcsin х. Эта функция,
будучи определена на интервале — 1 < x<Z + 1, служит обратной для
функции x = siny, определенной на интервале —	+ По-
скольку для функции x = siny в окрестности любой точки у интер-
вала ~выполнены все условия теоремы 5.4, то, согласно
этой теореме, функция у — arcsinх дифференцируема в любой точке
х= siny и для ее производной справедлива формула
(arc sin х)' =	= -— — г J. -.	(5.29)
V	(SHI У) COS У /1 _ Sjn2 у	v 7
Мы взяли перед корнем знак +, ибо cosy положителен всюду на
интервале — у<у<у. Учитывая, что sin у = х, из формулы (5.29)
окончательно получим
(arcsinx),=7T=T-
Полученная формула, как уже отмечалось в процессе ее вывода, спра-
ведлива для всех х из интервала —	+ По аналогичной
схеме вычисляется производная функции у = arccos х. Эта функция,
будучи определена на интервале —	служит обратной
для функции х = cosy, определенной на интервале 0 <у <it. По-
скольку для функции х = cosy в окрестности любой точки у интер-
вала 0<у<тс выполнены все условия теоремы 5.4, то, согласно
этой теореме, функция у = arccos х дифференцируема в любой точке
Л —cosy и для ее производной справедлива формула
(arccos xj — —1— =-----— =------г 1	.	(5.30)
(cos у)' sin у У 1 — cos2 у
ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ
167
Мы учли, что sin=-f-1 — cos2ибо sin_y>0 всюду на интер-
вале 0<_у<к. Принимая во внимание, что cos_y = x, из формулы
(5.30) окончательно найдем
(arccos х) = — у===.
Полученная формула, как уже отмечалось в процессе ее вывода, спра-
ведлива для всех значений х из интервала — 1<х<1.
Перейдем к вычислению производной функции у = arctg х. Эта
функция, будучи определена на бесконечной прямой — оо <; х < +об-
служит обратной для функции x=tgy, определенной на интервале
—	Поскольку для -функции х — tg_y в окрестности любой
точки у интервала	выполнены все условия теоремы 5.4,
то, согласно этой теореме, функция у — arctg X дифференцируема в
любой точке x = tgy и для ее производной справедлива формула
<=гс‘8х),=1ет=1+тет-
Учитывая, что tgj/ = x, окончательно получим
(arctg
Полученная формула справедлива для всех точек х бесконечной
прямой.
Остается вычислить производную функции _y = arcctgx. Эта
функция, будучи определена на бесконечной прямой — оо < х < -|- оо,
служит обратной для функции x = ctg_y, определённой на интервале
0<_у<т. Поскольку для функции x = ctg_y в окрестности любой
точки у интервала	выполнены все условия теоремы 5.4,
то, согласно этой теореме, функция у = arcctg х дифференцируема
в любой точке x = ctg_y и для ее производной справедлива формула
<агсс|г^=<нЬг=-г+ает-
Учитывая, что ctg_y = x, окончательно получим
(arc ctgx)' = —
Эта формула справедлива для всех точек х бесконечной прямой.
Таким образом, мы вычислили производные всех простейших эле-
ментарных функций, за исключением степенной функции с любым
вещественным показателем.
Откладывая вычисление производной этой последней функции до § 8,
займемся обоснованием правила дифференцирования сложной функции.
168
ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[ГЛ. 5
§ 7. Правило дифференцирования сложной функции
Целью настоящего параграфа является установление правила, позво-
ляющего найти производную сложной функции у =/[<р (0], если из-
вестны производные составляющих ее функций y—f(x) и х = <о(?).
Теорема 5.5. Пусть функция x — y(t) дифференцируема в не-
которой точке tQ, а функций y—f(x) дифференцируема в соот-
ветствующей точке х0 = ср(/0). Тогда сложная функция /[<p(i)J
дифференцируема в указанной точке t0, причем для производной
этой функции справедлива следующая формула *):
{/[?W=№Wo).	(5.31)
Доказательство. Придадим аргументу t в точке t0 произволь-
ное, отличное от нуля приращение йЛ. Этому приращению соответ-
ствует приращение Дх функции x = f(Z). Приращению Дх в свою
очередь соответствует приращение йу функции y=f(x) в точке хп.
Поскольку функция у =/(х) предполагается дифференцируемой в точке
х0, приращение этой функции в точке х0 может быть записано в виде
(см. §2)
йу = f (х0) Дх + аДх,	(5.32)
где.
lim а = 0.
Ьх — о
Поделив равенство (5.32) на Д/, будем иметь
Дг/ ,,	. Дх . Дх	_
= /(*о)д7- + адг-	(5-33)
Пусть теперь в равенстве (5.33) Д£—>0. Так как из дифференцируе-
мости функций x = <f(t) в точке t0 вытекает непрерывность этой
функции в точке t0, то, в силу разностной формы условия непрерыв-
ности, Дх—-0 (при Д£—>0). Поэтому можно утверждать, что суще-
ствует предельное значение
lim а=0.	(5.34)
д/^о
Кроме того, в силу требования дифференцируемости функции x — <?(t)
в точке t0 существует предельное значение
А г
Hm ^ = <p'(Z0).	(5-35)
ы -> о
Существование предельных значений (5.34) и (5.35) обеспечивает су-
ществование предельного значения (при Д/ —0) всей правой части
(5.33), равного f (х0) <pr (t0). Стало быть, существует предельное зна-
чение (при1 Д^—-0) и левой части (5.33). По определению производной * 1
*) Символом	мы обозначаем производную сложной функции
1) = / If WI в точке t = l0.
§ 7]	ПРАВИЛО ДИФФЕРЕНЦИРОВАНИЯ СЛОЖНОЙ ФУНКЦИИ	169
указанное предельное значение равно производной сложной функции
в точке t0. Тем самым нами доказана дифференцируемость
сложной функции в точке t0 и установлена формула (5.31).
Теорема 5.5 доказана.
Замечание. Мы рассматривали сложную функцию y = f(x), где
x — т. е. брали х в качестве промежуточного аргумента, a t
в качестве окончательного аргумента. Эти обозначения, конечно, могут
быть изменены. Часто удобнее бывает рассматривать сложную функ-
цию вида _у = /(»), где и = ?(х), т. е. брать х в качестве окончатель-
ного аргумента, а некоторую переменную и в качестве промежуточ-
ного. Для этой функции формула дифференцирования (5.31) принимает
вид
У = W(W =/(")?'(*)	(5.36)
(мы опустили у соответствующих значений аргументов- х и и нули,
имевшие вспомогательный характер).
Приведем примеры использования только что доказанного правила
дифференцирования сложной функции.
1°. Вычислить Производную функции у = earct2x. Эту функцию
будем рассматривать как сложную функцию вида у = еи, где
и — arctg х. Используя формулу (5.36), получим
У = (е“У (arctg х)' = еи 	— earct2 * _!—
2°. Вычислить производную функции у = 2х2. Эту функцию будем
рассматривать как сложную функцию вида _у=2“, где и — х2. Исполь-
зуя формулу (5.36), получим
У = (2")' (х2)' = (2° 1п 2) 2х = 2*- + 'х In 2.
3°. При рассмотрении указанных двух примеров мы отдельно вы-
писывали функции, составляющие данную сложную функцию. В этом,
конечно, нет никакой необходимости, и на практике дифференциро-
вание сложной функции производится сразу без расчленения на отдель-
ные составляющие функции. Например,
у — arcsin 7 5л:; У =	1	— (7 5л:)' —	 75 —
V1 — (75х)2	/1 — (75х)2
(здесь |л:|<^1.
4°. Теорема 5.5 и содержащееся в ней правило последовательно
переносятся и на случай сложной функции, являющейся суперпозицией
трех и большего числа функций.
Рассмотрим пример такой функции. Пусть требуется вычислить
производную функции у = 5arccte*х" >. Последовательно применяя пра-
вило дифференцирования сложной функции, получим
У = (5ar«lg(л») ]п 5)	8л:’.
по
ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[ГЛ. S
§ 8. Логарифмическая производная. Производная степенной
функции с любым вещественным показателем.
Таблица производных простейших элементарных функций
1.	Понятие логарифмической производной функции. Пусть
функция y=f (х) положительна и дифференцируема в данной точке х.
Тогда в [этой точке существует 1п_у = 1п/(х). Рассматривая 1п/(х)
как сложную функцию аргумента х, мы можем вычислить производную
этой функции в данной точке х, принимая _у —f(x)' за промежуточный
аргумент. Получим
[1п/(х)]' = -^.	(5.37)
Величина, определяемая формулой (5.37), называется логарифмической
производной функции у —f(x) в данной точке х. В качестве примера
вычислим логарифмическую производную так называемой степенно-
показательной функции у —и (х)* Мы уже знаем из. п. 2 § 7
главы 4, что эта функция определена и непрерывна для всех значе-
ний х, для которых и(х) и v(x) непрерывны и и(х)>0. Теперь мы
дополнительно потребуем, чтобы и(х) и v(x) были дифференцируемы
для рассматриваемых значений х. Тогда, поскольку 1пу = г(х)1пи(х),
мы получим, что логарифмическая производная рассматриваемой функ-
ции равна
'J- = [и (х) In и (х)]' = v’ (х) In и (х) + v (х)	.	(5.38)
У	и \Л}
Из равенства (5.38), учитывая, что у = и (х)” получим следующую
формулу для производной степенно-показательной функции:
у' = и (x)v р (х) In и (х) + v (х)	.
2.	Производная степенной функции с любым вещественным
показателем. Приступим теперь к вычислению производной степенной
функции _у = х* с произвольным вещественным показателем а. Мы
будем вычислять производную этой функции для тех значений х, для
которых эта функция определена при любом а, а именно для значе-
ний х, принадлежащих полупрямой*) х>0. Имея в виду, что всюду
на полупрямой х>0 функция у — Х1 положительна, вычислим ло-
гарифмическую производную этой функции. Так как 1п_у = а1пх, то
*) В случае, когда а = —, где т — целое нечетное число, функция у = ха
определена на всей бесконечной прямой. Однако и в этом случае достаточно вы-
числить производную указанной функции лишь для значений х > 0, ибо ука-
занная функция является нечетной и ее производную для значений х <. О легко
получить из этого соображения.
ЛОГАРИФМИЧЕСКАЯ ПРОИЗВОДНАЯ,
171
логарифмическая производная равна
— —Га In хГ = -.
У L J х
Отсюда, учитывая, что у—ха, получим формулу для производной
степенной функции
(х“)' = ах”-1.
Таким образом, нами вычислены производные всех простейших эле-
ментарных функций. Собирая воедино все вычисленные производ-
ные, мы получим следующую таблицу, уже выписанную нами в
главе 1.
3.	Таблица производных простейших элементарных функций.
1°. (ха)' = ах"'1. В частности, (—=-----(l/’x),=—.
V	’ \х)	Х2’	7	2/х
2°. (loga х)'=logo е (х > 0, Q<Za^ 1). В частности, (In х/ =
= _£
х ‘
3°. (ax)' = axlna (0<a^ 1). В частности, (ех)’ = ех.
4°. (sin х/ = cos х.
5°. (cosx)' = — sinx.
6°. (tg x)’ = -^-x = 1 + tg2 x (x # ~ + rw, где n = 0, ± 1,...).
7°. (ctgx)' = ——= —(1+ctg2x)(x#K«, где n = 0, ±1,...).
8°. (arcsin x)' =	( - 1 < x < 1).
9°. (arccosx)' = — j1 g ( — 1 <x< 1).
10°. (arctg х/=—
11°. (arcctgx)' = —
В § 4 главы 4 мы ввели гиперболические функции _y = shx,
_y = chx, _y = thx и _y = cthx, которые являются простыми комбина-
циями показательных функций. Из определения этих функций эле-
ментарно вытекают следующие выражения для их производных:
12°. (shx)' = chx.
13°. .(chx)' = shx.
14°. (thx)' = -i-.
4	' ch2 x
15°. (cthx)' = -^(x^0).
Указанная таблица вместе с правилами дифференцирования суммы,
разности, произведения и частного (т. е. формулами (5.16)) и правилом
172	ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ'	[ГЛ S
дифференцирования сложной функции составляет основу дифферен-
циального исчисления.
Установленные нами правила и формулы дифференцирования по-
зволяют нам сделать один важный вывод.
В § 7 главы 4 мы ввели понятие элементарной функции как
такой функции, которая выражается через простейшие элементарные
функции посредством четырех арифметических действий и суперпо-
зиций, последовательно примененных конечное число раз. Теперь мы
можем утверждать, что производная любой элементарной функции
представляет собой также элементарную функцию. Таким обра-
зом, операция дифференцирования не выводит нас из класса эле-
ментарных функций.
§ 9. Инвариантность формы первого дифференциала.
Некоторые применения дифференциала
1. Инвариантность формы первого дифференциала. В конце § 2
мы установили, что для случая, когда аргумент х является независи-
мой переменной, дифференциал функции y==f(x) определяется фор-
мулой
dy—f (х) dx.	(5.39)
В этом пункте мы докажем, что формула (5.39) является универсаль-
ной и справедлива не только в случае, когда аргумент х является
независимой переменной, но и в случае, когда аргумент х сам является
дифференцируемой функцией некоторой новой переменной t. Указан-
ное свойство дифференциала функции обычно называют инвариант-
ностью его формы.
Итак, пусть дана дифференцируемая в некоторой точке х функ-
ция y=f(x), аргумент х которой представляет собой дифференци-
руемую функцию х = <р(г“) аргумента t. В таком случае мы можем
рассматривать у как сложную функцию y=f [у (t)] аргумента t, а х
как промежуточный аргумент. В силу теоремы 5.5 производная у по t
определяется формулой
У=/'(х) ?'(/)•	(5.40)
Поскольку переменную t мы можем рассматривать как независимую,
производные функций x = <f>(f) и _у=/[<р(£)] по аргументу t, согла-
сно установленному в конце § 2, равны отношению дифференциалов
этих функций к dt, т. е.
?'W = g. У^[/М)1Г = г?'
Вставляя эти значения производных в формулу (5.40), придадим этой
ИНВАРИАНТНОСТЬ ФОРМЫ ПЕРВОГО ДИФФЕРЕНЦИАЛА
173
§ 9]
формуле вид
(5.41)
Умножая обе части равенства (5.41) на dt, получим для dy выраже-
ние (5.39). Тем самым доказана инвариантность формы первого диф5-
ференциала функции, т. е. доказано, что как в случае, когда аргу-
мент х является независимой переменной, так и в случае, когда
аргумент х сам является дифференцирумой функццей другой
переменной, дифференциал dy функции y=f(х) равен производной
этой функции, умноженной на’ дифференциал аргумента dx.
По-другому свойство инвариантности дифференциала можно сфор-
мулировать так: производная функции У=/(х) всегда*) равна от-
ношению дифференциала этой функции dy к дифференциалу аргу-
мента dx, т.е.
f'W = %x-	(5-42)
Доказанное равенство (5.42) позволяет нам в дальнейшем использо-
вать отношение^ для обозначения производной функции у =f(x)
по аргументу х.
Заметим в заключение, что после того, как доказано равенство (5.42),
правило дифференцирования сложной функции принимает вид простого
тождества:
dy_dydx	/=4Ч>
dt~dxdt'
Столь же простой вид приобретает правило дифференцирования обрат-
ной функции:
? =	(5.44)
dx dx	'	'
dy
Подчеркнем, однако, что равенства (5.43) и (5.44) нельзя рассматри-
вать как новые методы доказательства теорем 5.5 и 5.4, ибо фор-
мулы (5.43) и (5.44) существенно используют факт инвариантности
первого дифференциала, установленный нами именно при помощи тео-
ремы 5.5.
2. Формулы и правила вычисления дифференциалов. Мы дока-
зали, что дифференциал dy. функции _у=/(х) всегда равен производ-
ной этой функции /' (х), умноженной на дифференциал аргумента dx.
*) То есть как в случае, когда аргумент х является независимой пере-
менной, так и в случае, когда х сам является дифференцируемой функцией
некоторой другой переменной.
174
ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[ГЛ. 5
Таким образом, таблица производных, выписанная нами в п. 3 § 8,
приводит к соответствующей таблице дифференциалов:
1°. d (х“) = ах®-1 dx. В частности, d(—\=—^, d (Ух) = ***_•.
v	\х)	Х2>	/ 2рлх
* 2°. d (log0 х) —dx (х^>0, 0<^a^l). В частности,
d(lnx)=^.
3°. d (а%) = ах In a dx (0<^а^1). В частности, d (ех) = ех dx.
4°. d (sin х) = cos х dx.
5°. d (cos x) = — sin x dx.
6°. d(tgx) = -^- = (l + tg2 x) rfx (x #:-^-+ то, гдел = 0,±1,
7°. d(ctgx)= -^7= “(1 + ctg2x)(Zx (х^то, где « = 0,
±1, ...).
8°. d (arcsin x) =	(— 1	x 1).
9°. d (arccos x) = —	' С-'У ')•
10°. d (arctg x) = j-^.
11°. d(arcctgx)=
Из формул (5.16) и из соотношения (5.39) непосредственно вытекают
следующие правила для вычисления дифференциала суммы, разности,
произведения и частного:
d (и ± п) — du ± dv, d (ип) — v du + и dv, d
v du — udv
3. Использование дифференциала для установления прибли-
женных формул. Хотя, как мы видели в § 2, дифференциал dy
функции y=f(x) не равен приращению Ду этой функции, но с точ-
ностью до бесконечно малой более высокого порядка, чем Дх, спра-
ведливо приближенное равенство
Ду «э dy.
(5.45)
Относительная * *) погрешность этого равенства становится сколь угодно
малой при достаточно малом Дх. Формула (5.45) позволяет прибли-
женно заменить приращение Ду функции у=/(х) ее дифференциа-
*) Относительная погрешность этого равенства определяется отношением
^Дх^~ ’ <-)тметим> чт0» по определению дифференциала! Ду — dy — o (Дх).
§ 101
ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
175
лом dy. Выгода такой замены состоит в том, что дифференциал dy
зависит от Дх линейно, в то время как приращение Ду, вообще
говоря, представляет собой более сложную функцию от Дх.
Имея в виду, что приращение функции Ду определяется форму-
лой (5.1), а дифференциал dy определяется формулой (5.14), мы при-
дадим приближенному равенству (5.45) следующий вид:
/(х + Дх) -/(х)	(х) Дх
или
/(х + Дх) (х) +/' (х) Дх.
(5.46)
По формуле (5.46) функция / для значений аргумента, близких к х
(т. е. для малых Дх), приближенно заменяется линейной функцией.
В частности, из формулы (5.46) может быть получен ряд уже из-
вестных нам из главы 4 приближенных формул. Так, полагая /(х) =
— (1 4-х)1/'1, х=0, получим, что
(1 +Дх)’/"№ 1 +^,	(5.47)
Полагая /(x) = sinx, х — 0, получим
51пДх^Дх.	(5.48)
Полагая, f(x) = ex, х — 0, получим
eLx «и 1 + Дх.	(5.49)
Полагая /(х) == In (1 + х), х = 0, получим
1п(1-|-Дх)я«Дх.	(5.50)
Каждое из равенств (5.47) — (5.50) .справедливо с точностью до бес-
конечно малой более высокого порядка, чем Дх.
Равенства (5.47) —(5.50) в форме точных оценок уже были уста-
новлены нами в конце § 7 главы 4.
§ 10.	Производные и дифференциалы высших порядков
1.	Понятие производной n-го порядка. Как уже отмечалось
в п. 2 § 1, производная f (х) функции _у = /(х), определенной и
дифференцируемой на интервале (а, Ъ), представляет собой функ-
цию, также определенную на интервале {а, Ъ). Может случиться,
что эта функция f (х) сама является дифференцируемой в некоторой
точке х интервала (а, Ь), т. е. имеет в этой точке производную.
Тогда указанную производную называют второй производной (или
производной 2-го порядка) функции y=f(x) в точке х и обозна-
чают символом /<2) (х) или у<2>(х)*).
*) Вторую производную функции y = f(x) обозначают также символом
Г' (х) или у" (х).
176
ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[ГЛ 5
После того как введено понятие второй производной, можно по-
следовательно ввести понятие третьей производной, затем четвертой
производной и т. д. Если предположить, что нами уже введено по-
нятие (и—1)-й производной и что (я—1)-я производная дифферен-
цируема в некоторой точке х интервала (а, Ь), т. е. имеет в этой
точке производную, то указанную производную называют п-й про-
изводной (или производной п-го порядка) функции y=f(x)n точке х
и обозначают символом (х) или	(х).
Таким образом, мы вводим понятие л-й производной индуктивно,
переходя от первой производной к последующим. Соотношение, опре-
деляющее .я-ю производную, имеет вид
У") =	(5.51)
Функцию, имеющую на данном множестве {х} конечную произ-
водную порядка п, обычно называют п раз дифференцируемой на
данном множестве. Понятие производных высших порядков находит
многочисленные применения в физике. Здесь мы ограничимся тем, что
укажем механический смысл второй производной. Если функция
y=f(x) описывает закон движения материальной точки по прямой
линии, то, как мы уже знаем, первая производная f (х) дает мгновен-
ную скорость движущейся точки в момент времени х. В таком слу-
чае вторая производная /(2) (х) равна скорости изменения скорости,
т. е. равна ускорению движущейся точки в момент времени х.
Заметим, что методика вычисления производных высшего порядка
предполагает умение вычислять только производные первого порядка.
В качестве примеров вычислим производные и-го порядка некоторых
простейших элементарных функций.
2.	Л-е производные некоторых функций. 1°. Вычислим n-ю про-
изводную степенной функции у = хх (х^>0, а —любое вещественное
число). Последовательно дифференцируя, будем иметь
у'= а.ха~1,	= а(а — 1)ха“2, У3) = а(а — 1)(а — 2)х“~3, ...
Отсюда легко уяснить общий зако’н
(х“)<л> = а (а - 1) (а - 2)... (а - я + 1) хаЛ
Строгое доказательство этого закона легко проводится методом
индукции.
В частном случае а = т, где т — натуральное число, получим
(хт)(т) — от!, (xm)(n) = 0 при п^>т.
Таким образом, л-я производная многочлена т-ro порядка при
я^>т равна нулю*).
*) При этом мы используем еще следующую очевидную формулу [Ди (х) -|-
+ В&(х)['я> = Аи,п> (х) Bvmi (х), где А и В — постоянные.
§ Ю]
ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
177
2?. Далее вычислим п-ю производную показательной функции
у = ах (0<а^1). Последовательно дифференцируя, будем иметь
у' = ах\па, у^ = ах1пга, = а*Тп3а, ...
Общая формула, легко устанавливаемая по методу индукции, имеет
вид
(ax)w — ах In" а.
В частности,
(ех)<л> = е\
3°. Вычислим n-ю производную функции _y = sinx. Первую про-
изводную этой функции можно записать в виде _y' = cosx =
= sin^x+y^. Таким образом, дифференцирование функции у —
= sinx прибавляет 'К аргументу этой функции величину тс/2.
Отсюда получаем формулу
(sin Х)(Л) — sin (х -ф п у У
4°. Совершенно аналогично устанавливается формула

(cos х)(л) = coslx
.5°. В заключение вычислим n-ю производную так называемой
дробно-линейной функции у= где а, Ь, с и d г- некоторые
постоянные. Последовательно дифференцируя эту функцию, будем
иметь
У =	= ОЧ - М (сх + 4П
_у(2) = (ad — bc)(—2) (сх + d)~3 с,
_у(3) = (ad — be) (— 2) (— 3) (сх -ф d)~l с2, ...
Легко усмотреть и общий закон
Уп) = (ZT+^Г’ ={ad ~ bc) 1)П~1 п' + ^("+1) с”-1’
который может быть обоснован по методу индукции.
3.	Формула Лейбница для n-й производной произведения
двух функций. В то время как установленное ваше правило вычис-
ления первой производной от суммы или разности двух функций
(и ± v)' — и' ± v' легко переносится (например, по методу индукции)
на случай n-й производной (и ± ц)(я) = и(л> ± возникают боль-
шие затруднения при вычислении n-й производной от произведения
двух функций UV. 
178
ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[ГЛ. Б
Соответствующее правило носит название формулы Лейбница
и имеет следующий вид:
(ot)W ^u^v + Cku^v' +Cu<n-2M2> +С^("-8М3)-|-.	(5.52)
Легко подметить закон, по которому построена правая часть фор-
мулы Лейбница (5.52): она совпадает с формулой разложения би-
нома (u4-v)n, лишь вместо степеней и и v стоят производные
соответствующих порядков. Это сходство становится еще более
полным, если вместо самих функций и и v писать соответственно
и г»(0) (т. е. если рассматривать саму функцию как производную ну-
левого порядка).
Докажем формулу Лейбница по методу индукции. При п=1 эта
формула принимает вид (uv)' = u'v + uv', что совпадает с установлен-
ным выше (в § 3) правилом дифференцирования произведения двух
функций. Поэтому достаточно, предположив справедливость фор-
мулы (5.52)'для некоторого номера л, доказать ее справедливость для
следующего номера «+1. Итак, пусть для некоторого номера п
формула (5.52) верна. Продифференцируем эту формулу и объединим
слагаемые, стоящие в правой части, так, как это указано ниже:
(от)(л+‘) = н(я+*)г, + [C°n(nV +C^<"V] +	+ C^(ra-1M2)] +
+ [С2и<”-2М3> +	+.+ OT(n+1).	(5.53)
(При этом мы воспользовались тем, что 1 = С’г.) Из элементарного
курса известно, что для любого номера k, не превосходящего п,
справедлива формула *)
Ck I S-yk — 1 _
Пользуясь этой формулой, мы можем следующим образом переписать
равенство (5.53):
(uv)^ = и<л+1>ц + С'„+	+ С*п+ xu^-^v^ +... + №?(л+1).
Тем самым доказана справедливость формулы (5.52) для номера
(п+1). Вывод формулы Лейбница завершен.
Пример 1. Вычислить n-ю производную функции _y = x2cosx.
Воспользуемся формулой Лейбница, положив в ней и = cosx, v — x2.
В таком случае для любого номера k «(ft) = cos|^x + Ay^, т>' = 2х,
•ц(2) = 2, +3) ==... = 0. Получим
yW = X2 cos (х +	+ 2nx cos [х + (п — 1)	+
+ п (п — 1) cos [х + (л — 2) у
*) Впрочем, эта формула элементарно проверяется.
§ 10] ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 179
Пример 2. Вычислить и-ю производную функции у = х?ех.
Воспользуемся формулой Лейбница, положив в ней и = ех, v = x3.
Тогда для любого номера А =	т>' = 3х2, и(2) = 6х, г»(3) = 6,
^(4) — -у(5) = < 0. Получим
у(п) = (х3 + 3пх2 + 3п(п-1)х + п(п- 1)(п — 2))ех.
Рассмотренные примеры показывают, что формула Лейбница особенно
эффективна в случае, когда одна из двух перемножаемых функций
имеет лишь конечное число отличных от нуля производных.
4.	Дифференциалы высших порядков. В рассуждениях настоя-
щего пункта мы будем использовать для обозначения дифференци-
ала наряду с символом d также и символ 8 (т. е. будем писать там,
где это удобно, вместо dx и dy символы 8х и 8jz).
Предположим, что функция y—f(x) дифференцируема в некото-
рой окрестности точки х0. Тогда первый дифференциал dy этой
функции имеет вид*) dy—f'(x)dx и является функцией двух пере-
менных: точки х и величины dx.
Предположим дополнительно, что функция /' (х) также является
дифференцируемой в точке х0 и что величина dx имеет одно и то
же фиксированное значение для всех точек х рассматриваемой окрест-
ности точки х0.
При этих предположениях существует дифференциал функции
dy—f'(x)dx в точке х0, который мы будем обозначать символом
8 (dy), причем этот последний дифференциал определяется формулой
8 (dy) = 8 \f' (х) dx] |л=АГо = [f (х) dx]' |х=Хо 8х=/" (х0) dx 8х. (5.54)
Определение. Значение 8 (dy) дифференциала от первого диффе-
ренциала dy, взятое при Ъх — dx, называют вторым диффе-
ренциалом функции у = f (х) (в точке х0) и обозначают сим-
волом d2y.
Из формулы (5.54) и из определения второго дифференциала вы-
текает, что
d2y =f" (x0)(dx)2.	(5.55)
Заметим, что так как мы считаем величину dx фиксированной,
то из определения второго дифференциала сразу же вытекает, что
второй дифференциал независимой переменной d2x равен нулю.
Совершенно аналогично последовательно определяются дифферен-
циалы более высоких порядков. Предполагая, что производная по-
рядка (и—1) функции y=f(x) дифференцируема в точке х0 (т. е.
предполагая, что функция y—f(x) имеет в точке х0 производную
порядка п), мы определим дифференциал н-го порядка dny
функции у = f(x) (в точке <х0) как дифференциал 8 (dn~1y) от диф-
ференциала (п— 1)-го порядка взятый при Sx = dx.
*) См. п. 1 §9, формулу (5.39).
180
ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[ГЛ 5
Для дифференциала n-го порядка dny методом индукции элемен-
тарно устанавливается формула
dny = /(") (х0) (dx)n.	(5.56)
В самом деле, при п—.\ и и = 2 формула (5.56) справедлива.
Предположим, что эта формула справедлива для некоторого номера
(н—1), т. е. предположим, что о!"-1)/(x)(dx)"-1.
Тогда, согласно определению dny, получим *)
dny = 8 (d^y) \,x_dx = 8 [/<«-> > (х) (dx)"’1] \ъх-ах =
=/И) (х) (rfx)”-1 6Х =/l?) (х) (dx)n,
т. е. справедливость формулы (5.56) установлена.
Из формулы (5.56) вытекает следующее выражение для произ-
водной порядка п:
=	(5.56-)
Очень важно отметить, что при я>1 формулы (5.56) и (5.56')
справедливы, вообще говоря, лишь тогда, когда х является неза-
висимой переменной (т. е. второй и последующие дифферен-
циалы не обладают, вообще говоря, свойством инвариантности
формы).
Чтобы убедиться в этом, рассмотрим вопрос о вычислении вто-
рого дифференциала (дважды дифференцируемой) функции у — f (х)
в предположении, что переменная х является дважды дифференци-
руемой функцией некоторого аргумента t. Используя равенство (5.39)
и формулу 8 (uv) — vlii и8и, получим:
d*y = 8 (dy) \ix_dx = 8 \f (x) dx] \ix_dx =
= {dx 8 [/'(x)| + f' (x) 8 (dx)} |г.г_,м = [dx • f' (x) 8 (x)J +f(x) <Px.
Итак, d*y = f'(x) (dx)* 4-/' (x) d*x.
Последняя формула отличается от (5.55) наличием в ней допол-
нительного и, вообще говоря, не равного нулю члена /' (х) d*x.
§ 11. Дифференцирование функции, заданной параметрически
В этом параграфе мы остановимся на методике вычисления про-
изводных функции, заданной параметрически.
Пусть х и у заданы как функции некоторого параметра t:
x = if(t), y = ty(t). При этом мы предположим, что функции <р (t) и
ф(Ч,имеют нужное число производных по переменной t в рассматри-
ваемой области изменения этой переменной. Кроме того, мы предпо-
лооким, что функция x — <f(t) в окрестности рассматриваемой точки
*) Мы опускаем индекс 0 у точки х.
ФУНКЦИЯ. ЗАДАННАЯ ПАРАМЕТРИЧЕСКИ
181
4 н|
имеет обратную функцию t — <р-1 (х) *). Последнее предположение
дает нам возможность рассматривать у как функцию аргумента х.
Поставим задачу о вычисления- производных у по аргументу х.
Эти производные договоримся обозначать символами
у'х, У& У1^, • • •
В силу свойства инвариантности первого дифференциала можем
записать **)
у'х — ~х, dy — ф' (t) dt, dx = (f) dt.	(5.57)
Из этих формул получим следующее выражение для .первой про-
изводной:
Л =	(5.58)
Аналогично вычисляются производные высших порядков. Так, для вы-
числения второй производной у'х'г достаточно представить ее в виде
и воспользоваться формулой (5.58), третьей из формул (5.57) и прави-
лом дифференцирования частного.
Пример. Вычислить первую и вторую производные функции,
заданной параметрически:
{х— a (t — sin /),
у = а(1— cos 0, —оо<^<оо.
Кривая, определяемая этими уравнениями, называется циклоидой ***).
Получим
Ух = ~a(l^cLz)~ = Ctg 4 2ltA> где k ~ целое)-
„<2 _ [Ctg^] _	—1
a(l-coS0 -4asinl| •
*) Это обеспечивается существованием первой производной -/(/), отлич-
ной от нуля в некоторой окрестности рассматриваемой точки t (см. п. 4 § 2
главы 15).
**) При этом мы берем dy и dx в одной и той же точке t и для одного
и того же dt.
***) Циклоида представляет собой траекторию некоторой фиксированной
точки окружности, катящейся без скольжения по прямой линии.
ГЛАВА 6
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
В этой главе будет рассмотрена задача о восстановлении функ-
ции по известной производной этой функции. Актуальность этой
задачи была выяснена в главе 1.
§ 1.	Понятие первообразной функции
и неопределенного интеграла
1.	Понятие первообразной функции. - К числу важных задач
механики относится задача об определении закона движения матери-
альной точки по заданной ее скорости, а также задача об определе-
нии закона движения и скорости материальной точки по заданному
ее ускорению *).
Эти задачи приводят к математической проблеме отыскания
функции по заданной производной этой функции.
Переходим к рассмотрению этой проблемы.
Определение. Функция F(х) называется первообразной
функцией (или просто первообразной) для функции f(x)
на интервале (а, Ь), если в любой точке х интервала (а, Ь)
функция F (х) дифференцируема и имеет производную F' (х), рав-
ную f(x).
Замечание. Аналогично определяется первообразная для функ-
ции f(x) на бесконечной прямой и на открытой полупрямой **).
Примеры. 1) Функция F (х) = У1 — х2 является первообразной
для функции f(x) —---у* — на интервале (—1, -J-1), ибо в любой
точке х этого интервала (]/1 — х2)'=--х
*) Вместо ускорения материальной точки можно задать действующую
на эту точку силу (ибо, согласно второму закону Ньютона, сила определяет
ускорение этой точки).
**) И вообще на любом плотном в себе множестве {х}, Определение
плотного в себе множества см. в § 3 главы 2.
5 1)	' ПЕРВООБРАЗНАЯ И НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ	183
2)	Функция F(x) = sinx является первообразной для функции
/(x) = cosx на бесконечной прямой (—оо, оо), ибо в каждой точке х
бесконечной прямой (sin х)' = cos х.
3)	'Функция F(x) = lnx является первообразной для функции
f (х) = — на открытой полупрямой х > 0, ибо в каждой точке х
этой полупрямой (1ПХ)'=у.
Если F(x) является первообразной для функции f(x) на интер-
вале (а, Ь), то, очевидно, и функция F (х) + С, где С — любая посто-
янная, является первообразной для функции /(х) на интервале (а, Ь).
Естественно, возникает вопрос, как связаны между собой различ-
ные первообразные для одной и той же функции /(х). Справедлива
следующая основная теорема.
Теорема 6.1. Если Fx(x) и Es(x) — любые первообразные для
функции f (х) на интервале (а, Ь), то всюду на этом интервале
F1 (х) — F2 (х) = С, где С — некоторая постоянная.
Другими словами, две любые первообразные для одной и той же
функции могут отличаться лишь на постоянную.
Доказательство. Положим Ф(х) = F\(х) — F2(х). Так как
каждая из функций Fj (х) и F2 (х) дифференцируема на интервале
(а, Ь), то в силу теоремы 5.3 и функция Ф(х) дифференцируема на
интервале (а, Ь), причем всюду на этом интервале Ф' (x) = Fj(x)—
-К(х)=/(х)-/(х) = 0.
В § 10 главы 8 методами, не использующими результатов этой
главы*), будет доказана теорема 8.13 следующего содержания: если
функция Ф(х) дифференцируема всюду на интервале (а, Ь) и если
всюду на этом интервале Ф'(х) = 0, то функция Ф(х) является посто-
янной на интервале (а, Ь).
Из этой теоремы получим, что Ф(х) = Дх(х) — F2(x) = C = const,
что и требовалось доказать.
Следствие. Если F(x) — одна из первообразных функций для
функции /(х) на интервале (а, Ь), то любая первообразная Ф(х) для
функции /(х) на интервале (а, Ь) имеет вид Ф (х) = F (х) + С, где
С — некоторая постоянная.
2. Неопределенный интеграл.
Определение. Совокупность всех первообразных функций для
данной функции f(x) на интервале (а, Ь) называется неопре-
деленным интегралом от функции f(x) (на этом интер-
вале) и обозначается символом
^f(x)dx.	(6.1)
*) Заметим, что главы 6 и 7 без ущерба для понимания этой книги могут
читаться после главы 8. Мы выдвигаем главы 6 и 7 вперед, чтобы ускорить
знакомство читателя с техникой интегрирования.
184
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
[ГЛ. 6
В этом обозначении знак называется знаком интеграла, выражение
f(x)dx — под интегральным выражением, а сама функция f(x)—
подынтегральной функцией.
Если F(x) — одна из первообразных функций для функции f(x)
на интервале (а, Ь), то, в силу следствия из теоремы 6.1,
\f(x)dx = F(x) + C,	(6.2)
где С —любая постоянная.
Подчеркнем, что если - первообразная (а стало, быть, и неопре-
деленный интеграл) для функции f(x) на интервале (а, Ь) сущест-
вует, то подынтегральное выражение в формуле (6.1) представ-
ляет собой дифференциал любой из этих первообразных. В самом
деле, пусть F(x) — любая из первообразных для функции f(x) на
интервале (а, Ь), т. е. для всех х из интервала (а, b) F'(x)=*f(x).
Тогда f(x)dx^F’ (х) dx = dF.
Примеры. 1) х _dx = 1 — х2 + С на интервале — 1 <
k<Z 1, ибо функция F (х) = У 1 — х2 является одной из первооб-
разных для функции f (х) —  -.....на указанном интервале.
У 1 — х2
2)	cos х <Zx = sin х + С на всей бесконечной прямой —оо<х<;
<со, ибо функция F(x) = sinx является одной из первообразных
для функции /(x) = cosx на бесконечной прямой.
В этой главе мы не будем заниматься вопросом о существова-
нии первообразных (или неопределенных интегралов) для широких
классов функций. Здесь мы лишь отметим, что в § 7 главы 10 будет
доказано, что для всякой функции f(x), непрерывной на интервале
(а, Ь), существует на этом интервале первообразная функция
(и неопределенный интеграл).
Операцию нахождения первообразной или неопределенного интег-
рала (от функции /(х)) принято называть интегрированием
(функции f (х)).
3.	Основные свойства неопределенного интеграла. Прежде
всего отметим два свойства, непосредственно вытекающие из опреде-
ления неопределенного интеграла:
1 °, d § f (х)dx—f (х)dx.
2°. dF (x) = F (x) + C.
Свойство 1° означает, что знаки d и § взаимно сокращаются
в случае, если знак дифференциала стоит перед знаком интеграла.
Свойство 2° означает, что знаки J и d взаимно сокращаются и
в случае, если знак интеграла стоит перед знаком дифференциала,
но в этом случае к F (х) следует добавить произвольную постоян-
ную С.
ПЕРВООБРАЗНАЯ И НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
185
§ И
Для установления свойства 1° достаточно взять дифференциал от
обеих частей формулы (6.2) и учесть, что dF (х) = F' (х) dx = f\x) dx.
Для установления свойства 2° достаточно в левой части (6.2)
воспользоваться равенством dF (х) = f (х) dx.
Следующие два свойства обычно называют линейными свойствами
интеграла:
3°. $ [/ (х) ± g (х)] dx — \f (х) dx±\g (x)dx.
4°. jj [А/(х)] dx= A ^f(x)dx (А = const).
Подчеркнем, что равенство в формулах 3° и 4° имеет условный
характер: его следует понимать как равенство правой и левой частей
с точностью до произвольного постоянного слагаемого (это понятно,
поскольку каждый из интегралов, фигурирующих в формулах 3° и 4°,
определен с точностью до произвольного постоянного слагаемого).
Поскольку две первообразные для одной и той же функции
могут отличаться лишь на постоянную, то для доказательства свой-
ства 3° достаточно доказать, что если F (х) — первообразная для/(х),
а G(x) — первообразная для g(x), то функция [F(x)±G(x)] является
первообразной для функции /'(x)±g(x). Это последнее непосредст-
венно вытекает из того, что производная (алгебраической) суммы
функций равна сумме производных этих функций, т. е. [F(x)±G(x)]' =
= F' (х)± G' (х)=/(х)±g(x). Аналогично доказывается свойство 4°.
В этом случае используется равенство [AF(xJ]'= AF'(х) = А/(х).
4.	Таблица основных неопределенных интегралов. В главе 5
мы получили таблицу производных простейших элементарных функций
(см. § 8 главы 5), представляющую собой вычислительный аппарат
дифференциального исчисления. Каждая формула этой таблицы, уста-
навливающая, что та или иная функция F(x) имеет производную,
равную /(х), приводит нас, в силу определения неопределенного
интеграла, к соответствующей формуле интегрального исчисления
J/(x)<Zx = F(x) + C.
Таким путем мы приходим к следующей таблице основных неоп-
ределенных интегралов:
1°. ^O-dx — C.
2°. j 1 -dx = x + C.
3°.	x“dx = ^j + C ,.(а^ -1).
4°. j^ = ln|x| + C; (х^О).
5°. J axdx = ~ + C (0<а#1), J exdx = ex + C.
6°. sin x dx = — cos x + C.
7°. ^cosx(/x = sinx4-C.
186
НЕОПРЕДЕЛЕННЫЙ интеграл
[ГЛ. 6
8°'	О + tg2x)dx = tgx + C (х^^ + кп, где л—О,
.1 L-Uo Л	1	\	£
±1,...).
С* dx (*
9°. \ ^23с= \ О + ctg2x)dx= — ctgx-фС (х^яи, где n — 0,
± 1, ...).
„ p r/x ( arcsin x 4-C,
10°. \	{	(—l<x<l).
j 1^1— x2	(—arccos х-фС
11° C dx - f arctg* + c>
J 1+x2 I —arcctgx + C.
12°- $/^т=1п^ + /^±Т| + С
|x|>lj.
13". $ст=-Н^|+с (W*
К этим формулам можно присоединить
мулы для гиперболических функций;
14°. sh х dx = ch х + С.
(в случае знака —
1).
и соответствующие фор-
150, ch х dx = sh х -ф С.
16°. ^T^-^thx + C.
j ch2 x 1
17°.	~^~ = —cthx-фС (x#0).
J sh2x	1	\ -r- >
Сделаем замечания в отношении формул 4, 12 и 13. Формула 4
справедлива для любого интервала, не содержащего значения х = 0.
В самом деле, если х > 0, то из формулы (In х)' = заключаем, что
С dx	.	1
\— = 1пх + С, а если х<0, то из формулы [In (—х)] = —
J X	X
заключаем, что ^у = 1п(—х) + С. Тем самым формула 4 оправ-
дана для любого х 0.
Формулы 12 и 13 занимают исключительное положение в нашей
таблице, ибо эти формулы не имеют аналогов среди формул таблицы
производных.
Однако для проверки формул 12 и 13 достаточно убедиться в том,
что производные выражений, стоящих в правых частях этих формул,
совпадают с соответствующими подынтегральными функциями.
Наша ближайшая цель — дополнить таблицу неопределенных интег-
ралов основными приемами и методами интегрирования. Но прежде
чем приступить к реализации этой цели, сделаем одно важное за-
мечание.
В § 7 главы 4 мы ввели понятие элементарной функции,
а в п. 3 § 8 главы 5 установили, что производная любой элементар-
ной функции представляет собой также элементарную функцию.
ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ
187
§ 21
Иными словами, мы установили, что операция дифференцирования
не выводит нас из класса элементарных функций.
Отметим сразу же, что с операцией интегрирования дело обстоит
иначе. Можно доказать, что интегралы от некоторых элементарных
функций уже не являются элементарными функциями. Примерами
таких интегралов могут служить следующие:
1°. \e~x2dx.
2°. cos (№) dx.
3°. sin (№) dx.
4°.'	(0<х=£1).
J In X Л	7
5°.	(x^O).
6°. £ “Hrfx.
J x
Каждый из указанных интегралов представляет собой функцию,
не являющуюся элементарной. Указанные функции не только реально
существуют*), но и играют большую роль в различных вопросах
физики. Так, например, интеграл 1, называемый интегралом Пуассона
или интегралом ошибок, широко используется в статистической
физике, в теории теплопроводности и диффузии, интегралы 2 и 3,
называемые интегралами Френеля, широко применяются в оптике.
Часто встречаются в .приложениях и интегралы 4—6, первый из кото-
рых называется интегральным логарифмом, а последние два— инте-
гральными косинусом й синусом.
Для всех перечисленных новых функций (интеграла Пуассона,
интегралов Френеля, интегрального логарифма, синуса и косинуса)
составлены таблицы и графики.
Ввиду важности для приложений, эти функции изучены с такой же
полнотой, как и простейшие элементарные функции. Вообще следует
подчеркнуть условность понятия простейшей элементарной функции.'
§ 2. Основные методы интегрирования
1. Интегрирование заменой переменной (подстановкой). Замена
переменной — один из самых эффективных приемов интегрирования.
Этот прием базируется на следующем элементарном утверждении.
Пусть функция t = rz(x) определена и дифференцируема на неко-
тором множестве {х} **), и пусть {t} — множество всех значений
*) Мы уже отмечали, что в § 7 главы 10 будет доказано существование
неопределенного интеграла от любой непрерывной функции. Существование
интегралов 1—6 обеспечивается непрерывностью подынтегральных функций.
**) Это множество представляет собой либо интервал, либо сегмент, либо
полупрямую, либо бесконечную прямую.
188	НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ	[ГЛ. 6
этой функции. Пусть далее для функции g(t) существует на
множестве {Z} первообразная функция G(t), т. е.
\g(t)dt = G(t)+C.	(6.3)
Тогда всюду на множестве {х} для функции g[<p (х)] <р' (х) суще-
ствует первообразная функция, равная О [<р (х)], т. е.
5 g [? (*)1 ?' (*)dx = ° [? (*)] + С.	(6.4)
Для доказательства этого утверждения достаточно воспользоваться
правилом дифференцирования сложной функции *)
{<3 [? (х)]} = G' [ср (х)] ср' (х)
и учесть, что, по определению первообразной, G'(f) — g(t). Предпо-
ложим теперь, что, нам требуется вычислить интеграл
\f(x)dx.	(6.5)
В ряде случаев удается выбрать в качестве новой переменной такую
дифференцируемую функцию f —<р(х), что имеет место равенство
/(*) = £ [ср (х)] ср' (х),	(6.6)
причем функция g(f) легко интегрируется, т. е. интеграл
^(^ = G(0 + C
просто вычисляется. Доказанное выше утверждение позволяет нам
написать следующую формулу для интеграла (6.5):
$/(x)dx = G[<p(x)] + C.	(6.7)
Этот прием вычисления интеграла (6.5) и называется интегрирова-
нием путем замены переменной.
Конечно, такой прием применим не ко всякому интегралу. Кроме
того, следует подчеркнуть, что выбор правильной подстановки в зна-
чительной мере определяется искусством вычислителя. Приведем ряд
примеров, иллюстрирующих только что изложенный метод.
1°. Вычислить Jcos2x dx. Для вычисления этого интеграла сле-
дует сделать простейшую подстановку t = 2х, dt = 2dx. В резуль-
тате этой-замены получим
С о л С 1 \ cos 2х dx = \ у //у 2°. Вычислить \ —:—. J х -|- а замены t — x-\-a, dt — dx. *) См. § 7 главы 5.	cos t dt = sin t + С = у sin 2х + С. Этот интеграл вычисляется посредством
§ 2]
ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ
189
При этом получим
5т = Ь1|И + С-1п|х + а| + С. (хуЬ — а).
3°. Вычислить § ecos х sin х dx. Легко видеть, что этот интеграл
вычисляется путем замены Z = cosx.
В самом деле, при этом dt =— smxdx и
J ecos х sin х dx = — J e‘ dt = — e* + C = —ecos x + C.
(* (arctg
4°. Вычислить \ д —dx. Для вычисления этого интеграла
удобна замена t — arctg х. В самом деле, при такой замене dt—
dx С (arctg х)100 , _ С ,, _ Z101 . г_ (arctg x)i“ с
— Г+хз J ~1+'х®- ах~ у а1~ 101^	101	+Ь--
5°. Вычислить § (7х— 9)2999 dx. Конечно, этот интеграл можно
свести к сумме трех тысяч табличных интегралов, расписывая подын-
тегральную функцию по формуле бинома Ньютона. Несравненно
проще сделать замену t = lx— 9, dt — ldx, в результате которой
мы получим
J (7х-9)2989 Дг = у jj ^9"^-24ооо + С- 21 000 +С.
6°. Вычислить	.Чтобы усмотреть ту замену, посредством
которой может быть взят этот интеграл, перепишем его в виде \
f dx	\ cos х dx	(* cos x dx
j cos x	J cos2 x	J 1 — sin2 x ’
После этого понятно, что следует положить t = sinx, dt = cos xdx.
В результате получим
7°. Вычислить \ ,9 ,8	. Удобна замена t = (2х)4, dt = 64х3 dx.
При этом
0 х3 dx _ 1 Г dt ________arctg t „ _ arctg (2х)4	„
J (2х)8 + 1 “ 64 J Z2 + 1 — 64 +c—	64
8°. Вычислить £-------——ту. Для вычисления этого интеграла
} (х2 + п2) /а
оказывается удобной тригонометрическая подстановка t = arctg ,
хх,	dt
х — a tg t, dx — a —.	i
b ’	cos2 Z	-1
190
неопределенный интеграл
[ГЛ. 6
В результате этой подстановки интеграл принимает вид
С dx 1 г , ,,_sin/ . г_______________________tg* , г
J (х2 + а2)’/г a2 J	+ а2 /1 4- tg2/ +
=—гХ-^ +£
а2 У х2 + а2
9°. Вычислить С--------—	. Здесь оказывается удобной подста-
J (а2 — х2)3/*
новка t — arcsin — , х = a sin/, dx — a cos t dt. При этом
а	г
С dx = — С di —	4- с =
' (а2 — Х2)3/г а2 ' cos2 / а2 +
— 1 sin z 4- С —___________-________I- С
~ а2 V1 — sin21 "Г ~ а2 /а2 — х2
10°. Вычислить j/^^~~^dx. Для вычисления этого интеграла
оказывается удобной замена 2/ — arccos у, x = acos2/, dx =—
— 2а sin 2t dt. Мы получим
J ]/= cos2/rf/ =
= — 4a + У C0S	— 2a f C°S =
= — 2at — a sin 2t 4- C=
2. Интегрирование по частям. К числу весьма эффективных ме-
тодов интегрирования относится метод интегрирования по частям.
Этот метод основывается на следующем утверждении.
Пусть каждая из функций и(х) и т>(х) дифференцируема на
множестве {х} и, кроме того, на этом множестве существует
первообразная для функции v (х) и' (х). Тогда на множестве {х}
существует первообразная и для функции и (х) и' (х), причем
справедлива формула
и (х) v' (х) dx = и (х) v (х) —	(х) и' (х) dx. (6.8)
Замечание. Определение дифференциала и свойство инвари-
антности его формы позволяет записать формулу (6.8) в виде
^udv = и (х) v (х) — J к du.	(6.9)
Для доказательства сформулированного утверждения запишем фор-
мулу для производной произведения двух функций и(х) и v(x)
[zz (х) V (х)]' = и (х) v' (х) + и' (х) V (х).	(6.10)
5 2)
ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ
191
Умножим равенство (6.10) на dx и возьмем интеграл от обеих частей
полученного таким путем равенства. Так как по условию для всех х
из множества {х} существует jj v (х) и' (х) dx и [и(х)в(х)]' dx =
= и (х) v (х) + С (см. свойство 2° из п. 3 § 1), то для всех х из
множества {х} существует и интеграл и (х) v' (х) dx, причем спра-
ведлива формула (6.8) (или (6.9)).
Формула (6.9) сводит вопрос о вычислении интеграла J и dv
к вычислению интеграла ^vdu. В ряде конкретных случаев этот
последний интеграл без труда вычисляется.
Вычисление интеграла § и dv посредством применения формулы (6.9)
и называют интегрированием по частям. Заметим, что при конкрет-
ном применении формулы интегрирования по частям (6.9) очень удобно
пользоваться таблицей дифференциалов, выписанной нами в п. 2 § 9
главы 5.	'
Переходим к рассмотрению примеров.
1°. Вычислим интеграл l—^xnlnxdx(nj^ — 1). Полагая и = 1пх,
dx
dv = xndx и используя формулу (6.9), получим du= —, v
vn+1	1 г	v-n+1 /	i \
/ = ——г 1п х — —г-г- \ xndx = —р-г (In х  -—г) + С.
n + 1	(« + 1)J	п +1 \ п + 1у
2°. Вычислим далее интеграл 1= х arctg xdx. Полагая и == arctg х,
dv = х dx и используя формулу (6.9), будем иметь du — f = у,
. х2 ,	1 С х2 , ха ,	1 Г 1(1 + х2) —-11 ,
] = у arctg х - т	dx = 2- arctg х - у --q-^ dx =
х2 ,	1 С ,	. 1 (* dx х2 +1	, х , „
= yarctgx-y \ dx +у \	arctgх-у + С.
3°. Вычислим интеграл I = х2 cos х dx. Сначала применим фор-
мулу (6.9), полагая и = хг, dv = cosxdx. Получим du—2xdx,
v = sinx, / = x2sinx—2 ^xsinxtZx. Для вычисления последнего
интеграла еще раз применим формулу (6.9), полагая на этот раз
и — х, dv = sin х dx. Получим du = dx, v = — cosx, /=x2sinx +
+ 2x cos x — 2 cos x dx = (x2 — 2) sin x + 2x cos x + С. Tаким образом,
интеграл Jx2cosxdx вычислен нами посредством двукратного интег-
рирования по частям. Легко понять, что интеграл хл cos х dx
(где п — любое целое положительное число) может быть вычислен
по аналогичной схеме посредством д-кратного интегрирования по
частям.
192
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
[ГЛ. 6
4°. Вычислим теперь интеграл / = еахcosbxdx(a = const, b =
— const). Сначала применим формулу (6.9), полагая и — eeJf, dv =
= cos bx dx. Получим du = aeax dx, v = -in^*,
, eOJC sin bx a ? ax , ,	,
I =---g—- — у \ ea sin bx dx.
Для вычисления последнего интеграла еще раз применим формулу (6.9),
полагая на этот раз и = еах, dv = sin bxdx. Получим dit = аеах dx,
cos bx
b~>
, eax sin bx , a ax . a? ,	.
/ =----b---eax cos bx-^1.	(6.11)
Таким образом, посредством двукратного интегрирования I по частям
мы получили для интеграла / уравнение первого порядка (6.11). Из
этого уравнения находим
а2 + &2
Практика показывает, что большая часть интегралов, берущихся по-
средством интегрирования по частям, может быть разбита на следую-
щие три группы'.
1)	К первой группе относятся интегралы, подынтегральная функция
которых содержит в качестве множителя одну из следующих функций:
lnx, arcsinx, arccos х, arctg х, (arctg х)2, (arccos х)2, In ср (х), ...
(см. рассмотренные выше примеры 1° и 2°). Для вычисления интег-
ралов первой группы следует применить формулу (6.9), полагая в ней
и(х) равной одной из указанных выше функций*).
2)	Ко второй группе относятся интегралы вида (ах &)" cos (ex) dx,
$ (ах-Ь/>)я sin(cx)dx, § (ах + b)necxdx, где а, Ь, с—некоторые по-
стоянные, п— любое целое положительное число (см. рассмотренный
выше пример 3°). Интегралы второй группы берутся путем «-крат-
ного применения формулы интегрирования по частям (6.9), причем
в качестве и(х) всякий раз следует брать (ах + &) в соответствую-
щей степени. После каждого интегрирования по частям эта степень
будет понижаться на единицу.
3)	К третьей группе относятся интегралы вида § еах cos bx dx,
J еах sin bx dx, § sin (in x) dx, ^cos(lnx)</x, ... (см. рассмотренный
выше пример 4°). Обозначая любой из интегралов этой группы через
*) В случае, если подынтегральная функция содержит в качестве множителя
(arctg*)2, (arccos*)2, ...j формулу интегрирования по частям (6.9) придется
применить дважды.
§ 2]
ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ
193
I и производя двукратное интегрирование по частям, мы составим
для / уравнение первого порядка.
Конечно, указанные три группы не исчерпывают всех без исклю-
чения интегралов, берущихся посредством интегрирования по частям.
Приведем примеры интегралов, не входящих ни в одну из перечис-
ленных трех групп, но вычислимых при помощи формулы (6.9).
~ xdx
— интеграл не входит
менее, применяя фор-
получим du = dx,
5°. Вычислим интеграл / = \ —z—. Этот
к	J COS2X
ни в одну из упомянутых трех групп. Тем не
мулу (6.9) и полагая в ней и = х, dv=='crfs2x<
v — tg х,
S,	,	, Г sin xdx
tgxdx = xtgx — \----=
°	b J COS X
— x tg xa^SxX) = X tg X + In I COS X I + C-
6°. Вычислим, наконец, весьма важный для дальнейшего интеграл
К\= \———, где а = const, Х=1, 2, ... Этот интеграл также
J (/2 + а2)>ч
не входит ни в одну из упомянутых выше трех групп. Для вычисле-
ния этого интеграла установим для него рекуррентную формулу, сво-
дящую вопрос о вычислении к вычислению Kx.i-
Можно записать (при X ф 1)
1 Р a2 dt _ jf К<2 + °2) ~ /81 dt
а2 ' (/2 + а2^ — а2 J (i!2 +<z2)k
_ ( dt __________________L C t 2tdt
~ a2 J (/2 + a2)k‘‘	2a2 J (/2 + a2)x '
1 {id^ +
a2 2a2 J (/2 + a2)x *
Для вычисления последнего интеграла применим формулу
zc	и / j d (/2 + а2)
рования по частям (6.9), полагая в ней u — t, dv=——1
(/2 + а2)х
1
интегри-
Полу-
чим du — dt, v =	,
(л— 1) (<2 + a2)*-i ’
=1 Кх_х +----------------1------—-------------1----/<х v
a2	2a2 (X — 1) (/2-f-a2)x-1	2a2 (X — 1)
Из последнего равенства получим рекуррентную формулу
К =________________t______________ , 1 (2Х - 3) к
Х 2a2 (X — 1) (/2 + а2)х-1 "Г a2 (2Х — 2) Х v
Убедимся в том, что рекуррентная формула (6.12) позволяет
194
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
[гл. е
вычислить интеграл Ку для любого Х = 2, 3, ... В самом деле, инте-
грал вычисляется элементарно
<»	.,	, »	Л-М 1	у
,,	£	dt	If \а 1	-	t	, п
K, =	\	\	FTi ——’ = — arctg--И O.
1 J t2 + a3 a J , j a 6 a
\aj +
После того как вычислен интеграл Klt полагая в формуле (6.12)
X = 2, мы без труда вычислим К2. В свою очередь, зная К2 и полагая
в формуле (6.12) Х = 3, мы без труда вычислим К3. Продолжая дей-
ствовать таким образом дальше, мы вычислим интеграл К/. для любого
натурального X.
ГЛАВА 7
КОМПЛЕКСНЫЕ ЧИСЛА. АЛГЕБРА МНОГОЧЛЕНОВ.
ИНТЕГРИРОВАНИЕ В ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ
В предыдущей главе было указано, что неопределенный интеграл
от элементарной функции, вообще говоря, не является элементарной
функцией. Тем не менее существуют довольно широкие классы функ-
ций, интегралы от которых представляют собой элементарные функ-
ции. (Такие классы функций му будем называть интегрируемыми
в элементарных функциях.) Изучение указанных классов функций
и составляет основную цель настоящей главы. Поскольку среди
указанных классов функций одним из основных является класс
рациональных функций, мы должны прежде всего уточнить на-
ши представления о многочленах и рациональных функциях. Для
этого в свою очередь требуется уточнить наши сведения о комп-
лексных числах.
1. Краткие сведения о комплексных числах
Два вещественных числа х и у мы будем называть упорядо-
ченной парой, если указано, какое из этих чисел является пер-
вым, какое вторым. Упорядоченную пару вещественных чисел х
и у будем обозначать символом (х, у), записывая на первом месте
первый элемент пары х.
Комплексным числом называется упорядоченная пара (х, у)
вещественных чисел, первое из которых х называется действи-
тельной частью, а второе у —мнимой частью этого комплекс-
ного числа.
В случае, когда мнимая часть у равна нулю, соответствующую
пару (х, 0) договариваются отождествлять с вещественным числом х.
Это позволяет рассматривать множество всех вещественных чисел как
часть множества комплексных чисел.
Два комплексных числа zt = (xlt уг) и z2 — (x2, у2) называются
равными, если xt — xit у^^у^- Говорят, что комплексное число
z = (x, у) равно нулю, если х — 0 и у = 0.
196
ИНТЕГРИРОВАНИЕ В ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ
[ГЛ. 7
Определим операции сложения и умножения комплексных чисел.
Поскольку вещественные числа являются частью множества комплекс-
ных чисел, эти операции должны быть определены так, чтобы в при-
менении к двум вещественным числам они приводили к уже извест-
ным нам из § 2 главы 2 определениям суммы и произведения веще-
ственных чисел.
Суммой двух комплексных чисел z1 — (x1, yj и г2 = (х2, у2)
назовем комплексное число z вида
г = (х1 + х2, л+-Уг)-	(7Л)
Произведением двух комплексных чисел zt = (xv уг) и z2 = (х2, у2)
назовем комплексное число z вида
z = (x1x2-y1y2, х^ + х^]).	(7.2)
Легко проверить, что сумма и произведение комплексных чисел об-
ладают теми же самыми свойствами, что и сумма и произведение
вещественных чисел. Именно справедливы следующие свойства:
1°. zY + z2 = z2 -f- zx (переместительное свойство суммы).
2°. (гх + zs)'+ z3 =	-f-(z2 + z8) (сочетательное свойство суммы).
3°. z -|- (0, 0) = z (особая роль числа (0, 0)).
4°. Для каждого числа z — {x, у) существует противоположное
ему число z' — {—х, —у) такое, что z + z' — (Q, 0).
5°. zL • z2 — z2 • zr (переместительное свойство произведения).
6°. (zt  z2)  z3 = z1- (z2 • z3) (сочетательное свойство произведения).
7°. z-(l, 0) — z (особая роль числа (1, 0)).
8°. Для любого комплексного числа z = (x, у), не равного нулю,
существует обратное ему число у = (	~
такое, что г-у = (1,0).
9°. (Zj-I- z2)- z3— zt • z3 + z2 • z3 (распределительное свойство про-
изведения относительно суммы).
Свойства 1°—9° позволяют утверждать, что для комплексных
чисел полностью сохраняются все правила элементарной алгебры,
относящиеся к арифметическим действиям и к сочетанию равенств.
Кроме того, эти свойства полностью решают вопрос о вычита-
нии комплексных чисел как о действии, обратном сложению, и о де-
лении комплексных чисел как о действии, обратном умножению.
Разностью двух комплексных чисел zx — (хр yj и z2 = (х2, _у2)
называется такое комплексное число z, которое в сумме с z2
daent zv С помощью свойств 1°—4° элементарно устанавливается
существование и единственность разности двух любых комплексных
чисел *).
*) Это делается точно так же, как и для вещественных чисел (см. п. 3
§ 2 главы 2).
§ И
197
КРАТКИЕ СВЕДЕНИЯ О КОМПЛЕКСНЫХ ЧИСЛАХ
Легко проверить, что разностью двух комплексных чисел z± — (xv
и г2 = (х2, j/2). является комплексное число z вида
z = (x1-x2, Л-Л)-	G-З)
Частным двух комплексных чисел z1 = (xl, у^) и z2 = (x2, у2),
второе из которых не равно нулю, называется такое комплекс-
ное число z, которое при умножении на z2 дает zv С помощью
свойств 5° — 8° легко установить, что единственным частным двух
указанных комплексных чисел является комплексное число z вида

— Х1У2\
xl+yl г
(7.4)
В операциях с комплексными числами особую роль играет число,
представимое парой (0,1) и обозначаемое буквой I. Умножая эту пару
самое на себя (т. е. возводя ее в квадрат), получим в силу определе-
ния произведения комплексных чисел:
(0, 1) • (0, 1) = (— 1,0) = — 1, т. е. i2 = — 1.
Заметив это, мы можем любое комплексное число z — (х, у) пред-
ставить в виде
z = (x, у) = (х, 0) + (0, j) = (x, 0) + (j/, 0).(0, 1) = х-Н>.
В дальнейшем мы будем широко использовать для комплексного
числа z = (x, у) представление z — xy-iy. Это представление и рас-
смотрение i в качестве множителя, квадрат которого равен — 1,
позволяет производить операции с комплексными числами так же, как
они производятся с алгебраическими многочленами.
Комплексное число z = (x, — у) = х — iy принято называть сопря-
женным по отношению к комплексному числу z = (x, y) = x.+ iy.
Очевидно, что комплексное число равно нулю тогда и только
тогда, когда равно нулю сопряженное ему число *).
Для геометрического изображения комплексных чисел удобно
пользоваться декартовой прямоугольной системой координат. При этом
комплексное число z = (х, у) изображается или точкой /И с коорди-
натами (х, _у), или вектором ОМ, идущим из начала координат
в точку М.
При таком способе изображения сложение и вычитание комплек-
сных чисел сводится к сложению и вычитанию соответствующих им
векторов (это понятно из формул (7.1) и (7.3)).
Если наряду с декартовой системой координат ввести полярную
систему координат так, чтобы полюс находился в начале О декарто-
вой системы, а полярная ось была направлена вдоль положительного
направления оси Ох, то декартовы координаты (х, у) и полярные
*) Ибо равенства х = 0,) х = 0, ]
) и „ > эквивалентны,
у = 0 // -z/ = 0 /
198	ИНТЕГРИРОВАНИЕ В ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ	[ГЛ. 7
Координаты (р, 6) любой точки М, как известно, связаны формулами
Р = Ух2+у2,
x-pcosS, |	(arctg— прих>0,
_У = Р8ш9 J	х	(75)
0=- arctgу4-1С sgnyприx<fi,
у sgn у при х— 0.
Формулы (7.5) приводят нас к тригонометрической форме пред-
ставления комплексного числа z = (х, у)
z = (x, y) = x-\-ly — (p cos 0, р sin 0) = p (cos 0 +1 sin 0).	(7.6)
В тригонометрической форме представления (7.6) число р называют
модулем, а угол 0 аргументом комплексного числа. Аргумент 0 опре-
делен неоднозначно: вместо значения 0 можно брать значение 0 + 2вд
(где л = 0, ±1, ±2, ...).
В тригонометрической форме удобно производить операции умно-
жения и деления комплексных чисел.
Пусть даны два произвольных комплексных числа
г1 = (X1> J1) = (Pl cos PiSinOj) и z2 = (х2, у2) — (р2 cos 02, p2sinO2).
Тогда, по определению умножения (в силу формулы (7.2)), произ-
ведение этих чисел имеет вид
• г2 = (ххх2 -yty2, х^ + х2Уг) =
= (pjp2 cos 02 cos 92 — р2р2 sin 9j sin 02, p1p2 cos 9X sin 02 + pxp2 sin 9г cos 02) =
= [(PiP2)cos(914-92), (pxpa) sin (0X + 92)].	(7.7)
Аналогично из формулы (7.4) заключаем, что частное — двух комплекс-
^2
ных чисел г1 = (х1, J1) = (p1cos01, p1sin01) и z2 = (х2, у2) = (р2 cos 0.2,
р2 sin ©J имеет вид*)
а = cos (0, - 02), (₽J) sin (0j - 02)1.	(7.8)
г2 1_\?2/	\Ра/	J
Из формул (7.7) и (7.8) заключаем, что при умножении двух ком-
плексных чисел их модули перемножаются, а аргументы скла-
дываются (при делении двух комплексных чисел их модули де-
лятся, а аргументы вычитаются). Это свойство последовательно
переносится на случай произведения любого конечного числа комп-
лексных чисел. В частности, если перемножаются п равных комплекс-
ных чисел (т. е. если комплексное число возводится в степень п), то
(р cos 9, р sin 0)" = (рл cos 0л, p”sin 9л).	(7.9)
*) При этом предполагается, что комплексное число г2 не равно нулю, т. е.
§21
АЛГЕБРАИЧЕСКИЕ МНОГОЧЛЕНЫ
199
Из формулы (7.9) при р = 1 получим так называемую формулу
Муавра *)
(cos 9, sin 9)я = (cos 0n, sin 9л).	(7.10)
t
Формулу (7.10) можно записать и в другом представлении:
(cos 9 + /sin 9)" = cos 9л +1 sin On.	(7.11)
В заключение заметим, что комплексное число, записанное в триго-
нометрической форме, равно нулю в том и только в том случае,
когда равен нулю его модуль. Отсюда и из того, что при перемно-
жении комплексных чисел их модули перемножаются, вытекает, что
произведение нескольких комплексных чисел равно нулю лишь
в том случае,. когда равен нулю хотя бы один из сомножителей.
§ 2. Алгебраические многочлены
1. Алгебраическим многочленом л-й степени называется выраже-
ние вида
/ (г) = сйгп + qz"-1 +... + cn-rz + сп,	(7.12)
где z = (х, 1у) = х + (у — переменное комплексное число, а с0, cv ...
.. .,сп — некоторые постоянные комплексные числа, первое из которых
отлично от нуля. Как известно, любой алгебраический многочлен сте-
пени п можно поделить «столбиком» на другой алгебраический мно-
гочлен степени не выше чем п. Таким путем мы приходим к следу-
ющему утверждению: каковы бы ни были два многочлена f (z) и
<р (г) такие, что степень ср (г) не выше, чем f(z), справедливо
равенство
fW = 4(zYq(z) + r(z),	(1AZ)
в котором q (z) и г (z) — некоторые многочлены, причем степень
q(z) равна разности степеней многочленов f{z) и <p(z), а сте-
пень г (z) ниже степени <р (z).
По отношению к фигурирующим в равенстве (7.13) многочленам
/(?), ср (г), q(z) и г (z) обычно применяют вполне понятные термины
«делимое», «делитель», «частное» и «остаток».
Говорят, что многочлен f(z) делится на многочлен <p(z), если
в полученной посредством деления столбиком формуле (7.13) остаток
r(z) = 0.
Договоримся называть многочленом нулевой степени любую ком-
плексную постоянную. Тогда совершенно ясно, что любой многочлен
делится на отличный от нуля многочлен нулевой степени.
*) А. де Муавр — английский математик, по национальности француз
(1667-1754).
200
ИНТЕГРИРОВАНИЕ В ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ
[ГЛ. 7
Изучим вопрос о делимости многочлена f(z) на многочлен первой
степени (z — b).
Определение. Назовем комплексное число b корнем мно-
гочлена f(z), если f(b) равно нулю.
Теорема 7.1. Многочлен нулевой степени f(z) делится на
двучлен (z—b) тогда и только тогда, когда b является корнем
многочлена f(z).
Доказательство. Запишем для многочленов f(z) и <?(z) =
= (z—b) формулу (7.13). Поскольку степень остатка г (г) в этой
формуле обязана быть ниже степени делителя <p(z)^z — Ь, то
г (г) — многочлен нулевой степени, т. е. г (г) = с = const. Таким об-
разом, формула (7.13) принимает вид
f(z)^(z-b)-q(z) + c.	(7.14)
Полагая в формуле (7.14) z — b, найдем, что c=f(b). По определе-
нию f (г) делится на z — b тогда и только тогда, когда остаток
в формуле (7.14) с — f (b) равен нулю, т. е. тогда и только тогда,
когда b является корнем f(z). Теорема доказана.
2. Естественно, возникает вопрос: всякий ли алгебраический мно-
гочлен имеет корни? Ответ па этот вопрос дает основная теорема
алгебры *): всякий многочлен ненулевой степени имеет хотя бы
один корень.
Опираясь на эту теорему, докажем, что алгебраический много-
член п-й степени имеет точно п корней **). В самом деле, пусть
f (z) — многочлен n-й степени. Согласно основной теореме алгебры
f(z) имеет хотя бы один корень bv т. е. для /(z) справедливо пред-
ставление
*	/(г) = (г-^)Л(г),	(7.151)
в котором через (z) обозначен некоторый многочлен степени (я — 1).
Если я 1, то> согласно основной теореме алгебры,(z) имеет хотя
бы один корень Ьг, т. е. для fr(z) справедливо представление
/x(z) = (z-ft2)/2(z),	(7.152)
в котором через/2(z) обозначен некоторый многочлен степени (л —2).
Повторяя указанные рассуждения далее, мы получим представления
A(z) = (z-t3)/3(z),	(7.153)
(7.15")
*) Доказательство этой теоремы см. в выпуске «Функции комплексной
переменной».
**) При этом, конечно, мы считаем, что п>0.
АЛГЕБРАИЧЕСКИЕ МНОГОЧЛЕНЫ
201
§ 2)
В последнем из этих представлений через fn(z) обозначен некоторый
многочлен нулевой степени, т. е. /„ (г) = с = const. Сопоставляя между
собой равенства (7.1 б1) — (7.15я) и учитывая, что fn(z) — c, Ъул&л
иметь
f(z) = (.z-b^(z-b^ ... (z-bn)c:	(7.16)
Отметим, что комплексная постоянная с не равна нулю, ибо_в про-
тивном случае многочлен f(z) был бы тождественно равен нулю и
не являлся бы многочленом n-й степени *).
Из равенства (7.16) очевидно, что f(bt) =f(b2) = ...—f(bn) — 0,
t. e. каждое из чисел bv b2, ..., bn является корнем многочлена f(z).
Кроме того, из (7.16) очевидно, что, каково бы ни было комплекс-
ное число Ь, отличное от bv b2......Ьп, комплексное число f(b) не
равно нулю**). Таким образом,'многочлен /(г) имеет ровно п кор-
ней: Ьх, Ь2, ..., Ьп.
Равенство (7.16) дает разложение многочлена f(z) на множители.
Если известен вид многочлена f(z) (7.12), то мы можем определить
постоянную с в равенстве (7.16). Сравнивая в равенствах (7.16) и
(7.12) коэффициенты при zn, получим с = с0***). .
Многочлен (7.12), у которого с0= 1, называется приведенным.
Для приведенного многочлена формула разложения (7.16) принимает
вид
/(г) = (г-^)(г-Л)...(г-Ья).	(7.17)
Сравнивая формулу (7.17) с формулой (7.12) (при сй — 1), получим следующие
соотношения:
ci — — (bi + b2 + ... -|- Ьп),
с2 = + (bib2 + Ьф3 + ... + bn_ibn),
cn = (-\)n.bib2 ... bn.
В дальнейшем, если не оговорено .противное, мы будем рассматривать
приведенные многочлены.
*) Здесь мы используем следующее утверждение: если многочлен f (г) =
= аогл + а1гя-1+ an_iz + ап тождественно равен нулю, то все его коэф-
фициенты равны нулю. В самом деле, если f(z) = O, то при г = 0 получим
ал—0. Но тогда f (г) = г [аогп-1 + fljz'1-2-)-... + on_i] = 0. Так как г ^0, то
выражение й" квадратных скобках тождественно равно нулю, откуда при z = 0
получим an_i ~ 0. Продолжая аналогичные рассуждения далее, докажем, что
все коэффициенты равны нулю.
**) Ибо произведение нескольких комплексных чисел равно нулю лишь
в том случае, когда равен нулю хотя бы один из сомножителей (см. § 1).
***) Здесь мы используем утверждение: если два многочлена aoz'l-^-aiZn'~1-\-
+ ... + ап и bazn +	+ •   + bn тождественно равны друг другу, то а0 = Ьо,
«х = bi,	, ап = Ьп. Для доказательства достаточно к разности указан-
ных многочленов применить утверждение, отмеченное в сноске *) на этой
странице.
202
ИНТЕГРИРОВАНИЕ В ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ
[гл. г
§ 3. Кратные корни многочлена. Признак кратности корня
Среди корней многочлена f[z) могут быть совпадающие корни.
Пусть а, Ь, ..., с — различные корни приведенного многочлена /(г).
Тогда в силу результатов предыдущего параграфа для f(z) справед-
ливо разложение
f(z) = (z-a'f(z-b'f ... (z-c)\	(7.18)
В этом разложении а, £....f — некоторые целые числа, каждое из
которых не меньше единицы, причем а-|-р-|-...-|-у = л, где п—
степень многочлена /(z).
Если для многочлена f(z) справедливо разложение (7.18), то
говорят, что комплексное число а является корнем f(z) крат-
ности а, комплексное число b является корнем f(z) кратности
р, ..., комплексное число с является корнем f(z) кратности у.
Корень, кратность которого равна единице, принято называть
однократным, а корень, кратность которого больше единицы,
принято называть кратным.
Можно дать и другое эквивалентное определение корня данной
кратности: комплексное число а называется корнем многочлена
f(z) кратности а, если для f(z) справедливо представление
f(z) = (z-a')^(z), где ф(а)^0.	(7.19)
Наша цель — указать необходимое и достаточное условие для
того, чтобы комплексное число а являлось корнем многочлена /(z)
кратности а.
Назовем производной многочлена f(z) многочлен f(z), получен-
ный формальным дифференцированием *) f(z) по z. Прежде всего
докажем следующее утверждение.
Лемма 1. Если комплексное число а является корнем крат-
ности а многочлена f (z); то это же число а является корнем
кратности (а — 1) многочлена f (z).
Замечание. В частности, при а=1 число а, будучи однократ-
ным корнем f(z), совсем не является корнем f (z).
Доказательство. По условию для /(z) справедливо пред-
ставление (7.19). Дифференцируя формулу (7.19), будем иметь
Г (z) = a (z - а)1"1 <р (z) + (z - о)а <?' (z),
ИЛИ
Г (z) = (z — я)”-1	(z),	(7.20)
где
<f>i (г) = аср (z) + (z - а) <р' (z).
*) То есть дифференцирование f (г) по г производится так, как если бы г
была вещественной переменной.
§ 4] ВЫДЕЛЕНИЕ КРАТНЫХ КОРНЕЙ. АЛГОРИТМ ЕВКЛИДА	203
Поскольку срх (а) = а<р (а)	0, то представление (7.20) означает, что
число а является корнем кратности (а — 1) многочлена f (г). Лемма
доказана.
Теорема 7.2. Для того чтобы комплексное число а являлось
корнем кратности а многочлена f(z), необходимо и достаточно,
чтобы были выполнены следующие условия:
f(a)=f’{a) = ...=^{d) = Q, /а’(а)#0.	(7.21)
Доказательство. 1) Необходимость. Пусть а является
корнем кратности а многочлена f(z). Тогда, согласно лемме 1, это же
число а является корнем кратности (а—1) многочлена f (г~), корнем
кратности (а — 2) многочлена (г), ,.., корнем кратности единица
многочлена (г), т. е.
f(a) (а) = ... =/(“-« (а) = 0.
Согласно замечанию к лемме 1 число а совсем не является корнем
многочлена /(“>(г), т. е. /(а)(а)^0. Выполнение условий (7.21)
доказано.
2) Достаточность. Пусть выполнены условия (7.21). Требуется
доказать, что число а является корнем кратности а многочлена f(z).
Так как (а) — 0, число а является корнем многочлена (?)
кратности не ниже единицы. Стало быть, на основании леммы 1
число а является корнем многочлена (г) кратности не ниже
двух, корнем многочлена (г) кратности не ниже трех, ...,
корнем многочлена f(z) кратности не ниже а.
Остается доказать, что кратность корня а многочлена f(z) не выше а.
Если бы эта кратность была выше а, то, согласно лемме 1, кратность
корня а многочлена /(а-1)(г) была бы выше единицы, откуда следо-
вало бы, что а является корнем (г), т. е. (а) = 0, что проти-
воречит последнему из условий (7.21). Теорема доказана.
§ 4. Принцип выделения кратных корней.
Алгоритм Евклида
1. Принцип выделения кратных корней. Поставим перед собой
цель —для данного многочлена /(г), имеющего, вообще говоря, крат-
ные корни, найти такой многочлен F(z), который имеет те же
самые корни, что и f (z), но все кратности единица. Для достижения
этой цели введем некоторые новые понятия.
Определение 1. Назовем делителем двух многочленов f (z)
и <р (г) любой многочлен, на который делятся оба многочлена f(z)
и <р(2).
Определение 2. Назовем наибольшим общим делите-
лем двух многочленов f(z) и а> (z) такой их делитель, который
делится на любой другой делитель этих двух многочленов.
204
ИНТЕГРИРОВАНИЕ В ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ
[ГЛ. 7
Договоримся обозначать наибольший общий делитель двух много-
членов /(г) и ср (z) символом D [/(z), ср (z)].
Заметим, что из определения наибольшего общего делителя выте-
кает, что он определен с точностью до произвольного постоянного
множителя.
Возвращаясь к цели, сформулированной в начале настоящего пара-
графа, мы теперь легко можем проверить, что искомый многочлен F (z)
имеет вид
(7'22)
В самом деле, пусть
/ (z) = (z - а)л (z—bf ... (z — с)\	(7.23)
где а, Ь, ..., с —различные корни. Тогда, согласно теореме 7.2, для
многочлена f (z) справедливо представление
Г (г) = (z — о)2”1 (? —	• • • (г — с)т-1 ф (z)<	(7.24)
где ф (z) не содержит множителей (г — a), (z — Ь), ..., (z — с).
Из сопоставления формул (7.23) и (7.24) очевидно, что
D [f(z), f (г)] = (z - аГ1 {г - bf1 ..• (г - с)1’1.	(7.25)
Из сопоставления формул (7,23) и (7.25) в свою очередь очевидно,
что многочлен F (z), определяемый формулой (7.22), имеет вид
F(z) = (z — a)(z — b) ... (z-c).	(7.26)
Тем самым доказано, что многочлен F (z), определяемый формулой
(7.22), имеет те же самые корни, что и многочлен f(z), но все
кратности единица.
Таким образом, задача выделения кратных корней сводится к по-
строению по данному многочлену /(z) многочлена F (z), определимого
формулой (7.22).
Поскольку знаменатель формулы (7.22) содержит наибольший
общий делитель двух многочленов f(z) и f (z), возникает задача
о нахождении наибольшего общего делителя двух многочленов. Пере-
ходим к решению этой задачи.
2. Нахождение наибольшего общего делителя двух многочле-
нов (алгоритм Евклида). Пусть даны два совершенно произвольных
многочлена /(z) и ср (z)' и требуется найти их наибольший общий
делитель. Не ограничивая общности, будем считать, что степень ср (z)
не выше степени f(z). Тогда, поделив /(z) на cp(z) столбиком, мы
придем к формуле (7.13) (см. § 2)
/(Z) = ?(z)?(z)+r1(z),	(7.27’)
в которой, как установлено в § 2, степень остатка rx (z) меньше
степени делителя ср (z). Это дает нам право снова поделить столбиком
§4]
ВЫДЕЛЕНИЕ КРАТНЫХ КОРНЕЙ. АЛГОРИТМ ЕВКЛИДА
205
<Р (г) на гг (z). В результате этого деления мы получим формулу,
аналогичную формуле (7.13):
<Р (г) = rj (z) (г) + г2 (г),	(7.2 72)
в которой степень остатка г2 (z) ниже степени делителя гг (г).
Далее мы делим столбиком ц (z) на r2 (z) и т. д. В результате
получим
П (г) = r2 (г) (z) + r3 (z),	(7.27s)
Tk-2 GO = rk^ (z) qk^ (z) + rk (z).	(7.27*)
Поскольку при каждом делении столбиком степень остатка будет
снижаться по крайней мере на единицу, повторив описанный процесс
достаточно большое число k раз, мы на (&4-1)-м шагу получим
остаток, равный нулю *), т. е.
rk-Az)^rk(z)qk(z).	(7.27*+1)
Докажем, что последний отличный от нуля’ остаток r*(z) является
наибольшим общим делителем многочленов f(z) и 'f(z).
Достаточно доказать два утверждения:
1) многочлены /(z) и cp(z) делятся на rft(z) (это означает, что
rk(z) является одним из делителей/(z) и cp(z));
2) многочлен rft(z) делится на любой делитель r0(z) многочленов
/(z) и <p(z) (это означает, что rk (z) — наибольший общий делитель
указанных многочленов).
Для доказательства утверждения 1) заметим, что, в силу (7.27*+1),
(z) делится на г* (z), а тогда, в силу (7.27*), rft_2 (z) делится на
rA(z)... Поднимаясь вверх по цепочке равенств (7.271) — (7.27*), мы,
наконец, докажем, что <р (z) и /(z) делятся на rA(z).
Докажем теперь утверждение 2). Пусть r0 (z) — любой делитель
многочленов /(z) и <p(z). В силу равенства (7.271) rx(z) делится на
r0(z), а тогда, в силу равенства (7.272), r2(z) делится на r0(z), в СИЛУ
равенства (7.273) r3(z) делится на r0(z)... Опускаясь по цепочке
равенств (7.271) — (7.27*), мы, наконец, докажем, что rA(z) делится
на r0(z).
Тем самым мы полностью обосновали описанный выше процесс
нахождения наибольшего общего делителя двух многочленов. Этот
процесс обычно называют алгоритмом Евклида.
Пример. Найдем наибольший общий делитель двух много-
членов **)
/(z) = z4-2z3 + 3z2-2z+l и ср (z) 4z3 — 6z2 + 6z — 2.
*) Если остаток не обратится в нуль в одном из промежуточных звеньев
описанного процесса, то после некоторого количества k шагов мы получим
остаток г* (г) нулевой степени. Тогда следующий остаток rft+1 (г) заведомо
равен нулю (ибо любой многочлен делится на многочлен нулевой степени).
**) Легко видеть, что <f (г) = f (г).
206
ИНТЕГРИРОВАНИЕ В ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ
,[ГЛ. Z
Поделив f(z) на ®(г) столбиком, будем иметь	.
_ г4 - 2г3 + Зга - 2z + 1	| 4г3 - 6га + 6г -2
О	О	1	—'	--------
1 о , 3	2	3	, ,
2	+ 2 г 2	1
1	о , 3	2	3.1
— -A- Z3 + -г- Z2 — -J- Z + -т-
2	4	4'4
	з	2 з	,3 -r-z2 — -г- г + -у 4	4	'4
Далее мы должны были бы поделить <р (z) на обведенный пунктиром
многочлен. Однако, поскольку наибольший общий делитель определен
с точностью до произвольного постоянного множителя, удобно
4
умножить обведенный пунктиром остаток на -х- и поделить <р (г) на
О
многочлен г2 —г + 1. В результате получим
4г3-•’бг2 + 6г - 2 [га-г + 1
4г3 — 4г2 + 4г	4г — 2
_ - 2г2 + 2г - 2
— 2г2 + 2г — 2
остаток равен нулю.
Таким образом, наибольший общий делитель многочленов /(г) и
<р(г) равен г2 —г + 1, т. е.
D[f(z), <р(г)] = г2-г + 1.
Замечание 1. В приведенном выше примере мы для простоты
взяли многочлены /(г) и ср (г) с вещественными коэффициентами.
Та же методика сохраняет силу и для многочленов с комплексными
коэффициентами.
Замечание 2. Следует отметить, что до настоящего времени
практически отсутствуют устойчивые численные методы вычисления
корней произвольных многочленов с заданной точностью. Однако,
имея предварительную информацию о расположении искомого корня
многочлена на некотором сегменте числовой оси, мы можем вычис-
лить этот корень с интересующей нас точностью с помощью мето-
дов, изложенных в § 1 главы 12.
§ 5. Разложение правильной рациональной дроби
с комплексными коэффициентами на сумму простейших дробей
Рациональной дробью называется отношение двух алгебраи-
ческих многочленов. Рациональная дробь называется правильной, если
степень многочлена, стоящего в числителе, меньше степени многочлена,
стоящего в знаменателе. В противном случае рациональная дробь
§ 5]
РАЗЛОЖЕНИЕ ПРАВИЛЬНОЙ РАЦИОНАЛЬНОЙ ДРОБИ
207
Р (г)	,	,
—правильная рациональная дробь, зна-
Ч (Z)
имеет корнем кратности а комплексное
называется неправильной. Как правило, мы будем обозначать рацио
Р (г)
нальную дробь символом q-^-> понимая под P(z) и Q(z) алгебраи-
ческие многочлены.
Лемма 2, Пусть
менатель которой
число а, т. е.
Q (г) == (г — а)я (г), где у (а)	0.	(7.28)
этой дроби справедливо следующее представление:
Р(г) = А	ф (?)
Q (г) (г — и)" (г — а)и h ср (z) '
представлении А — комплексная постоянная, равная
k —целое число ^1, а ф (г) — некоторый многочлен,
Тогда для
(7.29)
В этом
А = ^-,
У (а)
причем последняя дробь в правой части (7.29) является правильной.
Доказательство. Обозначив через А постоянное число вида
А =	*), рассмотрим разность
? в А
Q(z) (г — а)а'
Приводя указанную разность к общему знаменателю, будем иметь
Р(?) А = Р(г)-А^(г) _ Ф (?)
<2 (z) (z — а)* (г — а)».<р (г) (г — аД ср (г) ’	1
где через Ф (г) обозначен многочлен вида Ф (г) = Р (z) — Ay (z).
Поскольку Ф (а) = Р(а) — Лф (а) — 0, комплексное число а является
корнем многочлена Ф(?) некоторой кратности k~^\, т. е.
Ф (г) = (z — a)k ф (г), где ф(а)^0.	(7.31)
Вставляя представление (7.31) в формулу (7.30), будем иметь
Р (z)_____А _________Ф (z)___ орх
Q (г)	(г — а)1	(г — а)“~л ср (г) ’	1-7
Тем самым формула (7.29) доказана. Остается только убедиться в том,
что дробь, стоящая в правой части (7.32), является правильной. Это
непосредственно вытекает из того, что разность двух правильных
дробей является правильной дробью **).
Лемма 2 доказана.
Из леммы 2 непосредственно вытекает следующая замечательная
теорема, устанавливающая факт разложимости правильной рациональ-
ной дроби на сумму простейших дробей.
*) Число А имеет смысл, ибо ср (а) ф 0 в силу (7.28).
**) В этом легко убедиться, приводя разность правильных' дробей к об-
щему знаменателю.
208
ИНТЕГРИРОВАНИЕ В ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ
[ГЛ. 7
Р (г)
Теорема 7.3. Пусть —
знаменатель которой, имеет вид
правильная рациональная дробь,
Q (z) = (z - а)“ (z - Ь/ ... (z - с)\	(7.33)
Тогда для этой, дроби справедливо следующее представление:
Р (?)  	। А2 ।	I	।
Q (г)	(г — а)а ' (г — а)а~1 'г ’' * - (г — а) ,
I В1_| Й2 |	[	
^(г —6)? (г —(г —Ь) 
+.................+
+^+(^+---+-Дг <7-34)
В этом представлении А2,..., Аа, BL, В2, ..., В^ ..., Cv С2,...
, Ст — некоторые постоянные комплексные числа, часть из
которых может быть равна нулю.
Доказательство. Сначала применим лемму 2 к дроби
Р(г)
<2(г) ’
имея в виду, что комплексное число а является корнем Q(z) крат-
ности а. При этом получим равенство (7.32). К правой части этого
равенства снова применим лемму 2, имея в виду, что либо комплекс-
ное число а является корнем знаменателя указанной правой части
кратности a — k (при а —А>0), либо, в силу разложения (7.33),
комплексное число b является корнем этого знаменателя кратности 8
(при 4—AsgO). В результате получим равенство, аналогичное (7.32),
к правой части которого снова можно применить лемму 2. Продол-
жая аналогичные рассуждения далее (т. е. последовательно применяя
лемму 2 по всем корням Q(z)), получим
ление (7.34). Теорема доказана.
Замечание. Поскольку в лемме 2
х Р(А
для дроби
представ-
число k может быть больше
единицы и многочлен Р (z) может иметь корни, совпадающие с кор-
нями Q (г), то часть коэффициентов Alt ..., Аа, В±, ..., В&, ..., Cv ...
..., Ст в формуле (7.34) может быть равна нулю.
§ 6. Разложение алгебраического многочлена
с вещественными коэффициентами
на произведение неприводимых вещественных множителей
Выше мы изучали разложение на сумму простейших дробей’ рацио-
нальной дроби с комплексными коэффициентами. Нашей окончатель-
ной целью является разложение рациональной дроби с веществен-
ными коэффициентами на сумму простейших дробей с всэдес/иеелг-
ными коэффициентами.
$ 6J	РАЗЛОЖЕНИЕ АЛГЕБРАИЧЕСКОГО МНОГОЧЛЕНА	209
Для достижения этой цели мы должны прежде всего найти разло^
жение алгебраического многочлена с вещественными коэффициентами
на произведение неприводимых вещественных множителей. Этому и
посвящен настоящий параграф.
Пусть
/(г) = zn +	+ с2гл-3 + ... + сп	(7.35)
— приведенный алгебраический многочлен с вещественными коэф-
фициентами сх, с2, .сп.
Прежде всего докажем следующую теорему.
Теорема 7.4. Если комплексное число а является корнем
алгебраического многочлена с вещественными коэффициентами
(7.35), то и сопряженное ему комплексное число *) а также яв-
ляется корнем многочлена (7.35). Более того, если комплексный
корень а имеет кратность, \ то и корень а имеет крат-
ность X.
Доказательство. Прежде всего докажем следующее вспомо-
гательное утверждение: если /(г) —многочлен с вещественными коэф-
фициентами, то комплексная величина f(z) является сопряженной
по отношению к величине f (г). Достаточно доказать, что для любого
номера п величина (2)” является сопряженной по отношению к вели-
чине zn. Это последнее непосредственно вытекает из тригонометри-
ческой формы комплексного числа. В самом деле, пусть
z = р (cos 9 +1 sin 0).
Тогда
z — р [cos (— 9) + i sin (— 9)].
В силу формулы Муавра (7.11)
zn = р" (cos 8п 4- i sin 9/г),
(z)n = р" [cos (— 0л) +1 sin (— 9л)] — р” (cos 9л — I sin 9л).
Из сопоставления двух последних формул вытекает, что (г)” является
величиной, сопряженной по отношению к гп. Вспомогательное утвер-
ждение доказано.
Пусть теперь комплексное число а является корнем многочлена
f (г), т. е. f(a) = 0. В § 1 этой главы мы установили, что ком-
плексное число равно нулю тогда и только тогда, когда равно нулю
сопряженное ему число. Стало быть, из равенства /(а) = 0 и из
доказанного выше вспомогательного утверждения вытекает, что
/(а) = 0, т. е.-число а является корнем f(z).
*) Всюду в дальнейшем мы будем обозначать комплексное число, сопря-
женное данному, тем же символом, что и данное число, но. с черточкой
наверху.
210
ИНТЕГРИРОВАНИЕ В ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ
[ГЛ. 7
Пусть дано, что кратность корня а равна X. Тогда в силу тео-
ремы 7.2
f{a) =f (a) =f^ (а) = ... =fW (а) = 0;	(а)	0. (7.36)
Так как комплексное число равно нулю тогда и только тогда, когда
равно нулю сопряженное ему число, то из доказанного выше вспо-
могательного утверждения и из соотношений (7.36) вытекают сле-
дующие соотношения *):
/(й) =/' (й) =JW	(й) = 0,	(й) # 0. (7.37)
В силу теоремы 7.2 соотношения (7.37) означают, что число й яв-
ляется корнем f(z) кратности X. Теорема 7.4 доказана.
Пользуясь теоремой 7.4, найдем разложение многочлена с веще-
ственными коэффициентами **) f(x) на произведение неприводимых
вещественных множителей. Пусть многочлен f(x) имеет вещественные
корни bv b2, ..., Ьт кратности рх, f32, ..., рот соответственно и ком-
плексно сопряженные пары корней аг и йх, а2 и й2, ..., ап и ап
кратности Х1( Х2, ..., Хя каждая пара соответственно.
Тогда, согласно результатам § 3, многочлен f(x) может быть
представлен в виде
f (Х) = (Х- (X - b2fc ... (X — Ь'п/'П (х - йх)х1 (х - йх)х1 X
X (х - «г/2 Iх — sz?2  •  (х- ап)'п (х - й„)хл. (7.38)
Обозначим вещественную и мнимую части корня ak(k = \, 2, ..., ri)
соответственно через uk и vk, т. е. пусть ак = uk + ivk. Тогда
ak = uk — ivk. Преобразуем для любого А=1, 2, ..., п выражение
(х - aktk (х - йА)х* = [(х - ak) (х - й*)]х* =
= [(х — Uk — iVk) (х - Uk + гоА)]х* = [(х — и*)3 + u*]xft =
= (х2+рАх + ^)Ч (7.39)
где
pk = — 2uk, Qk^ul + Vk.
Вставляя (7.39) в (7.38), окончательно получим следующее разложе-
ние многочлена /(х) на произведение вещественных неприводимых
множителей:
/(х) = (х - ix)₽i (х - fc2)p2 ... (х - bm)?™ (х2 +рхх + qrfi X
X (х2 + Рчх + ?2)х2 ... (х2 + рпх + qn)\ (7.40)
*) При этом мы учитываем, что производная многочлена с. веществен-
ными коэффициентами представляет собой многочлен также с вещественными
коэффициентами.
**) В дальнейшем нам придется иметь дело с многочленами от перемен-
ной, принимающей лишь вещественные значения. Поэтому для ее обозначения
удобнее пользоваться буквой хг а не г.
§7]	РАЗЛОЖЕНИЕ ПРАВИЛЬНОЙ РАЦИОНАЛЬНОЙ ДРОБИ	211
Мы приходим к выводу, что многочлен f(x) с вещественными коэф-
фициентами распадается на произведение (7.40) неприводимых веще-
ственных множителей, причем множители, соответствующие вещест-
венным корням, имеют вид двучленов в степенях, равных кратности
корней, а множители, соответствующие комплексным парам корней,
имеют вид квадратных трехчленов в степенях, равных кратности этих
пар корней.
§ 7. Разложение правильной рациональной дроби
с вещественными коэффициентами на сумму
простейших дробей с вещественными коэффициентами
Имеют место следующие два утверждения.
Лемма 3.
шественными
вещественное
р /и
Пусть — правильная рациональная дробь с ве-
коэффициентами, знаменатель .которой имеет
число а корнем кратности а, т. е.
Q (х) = (х — а)а <р (х), где ср (а)	0.
Тогда для этой дроби справедливо следующее представление:
Р(х):	А	ф(х)
Q (х) (х — ар (х — ар k ср (х)'
(7.41)
В этом представлении А — вещественное число, равное А =	,
k —целое число ^1, а ф (х) — некоторый многочлен с веществен-
ными коэффициентами, причем последняя. дробь в правой части
(7.41) является правильной. Лемма 3 доказательства не требует,
так как непосредственно вытекает из леммы 2. Следует только учесть,
что, поскольку Р(х) и Q (х) — многочлены с вещественными коэффи-
циентами, а а — вещественный корень, многочлены ср (х) и <р (х)
также имеют вещественные коэффициенты и, стало быть, постоянная
Л = —Н является вещественной.
<р (а)
р АЛ
Лемма 4, Пусть
Q(x)
щественными коэффициентами, знаменатель которой
имеет комплексные числа a = u-\-iv и a = u — iv корнями
ности X, т. е.
Q(x) = (x2+px + #<p(x), где ср(а)^О, ср (й) # 0,
р == — 2«, q — и2 ф- V2.
правильная рациональная дробь с ве-
Q(x)
крат-
(7-42)
Тогда для этой дроби справедливо следующее представление:
Р (х) _ Мх + тУ_________________ф(х)_________
Q (х)	(х2 + рх + qp (х2 + рх + qp~k <f (х)
(7.43)
212
ИНТЕГРИРОВАНИЕ В ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ
[ГЛ. 7
В этом представлении М и N — некоторые вещественные' посто-
янные, k —целое число 1, а ф (х) — некоторый многочлен с веще-
ственными коэффициентами, причем последняя -дробь в правой
части (7АЗ) является правильной.
Доказательство леммы 4. Договоримся обозначать веще-
ственную часть комплексной величины А символом Re [А], мнимую
часть комплексной величины А символом Im [А]. Положим *)
..	1. ГР(а)1	о ГР(а)1 “i Г Р (“) 1
7И —— Im —И- , N=Re —-----------Im —.
v |_<p(a)J	L ? (a) J v L?(a)J
Нетрудно проверить, что указанные Л и W являются решением сле-
дующего уравнения:
P(a)-.(Ala + N)<P(fl) = O.	(7.44)
В самом деле, поделив это уравнение на ср (а), и приравняв нулю
действительные и мнимые части, мы получим два равенства
Ми + N=Re ИД1,
Мх>=1тГ-^-1,
L<p(o)J
из которых определяются написанные выше М и N. Рассмотрим
теперь разность
Р (х) __ Мх 4- N
V	Q W (ха + Рх 4- <?)х ’
Приводя указанную разность к общему знаменателю, будем иметь
Р(х) Mx + N =Р (х) — (Мх + N) ср (х) _
Q W (^2 + рх 4- <?)х	(х2 4- рх 4- <?)х <f (х)
=--------.	(7.45)
(х2 4- рх 4- <?)х <р W
Здесь через Ф(х) обозначен многочлен с вещественными коэффи-
циентами вида Ф (х) = Р (х) — (Л1х 4- N) <р (х). Равенство (7.44) позво-
ляет- утверждать; что комплексное число а, а стало быть, в силу
теоремы 7.4, и сопряженное ему число й являются корнями много-
члена Ф(х) некоторой кратности А^1. В таком случае для много-
члена Ф(х) справедливо представление
Ф (х) = (х2 4- рх 4- q)k ф (х),	(7-46)
где ф (х) — некоторый многочлен с вещественными, коэффициентами,
не имеющий ^качестве корней числа а и а. Вставляя представление
*) В силу (7.42) <f (а)	0, так что отношение —— рассматривать можно.
§ 71
РАЗЛОЖЕНИЕ ПРАВИЛЬНОЙ РАЦИОНАЛЬНОЙ ДРОБИ
213
(7.46) в формулу (7.45), получим представление (7.43). Тот факт, что
последняя дробь, стоящая в правой части (7.43), является правильной,
вытекает из того, что эта дробь равна разности двух правильных
дробей.
Лемма 4 доказана.
Р (х)
Последовательное применение лемм 3 и 4 к дроби по всем
корням знаменателя приводит нас к следующему замечательному
утверждению.
Р (х)
Теорема 7.5. Пусть -—- — правильная рациональная дробь
с вещественными коэффициентами, знаменатель которой
имеет вид
Q (х) = (X -	(х -	... (X — bmft* (х2 +ptx +	...
 (х?+рпх + дпУп.
Тогда для этой дроби справедливо следующее разложение на сумму
простейших дробей:
Р(х)= В В о	В£
Q(x) (x-bj + (х-fei)2^ "+(х-А)р? + '*
В(«)
д(т)
° 2
(X-6m)2	(X-bJ*
(x2 + PjX + <7i)X1
Al?>x +
 • • H-----2-------V • (7-47)
(x2 + p„X + qn) n
(* — Ът)
Af/’x+A?;11 Afi/’x + W;1'
(х2 4- ptx + <?i),	(x2 + pLx + pj2 '
M^x+N^ M[^x + N^
(x2 + pnx + qn) (x2 + pnx + qn)2
В этом разложении B^\ В^\ ..., ВЬт\ A1W, .... тИ(А М’) —
12	1	1	кп кп
некоторые вещественные постоянные, часть из которых может
быть равна нулю.
Замечание. Для конкретного определения только что указан-
ных постоянных следует привести равенство* (7.47) к общему знаме-
нателю и после этого сравнить коэффициенты при одинаковых сте-
пенях х в числителях.
Примеры и разъяснения.
1°. Разложить на сумму простейших правиллную дробь
2х2 + 4х2 + х + 2’'
(х-1)2(х2 + х+1)-
Убедившись в том, что квадратный трехчлен х2 + х+1 имеет ком-
плексные корни, ищем, согласно теореме 7.5, разложение в виде
2х3 + 4х2 + х + 2 Вг Вг Mxy-N
(х-Г)2(х2 + х+1)~х-1 +(х-1)2+ х2 + х+1 •
(7.48)
214
ИНТЕГРИРОВАНИЕ В ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ
[ГЛ. 7
Приводя равенство (7.48) к общему знаменателю, получим
2x3 + 4x2 + х + 2 (хз — 1) + В2 (х2 + х + 1) + (Мх + N) (х2 — 2х + 1)
(X— 1)2(х2 4-х+ 1)“	(X — 1)2 (х2 + X + 1)
Сравнивая в числителях коэффициенты при х°, х1, х2 и х3, придем
к системе уравнений*)
B± + M = 2,
B2 + N-2M = 4,
B2 + M-2N=1,
Решая эту систему, найдем Вг = 2, В2 = 3, М = 0, N=l. Оконча-
тельно получим
2х3 Ц- 4хг + х + 2 _	2	.	3	.____1______ . д,
(х—1)2(х2 + х+1) х— 1 (х — 1)2"f" х2 + х+1 •	'	'
Только что проиллюстрированный метод отыскания разложения пра-
вильной рациональной дроби называется методом неопределенных
коэффициентов. Этот метод приводит к цели всегда; доказывать
разрешимость полученной в результате применения этого метода
системы уравнений не нужно — разрешимость вытекает из теоремы 7.5.
2°. Проиллюстрируем метод неопределенных коэффициентов еще
одним примером. Требуется найти разложение правильной дроби
3x4 + 2x3 + 3x2—1
(X-2)(X2 + 1)2 •
Так как квадратный трехчлен х2 + 1 имеет комплексные корни,
ищем, согласно теореме 7.5, разложение в виде
3x4 + 2x2 + 3x2 — 1 в М±х + А\ М2х + Nt
(х —2)(ха + 1)2	—х —2+ х2+1 + (х2 + I)2 *
Последнее равенство приводим к общему знаменателю и после этого
сопоставляем числители. Получим
Зх4 + 2х3 + Зх2 - 1 = В (х4 + 2х2 4-1) +
+ (МiX + Д\) (х3 - 2х2 + х - 2) + (7И2х + NJ (х - 2).
Сравнивая коэффициенты при х°, х1, х2, х3 и х4, придем к системе
*) При этом мы используем утверждение, сформулированное в сноске ***)
на стр. 201.
§ 71
РАЗЛОЖЕНИЕ ПРАВИЛЬНОЙ РАЦИОНАЛЬНОЙ ДРОБИ
215
уравнений
В + Afi= 3,
^-2М1 = 2,
25 + тИ1-2^ + тИ2 = 3,
Д^-2^ + ^-27412 = 0, |
B-2Nl-2Ni = — 1, J
Решая эту систему, найдем 5 = 3, тИ1 = 0, Nx = 2, тИ2=1, Лг2 = 0.
Окончательно получим
Зх1 + 2х3 + Зх2 — 1 _ з ,	2 х
(х — 2) (х2 + I)2 — х — 2 + х2 + 1 + (х2+ 1)а '
(7.50)
3°. Метод неопределенных коэффициентов, как видно из рассмот-
ренных примеров, является довольно громоздким. Естественно поэтому
в тех случаях, когда это возможно, найти другой, более простой метод
отыскания коэффициентов в разложении правильной рациональной
дроби на сумму простейших. Пусть знаменатель Q(x) правильной
рациональной дроби \ имеет вещественное число а корнем крат-
ности а. Тогда среди простейших дробей, на сумму которых раскла-
дывается дробь , будет фигурировать дробь
А
(х— а)л'
(7.51)
Укажем совсем простой метод вычисления коэффициента А при этой
простейшей дроби. Привлекая лемму 3 и формулу (7.41), мы убедимся
в том, что коэффициент А равен
. Р(а) . <
Л = 7^) - где
(х —а)а'
Мы приходим к следующему правилу: для вычисления коэффициента А
при простейшей дроби (7.51), соответствующей вещественному
корню а многочлена Q(x) кратности а, следует вычеркнуть в зна-
, Р (х)	-
менателе дроби скобку
(х — а)* и в оставшемся выражении
положить х — а.
Указанный прием нахождения коэффициента А обычно называют
методом вычеркивания. Отметим, что этот прием применим лишь
для вычисления коэффициентов при старших степенях простейших
дробей, соответствующих вещественным корням Q(x).
Метод вычеркивания особенно эффективен в случае, когда зна-
менатель Q (х) имеет лишь однократные вещественные корни, т. е.
когда Q (х) ?= (х — aj (х — а2)... (х — а„). Тогда, как мы знаем,
216
ИНТЕГРИРОВАНИЕ В ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ
1ГЛ. ?.
справедливо разложение
Р (х)___ Лх . А2 .	। Аь .	। Ап
Q (х) х — х — аг ' х —	‘ " х — ап’
все коэффициенты которого могут быть вычислены по метоДу вычер-
кивания. Для вычисления коэффициента Ak следует вычеркнуть в зна-
л Р (х)	,	, ч
менателе дроби скобку (х — ak) и в оставшемся выражении
положить х<=ак.
Пример. Найти разложение дроби
х -р 1
(х — 1)х(х —2) •
Согласно теореме 7.5 пишем
(7-52)
х 4~ 1______ Aj . Д2 । Д»
(х — 1) х (х — 2) х — Р х х - 2 '
/
Для отыскания вычеркиваем в выражении (7.52) скобку (х— 1)
и в оставшемся выражении берем х=1. Получим Аг = — 2. Анало-
.	1	.	3
гично находим Д2 = у, =
Окончательно получим
х-р 1	— 2.1.	3
(х-1)х(х-2):=х-1 + 2х +2(х-2)‘
(7.53)
§ 8. Проблема интегрирования рациональной дроби
Теперь мы подготовлены к тому, чтобы в общем виде решить
проблему интегрирования рациональной дроби с вещественными коэф-
фициентами.
Прежде всего, отметим, что эта проблема сводится к проблеме
интегрирования только правильной рациональной дроби, ибо всякую
неправильную рациональную дробь можно (посредством деления числи-
теля на знаменатель «столбиком») представить в виде суммы алге-
браического многочлена и правильной рациональной дроби.
Пример.
**-*3 + 1 _	_ 2х) ,	4х+1
х2 + х4-2	-,+ х2 + х + 2’
х4 — х3 + 1
— X4 + х3 + 2х3
—2х3 — 2х3 + 1
— —2х* — 2x2 — 4х
остаток 1 4х
I х2 4- X + 2
х2 —2х
§ 8]
ПРОБЛЕМА ИНТЕГРИРОВАНИЯ РАЦИОНАЛЬНОЙ ДРОБИ
217
Интегрировать многочлен мы умеем (напомним, что неопределен-
ный интеграл от многочлена представляет собой некоторый многочлен
степени, на единицу более высокой). Остается научиться интегриро-
вать правильную рациональную дробь. В силу теоремы 7.5 проблема
интегрирования правильной рациональной дроби сводится к интегри-
рованию простейших дробей следующих четырех типов:
1. -5-г, II.	HL ,	IV-	(7-54)
х — Ь’ (х — Ь)9’	(х2 +рх q) ’	(х2 + рх + v 7
Здесь Р = 2, 3,...; X = 2, 3,...; В, М, N, Ь, р и q — некоторые веще-
ственные числа, причем трехчлен x2-\-px-\-q не имеет вещественных
р2
корней, т. е. q— > 0.
Докажем, что каждая из четырех указанных дробей интегрируема
в элементарных функциях.
Дроби вида 1 и II элементарно интегрируются при помощи под-
становки t — x—b. Мы получим
= B J у = Д1п|1']-|-С = 51п]х-&] 4-С,	(7.55)
f В	о С Л	В
3 (х -Ь)₽ ах ~ J “	(р- 1) /Г» + с -
(7-56>
Для вычисления интеграла от дроби вида III представим квадратный
трехчлен в виде (х2 + рх + q) = ( х -)- ) + \q — и, учитывая, что
п2	7
9 — у > 0, введем в рассмотрение вещественную постоянную а =
—	j/"q — ^. Сделав подстановку t = x-\~, будем иметь
Mt + lNMp\
----dt
12(у+5-. dx=
(Х2 + px+q)
_Л4 г 2/ di / „ Мр\ у dt _
2‘ J /2 + а2 .	2 /' J /2 + а2 ~
М f d(t2 + a2) , ( v Мр\ 1 f
“ 2 J t2a2	2~ / a J ^_Lj2	~
M.	, 2/V — Mp , t .
= y in (t2 + a2) +	2-a arctg - + C =
X -I—~
M , . . ,	...	2/V — Mp '	^2	. _ 
= vln	+ Px + 9) H--7^—-i arctg-- ---- + C. (7.57)
218
ИНТЕГРИРОВАНИЕ В ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ
1ГЛ. 7
Остается вычислить интеграл от дроби вида IV. Используя введен-
ные выше обозначения / = х4-у, л=1/"? —	будем иметь
Mx + N -dx- С \	2 ! dt -
(№ + px + 9)x J (/2 +	“
M. C d (/« + a2)
2 J O2 4- a3)*
Введем обозначения
C d(t3 + a3)
J (/3 + а2)Х >
rz   C dt
x	} (/2 + a3}* ’
Интересующий нас интеграл будет вычислен, если будут вычислены
интегралы I и Кх. Интеграл 1 берется элементарно:
I —______!________*	4- С —_______-___________1	4- С
(X — 1) (/2 + а2)л-1Т'-—	(X— 1)
Интеграл К\ вычислен нами в примере 6 в конце § 2 главы 6. Там
мы получили для этого интеграла рекуррентную формулу (6.12), позво-
ляющую последовательно вычислить для любого Х = 2, 3, ....опи-
раясь на то, что
К,= ?	= -arctg-4-С.
1 J /2 а2 а Ь а I
Итак, нами вычислены интегралы от всех четырех простейших дро-
бей (7.54) и доказано, что каждый из этих интегралов представляет
собой элементарную функцию *). Тем самым мы приходим к следую-
щей теореме, исчерпывающей проблему интегрирования рациональной
дроби.
Теорема 7.6. Всякая рациональная дробь интегрируема в эле-
ментарных функциях.
В заключение этого параграфа мы остановимся на примерах
вычисления неопределенных интегралов от рациональных дробей.
Вычислим неопределенные интегралы от трех дробей, рассмотренных
в предыдущем параграфе (7.49), (7.50) и (7.53). Пользуясь указан-
ными тремя формулами, а также формулами (7.55), (7.56) и (7.57),
*) Точнее, выражается через логарифм, арктангенс и рациональную
функцию.
§ 9)
МЕТОД ОСТРОГРАДСКОГО
219
будем иметь:
2х? + 4х2 + х + 2	,
(х_1)2(Х2 + х+1)а*~
dx
1Д—I-
Г ' (X— I)2
— 2 In х — 1---h-г^arctg—-d=—НС.
1	1	х-1 /3	6 у3
9 f Зх* + 2x3 + 3x2-1
' (х — 2) (х2 + 1)2 х~
С 3 л.. । С 2 dx , f xdx _
— ' X^2dx + J x2 + 1 + J (x2+ 1)2“
= 31n |x - 2 | + 2 arctg x + ~ J yffjr =
= 3 In |x— 2 | + 2 arctg+ C.
3.	7--iT^7~-oV^x— f ~~2. dx+ f ^ +	57 3 -~rdx —
J (x — 1) x (x — 2) J x — 1	1	J 2x 1 J 2 (x — 2)
= — 2 In | x — 1 | + -g- In | X | + -g- In X — 2|+C.
§ 9. Метод Остроградского
M. В. Остроградским*) предложен остроумный метод выделе-
ния рациональной части интеграла от правильной рациональной
Анализируя вид интегралов от четырех простейших дробей (7.54),
можно сделать следующие выводы:
1)	Интегралы от дробей вида I и III, знаменатели которых содер-
жат двучлен или соответственно трехчлен в первой степени, являют-
ся нерациональными функциями (они равны логарифму или арк-
тангенсу).
2)	Интеграл от дроби вида II, знаменатель которой содержит
двучлен в степени (3 > 1, является правильной рациональной
дробью со знаменателем, равным тому же двучлену в сте-
пени р 2- 1.
3)	Интеграл вида IV, подынтегральная функция которого содер-
жит в знаменателе трехчлен в степени X, в конечном итоге **) равен
*) Михаил Васильевич Остроградский — русский математик (1801 — 1861).
**) С учетом рекуррентной формулы (6.12), полученной в конце § 2
главы 6,
220
ИНТЕГРИРОВАНИЕ В ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ
(ГЛ. 7
равным
арктан-
сумме правильной рациональной дроби со знаменателем,
тому же трехчлену в степени X — 1, и приводящегося к
, С dx
генсу интеграла const j_ рх .
Выводы 1), 2), 3) позволяют заключить, чему равна рациональ-
, Р (х)
ная часть всего интеграла от правильной дроби 777-т, которую мы,
х W
кроме того, будем считать несократимой. Пусть знаменатель Q(x)
имеет вид
Q (х) = (х - by)... (х - bm)?"> (х2 +ргх + gx)Ai ... (х2 4- рпх + qrf".
(7.58)
Тогда рациональная часть интеграла от правильной рациональной дроби
Р (х)
равна сумме правильных рациональных дробей, знаменатели кото-
рых соответственно равны
1

.... (х2 +pnx + qn)А«-'.
Указанная сумма *) представляет собой, очевидно, правильную рацио-
пальную дробь , знаменатель которой Qx(x) имеет вид
vi W
Qx (х) = (х- ^-1... (х - Ьт)^~1 (х3 + Рух + ?1)xt-‘...
...(x*+pnx + qn)xn-1. (7.59)
Подсчитаем теперь сумму тех простейших дробей, интегралы от
которых представляют собой нерациональные функции. Из выводов
1) и 3) вытекает, что эта сумма равна правильной рациональной
Р М
дроби -л-Л, знаменатель 02(х) которой равен
V2 (х)
Q2 (х) = (х - by)... (х - bm) (х2 + руХ + <?!)... (х2 +-рпх + qn). (7.60)
Таким образом, мы приходим к следующей формуле, впервые
полученной М, В. Остроградским:
С
' Q(x) Ql{x)
В формуле Остроградского многочлены Qx (х) и Q2 (х) определяются
формулами (7.59) и (7.60) и могут быть вычислены без разложения
многочлена Q(x) на произведение неприводимых множителей.
В самом деле, в силу результатов § 4 (см. формулу (7.25)), мно-
гочлен Qi (х) представляет собой наибольший общий делитель двух
(7.61)
„ т	л р<х)
*) 1о есть рациональная часть_интеграла от дроби
§9]
МЕТОД ОСТРОГРАДСКОГО
221
многочленов Q(x) и Q' (х) и может быть вычислен при помощи
алгоритма Евклида (см. §4).
Многочлен Q2(x), в силу формул (7.58), (7.59) и (7.60), пред-
А „	Q (х)	-
ставляет собой частное д . \ и может быть вычислен посредством
41 w
деления Q(x) на Qx(x) «столбиком».
Остается вычислить многочлены Рт (х) и Р2 (х). Поскольку дроби
Pi (х) Р2 (х)	„ . .
 *; . и  , : являются правильными, многочлен Pi(x) естественно
4i W 4а Vе)
задать как многочлен с неопределенными коэффициентами степени
на единицу ниже, чем 0х(х), а Р2(х) — как многочлен с неопреде-
ленными коэффициентами степени на единицу ниже, чем Q2 (х). Для
вычисления указанных неопределенных коэффициентов следует про-
дифференцировать формулу Остроградского (7.61), привести резуль-
тат дифференцирования к общему знаменателю и сопоставить коэф-
фициенты при одинаковых степенях х в числителях.
Таким образом, метод Остроградского представляет собой остро-
умный прием интегрирования рациональной дроби без предваритель-
ного разложения этой дроби на сумму простейших. Этот прием
особенно эффективен в том случае, когда корни Q(x) в основном
являются кратными или когда вызывает затруднение нахождение кор-
ней Q (х).'
Пример. Методом Остроградского вычислить
Имеем
6 — 7х — х2
х« — 2х» -ф Зх2 — 2х + 1
Q (х) = х4 — 2х3 + Зх2 — 2х + 1,
Q' (х) = 4х3 — 6х2 + 6х — 2.
Ищем (х) как наибольший общий делитель многочленов Q (х) и Q' (х).
Заметим, что наибольший общий делитель именно этих двух много-
членов уже найден нами в примере, рассмотренном в конце § 4.
Он равен
Q* (х) = х2 — хф-1.
Поделив Q (х) на Qj (х) «столбиком», найдем
Q2 (х) = х2 — х + 1.
Pj (х) и Р2 (х) задаем как многочлены первой степени с неопреде-
ленными коэффициентами.
Формула Остроградского (7.61) принимает вид
6 — 7х — х2	, Ах + В , С Сх + D
х* — 2х? + Зх2 - 2х + 1 ах ~ л2 — х + 1 + J X2 —х+ 1
(7.62)
222
ИНТЕГРИРОВАНИЕ В ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ
(ГЛ. 7
Для определения коэффициентов А, В, С, D продифференцируем
формулу (7.62). Получим
6 — 7х — х2
х4 — 2х3	3x2 _ 2х + 1
Л (х2 —х + 1) — (4х + В) (2х—1) CxA-D
(Х2—Хф!)2	+(Х2_х+1)-
Результат дифференцирования приводим к общему знаменателю, после
чего сопоставляем числители. Получим
6 — 7х —х2 =
= Л(х2-х+1)-(ЛхфВ)(2х-l) + (Cx + D)(x2-x+ 1).
Сравнивая коэффициенты при х°, х\ х2 и х3, получим систему
уравнений
С = 0,
— A + D-C = — 1,
— 2B-D + C=— 7,
А + В 4- D = 6.
Решая эту систему, найдем А —2, В = 3, С = 0, D = l. Таким обра-
зом, формула (7.62) принимает вид
С 6 — 7х —- х2 , ____________ 2х + 3 С dx
J X4 — 2x3 + Зх2 — 2х + 1ах ~ х2 — X + 1 + } х2 — х + ! •
Вычислив интеграл в правой части, окончательно найдем
С 6 — 7х — х2	, 2х + 3	,2	. 2х — 1 .
} х4 — 2x3 + 3x2 _ 2х + 1 dx ~ х2 — х + 1 /з arCtg +
§ 10. Интегрирование некоторых иррациональных
и трансцендентных выражений
В предыдущих параграфах мы установили, что интеграл от любой
рациональной дроби представляет собой элементарную функцию.
В настоящем параграфе мы рассмотрим некоторые другие классы
функций, интегрируемых в элементарных функциях. Как правило,
мы будем посредством некоторой подстановки сводить интеграл от
рассматриваемой функции к интегралу от рациональной дроби. Отно-
сительно указанной подстановки мы будем говорить, что она рацио-
нализирует интеграл от рассматриваемой функции.
§ 10]
ИНТЕГРИРОВАНИЕ ИРРАЦИОНАЛЬНЫХ ВЫРАЖЕНИЙ
223
1. Интегрирование некоторых тригонометрических выраже-
ний. Договоримся всюду в дальнейшем символом R (х, у) обозначать
любую рациональную функцию от двух аргументов х и у *).
В этом пункте мы докажем интегрируемость в элементарных
функциях любой функции вида
R (sin х, cosx).	(7.63)
Докажем, что интеграл от этой функции рационализируется подста-
новкой Z = Действительно,
2 tg 2"	2/	1 — tg2 1/2
sinx=--------Г = ТТК’ cosx =-----------Г=Т+Г2’
i+tg2|	i + tg’y +
х = 2 arctg t, dx =	,
так что
Го/-	хл f п/ 2/	1 —/2\ 2Л
у Я (sin х, cosx)dx=
Поскольку рациональная функция от рациональной функции пред-
ставляет собой также рациональную функцию, то интеграл, стоящий
в правой части последнего равенства, является интегралом от рацио-
нальной дроби.
Подстановка t = tg ~, хотя и является универсальной подстанов-
кой, рационализирующей интеграл от функции (7.63), часто приводит
к громоздким выкладкам. В связи с этим мы укажем несколько част-
ных случаев, в которых интеграл от функции (7.63) может быть
рационализирован с помощью других более простых подстановок.
Прежде всего, отметим два элементарных свойства рациональной функции
двух аргументов R (и, V):
Р. Если рациональная функция R (и, v) не меняет своего значения при
изменении знака одного из аргументов (например, и), т. е. если R (—и, v) =
— R (и, v), то эта рациональная функция может быть приведена к виду
R (и, v) = R1 (и2, v), где R± — некоторая рациональная функция своих двух
аргументов. (Эта функция содержит лишь четные степени и.)
*) Рациональная функция от двух аргументов определяется следующим
образом. Многочленом n-й степени от двух аргументов хну называется вы-
ражение вида
Рп (х, У) — аоо + °юх + апУ + а2о%2 + ОцХу -|- аа2у2 -(-...+ a0Z!J/ra> гДе аоо> а1о>
«01, ..., а0„ — некоторые постоянные числа. Рациональной функцией от двух
R (х и)
аргументов называется отношение вида п\ ’ где Рп(х, у) — произволь-
„	Qm \х> У)
ныи многочлен от двух аргументов степени п, a Qm (х, у) — произвольный
многочлен от двух аргументов степени т.
224
ИНТЕГРИРОВАНИЕ В ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ
[ГЛ. 7
2°. Если же при изменении знака и функция R (и, о) также меняет знак,
т. е. R (— и, о) = — R (и, v), то она приводится к виду R (и, v) = R2 (и2> v) и-
(Свойство 2° сразу вытекает' из свойства Iй, если применить его к функции
R(u, о) \
и /
Рассмотрим теперь вопрос о рационализации интеграла от функции (7.63)
для некоторых частных случаев.
I.	Пусть R (и, v) меняет знак при изменении знака и. Тогда, согласно
свойству 2й,
j R (sin х, cos х) dx = J R2 (sin2 x, cos x) sin x dx =
= — J R2 (1 — cos2 x, cos x) d (cos x).
Таким образом, интеграл от функции (7.63) рационализируется подстановкой
t — cos х.	у
II.	Пусть, далее, функция R (и, v) меняет знак при изменении знака V.
Тогда, согласно тому же свойству 2°,
J R (sin х, cos х) dx = j R3 (sin x, cos2 x) cosx dx = j Ra (sin x, 1 — sin2 x) d (sin x),
t. e. интеграл от функции (7.63) рационализируется подстановкой t — sin х.
III.	Пусть, наконец, функция R(u, о) не меняет своего значения при
одновременном изменении знаков и и v, т. е.
R (—и, —v) = R (и, v).	<
Докажем, что в этом случае интеграл от функции (7.63) рационализируется
подстановкой t — tg х. В самом деле, в этом случае
R (и, v) — R^~ v, = Ri ,
R(—u, — v) = r[~(—v), — ^ = Ri (-1, —vj.
Таким образом,
Но тогда, согласно свойству Iй,
Окончательно получим
R(u, v) — R2 v^.
Отсюда
J R (sin x, cos x) dx = j R2 (tg x, cos2 x) dx —
= (tg x, 1+tg2x ) dx = R2 [t, J J +p-,
где t = tgx, x = arctgt, dx =
§10]	ИНТЕГРИРОВАНИЕ ИРРАЦИОНАЛЬНЫХ ВЫРАЖЕНИЙ
225
dx
Примеры. 1) Вычислить интеграл /, = \ -гп--------. гДе а>0,
1 н	н 1 j 1 + a cos х ’
а/1. Применяя универсальную тригонометрическую подстановку
,	, X
t= tg у, получим
п	, 2dt	I—/2 *
х — 2 arctg t, dx —	, cos x —	,
®	1	12	1 +12
7 2 C dt _ 2 t dt
1	У(а+1)-Н2(1-а) Hl J , , 1~«,. ‘
Далее нужно отдельно рассмотреть два случая: 1) 0<а<1,
2)а>1. .
В случае 0 <а <1
и=*а,с'в (' / Ы)+с=гт=^1гс‘8(УМ‘8 г) +с-
В случае а > 1
sin х dx
sin2 х + 1 Ф
2) Вычислить интеграл ft =
Так как подынтегральная функция меняет знак при изменении знака
sinx, то, согласно I, следует сделать подстановку 7 = cosx. В результате
получим	/
/2 —
dt
1 — Г- + 1
C dt
J Za —2
-Lin
2 K2
/+ /2
t— /2
1 . cos x + У 2
=-------- In ------!———
2 У 2	cos x — У 2
3)	Вычислить интеграл !3 = \ . .Sln x cos x - dx.
'	J sm4 *x + cos4x
Так как подынтегральная функция сохраняет значение при одновремен-
ном изменении знаков sinx и cosx, то, согласно III, следует сделать подста-
новку t = tg х. В результате получим
- 4 $	- 4 ‘"=‘8 + С - 4 w «I + с-
226	ИНТЕГРИРОВАНИЕ В ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ	[ГЛ. 7
2. Интегрирование дробно-линейных иррациональностей. В
этом пункте мы докажем интегрируемость в элементарных функциях
любой функции вида
(7-64)
где а, Ь, с и d — некоторые постоянные, п — любое целое положи-
тельное число. Функцию такого вида мы будем называть дробно-ли-
нейной, иррациональностью.
Докажем, что интеграл от функции (7.64) при ad — be =£ 0 рацио-
нализируется
подстановкой t
ах + Ь
exd
самом деле,
. В
ах -f- Ь _ _ dtn — b , (ad — be) ntn 1
— cx + d ' Х ~ a-c-tn ’ йХ — (а — с/л)2
так что
dtn — Ь
а — cin ’
Д (ad — be) nt™
} (a — ctny-
ГТоскольку рациональная функция от рациональной функции пред-
ставляет собой также рациональную функцию, то интеграл, стоящий
в правой части последнего равенства, является интегралом от рацио-
нальной дроби. Тем самым доказано, что интеграл от дробно-линей-
ной иррациональности (7.64) рационализируется подстановкой t —
__ах-\-Ь
V cx-)-d'	___
Пример. Вычислить интеграл 1— у/~ 127 j- j ~ • Сделав под-
становку
f=l/I+Z /2-1+Л	dx- 4tdt
V 1— х’ 1 — X’ Х~ Р + 1’ (Р + 1)2’
получим
/=2 $	J ^ = 2^-2агс1ё^ + С =
= 2/гЙ-2’'^/^ + с-
3.	Интегрирование биномиальных дифференциалов. Биномиальным диффе-
ренциалом называют выражение вида
хт (а + bxn)P dx,
где а и b — любые постоянные, а показатели степеней т, п и р — некоторые
рациональные числа. Изучим вопрос об интегрируемости в элементарных
функциях биномиальных дифференциалов.
Прежде всего отметим три случая, когда интеграл от биномиального диф-
ференциала допускает рационализирующую подстановку.
§ 10]
ИНТЕГРИРОВАНИЕ ИРРАЦИОНАЛЬНЫХ ВЫРАЖЕНИИ
227
1?. Первый случай соответствует целому р. В этом случае биномиальный
дифференциал представляет собой дробно-линейную иррациональность вида
R (х, х) dx, где г — наименьшее общее кратное знаменателей рациональных
чисел тип. Стало быть, интеграл от биномиального дифференциала в этом
случае рационализируется подстановкой t = у/~х.
2®. Второй случай соответствует целому числу	В этом случае,
„	т 4- 1	,
сделав подстановку г = хп и положив для краткости —----------1 = q, будем
иметь
хт (а + bxn) р dx = (a+bz)Pz9dz.	(7.65)
Подынтегральная функция в правой части (7.65) представляет собой дробно-
линейную иррациональность вида R (г, у/а-^-Ьг), где s—знаменатель ра-
ционального числа р.
Таким образом, во втором случае биномиальный дифференциал рациона-
лизируется подстановкой
/ = уa -J- bz = |/ а + Ьхп-
3°-. Третий случай соответствует целому числу + *- -ф р). В этом слу-
чае подынтегральная функция в правой части (7.65) представляет собой дроб-
-	п ( т /а + bz\
но-линеиную иррациональность вида R I z, у —-—I, так что интеграл от
биномиального дифференциала рационализируется подстановкой вида
В середине прошлого века П. Л. Чебышев*) доказал, что указанными
выше тремя случаями исчерпываются все случаи, когда биномиальный диффе-
ренциал интегрируется в элементарных функциях.
Примеры. 1) Вычислить интеграл
/ = ( —, dx = \ ж"2 (а + &х2)- dXi
ix^a + bx^ J
Г»	л г»	1	/М "4“ 1 •	1
В данном случае /п = — 2, п=2, р = —так что —-------------1- р = — I (тре-
тий случай). Сделав подстановку
.	т/~а t ч ’	я Vatdt
f = I/ т + р, х —	, dx =------ ,
Г х*	yt^-^b	У (/а — 5)3 ’
будем иметь
' “ И-	— •‘° +С “ -	+ &
________________ 1
*) Пафнутий Львович Чебышев —великий русский математик (1821—1894),
228
ИНТЕГРИРОВАНИЕ В ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ	[ГЛ. 7
2) Вычислить интеграл 1 = J х6 (1 — х2) 2 dx. В данном случае т = 5,
п = 2, р ——	, так что m = 3 (второй случай). Сделав подстановку
/ = /Г^х2, х = /К=Т2, dx = —	,
К1-/2
будем иметь
/ = —J(l —/2)2Л = —+
= - t + | /з _ *L + с = -	~ /(1-хЗ)з-У	х2)6 + с.
О О	о	о	z
4. Интегрирование квадратичных иррациональностей посред-
ством подстановок Эйлера. В этом пункте мы докажем интегри-
руемость в элементарных функциях любой функции вида
R (х, ]/"ах2 + Ьх 4- с ),	(7.66)
где а, Ь и с — некоторые постоянные. Функцию такого вида будем
называть квадратичной иррациональностью. При этом мы, конечно,
считаем, что квадратный трехчлен 1 ах2 4- Ьх 4- с не имеет равных
корней (иначе корень из этого трехчлена может быть заменен рацио-
нальным выражением).
Мы докажем, что интеграл от функции (7.66) всегда рационали-
зируется одной из так называемых подстановок Эйлера.
Сначала рассмотрим случай, когда квадратный трехчлен ах2 4-
-j-bx + c имеет комплексные корни. В этом случае знак квадратного
трехчлена совпадает со знаком а, и поскольку по смыслу квадрат-
ный трехчлен (из которого извлекается квадратный корень) положи-
телен, то а > 0.
Таким образом, мы имеем право сделать следующую подстановку:
t = У ах2 4- ftx 4- с 4- х У а.	(7.67)
Подстановку (7.67) обычно называют первой подстановкой Эйлера.
Докажем, что эта подстановка рационализирует интеграл от функции
(7.66) для рассматриваемого случая. Возвышая в квадрат обе части
равенства У ах2 + Ьх + с = t — хУ а, получим bx-[-c = t2 — 2]Ла tx,
так что
t2 — c
2/«Z4-Z>’
У ах2 4- Ьх 4- с =
dx= 2
Таким образом,
у-а12 + Ы+сУа dt
(2V~at+b)2
Уа12-\-Ь(-\-сУа
2Уа1 + Ь
$ R (х, У ах2 Ьх + с) dx =
Уа^+Ы + сУаХ 2 /о/»4-И4-сУг5 d
2Уа1-]-Ь	)	(2Уа/-\-Ь)2
R(
\2yat + b
В правой части под знаком интеграла стоит рациональная дробь.
§ 10]	ИНТЕГРИРОВАНИЕ ИРРАЦИОНАЛЬНЫХ ВЫРАЖЕНИИ	229
Рассмотрим теперь случай, когда квадратный трехчлен ax2A~bx~j-o
имеет вещественные корни хх и х2.
В таком случае ах2 + Ьх -f- с = а (х — хД(х — х2). Докажем, что в
этом случае интеграл от функции (7.66) рационализируется посред-
ством подстановки
(7.68)
X —
называемой обычно второй подстановкой Эйлера. В самом деле,
возводя в квадрат равенство Уах2 + bx -|-с — t (х — xt) и сокращая
полученное равенство на (х — хх), получим а (х — х2) = t2 (х — х^,
так что
dx^(xt-x3) t d
ax— — r-
Таким образом,
j R (x, ax2 + bx + c ) dx =	*
_ С о/—QX2 + a (a — x3) П 2a (xt — x2) t .
J /2 — a ’	/2 — a j (t2 — a)2
В правой части под знаком интеграла стоит рациональная дробь.
Г* dx
Примеры. 1) Вычислить интеграл 7= \ -------—. По-
h+/x! + *+l
скольку квадратный трехчлен х2 + х+ 1 имеет комплексные корни,
сделаем первую подстановку Эйлера х
t = У х2 + х + 1 + х.
Возвышая в квадрат обе части равенства Ух2 + х+ 1 —t — х, полу-
чим х2 +х+ 1 = t2 — 2/х -|-х2 или х + 1 = t2 — 2/х, так что
/2—1	, о /а + / + 1 ,,
Х~~ 1 + 2/ ’ dx~ 2 (1 + 2/)2 dt-
Таким образом,
?—2 f +	ПЛ , В С 7
' Hl + 2/)2 J L t 1 + 2/ "* (1 + 2/)з] al-
Неопределенные коэффициенты А, В и С легко вычисляются:
А — 2, В — — 3, С = — 3. Окончательно получим
7 = 21n |/|-|lnl 1 4-2/1+^р^ + С^
= 21п |Ух2 + х+ 1 + х] -1 In | 1 + 2х+ 2 Ух2 + х+ 1 И
J__________-2___________I Q
2(1 +2x + 2Kx2 + x + о *
230
ИНТЕГРИРОВАНИЕ В ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ
[ГЛ. 7
2) Вычислить интеграл / = —р - —-. Поскольку ква-
дратный трехчлен 1 — 2х — х2 имеет вещественные корни	= —14-
У 2 и х2 ——1—1^2, сделаем вторую подстановку Эйлера (7.68)
_ У1 — 2х — х2
“ Х+1+/2 ’
Возвышая в квадрат обе части равенства 1 — 2х — х2 = /(х+ 1 4-
4- У 2), будем иметь (—1) (х4- 1 — 1^2) = t2 (х 4- 1 4- У %), так что
Таким образом,
1= — 41/2’f -----------------------—— -------
J (t2 4-1) О2 + 2 К214-1)
Получаем интеграл от рациональной дроби, вычисление которого
предоставляем читателю.
5. Интегрирование квадратичных иррациональностей другими способами.
Хотя подстановки Эйлера всегда рационализируют интеграл от функции (7.66),
но обычно эти подстановки приводят к весьма громоздким и сложным выклад-
кам. Ввиду этого на практике часто пользуются другими способами интегри-
рования функции (7.66). Этим способам и посвящен настоящий пункт.
Вводя обозначение у = у ах2 + Ьх 4- с и имея в виду, что у2 представ-
ляет собой многочлен, мы можем представить функцию (7.66) в виде суммы
R(x, y) = R1(x)+^,
где 7?! (х) и R2 (х) — некоторые рациональные функции одной переменной.
Поскольку интеграл от Rt (х) берется (в элементарных функциях), нам доста-
, R, (х)
точно заняться вычислением интеграла от функции 	.
Мы уже знаем *), что всякую рациональную дробь R2 (х) можно предста-
вить в виде суммы многочлена Р (х) и правильной рациональной дроби R3 (х).
Правильную рациональную дробь R3 (х) в свою очередь можно разложить на
сумму простейших дробей. Имея это в виду, мы можем утверждать, что про-
,	.	J.	7?, (х)
блема интегрирования функции - - сводится к вычислению интегралов сле-
дующих трех типов:
Т ? Р М	П I \
I. \ —— dx, где Р (х) — многочлен.
Л у
В ,	л п
---. -tll ах, где А и В — некоторые постоянные, а — натуральное
71) у
II.
число.
*) См. начало § 8.
§ 101	ИНТЕГРИРОВАНИЕ ИРРАЦИОНАЛЬНЫХ ВЫРАЖЕНИИ	231
р Мх ц- jv
III. \	тdx, где М, N, р и а —некоторые постоянные,
J (х* + рх + q)* у	г 7
п2
X — натуральное число, причем q — ^->0.
Остановимся на вычислении интегралов типа 1, II и III в отдельности.
I. Для вычисления интеграла типа I прежде всего установим рекуррент-
ную формулу для интеграла
, С xmdx	п , л
1т = \ -----, где т = 0, 1, 2, ...
J У
Для этого, предполагая, что т2г1, проинтегрируем следующее проверяемое
посредством дифференцирования тождество:
/	1 \	1	v/7t“2
(хт~1 у)' = та — + \m — -^}b — + (т—1)с
Интегрирование этого тождества приводит нас к равенству
хт~яу = malm + {rn — ^b 1т_х + (т — 1) с/т_2.	(7.69)
Беря в равенстве (7.69) т = 1, найдем
'-4 «-s'*	р-70'
Полагая затем в равенстве (7.69) т = 2 и используя уже вычисленное значе-
ние (т.-е. формулу (7.70)), найдем
- ЗЬ) у + ± (36® - 4пс) 19.
Продолжая аналогичные рассуждения далее, мы придем к следующей общей
формуле:
! т = Р т-1 (х) У "Ь стЛ>»	(? .71)
где Pm-i (х)— некоторый многочлен степени т — 1, а ст — некоторая посто-
янная. Если в интеграле типа I Р (х) представляет собой многочлен степени п,
то интеграл типа I будет равен сумме интегралов 10, Ц,..., 1п с некото-
рыми постоянными множителями (коэффициентами многочлена Р (х)). Стало
быть, в силу равенства (7.71) мы окончательно получим для интеграла типа I
следующую формулу:
(• р м	(• dx
\_¥Ldx = Qn~i (х) у + Со \	(7.72)
V  У	V У
В этой формуле Qn-i (х) есть некоторый многочлен степени п—1, а Со—
некоторая постоянная. Для определения многочлена Qn_i (х) и постоянной Са
используется метод неопределенных коэффициентов. Многочлен Q„_i (х) записы-
вается как многочлен с буквенными коэффициентами
<2л-1 (х) = Ао + AiX 4-... + Лл_1Хл-1.
Дифференцируя равенство (7.72) и умножая результат дифференцирования
на у, получим
Р (х) = О.п-1 {х) (ах2 + Ьх + с) + j Qn-i (х) (2ах -J- Ь) 4- Сс. (7.73)
232
ИНТЕГРИРОВАНИЕ Й ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ
[ГЛ. 7
В обеих частях равенства (7.73) стоят многочлены степени п. Приравнивая
их коэффициенты, получим систему п + 1 линейных уравнений, из которых
определяются Ло, Л1( ..., Лп_1 и Са. Разрешимость полученной системы выте-
кает из справедливости формулы (7.72), уже доказанной нами. Остается доба-
вить, что интеграл, стоящий в правой части (7.72), приводится к табличному
посредством линейной замены переменной ~ х ^а,- При помощи указанной
(* dx
замены интеграл \ — с точностью до постоянного множителя сводится
л У
к одному из следующих двух интегралов:
или
-у-— : = 1П ] / + JA2 ± Й2 J + С
/t2±A2	'
(k = const > 0)
dt	. t
,	= arcsin -г- -f- C.
jA2 —t2	k
Пример. Вычислить интеграл
О х3 .
\ —	— dx.
J VI + 2x — x2
Для рассматриваемого интеграла формула (7.72) имеет вид
С & а
\ г.______, = dx =
J /1 + 2х — х2
= (Ло + А1Х 4- Л2х2) /1 +2х-х2 + Со f	(7.74)
J V 1 + 2х — х2
Дифференцируя эгу формулу и умножая результат дифференцирования на
+ 2х — х2, получим
х3 = (Аг + 2Л2х) (1 + 2х — х2) + (Ло + Лхх + Лах2) (1 — х) + Со.
Сравнивая коэффициенты при х3, х2, х* 1, х° в правой и левой частях, получим
систему уравнений
— ЗЛ2= 1,
5Л2 — 2Лх = 0,
2Л2 + ЗЛ х — Ло == 0,
Лх + Ло + Со = 0.
1	5	19
Решая эту систему, найдем Л2 =-----Лх =--------у, Ло =----Со — 4.
о	и	О
Интеграл, стоящий в правой части (7.74), вычисляем посредством замены
t = x—1. Получим	I
С	С	1 । п • х — 1 , _ '
\ .	= \	_ __ = arcsin -у- + С = arcsin —=—Р С- -
J/1+2X —х2 J У2 —/2	ф2	/2
Окончательно будем иметь
р гз	/	19	5	1	,__________
\ f 	...^dx = -	| х - 4х2 ) /1 + 2х -х2 +
JJ/1 + 2X-х2 \	6	6	3	у'1
J	__ I
4- .4 arcsin —С.
J/2
§ 10]	ИНТЕГРИРОВАНИЕ ИРРАЦИОНАЛЬНЫХ ВЫРАЖЕНИЙ	233
II. Переходим к вычислению интеграла типа 11. Покажем, что этот
интеграл сводится к интегралу типа 1 посредством замены Z =В самом
X — /I
деле, поскольку
, dt 2i а । (А2а 4- Ab с) I2 -f- (2а А 4- b) i 4- а
dx = —. —2, ах2 4- Ьх + с =	11----------!—>.—!—
/2
мы получим
С В	С	Bt“~\dt
\ ------ТТГ- dx = — \	'	. .
J (х — А)л у	J /(Л2в + ЛЬ + с)/2 + (2аД + fc) / + а
III. Займемся, наконец, вычислением интеграла типа Ill. Прежде всего
вычислим интеграл типа III для частного случая р = 0, i!r= 0, т. е. вычислим
интеграл
Мх + N
----------;—,	dx.
(х2 + д)'- у ах2 4- с
Этот интеграл распадается на сумму двух интегралов
(*	х dx	,,	,, С	dx
\ --------;—>—  и К2 = N \ --------------—
J (х2 4- V ах2 4-е	J (х2 4-	1^ах2 4- с
Первый из .этих интегралов может быть записан в виде
л = М С d (х2)
1	2 ' (х2 4- <?)х j/ox2 4- с’
из чего видно, что подынтегральная функция представляет собой линейную
(а не квадратичную) иррациональность относительно х2. В силу доказанного
в п. 2 интеграл Ki рационализируется подстановкой I = \Аах2с. Интеграл
/<2 может быть записан в виде*)
из чего видно, что подынтегральная функция представляет собой линейную
иррациональность относительно —. Стало быть, интеграл К2 рационализи-
руется подстановкой г = ~у а-\-	. Итак, для частного случая, когда у обоих
квадратных трехчленов отсутствуют члены первой степени, интеграл типа III
вами рационализирован.' >
Рассмотрим теперь интеграл типа III в общем случае и покажем, что его
можно свести к интегралу изученного выше частного вида. Если коэффици-
енты квадратных трехчленов удовлетворяют соотношению
Ь = ар,	(7.75),
то для сведения интеграла типа III к интегралу изученного выше частного
вида достаточно сделать замену х = 1—|г. В самом деле, при этом мы
*) Мы считаем, что x^-Q.
234
ИНТЕГРИРОВАНИЕ В ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ
[ГЛ. 7
получим
г _______(Мх 4- #) dx_________
j (х2 4- рх 4- qY' Vах2 4* Ьх 4- с
+ JV
dt.
Сложнее осуществляется ' сведение интеграла типа III к интегралу изучен-
ного выше частного вида для случая, когда коэффициенты квадратных трех-
членов не удовлетворяют соотношению (7.75). В этом случае мы сначала сде-
лаем дробно-линейную подстановку
р£+д
(7.76)
выбрав постоянные р и м так, чтобы в полученных квадратных трехчленах
отсутствовали члены первой степени относительно t. Покажем, что такие р
и \ выбрать можно. В самом деле, сделав замену (7.76), будем иметь
№ + Р’.1 + ?) t2 + [2р^ + р (р + 4 + 2q] t + (№ -J- pi + q)
х -b px-\-q-------------------------------П~-Нр :	’
r + &P + c)<2 + 12рча 4- & (p + м) 4- 2c]f -j- (ач2 + Ь 4- с)
Un | (/л In c*
(7.77)
(l-H)2
Таким образом, коэффициенты p и м определятся из системы уравнений
2р> 4- Р (Р 4* 4 4- 2<? = 0, )
2рча 4-5(p4-v)4-2c = 0 J
или из системы эквивалентных уравнений
2 (с — aq)
р 4- * =----г----—,
Ь — ар'
ср — bq
Р1 — ~г------•
b — ар
Стало быть, р и м являются корнями квадратного уравнения
г 2£-щ?) г+ер-Ь1=0
Ь — ар Ъ — ар
Остается доказать, что квадратное уравнение (7.77) имеет вещественные
и различные корни. Для этого достаточно доказать, что дискриминант этого
уравнения положителен, т. е. достаточно установить неравенство
(с — aq)2 > (ср — bq) (b — ар).	(7.78)
Легко убедиться в том, что неравенство (7.78) эквивалентно следующему
неравенству:
[2 (с 4- aq) — bp]2 > (4q — р2) (4ас — b2).
(7.79)
Поскольку квадратный трехчлен
4q — р2 > 0.
Неравенство (7.79) заведомо
что это неравенство справедливо
чае q > 0, ас > 0 и 4 J^acq > pb.
(х2 4* рх 4- q) имеет комплексные корни, то
имеет место, если 4ас — Ь2 <. 0. Докажем,
и в случае, когда 4ас — Ь2 > 0. В этом слу-
Поэтому, учитывая, что —у caq,
х =
q —
5 ю]
ИНТЕГРИРОВАНИЕ ИРРАЦИОНАЛЬНЫХ ВЫРАЖЕНИИ
235
будем иметь
[2 (с + aq) — 5р]2^ 14 У qac — pb]2 =
= (4q — р2) (4ас — b2) + 4 (р У~ас — b W)2 3“ (4q — р2) (4ас — Ь2).
В написанной цепочке неравенств имеется хотя бы один знак строгого
неравенства >, ибо первый знак Js обращается в знак = лишь при с = aq,
но при с — aq, в силу того, что Ьф ар, заведомо (рУас — ЬУд)^-.О, и по-
этому второй знак не обращается в знак = . Итак, нами доказано нера-
венство (7.79), т. е. доказана возможность выбора таких р. и
в полученных, квадратных трехчленах отсутствуют члены
относительно i. Сделав замену (7.76) с указанными р. и ч, мы
рал типа III к виду
Р (/) dt
(^ + <?i)x/^2 + c1’
V, при которых
первой степени
приведем интег*
(7.80)
где а<, Ci и — некоторые постоянные, а Р (t)— многочлен степени 2Х—1.
рн\
Разложив *) дробь------	?  на сумму простейших, мы сведем вопрос о вы-
числении интеграла (7.80) к вычислению суммы интегралов вида
С -----Mkt ±Nk  dt =	2...
J (t2 + qi)kVa1t2 + cl
Каждый из этих интегралов относится к изученному выше, частному виду.
Тем самым мы доказали интегрируемость (в элементарных функциях) интег-
ралов всех трех типов I, II и III. Таким образом, еще раз помимо подста-
новок Эйлера доказана интегрируемость функции (7.66) в элементарных
функциях.
Пример. Вычислить интеграл I — V--------Этот ин-
J (х2 — х + 1) Кх2 + х + 1
теграл относится к типу III. Поскольку для него нарушено соотношение
(7.75), мы должны прежде всего сделать замену (7.76). В результате этой
замены получим
,2 л , l | _ (р2 + р+1)/2 + [2^ + (F+^) + 2]/ + fr8 + ^+l)
-t- х -t -	(1 + I)2
v2 r,|_ (^-P+I^+^-^+vJ + ^+^-^+I) '
X X + 1 “	(1 + t)2	*
Постоянные p. и v находим из системы уравнений
2(^4* (1х + *) + 2 = 0,
2^_((1+v) + 2 = 0.
Легко убедиться в том, что **) р= 1, м = — 1. Таким образом, замена (7.76)
имеет вид х = —_р-р так что
. х +1	.	2d/	з<2 + 1
Z-l—х’ dx (1+Z)2’ Х	- (1 + /)2’
Рассматриваемый интеграл принимает вид
/ = 2 f (1 + dt
J (/2 + 3)/3/2+ 1
Z2 + 3
(1 + 02
*) При X > 1.
♦*) Можно было бы положить наоборот р = — 1л v = 1,
236	ИНТЕГРИРОВАНИЕ В ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ	[ГЛ. 7
где
р	t dt	р	dt
/1 = 2 \	/2== 2 \	------г
J (/2 + 3) /З/2 + 1	J (/2 + 3) /З/2 + 1
Для вычисления интеграла /* делаем подстановку ц = ]/ З/2 + 1, а для вы-
числения интеграла /2 делаем подстановку v =	3 + , В результате по-
лучим
— 2 f du - = —arctg + C = arctg
J u2 + 8	/2	/8	/2
—+ с
Х)2
+ 1/A
/ (x+ I)2 Г 3
i/~x2 + x+1	-./T
V (x + 1/’ V 3
§ 11. Эллиптические интегралы
К интегралам от квадратичных иррациональностей естественно примы-
кают следующие интегралы:
J R (х, /ах» + bx2 -^-cx + d) dx,	(7.81)
\R(x, Vах* + Ьхз ex* + dx + е )dx,	(7.82)
подынтегральные функции которых содержат корень квадратный из много-
членов третьей или четвертой степени.
Эти интегралы весьма часто встречаются в приложениях. Отметим сразу
же, что интегралы (7.81) и (7.82), вообще говоря,' не являются элементарными
функциями.
Оба эти интеграла принято называть эллиптическими в тех случаях,
когда они не выражаются через элементарные функции, и псевдоэллипти-
ческими в тех случаях, когда они выражаются через элементарные
функции *).
Ввиду важности для приложений интегралов (7.81) и (7.82) возникла не-
обходимость составления таблиц и графиков функций, определяемых этими
интегралами. При произвольных коэффициентах a, b, с, d и е такие таблицы
и графики составить очень трудно. Поэтому возникла задача о сведении всех
интегралов вида (7.81) и (7.82) к нескольким типам интегралов, содержащих
по возможности меньше произвольных коэффициентов (или, как говорят,
о приведении интегралов (7.81) и (7.82) к канонической форме).
Прежде всего, заметим, что интеграл (7.81) сводится к интегралу (7.82).
В самом деле, кубичный трехчлен заведомо имеет хотя бы один веществен-
*) Эти названия происходят оттого, что впервые с этими интегралами
встретились при решении задачи о спрямлении эллипса (см. пример 3 п. 6 § 1
главы 11).
§ Н]
ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ
237
ный корень х0, а поэтому его можно представить в виде ах3 -ф Ьх2 -\-cx-\-d —
= а (х — xfl) (х2 -ф рх + <?)•
Сделав подстановку х — ха = ±t2, мы, как легко видеть, ' преобразуем
интеграл (7.81) в (7.82).
Таким образом, нам достаточно рассмотреть лишь интеграл (7.82).
В силу результатов § 6 многочлен четвертой степени можно разложить
на произведение двух квадратных трехчленов с вещественными коэффициен-
тами
ах* -ф Ьх3 -ф сх2 -ф dx -ф е = а (х2 -ф рх -ф д) (х2 + р'х -ф д').
Всегда найдется некоторая линейная или дробно-линейная подстановка, уни-
чтожающая у обоих квадратных трехчленов линейные члены *). Сделав такую
подстановку, мы с точностью до слагаемого, представляющего собой элемен-
тарную функцию, преобразуем интеграл (7.82) к виду
f __________R(t2\ dt________
J /А (1 -ф mt2) (1 -ф m'<2) ’
(7.83)
где R— некоторая рациональная функция. Далее можно показать, что при
любых комбинациях абсолютных значений и знаков постоянных Д, т и т‘
найдется замена, сводящая интеграл (7.83) к так называемому каноническому
интегралу	г
( — Мг - —,	(7.84)
J К(Г^г2) (1 _ *2Z2)
в котором через k обозначена постоянная, удовлетворяющая условию 0<k< 1.
Любой канонический интеграл (7.84) с точностью до слагаемого, пред-
ставляющего собой элементарную функцию, может быть приведен к следую-
щим трем стандартным интегралам:
и
______dz_____ р__________г2 dz___
/Д — Z2) (1 — k2Z2) ’ J	/(1 —22)71^*222)
£ -----7=^==	(0 < * < 1).
J (1 -ф hz2) /(1—22) (l—/i222)
Интегралы (7.85) принято называть эллиптическими интегралами соответст-
венно 1-го, 2-го и 3-го рода. Каждый из этих интегралов, как показано
Лиувиллем •*), представляет собой неэлементарную функцию. Эллиптические
интегралы 1-го и 2-го рода содержат только один параметр ft, принимающий
вещественные значения из интервала 0 < ft < 1, а эллиптический интеграл
3-го рода, кроме того, содержит параметр h, который может принимать и
комплексные значения.
Лежандр ***) подверг интегралы (7.85) дальнейшему упрощению, сделав
/	я \
замену z = sin ср 10 <р -й- -% ).
С помощью этой замены первый из интегралов \ (7.85) преобразуется
к виду
_______dtp ________
Y1 — ft2 sin2 ср
(7.86)
*) Это доказывается точно так же, как в п. 5 § 10.
**) Жозеф Лиувиллъ — французский математик (1809—1882).
***) Адриан Мари Лежандр — французский математик (1752—1833).
238	ИНТЕГРИРОВАНИЕ В ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ	[ГЛ. 7
Второй из интегралов (7.85) при этой замене с точностью до постоянного
множителя оказывается равным разности интеграла (7.86) и следующего ин-
теграла:
$ /1 — й3 sin3 <р d?.	(7.87)
Третий из интегралов (7.85) преобразуется к виду
d<f
(14-ft sin3 <р) У I — й2 sin <р ’ k
(7.88)
Интегралы (7.86), (7.87) и (7.88) принято называть эллиптическими интегра-
лами соответственно 1-го, 2-го и 3-го рода в форме Лежандра.
Особенно важную роль в приложениях играют интегралы (7.86) и (7.87).
Если считать, что оба эти интеграла обращаются в нуль при <р = 0, то по-
лучатся две вполне определенные функции, которые обычно обозначают
символами F (k, ср) и Е (k, tp). Для этих функций составлены обширные таблицы
и графики. Лежандром и другими математиками изучены свойства этих функ-
ций, для них установлен ряд формул.
Наряду с элементарными функциями функции Е и F прочно вошли в се-
мейство функций, часто используемых в анализе. Здесь еще раз стоит отме-
тить условность понятия элементарной функции. Вместе с тем следует под-
черкнуть, что задачи интегрального исчисления вовсе не ограничиваются
изучением функций, интегрируемых в элементарных функциях.
ГЛАВА 8
ОСНОВНЫЕ ТЕОРЕМЫ О НЕПРЕРЫВНЫХ
И ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ
Понятия непрерывной функции и дифференцируемой функции уже
известны нам из глав 4 и 5. В настоящей главе будет установлен ряд
важных свойств произвольных непрерывных и дифференцируемых
функций. Для вывода этих свойств мы введем новое определение
предельного значения функции и докажем эквивалентность этого опре-
деления старому определению, данному в главе 4.
§ 1. Новое определение предельного значения функции
1. Новое определение предельного значения функции. Его экви-
валентность старому определению. Пусть, как и в § 2 главы 4,
функция _У=/(х) определена на некотором множестве {х}, и пусть
а — некоторая точка, быть может, и не принадлежащая множеству {х},
но обладающая тем свойством, что в любой е-окрестности точки а
имеются точки множества {х}.
Напомним старое определение предельного значения функции,
введенное в главе 4: число b называется предельным значением
функции f(x) в точке х = а, если для любой сходящейся к а по-
следовательности хр х2, ..., х„, ... значений аргумента х, эле-
менты которой отличны от а, соответствующая последователь-
ность /(хх), /(х2), ..., /(хп), ... значений функции сходится к Ь.
Сформулируем теперь
Новое определение предельного значения функции. Число b
называется предельным значением функции /(х) в точке х = а,
если для любого положительного числа в найдется положитель-
ное число В *) такое, что для всех значений аргумента х, удов-
летворяющих неравенству 0<;|х — а|<;8, справедливо неравен-
ство |/(х) —&|<е**).
*) Так как 6 зависит от е, то иногда пишут 6 = В (е).
**) Старое определение предельного значения функции называют также
определением предельного значения по Гейне, а новое определение — опре-
делением предельного значения по Коши.
240
ОСНОВНЫЕ ТЕОРЕМЫ О НЕПРЕРЫВНЫХ ФУНКЦИЯХ
[ГЛ. 8
Замечание I. Ограничение 0 <; | х — а | означает, что рассматри-
ваются значения аргумента х, отличные от а. Это ограничение
становится понятным, если вспомнить, что изучаемая функция f(x)
может быть не определена в точке а. Отсутствие этого ограниче-
ния сделало бы невозможным определение производной f (а) как
, с / \ f (х) — f(a)
предельного значения функции г(х) = х~а ' в точке а-
Замечание 2. С логической точки зрения главным в новом
определении является то, что для каждого е > 0 найдется отве-
чающее этому е положительное число В, гарантирующее справед-
ливость неравенства |/(х)—/>| <; е для всех значений аргумента х,
удовлетворяющих неравенству 0 < ] х— а | < 8.
Замечание 3. Привлекая идею приближения функции /(х) в ок-
рестности точки х = а с наперед заданной точностью е, мы Можем
следующим образом переформулировать новое определение предель-
ного значения функции: число b называется предельным значением
функции f(x) в точке а, если для любой наперед заданной точ-
ности е, можно указать _ такую ^-окрестность точки а, что
для всех значений аргумента х, отличных от а и принадлежащих
указанной ^-окрестности, число Ь приближает значение функции
f(x) с точностью s (рис. 8.Г).
Теорема 8.1. Старое и новое определения предельного значе-
ния функции эквивалентны.
Доказательство. 1) Пусть сначала число b является пре-
дельным значением /(х) в точке а по новому определению. Докажем,
что это же число b является предельным значением /(х) в точке а
и по старому определению. Пусть {х„} —любая сходящаяся к числу
а последовательность значений аргумента, все элементы которой от-
личны от а. Требуется доказать, что соответствующая последователь-
ность {/(х„)} значений функции сходится к числу Ь. Фиксируем
любое е > 0. Согласно новому определению предельного значения
§ I] НОВОЕ ОПРЕДЕЛЕНИЕ ПРЕДЕЛЬНОГО ЗНАЧЕНИЯ ФУНКЦИИ 24J
функции, для этого s найдется 8>0 такое, что |/(х) — й|<е для
всех значений аргумента х, для которых 0<|х — а] <8. Так как
последовательность {хп} сходится к числу а, то для указанного чис-
ла 8>0 найдется номер N такой, что 0<|хл —а|<8 при n^N.
Стало быть, |/(х„) — b | < s при N, а это и означает сходимость
последовательности {/(х„)} к числу Ь.
2) Пусть теперь число b является предельным значением /(х)
в точке а по старому определению. Докажем, что это же число Ь
является предельным значением f(x) в точке а и по новому опреде-
лению. Предположим, что это не так. Тогда для некоторого поло-
жительного числа е не найдется гарантирующего положительного
числа 8, указанного в новом определении, т, е. для этого в и для
сколь угодно малого положительного 8 найдется хотя бы одно
значение аргумента х такое, что 0<|х — а|<8, но \f(х)— Ь\^г.
В силу сказанного мы. можем взять последовательность 8Л = -^-
(п = 1, 2, 3, ... ) и утверждать, что для каждого ее элемента 8Л=-^
найдется хотя бы одно значение аргумента хп такое, что
0<|хя-а[<1, н0
(8.1)
Левое из неравенств (8.1) означает, что последовательность {хя} схо-
дится к числу а и состоит из элементов, отличных от а. Но тогда,
согласно старому определению предельного значения функции, соот-
ветствующая последовательность {/(хя)} значений функции сходится
к числу Ь, а этому противоречит правое из неравенств (8.1), спра-
ведливое для всех номеров п. Полученное противоречие доказывает
теорему.
Новое определение предельного значения функции позволяет нам
сформулировать
Новое определение непрерывности функции в точке х = а*).
Функция f (х) называется непрерывной в точке х = а, если для
любого положительного числа е найдется положительное число 8
такое, что для всех значений аргумента х, удовлетворяющих
неравенству | х — а | < 8, справедливо неравенство
|/(х) —/(а) | < е.
(8.2)
Замечание 4. В этом определении нет необходимости накла-
дывать ограничение 0<|х—а|, ибо при х — а левая часть нера-
венства (8.2) обращается в нуль и неравенство (8.2) заведомо спра-
ведливо.
По аналогии с вышеизложенным формулируется новое определе-
ние предельного значения функции и доказывается эквивалентность
*) Конечно, при этом предполагается, что функция у = f (х) определена
и в самой точке а.
242
ОСНОВНЫЕ ТЕОРЕМЫ О НЕПРЕРЫВНЫХ ФУНКЦИЯХ [ГЛ. 8
этого определения старому определению и для случая, когда одно
или оба числа а и b обращаются в -|-оо или—со. Ограничимся
тем, что сформулируем новое определение предельного значения
функции для случая, когда а= -|-оо: число b называется предель-
ным значением f(x) при х->4-оо, если для любого положитель-
ного числа е найдется положительное число А такое, что для
всех значений аргумента х, удовлетворяющих неравенству xZ> А,
справедливо неравенство \f(x) — b | < е.
Рис. 8.2 разъясняет указанное определение.
В заключение сформулируем новое определение правого и левого
предельных значений функции f(x) в точке а: число Ь называется,
правым (левым) предельным значением функции f(x) в точке а.
если для любого положительного числа е найдется положитель-
ное число 8 такое, что для всех значений аргумента х, удовлет-
воряющих неравенству 0 < х — а <; 8 (0 < а — х <; 8), справедливо
неравенство |/(х) — b | < е.
Доказательство эквивалентности этого определения старому опре-
делению правого (левого) предельного значения совершенно анало-
гично доказательству теоремы 8.1.
2. Необходимое и достаточное условие существования пре-
дельного значения функции (критерий Коши). Пользуясь эквива-
лентностью старого и нового определений предельного значения
функции, установим необходимое и достаточное условие существова-
ния у функции f(x) предельного значения в точке а.
Определение. Будем говорить, что функция f(x) удовлетво-
ряет в точке х = а условию Коши, если для любого положитель-
ного числа е найдется положительное число 8 такое, что, каковы
бы ни были два значения аргумента х' и х", удовлетворяющие
неравенствам 0 < | х' — а | < 8, 0 < | х’ — а | < 8, для соответст-
вующих значений функции справедливо неравенство

§ 1] НОВОЕ ОПРЕДЕЛЕНИЕ ПРЕДЕЛЬНОГО ЗНАЧЕНИЯ ФУНКЦИИ 243
Теорема 8.2 (критерий Коши). Для того чтобы функция
f(x) имела конечное предельное значение в точке х = а, необхо-
димо и достаточно, чтобы функция f(x) удовлетворяла в этой
точке условию Коши.
Доказательство. 1) Необходимость. Пусть существует
конечное предельное значение lim/(x) = b. Докажем, что функция
х -* а
f(x) удовлетворяет в точке х — а условию Коши. Возьмем произ-
вольное е > 0. Согласно новому определению предельного значения
функции для положительного числа е/2 найдется положительное
число 8 такое, что, каковы бы ни были значения аргумента х' и х",
удовлетворяющие неравенствам 0 < | х' — а | < 8, 0 <; | х" — а | < 8,
для соответствующих значений функции справедливы неравенства
]/(х')—|/(х") — b | < Так как модуль суммы двух вели-
чин не превосходит суммы их модулей, то из последних неравенств
получим
]Ж)- /(х") I = I [/(х')- Ь\ - [/(ХЭ -b] I
</(x')-£| + |/(x’)-&l<s-
Тем самым доказано, что функция /(х) удовлетворяет в точке х — а
условию Коши.
2) Достаточность. Пусть функция f (х) удовлетворяет в точке
х = а условию Коши. Докажем, что функция /(х) имеет предельное
значение в точке х = а. Пусть {х„} — любая сходящаяся к а после-
довательность значений аргумента, все элементы хп которой отличны
от а. В силу старого определения предельного значения функции
достаточно доказать, что соответствующая последовательность {/(х„)}
значений функции сходится к некоторому числу Ь, причем это число
Ъ одно и то же для всех сходящихся к а последовательностей {х„}
таких, что х„ а.
Докажем сначала сходимость любой последовательности {/(хл)}.
Пусть задано произвольное е > 0. Возьмем то положительное число 8,
которое соответствует этому е согласно условию Коши, и, пользуясь
сходимостью последовательности {хй} к а, выберем для этого 8
номер 7V такой, что
0 < | хп — а | < 8 при n^N.
При этом для любого натурального р(р—1, 2, ...) и подавно
0.< Iхп+р — а | < S при n^N.
Последние два неравенства в силу условия Коши приводят к нера-
венству |/(х„+р) — /(х„) | < s при n^N, т. е. доказывают фунда-
ментальность последовательности {/(х„)}. Ц силу критерия Коши
244	ОСНОВНЫЕ ТЕОРЕМЫ О НЕПРЕРЫВНЫХ ФУНКЦИЯХ	[ГЛ. 8
для последовательности (т. е. теоремы 3.19) последовательность {/(х„)}
сходится к некоторому числу Ъ.
Докажем теперь, что все последовательности {/(х„)}, соответст-
вующие всевозможным сходящимся к а последовательностям {хя},
имеют один и тот же предел Ь.
Пусть {хя} и {Хп} —любые две сходящиеся к а последователь-
ности значений аргумента, все элементы которых отличны от а.
В силу доказанного выше обе последовательности {/(хя)} и {/(х„)}
сходятся. Обозначим предел первой из этих последовательностей
через Ь, а второй — через Ь'. Докажем, что b = Ь'. Рассмотрим схо-
дящуюся к а последовательность
Xj, *^2’	• • • >	^П9 • • •
В силу доказанного выше соответствующая последовательность зна-
чений функции
/(Xi), /(xj), /(x^, /(х0.../(хл),	/(хД ...
является сходящейся. Но тогда в силу п. 1 § 4 главы 3 все подпо-
следовательности этой последовательности, в том числе {/(хя)}
и {/(хя)}, сходятся к одному и тому же пределу, т. е. b = b'.
Теорема 8.2 доказана.
Аналогично формулируется условие Коши и устанавливается необ-
ходимое и достаточное условие существования предельного значения
функции /(х) при х—>-4-оо и при х —> — оо. Ограничимся формули-
ровками для случая х->4-оо.
Будем говорить, что функция f(x) удовлетворяет при
х -> 4~ условию Коши, если для любого положительного числа е
найдется положительное число А такое, что для любых двух
значений аргумента х' и х", превосходящих А, справедливо нера-
венство | f (х') — f (х') | < е.
В полной аналогии с теоремой 8.2 доказывается следующее утвер-
ждение: для того чтобы функция /(х) имела конечное предельное
значение при х—>4-оо, необходимо и достаточно, чтобы она
удовлетворяла при х-> 4-°° условию Коши.
§ 2. Локальная ограниченность функции, имеющей
предельное значение
В полном соответствии с определением множества вещественных
чисел, ограниченного сверху (снизу) *), введем понятие функции,
ограниченной на данном множестве сверху (снизу)."
Определение 1. Функция f(x) называется ограниченной
сверху (снизу) на множестве {х}, если найдется такое веще-
*) См. п. 5 § 1 главы 2.
§ 21	ЛОКАЛЬНАЯ ОГРАНИЧЕННОСТЬ ФУНКЦИИ	245
ственное число М (число т), что для всех значений ар-
гумента х из множества {х} справедливо неравенство f(x)^,
az M(f(x)^ т).
При этом число М (число т) называется верхней (нижней) гранью
функции f (х) на множестве {х}.
Определение 2. Функция f (х) называется ограниченной с обеих
сторон или просто ограниченной на множестве {х}, если
она ограничена на этом множестве и сверху, и снизу, т. е. если
найдутся такие вещественные числа т и М, что для всех зна-
чений аргумента х из множества {х} справедливы неравенства
m^f(x)^M.
Таким образом, ограниченность функции f (х) на множестве {х}
фактически означает ограниченность множества всех значений этой
функции.
Примеры. 1) Функция f(х) = secх — на полусегменте
|^0э сверху не ограничена, а снизу ограничена (в качестве нижней
грани может быть взято любое число m'^sz 1).
2) Функция Дирихле *) ограничена с обеих сторон на любом
сегменте [а, (в качестве нижней грани можно взять любое число
т '<0, а в качестве верхней грани любое число Л1 1).
Теорема 8.3. Если функция f(x) имеет конечное предельное
значение в точке х = а, то существует некоторая ^-окрест-
ность точки а * **), такая, что для всех значений аргумента из
указанной Ъ-окрестности функция /(х) ограничена ***).
Доказательство. Пусть &= lim/(x). Согласно новому опре-
х -* а
делению предельного значения функции, для некоторого положитель-
ного числа s найдется положительное число В такое, что \f(x) — b\ <е,
как только 0 < | х — а | < 8, или
Ь — е</(х)</>ф-е, как только а — 8<х<а+8 и х # а.
(8.3)
Если значение х=а не входит в область определения функции,
то теорема доказана (ибо неравенства (8.3) означают, что для всех
значений аргумента х из 8-окрестности точки а значения функции
/(х) заключены между b — е и b ф- е).
' *) Напомним, что функцией Дирихле называется функция, равная еди-
нице для всех рациональных значений аргумента и нулю для всех Иррацио-
нальных значений аргумента.
**) Напомним, что 8-окрестностью точки а называется интервал (а — 8,
а ф- 8), где В > 0.
***) Мы не исключаем случая, когда функция у = f (х) задана на некото-
ром множестве {х}, не заполняющем сплошь никакой 8-окрестности точки а.
246
ОСНОВНЫЕ ТЕОРЕМЫ О НЕПРЕРЫВНЫХ ФУНКЦИЯХ
[ГЛ. 8
Если же функция f(x) определена и при х = а и принимает
в точке а некоторое значение /(а), то, обозначив через т наимень-
шее из двух чисел (Ь — е) и
/(а), а через М наибольшее из двух
чисел (# + е) и /(а), мы можем
извлечь из неравенств (8.3) сле-
дующие неравенства:
m^f(x)^M, как только
а — 8 < х < а 4- 8.
Последние неравенства означают,
что функция f(x) ограничена всю-
ду в 8-окрестности точки а. Теоре-
ма доказана. Иллюстрацией к тео-
реме 8.3 может служить рис. 8.3.
Замечание. Свойство функции, устанавливаемое теоремой 8.3,
называют локальной ограниченностью функции, имеющей предель-
ное 'значение.
Следствие из теоремы 8.3. Если функция f(x) непрерывна
в точке х = а, то эта функция ограничена для всех значений
аргумента из некоторой Ъ-окрестности точки а. (Непрерывная
в точке х — а функция имеет в этой точке конечное предельное
значение.)
§ 3. Теорема об устойчивости знака непрерывной функции
Теорема 8.4. Если функция f(x) непрерывна в точке х = а и
если /(а)^0, то существует такая ^-окрестность точки а,
что для всех значений аргумента из указанной Ъ-окрестности
функция f(x) не обращается в нуль и имеет знак, совпадающий
со знаком f(a).
Доказательство. Так как функция непрерывна в точке а,
то существует lim f(x) = b, причем b=f(a)^Q. Согласно новому
х -» а
определению предельного значения функции, для любого е >0 най-
дется 8 > 0 такое, что
Ь — е</(х)<С& + е> как только*) a — 8<x<a4-8.	(8.4)
Возьмем в качестве е положительное число, удовлетворяющее требо-
ванию е < | b |. При таком выборе е все три числа b — е, #-|-е и Ь
будут одного знака. Стало быть, в силу (8.4) всюду в 8-окрестности
*) При этом нет необходимости исключать значение х = а, ибо для непре-
рывной функции f (х) значение / (а) = b также удовлетворяет левым из нера-
венств (8.4).
S -t]
ПРОХОЖДЕНИЕ НЕПРЕРЫВНОЙ ФУНКЦИИ
247
точки «функция f(x) сохраняет знак числа b=f(a). Теорема доказана.
Иллюстрацией к теореме 8.4 может служить рис. 8.4.
Замечание к теореме 8.4. Теорему 8.4 можно перенести на
случай функции f(x), непрерывной в данной точке х = а справа
(слева). Пусть 8 — некоторое положитель-
ное число. Договоримся называть полу- &‘
сегмент [а, «4-8) правой по лу-
окрестностью точки х=а, а полу-
сегмент (а—8, а] ле в ой по лу окрест-
ностью точки х = а. Имеет место сле-
дующее утверждение: если функция f(x)
непрерывна в точке х= а справа (слева) и
если /(а) 0, то найдется правая (левая)
полуокрестность точки х = а такая,
что для всех значений аргумента из
указанной полуокрестности функция f(x) не обращается в нуль
и имеет знак, совпадающий со знаком f(a).
Доказательство этого утверждения почти дословно повторяет дока-
зательство теоремы 8.4, только вместо правых неравенств (8.4) мы
получим неравенства а х «< а 4- 8 (а — 8 <; х а).
§ 4. Прохождение непрерывной функции через любое
промежуточное значение
1. Прохождение непрерывной функции через нуль при смене
знаков.
Теорема 8.5. Пусть функция f(x) непрерывна на сегменте
|а, Ь], и пусть значения этой функции на концах сегмента f(a)
у.	и f(b) суть числа разных знаков. Тог-
н	да внутри сегмента [а, Ь] найдется
такая точка В, значение функции в
которой равно нулю.
Доказательство. Ради опреде-
ленности предположим, что /(«)<; О,
/(b) >0. Рассмотрим множество {х} всех
значений х из сегмента [а, Ь], для ко-
торых f(x)<Z0. Это множество имеет
хотя бы один элемент х = а (ибо f(a) <Z 0),
и ограничено сверху (например, значе-
нием х = Ь). Согласно теореме 2.1 у мно-
Рис. 8.5.
жества {х} существует точная верхняя грань, которую мы обозначим
через В.
Прежде всего, заметим, что точка В является внутренней точкой
сегмента [а, Ь], ибо из непрерывности функции f(x) на сегменте
[а, Ь] и из условий /(а)<0, /(b) >0 в силу замечания к теореме
8.4 вытекает, что найдется правая полуокрестность точки х = а,
248	ОСНОВНЫЕ ТЕОРЕМЫ . О НЕПРЕРЫВНЫХ ФУНКЦИЯХ [ГЛ, 8
в пределах которой /(х)<;0, и левая полуокрестность точки х—Ь,
в пределах которой /(х)>0. Докажем теперь, что /(£) = 0. Если
бы это было не так, то по теореме 8.4 нашлась бы 8-окрестность
£ —8<;х<;£ + & точки £, в пределах которой функция f(x) имела
бы определенный знак. Но это невозможно, ибо, по определению
точной верхней грани, найдется хотя бы одно значение х из полу-
сегмента 5 — 8 < х sg I такое; что f(x) < 0, а для любого значения х
из интервала !; < х <; £ + 8 /(х)^0. Итак = Теорема дока-
зана. Иллюстрацией к теореме 8.5 может служить рис. 8.5.
2. Прохождение непрерывной функции через любое проме-
жуточное значение.
Теорема 8.6. Пусть функция f(x) непрерывна на сегменте
[а, Ь], причем f(a) = A, f(b)=B. Пусть далее С —любое число,
заключенное между А и В. Тогда на сегменте [а, Ь] найдется
точка Н такая, что —
Доказательство. Следует рассмотреть лишь случай, когда
АаВ и когда С не совпадает ни с одним из чисел А и В. Пусть
ради определенности A<zB, A<^C<ZB. Рассмотрим функцию
<р (х) = f (х) — С. Эта функция непрерывна на сегменте [а, Ь} (как
разность непрерывных функций) и принимает на концах этого сег-
мента значения разных знаков
<р(а)=/(а)-С = Д-С<0, ?(b)=f(b)-С=^В-С> 0.
По теореме 8.5 внутри сегмента [а, Ь] найдется точка $ такая, что
<f> (I) =/(Е) — С = 0. Стало быть, /(;) = С. Теорема доказана.
§ 5. Ограниченность функции, непрерывной на сегменте
Теорема 8.7 (первая теорема Вейерштрасса). Если функ-
ция f(x) непрерывна на сегменте [а, Ь], то она ограничена на
атом сегменте.
Доказательство. Докажем, что функция f(х) ограничена
сверху на сегменте [а, Ь] (ограниченность снизу доказывается совер-
шенно аналогично).
Предположим противное, т. е. допустим, что f(x) не является
ограниченной сверху на сегменте [a, £>].
.Тогда для любого натурального числа п(п=1, 2, ...) найдется
хотя бы одна точка хп из сегмента [а, Ь] такая, что /(х„)>л
(иначе /(х) была бы ограничена сверху на сегменте [а, £>]).
Таким образом, существует последовательность значений хп из
сегмента [а, Ь] такая, что соответствующая последовательность зна-
чений функции {/(х„)} является бесконечно большой. В силу теоремы
Больцано — Вейерштрасса (см. теорему 3.17 из п. 4 § 4 главы 3)
из последовательности {хл} можно выделить подпоследовательность,
§6]
ТОЧНЫЕ ГРАНИ ФУНКЦИИ
249
сходящуюся к точке принадлежащей, в силу замечания 2 к указан-
ной теореме, сегменту [a, Z>], Обозначим эту подпоследовательность
символом {-£лп}	2, ...). В силу непрерывности функции f(x)
в точке £ соответствующая подпоследовательность значений функции
{/(х*л)} обязана, сходиться к /(I). Но это невозможно, ибо подпо-
следовательность {/(**„)}> будучи выделена из бесконечно большой
последовательности {/(хл)}, сама является бесконечно большой (см. п. 1
§ 4 главы 3). Полученное противоречие доказывает теорему.
Замечание. Для интервала (или полусегмента) утверждение,
аналогичное теореме 8.7, уже несправедливо, т. е. из непрерывности
функции на интервале (или полусегменте) уже не вытекает ограничен-
ность этой функции на указанном множестве. Рассмотрим, например,
функцию /(x) = -i- на интервале (0, 1) (или на полусегменте (0, 1]).
Эта функция непрерывна на указанном интервале (или полусегменте),
но не является на нем ограниченной, ибо существует последователь-
ность точек хл = -^ (л = 2, 3, ...), принадлежащих указанному интер-
валу (или полусегменту), такая, что соответствующая последователь-
ность значений функции {/(хл)} = {л} является бесконечно большой.
§ 6. Точные грани функции и их достижение функцией,
непрерывной на сегменте
1. Понятие точной верхней и точной нижней граней функции
на данном множестве. Рассмотрим функцию f(x), ограниченную
на данном множестве {х} сверху (снизу) *). Используя для множества
всех значений этой функции введенное в п. 5 § 1 главы 2 понятие
точной верхней (точной нижней) грани, мы придем к следующему опреде-
лению. Число М (число т) называется точной верхней (точ-
ной нижней) гранью функции f(x) на множестве {х}, если
выполнены следующие два 'требования: 1) для каждого значения х
из множества {х} справедливо неравенство f (х) М (f (х) т), 2)
каково бы ни было положительное число е, найдется хотя бы
одно значение х из множества {х}, для которого справедливо
неравенство
f(x)>M-z (f(x)<m + s).
В этом определении требование 1) утверждает, что число М (число tri)
является одной из верхних (нижних) граней функции f(x) на мно-
жестве {х}, а требование 2) говорит о том, что эта грань является
наименьшей (наибольшей) и уменьшена (увеличена) быть не может.
♦) Определение функции, ограниченной на данном множестве сверху
(снизу), было дано в начале § 2 этой главы.
250
ОСНОВНЫЕ ТЕОРЕМЫ О НЕПРЕРЫВНЫХ ФУНКЦИЯХ
[ГЛ 8
Для обозначения точной верхней и точной нижней граней функции
f (х) на множестве {х} употребляют следующую символику;
М = sup {/(х)}, т = inf {/(х)}.
{*> {*}
Из доказанной в п. 5 § 1 главы 2 теоремы 2.1 непосредственно
вытекает следующее утверждение: если функция f(x) ограничена
на множестве {х} сверху (снизу), то у функции f(x) существует
на этом множестве точная верхняя (точная нижняя) грань.
Естественно, возникает вопрос, является ли точная верхняя
(точная нижняя) грань функции достижимой, т. е. существует ли
среди точек множества {х} такая точка х, значение функции в кото-
рой равно этой грани. Следующий пример показывает, что точная
верхняя и точная нижняя грани, вообще
говоря, не являются достижимыми.
Рассмотрим на сегменте |^0, у]
функцию
/(*) =
sinx при0<х<у,
1	г,	ГС
-% при х = 0 и х = у.
Эта функция ограничена на сегменте |0, yj и сверху и снизу и имеет
на этом сегменте точную верхнюю грань М = 1 и точную нижнюю
грань т — 0. Однако ни в одной точке сегмента ^0, yj эта функция
не принимает значений, равных этим граням (рис. 8.6). Таким образом,
рассмотренная нами функция не имеет на сегменте |j), yj ни макси-
мального, ни минимального значений.
Обратим внимание на то, что рассмотренная нами функция не
является непрерывной на сегменте £о, yj. Это обстоятельство не
является случайным, ибо, как мы докажем в следующем пункте, функ-
ция, непрерывная на сегменте, обязательно достигает в некоторых
точках этого сегмента своих точных верхней и нижней граней.
2. Достижение функцией, непрерывной на сегменте, своих
точных граней. Пусть функция f(x) непрерывна на некотором сег-
менте [а, &]. Тогда в силу теоремы 8.7 эта функция ограничена на
этом сегменте и сверху, и снизу. Стало быть, в силу утверждения,
сформулированного в предыдущем пункте, у этой функции сущест-
вуют на сегменте [а, Ь] точная верхняя грань М и точная нижняя
грань т. Докажем, что эти грани достижимы.
§6]
ТОЧНЫЕ ГРАНИ ФУНКЦИИ
251
Теорема 8.8 (вторая теорема Вейерштрасса). Если функ-
ция f(x) непрерывна на сегменте [а, Ь], то она достигает на
этом сегменте своих точных верхней и нижней граней (т. е.
на сегменте [а, Ь] найдутся такие точки хх и х2, что ф(хг) = М,
f(x2)=m).
Доказательство. Докажем, что функция f(х) достигает на
сегменте [а, Ь] своей точной верхней грани М (достижение точной
нижней грани доказывается аналогично).
Предположим противное, т. е. предположим, что функция f(x)
не принимает ни в одной точке сегмента [а, значения, равного М.
Тогда для всех точек сегмента [а, Ь] справедливо неравенство
f(x) < М, и мы можем рассмотреть на сегменте [а, Ь] всюду поло-
жительную функцию
F (х) = —Цтт •
v ’ М — f (х)
Так как знаменатель M—f(x) не обращается в нуль и непрерывен
на сегменте [а, />], то по теореме 4.2 функция F (х) также непрерывна
на сегменте [а, Ь]. В таком случае, согласно теореме 8.7, функция
F (х) ограничена на сегменте [а, &], т. е. найдется положительное
число В такое, что для всех х из сегмента [а, Ь]
F(x)
1
M-f(x)
Последнее неравенство (с учетом того, что М— /(х)>0) можно
переписать в виде
Написанное соотношение, справедливое для всех точек х из сег-
мента [a, h], противоречит тому, что число 714 является точной
верхней гранью (наименьшей из всех верхних граней) функции
f(x) на сегменте [а, Ь]. Полученное противоречие доказывает
теорему.
Замечание 1. Для интервала и полусегмента утверждение,
аналогичное теореме 8.8, не имеет места. В самом деле, в замечании
к теореме 8.7 (см. § 5) мы привели пример функции, непрерывной
на интервале (полусегменте) и не являющейся на нем ограниченной
(у такой функции точная верхняя (или нижняя) грань не только не
достигается, но даже не существует!).
Замечание 2. После того как доказано, что функция f(x),
непрерывная на сегменте, достигает на этом сегменте своих точных
верхней и нижней граней, мы можем назвать точную верхнюю грань
максимальным значением, а точную нижнюю грань минимальным
значением функции f(x) на этом сегменте и сформулировать теорему
252
ОСНОВНЫЕ ТЕОРЕМЫ О НЕПРЕРЫВНЫХ ФУНКЦИЯХ
[ГЛ. 8
8.8 в виде: непрерывная на сегменте функция имеет на этом
сегменте максимальное и минимальное значение *).
Замечание 3. К числу других свойств функции, непрерывной
на сегменте, относится свойство, называемое равномерной непрерыв-
ностью. Это свойство мы изучим в § 4 главы 10. Здесь мы лишь
отметим, что весь материал пп. 1 и 2 § 4 главы 10 может быть
прочитан непосредственно вслед за материалом настоящего параграфа.
§ 7.	Возрастание (убывание) функции в точке.
Локальный максимум (минимум)
1.	Возрастание (убывание) функции в точке. Будем предпо-
лагать, что функция /(х) определена всюду в некоторой окрестности
точки с.
Определение. Говорят, что функция f(x) возрастает
(убывает) в точке с, если найдется такая окрестность
точки с, в пределах которой
f(X) > f(c) при х>с uf(x) cf (с)
при X<z с (f(x) <.f(c) при Х> с
и f(x)>f(c) при X<Zc).
На рис. 8.7 изображена функ-
ция, возрастающая в точке с и
убывающая в точке d.
Установим достаточное ус-
ловие возрастания (убывания)
функции f(x) в точке с.
Теорема 8.9. Если функция
f(x) дифференцируема в точке
с и f'(c)>0 (/'(с)<0), то эта функция возрастает (убывает)
в точке с.
Доказательство. Докажем теорему для случая f(c) > 0 (слу-
чай f (с) < 0 рассматривается совершенно аналогично). Поскольку
г, , .	.. f(x) — f(c)
f (с)= lim
Х—С х с
то, по новому определению предельного значения функции, для лю-
бого s > 0 найдется положительное S такое, что
/' (с) — е <	< f (с) + е при 0<|х—с|<8.	(8.5)
*) Отметим, что и разрывные на некотором сегменте функции могут иметь
на этом сегменте максимальное и минимальное значения. Так, например, уже
известная нам из § 1 главы 4 функция Дирихле
(1, если х рационально,
(0, если х иррационально,
разрывна в любой точке любого сегмента [а, &], но имеет на этом сегменте
максимальное значение, равное единице, и минимальное значение, равное нулю.
§ 7]	ВОЗРАСТАНИЕ (УБЫВАНИЕ) ФУНКЦИИ В ТОЧКЕ
253
Возьмем в качестве е положительное число, меньшее /' (с). Тогда
/' (с) — е > 0 и, стало быть, из (8.5) получим
(с)
х — с
>0 при 0<|х—с|<5.
(8.6)
(8.6) означает, что всюду в ^-окрестности точки с /(х)>/(с) при
х>с и f{x)<Z.f{c) при х<с. Возрас-
тание функции /(х) в точке с доказано.
Замечание. Подчеркнем, что поло-
жительность {отрицательность) про-
изводной f (с) не является необходимым
условием возрастания {убывания) функ-
ции f{x) в точке с. В качестве примера
укажем на функцию f{x) — x3, которая
возрастает в точке х = 0 и тем не ме-
нее имеет в этой точке производную
f (0) = 0 (график этой функции изобра-
жен на рис. 8.8).
2. Локальный максимум и локаль-
ный минимум функции. Пусть снова
функция f{x) определена всюду в неко-
торой окрестности точки с.
Определение. Говорят, что функ-
ция f{x) имеет в точке: с локаль-
ный максимум {минимум), если найдется такая окрест-
ность точки с, в пределах которой значение f{c) является наи-
большим {наименьшим) среди всех
значений этой функции.
На рис. 8.9 изображена функция
f {x), имеющая локальный максимум в
точке с.
Локальный максимум и локальный
минимум объединяются общим назва-
нием локальный экстре му м.
Установим необходимое условие экс-
тремума дифференцируемой функции.
Теорема 8.10. Если функция f{x) дифференцируема в точке с
и имеет в этой точке локальный экстремум, то f'{c) = O.
Доказательство. Так как функция f{x) имеет локальный,
экстремум в точке с, то f{x) не может в этой точке ни возрастать,
пи убывать. Стало быть, в силу теоремы 8.9 производная f {с) не
может быть ни положительна, ни отрицательна, т. е. /' (с) = 0.
Теорема 8.10 имеет простой геометрический смысл: она утверждает,
что если в точке кривой _у=/(х), которой соответствует локальный
экстремум функции f{x), существует касательная к графику функ-
ции y—f{x), то эта касательная параллельна оси Ох (см. рис. 8.9).
254
ОСНОВНЫЕ ТЕОРЕМЫ О НЕПРЕРЫВНЫХ ФУНКЦИЯХ
[ГЛ. 8
§ 8.	Теорема о нуле производной
Теорема 8.11 (теорема Ролля * *)). Пусть функция f(x) не-
прерывна на сегменте [а, Ь] и дифференцируема во всех внутрен-
них точках этого сегмента. Пусть, кроме того, f(a)=f(b). Тогда
внутри сегмента [а, Ь] найдется 'точка £ такая, что значение
производной в этой точке f (?) равно нулю.
Кратко можно сказать, что между двумя равными значениями диф-
ференцируемой функции обязательно лежит нуль производной этой
функции.
Доказательство. Так как функция f(x) непрерывна на
сегменте [а, &], то, согласно теореме 8.8, эта функция дости-
гает на этом сегменте своего макси-
мального значения /И и своего мини-
мального значения т. Могут пред-
ставиться два случая: 1) М = т,
2) М>т. В случае 1) f(x) — M =
= т — const. Поэтому производная
/' (х) равна нулю в любой точке
сегмента [а, Ь]. В случае М > т, по-
скольку f(a)=f(b), можно утверждать,
что хотя бы одно из двух значений
М или т достигается функцией в неко-
торой внутренней точке ? сегмента [а, Ь]. Но тогда функция f(x)
имеет в этой точке ? локальный экстремум. Поскольку функция f(x)
дифференцируема в точке ?, то по теореме 8.10 f (?) = 0. Теорема
полностью доказана.
Теорема Ролля имеет простой геометрический смысл: если край-
ние ординаты кривой y=f(x) равны, то, согласно теореме Ролля,
на кривой у — f(x) найдется точка, в которой касательная к кривой
параллельна оси Ох (рис. 8.10).
Как мы увидим ниже, теорема Ролля лежит в основе многих фор-
мул и теорем математического анализа.
§ 9.	Формула конечных приращений (формула Лагранжа)
Большое значение в анализе и его приложениях имеет следующая
теорема, принадлежащая Лагранжу**).
Теорема 8.12 (теорема Лагранжа). Если функция f(x) не-
прерывна на сегменте [a, Z>] и дифференцируема во всех внутрен-
них точках этого сегмента, то внутри сегмента [а, Ь] най-
дется точка ? такая, что справедлива формула
 f(b)-f(a)=f(\)(b-a).	(8.7)
*) Мишель Ролль — французский математик (1652—1719).
**) Жозеф Луи Лагранж — великий французский математик и механик
(1736—1813).
§ 9]
ФОРМУЛА КОНЕЧНЫХ ПРИРАЩЕНИЙ
255
Формулу (8.7) называют формулой Лагранжа или формулой ко-
нечных приращений.
Доказательство. Рассмотрим на сегменте [а, Ь] следующую
вспомогательную функцию:
F (х) =/(х) —/(а) -	(х - а>-	(8-8)
Проверим, что для функции F (х) выполнены все условия теоремы
Ролля. В самом деле, F (х) непрерывна на сегменте [а, Ь] (как раз-
ность функции f(x) и линейной функции) и во всех внутренних точ-
ках сегмента [а, Ь] имеет производ-
ную, равную
Fr(x)=f'(x)-f{bl~fa(a\
Из формулы (8.8) очевидно, что
F(d) = F(b) = O.
Согласно теореме Ролля внутри сег-
мента [а, Ь] найдется точка 5 такая, что
=	(8.9)
Из равенства (8.9) вытекает формула Лагранжа (8.7). Подчеркнем,
что в формуле (8.7) вовсе не обязательно считать, что b > а.
Замечание. Мы получили теорему Лагранжа как следствие
теоремы Ролля. Заметим вместе с тем, что сама теорема Ролля
является частным случаем теоремы Лагранжа (при /(а) =/(/>)).
Для выяснения геометрического смысла теоремы Лагранжа заме-
тим, что величина	есть угловой коэффициент секущей,
проходящей через точки A (a, f(a)) и В (b, f(b)) кривой у —f(x),
a f (£) есть угловой коэффициент касательной к кривой y=f(x),
проходящей через точку С (£, /(£)). Формула Лагранжа (8.7) означает,
что на кривой у =f(x) между точками А и В найдется такая точка С,
касательная в которой параллельна секущей АВ (рис. 8.11).
Часто бывает удобно записывать формулу Лагранжа в виде, не-
сколько отличном от (8.7). Пусть f(x) удовлетворяет условиям тео-
ремы 8.11. Зафиксируем любое х0 из сегмента [а, £] и зададим ему
приращение Дх произвольное, но такое, чтобы значение (х0 4- Дх)
также лежало на сегменте [а, £]. Тогда, записывая формулу Лагранжа
для сегмента [х0, х0 -ф Дх], будем иметь
/(х0 + Дх)-/(х0) = Дх/'(5),	(8.10)
где 5 — некоторая точка, лежащая между х0 и х0 + Дх. Можно утвер-
ждать, что найдется такое (зависящее от Дх) число 6 из
256
ОСНОВНЫЕ ТЕОРЕМЫ О НЕПРЕРЫВНЫХ ФУНКЦИЯХ
[ГЛ. 8
интервала 0 < 9 < 1, что
£ = х0 + 9 Дх.
Таким образом, формуле (8.10) можно придать вид
/(х04-Дх) -/(х0) = Дх/,(х04-9Дх),	С8-11)
где 9 — некоторое число из интервала 0 <9 <1. Формула Лагранжа
в виде (8.11) дает точное выражение для приращения функции через
вызвавшее его произвольное конечное приращение Дх аргумента.
Этот вид формулы Лагранжа оправдывает термин «формула конечных
приращений».
§ 10.	Некоторые следствия из формулы Лагранжа
1.	Постоянство функции, имеющей на интервале равную нулю
производную.
Теорема 8.13. Если функция f (х) дифференцируема на интервале
(а, Ь) и если всюду на этом интервале /'(х) = С>, то функция f(x)
является постоянной на интервале (а, Ь).
Дока.зательство. -Пусть х0 — некоторая фиксированная точка ’
интервала (а, Ь), а х — любая точка этого интервала.
Сегмент [х0, х] целиком принадлежит интервалу {а, Ь). Поэтому
функция /(х) дифференцируема (а стало быть, и непрерывна) всюду на
сегменте [х0, х]. Это дает право применить к функции /(х) на сег-
менте [х0, х] теорему Лагранжа. Согласно этой теореме внутри
сегмента [х0, х] найдется точка $ такая, что
/(х)-/(х„) = (х-хо)/'(О.	(8.12).
По условию производная функции /(х) равна нулю всюду в интервале
(а, Ь). Стало быть, /'(£) = 0 и из формулы (8.12) мы получим
/(х)=/(х0).	(8.13)
Равенство (8.13) утверждает, что значение функции /(х) в любой
точке х интервала (а, Ь) равно ее значению в фиксированной точке х0.
Это и означает, что функция /(х) постоянна всюду на интер-
вале (а, Ь). Теорема доказана.
Теорема 8.13 имеет простой геометрический смысл: если касатель-
ная в каждой точке некоторого участка кривой y — f(x) параллельна
оси Ох, то указанный участок кривой _у=/(х) представляет собой
отрезок прямой, параллельной оси Ох.
Замечание. Теорема 8.13 уже-была использована нами в главе 6
при доказательстве теоремы 6.1. Здесь мы еще раз подчеркнем, что
весь материал настоящей главы (в том числе и теорема 8.13) совер-
шенно не использует результатов глав 6 и 7. При повторном чтении
этой книги главу 8 можно читать непосредственно вслед за главой 5,
а уже затем возвратиться к чтению глав 6 и 7.
§ 10] НЕКОТОРЫЕ СЛЕДСТВИЯ ИЗ ФОРМУЛЫ ЛАГРАНЖА	257
2.	Условия монотонности функции на интервале. В качестве
второго следствия формулы Лагранжа рассмотрим вопрос об условиях,
обеспечивающих неубывание (невозрастание) функции на данном ин-
тервале.
Прежде всего, напомним определения неубывания, невозрастания,
возрастания и убывания функции на данном интервале.
1°. Говорят, что функция f (х) не убывает (не возрастает) ш
интервале (а, Ь), если для любых двух точек хх и х3 интервала
(а, Ь), удовлетворяющих условию хг < х2, справедливо неравенство
2°. Говорят, что функция f(x) возрастает (убывает) на интервале
(а, Ь), если для любых точек хх и х2 интервала (а, Ь), связанных
условием xt < х2, справедливо неравенство
f (*1) < f (х2)	(J (хх) > f (х2)).
Теорема 8.14. Для того чтобы дифференцируемая на интервале
(а, Ь) функция f(x) не убывала (не возрастала) на этом интер-
вале, необходимо и достаточно, чтобы производная этой функции
была неотрицательной (неположительной) всюду на этом ин-
тервале.
Доказательство. 1) Достаточность. Пусть /'(х)^0
(^0) всюду на интервале (а, Ь). Требуется доказать, что f(x) не убы-
вает (не возрастает) на интервале (а, Ь). Пусть хх и х2 — любые две
точки интервала (а, Ь), удовлетворяющие условию хх < х2. Функ-
ция f(x) дифференцируема (а стало быть, и непрерывна) всюду на сег-
менте [хх, х2]. Поэтому к f(x) можно применить на сегменте [хх, х2]
теорему Лагранжа, в результате чего получим
f(x2) -/(хх) = (х2 - xjf О,	(8.14)
где хх<$<х2.
По условию /’(5)^0 (s^O), х2 — хх > 0. Поэтому правая часть
(8.14) неотрицательна (неположительна), что и доказывает неубывание
(невозрастание) /(х) на интервале (а, Ь).
2) Необходимость. Пусть функция f(x) дифференцируема на
интервале (а, Ь) и не убывает (не возрастает) на этом интервале.
Требуется доказать, что /' (х)^0 (=С0) всюду на этом интервале.
Так как f (х) не убывает (не возрастает) на интервале (а, Ь), то эта
функция не может убывать (возрастать) ни в одной точке интер-
вала (а, Ь). Стало быть, в силу теоремы 8.9, производная fr(x) ни
в одной точке интервала (а, Ь) не может быть отрицательной
(положительной), что и требовалось доказать.
Теорема 8.15. Для того чтобы функция. f (х) возрастала
(убывала) на интервале (а, Ь) достаточно, чтобы производная f’(x)
была положительной (отрицательной) всюду на этом интервале.
258
ОСНОВНЫЕ ТЕОРЕМЫ О НЕПРЕРЫВНЫХ ФУНКЦИЯХ
[ГЛ. 8
Доказательство проводится по той же схеме, что и доказа-
тельство достаточности в теореме 8.14. Пусть А\ и х2 —любые две
точки интервала (а, Ь), удовлетворяющие условию xl<Z.xi. Запи-
сывая для сегмента [хр х2] формулу Лагранжа, получим равенство
(8.14), но на этот раз в этом равенстве /'(?)>О (<0).
Вследствие этого левая часть (8-14) положительна (отрица-
тельна), что и доказывает возрастание (убывание) f(x) на интер-
вале (а, Ь).
Замечание. Подчеркнем, что положительность (отрицательность)
производной f'(x) на интервале (а, Ь) не является необходимым
условием возрастания (убывания) функции f(x) на интервале (а, Ь).
Так, функция _у = х3 возрастает на интервале (—1, +1), но произ-
водная этой функции f (х)~3хг не является всюду положительной
на этом интервале (она обращается в
нуль в точке х = 0). Вообще, легко
доказать, что функция f(x) возрастает
(убывает) на интервале (а, Ь), если
производная этой функции f (х) поло-
жительна (отрицательна) всюду на
этом интервале, за исключением ко-
нечного числа точек, в которых эта
производная равна нулю. (Для дока-
зательства достаточно применить тео-
рему 8.15 к каждому из конечного
числа интервалов, на которых f (х)
строго положительна (отрицательна) и
в тех точках, в которых производная
учесть непрерывность f(x)
равна нулю.) Установленную теоремой 8.15 связь между знаком произ-
водной и направлением изменения функции легко понять из геометри-
ческих соображений. Поскольку производная равна угловому коэффи-
циенту касательной к графику функции у =f(x), знак производной
указывает острый или тупой угол с положительным направлением
оси Ох составляет луч касательной, лежащий в верхней полуплоскости.
Если /' (х) > 0 всюду на интервале (а, Ь), то всюду на этом интервале
луч касательной, лежащий в верхней полуплоскости, составляет с Ох
острый угол, стало быть и кривая y—f(x) идет вверх всюду на этом
интервале (рис. 8.12).
3. Отсутствие у производной точек разрыва 1-го рода и
устранимого разрыва. Применим теорему Лагранжа для выяснения
одного замечательного свойства производной. Прежде всего докажем
следующее утверждение. Пусть функция f(x): 1) непрерывна в точке с
справа (слева), 2) имеет конечную производную всюду в правой
(левой) полуокрестности точки с и правую (левую) производную
в самой точке с. Тогда, если производная Г(х) имеет в точке с
правое (левое) предельное значение, то это предельное значение
равно правой (левой) производной в точке с.
§ 10]	НЕКОТОРЫЕ СЛЕДСТВИЯ ИЗ ФОРМУЛЫ ЛАГРАНЖА	259
Для доказательства этого утверждения рассмотрим любую после-
довательность {хп} значений аргумента, сходящуюся к с справа (слева).
Учитывая, что, начиная с достаточно большого номера я, все хп при-
надлежат той полуокрестности, в которой функция f(x) имеет конеч-
ную первую производную, применим теорему Лагранжа к функции
f(x) по сегменту *) [с, хп] ([хда с]). При этом получим
(8.15)
где через обозначена некоторая точка, лежащая между с и хп.
Пусть теперь в равенстве (8.15) я —оо. Тогда, очевидно, —"С справа
(слева). Поскольку по условию fr(x) имеет в точке с конечное правое
(левое) предельное значение, правая часть (8.15), по определению
предельного значения, обязана при я—-оо стремиться к указанному
предельному значению. Стало быть, существует предел при я — оо
и левой части (8.15). По определению правой (левой) производной
этот предел равен f (с 4- 0) (f (с — 0)). Итак, в пределе при я —оо
равенство (8.15) дает
Г(с4-0)= lim f'(x\	(/'(с—0) = lim f'(х)).
Jf-»c + o	х — с- 0
Тем самым доказано, что функция /' (х) непрерывна в точке с справа
(слева).
Применяя только что доказанное утверждение в каждой точке с
некоторого интервала (а, Ь), мы придем к следующему утверждению:
если функция f(x) имеет конечную производную всюду на интер-
вале (а, Ь), то f (х) не может иметь на этом интервале ни
точек устранимого разрыва, ни точек разрыва 1-го рода.
В самом деле, если в некоторой точке с интервала (а, Ь) сущест-
вуют конечные правое и левое предельные значения/'(х), то fr(x) не-
прерывна в точке с (в силу доказанного выше утверждения). Если же
хотя бы одного из указанных двух предельных значений не существует,
то /'(х) имеет в точке с разрыв 2-го рода. Приведем пример функ-
ции, производная которой существует .и конечна всюду на некотором
интервале и имеет в некоторой точке этого интервала разрыв 2-го
рода. Рассмотрим на интервале (—1, 4-1) функцию
Дд.)=/ *2 cos Т ПРИ х °’
[	0 при х = 0.
*) Все условия теоремы Лагранжа выполнены, ибо функция ((х) диф-
ференцируема (а стало быть, и непрерывна) в любой точке сегмента [с, хп]
(|хп, с]), за исключением точки с. Непрерывность / (х) в точке с справа (слева)
предполагается.
260	ОСНОВНЫЕ ТЕОРЕМЫ О НЕПРЕРЫВНЫХ ФУНКЦИЯХ [ГЛ. 8
Очевидно, что для любого х ф 0 производная этой функции суще-
ствует и определяется формулой f {х) = 2х cos — -J-siny. Суще-
ствование производной /'(0) в точке х — 0 непосредственно вытекает
из существования предельного значения
,.m f(0 + y-f(0) =
Дх — 0	^Х
lim Дх cos т- = 0.
дл-о &х
Производная f (х) не имеет в точке х = 0 ни правого, ни левого
предельного значения, ибо у слагаемого 2xcosy существует в точке
х = 0 равное нулю предельное значение, а слагаемое sin-^ не имеет
в этой точке ни правого, ни левого предельного значения (см. пример
в конце п. 1 § 8 главы 4).
4. Вывод некоторых неравенств. В заключение покажем, как
с помощью теоремы Лагранжа могут быть получены некоторые весьма
полезные неравенства. В качестве примера установим следующие два
неравенства:
|sinx1 — sin ха | sg | хг — ха|,	(8.16)
| arctg Xj — arctg хя [ «С | xx — xa	(8.17)
(Здесь под хг и xa можно понимать любые значения аргумента.)
Для установления неравенства (8.16) применим теорему Лагранжа
к функции /(х)= sin х по сегменту [хр r2J. Получим
sin хг — sin ха = (хх — х2)/' ($).	(8.18)
Учитывая, что /'(£)= cos £ и что ] cos $ |	1 для любого 5, получим,
переходя в (8.18) к модулям, неравенство (8.16).
Для установления неравенства (8.17) следует принимать теорему
Лагранжа по сегменту [х1, ха] к функции /(х) = arctg х и учесть,
что /'(?) = г-к5^1.
§11. Обобщенная формула конечных приращений
(формула Коши)
В этом параграфе мы докажем теорему, принадлежащую Коши и
обобщающую установленную выше теорему Лагранжа.
Теорема 8.16 {теорема Коши). Если каждая из двух функ-
ций f(x) и g(x) непрерывна на сегменте [а, 6] и дифференцируема
во всех внутренних точках этого сегмента и -если, кроме того,
производная g' (х) отлична от нуля всюду внутри сегмента [a, £>|,
то внутри этого сегмента найдется точка 5 такая, что спра-
ведлива формула
РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ
261
$ 12]
Формулу (8.19) называют обобщенной формулой конечных прираще-
ний или формулой Коши.
Доказательство. Прежде всего докажем, что g(a) g(b).
В самом деле, если бы это было не так, то для функции g(x) были
бы выполнены на сегменте [а, Ь] все условия теоремы 8.11 (Ролля)
и по этой теореме внутри сегмента [а, Ь] нашлась бы точка $ такая,
что g' (?) = 0. Последнее противоречит условию теоремы. Итак,
g(a) g(b), и мы имеем право рассмотреть следующую вспомогатель-
ную функцию:
F(x)=/(x)-/(n) -	[g(x) - g(a)].	(8.20)
В силу требований, наложенных на функции f(x) и g(x), функция F (х)
непрерывна на сегменте [а, Ь] и дифференцируема во всех внутрен-
них точках этого сегмента. Кроме того, очевидно, что F (а) = F (&)== 0.
Таким образом, для F(x) выполнены все условия теоремы 8.11 (Ролля).
Согласно этой теореме внутри сегмента [а, &] найдется точка $ такая,
что
F'C) = 0.	(8.21)
Имея в виду, что F' (x)~f (x') — ^~^~^g' (_х), и используя равен-
ство (8.21), будем иметь
(8М)
Учитывая, что	из равенства (8.22) получим формулу Коши
(8.19). Теорема доказана.
Замечание 1; Формула Лагранжа (8.7) является частным слу-
чаем формулы Коши (8.19) при g(x) = x.
Замечание 2. В формуле (8.19) вовсе не обязательно считать,
что Ь>а.
§ 12. Раскрытие неопределенностей (правило Лопиталя)
1. Раскрытие неопределенности вида Будем говорить, что
отношение двух функций представляет собой при х -> а неопре-
0
деленность вида -д-, если
lim У(х) = lim g(x) = 0.
л-+а	х-+а
Раскрыть эту неопределенность — это значит вычислить предельное
262
ОСНОВНЫЕ ТЕОРЕМЫ О НЕПРЕРЫВНЫХ ФУНКЦИЯХ
[ГЛ. 8
,. f (х) ,
Um (при условии, что это предельное значение суще-
х-.аё W
значение
ствует).
Следующая теорема дает правило для раскрытия неопределенности
О
вида -у.
Теорема 8.17 (правило Лопиталя*)). Пусть две функции
f(x) и g(x) определены и дифференцируемы всюду в некоторой
окрестности точки а, за исключением, быть может, самой
точки а. Пусть, далее,
Um /(х)= lim g(x) = 0
х->а
и производная g' (х) отлична от нуля всюду в указанной выше
окрестности точки а. Тогда, если существует (конечное ила
бесконечное) предельное значение **)
lim Ш
х~аё'(х)'
(8.23)
f (х)
то существует и предельное значение lim , причем справед-
х а ё W
лива формула
.. f(x) ..	f'(x)
lim -Д-Д= lim '.
х~аё(х) х-аё'Ю
(8.24)
Теорема 8.17 дает нам правило для раскрытия неопределенности
О
вида -у, сводящее вычисление предельного значения отношения двух
функций к вычислению предельного значения отношения их произ-
водных.
Доказательство. Пусть {хл} — произвольная последователь-
ность значений аргумента, сходящаяся к а и состоящая из чисел,
отличных от а. Будем рассматривать эту последовательность, на-
чиная с того номера п, с которого все хп принадлежат окрест-
ности точки а, указанной в формулировке теоремы. Доопре-
делим функции f(x) и g(x) в точке а, положив их равными
нулю в этой точке. Тогда, очевидно, f(x) и g(x) будут непрерывны
на всем сегменте [а, и дифференцируемы во всех внутренних
точках этого сегмента. Кроме того, g' (х) отлична от нуля всюду
внутри этого сегмента. Таким обра'зом, для f(x) и g(x) на сегменте
*) Гильом Франсуа де Лопиталь — французский математик (1661—1704).
**) Отметим, что предельное значение (8.23) может не существовать, тогда
f (х)
как предел отношения функций lim существует. Например, можно взять
х—аё W
а — 0, f (х) = х2 sin —, g (х) = sin х. Таким образом, правило Лопиталя «дей-
ствует» не всегда.
§ 12]
РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ
263
(8.26)
[а, хп] выполнены все условия теоремы 8.16 (Коши). Согласно этой
теореме внутри сегмента [а, хп] найдется точка Чп такая, что
f (хп) — f (а)  Г (%л)	го 9 кч
g(xn)-g(a)~g'(^Y	1	'
Учитывая, что, по нашему доопределению, f(a) = g(а) = 0, мы можем
следующим образом переписать формулу (8.25):
f(xn) _Г(Ц
g(xn) g'(in)'
Пусть теперь в формуле (8.26) в->оо. Тогда, очевидно, Ея->а. Так
как мы предположили существование предельного значения (8.23),
правая часть (8.26) при л—>оо обязана стремиться к этому предель-
ному значению. Стало быть, существует предел при п —>оо и левой
части (8.26). По определению предельного значения функции этот
.. f (х) гг	л
предел равен lim -у-у. Таким образом, в пределе при я—>оо равен-
х -*• a g (х>
ство (8.26) переходит в равенство (8.24). Теорема доказана.
Замечание 1. Если к условиям теоремы 8.17 добавить требо-
вание непрерывности производных f (х) и £ (х) в точке а, то при
условии g' (a)yi О формула (8.24) может быть переписана в виде .
НтШ = 4^.	(8.27)
g (а)
Замечание 2. Если производные /' (х) и g' (х) удовлетворяют
тем же требованиям, что и сами функции f(x) и g(x\ то правило
Лопиталя можно применять повторно (т. е. предельное значение отно-
шения первых производных функций /(х) и g(x) можно заменить
предельным значением отношения вторых производных этих функ-
ций). Мы получим при этом
f (х) f' (х)	.. f" (х)
lim 44= lim -44 = lim ,,, <
X~ag(x) х~а& (x) x-.ag W
Замечание 3. Теорема 8.17 легко переносится на случай, ког-
да аргумент х стремится не к конечному, а к бесконечному пределу
а=-|-оо или а=—оо. Ограничимся тем, что сформулируем теорему 8.17
для случая, когда a = -f-oo. Пусть две функции /(х) и g(x) определе-
ны и дифференцируемы всюду на полупрямой с<х<со. Пусть,
далее, lim /(х) = lim g(x) = 0 и производная g' (х) отлична от
х—+а>	х — 4-00
нуля на указанной полупрямой. Тогда, если существует предель-
Р (х)
ное значение lim \, то существует и предельное значение
г 7W	а
Jim 4-т, причем справедливо равенство
X--ycog W
.. И*) 1im f' (x)
lim — = lim .  . . .
^+oogW x- + oog W
264
ОСНОВНЫЕ ТЕОРЕМЫ О НЕПРЕРЫВНЫХ ФУНКЦИЯХ
[ГЛ. В
sinx 1
1™— -т-
Примеры.
' 1 — cosx
1) lim---»—
х — 0	х
2) Следующее предельное значение вычисляется двукратным при-
менением правила Лопиталя:
.. х — sin х
lim —
z-0
3) Трехкратным
дельное значение
х‘
---------= lim„
л х -> О
применением
1 — cos х ,. sin х
правила Лопиталя
вычисляется пре-
lim , , о--------п
х_0 х2 + 2cosх — 2
,.	4хз
lim-75---п	'
2х —2sinx
12*2
— 2 cos х
..	24х
= lim^—= 12.
02 sin х
1
6 '
(8.28)
2. Раскрытие неопределенности вида Будем говорить, что
/ (х)
отношение двух функций '-^4 представляет собой при х -> а неопре-
ё У.Х)
деленность вида —, если
оо
lim/(x) = lim g (х) = оо *).
Для раскрытия этой’ неопределенности, т. е. для вычисления пре-
,. f (х)
дельного значения lim . : , справедливо утверждение, совершенно
х-^а& W
аналогичное теореме 8.17, а именно: если в формулировке тео-
ремы 8.17 заменить требование lim/(x) — limg(x) = 0 на уело-
х—а	х — а
вие (8.28), то теорема 8.17 останется справедливой.
Для доказательства рассмотрим произвольную последовательность {хп}
значений аргумента, сходящуюся к а справа (или слева). Пусть хт и хп —
любые два элемента этой последовательности с достаточно большими номе-
рами т и п, удовлетворяющими условию п > т.
Применяя формулу Коши (8.19) по сегменту [хт, х„], мы можем утвер-
ждать, что на этом сегменте найдется точка Еотп такая, что
,___ f (*Л1)
f (хп) — f (хт) _ f (хп)__f (хп) _ f (Smn)
ё (хп) — ё (хт) ё (хп) ,  ё(хт) ё' (Ъпп) ‘
ё (Хп)
, ё (Хт)
f (хп) _ f (%тп)___ё (хп)
ё (хп) ё' (^тп) < _ f (хт)
f(Xn)
(х)
Если существует lim - ,) '  = Д, то для любого е>0 можно фиксировать
х-*а ё (х)
Отсюда .
*) Вместо со можно брать 4- оо или — оо.
§ 12]
РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ
265
номер т СТОЛЬ большим, ЧТО при любом п > т дробь  будет откло-
няться от числа А меньше чем на -у-. Далее, учитывая (8.28), мы можем
для данного фиксированного т найти номер п0 такой, что при л л0 Дробь
. ё(хт)
Ч ।  / (хт)
будет отклоняться от единицы меньше чем на -------. Но тогда при п^п0
1Л1 + ^
дробь будет отклоняться от числа А меньше чем на + | А |------------1-
«{Хл)	|Л|+у
. е- е	3	.	,•/(*)
+ -г---------= —е. А это означает, что предельное значение lim '
2 । л । х! 2	8 W
существует и равно А.
Примеры. 1) lim pxlnx = lim --------г = lim --------§-=
t-o + o	x —0+0 -4	x^0+0 , n - —
X	\ 2)X
= —2 lim fx=0.
x-0+0
2) л-кратным применением правила Лопиталя вычисляется пре-
дельное значение
х"	лх”-1	п(п — 1)хл~а	л! п
lim -?= lim —?—= lim —--------Н----= ...= hm —? —0.
рХ	рХ	рХ	рХ
X— + со^ Х->4-О0 е	X —4-00	Х — 4-С0 к
3. Раскрытие неопределенностей других видов. Кроме изучен-
„	0 со
них выше неопределенностей видов -д- и —, часто встречаются не-
определенности следующих видов: О-оо, оо — оо, Iю, 0°, со0.
Все эти неопределенности сводятся к изученным выше двум не-
определенностям путем алгебраических преобразований. Покажем это,
например, по отношению к последним трем из указанных выше
неопределенностей. Каждая из этих неопределенностей имеет вид
(8.29)
где при х—a f(x) стремится соответственно к 1, 0 или оо, a g(x)
стремится соответственно к оо, 0 или 0. Логарифмируя выражение
(8.29), получим (считая, что /(х)^>0)
lnj = g(Jf)ln/(x).
(8.30)
266
ОСНОВНЫЕ ТЕОРЕМЫ О НЕПРЕРЫВНЫХ ФУНКЦИЯХ
[ГЛ. 8
Для нахождения предельного значения выражения (8.29) достаточно
найти предельное значение выражения (8.30).
Заметим, что в любом из трех рассматриваемых случаев выраже-
ние (8.30) представляет собой при х->оо неопределенность вида
0 • оо. Стало быть, достаточно научиться сводить неопределенность
вида 0-оо к неопределенности вида -д- или Ц. Покажем, как это
делается. Итак, пусть
z = ср (х) • ср (х),	(8.31)
причем
lim <р (х) = 0, lim ср (х) = ± оо.
Перепишем (8.31) в виде
г = <р(х)-ср(х) = -^-.
' Ф(*)
(8.32)
Очевидно, выражение (8.32) представляет собой при х->а неопреде-
0 и
ленность вида -у. Наша цель достигнута.
Примеры. 1) Вычислить lim Xх. Обозначим у = хх. Тогда
Х-ОЧ-.О
1п_у = хInх	Применяя правило Лопиталя, будем иметь
X
_1_
lim (1п_у) = lim -Ц^-= lim х. = — lim х = 0.
х-~ 0-f-0	х-^ОЧ-О 1	х-»0+0 L	х — ОЧ-О
х	х2
Отсюда ясно, что lim _у = 1.	i
Х-О4-О	/
I	1
2) lim (1 4-х2) е*-1-* . Пусть _у = (14-х2)1 — х . Тогда
х —* 0
lnj=FJf2_^-ln(14-x2).
2х
Пользуясь правилом Лопиталя, получим
2х
.. .	,. In (1 4- х2)'	,.	1 4" х2 ,.
lim In v = hm „	,—- = lim —г =hm	..-г
x->o л x-o^-l-* x^oe —1 x-o (eX — ’)(! + *3)
2
^(1 +*2) + (ех~ 1)2* - 2’
Отсюда ясно, что lim у — е2.
х — 0
§ 13]
ФОРМУЛА ТЕЙЛОРА
267
§ 13. Формула Тейлора
Устанавливаемая в этом параграфе формула является одной из
основных формул математического анализа и имеет многочисленные
приложения как в анализе, так и в смежных дисциплинах.
Теорема 8.18 (теорема Тейлора *)). Пусть функция f(x)
имеет в некоторой окрестности точки а производную порядка**)
«4-1 (п — любой фиксированный номер). Пусть, далее, х — любое
значение аргумента из указанной окрестности, р — произвольное
положительное число. Тогда между точками а и х найдется
точка $ такая, что справедлива следующая формула:
f(x) =f(a) + ф- (х _ а) + М- (х - а)* +...
+	(8.33)
где *
Япъ (*) =	/(Л+1) ©•	(8-34)
\ Л v /	г
Формула (8.33) называется формулой Тейлора (с центром в точке а),
а выражение Rn+l(x) называется остаточным членом. Как мы уви-
дим ниже, остаточный член может быть записан не только в виде
(8.34), но и в других видах. Принято называть остаточный член
записанный в виде (8.34), остаточным членом в общей форме****).
Доказательство. Обозначим символом <р(х, а) многочлен
относительно х порядка п, фигурирующий в правой части (8.33),
т. е. положим
ср(х, а) —
=f(a)+^(x-a) + f-^(x-a)^ + ... + f-^-(x-a)n.	(8.35)
Далее обозначим символом /?га+1(х) разность
Rn+1(x)=f(x)-<?(x, а).	(8.36)
Теорема будет доказана, если мы установим, что Rn+1 (х) опреде-
ляется формулой (8.34).
Фиксируем любое значение х из окрестности, указанной в форму-
лировке теоремы. Ради определенности будем считать, что х>а.
*) Брук Тейлор — английский математик (1685—1731).
**) Отсюда вытекает, что сама функция f (х) и ее производные до по-
рядка п непрерывны в указанной окрестности точки а.
***) Так как £ лежит между х и а,
I х — а\Р	, п
I ——£-1 определено для любого р > 0.
*’**) эТу фОрМу остаточного члена
мильха — Роша.
х — а _
то-----г- > 0, так что выражение
X ““ с
называют также формой Шле-
268
ОСНОВНЫЕ ТЕОРЕМЫ О НЕПРЕРЫВНЫХ ФУНКЦИЯХ
[ГЛ. 8
Обозначим через t переменную величину, имеющую областью своего
изменения сегмент [a, xj, и рассмотрим вспомогательную функцию
ф(?) следующего вида:
Ф (О =/(*) - ? (х, 0 - (х - ty Q (х),	(8.37)
где
= <8-38>
V* — ajr
Подробнее ф(£) можно записать так:
ф (0 =/(х) -/(0 - ПО (х - о -...
,..-Пр-(х-0п-(х-<ГО(х).	(8.39)
Наша цель — выразить Q (х), исходя из свойств введенной нами
функции ф (t).
Покажем, что функция ф(/) удовлетворяет на сегменте [а, х] всем
условиям теоремы 8.11 (Ролля).
Из формулы (8.39) и из условий, наложенных на функцию /(х),
очевидно, что функция ф(0 непрерывна на сегменте [а, х] и диффе-
ренцируема на этом сегменте *). Убедимся в том, что ф(а) = ф(х) = 0.
Полагая в (8.37) t = а и принимая во внимание равенство (8.38),
будем иметь
Ф (a) -f(x) - (х, а) - Яп+1 (х).
Отсюда на основании (8.36) получим ф(а) = О. Равенство ф(х) = 0
сразу вытекает из формулы (8.39).
Итак, для функции ф(0 на сегменте [а, х] выполнены все условия
теоремы 8.11 (Ролля). На основании этой теоремы внутри сегмента
[а, х] найдется точка $ такая, что
ф'(0 = 0.	(8.40)
Подсчитаем производную ф' (0. Дифференцируя равенство (8.39), будем
иметь
  • +	- 'Г1 - (х - 0"+р (х - if Q (х). (8.41)
Легко видеть, что все члены в правой части (8.41), за исключением
последних двух, взаимно уничтожаются. Таким образом,
ф' (0 = _ (х - /)’+Р (х - Q (х).	(8.42)
*) Ибо f (/) и ее производные до порядка п непрерывны на сегменте
(а, х], a f,n+v (t) существует и конечна на этом сегменте (см. сноску**)
на стр. 267).
§ 14]	РАЗЛИЧНЫЕ ФОРМЫ ОСТАТОЧНОГО ЧЛЕНА	269
Полагая в формуле (8.42) t — K и используя равенство (8.40), получим
Q (х) =	(0-	(8-43)
Сопоставляя (8.43) и (8.38), окончательно будем.иметь
Rn+1 (X) = (х - a? Q (х) = (Х~а)Р^~£)П~Р+1/"+1) С).
Теорема доказана.
Найдем разложение по формуле Тейлора простейшей функции —
алгебраического многочлена п-го порядка. Пусть
/.(х) —	+ Сххп~1 +... 4- Сп_гх + Сп.
Тогда, поскольку /(л+1) (х) = О, остаточный член /?п+1(х) = 0 и фор-
мула Тейлора (8.33) принимает вид
/(х) =/(fl) + ф(х - а) + М(х - а)* + ... +	(х - а)л. (8.44)
(Здесь в качестве а можно взять любую точку бесконечной прямой.)
Таким образом, формула Тейлора позволяет представить любой мно-
гочлен f(x) в виде многочлена по степеням (х — а), где а —любое
вещественное число.
Пусть теперь f (х) — произвольная функция, удовлетворяющая
условиям теоремы 8.18. Постараемся выяснить, какими свойствами
обладает многочлен (8.35), фигурирующий в формуле Тейлора для
этой функции. Как и.выше, будем обозначать этот многочлен симво-
лом у(х, а). Символом ср(л)(х, а) обозначим л-ю производную <f(x, а)
по х. Дифференцируя формулу (8.35) по х и затем полагая х = а,
мы получим следующие равенства:
<р (а, а)=/(а),
ср'(a, a)—f'(a),
cp<2)(fl, a)=/(2)(a),
cp(n)(a, a)=/tn)(a).
Таким образом, фигурирующий в формуле Тейлора для произвольной
функции f (х) многочлен ср (х, а) обладает следующим свойством: он
сам и его производные до порядка л включительно равны в точке
х = а соответственно /(х) и ее производным до порядка л.
§ 14.	Различные формы остаточного члена. Формула Маклорена
1.	Остаточный член в форме Лагранжа, Коши и Пеано. Выше
мы установили формулу Тейлора с остаточным членом в общей форме.
Здесь мы установим другие возможные представления для остаточного
члена. Два из этих представлений мы получим в качестве частных
случаев из общей формы остаточного члена.
270
ОСНОВНЫЕ ТЕОРЕМЫ О НЕПРЕРЫВНЫХ ФУНКЦИЯХ
[ГЛ. 8
Прежде всего несколько преобразуем формулу для остаточного
члена (8.34), Поскольку точка $ лежит между точками а и х, найдется
такое число 6*) из интервала 0<9<1, что $ — а = 6(х — а).
При этом £ = а + 9 (х — а), х — 5 = (х — а)(1 — 6). Таким образом,
формула (8.34) может быть переписана в виде
/?„+1 (X) = (х~а)В+1п(|1рТ-9),,Г;,+7(^1) [а + о (х _ а)].	(8.45)
Рассмотрим теперь два важных частных случая формулы (8.45):
1) р = п 4-1, 2) р=\ (напомним, что в формулах (8.34) и (8.45)
в качестве р может быть взято любое положительное число). Первый
из этих частных случаев (/> = n-|-l) приводит нас к остаточному
члену в форме Лагранжа
W = 7ЯПЗГ^(я+1> [« +6 - «)]•	(8-46)
Эта форма остаточного члена наиболее употребительна в приложениях.
Остаточный член в форме Лагранжа напоминает следующий, очеред-
ной член формулы Тейлора, лишь только («4-1);я производная функ-
ция f(f) вычисляется не в точке а, а в некоторой промежуточной
между а и х точке $ = а 4- 6 (х — а). Второй из указанных выше
частных случаев (р=1) приводит нас к остаточному члену в форме
Коши
Rn+1 (*)= (^-°)в+Ч1-б)»./(я+1) [а + 9 (Х _ а)]	(8 47)
Так как формы Лагранжа и Коши отвечают разным значениям р,
а 9 зависит от р, то значения 9 в формулах (8.46) и (8.47) являются,
вообще говоря, различными. Для оценки некоторых функций форма
Коши является более предпочтительной, чем форма Лагранжа. Обе
формы остаточного члена (Лагранжа и Коши) обычно используются
в тех случаях, когда требуется при тех или иных фиксированных
значениях х, отличных от а, приближенно вычислить функцию f(x).
Естественно приближенно заменить /(х) многочленом <р(х, а) и
численно оценить сделанную при этом ошибку. Наряду с этим встре-
чаются задачи, в которых нас интересует не численная величина
указанной ошибки, а лишь порядок ее относительно малой вели-
чины (х — а). Для этой цели удобна другая форма записи остаточного
члена (так называемая форма Пеано **)), к установлению которой
мы и переходим.
*) Следует подчеркнуть, что а стало быть, и в зависят не только от х
и п, но также и от р.
**) Джузеппе Пеано — итальянский математик (1858—1932).
§14]	РАЗЛИЧНЫЕ ФОРМЫ ОСТАТОЧНОГО ЧЛЕНА	271
Пусть функция f (х) имеет производные до порядка (п — 1)
в некоторой окрестности точки а и производную порядка п
в самой точке а *).
Обозначим, как и выше, символом R„+1(x) разность функции /(х)
и многочлена (8.35) и докажем, что для Rn^tx) справедливо следую-
щее равенство **):
Яп+1(*) = о[(*- <*П	(8.48)
Это последнее равенство и называют остаточным членом, пред-
ставленным в форме Пеано.
Так как при сделанных нами предположениях многочлен (8.35) и
его производные до порядка п включительно совпадают в точке х — а
соответственно с функцией f(x) и ее производными, взятыми в той же
точке х = а, то справедливы равенства
Rn+i(a) = 0, я;н(«) = о, /?£+1(а) = 0.... R^(a) = 0, (8.49)
и нам остается доказать, что из равенств (8.49) вытекает представ-
ление (8.48). Это последнее мы докажем методом индукции. Сначала
мы убедимся в том, что из равенств (8.49) вытекает представление
(8.48) при п = 1.
При л=1 соотношения (8.49) превращаются в два равенства
(а) = 0,	(а) = О,
из которых следует, что
lim = lim	R (а) = 0.
х^а	х~а	
Но это и означает, что R2 (х) = о (х — а), т. е. при п = 1 формула
(8.48) справедлива.
Предположим теперь, что представление (8.48) вытекает из ра-
венств (8.49) для некоторого номера и убедимся, что в таком
случае представление (8.48) вытекает из равенств (8.49) и для номера
(п-\- 1). Действительно, если равенства (8.49) справедливы при замене п
на (п + 1), то для функции R'n+2(x) справедливы равенства
R’n+i (а) = 0, R"n+2 (а) = 0, ..., R<%" (а) = О,
из которых в силу сделанного предположения вытекает, что
R^(x) = o[(x-a)n].	(8.50)
Вместе с тем, применяя к функции Rn+i (х) на сегменте [а, х]
формулу Лагранжа (8.14) и учитывая, что Ял+2(а) = 0, мы получим,
*) Таким образом, мы подчиняем функцию f (х) требованиям более
слабым, чем в теореме 8.18.
*•) Символ о [(х— а)п] означает бесконечно малую при х—*а величину
более высокого порядка чем (х — а)п (см. п. 3 § 2 главы 4).
272
ОСНОВНЫЕ ТЕОРЕМЫ О НЕПРЕРЫВНЫХ ФУНКЦИЯХ
ГГЛ. 8
ЧТО
^л+2 (•*) = ^п+2 (Х) — Rn+2 (°) == ^»+2 (0 ' & ~~ а)>	(8.51)
где точка $ лежит между х и а. Имея в виду, что о [(£ — а)п] =>
= о[(х — а)а], и сопоставляя равенства (8.51) и (8.50), мы оконча-
тельно найдем Ря+2(х) = о [(х —а)'1'1’1].
Тем самым вывод представления (8.48) завершен.
В заключение запишем полностью формулу Тейлора с остаточным
членом в форме Пеано
f[x) =/(а) + ф (х - а)'+... +	(х -а)п + о [(х - а)п]. (8.52)
2.	Другая запись формулы Тейлора. Часто записывают формулу
Тейлора (8.33) в несколько ином виде. Положим в (8.33) а — х0,
(х — а) = Дх и возьмем остаточный член в форме Лагранжа (8.46).
При этом х = х0 + Дх, и мы получим
/(х0 + Дх) -/ (х0) =	Дх +	(Дх)2 +...
... +ф! (Дх)" +	<Дх)Я+1- (8‘53)
1*1	\ft “У” kjl
(Здесь 9 — некоторое число из интервала 0 < 9 < 1). Формула Тей-
лора (8.53) является естественным обобщением формулы Лагранжа (8.11)
(см. § 9). Фортиула Лагранжа (8.11) получается из формулы (8.53)
в частном случае и = 0.
3.	Формула Маклорена. Принято называть формулой Макла-
рена*) формулу Тейлора'(8.33) с центром в точке а = 0. Таким обра-
зом, формула Маклорена дает представление функции в окрестности
точки х = 0. Запишем формулу Маклорена для произвольной функ-
ции /(х) с остаточным членом в форме Лагранжа, Коши и Пеано **):
f{x) ==7(0) + ф х + М х2 +... + Xя + Rn+1 (х), (8.54)
где остаточный член имеет вид:
1)	в форме Лагранжа
W - (ЯЛ)Т/(Л+1) (0Х)	(° <9 < П <8-55)
2)	в форме Коши ***)
Ян-1 (х) = (ф 9)--- /(п+1)(9х)	(0 < 9 < 1),	(8.56)
*) Колин Маклорен — английский математик (1698—1746).
**) При этом предполагается, что fix) имеет в окрестности точки х = 0
(п + 1)-ю производную, а для остаточного . члена в форме Пеано — в окрест-
ности точки х = 0 (п — 1)-ю производную, а в самой точке х = 0 п-ю произ-
водную.
**•) Еще раз подчеркнем, что значения в в формулах (8.55) и (8.56), во-
обще говоря, различны.
$ 15}	ОЦЕНКА ОСТАТОЧНОГО ЧЛЕНА	273
3)	в форме Пеано
Лп+1(х) = о(хя).	(8.57)
(М.ы использовали формулы (8.46), (8.47) и (8.48).)
Перейдем к оценке остаточного члена в формуле Тейлора — Макло-
рена, к отысканию разложения по формуле Маклорена важнейших
элементарных функций и к рассмотрению различных приложений этой
формулы.
§ 15. Оценка остаточного члена. Разложение некоторых
элементарных функций
1. Оценка остаточного члена для произвольной функции. Оце-
ним для произвольной функции f(x) остаточный член в формуле
Маклорена (8.54), взятый в форме Лагранжа (8.55).
Предположим,'что рассматриваемая нами функция /(х) обладает
следующим свойством: существует такое вещественное число М,
что для всех номеров п и для всех значений аргумента х из
рассматриваемой окрестности точки х = 0 справедливо неравен-
ство
| /<"> (х) |	М.	(8.58)
Функцию, обладающую указанным свойством, будем называть функ-
цией, совокупность всех производных которой ограничена в окре-
стности точки х = 0.
Из неравенства-.(8.58) вытекает, что
|/W(0x)]<M	(8.59)
и поэтому из формулы (8.55) следует, что
Итак, мы получаем следующую универсальную оценку остаточ-
ного члена для функции, совокупность всех производных которой
ограничена числом М в- окрестности точки х = 0:
|/?п+1(х)|^Л411кщ.	(8.6О)
Напомним, что при любом фиксированном х
(см. пример 3 п. 3 § 3, главы 3). Отсюда вытекает, что, выбирая
достаточно большой номер п, мы можем сделать правую часть (8.60)
как угодно малой. Это дает нам возможность применять формулу
Маклорена для приближенного вычисления функций, обладающих ука-
занным свойством, с любой наперед заданной точностью. Приведем
274
ОСНОВНЫЕ ТЕОРЕМЫ О НЕПРЕРЫВНЫХ ФУНКЦИЯХ
[ГЛ. 8
примеры функций, совокупность всех производных которых ограни-
чена в окрестности точки х = 0.
1) f(x) = ex, /(я) (х) = ех. Совокупность всех производных этой
функции ограничена на любом сегменте [— г, г] (г >• 0) числом М — ^.
2./(x)=cosx или /(x) = Sinx. Совокупность всех производных
каждой из этих функций ограничена всюду на бесконечной прямой
числом М = 1.
2. Разложение по формуле Маклорена некоторых элементар-
ных функций.
А./(х) = е*. Поскольку /(П) (х) = е*, /W(Q)=1 для любого п,
формула Маклорена (8.54) имеет вид
^=l+^ + ^ + ... + Ji + Rn+1(x)>	(8.61)
где остаточный член в форме Лагранжа равен
yrt+L ь
^(х) = (НТ1)Г (0<9<1).
На любом сегменте [— г, + г] (г > 0), в силу того, что | еЬх | ег,
получим следующую оценку для остаточного члена:
г П+1
(8-62)
Б. /(х) = sin х. Поскольку /<") (х) = sin (х + п уj,
(0 при четном п,
п-1
(— 11 2 при нечетном п,
формула Маклорена (8.54) имеет вид
л	„	п — 1 „
уЗ у5 у7	—।  у^
sinx = x-^ + ^-^ + ... + (-l) 2 7й+Ял+2(.4	(8.63)
где и—нечетное число, а остаточный член в форме Лагранжа равен
Rn+z (*) =	sin (бх + п~ + к)	(0 < 9 < 1).
Очевидно, что на любом сегменте [—г, -|-г] (г>0) для остаточного
члена справедлива следующая оценка:
<8-64>
В. f (х) = cos х. Поскольку /(П) (х) = COS [х + п уj,
(0 при нечетном п,
п
(__jp при четном п,
5 15)
ОЦЕНКА ОСТАТОЧНОГО ЧЛЕНА
275
формула Маклорена (8.54) имеет вид
cosx=l--g- + ^--g- + ... + (-l)^ + /?n+2(x),	(8.65)
где п — четное число, а остаточный член в форме Лагранжа равен
Ял+2(*) = тАг5йс08 (9х + »4 + 1'}	(°<9<1)-
На любом сегменте [—г, + г] (г > 0) получаем для остаточного
члена оценку (8.64).
Г. f(x) — In (1 + х). Поскольку
fm (X) = (-1)”-1	, /(0) = 0, /(") (0) = (- l)"-1 (я - 1)!,
V т л)
формула Маклорена (8.54) имеет вид
Ш(1+х) = х-4 + т- Т +••• + (-	+	(8.66)
Остаточный член на этот раз запишем и оценим и в форме Лагран-
жа, и в форме Коши:
Rn+i (х) = (п влуй-Г (в Ф°Рме Лагранжа),	(8.67)
Rn+i(x) = (— I)”-*"4-1 (1(ipxp+i *) (в Форме Коши).	(8.68)
Для оценки функции 1п(1+х) для значений х, принадлежащих сег-
менту OsgxsCl, удобнее исходить из остаточного члена в форме
Лагранжа (8.67). Переходя в формуле (8.67) к модулям, получим для
всех х из сегмента 0 х 1
(8-69)
Из оценки (8.69) очевидно, что для всех х из сегмента 0 х 1
R„+1(x)->0 при л->со.
Оценим теперь функцию 1п(1-(-х) для отрицательных значений
х из сегмента — г sg: х 0, где0<г<1. Для этого будем исходить
из остаточного члена в форме Коши (8.68).
Перепишем этот остаточный член, в виде
/ 1 ___________________________ А \П уП+1
^w=(-Dn(r+^) да -	(870)
Принимая во внимание, что для рассматриваемых значений х
< 1 и переходя в формуле (8.70) к модулям, будем иметь
(8-71)
Так как г < 1, то оценка (8.71) позволяет утверждать, что lim Rn+1 = 0.
п — со
*) Еще раз отметим, что в формулах (8.67) и (8.68) значения в являются,
вообще говоря, различными.
276
ОСНОВНЫЕ ТЕОРЕМЫ О НЕПРЕРЫВНЫХ ФУНКЦИЯХ
[ГЛ. 8
Д.	4-х)“, где а — вещественное число. Поскольку
/(«) (X) = а (а - 1)... (а - я + 1) (1 + х)в1",
fW (0) = а (а -1)... (а - л + 1),
формула Маклорена (8.54) имеет вид
(1+х)а=1+^х + ^=±1х2 + ...
... + -(a~-1)'-^g~--+U	(*). (8.72)
где остаточный член в форме Лагранжа равен
Ян-i (х) =	(1 + М“"<"+1>	(0 <9< 1). (8.73)
В частном случае, когда а = я—целое число, /?л+1(х) = 0, и мы полу*
чим известную из элементарного курса формулу бинома Ньютона
(1+х)я=1 + ^х-1-^2^ха + ... + хл.	(8.74)
Если нужно получить разложение не двучлена (1 + х)п, а двучлена
(a-f-x)", то можно вынести ап за скобку и воспользоваться форму-
лой (8.74). При этом получим
(« + ХГ = а" (1 + I)' = а" [ 1 + i (i) +	(i)’ +... + (i)"].
Таким образом, общий случай бинома Ньютона является частным
случаем формулы Маклорена.
Е. f (х) = arctg х. Можно убедиться в том, что
/™(0) =
0	при четном л,
fl — 1
(—1) 2 (л—1)! при нечетном п.
Таким образом, формула Маклорена (8.54) с остаточным членом
в форме Пеано (8.57) имеет вид
о	ft	ч	м
ya vO у7	— уЛ	_
arctgx = x— | +	+ . + (_1) 2 ^ + о(хл).
(Здесь п — нечетное число.)
(	§ 16. Примеры приложений формулы Маклорена
1.	Алгоритм вычисления числа е. В п. 4 § 3 главы 3 мы ввели
/	1 \л
число е как предел lim ( 1 Н— и получили для е грубую оценку *)
п-»оо \	п )
2=^е=с;3. Теперь мы укажем, как вычислить число е с любой инте-
*) См. формулу (3.7) из главы 3.
§ 16]
ПРИМЕРЫ ПРИЛОЖЕНИИ ФОРМУЛЫ МАКЛОРЕНА
277
ресующей нас степенью точности. Воспользуемся формулой Макло-
рена (8.61) и оценкой остаточного члена (8.62), положив в этих фор-
мулах х=г=1. Получим
г=1+т1+1+---+ы+/?«+1(1)’	(8-75)
где
Выбирая в формулах (8.75) и (8.76) достаточно большое п, мы мо-
жем оценить с помощью этих формул число е с любой интересующей
нас степенью точности.
2.	Реализация (алгоритма) вычисления числа е на электрон-
ной машине. Указанный в предыдущем пункте алгоритм вычисления
числа е легко реализуется на электронно-вычислительных машинах.
Мы приведем результат вычисления числа е по формуле (8.75)
при /1=400 на электронно-вычислительной машине БЭСМ-6. Вычисле-
ния велись с 600 знаками после запятой. Учитывая возможные ошибки
округления, мы отбросили последние 10 знаков и приводим результат
вычисления с 590 знаками после запятой *):
2,718281 828459 045235 360287 471352 662497 757247 093699
959574 966967 627724076630353547 594571 382178 525166 427427
*) Для Читателей, знакомых со стандартным алгоритмическим языком
АЛГОЛ, приведем записанную на этом языке программу вычислений:
Система Алгол—БЭСМ.6, -вариант 10—12—69
begin integer i, с, р, п, т; integer array а, b, е [0:601.];
т : = 400; marg (39, 50, 39, 10, 0, 0);
е[0]:==1; Ь|0]:=1;
for i: = 1 Step I until 601 do
a p]: = b p]: = e p]: = 0;
for n: = 1 step 1 until m do
begin for i: = 0 step 1 until 600 do
a [»]: = b p]; c : = a [0];
for 1 = 0 step 1 until 600 do
begin b p]: = c-Z-n;
c: = (c — n xb pj) X 10 + a p 4-1] end
p: = 0
for I: = 600 step — 1 until 0 do
begin c : = e [i] + b p] + p;
p: = 0
if c < 10 then e p]: = c else
begin e p]: = c — 10; p: = 1 end
end
end
for n: = I step 1 until 6 do
begin output (‘10/’, ‘zd.’, e [0]);
for i: = 1 step Г until 590 do
output (‘zd’, e p])
end
end
278
ОСНОВНЫЕ ТЕОРЕМЫ О НЕПРЕРЫВНЫХ ФУНКЦИЯХ
[гл. а
466391 932003 059921 817413 596629 043572 900334 295260 595630
738132 328627 943490763233 829880 753195 251019 011573 834187
930702 154089	149934	884167 509244	761460 668082	264800	168477
411853 742345	442437	107539 077744	992069 551702	761838	606261
331384 583000	752044	933826 560297	606737 113200	709328	709127
443747 047230	696977	209310 141692	836819 025515	108657	463772
111252 389784	425056	953696 770785	449969 967946	864454	905987
931636 889230	098793	127736 178215	424999 229576	351482	208269
895193 668033	182528	869398 496465	105820 939239	829488	793320
36...
Отметим, что на проведение всех вычислений ушло около одной
минуты машинного времени.
3.	Использование формулы Маклорена для асимптотических *)
оценок элементарных функций и вычисления пределов. Формула
Маклорена является мощным средством для получения асимптотиче-
ских оценок элементарных функций и вычисления пределов.
В главе 4 мы установили следующие асимптотические формулы
для элементарных функций:
sin х — х + о (х),	:
У Ц-х=1 + -£ + о(х),
In (1 + х) = X + о (х),
ех = 1 + х -}- о (х),
COS X = 1 — у + о (х2).
(8.77)
Формулы (8.77) дают представление элементарных функций при малых
значениях | х Первые четыре из формул (8.77) оценивают соответ-
ствующие элементарные функции с точностью до членов 1-го
порядка относительно малой величины х, а последняя из формул
(8.77) — с точностью до членов 2-го порядка относительно х.
Оценок (8.77) оказывается достаточно для вычисления простей-
ших пределов. Однако для вычисления более сложных пределов,
в которых определяющую роль играют члены более высокого.порядка
относительно малой величины х, формул (8.77) оказывается уже
недостаточно. Так, например, при помощи формул (8.77) невозможно
вычислить предельное значение
llm—,	(8.78)
Х-.0 л'
ибо по виду знаменателя можно заключить, что здесь определяющую
роль играют члены 3-го порядка относительно х.
*) Формулу или оценку, характеризующую поведение f (х) прих—
(здесь при х-»0), называют асимптотической.
§ 16]	ПРИМЕРЫ ПРИЛОЖЕНИЙ ФОРМУЛЫ МАКЛОРЕНА	279
Таким образом, для вычисления тонких пределов необходимо
получить более точные асимптотические оценки для функций, стоящих
в левых частях формул (8.77).
Такие оценки немедленно вытекают из формулы Маклорена (8.54),
если в этой формуле взять остаточный член в .форме Пеано (8.57).
Записывая формулы Маклорена (8.63), (8.72), (8.66), (8.61) и (8.65)
и беря в каждой из этих формул .остаточный член в форме Пеано,
получим следующие асимптотические оценки:
sinx = x-J + g-... + (-in1^ + 0(x-i),
(1+х)‘=1+±х+1<^=2)Л2+...+
+	Xя + о (Xя),
1п(1+х) = х-5 + ^-... + (- 1Г-^ + о(хя),
х i I х . X2 ,	, Хп .	, п.
е =1+тГ + 2Г+-" + п! + 0(А;
cosx=l-^ + x^-... + (-l)2^ + o(xn+1).
(8.79)
(Здесь в первой из формул (8.79) п — любое нечетное число, а в послед-
ней из формул (8.79) п — любое четное число.) Формулы (8.79)
оценивают соответствующие элементарные функции с точностью до
членов любого порядка п относительно малой величины х. Эти фор-
мулы являются эффективным средством для вычисления ряда тонких
предельных значений.
Приведем примеры использования асимптотических формул (8.79).
1°. В качестве первого примера рассмотрим уже записанное выше
предельное значение (8.78). Привлекая первую из формул (8.79) (взя-
тую при п = 3), будем иметь
х — 4- о (х*) — х r , п ,
.. sinx- х ..	31	'	Г 1 , г	1
1Т» -г = J”--------------?-------“ 1'”» Г 31+° WJ = - я 
2°.
1= lim
ж—О
_ X»
g 2 — COSX
х3 sin х
Исходя из вида знаменателя, можно заключить, что определяющую
роль должны играть члены 4-го порядка относительно х (ибо
2g0	ОСНОВНЫЕ ТЕОРЕМЫ О НЕПРЕРЫВНЫХ ФУНКЦИЯХ [ГЛ. 8
sin х = х + о (х)). Пользуясь формулами (8.79), можем записать
' (8.80)
(8.81)
у2
cos х =1 - 2j + 4i + о (х6),
sin х = х + о (х),
ег = 1 + * + у + »(г2).
Стало быть, при z = — у получим
X2
—Т	. X2 . X4 ,	. ..
е 2 = 1 - у + у + о (х4).
В силу формул (8.80), (8.81) и (8.82) искомое предельное значение
может быть переписано в виде
у2 v4	у2
1-т + 7г + °(х‘)-1+т-й_
X4 + о (х4)
(8.82)
1= lim
х—0
1	1	,	, ч
..	8	24 +	_ 1	1 — 1
=	1 + « (х)	~ 8	24 — 12'
(Здесь символом а(х) мы обозначили величину °** , являющуюся
бесконечно малой при х -> 0.)
ОО	,	..	[	, Х2\* (sin X - х)
3 .	7= lim Icosx-f- -=-l
х—о\ гZ
Обозначим через у величину *) у = ^cos х + у ls'” . Тогда I =
= lim у. Логарифмируя выражение для у, будем иметь
х-»0
1	/	х2\
In у = —г-.----Г- In COS X 4- Т5- .
x(sinx — х) - \	' 2 /
Вычислим
/	х2\
In (cosx4-у \
limlnv= lim — --------г-
х^0 л	x(sinx —х) •
Лк* Л	Л**	л
Поскольку COS X = 1 — у + 24 + о (хБ), Sin X = X — у + о (х4), получим
lim ln_y= lim
х-»0	Х-.0
1п(1+й+о(х8))
*
-^+о(*6)
*) При малых х выражение
заведомо положительно.
ДОПОЛНЕНИЕ К ГЛАВЕ 8
281
Учтем теперь, что In (1 + ~ + о С?)- Из этой формулы
Таким образом,
X* ,	.	1 . о (х*)
,. ,	,.	24 +	24+
lim ln_y = lim --*-----= lim —:---------= —
«-♦о ж-о _£. + о(жб) *-о_2.+ о(х)
Отсюда
1= lim_y — е 4‘
х — 0
ДОПОЛНЕНИЕ К ГЛАВЕ 8
ВЫЧИСЛЕНИЕ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
В настоящем Дополнении мы изучим вопрос о вычислении значений про-
стейших элементарных функций.
Для вычисления значений всех указанных функций используется два
вида алгоритмов, первый из которых основан на разложении вычисляемой
функции по формуле Тейлора, а второй —на разложении ее в цепную или
непрерывную дробь *). Первый алгоритм позволяет составить единую про-
грамму вычислений значений логарифмической и обратных тригонометриче-
ских функций. Второй алгоритм лежит в основе универсальной программы
вычислений остальных простейших элементарных функций.
Помимо обоснования указанных алгоритмов, мы проведем оценку числа
итераций, обеспечивающих заданную точность вычислений.
1. Вычисление логарифмической и обратных тригонометрических функций.
Вычисление этих функций основано на применении формулы Тейлора. Мы
подробно рассмотрим вопрос о вычислении логарифма и арктангенса. Вычисле-
ние значений arcctg х, arcsin х и arccos х легко сводится к вычислению арктан-
генса с помощью следующих известных формул:
. П	.	. X
'	arcctg х =	— arctg х, arcsin х =arctg ..	,
. X
arccos х = arcctg	,
У 1 —х*
I. Вычисление 1пя. Представим число а>0'в следующей форме:
а == 2РМ,	(8.83)
где р — целое число, а М удовлетворяет условиям
ysSMCl.	(8.84)
Отметим, что представление а в форме (8.83) единственна Используя фор-
мулу (8.83), получим для In а следующее выражение:
In а — р In 2 + 1пЛ4.	(8.85)
*) Сведения о непрерывных дробях читатель может найти в учебнике
А. П. Киселева <Алгебра> (Учпедгиз, 1959, стр. 188 — 201).
282
ОСНОВНЫЕ ТЕОРЕМЫ О НЕПРЕРЫВНЫХ ФУНКЦИЯХ
[ГЛ. 8
Полагая
1 14-х
/2 1 — х
(8.86)
и подставляя это выражение для М в (8.85), преобразуем формулу (8.85)
для 1па к следующему виду:
1	/	1 \  п । 1 1 4- х
In а = \р — 7Г) In 24- In-r-1—
\	2 /	1 — х
(8.87)
J J--
Разложим функцию In по формуле Маклорена. Легко убедиться, что
это разложение с остаточным членом в форме Лагранжа имеет следующий
вид:
14-х о , 2хз 2x6	2x2n+i
1пТ^=2х + -Г + ^Г + ,-'+2мл + 7?г,г+2(х)’	(8>88)
где.	1
/?2Я+а (*) = — 2rt + 2 [(1 4- 0х)2«+з ~ (1 — ех)а«+2] ’	^’89)
а число 6 заключено строго между нулем и единицей.
Для приближенного вычисления 1п <з используется следующая формула
f 1 \	/ v3 vB	1-2П+1 \
1па^ р_ * 1п2 + 2 х + ^-4-^-4-...4-^Т7 ,	(8.90)
z /	у tj и	~р I!
1 х
которая получается из (8.87) путем замены In - частью формулы Макло-
рена (8.88) для этой функции без остаточного члена Т?2Я+2 (х). Заметим, что
число х в приближенной формуле (8.90) для In а определяется из формулы
(8.86) с учетом ограничений (8.84), наложенных на М.
Перейдем к оценке погрешности формулы (8.90). Так как приближенное
значение In а, вычисляемое по формуле (8.90), отличается от точного значения,
вычисляемого по формуле (8.87), на величину остаточного члена /?2л+2 (х).
то для выяснения погрешности достаточно оценить этот остаточный член.
Во-первых, выясним границы изменения х. Из формулы (8.86) получаем
Л4/2 — 1
М /2 4- Г
(8.91)
Из (8.91) следует, что для значений М, удовлетворяющих неравенствам (8.84),
абсолютная величина х удовлетворяет условию ♦)
|х| <0,172.	(8.92)
Заметим теперь, что структура остаточного члена /?2л+2 (х) такова, что
оценка для отрицательных и положительных значений х может быть прове-
дена одинаковым способом (из формулы (8.89) видно, что замена х на — х
не изменяет структуры /?2П+2 (*))• Поэтому достаточно получить оценку
/?2л+2 (х) для х5г0. Учитывая это и неравенство . (8.92), получим, заменяя
в правой части (8.89) величину х числом 0,172, величину у-q—— единицей,
*) Так как х является функцией от М, то вопрос сводится к разысканию
максимального значения модуля функции (8.91) на сегменте Гу, 11.
ДОПОЛНЕНИЕ К ГЛАВЕ 8
283
1
(8.93)
1 1
а величину •=-------числом -j------	, следующую оценку:
1	' vX	1 — vj 11 it
(0,172)^2	______________
I W I 2n + 2 L1 'Г (1 — 0,172)2«+2j-
В последней формуле внесем (0,172)2П+2 в квадратные скобки. Так как
0 172
j—< 0,208, то в результате получим следующую оценку для Т?2я+г (х):
(0,172)2«+2 + (0,208)2П+2
I «гл+2 W I =&	2п+~2
При вычислении Ina на электронно-вычислительной машине *) формулу
(8.90) берут обычно при п = 6. Точность вычислений для этого случая оцени-
/оаоч	(0,172)1*4-(0,208)14
вается, как это видно из (8.93,) числом —-----—, которое не пре-
вышает 1,625 • 10-10.
2. Вычисление arctgа. Очевидно, можно ограничиться случаем поло-
жительных значений аргумента, ибо, полагая | а | = х, найдем
arctg а = sgn а • arctg х.
Укажем теперь стандартные преобразования, с помощью которых вычис-
ление arctg х для значений аргумента х, не меньших 4-, приводится к вычис-
О
лению арктангенса для значений аргумента, меньших -5-.
О
Пусть сначала х^1. Положим у — arctg х, т. е. x = tgy, и хг =
.	tg у—1 х—1
= tg (у — arctg 1). Из последней формулы получаем хх = а -г = -—— < 1.
tg У 4- 1 х 4-1
Так как arctg х— arctg 1 4- arctg хх = arctg хх, то вычисление arctg х для
значений х^1 приводится к вычислению arctg хх при 0<хх<1.
Обратимся теперь к случаю, когда аргумент удовлетворяет неравенствам
4^х<1.
Пусть k4 = 1, k2 = i,'k3 = 4- k4 = 4-. Очевидно, для некоторого i = 1,
2	4	о
2, 3, 4 выполняются неравенства
kt^x<2ki.	(8.94)
Положим у = arctg х, т. е. х — tg у и хг = tg (у — arctg &,). Из этой фор-
мулы получаем
= tg г/ — fej X — kj
‘	1 + kiigy l+fe;X’
Так как х>0, то	1, кроме того, согласно правому из неравенств
(8.94), х — ki<z2ki — ki — ki. Поэтому из последнего выражения для х, полу-
чаем неравенство х, < й,-. Поскольку arctg х = arctg -f- arctg Xt, то вычисле-
ние arctg x для значений х, удовлетворяющих неравенствам (8.94), приводится
к вычислению arctg х, при 0 < х(- < k^.
*) Именно так вычисляется Ina на электронно-вычислительной машине
БЭСМ-6.
284
ОСНОВНЫЕ ТЕОРЕМЫ О НЕПРЕРЫВНЫХ ФУНКЦИЯХ
[ГЛ. 8
Повторяя описанные преобразования аргумента х самое большее четыре
раза, мы приведем вычисление arctg х для значений х из полуинтервала
1  1
к вычислению арктангенса для значений аргумента, меньших
О	о
Для вычисления arctg х при х < 4- используется формула Маклорена
О
уЗ	у2М+1
к	arctgx = x — у + у —...+ (— 1)п g—р-+ J?2„+2 (X).
При вычислениях обычно последнюю формулу берут при п = 6 и отбра-
сывают остаточный член *). Программа вычислений для логарифма и арктан-
генса общая. При пользовании этой программой для арктангенса надо лишь
х2Л+1
2га + Г
позаботиться о перемене
знаков у соседних членов
2. Вычисление тригонометрических функций, показательной функции и
гиперболических функций. Вычисление этих функций основано на применении
цепных (или, как их еще называют, непрерывных) дробей. Необ-
ходимые нам свойства этих дробей приводятся ниже в п. 1.
Вычисление всех перечисленных функций связано с определенной цепной
дробью, которая получается при разложении функции thx. Поэтому мы под-
робно рассмотрим вычисление значений функции th х, а затем укажем, каким
образом вычисляются остальные функции.
[.Некоторые сведения о цепных д р о б я х. Ко н е ч н о й
цепной дробью ^5 называется выражение вида
Qn
(8.95)
Величины at, о2, ..., ап обычно называются частными числителями, а &0,
Ь2, b„ — частными знаменателями.
Цепные дроби
Р а_
Qo 1 ’
_h I	^а _и I
QT-&o+V ^-6о +
£1___
+ &’
+ b2
(8.96)
называются подходящими
дробями для дроби
Рп
Qn'
 Если положить P_i = 1, (?_! = 0, то из выражений (8.96) для подходящих
дробей (k = 1, 2, ..
щие Pk с и Pk_2
., га) можно получить
И Qk с <2*_1 И Q*_a:
следующие формулы, связываю-
Pk = bkPk-i + ^kPk-i, "1
Qk = bkQk-i + o-kQk-i- i
(8.97)
*) Именно так поступают, например, при вычислениях на электронной
машине БЭСМ-6.
ДОПОЛНЕНИЕ К ГЛАВЕ 8
285
Нам понадобится специальная формула для дроби определяемой со-
хл
отношением (8.95). Для установления этой формулы сравним две подходящие
дроби и . Разность этих дробей, очевидно, равна
У* Ул-1
Pk	Pk-i _ PkQk-i — Qkpk-i
Qk	Qk-i Qk-iQk.
Числитель правой части (8.98) в силу (8.97) может быть записан в виде
. (8.98)
PkQk-i — QkPk-1 = (M^-l + akPk-z№k-i — (,bkQk-i + akQk-z) Pk-1 —
= — dk [Pk-iQk-2 — Qk-iPk-z]'	(8.99)
Последовательно .используя соотношение (8.99) для значений k, (k—1),
(k — 2), .... 1 и учитывая, что Р_1 = Т, Q_i = 0, Q0 = l, мы придадим дроби
(8.98) следующий вид:
Pk Pk-i
_	Qk Qk-i ~ ( 1)4+1 ал'1 - 01 Qk-iQk'
Так как
P n fo x fPi Pq\ i ! Рг Pi\ I	if Pn P n-i\
Qn~Q<i‘\Qi Qj^\Q2 QtK *" MQ* Qn-J
то с помощью (8.100) мы и получим необходимую нам специальную формулу
„ Рп	'
для дроби ~ :
Чп
ё=^+йг-^ + - + (-1)Я+1-та
(8:100)
... ап
(8.101)
2. Разложение функции thx в цепную дробь. Используе-
мый в этом пункте способ разложения функций th х в цепную дробь был
предложен Шлёмильхом *) для разложения в цепную дробь функции tgx.
Рассмотрим функцию у — ch Vx для значений х>0. Очевидны следую-
щие тождества, получаемые последовательными дифференцированиями данной
функции и простыми преобразованиями:	'
2Vx/ = sh/£ 2/Г«/"+-^--^ = 0.
ух 2ух
Из последнего соотношения получаем тождество, справедливое для всех х >> 0:
4ху"-{-2у'—у — 0.	(8.102)
Последовательно Дифференцируя тождество (8.102), будем иметь
4ху'" + &у" — у' =0,
(8.103)
4^<«+2> + (4rt 4. 2) (/<«+11 — (/<»> = 0. J	‘
u<n+i>
Обозначим отношение g ^пГ чеРез “л+i- Тогда из последнего соотношения
У 1
(8.103) получим тождество 4хил+2 + 4я + 2 =-------, из которого вытекает
“л+1
*) Schlomilch О. Ueber den Kettenbruch fur tgx. Zs. Math. u. Phys.
2(1857), 137-165.
286
ОСНОВНЫЕ ТЕОРЕМЫ О НЕПРЕРЫВНЫХ ФУНКЦИЯХ
(ГЛ. 8
th у х — —
н
соотношение
1
9
“n+i = 2n + 1 + 2х ил+а ’	(8Л04)
Так как и< = — =	, то соотношение (8.104) при п = 0 может быть
У 2/х
записано в следующей форме:
1 + 2xu2
В правой части этой формулы заменим и2 его выражением, полученным с по-
мощью (8.104) при п = 1. В результате получим формулу
х
3 -|- 2XUg
В последнем соотношении мы можем заменить и3 его выражением, полу-
ченным с помощью (8.104) при п = 2. Такого рода операции мы можем про-
вести любое конечное число раз. В результате получим разложение функции
th Vx в цепную дробь. Заменяя в этом разложении Vх на х, найдем нуж-
ное нам разложение функции th х в конечную цепную дробь. Это разложение
имеет вид
-	(8.105)
+_________*________
2п 1 4“ 2х3пя+а
3. Вычисление значений функции th х. Оценка погреш-
ности вычислений. Вычисление значений функции thx на электронно-
вычислительной машине обычно производится с помощью формулы (8.105),
в которой отбрасывается член 2х2ц„+2. При этом п обычно берется равным 6
(/I = 6), значения же х по абсолютной величине ограничиваются числом .
Мы проведем оценку погрешности для любого номера п.
Обозначим приближенное значение функции thx, полученное из (8.105)
путем отбрасывания члена 2х2ип+2 через th х. Для выяснения точности вычи-
слений мы должны, очевидно, оценить разность th х — th х. Заметим, что th х
и th х представляют собой цепные дроби, которые мы обозначим соответ-
р	р
ственно через —— и •
Qn+i	Qn+i
Выпишем значения частных числителей a-lt Si и частных знаменателей bi,
5,- для этих дробей ^черточкой сверху мы будем обозначать величины, отно-
р \
сящиеся к дроби _.п+1). Имеем
Qn+t)
а1 — а1=х,	а8 = Д2 = х2...an+l = Sn+i — х2,
bo = b0 = 0, bl = b1 = \,	bn=bn — 2n — \, .
bn+i — 2n + 1 + 2х2«л+2, bn+i = 2n + 1.
(8.106)
ДОПОЛНЕНИЕ К ГЛАВЕ 8
287
Так как для дробей ^”+1 и ^*”+1 Q_1=Q_1 = 0, Q0=Q0=1, то с по-
Qzi+i Фп+1
мощью формул (8.106) и соотношений (8.97) получаем следующие равенства:
Q1 = £?1> ОЗ = ^2>	> Qn — Qn<	1 ,g JQ~
Q«+i = (2n + 1 + 2x2«„+2) Qn + x2Qn_i, Q„+1 = (2n + 1) Qn + x*Qn_i. Г ’
P	P	
Представим теперь каждую из дробей —2±1 и в виде (8.101). Из фор-
*2п+1	Qn+i
мул (8.106) , и (8.107) ясно, что эти представления будут отличаться лишь
гр р
последними слагаемыми. Поэтому разность  Я+1 — будет равна разности
Qn+i Qn+i
последних слагаемых представлений этих дробей по формуле (8.101). Так как
разность рассматриваемых дробей равна th х—th х, то, используя (8.106),
получим следующую формулу:
thx — thx = (- 1)л+г х2л+1
1
1 1
QnQn+i CnCn+iJ
Это соотношение с помощью формул (8.107) легко, преобразовывается к сле-
дующему виду:
2х20лПл+а
th х —thx = (—1)',+1——
Qn1
. (8.108)
2х2флия+3 + (2п + 1) Qn + x2Qn-i _
Для получения нужной нам оценки воспользуемся следующими двумя нера-
венствами, которые будут доказаны ниже.
При х^>0 для любого Ajsl справедливо неравенство:
<2^(26-1)11	(8.109)
При х > 0 величина ип+2 положительна:
и„+3>0.	(8.110)
Перейдем теперь к оценке разности thx— thx при х>0. Так как при
х>0 ил+2>0 (см. (8.110)) и любое Qk>0 (см. (8.109)), то выражение
в квадратных скобках в правой части равенства (8.108) не превосходит еди-
ницы. Далее, из (8.109) получаем следующее неравенство.
w (2п+1).
Поэтому при х > 0 для любого номера п справедлива следующая оценка по-
грешности:
thx-thxlsc [(2п_1)||]2(2п+!) 1	(8>
Остановимся на оценке погрешности при п = 6 и для значений х, удовлетво-
ряющих неравенствам 0 <х . При п = 6 число 2п— 1 равно 11, а число
2n + 1 равно 13. Так как -^-<0,8, то х13 < (0,8)13 < 5,6  10-2. Легко под-
считать, что 111! = 10 395. Поэтому, учитывая, что 2-6-f-1 = 13, из формулы
(8.111) получим, что ошибка в приближенном вычислении thx для п = 6 не
превышает 4  10'и,
288
ОСНОВНЫЕ ТЕОРЕМЫ О НЕПРЕРЫВНЫХ ФУНКЦИЯХ
(ГЛ. 8
Докажем . теперь неравенства (8.109). и (8.110).
Доказательство неравенства (8.109).
Докажем сначала неотрицательность любого Q/,. Из формул (8.106) выте-
кает неотрицательность bk и Sk при х^О для любого k^n. Мы уже отме-
чали, что O-i = 0, Q0=l. Отсюда и из второй из формул (8.97) вытекает
неотрицательность 0* для любого k п.
Из второй формулы (8.97), а также из неотрицательности ak и 0л выте-
кает неравенство
Qk bkQk-i-	(8-112)
Так как ф0=1, а й* =_2£—1 при lsgfesgn, то последовательно из
неравенства (8.112) получаем 01^=1, 0а>3, ..., 0ftХ2й—1)11. Справедли-
вость неравенства (8.109) установлена.
Доказательство неравенства (8.110).
Достаточно доказать, что все производные функции y = chjlx при х>0
положительны. Очевидно, тем самым мы докажем неравенство (8.110), ибо
уШ+2>
uo+i — yi.n+i> <
"-у
х А	*
Умножая последнее соотношение (8.103) на —, мы можем перепи-
сать это соотношение в виде
1
Г 4-1 Т п~~2
|х" + 2у(п+1>J = yW	(8<ПЗ)
Убедимся теперь в том, что
lim [х"+V'1+1>(x)] = 0.	(8.114)
x-*0-f-0
Для этого достаточно убедиться в том, что величина
xVn+11W	(8.115)
-_	gli 1/"
ограничена при х —»0-|-0. Из соотношений у = ch ух и у' = g j/~~~ выте*
кает, что у (х) и у' (х) ограничены при х—*0-|-0. Но тогда из (8.102) выте-
кает, что и величина х«/2(х) ограничена при х—-0-|-0.
После этого из последнего соотношения (8.103) по индукции получается,
что величина (8.115) ограничена при х —0-|-0 для любого номера п. Тем
самым соотношение (8.114) доказано.
Докажем теперь, что для любого номера п производная
у1П'(х)	(8.116)
положительна при х>0. Очевидно, что у,0> (х) = у (х) = ch Ух положительна
при х>0. Предположим, что для некоторого номера п величина (8.116) поло-
жительна при х>0. Убедимся тогда, что и у (л+1, (х) положительна при х>0.
Из (8.113) заключаем, что производная в левой, части (8.113) положительна
п+о- (П-М)
при х>0, т. е. функция х у (х) возрастает при х>0. Но тогда из
(8.114) следует, что эта функция положительна при х>0. Итак, t/,n+1'(x) > 0
при х>0, и неравенство (8.110) доказано.
ДОПОЛНЕНИЕ К ГЛАВЕ 8
289
4. Вычисление гиперболического синуса, гиперболи-
ческого косинуса и показательной функции. В дальнейшем
символом Sn (0 мы будем обозначать следующую цепную дробь:
S„W = 1 +---Ц— .
3 + f-^--
2п+ 1
Обычно для электронно-вычислительной машины составляют программу вычи-
сления этой цепной дроби. Используя эту программу, можно без затруднений
составить программу вычислений гиперболического тангенса, ибо, как было
выяснено в предыдущем пункте, приближенное значение thx может быть
вычислено по формуле •	'
(8.118)
причем в предыдущих пунктах было также выяснено, что с увеличением п
точность вычислений возрастает и погрешность стремится к нулю.
Вычисление функций sh 2х, ch 2х, егх может быть редуцировано к вычи-
слению гиперболического тангенса с помощью формул
sh 2х =
2 thx
1 — th2x ’
ch х =
1 +th2x
1 — th2 x ’
e2x =
1 + th x
1 - thx-
Из этих формул и из соотношения (8.118) получаются следующие формулы
для приближенных значений перечисленных функций:
23л (х2) • х	S2 (х2) + х2	Sn(x2)-Srx
S Х~ S2(x2) —х2 ' С *~S2(x2)-x2’ в ~S„(x2)-x‘
Ясно, что с помощью этих формул и программы вычислений для S„ (t)
легко составляются программы для вычисления sh 2х, ch 2х и егх.
5. Вы числениетригонометрических функций. По аналогии
с разложением в цепную дробь функции th х строится разложение для функ-
ции tg х.
Рассмотрим функцию у — cos Ух для значений х > 0. Очевидны следующие
соотношения, получаемые последовательными дифференцированиями этой функ-
ции и простыми преобразованиями:
2/х/ = — sin/x; 2Уху" +	= —
ух 2 у х
Из последнего соотношения получаем тождество
4x1/" + 2у' + у = 0.
Последовательно дифференцируя это тождество, будем иметь
4ху'" + бу" + у' = 0,
4x(/,ra+21 + (4п + 2)	+ yin> = 0.
Обозначим
и<»+1>
отношение а
у,п'
через
ил+1-
Тогда из последнего равенства
290
ОСНОВНЫЕ ТЕОРЕМЫ О НЕПРЕРЫВНЫХ ФУНКЦИЯХ
[ГЛ. 8
получим равенство 4хпл+2 4п + 2 =------------, из которого вытекает соотно-
ыл+1
шение	1 	2 n+1 2п + 1 + 2х Wrt4-2 *
Отсюда, в полной аналогии с рассуждениями для гиперболического тангенса,
получаем следующее разложение функции tgx в цепную дробь:
tgx =
— х2
2/г + 1 + 2х2ил+2
Приближенное значение tgx получается из этой формулы путем отбрасывания
члена 2x2u„+2. С учетом выражения (8.117) это приближенное значение может
быть найдено по формуле
Как и в случае гиперболического тангенса, можно убедиться, что с увели-
чением п точность вычислений по формуле (8.119) возрастает и погрешность
стремится к нулю.
С помощью известных из курса элементарной математики формул sin 2х =
2tg х	1 ’ -  - tg^ %
= 1	и cos 2* = ।	|g2 х и соотношения (8.119) получаем следующие
формулы для вычисления приближенных значений sin 2х и cos 2х:
sin 2х
2Sn (- х*)  х
(— х2) —х2’
cos 2х
S^(-x2) + x2
S2 (—х2) — х2 *
В заключение заметим, что точность вычислений всех функций, указан-
ных в последних двух пунктах, для шести итераций (п = 6) будет не меньше
10-11 при условии, что аргумент х по абсолютной величине не превышает it/4.
ГЛ А ВA 9
ГЕОМЕТРИЧЕСКОЕ ИССЛЕДОВАНИЕ ГРАФИКА ФУНКЦИИ.
НАХОЖДЕНИЕ МАКСИМАЛЬНОГО И МИНИМАЛЬНОГО
ЗНАЧЕНИЙ ФУНКЦИИ
§ 1. Участки монотонности функции.
Отыскание точек экстремума
1. Отыскание участков монотонности функции. В § 10 пре?
дыдущей главы мы уже установили ряд условий, обеспечивающих
возрастание (или соответственно убывание, невозрастание и неубы-
вание) функции f(x) на некотором
интервале (а, Ь). Для удобства
сформулируем еще раз найденные
условия:
1°. Для того чтобы дифферен-
цируемая на интервале (а, Ь) функ-
ция fix) не убывала (не возраста-
ла) на этом интервале, необходимо
и достаточно, чтобы производная
этой функции f'(x) была неотри-
цательна (неположительна) всюду на
этом интервале.
2°. Для того чтобы дифферен-
цируемая функция f(x) возраста-
ла (убывала) на интервале (а, Ь),
достаточно, чтобы производная
f(x) была положительна (отрица-
тельна) всюду на этом интервале.
Таким образом, изучение вопроса об участках монотонности диф-
ференцируемой функции f(x) сводится к исследованию знака первой
производной этой функции.
В качестве примера рассмотрим вопрос об отыскании участ-
ков монотонности функции /(х) = я3—3№ —4. Поскольку
292
ГЕОМЕТРИЧЕСКОЕ ИССЛЕДОВАНИЕ ГРАФИКА ФУНКЦИИ
[ГЛ. 9
У (•*) = Зха — 6х = Зх (х— 2), то, очевидно, f (х)
положительна при — оо < х <; О,
отрицательна при 0 < х < 2,
положительна при 2 <z х < -ф оо.
Таким образом, рассматриваемая функция возрастает на каждой из
полупрямых ( — со, 0) и (2, ф-оо) и убывает на интервале (0, 2). График
этой функции изображен на рис. 9.1.
2.	Отыскание точек возможного экстремума. В п. 2 § 7 пре-
дыдущей главы мы ввели понятие локального максимума (минимума)
функции f(x) и установили необходимое условие наличия у функции
f(x) в данной точке локального максимума (минимума). Для удобства
сформулируем еще раз определения и результаты, установленные
в указанном пункте.
Пусть функция f(x) определена всюду в некоторой окрестности
точки с. Говорят, что функция f(x) имеет в точке с локальный
максимум (минимум), если найдется такая окрестность точки с,
в пределах которой значение f(c) является наибольшим (наименьшим)
среди всех других значений этой функции.
Локальный максимум и локальный минимум объединяются общим
названием экстремум.
Следующая теорема устанавливает необходимое условие экстре-
мума дифференцируемой функции: если функция f(x) диф-
ференцируема в точке с и имеет в этой точке экстремум, то
f'(c) = Q.
- Таким образом, для отыскания у дифференцируемой функции f(x)
точек возможного экстремума, следует найти все корни уравнения
f (x) — Q (т. е. найти все нули производной f'(x)). Впредь мы будем
называть корни уравнения f (х) = 0 точками возможного экстремума
функции f(x)*).
Заметим, однако, что, поскольку равенство нулю первой произ-
водной является лишь необходимым **) условием экстремума, нужно
дополнительно исследовать вопрос о наличии экстремума в каждой
точке возможного экстремума. Для проведения такого дополнительного
исследования следует установить достаточные условия наличия
экстремума, к чему мы и переходим.
3.	Первое достаточное условие экстремума.
Теорема 9.1. Пусть точка с является точкой возможного
экстремума функции f(x), и пусть функция f(x) дифферен-
цируема всюду в некоторой окрестности точки с. Тогда, если
*) Иногда корни уравнения f (х) = 0 называют стационарными точками.
**) Что это условие не является достаточным, видно хотя бы из рас-
смотрения функции у = х3. Эта функция не имеет экстремума в точке х — 0,
в которой /' (х) 0.
ОТЫСКАНИЕ ТОЧЕК ЭКСТРЕМУМА
293
Л п
в пределах указанной окрестности производная f'{x) положительна
{отрицательна) слева от точки с и отрицательна {положительна)
справа от точки с, то функция f{x) имеет в точке с локальный
максимум {минимум). Если же производная f'{x) имеет один и
тот же знак слева и справа от точки с, то экстремума
в точке с нет.
Доказательство. 1) Пусть сначала производная f {х) в пре-
делах "рассматриваемой окрестности положительна (отрицательна) слева
от с и отрицательна (положительна) справа от с. Требуется доказать,
что значение f{c) является наибольшим (наименьшим) среди всех зна-
чений f{x) в рассматриваемой окрестности. Обозначим через х0 любое
значение аргумента из рассматриваемой окрестности, отличное от с.
Достаточно доказать, что
f{c)-f{x0)>Q	(<0).
Функция f{x) дифференцируема (а стало быть, и . непрерывна) на
сегменте [с, х0]. Применяя к f{x) по сегменту [с, х0] теорему 8.12
Лагранжа, будем иметь
f(c)~f{x0)=f{\){c-x0),	(9.1)
где 5 — некоторое значение аргумента между с и хй. Поскольку про-
изводная /' (5) положительна (отрицательна) при х0 < с и отрицательна
(положительна) при х0> с, правая часть (9.1) положительна (отрица-
тельна).
2) Пусть теперь производная f (х) имеет один и тог же знак
слева и справа от с. Обозначая, как и выше, через х0 любое значе-
ние аргумента, отличное от с, и повторяя проведенные выше рассуж-
дения, мы теперь докажем, что правая часть (9.1) имеет разные знаки
при х0 < с и при х0 > с. Это доказывает отсутствие экстремума
в точке с.
Вытекающее из теоремы 9.1 правило можно кратко сформули-
ровать так: 1) если при переходе через данную точку с возможного
экстремума производная f {х) меняет знак с плюса на минус
{с минуса на плюс), то функция f {х) имеет в точке с локаль-
ный максимум {минимум)', 2) если же при переходе через данную
точку с возможного экстремума производная f {х) не меняет
знака, то экстремума в точке с нет.
Примеры. 1) Предполагая, что консервная банка имеет форму
круглого цилиндра радиуса г и высоты й, определить, при каком
соотношении между г и й консервная банка с постоянной площадью
полной поверхности имеет наибольший объем.
Обозначим площадь полной поверхности консервной банки через 5.
Тогда
2кг2 + 2ягй = S’ = const.	(9.2)
294
ГЕОМЕТРИЧЕСКОЕ ИССЛЕДОВАНИЕ ГРАФИКА ФУНКЦИИ
[ГЛ. 9
Из этого равенства находим, что
Таким образом, мы можем выразить объем V консервной банки как
функцию радиуса г
У=ЛГ2Й = у г — г.г3.
Задача сведена к отысканию максимума функции
V(r) = 4r-w3.
£
Приравнивая нулю производную V'(r) = -g—Злг2 и учитывая, что
г > О, находим точку возможного экстремума
г=/4-	(9.3)
Хотя по смыслу задачи и ясно, что единственная точка возможного
экстремума является точкой максимума функции V(г), мы можем
строго убедиться в этом, используя теорему 9.1 и замечая, что про-
изводная V (г) — Зт —г2^ положительна при г <Z - и отри-
цательна при	Установим теперь, при каком соотношении
у,	между радиусом г и высотой h реализуется
.	} наибольший объем V(r) консервной банки.
Для
этого поделим равенство (9.2) на г2 и
/	в правой части полученного при этом ра-
/	венства воспользуемся соотношением (9.3).
/	При этом получим
h п , о
/	— = 2, т. е. h — 2г.
г	г
/	Таким образом, наибольший объем будет
I	у той консервной банки, у которой вы-
сота равна диаметру *).
Рис. 9.2.	2) Найти точки экстремума функции
'	f(x) = (x — 2)5. Поскольку f (х) = 5 (х — 2)4,
то единственной точкой возможного экстремума является точка х = 2.
Так как/'(х) положительна как слева, так и справа от этой
точки, то функция /(х) = (х —2)5 вовсе не имеет точек экстремума
(график функции /(х) —(х —2)5 изображен на рис. 9.2).
4.	Второе достаточное условие экстремума. Иногда вызывает
затруднение исследование знака первой производной /'(х) слева
*) Решенная нами задача показывает, что в интересах экономии жести
целесообразно изготовлять консервные банки с высотой равной диаметру.
§ 1]
отыскание точек экстремума
295
с
в
с
с
Рис. 9.3.
случае для
решения вопроса о нали-
в точке с производных
в § 4 этой главы.
и справа от точки возможного экстремума. На этот случай мы ука-
жем другое достаточное условие наличия экстремума в данной точке
возможного экстремума, не требующее исследования знака f (х)
окрестности с, но зато предполагающее 'существование в точке
отличной от нуля конечной второй производной /(2) (х).
Теорема 9.2. Пусть функция fix) имеет в данной точке
возможного экстремума конечную вторую производную. Тогда
функция f(х) имеет в точке с максимум, если /(2)(с)<;0, и
минимум, если /(2) (с) > 0.
Доказательство. Из условия /(2)(с)<0 (>0) и из теоремы
8.9 вытекает, что функция /' (х) убывает (возрастает) в точке с.
Поскольку по условию /' (с) = 0, то найдется такая окрестность точки с,
в пределах которой /' (х) положительна (отрицательна) слева от с и
отрицательна (положительна)
справа от с. Но тогда по пре-
дыдущей теореме fix) имеет
в точке с максимум (минимум).
Замечание. Теорема 9.2
имеет, вообще говоря, более
узкую сферу действия, чем тео-
рема 9.1. Так, теорема 9.2 не
решает вопроса об экстремуме
для случая, когда вторая про-
изводная /(2) (х) не существует
в точке с, а также для случая,
когда /(2) (с) = 0. В последнем
чии экстремума нужно изучить поведение
высших порядков, что будет сделано нами
Примеры. 1) В чашку, имеющую форму полушара радиуса г,
опущен однородный стержень длины I (рис. 9.3). Предполагая, что
2г < I < 4г, найти положение равновесия стержня.
Положению равновесия стержня соответствует минимальное значе-
ние его потенциальной энергии, т. е. наинизшее положение центра его
тяжести О (поскольку стержень является однородным, центр тяжести
его совпадает с его серединой). Обозначая через ОК перпендикуляр
к плоскости, на которой стоит чашка, мы сведем задачу к отысканию
того положения стержня АВ, при котором отрезок ОК имеет мини-
мальную длину. Прежде всего вычислим длину отрезка ОК как функ-
цию угла а наклона стержня к плоскости, на которой стоит чашка.
Пусть DL параллельно ОК, а ОС перпендикулярно OK (D — точка,
в которой стержень опирается на край чашки).
Из прямоугольного треугольника BAD AD = ED cos a = 2r cos a.
По условию АО =-L. Таким образом,
OD — AD — AO = 2r cos a —,
296
ГЕОМЕТРИЧЕСКОЕ ИССЛЕДОВАНИЕ ГРАФИКА ФУНКЦИИ
[ГЛ. 9
С другой стороны, DC = DL — ОК = г — ОК. Поэтому из прямо-
угольного треугольника ODC
Таким образом, длина отрезка ОК, которую мы обозначим /(а), равна
/(а) = г у sin а — г sin 2а.
Переходим к отысканию того значения угла а, которое доставляет
минимум /(а). (Понятно, что мы можем ограничиться значениями
угла а из первой четверти.) Так как
/' (а) = у cos а — 2r cos 2а = у cos а 4- 2г — 4r cos2 а,
то точки возможного экстремума находятся как решения квадратного
уравнения
4г cos2 а — ycos а — 2г = 0.
Поскольку cos а в первой четверти положителен, то нам пригоден
только положительный корень этого уравнения
, I 4- //2 4- 128г2
cosa0=	.	(9.4)
Хотя по смыслу задачи и ясно, что единственная точка возможного
экстремума а0 является точкой минимума функции /(а), мы установим
это строго при помощи теоремы 9.2. Достаточно убедиться в том,
что /(2) (а0) > 0. Поскольку
/(2) (а) = — ~ sin а 4- 4r sin 2а = 8r sin a ^cos а —,
то, в силу (9.4),
/(2) (ао) = 8r sin а0 ^cosa0 —-^\ = ^^]//24- 128г2>0.
Тем самым установлено, что положению равновесия стержня отвечает
угол наклона его к плоскости, на которой стоит чашка, определяемый
формулой (9.4).
2)	Найти экстремальные значения функции /(х) = х3 — Зх2 — 4.
Эту функцию мы уже исследовали в пункте 1 настоящего параграфа
(см. рис. 9.1). Так как
/' (х) = Зх2 — 6х = Зх (х — 2),
то функция Дх) имеет две точки возможного экстремума: х1 = 0 и
ха — 2. Поскольку знак /' (х) слева и справа от этих точек легко
выясняется, -можно рерить вопрос об экстремуме при помощи тео-
§ 1]
ОТЫСКАНИЕ ТОЧЕК ЭКСТРЕМУМ^
297
ремы 9.1 (первого достаточного условия). Но мы предпочитаем при-
влечь теорему 9.2 (второе достаточное условие). Имеем
/(2)(х) = 6х-6, /2)(0) = — 6<0, /2)(2) = 6>0.
Таким образом, функция f(x) имеет максимум в точке 0 и минимум
в точке 2. Экстремальные значения этой функции равны
Утах =/(0) = — 4, /т,п =/(2) = — 8.
5.	Экстремум функции, недифференцируемой в данной точке.
Общая схема отыскания экстремумов. До сих пор мы решали
вопрос о наличии у функции f(x) экстремума в такой точке с,
в которой функция f(x) дифференцируема. В этом пункте мы
изучим вопрос о наличии в точке с экстремума у такой функции,
которая не дифференцируема в точке с, но дифференцируема всюду
в некоторой окрестности справа и слева от с.
Оказывается, теорема 9.1 может быть обобщена на случай такой
функции. Именно имеет место следующее утверждение.
Теорема 9.3. Пусть функция f(x) дифференцируема всюду
в некоторой окрестности точки с, за исключением, быть может,
самой точки с, и непрерывна в точке с.
Тогда, если в пределах указанной окрестности производная
f (х) положительна (отрицательна) слева от точки с и отри-
цательна (положительна) справа от точки с, то функция f(x)
имеет в точке с локальный максимум (минимум). Если же
производная f (х) имеет один и тот же знак слева и справа от
точки с, то экстремума в точке с нет.
Доказательство в точности совпадает с доказательством тео-
ремы 9.1. Только на этот раз применимость к функции f(x) по
сегменту [с, х0] теоремы Лагранжа
устанавливается следующим обра-
зом: по условию функция f (х) диф-
ференцируема (а стало быть, и
непрерывна) всюду на полусегменте
(с, х0] и, кроме того, непрерывна
в точке с. Тем самым f(x) непре-
рывна всюду на сегменте [с, х0] и
дифференцируема во всех внутрен-
них точках этого сегмента.
Примеры. 1) Найти точки
экстремума функции f(x) = | х ]. Эта
функция дифференцируема всюду на
бесконечной прямой, кроме точки х=0, и непрерывна в точке х=0,
причем производная /'(х)=1 при х>0 и равна—1 при х<0.
Теорема 9.1 к этой функции неприменима, а согласно теореме 9.3
она имеет минимум при х=0 (рис. 9.4).
298
ГЕОМЕТРИЧЕСКОЕ ИССЛЕДОВАНИЕ ГРАФИКА ФУНКЦИИ
ГГЛ. 9
2) Найти точки экстремума функции у = х2/\ Эта функция непре-
рывна на всей бесконечной прямой и дифференцируема всюду на
этой прямой, за исключением точки х = 0. Производная при х # О
равна
В предыдущем примере производная имела в точке х = 0 разрыв
1-го рода*); на этот раз производная имеет в точке х = 0 разрыв
2-го рода («бесконечный скачок»). Из выражения для производной
заключаем, что эта производная отрицательна слева от точки х = 0
и положительна справа от этой точ-
ки. Стало быть, теорема 9.3 позво-
ляет утверждать, что рассматривае-
мая функция имеет минимум в точке
х = 0 (график рассматриваемой функ-
ции изображен на рис. 9.5).
3) Найти точки экстремума функ-
ции
J = /(x) = .
^при х#0,
О при х — 0.
Легко видеть, что эта функция непрерывна на всей бесконечной пря-
мой. В самом деле, единственной «сомнительной» точкой является
точка х = 0, но и в этой точке функция непрерывна, ибо
lim у = lim _у = 0.
Х-.0+0	л-»0 —О
Далее, очевидно, что рассматриваемая функция дифференцируема
на всей бесконечной прямой, кроме точки х = 0. Всюду, кроме этой
точки, производная определяется формулой
1 1
1 + е* х +-^ех
У =-----7—
\1 +ех]
п	.. f (х) — /(0)	1
Легко видеть, что предел lim	!—:L-i-J-=:lim---г не существует,
х->0	Х	л —0	—
1 + е х
так что функция y=f(x) недифференцируема в точке х = 0. По-
*) В том смысле, что эта производная хоть и не существовала в точке
х = 0, но имела в этой точке конечные правое и левое предельные значения^
не совпадающие между собой.
§2]
НАПРАВЛЕНИЕ ВЫПУКЛОСТИ ГРАФИКА ФУНКЦИИ
299
скольку производная у положительна и слева, и справа от точки
х = 0, рассматриваемая функция, согласно теореме 9.3, не имеет
экстремума в точке х = 0, а стало быть, и вообще не имеет экстре-
мумов. (График рассматри-
ваемой функции изображен
на рис. 9.6.)
Переходим к общей схе-
ме отыскания точек ло-
кального экстремума. Пред-
положим, что функция /(х)
непрерывна на интервале *)
(й, Ь) и ее производная
f (х) существует и не-
прерывна на этом интервале всюду, кроме конечного числа точек.
Кроме того, предположим, что производная f (х) обращается
в нуль на интервале (а, Ь) лишь в конечном числе точек. Иными
словами, мы предполагаем, что на интервале (а, Ь) имеется лишь
конечное число точек, в которых производная /(х) не существует
или обращается в нуль. Обозначим эти точки символами xv х2, ...
..., хп (й < хх <; х2 <... < х„ <; ft). В силу сделанных предполо-
жений производная f (х) сохраняет постоянный знак на каждом из
интервалов (й, хД (хр х2), ..., (хл, ft). Стало быть, вопрос о нали-
чии экстремума в каждой из точек х1г х2, ..., х„ может быть
решен (в утвердительном или отрицательном смысле) при помощи
теоремы 9.3.
Здесь мы не будем приводить примера, иллюстрирующего общую
схему отыскания точек локального экстремума. Такой пример будет
приведен нами в § 6.
§ 2. Направление выпуклости графика функции
Предположим, что функция /(х) дифференцируема в любой точке
интервала (a, ft). Тогда, как установлено в п. 4 § 1 главы 5, суще-
ствует касательная к графику функции y=f(x), проходящая
через любую точку М(х, f (х)) этого графика (й<х<Д), причем
эта касательная не параллельна **) оси Оу.
Определение. Будем говорить, что график функции у=/(х)
имеет на интервале (а, Ь) выпуклость, направленную вниз (вверх),
если график этой функции в пределах указанного интервала
лежит не ниже (не выше) любой своей касательной.
Замечание 1. Термин «график лежит не ниже (или не выше)
своей касательной» имеет смысл, ибо касательная не параллельна
оси Оу.
*) Вместо интервала (а, Ь) можно рассматривать полупрямую, бесконеч-
ную прямую и другое множество.
**) Ибо угловой коэффициент ее, равный производной f (х), конечен,
300
ГЕОМЕТРИЧЕСКОЕ ИССЛЕДОВАНИЕ ГРАФИКА ФУНКЦИИ
(ГЛ. 9
На рис. 9.7 изображен график функции, имеющий на интервале
(а, Ь) выпуклость, направленную вниз, а на рис. 9.8 изображен гра-
фик функции, имеющий выпуклость, направленную вверх.
Теорема 9.4. Если функция y=f(x) имеет на интервале
(а, Ь) конечную вторую производную и если эта производная
неотрицательна (неположительна) всюду на этом интервале, то
график функции y=f(x) имеет на интервале (а, Ъ) выпуклость,
направленную вниз (вверх).
Доказательство. Ради определенности рассмотрим случай,
когда вторая производная /(2)(x)5s0 всюду на (а, Ь). Обозначим
через с любую точку интервала (а, Ь) (рис. 9.9). Требуется доказать,
что график функции y—f(x)
лежит не ниже касательной,
проходящей через точку
М(с, f(c)). Запишем уравнение
указанной касательной, обоз-
начая ее текущую ординату
через У. Поскольку угловой
коэффициент указанной каса-
тельной равен f (с), то ее
уравнение имеет вид*)
Рис. 9.9.
Y-f(c)=f(c)(x-c). (9.5)
Разложим функцию f(x) в окрестности точки с по формуле Тейлора,
беря в этой формуле п = 1. Получим
У(х) —f(c) + (х - с) +-^- (х - с)\	(9.6)
где остаточный член взят в форме Лагранжа, 5 заключено между
сих. Поскольку по условию f(x) имеет вторую производную на
*) В выпуске 8 настоящего курса доказано, что уравнение прямой,
проходящей через точку М (а, Ь) и имеющей угловой коэффициент k, имеет
вид У — b = k (х — а).
5 31	ТОЧКИ ПЕРЕГИБА ГРАФИКА ФУНКЦИИ	301
интервале (а, Ь), формула (9.6) справедлива для любого х из интер-
вала (а, Ъ) (см. § 13 главы 8).
Сопоставляя (9.6) и (9.5), будем иметь
У- У=^®(х-с)2.	(9.7)
Поскольку вторая производная по условию ^0 всюду на (а, Ь), то
правая часть (9.7) неотрицательна, т. е. для всех х из (а, Ь)
у - Y^Q или у Y.
Последнее неравенство доказывает, что график функции y=f(x)
всюду в пределах интервала (а, Ь) лежит не ниже касательной (9.5).
Аналогично доказывается теорема для случая /(2) (х)	0.
Замечание 2. Если всюду на интервале (а, Ь) /(2) (х) — 0,
то, как легко убедиться, y=f(x) — линейная функция, т. е. график
ее есть прямая линия. В этом случае направление выпуклости можно
считать произвольным.
Теорема 9.5. Пусть 'вторая производная функции y=f(x)
непрерывна и положительна (отрицательна) в точке с. Тогда
существует такая окрестность *) точки с, в пределах которой
график функции y=f(x) имеет выпуклость, направленную вниз
(вверх).
Доказательство. По теореме 8.4 об устойчивости знака
непрерывной функции найдется такая окрестность точки с, в пределах
которой вторая производная /(2) (х) положительна (отрицательна).
По предыдущей теореме график функции y—f(x) имеет в пределах
этой окрестности выпуклость, направленную вниз (вверх).
Таким образом, направление выпуклости графика функции
полностью характеризуется знаком второй производной этой
функции.
Пример. Исследовать направление выпуклости графика функ-
ции y=f(x) = х3 — Зх2 — 4. Эту функцию мы уже рассматривали
в пп. 1 и 4 предыдущего параграфа (см. рис. 9.1). Из вида второй
производной /(2) (х) = 6х —6 = 6(х—1) вытекает, что эта производ-
ная отрицательна при х<1 и положительна при х>1. Таким
образом, выпуклость графика функции у = х3 — Зх2 — 4 направлена
вверх на участке (—оо, 1) и вниз на участке (1, оо).
§ 3.	Точки перегиба графика функции
1.	Определение точки перегиба. Необходимое условие перегиба.
Предположим, что график функции у = f(x) имеет определенное
направление выпуклости на каждом из интервалов (а, с) и (с, Ь), где
а, Ъ и с — некоторые три числа, связанные неравенствами а <. с < Ь.
*) Напомним^ что окрестностью точки с называется интервал, содержа-
щий точку с.
302
ГЕОМЕТРИЧЕСКОЕ ИССЛЕДОВАНИЕ ГРАФИКА ФУНКЦИИ
(ГЛ. 9
Кроме того, предположим, что существует касательная к графику
функции y=f(x) в точке М(с, f(c')).
Определение. Точка М(с, f(c)) графика функции y=f(x)
называется точкой перегиба этого графика, если сущест-
вует такая окрестность точки с оси абсцисс, в пределах кото-
рой график функции y—f(x) слева
и справа от с имеет разные нап-
равления выпуклости.
На рис. 9.10 изображен график
функции, имеющий перегиб в точке
Л1 (с, f(e)).
Теорема 9.6 (необходимое ус-
ловие перегиба графика функции,
имеющей непрерывную вторую про-
изводную).
Если график функции y=f(x)
имеет перегиб в точке M(c,f(c))
и если функция y=f(x) имеет в точке с непрерывную вторую
производную, то f^(c) = Q.
Доказательство. Предположим противное, т. е. допустим,
что /(2)(с)^0. Тогда в силу теоремы 9.5 найдется окрестность
точки с, в пределах которой график функции у— f(x) (и слева, и
справа от с) имеет определенное направление выпуклости, а это
противоречит наличию перегиба в точке М (с, f (с)). Полученное про-
тиворечие доказывает теорему.
Таким образом, для отыскания всех точек перегиба графика функ-
ции y=f(x), имеющей непрерывную вторую производную, нужно
рассмотреть все корни уравнения /<2>(х)==0.
Поскольку равенство нулю второй производной является лишь
необходимым *) условием перегиба, то нужно дополнительно иссле-
довать вопрос о наличии перегиба в каждой точке, для которой
/(2) (х) _ о. Для проведения такого исследования следует установить
достаточные условия перегиба, к чему мы и переходим.
2.	Первое достаточное условие перегиба.
Теорема 9.7. Пусть функция y=f(x) имеет вторую произ-
водную в некоторой окрестности точки с и (с) = 0. Тогда,
если в пределах указанной окрестности вторая производная /(2) (х)
имеет разные знаки слева и справа от с, то графт этой функ-
ции имеет перегиб в точке
Доказательство. Заметим, во-первых, что график функции
y=f(x) имеет касательную в точке М(с, /(c)), ибо из условий тео-
ремы вытекает существование конечной производной f (с). Далее,
из того, что /(2) (х) слева и справа от с имеет разные знаки, и из тео-
*) Что это условие не является достаточным, видно хотя бы из рассмот-
рения функции у = xi. График этой функции не имеет перегиба в точке (0, 0),
хотя /'з- (х) = 12х2 = 0 при х = 0.
§ 3]	ТОЧКИ ПЕРЕГИБА ГРАФИКА ФУНКЦИИ	303
ремы 9.4 заключаем, что направление выпуклости слева и справа от с
является различным. Теорема доказана.'
Пример. Найти точки перегиба графика функции у = х3 — Зх2 — 4.
Эту функцию мы неоднократно рассматривали выше (график ее изо-
бражен на рис. 9.1). Поскольку /(2) (х) — 6х — 6 = 6 (х — 1), то един-
ственное значение аргумента, для которого- возможен перегиб, есть
х=1. Этому значению аргумента соответствует точка графика
М (1, —6). Так как /(2)(х) имеет разные знаки при х>1 и при
х<1, то точка М (1, —6) является точкой перегиба графика рас-
сматриваемой функции.
3.	Второе достаточное условие перегиба. На случай, когда
нежелательно исследование знака второй производной в окрестности
точки с, мы сформулируем второе достаточное условие перегиба,
предполагающее существование у функции у=/(х) в точке с конеч-
ной третьей производной.
Теорема 9.8. Если функция y—f(x) имеет в точке с конеч-
ную третью производную и удовлетворяет в этой точке усло-
виям (с) = 0, /,3) (с)	0, то график этой функции имеет
перегиб в точке
Доказательство. Из условия /(3) (с) ф 0 и из теоремы 8.9
вытекает, что функция /(2) (х) либо возрастает, либо убывает в точке с.
Так как /(2)(с) = 0, то и в том, и в другом случае найдется такая
окрестность точки с, в пределах которой /(2) (х) имеет разные знаки
слева и справа от с. Но тогда по предыдущей теореме график
функции y=f(x) имеет перегиб в точке М(с, f(c)).
Замечание. Конечно, теорема 9.8 имеет более узкую сферу
действия, чем теорема 9.7. Так, теорема 9.8 не решает вопроса о нали-
чии перегиба для случая, когда у функции y—f(x) не существует
конечной третьей производной, а также для случая, когда /(3) (с) = 0.
В последнем случае для решения вопроса о наличии перегиба нужно
изучить поведение в точке с производных высших порядков, что
будет сделано нами в § 4 этой главы.
Возвратимся к примеру, рассмотренному в предыдущем пункте,
и покажем, что вопрос о наличии перегиба у графика функции
у — х3 — Зх2 — 4 может быть решен и при помощи теоремы 9.8.
В самом деле, /(3) (х) = 6	0, стало быть, точка 7И(1, —6) является
точкой перегиба согласно теореме 9.8.
4.	Некоторые обобщения первого достаточного условия перегиба. Прежде
всего, заметим, что в условиях теоремы 9.7 можно отказаться от требования
двукратной дифференцируемости функции у = f (х) в самой точке с, сохраняя
это требование лишь для точек, лежащих в некоторой окрестности слева и
справа от с. При этом следует дополнительно предположить существование
конечной производной f' (с).
Доказательство теоремы 9.7 с указанными изменениями дословно совпадает
с доказательством, приведенным выше.
Далее можно договориться при определении точки перегиба не исключать
случая, когда касательная к графику в рассматриваемой точке параллельна
304
ГЕОМЕТРИЧЕСКОЕ ИССЛЕДОВАНИЕ ГРАФИКА ФУНКЦИИ
(ГЛ. 9
оси Оу *). При такой договоренности в теореме 9.7 можно отказаться даже
от требования однократной дифференцируемости функции f (х) в самой точке с
и сформулировать эту теорему следующим образом.
Пусть функция у = f (х) имеет конечную вторую производную всюду в неко-
торой окрестности точки с, за
исключением, быть может, самой точки с.
Пусть, далее, функция у = f (х) непрерывна
в точке с и график этой функции имеет ка-
сательную**) в точке М(с, f (с)). Тогда,
если в пределах указанной окрестности вто-
рая производная /'2' (х) имеет разные знаки
слева и справа от точки с, то график функ-
ции у = f (х) имеет перегиб в точке
М (с, f (с)).
Доказательство сформулированного ут-
верждения полностью аналогично доказа-
тельству теоремы 9.7.
Пример. Найти точки перегиба гра-
фика функции у = х1/». Эта функция имеет
вторую производную всюду на бесконечной
прямой, за исключением точки х = 0. В точ-
ке х — 0 рассматриваемая функция непре-
рывна, но уже первая производная обращается в бесконечность. Однако гра-
фик функции у = х1/в имеет в точке (0, 0) касательную, параллельную оси Оу ***)
(рис. 9.11). Так как вторая производная
р12’ =
2 1
9 х5/«
имеет слева и справа от точки
у = х*^ имеет перегиб в точке (0,
х = 0 разные знаки, то график функции
0).
§ 4.	Третье достаточное условие экстремума и перегиба
Теорема 9.9. Пусть п —некоторое целое положительное
число, и пусть функция у =f (х) имеет в некоторой окрестности
точки с производную порядка (п 4-1), причем указанная производ-
ная непрерывна в самой точке с. Пусть, далее, справедливы сле-
дующие соотношения
/(2) (с) =/<з) (С) = ... =/(«) (с) = 0,	(с)	0.	(9.8)
Тогда, если (п+1) —нечетное число, то график функции у =f(x)
имеет перегиб в точке М(с, f(c)). 'Если же («4-1)— четное
число и, кроме того, f (с) = 0, то функция y—f(x) имеет локаль-
ный экстремум в точке х = с, точнее, максимум, если (с) <; 0,
и минимум, если	(с) > 0.
*) Этот случай соответствует бесконечному значению первой производ-
ной f (с).
**) Хотя бы параллельную оси Оу.
***) Это вытекает, например, из того, что график обратной функции х =
имеет в этой точке касательную х = 0.
§ 41 ТРЕТЬЕ ДОСТАТОЧНОЕ УСЛОВИЕ ЭКСТРЕМУМА И ПЕРЕГИБА
305
Доказательство. 1) Пусть сначала (и +1) — четное число
и, кроме того, /' (с) — 0. Разложим функцию y=f(x) в окрестности
точки х = с по формуле Тейлора. Учитывая соотношения (9.8) и
равенство f (с) = 0 и записывая остаточный член в форме Лагранжа,
будем иметь
/(*)=/(') + (X -	(9.9)
Здесь £ лежит между сих. Для удобства перепишем формулу (9.9)
в виде
/(х) _/(c)=&g (X-с)"Ч	(9.10)
Так как производная /1”+1>(х) непрерывна в точке с и положительна
(отрицательна) в этой точке, то по теореме об устойчивости знака
непрерывной функции найдется некоторая окрестность точки х = с,
в пределах которой эта производная сохраняет тот же знак, что и
в точке с. Таким образом, значение /(л+1)(£) в формуле (9.10) поло-
жительно (отрицательно) для всех х, достаточно близких к с. Но
тогда, поскольку (п+1) —четное число, правая часть (9.10) поло-
жительна (отрицательна) для всех х, достаточно близких к с. Иными
словами, разность f(x)—f(c) положительна (отрицательна) для всех х,
достаточно близких к с. Это и доказывает, что функция f(x) имеет
в точке с локальный минимум (максимум).
2) Пусть теперь (n+ 1) — нечетное число. Докажем, что в этом
случае график функции имеет перегиб в точке М (с, f (с)). Прежде
всего заметим, что условия теоремы гарантируют существование
касательной к графику в точке М (с, Поэтому достаточно дока-
зать, что направление выпуклости графика является различным справа
и слева от точки с. Для этого, в силу теоремы 9.7, достаточно дока-
зать, что всюду в некоторой окрестности точки с вторая производ-
ная (х) имеет разные знаки при х < с и х > с. Чтобы убедиться
в этом, разложим функцию /<2)(х) в окрестности точки х — с по
формуле Тейлора. Учитывая соотношения (9.8) и записывая остаточ-
ный член в форме Лагранжа, будем иметь
/2)(*)=£^(*-оп-1,	'	(9.П)
где £ лежит между сих. Точно так же, как выше, устанавливаете,я,
что (£) сохраняет определенный знак для всех х, достаточно
близких к с. Но тогда, поскольку (д — 1) — нечетное число, для всех
достаточно близких к точке с значений х правая часть (9.11) имеет
разные знаки при х < с и х > с.
Теорема 9.9 полностью доказана.
Пример. Исследовать на экстремум и перегиб функцию f (х) =
= (х — с)”+1. Легко видеть, что /' (с) =	(с) = ... = /<л) (с) = 0,
306
ГЕОМЕТРИЧЕСКОЕ ИССЛЕДОВАНИЕ ГРАФИКА ФУНКЦИИ
(ГЛ 9
у(п+1) (с) — (n-f- 1)! > 0. Согласно теореме 9.9 при четном (л 4-1)
функция имеет минимум в точке х — с (рис. 9.12), а при
нечетном (»+1) график функции имеет перегиб в точке М(с, 0)
(рис. 9.13).
§ 5. Асимптоты графика функции
Определение 1. Говорят, что прямая х = а является верти-
кальной асимптотой графика функции y=f (х), если хотя
дем рассматривать сколь угодно
бы одно из предельных значений
lim f(x) или lim f(x)
+ 0	x-t-a — О
равно ф-оо или — оо.
Пример. График функции
1
у — — имеет вертикальную асимп-
тоту х — 0, ибо lim — = 4- оо,
х—о+ох
lim — — — оо (рис. 9.14).
*-»о — о х
Предположим далее, что функ-
ция у =f(x) определена для сколь
угодно больших значений аргу-
мента. Ради определенности бу-
большие значения положитель-
ного знака.
Определение 2. Говорят, что прямая
Y = kxyb
(9-12)
АСИМПТОТЫ ГРАФИКА ФУНКЦИИ
307
является наклонной асимптотой графика функции у =f(x)
при х~>4-оо, если функция /(х) представима в виде
f{x) = kx + b-{-a(x),	(9.13)
где lim а(х) = 0.
х—* Н- оо
Теорема 9.10. Для того чтобы график функции у —f (х) имел
при х—>4-оо наклонную асимптоту (9.12), необходимо и доста-
точно, чтобы существовали два предельных значения
lim	и lim [/(х)-kx] = b. (9.14)
х->4-со Х	л-^ + со
Доказательство. ^Необходимость. Пусть график функ-
ции y=f(x) имеет при х->4-оо асимптоту
справедливо представление (9.13). Тогда
lim
и kx +,b 4- а (х) =
_1_ го	X
X 1 X I
(9.12), т. е. для /(х)
lim
lim [/(х) — kx}~
lim [b 4- а (x)] — b.
2) Достаточность. Пусть суще-
ствуют предельные значения (9.14). Вто-
рое из этих предельных значений дает право
утверждать, что разность /(х) — kx — b
является бесконечно малой при х—>4-°°-
Обозначив эту бесконечно малую через
а(х), получим для /(х) представление
(9.13). Теорема доказана.
Замечание. Аналогично опреде-
ляется наклонная асимптота и доказы-
вается теорема 9.10 и для случая х -> — оо.
2х2 4- х
.Пример. График функции _у = ——-j—
х + 1
наклонную асимптоту Y = 2х — 1 и при х -> 4- °о> и при х -> — оо
и, кроме того, имеет вертикальную асимптоту X ——1 (рис. 9.15).
В самом деле,
2х — 1 -J--имеет
1 v J_ 1
.. f (х)	..	2х2 4- х „
hm	lim - . У ,. =2,
lim [/(х)-2х]= lim Г— 1 4-—1-1 = — 1,
Л-»±0Э	л->±соЬ *4-1.1
lim f(x) = 4- co, lim /(x) = — co.
x-* —14-0	x~*— 1— о
308
ГЕОМЕТРИЧЕСКОЕ ИССЛЕДОВАНИЕ ГРАФИКА ФУНКЦИИ
(ГЛ. 9
Наряду с линейной асимптотой (9.12) рассматривают также и асимптоты
более сложного вида.
Говорят, что парабола n-го порядка, определяемая многочленом
Г = апхп +	... + atx + аа,	(9.12*)
является асимптотой графика функции у = f (х) при х —--}-оо, если функ-
ция f (х) представима в виде
f (х) = апхп + Оп^х"-1 + ... + а^ + аа + а (х), где lim а(х) = 0.
Х-+4-00
Легко доказать следующее утверждение.
Для того чтобы график функции у = f (х) имел при х —» + оо асимп-
тоту (9.12*), необходимо и достаточно, чтобы существовали следующие п-ф 1
предельных значений:
Нт 7 W — (апхп + ап-1Хп 1 + ••• + а2х2)
х —+со	х
lim [/(х) — (апхп + ал_1хл » + ... + агх)] = а0.
§ 6. Схема исследования графика функции
В этом параграфе мы изложим схему, по которой целесообразно
проводить исследование графика функции, и приведем пример, иллю-
стрирующий эту схему.
Для качественного исследования графика функции y—f(x) целе-
сообразно прежде всего провести следующие исследования:
1°. Определить область задания функции.
2°. Выяснить вопрос о существовании асимптот (вертикальных и
наклонных).
3°. Найти области возрастания и убывания функции и точки
экстремума.
4°. Найти области сохранения направления выпуклости и точки
перегиба.
5°. Найти точки пересечения графика функции с осью Ох.
По полученным данным легко строится эскиз графика функции.
В качестве примера построим график функции
2х® — 5ха + 14х — 6	zn 1
v =--------.	(9.16)
Будем следовать изложенной выше схеме.
1°. Поскольку функция (9.15) представляет собой рациональную
дробь, то она определена и непрерывна всюду на бесконечной пря-
мой, кроме точки х—0, в которой обращается в нуль знаменатель.
2°. Выясним вопрос о существовании асимптот. Очевидно, что
2х3 — 5ха + 14х — 6 _
4ха —
оо,
lim
х — 0 + 0
§ 61
СХЕМА ИССЛЕДОВАНИЯ ГРАФИКА ФУНКЦИИ
809
поэтому график функции имеет вертикальную асимптоту х = 0.
Далее, из существования пределов
f(x)	2х’ — 5х2 + 14х — б
lim LU-= lim ---------------------- hm
X ± CO	X — ± CO	X -> i co
5, 14_ 6
X "I X2 X3
4
2x3 _ 5X2 4. 14X _ 6 — 2x3 _
4x2	—
вытекает, что и при х -> + оо, и при х—>— со график функции
,, х 5
имеет наклонную асимптоту Y —
3°. Для нахождения областей возрастания и убывания вычислим
первую производную функции (9.15)
хз_7х + 6 _ (х _ 1) (х _ 2) (х + 3)
у ~	2х3	—	2хз
Имея в виду, кроме того, что сама функция и первая производная
не существуют при х = 0, мы получим следующие области сохране-
ния знака у':
Область значений х	— со < х < — 3	—3<х<0	0<х< 1	1 <х<2	2 < х < со
Знак у’	+	— .	.+	—	+
Поведение функции	возрастает	убывает	возра- стает	убывает	возрастает
Из приведенной таблицы очевидно, что функция имеет следующие
точки экстремума:
49
1)	максимум при х =— 3, причем /(—3) = —
5
2)	максимум при х=1, причем /(1) = -^-,
9
3)	минимум при х — 2, причем f(2) — -^.
4°. Для нахождения областей сохранения направления выпуклости
вычислим вторую производную
310
ГЕОМЕТРИЧЕСКОЕ ИССЛЕДОВАНИЕ ГРАФИКА ФУНКЦИИ
ГГЛ. 9
Имея в виду, что сама функция и ее производные не существуют
в точке х — 0, мы получим следующие области сохранения знака _у(2):
Область значений х	— со < х <0	0<х< —	9 -?-<х<оо
Знак у^	—	—	+
Направление выпуклости графика	вверх	вверх	вниз
Из приведенной таблицы очевидно, что график функции имеет
/ 9	/9\\	/ 9 \ 913
перегиб в точке v, / v . Легко, подсчитать, что / -=- ==—.
\ /	\ / //	\ / / /00
5°. Остается найти точки пересечения графика с осью Ох. Эти
точки соответствуют вещественным корням уравнения
2х3 - 5х2 + 14х - 6 = 0.
Легко видеть, что 2xs — 5ха + 14х — 6 = 2 (х —j (х2 — 2х + 6). По-
скольку квадратный трехчлен (х2 —2x4-6) имеет комплексные
корни, то рассматриваемое уравнение имеет только один веществен-
§ 7] ОТЫСКАНИЕ МАКСИМАЛЬНОГО И МИНИМАЛЬНОГО ЗНАЧЕНИЙ
311
ный корень x = -i-, так что график функции пересекает ось Ох
в точке 0^. По полученным данным строим эскиз графика рас-
сматриваемой функции (рис. 9.16).
§ 7. Отыскание максимального и минимального значений
функции. Краевой экстремум
1. Отыскание максимального и минимального значений функ-
ции. Рассмотрим функцию y—f(x), определенную и непрерывную
на сегменте [a, Z>], До сих пор мы интересовались лишь отысканием
локальных максимумов и минимумов этой функции, а теперь поста-
вим задачу об отыскании максимального и минимального значе-
ний f(x) на сегменте [а, Ь]. Подчеркнем, что в силу теоремы Вейер-
штрасса.(см. § 6 главы 8) функция f(x) обязательно достигает в не-
которой точке сегмента
[a, Z>] своего максималь-
ного (минимального) зна-
чения. Ради определенно-
сти остановимся на оты-
скании максимального
значения f(x) на сегмен-
те [а, Ь].
Максимальное значе-
ние функции f(x) может
достигаться либо во внут-
ренней точке х0 сегмента
из локальных максимумов
одном из концов сегмента
[а, Ь] (тогда оно совпадает с одним
функции f(x), см. рис. 9.17), либо на
[о, й] (рис. 9.18). Отсюда ясно, что для
нахождения максимального зна-
чения функции f(x) на сегменте
[а, Ь] нужно сравнить между со-
бой значения /(х) . во всех точках
локального максимума и в гра-
ничных точках сегмента а и Ь.
Наибольшее из этих значений и
будет максимальным значением
f(x) на сегменте [а, Ь]. Анало-
гично находится и минимальное
значение f(x) на сегменте [а, Ь].
Если желательно избежать исследования точек возможного экстре-
мума, то можно просто сравнить между собой значения f(x) во всех
точках возможного экстремума и в граничных точках а и Ь. Наиболь-
шее (наименьшее) из этих значений, очевидно, и будет максимальным
(минимальным) значением функции /(х) на сегменте [a, 6J.
312
ГЕОМЕТРИЧЕСКОЕ ИССЛЕДОВАНИЕ ГРАФИКА ФУНКЦИИ
[ГЛ. 9
Отметим далее, что если f(x) имеет на сегменте [а, Ь] лишь
одну точку локального экстремума *), являющуюся точкой локального
максимума (минимума), то без сравнения значения f(x) в этой точке
с /(а) и f (b) можно утверждать, что это значение является максималь-
ным (минимальным) значением f(x) на сегменте [а, Ь] (рис. 9.19).
Аналогичными средствами решается вопрос об отыскании макси-
мального (и минимального) значения функции у =f(x) на интервале,
полупрямой и бесконечной прямой (при условии, что это значение
существует).
Может случиться так, что функция / (х) вовсе не имеет на сегменте
[а, Ь] (или полупрямой а «С х < оо) точек возможного экстремума.
В таком случае /(х) является монотонной на этом сегменте (полу-
прямой) и ее максимальное и
минимальное значения достигаются на
концах этого сегмента (на конце
этой полупрямой). Этот последний
случай мы проиллюстрируем физи-
ческим примером. Пусть требуется
Рис. 9.20.
определить, какое сопротивление х нужно включить в цепь последо-
вательно с данным сопротивлением г, чтобы на г выделилась наи-
большая мощность (при этом напряжение т>0 батареи считается по-
стоянным, см. рис. 9.20). По закону Ома ток / в цепи равен
г -|-х
Стало быть, по тому же закону падение напряжения vr на сопротив-
лении г равно
Таким образом, мощность w(x), выделяемая на сопротивлении г,
равна
, ,	, v$r
W (х) = IVг —  г—гтг .
v ' г (г + х)2
Поскольку по физическому смыслу сопротивление х не может быть
отрицательно, то задача сводится к отысканию наибольшего значе-
ния функции w(x) на полупрямой х^гО. Вычислив производную
*) Именно такой случай часто встречается на практике.
§ 7] ОТЫСКАНИЕ МАКСИМАЛЬНОГО И МИНИМАЛЬНОГО ЗНАЧЕНИЙ
313
этой функции
, г \ 2о?г
убедимся в том, что со' (х)<0 всюду на полупрямой х^О и точек
возможного экстремума нет. Таким образом, функция w(x) убывает
всюду на полупрямой х^О и ее максимальное значение на этой
полупрямой достигается при х —0 и равно v%/r (рис. 9.21). Это со-
вершенно ясно и из физических соображений.
В качестве второго примера рассмотрим задачу об отыскании
максимального и минимального значений функции у = sin (х2) на сег-
менте —у ~	•
Поскольку _y' = 2xcosx2, указанная функция имёет на рассма-
триваемом сегменте три точки возможного экстремума х — 0 и
х = — J/ у- Сравнивая значения функции в указанных точках и на
концах сегмента
7(0) = 0,/(±|Л^ = 1, /(_у7) = 0, /(^=sin^ = -^,
убедимся в том, что максимальное значение рассматриваемой функции
равно -|-1 и достигается в двух внутренних точках сегмента хг =
=♦- у и х2= + j/" у, а минимальное значение рассматриваемой
.	/2
функции равно —и достигается на правом конце сегмента.
График рассматриваемой функции изображен на рис. 9,22.
2. Краевой экстремум. Пусть функция y=f(x) определена на
некотором сегменте [а, &]. Будем говорить, что эта функция имеет
в граничной точке b этого сегмента краевой максимум (краевой
минимум), если найдется левая полуокрестность точки Ь, в пределах
которой значение f(b) является наибольшим (наименьшим) среди всех
других значений этой функций. Аналогично определяются краевой
314
ГЕОМЕТРИЧЕСКОЕ ИССЛЕДОВАНИЕ ГРАФИКА ФУНКЦИИ
[ГЛ. 9
максимум и краевой минимум в граничной точке а сегмента [а, 6].
Краевой максимум и краевой минимум объединяются общим названием
краевой экстремум. Имеет место следующее достаточное условие
краевого экстремума-, для того чтобы функция у = f (х) имела
в точке b сегмента [а, Ь\ краевой максимум (краевой минимум)
достаточно, чтобы эта функция имела в точке b положитель-
ную (отрицательную) левую производную *). (Доказательство анало-
гично доказательству теоремы 8.9.) Из указанного достаточного усло-
вия краевого экстремума непосредственно вытекает следующее необ-
ходимое условие краевого экстремума функции, имеющей в точке b
левую производную: для того чтобы, функция у =f (х), обладающая
в точке b левой производной, имела в этой точке краевой мак-
симум (краевой минимум), необходимо, чтобы указанная произ-
водная была неотрицательной (неположительной).
В заключение докажем следующее замечательное утверждение.
Теорема 9.11 (теорема Дарбу **)). Пусть функция f (х) имеет конечную
производную всюду на сегменте [а, &]***), и пусть f' (а + 0) — A, f (Ь—0) = В.
Тогда, каково бы ни было число С, заключенное между А и В, на этом сег-
менте найдется точка $ такая, что f (i) = С ****).
Доказательство. Сначала докажем следующее утверждение: если
F (х) имеет конечную производную на [а, Ь| и если F' (а + 0) и F' (Ь — 0) —
числа разных знаков, то на сегменте [а, Ь] найдется точка £ такая, что
F' ® = о.
Пусть ради определенности F' (а + 0) < 0, F’ (Ь — 0) > 0. Тогда функция
F (х) имеет краевой максимум на обоих концах сегмента [а, Ь]. Но это озна-
чает, что минимальное значение F (х) на сегменте [а, Ь] достигается в неко-
торой внутренней точке 5 этого сегмента (функция F (х) дифференцируема,
а стало быть, и непрерывна на сегменте [а, Ь] и поэтому достигает на этом
сегменте своего минимального значения). В указанной точке Е функция F (х)
имеет локальный минимум, и поэтому F' (?) = 0.
Для доказательства теоремы 9.11 остается положить F (х) = f (х) — Сх
и применить к F (х) только что доказанное утверждение.
*) Для граничной точки а достаточным условием краевого максимума
(краевого минимума) является отрицательность (положительность) правой про-
изводной в точке а.
**) Гастон Дарбу — французский математик (1842—1917).
***) Под этим понимается, что f (х) имеет производную в любой внутрен-
ней точке сегмента [ц, Ь] и, кроме того, имеет левую производную в точке b
и правую производную в точке а.
****) Подчеркнем, что непрерывность производной f (х) при этом не пред-
полагается.
ГЛАВА 10
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
В главе 1 мы рассмотрели физическую задачу о вычислении пути
пройденного материальной точкой, двигающейся вдоль оси Оу, по
известной скорости этой точки и геометрическую задачу о вычисле-
нии площади криволинейной трапеции (т. е. фигуры, лежащей между
графиком функции у =f(x) и сегментом [а, Ь] оси Ох). Рассмотре-
ние указанных двух задач естественно привело нас в главе 1 к не-
обходимости введения нового математического понятия — понятия
определенного интеграла. Кроме рассмотренных двух задач к поня-
тию определенного интеграла приводит и ряд других важных физи-
ческих и геометрических задач. Настоящая глава посвящена (изложе-
нию теории определенного интеграла, а в следующей главе дается
применение этой теории к некоторым геометрическим и физическим
задачам.
§ 1. Интегральные суммы. Интегрируемость
Пусть функция f(x) задана на сегменте [a, b], a<ib. Обозначим
символом Т разбиение сегмента [а, Ь] при помощи некоторых не
совпадающих друг с другом точек a = x0<Zx1<Z- ..<.xn = b на п
частичных сегментов [х0, хх], [хх, х2], , [xn-i’ хп1- Точки хп,
х1г ..., хп будем называть точками разбиения Т. Пусть — произ-
вольная точка частичного сегмента	х;], а Дхг — разность
х, — Xi_v которую мы в дальнейшем будем называть длиной частич-
ного сегмента [хг_х, х,-].
Определение 1. Число l\xi, где
п
I К ?/} =/&) Дхх +/(У Дх2 +... +/(U Дх„ = 2 Ш Ахг,
/=1
называется интегральной суммой функции f(x), соответ-
ствующей данному разбиению Т сегмента [а, Ь] и данному выбору
промежуточных точек на частичных сегментах [хг_х, хх].
В дальнейшем через Д мы будем обозначать длину максималь-
ного частичного сегмента разбиения Т, т. е. Д = тахДхх.
316
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
(ГЛ. 10
Выясним геометрический смысл интегральной суммы. Для этого
рассмотрим криволинейную трапецию, т. е. фигуру, ограниченную
графиком функции f(x) (для простоты будем считать эту функцию
положительной и непрерывной), двумя ординатами, проведенными в
точках а и b оси абсцисс,
и осью абсцисс (рис. 10.1).
Очевидно, интегральная сум-
ма I {xi, 5,-} представляет
собой площадь ступенчатой
фигуру, заштрихованной на
рис. 10.1.
Определение 2. Число
I называется пределом
интегральных сумм
I{xi, $,} при Д-+0, если
для любого положитель-
ного . числа е >» 0 можно
указать такое положительное число 8 *), что для любого раз-
биения Т сегмента [а, Z>], максимальная длина Д частичных сег-
ментов которого меньше 8, независимо от выбора точек 5/ на
сегментах [Х;_р xj
выполняется неравенство

Для обозначения
волика
предела интегральных сумм употребляется сим-
I =lim I {xi, £;}.
Д-0
Определение 3. Функция /(х) называется интегрируемой
(по Риману **)) на сегменте [а, Ь], если существует конечный
предел I интегральных сумм этой функции при Д -> 0. Указанный
предел I называется определенным интегралом от функции f(x)
по сегменту [а, Ь] и обозначается следующим образом:
ь
I^=^f(x) dx.
а
Наглядные геометрические представления показывают***), что опре-
деленный интеграл численно равен площади криволинейной трапеции,
определяемой графиком функции f (х) на сегменте [а, &]. В главе 11
мы докажем справедливость этого утверждения.
Приведем пример интегрируемой функции. Докажем, что функ-
ция /(х) = с — const' интегрируема на любом сегменте [а, 6], причем
*) Так как число В зависит от е, то иногда пишут 8 = 8 (е).
**) Бернгард Риман — немецкий математик (1826—1866).
***) См. § 4 главы 1.
§ 2]	ВЕРХНИЕ И НИЖНИЕ СУММЫ	317
ь
\>cdx = c(b-~a). В самом деле, так как /($;) = с при любых то
а
I {х.-> 5,-} = сДхх + сДх2 + ... + «Дхл =
— с (Дхх Дх2 -|- • • * “В Дхл)т= с (Ь а),
и поэтому lim I {х,-, 5;} = с(й — а).
д-.о
Выясним вопрос об интегрируемости неограниченных на сегменте
[а, Ь] функций.
Докажем следующее утверждение: неограниченная на сегменте
[а, Ь] функция f(x) не интегрируема на этом сегменте.
Доказательство. Пусть функция f(x) не ограничена на сег-
менте [а, Ь]. Тогда она не ограничена на некотором частичном сег-
менте [х*_х, х*] любого данного разбиения Т сегмента [а, Ь]. Поэтому
слагаемое /(?А)ДхА интегральной суммы /{х,-, £,}, отвечающей этому
разбиению Т, может быть сделано как угодно большим по абсолют-
ной величине за счет выбора точки 5*. Отсюда вытекает, что интег-
ральные суммы I {х;, £;}, отвечающие любому разбиению Т, не огра-
ничены*) и поэтому не существует конечного предела интегральных сумм.
Сообразуясь с доказанным утверждением, будем рассматривать
лишь ограниченные на сегменте [а, Л] функции. Возникает вопрос:
всякая ли ограниченная на сегменте [a, Z>] функция является
интегрируемой на этом сегменте? Следующий пример показывает,
что это, вообще говоря, не так. Убедимся, что заведомо ограничен-
ная на сегменте [а, Ь] функция Дирихле, значения которой в рацио-
нальных точках равны единице, а в иррациональных — нулю, не ин-
тегрируема на сегменте [я, й]. Действительно, если для любого раз-
биения Т со сколь угодно малым Д выбрать точки 5,- рациональными,
п	п
то, очевидно, /{хг, £г} = У, &Xi = У Дх, = b — а, если же для
i — 1	i == 1
того же разбиения Т точки <j; выбрать иррациональными, то Цх;, $,} =
= 0. Поэтому для функции Дирихле не существует предела интег-
ральных сумм, т. е. эта функция не интегрируема.
В дальнейшем мы докажем интегрируемость всех непрерывных
функций и широкого класса разрывных функций.
§ 2. Верхние и нижние суммы
1. Понятие верхней и нижней сумм. Пусть функция /(х) огра-
ничена на сегменте [а, б] и Т — разбиение этого сегмента точками
а = х0<х1<;...<Хп = &. Обозначим через и гщ соответственно
*) Чтобы убедиться в этом, достаточно фиксировать точки на всех
частичных сегментах разбиения Т, за исключением сегмента [хА_х, xfe]. Тогда
в интегральной сумме I {х;, будет изменяться лишь слагаемое f (£д) Дх^,
которое может быть как угодно большим по абсолютной величине.
318
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
(ГЛ 10
точную верхнюю и точную нижнюю грани этой функции на сегменте
[Х|_х, ATj]. Суммы
п
M1Sx1 + Л12Дх2 + • • • + Mnisxn — 2 Mi^xi
'	i= 1
U
п
s =	+ т2±х2 +... + тпйхп = У, т^х{
»=i
называются соответственно верхней и нижней суммами
функции f(x) для данного разбиения Т сегмента [a, Z?].
Очевидно, что любая интегральная сумма I {xit (,} данного
разбиения Т сегмента [а, Ь] заключена между верхней и нижней
суммами Sus этого разбиения.
Понятия верхней и нижней сумм становятся особенно ясными,
если обратиться к геометрическим представлениям. Для простоты рас-
смотрим положительную и непрерывную функцию f(x) и криволи-
нейную трапецию, определяемую этой функцией (рис. 10.2 и 10.3).
Если Т — некоторое разбиение сегмента [а, Ь], то числа Mt и mt
представляют собой в случае непрерывной функции /(х) максималь-
ное и минимальное значения этой функции на частичном сегменте
[х/-!, Xt] разбиения Т. Поэтому верхняя сумма 5 равна площади,
заштрихованной на рис. 10.2 ступенчатой фигуры, которая содержит
криволинейную трапецию, а нижняя сумма 5 равна площади, заштри-
хованной на рис. 10.3 ступенчатой фигуры, которая содержится
в криволинейной трапеции (эта трапеция на рис. 10.2 и 10.3 обведена
жирной линией).
Как уже говорилось, из наглядных геометрических представлений
вытекает, что интеграл численно равен площади криволинейной тра-
пеции. С другой стороны, очевидно, что если разность между верх-
ними и нижними суммами может быть сделана как угодно малой, то
эти суммы могут стать как угодно близкими к площади криволиней-
ной трапеции. Поэтому можно ожидать, что для интегрируемости
ВЕРХНИЕ И НИЖНИЕ СУММЫ
319
§ 2]
функции необходимо и достаточно, чтобы разность между верхней и
нижней суммами могла быть как угодно малой. Строгое доказатель-
ство этого будет дано в следующем параграфе.
2. Свойства верхних и нижних сумм. Докажем справедливость
следующих свойств верхних и нижних сумм:
1°. Для любого фиксированного разбиения Т и для любого
е > 0 промежуточные точки на сегментах [xi-v xt] можно
выбрать так, что интегральная сумма 1 {х{, £;} будет удовлет-
ворять неравенствам 0^S—I{Xi, £,•}<£. Точки Ег можно выб-
рать также и таким образом, что интегральная сумма будет
удовлетворять неравенствам 0 sg / {хг, I,-} — s < е.
Пусть Т — некоторсе фиксированное разбиение сегмента [а, £].
Докажем, например, возможность выбора по данному е > 0 точек
так, что будет выполняться неравенство OsgjS — /{х^	По
определению точной грани 7Иг для данного е > 0 на сегменте [х,_р х,]
можно указать такую точку что
г2—, /=1, 2.......п.
1 v Ь — а' ’	’
Умножая эти неравенства на Дх, и затем складывая, получим
O^S— I{Х[,	< е.
Справедливость свойства 1° установлена.
2°. Если разбиение Т' сегмента [а, Ь] получено путем добав-
ления новых точек к точкам разбиения Т этого сегмента, то
верхняя сумма S' разбиения Т' не больше верхней суммы S раз-
биения Т, а нижняя сумма s' разбиения Т' не меньше нижней
суммы s разбиения Т, т. е.
s s', S' S’.
Так как разбиение Т' может быть получено из разбиения Т путем
последовательного добавления к последнему новых точек, то, оче-
видно, сформулированное свойство достаточно доказать для случая,
когда к разбиению Т добавляется одна точка. Пусть эта точка х'
располагается на сегменте [х,_1; х,-] разбиения Т сегмента [а, &]. Обо-
значим через и М'[ точные верхние грани функции /(х) на сег-
ментах [Xj-p х'] и [х', Xt], через Дх,: и ДхГ длины этих сегментов
и через S и S' верхние суммы разбиения Т и разбиения Т', получен-
ного добавлением к разбиению Т точки х'. Отметим, что Дх, =
— Sx't 4- Дх,". Кроме того, если — точная верхняя грань значений
функции /(х) на сегменте [хг_х, х,-], то	и Л1г^Л1ь по-
скольку очевидно, что точная верхняя грань функции на части
сегмента [х,-_р х,] не превосходит точную верхнюю грань этой
функции на всем сегменте [х^-х, x,j. Поэтому, учитывая, что суммы
320
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
[ГЛ. 10
S и S' различаются лишь слагаемыми Mi &Xi и Mi kxi + М? Ьх{,
получим
S-S' = Mi &Xi - (Mi Axi + Mi Дх') =
= (Mi - Mi) i^xi+(Mi - M-) Дх;	o,
t. e. S' CS. Доказательство для нижних сумм проводится аналогично.
3°. Пусть Т' и Т" — любые два разбиения сегмента [а, Ь].
Т огда нижняя сумма одного из этих разбиений не превосходит
верхнюю сумму другого. Именно, если s', S' и s", S" —соответ-
ственно нижние и верхние суммы разбиений Т' и Т", то
s'^S",	s''=CS'.
Выше мы установили, что нижняя сумма данного разбиения не пре-
восходит верхнюю сумму этого разбиения. Пусть Т — разбиение сег-
мента [а, &], полученное объединением разбиений *) Т' и Т", a s и
S— верхняя и нижняя суммы разбиения Т. Так как разбиение Т мо-
жет быть получено из разбиения Т’ добавлением к нему точек раз-
биения Т", то по свойству 2° и отмеченному свойству нижней, и верх-
ней суммы одного и того же разбиения имеем
s' -is
Но разбиение Т может быть также получено из разбиения Т" добав-
лением к нему точек разбиения Т. Поэтому
•	s" -С s S".
Сравнивая установленные выше неравенства с только что получен-
ными, убедимся, что s's^S", s"^S'.
Справедливость свойства 3° установлена.
4°. Множество {5} верхних сумм данной функции f(x) для
всевозможных разбиений сегмента [a, fc] ограничено снизу. Мно-
жество {$} нижних сумм ограничено сверху.
Это свойство непосредственно следует из свойства 3°. Действи-
тельно, любая верхняя сумма не меньше некоторой фиксированной
нижней суммы, следовательно, множество {Д’} верхних сумм ограничено
снизу. Любая нижняя сумма не превосходит какую-либо верхнюю
сумму, и поэтому _ множество {s} нижних сумм ограничено сверху.
Обозначим через I точную нижнюю грань множества {£} верхних
сумм, а через I — точную верхнюю грань множества нижних сумм:
Z = inf{S}, I — sup {s}.
Числа / и I называются соответственно верхним и нижним интег-
ралами Дарбу от функции f(x). Докажем, что 1^1. Пусть />/•
Тогда разность I—I есть положительное число, которое мы обо-
значим через е, так что I — /=е>0. Из определения точных граней
♦) При этом общие точки разбиений Т' и Т" учитываются один раз.
ВЕРХНИЕ И НИЖНИЕ СУММЫ
321
§ 2]
I и I вытекает, что существуют числа 5' и s", представляющие собой
соответственно верхнюю и нижнюю суммы некоторых разбиений Т' и
Т" сегмента [а, Ь], такие, что/4--|->5' и 1 —	<з". Вычитая вто-
рое неравенство из первого и учитывая, что ! — !=&, получим з"
Но это последнее неравенство противоречит свойству 3° верхних и
нижних сумм.
5° Пусть разбиение Т сегмента [а, Ь] получено из разбиения Т
добавлением к последнему р новых точек, и пусть s', S' и з, 5 —
соответственно нижние и верхние суммы разбиений Т' и Т. Тогда
для разностей S — S' и s' — s*) может быть получена оценка,
зависящая от максимальной длины Д частичных сегментов разби-
ения Т, числа р добавленных точек и точных верхней и нижней
граней Мит функции f(x) на сегменте [а, &]. Именно,
S— S' =С(Л1 — т)рЬ, s' — №g (/И — m)pS.
Для того чтобы убедиться в справедливости этого свойства, доста-
точно доказать приведенные неравенства для случая, когда к разбие-
нию Т добавляется одна точка х'. Пусть эта точка находится на
сегменте [х,^, X;] разбиения Т. Тогда этот сегмент разделится на два
сегмента [х,-!, х'] и [х', xj, длины которых мы обозначим соответ-
ственно через Дх/ и Дх/. Пусть Mit Ml и Ml — соответственно
точные верхние грани функции /(х) на сегментах [х,_р х,], [х/_г, х’]
и [х', Х(]. Так как Дх,- = Дх,: + Дх," и верхние суммы S и S' раз-
биений Т vlT' различаются лишь слагаемыми М, &Х{ и Ml SxJ + Ml Дх[,
то 5 - s'=Mt (Дх; + Дх;) - (ти; Дх; + mi &xi)=(Mt-м;) дх; +
+ (Mi — Ml) Axf. Далее, m Mi sg Mi -g M и m sg Ml ^M-t^M **),
поэтому Mi — M[ sgM — m и Mi — Ml^szM — m. Следовательно,
S— S' ^z(M — m) (Sx'i + ДхГ) — (M — m) Sxt. Поскольку Дх, =g Д, то
S — 5' =g (M — m) Д. Это неравенство совпадает с первым из нера-
венств, приведенных в формулировке свойства б01, при р=1. Доказа-
тельство для нижних сумм проводится аналогично.
6°. Лемма Дарбу. Верхний и нижний интегралы Дарбу I и I
от функции f(x) по сегменту [а, /»] являются соответственно
пределами ***) верхних и нижних сумм при
*) Отметим, что в силу свойства 2° эти разности неотрицательны.
**) Выше, при доказательстве свойства 2°, мы уже отмечали, что точная
верхняя грань функции на части сегмента не превосходит ее точной верхней
грани на всем сегменте. Отметим также, что точная нижняя грань функции
на всем сегменте не превосходит ее точной верхней грани на любой части
этого сегмента.
***) Понятие предела верхних иди нижних сумм определяется в полной
аналогии с понятием предела интегральных сумм. Именно, число / называется
пределом верхних сумм S при Д — О, если для любого положительного числа г
можно указать такое положительное число 8, что при Д < 8 выполняется не-
равенство | S —7 | < е.
322
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
ТГЛ. 10
Доказательство. Докажем, например, что lim S=7. Для
д-*о
случая А1 = /я, т. е. для случая /(x) = c = const, лемма очевидна,
поскольку S = I = I = $. Будем поэтому считать, что М > т. Так как
7— точная нижняя грань множества верхних сумм, то для любого дан-
ного е > 0 можно указать такое разбиение Т* сегмента [а, Ь], что
верхняя сумма S* этого разбиения будет отличаться от 7 меньше чем
на
(Ю.1)
Обозначим через р число точек разбиения Т*, лежащих строго внутри
сегмента [а, />]. Пусть Т — любое разбиение сегмента [а, £»], макси-
мальная длина Д частичных сегментов которого подчинена условию
Д<8
е
2 (М — т) р
(Ю.2)
и S—верхняя сумма этого разбиения. Добавим к этому разбиению
внутренние точки разбиения Т*. В результате мы получим разбие-
ние Т', верхняя сумма S’ которого в силу свойства 5° и условия (10.2)
для Д удовлетворяет неравенству
0 S—S'(М - mjуД < у..
(10.3)
С другой стороны, это разбиение Т можно рассматривать как раз-
биение, полученное в результате добавления к разбиению Т* внут-
ренних точек разбиения Т. Поэтому,' в силу свойства 2°,
7<S'^S*.
Отсюда следует, что 0«gS' — 7«cS* — 7, т. е., согласно неравен-
ству (10.1),
0^S'-7<{.
Складывая это неравенство с неравенством (10.3), получим
0^5-7<е.	(10.4)
Таким образом, мы установили, что для любого данного е>0 можно
указать такое 8>0 ^можно, например, положить 8 = 2 (М — т) р )’
что верхние суммы S разбиений Т сегмента [а, Ь], для которых мак-
симальная длина Д частичных сегментов меньше 8 (см. (10.2)), удов-
летворяют неравенству (Ю.4). Но это означает, что верхний инте-
грал 7 Дарбу является пределом верхних сумм. Для нижних сумм
доказательство аналогично. Лемма Дарбу доказана.
§ 3] НЕОБХОДИМОЕ И ДОСТАТОЧНОЕ УСЛОВИЕ ИНТЕГРИРУЕМОСТИ 323
§ 3. Необходимое и достаточное условие интегрируемости
Установленные свойства верхних и нижних сумм позволяют сфор-
мулировать в весьма простой форме необходимое и достаточное
условие интегрируемости функции. Именно, имеет место следующая
основная теорема.	t
Теорема 10.1. Для того чтобы ограниченная на сегменте
[а, функция f(x) была интегрируемой на этом сегменте, не-
обходимо и достаточно, чтобы для любого s>0 нашлось такое
разбиение Т сегмента [а, Ь], для которого
S-s==Se.
Доказательство. 1) Необходимость. Пусть функция
/(х) интегрируема на сегменте [а, £>]. Обозначим через I предел инте-
гральных сумм этой функции. По определению предела интегральных
сумм для любого s>0 можно указать такое 8 > 0, что для любого
разбиения Т, удовлетворяющего условию Д <; 8, независимо от выбора
точек на частичных сегментах разбиения выполняется неравенство
|/ЫН1<Р	<10-5>
Зафиксируем одно такое разбиение Т. По свойству 1° (см. п. 2 пре-
дыдущего параграфа) для данного разбиения Т можно указать такие
две интегральные суммы (иными словами, можно так выбрать точки
и в каждом частичном сегменте [Xj_x, xj), что
s-i{xb	i{xb
Отметим, что обе интегральные суммы 1{хь и 1{хь 11} удовлетво-
ряют неравенству (10.5). Из соотношения
5-s = (5-7{xft ?;}) + (/{xb ll}-D + U-I{Xi, Vt}) + (I{Xi, X}-s),
неравенства (10.5) и неравенств S — 1{хь 5/}1 {xit —
вытекает, что
<S—s<e.
Необходимость условий теоремы доказана.
2) Достаточность. Так как для любого разбиения Т спра-
ведливы неравенства	и для любого е>0, согласно
условию теоремы, можно указать такое разбиение, что S —ssgs, то
OsSJ —/гСг. В силу произвольности е получим, что 1 = 1.
Общее значение чисел 1 и / обозначим через I и докажем, что
это число 1 является пределом интегральных сумм функции f(x).
324
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
[ГЛ. 10
Действительно, в силу леммы Дарбу (см. п. 2 предыдущего параг-
рафа) это число I есть общий предел при Д->0 верхних и нижних
сумм. Поэтому для любого .е можно указать такое 8, что при Д<о
выполняются неравенства / — $ < у и S — I , т. е. при Д<8,
5— s<e, причем ssg/sgS. Любая интегральная сумма /{х,-, дан-
ного разбиения Т заключена между верхней и нижней суммами
s^I{x;, SijsC'S'. Таким образом, при Д<8 обе величины I и I {х„
заключены между числами S и $, разность между которыми меньше е.
Отсюда вытекает, что при Д <; 8
\Г{ХЬ М-/|<е.
Следовательно, число 1 есть предел интегральных сумм. Теорема до-
казана.
В дальнейшем нам понадобится несколько иная форма записи не-
обходимого и достаточного условия интегрируемости. Пусть Mi и
mt — точные грани значений функции /(х) на [х,-х, xj. Число
OJ; = Mi — Hit
называется колебанием функции /(х) на сегменте [Xz-j, X;]. Отме-
тим, что так как Mt mit то колебание <о(- является неотрицательным
числом. Запишем теперь разность S-s в следующей форме:
п	п	п	п
S— S = 2 Mi ^Х1 — У. «г bxt ^^(Mi- mi)&Xi = У шг Дхг.
i = l	i = l	j=l	i = l
Поскольку e>j$:0n Дхг >0, то каждое слагаемое в последней сумме
неотрицательно.
Можно сформулировать необходимое и достаточное условие инте-
грируемости функции в следующей форме.
Для того чтобы функция fix) была интегрируемой на сег-
менте [a, ft], необходимо и достаточно, чтобы для любого е>0
нашлось такое разбиение Т сегмента [а, Ь], для которого
п
У «)(Дхг е.
z= 1
§ 4.	Некоторые классы интегрируемых функций
В этом параграфе мы докажем интегрируемость непрерывных на
сегменте функций, некоторых разрывных функций и монотонных функ-
ций. Для доказательства интегрируемости непрерывных функций нам
понадобится важное свойство непрерывных на сегменте функций, ко-,
торое устанавливается в ближайшем пункте.
§4]
НЕКОТОРЫЕ КЛАССЫ ИНТЕГРИРУЕМЫХ ФУНКЦИЙ
325
1.	Свойство равномерной непрерывности функции.
Определение. Функция f(x) называется равномерно не-
прерывной на множестве {х} *), если для любого положитель-
ного числа i можно указать такое положительное 8, зависящее
только от е, что для любых двух точек х' и х" множества {х},
удовлетворяющих условию \х" — х'|<;8, выполняется неравен-
ство |/(х”) — f(x’) | < е.
Замечание. Главное в этом определении то, что для любого
е >0 найдется 8 >» 0, гарантирующее выполнение неравенства \f(x")—
—f(x') | < е сразу для всех х' и х" из множества {х} при един-
ственном условии | х" — х' | < 8.
Для разъяснения свойства равномерной непрерывности рассмотрим
следующие примеры:
1)	Функция /(х) = ф/х равномерно непрерывна на полупрямой
Х51. В самом деле, по теореме Лагранжа имеем для любых х'5= 1
и х" 5s 1
|/(*") ~/(О | = \Г (5) II х" - х' |	| х" - х' | <у | х" - х' |
(последнее неравенство вытекает из того, что 5 заключено между х'
и х", и поэтому 5>1). Следовательно, если по данному е>0 вы-
брать любое 8, удовлетворяющее условию 0<8^2в, то при
|х"-х'|<8 выполняется неравенство |/(х'') —/(х') | < s, т. е. на
множестве хЭэ1 функция /(х) = рлх равномерно непрерывна.
2)	Функция /(х) = ха не является равномерно непрерывной на
множестве X5sl. Достаточно доказать, что для некоторого s>0
нельзя выбрать 8 > 0, гарантирующего выполнение неравенства
|/(х") — /(х')| < е для всех х' 5= 1 и х''51 при единственном усло-
вии |х"-х'|<8. Мы докажем, что на самом деле даже для любого
е 5> 0 нельзя выбрать указанного выше 8. Фиксируем е>0 и рас-
смотрим любое положительное 8. Выберем х'>-^-, х" = х'4--у.
Тогда |х" — х'| = у<8. Используя теорему Лагранжа, получим
|/(х") - f(x') | = 25 | х" - х' | = 58.
Так как 5 заключено между х' и х", то 5>у, и поэтому из по-
следнего равенства вытекает неравенство
|/(х")-/(х')|>е,
*) При этом предполагается, что множество {%} плотно в севе (см. ко-
нец § 3 главы 2).
326
определенный интеграл
4ГЛ. 10
хотя |х" — х'|<8. Таким образом, функция/(х) = х2 не является
равномерно непрерывной на множестве х^\.
3)	Функция /(x) = siny не является равномерно непрерывной
на интервале (0, 1). Докажем, что для любого е, удовлетворяющего
условиям 0 < е <; 2, нельзя указать 8 > 0, гарантирующего выполне-
ние неравенства \f(x") — f(x') | < в < 2 для всех х' и х" из интер-
вала (0, 1) при единственном условии \х" — х' I < 8. Чтобы убедиться
•	2	2
в ЭТОМ, достаточно ПОЛОЖИТЬ X — 77Г~Г~^— И X = ... ,	 и для
’	(46 4-3) тс	(46 4-1)к
любого 8>0 выбрать k столь большим, что |х"— х'|<8. Для
указанных точек х' и х" при любом k разность
|/ (*") -fix') | = | sin ~ - sin — | = 2 > e.
Докажем следующую основную теорему.
Теорема 10.2. (теорема о равномерной непрерывности).
Непрерывная на сегменте [а, Ь] функция f(x) равномерно непре-
рывна на этом сегменте.
Доказательство. Предположим, что непрерывная на сег-
менте [а, 6] функция f(x) не является равномерно непрерывной на
этом сегменте. Тогда для некоторого е>0 не выполняются условия,
сформулированные в определении равномерной непрерывности. Это
означает, что для указанного е>0и любого положительного числа 8
на сегменте [а, Ь] найдутся точки х' и х” такие, что | х” — х' | < 8,
но \f(x")—f(x') | e. Поэтому для каждого 8 =	и=1, 2, ...,
найдутся точки х'п и х’п сегмента [а, Ь] такие, что | х’п — х'п | < ,
но	/(Xn)|5se. Так как {х'п} — последовательность точек
сегмента [а, Ь], то из нее, согласно теореме Больцано—Вейерштрасса,
можно выделить сходящуюся к некоторой точке с этого сегмента
подпоследовательность {х&п} (см. замечание 2 п. 4 § 4 главы 3). Оче-
видно, подпоследовательность последовательности {х„} также
сходится к с. Так как функция f(x) непрерывна в точке с, то пре-
делы последовательностей	и	равны /(с), и поэтому
последовательность	является бесконечно малой. Но
этого не может быть, поскольку все элементы /(х£п) — /(хьп) ука-
занной последовательности удовлетворяют неравенству ]/(хап) —
— /(х*п) | е. Таким образом, предположение о том, чтсГнепрерыв-
ная на сегменте [а, Ь] функция не является равномерно непрерывной,
ведет к противоречию. Теорема доказана.
Следствие. Пусть функция f(x) непрерывна на сегменте
[а, Ь]. Тогда для любого положительного числа е можно указать
такое 8 > 0, что на каждом принадлежащем сегменту [а, Ь]
§4]	. НЕКОТОРЫЕ КЛАССЫ ИНТЕГРИРУЕМЫХ ФУНКЦИИ	327
частичном сегменте [с, d], длина d — c которого меньше В, коле-
бание «) *) функции f(x) меньше е.
Доказательство. В силу только что доказанной теоремы не-
прерывная на сегменте [а, Ь] функция /(х) равномерно непрерывна
на этом сегменте. Поэтому для любого е > 0 можно указать 8 > О
такое, что для любых х' и х" из сегмента [a, Z>j, удовлетворяющих
условию |х"-х'|<8, выполняется неравенство ]/(х")—/(х')| <е.
Докажем, что на каждом принадлежащем сегменту [а, Ь] частичном
сегменте [с, d], длина d — c которого меньше указанного 8, колеба-
ние ш функции f(x) меньше е. В самом деле, поскольку функция f(x)
непрерывна на сегменте [с, d], то на этом сегменте можно-указать
такие точки х* и х", что f(x') = m, а /(х") = М, где т и М — точ-
ные нижняя и верхняя грани функции f(x) на сегменте [с, d]
(см. теорему 8.8). Так как \х" — х'|<8 (ибо длина сегмента [с, d]
меньше 8), то \f(x”) — /(х')| < е. Но f(x") — f(x') = M — m = w.
Поэтому о> < е.
Замечание. Множество {х} точек числовой прямой называется
замкнутым, если оно содержит все свои предельные точки **). Справедливо
следующее утверждение. Непрерывная на замкнутом ограниченном***) мно-
жестве {%} функция f (х) равномерно непрерывна на этом множестве. Доказа-
тельство этого утверждения аналогично доказательству теоремы 10.2.
2.	Лемма Гейне — Бореля. Другое доказательство теоремы о равномерной
непрерывности. Точка х множества {х} называется внутренней точкой этого
множества, если она принадлежит некоторому интервалу, все точки которого
принадлежат множеству {х}. Множество {х} называется открытым, если все
точки этого множества внутренние.
Мы будем говорить, что данное множество {%} покрыто системой S
открытых множеств ****), если каждая точка х этого множества принадлежит
по крайней мере одному множеству системы £. Докажем следующую лемму.
Лемма Гейне — Бореля*****). Если сегмент[а, Ь] покрыт бесконечной
системой £ открытых множеств, то из этой системы можно выделить конеч-
ную подсистему £ множеств, которая также покрывает сегмент [а, 6].
 Доказательство ******), Пусть {х} — множество таких точек сегмента
[а, Ь], что если х принадлежит этому множеству, то сегмент [а, х] покры-
вается некоторой конечной подсистемой £' множеств системы £. Докажем,
что множество {х} совпадает с сегментом [а, 6]. Так как точка а покрыта
*) Напомним, что колебание а функции f (х) на сегменте [с, d] назы-
вается разность М — т между точной верхней и точной нижней гранями
функции f (х) на этом сегменте.
**) Определение предельной точки множества данов п. 6 § 4 главы 3.
***) Определение ограниченного множества дано в п. 6 § 4 главы 3.
****) Если множество {х} состоит из одной точки, а система £ содержит
лишь одно открытое множество, то мы будем говорить, что это множество
покрывает указанную точку.
*****) Э. Гейне (1821—1881 гг.) — немецкий математик.’Эмиль Борель
(1871—1956 гг.)—французский математик.
******) Это доказательство леммы Гейне— Бореля принадлежит француз-
скому математику Анри Лебегу (1875—1941). Отметим, что Лебегом был ука-
зан и обоснован более общий, чем излагаемый в этой главе, подход к про-
блеме интегрирования. Соответствующее понятие интеграла носит наименование
интеграла Лебега.
328
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
(ГЛ. 10
некоторым множеством системы £ и это множество открытое, то оно покры-
вает также некоторый сегмент [о, х], все точки которого, согласно вышеска-
занному, принадлежат множеству {х}. Множество {х}, очевидно, ограничено.
Пусть х = sup {х}. Убедимся, что X принадлежит множеству {х} и что Х = Ь.
В самом деле, X покрыто некоторым множеством системы £ и, следовательно,
этим же множеством покрыты все точки некоторого интервала {X — е, X + е).
Так как x = sup{x}, то имеются точки множества {х}, как угодно близкие
к X, и поэтому найдется точка х' этого множества, принадлежащая интервалу
(X — е, X-f-e). Из определения множества {х} вытекает, что сегмент [а, х']
покрывается некоторой конечной подсистемой 2' множеств системы £. При-
соединяя к S' множество, покрывающее точку X, мы получим конечную под-
систему £ множеств системы £, которая покрывает сегмент [а, х]. Следова-
тельно, X принадлежит {х}. Если допустить, что X < Ь, то подсистема £ покры-
вала бы все точки некоторого сегмента [а, х"], где X <х" <x-f- е, и поэтому
точка х" принадлежала бы множеству {х}. Но этого не может быть, так как
X — точная верхняя грань множества {х}. Таким образом, множество {х}
совпадает с сегментом [а, Ь]. Лемма доказана.
Замечание. Можно следующим образом обобщить лемму Гейне —
Бореля. Если замкнутое * **)) ограниченное множество {х} покрыто бесконеч-
ной системой £ открытых множеств, то из этой системы можно выделить
конечную подсистему £ множеств, которая также покрывает множество {х}.
Дадим теперь другое доказательство теоремы 10.2.
Доказательство теоремы о равномерной непрерывно-
сти. Продолжим f (х) на всю прямую, положив ее равной f (b) при х > b и рав-
ной f (а) при х<а. Так как / (х) непрерывна в каждой точке сегмента [а, Ь], то для
любой точки х этого сегмента и любого заданного е > 0 можно указать та-
кое В'>0, зависящее, вообще говоря, от х, что для всех точек х', удовлет-
воряющих 'условию |х' — х|<8', выполняется неравенство | f (х') — f (х) | <
<'у. Таким образом, сегмент [а, 6] покрыт бесконечной системой £ интер-
валов (х---2 ’ Х^”'27	’ И3 КОТОРОИ можно выделить, в силу леммы
Гейне — Бореля, конечную подсистему £ интервалов, также покрывающую
сегмент [а, 6]. Обозначим через 8 минимальное значение -% для этой конеч-
ной подсистемы £ интервалов. Пусть теперь х' и х"— любые точки сег-
мента [а, Ь], удовлетворяющее условию | х"—х' | < 8, и х— центр того
8' В' \	8'	-
интервала 1х----%-, х + -%-), В^-^-, системы £, который покрывает точ-
8'	е
ку х'. Так как | х'— х | <-к-< В' и | х" — х|<8', то | f (х') — f (х) | < —
Я If (x")—f (х) I < у и поэтому
|/(X")— /(X') |^|/(х")-/(X) 1 + |/(х') —/(X) |<у + у = е.
Итак, для любого заданного е > 0 мы указали
точек х' и х" сегмента [а, &], удовлетворяющих
*) См. замечание в предыдущем пункте.
**) Мы берем интервалы ^х---1-, * + у
удобства дальнейших рассуждений.
такое В > 0, что для любых
условию | х" — х' | < 6, вы-
вместо (х — 8', х -f-6') для
§4]
НЕКОТОРЫЕ КЛАССЫ ИНТЕГРИРУЕМЫХ ФУНКЦИИ
329
полняется неравенство | f (х") — f (х') | < е. Следовательно, функция f (х) равно-
мерно непрерывна на сегменте [а, 6]. Теорема доказана,
3.	Интегрируемость непрерывных функций. Докажем следую-
щую основную теорему.
Теорема 10.3. Непрерывная на сегменте [а, Ь] функция f(x)
интегрируема на этом сегменте.
Доказательство. Пусть дано любое в> 0. В силу равномер-
ной непрерывности функции f(x) на сегменте [а, для положитель-
ного числа	можно указать такое 8 > 0, что при разбиении Т
сегмента [а, Ь\ на частичные сегменты [хг_о х,-], длины Дхг которых
меньше 8, колебание шг функции f(x) на каждом таком частичном
сегменте будут меньше а (см. следствие из теоремы 10.2). По-
этому для таких разбиений Т
S — 5 =	СО; Дх, < ь д- Дх,- = В.
i = 1	i = 1
Следовательно, для непрерывной на сегменте [а, Ь] функции f(x)
выполнены достаточные условия интегрируемости.
4.	Интегрируемость некоторых разрывных функций. Мы будем
говорить, что точка х покрыта интервалом, если эта точка принад-
лежит указанному интервалу. Докажем следующую теорему.
Теорема 10.4. Если функция f(x) определена и ограничена на
сегменте [а, Ь] и если для любого положительного числа е можно
указать конечное число интервалов, покрывающих все точки раз-
рыва этой функции и имеющих общую сумму длин меньше в, то
J (х) интегрируема на сегменте [а, д].
Доказательство. Пусть дано любое в>0. Покроем точки
разрыва функции f(x) конечным числом интервалов, сумма длин ко-
торых меньше 2	, где гИ и т — точные верхняя и нижняя
грани f{x) на сегменте [а, д] (случай М — т можно исключить, так
как тогда f(x) = с = const). Точки сегмента, не принадлежащие ука-
занным интервалам, образуют множество, состоящее из конечного
числа непересекающихся сегментов. На каждом из них функция /(х)
непрерывна и поэтому равномерно непрерывна. Разобьем каждый такой
сегмент так, чтобы колебание о>,- функции /(х)' на любом частичном
сегменте разбиения было меньше
-х-тт--г-. Объединяя эти разбиения
2 (о — а)	г
и интервалы, покрывающие точки разрыва функции /(х), мы получим
разбиение Т всего сегмента [а, />]. Для этого разбиения слагаемые
п
суммы У о)гДхг (равной S—s) разделяются на две группы ш;Дх;
; = 1
и У о)/Дх;, причем в первую группу входят все слагаемые, отвечающие
330
определенный интеграл
[ГЛ. 10
частям разбиения Т, образованным из интервалов, покрывающих точки
разрыва, а во вторую — остальные слагаемые. Так как колебания
=	— mi для слагаемых первой группы удовлетворяет неравен-
ству шг М — т, то
2' ^xi ^(М-т) 2'	<(М-т)	J
Для слагаемых второй группы и>;<
2(6 — а) •
Поэтому
2	2(6 —а) 2	2ф-а)^Ь
£
Таким образом,
п
S— s= У, <огДх/ = 2' Wi^Xi 4- 2” и)гДХ( < е.
1 = 1
Итак, для указанной в условии
Рис. 10.4.
конечное число точек разрыва,
функция f(x) (рис. 10.4)
теоремы функции f(x) выполнены
достаточные условия интегрируе-
мости. Теорема доказана.
Следствие. Ограниченная на
сегменте [a, ft] функция f(x),
имеющая лишь конечное число
точек разрыва, интегрируема на
этом сегменте *). В частности,
кусочно непрерывная на данном
сегменте функция интегрируема
на этом сегменте.
Замечание. Очевидно, что
если функция f(x) интегрируема
на сегменте [a, ft], а функция g(x)
отличается от функции /(х)лишь
в конечном числе точек, то
функция ‘ g(x) также интегри-
руема на сегменте [a, ft], причем
ь	ь
$ f(x) dx —	(х) dx.
а	а
Рассмотрим пример интегри-
руемой функции, имеющей бес-
Пусть на сегменте [0, 1] задана
1
/(*) =  _!
0
на полусегментах
на полусегментах
в точке х = 0.
/ 1	11
\ 2п ’ 2п — 1
/1 1 :
\2n + 1 ’ 2п
п=1, 2,
л=1, 2,
*) Если р — число точек разрыва, то достаточно покрыть каждую точку
разрыва интервалом длины е/2р.
§ 5]	ОСНОВНЫЕ СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА	331
Указанная функция имеет разрывы 1-го рода во всех точках хп — ~,
п = 2, 3, ... Фиксируем любое е > 0. Покроем точку х = 0 (в любой
окрестности этой точки находится бесконечное число точек разрыва
функции) интервалом (----Вне этого интервала находится
лишь конечное число р*) точек разрыва функции, каждую из ко-
торых мы покроем интервалом длины меньше . Сумма длин интер-
валов, покрывающих все точки разрыва рассматриваемой функции,
6 । е
меньше
Следовательно, функция f(x) интегрируема на
сегменте [0, 1].
5.	Интегрируемость монотонных ограниченных функций.
Теорема 10.5. Монотонная на сегменте [а, й] функция fix)
интегрируема на этом сегменте **).
'Доказательство. Ради определенности докажем теорему для
неубывающей на сегменте [а, Ь] функции f(x). Зададимся произвольным
положительным числом е и разобьем сегмент [а, Ь] на равные части,
длины которых меньше	(случай f(a) —f(b) можно исклю-
чить, так как тогда f(x) = const). Оценим для этого разбиения раз-
п
ность S—J1, Имеем
!=1
П	П
1 = 1	1 = 1
п
Но для неубывающей функции У, и, — /(b) — f (а), поэтому £ — $ < е.
i = 1
Теорема доказана.
§ 5. Основные' свойства определенного интеграла
Докажем справедливость следующих свойств определенного интег-
рала:
1°. Мы будем считать, что
]f(x)dx = 0.	(10.6)
а
Отметим, что формула (10.6) должна рассматриваться как соглашение.
*) Это число р зависит, конечно, от г.
**) Отметим, что если функция монотонна на сегменте [a, t>], то ее зна-
чения заключены между f (а) и f (b). Поэтому определенная на сегменте [a, i]
монотонная функция ограничена на этом сегменте.
332
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
[ГЛ. 10
Ее нужно рассматривать как естественное распространение понятия
определенного интеграла на сегмент нулевой длины.
2°. Мы будем считать, что при а < Ь
а	b
^f(x)dx = — § /(х) dx.	(10.7)
Ь	а
Эта формула также должна рассматриваться как соглашение. Она
представляет собой естественное обобщение понятия интеграла на
случай, когда сегмент [а, 6] при a b пробегается в направлении
от b к а (в этом случае в интегральной сумме все разности
Дх; = Xi — х(--х имеют отрицательный знак).
3°. Пусть функции /(х) и g(x) интегрируемы на сегменте [а, £>].
Тогда функции /(x)+g(x), f(x) — g(x~) и f(x)g(x) также интегри-
руемы на этом сегменте, причем
ь	ь	ь
[/ (х) ± g (х)] dx=\f(x}dx±\g (х) dx.	(10.8)
а	а	а
Докажем сначала интегрируемость функции f(x)±g(x) и справедли-
вость формулы (10.8). При любом разбиении сегмента [а, Ф] и любом
выборе точек для интегральных сумм справедливо соотношение
п	п	п
2 [/&•) Дхг = 2	± 2 S (U
>=1 ( = 1	1 = 1
а поэтому из существования предела правой части следует существо-
вание предела левой части. Следовательно, функция /(x)±g(x) интег-
рируема и имеет место формула (10.8).
Докажем теперь, что произведение интегрируемых функций является
интегрируемой функцией. Так как функции /(х) и g(x) интегрируемы
на сегменте [а, Ь], то они и ограничены на этом сегменте (см. утвер-
ждение п. 1 § 1), так что |/(х)|<Л и |g(х)|«СВ. Рассмотрим
любое заданное разбиение Т сегмента [а, Ь]. Пусть х' и х" — произ-
вольные точки частичного- сегмента [Xf-X, xj. Имеем тождество
f (х") g (х'') - f (х') g (х') =
= [f(x”)-f(x’)]g(x") + [g(x'')-g(x')]f(x').
Так как
|/(x")g(x") -/(x')g(x') | < о),-,	\f(x") -f(x') | < оз,-,
\g(x")-g(x')\^ ш;,
где о>г, в>г, — соответственно колебания функций /(x)g'(x), /(х),
g(x) на сегменте [х;-1( xj, то, согласно указанному тождеству*),
ш, sS B<Si Д’®,.
*) В этом тождестве точки х' и х" можно выбрать так, что левая часть
будет как угодно мало отличаться от <ог.
§ 5]	ОСНОВНЫЕ СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА	333
Поэтому
У, W/Дх, < В У в^Дх, 4- А У ^Дх,.
1 = 1	1 = 1	1 =1
Поскольку f(x) и g(x) интегрируемы на сегменте [а, Ь\, для любого
заданного е > 0 можно указать такое разбиение Т этого сегмента, что
п	п,
У а5;Дхг<я^- и У ш;Дхг <Z Д-. Следовательно, для этого разбиения
Л £5	лшл	ЛА
1=1	1=1
п
S-s= 2 ^xi<B^ + A~ = z.
i = i
Поэтому произведение интегрируемых функций является интегрируе-
мой функцией.
4°. Если функция f(x) интегрируема на сегменте [а, &], то функ-
ция cf(x) (с = const) интегрируема на этом сегменте, причем
ь	ь
^cf(x)dx — c^f(x')dx.	(10.9)
а	а
Действительно, интегральные суммы функций f(x) и cf(x) отличаются
постоянным множителем с. Поэтому функция cf(x) интегрируема и
справедлива формула (10.9).
5°. Пусть функция f(x) интегрируема на сегменте [а, Ь]. Тогда
эта функция интегрируема на любом сегменте [с, d], содержащемся
в сегменте [а, Ь].
Так как функция f(x) интегрируема на сегменте [а, Ь], то для
любого е>0 существует такое разбиение Т сегмента [а, Ь], что
S’ —(см. теорему 10.1). Добавим к точкам разбиения Т точки с
и d. В силу свойства 2° верхних и нижних сумм (см. п. 2 § 2)
для полученного разбиения Т* тем более справедливо неравенство
S — 5 < е. Разбиение Т* сегмента [а, &] порождает разбиение Т
сегмента [с, dj. Если S и s - верхняя и нижняя суммы разбиения Т,
то S —	— s, поскольку каждое неотрицательное слагаемое и>/Дхг
в выражении S — $ = о^-Дх/ будет также слагаемым в выражении
для S — s. Следовательно, $<е, и поэтому функция f(x) интег-
рируема на сегменте [с, d],
6°. Пусть функция /(х) интегрируема на сегментах [а, с] и [с, Ь].
Тогда эта функция интегрируема на сегменте [а, Ь\, причем
Ь	с	b
^/(x)dx = $/(x)tZx-|-§/(x)</x.	(10.10)
а	а	С
Рассмотрим сначала случай, когда a<Zc<Zb. Так как функция /(х)
интегрируема на сегментах [а, с] и [с, Ь}, то существуют такие
334
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
[ГЛ. 10
разбиения этих сегментов, что разность 5— s для каждого из них
меньше Объединяя эти разбиения, мы получим разбиение сегмента
[а, />], для которого разность 5— s будет меньше е. Следовательно,
функция f(x) интегрируема на [а, Ъ\. Будем включать точку с в число
делящих точек сегмента [а, Ь} при каждом его разбиении. Тогда
интегральная сумма для f(x) на [а, Ь] равна сумме интегральных сумм
для этой функции на [а, с] и [с, &]. В пределе мы получим фор-
мулу (10.10).
Если точка с лежит вне сегмента [а, &], то сегмент [а, &] есть
часть сегмента [а, с] (или [с, £>]) и поэтому, в силу свойства 5°,
функция f(x) интегрируема на [а, &]. Рассмотрим случай
Тогда
§ f(x) dx + $Z(x) dx = ^f(x) dx.
aba
Отсюда, используя свойство 2° и формулу (10.7), мы опять получим^
соотношение (10.10). Легко- убедиться в справедливости этого соот-
ношения и при с < a <z b.
§ 6.	Оценки интегралов. Формулы среднего значения
1.	Оценки интегралов. В этом пункте мы получим некоторые
оценки для определенных интегралов, подынтегральные функции
которых подчинены тем или иным условиям.
1°. Пусть интегрируемая на сегменте [a, Z>] функция f(x)
неотрицательна на этом сегменте. Тогда
ь
J/(x)rfx^0.
а
Действительно, каждая интегральная сумма такой функции неотрица-
ь
тельна, и поэтому предел 7=^/(х)йх интегральных сумм также не-
а
отрицателен *).
Замечание 1. Если f(x) интегрируема на сегменте [a, Z>] и
f (х) т, то
ь
^f(x)dx^m(b — а).
а
*) Допустим, что предел I интегральных сумм отрицателен. Тогда,
согласно определению предела I, для числа е = | /1 найдется интегральная
сумма / {х(-, £,•}, для которой | / {х;,	— / | < | / |. Из этого неравенства
вытекает, что I {х,, $,•} <0, а мы только что убедились, что каждая интег-
ральная сумма неотрицательна. Следовательно, предел I неотрицателен.
S 6]	ОЦЕНКИ ИНТЕГРАЛОВ. ФОРМУЛЫ' СРЕДНЕГО ЗНАЧЕНИЯ	835
В самом деле, функция f(x) — т^ 0 и интегрируема на сегменте
ь
[а, &]. Поэтому J [/(х) — т\ dx 0. Отсюда
. ' °
ь	ь	ь
^f(x)dx^^mdx= т ^dx = m(b — а)
а	а	а
(см. свойство 3° и пример из § 1).
2°. Если функция /(х) непрерывна, неотрицательна и не равна
тождественно нулю на сегменте [а, Ь], то
ь
J/(x) dx Э- с > 0.
а
Действительно, так как функция /(х) неотрицательна и не равна
тождественно нулю, то на сегменте [а, Ь] найдется такая точка 5,
что /(Е) = 2А>0. Тогда по теореме об устойчивости знака непре-
рывной функции можно найти такой сегмент \р, д], содержащий
точку 5, в пределах которого значения функции /(х} будут не меньше
числа k > 0, Поэтому, в силу только что сделанного замечания,
ч
\f(x)dx^k(q-p)> 0.
р
Согласно свойству 6° определенных интегралов
J/(x)dx — ^f(x)dx + ^f(x)dx + \f(x)dx.
a	a	p	q
<7
Поэтому, поскольку /(x) о и §/(x) dx c > 0, где c — k (q — p),
p
b
\jf(x)dx'^c>Q.
a
3°. Если функции f(x) и g(x) интегрируемы на сегменте [а, &]
и /(x)^g(x) всюду на этом сегменте, то
ь	ь
J/(x) dx § g(x) dx.
а	а
Действительно, функция/(x) — g(x)^0 и интегрируема на сегменте
[a, Z>J. Отсюда, в силу свойства 1°, и вытекает справедливость
указанной оценки.
Замечание 2. Если функция f(х) интегрируема на сегменте
[а, д], то функция [f (х)| также интегрируема на этом сегменте,
336
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
[ГЛ. 10
причем
b	Ь	
J/(x)dx	$	|/(х)| dx.
а	а
Докажем сначала интегрируемость модуля |/(х) | интегрируемой
функции /(х). Обозначим через Л4; и пц точные грани /(х) на сег-
менте [хг_и xj, а через М[ и т\ точные грани |/(х)| на том же
сегменте. Легко убедиться в том, что M't — rn'i^Mi — mt (достаточно
рассмотреть три возможных случай: 1) случай, когда Mt и mt не-
отрицательны, 2) случай, когда Mi и пц неположительны, 3) случай,
когда Mt > 0, /я,	0). Из полученного неравенства вытекает, что
5' — s'^S- s. Таким образом, если для некоторого разбиения
S—-s<;e, то для этого разбиения S' — s'<e, т. е. для |/(х)| выпол-
нено достаточное условие интегрируемости *).
Докажем теперь интересующую нас оценку. Так как — [/(х)|^
Ь	 b	ь
=^/С*0^|/(х)|, то — $ |/(х) | dx^z ^f(x)dx^ $ |/(х)\dx, а это и
а	а	х а
b	ь
означает, что Ц/(х) dx |	|/(х) | dx.
а	а
4°. Пусть функции f(x) и g(x) интегрируемы на сегменте [а, Ь]
и g(x)^0. Тогда, если М и т —точные грани f(x) на сегменте
[а, й], то
ь	ь	ь '
т ^g(x)dx^z \f(x)g(x)dx^ М §g(x)dx.	(10.11)
а	а	а
Справедливость (10.11) вытекает из того, что для всех х из
сегмента [а, Ь] справедливы неравенства mg(x)^f (х) g(x)<: Mg(x)
(см. оценку 3° из настоящего пункта и свойство 4° из § 5).
Замечание 3. В дополнении 1 к этой главе мы получим не-
сколько важных неравенств для сумм и определенных интегралов.
2.	Первая формула среднего значения. Пусть функция /(х)
интегрируема на сегменте [а, Ь], и пусть т и М точные грани
f (х) на сегменте [а, Ь]. Тогда найдется такое число р, удовлет-
воряющее неравенствам	что
ь
^/(x)t/x = p(Z> — а).	(10.12)
' а
b
В самом деле, полагая g(x)=l и учитывая, что ^l-dx — b — a (см.
а
*) Из интегрируемости функции | / (х) | не следует, вообще говоря, интег-
рируемость f (х), Например, функция F (х) = { _ } для^р^ционалмых х,
неинтегрируема на сегменте [0, 1], тогда как |/(х) | = I—интегрируемая на
этом сегменте функция.
§ 6]
ОЦЕНКИ ИНТЕГРАЛОВ. ФОРМУЛЫ СРЕДНЕГО ЗНАЧЕНИЯ
337
пример п. 1 § 1) получим из (10.11)
ь
m(b — а) /(х) dx -С М (Ь — а),
а
b
Обозначая через р число j /(х) dx, мы и получим форму-
лу (10.12).	“ .
Если функция'/(х) непрерывна на сегменте [a, Z>], то существуют
такие точки р и q этого сегмента, что f(p) = m и f(q) = M (см.
теорему 8.8), и поэтому, в силу теоремы 8.6, на сегменте [р, q],
а стало быть, и на [а, Ь] найдется точка 5 такая, что /(!•) = р. В этом
случае формула (10.12) примет вид
ь
^f(x)dx=f(t)(b — a).
а
(10.13)
Эта формула называется первой формулой среднего значения.
3.	Первая формула среднего значения в обобщенной форме.
Докажем следующее утверждение. Пусть функции f(x) и g(x)
интегрируемы на сегменте [а, &], и пусть т и М — точные грани
f (х) на сегменте [а, &], Пусть, кроме того, функция g(x)^0
(или g(x)-^zQ) на всем сегменте [a, &|. Тогда найдется такое
число р, удовлетворяющее неравенствам	что
ь	ь
\f(x)g(x)dx=^\g(x)dx.	(10.14)
а	а
В частности, если f(x) непрерывна на сегменте [а, Ь], то на
этом сегменте существует такое число £, что
ь	ь
\f(x)g(x)dx=f($)\g(x)dx.	(10.15)
а	а
Формула (10.15) называется первой формулой среднего значения
в обобщенной форме.
ь
Докажем справедливость формулы (10.14). Если \ig(x)dx = fd, то,
а
b
в силу неравенств (10.11), ^f(x)g(x)dx = 0 и поэтому в качестве р
а
b
мы можем взять любое число. Если ^g(x)dx~y>0, то, разделив все
338
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
[ГЛ. 10
b
части неравенств (10.11) на ^g(x)dx, получим
а
Ъ
j f (X) g (х) dx
m sC --------T- 'S M.
$g(x)dx
a
b
\ \{x}g (x)dx
Обозначая через p. число	, мы и получим формулу (10.14),
\g(x)dx
а
Если f(x) непрерывна на сегменте [а, Ь], то, каково бы ни было
число р, заключенное между т и М, на этом сегменте найдется точка $
такая, что /(Е) = р, т. е. формула (10.14) переходит в формулу (10.15).
Замечание 4. Если функция f(x) не является непрерывной,
то формула (10.15),. вообще говоря, неверна. В самом деле, пусть,
например, /(х) =
1 при 0«gx<^,
r	ag(x) =
1 при у < xsC 1,
1 при
1. 1
у при у<Х<1.
Тогда, как легко убедиться, число р. в формуле (10.14) равно у.
Таким образом, для любого 5 из сегмента [0, 1] /($)^р..
4,	Вторая формула среднего значения. Справедливо следующее"
утверждение. Если на сегменте [а, &] функция g.(x) монотонна,
a f(x) интегрируема, то на этом сегменте существует такое
число что
ь	е •	ь
5 f (*) £ W dx = 8 (а) /(•*)dx + g dx-	О °-16)
а	a	t
Формула (10.16) называется второй формулой среднего значения
или формулой Бонне *). Сформулированное утверждение доказывается
в дополнении 2 к настоящей главе.
§ 7. Существование первообразной для непрерывной функции.
Основные правила интегрирования
1. Существование первообразной для непрерывной функции.
Прежде чем перейти .к доказательству теоремы о существовании
первообразной для непрерывной функции, введем понятие интеграла
с переменным верхним пределом.
*) Бонне (1819—1892) — французский математик.
§ 7J	СУЩЕСТВОВАНИЕ ПЕРВООБРАЗНОЙ	339
Пусть функция fix) интегрируема на любом сегменте, содержа-
щемся в интервале (а, Ь), и пусть с — некоторая фиксированная точка
этого интервала. Тогда, каково бы ни было число х из интервала
(а, Ь), функция fix) интегрируема на се,гменте [с, х]. Поэтому на
интервале (а, Ь) определена функция
X
Д(х) = $/(Г).Л *),
С
которую называют интегралом с переменным верхним пределом.
Докажем следующую теорему.
Теорема 10.6. Любая непрерывная на интервале (а, Ь) функ-
ция fix) имеет на этом интервале первообразную. Одной из пер-
вообразных является функция	,
F(x)=\f(f)dt,
€
где с —любая фиксированная точка интервала (а, Ь).
‘ Доказательство. Достаточно доказать, что для любого фик-
сированного х из интервала (а, Ь) существует предельное значение
.. F (х + Дх) — F (х)	, , .
Jim —Д—!—тЛ —, причем это предельное значение равно fix).
Ьх-fO	м
Имеем, в силу свойства 6° определенных интегралов (см. § 5) **),
F (х^х) — F (х) — § f[t)dt — ^f{t)dt =
С	с
X	X	х+Ь.Х
=\fit)dt+ 5 fit)dt-\fit)dt = 5 fit) di.
C	X	C	X
По формуле (10.13) среднего значения находим
F(x + bx)-F{x)= +$ fit)dt=fi£)bx,
X
где $ — число, заключенное между числами х и х + Ьх. Поскольку
функция fix) непрерывна в точке х, то при Дх->0 /(£)->/(х).
Поэтому из последней формулы находим
]im F(x + Дх) — Г (х)  lim /(5)==/(х).
Дх->0	Дх-»о
Теорема доказана.
Замечание 1. Аналогично доказывается теорема о существо-
вании первообразной у непрерывной на сегменте [a, £>] функции.
*) Мы обозначили переменную интегрирования буквой t, поскольку
буквой х обозначен верхний предел интегрирования.
**) Приращение Дх мы берем столь малым, что (х-)-Дх) принадлежит (а, Ь).
340
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
[ГЛ. 10
Отметим, что в этом случае в качестве нижнего предела интегриро-
вания с можно взять а.
Замечание 2. При доказательстве теоремы 10.6 мы установили
существование производной от интеграла с переменным верхним пре-
делом и доказали, что эта производная равна подынтегральной функции
(10.17)
Замечание 3. Отметим, что если функция f(x) интегрируема
на любом сегменте, содержащемся в интервале (а, F), то интеграл
с переменным верхним пределом представляет собой непрерывную на
интервале (а, Ь) функцию от верхнего -предела. Чтобы убедиться
в этом, докажем, что приращение ДР = F (х + Дх) — F (х) функции
X
F(x)=^f(t)dt стремится к нулю при Дх->0. Имеем, в силу фор-
мулы (10.12),
^F = F(x + Дх) — F(x) = J f(t) dt = р.Дх,
X
где число [а заключено между точной верхней и нижней гранями
функции /(х) на сегменте [х, х + Дх]. Из последней формулы выте-
кает, что и Др —► 0 при Дх 0.
Замечание 4. Интеграл с переменным верхним пределом часто
используется для определения новых функций. Мы уже отмечали
в главе 6, что первообразные некоторых элементарных функций не
выражаются через элементарные функции и не являются поэтому
элементарными функциями. Напомним, что к числу неэлементарных
X	X
функций относятся, например, функции е~dt, JcosFcF.
о	о
2. Основная формула интегрального исчисления. Мы доказали,
что любые две первообразные данной функции /(х) отличаются на
постоянную (см. теорему 6.1). Поэтому, согласно теореме 10.6 и за-
мечанию 1 к этой теореме, можно утверждать, что любая первообраз-
ная Ф(х) непрерывной на сегменте [а, Ь] функции /(х) имеет вид
<b(x) = \f(.f)dt + C,
а
где С —некоторая постоянная.
Полагая в последней формуле сначала х = а, а затем х = Ь и
используя свойство 1° определенных интегралов, найдем
ь
Ф(а) = С,	Ф(&) = $/(х)dx + С *).
________________ а
*) В этой формуле переменную интегрирования мы обозначили буквой х,
поскольку верхний предел имеет фиксированное значение Ь.
§ Л
СУЩЕСТВОВАНИЕ ПЕРВООБРАЗНОЙ
341
Из этих равенств вытекает соотношение
ь ,
$/(х)б/х = Ф(£)-Ф(а),	(10.18)
а
называемое основной формулой интегрального исчисления *).
Итак, для вычисления определенного интеграла от непрерывной
функции f(x) нужно составить разность значений произвольной
ее первообразной для верхнего и нижнего пределов интегрирования.
Отметим, что основная формула интегрального исчисления откры-
вает широкие возможности для вычисления определенных интегралов,
поскольку задача вычисления определенного интеграла сводится
к задаче разыскания первообразной функции. Методы разыскания
первообразных были достаточно полно разработаны нами в главах
6 и 7 этого курса.
Так как во многих случаях разыскание первообразных представляет
собой трудную задачу, естественно поставить вопрос о приближенных
методах вычисления определенных интегралов. В главе 12 будут
указаны некоторые методы приближенного вычисления определенных
интегралов.
Формулу (10.18) иногда записывают в иной форме. Именно, раз-
ность Ф(6) —Ф(а) обозначают символом Ф(х)|*. Тогда
ь
$/(х)</х = Ф(х)|*.	(10.19)
а
Рассмотрим несколько примеров:
6
1)	§ sin х dx — — cos х | * = cos a — cos b,
a
2
2)	J ^- = 1пх|^1п2-1п1=1п2,
1
1
3)	e~x dx— — e~x 11 = 1 —-,
I» e
о
4)	j ГТ^ = агсМ: = Ь
0
1
J	i_
5)	\ Лх.___= arcsin x I 2 = —
'J/1-х2	Io 6’
8
6)	1-л^ = 1п(х + ГТ+^) 3=1п(3+ГТо).
J у 1 + №	0
*) Эту формулу называют также формулой Ньютона—Лейбница.
342
ОПРЕДЕЛЕННЫЙ интеграл
[ГЛ. to
3.	Замена переменной под знаком определенного интеграла.
Пусть выполнены следующие условия:
1)	функция f (x) непрерывна на сегменте [а, Ь];
2)	сегмент [а, Ь] является множеством значений некоторой
функции x — g(t), определенной на сегменте	и имеющей
на этом сегменте непрерывную производную',
3)	£(₽) = &
При этих условиях справедлива формула
ь	₽
' 5/(х) dx = J/[g(()] g' (0 dt.	(10.20)
a	a
Формула (10.20) показывает, что если вычислен интеграл, стоящий
в левой части этой формулы, то вычислен и интеграл, стоящий в
правой части, и наоборот. Указанная формула называется формулой
замены переменной под знаком определенного интеграла.
Рассмотрим некоторую первообразную Ф(х) функции f(x). По
формуле (10.18) имеем
ь
$/(х)</х = Ф(6)-Ф(а).	(10.21)
а
Так как функции Ф(х) и x = g(t) дифференцируемы на соответст-
вующих сегментах, то сложная функция ®(g(0) дифференцируема
на сегменте [а, р]. Поэтому, применяя правило дифференцирования
сложной функции, получим
^,Ф(£(0) = Ф'(£(0)т	(10.22)
причем производная Ф' вычисляется по аргументу х: Ф'(g(0) = Ф'(х),
где x = g(f). Поскольку Ф'(х)=/(х), то при x = g(t) получим
Ф' (§ (0) — f(g (0)- Подставляя это значение Ф' (g(f)) в правую часть
равенства (10.22), получим
^®(g(O)=/(g(O)g'(0.
Следовательно, функция Ф(§(0), определенная на сегменте [а,
является на этом сегменте первообразной для функции f (g (t)) g1 (t),
и поэтому, согласно формуле (10.18),
$ f (g (0) g' (t) dt = Ф (g (P)) - Ф (g (a)),
a	*
Так. как ,g(P) = Z?, a g(a) = a, то
§ 7]
СУЩЕСТВОВАНИЕ ПЕРВООБРАЗНОЙ
343
Сравнивая последнюю формулу с формулой (10.21), мы убеждаемся
в справедливости формулы (10.20).
а 
Примеры. 1) Рассмотрим интеграл ^1пхД Положим х = е*.
1
Так как f = 0 при х=1, < = 1п2 при х — 2, то
2	|П2
(lnx^= i tdt=Z |1П2=41п*2.
J % J * [ 0	*“
1	о
2	) Рассмотрим интеграл sin]/x^L. Пусть x — t2. Тогда
т
х = ^- при t — ~, х = п2 при t = It.'Поэтому
1С2	К
C'sin]/x-^ = 2 С sin t dt —— 2 cos 11 =2.
J Vx J	L
«3	z •	2
T	"2
4. Формула интегрирования по частям. Пусть функции и(х)
и v(x) имеют непрерывные производные на сегменте [а, &]. Тогда
имеет место следующая формула интегрирования по частям для
определенных интегралов:
ь	ь
J и (х) v' (х) dx — [и (х) v (х)] — $ v (х) и' (х) dx.	(10.23)
а	а
Так как v' (х) dx — dv и и' (х) dx = du, то эту формулу записывают
еще следующим образом:
ь	ъ
§ и dv = [пи] j* — $ v du.	(10.24)
,	a	a
В справедливости этих формул убедиться нетрудно. Действительно
функция u(x)v(x) является первообразной для функции и(г)и'(х)-[-
4~ v (х) и' (х). Поэтому, в силу (10.19):
ь
$ [«(х) v' (х) + v (х) и' (х)] dx = [и (х) v (х)]
а
Отсюда, используя свойство 3° определенных интегралов (см. § 5),
мы и получим формулы (10.23) и (10.24).
Примеры.
2	2
1)	In х dx — х In х Р — х у = [х In х — х] Р = 2 In 2 — 1,‘
1
344
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
[ГЛ. 10
I1 v xdx
о J 1 + X2
2	2
2)	хех dx = хех — jj ех dx = ех (х — 1) |, = е2,
1	1
1 1
3)	arctg xdx — x arctg х
о	о
= |^х arctg х —in (1 + х2)^	— In V~2‘
5. Остаточный член формулы Тейлора в интегральной форме.
Применим формулу (10.23) для вывода формулы Тейлора функ-
ции f (х) с остаточным членом в интегральной форме. Пусть функ-
ция fix') имеет в некоторой е-окрестности точки а непрерывную
производную (п-|-1)-го порядка, и пусть х — любая данная точка из
этой е-окрестности. Убедимся, что число
X
Rn+l (х) = ± J /1"+1) (0 (х - ty dt	(10.25)
а
является остаточным членом формулы Тейлора для функции f(x)
с центром разложения в точке а. Таким образом, формула (10.25)
дает представление остаточного члена, формулы Тейлора для
функции f(x) в интегральной форме.
Для доказательства заметим, что
f(x) = f(a)+\f'(t)dt.
а
х
К интегралу (t)dt применим формулу (10.23) интегрирования по
а
частям, полагая u(t\=f (t) и v(t)~— (x — t) (так как х фиксиро-
вано, то t>' dt — dt). Имеем
\f (t) dt=-f' (0 (х -1) I* + $ г (0 (x -1) dt=
a	a
x
=f (a) (x - a) + $/" (0 (x - 0 dt.
a
Подставляя найденное ^выражение для (f)dt в приведенную выше
a
формулу для /(х), получим
/(х) =/(а) -ь f (а) (х - а) + jj f ’ (0 (х - 0 dt.
а
х
К интегралу J/"(0(x — t)dt также можно применить формулу интег-
§ 7]
СУЩЕСТВОВАНИЕ ПЕРВООБРАЗНОЙ
345
рирования по\ частям, полагая u(t) — f" (t) и v(t) —-^-{x — t)2 (так
как х фиксировано, то v' dt — (х — t) dt). После несложных преобра-
зований найдем
J f" (О {X -t)dt = (х - а)2 +1 J fV (t) (X -1)2 dt,
a	a
и поэтому
/(x) = f(a) + ф (x - a) + (x - а)2 +1 $ /<3’ (t) (x -1) dt.
a
Дальнейшее интегрирование по частям будем производить до тех пор,
пока не придем к формуле
/(х)=/(а) + ^-(х-а) + ^-(х-а)2+ ... + (х- а)п +
+ ^fn+V(t)(x-t)ndt.
а
Эта формула показывает, что Rn+1(x) действительно является оста-
точным членом формулы Тейлора для функции /(х) с центром раз-
ложения в точке а (см. § 13 главы 8). Используя интегральную
форму (10.25) остаточного члена формулы Тейлора, легко получить
остаточный член формулы Тейлора в форме Лагранжа. Именно по
обобщенной форме (10.15) формулы среднего значения получим
(х) = ± J (t) (х - 0я dt =	$ (х - t)n dt =
а	а
_	/(Л+1) (£)(*-/)"« И _(|Л+1>(Е),	яу1+1
nl (п+1) |о (п+1)!'Х	' ’
Полученное выражение и представляет собой остаточный член в форме
Лагранжа*) (см. формулу (8.46) из § 14 главы 8).
*) Отметим, что при указанном выводе остаточного члена в форме Лаг-
ранжа на производную (п -f- 1)-го порядка накладываются несколько боль-
шие ограничения, чем в § 14 главы 8. Однако, если использовать доказанную
в конце главы 9 теорему Дарбу (о прохождении производной через все
промежуточные значения), то получим остаточный член в форме Лагранжа
лишь при условии существования и интегрируемости /|Л+11 (х).
346
определенный интеграл
[ГЛ. 10
ДОПОЛНЕНИЕ 1 К ГЛАВЕ 10
НЕКОТОРЫЕ ВАЖНЫЕ НЕРАВЕНСТВА ДЛЯ СУММ И ИНТЕГРАЛОВ
1.	Вывод одного предварительного неравенства. Пусть А и В — любые
неотрицательные числа, а р и р' — любые- два числа, оба превосходящие
1,1,/
единицу и связанные соотношением — 4- — = 1 (такие числа будем называть
сопряженными). Тогда
ЛР Вр'
АВ^ + ^г.	(10.26)
£
Найдем максимальное значение функции f (х) = хр —— на полупрямой х2s0.
Поскольку f (х) = —\х>Р — 1) = — (х Р — 1 к то /' (х) >0 при 0<х<1
и f'(x)<0 при х>1. Поэтому функция имеет максимум в точке х= 1, при-
чем ее максимальное значение f (1) = 1---- = Д-. Итак, для всех х^О
Положив в последнем неравенстве х =	*) и умножив обе части этого не-
равенства на Вр', получим неравенство (10.26).
2.	Неравенство Гёльдера **) для сумм. Пусть at, Оа,..., ап и 62, •••, Ьп—
какие угодно неотрицательные числа, а р и р'- имеют тот же смысл, что и
выше. Тогда справедливо следующее неравенство:
п
2
/=1
(10.27)
которое называется неравенством Гёльдера для сумм.
Докажем сначала, что если Alf Л2......Ап; Вь ..., Вп — какие угодно
неотрицательные числа, удовлетворяющие неравенствам
п	п
2^1 И £<^1,
1 = 1	Z=l
(10.28)
то для этих чисел справедливо неравенство
п
2 AiBi^l-
(10.29)
В самом деле, записывая для
всех пар чисел Л/ и Bi неравенства (10.26) и
*) Здесь мы считаем, что В >• 0, ибо при В = 0 справедливость нера-
венства (10.26) не вызывает сомнений.
**) Гёльдер (1859—1937) — немецкий математик.
ДОПОЛНЕНИЕ 1 К ГЛАВЕ 10
347
суммируя эти неравенства по всем i от 1 до п, получим
Тем самым неравенство (10.29) доказано.
Положим теперь
Легко видеть, что числа Д/ и fi; удовлетворяют неравенствам (10.28), а поэ-
тому для этих чисел справедливо неравенство (10.29), которое в данном случае
можно записать так:
S aibl
1=1
.<=1
Из последнего неравенства вытекает неравенство Гёльдера (10.27).
Замечание. В частном случае р = р' = 2 неравенство Гёльдера пере-
ходит в следующее неравенство
Неравенство (10.30) называется неравенством Буняковского **) для сумм.
3.	Неравенство Минковского ***) для сумм. Пусть alt а2, .... ап; blt b2, ...,
Ьп — какие угодно неотрицательные числа, а число р>1. Тогда справедливо
следующее неравенство:
1 1.1
|.31)
Гл	Г Г л "Гл
2 (а£ + й,)₽	aPi + S b?
J=l	J »=1 J	1 = 1
называемое неравенством Минковского для сумм. Прежде всего преобразуем
сумму, стоящую в левой части (10.31). Можно записать
£ (а; + bt)P = S «i fa + *1)р-1 +^Ь1	+ bi)P~i.
1=1	1=1	1 = 1
К каждой из сумм, стоящих в правой части, применим неравенство Гёльдера.
*) Мы считаем, что хотя бы одно из чисел аг и хотя бы одно из чисел Ь[
отличны от нуля, ибо в противном случае формула (10.27) доказательства не
требует.
**) Виктор Яковлевич Буняковский (1804—1889) — русский математик.
***) Герман Минковский (1864—1909) — немецкий математик и физик.
348
определенный интеграл
[ГЛ. 10
П	/	1\	/	1 Р ------ 1
При этом, так как (р — р' = р и = ———
получим
Гл 1Р
.1 = 1
п
iwl
Р-1
1 Р
(at + bi)P)
Поделив обе части последнего неравенства на
неравенство Минковского (10.31).
S (ai+bi)P
получим
4. Интегрируемость произвольной положительной степени модуля интег-
рируемой функции. Докажем, следующую теорему.
Теорема 10.7. Если функция f (х) интегрируема на сегменте [а, 6], то
и функция | f (х) |г, где г — любое положительное вещественное число, также
интегрируема на сегменте [а, £>].
Доказательство. Достаточно доказать теорему для случая г<1,
ибо если r> 1, то функцию | f (х) |г можно представить в виде произведения
|f(x)|M |/(х)|г-И, где [г] — целая часть г, аг— [г] < 1. В силу замечания 2
п. 1 § 6 функция \f (х) | интегрируема на сегменте [а, Ь], а поэтому, в силу
свойства 3° § 5, функция | f (х) |lfl интегрируема на этом сегменте. Но тогда,
в силу того же свойства и интегрируемости функции |f(x)|r~функция
| f (х) |г также интегрируема на сегменте [а, ft], Итак, докажем теорему для
случая г<1. Положим г = — и заметим, что р>1. Так как функция | f (х) |
интегрируема на сегменте [a, ft], то для любого е>0 найдется такое раз-
биение Т этого сегмента, для которого
2 (Mi — mJ bxi < еР (6 — а)"-Р>.
i=i
(10.32)
Здесь через и т( обозначены точные грани функции | f (х) | на частичном
сегменте [х/^, хг]. Достаточно доказать, что сумма
л / 1 П
S — s = J] [МР — тР) bxi
i=l
(10.33)
меньше е.
Оценим эту сумму с помощью неравенства Гёльдера (10.27), полагая в нем
/ -L 1\	1	1
ai = \M{'—mPj(Mci)P, bi = (&Xi)p'’ Получим
1 1
(10.34)
ДОПОЛНЕНИЕ 1 К ГЛАВЕ 10
349
Докажем, теперь, что
/ 1 1\₽
[м? — т?) (Mi — mt).	(10.35)
Последнее неравенство посредством деления на Mi *) приводится к следую-
щему:
\Mj J " Mt'
В справедливости последнего неравенства легко убедиться, учитывая, что
0:£1, а р>1. Используя неравенство (10.35) и учитывая, что
У Дх, = Ь — а,
i=l
мы получим из неравенства (10.34) следующее неравенство:
П	L	_
2 (Mi-m-iKxi Р(Ь-а)Р'.
Отсюда, используя неравенство (10.32) и учитывая, что А.-|-А-=1, найдем
Теорема доказана.
5. Неравенство Гёльдера для интегралов. Пусть f (х) и g(x) — любые две
интегрируемые на сегменте [а, Ь] функции, а р и р' — любые два числа, оба
превосходящие единицу и связанные соотношением — + —7=1- Тогда спра-
ведливо следующее неравенство:
ъ
Р W g (х) dx
а
‘ 2 Г»	'll
IZWlPdx р $|g(x) |P'dxF
J L®	J
(10.36)
называемое неравенством Гёльдера для интегралов. Отметим, что существование
интегралов в правой части неравенства (10.36) гарантируется теоремой 10.7,
а интеграла в левой части — свойством 3“ § 5.
Докажем сначала, что если А (х) и В (х) — две неотрицательные и интег-
рируемые на сегменте [а, &| функции, удовлетворяющие неравенствам
то
ь	ь
АР (х) dx sg 1, ВР' (х) dx =5 1,
а	а
(10.37)
ь
А (х) В (х) dx =g 1.
а
(10.38)
В самом деле, в любой точке х сегмента [а, Ь] справедливо неравенство (10.26)
А(х)В(х)^^ + ^.
Р Р
*) Можно считать, что Mi > 0, ибо если Mi = 0, то т, = 0, и неравен-
ство (10.35) справедливо.
350
определенный интеграл
1ГЛ. 10
Отсюда, в силу оценки З2 из § 6 и формул (10.37),
о	. ь	ь
А (х)В (x)dx==Sy § Ар (х) dx + -L^ BP' (х) dx ~ = 1.
а	а	а
Неравенство (10.38) доказано.
Полагая
А (х) =
J f (х) I
ft	11
\]f(x)\Pdx Р
]g-(x)\
-ь -12
$|g(x)|P'dx ₽'
мы придем к следующему неравенству:
ъ
ъ	_ „
\\f(x)\PdxP $|g(x)|P'dx P'
a	~
О,
Так как, в силу замечания 2 п. 1 § 6/
ъ
J f W g (х) dx
а
b
< J I f (X) 11 g (х) I dx,
a
то неравенство Гёльдера (10.36) для интегралов установлено.
Замечание. В частном случае р = р' = 2 неравенство Гёльдера для
интегралов переходит в следующее неравенство;
ь	/ь - Гь
\f(x)g(x)dx =ё|/ j|f(x)|Mx]/ J | g (x) dx, (10.39)
a	' a	• a
называемое неравенством Коши — Буняковского для интегралов.
6. Неравенство Минковского для интегралов. Для любых неотрицательных
и интегрируемых на сегменте [а, й] функций f (х) ng (х) и для любого числа
р > 1 справедливо следующее неравенство:
[f(x) + g(*)lp<Mp*S
"ft	11
pp(x)dx ₽ +
а
Г* I1
j gp (X) dx P,
a
(10.40)
11 р
11
а
называемое неравенством Минковского для интегралов. Для получения этого
неравенства нужно исходить из формулы
ft	ft	ft
J [/ (x) + g (x)]P dx = p (x) [f (x) + g (x)]P-i dx + $ g (x) [/ (x) + g (x)]P-i dx
и применить неравенство Гёльдера к интегралам, стоящим в правой части
этой формулы. Детали рассуждений предоставляем читателю.
По индукции из неравенства (10.40) можно получить следующее неравен-
ство для п функций fi (х), /г(х),.... fn(x) неотрицательных и интегрируемых
на сегменте [а, ftj:
р	11
Л [/1(*) + fa W + - + fn WIP dx\P
w	/
f?(x)dx p
tb	11 rft 11
[f? (x)dx p + ...+ j/J(x)dx P.
®	La 1
ДОПОЛНЕНИЕ 2 К ГЛАВЕ 10
351
ДОПОЛНЕНИЕ 2 К ГЛАВЕ 10
ДОКАЗАТЕЛЬСТВО УТВЕРЖДЕНИЯ ИЗ П. 4 § в
Для удобства сформулируем еще раз утверждение из п. 4 § 6.
Если на сегменте [а, Ь] функция g (х) монотонна, a [ (х) интегрируема,
то на этом сегменте существует такое число 5, что
ъ	Е	ъ
\f(x)g (х) dx = g (а) $ /(х) dx + g (b) ( / (x) dx. (10.16) *)
a	a	t
Предварительно докажем следующее вспомогательное предложение.
Лемма Абеля **) Пусть t>i i.- v2 оп0 и щ, и2,..., ип — любые
числа. Если суммы Si — «1 4- u2 4- ... +«, при любом i заключены между А и В,
то сумма t>1u14~f2“2 + ••~i~vnun заключена между числами Ащ и BvY.
Доказательство. Имеем щ — Slt щ = S, — Sj-j. Поэтому
OjUi + v2u2 +... + vnun = vjSj + v2 (S2 — SJ +... -|- vn (Sn — Sn_j) =
= Si (Oj — v2) + S2 (o2 — О3) + ... + Sn_i (оя._1 vn) + Snvn.
Так как о;5=0 и vi— vi+1^0, то, заменяя в последнем соотношении каждое
Sj сначала на А, а потом на В, получим неравенства
A [(Vi — »2)+ (»г— Os)+--- + (^-i — y/i) + w«]=S
=sS fjЩ + v2 u2 + ... + vn un -< В [(vL — o2) +	— fs) + • • • + (Уп-1 — vn) + fn] •
Отсюда, замечая, что выражения в квадратных скобках равны vlt получим
Av,, ==£ OjUi + v2u2 4- ... + vnun sz Bvt.
Лемма доказана.
Замечание. При доказательстве леммы Абеля мы использовали пре-
п
образование суммы vkuk< которое обычно называют преобразованием Абеля.
*=1
Более полные сведения о преобразовании Абеля и важные применения этого
преобразования можно найти в п. 2 § 5 главы, 13.
Доказательство утверждения из п. 4 § 6. Допустим, что
функция g (х) не возрастает на [а, &} и • неотрицательна на этом сегменте.
Имеем, в силу интегрируемости f (х) g (х) ***),
&	п
\f (X) g (х) dx = lim 2 f g &Xi, где Д = max Дх;.
a	4 — °1 = 1
Пусть Mi и m, — точные грани f (x) на [x,_i, x,]. Тогда, поскольку g (x)
неотрицательна, справедливы неравенства
п	л	п
mig	S / (x<-x) g (x«-i) Дх£ S Mig (Xi_!) Ax;. (10.41)
«•=1 r	i = i	1=1
Так как g(x) не возрастает на [а, Ь], то'разность
У Mig (Xi-i) Дх,- — 2 mig (Xi-J bXi = (Mi — mi) g (x^) b.Xi
i = 1	i = 1	1=1
*) Для удобства мы сохраняем нумерацию приведенной формулы.
**) Нильс Генрих Абель — норвежский математик (1802— 1829).
***) См. свойство Зч § 5.
352
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
[ГЛ. 10
п
не превышает числа g (а) У] (44,- — m,) Дх,. Поскольку функция f (х) интегриру-
1=1
п	п
ема, сумма (Mi — пц) Дх,- = У а, Дх,- стремится к нулю при Д —► 0. Отсюда
1=1	1=1
и из неравенств (10.41) вытекает, что для любых чисел удовлетворяющих
неравенствам т,-^р;^44(, каждая из сумм
п х	п	п
У mig (х(_!) Дхг, 2 p,-g (х;_,) ДХ/, . У Mig (х,-—1) Дх,-
1=1	1=1	1=1
ъ
имеет своим пределам при Д—>0 интеграл $ f (х) g (х) dxt Согласно формуле
а
Х1
(10.12) числа р,-, mi =Gpj $£ М^ можно выбрать так, что J f (х) dx = р,- Дхр
*1-1
Так как функция F (х) = f(f)dt непрерывна на сегменте [а, &] (см. замеча-
а
i	xi
ние 3 п. 1 § 7), то числа S,- = У р* Дх* = ( f (!) dt заключены между точной
й = 1	а
нижней гранью т и точной верхней гранью М функции F (х) на сегменте
[а, Ь]. Положим t’1 = g(a), v2 — g(x1),	, o„ = g(x„_1), u, = px Дх,...un =
i
= pnbxn. Так как v1^v2's?...'^vn>^) и суммы S; = V u* заключены
”	fc=l.
между m и M, то, в силу леммы Абеля, сумма V g (Xi_j) р,- Дх; заключена
i — 1
между mg (а) и Mg (а). Но тогда и предел при Д —0 этой суммы заключен
между mg (а) и Mg (а), т. е. справедливы неравенства
ь
g(a) m^\j (х) g (х) dx^g (а) М.
а
х
Непрерывная функция F (х) = f (t) dt принимает любое значение А, заклю-
а
ченное между ее точными гранями т и /И, т. е. найдется такая точка что
ъ
£	5 f (X) g (*)
F(i) = y(t)dt = A = a g(a) -.
Поэтому
b	E
\f{x)g(x)dx = g(a)\jf(x)dx. -	(10.42)
a	a
Если невозрастающая функция g (x) имеет и отрицательные значения, то функ-
ция h (х) = g(x).— g(b) невозрастающая и имеет неотрицательные значения.
Поэтому, в силу (10.42), получаем
ь	Е
$ f (х) [g (х) — g (&)] dx = |g (a) — g (6)1 \ f (x) dx.
a	a
Отсюда путем несложных преобразований мы и получим формулу (10.16).
ГЛАВА И
ГЕОМЕТРИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ
ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
§ 1.	Длина дуги кривой
1.	Понятие плоской, кривой. Наиболее естественно рассматри-
вать кривую как след движущейся точки. В этом пункте мы прида-
дим этому представлению о кривой отчетливый математический смысл
и введем понятие так называемой
простой кривой.
Пусть. функции <р(0 и ф(7) не-
прерывны на сегменте [а, р] (аргу-
мент этих функций в дальнейшем
будем называть параметром). Если
рассматривать параметр t как вре-
мя, то указанные функции опреде-
ляют закон движения точки М с
координатами
х = <р(9, 7 = Ш (ПЛ)
a t р
по плоскости (рис. 11.1)*). Множество {44} точек М, отвечающих
всевозможным значениям параметра t из сегмента [a, р] естественно
рассматривать как след точки М, движущейся по закону (11.1). От-
метим, цто множество {А1}, представляющее собой след движущейся
точки, может не соответствовать нашим наглядным представлениям
*) Здесь и в дальнейшем мы будем называть плоскостью совокупность
всевозможных упорядоченных пар (х, у) чисел хну (каждую такую пару
мы будем называть точкой плоскости). Числа х и у называются координа-
тами точки (х, у). Для краткости мы будем также обозначать точку (х, у)
одной буквой М. Запись М (х, у) означает, что точка М имеет координаты
X и у.
354
ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
[ГЛ. 11
о кривой. Можно, например, указать такие непрерывные функции ср (/)
и tp (f), заданные на сегменте [0, 1], что след точки М, движущейся
по закону х — ср(0, _У=='р(О, будет заполнять целый квадрат*).
Поэтому естественно выделить такие множества {7И}, которые соот-
ветствуют нашим наглядным представлениям о кривой. Таким образом,
мы приходим к понятию, простой кривой.
Множество {А1} всех точек М, координаты х и у кото-
рых определяются уравнениями (11.1), будем называть простой
плоской кривой L, если различным значениям параметра t
из сегмента [а, р] отвечают различные точки этого мно-
жества.
Мы будем также употреблять следующую терминологию: «.урав-
нения (11.1) определяют простую плоскую кривую L» и «простая
плоская кривая L параметризована при помощи уравнений (11.1)».
Каждую точку множества {тИ}, фигурирующего в определении
простой плоской кривой, мы будем называть точкой этой кривой,
причем точки, отвечающие граничным значениям аир параметра t,
будем называть граничными точками простой, кривой.
Примером простой кривой может служить график непрерывной
на сегменте [а, р] функции y=f(x). В самом деле, этот график
можно рассматривать как след точки М, движущейся по закону
x — t, у = f(t),	причем, очевидно, различным значениям
параметра t отв.ечают различные точки графика.
Замечание 1. Простые кривые не исчерпывают всех точечных
множеств, заслуживающих наименования «кривая». Однако для наших
целей достаточно понятия простой кривой.
Замечание 2. Одна и та же простая кривая L может быть
параметризована различными способами. Мы будем рассматривать
всевозможные параметризации простой кривой L, получающиеся из
данной параметризации путем представления параметра t в виде не-
прерывных строго монотонных функций другого параметра s.
Замечание 3. Важным понятием является понятие простой
замкнутой кривой. Такая кривая образуется следующим образом.
Пусть Lx и Т2—две простые кривые, причем: 1) граничные точки
кривой Li совпадают с граничными точками кривой Т2; 2) любые не
граничные точки кривых Lx и Т2 различны. Кривая L, полученная
объединением кривых Lx и L2 и называется простой замкнутой
кривой.
2.	Параметрическое задание кривой. В математическом анализе
и его приложениях удобно рассматривать кривые, задаваемые пара-
метрически. Наглядными истоками такого способа задания кривой
служит представление о кривой как о геометрическом месте по-
следовательных положений движущейся точки. Например, геомет-
*) См. Бибербах, Дифференциальное и интегральное исчисление,
часть 1, стр. 156.
§ 11
ДЛИНА ДУГИ КРИВОЙ
355
рическое место последовательных положений точки Л1 с координа-
тами х и у, движущейся по закону
z2 — 1
х~а^ + 1>
/2_ 1
y = atF+i’
— оо < t < оо,
(И-2)
представляет-собой кривую, называемую строфоидой (рис. 11.2).
Заметим, что движущаяся по строфоиде точка М попадает в одно и
то же положение х = 0, _у = 0 дважды при t = —1 и <=1. Так
как мы рассматриваем последовательные положения движущейся точки,
то естественно считать различными точки
различным значениям параметра t.
Строфоида не является простой кри-
вой. Нетрудно, однако, убедиться, что.
область изменения параметра t можно
разбить на части таким образом, что соот-
ветствующие части строфоиды будут про-
стыми кривыми. Именно, разобьем число-
вую прямую — оо < t < оо на сегменты
[и—1, п], где л—любое целое число.
Очевидно, если мы будем рассматривать
параметр t на таком сегменте, то соот-
ветствующая часть строфоиды будет про-
стой кривой.
Мы воспользуемся этой идеей разбие-
ния на части для математического опре-
деления понятия кривой, задаваемой пара-
строфоиды, отвечающие
метрически.
Будем считать, что множество {/} представляет собой либо сегмент,
либо полусегмент, либо интервал, либо числовую прямую, либо от-
крытую или замкнутую полупрямую.
Введем понятие разбиения множества {^}. Будем говорить, что
конечная или бесконечная Система сегментов	разбивает мно-
жество {/}, если: 1) объединение всех этих сегментов представляет
собой все множество {^} и 2) общими точками любых двух сегмен-
тов системы мсгут быть лишь их концы.
Рассмотрим примеры
множеств {^}.
1. Система сегментов
бивает сегмент [0, 1].
разбиений некоторых из указанных выше
очевидно, раз-
Система сегментов 0, 4- ,	4-, 4- ,
I 2 J * 12*	41’
2«+i 1 т
 2д , —2л+1— > ••• разбивает полусегмент [0, 1).
3. Система сегментов {[л—1, я]}, где л —любое целое число,
очевидно, разбивает всю числовую прямую.
2.
2п— 1
8 I. ••• ,
356
ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
[ГЛ. И
Перейдем теперь к определению понятия кривой, задаваемой па-
раметрически.
Пусть функции ср (0 и (0 непрерывны на множестве {£} *). Бу-
дем говорить, что уравнения
х = ср(0, _у = ф(/)	(11.3)
задают параметрически кривую L, если существует такая си-
стема сегментов	разбивающих множество {/}, что для
значений t из каждого данного сегмента этой системы уравне-
ния (Н.З) определяют простую кривую.
При этом точки кривой L рассматриваются в определенном
порядке в соответствии с возрастанием параметра t. Именно,
если точка М1 соответствует значению параметра tv а точка М2 —
значению t2, jo считается предшествующей М2, если < t2. От-
метим, что точки, отвечающие различным значениям параметра,
всегда считаются различными.
Иными словами, кривую, задаваемую параметрически, можно рас-
сматривать как объединение простых кривых, причем эти простые
кривые последовательно пробегаются точкой М, координаты которой
определяются соотношениями (11.3), когда параметр t монотонно про-
бегает множество {/}.
Замечание 1. Простую кривую можно рассматривать как кри-
вую, заданную параметрически. В этом случае система сегментов,
разбивающих сегмент [а, р], сводится к одному этому сегменту.
В качестве примера рассмотрим кривую L, задаваемую парамет-
рически уравнениями
_r=cosi, _y = sin£,	(11.4)
где t изменяется на сегменте [0, 4л]. Очевидно, система сегментов
[О, л], [л, 2л], [2л, Зл], [Зл, 4л] разбивает сегмент [0, 4л], причем
для значений t из каждого указанного сегмента данной системы
уравнения (11.4) определяют простую кривую (полуокружность). На-
глядно ясно, что в рассматриваемом примере кривая L представляет
собой дважды обходимую окружность.
Замечание 2. Рассмотренный пример и пример строфоиды
показывают, что кривая, задаваемая параметрически, может иметь
точки самопересечения и даже целые участки самоналегания.
Замечание 3. В случае кривой, задаваемой параметрически
при помощи уравнений (Н.З), мы будем также говорить о парамет-
ризации указанной кривой при помощи этих уравнений. Одна и та
же кривая L может быть параметризована различными способами.
Мы будем рассматривать всевозможные параметризации кривой L,
получающиеся из любой данной параметризации путем представления
*) Множество {/} представляет собой одно из указанных выше мно-
жеств.
ДЛИНА ДУГИ КРИВОЙ
357
параметра t в виде непрерывных, строго возрастающих функций
другого параметра s. Отметим, что лишь при таких преобразованиях
параметра сохраняется порядок следования точек на кривой L.
3.	Понятие пространственной кривой. Понятие пространствен-
ной кривой вводится в полной аналогии с понятием плоской кривой.
Первоначально вводится понятие простой пространственной кривой
как множества {714} точек пространства, координаты х, у и z которых
определяются уравнениями
х=<р(0, > = <р(0, z = x(0> а=С^=СР,
(И.5)
при условии непрерывности функций <р (7), ф (£), у (/) и условии не-
совпадения точек множества {Д4}, отвечающих различным значениям
параметра t.
Понятие простой пространственной кривой и понятие разбиения
множества {£} изменения параметра, так же как и в плоском случае,
приводят к понятию пространственной кривой, задаваемой парамет-
рически уравнениями (11.5) при
условии монотонного изменения
параметра t на множестве {£}.
Отметим, что вся терминоло-
гия, введенная в предыдущих
пунктах, естественным образом
переносится на пространствен-
ные кривые.
4.	Понятие длины дуги
кривой. В этом пункте мы вве-
дем понятие-длины дуги кри-
вой, заданной параметрически.
Пусть кривая L задается
параметрически уравнениями
*=?(0. ^=ф(0, (11.3)
где параметр t изменяется на
сегменте [а, р].
Пусть Т—произвольное раз-
биение сегмента [а, р] точками
=	= . Обозначим через Мо, Mlt М2, ..., Мп
соответствующие точки кривой L (рис. 11.3). Возникающую при.
этом ломаную Л10Л41Л42...Мп будем называть ломаной*), вписанной
*) Будем называть прямой линию, определяемую параметрическими
уравнениями x = at-\-b, y=ct-]-d. Постоянные а, Ь,с и d заведомо можно
выбрать так, чтобы прямая проходила через две данные точки (xlt уг)
и М3 (х2, уг). Участок прямой между точками Mi и Л4а естественно назвать
отрезком, а совокупность конечного числа примыкающих друг к другу отрез-
ков естественно назвать ломаной.
358
ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
[ГЛ 11
в кривую L и отвечающей данному разбиению Т сегмента [а, р]. Так
как длина 7, звена	этой ломаной равна
Vl ? (ft) - ? (Л--1)]2+[ф (Ы - ф ft-J]2 *),
то длина l(ti) всей этой ломаной равна
7 ft) = 2 7Z = £ V1<р (Ы -«, ft_T)p + [Ф ft) - Ф ft-J]2.	(И.6)
i = l	Z=1
Определение. Если множество '{1(1$} длин вписанных в кри-
вую L ломаных, отвечающих всевозможным разбиениям Т сег-
мента [а, р], ограничено, то кривая L называется спрям-
ляемой, а точная верхняя грань I множества {/ ft)} называется
длиной дуги кривой L. -<
Замечание 1. Из определения кривой L, заданной параметри-
чески, и определения длины дуги I такой кривой следует, что длина I,
положительна, I > 0.
Замечание 2. Существуют неспрямляемые кривые. В допол-
нении к этой главе мы приведем пример плоской кривой, любая часть
которой неспрямляема.
В дальнейшем мы будем часто пользоваться следующей леммой.
Лемма. Пусть I* — длина ломаной, вписанной в кривую L
и отвечающей разбиению Т* сегмента [а, р], a l(t?) — длина лома-
ной, вписанной в кривую L и отвечающей разбиению Т, получен-
ному из разбиения Т* посредством добавления нескольких новых
точек. Тогда 1*	7 (t{).
Доказательство. Очевидно, достаточно рассмотреть случай,
когда к разбиению Т* добавляется одна точка у. Ломаная, отвечаю-
щая разбиению Т, отличается от ломаной, отвечающей разбиению Т*,
лишь тем, что одно звено	заменяется двумя звеньями Aftj С
и СА1г(С —точка кривой, соответствующая значению у параметра t).
Так как длина стороны Afi-1Afi треугольника M^CMi не превос-
ходит суммы длин двух других его сторон **) Afj—j С и CMit то
7* ft) 7ft).
Перечислим некоторые свойства спрямляемых кривых:
1°. Если кривая L спрямляема, то длина I ее дуги не зависит
от параметризации этой кривой.
*) Мы использовали формулу для расстояния между двумя точками
М,-_1 и координаты которых равны соответственно
*.-1 = <Р У{-1 = ф ft_i) и xt = <р (ti), у: = ф (/,•).
»*) Этот геометрический факт легко может быть доказан чисто аналити-
ческим способом.
ДЛИНА ДУГИ КРИВОЙ
359
§ 11
2°. Если спрямляемая кривая L разбита при помощи конечного
числа точек Л10,	Мп*) на конечное число кривых 'Li, то
каждая из этих кривых Li спрямляема и сумма длин It всех
кривых Li равна длине I кривой L.
3°. Пусть кривая L задана параметрически уравнениями (11.3).
Обозначим через I (f) длину дуги участка Lt кривой L, точки
которого определяются всеми значениями параметра из сег-
мента [a, t\. Функция I (0 является возрастающей и непрерывной
функцией параметра t. Эту функцию 1=1 (t) будем называть пере-
менной дугой на кривой L.
4°. Переменная дуга I может быть выбрана в качестве пара-
метра. Этот параметр называется натуральным параметром.
Справедливость свойства 4°-непосредственно вытекает из свойства 3°.
В самом деле, так как переменная дуга /=/(/) является возрастаю-
щей и непрерывной функцией параметра t, то и параметр t может
быть представлен в виде монотонной и непрерывной функции t=f(l)
переменной дуги I, и поэтому переменная дуга I может быть Ьыбрана
в качестве параметра.
Доказательство свойств I9 — З9.
I9. Пусть имеются две параметризации кривой L, а Л и s — параметры этих
параметризаций, определенные соответственно на сегментах [а, 3] и [а, й].
Так как t представляет собой строго монотонную и непрерывную функцию
от s, a s — строго монотонную и непрерывную функцию от t, то каждому
разбиению Т сегмента [а, 31 соответствует определенное разбиение Р. сегмента
[а, &] и наоборот. Очевидно, что вписанные в L ломаные, отвечающие соот-
ветствующим разбиениям сегментов [a, р] и [а, 6], тождественны, и поэтому
их длины I (ti) и /(О равны. Следовательно, множества {/(Л)} и {I(s/)} тож-
дественны. Отсюда вытекает, что длина дуги кривой не зависит от параметри-
зации этой кривой.
23. Очевидно, свойство 23 достаточно доказать для случая, когда кри-
вая L разбита точкой С на две кривые О и L2. Обозначим через 7 значений
параметра t, которому отвечает точка С. Тогда точки кривой Lt, соответст-
вуют значениям параметра t из сегмента [а, 7], а точки кривой L2 соответст-
вуют значениям параметра t из сегмента [7, р]. Пусть 7\ и Т2— произволь-
ные разбиения указанных сегментов, а Т — разбиение сегмента [о, 0], полученное
объединением разбиений T) и Т2. Если 7j (ti), l2(ti) n~l(ti) длины ломаных,
вписанных в кривые Llt L2 и L и отвечающих разбиениям 7\, Т2 и Т ука-
занных выше сегментов, то очевидно,
МО + МО = ЙО- •	(11.7)
Поскольку числа МО. МО и ЙО положительны, то из равенства (11.7) и
спрямляемости кривой L следует, что множества (/,•)} и {Г2 (Of длин
вписанных в кривые Li и L2 ломаных, отвечающих всевозможным разбиениям
сегментов [а, 7] и [7, р], ограничены, т. е. кривые Lt и L2 спрямляемы.
Отметим, что из равенства (11.7) и из определения длины дуги кривой следует,
*) При этом точки 7И0, Mt, .... Мп соответствуют значениям ta, tt, ...
... , tn параметра t, удовлетворяющим условиям а =19 </х <... <tn = р.
360
ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
[ГЛ. 1!
.что длины l2, 12 и I дуг кривых Lit L2 и L удовлетворяют неравенству *)
k +	(11.8)
Предположим, что /х -J- /2 < I. Тогда число
Z — (Zt+ Z2) = в
(И.9)
положительно. Из определения длины I дуги кривой L вытекает, что для
положительного числа е можно указать такое разбиение Т* сегмента [а; р],
что длина 7* (/,) ломаной, вписанной в кривую L и отвечающей этому разби-
ению, удовлетворяет неравенству I—1*1Ц)<С£. Добавим к разбиению Т*
точку 7 и обозначим полученное при этом разбиение через Т. Тогда, в силу
леммы этого параграфа, длина I (1,) ломаной, отвечающей разбиению Т, удов-
летворяет неравенству I — 7((;)<е. Так как разбиение Т сегмента [а, р]
образовано объединением некоторых разбиений Тг и Т2 сегментов [а, 7] и
[7, ₽]» то длины (4) и Т2 (0) ломаных, отвечащих этим разбиениям, удовлет-
воряют соотношению (11.7). Поэтому справедливо неравенство I—[/i(0)4"
4~ 7а (0)] < е- Так как (4) + /2 (tt) 1г 4- 12, то тем более справедливо нера-
венство 7	(/т + Z2) < е. Но это неравенство противоречит равенству (11.9).
Поэтому предположение, что 1г 4- 12 < /, неверно, а следовательно, в силу
(11.8), /j + /2 = I. Справедливость свойства 2° установлена.
3°. Из свойства 2Ч и замечания 1 этого пункта следует, что переменная
дуга I = 1(f) является строго возрастающей положительной функцией пара-
метра t. Для доказательства непрерывности функции I (/) воспользуемся следу-
ющими утверждениями:
1)	Пусть е — любое фиксированное положительное число, t — произвольная
точка сегмента [а, р], а М—соответствующая точка кривой L. Существует
такая ломаная, вписанная в кривую L, которая имеет точку М своей вершиной,
и длина которой отличается от длины кривой L меньше чем на е/2.
2)	Указанная ломаная может быть выбрана так, что длина каждого ее
звена будет меньше е/2.
3)	Пусть ломаная выбрана так, как указано в утверждениях 1) и 2).
Тогда часть кривой L, стягиваемая любым звеном рассматриваемой ломаной,
имеет длину меньше е.
Убедимся, что из сформулированных утверждений и монотонности функ-
ции I (I) вытекает ее непрерывность в любой фиксированной точке t этого
сегмента (в точках аир функция I (t) непрерывна соответственно справа
и слева).
Нам нужно доказать, что для любого е > 0 можно указать такое S > 0,
что при | Д/ | < & выполняется неравенство 1I (i 4- Д7) — I (f) | < е.
Рассмотрим то разбиение Т сегмента [а, р], которому отвечает ломаная,
обладающая перечисленными в утверждениях 1) и 2) свойствами. Обозначим
через 6 минимальную из длин двух частичных сегментов [Z&_i, /*], [/*, /^+1]
разбиения Т, примыкающих к точке t = tk сегмента [а, р]. Пусть приращение
Д/ аргумента удовлетворяет условию | Д/ | < В. Ради определенности будем
считать, что Д/>0. Так как t < t 4- М < t 4- 6 sg4t+i, то в силу строгого
возрастания функции I (t), справедливы неравенства
I (0 < I (t 4- до < / (7 4-») «U (^+1).
*) Из равенства (11.7) вытекает, что для любых разбиений и. Т2 сег-
ментов [а, 7] и [7, р] справедливо неравенство \ (4) 4- 72 (4) I. Отсюда и из
определения точной верхней грани получим неравенство (11.8).
5 и
ДЛИНА ДУГИ КРИВОЙ
361
В силу утверждения 3 справедливо неравенство
Отсюда и из предыдущих неравенств вытекает, что при 0 < А/ < 8 справед-
ливо неравенство
I (I + ДО — I (0 < в-
Случай А/ < О рассматривается -аналогично.
Перейдем теперь к доказательству утверждений 1), 2) и 3).
Доказательство утверждения 1). Пусть е — любое фиксиро-
ванное положительное число. Так как длина I (ф) всей кривой L, определяе-
мой параметрическими уравнениями (11.3), является точной верхней гранью
длин вписанных в эту кривую1 ломаных, отвечающих всевозможным разбиениям
сегмента [о, (3], то для данного е>0 можно указать такое разбиение Т**
сегмента [а, 0], для которого длина соответствующей ломаной, вписанной
в кривую L, отличается от I (Р) меньше чем на е/2. Добавим к разбиению Т**
точку t. В силу леммы этого- параграфа и определения длины дуги длина
ломаной, отвечающей полученному разбиению Т* сегмента [а, 0], отличается
от I (р) меньше чем на е/2, и эта ломаная имеет своей вершиной точку М
кривой, которая соответствует точке t сегмента [а, 0].
Доказательство утверждения 2). Так как непрерывные на
сегменте [a, 0] функции ср (/) и ф (0 равномерно непрерывны на этом сегменте,
то по заданному е > 0 можно указать такое 8 > 0, что для любого разбие-
ния Т сегмента [а, р] с длинами частичных сегментов Z(] меньшими 8
выполняются неравенства | <р ((;) — ср (^_г) I <
Поскольку длина 7,- звена ломаной, отвечающей данному разбиению, равна
/I? &) - <Р &-1)]2 + [ф (<,)— Ф (^«-1)12> т0. очевидно,	Рассмотрим те-
перь любое фиксированное разбиение Т' сегмента [а, р] с длинами частичных
сегментов меньшими 8 и добавим к нему точки разбиения Т* (см. доказатель-
ство утверждения 1). В результате мы получим разбиение Т, которому отве-
чает ломаная, вписанная в кривую L и удовлетворяющая всем условиям
утверждения 2).
Доказательство утверждения 3). Пусть ломаная	...
...	... Мп удовлетворяет условиям утверждений 1) и 2). Убедимся,
что длина каждой части кривой L, стягиваемой любым звеном рассматриваемой
ломаной, меньше^ е. В самом деле, пусть — длина части	кри-
вой L, a 1к— длина звена Мк-1Мк ломаной. Тогда, в силу условий утвержде-
я	i
ния 1), выполняется неравенство — 7^) < -у. Поскольку каждое слагае-
й = 1
мое 1к— последней суммы неотрицательно, то 1к — 1к<.~. Отсюда и
е
из неравенства lk < и вытекает требуемое неравенство lk < г.
Понятие длины дуги пространственной кривой, заданной параме-
трическими уравнениями (11.5), вводится в полной аналогии с поня-
тием йлины дуги плоской кривой. Рассматриваются длины l(ti) ло.ма-
ных, вписанных в кривую L, причем очевидно, что
Н*д= £ Vl<p (Ы - <?	+ [ф й) - ф (WP + lx &) - х
362
ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
[ГЛ. II
Пространственная кривая L, определяемая уравнениями (11.5), назы-
вается спрямляемой, если множество {/(7/)} длин ломаных, вписанных
в эту кривую, ограничено. Точная верхняя грань I этого множества
называется длиной дуги кривой L.
Отметим, что пространственные спрямляемые кривые обладают
перечисленными в этом пункте свойствами 1°, 2°, 3° и 4°. Доказа-
тельство этих свойств проводится совершенно аналогично доказатель-
ству для плоских кривых.
5. Достаточные условия спрямляемости кривой. Формулы для
вычисления длины дуги кривой.
Теорема 11.1. Если функции x — <p(t) и _у = ф(7) имеют на
сегменте [а, 8] непрерывные производные, то кривая L, определяе-
мая параметрическими уравнениями (11.3), спрямляема и длина I
ее дуги может быть вычислена по формуле
I = $	+	(11.10)
а
Доказательство. Докажем сначала, что кривая L спрямляема.
Для этого преобразуем выражение (11.6) длины 7(7/) ломаной, впи-
санной в кривую L и отвечающей произвольному разбиению Т
сегмента [а, р]. Так как функции <р (7) и ф(7) имеют на сегменте [а, р]
производные, то, в силу формулы Лагранжа, (t;) — ср (7/_т) = <?' (т/) Mt,
где 7/_г << tt, М{ = tt — ti_lt и ф (tt) — ф (7М) = ф' (tf) М(, где
< т* < tit Подставляя найденные выражения для ? (7/)—ср (7/_j) и
ф (t,) — ф (t(_j) в правую часть выражения (11.6), получим
7 = 2 к?/2(^)+Ф'2еп	(н.п)
>=1
По условию функции ср (7) и ф(7) имеют на сегменте [а, [3] непрерыв-
ные производные. Следовательно, эти производные ограничены, и
поэтому существует такое /И, что для всех t из сегмента [а, р] спра-
ведливы неравенства |ср' (t)[^M и | ф' (t) |	М-. Но тогда из фор-
мулы (11.11) вытекает, что
0<7(7/)==S J] УМ2 + М2 Д7г = ж/2 2 Mi = M /2 (р-а).
1=г	г=1
Таким образом, множество {7(7/)} длин вписанных в кривую L лома-
ных, отвечающих всевозможным разбиениям Т сегмента [а, р], огра-
ничено, т. е. кривая L спрямляема. Обозначим через I длину этой
кривой. Докажем, что длина I кривой L может быть вычислена по
формуле (11.10). Заметим, что правая часть формулы (11.11) похожа
ДЛИНА ДУГИ КРИВОЙ
363
«11
на интегральную сумму
п ___________________________________________
+	(11-12)
/ '=1
интегрируемой функции 1/Л<р'2(0 + ф,!! (0> причем эта сумма I {tiy
отвечает разбиению Т сегмента [а, ЭД и данному выбору точек на
частичных сегментах [£г_р Z;] этого разбиения. Докажем, что для
любого положительного е > 0 можно указать такое 8 > 0, что
при Д <3 (Д = шах Д^) выполняется неравенство
|^)-/|<у,	(И-13)
₽ _____________ s
где 1= ]Ар'2 (t) -ф ф'2 (t)dt — предел при Д->0 интегральных сумм
а
(11.12). Иными словами, докажем, что при достаточно «мелких»
разбиениях Т сегмента [а, ЭД длины l(ti) ломаных, вписанных
в кривую L и отвечающих этим разбиениям, как угодно мало
отличаются от интеграла I, стоящего в правой части формулы
(11.10). Отметим, во-первых, что
| /?'2(Ч) + Р(^) -	| <
< | ф' (Ф - ф' (тг) 1 Mi - mi *), (11-14)
где Mi и mi — точные грани функции ф' (t) на частичном сегменте
[/,_!, £,•]. В силу (11.11), (11.12) и (11.14) справедливы неравенства
\i(ti)-i{th Ml = | S (/т'2(т,.) + ф'2(т*)-
i — 1
-	Mi।< 2 |K<p'a(4)+f2(^)-
/ « =1
- V<?'2 eo + F (X/)| Ml ^j\(Mi- mi) Mi = S- s,	(.11.15)
i = 1
*) Для получения неравенств (11.14) мы воспользовались неравенством
| /а2 + 6*2 — У а2 4- 62 | sS ( b* — Ь |, где а2 = <р'2 (?,•), 6*2 = ф'2 (xf) и. 62 =
= ф'2 (х;) и неравенством | ф' (x?j — ф' (xj | Мt
Второе из этих неравенств очевидно, так как разность любых значений
функции не больше разности ее точных граней. Докажем первое из указанных
неравенств. Имеем
I к* 9. К9 1
I yai £*2 _ )/а2 + 62 I - -------, 1 —
/а2 + 6*2 + У а2 + 62
|&*-НР* + Ь| < |fe*-&|(| t>*| + IN)
4-"	p*[4-|6|
364
ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
[ГЛ. и
где S и s—верхняя и нижняя суммы функции ф' (t) для разбиения
сегмента [а, р]. Так как функции W! (t) -j-ф'2 (t) и ф' (t) интегри-
руемы на сегменте [а, р] (это вытекает из непрерывности производ-
ных <f>' (t) и ф' (/)  на сегменте [а, р]), то из определения интегрируе-
мости и из теоремы 10.1 (см. § 1 и § 3 главы 10) вытекает, что для
любого е>0 можно указать такое 8>0, чуо при Д < 8 (Д = max Д/г)
выполняются неравенства
М-/К-Г и $-«<-£.	(11.16)
Поэтому при Д<8, в силу (11.15) и (11.16), справедливы неравен-
ства 17 (ti) = (ti) - I {tb M +1 {th xj - /1< 7 ft) - I ft, T/} | +
4- ]/ft, t;} — Zj < -j- + -£- = у. Таким образом, справедливость не-
равенства (11.13) доказана.
Докажем теперь, что среди всевозможных ломаных, длины
l(ti) которых удовлетворяют неравенству (11.13), имеются ло-
маные, длины которых отличаются от длины I дуги кривой L
меньше чем на е/2.
Так как Z—точная верхняя грань множества {/ft)} длин лома-
ных, вписанных в кривую L* и отвечающих всевозможным разбиениям
сегмента [а, р], то найдется такое разбиение Т* этого сегмента, что
длина I* (ti) соответствующей ломаной удовлетворяет неравенствам
0</-7*ft)<|.	(11.17)
Разобьем теперь каждый из частичных сегментов ft_x, /J разбиения Т*
на столь мелкие части, чтобы максимальная длина Д разбиения Т
сегмента [а, р], полученного объединением указанных разбиений, была
меньше 8, Д<8. Очевидно, что длина 7 ft) ломаной, отвечающей раз-
биению Т, удовлетворяет неравенству (11.13). Так как вершины лома-
ной, отвечающей разбиению Т*, являются также вершинами ломаной,
отвечающей разбиению Т, то в силу леммы этого параграфа длина
7 ft) удовлетворяет неравенствам 0 < 7* ft) sS / ft) ^ /, и поэтому
в силу неравенства (11.17) выполняется неравенство
0^/-7ft)<y.	(11.18)
Итак, мы доказали, что среди ломаных, длины /ft) которых удовле-
творяют неравенству (11.13), имеются ломаные, длины 7ft) которых
удовлетворяют неравенству (11.18). Сопоставляя неравенства (11.13) и
(11.18), получим следующее неравенство:
1/-/|<®-
511
ДЛИНА ДУГИ КРИВОЙ
365
В силу произвольности е отсюда вытекает, что 1=1. Теорема до-
казана.
Замечание 1. Если функции <р (t) и ф (t) имеют на сегменте [а, |3|
ограниченные производные, то кривая L, определяемая уравнениями (11.1),
спрямляема. В самом -деле, в процессе доказательства теоремы (11.1) мы уста-
новили, что при условии ограниченности производных функций о (Z) и ф (О
длины I (tt) ломаных, вписанных в кривую L и отвечающих всевозможным
разбиениям Т сегмента [а, £], ограничены.
Замечание 2. Формула (11.10) для вычисления длины дуги справедлива,
если производные <f' (t) и ф' (I) определены и интегрируемы на сегменте [а, р].
В самом деле, из интегрируемости этих производных следует рх ограниченность
и поэтому, в силу замечания 1, спрямляемость кривой L. Заметим далее, что
для вывода неравенств (11.14), (11.15) и (11.16), а следовательно, и неравен-
ства (11.13) достаточно лишь существования и интегрируемости производных
ip' (/) и <|/(0, так как отсюда, согласно дополнению 1’к главе 10, вытекает
интегрируемость функции (t) + ф'2 (/). Все остальные рассуждения такие
же, как и в доказательстве теоремы 11.1.
Замечание 3. Если кривая L является графиком функции
y=f(x), имеющей на сегменте [а, Ь] непрерывную производную
f (х), то кривая L спрямляема и длина I дуги L может быть
найдена по формуле
ь
/ = $ /1 +/'2(х) dx.	(11.19)
а
Для доказательства заметим, что график рассматриваемой функции
представляет собой кривую, определяемую параметрическими уравне-
ниями x = t, у = f(t), a^t^b , и при этом, очевидно, выполнены
все условия теоремы 11.1. Поэтому, полагая в формуле (11.10)
<р (£) = /,	и заменяя переменную интегрирования t на х,
мы получим формулу (11.19). Отметим также, что если кривая L
определяется полярным уравнением г = г (9), 9й sg 9 sg 9г и функция г (9)
имеет на сегменте [9^ 62] непрерывную производную, то ,кривая L
спрямляема и длина I дуги L может быть найдена по формуле
_______
1= $ Кг2 (6) + г'2 (9) (Z9.	(11.20)
о<
Для доказательства воспользуемся формулами перехода от полярных
координат к декартовым
х = г (9) cos 9,	у = г (9) sin 9.
Таким образом( мы видим, что кривая L определяется параметриче-
скими уравнениями, причем функции ф = г (9) cos 9 и ф = г (9) sin 9
удовлетворяют условиям теоремы 11.1. Подставляя в (11.10) указан-
ные значения <р и <|), мы получим формулу (11.20).
Сформулируем достаточные условия спрямляемости пространствен-
ной кривой.
366
ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
[ГЛ. И
Если функции <f> (t), ф (t) и у (t) имеют на сегменте [a, pj не-
прерывные производные, то кривая L, определяемая уравнениями
(11.5), спрямляема и длина I ее дуги может быть найдена по
формуле
₽ ____________________
/ = $]Лр'2(0 + ф'гЮ+х,2СТ^- (11-21)
а
Доказательство аналогично доказательству теоремы 11.1.
Замечание 4. Если функции ср (I), ср (0 и у (t) имеют ограниченные
на сегменте [а, [1] производные, то кривая L, определяемая уравнениями (11.5),
спрямляема. Если при этом производные указанных функций интегрируемы
на сегменте [а, 0], то длина I дуги кривой L может быть вычислена по фор-
муле (11.21) (см. замечания 1 и 2),
6. Дифференциал дуги. Пусть функции x—<p(t) и у = ф(t)
имеют на сегменте [а, р] непрерывные производные. В этом случае,
в силу теоремы 11.1, переменная дуга 1(f) представляется следующей
формулой:
t _______________
+	(11.22)
Так как подынтегральная функция в правой части формулы (11.22)
непрерывна, то функция 1(f) дифференцируема, причем
/'(0 = К?'2(0 + Г(0
(см. п. 1 § 7 главы 10). Возводя обе части последнего равенства
в квадрат и умножая затем на eft2, получим формулу
[Г (f) dt]2 = [<?'(f) dt]2 + [ф' (t) dt]2.	(11.23)
Поскольку Г (f)dt = dl, <р' (t)dt = dx, ty'(f)dt = dy, то из (11.23)
найдем
dl2 = dx2 + dy2.	(11.24)
Из формулы (11.24), в'частности, следует, что если за параметр вы-
брана переменная дуга I, т. е. x — g(l) и у = h(l), то
Ш\2 , {dy\y
сЗг) =
(11.25)
Отметим, что при условии непрерывности производных функций
x = <o(f), y = ty(f) и z = -/(t) для дифференциала dl дуги простран-
ственной кривой, определяемой параметрическими уравнениями (11.5),
ДЛИНА ДУГИ КРИВОЙ
367
справедлива формула
dl2 = dx2	+dy2 + dz2.	(11.26)
Из	формулы	(11.26) следует, что	если за параметр выбрана перемен-
ная	дуга	I,	то	,
G-'MIWS)1’1-	<"-27>
7. Примеры вычисления длины дуги. 1°. Длина дуги циклоиды *)
x = a(t — sinУ — а (1 — cos О, 0^Z^2it. В рассматриваемом
случае <?' = а (1 — cos t), <]/= a sin £. Поэтому по формуле (11.10)
2ft	2ft
I = ( а 1^(1 — cos t)2 4-sin27dZ = 2а sin—dt = — 4а cos у = 8d.
о	о	-
2°. Цепной линией называется график функции j = a ch-^-**).
Найдем длину участка цепной линии, отвечающего сегменту [0, х].
Имеем по формуле (11.19)
Z(x) = jj /1 +у'2 (6) di - J j/" 1 + sh2~-di = ( ch^di = ash
DOO
3 . Найдем переменную дугу эллипса + р- = 1, а > i, отсчиты-
ваемую от точки 7И0 (0, й). Рассмотрим параметрические уравнения
эллипса х — a sin t, у — b cos t, 0=CZsC2k. По формуле (11.22) имеем
i _____________ t ______________________
I (Z) = J У®'2 (-t) -|- p (т) dx = У a2 cos21 + b2 sin21 dx =
о	0
t ____________
= a У1 — e2 sin2 x dx = aE (e, t).
e
TTa2 _ /,2
Число e — -—   называется эксцентриситетом эллйпса. Неопреде-
ленный интеграл $ 1^1 — е2 sin2 tdt, обращающийся в нуль при t = О,
называется эллиптическим интегралом 2-го рода и обозначается Е (е, t)
(см. § 11 главы 7).
*) Циклоида — плоская кривая, которую описывает точка окружности
радиуса а, катящейся без скольжения по прямой линии.
**) Наименование цепная линия связано с тем, что форму рассматриваемой
кривой имеет тяжелая цепь, подвешенная за концы.
368
ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
[ГЛ. 11
§ 2. Площадь плоской фигуры •)
1. Понятие квадрируемости плоской фигуры. Площадь ква-
дрируемой плоской фигуры. Понятие площади плоской фигуры,
ограниченной многоугольником *) **), известно из курса элементарной
математики. В этом пункте мы введем понятие площади плоской фи-
гуры Q —части плоскости, ограниченной, простой замкнутой кри-
вой L ***). При этом кривую L мы будем называть границей фигуры Q.
Мы будем говорить, что многоугольник вписан в фигуру Q, если
каждая точка этого многоугольника принадлежит фигуре Q или ее
границе. Если все точки плоской фигуры и ее границы принадлежат
некоторому многоугольнику, то мы будем говорить, что указанный
многоугольник описан вокруг фигуры Q.
Ясно, что площадь любого вписанного в фигуру Q многоуголь-
ника не больше площади любого описанного вокруг фигуры Q мно-
гоугольника.
Пусть {S;} — числовое множество площадей вписанных в плоскую
фигуру Q многоугольников, a — числовое множество площадей
описанных вокруг фигуры Q многоугольников. Очевидно, множество
{£<} ограничено сверху (площадью любого описанного вокруг фи-
гуры Q многоугольника), а множество {Sd} ограничено снизу (напри-
мер, числом нуль). Обозначим через Р точную верхнюю грань мно-
жества {SJ, через Р точную нижнюю грань множества {Sd}. Числа
Р и Р называются соответственно нижней площадью и верхней
площадью фигуры Q. Отметим, что нижняя площадь.Р фигуры Q не
больше верхней площади Р этой фигуры, т. е. Р Р. В самом деле,
предположим, что верно противоположное неравенство Р>Р. Тогда,
Р — Р
полагая — = в > 0 и учитывая определение точных граней, мы
найдем такой вписанный в фигуру Q многоугольник, площадь кото-
Р-\-Р	Р-ур
рого будет больше числа Р— & —	, т- е-	и такой
описанный вокруг фигуры Q многоугольник, площадь Sd которого
Р+Р	Р + Р
меньше числа Р -ф в =	, т. е. Sd < —. Сопоставляя получен-
ные два неравенства, найдем, что Sd<S,-, чего не может быть, так
*) Во второй части настоящего курса читатель найдет широкое при-
менение понятий площади плоской фигуры и произвольного множества точек
плоскости.
**) Многоугольником мы будем называть часть плоскости, ограниченную
простой замкнутой ломаной линией.
***) Отметим, что простая замкнутая плоская кривая L разделяет пло-
скость на две части — внутреннюю и внешнюю. Это утверждение было дока-
зано французским математиком Жорданом (1838—1922).
§ 2]	ПЛОЩАДЬ ПЛОСКОЙ ФИГУРЫ	369
как площадь Sd любого описанного многоугольника не меньше пло-
щади любого вписанного многоугольника.
Введем понятие квадрируемости плоской фигуры.
Определение. Плоская фигура Q называется квадрируе-
мой, если верхняя площадь Р этой фигуры совпадает с ее ниж-
ней площадью Р. При этом число Р = Р — Р называется пло-
щадью фигуры Q.
Замечание. В дополнении к этой главе будет приведен пример
неквадрируемой фигуры.
Справедлива следующая теорема.
Теорема 11.2. Для того чтобы плоская фигура Q была ква-
дрируемой, необходимо и достаточно, чтобы для любого положи-
тельного числа е можно было указать такой описанный
вокруг фигуры Q многоугольник и такой вписанный в фигуру Q
многоугольник, разность Sd — St площадей которых была бы
меньше е, Sd — St<Zs-
Доказательство. 1) Необходимость. Пусть фигура Q
квадрируема, т. е. Р = Р = Р. Так как Р и Р — точные верхняя и
нижняя грани множеств {5/} и {S^}, то для любого числа е > О
можно указать такой Вписанный в фигуру Q многоугольник, площадь S;
которого отличается от Р = Р меньше чем на е/2, т. е. Р — 5/<е/2.
Для этого же е>0 можно указать такой описанный многоугольник,
площадь Sd которого отличается от Р = Р меньше чем на е/2, т. е.
Sd — Р <_ г/2. Складывая полученные неравенства, найдем, что
Sd — 5/ < s.	’
2. Достаточность. Пусть Sd и Si —площади многоугольни-
ков, для которых Sd — S,<e. Так как Si^P^P^Sd, то
Р — Р < е. В силу произвольности е отсюда вытекает, что Р = Р.
Таким образом, фигура квадрируема. Теорема доказана.
Мы будем говорить, что граница плоской фигуры Q имеет пло-
щадь, равную нулю, если для любого положительного числа е > О
можно указать такой описанный вокруг фигуры Q многоугольник и
такой вписанный в фигуру Q многоугольник, разность Sd — пло-
щадей которых меньше е. Очевидно, теорему 11.2 можно также сфор-
мулировать следующим образом.
Для того чтобы плоская фигура Q была квадрируемой, необхо-
димо и достаточно, чтобы ее граница имела площадь, равную нулю.
Замечание. Во всех приведенных нами рассуждениях вместо
плоской фигуры можно рассматривать произвольное множество то-
чек плоскости.•-
Установим достаточный признак квадрируемости плоской фигуры.
Теорема 11.3. Если граница L плоской фигуры Q представляет собой
спрямляемую кривую, то фигура Q квадрируема.
Доказательство. Пусть /*—длина кривой L. Будем считать, что
кривая L параметризована с помощью натурального параметра I,
370
ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
ГГЛ. 11
причем, поскольку кривая L замкнута, ее граничные точки, отвечающие
значениям 0 и Z* параметра I, совпадают. Пусть е — произвольное положи-
тельное число. Разобьем сегмент [0,./*] точками 0 = Zo<
на п равных частей длины меньше е/9/*. Рассмотрим ломаную М0М^,	, Мп
(Мп = Мп), вписанную в кривую L и отве-
чающую указанному разбиению сегмента
(0, /*]. Точки Мо, Afj, .... Мп разбивают
кривую L на части Llt L2,	£„, длины
I* £
которых равны — <	. Очевидно, дли-
ны звеньев Mj_iMi указанной выше лома-
ной M0Mt ... Мп не больше /*/п. Поместим
каждое звено М{_1М{ внутрь квадрата со
стороной 31*1». так, как это указано на
рис. 11.4. Легко убедиться, что дуга L;,
стягиваемая звеном	располагается
внутри этого квадрата, ибо расстояние от
любой точки, расположенной вне или
на границе этого квадрата, до каждой
из точек Mi-1 и Mi не меньше 1*/п, и по-
этому, если бы какая-либо точка М дуги Li
была вне или на границе указанного квад-
рата, то вписанная в эту дугу ломаная
Mi^MMi имела бы длину, не меньшую 21*/п, т. е. большую, чем длина 1*/п
дуги L{, чего не может быть. Объединение всех таких квадратов, построен-
ных на всех звеньях ломаной MriMi ... Мп, представляет собой многоугольную
фигуру, содержащую кривую L, причем очевидно, что граница этой фигуры
представляет* собой объединение границ вписанного в фигуру Q многоуголь-
ника и описанного вокруг Q многоугольника. Очевидно также, что разность
Sd — St площадей этих многоугольников равна площади указанной фигуры,
а площадь этой фигуры не пре-
восходит суммы 8 площадей опи-
санных выше квадратов. Так как
9/*3	I*
S — п —— = 91* — < е (последнее
п2	п
неравенство следует из того, что
I* е \
— <, то Sd — Si Се. Поэто-
fi ^91*/ а 1
му, согласно теореме 11.2, фигура
Q квадрируема. Теорема доказана.
2. Площадь криволиней-
ной трапеции. Криволинейной
трапецией называется фигура,
ограниченная графиком задан-
ной на сегменте [a, Z>] непрерывной и неотрицательной функции
f(x), ординатами, проведенными в точках а и Ь, и отрезком оси
Ох между точками а и b (рис. 11.5). Докажем следующее утверж-
дение.
Криволинейная трапеция представляет собой квадрируемую
фигуру, площадь Р которой может быть вычислена по формуле
ь
P = ^f(x)dx.	(11.28)
§2]
ПЛОЩАДЬ ПЛОСКОЙ ФИГУРЫ
371
Доказательство. Так как непрерывная на сегменте [а, й]
функция интегрируема, то для любого положительного числа е мож-
но указать такое разбиение Т сегмента [а, Ь], что разность 5—у<е,
где S и s- соответственно верхняя и нижняя суммы разбиения Т. Но 5
и з равны соответственно' Sd и Si, где Sd и 5,- — площади ступенчатых
фигур (многоугольников), первая из которых содержит криволиней-
ную трапецию, а вторая содержится в криволинейной трапеции
(на рис. 11.5 изображены также и указанные ступенчатые фигуры). Так
как Sd —St<C.s, то, в силу теоремы 11.2, криволинейная трапеция
квадрируема. Поскольку предел при Д -> О верхних и нижних сумм
ь
равен ^f(x)dx и s^P^S, то площадь Р криволинейной трапеции
а
может быть найдена по формуле (11.28).
Замечание. Если функция f(x) непрерывна и неположительна
на сегменте [а, Ь], то значение интеграла ^f(x)dx равно взятой с от-
а
рицательным знаком площади криволинейной трапеции, ограниченной
графиком функции f(x), ординатами в точках а п b и отрезком
оси Ох между точками а и Ь. Поэтому, если f(x) меняет знак, то
ь
^f(x)dx равен сумме взятых с определенным знаком площадей кри-
а
волинейных трапеций, расположенных выше и ниже оси Ох, причем
цлощади первых берутся со зна-
ком 4*> а вторых — со знаком—.
3. Площадь криволинейного
сектора. Пусть кривая L задана
в полярной системе координат
уравнением г = г(0), а^0^р
(рис. 11.6), причем функция г (0)
непрерывна и неотрицательна на
сегменте [а, р]. Плоскую фигуру,
ограниченную кривой L и двумя
лучами, составляющими с поляр-
ной осью углы аир, мы будем на-
зывать криволинейным сектором.
Докажем следующее утверждение. Криволинейный сектор пред-
ставляет собой квадрируемую фигуру, площадь Р которой может
быть вычислена по формуле
р = 1 J r2(8)dd.	(11.29)
а
Доказательство. Рассмотрим разбиение Т сегмента [а, р]
точками а = 0О << 0Х . <; 0„ = р и для каждого частичного
372
ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
[ГЛ. II
сегмента 0J построим круговые секторы, радиусы которых равны
минимальному г, и максимальному Rt значениям г (9) на сегменте
lA-i, 6/]- В результате мы получим две веерообразные фигуры, пер-
вая из которых содержится в криволинейном секторе, а вторая содер-
жит криволинейный сектор (эти веерообразные фигуры изображены
на рис. 11.6). Площади St и Sd указанных веерообразных фигур
п	' п
равны соответственно у г?Двь- и -% JP Rj^i. Отметим, что первая
( = 1	г=1
из этих сумм является нижней суммой s для функции у г2 (9) для
указанного разбиения Т сегмента [я, р], а вторая сумма является верх-
ней суммой к? для этой же функции и этого же разбиения,- Так как
функция у г2 (9) интегрируема на сегменте [я, 0], то разность S— з =
= Sd — может быть как угодно малой. Например, для любого
фиксированного е>0 эта разность может быть сделана меньше е/2.
Впишем теперь во внутреннюю веерообразную фигуру многоуголь-
ник Qi с площадью S/, для которого Sf —Si'<y, и опишем во-
круг внешней веерообразной фигуры многоугольник Qa с площадью
,	— е
Sd для которого Sd — Sd<Z.-£ • Очевидно, первый из этих много-
угольников вписан в криволинейный сектор, а второй описан вокруг
него. Так как справедливы неравенства
S, < Si 4 V2 (9) dQ < Sd < s* (11 -30)
а
то, очевидно, Sd — Si<Z&. В силу произвольности е, отсюда вытекает
квадрируемость криволинейного сектора. Из неравенств (11.30) выте-
кает справедливость формулы (11.29).
4. Примеры вычисления площадей. 1°. Найти площадь Р фигу-
ры Q, ограниченной графиками функций у = хл и х==ух, я^1
(рис. 11.7). Поскольку фигура Q симметрична относительно биссект-
рисы первого координатного угла, то ее площадь может быть полу-
чена' посредством вычитания из 1 (площадь квадрата) удвоенной пло-
щади криволинейной трапеции, определяемой графиком функции _у = №
на сегменте [0, 1]. Таким образом, по формуле (11.28)
₽ = 1-2^“>-2[^Н=1
о
2 _а— 1
а+ 1 —а+ Г
*) Рассматриваемые веерообразные фигуры состоят из круговых секто-
ров. Каждый сектор квадрируем, и поэтому квадрируемы и веерообразные
фигуры. Поэтому для этих фигур можно найти многоугольники, площади 5,-
и Sd которых удовлетворяют указанным неравенствам.^
§ 2]
ПЛОЩАДЬ ПЛОСКОЙ ФИГУРЫ -
373
2°. Через три точки с координатами (— h, у0), (0, Jx), (h, у2)
проходит только одна парабола у — Ах2 -f- Bx -f- D (или прямая, если
эти точки лежат на одной прямой).
Действительно, система уравнений
относительно А, В, D *)
Ah2 — Bh 4- D = _у0,
D=yb
Ah2 + BhA-D=y2 .
имеет единственное решение. Именно:
д__Уо — 2^1 + Уг о__У-i — Уо
А~ 2h2	’ 2А ’
D=yy
Выразим площадь Р криволинейной трапеции, определяемой указан-
ной параболой, ординатами в точках (—h, 0) и (й, 0) и отрезком
оси Ох между этими точками (рис. 11.8), через ординаты у0, уг и у2.
Так как по формуле (11.28)
л
Р= J (^ + 5x+£>)rfx = [^ + v + Z?x]|lb=?T3 + 2L,/z’
— h
то, учитывая выражения для А и D, найдем
р = 4 Оо + 4Л + л)-
*) Эти уравнения представляют собой условия расположения точек
(— !li УоЪ (0< Уз) и (й, yd на параболе у = Ах2 Вх D.
374
ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
ГГЛ. И
3°. Найти площадь Р трилистника r = acos3S (рис. 11.9). Из
чертежа ясно, что вся площадь трилистника равна увеличенной в
шесть раз площади заштрихованной части трилистника, которая отве-
чает изменению 6 от 0 до л/6. Поэтому по формуле (11.29)
я /6
Р = 6^С cos2 39^9 = ^.
2 J	4
о
§ 3.	Объемы тел и площади поверхностей
1.	Понятие кубируемости и объема. Пусть Е— Некоторое конеч-
ное тело *). Рассмотрим всевозможные многогранники, вписанные в
тёло Е, и всевозможные многогранники, описанные вокруг тела Е.
Вычисление объема многогранника сводится к вычислению объемов
тетраэдров (треугольных пирамид). Поэтому мы будем считать извест-
ным понятие объема многогранника.
Пусть {V,-} — числовое множество объемов вписанных в тело Е мно-
гогранников, а {Vd} — числовое множество объемов описанных вокруг Е
многогранников. Множество {У,} ограничено сверху (объемом любого
описанного многогранника), а множество {Vrf} ограничено снизу
(например, числом нуль). Обозначим через V точную верхнюю грань
множества {У;}, а через V точную нижнюю грань множества
Числа V и V называются соответственно нижним объемом и верх-
ним объемом тела Е.
Отметим, что нижний объем V тела Е не больше верхнего объ-
ема V этого тела, т. е. V. Для того чтобы убедиться в справед-
ливости этого, достаточно провести рассуждения, аналогичные тем,
которые были сделаны для доказательства неравенства Р^Р
(см. п. 1 § 2).
Введем теперь понятие кубируемости тела.
Определение. Т ело Е называется к у бир у е м ы м, если верх-
ний объем V этого тела совпадает с нижним объемом V. При
этом число V=V=V называется объемом тела Е.
Справедлива следующая теорема.
Теорема 11.4. Для того чтобы тело Е было кубируемым,
необходимо и достаточно, чтобы для любого положительного
числа в можно было указать такой описанный вокруг тела Е
многогранник и такой вписанный в тело Е многогранник, разность
Vd—Vi объемов которых была бы меньше в. Доказательство этой
теоремы вполне аналогично доказательству теоремы 11.2 (см. п. 1 § 2).
*) Телом мы будем называть часть пространства, ограниченную замкну-
той непересекающейся поверхностью.
§ 3]
ОБЪЕМЫ ТЕЛ И ПЛОЩАДИ ПОВЕРХНОСТЕЙ
375
2.	Кубируемость некоторых классов тел. Будем называть
цилиндром тело, ограниченное цилиндрической поверхностью с об-
разующими, параллельными некоторой оси, и двумя плоско-
стями, перпендикулярными этой оси. Эти
плоскости в пересечении с цилиндриче- _________________*" " 4
ской поверхностью	образуют плоские	[	xnflfillf /г
фигуры, называемые основаниями цилинд-	k,	(Г
ра, а расстояние h между основаниями | Tn.	|1
цилиндра называется высотой цилиндра Ш РТТТТП
(рис. 11.10).	'•ЦЦЩ I
Докажем следующее утверждение. Если	^ч|Ц Ж
основанием цилиндра Е является квад-	Рис
рируемая фигура Q, тег цилиндр пред-
ставляет собой кубируемое тело, прицеле
объем V цилиндра Е равен Ph, где Р — площадь основания Q, а
h — высота цилиндра.
Так как фигура Q квадрируема, то для любого положительного
числа е можно указать такие описанный и вписанный в эту фигуру
многоугольники, разность Sd — S, площадей которых будет мень-
ше е/Л. Объемы Vd и Vt призм с высотой 1г, основаниями кото-
рых служат указанные выше многоугольники, равны соответственно
Sdh и Sth. Поэтому Vd — Vi = (Sd — Si)h<Z^h = e. Так как эти призмы
являются соответственно описанным и вписанным в рассматриваемое
тело Е многогранниками, то в силу
теоремы 11.4 тело Е кубируемо.
Поскольку Vi <zPh^ Vd, то объем
цилиндра равен Ph.
Из доказанного утверждения вы-
текает кубируемость ступенчатых
тел (ступенчатым телом назы-
вается объединение конечного числа
цилиндров, расположенных так, что
верхнее основание каждого преды-
дущего из этих цилиндров находится
в одной плоскости с нижним осно-
ванием последующего цилиндра, см.
рис. 11.11).
Замечание. Справедливо сле-
дующее очевидное утверждение.
Если для любого положительного числа е можно указать такое
описанное вокруг тела Е ступенчатое тело и такое вписанное
вЕ ступенчатое тело, разность Vd— Vi объемов которых мень-
ше е, то тело Е кубируемо.
Используем это замечание для доказательства кубируемости тела
вращения (рис. 11.12). Именно, докажем следующее утверждение.
376
ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
[ГЛ. П
Пусть функция y—f(x) непрерывна на сегменте [а, Ь]. Тогда
тело Е, образованное вращением вокруг оси Ох криволинейной
трапеции, ограниченной графиком функции f(x), ординатами в точ-
Рис. 11.12.
ках а и Ъ и отрезком осц Ох от
а до Ь, кубируемо и его объем V
может быть найден по формуле
ь
V — (x)dx. (11.31)
а
Доказательство. Пусть
л Т — разбиение сегмента [а, Ь] точ-
ками а — х0 < хг <... < хп — Ь,
mi и Mt — точные грани /(х) на
сегменте [Х;_р х,]. На каждом та-
ком сегменте построим два прямо-
угольника с высотами mi и Mt
(на рис. 11.12 изображены эти пря-
моугольники только на одном сег-
менте [х/_х, х(-]). Мы получим две
ступенчатые фигуры, одна из которых содержится в криволинейной
трапеции, а другая содержит ее. При вращении криволинейной тра-
пеции и этих ступенчатых фигур мы получим тело Е и два ступен-
чатых тела, одно из которых содержится в Е, а другое содержит Е.
Объемы Vi и Vd этих ступенчатых тел
равны соответственно
it J1, mj &Xi и л У Ml &х{.
i=i	г=1
Очевидно, эти выражения представляют
собой верхнюю и нижнюю суммы для
функции л/2(х). Так как эта функция
интегрируема, то разность указанных
сумм для некоторого разбиения Т сег-
мента [а, Ь] будет меньше данного по-
ложительного числа е. Следовательно,
тело Е кубируемо. Поскольку пре-
ь
дел указанных сумм равен u^/2(x)dx, то объем V тела Е может
быть найден по формуле (11.31).
3.	Примеры вычисления объемов.
1°. Объем тела, полученного вращением вокруг оси Ох астроиды
х2/з 4*>2/’= (рис. 11.13). Так как у = (аг/‘ — х*/»)’/*, то
а	49
V ='гс \ (а2/з	tZx = Га-- ла3.
— а
§3]
ОБЪЕМЫ ТЕЛ И ПЛОЩАДИ ПОВЕРХНОСТЕЙ
377
2°. Объем тела, полученного вращением вокруг оси Ох синусоиды
на сегменте [0, it]. Имеем
,, С. 9	,	С 1 — cos 2х ,
V= it \ sin2 х dx = it \	-----dx = -g-.
и	и

Рис. 11.14.
4.	Площадь поверхности вращения. Рассмотрим поверхность П,
образованную вращением вокруг оси Ох графика функции у =/(х),
заданной на сегменте [а, Ь] (рис. 11.14). Определим понятие квадри-
руемости поверхности вращения П. Пусть 7" — разбиение сегмента
[а, b] точками а = х0<х1 <;...<хп = Ь, и пусть Д, Д, ..., Ап—
соответствующие точки графика функции f(x). Построим ломаную
А^А^.. Ап. При вращении этой ломаной вокруг оси мы получим
поверхность П (Д), составленную из
боковых поверхностей усеченных ко-
нусов. Обозначим через Р (х{) пло-
щадь поверхности П (Д), Если yt —
ординаты f(x) в точках Х{, a /г — дли-
на звена Лг-1 Д ломаной А^... Ап,то
P(x0=2it ^.Уы+У11(==
1 = 1
п
= к (yi-i+yi)k- (П-32)
i = 1
Сформулируем следующие опреде-
ления.
1°. Число Р называется пре-
делом площадей Р (х,), если для
любого данного положительного числа s можно указать такое
положительное число 3, что для любого разбиения Т сегмента
[а, Ь], максимальная длина Д частичных сегментов которого
меньше 8, выполняется неравенство | Р (х;) — Р | < г.
2°. Поверхность вращения П называется квадрируемой, если
существует предел Р площадей Р (х,). При этом число Р назы-
вается площадью поверхности П.
Докажем следующее утверждение.
Если на сегменте [а, д] функция f(x) имеет непрерывную про-
изводную f (х), то поверхность П, образованная вращенцем гра-
фика этой функции вокруг оси Ох, квадрируема и ее площадь Р
может быть вычислена по формуле
ь _____________
P = 2it J/(x)/l+/'2(x)dx.	(11.33)
а
378
ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
[ГЛ. И
Доказательство. Длина Ц звена ломаной А0А1...А„
равна К(Л — Л-i)2 + (Л — Ji-i)2 • По формуле Лагранжа имеем
Д; - Л-i =/(*/) ~ /(Л-i) =Г (U (Л — Л-i)- Полагая х/-х^_1 = Дх,-,
получим /г =	1 +/'2 (У Дх,. Поэтому, согласно (11.32),
Р (Xi) = 2к 2 f&) V1 + Г (U Дл +
г= 1
+ 4 £ [(л-i - /&)) + (л -/&))] Ki +/'2&) Дл1 (11.34)
4 = 1	>
Первая сумма в правой части соотношения (11.34) представляет
собой интегральную сумму функции 2к/(х) 'V1 + /'2 (х), которая,
в силу условий утверждения, интегрируема'и имеет предел Р =
ь ___________________
= 2тс ^/(х) 1^1 +/'2(х) dx. Докажем, что выражение в фигурных
а
скобках в правой части соотношения (11.34) имеет предел, равный
нулю. В самом деле, пусть е —любое положительное число. Так как
функция f(x) равномерно непрерывна на сегменте [а, &], то по дан-
ному г > 0 можно указать такое 8 > О, что при Д <; 8 (Д = шах Дх;)
выполняются неравенства | Ji_i —/(?;) | < е и |jf —/(В,)| <е. Если
М — максимальное значение функции V^l +/'2 (х) на сегменте [а, Ь],
то для выражения в фигурных скобках в правой части соотношения
(11.34) получаем оценку
Z [(у.-i -/&)) + (Jz -/&))] Ki +/'2 (?i) Дл
i = I
= 2M(b - a)s.
В силу произвольности e > 0 предел указанного выражения равен
нулю. Итак, мы доказали существование предела Р площадей Р (xt)
и установили, что этот предел может быть вычислен по формуле (11.33).
Утверждение доказано.
Замечание 1. Квадрируемость поверхности вращения можно дока-
зать при более слабых условиях. Достаточно потребовать, чтобы функция
f (х) была определена и интегрируема на сегменте [а, 6]. Из этого предпо-
ложения вытекает интегрируемость функции / (х) р'Д + /'2 (х) (см. дополне-
ние 1 к главе 10). Дальнейшие рассуждения ничем не отличаются от рас-
суждений, проведенных при доказательстве утверждения этого пункта.
Замечание 2. • Если поверхность П получается посредством враще-
ния вокруг оси Ох кривой L, определяемой параметрическими уравнениями
x = <f(/), у = ip (t),	то4 осуществляя замену переменных под знаком
§ 4]
НЕКОТОРЫЕ ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ
379
определенного интеграла в формуле (11.33), получим следующее выражение
для площади Р этой поверхности:
3	_______________
Р = 2л $ ф (0 /ср'2 (0 _|_ ф'2 (0 dt.
(11.35)
Рассмотрим примеры вычисления площадей поверхностей вращения.
1°. Найдем площадь Р поверхности эллипсоида вращения. Пусть эллипс
4^2 у2
4-	= 1 вращается вокруг оси Ох. Рассмотрим сначала случай а > b
а2 о2
(вращение вокруг большой оси эллипса). Так как в этом случае f (х) =
р,  ______ _ Гаа t>2
—— 1/ а2 — х2, то, полагая е= I/ --------—, найдем
а ’	' v "2
а2 — Ь2
а2
а
a	b С	/	1
р = 2л / (х) }^1 + /'2 (х) dx = 2л — \ ]/ а2 — е2х2 dx = 2лЬ — arcsin е
а	—а
Если а < Ь, то, полагая е =
и проводя соответствующие вычисле-
ния, получим
п о , !. I 412 1 . 1 -|- е\
Р = 2л6 6 +	— In -j—!— .
\ 2b е 1 — е /
2°. Найдем площадь Р поверхности, образованной вращением вокруг
оси Ох циклоиды, определяемой параметрическими уравнениями х =
= a (t—sin t), у = а(\—cast), 0^<^2л. По формуле (11.35) имеем
3	2л
Р = 2л f ф (0 /?'2 (0 + ф'2 (0 dt = 2 /2 ла2 ( (1 — cos 0s/« dt = ла2.
V	•)	о
а	О
§ 4. Некоторые физические приложения
определенного интеграла
1. Масса и центр тяжести неоднородного стержня. Рассмот-
рим неоднородный стержень, расположенный на сегменте [a, ft]
оси Ох Пусть р(х) — линейная плотность стержня*). Обозначим
через Т.разбиение сегмента [a, ft] точками а = хй <Zхх <...<хп = ft.
Выберем на каждом частичном сегменте х(] точку и составим
п
сумму У] р(£;)Дхг. Так как каждое слагаемое этой суммы представ-
i = 1
ляет собой приближенное значение массы части стержня на сегменте
*) Если Am— масса части стержня на сегменте [х, х-рДх], то отноше-
Д/п	,	„ „
ние называется средней линейной плотностью стержня на этом сегменте.
„	. .	. .	.. Д/п
Линеинои плотностью о (х) называется предел р (х) = lim -т—.
380
ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
(ГЛ. 11
[xuj, xt], то указанную сумму естественно принять за приближенное
значение массы всего стержня. Согласуясь с этими предварительными
рассуждениями, мы определим массу М всего стержня как предел
п	4
сумм 2 Р (W ^xi- пРи стремлении к нулю Д = шах Дх,-, т. е. как
i = 1
b
интеграл ^p(x)dx. Таким образом,
а
b
M^\t>(x)dx.	(11.36)
а
Для определения центра тяжести неоднородного стержня воспользу-
емся формулой для координаты центра тяжести системы {/И/ (х,-)}
материальных точек, имеющих массы mt и расположенных в точках
х,- оси Ох. Именно, координата хс центра тяжести системы {тД
может быть найдена по формуле
S т‘х‘
OTjXi + ffl2x2+... + wnx„ i=i	ш 371
У mi
i=i
Рассмотрим разбиение T сегмента [а, b] точками а = ха<^х1<^...
...<Zxn = b и вычислим массу mt части стержня, расположенной
xi
на сегменте [хг_х, хг]. Имеем по формуле (11.36) т,— р(х)Нх.
*	'	xi-l
Применяя формулу (10.13) среднего значения, получим также, что
т, — р (£;) Дх,-. Считая, что масса пц сосредоточена в точке сег-
мента [хг_1( хг], мы можем рассматривать неоднородный стержень
как систему материальных точек с массами mit расположенных в точ-
ках $г сегмента [а, Ь]. Поскольку-
п	п xi	Ъ
 у mt — У, J р (х) dx — J р (х) dx — М,
1 = 1	i = 1	а
то по формуле (11.37) найдем приближенное выражение для коорди-
наты хс центра тяжести неоднородного стержня
п
Л Е.-Р fc)
------•	(11-38)
Выражение, стоящее в числителе правой части соотношения (11.38),
ДОПОЛНЕНИЕ К ГЛАВЕ 1!
381
представляет собой интегральную сумму для функции хр(х) на сег-
менте [а, &]. В соответствии с проведенными рассуждениями мы' оп-
ределим координату хс центра тяжести неоднородного стержня по
формуле
ь
§ хр (х) dx
хс = —ь----------.	(11.39)
j р (х) dx
а
2. Работа переменной силы.' Пусть материальная точка переме-
щается из точки а оси Ох в точку b этой оси под действием силы
F, параллельной оси Ох. Будем считать, что эта сила является функ-
цией от х, определенной на сегменте [а, Ь]. Пусть Г —разбиение
сегмента [а, Ь] точками а = xn<^x1<Z- • - <Zxn = b. Выберем на каж-
дом частичном сегменте хг] точку Ег и будем считать прибли-
женным значением работы А переменной силы F (х) на сегмент^ [а, Z?]
п
выражение У, F (^,-) Ах,. Согласуясь с этими предварительными рас-
суждениями, мы определим работу А переменной силы F (х) на сег-
ь	.	-
менте [а, Ь] как интеграл ^F(x)dx. Таким, образом,
<	а
Ъ
A==\F(x)dx.	(11.40)
а
S
ДОПОЛНЕНИЕ К ГЛАВЕ И
ПРИМЕР НЕКВАДРИРУЕМОЙ ФИГУРЫ
1. Будем называть полуоткрытым треугольником множество точек
треугольника, из границы *) которого удалены точки двух его сторон и двух
вершин, прилегающих к этим сторонам. Рассмотрим построение кривой L,
которая будет частью границы неквадрируемой фигуры Q. Это построение
производится путем последовательных удалений определенных полуоткрытых
треугольников из некоторого данного равнобедренного прямоугольного тре-
угольника Т, который для удобства дальнейших рассуждений мы обозначим
Т [0, 1]. Координаты вершин этого треугольника равны (0, 0), (1, 1), (2, 0)
(рис. 11.15). Опишем теперь процесс последовательных удалений из треуголь-
ника Г [0, 1] определенных полуоткрытых треугольников:
1.	Удаляется полуоткрытый треугольник, одна вершина которого имеет
координаты (1, 1), а две другие расположены на оси Ох. Площадь Si уда-
ляемого треугольника равна х/4. Полученная в результате фигура изображена
*) Г^ница треугольника — множество точек его сторон и вершин.
382
ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
[ГЛ. И
на рис. 11.16. Она состоит из двух треугольников 7^0, 1] и Т ^1, lj, пло-
щади которых равны друг другу.
2.	Из треугольников 7^0, lj и lj удаляется по одному треуголь-
нику, сумма S2 площадей которых равна Vs- Полученная в результате фигура
изображена на рис. .11.17. Она состоит
ГГ1 11 ?Г1 11	гГ1 11
[4 ’ 2 J ’	[2 ’ 4]’ L 4 ’ J’
из четырех треугольников:
площади которых равны друг другу.
3.	Из каждого указанного треугольника удаляется по одному треуголь-
нику, сумма S3 площадей которых равна 1/1й. Полученная в результате фи-
гура изображена на рис. 11.18. Она состоит из восьми треугольников:
площади которых равны друг другу.
4.	Из каждого указанного треугольника удаляется по одному треуголь-
нику, сумма <S4 площадей которых равна !/32. Полученная в результате фи-
ДОПОЛНЕНИЕ К ГЛАВЕ II
383
гура изображена на рис. 11.19. Она состоит из шестнадцати треугольников
равной площади. Каждый из этих треугольников мы обозначим символом
г[£. Ц1]. Р-». .........
Дальнейший процесс удаления треугольников очевиден. Перейдем теперь
к определению кривой L. Треугольники
отрицательные целые - числа, удовлет-
воряющие условию р<2л), получен-
ные в описанном выше процессе, об-
ладают следующим свойством: пусть
у Г Pi Pi + И и у Г Рг Рз + П_____________
I 9 2rei I I 2n*
’ 2Лг J
что -£j—
2».
Тогда вто-
два треугольника таких,
__Ра Рз + 1 Pi 4~ 1
2711
рой из этих треугольников содержится
в первом. Отметим также следую-
щее очевидное свойство треугольников
7-ГХ р+11.
L 2™ ’ 2Л J ‘
/у Г Ра Ра ~
I L 2Л* ’ 2”ft
2П3
при п—*со их диаметры *)
стремятся к нулю. Пусть
, k=l, 2, ..., стягивающаяся система треугольников (это
означает, что треугольник, отвечающий индексу k, содержит треугольник,
отвечающий индексу fe-J-1, и при й—-со диаметры треугольников стремятся
к нулю). Каждая такая стягивающаяся система треугольников имеет ровно
одну общую точку**). Рассмотрим всевозможные стягивающиеся системы ука-
занных выше треугольников. Кривую L мы определим как множество {М}
всевозможных точек, каждая из которых представляет собой общую точку не-
-	-	т Г Р Р + 1 I
которой стягивающейся системы указанных выше треугольников Т I	.
Отметим, что множеству {Л1} (кривой L) принадлежат вершины всех
треугольников	j • Чтобы убедиться в этом, заметим, что вер-
шина каждого такого треугольника принадлежит стягивающейся системе тре-
(_ Г 2*р	2*р+1Д	f Г2^р — 1	2»р 1) п
угольников 1Т -----—, ——:— }• и системе -IT —-—:—,  —И. Для
I L 2л+* 2л+а JI	' L 2Л+* 2n+ftJJ
того чтобы убедиться, что построенное нами множество {УИ} является простой
кривой в смысле определения, данного в п. 1 § 1 этой главы, мы должны
*) Диаметром треугольника называется длина его максимальной сто-
роны.
**) В главе 3 (см. п. 2 § 3) мы доказали, что стягивающаяся система
сегментов имеет ровно одну общую точку. Проектируя стягивающуюся си-
стему треугольников на оси Ох и Оу, мы получим стягивающиеся системы
сегментов на координатных осях. Пусть х и у — соответственно общие точки
указанных стягивающихся систем сегментов на осях Ох и Оу. Читатель легко
убедится, что точка М с координатами х и у является единственной общей
точкой рассматриваемой стягивающейся системы треугольников.
384
ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
(ГЛ. И
доказать, что все точки множества М определяются параметрическими урав-
нениями х = ср (1), у ф (/), a^t^b, где <р (() и ф (()— непрерывные
функции *).
Рассмотрим сегмент [0, 1] оси t. Каждому сегменту	где Р и
п — любые неотрицательные целые числа, р < 2Л, поставим в соответствие
треугольник	И **)• На рис. 11.20 изображены сегменты, которым
О 1/8 1/4 3/8 1/2 8/8 3/4 7/8 1 t
j----------1----1-----1---->----------1----1-------
Рис. 11.20.
отвечают треугольники 7^-^-,	Любая точка t сегмента [0, 1] принад-
«	-	(Г Pk Pk Н-1 "11
лежит всем сегментам некоторой стягивающейся системы г -£=-,	;>
U 2я*	2 k Я
***). Поставим в соответствие этой точке t общую точку М сгяги-
Pfc 4~ 1 11 Таким образом, каж-
2V Я
сегментов
вающейся системы треугольников
дому значению t из сегмента [0, 1] ставится в соответствие два числа х и у —
координаты точки М. Следовательно, х и у являются функциями параметра t.
Убедимся, что эти функции х = <р (/) и у = ф (t) непрерывны на сегменте [0, 1].
& самом деле, пусть г— любое данное положительное число, t — данная точка
сегмента [0, 1] и М — точка кривой L, определяемая этим значением пара-
метра t. Из стягивающейся системы Г-^- ~Я 1
треугольников, опре-
2я* Я
деляющих точку М, выберем треугольник, диаметр которого меньше в и
[Pk Pk 11	-	*
— , который содержит точку г, определяю-
2пй 2М
щую М (а следовательно, х и у). Все точки кривой L, определяемые значе-
ниями t из этого сегмента, расположены в указанном выше треугольнике,
и поэтому их координаты отличаются от координат точки М не более чем
на е. Но это означает, что функции tp (() и ф (<) непрерывны в указанной
точке.
2. Перейдем к построению неквадрируемой фигуры Q. Рассмотрим
квадрат Q, сторона которого равна 2. На каждой стороне этого квадрата
построим равнобедренные прямоугольные треугольники 71, Г2, Т3, Tt, в ре-
*) То-, что различным t отвечают различные точки множества М, оче-
видно из построения кривой L.
**) Отметим, что каждому такому треугольнику отвечает только один
*** Пусть t — любая точка сегмента [0, 1] и п — любое целое положи-
тельное число; Тогда, очевидно, точка t принадлежит некоторому сегменту
|^,	1J, причем каждый такой сегмент, отвечающий номеру п + 1, со-
держится в сегменте, который отвечает номеру п.
ДОПОЛНЕНИЕ К ГЛАВЕ И
385
зультате мы получим квадрат <2 со стороной 2]/? (рис. 11.21). Затем из
каждого такого треугольника произведем удаление полуоткрытых треуголь-
ников так, как это описано выше, в пункте 1. В результате мы получим
фигуру Q, ограниченную замкнутой кривой, состоящей из четырех кривых,
конгруэнтных * **)) кривой L (см. п. 1). Докажем, что полученная фигура Q
неквадрируема. Рассмотрим две специаль-
ные последовательности многоугольников
{•Зл} и {Qn}. первая из которых со,стоит
из вписанных в фигуру Q многоугольни-
ков, а вторая из описанных вокруг Q
многоугольников. Последовательность |<2Я|
получается посредством присоединения к
квадрату Q полуоткрытых треугольников,
удаляемых из треугольников 7\, Т2, Т3,
на каждом нечетном шаге процесса, опи-
санного в п. 1. Последовательность
получается посредством удаления из квадрата
Q полуоткрытых треугольников, удаляемых
из треугольников Tlt Т2, Т3, Tt на каждом
четном шаге процесса, описанного в п. 1.
Очевидно, что любой вписанный в фигуру Q
многоугольник содержится в каком-нибудь
многоугольнике Qn, а любой описанный вокруг
фигуры Q многоугольник содержит какой-нибудь многоугольник Qn. Поэтому
предел последовательности площадей многоугольников Q„ равен нижней
площади Р фигуры Q, а предел последовательности {sn} площадей много-
угольников Q„ равен верхней площади Р фигуры Q. Легко убедиться, что
п	п .
?П = 4 + 2 4^Г’ а Зп = 8 “ Т 2 4^ П0ЭТ0МУ - = “"Jo = ¥’
* = 1	ft = l	а~"°°
—	-	22	—
а Р = lim Sn = -g-. Так как Pz£P, то фигура Q неквадрируема. Отметим,
Л-^-ОО	—
что разность Р — Р = 2. Таким образом, граница рассматриваемой фигуры Q
имеет площадь, равную 2.
3. Докажем, что любая часть кривой L, ограниченная двумя различными
точками, неспрямляема. Докажем сначала, что такая часть L' кривой L имеет
отличную от нуля площадь, т. е. любой многоугольник, покрывающий L',
имеет площадь, большую некоторого положительного числа. Заметим, что L'
содержит часть L", отвечающую точкам некоторого сегмента
Р Р+1
2я > 2я
*) Множества А и В называются конгруэнтными, если они могут быть
совмещены движением.
**) Эти формулы легко получить, если учесть, что суммы площадей
треугольников, удаляемых на нечетных шагах процесса, образуют гео-
метрическую прогрессию 1,	а суммы площадей треугольников,
удаляемых на четных шагах процесса, образуют геометрическую прогрес-
сию Т’ •••
386
ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
1ГЛ. И
и поэтому L” содержится в треугольнике Т	и м°жет быть по-
лучена посредством удаления из этого треугольника определенных полуоткры-
тых треугольников (см. п. 1 настоящего дополнения). Легко подсчитать, что
сумма S площадей всех удаляемых полуоткрытых треугольников меньше пло-
щади S т треугольника Т | ~	j. Следовательно, часть L" имеет пло-
щадь, равную ST— S >0. В § 2 этой главы при доказательстве квадрируемости
фигуры, ограниченной спрямляемой кривой, мы доказали, что площадь спрям-
ляемой кривой равна нулю (спрямляемую кривую можно покрыть многоуголь-
ником сколь угодно малой площади). Поэтому часть L” кривой L, а следо-
вательно, и часть L', содержащая L", неспрямляема.
Замечание. Каждая из построенных функций <j>(t) и Ф(Z) не имеет
производной ни в одной точке сегмента [0, 1].
ГЛАВА 12
ПРИБЛИЖЕННЫЕ МЕТОДЬ! ВЫЧИСЛЕНИЯ КОРНЕЙ
УРАВНЕНИЙ И ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
В этой главе рассматриваются приближенные методы нахождения
корней алгебраических и трансцендентных уравнений и вычисления
определенных интегралов.
§ 1.	Приближенные методы вычисления корней уравнений
В этом параграфе мы займемся приближенным вычислением одного
из корней уравнения /(х) = 0, где y — f(x) — некоторая непрерывная
или дифференцируемая функция. Мы будем считать, что интересующий
нас корень с этого уравнения изолирован на некотором сегменте
[а, Ь], т. е. будем считать, что этот корень является внутренней точ-
кой сегмента [а, Ь], не содержащего других корней рассматриваемого
уравнения. На практике обычно путем грубой прикидки определяют
размеры указанного сегмента [а, 6] *).
1.	Метод «вилки». Мы начнем с метода, который часто исполь-
зуется для приближенного вычисления корней на современных быстро-
действующих математических машинах.
Пусть интересующий нас корень с уравнения /(х) = 0 изолиро-
ван на некотором сегменте [а, />]. Относительно функции / (х) мы
предположим, что она непрерывна на сегменте [а, Ь] и имеет на кон-
цах этого сегмента значения разных знаков. В дальнейшем для крат-
кости мы будем называть «вилкой» всякий сегмент, на концах кото-
рого f (х) имеет значения разных знаков.
Перейдем к описанию метода отыскания корня уравнения/(х)=0,
называемого методом «вилки».
Ради определенности будем считать, что /(а)<0, /(6)>0. Раз-
делим сегмент [а, пополам. При этом может представиться два
*) При этом может быть использована вытекающая из физического со-
держания задачи дополнительная информация о расположении корня.
388
ПРИБЛИЖЕННЫЕ МЕТОДЫ
[ГЛ. 12
случая: 1) значение функции в середине сегмента [а, Ъ] равно нулю
(в этом случае искомый корень найден), 2) указанное значение' не
равно нулю. В этом случае одна из половин сегмента [а, Ъ] является
вилкой. Эту половину мы обозначим [а1( Z^]. Очевидно, что /(ai)<0,
f (^i) > 0. С сегментом [ах, поступим точно так же, как с сегмен-
том [а, Ь], т. е. разделим сегмент [ах, пополам. Продолжая ана-
логичные рассуждения далее, мы будем иметь две возможности: 1) либо
описанный выше процесс оборвется вследствие того, что значение
функции в середине некоторого из сегментов окажется равным нулю
(в этом случае искомый корень найден), 2) либо описанный процесс
можно продолжать неограниченно, и мы получим стягивающуюся си-
стему сегментов — вилок [а1; &х], [а2, &2], ..., [ап, Ьп],причем для
любого номера п f (a„)<0, f (Ьп)>0. Указанная стягивающаяся си-
стема сегментов имеет одну общую точку с, к которой сходится
каждая из последовательностей {а„} и {£„} (см. следствие-из тео-
ремы 3.15). Докажем, что с и является искомым корнем, т. е./(с)=0.
Поскольку функция J(x) непрерывна в точке с, то каждая из после-
довательностей {/(а„)} и {/(&„)} сходится к /(с). Но тогда из усло-
вий /(ая)<;0, /(&„)> 0, в силу теоремы 3.13 и замечания к этой
теореме, получим, что одновременно справедливы неравенства /(с)=С0
и f(c) 5э 0, т. е. /(с) = 0.
Проведенные выше рассуждения дают алгоритм отыскания иско-
мого корня с. За приближенное значение этого корня можно взять
точку а” я, т. е. середину сегмента [ап, Ьл]. Поскольку длина сег-
г i. 1	д  О	Ufl ~1“
мента [ап, Ьп] равна , то число	—- отличается от точного
значения корня не более чем на 2~1а. Таким образом, описанный
выше процесс последовательного деления сегментов-вилок пополам
позволяет вычислить искомый корень с с любой наперед заданной
степенью точности. Так как описанный процесс приводит к много-
кратному повторению однотипных вычислительных операций, он
особенно удобен для проведения вычислений на быстродействующих
математических машинах.
2.	Метод касательных *). Метод касательных является одним из
самых эффективных приближенных методов вычисления корней урав-
нения /(х) = 0.
Пусть искомый корень с уравнения /(х) = 0 изолирован на сег-
менте [а, />]. Перейдем к описанию метода касательных, не выясняя
пока условий, при которых применим этот метод.
Обратимся к рассмотрению графика функции f(x) на сегменте
[а, Ь] (рис. 12.1). Возьмем за нулевое приближение искомого корня
некоторое значение х0 из сегмента [а, £] и обозначим через Во точку
*) Этот метод называют также методом Ньютона.
§ I]
ВЫЧИСЛЕНИЕ КОРНЕИ УРАВНЕНИЙ
389
графика функции с абсциссой х0. Проведем через точку Во касатель-
ную к графику функции и возьмем за первое приближение искомого
корня абсциссу Xj точки пересечения этой касательной с осью Ох *)
(см. рис. 12.1). Далее проведем касательную к графику функции через
точку с абсциссой хх и возь-	д
мем за второе приближение абс-	Л
циссу х2 точки пересечения этой	Вд /1
касательной с осью Ох. Продол-	У! i
жая этот процесс неограниченно,	д //] j
мы построим последовательность	/ i 1
х0, xlt ..., х„, ... приближенных	У\ / I i
значений искомого корня.	д \	' '
В практических целях удобно	________________________У	1
получить рекуррентную форму-	а\	х,	хд
лу, выражающую хл+1 через хп.
Для этого возьмем уравнение	А
У = f (х^(х-хп) каса-	Рис. 12.1.
тельной к графику функции в
точке Вп и вычислим абсциссу х„+1 точки пересечения этой каса-
тельной с осью Ох. При этом получим
Хп+1 = Х"~Н^Г-
Формула (12.1) определяет алгоритм метода касательных. Таким обра-
зом, метод касательных представляет собой метод последовательных
приближений (или, как говорят, метод итераций), которые строятся
при помощи рекуррентной формулы (12.1). Нашей дальнейшей зада-
чей является обоснование метода касательных.
В п. 5 мы выясним условия, при которых последовательность
значений хп, определяемых формулой (12.1), сходится к искомому
корню с, и дадим оценку погрешности, т. е. отклонения приближен-
ного значения хп от точног^о значения корня с.
3.	Метод хорд. К числу широко распространенных приближен-
ных методов решения уравнения /(х) = 0 относится метод хорд.
Перейдем к описанию этого метода, не выясняя пока условий,
при которых он применим.
Предположим, что искомый корень с уравнения f[x) = Q изоли-
рован на сегменте [а, Ь], и обратимся к рассмотрению графика функ-
ции f(x) на этом сегменте (рис. 12.2). Возьмем за нулевое прибли-
жение искомого корня некоторое число х0 из сегмента [а, &] и обо-
значим через Ло и В точки графика функции с абсциссами хй и Ь.
*) Так как касательная в точке Ва представляет собой график диффе-
ренциала функции у = f (х) в точке х0, то указанный прием отыскания пер-
вого приближения Xj основан на замене функции ее дифференциалом в точке х0.
390
приближенные методы
[ГЛ. 12
Проведем
за первое
ния этой
Рис. 12.2.
через точки Ло и В графика функции хорду А0В и возьмем
приближение искомого корня абсциссу хх точки пересече-
хорды с осью Ох (см. рис. 12.2). Далее проведем хорду
через точки графика функции А1
с абсциссой xt и В. За второе
приближение возьмем абсциссу х2
точки пересечения хорды АгВ
с осью Ох. Продолжая этот про-
цесс неограниченно, мы построим
последовательность х0, xlt х2, ...
..., хп, ... приближенных значе-
ний искомого корня.
В практических целях удобно
получить рекуррентную фор-
мулу, выражающую х„+1 через хп.
Для этого возьмем уравнение
У — f (хп) х — хп
Х°РДЫ> "Ро-
дящей через точки Ля(хл, /(хл)) нВ(Ь, /(b)), и вычислим абсциссу
хл+1 точки пересечения этой хорды с осью Ох. При этом получим
„	_ v (Ь — хл) f (х„)
Xn+1-xn
(12.2)
Формула (12.2) определяет алгоритм метода хорд. Таким образом,
метод хорд представляет собой метод итераций, которые строятся
при помощи рекуррентной формулы (12.2). Нашей дальнейшей зада-
чей является обоснование метода хорд.
В пункте 6 мы выясним условия, при которых последовательность
значений хп сходится к искомому корню с, и дадим оценку погреш-
ности метода хорд.
4.	Метод итераций (последовательных приближений). Из пп. 2
и 3 ясно, что методы касательных и хорд связаны общей идеей по-
строения последовательных приближений к искомому корню. Эта идея
и лежит в основе излагаемого в настоящем пункте метода.
Этот метод мы рассмотрим в применении к уравнению
x = F(x).
(12.3)
Введем понятие итерационной последовательности.
Последовательность х0, хг, ..., хп, ... будем называть итераци-
онной, если для любого п1 элемент хп выражается через элемент
Хп_г по рекуррентной формуле x„ = F(xn_1), а в качестве х0 взято
любое число из области задания функции F (х). Мы докажем, что
при определенных условиях итерационная последовательность сходится
к корню уравнения (12.3) и, стало быть, ее элементы могут быть
взяты за приближенные значения этого корня.
ВЫЧИСЛЕНИЕ КОРНЕЙ УРАВНЕНИЙ
391
§ И
Справедливо следующее утверждение.
Утверждение 1. Пусть функция F (х) непрерывна на сегменте
[a, t], и пусть все элементы итерационной последовательно-
сти х0> xlt .хп, ... лежат на этом сегменте. Г огда, если эта
последовательность сходится к некоторому числу с, то указан-
ное число с является корнем уравнения (12.3).
Доказательство. Так как последовательность {хл} сходится
кси все ее элементы принадлежат сегменту [a, h], то и предел с
принадлежит сегменту [а, £>] (см. следствие 2 из теоремы 3.13). По
условию функция F (х) непрерывна в точке с, и поэтому последова-
тельность {Д(хл_1)} сходится к F (с). Таким образом, равенство
xn = F(х„_1) в пределе при л->со переходит в равенство c — F(c),
т. е. с является корнем уравнения (12.3). Доказанное утверждение
будет существенно использовано нами в пп. 5 и 6 для обоснования
метода касательных и хорд.
Докажем еще одно утверждение, часто используемое для прибли-
женного вычисления корня уравнения (12.3) с помощью итерацион-
ной последовательности.
Утверждение 2. Пусть с —корень уравнения (12.3), и пусть
в некотором симметричном относительно точки с сегменте
[с —е, с -|- е] производная функции F (х) удовлетворяет условию
\F' (х) а< 1. Тогда итерационная последовательность х0,
Xt....х„, ..., у которой в качестве х0 взято любое число из
сегмента [с — е, с -|- е], сходится к указанному корню с.
Доказательство. Прежде всего докажем, что все элементы
итерационной последовательности {хл} принадлежат указанному сег-
менту [с — е, с + е]. В самом деле, х0 принадлежит этому сегменту
по условию. Поэтому достаточно, предположив, что х^ принадле-
жит этому сегменту, доказать, что и хп ему принадлежит. Для этого
применим формулу Лагранжа к разности F (хл_х) — F (с) и учтем, что
F(c) = c, Xn — Fix^j). Получим
хЛ - с = F (хл_х) - F (с) = F' (?) (x„_t - с),	(12.4)
где $ — некоторая точка, лежащая между хп^ и с и, стало быть,
принадлежащая сегменту [с—г, с + е]. Так как [ F' (?) | а < 1, то
из равенства (12.4) получим
|x„-c|<a|x„_x-c|.	(12.5)
Из (12.5), поскольку 0<а<1, в свою очередь получим
|x„-c|<|Xb_i-c|.	(12.6)
Неравенство (12.6) устанавливает, что каждый последующий элемент хп
расположен к с ближе, чем предыдущий элемент хл_х, и, стало быть,
так как хл_х принадлежит сегменту [с — е, с + г| и так как этот
сегмент симметричен относительно точки с, то и хп принадлежит
392
ПРИБЛИЖЕННЫЕ МЕТОДЫ
[ГЛ. 12
этому сегменту. Остается доказать, что последовательность {хп} схо-
дится к с. Поскольку неравенство (12.5) справедливо для всех номе-
ров п, то с помощью этого неравенства получим
|x„-c|==Sa"|x0-c|;	(12.7)
Из последнего неравенства очевидно, что х„->с, ибо ап->0. Утвер-
ждение 2 доказано.
Сделаем практические замечания относительно только что доказанного
утверждения. Предположим, что путем предварительной прикидки мы устано-
вили, что интересующий нас корень уравнения (12.3) изолирован на некото-
ром сегменте [а, Ь], на котором производ-
_______с 2с-а	 , ная функции F (х) удовлетворяет условию
ао °	°	0 ° | F (х) | sg«< 1.
Так как сегмент [а, 6], вообще говоря,
а 0	о £ с не является симметричным относительно
искомого корня, то, естественно, возникает
Рис. 12.3.	вопрос о том, как выбрать нулевое приближе-
ние х0, с тем, чтобы можно было применить
доказанное выше утверждение 2. Заметим, что где бы внутри сегмента [а, &] ни
находился искомый корень с, хотя бы один из двух симметричных относительно
с сегментов [а, 2с — а] или [2с — Ь, 6] (рис. 12.3) целиком принадлежит сегменту
[а, 6]. Поэтому хотя бы одна из точек а или Ь принадлежит симметричному
относительно корня с сегменту, всюду на котором | F' (х) | sg а < 1. Стало
быть, по крайней мере одну из точек а или b можно, согласно доказанному
выше утверждению 2, выбрать за х0. Конкретно за х0 следует выбрать ту из
двух точек а или Ь, для которой приближение хг = F (х0) не выходит за пре-
делы сегмента [а, &].
На практике чаще всего встречается случай, когда производная
F' (х) имеет на сегменте [a, Z>] определенный знак. Если этот знак
положителен, то из формулы (12.4) следует, что последовательность
{х„} монотонна. Этот случай приводит к так называемой ступенча-
той диаграмме, изображенной на рис. 12.4. Если же производная
F' (х) отрицательна на сегменте [a, fcj, то из той же формулы (12.4)
ВЫЧИСЛЕНИЕ КОРНЕИ УРАВНЕНИИ
393
§ 1]
видно, что любые два последовательных элемента хп_х и х„ лежат
по разные стороны от корня с. Этот случай приводит к так назы-
ваемой спиралеобразной диаграмме, изображенной на рис. 12.5.
Замечание. Возникает вопрос об оценке погрешности метода
итераций, т. е. об оценке отклонения я-го приближения хП от точ-
ного значения корня с. Из формулы (12.7) непосредственно вытекает
следующая оценка:
I Хп. — с | а.п (Ь — а),
где а — точная верхняя грань функции | F' (х) | на сегменте [а, Ь],
на котором изолирован рассматриваемый корень. Если производная
F (х) отрицательна на сегменте [а, Ь], то, как указано выше, и
хп лежат по разные стороны от корня с, и поэтому справедлива
следующая оценка:
|хя-с|<|хп-х„_1|.
Если же в рассматриваемом случае взять за приближенное значение
корня полусумму двух последовательных приближений
____ХП ХП-1
Хп— 2	’
то получим следующую оценку погрешности:
5.	Обоснование метода касательных.
1°. Рассмотрим сначала случай, когда искомый корень с уравне-
ния /(х) = 0 изолирован на некотором сегменте [а, Ь], на котором
функция f(x) имеет не обращающуюся в нуль первую производную
и ограниченную вторую производную. Докажем, что в этом случае
найдется такая достаточно малая окрестность корня с, что если нуле-
вое приближение лежит в этой окрестности, то последователь-
ность {х„}, определяемая рекуррентной формулой (12.1), сходится
к корню с.
Прежде всего, заметим, что уравнение
x = F(x), где Р(х) = х-^	(12.8)
имеет на сегмент.е [а, Ь] только один корень с, совпадающий с кор-
нем уравнения /(х) = 0. Поэтому вместо уравнения f(x) = 0 мы
будем решать уравнение (12.8). Для этого, взяв некоторое х0, по-
строим итерационную последовательность
xn+1 = F(x„) = x„—(12.9)
Заметим, что рекуррентная формула (12.9) в точности совпадает
с рекуррентной формулой (12.1).
394
ПРИБЛИЖЕННЫЕ МЕТОДЫ
(ГЛ. 12
Для того чтобы доказать сходимость итерационной последователь-
ности {хп} к искомому корню с, достаточно доказать, что в неко-
торой е-окрестности корня с производная F' (х) удовлетворяет усло-
вию | F' (х) |	< 1, и взять х0 в указанной е-окрестности (см. утвер-
ждение 2 из п. 4), В силу требований, наложенных на функцию f(x),
найдутся положительные числа т и N такие, что всюду на сегменте
[а, />] выполняются неравенства
Поскольку

(12.10)
то из неравенств (12.10) вытекает следующая оценка:

LLWJJv
тг
(12.11)
Из непрерывности функции f(x) вытекает, что в некоторой е-окрест-
ности корня с эта функция удовлетворяет неравенству
(12.12)
где а — фиксированное число из интервала 0<а<1. Сопоставляя
неравенства (12.11) и (12.12), мы получим, что всюду в указанной
е-окрестности корня
\F' (х)|<а< 1.
Тем самым сходимость последовательности (12.9) к корню с доказана.
Замечание 1. Мы доказали сходимость последовательности
{х„} к корню с лишь при условии, что нулевое приближение х0
лежит в достаточно малой е-окрестности корня с. Выбор нужного х0
без труда осуществляется на современной быстродействующей элек-
тронно-вычислительной машине при помощи нескольких проб. ’
Замечание 2. Оценим отклонение приближенного значения
корня хл+1 от точного значения с. С этой целью разложим функцию
f(x) в окрестности хл по формуле Тейлора с остаточным членом
в форме Лагранжа:
/(х) =/(х„) +/' (хл) (х - х„) + ^f" (0 (х - хл)2.
# -
Полагая в этой формуле х = с и учитывая, что /(с) = 0, будем иметь
0 =/(х„) +/' (х„) (с - хл) +1/" (?) (с - хл)2.
*) Эти неравенства вытекают из того, что производная /' (х) непрерывна
и не обращается в нуль на рассматриваемом сегменте.
§ и
ВЫЧИСЛЕНИЕ КОРНЕЙ УРАВНЕНИЙ
395
Вычитая из последней формулы формулу	(хл)(хя+1 — х„)=0,
которая вытекает из рекуррентного соотношения (12.9), получим
1 f" (?) /	42
с ~ 2 f' (х„)	•
Отсюда, используя принятые выше обозначения (12.10), придем к сле-
дующему неравенству:
I xn+i с I '?5 I хп с |2-
Последовательно применяя эту оценку для л = 0, 1, 2, ..., получим
следующую оценку:
2°. Дадим обоснование метода касательных при несколько иных
предположениях.
Пусть искомый корень с уравнения /(х) = 0 изолирован на сег-
менте [а, £], на котором /(х) имеет монотонную первую производ-
ную, сохраняющую определенный знак.
Ради определенности предположим, что производная не убывает
и положительна на сегменте [a, Z»]. Докажем, что итерационная
последовательность { х„ }, у которой х0 = Ь, а хя+1 определяется через
хп с помощью формулы (12.9), сходится к корню с. Для этого доста-
точно доказать, что все хп лежат на сегменте [а, Ь] и что последо-
вательность {хп} сходится (см. утверждение 1 из п. 4). Применяя
метод индукции, докажем, что все хп лежат на сегменте [а, Ь],
точнее, на сегменте [с, £], где с — искомый корень. Так как хй — Ь
лежит на сегменте [с, Ь], то для проведения индукции достаточно,
предположив, что хп лежит на сегменте [с, Ь], доказать, что и хл+1
также лежит на этом сегменте. Если х„ — с, то / (хя) = / (с) — О и
из формулы (12.9) следует, что xnJtl = хп = с, т. е. индукция прове-
дена. Пусть теперь хл>с. Тогда из формулы (12.9), учитывая, что
/(с) = 0, получим
r г  Нхп) — Цс)
Применяя к выражению, стоящему в числителе последней дроби,
формулу Лагранжа, найдем
Хп ХП+1 ~ (.Хп О fr >
где с <£„<*„.
НОЙ дробь 7Г7-V
f (Х„)
В силу неубывания и положительности производ-
положительна и не превосходит единицы, т. е.
396
ПРИБЛИЖЕННЫЕ МЕТОДЫ
(ГЛ. 12
хп — хп+1 хп — с или	Итак, индукция проведена.. Из поло-
жительности производной f (х) следует возрастание функции f (х),
а поэтому из неравенства с^хп следует, что 0 = /(с)^/(х„).
Таким образом,  {/?".	0. Отсюда, в силу формулы (12.9), х„+1^х„,
I {хп)
т. е. последовательность {х„} не возрастает. Так как эта последо-
вательность, кроме того, ограничена снизу числом с, то она сходится
(см. теорему 3.15). В силу утверждения 1 из п. 4 пределом ее
является искомый корень с.
Замечание 3. Мы рассмотрели случай, когда f (х) не убывает
и положительна на [а, £]. Возможны еще три случая: 1) /'(х) не
возрастает и отрицательна на [а, &], 2) /' (х) не возрастает и поло-
жительна на [а, й], 3) f (х) не убывает; и отрицательна на [а, &].
В каждом из этих трех случаев обоснование метода касательных
проводится в полной аналогии со случаем, рассмотренным выше. Отме-
тим лишь, что в случае 1) за нулевое приближение следует взять
значение х0 = Ь, а в случаях 2) и 3) —значение х0 — а. Это обеспе-
чит принадлежность всех членов итерационной последовательности
{х„} сегменту [а, &] и сходимость этой последовательности к иско-
мому к<)рню с.
Замечание 4. Укажем оценку отклонения п-го приближения хп
от точного значения корня с (при сформулированных в этом пункте
предположениях).
Применяя к выражению /(хл) = /(хп) —/(с) формулу Лагранжа,
будем иметь /(хл) = (х„ — c)f (?„). Отсюда получим следующую
оценку:
\хп-(12.13)
где т — минимальное значение \f (х)| на сегменте [а, Ь]. Фор-
мула (12.13) позволяет оценить отклонение хп от точного значения
корня с через значение модуля заданной функции у=/(х) в точке хя.
6. Обоснование метода хорд. Предположим, что искомый корень с
уравнения /(х) = 0 изолирован на некотором сегменте [а, Ь], на ко-
тором /(х) имеет монотонную первую производную, сохраняющую
постоянный знак. Ради определенности будем считать, что .эта про-
изводная не убывает и положительна на сегменте [а, 6]. Заметим,
что уравнение
x = F(x), где f(x) = x^(A=^-J*)	(12.14)
имеет на сегменте [а, Ь] только один корень с, совпадающий с кор-
нем уравнения /(х) = 0. Поэтому вместо уравнения /(х) = 0 мы
*) При этом мы считаем, что F (b) = b
дет непрерывна на всем сегменте [а, 6].
f(b)
ГФ)’
Тогда функция F (х) бу-
§ 1]
ВЫЧИСЛЕНИЕ КОРНЕЙ УРАВНЕНИИ
397
будем решать: уравнение (12.14). Для этого, взяв х0 — а, построим
итерационную последовательность
(12.15)
Заметим, что рекуррентная формула (12.15) в точности совпадает
с рекуррентной формулой (12.2).
Докажем, что последовательность {хп} сходится к искомому
корню с. Для этого достаточно доказать, что все хп лежат на сег-
менте [а, Ь] и что последовательность {хп} сходится (см. утвержде-
ние 1 из п. 4). Применяя метод индукции, докажем, что все хп
лежат на сегменте [а, Ь], точнее, на сегменте [а, с], где с —
искомый корень. Так как хй — а лежит на сегменте [а, с], то для
проведения индукции достаточно, предположив, что хп лежит на сег-
менте [а, с], доказать, что >*л+1 также лежит на этом сегменте. Исполь-
зуя формулу (12.15) и учитывая, что /(с) = 0, будем иметь*)
_	_ _ (b — х„) f (х„) _ (b — хп) [f (с) — f (хл)]
rt+1 хп f(b)-l(xn) [f(b)-f(c)} + [f(c)-l(Xn)]‘
Применяя к выражениям в квадратных скобках формулу Лагранжа,
получим
_ (b — хп) f (Е„) (с — хп)
П+1 Хп (Ь_с)/(й) + (с_Хп)/(г„) ’
(12.16)
где хп < Ел < с, с < I* < b, т. е. ?л < 5* В силу неубывания и поло-
жительности производной f (х) можем записать 0 <;/'(;л) sC/'^’j).
А отсюда, так как Ь — с > 0 и с — хл > О, получим
(b - С) f (?*) 4- (С - xn)f' (U [(й - с) 4- (с - Xn)]f' (U =
= (^-хл)/' (Q.
Таким образом, из равенства (12.16) найдем — хп sg с — хп или
хл+1^с, т. е. индукция проведена.
Докажем теперь, что последовательность {хп} является
неубывающей. Для этого достаточно доказать, что дробь, стоящая
в правой части равенства (12.15), является неположительной. Так как
производная /'(х) положительна на.сегменте [а, Ь], то функция f (х)
возрастает на этом сегменте, и поэтому из неравенств хп^с <.Ь
следует, что f(xn)^f(c) = 0, /(b)—/(хл) > 0. Отсюда и вытекает
неположительность указанной дроби. .
Итак, последовательность {хп} не убывает и ограничена сверху
числом с. По теореме 3.15 эта последовательность сходится. В силу
утверждения 1 из п. 4 пределом ее является корень с.
*) В дальнейшем мы предполагаем, что хп<с, ибо если х„=с, то
f (хл) = / (с) = 0 и, стало быть, хл+1 = хп = с, т, е. принадлежность хл+1
сегменту [a, cj установлена.
398
ПРИБЛИЖЕННЫЕ МЕТОДЫ
(ГЛ. 12
Замечание 1. Мы рассмотрели случай, когда f (х) не убывает
и положительна на [а, Ь]. Возможны еще три случая: 1) f (х)
не возрастает и отрицательна на [а, 6], 2) f (х) не возрастает
и положительна на [а, Ь], 3) f (х) не убывает и отрицательна
на [а, Ь\.
Эти три случая аналогичны рассмотренному выше. В случае 1)
уравнение /(х) = 0, так же как и выше, заменяется уравнением (12.14)
и в качестве нулевого приближения берется х0 = а (при этом после-
довательность {хп} также оказывается неубывающей). В случаях 2)
и 3) уравнение f(x) — 0 заме-
няется не уравнением (12.14),
а уравнением
x = F(x),
где
F(x)=X-^—^l^l
W х /(Q)_f(x)
и в качестве нулевого прибли-
жения берется точка х0 = &
(при этом последовательность
{ х„ } оказывается невозрастаю-
щей).
Замечание 2. Укажем,
лива та же самая оценка (12.13)
и Для метода касательных.
что для метода хорд справед-
отклонения хп от корня с, что
Замечание 3. На практике часто используют комбинированный
метод, заключающийся в поочередном применении метода хорд и ме-
тода касательных.. Ради определенности предположим, что f (х) не
убывает и положительна на сегменте [а, &] (рис. 12.6). Определим х1
по методу касательных, взяв за нулевое приближение точку Ь. После
этого определим х2, применяя метод хорд, но не к сегменту [а, Ь\,
а к сегменту [a, Xj]. Далее, определим х3 по методу касательных,
исходя из уже найденного хр а х4 по методу хорд, применяя
его к сегменту [х2, х3]. Указанный процесс иллюстрируется на
рис. 12.6.
Преимущества комбинированного метода состоят в следующем:
во-первых, он дает более быструю сходимость, чем метод хорд, и,
во-вторых, поскольку последовательные приближения хл и хп+1 ком-
бинированного метода с разных сторон приближаются к корню, то
разность | х„+1 — хп | дает оценку погрешности этого метода. Если
за приближенное значение корня взять х* = Хп , то для погреш-
ности получим оценку
I хп+1 хп I
2
§ 2]
ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
399
§ 2.	Приближенные методы вычисления определенных
интегралов
Рис.
12.7.
1.	Вводные замечания. При решении ряда актуальных физических
и технических задач встречаются определенные интегралы от функций,
первообразные которых не выражаются через элементарные функ-
ции. Кроме того, в приложениях приходится иметь дело с опреде-
ленными интегралами, сами подынтегральные функции которых
не являются элементарными. Это приводит к необходимости раз-
работки приближенных методов вычисления определенных интег-
ралов *).
В этом параграфе мы познакомимся с тремя
наиболее употребительными приближенными мето-
дами вычисления определенных интегралов: ме-
тодом прямоугольников, методом трапеций, и
методом парабол.
Основная идея этих методов заключается в за-
мене подынтегральной функции f(x) функцией
более простой природы — многочленом, совпадаю-
щим с f (х) в некоторых точках. Для уяснения
этой идеи рассмотрим при малых h интеграл
й
f(x)dx, представляющий собой площадь узкой
—h
криволинейной трапеции, лежащей под графиком
функции y—f(x) на сегменте [—h, h] (рис. 12.7).
Заменим функцию f(x) многочленом нулевого
порядка, а именно константой /(0). При этом ин-
' й
теграл J f (х) dx приближенно заменится площадью
—й
прямоугольника, заштрихованного на рис. 12.8.
Ниже мы покажем, что при определенных требованиях
ошибка, совершаемая при такой замене, имеет порядок й3. Заменим,
далее, функцию f(x) многочленом первого порядка, а именно линейной
функцией y = kx-\-b, совпадающей с /(х) в точках — h и h. При
й
этом интеграл ^f(x)dx приближенно заменится площадью прямо-
—й
линейной трапеции, заштрихованной на рис. 12.9. Ниже мы покажем,
что при определенных требованиях на /(х) ошибка, совершаемая
при такой замене, также имеет порядок Л3. Заменим, наконец, функ-
цию /(х) многочленом второго порядка, т. е. параболой у — АхгА-
+ Вх + С, совпадающей с /(х) в точках — h, 0 и h. При этом
на /(л)
*) Заметим, что приближенными методами часто пользуются и для инте-
гралов, выражающихся через элементарные функции.
400
ПРИБЛИЖЕННЫЕ МЕТОДЫ
[ГЛ. 12
Л
интеграл § f (х) dx приближенно заменится площадью фигуры, ле-
— h.
жащей под параболой и заштрихованной на рис. 12.10.
Ниже мы покажем, что при определенных требованиях на функ-
цию f (х) ошибка, совершаемая при такой замене, имеет порядок ft5.
ь
Если требуется вычислить интеграл ^f(x) dx по любому сегменту
а
[а, Ь], то естественно этот сегмент разбить на достаточно большое
число малых сегментов и к каждому из этих сегментов применить
Рис. 12.9.
-fi О h
аг
Рис. 12.10.
изложенные выше рассуждения. При этом мы и придем к методам
прямоугольников, трапеций и парабол в их общем виде.
Детальное изложение каждого из этих трех методов дается ниже.
Здесь же мы сделаем одно важное для дальнейшего замечание.
Замечание. Пусть функция f(х) непрерывна на сегменте
[а, Ь], а хг, х2,	, хп — некоторые точки сегмента [а, ft], Тогда
на этом сегменте найдется точка £ такая, что среднее ариф-
метическое	2 	равно /(?).
В самом деле, обозначим через т и М точные грани функции f (x)
на сегменте [a, ft], Тогда для любого номера k справедливы неравен-
ства m^f{Xk)^M (k— 1, 2,..., п). Просуммировав эти неравен-
ства по всем номерам А = 1, 2....п и поделив результат на п,
получим
т_^ f(ХД + f fe) + • • • + /(хп) ум
п	'
§ 2]
ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
401
Так как непрерывная функция принимает любое промежуточное зна-
чение, заключенное между т и М, то на сегменте [a, й] найдется
точка £ такая, что
+ f,	+ • • • ~Ь / (хп)	(12 j7)
2.	Метод прямоугольников. Пусть требуется вычислить интеграл
ь
\f(x)dx.	(12.18)
а
Разобьем сегмент [а, Ь] на п равных частей при помощи точек
а — х0 < х2 <... < xin = b. Обо-
значим через среднюю точку
сегмента [x»*-j, х3*] (рис. 12.11).
Метод прямоугольников заключается
в замене интеграла (12.18) суммой
[/(*i) +/(х3) +... +/(Х3л_1)]
площадей прямоугольников с вы-
сотами, соответственно равными
/(Xsfc-j), и основаниями, равными
Ь — а ,
x3ft — x3fe_3=—— (эти прямоуголь-
ники заштрихованы на рис. 12.11). Таким образом, справедлива фор-
мула
ь
$ /(х) dx =	[/(Xi) +/(Х3) +... +/(x3„-i)] + R, (12.19)
где R —• остаточный член. Формула (12.19) называется формулой
прямоугольников.
Докажем, что если функция /(х) имеет на сегменте [а, Ь] непре-
рывную вторую производную, то на этом сегменте найдется такая
точка 1], что остаточный член R в формуле (12.19) равен
(12.20)
h
С этой целью оценим сначала интеграл J / (х) dx, считая, что
—л
функция /(х) имеет на сегменте [—h, ft] непрерывную вторую про-
изводную. Обозначим через F (х) первообразную функции /(х). Тогда
л
$ f(x)dx — F (h) — F(—й). Имея в виду, что функция F (x) имеет
на сегменте [—ft, ft] три непрерывных производных, разложим эту
402
ПРИБЛИЖЕННЫЕ МЕТОДЫ
[ГЛ. 12
функцию по формуле Маклорена с остаточным членом в форме Лаг-
ранжа. Получим
F (х) = F (0) + F' (0) х + F<2> (0) J + f о) ф 2L3,	(12.21)
где $ — некоторая точка сегмента [— h, h]. Учитывая, что F' (0) =
= 7(0), F(2) (0) =/' (0), Fw (5) =/(2) (;), и беря формулу (12.21) для
x = h и х — — h, получим
h
J /(х) dx = F (h) - F (- h) = [f (0)+7(0) h+f'	+/<2) (y _
— Л
-1> (0) - 7(0) h+f (0) - 7(2) (?2) =
= 27(0)^ + ^^+^).
В силу замечания в конце п. 1 на сегменте [—h, h] найдется точка т]
такая, что -——— = fz) (tj). Таким образом,
л
5 7(х) dx = 27(0) h + R,	(12.22)
-л
где
£=~7(2)01)(W	(12.23)
Так как величина 27(0) -й представляет собой площадь прямо-
угольника, заштрихованного на рис. 12.8, то формулы (12.22) и (12.23)
h
доказывают, что ошибка, совершаемая при замене j f(x) dx указан-
-л
ной площадью, имеет порядок й3.
л
Таким образом, формула ^f(x)dx^2f(Q)h тем точнее, чем
—к
ь
меньше й. Поэтому для вычисления интеграла ^f(x)dx естественно
а
представить этот интеграл в виде суммы достаточно большого чи-
сла п интегралов
X,	xt	xsn
$7(*М*+ $7(X)^ + ---+ J f(x)dx
X.	X,	xin_t
и к каждому из указанных интегралов применить формулу (12.22).
Учитывая при этом, что длина сегмента [х^-я, х8А] равна мы
§ 2]
ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
403
получим формулу прямоугольников (12.19), в которой
R - Ях + Я2 +... + Я,=[Л2 > (%) +/2> (%) +... +/2> (т)„)] =
_(fe-g)3 Гг,(Л1) + Л8>0i2) + - + P'fr)n)_(fe-g)3 Л2)/-А
24rt2	п	24п2 J v
(Здесь	Мы воспользовались формулой (12.17) для функ-
ции /(2) (х).)
3.	Метод трапеций. Пусть, как и выше, требуется вычислить
интеграл
ь
^f(x)dx.	(12.18)
а
Разобьем сегмент [а, &] на п равных частей при помощи то-
чек а = хв < Xj < х2 <... < хп = b
.(рис. 12.12). Метод трапеций заклю-
чается в замене -интеграла (12.18)
суммой
+• •• +	+/(хп)1} =
д — 1
= Ц^{/(«)+/(^) + 2 2/(М,
* = 1
площадей трапеций с основания-	кис- 1Z-1Z-
ми, соответственно равными /(xft_x)
и /(Хй), и с высотами, равными х^ —	(эти трапеции за-
штрихованы на рис. 12.12).
Таким образом, справедлива формула
!п— 1
/(a)+/W + 2 J/(x*)+R
Л = 1
(12.24)
где R —остаточный член. Формула (12.24) называется формулой
трапеций.
Докажем, что если функция f(x) имеет на сегменте [а, Ь\ непре-
рывную вторую производную, то на этом сегменте найдется такая
точка т), что остаточный член Д в формуле (12.24) имеет вид
R = —(12.25)
404
ПРИБЛИЖЕННЫЕ МЕТОДЫ
[ГЛ. 12
Л
С этой целью оценим сначала интеграл J f(x) dx, считая, что
-л
функция /(х) имеет на сегменте [—h, h] непрерывную вторую про-
изводную. Последовательно производя интегрирование по частям, по-
лучим
л	л	л
\f(x)dx = ^f(x)d(x + h)=f(x)(x + h)\h_/t - $ f (х) (х + h) dx =
-л	-л	-Л
л
=/(ft)2ft — У (X)(x + h)d(x-h) =
— л
л
=f(h) 2h - f (х) (х + ft) (х - ft) |1д +	(x) (x - ft) (x + ft) dx +
-A
A
4- f (x) (X — ft) dx.
— A
Имея в виду, что последний интеграл равен
л	к
J /' (*)(х — h)dx=f(— h'jZh— $/(х)dx,
-л	-л
г
получим
л	л
J /(X) dx = [/(- ft) +/(ft)] ft + у /(2) (х) (х* - ft2) dx. (12.26)
—л	—л
Так как функция (х2 —ft2) не положительна на сегменте [—ft, ft], то
по теореме о среднем на этом сегменте найдётся точка •>] такая, что
h	Л
4 $ /(2) (*) (*а - h*) dx = 1/2> (7)) t (X2 - ft2) dx = - ^/l2) (*|)
— A	-A
Итак,
A
J / (x) dx =	2ft + R,	(12.27)
— A
где
^ = -^/2>(7j)(2ft)3 (-ft^Tj^ft).	(12.28)
т	/(— h) + f(h) n.	, u
Так как величина	представляет собой площадь
трапеции, заштрихованной на рис. 12.9, то формулы (12.27) и (12,28)
§2]
ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
405
h
доказывают, что ошибка, совершаемая при замене § f(x)dx указан-
—л
ной площадью, имеет порядок /г3.
ъ
Для вычисления интеграла ^f(x)dx, как и в методе прямоуголь-
а
ников, представим этот интеграл в виде суммы достаточно большого
числа п интегралов
xt	хг	* Хп
$ fix)dx + $/(х) dx +... + \ fix) dx.
Применяя к каждому из этих интегралов формулы (12.27) и (12.28),
мы и придем к формуле тра-
пеций (12.24) с выражением
для остаточного члена (12.25).
4. Метод парабол. Для вы-
числения интеграла
ь
\f(x)dx (12.18)
а
снова разобьем сегмент [а, Ь]
на п равных частей при помо-
щи точек а = х0<хг<...<	Рис. 12.13.
<fxin — b и обозначим через
Хай-i середину сегмента	Метод парабол заключается
в замене интеграла (12.18) суммой
6^ {[/(*о) + Wi) +/(хг)] + [/(ха) + 4/(х3) +/(x4j] +
+ • • • + [/(^Sn-a) + 4/ iXtn-l) + f (-*5Ь1)1} =
f	Л—l	л—1
= —(a)+/(^) + 2 ^/(•уза)4-4 /(Хзй+i)
I	A = 1	fc=0
площадей фигур, заштрихованных на рис. 12.13 и представляющих
собой криволинейные трапеции, лежащие под параболами, проходя-
щими через три точки графика функции fix) с абсциссами х2ь-ъ
Xik-t и х2й*).
*) Из примера 2 п. 4 § 2 главы 11 вытекает, что выражение —g~~ X
X [/ (х2й-2) + 4/ (х2й_1) + f (xaft) 1 с учетом того, что	, пред-
ставляет собой площадь, лежащую под параболой, проходящей через три
точки графика функции / (х) с абсциссами х2к_2, x2a-i и х2й-
406
ПРИБЛИЖЕННЫЕ МЕТОДЫ
(ГЛ. 12
Ъ
а
Таким образом, справедлива формула
л —1	л —1
/(а)+/(*) +2	/(*«) +4 J /(*««) +R,
*=1	*=о
(12.29)
где R — остаточный член. Формула (12.29) называется формулой па-
рабол или формулой Симпсона *).
Докажем, что если функция f(x) имеет на сегменте [а, Ь] непре-
рывную четвертую производную, то на этом сегменте найдется такая
точка т], что остаточный член R в формуле (12.29) равен
h
С этой целью оценим сначала интеграл J f(x)dx, считая, что
-л
функция f(x) имеет на сегменте [—ft, h] непрерывную четвертую
производную. Производя последовательное интегрирование по частям,
получим
л	л	л
$/(х) dx = J f (х) d(x — h) =/(0) h — $ f (x) (x — h)dx =
0	0	0
h	h
=/(0) h — X(x — h)f (x) I* + J/' (x)xdx + §/(2) (x)x(x — h)dx =
о	0
л	л
=/(0) h + J f (x) x dx + §/l2) (x) x (x — ft) dx.
о	о
Аналогично
о	oo
J /(x) dx =/(0) ft 4- J f (x) xdx + $ /(2) (x) x (x + ft) dx.
-h.	—h	— Л
Таким образом,
л	о
$ /(х)dx = 2/(0) ft + /(2) (х) х (х + ft) dx +
-л	—л
л	л
+ §/(2) (х)х(х — h}dx-\- $ f (x)xdx. (12.31)
о	-л
Последний интеграл в правой части (12.31) равен
л	л
$/, (x)xdx = ft[/(A)+/(-ft)]- J f(x)dx. (12.32)
—л	—л
•) Т, Симпсон — английский математик (1710—1761).
§2]
ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
407
Из формул (12.31) и (12.32) получим
л
4 J /(х) dx = 4/(0) h + 2 ]/ (— h) +f(h)] h +
—л
h	О
+ 2 J/«)(x)x(x-A)dx + 2 J /(2) (x) x(x-\-h)dx.	(12.33)
о	-ft
Вычитая из формулы (12.33) формулу (12.26), будем иметь
л
3 f(x) dx = ]f(-h) + 4/(0) +/(й)] h + 4 +12,	(12.34)
— л
где
о
4 = J /(2) (x) [f x2 + 2ЙХ + 4 й2] dx,
— h
h
12=\ f*} (x) [4x2- 2hx 4- 4Й2] dx.
Интегрируя /х по частям, будем иметь
о
4 =/(2) (х) ~ х (х + й)2 Г h -1 § /(3) (х) [(х + й)3 - h (х + й)2] X
—л
о
X d (х + й) =/(«> (0) g +1 J /(4) (х) (х + й)3 (х - 4) dx.
—*л
Совершенно аналогично
л
4 = -/(8) (0) § + 4 $ fw (х) (х - й)3 (х + A) dx.
о
Учитывая, что функции (х + й)3(х —4Д и (х —й)3(х + 4] сохра-
\ о /	у о /
няют знаки на сегментах [— й, 0] и соответственно [0, й], и приме-
няя теорему о среднем, найдем
+/(4,(U J (х-й)3(х +
о
Й6 fl4>(Si)+fl4,fa)
30	2

где $2 и т] —некоторые точки сегмента [—й, й].
408
ПРИБЛИЖЕННЫЕ МЕТОДЫ
(ГЛ. 12
Таким образом, из формулы (12.34) получим
л
С /(х)dx =	2ft+(12 35)
—л
где
<12-36>
-г	иA) + 4f(0)+f (MJ '	л„
Так как величина --------  -g- - 2д представляет собой
площадь фигуры, лежащей под параболой и заштрихованной на
рис. 12.10, то формулы (12.35) и (12.36) доказывают, что ошибка,
л
совершаемая при замене jj f(x)dx указанной площадью, имеет
— л
порядок ЛБ.
ь
Для вычисления интеграла ^f(x)dx, так же как и в методах пря-
а
моугольников и трапеций, представим этот интеграл в виде суммы
п интегралов
Х2	Х4	Х2П
ч	§ /(x)rfx+^ f(x)dx-j- ... + § f(x)dx.
Х0	Х2	Х2П~2
Применяя к каждому из этих интегралов формулы (12.35) и (12.36),
мы и придем к формуле Симпсона (12.29) с выражением для оста-
точного члена (12.30).
Сравнивая остаточный член (12.30) с остаточными членами (12.20)
и (12.25), мы убеждаемся в том, что формула Симпсона дает ббль-
шую точность, чем формулы прямоугольников и трапеций.
В качестве иллюстрации применения формулы Симпсона обратимся
к вычислению интеграла /(x0)=J e~x,dx*), ограничиваясь для про-
о
стоты значениями хе из сегмента 0^хо^1. Полагая f(x) = e~ х‘ и
вычисляя производную /<4> (х) = 4 (4х4 — 12х2-|-3)е— х‘, без труда
убедимся в том, что для всех х из сегмента 0 х х0 1 во вся-
ком случае |/(4) (х)| <; 20. Исходя из оценки (12.30), можем утверж-
дать, что | R | <z • Стало быть, разбив сегмент [0, х0] всего на
пять равных частей и заменив рассматриваемый интеграл суммой.
*) Рассматриваемый интеграл не выражается через элементарные функции,
но имеет большое значение в статистической физике, теории теплопроводности
и диффузии.
§ 2]	ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ	409
стоящей в правой части формулы Симпсона, мы вычислим этот инте-
грал с точностью до —1^.=^.,
5. Заключительные замечания. Каждый из изложенных в этой
главе методов вычисления корней уравнений и определенных инте-
гралов содержит четко сформулированный алгоритм для прове-
дения вычислений. Другой особенностью изложенных методов является
стереотипность тех вычислительных операций, которые приходится
проводить на каждом отдельном шаге. Эти две особенности обеспе-
чивают широкое применение изложенных методов для проведения
вычислений на современных быстродействующих вычислительных
машинах.
Выше для приближенного вычисления интеграла (12.18) от функ-
ции f(x) мы исходили из разбиения основного сегмента [а, 6] на
достаточно большое число п равных частичных сегментов одина-
ковой длины h и из последующей замены функции f(x) на каждом
частичном сегменте многочленом соответственно нулевого, первого
или второго порядка.
Погрешность, возникающая при таком подходе, никак не учиты-
вает индивидуальных свойств функции f(x). Поэтому, естественно,
возникает идея о варьировании точек разбиения основного сег-
мента [а, Ь] и выборе для каждой фиксированной функции /(х)
такого оптимального разбиения основного сегмента [а, Ь] на п, вообще
говоря, не равных друг другу частичных сегментов, которое обеспе-
чивало бы минимальную величину погрешности данной приближенной
формулы.
В Дополнении к главе 14 мы остановимся на реализации указан-
ной идеи, принадлежащей А. Н. Тихонову и С. С. Гайсаряну.
ГЛАВА 13
ТЕОРИЯ ЧИСЛОВЫХ РЯДОВ
Еще в элементарном курсе приходилось сталкиваться с суммами,
содержащими бесконечное число слагаемых (например, с суммой бес-
конечного числа элементов геометрической прогрессии). Такого рода
суммы, называемые рядами, и изучаются в настоящей главе. Мы уста-
новим, что при некоторых условиях ряды обладают свойствами,
аналогичными свойствам конечных сумм.
§ 1. Понятие числового ряда
1. Ряд и его частичные суммы. Сходящиеся и расходящиеся
ряды. Рассмотрим бесконечную числовую последовательность ир
н2....uk, ... и формально образуем из элементов этой последова-
тельности выражение вида
ОО
«1 + «г+ +на+ ••• — X, 11 ь-	(13.1)
fe = l
Выражение (13.1) принято называть числовым рядом или просто
рядом. Отдельные элементы uk, из которых образовано выраже-
ние (13.1), принято называть членами данного ряда. Как правило,
мы будем пользоваться для обозначения ряда символом суммы
Сумму первых п членов данного ряда будем называть п-й час-
тичной суммой данного ряда и обозначать символом Sn. Итак,
п
sn = 4-w2-|- ... -\-ип= X «*• Ряд (13.1) называется сходя-
Й=1
«4гг м с я, если сходимся последовательность {£„} частичных сумм
этого ряда. При этом предел S последовательности частичных
сумм {£„} называется суммой данного ряда. Таким образом,
для сходящегося ряда, имеющего сумму S, мы можем формально за-
писать равенство
СО
<S= S и*.
*=i
§ п
ПОНЯТИЕ ЧИСЛОВОГО РЯДА
411
В случае, если lim не существует, ряд называется рас X о-
п-*-оэ
д я щи м с я.
Подчеркнем, что понятие суммы определено лишь для сходящегося
ряда и, в отличие от понятия конечной суммы, вводится посредством
предельного перехода *).
Заметим, что рассмотрение числовых рядов есть новая форма
изучения числовых последовательностей, ибо: 1) каждому данному
ряду однозначно соответствует последовательность его частичных сумм,
2) каждой данной последовательности {5га} однозначно соответствует
ряд, для которого эта последовательность является последователь-
ностью его частичных сумм (достаточно положить члены ряда рав-
ными uk = Sk — Sk-i при k > 1 и нх = «Sj).
Одной из главных задач теории числовых рядов является установ-
ление признаков, по которым можно решить вопрос о сходимости
или расходимости данного ряда.
Примеры числовых рядов.
1.	Изучим вопрос о сходимости ряда
СО
1-1 + 1-14-... =	(13.2)
s=i
Поскольку последовательность его частичных сумм <SX = 1, S2 = 0,...
..., 5'3л_1= 1, S2n=0,... не имеет предела, ряд (13.2) расходится.
2.	Рассмотрим ряд, составленный из элементов геометрической
прогрессии:
СО
1+? + ?2+ ... +^+ ... = J] qk-\ (13.3)
Л=1
и-я частичная сумма этого ряда при q 96 1 имеет вид
5я=1+?+...+9»-1 = ^=г^-т^.	(13.4)
Очевидно, что при -1 q | <; 1 последовательность частичных сумм Sn
сходится и имеет предел, равный Таким образом, при |^|<1
рассматриваемый ряд сходится и имеет сумму, равную t •
При |9|>1 из равенства (13.4) очевидно, что последователь-
ность S„ (а стало быть, и рассматриваемый ряд) расходится. При
|?| = 1 расходимость ряда (13.3) усматривается непосредственно.
*) В. современной математике, наряду с указанным выше понятием суммы,
вводится понятие суммы ряда в различных обобщенных смыслах. Это позво-
ляет суммировать в обобщенных смыслах многие расходящиеся ряды (см. допол-
нение 3 к этой главе).
412
ТЕОРИЯ ЧИСЛОВЫХ РЯДОВ
[ГЛ. 13
В самом деле, при <7=4-1 Sn — n, расходимость последователь-
ности S„ очевидна, а при q ——1 ряд (13.3) переходит в изученный
выше ряд (13.2).
3.	Пусть х — любое фиксированное число. Докажем, что ряд
1 +ir+sr + •••+£+••• = 2(Йг’)	<13S>
Й = 1
сходится и имеет сумму, равную е*.
В п. 2 § 15 главы 8 мы получили разложение по формуле Мак-
лорена функции ех
г 1*2
еЛ=1+к+21 + •••+f^I)F+^(x)’	<13-6)
где
Я„(х) = ^Л (О<0<1),	(13.7)
Из формул (13.6) и (13.7) мы получим
<138>
Обозначая через S„ п-ю частичную сумму ряда (13.5), мы можем
переписать неравенство (13.8) в виде
(13.9)
Поскольку при любом фиксированном х
то правая часть неравенства (13.9) представляет собой элемент бес-
конечно малой последовательности. Но это и означает, что последо-
вательность {S„} сходится к числу ех. Стало быть, и ряд (13.5)
сходится и имеет сумму ех.
4.	Совершенно аналогично, используя формулу Маклорена для
функций sin дс и cos .г, можно доказать, что ряды
х’ . х5 х’ _	(— l^-’x2**1
Х 3! +5!	71 +-------Z (2k — 1)!
ft = i
И
X2 X1 Х«	_ yi
1	21 + 4!	61 +-------Z (2k — 2)!
ft=l
*) Символом 0! мы обозначили число 1.
*♦) См. пример 3 из п. 3 § 3 главы 3.
$ 1]
ПОНЯТИЕ ЧИСЛОВОГО РЯДА
413
при любом фиксированном значении х сходятся и имеют суммы
соответственно равные sinx и cosx. (Предоставляем читателю самому
убедиться в этом.)
2. Критерий Коши сходимости ряда. Так как вопрос о сходи-
мости ряда, по определению, эквивалентен вопросу о сходимости
последовательности его частичных сумм, то мы получим необходимое
и достаточное условие сходимости данного ряда, сформулировав кри-
терий сходимости Коши для последовательности его частичных сумм.
Ради удобства приведем формулировку критерия Коши для последо-
вательности. Для того чтобы последовательность была схо-
дящейся, необходимо и достаточно, чтобы для любого положи-
тельного числа е нашелся номер N такой, что для всех номе-
ров п, удовлетворяющих условию n^N, и для всех натуральных
p(p=i, 2, 3, ...)
I Sn+p — Sn | < е-
В качестве следствия из этого утверждения мы получим следующую
основную теорему.
Теорема 13.1 (критерий Коши для ряда). Для того чтобы
СО
ряд У, Uh сходился, необходимо и достаточно, чтобы для любого
ь=\
положительного числа е нашелся номер N такой, что для всех
номеров п, удовлетворяющих условию n^N и для всех нату-
ральных чисел р
п + р
k — п Ч-
(13.10)
1

Для доказательства этой теоремы достаточно заметить, что величина,
стоящая под знаком модуля в неравенствЬ (13.10), равна разности
частичных сумм Sn+p — Sn. Подчеркнем, что критерий сходимости
Коши представляет в основном теоретический интерес. Его исполь-
зование для практических потребностей установления сходимости или
расходимости тех или иных конкретных рядов, как правило, сопря-
жено с трудностями. Поэтому наличие критерия Коши не снимает
вопроса об установлении других практически эффективных признаков
сходимости и расходимости рядов.
Из теоремы 13.1 легко извлечь два элементарных, но важных
следствия.
ОО
Следствие 1. Если ряд У п* сходится, то последователь-
Л = 1
ОО
ность гп — У иь является бесконечно малой. Принято назы-
fe=n+l
со
вать величину гп п-м остатком ряда У uk. Чтобы доказать
Л = 1
414
ТЕОРИЯ ЧИСЛОВЫХ РЯДОВ
[ГЛ. 13
следствие 1, достаточно доказать, что для любого е>0 найдется
номер N такой, что | гп | е при n^N. Последнее неравенство
непосредственно вытекает из неравенства (13.10), справедливого для
любого р—\, 2, 3, ... и из теоремы 3.13.
Следствие 2 (необходимое условие сходимости ряда). Для
СО
сходимости ряда J1, ик необходимо, чтобы последовательность
4 = 1
нх, и2, и&, ... членов этого ряда являлась бесконечно малой.
Достаточно доказать, что для данного сходящегося ряда и для
любого е> 0 найдется номер No такой, что при n^N9 | н„| <е.
Пусть дано любое е>-0. Согласно теореме 13.1 найдется номер Af
такой, что при n^N и для любого натурального р выполняется
неравенство (13.10). В частности, при/?=1 это неравенство имеет вид
1 нл+11 <е (при n^N).	(13.11)
Если теперь положить номер No равным No = N -{-1, то при n^-N0
в силу неравенства (13.11) получим | ип | < е, что и требовалось
доказать.
По другому следствие 2 можно сформулировать так: для сходи-
ОО
мости ряда У uk необходимо, чтобы lim uk = G. Таким образом,
4=1	fc—от
при исследовании на сходимость данного ряда следует прежде всего
посмотреть, стремится ли к нулю А-й член этого ряда при k —► оо.
Если это не так, то ряд заведомо расходится. Так, например, ряд
у
Z 5^ + 300/г
4 = 1
заведомо расходится, ибо
кг 1
lim uk— lim , onn:- = -g-	0.
4 = co 4_ot5^ + 300*	5^
CO
Аналогично расходимость уже изученного выше ряда У, (—1)й-1
4=1
вытекает из того, что lim (— 1)* не существует.
4 -► оо ч
Подчеркнем, однако, что стремление к нулю k-vo члена ряда при
А->оо является лишь необходимым, но не достаточным условием
сходимости ряда.
В качестве примера рассмотрим ряд
СО
2т = 1+т+1+-	<13Л2>
4=1
Этот ряд обычно называют гармоническим рядом. Очевидно, что
для гармонического ряда выполнено необходимое условие сходимости,
§2]
РЯДЫ С ПОЛОЖИТЕЛЬНЫМИ ЧЛЕНАМИ
415
ибо lim -£- = 0. Докажем, однако, что этот ряд расходится. Восполь-
зуемся критерием Коши. Докажем, что для положительного числа
е = 4- не существует такого номера N, что при n^N для любого
натурального р
п + р
2 4
1
< е— 2 .
(13.13)
В самом деле, если взять р — п, то
для сколь угодно большого п
» + р	2п
2 1- V	_ 1_
k — L	2пП~ 2-
k = п + 1	k == п 4- 1
^Мы учли, что в последней сумме п слагаемых и что наименьшее
из этих слагаемых равно .j
Итак, неравенство (13.13) оказывается невыполненным, каким бы
большим мы ни взяли номер N. В силу критерия Коши ряд (13.12)
расходится.
3. Два свойства, связанные со сходимостью ряда. 1°. Отбра-
сывание конечного числа членов ряда (или добавление к ряду конеч-
ного числа членов) не влияет на сходимость или расходимость
этого ряда.
Чтобы убедиться в этом, достаточно заметить, что в результате
указанного отбрасывания (или добавления) членов, все частичные
суммы этого ряда, начиная с некоторого номера, изменятся на одну
и ту же постоянную величину.
2°. Если с — отличная от нуля постоянная, u'k = cuk, то ряд
ОО	со
2 u'k сходится тогда и только тогда, когда сходится ряд м*-
*=1	•	Л=1
Если обозначить л-е частичные суммы рассматриваемых рядов
соответственно через S’n и Sn, то очевидно, что S'n — cSn. Из послед-
него равенства вытекает, что lim существует тогда и только
п -* со
тогда, когда существует lim
П-* СО
§ 2. Ряды с положительными членами
1. Необходимое и достаточное условие сходимости ряда
с положительными членами. В этом параграфе мы рассмотрим ряды,
все члены которых неотрицательны. Следуя установившейся тра-
диции, мы будем называть такие ряды рядами с положительными
'416
ТЕОРИЯ ЧИСЛОВЫХ РЯДОВ
[гл. 13
членами (хотя правильнее было бы употреблять термин «ряды с не-
отрицательными членами»). Что же касается рядов, все члены которых
строго больше нуля, то такие ряды мы будем называть рядами со
строго положительными членами.
Ряды с положительными членами сами по себе часто встречаются
в приложениях. Кроме того, их предварительное изучение облегчит
изучение рядов с членами любого знака. В дальнейшем, чтобы под-
черкнуть, что речь идет о ряде с положительными членами, мы Часто
будем обозначать члены такого ряда символом рк вместо ик.
Мы можем сразу же отметить основное характеристическое свой-
ство ряда с положительными членами: последовательность частич-
ных сумм такого ряда является неубывающей.
Это позволяет нам доказать следующее утверждение.
Теорема 13.2. Для того чтобы ряд с положительными чле-
нами сходился,''необходимо и достаточно, чтобы последователь-
ность частичных сумм этого ряда была ограничена.
Необходимость следует из того, что всякая сходящаяся
последовательность является ограниченной (в силу теоремы 3.8).
Достаточность вытекает из того, что последовательность ча-
стичных сумм не убывает и, стало быть, для сходимости этой после-
довательности достаточно, чтобы она была ограничена (в силу тео-
ремы 3.15).
2. Признаки сравнения. В этом пункте мы установим ряд при-
знаков, позволяющих сделать заключение о сходимости (или расходи-
мости) рассматриваемого ряда посредством сравнения его с другим
рядом, сходимость (или расходимость) которого известна.
СО	00
Теорема 13.3. Пусть y^pft и У р* — два ряда с положи-
, *=i	fe = i
тельными членами. Пусть, далее, для всех номеров k справедливо
неравенство
Pk^Pk.	(13.14)
’ 00
Тогда сходимость ряда ^р^ влечет за собой сходимость ряда
к — 1
00	оо
Ур^; расходимость ряда Pk влечет за собой расходимость
k=i	k=i
ОО
ряда У р*.
й=т .
Доказательство. Обозначим n-е частичные суммы рядов
00	со
У р* и ^р’к соответственно через и S’n. Из неравенства (13.14)
k=i	k=i
заключаем, что Sn^S’n. Последнее неравенство означает, что ограни-
ченность последовательности частичных сумм влечет за собой
ограниченность последовательности частичных сумм {£„} и, наоборот,
§ 21
РЯДЫ С ПОЛОЖИТЕЛЬНЫМИ ЧЛЕНАМИ
417
неограниченность последовательности частичных сумм {£„} влечет за
собой неограниченность последовательности частичных сумм {5^}.
В силу теоремы 13.2 теорема 13.3 доказана.
Замечание 1. В условии теоремы 13.3 можно требовать, чтобы
неравенство (13.14) было выполнено не для всех номеров k, а лишь
начиная с некоторого номера k. В самом деле, в силу п. 3 § 1,
отбрасывание конечного числа членов-не влияет на-сходимость ряда.
Замечание 2. Теорема 13.3 останется справедливой, если
в условии этой теоремы заменить неравенство (13.14) следующим
неравенством:
pk^cp'k,	(13.15)
где с — любая положительная постоянная. В самом деле, в силу
ОО
п. 3 § 1, вопрос о сходимости ряда У ph эквивалентен вопросу
* = !
ОО
о сходимости ряда У, (ср'ь). При этом, конечно, можно . требовать,
k = i
чтобы неравенство (13.15) было выполнено, лишь начиная с некого-
рого достаточно большого номера k.
СО
Следствие из теоремы 13.3. Если У pk — ряд с положи-
k = i
со
тельными членами, У — ряд со строго Положительными чле-
k = t	.
нами и если существует конечный предел
lira 4 = L,
fe-*OO pk
00
то сходимость ряда У ph влечет за собой сходимость ряда
* = 1
00	00	_
У р^, расходимость ряда У рк влечет за собой расходимость
k = l	А = 1
СО
ряда У р'к.
4 = 1
Доказательство. Так как lim 4 = L, то, по определению
k -* ОО pk
предела, для некоторого е>• 0 найдется номер Nтакой, что при k^N
E — e.<Z^<iL + e.
Pk
Стало быть, при k^N справедливо неравенство pk<Z(L + t)p'k.
Последнее неравенство совпадает с неравенством (13.15) при c = L 4-е.
В силу замечания 2 к теореме 13.3 следствие доказано.
418
ТЕОРИЯ ЧИСЛОВЫХ РЯДОВ
(ГЛ. 13
Теорема 13.4. Пусть У и У р'к — два ряда со строго по-
fe = l л = 1
ложительными членами. Пусть, далее, для всех номеров k спра-
ведливо неравенство
(13.16)
Pk pk
СО
Тогда сходимость ряда pit влечет за собой сходимость ряда
fe = 1
СО	00
2 Pk! расходимость ряда У pk влечет за собой расходимость
fe = l	/г = 1
00
ряда Pk-
s = i
Доказательство. Запишем неравенство (13.16) для k = l,
2,	...» и—1, где п — любой номер. Будем иметь
Ра Pi
Pl Pl ’
Рз Рз
Ра Рз ’
Рп рп
Рп-1 p'n—l *
Перемножая почленно все написанные неравенства, получим
Рп
Pi
или
Рп^^-Рп-
Поскольку в последнем неравенстве величина с = ~ представляет
Pi
собой положительную постоянную, не зависящую от номера п,
то, в силу замечания 2 к теореме 13.3, теорема 13.4 доказана.
Замечание 3. В условии теоремы 13.4 можно требовать, чтобы
неравенство (13.16) было выполнено не для всех номеров k, а лишь
начиная с некоторого номера k (ибо отбрасывание конечного числа
первых членов не влияет на сходимость ряда).
Обе доказанные в настоящем пункте теоремы называют теоре-
мами сравнения или признаками сравнения.
Приведем примеры применения признаков сравнения.
1.	Исследуем вопрос о сходимости ряда
оо
2 зт^’ где ь>0-
k—i
§ 2]
РЯДЫ С ПОЛОЖИТЕЛЬНЫМИ ЧЛЕНАМИ
419
Если 5^1, то Л-й член рассматриваемого ряда не стремится к нулю
при k—► оо. Стало быть, нарушено необходимое условие сходимости
ряда и ряд расходится. Если же &>»1, то, поскольку для любого
номера k справедливо неравенство
1	1
3 +	6s
ОО
и поскольку ряд 2 сходится, теорема сравнения 13.3 позволяет
k = i
утверждать сходимость рассматриваемого ряда.
2.	Исследуем вопрос о сходимости для любого а 1 следующего
ряда:
оо
2₽-1 + i+-+js+-
fe=l
Этот ряд часто называют обобщенным гармоническим рядом. По-
скольку при а 1 для любого номера k справедливо неравенство
со
и поскольку гармонический ряд у расходится *), то теорема
* = 1
сравнения 13.3 позволяет утверждать расходимость ряда (13.17) для
любого 1.
3.	Признаки Даламбера и Коши. К признакам сравнения непо-
средственно примыкают два весьма употребительных признака схо-
димости рядов с положительными членами — Даламбера и Коши. При-
знаки Даламбера и Коши основаны на сравнении рассматриваемого
ряда с рядом, составленным из элементов геометрической прогрессии,
а именно со сходящимся рядом
У ?fe = ? + 9a + ?3 + ..., |?|<1,
(13.18)
или с расходящимся рядом
£1 = 14-1 + 1+...	(13.19)
Теорема 13.5 (признак Даламбера) **). I. Если для всех
номеров k, или по крайней мере начиная с некоторого номера k,
♦) Расходимость гармонического ряда установлена в п. 2 § 1.
**) Жак Лерон Даламбер — французский математик и философ (1717^1783).
420
ТЕОРИЯ ЧИСЛОВЫХ РЯДОВ
(ГЛ. 13
справедливо неравенство
(13.20)
то ряд У, ph сходится (расходится).
t = i
II. Если существует предел
(13.21)
Pk
СТВО
lim ^±1 = £,
Л-юэ Pk
оо
то ряд У рк сходится при L<Z 1 и расходится при L > 1.
Л = 1 .
Теорему II обычно называют признаком Даламбера в предельной форме.
В этой форме он наиболее Аасто используется.
Доказательство. Разберем отдельно теоремы I и II.
1) Для доказательства теоремы I положим р'к = qk(ph = 1). Тогда
Pk+i- = q, где #<1, 1 t~!~1 — 1), и мы можем переписать неравен-
\ Pk /
(13.20) в виде
Pk+i __ P'k + t /Pk+i Р£-н\
Pk	Pk	\ Pk Pk /'
ОО
как ряд pi совпадающий с рядом (13.18) ((13.19)), сходится
л = 1
(расходится), то неравенство (13.22) на основании теоремы сравне-
ОО
ния 13.4 гарантирует сходимость (расходимость) ряда У ph. Теорема I
-*=1
(13.22)
Так
доказана.
2) Докажем теперь теорему II. Если L <; 1, то найдется положи-
тельное число е такое, что £ = 1 — 2е и £ -]- е = 1 — е. По опре-
делению предела последовательности для указанного е найдется
номер N такой, что при k^N
L-&<^-CL + &=l-e.	(13.23)
Число £-|-е=1— е играет роль q в теореме I. Ряд сходится.
Если же £>1, то найдется положительное число е такое, что
£ = 1 е и £ — е=1. В этом случае на основании левого из нера-
венств (13.23) получим
> L — е = 1 (при k N).
ОО
*) При этом, конечно, предполагается, что все члены ряда S Pk (по
k=l
крайней мере начиная с некоторого номера) строго положительны.
§ 2]
РЯДЫ С ПОЛОЖИТЕЛЬНЫМИ ЧЛЕНАМИ
421
Ряд расходится на основании теоремы I. Теорема 13.5 полностью
доказана.
Замечания к т е о р е м е . 13.5. 1) Обратим внимание на то,
что в теореме 13.5 (I) неравенство	<11 (для всех k, начиная
с некоторого) нельзя заменить на^^-<.1-
В самом деле, как доказано выше, гармонический ряд (13.12) рас-
ходится, но для этого ряда -^±1 = j < 1. (для всех номеров k).
2)	Если в условиях. теоремы 13.5 (II) L = 1, то нельзя сказать
ничего определенного о сходимости ряда (т. е. при L = 1 признак
Даламбера «не действует»), В самом деле, для гармонического ряда
(13.12) L=l,-причем этот ряд, как мы знаем, расходится. Вместе
с тем для ряда
(13.24)
* = |
также Т=1, но этот ряд, как будет показано в следующем пункте,
сходится.
Теорема 13.6 (признак Коши). I. Если для всех номеров k,
или по крайней мере начиная с некоторого номера k, справедливо
неравенство
^Рк^<1<1 (^Р^1)>	(13.25)
ОО
то ряд 2 Рь сходится (расходится).
k = i
II. Если существует предел
kr-
limy/7ft — L,	.	(13.26)
k 00
oo
то ряд pk сходится при L •< 1 и расходится при L > 1.
fe = i
Теорему II обычно называют признаком Коши в предельной
форме.
Доказательство. Разберем отдельно теоремы I и И.
1)	Для доказательства теоремы I положим p'k = qk (p'k = \). Тогда
из неравенства (13.25) получим
Pk^Pk (Pk^Pk).	(13.27)
СО
Так как ряд pk, совпадающий с рядом (13.18) ((13.19)), сходится
ft=l
(расходится), то неравенство (13.27) на основании теоремы сравне-
00
ния 13.3 гарантирует сходимость (расходимость) ряда X pk.
Й = 1
422
ТЕОРИЯ/ ЧИСЛОВЫХ РЯДОВ
ТТЛ. 13
Теорема 13.6 (I) доказана.
2)	Для доказательства теоремы 13.6 (II) следует дословно повто-
рить схему доказательства теоремы 13.5 (II), заменив во всех рас-
суждениях на рк.
Теорема 13.6 полностью доказана.
Замечания к теореме 13.6. 1) Как и в предыдущей теореме,
k_______________________________
в теореме (13.6) (I) неравенство урд, «С <? <; 1 нельзя заменить на
frpkC К
2)	При L = 1 признак Коши в предельной форме «не действует».
Можно сослаться на два примера, указанные в соответствующем заме-
чании к признаку Даламбера.
3)	Возникает вопрос о том, какой из двух признаков, Даламбера или
Коши, является более сильным. Проанализируем этот вопрос в отношении
признаков Даламбера и Коши, взятых в предельной форме. Можно доказать,
что из существования предела (13.21) вытекает существование предела (13.26)
и факт равенства этих пределов. (Доказательство приведено в дополнении I
к этой главе.) Обратное неверно. В самом деле, легко убедиться в том, что
для ряда
J	(13.28)
Л=1
предел (13.26) существует и равен i, в то время как предел (13.21) вообще
не существует. Таким образом, признак Коши является более сильным, чем
признак Даламбера, ибо всякий раз, когда действует признак Даламбера,
действует и признак Коши и вместе с тем существуют ряды (например,
ряд (13.28)), для которых действует признак Коши и не действует признак
Даламбера. Несмотря на это, признак Даламбера на практике употребляется
чаще, чем признак Коши.
Примеры. 1) Исследуем вопрос о сходимости ряда
2 т-	а ад
А=1
Применим признак Даламбера в предельной форме. Имеем
(/йЛ pft+1._(/feTD*+1 fei____1 и  Ц2
Рк *1 ’ Рь (*+1)1 (/й)*~уТ+Т\
На основании (13.30)
k
(13.30)
lim ^±1
Л-*ОО Pk
k -f- 1
т. e. ряд (13.29) сходится.
§ 2]
РЯДЫ С ПОЛОЖИТЕЛЬНЫМИ ЧЛЕНАМИ
423
2) Изучим вопрос о сходимости ряда
, оо
2	о3-31)
л=1
Применим признак Коши в предельной форме. Имеем
Vpk^.-	(13.32)
На основании (13.32) lim yfPk = -7r l>m *) = 4~'\ 1- Таким обра-
k—►со	А-*оо	*
зом, признак Коши устанавливает сходимость ряда (13.31).
4. Интегральный признак Коши — Маклорена. Признаки Далам-
бера и Коши оказываются непригодными для выяснения вопроса
о сходимости некоторых часто встречающихся рядов с положитель-
ными членами. Так, например, с помощью этих признаков нельзя
выяснить вопрос о сходимости обобщенного гармонического ряда
СО
<13.33)
k = l
(а — любое вещественное число).
Правда, в конце пункта 2 мы установили, что при а 1 ряд
(13.33) расходится, но остается открытым вопрос о сходимости этого
ряда при а>1. В этом пункте мы установим еще один общий при-
знак сходимости ряда с положительными членами, из которого,
в частности, будет вытекать сходимость ряда (13.33) при а>1.
Теорема 13.7 (теорема Коши — Маклорена). Пусть функ-
ция f(x) неотрицательна и не возрастает всюду на полупрямой
х^т, где т — любой фиксированный номер. Тогда числовой ряд
ОО
S f(k) =f(m)+f(m 4-1) +f(m+ 2) + ...	(13.34)
k = m
сходится в том и только в том случае, когда существует пре-
дел при п-^-оо последовательности
an = \f(x)dx.	(13.35)
т
Доказательство. Пусть k — любой номер, удовлетворяющий
условию k т 4-1, а х— любое значение аргумента из сегмента
♦) Для вычисления lira х1^ следует прологарифмировать выражение
х11х и применить правило Лопиталя,
424
ТЕОРИЯ ЧИСЛОВЫХ РЯДОВ
[ГЛ. 13
k— l^x^k. Так как по условию функция /(х) не возрастает на
указанном сегменте, то для всех х из указанного сегмента справед-
ливы неравенства
/(А)</(х)</(Л-1).	(13.36)
Функция f(x), будучи ограниченной и монотонной, интегрируема на
сегменте k—i^x^k (см. п. 5 § 4 главы 10). Более того, из
неравенств (13.36) и из свойства 3° (см. и. 1 § 6 главы 10) вытекает,
что
k
§ f(k~)dx^
k—i
или
k	k
$ f(x)dx^ j f(k—\)dx
k-\	k—i
k
W 5 f(x)dx^f(k-\).
ft—1
(13.37)
Неравенства (13.37) установлены нами для любого	Запи-
шем эти неравенства для значений k, равных лг-(-1, л*+ 2,. ..,’л,
где л — любой номер, превосходящий т.
т+ 1
/(/л + 1)^ j f(x)dx^f(m),
т
m + 2
f(m 4-2)=с $ f(x)dx^f(m + 1),
т 1
/(я)^ 5 f&)dx^f(n-\).
n—1
Складывая почленно записанные неравенства, получим
f(k) $ /(х) dx J] f(k).	(13.38)
ft=m-|-l	т	к = т
Договоримся обозначать символом Sn п-ю сумму ряда (13.34), равную
Sn= S f(k).
к = т
Приняв это обозначение и учитывая обозначение (13.35), мы можем
следующим образом переписать неравенства (13.38):
Sn—fkrnj^a^Sn-^	(13.39)
Неравенства (13.39) позволяют без труда доказать теорему. В само.^
деле, из формулы (13.35) очевидно, что последовательность {a„|
является неубывающей. Стало быть, для сходимости этой последова-
тельности необходима и достаточна ее ограниченность. Для сходи-
§ 2]
РЯДЫ С ПОЛОЖИТЕЛЬНЫМИ ЧЛЕНАМИ
425
мости ряда (13.34) в силу теоремы 13.2 необходима и достаточна
ограниченность последовательности {«?„}. Из неравенств (13.39) выте-
кает, что последовательность {£„} ограничена тогда и только тогда,
когда ограничена последовательность {ап}, т. е. тогда и только тогда,
когда последовательность {а„} сходится. Теорема доказана.
Примеры. 1) Прежде всего применим интегральный признак
Коши — Маклорена для выяснения сходимости обобщенного гармони-
ческого ряда (13,33). Поскольку ряд (13.33) можно рассматривать
как ряд вида (13.34) при т = \, /(х) = ^ и функция f(x) убывает
и положительна на полупрямой х^1, вопрос о сходимости ряда
(13.33) эквивалентен вопросу о сходимости последовательности {ал},
где
и = л	ni-« _ 1
—aUl = -T^- ПРИ
|-Г=Д
Inx = 1пи при a= 1.
п
ап = \ ^х =
Из вида элементов ап вытекает, что последовательность {а„} расхо-
дится при asg 1 и сходится при а>1, причем в последнем случае
lim ап— —_2~г- Таким образом, ряд (13.33) расходится при a=g 1
n-»oo a 1
(это мы уже установили выше другим способом) и сходится при
a> 1. В частности, при а = 2 ряд (13.33) переходит в ряд (13.24),
сходимость которого мы теперь можем утверждать.
2) Исследуем вопрос о сходимости ряда
2 А1п₽А’
* = 2
(13.40)
где р — фиксированное положительное вещественное число. Ряд (13.40)
можно рассматривать как ряд вида (13.34) при m = 2n f(x) = x
Поскольку функция f (х) неотрицательна и не возрастает на полупря-
мой х~^2, вопрос о сходимости ряда (13.40) эквивалентен вопросу
о сходимости последовательности {an}, где
п
С 1 л
ап= \ . а-- ах =
п 1 х 1п₽х
]П1-Рп— 1п1—₽2
1 — ₽ |х=2=	1 — ₽
при р 96 1,
In In х Г _” = In In п— In In 2 при P=l.
Из вида элементов ап вытекает, что последовательность {а„} сходится
при р>1 и расходится при р sg 1. Таким образом, ряд (13.40) схо-
дится при р> 1 и расходится при p«g 1.
5.	Признак Раабе. Признаки 'Даламбера и Коши были основаны на
сравнении рассматриваемого ряда с рядом, представляющим собой сумму
426
ТЕОРИЯ ЧИСЛОВЫХ РЯДОВ
[ГЛ. 13
геометрической прогрессии. Естественно, возникает идея о получении более
тонких признаков, основанных на сравнении рассматриваемого ряда с другими
стандартными рядами, сходящимися или расходящимися «медленнее», чем ряд
для геометрической прогрессии.
В этом пункте мы установим признак, основанный на сравнении рассма-
триваемого ряда с изученным в предыдущем пункте стандартным рядом
ОО
2 i = 1+F + i + -	<13-41)
fe=l
Теорема 13.8 (признак Раабе) *). I. Если для всех номеров k, или по
крайней мере начиная с некоторого номера k, справедливо неравенство
**)	(13.42)
ОО
то ряд У Ph сходится (расходится),
А=1
II. Если существует предел
lim k( 1 — ^±1') = L,	(13.43)
СО
то ряд Pk сходится при L> 1 и расходится при L< 1. Теорему II обычно
Й = 1
называют признаком Раабе в предельной форме.
Доказательство. Разберем отдельно теоремы I и II.
1) Для доказательства теоремы I перепишем неравенство (13.42) в виде
4 j^-Ssl-----------Ц.	(13.44)
Pk * I Pk fe J
Так как q> 1, то найдется некоторое число а, удовлетворяющее неравенствам
д>а>1. Разложив функцию (1 + х)Л по формуле Маклорена с остаточным
членом в форме Пеано (см. п. 2 § 15 главы 8), будем иметь
(1 + х)а = 1 + ах + о (х).
Полагая в последней формуле х = —i-, получим
Поскольку последовательность —    является бесконечно малой, то, начиная
k
с некоторого номера k0, справедливо.неравенство
^q — а.	(13.46)
____________ k
*)	Иозеф Людвиг Раабе — швейцарский математик (1801—1859).
ОО
**	) Конечно, при этом предполагается, что ряд У] pft, по крайней мере
k=i
начиная с некоторого номера, имеет строго положительные члены.
§21
РЯДЫ С- ПОЛОЖИТЕЛЬНЫМИ ЧЛЕНАМИ
427
Сопоставляя (13.45) и (13.46), получим неравенство
1— у) ^1— (при
Сравнение неравенств (13.44) и (13.47) дает
(13.47)
P*±i 1 V 1 -11
Pfe-"\ k) \рк	И
(при й^й0).
Последние неравенства можно переписать в виде
Pfe+i
Pk ~~	1
(k - 1?
1 '
Pfe+i
Pk " 1
k~V
(при k Ss fc0).
(13.48)
Поскольку ряд (13.41) сходится при а>1 и расходится при о=1, то нера-
венства (13.48) и теорема сравнения 13.4 позволяет утверждать, что ряд
ОО
2 Рь сходится (расходится). Теорема 1 доказана.
* = 1 .
2) Точно так же, как и в признаках Даламбера и Коши, мы сведем
теорему II к теореме I. Пусть сначала L>\. Положим е=—gl,
<? = 1 е = L — е. По определению предела (13.43) для этого е можно указать
номер Ло, начиная с которого Л (1 —	— L < е, и, стало быть, спра-
I \ Pfe / I
ведливо левое неравенство (13.42). Если же L<1, то мы положим е=1—L
и, используя определение предела (13.43), получим, что, начиная с некоторого
номера 7е0, справедливо правое неравенство (13.42). Теорема 13.8 полностью
доказана.
Замечание. Отметим, что в теореме 13.8 (I) в левом неравенстве (13.42)
нельзя взять q = 1 (при этом сходимость ряда может не иметь места). При
L = 1 теорема 13.8 (II) «не действует» (возможна и сходимость, и расходи-
мость ряда).
Пример. Исследовать вопрос о сходимости ряда
со	_\
2 Pfe, где pk = а '	9	9	*-1/ (а = const >0).
* = S
Легко проверить, что признаки Даламбера и Коши в применении к этому ряду
«не действуют». Применим признак Раабе. Легко проверить, что
_ 1
\ Pk 1 f_l\
\ k)
Нетрудно сообразить, что последняя дробь при k —► оо стремится к производ-
ной функции ах в точке х = 0, т. е. стремится к In а. В силу признака Раабе
рассматриваемый ряд сходится при 1па>1, т. е. при а>е, и расходится
при 1па< 1, т. е. при а <е. При а = е вопрос о сходимости ряда требует
дополнительного исследования, так как признак Раабе «не действует». Другим
примером ряда, в применении к которому «не действует» признак Раабе,
может служить ряд (13.40).
6. Отсутствие универсального ряда сравнения. Мы уже отмечали, что
признаки' Даламбера и Коши основаны на сравнениях рассматриваемого ряда
428
ТЕОРИЯ ЧИСЛОВЫХ РЯДОВ
[ГЛ 13
с рядом для геометрической прогрессии, а признак Раабе — на сравнении
с более медленно сходящимся (или расходящимся) рядом (13.41).
Естественно, возникает вопрос о том, не существует ли такой универ-
сальный (предельно медленно}) сходящийся (или расходящийся) ряд, сравнение
с которым позволило бы сделать заключение о сходимости (или расходимости)
любого наперед взятого ряда с положительными членами.
Докажем, что такого универсального ряда не существует. Пусть даны
со	со
два сходящихся ряда 2 Pk и 2 обозначим символами гп и г'п соот-
fe=i	* *=1
СО
ветственно их n-е остатки. Будем говорить, что ряд У р'к сходится медленнее,
“ г *=1
чем ряд У рщ если lim -Д = 0. Докажем, что для каждого сходящегося ряда
k=i	п~>со гп
существует ряд, сходящийся медленнее этого ряда. В самом деле, пусть
оо
2 Ph — любой сходящийся ряд; гп — его n-й остаток. Докажем, что ряд
*=1
оо	__ оо
2 Р'ь> где*) Р* = Усходится медленнее, чем ряд 2 Pk-
А=1	fc=l
СО
В самом деле, если т’п— n-й остаток ряда 2 РУ то
й = 1
lim £?= Пт =0.
П-Ю&Гп	п — оэугп
Докажем теперь отсутствие универсального сходящегося ряда, сравнение с ко-
торым позволило бы сделать заключение о сходимости любого наперед взятого
сходящегося ряда. В самом деле, если бы такой универсальный сходящийся
ряд 2 Pk существовал, то, взяв для него построенный выше ряд 2 Р*>.
fe=i	k=i
мы получили бы, что
lim ^- = lim	= Пт-(У 4-/7^) = 0.
k^-coPh k-^cayrh-i — У Гь k-юэ
СО
Таким образом, из сравнения с рядом 2 Pk нельзя сделать заключения о схо-
k=t
ОО
димости ряда 2 Pk- Аналогично доказывается отсутствие универсального
расходящегося ряда, сравнение с которым позволило бы сделать заключение
о расходимости любого наперед взятого расходящегося ряда. .
§ 3. Абсолютно и условно сходящиеся ряды
1. Понятия абсолютно и условно сходящегося ряда. Теперь
мы перейдем к изучению рядов, члены которых являются веществен-
ными числами любого знака.
ОО
*) За г0 принимаем всю сумму 2 Pk'
Л = 1
§ 3]
АБСОЛЮТНО И УСЛОВНО СХОДЯЩИЕСЯ РЯДЫ
429
Определение 1. Будем называть ряд
ОО
У «л
л = 1
абсолютно сходящимся, если сходится ряд
У 1«л|-
Л = 1
(13.49)
(13.50)
Заметим, что в этом определении ничего не сказано о том, предпо-
лагается ли при этом сходимость самого ряда (13.49). Оказывается,
такое предположение оказалось бы излишним, ибо справедлива сле-
дующая теорема.
Теорема 13.9. Из сходимости ряда (13.50) вытекает сходи-
мость ряда (13.49).
Доказательство. Воспользуемся критерием Коши для ряда
(т. е. теоремой 13.1). Требуется доказать, что для любого ,е >• 0 най-
дется номер N такой, что для всех номеров п, удовлетворяющих
условию n^N, и для любого натурального р
п+р
X''
<е.
(13.51)
Фиксируем любое е>0. Так как ряд (13.50) сходится, то, в силу
теоремы 13.1, найдется номер N такой, что для всех номеров 'п,
удовлетворяющих условию n^N, и для любого натурального р
п+р
|«л|<е-
Л = л + 1
(13.52)
Имея в виду, что модуль суммы нескольких слагаемых не превосходит
суммы их модулей, можем записать
л+р
< 5 |«л|-
Л —л+1
(13.53)
Сопоставляя неравенства (13.52) и (13.53), получим неравенство (13.51).
Теорема доказана.
Определение 2. Ряд (13.49) называется условно сходя-
щимся, если этот ряд сходится, в то время как соответст-
вующий ряд из модулей (13.50) расходится.
Примером абсолютно сходящегося ряда может служить ряд
2(— 1)*-»	,	1,1	1 ,	'	. ,
— 1	2“ + 3“	4» + • • • > гДе а
430
ТЕОРИЯ ЧИСЛОВЫХ РЯДОВ
Ггл. 13
Этот ряд сходится абсолютно, ибо при а>1 сходится ряд (13.33).
Приведем пример условно сходящегося ряда. Докажем условную
сходимость ряда
+	+ - +	+ - 03.54)
Л = 1
Так как соответствующий ряд из модулей (гармонический ряд), как
мы уже знаем, расходится, то для доказательства условной сходи-
мости ряда (13.54) достаточно доказать, что этот ряд сходится.
Докажем, что ряд (13.54) сходится к числу In 2. В п. 2 § 15 главы 8
мы получили разложение по формуле Маклорена функции In (1 х)
у2 уЗ у4	уЛ
1п(1+х) = х-| + у-|+... + (-1Г-1^ + /?п+1(х). (13.55)
Там же для всех х из сегмента О^х^ 1 получена следующая оценка
остаточного члена:
Полагая в формулах (13.55) и (13.56) х=1, будем иметь
1п2=1-1 + 1-1 + <=^4-/?„+1(1),
где
|Rm(DI<4t
или
1Г1-1 + 1-1+ I (- П"-1] 1П 2 I 1
It1 2 + 3	4 +•••+ п J 1П 2 j < п + 1 '
Обозначая через л-ю частичную сумму ряда (13.54), мы можем
переписать последнее неравенство в виде
Таким образом, разность S„ — In 2 представляет собой бесконечно
малую последовательность. Это и доказывает сходимость ряда (13.54)
к числу In 2.
2. О перестановке членов условно сходящегося ряда. Одним
из важнейших свойств суммы конечного числа вещественных слагае-
мых является переместительное свойство. Это свойство утверждает,
что от перестановки слагаемых сумма не меняется. Естественно,
возникает вопрос, остается ли справедливым это свойство для суммы
сходящегося ряда, т. е. может ли измениться сумма сходящегося
ряда от перестановки членов этого ряда? В этом пункте мы
выясним этот вопрос в отношении условно сходящегося ряда. Мы
начнем наше рассмотрение с изучения некоторой конкретной переста-
§31
АБСОЛЮТНО И УСЛОВНО СХОДЯЩИЕСЯ РЯДЫ
431
новки членов ряда (13.54). Для удобства запишем ряд (13.54) в виде
1-| + 4-т + - + 2Й-я+-	<13-56’
В конце предыдущего пункта мы доказали, что ряд (13.54) сходится
условно и имеет сумму S=ln2. Переставим теперь члены ряда (13.54)
так, чтобы после одного положительного члена стояли два отрица-
тельных члена. В результате такой перестановки членов получим ряд
(13.67)
Докажем, что полученный в результате указанной перестановки членов
ряда (13.54) ряд (13.57) сходится и имеет сумму, вдвое меньшую, чем
ряд (13.54). Будем обозначать т-е частичные суммы рядов (13.54) и
(13.57) символами Sm и S'm соответственно. Можем записать:
т
fc = l
Итак,
Далее, очевидно, что
'Зт-1 — 2	4/п ’
*$М1-2 — •Ssm-l 4т_______2‘
1\_.1е
2k) ~ 2 2№
(13.58)
(13.59)
(13.60)
*$3т — 2
Поскольку lim S2m = S, в пределе при ти->со из формул (13.58)
(13.59) и (13.60) получим
lim S3m = -nS, lim	Um S3m_a = -yS.
m—>оо	41 m-^co	*	гп—*со
Тем самым окончательно доказано, что ряд (13.57) сходится и' имеет
сумму, равную у S'. Поскольку S=ln2 0, ясно, что у S. Стало
быть, в результате указанной выше перестановки членов сумма
условно сходящегося ряда (13.54) изменилась. Рассмотренный нами
конкретный пример показывает, что условно сходящийся ряд не обла*
дает переместительным свойством. Полную ясность в вопроа
432
ТЕОРИЯ ЧИСЛОВЫХ РЯДОВ
[ГЛ. 13
о влиянии перестановок членов на сумму условно сходящегося ряда
вносит следующее замечательное утверждение, принадлежащее Риману.
Теорема 13.10 {теорема Римана). Если ряд сходится условно,
то, каково бы ни было наперед взятое число L, можно так
переставить члены этого ряда, чтобы преобразованный ряд схо-
дился к числу L.
• Доказательство. Пусть
СО
Л = 1
— произвольный условно сходящийся ряд. Обозначим через plt р2, Рз,...
положительные члены ряда (13.61), выписанные в таком порядке,
в каком они стоят в этом ряде, а через qlt q2, q3, ... модули отри-
цательных членов ряда (13.61), выписанные в таком же порядке,
в каком они стоят в этом ряде. Ряд (13.61) содержит бесконечное
число как положительных, так и отрицательных членов, ибо
если бы членов одного знака было конечное число, то, отбросив не
влияющее на сходимость конечное число первых членов, мы бы полу-
чили ряд, состоящий из членов одного знака, для которого сходи-
мость означала бы абсолютную сходимость. Итак, с рядом (13.61)
ОО
связаны два бесконечных ряда с положительными членами У pk и
*=i
СО
У, qk. Будем обозначать первый из этих рядов символом Р, а вто-
л=1
рой — символом Q. Докажем, что оба ряда Р и Q являются расхо-
дящимися. Обозначим символом Sn п-к> частичную сумму ряда (13.61),
символом Рп — сумму всех положительных ' членов, входящих в Sn,
символом, Q„ сумму модулей всех отрицательных членов, входящих
в Sn- Тогда, очевидно, Sn = Pn — Qn, и так как по условию ряд (13.61)
сходится к некоторому числу S, то
lim (P„-Q„) = S.	(13.62)
п-*со
С другой стороны, так как ряд (13.61) не сходится абсолютно, то
lim (P„ + Q„) = oo.	(13.63)
n->GO
Сопоставляя (13.62) и (13.63), получим lim Р„ = оо, lim Qn = oo,
п—>00	/I—►СО
т. е. доказано, что оба ряда Р и Q расходятся. Из расходимости
рядов Р и Q вытекает, что даже после удаления любого конечного
числа первых членов этих рядов, мы можем взять из оставшихся
членов как ряда Р, так и ряда Q столь большое число членов, что их
сумма превзойдет любое. наперед взятое число. Опираясь на этот
факт, докажем, что можно так переставить члены исходного ряда
§ 3]
АБСОЛЮТНО И УСЛОВНО СХОДЯЩИЕСЯ РЯДЫ
433
(13.61), что в результате получится ряд, сходящийся к наперед взятому
числу L. В самом деле, мы получим требуемый ряд следующим
образом. Сначала выберем из исходного ряда (13.61)’ равно столько
положительных членов р2, р2, р3....pkl, чтобы их сумма Pi + • • •
• ••+ Pki превзошла L. Затем добавим к выбранным членам ровно
столько отрицательных членов —qY, — q2,..., —qks, чтобы общая
сумма рг +р2 + • • •	— Яг — <72—	~ оказалась меньше L. Затем
снова добавим ровно столько положительных членов pkl+i, pt^+i, • • •
..., ркз, чтобы общая сумме pJ+p2 + ...+pkl — q1 — q2 — ... — qks +
+ Pfej+i+• • •+^*3 сказалась больше L. Продолжая аналогичные рас-
суждения далее, мы получим бесконечный ряд, в состав которого
войдут все члены исходного ряда (13.61), ибо каждый раз нам придется
добавлять хотя бы один положительный или отрицательный член
исходного ряда. Остается доказать, что полученный ряд сходится к L.
Заметим, что в полученном ряде последовательно чередуются группы
положительных и группы отрицательных членов. Если частичная
сумма полученного ряда заканчивается полностью завершенной груп-
пой, то отклонение этой частичной суммы от числа L не превосходит
модуля последнего его члена *). Если же частичная сумма заканчи-
вается не полностью завершенной группой, то отклонение этой
частичной суммй от числа L не превосходит модуля последнего члена
предпоследней из групп. Для установления сходимости ряда к L
достаточно убедиться в том, что модули последних членов групп
образуют бесконечно малую последовательность, а это непосредственно
вытекает из необходимого условия сходимости исходного ряда (13.61).
Теорема Римана доказана.
3. О перестановке членов абсолютно сходящегося ряда. В пре-
дыдущем пункте мы доказали, что условно сходящийся ряд не обла-
дает переместительным свойством. В этом пункте мы докажем,
что для всякого абсолютно сходящегося ряда справедливо переме-
стительное свойство.
Теорема 13.11 {теорема Коши). Если данный ряд сходится
абсолютно, то любой ряд, полученный из данного ряда посредст-
вом некоторой перестановки членов, также сходится абсолютно
и имеет ту же сумму, что и данный ряд.
Доказательство. Пусть ряд
СО
2	(13.64).
fe==i
сходится абсолютно и сумма этого ряда равна 5. Пусть, далее,
СО
л 4	(13.65)
А=1
.6______________
*) Ибо мы добавляем в данную группу члены ровно до тех пор, пока
общая сумма «не перейдет» через число L.
434
ТЕОРИЯ ЧИСЛОВЫХ РЯДОВ
[ГЛ. 13
— ряд, полученный из ряда (13.64) посредством некоторой переста-
новки членов. Требуется доказать: 1) что ряд (13,65) сходится и имеет
сумму, равную 5, 2) что ряд (13.65) сходится абсолютно. Докажем
сначала 1). Достаточно доказать, что для любого е>0 найдется номер N
такой, что при

< £.
(13.66)
Фиксируем произвольное е>0. Так как ряд (13.64). сходится абсо-
лютно и имеет сумму, равную S, то для выбранного е > 0 можно
указать номер No такой, что будут справедливы неравенства
Nd+p
У	(р —любое натуральное число) (13.67)
* = tfo + l
и
(13.68)
Выберем теперь номер N столь большим, чтобы любая частичная
сумма S'„ ряда (13.65) с номером п, превосходящим N, содержала
все первые No членов ряда (13.65) **).
Оценим разность, стоящую в левой части (13.66), и докажем, что
при для этой разности справедливо неравенство (13.66).
В самом деле, указанную разность можно представить в виде
в	г п	Nq \	\
u'b-s= 2 н*~	+ LS u*~s •	(13-69)
£=i	\fe=i	л=1 / \fe=i	/
Так как модуль суммы двух величин не превосходит суммы их моду-
лей, то из (13.69) получим
А = 1
а	No
У, Uk- 2
fc = l	Л = 1
Nd
S uk-S
(13.70)
Из неравенств (13.68) и (13.70) очевидно, что для доказательства
неравенства (13.66) достаточно доказать, что при n^N
п	Nd
2 й- 2»«
Л = 1	Л = 1
е
У
(13.71)
*) Номер Nd в неравенствах (13.67) и (13.68) можно взять один и тот же.
В самом деле, предварительно записав указанные два неравенства с разными
номерами Af0, мы затем можем взять наибольший из двух номеров No.
**) Такой номер N выбрать можно, ибо ряд (13.65) получается из ряда
(13.64) посредством некоторой перестановки членов.
§ 4] АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ НАД СХОДЯЩИМИСЯ РЯДАМИ 435
Для доказательства неравенства (13.71) заметим, что при N
первая из сумм, стоящих в левой части (13.71), содержит все No
первых членов ряда (13.64). Вследствие этого разность
п	No'
*=1	k=i
(13.72)
представляет собой сумму (п — No) членов ряда (13.64) с номерами,
каждый из которых превосходит No.
Если выбрать натуральное р столь большим, чтобы номер N0+p
превосходил номера всех (п — AQ членов только что указанной
суммы, то для разности (13.72) во всяком случае справедливо нера-
венство
л	No	No+p
'Яиь-'^иь £ 1»*1-	(13.73)
* = 1	Л = 1	й = ЛГ0 + 1
Из неравенств (13.73) и (13.67) вытекает неравенство (13.71). Тем
самым доказано неравенство (13.66), т. е. доказано, что ряд (13.65)
сходится и имеет сумму, равную 5. Остается доказать утверждение 2)
о том, что ряд (13.65) сходится абсолютно. Доказательство этого
утверждения следует из утверждения 1), если его применить к рядам
У |«41 и uk
*=i	*=i
(13.74)
При этом мы докажем сходимость второго из рядов (13.74), т. е.
докажем абсолютную сходимость ряда (13.65). Теорема 13.11 пол-
ностью доказана.
§ 4. Арифметические операции над сходящимися рядами
В этом параграфе мы рассмотрим вопрос о возможности почлен-
ного сложения и перемножения сходящихся рядов,
со	СО
Теорема 13.12. Если два ряда У иь и У сходятся и имеют
Й = 1	А = 1
00
суммы, соответственно равные U и V, то и ряд У
сходится и имеет сумму, равную U±V.
Доказательство. Обозначим n-е частичные суммы рядов
Xuk, и (ltk соответственно через Un, Vn и Sn. Тогда,
очевидно, Sn— Un± Vn. Так как lim Un — U, lim V„ = V, то, согласно
n—>00	П-+С&
теоремам 3.9 и 3.10, существует предел lim Sn= U±V. Теорема
Л-+СО
доказана.
436
ТЕОРИЯ ЧИСЛОВЫХ РЯДОВ
ГГЛ 13
Таким образом, любые сходящиеся ряды можно почленно скла-
дывать и вычитать.
Переходя к вопросу о возможности почленного перемножения
рядов, докажем следующее утверждение.
ОС	оо
Теорема 13.13. Если два ряда У, ик и У сходятся абсо-
*=1	г=1
лютно и имеют суммы, соответственно равные U и V, то ряд,
составленный из всех произведений вида ukVi (Л=1, 2,
1—\, 2, ...), занумерованных в каком угодно порядке, также
сходится абсолютно и его 'сумма равна UV.
Доказательство. Обозначим через wv w2, w3, ... произве-
дения вида ukV[ (Л=1, 2, ...; /= 1, 2, ...), занумерованные в каком
ОС
угодно порядке. Докажем, что ряд у I wi I сходится. Пусть — и-я
I-1
частичная сумма этого ряда. Сумма Sn состоит из членов вида | ukVi |.
Среди индексов Ли/ таких членов, входящих в сумму найдется
наибольший индекс, который мы обозначим через т. Тогда во всяком
случае
*$л=^ (] | + | I + • +| ит|)(|т»11 +1 14- ... + | vm |). (13.75)
В правой части неравенства (13.75) стоит произведение т-х ча-
стичных сумм рядов . I uk I и 2dI vi L В силу сходимости ука-
занных рядов с положительными членами все их частичные суммы
(а стало быть, и их произведение) ограничены. Поэтому ограни-
чена и последовательность частичных сумм -{Sn}, а это и дока-
зывает сходимость ряда У, | Wi |, т. е. абсолютную сходимость
ряда £
Остается доказать, что последний ряд имеет сумму S, равную UV.
Так как этот ряд сходится абсолютно, то в силу теоремы 13.11 его
сумма S не зависит от порядка, в котором мы его суммируем.
Какую бы мы ни взяли последовательность (а стало быть, и подпо-
следовательность *)) частичных сумм этого ряда, она сходится
ОО
к числу S. Но в таком случае сумма 5 ряда У W; заведомо равна
1=1
UV, ибо именно к этому числу сходится подпоследовательность
частичных сумм этого ряда вида
WOT=(«l + «2+ ••• + Um) (Т>1 + V2 + ... +^m).
Теорема 13.13 доказана.	"
*) В силу п. 1 § 4 главы 3.
§ 5]
ПРИЗНАКИ СХОДИМОСТИ ПРОИЗВОЛЬНЫХ РЯДОВ
437
СО	00
Замечание. Произведение рядов У, ик и У vk для многих
А=1	*=1
целей удобно записывать в виде
(4-со \ 14- с° \
У «л S vk =
fe=l / \*=1	/
=	+ («^2 + U2Vj) + • • • + (!hVk-l + • • • + Hfe-1'01) + • • •
Отметим без доказательства, что ряд, полученный почленным пере-
множением двух рядов указанным специальным образом, сходится и
в случае, когда только один из двух перемножаемых рядов сходится
абсолютно (а другой ряд может при этом сходиться только услов-
но). В случае, когда оба ряда сходятся условно, почленное перемно-
жение их даже по этому правилу приводит, вообще говоря, к рас-
ходящемуся ряду.
§ 5. Признаки сходимости произвольных рядов
В § 2 мы установили ряд признаков сходимости для рядов
с положительными членами. В этом параграфе мы изучим вопрос
о признаках сходимости для рядов с членами любого знака. Итак,
пусть
00
2 «А	(13.76)
— ряд, члены которого имеют какие угодно знаки. Прежде всего,
заметим, что для установления абсолютной сходимости этого ряда,
т. е. для установления сходимости ряда с положительными членами
k=\
можно применять любой из признаков § 2 (признак Даламбера, Коши,
Раабе или интегральный признак). Однако ни один из указанных приз-
наков не дает возможности выяснить более тонкий вопрос об услов-
ной сходимости ряда (13.76)*).
*) Заметим, впрочем, что признаки Даламбера и Коши можно применять
для установления расходимости ряда с членами любого знака (13.76). В самом
деле, всякий раз, когда признак Даламбера или Коши констатирует расходи-
со
мость ряда из модулей 2 I °а 1> й-й член РяДа (13.76) uk не стремится
А=1
к нулю при й —со, т. е. ряд (13.76) расходится. В качестве примера устано-
00
2. . / X \k	,	.
й! 1-^-1 расходится для любого фиксированного значения х,
А = 1
438
ТЕОРИЯ ЧИСЛОВЫХ РЯДОВ
(ГЛ. 13
Ниже мы и займемся отысканием более тонких признаков, позво-
ляющих устанавливать сходимость ряда (13.76) и в тех случаях,
когда этот ряд не является абсолютно сходящимся.
1. Признак Лейбница. Признак Лейбница относится к весьма
распространенному частному виду ряда (13.76), к так называемому
знакочередующемуся ряду. Ряд называется знакочередующимся, если
члены этого ряда поочередно имеют то положительный, то отрица-
тельный знаки. Знакочередующийся ряд удобно записывать так, чтобы
были выявлены знаки всех его членов, т. е. в виде
Л-Рг+Л-...+(-1)*’1Л+...,	(13.77)
где все p*2s0.
Теорема 13.14 {признак Лейбница). Если члены знакочере-
дующегося ряда, будучи взяты по модулю, образуют невозрастаю-
щую бесконечно малую последовательность, то этот ряд схо-
дится.
Замечание 1. Ряд, удовлетворяющий условиям теоремы 13.14,
часто называют рядом Лейбница.
Доказательство теоремы 13.14. Пусть дан ряд (13.77)
и известно, что последовательность {ph} является невозрастающей и
бесконечно малой. Частичную сумму этого ряда четного Порядка .S^
можно записать в виде
’San = (Pi ~ Pi) + (Рз — Pi) + • • • + (P«n-i ~ Pin)-	(13.7 8)
Так как каждая круглая скобка в (13.78) неотрицательна *), то
ясно, что при возрастании п последовательность {	} не убывает.
С другой стороны, можно переписать в виде
San = Pi — (р^ — pi) — (Pi — pi) — ••• — (Рзп-з — Pin-i) — Pint
откуда очевидно, что для любого номера п будет Stn^pi. Таким
образом, последовательность четных частичных сумм не убывает
и ограничена. сверху. В силу теоремы 3.15 эта последовательность
сходится к некоторому числу 5, т. е. limS2„ = 5. Из очевидного
п-*оо
удовлетворяющего неравенству | х | > е. Подчеркнем, что непосредственная
проверка того, что fe-й член рассматриваемого ряда не стремится к нулю при
k —> оо, является затруднительной. Применим к рассматриваемому ряду при-
знак Даламбера. Обозначая й-й член этого ряда через ak, будем иметь
। — —L£-L— откуда lim = bSl > 1. Расходимость ряда до-
казана.
*) Вследствие того, что {/>*} не возрастает, т. е.
§5]
ПРИЗНАКИ СХОДИМОСТИ ПРОИЗВОЛЬНЫХ РЯДОВ
439
равенства	+ р2п и из того, что limpa„=0, вытекает, что
п->со
и последовательность нечетных частичных сумм {Sin-i} сходится
к тому же числу 5, т. е. lim ^„-i = <$. Таким образом, вся после-
п-»оо
довательность {Sn} сходится к 5. Теорема доказана.
Замечание 2. При доказательстве теоремы 13.14 мы обнару-
жили, что последовательность четных частичных сумм {S2n} схо-
дится к пределу S не убывая. Аналогично из равенства
Sin-1 = pl- (Pi - Рз) - (Pi - Pn) - ... - (Pin-i - Pin-1)
вытекает, что последовательность нечетных частичных сумм {}
сходится к пределу «S’ не возрастая.
Таким образом, для любого номера п
Sin^S^Stn-i.	(13.79)
Поскольку Sin-i —	= р^ из неравенств (13.79) вытекает, что
— Sin pin
и
— S Pin £5 Pin-1-
Тем самым мы получаем, что для любого номера п справедливо
неравенство
|5„- S\^pn.	(13.80)
Неравенство (13.80) широко используется для приближенных вычи-
слений с помощью рядов.
В качестве примера рассмотрим уже неоднократно фигурировав-
ший выше ряд
2fcF=‘-4+l-l+-+tF+- о’»»
*=1
Заметим, что ряд (13.81) является рядом Лейбница, а поэтому сходи-
мость его вытекает из теоремы 13.14. Пусть, например, нужно вычи-
слить сумму ряда (13.81), т. е. число In 2, с точностью до В силу
оценки (13.80) эта сумма с требуемой точностью совпадает с Sl0n =
= i_l + ±_l + „ __L
2^3	4	10"'
2. Признак Дирихле — Абеля. Для установления еще одного
тонкого признака сходимости рядов выведем одно интересное тож-
дество, представляющее собой аналог формулы интегрирования по
частям. Пусть их, и2, и3.vv v2, v3, ... — совершенно произволь-
ные числа, 5л = И1 + и24-,,,+«де п и р — любые номера. Тогда
440
ТЕОРИЯ ЧИСЛОВЫХ РЯДОВ
[ГЛ. 13
справедливо следующее тождество:
п + р	п+р—I
У, ВД = У, Sfe (ук - nm) + Sn+pvn+p -	’ (13.82)
k = n	k = n
Тождество (13.82) обычно называют тождеством Абеля*).
Вывод тождества Абеля. Учтем, что ик — Sk — Sk-V и
подставим это значение ик в левую часть (13.82). Получим
п+р	п + р	п + р
У, = У Skvk — У
k — tl	k~n	k = п
В последней сумме уменьшим на единицу индекс суммирования k.
Получим
п + р	п+р	п+р—1
S ”i>vk = У, $kvk - У SkvkJrl =
k = п	k—n	Л = П— 1
п+р—1	п+р—1
“	~Т ^л+р^л+р 'jS.	=
k — n	k = n
n+p — 1
“	tyk	"h *$nH-p^n+p
k = n
Мы получили выражение, совпадающее с правой частью (13.82). Тем
самым тождество Абеля доказано.
Теорема 13,15 [признак Дирихле — Абеля), Пусть дан ряд
со
2 "А-	(13.83)
k = l
Этот ряд сходится, если выполнены следующие два условия:
1) последовательность {vk} является невозрастающей и бес-
конечно малой;
' '	со ’
2) ряд У ик имеет ограниченную последовательность частич-
k=i
них сумм.
Доказательство. Обозначим через Sn п-ю частичную сумму
ОО
ряда У ик. По условию существует такое число М > 0, что | <$„ | М
*=i
*) Если равенство (13.82) переписать в виде
п+р	-	।	п+р—1
У vk (8к — Sp_i) = Sn+pVn+p — Sn-iVn — У 8к (w*+i — vk),
k=n	k=n
то становится очевидным, что преобразование Абеля является по существу
формулой суммирования по частям, представляющей собою разностный аналог
формулы интегрирования по частям.
§51
ПРИЗНАКИ СХОДИМОСТИ ПРОИЗВОЛЬНЫХ РЯДОВ
441
для всех номеров п. В силу критерия Коши достаточно доказать,
что для любого е > 0 найдется номер N такой, что при п N и
для любого натурального р
п+р
У, Wk
k=n
(13.84)
Пусть дано любое е>0. Так как последовательность {vk} является
бесконечно малой и не возрастает, то для положительного числа
найдется номер N такой, что
(npH«^N).	(13.85)
Применим теперь для оценки величины, стоящей в левой части (13.84),
тождество Абеля (13.82). Учитывая, что модуль суммы нескольких
величин не превосходит суммы их модулей, модуль произведения
равен произведению модулей и что Vk^Wv получим
п+р	п+р—1
^Wk^JZ \Sk\('vk-Vk+1) + \S^p\vn+p + \Sn-1\vn.	(13.86)
k=п	' k = n
В правой части (13.86) воспользуемся неравенством 15Л | М, спра-
ведливым для всех номеров п. Получим
п+р
У, Wk
k — n
(п+р — 1
v	= n
(Vk - fft+i) + Vn+p > + Mvn
(13:87)
Далее, заметим, что сумма, стоящая в фигурных скобках, точно
равна т>л. В таком случае неравенство (13.87) принимает вид
п+р
У Wk
k = n
< 27Ицл.
(13.88)
Теперь, если в правой части (13.88) воспользоваться неравенст-
вом (13.85), получим, что при n^N и для любого натурального р
справедливо неравенство (13.84). Теорема доказана.
Замечание. Теорема 13.14 (признак Лейбница) является част-
ным случаем теоремы 13.15 при*) uk = (—1)А-1.
Примеры. 1. Исследовать на сходимость следующий ряд:
^Зп — г + зп — 1
2
Зп
00	со
*) Очевидно, что ряд У иь = У (— I)*-1 = 1 — 1 + 1 — 1 + ... имеет
k=\	k=i
ограниченную последовательность частичных сумм.
442
ТЕОРИЯ ЧИСЛОВЫХ РЯДОВ
(ГЛ. 13
Указанный ряд можно рассматривать к,ак ряд вида (13,83) при
^ = у> M1=1> w2 = 1> «з = —2, и4=1, И5=1, и6 = — 2, ...
СО
Очевидно, что: 1) ряд У, uk обладает ограниченной последователь-
*=1
ностью частичных сумм: <$i=l, 5г = 2, S3 = 0, S4=l, 56 = 2,
5в = 0, ...; 2) последовательность { vk } не возрастает и является
бесконечно малой. По теореме 13.15 рассматриваемый ряд сходится.
„ г,	Xi cos fox
2. Выясним вопрос о сходимости ряда Л-, где х — неко-
k=\
торое фиксированное вещественное число. Пользуясь обозначениями
теоремы 13.15, положим nft = cos^x, дл = -^-. Оценим последователь-
СО
ность частичных сумм 5Л ряда У uk. Поскольку для любого номера k
л=1
sin I k + у) х — sin I k — у j x = 2 sin у cos kx,
то, суммируя это соотношение no k от 1 до я, получим
п
sin (я + 44 х— sin 4- х = 2 sin У cos kx = 2Sn sin ~.
k=l
Отсюда
c  x
2 sin -y
Таким образом, для любого х, не кратного 2к, последовательность
частичных сумм Sn ограничена:
l^rAr
I ИП 2 |
По теореме 13.15 рассматриваемый ряд сходится для любого зна-
чения х, не кратного 2л. Если же х кратно 2л, то рассматривае-
мый ряд превращается в гармонический и, как доказано выше, рас-
ходится.
§ 6. Бесконечные произведения
1. Основные понятия. К понятию числового ряда близко при-
мыкает понятие бесконечного числового произведения. Пусть дана
бесконечная числовая последовательность vx, да, г»*, ,,, Записан-
§61
БЕСКОНЕЧНЫЕ ПРОИЗВЕДЕНИЯ
443
ное формально выражение вида
... vk
(13.89)
t-1
принято называть бесконечным произведением. Отдельные элементы и*
принято называть членами данного бесконечного произведения. Про-
изведение первых п членов данного бесконечного произведения при-
нято называть гг-м частичным произведением и обозначать символом Рп:
п
4 = 1
Бесконечное произведение (13.89) называют сходящимся, если после-
довательность частичных
отличный *) от нуля.
дения (13.89) указанный
конечного произведения,
произведений Рп имеет конечный предел Р,
В случае сходимости бесконечного произве-
предел Р называют значением этого бес-
т. е. пишут
(13.90)
4 = 1
Подчеркнем, что равенство (13.90) имеет смысл лишь для сходяще-
гося бесконечного произведения. Ясно, что рассмотрение бесконечных
произведений по существу представляет собой новую форму изучения
числовых последовательностей, ибо каждому данному бесконечному
произведению однозначно соответствует последовательность его частич-
ных произведений и каждой числовой последовательности {Рл}, все
элементы которой отличны от нуля, однозначно соответствует беско-
нечное произведение, для которого эта последовательность является
последовательностью частичных произведений (достаточно
х	Pk
члены бесконечного произведения равными vk=   при
^4-1
= PJ
Теорема 13.16. Необходимым условием сходимости
ного произведения (13.89) является стремление к единице его k-го
члена при k -> 00.
"Доказательство. Пусть бесконечное произведение (13.89)
сходится и имеет значение Р, отличное от нуля. Тогда lim Pft l _
k 0000
Рь
= lim Pk = P yh 0, Поскольку vk = -^~, то lim vk существует и
k —>co	*k-l k-+<x>
равен единице.
Заметим, что на сходимость бесконечного произведения не влияет
удаление любого конечного числа членов этого произведения (если,
•) Тот факт, что при Р = 0 бесконечное произведение принято считать
расходящимся, хотя и носит условный характер, но, как мы увидим ниже,
позволяет провести четкую аналогию между сходимостью рядов и бесконечных
произведений.
положить
и
бесконеч-
444
ТЕОРИЯ ЧИСЛОВЫХ РЯДОВ
[ГЛ. 13
конечно, среди этих членов нет равных нулю). Поскольку бесконеч-
ное произведение, у которого хотя бы один член равен нулю, согласно
принятому выше определению, считается расходящимся, то мы
в дальнейшем вообще исключим из рассмотрения бесконечные
произведения, у которых хотя бы один член равен нулю.
Примеры бесконечны х*произведений.
,	ТТ х х х х
1.	I I cos = cos у cos . cos 2^...	(13.91)
* = t
(х любое фиксированное число).
Докажем, что бесконечное произведение (13.91) сходится и имеет
sin х „
значение ——. Подсчитаем n-е частичное произведение
Рп = coscos ^... cos	(13.92)
Умножая обе части (13.92) на sin и последовательно используя
формулу для синуса двойного угла sin 2_у = 2 sin у cos_y, получим
^nsin^ = ^sinx.
Из последней формулы *)
Поскольку выражение в фигурных скобках стремится к единице при
п->оо (в силу первого замечательного предела), то lim Рп существует
«—♦со
и равен Тем самым доказано, что бесконечное произведе-
ние (13.91) сходится и имеет значение -у~.
9 I I Г1	2 I _ тт(4 - 1) (k + 2) _ -
•ILL	k (k + 1)J “ 11 k (k + 1) “
k = 2	fe = 2
-1 1 1 A (fe-1) (fe + 2)
“ 2’3’3 ’4”\ k (£+!);••
Докажем, что бесконечное произведение (13.93) сходится и имеет
значение у. Подсчитаем частичное произведение Рп:
р_1 2 3 n—1 4 5 6 я + 2 _ 1 п + 2
Рп~ 2 ’ 3 ' 4 • ‘ • п ’ 3 ’ 4’ 5 •' • я + 1 ~ п' 3 *
После этого очевидно, что lim P„ = lim ——существует и равен
п-юз п-»со	V-r
*) Мы считаем, что xyiO. Если х = 0, то все члены (13:91) и его значе-
ние равны единице.
§ 6]	БЕСКОНЕЧНЫЕ ПРОИЗВЕДЕНИЯ	445
2. Связь между сходимостью бесконечных произведений и
рядов. Если бесконечное произведение (13.89) сходится, то в силу
теоремы 13.16 все члены его начиная с некоторого номера k,
положительны *). Поскольку конечное число первых членов вообще
не влияет на сходимость бесконечного произведения, то при изуче-
нии вопроса о сходимости бесконечных произведений мы, не ограни-
чивая общности, можем рассматривать лишь такие бесконечные про-
изведения, у которых все члены положительны.
Теорема 13.17. Для того чтобы бесконечное произведение (13.89)
с положительными членами сходилось,-необходимо и достаточно,
чтобы сходился ряд
СО
£1п^.	(13.94)
fe = l
В случае сходимости сумма S ряда (13.94) и значение Р произ-
ведения (13.89) связаны формулой
P = eS.	(13.95)
Доказательство. Обозначив через Рп п-е частичное произве-
дение бесконечного произведения (13.89), а через п-ю частичную
сумму ряда (13.94), можем записать
S„ = lnP„, Pn = eSn.
В силу непрерывности показательной функции для всех значений
аргумента и непрерывности логарифмической функции для всех поло-
жительных значений аргумента, последовательность Рп сходится тогда
и только тогда, когда сходится 8п, причем если lim •$’„ = »$’, то
л-* со
lim Pn — es. Теорема доказана.
Я->СО
При исследовании на сходимость бесконечного произведения ока-
зывается очень удобным представить это бесконечное произведение
в виде
ОО
П t1+«*) = о+ «1)(1+и2)---(1+"*)••.	(13.96)
Л = 1
При этом, конечно, в соответствии с принятым выше предположением,
мы считаем, что все и*> —1.
Теорема 13,17 утверждает, что вопрос о сходимости произведе-
ния (13.96) эквивалентен вопросу о сходимости ряда
ОО
Е1п(1+“л)-	(!3.97)
' £
Теперь мы можем доказать еще одно утверждение.
*) Ибо lim vk = 1.
Л-юо
446
ТЕОРИЯ ЧИСЛОВЫХ РЯДОВ
[ГЛ. 13
Теорема 13.18 Если все uk (по крайней мере начиная с неко-
торого номера k) сохраняют один и тот же знак, то для схо-
димости бесконечного произведения (13,96) необходимо и доста-
точно, чтобы сходился ряд
ОО
5 «л-	(13.98)
*=1
Доказательство. Поскольку условие lim uk = 0 является
k —► оо
необходимым и для сходимости ряда (13.98), и для сходимости про-
изведения (13.96), мы можем считать это условие выполненным как
при доказательстве необходимости, так и при доказательстве доста-
точности. Но из указанного условия и из асимптотической формулы *)
вытекает, что
и
In (1 +j) =у + о (у)
.. In (1 + Ub) ,
lim —J1—— = 1
* — ОО “*
lim ,	—r = 1.
* —oo 1° (1 + “*)
(13.99)
(13.100)
Поскольку по условию теоремы все члены рядов (13.97) и (13.98),
начиная с некоторого номера k, сохраняют один и тот же знак,
условия (13.99) и (13.100), в силу следствия из теоремы сравне-
ния 13.3, позволяют утверждать, что ряд (13.98) сходится тогда и
только тогда, когда сходится ряд (13.97). Теорема доказана.
Примеры. 1) Из расходимости гармонического ряда й из теоре-
мы 13.18 вытекает расходимость следующих бесконечных произведений:
СО
П(‘+т)=<*+'>('+4) +!) +т)—
* = 1
Легко понять, что первое из указанных произведений расходится к -|-оо,
а второе к нулю.
2)	Из той же теоремы 13.18 и из сходимости ряда (13.33) при а> 1
вытекает сходимость при а > 1 следующих бесконечных произведений:
ОО
ft= 1
00
П ~ (k+ 1)«] = (1 — 2s) — • • • (1 —(й-нг) •”
k = 1
*) См. § 7 главы 4.
§ 6J
БЕСКОНЕЧНЫЕ ПРОИЗВЕДЕНИЯ
447
Так же как и для рядов, для бесконечных произведений вводится
понятие абсолютной и условной сходимости. Бесконечное произве-
дение (13.96) называется абсолютно сходящимся в том и только
том случае, когда сходится абсолютно ряд (13.97). Теоремы Коши 13.11
и Римана 13.10 позволяют заключить, что абсолютно сходящееся
произведение обладает переместительным свойством, в то время
как условно Сходящееся произведение заведомо им не обладает.
Справедливо следующее утверждение.
Теорема 13.19. Бесконечнее произведение (13.96) сходится
абсолютно тогда и только тогда, когда сходится абсолютно
ряд (13.98). Для доказательства этой теоремы достаточно доказать,
ОО
что ряд У ] iih | сходится тогда и только тогда, когда сходится ряд
t=i
ОО
У |1п(1 +»*)]. Это последнее легко вытекает из существования пре-
fe=i
делов (13.99) и (13.100). Детали рассуждений предоставляем читателю.
В заключение рассмотрим еще несколько примеров.
1°. Рассмотрим бесконечное произведение
fe = l
оо
Так как ряд сходится, то, в силу теорем 13.18 и 13.19, беско-
*=1
нечное произведение (13.101) сходится абсолютно для любого фикси-
рованного значения х, отличного от Zir (где 1—0, ±1, ...). В допол-
нении 2 к этой главе мы докажем, что это произведение сходится
к значению sinx. Тем самым будет обосновано разложение функ-
ции sinx в бесконечное произведение
СО
sinx = xJJ(l-^-2).	(13.102)
ь= i '
2°. Из разложения (13.102) путем использования соотношения
sin 2х
cos х == 2 sin элементарно получается следующее разложение:
СО
COS X = JJ [1 — (2й_1)яяа]-	(13.103)
Абсолютная сходимость произведения, стоящего в правой части
(13.103), для любого х, отличного от ~(21 — 1) (7=0, ±1, .,.),
СО
вытекает из теорем 13.18 и 13.19 и из сходимости ряда У жт-1 па.
448
ТЕОРИЯ ЧИСЛОВЫХ РЯДОВ
[ГЛ. 13
3°. Полагая в разложении (13.102) х—^-, получим
2.-117!__________И ТТ4^-1 _~n'(2fe-l)(2fe + l)
л 117 4^/ 1J 4А2 LL (2й)3
k=1	*=1	fe= 1
Отсюда получается так называемая формула Валлиса *)
я _ ТТ	(2й)3 '	2 2 4 4 2k 2k
2 ~ 11 (2k — 1) (2k + 1) “ 1 ' 3 ' 3 ‘ 5 "’2k— 1 ’ 2fe.-f-1 •”
k = 1
Путем несложных преобразований формулу Валлиса можно привести
к виду
к _	1	Г22й(*1)2]3
2 “Д” 2fe+l L (2А)! J •
(13.104*)
Первоначально формулу Валлиса использовали для приближенного
вычисления числа it. В настоящее время для вычисления числа к су-
ществуют более эффективные методы. Формула Валлиса. (13.104) пред-
ставляет интерес для ряда теоретических исследований **).
ДОПОЛНЕНИЕ 1 К ГЛАВЕ 13
ВСПОМОГАТЕЛЬНАЯ ТЕОРЕМА ДЛЯ П. 3 § 2
Теорема 13.20. Пусть р^ — какие угодно положительные числа. Тогда,
если существует предел
lim_E*±L=L)	(13.105)
k —►со Pk
то существует, и
предел lim & pk, причем справедлива формула
k—*(X)
lim V pit = lim —k+1 • = L.
k—a> y	Pk
(13.106)
Доказательство. Прежде всего докажем следующее вспомогатель-
ное утверждение ***): если последовательность положительных чисел щ,
а2, ..., а*, ••• сходится к некоторому числу L, то к этому же числу L
сходится и последовательность средних геометрических этих чисел
bk = -j/a^ ... а^. Для доказательства вспомогательного утверждения за-
метим, что, в силу непрерывности логарифмической функции, для L > 0
lim lna* = ln£. (Последнее равенство формально справедливо и при £ = 0,
А-*оо
*) Джон Валлис — английский математик (1616—1703).
**) В частности, она может быть использована для установления таи
называемой формулы Стирлинга (см. часть 2 настоящего курса). Джемс Стир-
линг — английский математик (1692—1770).
***) Подчеркнем, что это утверждение имеет и самостоятельный интерес.
ДОПОЛНЕНИЕ 2 К ГЛАВЕ 13
449
когда In L = — оо.) Но тогда по теореме о пределе среднего арифметического
(см. дополнение к главе 3, пример 1) существует предел
, к/---------Inaj + In 02 + ... + In ak , ,
lim In т/ ... ak = lim --------—-----1-------------- = In L.
4 ->oo r	fe —► оо	й
(Последнее равенство справедливо и при L = 0, когда In L = — со.) Из послед-
него равенства, в силу непрерывности показательной функции, получим
*_______
lim р/Га1а2 ... а* — lim е'пak = e\nL_^^
/г —* со	/г—>со
(Эти рассуждения справедливы и при L = 0.)
Вспомогательное утверждение доказано. Применяя это утверждение
D»	Од	Ph
к числам — Pi, а2 = —, а3 = —,	, •••» мы установим су-
pl	Pi	Pk-1
ществование предела lim т/7>й и равенство (13.106). Теорема 13.20 доказана.
k—» со
ДОПОЛНЕНИЕ 2хК ГЛАВЕ 13
РАЗЛОЖЕНИЕ ФУНКЦИИ sinx В БЕСКОНЕЧНОЕ ПРОИЗВЕДЕНИЕ
(13.107)
Ради удобства разобьем вывод формулы (13.102) на отдельные пункты.
I9.	Пусть т — любое положительное нечетное число: т = 2п + 1. Прежде
всего докажем, что для любого отличного от k~ (k = 0, ± 1, ...) значения 0 *)
справедлива следующая формула:
sin т9 /, sin2 0 \ /, sin2 0 \	/, sin2 0 \	т — 1
—= 11-----------------\ 1-------о" 1 ••• 11 -----1, п = —й—.
т sin 0	. „ к	. „ 2тс	'	. , пг.	2
\ sin2 — I I sin2 — I I sin2 — /
\ т / \ т /	\ т /
Для установления формулы (13.107) будем исходить из формулы
(см. § 1 главы 7)
cos m0 + i sin m0 = (cos 0 + i sin 0)171.
Расписывая правую часть этой формулы с помощью бинома Ньютона
нивая мнимые части, получим
sin m0 = т cos"1-1 0 sin 0--W ; „ -------— cosm-3 0 sin3 0 + ...
Муавра
И срав-
1 -2-3
Учитывая, что m = 2n-|-l, будем иметь
= cos2" 0 — ——cosM’2 9 sin2 9 + • • •	(13-108>
msm 0	1-2-3	1 v
В правой части (13.108) все показатели при косинусах и синусах четные, так
что если заменить cos2 0 на 1 — sin20, то в правой части (13.108) получится
многочлен степени п относительно sin2 0. Положив г = sin2 0, обозначим этот
многочлен символом F (г), а его корни символами аг, а2. ап. Так как
z = sin20—>0 при 0 —> 0 и поскольку левая часть (13.108) стремится к еди-
нице при 0 —<• 0, многочлен F (г) можно представить в виде
“^ = f(2) = (1-AWi-^.Ji-^.
т sin 0	\	«1 / \	а2 /	\
*) Нас в дальнейшем будут интересовать значения 0 лишь из интер-
вала 0 < | 0 | < л.
450
ТЕОРИЯ ЧИСЛОВЫХ РЯДОВ
[ГЛ. 13
Остается определить корни а1( а2, .... ап. Замечая, что эти корни соответст-
вуют нулям функции sin mO, получим
. о 71
«1 = sm2 —,
т ’
а, = sin2 —
т
ап = sin2
пл
т ‘
Тем самым формула (13.107) установлена.
2°- Положив в формуле (13.107) 0 = — и считая, что
дадим этой формуле вид
sin х
х
т sin —
tn
0 < | х | < лиг, при-
(13.109)
Фиксируем любое (отличное от нуля) значение х и возьмем два произ-
„ I х | _
вольных натуральных числа р и п, удовлетворяющих неравенствам z <
tn 1
< р < n =—2—. Тогда формулу (13.109) можно записать в виде
где
sin2 —\
_____т_ '
sin2 — /
т /
Rp (х),
(13.110)
п /
RP (х) = J[ 1
k=p+i\
sin2 —\
m 1
. . kn / ’
sin2 — /
m /
(13.111)
n	r, , . t,	„ x	m — 1
Прежде всего, оценим RB(x). Поскольку 2 -—-<p<_ n= —, to apry-
F	л	z
менты всех синусов, стоящих в формуле (13.111), принадлежат интервалу
j. Кроме того, ясно, что для всех k, участвующих в этой фор-
. . kr.
муле, | х | < у и, стало быть,
• а X
sin2 —
т
. , £л
sin2 —
т
 9
Sin2-=r—
2т
sin2---
т
1 1
Л 2 kn< 2
4 cos2
2т
(ибо — <; 4г, т. е. н— < -г-, и поэтому cos2	1. Так как для любого В
\ т 2 ’ 2m 4	J 2т 2 j
из интервала 0 < р < -% справедливы неравенства 1 > 1 — 0 >• е~^ *), то для
*) Правое из этих неравенств элементарно вытекает из формулы Макло-
рена:	= 1 — 2,3	----... < 1 — 2р 2р2 < 1 — р, так как 2?2 < р.
ДОПОЛНЕНИЕ 2 К ГЛАВЕ 13
451
всех номеров k, превосходящих р,
• 2 х
sin2 —
т
sin2 —
т
sin’ —
т
sin2 —
т
(13.112)
Почленно перемножая неравенства (13.112), записанные для значений А = р+1,
р + 2, и,
получим следующую оценку для Rp(x):
у '
т +_|	, . kx
Ь — „4- | Sill* —
1	«—₽.+ • т
(13.113)
Имея в виду,
из первой четверти 1
k-K
что аргумент лежит
sin В	2
о	—	), получим
р	тс
в первой четверти и что для
любого 3
1^1	т2
. , Ал < / 2\2 /Ал\2 - 4А2
sin2 —	—	—
т	\тг \т
Таким образом,
п
-2 sin*— V
tn
А = р+
1
А—1 Al'
sin2 —
tn
тг , . х	\1 Г 1	1 1	т‘
2 S п т	[а — 1 к J	2р
е	-	m	—р +1	_ е
Последнее неравенство позволяет следующим образом усилить оценку (13.113):
т‘ , . х
— -s- sin* ---------------------------------------•
1	£> «Л 2₽ т
. в Ате
1 sin2 ----
* т
(13.114)
З4. Устремим теперь в формуле (13.110) число т к бесконечности, остав-
ляя фиксированными значение хи номер р. Поскольку lim tn sin — = х,
т-*оэ M
lim m2 sin2 — == k2x2, то существует предел левой части (13.110), равный ^12?
яг-* со	т	х
р /
и предел конечного произведения JJ I 1
а== 1 \
Далее мы будем считать, что последний
он равен нулю, sin х — 0 и разложение
sin2 —\	Р .
’равныйП^-Д2 •
sm2—/	t=i
т /
предел отличен от нуля, ибо когда
(13.102) установлено.
Но тогда
sm 8
*) Эти неравенства вытекают из того, что отношение ——•
р
тс	2
нии от 0 до *77 убывает от 1 до —. Факт убывания функции
2	тс
cos 8 .л . л. л
—- (р — tg р) < 0 всюду на интер-
г
при измене*
sin 3
о в свою
очередь вытекает из того, что
вале0<р<у.
452
ТЕОРИЯ ЧИСЛОВЫХ РЯДОВ
[ГЛ. 13
существует и предел lim Rp (х). Обозначим этот предел через $р (х). Из нера-
т-*оо
венств (13.114), справедливых для любого номера т, и из теоремы 3.13 выте-
кает, что
_ л»
1^Лр(х)>е 2₽.	(13.115)
Формула (13.110) в пределе при /п-*оо дает
р
k = l
4°. Остается, сохраняя фиксированным х, устремить в формуле (13.116)
номер р к бесконечности. Поскольку левая часть (13.116) от р не зависит,
а предел lim Rp(x), в силу неравенств (13.115) и теоремы 3.14, существует
р —» со
и равен единице, то существует и предел
р
,. ТТ /1 х2 \ sin х
11
6 = 1
Тем самым разложение для sinx (13.102) установлено.
Замечание. В полной аналогии с разложениями (13.102) для sinx и
(13.103) для cosx можно получить разложения в бесконечные произведения
гиперболических функций
8Ьх=хД(1+^) и сЬх = Д[1 + (2^)2яг].
6 = 1	6=1
Заметим, что из разложений для sin х, cos х, sh х, ch х немедленно получаются
разложения в бесконечные произведения функций tgx, ctgx, и thx, cthx.
ДОПОЛНЕНИЕ 3 К ГЛАВЕ 13
ОБОБЩЕННЫЕ МЕТОДЫ СУММИРОВАНИЯ РАСХОДЯЩИХСЯ РЯДОВ
Во всей главе 13 мы называли суммой ряда
СО
2	= “1 + и2 + “з + ••• + “л + •••	(13.117)
6 = 1
предел S последовательности {5Л} частичных сумм этого ряда (при условии,
что этот предел существует).
В ряде задач математического анализа, представляющих как теоретиче-
ский, так и практический интерес, приходится оперировать с рядами, у ко-
торых последовательность частичных сумм не сходится и суммы в указанном
в главе 13 обычном смысле не существует. Естественно, возникает вопрос
об обобщении понятия суммы ряда и о суммировании расходящегося в обыч-
ном смысле ряда (13.117) с помощью каких-либо обобщенных методов. В на-
стоящем дополнении мы и остановимся на некоторых обобщенных методах
суммирования расходящихся рядов.
Прежде всего дадим общую характеристику тех методов суммирования,
с которыми мы будем иметь дело. Разумно требовать, чтобы обобщенное по-
нятие суммы включало в себя обычное понятие суммы. Точнее, ряд, сходящийся
ДОПОЛНЕНИЕ 3 К ГЛАВЕ 13
453
в обычном смысле и имеющий обычную сумму S, должен иметь обобщенную
сумму, и притом также равную S. Метод суммирования, обладающий ука-
занным свойством, называется регулярным.
Далее естественно подчинить понятие обобщенной суммы следующему
СО	00
условию: если ряд У, uk имеет обобщенную сумму (7, а ряд	имеет
k=A	k=l
СО
обобщенную сумму V, то ряд У, (Ли* + Bvk), где А и В — любые по-
k= 1
опаянные, имеет обобщенную сумму (AU + BV). Метод суммирования, удо-
влетворяющий указанному условию, называют линейным. В анализе и в его
приложениях, как правило, имеют дело лишь с регулярными линейными мето-
дами суммирования. Остановимся на двух методах обобщенного суммирования,
представляющих особый интерес для приложений.
1. Метод Чезаро*) (или метод средних арифметических). Говорят, что
ряд (13.117) суммируем методом Чезаро, если существует предел средних
арифметических частичных сумм этого ряда
lim 51 +Л + ": + \	(13 И8)
п-*оо	п
При этом предел (13.118) называется обобщенной в смысле Чезаро суммой
ряда (13.117).
Линейность метода суммирования Чезаро очевидна. Регулярность метода
Чезаро вытекает из примера 1, рассмотренного в дополнении 1 к главе 3.
В самом деле, из указанного примера вытекает, что. если последователь-
ность {£„} частичных сумм ряда (13.117) сходится к числу S, то предел
(13.118) существует и также равен S.
Приведём примеры рядов, не сходящихся в обычном смысле, но сумми-
руемых методом Чезаро.
1) Рассмотрим заведомо расходящийся ряд
ОО
2 (- I)*-1 = 1-1 + 1-14-...
А = 1
Поскольку все четные частичные суммы Strt этого ряда равны нулю, а все
нечетные частичные суммы S2n_i равны единице, то предел (13.118) сущест-
вует и равен -g-. Таким образом, рассматриваемый ряд суммируем методом
Чезаро и его сумма в смысле Чезаро равна -i-.
2) Считая, что х — любое фиксированное вещественное число из интер-
вала 0<х<2л, рассмотрим заведомо расходящийся**) ряд
СО
У cos kx — cos х + cos 2x + cos Зх + ...	(13.119)
fe= 1
Частичная сумма этого ряда Sn уже подсчитана нами в примере 2'в конце § 5
о • х
2smy
*) Эрнесто Чезаро — итальянский математик (1859—1906).
**) Расходимость ряда (13.119) без труда усматривается из приведенного
ниже выражения для его частичной суммы.
454
ТЕОРИЯ ЧИСЛОВЫХ РЯДОВ
[ГЛ. 13
Подсчитаем среднее арифметическое частичных сумм:
S1 4~	+ •• + Sn
п
1
4п sin2 -g-
(cos тх — cos (т + 1) х)
1	_ cos х — cos (n + 1) х
2	~	. . x
4n sm2 -g-
Отсюда очевидно, что
lim ,Si + 'S2 + --- + Sn
Л-+О0
Таким образом, ряд (13.119) суммируем методом Чезаро и его сумма в смысле
Чезаро равна ~.
2.	Метод суммирования Пуассона *) — Абеля. Этот метод суммирова-
ния состоит в следующем. По данному ряду (13.117) составляется степен-
ной ряд
и^х^ 1 ~ и2х UgX2 .. -]- и^х^ 2	. •	(13.120)
4 = 1
Если указанный степенной ряд сходится для всех х из интервала 0 < х < 1
и если сумма S (х) этого ряда имеет левое предельное значение lim S (х)
я— 1 —0
в точке х— 1, то говорят, что ряд (13.117) суммируем методом Пуассона —
Абеля. При этом указанное предельное значение называется суммой ряда
(13.117) в смысле Пуассона—Абеля.
Линейность метода суммирования Пуассона — Абеля не вызывает сомне-
ний. Докажем регулярность этого метода. Пусть ряд (13.117) сходится в обыч-
ном смысле и имеет сумму, равную S. Требуется доказать: 1) что ряд (13.120)
сходится для любого х из интервала 0<х< 1, 2) что сумма S (х) ряда
(13.120) имеет в точке х= 1 левое предельное значение, равное S.
Докажем сначала утверждение 1). Так как ряд (13.117) сходится, то
последовательность его членов является бесконечно малой и, стало быть,
ограниченной, т. е. найдется такое число М, что для всех номеров k
(13.121)
Используя неравенство (13.121), оценим модуль й-го члена ряда (13.120),
считая, что х — любое число из интервала 0<х<1. Получим
I «л**-1 | М | х |*-1.
СО
Так как | х | < 1, то ряд У lx)*'1 сходится. Стало быть, в силу замеча-
fe = i
ния 2 к теореме сравнения 13.3, сходится и ряд (13.120).
Докажем теперь утверждение 2). Пусть 5П — n-я частичная сумма ряда
(13.117), a S — его обычная сумма. С помощью преобразования Абеля *♦) легко
*) Симон Дени Пуассон — французский математик (1781—1840).
**) Преобразование Абеля (13.82) установлено нами в п. 2 § 5. В рассмат-
риваемом случае следует положить в (13.82) п = 1,	= 0 и затем устре-
мить р к бесконечности.
ДОПОЛНЕНИЕ -3 К ГЛАВЕ 13
455
убедиться в том, что для любого, х из интервала 0 < х < 1 справедливо тож-
дество
со	оо
2 W*'1 = (1 - х) 2 Skx»-\	(13.122)
А = 1	А=1
Вычтем тождество (13.122) из следующего очевидного тождества:
S = (l—х)2 Sx*"1.
A = l
При этом, обозначая через г* й-й остаток ряда (13.117), будем иметь
00	оо
5—2 “а**"1 =(»-*) 2 V*'1’
А=1	А = 1
или
S — S (х) = (1 — х) 2 V*"1-	(13.123)
А = 1
Наша цель доказать, что для любого е > 0 найдется 8 > О такое, что левая
часть (13.123) меньше е для всех х, удовлетворяющих неравенствам Г—8 <
<х-<1. Так как остаток ряда (13.117) стремится к нулю при й —оо, то
для положительного числа найдется номер й0 такой, что г* < при
k й0. Таким образом,
СО	00
|(1— *) 2 'а**'1 | < у |о — *) 2
k = kQ
Остается доказать, что для х, достаточно близких к единице,
(1—*) У rkXk~l <у,
А = 1
по это очевидно, ибо сумма, стоящая в последнем неравенстве, ограничена.
Регулярность метода Пуассона — Абеля доказана. В качестве примера снова
рассмотрим расходящийся ряд
У (— I)*"1 = 1 - 1 + 1 — 1 + ...	(13.124)
А = 1
Для этого ряда составим степенный ряд вида (13.120)
У (— 1)*-1х*-1 = 1 — х + х2 — хз + ...
А = 1
Очевидно, что последний ряд сходится для всех х из интервала 0<х<1
и имеет сумму, равную S (х) =
1
1 +*
_ Так как
lim S (х) = lim
х-*1—о	х-+1 — о
1 1
+ х~ 2’
456	ТЕОРИЯ ЧИСЛОВЫХ РЯДОВ	1ГЛ. 13
то ряд (13.124) суммируем методом Пуассона—Абеля и его сумма в смысле
Пуассона — Абеля равна
Обратим внимание на то, что сумма ряда (13.124) в смысле Пуассона —
Абеля совпадает с его суммой в смысле Чезаро. Этот факт не является слу-
чайным: можно доказать, что если ряд суммируем - методом, Чезаро, то он
суммируем и методом Пуассона—Абеля, причем сумма этого ряда в смысле
Чезаро совпадает с его суммой в смысле Пуассона—Абеля. Более того, суще-
ствуют ряды, суммируемые методом Пуассона—Абеля, но не суммируемые
методом Чезаро *). Детальное изучение всевозможных методов обобщенного
суммирования расходящихся рядов проводится в монографии Г. Харди «Рас-
ходящиеся ряды», ИЛ, 1951 г.
*) Таким образом, можно сказать, что метод Пуассона—Абеля является
более «сильным» методом суммирования, чем метод Чезаро.
ГЛАВА 14
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
§ 1.	Понятие функции нескольких переменных
1.	О функциональных зависимостях между несколькими пере-
менными величинами. При изучении многих вопросов естествознания
встречаются такие зависимости между несколькими переменными ве-
личинами, когда значения одной из этих переменных величин полно-
стью определяются значениями остальных переменных. Так, .при рас-
смотрении каких-либо физических характеристик тела (например, его
плотности р или температуры Т) нам приходится учитывать изменение
этих характеристик при переходе от одной точки тела к другой. По-
скольку каждая точка тела определяется тремя декартовыми коорди-
натами х, у и z, то рассматриваемые характеристики (плотность р или
температура Г) определяются значениями трех переменных х, у и z.
При рассмотрении физических процессов, меняющихся во времени,'
значения физических характеристик определяются значениями четырех
переменных: трех координат точки х, у, z и времени t. Например,
при изучении звуковых колебаний газа плотность р этого газа и
давление р определяются значениями четырех переменных х; у, z и t.
Для изучения такого рода зависимостей в этой главе вводится поня-
тие функции нескольких переменных и развивается аппарат для иссле-
дования таких функций.
В теории функций нескольких переменных удобно пользоваться ге-
ометрической терминологией. Непосредственно ясно, что областью зада-
ния функции двух (или трех) переменных является некоторое множество
точек плоскости (или пространства). Для геометризации наших пред-
ставлений о функции т переменных удобно ввести понятие, /«-мер-
ного пространства, обобщающее хорошо известные понятия двумерной
плоскости и трехмерного пространства. Наше последующее изложе-
ние мы начнем с выяснения необходимых нам геометрических понятий.
2.	Понятия евклидовой плоскости и евклидова пространств^.
Известные из аналитической геометрии понятия координат точек на
плоскости и в пространствен формула для определения расстояния
458	ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ	[ГЛ. 14
между двумя точками могут быть использованы для аналитического
введения понятий плоскости и пространства. Множество всевозмож-
ных упорядоченных пар (х, у) вещественных чисел х и у назы-
вается координатной плоскостью.
При этом каждую пару (х, у) мы будем называть точкой этой
плоскости и обозначать одной буквой М. Числа х и у называются
координатами точки М. Запись М (х, у) означает, что точка М имеет
координаты х и у.
Координатная плоскость называется е в к лид о в ой плос-
костью, если между любыми двумя точками М' (х', у’) и
М"(х",у") координатной плоскости определено расстояние
р(ЛГ, М") по формуле
р (М', М’') = У(х" -х')2 + (у"-у')2.
Совершенно аналогично вводится понятие координатного и евклидова
пространств. Множество всевозможных упорядоченных троек
(х, у, z) чисел х, у и z называется координатным прост-
ранством. При этом каждую тройку (х, у, z) мы будем называть
точкой этого пространства и обозначать одной буквой М. Числа х, у
и z называются координатами точки М. Запись М (х, у, z) означает,
что точка М имеет координаты х, у и z.
Координатное пространство называется евклидовым про-
странством, если между любыми двумя точками М'(х', у',
z') и М" (х', у”, z") координатного пространства определено рас-
стояние по формуле
р (ЛГ, М") — ]/ (х” — х')2 + (у" —у’)2 + (г" — z’)2.
Введенные нами понятия координатной плоскости и координатного
пространства представляют собой аналоги числовой прямой, а евкли-
дова плоскость и евклидово пространство представляют собой ана-
логи евклидовой прямой, которую можно определить как числовую
прямую, между любыми двумя точками х' и х" которой определено
расстояние р(х', х") по формуле р(х', х") = У(х'' — х')2 = \х" — х' |.
Рассмотрим некоторые множества {Л4} точек евклидовой плоско-
сти и евклидова пространства.
1°. Множество {Л4} точек евклидовой плоскости, координаты х
и у которых удовлетворяют неравенству (х — а)2 4- (у — b)2	R2, как
известно, называется кругом радиуса R с центром в точке Ма(а, Ь).
Если координаты х и у удовлетворяют строгому неравенству (х — a)2 4-
+ (У ~ Ь)2 < Z?2, то множество {Л1} называется открытым кругом.
В евклидовом пространстве множество {М} точек, координаты х, у
и z которых удовлетворяют неравенству (х — а)2 + (у — Ь)2 4-
4- (z — с)2 -с; R2, как известно, называется шаром радиуса R. с цент-
ром в точке ’ Л10 (а, Ь, с). Если координаты х, у и z удовлетворяют
§ 1]	ПОНЯТИЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ	459
соответствующему строгому неравенству, то множество {Л1} назы-
вается открытым шаром *).
2°. Множество {Л4} точек евклидовой плоскости (евклидова про-
странства), координаты х и у (х, у и z) которых удовлетворяют
неравенствам | х — а | -С d± и |_у — b | -С d2 (| х — а | db \у — b\^di
и | z — с |	d3), называется координатным прямоугольником (коор-
динатным параллелепипедом) с центром в точке Мо (а, Ь) (в точке
/Ио (а, Ь, с)).
3.	Понятие функции-двух и трех переменных. Используя гео-
метрическую терминологию, можно следующим образом сформулиро-
вать уже известное нам понятие функции одной переменной.
Если каждой точке М из некоторого множества {7И} точек
евклидовой прямой ставится в соответствие по известному за-
кону некоторое число и, то говорят, что на множестве {/И}
задана функция и = и(М) или u=f(M).
Введем теперь понятие функции двух переменных.
Если каждой точке М из некоторого множества {7И} точек
евклидовой плоскости ставится в соответствие по известному
закону некоторое число и, то говорят, что на множестве {Л4}
задана функция и = и(М) или и= /(?И).
Заметим, что понятие функции двух переменных отличается от
сформулированного выше понятия функции одной переменной лишь
тем, что вместо слов «евклидова прямая» используется термин «евк-
лидова плоскость». Совершенно аналогично вводится понятие функции
трех переменных. Для этого вместо множества {/И} точек евклидовой
плоскости нужно взять множество {Л4} точек евклидова пространства.
Так как точка М евклидовой плоскости определяется двумя коор-
динатами х и у, а точка М евклидова пространства — тремя коорди-
натами х, у и z, то для функций двух и трех переменных мы будем
употреблять соответственно обозначение u = f(x, у) и u=f(x,y, z).
Если функция u=f(M) задана на множестве {7И}, то это множество
называется областью задания функции u—f \M). Число и, соответ-
ствующее данной точке М из множества {М}, будем называть част-
ным значением функции в точке М.
Совокупность {н} всех частных значений функции гг=/(А4) назы-
вается множеством значений этой функции.
Для функции двух переменных можно ввести понятие графика,
именно: графиком функции u=f(x, у) называется поверхность,
точки которой имеют координаты (х, у, f (х, у)).
Рассмотрим примеры функций двух и трех переменных.
1°. н = рл4 — х2 — у2. Областью задания этой функции является
круг радиуса 2 с центром в начале координат, а множество значе-
ний представляет собой сегмент 0=Си=с2.
*) Очевидно, круг и шар представляют собой множества {44} точек пло-
скости и пространства, для которых р (41,
460
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[ГЛ. и
2°. я = .	Областью задания этой функции является
/х2 + у2 — 4	7
множество точек, лежащих вне круга радиуса 2 с центром в начале
координат, а множество значений представляет собой открытую полу-
прямую и > 0.
3°. и = У cos (№ У _у2). Областью задания этой функции является
множество {44} точек, координаты которых удовлетворяют неравен-
ству cos (х2 у у2) 0. Это неравенство эквивалентно неравенствам
Рис. 14.1.
0 х2 У у2 -С ~, 2Атс — у х2 +у2 -С 2Ая у ~, Л=1, 2, ... Таким
образом, {44} состоит из круга радиуса Vtc/2 с центром в точке
0(0, 0) и кольцеобразных областей (рис. 14.1).
4°. и — In xyz. Областью задания этой функции является множество
{44} точек, координаты которых удовлетворяют неравенству xyz > О,
а множеством значений —вся числовая прямая —оо<;м<Уоо.
5°. и — х2 у у2 у z2. Областью задания этой функции является все
евклидово пространство, а множеством значений — полупрямая
4.	Понятия /«-мерного координатного пространства и /«-мер-
ного евклидова пространства. Множество всевозможных упоря-
доченных совокупностей, (хх, х2, ..., хт) т чисел хх, х2.хт
называется т-'ме.рным координатным пространст-
вом Ат.
При этом каждую упорядоченную совокупность (хх, х2, ..., хт)
мы будем называть точкой этого пространства и обозначать одной
буквой 44. Числа хх, х2, ...» хт называются координатами точки М.
§ П
ПОНЯТИЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
461
Запись Л1 (хх, х2, хт) означает, что точка М имеет координаты
Хх, х2,..,, хт. Введем понятие т-мерного евклидова пространства.
Координатное пространство Ат называется т-мерным евкли-
довым пространством Ет, если между любыми двумя
точками М' (х[, х2, ..., х'т) и М" (х{, х2, ..., Хщ) координатного
пространства Ат определено расстояние *) р (М', М") по формуле
р(м', м")=V(х?- х^ + (х; - хд* +...+(х"т-х'ту. (14.1)
Введенные нами понятия /«-мерного координатного пространства Ат
и /«-мерного евклидова пространства Ет представляют собой обоб-
щения указанных выше понятий координатного пространства и евкли-
дова пространства.
5.	Множества точек /«-мерного евклидова пространства Ет.
Символом {/И} мы будем обозначать некоторое множество точек
/«-мерного евклидова пространства Ет. Рассмотрим несколько при-
меров множеств в «/-мерном евклидовом пространстве Ет.
1°. Множество {Л4} всевозможных точек, координаты xv х2, ...
..., хт которых удовлетворяют неравенству (xt — х$)2 4- (х2 — х2)2 4-...
... 4- (хт — х„)г R2, называется т-мерным шаром радиуса R
с центром в точке Л40(х{,	Хт)- Таким образом, ///-мерный
*) Евклидово m-мерное пространство представляет собой так называемое
метрическое пространство. Произвольное множество {Л4}, элементы которого
именуются точками, называется метрическим пространством, если существует
правило, с помощью которого любым двум точкам М' и М" множества (Л4)
ставится в соответствие некоторое число р (М', М"), называемое расстоянием
между этими точками. При этом указанное правило должно быть таким, чтобы
выполнялись следующие аксиомы (аксиомы метрического пространства)’. 1) для
любых М' и М" р (Л1'> М") — р (Л4", М‘) (симметрия расстояния); 2) для
любых М' и М" р (ЛГ, Л4")	0, причем, если р (М', М") = 0, то. точки М'
и М" совпадают; 3) для любых трех точек М', М" и М"' выполняется не-
равенство р (М', Л4"')^р(Л4', /И")-|-р (М", М'") (неравенство треугольника).
Убедимся, что введенное нами евклидово m-мерное пространство действи-
тельно является метрическим пространством. В самом деле, справедливость
первых двух аксиом метрического пространства очевидна (см. формулу (14.1)).
Убедимся в справедливости третьей аксиомы.
Пусть Хр xf, х’-‘ — координаты точек М', М", М'". Имеем р2 (М’, М"')~
= 2 [(*Г ~ XD + (xi - x’i)]2 = 2 (x’l" ~ xi)2 + 2 2 (x'i" ~ xi) (x'i ~ x'i) +
j=l	i=l	i=l
m
4- У (х[ — x-)2. Полагая x'i’ — x- — а. и x’t — x't = &г и используя неравен-
i= 1
ство Буняковского (см. неравенство (10.30) в дополнении 1 к главе 10), найдем,
что У (x't — xi) (х? — х))^ р/ J] (xf — х!')2 J/ 2 (х/ “ х'д2’ Отсюда
(Г т	/ т	\2
2 (Х1 — х«")2 +1/ 2 (xi ~л/)2) т-е>
Р (М’, М'") Sg Р (Л4', М") 4- Р (М'’Гм'").
462
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
(ГЛ. 14
шар определяется как множество М всевозможных точек, расстояние р
от каждой из которых до некоторой точки 7И0 (центр шара) удов-
летворяет неравенству р (М, M0)^R. Если расстояние ,р (Ж, /Ио) от
каждой точки множества {7И} до точки А10 удовлетворяет строгому
неравенству р(М, M0)<zR, то множество {/И} называется откры-
тым т-мерным шаром.
2°. Множество {тИ} точек, расстояние от каждой из которых до
некоторой точки Мо удовлетворяет соотношению р (Af, Л1о) = R, назы-
вается т-мерной сферой радиуса R с центром в точке /Ио.
3°. Множество {AI} точек, координаты хх, хг, ..., хт которых
удовлетворяют неравенствам | хг — xj |	| Jv2 — xj |	d2,
| хт — х°т j --С dm, называется т-мерным координатным параллелепи-
педом. При этом точка Мо (х£, х2,..., х‘т) называется центром этого
/«-мерного параллелепипеда. Если координаты xv х2, ..., хт точек
множества {/И} удовлетворяют строгим неравенствам |х! — х?|<^1»
|х2 — x2|<rf2,	| хт — Хт | < dm, то множество {М} называется
открытым т-мерным координатным параллелепипедом.
Введем понятия z-окрестности точки Af0 евклидова /«-мерного
пространства и прямоугольной окрестности этой точки Мо. Будем
называть ^окрестностью точки 7И0 (xj, х* ..., х°т) т-мер-
ного евклидова пространства Ет открытый т-мерный шар ра-
диуса е с центром в точке Мй. Прямоугольной окрест-
ностью точки 7И0(х}, х2, ..., х^>) т-мерного евклидова
пространства называется любой открытый т-мерный координат-
ный параллелепипед с центром в точке Мо.
Справедливо следующее очевидное утверждение.
Любая е.-окрестность точки Мо евклидова т-мерного про-
странства Ет содержит некоторую прямоугольную окрестность
этой точки. Любая прямоугольная окрестность точки Мо со-
держит некоторую е-окрестность точки Мо.
Пусть {Л4} — некоторое множество точек евклидова /«-мерного
пространства Ет. Введем следующие понятия.
Точка М множества {7И} называется в ну тр е н не й‘точкой
этого множества, если существует некоторая г-окрестность
точки М, все точки которой принадлежат множеству {/И}.
Т очка М *) называется граничной точкой множества {М},
если любая ^-окрестность этой точки содержит как точки,
принадлежащие Множеству {Л4}, так и не принадлежащие ему.
Множество {/И} пространства Ет называется открытым
множеством или об лас тью, если любая точка этого
множества внутренняя.
Если каждая граничная точка множества {7И} является точ-
кой этого множества, то множество {Л4} называется замк-
нутым.
*) Отметим, что при этом точка М может не принадлежать множеству {Л4}.
§ 1]	ПОНЯТИЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ	463
Если множество {44} представляет собой область, то множество
{44}, полученное присоединением к {А1} всех граничных точек этого
множества, называется замкнутой областью.
Отметим, что если все точки области {44} находятся внутри неко«
торого шара, то эта область называется ограниченной.
В дальнейшем нам понадобится понятие связного множества.
Предварительно мы введем понятие непрерывной кривой в многомер-
ном пространстве Ет.
Непрерывной кривой L в пространстве Ет мы будем называть
множество \М] точек этого пространства, координаты xv х2,...
..., хт которых представляют собой непрерывные функции пара-
метра t:
= x2 = <?2(t), ..., xm = <?m(t),	(14,2)
Мы будем говорить, ЧТО ТОЧКИ М'(х[, Х2, ..., Хт) и ЛГ(Х%, Х2,. ,,,Хт)
пространства Ет можно соединить непрерывной кривой L, если
существует такая непрерывная кривая L, определяемая параметриче-
скими уравнениями (14.2), что
=	x;=<p2(a), ..., х'т=?т(а),
*1=?1(Р)>	*2 = ?2(₽)>	4 =
Сформулируем понятие связного множества. Множество {44} про-
странства Ет называется связным, если две любые его точки
можно соединить непрерывной кривой, все точки которой принад-
лежат этому множеству.
Замечание. Отметим, что иногда областью называют открытое
и связное, а не просто открытое множество.
Рассмотрим следующий пример.
Множество {44} точек Ет, определяемое уравнением
называется «-мерным эллипсоидом. Точки «-мерного эллипсоида
являются граничными точками множества {41} точек 44, координаты
которых удовлетворяют неравенству
Это множество является множеством внутренних точек «-мерного
эллипсоида.
Читатель легко убедится сам, что множество внутренних точек
«-мерного эллипсоида является открытым и связным множеством.
Отметим, что «-мерный эллипсоид, определяемый соотношением (14.3),
представляет собой замкнутое множество.
Область задания функции
н = ]/ cos (х2 +>2)
464
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
|ГЛ. 14
представляет собой несвязное множество (см. пример 3° п. 3 и
рис. 14.1).
В заключение договоримся называть окрестностью точ-
к и М любое открытое связное множество, содержащее М.
6.	Понятие функции т переменных. Введем понятие функции т
переменных.
Если каждой точке М из множества {Af} точек т-мерного
евклидова пространства Ет ставится в соответствие по из-
вестному закону некоторое число и, то говорят, что на мно-
жестве задана функция и = и(М) или u—f{M). При этом,
множество {7И} называется областью задания функции u—f(M).
Число и, соответствующее данной точке М из множества {Л1},
будем называть частным значением функции в точке М. Совокуп-
ность {и} всех частных значений функции и=/(7И) называется мно-
жеством значений этой функции. Так как точка М определя-
ется координатами xv х2, ..., хт, то для функции u—f(M) т пере-
менных используется также обозначение u=f(xY, xv ..., xm).
Рассмотрим примеры функций т переменных.
1°. Пусть и = 1^1 — х'{ — х$ —.— х2т. Областью задания этой
функции служит, очевидно, zn-мерный шар радиуса 1 с центром в точке
О (0, 0, ..., 0). Множеством значений рассматриваемой функции
является сегмент [0, 1].
2°. Пусть и = —	1 	. ----:. Областью задания функ-
|/ a? af "• <4
ции является множество {/И} внутренних точек /«-мерного эллипсо-
ида. Множеством значений этой функции является полупрямая «1.
§ 2.	Предельное значение функции нескольких переменных
1.	Сходящиеся последовательности точек в /«-мерном евкли-
довом пространстве Ет. Критерий Коши сходимости последова-
тельности. Рассмотрим в ///-мерном евклидовом пространстве Ет по-
следовательность точек {Л4П} *). Сформулируем следующее определение.
Последовательность {/Ил} точек евклидова пространства Ет
называется сходящейся, если существует такая точка А, что
для любого положительного числа е можно указать номер N **)
такой, что при n^N выполняется неравенство р (Mn, Д) < е.
*) Понятие последовательности точек в евклидовом пространстве Ет
определяется следующим образом. Пусть каждому числу п натурального ряда
чисел 1, 2, ..., п, ... ставится в соответствие точка Л4п евклидова простран-
ства Ет. Возникающий при этом ряд точек Мг, Л12.Мп, ..., рассматри-
ваемый в указанном порядке, называется последовательностью точек евклидова
пространства Ет. Мы будем кратко обозначать эту последовательность симво-
лом {Мя}.
**) Так как номер N зависит, вообще говоря, от е, то иногда пишут
N = N (е).
§2]
ПРЕДЕЛЬНОЕ ЗНАЧЕНИЕ ФУНКЦИИ
465
При этом точка А называется пределом последовательности
{Л4„}. Для обозначения предела А последовательности {Л4П} исполь-
зуется следующая символика:
lim Мп = А, или М„-*-А при п->оо.
,	п -* 00
Докажем следующую лемму.
Лемма 1. Пусть последовательность {Мп} точек евклидова
пространства Ет сходится к точке А. Тогда последовательности
{Х2Я>}>  • • > {хт>} координат точек Мп сходятся к соответ-
ствующим координатам av а2, ат точки А, и наоборот, если
последовательности рср>},	> {*?} координат точек Мп
сходятся соответственно к числам дх, а2, ат, то последова-
тельность {А4Л} сходится к точке А с координатами av а2, ..., ат.
Доказательство. Докажем первую часть леммы. Если после-
довательность {А1„} сходится к точке А, то для любого е > 0 можно
указать номер N такой, что при n^N выполняется.неравенство
р (Мп, А) < е. Пусть (хр>,	...,	— координаты точки Мп, а
(а1( а2, . ат) — координаты точки А. Тогда неравенство р(Мп, А) <в
можно записать следующим образом:
VWn) - ai)2+W	++W ~<е- о4-4)
Отсюда следует, что при n^N выполняются неравенства
I -*1Л) — «11 < | Хя) — а21 < г.| х„} — ат | < е.
Иными словами, последовательности рср>|, рср>}, •••, коорди-
нат точек Мп сходятся соответственно к числам alt d2, ...', ат. Дока-
жем теперь обратное утверждение. Предположим, что указанные
последовательности координат точек Мп сходятся соответственно
к числам а1, а2, ..., ат. Тогда для любого е>0 можно указать
номера Nlt N2, ...., Nm такие, что при п'^Пг, n^N2, ..., n^Nm
соответственно выполняются неравенства
- а, | <	...
У т	ут	Ут
Отсюда следует, что при n^N=max{M1, П2, ..., Nm} выполняется
неравенство (14.4). Иными словами, при n>;N выполняется нера-
венство р(2И„, А)<е, где А —точка Ет с координатами а1г а2, ...
..., ат. Таким образом, последовательность {Л4л} сходится к точке А.
Лемма доказана.
Сформулируем определение фундаментальной последовательности
точек в щ-мерном евклидовом пространстве. Последовательность {А1л}
точек т-мерного евклидова пространства, называется фунда-
ментальной или последовательностью Коши, если для любого
468
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[ГЛ. 14
положительного числа г можно указать такой номер N, что при
ny^N и для любого натурального р выполняется неравенство
р(Мп+р, Мп) Справедлив следующий критерий сходимости после-
довательности (критерий Коши).
Для 'того чтобы последовательность {/Ил} точек т-мерного
евклидова пространства была сходящейся, необходимо и доста-
точно, чтобы она была фундаментальной. Чтобы убедиться в спра-
ведливости' сформулированного критерия, достаточно заметить, что из
условия фундаментальности последовательности {Л4л} следует, что
последовательности ^х<л)|, {х<")|, • • • > {хт)} координат точек Мп
также фундаментальны, и наоборот, если указанные последовательности
координат фундаментальны, то фундаментальной будет и последова-
тельность	и затем применить критерий Коши для числовых
последовательностей к последовательностям координат точек {Л1„}
и лемму 1 этого пункта.
2.	Некоторые свойства ограниченных последовательностей
точек в /n-мерном евклидовом пространстве. Введем понятие огра-
ниченной последовательности точек в /«-мерном евклидовом простран-
стве. Последовательность {Л4Л} точек т-мерного евклидова про-
странства называется ограниченной, если существует такое
число а ~у> 0, что для всех п выполняется неравенство р (О, Л4л) а,
где О — точка, все координаты которой равны нулю. Иными сло-
вами, последовательность {Л4л} является ограниченной, если все точ-
ки Мп этой последовательности находятся внутри или на границе
некоторого шара с центром в начале координат.
Справедлива следующая основная теорема.
Теорема 14.1 {теорема Больцано — Вейерштрасса). Из
любой ограниченной последовательности {А/л} точек т-мерного
евклидова пространства можно выделить сходящуюся подпосле-
довательность.
Доказательство. Убедимся, во-первых, что последователь-
ности |х*л>|, |х<п>}, •••’ {*«’} координат точекМп являются ограничен-
ными. Действительно, так как последовательность {7ИЛ} ограничена,
то для всех п выполняется неравенство р (О, Мп) а. Поскольку
р (О, Мп) = х(л>2 + х{">‘ +... + то отсюда следует, что для всех
п выполняются неравенства | х*л> | а, | х(£} | sg а. |х^>|е5а.
Иными словами, последовательности	• •  > коорди-
нат точек Мп ограничены. В силу теоремы Больцано — Вейерштрасса
для числовых последовательностей (см. п. 4 § 4 главы 3) из после-
довательности {х<л>} можно выделить последовательность {х^*?},
сходящуюся к некоторому числу av Рассмотрим соответствующую
подпоследовательность {х<л*1>} последовательности вторых координат
точек Мп. В силу той же теоремы из подпоследовательности {х<л*1>}
можно выделить подпоследовательность {х*л*Р}, сходящуюся к неко-
торому числу а2. Заметим, что подпоследовательность {х^л^)} после-
ПРЕДЕЛЬНОЕ ЗНАЧЕНИЕ ФУНКЦИИ
467
§ 2]
довательности	сходится к числу av Итак, подпоследовательно-
сти {x^fta1} и {х*яй2>} сходятся к числам аг и а2 соответственно. Оче-
видно, что если мы из подпоследовательности {х(3лйа>} последователь-
ности третьих координат точек Жя выделим сходящуюся к некоторому
числу а3 подпоследовательность {хО*а>}, то подпоследовательности
{xOftj)}, {х<пМ}, {х(8лй8)} сходятся соответственно к числам alt аг, а3.
Продолжая эти рассуждения, мы, наконец, получим сходящуюся к неко-
торому числу ат подпоследовательность	последовательности
m-х координат точек Мп, причем подпоследовательности {х^я,)},
{х(л*т)|,	сходятся к числам Др а2,.... ат соответственно.
Но тогда, в силу леммы 1, подпоследовательность {Ж„л } последо-
вательности точек {Ain} сходится к точке А с координатами а1г
а2, ..., ат. Теорема доказана.
Замечание. Предел А последовательности {Жя} точек, принад-
лежащих замкнутому множеству {Ж}, также принадлежит этому
множеству. Чтобы убедиться в этом, достаточно заметить, что в любой
е-окрестности точки А имеются точки Жя, т. е. точки множества {А1},
и поэтому точка А является либо внутренней, либо граничной точ-
кой {Ж}, а следовательно, принадлежит {Ж}. •
3.	Понятие предельного значения функции нескольких пере-
менных. Рассмотрим функцию д=/(Ж), определенную на множестве
{Ж} /«-мерного евклидова пространства, и точку А этого множества,
быть может, и не принадлежащую множеству {Ж}, но обладающую
тем свойством, что в любой е-окрестности этой точки содержится
хотя бы одна точка множества {Ж}, отличная от А.
Определение 1. Число b называется предельным значе-
нием фу нкц и и и — f(M) в точке А (или пределом функ-
ции при Ж-> А), если для любой сходящейся к А последовательно-
сти Жх, Ж2, ..., Жя,... точек множества {Ж}, элементы М„ кото-
рой отличны от А *) (Жя Л), соответствующая последователь-
ность f(M^), f(M^, ..., /(Ж„), ... значений функции сходится к Ь.
Приведенное определение называется определением предельного
значения функции с помощью последовательностей. Сформулируем
другое определение предельного значения функции, используя «е —Sb-
терминологию.
Определение 2. Число b называется предельным значением
функции u=f (Ж) в точке А, если для любого положительного
числа е можно указать такое положительное число 8, что для
всех точек М из области задания функции, удовлетворяющих
условию 0<р(Ж, А) <8, выполняется неравенство |/(Ж) —£|<е.
Замечание. Определения 1 и 2 предельного значения функции
эквивалентны. Справедливость этого утверждения может быть доказана
*) Это требование объясняется, в частности, тем, что функция и — f (М)
может быть не определена в точке А.
468
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[ГЛ. 14
точно так же, как и эквивалентность двух определений предельного
значения функции одной переменной. Для обозначения предельного
значения b функции u=f(M) в точке А используется следующая
символика:
lim f(M) = b, или lim f(xv хг, хт~) = Ь,
М-+А
т т
где а2, ат — координаты точки А.
Сформулируем определение предельного значения функции при
стремлении точки Л4 к бесконечности.
Определение 3. Число b называется предельным значе-
нием функции u=f(M) при М->со(или пределом функ-
ции при Л4 —> оо), если для любого положительного числа е можно
указать такое положительное число а, что для всех М из обла-
сти задания функции, удовлетворяющих условию р (О, М) > а,
выполняется неравенство | f(M) — b | < е.
Арифметические операции над функциями т переменных, имею-
щими предельное значение в точке А, приводят к функциям, также
имеющим предельное значение в точке А. Именно, справедливо сле-
дующее утверждение.
Пусть функции f(M) и g(M) имеют в точке А предельные
значения b и с. Тогда функции /(A4) + g(Al), f (М) — g(M),
f(M)-g(M) и имеют в точке А предельные значения (част-
ное при условии с 0), равные соответственно b-\-ct b — c,
< b
Ь-с, —.
с
Доказательство этого утверждения совершенно аналогично дока-
зательству теоремы 4.1.
4.	Бесконечно малые функции. Функция u=f (Л4) называется
бесконечно малой в точке А (при М-> А), если lim /(Л1) = 0.
М->А
Легко убедиться, что функция f(M) = (x1-ai)n'A-...
... А~ (хт — ат)Пт, где и1; ..., пт — положительные числа, является
бесконечно малой в точке A (alt а2, ..., ат) *).
Если функция u—f(M) имеет равное b предельное значение
в точке А, то функция a(M)=f(M) — b является бесконечно
малой в точке А. Действительно, lim а(7И)= lim (f(M) — b)—
Л1 — л	м -> А
= lim f(M)— lim b — Q. Используя этот результат, мы получим
AI —А	М-.А
специальное представление для функции, имеющей равное b предель-
*) Достаточно учесть, что каждая из функций одной переменной / (хк) =
= (xk — а^)п,г является бесконечно малой в точке xk =
§ 2]
ПРЕДЕЛЬНОЕ ЗНАЧЕНИЕ ФУНКЦИИ
469
ное значение в точке А:
/(M) = Z> + <x(7H), где lim а(М) = 0.
•М —А
Сравнение бесконечно малых функций нескольких переменных про-
изводится точно так же, как это указано в п. 3 § 2 главы 4 для
бесконечно малых функций одной переменной. Отметим, что, как и
в случае одной переменной, под символом о (9) мы будем пони-
мать любую бесконечно малую в данной точке А функцию более
высокого порядка малости, чем бесконечно малая в данной точке А
функция р (Л4).
5.	Необходимое и достаточное условие существования пре-
дельного значения функции (критерий Коши). Будем говорить,
что функция f(M) удовлетворяет в точке М = А условию Коши,
если для любого положительного числа е найдется положительное
число 8 такое, что, каковы бы ни были две точки М' и 1Л" из об-
ласти заданця функции /(Л4), удовлетворяющие неравенствам
0<;р(ЛГ, Д)<8, 0<р(Л4", А)<8, для соответствующих значений
функций справедливо неравенство
|/(М')-/(Ж")| <е.
Справедлива следующая основная теорема
Теорема 14.2 (критерий Коши). Для того чтобы функция
f (Л4) имела конечное предельное значение в точке М = А, необхо-
димо и достаточно, чтобы функция f(M) удовлетворяла в этой
точке условию Коши. Доказательство этой теоремы совершенно
аналогично доказательству теоремы 8.2 и получается из него путем
замены букв х и а на буквы М и А и замены выражений типа
| х — а | на символ р (М, А).
6.	Повторные предельные значения. Для функции u=f(xlt х2, ... , хт)
нескольких переменных можно определить понятие предельного значения
по одной из переменных при фиксированных значениях остальных пере-
менных. В связи с этим возникает понятие повторного предельного значения.
У ясним это понятие на примере функции и = / (х, у) двух переменных х и у.
Пусть функция, и =[ (х, у) задана в некоторой прямоугольной окрестности
|х —	\у — у{) | <Zdt точки Мо (х0, р0), за исключением, быть может,
самой точки Ма. Пусть для каждого фиксированного у, удовлетворяющего
условию 0 < | у — уа | < d2, существует предельное значение функции u=f(x, у)
одной переменной х в точке х = х0:
lim f(x, y)=<f(y),
X — XQ
у — фикс
и пусть, кроме того, существует предельное значение b функции <р (у) в точ-
ке у = уа:
,	lim <р (у) = Ь.
у—у«
В этом случае говорят, что существует повторное предельное значение b
470
ФУНКЦИИ НЕСКОЛЬКИХ’ПЕРЕМЕННЫХ
[ГЛ. 14
для функции и = / (х, у) в точке Мо, которое обозначается следующим об-
разом:
lim lim / (х, у) = Ь.
У—Ун х —
Аналогично определяется повторное предельное значение
lim lim f (х, у).
х-+х<,у^>у.
Установим достаточные условия равенства двух введенных повторных
предельных значений.
Теорема 14.3. Пусть функция и = / (х, у) определена в некоторой пря-
моугольной окрестности |х— х0 | < dj, | у — у0 | < d2 точки М0(х0, у„)
и имеет в этой точке предельное значение Ь. Пусть, кроме того, для любого
фиксированного х, 0 <с | х — х0 \ <zdi, существует предельное значение ф (х) =
= lim / (х, у) и для любого фиксированного у, 0 < | у — уа | < d2, существует
у-^у»
предельное значение <р (у) — lim / (х, у). Тогда повторные предельные значения
Х—*Х0
lim lim / (х, у) и lim lim f (х, у) существуют и равны Ь.
х — х,у — уа	У—Уо х->х„
Доказательство. Так как функция u—f(x, у) имеет в М0(х0, yQ)
предельное значение Ь, то для любого е>0 можно указать такое 8 > 0, что
при |х— х0 | < 8 и | у — у0 | < 8 выполняется неравенство |/(х, у) — b | < е.
Таким образом, в прямоугольной окрестности |х — Хр | < 8 и \у — уй | < 8
точки Л10 значения функции f (х, у) отличаются от й не больше чем на е.
Но тогда предельные значения ф (х) и <р (у), указанные в формулировке тео-
ремы при х и у, удовлетворяющих неравенствам |х—х01 < 8 и |</ — у0|<8,
также отличаются от b не больше чем на е. Следовательно, и предельные
значения этих функций в точках х0 и уа соответственно существуют и равны
Ь. Теорема доказана.
Можно определить понятие повторного предела для так называемых
двойных последовательностей {ат„}, элементы атп которых определяются
двумя индексами т и п. -Именно, символ lim lim атп означает, что сна-
л-*со т—-от
чала определяется последовательность {Ь„}, Ьп = lim атп, а затем нахо-
т —- со
дится предел этой последовательности {Ьп}.
Рассмотрим, например, двойную последовательность {ата}, где атп =
= cos'" 2лл!х, х — фиксированное число. Докажем, что
( 1, если х рациональное число,
lim lim cos'” 2яп1х = < „
„-►со т —оо	10, если х иррациональное число.
В самом деле, если х = —, где р и q — целые числа, то при n^q имеем
соз2тгп1х=1, и поэтому lim cos'”2nn!x = 1. Иными словами, если х—ра-
т — оо
циональное число, то lim lim cos'” 2лп! х = 1. Если же х — иррациональ-
п—»оо т —* оо
ное число, то при любом п справедливо неравенство | cos 2iml х | < 1, и по-
этому lim cos'” 2яп! х = О, т. е. lim lim cos'” 2лп! х = 0.
m —оо	л—*oo m—»oo
Замечание. Используя полученный результат, мы можем аналитиче-
ским способом задать функцию Дирихле (см. п. 1 § 1 главы 4) как повторный
предел lim lim cos'” 2wi! х.
п~» оо т -» от
§ 3]	НЕПРЕРЫВНЫЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ	471
§ 3.	Непрерывные функции нескольких переменных
1.	Определение непрерывности функции нескольких перемен-
ных. Пусть точка А принадлежит области задания функции и = f(M)
нескольких переменных и любая s-окрестность точки А содержит
отличные от А точки области задания этой функции.
Определение 1. Функция u=f(M) называется непрерыв-
ной в точке А, если предельное значение этой функции в точке
А существует и равно частному значению f(A). Отметим, что так
как А = lim М, то условие непрерывности функции можно записать
м — а
в следующей форме:
lim /(Л4)=/( lim М).
М — А	М — А
Точки, в которых функция не обладает свойством непрерывности
называются точками разрыва этой функции.
Сформулируем определение непрерывности функции, используя
определение предельного значения функции с помощью е и 8.
Определение 2. Функция u=f(M) называется непрерывной
в точке А, если для любого положительного числа е можно ука-
зать такое положительное число 8, что для всех точек М из
области задания функции, удовлетворяющих условию р (М, А) < 8,
выполняется неравенство |/(уИ) — f (А) | <; е.
Определение 3. Функция u=f(M) называется непрерыв-
ной на множестве {М}, если она непрерывна в каждой точ-
ке этого множества.
Назовем приращением или полным приращением функции u=f (7И)
в точке А функцию &и, определяемую формулой
Ьи — f (М) — f (А),	(14.5)
где М — любая точка из области задания функции. Пусть точки А
и М имеют соответственно координаты alt as, , ат и хь хг, ....
хт. Обозначим хг — at = Ajq, х2 — а2 = Дх2, ..., хт — ат = Дхт.
Используя эти обозначения, получим для приращения функции Дц,
соответствующего приращениям аргументов &xv ..., Дхет, следующее
выражение:
Ди=/(а1-|-ДХ1, а2 + Дх2, ..., am + ^xm)-f(alt av .... am). (14.6)
Очевидно, для непрерывности функции u=f(M) в точке А необ-
ходимо и достаточно, чтобы ее приращение &и представляло
собой бесконечно малую в точке А функцию, т. е. необходимо и
достаточно, чтобы
lim Аи= lim (/(7И) — /(Д)) = 0 или lim Ди = 0.	(14.7)
М-»А	Длг,->0.
4х,->0,
Ах_-0
tn
472
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[ГЛ. 14
Условие (14.7) мы будем называть разностной формой условия не-
прерывности функции u=f(Л1) в точке А.
Для функции u=f (хг, х2, ., хт) нескольких переменных можно
определить понятие непрерывности по одной из переменных при
фиксированных значениях остальных переменных. Для определения
этого понятия рассмотрим так называемые частные приращения
функции u=f(x1, х2, хт) в точке M(xv х2, хт), принад-
лежащей области определения функции. Зафиксируем все аргументы,
кроме первого, а первому аргументу придадим произвольное прира-
щение Дхх такое, чтобы точка с координатами xt + Дхр х2, ..., хт
находилась в'области задания функции. Соответствующее приращение
функции называется частным приращением *) функции в точке
М (хр х2, ..., хт), соответствующим приращению Дхх аргумента xv
и обозначается ДЛ1п. Таким образом,
Д_у1н ==У^(х-£ДХ1, х2> ..., Хгп) — f (X\t х2, ..., xm). (14.8)
Аналогично определяются частные приращения функции, соответ-
ствующие приращениям других аргументов:
Введем теперь понятие непрерывности функции u=^f (xv х2, ..., хт)
по одной из переменных.
Функция u—f(xv х2, ..., хт) называется непрерывной в точке
М(хр х2..., хт) по переменной xk, если частное приращение ^Xfit
этой функции в точке М представляет собой бесконечно малую
функцию от &Xk, т. е. если
lim Дх и = 0.
(14.10)
При фиксированных значениях всех переменных, кроме переменной xft,
функция и=/(Хр х2, ..., хт) представляет собой функцию одной
этой переменной. Отметим, что непрерывность функции по перемен-
ной х* означает непрерывность указанной функции одной переменной.
Очевидно, из условия непрерывности функции tt—f(x1,x2, xm)
в данной точке М вытекает непрерывность этой функции в точке М
по каждой из переменных хр х2, ..., хт. Однако из непрерывности
функции в точке М по каждой из переменных xv х2......хт не вы-
текает, вообще говоря, непрерывность функции в этой точке. Чтобы
убедиться в этом, рассмотрим следующие примеры:
*) Термин «частное приращение» употребляется для того, чтобы отли-
чить это приращение от полного приращения (14.6), соответствующего про-
извольным приращениям Дх2............Дхт всех аргументов х2.............
§ 3]
НЕПРЕРЫВНЫЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
473
1°. Мы будем говорить, что функция и=f (Л4) = f(x, у) непрерыв-
на в точке М на некоторой прямой, проходящей через эту точку, если
для любой последовательности точек {Мп} этой прямой, сходящейся
к точке М, соответствующая последовательность {/(Л4П)} значений
функции имеет пределом частное значение f(M) функции в точке М.
Так как на прямой функция u=f(x, у) представляет собой функцию
одной переменной, то понятие непрерывности функции на прямой сов-
падает, очевидно, с понятием непрерывности указанной функции одной
переменной. В частности, непрерывность функции в точке М по отдель-
ным переменным х и у представляет собой непрерывность ее на пря-
мых, проходящих через точку М и параллельных координатным осям.
Докажем, что функция
при х2+У#0,
О при х2 -\-у2 = О
каждой из переменных х и у, т. е.
в точке 0(0, 0) по
на каждой из координатных осей, но не является непре-
всех остальных прямых, проходящих через эту точку, и
непрерывна
непрерывна
рывной на
поэтому не является непрерывной в точке О. Каждая прямая, отлич-
ная от координатных осей и проходящая через точку 0(0,0), может
быть представлена уравнением у — kx, где k уЬ 0. Очевидно, на такой
прямой все значения функции постоянны и равны	Поэтому,
если последовательность {Мп} отличных от О точек такой прямой
сходится к точке О, то соответствующая последовательность значений
k
функции имеет предел Так как при k 0 этот'предел отличен
от нуля и не совпадает с частным значением функции в точке О,
то функция разрывна в этой точке на рассматриваемой прямой. Не-
прерывность функции на координатных осях вытекает из того, что
ее значения на этих осях равны нулю.
Может сложиться впечатление, что если функция дзух переменных
непрерывна на любой прямой, проходящей через данную точку, то
эта функция непрерывна в указанной точке. "Следующий пример по-
казывает, что это, вообще говоря, не так.
2°. Рассмотрим функцию
( х2У
и =f(M) = J х4 + ^а
О
при х4 + у2 ф О,
при х4 + у2 = 0.
Докажем, что, хотя указанная функция
ходящей через точку О (0, 0) она не
В самом деле, значения функции на прямой у = kx равны	,
непрерывна на любой прямой, про-
является непрерывной в этой точке.
kx
и по-
этому при х —* 0 и —> 0. Непрерывность этой функции на оси Оу вытекает
из того,- что ее значения на этой оси равны нулю. С другой стороны, зна-
чения функции на параболе у = рх2 постоянны и равны
Р
1+Р2’
поэтому
474
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
(ГЛ. 14
предельное значение функции при стремлении точки М к точке О по ука-
Так как при рт^О этот предел отли-
частным значением функции в точке О’, то
занной параболе также равно
чен от нуля и не совпадает с
функция разрывна в этой точке.
2.	Основные свойства непрерывных функций нескольких
переменных. В этом пункте мы перечислим основные свойства непре-
рывных функций нескольких переменных. Поскольку доказательства
этих свойств в основном аналогичны доказательствам соответствующих
свойств функций одной переменной, то, как правило, мы будем давать
лишь краткие пояснения, предоставляя детали доказательств читателю.
1°. Арифметические операции над непрерывными
функциями. Справедливо следующее утверждение.
Пусть функции f(M) и g(Af) непрерывны в точке А. Тогда
функции f(M) + g (Af), f (Al) - g (/И), f(M)-g (Ж) и непрерывны
в точке А (частное при условии g(A) 0). Доказательство этого
утверждения совершенно аналогично доказательству теоремы 4.2.
2°. Непрерывность сложной функции. Введем понятие
сложной функции нескольких переменных. Пусть функции
Xn^Vl(^V (2’ •••>
Х2 ~ (^1 ?2’ •••> t/i)> I	(14 11)
= t2........h) J
заданы на множестве {А/} евклидова пространства Ek (tt, t2,...,tk—
координаты точек в этом пространстве). Тогда каждой точке
N(^> /2, .... tk) из множества {А/} ставится в соответствие с по-
мощью формул (14.11) точка М (xv х2........ хт) евклидова прост-
ранства Ет. Обозначим через { М } множество всех таких точек. Пусть
u=f(xv х2, ..., хт) — функция zn-переменных, заданная на указан-
ном множестве {М}. В этом случае мы будем говорить, что на мно-
жестве {N} евклидова пространства Ек определена сложная функ-
ция и— f(xv х2, хт), где xv х2, хт являются функциями
переменных t\, t2, ..., tk, причём эти функции определяются соотно-
шениями (14.11). Справедливо следующее утверждение.
Пусть функции x1 = <pi(/i, /2> •••> **)> х2 = Тгf2> •••>
..., хт = <pm (lx, t2, ..., tk) непрерывны в точке А (аь а2, ак),
а функция и = f(xb х2,хт) непрерывна в точке В (blt Ьг,Ьт),
где	а2....ак), I— 1, 2, т. Тогда сложная функция
u=f(x1, х2...... хт), где хь х2, хт представляют собой
определенные выше функции аргументов tlt .........tk, непрерывна
в точке А(ах, а2, ..., ак). Наметим основные этапы доказательства
этого утверждения. Пусть { N„ }, NnjA А,— произвольная сходящаяся
к А последовательность точек из области {N} задания функций
НЕПРЕРЫВНЫЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
475
§ 3]
(ti, t2, .... tk)> a { Af„ } — соответствующая последовательность то-
чек, координаты которых равны	..., В силу не-
прерывности функций <р, в точке А, последовательность {Мп} схо-
дится к точке В (Ь1г Ь2, .... Ьт) (не исключена возможность совпа-
дения точек Мп с точкой Б). В силу непрерывности в точке В
функции их2, хт), последовательность {f{Mn)} сходится
к f(B). Но эта последовательность представляет собой последова-
тельность значений сложной функции, отвечающую • сходящейся к А
последовательности { Nn\ точек области ее задания. Так как мы убеди-
лись, что последовательность {/(7ИП)} сходится к частному значению
f(B), то тем самым непрерывность сложной функции доказана.
Замечание. Приведенное здесь доказательство представляет
собой обобщение на случай нескольких переменных доказательства
теоремы 4.5 о непрерывности сложной функции одной переменной.
3°. Теорема об устойчивости знака непрерывной
функции.
Теорема 14.4. Если функция u—f(M) непрерывна в точке А
евклидова пространства Ет и если f (Л) 0, то существует
такая Ъ-окрестность точки А, в пределах которой во всех точ-
ках области своего задания f(M) не обращается в нуль и имеет
знак, совпадающий со знаком f(M). Справедливость этой теоремы
непосредственно вытекает из определения непрерывности функции в
терминах «е — 8».
4°. Теорема о прохождении непрерывной функции
через любое промежуточное значение.
Теорема 14.5. Пусть функция u=f(M) непрерывна во всех
точках связного множества {М} евклидова пространства Ет,
причем и f(B) — значения этой функции в точках А и В
этого множества. Пусть, далее, С — любое число, заключенное
между f(A) и f(B). Тогда на любой непрерывной кривой L, соеди-
няющей точки А и В и целиком располагающейся в { М }, найдется
точка N такая, что f(N) — C.
Доказательство. Пусть
=	^2 = ?2(0> ....
— уравнения непрерывной кривой L, соединяющей точки АиВ мно-
жества {М} и целиком располагающейся в {М} (см. п. 5 § 1).
На сегменте [а, р] определена сложная функция u=f (хх, х2, ...,хт),
где х; = <р;(0, t = 1, 2,..., т,	Очевидно, значения этой
функции на сегменте [а, {3] совпадают со значениями функции u—f (М)
на кривой L. Указанная сложная функция одной переменной t, в силу
утверждения раздела 2° этого пункта, непрерывна на сегменте [а,
и, согласно теореме 8.6, в некоторой точке В сегмента [a, 8| прини-
мает значение С. Поэтому в точке N кривой L с координатами <рх (£),
Та©» •••> ?т(£) справедливо равенство — Теорема доказана.
476
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[ГЛ. 14
5°. Ограниченность функции, непрерывной на
замкнутом ограниченном множестве.
Теорема 14.6 (первая теорема Вейерштрасса). Если функ-
ция u—f(M) непрерывна на замкнутом ограниченном множестве
{М}, то она ограничена на этом множестве. Остановимся на
доказательстве ограниченности u=f(M) сверху. Предположим, что
u—f(M) не ограничена сверху на {41}. Выделим (как и в дока-
зательстве аналогичной теоремы 8.7) последовательность { М„ } точек
множества {44}, для которых /(44„)>л. В силу теоремы Боль-
цано — Вейерштрасса (см. п. 2 § 2) из {44л} можно выделить
сходящуюся подпоследовательность { 44}, предел" М которой, в силу
замечания к теореме Больцано-Вейерштрасса, принадлежит множеству
{М}. Очевидно, последовательность {/(44^) | бесконечно большая.
С другой стороны, в силу непрерывности функции в точке М, эта
последовательность {/(Л4ал)} должна сходиться к f(M). Полученное
противоречие доказывает теорему.
6°. Достижение функцией, непрерывной на замк-
нутом ограниченном множестве, своих точных
граней.
Теорема 14.7 (вторая теорема Вейерштрасса). Если функ-
ция u=f(M) непрерывна на замкнутом ограниченном множестве
{М.}, то она достигает на этом множестве своих точных
верхней и нижней граней. Доказательство этой теоремы совершенно
аналсгично доказательству теоремы 8.8 (вторая теорема Вейерштрасса
для функции одной переменной).
7°. Понятие равномерной непрерывности функции
нескольких переменных. Функция u=f(M) называется
равномерно непрерывной на множестве {44}*) евклидо-
ва пространства Ет, если для любого положительного числа s
можно указать такое положительное 8, зависящее только от е,
что для любых двух точек М' и М" множества {44}, удовле-
творяющих условию р(41', 41") <8, выполняется неравенство
\f(M")—f(44')|<;е. Имеет место следующая теорема.
Теорема 14.8 (теорема о равномерной непрерывности).
Непрерывная на замкнутом ограниченном множестве { 44 } функ-
ция равномерно непрерывна на этом множестве. Доказательство
этой теоремы совершенно аналогично доказательству теоремы 10.2 и
получается из него путем замены термина «сегмент [а, £]» термином
«множество { 44}», замены’буквы х на букву М и замены выраже-
ний типа |х" — х'\ на символ р (41', 44").
Замечание. Назовем диаметром ограниченного множества
{44} точную верхнюю грань чисел р'(44', 41"), где 44' и 44" — все-
*) При этом предполагается, что множество { 44 } плотно в себе, т. е.
в любой е-окрестности каждой точки 44 этого множества имеются отличные
от 44 точки множества { 44
§ fl	ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ	-477
возможные точки множества {М}. Используя понятие диаметра мно-
жества, отметим следующее свойство непрерывных на замкнутых ог-
раниченных множествах функций. Пусть функция u=f(Л4) непре-
рывна на замкнутом ограниченном множестве {М }. Тогда для
любого положительного, числа, е можно указать такое 8 > О,
что на каждом принадлежащем множеству { М} замкнутом под-
множестве {М}, диаметр .которого меньше 8, колебание ш*)
функции f(M) меньше е. Доказательство этого свойства совершенно
аналогично доказательству следствия из теоремы 10.2.
§ 4.	Производные и дифференциалы функции
нескольких переменных
I.	Частные производные функции нескольких переменных.
Пусть точка М (хр х2, ..., хот) является внутренней точкой области
задания функции u=f(x1, x2, •••, хт). Рассмотрим в данной фикси-
рованной точке M(xv х2, хт) отношение частного приращения
&Х/и (см. пункт 1 § 3, формулы (14.8) и (14.9)) к соответствующему
приращению Дх* аргумента хк:
bXku _ /fa. х2..xk_lt	xk+l...xm)—f(xi, x2....xm)
&xk ~	ДхА	•
(14.12)
Отношение (14.12) представляет собой функцию от ДхА, определен-
ную для всех, отличных от нуля значений Дх*, для которых точка
М (хх, х2,	, Xii-y xk-\-ixxk, xk+1> ..., хт) принадлежит^ области
задания функции и.
Определение. Если существует предел отношения (14.12)
частного приращения Д^и функции в точке М(хг, х2, ..., хт)
к соответствующему приращению &хк аргумента хк при &хк —> 0,
то этот предел называется частной производной функции
u=f (хр х2, ..., хт) в точке М по аргументу хк и обозначается
одним из следующих символов:
°L и' Г
dxk’ dxk’ xk’ 'xk‘
Таким образом,
Отметим, что частная производная функции u=f(x1, х2, ..., хш)
по аргументу хк представляет собой обыкновенную производную
*) Колебанием <о функции f (М) на множестве { М } называется разность
между точной верхней и точной нижней гранями функции f (М) на этом
множестве.
478
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[ГЛ. 14
функции одной переменной х* при фиксированных значениях осталь-
ных переменных. Поэтому вычисление частных производных произ-
водится по обычным правилам вычисления .производных функций
одной переменной.
Примеры.
1° и -arctg-	= —У— ЁУ = -~Х .
дх х2 + у2’ ду х2 + ^'
2°. и = хе>г4-In(х—y + z),	—	----,
1	4	1 л дх ' х — у + z’
— ^xze?’-  1	— = х\>еуг +__!___
ду XZe x-y-j-г’ дг хуе ^х-у + г'
3°. U— tg|/xa — yz, = -7=:_________ Х--	,
й* у & — уг cos2 У к? — уг
ди _	_________г_________ ди___.	__________у________
ду 2 Ух2 — уг cos2 Ух2 — уг' дг	2 Ух2 — уг cos2Ух2 — уг
Замечание 1. Из существования у функции в данной точке
всех частных производных, вообще говоря, не вытекает непрерывность
функции в этой точке. Мы уже убе-
дились, что функция
( при +у* °’
и = < А т У
I 0 при х2+_уг = 0
не является непрерывной в точке
0(0, 0) (см. пример 1° п. 1 § 3). Од-
нако в этой точке указанная функ-
ция имеет частные производные по
х и у. Это следует из того, что
/(х, 0) = 0 и /(0,_у) = 0, и поэтому
Я =Ои?1 =°-
дх |(о, 0) ду |(о, 0)
Замечание 2. Мы опреде-
лили понятие частных производных
для внутренних точек области задания функции. Для граничных точек
области задания данное нами определение частных производных
является, вообще говоря, непригодным. В частности, это связано
с тем, что в граничных точках области задания функции не всегда
можно вычислить частные приращения этой функции (так, например,
обстоит дело с граничной точкой Л10 области, изображенной на
рис. 14.2). Поэтому обычно частные производные в граничных точках
области задания функции определяются как предельные значения
этих производных.
§ 4]	ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ	479
2.	Понятие дифференцируемости функции нескольких, пере-
менных. Напомним, что приращением (или полным приращением)
функции u—f(xv х2, хт) в точке М(х1У х2, хт), соответ-
ствующим приращениям Дхх, Дх2, ..., &хт аргументов, называется
выражение
Ди=/(х14-Дх1, х24-Дх2, ..., xm + &xm)-f(xv х2....хт).
Определение. Функция и = f (xv х2, .хт) называется
дифференцируемой в данной точке М (хр х2, хт), если
ее полное приращение в этой точке может быть представлено
в виде
Ди = >1^X1 + Л2Дх2 4- ... 4- Ат&хт axAxj4-	4"
4- ... -Гат^хт> (14.14)
где Лр А2, ..., Ат— некоторые не зависящие от Дхр Дх2, ..., Дхт
числа, а ах, а2, ..., чт — бесконечно малые при Дхх 0, Дх2 —> О,
..., Дхт —► 0 функции, равные нулю при Дхх = Дх2 = ... = Дхт = 0.
Соотношение (14.14) называется условием дифференцируемости функ-
ции в данной точке М. Условие (14.14) дифференцируемости функции
можно записать также в иной форме. Для этого рассмотрим беско-
нечно малую при Дхх —► 0, Дх2 —► 0 &хт —> 0 функцию р =
=}/~bxf 4- Дх2 4- ... 4- Дхт *) и отметим, что эта функция обращается
в нуль лишь при Дхх = Дх2 = ... =Дхт = 0. Убедимся теперь, что
входящая в правую часть соотношения (14.14) сумма ахДхх 4-а2дх2 +
4- ... 4- атАхт представляет собой бесконечно малую более высокого
порядка функцию по сравнению с р. Иными словами, убедимся, что
эта сумма представляет собой выражение о(р). В самом деле, при
, п	| ДХ; I _ .
р ф 0 справедливо неравенство — р ”	1, и поэтому
I а1Д*1 + а2Д*2 4- • • • 4- «тдхт I <
^ .{ I “1 I + I а2 I + • • • 4“ I ат | } Р — ° (р)-
Таким образом, условие (14.14) дифференцируемости функции может
быть записано в следующей форме
Ди = ЛхДхх 4-Д2Дх2 + • • • + Ат&хт 4- о (р).	(14.15)
При этом величину о(р) мы считаем равной нулю при р = 0.
Чтобы доказать, что условие (14.15) эквивалентно условию (14.14),
нужно убедиться, 'что из представления (14.15) в свою очередь вы-
текает представление (14.14). Для этой цели, считая, что не все Дхх,
*) Геометрически эта функция представляет собой расстояние между
точками М (хх, ха, ..., хот) и М' (хх4- Дхх, х2 4- Дх2, ..., хт4- Дхт).
480
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[ГЛ. 14
Дх2, ^хт равны нулю*), представим о(р) в виде
0(р)р2	о(р)Д^+Дх’+ ... +Дх^_
о(р) =------=-------5--------- --------
Р ? Р
[о (р)Дхх
Нтт]^+-+[тт]4'-
„ О (р) Дх,-	,
Полагая —— = а; и учитывая, что а,- является бесконечно малой
при р->0 (а стало быть, и при Axj-^О, Дх2->0, .... Дхт->0)
функцией, мы придем к представлению (14.14).
Итак, условие дифференцируемости функции можно записать как
в виде (14.14), так и в виде (14.15).
Если хотя бы одно из чисел Лх, А2, ..., Ат отлично от нуля, то
сумма ЛхДхх4- Л2Дх2 -ф ... -ф Ат&хт представляет собой главную,
линейную относительно приращений аргументов часть приращения
дифференцируемой функции. Отметим, что при определении понятия
дифференцируемости функции мы не исключали возможности обраще-
ния всех чисел Лх', Л2, ..., Ат в нуль, и поэтому, если приращение
Дн функции может быть представлено в виде (14.14) или (14.15) при
Лх = Л2 — ... = Ат — 0, то функция дифференцируема в данной точке.
Справедлива следующая теорема.
Теорема 14.9. Если функция u—f(xv х2, .... хт) дифферен-
цируема в точке Л1 (хх, х2, ..., хт), то в этой точке сущест-
ди .
вуют частные производные по всем аргументам, причем = Лц
где At определяются из условия (14.14) или (14.15) дифференци-
руемости функции.
Доказательство. Из условия (14.14) дифференцируемости
функции в точке М (хх, х2, ..., хт) вытекает, что ее частное при-
ращение Дх.и в этой точке равно Дх.м = Л(-Дх/ -ф а;Дх(. Отсюда вы-
Дх,и
текает, что	— А + аь и поэтому, так как а;->0 при Дх,—>0,
Дх; и ди
lim — = — = Л;.
Дхг дх.
Следствие 1. Условие (14.15) дифференцируемости функции
в данной точке М можно записать в следующей форме:
4» = |4* **). +М4х’+ - +£4х- + "<1,>*^	<’4Л6>
Следствие 2. Если функция u—f (хх, х2, ..., хт) дифферен-
цируема в точке М (xv х2, .хт)',' то представление ее прира-
Дх.
*) Если все Дх; равны нулю, то все члены в правой части формул
(14.14) и (14.15) равны нулю.
**) Здесь все частные производные берутся в данной точке М.
§ 41
ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
481
щения Дгг в форме (14.14) или (14.15) единственно. В самом деле,
коэффициенты At этих представлений равны частным производным
ди .	_	..
в данной точке М и поэтому определяются единственным образом.
Убедимся в справедливости следующего важного свойства диф-
ференцируемых функций.
Если функция u—f(xv х2, хт) дифференцируема в точке
М(xv х2, .хт), то она и непрерывна в этой, точке. В самом
деле, из условия (14.14) дифференцируемости функции в точке вы-
текает, что lim Ди — 0, а это и означает, что функция непрерывна
Дх, -<• о,
Сх, -* о.
в точке М (см. п. 1 § 3, формула (14.7)).
В случае функции u=f(x, у) двух переменных условие диффе-
ренцируемости может быть иллюстрировано геометричес-ки. Введем
понятие касательной плоско-
сти к поверхности в точке
А'о. Плоскость тс, проходя-
щая через точку No поверх-
ности, называется каса-
тельной плоскостью
в этой точке, если угол
между этой плоскостью
и секущей, проходящей че-
рез точку Na и любую
точку поверхности,
стремится к нулю, когда
точка стремится к
No (рис. 14.3).
Если в точке суще-
ствует касательная плос-
кость, то очевидно, что ка-
сательная в точке No к лю-
бой кривой, расположенной
на поверхности и проходящей через No,
лежит в указанной плоскости.
Убедимся, что из условия дифференцируемости функции u—f(x, у)
в данной точке Л40(х0, у0) вытекает существование касательной пло-
скости к графику £ этой функции в точке No (х0, у0, zQ). Положим
Дх = х-х0, 4у=^-Л> Аи = и-и0, где u0=f(x0, у0), u=f(x, у).
Очевидно, условие (14.14) дифференцируемости в рассматриваемом
случае можно записать следующим образом:
« — «о = А (х — х0) + В (у — у0) 4- аДх -ф рДу =
= А (х - х0) + В (у - у0) + о (р),
где А и В — постоянные, равные частным производным и
482
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
|ГЛ. 14
в точке Л40, а а и р — бесконечно малые при Дх->0 и Ду—>0
функции, р = ]/Д№-|-Ду2.
Рассмотрим следующее уравнение:
U- иа = А(х- хл) + В (у -у0).
Из аналитической геометрии известно, что это уравнение опреде-
ляет в декартовой системе координат (х, у, U) некоторую плоскость
it, проходящую через точку No (х0, у0, п0) и имеющую нормальный
вектор п = {А, В, — 1}*).
Докажем, что эта плоскость it является касательной плоскостью
в точке No поверхности. 5. Для этого достаточно убедиться, что:
1) плоскость тс проходит через точку No поверхности S и 2) угол ср
между нормалью п к этой плоскости и любой секущей N0N1 стремится
к тс/2, когда точка поверхности S стремится к точке ^.Утверж-
дение 1) очевидно. Перейдем к доказательству утверждения 2). Вы-
числим косинус угла ср, воспользовавшись известной формулой для
косинуса угла между двумя векторами. Так как координаты вектора п
равны А, В, — 1, а координаты вектора NONX секущей равны х — хй,
у— у0, и— и0 (см. рис. 14.3), то
сок fp = Л (х — х0) + 5 (у — Уо) — (и — »0)
?	/Л2 + В2 + 1 V(X - Хо)2 + (у - у0)2 + (а - и0)2 
Преобразуем выражение для cosep. Из условия дифференцируемости
функции и = f (х, у) вытекает, что
Д (х - х0) + В (у-у0) - (и - w0) = о (р).
Далее,
__________ 1		1__
]Д(х — х0)2 4- (у — Уо)2 + (и — и0)2___________VДх2 + Ду2 + Ди2
__________1_____________1	_ | cos у1
р j/” 1 + j2 р 1 + tg21 р
где f — угол между секущей и плоскостью (х, _у). Поэтому
| cos 7 | о (р)
cos <р —
/Л2 + В2 + 1 р
Из этой формулы вытекает, что lim cos ср = 0, т. е. lim ср——,
р—>-0	р->0
Утверждение 2) доказано.
Таким образом, дифференцируемость функции u_=f(x, _у) в точке
Л40 (х0, Уо) с геометрической точки зрения означает наличие каса-
тельной плоскости к графику функции u—f(x, у) в точке
No (х0> З'о- «о)-
*) Нормальным вектором плоскости называется любой ненулевой век-
тор л, перпендикулярный к этой плоскости.
§ 41
ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
483
Так как коэффициенты А и В равны соответственно частным
производным, вычисленным в точке 7И0(х0, j0), то уравнение каса-
тельной плоскости может быть записано в виде
y-no=|“(x-xo)+g(j-jo).	(14.17)
Нормальный вектор п=={^>	—Q касательной плоскости
принято называть нормалью к поверхности u—f(x, у) в точке
Ло С^О’ У О’ "о)-
Выясним достаточные условия дифференцируемости функции не-
скольких переменных.
Теорема 14.10. Если функция u=f(xlt х2, .... хт) имеет
частные производные по всем аргументам в некоторой окрест-
ности точки Мо (хр х2, хт), причем все эти частные произ-
водные непрерывны в самой точке /Ио, то указанная функция
дифференцируема в точке Мо.
Доказательство. Для сокращения записи проведем доказа-
тельство для функции двух переменных u=f(x,y). Итак, пусть обе
частные производные Л и fy существуют в окрестности точки
Af0(x0, у0) и непрерывны в этой точке. Дадим аргументам х и у
столь малые приращения Дх и Ду, чтобы точка Af (х0 + Дх, j0 + Ду)
не выходила за пределы указанной окрестности точки Л40. Полное
приращение Дп=/(х0 + Дх, Jo + Aj) — f (xo> Jo) можно записать
в виде
Д« = [/(х0 + Дх, у0 + Ьу) - f (х0, уа + Ду)] +
+ I/ (*о> уо	(х0, j0)].
Выражение [/(х0 + Дх, y0 + by)—f(x0, у0 4- Ду)] можно рассмат-
ривать как приращение функции /(х, _У0 + Ау) одной переменной х
на сегменте [х0, х04-Дх]. Поскольку функция u=f(x, j) имеет
частные производные, указанная функция f (х, у0 + Ду) дифферен-
цируема и ее производная по х представляет собой частную произ-
водную f'x. Применяя к указанному приращению формулу Лагранжа,
найдем такое из интервала	что
[/(х0 + Дх, yQ + Ду) - f (х0, у0 + Aj)] =Л (х0 + SjAx, j0 + by) bx.
Рассуждая совершенно аналогично, получим, что для некоторого
0а из интервала 0<62< 1,
1/(Л» Уо + by) -/(х0, j0)] =fy (х0, j0 + 02Ду) Aj.
Так как производные fx и f’y непрерывны в точке 7И0, то
Л (х0 + 6^x, Jo + by) =fx (х0, Jo) + а,
Л (^o> У о + 62AJ) = Л (Хо> У о) +
484
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
(ГЛ 14
где а и р — бесконечно малые при Дх —► 0 и Ду -> О функции. Отсюда,
учитывая приведенные выражения для
[/(*о + Дх, Jo + АУ) - / (*о> Jo + 4y)] и [/(х0, у0 +Ду) —/(-х0, Jo)]
и выражение для Ди, найдем
Ди = Л (х0, j0) Дх +4(х0, j0) Aj + аДх + ₽Aj.
Следовательно, функция м=/(х, j) дифференцируема в точке Л10.
Теорема доказана.
3.	Понятие дифференциала функции нескольких переменных.
Определение. Дифференциалом du дифференцируемой
в точке М (хр х2,..., хт) функции и — f (хг х2, ...., хт) называется
главная линейная относительно приращений аргументов часть
приращения этой функции в точке М. Если все коэффициенты.
Ate представлении (14.14) приращения дифференцируемой функции
равны нулю, то дифэференциал du функции в точке М считается
равным нулю.
Таким образом, дифференциалом du дифференцируемой в точке М
функции н=/(х1,-х2,...» хст) называется выражение
= AtAXi 4- Д2Дх2 + -. • + АтДхт.	(14.18)
Используя теорему 14.9, мы можем, очевидно, переписать выражение
(14.18) для дифференциала du следующим образом:
, ди .	, ди .	,	, ди .	,, , , л.
dll~ ~дъ ДХ1 + ах2'Дх2 + ---+ а^ДХт- (14.19)
Введем понятие дифференциала dxi независимой переменной x-t.
Под дифференциалом dxi независимой переменной хг можно пони-
мать любое (не зависящее от хр х2,...,хт) число. Договоримся
в дальнейшем брать это число равным приращению Дх; независимой
переменной х,-. Эта договоренность позволяет нам переписать фор-
мулу (14.19) в виде
du = dx! + dx„ +	+ dxm.	(14.20)
dxt 1 1 дх3 21	1 дхт т	'	’
Подчеркнем, что формула (14.20) установлена нами лишь для слу-
чая, когда аргументы хр х2,..., хт являются независимыми перемен-
ными. Однако ниже, в пункте 5 этого параграфа, мы докажем, что
формула (14.20) остается справедливой и для случая, когда аргу-
менты х1( х2, ..., хт не являются независимыми переменными, а сами
представляют собой дифференцируемые функции некоторых новых
переменных.
4.	Дифференцирование сложной функции. В этом пункте мы
рассмотрим вопрос о дифференцировании сложной функции вида
5 41
ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
485
и—f (Хр -^г* •••> -^т)> где
Xj — Ф 1 (^р ^2’ • • • > ^/г)>
х2 — <f>2 (tp f2> • • • >
(14.21)
хт — 'fm (fv ^2> • •  > ^k)-
Мы докажем, что при определенных условиях эта сложная функ-
ция является дифференцируемой функцией своих аргументов tv t2 ...
tk. При этом частные производные указанной сложной функции
по аргументам tv t2,..., tk выражаются через частные производные
функции ii=f(x1, х2,..., хт) и через частные производные функций
(14.21) по следующим формулам:
(JU OU (IX} д UU иХ2 ।	।	<7U
dtL dxY dt2 dx2 dti	dxm ’
du ___du dxx du dx2	,	,	-du dxm
дГ2	дхг dt2	' dx2dt2	‘	‘	dxm dt2	’
(14.22)
du  du dxt du dx.2 ,	, du dxm
dtk dxL dtk dxa dt к ’ ’ ‘ ' dxm dtk
Докажем следующую основную теорему.
Теорема 14.11. Пусть функции (14.21) дифференцируемы в неко-
торой точке М (t v 12, .t ь), а функция u=f(xv х2,...,хт)
дифференцируема в соответствующей точке N (xv х2, ..., хт),
где xi = <t>J(f1, t2,tk), 1=1, 2,..., т. Тогда сложная функция
u=f(xlt ха. хт), где xv х2, ...,хт определяются соотноше-
ниями (14.21), дифференцируема в точке М. При этом частные
производные этой сложной функции в точке М определяются
формулами (14,22), в которых все частные производные
ди , 	, дх;
— берутся в точке N, а все .частные производные ~
ихт	и* I
функций (14.21) по аргументам 11г12,..., tk берутся в точке М.
Доказательство. Придадим аргументам tx, t2, ..., tk в точке
M(tlt t2, ..., fft) произвольные приращения Д^х, Д^2, Д^А, не рав-
ные одновременно нулю. Этим приращениям соответствуют прираще-
ния Дхх, Дх2,..., Дхт функций (14.21) в точке М. Приращениям
Дхг, Дх2,..., Дхт в свою очередь соответствует приращение Ди
функции и=/(хг, х2,..., хт) в точке N. Поскольку функция и =
= /(Хр х2,..., хт) предполагается дифференцируемой в точке N, ука-
занное приращение Ди этой функции может быть записано в виде

4 ^Дх! + а2Дх2 +... + атДхго	(14.23)
486
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[ГЛ. 14
ди ди ди -	..
где частные производные ..........берутся в точке N, а ах,
а2, ..., ат — бесконечно малые при Дхх -> 0, Дх2 -> 0, ..., ’ Дхт -> О
функции, равные нулю при Дхх = Дх2 =... = Дхт = 0. Подчеркнем,
что в соотношении (14.23) Дх1; Дх2, ...Дхт представляют собой
приращения функций (14.21), отвечающие выбранным приращениям Д<1(
Д1“2, ..., Д^ аргументов этих функций. В силу дифференцируемости
функций (14.21) в точке Л1 (1х, Za, ..., lb) указанные приращения
Дх; можно записать в следующей форме:
Лх‘=$ “•+s?'-+ +а;"»+ » (Л <14-24)
I — 1, 2,..т,
dxi dxi dxi ,	..
где частные производные	берутся в точке М, а р =
= /(Д^ + (Д/2)2 + ... + (дЬ. 2
Мы должны убедиться в том, что после подстановки в правую
часть (14.23) выражений (14,24) приращение Дп может быть приве-
дено к виду
Дц = /^Д^х +	-(-... + ''^Д/* 4- о (р),	(14.25)
где
+	л7-+---+А^. /=1’ 2’->k (14.26)
‘ дхг dti 1 дхг dtj 1	1 дхт dt, '	’ v ’
Тем самым доказательство теоремы будет завершено, ибо формула
(14.25) устанавливает факт дифференцируемости сложной функции,
а выражение (14.26) представляет собой частную производную ука-
занной сложной функции (см. теорему 14.9).
При подстановке в правую часть (14.23) выражений (14.24), кроме
группы слагаемых ^Д^ + Л2Д/2 +... + Ак№к, мы получим и другие
группы слагаемых. Нам нужно убедиться в том, что все другие группы
слагаемых представляют собой величину о (р). Это вытекает из сле-
дующих соображений:
1°. Все частные производные в формуле (14.23) берутся
в точке N, т. е. представляют собой постоянные числа, кото-
рые при умножении на о(р) дают снова величину о(р).
2°. Все kxt (i = 1, 2,..., т) удовлетворяют неравенству | Дх; |
const р. Это непосредственно вытекает из формул (14.24).
3°. Все rj-i в формуле (14.23) представляют собой бесконечно
малые при р —► 0 функции. В самом деле, все а; являются бесконечно
малыми при ДХ1->0, Дх2->0,..., Дхт->0. Но все функции (14.21)
дифференцируемы, а стало быть, и непрерывны в точке М, и поэтому
Дхр Дх2, ..., Дхт стремятся к нулю при р -> 0.
4°. Каждое произведение представляет собой величину
о(р). Это непосредственно вытекает из пп. 2° и 3°. Теорема доказана.
§ 4]
ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
487
Замечание. Рассмотрим важный частный случай, когда функции
(14.21) зависят от одного аргумента t. Тогда мы имеем сложную
функцию одной переменной t: u=f(xv х2......хт), где X/= ?,(/).
Производная этой сложной функции определяется следующей фор-
мулой:
du _ ди dxL , ди dx2 .ди dxm	... .
dt — дхг dt + dx2 dt + *” + dxm dt ’	V4-2'/
Применим формулу (14.27) для доказательства теоремы Эйлера
об однородных функциях.
Функция u—f{xv х2,хт), заданная на множестве {Л4}, назы-
вается однородной функцией степени р на этом множестве, если
для каждой точки М (хг, х2...хот) множества {2И} и для каждого
числа t, для которого точка N(txv tx2,..., txm) принадлежит мно-
жеству {7И} выполняется равенство
f (fxlt tx2,txm) = tpf (хр x2,..., xm). (14.28)
Теорема 14.12 (теорема Эйлера об однородных функциях).
Если u=f(xY, х2,...,хт) является в некоторой области {Л4}
дифференцируемой однородной функцией степени р, то в каждой
точке М (хь х2,..., хт) области {М} справедливо равенство
-5— xi +	. + -ч— хт = ри.	(14.29)
dxt 1 1 дх2 2 1	1 дхт т е	\	>
Доказательство. Пусть Af0(xlt х2, ..., хт) — произвольная
точка области {А1}. Рассмотрим сложную функцию и =f(xlt х2,..., хт),
где Xi — txi (1=1, 2..т),	т. е. функцию u=f(fxb tx2, ..., txm).
Так как при 1 функции Xt = txi дифференцируемы и функция
и —f (хх, х2, ..., хт) дифференцируема в соответствующей точке /Ио,
то, согласно теореме 14.11 и замечанию к этой теореме, мы можем
вычислить производную указанной сложной функции в точке t = 1
по формуле (14.27). Так как ~- = Xi, то
SI =^Lxl + ~x2 + ...^^-xm,	(14.30)
dt |/ = i dxi 1 1 дх2 21	1 дхт 	v 7
где производные берутся в точке Мо. С другой стороны, в силу
О%1
(14.28) рассматриваемая сложная функция может быть представлена
следующим образом:
«=/(^х, tx2,..., txm) = tpf(xv х2,..., хт). (14.31)
Из (14.31) вытекает, что	= ptp~'Lf(x1, х2....хш), т. е.
J|/=1 =pf(Xi> х2, .... хт)=ри.	(14.32)
488
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[ГЛ. 14
Сравнивая (14.30) и (14.32), мы получим соотношение (14.29) для
точки Л10. Так как точка Л40 — произвольная точка области {УИ}, то
теорема доказана.
5. Инвариантность формы первого дифференциала. В п. 3 мы
ввели понятие первого дифференциала du функции нескольких пере-
менных и установили, что когда аргументы х1( х2,..., хт являются
независимыми переменными, то дифференциал du можно представить
в виде
du — ~ dxy + ~ dx2 +... -|- 4^- dxm.	(14.20)
дхг 1 1 дх2 21	' дхт т	v '
В этом пункте мы докажем, что формула (14.20) является универ-
сальной и справедлива также и в том случае, когда • аргументы xlt
х2, .хт сами являются дифференцируемыми функциями новых
переменных tv tk. Указанное свойство первого дифференциала
обычно называют свойством инвариантности его формы..
Итак, пусть аргументы хх, х2, ..., хт функции u=f (хг, х2,..., хт)
представляют собой дифференцируемые в точке A(t р 12,..,, tk) функ-
ции xi — ^i(tv t2,..., tk), а сама функция u=f(xv х2,..., хт) диф-
ференцируема в точке В(хг, х2,..., хт), где х-, — ср; (^, t2,..., tk).
В таком случае мы можем рассматривать и как сложную функцию
аргументов tr, t2,..., tk, которая, в силу теоремы 14.11, является диф-
ференцируемой в точке А. Поэтому дифференциал du этой сложной
функции можно представить в виде
du = ^dt1 + ^dt2+... + -^dt/l,	(14.33)
где определяются из соотношений (14.22). Подставляя из (14,22)
в (14.33) и собирая коэффициенты при получим
•••+^(^ + ^++^‘4
Остается заметить, что в последнем соотношении коэффициент при
равен дифференциалу dxt функции х; = <pf (tv t2,..., tk). Мы
получим для дифференциала du сложной функции формулу (14.20),
в которой дифференциалы dxt будут дифференциалами функций
х: = ф,-(/1, t2,..., tk). Инвариантность формы первого дифференциала
установлена.
Свойство инвариантности формы первого дифференциала позво-
ляет установить следующие правила дифференцирования. Пусть и
« 41
ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
489
и v — дифференцируемые функции каких-либо переменных. Тогда
d (си) — с du (с = const),
d (и ±v) = du± dv, d (uv) — udv + v du, d(^ = v_du—_udv_.
(В последней из написанных формул v не обращается в нуль).
Дбкажем, например, справедливость третьей из указанных формул.
Рассмотрим функцию w — uv двух переменных и и v. Дифференциал
этой функции dw равен
, dw , . dw ,
dw = du 4- 5- dv,
du dv
Так как |~ = v и ^ — u, to dw = и dv -f- v du. В силу инвариантно-
сти формы первого дифференциала выражение udv-\-vdu будет диф-
ференциалом функции uv и в случае, когда и и v сами являются диф-
ференцируемыми функциями каких-либо переменных.
6. Производная по направлению. Градиент. Пусть функция
u=f(x, у, z) трех переменных х, у и z задана в некоторой окре-
стности точки A40(.r0, у/0, z0). Рассмотрим некоторое направление,
определяемое единичным вектором а с координатами cos a, cos р,
cos 7 *). Проведем через точку Мо ось 1, направление которой совпа-
дает с направлением вектора а, возьмем на этой оси произвольную
точку М (х, у, z) и обозначим через I величину направленного отрезка
/И0Д4 указанной оси **). Из аналитической геометрии известно, что
координаты х, у, z точки М определяются равенствами
х — х0 +1 cos а, у =у§ +1 cos р, z — z0 +1 cos (14.34)
На указанной оси 1 функция u=f(x, у, z), очевидно, является слож-
ной функцией одной переменной величины I. Если эта функция имеет
в точке 1~0 производную по переменной I, то эта производная
называется производной по направлению 1 от функции
u~f(x, у, z) в точке Мо и обозначается символом Согласно
замечанию к теореме 14.11, в случае дифференцируемости функции
u=f(x, у, z) в точке Мо производная может быть вычислена
по формуле (14.27), в которой аргумент t нужно заменить на I. Таким
образом,
ди_______________________du_dx ди dy . ди dz
dl дх dl ' ду dl ' dzdl ’
*) Из аналитической геометрии известно, что если единичный вектор а
составляет с осями координат углы а, (3, у, то координаты этого вектора равны
cos a, cos р, cos f.
**) Величиной / направленного отрезка М0М оси 1 называется число, рав-
ное его длине,, взятой со знаком плюс, если направление этого отрезка совпа-
дает с направлением оси 1, и со знаком минус, если направление этого отрезка
противоположно направлению оси 1.
490
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
ГГЛ. 14
~	dx	dy Q dz	„ .
Так как = cos а, = cos р, = cos 7, то из последней формулы
находим
5» ди .ди а	, ди
зг = з- cos а 4- ч- cos В	4- — cos	г.	(14.35)
д1 дх 1 ду “	1 дг	1	'	'
Введем понятие градиента дифференцируемой в точке Мо (х0, у0, z0)
функции u=f(x, у, г).
Градиентом функции u—f (х, у, z) в точке Л40 называется
вектор, обозначаемый символом grad» и имеющий координаты,
, ди ди ди
соответственно равные производным	взятым в точке
Мй. Таким образом,
, [ди ди ди\
^du={dx’ ду’ д1Г
(14.36)
Используя понятие градиента функции и учитывая, что вектор а,
определяющий направление оси 1, имеет координаты cos a, cos р, cos f,
представим выражение (14,35) для производной ~ по направлению 1
в виде скалярного произведения векторов grad» и а:
Oi = a grad и *).
(14.37)
Покажем, что градиент функции u=f(x,y, z) в точке Мо харак-
теризует направление и величину максимального роста этой
функции в точке /Ио. Именно, убедимся, что производная функции и
в точке 714О по направлению, определяемому градиентом этой функции
в указанной точке, имеет максимальное значение по сравнению с произ-
водной по любому другому направлению в точке Л40, а значение
указанной производной равно | grad и |, т. е. длине вектора grad».
Перепишем формулу (14.37) в виде
J = I а 11 grad и | cos ср,
где ср —угол между векторами а и grad». Так как
| а | = 1, то = | grad и | cos ср.
,,	„ ,	!ди\
Из последней формулы вытекает, что максимальное значение 5-
\О1 /щах
производной по направлению будет при cos<p = i, т. е. когда напра-
*) Напомним, что скалярное произведение двух векторов, определяемое
как' произведение модулей (длин) векторов на косинус угла между ними,
в случае, когда векторы заданы координатами, равно сумме произведений
одноименных координат этих векторов.
§ 41
ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
491
вление вектора а совпадает с направлением grad и, при этом
= | grad и |.
\д1 /шах 16	1
Для выяснения геометрического смысла вектора grad и введем понятие
поверхности уровня функции u = f(x, у, г).
Назовем поверхностью уровня функции и = j (х, у, г) каждую поверх-
ность, на которой функция и = f (х, у, г) сохраняет постоянное значение,
f (х, у, г) = с = const.
Нетрудно убедиться в том, что вектор grad и в данной точке Ма (х0, </0> го)
ортогонален к той поверхности уровня функции и = f (х, у, z), которая про-
ходит через данную точку Ма.
Замечание. В случае функции u—f(x, у) двух переменных х
и у единичный вектор а, определяющий направление в точке Мо,
имеет координаты cos а и sin а. Поэтому в указанном случае фор-
мула (14.35) принимает вид
ди	ди	, ди .
sr = д- cos а + д- sin а.
о/	дх	' ду
Отметим, что в случае функции двух переменных градиент дифферен-
цируемой функции и (х, у) определяется как вектор, имеющий коор-
ди' ди .	...
динаты и Формула (14.37), очевидно, справедлива и в случае
двух переменных. Для функции и =/(х1( х2, .хт) т переменных
х1: х2, ..., хт производная по направлению и градиент определяются
аналогично. Именно, производная в точке Af0 (хъ х2, ..., хт) по
направлению 1, которое задается единичным вектором a = {cosa1,
cos <х2, ..., cosam}*), определяется как производная по I сложной
функции п=/(х1; х2, ..., хт), где Xj = х2 +1 cos alt x2=x24~
4-1 cos a2,..., xm = xm +1 cos am. В случае, если и =f(xb х2.хт) —
дифференцируемая функция, для производной по направлению имеет
место формула
ди ди , ди ,	, ди
= 5— cos «1 + 5— cos а» 4-... 4- з— cos <xm.
dl	1 1 dxa 21	1 dxm m
Градиентом функции в данной точке 2H0(xx, х2, ..., xm) называется
вектор, обозначаемый символом grad и и имеющий координаты ~,
ди	ди	а
ч—,	причем указанные производные берутся в точке /Ио.
OXg	vXm
Для производной по направлению дифференцируемой функции и —
=/(х1, х2....хот) справедлива формула (14.37).
*) В аналитической геометрии m-мерного евклидова пространства единич-
ный вектор а определяется как вектор с координатами cosq, cosa2, ..., cosam,
где cos2 а2 -j- cos2 a2 -f- ... 4- cos2 am = I.
492
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[ГЛ. 14
§ 5. Частные производные и дифференциалы
высших порядков
1, Частные производные высших порядков. Пусть частная про-
изводная
деленной в области {Л4},
В этом
функцию переменных xv х.
Может случиться, что эта
по аргументу хк в некоторой точке 7И области {Л4}. Тогда указан-
ии
•V- по аргументу
ОХ}
случае указанная
х, функции и = f (х1; х2, хт), оире-
существует в каждой точке области {Ж},
частная производная представляет собой
..., хт, также определенную в области {Ж}.
.	ди
функция имеет частную производную
ную частную производную по аргументу xk называют второй частной
производной или частной производной второго порядка функции
u=f(x1, х2.....хт) в точке М сначала по аргументу Х{, а затем
по аргументу хк и обозначают одним из следующих символов:
d»U Г( о ,
dxkdxi ’ Jxixk'
it
(2 >
XiXk‘
При этом, если I k, то частная производная
&и
dxkdxi
называется сме-
шанной частной производной второго порядка. После того как введено
понятие второй частной производной, можно последовательно ввести
понятие третьей частной производной, затем четвертой и т. д. Если
предположить, что нами уже введено понятие (л—1)-й частной про-
изводной функции ti—f (хх, х2, .... хт) по аргументам X;,, х,2, ...
..xln j (отдельные или даже все номера которых могут совпадать) и
что эта (и — 1)-я частная производная имеет в точке М частную про-
изводную по аргументу xin, то указанную частную производную назы-
вают п-й частной производной (или частной производной л-го по-
рядка) функции и = /(хр х2, ..., хт) в точке М по аргументам Xi
Xi, ..., Xin , Х(л> Таким образом, мы вводим понятие л-й частной
производной индуктивно, переходя от первой частной производной
к последующим. Соотношение, определяющее л-ю частную производ-
ную по аргументам X;, х^, .... Xi , xi, имеет вид
дпи	__ д ! дп lu
дх, дх, ...дх.дх, дх, дх, ... дх, дх,
‘л ‘л-i ‘г ‘1 ‘л \ ‘л-i ‘г ‘1
Если не все индексы 1Г, 12, ..., 1п совпадают между собой, то част-
д"и	„
ная производная	3— называется смешанной частной про-
ОХ: • «. ОХ} ОХ}
‘л 'г ‘1
изводной л-го порядка. Так как частная производная функции по
аргументу х, определяется как обыкновенная производная функции
одной переменной х, при фиксированных значениях остальных пере-
менных, то методика вычисления частных производных высших поряд-
ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
493
ков предполагает умение вычислять только обыкновенные производ-
ные первого порядка. В качестве примера вычислим частные произ-
водные второго порядка функции и = arctg—. Имеем
У
ди _	_ У	ди	X
дх	х2 + у2 ’	ду	Х2 + у2'
д2и	2ху	д2и._	х2 — у2
дх2 ~	"	(х2 + у2)2 ’	дхду	(х2 + у2)2 ’
д2и _	X2— у2	д2и	2xi/
дудх	(х2 + у2)2’	ду2	(х2 + у2)2 •
В рассмотренном примере смешанные частные производные и
<32и	о л
равны друг другу. Вообще говоря, значения смешанных произ-
водных зависят от порядка, в котором производятся последователь-
ные дифференцирования. Убедимся, например, что смешанные частные
д2и д2и .
производные и функции
х2__ п2
ху Х2 + у2 при -X2 + У2 О,
О при х2 + _у2 = 0
в точке (0, 0) существуют, но не равны друг другу. Действительно,
г у (xi — у4 + А.х2у2)	, , 2	„
ди___|	(х2 _|_ у2-р при х + у 7^ 0,
1 О' при х2 -\-у2 = 0.
Поэтому
ди. I	ди I
д2и I	_.. дх }х=о. дх |х=о, у=о_____________1
дудх\х=о, >=о	^,.,0	у
тт	I	.	~
Проводя аналогичные вычисления, получим	0	0=1. „Таким
$2и
образом, в точке (0,0) дудх' ®ыясним достаточные условия неза-
висимости значений смешанных производных от порядка, в котором
производятся последовательные дифференцирования. Предварительно
введем понятие п раз дифференцируемой функции нескольких перемен-
ных. Функция u=f (Хц xv...,хот) называетсяп раз дифференци-
ру е мой в точке Л40 (хх, х2,..., хт), если все частные производные
(п— 1)-го порядка этой функции являются дифференцируемыми
функциями в точке Мй. Отметим следующее утверждение. Для
того чтобы функция u=f(xlt х2, ...,xm) была п раз дифферен-
цируемой в точке Af0 (х1( х2,..., хт), достаточно, чтобы все ев
частные производные п-го порядка были непрерывными в точке Л10.
494
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
ГГЛ. 14
Справедливость этого утверждения вытекает из определения диффе-
ренцируемости функции и теоремы 14.10 о достаточных условиях
дифференцируемости.
Теорема 14.13. Пусть функция u=f(x, у) дважды дифферен-
цируема в точке Л40(х0, j0). Тогда в этой точке частные произ-
водные и f-yx равны.
Доказательство. Так как функция u—f(х, у) дважды диф-
ференцируема в точке Af0(x0, j0), то частные производные fx и fy
определены в некоторой окрестности точки /Ио и представляют собой
дифференцируемые функции в этой точке. Рассмотрим выражение
Ф =f(x0 + h, у0 + h) -f(x0 + h, j0) -
-/(-vo, Уо + h) +/(x0, Jo), (14.38)
где й — любре столь малое число, что точка М (х0 + h, j0 + й) нахо-
дится в указанной окрестности точки Мо. Выражение Ф можно рас-
сматривать как приращение Дер = <р (х0 -|- h) — <р (х0) дифференцируе-
мой на сегменте [х0, х0 + й] функции <р (x)=f(x, j0 + й) —f(x, j0)
одной переменной х. Поэтому по формуле Лагранжа, обозначая
через в некоторое число из интервала 0 •< 0 •< 1, можем записать
Ф = Д? = ср' (х0 + 0й) й = [Д (х0 + 0й, у0 + й) - fx (х0 + Ой, j0)] й =
= {(Л (*о + е/г> У о + h) - Л (х0, Jo)] -
- [ Д (ХО + Ой, у0) -fx (х0, j0)]} й. (14.39)
Так как частная производная fx является дифференцируемой в точке
/Ио функцией, то
[Д (-v0 + е/г> Jo + h) - Л (х0, Jo)] =
=Лх (х0, Jo) Ой + ffy (х0, уа) h + ах0й + ^й,
[Л (*о + 9/г> Jo) - Л (-Vo> Jo)] = Лх (х0, Jo) Ой + а20й,
где ах, рх и а2 — бесконечно малые при й -> 0 функции. Подставляя
найденные выражения для [Д (х0 + Ой, у0 + й) — Л (х0, j0)] и \fx (х0 +
Ч-Ой, Jo)—Л Л о, Jo)] в формулу (14.39), получим
Ф = [/Д(*о, Jo) + «m	(14.40)
где а = ах0-(-рх — а20 — бесконечно малая при й->0 функция. С дру-
гой стороны, выражение Ф, определяемое соотношением (14.38), можно
рассматривать как приращение Дф = ф (j0 + й) — ф (j0) дифференциру-
емой на сегменте [j0, Jo + ^l функции ]>(j) =/(х0 + й, j) —/(х0, j).
Применяя формулу Лагранжа и учитывая дифференцируемость част-
ной производной fy в точке Мо, мы получим совершенно аналогично
предыдущему следующее выражение для Ф:
Ф = [/$(Хо- Jo) + ₽]ft2,	(14.41)
где § —бесконечно малая при й->0 функция. Приравнивая правые
части соотношений (14,40) и (14.41) и сокращая обе части получен-
§ 5] ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 495
ного равенства на й2, найдем, что fxy (х0, _у0) + a=fyi(xa, y0) + fk Так
как -а и р —бесконечно малые при /г—>-0 функции, то из последнего
равенства следует, что Л^(х0, Уо)—/ух{хй, у^. Теорема доказана.
Замечание. Теорема 14.13 утверждает, что в данной точке
Д40(х0, J'o) имеет место равенство fx'y=fyx, если в этой точке диф-
ференцируемы fx и fy. Из дифференцируемости fx и fy в точке Мо
вытекает существование в этой точке всех частных производных
второго порядка. Однако равенство fxy~fyx имеет место и при усло-
вии существования лишь производных fxy и f'ff но при дополнитель-
ном требовании непрерывности этих производных в рассматриваемой
точке. Именно, справедливо следующее утверждение.
Пусть в некоторой окрестности точки А40(х0, _у0) функция
u=f(x, у) имеет частные производные f’x, fy, ffy, fff Пусть,
кроме того, производные ffy и f'fx непрерывны в точке 2И0. Тогда
в этой точке ff^=fff
Для доказательства воспользуемся выражением Ф, определенным’соотно-
шением (14.38). Из (14.39) вытекает, что Ф представляет собой умноженную
на h разность значений функции fx (х, у) в точках (х0 + 6ft, у0 -j- h) и (х0 +
+ вй, уа). Применяя к этой разности формулу Лагранжа конечных прираще-
ний по переменной у на сегменте [j/0, yQ + ft], получим
ф = fxy (*<> + 6Л- Уо + М) Л2, где 0 < < 1.
В силу непрерывности f'fy в точке Л40 (х0, yQ), из последнего равенства полу-
чаем
ф=[/!?И*о. 1/о) + »(Л)]л2,
где a (ft) — 0 при ft —> 0.
С другой стороны, эта же величина Ф представляет собой умноженную
на ft разность значений функции f' (х, у) в точках (х0 + ft, у0 + Огй) и (х0,
у0 + М). Применяя к этой разности формулу Лагранжа конечных прираще-
ний по переменной х на сегменте [х0, х0 + ft] и учитывая непрерывность f'f.
в точке Л40 (х0, у0), получим
Ф = (хо, Уо) + 3 (Л)] ft2,
где ₽ (ft) —< 0 при Л — 0.
Приравнивая последние два выражения для Ф и рассуждая так же, как
и в конце доказательства теоремы 14.13, мы убедимся в справедливости нуж-
ного нам равенства
fxy (хо, Уо) = ffx (*о> Уо)-
Докажем теперь теорему о независимости значения любой смешанной
частной производной n-го порядка от порядка, в котором производятся по-
следовательные дифференцирования.
Теорема 14.14. Пусть функция и = f (хь х2.....xm) п раз дифференци-
руема в точке Л40(хь х2, ... , хт). Тогда в этой точке значение любой смешан-
ной частнсй производной п-го порядка не зависит от порядка, в котором про-
изводятся последовательные дифференцирования.
Доказательство. Очевидно, достаточно доказать независимость зна-
чения любой n-й смешанной производной от порядка проведения двух последо-
вательных дифференцирований. Иными словами, достаточно доказать равенство
__________________________________=____________дПи _________ Д4 42)
dxin...dxihJ[1dxik...dxil dxin...dxik.dxill+l...dxli-
496
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
ГГЛ. 14
дя~* 1и
Рассмотрим функцию 33. Эта функция представляет собой дважды
l ...дх^
дифференцируемую функцию переменных и Х;А+1- Поэтому, в силу
теоремы 14.13,
дк+1и______________________________________дк+1и___________
dx<k+i dx‘k dxik-i -dxii = dxik dxik+i dxik-i	
Отсюда и вытекает справедливость равенства (14.42). Теорема доказана.
Отметим, что в случае п раз дифференцируемой в точке Л1о функ-
ции u=f(xv х2, ..., хт) любую ее частную производную л-го по-
рядка можно записать в виде
дпи
_ а, а _ а
дх,1 дх2г ...дх™
где и ai + a2 + ... + <*m =п.
2. Дифференциалы высших порядков. Введем понятия билиней-
ной и квадратичной форм. Функция
Ф(х, 3’) = Ф(х1, ..., хт; у1г
т
ут)= У,	а,* = const,
i. ft = 1
зависящая от переменных xv ..., хт; у2, .... ут, называется били-
нейной формой от указанных переменных. Наименование билинейная
форма объясняется тем, что при фиксированных значениях беремен-
ных х функция Ф(х,у) будет линейной относительно переменных у
и наоборот.
Функция
т
Ф (X, X) = Ф (Xj, ..., Xm, Xj, . .., Xm) = У UikXiXk
,	I. ft = I
называется квадратичной формой, соответствующей данной билиней-
ной форме Ф (х, _у).
Если aik=aki, i, k—1, 2, ..., п, то билинейная форма Ф(х, у)
и соответствующая ей квадратичная форма Ф(х, х) называются сим-
метричными.
Мы будем использовать для обозначения дифференциалов наряду
с символом d также и символ В.. Например, для первого дифферен-
циала функции u = f(x, у) можно использовать выражения
du = dx + dy и 8« = ох ф- 8_у.
дх ' ду	дх ду
т
♦) Символ У Ь[1г обозначает сумму т2 однотипных слагаемых: (Ьп ф-
i. ft = 1
+ &12 + ••• + ^im) + ('’ai + b№ 4"	+ b2m) +	+ ('’ml + '’ma + ••• + bmm)-
§ 5] ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 497
Введем понятие дифференциала второго порядка в точке Af0 для
функции u—f(xt, хт), дифференцируемой в некоторой окрест-
ности точки Л40 и дважды дифференцируемой в самой точке Мо.
Для сокращения записи проведем рассуждения для функции двух
переменных и = f(x, _у). Итак, пусть функция и = f (х, у) дифферен-
цируема в некоторой окрестности точки Мо (х0, _у0) и дважды диф-
ференцируема в этой точке. При этих условиях в каждой точке
указанной окрестности существует первый дифференциал du, опреде-
ляемый формулой
du = ^dx+~dy.	(14.43)
дх 1 ду J	\	>
Будем считать, что dx и dy имеют фиксированные значения одни
и те же длр всех точек рассматриваемой окрестности Мо. Тогда в
этой окрестности дифференциал du представляет собой функцию
от х и у, дифференцируемую в точке AlJ). Вычислим дифференциал
этой функции в точке тИ0, используя для обозначения дифференциа-
лов символ 8. Из формулы (14.43) и из правил дифференцирования
(см. п. 5 § 4 этой главы) вытекает, что
Так как, во-первых,
„ 1ди\ д /ди\ 5	. д /ди\ - д2и s . д2и „
5Ы==^Ы8х+^Ы8з'=^8х+^8-у>
df}=^^hx + ^^^y = ^x + d^y
\ду) дх\ду) ду \ду j J дх ду ду3
и, кроме того, в силу двукратной дифференцируемости функции
и в точке Мо, согласно теореме 14.13,
д2и _ д2и
ду дх дхду’
то для 8 (du) получим выражение
5 (dd> = S dx Ъх + (dx + 8х d? 8-У>
в котором все производные берутся в точке 7И0.
Таким образом, 8 (du) представляет собой симметричную билиней-
ную форму переменных dx, dy, 8х, 8_у.
Квадратичная форма, соответствующая этой билинейной форме,
называется вторым дифференциалом функции u~f(x, у) в точке
.	ди ди
*) При сформулированных условиях и являются дифференцируемы-
ми в точке Мо функциями. Поэтому, согласно (14.43), дифференциал du пред-
ставляет собой дифференцируемую в точке Л40 функцию.
498
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[ГЛ. И
Л40 (х0, _у0) и обозначается d2u. Итак,
д2и , „ . с, д2и ,	,	, 52и , .	t ...
d2u — ^dx2 + 2-^—rdxdy + ^-,dy2.	(14.44)
дх2 1 дхду . J 1 ду2	'	’
Таким образом, для того чтобы получить дифференциал второго по-
рядка нужно сначала, считая dx и (/у фиксированными, вычислить
дифференциал 8 (Фи) от дифференциала du, а затем положить 8х = Фх
и 8у = Фу. Отметим, что обычно при вычислении вторых дифферен-
циалов совмещаются оба шага—вычисление дифференциала 8(Фи)
и приравнивание дифференциалов аргументов 8х = Фх и 8_у = Ф_у.
Для, функции, трижды дифференцируемой в точке Д40, вводится
понятие третьего дифференциала Ф3н в этой точке: сначала, считая
dx и dy фиксированными, вычисляют дифференциал 8 (Ф2и) от вто-
рого дифференциала Ф2и, после чего получают третий дифференциал dPa,
полагая 8х = Фх и 8j/ = dy.
Для функции, п-|- 1 раз дифференцируемой в точке 7И0, по индук-
ции вводится понятие дифференциала п 4-1 порядка Фя+1и в этой
точке: для того чтобы получить Ф”+1н, нужно сначала, считая dx и dy
фиксированными, вычислить дифференциал 8 (Фли), а затем положить
8х = Фх и 8_у = фд/.
Для сокращения записи второго и последующих дифференциалов
функции введем символ дифференциала d при помощи соотношения
d=kdx+Tydy	<14-45>
и определим операцию возведения этого символа в степень п как
обычную операцию возведения двучлена ^.dx -y^dy в степень п.
Например:
d2 = (3- dx + 3- dy\2 = dx2 4- 2 dx dy 4- dy2.
\дх ду ,1 ду2 1 дхду ' dy2 J
Мы можем теперь записать выражения (14.43) и (14.44) для первого
и второго дифференциалов функции двух переменных в виде произ-
ведения символов d и d.2 на и:
• j /д , , д , \	ди , .ди ,
du == И- dx 4- 5- dy\u = ч- dx 4-	dy,
\dx ay - /	dx 1 dy
/ д , , d . \2 I d2 , „ ,	„	d2	, ,	. д2 , A
d2u = \-3~ dx 4- 5- dy] и = k-z- dx2 4- 2	ч—ч-	dx dy	+	dy2] и =
\dx dy ] \dx2 1	дхду	1 dy2 ]
= 3-5 dx2 4- 2 5-3- dx dу 4- -x-x dy2.
dx2 1 дхду ?' dy2
Легко убедиться, что выражение для п-го дифференциала dnu
функции u—f(x, у) можно записать в следующей форме:
= (Й dx + Ту dySU’ (14’46)
§ 5]
ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
499
В полной аналогии с рассмотренным случаем функции двух пере-
менных индуктивно вводится понятие дифференциала н-го порядка
dnu для функции u=f(x1,x2,...,xm) нескольких переменных. Для
сокращения записи удобно пользоваться символом d дифференциро-
вания, полагая по аналогии с (14.45)
d ~ дХ1 dX1 + дх2 dx* + • • •+ дхт dXm'
Если определить операцию возведения этого символа в степень п как
обычную операцию возведения
д ,	, д ,
многочлена -ч— dx, -|- -x— dx2 + ...
иХ}	ОХ^
-г— dxm в степень п, то для d"u легко получить следующие вы-
иХт
ражения, аналогичные выражению (14.46):
dn“=Udx*+• • •+dx*}n u>
dl*a = [dx[ dX1	dx- + • • • + dx^ dXm) ?x2> • • • ’ x^'
(14.47)
В проведенных выше рассуждениях мы предполагали, что значения
дифференциалов dxlt dx2, ..., dxm фиксированы. Это предположение
может быть выполнено в случае, когда аргументы х2, хт
функции u—f(xl,x2,...,xm) являются независимыми переменными.
Если же аргументы xv х2, .хт представляют собой дифферен-
цируемые функции каких-либо других переменных Zp t2, ..., tk, то
выражение дифференциала dnu при отличается, вообще говоря,
от его выражения в форме (14.47). Убедимся в этом на примере диф-
ференциала второго порядка для функции u=f(x, у). Пусть, напри-
мер, x = x(tv t2) и y=y(tv t2). В силу инвариантности формы пер-
вого дифференциала имеем
da — dx + dy.
дх 1 ду J
Найдем теперь дифференциал 8 (</и), считая 'dtx = dtx и Zt2 — dt2 (при
этом мы будем пользоваться свойством инвариантности первого диф-
ференциала). Получим
da« = 8 (dii} = 8 dx +	..
x f	\0x du "J
6t2=dt2	4	.	*	'
= b(d^\dx+^(~\dy + ^b (dx) + Jf8(rfy)
\dxj 1 \ду/ ' dx v ' dy v
dti
dt,

(14.48)
500
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
(ГЛ. 14
Для второго дифференциала функции т переменных и =
—f(xi> xv • • • > xm)> аргументы xlt х2, хт которой являются
функциями переменных tlr t2, tk, мы получим следующее выра-
жение, аналогичное формуле (14.48);
л,=(ж; dx>+•  •+4; Лг")'”+'й	'
Замечание. Если переменные х1У х2, ..., хт являются линей-
ными функциями переменных t2, .... tk, то дифференциал и-го
порядка функции u=f (xlt х2, ..., хт) может быть записан в форме
(14.47). В самом деле, если
х, = bt +	+ ai2t2 +...4-aiktk, 1= 1, 2, т,
то, так как d41 = d2t2 ==...= d2tk = 0 (напомним, что дифференциалы
dtlt dt2, ..., dtk считаются фиксированными), получим
d2Xi = aild2t1 + ai2dst2 4-... + aikd2tk = 0,
и тем более dsxi = d*xt =... = dnXi = 0. Следовательно, в указанном
случае дифференциал dnu может быть записан в форме (14.47).
3. Формула Тейлора для функции нескольких переменных.
Мы будем обозначать дифференциал А-го порядка функции и = f(xlt
х2, ..., хт) в точке М символом dku |Af. Докажем следующую теорему.
Теорема 14.15. Пусть функция u=f(M)=f(x1, х2, ..., хт).
задана в некоторой ^-окрестности точки Л10 (хь х2...... хт) и
1 раз дифференцируема в указанной ^-окрестности. Тогда пол-
ное приращение Ди = f (Al) — f (7И0) этой функции в точке Л40
для любой точки М из указанной ^.-окрестности может быть
представлено в следующей форме:
£м = du I +id2u| -j-.. .-j-^-idnu I +7—^-TrTd”+1w| , (14.50)
|Af0 21	\m,	' nl |M0 ' («+1)1 k’ v
при этом N —некоторая точка указанной г-окрестности, завися-
щая, вообще говоря, от Af(xx, х2, хт), а дифференциалы dxt
переменных x]t входящие в выражения dku\M> и йп+1и\н, равны
hXi — Xi — Xi. Формула (14.50) называется формулой Тейлора для
функции u — f(M) с центром разложения в точке Мо.
Доказательство. Для сокращения записи проведем рассужде-
ния для функции u—f{x, у) двух переменных х и у. Предварительно
запишем в специальной форме формулу Тейлора для «4-1 раз диф-
ференцируемой в некоторой окрестности точки /0 функции n = f(l)J
одной переменной t. Напомним,, что формула Тейлора с центром раз-
ложения в t0 для функции и = F (t) одной переменной имеет следую-
§ 5] ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 501
щий вид (остаточный член взят в форме Лагранжа):
F (0 = F (U + F' (t0) (t -	+ -2, FM (t0) (t - ter +
+ ... +1	(t0) (t - t0? + F^ (t0 + 9 (t - tg)) (t -
0<9<l.	(14.51)
Так как аргумент t является независимой переменной, то приращение
М = t —t0 представляет собой дифференциал dt независимой пере-
менной t. Поэтому
F™ (Q (t ~ to)k = F^ (Q dtk = dkF (tg) = dku\t,
и
F(n+V (to + 9 (t - Q) (t -t0)™ = d™ и \t, + e {t _ /o).	(14.52)
Если мы обозначим разность F(f) — F(t0) через Д«, то, согласно
(14.52), формулу Тейлора (14.51) можно записать в следующей спе-
циальной форме:
Ди = du I	+  • • + ~г dnu | -Н—i-т-т й(л+1) и I
И. 21	п\ |/„ (и +1)1 ро + 9(^о)
(14.53)
Рассмотрим теперь в е-окрестности точки Л40(х0, +0) произвольную
точку М (х0 + Дх, уд + Ду) и соединим точки 7И0 и М прямой линией.
Очевидно, координаты х и у точек указанной прямой представляют
собой следующие линейные функции новой переменной t\
х = х0 + /Дх, у— y0 + t^y,	(14.54)
при этом координаты точек отрезка М0М соответствуют значениям
переменной t из сегмента [0, 1]. Отметим, что значению t = Q отвечает
точка Мд, а значению (=1— точка М. Так как по условию функ-
ция u=f (х, у) двух переменных х и у в рассматриваемой окрест-
ности точки Мд »+1 раз дифференцируема, то из формул (14.54)
вытекает, что на прямой ?ИоуИ эта функция является сложной функ-
цией переменной t, («+1) раз дифференцируемой по крайней мере
для всех значений / из сегмента [0, 1]. Обозначим эту сложную функ-
цию через F (t) и запишем для нее формулу Тейлора с центром раз-
ложения в точке /0 = 0 в специальной форме (14.53) при
A«=F(l)-F(0)= /(М)-/(Мд).
Фигурирующие в формуле (14.53) дифференциалы различных поряд-
ков представляют собой дифференциалы сложной функции и =f(x, у),
где хтлу являются линейными функциями (14.54). Согласно замечанию
предыдущего пункта при этих условиях дифференциалы любого порядка
502
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
(ГЛ. 14
функции u—f(x, у) могут быть записаны в форме (14.47). Поэтому
,ft	/ д . , д . \*
du\ = -s- dx 4- л- dy\ и
6, = о \5х ду J) м0 (л-»,
Г/о)
</л+1и|	„
Ре (Г-------/0)
[аг (хо4-0Дх, tfc + OAj/)
=<7Л+1«|ЛГ,
(14.55)
причем в формулах (14.55) dx и dy находятся из соотношений (14.54)
при (# = Д£= 1—0=1. Таким образом, в формулах (14.55)
dx = dthx = bx и dy = dt by = by.	(14.56)
Подставляя dku\t„ и dn+1 и 4.0 « _ /о) из (14.55) в формулу (14.53) и
учитывая соотношения (14.56), мы получим формулу Тейлора (14.50).
Теорема доказана.
Приведем развернутое выражение формулы Тейлора (14.50) для
функции u=f(x1, х2, хт):
f (x-i, х2, ..., хт) — f(x^, х2, ..., Хт) +
п
k = 1
+ дх^ (Хт ~	^2’ • • • ’ Х"^ + (п+ 1)1 [c£q (X1 ~ XJ +
+	(Х2 - *2) + • • • + д~ (Хт - -*т)]”+1 /[^1 + 6 (Хх - Хх),
х2 + 6 (х2 - Хг),  , хт + 6 (хт- хт)].	(14.57)
§ 6. Локальный экстремум функции нескольких переменных
1. Определение локального экстремума. Необходимые условия
локального экстремума. Пусть функция и = f(M)=f(xl, х2, ..., хт)
задана на множестве {Л4} и М0(х1, х2, ..., хт) — некоторая точка
этого множества.
Определение. Функция u-^f (хх, х2, ..., хт) имеет в точке А40
локальный максимум (минимум), если значения этой
функции во всех точках множества {7И}, принадлежащих неко-
торой окрестности точки Л10, не больше (не меньше) ее значения
в точке Мо.
Локальный максимум и локальный минимум объединяются общим
наименованием локальный экстремум. Если функция и =f (M) имеет
локальный экстремум в точке тИ0,' то полное приращение
bu = f(M)-f(M0)
этой функции в точке Мо (Л4 — любая точка множества {ЛГ}, при-
надлежащая указанной в определении окрестности точки Л40) удовле-
§ 6) ЛОКАЛЬНЫЙ ЭКСТРЕМУМ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 503
I
творяет одному из следующих условий:
Azz^O (в случае локального максимума),	(14.58)
Azz^O (в случае локального минимума).	(14.59)
Очевидно и обратное: если полное приращение Дм =/(7И) —/(Л10)
функции u — f(M) в точке Ма(М — любая точка множества {Л4},
принадлежащая некоторой окрестности точки 7И0) удовлетворяет усло-
вию (14.58) (условию (14.59)), то в этой точке функция имеет локаль-
ный максимум (локальный минимум). Установим необходимые условия
локального экстремума. Справедливо следующее утверждение.
Пусть функция u=f(xlt ха, ..., хт) имеет в точке
7И0(•*!»	т) локальный экстремум. Тогда, если в этой
точке существуют частные производные первого порядка, то все
эти частные производные равны нулю.
Докажем, например, равенство нулю частной производной
ди
dxi '
Для доказательства зафиксируем значения переменных х2, .... хт,
положив их соответственно равными х2, ..., хт. Мы получим функ-
цию u=f(хх, х2, ..., хт) одной переменной xv Эта функция имеет
в точке хх = хх локальный экстремум и имеет в"этой точке произ-
ди
dXi'
2 § 1 главы 9 эта производная указанной функции
= 0 в точке 7И0.
произ-
ди
нулю. 1аким образом, -ч—
равенство нулю остальных частных
водную по аргументу хх, которая и является частной производной
Согласно п.
одной переменной равна
Аналогично доказывается
водных. Итак, условие
$-1 =0,	1, 2, ..., т,	(14.60)
является необходимым условием локального экстремума.
Замечание 1. Если функция zz—/(хх, х2, ..., хт) имеет
в точке уИ0 (хх, х2..Зст) локальный экстремум и дифференцируема
в этой точке, то, очевидно, условие (14.60) влечет за собой сле-
дующее равенство:
du\Mt = 0.	(14.60')
Обратно, если в точке Мо дифференциал du тождественно (отно-
сительно дифференциалов dx,) равен нулю, то все частные производ-
ди	п
ные в этой точке равны нулю. В самом деле, так как
. | ди I ,	, ди I ,	.	, ди I , л
dzz = д— dx, + -5— dx2 +... + д—	dxm = 0,
|м0 d*i |м,- 1	5х2|м0	2 дхт т ’
то, полагая, например, dxx ф 0, a dx2 = ... = dxm = 0, мы получим
5—	=0. Из проведенных рассуждений вытекает, что соотношение
504
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
|ГЛ 14
(14.60') является необходимым условием локального экстремума
дифференцируемой в Л40 функции.
Замечание 2. Условия (14.60) и (14.60') не являются доста-
точными условиями локального экстремума. Например, частные про-
изводные функции и = ху равны нулю в точке 7Ио(О, 0), но эта
функция не имеет экстремального значения в этой точке, так как она
равна нулю в точке Л40 и в любой окрестности точки Л40 имеет как
положительные, так и отрицательные значения.
В дальнейшем точки, в которых выполняются условия (14.60) или
(14.60'), мы будем называть точками возможного экстремума*).
2. Достаточные условия локального экстремума. Рассмотрим
симметричную квадратичную форму (см. п. 2 § 5 этой главы)
т
Ф = У, aihhihk, aik = aki,	(14.61)
i, fe —1
зависящую от переменных hlt hz, hm. Квадратичная форма
т
называется положительно определенной {отрицательно определен-
ной), если для любых значений переменных hlt h2, ...,- hm, не равных
одновременно нулю, эта форма имеет положительные (отрицательные)
значения. Положительно определенные формы и отрицательно опре-
деленные формы объединяются общим наименованием знакоопре-
деленные формы. Квадратичная форма Ф называется знакоперемен-
ной, если она имеет как положительные, так и отрицательные
значения.
Квадратичная форма Ф называется квазизнакоопределенной, если
она имеет либо только неотрицательные значения, либо только непо-
ложительные значения, но при этом она имеет нулевые значения
также и для не равных одновременно нулю значений переменных
hv h2, ..., hm. Сформулируем критерий знакоопределенности квадра-
тичной формы. Этот критерий был установлен Сильвестром и назы-
вается критерием Сильвестра знакоопределенности квадратичной
формы**). Мы будем называть симметричную матрицу ***)

'Сц а12 ... а1т
fl21 а22 • • • a2tn
,ат1 amz • • • атт'
*) Такие точки называются также стационарными точками.	.-кш
**) Дж. Дж. Сильвестр — английский математик (1814—1897). Доказа-
тельство критерия Сильвестра приводится в курсе линейной алгебры.
***) Матрица называется симметричной, если ац, = ащ.
§ 61 ЛОКАЛЬНЫЙ ЭКСТРЕМУМ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 505
матрицей квадратичной формы (14.61). Определители
				а11	й12 й13
— й11> Д2 —	Й11	й12		Й21	й22 й23
	Й21	° 22			
				°31	й32 й33
		Й11	й12	а	1Г71	
Д		Й21	а22 ... а	2т	
	п - 				
		ат1		тт	
называются главными минорами матрицы А квадратичной формы.
Для того чтобы квадратичная форма (14.61) была положительно
определенной, необходимо и достаточно, чтобы были выполнены
неравенства
Xj>0, Д2>0, Д3>0, ..., Дт>0.	(14.62)
Для того чтобы квадратичная' форма была отрицательно опре-
деленной, необходимо и достаточно, чтобы знаки главных мино-
ров Др Д2, ..., Ат чередовались, причем А]^ <; 0. Мы используем
понятия знакоопределенной и знакопеременной квадратичной формы
для формулировки достаточных условий наличия локального экстре-
мума и достаточных условий отсутствия локального экстремума
в точке А10 возможного экстремума.
Теорема 14.16. Пусть в некоторой окрестности точки
Л10 (х1; х2, ..., хт) возможного экстремума функция u=f (х1(
х2,	, хт) дважды дифференцируема и все вторые частные про-
изводные этой функции непрерывны в точке Л1о. Тогда, если в этой
точке второй дифференциал <Ри |м0 представляет собой знакооп-
ределенную квадратичную форму от дифференциалов dxlt dx2; ...
... , dxm независимых переменных, то функция и = f(xlt х2,..., хт)
имеет в точке /Ио локальный экстремум. При этом, если d2u < 0,
то в точке Л10 рассматриваемая функция имеет локальный макси-
мум, а если d2u > 0, то — локальный минимум. Если же в точке 2И0
второй дифференциал d2u является знакопеременной формой, то
в этой точке функция u—f^x^ х2, ..., хт) не имеет локального
экстремума.
Доказательство. Согласно формуле Тейлора (14.50), взятой
для п— 1, полное приращение Ди=/(7И) — /(Д40) функции и = f(M) =
= f (xlt х2, .... хт) в точке 7И0 можно записать в виде
Ди = du | +^-d2ul .	(14.63)
|м„ 2! pv	’
При этом N — некоторая точка рассматриваемой окрестности, завися-
щая от М, а дифференциалы dx; переменных Xi, входящие в выра-
жения du\ju0 и d2u pv, равны приращениям Дд^ = Л/ —х, этих пере-
менных.
506
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
ГГЛ. 14
Отметим, сразу же, что так как /Ио является точкой возможного
экстремума, то du [д, = 0 (см. предыдущий пункт этого параграфа).
Преобразуем теперь выражение d2u |jy. В это выражение входят все-
возможные частные производные второго порядка рассматриваемой
функции, которые берутся в точке N. Так как все эти частные про-
изводные
д2и
дх, dxk
непрерывны в точке А10, то, обозначая значения этих
частных производных в точке Мо через zzift, aik = akt, получим
<32u I	,
дх, дхк aik а,к'
(14.64)
где a-ik — бесконечно малые при Дхх -> 0, Дх2 -► 0, .,., Дхт —► 0 функ-
ции. Поскольку
т
d2u — У — I Дх/ Дхй,
|/v Li дх;дхк ‘
i, k as 1
то, согласно (14.64), получим
m	m
d2u\N= У aik^Xi^xk+ У «z* Д*.-Д*й. (14.65)
i, fe= I	i, k=\
Для преобразования правой части (14.65) введем обозначения
р = /Дх? + Дх1+...+Дх8т*)>	,1466)
Дхг — рЛ/,	I = 1, 2, ..., т.
Очевидно, при р # О
^ + ^+...+^ = 1.	(14.67)
Заметим также, что
|/2z|sSl,	/=1, 2, ..., от.	(14.68)
Преобразуем теперь первую сумму в правой части равенства (14.65),
которая, очевидно, представляет собой второй дифференциал d2u |д10
рассматриваемой функции, вычисленный в точке Имеем, со-
гласно (14.66),
т	т
^2и|д1.= У aikbXibxk = f У aikhihk. (14.69)
i, k = 1	i, k = 1
Для второй суммы в правой части (14.65) имеем, согласно (14.66),
т	т
У, ^Xt й.хк = Р2 У aikhihk.	(14.70)
' I, k = 1	i, k « 1
m
Согласно (14.68) сумма У a-ikhthk представляет собой бесконечПд
z, л = 1
*) Отметим, что р = 0 лишь при Дхг= Дх2= ... =йхт = 0.
§ 6] ЛОКАЛЬНЫЙ ЭКСТРЕМУМ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 507
малую при Дл'! -> 0,	-> 0, ..., Дхт -> 0 (т. е. при р -> 0) функ-
цию. Эту функцию мы обозначим символом а(р). Таким образом,
У, a-ikhihk = a-(p), а(р)—>0 при р->0.	(14.71)
>, * = 1
Используя (14.71) и (14.70), найдем
У я/йДх/Дх* = р2а(р).	(14.72)
it k = 1
Согласно (14.69) и (14.72) выражение (14.65) примет вид
о!2и|Лг = р2
т
У, aikhihk + а (р)
_1, * = 1
Учитывая равенство du |м„ = 0 и только что полученную формулу,
мы получим из (14.63) следующее выражение для Ди:

г- т
У aikhihk + а(р)
.<•* = !
(14.73)
Пусть ради определенности второй дифференциал d2u |ai0 представ-
ляет собой положительно определенную квадратичную форму, так
что й2п|мо>0. Тогда из соотношения (14.69) вытекает, что выра-
жение
т
Ф= S a^hihk	(14-74)
i, k = 1
положительно при всех значениях hlt h2, ..., hm, не равных одно-
временно нулю, т. е. Ф > 0. В рассматриваемом случае переменные
ftp й2, .... hm связаны соотношением (14.67) и поэтому одновременно
не равны нулю. Будем рассматривать Ф как функцию от перемен-
ных hv h2, ..., hm, заданную для всех значений этих переменных,
удовлетворяющих условию (14.67). Очевидно, функция Ф, определяе-
мая соотношением (14.74), представляет собой непрерывную функ-
цию  переменных й1( h2, ..., hm, принимающую только положитель-
ные значения и заданную на сфере единичного радиуса с центром
в начале координат. Поскольку эта сфера представляет собой замк-
нутое ограниченное множество (см. п. 5 § 1), то, в силу теоремы 14.7,
эта функция достигает своей точной нижней грани р, а так как
цсе значения функции Ф положительны, то р>0. Таким образом,
для всех значений hb h2, hm, удовлетворяющих условию (14.67),
^дополняется неравенство
т
ф= У, Aikhihk =& р > о.	(14.75)
i, А = 1
508
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[ГЛ. 14
Выберем теперь р0 столь малым, чтобы при 0 < р < рд выполнялось
неравенство | а (р) | <; р. Тогда для всех указанных значений р, в силу
неравенства (14.75) и соотношения (14.73), выполняется неравен-
ство Ди > 0.
Следовательно, если <72zz ]jm0 представляет собой положительно
определенную форму, то функция zz=/(x1, х2, хт) имеет
в точке Мо возможного экстремума локальный минимум. Аналогично
устанавливается, что если d2u |м, представляет собой отрицательно
определенную форму, то функция и имеет в точке Мд локальный
максимум.
Убедимся теперь, что если d2u |м, представляет собой знакопе-
ременную форму, то функция и не имеет локального экстремума
в точке Л10.
Пусть для значений Ьх[, Дх2, ..., Ьх'т приращений аргументов
хг, х2....хт второй дифференциал dPa |м, имеет положительное
значение, а для значений Дх[, Дх2, ..., Дх„ — отрицательное. Обо-
значим через р' и р” соответствующие значения р, а через h[, h'it...
, h'm и h^, h2, ..., h’m соответствующие значения величин h(
(см. (14.66)). Из соотношения (14.69), очевидно, вытекает, что
У чцМ^'Х), aikh?hrk = q’<0-	(14.76)
i. k = \	i, k = \
Отсюда и из соотношения (14.69) вытекают неравенства
m
d2u 1л!, = р2 У aMh'k >0 при 0 < р < р’,
" 1=‘	(П.77)
d2u 1м, =.р2 У alkhlhk<0 при 0<р<р".
I. А = 1
Выберем теперь р0 столь малым, чтобы выполнялись неравенства
О<Ро<р'> О<ро<р", | я (р) | < min {/, |9"|} при О<р<ро.
(14.78)
Тогда, при 0 < р <; р0, в силу (14.73), (14.76), (14.77) и
справедливы неравенства
(14.78),
a-ikh'ih'k + а (р)
Из этих неравенств, справедливых для как угодно малых р, вытекает,
что функция и —f (xv х2, ..., хт) не имеет локального экстремума
в точке Мо. Теорема доказана.
§ 6) ЛОКАЛЬНЫЙ ЭКСТРЕМУМ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 509
Замечание. - Если второй дифференциал d2u |уи0 является квази-
знакоопределенной формой, то функция и в точке Л40 возможного
экстремума может иметь локальный экстремум, но может и не иметь
его. В указанном случае для выяснения вопроса нужно дополнитель-
ное исследование.
3. Случай функции двух переменных. На практике часто встре-
чается задача об экстремуме функции двух переменных u=f(x, у).
В этом пункте мы приведем результаты, относящиеся к этой задаче.
Q2U
Договоримся обозначать частные производные g~-a,	, -g--2-
в некоторой точке М0(х0, у0) символами а11; а12, а22 соответственно.
Имеет место следующее утверждение.
Пусть в некоторой окрестности точки М0(х0, у0) функция
u=f(x,y) дважды дифференцируема и все вторые частные произ-
водные этой функции непрерывны в точке Мо. Тогда, если в точке
возможного экстремума Л10 выполнено условие . аХ1а22 — af2 > 0,
то функция u—f(x, у) имеет в точке Л10 локальный экстремум
(максимум при аи<0 и минимум при ап > 0). Если же в точке
возможного экстремума ana22 — af2< 0, то функция u=f(x,y)
не имеет в этой точке локального экстремума *). Справедливость
первой части сформулированного утверждения непосредственно выте-
кает из теоремы 14.16 и критерия Сильвестра знакоопределенности
квадратичной формы, ибо Аг = ап, А2 = а1Хй22— ап-
Убедимся в справедливости второй части утверждения. Итак, пусть
в точке Мо справедливо неравенство ana22 — а‘9' < 0. Докажем, что
в этом случае второй дифференциал d?ti в точке 7И0 представляет
собой знакопеременную форму. Рассмотрим .сначала случай а1г ^0.
Из формулы (14.69) предыдущего пункта имеем
2
dsu = Р3 У aikhthk = р2 (anhl + 2alih1h2 + a22h$ =
i, k «1
р2
= IfaiA + л12/г2)3 + (аца22 - af2) ^]-
Отсюда видно, что при йх=1, й2 = 0 и при h1——— 012	, /г2 =
УАЧЧ
—-----°п **) дифференциал d?u имеет разные знаки, т. е.
У аД + а?а
является знакопеременной формой и поэтому, согласно теореме 14.16,
функция не имеет в Мо локального экстремума.
Рассмотрим теперь случай а1У — 0. Тогда из условия апа22 — а^ < 0
вытекает, что а12	0. Из (14.69) имеем
<Ри |Жо = р2/г2 (2a12hx-\- a22hj).	(14.79)
*) Случай апа32 —	= 0 требует дополнительного исследования.
**) При этом р может быть как угодно малой величиной. Условие h{ +
+ — 1 выполнено.
510
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
(ГЛ. 14
Пусть Л19^ 0 и величина | Л21 столь мала *), что. выражение
(2а12йх-|-а22/г2) сохраняет знак величины 2alih1. Тогда из формулы
(14.79) вытекает, что йги\ма имеет разные знаки при Л2 > 0 и h2 •< 0,
т. е. функция не имеет локального экстремума в точке Л1о.
4. Пример исследования функции на экстремум. На плоскости
даны п точек Л4/(а,-, bi), 2 = 1, 2, .... п, в которых сосредоточены
массы mt>0. Найти точку М0(ха, _у0) такую, относительно которой
момент инерции J(x0, _у0) указанной системы материальных точек
минимален.
Пусть J(x, у) — момент инерции этой системы относительно
точки Af (х, у). Очевидно,
п
J{x,y)=^^ mi[{x — ai)2(у — b-i^].	(14.80)
i = i
Найдем экстремальные значения функции J(x, у). Для этого предва-
рительно найдем точки возможного экстремума. Так как в этих точ-
ках |~ = 0 и |^- = 0, то из (14.80) получаем уравнение для опреде-
ления координат этих точек. Имеем
п	п
^- = 2 2 »гг(х-аг) = 0. ^- = 2 2 mi(y-bi) = 0.
i = 1	i — 1
Отсюда вытекает, что единственной точкой возможного экстремума
будет точка Мо (х0, у0), координаты которой равны
х0 =
т1а1 + т2аг+ ... + тпап _ т1Ь1 Ч- m2fr3 + ... -р тпЬп
т1 + т2+...+тп	’ •Уо гщ + т2 + ... + тп
п	п
Так как an = g3- = 2 2 Wi>0, ам = ~ = 2 2 гщ> 0 и а12 =
«=1	1=1
d2J п	______
= •^-^- = 0, то апа22 — а;2 > 0, и поэтому, согласно предыдущему
пункту; в точке А40 (х0, у0) функция J (х, у) имеет локальный мини-
мум **). Заметим, что х() и у0 представляют собой координаты центра
тяжести рассматриваемой системы материальных точек.
§ 7. Градиентный метод поиска экстремума выпуклой функции
В этом параграфе мы познакомимся с так называемым градиент-
ным методом поиска экстремума функции нескольких переменных.
Этот метод широко используется для приближенного поиска экстре-
мума. В общих чертах этот метод состоит в том, что в области
*) Из условия hj -j- hf = 1 вытекает, что такой выбор и h2 возможен.
**) Читатель легко убедится, что значение J (х, у) в этой точке будет
наименьшим из всех возможных.
§ 7]	ГРАДИЕНТНЫЙ МЕТОД ПОИСКА ЭКСТРЕМУМА	511
задания функции строится специальная последовательность точек,
сходящаяся к точке экстремума. При этом отрезок, соединяющий
данную и следующую точки этой последовательности, направлен по
градиенту функции в данной точке.
1. Некоторые сведения о выпуклых множествах в евклидо-
вых пространствах. Для упрощения изложения мы будем рассмат-
ривать евклидово пространство Ет как линейное пространство *),
в котором введено скалярное произведение элементов. При этом эле-
ментами или векторами х, у, ... этого линейного пространства слу-
жат точки (xlt х2,	хт), (yv у2, .... ут), ... пространства Ет,
а операции сложения векторов и умножения векторов на числа опре-
деляются следующим образом: вектор	есть точка (•^i+j'i,
х2+_у2> Хт+Ут)> а вектор лх —точка (Лхх, >-х2, ..., кхт). Нуле-
вым вектором является точка с координатами (0, 0, ..., 0). В даль-
нейшем мы не будем различать термины «вектор» и «точка».
Скалярное произведение (х, у) двух векторов х и у определяется
равенством
(х,у) = х1у1+зд+...-Ьхяуя.	(14.81)
Отметим следующие очевидные свойства скалярного произведения:
1) (х, У) = (У> х), 2) (х+у, z) = (x, z) + (y, z), 3) (kx, y) = k(x, у),
4) х2 — (х, х)^0, причем х2 — 0 лишь при х = 0.
С помощью скалярного произведения определяется длина вектора,
расстояние между точками и угол между векторами. Именно, длина
| х | вектора х определяется соотношением
[х1 = У(хГх) = Ух~2,	(14.82)
расстояние р(х; _у) между точками х и у по определению равно
длине вектора у — х. Поэтому, согласно (14.82),
Р(х, у) - У(у-х, у-х) = KCv -х)2.	(14.83)
Косинус угла у между ненулевыми векторами х и у может быть
найден по формуле
cosy — .	.	(14.84)
т 1*1- 1у!	4	’
Из формулы (14.84) и очевидного неравенства | (х, у) |	| X | • |_у1 **)
вытекает, что |cosy|^l. Из формулы (14.84) получаем следующую
формулу для скалярного произведения ненулевых векторов:
(х, у) — |x|.|j|-cosy.	(14.85)
*) С понятием линейного пространства читатель может познакомиться,
например, в выпуске «Линейная алгебра» настоящего курса.
**) Это неравенство вытекает из неравенства Коши — Буняковского
(х, у)2 sg х2 • у2, которое в свою очередь выражает необходимое и достаточное
условие очевидной неотрицательности квадратного трехчлена к2х2 -j- 2л (х, у) -}-•
-ф У2 —	+ У> + У) относительно переменной К.
512
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
(ГЛ. 14
В дальнейшем мы будем называть ортогональными векторы, скаляр-
ное произведение которых равно нулю.
Введем понятие отрезка, соединяющего данные точки.
Определение 1. Отр-езком ху, соединяющим точки х и у,
называется множество точек х -\- t(y — х), где t —любое число
из сегмента [0, 1].
Введем теперь понятие выпуклого множества евклидова про-
странства.
Определение 2. Множество Q точек евклидова пространства
называется выпуклым, если вместе с любыми его точками
х и у этому множеству принадлежарг все точки отрезка ху.
Очевидно, все пространство, полупространство, шар, любой отре-
зок, представляют собой примеры выпуклых множеств.
Пусть Q — некоторое непустое множество точек пространства Ет.
Расстоянием р(х, Q) точки х пространства Ет
до множества Q называется точная нижняя грань расстоя-
ний от х до всевозможных точек этого множества. Таким
образом,
р(х, Q) = infp(x, >).
Поскольку множество расстояний от х до всевозможных точек у
множества Q ограничено снизу числом нуль, то указанная грань
существует.
Точку множества Q, для которой расстояние до х равно расстоя-
нию от х до Q, будем называть проекцией х на Q и обозна-
чать символом PQ(x).
Замечание. Если х — точка множества Q, то, очевидно, ее
проекция Pq(x) совпадает с х, т. е. Pq(x) = x.
Отметим, что проекция точки на множество Q может и не суще-
ствовать, Если, например, Q —интервал числовой оси, а х — точка
этой оси, лежащая вне интервала, то, очевидно, на Q нет точки,
представляющей собой проекцию х. Проекция может быть неедин-
ственной: если, например, Q — окружность, а х — ее центр, то Pq (х) —
любая точка Q.
Справедливо следующее утверждение.
Лемма 1. Если Q — замкнутое выпуклое множество прост-
ранства Ет их — произвольная фиксированная точка этого про-
странства, то существует единственная проекция Pq(x) точки
х на множество Q.
Доказательство. Существование по крайней мере одной
проекции точки х на Q вытекает из замкнутости множества Q *).
*) Чтобы убедиться в этом, проведем следующее рассуждение. Пусть
р (х, Q) = inf р (х, у) = d. Из определения точной нижней грани следует, что
ГРАДИЕНТНЫЙ МЕТОД ПОИСКА ЭКСТРЕМУМА
513
§ 71
Убедимся теперь, что существует лишь единственная проекция х на
Q. Допустим, что это не так. Пусть y1 = Pq(x) и у2 = Pq (х) — раз-
личные проекции х на Q. В силу выпуклости Q все точки у2 4-1 (j1 — у2)
отрезка j/1^2 принадлежат Q. Найдем расстояние р (х, -^(у1 +j2)^ от
х до середины у (.у1 +_у2) этого отрезка (для середины t = -i-j. Из
(14.83) и из свойств скалярного произведения получим
Р2	~ (У + у2)\ = (у (у1 +ys) ~х,~ (у1 + У2) - х) =
= (4 О'1 - *)+4о2 - А ±(у2 - *)) =
= ^;{(У1—х>У1 — х) + 2(у1 — х,у2 — х) + (у2 — х,у2 — х)}. • (14.86)
Так как (у1 — х, у1 — х) = (у2— х, y2 — x) = d2, где d = p(x, Q) и при
дЛуб-У2 справедливо соотношение*)
I (У1 — х, у2 — х) | < У(уг — х, у1 — х)-У(у2 — х, y2 — x) — d2,
то из формулы (14.86) вытекает неравенство
р(лг,1(У +y2^<d,
которое противоречит определению расстояния d = р (х, Q) как
infp(x, у). Таким образом, предположение, что у1 и у2 различны,
ведет к противоречию. Единственность проекции также доказана.
Нам понадобится еще одно свойство выпуклых множеств.
Лемма 2. Пусть Q —замкнутое выпуклое множество, х —
произвольная фиксированная точка Ет, а у —любая точка Q.
Тогда
(х - Pq (х), у - PQ (х)) < 0.	(14.87)
для любого числа — , п=1, 2, ... существует точка уп е Q такая, что
d «5 р (х, уп) =5 d +	• Последовательность { уп } точек Q ограничена (она
лежит в шаре радиуса d + 1 с центром в х). Поэтому существует предельная
точка у последовательности { уп }, принадлежащая Q в силу замкнутости этого
множества. Отсюда и из приведенных выше неравенств следует, что р (х, у) — d,
т. е. у = Pq (х).
*) Для неколлинеарных векторов г1 = у1 — х и г2 = р2 — х справедливо
«неравенство ( (г1, г2) | < ]/ (г1, г1) • У (г2, г2). В самом деле, если г1 и г2 не
коллинеарны, то при любом вещественном X вектор Хг1 + г2 не нулевой, а
поэтому квадратный трехчлен (Хг1 + z2, Xz1 + г2) = X2 (z1, г1) + 2Х (г1, г2) +
+ (г2, г2) строго положителен, т. е. его дискриминант (г1, г2)2 — (г1, г1) (z2, г2)
строго отрицателен.
514
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[ГЛ. 14
С геометрической точки зрения указанное свойство означает, что
угол между векторами, ведущими из точки Pq (х) в точки х и у,
не может быть острым (рис. 14.4).
Доказательство леммы 2. Допустим, что утверждение
леммы несправедливо. Тогда существует точка у множества Q такая,
что для этой точки выполняется нера-
венство
(х - PQ (х), у - PQ (х)) > 0.
Из этого неравенства вытекает, что точка
у не совпадает с Pq(x).
Пусть z = Pq (х) +1 (у - Pq (х))— про-
извольная точка отрезка pQ(x)y. В силу
выпуклости Q точка z принадлежит Q.
Найдем расстояние между точками х и z.
Имеем р2(г, х) = (х — Pq(x) — t(y —
— Pq (х)), х - Pq (х) - t (у - PQ (x))) =
= P2 (x, Pq (x)) - 2t (x — Pq (x), у —
—Pq (*)) + ^2P2 (V, Pq (x)). Из этого равен-
ства и из неравенства (х—Р0(х), _у —Ро(х))>0 вытекает, что при
всех достаточно малых t выполняется неравенство р2 (г, х) < р2 (х, Ро (х)),
которое противоречит определению расстояния р(х, Р0(х)) как
inf р (х, у). Лемма доказана.
2. Понятие выпуклой функции. Некоторые свойства выпуклых
функций. Напомним, что графиком функции /(х), заданной на мно-
жестве Q евклидова пространства Ет, называется множество точек
евклидова пространства Ет+1 с координатами (х, /(х)).
Будем говорить, что график функции /(х), заданной на выпук-
лом множестве Q, обращен выпуклостью вниз на этбм множе-
стве, если для любых двух точек х1 и х2 множества Q и для любого t
из сегмента [0, 1J выполняется соотношение
/(х1 +1 (х2 - х1)) ^/(х1) +1 (f(x2) -/(х1)).	(14.88)
Аналогично определяется понятие выпуклости вверх графика функции
(в этом случае в соотношении (14.88) знак неравенства нужно заме-
нить на противоположный).
Если в соотношении (14.88) для всех х1 и х2 из Q и для всех t
из интервала (0, 1) имеет место знак строгого неравенства, то в этом
случае говорят о строгой выпуклости вниз (вверх).
Геометрически условие выпуклости вниз графика функции /(х)
на множестве Q означает, что точки графика этой функции, отвечаю-
щие точкам отрезка, соединяющего любые точки х1 и х2 множества
Q, лежат не выше хорды, соединяющей точки (х1, /(х1)) и (х2, /(х2))
указанного графика (рис. 14.5).
§ 71
ГРАДИЕНТНЫЙ МЕТОД ПОИСКА ЭКСТРЕМУМА
515
на этом множестве. Если
Функцию, график которой на данном множестве Q обращен
выпуклостью вниз (вверх) будем называть выпуклой вниз (вверх)
на множестве Q.
Ниже мы будем рассматривать только выпуклые вниз функции.
Для краткости такие функции мы будем называть просто выпуклыми.
Отметим, что все результаты для
выпуклых вниз функций легко пере-
носятся на случай выпуклых вверх
функций, ибо каждая выпуклая
вверх функция после умножения на
минус единицу переходит в выпук-
лую вниз функцию.
Познакомимся с некоторыми свой-
ствами непрерывных и дифференци-
руемых выпуклых функций *).
В следующей теореме устанав-
ливаются достаточные условия вы-
пуклости дважды дифференцируемой
функции.
Теорема 14.17. Пусть функ-
ция f(x) задана на выпуклом мно-
жестве Q и дважды дифференцируема
во всех точках множества Q второй дифференциал d2f представ-
ляет собой положительно определенную форму, то f(x) является
выпуклой функцией на множестве Q.
Доказательство. Требуется доказать справедливость неравен-
ства (14.88) для любых точек х1 и х2 множества Q. Пусть х1 их2—
любые фиксированные точки множества Q. Рассмотрим на сегменте
[О, 1] дважды дифференцируемую функцию
F(0=/(x1 + / (х2- ^-/(х1) - t(J(x2) -/(х1)) (14.89)
аргумента t. Заметим, что F(0) = F(l) = 0. Применяя правило диффе-
ренцирования сложной функции, легко убедиться, что F" (t) = d2f.
Следовательно, согласно условиям теоремы	Поэтому пер-
вая производная F' (f) не убывает на сегменте [0, 1]. Нетрудно дока-
зать, что F'(0)=C0, a F' (1)^0**). Рассмотрим сначала случай
F' (0) = 0. Так как F' (t) не убывает на сегменте [0, 1], то в этом
*) Выпуклая функция может быть и разрывной. Например, функция,
равная нулю на интервале (0, 1) и единице в точках 0 и 1, выпукла на сег-
менте [0, 1].
**) Докажем, например, что F' (0)^0. Применяя для F (/) формулу Тей-
лора с центром в нуле, получим F (/) = IF’ (0) -|- -i- d2f (черточка над f озна-
чает, что d2f вычисляется в промежуточной точке). Полагая в этой формуле
/ = 1 и учитывая, что F(l) = 0, a d2f 2э0, получим, что F'(0)^0. Анало-
гично доказывается, что F' (1) Ss 0.
516	ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ	ГГЛ. 14
случае F' (t)	0 на этом сегменте, и поэтому F (t) не убывает на
[О, 1]. а так как F (0) = F (1) = 0, то ясно, что F(t) = O на сегменте
[О, 1]. Обратимся теперь к случаю F' (0)<0. Поскольку F' (t) не
убывает и F' (1)^=0, то найдется единственная точка /0 сегмента
[О, 1] такая, что на полуинтервале [О, Q производная F' (£)<0, а на
сегменте [/0, 1] производная F' (^)^О. Но тогда можно утверждать,
что на сегменте [О, функция F (t) убывает от своего нулевого зна-
чения в точке 0 до некоторого отрицательного значения в точке t0
и возрастает (с возможным .участком неубывания) на сегменте [/0, 1]
от этого отрицательного значения до нулевого значения в точке 1.
Итак, в рассматриваемом случае F(t)^.O на сегменте [0, 1]. Обра-
щаясь к конкретному виду (14.89) функции F (t), мы получим для
точек х1 и х2 неравенство (14.88). Теорема доказана.
Замечание. Если второй дифференциал (Pf представляет
собой строго положительную на множестве Q квадратичную
форму, то функция f (х) является строго выпуклой на этом
множестве.
Чтобы убедиться в. справедливости этого утверждения, достаточно
заметить, что первая производная F' (t) в этом случае будет строго
возрастать от отрицательного значения при ^ = 0 до нулевого значе-
ния при некотором t0, 0 < ta < 1, и далее при t > t0 — до положи-
тельного значения при /=1. Отсюда и из условия F(0) = /7(l) = 0
вытекает, что F (t) < 0 на интервале (0, 1).
Нам понадобится необходимое и достаточное условие локального
экстремума’ дифференцируемой выпуклой функции. Мы сформулируем
это условие для случая локального минимума. Случай локального
максимума сводится к случаю локального минимума путем умножения
функции на минус единицу.
Теорема 14.18. Пусть на выпуклом множестве Q задана диф-
ференцируемая выпуклая функция f (х). Для того чтобы в точке
х° множества Q эта функция имела локальный минимум *), необ-
ходимо и достаточно, чтобы в этой точке для любого доста-
точно малого по модулю вектора Дх выполнялось соотношение
grad/(x0)- Дх^О.	(14.90)
Доказательство. 1) Необходимость. Левая часть соот-.
ношения (14.90) может быть представлена в виде произведения про-
изводной от функции /(х) по направлению вектора Дх на длину
| Дх | этого вектора (см. п. 6 § 4 этой главы). В точке минимума
производная по любому направлению неотрицательна. Поэтому спра-
ведливость неравенства (14.90) установлена.
2) Достаточность. Так как /(х) — выпуклая функция, то мы
можем воспользоваться соотношением (14.88). Полагая в этом соот-
*) Отметим, что этот минимум может быть и краевым, т, е. может дости-
гаться в граничной точке множества Q.
§ 7]	ГРАДИЕНТНЫЙ МЕТОД ПОИСКА ЭКСТРЕМУМА	517
ношении х1 = х°, х2 = х°4-Дх, после несложных преобразований
получим
f(x° + Дх) -f(x°)	7 (х° + *	~f (л0).	(14.91)
В пределе при t—-0 первая часть неравенства (14.91) дает произ-
водную функции f(x) по направлению вектора Дх, умноженную на
| Дх |. В силу неравенства (14.90) эта производная неотрицательна, и
поэтому, согласно (14.91), для всех приращений Дх аргумента выпол-
няется неравенство /(х°Н-Дх)—</(х°)^0, означающее, что в точке
х° функция /(х) имеет минимум. Теорема доказана.
Замечание 1. Если х° — внутренняя точка множества <2, то
условие (14.90) принимает вид
grad f (х°) • Дх = 0.	(14.92)
В самом деле, во внутренней точке х° локального экстремума про-
изводная по любому направлению равна нулю, и поэтому (14.92) имеет
место. Достаточность условия (14.92) для внутренней точки доказы-
вается так же, как и в теореме 14.18.
Замечание 2. Условие (14,90) (соответственно для внутренней
точки (14.92)) является необходимым условием локального минимума
любой дифференцируемой функции.
Возникает вопрос о единственности минимума выпуклой
функции. Ответ на этот вопрос дает следующая теорема.
Теорема 14.19. Дифференцируемая строго выпуклая функция
f(x), заданная на выпуклом множестве Q, может иметь локаль-
ный минимум лишь в одной точке этого множества.
Д о к а з ат е л ь ст в о. Пусть функция /(х) имеет локальный мини-
мум в различных точках х1 и х2 множества Q. Из соотношения
(14.88) имеем
У (х2) / (х1) < f(xl + ‘(xi ~ х1)) ~ 7	,
f С*1) - f (х2)	.
В пределе при t —»- 0 правые части последних неравенств дают соот-
ветственно производные /(х) в точках х1 и х2 по направлениям
векторов х2 —х1 и х1 —х2, умноженные на |х2 — х11. Так как х1 и
х2 —точки локального минимума /(х), то эти производные неотрица-
тельны, и поэтому из полученных в пределе неравенств вытекает
соотношение
/(х1)=/(х2).
Используя это равенство и условие строгой выпуклости, получим
из (14.88) следующее неравенство, справедливое для всех значений t
из интервала (0, 1):
/(х1 + Цх2 - х1)) </(х1).
518
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
ГГЛ. 14
Из этого неравенства вытекает, что существуют как угодно близкие
к х1 точки множества Q (эти точки отвечают как угодно малым
значениям t), в которых значение функции меньше /(х1), а это про-
тиворечит условию локального минимума функции в точке х1.
Итак, строго выпуклая функция, заданная на выпуклом множестве,
может иметь локальный минимум лишь в одной точке. Теорема доказана.
В дальнейшем мы будем рассматривать так называемые сильно
выпуклые функции.
Дважды дифференцируемая функция fix'), заданная на выпук-
лом множестве Q, называется сильно выпуклой на этом
множестве, если второй дифференциал dftf во всех точках
множества Q удовлетворяет условию
k (Дх)2 < К (Дх)2,	(14.93)
где 0<А<К*).
Отметим следующее важное свойство сильно выпуклых функций.
Теорема 14.20. Сильно выпуклая функция, заданная на зам-
кнутом выпуклом множестве Q, имеет в некоторой точке х°
этого множества минимальное значение.
Прежде чем перейти к доказательству этой теоремы, подчеркнем,
что в силу замечания к теореме 14.17 и теоремы 14.19 точка х° бу-
дет единственной.
Д о к а з ате л ь ст в о т е о р ем ы 14.20. Если Q—ограничен-
ное множество, то в силу непрерывности /(х) и теоремы 14.7
эта функция в некоторой точке х° множества Q имеет минимальное
значение.
Пусть Q— неограниченное множество и х1—любая фикси-
рованная точка Q. По формуле Тейлора с центром в точке х1 имеем **)
/(х) =/(хт) + grad /(х1) • Дх 4- у d2f. (14.94)
Так как </2/^ Л (Дх)2 и | grad/(х1) • Дх |	| grad/(х1) | • | Дх |, то из
*) Второй дифференциал представляет собой квадратичную форму от коор-
динат вектора Дх, коэффициенты которой — вторые частные производные от f.
Отметим, что (Дх)2 = (Дх, Дх) также является квадратичной формой от коор-
динат вектора Дх.
**) Используя ранее введенное скалярное произведение векторов, можно,
очевидно, записать первый дифференциал функции f в виде df = (grad f, Дх) =
= grad/-Ax, где grad/ и Дх — соответственно векторы, с координатами
и (дХх, Дх2, ..., Дхт). С помощью этой записи df фор-
OX% uXjn)
мула Тейлора для дважды дифференцируемой функции f (х) может быть запи-
сана в следующей форме:
/(x + Ax)=/(x) + grad/(x)-Ax4-ld7
(черточка над f в выражении для d2/ означает, что значение этого дифферен-
циала вычислено в промежуточной точке).
§ л
ГРАДИЕНТНЫЙ МЕТОД ПОИСКА ЭКСТРЕМУМА
519
(14,94) получим следующее неравенство:
+ k-1 Дх| — |grad/(x1) Дх|. (14.95)
Выберем число R так, чтобы при | Дх | > R выполнялось неравен-
ство ~ k [ Дх | — | grad/^x1) | > 0. При таком выборе R, как это
видно из (14.95), значения функции /(х) вне шара С с центром в х1
радиуса R больше /(х1). С другой стороны, функция /(х) имеет
минимальнее значение в некоторой точке х° части множества Q, рас-
положенной в шаре С. Из проведенных рассуждений вытекает, что
значение функции в точке х° является минимальным значением функ-
ции на всем множестве Q. Теорема доказана.
3. Вспомогательные предложения. В этом пункте мы докажем
вспомогательные предложения, которые будут использованы при дока-
зательстве основной теоремы о поиске минимума сильно выпуклой
функции.
Лемма 1. Пусть f(x)— дифференцируемая выпуклая функция,
заданная на выпуклом множестве Q. Если при некотором поло-
жительном а проекция Pq(x° — agrad/(x0)) течки х°—agrad/(x°)
на множество Q совпадает с точкой х° этого множества, то
в точке х° функция f(x) имеет минимум. Иными словами, если
при а >> 0 имеет место равенство
Ро (х° — а grad /(х0)) == х°,
то в точке х° функция имеет минимум.
Доказательство. Воспользуемся леммой 2 п. 1 этого параг-
рафа для множества Q и точек х = х°— <х grad/(х°), Ро (х) — Pq(x°—
-—agrad/(x0)) и у = х\ Согласно неравенству (14.87), указанному
в формулировке этой леммы, получим
(х° — a grad/(х°) — Pq (х° — а grad/(х0)), х1 — PQ (х° — а grad/(х0)) -С 0.
Так как х° = PQ (х° — a grad f (х0)), а > 0 и х1 — х° = Дх, то послед-
нее неравенство перейдет в неравенство
grad f (х°) • Дх 0.
Из последнего неравенства и из теоремы 14.18 следует, что в точке
х° функция /(х) имеет минимум. Лемма доказана.
Пусть число р. превышает минимальное значение выпуклой функ-
ции с непрерывными частными производными на ограниченном выпук-
лом множестве Q:
р. >min/(х),
и пусть число v удовлетворяет условию р.^г Обозначим через Q
520
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[ГЛ. 14
множество точек Q, для которых значения функции /(х) удовлетво-
ряют неравенствам
=sg/(x)sgv.
Справедливо следующее утверждение.
Лемма 2. Пусть х— любая точка множества Q, а>0 «
Дх = Ро (х —• а grad /(х)) — х. Существует такая константа ц2 > 0,
что для всех точек х множества Q выполняются неравенства
(Дх)3^т)в,	(14.96)
grad/(х) • Дх	(Дх)2.	(14.97)
Доказательство. Так как Q—замкнутое множество*), то
непрерывная неотрицательная функция (Дх)2 = (Ро (х — a grad/(х)) — х)а
имеет на этом множестве минимальное неотрицательное значение т]2.
Число к;2 не равно нулю, ибо в противном случае в некоторой точке
х° мы получили бы Дх = Р0(х°—agrad/(x0))—х° = 0 и, согласно
только что доказанной лемме 1, в точке х° множества Q функция/(х)
имела бы минимум, чего не может быть. Итак, неравенство (14.96)
доказано.
Докажем теперь неравенство (14.97). Воспользуемся леммой 2 п. 2
этого параграфа. Подставляя в левую часть неравенства (14.87)
х— a grad/(х) вместо х, Ро (х — а grad/(x)) вместо Р0(х) и х
вместо у, получим
(х — a grad f (х) — PQ (х — а grad f (х)), х — PQ (х — а grad f (х)) =sg 0.
Учитывая обозначение Pq(x—agrad/(x)) — х = Дх и свойства ска-
лярного произведения, перепишем последнее неравенство в форме
(Дх)2 + a grad /(х) • Дх sg 0.
Последнее неравенство,' очевидно, эквивалентно неравенству (14.97).
Лемма доказана.
Лемма 3. Пусть выполнены условия леммы 2, функция f
является сильно выпуклой на выпуклом множестве Q и положи-
2
тельная константа а удовлетворяет условиям 0 < a <g , где
К—константа, фигурирующая в неравенствах (14.93). Тогда при
переходе из точки х в точку х* = Р0(х —а grad/(x)) значение
функции f(x) уменьшается, причем приращение функции f(x)
удовлетворяет соотношению
<14-98)
*) Легко убедиться, что для непрерывной функции множество значений
аргумента, для которых |л^/(х)^м, замкнуто.
§ 7]	ГРАДИЕНТНЫЙ МЕТОД ПОИСКА ЭКСТРЕМУМА	521
Доказательство. Используя формулу Тейлора, неравенство
2
условие (14.93) и неравенство (14.97), получим
Д/= f(x*) - /(х) = grad/(x) • Дх + 4	- у (М2 + (Дх)2 = -
Из этого соотношения получаем |Д/|^^—у) (Дх)2. Отсюда и из
неравенства (14.96) получаем неравенство (14.98). Лемма доказана.
4. Поиск минимума сильно выпуклой функции. Мы доказали
(см. теорему 14.20), что сильно выпуклая функция /(х), заданная
на выпуклом множестве Q, имеет на этом множестве единственный
минимум. Естественно поставить вопрос о построении алгоритма,
с помощью которого можно было бы найти точку х° множества Q,
в которой /(х) имеет минимум. Мы докажем, что если х1 —любая
точка множества Q, то последовательность {х*}> определенная рекур-
рентным соотношением
x*+1 = (xft — agrad/(xfc)),	(14.99)
где а удовлетворяет условию
0<а<^-,	(14.100)
сходится к точке х° минимума /(х). Итак, справедлива следующая
основная теорема.
Теорема 14.21. Пусть сильно выпуклая функция f(x) задана
на выпуклом множестве Q и х1 — любая точка этого множе-
ства. Тогда последовательность {х*} значений аргумента этой
функции, определенная соотношением (14.99), сходится к точке
х° минимума функции f (х).
Доказательство. Отметим, что можно остановиться лишь на
случае ограниченного замкнутого выпуклого множества Q. Чтобы
убедиться в этом, проведем следующие рассуждения.
Пусть х1 — любая фиксированная точка неограниченного множе-
ства Q. При доказательстве теоремы 14.20 мы установили, что
точка х° минимума функции /(х) /лежит на части Q множества Q,
расположенной в шаре С с центром в х1 такого радиуса R, что при
| х — х11 > R выполняется неравенство у k |х — х11 — | grad/(x1) | > 0.
Ясно, что Q представляет собой замкнутое, ограниченное, выпуклое
множество.
Так как по лемме 3 при переходе от точки х* к х*+1 значе-
ние функции уменьшается, то при любом k 1 выполняется нера-
венство /(xft)^/(x1). Следовательно, все точки xk принадлежат
522
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[ГЛ. 14
множеству Q *), и поэтому
(xft - a grad / (xft)) = Р (Xй - а gra d / (хй)).
Таким образом, в случае неограниченного множества Q, мы можем
указать выпуклую ограниченную замкнутую часть Q множества Q,
содержащую точку х° минимума /(х), причем точки последователь-
ности {хй} принадлежат множеству Q и могут быть определены
рекуррентным соотношением
хйм = Р$ (хь — a grad f{xh)).
Итак, будем считать, что Q—замкнутое ограниченное выпуклое
множество. Рассмотрим последовательность {/.(хй)}. По лемме 3 эта
последовательность убывающая и, кроме того, она ограничена снизу
минимальным значением т функции /(х) на множестве Q. Следова-
тельно, последовательность {/(хй)} сходящаяся. Пусть р — предел
этой последовательности. Отметим, что р=С/(хй) для любого k.
Докажем, что p.= «z. Допустим, что у. > т = inf/(x), и обозначим
xeQ
через ч максимальное значение функции /(х) на множестве Q. Рас-
смотрим множество Q* точек выпуклого множества Q, для которых
[isC/(x)sgv. Воспользуемся теперь леммами 2 и 3 предыдущего
пункта. В силу этих лемм существует такое число т]2 > 0, что при
любом k
/(хй)-/(хй+1)^(1-^-)т12.	(14.101)
Выберем теперь номер k столь большим, чтобы для этого номера
выполнялось неравенство
/(хй)(14.102)
(такой выбор k возможен, так как последовательность {/(хй)} убывает
и сходится к р). Вычитая из неравенства (14.101) неравенство (14.102)
и учитывая, что в силу условия (14.100) число —положи"
тельно, получим неравенство
р -/(хй+1) > О,
которое противоречит отмеченному ранее неравенству р=С/(хй),
справедливому для любого k. Итак,
р = rra = miti /(х).
*) При доказательстве теоремы 14.20 мы установили, что вне шара С
значения функции / (х) превосходят / (х1).
ДОПОЛНЕНИЕ К ГЛАВЕ 14
523
Докажем теперь, что последовательность {хк} сходится к точке х"
минимума функции fix'). Обозначим через Qs любую фиксированную
g-окрестность точки х°. Рассмотрим часть Q — Qe множества Q, кото-
рая не содержит точек Qe. Очевидно, Q — Qs.— замкнутое ограниченное
множество, и поэтому на Q—Qs функция f(x) имеет минимальное
значение тие, причем, очевидно, /пе> т. Если на множестве Q— Qe
имеются точки последовательности {х*} с как угодно большими
номерами, то значения функции /(х) на множестве Q— Qe в силу
сходимости последовательности {/(х*)} к т могут быть как угодно
близки к т. А это противоречит только что отмеченному неравен-
ству	Таким образом, для данной е-окрестности Qe точки х°
можно указать номер А/ такой, что при k^N все точки последова-
тельности {х*} находятся в Qs. Это и означает сходимость последо-
вательности {хк\ к х°. Теорема доказана.
Замечание. Если множество Q совпадает со всем простран-
ством Ет, то PQ(xk— agrad/(xft)) = xft — agrad/(xft), и поэтому
рекуррентная формула (14.99) для этого случая принимает следующий
вид:
xfe+1 = х* — a grad / (хА).
- Развитие и обобщение изложенной в этом параграфе теории
можно найти в монографии Б. М. Будака и Ф. П. Васильева «При-
ближенные методы решения задач оптимального управления», вып. И,
Ротапринт, МГУ, 1969 г.
ДОПОЛНЕНИЕ К ГЛАВЕ 14
О ВЫБОРЕ ОПТИМАЛЬНОГО РАЗБИЕНИЯ СЕГМЕНТА
ДЛЯ ПРИБЛИЖЕННОГО ВЫЧИСЛЕНИЯ ИНТЕГРАЛА
В главе 12 для приближенного вычисления интеграла
*
\f(x)dx	(14.103)
а
мы разбивали сегмент [а, &] на достаточно большое число п равных частичных
сегментов и на каждом из этих сегментов заменяли функцию f (х) многочленом
нулевого, первого или второго порядка. Возникавшая при этом погрешность
никак не учитывала индивидуальных свойств f (х). Поэтому, естественно, встает
вопрос о варьировании точек разбиения основного сегмента [а, 6] и выборе
для каждой фиксированной функции /(х) такого оптимального разбиения
основного сегмента на п, вообще говоря, не равных друг другу частичных
сегментов, которое обеспечивало бы минимальную величину погрешности дан-
ной приближенной формулы.
В настоящем дополнении мы остановимся на решении указанного вопроса,
принадлежащем А. Н. Тихонову и С. С. Гайсаряну *).
*) См. работу А. Н. Тихонова и С. С. Гайсаряна «О выборе оптимальных
сеток при приближенном вычислении квадратур» (Журнал вычислительной
математики и математической физики, том 9, № 5, 1969).
524
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[ГЛ 14
Для приближенного вычисления интеграла (14.103) разобьем сегмент [а, Ь]
на п частичных сегментов при помощи точек
а = х0 < xt < х2 < ... < хп = Ь.
Длину й-го частичного сегмента [x*_i, х*] (й=1, 2, ..., п) обозначим
символом hk, так что hk = х^ — х^.
Представив интеграл (14.103) в виде суммы интегралов
*	п Xk
p(x)dx= 2 $ f(*)dx,	(14.104)
приблизим каждый из интегралов, в правой части (14.103) с помощью одной
из трех приближенных формул (прямоугольников, трапеций или парабол).
Любую из указанных трех формул можно записать в виде
т — 1
f(x)dx = hk 2 4if (xk + tihk) + Rs, m> k (f),	(14.105)
xk-i	'=0
где узлы и веса q, (i = 0, 1, ... , m— 1) выбираются так, чтобы остаточный
член Rs,m,k(f) имел порядок hsk при некотором s>l *).
Вставляя (14.105) в (14.104), мы получим, что
b	п	т — \
\ f (х) dx = 2 hk 2 Qif + tihk) + Rs> m (f),	(14.106)
a	k=l	/=0
где
S	(14.107)
k = 1
Поставим вопрос о выборе такого разбиения {xfc} сегмента [а, 6], при ко-
тором квадрат погрешности (14.107) достигал бы минимума при фиксирован-
ном числе точек разбиения п, фиксированной функции f (х) и фиксированной
приближенной формуле (14.105). При такой постановке вопроса квадрат по-
грешности /?’ т (() зависит только от выбора промежуточных Точек разбиения,
т. е. является функцией (п — 1) переменных хх, х2, .... xn_lt определенной
в тетраэдре а < xt < х2 С... <xn_j < Ь. Поскольку указанный тетраэдр яв-
ляется открытой областью, то минимум функции 7?’, т (/) в этом тетраэдре
может, вообще говоря, и не достигаться (т. е. оптимального разбиения сег-
мента [а, Ь] может, вообще говоря, и не существовать).
Можно, однако, доказать, что если производная f{si (х) сохраняет знак. на
сегменте [а, &], то минимум квадрата погрешности Rs, т (/) достигается на
таком разбиении сегмента [а, Ь], узлы Х^ которого удовлетворяют (п—1)
уравнениям
dRs' т ® =0 (й = 1, 2...........п - 1)	(14.108)
OXk
и дополнительным условиям х0 = а, хп = Ь **).
*) В частности, для формулы трапеций в (14.105) следует положить
т = 2, s = 2, <0 = 0, <1=1,	= gi =
.**) Доказательство этого утверждения можно найти в работе А. Н. Тихо-
нова и С. С. Гайсаряна, отмеченной в сноске на стр. 523,
ДОПОЛНЕНИЕ К ГЛАВЕ 14
525
Остановимся более подробно на случае формулы трапеций. В этом
случае в формуле (14.106) следует положить s = 2, т = 2, ta = 0, /х=1,
q0 = q1 = -Ь( в результате чего формула (14.106) принимает вид
Ь	п
V (X) dx = 2 (xk) +f(xk + fik)] + /?212 ff). (14.109)
a	k = l
Уравнения (14.108), в силу (14.109) и (14.104), приводятся для этого
случая к виду
F (*й+1) — f = Г (Xk) (Xk+i — Xk-i) (k = 1 > 2, ..., n — 1). (14.110)
Существование решения системы уравнений (14.110) обеспечивается сохра-
нением знака второй производной f" (х) на сегменте [а, 6], т. е. сохранением
направления выпуклости кривой у = f (х) при а^х^Ь. Узлы оптималь-
ного разбиения сегмента [а, 6], определяемого уравнениями (14.110), обладают
следующим геометрическим свойством: секущая, проведенная через точки гра-
фика функции, у — f (х) с абсциссами Хк+1 и Xk_lt параллельна касательной
к указанному графику, проведенной через его точку с абсциссой Хк.
Это свойство является прямым следствием равенств (14.110) и иллюстри-
руется на рис. 14.6 (рассуждения те же самые, что и в § 7 главы 8).
Можно доказать, что узлы «приближенного разбиения» {xft} (й = 0,1,..., п),
определяемые рекуррентными равенствами
__1_
х0 = а\ xft+1 = х* + X | f" (х*) | 3 (й = 0, 1, ... , п — 1), (14.111)
при X — - а удовлетворяют уравнениям (14.110) с ошибкой (или, как гово-
рят, с невязкой) порядка X2. Это означает, что при больших п разбиение
(хй) близко к оптимальному разбиению {JCj}. Таким образом, при больших
п вычисление интеграла (14.103) по формуле трапеций с разбиением {л>},
узлы которого последовательно определяются рекуррентными соотношениями
(14.111), обеспечивает погрешность, близкую к минимальной.
ГЛАВА 15
ТЕОРИЯ НЕЯВНЫХ ФУНКЦИЙ И ЕЕ ПРИЛОЖЕНИЯ
§ 1. Понятие неявной функции
В математике и в ее приложениях приходится сталкиваться с та-
кими задачами, когда переменная и, являющаяся по смыслу задачи
функцией аргументов х, у, ..., задается посредством функциональ-
ного уравнения
F(u, х, у, .. .) = 0.	(15.1)
В этом случае говорят, что и как функция аргументов х, у, ...
задана неявно. Так, например, функция и = — У1 — х2 — у2, рассмат-
риваемая в круге х2+у2^ 1, может быть неявно задана посредст-
вом функционального уравнения
F (и, х, у) = и2 + х2 +_у2 — 1=0.	(15.2)
Естественно, возникает вопрос, при каких условиях функциональное
уравнение (15.1) однозначно разрешимо относительно и, т. е. одно-
значно определяет явную функцию и = <р (х, у, ...) и более тонкий
вопрос, при каких условиях эта явная функция является непрерывной
и дифференцируемой. Эти вопросы не являются простыми. Так функ-
циональное уравнение (15.2), вообще говоря, определяет в круге
х2 -\-у2	1> кроме указанной выше явной функции и = — у/1 — х2 —у2,
бесконечно много других функций. Таковыми являются функция и =
= +	— х2 — у2, а также любая функция и, равная -|- У1 — х2 — у2
для некоторых точек (х, у) из круга х2 + у2 «С 1 и равная — У1 — х2 — у2
для остальных точек этого круга. Для выяснения вопроса об усло-
виях, обеспечивающих однозначную разрешимость уравнения (15.2)
относительно и, обратимся к геометрической иллюстрации. Уравне-
ние (15.2) определяет в пространстве (и, х, у) сферу S радиуса 1
с центром в начале координат (рис. 15.1). Возьмем на сфере Сточку
Л10 (й, х, _у), не лежащую в плоскости Оху, т. е. такую, для которой
й =£ 0. Очевидно, часть сферы S, лежащая в достаточно малой
§ 2J
ТЕОРЕМА О СУЩЕСТВОВАНИИ И ДИФФЕРЕНЦИРУЕМОСТИ
527
окрестности точки 7И0, однозначно проектируется на плоскость
Оху. Аналитически это означает, что если рассматривать функцию
F (и, х, у) = и2 ф х2 ф_у2 — 1 только в указанной окрестности точки Мо>
то уравнение (15.2) однозначно разрешимо относительно и и опре-
деляет единственную явную функцию и— ф 1 — х2 — у2 при й>0
и и — — У" 1 — х2 — у2 при й < 0.
Если же на сфере 5 взять точку
Л/11 (О, х, у), лежащую в плоскости Оху
(рис. 15.1), то очевидно, что часть
сферы 5, лежащая в любой окрестно-
сти М1г неоднозначно проектируется
на плоскость Оху. Аналитически это
означает, что если рассматривать функ-
цию F (и, х, у) = и2 + х2+у2— 1 в лю-
бой окрестности точки 7И1, то уравне-
ние (15.2) не является однозначно разре-
шимым относительно и. Обратим внима-
ние на то, что частная производная
дЕ
v-= 2н функции F(u, х, у) = и2 + х2Рис. 15.1.
-фу2 — 1 не обращается в нуль в точке
Мо и обращается в нуль в точке Ниже мы установим, что для одно-
значной разрешимости в окрестности точки 7И0 общего функциональ-
ного уравнения (15.1) относительно и принципиальную роль играет
dF
необращение в нуль в точке Л10 частной производной . Попут-
но мы установим условия, при которых явная функция, представляю-
щая собой единственное решение уравнения (15.1), является непре-
рывной и дифференцируемой.
В дальнейшем мы будем обозначать пространство переменных
(и, х, у, ...) символом R, а пространство переменных (х, у, ...) сим-
волом R'. Ради сокращения записи и для удобства геометрической
иллюстрации будем рассматривать две переменные х, у.
§ 2. Теорема о существовании и дифференцируемости
неявной функции и некоторые ее применения
1. Теорема о существовании и дифференцируемости неявной
функции.
Теорема 15.1. Пусть функция F (и, х, у) дифференцируема
в некоторой окрестности точки M0(ii, х, у) пространства R,
dF
причем частная производная непрерывна в точке Мй. Тогда,
если в точке Мо функция F обращается в нуль, а частная про-
, dF ,	,	-	,
изводная не обращается в нуль, то для любого достаточно
528
ТЕОРИЯ НЕЯВНЫХ ФУНКЦИЙ И ЕЕ ПРИЛОЖЕНИЯ
{ГЛ 15
малого положительного числа е найдется такая окрестность
точки у) пространства R', что в пределах этой окрест-
ности существует единственная функция и = <?(х, у), которая
удовлетворяет условию |и— й|<е и является решением урав-
нения
F(u,x,y) = 6,	(.15.3)
причем эта функция п = <р(х, у) непрерывна и дифференцируема
в указанной окрестности точки М’й.
Замечание 1. В условиях теоремы 15.1 можно опустить тре-
dF
бование непрерывности частной производной д— в точке Мй, но тогда
придется дополнительно потребовать,
чтобы эта производная не обращалась
в нуль не только в самой точке А/о,
но и в некоторой окрестности этой
точки и сохраняла определенный знак
в этой окрестности.
Доказательство теоремы 15.1.
1. Прежде всего докажем, что для
достаточно малого е > 0 в окрест-
ности точки №]>(&,у) существует
единственная функция и = <?(х, у),
удовлетворяющая условию | и — ii | < в
и являющаяся решением уравнения
(15.3). Чтобы сделать доказательство
более наглядным, будем сопровождать
ёго геометрической иллюстрацией. Из
аналитической геометрии известно, что
уравнение (15.3) определяет в прост-
ранстве R некоторую поверхность S
(рис. 15.2), причем, в силу условия
/= (УИ0) = 0, точка 7И0 лежит на этой
поверхности. С геометрической точки
зрения однозначная разрешимость урав-
нения (15.3) относительно и означает,
что часть поверхности S, лежащая в непосредственной близости
к точке 7Й0, может быть однозначно спроектирована на координат-
ную плоскость Оху.
Ради определенности будем считать, что частная производная
положительна в точке Af0. Тогда из непрерывности указанной про-
изводной в Мо и из теоремы об устойчивости знака непрерывной
функции вытекает, что найдется такая окрестность точки /Ио,
всюду в пределах которой положительна. Эту окрестность мы
можем взять в виде шара 2 достаточно малого радиуса с центром
5 2J
ТЕОРЕМА О СУЩЕСТВОВАНИИ И ДИФФЕРЕНЦИРУЕМОСТИ
529
в точке 7И0. Фиксируем далее положительное число е настолько малым,
чтобы каждая из точек Л11 (м — s, х, у) и 7Иа (й -f-е, х, у) лежала
внутри шара Q (для этого достаточно взять в меньшим радиуса
шара 2). Подчеркнем, что при этом снизу в ограничено лишь нулем,
и мы можем брать его как угодно малым — это будет использовано
нами ниже.
Рассмотрим функцию F (и, х, у) одной переменной на сегменте
li -к 4-е. С геометрической точки зрения это означает, что
мы рассматриваем функцию трех переменных F (и, х, у) вдоль от-
dF
резка AJtM2 (см. рис. 15.2). Так как производная ^(и, х, у) поло-
жительна на сегменте й — е и и + в, то функция F (и, х, J») воз-
растает на этом сегменте. Но тогда, поскольку эта функция равна
нулю в середине указанного сегмента (т. е. при и = н), то F (и, х,у)
имеет отрицательное значение на левом конце и положительное
значение на правом конце указанного сегмента, т. е.
F^XO, F(Al2)>0.
Далее рассмотрим функции F (й — в, х, у) и F (и 4-е, х, у) двух пере-
менных х и у, т. е., выражаясь геометрическим языком, рассмотрим
функцию F (и, х, у) на двух плоскостях, параллельных координатной
плоскости Оху, первая из которых проходит через точку Мг, а вто-
рая—через точку ТИ2; Поскольку F (.Mj) <; О, Д(Ж2)>0 и функции
F (и, х, _у) непрерывна всюду в шаре 2, то по теореме об устой-
чивости знака непрерывной функции на указанных плоскостях най-
дутся такие окрестности точек М2 и Л12, в пределах которых
функция F' сохраняет те же знаки, что и ц, точках Л1Х и ЛГ2. Эти
окрестности мы можем взять в виде открытых квадратов с центрами
в точках Afj и М2 и с достаточно малой стороной 28 < (на рис. 15.2
указанные квадраты заштрихованы). Аналитически тот факт, что функ-
ция F(и, х, у) сохраняет постоянный знак на указанных квадратах
выражается неравенствами
F(й — е, х, у) <0,1
_ ( при lx —	|у—V I < 8. j (15.4)
F(ti 4-е, х, _у)> 0 j r 1	I-- > i-л	j v i
Выбор стороны, указанных квадратов мы подчиним и еще одному
условию: возьмем 8 столь малым, чтобы оба указанных квадрата
лежали внутри шара 2 (это заведомо можно сделать, ибо центры
квадратов 7ИГ и Л12 являются внутренними точками шара 2). При
таком выборе 8 любая точка пространства (W, х, у), координаты ко-
торой удовлетворяют неравенствам
|х —х|<8, |_У—_у|<8, |w — й|<е,	(15.5)
будет лежать внутри шара 2. С геометрической точки зрения нера-
венства (15.5) определяют открытый прямоугольный цараллелепипед
530
ТЕОРИЯ НЕЯВНЫХ ФУНКЦИЙ И ЕЕ ПРИЛОЖЕНИЯ
(ГЛ. 15
с центром в точке 7И0 и со сторонами, параллельными осям коорди-
нат и, х, у и соответственно равными 2е, 28 и 28. Этот параллеле-
пипед мы будем обозначать символом П. Так как параллелепипед П
лежит внутри шара 2, то всюду в параллелепипеде П *) производ-
ная положительна. Кроме того, в силу неравенств (15.4), функ-
ция F (и, х, у) отрицательна на нижнем основании и положи-
тельна на верхнем основании П.
Докажем теперь, что уравнение (15.3) однозначно разрешимо от-
носительно и, если функцию F (и, х, у) рассматривать лишь для зна-
чений и, х, у, лежащих внутри параллелепипеда П. Уясним, что тре-
буется доказать. Пусть М' (х, у)— любая точка пространства R',
координаты которой удовлетворяют неравенствам
|х — х|<8, |_У — J) | < 8.	(15.6)
Иначе говоря, пусть М' (х, у) — любая точка плоскости Оху, лежащая
внутри квадрата с центром в течке М'0(х, _у) и со сторонами, рав-
ными 28. Требуется доказать, что для координат х, у точки М'
найдется, и притом единственное, число и из интервала й — е<и<й + е
такое, что F (и, х, y) = Q. (С геометрической точки зрения это озна-
чает, что любая прямая, параллельная оси и и пересекающая парал-
лелепипед П, пересекает поверхность 5 внутри параллелепипеда П
в одной и только в одной точке.)
Зафиксировав значения х иу, удовлетворяющие неравенствам (15.6),
рассмотрим функцию F (и, х, у) аргумента и на сегменте й —
и и + е, т. е. рассмотрим функцию F (и, х, у) на отрезке
где Afj и М’г — точки пересечения прямой, проходящей через точку
(х> У) и параллельной оси Ои, с основаниями параллелепипеда П
dF
(см. рис. 15.2). Так как производная (и, х, у) положительна на сег-
менте й — е sC и sS й + е, то функция F (и, х, у) возрастает на этом
сегменте (или, что то же самое, возрастает на отрезке AfjAf^). Но
тогда из условий F (714j) < 0, F (AQ > 0 вытекает, что внутри сег-
мента й — г п й + е найдется одно единственное значение и такое,
что F (и, х, у) = 0 (или, выражаясь геометрически, внутри отрез-
ка AljAia найдется единственная точка М, лежащая на поверх-
ности 5).
Пусть теперь функция ц = <р(х, у) символизирует то правило, по-
средством которого каждой точке М' (х, j<) из окрестности (15.6) ста-
вится в соответствие единственное число и из интервала й — е < и <
< й + е, для которого F (и, х, у) = 0. Мы доказали, что в окрестности
(15.6) существует единственная функция и = ф (х, ^.удовлетворяющая
условию |и—й|<е и являющаяся решением уравнения (15.3).
’) Включая открытые квадраты, лежащие в его основаниях.
§ 2]
ТЕОРЕМА О СУЩЕСТВОВАНИИ И ДИФФЕРЕНЦИРУЕМОСТИ
531
2, Докажем теперь, что функция и = <р(х, у) непрерывна в любой
точке Л4'(х, у) окрестности (15.6). Так как для любой точки
М’ (х, у) из окрестности (15.6) выполнены те же условия*), что и
для точки М\)(х, у), то достаточно доказать непрерывность функции
и — ^(х, у) лишь в точке Л4д(х, у). Требуется доказать, что для
любого достаточно малого положительного е существует положитель-
ное число 8 такое, что для любых х и у, удовлетворяющих неравен-
ствам |х — х|<8, |у — у |<8, справедливо неравенство |и—w|<e,
где и = <?(х, у), й=<?(х, у). Если взять в качестве е то число,, ко-
торое выбрано выше при рассмотрении пункта 1, то существование 8
обеспечивается неравенствами (15.5). Остается заметить, что в рас-
суждениях пункта 1 положительное число е может быть взято как
угодно малым (это отмечалось в пункте 1).
Тем самым непрерывность функции и = ю(х, у) установлена. За-
пишем условие непрерывности функции и = ^(х, у) в точке У1о(х, у)
в разностной форме. Обозначая через Д« полное приращение функ-
ции и = ф(х, у) в точке Л1 g (х, у), соответствующее приращениям
( Дх -> О,
аргументов Дх и Ду, мы получим, что Дн -> 0 при | д
3. Остается доказать дифференцируемость функции и = <р (х, у)
в любой точке М’ (х, у) окрестности (15.6). В силу замечания, сде-
ланного в пункте 2, достаточно доказать дифференцируемость функ-
ции и = <р(х, у) в самой точке Alf,(x, у). Чтобы это сделать, вычис-
лим полное приращение Д/z функции п = у(х, у) в точке Л1о(х, у),
соответствующее приращениям аргументов Дх и Ду. Поскольку
F(u, х, y) — Q и F (и + Ди, х + Дх, у + Ду) = 0, то полное прира-
щение liF функции F (и, х, у) в точке М0(н, Л у), соответствующее
приращениям аргументов Ди, Дх и Ду, равно нулю. Но в силу усло-
вия дифференцируемости функции F (и, х, у) в точке Л10(и, х, у)
это полное приращение имеет вид

Здесь все частные
г
, dF dF dF
производные -г-, и з—
	ди ’ дх ду
берутся в точке
7И0(й, х, у); а, р и 7-*- 0 при
Ду-* О,
Ди -> 0.
*) Именно, любой точке М'(х, у) из окрестности (15.6) соответствует
точка М {и, х, у) пространства 7? такая, что функция F (и, х, у) обращается
в нуль в точке М, дифференцируема в некоторой окрестности точки М и
имеет в этой окрестности отличную от нуля частную
dF
производную
532
ТЕОРИЯ НЕЯВНЫХ ФУНКЦИИ И ЕЕ ПРИЛОЖЕНИЯ
[ГЛ. 15
Итак, мы получаем
(15.7)
Согласно разностной форме условия непрерывности функции и =
(	0,	•
= <р(х, у) в точке М’о(х, у) Ди-+0 при ( Ду^д Таким образом,
можно утверждать, что из условия < д
По условию теоремы частная производная
следует, что
dF
отлична от нуля
то при достаточно ма~
в точке Л40. Поскольку 7—>0 при
лых Ьх и Ду выражение + 7 не обращается в нуль. В таком
IdF \
случае формулу (15.7) можно поделить на + в результате че-
го мы получим
/ . а \ / . й \
.	|	. I ду + Р \ А
дн=	- Дх+ -	- Ду.
\ asr+v \ ai?+V
(15.8)
По теореме о предельном значении
утверждать, что
частного двух функций’ можем
dF
дх
dF
ди
dF
дх  ,
df+*
ди
dF
dF
du
dF
ду
dF
ди
(15.9)
где р. и v -> 0 при I ду 0
Сопоставляя формулы (15.8) и
(15.9), окончательно получим
А	I	U*
\	дг
\	ди
dF_ \
! Ду + р.Дх-НДу. (15.10)'
да /
Формула (15.10) доказывает дифференцируемость функции и = <р(х, у)
в точке Л1'6(х, у). Тем самым теорема 15.1 полностью доказана.
Замечание 2. Приведенное доказательство без всяких затруд-
нений переносится на случай неявной функции, зависящей не от двух,
§ 2] ТЕОРЕМА О СУЩЕСТВОВАНИИ И ДИФФЕРЕНЦИРУЕМОСТИ 533
а от любого конечного числа аргументов xlt х2, .хт *). Случай
двух аргументов х и у имеет лишь то преимущество, что допускает
наглядную геометрическую иллюстрацию в пространстве (и, х, у).
2. Вычисление частных производных неявно заданной функ-
ции. Остановимся на вычислении частных производных функции, не-
явно заданной посредством уравнения (15.3). Пусть выполнены усло-
вия теоремы 15.1. Тогда для полного приращения функции и — у (х,у)
справедливо представление (15.10). Это представление и теорема 14.9
позволяют утверждать, что частные производные функции и = <р(х, у)
определяются формулами
dF	dF
¥ =	=	(15.11)
dx dF ' ду dF	v '
du	du
Аналогичные формулы справедливы и для случая, когда неявно задан-
ная функция зависит не от двух, а от любого конечного числа аргу-
ментов х2, хт. В этом случае
dF
ди   dxk
dxk	dF
du
(k = l, 2, .... m).
Если мы хотим обеспечить существование у неявно заданной функ-
ции и = <р(х, у) частных производных второго порядка, то, естест-
венно, приходится усилить требования, наложенные на функцию
F (и, X, у) в теореме 15.1, именно приходится дополнительно тре-
бовать, чтобы функция F (и, х, у) была два раза дифференцируема
в рассматриваемой точке. В этих предположениях остановимся на
вычислении частных производных второго порядка.
Введем полезное в дальнейшем понятие полной частной произ-
водной функции. Предположим, что нам дана дифференцируемая функ-
ция трех аргументов Ф (и, х, у), причем один из этих аргументов и
сам является дифференцируемой функцией двух других аргументов х
и у. Тогда функцию Ф(«, х, у} можно рассматривать как сложную
функцию двух аргументов х, у. Частные производные этой сложной
функции по х и у будем называть полными частными производными
,	/Г. ,	,	-	ОФ ОФ т-г
функции Ф(н, х, у) по х и у и обозначать символами и По
правилу дифференцирования сложной функции мы получим следую-
щие формулы для указанных полных частных производных:
ОФ 0Ф ди . <5Ф ОФ ЗФ ди . дФ
Dx	ди дх "г дх ’ Dy	ди ду' ду *
') И, в частности, от одного аргумента.
534
ТЕОРИЯ НЕЯВНЫХ ФУНКЦИИ И ЕЕ ПРИЛОЖЕНИЯ
[ГЛ. IS
О3Ц тт , ,
ную дудх' ЛиФФеРенш1РУя
Переходим к вычислению частных производных второго порядка
неявно заданной функции. Ради определенности вычислим производ-
первую из формул (15.11) по у и прини-
dF dF
мая во внимание, что каждая из частных производных и зави-
сит от трех аргументов и, х, у, первый из которых сам является
функцией х и у, будем иметь
д2и __
дудх
0F -
дх
ди -
Вставляя в полученную
рой из формул (15.11),
D
dF P[dx] dF
ди Ру ~г~ дх Ру
_ dF ! d2F ди Э2Г \ dF (cPF ди d2F \
 ди ди ду’' дхду]~' дх \ди2 ду ' диду)
,	ди
формулу выражение определяемое вто-
окончательно будем иметь
d2F d£dF__ d2F fdP\z	<32F <9F gF । d2F dF dF
d2u  dx du dy du dx dy \du /	du2 dx dy dy du dx du	... _ . „
дудх ~	7dF\3	• (1 1
\du /
~	d2u d2u
Совершенно аналогично вычисляются частные производные и
Аналогичным методом могут быть вычислены и частные производ-
ные третьего и последующих порядков *).
Примеры. 1) Вычислить частную производную фуНКЦИИ
и = ср (х, у), заданной, посредством уравнения
х+_у + я-е-^+“) = 0.
Прежде всего, пользуясь формулами (15.11), вычислим частные про-
изводные первого порядка
ди ди_ 1 +	_
дх = ду ~ l-ф- e-lJC+>+«i— ъ
тт	d2U п
Далее очевидно, что — 0.
*) При условии, что функция F (и, хг у) дифференцируема в данной точке
соответствующее число раз.
§ 2] ТЕОРЕМА О СУЩЕСТВОВАНИИ И ДИФФЕРЕНЦИРУЕМОСТИ 535
2) Тот же вопрос для функции, заданной уравнением
и2 4- х2 _у2 — а2 = 0.
Используя формулы (15,11), получим
ди  х ди   у
дх	и ’ ду	и '
Далее, будем иметь
„(ди\	х\ ди
д	D------х-
o2u __	\ дх /_	\ и /__ ду__ ху
ду дх Dy Dy u2 и3 ‘
3. Особые точки поверхности и плоской кривой. Рассмотрим
некоторую поверхность S’ (плоскую кривую L), определяемую в за-
данной декартовой прямоугольной системе координат уравнением
F (х, у, z) = 0 (F(x, j/) = 0). Относительно функции F (х, у, г)
(F (х, у)) предположим, что она имеет непрерывные частные произ-
водные первого порядка по всем аргументам всюду в некоторой
окрестности любой точки поверхности S (кривой L). Будем назы-
вать данную точку поверхности S (кривой L) особой, если в этой
точке обращаются в нуль все частные производные первого порядка
функции
F(x, >, г) (F(x,y)).
В окрестности особой точки нельзя применить к уравнению
F (х, у, г) = 0 (F(x,y) — 0) теорему 15.1, т. е. нельзя утверждать,
что это уравнение разрешимо хотя бы относительно одной из пере-
менных х, у, Z'(x, у). Таким образом, участок поверхности S (кри-
вой L), прилегающий к особой точке, может не допускать однознач-
ного проектирования ни на одну из координатных плоскостей (ни
на одну из осей координат). Структура поверхности X (кривой L)
в окрестности особой точки может быть очень сложной и требует
дополнительного исследования.
Точки поверхности X (кривой L), не являющиеся особыми, при-
нято называть обыкновенными. В окрестности обыкновенной точки
действует теорема 15.1, так что прилегающий к обыкновенной точке
участок поверхности X (кривой L) допускает однозначное проекти-
рование хотя бы на одну из координатных плоскостей (хотя бы на
одну из осей координат), что существенно облегчает исследование
этого участка.
Примеры. 1) Найти особые точки кругового конуса х2 +>2 —
— z2 = 0. Поскольку F(x, у, z) = x2-f-_y2 — z2, то ~ = 2х, ~- = 2у,
dF
— — 2г. Единственной особой точкой является начало координат.
Хорошо известно, что в окрестности этой точки поверхность конуса
536
ТЕОРИЯ НЕЯВНЫХ ФУНКЦИИ И ЕЕ ПРИЛОЖЕНИЯ
ГГЛ 1S
не может быть однозначно спроектирована ни на одну из коорди-
натных плоскостей (рис. 15.3).
2)	Тот же вопрос в отношении плоской кривой х2 — у2 + Xs = 0.
Частные производные имеют вид	= 2х + Зх2 = х (2 -ф- Зх), ^ ==
= — 2у. Обе частные производные обращаются в нуль в двух точ-
ках плоскости (0, 0) и I — -у, 01. Из этих двух точек только пер-
вая принадлежит рассматриваемой кривой, т. е. является особой.
Построив кривую х2—у2 + х3 = 0 в окрестности точки (0, 0), мы убе-
димся в том, что эта точка является точкой самопересечения графика
(рис. 15.4). Ясно, что в окрестности этой точки кривую нельзя одно-
значно спроектировать ни на ось Ох, ни на ось Оу.
4.	Условия, обеспечивающие существование для функции
_у=/(х) обратной функции. Применим теорему 15.1 для выясне-
ния условий, при выполнении которых функция у =f(x) имеет в не-
которой окрестности точки х0 обратную функцию х =f-1 (у), опре-
деленную в некоторой окрестности точки _у0, где _у0=/(х0). Будем
рассматривать _у=/(х) как функцию, определяемую функциональным
уравнением вида F (х, y)—f(x)~y = 0.
Тогда вопрос о существовании обратной функции совпадает с во-
просом о разрешимости относительно х указанного функционального
уравнения. Кдк следствие теоремы 15.1 и замечания 1 перед доказа-
тельством этой теоремы, мы получим следующее утверждение: если
функция y=f(x) имеет отличную от нуля производную в неко-
торой окрестности точки х0, то для этой функции в окрест-
ности xQ существует обратная функция х = f~x {у), определенная
и дифференцируемая в некоторой окрестности точки у9, где
y0—f(xQ). Производная указанной обратной функции в точке у0
в силу второй из формул (15.11) равна тгт-т.
§ 3]
СИСТЕМЫ ФУНКЦИОНАЛЬНЫХ УРАВНЕНИИ
537
§ 3.	Неявные функции, определяемые системой функциональных
уравнений
1.	Теорема о разрешимости системы функциональных урав-
нений. В предыдущем параграфе мы рассматривали вопрос о сущест-
вовании и дифференцируемости неявной функции, определяемой по-
средством одного функционального уравнения. В этом параграфе мы
рассмотрим аналогичный вопрос для совокупности т (т — любое
натуральное число) неявных функций, определяемых посредством
системы функциональных уравнений.
Итак, предположим, что т функций
Wj —	(Х\, х2, ..., хп),
н2 = ?2 (Xj, Х2, • • • > Хп),
(15.13)
Um — Тт (Xj, Х2, • • • ’	.
ищутся как решение системы т функциональных уравнений'
«2......
F2	^2» • • • > Чт>
хг ха......х„) = 0,
1щ> Хр JVg, ...» Хп,
(15.14)
Fm(«p »2, .... ит, Хр xv ..., х„) = 0.
Изучим вопрос о разрешимости системы функциональных уравнений
(15.14) относительно uv иг, .... ит. Под термином «решение системы
(15.14)» мы в дальнейшем будем понимать совокупность т функций
(15.13) таких, что при подстановке этих функций в систему (15.14)
все уравнения этой системы обращаются в тождества. Это решение
мы будем называть непрерывным и дифференцируемым в некоторой
области D изменения переменных xv х2, ..., х„, если каждая из
функций (15.13) непрерывна и дифференцируема в области D. Дого-
воримся обозначать символом R пространство (тп-фя) переменных пр
п2, ..., ит, xv х2, ..., хп, а символом R' пространство п перемен-
ных xlt х2, ..., хп-
Рассмотрим т функций Flt F2, ..., Fm, стоящих в левых частях
системы (15.14), и составим из частных производных этих функций
следующий определитель:
Д =
д!\ dh
dut ди2
dF2 dF2
диг ди2
dFt
дит
dF2
дит
(15.15)
dFm dFm dFm
dut du2 ‘ * dum
538
ТЕОРИЯ НЕЯВНЫХ ФУНКЦИЙ И ЕЕ ПРИЛОЖЕНИЯ
[ГЛ. 15
Будем называть определитель вида (15.15) определителем Якоби*)
(или кратко якобианом) функций Ft, F2, •••> Fm по переменным ult
и2....ит и кратко обозначать символом
О (Л, F,...F т)
D (ut, и2, ..., ит) ’
Имеет место следующее замечательное утверждение. °
Теорема 15.2 (обобщение теоремы 15.1). Пусть т функций
ДхСд и2, ..	., 11т> Хр ..	Хп), '	
F2(uv «2- ••	• > • •	 > хп),	(15.16)
Рт(.Щ, и2, ..	• > ttnti	• •	 > хп)	
дифференцируемы в некоторой окрестности тонки Мй(йу, гг2,..<,
..., йт, xv .хп) пространства R, причем частные производные
этих функций по переменным uv и2, .ит непрерывны в точке тИ0.
Тогда, если в точке Л40 все функции (15.16) обращаются в нуль,
* D (fj, Г2, ..., Fm)	,
а якобиан	отличен от нуля, то для достаточно
D(ui, и2..ит)
малых положительных чисел ер е2,..., zm найдется такая окрест-
ность точки ТИо (л‘1..хп) пространства R', что в пределах
этой окрестности существуют единственные т функций (15.13),
которые удовлетворяют условиям | их — й j | < ер | и2 — й21 < е2,...
..., | ит — йт | < ет и являются решением системы уравнений (15.14),
причем это решение непрерывно и дифференцируемо в указанной
окрестности точки Al0.
Замечание. При /и=1 теорема 15.2 переходит в доказанную
выше**) теорему 15.1, ибо в этом случае якобиан (15.15) обращается
в частную производную дР^дщ.
Доказательство теоремы 15.2 проведем методом матема-
тической индукции. При т = Л теорема уже доказана. Поэтому доста-
точно, предположив теорему 15.2 справедливой для системы т— 1
функциональных уравнений, доказать справедливость этой теоремы и
для системы /п функциональных уравнений. Поскольку, по предполо-
жению, якобиан
dFt......"dFj"
диг ‘' di/fn-i
dFt
дит
Д-=Р(Л, Гг. Fm)
D(ult и2, .... ит)
dF т_2	dFm_t
ди,, '' • dum_i
dFm.....dFm
dut
dFm^
дит
dFm
дит
(15.17)
*) Карл Густав Яков Якоби — немецкий математик (1804—1851).
**) При этом следует учесть замечание 2 к теореме 15.1.
§ 3]
СИСТЕМЫ ФУНКЦИОНАЛЬНЫХ УРАВНЕНИЙ
539
отличен от нуля в точке Жо, то хотя бы один аз миноров (т — 1)-го
порядка *) этого якобиана отличен от нуля в точке >И0. Не ограни-
чивая общности, будем считать, что в точке /Ио отличен от нуля
обведенный пунктиром минор, стоящий в левом верхнем углу. Тогда,
в силу предположения индукции, первые т — 1 уравнений системы
(15.14) разрешимы относительно их, и2, ..., Точнее, для доста-
точно малых положительных чисел ех, е2, ет_х найдется такая
окрестность точки (ит, xlt х2, ..., хп) пространства/?” перемен-
ных (ит, xv xv ..., хп), что в пределах этой окрестности опреде-
лены т — 1 функций
хь х2, .... хл),
(15.18)
М-т-1 —'	(^т>	-^а> • • • >
которые удовлетворяют условиям | их — йх | < ех,..., | zz^j — йт_1 I <
< em-i и являются при наличии этих условий единственным непрерывным
и дифференцируемым решением системы первых от—1 уравне-
ний (15.14).
Подставим найденные функции (15.18) в левую часть последнего
из уравнений (15.14). При этом левая часть последнего из уравнений
(15.14) превращается в функцию, зависящую только от ит, xv...,xn
Fт (я1> • •  > ят-1> ят> •  • >	— Рщ [®1 (ят> • • • > Л-п), • • • >
.	(15.19)
(ят> • • • > %п)> Мт> %1> • •  > ^п] — (ят> -^1> • • • >
(эту функцию мы обозначили символом Ф). Таким образом, последнее
из уравнений системы (15.14) приводит нас к уравнению
Г(«т, Х1, .... х„) = 0.	(15.20)
В силу равенства (15.19) Ф(ит, хг, ..., х„) можно рассматривать как
сложную функцию своих аргументов. Тогда, применяя теорему о диф-
ференцируемости сложной функции, мы можем утверждать, что функ-
ция Ф(ит, хг, ..., хп) дифференцируема в некоторой окрестности
точки М"9(ит, хг, ..., хя) пространства R”. Равенство (15.19)
и последнее из уравнений (15.14) позволяет утверждать, что
Ф (ит, хь ..., х„) = 0. Поэтому, для того чтобы доказать, что к урав-
нению (15.20) применима теорема 15.1 и это уравнение разрешимо
относительно ит, достаточно установить, что частная производная —
непрерывна и отлична от нуля в точке М^. Для того чтобы сделать
*) Напомним, что минором (от — 1)-го порядка данного определителя т-го
порядка называется определитель (от—1)-го порядка, полученный из данного
определителя m-го порядка вычеркиванием одной строки и фщого столбца.
540
ТЕОРИЯ НЕЯВНЫХ ФУНКЦИЯ И ЕЕ ПРИЛОЖЕНИЯ
1ГЛ. 15
это, вычислим указанную частную производную. Подставим в пер-
вые от—1 уравнений системы (15.14) функции (15.18), являющиеся
решением этих уравнений, и продифференцируем полученные при
этом тождества по ит. Получим
, I dFl дФт-1 |	— О
5«1 дит "Г •' • *1' дит_г дит дит
(15.2 Р)
+	(15.2lm-i)
дит	дит_г дит ' дит	4	>
Далее продифференцируем по ит равенство (15.19). Получим
.	(i5.2im)
дит	дит_! дит дит дит	4	7
Умножим теперь равенства (15.211)—(15.21т) на соответствующие
алгебраические дополнения Дх, Д2, ..., Дт элементов последнего
столбца якобиана (15.17) и после этого сложим эти равенства. По-
лучим
т — 1
VI дФд Гд dFi . д dfi	д d-Ffril .
Л = 1
_i_ f Д Д
- д ^\ = Д
"+ тдит) тдит‘
Так как сумма произведений элементов данного столбца определи-
теля на соответствующие алгебраические дополнения элементов этого
(другого) столбца равна определителю (нулю), то каждая квадратная
скобка равна нулю, а круглая скобка равна якобиану (15.17).
Таким образом, мы получим
Д = Дт^.	(15.22)
иит
Здесь символом Д обозначен якобиан (15.17), а Дст — алгебраическое
дополнение последнего элемента последнего столбца, которое совпа-
дает с минором, обведенным пунктиром и, по предположению, отлич-
ным от нуля в точке 7И0. Поделив равенство (15.22) на Дт, окон-
чательно найдем
дчг _ Д
дит
Формула (15.23), справедливая в точке доказывает непрерывность
частной производной в точке (ибо Д и Дт состоят из част-
оит
ных производных функций (15.16) по «х, и2, ..., ит> непрерывных в
дФ"
точке Л40). Кроме того, из формулы (15.23) вытекает, что ч—в точ-
ке Mq отлична от нуля (ибо якобиан А отличен от нуля в точке Л40).
СИСТЕМЫ ФУНКЦИОНАЛЬНЫХ УРАВНЕНИИ
541
§ 31
Тем самым мы доказали, что к уравнению (15.20) можно применить
теорему 15.1.
Согласно этой теореме для достаточно малого положительного
числа найдется такая окрестность точки Л4о (хх............х„) прост-
ранства R', что всюду в пределах этой окрестности определена функция
nm = <pm(Xi, х2, ..., хп),	(15.24)
которая удовлетворяет условию j ит — iim | < sm и является при нали-
чии этого условия единственным непрерывным и дифференцируе-
мым решением уравнения (15.20). Имея в виду, что функции (15.18)
являются решениями первых т— 1 уравнений (15.14) при любых
ит, хр..., хп из окрестности точки Л4о, и вставляя найденную функ-
цию (15.24) в (15.18), мы получим функции, зависящие только от пе-
ременных хр ..., хп:
«1 = Ф1 [<Pm (*1,... > Хп), Х1г ..., Х„] - <рх (Хх.Xn),
«ш-1 ~ Фт-1 [’Pm (.Xi> •  •, Хп), Хр ..., Хл] —	(-*"1' • • • > Х^).
(Эти функции мы обозначили символами tpv ..., срщ.р) Теорема о диф-
ференцируемости сложной функции дает право утверждать, что каж-
дая из функций срр ..., (fm.! дифференцируема в окрестности точки
Мо (хр ..., хя). Таким образом, мы окончательно доказали, что т
функций
«i = tPi(^v	х^,
«2 = ?2(*1....хп),
— ?т (Х±, ..., Хп)
(15.25)
удовлетворяют в окрестности точки Мо условиям ]ях — ах | < sx, ...
..., |ит — ит | <ет и представляют собой при наличии этих условий
единственное непрерывное и дифференцируемое в некоторой окрестности
точки Мо(х...х„) решение .системы (15.14). Теорема 15.2 доказана.
2.	Вычисление частных производных функций, неявно определяемых по-
средством системы функциональных уравнений. В этом пункте мы предположим,
что выполнены условия теоремы 15.2, и займемся вычислением частных произ-
водных функций (15.25). Подставим функции (15.25) в систему уравнений (15.14),
решением которой эти функции являются, и продифференцируем получившиеся
тождества no х{ (I = 1, 2, ..., п). Получим
. I дит । dFi _р
диг dxi r'"r дит dxi ”г dxi ’
dFm ди-t	dF^ du„	dF**
dux dxi	dum dX{	dxt =
(15.26)
542
ТЕОРИЯ НЕЯВНЫХ ФУНКЦИИ И ЕЕ ПРИЛОЖЕНИЯ
(ГЛ. 15
Равенства (15.26) представляет собой линейную систему уравнений относи-
ли, дит ~
тельно т неизвестных .........."дх" <АПРеделитель этои системы якобиан
(15.17) отличен от нуля в окрестности точки Мо. Стало быть, система (15.26)
имеет единственное решение, определяемое формулами Крамера:
Wi.^2........Fm)
duk _ D («1, . uk_j, Xi, uk+1, ..., um)
dxt	D(F1, F2, ...,Fm)
D (ult u2....um)
Выражения для частных производных второго и последующих порядков *)
можно получить посредством дифференцирования этих формул.
3.	Взаимно однозначное отображение двух множеств zn-мерного простран-
ства. Рассмотрим в некоторой окрестности точки Мо (xlt ..., хт) т функций
и1 — ?1 (Х1..хт)’
“2.= 'f.2^’;,;/.'n.\ 	(!5.27)
Пщ ~ ?т (*1> ••• > xmF .
Рассматриваемые zn функций осуществляют отображение указанной окрестности
точки Л1о на некоторое множество {/V} zn-мерного пространства переменных
ut, и2.....ит. Это отображение называется взаимно однозначным, если каж-
дой точке из указанной окрестности точки Мо соответствует только одна точка
множества {.V}, так что при этом каждая точка множества {N} соответствует
только одной точке указанной окрестности точки Л40.
Из теоремы 15.2 непосредственно вытекает следующее утверждение.
Если функции (15.27) дифференцируемы в окрестности точки Л40, причем
все частные производные первого порядка непрерывны в самой точке Мо, а якобиан
fe1 — отличен от нуля в этой точке, то функции (15.27) осуществля-
и (хп .... хт)
ют взаимно однозначное отображение некоторой окрестности точки Л40(х1(...
..., xm) на некоторую окрестность точки No (иъ ..., ит), где U{ = <р(- (хх,..., хт)
(1=1, 2, ..., т).
В самом деле, соотношения (15.27) можно рассматривать как систему
функциональных уравнений относительно хк, х2,	, хт, для которой выпол-
нены условия теоремы 15.2. Но тогда эта система всюду в некоторой окрест-
ности точки Л'о («j...ит) имеет единственное решение:
Xj =	(«!,..., um), 1
..................... >	(15.27')
хт — Фт (н1> ••• > ит)- J
Очевидно, что функции (15.27') осуществляют обратное отображение.
Заметим, что в условиях сформулированного утверждения как функции
(15.27), осуществляющие прямое отображение, так и функции (15.27'), осуще-
ствляющие обратное отображение, являются непрерывными. Взаимно однознач-
ное отображение, обладающее таким свойством, называется гомеоморфным.
*) Существование этих частных производных обеспечивается дополнитель-
ными ограничениями на функции (15.16).
§4]
ЗАВИСИМОСТЬ ФУНКЦИЙ
543
§ 4.	Зависимость функций
1.	Понятие зависимости функций. Достаточное условие неза-
висимости. Пусть т функций от одних и тех же п переменных
“1 =	^2’ • • • > -^л),
tl2 ~ ?2 (Х1> Х2' •••> Хп)> ,	(15.28)
Um = 9 m (,xlt х& • • • > хп)
определены и дифференцируемы в некоторой открытой д-мерной об-
ласти *) D.
Будем говорить, что одна из этих функций, например ик, зави-
сит в области D от остальных функций, если сразу для всех
точек (хг, х2, хп) области D
ИЛ = Ф(И1,	Ий_1> «*+1> •••> ит\	(15.29)
где Ф — некоторая функция, определенная и дифференцируемая в
соответствующей области изменения своих аргументов. Функции ult
и2, ит будем называть зависимыми в области D, если одна из
этих функций (все равно какая) зависит в области D от остальных.
Если же не существует дифференцируемой функции Ф такой,
что сразу для всех точек области D справедливо тождество вида
(15.29), то мы будем называть функции uv и2, ..., ит независимыми
в области D.
Примеры. 1. Легко убедиться в том, что три функции четырех
переменных
И2 = Х1 + Х2 + Х3 4" Х4>
и3 = 2х1х2 + 2х1х3 + 2xrx4 + 2х2х3 + 2х2х4 + 2х3х4
зависимы в любой области D четырехмерного пространства, ибо для
всех точек (хр х2, х3, х4) этой области
Щ. = и% — и3.
2.	Покажем теперь, что две функции двух переменных иг = х +у
и и2 = х — у независимы в любой области D плоскости х, у, содер-
жащей начало координат. Ясно, что функция и± сохраняет постоянное
*) В частности, в качестве области D можно взять некоторую окрестность
фиксированной точки Мо n-мерного пространства.
544
ТЕОРИЯ НЕЯВНЫХ ФУНКЦИИ И ЕЕ ПРИЛОЖЕНИЯ
[ГЛ. IS
значение нуль на прямой = проходящей через начало коор-
динат (рис. 15.5). Но на этой прямой функция и2 имеет переменное
значение и2 = 2х. Поэтому на том участке этой прямой, который
лежит внутри D, и2 заведомо не зависит от wv Совершенно анало-
гично доказывается, что на лежащем
внутри области D участке прямой
х—у — 0 и2 = 0, и1 = 2х и, стало
быть, Wj не зависит от и2.
Замечание. В курсе линейной
алгебры вводится понятие линейной
зависимости функций: т функций ult
и2, ... , ит называются линейно зависи-
мыми в области D, если для всех
точек области D одна из этих функций
выражается в виде линейной функции
от остальных. Ясно, что линейная зави-
симость функций является частным
случаем зависимости этих функций, ибо,
если функции «1, и2, ... , ит линейно
зависимы в области D, то они зависимы в этой области, но существуют функ-
ции, зависимые в области D, но не являющиеся в D линейно зависимыми (на-
пример, функции, выписанные в примере I).
Теорема 15.3 (достаточное условие независимости функ-
ций). Пусть т функций от п~^т переменных
---Ф1 (j?l> • • • >	• • • >
И/п —	(-^i> • • • >	^т+1.-^л)
определены и дифференцируемы в окрестности точки Мо (х2, ..,
хт, хт+г,хп). Т огда если якобиан из этих функций по каким-
либо т переменным отличен от нуля в точке 7И0, то эти функ-
ции независимы в некоторой окрестности точки Мо.
Доказательство. Не ограничивая общности, будем считать,
что в точке 7И0 отличен-от нуля якобиан
D(ui, ц2, ит)
D (хъ х2, ..., xm)
(15.30)
Докажем теорему от противного.
м2, ..., ит зависимы в некоторой
из этих функций, например и*, для
ражается в виде
Предположим, что функции uv
окрестности точки Мо, т. е. одна
всех точек этой окрестности вы-
=	......ЙЛ-1, «ft+Р .... «т)>
где Ф —некоторая дифференцируемая функция. Пользуясь правилом
дифференцирования сложной функции, вычислим производную функции
§ 41
ЗАВИСИМОСТЬ ФУНКЦИИ
545
и* по любой из переменных xz(7=l, 2,	т). Будем иметь
диъ дФ ди! ,	.
dxi dut dxi '
<ЭФ
duk_! dxt
I ЗФ диА+1	<ЭФ дит
"г дим dxi	дит dxi
(7=1, 2, ..., т). (15.31)
Формулы (15.31), если их взять для каждого значения 7=1, 2,..., щ
в точке 7И0, говорят о том, что A-я строка якобиана (15.30) пред-
ставляет собой., линейную комбинацию остальных строк с коэффи-
<ЭФ <ЭФ	ЭФ дФ
циентами, соответственно равными	л. ...
г	диг ди2' ’	<Э“*+1’
.д—. Но в этом случае якобиан (15.30) равен нулю в точке Мо,
оит
что противоречит условию теоремы.
Пример. Уже рассмотренные выше две функции их = х-|-_у и
п2 = х— у независимы в окрестности любой точки М(х,у); ибо яко-
биан ! -! |=-2 °всюду-
2. Функциональные матрицы и их приложения. Снова рассмот-
рим т функций от п переменных (15.28):
Uj — <f>l (Хр -^2> • • • > -^п),
(Хр -^2’ * * • > Хл).
(15.28)
На этот раз предположим, что функции (15.28) определены и диф-
ференцируемы. в некоторой окрестности точки 7И0 (хр ..., хл),
причем все частные производные первого порядка этих функций
непрерывны в самой точке Л10.
Составим из частных производных функций (15.28) следующую
функциональную матрицу:
d<pi Aft	d?i
dxt дх2	' дхп
d?2	
дхг дхг	’ дхп
fym д,?т	d<fm
	
дхг дх2	' дхп
(15.32)
содержащую т строк и и столбцов.
Имеет место следующее утверждение.
Теорема 15.4. Пусть у функциональной матрицы (15.32):
1) некоторый минор г-го порядка*) отличен от нуля в точке
*) Напомним, что минором г-го порядка данной матрицы называется опре-
делитель, составленный из элементов, стоящих на пересечении каких-либо t
столбцов и г строк матрицы.	z
546
ТЕОРИЯ НЕЯВНЫХ ФУНКЦИЙ И ЕЕ ПРИЛОЖЕНИЯ
[ГЛ. 15
Мй (хх, х2, ..., хХ 2) все миноры, (г + 1)-го порядка равны, нулю
в некоторой окрестности точки А1о*). Тогда г функций, пред-
ставленных в указанном миноре т-го порядка, независимы в окрест-
ности точки Л40, каждая из остальных функций зависит в этой
окрестности от указанных г функций.
Доказательство. Не ограничивая общности, будем считать,
что в точке Мо. отличен от нуля минор, стоящий в левом верхнем
углу матрицы (15.32), т. е. отличен от нуля определитель
Арх Ctyi
дхх ’ ‘ ‘ дхг
d'fr drfr
dxL ‘' дхг
(15.33)
Тогда независимость в окрестности точки /Ио функций и1г и2, ..., иг
сразу вытекает из теоремы 15.3. Остается доказать, что любая из
функций иг+1....ит **) зависит в окрестности Мо от их, п2, ..., иг.
Докажем, например, что ur+1 зависит в окрестности точки Мо
от пх, и2, .. ., иг. Сосредоточим свое внимание на первых г функ-
циях (15.28). Если обозначить через uv ..., йг числа вида
Й1 = ох (хх, х2,..., хп),.. .,йг— vr (хх, х2, ..., х„), то всюду в некоторой
окрестности точки М0(йх, ..., йг, хх, ..., хл) (и + г)-мерного про-
странства первые г функций (15.28) представляют собой единственное
и дифференцируемое решение следующей системы уравнений ***):
Дх (их, ..., иг, Хр ...х„) = <f>! (Хр ..., х„) - их = О,
(15.34)
Fr («р ..., иг, Хр ..., хя) = <рг (Хр ..., х„) - иг = 0.
С другой стороны, поскольку якобиан
О (Л. Fr)
D (хр ..., хг)
совпадающий с минором (15.33), отличен от нуля в точке No, то
систему (15.34) можно в окрестности этой точки однозначно разре-
шить относительно хх, ..., хг. Иными словами, всюду в достаточно
*) В случае, если г = min (т, п), требование 2) следует опустить.
**) Конечно, при этом предполагается, что т>г.
***) В самом деле, в указанной точке No все функции Fx, .... Fr обра-
, D(Fi
щаются в нуль, а якобиан _ ;
D Щ
, •• , иг
условия теоремы 15.2.
= •(—1)г^£0, так что выполнены
§ 4]
ЗАВИСИМОСТЬ ФУНКЦИИ
547
малой окрестности точки No система (15.34) имеет единственное и
дифференцируемое решение
*1 = Ф1(г,1> •••> ип *г+1, > Хп},
(15.35)
хт = Фг(«1>  • • > «г> хг*п хп).
Подчеркнем, что равенства (15.35) и первые г равенств (15.28) пол-
ностью эквивалентны в окрестности точки No. В частности, если
подставить xv xv хг, определяёмые уравнениями (15.35), в пер-
вые г равенств (15.28), то указанные равенства обратятся в тождества
относительно хг+1, ..., хп, их, ..., иг. Дифференцируя эти тождества
по переменной xt (1= г 4- 1, ..., п) и замечая, что иь ..., иг не за-
висят от хг+1, ..., хп, будем иметь

Л^+..., + .^4^ + _^ = 0.	(15.369
dxt dxt 1 дхг дх; dxi .	4	'
Заметим, что равенства (15.361) (15.36г) справедливы для всех
значений переменных хр ..., хг, хг+1, ..., хп из некоторой окрест-
ности точки Мо.
Для того’ чтобы убедиться в том, что функция иг+1 зависит в не-
которой окрестности точки Мо от wx, ..., иг, подставим значения
хл, хг, определяемые уравнениями (15.35), в (г1)-е равен-
ство (15.28). При этом иг+1 превращается в функцию аргументов
И1....хг+1,	х„, ибо llr+i = <Pr+i (хь хг, хг+1, хп) =
= ?гц[Ф1(«1> •••> Х^у, ..., Хп)....... фг(«р ..Д 11г, Хг+р ..., Хп),
х^, ..., х„] = Ф(Ир ..., иг, хг+1, ..., хп) (эту функцию мы обозна-
чили символом Ф). Остается доказать, что для всех значений пере-
менных хх, ..., xr, xrV1> ..., хп, лежащих в достаточно малой
окрестности точки /Ио, функция. Ф не зависит от хг+1, ..., хп. Для
этого достаточно доказать, что для всех хх, ..., хп из достаточно
малой окрестности точки 7И0 справедливы равенства
-£- = 0	(/ = г+1, ..., п).	(15.37)
Продифференцируем функцию Ф по переменной xz(Z=r-]-l, ..., п)
как сложную функцию. При этом получим - 
+ ...+^±Ж+^±1 = ^.	(i5.36^+i)
dxt dxt 1	1 дхг дх{ 1 дХ{ dxi v 7
548
ТЕОРИЯ НЕЯВНЫХ ФУНКЦИЙ И ЕЕ ПРИЛОЖЕНИЯ
[ГЛ. 15
Рассмотрим теперь следующий минор (г4-1)-го порядка матри-
цы (15.32):
dtp!	<?<pi
дхг дхг dxi
d'tr	d'j}r	дч/г
дх,	' ‘	‘	дхг	dxi
d?r-n	d<?r+l	d?r+i
dxt	‘‘	dxr	dxi
(15.38)
По условию теоремы этот минор равен нулю всюду в окрестности
точки 7И0. Умножим равенства (15.361) — (15.36г+г) на соответ-
ствующие алгебраические дополнения Дх, ..., Дг, Дг+1 элементов
последнего столбца минора (15.38) и после этого сложим все эти
равенства. В силу теоремы о том, что сумма произведений элемен-
тов данного столбца на соответствующие алгебраические дополнения
элементов этого (другого) столбца равна определителю (нулю), по-
лучим *)
Д = ^Дг+1.	(15.39)
иЛ,1 ,
В равенстве (15.39) символ Д обозначает минор (15.38), равный нулю
всюду в окрестности точки Л10, а алгебраическое дополнение Дг+1
совпадает с минором (15.33), отличным от нуля в точке Л40, а стало
быть, и в некоторой окрестности этой точки**). Из равенства (15.39)
заключаем, что всюду в некоторой окрестности точки Мо справед-
ливы равенства (15.37). Теорема доказана.
Пример. Вернемся к исследованию зависимости функций
= + + +
и2 = хг -f- х2 4- х3 -ф х4,
и3 = 2хгх2 4- 2ххх3 4- 2ххх4 4- 2х2х3 + 2х2х4 + 2х3х4.
Функциональная матрица (15.32) имеет вид
2хх	2х2	2х3	2xt
1 1 1 1
2 (Х2 4- Х3 4- х4) 2 (хх 4- Х3 4- Х4) 2 (ХХ + х2 4- х4) 2 (хх 4- х2 4- х3)
Легко убедиться в том, что все определители 3-го порядка тожде-
ственно равны нулю, причем в любой точке пространства (х1, х2, х3, х4),
*) При этом мы повторяем рассуждения, подробно описанные на стр. 540.
**) Поскольку все частные производные, входящие в минор (15.33), не-
прерывны в точке Л40, то и сам минор (15.33) непрерывен в точке Мо.
Но тогда по теореме об устойчивости знака непрерывной функции этот
минор отличен от нуля не только в самой точке М9, но и в некоторой ее
окрестности.
§ 5]
УСЛОВНЫЙ ЭКСТРЕМУМ
549
у которой не все четыре координаты хь х2, х3, х4 совпадают, хотя
бы один из определителей второго порядка
2хг 2х2 2хг 2х3
11’ 11
2х2 2xt
1 1
отличен от нуля. Стало быть, в окрестности любой указанной точки
их и п2 независимы, а и3 зависит от и2 и и2.
§ 5. Условный экстремум
1. Понятие условного экстремума. В § 6 главы 14 мы занима-
лись отысканием локальных экстремумов функции, аргументы кото-
рой не связаны никакими дополнительными условиями. Вместе с тем
в математике и в ее приложениях часто встречается задача об отыс-
кании экстремумов функции, аргументы
которой удовлетворяют дополнительным
условиям связи. Экстремумы такого рода
мы будем называть условными, чтобы от-
личить их от (безусловных) экстремумов,
изученных в § 6 главы 14.
Приведем пример задачи об отыскании
условного экстремума. Пусть требуется
найти экстремум функции и — х2 +у2 при
условии, что аргументы этой функции удов-
летворяют условию связи х-\-у — 1 = 0. Та-
ким образом, экстремумы функции и —
— х2+у2 ищутся не на всей плоскости
Оху, а лишь на прямой х +у —1=0. Для
решения поставленной задачи подставим в
уравнение функции и = х2-|-у2 значение у,
определяемое из условия связи x-j-y— 1 = 0. Таким путем мы сведем
поставленную задачу к задаче об отыскании безусловного экстремума
функции и — 2х2 ~2х+ I.
Последний экстремум находится без труда: поскольку и' = 4 \ х —	,
п(2) _ 4, т0 фуНКцИЯ и — 2х2 -2x4-1 имеет минимум и = ~2 ПРИ х = -^-.
Таким образом, функция и = х24-_У2 с условием связи х+у— 1=0
1 /1 1 \
имеет условный минимум и = в точке (у, Отметим, что
безусловный минимум функции n = x24-J2 достигается в точке (0, 0)
и равен п = 0. Впрочем, даже из наглядных соображений (рис. 15.6)
очевидно, что минимум функции и = х24~_У2 (графиком которой слу-
жит параболоид вращения) на всей плоскости Оху не совпадает Фее
минимумом на прямой х +у — 1 = 0.
550
ТЕОРИЯ НЕЯВНЫХ ФУНКЦИИ И ЕЕ ПРИЛОЖЕНИЯ
ГГЛ. 15
Переходим к общей постановке задачи об отыскании условного
экстремума. Пусть требуется найти экстремум функции т 4- п пере-
менных
и =г=/(ХЬ	Хп, ух.....jm)	(15.40)
при наличии т условий связи
.... хп, у1г ..., ут) = 0, '
F2 (Х1,	Хп, У1, • ••> Ут) = 0,	(15 41)
Fm(xlt .... хп, ylt ут) = 0.
Прежде всего уточним само понятие условного экстремума функ-
ции (15.40) при наличии связей (15.41). Будем говорить, что функ-
ция (15.40) при наличии связей (15.41) имеет условный максимум
(минимум) в точке МДХр хп, уг..........._у™)> координаты кото-
рой удовлетворяют условиям связи (15.41), если найдется такая
окрестность точки Мо, в пределах которой значение функ-
ции (15.40) в точке Мв является наибольшим (наименьшим) среди
ее значений во всех точках, координаты которых удовлетво-
ряют условиям связи (15.41).
Для нахождения условного экстремума функции (15.40) при нали-
чии связей (15.41) предположим, что функции, стоящие в левых
частях равенств (15.41), дифференцируемы в некоторой окрестности
рассматриваемой точки Мо, причем в самой точке Л40 частные произ-
водные указанных функций по .......ут непрерывны, а якобиан
Д(Л.	Fm)
D (У ....Ут)
(15.42)
отличен от нуля.
В таком случае в силу теоремы 15.2 для достаточно малых поло-
жительных чисел вр е2, ..., ет найдется такая окрестность точки
Л4о(Хр ..., хп) пространства переменных (хь х„), что всюду
в пределах этой окрестности определены т функций
=	•••> хП),
У2 = Ъ(.х1....х„),
Ут~<?т(Х1> .... Х„),
(15.43)
удовлетворяющих условиям | Ji — Jl I < е1> • • • > IУт — Ут | <	И
являющихся при наличии этих условий единственным и дифференци-
руемым решением системы уравнений (15.41). Подставляя найденные
функции (15.43) в (15.40), мы сведем вопрос о существовании услов-
ного экстремума в точке Мо у функции (15.40) при наличии связей
(15.41) к вопросу о существовании безусловного экстремума в точке
§ 5]	УСЛОВНЫЙ ЭКСТРЕМУМ	551
Мд у сложной функции аргументов хь ..., хп
11 = / [-*"!> • • • >	91	• • • > -^л)> •  • > <?т (•#!>  • • > -^л)] ==
= Ф(ХХ, ..., хп). (15.44)
Вопрос о существовании безусловного экстремума функции (15.44)
может быть решен методами, указанными в § 6 главы 14 *). Изло-
женная нами общая схема сведения условного экстремума к безус-
ловному была реализована в рассмотренном выше частном примере.
Постараемся теперь, не прибегая к решению системы (15.41), уста-
новить по крайней мере необходимые условия существования услов-
ного экстремума в точке 7И0. Итак, пусть функция (15.40) дифферен-
цируема в точке А10 и имеет в этой точке условный экстремум при
наличии связей (15.41) или (что то же самое) функция (15.44) имеет
в точке Л4о безусловный экстремум. Согласно установленному в § 6
главы 14, необходимым условием безусловного экстремума функции
и — Ф (Xj...хп) в точке Мд является равенство нулю в этой точке
дифференциала этой функции
=	+	+	=	(15.45)
тождественное относительно dxit ..., dxn. В силу инвариантности
формы первого дифференциала и равенства (15.44) формулу (15.45)
можно переписать в виде
dll^^xldXi+-'-+6rndXn+'S{dyi+‘''+^dym^0- (15,46)
(В этой формуле все частные производные берутся в точке Af0.)
Подчеркнем, однако, что в равенстве (15.46) dyr... dym пред-
ставляют собой дифференциалы функций (15.43), так что равенство
(15.46) не является тождеством относительно dylt ..., dym. Предпо-
ложим, что в уравнения связи (15.41) мы подставили функции (15,43),
являющиеся решением системы (15.41). При этом уравнения (15.41)
обратятся в тождества, и мы получим, дифференцируя эти тождества,
............................................. (15.47)
^dx1 + ... + ^dxn + ^dy1 + ... + ^dym = O.
dxt 11 дхп n ' dt/i 1	1 dym	J
Так как якобиан (15.42), по предположению, отличен от нуля в точке Мо,
то из линейной системы (15.47) dylt dym могут быть выражены *•)
*•) При этом, конечно^ придется подчинить функцию (15.40) некоторым
условиям.
552
ТЕОРИЯ НЕЯВНЫХ ФУНКЦИИ И ЕЕ ПРИЛОЖЕНИЯ
ГГЛ. 15
как линейные функции dxlt dxn. Если найти эти выражения
и подставить их в (15.46), то, собирая в полученном равенстве члены,
содержащие dxlt ..., dxn, мы будем иметь
A^dXi +... + Andxn — О,
(15.48)
где через Аг, ..., Ап обозначены некоторые рациональные функции
частных производных /, Fv Fm в точке 7И0. Так как в равен-
стве (15.48) фигурируют лишь дифференциалы независимых пере-
менных, то из этого равенства заключаем, что Л1 = 0, Дл = 0.
Присоединяя к указанным равенствам т условий связи (15.41), мы
получим необходимые условия существования условного экстремума
функции (15.40) при наличии связей (15.41) в виде
41 = 0....А„ = 0, Fi = 0, FOT = 0.	(15.49)
Равенства (15.59) представляют собой систему от + п уравнений для
определения туп координат точки возможного экстремума.
2.	Метод неопределенных множителей Лагранжа. При изло-
женном выше методе отыскания точек возможного условного экстре-
мума мы нарушили симметрию в отношении переменных хь ...
...,хп,уь .ут. Часть из этих переменных .... хп мы рассмат-
ривали как независимые, остальные — как функции этих переменных.
В ряде' случаев это приводит к усложнению выкладок. Лагранжей
предложен метод, симметризирующий роль переменных. Изложению
этого метода и посвящен настоящий пункт. Умножим равенства
(15.47) соответственно на произвольные (и пока еще неопределенные)
постоянные множители ........Хот. Полученные после умножения
равенства сложим почленно с равенством (15.46). В результате
получим следующее равенство:
ЭФ ,	,	, № ,	, dW ,	.	, dV , Л
+	+	+	=	(15.50)
где символом Це (xx, .... хп, ylt ..., ут) обозначена следующая функ-
ция
W = /+X1Fi + -.- + XmFm-	(15.51)
Эту функцию мы в дальнейшем будем называть функцией Лагранжа.
Считая, что для функций (15.41) выполнены условия, сформули-
рованные в предыдущем пункте, и что функция (15.40) дифферен-
цируема, выберем множители ..., \т так, чтобы выполнялись ра-
венства
<w _n	&W_
dyt~   tym
(15.52)
Это заведомо можно сделать, ибо равенства (15.52) приводят к
S 51
условный экстремум
553
линейной системе
определитель которой (якобиан (.15.42)) отличен от нуля. В силу ра-
венств (15.52) равенство (15.50) принимает вид
aw	лчг
к«х1+... + ^.^ = °.	(15.53)
Поскольку при сделанных .выше предположениях переменные
х1г .... хп являются независимыми, то из равенства (15.53) заклю-
чаем, что
Присоединяя к уравнениям (15.52) и (15.54) условия связи
мы получим систему n-f-2(w уравнений
=	=0,^ = 0,..., ^ = 0,1
дх! ’ дха di/t	дут
Ft = O..... Fm = 0
(15.41),
(15.55)
для определения п-}-т координат точек возможного условного экст-
ремума и т множителей Хх, ..., ~кт. Практически при реализации
этого метода поступают следующим образом. Составляют функцию
Лагранжа (15.51) и для этой функции находят тонки возможного
безусловного экстремума. Для исключения множителей Хх, ..., Хт
привлекают условия связи (15,41). Такой путь отыскания точек воз-
можного условного экстремума является законным, ибо он приводит
нас как раз к системе и4-2от уравнений (15.55). Пример применения
метода множителей Лагранжа будет рассмотрен в п. 4.
3.	Достаточные условия. В этом пункте мы рассмотрим один
из путей дополнительного исследования точек возможного условного
экстремума. Предположим, что в точке Mo выполнены необходимые
условия экстремума (15.55). Кроме того, дополнительно потребуем
двукратной дифференцируемости функций (15.40) и (15.41) в окре-
стности точки Мо и непрерывности всех частных производных 2-го
порядка в самой точке Л10. Из конструкции функции Лагранжа
(15.51) очевидно, что при наличии связей (15.41) экстремумы функции
(15.40) и функции Лагранжа совпадают *). Но тогда из результатов § 6
главы 14 вытекает, что для получения достаточного условия экстремума
*) Это вытекает из того, что при наличии связей (15.41) разность
/ (М) — f (Mg) совпадает с разностью ЧГ (/И) — W ((Ио).
554
ТЕОРИЯ НЕЯВНЫХ ФУНКЦИИ И ЕЕ ПРИЛОЖЕНИЯ
[ГЛ. 1S
в точке 7И0 у функции (15,40) при наличии связей (15.41) следует,
присоединить к условиям (15.55) требование знакоопределенности
в этой точке d24'. При этом в соответствии с результатами § 6
главы 14 мы можем констатировать наличие, в точке Л40 минимума,
если при наличии связей (15.41) d2'i‘ |м0> 0, и максимума, если
<W|mo<0. Сделаем еще несколько замечаний практического ха-
рактера. Прежде всего отметим, что второй дифференциал о!2ЧГ
можно в данной точке Л1о возможного экстремума вычислять
так, как если бы все переменные хь ..., хп, ..., ут были
независимыми. В самом деле, в общем случае второй дифферен-
циал d2W функции ЧТ не обладает свойством инвариантности формы
и должен был бы с учетом зависимости	ут от xlt хп
определяться равенством
=	+-+^+<й,4 +---+*4;),'г +
+ — d2yt +... +	d2ym.
dyi 'Л1 ' п дут -Ут’
Но в точке возможного экстремума Мо справедливы равенства
^ = 0......^ = 0,
дУ1	дут
так что d2W определяется той же формулой
СТ = (^1Д + ... + ^ + <у, А +... + ЙЛ(15.56)
что и в случае, когда все переменные хь хп, ylt .... ут незави-
симы. Далее, заметим, что поскольку нам требуется установить
знакоопределенность d2}P лишь при наличии связей (15.41), то при
проведении вычислений следует в формулу (15.56) для й2Ф под-
ставить вместо dyb dym их значения, определяемые из системы
(15.47). После этого следует изучить вопрос о знакоопределенности
dW в данной точке Л40. Теперь мы можем перейти к рассмотрению
примера.
4.	Пример. Предположим, что нам требуется найти максимальное
и минимальное значения величины определителя
Xi Ух ...
Д — Xz У2 ••• Z2
(15.57)
Хп Уп ••• zn
причем известна сумма квадратов элементов каждой строки этого
определителя. Задача сводится к отысканий экстремальных значений
УСЛОВНЫЙ ЭКСТРЕМУМ
555
§ 5J
функции ла переменных (15,57) при наличии следующих п условий
связи *)
+ ••• +2’1 = й1,
Х1 + • • • 4- А — hz, .	(15 58)
Хп + Уп + • • • + z„ = hn,
где ftp ft2, hn— заданные положительные числа**). Для решения
поставленной задачи рассмотрим и решим более простую задачу.
Фиксируем у определителя (15,57) в экстремальной точке эле-
менты всех строк, за исключением одной k-й строки. В таком
случае определитель: (15.57) можно рассматривать как функцию п
переменных xk, yk, , zk. Явное выражение этой функции можно
получить, разложив определитель по элементам А-й строки:
Д =	••• -\~ZkZk-	(15.59)
Здесь через Xk, ..., Zk обозначены алгебраические дополнения
соответствующих элементов хк, ук, ..., zk. Так как элементы всех
строк определителя, кроме А-й, фиксированы в экстремальной точке,
то Хк, Уь-, ..., Zk можно рассматривать как постоянные числа.
Поставим задачу об отыскании экстремумов функции (15.59) при
наличии одного условия связи ***)
Xk 4~ yl + • • • 4~ Zk — hk-	(15.60)
Для решения этой задачи составим функцию Лагранжа •
ЧГ = XkXk + Уь Yk 4* ... + ZkZk 4- (х| 4-ук 4-... + z"k — hk), (15.61)
и для этой функции решим вопрос о безусловном экстремуме.
Из условий
лиг
а=^+2Лх,=о,
» = у,+2>.л»о.........»=г,+аг,=0
находим координаты точки возможного экстремума
h	Уb	Zh	л хълх
Хь~~1У' ^ = —2Х’’ •••’ 2* = —2Г"	(15.62)
*) Вопрос о существовании экстремальных значений не вызывает сом-
нений, ибо функция (15.57) является непрерывной функцией своих па пере-
менных на замкнутом множестве (15.58).
**) Мы опускаем тривиальный случай, когда хотя бы одно из чисел
Ль h2, ... , hn равно нулю. В этом случае определитель (15.57) тождественно
равен нулю.
»»•) В качестве этого условия мы берем й-е из условий (15.58).
556
ТЕОРИЯ НЕЯВНЫХ ФУНКЦИЙ И ЕЕ ПРИЛОЖЕНИЯ
ГГЛ. 15
Постоянный множитель X легко исключить из условия связи (15,60).
Из этого условия находим два значения:
^/Х8+^"-+гг>0. ч=_/5±Д™<0.
(При этом мы снова опускаем тривиальный случай, когда все Xk,
Yk, .... Zk равны нулю, ибо в этом случае определитель (15.59)
тождественно равен нулю.)
Таким образом, мы получаем две точки возможного экстремума:
лл ! Xjg	Yь	Zjf \	( Xk Y/g	Zb \
— 2X7’ •••’ — 2X7) и	~2V •••’
Докажем, что в точке Л4Х реализуется условный минимум, а в точке
А42 — условный максимум. Для этого вычислим второй дифферен-
циал d2W функции Лагранжа (15.61). Легко видеть, что
,d2W = 2Х [(dxft)3 + (dyk)2 + ... + (dzk)2].
Из последней формулы вытекает, что d2W представляет собой поло-
жительно определенную квадратичную форму при Х==Хг>0 (т. е.
в точке и отрицательно определенную — при X = Хг <; 0 (т. е.
в. точке ТИ2). Итак, функция (15.59) при наличии связи (15.60) имеет
условный минимум в точке М1 и условный максимум в точке Л12.
Не вычисляя наибольшего и наименьшего значений функции (15.59) при
наличии условия (15.60), заметим, что в той точке, в которой дости-
гаются эти значения, справедливы равенства (15.62), а стало быть,
справедливы равенства
*	*fe —Уь
Xk Yk
(15.63)
2Г
Возвратимся теперь к вычислению экстремальных значений опреде-
лителя (15.57) при наличии п связей (15.58). Сохраняя смысл при-
нятых выше обозначений Xk, Yk, ... , Zft, согласно известному
свойству определителя для любого I, отличного от k, можем записать
XiXb+ytYkA- ... +*,-Zft = 0	Ц^к).	(15.64)
Из равенствД 15.63) и (15.64) находим, что
XtXk+yiyk-^ ••• +^ = 0 (при l^k).	(15.65)
Равенства (15.58) и (15.65) и правило перемножения определителей
позволяют заключить, что при умножении определителя Д самого
на себя получается определитель, все элементы которого равны
нулю, за исключением элементов главной диагонали, которые равны
соответственно hlt h2, , hn. Таким образом,
Д.Д = Д2=;й1/г2 ... hn.
Стало быть, максимальное и минимальное значения величины опре-
ДОПОЛНЕНИЕ К ГЛАВЕ 15
557
делителя (15.57) при наличии условий (15.58) соответственно равны
+ рл/г1/г3 ... hn и — КМ*2 ••• hn. Тем самым мы получаем, что
... hn,
ИЛИ
|.А|V(xj + ... +zl)(xl+ ... +г|) ... (хН ... +г%. (15.66)
Последнее неравенство, справедливое для произвольного определи-
теля (15.57), называется неравенством Адамара*).
Замечание. При п = 3 неравенство Адамара (15.66) допускает
простую геометрическую интерпретацию. В этом случае | А | представ-
ляет собой объем параллелепипеда, построенного на отрезках 0Alt
ОА2 и ОА3, соединяющих начало координат О с точками Ах (xx, у2, zx),
А2 (х2, у.2, z2), А3 (х3, у3, z3). Неравенство (15.66) утверждает, что
из всех параллелепипедов, имеющих ребра данной длины, наиболь-
ший объем имеет прямоугольный параллелепипед.
ДОПОЛНЕНИЕ к ГЛАВЕ 15
ЗАМЕНА ПЕРЕМЕННЫХ
В ряде вопросов анализа и других разделов математики встречается
задача о замене переменных. Эта задача заключается в следующем. Предпо-
ложим, что нам задано некоторое выражение
(15.67)
содержащее независимые переменные х, у, функцию г — г(х, у) и ее част-
ные производные. Вместо независимых переменных х и у и функции z =
= z (х, у) вводятся новые независимые переменные и и v и новая функция
а> = w (и, v), причем заданы соотношения, посредством которых и, v и w
выражаются через х, у и г:
и = ¥ (х, у, г),
о = ф(х, у, г),
и> = Х(*. у, г).
(15.68)
Требуется преобразовать выражение (15.67) к новым переменным и, v и а>.
При этом мы будем предполагать, что функции (15.68) достаточное число
раз дифференцируемы и что систему (15.68) можно разрешить относительно
х, у и г, а первые дйа уравнения (15.68) — относительно х и у.
Очевидно, для решения поставленной задачи достаточно выразить част-
dz dz	dw ди>
ные производные 3-, ... через и, v, w,	, ... Укажем, как это
дх’ ду'	ди' dv ’
можно сделать.
') Жак Адамар — французский математик (1865—1963).
558
ТЕОРИЯ НЕЯВНЫХ ФУНКЦИИ И ЕЕ ПРИЛОЖЕНИЯ
[ГЛ. 15
Имея в виду, что г = г (х, у), a w = w (и, о), запишем первые дифферен-
циалы функций (15.68). Получим
,	д<? , , да , , <Эф .	дш , 5ф . . 5ф fdz , , дг , \
du = д5- dx + J- dy +-£- dz = dx + д1 dy + U- dx + =- dy I,	(15.69)
dx dy dz dx dy dz \dx ' dy a j ’	'	'
, dfy . , di/ , . dty дф , дф дф fdz , . дг \
du = д~ dx 4- д3- dy + -J- dz = dx + д!- dy + k- dx -ф д- dy], (15.70)
dx ' dy dz dx dy ' dz \dx 1 dy ]' 4	’
, dw , . dw , dy , . dy , , д'/ fdz , , dz , \
dw = 4— du + д— dv = д^ dx +	dy + -£ у dx + -^-dy .	(15.71)
du dv dx dy ' dz \dx dy yj
Подставляя в (15.71) du и dv, определяемые формулами (15.69) и (15.70), и
приравнивая коэффициенты при dx и dy, получим систему двух уравнений
da> Гд<Р	дер дг!	dw	Гдф	дф	дг 4	ду	ду	дг
ди [дх + дг дх] ’’’dv	[дх ' дг	дх] ~	дх ' дг	дх'
дю Гдер	.	дер дг!	дш	Гдф	дф	дг! _	ду	ду	дг
ди [ду	дг ду J	до	[ду	дг	ду J —	ду	дг	дх ’ .
дг	dz
из которой легко выразить	и д-; dy dw дер , dw дф ду
дг	ди дх dv дх дх
дх ~~	dw дер	dw дф	ду du дг	dv дг	дг dw дер	,	dw дф	ду
дг	ди ду dv ду ду
dy~	dw д<р dw дф ду ди дг ' до дг дг
Если выражение (15.67) зависит' также и от частных производных второго
порядка, то для определения этих производных через частные производные
w по и и v следует записать первые дифференциалы от уже вычисленных
производных первого порядка.
Замечание 1. Аналогично производится замена и в случае, когда
старые переменные связаны с новыми не соотношениями (15.68), а неявными
соотношениями вида *)
Фх (и, v, w, х,	у,	г) = 0,	1
Ф2 (и, v, w, х,	у,	г) = 0,	|	(15.72)
Ф3 (и, v, w, х,	у,	г) = 0.	)
Замечание 2. Мы ограничились случаем двух независимых перемен-
ных лишь для сокращения записи. Указанный прием применим для случая
любого числа независимых переменных (и, в частности, для случая одной
независимой переменной).
Пример. Пусть г есть функция переменных х и у. Преобразовать
выражение **)
г А д=г , д2г
F = Дг =	+ и-.
дх2 ду2
*) Допускающими, конечно, разрешимость как относительно и, о и w,
так и относительно х, у и г.
**) Указанное выражение называется оператором Лапласа. Оно играет
важную роль в математике и ее приложениях. Пьер Симон Лаплас — фран-
цузский астроном, математик и физик (1749—1827).
ДОПОЛНЕНИЕ К ГЛАВЕ 15
559
к полярным координатам и u v:
x — ucosv, y = usinv.	(15.73)
Отметим, что в данном примере производится лишь замена независимых
переменных. Функция г остается при этом неизменной. Из (15.73) вытекает, что
dx —cosvdu — и sin v dv, dy = sin v du 4- и cos v dv,
поэтому из соотношений
, дг . , дг , ’дг , . дг ,
dz = х- dx + dy = 5— du + =- dv
дх ' ду du dv
имеем
дг .	,	.	, , . дг , .	, ,	, . дг . , дг .
(cos v du — и sin v dv) + (sm v du 4- и cos v dv) = du 4- dv
Приравнивая коэффициенты при du и dv, найдем
дг , дг . дг
з— cos v + 5— sin v = v-,
дх ду ди ’
дг	.	, дг	дг
— з— и sm v 4- з— u cos и = =—,
дх	ду	dv
Отсюда
дг
— = C0S V
дх
дг
х— = sm v
ду
дг	1 . dz
	— sin V =—
du	и	dv
	1	dz
-i- ди "г	— COS V -=r- u	dv
(15.74)
d2z	д2г & (у
Найдем теперь Так как = . -—, то из первой формулы (15.74)
находим
d2z	\5x}	\dx)
dx2	dx	du
дг
1 д F
1 . \дх /
— sm v —5—- =
и dv
~ ।	1 . дг! 1 . д Г dz 1 . дг
= cos о 3— cos v 3---sin v 3-------sm v 5- cos v 5-----sin v
ди I ди и dv J и dv I ди и dv
du
После вычислений получим
д2г , д2г 2 .
з-- = COS2 V 5-5---sm V COS V a
дх2 ди2 и	dudv
д2г , 1 . , д2г ,
sm2 V 5-- +
и2 dv2
, 1 . „ дг . 2 . дг
4—- sm2 v 3—)- — sm v cos v
u ди и2	dv
Аналогично, из второй формулы (15.74) находим
„	5 ЬгЧ д л1 1 д F
52z	\ду /	. \ду /	, 1	\ду	/
-4 = -	= sm v -у  4--cos и  -V - =
ду2	ду	ди и	dv
. „ д2г 2 . д2г 1 д2г 1 дг 2 . дг
= sm2 v з-» 4-sm v cos v , ., 4- -= cos2 05-5-4-cos2 v 5-„ sm v cos v x-.
ди2	и	dudv ' и2 dv2 1 и ди	и2	dv
Таким образом, в полярных координатах и и v оператор Лапласа Дг =
д2г , д2г
=	имеет следующий вид:
_д2г_ 4- — — 4- — —
г ~~ ди2 и ди и2 dv2'
ГЛАВА 16
НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ
ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
§ 1.	Огибающая и дискриминантная кривая
однопараметрического семейства плоских кривых
1.	Предварительные замечания. Мы будем задавать плоские
кривые либо при помощи параметрических уравнений
X = <р(а), J = t|»(a),	(16.1)
где а—некоторый параметр, либо при помощи уравнений вида
F(-v,j) = 0.	(16.2)
В дальнейшем нам понадобятся понятия обыкновенной и особой то-
чек кривой.
Пусть кривая L определяется параметрическими уравнениями (16.1),
причем функции х = <?(а) и _у = <р(а) имеют при а = а0 непрерывные
производные. Точку Af0(x0,j/0) кривой L, координаты х0 и _у0 кото-
рой соответственно равны <р(а0) и ф(а0), назовем обыкновенной, если
?'а(«о) + Г(«в) 0.	(16.3)
Если же при а = % выполняется соотношение
ф'9(%) + ф'8(«о) = О,	(16.4)
то точку А10 мы назовем Особой точкой кривой L.
Пусть кривая L определяется уравнением (16.2), причем функция
F(x,y) дифференцируема в некоторой окрестности точки Д40(хй,у0)
этой кривой и имеет в указанной точке непрерывные частные произ-
водные по х и у. Точку Л!0(х0,_у0) назовем обыкновенной точкой кри-
вой L, если в этой точке выполняется соотношение *)
F'j + /7^0.	(16.5)
*) Понятия обыкновенной и особой точек для кривой (16.2) уже были вве-
дены в п. 3 § 2 главы 15.
§ 1]	ОГИБАЮЩАЯ И ДИСКРИМИНАНТНАЯ КРИВАЯ	561
Если же в точке Мв выполняется соотношение
+	=	(16.6)
то эту точку мы назовем особой точкой кривой L. Убедимся, что
если точка Л40 кривой L является обыкновенной, то в некоторой
окрестности этой точки кривая L представляет собой либо
график некоторой дифференцируемой функции у—f (х), либо гра-
фик некоторой дифференцируемой функции x=g(y). В самом
деле, пусть кривая L определяется параметрическими уравнениями
(16.1) и, кроме того, выполнено условие (16.3). Из непрерывности
производных <р'(а) и при 0- = % и из условия(16.3) вытекает,
что в некоторой окрестности. а0 хотя бы одна из этих производных,
например <р'(а), не равна нулю. Тогда функция х — <р(а) является
дифференцируемой строго монотонной функцией в отмеченной окре-
стности. При этих условиях существует дифференцируемая монотон-
ная обратная функция а — ®-1 (х). Подставляя эту функцию в выраже-
ние у — ф (а), мы убедимся, что кривая L в некоторой окрестности
точки Л40 представляет собой график дифференцируемой функции
у =/(х) = <р [ср-1 (х)]. Справедливость сформулированного утверждения
для случая, когда кривая задается при помощи уравнения (16.2),
вытекает из того, что в окрестности обыкновенной точки действует
теорема 15.1 о неявных функциях, и поэтому прилегающий к обык-
новенной точке участок кривой представляет собой график дифферен-
цируемой функции y—f(x) или функции x = g(j).
Замечание 1. В геометрии точку/Ио кривой L называют обыкновен-
ной, если в некоторой окрестности этой точки кривая L представляет собой
график некоторой дифференцируемой функции, и особой, если в любой окрест-
ности этой точки кривая L не может быть представлена в виде графика
дифференцируемой функции.' Мы видели, что точка кривой L, являющаяся
обыкновенной согласно нашему определению, будет также обыкновенной
с геометрической точки зрения. Можно привести примеры, когда точка кри-
вой, являющаяся особой по нашему определению, будет обыкновенной с гео-
метрической точки зрения. Таким образом, наше определение обыкновенной
точки является более узким, чем геометрическое, но более удобным для
приложений.
Введем теперь понятие касания кривых Li и 1ав их общей точке
Мо. Будем говорить, что кривые Li и La касаются в их общей
точке тИ0, если обе кривые имеют в точке Л10 касательные и эти
касательные совпадают.
В дальнейшем нам понадобится условие касания двух кривых
Li и L$
Пусть кривая Li определяется уравнением (16.1), а кривая Lt — урав-
нением (16.2) и Л/0(х0,_у0) — общая точка этих кривых (при этом
координаты ха и _у0 отвечают значению а = а0 параметра а). Будем
считать, что точка Мо является обыкновенной точкой кривых Li и La
и эти кривые касаются в точке 7И0. Тогда эти кривые представляют
562
ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ДИФФЕРЕНТ ИСЧИСЛЕНИЯ (ГЛ. IS
собой в окрестности Л10 графики дифференцируемых функций. Ради
определенности будем считать, что и L2 являются графиками
функций y = f\(x) и y=f2{x). Так как по условию кривые* Ьг и L2-
касаются в точке А10 (х0,у0), то угловые коэффициенты касательных
в Л,, к графикам функций /х(х) и /2(х) равны, т. е.
71 (АГо)=Х2(АГо).	(16.7)
Используя формулы дифференцирования функций, заданных парамет-
рически (см. § 11 главы 5), и формулы дифференцирования неявных
функций (см. п. 2 § 2 главы 15), получим
. F'x(Ma)
(cto). /2(х0)- jggg-	(16.8)
Формулы (16.8) позволяют придать равенству (16.7) следующий вид:
или
Fx (Жо) ? (а0) + F'y (Мо) ф' (а0) = 0.	(16.10)
Последнее соотношение мы будем в дальнейшем называть условием
касания в точке /Ио кривых Lr и L2, заданных соответственно урав-
нениями (16.1) и (16.2). Опуская аргументы функций и используя
, dx ,, dy
обозначения ? — и ф = мы запишем условие касания в следую-
щей форме:
=	(16.11)
Замечание 2. Если в общей точке 7И0 кривых и Z,2, задан-
ных соответственно уравнениями (16.1) и (16.2), выполнено условие
касания (16.10) (или, что то же самое, (16.11)) и если при этом
точка Мо является обыкновенной точкой кривых L± и L2, то кривые
и L2 касаются в точке Л10. В самом деле, из соотношений (16.3),
(16.5) и из условия (16.10) вытекает либо условие (16.9), либо условие
<?' («о) F (Мо)
у = —р? у, т‘ е‘ Равенств0 угловых коэффициентов касатель-
ных в общей точке 7И0 кривых и L2. Это и означает, что кривые
Li и L2 касаются в 7И0. Заметим, что условие касания выполняется
также и в случае, когда точка Мц является особой точкой по край-
ней мере одной из кривых Lx и L2.
Итак, условие касания (16.10) выполняется как в случае, когда
кривые Li и L2 касаются в точке Л10, так и в случае, когда Л10
является особой точкой по крайней мере одной из этих кривых.
§ 1]
ОГИБАЮЩАЯ И ДИСКРИМИНАНТНАЯ КРИВАЯ
563
2.	Однопараметрические семейства плоских кривых. Характе-
ристические точки кривых семейства. В различных геометрических
и физических задачах часто встречаются семейства плоских кривых.
В геометрической оптике
рассматриваются отражен-
ные и преломленные пучки
(семейства) лучей, в меха-
нике — семейства возмож-
ных траекторий материаль-
ной частицы в данном поле
сил, в геометрии — семейства
касательных к кривым ли-
ниям. Один из возможных
способов задания такого
рода семейства линий заклю-
чается в следующем. Рас-
сматривается функция F (х,у, а) трех переменных х, у, а и для
каждого значения параметра а из данного множества {а} *) определя-
ется кривая семейства при помощи
уравнения
F (х, у, а) = 0.	(16.12)
Мы будем говорить, что соотно-
шение (16.12) определяет однопара-
метрическое семейство плоских кри-
вых. Параметр а будем называть пара-
метром семейства.
Рассмотрим примеры однопарамет-
рических семейств плоских кривых.
1°. Уравнение у — (х— а)2 = 0 оп-
ределяет семейство парабол, получае-
мых сдвигом по оси Ох параболы
у — х2 = 0 (рис. 16.1).
2°. Уравнение (у — а)а — (х— а)3 = О
определяет семейство полукубических
Рис. 16.2.	парабол, полученных параллельным
сдвигом вдоль биссектрисы первого
координатного угла полукубической параболы _у2 = х3 (рис. 16.2).
Пусть функция F (х, у, а) является дифференцируемой функцией
в области ее задания. В этом случае можно ввести понятие характе-
ристической точки кривой семейства, определяемого соотношением
(16.12). Точка М(х, у) называется характеристической точкой
кривой семейства (16.12), отвечающей данному значению а параметра
) Обычно множество {а} представляет собой некоторый интервал.
564
ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ДИФФЕРЕНТ!. ИСЧИСЛЕНИЯ [ГЛ/ 16
семейства, если координаты х и у этой точки удовлетворяют системе
уравнений
F (х, у, а) = О, |
Fл(х, у, а) = 0. )
(16.13)
Рассмотрим геометрическую интерпретацию характеристической точки
кривой семейства (16.12). Для простоты ограничимся случаем, когда
любые две кривые семейства пересекаются * ). Пусть La и Ля+дя—две
кривые семейства (16.12), отвечающие зна-
чениям параметра а и а-}-Да (рис. 16.3).
Координаты точки М их пересечения удов-
летворяют следующей системе уравнений:
F (х,у, а) = 0, F (х,у, а 4- Да) = 0
или равносильной системе
F(x,y, а) = 0,
F (х, </, а 4-Да) — F (х.у.п) _0
Да
Если Да->0, то точка N, расположенная на кривой F(x,y, а) = 0,
стремится, вообще говоря, к некоторой точке М на этой кривой.
... F (х, у, a -J- Да)—F (х, у, а) _. .	.
Так как lim ————--------------———— = Рл(х,у, а), то координаты
Да — 0	Да
точки М удовлетворяют уравнениям (16.13), и поэтому точка М яв-
ляется характеристической точкой кривой семейства. Итак, характе-
ристическая точка данной кривой — это та точка, которая служит пре-
делом при Да->0 точек пересечения данной кривой La и близкой
к ней кривой
3.	Огибающая и дискриминантная кривая однопараметриче-
ского семейства плоских кривых. Пусть однопараметрическое семей-
ство плоских кривых определяется соотношением (16.12). При этом
мы будем считать, что функция F (х,у, а) является дифференцируе-
мой в области ее задания. Введем понятие огибающей, семейства кри-
вых (16.12).
Огибающей однопараметрического семейства кривых (16.12)
называется кривая О, которая 1) в каждой своей точке каса-
ется только одной кривой семейства (16.12), 2) в разных
точках касается различных кривых указанного семейства.
Наглядные геометрические соображения наводят на мысль о том, что
огибающая касается кривых семейства в характеристических точках
*) Существуют такие семейства кривых, любые две кривые которых не
пересекаются. Примером такого семейства может служить семейство парабол,
определяемых уравнением у— (х— а)з = 0.
§ И
ОГИБАЮЩАЯ И ДИСКРИМИНАНТНАЯ КРИВАЯ
565
а параметра семейства
значению
Рис. 16.4.
определенных условиях может рассмат-
место характеристических точек кривых
характеристических точек кривых
каких условиях дискриминантная
этих кривых и поэтому при
риваться как геометрическое
семейства. В самом деле, пусть М — точка касания огибающей О и
кривой £а семейства, отвечающей
(рис. 16.4), Р — точка касания
огибающей О и кривой £а+да се-
мейства, отвечающей значению
а-|-Да параметра, и N—точка
пересечения кривых £а и £а+да.
Наглядно ясно, что при Да —> О
точки Р и N стремятся к точ-
ке М, т. е. огибающая О ка-
сается кривой £я именно в
характеристической точке М
этой кривой.
Будем называть дискрими-.
нантной кривой семейства кри-
вых (16.1 2) геометрическое место
этого семейства. Выясним, при
кривая является огибающей. Предварительно докажем следующую
лемму.
Лемма. Пусть Мо (х0, _у0) — характеристическая точка семей-
ства F (х,у,а) = 0, отвечающая значению а0 параметра семейства.
Пусть, далее, функции F(х,у,а) и Fi(x,y,o.) дифференцируемы,
в некоторой окрестности точки (хо,уо,а9) и частные производ-
ные этих функций по х и у непрерывны в самой точке (xo,yq, ^)-
D Ю
Тогда, если в точке (х^, у0, а0) якобиан --г— отличен от нуля,
и У)
то дискриминантная кривая, проходящая через Л1о, в некоторой
окрестности этой точки может быть задана параметриче-
скими уравнениями х = <р (а) и у = ф (а), где <р (а) и ф (а) — дифферен-
цируемые в некоторой окрестности ао функции.
Доказательство. Так как точка Afe(xe,j/0) является харак-
теристической точкой кривой семейства, отвечающей значению ав па-
раметра семейства, то Fix^y^, а0) = О и F„ (хв, Уо,ао) = 0, и поэтому,
в силу условий леммы, система уравнений (16.13), определяющая ха-
рактеристические точки кривых семейства, удовлетворяет всем тре-
бованиям теоремы 15.2 о разрешимости системы уравнений относи-
тельно х и у. Следовательно, в некоторой окрестности точки а®
определены две функции
х = ср(а), _у = ф(а),
(16.14)
являющиеся единственным, непрерывным и дифференцируемым реше-
нием системы (16.13). Кривая, определяемая параметрическими урав-
нениями (16.14), состоит из характеристических точек и является
566
ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ДИФФЕРЕНЦ. ИСЧИСЛЕНИЯ [ГЛ. 16
поэтому дискриминантной кривой семейства, проходящей через точку /Ио.
Отметим, что в силу единственности решения системы (16.13), раз-
личные точки дискриминантной кривой, которая определяется пара-
метрическими уравнениями (16.14), являются характеристическими точ-
ками различных кривых семейства (16.12). Укажем теперь дополни-
тельные условия, при выполнении которых дискриминантная кривая,
проходящая через точку Л40, в некоторой окрестности этой точки
представляет собой огибающую.
Теорема 16.1. Пусть кроме условий, сформулированных в лемме,
выполняются следующие условия: 1) в некоторой окрестности
точки (х0, у0, а0) производные F'x, F'y, F"ax, F",y и F”M непрерывны;
2) в точке (х0, у0, а0) выполняются соотношения Fx+F'y # О,
^6 0. Тогда дискриминантная кривая, проходящая через харак-
теристическую точку тИ0(х0, _у0), является в некоторой
окрестности этой точки огибающей рассматриваемого семейства
кривых.
Доказательство. Мы уже убедились, что некоторый
участок дискриминантной кривой, проходящей через точку Мо, при
сформулированных условиях может быть задан параметрическими
уравнениями (16.14), которые представляют собой решение си-
стемы (16.13). Подставим это решение в уравнения (16.13) и продиф-
ференцируем по а полученные тождества F (х,у, а)= 0 и F' (х,у, а) = 0.
Получим
F' ~ -I- F' ~ -4- F' — 0
da da — U,
Так как F'a = 0, то первое соотношение (16.15) примет вид
р' -| р ' dy — о
da da~='U-
Мы видим, что в каждой точке рассматриваемой дискриминантной
кривой выполняется условие касания (16.11) этой кривой и соответст-
вующей кривой семейства. Поэтому, в силу замечания 2 из п. 1,
для завершения доказательства теоремы достаточно установить, что
каждая характеристическая точка кривой семейства, расположенная
в некоторой окрестности точки Мо, и каждая точка дискриминантной
кривой в этой окрестности являются обыкновенными. По условию
теоремы в точке (х0, у0, а0) выполняется соотношение Fx2-FFy2^0,
которое, в силу непрерывности частных производных Fx и F'y, будет
выполнено и в некоторой окрестности указанной точки. Следова-
тельно, в этой окрестности все характеристические точки кривых
семейства являются обыкновенными. Из соотношения F^ 0 (спра-
ведливого, в силу непрерывности этой производной, в некоторой
§ 1]	ОГИБАЮЩАЯ И ДИСКРИМИНАНТНАЯ КРИВАЯ	56'
окрестности точки (х0, у0, а0)) и из второго тождества (16.15) выте-
„	dx dy ~
кает, что в указанной окрестности производные и не обра-
щаются одновременно в нуль *). Таким образом, все точки дискри-
минантной кривой в некоторой окрестности Мо являются обыкновен-
ными. Из только что доказанной леммы вытекает также, что различ-
ные точки дискриминантной кривой являются характеристическими
точками различных кривых семейства. Теорема доказана.
Замечание 1. Рассуждения, проведенные при доказательстве
теоремы, показывают, что в случае, когда выполнены только условия
леммы, в каждой точке дискриминантной кривой выполнено условие
касания этой кривой и кривой семейства. Мы уже отмечали (см. за-
мечание 2 п. 1), что условие касания выполняется и тогда, когда
общая точка двух кривых является особой точкой по крайней мере
одной из них. Отсюда вытекает, что дискриминантная кривая может
представлять собой геометрическое место особых точек кривых се-
мейства (если в каждой характеристической точке выполняется усло-
вие F'x2 + fy2 — 0). Отметим, что и сама дискриминантная кривая
,	, dx dy
может иметь особые точки (если и равны одновременно
нулю).
Замечание 2. Теорема 16.1 геометрически может быть истол-
кована следующим образом. Если все кривые семейства и дискри-
минантная кривая не имеют особых точек, то указанная дис-
криминантная кривая является огибающей.
Рассмотрим примеры.
1°. Найти дискриминантную кривую семейства у — (х— а)а = 0.
Имеем F (х,у, а) —у — (х—а)2, К (х,у, а)= 2 (х—а). Таким образом,
система (16.13) имеет вид
у — (х — а)2 = 0, 2 (х — а) = 0.
Отсюда вытекает, что характеристические точки имеют координаты-
(а, 0) (см. рис. 16.1). Поэтому дискриминантная кривая задается пара-
метрическими уравнениями
х = а, у = 0.
Имеем, далее, F’x——2 (х—а), FJ,= 1. В точках дискриминантной
кривой F'x -FF'y— 1. Кроме того, F'a<x =—2^0. Таким образом,
дискриминантная кривая — ось Ох является огибающей.
*) Непрерывность этих производных непосредственно вытекает из непре-
рывности производных F'x, F'v, F"^, F''ay и F"ax и из соотношений (16.15),
dx „ du	. „
из которых эти производные —— и могут оыть найдены алгебраи-
uct	act
чески.
-558
ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ДИФФЕРЕНЦ. ИСЧИСЛЕНИЯ (ГЛ. 16
2°. Найти дискриминантную кривую семейства {у — а)2—(х—а)3 = 0.
Имеем F (х, у, а) = (у — а)2 — (х— а)3, Ев (х, у, а) == — 2 (_р—а) +
+ 3(х— а)2. Система (16.13) имеет вид
О —а)2-(х —а)3 = 0, — 2 (у — а) + 3(х — а)2 = 0.
Отсюда вытекает, что дискриминантная кривая представляет собой
две прямые линии, определяемые параметрическими уравнениями
4 .	8 .
х = а, у = а и х = -д + а> -У = "27+а
(см. рис. 16.2). Легко убедиться, что в точках прямой х = а, у —а
выполняется условие Fx4-Fjs = 0, т. е. эта часть дискриминантной
кривой представляет собой геометрическое место особых точек кри-
вых семейства. Читатель легко убедится, что прямая x = ~-j-a,
g
у — -у? + а является огибающей рассматриваемого семейства линий.
4.	Огибающая и дискриминантная поверхность однопараметрического се-
мейства поверхностей. Рассмотрим однопараметрическое семейство поверхно-
стей, определяемое уравнением
F(x, у, г, а) = 0.	(16.16)
При этом мы будем предполагать, что функция F (х, у, z, а) является диффе-
ренцируемой функцией в области ее задания. Линия L на поверхности семей-
ства (16.16), отвечающей значению а пара-
ч-	метра семейства, называется характеристи-
IГГГгк	ческой (или характеристикой), если коорди-
наты точек этой линии удовлетворяют
системе уравнений
У	F(x, у, г, а) = 0, 1
/	F'a (х, у, г, а) = 0. /	<16-17)
'	Геометрическое место характеристик назы-
р .j, с	вается дискриминантной поверхностью се-
’	’ '	мейства (16.17). Огибающей однопарамет-
рического семейства поверхностей (16.16)
называется поверхность О, которая касается всех поверхностей семейства.
Можно доказать следующее утверждение.
Если все поверхности семейства и дискриминантная поверхность не имеют
особых точек, то указанная дискриминантная поверхность является огибающей.
Отметим, что дискриминантная поверхность может представлять собой
геометрическое место особых точек поверхностей семейства и сама может
иметь особые точки.
Рассмотрим следующий пример. Найти огибающую семейства сфер по-
стоянного радиуса R, центры которых находятся в точках данной кривой
L*) (на рис. 16.5 изображена одна такая сфера с центром в точке М кривей
£), определяемой уравнениями
х = <р(а), У *= Ж, 2 = х(а).
*) Огибающие таких семейств сфер называются Качаловыми поверхностями.
СОПРИКОСНОВЕНИЕ ПЛОСКИХ КРИВЫХ
569
§ 2]
Рассматриваемое однопараметрическое семейство сфер определяется следую-
щим уравнением:
I* - <Р («) ]» + [У - Ф («) Р + к - X (а) I2 - R* = 0.	(16.18)
Характеристики указанного семейства сфер определяются из уравнения (16.18)
и уравнения
(X - ? (а) 1 ?' («) + [у - Ф (а) 1Ф' («) + V ~ Х(«) 1 X' (“) = 0.	(16.19)
Уравнение (16.19) представляет собой плоскость, проходящую через
центр М сферы перпендикулярно касательной к кривой L. Поэтому характе-
ристиками являются окружности, представляющие собой линии пересечения рас-
сматриваемых сфер с плоскостями (16.19) (см. рис. 16.5). Отметим, что если
L является окружностью, то огибающей будет тор.
§ 2.	Соприкосновение плоских кривых
1.	Понятие порядка соприкосновения плоских кривых. Пусть
две кривые Li и L2 касаются друг друга в некоторой точке Мо *)
(рис. 16.6). Пусть, далее, М — произвольная точка на общей .каса-
тельной к кривым Lj и La, а М, и
Мз — точки пересечения с кривыми Li	/ /
и La соответственно перпендикуляра к	I /
указанной касательной, восставленного	мЛ /
в точке М **) (см. рис. 16.6). Будем
говорить, что две кривые Li и Ьз
имеют в точке Мо порядок сопри- к
косновения п, если существует от-
личный от нуля предел
|Af Л40 ’”+1' ‘ ‘ (16 20)	рис. 16.6.
(При этом | Л11 Ма | обозначает длину отрезка Mi Мз, а 1Л4Л10| —
длину отрезка М Мо.)
Замечание 1. Если предел (16.20) равен нулю, то говорят, что
кривые Lt и La имеют порядок соприкосновения выше п.
Замечание 2. Если две кривые Lt и La имеют в точке Мо
порядок соприкосновения выше любого п, то говорят, что они
имеют в этой точке бесконечный порядок соприкосновения.
Примеры. 1°. Кривые, являющиеся графиками функций у — хг
и у — Зх2, касаются друг друга в начале координат О, причем их
общей касательной служит ось Ох. Взяв на оси Ох точку М с абс-
циссой х, мы получим, что | ОМ | = [ х |, а | Mi Мз | = | Зх2 — х2 | = 2х2„
*) То есть проходят через Л1о и имеют в этой Точке совпадающие каса-
тельные.
**)При этом предполагается, что если точка М достаточно близка к М9,
то перпендикуляр, восставленный в точке М к касательной, пересекает
каждую кривую и La лишь в одной точке.
570
ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ДИФФЕРЕНЦ. ИСЧИСЛЕНИЯ [ГЛ. 16
Поскольку
lim 1^..^
\°М I2
JimoW = 2^°’
то рассматриваемые кривые имеют в точке О порядок соприкоснове-
ния единица.
2°. Рассмотрим, далее, две кривые Lj и L2, первая из которых сов-
падает с осью Ох, а другая является графиком функции
1
е 1*1 при х 0,
0 при х = 0.
Убедимся, что указанные кривые имеют бесконечный порядок сопри-
косновения в начале координат О. Так как общей касательной в точке О
служит ось Ох, то, взяв на этой оси точку М с абсциссой х, мы
_ 1________________________________________
получим, что | ОМ | = | х |, а ] МгМ21 = е 1*1. Достаточно доказать,
1
X	,• I М,Мп I ,• О I * I	ГТ
что для любого п предел lim ' * .	= lim г______равен нулю. 11о-
м ->-о 1 илг I х-»0 | х 1л+1
1	/Л+1 г>
лагая t = ~.—г, мы сведем этот предел к пределу lim В конце
I х I	t ->• + оо е
п. 2 § 12 главы 8 доказано, что последний предел равен нулю.
2.	Порядок соприкосновения кривых, являющихся графиками
функций. Предположим, что две кривые Lx и L2 являются графиками
функций у =f\ (х) и у = /2 (х) соответственно. Предположим, далее,
что эти кривые касаются друг друга в некоторой точке ТИрСХр.Д^р)),
причем точка 7И0 является обыкновенной для каждой из этих кривых *).
Мы докажем, что при этих предположениях данное в предыдущем
пункте определение порядка соприкосновения кривых L1 и L2 можно
заменить другим эквивалентным определением, более удобным для
приложений.
Пусть Ал:—произвольное приращение аргумента в точке х0, а
х =	+ Будем говорить, что кривые и L2 имеют в точке
Л40 (х0,	(х0)) порядок соприкосновения п, если существует отлич-
ный от нуля предел
lim
Дх-> о
| /2 (х0 + Дх) —(х0 + Дх) | _ . .	| f2 (х) — h (х) |
|ДхГ>	“Д”	|х-х„|™ *
(16.21)
*) Определение обыкновенной точки кривой, заданной уравнением
F (х, у) = 0, было дано в и. 1 § 1. В частности, для кривой, заданной уравне-
нием y — f (х), точка Мр(х0, / (х0)) будет обыкновенной, если производная f (х)
лишь непрерывна в точке х0.
§2]
СОПРИКОСНОВЕНИЕ ПЛОСКИХ КРИВЫХ
571
Для того чтобы можно было говорить о порядке соприкосновения
рассматриваемых кривых Li и L2 в смысле определения, данного в пре-
дыдущем пункте, нужно прежде всего доказать, что в некоторой
окрестности Мл эти кривые однозначно проектируются на свою
общую касательную. Этому посвящена приводимая ниже лемма 1.
Остальная часть настоящего пункта посвящена доказательству еще
двух лемм, из которых непосредственно вытекает эквивалентность
двух определений порядка соприкосновения кривых Lj и L2.
Лемма 1. Если точка М0(х0, f(x0)) является обыкновенной точкой кривой
L, служащей графиком функции у — f(x), то кривая L в некоторой окрестности
Мо однозначно проектируется на свою
касательную.
Доказательство. Прежде все-
го, отметим, что существование каса-
тельной к кривой L в точке А40 выте-
кает из существования производной }'{хй).
Перейдем теперь к новой системе декар-
товых прямоугольных координат XY,
поместив новое начало в точку касания
А?о и направив ось X вдоль касательной
в Ма (рис. 16.7). Если через а обозна-
чить угол между осью х и осью X, то
очевидно, что новая система координат
получается из старой посредством пе-
реноса начала в точку MQ (х0, /(х0)) и по-
ворота осей на угол а. Используя извест-
Рис. 16.7.
ные формулы преобразования координат при переносе и повороте осей (см. вы-
пуск 8), получим следующее выражение новых координат X, Y точек кривой L
через старые координаты х и у = f (х);
X = (X — Хо) COS а + [/(X) — /(Хо)] sin а,	1
у = — (X — х0) sin а 4- If (х) — f (Хо)] COS а. J	1	'
Наша цель будет достигнута, если мы покажем, что из уравнений (16.22)
можно выразить Y как функцию X (это и будет означать, что участок кри-
вой L, примыкающий к MQ, однозначно проектируется на ось X, т. е. на
касательную). Для этого достаточно доказать, что в окрестности точки Afe
первое из уравнений (16.22) однозначно разрешимо относительно х. (В самом
деле, выразив х через X из первого уравнения (16.22) и подставив полученное
выражение во второе уравнение (16.22), мы и определим Y как функцию X.)
Согласно теореме 15.1 достаточно доказать, что производная по х правой части
первого из уравнений (16.22) отлична от нуля в точке х0 и непрерывна
в этой точке. Но это очевидно, ибо указанная производная имеет вид
cos а (X) sin а и в точке х0, в которой f (х0) = tg а, равна * . Так как
“ Ф , то cos а ф 0. Лемма доказана".
Пусть кривые Lj и L2, представляющие собой графики функций у = /\(х)
и У —fi (х), касаются друг- друга в точке Мо (х0, (х0)), которая является
обыкновенной для каждой из этих кривых, а х = х0 + Дх. Пусть, далее, из
точки М2(х, f2(x)) опущен перпендикуляр на касательную в Ма (рис. 16.8),
Mi —точка пересечения этого перпендикуляра с кривой Lj *), а М — с ка-
сательной. Тогда справедливы следующие утверждения.
') В силу леммы 1 при достаточно малом Дх такая точка будет только одна.
572	' ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ДИФФЕРЕНЦ. ИСЧИСЛЕНИЯ [ГЛ. 16
Лемма 2. Существует отличный от нуля предел
lim
Ах-*0
1/8 (X) —(X) I
(16.23)
Лемма 3. Существует отличный от нуля предел
lim
Ах-. О
|7ИОЛ4 |
|Дх|
(16.24)
Заметим, что из лемм 2 и 3 вытекает, что отличный от нуля предел
(16.21) существует тогда и только тогда, когда существует отличный от нуля
предел (16.20), а это й означает
эквивалентность двух определе-
ний порядка соприкосновения. Пе-
реходим к доказательству лемм
2 и 3.
Доказательство лем-
мы 2. Ради простоты обозначим
расстояние Mt М2 через р, и ради
определенности будем считать, что
кривые Lj и L2 расположены так,
как указано на рис. 16.8. Если X
и Y — координаты точки Mlf а
а — угол наклона касательной в
Л40 к оси Ох, то, очевидно,
X = х + р sin a, Y = Д (х) — р cos я.
Так как точка Мг лежит на кри-
вой то Y = fx (X) или
/2 W — Р cos я = Д (х + р sin я).
Применяя к правой части послед-
него равенства формулу Лагран-
жа по сегменту [х, х + р sin я],
будем иметь
fa (*) — Р cos я = (х) 4- р sin я /' (5),
где $ — некоторая точка, лежащая
внутри указанного сегмента. Так
как р—. 0 при Дх—-0 и произ-
водная f (х) непрерывна в точке
х0, то последнее раренство можно
переписать в виде
Д (х) — р созя = Д (х) +
+ Р sin я [/' (х0) + е], (16.25)
где е —»0 при Дх—»0. Учитывая, что /'(x0) = tgfl, мы получим из (16.25)
Л(^)-/х(х) =_j_ ,пя
р	COS Я 1
Лемма 2 доказана.
Доказательство леммы 3. Обозначим через р угол между
хордой Л40Л42 и касательной М0М (рис. 16.9). Очевидно, что 0—.0 при Дх—>0.
§ 21
СОПРИКОСНОВЕНИЕ ПЛОСКИХ КРИВЫХ
573
Из прямоугольных треугольников	и МаМ2М. (здесь МйР парал-
лельно оси Ох) находим
I М»М* I =	= |M°Ct|'.
1	Cos(a + P)	COS fi
Из последней формулы очевидно, что
lim hMg
Дх->0 IM.
3 доказана.
,. COS 0	1
lim  ----—!г-гт- =------
дл_о cos (“ + ₽) COSa
Лемма
3. Достаточные условия соприкосновения порядка и. Пусть,
как и выше, две кривые и Ь2, служащие графиками функций
(х) и /2 (х), касаются друг друга в Мо (х0, fr (х0)). Справедливо
следующее утверждение.
Теорема 16.2. Пусть функции у = Д (х) и у — f2(x) п + 1 раз
дифференцируемы в некоторой окрестности точки ха, причем
производные порядка л+1 непрерывны в самой точке х0. Тогда,
если в точке х0 выполняются соотношения
fi (*о) = Л М)> fi (*о) = Л (М.ff (*о) = Ля) М>).
/?+1)(*o)#/?+1)(*o)>	(16.26)
то кривые и L2 имеют в точке 7И0 (х0,	(х0)) порядок сопри-
косновения п.
Доказательство. Пусть F (х) = f2 (х) — Д (х). Достаточно
доказать, что существует отличный от нуля предел
lim -
X-.XQ
WI
|x-x0|«+i-
Так как, в силу (16.26), F (х0) = F (х0) = ... =	(х0) — О,
F(«+D (х0) ф 0, то, записывая для функции F (х) формулу Тейлора
с остаточным членом в форме Лагранжа, будем иметь
F (*) =-ёГр!)Г р("+1) (хо + 0 (х - х0)) (х - хоу+\ 0 < 9 < 1. (1-6.27)
В силу непрерывности производной порядка п +1 в точке х0
F{n+1) (х0 + 9 (х - х0У) = Fn+» (х0) + s,	(16.28)
где е->0 при х-*-х0. Из соотношений (16.27) и (16.28) получим,
что
Теорема доказана.
Замечание 1. Если выполнены все условия теоремы 16.2, за
исключением, быть может, условия Д"+1) (х0) ф Дя+» (х0), то можно
574
ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ДИФФЕРЕНЦ. ИСЧИСЛЕНИЯ (ГЛ. 16
утверждать, что кривые и имеют в точке Мо порядок сопри-
косновения не ниже п.
Замечание 2. Выясним порядок соприкосновения кривой L,
являющейся графиком функции _у=/(х) со своей касательной Т
в точке Л10(х0, /(х0))- При этом будем считать, что функция f(x) три
раза дифференцируема в окрестности точки х», а ее третья производ-
ная непрерывна в точке ха. Напомним, что касательная Т служит гра-
фиком линейной функции у = ср (х)*=р(х^ (х— хй) -|- f (х0). Так как
У^о) = /Uo), <р'Оо) =/'(*о) и <р"(хо) = О, то в случае f’ixfrf-b
кривая L имеет со своей касательной Т порядок соприкосновения
п = 1, а в случае /"(хй) = 0 указанный порядок соприкосновения
не ниже двух.
4. Соприкасающаяся окружность. Пусть А1о(хо, _у0) — точка кри-
вой L, являющейся графиком функции у = f(x), имеющей непрерыв-
ную третью производную в точке х0. Через точку 7И0 можно провести
бесконечно много окружностей, касающихся кривой L в этой точке.
Легко убедиться в том, что часть каждой такой окружности, распо-
ложенная в некоторой окрестности точки Мо, представляет собой гра-
фик функции вида у=у(х). Поэтому мы можем говорить о порядке
соприкосновения кривой L и любой из этих окружностей в их общей
точке Мо. Та из этих окружностей, которая имеет с кривой L порядок
соприкосновения не ниже двух, называется соприкасающейся окруж-
ностью для кривой L в точке Af0. Следующее утверждение уста-
навливает достаточные условия для существования у кривой L в то-
чке соприкасающейся окружности.
Теорема 16.3. Пусть кривая L является графиком функции
у = f (х), причем f(x) имеет в точке ха не равную нулю вторую
производную и непрерывную третью производную. Тогда для
кривой L существует в точке Л10(х0, /(х0)) соприкасающаяся
окружность.
Доказательство. Будем искать уравнение соприкасающейся
окружности в виде
(х — а)2 + (у — Ь)* = р2,	(16.29)
где а, b и р — постоянные, подлежащие определению. Разрешим урав-
нение (16.29) относительно у и найденное решение у — у(х) подставим
в левую часть (16.29). Тогда мы можем рассматривать (16.29) как тож-
дество относительно х (считая при этом, конечно, что _р=у(х)).
Продифференцируем тождество (16.29) два раза по х и потребуем
чтобы в полученных при этом соотношениях и в самом соотношении
(16.29) значения у0, уо, уо функции у =у (х) и ее первых двух производ-
ных в точке х0 равнялись соответственно f (xg), f'(х0),/" (х0):
Л=/(^о)> j6=/(a;0), ^'=Л(^о).
Таким образом, мы получим следующую систему уравнений относи-
КРИВИЗНА ПЛОСКОЙ КРИВОЙ
575
§ 3]
тельно а, b и р:
(х0 — а)2+О0 — ^=Р9>
(х0 —а)+(Л —^)А== О.
1+су;)84Луо-*)у;=о.
При условии _у" =/"(хо)^:О, р 0 эта система имеет единственное
решение:
1 + у'2	1 + у'2	(1 + у°-}*Ь
а = х0----+	=	°	• (16.30)
Уо	У о
Из проведенных рассуждений вытекает, что для окружности,
координаты (а, Ь) центра и радиус р которой определяются форму-
лами (16.30), и кривой L выполняются все условия замечания 1
к теореме 16.2. Поэтому указанная окружность будет соприкаса-
ющейся.
Замечание. Если в условиях теоремы 16.3 требование
/"(хо)е^О заменить противоположным требованием /” (хо) = 0, то
у кривой L в точке Мо не существует соприкасающейся окруж-
ности.
Однако, в силу замечания 2 к теореме 16.2, в этом случае кри-
вая L и касательная к ней в точке Мй имеют в этой точке порядок
соприкосновения не ниже двух. Таким образом, можно считать, что
в указанном случае соприкасающаяся окружность в точке Мо вырож-
дается в прямую.
' § 3. Кривизна плоской кривой
1. Понятие о кривизне плоской кривой. Пусть кривая L задана
посредством параметрических уравнений х = <р (t), у — ф (/). Будем
считать, что для кривой L выполнены условия, оговоренные в § 1
главы И *). В таком случае в любой точке М кривой L можно
выбрать положительное направление. Договоримся называть положи-
тельным направлением в данной точке М кривой L то направление,
в котором будет перемещаться точка М при увеличении пара-
метра t.
Фиксируем теперь на кривой L некоторую точку M<)t отвечающую
значению параметра t0, и предположим, что эта точка! является обыкно-
венной тонкой кривой L.
Тогда участок кривой L, примыкающий к точке Мо, представляет
собой график функции вида либо y=f(x), либо x=fi(y), причем
существует касательная к кривой L в точке 7И0. На этой касательной
*) То есть будем считать, что кривая L не имеет точек самопересечения и
участков самоналегания.
576 ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ДИФФЕРЕНЦ. ИСЧИСЛЕНИЯ [ГЛ. 16
мы введем положительное направление, соответствующее положитель-
ному направлению в точке Л40 кривой L *).
Всюду в дальнейшем мы будем рассматривать только направленную
касательную. На рис. 16.10 направление касательной указано стрелкой.
Предположим теперь,
в некоторой окрестности
что все точки кривой L, расположенные
фиксированной нами точки Л40, являются
обыкновенными. Пусть М — одна из ука-
занных точек. Введем понятие угла смеж-
ности участка кривой М^М. Ради опре-
деленности будем считать, что точка М
соответствует большему значению пара-
метра, чем Мо.
Углом смежности участка кривой
МйМ назовем угол между направленными
касательными к кривой L в точках М и
Мо, взятый со знаком плюс в случае, если
касательную в точке 440 для совмеще-
ния кратчайшим путем с касательной в точке М следует повернуть
против часовой стрелки, и со знаком минус — в противном случае.
На рис. 16.11 изображен участок Л4ОЛ4, имеющий положительный
угол смежности, а на рис. 16.12 —участок МйМ, имеющий отрица-
тельный угод смежности.
Введем далее понятие средней кривизны участка кривой М^М.
Средней кривизной участка кривой М^М назовем отношение угла
смежности этого участка к длине этого участка.
Так как точку кривой L мы считаем фиксированной, то сред-
няя кривизна участка МйМ будет функцией точки М или функцией
параметра i. Эту функцию мы обозначим символом (44) или (f).
*) То есть договоримся называть положительным направлением на каса-
тельной то направление, в котором будет перемещаться при увеличении пара-
метра точка, представляющая собой проекцию на касательную точки кривой L.
§ 3]	КРИВИЗНА ПЛОСКОЙ КРИВОЙ	577
Естественно, возникает вопрос о рассмотрении предела этой функ-
ции при стремлении точки М. вдоль кривой L к точке /Ио' (или, что
то же самое, при стремлении параметра t к /0).
Определение. Предельное значение средней кривизны участка
кривой М0М при стремлении точки М вдоль кривой к точке 7И0
называется кривизной в данной точке Мй кривой L и обозна-
чается символом k(MQ).
Таким образом, по определению
k (7И0) = lim х,м0 (/И)=lim	(t).
м-м0	t_tt>
Предоставим читателю самому убедиться в том, что: 1) как сред-
няя кривизна любого участка прямой линии, так и кривизна в любой
точке этой линии равны нулю, 2) как средняя кривизна любого
участка окружности радиуса R, так и кривизна в любой точке этой
1
окружности равны .
Установим формулу для вычисления кривизны в любой точке про-
извольной кривой L.
2. Формула для вычисления кривизны. Пусть кривая L задана
параметрическими уравнениями	y=ty(t), Мй—некоторая фикси-
рованная точка этой кривой, отвечающая значению параметра Пред-
положи^, что все точки кривой L из некоторой окрестности ТИо
являются обыкновенными и что функции ср(£) и tp(f) имеют в точ-
ке вторые производные. При этих предположениях мы ус-
тановим общую формулу для вычисления кривизны в точке Мй
кривой L.
Пусть х и х— значения первой и второй производной функции
x = <f(t) в точке /в, а х + Дх — значение первой производной этой
функции в точке 4- AZ (Д£ — произвольное приращение параметра £).
Такцм образом, Дх — приращение первой производной функции
х = ср (t). Пусть у, у и АР — соответствующие значения производ-
ных функции у = Ср (t).
Если считать, что точка /Ио, отвечающая значению параметра tn,
фиксирована, а точка М отвечает значению параметра t = Zo + Д£,
то угол смежности участка Л1оЛ4 и длину этого участка можно рас-
сматривать как функции аргумента М. Эти функции мы обозначим
соответственно через a(AZ) и Z(AZ).
По определению кривизна й(/И0) в точке /Ио кривой равна пре-
дельному значению
А(Ж0) = Ит^.	(16.31)
I (Д<)	v '
Докажем, что предельное значение (16.31) существует и вычислим
это предельное значение.
578
ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ДИФФЕРЕНЦ. ИСЧИСЛЕНИЯ [ГЛ. 16
Обозначим через <р0 и <р углы наклона к оси Ох касательных к кри-
вой L, проведенных через точки Мй и М соответственно (рис. 16.13).
Тогда, очевидно, при любом расположении точек 7И0 и М для угла
ции, заданной параметрически
смежности a (Af) будет справедливо
соотношение
а (ДО = «р — ср0.
Из последнего соотношения вытекает,
что
- tg а (ДО =	5 —. (16.32)
& 4 ' l + tg?tg=p0 4	’
Исходя из геометрического смыс-
ла производной (см. п. 4 § 1 главы 5)
и из выражения для производной функ-
(см. § И главы 5), мы можем записать
tg<Po = |,
Таким образом, формулу (16.32) можно переписать в виде
g ( I _i_ 2X£+Jy) х(х + дх)+5-(^4-дя’ (  )
1 "Г х(Л4-Дх)
Поскольку функции х = ср (0 и _у = ф(О имеют в точке вторые
производные, то первые производные этих функций в точке О не-
прерывны и, стало быть,
lim Д_р = 0,	lim Д.£ = 0.
дг—0	ы-Л
Но тогда, в силу равенства (16.33),
limtga(Af)= 0.
nt—о
Из последнего равенства и из непрерывности арктангенса выте-
кает, что
lim а (ДО = 0.
дг—о
Поэтому справедливо равенство
Ит л = Нт [cos а (ДО -? (*Ц-. 1=1.	(16.34)
д/_,о18а(АО iZ_0L	Sin а (ДО J	v
Равенство (16.34) и теорема о предельном значении произведения
сводит вопрос о вычислении предельного значения (16.31) к вычис-
§ 3]
КРИВИЗНА ПЛОСКОЙ КРИВОЙ
579
лению следующего предельного значения:
k (Мо)	*	(16.35)
Для вычисления этого предельного значения заметим, что длина / (ДО
участка кривой МаМ определяется формулой
f о+А f ___________
I (Д0 =	х2 (т) + у2 (т) dx.
Применив к интегралу, стоящему в правой части последнего равен-
ства, формулу среднего значения, будем иметь
I (At) = Д/ K^2(/*)+j>\/*)>	(16.36)
где tQ t* t0 -J- Д/.
Соотношения (16.35), (16.33) и (16.36) позволяют заключить, что
вычисление кривизны сводится к вычислению предельного значения
. Ду, . Дх
4(М0) = Пп,---------------О6-”)
д/-о [^(Л + Дх)+У (У4-Ду)]]Сх2(/*)4-у2 (/*) •
Так как функции х = ср'(/) и у = <])(/) имеют в точке t0 вторые
производные, то существуют предельные значения
lira дт = х и lim =JJ.	(16,38)
Д1-+0	Д/_0	1
Далее, из непрерывности первых производных функций x = <?(t)
и у = ф(() заключаем, что
lim ДХ = 0, lim Ду = О, lim/x2(f*)-|-ji2(H = ]/гх2 + у2. (16 39)
д<-»о	дг—д	д<-»о	' ’ ’
Из существования предельных значений (16.38) и (16.39) вытекает,
что предельное значение, стоящее в правой части (16.37), существует
и равно
Ху-Ху
[Х2+У2]’/а ’
Таким образом, мы доказали, что кривизна в точке Ло кривой L
существует и определяется формулой
*(М>) =
Ху — Ху
[X2 +У2]3/’
(16.40)
Замечание. Пусть требуется вычислить кривизну k(ЛГ0) в дан-
ной точке Л40 кривой L, представляющей собой график дважды
дифференцируемой функции y=f(x).
580 ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ДИФФЕРЕНТ ИСЧИСЛЕНИЯ [ГЛ. 18
Положив в формуле (16.40) x — t, y—f (t), мы получим для иско-
мой кривизны следующую формулу:
k = [1 + V' (*))21,|а '
В качестве примера вычислим кривизну в произвольной точке цеп-
ной линии у = a ch—.
Поскольку
l+lf«l’=ch-5=g.
то кривизна равна
§ 4. Эволюта и эвольвента
1. Нормаль к плоской кривой. Пусть плоская кривая L задана
посредством параметрических уравнений
y=’]>(t).	(16.41)
Будем считать, что кривая L не имеет точек самопересечения и
участков самоналегания. Кроме того, будем считать, что каждая
точка кривой L является обык-
новенной *).
Введем понятие- нормали к
кривой в данной ее точке М.
Прямая, расположенная в
плоскости кривой L и проходя*
тая через точку М кривой пер-
пендикулярно касательной к L
в точке М, называется нор-
малью к L в точке М
(рис. 16.14).
Найдем уравнение нормали к
кривой. Пусть х и у — коорди-
наты точки М кривой L, а X и
У — координаты любой точки W
нормали к кривой. Согласно оп-
ределению нормаль перпендику-
лярна касательной, и поэтому угловой коэффициент kn нормали свя-
зан с угловым коэффициентом kt касательной соотношением **)
knkt = — 1.
(16.42)
*) Отметим, что при этих условиях в каждой точке кривой £ существует
уасательная.
**) Это соотношение известно из курса аналитической геометрии (см.,
например, выпуск «Аналитическая геометрия» настоящего курса).
§ 4]
ЭВОЛЮТА И ЭВОЛЬВЕНТА
581
Так как угловой коэффициент kt касательной в случае параметри-
ческого задания кривой (16.41) равен то из (16.42) получаем
*л=-£.-	(16.43)
Используя известное из курса аналитической геометрии уравнение
прямой с данным угловым коэффициентом km получим следующее
уравнение нормали к кривой L:
(16.44)
Учитывая, что x — 's>(t) и j = cp(/), перепишем уравнение (16.44)
в следующей форме:
<?'(Х — т) + ф'(У — ф) = 0.	(16.45)'
Замечание. В случае, если касательная в точке М парал-
лельна оси абсцисс, ее угловой коэффициент kt равен нулю, и поэтому
соотношения (16.42), (16.43) и (16.44) не имеют, смысла. Однако в
этом случае уравнение (16.45) все же представляет собой уравнение
нормали. Действительно, если
kt = 0 (касательная парал-
лельна оси абсцисс), то
<]>' = 0, а ср' ф 0 *) и поэтому
соотношение (16.44) прини-
мает вид X—<р = 0. А это
есть уравнение прямой, пер-
пендикулярной оси Ох и
отсекающей на этой прямой
отрезок, равный ср. Ясно,
что эта прямая совпадает в
рассматриваемом случае с
нормалью в точке М.
2. Эволюта и эвольвен-
та плоской кривой. Пусть
кривая L удовлетворяет тем
же условиям, что и в пре-
дыдущем пункте. Обратимся
к уравнению (16.45). Если в
этом уравнении рассматривать t как
параметр, то оно представляет собой уравнение однопараметриче-
ского семейства всех нормалей плоской кривой L. Представление
о семействе нормалей плоской кривой дает рис. 16.15.
При определенных условиях однопараметрическое семейство нор-
малей имеет огибающую, которая называется эволютой кривой L.
•) Напомним, что k/ = \ и для обыкновенной точки <р'2	ф'2	0.
582 ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ДИФФЕРЕНЦ. ИСЧИСЛЕНИЯ [ГЛ. 16
Итак, эволютой плоской кривой L называется огибающая
однопараметрического семейства нормалей этой кривой. Кривая L
по отношению к своей эволюте называется эвольвентой.
Выясним условия существования эволюты плоской кривой L
и найдем ее параметрические уравнения.
Будем считать, что кривая L без особых точек задана посредством
параметрических уравнений (16.41). Для простоты предположим, что
параметр t изменяется на интервале (0, 1). Допустим также, что
функции <р(0 и ф(0, фигурирующие в соотношениях (16.41), имеют
непрерывные третьи производные на интервале (0, 1). При этих
предположениях справедлива следующая теорема.
Теорема 16.4. Пусть во всех точках кривой L ее кривизна k
и производная кривизны *) не равны нулю. Тогда существует
эволюта кривой L, причем параметрические уравнения эволюты
имеют вид
• т ““ V т '
,2 . г,9
1 Т ?'<|Z — Т •
(16.46)
Доказательство. Мы определили эволюту как огибающую
однопараметрического семейства нормалей кривой L. Это семейство
задается уравнением (16.45). Таким образом, функция F {X, Y, f), за-
дающая семейство, определяется соотношением
Д(Х У, 0 = <р,(^-ср) + ф'(У-ф),	(16.47)
причем t играет роль параметра.
Применим теперь выводы § 1 этой главы о существовании оги-
бающей для выяснения вопроса о существовании эволюты (т. е. оги-
бающей семейства (16.45)). Мы должны проверить выполнение усло-
вий леммы п. 3 § 1 этой главы и условий теоремы 16.1. Перейдем
к проверке указанных условий. Остановимся сначала на проверке
условий леммы. Очевидно, при сформулированных требованиях на
функции ср и ф функции F (X, Y, f) и F}(X, У, t) дифференцируемы.
Убедимся
> Л 1
выражение (16.40) для кривизны k кривой L, можно представить
этот якобиан в следующей форме:
D (F, Fa
теперь, что якобиан п. у у отличен от нуля. Используя
О(Д Ft)
D(X, У)
= Л[ср,2+ф,2]3/2.
По условию теоремы кривизна k отлична от нуля. Кроме того, так
как все точки кривой L обыкновенные, то ср'* ф'’	0. Таким обра-
*) При условиях, наложенных на функции <р и ф, кривизна k представляет
собой дифференцируемую функцию параметра t.
§fl
ЭВОЛЮТА И ЭВОЛЬВЕНТА
683
зом, указанный якобиан отличен от нуля, и стало быть, все условия
леммы выполнены.
Проверим теперь условия теоремы 16.1. Очевидно, что при сфор-
мулированных требованиях на функции <р и ф производные F'x, Fy>
Fix, Fly, Fit непрерывны. Остается лишь убедиться в справедливости
соотношения Fit 0 для всех значений t из интервала (0,1) и для
характеристических точек на нормалях к кривой L.
Так как
Fit = (*-?) + ф'" ( У- Ф) - з (cpY + ф'ф')	(16.48)
и согласно п. 2 § 1 этой главы и формулам (16.13), характеристи-
ческие точки для рассматриваемого случая определяются соотноше-
нием
<р'(Х-<р)+Ф'(г~ф)=(И
- ?) + ФЧ у - Ф) - (/+ Ф'3)=о, J
то значение производной Fit в характеристических точках в силу
(16.48) и (16.49) равно
=Уф"~~?У(<р,а+ф,2) ~3 (?v+w • (1б-50)
Обратимся к выражению (16. 40) для кривизны k кривой L. С уче-
том обозначений (16. 41) из формулы (16. 40) путем дифференцирования
получаем
* =	• л'’+л -3 <л"+m} 
С помощью этого соотношения и выражения (16.40) для кривизны
придадим выражению (16.50) следующую форму:
*1(^ + ф'*).
Так как по условию теоремы k и А' не равны нулю и, кроме того,
<р'9 _|_ ф'2 о, то из последнего выражения для Ftt следует, что для
всех значений t из интервала (0, 1) и для характеристических точек
на нормалях к L F"(t^0. Таким образом, условия теоремы 16.1
также выполнены.
Найдем теперь параметрические уравнения эволюты. Так как при
сформулированных условиях эволюта есть геометрическое место
характеристических точек семейства нормалей, то координаты X и У
точек эволюты определяются из соотношений (16. 49). Находя из
этих соотношений X и У,-мы и получим параметрические уравнения
(16.46). Теорема доказана.
Замечание. В геометрии часто используются понятия радиуса
кривизны и центра кривизны. Радиусом R кривизны кривой L назы-
вается величина 1/А, где k— кривизна L, а центром кривизны —
584
ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ДИФФЕРЕНЦ. ИСЧИСЛЕНИЯ [ГЛ. 16
та точка нормали к кривой, которая отстоит от данной точки кривой
L в направлении вогнутости L на расстоянии R.
Отметим, что радиус кривизны кривой равен радиусу соприкаса-
ющейся окружности, а центр кривизны совпадает с центром соприка-
сающейся окружности.
Убедимся, что эволюта представляет собой геометрическое ме-
сто центров кривизны кривой. В самом деле, из соотношений (16.46)
Рис. 16.16.
получаем
т. е. точка эволюты с координатами
(X, У) отстоит от точки кривой L
с координатами (®, ф) на расстоя-
нии R. Из геометрического смысла
эволюты (см. рис. 16.15) ясно, что
точка (X, У) расположена на норма-
ли в сторону вогнутости кривой L.
Пример. Найдем уравнения эво-
люты эллипса ABCD (рис. 16.16),
определяемого параметрическими
уравнениями
х = ср (/) = a cos t, у = tp(f) = &sin£
Так как ср' = — asinf, t/ = £cosf, <р" = — a cost, ф" =— b sin t, то
?,a + ’/? = aesina^ + Z/icos2£, а <р'ф"— <р"ф' = ab. Поэтому, согласно
(16.46), параметрические уравнения эволюты эллипса имеют вид
v а2 — b2 . а ,	,, b2 — a2 . о ,
X =--------COS3 t, У == —г— sin3 /.
a	b
Таким образом, эволюта эллипса представляет собой так называемую
удлиненную астроиду (см. рис. 16.16).
Отметим, что в точках А, В, С, D эллипса (т. е. в его вершинах)
производная кривизны равна нулю. Поэтому в этих точках не выпол-
нены условия теоремы 16.4. В соответствующих точках А', В', С, D
эволюта эллипса имеет особенности — так называемые точки возврата
ПРИЛОЖЕНИЕ
ДАЛЬНЕЙШЕЕ РАЗВИТИЕ ТЕОРИИ ВЕЩЕСТВЕННЫХ ЧИСЕЛ
В главе 2 для введения вещественных чисел мы использовали
множество бесконечных десятичных дробей. Определив для множе-
ства этих дробей правила сравнения, сложения и умножения, мы уста-
новили, что элементы этого множества обладают 13 основными,
свойствами (перечисленными1 в п. 1 § 1 главы 2 для рациональ-
ных чисел). Описанный метод введения вещественных чисел, хотя
и обладает несомненными эвристическими и методическими достоин-
ствами, не является единственно возможным. Можно было бы ввести
вещественные числа с помощью бесконечных двоичных дробей, с по-
мощью так называемых дедекиндовых сечений в области рациональ-
ных чисел *), с помощью последовательностей рациональных чисел **)
и другими методами. Чтобы выяснить взаимосвязь между различными
методами введения вещественных чисел, привлечем некоторые новые
понятия и установим еще одно важное свойство множества изученных
нами вещественных чисел.
1. Полнота множества вещественных чисел. Два множества,
для элементов каждого из которых определены правила сравнения,
сложения и умножения, мы будем называть изоморфными друг другу
относительно этих правил, если между элементами этих множеств
можно установить взаимно однозначное соответствие ***) так, что если
элементам а и Ь первого множества соответствуют элементы а' и Ь'
второго множества, то: 1) элементы а' и Ь' связаны тем же знаком
(^>, <^ или = ), что и элементы а и Ь; 2) элементу аУ-b соответ-
ствует элемент а'-[-Ь'\ 3) элементу а -Ь соответствует элемент а'-Ь'.
*) Способ введения вещественных чисел с помощью сечений принадлежит
немецкому математику Р. Дедекинду (1831—1916). Этот способ изложен,
например, в главе I книги Ф. Франклина «Математический анализ» или
в главе I книги Г. М. Фихтенгольца «Основы математического анализа».
**) Этот способ введения вещественных чисел принадлежит Г. Кантору.
Его изложение можно найти в книге В. В. Немыцкого, М. И. Слудской и
А. Н. Черкасова «Курс математического анализа», том I, глава 2.
***) По поводу взаимно однозначного соответствия между элементами
двух множеств см. первую сноску на стр. 87.
586
ПРИЛОЖЕНИЕ
Аналогично можно было бы говорить не о правилах сравнения
сложения и умножения, а о каких-либо других правилах, характери-
зующих соотношения между элементами, и ввести понятие множеств,
изоморфных друг другу относительно указанных правил.
Примером двух множеств, изоморфных друг другу относительно
правил сравнения, сложения и умножения, могут служить множество
рациональных чисел, введенных в виде отношения целых чисел,
с правилами сравнения, сложения и умножения, указанными в сносках
на стр. 36, и множество рациональных чисел, записанных в виде беско-
нечных десятичных дробей, с обычными правилами сравнения, сложе-
ния и умножения вещественных чисел.
Рассмотрим более внимательно два множества: множество всех ра-
циональных чисел и множество всех вещественных чисел. Для каж-
дого из этих множеств определены правила сравнения, сложения и
умножения и справедливы 13 основных свойств. Вместе с тем ясно,
что множество всех вещественных чисел является более «широким»,
чем множество всех рациональных чисел, ибо в целом множество
всех вещественных чисел не изоморфно относительно правил
сравнения, сложения и умножения множеству всех рациональных
чисел *), но в множестве вещественных чисел можно выделить
часть, изоморфную относительно указанных правил множеству
всех рациональных чисел.
Естественно, возникает вопрос, нельзя ли и для множества всех
вещественных чисел построить более «широкое» множество объектов,
обладающее следующими свойствами: 1) в этом более «широком»
множестве определены правила сравнения, сложения и умножения и
справедливы 13 основных свойств; 2) в целом более «широкое»
множество не изоморфно относительно указанных правил множеству
всех вещественных чисел; 3) в более «широком» множестве можно
выделить часть, изоморфную относительно указанных правил мно-
жеству всех вещественных чисел.
Мы докажем, что такого более «широкого» множества не суще-
ствует, т. е., как принято говорить в математике, множество всех
вещественных чисел является полным относительно правил
сравнения, сложения и умножения и 13 основных свойств.
Вообще произвольное множество объектов, для' которого
определены некоторые правила и справедливы некоторые свойства,
называется полным относительно этих правил и свойств, если
нельзя построить более «широкое» множество объектов такое,
чтобы: 1) в этом, более «широком» множестве были определены
те же правила и справедливы те же свойства; 2) в целом это
более «широкое» множество не было изоморфно данному отно-
*) Это вытекает из того, что между множеством всех рациональных чисел
и всех вещественных чисел нельзя установить взаимно однозначного соответ-
ствия (см, п. 6 § 4 главы 3).
ДАЛЬНЕЙШЕЕ РАЗВИТИЕ ТЕОРИИ ВЕЩЕСТВЕННЫХ ЧИСЕЛ
587
сительно указанных правил; 3) в этом более «широком» мно-
жестве существовала часть, изоморфная данному множеству
относительно указанных правил.
Можно утверждать, что множество всех рациональных чисел не
является полным относительно правил сравнения, сложения и
умножения и 13 основных свойств, ибо существует более «ши-
рокое» множество (множество вещественных чисел), удовлетворяю-
щее требованиям 1), 2) и 3) из только что сформулированного опре-
деления.
Докажем теперь, что множество всех вещественных чисел
является полным относительно правил сравнения, сложения и
умножения и 13 основных свойств.
Предположим противное, т. е. предположим, что существует бо-
лее «широкое» множество объектов {л/} такое, что: 1)для элементов
множества {х'} определены правила сравнения, сложения и умноже-
ния и справедливы 13 основных свойств, 2) в целом множество {х7}
не изоморфно относительно указанных правил множеству {х} всех
вещественных чисел, 3) существует часть множества {х7} (дбозна-
чим ее символом {X7}), изоморфная относительно указанных правил
множеству {х} всех вещественных чисел.
Заметим, прежде всего, что у множества {х7} существует един-
ственная пара элементов О' и 1', играющих особую роль нуля и
единицы *). Далее, можно утверждать, что элементы 0' и 1' вхо-
дят в состав множества {X7} и находятся во взаимно однознач-
ном соответствии с вещественными числами 0 и 1 **). Пусть
а7 — какой-либо элемент множества {х7}, не принадлежащий множе-
ству {X7}.
В силу правила сравнения мы можем разбить все элементы X7
множества {X7} на два класса — верхний и нижний, отнеся' к вер-
хнему классу все элементы X7, удовлетворяющие неравенству Х^>а7,
а к нижнему классу все элементы X7, удовлетворяющие неравенству
X7<jx7. Оба эти класса не являются пустыми. В самом деле, докажем,
например, что верхний класс не пуст. Повторив элемент Г слагаемым,
достаточное число раз, мы, в силу свойства 13°, получим элемент п
*) Если бы нашлось два элемента и О^, играющих особую роль нуля,
то, в силу свойств суммы, мы получили бы 0[ = О;-|-Oj = ОзО; = Oj, т. е.
О; = Oj. Аналогично доказывается единственность элемента V, играющего особую
роль единицы.
**) Докажем, например, что элемент 0' входит в состав множества {X'} и
находится во взаимно одонозначном соответствии с вещественным числом 0.
Предположим, что вещественному числу 0 соответствует некоторый элемент О'
множества {X}, и пусть а’ — любой элемент этого множества, соответствующий
вещественному числу а. В силу изоморфности относительно сложения элементу
а' + 0' соответствует вещественное число а + 0 = а, т. е. элемент а' + 0’ сов-
падает с элементом а', но это означает, что 0' (единственный!) нулевой эле-
мент, т. е. О' = 0'. Аналогично проводятся рассуждения и для единичного эле-
мента.
588
ПРИЛОЖЕНИЕ
множества {£'}, удовлетворяющий неравенству ft > а', т. е. принад-
лежащий верхнему классу. Из свойства 1° вытекает, что каждый
элемент нижнего класса меньше любого элемента верхнего
класса. В силу изоморфизма множества {х7} и множества {х} всех
вещественных чисел можно утверждать, что множество всех вещест-
венных чисел также разбивается на два класса, причем каждое
число из нижнего класса меньше любого числа из верхнего класса.
Но это означает, что нижний класс вещественных чисел ограни-
чен сверху и имеет (в силу теоремы 2.1) точную верхнюю грань т,
а верхний класс имеет точную нижнюю грань М. Из определения
точных граней вытекает, что обе грани т и AI заключены между
вещественными числами, как угодно близкими между собой, а поэтому
т — М. Так как число т = М является одним из вещественных
чисел, то оно принадлежит одному из классов, т. е. существует
либо наименьший элемент в верхнем классе, либо наибольший
элемент в нижнем классе. Докажем, что оба .эти утверждения
абсурдны. Пусть (ради определенности) существует наименьший
элемент в верхнем классе вещественных чисел. Тогда существует
наименьший элемент т' и в верхнем классе, отвечающем разбиению
множества {X'}. По определению верхнего класса ni > а'. Согласно
свойствам суммы существует разность т! — а', причем, согласно этим
свойствам, ni — а' > О'. Но тогда, в силу свойства 9°, для элемента
т' — ai существует обратный, который, в силу свойств, произведения,
Г~
равен частному —, . Согласно свойству 13° элемент г можно
повторить слагаемым столько раз, что полученный при этом «целый»
элемент ri будет принадлежать {х'} и удовлетворять неравенству
л' > ,а,. Из последнего неравенства,, в силу свойств произведе-
ния и суммы, получим *)
т'—1-,>а.'.	(П.1)
Так как элементы т’, 1' и п' принадлежат множеству {х'}, то и
элемент 1/л ——Л также принадлежит этому множеству и, очевидно,
удовлетворяет неравенству ni—^,<Zm'. Но тогда неравенство (П.1)
означает, что в верхнем классе имеется элемент, меньший т\
т. е. т' не является наименьшим элементом. Полученное проти-
воречие доказывает полноту множества вещественных чисел.
2. Аксиоматическое введение множества вещественных чисел.
Полное логическое завершение наших представлений о вещественных
числах дает аксиоматический метод введения этих чисел. Этот метод
заключается в следующем.
*) Эти свойства обеспечивают применимость всех правил алгебры.
ДАЛЬНЕЙШЕЕ РАЗВИТИЕ ТЕОРИИ ВЕЩЕСТВЕННЫХ ЧИСЕЛ 589
/
Множество вещественных чисел вводится как совокупность
объектов любой природы, удовлетворяющих 17 аксиомам, в ка-
честве которых берутся, правила сравнения, сложения и умно-
жения*), 13 основных свойств и аксиома о полноте относи-
тельно указанных правил и свойств.
Указанные 17 аксиом обычно называют аксиомами веществен-
ного числа. Конкретной реализацией совокупности объектов, удов-
летворяющих ,17 аксиомам вещественного числа, является изученное
нами в главе 2 множество бесконечных десятичных дробей. Возможны
и другие реализации указанной совокупности объектов **). Полное
выяснение вопроса о связи между этими реализациями дает следую-
щей замечательное утверждение.
Любая реализация {х'} совокупности объектов, удовлетворяю-
щих 17 аксиомам вещественного числа, изоморфна относительно
правил сравнения, сложения и умножения изученному выше мно-
жеству {х} бесконечных десятичных дробей.
Доказательство. Ради удобства разобьем доказательство на
отдельные пункты.
1°. Прежде всего, заметим, что аксиомы гарантируют существова-
ние у множества {x'i элементов О' и Г, играющих особую роль нуля
и единицы. В силу аксиомы Архимеда Г^>0'***). Выделим у мно-
жества {х’\ совокупность «рациональных объектов». Для этого заме-
тим, что любое рациональное число может быть получено из чисел
О и 1 посредством операций сложения, вычитания и деления. В самом
деле, повторяя число 1 слагаемым нужное число раз, мы получим
любое положительное целое число л; вычитая из числа 0 число 1 нужное
число раз, мы получим любое отрицательное целое число; делением
двух целых чисел получим' любое рациональное число. Так как в
множестве {х'}> согласно аксиомам, определены операции сложения,
вычитания и деления, то с помощью этих операций мы получим
из 0' и Г все «рациональные объекты». Эти объекты мы будем обозна-
чать теми же символами, что и рациональные числа, но снабжать
штрихами.
Докажем, что построенная нами совокупность «рациональных объ-
ектов» множества {х'} изоморфна относительно правил сравнения, сло-
жения и. умножения совокупности рациональных чисел множества {х}.
*) Постулируется лишь факт существования правил сравнения, сложения
и умножения. Конкретный вид этих правил при этом не указывается.
**) Мы уже указывали во введении к настоящему приложению, что вещест-
венные числа могут быть введены различными способами (с помощью беско-
нечных двоичных дробей, с помощью так называемых дедекиндовых сечений и
другими способами).
***) В самом деле, если бы было верно противоположное неравенство Г^О',
то из него, в силу аксиом, мы получили бы Г 4- 1' 4~ ... + 1'^0'4~0' 4-... +
+ 0' = 0' (сколько бы раз число Г ни было повторено слагаемым), а это про-
тиворечит аксиоме Архимеда.
590
приложение
<7	,	Г
~ и Остается убедиться в том, что Д- и А- связаны
п q	nq
т р
же знаком, что и — и —
нашем
В самом деле, поставим в соответствие рациональному числу — «ра-
циональный объект» Из способа построения «рациональных объ-
ектов» вытекает, что сумме и произведению рациональных чисел
т р	,
— и — соответствует сумма и произведение «рациональных объек-
тов»
тем
п Я	' ’
«рациональных объектов» правило сравнения любых «рациональ-
ных объектов» посредством умножения на «целые объекты» сво-
дится к сравнению «целых объектов», то нам достаточно убедиться
в том, что для любых «целых объектов» т' и rl т,'^>п' при т~^>п.
Для того чтобы убедиться в этом, достаточно в силу аксиом доказать,
что (и + 1)'>п'. Последнее вытекает из того, .что Г^>0' и, стало
быть,
(я -|- 1 у = ri + 1' п' + О' = п'.
2°. Пусть теперь а' — любой объект множества {а/}. Покажем, что
этому объекту можно поставить в соответствие вполне опре-
деленную «бесконечную десятичную дробь». Ради определенности
предположим, что	В силу аксиомы Архимеда из «целых объ-
ектов», строго меньших а', найдется наибольший объект, который
мы обозначим через а'; из тех «рациональных объектов»
а;, О'; а'й, Г; ...; а'о, 9',
которые строго меньше а', найдется наибольший объект, который
мы обозначим через а', а[, и т. д.
Таким путем мы поставим в соответствие любому объекту беско-
нечную совокупность «рациональных объектов»
aj, a'p a'o, а’ ... ап;...,	-	(П.2)
или, что то же самое, «бесконечную десятичную дробь»
<, а\а2 ... ап ...	(П.З)
Те же рассуждения справедливы и для а'<^0', но в этом случае
как все объекты (П.2), так и «бесконечная десятичная дробь» (П.З)
будут иметь знак минус.
Из построения совокупности объектов (П.2) очевидно, что для
любого номера п справедливы неравенства
“1“ У П^-4)
т. е. любой объект а' заключен между двумя «рациональными объ-
ДАЛЬНЕЙШЕЕ РАЗВИТИЕ ТЕОРИИ ВЕЩЕСТВЕННЫХ ЧИСЕЛ
691
ектами», разность между которыми -цдну' может быть сделана
ше любого наперед взятого «положительного» объекта*).
мень-
3°. Докажем теперь, что если два объекта а’ и Ь' могут
быть заключены между двумя «.рациональными объектами» а! и
Р'	разность между которыми {Г — а' может быть сде-
лана меньше любого наперед взятого «положительного» объекта,
то d = Ь’. Предположим, что а' ф Ь'. Пусть, например, а'<Д}'.
Тогда а' d b' [У. Из этих неравенств, в’ силу аксиом, получим
О'< &' —«У [У—а'.	(П.5)
Но тогда для объекта b' — d найдется обратный _~ ат-, а для него
найдется «целый объект» п' такой, что
так что
Сопоставляя последнее неравенство с (П.5), получим
что противоречит тому, что разность {У — d может быть сделана
меньше любого наперед взятого «положительного» объекта.
4°. Убедимся в том, что двум неравным объектам множества
{х'} ставятся в соответствие различные «бесконечные десятич-
ные дроби». В самом деле, предположим, что двум объектам из {У}
ставится в соответствие одна и та же «бесконечная десятичная дробь»
(например, (П.З)). Тогда в силу неравенств (П.4) оба эти объекта
могут быть заключены между «рациональными объектами», разность
между которыми может быть сделана меньше любого наперед взя-
того «положительного» объекта. На основании пункта 3° рассматри-
ваемые объекты равны. Доказанное утверждение оправдывает
представление любого объекта множества {х7} «бесконечной деся-
тичной дробью».
5°. Согласно первым трем аксиомам для объектов множества {х'}
определены правила сравнения сложения и умножения.' Докажем, что
если все объекты множества {У} представить «бесконечными
*) В самом деле, для любого объекта е' > 0' в силу аксиом существует
обратный элемент 4- , а для него найдется «целый объект» п' такой, что
, Г	1'	1'
л > —, так что -J7— < — <«',
«	(10") п
592
ПРИЛОЖЕНИЕ
десятичными дробями», то для этих «дробей» правило сравнения
и определения суммы и произведения формулируются точно так же,
как для обычных бесконечных десятичных дробей, изученных выше.
Пусть аг и Ь' — любые два объекта множества {л/}, и пусть этим
объектам соответствуют «бесконечные десятичные дроби» *)
а'о, a't ... а'п ... и Ь'о, Ь[ ... Ь’а ...	(П.6)
Прежде всего выясним правило сравнения объектов а' и У, представ-
ленных в виде «бесконечных десятичных дробей» (П.6). Достаточно
доказать следующие два утверждения: 1) если дроби (П.6) совпадают,
т. е. если
Д() = ^в>	=	•”>
то объекты а' и V равны; 2) если найдется номер п такой, что
справедливы соотношения
d; = £>;, а[ = Ь[, .... a;_i = b^i, а'п<Ь’п, (П.7)
то объекты а' и Ь’ связаны неравенством a'<Cb’.
Утверждение 1) уже доказано в п. 4°. Докажем утверждение
2). Последнее из соотношений (П.7) можно переписать в виде
Un~\~ У^Ьп.
Пользуясь этим соотношением и остальными соотношениями (П.7) и
записывая для а' правое из неравенств (П.4), а для Ь' левое из не-
равенств (П.4), будем иметь
д ио, а± ... йд. 1ДЯ 4"	= а0>	(®л 4~ 1
д', д' ... ап_ф'л < &', т.е. а'<Ь'.
Докажем теперь, что для обьектов д' и Ь' справедливы те же
определения суммы и произведения, что и для обычных вещественных
чисел. Ограничимся случаем суммы. Пусть, а', а' р' и р' —всевоз-
можные «рациональные объекты», удовлетворяющие неравенствам
< < д' a', pi Z>' Р'.	(П. 8)
Тогда сумма а' 4- Ь’ объектов д' и У представляет собой единствен-
ный объект, удовлетворяющий неравенствам
+ + (п-9)
В самом деле, из аксиом вытекает возможность почленного сложе-
ния неравенств, а отсюда следует, что сумма д' 4- Ь' удовлетворяет
*) При установлении правила сравнения можно ограничиться случаем
«положительных» объектов д' и Ь', ибо общий случай сводится к этому слу-
чаю с помощью правила знаков.
ДАЛЬНЕЙШЕЕ РАЗВИТИЕ ТЕОРИИ ВЕЩЕСТВЕННЫХ ЧИСЕЛ
593
неравенствам (П. 9). Кроме того, эта сумма является единственным
объектом, удовлетворяющим неравенствам (П. 9), ибо каждая из раз-
ностей
< —и
а стало быть, и разность
(а2 + Рг) — (аг + Pi)
может быть сделана меньше любого наперед взятого «положитель-
ного» объекта (в силу п. 2°). Аналогично рассматривается случай
произведения.
6°. Докажем, наконец, что множество {%'} изоморфно относительно
правил сравнения, сложения и умножения множеству {х}. Каждому
объекту а' множества {х'}, представляемому «бесконечной десятичной
дробью»
±а;, а; ...а;
поставим в соответствие вещественное число
а= ±ай, 01 ...ап ...
Пусть двум объектам а' и Ь' соответствуют вещественные числа а
и Ь. Из результатов пункта 5° вытекает, что: 1) d и Ь' связаны
тем же знаком, что и числа а и Ь\ 2) сумме а' + Ь' соответствует сумма
а + Ь‘, 3) произведению а' • Ь' соответствует произведение а • b *).
Остается доказать, что при установленном нами соответствии
каждому вещественному числу отвечает некоторый объект множества
{./}. Если бы это было не так, то мы могли бы расширить множе-
ство {х'}, дополнив его недостающими «бесконечными десятичными
дробями» с сохранением правил сравнения, сложения и умножения
и 13 основных свойств, и пришли бы к противоречию с тем, что
множество {d} является полным относительно указанных правил и
свойств. Утверждение доказано.
3. Заключительные замечания. В заключение заметим, что аксио-
матический метод и понятие изоморфных (относительно различных
правил) совокупностей объектов широко используются в разнообраз-
ных разделах современной математики и физики (при построении гео-
метрии, теории вероятностей, классической механики, статистической
физики, квантовой механики * **) и других разделов).
.	*) Ибо сравнение, сложение и умножение объектов а' и Ь' и веществен-
ных чисел ан b определяются одними и теми же правилами.
**) Так, квантовая механика первоначально возникла в виде двух внешне
различных теорий: «Матричной механики» Гейзенберга и «Волновой механики»
Шредингера. Позже было доказано, что эти две теории используют две
изоморфные друг другу конкретные реализации одной общей совокупности
объектов, вводимой аксиоматически и называемой абстрактным гильбертовым
пространством (см. по этому поводу часть 2 настоящего курса).
594	ПРИЛОЖЕНИЕ
Например, в геометрии множество точек прямой вводится как
совокупность объектов, удовлетворяющих некоторым аксиомам, среди
которых фундаментальную роль играет аксиома о полноте этой сово-
купности относительно остальных аксиом. Упомянутые аксиомы позво-
ляют установить взаимно однозначное соответствие между множеством
всех точек прямой и множеством всех вещественных чисел*). Это со-
ответствие позволяет изображать вещественные числа точками на пря-
мой (числовой оси), чем широко пользуются в курсе анализа в иллю-
стративных целях.
*) См. Приложение к выпуску 5 настоящей серии «Аналитическая гео-
метрия» и в более подробном изложении книгу Н, В. Ефимова «Высшая
геометрия», изд. 1961 г. §§ 20—23.
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Абель 351
Абеля преобразование 351, 427
Абеля—Дирихле признак 439
Абеля—Пуассона метод суммирования
454
Абсолютная сходимость бесконечного
произведения 447
Абсолютно сходящийся ряд 429
Адамар 530
Адамара неравенство 530
Алгебраический многочлен 199
Алгоритм 33
— Евклида 203
Аналитический способ задания функ-
ции 19, 97
Аргумент 18, 96
— промежуточный 19
Архимеда аксиома 37
Асимптота графика вертикальная 306
----- наклонная 307
Астроида 376
Бесконечная десятичная дробь 39
Бесконечно большая последователь-
ность 60
-----функция в точке 102
— малая последовательность 60
-----функция в точке 102, 468
— малые функции эквивалентные
103
Бесконечное произведение 442
Билинейная форма 496
Бином Ньютона 21
Больцано 82
Больцано—Вейерштрасса теорема 82,
466
Бонне 338
Борель 327
Бореля—Гейне лемма 327
Буняковский 347	,
Буняковского—Коши неравенство (для
Интегралов) 350
Буняковского неравенство (для сумм)
347
Валлис 448
Валлиса формула 448
Вейерштрасс 82
Вейерштрасса теорема вторая 251,
476
-----первая 248, 476
Вейерштрасса—Больцано теорема 82,
466
Векторная функция 153
Векторной функции производная 154
Величина (переменная, постоянная) 17
Вертикальная асимптота 306
Верхняя площадь 368
— сумма 318
Вещественное число 35, 40, 585
-----, модуль 42
-----, правило сравнения 40
Взаимно однозначное отображение 542
— — соответствие 87
«Вилки» метод 387
Внутренняя точка множества 462
-----сегмента 54
Возрастание функции в точке 252
Выпуклая функция 514
Выпуклое множество 511
Гармонический ряд 414
-----обобщенный 419
Гармоническое колебание 20
Гейне 327
Гейне—Бореля лемма 327
Гёльдер 346
Гёльдера неравенство для интегралов
349
--------сумм 346
Геометрическая прогрессия 411
Гиперболические функции 117
Гомеоморфное отображение 512
Градиент 489
596
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Градиентный метод поиска экстремума
510
Граничная точка множества 462
Грань функции (точная верхняя, точ-
ная нижняя) 249
— числового множества (верхняя,
нижняя)-44
График функции 26, 459
----, направление выпуклости 299,
514
----, точка перегиба 301
Графический способ задания функции
19, 98
Даламбер 419
Даламбера признак 419
Дарбу 314
—	интегралы 320
—	лемма 321
—	теорема 314
Движения закон 18
Диаметр множества 476
Дирихле 96
—	функция 96
Дирихле—Абеля признак 439
Дискриминантная кривая 565
—	поверхность 568
Дифференциал 156, 484
—	высших порядков 175, 492
— дуги 366
Дифференциала инвариантность формы
172, 488
Дифференцирование 20, 156
— сложной функции 24, 168, 484
— суммы, разности, произведения,
частного 25, 158
Дифференцируемая функция 155, 479
----п раз 176, 493
Длина дуги кривой 358
— максимального частичного сегмента
316
Евклида алгоритм 203
Евклидова плоскость 458
Евклидово пространство 458, 461
Жордан 368
Замечательный предел второй 23, 127,
----первый 22,126
Замкнутое множество 462
Знакочередующийся ряд 438
Изоморфные множества 585
Инвариантность формы дифференциала
172, 488
Интеграл неопределенный 28, 182
— определенный 30, 316
—	эллиптический 236
Интегральная сумма 315
Интегральный косинус 187
—	логарифм 187
—	синус 187
Интегрирование биномиальных диффе-
ренциалов 226
— дробно-линейных иррационально-
стей 226
— по частям 190, 343
— рациональной дроби 216
— с помощью замены переменной 187,
342
Интегрируемости условие 323
Интегрируемость функции 316
Интервал 54
Иррациональные числа 40
Итераций метод 390
Итерационная последовательность 390
Итерация 92
Касание кривых 561
Касательная к графику функции 27
—	плоскость 481 
Касательных метод (метод Ньютона)
388, 393
Квадратичная форма 496
--- знакоопределенная 504
Квадрируемая плоская фигура 368
Классификация точек разрыва функ-
ции 136
Колебание функции 324, 477
Комбинированный метод отыскания
корней 398
Комплексные числа 195
Координатная плоскость 458
Координатное пространство 458, 460
Корень многочлена 200
---кратный, однократный 202
Коши 84
—	критерий существования предель-
ного значения функции 242, 469
--- сходимости последовательности
85, 466
—	последовательность 465
—	признак сходимости рядов 421
—	условие 242, 469
—	форма остаточного члена 270
—	формула 260
Коши—Буняковского неравенство 350
Коши—Маклорена признак 423
Кривая простая 354
Кривизна кривой 575
Криволинейная трапеция 30, 370
Кубируемое тело 374
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
.597
Кулона закон 19
Кусочно-непрерывная функция 139
Лагранж 254
Лагранжа метод неопределенных мно-
жителей 552
—	форма остаточного члена 270
—	формула конечных приращений
254
—	функция 552
Лаплас 558
Лапласа оператор 558
Лебег 327	*
Лежандр 237
Лейбниц 32
Лейбница признак 438
—	ряд 438
—	формула 178	'
Лейбница—Ньютона формула 32, 341
Лиувилль 237
Логарифм интегральный 187
— натуральный.116
Логарифмическая функция 115
Локальная ограниченность функции
244, 246
Локальный максимум функции 253,
 502
— минимум функции 253, 502
— экстремум 253, 502
Лопиталя правило 261
Маклорён 272
Маклорена формула 272
Маклорена—Коши признак 423
Минковский 347
Минковского неравенство для инте-
гралов 350
------- сумм 347
Множества внутренняя точка 462
—	граничная точка 462
—	диаметр 476
—	предельная точка 86
Множество вещественных чисел 44,
53
—	всех значений функции 96
—	конечное, бесконечное 86
—	мощности континуума 87
—	ограниченное 86
---сверху, снизу 44
—	, плотное в себе 54
—	связное 463
—	счетное 87
Модуль вещественного, числа 42
Монотонная последовательность 70
—	функция 106
Муавр 199
Муавра формула.199
Наклонная асимптота 307
Натуральный логарифм 116
— параметр на кривой 359
Начальное понятие 18
Неопределенный интеграл 28, 182
Неопределенных коэффициентов метод
214
— множителей метод (метод Лагран-
жа) 552
Неправильная рациональная дробь
207
Непрерывность функции 22, 104, 471
— — в точке 105, 241, 471
-----на множестве 106, 471
------- прямой 473
----- односторонняя 105
-----равномерная 325, 476
-----, разностная форма 150, 472
Неявная функция 526
Нижняя сумма 318
Нормаль к поверхности 483
Ньютон 18
Ньютона бином 21
— метод касательных 388, 393
Ньютона—Лейбница формула 32, 341-
Область 462
— задания функции 96, 464
— замкнутая 463
— ограниченная 463
Обобщенный гармонический ряд 419
Обратная тригонометрическая функ-
ция 124 
— функция 107, 536
Объем тела (верхний, нижний) 374
Обыкновенная точка кривой 535; 560
-----поверхности 535
Огибающая семейства кривых 564
-----поверхностей 568
Ограниченная область 463
— последовательность 59, 466
— функция 245
— — сверху, снизу 244
Ограниченное множество 86
----сверху, снизу 44
Ограниченность локальная функции
246
Однопараметрическое семейство кри-
вых 563
Однородная функция 487
Односторонний^ предел 99
Односторонняя непрерывность 105
— производная 153
Окрестность точки 54, 462, 464
Определенный интеграл 30, 316
Особая точка кривой 535, 560
----- поверхности 535
598
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Остаток ряда 413
Остаточный член формулы Тейлора
267
----------в интегральной форме 344
----------в форме Коши 270
----------------Лагранжа 270
----------------Пеано 271
----------------Шлемильха—Роша
267
Остроградский 219
Остроградского метод 219
Открытая полупрямая 54
Отображение взаимно однозначное 542
—	гомеоморфное 542
Отрезок в евклидовом пространстве
512
Парабол метод (формула Симпсона)
405, 406
Пеано 270
—	форма остаточного члена 271
Первообразная 182
Переменная величина 17, 95
Площадь верхняя 368
—	криволинейного сектора 371
—	криволинейной трапеции 370
—	нижняя 368
—	поверхности вращения 377
Поверхность уровня 491
Повторное предельное значение 469
Повторный предел 470
Подпоследовательность 78
Показательная функция 112
Полнота множества вещественных чи-
сел 586
Полупрямая 54
Полусегмент 54
Порядок соприкосновения кривых 569
Последовательность бесконечно боль-
шая 60
—	— малая 60
—	итерационная 390
—	неограниченная 60
—	ограниченная 59, 466
—	сходящаяся 64, 464
—	фундаментальная 83, 465
—	числовая 58
Правило сравнения вещественных чи-
сел 41
Правильная рациональная дробь 206
Предел верхний 80
—	нижний 80
—	повторный 470
— последовательности 64, 465
Предельная точка 78
Предельное значение функции 98,
239, 467
Приведенный многочлен 201
Признаки сравнения для рядов 416
Приращение функции 149
--- полное 471
--- частное 472
Проекция точки на множество 512
Произведение бесконечное 442
---абсолютно сходящееся 447
---сходящееся 443
---условно сходящееся 447
—	вещественных чисел 50
Производная 20, 150
—	высшего' порядка 175
—	по направлению 489
—	правая, левая 153
—	частная 477
---высшего порядка 492
Промежуточный аргумент 19
Пространство евклидово 458, 461
—	координатное 458, 460
—	метрическое 461
Прямоугольная окрестность точки 462
Прямоугольников метод 401
Пуассон 454
Пуассона интеграл 187
Раабе 426
—	признак 426
Радиус кривизны 583
Разность вещественных чисел 51
Разрыв 1-го рода 137
—	2-го рода 138
— устранимый 136
Расстояние точки до множества 512
Рациональная дробь 206
--- неправильная 207
--- правильная 206
Рациональное число 35
Риман 316
Римана теорема о перестановках ря-
дов 432
Ролль 254
Ролля теорема 254
Роша—Шлемильха форма остаточного
члена 267
Ряд абсолютно сходящийся 429
— гармонический 414
—	знакочередующийся 438
—	Лейбница 438
—	расходящийся 411
—	сходящийся 410
—	условно сходящийся 429
—	числовой 410
Ряда сумма 410
—	частичная сумма 410
Сегмент 54
Секущая 27
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
699
Сильвестр 504
Сильно выпуклая функция Б18
Симпсон 406
Симпсона формула (метод парабол) 406
Скорость мгновенная 20
—	средняя 20
Сложная функция 24, 130, 474
Соприкасающаяся окружность 574
Способ задания функции 97
•-------аналитический 19, 97
-------графический 19, 98
--------табличный 19, 98
Спрямляемая кривая 358
Среднего значения формула вторая
338
--------первая 336, 337
Степенная функция 117
Строфоида 355
Сумма верхняя 318
— вещественных чисел 48
— нижняя 318
— ряда 410
Суммирования методы 452
Сходящаяся последовательность 64,
464
Сходящееся произведение 443
Сходящийся ряд 410
Табличный способ задания функции
19, 98
Тейлор 267
Тейлора формула 267, 500
Точка разрыва функции 105
--------, классификация 136
Трапеций формула 403
Тригонометрические функции 120
----обратные 124
Убывание функции в точке 252
Угловой коэффициент прямой 27
Условно сходящееся произведение 447
— сходящийся ряд 429
Френеля интегралы 187
Фундаментальная последовательность
83, 465
Функция 18, 96, 464
Характеристика 568
Характеристическая точка 563
Хорд метод 389, 396
Центр кривизны 583
Цепная линия 367
Циклоида 181, 367
Частичная сумма ряда 410
Частное вещественных чисел 52
— значение функции 96, 464
Частная производная 477
Чебышёв 229
Чезаро 453
—	метод суммирования 453
Число е 23, 75, 277
Числовая прямая 54
Числовой ряд 410
Шлемильха—Роша форма остаточного
члена 267
Штольца теорема 88
Эвольвента 582
Эволюта 582
Эйлер 23
Эйлера подстановка 228 '
—	теорема 487
Эквивалентные бесконечно малые
функции 103
—	множества 87
Экстремум краевой 313
—	локальный 253
----, достаточное условие 292, 294,
297, 304
----, необходимое условие 253
---- функций нескольким перемен-
ных 502
•------------, достаточное условие
504
-------------, необходимое условие
503
Элементарная функция 136
Эллипс 367
Якоби 538
Якобиан 538
Владимир Александрович Ильин;
Эдуард Генрихович Позняк
ОСНОВЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА
Часть 1
(Серия: <Курс высшей математики
и математической физики>)
М., 1971 г., 600 стр. с илл.
Редактор Ш. А. Алимов
Техн, редактор В. Н. Кондакова
Корректоры Т. С. Вайсберг, О. А. Сигал
Сдано в набор 29/ХП 1970 г. Подписано к печати
20/V 1971 г. Бумага 60Х901/!,. Физ. печ. л. 37,5.
Условн. печ. л. 37,5. Уч.-изд. л. 38,98.
Тираж 97 000 экз. Т-06594. Цена книги 1 р. 25 к.
Заказ Xs 1544.
Издательство <Наука>
Главная редакция
физико-математической литературы.
Москва, В-71, Ленинский проспект, 15.
Ордена Трудового Красного Знамени Ленинград-
ская типография Xs 1 «Печатный Двор»
им. А. М. Горького Главполиграфпрома Комитета
по печати при Совете Министров СССР,
г. Ленинград, Гатчинская ул., 26.