Г. Д. Ким, Л. В. Крицков
АЛГЕБРА
И АНАЛИТИЧЕСКАЯ
ГЕОМЕТРИЯ
ТЕОРЕМЫ И ЗАДАЧИ
ТОМ II (1)

КЫч 22.147
Рекомендовано
Советом по прикладной математике и информатике
\ \(0 по кчассическоллу университетскому образованию
Лм студентов высших учебных заведений,
обучающихся по специальности 010200
"Прикладная математика и информатика “ и направлению 5/0200
"Прикладная математика и информатика"
Ким Г. Д., Крнцков .1. В.
Алгебра н аналитическая геометрия: Теоремы и задачи. Том II
часть 1. М.. 11КД “Зерцало-М”, 2003.— 170 с.
I5ВN 5-94373-068-0
Книга представляет собой первую часть второго тома задачника по объели-
ненному курсу линейной алгебры и аналитической геометрии. Каждый раздел со-
держит теоретическое введение, примеры решения типовых задач и большое чис-
ло задач для семинарских занятий и самостоятельной работы студентов. Задачи снаб¬
жены ответами и указаниями. Книга тесно связана с учебником Ильина В. А,
Ким Г Д -Линейная алгебра и аналитическая геометрия".
Для с(удентов физико-математических специальностей университетов.
I5ВN 5-94373-068-0
О Ким Г. Д., Крнцков Л. В.. 2003
О Издательство “Зерцало”, 2003

ОГЛАВЛЕНИЕ
Предисловие	 4
Список литературы			 5
Глава XII. Линейное пространство над произволь¬
ным полем	 б
§44. Определение и основные свойства	   6
§45. Линейное подпространство	 22
§46. Линейное аффинное многообразие	 38
Глава XIII. Евклидовы и унитарные пространства., 50
§47. Скалярное произведение. Матрица Грама	 50
§ 48. Ортогональные векторы	 60
§49. Ортогональные подпространства	 71
§50. Метрические задачи	 83
§51. Линейные аффинные многообразия в евклидовом (уни¬
тарном) пространстве	   93
Глава XIV. Линейные операторы в линейных про¬
странствах	100
§52. Понятие линейного оператора. Матрица линейного
оператора	100
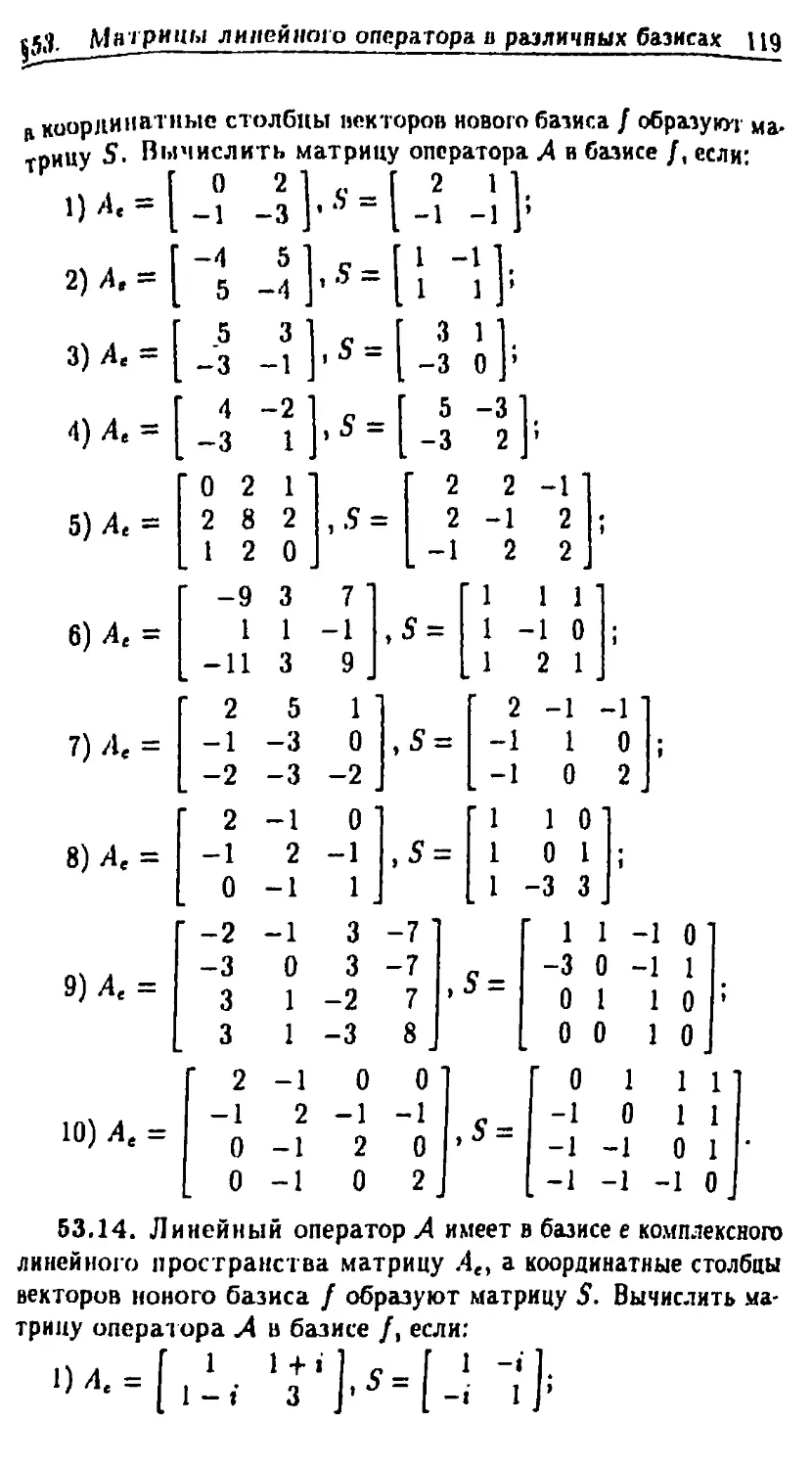
§53. Матрицы линейного оператора в различных базисах.
Эквивалентные и подобные матрицы	115
§54. Образ и ядро линейного оператора	123
§55. Линейное подпространство линейных	операторов	131
§56. Умножение линейных операторов. Обратный оператор 136
Ответы и указания	,.	147

ПРЕДИСЛОВИЕ
Настоящее учебное пособие представляет собой первую часть в-ц>.
рого тома сборника задач по объединенному курсу алгебры и аналити.
ческой геометрии. Оно содержит подборку задач по теории линейны^
пространств над произвольным полем, теории евклидовых и унитар.
ных пространств, а также задачи, касающиеся алгебры линейных опе¬
раторов в конечномерных пространствах.
Вудучи непосредственным продолжением первого тома [8), посо.
бис наследует его структуру. Задачи сгруппированы в параграфы,
нумерация которых продолжает нумерацию первого тома. В начале
каждого параграфа приводятся определения и формулировки теорем,
касающиеся рассматриваемых понятий, а также примеры решений ти¬
повых задач. Теоретической поддержкой задачника являются учебник
В.В.Воеводина [2], в котором заложены методические основы объедине¬
ния курсов алгебры и геометрии, и учебник В.А.Ильина, Г.Д.Ким [7].
Последовательность разделов, а также определения и обозначения со¬
ответствуют учебнику [7]. В конце задачника помещены ответы к
задачам, к некоторым из них даются рекомендации.

Список литературы
1.	Беклсмишева Л.А., Петрович А.Ю., Чубаров И.А.
Сборник задач по аналитической геометрии и линейной алгебре.- М.:
Наука, 1987.
2.	Воеводин В.В. Линейная алгебра,- М.: Наука, 1974.
3.	Воеводин В.В., Кузнецов Ю.И. Матрицы и вычисления.-
М.: Наука, 1984.
4.	Гантмахср Ф. Р. Теория матриц - М.: Наука, 1988.
5.	Г лазман И. М., Л юбич 10. И. Конечномерный линейный ана¬
лиз- М.: Наука, 1969.
6.	И крамов Х.Д. Задачник по линейной алгебре.- М.: Наука,
1975.
7.	Ильин В.А., Ким Г.Д. Линейная алгебра и аналитическая
геометрия,- М.: Изд-во Моек, ун-та, 1998.
8.	Ким Г.Д., Кринков Л.В. Алгебра и аналитическая геоме¬
трия: теоремы и задачи. Том 1.- М.: Зерцало, 2003.
9.	Кострикин А.И. Введение в линейную алгебру,- М.: Наука,
1977.
10.	Костр и к ин А. И., М ан ин Ю.И. Линейная алгебра и геомет¬
рия- М.: Наука, 1986.
11.	К у рош А. Г. Курс высшей алгебры.- М.: Наука, 1971.
12.	Полна Г., Сеге Г. Задачи и теоремы из анализа (в 2-х
частях).- М.: Наука, 1978.
13.	Прасолов В. В. Задачи и теоремы линейной алгебры.- М.:
Наука, 1996.
14.	Проскуряков И. В. Сборник задач по линейной алгебре.-
М.: Наука, 1967.
15.	Сборник задач по алгебре / Под ред. Кострикина А. И.- М.:
Факториал, 1995.
16.	Халмош П. Конечномерные векторные пространства - М.:
Физматгиз, 1963.
17.	Хорн Р., Джонсон Ч. Матричный анализ,- М.: Мир, 1989.
18.	Шилов Г.Е. Математический анализ (конечномерные линей¬
ные пространства).- М.: Наука, 1969.

Глава XII. Линейное пространство над
произвольным полем
§44. Определение и основные свойства
Пусть дано поде Р. Непустое множество V называется линейны* н
векторным пространством над полем Р, если на этом множестве опр^*
лены внутренний закон композиции I' х V -* V, называемый сложением*
внешний закон композиции Р х V -* V, называемый умножением на чиЛ*
из поля Р, удовлетворяющие следующим аксиомам: для любых а, 6, е ^ V °
о,0 еР	*
1)	о + ^ — 6 + в $
2)	(а + 6) + с = в + (5 + с);
3)	существует элемент в € V такой, что а + 0 = 0 + а:=а;
4)	для любого элемента а <• V существует элемент -а е V такой,
а + (-а) — (—а) + а = б ;
5)	1 • а — а ;
6)	а(Яо) = (о0)а ;
7)	(о + 0)а = а« +Дв;
8)	о(а + Ь) = аа + аЬ.
Линейное пространство над полем называется рациональным, нал по¬
лем Я - вещественным, а над полем С - комплексным линейным простран¬
ством.
Понятия линейной зависимости, базиса и размерности линейного про¬
странства, линейного подпространства и линейного многообразия, рассмо¬
тренные применительно к вещественным линейным пространствам в гла¬
ве IV части 1, сохраняются и в линейном пространстве над произвольным
полем. Практически неизменными остаются и все теоремы (а также нх до¬
казательства), касающиеся этих понятий. Незначительное изменение кос¬
нется лишь формулировок: в них добавится уточнение, какое именно поде
рассматривается. Безусловно, это сходство с вещественными линейнымх
пространствами относится к тем общим свойствам линейных пространств,
которые опираются лишь на аксиомы поля. Частные же особенности полв
(такие, например, как конечность поля или отличие от нуля его характери¬
стики) могут сделать свойства линейного пространства исключительными
(пример 44.4, задачи 44.11-44.15, 44.93, 45.26, 45.48).
Приведем теперь некоторые дополнительные понятия н факты, связан¬
ные с линейными пространствами над произвольным нолем.
Линейно независимая подсистема системы векторов, через которую як-
иейио выряжается любой вектор системы, называется базой этой системы
векторов
Теорема 44.1. Подсистема системы векторов является базой
системы векторов тогда и только тоес!а, кояда образует максимальную
линейно независимую подсистему

7
§•('/. Определение и основные свойства
Следствие. Псе базы одной системы осктороа соетомт из одина¬
кового числа векторов, равного максимальному числу линейно независимых
векторов системы.
Число векторов базы называется рангом системы векторов. Очевидно,
ранг системы векторов равен максимальному числу линейно независимых
векторов системы. Обозначение: г^(а(,...,а„).
Две системы векторов линейного пространства называются эквивалент¬
ными, если любой вектор каждой из этих систем линейно выражается через
другую систему. Из определения следует, что база системы векторов экви¬
валентно самой системе.
Теорема 44.2. Если система векторов в),..., а» линейно выра¬
жается через 6|,..., Ьт , то гв(а|,..., а*) < гв(6|	6т).
Следствие 1. Ранги эквивалентных систем совпадают
Следствие 2. Эквивалентные линейно независимые системы век¬
торов состоят из одинакового числа векторов.
Говорят, что система векторов в\	е„ линейного пространства V
порождает пространство V, если любой вектор х € V является линейной
комбинацией с\,...,е„.
В этой терминологии базис линейного пространства V - это линейво
независимая система векторов, порождающая все пространство V.
Теорема 44.3 (о неполном базисе). Вп-мерном пространстве
любую линейно независимую систему из к, где к < п, векторов можно
дополнишь до базиса.
Пример 44.1. Арифметическое пространство Рп. Пусть Р
- поле, а В" - множество всевозможных упорядоченных наборов п чисел из
ноля Р, т.е. В" = {а = (а\, аз,... ,а„)| а, е В, I = 1, п). Два арифметических
вектора а = (а| ,аз,..., а„) и Ь = (4|, 6э,... ,Ь„) называются равными, если
а, = Ь,, I = 1,л. Введем в В" операции по следующим правилам:
а)	если а = (а\, аз,..., а„), 6 = (6| , 4з,..., 6П)■ то
а + Ь = (а| + Ь\,аз -Г4з,..., а„ + 6П);
б)	для любого числа о 6 В
аа = (аа[, ааз,..., аа„).
Нетрудо проверить, что В" линейное пространство над полем В.
Единичные векторы
е, =(1,0,...,0), е2 = (0,1,... ,0), .... е„ = (0,0	1)	(44.1;
образуют базис В" (см. пример 17.2), называемый естественным базисом
пространства В", координатами вектора а = (01,03	а„) в естественном
базисе служат его компоненты 01,03,...,о„.
В частности, С" ■ комплексное линейное пространство, <Ит = п и
векторы (44.1) образуют его базис.
При мер 44.2. Арифметическое пространство С^. В линей¬
ном пространстве С" векторы умножаются на комплексные числа. Однако
можно было бы ограничиться умножением только на вещественные числа,
при этом результат умножения, несомненно, останется арифметическим век¬
тором из С" . Э го означает, что внешний закон композиции можно вводится
как умножение на вещественные числа, т.е. как отображение ах. — с-
Символом Сщ будем обозначать множество С", в котором внешний закон
композиции определен как К к Г" -• С". Нетрудно проверить, что
вещественное линейное пространство.

8 Глава XII.Линейное пространство над произвольны^
В арифметическом пространстве векторы (44.1) не могут бы*
эксом, так как умножением этих векторов только на вещественные ^
нельм получить любой комплексный арифметический вектор а -- ^Сл*
+ |0„), гле о*,0* 6 К. * = 17". Добавим к векторам (44.П **' +
векторов:	' е,Ие ,,
/.={«, о	о), и = (0,1	0)	/„ = (0,0	,).
Покажем, что система векторов е>,..., е„, /ь ■ • • • /п образует базис р*
Действительно, линейна» комбинация этих векторов с вещественными
эффиииеитами о», имеет вил	и *о.
(44.2)
П	П
53а|,г*+53 ^к ~ (°‘+«л > * •.. «*п+|Д».)
1>|	1*1
и равна нулевому вектору 8 = (0,...,0) тогда и только тогда, когда
= 0, к = 1, п, т.е. а* = /0* = 0, к = 1,п. Следовательно, вектоп+
е».....еп,/»,..-|/п линейно независимы. Они порождают псе пространств
С^, так как любой вектор (аз +|Л		 	 а'/7п) из С|^ согласно (44
является линейной комбинацией этих векторов с вещественными коэффИци
ентами 01,...1оп,Д|,....^п.
Итак, <Нт = 2п.
В частиости, само поле С можно рассматривать как вещественное лц.
иейное пространство Сд.. В этом случае сИш = 2, а естественным 613^
сом служат числа 1 н I.
Пример 44.3. Множество На — (0,1), в котором операции сложения
и умножених выполнлются по правилам
0
1
0
0
0
1
0
1
+
0
1
0
0
1
1
1
0
соответственно, образует, как нетрудно проверить, поле. Как и любое поле
оно авлхетси линейным пространством над самим собой.
Заметим, что это поле есть ничто иное как поле вычетов (Со,СЛ по
модулю 2, в котором каждый из классов представлен своим элементом. Опе¬
рации сложении и умножених в На введены по правилам:
1)	сумма шил есть остаток от делении обычной суммы ш + п на 2,
2)	произведение тип есть остаток от деления обычного пронэведени*
тп на 2.
Таках операции сложении (умножения) называется сложением (соответ¬
ственно умножением) по модулю 2 н обозначается (т + п) тод 2 (соответ¬
ственно (тп) тод 2).
Аналогичным образом могут быть введены алгебраические операции и
в — (0,1,... ,р — 1}.
Пример 44.4. Пусть М = (аьоа	а„} - множество, состоящее из
п элементов. На множестве всех его подмножеств V определим операции
сложении и умножении на числа из поли На (см. предыдущий пример) по
правилам:

9
§44. Определение и основные свойства
X + У = (ХоУ)\(ХпУ),
1-Х = Х, 0 Х = ф.
Нетрудно проверить (например, на круга* Эйлера), что относительно ути*
операций множество V является линейным пространством нал полем 2г.
Отметим, что в этом пространстве в = ф -X = X.
Покажем, что подмножества Л'| = (ад), Xз = (аз),..., А'„ = (в„)
образуют базис V. Во-первых, они образуют линейно независимую систему,
так как никакая нетривиальная линейная комбинация (т.е. с коэффициен¬
тами, равными 1) этих подмножеств не равна 0: 1 • X,, + 1 • X,, + ... +
1 • Х,к = {а,,,а,э,...,а,ь) / ф. Во-вторых, как следует из последнего ра¬
венства, любое подмножество является линейной комбинацией подмножеств
X,, Я,
Таким образом, (Вт V = п.
Отметим также, что число всех векторов в пространстве V конечно н
равно 2".
Пример 44.5. Доказать, что линейное пространство йф веществен¬
ных чисел над полем рациональных чисел бесконечномерно.
Решение. Покажем, что для любого натурального числа п можно
указать п вещественных чисел, линейно независимых над полем {$.
Пусть р1,рз,... ,р„ - произвольные различные простые числа и
II = 1°8з Р1 ■ 12 = 1°8з Р2| • • ■ I *п = Рп.
Покажем, что если
ад!) + 0(2*3 +... + Оп1п = 0	(44.3)
для некоторых рациональных коэффициентов ад,0!2,...,ап, то екз = аг =
... = а„ = 0.
Без ограничения общности можно считать, что все коэффициенты в ле¬
вой части (44.3) целые: а, = к, 6 2, 1 = 1, п (в противном случае, т.е. если
а, = —, к, € 2, ш, 6 N. I = 1, п, достаточно умножить обе части равенства
т,
(44.3) на наименьшее общее кратное знаменателей шд,Ш2	т„). Таким
образом, выполнено равенство
(44.4)
к\ 1о&2 Р1 + кз 1о§2 р7 4-... + *„ Цз Рп = 0
или, что тоже самое,
Р*1 -Рз3 ■■ - Рп’ =1-	(44-5)
Если все показатели степени к\,кз,...,кп в левой части (44.5) неотри¬
цательны, то так как р, ф ], д = 1, п, то к\ = к7 = ... = кп = 0.
Если же среди чисел Ад,..., кп есть отрицательные - например,
к] < 0, ...,*,< 0, *,+! > 0, .... кп>0,
то из (44.5) следует, что
„1*<1
• •р^рГ11
что противоречит единственности разложения натурального числа на про¬
стые множители.
Таким образом, равенство (44.3) с целыми, а следовательно, и с рацио¬
нальными коэффициентами возможно тогда н только тогда, когда все эти
коэффициенты нулевые. ■

10 Глава ХПЛнш'йноо пространство на а произвольным
Двя линейных прострвнггпв Ц и 1а мал общим полем Р цМЬ|
изоморфными, гели существует биективное отображение ^ : Ц -»
торос сохраняет законы композиции, т.е. если для любых векторов * 1 > * *
и любого числа о € Р	'1 ^ ь
0 *(* + *) = *>{*) +р(у);	1
2) у>(ох) = п^(х).
Обозначение: VI 3 Vз. Само отображение уз Называется изом0
мом линейных пространств.
Пример 44.6. Геометрические пространства Ц, V), Кз вектор
прямой, на плоскости и в пространстве изоморфны арифметическим рр" Н*
рансгаам Я1, Я* и Я1 соответственно. Действительно, поставим в НОс>.
ветствме каждому вектору х С V, набор его координат в каком-либо б»00*,
е, т.е. арнфметнческий вектор г, 6 К , где п = 1,2, .4. Это соотвсгГЧ(,
взаимно однозначно и сохраняет законы композиции, так как коордИк1\
вектора обладают свойством линейности.	|*4Т|4
Пример 44.7. V} =	= Ж2.
Пример 44.8. Рт*Л « />">«, н в частности Жтхп “Жтп.
Теорема 44.4. Отношение изоморфизма есть отношение Э|г
валентности на множестве всех линейных пространств над полем
Теорема 44.5. В изоморфных пространствах
а)	образ (и прообраз) линейной комбинации векторов есть линец
комбинация образов (прообразов) с теми же коэффициентами;
б)	образ (и прообраз) нулевого вектора есть нулевой вектор;
в)	образ (и прообраз) линейно независимой системы векторов образ
линейно независимую систему;
г)	образ (и прообраз) базиса есть базис.
Нцл
<У%
Теорема 44.6 (критерий изоморфизма). Два конеинамерНы
линейных пространства над общим полем изоморфны тогда и только щ
гда, когда их размерности совпадают.
Следствие. Любое п-мерное вещественное пространство изомоп*
но арифметическому пространству Ж", а любое п-мерное комплексное пр0
странство - арифметическому пространству Сп.
ЗАДАЧИ
44.1.	Доказать, что в линейном пространстве над полем Р
для выполнения равенства ах + (Зу = (Зх + ау, где а,(3 Е Р, х,у
- векторы пространства, необходимо и достаточно, чтобы либо
а = /3, либо х = у.
44.2.	Не пользуясь коммутативностью сложения векторов,
доказать, что правые противоположный и нулевой элементы бу¬
дут одновременно левыми.
44.3.	Доказать, что коммутативность сложения векторов
вытекает из остальных аксиом линейного пространства.
44.4.	На множестве Я2 упорядоченных пар действительных
чисел введена операция сложения по правилу:

§44. Определение и оснонныс свойства
II
если а = (а1, а2) и Ь = (Ь,, Ь2), то а + Ь = (а, + 6,, а2 + Ь2).
Ввести операцию умножения пары (я1,аа) на действительное
число а так, чтобы:
а)	были выполнены все аксиомы линейного пространства,
кроме аксиомы
1 • а = а, Ча еШ2;
б)	были выполнены все аксиомы линейного пространства,
кроме аксиомы
(а + /3)а = аа + 0Ь, Ча е К3, Ча,0 е К.
44.5.	На множестве К2 упорядоченных пар действительных
чисел введены следующие операции:
если а = (в|, а2) и 6 = (Ьх, Ь2), то а + 6 = (а, + 6|, а2 + Ь2)\
для любого комплексного числа а = А + {ц (А,// € К)
а(аиа2) = (Ав! + ца2,-цах + А а2).
Доказать, что множество К2 с так введенными операциями
является комплексным линейным пространством.
44.6.	На множестве К2 упорядоченных пар действительных
чисел введена операция сложения по правилу:
если а = (ах,а2) и Ь = (ЬХ,Ь2), то а + Ь = (ах + Ьх,а2 + Ь2).
Ввести операцию умножения пары (ах,а2) на комплексное чи¬
сло а так, чтобы были выполнены все аксиомы линейного про¬
странства, кроме аксиомы
а(0а) = (а0)а, Ча € Ж2, Ча,Р 6 С.
44.7.	В комплексном линейном пространстве V определе¬
на новая операция умножения на число по правилу а о х = ах,
Ч 6 С. Доказать, что V является комплексным линейным про¬
странством относительно старой операции сложения векторов и
новой операции умножения на число.
44.8.	Найти ошибку в следующем ''доказательстве" того,
что аксиома 1 • а = а Ча 6 V вытекает из других аксиом линей¬
ного пространства: "Пусть а = об, тогда 1 а = 1(о6) = (1 а)6 =
аЬ= а”.
44.9.	На множестве К+ положительных действительных чи¬
сел определены следующие операции:
а)	"сложение” хфу = ху (т.е. обычное умножение х и у);
б)	"умножение на действительное число" а © х = х° (т.е.
возведение х в степень о).
Показать, что множество К+ относительно указанных опера¬
ций образует вещественное линейное пространство.

>2 Глава .V//. Линейное пространство нал произаилг.щ.ц.
44.10.	Пусть 1* - множество всех функций, заданных и
нимаюших положительные значения на отрезке [а, 6]. Оц ^Ч-
лим сложение двух функций н умножение функции на числ^®'
венетвами:	Рч
/ФР = /.<?. “0/=/",	/>Р € К,о е К.
а)	Проверить, что относительно указанных операций V
ется вещественным линейным пространством.
б)	Доказать, что пространство V изоморфно прострацСт
\\ всех действительных функций, заданных на отрезке (а,6],^
носителъно обычных операций сложения функций и умножен^
функции на число.	*
44.11.	Пусть Р - поле, Г - его подполе,
а)	Доказать, что Г является линейным пространством на
полем Г.
б)	Найти базис и размерность поля С над полем Ж.
в)	Пусть п*|,..., пц - различные натуральные числа, кажд^
из которых не делится на квадрат простого числа. Доказать, ч*0
числа 1,	..., у/тп^ линейно независимы в пространстве
г)	Пусть гь...,г„ • различные рациональные числа из ин-
тервала (0,1). Доказать, что числа 2Г*,...,2Г" линейно незави¬
симы в пространстве йф.
44.12.	Пусть р - простое число и 2Р = {0,1,... ,р - 1} -
множество, в котором операции сложения и умножения вводится
по правилам (сы. пример 44.3):
т ф у = (х + у) то<1 р, X о у = (ху) тос! р.
а)	Показать, что 2р образует поле, и следовательно, является
линейным пространством над самим собой.
б)	Ввести структуру линейного пространства на множестве
Ер всевозможных арифметических векторов, в которых каждая
компонента равна одному из чисел множества Ер.
в)	Найти общее число векторов в линейном пространстве^
и его размерность.
44.13.	Привести примеры линейных пространств, состоя¬
щих из п векторов, если: а) п = 1; б) п = 2; в) п = 3; г) п = 4.
44.14.	Показать, что если линейное пространство V содер¬
жит конечное число векторон, большее одного, то его основное
поде конечно.
44.15.	Существует ли линейное пространство, состоящее из

§//.). Определение и основные свойства
13
шести векторов?
44.16.	Пусть V - линейное пространство всех подмножеств
конечного множества Л/ из п элементов над полем (си. при¬
мер 44.4). Доказать, что если ни одно из подмножеств Хи...,Хк
этого множества нс содержится в объединении остальных, то эти
подможества составляют в V линейно независимую систему.
44.17.	Доказать, что пространство V всех подмножеств мно¬
жества М из п элементов (см. пример 44.4) и арифметическое
пространство И!\ изоморфны как линейные пространства над по¬
лем Указать какой-либо изоморфизм между ними.
44.18.	Два вектора а и 6 линейного пространства V над по¬
лем Р называются коллчнеарными, если существует такое число
а € Р, что либо а = аЬ, либо Ь = аа. Выяснить, являются ли
коллинеарными следующие пары векторов комплексных ариф¬
метических пространств:
а)	(1, 1 + «,2,2-30, (*, 1 - *, 2 + 1, -1);
б)	(1,1, 2 — *, 3 + *), (1 — 1, 1 + «, 1 — Зг, 4 — 2*).
Будут ли они коллинеарны как векторы соответствующих ве¬
щественных арифметических пространств?
44.19.	Пусть в пространстве V над полем Р задан неко¬
торый базис е|,...,еп. Тогда каждому вектору г 6 У можно
поставить в соответствие строку его координат в этом базисе:
и-> хе = (оь...,ал).
Доказать, что:
а)	линейная зависимость (линейная независимость) системы
векторов х, у,..., г равносильна линейной зависимости (соответ¬
ственно линейной независимости) системы строк хе,у„...,хе,
рассматриваемых как элементы соответствующего арифметиче¬
ского пространства
б)	ранг системы векторов х,у,...,г равен рангу системы
строк хе,&,...,ле;
в)	если вектор а линейно выражается через систему х,у,...,
г, т.е. а = Ах + ру + ... 4- иг, то это же верно и для строк ае, хе,
уе,..., ге, причем ае = X хс+ руе + ... +
44.20.	Выяснить, являются ли следующие системы матриц
линейно зависимыми:

14 Глада А71.Линейны пространстпо над проиэпольикп.
•1-: ;м::-;]■[•: и- (? -;]■
Запнгнт ли ответ от того, каким является пространство
ствснным или комплексным?
в°'%
44.21.	Выяснить, являются ли следующие системы мн0,.
членов линейно зависимыми:	°‘
а) р(Н), Р(~‘0. Р(0> Р(~0. , де Р(0 = <3 + Iя + I + 1;
б)	*-|\ < + |, о-О2, О + О8-
Зависит ли ответ от того, каким является пространство - Ве,1№
ственным или комплексным?
44.22.	Доказать, что если какой-либо вектор линейного пр0
странства единственным образом представляется в виде лине$
ной комбинации векторов е1,е3,..., ек, то эта система вектор^
линейно независима.
44.23.	Доказать, что если каждый вектор линейно неза
висимой системы 1),...,хп линейно выражается через вектору
ТО п < т.
Найти ранг следующих систем векторов и выяснить, зависит-
ли ответ от того, какому пространству - вещественному «ли
комплексному - принадлежат эти векторы:
*» = (1,4, 7, 10),
*а = (2, 5, 8, 11),
*з = (3, 6, 9, 12).
44.24. х, = (1,2,3),	44.25.
х, = (6, 5, 4),
*з = (7, 8, 9),
хч = (12, 11, 10).
44.26. х, =(1,-1, 0,0),
х? = (0, 1, -1, 0),
*з = (0,0, 1,-1),
*« = (0,0, 0,-1),
х5 = (7, -3, -4, 5).
44.28. х, =(1,10,0,0),
*» = (0, 1, Ю,0),
хз = (0, 0, 1, 10),
Х4 = (Ю-3,0, 0,1).
44.30.	х, = ( 3-1,1-21,-7+ 51,4 + 30,
хз = (1 + 3|, 1 + 1, —6 — 7»,	4*),
*» = (	0,	1,	1,	-3).
44.31.	р,(0 =*«-!, р,(0 = «»-!, р3(0= <г+1, рЛ0 = 1 + 1’
Рь( 0 = <-1.
44.27.
44.29.
х, = (1, -1,0,0),
х2 = (0, 1, -1,0),
Хз = (0, 0, 1, —1)1
х4 = (1, 0, 0,-1).
х, = (1, 1, 1, 1, 1)>
х2 = (1, г, -1, О.
х3 = (1, -1. !> -.1> 0»
хА = (1, -I, -1> 1> *)■

у,/. Определение и основные свойства
15
44.32.	р,(!) = (« + О’. ЫО = (I - I)5, Рэ(<) = (И- I)3,
р<(0 = (<-1)3, Рз(0 = (<+1)\ р6(1) = (1-1)4.
44.33.	р,(() = (1 - I)4, р,(1) = (1 - 1 )3(< + 1),
р3(1) = (<-1)2(1 + 1)2, р4(0 = (<-!)(< +1)3,
Р»(0 = (‘ + 1)4-
44.34.	р,(1) = 1 + г, р2(<) = 1-1, р3(0 = 1+1, р4(!) = 1-1.
44.35.	Л, Л2, Л3, Л4, где Л = II ! .
44.36.	Л1
Лз
44.37.	Л, =
1 I 1 + 1
2-1 0 1-1
Л2
-11 I
О 1 + 1 2 + I ’
1 + 1 -2 -1
1+21 -1-1 -1
Л4
11 + г
11-1
I -1 + 1
-1 1+1
Лз —
1 - I 21
2-1 -1+1
2-1 3+1
1+2: 1 - 31
44.38.	Существует ли система векторов из Сп, которые кол-
линеарны как элементы комплексного пространства, а как эле¬
менты вещественного пространства имеют ранг, больший двух?
44.39.	Известно, что система векторов а\,а^, ...,ап 6 С"
имеет ранг г как элементы комплексного пространства С". До¬
казать, что ранг этой системы в вещественном пространстве
не превосходит 2г.
Для каждой из следующих систем векторов найти ранг и
какую-нибудь базу:
44.40.	1, = (1,-4, 3,2),
х2 = (3, —7, 5, 3),
хз = (3, —2, 1, 0),
*« = (-4, 1,0, 1).
44.41. 1, = (0, 2,-1),
х2 = (3, 7, 1),
13 = (2, 0, 3),
х« = (5,1,8).
44.42.	Р1(1) = 3<2	+ 21	+ 1, 44.43. р,(1) = I3 + 2!2 + 31 + 4,
р2(1) = 4!2	+ 31	+ 2,	ра(1) = 213 +	З!2 + 41	+	5,
р3(1) = З!2	+ 21	+ 3,	Рз(1) = 313 +	412 + 51	+	6,
р4(!) = I2 + 1 +	1,	р4(!) = 413 +	512 + 61	+	7.
р5(1) = 412	+ 31	+ 4.
44.44.	Л, Лт, ЛЛТ, Л2, Л3, Л4, где Л =
!-!]
1 1 '
44.45.	Л, В, Вт, ЛВ, АВТ, В А, Вт А, ВВТ, ВТВ, где

16 Глава XII.Линейное пространство над нроизяолы»...г
10 0'
‘0 0 Г
0 1 0
, в =
0 1 0
0 0 0
0 0 0
/1 =
44.46.	В системе Х1,..-,хт первые г векторов образу^
зу, а х, - ненулевой вектор, не входящий в эту базу. Д0ца.
что среди векторов базы найдется вектор *>. 1 < ] < г,
что при замене его в подсистеме ж,,..., хР вектором х, полун*^,
новая база заданной системы х»,...^*,. Будет ли такой Век-)С*
Ж| единственным?	Г°Р
44.47.	Что можно сказать о системе векторов ранга г
она имеет: а) единственную базу; б) ровно две базы; в) р0ц и
три базы? Две базы, отличающиеся лишь порядком вектору
считаются одинаковыми.
Найти все базы следующих систем векторов:
44.48.	ж, = (4, -2, 12, 8),	44.49. ж, = (1, 2, 3, 0, -п
х2 = (-6, 12, 9, -3),	ж2 = (0, 1, 1, 1, 0) Л
*3 = (-Ю. 5, -30, -20),	х3 = (1, 3, 4, 1, -и
ж, = (-14,28,21,-7).
44.50.	Указать все базы системы векторов
ж, =(1 + «, 1-г,2 + 3»), х2 = ( *,	1,	2),
х3 = (1 - 1,-1 ~ *»3 — 2»),	= (4,-4», 10 + 2»),
рассматриваемых как: а) элементы комплексного пространства-
б)	элементы вещественного пространства.
44.51.	Даны две системы векторов:
х» =(1,1,1),	у, =(1,2,3),
х2 = (1, 0, —1),	Уг = (0,1,2),
*а = (1,3,5),	уз = (3, 4, 5),
У* = (4, 6, 8).
Определить, будет ли система УьУ2,Уз,У4 линейно выражаться
через систему ХьХ2,х3.
44.52.	Известно, что в системе векторов хх,..., хт, у,,.. . ,уп
векторы У),. ..,уп линейно выражаются через векторыж!,... ,жт.
Показать, что система Ж1,...,хт,Уь • • •,уп эквивалентна систе¬
ме ж,,...,жт.
44.53.	Доказать, что в каждой системе векторов Ж1,...,хт,
содержащей хотя бы один ненулевой вектор, можно выбрать
эквивалентную ей линейно независимую подсистему.

17
§44. Определение и основные свойства
44.54.	Ланы векторы:
а, = (0,1,0,2,0), а, = (7,4,1,8,3), а3 = (0,3,0,1,0),
а« = (1,9,5,7,1), а, = (0,1,0,5,0).
Можно ли подобрать числа с„, I,; = 173, так, чтобы векторы
Ь, = с,,<2, + с(2а2 + с,3а3 + с^а, + с,ва5, I = Т73,
были линейно независимы?
44.55.	Доказать, что вектор 6 тогда и только тогда линейно
выражается через векторы а|,я2,..,,а4, когда ранг последней
системы векторов не меняется от добавления к ней вектора 6.
44.56.	Доказать, что если две системы векторов имеют оди¬
наковый ранг и одна из этих систем линейно выражается через
другую, то эти системы эквивалентны.
44.57.	Доказать, что если пересечение двух систем векторов
А = {а1,...,а*} и В = {6|,...,6т} непусто, то
т$[А П В) + ге(Д II В) < г§ Д + щВ.
44.58.	Доказать, что для любых двух систем векторов Д =
{а1,...,а*} и В = {6ь...,6т} справедливо равенство
:%{АиВ) < г|Д + гвВ,
причем равенство в этом соотношении выполнено тогда и толь¬
ко тогда, когда ни один вектор одной системы не выражается
линейно через векторы другой системы,
44.59.	Доказать, что в п-мерном линейном пространстве лю¬
бые п линейно независимых векторов образуют базис.
44.60.	Доказать, что любой ненулевой вектор пространства
можно включить в некоторый базис этого пространства.
44.61.	Доказать, что в конечномерном пространстве суще¬
ствует базис, не содержащий ни одного вектора из заданной си¬
стемы векторов Я),..., а*.
44.62.	В пространстве I5 найти три различных базиса, име¬
ющих общие векторы ех = (1,0,0,1,1), е2 = (0,1,1,0,0). Верно
ли, что существует лишь конечное число таких базисов, в кото¬
рых системы добавляемых векторов попарно не эквивалентны?
44.63.	Систему многочленов <5 + 1Л, I3 - И3, 13 + 212, 15 - I
дополнить до базиса пространства Л/5.
допол-
'2 7 6'
2 1 Г
'4 8 7'
6 1 4
’
3 0 1
>
9 2 5
44.64.	Систему матриц
нить до базиса пространства К2*3.

18 Глав» ХИ.Линсйнос пространство над произвольным
1 1 0'
'0 0 2'
'2 0 0'
° 0 (п
44.65. Систему матриц
1 0 1
0 10,
0 1 0
1 0 1
0 1 0
2 0 1
0 0 0
.0 0 0
дополнить до базиса пространства К3*3. Можно Л((
0 2 0
0 0 0
0 2 0
выбрать все добавляемые матрицы кососимметрическими?
Показать, что векторы С|	образуют базис арифмети
ческого пространства и найти координаты вектора х в этом 64.
зисе:
44.66.	с, = (2,2,-1), с3 = (2,-1,2), е3 = (-1,2,2);
» = 0,1,1).
44.67.	е, = (1,5,3), е3 = (2,7,3), еа = (3,9,4);
х = (2 - 2», 7 — 4», 4 - 1).
44.68.	е, =(1,2,-1,-2), е, = (2,3,0,-1), е3 = (1,2,1,4),
«а = (1,3, —1,0); * = (7,14, —1,2).
44.69.	е, = (1,2,1,1), е, = (2,3,1,0), е3 = (3,1,1,-2),
«« = (-4,4,-1,6);* = (7,8,7,2).
44.70.	Построить какой-либо базис в вещественном про.
странстве С5 и найти координаты в этом базисе вектора
(1 + 1,1 — 2*).
44.71.	Арифметические векторы е1,..., е„ образуют базис в
комплексном пространстве С". Доказать, что:
а)	векторы 			*С|,...,«еп образуют базис в веществен¬
ном пространстве С$;
б)	векторы е1,...,е„,ое1	ае„ образуют базис в вещест¬
венном пространстве Сд тогда и только тогда, когда комплекс¬
ное число о не является вещественным.
44.72.	Найти координаты многочлена 1& - I4 + I3 - 0 - 1 + 1
в каждом из следующих базисов пространства Л/5:
а)	1, 1, I1, I3, 1\ 1*;
б)	1, 1-1, 1* + 1, I3 - 1, I4-И, 18 + «;
в)	1 +13, 1-М3, Г3-И3, I3, 14 + 13, 18 + 13-
44.73.	Доказать, что многочлены 21 + 18,13-!5,1 + 13 образуют
базис в пространстве нечетных многочленов степени не выше 5,
и найти координаты многочлена 51 - I3 + 218 в этом базисе.
44.74.	Показать, что последовательности
е, =(2,3,5,8,13,...), е, = (1,2,3,5,8,...)

19
$44- Определение и основные свойства
образуют базис пространства всех последовательностей веще¬
ственных чисел (01,02,...), удовлетворяющих условию о* =
а*_1 + а»-з, к > 3. Разложить по этому базису последователь¬
ность х = (1,1,2,3,15,8,...).
44.75.	Доказать, что система матриц
121 р -\2 2
12 ' ~ 11
,Яэ =
1 21 ,, [21
2 1 ' = 2 1
В,=
образует базис пространства К2ха. Построить другой базис это¬
го пространства так, чтобы ни одна из его матриц не выража¬
лась линейно через какие-либо две матрицы базиса Еи Ег, Е3,
Еа.
44.76.	Доказать, что матрицы
1 -Г
! -1
,Ег =
'2 5
1 3
, Е3 =
'1 Г
0 1
,Дч =
3 4'
.5 7
и наити координаты
в каждом из
образуют базис пространства
'5 14"
6 13
в этом базисе.
матрицы А =
44.77. Найти координаты матрицы
следующих базисов пространства С2х2:
б)
44.78. Доказать, что матрицы
1 г
1 Г
1 Г
1 Г
1 1
)
1 г
1 1
1
1 1
»
1 Г
0 г
1 0
2 1 + 1
г 0
1
г 3
1
0 1
>
1
0
0
Г
'1
2 2'
'1
2
3'
0
1
0
е2 =
2
1 -2
, Е3 =
2
3
4
1
0
0
2 -
-2 1
3
4
5
: -2
3
'
: 2
2 -Г
:о
1
1:
3
6
1
, Еь =
2
-1 2
, Е6 =
1
-1
-1
1
2
-1
2 2
1
-1
-2
матриц порядка
в этом базисе.
образуют базис пространства симметрических
[0 6 1
3, и найти координаты матрицы .4 =
3 -3
-3 -3

20 Глава X//.Линейное пространство нал нроизвольн>.,,т
44.79.	Доказать, что каждая из двух систем нектор0й
е, = (	1-1,3 + 21),	е',=(	1,	9 + 3«),
с, = (— 1 + 2«, 3 - 0,	е'а = ( -1 + 3»,	9)
является базисом пространства С*, и найти матрицу передо
первого базиса ко второму. Найти координаты вектора в „еЧа°т
базисе, если известны его координаты (х,,х2) во втором
44.80.	Доказать, что каждая из двух систем векторов Ксе
«, =	(1,0,0,	с',	= ( 1, 0,-0,
е} =	(0,1,1),	с'2	= ( 0,-«, 1),
с3 =	(«,1,0),	е,3	= (-1, 1,	0)
является базисом пространства С3, и найти матрицу переход^
первого базиса ко второму. Найти координаты вектора в перв°Т
базисе, если известны его координаты (х,,х2,х3) во втором б*1
зкее.
44.81.	Показать, что многочлены 1,1-е, (<-с)2,...,	^
образуют базис в пространстве Мп, и найти координаты Много,
члена
/(1) = во + 0\1 + а2<2 +-... + ап1п
в этом базисе.
44.82.	Найти матрицу перехода от естественного базиса пр0.
странства Мп к базису 1,1 - с, (/ - с)2, ...,(<- с)п.
44.83.	Доказать, что каждая из двух систем матриц
'1 2'
■ 0 Г
0
0'
‘0
0'
'3
1 '
'0 0'
3 0
»
-1 1
)
1
_2
1
0
1
)
2
1
1
0 0
0 2
0 0
0
1
0
2
1
0
0 1
’ 1
11
'4 3'
'3 0'
‘3
1'
' 0
1 ‘
'0
01
4
-1
1
5 1
*
3 0
1
0
5
)
-1
2
У
1 -1
0
2
1 2
1 0
1
-2
0
0
.0
4
является базисом пространства К3*2, и найти матрицу перехо¬
да от первого базиса ко второму. Найти координаты матрицы
размера 3 х 2 в первом базисе, если известны ее координаты
(х,,хг,...,хв) во втором базисе.
44.84.	Доказать, что каждая из двух систем матриц
■ 0 1 -2'
0 0 -Г
'0-1 2'
-10 3
I
0 0 4
»
1 0 -2
2-3 0
1 -4 0
-2 2 0

21
$44. Определение и основные свойства
■ 0 1 Г
‘ 0 2-2'
0 10'
-1 0 -1
)
-2 0 3
-1 0 -2
-1 1 0
2-3 0
0 2 0
является базисом в пространстве кососимметрических матриц
порядка 3, и найти матрицу перехода от первого базиса ко вто¬
рому. Найти координаты кососимметрической матрицы поряд¬
ка 3 в первом базисе, если известны ее координаты {х\,х3,х3) во
втором базисе.
44.85.	Доказать, что каждая из двух систем многочленов
1-0, 0, 1+5< + <3, (1 -И)3
(1 +03, (1-03, 1-0 + 0, 1 + 1 + 0 + 0
является базисом пространства М3. Найти координаты много¬
члена степени не выше 3 в первом базисе, если известны его
координаты (х1,хг,х3,х4) во втором базисе.
44.86.	Доказать, что каждая из двух систем многочленов
(1 + 0У, (1 -0У, 1
и
1 -И2 -И4, 1 - 0 + О, О
является базисом в пространстве четных многочленов степени
не выше 4, и найти матрицу перехода от первого базиса ко вто¬
рому. Найти координаты четного многочлена степени не выше 4
в первом базисе, если известны координаты (*!, х3, х3) во втором
базисе.
44.87.	Как изменится матрица перехода от одного базиса к
другому, если:
а)	поменять местами 1-й и )-й векторы первого базиса;
б)	поменять местами г-й и _?'-й векторы второго базиса;
в)	записать векторы обоих базисов в обратном порядке?
44.88.	Матрица 5 является матрицей перехода от перво¬
го базиса е,,..., е„ ко второму базису /1,..., /„ п-мерного про¬
странства V, а матрица ф - матрицей перехода от третьего
базиса	д„ ко второму базису /1,...,Найти матрицу
перехода:
а)	от второго базиса к первому;
б)	от первого базиса к третьему.
44.89.	Как связаны между собой базисы /ь-.-./п и е\,...,еп
пространства V, если матрица перехода от базиса е к /:

22 Глава ХП. Линейное пространств нал произвол!.»,....
-1*
а)	диагональная;
б)	скалярная;
в)	верхняя треугольная;
г)	ннжняя треугольная?
44.90.	В п-мерном линейном пространстие заданы некто
ет, причем т > п + 2. Доказать, что существуют так
числа а^..., лт, нс все равные нулю, что
Е," I = в и 22™, а, = 0.
44.91.	Доказать, что система векторов линейного простру
ства является базисом тогда и только тогда, когда она образу^
минимальную систему векторов, порождающую все простран
ство.
44.92.	Пусть си	- два базиса линейного
пространства V' и 1 < к < п. Доказать, что из векторов вто.
рого базиса можно выбрать такие к векторов, что после обмена
их с векторами ех,...,е* из первого базиса получатся снова цВ1
базиса пространства V'.
44.93.	Векторы хх,...,хк € V' линейно независимы, аба-
зис е],...,еп пространства V таков, что он остается базисов
после замены вектора е* на вектор х, при любом г = 1, к. Вер.
но ли, что векторы х1,...,хк)ек+х, ...,е„ тоже образуют базис
пространства V?
44.94.	Пусть V' - л-мерное линейное пространство над нолем
Р, состоящим из 9 элементов. Найти:
а)	число векторов в пространстве V;
б)	число базисов пространства V;
в)	число невырожденных матриц п-го порядка над полем Р.
§45. Линейное подпространство
Непустое подмножество Ь пространства V называется линейным под¬
пространством пространства й, если оно само является линейным прост¬
ранством относительно законов композиции, действующих в V. Другое опре¬
деление линейного подпространства, эквивалентное этому, устанавливаете!
теоремой 18.1, которая имеет место и в общем случае.
Как указывалось в $22, множество всех решений однородной системы
уравнений
Ах = 0	(45.1)
с п неизвестными образует линейное подпространство арифметического про¬
странства Ь“. В общем случае, ко!да А € рт*п) множество всех решения
системы (45.1) образует подпространство Л линейного пространства Р ,
причем его размерность также равна п - г%А.

уд. Линейное подпространство
23
О таком подпространстве говорят, что оно задано однородной системой
(45.1), и записывают это в виде
/,: Лх = 0.
Другой способ задания линейного подпространства связан с понятием
линейной оболочки.
Пусть 01,0],.,.,да - система векторов линейного пространства V над
полем Р. Линейной оболочкой системы векторов 0|,а],...,вя называ¬
ется множество всевозможных линейных комбинаций этих векторов. Го¬
ворят также, что линейная оболочка натянута на лекторы а),а]...,а*.
Обозначение: Д(а|,...,аа). Итак,
Д(о|,... ,ва) = |а =	а,а, |а, 6 Р, ■ = 1,й|.
Из определения следует, что каждое конечномерное пространство явля¬
ется линейной оболочкой векторов своего базиса.
Теорема 45.1. Если в|,...,а* - векторы линейного простран¬
ства V, то С[а\,..., а/,) является линейным подпространством простран¬
ства V.
Теорема 45.2. Две системы векторов линейного пространства
эквивалентны тогда и только тогда, когда их линейные оболочки совпа¬
дают.
Следствие 1. Линейная оболочка системы векторов совпадает с
линейной оболочкой своей базы.
Следствие 2. Размерность линейной оболочки системы векторов
равна рангу этой системы;
д>т Д(о|,...,ая) = г((о1,...,вя).
Пример 45.1. Найти размерность и какой-либо базис линейной обо¬
лочки Ь = Ё(а1,а],аз,а<), натянутой на векторы в! = (1,2,3,1,0), в] =
(1,1,2,4,1), а3 = (3,4,7,9,2), а, = (1,0,1,7,2).
Решение. Составим из векторов ая, а2, аз, а* матрицу, расположив
их компоненты по-строчно и указав в конце каждой строки наименование
соответствующего вектора:
' 1 2
3
1
0 '
1 1
2
4
1
а?
3 4
7
9
2
аз
1 0
1
7
2
а<
Отметим, что любое элементарное преобразование строк этой матрицы
приводит к новому набору строк, которые остаются в исходной линейной
оболочке Приведем матрицу (45.2) элементарными преобразованиями
строк к верхней ступенчатой форме:
'12 3
1
0'
а\
'1
2
3
1
0'
а]
0 -1 -1
3
1
аз
- 01
0
-1
-1
3
1
аа
-
0 -2 -2
6
2
а3
— Зо 1
—♦
0
0
0
0
0
аз
— 2аз - аз
0 -2 -2
б
2
а*
-01
0
0
0
0
0
а<
— 2а3 + а1
Из последней матрицы следует, что:
-	векторы аз, а< являются линейными комбинациями векторов 01 н аз:
аз = а1 + 2аз, а< = —а! 4- 2аз,
-	векторы 01, аз — Я|, а следовательно, и векторы в], оз линейно неза¬
висимы.

24 Глава XI/.Линейное пространство над
Титам образом, 4тш Ь — 2 м векторы а), а] образуют базу
векторов О), аз, аз, <ц, к поэтому каляютск базисом линейной оболо Ст'ц
Отметим, что в качестве базиса & может быть выбрана нс гол*и Г*4
за рассматриваемой системы векторов, но и, например, ненулевые Ь,<'1 О*,
полученной верхией ступснчаэгой формы, т.е. векторы а| =(12
аз -в, =(0,-1,-1,3,1). ■	’ "Но)*
Пример 45.2. Составить однородную систему алгебраически»
нений, множество решений которой совпадает с линейной оболочкой
смотренной в предыдущем примере.	**■
Решение. Вектор * = (х|,ха,хэ,х«,хз) принадлежит линейной
дочке Ь — <6(01,03, оз,а<) тогда и только тогда, когда найдутся посто.
СЫ| аа, аз, а«, а» такие, что	""ц
проиэволып.,ч
0|в| •+■ аэаэ + азаэ + а«а« + а&аз = х.	/,
		'45-3)
Равенство (45.3) относительно а,, > = 1,5, представляет собой сист
линейных алгебраических уравнений с расширенной матрицей	т*йу
Г 1 1 3 1
XI '
2 14 0
хэ
3 2 7 1
хз
14 9 7
х«
0 12 2
Хз .
а существование коэффициентов Од ] = 1,5, в этом соотношении равносщ.
но совместности системы с расширенной матрицей (45.4).
Исследуем совместность этой системы методом Гаусса:
Г 1
1
3
1
XI
-
Г 1
1
3
1
И
-1
0
1
2
2
хз
0
1
2
2
хз
0
-1
-2
-2
хз
— 3X1
—»
0
0
0
0
ха
— 2х
+ Ха
0
3
6
6
х«
- *1
0
0
0
0
хэ
— Зх
+ х&
0
-1
-2
-2
ха
— 2X1 ]
0
0
0
0
хз
- И
— Зха.
Таким образом, для совместности системы, и следовательно, для того
чтобы вектор х = (х), ха.хз, х«, х&) принадлежал линейной оболочке ^ ~
^(в1.аэ,аз, а4), необходимо и достаточно, чтобы вектор х был решением
системы
{—2x1 + Хз + хь = о,
-3X1 + Хз + хз = 0,	■
-XI + Ц - Зхз = о.
Теорема 45.3 (о монотонности размерности). Размерность
линейного подпространства не преаосходит размерности пространства
Подпространство той же размерности, что и все пространство, с ним
совпадает.
Суммой подпространств Ь\,...,Ьм называется множество
я
22	I х, € I, , 1=1,Л).
■ к 1
Представление х = Х| + ... + Х* вектора х называется его разложением
по подпространствам Ь\,..., Ьм .

25
уд. Линейное подпространство
Пересечением подпространств Ц,,‘,,,Ьь называете» множество
ц п...ги* = {г е ^|г. 61 = 17*}.
Теорема 45.4. Сумма и пересечение подпространств линейного
пространства V являются его линейными подпространствами.
Теорема 45.5. Сумма линейных подпространств есть линейная
оболочка совокупности базисов слагаемых подпространств.
Следствие. Размерность суммы линейных подпространств равно
рангу совокупности базисов слагаемых подпространств:
к
<Кт 5^ I, = г§(в|,...,ет,/,	/„...,у,	у,).,
|»1
где е1,...,ет)/1,,..,/,|...,у|1...|у| - базисы подпространств Ц, ...,
1*к>
Теорема 45.6. Для любых двух линейных подпространств Ц и
[*1 линейного пространства V имеет место соотношение
(Ит(11 + Ьз) = (Пт ^| + <Нт 6,2 - (Пт Ь\ П Ьз.
Пример 45.3. Найти размерность и какой-либо базис суммы подпро¬
странств 6,1 и Ьз, натянутых на системы векторов
01 =(1,1,1,1),
6| = (
02 =1,1, -1,-1),
И
Ьз = г;
о3 = (1,-1,1,-1)
бз = (;
соответственно.
Решение. В силу теоремы 45.5
6,1 + 6,2 = ^(01,02,03,61,62,63).
Найдем базис этой линейной оболочки методом, описанным в примере
■ 0)
1-1111-
01
02
0 0-2-2
02 - 01
Оз
0-2 0-2
03 “01
61 -
0-2-2 0
61 -01
Ьз
0 -6 -4 -2
Ьз — За 1
1ьз
.0 -4 -2 -2.
6з — За]
Г1 1 1
1-]01
1111
1 1-1-1
1-1 1-1
1-1-1 1
3-3-1	1
3-111
45.1
оз -01
61	-03
02 - 01 + оз - 6]
62	— 261 — оз
63	- 61 - 01 - Оз
0-2 0-2
О -2	2
0	0-4
О О О
О О О
01
оз - 01
02 — О]
61	- оз
62	— За ]
63	— О] — 2оз
1	1	1 И
0-2 0-2
О 0-2-2
0 0-22
0	0-44
О 0-2	2 ^
Следовательно, (Лт(6,| + 6,3) = 4 и базис суммы 6.1 + 62 образуют, на¬
пример, векторы
(1,1,1, 1), (0, -2,0, -2), (0,0, -2,2), (0,0,0, -4)
или векторы 01, аз, оз, 61 исходных систем. •
Пример 45.1. Найти размерность и какой-либо базис пересечения
подпространств Ь\ и 1з из предыдущего примера.

26 Глава ХИ.Линейное пространство нал произвольным Пол
			 .й способ. Опишем каждое ия подпространств ц
I ешеикс. 1 «	„		с», и ног» и V Vг»аI>>IС)IН н Г гм
45.2):
Г 1 I 11*0 Г1 1 ^
1 I -1 *» I _ 0 0
1-1 1 *» Р “2 2
|_ 1 -1 -1|*. \ 1° “2 ~2
Г 1 3 31 *т 1	Г1 з 3
-1 -3 — 11 *а _ Р 0	2
1—1—1 1 хз	I 0 2 4
I. 1	1	1|гч]	[0-2-2
П
Хз ~ *1
X] — *1
*< - XI
Х|
*а 4- Х|
Хз + Х|
Х« — Х| ,
чгских
урапнснин
' 1
1
1
XI
0
-2
0
ХЗ — X!
0
0
-2
Хз — XI
0
0
0
Х« — Хз
" 1
3
3
XI
0
2
4
Хз 4- XI
0
0
2
*2 + XI
0
0
0
х« 4- Хз
-XI
— га 4- хз + х*
Таким образом,
г Х| — х» — хз 4- х« = 0; Ьз
Вектор х = (х1,хг.хЭ|хО принадлежит пересечению I,, П Ьз тогда н
только тогда, когда его компоненты удовлетворяют обеим системам, описи,
ваюшим подпространства Ь\ и 1*з-
. _ . Г	х, -ха-гэ + х« = о,
^1 П ^ • ■[ —*! — Хз + *3 + Х« =0.	\45-5)
Тем самым, базисом пересечения 1*\ О /»з является фундаментальная си*
стсма решений однородной системы (45.5). Построим ее методом I аусса:
Г 1-1-1 1101 Г 1 —1 —1 1| 0]
1-1-1 1 11 0 ] —* [б —2 0 21 0 ] '
Следовательно, векторы в! =(0,1,0,!), е» = (1,0, 1,0) образуют базис пере¬
сечения и сНт(1,| П Ьз) — 2.
2-й способ. Вектор г принадлежит пересечению Ь\ п^г тогда и толь¬
ко тогда, когда он представим в виде линейной комбинации как векторов
01.02.03,	так и векторов 61,63,63, т.е. найдутся постоянные сну, 0}, ] = ТД
такие, что
х = 0)01 + аза» 4- азоз = 0\Ь\ 4- 0зЬз 4- 0зЬ$.	(45.6)
Правое равенство в (45.6) представляет собой однородную систему ли¬
нейных алгебраических уравнений относительно коэффициентов а,, 0}, ) =
1.3.	Найдем ее фундаментальную систему решений:
'1 1 1 -1 -3 -3
0'
‘ 1 1 1-1 -3 -3
0 '
11-1131
0
0 0 -2 2 6 4
0
1-1 1 1 1-1
0
0 -2 0 2 4 2
0
1 -1 -1 -1 -1 -1
0
0 -2 -2 0 2 2
0
"1
1
1
-1 -3 -3
0'
‘ 1
1
1
— 1 -3 —3
0'
0
1
1
0 -1 -1
0
0
1
1
0—1 — 1
о
0
0
1
-1 -3 -2
0
0
0
1
— 1 —3 —2
о
0
1
0
-1 -2 -1
0
0
0
0
-2 -4 -2
0
жмт два решения:
системы уравнений содер-
0|
о> Оз
01
03
0л
1
0 ]
-1
0
1
]
0
0 1
-2
0

27
§4Д. Линейное подпространство
Из равенства (45.6) получим, что набору а\ = 1, а» = 0, щ = 1 (а также
набору 01 = — 1, 02 = 0, 0з = 1) соответствует вектор е> = (2,0,2,0), а набо¬
ру О] = «з = 0, аз = 1 (01 = —2, 01 = 1, 0з = 0) - вектор е» = (I,—1,1, — 1).
Эз н векторы линейно независимы и, как следует из определения фундамен¬
тальной системы решений системы (45.6), через них линейно выражаются
все векторы х, представимые в виде (45.6). Следовательно, с\, ез - базис
7,1 П 1<з и (11т(11 П 7,з) = 2.
Заметим, что для построения С| и ез достаточно определить только на¬
бор значений 01,01,01 (или только ог|,аз,а]). ■
Сумма подпространств линейного пространства называется прямой сум¬
мой, если разложение каждого вектора в ней по слагаемым подпростран¬
ствам единственно. Обозначение: 7,| 0 ... ф 7>к .
Теорема 45.7 (критерии прямой суммы). Для под прост¬
ранств 1,1,..., I,), конечномерного линейного пространства V следующие
утверждения равносильны:
1)	сумма подпространств 7,1,...,7,к - прямая;
2)	совокупность базисов подпространств 1,1,..., Ь* линейно независи¬
ма;
3)	совокупность базисов подпространств 1,1,..., Ьк образует базис
суммы Е*„| 7,,;
4)	<Ит^в1 7м = Е*=1 ‘К™ 7м
5)	существует вектор а 6 Е,ж1 7м» для которого разложение по под¬
пространствам 1,1,..., I,/, единственно;
6)	произвольная система ненулевых векторов в!,..., а/,, взятых по од¬
ному из каждого подпространства 7,,, I = 1,7;, линейно независима;
7)	7,, П Ц = {в) (для к = 2).
Теорема 45.8. Линейное пространство V является прямой сум¬
мой своих подпространств 1,1 и 7.2 тогда и только тогда, когда:
1) с1ип V' = сПт 7,1 + <Пт 7,з,*
2^ 7,1 П Ц = {6} .
Если пространство V является прямой суммой 7,1 и 7,2, то в разложении
произвольного вектора х Е V по этим подпространствам: г = X) + гг, хг Е
7,1,	гз Е 7,2( вектор Х1 называется проекцией х на 7м параллельно 7,2, а
вектор хз, соответственно, - проекцией х на 7,2 параллельно Ь1.
Пример 45.5. Ланы многочлены
Л(7) = 73 + 27 + 4,	у,(7) = 73 + 7* + 27,
МО = 313 + 1* - 1,	и уг(0 = 273 + 72-М + 3,
МО = 573 + I2 + 47 + 7	уз(7) = 73 + 273 + 57-3.
Показать, что подпространства 7,1 = ^(Л./г./з) и 7г = ^(91,92,91) в пря¬
мой сумме образуют все пространство Л/з, и найти проекцию многочлена
р(7) = 673 + 27г + 67 + 7 на 7,1 параллельно Ц.
Решение. В силу изоморфизма линейных пространств Мз и Ж4 ре¬
шим ту же задачу для линейных подпространств 7,1 и 7,з, натянутых на
арифметические векторы
6, = (1, 1,2,0),
и 62 =(2,1, 1,3),
Ьз = (1,2, 5,-3)
а, =(1,0,2,4),
аз = (3,1,0,-1),
аз =(5.1,4, 7)

28 /лада ХП.Лимойнсиу прастрапстпо нал произвол 1.111.1м пол„(
соотмтсткино, и ап гор* » = (в, 2.6, 7).
В силу поромы 45.7 достаточно покатать, что
Н»т /.1 + Лт Аз = Лт(4| + /.») = 4.
И МРСМ
Дл. нахождспна Н!т(А, 4- Аз) воспользуемся алгоритмом, описанным „
примере 45.3:
1 0 2 4 ’
' 1 0 2 4 '
' 1 0 2 4
0 1 —6 —13
0 1 —6 —13
0 1—6 —13
112 0
	*
0 10—4
—♦
0 0 6 9
0—1—3 3
0 0 —9 —10
О 0 9 10
Тем самым, <11(п(^1 4- Аз) — 4м А , Ф Аз — Ж .
Найдем теперь проекцию вектора х = (6, 2, 6, 7) на А, параллельно
Дла этого разложим осктор х по базису «и, аз, 6», 6» пространства К :
г = о ] а 1 + азаз + 0\Ь\ 4- /ЗзЪз.
(45.7)
Из этого разложения следует, что искомая проекция — это вектор 01121 4-с*за,.
Решим систему (45.7) метолом Гаусса:
3
1
2;
61
Г1
3
1
2
6'
" 1
3
1
2
6 '
1
1
1
2
0
;
1
1
2
0
1
1
1
2
О
2
1
б
О
—6
0
—
3
— 6
*
0
О
6
3
6
1
0
3
[о
-13
— 4
—
5
— 17
О
0
9
8
9
р
3
1
2
6"
= о.
0
1
1
1
2
0\
= 1,
0
0
2
1
2
ОГ2
= 1,
1°
0
0
25
0
О 1
= 2.
Таким образом, проекцией х на А, параллельно /,] является вектор
2а, 4- а3 = (5, 1,4, 7),
а следовательно, проекцией многочлена р(|) на подпространство 1^1 парал¬
лельно подпространству Аэ, заданным в условии задачи, является многочлен
513 4- *3 4- 4/ 4- 7.
Замечание. Можно отказаться от вычисления сПт(/,1 4- Аз), а сразу
искать разложение вектора х по совокупности базисов а], аз и Ь,,6з полпро-
ст ранет в А1 и Аз, решая систему (45.7). Эта система имеет решение при
любой правой части (следовательно, К* =
ное решение (как крамеровская система), и
х € К. имеет единственное разложение по
Л* = А, 0 Аз- а
А1 4- Аз), она имеет единстпен-
следавательно, каждый вектор
подпрост ранствам А, и Аз, т.е.

§45. Линейное подпространство
29
Пусть Ь - линейное полпространство пространства V. Полпространство
называется дополнительным подпространством к 1, если I* ф 1* = V.
Теорема 45.0. Для любого подпространства Ь линейного
пространства V существует дополнительное подпространство.
Пример 45.6. Найти какие-либо лва различных дополнительных пол-
пространства к подпространству Ь\ =	из предыдущего примера.
Решение. Воспользуемся изоморфизмом линейных пространств М)
и К4 и тем, что, как было показано в предыдущем примере, 1\ является
линейной оболочкой своего базиса из векторов
а, =(1,0,2,4), а,-За, = (0,1, -6,-13).
Дополним эти два вектора до базиса всего пространства К4, для чего до¬
пишем к матрице, составленной из компонент векторов а, и аз — За,, строки
так, чтобы в результате получилась невырожденная матрица. Это можно
сделать, например, построив следующую верхнюю треугольную матрицу:
10	2	4
0	1	-6	-13
0 0 10
0 0 0 1
(45.8)
Отсюда следует, что векторы 6, = (0,0,1,0) и &з = (0,0,0,1) обладают
требуемым свойством, и подпространство ^(5,,6з) - дополнительное к 1\.
Для построения другого дополнительного подпространства перейдем от
матрицы (45.8) к новой невырожденной матрице, прибавив к ее третьей
строке первую:
Г 1	0	2	4	'
0	1	-6	-13
10	3	4
0	0	0	1
Строки матрицы останутся линейно независимыми н, следовательно, бу¬
дут базисом пространства К4. Таким образом, линейная оболочка ^(&з,6«),
натянутая на векторы 6з = (1,0,3,4), 6, = (0,0,0, 1), образует, очевидно,
другое дополнительное подпространство к Ь\. *
ЗАДАЧИ
45.1.	Доказать, что в изоморфных пространствах образ и
прообраз линейного подпространства являются линейными под¬
пространствами, изоморфными исходному.
Доказать, что следующие множества арифметических векто¬
ров из Рп образуют линейные подпространства, и найти их базис
и размерность.
45.2.	Все векторы, у которых первая и последняя компонен¬
ты равны между собой.
45.3.	Все векторы, у которых компоненты с четными номе¬
рами равны нулю.

30 Глава ХП.Лннейное пространство над произвольным полец
45.4.	Все векторы, у которых компоненты с четными номе¬
рами равны между собой.
45.5.	Все векторы вида (а,/3,а,/?,...), где а, 0 произвольны
45.6.	Доказать, что все симметрические матрицы образуют
линейное подпространство пространства матриц Рп*п. Найтц
размерность и какой-либо базис этого подпространства.
45.7.	Доказать, что все кососимметрические матрицы обра-
зуют линейное подпространство пространства матриц РпХп1
Найти размерность и какой-либо базис этого подпространства.
45.8.	Доказать, что все матрицы, перестановочные с данной
матрицей А € Л"*", образуют линейное подпространство про-
странства матриц Рп*п. Найти размерность и какой-либо базис
_	_	. Г 1 Г
этого подпространства в случае, когда г = С и Л -	^ .
45.9.	Доказать, что если линейное подпространство Ь про-
странства многочленов Л/„ для любого к = 0,р содержит хотя
бы один многочлен степени к и не содержит многочленов степени
к > р, то оно совпадает с подпространством Мр всех многочле¬
нов степени не выше р.
Доказать, что следующие множества многочленов из Мп об¬
разуют вещественные линейные подпространства, и найти их
базис и размерность.
45.10.	Все четные многочлены.
45.11.	Все нечетные многочлены.
45.12.	Все многочлены, имеющие корень а 6 К.
45.13.	Все многочлены, имеющие корень а 6 С \ Е.
45.14.	Все многочлены, имеющие своими корнями не равные
между собой числа 01,а2,...,а* Е Е.
45.15.	Многочлен /(х1,12,...,1п) от п неизвестных с коэф¬
фициентами из произвольного поля Р называется однородным
многочленом, если можно указать такое натуральное число т,
что
/(*х1|*2а1...,**в) = г/(х1,ха,...,хп) Щ е Р.
Показать, что все однородные многочлены степени к от п неиз¬
вестных хьх2,...,хп с коэффициентами из произвольного поля
вместе с нулевым многочленом при обычных операциях над мно¬
гочленами образуют линейное пространство, и найти его размер-
илгть	г	г

31
§45. Линейное подпространство
45.16.	Найти размерность и какой-либо базис комплексного
арифметического подпространства, заданного системой линей¬
ных алгебраических уравнений:
Л (1 + 0*1 +(1 + 30*2=0, Л (I-«)!,+ (2 + 1)13=0,
' 1 (1 - 2«>, + (1 + 2012=0;	\ (6 - 40*1 + (9 + 70*2=0;
(	(1 - *)®, + (-3 + 20*2 + (2 - 0x3 = 0,
в) < (-4 + б*)х, + (4 - 3|)х2 -	З|'х3 = 0,
[ (-9 + »)*!+	(5-0*2+	4х3 = 0;
[	*| + (1-0*2+	(2 + |)х3 = 0,
г)	< (1 - 30*1 - (2 + 4|)х2 + (5 - 5|)х3 = 0,
I 2»Х| + (2 + 21)х3 + (-2 + 4»)*3 = 0;
*1-	2*2+ (1 +20х3- (1 — *)х4 = О,
-Х| + Зх2 - (1 + З*)х3 + (2 -0*4 = 0,
Д) 1Х1-+(1 + 0*2+	*3+	21Х4	=	0,
21*1+	2»х3-(2-2|>< = 0,
(2-0*2-(1 + 2»)*з+ (2-«)*4 = 0.
Найти размерность и какой-либо базис линейных оболочек,
натянутых на следующие системы векторов соответствующих
линейных пространств.
45.17.	а, =(1,0,0,-!), а2 = (2,1,1,0), а3 = (1,1,1,1),
а-» = (1,2,3,4), а5 = (0,1,2,3).
45.18.	Й1 =(1,1,1,1,0), а2 = (-1,-1,1,1,1), а3=(2,2,0,0,-1),
а4 = (1,1,5,5,2), о8 = (1,-1,-1,0,0).
45.19.	/»(!) = I6 + 1\ /2(0 = I6 + 3<4 - I, /3(0 = <6
/4(0 = I6 - 414 + 21.
45.20.	С1 = (-3 + 2г, -1), с2 = (3 + г,7 — 60-
45.21.	с, = (1, -2,0, с2 = (2 -1,-4 + 21,1 + 20,
С3 = (31, —6», -3).
45.22.	с, = (0,3 + г,4-1,-3), са = (1,1,1,1-0,
с3 = (1,7 + 61,9 - 21,-5 - 0-
45.23.	С1 = (1,1,1,1), с2 = (1,1,1,1 - 0, с3 = (1,2,1,3),
с4 = (0,0,0,1), с5 = (2,3,2,4-0.
■ 2(4 + (,
2 7 6
-6 1 4
, А3 -
2 1 1
3 0 1
А2 -
б 9 8
0 1 6
45.24. Ах =
45.25.	Линейное подпространство Ь натянуто на систему
векторов XI,...,**. Доказать, что размерность Ь равна рангу
системы *!,...,х*, а базисом может служить любая база этой

32 Глава Л7/.Линейное прострянстно нал произвольным пол«ц,
системы.
45.28.	Пусть Г - л-мернос линейное пространстио над ц0.
лем Р, состоящим из 9 элементов. Найти количество А-мерных
подпространств пространства V.
Найти системы линейных алгебраических уравнений, онисы.
пахших линейные оболочки, натянутые на следующие системы
векторов.
45.27.	Л) = (1, —1,1,0), о3 = (1,1,0,1), вз = (2,0, 1,1).
45.28.	а,=(1,-1,1,-1,1),0} = (1,1,0,0,3), а3 = (3,1,1,-1,7),
он = (0,2,-1,1,2).
45.29.	с, = (1 + 1,3), с, = (3 - *, 3 - б*).
45.30.	с, = (1,1,1,1 — *).
45.31.	с, = (0,3 + 1,4- 1,-3), с3 = (1,7 + 2*',9 — 2*, —5 — *),
= (1*4 + 1,5 — I, —2 — 1), С4 = (1,1,1,1 “• *')■
45.32.	Пусть I - т-мерное линейное подпространство п-
мерного пространства 1‘. Доказать, что можно найти такой
базис в!,..., е„ пространства V, в котором первые тп векторов
е1,...,е,„ принадлежат подпространству Ь.
45.33.	Доказать, что каково бы ни было ш-мерное подпро¬
странство I п-мерного пространства К, где тп < п, найдется
базис Г, в котором: а) не содержится ни одного вектора из Ц
б)	содержится ровно к векторов из Ь, к < тп.
45.34.	Можно ли составить базис пространства Мъ из мно¬
гочленов пятой степени? Можно ли, наоборот, найти базис этого
пространства, в котором бы не содержалось ни одного многочле¬
на пятой степени?
45.35.	Доказать, что линейная оболочка системы векторов
•..,** является пересечением всех подпространств, содержа¬
щих векторы 11,...,х*, и в этом смысле является наименьший
подпространством, содержащим эти векторы.
45.36.	Пусть V - л-мерное линейное пространство. Если е-
какоя-либо базис пространства I , то для каждого вектора л б V
обозначим через ае строку из его координат в базисе е. Доказать,
что две линейно независимые системы а,, а2,..., ак и Ьг, Ь2,..., Ьк
(к < л) пространства V эквивалентны тогда и только тогда,
когда в любом базисе е соответствующие миноры А:-го порядка
!*.аТри“ И В" доставленные из строк (л,)«, («,)„..., (а*), и
1°и«1102)0 • •., (5*)«, пропорциональны.

33
§4Д. Линейное подпространство
45.37.	Доказать, что для любого ре 14
Н1т(/,) + . .. + Ьр) < «Пт -+- . .. + «Ит /.р.
45.38.	Пусть А,, - линейная оболочка векторов а,,...,ак,
Ьз - линейная оболочка векторов	Доказать, что бази¬
сом суммы А| + Аг может служить любая база системы а,,... ,ак,
&!,..., Ь|. И частности, базис А. 1 + Ь2 можно получить дополне¬
нием как базиса Л), так и базиса А.а.
Найти размерность и какой-либо базис суммы подпрост¬
ранств = С(ах,..., ак) и А/3 = С(ЬХ,..., Ь|) для каждой из
следующих систем векторов соответствующих линейных про-
ах =(0,1, 1,1), а2 = (1,1,1,2), а3 = (-2,0,1,1);
Ьх = (—1,3,2,—1), Ь2 = (1,1,0, —1).
а, = (2,-5, 3,4), а2 = (1,2,0,-7), а3 = (3,-6,2,5);
й, = (2, О,-4,6), Ь, = (1,1,1,1), Ь3 = (3,3,1,5).
странств.
45.39.
45.40.
45.41.
45.42.
45.43.	Доказать, что сумма Ьх + Ь2 двух линейных под¬
пространств равна пересечению всех линейных подпространств,
содержащих как А,!, так и А,г.
45.44.	Доказать, что для любого р € N
сПш(А.1 + ... + Ьр) > тах(<Нт Ьь ... ,<Пш Ьр),
причем знак равенства в этом неравенстве достигается тогда и
только тогда, когда одно из подпространств Ь, содержит все
остальные подпространства.
45.45.	Пусть V — линейное пространство над бесконечным
полем. Доказать, что объединение конечного множества подпро¬
странств в V является подпространством тогда и только тогда,
когда одно из подпространств содержит все остальные.
45.46.	Пусть V - линейное пространство над бесконечным
полем Р и V'),..., V* - его подпространства, причем V*! и.. .11V’* =
V. Доказать, что V = V) для некоторого ] = 1,...,Аг.
45.47.	Пусть V линейное пространство над полем Р, и
2	7470

34 Глав» ХП.Линейное пространство нал проинюльнын полем
1'э - его подпространства, причем V, и V» = V. Доказать, что
либо V' = Ц, либо Г = У3.
45.48.	Привести пример такого пространства V над конеч¬
ным полем, что V = V', и \'3 I) 1'3, где все Ц, Ц, У3 являются под.
пространствами, отличными от V' и от нулевого подпростран¬
ства.
Найти размерность и какой-либо базис пересечения двух под.
пространств = >С(«|,...,а*) и [} = С(ЬХ,... ,Ь,) для каждой
из следующих систем векторов.
45.49.	а, = (2,1,0), в, = (1,2,3), а3 = (-5,-2,1);
6, = (1,1,2), Ь3 = (-1,3,0), Ь3 = (2,0,3).
45.50.	а, = (1,2,1,1), а, = (2,3,1,0), а3 = (3,1,1,-2);
6, = (0,4,1,3), Ь3 = (1,0,-2,-6), Ь3 = (1,0,3,5).
45.51.	а, = (1,1,0,0), в, = (0,1,1,0), в3 = (0,0,1,1);
Ь■ = (1,0,1,0), Ь3 = (0,2,1,1), Ь3 = (1,2,1,2).
Найти размерности и какие-либо базисы суммы и пересече¬
ния подпространств Ьх = Да],...,»»*) и Ь3 = С(ЬХ,..., Ь(), на¬
тянутых на следующие системы комплексных арифметических
векторов; рассмотреть два случая: когда основным полем явля¬
ется поле К вещественных чисел и когда - поле С комплексных
чисел.
45.52.	а, = (1,2,3), а3 = (1,-2,»), а3 = (2,0,3 + »);
6, = (1,0,3»),	= (1,4,3 + 2*), Аз = (-1,4,3-40.
45.53.	а, = (1,1,1,1), а, = (1,2,1,3-»), а3 = (2,3,2,4-»),
а, =(1,1,1,1-0; А»=(0,1,0,3- 0, = (0,2,0,5 - 2»),
Ь3 = (0,2 + *, 0,6 + »), Ьл = (1,4 + »,5 - », -2 - »)•
Найти размерность и какой-либо базис пересечения двух под¬
пространств Ьх и Ь3, если первое задано однородной системой
уравнений, а второе - как линейная оболочка системы векторов
а1 = (2,3,-1),
«я = (1,2,2),
а3 = (1,1,-3).
а, = (1,1,1,1),
а2 = (1,0,1,-1),
д3 = (1,3,0,-4).
а1,а2,вз-
Г 9X1 - 6хг + Зх3 = о,
\6Х1 - 4х3 + 2х3 = 0;
45.54.
45.55. { -5x1 + Зх2 + х3 + хл = 0;

§45. Линейное подпространство
35
45.56
•{
х, + х3-2х4	=0,
2х, + 2х3-5х4 + х6 = 0;
а, = (-1,6,4,7,-2),
а3 = (—2,3,0,5,—2),
а3 = (-3,6,5,6,-5).
45.57. Найти размерности и какие-либо базисы суммы и
пересечения подпространств 1ц и 7,3, если первое задано одно¬
родной системой уравнений, а второе - как линейная оболочка
системы комплексных арифметических векторов а\,а3,а3 (рас¬
смотреть два случая: когда основным полем является поле Я
вещественных чисел и когда - поле С комплексных чисел):
Зх,+(1 - 2!')х3 + »х3 = 0,
(3 + 6»')*1 + 5х3 - (2 - 0*з = 0;
«I = 0,-2,0.
аг = (2,1 + 1,-0,
д3 = (0,5+ 1,-3»).
Найти какие-либо базисы суммы и пересечения двух подпро¬
странств Ь1 и Ь-2, заданных однородными системами уравнений.
х3-х3- х4 =0,
45.58.
Гх, ■
- *3 +
*5
= 0,
/ X:
1*1 •
“*2 +
х3 — х4
= 0;
\2х
45.59.
Г 2Х|
*2
- х3 = 0,
'Зх, •
1
*з -
- х4 = 0;
1
. *»■
45.60.
Г 2х,
1
+ *2
+ 2х3
-	2х3 -
-	*з-
х4
2х4
II II
О
Зх3 = 0,
/ *2
1 -Зх3
- х4 = 0,
+ 3х4 = 0.
45.61. Найти размерности и базисы суммы и пересечения
подпространств пространства К3*3, натянутых на системы ма¬
триц
А, =
А 4 =
2 2
1 -2
, Аг —
1 -1
1 -2
. -4з —
1 -3 -1
-2	7 2
-2
3
1
2 1
[1 0 1 ]
3 2 -4
3 Г
’0 0 Г
1 2 3
6 2
2 1
;Я. =
0 2 6
1 6 4
,в,=
2	3 4
3	4 5
'0 5 4]	Г 0 5 3
В3 = 4-4	2 , В4 =	4-6-4
.0 2 9}	1-1-4 5.
45.62. Найти размерности и базисы суммы и пересечения
подпространств пространства Л/3, натянутых на системы мно¬
гочленов 1+21-М3, 1 + I + I3, I - I2 + ? и 1 + I2, 1 + 31 + I3,
31 - I1 + I3 соответственно.
I'

36 Глава XI/.Линейное пространства нал пронзнолы/ым полем
45.63.	Доказать, что если размерность суммы двух подпро
странств на единицу больше размерности их пересечения, то
сумма совпадает с одним из этих подпространств, а пересече¬
ние - с другим.
45.64.	Доказать, что если размерность суммы двух подпро¬
странств больше размерности всего пространства, то пересече-
иие этих подпространств содержит ненулевой вектор.
45.65.	Матрицы .4» и .42 имеют одинаковые размеры. Про¬
странства Ц, Г2 порождены их строками, а пространства И7,,
И 3 - их столбцами. Доказать, что следующие условия эквива¬
лентны:
а)	гб(Л, + Лз) = гвЛ, + ге Л2;
б)	V, П Г3 = {&};
в)	И', П И'з = {0}.
45.66.	Доказать, что
а)	(1П1,) + (1П13) С 1,П(Ь} + 12);
б)	1 + (I, п Ь2) С (Ь + Ьх) П (/, + Ь2).
Привести примеры подпространств Ь, Ьх, Х2, для которых в
этих соотношениях включения являются строгими.
45.67.	Доказать, что
а)	если Ьх С I, то (Ь П /,,) + (Ь п Ь2) = Ь п (Ьх + Ь2)\
б)	если Ь С Ь\,то Ь + (Ьх п Ь2) = (I + Ьх) п (Ь + Ь2).
45.68.	Для вектора х = (1,0,1) найти два различных раз¬
ложения по подпространствам Ьх и Ь2, рассмотренным в задаче
45.49.
45.69.	Пусть V - линейное пространство над бесконечным
полем. Доказать, что если его вектор х имеет два различных
разложения по подпространствам 1/1,...,!,*, то он имеет беско¬
нечно много таких разложений.
45.70.	Доказать, что пространство К" арифметических век¬
торов х = (хь...,хп) есть прямая сумма подпространства Ьх,
описываемого уравнением г, + ... 4- х„ = 0, и подпространства
Ь2, описываемого системой уравнений хх = х2 = ... = хп. Най¬
ти проекции единичных векторов ех,... ,е„ естественного базиса
пространства К" на Ьх параллельно Ь2 и на Ь2 параллельно Ьх.
45.71.	Доказать, что пространство К"х" есть прямая сумма
подпространств Ьх - симметрических и Ь2 - кососимметриче-

§45. Линейное иодпрострлиство
37
ских матриц. Найти проекции А, и А3 матрицы
А =
1 1
О 1
О О
на А| параллельно Ь3 и на Ь3 параллельно Ь\.
45.72.	Показать, что линейные подпространства и Ь3,
натянутые на системы векторов Д) = (2,3,11,5), д3 = (1,1,5,2),
д3 = (0,1,1,1) и 5, = (2,1,3,2), Ьг = (1,1,3,4), Ь3 = (5,2,6,2) со¬
ответственно, дают в прямой сумме все пространство и найти
разложение вектора х = (2,0,0,3) по этим подпространствам.
45.73.	Доказать, что пространство М„ является прямой сум¬
мой подпространства всех четных и подпространства всех нечет¬
ных многочленов степени не выше п.
45.74.	Доказать, что пространство М3 является прямой сум¬
мой следующих подпространств Ь1 и Ь2, и найти проекцию мно¬
гочлена р(1) = I3 + 1 на параллельно Ь3:
а)	Ь\ = {/(<) 6 Л/з I /(1) = 1'{У) — 0},
*2 = {/(ОеМ3|ЯО) = /'(0) = 0};
б)	1\ = {/(<)б Л/3|/(0) = /(1)},
^ = {/(0 € Л/з | /(20 = 2/(0 V* 6 К};
В) />1 = {/(0 е Л/з I /(-1) = /(0) = /(1) = 0},
^2 = {/(0б Л/3|/'(1) = 0}.
45.75.	В пространстве Сг подпространство Ь\ натянуто на
вектор (г, 2), а подпространство - на вектор (1 +1,3). Найти
проекцию вектора а на параллельно Ьг, если:
а)	а = (-1,20; б) а = (3 — *,3 — 6г); в) а = (10+ 151,-Ш).
45.76.	Доказать, что для того, чтобы сумма более чем двух
подпространств /,,+/,2+- • -+Лр была прямой, необходимо, чтобы
выполнялось условие Ь; П	= {0} для всех { ф /. Является ли
это условие достаточным?
45.77.	Для подпространства Ь, натянутого на векторы Д1 =
(1,3,0,-1), д2 = (2,5,1,2), д3 = (1,2,1,3), найти два различных
дополнительных подпространства.
45.78.	В пространстве Л/„ найти два различных дополни¬
тельных подпространства для подпространства Ь многочленов,
удовлетворяющих условию /(1) = 0.

38 Глана ХП.Линейное пространство нал произвольным
45.79.	Н пространство К3*3 найти два различных дог,0
нитсльных подпространства для подпространства ^ кососими^
тричсских матриц.
45.80.	Пространство V разложено в прямую сумму подцр0
странств 1. \,... у 1*р. Доказать, что:
а)	сел и вектор о имеет разложение а — ах + ... + ар, а; ^ /
то разложение вектора Да по подпространствам 1Х,..., /,р имоет'
вид
Да = Да1 + ... + Дар;
б)	егли вектор Ь имеет разложение Ь = Ьх + ... +ЬРу ^ То
разложение вектора а + Ь по подпространствам Ьх,..., /,р имеет
вид
в + 6 = (ах +61) + ... + (ар + Ьр).
45.81.	Пусть Р поле из к элементов, (У подпространство
размерности тп в пространстве V' размерности п нал полем Р.
Найти число всех дополнительных к V подпространств.
45.82.	Доказать, что подпространства Ьх,..., Рр имеют об¬
щее дополнительное подпространство в том и только том случае,
когда их размерности равны.
45.83.	Известно, что функционал Л{Ь) на множестве всех
подпространств линейного пространства V обладает следующи¬
ми свойствами:
а)	если подпространства Ьх и имеют нулевое пересечение,
то
(1(ЬХ + Ьз) = <1{Р\) +
б)	если (Пт Ь = 1, то й{Ь) - 1.
Доказать, что <1(1) = (Пт I для всех подпространств
§46. Линейное аффинное многообразие
Приведенные в §18 определение и элементарные свойства линейного мно¬
гообразия (применительно к вещественным линейным пространствам) со¬
храняются и в линейном пространстве над произвольном полем. Воспроиз¬
ведем известные факты и дополним их рядом новых.
Из определения линейного аффинного многообразия вытекают следую¬
щие <^>акты.
1*. Вектор сдвига хп принадлежит линейному многообразию.
2е. Разность двух векторов линейного многообразий принадлежит на-
правляющему подпроетранству.
Теорема 46.1. Два линейных аффинных многообразия IIх = хх +
и Нг = х? + Ьз совпадают тогда и только тогда, когда Ьх =/,] = /. и

39
	Линейное нффинное многообратие
г, - ха € 1>.
Следствие 1. Вектором сдвига может быть любой вектор линей¬
ного многообразия.
Следствие 2. Линейное многообразие может быть получено сдви¬
гом единственного направляющего подпространства.
Размерностью линейного аффинного многообразия называется размер¬
ность его направляющего подпространства. Линейное многообразие раз¬
мерности 1 называется прямой в линейном пространстве, размерности 2 -
плоскостью, размерности (п — 1), где п = <Нт V, - гиперплоскостью.
Очевидно, что прямая в линейном пространстве определяется уравнени¬
ем
х = хо + 1а, I е Р,
где хо вектор сдвига и а базис направляющего подпространства, а плос¬
кость - уравнением
х = го + ир1 + ера, и, г € Р,
где хо ~ вектор сдвига и рьРз - базис направляющего подпространства.
Теорема 46.2. Множество всех решений неоднородной системы
линейных уравнений с п неизвестными и с коэффициентами из произволь¬
ного поля Р является линейным аффинным многообразием в арифмети¬
ческом пространстве Рп, полученным сдвигом подпространства решений
приведенной однородной системы на частное решение неоднородной систе¬
мы.
Отметим, что вытекающее отсюда утверждение о размерности линей¬
ного многообразия решений неоднородной системы остается в силе и для
случая произвольного поля.
Пример 46.1. Линейное многообразие Н арифметических векторов
пространства 2&а описывается системой
{х\ + ха + хз + х$ = 1,
XI	+ хз + х« + хь = 1,
ха + хз + хз =1.
х 1 + ха	+ хз = 0.
Найти его размерность и показать, что общее количество векторов в Я ко¬
нечно.
Решение. Применим метод Гаусса:
1 1 10 1
10 111
0 1110
110 0 1
1110 1
0 10 10
0 1110
0 0 10 0
1110 1
0 10 10
0 0 10 0
0 0 10 0
XI + ха + хз + хз = 1,
ха + х« = 0,
хз = 1.
Вектор сдвига многообразия Я это частное решение последней систе¬
мы: например, вектор а = (0,0, 1,0,0), а направляющее подпространство и
это множество решений однородной системы
Х| + ха + хз +
ха + т« = 0,
хз = 0.
(46.1)

40 I лова XII.Линейное пространство ила произвольным поле».
Ее фундаментальную систему образуют векторы
Х| хз
X»
х«
х&
1 1
0
1
0
1 0
0
0
1
Таким обратом, общее решение системы (46.1) задаетск соотношением
* = С|(1,1,0,1,0) + С}(1,0, 0,0, 1), с.сз 6 2т.
Отсюда следует, что 61т Ь = 2 и, так как каждый коэффициент с, в зтоц
соотношении принимает только два значении, то 2 содержит 4 вектора.
Тем самым, «Пт // = 2 и обшее количество векторов в многообразии
Н = а + Ь конечно и равно 4. ■
Пример 46.2. Показать, что множество
н = МО е М* 1/(1) = I,/'(о) + 2/(0) = 2}
образует линейное многообразие в пространстве М«. Найти его размер,
ность.
Решение. Опишем множество И системой линейных соотношений,
которым удовлетиорают коэффициенты многочлена /(0 = ао + а\1 + от!1 +
оз13 + а,<‘ € Н:
/(1) = 1	< 3 ао + Я| + 03 + 03 + 04 — 1,
/'(0) + 2/(0) = 2	«=>	2ао+а1=2.
Решим аналогичную задачу дли арифметических векторов (00,01,03,01,
о<) из пространства Я1, изоморфного пространству М\.
Множество решений неоднородной системы
Г ао	+	О]	+ 02 + Оз + 04	= 1,	,
\	2о0 + 01	= 2	(46-2)
образует линейное многообразие с направляющим подпространством, опи¬
сываемым соответствующей (46.2) приведенной однородной системой, и век¬
тором сдвига, являющимся частным решением системы (46.2). Таким обра¬
зом, направляющее подпространство - это множество решений системы
/00	+	01+03+03 + 04	=0,
\	2оо + 01	=0,
размерность которого равна 5 — 2 = 3, а вектор сдвига - это, например,
вектор
Оо = 1,0] = аз = аз = 04 = 0.
Это означает, что исходное множество Н образует линейное аффинное мно¬
гообразие с вектором сдвига /0(<) = 1 и «Пт Н = 3. ■
Пример 46.3. Описать линейное многообразие И = а + / системой
уравнений, если а = (2,0,0,1,1), а направляющее подпространство Ь натк¬
нуто на векторы о, = (1,1,0,2,1), оз = (0, 2,1,1,0), оэ = (2,4,1,5,2).
Решение. Вектор х = (г|, гз, х3, х4, х&) принадлежит линейному мно¬
гообразию М — о +А тогда и только тогда, когда вектор х — а принадлежит
линениои оболочке I = 2(01,03,03). Как было показано в примере 45.2, это

•и
§*<6. Линейное аффинное многообразие
равносильно совместности следующей системы относительно неизвестных
°1. а,. 01:
0| +	+ 2а, = *| - 2,
о | + 2а, + 4а, =
а, + о, = *,,	(46.3)
2в| + 6} + 5ог) = х* — 1,
а|	— 2аз * п — I.
Совместность этой системы исследуем методом Гвусса:
4 0 2
XI -2-
10 2
XI - 2 1
Г 1 0 2
х» - 2 -1
1 2 4
га
0 2 2
X, - XI + 2
0 1 1
*,
0 1 1
О
0 1 1
Хз
—♦
0 0 0
-2х3 + хз - Х| + 2
2 15
г« - 1
0 1 1
Хя — 2X1+3
0 0 0
-2хя + X, + Зх( - 4
.10 2
х» - 1 .
.0 0 0
Х5 - X] + 1
.0 0 0
X» - II + 1
Таким образом, лля совместности системы (46.3), и слеповательпо, лл«
того, чтобы вектор х = (х,,х,,х,,х,, х5) принадлежал линейному много¬
образию // необходимо и достаточно, чтобы выполнялись соотношения
2,
Г1 - Г, + 2хз
Зх| + х, — 2х« = 4,
И - 14 = 1-
Пример 46.4. Описать линейное многообразие Н = а + Ь системой
уравнений, если а = (1,1,1,1,1), а направляющее подпространство Ь задано
однородной системой
( 21] + х, — хэ - х<	=0,
< ц - хз	+ Хя + х, = 0,
(.—X]	+ Хэ	+2X5=0.
Решение. Из теории систем линейных алгебраических уравнений сле¬
дует, что данная однородная система является приведенной для искомой
системы
{2ц + хз-хз-х« =6»,
Х| - Хз	+ Хя + Х5 =Ьз,
-XI	+ Хз	+ 2x5=6,.
Константы 61,63,63 в правых частях надо подобрать так, чтобы век¬
тор сдвига а = (1,1,1,1,1) был одним из решений системы. Тривиальной
подстановкой получим: 61 = 1, 63 = 0, 63 = 2. •
Линейные аффинные многообразия Н\ = х, + и Яз = Хз + ^з в
линейном пространстве V называются параллельными, если либо Ь\ С 1.2,
либо 1.1 С Е1 •
Теорема 46.3. Если два линейных аффинных многообразия с не¬
пустым пересечением параллельны, то одно из них содержит другое.
Следствие . Если линейные многообразия параллельны, то либо они
не пересекаются, либо одно из них содержится в другом.
Теорема 46.4. Непустое пересечение линейных аффинных мно¬
гообразий Н\ = ц + Ь\ и Н1 = Хз + 1.1 является линейным многообразием
с направляющим подпространством П ^з.
Теорема 46.5. Всякое к-мерное линейное аффинное многообра¬
зие а п-мерном пространстве можно задать в виде пересечения п — к ги¬
перплоскостей.

42
/лапа XИ.Линейное пространство нал произвольным полр
Теорема 40.0. //гргсечемиг линейного аффинном миоеообрп
// = гр + I с любым по&прпстпрпнстоом, дополнительны* к состо31^
рол но из одного лектора	N
ЗАДАЧИ
46.1.	Что представляет собой линейное многообразие р^
мерности О?
46.2.	Что представляет собой линейное многообразие
мерности п в п-мерном пространстве VI
46.3.	Доказать, что линейное многообразие Н = а + I явля.
ется подпространством тогда и только тогда, когда его вектор
сдвига я принадлежит направляющему подпространству.
46.4.	Доказать, что для того, чтобы линейное многообразие
// = а 4- Ь было подпространством, необходимо, чтобы сумма
любых двух его векторов принадлежала направляющему под.
пространству Ь.
46.5.	Пусть V - линейное пространство над полем Р ха¬
рактеристики, большей двух. Доказать, что для того, чтобы
линейное многообразие Н = я + Ь в V было подпространством,
достаточно, чтобы сумма каких-либо двух его векторов принад.
лежала направляющему подпространству Ь. Верен ли этот ре-
эультат, если характеристика поля Р равна двум?
46.6.	Пусть линейное многообразие И = а + Ь не являет¬
ся подпространством. Может ли объединение линейного мно¬
гообразия Н и его направляющего подпространства Ь являться
подпространством?
Найти вектор сдвига и направляющее подпространство для
линейного многообразия, описанного системой.
46.7.
11+2х2- х3 =0,
Х\ — хг+2х3-3х<=3,
2х,+ х2-Зх3+Зх4=-1,
х2- х3+ х< = -1.
46.8.
х | х3 Зхц — 1,
2х!-|-х2	-7х,,=4,
X] — х2 — Зх3 — 2х< = -1,
х2 + 2х3- х4=2.
Найти вектор сдвига и направляющее подпространство для
линейного многообразия в пространстве комплексных арифме¬
тических векторов, если это многообразие описано неоднородной
системой) рассмотреть два случал: когда основное поле - ноле
С комплексных чисел и когда поле Ж вещественных чисел.

§46. Линейное аффинное многообразие
43
Г (1 - |)Х| + (1 + «)х}-	35;, = 1,
46.9. <	2х, +	2»х3-(1 + »)*з= -1 + >>
| (3 — |')х, + (1 + 3|>,-(2 + «>з=-1 + 21.
(х, - «х2 + х3 + х4 = 2 - I,
IX, + «Х2 - Хз = -2 + «,
х, - х2 - «хз - х4 = -2 + «.
Найти вектор сдвига и направляющее подпространство ли¬
нейного многообразия, описанного следующими системами, в за¬
висимости от значения Л (считать, что основное поле - С).
46.11
•{
Ах, + «х2 - 2хз = -2А,
—х, «х2 2Ах3 = 2А.
(Х,+2х7- х3+ х4 = А,
х, + х2 4- 2х3	= А — «,
-х, + х3 - 8х3 4-Ах4 = 3« - 2.
46.13.	Доказать, что в изоморфных линейных простран¬
ствах образ (прообраз) линейного многообразия Н = х0 + Ь
является линейным многообразием, вектором сдвига которого
служит образ (прообраз) вектора х0, а направляющим подпро¬
странством - образ (прообраз) подпространства Ь.
46.14.	Доказать, что в пространстве многочленов М„ следу¬
ющие множества многочленов /(I) являются линейными много¬
образиями, и найти их размерности:
а)	/(М = с> где <1,с€ 1 произвольны;
б)	/'(!«) = с, где 1,,с 6 Ж произвольны;
в)	+	= с, где Од + а? / 0 и 1,,с6 К произволь¬
ны;
к
г)	^2 а, /(<,) = с, где к < п и а\ + ... + а\ / 0, <,,с € Я
1=0
произвольны;
*
д)	51 Ж) = с> где а? + • • • + а1 / °> с, и 6 й (« = 1, *)
произвольны;
е)	51 а< / ЛОЛ = с, где а? + ... +	/ 0 и с,а,, А, е Я
1 = 1	•'<4
(« = 1 ,к) таковы, что а, < 6, < а2 < 62 < ... < ак < Ьк.
46.16. Доказать, что в пространстве квадратных матриц

Л7/.Линейное пространство нал проилпольн
44 Глав»
Кпяп соотвсгсгвуюшего порядка п следующие множества
триц .V являются линейными многообразиями, и найти и* ■**'
мерности:
а)	1г Л’ = с, где с Е Я;
б)	.4Л’ = В, где матрицы Л, В Е Кт*п таковы, что г» .
<*М1 В);	*4 ■
в)	Л'Л = В, где матрицы А, В Е Жпхт таковы, что ге
*М*|яг]:
г)	АХ В = С, где матрицы Л Е Глхп, В Е Кп*‘, С е ^
таковы, что гд Л = г{;(Л | С] и г($ В = г§[ пТ 1 г'тл-
Вт | Ст);
2 1
-2 -2
1 О
О -1
, В =
, Я =
д) [.V,Л] = В, где Л = [2 2
») [А\Л]= Я, где Л = [} }
46.16.	Доказать, что в пространстве матриц к"*"
а)	все стохастические матрицы;
б)	все дважды стохастические матрицы
образуют линейное многообразие, и найти его размерность.
Построить системы линейных уравнений, описывающие^
нейные многообразия Н = а + Ь со следующими векторами сдв^
га а и направляющими подпространствами I;, натянутыми^
указанные системы векторов.
46.17.	б] = (0,1,3,—4), е2 = (2, -1,0,2), е3 = (2,1,6,-6),
а = (1,-2,-1,0)
46.18.	е, =(1,-1,2,1), е2 = (0,-1,1,1 + *), е3 = (-3,1,-2,()
а = (1,0,1,0)
46.19.	е, =(1,1,2,2), е2 = (0,3,1,-1), е3 = (2,0,1,0),
а = (1,2,1,-1)
46.20.	е, = (1,«,2,1), е2 = (», 0,1,2*), е3 = (2*. -1,1 + 2.,31),
а = (1,3*, 7,-1)
Построить системы линейных уравнений, описывающие^
нейные многообразия // = а+1 со следующими векторами®#
га а и направляющими подпространствами Ь, заданными одно
родными системами.
( 2x1 — Х2	+2X4 = 0,
{ -х, + Зх2 - х3 - х4 = 0,
I XI + х2 + 2х3	=°-
46.21. а = (1,0,-2,-1), Ь :

§46. Линейное аффинное многообразие
45
( х, + 1х3+ (1 - |)*3 = О,
46.22.	а = (1,-2,-2), I : < 2»х, - х3 + .хл = 0,
I 3|х, - 2х, + (1 + 2|)х3 = О.
46.23.	Что можно сказать о матрице А е ВТ**", если извест¬
но, что для любого Ь е Ктх‘ система Ах = Ь описывает линейное
многообразие размерности 1? размерности 2?
46.24.	Доказать, что в линейном многообразии размерно¬
сти к, не являющемся подпространством, можно найти линейно
независимую систему, состоящую из к + 1 векторов.
46.25.	Доказать, что в линейном многообразии размерности
к всякая система, состоящая из к + 2 векторов, линейно зависима.
46.26.	Доказать, что для любых к + 1 линейно независи¬
мых векторов существует, причем единственное, линейное мно¬
гообразие размерности А:, содержащее эти векторы.
46.27.	Доказать, что линейное многообразие размерности к,
содержащее линейно независимые векторы х0,	х4, может
быть описано как множество всех линейных комбинаций а020 +
01X1+• • .+а*х*, коэффициенты которых удовлетворяют условию
Оо + О) + ... + оц = 1.
46.28.	Описать все линейные многообразия п-мерного ли¬
нейного пространства V, содержащие линейно независимые век¬
торы х0| Х|,..., х», где к < п — 1.
46.29.	Пусть V - п-мерное пространство над полем Р, со¬
стоящим из ^ элементов. Найти число А-мерных линейных мно¬
гообразий пространства V.
46.30.	Пусть Н - произвольное линейное многообразие в
линейном пространстве V. Доказать, что бинарное отношение,
определенное правилом:
х ~ у <=> х 6 Я, у 6 //
является отношением эквивалентности на множестве всех век¬
торов пространства V.
46.31.	Суммой Н1 + #2 линейных многообразий Нх = <4 +
Ьх и Я2 = а2 + Ь2 называется множество всех векторов вида
г, + г2, где 21 6 #ь Ъ 6 Н2. Доказать, что сумма линейных
многообразий //1 и //г также является многообразием. Найти
его направляющее подпространство.
46.32.	Произведением АН линейного многообразия Н = а + Ь
на число называется множество всех векторов вида Аг, где г €
//. Доказать, что произведение многообразия Н на число А так¬

<1
Глава XII.Линейное пространств нал произвольным нгщ
•16
же является многообразием. Найти его направляющее копир,
сзранство.
46.33.	Н линейном пространстве Г фиксировано нодпрг,
стране!во /.. Будет множество Л/ всех линейных многообразие
пространства Г, полученных сдвигом подпространства I, Ли
нейным пространством относительно операций сложения и умно
ження на число, определенных в предыдущих двух задачах?
46.34.	Показать, что если умножение многообразия Н ^
а. + Ь на число А ввести по правилу А// = Аа + Ь, то множество
М из предыдущей задачи будет линейным пространством. (По.
лученное пространство Л/ называется фактор-пространствоц
пространства Г по подпространству Л.
46.35.	Пусть в условиях предыдущей задачи I мерное
подпространство п-мерного пространства V. Какова в такой
случае размерность фактор-пространства Л/?
46.36.	В пространстве К5 дана плоскость х = хо + ^Д] -И2а}
где 10 = (2,3,-1,1,1), а, = (3,-1,1,-1,1,), а2 = (-1,1,1,1,-1)!
Установить, принадлежат ли ей векторы и = (1,6,4,4, -2) и
V = (1,6,5, 1,-2).
46.37.	Доказать, что если прямая имеет два общих вектора
с плоскостью, то она содержится в этой плоскости.
46.38.	Определить взаимное расположение многообразна
// = х0 + где х0 = (1,0,0,1), а I натянуто на векторы у} г
(5,2,-3.1), уз = (1,1. -1,0), у3 = (-1,2,-5,3), и прямой х =
То + (я, если:
а)	х0 = (3,1,-4,1), ц = (-1,1,2,1);
б)	Хо = (3,0,-4,1), д = (-1,1,2,1);
в)	т0 = (-2,0,-1,2), д = (1,1,-2,1).
46.39.	Найти условия, необходимые и достаточные для то¬
го, чтобы две прямые х = Х| -|- 1у\ и х = х2 + линейного
пространства V’ размерности п > 1 лежали в одной плоскости.
46.40.	Найти условия, необходимые и достаточные для то¬
го, чтобы две прямые х = Х| + и х = х2 + 1ц2 линейного
пространства V имели один общий вектор, но не совпадали.
Доказать, что прямые х = Х1 + 191 и х = х2-Ид2 пересекаются,
и найти их пересечение. Указать плоскость, в которой лежат эти
прямые.
46.41.	х, =(9,3,6,15,-3), 91 = (7,-4,11,13,-5),
*г = (-7,2,-6,-5,3), яз = (2,9,-10,-6,4).

§46- Линейное аффинное лтопэобрачис
47
46.42.	х, =(2.1,1,3,-3), у, = (2,3,1,1, - 1),
х2 = (1,1,2,1,2), у2 = (1,2,1,0,1).
46.43.	х, = (3,1,2,1,3), у. = (1,0,1,1,2),
= (2,2,-1,-1,-2), <7, = (2,1,0,1,1).
46.44.	Выяснить, при каком значении параметра Л прямые
х = Х] + <у, и х = х2 + <92, где х, = (1,1,1,1), у, = (2,3,0,0), х2 =
(1,1,1, Л), 92 = (3,2,0,0), принадлежат линейному многообразию
наименьшей размерности.
46.45.	Найти условия, необходимые и достаточные для то¬
го, чтобы существовала единственная прямая, пересекающая две
данные прямые х = Х| + <91, х = х2 + 1у2 и содержащая заданный
вектор с.
Найти прямую, содержащую вектор с и пересекающую пря¬
мые х = Х!-И9|,х = х2 + <92. Найти пересечения искомой прямой
с обсми заданными прямыми.
46.46.	с = (8,9, -11, -15), х, = (1,0, -2,1), 9, = (1,2, -1, -5),
х2 = (0,1,1,-1), 92 = (2,3,-2,-4).
46.47.	с = (4,5,2,7),*, = (1,1,1,1), 9, =(1,2,1,0),
х, = (2,2,3,1), 9» = (1,0,1,3).
46.48.	Доказать, что любые две прямые линейного про¬
странства V размерности п > 3 содержатся в некотором трех¬
мерном линейном многообразии пространства V.
46.49.	Доказать, что прямые 2 = 21+191 и х = х2 + 1у2, где
х, = (8,2,5,15,-3), 9; = (7,-4,11,13,-5), х2 = (-7,2,-6,-5,3),
92 = (2,9, -10, —6,4), не пересекаются. Построить линейное мно¬
гообразие размерности 3, содержащее эти прямые.
46.50.	Доказать, что любые две плоскости линейного про¬
странства V, (Пт V = п > 3, содержатся в некотором линейном
многообразии размерности не выше 5.
Определить взаимное расположение плоскостей Хо + <1Р1 + ^Рг
и Уо + 1101 + <292-
46.51.
20 = (3,1,2,0,1),р, = (2, -6,3,1,-6), ра = (0,5,-2,-1,6),
у0 = (1,0, 1,1,0), 9. = (-1-1.-1,0,1), 92 = (-1,3,-1,-1,2).
46.52.
х0 = (7, -4,0,3,2), р, = (-1,1,1,1,1), Р2 = (1,-1,1,», 1),
Уо = (6, -5, -1,2,3), (/] = (1,1, — 1,1,1), 9г = (1.1.1> -1> !)•

48	/ лала XII.Линейное пространстио паи прпи-*полпш.ии „
			^
46.53.
х0 = (2,-3, 1.5,0), р, = (3.-2, 1,0, 1), ра = (- 1,5,-2,0,3)
Уо = (0.-1,0,4,1), </, = (1,2,4,0,-2), д3 = (6, 3, 4,0, 3).	'
46.54.
х0 = (-3, -2, 1,-1,2), р, =(1,-1, 1, 1,3), р2 = (- 1,2, 1,2,-2)
Уо = ( —1» 0,3,3,8), дх =( 1.1, —3, —3, 1), 9э = (0, 1,2,3, 1).
46.55.	Описать все случаи взаимного расположения дцу^
плоскостей х = х0 4- 1,р, + 13р3 и х = у0 4- <1^1 +	11 п-мерн01)
пространстве и указать необходимые и достаточные условия д.^
каждого из этих случаев.
46.56.	Доказать, что два линейных многообразия прострац.
ства размерностей к и / соответственно содержатся в некот0.
ром линейном многообразии размерности не выше к 4- / + 1.
46.57.	Пусть Н\ и //2 - дна линейных многообразия размер,
ностей кI и к3 н-мерного пространства V имеют общий вектор
причем А4 4- Аг2 > п. Доказать, что их пересечение есть линейно*
многообразие размерности не меньше к + I — п. Сформулиро.
вать утверждения, которые вытекают отсюда для трехмерного
и четырехмерного пространств.
46.58.	Найти уравнение линейного многообразия минималь¬
ной размерности, содержащего векторы ах = (1, 1, 1, 1), а2 «
(2,4, 1,3), аа = (4,8,0,3), ал = (3,5,0, 1), и найти пересечение
этого многообразия с прямой х = х0 4- Я?, где
а)	х0 = (0,0,1,3), Я = (0,0,1,0);
б)	х0 = (0,0,1.3), я = (1.3,0,2).
46.59.	Доказать, что в линейном пространстве V' над полем
характеристики 2 объединение любого линейного многообразия
Н = а 4- Ь и его направляющего подпространства /. является
линейным подпространством.
46.60.	Доказать, что два линейных многообразия II х = а, +
Ь\ и //2 = а2 4- Ь3 пересекаются тогда и только тогда, когда
Я| — а, Е кх 4~ 1>3.
46.61.	Пусть III = а, 4- к\ и И2 = а2 + Ь3 два непересе-
кающихся линейных многообразия. Доказать, что минимальная
размерность линейного многообразия, содержащего //, и парал¬
лельного //2, равна
Фт У/1 4- Фт Н3 — Фгп(Л, П Ь3).
46.62.	Пусть II1 =01-4-1.1 и П3 = а2 4- 1>3 две иепсресекаю-
шисся прямые в линейном пространство V' над полем Р и пусть

§•/6. Линейное аффинное многообразие
49
А - фиксированный элемент иэ Я, отличный от нуля и единицы.
Выяснить, что представляет собой множество всех векторов ви¬
да Аа, + (1-А)а2, где а, и а2 пробегают соответственно 11х и
Я3.
46.63.	Пусть V - линейное пространство над полем Р ха¬
рактеристики, не ранной 2. Доказать, что Я является линейном
многообразием в пространстве V тогда и только тогда, когда
имеете с любыми двумя различными векторами а,Ьб Я в Я со¬
держится прямая, содержащая а и Ь. Верно ли это утверждение,
если характеристика поля Р равна 2?
46.64.	Доказать, что если прямая х = х0 + и гиперплос¬
кость а + /. не пересекаются, то ц € Ь.
46.65.	Доказать, что если гиперплоскости в| + /м и а2 + Ц
нс пересекаются, то = /,2.
46.66.	Доказать, что если пересечение гиперплоскостей Нх,
..., Я * п-мерного пространства непусто, то оно есть линейное
многообразие, размерность которого не меньше п - к.
46.67.	Доказать, что всякое линейное многообразие размер¬
ности & в п-мерном пространстве можно задать как пересечение
п - к гиперплоскостей.
46.68.	Пусть ап, а,,..., а* - любые вектора линейного про¬
странства V над полем Р. Доказать, что все векторы вида
I = ОрДо + ОЦЙ1 + . . . + ОцОь,
где числа а0,а,,... ,а* б Р удовлетворяют условию о0 + оц +
• ■. + а* = 1) образуют линейное многообразие Я, размерности
равной рангу системы векторов а1 - а0,...,а* - а0.
Показать, что Я есть многообразие наименьшей размерно¬
сти, содержащее все векторы а0,а1,. . ,,а4.

Глава XIII. Евклидовы и унитарные
пространства
§47. Скалярное произведение. Матрица Грама
Пусть V - вещественное или комплексное линейное пространство (т.с
Р = С или Р = Я). Отображение
(.,•):	КхР' -
называется скалярным произведением, если оно удовлетворяет следующие
аксиомам: для любых х.у.х С V н любого о € Р
О (х,у) = (у.*);
2)	(ох,у) = о(г,у);
3)	(х + У.х) = (х, х) + (у, х);
4)	(х. х) > 0 для любого х 6 V,
(х,г) = 0 тогда и только тогда, когда х = в.
Число (х,у) называется скалярным произведением векторов гну, ак¬
сиомы 1-4 называются аксиомами скалярного произведения.
Замечание. В вещественном случае черта комплексного сопряжения
в первой аксиоме может быть опущена.
Вещественное линейное пространство со скалярным произведением
называется евклидовым пространством, а комплексное - унитарным.
Обозначение: Е и и соответственно.
Пример 47.1. Скалярное произведение геометрических векторов, вве¬
денное в §24 на основании метрики, имеющейся на прямой, на плоскости
и в пространстве, удовлетворяет всем аксиомам скалярного произведения
(теорема 24.2) и превращает пространства К., я = 1,2, 3, в евклидовы про¬
странства. Аксиоматическое определение скалярного произведения говорит
о том, что это не единственный способ введения скалярного произведения.
Пример 47.2. В арифметическом пространстве И" скалярное про¬
изведение векторов х = (ц. г?,..., 1п) и у = (у 1, Уз, * ■ • ■ Уп) может быть
введено по правилу
(х.у) = ^г.у,	(47.1)
НЛП. что то же с&мос,
(х.у ) = ХТУ,	(47.2)
где X = (х|, х?	х„)т, V = (у| ,уз	у„)т■ Такой способ введения ■ ка-
ляриого произведения в Л" будем называть стандартным.
Пример 47.3. В арифметическом пространстве С" скалярное про¬
изведение векторов х = (х|,хз	гп) и у = (уьУг	Уп) может Сыть
введено по правилу
(х.у) =
1*1
(47.3)

§47. Скалярное проиэипление. Матрица Г’рама
51
или, что то же самое,
(х,у) = Хт7,	(47.4)
где X = (*|, хз,..., Гп)т, У = (уГ, 5з	уч)т. Такой способ введения ска-
ляриого произведения я С" будем называть стандартным.
Пример 47.4. В вещественном арифметическом пространстве
скалярное произведение лекторов х = (о) + >^|,...1п„ + 10„) и у = (о^ +
\0[,... ,а'„ + \Р'„) может Быть апедсио по правилу
(*. У) =	+	(47.5)
Пример 47.5. В пространстве матрии К"’1’1" (Ст1<") скалярное про¬
изведение матриц А = (а,,), В = (Ь,,) может быть введено по правилу
(Л.В) = ^^а,)6„,	(47.6)
. = 1
или, что то же самое,
(Д, В) = 1г(/?тД),
если Л, В 6 1Ктхп, и
(Л,В) =	а„г„	(47.7)
'=1 Т-1
или, что то же самое,
[А, В) = а(ВнЛ),
если А, В 6 Стхп. Эти способы введения скалярного произведения в про¬
странствах №ткп и Стхп будем называть стандартными.
Пример 47.6. В пространстве многочленов степени не выше п с ве¬
щественными коэффициентами скалярное произведение многочленов р(() =
1 и д{1) = 52"_0Ь|1‘ может быть введено одним из следующих пра-
вил:
П
{р,ч) = ^а,Ь,
(47.8)
или
(р.«)= / Р (09(0*,
(47.9)
где <1 < (э ~ произвольные фиксированные числа. Скалярное произведение,
введенное в Л/„ по правилу (47.8), будем называть стандартным.
Пример 47.7. В комплексном линейном пространстве многочленов
степени нс выше п скалярное произведение многочленов может быть введено
по правилу
(Р. я) =
(47.10)

52
Глав» XIII. Евклидовы и унитарные пространств
Скалярное произведение, введенное в комплексном пространстве Мп по это.
му правка)’, будем называть стандартным.
Пример 47.8. В функциональном пространстве С[0, I] скалярное про.
кзаеденне функций /(г) и у(х) может быть эалаио равенством:
(/.«) = [ Я*)у(*М*
Го
Теорема 47.1. Скалярное произведение обладает следующими
спайстлами:
>) (*,у + *) = (*>у) + (*>*)> у*.у. * е е (и);
I) (х.ох) = а(х,у), Ух, у 6 Е (V), Уо е К (соответственно С);
У/(«,х) = (х,«) = 0, Ух € Е (11 У,
4)	(*, у) = 0 для любого вектора у в Е (I/) тогда н только тогда,
когда х = в;
5)	любое подпространство Б евклидова (унитарного/ пространства
является евклидовым (соответственно унитарным/ пространством.
Теорема 47.2. Для любых векторов х,у € Е (И) имеет место
неравенство
или, в другой форме,
1(*.у)1’ < (*,*)(У,У)
(*.*)
(У.*)
(*.у)
(У, У)
> 0.
Это неравенство называется неравенством Коши-Бунмковского.
Теорема 47.3. Неравенство Коши-Буняковекого обращается в
равенство тогда и только тогда, когда векторы х и у коллинеарны.
Длиной вектора г в евклидовом и унитарном пространстве называется
число
1*1 = >/(*.*)■
Вектор х называется нормированным, если его длина равна единице:
1*1 = I-
Из аксиом скалярного произведения следует, что
1)	любой вектор х евклидова (и унитарного) пространства имеет длину,
при этом |х| > 0, Ух е Е (I/) и |х| = 0 о х = 8;
2)	|аг| = |о||х|, Ух 6 Е (II), Уо 6 М (соответственно С).
С помощью длин векторов неравенство Коши-Ьуняконского может быть
переписано в виде
1(*.У)1 < 1*1 • 1у1
Теорема 47.4. В евклидовом (унитарном) пространстве для лю¬
бых векторов х,у имеют место неравенства
11*1 - М1 <1* + у1< 1*1+ М-	(47.11)
Неравенства (47.11) называются неравенствами треугольника в евкли¬
довом (унитарном) пространстве.
Матрицей Грома системы векторов а1,...,а* евклидова (унитарного)
пространства называется матрица
(01.01)	(01,03)	... (а1,а*)
(04.01)	(04,03)	...	(04,04)
С(аи...,ак) =

53
§47. Скалярное произволение. Матрица / рама
Определитель матрицы Грама называется определителей (рама.
Теорема 47.5. Система векторов о», .. ,ои елилиоово (унитор*
ного) пространства линейно зависима тогда и только тогда, когда
Не1 С(а1,... , а*) = 0 .
Теорема 47.0. Матрица /рама системы векторов евклидова
(унитарного) пространства эрмитова.
Теорема 47.7. Определитель Грома линейно независимой систе¬
мы векторов в евклидовом (унитарном) пространстве положителен.
Если С(еьез	е„) = (у.,) - матрица Грама базиса уфостранства V,
то скалярное произведение векторов г =	11*1 и у ='^1в, у,е, связано
с их координатами соотношением
(г,у) = ^^Я.1х,у1 = гТсСуе>	(47.12)
«И ,•!
если V - евклидово пространство, и
(г. у) = 5^	“ Х*СУ*'	(47.13)
.»! ]* 1
если V - унитарное пространство.
Евклидовы пространства Е, и Е-г называются изоморфными, если су¬
ществует биективное отображение : Е, —> Ез , которое сохраняет законы
композиции и скалярное произведение, т.е. если:
1)	+ У) = Ж) + 4>{у), VI, у б ^1 ;
2)	у>(аг) = ау)(х), VI е Е, , Уа € К;
3)	М*).р(у)) = (х,у), Чх,у€Е,.
Само отображение у> при этом называется изоморфизмом евклидовых
пространств или иэожешрией.
Точно так же определяется изоморфизм унитарных пространств II, и (I,
(с очевидным отличием в свойстве 2: а С !-). Из определения следует, что
изоморфные евклидовы (унитарные) пространства изоморфны как линейные
пространства.
Теорема 47.8. Два евклидовых (унитарных) пространства изо¬
морфны тогда и только тогда, когда равны их размерности.
ЗАДАЧИ
47.1.	Доказать, что в евклидовом (и в унитарном) простран¬
стве для любого вектора х выполнено соотношение
(в,х) = 0.
47.2.	Доказать, что в любом конечномерном вещественном
или комплексном линейном пространстве можно определить ска¬
лярное произведение.
47.3.	Пусть V - евклидово пространство со скалярным про¬
изведением (х,у). Показать, что если положить
(х, у) = А(х,у),

54
Глава А'///. Епкли/юаы и унитарные пространств
где А - фиксированное положительное число, то для (х, у) также
выполнены все аксиомы скалярного произведения. Какой геоме-
тричегкнй смысл имеет переход от (х,у) к {х,у) в пространстве
1з геометрических векторов?
47.4.	Доказать, что если (х,у)| и(х,у)2-лва различных ска¬
лярных произведения в одном и том же линейном пространстве
Г, то скалярным произведением в Г будет и величина
*) (*1!/) = (*.У)| +(*,у)з;
б)	(х,у) = А(х,у)| + р(х,у)2,
где А и /1 - произвольные положительные числа.
47.5.	Пусть хих2 и у!,у2 - координаты векторов х и у в не
котором базисе двумерного вещественного линейного простран¬
ства V. Определить, можно ли скалярное произведение в V опре¬
делить формулой:
а)	(х,у) = х2у,;	б) (х,у) = 2х!у, + Зх2у2;
в)	(х,у) = х,у, - 2х,у2 - 2х3у| + 5х2у2;
г)(*,у)=[*1*»1[о 4] [у2]: д) (*•») = [*! **]
е)(а-.У) = [*13-а][_з	[у‘]^ж) (г.УЫ*! *г]
' 1 2'
У| ‘
.0 9.
. Уг.
'2 2
У1
2 1
.Уг.
47.6.	Доказать, что в двумерном вещественном линейном
пространстве Г равенство
(х.у) = х[/4ус, Л =
где г, и у, - координатные столбцы векторов х и у в некотором
базисе е, задает скалярное произведение в V тогда и только то¬
гда, хогда
АТ = Л, ам > 0,	<1е1 Л > 0.
47.7.	Доказать, что в п-мерном вещественном линейном про¬
странстве Г равенство
[х,у) = **ЛУ', А = (а0) 6 ®пхп,
где I, « у, - координатные столбцы векторов х и у в некотором
базиер е, задает скалярное произведение в V, если
П
Лт = Л, а,, > ^ ^ 1ао||	= 1,п.
3 = 1
°11 Н12Т
а21 о22 I ’

§47. Скалярной произведение. Матрица Грама
55
47.8.	Пусть ХцХз и у(,у2 координаты векторов х и у в неко¬
тором базисе двумерного комплексного линейного пространства
V. Определить, можно ли скалярное произведение в V опреде¬
лить формулой:
а) (х,у) = х,у! -(- х2у2; б) (х,у) = х,]й;
в)	(х, у) =	+ «х2у7; г) (х, у) = 1х(Щ - \х7у{\
Д) (х,у) = 1х1х,1[3“ .3 + ‘][{1];
е)= I1' о 5] [й]' ж) <*•») = **1 [5 °] [к]:
з)	(х,у) = [х,х2]	|] [|1];
и)	(х, у) = Х1УГ + 1Х)Щ - «Х2у7 + х2уа.
47.9.	Пусть I, и у, - координатные столбцы векторов х
и у в некотором базисе е двумерного комплексного линейного
пространства V. Найти условия, необходимые и достаточные
для того, чтобы равенство
(х,у) = хГдк, д
задавало скалярное произведение в V.
47.10.	Выяснить, можно ли скалярное произведение в про¬
странстве к"*" квадратных матриц порядка п > 2 ввести по
формуле:
а)(А,У) = иАУ;	б) (А, У) = 1г АУТ;
в)	(А, У) = 1т X • 1гУ;	г) (X,У) = (1е1 ХУ;
д)	(.V, У) = 1г АГСУ, где О - диагональная матрица порядка
п с положительными элементами на главной диагонали.
47.11.	Выяснить, какие из следующих правил определяют
скалярное произведение в пространстве матриц Стхп:
а) (А, У) = »г(ХУТ); б) (А,У) = 1г(АУи);
в)	(А, У) = 1г(АУ7’).
47.12.	Установить, какие из следующих правил определяют
скалярное произведение в пространстве многочленов Л/„ с веще¬
ственными коэффициентами:
0 (Р.Ч)= 53р(0(“)9<4,(а).
*=0
(47.14)

56
Глава ХШ. Кньлнповы и унитарные пространства
где точка л е К произвольна;
2)	(р,?) = Х^р(*М*)-	(47,,5)
47.13. В вещественном п-мерном пространстве V скаляр,
ное произведение (х, у) задано как функция координат ,•..,хв
и У|,...,у„ векторов х и у в некотором базисе е пространства.
Вычислить матрицы Г рама базиса с и базиса, составленного из
векторов /1,...,/п. Найти выражение для скалярного произве-
дения (г, у) через координаты векторов х и у в базисе /:
1)	(х,у) = 1,у, + х2у2;
а)	(/|)« = (1>2)т, (/,)« = (2,1)т;
б)	(/,)-= (М)Т, (/,)« = (1,-1)т;
2)	(г,у) = х,у! + х,у2 + х2у1 + Зх2у2;
а)	(/,). = (1.-1)М/,). = (1,1Г;
б)	(/,). = (1,-1)т, (/,). = (1,0)т;
3)	(г,у) = 4х,у, - 2х,у2 - 2х2у, + 4х2у2;
а)	(/,). = (1.0Г, (/г)« = (1|_1)Т;
б)	(/,)« = (1/2.1/2Г, (/г)е = (-1/2,1/2)т;
4)	(х,у) = 4х,у! + 2х,у2 + 2х2у1 + 2х2у2 - х2у3 - х3у2 4- Зх3у3;
а) (/,)« = (1,0,0)т, (/,)« = (1, ■-1,0/, (/»). = (0,1,1)т;
б) (/.)« = (1,0,0/, (/,), = (-1,2,0/, (/,), = (-1,2,2)т.
47.14.	В комплексном п-мерном пространстве V скалярное
произведение (х,у) задано как функция координат х1,...,х„ и
Уь • • •, Уп векторов х и у в некотором базисе е пространства. Вы¬
числить матрицы Г рама базиса е и базиса, составленного из век¬
торов	Найти выражение для скалярного произведения
(х,у) через координаты векторов х и у в базисе /:
1)	(г,у) = 2х,уГ + (1 + 1>,й + (1 - »>*УГ + Зх2уг;
а)	(/,). = (1,0/, (/а). = (1,-1/;
б)	(/|). = 0,0/, (/*), = (-1,1 + ./;
2)	(х,у) = х,у,-1х,уЛ-|'х2уГ + 2х2у2 + (2-И)х2у3 + (2-1')х3й-(-
6х3у»;
а)	(/,). = (1,1,0/, (/,)« = (-1,1,0)т, (/3). = (0,0,1)^;
б)	(Л), = (1,0,0) , (/2), = (-», 1,0)т, (/з), = (1+2«, —2+1,1/.
47.15.	Вычислить матрицу Грама С базиса 1,1,г в ев¬
клидовом пространстве Л/„ многочленов со скалярным произве¬
дением, заданным:

57
§,/ 7. Скалярное, произведение. Матрица Г рама
а)	равенством (47.8);
Г>) равенством (47.9), в котором 1| = 0,1} - 1!
в)	равенством (47.9), в котором I) - -1,1г = 1;
г)	равенством (47.14) (отдельно рассмотреть случай а = 0);
д)	равенством (47.15), в котором т > п.
47.16.	Пусть С и С - матрицы Грама базисов сие' евкли¬
дова (унитарного) пространства, связанных матрицей перехода
5: е' - е8. Доказать, что:
1)	в евклидовом пространстве С = 8ТС8\
2)	в унитарном пространстве С = 5ТС5.
Как связаны между собой определители матриц С и 6’'?
47.17.	Доказать положительность определителя матрицы
А = (а^) порядка п с элементами:
а)	а<; = 2/(1 + ] - 1), если I + ] четно, и а,, = 0 иначе;
б)	а,; = 1/(1 + ] - 1) для всех »,;=17п.
47.18.	Векторы хну евклидова пространства заданы в бази¬
се е координатными столбцами х< и уе соответственно, и извест¬
на матрица Грама С(1) базиса /. Вычислить матрицу Грама
С(е) базиса е и скалярное произведение векторов х и у, если:
0 /1 = С1 ~ е5> I? - е\ ~ 2еа,
, хе = [1 0]Т, уе = [0 -1
2	3
3	6
ад=
2) /1 - 2б| + ег, /2 - С| -(- е2,
,*. = (! *]Т. ». = [0 1]Т;
3 2
2 2
0(1) =
3) /1 - е1 “ ^2, /2 - С] + Ё2,
5 3
3 5
, хе - [ 1 1 ] , уе - [ 1 3] ;
'О /1 = еь /а = е1 + е2, /з = С2 -Г е3,
’ 3 1 -Г
1 2 1
-1 1 2
5)	/1 = е[ + е2, /2 = е, + е3, /3 = е7 + е3,
’5 2 3'
'.*. = [! -2 1]т,л = (1 1 1]т.
, хе = [1 2 1]Г, у, = [1 1 -1]Т;
2	3 1
3	1 4
ед=
/| - е1,
ад=
/1 = е, -
0(1) =
47.19.	Векторы х и у унитарного пространства заданы в
жзисс е координатными столбцами хе и уе соответственно, и

58
Глава ХШ. Квклкловы и унитарный продрана цл
известна матрица Грана С(Л базиса /. Вычислить матрицу
Грама С?(с) базиса е и скалярное произведение лекторов х и у(
если:
О /1 = «I + »>*, Ь = -3»С| + 4с2,
«?(/)=[_,,® 141;],*.=(1 •■)т.»«:=[1+‘2]
2) Л = е,, /2 = — »с, + 2ег + |'с3, /а = -ге3 + е3,
1	31	-1
(?(/) = -3»	22	10*
-1 -101	5
, х, = [0 1 0]Т, ус = [ 1 -2. Г
47.20.	Пусть а - фиксированный вектор евклидова простран-
ства V, а - заданное вещественное число. Будет ли множество
всех векторов х, для которых (х,а) = а, линейным подпростран¬
ством пространства Г?
47.21.	Доказать, что всякое подпространство евклидова про¬
странства V' само является евклидовым пространством в смысле
скалярного произведения, заданного в V.
47.22.	Линейное пространство V разлагается в прямую сум¬
му подпространств Г,,...,Ьр. На каждом из подпространств
определено скалярное произведение (ж, у),, Ух, у е Доказать,
что можно ввести скалярное произведение во всем пространстве
Г, положив
(г,у) = (х,,у,)1 + --- + (1р,1/р)р,
если векторы х и у имеют разложения по подпространствам со¬
ответственно: X = XI + ... + хр и у = у, + ... + ур.
47.23.	На подпространстве Ь линейного пространства V вве¬
дено скалярное произведение (х, у). Доказать, что можно опре¬
делить скалярное произведение во всем V так, что для векторов
х и у из I оно будет совпадать с первоначально заданным ска¬
лярным произведением (х,у).
47.24.	Пользуясь неравенством Коши-Буняковского, дока¬
зать следующие неравенства:
‘КНЧй (14
Здесь числа а,,0, € №, I = 1,п, произвольны, а числа А, 6 И,

59
§47. Скалярное произведение. Матрица Грлмя
« = Т7п, произвольны и положительны.
47.26.	Пользуясь неравенством Коши-Буняковского для уни¬
тарного пространства, доказать неравенство
Л
2 /
53
»=1
<
где числа а,,Д 6 €, г = Туп, произвольны.
47.26.	Пользуясь неравенством Коши-Буняковского, дока¬
зать неравенство
где /(I), д(1) - произвольные непрерывные на [а,6] функции.
47.27.	Доказать, что неравенство
[1г(ЛтЯ)]а < и{АтА)1т(ВтВ)
выполнено для любых матриц А и В одинакового размера.
47.28.	Доказать, что для любых квадратных матриц А и В
одинакового порядка выполнено неравенство:
а)	[1т(АВ)}2 < и{АтА)1г{ВтВУ,
б)	1г(ЛтА) > —(1гЛ)г.
71
47.29.	Пусть в определении скалярного произведение четвер¬
тая аксиома заменена на более слабое требование: (х,х) > 0 для
любого х 6 V. Доказать, что в пространстве V с таким "ска¬
лярным произведением”:
а)	выполняется неравенство Коши-Буняковского;
б)	выполняется неравенство треугольника;
в)	множество М векторов х, для которых (х,х) = 0, образует
подпространство;
г)	для любого х € А/ и любого вектора у Е V скалярное
произведение равно нулю;
д)	если N произвольное дополнительное к М подпростран¬
ство, и х = хд/ + Жуу, у = Ум + Уы ~ разложения векторов х и
у по подпространствам Л/ и ТУ, то знак равенства в неравен¬
стве Коши-Буняковского для векторов ли у имеет место тогда
и только тогда, котла Х/у и ум линейно независимы.

60	Глава XIII. Евклилоны и унитарные просграигтц
47.30.	Сохранится ли неравенство Коши Пуняковского Г1
случае, если в определении скалярною произведения откалатьсц
от четвертой аксиомы?
47.31.	Найти длину вектора:
1)	а = (5,4,3) в пространстве К3 со стандартным скалярным
произведением;
2)	а = (1, -2,3,4) в пространстве К* со стандартным скаляр,
ным произведением;
3)	о = (1,1) в пространстве Ка со скалярным произведением
(х, у) = г,у, +т,у,+ 1}У, + 3х2у,;
4)	а — (1, —1,2) в пространстве К3 со скалярным произведе-
нием (х,у) = х
'4	2
2 2
2 -1
2'
-1
3
У
т.
У
5) а = (1,1*) в пространстве С* со скалярным произведением
'2 1 -I- Г
1-1 2
6) а =
дением (х,у) = х
—Т
у \
6) а = (1 + |, 1,-|) в пространстве С3 со скалярным произве-
Г1 -1* О
» 2 2 + 1
0 2-1 6
—т
у•
47.32. Доказать, что для любых векторов х и у выполнено
равенство
|х + у|г + |х-у|3 = 2|х|а + 2|у|а.
Какой смысл имеет это соотношение в пространстве Уз геоме¬
трических векторов?
47.33. Показать, что для любого вектора х конечномерною
евклидова (унитарного) пространства V выполнено соотношение
И =
$1ф
1(«.у)1
|у| *
§48. Ортогональные векторы
цм вектор* ж,у € 4’ (1/) иашааютс» ортоеома^ными, если (ж, у) = 0.
Систем* вес торов х,	..*» 6 К (V) называете* ортогональной, если
(х,,х;) = 0 при \ф).
Свете*** вех торов 		,х. € Е (У) и**ы*апс* ортоморвироооммов

Ортогональные пек горы
61
системой, если
*.,*2
1,
О,
' = У,
• ф)’
Теореме 48.1. Ортогональная система ненулевых векторов ли¬
нейно независима.
Следствие 1. Ортонормиропанная система векторов линейно не¬
зависима.
Следствие 2. И п-мерном евклидовом (унитарном) пространстве
любая ортонормирооанная система из п векторов образует базис. Этот
б&эис называется ортонормированным базисом.
Пример 48.1. Известно, что скалярное произведение в пространстве
К4 задано стандартным образом. Лополнить векторы с\ =
сз = ( Д=,	—7=, 0 ) до ортонормированного базиса пространства Я1.
\у/6 у/6	у/6	)
Решение. Найдем какой-либо ненулевой вектор х = (ц,Х2,хз,х4),
ортогональный лекторам е\ и с?:
Г XI - XV + хэ + X, =0, л.(х\- XI + Х|+ X, = 0,
\2х,+Х2-Гз	=0 ^ \	3X2 -Зхэ-2х, =0.
Решением зтой системы является, например, вектор х = (0,1,1,0). По¬
сле нормировки получим вектор еэ =
)'
Найдем теперь новый ненулевой вектор х так, чтобы он был ортогонален
векторам в|, сз и ез:
х. еП = 0,
1,021 = 0,
I,ез) = 0
Г ц - х2 + хз + х4
<=> < 2х| 4- хз — хз
I	Х2 + Хз
О,
0,
0
{Ц - XV + Хз +х, =0,
XV + хз =0
Зхз + х« =0.
Отсюда х = ( — 1, 1,—1,3). Положим в\ =
Тогда система векторов е|,ез,ез,е« ортонормирована и, так как еЛш Я* = 4,
она образует ортонормированный базис пространства Я*. •
Теорема 48.2. В евклидовом (унитарном) пространстве ко¬
ординаты XI,...,хп вектора х в базисе е = (е»	е„) вычисляются по
правилу
х, = (х, е.),	1 = 1,п,
тогда и только тогда, когда е - ортонормированный базис.
Теорема 48.3. В евклидовом (унитарном) пространстве ска¬
лярное произведение векторов х =	х,е,, у = Е"„| У,*, ■ заданных сво¬
ими координатами в базисе е, вычисляется по правилу
П
(*.») = Е*•*
•«I
тогда и только тогда, когда е ортонормированный базис.
^	1	1	3_\
2л/3* 2з/3' 2\/з’2уД)‘

Глава Л'Ш. Евклидовы и унитарные пространства
62
В стел к ловом простркнстпг черта комплексного соприжения и последнем
равенстве может быть опушена: (к,у) = )П"в1 *,У, ■
Теорема 48.4. В конечномерном евклидовом (унитарном) про.
странстое существует ортонормиропанныЛ базис.
Процесс ортоеонализаиии позволяет построй и. Н1 произвольной линей-
но независимой системы векторов /з,	ортогональную систему ненуле¬
вых векторов !■ — и состоит в следующем. Полагаем д\ = Д. После¬
дующие векторы }■	ут находятся из рекуррентных формул
к-1
9> = /> - У ак)9,.
3-1
Коэффициенты о», однозначно определаютск условием ортогональности вех-
тора уз векторам 91,...,93-1:
(А.Зз)
(Яз.Зз)’
о зз
Нормнрув векторы 			 приходим к ортонормированному базису
подпространства С{!/т).
Пример 4В.2. В пространстве К4 со стандартным скалярным произ¬
ведением построить ортокормированный базис линейного подпространства
I, наткнутого на векторы аз = (1,1,0,0), аз = (2, 0,1,-1), а3 = (4, 2,3,1).
Решение. Векторы аз,аз,аз, как нетрудно проверить, линейно не¬
зависимы. Для построения ортонормироаанного базиса подпространства Л
применим процесс ортогоналмзации к системе векторов аз,аз, ад.
1)	Положим /з = аз и возьмем ез =	/, = (	, Д=,0,0V
\П \х/2 Л )
2)	Построим вектор /> так, чтобы он линейно выражался через векторы
аз, 0] и был ортогонален вектору аз. Согласно описанному выше алгоритму
этого можно добиться, определив /а равенством
(аа,а|)
(оз.аз)
/з = аз -
Отсюда /з = (2,0,1,-1) -(1,1,0,0) = (1,-1,1,-1).
Так как (/з./з) = 4, то возьмем ез = ^/з =	•
8) Построим вектор Д так, чтобы он лиззейно выражался через векторы
аз, аз, аз или, что то же самое, через векторы /з, /з, аз и был ортогоззалеи
векторам аз, /з- Этого можно добиться, определив Д равенством
/з.
(°з, /з)
(аз«аз)
: ад - ;	г/з
(аз,аз)
(/з,/зГ
Отсюда Д = (4,2,3,1) - 3(1,1,0,0) - (1, -1,1,-1) = (0,0, 2,2).
Так как (/з,/з) = 8, то возьмем ез = Д
-(“я-яУ
Тем самым, система ез,ез,ез ортонормирована, принадлежит Подпро¬
странству I н. следовательно, образует ортонормиронанный базис /, ,
Матрица У 6 С’""" называется унитарной, если
иин = инц = /.

§4Й. Ортогональные векторы
63
Матриц» С/ € Л"*" называется ортогональной, если
д«г = дТд = /.
Теорема 48.5. Л/атрицо ортогональна (унитарна) тогда и
только тогда, когда она является матрицей перехода от одного орто-
нормированного базиса к другому артомормироланному базису евклидова
('унитарного,) пространства.
Две системы векторов Х|,...,Хк и 		у» в унитарном (евклидовом)
пространстве называются биортогональными, если
(*••»!) =*{ о; !/]■!
Теорема 48.6. Каждая система из пары биортогональных си¬
стем оекторов линейно независима.
Бнортогональные системы е1,...,ел и Д,образующие базисы
пространства V, называют биортогональной парой базисов.
Теорема 48.7. Иля любого базиса с\,... ,г„ унитарного (евкли¬
дова) пространства существует, и притом единственный, биортоганаль-
нмй базис
Пример 48.3. Построить базис пространства Мз, бнортогональкый
базису
е,(0 = 1 + 21 + еа(0 = 1 — 1, ез(«) = 2 + 21 + 1’.
если известно, что скалярное произведение в пространстве Мз задано сооот-
ношением (47.8).
Решение. Так как пространство Мз со скалярным произведением
(47.8) изоморфно пространству К5 со скалярным произведением (47.1), то
решим аналогичную задачу для базиса с\ = (1,2,1), еа = (1,-1,0), ез =
(2,2,1) пространства К3.
Пусть система векторов /ь/з./з биортогональна к системе в],ез.ез. То¬
гда
Г(в1>/|)=1|	Г(е1|/з) = °.	((е1./э)=0,
< («з,/|) = 0>	я(«з,/з)=1,	<(ез,/э) = 0,
I ('•-з,/з) = 0,	1(«з>/з) = 0,	1(ез,/з) = 1,
и следовательно, нужно решить три системы уравнений
С 11+2X1+13 = 1,	С Х1+2Х1+Гз=0,	Г Г] + 2г! + Г) = 0,
< XI - Хз =0,	< ц - ГЗ =1,	{ и - хз	=0,
I 2ц + 2хз + хз = 0,	I 2х| + 2хз + хз = 0,	(. 2х] + 2хз + хз = 1.
Так как матрица коэффициентов одинакова у всех этих трех систем, то
решим их одновременно, составив следующую расширенную матрицу:
2 1
1 0 0
Г 1 2 1
1 0 01
Г1 2 1
1 0
0 1 0
-. 0-3-1
-1 1 0
0-10
2 1
0 0 1
[О -2 -1
-го и
0 0-1
Г I	0	0	-1	0	11
-.010-1-1 1 .
I 0	0	1	4	2	—3 Л
Отсюда /, = (-1,-1,4), /, = (0,-1,2), /э = (I, 1,-3).
Таким образом, искомый биортогональный базис образуют многочлены
/,(<) = -!-[ + |(3, /3(1) = -I + 211, /з(») = 1 + < — 3(а. .

64
Глава XIII. Евклидовы и унитарные пространства
ЗАДАЧИ
48.1.	Доказать, что в евклидовом пространстве Е:
1)	вектор / ортогонален всем векторам из Е тогда и только
тогда, когда вектор / нулевой;
2)	векторы / и у удовлетворяют соотношению (/,х) = (у,х)
для любого вектора х € Е тогда и только тогда, когда / = у.
Верны ли эти утверждения в унитарном пространстве?
48.2.	Доказать, что если хь...,х4 - ортогональная система
векторов, то для любых чисел А<, » = 1,&, система векторов
А^,..., А*х* также будет ортогональна.
48.3.	Пусть вектор х евклидова или унитарного простран¬
ства ортогонален каждому из векторов	Д. Доказать, что
х ортогонален и любому вектору из линейной оболочки векторов
/|г'м/ь
48.4.	Доказать, что если в евклидовом пространстве для
любого числа а выполнено неравенство |х + ау| > |х|, то векторы
х и у ортогональны.
48.5.	Доказать, что в евклидовом пространстве выполнено
тождество
2(г,у) = |*+ у|2 - |х - у|2.
48.6.	Доказать, что в унитарном пространстве выполнено
тождество
4(х,у) = \х + у|2 - |х - у|2 + «|х + 1у|2 - |‘|х - ?у|2.
48.7.	Последовательность векторов {а*} п-мерного евклидо¬
ва (унитарного) пространства называется сходящейся к вектору
а, если 1нп |а* - а| = 0. Доказать, что
4-«®
1)	если последовательность векторов {/*} сходится к вектору
/, то числовая последовательность {|Д|} сходится к |/|;
2)	если последовательности векторов {/*} и {у*} сходятся
соответственно к векторам / и у, то
Нт(/*,у4) = (/.у).
48.8.	Верно ли, что произвольная система попарно ортого¬
нальных векторов линейно независима?
48.9.	Пусть /|,...,/т И У1,...,Ут * две линейно независимые
ортогональные системы векторов евклидова или унитарного про¬
странства, которые обладают следующим свойством: при любом
к = 1,т линейная оболочка	.., /*) совпадает с линейной

65
§48. Ортогональные некторы
оболочкой С{д\,...,дь). Доказать, что дк - •>*/», к = 1,т, при
некоторых отличных от нуля коэффициентах 7*.
48.10.	Доказать, что если система арифметического про¬
странства 1КП
х\ = (®М| 0|2>а13| • • •
• ^10)1
х2— (0« Озг^аз,...
>°гп)»
хз — (0, 0, Озд,...
> **3п)«
хп= (0, 0, 0, ...
, ®пл)
образует ортогональный базис этого пространства, то: а) а,< ф
О, I = 1, л; б) а^ = 0, если * ф
48.11.	Доказать, что естественный базис арифметического
пространства 1Р.” (Сп, С^) со стандартным скалярным произве¬
дением является ортонормированным базисом.
48.12.	Пусть относительно стандартного скалярного произ¬
ведения арифметического пространства вектор-столбцы и]уи2,и3
образуют ортонормированный базис Я3, а вектор-столбцы В1,»г
- ортонормированный базис К2. Показать, что если А =	+
и2е^, то АтА = I.
48.13.	Известно, что в пространстве К" (п > 1) имеется
ортогональный базис е1,...,еп такой, что все компоненты ка¬
ждого из векторов е, равны 1 или —1. Доказать, что п равно 2
или кратно 4.
48.14.	Построить какой-либо ортонормированный базис ев¬
клидова (унитарного) пространства Ятхп (Стхп) со стандарт¬
ным скалярным произведением.
48.15.	Построить какой-либо ортонормированный базис ев¬
клидова пространства Л/п со скалярным произведением, опреде¬
ляемым:
1)	равенством (47.8);
2)	равенством (47.13);
3)	равенством (47.14) при тп — п + I.
48.16.	Доказать, что координаты х, произвольного вектора
х п-мерного евклидова (унитарного) пространства в ортогональ¬
ном базисе еь ..., е„ можно вычислить по формуле
— (х, е, )/(е,’, ), I — 1, п.
|(*.е,)|2
П
Иывести отсюда равенство |х|2 =
1 = 1
3	7470

66
/лапа .УIII. Евклидовы и унитарные /тросграцг-.
-Л
48.17.	Доказать, что в евклидовом (унитарном) простру
стве длина вектора т, заданного своими координатами 11,...^'
в базисе е, вычисляется по правилу	'
. = 1
тогда и только тогда, когда е - ортонормированный базис пРо
странстпа.
48.18.	Пусть С|,... ,сп ортонормированный базис свклид0.
ва пространства. Найти выражение для скалярного произведи
ния произвольных векторов х и у через их координаты:
а)	в базисе А|С,, А2с2,.... Апс„, где Аь А2,..., А„ - ненулевьд,
числа;
б)	в базисе е, + е2, с2, е3,..., е„.
48.19.	Пусть Г - вещественное или комплексное линейно^
пространство и е4- некоторый базис в нем. Доказать
что в Г можно ввести скалярное произведение так, чтобы этот
базис был ортонормированным относительно введенного скаляр,
кого произведения.
48.20.	В пространстве М„ многочленов степени не выше п с
вещественными коэффициентами произвольным образом введено
скалярное произведение. Доказать, что в полученном евклидо.
вом пространстве:
а)	существует ортогональный базис, содержащий по одному
многочлену каждой степени к = 0, гг;
б)	если /о(О, МО	МО и $о(0. М0>---> МО ~ •ава °Р‘
тогональных базиса, обладающих указанным свойством, то (при
соответствующей нумерации) многочлены, входящие в эти бази¬
сы, различаются лишь скалярным множителем: д^(^) = »,/,(/),
I = О, Л.
48.21.	В пространстве Л/„ ввести скалярное произведение
так, чтобы базис
I7	Г
М’ 2!*	^
стал ортонормированным.
48.22.	Найти какой-нибудь нормированный вектор, ортого¬
нальный к указанной системе векторов веществен кого арифме¬
тического пространства с соответствующим скалярным произ¬
ведением:
1)	(2,2,1), (-2,2,3), скалярное произведение стандартное;

§48. Ортогональные пскторы
67
2)	(1,2,1,0), (1,1,1,1), скалярное произведение стандартное;
3)	(1, —1,2), скалярное произведение стандартное;
•1) (1,1), скалярное произведение задано равенством (х,у) =
Х\У\ + *\У7 + Х1У\ + Уъ
5) (1,2,0), (2,0,-1), скалярное произведение задано равен¬
ством (х, у) = 4x12/1 + 2x1 У7 + 2х22/1 + 2х2у2 - х2у3 - х3у2 + Зх3у3.
48.23.	Найти какой-нибудь нормированный вектор, ортого¬
нальный к указанной системе векторов комплексного арифмети¬
ческого пространства с соответсвуюшим скалярным произведе¬
нием:
1)	(1 + 1,1 — г), скалярное произведение стандартное;
2)	( —1,1 + 1,0), (0,1,1), скалярное произведение стандартное;
3)	(1,»\0), ((, 1,0), скалярное произведение задано равенством
(х, у) = х,у7 + 5х2уг + х3у1 + 1Х2уз - хх3Щ.
48.24.	Доказать, что процесс ортогонализапии, применен¬
ный к линейно независимой системе векторов /Ь...,Д, приво¬
дит к ортогональной системе ненулевых векторов У|,...,у*.
48.25.	Применить процесс ортогонализапии к линейно неза¬
висимой системе векторов вещественного арифметического про¬
странства со стандартным скалярным произведением:
1)	/, = (1,-3,1), /а = (4, -5,3);
2)	!\ — (1.0, — 1,2), /2 = (2,1, —1,3);
3)	/, = (2,0, -1), /2 = (5, -1,0), /э = (1,7,-3);
•ОЛ =(1,2,2), /а = (1,1,0), /3 = (0,1,-4);
5)	/1 = (2,1,-2), /а = (4,1,0), /3 = (0,1,0);
6)	/, = (1,1, -1,0), /2 = (1,2,0,-1), /3 = (0,0,1,0).
48.26.	Пусть в результате применения процесса ортогонали-
эации к системе векторов /ь ...,/* получается системад1г ... ,у*.
Доказать, что:
1)	если система векторов /ь-..,Л линейно зависима, а ее
подсистема /1	г линейно независима, то векторы дх...,
у*_, ненулевые, а дк = 0;
2)	если векторы </],.. -, дк-1 в получаемой системе ненулевые,
а дк = в, то и исходной системе векторы	линейно
независимы, а вектор /* через них линейно выражается.
48.27.	Показать, что тригонометрическая система функций
1, сое /, 5ш сое п1, 81п п1 ортогональна относительно скаляр¬
ною произведения (47.9) с 1| = -л и *2 = л\
)•

68
Глава XIII. Евклидовы и унитарные пространен^
48.28.	Н пространстве многочленов Мя го скалярным про.
изволением (47.9), п котором /, = -1, (, = 1, построит!, орто,
тональный Палке, применив процесс ортотоналилацин к систем*
многочленрв 1, <, /*, *э.
48.29.	Докидать, что в пространстве многочленов М„ со ска.
лярным произведением (47.9), в котором (, = -1, (2 = 1, много,
члены Лежандра
П(0=1.	* =
образуют ортогональный базис.
48.30.	Доказать, что:
а)	любой ненулевой вектор можно включить и некоторый ор.
тогональный базис евклидова пространства;
б)	любую ортогональную систему ненулевых векторов можно
дополнить до ортогонального базиса пространства.
48.31.	Дополнить следующие системы векторов до ортого.
нальных базисов пространства К* (скалярное произведение в К*
введено стандартным образом):
1)	а, =(1,-2,1,3), а, = (2,1,-3,1);
2)	а, =(1,-1,1,-3), а, = (-4,1,5,0);
3)	в, = (1,1,1,2), в, = (1,0,1,-1);
4)	в, =(1,2,1,2), а2 = (1,1,—1, —1).
48.32.	Дополнить следующие системы векторов до ортого-
нальных базисов пространства С3 (скалярное произведение в С3
введено стандартным образом):
1)	о, = (1,1 -1,2), а2 = (2,-5 +31,3+ *);
2)	а, = (-«',2,-4+ «), а3 = (4 - 1,-1,0-
48.33.	Дополнить следующие системы векторов до ортонор.
мированных базисов соответствующего арифметического про¬
странства (скалярное произведение считается введенным стан-
11 2 2
\ / 2 14
_15’_15’3
)'аг~{ 15’ 15’
1111
\ 111
2’ 2'2’ 2
),а2 V 2’2’2’
1 1
1 \ / 1 1
N/3’ у/3' '
7з],а’~ ^/З’л/З1

69
§‘<8. Ортогональные векторы
_1	1	’2_
уП'Л'Л'
/2,0,^2'),аг" (
48.34.	Н пространстве Л* со стандартным скалярным произ¬
ведением построить ортогональный базис подпространства, на¬
тянутого на систему векторов:
1)	а, = (2,3,-4,-6), а2 = (1,8,-2,-16),
а3 = (12,5, -14,5), я4 = (3,11,4,-7);
2)	а, = (1,1, —1,-2), а2 = (—2,1,5,11),
а3 = (0,3,3,7), а4 = (3,-3,-3,-9).
48.35.	И пространстве С3 со стандартным скалярным произ¬
ведением построить ортогональный базис подпространства, на¬
тянутого на систему векторов:
1)	а, = (2,1, - а2 = (3 + г, 0, -2), а3 = (0,6 - 1);
2)	а, = (0,1 - *,2), а, = (1,2,2 - «), а3 = («,2,5+ 2г).
48.36.	Найти размерность подпространства, образованного
всеми векторами х, для которых (а, х) = 0, где а - некоторый
фиксированный ненулевой вектор рассматриваемого п-мерного
евклидового пространства.
48.37.	Подпространство I; арифметического пространства
со стандартным скалярным произведением описано системой ли¬
нейных уравнений. Найти какой-либо ортонормированный базис
если:
1)	х, - х2 - х3 = 0;	2) Х1 + х2 + х3 + х4 = 0;
1
(*|
- хг -
х3 — х4 — 0,
3)|
*.
- 2х2 +
х3 + 4х4 =0,
1*1
-
Зх3 — 6х4 = 0;
«I
X
1 - 2х2 -
- х3 + 2х4 + 14х5 =
= 0
.ЗХ;
1 + х2 ~
И
г*-
1
н
00
1
«
н
= 0;
1
Г х \
+ Зх2 -
х3 — Зх4 4- 4x5 — 0)
5,|
- х2-
х3 + х4 = 0,
[*1
+ 2х2 +
хз ~ 5х5 = 0;
1
Г X
1 + х2 -
- Xз — Х4 + х5 ~
0,
4
X
, - 2х2 -
- 4х3 + Зх4 =
0,
1 3*
1 —
6х3 + х., + 2х5 =
0.
48.38. ПустьЛ -линейно независимая система векто¬
ров евклидова (унитарного) пространства, ди..-,дк ~ система,
полученная из нее процессом ортогонализадии. Доказать, что
<1е1 <?(/,,. ..,/*) =6е1С(ди...,дк) = Ыа-.-Ы2-

70
Глава XIII. Евклидовы и унитарные пространств
48.30.	Пусть С = С(с[,..., е„) - матрица Грама базис*
с,....,г„ евклидова пространства Е. Найти матрицу переход^
к биортогональному базису /,,...,/„ и его матрицу Грама.
48.40.	Пусть 5 матрица перехода от базиса е к базису
г'. Найти матрицу перехода от базиса /, биортогонального дл„
базиса е, к базису /', биортогонального к /:
а)	в евклидовом пространстве;
б)	в унитарном пространстве.
48.41.	Доказать, что определитель Грама любой системы
векторов не превосходит произведения квадратов длин век ейров
системы, причем равенство имеет место только в случае, когда
либо векторы попарно ортогональны, либо один из них нулевой,
48.42.	Доказать, что в евклидовом (унитарном) простран¬
стве каждая из двух биортогональных систем векторов в|,... , е*
и /ь-линейно независима.
48.43.	Пусть	е„ и /|,...,/п - биортогональная пара
базисов в евклидовом (унитарном) пространстве Е (I/). Дока¬
зать, что координаты произвольного вектора х в базисе ех,.. •, еп
вычисляются по формулам
2,	— (^1/1))	* = 1|П.
48.44.	Пусть хе и уу - координатные столбцы векторов 1
и у соответственно в базисах ей/ евклидова пространства Е.
Доказать, что равенство
(г,у) = хтсУ]
выполнено тогда и только тогда, когда базисы ей/ образуют
биортогональную пару. Сформулировать и доказать аналогич¬
ное утверждение в унитарном пространстве II.
48.45.	Пусть Е - п-мерное евклидово (унитарное) простран¬
ство. Доказать, что для всякой линейно независимой системы
векторов е!,..., е*, к < я, существует биортогональная система.
Как отличаются друг от друга системы векторов, каждая из
которых образует с системой ех,.. . ,е* биортогональную пару?
48.46.	Пусть Е - конечномерное евклидово (унитарное) про¬
странство. Доказать, что система векторов ех,..., ек имеет един¬
ственную биортогональную систему тогда и только тогда, когда
векторы ех,...,ек образуют базис пространства Е.
48.47.	Пусть ей/ биортогональная пара базисов в евкли¬
довом (унитарном) пространстве Е (II), хс и х/ - координатные
столбцы произвольного вектора х в базисах ей/ соответствен-

§4». Ортогональные подпространства
71
но, а С(е) и С(/) - матрицы Грама этих базисов. Доказать,
Ч,01)/ = е6"'(/);	2 )х/ = (Гг[с)х..
Найти биортогональнме базисы для следующих базисов ве¬
щественного арифметического пространства со стандартным
скалярным произведением:
48.48.	е, = (1,3), е2 = (1,5).
48.49.	е,	= (1,0,0),	е,	=	(0,2,0),	е3 = (0,0,3).
48.50.	с 1	= (1,1,1),	е2	=	(1,2,3),	е3 = (1,4,9).
48.51.	в!	= (1,0,0),	с,	=	(3,1,0),	е3 = (-2,-5,1).
48.52.	е,	= (1,0,1,0),	е2	= (0,1,2,0), е3 = (0,0,3,1),
е4 = (0,0,2,1).
48.53.	с, = (-2,1,1,1), е2 = (1, -2,1,1), е3 = (1,1, -2,1),
е4 = (1,1,1,-2).
48.54.	е, = (1,1,1,1),е2 = (1,1,1,0), е3 = (1,1,0,0),
е< = (1,0,0,0).
48.55.	Найти биортогональный базис для базиса е, =(1,0,1),
е2 = (1,1,0), е3 = (0,1,1 + *) пространства С3 со стандартным
скалярным произведением.
48.56.	В арифметическом пространстве К4 со стандартным
скалярным произведением построить систему векторов, биорто-
гональную указанной системе векторов и принадлежащую их ли¬
нейной оболочке:
а)	е, = (1,1,1,1), е2 = (1,1,1,0);
б)	е, = (1,1,0,1), е2 = (1,0,-1,0), е3 = (0,0,-1,1).
48.57.	Пусть в пространстве многочленов М3 скалярное про¬
изведение задано формулой (47.9), в котором 11 = -1, <2 = 1.
1)	Построить систему векторов, биортогональную системе 1,
I, 12 и принадлежащую линейной оболочке этих векторов.
2)	Построить базис Л/3, биортогональный базису 1, I, I3, I3.
§49. Ортогональные подпространства
Пусть X - линейное подпространство евклидова (унитарного) простран¬
ства Е ((/). Вектор х называется ортогональным к подпространству X,
если он ортогонален любому вектору у 6 X ■ Обозначение: гХХ.
	Очевидно, что г X Х(а,,..., а») тогда и только тогда, когда г X а,, I =
1,*. Совокупность всех векторов г 6 Е ((/), ортогональных подпростран¬
ству X , называется ортогональным дополнением к X . Обозначение: ХА.

72
Глада Л'///. Гяклидояы к унитарные просгрансть»
Теорема 40.1. Ортоаомольное дополнение к подпространств
валяется лингЛнмж подпростронстпом.
Пример 49.1, Найти ортогональное дополнение и линейному пол про.
страистшу /., натянутому на векторы в| = (1,4,-2,1), аэ = (2,5, —1,-2),
«л = (I, —2,4, —Т), а, = (1,7, -5,5). Сиалирное произведение в простран,
стае К4 ааедено стандартным образом.
Решен ие. Вектор т = (*,, *з, хз, *«) принадлежит ортогональному до.
полнеиню к подпространству I — ^(01,03,03,01) в том и только том случае,
когда он ортогонален каждому вектору а,, I = 1,4:
{
г,О|) = 0,	( Х|+4*э — 2*э + х« = О,
х,«з) = 0,	.	.	12х|+5**- хз-2х«=0,
х, аз) = 0, ^ 7 Х| -2*з + 4*з - 7х« =0,
*, О1) = 0	I ц + 7х* - 5*э + 5х« = 0.
Опишем множество решений этой системы, построив ее фундаменталь¬
ную систему решений:
' 1 4-2
1
1°1
' 1
4
-2
1
0
‘ 1
4
-2
1
0 ■
2 5-1
-2
0
0
-3
3
-4
0
0
-3
3
-4
0
1 -2 4
-7
0 “*
0
-6
6
-8
0
0
0
0
0
0
1 7 -5
5
о]
0
3
-3
4
0
0
0
0
0
0
=> е( = (13,-4,0,3), е* = (-2, 1,1,0).
Построеккал фундаментальна! система решений ег, е* образует базис
пространства решений системы, и следовательно, является базисом ортого-
нального дополнения Таким образом, Iх =^(е|,е*). ■
Пример 49.2. Найти ортогональное дополнение к подпространству
и. заданному системой
Х| + 4х* — 2хэ + х« = 0,
2*1+5**- *з — 2*4 = 0,
* 1 - 2х* + 4*3 - 7х« = 0,
х 1 + 7г* — 5*з + 5х« = 0.
Скалярное произведение в пространстве А4 введено стандартным образом.
Решение. Обозначим через 01,03,03,04 векторы, компоненты которых
являются коэффициентами заданной системы уравнений: а> = (1,4,—2,1),
в, = (2,5,-1,-2), аз = (1.-2,4,-7), а< = (1,7,-5,5). Из правила (47.1),
задающего скалярное произведение, следует, что вектор х = (*■, г*, хз, х,)
принадлежит подпространству I тогда и только тогда, когда
х ± С(а,, а*, Оз, а,).
Это означает, что I= 1(о|,аз,аз,а<) и для построения базиса ортогональ¬
ного дополнения достаточно найти базис указанной линейной оболочки:
■ 1 4-2 1
а( Г 1 4-2 1 '
2 5-1-2
а* 0-3 3-4
1-2 4-7
аз — 0 0 0 0
17-55
а« [ 0 0 0 0
0|
а* - 2а1
За| — 2аз + а*
—За) + а* + а*

*И9. Ортогональные подпрастрянстня
73
Отсюда следует, что базис I,1 образуют векторы
е, = (1,4. -2.1), е, = (0,-3,3,-4)	.
Т еоромп 40.2. Если I. линейное подпространство Е(11), то
I. © /.А = Е ((/).
Следствие. Если I. - линейное подпространство Е (II), то для лю¬
бого вектора / 6 Е (II) существует, и притом единственное, разложение
/ = 9 + Л,	(49.1)
где д Е Е, Л X Е.
Вектор д п разложении (49.1) называется ортогональной проекцией век¬
тора / на подпространство Ь, а вектор А ортогональной составляющей
вектора /.
Задачу разложения (49.1) вектора на ортогональную проекцию и орто¬
гональную составляющую называют задачей о перпендикуляре. Ортого¬
нальную составляющую А в разложении (49.1) называют также перпенди¬
куляром, опущенным из вектора / на подпространство I., а сам вектор /
- наклонной к подпространству I,.
Подпространства Ь\ и Ез евклидова (унитарного) пространства назы¬
ваются ортогональными, если любой вектор каждого из них ортогонален
другому подпространству. Сумма конечного числа попарно ортогональных
подпространств называется ортогональной суммой.
Пример 49.3. Найти ортогональную проекцию и ортогональную со¬
ставляющую вектора / = (5,8,-4,-1) на подпространство Е, натянутое
на векторы а) = (1,4, —2,1), аз = (2,5, —1,-2). Скалярное произведение в
пространстве 1Я4 введено стандартным образом.
Решение. Заметим, что векторы а\,аз образуют базис I. В силу
определения ортогональной проекции требуется построить разложение / =
3 + Л, где з 6 Е, А 6 Ех, или, что то же самое, найти такие числа а), аз € Я
и такой вектор Л 6 Е^, что
/ — 0)0) + ОзОз + Л.
Умножим скалярно обе части этого равенства на векторы аз и аз. Так
как (А, 01) = (А, аз) = 0, то получим
Г 22а 1 + 22аз = 44,
^ 22а! 4- 34оз — 56
<=> а х = аз — 1.
Таким образом, вектор д = щ + аз = (3, 9, -3,-1) - ортогональная про¬
екция вектора / на подпространство Е, а вектор Л = / — д = (2, — 1, —1,0) -
его ортогональная составляющая.
Замечание. Отметим, что в этом решении сначала найдена проекция
3 = и|С1 +азсз, а мотом перпендикуляр Л = /-д. Очевидно, что можно было
бы сначала искать перпендикуляр Л = +&зЬз, предварительно построив
базис Ь\ ,Ьз подпространства Iх. В данной задаче базис Е уже дан (это
векторы в), аз), этим оправдано то, что поиск ортогональной проекции и
перпендикуляра начат с проекции
Вообще гоноря, построение базиса как I, гак и Ьх, не столь затрудни¬
тельно. Полое трудоемко составление и решение системы с матрицей Грама
базисных векторов. Поэтому при выборе вектора, с которого надо начинать

7-5
Глава ХШ. Еяклидопы и унитарные пространств^
разложение вектора /, желательно учитывать размерности этих молпр^
странств: если <Ит А < <Лт Iх, то лучше начинать разложение г. проекцЦц
д, а если (Нш А > еИтп АА, то с А. ■
Пример 49.4. Найти ортогональную проекцию матрицы Р —
5 3
4 3
на подпространство А всех квадратных матриц второго порядка с нулсвы*,
следом. Скалярное произведение н пространстве К3*3 введено стандартны*,
образом.
Решение. В силу изометрии евклидовых пространств К3*1 и К4 Со
стандартными скалярными произведениями поставленная задача экпиналец.
тиа следующей задаче:
найти ортогональную проекцию вектора / = (5,3,4,3) на подпрострц,|.
ство А; п + г« = 0.
Как следует из решения примера 49.2, ортогональное дополнение I-1
является линейной оболочкой, натянутой на вектор О] = (1,0,0,1). Поэтому
(см. замечание к примеру 49.3) разложение / = $ + А, д 6 А, А 6 Ах, будем
искать в виде
/ = д + о 101, д е а, сы е К.
Умножим скалярно обе части этого равенства на вектор аь Так как
(д, 011 = 0, то получим
(/.01) = 01(01,01) <=> 2о) — 8 <=> 1*1 = 4.
Таким образом, вектор Л = 401 = (4,0,0,4) - ортогональная составляю-
ш&я вектора / а вектор д = / - А = (1,3,4,-1) - ортогональная проекция
вектора / на подпространство А.
Итак, ортогональной проекцией матрицы Р на указанное подпростран¬
ство квлиется матрица С = I .	,	. ■
Пример 49.5. Найти ортогональную проекцию многочлена /(0 =
2 + 4< + 213 на подпространство А многочленов степени не выше 4, имеющих
корим I = — I, I = 0 к I = 1. Скалярное произведение в пространстве Л/4
введено стандартным образом.
Решение. .Многочлен /(<) =- во + <МI + щ!3 + аз<э + а«/4 имеем корни
1 = — 1. 1 = 0 и I = 1 в том и только том случае, если
Г а0 = 0,
<	во 4- а| + а? + аз 4 о* = 0,
( ао — 01 + а? — аз + а4 =0.
Поэтому в силу кзометрии пространств Л/« и М8 со стандартными ска¬
лярными произведениями поставленная задача эквивалентна следующей за-
даче:
найти ортогональную проекцию вектора / = (2,4,2,0,0) на подпро¬
странство А, заданное системой
Г XI	=0,
<	XI + г* + Ха + х4 + х6 = 0,
1x1 — Ха + ха — х4 + х& = 0.
Исследуем пространство решений последней системы:
I
1
1
1
0 0 0 0 ' 0 •
[10 0 0
0
0
11 1110
-4
0 111
1
0
1 1 -1 1 1 0 .
0 0 10
1
0.
(49.2)

§•<9. Ортогональные полпространстпа
75
Отсюда Лш 7. = 2 и Лгп = 3. Так как Лш 1 < <5т А'*' (си- экмечкние
к примеру 49.3), то будем искан, ратложсиие / = в + А, 9 € А, А 6 А ,»
виде
/ = ®|С1 +	+ Л, а|,а] С 6	(49.3)
где в], е.1 - какой-либо базис пространства А. Построив фундаментальную
систему решений системы (49.2), получим
е] = (0,0,-1,0,1),	= (0,-1,0,1,0).
Ит (49.3) следует:
«/,С]1 = ог|(е|,еИ + аЛез.еЛ,
/,еа) = оп(е1,ез) + аг(ез,е])
2а,
2оз
2,
4
О] = —1, О] — —2.
Таким обратом, вектор д — -с, - 2ез = (0,2,1,-2,-1) явлкетск ортого¬
нальной проекцией вектора / на подпространство А.
Итак, ортогональная проекция многочлена /(I) на укатанное подпро¬
странств А - это многочлен }(() = 24 + I* - 213 - (V •
ЗАДАЧИ
49.1.	Доказать, что ортогональная сумма подпространств
является прямой суммой.
49.2.	Доказать, что если сумма размерностей подпрост¬
ранств в ортогональной сумме I,] © ... © Ьр равна размерности
всего пространства Е, то Е =	© ... ® Ьр.
49.3.	Доказать, что сумма Ь подпространств 1ц,..., 1р явля¬
ется их ортогональной суммой тогда и только тогда, когда сово¬
купность ортогональных базисов этих подпространств дает ор¬
тогональный базис /у.
49.4.	Пусть Е = /,!©.. .©1р. Доказать, что эта сумма будет
ортогональной тогда и только тогда, когда для скалярного про¬
изведения любых векторов х и у из Е, имеющих по подпростран¬
ствам ,..., Ер разложения х = х( + ... + хр и у = у, + ... + ур
соответственно, справедливо равенство
(*.у) = (*1,У|) + ...+ (*,>%>)•
49.5.	Линейное пространство V разложено в прямую сумму
подпространств: V = ^ ©...©^. Доказать, что скалярное
произведение в V' можно определить таким образом, чтобы под¬
пространства Л, в этом разложении были все попарно ортого¬
нальны.
49.6.	Доказать, что если Ли В - матрицы одного размера и
Вг Л = О, то ге(Л + В) - г|»Л + щВ.

76
I лава А///, Епклилопы и унитарные »ростра»гта
49.7.	Доказать, что ортогональное дополнение и евклидов^
(унитарном) нрогтрннстпс Е облапает следующими свойствами.
а)	(/>)х = *.;	б) сели /., С / », то 14 С
п) (^, + / э)А = 14 п 14. О (/-. П Д,)^ = 14 + 14;
л) *ГХ - {<?}, {0}х = Е.
49.8.	Пусть .4 н В матрицы размера т х п и Аг х л соот.
ветственно, причем если .4т = О лля некоторого столбца х, то и
Вх = О. Доказать, что В = С-4, где С матрица размера к х щ
49.9.	Подпространства Л, и Дэ лают в прямой сумме псо
евклидово (унитарное) пространство Е. Доказать, что этим жс
свойством обладают и их ортогональные дополнения, т.е.
Е = Дх ф 1и$.
49.10.	Пусть /. и Ь\ линейные подпространства евклидова
(унитарного) пространства Е, причем Ьх С Д- Обозначим через
Д.х ортогональное дополнение подпространства Ь\ в Е, через Д,А
— ортогональное дополнение Ьх в Д. Показать, что Ьх = Дх ПД.
49.11.	Пусть Ьх н Ь3 линейные подпространства евклидова
^унитарного) пространства, причем еЛт Д| < сПгп Дг. Доказать,
что в Д3 найдется ненулевой вектор, ортогональный всем векто¬
рам из
49.12.	В пространстве Ж4 со стандартным скалярным произ¬
ведением найти базис ортогонального дополнения линейной обо¬
лочки системы векторов:
а а. = '1,0,2.1), а3 = (2,1,2,3), а3 = (0, 1,-2, 1);
6)	а, = (1, 1,1,1), а3 = (-1,1,-1,1), а3 = (2, 0,2,0);
в; о, = (1,3,0,2). а3 = (3, 7, - 1,2), а3 = (2,4,-1,0).
49.13.	В пространстве комплексных арифметических векто¬
ров найти базис ортогонального дополнения линейной оболочки
системы векторов <11 = (0,1 + 2»',—*), а3 = (1, —1,2 — «) в двух
случаях:
а» когда пространство комплексное со стандартным скаляр¬
ным произведением;
б)	когда пространство вещественное, а скалярное произведе¬
ние задано равенством (47.5).
49.14.	В арифметических пространствах '•?* (для пунктов а)
и 6]| и Сэ (для пункта в)) со стандартными скалярными произ¬
ведениями най: и системы уравнений, задающие ортогональные

77
З'О. Ортогональные подпространства
пополнения к подпространствам, описанным каждой из следую¬
щих системой уравнений;
49.15.	Доказать, что системы линейных уравнений, зада¬
ющие линейное подпространство Ь в пространстве К" со стан¬
дартным скалярным произведением и его ортогональное допол¬
нение Ь1, связаны следующим образом; коэффициенты системы,
задающей одно из этих подпространств, являются координата¬
ми векторов, порождающих другое подпространство.
49.16.	Найти системы линейных уравнений, описывающие
подпространство /,, заданное в задаче 49.12(в), и его ортогональ¬
ное дополнение /,х.
49.17.	В пространстве многочленов А/„ скалярное произве¬
дение введено стандартным образом. Найти ортогональное до¬
полнение подпространства;
а)	многочленов, удовлетворяющих условию /(1) = 0;
б)	многочленов, удовлетворяющих условию Д-1) = /(1);
в)	многочленов, удовлетворяющих условию /(1) + /'(1) = 0;
г)	всех четных многочленов пространства Л/„.
49.18.	В пространстве Ж"*п со стандартным скалярным про¬
изведением найти ортогональное дополнение к подпространству:
в)	кососимметрических матриц;
г)	верхних треугольных матриц.
49.19.	Квадратная матрица А порядка п такова, что для
любой матрицы X порядка п с нулевым следом 1г .4 .V = 0. До¬
казать, что А - скалярная матрица.
49.20.	Квадратная матрица Л порядка п такова, что для лю¬
бой симметрической матрицы Л” €КП><,> выполнено соотношение
в) (	11 + 0 ~ *)** “	= 0,
\ —1Х\ -(-	4ж2	=0.
а)	матриц с нулевым следом;
б)	симметрических матриц;
1г /1 А’ = 0.
1.	Доказать, что .4 кососимметрична.

78
Глада .VШ. Евклидовы и унитарные пространства
2.	Что можно сказать о квадратной матрице А, если соот.
ношение 1г.4ДГ = 0 выполнено для любой кососимметрической
матрицы X порядка п?
40.21.	Ненулевая квадратная матрица А порядка п такова,
что для любой стохастической матрицы X порядка п выполнено
соотношение 1г ЛА' = 1г А. Доказать, что ранг матрицы А равен
единице.
49.22.	Квадратная матрица А порядка п такова, что для
любой дважды стохастической матрицы X порядка п выполнено
соотношение 1гЛА' = 1гА. Доказать, что ранг матрицы А не
превосходит двух.
49.23.	Найти базис ортогонального дополнения линейной
оболочки системы векторов евклидова пространства Е, задан¬
ных в некотором ортонормированном базисе Е координатными
столбцами:
а)	(10,1, —7)т;	б) (1,1,1)т, (1,-4, -1)т;
в)	(1, -5,2,-9)т; г) (1,1, -5,1)т, (2, -7,2,1)т;
а)	(-1,3,0,1)7-, (4,2,1,1)т, (3,5,1,2)т.
49.24.	В арифметическом пространстве со стандартным ска¬
лярным произведением найти ортонормированный базис ортого¬
нального дополнения линейной оболочки следующих систем век¬
торов:
а)	а, = (1,2,1);	б) а, = (1,-1,1,-1);
в)	а» = (1,3,-1,1), в, = (2,5,-2,3);
г)	а, = (1,2,-1,-3), а2 = (2,1,1,-9), а3 = (1,4,-3,-1);
д)	а1 = ( —1,0,1,2,1), а* = (2, -3,1,-1,4), а3 = (-1,-1,2,3,3).
49.25.	Найти базис ортогонального дополнения подпростран¬
ства векторов, координаты Х\,..., х„ которых в некотором орто¬
нормированием базисе евклидова пространства удовлетворяют
системе линейных уравнений:
Г *1
+
Х2 Х3 +
хч = 0,
а) <
7х,
-
2х2 + Зх3 -
5х4 = 0,
[ю*,
+
Хз —
2х4 = 0;
Г 2т,
+
9х3+5х3-
II
ы
со
1
0,
б) <
+
2х2 +
х4 =
0
1 Юх1
+
19х2 - х3 + 11х4 =
0

79
§•>9. Ортогональные поппростраипва
(X) •+■ 2х, + х3 + 2х4 + 6x5 = О,
2х| + Зх, +	х4 + 6х5 = О,
Зх,+ х, - 7х3 - 9х4 - 5хц = О,
5х| + 4х, — 7хз - 8х4 + х5 = 0.
49.26. Найти систему линейных уравнений, описывающую
ортогональное дополнение линейного подпространства, тяпанно¬
го в некотором ортонормированием батисе евклидова простран¬
ства системой уравнений:
б)	х( + 2х, + 5х4 = 0;
( х,+ х,-4х3	=0,
г)	< х1 - Зх, -	8х4 = 0,
I 2х! + Зх, - 9х3 + 2х4 = 0;
^ Г г1 + ~ хз — 0,
' \х, - х, + 2х3 = 0;
Ч Г II - I? -	2х4 = 0,
' \ 2х, - 2х, + х3 - Зх4 = 0;
(X, - х3 + х4 = 0,
X) - 2х, - х3 - х4 = 0,
3x1 + 5х, - х3 + 2х4 = 0.
49.27.	Пусть Ах = 6 - вещественная система т линейных
уравнений с п неизвестными, а\,...,а'т строки, а|,...,ап -
столбцы матрицы Л. Будем рассматривать решение х системы
и строки матрицы А как векторы арифметического простран¬
ства К", а столбец правых частей Ь и столбцы матрицы А как
векторы арифметического пространства Ет. Пусть в простран¬
ствах Е" и Ет скалярные произведения введены стандартным
образом. Обозначим через А и М линейные оболочки соответ¬
ственно векторов а\,...,а'т и а\,...,ап. Показать, что:
1)	множество всех решений однородной системы уравнений
Ах = 0 совпадает с А1;
2)	множество всех решений сопряженной однородной системы
уравнений АТу = 0 есть М-1;
3)	система уравнений Ах = Ь разрешима тогда и только то¬
гда, когда 6 е М;
4)	опираясь на предыдущие пункты, доказать теорему Фред¬
гольма: система уравнений Ах = Ь разрешима тогда и только
тогда, когда столбец Ь ортогонален любому решению у сопря¬
женной однородной системы;
5)	доказать альтернативу Фредгольма: либо система урав¬
нений Ах = Ь разрешима при любой правой части 6, либо сопря¬
женная однородная система имеет нетривиальное решение.
49.28.	Пусть е,,... ,е„ и /|,..., /„ - биортогональные базисы

80
Глава А’Ш. Евклидовы и унитарные пространства
евклидова (унитарного) пространства и /,* = С{гЛ,...,«*), к <
п. Доказать, что ^ = Г(А.ц,..../„).
40.29.	Доказать, что в любых двух подпространствах ев¬
клидова (унитарного) пространства можно выбрать ортонорми-
рованные базисы е.\,..., с* и	так, чтобы (е,-, /;) = 0 при
1 ф з и (с,,/,) > 0 для всех I.
В пространстве К4 со стандартным скалярным произведени¬
ем найти ортогональную проекцию д и перпендикуляр к, опу-
шенкый из вектора / на подпространство /,, натянутое на век¬
торы 0|, а2, о3.
49.30.	а, = (-3.0,7,6), а2 = (1,4,3,2), а3 = (2,2,-2,-2),
/ = (14,-3,-6,-7).
49.31.	а, = (1,3.3,5), а2 = (1,3,-5,-3), а3 = (1, —5,3, —3),
/ = (2,-5,3,4).
49.32.	а, =(1,1,1,1), а2 = (1,2,2,-1), а3 = (1,0,0,3),
/ = (4,-1,-3,4).
49.33.	а, = (2,1,1,-1), а2 = (1,1,3,0), а3 = (1,2,8,1),
/ = (5,2,-2,2).
49.34.	В пространстве С3 со стандартным скалярным произ¬
ведением найти ортогональную проекцию д и перпендикуляр к,
опущенный из вектора / = (0,-1 + 1, —1 + 6*) на подпространство
Ь, натянутое на векторы а! = (-1,2 + 1,0), а2 = (2,-3 - 1,1).
В пространстве К4 со стандартным скалярным произведени¬
ем найти ортогональную проекцию д и перпендикуляр к, опу¬
шенный из вектора / на подпространство Л, заданное однород¬
ной системой уравнений.
{Зх! + 2х2 + х3 — 2х4 = 0,
5X1+4х2 + Зх3+ 2х4 = 0,
Х| + 2х2 + Зх3 -I- Юх4 = 0.
!2х1 + х2+ х3 + Зх4 = 0,
Зх!+2х2 + 2х3+ х4 = О,
X] + 2х2 + 2х3 - 9х4 = 0.
49.37.
/ = (8,-2,8
(х!-2х2+ х3 =0,
\ X) х2 + 4х3 + х4 = 0.
{XI + х2 + х3- Х4 = 0,
2X1 + 12 + Зх3	=0,
4Х) 4- Зх2 -I- 5х3 - 2х4 = 0.

81
§49. Ортогональные полпространства
В пространстве Сп со станпартным скалярным произволени¬
ем найти ортогональную нроекиию д и перпендикуляр /», опу¬
шенный из вектора / на подпространство А, заданное однород¬
ной системой уравнений.
49.39.	/ = (0, -71,7 + 7»), А :	- (2 - >)х3 = 0.
49.40.	/ = (4, -4,4»), А : х, 4- (1 + |)х* - |'х3 = 0.
(2 + 1)х» + Хз + 2х3-Нх,| = 0,
5х,-21'х2 + Зх3+2х^ = 0.
49.41. / = (3-1,14-21,2,-1), А
В пространстве МЛ со стандартным скалярным произведе¬
нием найти ортогональную проекцию и перпендикуляр, опущен¬
ный из многочлена /(<) на подпространство А.
49.42.	/(«) = Ы + 612 + 81я + 1\ А : {д'(\) = 0};
49.43.	/(0 = 3 4- 31 + Ыг + З13 - 1\ А : {</(-1) = д(1) = $(2)};
49.44.	/(0 = 2 + 4*2 - 7(\ А : {2д(-1) - /(-1) = 0,
9(0) = 0,2$(1) + в'(1) = 0}.
49.45.	Найти ортогональную проекцию д(1) многочлена 1 +
1 + 12 + I3 на линейное подпространство Мх многочленов степени
не выше первой, если скалярное произведение в М3 задано:
а)	стандартным образом равенством (47.8);
б)	равенством (47.9), в котором 1Х = 0,13 = 1;
в)	равенством (47.14), в котором а = 1;
г)	равенством (47.15), в котором т = 4.
49.46.	Доказать, что если в процессе ор гогонализации систе¬
ма векторов ах,..., ап переходит в систему ..., 6„, то вектор
Ьк есть перпендикуляр, опущенный из вектора а* на линейную
оболочку системы а1,...,а*_1 (к > 1).
49.47.	Пусть ех,...,ет - ортогональный базис линейного
подпространства А евклидова (унитарного) пространства Е, / —
произвольный вектор из Е, а д - его ортогональная проекция на
А. Доказать, что:
, \ (/<е*) .
1)	9 =	-/	ге*.
^(ек,ек)
т I/ г ч 12
2)	/ ’ *	< |/|2 (неравенство Бесселя);
*=: (е*>е*)
3)	равенство Иарсеваля У' , ’	= |/|2 справедливо для
(е*>е*)
всех векторов / из А тогда и только тогда, когда А = Е.

82
Глав» XIII. Евклидовы и унитарные просгрансти»
49.48.	Доказать, что если для системы ненулевых век горец,
а,,...,ат равенство Парссналя ) -	г- = |/| выполнено
, = 1 (а*>а0
для всех векторов / € Г(а|,...,ат), то система а|,...,ат орто,
гональна.
49.49.	Пусть а|,...,а1Л - линейно независимая система век-
торов евклидова пространства Е и С = С(а{1..., ат) - ее матри-
ца Грама. Обозначим через С~х = (-у,-*) обратную к С матрицу.
Тогда для всех векторов / е Е выполнено неравенство
Е 7и(/,«.■)(«*,/) <(/,/)•
|,к=1
Знак равенства в этом неравенстве достигается тогда и только
тогда, когда / € Г(а,,..., ат).
49.50.	Пусть а,,...,ат - линейно независимая система век¬
торов евклидова пространства Е и С = С(а,,..., ат) - ее матри¬
ца Грама. Обозначим через С~х = (7,*) обратную к О матри¬
цу. Тогда система векторов а,,..., ат образует базис Е тогда и
только тогда, когда / 6 Е выполнено равенство
]С 7.*(/,вО(в*,/) = (/,/)•
1,4=1
49.51. Доказать следующие свойства определителя матри¬
цы Грама системы векторов	евклидова (унитарного)
пространства:
1)	с!ег С?(/,	/„) < |/,|а -... -
2)	равенство <1е1С(/,,...,/т) = |/,|2 •... • |/т|2 справедливо
тогда и только тогда, когда либо векторы	/т образуют
ортогональную систему, либо хотя бы один из этих векторов
нулевой.
49.52.	Используя предыдущую задачу, доказать для опреде¬
лителя матрицы А = (а,;) € Спхп следующие утверждения:
1)	| с!е1 А\2 < П ^ М2^
2)	равенство |<1е1Л|2 = Ц
(неравенство Адамара);
справедливо тогда и
только тогда, когда либо А11 А является диагональной матрицей,
либо один из столбцов матрицы А нулевой.

83
§50. Метрические задачи
49.53.	Пусть Ь - линейное подпространство евклидова про¬
странства Е,	/т базис вй С = 0(/и...,1т) его
матрица Грама. Пусть для произвольного вектора / е /. вектор
д является его ортогональной проекцией на />, Н ортогональной
составляющей. Доказать, что:
|/4|2 _	^(/1 1 • • • ) /пи /)
с1е1 С	’
, где с - строка из скалярных
С ст
с 0
4е1
г1е10
(/./.)	(/,/-.)■
2) Ы’ = -
произведений
49.54.	Пусть/.] и Ц - линейные подпространства евклидова
(унитарного) пространства Е такие, что С /.3, и пусть д1 и
д7 - ортогональные проекции вектора / € Е на I] и Ц, а Л,
и Н7 - перпендикуляры, опущенные из вектора / на и /,3
соответственно. Доказать, что |</]| < |з2|, |Л]| > |Л7|.
49.55.	Доказать следующие свойства определителя матрицы
Грама системы векторов /1, ...,/*, д\,... ,д\ евклидова (унитар¬
ного) пространства:
1)	для любых к,1 > 0 выполнено неравенство
ае1С(/],...,Л,17ь.-.,д/) < Ае1С{/и...,/к)Ае1С(ди...,д,)-,
2)	равенство
6е1С(/и...,/к,дх,...,д,) = с!е1 С(/ь../к)йаС(ди.. .,д,)
справедливо тогда и только тогда, когда либо линейные обо¬
лочки систем векторов /],...,/* и ди... ,д, ортогональны, либо
одна из этих систем линейно зависима.
§50. Метрические задачи
Множество Л/ называется метрическим пространством, если задано
отображение
р : М х М - Е,
которое каждой упорядоченной паре элементов х,у 6 Л/ ставит в соответ¬
ствие число р(х, у) е Ж такое, что:
1)	Р(х,у) >0, VI, у 6 Л/,
р(х,у)~0 *=> х = У ;
2)	р{х,у) = />(». г). Ух.уеЛ/;
3)	Р(г1 *) < р(*, у) + р(у, *) 1 Уг, у, г е Л/ .
Число р{х,у) называется расстоянием меж<?!/ х и у; отображение р -
метрикой, аксиомы 1-3 - аксиомами метрики /расстояния/

84
/ лапа XIII. Е'нклн/юпы и унитарные пространства
Расстоянием между множествами X н V я метрическом пространстве
называется число
Теорема 50.1. В еаклидовом (унитарном) пространстве V про.
лило
/>(*.») = I* — у|	(50-1)
зодагт метрику.
В дальнейшем, говоря об евклидовом (унитарном) пространстве как о
метрическом, будем иметь в виду именно эту метрику.
Теорема 50.2 (о кратчайшем расстоянии). Расстояние меж¬
ду вектором / и линейным подпространством А о евклидовом (унитар.
ном) пространстве равно длине перпендикуляра, опущенного из вектора /
на А или, в других терминах:
1)	расстояние между век тором / и подпространством А равно рае.
стоянию между лектором / и его ортогональной проекцией на А;
2)	среди всех векторов подпространства А ближе всего к вектору /
расположена его ортогональная проекция на А.
П рн мер 50.1, В пространстве К* со стандартным скалярным произ¬
ведением найти расстояние от вектора / = (7,-3,1,-1) до линейного под.
пространства А, натянутого на векторы
а, =(1,1,1,1), аз = (2,-1,3,2), а3 = (1,0,-1,1).
Решение. Так как
Г 1	1	1 П а, Г 1 1 1 Па,
2-1	3 2 а3 — 0 1 2 -2 а, -а3
1.1	0—11) аз 1.007	0 .1 а, + аз — Заз
то (Вт А = 3 и векторы а,,аз,аз образуют базис А. Следовательно, Лт Ах =
1 и будем искать разложение / = у+Л вектора / на ортогональную проекцию
у и перпендикуляр А в виде
/ = у + ое,,	(50.2)
где е, - базис ортогонального дополнения Iх. Как следует из примера 49.1,
вектор е, является фундаментальной системой решений системы с расши¬
ренной матрицей
Г 1 1	1 1 101	Г 1 1 1	10 1
2-1	320—012-20	.
[1 0-1 1 |01	1.0 0 7	0 0.
Отсюда е, =(—3,2,0,1).
Из равенства (50.2) получим
(/,е.з) = а(е1>о) <=> а = —2.
Поэтому Л = —2е, = (6, -4,0, -2) и р(/, А) = |Л| = 4л/Т4. ■
Пример 50.2. В пространстве многочленов Мз со стандартным ска¬
лярным произведением найти расстояние от многочлена /(1) = 4 + 1 + З13
до линейного подпространства Л всех четных многочленов, обращающихся
в нудь при I = 1.
Решение. Многочлен /(<) = а0 + а,1 + аз!2 + азI3 принадлежит под¬
пространству А тогда и только тогда, когда а, = аз = 0, ао + а, + аз + аз =

85
$50. Метрические задачи
0. Тем самым, Ь - одномерное подпространсию, натянутое на многочлен
е,(«) = I - I2. Разложение /(1) = р(1)4- 40 многочлена на ортогональную
проекцию д{1) н перпендикуляр А(1) будем мгкать в пиле
/(0 = °,е,(0 + М0
Отсюда (/,с 1) = «|(с 1,с|) е=> П| =■ 2. Поэтому А(1) = /(0 - 2«|(0 =
2 + I 4- 217 4- З<3, и следовательно, р{/, I.) = |А| = 3>/2. я
Упорядоченная тройка вектороп х, у, х-у произвольногоевклидова (уни¬
тарного) нространстпа называется треугольником, натянутым на лекторы
гну.
Точно также упорядоченная пара векторов х, у произвольного евклидона
(унитарного) пространства называется параллелограммом, натянутым на
векторы х и у с диагоналями х 4- у и х — у.
Упорядоченная совокупность п линейно независимых векторов
хп п-мерного евклидова (унитарного) пространства называется п-мерным
параллелепипедом, натянутым на лекторы х\	х„. В частности, парал¬
лелограмм, натянутый на пару линейно независимых векторов, является
двумерным параллелепипедом.
Объем п-мерного параллелепипеда, натянутого на векторы х\,,.., х„
евклидова пространства, определяется по индукции:
О !'(*,) = М;
2) 1/(х1,...,х„) = У(х1,...,х„_1) |/1п|, где А„ - ортогональная соста¬
вляющая вектора х„ относительно подпространства, натянутого на векторы
Г1	1п-1.
В евклидовом пространстве углом между ненулевыми векторами х и у
называется угол <р, 0 < <р < г, для которого
(*. У)
М-Ы
сов =
В евклидовом пространстве углом между ненулевым вектором х и не¬
нулевым подпространством Ь называется точная нижняя грань значений
угла, который образует вектор х с ненулевыми векторами из Ь.
Углом между ненулевыми линейными подпространствами Ь\ и Ьз ев¬
клидова пространства, не имеющими общих ненулевых векторов, называет¬
ся точная нижняя грань значений угла между ненулевыми векторами X] € Ь\
и 12 6 Ьг- Если Ь\ П Ь3 = П ф {в) и О ф Ь\, Д ^ Ьз, то углом между
Ь\ и Ьз называется угол между ортогональными дополнениями и О?
подпространства П в подпространствах Ь\ и Ьз соответственно. Если од¬
но из подпространств Ь\ и Ьз содержится в другом, то угол между ними
считается равным нулю.
Пример 50.3. В пространстве Ж4 со стандартным скалярным про¬
изведением найти угол между подпространствами Ь\ = С[а\,аз), где а| =
(1,1, —1, 1), аз = (2, 2, —2, 2), и Ьз, описанным системой | ** = о* ~~
Решен и е. Заметим, что сПт Ь1 = I, сЛт Ьз = 2 и Ь\ П Ьз = {$}. Так
как косинусы углов, которые образуют векторы из Ь\ с подпространством
Ьз отличаются только знаком (см. задачу 50.14, пункт 3), то точная нижняя
грань этих углов совпадает с углом между вектором а\ и подпространством
Ьз, который, н свою очередь, равен углу между вектором а! н проекцией а(
на подпространство Ьз (см. задачу 50.14, пункт 1). Найдем эту проекцию.
Имеем: а] = д 4- А, д 6 Ьз, Л € Ьз или а] = а)в) 4- азвз 4- Л, где
С| = (I, 0, — 1,0), е» = (0, 0, 0, 1) - базис Ьз. Умножая почленно обе части по-

86
Глава XIII. Евклидовы и учи гарные пространств
слсдкега равенства на «| и на ел. получим систему уравнений относи тельцу
<*1, «>: 2в| = 2, аа = 1. Отсюда следует, что 9 = «| + е» = (1,0, -1, I).
Следовательно, если <р - угол между 1| к л (т.е. искомый угол),
со* 0 — л/З/2 и 0 = г/6. ■
Пример 50.4. В пространстве Ж* со стандартным скалярным про.
изведенном найти угол между подпространствами 1.\ = А(а1,аз), где а, в
(1,1,-1, 1), а? = (0,0, —1, I), и Аз, описанным системой |	= о3 ~
Решение. Заметим, что Фт /.1 = 2, Фт Аз = 2, 1.\ П Л.? = (б). Путь
решения, описанный в примере 50.3, не может быть применен и данной
задаче, так как (Вт 1*\ > 1, Фт Аз > 1. Будем исходить из опрсделсни!
угла между подпространствами с нулевых» пересечением. Обозначим черс1
*р(г,у), <0{х,Ц и р(А],Аз) угол между векторами г,у, угол между вектором
х и подпространством А и угол между подпространствами А] и Аз соответ¬
ственно.
Пусть г - произвольный вектор из А», д его ортогональная проскцнд
на Аз, д\ - ортогональная проекция у на А». Имеем
»р(А,,Аз)= тГ у>(г,у)=	( шГ йо(г,у)] = шГ <е(х,д) =
= Ч>{9< А1) = ^(9,9|)-
Таким образом,
0(Ь\. Аз) = 0(д,9\),	(50.3)
где д - ортогональная проекция произвольного ненулевого вектора х 6 А>
на Аз, а 9з - ортогональная проекция вектора д на Аь
Возьмем г = 01. Как следует из примера 50.3, д — (1,0,—1,1). Разло¬
жение 9 = 91 + А, где 91 € А1, А 1 Аь находим в виде
9 = 0101 + вэОэ + А,
где коэффициенты а|,аз являются решением системы
т.е. а, = 1/2, аз = 1/2 и д = 1(1,1, -2,2).
Г 40] + 2а3
\ 2«1 + 2аз
3,
2,
Следовательно, если 0 - искомый угол, то согласно (50.3) соз 0 = з/30/б
и 10 — агссоб(У30/6). ■
Пример 50.5. В пространстве Ж4 со стандартным скалярным произ¬
ведением найти угол между подпространствами А| = А(а),аз,аз) н Аз =
А(Ь!, Аз,6э), где 01 = (1,0,0,0,0), а3 = (0,1,0,0, 0,0), а3 = (0,0,1,0,0),
6, = (0,0,0,1,0), Ьз =(0,0,0,0,1), Ь> = аз.
Решение. Заметим, что Фт Ь\ = 3, Фт Аз = 3, А = А, П Аз =
А(оз), <Пт А = 1. Согласно определению ^(А^Аэ) = у>(А1,Аэ), где Т\ -
ортогональное дополнение А до А], Аз - ортогональное дополнение А до
Аз. Имеем: А1 = А(а1,аз) ,Аз = А(А),Аз), при этом Фт А) = Фт Аз =2,
А» Л Аз = (в). Этот случай рассмотрен в примере 50.4. Впрочем можно нс
прибегать к вычислениям, описанным в этом примере, так как Т[ 1 Ту, и
потому искомый угол 0 = аг/2. ■

87
(|50- Метрические шлачи
задачи
60.1.	Найти угол между лекторами я и Ь в пространстве:
1)	1Ла со стандартным скалярным произведением, если:
а)	а = (2, -3,1), Ь = (4, -6,2); б) а = (1,-1,2), 6 = (1,0,1);
в)	а = (1,0,— 1), Ь = ( — 1,2,2);
2)	1К4 со стандартным скалярным произведением, если:
а)	я = (1,-1,1,-1), 6 = (-1,1,-1,1);
б)	а = (-1,2,3,-4), Ь = (5,0, -2,1);
и) а = (1,2,2,1), Ь = (1,1,1,2);
3)	К2 со скалярным произведением (х, у) = х^, + х,у2 + х2у, +
ЗхаУа, если:
а)	а = (1,0), Ь = (0,1); б) а = (1,0), 6 = (-1,1);
'4	2	21
4) Л3 со скалярным произведением (х,у) = х 2	2-1
2-1	3
если:
а)	а = (1,0,0), Ь = (0,1,0); б) а = (-1,0,0), Ь = (-1,2,2).
50.2.	Как изменится угол между ненулевыми векторами х и
у, если:
а)	умножить вектор х на положительное число;
б)	умножить вектор х на отрицательное число;
в)	умножить оба вектора х и у на отрицательные числа?
50.3.	Доказать, что треугольники, натянутые соответствен¬
но на векторы х, у и ох, оу, где о - произвольное ненулевое
число, имеют одинаковые углы.
50.4.	В треугольнике, натянутом на векторы:
а)	х = (2,-1,3,-2) и у = (3,1,5,1);
б)	х = (4,0,2,0,4) и у = (3,3,3,3,0)
в арифметическом пространстве со стандартным скалярным про¬
изведением, найти длины сторон. Определить углы между сто¬
ронами треугольника - векторами х, у, х - у. Какие из этих
углов естественно считать внутренними углами треугольника,
а какие - внешними?
50.5.	Доказать, что в евклидовом пространстве:
1)	сумма внутренних углов любого треугольника равна т;
2)	сумма квадратов диагоналей параллелограмма равна сум¬
ме квадратов его сторон;
3)	квадрат стороны треугольника равен сумме квадратов
двух сторон без удвоенного произведения этих сторон на косинус

88
Глава Л’.Ш. Евклидовы и унитарные прострянсщ
угла между ними (теорема косинусов);
Л) стороны треугольника пропорциональны синусам проти.
воположных внутренних углов (теорема синусов).
50.6.	Пусть	система попарно ортогональных век.
торов евклидова или унитарного пространства. Доказать, что
|/, +	-+■ /*|э = |/| |а + • • ■ + |Л1* (обобщение теоремы Пифагора).
50.7.	Доказать, что в евклидовом пространстве верна теоре¬
ма, обратная теореме Пифагора: если \/х -4- /2|а = \/\\3 + |/г|а, То
векторы /х и /а ортогональны. Справедливо ли эго утверждение
в унитарном пространстве?
50.8.	Доказать, что векторы х и у унитарного пространства
ортогональны тогда и только тогда, когда равенство \ах + Ру\2
|ах|э + |/Зу|а выполнено для любых а.,0 € С.
50.9.	1. Доказать, что в евклидовом пространстве равенство
|х + у| = |х — з/| имеет место тогда и только тогда, когда век¬
торы х и у ортогональны. Каков геометрический смысл этого
утверждения?
2. Показать, что в унитарном пространстве утверждение
предыдущего пункта уже неверно. Для каких векторов х и у
имеет место равенство |х + у| = |х — у| ?
50.10.	В «-мерном евклидовом пространстве Е заданы век¬
торы еХг— , еп+1, попарно образующие тупые углы. Доказать,
что любые п из этих векторов образуют базис Е.
50.11.	Доказать, что в п-мерном евклидовом пространстве
т* + 2 вектора не могз'т попарно образовывать тупые углы.
50.12.	Доказать, что в п-мер ном евклидовом пространстве
п + 1 вектор не могут попарно образовывать углы, все равные
7Г /3.
50.13.	Может ли угол между вектором и линейным подпро¬
странством быть больше, чем 7г/2?
50.14.	Пусть / — ненулевой вектор евклидова пространства
Е, Ь — линейное подпространство Е, — угол между / и Ь, д -
ортогональная проекция вектора / на Ь. Доказать, что:
1)	если д = в, то = тг/2;
2)	если д ф в, то угол </? равен углу между векторами / ид;
3)	если д ф в, то для всякого вектора у 6 Ь, образующего
угол V7 с вектором /, имеет место равенство у — ад, где а > 0.
50.15.	Доказать, что в евклидовом пространстве углы, ко¬
торые вектор / образует с произвольным подпространством Ь и

$Л0. Метрические задачи
89
его ортогональным дополнением А1, и сумме равны г/2.
50.16.	Пусть С|,...,еп - ортонормированный базис евкли¬
дова пространства, х - произвольный нормированный вектор.
Доказать, что координаты вектора I в базисе е,,...,еп равны
косинусам углов о,,.. . ,а„, которые г образует с базисными век
торами. Вывести отсюда соотношение:
сов2 + соя2 аз 4- ... + соя2 а„ = 1.
50.17.	Евклидово пространство Е разложено в ортоюналь-
ную сумму подпространств	Доказать, что для углов
оп-.-^Р! которые произвольный вектор / образует с подпро¬
странствами	справедливо соотношение
сов2 а( 4- соз2 йз + ... + сов2 а? - 1.
50.18.	Подпространство I есть ортогональная сумма под¬
пространств и /,3. Вектор / ортогонален подпространству
1\. Доказать, что угол между / и Ь равен углу между / и
В пространстве ®4 со стандартным скалярным произведени¬
ем найти угол между вектором / и линейным подпространством
/,, натянутым на векторы а1,аг,а3.
50.19.	а1 = (2,3,-4,-6),аз = (-1,-8,2,16),д3 = (3,-2,-6,4),
/ = (-3,15,1,-5).
50.20.	а, = (2, -1,2,1), а2 = (-1,2, -2,1), а3 = (-1,1, -1,0),
/ = (3,1, >/5,-2).
50.21.	а, = (3,4,-4,-1), а2 = (0,1,-1,2), а3 = (3,5,-5,1),
/ = (2,2,1,1).
50.22.	а, =(5,3,4,-3),аз = (1,1,4,5),а3 = (2,-1,1,2),
/ = (1,0,3,0).
В евклидовом пространстве Е выбран некоторый ортонор¬
мированный базис е. Найти угол между вектором /, заданным
координатным столбцом в этом базисе, и подпространством I,
описанным в базисе е однородной системой уравнений.
50.23.	/е = (1, -2,1)т, Ь : Х[ -2х2 + 5х3 = 0.
50.24.	/е = (1,0,0,0)т, Ь : 11 - х2 + х3 - х4 =0.
50.25.	Л = (3,,,-1.-|)М:{2^*;-21>г);2:
( X!-)- Х2 + Х3+ Х4 = 0,
50.26.	/„ = (0,2,1,1)г, I : <3x1+ х2 - х3 4- х4 = 0,
(5x1 + Зх2 4-	2х4 = 0.

90
Глава XIII. Евклидовы и унитарные пространств
50.27.	В пространстве К" со стандартным скалярным произ¬
ведением линейное подпространство I. описано системой Лх = о
с некоторой матрицей А е Ктхп. Найги угол между вектором
(С|,...,с„) и подпространством Ь, если с; =
В арифметическом пространстве со стандартным скалярным
произведением найти расстояние от вектора / до подпростран¬
ства //, натянутого на векторы а(,...,а1.
50.28.	а, =(4,3,2,1),/ = (1,-1,1,-1).
50.29.	а, =(1,1,1),а, = (4,0,5),/ = (7,-3,-1).
50.30.	в, = (1,-1.1,0), а, = (2,-1,0,1), / = (1,0,2,-2).
50.31.	в, =(-2,0,1, !),«, = (1,-1,1,-1), аа = (1,1,-1,-1),
/ = (1,2,0,-1).
50.32.	в, =(1,1,1,1), а2 = (5,1,1,3), а3 = (3,-1,1,0),
/=(5,4,-3.-2).
В пространстве К4 со стандартным скалярным произведени¬
ем найти расстояние от вектора / до подпространства I^, задан¬
ного однородной системой уравнений.
50.33. / — (1,-2,3,-4), Ь : (х1 + х2 + хз + х4 — 0.
50.34.	/ = (8, -2,8,3), Ь : |
50.35.	/ = (2,3,-1,-2),Ь:
Х1-2хг+ х3 =0,
XI- Х2 + 4Х3 + Х4 = 0.
!Х1 + х2 + Х3- х4=0,
2x1+ х2 + Зх3 = 0,
4x1 + Зх2 + 5х3 - 2х4 = 0.
{2X1 +х2 + х3 + х4 = 0,
бХ] + х2 - х3 + х4 = О,
х2 + х3-х4 = 0.
50.37.	Доказать, что квадрат расстояния от вектора / ев¬
клидова пространства до подпространства Ь, натянутого на ли¬
нейно независимую систему векторов /1,...,/*, равен отноше¬
нию определителей Грама систем Л,---,/*,/ и /1 ,...,/*.
50.38.	Пусть Ь - линейное подпространство и / - некото¬
рый вектор евклидова (унитарного) пространства. Доказать,
что наименьшее значение величины |/ — р| среди всех векторов
д € Ь достигается на единственном векторе, являющемся ор¬
тогональной проекцией вектора / на подпространство и оно
равно длине перпендикуляра, опушенного из / на Ь.
50.39.	В пространстве многочленов Л/„ скалярное произведе¬
ние введено стандартным образом. Для заданных многочленов:

$50. Метрическис задачи
91
/|(0 - 31* + 21 + 1, /г(1) = -I3 +21+1,
МО = 31»+ 21 +5, Ш = 31» + 21 + 2
а)	найти многочлен /0(1) степени нс выше 2, равноудаленный
от /,(/), МО, МО. МО;
б)	определить расстояние между /0(1) и каждым из много¬
членов /| (1), МО. МО, МО;
в)	докатать, что всякий многочлен вида
МО + «3(3 + ...+ а„Г
равноудален от /1(1), МО, МО, МО. и определить расстояние
от него до этих многочленов.
50.40.	Докатать, что в евклидовом пространстве Е для лю¬
бого подпространства Е и любого вектора х С Е выполнено ра¬
венство
р(х + у, Е) = р(х,Е),
где у произвольный вектор подпространства Е.
50.41.	Подпространство I. является ортогональной суммой
подпространств Ех и Доказать, что если вектор х ортогона¬
лен подпространству ^\,'то
р{х,Ь) = р(х,12).
50.42.	Пусть а фиксированный вектор евклидова простран¬
ства, Е - подпространство всех векторов, ортогональных а. До¬
казать, что для произвольного вектора х расстояние до подпро¬
странства Е можно вычислить по формуле
п(г П КХ,Я)1
р{х,Е)-	)а|	.
50.43.	Н пространстве многочленов М„ скалярное произве¬
дение введено стандартным образом. Найти расстояние между
подпространством А/п_ 1 и
а)	многочленом 1";
б)	многочленом 1” + ап_)Г"1 + ... + ад! + о0;
в)	многочленом апГ + йп-П"-1 + .. ■ + аП + о0-
50.44.	И пространстве многочленов Мп со стандартным ска¬
лярным произведением рассматривается подпространство А всех
многочленов, удовлетворяющих условию/(1) = 0. Доказать, что
расстояние от произвольного многочлена д(1) до подпростран¬
ства Е равно
9( 0
\/п + 1
р{уЛ) =

92
Глава XIII. Евклидовы я унитарные пространства
50.45.	Показать, что угол между любыми линейными иод.
пространствами всегда определен и равен нулю тогда и только
тогда, когда одно из этих подпространств содержится в другом.
50.46.	Найти угол между подпространствами векторов *
евклидова пространства, удовлетворяющими условию (х,а,) = о
и (х,а3) = 0 соответственно, где а,,а3 - заданные ненулевые
векторы.
50.47.	Подпространства 1ц и Ь7 являются линейными обо-
лочками систем векторов, заданных в некотором ортоноромиро-
ванном базисе евклидова пространства координатными столбца-
ми а!,...,а* и Л,,..., 6,. Найти угол между подпространствами
и Ь-2, если:
1)	о, = (0,3,-1,0)г, а3 — (1,-2,1,1)т,
Ь, = (0,0,1,-3)т, Ь3 = (1,1,0,1)т;
2)	о, = (1,1,2,0)т, а3 = (2,0, —1,-1 )т,
Ь\ — (1,1.0, -2)г, Ь2 = (1,1,-3,1)т;
3)	0, = (1,2,0,1)т, а7 = (0,1,1,1)т,
6, = (1,0,1,0)т, Ьг = (1,1,2,0)т, 63 = (1,0,1,-1);
4)	а, = (1,1,1,1)7, аг = (1,0,1,2)т, аэ = (0,1,0,-1)т,
6, = (1,1,0,0)т, Ьг = (1,0,0,1)т, Ь3 = (0,1,1,0).
50.48.	В пространстве М„ рассматриваются одномерные
подпространства Ь0, /-!,•••> Ьп> натянутые на многочлены 1,
1п соответственно. Для каждого к = 1, п найти угол между
подпространствами и /.*, если:
а)	скалярное произведение в М„ введено стандартным обра¬
зом;
б)	скалярное произведение в М„ введено равенством (47.9), в
котором <1 = 0, <2 = 1.
50.49.	В пространстве Мп со стандартным скалярным про¬
изведением найти угол между подпространствами:
а)	Ьх = {/(0 | /(1) = 0} и = {/(0 | /'(1) = 0};
б)	Ьх = {/(0 | /(1) = 0} и Ьг = {/(0 | /(2) = 0};
в)	Ьх = {Л0 I Л») = /(1) = 0} и 1г = {Л О I /'(0) = 0}.
50.50.	Доказать, что объем п-мерного параллелепипеда, на¬
тянутого на линейно независимые векторы а1,...,а„, может
быть вычислен по формуле
1''(а,,...,о„) = х/с!е1 С(а1,.. .,а„) = Ие1 Л|,
где С(аь...,ап) - матрица Грама векторов а,,...,^, а Л -I

$51. Линейные аффинные многообразия
93
матрица, строками которой являются координаты рассматри¬
ваемых векторов п каком-нибудь ортонорм и ропан ном базисе п-
мерного подпространства, натянутого на векторы а|,...,а„.
60.51.	В пространстве многочленов Л/„ со скалярным про¬
изведением (47.9) с /, = -1 и «2 = 1, найти:
а)	объем параллелепипеда, натянутого на многочлены 1, 1,
I3,..., Г;
б)	наименьшее значение интеграла
/V -мул
на множестве всех многочленов /(I) степени не выше п — I.
50.52.	Доказать, что объем п-мерного параллелепипеда не
превосходит произведения длин его ребер, выходяших из одной
вершины:
У(аь...,ап) < П |а(|,
1=1
и равен этому произведению тогда и только тогда, когда эти
ребра попарно ортогональны, т.е. параллелепипед прямоуголь¬
ный.
50.53.	Доказать, что объем параллелепипеда удовлетворяет
неравенству:
У(а,,...,а*,Ьь...,Ь,) < К(аь...,ак)^(Ь1,...,Ь|),
причем знак равенства в нем имеет место тогда и только то¬
гда, когда линейные подпространства, натянутые на векторы
а!,...,ак и Ь!,...,Ь|, ортогональны.
50.54.	Доказать, что если аь...,а„ - нормированная систе¬
ма векторов и У[а.\,... ,а„) = 1, то эта система ортонормирова-
на.
50.55.	Доказать, что среди всех параллелепипедов, натяну¬
тых на нормированную систему, параллелепипед, натянутый на
ортонормированную систему, имеет максимальный объем.
§51. Линейные аффинные многообразия
в евклидовом (унитарном) пространстве
Пусть // = 1о + />- линейное многообразие в евклидовом (унитарном)
пространстве. Нектор п 6 //, ортогональный Ь, называется нормальным
вектором линейного многообразия И .

Глава Л’Щ. Едклилопы и унитарные пространств
9-1
Теорема 51.1. Для любого линейного многообразия о евклидово*
(унитарном) пространстве существует, и притом единственный, нор.
мальный вектор.
Теорема 51.2. Нормальный вектор линейного многообразия со.
впадает с перпендикуляром, опущенным из любого вектора линейного мно.
вообразив на направляющее подпространство.
Следствие. Среди всех векторов линейного многообразия нормаль.
ный вектор имеет наименьшую длину.
Пример 51.1, Найти нормальный вектор линейного многообразия
Н — ао + Ь, если ао = (—1,0,0,3), а I натянуто на векторы а| = (1, 1,1,1),
аз = (1,0,2,-1). Скалярное произведение в К4 задано стандартным обра¬
зом.
Решение. Нормальный вектор п линейного многообразия // удовле¬
творяет условиям:
п = ао +0)01 + о»аз,
Гп,аИ = 0,	<=>
(п,а3) = О
Г п = ао + ОЮ1 + азаг, 	.
\ *=*
{П = ао +0101 + о2аз,
а» (вз •а») +	= -(ао.аП,
оцв!, а») + аг(аз,аг) = -(ао.аз).
Из последней системы следует, что 01 = -1, аз = 1, и следовательно,
п =(-1.0,0,3) -(1,1,1,1) + (1,0,2,-1) = (-1,-1,1,1). .
Пример 51.2. Найти нормальный вектор линейного многообразия //,
заданного системой
/*1 + 1г + 2хз +п =3,
\х1-2хз- хз + х« = -3.
Скалярное произведение в ®4 задано стандартным образом.
Решение. Направляющим подпространством Л линейного многообра¬
зия Н ~ ао+1> служит множество решений приведенной однородной системы
Г XI + хз + 2хз + Х4 = О,
\*1 — 2хз - Хз + х< = О,
фундаментальная система решений
е, =(1,0,0,-1), сз = (1,1,-1,0)
которой, очевидно, образует базис в Ь.
Согласно определению нормального вектора п многообразия //, он ор¬
тогонален направляющему подпространству Ь или, что то же самое, его
базису С], ез- Тем самым, координаты (ц, хз, хз, х<) нормального вектора
п удовлетворяют системе
X! +
хз + 2хз + Х4 = 3,
XI -
2хз - Хз + Х4 = -
XI -
X 4 = 0,
XI +
н
1
н
и
II
о
XI + Хз+2ХЗ + Х4
XI -2хз - ХЗ + Х4
Отсюда п = (0,1,1,0). ■
Теорема 51.3. Пусть Н = хц + Ь - линейное аффинное много¬
образие в евклидовом (унитарном) пространстве. Тогда
р(/,И) = р(/-х0,Ц.

95
|[51 Линейные аффинные многообразия
Пример 51.3. Найти расстояние от многочлена /(*) = —4 + 31 -
17 + (’ по линейного многообразия // всех многочленов степени не выше 3,
удовлетворяющих условиям /(1) = 1, /'(1) = 2. Скалярное произведение в
Мз задано стандартным образом.
Решение. Многочлен /(I) = ао + а| 1 + азР + аз!3 принадлежит много¬
образию II тогда и только тогда, когда
Г во + в| + аз + аз = 1,
\	0| + 2оа + За» = 2.
Вектором сдвига *о многообразия Н является многочлен, коэффициенты
которого удовлетворяют этой системе например, ао = — 1, 0| = 2, а3 = аэ =
О, т.е. многочлен го(<) = — 1 + 21.
Расстояние от многочлена /(1) до рассматриваемого линейного много¬
образия II равно расстоянию от многочлена /(<) - го(0 = —3 + I - I1 + г1
до направляющего подпространства I многообразия )/, которое в данном
случае описывается однородной системой
{Оо + а1+ аз + аз = О,
01 + 2аз + Заз = 0.
Отсюда следует, что ортогональное дополнение А1 является линейной
оболочкой, натянутой на многочлены, коэффициенты которых совпадают с
коэффициентами однородной системы, описывающей А, т.е. на многочлены
е 1 (<) = 1 + I + I3 + <3, сз(0 = I + 21г + З13. Поэтому разложение многочлена
/(1) - хо(0 на ортогональную проекцию д{1) и перпендикуляр Л(<) будем
искать в виде
Л0 - *о(0 = 5(0 + МО <=> Л‘)-го(0 = 3(0+а1е1(0 + “2С2(0-
Из последнего соотношения следует
П/ - го, еИ = а^сьеП + аз(ез,е^), .. Г 4»! + баз = -2, .. а! = -2,
\ (/— Ю, ег) = в! («1, «г) + «^(еа.ез)	\6а1 + 14аз = 2	аз	= 1.
Следовательно, А(<) = -2е](<) + ез(<) = -2 - I + I3. Отсюда р(/, Н) =
р(/ - *о, I) = |Л| = 'Л- •
Теорема 51.4. Пусть Н\ = х\ + 1\ и Нз = гг + Ьз - линейные
аффинные многообразия в евклидовом (унитарном) пространстве. Тогда
р{И\, Нз) = р(II - хз, Ь\ + Аз).
Пример 51.4. Найти расстояние между линейным многообразием
Н\ всех четных многочленов степени не выше 3, удовлетворяющих условию
/(1) = 1, и линейным многообразием #з всех нечетных многочленов степени
не выше 3. Скалярное произведение в М] задано стандартным образом.
Решен и е. Линейное многообразие Н\ имеет вектор сдвига х\(1) = 1 н
направляющее подпространство состоящее из всех четных многочленов,
обращающихся в нуль при I = 1. Таким образом, А| одномерно н натянуто
на многочлен О] (<) = 1 — I7.
Линейное многообразие Из является линейным подпространством, по¬
этому его вектор сдвига хз(1) можно выбрать нулевым, а направляющее
подпространство А двумерно и натянуто на многочлены Ь\(1) = I, Ьз(1) = <3.
Расстояние между Н\ и Из согласно теореме 51.4 равно расстоянию от
вектора 11(1) — хг(<) = Х1(<) до подпространства А1 + Аз = ЛшА.бз)-
Найдем ортогональное дополнение подпространства А| +/3. Многочлен
/(I) = 00+01 / + а217 + <Ы3 принадлежит (А] + Ьз)х тогда н только тогда,

Глава Л'Ш. Евклидовы и унитарные пространств
96
во - аа = О, О] = Я] = 0.
когда
Спсломтсдкно, тшпростраисгоо (Л| + /•г)'1' одномерно н наткнуто на мня.
гочлен е.(г) = 1 + I3, и разложение
П(1) = ®(0 + А(1). 9(0 € I, + Ьи МО 1 (/-I + М)-
будем игкать я пндс Х|(1) = д[1) + ог(0-
Имеем (г|,е) = а(е,е), т.е. а = 1/2. Следовательно, МО = (I + I1)/2 к
Р(/Л.Я,) = |Л| = 1/ч/2- ■
Углол леж^у линейными мно?оо5/юэи*,ми н&зыпастся угол между и*
направляющими подпространстпамн.
ЗАДАЧИ
51.1.	Доказать, что множество всех векторов евклидова
(унитарного) пространства Е, удовлетворяющих условию
(я,*) = Ь, где п - фиксированный ненулевой вектор, Ь - заданное
число, есть гиперплоскость этого пространства. В каком случае
эта гиперплоскость является подпространством?
51.2.	Показать, что гиперплоскость, заданную условием
(п,х) = 6, можно описать и условием (п,х - х0) = 0, где хо ~
произвольный вектор этой гиперплоскости.
51.3.	Доказать, что всякую гиперплоскость евклидова про¬
странства можно задать условием (п,х) = Ь.
51.4.	Доказать, что если условия (п,,х) = Ь| и (п2,г) = Ь7
определяют одну и ту же гиперплоскость, то пг = ап2, М = аЬг
для некоторого ненулевого числа а.
51.5.	В пространстве многочленов Л/„ со стандартным ска¬
лярным произведением для гиперплоскости, заданной условием
/(с) = </, найти представление (п,/) = Ь. Указать соответству¬
ющий многочлен п(1).
51.6.	Всякую ли гиперплоскость пространства многочленов
А/„ можно задать условием вида /(с) = сП
51.7.	Пусть <1 е К произвольно. Доказать, что любую гипер¬
плоскость в пространстве многочленов Л/„ можно задать усло¬
вием
во/(М+ «*./'(».)+ -- + “»/(",(М = е
с соответствующим образом подобранными коэффициентами
ео|®1г-м®п»^ € Л.
51.8.	Пусть	произвольные различные между
собой действительные числа. Доказать, что любую гиперплос-

97
Ш.
Линейный
аффиннмр многообразия
кость в пространстве многочленов М„ можно задать условием
Ого/Оо) +	/С^г) + • • • + °п/(^п) = С
с соответствующим образом подобранными коэффициентами
О01°Ь • • • 1 ИП( с € К.
51.9.	Пусть ак, к = 0,п + 1 - произвольные действительные
числа, удовлетворяющие условию а0 < «ц < ... < а„ < ап+|. До¬
казать, что любую гиперплоскость в пространстве многочленов
Мп можно задать условием
«о/ 1{1)й1 + аI /(*)<Д + ... + ап /	1{1)И = с
с соответствующим образом подобранными коэффициентами
Оо, С*1> • • ■ ) ®п» ^ 6 К.
51.10.	Доказать, что в каждом ортонормированием базисе
пространства всякая гиперплоскость может быть описана урав¬
нением первой степени
^1°! + Л2о2 + ... + /1„ап = 6
относительно координат О), а2,..., а„ векторов этой гиперплос¬
кости.
51.11.	Доказать, что если пересечение гиперплоскостей п-
мерного евклидова (унитарного) пространства
(пь1)= 6,, (п2,х) = Ь2,..., {пк,х) = Ьк
непусто, то оно представляет собой линейное многообразие раз¬
мерности п - г, где г - ранг системы векторов л.1,...,п*.
51.12.	Найти нормальный вектор для гиперплоскости, за¬
данной условием (п,х) = Ь.
51.13.	Пусть п - нормальный вектор многообразия Я (не
совпадающего со всем пространством). Доказать, что много¬
образие Я содержится в гиперплоскости (п,х) = (п,л).
51.14.	В пространстве многочленов Мп со стандартным ска¬
лярным произведением определить нормальный вектор для мно¬
гообразия, заданного условиями:
а)	/(0) = 1, /(1) = 1;	б)/'(0)=1,/'(1)=1;
в)/(0= 1,/'(1)= 1;	г)/(0) + Л0) = 1,/(1) = 0.
51.15.	Подпространство Ь натянуто на линейно независи¬
мую систему векторов а|,...,ак, Доказать, что расстояние от
вектора х до линейного многообразия Я = х0 + I равно
р{х,Н)
ое1 С(а{,...,ак,х-х0)
(1е1 С(аи...,ак)
* пп

98
Глава Л'Ш. Евклидовы и унитарные пространств
51.16.	В пространстве К4 со стандартным скалярным произ.
велением найти расстояние от вектора х = (5,3, -1, -1) до мно.
гообразия // = х0 + /„, где х0 = (0,0, -3,6), а Ь натянуто на си.
схему векторов а, = (1,0,2,-2), а, = (0,1,2,0), о3 = (2,1,6,-4),
51.17.	В пространстве Л/„ со стандартным скалярным про.
изволением найти расстояние от многочлена х(/) = 1 +1 +... + р
до многообразия, заданного условием:
»)/(!) = »; 6) /(0) = /(1)= 1; в) /(0) = /'(1) = 1.
51.18.	В пространстве Кпхп со стандартным скалярным про.
изведенном найти расстояние от матрицы А', все элементы ко.
торой равны 1, до многообразия:
а)	матриц А с единичным следом: 1гЛ = 1;
б)	всех стохастических матриц;
в)	всех дважды стохастических матриц.
51.19.	Доказать, что квадрат расстояния между прямыми
/| : х = X) +{д, и /2 : х = х2 + (д2 может быть вычислен по
формуле:
1)	РЛЛ)
раздельны;
2)	МЛ)
ны.
^С[дид2,Х1-х7)
&\С{дид2)
кЩдих{-х2)
, если прямые /1 и /2 не па-
, если прямые 1\ и /2 параллель-
Найти расстояние между прямыми 11 : х = XI + ^ и /2 ;
х = х2 + 1д2 (скалярное произведение в Е4 считается введенным
стандартным образом).
51.20.	XI = (5,2,0,3), д, = (1,2,-4,1);
х2 = (3,-1,3,1), д2 = (1,0,-1,0).
51.21.	XI = (5,4,3,2),д, = (1,1,-1,-1);
Хг = (2,1,4,3), д2 = (-3,-3,3,3).
Найти расстояние между плоскостями Р1 : х = X! + 1\р^ + /2р2
и Р7: х = х2 + 1|д! +<2?2 (скалярное произведение в К5 считается
введенным стандартным образом).
51.22.	X) = (89,37, Ш, 13,54), х2 = (42,-16, -39,71,3),
Р1 = (1,1,0,-1,-1),Р2 = (1,-1,0,-1,1);
д, =(1,1,0,1,1), д2 = (1,-1,0,1,-1).
51.23.	х, =(5,0,-1,9,3), *2 = (3,2,-4,7,5),
Р, = (1,1,0,-1,-1), р2 = (1,-1,0,-1,1);
Я\ =(1.1.0,1,1), 9а = (0,3,0,1,-2).

Линейные аффинные многообразия	99
61.24.	х, =(4,3,3,3,0), х, = (-1,1,-1,0,2),
р, =(1,2,2,-1,1), р3 = (2,1,-2,1,-1);
7» = (8,7,-2,1,-1),	= (5,4,-2,1,-1).
61.25.	Доказать, что в любом базисе линейного простран¬
ства любая гиперплоскость может быть описана уравнением пер¬
вой степени относительно координат векторов этой гиперплос¬
кости (ср. с задачей 51.10).,
51.26.	Доказать, что в любом базисе линейного простран¬
ства всякое линейное многообразие размерности г может быть
описано системой п-т линейных уравнений относительно коор¬
динат векторов этого многообразия.
51.27.	Пусть Я - некоторое линейное многообразие линей¬
ного пространства, не являющееся подпространством; х - произ¬
вольный вектор этого многообразия. Показать, что в простран¬
стве можно ввести скалярное произведение таким образом, что¬
бы х был нормальным вектором многообразия Я.
51.28.	В пространстве I4 со стандартным скалярным произ¬
ведением найти угол между плоскостями Р\ : х = Х\ -Игр! + *аРг
и Рз: х = х2 + 1^1 + *202. где
х, =(3,1,0,1), р, =(1,0,0,0), р2 = (0,1,0,0),
ха = (2,1,1,3), «?, =(1,1,1,1), </2 = (1,-1,1,-1).
4*

Глава XIV. Линейные операторы в
линейных пространствах
§52. Линейный оператор и его матрица
Пусть V к И' - линейные пространства над общим полем Р. Отобр4
жение
А : V' - И7	(52.1)
называется линейны* отображение* пространства К о пространство И'
если для любых г, у 6 I', о 6 Р
1)	А(х + у) = Ах +Лу;
2)	,4(ах) = аАх .
Линейное отображение (52.1) называют также линейны* преобразова.
ние* пространство V в пространство И7 нлн линейным оператором, <?ей.
ствующим из пространства V в пространство И7.
Если V’ = И7, то линейное отображение А : V — V называют линей.
ны« отображением (преобразованием) пространство V в себя, а чаще -
линейны* оператором, действующим в I7 .
Если И' = Р, то линейное отображение (52.1) называют линейной фор.
*ой или линейным функционалом в пространстве V. Линейный функци.
онад обозначают строчными латинскими буквами (например, /), при этом
образ вектора х - символом /(х).
Множество всех линейных операторов, действующих из пространства V
в пространство И’, будем обозначать символом С\У, И7).
В соответствии с определением равенства отображений (§11) операторы
А, В е ЦУ, И') равны, если Ах = Вх, Ух 6 I7.
Пример 52.1. Пусть М„ - пространство вещественных многочленов
степени не выше п. Отображение V : М„ —> Л/„, определенное правилом
Vр(^) = р'(^),
является линейным и называется оператором дифференцирования.
Пример 52.2. Пусть V = Ц © Ь? . Отображение V : V —< V, опреде¬
ленное правилом
Тх = I)
для вектора х 6 V7 с разложением х = х\ + х», где XI 6	, хз € Ц,
является линейным и называется оператором проектирования (проекто¬
ром) пространства I' на параллельно Ьз .
Отображение "Я : V —• V , определенное правилом
%х — х\ - хг ,
также является линейным и называется оператором отражения простран¬
ства V относительно	параллельно 1,3.
Пример 52.3. Отображение О : V' —• И7, которое каждый вектор
х € I7 переводит в нулевой вектор в 6 И7, является линейным и называется
нулевым оператором.

101
Линейный оператор и его матрица
Пример 52.4. Отображение I : У -» И, которое каждый вектор
^ К переводит и г, являете» линейным и называете» тождественным
Циничным,/ оператором.
Пример 52.5. Изоморфизм линейных пространств V и IV (§44),
очевидно, является линейным оператором, действующим из V в И'.
Из определения оператора следует, что
)) линейный оператор переводит нулевой вектор в нулевой вектор;
2)	линейный оператор сохраняет линейные комбинации, т.е. переводит
линейную комбинацию векторов в линейную комбинацию образов с теми же
коэффициентами: Л(Е*=1 °‘г0 = Е*«1 а'Лх' I
3)	линейный оператор сохраняет линейную зависимость, т.е. перево¬
дит линейно зависимую систему векторов н линейно зависимую.
Теорема 52.1. Пусть с\,...,еп - базис пространства V, а
л|,...,Уп произвольные векторы пространства [V. Тогда существует,
и притом единственный, линейный оператор А 6 С(У, IV), который пере¬
водит век торы е ],..., еп в векторы д\,... ,д„ соответственно.
Следствие . Линейные операторы А, В 6 С(У,\У) равны тогда и
только тогда, когда они совпадают на векторах базиса V.
Пусть е = (в1,..., е„) и / = (/],.. .,1т) - базисы пространств V и V/.
Как следует из теоремы 52.1, линейный оператор А 6 С.(У, V/) однознач¬
но определяется заданием векторов Асг,..., Ае„. В свою очередь, векторы
Ас,, I = 1, п, однозначно определяются своими координатами в базисе /, т.е.
коэффициентами разложений
Ае 1 = ац/] + аз] /г 4-... + ат]/т ,
Ав2 = 012/1 + агг/г + ... + атз/т ,
«4еп = 01п/1 + 02п/2 + . . . + ат„/т .
ац
012
ам
021
022
Д2п
Пт1
От2
Ятп
Матрица
называется матрицей оператора А в паре базисов ей}. Для обозначения
этой матрицы используется также символ («4)/».
Из единственности разложения вектора по базису следует, что при фик¬
сированных базисах г и / матрица линейного оператора определена одно¬
значно.
Теорема 52.2. Пусть (Пт V = п, сЛт 1У = т. Тогда существу¬
ет взаимно однозначное соответствие между линейными операторами из
С(У, Щ и матрицами из ртхп.
Теорема 52.3. Пусть А 6 С[у, И'), е и / базисы пространств
V и соответственно. Тогда если у = Ах , то
у/ = А/схс .
Пусть / 6 С.{У, И) - линейная форма в пространстве V над полем Р.
Если е 1,..., е„ базис пространства V', то линейная форма / однозначно
определяется числами
О ] = /(«1) , .... а„ = }(сп).

102Глава .УН'. Линейные операторы в линейных пространств*^
При этом для произвольного вектора г =	*>*• выполнено равенство
/(х) = й|Х1 + .. . + впГ„ .
Это представление называете* общим видом линейной формы / в баэцСе
С|,...,еп. Числа оь...,о„ называются коэффициентами линейной форМы
/ а базисе
Если И’ = V, то при построении матрицы линейного оператора А ^
С(У, К) используется один базис е пространства V: столбцами этой матр*.
цы являются коэффициенты разложений векторов Ас1,...,Аг.п по базису
еь..., е„; матрица обозначается символом Аг или {А)г и называется матри.
цей оператора А а базисе е. Очевидно, 6 Рп*п.
Пример 52.6. Выяснить, являются ли линейными следующие пре.
образования.
1.	Преобразование .4(х|,1э,гз) = (хз,-хз,Х|) арифметического про.
странства К3 в себя.
2.	Преобразование А(х\,хз) = (х| + хз,хз + 1) арифметического про¬
странства Ж3 в себя.
3.	Преобразование АХ = 1гЛ' пространства квадратных матриц К"*"
в пространство К.
4.	Преобразование АХ = йе1 А' пространства квадратных матриц К"*’’
в пространство Я.
5.	Преобразование Ар({) = р(2/ + 1) пространства многочленов Мп в
себя.
6.	Преобразование Ар(1) =	~ ^ пространства Л/„ в про-
странство Мп-1 •
Решение. 1. Преобразование А является линейным, так как если
* = (*1, х3, х3), у = (у!, уз, уз) и а € Я, то
А(х + у) = (х3 + уз, -хг - уз,и +У1) = Ах + Ау,
А(ах) = (ахз, -013,0x1) = о Ах.
2.	Преобразование А нс является линейным, так как оно нулевой вектор
(0,0) переводит в ненулевой вектор (0,1).
3.	Преобразование А является линейным, так как в силу определения
следа матрицы:
А(Х + У) = 1г(Л’ + У) = и А + 1г V = АХ + АУ,
А(аХ) = 1г(оЛ’) = о 1г X = аАХ.
Таким образом, это преобразование - линейная форма в пространстве Жпхп.
4.	Преобразование А является линейным лишь в случае п = 1, так как
при п > 2 для любого а € Я выполнено равенство
А{аХ) = 4е1(аАГ) = а” <1е1 X = а" АХ,
что, например, при от = 2 противоречит пункту 2 определения линейного
оператора.
5.	Преобразование А является линейным, так как для любых р((), д(1) €
Мп и о 6 Я
А{р( I) + у(0) = />(2< + 1) + 9(21 + 1) = Ар(1) + Ая(1),
А{ар(1)) = ар(21 + 1) = аАр{1).
6.	Убедимся сначала, что преобразование А переводит любой многочлен
р(0 степени не выше п в многочлен степени не выше п - 1. Действительно,
при 1 = 0 многочлен р(1 + () — р(1 — I) обращается в нуль, и следовательно,
в силу теоремы Безу его можно записать в виде р(1 + I) — р(1 — I) = (р 1(0,

сиз. Линейный оператор и его матрица
103
гпе Р1 (<) " многочлен на единицу меньшей степени, чей многочлен р(1 + 1) -
(! _ (). Поэтому Лр(«) = р,(|) е А1 г,—I.
Линейность вытекает из того, что для любых р(0,ч(0 € М„ и а € Л
лмо+.О)-	+А(|),
Пример 52.7. Построить матрицу линейного оператора А, дей¬
ствующего из пространства М» в пространство М, по правилу Ар{1) =
	—, в парс естественных базисов пространств М, и Л/| (см.
пример 52.6(6)).
Решение. Итак, в пространстве Л/3 выбран базис в| = 1, е3 = (,
(з = I*, а в пространстве М| - базис /1 = 1, /а = I. Тогда имеем:
«Лег = - д — = 0 = 0/г + 0/д,
Ии -	„ г = 2/, + 0/,.
Отсюда следует, что
А1‘= [ 0 0 0 ]• '
Пример 52.8. Построить матрицу линейного оператора Л, действую¬
щего из пространства К3х3 в пространство К по правилу АХ = 1гХ, в паре
базисов
пространства Ж3*3 и /1 = 1 пространства К.
Решение. Так как
АЕ\ = 1 = 1/,,	=0 = 0/,, АЕ} =0 = 0/,, АЕ< = 1 = 1/1
то матрица оператора А имеет вид
Л/е = [ 1 0 0 1 ]. •
Пример 52.9. Построить матрицу линейного оператора А умножения
[ а Ь 1
квадратных матриц второго порядка слева на заданную матрицу с ^
в естественном базисе (52.2) пространства Я3*2.
Решение. Так как
АЕ' = [ с 4 ) [ 0 0 1
Л[2 о]
^-[“с !][? 81
= [ с 0 ]=■*+**•
= [о с]=°Ь+сЕ'>
= 5 о]=№+^'

101/лапа А/1'. Линейные операторы в линейных пространства*
-«*•«[; 5][о ?] = (о
то матрица оператора А я базисе с имеет пил
Г а	0	6	0	'
.	О	а	О	Ь
л‘ = е	0	4	0	•	*
О	с	0	</	.
Пример 52.10. Пусть линейный оператор .4, действующий в п.
мерном линейном пространстве V, переводит линейно независимые векторы
/«■•••«/я ■ векторы 	у„ соответственно. Пусть «з,...,еп - некото¬
рый базис пространства V, а Р и С - матрицы, столбцы которых являются
координатными столбцами векторов /)	/„ и д\,...,дп соответственно в
базисе е. Доказать, что матрицу оператора А в базисе е можно найти из
соотношения
А, = СР~1.
Решение. В силу теоремы 52.3 выполнены равенства
($.)« = 4, (/,)е, 1 = 17".
которые можно объединить в одно матричное соотношение
С = А'Г.
Так как векторы /1	линейно независимы, то и столбцы матрицы
Р линейно независимы, и следовательно, матрица Р невырождена и Ас =
СР~'. .
Пример 52.11. Построить матрицу оператора проектирования V
пространства К2*2 на подпространство Ь\ симметрических матриц парал¬
лельно подпространству Ь, кососимметрических матриц в базисе (52.2) про¬
странства К2*2.
Решение. Воспользуемся тождеством
А = %{Х + А"г) + ';[х - Хт),
которое, по существу, является разложением произвольной матрицы X 5
й2*2 по подпространствам Ц и Ь,, так что Аз = ^(А + Ат) и Х-г =
1(А — Хт). Отсюда следует, что рассматриваемый здесь оператор про¬
ектирования действует по правилу
ТХ = %(Х + Хт).
Так как
РЕ> = [ I 5 ] = 1 Ей РЕ, = [ х°/2 1/02 ] = (Е, + Е3)/2,
РЕ, = [ 1/2 Ч2 ] = (& + Яэ)/2. РЕ, = [ ° ° ] = 1 Еи
то
Г 1	0	0	0 '
Пример 52.12. Построить матрицу оператора отражения П про.
странства многочленов М, относительно подпространства /.) = {/(<) ^
А/з|/(0) = /'(О) = 0) параллельно подпространству Ь, = {/(0 6 Л/з | /(]) =

105
^2. Линейный оператор и его матрица
(I - 0’.
1'(\) - 0) 0 естественном базисе пространств» ЛЬ.
Решение. Выберем базисы: /| = I5, /1 = I5 в I., и /|
I( в 1(1 - 0* п />»• Нетрудно проверить, что 1| © Ц = ЛЬ.
Способ /. Разложим произвольный многочлен р(1) = а» + а<( + а»!1 +
-3(5 по базису /11/31/31/4- Решая соответствующую неоднородную систему
линейных уравнений, получим
р(0 = (0з +	+ Зао)13 + (аз — а1 — 2ао)1* + ао(1 — I)1 + (01 + 2ао)((1 - 0*
Отсюда следует, что
Яр(0 = (°3 + 3в1 + Зао)!1 + (аз — а; — 2ао)(5 — ао( I — I)1 — (°> + 2ао)1(1 - О*-
Таким образом, оператор Я действует на векторы естественного базиса
е) = 1, ез = I, г.з = (3, е« = I3 пространства Л/з следующим образом:
— —14- 613 — 41** = —е] +6еэ —4ез, Яе2 = — ( + 413 — 2(3 = — ез -Мез — 2е|,
Яез = I3 = ез,	Яе, — 0 = е<.
Следовательно, матрица оператора Я в базисе е имеет вид
-1	0 0 0
0-100
6	4 10
-4 -20 1
Способ 2. Воспользуемся результатом примера 52.10.
Согласно определению оператора отражения Я его действие на векторы
базиса /1./а, /з, /я описывается соотношениями
Я/1 =/■, Я/* = /а, Я/з = -/3, Я/, = -/„
В силу соотношения примера 52.10 Я< = СР~Х, где
Р =
Найдем матрицу Яе методом Гаусса-Жордана (§9):
Я. =
' 0
0
1
0 '
' 0
0
-1 0 '
0
1
0
0
-2
1
1
-2
, с =
0
1
0
0
2 -1
-1 2
0
1
0
1
0
1
0 -1
ГО
0
1
01
Г 1
0
0
01
Г 1
0
0
01
0
0
-2
1
-2
1
0
0
элементарные
0
1
0
0
1
0
1
-2
1
-2
1
0
преобразования
0
0
I
0
0
1
0
1
0
1
0
1
столбцов
0
0
0
1
0
0
-1
0
- 1
0
0
0
-1
0
0
0
0
0
2
-1
2
-1
0
0
0
-1
0
0
1
0
-1
2
-1
2
1
0
6
4
1
0
0
1
0
-1
0
-1
0
1
-4
-2
0
Ч
Следовательно,
0 0
0 0
1 0
0 1
0
-1
4
-2
Я, =
ЗАДАЧИ
52.1.	Доказать, что всякий линейный оператор, действую¬
щий в одномерном пространстве, сводится к умножению всех

106/лана XIV. Линейные операторы и линейных пространства>
нскторов и рос 1ранства па фиксированное (для данного операто.
ра) число (такие операторы называют скалярными).
52.2.	Описать все линейные операторы пространства ®;+
введенного в задаче 44.9.
52.3.	Выяснить, какие из следующих отображений линейно,
го пространства V нал полем Р являются линейными операто.
рами:
а)	Их = а (а - фиксированный вектор);
б)	Их = х + а (а - фиксированный вектор);
в)	Ах = ох (а - фиксированное число из поля Р).
52.4.	Выяснить, какие из следующих отображений геоме¬
трического пространства 13 являются линейными операторами
(здесь а и Ь - некоторые заданные векторы):
а)Их = (х, а)а;	б) Их = (а, х) Ь;
в)Их = (а, х)х;	г)Их = [х, а];
д)	Их = [а,(х, Ъ]].
52.5.	Пусть а, п - фиксированные ненулевые векторы гео¬
метрического пространства Ц или У3. Показать, что следующие
преобразования являются линейными, и выяснить их геометри¬
ческий смысл:
а)	Их = (х, а) — ;
а, если (а, п) ф 0;
(*, п)
(а, п)
б) Их =
в)	Их = х- (х, п)^;
1“Г
г)	И х = х - - Х‘ а, если (а, п) ф 0;
(а, п)
д)	Их = х — 2(х, п)—;
I П1
е)	Их = 2( х, а)— - х;
I аг
ж)	Их = [х, а], где а - заданный единичный вектор.
52.6.	Пусть х = (х^ха,...,*,,) - произвольный вектор про¬
странства К". Выяснить, какие из следующих преобразований
пространства Ж" являются линейными операторами:
а)	Их = (хз.хьхг) (п = 3);
б)	Их = (х3,х,,хг - 1) (п = 3);
в)	Их = (хг,х, - х2) (п = 2);

107
^5? Линейный оператор и его матрица
г)	Ах = (*).*».*э) (п = 3);
д)	.А* = (*1 + 3*2 — 2х3,Зх, + 1} - Х3,2/, + Зхг - х3) (л = 3);
с) Ах = (8'П Х|,С05Х2,13) (л = 3);
ж)	Ах = (хп, 1п-) 1 • • • > 11);
з)	Ах ~ (а:1! 2|з:г|) ~ Зх3) (п = 3).
52,7.	Выяснить, какие из следующих преобразований про¬
странства многочленов А/„ являются линейными операторами:
а)И/(0 = Я-0;	бМ/(1) =/(« + 1);
в)	А/{1) = Д°‘ + Ь), где а ф 0, Ь — фиксированные числа;
г)	А К 0 = ДНО. где ЛЕН фиксировано;
д)	Л/(0 = /(' + !)-ДО;
е)	А/{1) — Д‘ + 0 _9(0> где 5(0 " фиксированный ненулевой
многочлен;
ж) >1/(0 = ‘ДО; 0 л/(‘) = ‘ДО;
„) >1/(0 = Д«)+^(‘-“)+ф(‘-^+...+^((-а)‘,
где А: € N и а € К фиксированы;
. ..п. /(-0-/(о) + /(0.
к) АД О =	^	■
л) А/(0 = КП
М) ДДО = 7/0‘ ДО^-
52.8.	Показать, что дифференцирование определяет линей¬
ное отображение:
а)	пространства многочленов М„ в пространство многочле¬
нов Мп-\>
б)	пространства четных многочленов степени не выше 2л в
пространство нечетных многочленов степени не выше 2л - 1;
в)	пространства нечетных многочленов степени не выше 2я+
1 в пространство четных многочленов степени не выше 2л.
52.9.	Показать, что отображение /(<) н* /((г) определяет
линейное отображение пространства А1„ в пространство много¬
членов М2п-
52.10.	Показать, что отображение/(/) н-* ^ К0^ при лю¬
бом а € К определяет линейное отображение пространства мно¬
гочленов Мп в пространство Л/п+1.
52.11.	Ныяснить, какие из следующих отображений про¬
странства матриц Кпхт являются линейными операторами:
а) АХ = Хг;

108Глая а А7Г. Лингйиые операторы н линейных пространства»
б)	ИЛ' = ВХ, где Л - заданная кпапратная матрица п-го
порядка;
и)	ИЛ' = ВХС, где В, С - заданные квадратные матрицы
п-го и т-го порядков соответственно;
г)	АХ = ЛХ + ХВ, где В, С-заданные квадратные матрицы
п-го и т-го порядков соответственно;
д)	ИА' = Л’|, где А1 получена из матрицы Л' перестановкой
первого и последнего столбцов.
52.12.	Выяснить, какие из следующих отображений явля¬
ются линейными операторами, действующими из пространства
квадратных матриц К"*" в подходящее линейное пространство
V (в каждом случае указать это пространство V):
а)	ИА = ±(А + Ат); б) ИА = 1(А - Аг);
в)	ИА = 1г А;
г)	ИЛ” = 1г(ВХ), где В - заданная квадратная матрица п-го
порядка;
д)	ИА = йе1 А;
е)	ИА" = 6е1(ВХ), где В - заданная квадратная матрица п-го
порядка;
ж)	ИА = г§ Л";
з)	ИА = ХС, где С - заданная матрица размера л х т;
и)	АХ = [.V, В] - коммутатор матрицы А и заданной ква¬
дратной матрицы В порядка п;
к)	АХ = X ® В - кронекерово произведение матрицы А и
заданной матрицы В размера т х к.
52.13.	Доказать линейность отображения И и выяснить,
является ли оно сюръективным, инъективным или биективным,
если:	^
а)	И - нулевое отображение;
б)	И тождественное отображение;
в)	И сводится к умножению вектора на фиксированное число
из поля.
52.14.	Пусть	- линейно независимые векторы ли¬
нейного пространства V', а <7ь...,д* - некоторые векторы про¬
странства И'. Доказать, что существует линейный оператор
А € С.(У, IV) такой, что А/, = 5, для всех г = 1 ,к. В каком
случае оператор А единствен?
52.15. Пусть	- векторы линейного пространства
V, а д\,...,дк - векторы пространства IV. Найти необходимые

109
^3. Линейный оператор и его матрица
„ достаточные условия, при которых:
а)	существует линейный оператор А € С{У,\У) такой, что
//, = для всех « = IД;
б)	такой линейный оператор А единствен.
62.16.	Пусть I линейное подпространство пространства
V', А - произвольный линейный оператор, действующий из /, в
некоторое линейное пространство IV.
1.	Доказать, что найдется оператор из V, И^), действие
которого на подпространстве I совпадает с оператором А.
2.	Показать, что если поле Р бесконечно, то таких линейных
операторов существует бесконечно много.
52.17.	В пространстве многочленов А/„ построить два раз¬
личных оператора, совпадающих на подпространстве Л/„_, с
оператором д ифферен ни рован и я.
52.18.	Пусть пространство V есть прямая сумма подпро¬
странств	/>р. Показать, что действие линейного операто¬
ра А на любой вектор пространства определяется единственным
образом, если известно действие этого оператора на каждом из
подпространств
52.19.	Выяснить, какие из следующих отображений про¬
странства являются линейными формами:
а)	/( х) = о, где а 6 К задано;
б)	/( х) = ( х, а), где а - заданный вектор;
в)	/( х) = соя( зГра), где а - заданный вектор;
г)	/( х) = ( х, х);
д)	/(х) = (а, х, Ь), где а, Ь - заданные векторы;
е)	/(х) = ( х,[а, х]), где а заданный вектор.
52.20.	В пространстве У фиксирован базис е1,...,еп. Дока¬
зать, что отображение, ставящее в соответствие каждому векто¬
ру х пространства V его 1-ю координату в этом базисе, является
линейной формой.
52.21.	Пусть а 6 К - некоторое фиксированное число. Пока¬
зать, что отображение /(()	/(а) задает в пространстве мно¬
гочленов Мп линейную форму. Верно ли обратное: всякую ли¬
нейную форму в пространстве М„ можно задать таким образом
при подходящем выборе числа а ?
52.22.	Пусть а, Ь 6 К - некоторые фиксированные числа. По¬
казать, ч го отображение /(<) »-*	/(/) &Х задает в пространстве

1 ЮГлала XIV. Линейные операторы в линейных пространству
многочленов Мп линейную форму. Верно ли обратное: всякую
линейную форму в пространстве Л/„ можно задать таким обра.
зом при подходящем выборе чисел а и Ь ?
52.23.	Может ли линейная форма на комплексном линейном
пространстве принимать только действительные значения?
Оператор А задан твоим действием на произвольный вектор
х = (*1,хг,х3) арифметического пространства Ж3. Построить
матрицу этого оператора: а) в естественном базисе е), е7, е3; б) ц
базисе С] + е2, е2 + е3, е, + е3.
52.24.	Ат = (х2 + х3,2х, + х3, Зх, - х2 + х3).
52.25.	Ах = (х, - х, + х3, х3, х7).
52.26.	Ах = (х, - х2,х2 - х3,х3 - х,).
Оператор А, действующий в пространстве I3, переводит век¬
торы /1,/г,/з соответственно в векторы 91,д7,д3- Построить ма¬
трицу этого оператора: а) в естественном базисе пространства
К3, б) в базисе , /2, /з-
52.27.	/, =(2,3,5),/2 = (0,1,2),/3 = (1,0,0),
0. =0,1,1). Л = (1,1,-1), Л = (2,1,2).
52.28.	/, =(2,0,3), /2 = (4,1,5), /3 = (3,1,2),
9, = (1,2, -1), 91 = (4,5, —2), д3 = (1,-1,1).
52.29.	/, = (5,3,1),/2 = (1,-3,-2), /3 = (1,2,1),
д, = (-2,1,0), д7 = (-1,3,0), д3 = (-2,-3,0).
Оператор А, действующий из пространства Ж" в простран¬
ство Жт, переводит линейно независимые векторы ,...,	6 Ж"
соответственно в векторы 01,..., 0„ Е Жт. Построить матрицу
этого оператора в паре естественных базисов пространств Ж" и
52.30.	п = 2, тп = 3,
/, =(2,-1),/2 = (1,-1),
9х =(—4,2,—1),Л = ( — 1,1,-1).
52.31.	п = 3. тп = 2,
Л = (0,1,1), /а = (1,1,1), /з = (1,0,1),
Л =(3,-1), й = (2,0), * = (0,1).
52.32.	п = 2, тп = 5,
/.=(2,1), /2 = (1,1),
0, = (-2,-2,2,3,0), д7 = (5,-1,-2,0,3).
52.33.	п = 4, тп = 2,
/. = (4,3,-1,7), /2 = (5,2,3,7), /* = (9,7,2,6),

111
^Л' Линейный оператор и его матрица
д —	2 2 1)
9. = (0,8)|,д3,= (Я5,33),дз = (19,19),54 = (-2,0).
52.34.	п = 3, тп = 4,
/, =(1,1,2),/, = (1,2,3),/3 = (1,2,4),
01 = (-4,2,14, -6), д7 = (-2,1,7, -3), № = (-6,3,21,-9).
52.35.	п = 4, т = 3,
/. = (1,1,1,1), л = (1,/э = (1,-1,1,-1),
и = (-1,1,1,-1),
у, = (0,8,0),л = (-2,8,4),®з = (2,24,-4),®4 = 0,8,-8).
Оператор А, действующий в комплексном арифметическом
пространстве С2, переводит векторы /,/а соответственно в век¬
торы дх, <7з. Построить матрицу этого оператора в естественном
базисе пространства С2.
52.36.	/, = (*\1),/а = (1,0,01 М«-М+1).й = (»+!,»“!)■
52.37.	/, =(1,-0,/а = (-*,!), 01 = (0,0),	= (2,2.).
52.38.	/, = (1,0, /а = (0,1), 01 = (*, "0,0з = (1,20-
Оператор А действует в пространстве многочленов М„. По¬
строить матрицу этого оператора в естественном базисе этого
пространства.
52.39.	А = V - оператор дифференцирования.
52.40.	А = Т>2 - оператор двукратного дифференцирования.
52.41.	-4/(0 =	^- разностный оператор (к ■
п
фиксированное положительное число).
52.42.	-4/(0 = у^'/(О#.
/(а + 0 - /(а - О
, где а - произвольное фик-
21
52.43. -4/(0 =
сированное число.
52.44.	Рассматривая оператор дифференцирования V как
оператор, действующий из Мп в Мп-\, построить его матрицу
в паре базисов 1,1,12,... ,Г и	В этой же паре
базисов найти матрицу оператора интегрирования
-4/(0 = / жк
Л
как оператора из Л/„_, в А/„.
52.45.	Пространство V является прямой суммой подпро¬
странств /-! и Ь7. Базис еи...,еп выбран таким образом, что

112Глава Л71\ Линейные операторы в линейных пространства*
векторы	образуют базис подпространств Аь а некто,
ры е4+|,...,с„ - базис подпространства Л2. В базисе с
составить:
а)	матрицу оператора проектирования на 1\ параллельно Аг>
б)	матрицу оператора проектирования на А2 параллельно
в)	матрицу оператора отражения относительно парал.
лсльно А2.
52.46.	Пусть в пространстве У3 задана прямоугольная де.
картова система координат {О; еь е2, е3}, Для линейного опе¬
ратора А, действующего по правилу:
Ах = [х, а],
где а = {а!,а2,а3} - фиксированный ненулевой вектор, найти
матрицу в базисе еь е2, е3.
52.47.	Пусть а = {аьа2,а3}, п = {п1,п2,п3} - некоторые
единичные векторы геометрического пространства К3, коорди¬
наты которых заданы в прямоугольной декартовой системе ко¬
ординат {О;	е2, е3}. Найти матрицу линейного оператора А
в базисе в1, е2) е3, если А осуществляет:
а)	ортогональное проектирование на плоскость ( г, п) = 0;
б)	ортогональное проектирование на прямую [г, а] = 0;
в)	проектирование на плоскость ( г, п) = 0 параллельно век¬
тору а (( а, п) ф 0);
г)	проектирование на прямую [г, а] = 0 параллельно плос¬
кости (г, п) = 0 ((а, п) ф 0);
д)	ортогональное отражение относительно плоскости ( г, п) =
0;
е)	ортогональное отражение относительно прямой [ г, а] = 0;
ж)	отражение относительно плоскости ( г, п) = 0 параллель¬
но вектору а ((а, п) ф 0);
з)	отражение относительно прямой [г, а] = 0 параллельно
плоскости ( г, п) = 0 ((а, п) ф 0).
52.48.	Пусть в геометрическом пространстве У3 задана пря¬
моугольная декартова система координат {О; еь е2, е3}. В ба¬
зисе е,, е2, е3 найти матрицу оператора V ортогонального про¬
ектирования на подпространство А , если 1; является:
а)	прямой 1 = г = 0;
б)	прямой г = у = г\
в)	плоскостью I -I- у + г = 0;

Линейный оператор и его матрица
ИЗ
г)	плоскостью, натянутой на векторы а = {-1,1,-1} и Ъ =
{1| -3,2}.
52.49.	Пусть в геометрическом пространстве У3 ладана пря-
цоУГОЛЬная декартова система координат {О; е|,е2,е3}. В ба¬
зисе в1,е2,е3 найти матрицу оператора V проектирования на
подпространство параллельно подпространству А2, если:
а)	Ь\ определено уравнением х = 0,л Ц - уравнениями 2х =
2у=
б)	имеет уравнение х = у, а Л2 определяется системой
уравнений х + у + г = 0, 2х 4- у + 4г = 0;
в)	Ь\ определено уравнениями -20х = 15у = 12г, а Ь7 -
уравнением 2х + Зу - г = 0;
г)	/,1 определено системой уравнений х - у + г = 0, 2х - Зу +
4г = 0, а Ь7 - уравнением 2х + Зу - <\г = 0.
52.50.	Пусть в геометрическом пространстве У3 задана пря¬
моугольная декартова система координат {О; в|, е2,е3}. В ба¬
зисе еь е2| е3 найти матрицу оператора 72. ортогонального от¬
ражения относительно:
а)	плоскости 1 = 0;
б)	прямой х = 2у = г;
в)	плоскости, натянутой на векторы а = {1,0,-1} и Ь =
{1,1,-2}.
52.51.	Пусть в геометрическом пространстве У3 задана пря¬
моугольная декартова система координат {О; вз, е2, е3}. В ба¬
зисе в!, е2, е3 найти матрицу оператора 72 отражения:
а)	относительно плоскости 1 = 0 параллельно прямой 2х =
У=~2]
б)	относительно прямой х = х, х - у + г = 0 параллельно
плоскости х + у = 0.
52.52.	В геометрическом пространстве У3 задан ортонорми-
рованный базис в|, е2, е3. Построить в этом базисе матрицу
оператора поворота пространства:
а)	на угол а вокруг вектора е3;
б)	на угол 7г/2 вокруг вектора в|;
в)	на угол 2тг/3 вокруг прямой х = у = г.
52.53.	И естественном базисе (52.2) пространства X2*1 ква¬
дратных матриц второго порядка найти матрицу:
а) оператора умножения слева на заданную квадратную ма¬
трицу Л = (а|;) второго порядка;

1НГлава А7У. Линейные операторы в линейных пространствах
б)	оператора умножения справа на заданную квадратную ма¬
трицу А = (я,у) второю порядка.
52.54.	В естественном базисе (52.2) пространства К2*1 ква¬
дратных матриц второго порядка найти матрицу:
а)	оператора транспонирования,
б)	оператора (/, который каждой матрице X ставит в соот¬
ветствие матрицу АХ В, где А = (а,у) и В = (6,,) - заданные
квадратные матрицы второго порядка,
в)	оператора определенного соотношением
ТХ = АХ + X В,
где .4 = (оу) и В = (6у) - заданные квадратные матрицы вто¬
рого порядка.
52.55.	Пусть в пространстве Кт*п фиксирован естественный
базис из матричных единиц Ец,Ец,...,Е,П} I = 1,т. Пусть
далее А и В - заданные квадратные матрицы соответственно
порядков тип. Рассмотрим операторы д и Т, определенные
соотношениями
дх = АХ В,
ТХ = АХ + А' В.
Доказать, что в указанном базисе матрица:
а)	оператора есть кронекерово произведение А® Вт\
б)	оператора Т есть А ® /„ + /т ® Вт.
Найти матрицы тех же операторов в естественном базисе,
занумерованном другим образом: Е^,Ец,..., Ет], ] — 1,п.
52.56.	Отображение А арифметического пространства К2 в
пространство матриц К2*2 задано соотношением
-У
х
X
У
А[х,у)
Показать линейность и инъективность этого отображения и по¬
строить его матрицу в естественных базисах пространств К2 и
Ж7Ж2
52.57. Отображение А арифметического пространства М3 в
пространство матриц К2*2 задано соотношением
Показать линейность и инъективность этого отображения и по¬
строить его матрицу в естественных базисах пространств К3 и
2x3
7.

Матрицы линейного оператора в различных блзислх 115
62.58. Отображение А арифметического пространства Я
задано
■2x2
вещественное пространство комплексных матриц С
соотношением
II + Из
-1з
*з
I, - IX]
А(Х1,Х7,Х3) =
Показать линейность и инъективность этого отображения и по¬
строить его матрицу в естественном базисе пространства Я3 и
базисе Еи, гЕп, Е2и *Е2Х,Е12, \ЕХ2, Е»,\ЕП пространстваСи7.
52.59. Отображение А арифметического пространства й*
в вещественное пространство комплексных матриц С7х7 задано
соотношением
а Ь '
-Ь а ’
А[хихъх3,хл) =
где а = I! + Иг, Ь = х3 + *х4. Показать линейность и инъек¬
тивность этого отображения и построить его матрицу в есте¬
ственном базисе пространства й3 и базисе пространства С7х7,
указанном в предыдущей задаче.
§53. Матрицы линейного оператора в различных
базисах. Эквивалентные и подобные матрицы
Матрицы А, В € Рп*п называются подобными, если существует невы¬
рожденная матрица ^ такая, что
л = я~1вя.
Теорема 53.1. Матрицы А)С и А„ линейного оператора А 6
С(\\ IV) в парах базисов е, / и I = еС, з = /й связаны соотношением
А к = О 1 А)гС.
Следствие 1. Матрицы линейного оператора в различных парах
базисов эквивалентны (§16).
Следствие 2. Ранг матрицы линейного оператора не зависит от
выбора базисов.
Теорема 53.2. Две матрицы А и В над полем Р одинакового
размера т х п эквивалентны тогда и только тогда, когда они являются
матрицами одного и того же линейного оператора А 6 С(У, IV), где V и
И' - линейные пространства над полем Р размерностей пит соответ¬
ственно.
Если IV = V, то при переходе от базиса е к базису ] = е^ матрица
оператора А 6 С(У, V) изменяется по закону:
/*/=<?■'/!,<?.	(53.1)
Таким образом, одному и тому же линейному оператору А €
соответствует целый класс матриц, подобных друг другу.

1161 лава я/У. Линейные операторы о линейных пространствах
Очевидно, что две матрицы Л, й € й""" подобны тогда н только тогд»|
когда они являются матрицами одного к того же линейного оператора, дей¬
ствующего в п-мерном линейном пространстве нал полем й (теорема 53.2).
Ик соотношении (53.1) следует, что все матрицы одного и того же линей¬
ного оператора имеют одинаковый определитель. Определителем линейного
оператора А Е С(У, I/) называется определитель матрицы этого оператора
в произвольном базисе. Обоз н а ч ен н е: с1е1.4. Итак,
4е1.4 = йе1 А, .
Пример 53.1. Пусть оператор А, действующий в п-мерном про¬
странстве К, переводит линейно независимые векторы /|,...,/п в векторы
01,...,9п соответственно. Пусть е1,...,еп - некоторый базис пространства
V, > Г и С - матрицы, столбцы которых являются координатными столбца¬
ми соответственно векторов	и д\	д„ в базисе е. Доказать, что
матрицу оператора А в базисе / можно найти из соотношения
А, = У'С.
Решение. Как показано выше в примере 52.10, выполнено соотноше¬
ние А, = СР~*.
Так как матрица перехода от базиса е. к базису / совпадает с матрицей
Р, то в силу соотношения (53.1)
А, = р-'{СР~')Р = Р~1С. .
ЗАДАЧИ
53.1.	Как изменится матрица линейного оператора А €
в базисе е,,...,еп, если в этом базисе:
а)	поменять местами два вектора е, и е*;
б)	умножить вектор е, на число а ф 0 ?
53.2.	Доказать, что матрицы одного и того же линейного
оператора в двух базисах совпадают тогда и только тогда, ко¬
гда матрицы перехода от одного из этих базисов к другому пе¬
рестановочна с матрицей линейного оператора в одном из этих
базисов.
53.3.	Линейный оператор А в базисе е1,...,еп имеет верх¬
нюю треугольную матрицу. В каком базисе его матрица будет
нижней треугольной?
53.4.	Линейный оператор А в базисе е^ег^з, е4 имеет ма¬
трицу
' 1
2
0
1 '
3
0
-1
2
2
5
3
1
1
2
1
3
Найти матрицу этого оператора в базисе:
а) еье3,е2,е4;

Матрицы линейного оператора н различных базигах 117
б) е1( С1 + е2, в! 4- с, 4 е3, б| + с, + сэ + е,.
53.5.	Линейный оператор А в базисе е,,е2,е3 имеет матрицу
15
-11
5
20
-15
8
8
-7
6
Найти матрицу этого оператора в базисе
/1 = 2в| 4 Зе2 4- с'з, /2 = Зе 1 4- 4с2 4 е3, /3 = е, + 2е2 4 2е3.
53.6.	Линейный оператор А в базисе
1х = (8,-6,7), /2 = (-16,7,-13), /3 = (9,-3,7)
имеет матрицу
1
-18
15
-1
-22
15
1
-25
22
Найти матрицу этого оператора н базисе
9х = (1,-2,1), д2 = (3,-1,2), д3 = (2,1,2).
53.7.	Дан вектор а = {1,2,3}. Найти матрицу линейного
оператора .4 х = ( х, а) а геометрического пространства К3:
а)	в ортонормированном базисе е1,е2, ея, в котором даны
координаты всех векторов;
б)	в базисе Ь, = {1,0,1}, Ь2 = {2,0,-1}, Ъ3 = {1,1,0}.
53.8.	В геометрическом пространстве У2 задана аффинная
система координат {О; е», е2}. В базисе в!, е2 найти матрицу
оператора А, если А осуществляет:
а)	отражение плоскости относительно прямой х 4 2у = 0 па¬
раллельно прямой х 4 Зу = 0;
б)	проектирование плоскости на прямую х+у = 0 паралельно
прямой 4х + 5у = 0;
в)	сжатие с коэффициентом А = 2 к прямой Зх — 2у = 0
параллельно прямой х — у = 0.
53.9.	В геометрическом пространстве У3 задана прямоуголь¬
ная декартова система координат {О; е1( е2, е3}. В базисе е^е2,
е3 найти матрицу линейного оператора .4, если А осуществляет:
а)	проектирование на плоскость Зх - у = 0 параллельно пря-
мой х 4 г = 0, х 4- у 4 2г = 0;
б)	отражение пространства относительно прямой х = у =
-2г параллельно плоскости х 4 у 4 Зг = 0;
в)	сжатие с коэффициентом А = 2 к плоскости х - 2г = 0
параллельно прямой х = у = г;

ПВГлава .УД . Линейные операторы и линейных пространства.у
г) поворот вокруг прямой х = у = -г на угол ж/2\
д) поворот вокруг прямой х + у = 0, у - г = 0 па такой угол,
что первая из данных плоскостей переходит по вторую.
53.10.	Пусть линейный оператор А, действующий п п-мер-
ноы линейном пространстве V, переводит линейно независимые
векторы	в векторы <71,..., 0„ соответственно. Пусть
е1(...,еп - некоторый базис пространства V', а /•’ и С - матри¬
цы, столбцы которых являются координатными столбцами со¬
ответственно векторов	и д\,...,дп в базисе е. Найти
матрицу оператора А:
а)	в базисе е;
б)	в базисе / из столбцов матрицы Р;
в)	в базисе д из столбцов матрицы О (при условии, что О
невырождена).
53.11.	Пусть А - невырожденная матрица порядка п, В -
матрица размера т х л. Доказать, что найдется единственное
линейное отображение А пространства К" в пространство Жт,
при котором образами столбцов матрицы .4 являются соответ¬
ствующие столбцы матрицы В. Найти матрицу оператора А-
а)	в естественных базисах пространств;
б)	в базисе пространства К" из столбцов матрицы А и есте¬
ственном базисе пространства Кт;
в)	в базисе пространства Ж" из столбцов матрицы А и базисе
пространства Жт из столбцов матрицы В (при условии, что тп =
пи В невырождена).
53.12.	Координаты векторов /|,/а>/з и 01102.03 трехмерного
линейного пространства V' заданы в некотором базисе е),е2,е3.
Линейный оператор А переводит векторы /, в д, (| = 1,2,3).
Построить матрицу оператора А', а) в базисе е\,е7, е3; б) в базисе
/ь/а./э, если:
1)	/« =(1,1,1),/а = (1,0,-3),/3 = (0,1,3),
3. = (1,1,1), <7а = (2,0,-6), </з = (0,2,6);
2)	/, = (1,1,-1),/а = (2,1,0),/3 = (3,0,2),
0. = (0,0,0), у, = (2,1,0), <7з = (3,0,2);
3)	/, = (0,2,1), /, = (-1,1,-1), /3 = (1,-2,0),
91 = (0,0,0), 0а = (-2,2,-2), 0з = (1.-3.-1);
4)	/, = (2,0,-1), /, = (—1,2, -1), /3 = (0,-1,1),
0. = (-6,0.3), д, = (5,-6,2), д3 = (0.-2.2).
53.13.	Линейный оператор А имеет в базисе е матрицу .4,,

1|ДД. Матрицы линейного оператора и различных базисах
5 координатные столбцы векторов нового батиса / обратуют ма*
-1 О
-1 1
1 О
1 О
1 1
1 1
О 1
0 2 1
,5 =
Г 2
1 1
. -1 -З]
1-1
-1]
;
-4 5 1
,5 =
Г 1
1 1
5-4
ь
1 Г
Г 5 3
,5 =
Г 3
1 1
1-3 -1 .
1-
3
о Г
Г 4 -2
,5 =
г
5
-3
1
1-3 1
1-
3
2
];
' 0 2 1
■
2
2
-1 ‘
2 8 2
,5 =
2
-1
2
*
12 0
1
2
2
' -9 3
7 '
1
1 1
•
1 1
-1
5 =
1
-1 0
-П 3
9 _
1
2 1
' 2 5
1 ‘
’ 2
-1
-1 -3
0
,5 =
-1
1
-2 -3
-2
. -1
0
' 2 -1
0 ‘
' 1
1 0
‘
-1 2
-1
,5 =
1
0 1
0 -1
1
1
-3 3
' -2 -1
3
-7 '
’ 1
1
-3 0
3
-7
,5 =
-3
0
3 1
-2
7
0
1
3 1
-3
8
0
0
' 2 -1
0
0
' 0
-1 2
-1
-1
-1
0 -1
2
0
•
5 =
-1
0 -1
0
2
-1
1)	Ас =
2)	А, =
<)-». = [
5)	А, =
6)	Ае =
7)	Ае =
8)	Ас =
9)	Ас =
10)	Ас =
53.14.	Линейный оператор А имеет в базисе е комплексного
линейного пространства матрицу ,4С, а координатные столбцы
векторов ноного базиса / образуют матрицу 5. Вычислить ма¬
трицу оператора А в базисе /, если:

120Глаял А'1\\ Линейные операторы н линейных пространств^
*
'1 1 + 1
1 - * '
,5 =
1 1
1
-I -1
1
3 -3 I
3 -2 2
-1 2 0
3«
‘ 1 1 1
1
' 2
1
-1
0 '
1 1-1
1
,5
1
0
1
1
-1
1 -1 1
-
1
—
0
1
0
.1 -г -1
«
1
0
1
1
-5 -2 -3
-1
Г 1
0
1
4 2 2
6 3 3
1
1
,5 =
:
1
1
1
-I
-1
-1
2-3 4
0
-
\
3»-
3
г -
2)	А. =
3)	А, =
4)	Аг =
53.15.	Линейный оператор, действующий из пространств
К" в пространство Кт, задан матрицей .4/* в паре естественна
базисов этих пространств. Координатные столбцы новых базис.
ных векторов д и Л составляют соответственно матрицы 5 и 7’
Вычислить матрицу линейного оператора А в паре базисов д и
А, если:
5 -8
2 -3
2 5
1 3
>Т =
,Т =
5	4	4
2	6	4
-3 -5 -3
1110
0 111
-10-1 1
1-1 0-1
1 1 1
1 2 2
2 3 4
,Т =
-5
3
,5 =
,5 =
9
-5
1) п = 3, т = 2,
.4/с =
-1 2 1
1 -1 О
2) п = 4, т = 2,
117-3
1-1-1 1
Аи =
3) п = 2, т = 3,
1 2
,5 =
А,< =
1	1	О
0	1	1
1	-1	-1
1	1	0
,Т =
2-1 0
-1 2 -1
0 -1 1
,5 =
2	3
3	4
4) п = 3, тп = 4,
2	3-1
4	7 5
-1 -2 -3
2	5 13
Аи =
53.16.	Пусть V - оператор дифференцирования в простран¬
стве М„. Вычислить матрицу оператора V в следующих базисах

121
линейного оператора и различных базисах
Матричы
_го пространства:
9	!)!+<,< + 2(а, З*2 - 1 (п = 2);
2)	е» + 1, 1 - I, 1 - I + «2, 1 - * + I7 - I3 (п = 3);
3)	1, *,	I" (п > 1);
4)	1>^> а?» ■ • пТ (п — О?
5)	1, 1 + *. 1 4-< + ^т,..., 1 + < + -- .+ ^7(п>1);
6)	I, 1 + <, 1 + I + I2,. ■	1	+	* + -.. + Г (п > I);
7)	1, < - «о, (< - «о)а, • • м (< ~ *о)" (« > 1, «о € ®);
8)	1, * - 1,	Г - <п~‘ (п > 1).
53.17.	В базисе I,*,*2 пространства М2 оператор А задан
матрицей
0 0 1
0 1 0
10 0
Найти матрицу этого оператора в базисе, составленном из мно¬
гочленов З*2 -Ь 22, 512 -|- 31 *{■ 1, 7^2 -Ь 5^	3.
53.18.	Пусть А — оператор траиспонирования в простран¬
стве К3*2. Построить матрицу этого оператора в базисе:
а)
1
01
Г 1
1 1
Г 1
1 1
Г
0
о 1
1 0
0 ]•
1 1
о ]
’1
б)
0
01
Г 0
0 1
Г 0
1 1
г
0
1 ]’
[ 1
1 ]’
1 1
1
К
в)
1 1
01
Г 0
1 1
Г 0
-1 1
[ о
1 Г
1 1
0 ]’
1 1
0 ]’
53.19.	Пусть С — оператор в пространстве Э12х2, ставящий в
соответствие каждой матрице X значение ее коммутатора [X, Л]
с матрицей А
базисе:
Найти матрицу этого оператора а
-[5 ?]•
Г 1
01
1 Г 0
1 1
1 [ 0
01
1 [ 0
01
1 °
0 ]
1’ 1 0
о ]
1* 11
о ]
1’ 1 о
1 ]
0
1 1
1 1
1 [1
01
1 [ 1
1 1
1 о
1 1
г 1 о
1 ]
1* 1 1
1 ]
г 11
2 ]
53.20.	Доказать, что отношение подобия на множестве всех
невырожденных матриц одного порядка является отношением
эквивалентности.

122Глава XIV. Линейные операторы в линейных пространства*
53.21.	Пусть матрицы /1 и В подобны: В = 5~ХАХ. Одно,
значно ли при этом определена матрица преобразования 5 ?
53.22.	Показать, что скалярная матрица подобна только са¬
мой себе. Доказать, что этим свойством обладают только ска¬
лярные матрицы.
53.23.	Пусть .4 - фиксированная квадратная матрица. До¬
казать, что множество матриц 5, для которых А — 5~М5 явля¬
ется группой но умножению?
53.24.	Пусть А и В - подобные матрицы. Доказать, что если
матрица 50 такова, что В =	то все множество матриц
5, осуществляющих преобразование подобия: В = 5-1 Л5, полу,
чается из множества матриц {Р | А = Р~х АР) путем умножения
этих матриц справа на матрицу 50-
53.25.	Показать, что матрица А переходит в подобную, если
над ней выполняется любое из следующих преобразований:
а)	«-я строка умножается на число а ф 0, а затем 1-й столбец
умножается на число 1 /а;
б)	к 1-й строке прибавляется ^-я, умноженная на число /7, а
затем из ]-го столбца вычитается 1-й, умноженный на /?;
в)	переставляются 1-я и ]-я строки, а затем *'-й и ^-й столбцы;
г)	каждый элемент матрицы заменяется на симметричный
ему относительно "центра” матрицы.
53.26.	Доказать, что если хотя бы одна из двух матриц А
или В невырождена, то матрицы АВ и В А подобны. Верно ли
это утверждение, если обе матрицы вырождены?
53.27.	Доказать, что преобразование подобия сохраняет сле¬
дующие свойства матриц:
а)	невырожденность;
б)	нильпотентность;
в)	периодичность;
г)	ортогональность.
53.28.	Пусть А - симметрическая матрица, а матрица В по¬
добна матрице А. Доказать, что для того, чтобы В была симме¬
трической матрицей достаточно, чтобы матрица преобразования
была ортогональна. Является ли это условие необходимым?
53.29.	Матрица В получена из матрицы А преобразованием
подобия. Выяснить, верны ли следующие утверждения:
а) если А - треугольная матрица, то В - также треугольная;

123
Пбра-э и ядро линейного оператора.
б) если Л стохастическая матрица, то В - также стохасти¬
ка*.	,
53.30.	Пусть матрицы Л к В подобны кВ — 5~ХА8. Дока¬
зать, что:
а)	4е1 В = с!е1 Л;
б)	1г В = 1г А;
в)	В = I тогда и только тогда, когда А = /;
г)	В = А тогда и только тогда, когда А и 5 перестановочны;
д)	Вк = 5"'Л*5 для любого к е М;
е)	/(В) = 8~} /(А)8 для любого многочлена /(<);
ж)	В-1 = 5Л-15-‘.
53.31.	Если квадратные матрицы А и В п-го порядка экви¬
валентны, то означает ли это, что эквивалентны и матрицы Л2
и я3?
53.32.	Матрицы Л и Л порядков пит подобны соответ¬
ственно матрицам С и I). Доказать, что:
а)	произведения Л ® В и С ® И подобны;
б)	матрицы Л ® /п <8 +/т ®ВТиС®/„0 +/т ® ДТ подобны.
53.33.	Показать, что если комплексные матрицы Л1 = В1 +
1С1 и Л2 = Д2 + подобны, то подобны и действительные
матрицы
Ох
Д, -С,
. С]	В,
Д2 =
Д2
С2
-С2
Д2 •
§54. Образ и ядро линейного оператора
Образом линейного оператора А 6 /^(У, И/) называется множество
1гп Л = {у € кУ | Зг С V : Лг = у},
адрон оператора А - множество
кег А = {х 6 V | Лг = в).
Пример 54.1. В пространстве многочленов Мп для оператора диф¬
ференцирования (§52): 1т V = Л/„_ 1, кег V = Л/о.
Пример 54.2. Для оператора проектирования (§52): хтР = 1.\,
кег? = Ц.
Пример 54.3. Для оператора отражения (§52): 1ш К = V, кег V. = {в}.
Теорема 54.1. Если А 6 С(У,\У), то кегЛ - линейное под¬
пространства пространства V, ,т Л - линейное подпространство прост¬
ранства И'.
Рангом линейного оператора называется размерность его образа а де¬
фектом - ризмсрностъ яцра.. Обозначения: геЛ, беГЛ. Итак геЛ =
Фш 1ш Л, беГ Л = сПт кег Л.

124Глава XIV’. Линейные операторы в линейных пространства»
Теорема 54.2. Если е|,...,гп - базис пространства и, то
"|тЛ = ^(Ле1,...,.4сп).
Теорема 54.3. Ранг линейного опе.ратора равен рангу его мат.
рш|ы в произвольной паре базисов.
Теорема 54.4 (о ранге и дефекте). Если А € С(\',\№), то
гв А + беГ .4 = 61т V .
Пример 54.4. Пусть С - оператор, действующий в пространстве К3х1(
ставит в соответствие каждой матрице А' значение се коммутатора [X, Л] с
заданной матрицей А — | ®	^ |. Найти образ оператора С.
Решение. Выберем в пространстве К3*2 естественный базис из ма-
трип (52.2). Тогда
и
и
о о
0 6
—с 0
]■
гэ
О о
1
0
II
О О
]
0
0 1 _ 1
: -ь
0
1 г [
0
о 1 [
0 -Ь 1
1 1
о ) - 1
а — 6.
6
1- С1
0
1 1 = [
с 0 ]
Для нахождения базиса линейной оболочки, натянутой на найденные
образы базисных матриц, воспользуемся изоморфизмом пространства К
пространству К и исследуем линейную оболочку, натянутую на арифмети¬
ческие векторы
(0,6, -с,0), (с, б - а, 0, -с), (-6,0, а - б, 6), (0, —6, с, 0).
Составим матрицу из координат этих векторов:
‘ 0 6 -с 0 "
с б — а 0 —с
с б — а 0 —с
—6 0 а — б 6
-6 0 а-б 6
—♦
0 6 -с 0
0-6 с 0
0 0 0 0
Если а = б, Ь = с = 0, то ранг этой матрицы равен нулю, и следователь¬
но, образ оператора С - кулевое подпространство.
В противном случае первые три строки последней матрицы линейно
зависимы, так как их линейная комбинация с коэффициентами Ь, с, а — 4
равна нулевой строке. Поэтому ранг последней матрицы не превосходит 2.
Если 6 ф 0, то г^С = 2 и базис образа образуют матрицы
[5 *::}■[ Л »]•
Если с / 0, то гцС = 2 и базис образа образуют матрицы
[ -6 0 1 Г 0 6 1
(а — б 6 ] ’ ( — с 0]‘
Если 6 = с= 0иа^б, то г§ С = 2 и базис образа образуют матрицы
(0 11 [0 0 1
[ 0 0 ]• [ 1 0 ]• *
Теорема 54.5 (о канонической паре базисов). Пусть А С
С(У, IV), г%А = г, б'ип V = п, бнп IV = т. Тогда существуют базисы е и
/ пространств V' и IV, о которых оператор А имеет матрицу 1Г € РтХп

125
Образ и ядро линейного оператора
1
0
0
1
О
О
о
в которой осе элементы равны нулю, кроме первых г диагональных элемен¬
тов, равных 1.
ЗАДАЧИ
64.1.	Что можно сказать о матрице оператора А ранга г,
если в базисе е4,. .. , е„ пространства V векторы ег+1,	, еп при¬
надлежат ядру этого оператора?
54.2.	Что можно сказать о матрице оператора А ранга г,
если в базисе е1,...,еп пространства V векторы ех,...,ег при¬
надлежат образу этого оператора?
54.3.	Найти образ и ядро линейного оператора А в геоме¬
трическом пространстве У3, если:
а) А х = [ х, а]; б) А х = [ а, [ х, Ъ]].
Для следующих линейных преобразований арифметического
пространства К3 построить базисы образа и ядра, найти ранг и
дефект.
54.4.	А(Х1, Х2, х3) = (хх + Х2 + 13,3=1 + Х-2 + Х3,Хг + Х-2 + х3).
54.5.	Л(хх,х2,х3) = (2х, -х2— х3,хх— 2х2+х3,хг+х2— 2х3).
54.6.	А{хх, х2, х3) = (—Хх Ч- х2 -1- х3, хх — х2 + х3, Хх + х2 — х3).
54.7.	Л(хх,х2,х3) = (4хх+х2-х3,2хх + 8х2 —8х3,4хх + х2 —х3).
54.8.	-4(хх, х2, х3) = (Зхх — Зх2 + х3, Зхх + 2х3, —хг + 2*а)-
54.9.	Линейный оператор, действующий из Ж" в Жт, задан
матрицей А в паре естественных базисов пространств. Найти
образ вектора а, если:
, а = (4,-1,-1,3);
, а = ( —1,1,1,-1);
' 1
3
4
1 '
2
2
3
1
4
0
1
1
' 1
2
3
4 '
2
3
4
5
3
4
5
6
4
5
6
7
1)	т = 3, д = 4, А =
2)	т = 4, п = 4, А =

126/'дам А7\'. Линейные операторы в линейных пространп ва»
' 1
0
-2
0
2
1
-1
5
-1
1
0
0
0
2
1
5
4
-1
1
7
0 = (-2,1,3,-!).
54.10. Линейный оператор А действующий в п-мерном про-
странстве V, задан матрицей А в некотором базисе е. Найти его
ядро и образ и выяснить, является ли этот оператор изоморфиз¬
мом, если:
1) п = 2, Л =
25 60 ]
60 144 ;
2) п = 3, .4 =
-2	5	3 ‘
-2	5 .3 ;
2-5-3]
3)	п = 3, Л =
0 1 Г
110;
-1 0 1
4)	п = 4, Л =
5)	п = 4, Л =
‘ 1 1
1 -1
-3 -1
-3	1
1 1
2 -1
О 1
3 -1
ГЗ -1
6)	п = 5, Л =
2 -5
1 0
0 2
1 1
-1
1
1
-1
1
-1
-1
1
-1
1 '
3
-2
-1
2
1
-1
1
0
0
1
0
-1
1
1
-3
1
54.11. Линейный оператор А, действующий из п-мерного
пространства V в т-мерное пространство И', задан матрицей
Л в некоторой паре базисов е и / пространств V и 1У соответ¬
ственно. Найти его ядро и образ и выяснить, задает ли данный
оператор сюръективное, инъективное отображение, если:
-2	1	3 -2 ‘
4 -6	2	3;
2 -3 -11 -15
1) яг = 3, п = 4, Л =

127
Образ и млро линейного оператора.
4
5 9 ‘
3
2 7
1
3 2
9
7
1
СО
г-
2
6
-4 '
1
-3
2
7
-21
14
3
9
-6
2) гп = -1, п = 3, /1 —
3) тп = 4, п = 3, А =
4) т = 2, п = 5, А =
5) т = 5, п = 3, /1
6) т = 3, п = 5, А =
54.12. Найти ранг оператора Т, действующего в простран¬
стве К2*2
1
2
-1 1
1 '
1
-2
1 3
-1
*
-2
-2
2 '
-2
-2
2
-3
-2
2
•
I
4
-1
1
6
5
-5 я
1
-1
2
4 -2
-
3
9
-14
2 1
3
6
-9
1 1
-3 I
-4 1
Х + Х
2 -1
1 О
по правилу
ТХ =
54.13.	Доказать, что ранг оператора С, действующего в про¬
странстве К2х2 по правилу СХ = [X, Л], где А - заданная матри¬
ца, не превосходит 2.
54.14.	Доказать, что ранг оператора О, действующего в про¬
странстве !пхп по правилу ОХ = АХ} где А - заданная матрица,
равен пт%А.
54.15.	Доказать, что ранг оператора О, действующего в про¬
странстве Жпхп по правилу ОХ = ХВ, где В - заданная матри¬
ца, равен л В.
54.16.	Доказать, что ранг оператора Л, ставящего в соответ¬
ствие каждой квадратной матрице А' 6 Кпхп кронекерово произ¬
ведение А' ® В с заданной матрицей В 6 Ктх*, равен п2т%В.
54.17.	Описать образ и ядро оператора дифференцирования
V в пространстве М„.
54.18.	Описать образ и ядро разностного оператора Л в про-

128/ лала А7У. Линейные операторы в линейных пространству
странстве .М„, действующего по правилу
<4/(0 =
/(г -н Л) — /(/)
54.19.	Линейный оператор А действует из пространства Л/^
в пространст во Я* по правилу А/(1) = (/(01),... ,/(а*)), где
Я|,...,а( различные числа. Найти дефект этого оператора.
54.20.	Описать образ и ядро оператора Л в пространстве
Л/я, действующего по правилу
им /(° + 0-/(а-0
Л/(')=	й	.
где о 6 й - заданное число.
54.21.	Найти дефект линейного функционала / на л-мерном
пространстве Г.
54.22.	Для каждого из линейных функционалов геометриче¬
ского пространства Г3, действующих по правилам Л( х) = ( х, а)
и /а(х) = ([а, х], Ь), найти ядро.
54.23.	Пусть /,,/г - два линейных функционала в линейном
пространстве Г, причем /1(х)/2(х) = 0 для всех х € V. Дока¬
зать, что один из функционалов нулевой.
54.24.	Пусть /ь...,Л - линейные функцоналы в линейном
пространстве Г над бесконечным полем. Доказать, что если
/,(х).../*(*) = 0 для всех х е V, то один из функционалов
нулевой.
54.25.	Линейный оператор А действует из V' в И', а у про¬
извольный вектор, принадлежащий его образу. Доказать, что
полный прообраз вектора у, т.е. множество всех векторов х 6 V,
для которых Ах = у, образует линейное аффинное многообразие
пространства V с направляющим подпространством кегА
54.26.	Пусть оператор А действует из V в \\;, а подпро¬
странство I удовлетворяет включению: I С 1т А. Доказать,
что множество векторов х € Г, образы которых принадлежат
Ь, (т.е. полный прообраз подпространства Ь) также является
подпространством, и его размерность равна сПш Ь + (1еГ А.
54.27.	Линейный оператор, действующий из К" в Кт, задан
в паре естественных базисов пространств матрицей А. Найти
полный прообраз вектора у, если:
Г -1	-5	-4	-3	'
2	-1	2	-1
5	3	8	1
1) п = 4, т = 3, А =
> У = (-1,0,1);

-V * (1,2,1);
7
-4
25
4
2
,У=(4,2,9,-20,-3);
Г 1	3
2) п = 5, т = 3, А =	1 -2
I 2 П
30	9
-24 -15
>У = (0,1,1,2,-1).
9
-20
-3
-2
-1
0
1
1
43
-50
-5
1
2
-1
0
4
3) п = 3, т = 5, А =
4) п = 4, т = 5, А =
54.28. Линейный оператор, действующий из ®п в Ж"1, задан
в паре естественных базисов пространств матрицей А. Найти
полный прообраз подпространства I С 1т, если:
I натянуто на
-1
1
Ь задано в есте-
-2
4
3
2
-2
3 1
6 -4
9 -6
1)	п = 5, т = 2, А —
вектор (3,-1);
2)	п = 4, т = 3, А =
ственном базисе системой уравнений х1 + хг = 0, Х\ - х3 = 0;
I задано в
1
-1
-1
1
0
0
-1
2
4
0
1
5
2
-3
-5
1
0
-4
0
1
3
1
1
5
0
1
3
1
0
4
1
0
2
2
1
5
3) п = т = 6, А =
естественном базисе системой уравнений 2х! - х3 = 0, хг + х3 -
2х< = 0, -х2 + 2хл - х6 = 0.
54.29.	Пусть линейное преобразование пространства всех
многочленов от I переводит каждый многочлен в 1п (к =
0,1,2,...). Убедиться в том, что это преобразование инъектив¬
но, но не сюръективно. Найти его образ.
54.30.	Найти образ и ядро линейного оператора умножения
матриц пространства ®2х3-
1) на матрицу А = ^	^ |

130/ лава XIV, Линейные операторы н линейных пространств.,^
справа.
3 2 '
3 1
-2 О
2)на матрицу А —
54.31.	Для каждой матрицы -V 6 1№тхп обозначим черСз
У 6 Ж"’**"-1) матрицу, составленную из первых п — 1 столбцу
матрицы А’. Определим отображение А равенством АХ = у
Доказать, что отображение А линейно, найти его ядро и обрц
54.32.	Пусть Л|,...,ЛП - заданные квадратные матрицу
порядка ш. Отображение А каждому вектору х = (х ],..., х„)^
Шп ставит в соответствие матрицу Ах = а:х А| 4- ... + з:пЛп.
1)	Доказать линейность отображения А.
2)	Найти ядро и образ этого отображения, если п = 4 и
1 1
' 1 Г
, Г 1 —1
' 0 -Г
1 1 .
•4
1!
0 1
> Лз “ [ 1 1
, А+ —
- 1 0
54.33.	Для оператора А € С{У, И7) построить взаимно од.
нозначное соответствие между его образом гаЛ и линейными
многообразиями пространства V вида Р = х0 + кегА
54.34.	Множество А/ всех плоскостей пространства V вида
Р = х0 + кег.4 является согласно задаче 46.34 линейным про¬
странством (фактор-пространством пространства V по подпро¬
странству кег Л). Доказать, что соответствие между многообра¬
зиями из А/ и векторами из ‘ил .4, построенное в предыдущей
задаче, является линейным оператором. Найти ядро и дефект
этого оператора.
54.35.	Пусть V - линейное пространство. Доказать, что
всякое линейное подпространство из V служит:
а)	ядром некоторого линейного оператора в V;
б)	образом некоторого линейного оператора в V.
54.36.	Доказать, что для любой ненулевой линейной формы
/ на п-мерном пространстве V над полем Р существует базис
е),...,еп пространства V, такой, что равенство
/(х,е, + ... + хпеп) = х,
выполнено для любых чисел х1(..., хп € Р.
54.37.	Привести пример линейного оператора, действующе¬
го в пространстве V, для которого пространство V не является
прямой суммой образа и ядра этого оператора.
54.36.	Пусть Ь - любое подпространство, дополнительное к
ядру кег.4 оператора А. Доказать, что:

Линейное подпространство линейных операторов 131
в) любая линейно независимая система векторов из Ь перево¬
де* оператором А в линейно независимую систему;
^ б) подпространство Ь отображается оператором А взаимно
„оэнамно на его образ 1т А.
54.30. Показать, что для любых двух подпространств: N
р. мер ном пространстве V и Т в пространстве таких, что
;1{ПДГ + (ВтТ = п, найдется линейный оператор А € С(У,IV),
которого ядро совпадает с N, а образ с Т.
54.40.	В пространстве Мп построить два различных линей-
йЬ1* оператора, имеющих одни и те же образ и ядро.
54.41.	В естественных базисах арифметических пространств
и Кт линейный оператор А имеет матрицу А. Найти кано-
1(Ическую пару базисов в каждом из следующих случаев;
= [х 31
[ 3 10 ]’
2) А
2
-2
4
4
4
4
2
-10
-1
1
-2
2
2
2
1
-5
1
-1
2
-2
-2
-3
4
6
4) А =
6) А =
-1
1
-1
0
-1
1
1 1
1 1
О
-1
-1
2
-2
1)Л =
3) А =
5) 4 =
§55. Линейное подпространство линейных
операторов
Пусть V и И/ - линейные пространства над полем Я.
Суммой линейных операторов А, В С	называется отображение
.4 +В : V —* [V , выполняемое по правилу
(Л + В)х = Ах + Вх, Ухе У.
Произведением линейного оператора А € С{у, IV) на число а € Я
называется отображение огИ ; V —* IV, выполняемое по правилу
(оД)г = аАх , Ух 6 V.
^Теорема 55.1. Для любых операторов А, В Е IV) и числа
А + В е С(У, IV), аЛеГ(ЦИ').
Следствие. Сложение операторов и умножение оператора на чи-
сяо являются внутренним и внешним законами композиции на множестве
5*

132Глава XIV, Линейные операторы в линейных простр&нств
Теорема 55.2. Множество С{у, IV) - динейнос пространен)
над полем г относительно введенных выше операций.
Теорема 55.3. При сложении операторов их матрицы склад)
ваютсл, при умножении оператора на число еео матрица умножается ,
это кисло, т.е. если ей/- базисы пространств V и IV, то
(.4 + В)/, = А/, + В/г, (а.4)/, — аА/ш.
Теорема 55.4. Если Лт V = п, «Пт И' = т, то линейно
пространство ^(1', И') изоморфно пространству матриц рт*п.
Следствие. «Пт^(1', IV) = сИт V • сНт IV.
ЗАДАЧИ
55.1. Линейный оператор А в базисе а! = (-3,7), а2
Г 2 —1
(1,-2) пространства К2 имеет матрицу
а оператор
-2
. Найти
5 -3
‘ 1
2 -3
В в базисе Ьх = (6, -7), Ь2 = (-5,6) - матрицу
матрицу оператора А + В:
а)	в естественном базисе пространства К2;
б)	в базисе 01,а2;
в)	в базисе ЬХ,Ь3.
55.2.	Линейный оператор А, действующий в трехмерном
пространстве, переводит векторы базиса еье2,е3 в векторы «1,
а2, а3| координаты которых в этом базисе равны (-2,-1,-2),
(11,7,1), (-6,-4,-1) соответственно. Линейный оператор В пе¬
реводит векторы аиа3,а3 в векторы Ьх,д2,63, координаты кото¬
рых в том же базисе е равны (1,5,0), (3,4, —3), (-1,-1,2) соот¬
ветственно. Найти матрицу оператора А — ЗВ в базисе е1,е2,е3.
55.3.	Линейные операторы А и В, действующие в арифмети¬
ческом пространстве Ж3, переводят векторы ах = (1,1 — 1), а2 =
(2,0,1), а3 = (2,-5,6) соответственно в векторы Ьх = (0,-2,2),
Ь, = (1,1,1), Ь3 = (-2,4,1) и с, = (1,3,-3), с2 = (0,1,-1),
с3 = (3,-4,2). Найти матрицу оператора А + В в естественном
базисе пространства К3.
55.4.	Пусть линейное пространство V является прямой сум¬
мой двух ненулевых подпространств Ьх и Ь2. Показать, что
единичный оператор пространства V представим в виде суммы
X = Г» + "Р2х где Тх и Р2 - операторы проектирования простран¬
ства V на Ьх параллельно Ь2 и на Ь2 параллельно Ь\ соответ¬
ственно.

133
Линейное полпространство линейных операторов
55.5» Доказать, что для произвольных операторов АЛВ €
.у \у) выполнено:
а)	|1Л	= ,т если А / О;
б)	|т(-4 -к В) С '|т А 4- 1гп В.
т1оИвести пример, когда включение пункта 6) является строгим.
55.в. Доказать, что для произвольных операторов А, В €
IV) выполнено:
а)	кег А.Д = кег .А, если А ф О;
б)	кег(А -+- В) 3 кег .А П кег В.
Привести пример, когда включение пункта б) является строгим.
55.7.	Доказать, что если операторы А, В Е С(У, IV) таковы,
цхо кег .А -к кег В = V, то выполнено равенство
1т(.А -к В) = 1 т А 4- «т В.
Является ли условие кег А -к кег В = V необходимым для спра¬
ведливости этого равенства?
55.8.	Доказать, что если операторы А, В Е С(Уг\У) таковы,
что "нп А П 1 пт В — {0}, то выполнено равенство
кег(А + В') — кет А П кег Д.
Является ли условие 1шЛ П \тп В = {в} необходимым для спра¬
ведливости этого равенства?
55.9.	Доказать, что ненулевые операторы А, В Е С.{У, И''),
образы которых различны, линейно независимы.
55.10.	Ненулевые операторы А, В, С Е &(У, XV) таковы, что
их образы попарно различны. Верно ли, что эти операторы ли¬
нейно независимы?
55.11.	Пусть /1, . - - , /т ~ базис пространства И', д — ненуле¬
вой вектор пространства V. Доказать, что операторы Дх,..., Вт
такие, что В,д — /,•, д = 1, т, линейно независимы.
55.12.	В пространстве \У задан базис	Доказать,
что для всякого оператора А Е /1(У,кУ) найдутся операторы
В|,..., Вт такие, что А — В1 -к ... -к Вт, причем:
а)	ранг каждого из операторов В} не превосходит единицы;
б)	образ ненулевого оператора Вл натянут на вектор /;.
55.13.	Пусть в!, . . . , е„ — базис пространства V', а д — некото¬
рый ненулевой вектор пространства. Доказать, что операторы
•Ах,.. ., .Ап, заданные на базисе е равенствами
_ / У, * = ],
"!«. * * з,

134 /"лава А'/\’. Линейные
операторы л линейных пространства^
линейно независимы.
55.14.	Доказать, что вгякий оператор ранга 1, образ кото,
рого содержит вектор д, есть линейная комбинация операторов
./4х,...,-4„, введенных в предыдущей задаче.
55.15.	Пусть в пространствах V и И' заданы соответственно
базисы	и /х,...,/то. Используя результаты предыду.
ших задач, показать, что всякий оператор, действующий из У в
IV, есть линейная комбинация операторов ,4х !>•••» -^тп * УДОВЛО-
творяюших соотношениям:
= { 'Ц	1 = 17^,7 = 17^.
55.16.	Показать, что система операторов Л^^, введенных в
предыдущей задаче, линейно независима. Вывести отсюда, что
эти операторы образуют базис пространства С(У, XV).
55.17.	Выяснить, образует ли данное множество линейных
операторов линейное подпространство в С(У, IV):
а)	множество всех операторов ранга к > 1;
б)	множество всех операторов ранга, на превосходящего чи¬
сла А: > 1;
в)	множество всех инъективных отображений;
г)	множество всех сюръективных отображений.
55.18.	Будет ли линейным подпространством пространства
/0(У, IV) множество всех операторов, имеющих:
а) один и тот же образ; б) одно и то же ядро?
55.10.	Показать, что если Т - подпространство простран¬
ства IV, то множество всех линейных операторов, образы кото¬
рых содержатся в Т, является подпространством пространства
V, IV). Найти его размерность, если сПт V = п, (11т Т = к.
55.20.	Показать, что если N — подпространство простран¬
ства V', то множество всех линейных операторов из /^(К, IV),
ядро которых содержит IV, является подпространством прост¬
ранства С(У, XV). Найти размерность этого подпространства,
если сПт V = п, сПт N = /, (Пт И7 = тп.
55.21.	Пусть Ь\ и	произвольные подпространства про¬
странства XV, причем Ь — Ьх + Ь2, Ь0 = Ьх п /,2. Доказать
следующие соотношения:
а)	С(У,Ь) = С{\',Ьх) + С{У,1,2у,
б)	С{У, Ь0) = С(У,ЬХ)П С(У, Ь2).
55.22.	Пусть пространство IV разложено в прямую сумму

135
Л и ней нос ноппрос; ра не 7 во линейных операторов
^пространств 1\,..., Д. Доказать, что
ДУ, IV) = Д У, Д) ф Д У, Д) ф ... 9 ДV, Д).
55.23.	Доказать, что ранг суммы операторов А, В Е ДУДУ)
„с превосходит суммы рангов этих операторов:
ге(Л + В) < гб^ + г^В.
55.24.	Пусть операторы А,В € ДУ,У) таковы, что
V = '|гп А ф т В = кег А ф кег В.
Доказать, что ранг суммы А + В этих операторов равен сумме
рангов гб-Д и г^В.
55.25.	Показать, что для любых операторов А,В Е ДУ,кУ)
дополнено соотношение
гб(Л + В) >\чА-т%В\.
55.26.	Пусть V - некоторое линейное пространство, а к1 и к2
-натуральные числа, удовлетворяющие условиям 0 < кик2 $
(Пт V,	+ к2 < сПтУ. Для каждого натурального числа к:
1&1-Д1 < к < Д+Д принести пример операторов А, В Е ДУ,У),
иля которых гб А = Д, гбВ = Д, гб(.Л + В) = к.
55.27.	Доказать, что любой оператор А Е ДУ, \У) ранга
г может быть представлен в виде суммы г операторов ранга 1,
но не может быть представлен в виде суммы менее чем г таких
операторов.
55.28.	Найти условие, необходимое и достаточное для того,
чтобы сумма двух операторов А и В ранга 1 была оператором
ранга не больше единицы.
55.29.	Пространство У имеет размерность п > 1. Доказать,
что в пространстве ДУ, У) всякое подпространство Ь размерно¬
сти л+1 содержит хотя бы один оператор ранга больше единицы.
55.30.	Пусть операторы А,В Е ДУДУ) таковы, что для
любого вектора х Е У векторы Ах и Вх коллинеарны. Значит
ли это, что операторы А и В коллинеарны?
55.31.	В условиях предыдущей задачи дополнительно пред¬
положить, что ранг оператора В равен размерности простран¬
ства У. Коллинеарны ли операторы А и В в этом случае?
55.32.	Доказать, что операторы А и В ранга 1, имеющие
один и тот же образ Т и одно и то же ядро N, коллинеарны.
55.33.	Доказать, что если два линейных функционала имеют
одинаковые ядра, то они коллинеарны.
55.34.	Доказать, что п линейных функционалов на п-мерном

136/лава XIV. Линейные операторы ь линейных пространству
пространстве линейно независимы тогда и только тогда, когда
пересечение их ядер есть нулевое подпространство.
55.35.	Доказать, что формы ^о(/) = /(а)> Ч>\(П — /Ча)> • • .,
рп(/) = /(пЧ°) ПРИ любом а 6 К образуют базис в пространстве
С(МПЛ).
55.36.	Доказать, что формы <р0(Л = Дао). ^(/) = /(«1 )>•••,
= Да„), где аи, аь..., а„ - произвольные попарно раз¬
личные действительные числа, образуют базис в пространстве
ДЛ/П,К).
/■°»+1
55.37.	Доказать, что формы у>*(/) = /	Д0<^> * =
_	-/о»
где а01а»,---»ап+1 - произвольные действительные числа, удо¬
влетворяющие неравенствам а0 < а) < ... < ап+ь образуют
базис в пространстве /С(Л/П,К).
55.38.	Доказать, что для любого проектора V оператор 2-Р
также является проектором. Найти, как связаны ядро и образ
оператора 2 — V с ядром и образом оператора V.
55.39.	Доказать, что если V - оператор проектирования про¬
странства V на параллельно то оператор И — 2 - 2Р
является оператором отражения.
§56. Умножение линейных операторов.
Обратный оператор
Пусть V', IV, 2 - линейные пространства над полем Р. Произведением
линейных операторов А 6 С(У, УУ) и В в С(УУ, 2) называется отображение
ВА : I' —• 2, выполняемое по правилу
(ВА)х = В(Ах), VI 6 V.
Теорема 56.1. Если А € С(У, IV), В €	2), то ВАС С(У,2).
Теорема 56.2. Операция умножения линейных операторов обла¬
дает следующими свойствами:
1)	(АВ)С — А(ВС) (ассоциативность),
2)	а(АВ) = (аА)В = Л(оВ),
3)	{А + В)С = АС + ВС,
А(В + С) = АВ + АС (дистрибутивность),
выполненными для любых операторов А, В, С, для которых левые части
равенств имеют смысл.
Теорема 56.3. При умножении линейных операторов их матри¬
цы умножаются, т.е. еслие,},д - базисы пространств V, УУ, 2, то
(ВА)" = Вд(А{с ■
Во множестве С(У, V) всех линейных операторов, действующих в прост¬
ранстве У, для любых операторов выполнимы операции сложения, умпоже-

Умножение линейных оперлтороп, Обратный оператор! 37
„и* на число н умножение друг на друга. Ка* следует из обшей теории
Линейных операторов,
1)	С(У, V) - линейное пространство над полем Р\
2)	С{У,У) - некоммутативное кольцо с единицей.
Линейное пространство над полем Р, которое (влкетск кольцом и для
дрбых своих элементов А, В удовлетворает условию
а(АВ) = (с,А)В = А(аВ), Уо 6 Р,
ддзываетса алгеброй (или линейной алгеброй) над полем Р. Размерность
^именного пространства при этом называетса также размерностью алгебры.
Т»ким образом, С{У, У) - алгебра над полем Р.
Как и п любом кольце, оператор А 6 С(У, У) можно возводить в степень
„ Е К, и если р(<) = до + в1< + ... + ап1п произвольный многочлен над
полем Р от переменной I, то однозначно определен оператор
р(А) — а о/ 4- а\А + ... + апАп ,	(56.1)
называемый многочленов от оператора А. Из свойств матрицы линейного
оператора следует, что матрицей многочлена (56.1) от оператора А авлаетса
тот же многочлен от матрицы Ае: (р(А))€ = р{Ае).
Пусть А 6 С(У, V). Отображение А~г : У —• V называетса обратным
оператором к оператору А, если
АА~1 = А-'А = I.
Теорема 56.4. Линейный оператор А 6 С[У,У) обратим тогда
и только тогда, когда он биективен.
Теорема 56.5. Обратный оператор единствен.
Теорема 56.6. Матрица обратного оператора А~* в произволь¬
ном базисе является обратной к матрице оператора А в этом же базисе.
Оператор А 6 С{У, V) называется невырожденным, если его ядро состо¬
ит только из нулевого вектора, т.е.
ксг А = {6} ,
и вырожденным в противном случае.
Теорема 56.7. В конечномерном пространстве У следующие
утверждения равносильны: для А € С(У, V)
1) АА~1=Т;	4) 1т .4 = V ,-	6) А обратим;
2) А~*А = X;	5)де\.АфО;	7) А биективен.
3)	А не вырожден;
Теорема 56.8. Произведение обратимых операторов обратимо,
при этом
(АВ)“* = В-1 А~\
Следствие 1. Умножение линейных операторов является алгебра¬
ической операцией на множестве всех обратимых операторов, действую¬
щих в пространстве V.
Следствие 2. Множество всех обратимых линейных операторов из
[.{V, К) образует неабелеву мультипликативную группу.

138/лава XIV. Линейные операторы в линейных пространства
ЗАДАЧИ
56.1. Линейный оператор А в базисе я1 = (-3,7), аг ^
(1,-2) пространства Д2 имеет матрицу ^ ^	а оператор
5 в базисе &! = (6, —7), 6г = (-5,6) - матрицу ^ -3 ]' ^а”ти
матрицу оператора АВ:
а)	в естественном базисе пространства К2;
б)	в базисе аьа2;
в)	в базисе />,, 62.
56.2.	В пространстве Д/3 заданы два оператора. Оператор
А всякий многочлен а0 + ах( + а2/2 + а3/3 переводит в многочлен
ар + а,* + а?*2- Оператор В многочлены <3 + 12, I3 + I, /3 + 1,
I3 + /2 + I + 1 переводит соответственно в I3 + /, /3 + 1, <3 + *2 +
1 + 1 и нулевой многочлен. В базисе 1, /, <2,13 составить матрицы
операторов АВ и ВА.
56.3.	Координатные столбцы векторов а^а^аз,
СьСз.Сз в некотором базисе трехмерном пространства V обра-
зуют соответственно матрицы
' -2 1 2 '
'2-1 0 '
'2-1 0 '
-10 2
, в=
0 2-1
, С =
-1 2 -1
-2 0 3
-1 -1 1
0 -1 1
А =
Линейный оператор Т переводит векторы а!,а2,а3 в ,62,63, а
линейный оператор О переводит векторы Ь\, Ь2, Ь3 в С1, с2, с3. Най¬
ти матрицу преобразования ОТ:
а)	в базисе, в котором заданы координаты всех векторов;
б)	в базисе аьа2,а3;
в)	в базисе ЬьЬ2,&з.
56.4.	Пусть А, В - линейные операторы, действующие в
' а	.	. _ Г 5 -1
пространстве м. , причем А имеет матрицу Ае —
естественном базисе е1,Сг, а В - матрицу И/ —
1
О
-2
базисе /, = (1,3), /а = (-1,-2). Найти матрицы следующих
операторов:
а)	А7 - 6А + 91 в базисе е;
б)	В7 + 4В + 42 в базисе е;
в)	А7 — В2 в базисе е;

{56. Умножение линейных операторов. Обратный о/тератор!39
г)	ААВ~Х п базисе /;
я) (4 + В)* в базисе дх = (1,2), д7 = (0,-1).
50.6.	Доказать, что всякое линейное отображение предста¬
вимо в виде произведения сюръективного и инъективного линей¬
ных отображений.
50.0. Верно ли, что перестановочность операторов являет¬
ся отношением эквивалентности на множестве операторов, дей¬
ствующих в пространстве V?
50.7.	Показать, что всякий оператор отражения V. удовле¬
творяет соотношению IV — X.
50.8.	Показать, что всякий проектор V удовлетворяет соот¬
ношению V2 = V.
50.9.	Доказать, что, наоборот, всякий оператор "Р, удовле¬
творяющий условию V2 = V, является проектором.
50.10.	Показать, что из условий + Р2 = 2, 'Р\'Р7 = О
следует, что:
а)	Р[, V? - проекторы;
б)	7>гр, = О.
58.11.	Пусть V - оператор дифференцирования, действую¬
щий в пространстве многочленов Мп. Показать, что 2>п+1 = О.
56.12.	Пусть V - оператор дифференцирования, действую¬
щий в пространстве многочленов М„. Найти матрицу оператора
Р‘ в базисе ех = 1, е2 = I, е3 = I2/2!,..., е„+1 = 1п/п\.
58.13.	В пространстве всех многочленов от переменной *
рассматриваются линейные операторы: А - умножения на I и
V - дифференцирования. Найти:
а)	оператор 42?;
б)	оператор 2?4;
в)	коммутатор [2?, А] = Т>А — АР.
56.14.	Для операторов А и 2?, рассмотренных в предыдущей
задаче, доказать равенство [2?*,.4] = кТ>к~1 (к = 2,3,...).
58.15.	Доказать, что коммутатор [А,В] = АВ - ВА двух
линейных операторов, действующих в конечномерном линейном
пространстве над бесконечным полем, не может быть единич¬
ным оператором. Объянить, как это утверждение согласуется с
результатом пункта в) задачи 56.13.
56.16.	Доказать, что если [4,6] = 4, то 4 - вырожденный
оператор.

140/лава Л7У. Линейные операторы в линейных пространств.*
56.17.	Показать, что любые два многочлена от одного опе¬
ратора А перестановочны.
56.18.	Показать, что множество всех многочленов от задан¬
ного оператора А образует коммутативную алгебру.
56.19.	Показать, что если операторы А и В перестановочны,
то перестановочны и любые многочлены /(А) и д(В) от этих
операторов.
56.20.	Доказать, что для перестановочных операторов А и
В выполнено соотношение
(А + В)" = А” + пАп-'В + —■"■■Л"-аВа + ... + Я".
56.21.	Доказать, что операторы ранга 1, имеющие одинако¬
вое ядро и одинаковый образ, перестановочны.
56.22.	Операторы А и В перестановочны. Доказать, что
ВкегАС кег А.
56.23.	Доказать, что если проекторы Р, и Р2 перестановоч¬
ны, то их произведение также является проектором. При этом:
а)	1тп Р)Р2 = 1Ш Р! П1Ш Р2;
б)	кег Р) Р2 = кегР, + кегР2.
56.24.	Доказать, что произведение проекторов Р, и Р2 также
является проектором тогда и только тогда, когда коммутатор
[Ра* Рз] отображает подпространство \т Р2 в подпространство
кег Р]. При этом:
а)	1шР]Р2 = та Р, П (1Ш Р2 + кегР1 П кегР2);
б)	кегР1Р2 = кегР1 + кегР2 П (шР, + 1тР2).
56.25.	Доказать, что если произведение проекторов Р =
Р, ...Р* не меняется при циклических перестановках сомножи¬
телей, то оно также является проектором, причем
1ШР = 1тР1 П .. .Л 1ШР*, кегР = кегР, + ... + кегР*.
56.26.	Доказать, что сумма проекторов Р1 и Р2 также явля¬
ется проектором тогда и только тогда, когда Р,Р2 = Р2Р, = О.
При этом:
а)	1ш(Р) + Р2) = 1Ш Р, © 1гп Р2;
б)	кег(Р| + Р2) = кегР, П кегР2.
56.27.	Пусть проекторы Р,,..., Р* удовлетворяют условиям:
Р,Р, = О при » ф ]. Доказать, что в этом случае их сумма
Р1 + ... + Р* также является проектором.
56.28.	Операторы >1,,...,>1* в пространстве V размерности
п таковы, что А\ + ... + Аь = 2. Доказать, что следующие

^56. Умножение линейных операторов. Обратный оператор!41
условия эквивалентны:
а)	все операторы А, являются проекторами;
б)	А,А} = О при всех * ^
в)	+ ...+ Гб А = л.
56.29.	Доказать, что если оператор А перестановочен с ка-
жпым оператором из ЦУ, V), то А1, С Ь для любого подпро¬
странства 1 из К. В частности, для любого вектора I € V
векторы х и Ах коллинеарны.
56.30.	Пользуясь предыдущей задачей, доказать лемму Шу¬
ра: если оператор А перестановочен с каждым оператором из
ДУ,У), то он - скалярный.
56.31.	Доказать, что для произведения В А операторов А и
В справедливы неравенства:
а)	гбВА < шш(гб А, гбВ);
б)	ёеГ ВА > с!еГ А\
в)	йеГ ВА > <1сГ В (если операторы А и В действуют в одном
пространстве).
56.32.	Доказать, что для произведения ВА операторов А и
В выполнены равенства:
а)	гб(0.Д) = гб А - сИш(1ш А П кег В);
б)	йеГ(ВЛ) = с!еГ А + <Ит(нп А П кег В).
56.33.	Доказать, что для любого оператора А € С(У, V)
выполнены равенства
П
<1еГ Лп+1 = йеГ А 4- ^ сПт(1т.Дк П кег Л),
к = 1
л
гб-4п+1 = гб-4 - ^ <Нт(|т.Лк П кег А).
к = I
56.34.	Доказать, что произведение ВА операторов А и В
удовлетворяет неравенству
с!еГ(#Л) < ДеГА + МВ.
56.35.	Пусть А> В, С - такие линейный операторы, что про¬
изведение ВАС определено. Доказать, что справедливо неравен¬
ство Фробениуса:
гб(ДД) + т&АС < гб Л + гб ВАС.
56.36.	Доказать, что для всякого оператора А € С(У, V),
ранг которого равен 1, найдется число а такое, что А1 = аА.

142Глава XIV. Линейные операторы в линейных пространствах
56.37.	Пусть А 6	V', И') и В 6 С(IV, 2) - линейные ото.
браження и (Пт И/’ = т. Доказать, что:
а)	те В А > Гб-4 + гб б - т (неравенство Сильвестра);
б)	если ВА = О, то т&А + г$В < т.
56.38.	Пусть А 6 С(У,У) - произвольный линейный опера¬
тор. Доказать, что для любого натурального числа к, удовле¬
творяющего условию гб^4 < к < (Пт К, существует линейный
оператор В 6 Д(К, У) такой, что Б А = О и г&В + гб-Д = к.
56.39.	Доказать, что для любых двух перестановочных ли¬
нейных операторов А и В имеет место включение
кег -4 + кег В С кег .4В.
Привести пример, когда это включение является строгим.
56.40.	Доказать, что если перестановочные операторы А и
В таковы, что кег .4 П кег В = {0}, то справедливо равенство
кегЛВ = кег Л © кег В.
56.41.	Пусть линейный оператор А, действующий в п-мер-
ыом пространстве, удовлетворяет соотношению А2 = 2. Дока¬
зать, что:
а)	гб(Л + 2) + г§(Л - I) = п]
б)	с!еГ(.4 + 2) + <1еГ(Л -2) = п.
56.42.	Пусть А,В € С{У>У) таковы, что ВА = О. Следует
ли отсюда, что АВ = О?
56.43.	Привести пример двух ненулевых операторов А и В,
таких, что АВ = ВА = О.
56.44.	Доказать, что если гб-4 = 1 и 1тАВ = 0, ТО-4В.Д = О.
56.45.	Пусть А - заданный линейный оператор, действу¬
ющий в линейном пространстве У. Доказать, что множество
всех линейных операторов В 6 С(У, V), удовлетворяющих усло¬
вию АВ = О, является подпространством пространства Д(У, К).
Найти размерность этого подпространства, если (Пт V = п и
ранг оператора А равен г.
56.46.	Тот же вопрос для множества операторов С € С(У,У),
удовлетворяющих условию СА = О.
56.47.	Пусть V - 2т-мерное пространство над бесконеч¬
ным полем. В пространстве С(У^ V) указать подпространство
размерности тп2 + 1, состоящее из попарно перестановочных опе¬
раторов.
56.48.	Пусть У - п-мерное пространство, А € С(У, V) - за¬
данный оператор ранга г. Преобразование пространства С{ V, У)

Уипожсние линейных о/шратпрон. ОКрлпшй олграгорНЛ
пятому оператору X ставит в соответствие оператор АХ. До-
II.'»гь, что это преобразование являете* линейный. Найти его
ранг и дефект.
56.49.	Пусть У - п-мерноо пространство, А € С.(У.У)
«данный ненулевой оператор. Преобразование Ь пространства
каждому оператору X ставит в соответствие его ком-
иутагор [Л, А1]. Доказать, что это преобразование является ли
нейным. Показать, что преобразование Ь обладает следующими
свойствами:
а)	6 является вырожденным и его ядро содержит все опера
горы, перестановочные с А\
б)	если /(А) многочлен от оператора А. то ё/(А) = О;
в)	для любых операторов В,С 6 С.{УХ V) выполнено сошно
шение
6(АВ) = (6А)В + А(6В)-,
г)	для любого оператора В 6 С{У, V ) выполнено соотношение
Л- I
<5(В") ■■= ^2вк{6В)Вп~1-к-,
к-о
д)	для любого обратимого оператора В € С{У, V) выполнено
соотношение
ё(В~1) = -В-'(6В)В-и,
о) для любых перестановочных операторов В,С 6 ЦУ, Г) вы¬
полнено соотношение
6{АВ-1) = В-'{В(6А) - А(6В))В~1.
56.50.	Показать, что если А невырожденный оператор, то
для любого подпространства Ь имеет место равенство сПт А1 =
сПт I.
56.51.	Пространство V является прямой суммой подпро¬
странств А.I	. Пусть .4, невырожденный оператор, за¬
данный на подпространстве Ь;, I = 1, Де. Показать, что оператор
А 6 С(У,У), совпадающий на каждом из подпространств I, с
соответствующим оператором Л;, также будет невырожденным.
56.52.	Проверить, что оператор дифференцирования V явля¬
ется:
а)	вырожденным в пространстве многочленов А/„ ;
б)	невырожденным па двумерном линейном пространстве,
натянутом па функции /1 = сон I и /2 = нт I (с обычными опера-

операторы в линейных пространств
144 Глава Л'/\'. Линейные
имямн сложения функций и умножения функции на число).
56.53.	Найти обратный оператор для оператора лиффСрс,
кнрования пункта б) предыдущей задачи.	(
56.54.	Найти обратный для оператора отражения 7^.
56.55.	Показать, что для невырожденного оператора а
любого числа а, отличного от нуля, выполнено равенство 11
(а./*)-1 = о“1	1.
56.56.	Доказать, что если А - оператор ранга 1, то хотя
один из операторов X + А или X — А невырожден.
56.57.	Доказать, что если оператор А невырожден, то дл
любого оператора В имеют место равенства
гк АВ = В А =	В.
56.58.	Доказать, что произведение операторов А и В тогда й
только тогда будет невырожденным оператором, когда каждый
из операторов А и В невырожден. При этом
(.4Я)-1 = В-'А~1.
56.59.	Доказать, что для невырожденного оператора А и
произвольного оператора В справедливо тождество
{А + В)А~'{А — В) = (А — В)А~1(А + В).
56.60.	Пусть А - нильпотентный оператор индекса ц. Дока
зать, что оператор X — А невырожден и
(Г -А)-1 = Х + А + А2 + ...+ А9-1.
56.61.	Операторы А и В связаны соотношением АВ + А +
X = О. Доказать, что А - невырожденный оператор, причем
А-1 = -X- В.
56.62.	Линейный оператор X, действующий в пространстве
Гхп, сохраняет определитель матриц. Доказать, что оператор
X невырожден.
56.63.	Ненулевой многочлен /(<) называют аннулирующим
оператор А, если /(А) = О. Доказать, что если у многочлена
/(/), аннулирующего оператор А, свободный член отличен от
нуля, то оператор А невырожден.
56.64.	Доказать, что у любого линейного оператора А, дей¬
ствующего в тт-мерном пространстве, существует аннулирую¬
щий многочлен степени не выше п2.
56.65.	Доказать, что для невырожденного оператора А, дей¬
ствующего в п-мерном пространстве, обратный оператор А~1
представляется многочленом от А степени не выше п2 — 1.

N миожение л н ной них опери / »ров, Обратный опорл׳юрМ*>
50.66.	Показать, что перестановочны любые пва многочлена
/(А) И ;/(Л1־), где А произвольный невырожденный оператор
56.67.	Пусть А £ £(У, W) и найдется оператор В 6 £(W, V)
такой, что В А = Zy (единичный оператор пространства V)
Значит ли это, что АВ = Iw ?
56.68.	Пусть операторы А £ £(Л/״_!,Л/П). В £ £(Л/״, Мг..!)
определен ы соотношен и я ми
ЛДО = «ДО, в/(0 = (/(0-/(0))/«•
Показать, что оператор ВЛ единичный, а оператор ЛВ ־ не!
56.69.	Пусть V линейная оболочка многочленов i,В, .,Г
IV пространство многочленов Л/״.!. Рассмотреть лифферен-
чирование многочленов как оператор V, действующий из V в
И׳, а также интегрирование / /(()d£ как оператор В, действу-
Jo
ющнй из И׳' в У. Показать, что
BV = Iv, VB = JW.
56.70.	Пусть в условиях задачи 56.67 dim IV > dim V До¬
казать, что оператор АВ будет оператором проектирования в
пространстве W.
56.71.	Пусть АВ 6 £(У, W) линейные операторы, причем
rg.4 < rgB. )!оказать, что существуют такие операторы С и 7?.
действующие соответственно в У и в И’, что А = VBC, причем
один из операторов С или D можно выбрать невырожденным.
56.72.	Пусть А, В £ £(У, И׳')■ Доказать, что следующие
условия эквивалентны:
а)	ker.4 С кег В;
б)	В = С А для некоторого оператора С £ £(1V, IV).
56.73.	Пусть А, В £ £(У, W). Доказать, что следующие
условия эквивалентны:
а)	im А С im В\
б)	А = ВТ) для некоторого оператора V £ £(У, У).
56.74.	Пусть А £ £(У, W). Доказать, что существует такое
линейное отображение В £ £(IV, У), что А = АВА и В - БАБ.
56.75.	Пусть в линейном пространстве У задан базис е.
Доказать, что следующие множества линейных преобразований
пространства У являются группами относительно операции
умножения п рсчзбразован и й:
а) множество всех невырожденных преобразований;
6 то

И6Глава XIV. Линейные операторы в линейных пространства*
б)	множество всех невырожденных преобразований с опредо.
л и телом, равным 1;
в)	множество всех невырожденных преобразований, матрицы
которых в базисе с верхние треугольные;
г)	множество всех невырожденных преобразований, задан-
ных в базисе е диагональными матрицами;
д)	множество всех скалярных операторов АХ, где А ф 0;
е)	множество всех преобразований, матрицы которых в бази¬
се е являются матрицами перестановок.
56.76. В линейном пространстве V дан базис е. Являются
ли мультипликативными группами следующие множества ли¬
нейных преобразований пространства V:
а)	множество всех линейных преобразований;
б)	множество всех преобразований, матрицы которых диаго-
нальны в базисе е;
в)	множество всех невырожденных преобразований, которые
в базисе е задаются целочисленными матрицами;
г)	множество всех преобразований, матрицы которых в бази¬
се целочисленны и имеют определители, равные 1 или —1;
д)	множество всех преобразований с одинаковыми определи¬
телями, равными <1\
е)	множество всех невырожденных преобразований, имеющих
в базисе е матрицы, каждая строка и каждый столбец которых
содержат ровно по одному ненулевому элементу?

Ответы и указания
§44
44.3.	Указание. Показа гь, что 0■! в, откуда вывести, что (- 1)х ־
Затем воспользоваться ассоциативностью сложения.
44.4.	Указание. Положить: а) А (а!,аз) = (а!,0); б) А(а! ,аз) =
(1вьат)•
44.6. Указание. Положить: А(а!, аз) = (Не Аа!, Кс Аа2).
44.8. Указание. Не доказана сюръективность умножения на чи¬
сло•
44.10.	Указание. Рассмотреть отображение у?(/) = 1п/(т).
44.11.	Указание, в,г) Воспользоваться индукцией поп.
44.12.	в) Содержит рП векторов, размерность равна п.
44.14.	Указание. Показать, что если числа а, £ Р, ! £ П, различны
к вектор а £ V ненулевой, то векторы а,а также различны.
44.15.	Нет. Указание. Рассмотреть порядки элементов аддитивной
группы векторов пространства.
44.16.	Указание. Нели * £ X,, но г Ху для всех } ф !, то г не
содержится ни в какой линейной комбинации подмножеств Х}, ] ф \
44.17.	Указание. Пусть Л/ = {х!,.	х״} Для каждого подмноже¬
ств» X С М положить V»(-V) = (а!,..., а״), где а, = 1, если г, £ X, и а, = 0
в противном случае.
44.18.	а) Линейно независимы; б) линейно зависимы. Обе пары линейно
независимы как векторы вещественных пространств.
44.20.	а) Линейно зависимы; б) линейно независимы Обе системы
линейно независимы как системы векторов вещественных пространств.
44.21.	а) Линейно независимы; б) линейно зависимы. Обе системы
линейно независимы как системы векторов вещественных пространств.
44.24. 2 в обоих случаях. 44.25. 2 в обоих случаях.
44.26. 4 в обоих случаях. 44.27. 3 в обоих случаях.
44.28.	3 в обоих случаях. 44.29. 4 в обоих случаях.
44.30.	2 в комплексном пространстве, 3 в вещественном.
44.31.	4 в обоих случаях. 44.32. 5 в обоих случаях.
44.33.	5 в обоих случаях.
44.34.	2 в комплексном пространстве, 3 в вещественном.
44.35.	2 в обоих случаях.
44.36.	2 н комплексном пространстве, 4 в вещественном.
44.37.	1 в комплексном пространстве, 2 в вещественном.
44.38.	Нет.
44.39.	Указание. Пусть а\,...,аг база, а аг+! — ома! + 01,2^2 +
... + а,гвг, 1 = 1, г + 1. Рассмотреть матрицу (1т а,2), ! = 1, г + 1, ] = 1, г, и
показать, что один из векторов аг+1,... , агг+1 представим в виде линейной
комбинации остальных с вещественными коэффициентами.
44.40.	Ранг ранен 2, база например, Х1,х2.
44.41.	Ранг равен 3, база например, х!, г2,	.
44.42.	Ранг равен 3, база например, Р! (0> Рз(0.	(*)-
6•

148
О гнеты н .указания к §^<
44.43.	Рянг ранен 2, Пазя — например, р» (<), рл (<).
44.44. Ранг ранен 2, бия например. Л, Ат.
44.45. Ранг ранен 5, база - например. Л, Д, От, Лйт, Нг Н.
44.40. Указание. Если Х| = <3|Х| + ,.. + агГг, то п качсстпе пек тор,
х} можно взять любой нсктор, у которого козффииненг о, н этом разложения
отличен от нуля.
44.47.	а) В системе ровно г нс к торов отличны от нуля; б) и систем
ровно г -+ 1 оектороп отличны от нуля, причем япа из них коллинеарнь:
в) либо в системе г + 2 вектора отличны от нуля, причем три из них колли
неарны, либо в системе отличны от нуля г + 1 векторов и существует тройк
линейно зависимых векторов, в которой никакие лва не холлинеарны.
44.48.	Г1,хз; Х],х«; гз.хэ; хз,х«. 44.49. Любые лпа лектора.
44.50.	а) п,х3; х3,х3; ха.х*; б) Х1,х3,х3; х,,ха,г4; х3,х3,хз.
44.51.	Да. 44.53. Указание. Рассмотреть базу системы.
44.54. Нет, нельзя. 44.62. Нет.	44.65. Нет, нельзя.
44.66. хе = (1/3, 1/3, 1/3)т.	44.67. г« = (1 + -1, 1 - «)Т.
44.68. х« = (0.2, 1,2)г.	44.69. х, = (6, 5,-7,-3)т.
44.72.	*) (1,_, 1,-1, 1, -1. 1)т; 6) (2,-1, -1, 1, -1, 1)Т;
в) (1, — 1, —1,2, —1, I)7 .
44.73.	(4,_1,_3)т.	44.74. х =-е, + е3.	,.
44.75.	Указание. Рассмотреть матрицы Е\ + Ел +
Е 1 4“ Ел 4- Е\, Ел + Ел + Е*~
44.76.	(-1,2,-1, 1)г.	44.77. а) (1, —1,1,1); 6) (1.1.—1.°2-	^
44.78. (1.1.-1, I, 1, 1)т.	44.79. (х',,х^)т=[ \	2	'
44.80.
44.81.
44.84.
44.85.
=
V
- | 1 -1
(ло.т-
1 -1
"(с)
2! ''
— » 1—1
/1п,(еЛ
1 —с
с1
-с3
... (-с)- -1
0 1
-сС\
с3Сз
... (-с)"-СД
0 0
1
-сс1
... (-с)"-3СД
0 0
0
1
... (—с)”-3СД
0 0
0
0
1
Г
1 1
0
0 0 0 з
-10-1 0 10
0	1	1	1 0	0
0	0	0	0	-2	1
Г 9
7
4
1
(*'|
.х'„х'з)т = -
3
-2
-2
1 (*1.Х»
8
5
3
0
-18
1 _Ю
(х*,
.х'2.х^,х;)т =
-0
-2
1 0
0
6
0 4
Г
1
-5
0 -з
(ц , Х3, Хз)
..,г;)т=«(х	гв:
*з)т
(Х|. ХЗ
X3•*«)

149
, Ы Ц Ука,л,,мя к §45
(*!,*7, *з)1
1/2
1/2
-1
1/4
3/4
О
3/4
1/4
О
,86. (*{,*а.*»)1
^,87. &) Поменяются местами I и к; < строки; 6) поменяются местами
. й столбцы; н) псе строки, а татем псе столбцы запишутся л обратном
) * *(•
У1\ЛЪ- *) 5׳־?>$ (6 ;'־.
44.80• а) Каждый лектор /, коллимеарен с,, ! = 1, п; б) /. = ое,, ! =
, каждый лектор /, линейно выражается через е!,ез	е,; г) каждый
\У'.п /! линейно выражается через е,,е, + |	сп
/״44.9׳■ Указание. Так как е!,е]	ет линейно зависимы, то суше
(Г не тривиальная линейная комбинация 0!е! +.	+/?8 = ,״»,״ Пусть
0. Тогда, так как ег,...,ет также линейно зависимы, то существует
)! ',״!шальная линейная комбинация ТзСз +	. + ттет = 8. Пусть 9 =
/е /?, и у =	отличны от нуля. Тогда линейная комбинация
Мц + • • • + 9тСт) 1״7 + . . . + 1^1)0 ־*т) ־ ИСКОМаЯ
!Г 44.92. Указание. Пусть матрица перехода от / к « Так как она
^рождена, то среди минороц *-го порядка, стоящих в первых * столб-
!(' обязательно есть ненулевой. Номера строк, в которых он находится,
I‘**, редел я ют требуемый набор векторов из базиса /. Чтобы убедиться а
Я достаточно составить матрицу перехода от / к вновь построенному
Л.
6*’ 44.93. Нет, нс обязательно. Можно, например, взять векторы /1 =
„ ез и /а = е3 - ез - е!. Тогда /! + /!+«!8 ־.
1' 44.94. а) 9"; б),н) (д" -1 ׳)(д" - <?) ■■(?"־Г‘)■
Н5
45.2.	(1,0, 0,... ,0, 1), (0, 1,0	0, 0),..., (0,0,0	1,0); размерность
р»*1־״*״•	гп + 1,
45.3.	(!,0,0,0,...), (0,0, 1,0,...), размерность равна [—^—]
45.4.	(0,1,0,1,0,	), (1,0,0,0, 0,...), (0,0,1,0,0,...),...; размерность
р..״‘ Р±±] + 1■
45.5.	(1,0,1,0,...), (0,1,0, 1,...); размерность равна 2.
45.6.	Базис образуют, например, матрицы Л; (• < }, *,) = I. ״). У кото¬
рых злементы {,, =	= 1, а все остальные элементы равны 0; размерность
п(п + 1)
45.7.	Базис образуют, например, матрицы С,, (! < ), г.} = 1,п). у
,огорых элементы уч = -д>х = 1, а нее остальные элементы равны 0; раэ-
п(п - 1)
„гриость равна —1—
45.8.	Размерность равна 2; базис образуют матрицы ] д ! |. | д ].
45.10.	1, I3, I4,...; размерность равна [־־־־־־־־]•
45.11.	(, Г1, I4,...; размерноезь равна [—у־־]•
45.12.	( - а, (1 — а)<, (< - а)!3	(< - о)!1-״; размерность равна п.

Ответы и указан и я к §4,$
150
45.13.	(I - а)(« - о), (<-«)(<-а)(, (1 - в)(« - 5)(»	(I - а)(1 - я)!"'1;
размерность равна п - I.
45.14.	При 1 < л: (I - а!)...(/ - о»), (< - о!)...(( - а*)!,..., (I -
«!)•	(<-“О*״"‘, размерность равна п + 1 - к. При к > п - это нулевое
подпространство.
45.15.	С&_,.
45.16.	а) Размерность равна 0;
б) размерность равна 1, базис (1 + 3•2- ,־);
п) размерность равна 1, базис (1,1,1);
г)	размерность равна 2, базис (1 - I, —1,0), (2 + 1,0, — 1);
д)	размерность равна 2, базис (—1,1,1, 0), (1 + I, ],0, -1).
45.17.	Размерность равна 3; базис образуют, например, 01,02,0!
45.18.	Размерность равна 3; базис образуют, например, 01,03,05.
45.19.	Размерность равна 3; базис образуют, например, /!, /з,/з-
45.20.	Размерность равна 2; базис образуют, например, С\,г.!.
45.21.	Размерность равна 1; базис образует, например, с!.
45.22.	Размерность равна 2; базис образуют, например, с!,сз.
45.23.	Размерность равна 3; базис образуют, например, с!,с!,ез.
45.24.	Размерность равна 2; базис образуют, например, Л!, Лз•
45.26. (?" - 1)(?־״9- ״?)	״м ‘)/I, где 6 = (чк - 1)(?* -?)...(?*-
?*-׳) число различных базисов в 1-мерном подпространстве.
45.27.	Например, I! —13 — 1« = 0, !2 + х3 — х! = 0.
45.28.	Например, х! -Х2-2!з = 0, Г1 -хз-(-2ц = 0, 2х! +хг —!5 = 0.
45.29.	Например, (3 — 3!)г! - 2хз = 0.
45.30. Например, х! — !2 = 0, х! - х3 = 0, (1 — {)х! — х4 = 0.
45.31. Например, (1 - 7!)!! + (-11 + 7|)хг + 10х3 = 0, (-19 + 13|)х! +
(9 - З|)х3 •+• 10х4 = 0.
45.33.	Указание. Произвольный базис подпространства £ допол¬
нить до базиса пространства V. Затем элементарными преобразованиями
получить базис, удовлетворяющий условию.
45.34.	Да. Нет.
45.36. Указание. При доказательстве необходимости использовать
равенство В, = САс, где С - невырожденная матрица, составленная из ко¬
эффициентов разложения второй системы через первую. При доказательстве
достаточности приписать к матрице Ле снизу строку координат вектора 6,
и показать, что ранг полученной матрицы равен г.
45.39.	Размерность I! + £3 равна 3, базис - например, 01,03,03.
45.40.	Размерность £1 + £з равна	4,	базис - например,	а!, аг, о3, 6!.
45.41.	Размерность £! + £2 равна	3,	базис - например,	01,02, 6!
45.42.	Размерность £! +£2 равна 3, базис - например, 01,02,6!.
45.49.	Размерность £! П £2 равна	1,	базис - например,	С1 =(3,5,7).
45.50.	Размерность £! П £2 равна	2,	базис - например,	с! = (0, 1,0,1),
Сз = (1,0,1,0).
45.51.	Размерность £! П£г равна 2, базис ־ например, С1 = (1,2,2,1),
сз =(1,1,1,1).
45.52.	И в вещественном, и в комплексном случаях: сЛт(£| + £3) = 3,
<Нт(£| П £2) = 1, базис суммы - например, 01,02.62, базис пересечения -
с, =(0,4,3-!).
45.53.	В комплексном случае; <Пш(£! + £г) = 4, сПт(!!П£з) = 2, базис
суммы - например, 01,02,01,61, базис пересечения с! — (0,1,0,0), а =
(0,0,0,1). В вещественном случае: сИт(£1 + £г) = 6, (Пт(£! П £2)= 1, базис

151
’Iн 11 УкаЗМННЯ К §'/в
0
.)■
^мЬ1 например, а^.а^,Ь^,Ь^,Ьз,Ь^, базис пересечения - е| = (0.1,0, 2
45.54. Размерность 1\ П/,2 раина 1, базис например, с> = (■*•*• *)'
45.65. Размерность П Ц раина 2, базис например, а\,<1з-
45.66.	Размерность ЬхПЦ раина 2, базис - например, с\ = (1. •< •> *• '/•
-(0,2,3,1,-1).
45.57.	В вещественном случае: сНт(/,| + Аз) = 6, А\т(Ь\ГМз) = базис
уМмМ * например, а,, а3,	= (|,0,-3), Ьз = (1,0,3»), 63 = (0, —I
(, = (0,1,2 + |). В комплексном случае: (Лт(Л| + /.3) = 3, А\т{Ь\ *"• ь?) ~ *<
00ИС суммы - например, Я|, аз, Л|, базис пересечения - С| = ( — 10 + 9в, 16 +
31,3“ Ш').
45.58.	Например, базис суммы - а] = (1,1,0,0,—I), аз = (0,1,1,0,1),
и = (0,0,1,1,1), а« = (1,0,1,0,1), базис пересечения с« = (1,1,1,1,0),
« = (1,0,0,1,-1).
45.50. Например, базис суммы а1 — (1,0,0,1), а3 = (0,1,0,0), аз —
(0,0,-1,1), базис пересечения С1 =(2,3,1,1).
45.60.	Например, базис суммы а] = (1,0, 1,0), аз = (0,1,0,1), а3 =
(0,0,1,0), базис пересечения - в],аз.
45.61.	Размерность суммы раина 5, размерность пересечения равна 2,
бикс суммы - например, Л1, Аз, Л3, Л«, В\, базис пересечения например,
Ль
45.62.	Размерность суммы раина 3, размерность пересечения равна 1,
бикс суммы - например, 1 + 21 + I3, 1 + I2, 1 + I + I1, базис пересечения -
кмример, 2 + 3< + /2 + *3.
45.65. Указание. Учесть, что <Нт(Ц + Уз) = сНт(И^1+ И/з) = гб(Л| +
Да)-
45.70.	Проекция вектора е, на параллельно Ьз имеет 1-ю коорли-
явту (п - 1)/п, а остальные координаты, равные — 1/п, проекция на Ьз
параллельно Ь\ имеет все координаты, равные 1/п.
45.71.	В матрице А\: {Л1},, = 1,1 = 1,та, остальные элементы равны
1/2; в матрице Аз: {ЛзЬ; = — {Аз}), = 1/2, 1 < ), »,у = 1,п, все диагональ¬
ные элементы равны 0.
45.72.	х = (-1,-2,-6,-3) + (3,2,6,6).
45.74.	а) 213 - 3<2 + I; б) I3 - I + 1; в) З(«3 - 1)/2.
45.75.	а] (—1,2«); б) (0, 0); в) (27 + 61,12 - 541).
45.77.	В качестве дополнительных подпространств можно взять, на¬
пример, линейные оболочки, натянутые на векторы с\ = (1,0,0,0), е3 =
(0,1,0,0) и е3 = (0,0, 1,0), е« = (0,0,0, 1).
45.78.	В качестве дополнительных подпространств можно взять, на¬
пример, подпространство Л/о и линейную оболочку, натянутую на много¬
член Г.
45.79.	В качестве дополнительных подпространств можно взять, на¬
пример, подпространство всех симметрических матриц и подпространство
все* верхних треугольных матриц.
45.81.
(*"• - 1)(*т - **)...(*"• - *”•-') ’
§46
46.1. Нек
гор. 40.2. Пространство V.

152
Отпеты и указания к
46.5. Нет, неверно. Если характеристика пола равна двум, то для
любого о 6 I-' выполнено в + а = $, и слелопатслыю, Ух, у С ь : (а + х) ■+ (а +
у) = х + у €	,
46.в. Может, например, если И - это лннсиное многообразие п линей,
ном подпространстве над полем 2з-
46.7.	Вектор сдвига (1,0,1,0), направляющее подпространство натк¬
нуто на вектор (1, 1,3,2).
46.8.	Вектор сдвига (1,2,0,0), направляющее подпространство натя¬
нуто на векторы (3,1, 0,1), (1, -2,1,0).
46.9.	В комплексном случае: вектор сдвига (0,1,—1), направляющее
подпространство двумерно и натянуто на векторы (1,1,0), (2|, 1, 1 + «). В
вещественном случае: вектор сдвига (0,1, —1), направляющее подпростран¬
ство четырехмерко н натянуто на векторы (1,1,0), (г, —1,0), (2*, 1,1 + г),
(-2,.,-М-.)-
46.10.	В комплексном случае: вектор сдвига (|,2,1 + 1,1 — г), напра¬
вляющее подпространство одномерно и натянуто на вектор (0,—1,1,0). В
вещественном случае: вектор сдвига (г, 2,1 +1,1 — |), направляющее подпро¬
странство двумерно н натянуто на векторы (0,-1,1,0) и (0, 1,1,0).
46.11.	Если А = 1, то вектор сдвига (2,0,0), направляющее подпро¬
странство натянуто на векторы (2,0,1), (—1,1,0). Если А ^ 1, то век¬
тор сдвига (—2, —2я, 1), направляющее подпространство натянуто на вектор
(-2,-21 -2гА, 1).
46.12.	Если А = 2, то вектор сдвига (2 - *, 0,0,»'), направляющее под¬
пространство натянуто на векторы (1, —1,0,1), (-5,3,1,0). Если А ф 2, то
вектор сдвига (А+1 — 2я, 1—1,0,1), направляющее подпространство натянуто
на вектор (-5,3,1,0).
46.14.	Все являются гиперплоскостями в Мп.
46.15.	а) п3 - 1; б) л(л - г^Л); в) л(п - ге А); г) л3 - т& А т& В, а) 1;
е)	2.
46.16.	а) п3 - п; б) п3 - 2п + 1.
Г Зх) + 6х, - 2ха = -7,
46.17. < *7- 2хз - 2х3 - 2ц = 7,
I. Зх> — 4хэ — Зх« = 7.
46.18.
46.19.
46.20.
46.21.
Т! + (2 + |)хз + Из + (1 - |)х4 =‘1 + «.
+ Х2 - 2хз + 2* = 0.
Г 2X1 + 1X2 - х« = О,
\12| - (1 - 2|)хз + хз = 1 — 2|.
Г 2X1 - 22 + 2х« = О,
< -XI + Зхз - Хз - Т\ = 2,
1х> + Х2 + 2гз — —3.
{*1 + 1X2 + (1 - |)хз = -1,
2»п - хз + из = 2,
Згх 1 — 2хз + (1 + 2|)хз = 2 — 1.
46.23.	г& Л = т, и л=т+1 или л = т + 2.
46.24.	Указание. Преобразовать систему из базиса направляюще,
го подпространства е1,...,ек и вектора сдвига а так, чтобы все векторы
принадлежали многообразию.
46.26. Если хо, XI,..., г» - заданная система векторов, то в качепве
вектора сдвига можно взять хо. а в качестве направляющею подпростран¬
ства - С(х 1 - 			 - хо)

153
46§ go 1 м и указания к ן.
40.28.	Если * = п 4• 1, то единственным многообразием является все
^сграиство V. Если к < n + 1, то многообразия имеют вид *о + С(хi -
'* ... ,** —*о, У!• • •. | V!)! где I < п + 1 -к и у!	у! произвольные векторы,
*At которых система го, z!,..., х», у!,у! линейно независима
'■ KUO.	- l)(?"	,"6/(' + *־, где Ь = (,‘ - I)(,‘ -
,)..V-f‘־‘)■
*	40.31. £,! + Lj. 46.32. L, если А / 0, {9), если А = 0.
40.33.	Да, если L— (0).
46.35.	dim М = л — к Указание. Установи гь изоморфизм между А/
.произвольным подпространством, дополнительным к L.
40.36.	Содержит вектор и, нс содержит вектор v.
40.38.	а) Прямая не пересекается с многообразием; б) прямая имеете
многообразием единственный общий вектор г = (2,1,-2,2); в) прямая лежит
1|Д многообразии.
40.39.	Векторы г! - 13,71,72 должны быть линейно зависимы.
46.40.	Векторы 71,72 должны быть лииейио независимы, а вектор z! -
tJ должен линейно выражать через 71,03.
46.41.	Общий вектор г = (-5,11,-16,-11,7), плоскость имеет вид
г + £(?!. 92 )•
46.42.	Общий вектор г = (-2, -5, -1,1, -1), плоскость имеет вид г +
Общий вектор z = (0,1,-1,-2,-3), плоскость имеет вид г 4•
£(71-72)•
46.43.
£( 71.72)•
46.44.
46.45.
При А = 1.
Векторы г! — с,хг — с,71,73 лииейио зависимы, а каждая из
систем X] - с, 7!, 73 и га - с, 71,72 линейно независима.
46.46.	! = с + 17, где 7 = (6, 7,-8,-11); векторы пересечения: (2,2,
-3,-4), (-4,-5,5,7).
46.47.	х = с + <7, где 7 = (1,1,0,3); векторы пересечения: (2,3,2,1),
(1,2,2,-2).
46.48.	Указание. Рассмотреть параметрические уравнения пря¬
мых.
46.49.	х! +£(хз — х!, ?!, 7з).
46.51.	Имеют один общий вектор я = (1,2, 1,0,1).
46.52.	Не пересекаются; направляющие подпространства пересекаются
по нулевому вектору.
46.53.	Не пересекаются; направляющие подпространства пересекаются
по одномерному подпространству, натянутому на вектор (5,1,0,0,5).
40.54.	Пересекаются по прямой х = го +7з<, где г0 = (-2, -1,6,6, 7).
46.55.	Введем две матрицы: А - матрица, по столбца.« которой запи¬
саны координаты векторов Р1,Рз,71,72| В матрица, полученная из А при¬
писыванием столбца координат вектора хо — уо■ Пусть г§ А = г!, Г£ В = г5.
Возможен один из шести случаев:
1)	г! = 4, Г2 = 5: плоскости не лежат в одном четырехмерном много¬
образии;
2)	г! = гз =4: плоскости имеют одну общую точку, и следовательно,
лежат в одном четырехмерном, но не лежат в одном трехмерном многообра¬
зии;
3)	г! = 3, г< = 4: плоскости не имеют общих точек, лежат в одном
четынехмерном, но не лежат в одном трехмерном многообразии;
'1) г! = Гз = 3: плоскости лежат в трехмерном многообразии и пересека¬
ются по прямой;

Ответы и указания к §47
15-4
5)	г! = 2, г! = 3: плоскости не имеют общих точек, но лежат в одном
трехмерном многообразии;
6)	г! = г! = 2: плоскости совпадают.
46.57.	Если две плоскости трехмерного пространства имеют общую
точку, то они имеют общую прямую. Если плоскость и трехмерное ли
неннос многообразие четырехмерного пространства имеют общую точку, то
они имеют общую прямую. Если два трехмерных линейных многообразия
четырехмерного пространства имеют общую точку, то они имеют общую
плоскость.
46.58.	Линейное многообразие имеет уравнение г = а! + <! (a! — a!) +
<j(e« - a!). Пересечение с заданной прямой; а) состоит из одного вектора
(0,0,3,3); б) пусто.
46.62.	Гиперплоскость, параллельная Я! и //; и проходящая через одну
из точек указанного вида.
46.63.	Если характеристика поля равна 2, то это утверждение неверно
Указание. Записать уравнение прямой, содержащей а и Ь, в виде Аа + (1 -
А)6, А ЕР.
46.66.	Указание. Показать, что dim(//!Л...ПЯ*) = dim(L!П.. •Л/,!,),
а затем по индукции показать, что в n-мерном пространстве размерность
пересечения к подпространств размерности п - 1 не меньше п — к.
46.67.	Указание. Дополнить базис направляющего подпространства
рассматриваемого многообразия до базиса всего пространст ва.
§47
47.2.	Пусть с произвольный фиксированный базис пространства. Для
любых векторов ! и у обозначим через !, и у, их координатные столбцы в
базисе е. Тогда скалярное произведение можно ввести равенствами (г, у) =
!Гу, в вещественном случае и (!,у) = !Гу7 в комплексном случае.
47.3.	Изменение масштабной единицы для измерения длин.
47.5.	а,д,е,ж) Нет; б,в,г) да.
47.7.	Указание. При проверке последней аксиомы воспользоваться
неравенством 2|а,аД < |а,|г + |а,|3.
47.8.	а,б,в,г,ж,и) Нет; д,е,з) да.
47.9. .4״ = А, а0 < ״, а0 < ״, det А > 0.
47.10.	а,в,г) Нет; б,д) да.
47.11.	Только правило б).	47.12. 1) Да; 2) да, если т > п + 1.
[£!]■*> С(/)=[^],б) С(/)״*]־־];
_ 1 3]׳ а) С(/)= [_2 1].״) С(Я=[о?|;
41]-
>с(Я=[б !г]•6)
Г 4 2 01
[4 2 2 1
2 2-1
10 -1 3
, a) C(/) =
2 2 1
.2 1 3
, 6) C(f) =
■״§]־6) С(Я.
./ = (/)6) С.
2 1 -
1+1	3
1 - 2! 2 + I
2 + 1
6
,a)G(/) =
9 1	Г з 1 -21 5
2 + . ,а) С(/)= 1+2.	3 з
6 J	L2-i2-i
2 1 +
11 - I 3
0
47.13.	1) С(е) =
2)	С(с) = [
3)	13(c) = |
4)	С(с) =
47.14.	1) G(e) = j
2)C(e)=f! 2׳
Lo 2 -i
47.15. a) G - 7; б) С = (у,,), где g,, = (i+j - 1)~*;

155
q,■петы И указания к §48
») G ־־ (®ч)• глг ®ч — (' + J ~ I)-', если I + ; четно, и у,, = 0, если ! + !
״четно;	>
״Ня(|-| j-|)
о с . (».,), г™	,,״
־•))־ ,-9 :0־־!)!),«.Г, т
я) G = (9ч). г״е 9ч = X]
ksl
47.16.	det G' = det G(dct S)2.
47.17.	Указание. Воспользоваться результатом тадачи 17.15׳ б, в).
47.18.	1)С(־) = [] а]• (*-») = 0 (1-2־(e) = [ _{ ־'],(х,у) = 2;
3)	С(е) = [ о °! ] - (*. У) = Т’ 1׳) С(е) = [ ־] Д ״ *) - [} ־) =
״J. (г׳ у) = 3־•
2 0 0
О 3
О О
5) С(е) =
Л*.У)=7..
1 I О
-!4 0
О 0 1
47.19. 1) G(e)= [q 2 ] > (1,!/)—I + 3»; 2) С(е) =
47.20. Будет, если а = 0.
47.23.	Указание. Внести произвольным образом скалярное произве¬
дение на I‘ и использовать предыдущую задачу.
47.28. Указание. Воспользоваться предыдущей задачей и свойства¬
ми следа матрицы.
47.30.	Нет.
47.31.	1) |я| = 5з/2; 2) |я| = >/30; 3) |а| = ч/б; 4) |а| = Зч/2; 5) |а| = У7׳;
6) |а| = ч/Го.
47.32.	Совпадает с тождеством параллелограмма.
§48
48.1.	Да.
48.8.	Нет. Если в системе есть нулевой вектор, то она линейно зависи¬
ма.
48.13. Указание. При п > 3 записать компоненты векторов базиса в
строки матрицы и проанализировать ее первые три строки.
48.15.	1) 1, <	Г; 2) (*!)־'(/ — я)*,* = 0^; 3) Д (<-д(<.-д־\
	 2=!о*‘
к = 1, п + 1.
48.17.	Указание. Воспользоваться задачами 48.5 и 48.6.
48.18.	Если хс = (*,	г״)г, ус = (у|,...,9п)Г, то: а) (!,у) =
Е^'Уч 6) (х,у) = (2г,у! + х,у■! +Х29!) + ^Аг1.9..
2=1 |־,
48.19.	Указание. См. задачу 47.2.

156
Ответы и указании к
48.21.	Для /(/) = а, +и! |+аа|}+.. .+ап1׳\ д(() - бо+Ь! М-б?/3 +.. ■+6״р
положи ть (/.у) - во*с + а!6! + (2!)5аг&1 + ... 4־ (п!)2а״Ьп.
48.22.	1) 1-,2)-^ (1 ;(1,1,0)^- (3 ;(1-,1 ,1- ,1)1 (2 ;(2.2-.1)־);
.(1.1־.!)^ (5
.(.5-,0,1)״^ (3 ;0-.1 ,«־ 1)1 (2 1+05־,.+ 1)1 (1 .48.23
48.24.	Указание. Предположить противное - хотя один из пектор0й
!9* кулевой.
48.25.	1) 2,1)1- ,(1 ,3— ,1)=^־. I); 2) -^(1,0. - 1,2), -1.2,1.0)=־);
3)	~(1,5,2);
4)	1(1.2.2), 1(2, 1.-2). 1(2,-2,1);
5)	5(2.1.-0.0.1־(- .(־), ^(-М.О;
6)	-1(1,1,-1,0), ^(0.1.1.-1), —(1.0.1.1).
48.28.	I,«,«2-!!1- |*.
48.29.	Указание. Выполнить интегрирование по частям.
48.31.	1) Например, векторами аз = (1,1,1,0), а. = ( — 1, 1,0,1);
2)	например, векторами аз = (2, 3,1,0), а. = (1, —1,1,1);
3) например, векторами а3 = (0, -3,1,1), а. = (11, -3, -10, 1);
4) например, векторами аз = (0, —5,4,3), а. = (2,1,10, —7).
48.32.	1) Например, вектором а3 = (11 — 3!, 1, —6 + <);
2) например, вектором аэ = (4 -+ 3!, 16 + 8!, 8 + 3»).
48.33.	1) Например вектором аэ = -(2,-1,2);
2)	например, векторами аз = 1(1,1,1,1), а. = 1(1,1,-1,-1);
3)	например, векторами а3 = -1= (1.0,1,-1), а, = -~(0, 1, 1, 1);
4)	например, а3 = -^=(-2,1,0,-1), а. = -|=:(2,2, 2- ,3־).
1)	Яг = (2,3,-4,-6),	= (-3,2,6,-4), 53 = (4, 6,2,3)•
2)	5, =(1,1,-1,-2), 53 = (2,5,1,3), д, =(2,-1, 1,0).
48.35.	1)5, = (2,1.-»). 52= (И2+0- ,1־ .־•־, д3 = (_]+,- 4_,- _1+2|х.
2)5. =(0,1 —.,2), д7 =(1,1 -И,-.).	1 ־ +
48.36.	п - 1.
48.34.
48.37.	1) Например, ^=(1,1,0), -^(1,-1,-2);
2)	например. -^(1,-1,0,0), -^(0,0,1,-!), 1(1,1,	_ ,).
3)	например, -^=(3, 2,1,0), -^(0,1, -2,1);

157
■Огяггы н указания к $■19
4)	например, --=(1,0,1,0,0), -~=(1,2,-1,1,0), —(2,1- ,2.3,2־),
5)	например, -(1,-1,1,-1,0), -^=(1,1,2,2,1);
Л) например, ~(2, -1,1,0,0), —^(1.3,1,3,0), -^4-.1- ,1-,1,1)־).
V (»	2 \/Ъ	1\]гэ
<18.38. Указание. Процессу ортогонали«иии соответствует тре¬
угольна* матрица перехода.
•18.39. Обе матрицы раины С-1.	48.40. а) (5Т)-1; б) (5Т)-1.
48.41. Указание. Воспользоваться задачей 48.38.
48.45. Если системы е!,..., с* и /!,..., /* биортогональкм, то система
Л,,.... Лк также образует с системой е!,... ,е* биорто!опальную пару тогда
и только тогда, когда векторы /! - А!,...,/я - п* ортогональны подпро-
гтраиству £(е!,.
• •,в»,)•
48.48.
/. =
(5/2,-1/2), /, = (-3/2,1/2).
48.49.
/. =
(1.0,0), /2 = (0.1/2,0), /з = (0,0,1/3).
48.50.
/. =
(3, —3,1), /, =(-5/2,4, -3/2), /, = (1/2,-1,1/2).
48.51.
/. =
(1,-3,-13), /, = (0,1,5), /3 = (0,0,1).
48.52.
/» =
(1,0, 0,0), /,= (0,1,0,0), /, = (-1,-2,
1.-2),
и =
(1,2,-1,3).
48.53.
и =
(0, 1/3, 1/3, 1/3),/, = (1/3,0,1/3,1/3),
/з —
(1/3, 1/3,0, 1/3), /4 = (1/3, 1/3,1/3,0).
48.54.
/. =
(0,0,0,1), /,= (0,0,1,-1), /з = (0,1,-
•1,0),
/♦ =
(1,-1,0,0).
48.55.
/. =
1(3-1,-1 -31,-1 +2|), /г = 1(2 + 1,
1+31,1-2!),
/з =
1(1 -21,2 + 1,2 + !).
48.56.
а) /!
1 =(0,0,0,1),/, = (1/3,1/3,1/3,-1);
б) /.
= (2/7, 3/7, 2/7,2/7), /, = (4/7,-1/7, -
,(3/7-,3/7־
/з
= (-3/7,-1/7,-3/7,4/7).
48.57.
»5
2) !(. 2)5 ־), у (5( - 7I3), -у(1 - 3<2), -у(31 - 513).
§49
49.6.	Указание. Воспользоваться результатом задачи 45.65.
49.8.	Указание. Показать, что строки .матрицы В линейно выража¬
ются через строки матрицы А.
49.12.	а) Например, 6! = (2, — 2, —1, 0), 63 = (1,1,0,-1); б) например,
6! = (0,1,0,-1), Ь, = (1,0,—1,0); в) например, 6! = (-3,1,-2,0), 4, =
(1,-1,-2,1).
49.13.	а) Например, 61 = (-4 + 2!, -1,1 - 2!); б) например, 5! = (!, 0,0),
42,0-) = 63 ,(1,0 + 2-,2-) = ־, I), 6, = (2,1,!).
49.14.	а) г, + г* = 0; 6) { _ ,״ + { \\ * ־'״**
в) 4г! - !г, + (1 + 5!)гэ = 0.

158
Отвиты и указания к $49
40.16. I: /Зг> “ *» + 3x1 ,
\ л - хз - 2ц + х,
= 0, »а. Г и + Зх» +	2х«=0,
= 0, * ‘ | Зх| ■
^ *1 - *1 - «) т м - "I ( Зх| + 7х» — хз + 2х, = 0.
49.17. а) Подпространство, натянутое на многочлен 1 + I + ... + 1";
б) полпространство, натянутое на многочлен ( + <*+...+ 13*+', где 2к +
1 - наибольшее нечетное число, не превосходящее п; в) подпространство,
натянутое на многочлен 1 +2Г + 3«’ + ... + (п + 1)1"; г) подпространство всех
нечетных многочленов из Л/„.
49.18.	а) Подпространство скалярных матриц; б) подпространство
кососиммстркческих матриц; в) подпространство симметрических матриц;
г)	подпространство нижних треугольных матриц с нулевой главной диаго¬
налью.
49.19.	Указанно. Учесть, что величина 1г(Л /1) задает скалярное
произведение в пространстве К"*".
49.23. а) (1. — 10,0)г, (0,7, |)г; б) (3,2. —5)г;
в) (5, 1,0,0)г, (2,0, -1,0)г, (9,0,0, 1)Г; г) (2,1,0, -3)г, (1,0,1,4)г;
д) (1.0, —5,1)7*, (0,0, 1,-3)г.
49.24.
49.25.
49.26.
49.30.
49.31.
49.32.
49.33.
49.34.
49.35.
49.36.
49.37.
49.38.
49.39.
49.40.
49.41.
49.42.
2уД
(1,-3,2,1,-3).
а)	>0.-1). -1(1,-1,1);
б)	-1(1,1,0,0), -1(0,0,1,1), ^(1,-1,-1,1);
г)	^(-1.1,1,0), -^(3.1, 2,1);
д)	-^(1,1,1,0,0), -1(1,0,-1,1,0),
а)	(1,1, -1,1)г, (10,1,0, —2)г;
б)	(0,1,1, -1)т, (1,0, -2,3)г;
в)	(1,1, -1, -1,1)г, (0,1,2,3,4)т.
( 2ц - хз = 0,
а) и - Зхз - 2ц = 0; б) < хз = 0,
I 5ц - х« = 0;
ч / 11+12=0,	, /ЗХ] + Хз+Ц=0,
*> \ 2х2 + 1з-х«=0; г> \ 2ц-2ц + х« = 0;
д)	2ц - хз + Зх3 + х« = 0.
9 = (5.2, -9, -8), А = (9,-5,3,1).
д = (0,-3,5,2), Л = (2,-2, -2,2).
9 = (1, “1, ~ 1,5), Л = (3,0, -2, — 1).
9 = (3,1,-1,-2), Л = (2,1, -1,4).
9 = (2 - '.-1,0, Л = (-2 + 1,1, -1 + 51).
, = (1,2,-5,1), А = (-4,-2,0,8).
9 = (5,-5,-2,-1), А = (2,1,1,3).
У = (5,2, -1,1), Л = (3, —4,9,2).
, = (1,1,—1,1), А = (1,2,0,-3).
, = (2+ 1,1 - 91,4 + За), А = (-2 - I,-1 + 2а, 3 + 4я).
, = (3 + I, -4 + 2|, -1 + 31), А = (1 - I, —2а, 1 + •').
, = (0,1,0,-1), А = (3	2,1 -,)•
,(<) = -2 + « + |», А(<) = 2 + 41 + 6(3 + 8<3.

159
0Гцргы и указания к §50
49.13.	д(<) = 3 4- 5I3 - /\ Л(<) = з/ + ц3.
40.44.	ff(l) = 6/J - 4/\ А(0 = 2-2/J - 3/V
40.45.	«) ff(/) = 1 + «; б) ff(/) =	в) ff(/) 6 + 2־ ־t;
40.52. Указание. 1) Рассмотреть определитель матрицы Л А.
40.55.	Указание. Воспользоваться результатами задач 48.38 и 49.54.
§50
50.1.	t) а) 0; б) 7г/6; в) Зя2 ;4/־) а) я־; б) 2х/3; в) arccos >/7/10;
3) а) arccos( 1 /\/3); б) ir/2; 4) а) х/4; б) я2/־.
50.2.	а) Не изменится; б) заменится на дополнительный до я•; в) не
тиснится.
50.4.	а) |г| = 3V2, |у| = 6, |z — у| = 3V2, поэтому треугольник
равнобедренный; (z,z- у) = х/2, поэтому треугольник прямоугольный.
(*Ту) = »/4 и является внутренним углом треугольника; (у, z - у) = Зх/4,
поэтому внутренним углом является (у, у — z);
б) |х| = |у| = |z - у| = 6, поэтому треугольник равносторонний; углы
(С!/) = (х, z - у) = (у, у — х) = гг/3 являются внутренними.
50.5.	Указание. 4) Воспользоваться теоремой косинусов из преды¬
дущего пункта.
50.7.	Нет.
50.9.	1. Параллелограмм, у которого равны диагонали, является пря¬
моугольником. 2. Равенство справедливо лишь тогда, когда Re(r,y) = 0.
50.10.	Указание. Показать, что если нетривиальная линейная ком¬
бинация векторов ei,...,en+i равна в, то все коэффициенты одного знака.
Далее показать, что в минимальную линейно зависимую подсистему входят
все векторы.
50.11.	Указание. От противного: если все углы тупые, то в равной
нулевому вектору нетривиальной линейной комбинации векторов ej,...,en+2
все коэффициенты одного знака; с другой стороны эти коэффициенты могут
быть подобраны так, чтобы их сумма равнялась нулю (см задачу 44.89).
50.13.	Нет.	50.19. х/4.	50.20. тг/З. 50.21. х/3.
50.22.	ir/6.	50.23. arccos(2/3). 50.24. х/6.	50.25. т/3.
50.26.	arccos( 1/\/б).	50.27. х/2.	50.28. >/58/15.
50.29.	>/42.	50.30. >/3.	50.31. 1.	50.32. 2\Д0.
50.33.	1.	50.34. v/TTÖ. 50.35. >/м.	50.36. >/22/3.
50.39. а) /3 + 3/ + 3; б) 3; в) (3 + а§ + ... + а
50.42.	Указание. Перпендикуляр из вектора г на £ холлинеарен
вектору а,
50.43.	а) 1; б) 1; в) а״.
50.44.	Указание. Использовать задачу 50.42.
50.46.	Косинус угла равен модулю косинуса угла между а! и ад
50.47.	1) arccos(2/7); 2) arccos(l/\/3 ;(3׳) х/2; 4) 0.
50.48.	а) х/2; б) arccos —у.

Огвсгы и УКазанял к §Й2
160
/	3(2"»1 - i)~
V(״
4 1)(2"+' + О'
/ 2(п + I) „
, / —б) лгссо*
V 2(2п + 1)• '
50.49. я) arccos
•S1
и) arccos
50.50.
V 71
У man ис. Использовать задачу •18.38,
50.51. «)Л
\(п 4
у.) ־ö)(c;ny
1}!(п4 2)К..(2п + 1)!,
Указан и с. Использовать результат задачи 49.51.
Указание. Использонать результат задачи 49.55.
Указание. Использонать результат задачи 50.52.
Указание. Использовать предыдущую задачу.
50.52.
50.53.
50.54.
50.55.
§51
51.1.	При 6 = 0.
51.2.	Указание. Найти хо п виде ап.
51.3.	Указание. Если гиперплоскость имеет вид ю + то п ״а,Ис
£х.
51.5. л(1) = 1 4־ с/4• с3<2 4• ... 4־ с"<", 6 = г(.	51.6. 'Нет.
51.7. Указание. Показать, что многочлены п*(1), Аг = 0, п, в пред¬
ставлении подпространства	= 0 равенством (я*,/) = 0 образуют
базис пространства А/„•
51.11.	Указание. Показать, что направляющее подпространство
этого многообразия есть ортогональное дополнение к £(«!,...,״*).
51.12.	Нормальный вектор равен ап, где а = Ь/(п, п).
51.14. а) 1; б) (;
4(п ־־ Л /, ,״..	״.״з	6(п —_2)	,,^212 + ... + пГ)■
(1 4-Н-...+ <")-■
п(п 4- 1)(п 4• 2)
^2(1 +1 + ... + <") -(п + 1)(,1 + 0J•
3(п 4 2)(п - 1)
(п -f 1)(п 4■ 2)
ля
\J6n(n + 1)(2п 41 ־)
51.20. 2.
б) у/п\ в)
а)
п(п - 1)
5	51.17
г)
51.16.
б) п - 1; в) ^(п - 1).
150.	51.23. 5.	51.24. 5.
Ввести в пространстве скалярное произведен:
*0־0*
51.18. а)
51.21. 2.	51.22.
51.25.	Указание
так, чтобы заданный базис стал ортонормированным.
51.26.	См. указание к предыдущей задаче.
51.27.	Указание. Пусть «!,...,е* - базис направляющего поди
страиства многообразия //. Линейно независимую систему еек, х
полнить до базиса всего пространства и ввести скалярное произведение
чтобы этот базис стал ортонормированным.
51.28.	1г/4.
§52
52.2. Всякий оператор состоит в возведении чисел в степень <:
роьанным (для данного оператора) действительным показателем.

Ответы и указании к §.52
161
52.3. а,б) Да, если о = в; в) л».	52.4. а,6,г,д) Да; в) нет.
52.5.	а) Ортогональное проектирование на прямую г » (и; 6| про¬
ектирование на прямую г = 1а параллельно подпространству (г, п) « 0;
и) ортогональное проектирование на подпространство (г, п) » 0; г) проек¬
тирование на подпространство (г, п) = 0 параллельно вектору а, д) орто¬
гональное отражение относительно подпространства (г, л) г 0; е) ортого¬
нальное отражение относительно прямой г « I а; ж) суперпозиция ортого¬
нального проектирования на плоскость (г, п) = 0 и поворота на угол */2
вокруг прямой г = (а.
52.6.	а,в,л,ж) Да; б,г,с,з) нет.
52.7.	а-л,э,и,к,м) Да; с,ж,л) нет. 52.11. а-д) Да.
52.12. а,б) Да, н пространство К"*"; в,г) да, о пространство Л;
д,е,ж) нет; э) да, в пространство 1Яп*т; и) да, в пространство &пя"; к) да,
в пространство 1^пгпХп*
52.13.	а) Нс яиляется ни сюръективным, ни иньективнмм; б,в) являете*
биективным.
52.14.	В случае, если /ь •.., Д - базис V.
52.15.	Пусть /»,... ,/г - база системы	Тогда векторы /к+ь
должны быть такими же линейными комбинациями векторов /*,...»
/г, как 0г+1,. •., дк векторов у),... , уг.
52.16.	Указание. Использовать задачу 52.14.
52.19. а) Да, если а = 0; б,д,с) да; в,г) нет.
52.21. Линейную форму в пространстве Мп можно задать таким
образом тогда и только тогда, когда для чисел с* = <?(**) выполнены соот¬
ношения: с0 = 1,	~ ду к =Т7п.
Ск-1
52.22.	Линейную форму «р в пространстве Мп можно задать таким
образом тогда и только тогда, когда для чисел с* = (* +1)^(1*) выполнены
/	\*+*	/	Ч*+1
соотношения:^,), с*	- (Д + |)	. * = ^
52.23.	Нет, если эта форма не равна тождественно нулю.
0 1 1 1
1/2
3/2
01
52.24. а)
2 0 1
; в)
3/2 -
•1/2
3 •
. 3 -1 1 .
1/2
1/2
1 ]
Г 1 -1 11
-
1/2
0
3/2 ‘
52.25. а)
0 0 1
; б)
1/2
1 -
-1/2
. 0 1 0
1/2
0
1/2
1 -1
0
1
-1
0
52.26. а)
0 1 -
-1
6)
0
1
-1
-1 0
1
-1
0
1
52.27.	а) Ас
52.28.	а) Ас
52.29.	а) Ас
2-116
1	-7	4
2-10
' -2	11/3	5/3
-4	13/3	10/3
2	-5/3	-5/3
5	-20	33
7	-24	38
0 0 0
ИА'*Ы :
б) А, =
3 0
8 1 .
5 2 .
-10/3 -7
3
2
; б) А, =
5/3
1/3
-5 -Ю -7
6	13	-Ю
17	36	-27
3
-2 .
1

162
Ответы
и указания к §,52
52.30.
52.33.
52.35.
52.37.
52.30.
52.40.
52.41.
52.42.
52.43.
Г “3
-2 1
1
0
. 52.
1 о
1
4 7
1 1
1 3 -
3 5
2 ]
-1
1
3 -
4
4
12 -
2
-2
-6
1
52.
— 1
• ]
Г 0 1
0
...
0 0
2
...
0 0
0
...
. 0 0
0
...
Г 0 0
1 •
2 0
0 0
0
2-
0 0
0
0
0 0
0
0
0 0
<]
0
0 1
н
к2
0 0
2
ЗЛ<
0 с
0
3<г
0 с
0
0
.0 с
0
0
сИ&е(1,1/2,1/3,...
г 0 1 2а За*
0 0 0
0
0
Э 0
1
0
0 (1
0
0
0 0 0
0
0 0 0
1 о
0
1 0
, если п нечетно, и
-о 1
0 0 .
0 0
2 0 .
х> =
0 0
0 3 .
г.31- [ “!	-? о ]•
52.32.
52.34.
-2
1
7
-3
6
-3
-21
9
52.30.
К ]'
О 1
О
,. п(п - 1)
О
О
Л""1	"
Оп"г<
с1нп~317
сх~Чп-'
4а
О
За
О
О
О
Сп-1а
О
.0 0 0 0
. Л =
Г -7
-1
1
3
-3
12
О
-6
-3
6
—1
2
14
-6
[т
а"-7
п —I
па
0
1
С
лЗ п—3
Сп(1
0
Г-6
Спа
О
О
п четно.
000
1	О О
О 1/2 О
0 0	1/3
О О
1/п
52.45.	а) Первые к элементов главной диагонали равны 1, все осталь¬
ные элементы равны 0; б) последние п — к элементов главной диагонали
равны 1, все остальные элементы равны 0; н) матрица диагональная, пер¬
вые к элементов ее главной диагонали равны 1, остальные равны —1.

163
Отпеты и указания к §52
О	аз	—о!
52.46.	Ле =	־־«з	О	я!
.	аз	-а!	О	л
52.47. 13ведем для любых двух векторов х = {г!, х3, гз). У = I!׳1״	׳ 1׳
матрицу .9( х, у) = (х, х2 хз)т(у, у, у,). Тогда матрица Ле имеет вил: а) I-
9( п, п); б) 9( а, а); в) 1 --±-Д(״, а); г) —Ц9(п,а); д)/29־(п, п);
1а■ П1	(а, п)
е) 29( а, а)-/; ж) 1 17) ־^)^ "• а): 3) ^^5( п, а) - /.
0 0
0
1 1 1
1
2 -1 -1 '
0 1
0
;6) \
1 1 1
; в) -
-1 2 -1
0 0
0
3
.111.
3 ׳
-1-1 2
52.48. а)
Указание. Использовать результат задачи 52.47
5	1	2
1	5 -2
2-2 2
г) Ъ
Г 0 0 0’
1
2 3 0
Г -6 -9 -3 '
-1 1 0
I б) {
2 3 0
i »)
8 12 -4
2 0 1
5
I -1 5
10 15 -5
Указание. Использовать результат задачи 52.47.
-2	-2
1	-2
-2	1
1
-2
-2
-1	4	8
4-7	4
8	4 -1
’ б> 9
-10 0
0	1	0
0	0	1
52.49.	а)
2	3-4
4	6-8
2	3-4
52.50.	а)
0J
Указание. Использовать результат задачи 52.47.
-1 2	0
4 1	О
2 2-3
-10 о
-4	1 О
4	0	1
52.51. а)
Г 1
0
0
1; 6) 0
0
Т1
L о
±1
0
0	0	1
1	О О
О 1 О
Указание. Использовать результат задачи 52.47.
cos <х Т sin or О
± sin a cos а О
О	0	1
О 1
0	О
1	О
О	О
О	О
ЯИ Я!2
Я21 Взз
О
О
0
1
' <*11
0
Я21
־ 0
;6)
0
“11
0
Я21
а!2
0
Я22
0
0
а!2
0
Я22
“״< Я,2 ВТ
а"В Я2з ДТ
!б)
я!1 Я]2
Я21	“22
О	О
О	о
1	О	о
О	0	1
О	1	О
0	0	0
auI + UT	»12/
Я21 /	Я22 I + ВГ
52.55.	а) ВТ®Л\ б) /„ ® Л + й'׳> /т.
52.52. а)
52.53. а)
52.54. а)
Г 1 0
0 1 0 1
0 1
0 -1
52.57.
0 0-1
0 0 1
1 0 .
L 1 0 0
52.56.

164
Ответы и указании к
52.58.
Г 0
0
1
г 1
0
0
0 т
п
0
0
0
1
0
0
1
0
0
0
0
-1
0
0
-1
0
52.59.
0
0
0
1
1
1
0
0
0
0
0
0
1
0
0
0
0
1
0
0
-1
1
0
0
0
. 0
0
0 .
. 0
-1
0
0 .
§53
53.1. а) В матрице персставятся 1-я и /-я строки и 1-й и _>-й столбцу,
б) в матрице »-й столбец умножится на число «, а 1-я строка разделится ц4
число а.
53.3. В базисе еп...,е|.
53.4. а)
‘ 1
0
2
1 ’
' -2
0
1
0 '
2
3
5
1
;б)
1
-4
-8
-7
3
-1
0
2
1
4
6
4
1
1
2
3
1
3
4
7
53.5.	2,3).	53.6.
2
-1
-3
2
-2
1
53.7.	а)
53.8.	а)
1
2
•6>1
20	-5	15
-16	4	-12
24	-6	18
-4	-5
4	5
Указание. Сначала выписать матрицу оператора в базисе из напра¬
вляющих векторов данных прямых.
2 3
4	6
3 6 9
-5	-12
2	5
]:«)['! '!]'»>[! :?]•
53.9. а)
1 2
• -1 101
Г 3 4 0'
Г 0 0 2 ■
-3 3 0 ;б)
4 3 3
; в)
-1 1 2
3 -1 2 ^
-2 -2 1 .
-10 3
1 1 + з/З —1 + \/3 '
1
и -
1 1 — \/3 —1 — \/3
1 - VI 1 -1 -у/2
1 + %/3 1 -1 +\Д
. -1 - \Д - 1 1 .
3
,-1+з/3 —1 — з/З 1.
0
0
-1 1
1
и -
2
-2
1 ‘
-I
0
0
1
2
2
0
1
0
3
. -2
-1
2 .
«о
О 1
Указание. Сначала построить матрицу оператора в базисе, соста¬
вленном из базисов данных подпространств.
53.10.
53.11.
а) = С/'"1; б) А/ = Р~'С; в) А, = Р~'С.
а) В А'1; б) В; в) I.
53.12. 1) а)
2) »)
[:!
Г -1	4
-2	5
12-4-
3 -1
5 -1
3 )
; б) <4186(1.2,2);
; б) сЬ&б(0,1,1);
3) а)
-1 -1 21
0
0 0
-5 -1 2
;б)
0
2 1
-7 -3 6
0
0 2 .

165
flggwj и указания к §53
Î 4)
-2 1
-12 7
3
-3 2
-2
5 -3
-3
5 -3 .
3) diag(2,2, —2,2»)
ו
ן 3 5-
H
[1 -il
-3	1
о -3
О о
2
1
-3 ]1 ’>
Г -1 4
ן 4
;6)
-10 -18
-20
9 13
15 .
1
-1
О -1
-1
о
о
;7)
) —2 ]* 2)
1 О
О
О
-2
0 ־
-1 0
2
1
2 -1
-1
0
1 4
0
0
-1 -2
2
1 + 1
1
1; 2) diag(
.1־
П 2
О О
10)
(0 а׳
53.13.	1)
4	0	5
0 0 0
5	0	4
1 О О О
;6)
0	О
1	1
О 1
О о
0 0 0 1 .
53.14.	1)
0
י 0
0
0
—1
1
0
— 1
г ас 	3 1	. [ —42 —13	20	48
1 .3.15־) [IS :SJ Hl 15 זי-י י
I I
О I
О о
о о
9
5
25	-31
1 כ
rO 1 0 ... 0
1 0-1־]
1
0 0 2 ... о
3 -5 -12
-3 9 18
;2)
2- ס 3-
1- 1 3
1
-4
;3,7)
0 0 0 ... n
2 -6 -12.
0 -1 1
1 .
0 0 0 ... 0
Г 0
1 -1
-1 ... -1
ך 0 ... ו
0
0 2
-1 ... -1
Г -3 -15
1	5
5
1
53.16. 1)
О О
О О
О О
порядка п + 1; 6)
О 1
ООО
.000
0 111
0 0 2 1
0	0 0 3
4.5)
О О
0
0
0
4
0
0
1
-15
-16
-20
4
9
12
16
1 ־
1
0
־ 0
1 ־
0
0
־ 2
0
-1
0
1
0
; в)
0
1
0
0
а,б]
0
1
0
0
0
1
0
0
0
0
1
0
0
0
-1
0
2
0
0 :
: 0
0
0
0 :
и
0
0
0
;6)
0
0
0
0
а)
-2
0
0
2
-2
0
0
2
0
-2
0
0
-2
-2
0
2
53.17.
53.19. а)

Огне 11.1 и укала ния к § Л 4
166
ч 53.21. Нет.
53.22.	> к азан не. Показать, что квадратная матрица А нереста-
новочна с любом невырожденной матрицей тогда и только тогда, когда А
скалярия
53.26.	Нет, неверно. 53.28. Нет, неверно.
53.31. Нет, не означает.
§54
54.1.	Последние п —г столбцоп матрицы нулевые, в то время как первые
г линейно независимы.
54.2.	Последние и—г столбцов матрицы нулевые, в то время как первые
г линейно независимы.
54.3.	а) Образ - плоскость ( х, а) = 0, ядро прямая [х, а] = О;
б) если (а, Ь) = 0, то образ прямая [х, Ь] = 0, а ядро плоскость
( х, а! = 0; если (а. Ь) ф 0. то образ - плоскость (х, а) = 0, а ядро прямая
[ ь] = 0
54.4.	!£.4 = 1. базис образа (1, 1,1); Ае{ А = 2, базис ядра (1, —1,0),
(1.0. -1).
54.5.	г§Д = 2, базис образа - (2,1, ]), ( — 1, -2, 1); веТ>1 = I, базис ядра
-0.1.1).
54.6.	ге -А = 3. <1еГА = 0.
54.7.	г§ Л — 2, базис образа (2,1,2), (1, 8,1); <1еГ А = 1, базис ядра
(0,1.1).
54.8.	А - 2, базис образа - (1,2,0), (—3,0,2); с!сГ А — 1, базис ядра
(2.1.-3)-
54.9.	1) (0,6, 18); 2) (0,0, 0,0); 3) (-8,-11,3,0,-13).
54.10.	В базисе < координатные столбцы базисных векторов: 1) ядра
(12,-5)т, образа - (5,12)т; 2) ядра - (1, 1, -1)т, (3,0, 2)т, образа (1,1,-1)т;
3) ядра - (1,-,1,1)т, образа (1.1,0)т, (0,1,-1)г; 4) ядра - (0, 1, 1,0)т,
(0.0 1,1)г, образа (1,1,-3,-3)т, (1,-1,-1,1)г; 5,6) кег«4 = (0), 1т А =
Г, А - изоморфизм.
54.11.	В соответствующих базисах е или / координатные столбцы
базисных векторов: 1) ядра - (0, 2,0,1)7 . (0, — 3,1,0)т, образа (0,1,О)7,
(1,0, -2)г; 2) образа - (4,3,-1,7)т, (5,2,3,7)г, (9,7,2,6)г, кег А = (0), А
инъективно: 3) ядра (3,1, О)7", (2,0, — 1)т, образа - (—2,1,7,-3)т; 4) ядра
- (2,0,1, —1,0)т (0,1,2,0,0)т. (0,0,1,0,1)7’, !тЛ = IV, А сюръективно;
5)	ядра - (0,1, 1)г, образа - (-2,-2,-3, 4, б)7", (2,2,2,1,-5)г; 6) ядра
(—23,1, 0, —3, 6)т, (—42,0,1,5, 10)т, !т А = И', А сюръективно.
54.12.	Гб7=2.
54.13.	Указание. См. пример 54.4.
54.14.	Указание. Составить матрицу оператора £/ в естественном
базисе пространства й״*".
54.15.	См. указание к задаче 54.14.
54.16.	См. указание к задаче 54.14.
54.17.	Образ -	ядро - Л/о•
54.18.	Образ Л/״-!, ядро Мо.
54.10. в + 1 - к, если к < п + 1, и 0, если к > п + 1.
54.20.	Образ все четные многочлены из Л/», ядро линейная оболоч¬
ка, натянутая на многочлены (I - а)''*, 0 < 2к < п.

167
Ответы и указания к §55
54.21.	п, если / нулевой, п - 1, если / ненулевой.
54.22.	Двумерное подпространство векторов, ортогональных а; дву¬
мерное подпространст во векторов, компланарных а и Ь
54.23.	Указание. Использовать результат задачи 45.47 для хлер
функционалов.
54.24.	Указание. Использовать результат задачи 45.46 для ядер
функционалов.
54.27.	1) (0,0,1/10,1/5) + а!(10,0, -7,6) + оз(0,5, -1, — 7);
2)	(7/2,0,-1/2,0,0)+ 01(19,2,-5,0,0)+ 0^41,0,-11,2,0) + а1(1,0,-2,0.1);
3)	(0,0,1) + а!(1, -2, —3);	4) (0,1,0,0) + о!(2,2,1, -1)
(здесь а, 6 К, ! = 1,2,3, произвольны).
54.28.	Линейная оболочка, натянутая на векторы:
1) (1,1,0,0,0), (0,1,2,0,0), (2,0, 1,-1,0), (0,0,1,0,1);
2)	(1,1,-1,-1), (0,2,1,0), (7,23,0,-11);
3)	(о, 3,-1,0,0,0), (0, 1,0,-1,0,0), (0,4,0,0,0,-1), (1,0,0,0,0,0),
(0,0,0,0,1,0).
54.29.	13се четные многочлены.
54.30.
1) Базис образа _2 о ]
' [ 0 -2 ] ׳ ®азис *״РЛ [
3
О с
О о
— и>
2) образ все пространство
ES.3 хг, базис ядра - j q
4
0
21
0 0
0 1
1 -2 4
з ]•
54.31. Ядро состоит из матриц, у которых первые п - 1 столбцов ну-
лсвыс, образ - все пространство К1 ״)*1״'.
54.32.	2) Ядро натянуто на вектор (1,-2,1,-2), образ все матрицы
из К32״ вида | “ аЬ ].
54.33.	Указание. Каждому вектору из !ш Л поставить в соответ¬
ствие линейное многообразие его прообразов.
54.34.	Ядро кегА дефект равен нулю.
54.36. Указание. Построить базис так, чтобы /(е!) = 1, /(с!) =
... = /(е„) = 0.
54.41. 1) (1,0), (-1,1) и (1,1), (0,1); 2) (1,0), (0,1) и (1,3), (3,10);
3)	(1,0,0), (0,1,0), (1,1,-1) и (0,-1,-1), (1,0,1), (0,0,1);
4)	(1,0,0), (1,1,0), (1,-1,-1) и (1, —1,2), (0,1,0), (0,0,1);
5)	(1,0,0, 0,0), (0, 1,0,0,0), (0, 1,2,0,0), (2,0, Г,-1,0), (0,0,1,0,1) и (1, 1),
(2,-2);
6)	(1,0,0), (0, 1,0), (0, 1,1) и (-2,-2,-3,4, 6), (2,2,2, 1,-5), (0,1,0,0,0),
(0,0,0, 1,0), (0,0,0,0, 1).
§55
55.1.
о[1
1HI
-7 1
-27 4
];в)
f -30
-35
27
31
-5
14
-3
5
-13
-9
55.2.
-1 4
5
55.3.
3
-6
-4
-5
7
-1
. -2
5
4
55.7. Нет, не является. Указание. Рассмотреть случай Л - В
55.8. Нет, нс является. Указание. Рассмотреть случай А = В
55.10. Нет, неверно.

Отпеты и указания к §.5б
168
55.12. У к в s а н к с. Пусть е!,..., е״ - базис V׳׳, и пусть Ас.) — &\,f\ +
... 4• amj/m Тогда положить В,с.} = а,,/,.
55.14. Указание. Множество всех операторов, отображающих п-
мерпое прост рапс г по и одномерное пространство, имеет размерность п.
55.16.	Указание. Учесть, что dim £(lr, И׳) = mn.
55.17.	а-г) Нет.
55.18.	а) Нет, если этот образ отличен от нулевого пространства;
б) ист, если это ядро нс совпадает со всем пространством V'.
55.19.	кп. 55.20. m(n - /).
55.21. Указание, а) Пусть е!	с״ некоторый базис V'. Лля
данного оператора А £ C(V, L) фиксируем какие-либо разложения векторов
.До,..., .4«■״ по подпространствам L\ и Ц: Ас, = u,+v,. Тогда А = А \ +-Д2,
где Не, = и,, Не, = в,, i = 1,п.
55.22.	Указание. Воспользоваться индукцией по к и результатом
предыдущей задачи.
55.23.	Указание. Использовать результат задачи 55.5, пункт б).
55.24.	Указание. Доказать, что im(H + В) = V.
55.27.	У к азан не. Использовать тот факт, что матрицу оператора
ранга г можно представить в виде суммы г матриц ранга 1, н результат
задачи 55.23.
55.28.	Либо кегИ = кег В, либо im H = im В.
55.29.	Пусть в L все операторы имеют ранг нс выше 1, и пусть Н £ L
- произвольный оператор ранга 1. Рассмотрим в L подмножество L\ всех
операторов В для которых кег В Э кегИ, и подмножество /2 всех операто¬
ров С, для которых im С С imH. Согласно 55.19 и 55.20 эти подмножест во
являются подпространствами I. размерности не выше п. Поэтому L\ ф L,
L■} ф L и существует оператор D £ L такой, что D & L\, V & Lг, т.е.
im V ф im A, ker V ф кегН. Но тогда в силу задачи 55.21 rg(H + V) = 2.
55.30.	Нет (см. задачу 55.13).
55.31.	Да Указание. Показать, что если для ненулевых векторов
х. у выполнено Az = Az, •Ду = ру, то А = р.
55.32.	Указание. Построить базис с!,...,еп в V так, чтобы векторы
е!,-• ,en-i образовывали базис кег А, и рассмотреть матрицу оператора в
этом базисе.
55.33.	'־казан и с. Использовать предыдущую задачу.
55.34.	Указание. Пусть ei,...,en - базис в V. Тогда вектор х =
а»е> + ... +а״е״ принадлежит ядру функционала /* тогда и только тогда,
когда од/*(<,)+ .+o״/k(en) = 0. Рассмотреть систему таких соотношений
с к = 1,п.
55.35.	Указание. Воспользоваться результатом задачи 55.34.
55.36.	См. указание к задаче 55.35.
55.37.	См. указание к задаче 55.35.
§56
-V) =
im V,
im(X
-V):
= кег V.
4 3
l6־)
[ 14
-3
\ f 27
-25 1
1 -1
1 51
-11
31 1 (“ ־
-28 J
0 ־
0
-1
־ 1
0
0
-1
־ 0
0
1/2
-1
-1/2
0
-1/2
1
1/2
; НА =
0
1/2
1-
1/2־
0
-1/2
0
0
0
0
а
°J
L-1/2
-1/2
-1/2
0
56.2. АН =

169
Ответы и указания к §56
-1 4 -2
-3
8 -5
2
8 -5
2 -1 -1
;6)
0
-5 -4
(״!
4
5 -4
. -1 о 1 .
. -2
5 -3
3
13 -8
56.4. а) О; 0)0; в) [ J® :JJ ];г) [ _jj }; ״) [ J ? ].
50.6. Нет, неверно.
56.9.	Указание. Показать, что ker Pnim V-(9) и V(\m P) = im V.
56.10.	Указание, а) Использовать задачу 56.9.
56.12.	Матрица порядка n + 1: | q q J, где А - единичная матрица
порядка п - Л + 1 при к < п, и нулевая матрица при к > п.
56.13.	a) (•42?)(ûod־Bil4־4־-־nnln) = flil־b2ct2l‘f4-...־fnanln;
б) (Т>Л)(ао •+־ а! ( + . . + апIя) = До + 2а! ( +... + (n -f 1)а„1"; u) [V, А] — 2
56.14.	Указание. Доказать по индукции, используя результат зада¬
чи 56.13, пункт в).
56.15.	Указан ие. Показать, что след матрицы коммутатора всегда
равен нулю.
56.16.	Пусть А невырожден. Тогда А~'АВ - A~lBA = 1. Но tr(B -
А~' ВА) = 0, a tri ф 0.
56.21.	Указание. Использовать результат задачи 55.32.
56.23. Указание. Использовать результат задачи 56.9.
56.25.	Указание. Использовать результат задачи 56.9.
56.26.	У к азан ие. Использовать результат задач 56.6 и 56.9.
56.27.	Указание. Использовать результат задачи 56.9.
56.28.	Указание. б)=*а) Домножить равенство А\ + ... + Ai = I на
А, и воспользоваться результатом задачи 56.9. а)=>в) Учесть, что в любом
базисе е: rg(A)c = tr(A)c в)=>б) Показать, что V = im Ai ® ... © im А!,.
Из равенства A,z = AiA,z +...+ AkA,z вывести, что А,А, = О при ! ф )
и А3, = А,.
56.29.	Указание. Использовать перестановочность оператора А с
любым проектором.
56.30.	Указание. Использовать результаты задач 55.31 и 56.29.
56.31.	Указание, а) Перейти к матрицам операторов; б,в) приме¬
нить теорему о ранге и дефекте.
56.32.	Указание, а) Использовать соотношение (BA)V = B(im А).
56.33.	Указание. В силу пункта б) задачи 56.32 справедливо соот¬
ношение dim(im Ак П ker Л) = de[Ak*' - del Ак.
56.34.	Указание. Воспользоваться соотношением из пункта б) зада¬
чи 56.32.
56.35.	Указание. Использовать соотношения: t%(BAC) = rg(AC)-
dim(im АС П ker В), rg(BA) = rg(>l) - dim(im А П ker B).
56.36.	У к аз ан ие. Если А־ ф О, то использовать результат задачи
55.31.
56.37.	Указание, а) Использовать неравенство Фробениуса из зада¬
чи 56.35.
56.38.	Указание. Перейти к матрицам операторов в некотором ба¬
зисе пространства V.
56.39.	Указание. Построить оператор В = А так, чтобы включение
ker А С ker А1 было строгим.
56.40.	Указание. Использоваться результаты задач 56.39 и 56.34.
56.41.	5 казание. а) Для операторов A -f 1 и А — Т воспользоваться
результатами задач 55.23 и 56.37, пункт б).

170
Отвогы и указании к §5б
56.44.	Указание Пусть 1т^4 = Л(в|). Проаналмзирова! ь млтрицу
оператора А8 и 6* шее г*, ...,е„.
56.45.	п(п - г).	56.46. п(п - г).
66.47. Указание. Учесть, чго матрицы I	1,глгЛ промэ-
вольная матрица пори два т, перестановочны.
56.48.	Ранг равен вг, дефект равен п(п — г).
56.53.	Оператор, ставящий в соответствие каждой функции се един¬
ственную первообразную, принадлежащую данному пространству.
56.54.	И**1 = П.
56.56.	Указание. Выбрать базис еь . ,.,еп пространства так, чтобы
векторы ез,образовывали базис ксг.4, и рассмотреть матрицы опера¬
торов I — А*7 + Ал этом базисе.
56.57.	Указание. Использовать соотношение из пункта а) задачи
56.31.
56.62. Указание. Пусть Т вырожден, тогда существует ненулевая
матрица А такал, что ТА = О. Положим г = г§; Л, тогда 0 < г < п и суще¬
ствуют невырожденные матрицы Р н С? такие, что РА(3 =
/г о
О О
В та¬
ком случае для любом матрицы X С Кпяп выполнено: |Р/и? +Х|-|Я(?|-1 =
1А + Р-,А'(?-‘| = |^(.4 4	= \Г{Р-'Х<Г‘)| = |Л'|.|Рд|-‘, т.е.
/Мф 4 Л'| = |А'|. Но это неверно, если, например, .V = [ ф / ^ 1 •
56.63.	Указание. Если х 6 кег.Л ненулевой, то /(А)х Ф в вопреки
условию, что /(<) - аннулирующий многочлен.
56.64.	Указание. Учесть, что ^(У, V) = п7.
56.65.	Указание. Использовать результат предыдущей задачи.
56.67. Да, если сИт V' = «Вт И’; нет, если (11т 1г > <Нт V.
56.71.	Указание. Выбрать базисы е в V' и / в IV, образующие
каноническую пару базисов для оператора А.
56.72.	Указание. Использовать построение задачи 56.71.
56.73.	Указание. Использовать построение задачи 56.71.
56.74.	У казанке. Использовать построение задачи 56.71.
56.76. а,б,в) Нет; д) нет при Л ф 1; г,с) да.

Ким I' Д., Кринкой Л. В
АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ:
Теоремы и калачи.
Том II (I)
ИКД "Зерцало-М"
Лицензия № 003601 от 20 ноября 2000 г.
Подписано в печать 28 01 2003.
Формат 60x90/16 Уел печ л. 11.0
Т и раж 2000 эю Заказ № 7470
Отпечатано с готового оригинал-макета
в ПГ1П “Типография “НАУКА"
121099, Москва. Шубинский пер., 6
15ВЫ 5-94373-068-0