В.А. Ясінський
Задачі математичних олімпіад та методи їх розв’язування
ТЕРНОПІЛЬ
НАВЧАЛЬНА КНИГА - БОГДАН


ББК 22.1я7
qoi
° Рецензенти:
завідувач кафедрою прикладної та вищої математики Миколаївського державного гуманітарного університету ім. Петра Могили, професор, заслужений учитель України Лейфура В.М.
завідувач кафедрою алгебри і методики викладання математики Вінницького державного педагогічного університету ім. Михайла Коцюбинського, кандидат педагогічних наук Матяш О.І.
Ясінський В.А.
Я81 Задачі математичних олімпіад та методи їх розв’язування. —
Тернопіль: Навчальна книга - Богдан, 2012. — 208 с.
ISBN 966-692-586-9
Книга розрахована на студентів спеціальностей «Математика», «Математика та інформатика», «Математика і фізика» педагогічних університетів та інститутів, вчителів математики та керівників математичних гуртків, а також учнів загальноосвітніх шкіл.
ББК 22.1я7
Охороняється законом про авторське право.
Жодна частина цього видання не може бути використана чи відтворена в будь-якому вигляді без дозволу автора чи видавництва.
Навчальне видання
Ясінський Вячеслав Андрійович Задачі математичних олімпіад та методи їх розв’язування
Головний редактор Б. Є. Будний Редактор Г.Р. Турчин Художник В.А. Басалига Комп’ютерна верстка О.В. Побережник
Підписано до друку 17.10.2011. Формат 60x84/16. Папір офсетний. Гарнітура Antiqua. Умови, друк. арк. 12,09. Умови, фарбо-відб. 12,09.
Видавництво «Навчальна книга - Богдан»
Свідоцтво про внесення до Державного реєстру видавців ДК №370 від 21.03.2001 р.
Навчальна книга - Богдан, а/с 529, м.Тернопіль, 46008 тел./факс (0352)52-06-07; 52-19-66; 52-05-48 publishing@budny. te.иа \vww.bohdan-books.com
© Навчальна книга - Богдан,
ISBN 966-692-586-9 майнові права, 2012
Друк ВВП «Місіонер». Зам. № 335


§ 1. Метод математичної індукції
Теоретичні відомості
При розв’язуванні багатьох олімпіадних задач іноді використовують метод математичної індукції. Суть цього методу полягає у наступному. Нехай Tv Т2, Т3, ... послідовність тверджень, причому відомо, що:
1) твердження Тх істинне;
2) якщо деяке твердження Tk істинне, то наступне твердження Tk+l також істинне.
Тоді принцип математичної індукції стверджує, що всі твердження цієї послідовності істинні.
Спосіб міркувань, оснований на принципі математичної індукції, називають методом математичної індукції. При цьому доведення істинності твердження Тх називають базою індукції, а доведення того, що з істинності твердження Tk випливає істинність твердження Тм, називають індукційним кроком.
Метод математичної індукції можна застосовувати не тільки для доведення, але і для задания послідовностей. Якщо ми задамо перший член послідовності і, припустивши, що £-й член вже заданий, за його допомогою задамо (k + 1 )-й, то згідно з принципом математичної індукції, вся послідовність буде заданою. Такий спосіб задания послідовності називають рекурентним.
Існують й інші форми принципу математичної індукції. Іноді зручно починати індукцію не з доведення істинності Tv а з доведення істинності деякого Tk. Принцип індукції еквівалентний такій аксіомі: в довільній непорожній множині натуральних чисел є найменше.
Метод доведення деякого твердження для довільного натурального п оснований на такому принципі: якщо твердження справедливе для п = 1 та із справедливості його для п = k випливає істинність цього твердження для п = k + 1, то це твердження справедливе для всіх натуральних п {принцип математичної індукції). Часто доведення за індукцією має форму «спуска»: доведення твердження для деякого натурального п зводиться до того, що твердження справедливе для деякого значення п{ < п\ тут використовується принцип індукції в такій формі: якщо твердження справедливе для п - 1 та (при п > 1) із справедливості його для всіх k< п випливає справедливість для k = п, то твердження справедливе


4
Задачі математичних олімпіад та методи їх розв’ язування
для всіх натуральних п. Іноді зручно починати індукцію не з п = 1, а з п - 0 чи деякого п = nQ.
Задачі
1.1 (7-8). Доведіть, що довільну суму, більшу 7 коп., можна сплатити
монетами вартістю в 3 коп. та 5 коп.
1.2 (8-9). Дійсне число х таке, щох + — — ціле. Доведіть, що для
х
довільного натурального h число хп +— також ціле.
1.3 	(9). Доведіть, що 1 + 3 + б +... +
п(п +1) 2
п(п + 1)(п + 2) 6
1.4 (9-10). Нехай а — ціле непарне число, х та у корені рівняння
t2 + at - 1 = 0. Доведіть, що числа х4 + у* та х5 + у5 — цілі і взаємно прості.
1.5 (9-10). Дано декілька квадратів загальної площі 1. Доведіть,, що їх
можна розмістити без накладань всередині квадрата зі стороною 2.
1.6 (9-10). Довести,-що число, яке записується за допомогою Зл оди¬
ниць, ділиться на Зп. (Мається на увазі десятковий запис).
1.7 (9). Доведіть, що число (і + >/2) можна подати у вигляді а + Ьуі2,
де а і b — взаємно прості цілі числа.
1.8 (9). Послідовність {aj задана рекурентним способом: а, = т, тє N
і 	ап+1 = ап+ 2ая для всіх натуральних п. Доведіть, що серед членів цієї послідовності знайдеться безліч чисел, які діляться на 3.
1.9
(10-11). Доведіть нерівність 1 + —= + —= + ... + —=< 2л/2 3V3 п4п
всіх натуральних п.
1.10 	(10-11). Послідовність {а) додатних чисел неспадна, а послідовність {&„}, де bk = ам - ак для всіх k є N, незростаюча. Доведіть, що
послідовність <
а,
• незростаюча.


Метод математичної індукції
5
1.11 (10-11). На площині задано набір із п векторів, довжина кожного
з 	яких не перевищує 1. Доведіть, що, замінивши деякі вектори цього набору на протилежні, можна одержати набір векторів, сума яких має довжину: а) яка не перевищує >/п; б) яка не перевищує 72.
1.12 (10-11). Опуклий многокутник будемо називати «красивим», якщо
виконуються такі умови: а) кожна його вершина пофарбована в один з трьох кольорів; б) будь-які дві сусідні вершини многокутника пофарбовані в різні кольори; в) для кожного з трьох даних кольорів знайдеться принаймні одна вершина многокутника, пофарбована в цей колір. Доведіть, що будь-який «красивий» я-кут- ник (я > 3) можна розрізати діагоналями, які не перетинаються, на «красиві» трикутники.
1.13 (10-11). Доведіть, що для довільного натурального я справедлива
рівність ^2 + у[2 + ... + уі2 + у/2 = 2cos-^r.
' v ' 2
* п знаків кореня
1.14 (10-11). Доведіть, що при кожному натуральному я число 13 • (-50)" +
+ 17 • 40" - 30 ділиться на 1989.
1.15 (11). Знайдіть натуральні числа а, Ь, с, які не діляться на 10 і такі,
щоб при будь-якому натуральному k у чисел ak + 6* та ск були однаковими дві останні цифри.
1.16 (11). Послідовність {ал} задана рекурентним способом: я, = 1,
а2 = 1 і ап+2 = ап+1 + для всіх я є N. Доведіть нерівність ап < З для будь-якого номера я.
1.17 (11). Послідовність {%п} задана рекурентним способом: х, = 0
і 	%л+1 = 5хл + yj2Axn +1 для всіх я є N. Доведіть, що всі члени послідовності, починаючи з другого, є натуральними числами.
1.18 (11). Дано я довільних квадратів. Доведіть, що їх можна розрізати
на частини так, що із одержаних частин можна було б скласти один великий квадрат.


6
Задачі математичних олімпіад та методи їх розв’ язування
1.19 	(11). На площині дано 2п + 1 точок, які є вершинами опуклого 2п + 1-кутника. Побудуйте 2п + 1-кутник, для якого ці точки є серединами його сторін.
1.20* (11). На скільки частин розбивають простір п сфер, кожні дві з яких перетинаються між собою?
Розв’язки, вказівки, відповіді
1.1. Індукцію ведіть по числу копійок. База. Суму в 8 коп., очевидно, можна сплатити. Крок. Припустимо, що нам вдалося сплатити суму в гі копійок вказаними монетами. Якщо серед них е монета в 5 коп., то замінимо її на дві монети по 3 коп. і одержимо суму в (п + 1) коп. Якщо ж всі монети суми по З коп., то їх не менше трьох і, замінивши три монети по 3 коп. на дві монети по 5 коп., ми також збільшимо суму на 1 коп.
1.2. Застосуйте індукцію по числу п. При цьому скористайтесь тотожністю
х" +
хп~' +
р
X А
х;
1
хл"2 +
1 V
,Л-1
V
1 „ т „ . ... п(л + І)(л + 2)
1.3. 	Індукційний перехід зводиться до перевірки рівності: +
(п + 1)(п + 2) _ (п + 1)(л + 2)(я + 3)
+ 2 б ‘
1.4. Доведіть індукцією по числу п, що числа х" + уп та хл+1 + г/л+1 — цілі та взаємно прості. База. х° + у° = 2; х1 + у1 = —а. За умовою а — непарне, тому а і 2 взаємно прості. Крок індукції. Нехай вже доведено, що хп + у" та хл+І + £/л+1 — цілі взаємно прості числа. Тоді хл+2 + г/л+2 = (хл+| + г/л+1) (х + у} - -хп+ху - хуп+ї = -а (хл+1 + #л+|) + (хл + уп} — ціле число. Нехай d — спільний дільник чисел хл+2 + уп+2 та хл+1 + уп+і. Тоді хл + уп = хл+2 + г/л+2 + а (хл+1 + #л+|)
ділиться на d, тобто d — спільний дільник чисел х” + уп та хл+1 + ул+1.
Отже, d = 1, тобто НСД(хл+1 + £/л+1;хл+2 + £/л+2) = 1.
1.5. Доведіть за допомогою індукції (по числу п) таке твердження: п квадратів загальної площі S можна розмістити всередині квадрата зі стороною 2>/S . Для цього розгляньте найбільший з п квадратів.


Метод математичної індукції
7
1.6. Доведіть за допомогою індукції (по числу п). Скористайтесь тим, що відношення числа, яке записане за допомогою Зя+1 одиниць до числа, яке записане за допомогою Зл одиниць дорівнює 1003" +103" +1 і ділиться на 3.
1.7. Методом математичної індукції доведіть більш загальне твердження: для кожного п є N існують такі взаємно прості числа ап і Ьп, що виконується рівність (і + 72)" =а„+Ь„у/2..
1.8. Доведіть за допомогою індукції (по числу п), що ая+1 = т + 2а' + 2°2 +... + 2а". Далі розгляньте остачі відділення на 3 чисел виду
2°, де ае N.
1.9. Індукційний перехід зводиться до доведення нерівності 2 2 1
-7= - І , —г= для всіх п є N.
Чп -ул +1 \п + lhjn
1.10. Доведіть за допомогою індукції (по числу п) таку нерівність:
/ІЄН
П Л + 1
1.11. 	Обидва твердження доводяться методом математичної індукції.
а) База. Якщо п = 1, то твердження очевидне: І сц |< 1 = >ІЇ. Крок індукції.
Припустимо, що твердження задачі справедливе для довільного набору з п векторів, довжини яких не перевищують одиниці. Розглянемо довільний набір
Г-> -> -» "І
з (л+ 1)-го вектора ш,; о,; ...; ап; ая+1>, довжини яких не перевищують 1. За
—> —»
припущенням, замінивши деякі з векторів а,;
; ап на протилежні, ми діс¬
танемо набір векторів
ність І с |< 7л, покладемо Ьп+1
шуканий,
6,; Ь.2;
для якого виконується нерів¬
де с = 6,+ 62+... + Ьп. Покладемо 6Я+1 = ая+1, якщо с- ая+1 < 0, і
-> -» -» г—> ->-»-> і
= -ая+і, якщо с-ая+1>0. Тоді набір р,; Ь2; ...; Ьп\ *Я+Л —
бо
с+М = М +2-c-WPn+l £
6j+ b.2+... + bn+ b.
л+1
-»
2
->
2
2
с
+
&л + .
< П +
= 1ї +
& n + v
< п + 1 .


8
Задачі математичних олімпіад та методи їх розв’язування
1.12. Скористаємось методом математичної індукції.
База. При п = 3 твердження задачі очевидне: вершини «красивого» трикутника пофарбовані в три різні кольори і ніяких розрізів не треба.
Крок індукції. Припустимо, що твердження задачі справедливе для довільного «красивого» л-кутника (п > 3). Розглянемо довільний «красивий» (п + 1)- кутник і доведемо, використовуючи припущення, що його можна розрізати вказаними діагоналями на «красиві» трикутники. Позначимо че- рез Д.Л^Л},...,Д,,ЛЯ+, — послідовні вершини (п + 1)-кутника. Якщо в деякий
з трьох кольорів пофарбована лише одна із вершин цього (п + 1)-кутника (а така ситуація можлива для «красивого» чотирикутника та п’ятикутника), то, з’єднавши цю вершину діагоналями зі всіма несусідніми з нею вершинами (п + 1 )-кутника, одержимо потрібне розбиття (п + 1 )-кутника на «красиві» трикутники. Якщо ж в кожний з трьох кольорів пофарбовані дві вершини (п + 1)-кутника, то в цьому випадку в фарбуванні довільних вершин (л + 1)- кутника обов’язково беруть участь всі три кольори. Позначимо цифрою 1 колір, в який пофарбована вершина Л,, а цифрою 2 колір вершини Л2. Нехай k (k > 3) — найменший номер, такий, що вершина Ак пофарбована в третій колір. Відріжи- мо від (л + 1)-кутника трикутник Ak_2Ak_xAk. Відповідно з вибором числа k всі вершини цього трикутника пофарбовані в три різні кольори (кожна в один з трьох), тобто цей трикутник «красивий». Многокутник AlA2...Atl_2AkAM:..An+l,
який залишився, також буде «красивим» і за припущенням розбивається на «красиві» трикутники.
1.13. Скористайтесь методом математичної індукції.
База. При л = 1 сформульоване твердження справедливе, бо cos—= —.
4 2
Крок індукції. Припустимо, що твердження справедливе при л = k, і доведемо його справедливість при л = k + 1. Скористаємося тотожністю:
1 + cos а = 2 cos2
а
ЇЇ
Використовуючи припущення індукції, одержуємо:


Метод математичної індукції
9
>/2 + 72+ У~2 + Т2 = ^2 + 2cos-^ - ^2 -2 cos2 = 2 ■ cos ,
Л+1 знаків кореня
тобто при п = k + 1 твердження справедливе. Отже, вказана в умові
задачі рівність, справедлива при всіх п є N.
1.14. 	Скористайтесь методом математичної індукції.
Нехай число хп = 13 • (-50)" + 17 • 40" - ЗО ділиться на 1989, тоді розглянемо число х„+1 = 3-13-17- (40л - (-50)") + хп. Другий доданок: хп — ділиться на 1989 за припущенням, а перший можна перетворити так
З • 13 • 17 • (40 - (-50)) • (40я-‘ + 40л~2 • (-50) +... + (-50)лЧ) =
= 1989-30- (40л~* +... + (—50)л_І).
Тут ми скористалися тотожністю:
ап - Ьп = (а - Ь) (ал_1 + ал’26 +... + abn~2 + Ьп~1),
яку також можна довести методом математичної індукції (зробіть це самостійно). Оскільки Xj = 0 ділиться на 1989, то хп ділиться на 1989 при всіх пе N.
1.15. а = 4, b = 25, с = 29. Далі, користуючись методом математичної
індукції, доведіть, що при всіх натуральних k число 4* + 25* - 29* ділиться на 100, тобто останні дві цифри чисел 4* + 25* та 29* однакові.
1.16. Для доведення твердження задачі достатньо довести нерівність
(»)
для всіх п > 3 (оскільки а, = 1 < 3 і а2 = 1 < 3). Доведемо (♦) методом математичної індукції.
База. При п = 3 маємо:
а3 = а2 +
= =
2* 2 23
При п = 4 маємо:
З 1 7 о 12 2 4 4 24
Крок індукції. Припустимо, що нерівність
аА.<3-? (**)
виконується при всіх k = 3, 4, 5,..., п, п + 1 (п 3). Доведемо, використовуючи це припущення, що нерівність (♦*) справедлива і для k = п + 2. Дійс-
Н0’ а»+2
= Я
п+1


10
Задачі математичних олімпіад та методи їх розв’язування
За припущенням індукції: ап < З
12 2" ’
л+1
<3-
12
2Й+1
Тому,
5і
2й
= ал+І + тг < 3 -
6 1
— 4- — 2" 2й
3-
12
2й
12
12
= 3- — - — <3- — = 3- „.
2й 4й 2й 2Й+2
ч "У
Звідси, згідно з принципом математичної індукції, випливає, що (*) має місце при всіх п є N.
1.17. Скористайтесь методом математичної індукції. Очевидно хп+і-5х„+1.
а
Звідси доведіть, що хл+1 > 1 при всіх п є N. Тоді хп+1 > хп + 1. Далі, з рівності
випливає, щохл+1 - 10хл+1хл + х2 = 1 для всіх п є N. Очевидно, що справедлива і
рівність х2 - 10хлхл_, + х2_, = 1 для всіхп = 2,3,4,.... Віднімаючи почленно від першої рівності другу, одержимо
х«+і “ 4-і ~ 10*л+Л + 10x„xn_, = 0, (хп+1 - х„_,) • (хл+1 + х„_, - 10хл) = 0.
Оскільки хл+1 - х„_, > 2, то хл+1 + хл_, - 10х„ = 0 для всіх п є N, п > 2. Із
рівності хл+1 =10хл -хл_, та умов х, =0, х2= 1, випливає, що х3 — також натуральне. Оскільки х2 та х3 — натуральні, то х4 — також натуральне число і т. д. За індукцією отримаємо хя+1 — натуральне число при всіх п є N.
1.18. 	Скористайтесь методом математичної індукції.
База. При п = 1 твердження задачі доводити немає необхідності.
Крок індукції. Припустимо, що твердження задачі вже доведено для п
квадратів, і нехай дано п + 1 квадратів Kv Kv ..., Кп, Кп+Г Виберемо довільні два квадрати, наприклад, Кп і /Ся+І. Нехай квадрат /Ся+1 більший за квадрат Кп, тобто його сторона х більша за сторону у квадрата Кп (див.рис.). На цьому рисунку показано, як потрібно розрізати квадрат /Сп+1 на частини (чотири рівних чотирикутники AMOQ, BNOM, CPON, DQOP), з яких та з квадрата Кп можна скласти квадрат A'B'C'D'.


Метод математичної індукції
11
Точки Л4, N, Р, Q вибрані так, що AM = BN = CP = DQ = • Далі, згідно
із зробленим припущенням, квадрати /С,, К2, ..., Kn_v A'B'C'D' можна розрізати на частини, із яких можна скласти один «великий» квадрат, що і потрібно було довести.
1.19. Скористайтесь методом математичної індукції.
База. При п = 1 задача зводиться до побудови трикутника по заданих серединах його сторін (достатньо провести через кожну з трьох заданих точок пряму, паралельну до прямої, що з’єднує дві других).
Крок індукції. Припустимо, що ми вміємо будувати (2п - 1)-кутник за серединами його сторін. Нехай нам дано точки Л,, Л2,.... Л2п+|. Побудуємо точку Л, яка є четвертою вершиною паралелограма Л^уДдЛ. Будуємо (2п - 1)- кутник ХхХ2...Х2п_х, для якого точки А, Л4, А5, ...,А,п+, є серединами сторін ХхХ2, Х2Х3, ..., Х2„_,Х, відповідно (його можна побудувати за припущенням (див. рис.)). Нехай Y — точка, симетрична точці X, відносно Л,, a Z — точка, симетрична Х2 відносно Л3. Тоді точки У та Z симетричні відносно Л2, тобто (2п + ^-кутник XxYZX2...X2n_x є шуканим, що і
треба було довести.
1.20. Розгляньте та розв’яжіть послідовно такі задачі, застосувавши індукцію.
А. На скільки частин ділять пряму п пар точок? (Пара точок — це «однови-
мірна сфера»). Відповідь. 2п різних точок прямої ділять її на 2п + 1 частин.
А'. Знайти число ф,(л) частин, на які ділять коло п пар точок, розташованих на ньому. Відповідь. Ф,(п) = 2п.
Б. Знайти число ф2(м) частин, на які ділять площину п кіл, кожні два з
яких перетинаються і розташовані на ній. Відповідь. <р2(п) = п2 - п + 2.
Б'. На скільки частин ділять сферу п кіл, кожні два з яких перетинаються, розташованих на ній? Відповідь. На <р2(л) = п2 - п + 2 частин.
В. Запропонована задача. Відповідь. Ф3(п) =
п(п2 - Зп + 8) З


§2. Цілі числа. Подільність
Теоретичні відомості
У різноманітних задачах про цілі числа використовуються основні поняття і теореми, пов’язані з подільністю. Кожне ціле число а можна розділити на натуральне число пг з остачею, тобто подати у вигляді а = mq + г, де q та г (остача) — цілі числа і 0 < г < пг.
Серед будь-яких т послідовних цілих чисел знайдеться рівно одне число, яке ділиться на пг. Якщо два цілих числа а і b при діленні на число т дають однакові остачі, то говорять, що а конгруентне b за модулем т. Записують це так а = b (mod пг).
•Якщо а і b — натуральні числа і а = bq + г (0 < г < Ь), то найбільший спільний дільник d цих чисел дорівнює найбільшому спільному дільнику чисел b і г; використовуючи це твердження декілька разів можна знайти d як останню не рівну нулеві остачу в ланцюгові ділення з остачею: а = = bq + г, Ь = rq, + г,, r = r,q2 + r2> r, = r2q3 + г3, .... гп-і = гЛи + г„ = ^Чп.2 (алгоритм Евкліда); звідси випливає, що існують цілі числа х та у, такі, що d = ах + by. Зрозуміло, що коли а та b взаємно прості, тобто d = 1, то існують такі цілі числа х та у, що ах + by = 1.
Кожне натуральне число єдиним чином подається у вигляді добутку простих чисел (основна теорема арифметики). Кількість простих чисел нескінченна; доведення цього твердження, запропоноване Евклідом, базується на тому, що добуток простих чисел, збільшений на 1, має відмінні від усіх цих простих чисел множники.
Якщо числа bv b2, ..., Ьп попарно взаємно прості, то для довільних остач гр г2, ..., гп(0 < г. < Ь() знайдеться число а, яке при діленні на Ь. дає остачу г., тобто а = r. (mod b) при і = 1, 2, 3, ..., п (китайська теорема про остачі).
Задачі
2.1 (8-11). Доведіть, що число 1 + 2 + 3 + ... + 1986 не розкладається у
суму квадратів двох цілих чисел.
2.2 (7-11). Доведіть, що не існує таких цілих чисел х, для яких число
1986 + х- є квадрат цілого числа.


Цілі числа. Подільність
13
2.3 (8-11). Доведіть, що число 431988 + б1988 ділиться на 41.
2.4 (7-8). Натуральне число п ділиться на 2 і на 9 та має 14 дільників
(включаючи 1 та п). Знайдіть це число.
2.5 (8-9). Числа piaq — прості. Знайдіть їх, якщо відомо, що рівняння
х4 - рх3 + q = 0 має цілі корені.
2.6 (8-10). Чи має рівняння 19/г + 86/n = 1986& розв’язок у простих
числах?
2.7 (7-8). Доведіть, що для довільного натурального п знайдеться нату¬
ральне т таке, що пт +1 — складене.
2.8 (7-8). Доведіть, що число 19792 + 21979 взаємно просте з числом
1979.
2.9 (8-9). Було 4 аркуші паперу. Деякі з них розрізали на 8 частин,
після деякі з цих частин знову розрізали на 8 частин і т. д. Коли підрахували загальну кількість аркушів, то з’ясувалося, що їх всього 1986. Доведіть, що підрахунок був неправильний.
2.10 (9). Скількома нулями закінчується число, що дорівнює добутку
всіх натуральних чисел від 1 до 1984 включно?
. . - 8/2 + 71
2.11 (8-9). При яких натуральних п дріб — є скоротним?
Ьп + 46
2.12 (8-9). Доведіть, що число я2 + 5я + 16 ні при якому натуральному
п не ділиться на 169.
2.13 (9). а) Знайдіть найменше натуральне число, таке, що його сума
цифр та наступного за ним числа ділиться на 7;
б) 	Доведіть, що серед будь-яких 13 послідовних натуральних
чисел знайдеться число з сумою цифр, яка ділиться на 7.
2.14 (9). Доведіть, що існують безліч цілих чисел, які є точними квадра¬
тами і залишаються такими ж після дописування до них справа одиниці (в десятковому записі).
2.15 (9). Знайдіть всі пари натуральних чисел х, у таких, що 2х +1
ділиться на у та 2у + 1 ділиться на х.
2.16 (9). Яких чисел більше серед цілих чисел від 1 до 1000000 включ¬
но: а) тих, що діляться на 11, але не діляться на 5, чи тих, що діляться на 12, але не діляться на 7? б) тих, що діляться на 13, але не діляться на 6, чи тих, що діляться на 15, але не діляться на 26?


14
Задачі математичних, олімпіад та методи їх розв'язування
2.17 (9). Числа х та у — цілі, причому число 6% + ііу ділиться на 31.
Доведіть, що число х + 7у також ділиться на 31.
2.18 (9). Відомо, що п - 1 ділиться на 15, а 1001 ділиться на п + 1.
Знайдіть значення п.
2.19 (9). Знайдіть всі натуральні числа я, для яких число п3 + 3 ділиться
на п + 3.
2.20 (9). Доведіть, що з довільних 100 натуральних чисел можна вибра¬
ти декілька чисел так, щоб їх сума ділилась на 100.
2.21 (9). Доведіть, що число п4 + 64 є складеним.
2.22 (9). Доведіть, що число 210 + 512 є складеним.
2.23 (9). Знайдіть всі цілі значення х, при яких вираз набуває
Зх + 4
цілих значень.
2.24 (9). Натуральні числа т і п такі, що т > п, т не ділиться на п і має
при діленні на п таку ж саму остачу, що і т + п при діленні на т - п. Знайдіть відношення т : п.
2.25 (9). Нехай т,п — різні натуральні числа, причому т — непарне.
Доведіть, що 2/л - 1 та 2Л + 1 взаємно прості.
2.26 (9). Доведіть, що число 1984 • 1985 • 1986 • 1987 + 1 є точним квадратом.
2.27 (9). Доведіть, що ні для якого натурального числа п число п4 + 2/г3 + 2гї2 + 2п + 1 не може бути точним квадратом.
2.28 (9-11). Доведіть, що число М = 19841984 + 19851985 + 19861986:
а) 	ділиться на 3; б) не є квадратом цілого числа.
2.29 (9-10). Доведіть, що не існує простих чисел А, В, С, D таких, що
Л2 + В2 + С2 + D2 = ABCD + 4.
2.30 (9-10). Число а + — — ціле. Доведіть, що число ап +— також
а ап
ціле при довільному цілому п.
2.31 (9-10). Доведіть, що існують 1988 попарно взаємно простих чисел
таких, що сума довільних декількох з цих чисел є число складене.
2.32 (9-10). Доведіть, що число 16я - 15/г - 1 ділиться на 25 для всіх
натуральних п.


Цілі числа. Подільність
15
2.33 (10). Знайдіть всі цілі числа я, для яких модуль тричлена я2 - 7п + 10 буде простим числом.
2.34 (10). У послідовності {ял}•: Щ = и2 = 1, яя+2 = ял+1 + и* (я > 1). Чи ділиться число я,986 на 7?
2.35 (10). Знайдіть найбільший спільний дільник чисел А = 21986 - 1 таВ = 21983 - 1.
2.36 (10). Знайдіть всі цілі k, для яких k5 + 3 ділиться на &2 + 1.
2.37 (10). Ціле число а має властивість: число За можна подати у виг¬
ляді х2 + 2р2, де х та у — цілі числа. Доведіть, що і число а можна подати в такому ж вигляді.
2.38 (11). Нехай р — просте число, більше 2. Знайдіть суму остач від ділення чисел 1Р, 2Р, ..., (р - 1)р на р2.
2.39 (10-11). Чи може число 101010... 10 (1983 одиниці і 1983 нулі) бути поданим у вигляді суми або різниці двох квадратів цілих чисел?
2.40 (10-11). Нехай ап — сума я перших простих чисел. Доведіть, що для будь-якого натурального я відрізок [яя; яя+І] містить квадрат натурального числа.
2.41 (10-11). Чи ділиться число на 1980?
2.42 (10-11). Всі натуральні числа довільним чином розбиті на дві мно¬
жини. Довести, що хоча б в одній з них знайдуться три числа, одне з яких є середнім арифметичним двох інших.
2.43 (11). Чи можна знайти 1984 натуральних числа, які ідуть підряд,
таких, що серед них немає жодного простого числа?
2.44 (11). Нехай Р(х) = х2 + ах + Ь, де а та b — цілі числа. Доведіть, що
знайдеться таке ціле N, що всі числа P(N + 1), P(N + 2), ..., P(N + 1989) — складені.
2.45 (11). Після декількох операцій диференціювання і множення на х + 1 виконаних у певному порядку, многочлен х8 + х7 перетворився в ях + Ь, де я та 6 — цілі числа. Доведіть, що різниця а - b ділиться на 49.


16
Задачі математичних олімпіад та методи їх розв’язування
Розв’язки, вказівки, відповіді
1 + 1986
2.1. Візьмемо до уваги, що 1 + 2 + 3 + ... + 1986 = • 1986 =
= 1987 • 993. Нехай існують такі цілі числа х та у, що 1987 • 993 = х2 + у2. Оскільки 1987 • 993 — число непарне, то одне з чисел повинно бути парним, а друге — непарним. Тоді число х2 + у2 при діленні на 4 дає остачу 1, а число 1987 • 993 при діленні на 4 дає остачу 3.
Отже, рівність 1987 • 993 = х2 + у2 не виконується при жодних цілих значеннях х та у.
2.2. Припустимо, що існує таке ціле число х, що 1986 + х2 = у2. Запишемо це рівняння у вигляді 1986 = у2 - х2 (*). Звідси випливає, що х і у повинні бути одночасно парними або непарними. В обох випадках у2 - х2 = (у - х)(у + х) ділиться на 4. Але права частина (*), тобто 1986, не ділиться на 4.0тже, не існує такого цілого числа х, щоб 1986 + х2 = у2.
2.3. 431988 + б1988 = 21988 + 21988 • З1988 = 21988 • (1 + З1988) = 21988 • (1 + 81497) = = 2’988 • (1 + 81) • N = 21988 • 82 • N а 0 (mod 41). Тут ми скористались відомим
фактом: (я2я+І + ft2n+l):(a + ft) при всіх п є N.
2.4. Відповідь. N = 2 • З6.
2.5. Відповідь, р = 3, q = 2.
2.6. Відповідь. Ні. Просте число п — парне, бо 19л = 1986& - 86/л, отже п= 2. Але тоді 43 • (т - k) = 19 • (50£ - 1). Права частина рівності непарне число, тобто т та k різної парності і, отже, k = 2 , але 19 • 99 не ділиться на 43.
2.7. Можна вибрати, наприклад, т = п + 2.
2.8. Кожний спільний дільник чисел 19792 + 21979 та 1979 є дільником числа 21979, але 1979 і 21979 взаємно прості.
2.9. При кожному розрізанні аркуша паперу, загальна кількісь аркушів збільшується на 7. Отже, після п розрізань ми дістанемо 7л + 4 аркушів. За умовою це число повинно дорівнювати 1986. Отже, 4 + 7л = 1986, тобто 7л = 1982. Оскільки число 1982 не ділиться на 7, то л не може бути цілим, тобто підрахунок був неправильний.
2.10. Кількість нулів, якими закінчується число N = 1 • 2 • 3 • ... • 1984, дорівнює кількості пар множників 2 і 5, які можна утворити після розкладу числа N на прості множники. Тому, необхідно підрахувати, скільки разів множ¬
ник 5 входить у такий розклад (виявляється, що
1984
625
1984
1984
25
разів), та переконатися в тому, що множників 2
1984
125
буде біль¬
+
+
ше ([%] — ціла частина числа х). Відповідь. 493 нулі.


Цілі числа. Подільність
.17
2.11. Зазначимо, що
8п + 71 Зл + 25
5л + 4б " 1 + + 46 ’ тому даний дріб буде скорот-
Зл + 25 5л + 46
ним тільки тоді, коли скоротним є дріб - —, а звідси й дріб т Далі,
5 л + 46 дп + 2о
послідовно одержуємо, що скоротність вихідного дробу еквівалентна скорот-
Зл + 25
ності дР°бів ТТїїї
5л + 46 _ 2л + 21 . 2л+ 21 Зл + 25 Зл + 25 ’ л + 4
(бо
Зл + 25 2л + 21
. л + 4 13 2л+ 21 о 13
= + ТТЇЇЇ ) 1 ЇЇ7Ї (б° 77Г її?4 >' Останній 3 одержаних дробів
скоротний тоді і тільки тоді, коли його знаменник ділиться на 13, тобто коли л = 136 - 4, де k є N. Зауваження-, фактично ми застосовували алгоритм Евкліда. Відповідь, л = 136 - 4, де 6 є N.
2.12. Зазначимо, що л2 + 5л + 16 = (л — 4)2 + 13л. Це число повинно ділитися на 13, тому л - 4 теж повинно ділитися на 13, тоді (л - 4)2 ділиться на ІЗ2 = 169 , але другий доданок 13л не ділиться на 169 при л = 136 + 4, 6 є N.
2.13. а) Нехай число а, яке має суму цифр 6, закінчується точно л дев’ятками (л = 1, 2, 3, ...). Тоді сума цифр числа а + 1 дорівнює 6 + 1 - 9л. Тому число 9л - 1 повинно ділитися на 7. Найменше таке число дорівнює 35. Далі підбором знаходимо відповідь: 6999; б) Серед 13 послідовних натуральних чисел, як мінімум, 7 належить одному і тому ж десятку. Суми їх цифр — 7 послідовних натуральних чисел, тому одна з них обов’язково ділиться на 7. Число 13, в умові задачі, не можна замінити меншим: серед дванадцяти чисел 994, 995, .... 1005 немає жодного з сумою цифр, що ділилась би на 7.
2.14. Будуємо безліч пар (лі; 6) натуральних чисел таких, які задовольняють умову Юлі2 + 1 = б2. Першу таку пару знаходимо підбором: т = 6, 6 = 19, (б2 = 36, 192 = 361). Далі достатньо показати, що коли Юлі2 + 1 = б2,то 10(2лі6)2 + 1 = = 40лі2(10лі2 + 1) + 1 =400лі4 + 40/л2 + 1 = (20лі2 + І)2. Отже, з пари (лі; 6), яка задовольняє умову задачі, можемо побудувати нову пару (2лг6; 20лі2 + 1) чисел, які, очевидно, будуть більшими за попередні і також будуть задовольняти умову задачі. Це і дозволяє створити нескінченну множину таких пар.
2.15. Число 2х + 1 непарне і ділиться на у, тому у непарне також; аналогічно х — непарне. Числа х та у взаємно прості: якщо х і у діляться на р, то 2х і 2х + 1 теж діляться на р, і , отже, 1 ділиться на р, тобто р = 1. Число 2х + 2у + 1 ділиться на х і на у, тобто воно Ділиться на ху. Тоді 2х + 2у + 1 > ху. Нехай х < у, тоді або 2х + 2у + 1 < 5р, або х = у = 1. В обох випадках ху < 5у, отже, х < 5. Тому, х = 1 і 2х + 1 = 3 ділиться на у або х = 3і2х+1=7 ділиться на у. Відповідь. (1; 1), (1; 3), (3; 1), (3; 7), (7; 3).


18 Задачі математичних олімпіад та методи їх розв’язування
2.16. 	Якщо р і q взаємно прості і N ділиться на pq, то серед чисел 1, 2, 3,....
N маємо рівно — чисел, що діляться на р і рівно —, що діляться на pq. Р РЯ
Отже, серед чисел 1, 2, .... N маємо рівно
N N N(q-1)
чисел, що ділять-
р pq pq
ся на р і не діляться на q. а) Число 997920 ділиться на 11 • 5 і на 12 • 7. Тому, 997920 • 4
згідно з зазначеним вище, серед чисел 1, 2,..., 997920 маємо
55
= 72576
чисел, що діляться на 11, але не діляться на 5 і
997920-6
12-7
= 71280 чисел, що
діляться на 12, але не діляться на 7. Отже, перших чисел більше, і 2080 чисел, що залишились до 1000000 цього балансу не, змінять: серед них, чисел, що діляться на 11 (також і на 12) менше ніж 200. б) Аналогічно до попереднього серед чисел 1,2,..., 999960 тих, що діляться на 13 і не діляться на 6, є 64100, а тих, що діляться на 15, але не діляться на 26 — стільки ж (тому, що
5 25
= ). Оскільки віднімання числа 999960 не змінює подільності ні
13-6 15-26
на жодне з чисел 13, 5, 15, 26, серед чисел, які залишились до 1000000, таких, що нас цікавлять стільки ж, скільки їх серед чисел 1, 2, ..., 40. А серед цих чисел перших маємо три: 13, 26, 39, а других — два: 15, ЗО. Відповідь, а) перших більше; б) перших більше.
2.17. Скористайтесь рівністю 6(х + Ту) = (6% + 11р) + Зір. Крім того, НСД(6;31)= 1.
2.18. 1001 = 7 • 11 • 13, тому всі дільники числа 1001 — це такі числа: 1, 7, 11, 13, 77, 91, 143, 1001. Перевіркою переконаємось, що умову задовольняє число 76. Відповідь. 76.
2.19. З рівності п3 + 3 = (п3 + 27) - 24 = (п + 3)(п2 - Зп + 9) - 24 випливає,
що число п + 3 є дільником числа 24. Відповідь. {1; 3; 5; 9; 21}.
2.20. Нехай а,, а2, а3, ..., а100 — дані числа. Розглянемо числа av ах + а,, а, + а2 + ау .... а, + а2 + ... + а100. Якщо жодне з цих чисел не ділиться на 100, то серед них знайдуться два, які при діленні на 100 дають однакові остачі. Залишається від більшого з них відняти менше.
2.21. гі* + 64 = (п~ +8) — 16п2 = (п2 + 4zi + 8) (п~ — 4п + 8).
2.22. 210 + 5'2 = (25 + 56)2 - 2 • 25 • 5s = (25 + 5s)2 - (23 ■ 53)’ =
= (25 + 5б + 23 ■ 53)(25 + 55 - 23 ■ 53).


Цілі числа. Подільність
19
7х +1
2.23. Якщо х < -6 або х > 7, то 2 < < 3.
Зх + 4
2.24. Нехай т = ап + с, т + п = Ь(т - п) + с, де а > 1, b > 1, с < п, с < т — п. Якщо а = 1, то с = т - п, що суперечить попередньому. Отже, а > 1, звідси
т > 2п, п <
Зт
~2
т
7;
т + п <
т
т
п>~^ і b < 3. Залишаються можливості b = 1
та b = 2. Якщо &=1,то/я + л = /л-п + стас = 2п, що не можливо, оскільки с < п. Отже, b = 2, т + п = 2(т - п) + с, т = Зп - с; звідки а = 2, т = 2п + с,
с = — і т = —. Відповідь. 2 2
5
2
2.25. Нехай d — спільний дільник чисел 2'" - 1 та 2" + 1, а саме 2т - 1 = Ad та 2й + 1 = Bd. Тому 2тп =(Ad + 1)й = (Bd - l)m. Бачимо, що число 2тй дає при діленні на d остачу 1 і в той же самий час остачу d - 1. Але зрозуміло, що d > 2; тому 1 * d - 1. Протиріччя.
2.26. Позначте 1984 через п, тоді 1984 • 1985 • 1986 • 1987 + 1 = п(п + 1) х х (п + 2)(л + 3) + 1 = (п2 + Зя)(/г2 + Зп + 2) + 1. Далі, позначте гі* + Зп + 1 = т, одержимо, що 1984 • 1985 • 1986 • 1987 + 1 = (т - 1)(/га + 1) + 1 = т2.
2.27. (гі2 +я)2 =п4 + 2я3 + л2 <п4 + 2п3 + 2п2 + 2п + 1<п4 + 2п3 + 3п2 +2п + 1 =
= (п2 + п +1)2.
2.28. а) При діленні на 3 перший доданок дає в остачі 1, а другий 2, а третій ділиться на 3. Отже, число М ділиться на 3. б) Число закінчується цифрою 7, а тому не може бути точним квадратом.
2.29. Покажіть, що хоча б одне з чисел A, В, С, D дорівнює 2 (інакше ліва частина рівняння ділиться на 4, а права — ні). Рівняння з трьома невідомими досліджується аналогічно.
= а* + і
а
2.30. При k = 1, 2 числа
— цілі, оскільки — ціле, а чис¬
ло b2=b2 - 2. Крім того, bM =bx-bk- bk_v для всіх цілих k.
2.31. Відповідь. Умову задачі задовольняють, наприклад, числа а{ = 1988! + 1, а2 = 1988! -2+1, ..., а1988= 1988! • 1988+ 1. Ці числа взаємно прості, бо спільний дільник двох чисел ділить І їх різницю, тобто є дільником числа 1988. Сума довільних п даних чисел ділиться на п.
2.32. Скористайтесь індукцією.
2.33. Добуток І п - 21 • І п - 51 буде простим числом тоді і тільки тоді, коли один із співмножників дорівнює одиниці, а другий при цьому є простим числом.


20
Задачі математичних олімпіад та методи їх розв’язування
2.34. Нехай vn — остача від ділення числа ип на 7. Легко підрахувати декілька перших членів послідовності {uj: и, = 1, о2 = 1, и3 = 2, v4 = 5, v. = 1, и6 = 5, v7 = 5, v3 = 1 і т.д. Оскільки пара (и4; и5) збігається з парою (и7; о8), то послідовність {ил}, починаючи з четвертого члена, періодична з періодом З, тобто ил+3 = vn при п > 4. Тому серед членів послідовності {о} немає нуля.
2.35. Оскільки А - В = 21986 - 2*983 = 7 • 21983 і числа А та В — непарні, то їх найбільший спільний дільник дорівнює 7 або 1. Але А = 21986 - 1 = = (23 - 1)(21983 + 21980 + ... + 2 + 1) (ми скористались формулою скороченого множення) ділиться на 7, а тоді і В = А - (А - В) ділиться на 7. Відповідь. 7.
2.36. Оскільки kb + 3 = (k3 + £)(£2 + 1) + (k + 3), то k5 + 3 ділиться на k2 + 1, тоді, коли £ + 3 = 0, тобто коли k = -3. Хоча при малих k може бути, що k + З ділиться на £2 + 1. Тому необхідно перевірити, що відбуватиметься при |£| < 3. Відповідь, k є {-3; -1; 0; 1; 2}.
2.37. Оскільки х2 + 2у2 ділиться на 3, то х2 - у2 також ділиться на 3, тому х + у (а тоді і х - 2у), або х - у (а тоді і х + 2у) діляться на 3. Тому одна з двох
х2 + 2у2
рівностей — =
О
дає розв’язок задачі.
2.38. При розкритті дужок у біномі Ньютона (р -т)р = рр - С'ррр~'т +...
множник р2 буде присутнім в усіх доданках, крім останнього: -тр. Отже, тр + (р - т)р ділиться на р2. Оскільки при т = 1, 2, 3,..., р числа т? та (р - т)2 на р2 не діляться, то сума остач від ділення цих чисел на р2 дорівнює р2. Тоді сума остач від ділення на р2 чисел Р, (р - 1)р, 2р, (р - 2)р (всього — пар)
V
V
'х-у^
х-2р
Х + у
х2 + 2у2
х + 2у
+ 2
+ 2
. 2 Р
дорівнює р • .
2
2.39. Це число ділиться на 3 і не ділиться на 9. Відповідь. Ні.
2.40. Достатньо показати, що ^а~п > у/ап_} +1. Остання нерівність еквівалентна нерівності (ая_, -ап +1)2 - 4а„_, > 0. Вираз зліва не спадає по п, починаючи з п > 4.
2.41. Вказане число не ділиться на 4.
2.42. Нехай М — одна з двох множин, а, b є М і а < b < 2а, а + b — парне (такі а та b знайдуться, інакше в другій множині будуть три послідовних чис-
\ л . 2Ь -а + а .
ла). Оскільки - = о, то можна вважати, що 2b - a g М; аналогіч-


Цілі числа. Подільність
21
но 2а - b £ М. Залишилось зауважити, що
2а-Ь + 2Ь-а
, причому це
число попадає або в множину ТИ, або в її доповнення до N.
2.43. Розгляньте 1984 натуральних числа, які йдуть підряд за числом 1985! + 1. Відповідь. Можливо.
2.44. Візьмемо натуральне число т, яке більше за довільний розв’язок рів¬
няння Р(х) = 0 і більше за
а
2’
та покладемо N = Р(т + 1) • Р(т + 2) •...
• Р(т + 1989) + т. Оскільки різниця Р(с) - P(d) ділиться на с - d, то різниця P(N + п) - Р(т + п) ділиться на N - т, і якщо 1 < п < 1989, то P(N + п) ділиться на Р(т + л). В той же час P(N + п) > Р(т + л), бо Р(х) зростає при х> т. Отже, P(N + л) — складене число.
Зауваження. Ці міркування можна застосувати до довільного многочлена, степінь якого не менший 1, з цілими коефіцієнтами та додатним старшим членом; вони показують, що для довільного такого многочлена знайдеться скільки завгодно послідовних натуральних чисел, значення многочлена в яких є складеними числами.
2.45. 	Зробіть заміну у = х + 1. Тоді вираз х8 + х7 (1) перетвориться в многочлен виду у8 - Ту1 + ... (2), а вираз ах + b у вираз ау - (а - Ь). Множенню виразу (1) на х + 1 відповідає множення виразу (2) на у.


§3. Цифри і системи числення
Теоретичні відомості
У задачах, де йдеться про цифри в десятковому записі натурального числа N - а • 10" + а • ІО"-1 + ... + а, • 10 + ап (цей запис іноді
позначають ) використовуються різні міркування: поділь¬
ність чисел, алгебраїчні перетворення, оцінки. Зокрема, допомагають ознаки подільності на 3 і на 9, а також таке її уточнення: число
N = дає при діленні на 9 (на 3) таку ж остачу як і сума
його цифр ап + ап_х + ... + ах + а0 (різниця N - (ап + ап_х ± ... + а, + а0) = = ап • (10л - 1) + ап_х • (10я-1 - 1) + ... + а, ♦ (10 - 1) + а0 очевидно ділиться на 9).
Іноді буває зручним запис натурального числа N в системі числення з основою р: N = ап • рп + ап_х • рп~х + ... + ах • р + а0, де а., 0<а.< р (і = 1, 2, ..., п) — «цифри» цієї системи числення.
Задачі
3.1 (7). Число а ділиться на 99. Доведіть, що сума його цифр не менша
за 18.
3.2 (7). Сказав Кощій Івану-царенку: «Жити тобі до завтрашнього ран¬
ку. Ранком з’явишся перед мої очі, я загадаю три цифри а, Ь, с. Ти назвеш мені три числа: х, у, z. Вислухаю я тебе і скажу, чому дорівнює вираз ах + by + cz. Тоді відгадай, які а, Ь, с я загадав. Не відгадаєш — голову зніму». Засмутився Іван-царенко, пішов думу думати. Треба йому допомогти. Як?
3.3 (7-9). Знайдіть найменше натуральне число, сума цифр якого дорів¬
нює 1982.
3.4 (7-8). В десятизначному числі N = а[а2...а10 цифра ах збігається з
кількістю одиниць в записі N, а2 — з кількістю двійок, а3 — трійок, ..., а10 — кількістю нулів. Знайдіть число N.
3.5 (7-8). Довести, що останні цифри в послідовності чисел 1-2-3,
2-3-4, ..., (п- 1) • п • (п + 1) періодично повторюються.


Цифри і системи числення
23
3.6 (8-9). Нехай р — просте число, р > 3. Відомо, що для деякого
натурального п число рп містить 20 цифр. Довести, що серед них принаймні 3 однакових цифри.
3.7 (8-9). Знайдіть всі двозначні числа, квадрат яких дорівнює кубу
суми цифр цих чисел.
3.8 (8-9). Знайдіть всі натуральні числа N = ala2...an такі, що
2aP..anl: Ц...ап2 = 21:12.
3.9 (8-9). Доведіть, що число 1010010...1...01, яке складається з 1982
одиниць і 1+2 + ... + 1981 нулів, можна помножити на деяке натуральне число таким чином, щоб в записі добутку не було жодного нуля.
3.10 (9). Доведіть, що коли А та В — довільні цифри, відмінні від нуля,
то ABBA - ВАВА = АВАВ - ВААВ.
3.11 (9). Чи можна з цифр: а) 1, 2, 3, ..., 9; б) 2, 3,. 4,..., 9 скласти
кілька чисел, сума яких була б точним квадратом? (Кожна цифра використовується лише один раз).
3.12 (9-10). Доведіть, що коли в десятковому записі числа —-—
99...92
' V '
1984
зустрічається 20 дев’яток записаних підряд, то така ж послідовність з 19 дев’яток присутня в записі числа - .
12499...9
v/
1984
3.13 (10-11). Доведіть, що всі натуральні числа від 1 до 1986 не можна
записати підряд у такому порядку, щоб число, яке утвориться, було квадратом цілого числа.
3.14 (11). Якщо в деякому натуральному числі, що не закінчується нулем, закреслити одну з цифр, то воно зменшиться в ціле число разів. На якому місці може стояти цифра, яку закреслили?
3.15 (11). З таблиць відомо, що lg7i = 0,4972.... Скількома знаками записується число [я100]?


24
Задачі математичних олімпіад та методи їх розв'язування
Розв’язки, вказівки, відповіді
3.1. Скористайтесь ознакою подільності на^ІІ. Якщо а = a„an_,...a,a0 ділиться на 99, то воно ділиться на 11, тобто (а0 + а2 + а4 + ...) - (а, + а3+ + а5 +...) — ділиться на 11. Далі, скористайтесь ознакою подільності на 9.
3.2. Потрібно, щоб Кощій дав відповідь у вигляді тризначного числа
abc = 100а +106 + с. Відповідь, х = 100, у = 10, z = 1.
3.3. Відповідь. N = 299. ..9 (всього 221 цифра).
3.4. Відповідь. 2100010006.
3.5. Доведіть, що число (п + 10 - 1)(п + 10)(п + 10 + 1) - {п - 1)л(л + 1) ділиться на 10.
3.6. Припустимо протилежне. Тоді число рп складається з цифр 0, 0, 1, 1,2,
2,..., 8, 8, 9, 9, а тому ділиться на 3.
3.7. Відповідь. 27.
3.8. Відповідь. N = 33...З (п цифр; п — довільне натуральне число).
3.9. Цифри множника можна підбирати послідовно, почавши з останньої.
3.10. Скористайтесь поданням xyuv = 1000% + 100 г/ + 10u + v.
3.11. а) Так; 1 + 2 + 3 +45+ 6 + 7 + 8 + 9 = 81. б) Ні. Квадрат натурального числа при діленні на 3 не дає в остачі 2.
3.12. Десятковий запис першого числа одержується з запису другого множенням на 8 і перенесенням коми.
3.13. Утворене число ділиться на 3, але не ділиться на 9. Отже, воно не може бути квадратом цілого числа.
3.14. Нехай число Y одержується з числа X викиданням т-ї цифри. Приклади показують, що т може дорівнювати 1 або 2 (можна взяти X = 66, У = 6). Припустимо, що т > 3. Запишемо: X = А • 10”+1 + В • 10" + С, У = А • 10” + С. Маємо С < 10”, В < 9 та якщо т > 3, то А > 10. Тоді X - 10У = В • 10” - 9 • С,
-9 • 10” < -9С < В • 10” - 9 • С < В • 10" < 9 •10", звідси
|Х- 10У| < У, 9- У<Х< 11 • У.
Тому, якщо X ділиться на У, то X : У = 10, що суперечить тому, що X не закінчується нулем.
3.15. 49 < lg(7i,0°) < 50. Відповідь. 50.


§4. Числа раціональні та ірраціональні
Теоретичні відомості
Будь-яке раціональне число а можна подати у вигляді а = —, де п
те Z, п є N, а також у вигляді періодичного десяткового дробу. Десяткові дроби, що представляють ірраціональні числа, не періодичні.
У багатьох задачах, разом з ірраціональним числом а + b4d (де а і b — раціональні числа, d — ціле, яке не є квадратом натурального числа) доцільно розглянути «спряжене» до нього число а - byfd : його
сума і добуток з даним — раціональні числа. Тому числа виду а ± b4d є коренями квадратного рівняння з цілими коефіцієнтами.
Задачі
4.1 (8-9). Числа р, q, Jp +y/q — раціональні (р > 0, q > 0). Доведіть,
що числа у[р та y[q — теж раціональні.
4.2 (9-10). Числа а і b — ірраціональні, а число г — раціональне. Які з
вказаних чисел можуть виявитися раціональними: а + Ь, а + г, 4а, 4r, ab, аг, -J a + r, yja + 4b, >]а + 4г, ^г + 4а ?
/ г—\1981
4.3 (9). Доведіть, що число 11 + V2 1 можна подати у вигляді а + b4%,
де а та b — цілі взаємно прості числа.
4.4 (10). Чи існують на площині точки А, В, С такі, що для будь-якої
точки Р цієї площини хоча б один з відрізків PA, РВ, PC був ірраціональним числом?
71
4.5 	(10-11). Доведіть, що число cos— при будь-якому пе N і п>2
ірраціональним числом.


26
Задачі математичних олімпіад та методи їх розв'язування
4.6 (10). Яким є число л/73 — 12л/зУ -773 + 12737 — раціональним
чи ірраціональним?
4.7 (9-10). Знайдіть всі цілі числа п, для яких число Уі 1 + бУп +
+7l 1 - бУя — натуральне.
4.8 (10-11). Із нескінченної послідовності 1; 0,1; 0,01; 0,001; ... викрес-
літь елементи, номери яких є квадратами натуральних чисел. Доведіть, що сума чисел, яка залишилась — число ірраціональне.
4.9(11). Знайдіть всі значення Ь, при яких вираз f{n) =
f.
Y
Y
1 + Тб
1-75
натуральних n.
4.10 	(11). Доведіть, що коли ф,, У^ф,, 72tg(p2, ...» T2tg(prt
приймає цілі значення при всіх
<Р2> •••, Ф„ — дійсні числа, такі, що раціональні, а суми ф1 + ф2 + ... + (рт
= b
не дорівнюють —+ 7С& при довільному т = 1, 2, 3, ..., п і довіль- 2
ному k є Z, то число72tg^ + ф2 +... + фп) також раціональне.
4.11 (11). Послідовність {хд} задана рекурентно в такий спосіб: х1 = 0
і 	ха+1 = 5хп +-у]24х2п +1 для пє N. Чи є серед її членів ірраціональні числа?
4.12 (11). Доведіть, що при будь-якому натуральному п рівняння
-(% + £/ 7з)"=7Г7Тз не має розв’язків у раціональних числах х та у.
4.13 (11). Доведіть, що число log418 є ірраціональним.
Розв’язки, вказівки та відповіді
4.1. 	Скористайтесь рівністю у[р =
Р ~ Я + (Ур + 7? )
2(Ур + 7?)


Числа раціональні та ірраціональні
27
4.2. Відповідь. а + b, yfr, ab, аг, yja + yfb, у/a + л/r. Для кожного з випадків вкажіть свої конкретні числа а, b та г.
4.3. Доведіть більш загальне твердження: для кожного п є N існують такі
взаємно прості цілі числа ап та Ьп, що виконується рівність (і + 72 = ап+ Ьп-^2.
Скористайтесь методом математичної індукції.
4.4. 	Відповідь. Такі точки існують. Нехай А і В — дві точки площини,
відстань між якими дорівнює 72, С — середина відрізка АВ. Нехай Р —
довільна точка площини, яка не лежить на прямій ЛВ. Добудуємо АЛРВ до паралелограма APBQ. Оскільки для довільного паралелограма має місце рівність: AB2 + PQ2 = = 2(РЛ2 + РВ2), то враховуючи PQ = 2РС, дістанемо:
ЛВ2 = 2РЛ2 + 2РВ2 - 4РС2 (*).
Оскільки ЛВ2 = у/2, а число у/2 — ірраціональне, то числа РЛ, РВ, PC не можуть бути одночасно раціональними. Якщо ж точка Р лежить на прямій ЛВ, то рівність (*) також справедлива (доведіть це самостійно), тому твердження задачі доведено.
л ті
4.5. 	Нехай ап = cos — , де п = 2, 3, 4, 5, ... Тоді сц - cos — = —- — число
2 4 2
ірраціональне. Далі доведіть, методом від супротивного, таке твердження: якщо число ап — ірраціональне, то число л;і+1 — також ірраціональне: а*+, = .
4.6. V73 -12Т37 - д/73 +12>/37 = (Т37 - б) - (Т37 + б) =-12 — раціональне число.
4.7. Відповідь, п = 2. Нехай а = у]іі + §4п + -\Д 1- бТл. Оскільки
11-бТл >0, то 0 < п < 4. Число а2 =22+ 27121-36л також натуральне.
Число 121 - 36л повинно бути непарним, бо а2 не може давати остачу 2 при діленні на 4. Тому, п — парне число, тобто п - 2 або л = 0. У першому випадку а = б. Другий випадок відпадає, бо а2 = 44 і тому а — не натуральне.
4.8. Припустимо, що вказана сума раціональна, тобто одержаний десятковий дріб — періодичний. Нехай довжина періоду дорівнює л і період починається після k-ro десяткового знака. Тоді {k + л + І)2 - (k + л)2 = 2л + 2k + 1 > л, тобто в цьому десятковому дробі зустрінуться л одиниць, що стоять поруч. Звідси випливає, що весь період складається із одних одиниць, тобто починаючи з {k + 1)-го знака після коми, в десятковому дробі, що є сумою чисел, які залишились, стоять одні одиниці. Протиріччя.


28
Задачі математичних олімпіад та методи їх розв’язування
л л тт 1 + 7б 1 ~ у/д
4.9. 	Легко перевірити, що числа = —-— і <72 = —z— є коренями
Z "
квадратного рівняння q2 - q - 1 = 0. Отже, користуючись цим рівнянням, можна записати, що f(n + 2) = b(qf+2 -q™2} = b(q" (7, +1)- q2 (q2 +1)) = f(n +1) +
+f(ri). З одержаної рівності випливає, що коли /(л + 1) та /(л) — цілі числа, то /(л + 2) — також ціле число. Тому, для того, щоб /(л) було цілим при всіх натуральних л, необхідно і достатньо, щоб вирази /(1) та /(2) були цілими. Оскільки, /(1) = /(2) = by/б, то /(л) буде цілим при довільному натуральному л
tH 1
тоді і тільки тоді, коли Ь = —=■, де т є Z. Хотілося б зазначити, що при Ь = —7=
75 75
V
формулою /(л) = X V5
1 + 75
1-75
буде задаватись послідовність
Фібоначчі: 1, 1, 2, 3, 5, 8,... Відповідь, b = -X, де т є Z.
75
4.10. Введемо позначення: а, » T2tg(pz, де / = 1, ..., л, а, = ф,, а2 = а, + ф2,
..., ал = ал_, + фп. За умовою для довільного / = 1, ..., л число b} - 72tga;- існує. Доведемо, що всі числа Ь. раціональні. Число bx = а, — раціональне за умовою
задачі. Для / = 2 маємо: tga2 - tg(a, + ф2) = ^а‘ + і тому
1 - tga, • tg<p2
Ь "V CL
b2 = —!-j—Оскільки числа bx і a2 раціональні, то звідси випливає, що чис- 1--Ь1а2
ло Ь2 також раціональне. Аналогічно отримуємо Ь3-—, t і взагалі
b- + а-.,
bj+l = ■ у , І =1,2, .... л - 1. Оскільки числа а,, а2, ..., ап раціональні
і Ьх = ах, то за індукцією доводиться, що числа Ь2, Ь3 Ьп також раціональні.
4.11, Очевидно, що *л+і^ 5х„ +1. З цієї нерівності та умови х, = 0 за індукцією одержуємо, що хл+, > 1 для довільного номера л. Тоді хп+, > хп +1. З рів¬
ності хл+1 - 5хп = у/24х2 +1 випливає, що хл+, - 10хл+,хл + хл = 1 для довільно-


Числа раціональні та ірраціональні
29
го п= 1, 2, .... Очевидно, що справедлива й рівність хя -10хлхл_, + х2_, = 1 для довільного п = 2, 3, .... Віднімаючи почленно від першої рівності другу, дістанемо: х2+1 - x2_, - 10xrt+1x„ + 10хлхл_, = 0, (xn+1 - хл_,)(хл+1 + x„_, - 10x„) = 0.
Оскільки. хл+, - xn_j > 2, to xn+1 + xn_, - 10x„ = 0 для довільного натурального n
> 2. З рівності хл+1 = 10хл - хл_, та умов х, = 0, х2 = 1 випливає, що х3 натуральне число. Оскільки х2 і х3 — натуральні, то х4 також натуральне, і т. д. Індукцією доводиться, що хл+1 — натуральне число для довільного натурального п.
4.12. 	Доведемо, що при п = 1 твердження задачі справедливе. Припустимо протилежне: існують такі раціональні числа х та у, що виконується рівність х + у>ІЗ = + л/з. Тоді (х + і/л/з^ = 1 + Л х + 2>у — 1 = (і — 2хр)>/3. Оскіль¬
ки числа х та у раціональні, а число Тз — ірраціональне, то остання рівність
рівносильна системі •
1 - 2ху = 0, х2 + Зу2 -1 = 0.
Але ця система розв’язків не має. Протиріччя. Покажемо, як випадок довільного п зводиться до розглянутого. Користуючись методом математичної індукції, легко довести, що коли х та у раціональні числа, то для кожного натурального п існують такі раціональні числа хл та уя, для яких виконується рівність
(х + у4з} = х„+ уп4з. Отже, якби для деякого натурального п виконувалась
рівність (х + у Л)" = 7і + 7з, де х, у є Q, то для деяких раціональних хя та уп
виконувалась би рівність хя + уп4з = л/і + л/З, що суперечить доведеному вище твердженню.
4.13. 	Доведення проведемо від супротивного. Припустимо, що log418 = —, я
де р є Z, q є N. Але тоді мала би місце рівність22р~ч = З2’, яка виконується
лише тоді, коли 2р - q = 0 \2q = 0. Отже, р = 0 і q = 0. Дістали протиріччя з умовою, що q є N. Отже, log418 є ірраціональним числом.


§5. Квадратний тричлен.
Неперервні функції, графіки і корені рівнянь
Теоретичні відомості
У більшості задач, що зводяться до дослідження квадратичної функції у - f(x) = ах2 + Ьх + с, корисно уявити собі її графік. Якщо він перетинає вісь Ох у двох точках (коренях) х{ та х2, то між цими точками значення функції у = f(x) протилежні по знаку з числом а. При цьому вершина параболи у = f(x) (абсциса якої дорівнює півсумі коренів) відповідає точці екстремуму функції у = f(x): мінімуму, якщо а > 0, і максимуму, якщо а < 0.
В ряді задач доцільно використати й такий факт: якщо неперервна на відрізку [а; Ь] функція у - f(x) приймає на кінцях цього відрізка значення різних знаків, то між точками а і Ь лежить хоча б один корінь рівняння f(x) = 0?
Задачі
5.1 (9). Функція у = а ІхІ + б|х - /г| перетворюється в нуль при
х = -1 та при х = 3 і має найбільше значення 2. Знайдіть параметри а, Ь та k.
5.2 (9). Параболи, що є графіками квадратичних функцій у = Д(х)
та і/ = /2(х), одержані одна з другої паралельним перенесенням і перетинають вісь абсцис: перша — у точках х0 та хр друга — у точках х0 та х2. Знайдіть точки перетину з віссю Ох графіка функції у = Д(х) + /2(х).
5.3 (9-10). Знайдіть всі квадратні тричлени /(х) = ах2 + Ьх + с такі, що
f(x + 1) = /(-х) для будь-якого дійсного значення х.
5.4 (9-11). Відомо, що х,, х2 — корені рівняння х2 + ах + Ь = 0 з
невідомими коефіцієнтами а, Ь. Знайдіть корені рівняння: Ьх2 + + a(b + 1)х + (Ь - І)2 + а2 = 0.
5.5 (9-10). Знайдіть всі значення параметра а, при яких множи¬
на {(х;у)|х2 + у2 + 2х < l}n{(x;z/)|x - у + а > 0} містить тільки одну точку. Знайдіть цю точку.


Квадратний тричлен. Неперервні функції, графіки і корені рівнянь 31
5.6 (9). Знайдіть множину значень функції:
ч 	<•> ч л З г/ ч х2 +2х-2
a) 	f(x) = 2х + —; б) /(х) = —5 —.
х х- - х +1
5.7 (9). Намалюйте графік функції у = tgx • ctgx.
5.8 (9). За графіком квадратичної функції у = ах2 + Ьх + с визначте
знаки коефіцієнтів а, Ь, с (див. рис.).
5.9 (10-11). Знайдіть найкоротшу відстань між точками параболи
у = х2 - 8х +16 і прямої у = -2х + 1.
5.10 (10-11). До параболи у = ах2 - х {а > 0) в її вершині та у двох
точках, розташованих по різні сторони від вершини, проведено дотичні. Точки перетину цих дотичних є вершинами правильного трикутника зі стороною ч/з. Знайдіть коефіцієнт а.
5.11 	(10-11). Доведіть, що параболи у2 = 2х і у = |х2 -5х + 6 перети-
2-і
наються у чотирьох точках, які лежать на одному колі. Знайдіть центр і радіус цього кола.
5.12 (10). Знайдіть рівняння спільної дотичної до парабол у = х2 + 4х + 8
та у = х2 + 8х + 4.
5.13 (10). При яких а та b рівняння х3 + ах + b = 0 має три різних
дійсних корені, які утворюють арифметичну прогресію?
5.14 (10). а) Знайдіть рівняння прямих, що дотикаються одночасно до пара¬
бол г/ = х2 + х~2таг/ = -х2 + їх - 11.6) Скільки спільних дотичних
мають параболи у = а,х2 + b{x + q та у - а2х2 + Ь2х + с2 ?
5.15 	(10). Чи існують функції f та g, що задані на всій числовій осі, такі, що для всіх х і у виконується рівність /(х) • g(y) = X + у + 1 ?


32
Задачі математичних олімпіад та методи їх розв’язування
5.16 	Побудуйте графік функції у =
5.17 	(10). Знайдіть /'(2), якщо: а) /(х) = (х - 2)2g(x), де g(x) — довільна диференційовна в точці х = 2 функція; б) /(х) = (х - 2)2g(x), де g(x) — довільна неперервна в точці х = 2 функція;
в) 	/(х) = (х - 2) {у]х + у/х -2 + (х - 2)2л]х5 + yfx ).
5.18 	(11). Функція /(х) задана і має похідну на [0; +<»). Доведіть, що коли для всіх х > 0 виконуються нерівності І /(х) І < 2 та /(х) • Г(х) > cosx, то не існує lim /(х).
5.19 	(11). Фігуру на координатній площині задано системою нерівнос¬
тей:
|ї/|>х2 +1.
Обчисліть площу цієї фігури.
5.20 (11). Розглянемо всі можливі параболи у = х2 + Ьх + с, що перети¬
нають осі координат у трьох різних точках. Для кожної такої параболи через ці три точки проведемо коло. Доведіть, що всі ці кола мають спільну точку.
5.21 (11). Кубічне рівняння і квадратне рівняння, обидва з більшими
коефіцієнтами 1, та з раціональними коефіцієнтами, мають спільний корінь. Доведіть, що у кубічного рівняння є раціональні розв’язки.
5.22 (11) Мінімум функції у = (х - а)4 + (х - Ь)4 + (х - с)4 дорівнює 0, а мінімум функції у = (х - а)4 + ^2(х + Ь)4 + (х - с)4 дорівнює 4. Знайдіть числа a, Ь, с.
5.23 (11). Доведіть формулу Сімпсона: Нехай площа перерізу тіла площиною Рх, що проведена перпендикулярно координатній вісі Ох через точку цієї вісі з координатою х, подається при х є [а; Ь] многочленом від х не вище другого степеня (тіло обмежене між площинами Ра та Рь); тоді об’єм тіла V можна обчислювати за формулою: V = ^(Sa+4Scp+Sb), де h = b - a, Sa = S(a\


Квадратний, тричлен. Неперервні функції, графіки і корені рівнянь 33
Sb = S{b), Scp — площа «середнього» перерізу — переріз площи¬
ною Р^
2
а + Ь
що відповідає координаті хср =
5.24 (11). Скільки коренів має рівняння (V3) = х?
5.25 (11). Нехай Р(х) = х3 - ах. При яких х існує у Ф х таке, що Р(у)=Р(х)?
5.26 (11). Знайдіть площу фігури, що обмежена графіком функції у = sinx
на відрізку [0; д], і дотичними до нього, що проведені в точках з абсцисами х = 0 та х = д.
5.27 (11). Намалюйте графік функції у = де [х] — ціла частина
дійсного числа х.
Розв’язки, вказівки, відповіді
5.1. 	у(-1) = у(3) = 0. Звідси випливає, що 13 - k | = 3- 11 + або b = 0. 4 2
Відповідь. а = —, b = -~, k = -3.
З З
5.2. Застосуйте теорему Вієта. Відповідь. х0; — -.
2
5.3. Відповідь, а = -Ь\ с — довільне.
5.4. Скористайтесь теоремою Вієта.
5.5. Відповідь, а = -3; Л(+1; -2).
5.6. Множина значень функції f збігається з множиною значень параметра а, для яких рівняння /(х) = а має хоча б один розв’язок.
З
а) Рівняння 2х + — - а має розв’язок тоді і тільки тоді, коли має розв’язок квадратне рівняння 2х2 - ах + 3 = 0, тобто коли дискримінант цього квадратного рівняння невід’ємний: а2 - 24 > 0, тобто |а, > 2л/б.
б) Рівняння /(х) = а рівносильне рівнянню (а - і)х2 - (а + 2) • х + (а + 2) = 0 (*). При а Ф 1 рівняння (*) квадратне і має хоча б один корінь при умові
(а + 2)2 - 4(а - 1)(а + 2) > 0. При а = 1 рівняння (*) лінійне і має корінь х = 1.
5.7. Відповідь. Графіком даної функції є пряма у = 1, з якої виколоті точки
- , А
, де k є Z.
7


34
Задачі математичних олімпіад та методи їх розв’язування
5.8. 	Вітки параболи напрямлені у випадку а) вгору, а у випадку б) вниз, звідки знаходимо знак а-, а) а > 0; б) а < 0. Знак числа с знаходимо з умови с = /(0): а) с < 0; б) с < 0. Для визначення знака числа b простіше і зручніше
скористатися формулою для абсциси вершини параболи: х0
Ь_
2а
. Відзначи¬
мо, що в пункті а) можна використати і теорему Вієта: сума коренів додатня,
а їх добуток від’ємний, тому числа — та - від’ємні: а) b < 0; б) b < 0. а а
Відповідь, а) а > 0, 6 < 0, с < 0; б) а < 0, 6 < 0, с < 0.
5.9. 	Знайдіть таке число с, при якому графіки у -х2 - 8% + 16 та у = -2х + с
дотикаються (з цією метою прирівняйте до нуля дискримінант квадратного рівняння: х2 - 8% + 16 = -2% + с). Потім обчисліть відстань між паралельними
прямими у = -2% + 1 та у = -2% + с. Відповідь, с-1', р = —=.
45
5.10. Відповідь. а = -.
2
5.11. Запишіть рівняння парабол у такому вигляді у2 - 2х (1), %2 = 2у + + 10% - 12 (2). Очевидно, що усі спільні точки цих парабол, лежать на лінії, рівняння якої ми отримаємо, якщо додати рівняння (1) і (2). В результаті ми дістанемо рівняння %2 + у2 = 2у +10% -12 + 2%, яке можна записати так:
(% - б)2 + (у -1)2 = 25. Це — рівняння кола радіуса 5, центром якого є точка (6; 1).
5.12. Запишемо рівняння дотичної до першої параболи в її довільній точці — точці з абсцисою %,: у = (2%, + 4)% - %2 +8, і рівняння дотичної до другої параболи в її довільній точці — точці з абсцисою %2: у = (2%, + 8)% - %2 + 4.
Одержані прямі збігаються при умові, що 2%, + 4 = 2%2 + 8, -%2 + 8 = -%2 + 4,
звідси, %, = 2, %2 = 0. Відповідь, у = 8% + 4.
5.13. Підставте с - d, d, с + d (d 0) в дане рівняння та з суми першої і третьої одержаних рівностей відніміть подвоєну другу. (Інший спосіб: скористайтесь формулами Вієта або дослідіть функцію у = %3 + ах + b за допомогою похідної). Відповідь, а < 0, b = 0.
5.14. а) Нехай пряма у = kx + b дотикається першої параболи в точці (%,; //,) та другої — в точці (%2; г/2). Отже, всього маємо шість невідомих. Запишіть:
— умови належності точок (%,; у^ та (%2; z/2) відповідним параболам (два співвідношення);
— умови проходження прямої через ці точки (ще два співвідношення);


Квадратний тричлен. Неперервні функції, графіки і корені рівнянь 35
■■■■■■■г-
— умови рівності кутового коефіцієнта прямої значенню похідної першої параболи при х = х, та значенню похідної другої параболи при х = х2 (ще два співвідношення).
Відповідь, у - х - 2\ у = 1 х - 11.
б) Якщо ах та а2 — числа одного знака, то параболи ахх2 + bxx + сх та а^х.2 + Ь2х + с2 мають дві спільні дотичні тоді і тільки тоді, коли вони перетинаються; якщо ж ах та а2 — числа різних знаків, то ці параболи мають спільну дотичну тоді і тільки тоді, коли вони не перетинаються (доведіть.!).
5.15. При х = у = 0 дістанемо /(0) • g(0) = 1, тобто /(0) Ф 0 та g(0) £ 0. Аналогічно, при х = 1, у = -1 матимемо /(1) • g(-l) = 1, тобто g(-l) £ 0. Але, це суперечить тому, що /(0) 1 g(-l) = 0. Відповідь. Не існують.
5.16. Область визначення даної функції — проміжок [1; +<»). Виконавши очевидні перетворення, дістанемо:
у = (V(Vx -1 - 7(Vx -1 -IF) = G/x-1 +1) - -і I Vx-1 -11.
& L и
Якщо 1 < x < 2,. то у = Vx -1, а якщо x > 2, to у = 1. Тепер вже легко побудувати графік функції.
5.17. а) Скористайтесь формулою для похідної добутку.
б) Для даного випадку застосувати формулу для похідної добутку неможна. За
. .. /(2 + Л)-/(2) h2g(2 + ti) ,L
означенням похідної / (2) = lim- — = lim—2 = lim(h • m2 + h)} =
Л—>0 fa A-»0 fa h-*Q ' '
= lim h • lim g(2 + h) = 0 • g(2) = 0.
Л->0 л-»о
в) 	Функція у = /(х) має вигляд /(х) = (х - 2) • g(x), де g(x) = yjx + >fx - 2 + +(х — 2)2^/х5 + Vx. Тому, враховуючи диференційовність g(x) в точці х = 2,
/
матимемо: ((х - 2) • g(x)) = g(x) + (х - 2) • g'(x). При х = 2 дістанемо:
/'(2) = g(2) = ’^2. Відповідь, а) 0; б) 0; в) *^2.
5.18. Функція р(х) - sinx не спадна і обмежена.
5.19. При заміні х на -х чи у на -у система не зміниться, тому задана фігура симетрична відносно осей Ох та Оу. А при х > 0, у > 0 система матиме
вигляд ■
z/ < 1 + х, г/ > х2 +1.
Відповідь. — кв. од. З
5.20. 	Нехай х,, х2 — корені квадратного рівняння х2 + ах + b = 0. Парабола у = х2 + ах + b перетинає вісь Ох у двох точках А(хх; 0) та В(х2; 0) і вісь Оу у точці С(0; Ь). Коло, яке проходить через точки А, В, С також проходить і через точку D(0; 1), бо ОА • ОВ = ОС • OD (точка О — початок координат).


36
Задачі математичних олімпіад та методи їх розв'язування
5.21. Нехай р(х) = х3 + ах- + Ьх + с = 0, q(x) = х2 + тх + п = 0 — дані кубічне і квадратне рівняння. Легко помітити, що £?(х) = р(х) - (х - (т - а)) • q(x) — многочлен з раціональними коефіцієнтами степеня, не вище першого. Спільний корінь многочленів р(х) і q(x) є коренем і многочлена R(x). Якщо R(x) 0 0, то цей корінь — раціональний, а якщо R(x) = 0, то р(х) = (х - (т- а)) ♦ q(x) і, отже, раціональне число т - а є коренем р(х).
5.22. Якщо мінімум першої функції дорівнює 0, то х-а = х- Ь = х~с = 0, тобто х = а - b = с. Отже, друга функція має вигляд У = 2((х - а)4 + (х + а)4) =
= 4(х4 + 6а2х2 + а4). Це парна функція, яка зростає при х > 0. Отже, тоді вона
досягає свого мінімуму при х = 0, і цей мінімум дорівнює 4а2. Звідси 4а4 = 4, тобто а = ± 1. Відповідь, а = b = с = ± 1.
5.23. 	Доведіть, що коли /(х) — квадратний тричлен, то має місце така
ь
рівність J f(x)dx =
а
f(a) + 4/
ґ а + Ьу о
+ f{b)
ч
1 2 J
У
In х In З
5.24. 	Перепишіть дане рівняння у вигляді і покажіть, що функ-
X о
ІПХ . /л ч / ч
ція у = на проміжку (0; е) — зростає, а на проміжку (е; °°) — спадає.
Відповідь. 2 корені.
5.25. 	Нехай х3 - ах = у3 - ау і х ■£ у. Тоді yz - х3 = а(у - х), у2 + ху + х2 = а, у2 + ху + (х2 - а) = 0. Останню рівність розгляньте як квадратне рівняння відносно у. Воно матиме розв’язки лише тоді, коли х2 - 4(х2 - а) > 0, тобто при
2 - 4а
0, то |х| < якщо a < 0, розв’язків немає. (Задачу можна розв’язати і в такий спосіб — дослідити за допомогою похідної графік
х < —. Отже, якщо а >
О
4а
функції у = х3 - ах). Відповідь. Якщо а > 0, то при |х| < якці° а 0, то ні при яких х.


Квадратний тричлен. Неперервні функції, графіки і корені рівнянь 37
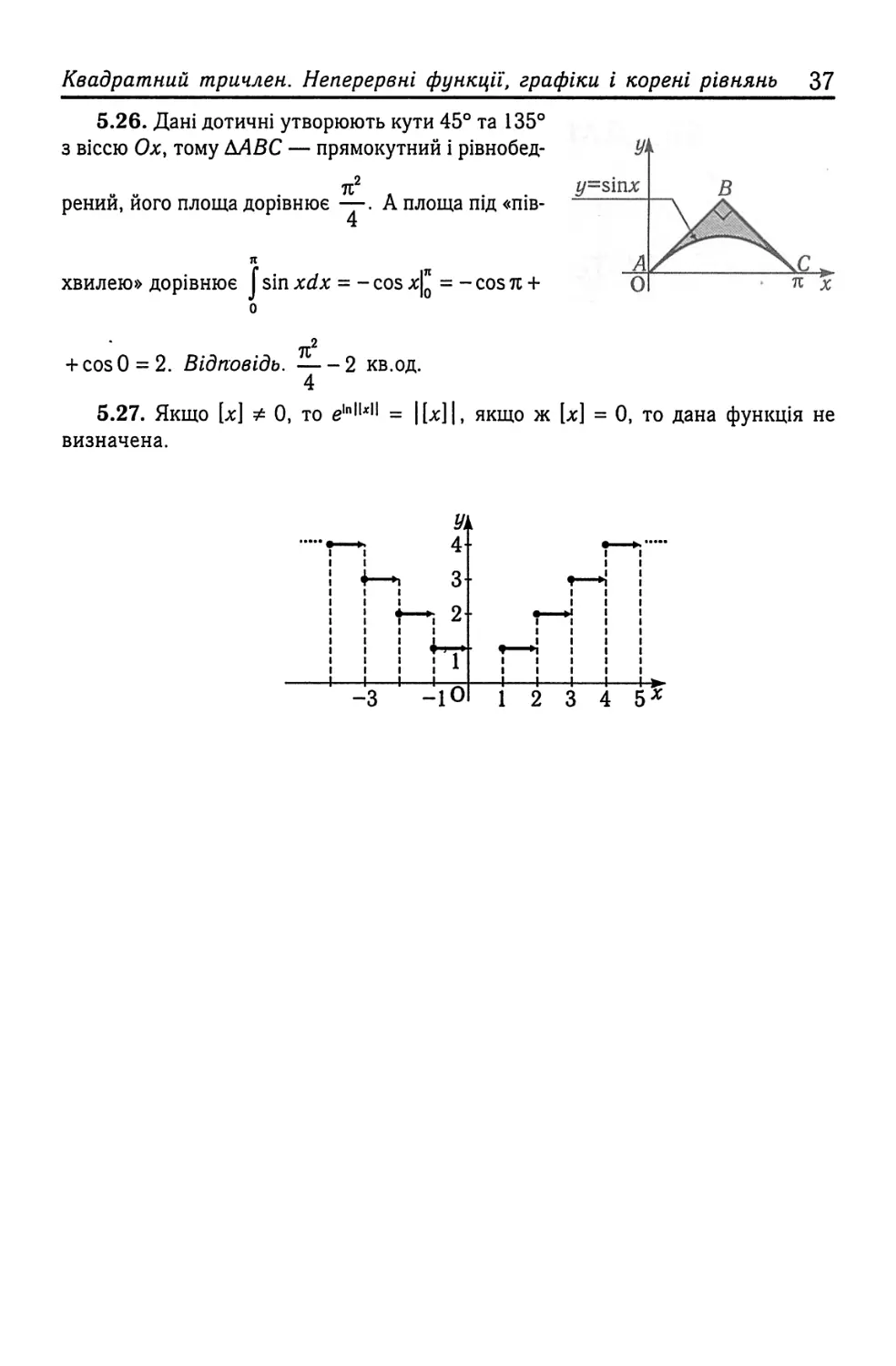
5.26. 	Дані дотичні утворюють кути 45° та 135° з віссю Ох, тому ДЛВС — прямокутний і рівнобед-
71
рений, його площа дорівнює —. А площа під «пів-
хвилею» дорівнює J sin xdx = - cos х|” = - COS 7t + о
+ cos 0 = 2. Відповідь. 2 кв.од.
4
5.27. 	Якщо [х] * 0, то е|п|1х|1 = |[х]|, якщо ж [х] = 0, то дана функція не визначена.


§6. Алгебра многочленів
Теоретичні відомості
Якщо многочлен Р(х) має корінь х = а, то він ділиться на двочлен х - а, тобто його можна подати у вигляді Р(х) = (х - а) • Q(x), де Q(x) — многочлен на одиницю меншого степеня.
Многочлен степеня п має не більше п дійсних коренів (навіть з урахуванням кратності). Звідси випливає, що коли два многочлени Р(х) та Q(x), степінь яких не більший п, набувають однакових значень більше ніж в п точках, то їх коефіцієнти при відповідних степенях рівні.
Часто використовують такі тотожності:
хп - уп = {х — у)(хп~1 + хп~2у +... + хуп~2 + г/л_1),
х2т+1 + у2т+ї = (х + у)(х2т - х2т~'у +... - хі/2'"-1 + у2т), а також формулу бінома Ньютона:
(х + у)п =хп+ C\xn~{y + С2хп~2у2 +... + Cnn-'xyn~' + уп, де біноміальні коефіцієнти обчислюються за формулою:
С„‘ =
п(п - 1)(я - 2) •... • (п - k +1) 1-2-3-...-& ~
, k = 1, 2, 3, ..., п.
Задачі
6.1 (7-9). Доведіть, що всі коефіцієнти у розкладі многочлена
(1 + 2х - х2 + 2х3 + х4)100 додатні.
6.2 (8-9). Розкладіть на множники многочлен х5 + х + 1.
6.3 (9). Доведіть, що суму квадратів двох різних натуральних чисел,
помножену на суму квадратів двох інших різних натуральних чисел, можна подати у вигляді суми квадратів двох натуральних чисел.
6.4 (9-10). Доведіть, що при цілих х, у, z число х3 + у3 + z3 - 3xyz
ділиться на число х + у + z.


Алгебра многочленів
39
6.5 (10-11). Розкладіть на множники многочлени:
а) 2(а° + Ь5 + с5) - 5abc(a2 + Ь2 + с2);
б) 6(а5 +Ь5+ с5) - 5(а3 + Ь3 + с3)(а2 + Ь2 + с2).
6.6 (10). Многочлен: а) ах2 + Ьх + с; б) ах3 + Ьх2 + сх + d набуває цілі
значення при довільному цілому х. Якими можуть бути його коефіцієнти (наприклад, чи обов’язково вони є цілими)?
6.7 (10). Многочленаохп +а1хп~ї + ... + ап набуває в усіх цілих точках х
цілі значення. Чи може один із його коефіцієнтів а. дорівнювати
13
6.8 (10). Розкладіть на множники многочлен (1+х + х2 + х3 +...+х”)2 -хп,
п — натуральне число, п > 3.
6.9 (10-11). Коефіцієнти многочлена хп + а1хл~І + а2хп~2 +... + ап_хх + ап
дійсні числа, які за модулем не перевищують 1985. Доведіть, що цей многочлей не має дійсного кореня, більшого за 1986.
6.10(11). Знайдіть суму коефіцієнтів при непарних степенях х у многочлена (х5 +х- 1)1986.
6.11 (10-11). Подайте многочлен х,985 +х + 1 у вигляді добутку двох
многочленів, степінь кожного з яких не менший за 2.
6.12 (10-11). Многочлен Р(х) = ах3 + Ьх2 + сх + d набуває цілих зна¬
чень при х = -1,х=0, х = 1,х = 2. Доведіть, що цей многочлен набуває цілих значень для всіх цілих х.
6.13 (11). Многочлен Р(х) = х4 + ах3 +Ьх + с має чотири різних дійс¬
них корені. Доведіть, що ab < 0.
6.14 (11). Графік многочлена Р(х) = ах4 - х2 + Ьх + с зображено на рисунку. Знайдіть знаки коефіцієнтів а, Ь, с.
6.15 (11). Доведіть, що при будь-якому значенні с многочлен Р(х) = х(х2 - 1)(х2 -10) - с не може мати п’ять цілих коренів.


40
Задачі математичних олімпіад та методи їх розв'язування
6.16 (10-11). Знайдіть многочлен з цілими коефіцієнтами, такий, щоб
число а = >/2 + V3 було його коренем.
6.17 (10-11). Обчисліть коефіцієнт при х,0° у многочлені (1 + х + х2 +
+х3 +... + х100)3 після зведення подібних доданків.
6.18 	(11). Нехай /(х) = хк + а{хк 1 +... + ak_{x + ak, g(x) = хт + b{xm~{ + +... + bm_{x + Ьт такі два многочлени, які задовольняють нерівності |/(х)| < 1980 • |g(x)| та |g(x)| < 1980 • |/(х)|, при всіх дійсних значеннях змінної х. Доведіть, що k = т.
Розв’язки, вказівки, відповіді
6.1. Розгляньте спочатку многочлен (1 + 2х - х2 + 2х3 + х4)2.
6.2. Маємо х5 + х + 1 = х5 - х2 + х2 + х + 1 = х2(х3 -1) + (х2 + х +1) = х2 х х(х - 1)(х- + х + 1) + (х” + X +1) = (х- + х + 1)(х3 — х~ + і).
6.3. Маємо (а2 + b2)(c2 + d2) = а2с2 + a2d2 + b2c2 + b2d2 = (а2с2 + 2abcd + +b2d2) + (a2d2 - 2abcd + b2c2) = (ас + bd)2 + (ad - be)2.
6.4. Розкладіть многочлен x3 + у3 + z3 - 3xyz на множники, одним з яких буде х + у + z.
Маємо х3 + у3 + z3 - 3xyz = (х + у)3 +z3 - Зху(х + у + z) = (х + у + z)x х((х + у)2 -(х + y)z + z2) -Зху(х + у + z) = (х + у + z)((x + у)2 - (х + y)z + 2? -Зху} =
= (х + у + z) (х2 + у2 + z2 - ху - yz - zx).
6.5. 	а) Скористайтесь многочленом Р(х) = 2х2(х - а)(х - Ь)(х - с), тобто Р(х) = 2х5 - 2(а + b + с)х4 + 2(аЬ + Ьс + са)х3 - 2abcx2. Тоді Р(а) + Р(Ь) + + Р(с) = 0.
б) Скористайтесь тією ж ідеєю та многочленом Q(x) = ЗР(х).


Алгебра многочленів
41
Відповідь.
а) (а + Ь + с)(2(а4 + Ь* + с4) - ЪаЬс(а + b + с)- 2(ab + Ьс + са) х х(а2 + Ь~ + с2 - ab - Ьс - са));
б) (а + Ь + с)(6(а4 + Ь4 + с4) - 9abc(a + Ь + с) -
~(6(ab + Ьс + са) + 5(а2 + Ь2 + с2))(а2 + b2 + с2 - ab - Ьс - са)).
6.6. 	а) Підставивши у многочлен 0 та ±1, дістанемо, що с та а ± Ь — цілі
числа. Отже, цілими є числа с, 2а, 2Ь та а + Ь. Навпаки, якщо вказані числа
цілі, то многочлен можна записати у вигляді: т + пх + р з цілими т =
2
= 2а, п = а - Ь та р = с, і набуває для цілих х цілі значення.
Зауваження. Многочлен &-го степеня, який набуває при цілих х цілі зна¬
чення, завжди можна подати у вигляді:
Р(х) = т
х(х - 1)...(х - (k -1))
k\
+ ТІ
х(х - 1)...(х - (k - 2)) (k-l)\
+... + px + q,
де т, п, ..., р, q — цілі числа.
Відповідь, а) с, 2а, 2Ь та а + Ь — цілі числа.
б) Числа 6а, 2Ь, а + Ь + с та d повинні бути цілими; многочлен подається
У
Р
х(х - 1)(х - 2) вигляді т
6
= а + b + с, q = d.
х(х -1) 2
+ px + q, з цілими т = 6а, п = 6а + 2Ь,
+ п
6.7. Многочлен
Р(х) = ^х(х ~ О-(х -12)
набуває в цілих точках цілих
значень, а коефіцієнт при х13
в нього дорівнює Відмітимо, що довільне 1 о
раціональне число може бути коефіцієнтом такого многочлена, але ніяке ірраціональне число бути ним не може. Відповідь. Так, може.
6.8. 	Припустимо, що х Ф 1 і скористаємося формулою суми геометричної 1 — хя+1
прогресії: 1 + х + х2 +... + хп = . Отже, наш многочлен можна записа-
1 - х
ти у такому вигляді:
Р(х) =
1-х
л+1
хп =
(1-хя)(1-хя+2) 1-х"
(1 - х)2
1 - хя+2 1 - X
(при х Ф 1). Випадок, коли х = 1, очевидний.
Відповідь. (1 + х +... + х'"1 )(1 + х + ... + х” + хл+1).
1 - X
1 - X
\2


42
Задачі математичних олімпіад та методи їх розв'язування
6.9. 	Запишемо даний многочлен у вигляді хп~1(х + а, -1) + хп 2(х + а2 -1) +
+... + х(х + ап_і -1) + (х + ап). Оскільки за умовою задачі|а,| 1985 (і = 1, 2, З,
.... я), то при значеннях х більших за 1986 значення виразів, записаних у дужках, будуть додатними. Отже, задане рівняння не має коренів, більших за 1986.
6.10. 	Розгляньте многочлен
Р(х) - Р(-х) 2
де Р(х) = (xs + х- 1)1986. Шука-
Р(1)-Р(-1) .а 1-31986
на сума дорівнює . Відповідь. .
2 2
6.11. 	Покажіть, що даний многочлен ділиться на х2 + х + 1. Для цього
скористайтесь тотожністю: ап -1 = (а - 1)(а"~* + я"-2 +... + а2 + а +1), яка має місце для будь-якого дійсного а та натурального п. Зауваження. Аналогічно доводиться, що при будь-яких невід’ємних цілих числах k, п, т многочлен х3*+2 + х3"+* + х3т ділиться на х2 + х + 1.
Відповідь, (х2 + х + 1)(х2(х - 1)(х1980 + х1977 + ... + х3 + 1) + 1).
6.12. 	Має місце тотожність
( % (х - 1)х(х +1) о, х(х -1) , . t х ,
Р(х) — D6Z h 26 Ь (й + Ь + С)Х + d.
6 2
Далі скористайтесь ідеями розв’язування задачі 6.6.
6.13. 	1-й спосіб. Нехай х, < х, < х3 < х4 — корені даного многочлена. Тоді
х* + ях3 + bxk + с = 0 і х^ + ях3 + Ьхт + с = 0. Віднявши ліві і праві частини
рівностей, дістанемо (xk - xm)(xk + xffl)(x2 + х2 + я(х2 + xkxm + х2) + b) = 0. Якщо k* т, то
х, + х = —а
к т
%к + Xk^tn + -Чи _ l 9 0 U
о 2
х: + х:
(1)
Крім того, за теоремою Вієта:
х,х2 + х,х3 + х,х4 + х2х3 + х2х4 + х3х4 = 0. (2)
Доведемо, що ab < 0. Припустимо протилежне, тобто, що ab > 0. Нехай, наприклад, а > 0, b > 0. (Випадки коли, а = 0, b — будь-яке число, або 6 = 0, а — будь-яке число, а також випадок а < 0, b < 0 розглядається аналогічно. Зробіть це самостійно.) Тоді з формули (1) маємо х, +х2<0. Аналогічно, одержуємо, що х, + х3 < 0, х, + X, <0, х2 + х3 < 0, х2 + х4 < 0, х3 + х4 < 0. А це означає, що серед чисел х,, х2, х3, х4 не більше одного додатного, тобто х, < 0, х2 < 0, х3 < 0 (бо х4 — найбільший серед цих коренів). Але тоді з рівності (2), яка має вигляд


Алгебра многочленів
43
х,(х2 + х4) + х3(х, + х4) + х2(х3 + х4) = О, випливає, щох2 + х4=х|+х4 =
= х3 + х4 = 0. Звідси х, = х, = х3. Дістали протиріччя.
Н-й спосіб. Нехай х, -< х2 < х3 < х4 — корені даного многочлена. Скориста¬
ємося графіком функції у = х4 + ах3 +6х + с (див. рис. 1). Її похідна
у' = 4х3 + Зах2 + b перетворюється в нуль у трьох різних простих точках р,,
р2, р3, які лежать між числами х,, х2, х3, х4: х, < р, < х2 < р2 < х3 < р3 < х4. При цьому на інтервалі (р,; р2) функція у' додатна, а на інтервалі (р2; р3) — від’ємна. Друга похідна у" = 12х2 + бах перетворюється в нуль у двох різних точках
а
q{ та qv причому точки р, та q2 збігаються з точками 0 та - —. Значення
першої похідної в цих точках має різні знаки. Це означає, що а * 0
сі 46^
і /(0)-/(—)<0, тобто Ь(4Ь + а3) < 0. Звідси випливає, що ab < г-.
2 а
4Ь2
Оскільки — > 0, то ab < 0. а2
Рис. 1.
6.14. З даного рисунка видно, що Р(х) -> °° при х -» Тому, а > 0. З рівності с = /(0) та з рисунка випливає, що с > 0. Для визначення знака числа Ь, слід помітити, що b = РЧО). Як видно з даного рисунка, в околі точки х = 0 даний многочлен спадає, тому Р'(О) < 0, тобто b < 0. Відповідь, а > 0, b < 0, с > 0.


44
Задачі математичних олімпіад та методи їх розв’язування
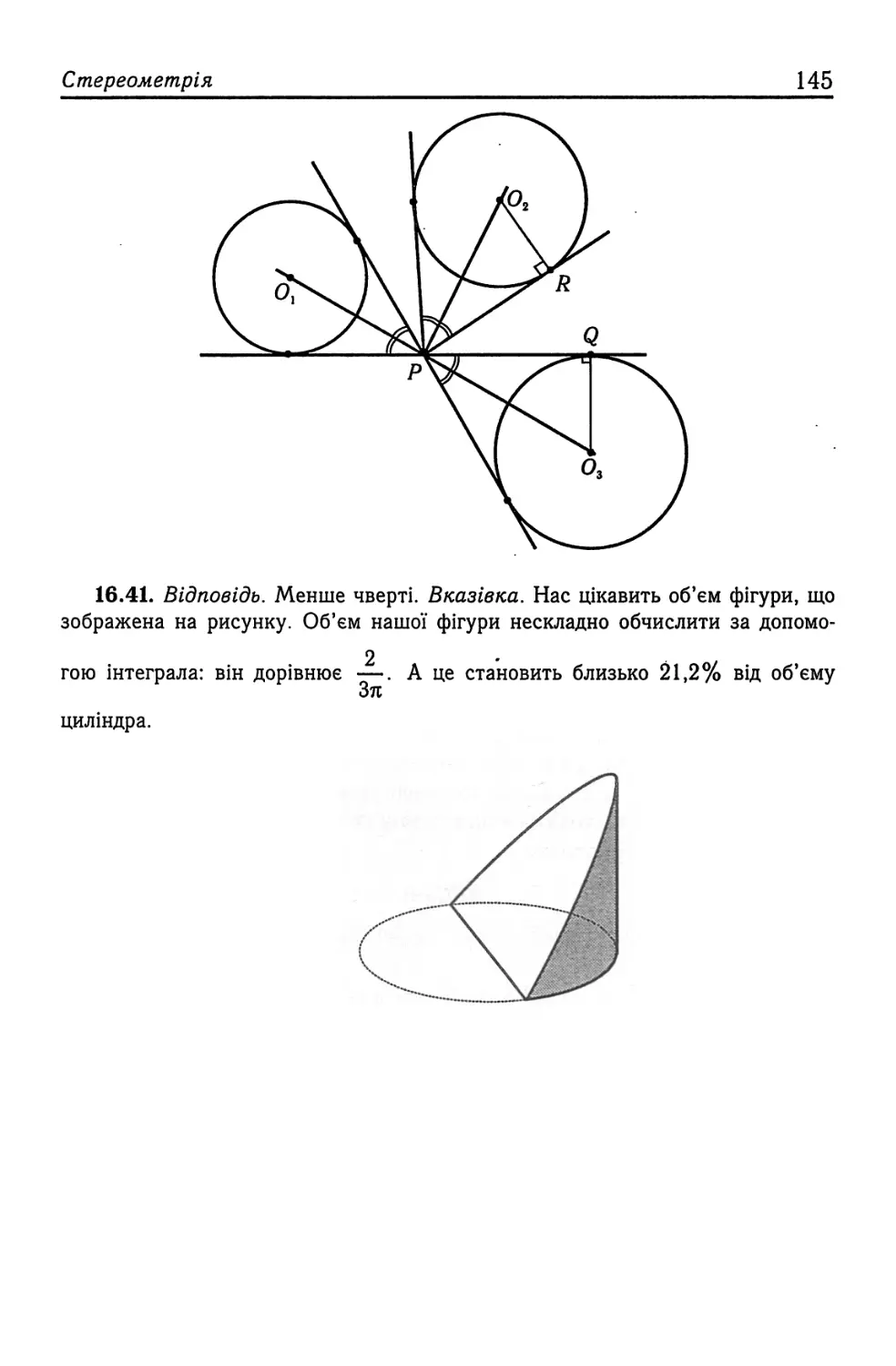
6.15. Розглянемо ескіз графіка функції у = /(%), де /(х) -х(х- - 1 )(х2 - 10) (див. рис. 2). При с = 0, многочлен Р(х) має лише три цілих корені: х = -1, х = 1, х = 0. При с*0 рівняння /(х) = с поза відрізком [-1; 1] має не більше трьох коренів, а на відрізку [-1; 1] цілих коренів не.має. Тому сумарна кількість цілих коренів многочлена Р(х) не перевищує три.
Рис. 2
6.16. Оскільки а3 = (л/2 + л/З)3 = 5 + Зл/2 • >/3(л/2 + л/з) = 5 + За^б, то (а3 - 5)3 = (З^ба)3 = 162а3, тобто а9 - 15а6 - 87а3 -125 = 0. Отже, шуканий
многочлен — Р(х) = х9 - 15х6 - 87 х3 -125.
6.17. Перемноживши без зведення подібних членів три многочлени (1 + X + х2 +... + х’°°) • (1 + X + х2 +... + х100)(1 + X + х2 +... + х‘°°),
дістанемо суму добутків виду xpxqxr, де р, q, г — цілі числа, які задовольняють умови 0 < р < 100, 0 < q < 100, 0 < г < 100, причому коефіцієнти при xpxqxr дорівнюють 1. Вирази х,0° одержаться лише при умові р + q + г = 100. Тому шуканий коефіцієнт при х100 дорівнює кількості цілочисельних роз’язків рівняння р + q + г = 100, де 0 < р < 100, 0 < q < 100, 0 < г < 100. Це рівняння має 101 розв’язок при р = 0, 100 розв’язків при р = 1, 99 розв’язків при р = 2 і т. д. Отже, шуканий коефіцієнт дорівнює
101 +100 + 99 +... + 2 +1 = 10-101 = 5151.
2
Відповідь. 5151.
6.18. Припустимо, що k Ф т. Нехай спочатку k > т. Тоді
gU) = 1 /(х) хк~т
-> 0


Алгебра многочленів
45
при X —>°°, але це неможливо, бо згідно з умовою
g(x)
1980
, для будь-якого X,
1
М
крім скінченної кількості тих значень х, для яких /(х) = 0. Якщо k < т, то f(x)
—> 0, при X —» о°, що суперечить другій нерівності. Одержані протиріччя
g(x)
і доводять, що k = т.


§7. Рівняння і системи рівнянь
Теоретичні відомості
При розв’язанні чи дослідженні рівнянь, крім звичайних «шкільних» методів (підстановки, заміни змінних, тотожних перетворень тощо), іноді користуються міркуваннями монотонності: якщо функція у = f(x) монотонно зростає чи монотонно спадає на R, то рівняння /(р(х)) = ~ /(<?(*)) та рМ = #(х) рівносильні.
При розв’язуванні системи рівнянь іноді бувають корисними геометрична інтерпретація, ідеї симетричності чи циклічності, вихід на лінійну комбінацію між змінними тощо.
Задачі
7.1 	(8-9). Обчисліть суму 2 —-2 —+ 1 —-2—+ —-7 —.
11 13 11 13 11 13
1 1
, 4
99
7.2 (8-9). Доведіть, що 1 - і + і - - +
2 3 4
7.3 (8-9). Знайдіть суму 1-3 + 3- 5 + 5- 7 + 7- 9 +
1 1 1
__ 1 h ... 4
100 51 52
100
... _ _ . . . ... + 999-1001.
7.4 (8-9). Відомо, що а + b + с = 0. Доведіть, що а3 + Ь3 + с3 = ЗаЬс.
7.5 (9-10). Відомо, що abc = 1, а + Ь + с = - + - + Доведіть, що хо¬
бі b с
ча б одне з чисел а, Ь, с дорівнює 1.
7.6 (10-11). Доведіть рівність ^20 +14>/2 + ^20-14л/2 = 4.
7.7 (10-11). Обчисліть суму —?—+ !—+...+
1-2-3-4 2-3-4-5
7.8 (10-11). Обчисліть добуток
1
1
it' (тї+1)- (л+2)- (п+3)
( 1 "і
7 1 'І
( 1 ї
1 4-
1 4-
1 4"
1.3J
2-4J
3-5J
х
х
99-101
1 +


Рівняння і системи рівнянь
7.9 	(10-11). Числа х, у, z задовольняють співвідношення х + у + z - а,
— + — + — = Доведіть, що принаймні одне з чисел х, у, z х у z а дорівнює а.
7.10 (10-11). Числа х, у, z, а, Ь, с такі, що х2 + ху + у2 = а2; у2 + yz + z2 =
= b2; z2 + zx + x2 = c2. Обчисліть xy + yz + zx.
7.11 (10-11). Знайдіть добуток: a) sin 10° • sin 50° • sin 70°; 6) cos — cos x
15 15
7д
X...-COS .
15
7.12 (10-11). Знайдіть суму tg4° • tg8° + tg8° • tgl2° + ... + tgl72° • tgl76°.
7.13 (10-11). Доведіть рівність (n > 2) tgx ♦ tg2x + tg2x ♦ tg3x + ... +
+ tg(n - 1 )x • tgnx
tgnx
— n.
tgx
7.14 (10-11). Відомо, що tgoq -tga2 -...-tgan =1. Знайдіть найбільше
можливе значення добутку sin a, -sina2 - ...-sinan.
7.15 (11). Обчисліть різницю 2’°Єз5 - 5‘°Єз2.
7.16 (11). Відомо, що log712 = a, log1224 = b. Знайдіть log54168.
X
7.17 	(10-11). Дано функцію /(х) = Знайдіть суму f
і -|- х
+... + /
П
+/
Id
+
m
W
Ґ100Л
+/
+f
100
100
+ ... + f
+ ... + f
+
J
+f
100
+ ... + /
Поо
100
7.18 (8-9). Розв’яжіть рівняння x3 - 9x2 + 27x = 19.
7.19 (9-10). Доведіть, що рівняння x10 - x7 + x2 - x + 1 = 0 не має
дійсних коренів.
7.20 (10-11). Розв’яжіть рівняння (х - 2)(х3 - 1) = 6х2 + х + 1.


48 Задачі математичних олімпіад та методи їх розв'язування
7.21 	(8-9). Розв’яжіть рівняння (х20 + 1)(1 + х2 + х4 + ... + х18) = 20х19.
9х2
7.22 (9-10). Розв’яжіть рівняння х2 +
= 16.
(х + З)2
7.23 (9-10). При яких а та b рівняння х2 + а ♦ |х| + b = 0 має 4 корені?
7.24 (9-10). Обчисліть Д + Д, де х та х„ корені рівняння х2 + (а - 1)х +
xf xf
+ 3 + а - 4а2 = 0. При яких значеннях параметра а ці корені існують?
7.25 (10-11). Відомо, що а < b < с. Доведіть, що рівняння —!— + —— +
х-а х-Ь
1
+ = 0 має рівно два корені х, та х2, причому а < х{< b < х2 < с.
х-с
7.26 (11). Скільки коренів (залежно від параметра а) має рівняння
І Іпх І = ах?
7.27 (11). Визначте кількість дійсних коренів рівняння х!3 = а(1 + х14)
для кожного дійсного а.
7.28 (10-11). Розв’яжіть рівняння у/і7-х~ = (З-л/х) .
7.29 	(10-11). Розв’яжіть рівняння у/а + у/а
+ х = х.
7.30 	(10-11). Розв’яжіть рівняння 4х2 - 4х - 3 = 4 частина числа а).
2х-1
([а] — ціла
7.31 (10-11). Розв’яжіть рівняння >/3 -х + у/х-І = 2 + (х - у)2.
7.32 (11). Розв’яжіть рівняння log2(x + у) + log2 ху +1 = 2iog2(x + у).
7.33 	(10-11). Розв’яжіть рівняння х +
х
35
7.34 	(10-11). Розв’яжіть рівняння ^/2-х + Vx -1 -1 = 0.
л/х2-! 12


Рівняння і системи рівнянь
49
7.35 (10-11). Розв’яжіть рівняння Ца-х + $]b-x = $ja + b-2x.
7.36 (10-11). Розв’яжіть рівняння:
а) (х2 - х + і)2 + 2(х3 +1) = (х +1)2;
б) ^(х +1)2 - ІЇх1 -1 = &І(х -1)2.
7.37 (10-11). Розв’яжіть рівняння sinx + sin2x + ... + sinnx = п, якщо
/г є N, п> 1.
7.38 (10-11). Розв’яжіть рівняння: a) sinx ♦ sin2x • ... • sinnx = 1;
б) 	cosx • cos2x ♦... • cosnx = 1, якщо n є N.
7.39 (10-11). Розв’яжіть рівняння 11 + lOcosx + cos2x + 2cos3x = 0.
7.40 (11). Розв’яжіть рівняння sin2x + cos24x = 2sin3x cos34x.
7.41 (11). Розв’яжіть рівняння 3sinx - 4cosx = cos5x - 7.
7.42 	(11). Розв’яжіть рівняння cos x + cos у - cos(x + y) = 1AZ (11). Розв’яжіть рівняння x2 +2xsinxr/ +1=0.
2 8
7.44 (11). Розв’яжіть рівняння arcsin—-— = 2arcsin —- —.
7.45 (11). Розв’яжіть рівняння 2arccosx = arccos(2x2 - 1).
7.46 (10-11). Розв’яжіть рівняння sinx = x2 + x + 1.
7.47 (10-11). Знайдіть всі розв’язки рівняння 4х + 1 = 2Х+1 • sinr/.
7.48 (10-11). Розв’яжіть рівняння 2^ = З*-*-* ([г/] — ціла частина числа у).
7.49 (11). Доведіть, що: а) числа tg220°, tg240°, tg280° — корені рівнян¬
1
1
1
ня х3 - ЗЗх2 + 27х - 3 = 0; б)
cos 20° cos2 40° cos2 60е
+ — = 40.
cos2 80°
7.50 (9-10). Розв’яжіть у цілих числах рівняння 1 + х + х2 + х3 = 2<
7.51 (9-10). Розв’яжіть у простих числах рівняння ху + 1 = z.
7.52 (10-11). Знайдіть всі розв’язки у цілих числах рівняння •
1986х3 = = 18 г/3 + z3 + 9х£/2.


50
Задачі математичних олімпіад та методи їх розв’язування
7.53 (10-11). Знайдіть всі трійки натуральних чисел х, у, z такі, що рівність хп + уп =zn+{ має місце при всіх п > 1989.
7.54 (10-11). Доведіть, що рівняння ху+ yz + zx = 1 має безліч розв’язків
у цілих числах.
7.55 (8-11). Доведіть, що рівняння х2 + у* + z5 = t7 має безліч розв’яз¬
ків у натуральних числах.
7.56 (10-11). Розв’яжіть у цілих числах рівняння (х + 1)(г/2-х2- - 4) = х2.
7.57 (11). Скільки цілочисельних розв’язків має рівняння (х - у)2 = х + у,
якщо |х| < 100, Ы < 100?
7.58 	(8-9). Розв’яжіть систему рівнянь
х + у = 1,
2 ,2 3-
х -ху + у = X .
7.59 	(10-11). Розв’яжіть систему рівнянь
х = у2 + ау + Ь, у = х2 + ах + Ь.
7.60 	(9-10). При яких значеннях параметра а система рівнянь
|2х + ш/ = а+ 2, , . _
1 не має розв язків?
І (а + 1)х + 2ау = 2а + 4
7.61 (11). Розв’яжіть систему рівнянь
х3 = lx + 2 г/, z/3 = 2х + Ту.
7.62 (10-11). Розв’яжіть систему рівнянь
7(х-1)2 + г/2 + 7(* + 1)2 +#2 - 2,
9 2 -2
Х“ + у = sin X.
7.63 (9-10). Розв’яжіть систему рівнянь
7.64 (9-10). Розв’яжіть систему рівнянь
х + 2у = 4,
2ху - 3z2 = 4.
х + у + z = З,
2ху -2y-z2 =4.


Рівняння і системи рівнянь
51
7.65 (10-11). Розв’яжіть у цілих числах систему рівнянь х3 + у3 + г3 = = x + y + z = 2.
7.66 (9-10). Розв’яжіть систему рівнянь
7.67 (9-10). Розв’яжіть систему рівнянь
7.68 (9-10). Розв’яжіть систему рівнянь
7.69 (9-10). Розв’яжіть систему рівнянь
- + - = 1985, х у
1 + 1 = 1986,
У г
1 + 1 = 1987.
Z X
х2 + у2 + z2 = З, ху + yz + zx = 3.
х2 + ху + у2 = 7,
« х2 + xz + z2 = 21, у2 + yz + z2 = 28.
1 | 1 = 1 х у + z 2’ 1 1^1 у х + z З’ 1 1^1 z х + у 4
7.70 (10-11). Розв’яжіть систему рівнянь -
ху + х + у = 1, yz + у + z = 5, zx + х + z = 2.


52
Задачі математичних олімпіад та методи їх розв'язування
7.71 (10-11). Розв’яжіть систему рівнянь
х- -yz = y-z,
• у2 -xz = z-y, z2 - ху = x-z.
x"z/9 9 + Зх2 -у2 = З,
7.72 (10-11). Розв’яжіть систему рівнянь -
х™у" + 2х2 -2у* = 1,
x"z/99-х2-Зг/2 =-3.
7.73 (10-11). Доведіть, що система рівнянь
в’язків не має.
1986z/jz + x2 +z = 0, 1986хг/ + г2 + х = 0,
1986xz + у2 + у +1 = 0
роз-
7.74 (10-11). Розв’яжіть у цілих числах систему рівнянь
ab + cd
• ас+ bd ad + be
-1,
-1,
-1.
7.75 (9-10). Розв’яжіть систему рівнянь
х,х2х3
х2х3х4
х3х4х5
1,
-1,
1,
X,qXjX2 — 1.
7.76 	(10-11). Розв’яжіть у додатних числах систему рівнянь х, +х2 + ... + хл = З,


53
Рівняння і системи рівнянь
7.77 	(10-11). Розв’яжіть систему рівнянь
Xj + 2х2 +... + 9xg +1 Oxjq = 55, х2 + 2х3 +... + 9х10 +1 Ох, = 55,
Xjq + 2х, +... + 9х8 +1 Охд = 55.
7.78 	(11). Розв’яжіть систему рівнянь xf2 = х3, х23 = х4, ..., х*г2' = хя,
vxtt — V YXl — V
лл_, — Л,, лп — л2.
Розв’язки, вказівки, відповіді
7.1. Вказівка. Позначте = а і = b і перепишіть суму у вигляді
(2 + а)(3 - Ь) + (1 + 2а)(2 + Ь) + (1 - а)(7 + Ь). Відповідь. 15.
70 о • , 1 1 1 11,111
7.2. Вказівка. 1 — + + ... + = 1 + — + — + — +
2 3 4 99 100 2 3 4
1 >
1 1 1
-2
1 1 Ь ... +
246 100
,11 1 = 1 + —і 1-... н
2 3 100
1
+ — + 52
1
100
J_ 1 + 99 + 100
П_1_ + ’ 50 51 +
' 1 1 1 + - + - +
2 З
(& + 2)3 - kz - 8
7.3. 	Використовуючи рівність k(k + 2) = , матимемо 1 • 3 +
+ 3-5 + 5-7 +
З3-І3 -8 53 -33 -8 73 -53 -8
+ 999-1001 = + + + ••• +
10013 - 9993 - 8 1 0013 -13 - 8 • 500 1002999000
= 167166500.
6 6 2
7.4. Вказівка. 0 = (а + b + с)3 = а? + б3 + с3 + 3(ад + Ьс + са){а + Ь + с)- ЗаЬс.
7.5. Вказівка. Домноживши праву частину другої рівності на abc = 1, матимемо а + b + с = Ьс + ас + ab, abc -bc-ac~ab + a + b + c- i=Q, (а - 1)(6 - 1)(с - 1) = 0, тобто принаймні одне з чисел а, Ь, с дорівнює 1.
7.6. Позначимо ліву частину рівності через х і піднесемо її до куба, скориставшись формулою (а + б)3 = а3 + b3 + ЗаЬ(а + Ь).
Дістанемо: х3 = 20 +14-72 + 20 -14-72 + Зхл/202 - 2 • 142 = 6х + 40.


54
Задачі математичних олімпіад та методи їх розв’язування
Очевидно, що х = 4 є розв’язком рівняння х3 = 6х + 40; інших розв’язків це рівняння не має, оскільки х3 - 6х - 40 = (х - 4)(х2 + 4х + 10).
1
7.7. Вказівка. Скориставшись представленням
BCD
1 о +
/г + 1 k + 2 /г + З
З 1
доведіть рівність
k(k + \)(k + 2)(k + 3) k
1 Ю 3
k k +1
k(k + i)(k + 2)(k + 3) 6
. Шукана сума дорівнює і 6
З п +1 п + 2 п + 3
k + 2 k + 3
1 2 +
1 > . я
J
= - +
1 +
7.8. 	Вказівка. Перетворіть числовий вираз у кожній дужці за формулою 1 (п +1)2
та скоротіть спільні множники чисельника та знамен¬
п(п + 2) п(п + 2) 200
ника. Відповідь.
101
7.9. 	Вказівка. З даних співвідношень випливає, що (x + r/ + z)x
х
G і і
- + —+ - чх У Z
= 1, звідси (х + у + z)(yz ’+ zx + ху) - xyz, (х + у + z)(yz + ZX +
+ ху) - xyz = 0, (х + у)(х + z)(y + z) = 0. Отже, або х + у = 0, або х + z = 0, або у + z = 0, а тоді відповідно або z, або г/, або х дорівнюють х + у + z = а.
7.10. 	З даної точки О на площині відкладемо такі три відрізки О А, ОВ, ОС, що утворюють попарно кути в 120°, і О А = z, ОВ = х, ОС =у. Тоді за теоремою косинусів х2 + ху + у2 = ВС2, у2 + yz + z2 = AC2, z2 + zx + х2 = АВ2. Тому, ВС - а, АС - b, АВ - с. Площа трикутника ABC дорівнює сумі площ трикутни¬
ків АОВ, СОА, ВОС, тобто S .вс = (ху + yz + zx)
sin 120°
. Отже,
4 о п а а а ір(р - а)(р - Ь)(р - с) а + Ь + с
xy + yz + zx = -j= S^BC. Відповідь. 4^— - , де р =
sin 20° • cos 20° • cos 40°
7.11. a) sinlO° • sin50° • sin70° = sinlO° • cos20° • cos40° =
sin 40° • cos 40° _ sin 80° _ 1 4 cos 10° 8 cos 10° 8
2 cos 10°
л 2ti 4л 7л л 2л 4л 8ті
б) cos — cos — cos — cos — = - cos — cos — cos — cos — = —
15 15 15 15 15 15 15 15 16
1


Рівняння і системи рівнянь
55
Зл 6л 1 5л лі
cos — cos — = —; крім того cos — = cos - = -.
15 15 4 15 3 2
Відповідь, а) б)
7.12. 	Відповідь. -45.
7.13. Вказівка. Скористайтесь тотожністю tg а • tg J3 = ~ 1 •
7.14. Вказівка. З умови випливає, що sin а, • sin<x2 •... • sina„ = cos а, х х cosa2 •... • cosa„. Тому 2Л sin2 а, • sin2 а2 •... • sin2 ал = sin2а, • sin2a2 • ...х
V
х sin 2а„ < 1. Отже, sin а, • sin а2 •... • sin ал <
_1_
72
Рівність досягається при
л
а, = а, =... = ал = —.
4
7.15. Скористайтеся (доведіть її самостійно) такою тотожністю: a'°g»c _ ciog»e, а > о, £ > о, с > 0, b * 1. Звідки й випливає, що 2log35 - 5log3 2 = 0. Відповідь. 0.
7.16. Перейдемо до логарифмів з основою 12. За умовою log712 = а, тому log,, 7 = -; log,2 (2 • 12) = b, тому log12 2 = 6-1. Тоді log54 168 = log|2168 =
1 1 A 1
_ 1 + log12 7 + log,, 2 _ +a+ _ 1 + ab
3-5 log,2 2 3 - 5(6 -1) 8a - 5a6
Примітка. Можна було перейти до логарифмів за основою, наприклад, 2 1 + ab
або 3. Відповідь. —-■
8а - 5а6
1
7.17. Зазначимо, що /(1) = — та /(х) + f 2
-1 при будь-яких ДІЙСНИХ X, х ї 0. У нашій сумі є деяка кількість (100) доданків /(1), а інші можна згрупу-


56
Задачі математичних олімпіад та методи їх розв'язування
і А
вати у пари /(х) + / — . Тому шукана сума дорівнює кількості доданків, по-
множеній на Відповідь. 5000. 2
7.18. Запишіть дане рівняння у такому вигляді х3 - 9х2 + 27х - 19 = 0. Оскільки сума коефіцієнтів даного рівняння дорівнює 0, то 1 є його коренем. Далі, розкладіть на множники многочлен: х3 - 9х2 + 27х - 19 = (х - 1 )(х2 - 8х + 19). Відповідь, х = 1.
7.19. Переконайтеся, що на кожному з проміжків (-°о; 0], (0; 1), [1;+°°), функція /(х) = х10 - х7 + х2 - х + 1 набуває лише додатних значень.
7.20. 	Вказівка. Зробіть заміну t = х + —, тоді дане рівняння зводиться до х
квадратного рівняння. Відповідь, х, = -1; х23 = 2 ± д/З.
7.21. Відповідь, х = 1.
9х2
7.22. Ліву частину рівняння подайте у вигляді х2 + - -у
х4 + 6х3 +18х2
6х2
+ Позначивши
X"
= у, дістанемо рівнян-
(х + 3)2 (х + З)2 х + 3 "" ” ” х + 3
ня у2 + 6у - 16 = 0, корені якого ух = -8 і у2 = 2. Залишилося розв’язати сукуп¬
ність двох рівнянь
о
х + 3
, друге з яких не має розв’язків. Відповідь.
1 + УІ7.
х
7.23. Число х тоді і тільки тоді є розв’язком даного рівняння, коли число |х| є розв’язком рівняння у- + ay + b = 0. Дане рівняння матиме 4 розв’язки лише тоді, коли вказане квадратне рівняння має 2 додатних різних корені. Відповідь, а2 > 4Ь, а < 0, b > 0.
7.24. Вказівка. Скористайтеся теоремою Вієта.
7.25. Перепишемо рівняння у вигляді /(х) = (х - Ь)(х - с) + (х - а)(х - с) + + (х - а)(х - Ь) = 0. За умовою задачі: /(а) = (а - Ь)(а - с) >0, /(6) = = (Ь - а)(Ь - с) < 0, /(с) = (с - а)(с - Ь) > 0. Отже, на інтервалах (а; Ь) і (6; с) маємо принаймні по одному кореню рівняння /(х) = 0. Але /(х) — квадратний тричлен, тобто рівняння /(х) = 0 не може мати більше ніж два корені.
7.26. Відповідь. При а < 0 коренів немає; при а = 0, х = 1; при 0 < а < -
е
1 	. . 1 . рівняння має три корені; при а = - рівняння має два корені; при а > - рів-
е е
няння має один корінь.


Рівняння і системи рівнянь
57
X
7.27. 	Вказівка. Достатньо побудувати графік функції у = ту. Відпо-
1 + х
відь. Немає коренів при | а | > Ь; один корінь при | а | = Ь\ два корені при 0 < 1 -
< І а І < Ь; один корінь при а = 0, де b = — 13й.
14
7.28. 	Позначимо и = 7х, v = 3 - 4х. Тоді и + v = 3, а рівняння буде мати вигляд 7і7-і? = v1  2  *, звідси и4 + v4 = 17. Отже, и та v задовольняють систему и4 + v4 =17,
рівнянь •
Для розв’язання цієї системи рівнянь перетворимо суму
и + v = 3.
четвертих степенів: (и2 + и2)2 - 2u2v2 =17, (9 - 2uv)2 - 2u2v2 = 17. Розв’язавши це квадратне рівняння відносно uv, дістанемо uv = 2, або uv = 16. Залиши¬
лося розв’язати дві системи рівнянь:
и+ и = 3, fu + о = 3, ми = 16; uv = 2.
ч
Перша система розв’язків не має. Розв’язок другої: (1 ;2) та (2;1)ю Отже,
або 7х = 1, звідки х = 1, або 7х = 2, звідки х = 4. Перевірка показує, що знайдені значення х є коренями рівняння.
Відповідь, х, = 1; х2 = 4.
£
4
7.29. Відповідь. Для
а <-
розв’язків немає
; для а>-- 4
розв’язок
1 + 740 + 1 X = .
2
7.30. 	Вказівка. Перепишіть дане рівняння у вигляді t2 - 1 = (/], де 2% — 1
Z = , та врахуйте, що при t < 1 та t > 2 рівність неможлива. Таким
2
чином, 1 < t < 2. В такому разі [/] = 1 і рівняння матиме вигляд t2 = 2. Відпо-
272+1 відь. х = .
2
7.31. 	Оскільки (73 - х + 7х -1) = 2 + 27-х2 + 4х - 3, то ліва частина досягає найбільшого значення тоді, і лише тоді, коли його досягає квадратний тричлен -х2 + 4х - 3, тобто при х = 2. Отже, найбільше це значення лівої частни дорівнює 2.


58
Задачі математичних олімпіад та методи їх розв’язування
Але цьому ж числу дорівнює найменше можливе значення правої частини рівняння, яке досягається при х = у. Відповідь, х = у = 2.
7.32. Вказівка. Дане рівняння запишіть у вигляді (log2(x + у) -1)2 + + \og2(xy) = 0. Відповідь, х = у = 1.
7.33. Вказівка. Піднесіть обидві частини рівняння до квадрата та вико-
v2 5 5
найте заміну t = . * Відповідь. х,=—, х2=—.
Vx2 -1 4 3
7.34. Вказівка. Взявши л/2 - х = а, Vx -1 = Ь, дістанете рівносильну си-
2 	- х = а3,
стему ’
х -1 = Ь2,
Звідси Ь- + 1 = 2 - (1 - Ь)\ Коренями цього рівняння
а = 1 - Ь, Ь>0.
будуть числа - 0, Ь2 = 1, Ь3 = 3. Отже, коренями вихідного рівняння будуть х, = 1, х2 = 2, х3 = 10.
7.35. Вказівка. Піднесіть обидві частини рівняння до 4-го степеня, дістанете рівняння: 2у/а - х • yjb- х • (2у/а - х + Зл/а - х • у/b- х + 2y/b - х) = 0.
Звідси х, = а, х0 = Ь. Необхідно зробити перевірку.
7.36. Вказівка, а) Легко перевірити, що х = -1 не є коренем рівняння. Тому можна обидві частини рівняння поділити на (х + І)2, внаслідок чого діс¬
танемо квадратне рівняння у2 + 2у - 2 = 0, відносно змінної у .
X + 1
Коренями цього рівняння будуть г/, 2 = -1 ± >/3. Після цього залишається роз-
в язати сукупність двох квадратних рівнянь:
х" - х +1 = (-1 + у/З) (х +1), х2 - х + 1 = ^-1 -у/з}(х + 1).
(Друге рівняння розв’язків не має.) б) Переконавшись, що х = 1 не є коренем даного рівняння, після ділення обох частин на у/(х -1)2, дістанемо квадратне рівняння у2 - 2у - 8 = 0 відносно
їх +1
змінної у = з/ , корені якого у = 4 та у9 = -2. Розв’язавши сукупність двох
V х — 1
рівнянь
х -1 Іх + 1
х -1
7 65
отримаємо х,=—, *2=—.
= 4,
= -2,


Рівняння і системи рівнянь
59
Відповідь, а) = — ± ./Тз - б) Xj =-^,
2 	V 4 У бо
7.37. 	Використавши нерівність sina< 1 і те, що дана сума sinx + sin2x + ...+ + sin/гх містить п доданків, де п > 1, приходимо до висновку, що sinx + sin2x + ...+
sin х = 1,
sin 2х = 1,
+ sin/гх < п, тобто рівняння рівносильне системі рівнянь:
sin пх = 1.
При п > 1, ця система розв’язків не має (всі розв’язки першого рівняння системи не є розв’язками другого). Відповідь. 0.
7.38. 	При дослідженні рівнянь а) і б) треба взяти до уваги, що при будь- яких дійсних значеннях ф | єіпф | < 1, | соэф | < 1. Тому розв’язками цих рівнянь можуть бути лише ті значення х, при яких кожний множник лівої частини рівності дорівнює +1 або -1. При п > 2 перше рівняння розв’язків не має, бо при тих значеннях х, при яких sinx дорівнює +1 або -1, sin2x дорівнює нулеві.
При п = 1 рівняння а) має вигляд sinx = 1, звідси х = — + 2я&, де k є Z.
&
Розв’язками рівняння б) при будь-якому натуральному п будуть числа х = 2nk, де & є Z; якщо ж п натуральне число виду п = 4т + 3 (де т = 0, 1,2,...), то крім вказаних розв’язків, рівняння б) має ще й такі розв’язки: х = п + 2пІ, де Z є Z.
7.39. Вказівка. Звести рівняння до вигляду 3cosx + cos3x + 4 = -(1 + cosx)2 і врахуйте, що 3cosx + cos3x + 4 > 0. Відповідь, х = я + 2nk, де k є Z.
7.40. Вказівка. З нерівності |2 sin3 х • cos3 4х| < 2 |sin х| • |cos4x| < sin2 х + cos2 4х
випливає, що
sin х = 1,
або
sinx = -l, п
л , Відповідь, х = — + 2я/г, де п є Z. cos 4х = -1. 2
cos 4х = 1
7.41. Вказівка. Розглянути функцію /(х) = 3sinx - 4cosx та переконатися в тому, що її найбільше значення дорівнює +5, а найменше — -5.
(Покажіть, що точками екстремуму є ті значення х, при яких tgx = - —;
3 4 З
виведіть звідси, що в точках екстремуму sinx = —, cosx = - — або sinx = —,
5 5 5
4
cosx = —
5
) •
Далі дослідіть множину значень функції cos5x - 7. Відповідь. 0.


60
Задачі математичних олімпіад та методи їх розв'язування
7.42. 	Вказівка. Рівняння можна звести до вигляду
z \2
' х+у х-у' 2 cos — - cos
2
х-у , COS — = 1,
cos2 ——— -1. Звідси ’ 2
COS
£+2 = 1. 2 2’
або
х-у і cos - = -1,
2
cos
x + # _ 1
Відповідь.
± — + я/я; ± — + я(/я + 4я) 6 6
± — + nk; ± — + n(k + 4/ + 2) З З
де
т, п, k, І є Z.
7.43. 	Вказівка. Запишіть рівняння у вигляді (х + sinx#)2 + (1 - sinx#)x х (1 + sinx#) = 0. Обидва доданки невід’ємні.
я
Звідси х = 1, # = + — + k е Z.
^2 __ g
7.44. 	По-перше, J х І <4. Далі, враховуючи, що 0 < arcsin + — < я, то
8 2
я
0 < arcsin — < —, тобто 0 < х < 4. Візьмемо косинус від обох частин рівняння:
1) cos
2) cos
. х2 - 8 я4 arcsin + —
8 2
= - sin
arcsin ■
x-8 8
8-х2
о • x 2 arcsin — 4
= 1 -2 sin2
ґ •
= 1-2
1 4J
w
8-х2
8
8
Відповідь. 0 < x < 4.
7.45. Косинуси лівої і правої частин рівняння однакові. Відповідь. 0 < х < 1.
7.46. Якщо х не належить відрізку [-1; 0], то х2 + х + 1 > 1 > sinx, а коли х належить цьому відрізку, то sinx < 0, а х2 + х + 1 > 0. Отже, для будь-яких х значення лівої частини менші за значення правої частини рівняння. Відповідь. 0.
71
7.47. Вказівка. Див. 7.43. Відповідь, х = 0, у = — + 2яя, де пе Z.
&
1А%. Цілий степінь двійки дорівнює цілому степеню трійки лише тоді, коли показники цих степенів дорівнюють нулеві:
[x-
- 4x] = 0, г
41'
«=> -
X
= 0;
2 < |х| < л/5,
X > 1.
Відповідь. 2 < х < -Тб.


Рівняння і системи рівнянь
61
7.49. 	а) Оскільки tg За = —, то для а = 20°, 40°, 80° маємо
-ді—з* 2 )2— = 3. Взявши и = tga, матимемо: и(3 - и)2 = 3(1 - Зл)2. Звідси и3 - ЗЗи2 + 27 л -3 = 0.
б) Покладемо л,= tg220°, л2 = tg240°, и3 = tg280°. Тоді за теоремою Вієта (з
пункту а)) маємо: и. + л„ + л, = 33. Оскільки tg2 a = —7 1, то —J—— +
J 12 3 ь cos2 a cos2 200
+ —5 + —5 + —5 = 33 + 3 + 4 = 40.
cos2 40° cos2 60° cos2 80°
7.50. Якщо у < 0, то ліва частина ціле число, а права — менша за 1. Якщо у = 0, то х = 0. Якщо у > 1, то записавши рівняння у вигляді (1 + х)( 1 + х2) = = 2у, робимо висновок, що 1 + х = 2р, 1 + х2 = 2у, де р + q = у. Звідси знаходимо, що р = q = 1, тобто х = 1, у = 2. Відповідь. {(0; 0), (1; 2)}.
7.51. Числа х та 2 мають різну парність, тоді менше з них, тобто х, дорівнює 2. Якщо у — непарне, то 2у + 1 ділиться на.З (доведіть!), причому 23 + 1 = = 9 > 3. Тоді у — парне, тобто у = 2 і z = 5. Відповідь, х = 2, у = 2, z = 5.
7.52. Єдиним розв’язком у цілих числах цього рівняння єх = # = 2 = 0. Скориставшись однорідністю рівняння, шукатимемо його розв’язок х = х0, у = yQ, z = z0, припустивши, що числа х0, z/0, z0 не мають спільного множника. Скориставшись рівнянням, послідовно доведемо, що число z0 кратне 3, далі доведемо, що х0 кратне 3, і нарешті yQ — кратне 3. Звідси робимо висновок (застосувавши «принцип крайнього»), що х0 = yQ = z0 = 0.
V
7.53. Перепишемо дану рівність у вигляді
у\
Z
= 2.
Якщо X > 2, то
вираз
нескінченно зростає з ростом п, а якщо х < z, то вираз
zxV
з ростом
7
п необмежено спадає. Подібне ж виконується і для у. Тоді рівність можлива лише при х = 2 та у = 2, тобто 2хл = хя+1. Звідси х = 2. Відповідь. х = у = z = 2.
7.54. Вказівка. Покладіть х = k, у = 1 - k і знайдіть 2.
7.55. Один розв’язок знаходимо підбором: 100 + 27 + 1 = 128, тобто х = 10,
у = 3, 2 = 1, t = 2.
Після цього знайдені х, у, z та t домножуємо відповідно на л105, л70, л42 та л30, де л — довільне натуральне число. Тоді довільний набір х = 10л105, у = Зл70, 2 = л42, t = 2л30, л є N дає розв’язок даного рівняння.


62
Задачі математичних олімпіад та методи їх розв’язування
7.56. 	Оскільки числа х2 та х + 1 взаємно прості, то наша рівність може виконуватися лише при х2 = х + 1, х2 = -(х + 1), х + 1 = 1, х + 1 = -1 або х2 - 0. Перші два рівняння не мають цілих розв’язків. Отже, х = 0 або х = -2.
Відповідь. {(0; 2), (0; -2), (-2; -2), (_2; 2)}.
-п • , , . п(п +1) _ п(п -1)
7.57. 	Покладемо х - у = п. Тоді х + у = п2, звідси х = —-—, у = —-—.
X X
Очевидно, що х та у — цілі для довільного цілого п, тобто цілочисельні розв’яз- f п(п +1) п(п - lP
ки нашого рівняння мають вигляд
, де п є Z.
Нерівності |х| < 100, |і/| < 100, виконуються при |л|<13. Відповідь. 27.
7.58. Вказівка. Перемножте рівняння системи. Відповідь. (1;0).
7.59. Вказівка. Віднявши друге рівняння системи від першого, дістанемо рівняння х - у = {у2 - х2) + а(у - х), з якого випливає: х = у або х + у + а+ 1 =0. Відповідь, («,; и2), (и2; и3), (и3; м4), («4; и3), де и2 — корені рівняння и2 + + (а - l)u + b = 0, и3, и4 — корені рівняння и2 + (а + 1)« + {а + b + 1) = 0.
Якщо одне з них (або обидва) мають розв’язки, що збігаються, або взагалі не мають розв’язків, то дана система має відповідно меншу кількість розв’язків. Отже, кількість розв’язків нашої системи дорівнює сумарній кількості розв’язків вказаних двох квадратних рівнянь.
7.60. Віднімемо від другого рівняння подвоєне перше; дістанемо (а - 3)х = 0. Отже, якщо а * 3, то х = 0 і для у матимемо рівняння ау = а + 2, яке має розв’язок в тому і тільки в тому випадку, коли а * 0. Якщо ж а = 3, то система перетворюється на пару рівносильних рівнянь 2х + Зг/ = 5, 4х- + 6у = 10, яка має (це очевидно) безліч розв’язків. Відповідь, а = 0.
7.61. Вказівка. Додавши та віднявши рівняння системи, отримаємо сис¬
тему: -
(х + у)(х2 - ху + у2 - 9) = 0, (х - у){х2 + ху + у2 - 5) = 0.
Система рівносильна сукупності чотирьох систем, розв’язки кожної з них нескладно знайти.
7П+7з 7П-7з
Відповідь. ■
(0; 0), (3; 3), (-3; -3), (75; -7б), (-75; Тб),'
Г7й-7з
ТГЇ + Тз^
'-ТГЇ-л/з. -л/ГЇ + Тз"
—7п + л/з — 7П — л/з
2 ’
2
7
2 ’
2
/
2 ’ 2
7.62. Вказівка. Геометрична інтерпретація першого рівняння системи призводить до висновку: у = 0. Відповідь, х = 0, у = 0.


Рівняння і системи рівнянь
63
7.63. Вказівка. Розв’яжіть систему відносно х та у. Відповідь, х = 2, у = 1, 2 = 0.
7.64. Вказівка. Виразіть х через у, z з першого рівняння і підставте його у друге рівняння. Після чого зведіть рівняння до вигляду: {у - 2)2 + (у + z)2 = 0. Відповідь. (3; 2; -2).
7.65. Візьмемо х = 1 + а, у = 1 + Ь, тоді z = -(а + Ь} і перше рівняння системи набуде вигляду (а + І)3 + (b + І)3 - (а + Ь)3 = 2, яке після перетворень зводиться до такого а2 + b? + а + b = ab(a + Ь), або а + b = (а + b + 2)(а + b - ab).
Отже, а + b ділиться на а + b + 2. Це залишає для а + b чотири можливі значення 0; -1; -3; -4. Для кожного з них з другого рівняння системи можна знайти ab, а після а і Ь. Зі знайдених розв’язків залишаємо лише цілі.
Відповідь. (0; 1; 1), (1; 0; 1), (1; 1; 0).
1.1 1
7.66. Вказівка, а + b + с = 3 • 993, де а = —, о = —, с = —.
xyz
і 1 1
Відповідь, х 993, У 992> z 994-
7.67. Вказівка. Віднявши від першого рівняння друге, дістанемо: х2 + у2 + + z2 - ху - xz - yz = 0. Звідси (х - у)2 + (у - z)2 + (z - х)2 = 0, що можливе лише при х = у = z. Відповідь, х = у = z = 1; х = у = 2 = -1.
7.68. Вказівка. Помножимо перше рівняння на х - у, друге на 2 - х, третє на у - 2 та додамо їх. 7(х - у) + 21 (2 - х) + 28(у - 2) = 0, звідси z = 3y - 2х. Підставляючи це значення z у друге і третє рівняння системи, одержуємо, що у = 0 або у - 2х. Відповідь, (77; 0; - 277), [~>І7; 0; 277), (1; 2; 4), (-1; -2; -4).
7.69. Перепишемо систему у вигляді
ху + xz- 2(х + у + 2), ху + yz = 3(х + у + 2), Х2 + yz = 4(х + у + 2).
1 З
З 	цих рівнянь знаходимо: ху = — (х + у + 2), Х2 = —(х + у + 2),
yz = — (х + у + 2). Оскільки х Ф 0, у ї 0, z Ф 0, ці рівності можна поділити одна
на одну. Виконавши це, знаходимо, що х : у : z = 3 : 5 : 15. Тоді кожне з наших рівнянь зводиться до квадратного рівняння відносно х. Скажімо, перше:
5 1
X • — X = — З 2
х + - х + 5х З
, 10х2 - 23х = 0. Звідси х = 0, що неможливо, або
23 D._ .д 23 23 23
х = -. В,дповідь. Х = -, у = -,г = -


64 Задачі математичних олімпіад та методи їх розв'язування
7.70. 	Вказівка. Додавши по 1 до обох частин рівнянь, дістанемо систему
(х + 1)(у +1) — 2,
■ (у + 1)(г +1) = 6, звідси ((х + 1)(у + l)(z + І))2 = 36, тобто (х + 1)(у + l)(z + 1) = (х + l)(z + 1) = З,
= ±6. Відповідь. {(0; 1; 2), (-2; -3; -4)}.
7.71. Додавши почленно рівняння системи, після нескладних перетворень, дістанемо: (х - у)- + (у- z)- + (х - z)2 = 0. Звідси знаходимо розв’язок: х = у = z.
7.72. Віднімемо від першого рівняння друге та від другого — третє. Діста¬
немо систему •
X2 + у- = 2, Зх2 + у~ = 4,
яка має чотири розв’язки: (1; 1), (-1; 1), (1; -1),
(-1; -1).
Ці розв’язки необхідно підставити в будь-яке з рівнянь системи, наприклад, у перше (якщо воно буде виконуватись, то і два інших виконуватимуться).
Легко бачити, що два розв’язки є розв’язками вихідної системи, а два інших — ні. Відповідь. (-1; -1), (1; 1).
1
у + - У 2
7.73. Оскільки у2 + у +1 =
ч 	"У
го рівняння системи випливає, що xz < 0.
А з перших двох рівнянь, записавши їх у вигляді (1986і/ + l)z + х2 = 0, (1986# + 1)х + z2 = 0, приходимо до висновку, що xz > 0. Прийшли до протиріччя.
7.74. Віднімаючи від першого рівняння друге, дістанемо (а - d)(b - с) = 0, тобто а = d або b = с. Аналогічно а = с або b — d. Бачимо, що в усіх випадках три з наших чотирьох чисел рівні. Нехай це числа b, с, d. Тоді кожне з рівнянь системи набуває вигляду ab + Ь2 = 1, тобто Ь(а + Ь) = -1. Тоді b- 1, а + Ь = —\ або b = -1, а + b = 1. Відповідь. Одне з чисел дорівнює ±2, решта дорівнюють ±1.
7.75. Вказівка. Поділивши перше рівняння на друге, матимемо х1 :х4 = -1, тобто х, = -х4 і т.д. Відповідь, х, = х3 = ... = х9 = -1; х2 = х4 = ... - х,0 = 1.
+ — > 0 при всіх дійсних у, то з третьо-
7.76. Додамо дані рівняння:
її
(
И
г и
Xj
+ —
+
Х2
+
+ ...
. +
ХП +
х,
X.,
и
<
2 J
< п J
= 6.
Але х + — > 2 при х > 0, причому х + — = 2 тільки при х = 1. Отже, п < 3. х
Якщо п = 3, то х, = х2 = х3 = 1. Випадки п = 2 та п = 1 не викликають трудно-


Рівняння і системи, рівнянь
65
щів. Відповідь. При л > 4 або п = 1 — розв’язків немає; при п = 3 — х, = х2 =
- х3= 1; при л = 2 —
х,
З + л/б 2
7.77. Додавши ліві і праві частини всіх рівнянь системи, дістанемо 55х, + 55х2 + ... + 55х,0 = 550, звідси х, + х2 + ... + х10 = 10.
Різниця другого та першого рівняння дорівнює 9х, - х2 - ... - хІ0 = 0. Додавши ці два рівняння, дістанемо 10xt = 10, тобто х, = 1. Аналогічно знаходимо х2,.... х,0. Відповідь, х, = х2 = ... = х10 = 1.
7.78. Нехай л непарне.
Якщох, = 1, тох3 = 1, х5 = 1,..., хп = 1, х2 = 1, х4 = 1,..., хй_, = 1. Якщох, > 1,
то всі х. більші за 1, й х, = х*і, > х„_, = х*п_^ > х„_3 =... > х,; випадок х, < 1
аналогічний.
Нехай л парне.
Якщо х, = 1, то х3 = х5 = ... хп_, = 1 та х2 = х4 = ... = хп. Якщо х2 = 1, то х4 = х6 = ... = 1 та х, = х3 = ... = хп _,. Припустимо, що х, * 1 та х2 Ф 1. Якщо, наприклад, х, < 1, то х3 < 1, х5 < 1, ... та х,х3х5... < 1, що суперечить рівності
х2'*3-*5 " = х2, яка випливає з системи.
Відповідь, х, = ... = хп = 1 при непарному л; х, = х3 = х5 = ..., х2 = х4 = ... та х, = 1 або х2 = 1 при парному л.


§8. Доведення нерівностей
Теоретичні відомості
Для доведення нерівностей часто використовують такі відомі нерівності:
I. |х + у\ < |х| + Iz/1, |х - у\ > |х| - |г/|;
II. 4аЬ < — для довільних а > 0, b > 0;
2
III. якщо av а2, ..., ап — невід’ємні числа, то
і а, + сь, +... + а , . . т. ...
ца,а2...ап < — (нерівність Коші між середнім геометрич-
п
ним і середнім арифметичним);
9 + а2 4*... + а% }
IV. (а, + Оз +... + ап)“ < (для довільних а,, а2,..., ап);
с + d с b
N. для додатних чисел а, b дріб лежить між дробами — і —
a + b ad
VI. sinx < х при х > 0.
Задачі
8.1 	(9). Доведіть нерівність у/2 + 7 < 8*^2.
8.2 (8-9). Доведіть, що - • і < —.
369 102 17
8.3 (7-8). Доведіть, що для будь-яких дійсних чисел х та у виконується
нерівність х2 - 2ху +1989г/2 > 0.
8.4 (9). Знайдіть всі трійки цілих чисел х, у, z, що задовольняють
систему нерівностей ’
х~ <у, у2 <г, z~ <х.


Доведення нерівностей
67
8.5 (9). Доведіть, що для довільних чисел а, Ь, с виконується нерівність
а2 +Ь2 +с2 > ab + bc + са.
8.6 (9). Доведіть, що для довільних дійсних чисел а, Ь, с виконується
нерівність а4 + b4 + с4 > abc{a + Ь + с).
8.7 (9). Доведіть, що коли а • (4а + 2Ь + с) < 0, то Ь2 > 4ас.
8.8 (9). Доведіть, шо коли добуток довільних додатних чисел о,, а2, ...,
ап дорівнює 1, то (1 + 4а,)(1 + 40%)...(1 + 4ол) > 4".
8.9 (9). Нехай а, Ь, с — додатні числа. Доведіть, що
a+b b+c а+с 1 1 1
+ ———< —• -4- — + —
а+Ь о + с а + с а Ь с
8.10 (8-9). Числа а, Ь, с такі, що | ах2 +bx + c |< 1 при |х| < 1. Дове¬
діть, що \сх2 -Ьх + а |< 2 для всіх | х | < 1.
8.11 (9). Позначимо через рп п-те просте число (р, = 2, р2 = 3, р3 = 5
і т. д.). Доведіть нерівність рп < 2рп-і-
8.12 (10). Доведіть нерівність — + — + — >x + y + z, при умові xyz > 0.
z х у
8.13 (10-11). Відомо, що розв’язком нерівності f(x) <0є відрізока<х<Ь
(а < Ь). Знайдіть розв’язок нерівності f
'с) \х J
< 0, де с Ф 0.
8.14 (10-11). Нехай bv b2,..., Ьп — довільна перестановка множини додат-
а, а9 а
них чисел а., а2, а . Доведіть нерівність - + -=- + ... + -^->/2.
1 1 п bi bn U
12 П
8.15 (9-10). Нехай < а2 < ... < ап неспадна послідовність чисел. Доведіть нерівність
(l + 2 + ... + n)(o, H-Og + ... + ол)< п-(а{ +2о2 + ... + пол).


68
Задачі математичних олімпіад та методи їх розв'язування
8.16 (10-11). Доведіть, що для будь-яких дійсних чисел <2р а2,-..., ап
таких, що при i^j І а. - а. | > 1, справджується нерівність
а2+... + а2 (а,+... + £„) >n — l п ■ п2 2п
8.17 (10). Додатним чи від’ємним є число sin 10000?
8.18 (10). Нехай х — дійсне число. Доведіть, що 2s,njc +2C0SJf >2 2.
8.19 (10). Доведіть, що при всіх допустимих значеннях а виконується
нерівність Vsina + Vcosa > 1.
8.20 (10-11). Дано декілька додатних чисел, сума яких дорівнює З, а сума квадратів дорівнює 1. Доведіть, що серед цих чисел знайдуться таких три числа, що їх сума не менша за одиницю.
8.21 (10-11). Нехай a, b, с, d — довільні числа, сума яких дорівнює 1.
Доведіть, що а2 + b2 + с2 + d2 - 2ab - 2bc - 2cd - 2da > .
4
8.22 (11). Нехай a, b, с — додатні числа. Доведіть, що виконується така нерівність (ааЬьсс^ > аь+сЬс+аса+ь.
8.23 (11). Доведіть нерівність In. — > -—- при а > b > 0.
V b а + Ь
8.24 (11). Доведіть, що для всіх х >0 і натуральних п виконується нерівність хп <
\п /г '
Vе J
8.25 	(11). Доведіть, що для всіх натуральних п виконується нерівність
12 3 п 1
1 Т "І «■ + ... н г < — •
З З4 З9 3я 2
8.26 	(11). Нехай п — натуральне число. Доведіть, що виконується
подвійна нерівність
— rijn < Vi + у/2 +... + J 3 . Л


Доведення нерівностей
69
8.27 	(11). Знайдіть всі дійсні числа х, для яких виконуються нерівності sinx < sin2x < ... < sin9x < sinlOx.
Розв’язки, вказівки, відповіді
8.1. Візьмемо ч/2 = а. Необхідно довести, що а2 - 8а + 7 < 0. Але це дійсно так, оскільки 1 < а < 7.
102
1 4 7
8.2. Позначте х =
3 6 9
100. _2 5 8 101. _3 6 9 102’ У 4 7 10 '*103’ Z 5*8*11'
104
ОСКІЛЬКИ > П
при k > п > 0, то маємо х < у < z. Тому,
х < хуг =
k + 2 /2 + 2
1 • 2 • 3 •... • 100 • 101 • 102 З • 4 • 5 •... • 102 • 103 • 104 103 • 104 ' 100 • 100 " 5000 ' 173 ’
1 1 <
звідси х < ■—, що і треба було довести.
8.3. Вказівка. Подайте ліву частину у вигляді (х - у)2 + 1988г/2.
8.4. Вказівка. З даних нерівностей видно, що числа х, у, z невід’ємні. Скориставшись цим, з даних нерівностей випливають нерівності х8 < х, у*<у та z8 < г. Звідси, кожне з чисел х, у, z дорівнює 0 або 1. Але тоді х2 = х, у2 = у та z2 = z відповідно х < у, у < z та г <х, тобто х = у = г. Відповідь. {(0; 0; 0), (1; 1; 1)}.
З.Ь.Вказівка. Скористайтесь тотожністю 2а2 + 2Ь2 + 2с2 - 2ab - 2Ьс - 2ас =
= (а - Ь)2 + (Ь- с)2 + (с - а)2. Оскільки для довільних а, Ь, с сума (а - Ь)2 +
+(д - с)2 + (с - а)2 > 0, тоді й 2а2 + 2Ь2 + 2с2 - 2ab - 2Ьс - 2са > 0. Звідси й
випливає справедливість нерівності а2 + b2 + с2 > ab + Ьс + са для довільних дійсних чисел а, Ь, с.
8.6. Вказівка. Скористайтесь результатом попередньої задачі для чисел х = а2, у = b2, г = с2.
Оскільки х2 + у2 + z2 > ху + yz + zx, то а4 + Ь4 + с4 > а2Ь2 + Ь2с2 + с2а2. Скориставшись тепер результатом попередньої задачі для чисел m = ab, п = Ьс,
k = ас, дістанемо: a2b2 + b2c2 + с2а2 > ab • be + Ьс • са + са • ab = abc(a + Ь + с).
8.7. Вказівка. При а > 0 значення квадратичної функції у - ах2 + Ьх + с у точці х = 2 від’ємне, а при а < 0 — додатне. Тому її графік перетинає вісь Ох. Звідси дискримінант додатний, тобто Ь2 - 4ас > 0.
8.8. Вказівка. Скористайтесь нерівностями 1 + 4af > 2^/а?, де і = 1, 2, ..., п.


70
Задачі- математичних олімпіад та методи їх розв’ язування
8.9. Вказівка. Зважте на те, що —: г- = —
а2+62 2
а + b а2 + Ь2 2
1Ґ1 1
— + ^а b
де а > 0,
b > 0.
8.10. Вказівка. Справедлива тотожність q(x} = сх2 - Ьх + а = /(0)(х2 - 1) +
+ /(-1) + /(1) , де /(х) = ах2 + Ьх + с. Звідси випливає, що
2 2
I q(x) |<| х2 -11 + -—— + — = 1+ І х2 -11< 2 при І х І < 1.
2 	2
8.11. Вказівка. Доведіть допоміжну нерівність рл+1 РхРч--Рп + 1, п = 1, 2, ....
8.12. Вказівка. Поділимо обидві частини нерівності на xyz та перенесемо
_1_ J_ _1__
всі доданки в ліву частину. Нерівність набуде вигляду: ч. + 2 + 2 2 х у
yz
>0, тобто
xz ху
2
\2
>0.
ч2\
X у
2_
У
8.13. Вказівка. Знаходимо розв’язки нерівності а < — < Ь, розглянувши
х
можливі знаки значень чисел а, Ь, с.
8.14. Вказівка. Скористайтесь нерівністю між середнім арифметичним та середнім геометричним додатних чисел.
8.15. Вказівка. Дана нерівність збігається з такою:
(1 + 2 +... + я)(bxn + Ь2(п -1) +... + Ьп) < п (6,(1 + 2 +... + я) + 62(2 +... + я) +... + Ьпп),
де bx = altb2 = а, - а, > 0, .... Ьп = ап - а„_, > 0, отже, достатньо порівняти коефіцієнти при bv ..., bn.
8.16. 	Вказівка. Домножте обидві частини даної нерівності на я2 і зробіть такі
перетворення: я (а2 +... + а2) - (а, +... + ап )2 > , (я -1) (а,2 +... + а2) -
2
— 2(п,Я2 + я,йз +... + ап_1ап) > - , (с, — #2) + (Ді — °з) + ••• + (ая-і ~ —
(я - 1)я
^С2 =
(ліва частина останньої нерівності містить С2 доданків).
2


Доведення нерівностей
71
при х
О 1-7 П • Q , А1С / / Q і А• 10000 10000 10000 А
8.17. Оскільки 3,1415 < п < 3,1416, тоді < < . Але
3,1416 п 3,1415
10000 91О9Л 10000 Q1QQ1 О,ОО. 10000 Q1OA X
=3183,0... та = 3183,1..., тому 3183 < <3184, тобто
3,1416 3,1415 п
3183л < 10000 < 3184л. Отже, кут в 10000 радіан знаходиться в 3-й або 4-й чверті, тобто sin 10000 < 0, є від’ємним числом. Відповідь. Є від’ємним числом.
8.18. Вказівка. Застосуйте нерівність Коші
2S'"X + 2C0SX > 2-72s,nx • 2C0SX = 2 2 ' 4' > 2 2. Знак рівності досягається Зл
+ 2л&, k є Z.
8.19. Вказівка. Очевидно, вираз Vsincc + Vcosa має зміст для
2л& < ос < ^ + 2л&, k є Z. Але для цих значень а маємо л/sin a > sin2 a,
л/cosa > cos2 а. Додавши їх почленно і врахувавши, що sin2 a + cos2 a = 1, дістанемо Vsina + л/cosa > 1.
8.20. Нехай х, > х2>х3> ... > хп — дані числа, тоді х,+х2+х3> > х, + х2 + х3 - (Xj - х3)(1 - х,) - (х2 - х3)(1 - х2) = х2 + х2 + х3(3 - X, - х2) =
= х,2 + х2 + х3(х3 + х4 +... + х„) > х,2 + х2 + х£ +... + х2 = 1, (тут ми скористались тим, що всі х. є (0; 1] та x3xk > x2k при всіх k = 3, 4, 5, ..., п).
8.21. Перепишіть нерівність у такому вигляді 4(a2 + b2 + с2 + d2 - - 2ab - 2bc - 2cd - 2da) + (а + b + с + d)2 > 0. Ліва частина цієї нерівності подається у вигляді суми квадратів: (а - b + с - d)2 + 2{а - Ь)2 + 2(Ь - с)2 + + 2(с - d)~ + 2(d - а)2 > 0.
8.22. Вказівка. Очевидно, що при довільних додатних х та у справедли¬
вою є така нерівність
Тому
\в-б
а'
7
b V“c ( с ^с~а г п
>1.
>1, що і означає, що > ай+с6с+всв+й.
уУ;


72
Задачі математичних олімпіад та методи їх розв’язування
8.23. 	Вказівка. Нехай — = х, тоді слід знайти найменше значення різни- b
ці лівої та правої частин при х > 1: /(х) = In 4х -
х -1 х +1
8.24. Вказівка. Неважко переконатись у справедливості цієї нерівності
при п= 1: х<ех~х. Підставимо в цю нерівність замість х вираз — і піднесемо п
обидві її частин до л-го степеня.
8.25. Вказівка. Доведіть спочатку, що я-З-"2 < З-", для л > 1, л є N.
1
А сума 3'" = - -q ■ = - — сума нескінченно спадної геометричної прогресії.
«=І
‘-з
8.26. 	Розглянемо графік функції у = 4х на відрізку [0; я]. Нехай S — площа криволінійного трикутника, обмеженого кривою у = у/х, віссю Ох та пря¬
мою
" 2 г~
х = п (рис. 1 ,а). Тоді S = J4xdx = — п4п. Нехай = Ті + у/2 + +... + у/п.
Легко бачити, що Sn — площа фігури, зображеної на рис. 1,6. Тому S < Sn. З іншого боку, площа 8п фігури, зображеної на рис. 1,в, дорівнює
8„ =у/ї + л/2 +... + 7л -1 +-^- = Sn- — , і очевидно, що 8я < S, тобто 2 2
1 Г Г~
< S. Таким чином, S„ - < S < S„, тобто S<Sn<S + —. Це і дає
2 2 2
необхідну нерівність.
рис.І.а
рис. 1,6


Доведення нерівностей
73
рис. 1,в
8.27. 	Оскільки всі функції, що входять у ланцюжок нерівностей, періодичні з періодом 2я, достатньо розв’язати задачу, припустивши, що 0 < х < 2п. Нерів¬
2/n + l ї .
ність sin/nx < sin(m + 1)х рівносильна нерівності 2 cos
sin
>0.
— X
У
• Л А
Оскільки sin — > 0 при 0 < х < 2я, остання нерівність на нашому інтервалі
рівносильна нерівності cos
2т +1
> 0. Розв’язком цієї нерівності є об’єд¬
нання відрізків
-7і + 4nk n + 4nk 2т+ 1 ’ 2т +1
Позначимо це об’єднання через А . Роз¬
в’язком задачі є перетин множин Л,, Л2 Л9. Використавши координатну
пряму (для всіх А., і=1, 2, ..., 9), знаходимо, що цей перетин складається
з відрізка
0; — 19
1 ТОЧКИ 71.
Відповідь. 2nk < х< n(2k + ~), х = тс(1 + 2k), k& Z. 1У


§9. Принцип Діріхле
Теоретичні відомості
У цьому розділі зібрано задачі, для розв’язання яких можна використати так званий «принцип Діріхле». Він має декілька формулювань.
Основне формулювання таке: якщо в k клітках більше ніж nk зайців, то хоча б в одній клітці сидять більше ніж п зайців.
Наведемо ще декілька схожих на «принцип Діріхле» тверджень, які використовуються в геометрії та аналітичних задачах:
якщо сума площ декількох фігур менша за S, то ними не можна покрити фігуру, площа якої дорівнює S;
якщо на відрізку довжиною 1 розташовано декілька відрізків з сумою довжин Z, то знайдеться точка цього відрізка, яка.буде накрита не більше ніж [Z] цими відрізками;
якщо середнє арифметичне декількох чисел більше а, то хоча б одне з цих чисел більше а.
Задачі
9.1 (7-8). У районі 15 шкіл. Доведіть, що як би не розподіляли між
ними 90 комп’ютерів, то обов’язково знайдуться дві школи, яким припаде однакова кількість комп’ютерів (можливо й жодного).
9.2 (7-8). У першості з хокею беруть участь 5 команд. Кожні дві з них
повинні зіграти між собою один матч. Доведіть, що у будь-який момент змагань є дві команди, які зіграли однакову кількість матчів.
9.3. (8-9). Чи можна вивезти 50 каменів вагою 370, 372, 374, ..., 468 кг на семи тритонних вантажівках?
9.4 (8-9). За 5 років навчання студент склав 31 екзамен, причому
кожного року він складав більше екзаменів, ніж у попередньому. На п’ятому курсі екзаменів втричі більше, ніж на першому. Скільки екзаменів на четвертому курсі?
9.5 (8-9). Яку максимальну кількість натуральних чисел від 1 до 50
можна вибрати так, щоб серед них не було двох чисел, одне з яких вдвічі більше за друге?


Принцип Діріхле
75
9.6 (9). Чи можна покрити квадрат зі стороною 1,5 трьома квадратами
зі стороною, що дорівнює 1?
9.7 (10). У квадрата 5x5 пофарбовано 16 клітинок. Доведіть, що знай¬
деться фігурка виду всі клітинки якої будуть пофарбованими.
9.8 (10). Прямокутник розміром 20x30 розбито на клітинки 1x1. Чи
можна провести пряму, яка перетинає (по внутрішніх точках) 50 клітинок прямокутника?
9.9 (11). Дано 70 різних натуральних чисел, кожне з яких не переви¬
щує 200. Доведіть, що деякі два з них відрізняються на 4, на 5 або на 9.
9.10(11). Після проведення шахового турніру в одне коло з’ясувалось, що всі партії були результативними і всі гравці знали імена тих гравців, які виграли у них, а також тих, хто виграв у їх переможців. Доведіть, що знайдеться шахіст, який знає імена всіх учасників турніру.
9.11 (11). Березовий гай має форму круга радіусом 215 м. Відстань між
двома деревами в цьому гаю не менша 10 м. Доведіть, що в гаю менше 1990 дерев.
9.12 (8-11). З чисел від 1 до 200 вибрали 101 число. Доведіть, що серед
них є два числа, одне з яких ділиться на друге.
9.13 (9-11). На дереві 15 листків. Доведіть, що можна зірвати 8 з них так,
7
що ті, які залишаться, даватимуть не менше — початкової тіні.
15
9.14 (10-11). Будують башту з чорних та білих кубиків, в основі якої
лежить прямокутник 3x4. Перший пласт — довільний, кожний наступний кладеться так, щоб довільний кубик у попередньому мав парну кількість чорних сусідів. Доведіть, що зустрінеться пласт, який складається лише з білих кубиків.
9.15 (10-11). Є 20 гирьок, вага кожної з яких виражається цілим чис¬
лом грамів. Сумарна вага гирьок не більша за тону. Доведіть, що їх можна розділити на дві групи однакової ваги (що не перетинаються).
9.16 (10-11). Доведіть, що існує число Фібоначчі, десятковий запис
якого закінчується на 0001.
9.17 (11). Підлога розміром 6x3м2 повністю покрита квадратними
ковдрами різних розмірів (краї ковдр паралельні до стін кімнати).


76
Задачі математичних олімпіад та методи їх розв’язування
Доведіть, що можна забрати частину ковдр так, щоб ковдри, які залишились, не перекривались і покривали більше 2 м2 підлоги.
9.18 (10-11). Яку найбільшу кількість клітинок може перетнути коло
радіусом 10, яке накреслили на папері в клітинку (сторона клітинки дорівнює 1).
9.19 (10-11). На площині розташовано п точок так, що довільний три¬
кутник з вершинами в цих точках має площу не більшу за 1. Доведіть, що всі ці точки можна накрити трикутником, площа якого дорівнює 4.
9.20 (11). У лісі всі дерева різної висоти в межах від 10 м до 50 м, причому відстань між будь-якими двома деревами не більша за різницю їх висот. Доведіть, що цей ліс можна обгородити парканом довжиною 80 м.
Розв’язки, вказівки, відповіді
9.1. Вказівна. Якщо в усіх школах буде різна кількість комп’ютерів, то всього комп’ютерів буде не менше ніж 0 + 1 + 2 + ... + 14 = 105 > 90. Протиріччя.
9.2. Вказівка. Припустимо, що всі команди зіграли різну кількість матчів.
Більше чотирьох матчів жодна команда зіграти не могла.
9.3. Якщо це можна зробити, то хоча б одну вантажівку потрібно буде завантажити принаймні 8 каміннями (бо 7 • 7 < 50). Але навіть найлегших 8 каменів мають сумарну вагу 370 + 372 + ... + 384 = 3016 > 3000 кг = 3 т. Протиріччя. Відповідь. Ні, не можна.
9.4. Нехай на першому курсі студент склав п екзаменів, тоді на другому курсі він склав не менше п + 1 екзаменів, на третьому — не менше п + 2 екзаменів, на четвертому — не менше п + 3 екзаменів. З іншого боку, на п’ятому курсі він склав Зл екзаменів, тому на четвертому курсі він склав не більше Зл - 1 екзаменів, на третьому — не більше Зл - 2; а на другому — не більше Зл - 3. Одержуємо систему нерівностей 7л + 6 < 31 < 13л - 6, яка, очевидно, має єдиний розв’язок л = 3. При цьому студент склав на п’ятому курсі 9 екзаменів, на четвертому — не більше 8. Якби на четвертому курсі він склав 7 екзаменів, то всього він склав би не більше 3 + 5 + 6 + 7 + 9 = 30 екзаменів. Протиріччя. Відповідь. 8 екзаменів.
9.5. Розіб’ємо всі числа від 1 до 50 на 33 групи таким чином: {1; 2}, {3; 6}, {5; 10},..., {25; 50}, {27}, {29},.... {49} (всього 25 груп), {4; 8}, {12; 24}, {20; 40}, {28}, {36}, {44} (6 груп), {16; 32}, {48}. У нас рівно 33 групи, причому з кожної групи можна взяти не більше одного елемента, тому всього буде не більше 33-х чисел. Взявши по першому елементу із кожної групи, ми одержимо шуканий набір, бо в розкладі кожного з цих елементів на прості множники двійка входить у парному степені (частка двох таких чисел або непарна, або ділиться на 4 і не може бути рівною 2). Відповідь. 33.


Принцип Діріхле 77
9.6. Дві вершини більшого квадрата не можуть бути покритими одним маленьким, бо 72 <1,5. Тому, для покриття більшого квадрата потрібно не
менше 4-х маленьких квадратів (по числу вершин великого квадрата). Відповідь. Ні, не можна.
9.7. Припустимо, що у нашому квадраті немає зафарбованих фігурок, тоді у будь-якому квадраті 2x2 не менше 2 чистих клітинок. Розглянемо квадрат Kv заштрихований на рис. 1. Оскільки він розбивається на 4 квадрати 2x2, то в ньому не менше 8 чистих клітинок. Отже, зовні нього не більше однієї чистої клітинки (бо всього чистих клітинок 25 - 16 = 9). Аналогічно, зовні квадрата К2 (рис. 2) також не більше однієї чистої клітинки. Доповнення до квадратів Кх і К2 утворюють разом «граничний пояс» (рис. 3), в якому знаходиться не більше двох чистих клітинок. Але цей «пояс» містить чотири вказаних фігурки, що не перетинаються, тому дві з них зафарбовані повністю. Протиріччя.
9.8. При переході із клітинки в сусідню пряма перетинає або вертикальну, або горизонтальну лінію сітки. Жодну з цих ліній вона не може перетнути двічі. Всередині прямокутника розташовано 19 + 29 = 48 ліній сітки. Отже, пряма не може перетнути більше 49 клітинок. Відповідь. Ні, не може.
Рис. 1 Рис. 2 Рис. З
9.9. Розглянемо нові 70 чисел, які дістааємо з вихідних додаванням до кожного з них 4. Якщо початкова і одержана множини перетинаються, то у початковій множині знайдеться пара чисел з різницею 4. Припустимо, що ці множини не перетинаються. Розглянемо ще 70 чисел, які дістаємо з другого набору чисел, збільшенням кожного його елемента на 5. Якщо ця третя множина чисел перетинається або з першою, або з другою множинами, то знайдеться два числа, які відрізняються одне від одного на 5 або на 9. Якщо ж цього не відбудеться, то є 210 різних натуральних чисел, кожне з яких не перевищує 200 + 4 + 5 = 209, що неможливо.
9.10. Нехай гравець А набрав менше всіх очок (точніше, не більше, ніж кожен інший). Цей гравець знає імена всіх, хто виграв у нього. Припустимо, що В програв А. Тоді В виграв у когось, хто виграв у А (інакше у В було б менше очок, ніж у А, а це суперечить вибору А). Тому, А знає й ім’я гравця В. Отже, А — шуканий учасник турніру.
9.11. Нехай в гаю п беріз. Опишемо навколо кожного дерева круг радіусом 5 м. За умовою задачі ці круги не перетинаються і розташовані у крузі радіусом 215 + 5 = 220 м. Отже, площа «збільшеного березового гаю» не менша сумарної площі маленьких кругів. Розв’язавши нерівність я • 2202 > я • 52 • п, дістаємо п<442= 1936.


78
Задачі математичних олімпіад та методи їх розв’язування
9.12. Вказівка. Розбийте числа від 1 до 200 на 100 груп, в кожній з яких всі числа діляться одне на одне і застосуйте принцип Діріхле.
9.13. Вказівка. Зведіть задачу до випадку, коли тіні листків не перекриваються.
9.14. Вказівка. Доведіть, що розфарбування пластів «зациклюється». Крім того, можна вважати, що «нульовий» пласт складається з білих кубиків.
9.15. Вказівка. Підрахуйте, скільки всього наборів можна утворити з 20 гирьок та застосуйте принцип Діріхле.
9.16. Вказівка. Скористайтесь тим, що остачі чисел Фібоначчі за модулем 10000 утворюють цикл.
я2
Рис. 4
Рис. 5
9.17. Відмітимо найбільшу ковдру Кг Нехай її площа дорівнює S,. Заберемо всі ковдри, які перекриваються з Kv При цьому звільниться від ковдр площа підлоги, яка не перевищує 8S, (див. рис. 5 ). Серед всіх ковдр, що залишились, крім Kv знову виділимо ковдру К2 максимальної площі S2 і заберемо з підлоги ті ковдри, які перекриваються з Кг При цьому ми звільнимо від ковдр площу підлоги, яка не перевищує 8S2. Продовжуючи цей процес, ми одержимо набір
1
ковдр Kv К2, .... які попарно не перетинаються і покривають більше ~ площі
підлоги (доведіть це самостійно).
9.18. Відповідь. Найбільше можливе число клітинок дорівнює 80.
9.19. Серед всіх трикутників з вершинами в даних точках виберемо трикутник найбільшої площі S < 1. Через кожну його вершину проведемо пряму, паралельну до протилежної сторони. Площа трикутника, утвореного цими прямими, як бачимо, дорівнює 4S < 4. Доведіть, що цей трикутник містить всі дані точки. При доведенні цього факту скористайтесь тим, що всі трикутники зі спільною основою а, які мають площу S (або меншу), розташовані в смузі між двома прямими, паралельними до основи а, які знаходяться від неї на відстані
h =
2S
а
9.20. 	Зауважте, що стежка, яка починається біля найвищого дерева, потім йде по прямій до наступного за висотою дерева, потім — до третього за висотою і т. д. до найнижчого дерева, має довжину, меншу 40 м. Огородивши парканом (довжиною 80 м) цю стежку, ми тим самим огородимо парканом увесь ліс.


§10. Комбінаторика
Основні поняття
Основний прийом у задачах на підрахунок кількості різних комбінацій елементів скінченної множини — встановлення взаємно однозначної відповідності між множинами, заданими за допомогою різних умов.
Зокрема, множина всіх впорядкованих наборів із п одиниць та нулів — всього таких наборів 2" — може бути поставлена у відповідність множині всіх підмножин даної множини, яка містить п елементів. Множина таких наборів, що містять k одиниць, відповідає множині всіх k- елементних підмножин л-елементної множини. Всього таких наборів
_ пі _ л(л-1)(л-2)...(л-& + 1) п ~ kb (n-k)l ~ 1-2-3-...-& '
При п - 2 це — число невпорядкованих пар елементів з даної п-
елементної множини:
С2 =
п
п(п -1) 2
Кількість перестановок (впорядкувань) даної множини, що містить п елементів, дорівнює п\ = 1 • 2 • 3 • ... (п - 1) • п.
Задачі
10.1 (8). Дерев’яний куб п х п х п пофарбували і розпиляли на кубики
1x1x1. Скільки кубиків матимуть: 3 пофарбовані грані? 2 пофарбовані грані? 1 пофарбовану грань? жодної пофарбованої грані?
10.2 (7-8). Скільки існує тризначних чисел, які при діленні на 8 дають
в остачі З?
10.3 (7-8). Скільки натуральних чисел, які не перевищують 500, не діляться ні на 2, ні на З?
1-0.4 (7-8). У класі 19 лижників, 8 плавців та 11 велосипедистів. Відомо, що кожен спортсмен займається двома видами спорту. Скільки в класі спортсменів?
10.5 	(7-8). Скільки існує натуральних чисел, менших за 100, цифри яких йдуть у порядку зростання?


80
Задачі математичних олімпіад та методи їх розв’язування
10.6 (8). Знайдіть кількість пар {а, Ь} натуральних чисел, які не переви¬
щують 20, для яких сума а + b непарна ({а, Ь} та {Ь, а} вважайте однією парою).
10.7 (8). Знайдіть суму всіх чисел від 1 до 100, у записі яких немає
цифр 4 і 5.
10.8 (9). Всі натуральні числа від 1 до 100 розбили на дві групи: парні
та непарні числа. Визначте, в якій з груп сума всіх цифр, що використовуються для запису їх чисел, більша і наскільки?
10.9 (9-10). Знайдіть суму квадратів всіх натуральних чисел від 1 до
1995.
10.10 (10-11). Скількома різними способами з аркуша паперу в клітинку розміром тхп можна вирізати прямокутник зі сторонами, що йдуть по лініях сітки?
10.11 	(9-10). Скільки різних чисел зустрічається серед чисел
І2
1980
' 22
’ з2
19792'
19802 ’
_1980_
>
198°
, • • •»
1980
J
.1980 _
числа х?
де [х] — ціла частина
10.12 	(9-10). Яку найбільшу кількість точок можна вибрати на відрізку [0; 1] так, щоб на довільному відрізку [а; Ь], який міститься в [0; 1], лежало б не більше 1 + 100(6 - а)2 вибраних точок?
10.13* (10-11). Множину чисел 1, 2, 3, ..., 1974, 1975 розбито на дві групи. До першої групи віднесли всі числа з непарною сумою цифр, а до другої — з парною. Що більше: сума всіх чисел першої групи чи сума всіх чисел другої групи?
10.14 (10-11). Яких шестизначних чисел більше: тих, які можна подати у вигляді добутку двох тризначних чисел, чи для яких це не можна зробити?
10.15 (10-11). Скількома способами можна покрити прямокутну дошку розміром 2х 12 прямокутними плитками розміром 1x2? (Плитки дозволяється класти так, щоб вони не перекривались і повністю вміщалися на дошці).
10.16 	(11). Коло радіусом 1 котиться по колу радіусом >/2, знаходячись зовні його. Липкою фарбою у момент часу t = 0 відмічено


Комбінаторика
81
точку дотику. При рухові зафарбовані точки меншого кола фарбують точки більшого і навпаки. Скільки точок нерухомого кола будуть пофарбовані до моменту часу t = 100, якщо центр рухомого кола здійснює один оберт за одиницю часу і коло рухається без пробуксовки?
10.17 (11). По кругу написано не менше трьох різних дійсних чисел. Кожне з цих чисел дорівнює добутку двох чисел, які стоять по обидва боки від нього. Скільки чисел може бути виписано?
10.18 (11). Дано правильний (2л + 1)-кутник. Знайдіть кількість трикутників, вершини яких співпадають з вершинами даного (2л + 1)- кутника і які містять його центр.
10.19 (11). Є набір гирьок масою І2 г, 22 г, ..., 10002г. Скількома способами їх можна-розділити на дві групи однакової маси, по 500 гирьок у кожній групі?
Розв’язки, відповіді, вказівки
10.1. Всього отримали л3 кубиків. З них 8 кубиків, які стоять у вершинах
«великого» куба, мають по 3 пофарбовані грані. На кожному ребрі є п - 2 кубики з двома пофарбованими гранями. Всього таких кубиків 12(л - 2). На кожній грані «великого» куба (л - 2)2 кубиків з однією пофарбованою гранню, всього їх 6(л - 2)2. Всередині «великого» куба знаходиться (л - 2)3 непофарбо- ваних одиничних кубиків.
10.2. Розіб’ємо всі 900 тризначних чисел на вісімки послідовних тризначних чисел: {100, 101,..., 107}, {108, 109,.... 115} У кожній вісімці лише одне
(а саме останнє) число при діленні на 8 дає остачу 3. Оскільки 900 = 112-8 + 4, то є 112 таких вісімок і одна «неповна вісімка», в якій потрібного числа немає. Відповідь. 112.
10.3. Вказівка. Числа, які не діляться ні на 2, ні на 3, дають при діленні на 6 остачу 1 або 5. Далі, розбийте числа від 1 до 500 на шістки послідовних чисел (див. попередню задачу). Відповідь. 167.
10.4. Вказівка. 19 + 8 + 11 = 38. За умовою задачі кожен спортсмен у цій сумі підрахований двічі. Отже, всього спортсменів 38 : 2 = 19. Відповідь. 19.
10.5. Будемо записувати однозначні числа у вигляді 01, 02, ..., 09. Викресливши з 99 двозначних чисел 9, які записуються однаковими цифрами, розіб’ємо 90 чисел, які залишились, на 45 пар, у кожній з яких числа відрізняються лише порядком цифр. У кожній парі одне число нам потрібне, одне — ні. Відповідь. 45.
10.6. Оскільки сума чисел в парі непарна, то доданки мають різну парність. Всього у нас 10 парних і 10 непарних чисел. Парне число можна вибрати в пару довільно, одним із 10 способів. Непарне — також 10 способами. Отже всього є 10 • 10= 100 пар з непарною сумою. Відповідь. 100.


82
Задачі математичних олімпіад та методи їх розв’язування
10.7. Вказівка. 1+2 + 3 + 6 + 7 + 8 + 9 = 36. Кожна з цих цифр зустрічається в кінці восьми чисел (в кожному десятку, за виключенням 4-го і 5-го, є рівно одне число, яке закінчується на кожну з цих цифр). Тому сума розряду одиниць всіх чисел дорівнює 36 • 8 = 288. Сума цифр розряду десятків буде такою ж. Тому шукана сума буде рівною 288 + 2880 + 100 = 3268. Відповідь. 3268.
10.8. Вказівка. Розбийте всі числа на пари {100; 1}, {2; 3}, {4; 5},..., {98; 99}. Всього 50 пар. В усіх парах, крім першої, у другого числа (непарного) сума цифр на 1 більша, ніж у першого числа (парного). Відповідь. Сума цифр в групі непарних чисел на 49 більша, ніж в групі парних чисел.
10.9. Знайдемо спочатку суму квадратів цифр всіх чисел від 0 до 999. Дописавши попереду нулі, можна вважати всі числа тризначними. Всього є З • 1000 = 3000 цифр. Очевидно, що кожна цифра зустрічається однакову кількість разів (по 300). Отже, наша сума дорівнює 300 • (І2 + 22 + ... + 92) = 300 • 285 = = 85500. Числа від 1000 до 1999 відрізняються від попередніх лише одиницею в старшому розряді. Тому сума квадратів їх цифр буде рівною 85500 + 1000 = = 86500. Залишилось відняти суму квадратів цифр чисел 1996, 1997, 1998, 1999, тобто 9 • 92 + 82+ 72 + б2 + 4 • 1 = 882.
Тому, всього одержимо 85500 + 86500 - 882 = 171118.
10.10. Вказівка. Пару горизонтальних ліній можна вибрати т^т + спо¬
собами; аналогічно пару вертикальних ліній можна вибрати
п(п + 1) Л — способа-
2
ми. Відповідь.
пт(т + 1)(п + 1) 4
10.11. 	Розглянемо множину чисел {у }, де и =——. п = 1, 2, ..., 1980.
" Уп 1980
Через хп позначимо n-е із заданих чисел: хп = [z/„], п = 1, 2, ..., 1980.
Якщо z/n+1 > уп + 1, то, очевидно, хл+1 = [і/л+)] > [ул] = хп. Залишилось знайти
всі п, які задовольняють цю умову: г/л+1 - уп
- > 1, тобто 2п > 1979. Одер 1980 Н
жуємо п > 990. Отже, якщо п > 990, то хл+І > хп, тобто х990 < х991 < ... < х1980. Зауважимо, що х990 = 495.
Якщо ул+1 < уп + 1, то або [ул+І] = [r/J, або [г/л+1] = [і/J + 1. Ми бачимо, що серед чисел х,, х2, ..., х989 зустрічаються всі цілі числа від х, = 0 до х989 = 494. Отже, серед даних чисел є 495 + (1980 - 989) = 495 + 991 = 1486 різних чисел.
Відповідь. 1486.
10.12. 	Якщо b — а < 0,1, то 1 + 100(6 - а)2 < 2. Отже, на відрізку, довжина якого менша за 0,1, може знаходитись не більше однієї вибраної точки. Звідси


Комбінаторика
83
випливає, що відстань між двома сусідніми вибраними точками більша або рівна 0,1.
Нехай av а2, ..., ап — вибрані точки. Нехай вони занумеровані так, що 0 < а, < а2 < ... < ал < 1. Згідно зі сказаним вище, мають місце такі нерівності: а2 - а, >0,1, а3 - а2 >0,1, .... ап - ап_{ >0,1. Додавши ці нерівності, одержимо ап - ах > (п - 1) • 0,1. З другого боку, 1 > ап - аГ Тому, 1 > (п - 1) • 0,1. Звідки п < 11, тобто максимальна кількість вибраних точок не може перевищувати 11, які задовольняють умову задачі: а, =0, а2 = 0,1, а3 = 0,2,..., а,о = О,9, ац = 1. Відповідь. 11.
10.13. 	Нехай А = {0, 1, 2, 3, .... 1974, 1975} (можна вважати, що це дана множина чисел, бо включивши до неї 0, не зміниться відповідь до питання задачі, В = {0, 1,2,3,.... 1974, 1975, 1976,..., 1998, 1999}).
Доведемо, що коли В розбити на дві групи так, як це вимагає умова задачі, то сума всіх чисел однієї групи буде рівною сумі всіх чисел другої. Знаючи цей результат, можна відповісти і на питання задачі відносно розбиття множини А, оскільки вона одержується з В вилученням всього 24-х чисел, відповідні суми яких легко обчислюються.
Всі числа з множини В мають вигляд pqab, р дорівнює 0 або 1, а цифри q, а, b можуть бути довільними. Розіб’ємо множину В на дві підмножини Н і П, включивши до Н всі числа із В з непарною сумою цифр, а в П — з парною. Позначимо через Ея та Еп суми чисел відповідно з Н та П. Доведемо, що Ея = Еп • Для нього, подамо Ея як суму YH + Ея. де — сума чисел pqab, в яких а + b непарне число (тому р + q — парне число), a EJ — сума чисел pqab, в яких а + Ь — парне число (тому р + q — непарне число). Аналогічно зробимо це з сумою Еп» поклавши Еп = Еп +Еп » Де Еп (Еп ) — сума чисел pqab, в яких і а + Ь, і р + q непарні (відповідно, і а + Ь, і р + q парні). Тоді Ея -Еп = (Ея - Еп) + (Ея - Еп). Де вираз Ея - Еп містить тільки ті числа
pqab, в яких а + Ь непарне, а вираз Ея “Еп — тільки ті числа pqab, в яких а + b парне.
Покажемо, що Ея - Еп =0- Зафіксуємо цифри а і b і розглянемо в сумах Ея і Еп доданки, запис яких закінчується цими цифрами. Вони мають відповідно вигляд pxqxab, де р, + qx — парне, і p2q2ab, де р2 +q2 — непарне, причому таких доданків у сумах Ея і Еп міститься порівну. Для них маємо p&ab - p2q2ab = 100(р,<7, - p2q2). Позначимо через ТИ, (відповідно через М2)


84
Задачі математичних олімпіад та методи їх розв’язування
суму всіх чисел pqt де р є {0; 1}, q є {0; 1; 9} і р + q парне (відповідно
непарне), і просумуємо всі такі різниці. Оскільки (це легко перевірити) Мі = М2, то сума всіх різниць дорівнює 100(.М, - М2). Це правильно для довільних а і Ь. Отже, -Е'п = 0.
Міркуючи аналогічно, одержимо, що E# -£п = 0» тобто = Еп • А тепер повернемося до множини А. Нехай SH і Sn — суми чисел, які належать до А, і мають відповідно парну і непарну суми цифр. Оскільки, В = Аи {1976, .... 1999}, то 2П = Sn + 1977 + 1979+ 1980+ 1982 + 1984 + 1986 + 1988 + 1991 + +1993 + 1995 + 1997 + + 1999, ZH=SH+1976 + 1978 +1981 +1983 +1985 +1987 + + 1989 + 1990 + + 1992 + 1994 + 1996 + 1998. Звідси £п - S„ +2, і
тому, + 2 = SH, бо Sn = •
Відповідь. 2.
10.14. 	Маємо всього 900 тризначних чисел. Випишемо їх всі можливі попарні добутки, позначивши самі числа х,, х2, .... хя_р хя, де п = 900:
х,-х„ х,-х2, х,-х3 Х,'ХЯ_„ х,-хя,
х2 • х2, х2 • х3, ...,х2 • хя_р х2 • хя,
Х3 ' ■£}» • Х„_,, Х3 ■ Хп’
Хп-\ ‘ Хп-І ’ Хп-1 " Хл>
Хп'Х«-
Нескладно підрахувати кількість виписаних добутків: п + (п - 1) + (п - 2) + л(л + 1) 900-901
+ ... + 2 + 1 = —-— = - = 405450. Серед цих добутків можуть бути
п’ятизначні (наприклад 100 • 100 = 10000), деякі з добутків можуть бути рівними один одному (наприклад 600 • 600 = 400 • 900). Отже, кількість шестизначних чисел, які можна подати у вигляді добутку двох тризначних чисел, менша ніж 405450.
Кількість всіх шестизначних чисел дорівнює 900000. Тому кількість шестизначних чисел, які не можна подати у вигляді добутку двох тризначних чисел, більша ніж 900000 - 405450 = 194550, тобто їх кількість більша, ніж тих, які можна подати у вигляді добутку двох тризначних чисел.


Комбінаторика
85
10.15. Розглянемо аналогічну задачу для дошки розміром 2 х п. Позначимо через хп кількість різних способів покриття цієї дошки кісточками доміно 1 х 2. Зрозуміло, що хоча б одним способом це можна зробити (наприклад всі домі- ношки розмістити вертикально). Таким чином, ха > 1 при всіх п є- N.
Дошка розміром 2 х 1 може бути покрита лише одним способом, тобто х, = 1. Дошка розміром 2x2 може бути покрита лише двома різними способами, тобто х2 = 2. Нехай п > 3. Початок дошки може бути накритий однією вертикальною чи двома горизонтальними кісточками доміно, а кінець — двома горизонтальними чи однією вертикальною, тому хп = хп_2 + хп_,.
За допомогою цього співвідношення та х, = 1, х2 = 2 знаходимо послідовно, х3 = 2 + 1 = 3, х4 = 3 + 2 = 5, і т. д., х12 = 233.
Відповідь. 233.
10.16. Нехай О — центр більшого (нерухомого) кола, В — зафарбована точка цього кола, на яку наїхало менше коло (з центром О,). Точка В пофарбує менше коло в точці В'. Коли менше коло проїде по більшому шлях, який дорівнює 2л (менше коло має радіус 1), точка В' меншого кола доторкнеться до більшого і пофарбує його в точці С. Нехай Z.BOC = а. Оскільки ОВ - ОС = 72, то
довжина дуги ВтС, на яку спирається цей кут, дорівнює 72а. Тому, 72а = 2л,
а = лТ2. Отже, пофарбована точка В' залишає свій перший слід на більшому
колі через кут а. Цей слід породжує новий слід через кут а і т. д.
Якщо менше коло повторно наїде на вже пофарбовану точку, то слід від цієї точки співпадатиме з вже відміченими точками більшого кола. Таким чином, пофарбовані точки нерухомого кола породжуються лише початковою точкою А = Ао (мал. зробіть самостійно): спочатку через кут а з’явиться точка Л,, тоді через кут а з’явиться точка Л2, далі — точка А3 і т. д.
Доведемо, що ці точки не співпадають. Припустимо, що Ak = Л, для деяких номерів k і I, i<k< І. Сумарний кут повороту від точки Ak до точки At дорівнює а(/ - k). Оскільки Ak = а(, то цей кут повинен бути кратним 2л, тобто
2д
а(/ - k) = 2пл, п є N. Звідки, 72 раціональне число, що неправильно.
І - k
Тепер неважко підрахувати число точок, які будуть пофарбованими за 100 обертів. За сто обертів центр О, меншого кола опише кут, рівний 100 • 2л. Кут а, який послідовно відкладається і відмічає точки А,, Л2, .... Лп, вміститься в цьому куті п разів, де лє N, таке, що ла < 2л • 100 < (п + 1)а. Звідси
одержуємо:
2л-1001 Г2л-100
а
лТ2
= [іООТй] = [100 ♦ 1,4142...] = 141.
(Не
забудьте про точку Лоі). Відповідь. 142.


86
Задачі математичних олімпіад та методи їх розе’язування
10.17. 	Зрозуміло, що жодне з написаних чисел не дорівнює нулеві. Одне з них позначимо через uv а числа, які безпосередньо слідують по колу за и,, в напрямі руху годинникової стрілки, — через и2, иу и4, ... Нехай их = а, и2 = Ь.
1
Тоді
Mj а
^. = А = І «з L b' а
м6
«5.= £ = £
и4 і b'
а
а
иь
а
Щ=—=Т= a,
«5 1
j. b
За умовою всі числа, записані по кругу, різні. Оскільки одер¬
жали, що и7 = uv то звідси випливає, що більше шести чисел розмістити по кругу неможливо. Безпосередньою перевіркою переконуємось, що вказаним чином можна розташувати лише шість чисел.
Відповідь. 6.
10.18. 	Вказівна. Спочатку підрахуйте, скільки є трикутників, які задовольняють умову задачі, одна з вершин яких співпадає з фіксованою вершиною (2 л + 1)-кутника.
• п(п + 1)(2л + 1)
Відповідь. - трикутників.
10.19. 	Вісім квадратів послідовних натуральних чисел — х2, (х + І)2, (х + 2)2, (х + 3)2, (х + 4)2, (х + 5)2, (х + 6)2, (х + 7)2 — можна розбити на вказані дві групи. Це можна зробити, наприклад, у такий спосіб: {х2, (х + З)2, (х + 5)2, (х + б)2} та {(х + 1 )2, (х + 2)2, (х + 4)2, (х + 7)2}. Поклавши х = 1 + 8k, де k = 0, 1, ..., 124 ми одержимо четвірки гирьок для однієї і для другої групи.
2-2*. ..-2
Тому число способів потрібного розбиття буде рівним -
£
Відповідь. 2124.
п125
— = 2124 2


§11. Графи. Відображення
Теоретичні відомості
Зображаючи елементи деякої множини точками і з’єднавши деякі пари точок відрізками, ми одержуємо наочне уявлення дуже популярного об’єкта дискретної математики, що називається графом', точки (елементи множини) називаються вершинами, відрізки (або дуги) — ребрами графа. Граф, з будь-якої вершини якого можна пройти у будь- яку іншу шляхом, який складається з ребер, називається зв'язним. Зв’язний граф без циклів — дерево — має вершин на одну більше, ніж ребер. Якщо всі цикли графа мають парну кількість ребер, то його вершини можна пофарбувати у два кольори так, що вершини одного кольору не з’єднані жодним ребром; такий граф називається дводольним. Якщо на ребрах графа поставити стрілки (задати напрям), то одержимо орієнтований граф {орграф). Будь-яке відображення f скінченої множини А в себе задає орграф, із кожної вершини а є А якого виходить одна стрілка — у вершину {{а). (При цьому можливі петлі — стрілки, які будуть йти з а в а; вони відповідають нерухомим точкам відображення /). Якщо f взаємнооднозначне відображення, то орграф розпадається на цикли (і петлі).
Одним із прикладів складного графа — є схема телефонної сітки. Можуть розглядатись графи, ребра чи вершини яких пофарбовані у декілька кольорів, чи помічені числами.
Задачі
11.1 (7-8). Є ЗО осіб, серед яких деякі знайомі між собою. Доведіть, що
кількість осіб, які мають непарну кількість знайомих, парна.
11.2 (7-8). У країні будь-які два міста з’єднані між собою або залізни¬
цею, або авіалінією. Доведіть, що один з видів транспорту дозволяє попасти з будь-якого міста у будь-яке інше.
11.3 (8). У деякій країні зі столиці виходять 89 доріг, з міста Дальнє —
1 дорога, а з інших 1988 міст — по 20 доріг. Доведіть, що із столиці можна доїхати в Дальнє.
11.4 (8). 20 школярів розв’язували 20 задач. Кожен розв’язав по дві
задачі, і кожну задачу розв’язали двоє. Доведіть, що можна влаш-


88 Задачі математичних олімпіад та методи їх розв’язування
тувати розбір задач так, щоб кожен розповідав одну, розв’язану ним задачу.
11.5 (8). Із повного 100-вершинного графа викинули 98 ребер. Доведіть,
що граф залишився зв’язним.
11.6 (8-9). На аркушу у клітинку пофарбували 25 клітинок. Чи може
кожна з них мати непарну кількість пофарбованих сусідів (клітинок, що мають спільну сторону).
11.7 (8-9). Чи можуть степені вершин графа бути рівними:
а) 8, 6, 5, 4, 4, 3, 2, 2;
б) 7, 7, б, 5, 4, 2, 2, 1;
в) 6, 6, б, 5, 5, 3, 2, 2?
11.8 (8-9). У графі кожна вершина — синя або зелена. При цьому
кожна синя вершина з’єднана з 5-ма синіми та 10-ма зеленими, а кожна зелена — з 9-ма синіми та 6-ма зеленими. Яких вершин більше: синіх чи зелених?
11.9 (8-9). У графа 100 вершин, причому степінь будь-якої з них не
менший за 50. Доведіть, що граф зв’язний.
11.10 (8-9). Є 20 карток, у кожної з яких на обох сторонах написано по числу. При цьому всі числа від 1 до 20 записані по два рази. Доведіть, що картки можна розкласти так, щоб всі числа зверху були різними.
11.11 (8-9). У царя Гвидона було 3 сини, з його нащадків 100 мали по
З сини, а інші померли бездітними. Скільки нащадків у царя Гвидона?
11.12 (8-9). У графа з кожної вершини виходять по 3 ребра. Чи може в
ньому бути 1990 ребер?
11.13 (8-9). У класі більше ЗО, але менше 40 учнів. Кожен хлопчик цього класу товаришує рівно з 3-ма дівчатками, а кожна дівчинка — з 5-ма хлопчиками. Скільки учнів у цьому класі?
11.14 (9). В орієнтованому графі 101 вершина. У кожної вершини кількість ребер, які з неї виходять, дорівнює кількості ребер, що в неї входять; причому ця кількість дорівнює 40. Доведіть, що з будь- якої вершини можна попасти у будь-яку іншу, пройшовши не більше ніж по трьох ребрах.
11.15 (9). Всі грані деякого многогранника пофарбовані у два кольори так, що сусідні грані мають різні кольори. Відомо, що всі грані,


Графи. Відображення
89
крім однієї, мають кількість ребер, яка ділиться на 3. Доведіть, що і ця остання грань також має кількість ребер, що ділиться на 3.
11.16 (9). У деякій країні будь-які два міста з’єднані шляхом з одностороннім рухом. Доведіть, що існує місто, з якого можна проїхати у будь-яке інше не більше ніж по двох дорогах.
11.17 (10). У деякій країні будь-які два міста з’єднані шляхом з односто¬
роннім рухом. Доведіть, що можна проїхати по всіх містах, побувавши в кожному по одному разу.
11.18 (10-11). У графа 20 вершин, степінь яких не менший 10. Доведіть,
що в ньому є гамільтоновий шлях (шлях, по якому можна обійти всі його вершини, побувавши у кожній по одному разу).
11.19 (10-11). Є волейбольна сітка 5 х 10. Яке максимальне число мотузок, з яких вона сплетена, можна розрізати так, щоб вона не розпалась?
11.20 (11). Ребра повного 17-ти вершинного графа пофарбовані в три кольори (кожне в один з трьох кольорів). Доведіть, що знайдеться однокольоровий трикутник.
11.21 (11). Ребра повного 18-ти вершинного графа пофарбовані у два кольори. Доведіть, що існує повний однокольоровий підграф з 4-х вершин.
11.22 (11). Яку найбільшу кількість ребер може мати 30-ти вершинний граф, в якому немає підграфа з трьох вершин?
11.23 (11). На площині відмітили В точок (вершин), з’єднали їх «ребрами», які попарно не перетинаються (з кожної вершини виходить хоча б одне ребро). Доведіть, що В - Р + Г = 2, де Р — кількість «ребер», Г — кількість областей (граней), на які граф ділить площину (включаючи зовнішню) [Теорема Ейлера].
Розв’язки, вказівки, відповіді
11.1. Розглянемо граф, який відповідає умові задачі і біля кожної його вершини напишемо по числу — кількості ребер, які з неї виходять (степінь вершини). Тоді сума всіх цих чисел — число парне (воно в 2 рази більше за кількість ребер). Звідси випливає, що непарних доданків у цій сумі мусить бути парна кількість, що і треба було довести.
11.2. Вказівка. Розгляньте граф (повний), який відповідає умові задачі, і кожне його ребро пофарбуйте в один з двох кольорів (залежно від виду транспорту). Далі, доведіть, що коли об’єднання двох графів — повний граф, то один з них зв’язний.


90
Задачі математичних, олімпіад та методи їх розв’язування
11.3. Вказівка. Скористайтесь тим, що коли б столиця та Дальнє не були зв’язані, то в компоненті зв’язності столиці була б непарна кількість (один) міст, із яких виходить непарна кількість доріг.
11.4. Вказівка. Якщо у графа степінь кожної вершини дорівнює двом, то він розбивається на цикли.
11.5. Вказівка. Врахуйте, що у повного 100-вершинного графа від кожної вершини виходить по 99 ребер.
11.6. Вказівка. Скористайтеся ідеєю розв’язування задачі 11.1.
11.7. Відповідь. Ні. а) Якщо граф має 8 вершин, то степінь 8 зустрітись не може, б) Якщо є дві вершини, що з’єднані з усіма іншими, то степінь інших вершин не менше двох, в) Сума степенів вершин повинна бути парною.
11.8. Відповідь. Зелених вершин більше. Вказівка. Ребра, що з’єднують однокольорові вершини, можна не враховувати.
11.9. Припустимо, що це не так, тоді він складається з граф (підграфи), не зв’язних між собою. Нехай k — кількість вершин одного з них, причому k — найменше. Тоді k < 50. Але тоді степінь кожної вершини такого графа не більше 49. Протиріччя.
11.10. Вказівка. Розгляньте граф з 20-ма вершинами: 1, 2, 3, ..., 20, ребра якого відповідають заданим карткам. Скористайтесь тим, що такий граф складається з декількох підграф, кожен з яких зв’язний, але між собою вони не зв’язні.
11.11. Відповідь. 303. Вказівка. Розгляньте відповідний граф (він складається з трьох незв’язних між собою дерев).
11.12. Відповідь. Ні. Вказівка. Якщо п — кількість його вершин, то з умови
3/2
випливає, що кількість ребер рівна — = 1990, що неможливо при п є N.
2
11.13. Відповідь. 32 учні. Вказівка. Нехай у класі т хлопчиків та п дівчаток; розгляньте відповідний граф, який матиме т + п вершин (ЗО < т + п< 40). Підрахуйте кількість ребер цього графа двома різними способами, одержите рівність: Зт = Зп.
11.14. Нехай а та b — дві вершини даного графа, А — множина, яка складається з 40 вершин, в які йдуть ребра з а, В — множина, яка складається з 40 вершин, з яких йдуть ребра у вершину b, С — множина вершин, які залишились.
Припустимо, що з а не можна попасти у вершину b по трьох ребрах. Тоді всі ребра, які виходять з А, йдуть в А чи в С. Таких ребер за умовою всього
40x40= 1600. Але ребер, які знаходяться в А не більше, ніж —-— = 780,
а ребер, які виходять з А в С не більше, ніж 40 х 19 = 760. Але 780 + 760 = 1540 < < 1600. Протиріччя.


Графи. Відображення
91
11.15. Вказівка. Розгляньте граф, вершинами якого є «грані» даного многогранника, а ребрами — спільні ребра «граней». Тоді він двокольоровий і число ребер, які виходять з вершин одного кольору, дорівнює числу ребер — з другого.
11.16. Вказівка. Розгляньте місто з якого виходить найбільша кількість доріг.
11.17. Вказівка. Потрібно довести, що в повному орієнтованому графі існує гамільтоновий шлях. Зробіть це за індукцією.
11.18. Виберемо найдовший шлях, в якому вершини не повторюються. Припустимо, що він містить не всі вершини. Тоді в ньому є дві сусідні вершини, одна з яких з’єднана з кінцем шляху, а друга — з вершиною, яка не належить цьому шляху. Маючи такі вершини, неважко збільшити шлях.
11.19. Відповідь. (5 • 11 + 10 • 6) - (6 • 11 - 1) = 50. Вказівка. Після такого розрізу залишиться «дерево» (в ньому кількість ребер на один менша за кількість вершин).
11.20. Виберемо одну вершину. З неї виходить 6 однокольорових ребер (принцип Діріхле). Якщо дві з цих 6-ти вершин з’єднані ребром цього ж кольору, то задача розв’язана, якщо ж ні, то ці 6 вершин утворюють повний двокольоровий граф, до якого застосуйте такі ж міркування.
11.21. Вказівка. Спочатку доведіть таке твердження: у повному 9-ти вершинному графі, пофарбованому в два кольори, знайдеться або однокольоровий трикутник, або повний 4-вершинний підграф іншого кольору. Потім дійте так, як і в попередній задачі (11.20).
11.22. Вказівка. У графі з п вершинами без трикутників є вершина з сте-
п
пенем, який не більший — • Відповідь. 225.
11.23. 	Вказівка. Скористайтесь індукцією по кількості вершин графа.


§12. Парність, Задачі на
арбування.
решітках
І
Теоретичні відомості
При розв’язуванні задач на графи часто доводиться використовувати поняття парності. Наприклад, число вершин, з яких виходить непарна кількість ребер, завжди парне. Подібні міркування використовуються і при розв’язуванні інших задач. Так, наприклад, для розв’язування класичної задачі: чи можна шахову дошку 8x8 клітинок без двох кутових клітинок у протилежних кутках покрити «доміношками» 1x2 — досить помітити, що кожна доміношка покриває дві клітинки різного кольору (при звичайноу шаховому пофарбуванні), а кутові клітинки — одного кольору. Інколи виникає необхідність пофарбування в більшу кількість кольорів.
Окрім парності та пофарбування, у задачах на аркуші в клітинку та інших плоских і просторових решітках часто використовують різні геометричні і комбінаторні міркування, метод координат. Доцільно розглянути аркуш у клітинку як числову площину, на якій вузли решітки — точки з цілочисельними координатами, чи квадрат з р2 вузлів, координати яких — пари остач (%, у) при діленні на р.
Задачі
12.1 (8-9). Набір доміно виклали в ряд за чинними правилами. На одно-
му кінці ланцюга — п’ятірка. Що на другому кінці?
12.2 (8-9). У виразі 0*1*2* 3*.. *9 зірочки замініть на «-» або «+».
а) Чи можна одержати 0?
б) Чи можна одержати 1?
в) Які числа можна одержати?
12.3 (9). Чи може ламана, яка має 25 ланок, перетинати кожну свою
ланку рівно 3 рази?
12.4 (9). Дошка 9x9 пофарбована в 9 кольорів, причому всіх кольорів
порівну, і пофарбування симетричне відносно головної діагоналі. Доведіть, що на цій діагоналі всі клітинки пофарбовані в різні кольори.
12.5 (9-10). На шаховій дошці стоять 8 тур, які не «б’ють» одна одну.
Доведіть, що число тур, які стоять на чорних клітинках, парне.


Парність, фарбування. Задачі на решітках
93
12.6 (10). У вершинах куба записані числа 1 і -1. Також на кожній
грані записано добуток чисел, які стоять у вершинах цієї грані. Чи може сума всіх записаних чисел дорівнювати 0?
12.7 (10-11). У таблиці 25x25 записані цілі числа так, що в кожному
стовпчику та кожному рядку зустрічаються всі числа від 1 до 25. При цьому таблиця симетрична відносно головної діагоналі. Доведіть, що на головній діагоналі зустрічаються по одному разу всі числа від 1 до 25.
12.8 (10-11). За круглим столом сидять п рицарів із двох ворогуючих
країн. Число пар сусідів-друзів дорівнює числу пар сусідів-воро- гів. Доведіть, що п ділиться на 4.
12.9 (10-11). По кругу записані 4 одиниці і 5 нулів. За один хід між
двома однаковими цифрами записують одиницю, а між різними — нуль (старі цифри стирають). Чи можуть через декілька ходів всі числа стати однаковими?
12.10 (11). У вершинах я-кутника записані числа 1 та -1. На кожній стороні написано добуток чисел, які записані на її кінцях. З’ясувалось, що сума всіх чисел, записаних на сторонах, дорівнює нулю. Доведіть, що п ділиться на 4.
12.11 (8-10). Чи можна розрізати квадрат 10x10 на 25 фігур виду
12.12 (8-10). Чи можна розрізати квадрат 10x10 на 25 фігур виду ГГГП?
12.13 (8-10). Чи можна розрізати квадрат 10x10 на 25 фігур виду
СЕ0?
12.14 (9-10). Квадрат: а) 5 х 5; б) 8 х 8 розбили на декілька прямокутників 3 х 1 і один квадрат 1x1. Де може знаходитись квадрат 1x1?
12.15 (10-11). Чи можна квадрат 16 х 16 розбити на 64 прямокутники 1 х 4, із яких 31 стоятимуть вертикально, а решта 33 — горизонтально?
12.16 (10-11). При яких натуральних п квадрат я х п можна розбити на фігурки виду:
.> ЯЕВ » “В’


94
Задачі математичних олімпіад та методи їх розв'язування
12.17 (10-11). Прямокутник mxk розбитий на прямокутники їх я. Доведіть, що або т ділиться на п, або k ділиться на п.
12.18 (10-11). Прямокутник тхп називають «міцним», якщо його можна розбити на доміношки так, що будь-який розріз прямокутника перетинає хоча б одну доміношку.
а) Доведіть, що прямокутник б х б не «міцний».
б) Які прямокутники будуть «міцними», а які ні?
12.19 (11). Чи можна дошку 2пх2п без кутової клітинки розбити на фігурки виду
12.20 (11). При яких натуральних п дошку (2я + 1)х(2я + 1) без кутової клітинки можна розбити на доміношки, серед яких однакова кількість вертикальних та горизонтальних?
12.21 (8-9). Яку найбільшу кількість: а) тур; б) королів можна розмістити на шаховій дошці 8x8 так, щоб вони не били одна одну?
12.22 Яку найбільшу кількість: а) слонів; б) коней можна розмістити на шаховій дошці 8x8 так, щоб вони не били одна одну?
12.23 (8-9). Яку найменшу кількість клітинок потрібно зафарбувати у квадраті бхб так, щоб із залишку, який не зафарбовано, не можна було б вирізати фігурку виду ч?
12.24 (9). На полі морського бою, розміром 10x10, стоїть корабель 1x4. Яку найменшу кількість пострілів потрібно зробити щоб в нього попасти?
12.25 (9-10). На шаховій дошці 8x8 стоять 20 тур, які «б’ють» всі поля. Доведіть, що з них можна вибрати 8 тур, які теж «б’ють» всі поля.
12.26 (9-10). На шаховій дошці 10 х 10 стоїть 51 тура. Доведіть, що можна вибрати б тур, які не «б’ють» одна одну.
12.27 (9-11). Яку найменшу кількість королів потрібно розмістити на дошці: а) 4 х 4; б) 10 х 10 так, щоб під «боєм» були всі клітинки дошки?
12.28 (10-11). Із квадрата 31x31 вирізали 99 квадратів 2x2 (по лініях сітки). Доведіть, що можна вирізати принаймні ще один.


Парність, фарбування. Задачі на решітках
95
12.29 (10-11). У деяких клітках дошки /ихп стоять фішки. Кожна фішка — єдина у своєму стовпчику чи своєму рядку. Яка максимально можлива кількість фішок?
12.30 (11). На дошці пхп стоять декілька тур так, що у будь-якому хресті, утвореному з вертикалі та горизонталі, центральна клітинка якого порожня, стоїть п тур. Доведіть, що всього тур не менше,
9
П~
НІЖ —.
2
12.31 (11). На дошці тхп розташовано декілька кісточок доміно. Жодну з них не можна зсунути (не зсуваючи інших). Доведіть, що
вільних клітинок у прямокутнику менше за
тп
Т’
Розв’язки, вказівки, відповіді
12.1. Відповідь. Також п’ятірка. Вказівка. П’ятірки всередині ланцюга розбиваються на пари.
12.2. Відповідь, а) Ні; б) так; в) всі непарні числа від -45 до 45. Вказівка. а) Серед всіх доданків 5 непарних; б) наприклад, 0+1 - 2 + 3- 4 + 5 + 6- - 7 + 8 - 9 = 1; в) при заміні доданка а на доданок -а, сума замінюється на -2а (парне число).
12.3. Відповідь. Ні. Вказівка. Спробуйте підрахувати кількість точок перетину.
12.4. Вказівка. Простіше довести, що кожен колір зустрічається на діагоналі.
12.5. Вказівка. Колір клітинки визначається сумою її координат (парністю цієї суми). Сума координат всіх тур парна (вона не залежить від їх розміщення і дорівнює 2(1 + 2 + 3 +... + 8)).
12.6. Відповідь. Ні. Вказівка. Чисел всього 14, а їх добуток дорівнює 1.
12.7. Вказівка. Скористайтесь розв’язком задачі 12.4.
12.8. Вказівка. Число пар сусідів-ворогів завжди парне.
12.9. Відповідь. Ні.
12.10. Вказівка. Порівняйте цю задачу із задачею 12.8.
12.11. Вказівка. Пофарбуйте дошку в шаховому порядку. Чорних клітинок буде парне число, а в кожну фігурку їх попаде одна або три. Відповідь. Ні.
12.12. Вказівка. Пофарбуйте дошку в чотири кольори (див. рис.). Кожна фігурка містить по одній клітинці кожного кольору, а клітинок першого і другого кольору різна кількість. Відповідь. Ні.


96
Задачі математичних олімпіад та методи їх розв’язування
1
2
3
4
1
2
3
4
1
2
2
3
4
1
2
3
4
1
2
3
3
4
1
2
3
4
1
2
3
4
4
1
2
3
4
1
2
3
4
1
1
2
3
4
1
2
3
4
1
2
2
3
4
1
2
3
4
1
2
3
3
4
1
2
3
4
1
2
3
4
4
1
2
3
4
1
2
3
4
1
1
2
3
4
1
2
3
4
1
2
2
3
4
1
2
3
4
1
2
3
12.13. Вказівка. Пофарбуйте вертикалі дошки через одну. Відповідь. Ні.
12.14. Відповідь, а) У центрі; б) на третій клітинці по діагоналі від будь- якого кута даного квадрата. Вказівка. Пофарбуйте дошку в 3 кольори так, як і в задачі 12.12.
12.15. Вказівка. Пофарбуйте кожну четверту вертикаль.
12.16. Відповідь. п = 4k, k є N.
12.17. Вказівка. Пофарбуйте даний прямокутник в п кольорів так, як це зроблено у задачі 12.12.
12.18. а) Вказівка. Кожна лінія розбиття квадрата 6 х 6 на одиничні квадрати перетинає парну кількість доміношок; б) Відповідь. Всі прямокутники т х п, де тп число парне, zn > 5, п>5, крім квадрата 6x6.
12.19. Відповідь. Так, можна. Вказівка. Доведіть по індукції.
12.20. Відповідь. При парних п.
12.21. а) Відповідь. 8. Вказівка. На кожній вертикалі стоїть не більше однієї тури; б) Відповідь. 16. Вказівка. У кожному квадраті 2x2 знаходиться не більше одного короля.
12.22. а) Відповідь. 14; б) Відповідь. 32.
12.23. Відповідь. 18. Вказівка. У кожному квадраті 2x2 необхідно зафарбувати 2 клітинки.
12.24. Відповідь. 24.
12.25. Вказівка. Тури є на всіх вертикалях чи всіх горизонталях.
12.26. Вказівка. Доведіть за індукцією більш загальне твердження: з nk + 1 тур на дошці п х п можна вибрати k + 1, які не «б’ють» одна одну. Для цього, виберіть туру, яка б’є не більше п + k - 2 інших.
12.27. Відповідь, а) 4; б) 16. Вказівка. Кожен король може бити лише одну з відмічених клітинок (див. рис.)


Парність, фарбування. Задачі на решітках
97
12.28. Вказівка. Якщо це не так, то квадрати 3 х 3 з тими ж центрами, що і вирізані квадрати 2x2, покривають квадрат ЗО х ЗО, що неможливо.
12.29. Вказівка. Доводьте по індукції. Відповідь, т + п~ І.
12.30. Нехай k — кількість тур в одній з горизонталей. Можна вважати,
п
що k < —. Нехай є І горизонталей з k турами і т вертикалей з (п - k) турами. &
Можна вважати, що це нижні І горизонталей і праві т вертикалей. Очевидно, що т>п - k і l> k. Крім того, лівий нижній прямокутник 1 х (п - т) цілком заповнений турами (інакше знайдуться ще вертикалі з п - k турами). Отже, всього тур не менше ніж І • (п - т) + т(п -k)> k(n -т) + т(п - k) = т(п - 2k) +
„2
+kn >(п- k)(n -2k) + nk = k2 + (п-k)2 > —.
2
12.31. 	Вказівка. Використайте такий план розв’язку. По-перше: на краю дошки не може бути вільних клітинок; по-друге: будь-які чотири клітинки, сусідні (через сторону) з однією вільною, повинні бути зайнятими. По-третє: у різних вільних клітинках набори сусідів не перетинаються.


§13. Операції та інваріанти
Теоретичні відомості
У задачах, де потрібно з’ясувати, чи можна за допомогою заданих операцій перейти від одного об’єкта до другого, часто корисно знайти «інваріант» — числову характеристику об’єктів (або функцію із якимись іншими значеннями на множині об’єктів), яка не змінюється при вказаних операціях. Якщо при цьому значення інваріанта на двох об’єктах різні, то перетворити один в інший неможна. У цілочисельних та інших «дискретних» задачах інваріантом може бути остача від ділення на 2 (парність) або на інший натуральний дільник.
Якщо всі задані операції оборотні, то вся множина об’єктів, над якими вони виконуються, розбивається на класи еквівалентності (два об’єкти еквівалентні, якщо один з них може бути одержаний з другого за допомогою даної операції (операцій)).
У задачах, де потрібно, оцінити кількість операцій чи довести, що їх не можна виконувати безліч разів (наприклад, впевнитись у відсутності «циклу»), іноді буває корисно придумати функцію, яка після кожної дії (операції) монотонно зростає (чи спадає).
Задачі
13.1 (7-8). Було 5 аркушів паперу. Деякі з них розрізали на 5 кусків
кожен. Потім деякі з одержаних кусків знову розрізали на 5 кусків і так зробили декілька разів. Чи можна в результаті виконання таких дій одержати 1975 кусків?
13.2 (8). В одній вершині куба написали число 1, в інших — нулі.
Можна додавати по 1 до чисел, записаних на кінцях одного ребра. Чи можна добитися того, щоб всі числа ділились на З?
13.3 (8). 1989 солдатів вишикувались у шеренгу. Чи завжди їх можна
вишикувати за зростом, якщо дозволяється міняти місцями двох солдатів, які стоять через одного?
13.4 (8-9). В одній кутовій клітинці квадрата 3x3 стоїть знак мінус, а в
усіх інших клітинках — плюси. Дозволяється змінювати всі знаки одного рядка чи стовпчика на протилежні. Чи можна в результаті таких операцій одержати таблицю лише з одних плюсів?


Операції та інваріанти
99
13.5 (8-9). Круг поділили на 6 секторів, в кожному з яких лежить по
цукерці. За один хід одну цукерку можна перемістити в сусідній сектор. Чи можна зібрати всі цукерки в одному секторі рівно за 20 ходів?
13.6 (9). На дошці виписали числа 2, 3, ...» 1975. Дозволяється стерти
будь-які два числа, записавши замість них їх різницю. Довести, що багатократним повторенням такої операції не можна досягти того, щоб на дошці залишився один нуль.
13.7 (8-10). Нехай т, п — взаємно прості натуральні числа. А —
операція, яка переводить дріб — в дріб -2 - (тобто А
т2 + 2 ч .г л . т
= ——Довести, що застосувавши Л-операцію до дробу —,
п +1 п
далі до одержаного результату і т. д., ми, після деякого скінченого числа застосувань Л-операції, отримаємо скоротний дріб.
13.8 (8-10). На координатній площині дано чотири точки з цілими коор¬
динатами. Дозволяється замінити будь-яку з цих точок на точку, симетричну їй відносно довільної іншої з цих точок. Чи можна за декілька таких операцій перейти від точок (0; 0), (0; 1), (1;0), (1; 1) до точок з координатами (0; 0), (1; 1), (3; 0), (2; -1)?
13.9 (9-10). На дошці записали декілька плюсів та мінусів. Дозволяєть¬
ся стерти будь-які два знаки і написати замість них плюс, якщо вони однакові, і мінус в іншому випадку. Довести, що знак, який
залишиться на дошці, не залежить від порядку, в якому здійснювалось стирання.
13.10 (9-10). У трьох вершинах квадрата знаходяться три коники. Вони грають в «чехарду». При цьому після стрибка через коника В коник А попадає в точку, симетричну точці А відносно точки В. Чи зможе після декількох стрибків один з коників попасти в четверту вершину даного квадрата?
13.11 (9-11). На дошці виписані числа від 1 до 20. Дозволяється довільну пару чисел (%; у) замінити на число х + у + 5ху. Чи можна наприкінці одержати число 19901989?
13.12 (9-11). Фігура ходить по діагоналі прямокутника 2хя (наприклад, для коня це 2 х 3). При якому п вона зможе попасти з будь- якої клітинки у будь-яку на необмеженій шаховій дошці?


100
Задачі математичних олімпіад та методи їх розе’язування
13.13 (10-11). На дошці записані числа від 1 до 20. Пару чисел (х; у) можна замінити на число х + у + ху. Яке число залишиться на дошці після 19 операцій?
13.14 (10-11). У шести секторах круга лежить по «снікерсу». Дозволяється одночасно пересувати два «снікерси» в сусідні сектори, рухаючи їх в протилежних напрямках. Чи можна одержати таке їх розташування: 5, 1,0, 0, 0, 0?
13.15 (10-11). У квадраті 8x8 стоять цілі числа. Можна додавати по одиниці до всіх чисел довільного квадрата 3x3 або 4x4. Чи завжди можна отримати таблицю, всі числа якої діляться на З?
13.16 (10). На дошці записані числа 1990, 1995, 1996. Будь-які два
. . . За-b . ЗЬ-а
числа а і о можна замінити на числа і —-—. Чи можна
2 	2
одержати набір чисел 1991, 1994, 1997?
13.17 (11). В ряд виписані числа від 1 до 1991. Дозволяється взяти будь- які 4 числа і переставити їх у зворотному порядку. Чи можна за допомогою таких операцій одержати ряд чисел 1991, 1990,..., 2, 1?
13.18 (11). Автомат працює з картками, на яких написані пари чисел. Із
картки (а, Ь) автомат може зробити
а b 2’2
якщо а і b парні,
або (а + 1, b + 1). Із карток (а, Ь) і (Ь, с) він може зробити картку {а, с). Попередні картки він також повертає. Спочатку є картка (З, 10).
а) Чи можна отримати картку (1, 100)?
б) Чи можна отримати картку (1, 50)?
в) Для яких натуральних іг можна отримати картку (1, л)?
13.19 	(11). На дошці записані числа: a, b, с, d. Щосекунди вони заміню- . ються на числа а + b, b + с, о + d, d + а. Через деякий час знову одержали початкові числа: a, b, с, d. Доведіть, що а = b =
= с = d = 0.
13.20 	(11). 239 автомобілів увесь день їздили по круговій дорозі в одному напрямку. І ввечері всі вони опинились на тих же місцях, звідки починали рухатись вранці. Доведіть, що вони здійснили парну кількість обгонів.


101
Операції та Інваріанти
Розв’язки, вказівки, відповіді
13.1. Відповідь. Ні. Вказівка. При розрізанні одного куска кількість кусків збільшується на 4. Тому остача від ділення кількості всіх кусків на 4 не змінюється. Але 5 при діленні на 4 дає остачу 1, а 1975 — остачу 3.
13.2. Вказівка. Пофарбуємо вершини у шаховому порядку. Після цього сума чисел у білих вершинах завжди буде відрізнятись на 1 від суми цифр у чорних вершинах, бо після додавання обидві суми збільшуються на 1.
Відповідь. Ні.
13.3. Відповідь. Не завжди. Вказівка. При перестановках зберігається парність номера місця. Тому, коли найвищий стоїть на парному місці, він ніколи не стане першим.
13.4. Відповідь. Ні. Вказівка. Кількість мінусів у кутовому квадраті 2x2 завжди буде непарною.
13.5. Відповідь. Ні. Вказівка. Пофарбуйте сектори в шаховому порядку.
13.6. Вказівка. Вказана операція не змінює парності суми написаних чисел.
2 	+1975
Оскільки сума заданих чисел 2 + 3 + ... + 1975 = 1974 = 1977 • 987 —
непарна, то в кінці залишиться непарне число.
13.7. Вказівка. Розглянувши остачі від ділення на 3, бачимо, що чисельник і знаменник на якомусь кроці будуть ділитися на 3.
13.8. Відповідь. Ні, не можна. Вказівка. Точки (0; 0), (1; 1), (3; 0) та (2; -1) є вершинами паралелограма, який на координатній площині породжує відповідну сітку. Тоді «зворотними» операціями ми завжди будемо попадати у вузли цієї сітки, а вона не містить точок (0; 1) та (1;0).
13.9. Вказівка. Замініть плюсй на 1, а мінуси — на -1 і зауважте, що вказана дія не змінює добутку всіх чисел.
13.10. Вказівка. Введіть на площині систему координат так, щоб вершини квадрата, в яких сидять коники, мали координати (0; 0), (1; 0) та (0; 1). Зрозуміло, що коники будуть стрибати по точках з цілими координатами. Легко перевірити, що після стрибка парність кожної координати не змінюється. Тому жоден з коників не зможе попасти в точку (1; 1), в якої обидві координати непарні.
13.11. Відповідь. Ні. Вказівка. Сума всіх записаних чисел завжди буде ділитися на 5.
13.12. Вказівка. Розгляньте різні випадки парності числа п. Відповідь. При партних п.
13.13. Відповідь. 21! - 1. Вказівка. Додайте до всіх чисел по 1.
13.14. Вказівка. Занумеруємо сектори числами від 1 до 6 за годинником вою стрілкою і напишемо на кожному «снікерсі» номер сектора, в якому він знаходиться (при переміщенні у сусідній сектор, номер «снікерса» змінюється на відповідний номер сектора). Тоді сума написаних чисел завжди ділитиметься на 3. Відповідь. Ні.


102 Задачі математичних олімпіад та методи їх розв’язування
13.15. Відповідь. Ні. Вказівка. Замініть всі числа таблиці на їх остачі за модулем 3. Тоді кількість різних таблиць, які можна одержати з нульової, не більша З61, а всього таблиць: З64.
13.16. Відповідь. Ні. Вказівка. Сума всіх чисел набору не змінюється: 1990 + 1995 + 1996 * 1991 + 1994 + 1997.
13.17. Відповідь. Ні, неможна. Вказівка. Назвемо «безпорядком» числового ряду — кількість пар (Z; /) чисел і та / ряду, для яких і < j, але число і стоїть після числа /. Тоді вказана дія не змінює парності «безпорядку» числового ряду.
13.18. Вказівка, в) Для всіх п виду 7k + 1, де k натуральне число.
13.19. Вказівка. Через секунду сума даних чисел збільшується вдвічі. Тоді через п секунд 2"(а + b + c + d) = a + b + c + d, тобто а + b + с + d = §. Далі, враховуючи одержаний результат, з четвірки чисел: a + b, b + с, с + d, а + d через 2 кроки одержуємо четвірку чисел: 2(а + b), 2(b + с), 2(с + d), 2(а + d). Продовжуючи далі, одержимо, moa + b = 0,b + c = 0,c + d = 0,a + d = Q, тобто a = b = c = d = Q.
13.20. Вказівка. Розріжте дорогу в довільному місці, і тоді автомобілі будуть утворювати деяку перестановку. Легко перевірити, що її парність співпадає з парністю числа кількості обгонів.


§14. Перестановки, розміщення
I
комбінації цілих чисел та цш
Р-
Турніри
Теоретичні відомості
У розв’язуванні задач на скінченні послідовності цифр, цілих чисел, букв, фішок, розміщення їх на колі або в таблиці проводяться міркування, пов’язані з подільністю, комбінаторикою, оцінками, які застосовують індукцію.
Задачі про турніри, набрані бали та зайняті місця учасниками спортивних змагань розв’язуються такими ж міркуваннями.
Задачі
14.1 (7-8). Чи можна в клітинках таблиці 5x6 (5- — рядків, 6 —
стовпців) розмістити числа від 1 до ЗО так, щоб суми чисел в усіх а) рядках; б) стовпчиках були рівними?
14.2 (7-8). Чи можна числа від 1 до 21 розбити на декілька груп, у
кожній з яких якесь одне число дорівнює сумі всіх інших?
14.3 (7-8). Чи можна числа від 1 до 32 розбити на групи з однаковими
добутками?
14.4 (7-8). В стопу склали декілька однакових трикутників, на кожно¬
му з яких біля вершин написані числа 1, 2, 3 (трикутники можна повертати, але не можна перевертати). З’ясувалось, що біля кожного вертикального ребра стопи сума чисел дорівнює п. Які значення може приймати число л?
14.5 (8-9). У вершинах 10-кутника в довільному порядку розмістили
числа від 1 до 10. На кожній стороні написали суму чисел, які знаходяться на її кінцях. Доведіть, що десятковий запис якихось двох з цих сум закінчується на одну й ту ж цифру.
14.6 (8-9). Є сім натуральних чисел, сума будь-яких шести з них крат¬
на п’яти. Доведіть, що всі ці числа кратні 5-ти.
14.7 (9). Чи можна числа від 1 до 9 розбити на три групи так, щоб
добуток в кожній групі був: а) не більший 70; б) не менший 72?


104
Задачі математичних олімпіад та методи їх розв'язування
14.8 (9-10). У таблицю 10 х 10 записали числа від 1 до 100. Доведіть,
що знайдуться дві сусідні (через сторону) клітинки, різниця чисел в яких більша 5.
14.9 (9-10). По колу виписали 20 цілих чисел, сума яких дорівнює 1.
Скільки буде ланцюжків (підряд записаних чисел) з додатною сумою?
14.10 (10). Чи можна один мільйон гривень розміняти на 500000 папірців по 1 грн, 10 грн, 100 грн, 1000 грн?
14.11 (10). Кожне число таблиці дорівнює добутку суми чисел свого рядка та суми чисел свого стовпчика. Доведіть, що сума всіх чисел в таблиці дорівнює 0 або 1.
14.12 (9-10). ЗО команд зіграли турнір за олімпійською схемою. Скільки всього було зіграно матчів?
14.13 (10-11). 50 команд зіграли турнір з волейболу в одне коло. Говорять, що команда А сильніша за команду В, якщо А виграла у В або є така команда С, що А виграла у С, а С виграла у В. Доведіть, що команда, яка набрала найбільшу кількість балів, сильніша за будь-яку іншу.
14.14 (10-11). 12 команд зіграли турнір з.волейболу в одне коло. Дві команди здобули 7 перемог. Доведіть, що знайдуться команди А, В, С такі, що А виграла у В, В виграла у С, а С виграла у А.
14.15 (10-11). Матч між двома футбольними командами закінчився з рахунком 8 : 5. Доведіть, що був момент в грі, коли перша команда забила стільки ж м’ячів, скільки другій залишилось забити.
14.16 (10-11). 12 шахістів зіграли турнір в одне коло. Потім кожен з них написав 12 списків. У першому тільки своє прізвище, у (k + 1)-му прізвища тих, які були в &-му та ті, у кого вони виграли. З’ясувалось, що у кожного шахіста 12-й список відрізняється від 11-го. Скільки було нічиїх?
14.17 (11). 20 команд зіграли турнір з волейболу в одне коло. Нехай V. — число партій, які виграла Z-та команда, Р. — число партій, які вона програла. Доведіть, що V2 + Ц2 +... + V£ - Р2 + Р2 +... + Р20.
14.18 (11). Нехай A(t) = х2 - 600 і Л,(0 = х2 - 600, тоді позначимо через A(t) = A(Ak(x)), де є N. Розв’яжіть рівняння: Л100(х) - х.


Перестановки, розміщення і комбінації цілих чисел та цифр. Турніри 105
14.19 (11). У клітинках таблиці 7x7 записані плюси та мінуси. Можна одночасно змінювати знаки в будь-якому стовпчику чи рядку. Доведіть, що можна зробити так, що у будь-якому стовпчику та рядку плюсів буде більше, ніж мінусів.
14.20 (11). На столі лежать 15 зошитів в декількох стопах. З ними виконують таку операцію: беруть з кожної стопи по зошиту і утворюють з них нову стопу. Доведіть, що буде момент, коли утвориться 5 стоп, в яких буде відповідно 1, 2, 3, 4, 5 зошитів.
14.21 (10-11) Під час проведення футбольного турніру в одне коло з’ясувалось, що серед кожних чотирьох учасників є принаймні одна команда, що зіграла з іншими трьома. Доведіть, що всього в турнірі не зіграно щонайбільше три матчі.
14.22 (11). У чемпіонаті країни з футболу беруть участь 16 команд. Кожна команда має свій стадіон. Усі команди повинні зіграти між собою; у кожному турі чемпіонату беруть участь усі 16 команд (тобто проводиться 8 ігор). Чи можна скласти розклад турів чемпіонату так, щоб кожна команда проводила одну гру на своєму полі, а наступну — на полі суперника?
Розв’язки, вказівки, відповіді
14.1. Відповідь, а) Так; б) ні. Вказівка. Сума всіх чисел від 1 до ЗО ділиться на 5, але не ділиться на 6.
14.2. Відповідь. Ні. Вказівка. Сума всіх чисел від 1 до 21 непарна.
14.3. Відповідь. Ні. Вказівка. Лише в одній групі добуток може ділитися на 29.
14.4. Відповідь, п — будь-яке число, кратне 6.
14.5. Вказівка. Сума всіх чисел на сторонах дорівнює 110, а сума десяти різних цифр закінчується на 5.
14.6. Вказівка. Доведіть спочатку, що сума всіх чисел ділиться на 5.
14.7. Відповідь. Ні. Вказівка. 9! = 70 • 72 • 72, що більше 703 і менше 723.
14.8. Вказівка. Найкоротший шлях від 1 до 100 містить не більше 19 клітинок (всього 18 кроків). Якби на кожному кроці число в клітинці змінювалось не більше ніж на 5, то в результаті воно не могло б змінитися більше, ніж на 90.
14.9. Вказівка. Ця кількість рівна половині всіх ланцюжків підряд записаних чисел.
14.10. Вказівка. Розгляньте остачі за модулем 3.
14.11. Вказівка. Нехай ST — сума чисел таблиці; S. — сума чисел г-го
стовпчика, R. — сума чисел /-го рядка. Тоді = £ аг = 22$ • Я = .
/=1,/=1 і=1 /=1
14.12. Відповідь. 29. Вказівка. їх кількість така, як і кількість вибувших команд.


106
Задачі математичних олімпіад та методи їх розв'язування
14.13. Вказівна. Нехай А — команда, яка набрала найбільшу кількість очок, а В — команда, яка виграла в А та виграла в усіх тих команд, у яких виграла команда А. Тоді кількість очок, які набрала команда В буде більшою за кількість очок, які набрала команда А. Протиріччя.
14.14. Вказівка. Якщо таких команд немає, то усі команди набрали різну кількість очок.
14.15. Вказівка. Позначимо через S різницю між кількістю м’ячів, які залишилось (на даний момент) забити другій команді, та кількістю м’ячів, забитих першою командою. При кожному забитому м’ячеві, в ті чи інші ворота S зменшується на 1. На початку гри S = 5, а в кінці S = -8. Тому, був момент, коли S = 0, тобто кількість м’ячів, які залишилось забити другій команді дорівнює кількості м’ячів, які вже забила перша команда. Зауваження. Використана ідея називається дискретною неперервністю.
14.16. Відповідь. 54. Вказівка. Доведіть, що кожен шахіст виграв рівно одну партію (якщо (k + 1 )-й та k-й списки співпадають, то всі наступні також співпадають).
14.17. Вказівка. Підставте Р. = 19 - V., де і = 1, 2, .... 20.
14.18. Відповідь, х = 25 або х = -24.
14.19. Вказівка. Зменшуйте загальну кількість мінусів, поки це можливо.
14.20. Вказівка. Впорядкуйте стопи по кількості зошитів, що входять до них. Тоді їх відмінність від набору 1, 2, 3, 4, 5 зменшуватиметься.
14.21. Вказівка. Доведіть від супротивного.
14.22. Відповідь. Такий розклад скласти неможливо. Вказівка. Якщо в одному турі команди А і В грають на своїх полях (зрозуміло, що такі команди знайдуться), то в наступному турі вони повинні грати на полі суперника, в третьому турі знову на своїх і т. д. Тому зустріч між А та В неможна включати в розклад (адже в ній або А прийматиме В, або В прийматиме А на своєму стадіоні).


§15. Планіметрія
Теоретичні відомості
Майже в кожному варіанті олімпіадних завдань зустрічається традиційна шкільна, хоча і не проста, задача з планіметрії. Серед найбільш поширених геометричних теорем, які використовуються для їх розв’язку, відмітимо такі:
0 кут між січною та дотичною кола дорівнює піврізниці величин дуг, розташованих між сторонами кута;
0 квадрат довжини дотичної дорівнює добутку відрізків січної від вершини кута до точок її перетину з колом;
0 дотичні, проведені з однієї точки до кола, рівні;
0 чотирикутник описаний навколо кола тоді і тільки тоді, коли суми його протилежних сторін рівні;
0 чотирикутник вписаний в коло тоді і тільки тоді, коли суми його протилежних кутів 180°;
0 площа описаного многокутника дорівнює половині добутку периметра на радіус кола.
Задачі
а) Коло та інші геометричні фігури
15.1 (8-9). Три кола О,, О3 одиничного радіуса перетинаються в точ¬
ці А. Нехай В, С, D — точки перетину кіл Oj і О2, О2 і О3, О3 і Ої відповідно, що не збігаються з А. Доведіть, що точки В, С і D лежать на колі радіусом 1.
15.2 (8-9). У трикутнику центри вписаного та описаного кіл симетричні
відносно однієї із сторін. Знайдіть кути трикутника.
15.3 (8-10). Відрізки АЕ та CD — бісектриси трикутника ABC. Дове¬
діть, що якщо Z.BDE: Z.EDC = /.BED: Z.DEA, то трикутник ABC — рівнобедрений.
15.4 (9). а) Відомо, що медіана та висота, проведені з однієї вершини
трикутника, ділять кут при даній вершині на три рівні частини. Доведіть, що даний трикутник — прямокутний, знайдіть його гострі кути.


108
Задачі математичних олімпіад та методи їх розв’язування
б) Відомо, що медіана, бісектриса та висота, проведені з однієї вершини трикутника, ділять кут при даній вершині на чотири рівних частини. Доведіть, що даний трикутник — прямокутний, та знайдіть його гострі кути.
15.5 (9). У шестикутнику ABCDEF сторони АВ та DE, ВС та EF, CD
та FA паралельні. Відомо також, що діагоналі AD, BE, CF рівні. Доведіть, що навколо цього шестикутника можна описати коло.
15.6 (9). Висоти трикутника ABC перетинаються в точці Н. Відомо, що
НС = АВ. Знайдіть кут при вершині С.
15.7 (9). Нехай ВВ{ та СС, — висоти гострокутного трикутника ABC
з 	кутом А = 30°, В2 та С2 — середини сторін АС та АВ відповідно. Доведіть, що відрізки В,С2 та В2С, перпендикулярні.
15.8 (9). На колі, описаному навколо правильного трикутника ABC, довільним чином вибрали точку. Знайдіть суму квадратів відстаней від цієї точки до вершин трикутника, якщо сторона трикутника дорівнює а.
15.9 (9). Нехай М — точка перетину бісектрис внутрішнього кута В
і зовнішнього кута С трикутника ABC, a N — точка перетину бісектрис зовнішнього кута В і внутрішнього кута С. Доведіть, що середина відрізка MN лежить на колі, описаному навколо трикутника ABC.
15.10 (9). У прямокутному трикутнику ABC (Z.C = 90°) проведена висота CD. Знайти: а) радіус кола, що вписане в трикутник ABC, якщо радіуси кіл, що вписані в трикутник ACD та трикутник BCD, дорівнюють відповідно г, та г2; б) периметр трикутника ABC, якщо периметри трикутників ACD та BCD дорівнюють Р, та Р2 відповідно.
15.11 (9). Два відрізки ЛЛ, та ВВХ перетинаються в точці М. Кола, описані навколо трикутників АВМ та АХВХМ перетинаються в точці К (К Ф М). Довести, що трикутники АКВ та АХКВХ подібні.
15.12 (9). Через точку перетину діагоналей трапеції проведено пряму, паралельну основам трапеції. Обчисліть довжину відрізка цієї прямої, розташованого між бічними сторонами трапеції, якщо основи трапеції мають довжини а та Ь.
15.13 (9). Основи трапеції мають довжини 3 см та 15 см. Чи може радіус кола, вписаного у трапецію, мати довжину 4 см?


Планіметрія
109
15.14 (9). На площині дано трапецію ABCD. Нехай Р, Q — середини основ ВС і AD, а точка М лежить зовні трапеції на прямій, що проходить через вершини А і С. Через точки М і Р, М і Q проведено прямі МР та MQ до перетину з бічними сторонами трапеції АВ і CD відповідно в точках L і N. Доведіть, що пряма LN паралельна основам.
15.15 (9). Пряма, що проходить через середини двох відрізків, які відтинаються на прямих /, та /2 кутом АОВ, містить вершину цього кута — точку О. Доведіть, що прямі /, і /2 паралельні.
15.16 (9-11). Діаметр АВ кола co радіусом Р поділено точками М і Nна три рівні частини. У півкола, що утворилися, вписані кола co, та со2, які дотикаються діаметра АВ в точках М та N. Обчисліть відстань між центрами кіл co, та со2.
15.17 (9). Доведіть, що круги, побудовані на сторонах опуклого чотирикутника, як на діаметрах, покривають цей чотирикутник.
15.18 (9). Доведіть, що серед діагоналей довільного опуклого п’ятикутника можна вибрати три діагоналі таким чином, що з них можна скласти трикутник.
15.19 (10). У гострокутному трикутнику ABC висоти ЛЛР ВВХ та СС, перетинаються в точці Н. Доведіть формулу для радіуса Р описа¬
ного кола: Р = — АН2 2
А,Н
В{Н • СХН *
15.20 (10). У трикутник ЛВС вписаний трикутник MNP (точки М, N, Р лежать на сторонах АВ, ВС, АС відповідно) таким чином, що сторона MN перпендикулярна до сторони ВС, а сторона МР перпендикулярна до сторони АС. Знайдіть положення точки М (на стороні АВ), при якому сторона PN буде найменшою.
15.21 (10). Яким буде трикутник (гострокутним, прямокутним чи тупокутним), якщо: а) його висоти рівні 3 см, 4 см та 5 см; б) його медіани рівні 3 см, 4 см та 5 см?
15.22 (10). У колі радіусом Р проведено два діаметри, кут між якими дорівнює а. Доведіть, що відстань між основами перпендикулярів, проведених з довільної точки кола на ці діаметри, не залежить від положення точки на колі, та знайдіть цю відстань.
15.23 (10). Нехай AD — бісектриса кута А в трикутнику ABC. Доведіть, що AD2 = AB • АС - BD • CD.


по
Задачі математичних олімпіад та методи їх розв’язування
15.24 (10). Нехай МА та MB — дотичні до кола. У середині кола взято точку С таку, що МС = МА. Доведіть, що відмінні від А та В точки перетину прямих АС та ВС з даним колом діаметрально протилежні.
15.25 (10). У трикутнику ABC ZB АС = а, ВС = а. Знайдіть відстань від середини сторони ВС до прямої PQ, де Р та Q — основи висот трикутника, проведених до сторін В А і СА.
15.26 (10). Дано прямокутну трапецію з основами а і Ь. Відомо, що існує пряма, паралельна основам і ділить трапецію на дві менші частини, у кожну з яких можна вписати коло. Знайдіть радіуси цих кіл.
15.27 (10). Проекції деякого відрізка на дві сторони правильного трикутника дорівнюють 2 та 3. Знайдіть проекцію цього відрізка на третю сторону.
15.28 (10-11). Діаметр кола поділено на п рівних частин. На колі взято точку М. Доведіть, що сума квадратів відстаней від точки М до точок поділу не залежить від вибору точки М на колі.
15.29 (10-11). На площині дано п точок, причому відомо, що кожні' чотири з них є вершинами опуклого чотирикутника. Доведіть, що всі п точок є вершинами опуклого п-кутника.
15.30 (10-11). В опуклому чотирикутнику ABCD діагоналі перпендикулярні і перетинаються в точці М. Доведіть, що проекції точки М на сторони чотирикутника лежать на одному колі.
15.31 (11). У коло вписаний п’ятикутник ABCDE. Відстані від точки Е до прямих АВ, ВС та CD дорівнюють відповідно а, b та с. Знайдіть відстань від точки Е до прямої AD.
15.32 (11). На стороні ВС трикутника ABC знайдіть таку точку D, щоб кола, вписані в трикутники ABD та ACD, дотикались одне одного.
15.33 (11). Відданого трикутника трьома прямими, паралельними сторонам трикутника, відрізаються три трикутники так, що утворюється рівносторонній шестикутник. Знайдіть довжину сторони шестикутника, якщо довжини сторін трикутника рівні а, b та с.
б) Площі фігур
15.34 (8). Дано опуклий чотирикутник ABCD, площа якого дорівнює S. На його сторонах АВ, ВС, CD, DA обрано точки Е, F, Р, Н


Планіметрія
111
так, що АЕ = 2££, ЕС = ЗЕВ, CP = PD, АН = 5HD. Знайдіть площу шестикутника AEFCPH.
15.35 (8-9). Довжина основи АВ трапеції ABCD вдвічі більша від довжини основи CD і вдвічі більша від бічної сторони AD. Довжина діагоналі ЛС дорівнює а, довжина бічної сторони ВС дорівнює Ь. Знайдіть площу трапеції ABCD.
15.36 (8-9). На площині лежить рівнобедрений прямокутний трикутник ABC з катетом а. Трикутник Л^С утворено поворотом трикутника ABC навколо вершини прямого кута С на 45°. Знайдіть площу спільної частини трикутників ABC і Л,В,С.
15.37 (8-10). Основи трапеції дорівнюють а і b {а < Ь). Діагоналі розбивають трапецію на чотири трикутники. Найменший з них (за площею) має площу S. Знайдіть площі трьох інших трикутників.
15.38 (9). Дано довжини а та b двох суміжних сторін чотирикутника і гострий кут а між ними. Крім того, відомо, що кути чотирикутника, прилеглі до кожної з даних сторін, прямі. Знайдіть площу чотирикутника.
15.39 (9). У середині кута з вершиною В дано точку Р. Проведіть через точку Р пряму, яка б відтинала від кута трикутник найменшої площі.
15.40 (9). Довжина бічної сторони трапеції дорівнює а, а відстань до неї від середини протилежної сторони дорівнює Ь. Знайдіть площу трапеції.
15.41 (9). У трикутнику ABC проведено медіану AM, точка К лежить на AM, причому АК: AM =1:3. Через точку К і вершину В проведено пряму, що перетинає АС в точці L. Знайдіть площу трикутника AKL, якщо площа трикутника ABC дорівнює S.
15.42 (9). Доведіть, що-довільний трикутник розбивається своїми медіанами на б рівновеликих трикутників.
15.43 (9). Доведіть, що якщо у двох опуклих чотирикутників середини сторін збігаються, то їх площі рівні.
15.44 (9). Чи існують трикутники з висотами л/2, л/З, л/2 + 7з?
15.45 (9). В опуклому чотирикутнику ABCD знайдіть т„аку точку О, щоб площі чотирикутників, що утворюються при з’єднанні точки О з серединами сторін чотирикутника ABCD, були рівні.


112
Задачі математичних олімпіад та методи їх розв’язування
15.46 (9). На сторонах АВ та ВС трикутника ABC дано точки М та N такі, що AM : MB = BN: NC. Нехай Q — точка перетину прямих AN та CM. Доведіть, що площа чотирикутника MBNQ дорівнює площі трикутника ACQ.
15.47 (9). Кожна діагональ чотирикутника ділить його на трикутники однакової площі. Доведіть, що цей чотирикутник — паралелограм.
15.48 (9-10). Довжини сторін чотирикутника, описаного навколо кола радіуса г, взяті послідовно, утворюють геометричну прогресію. Обчисліть площу чотирикутника, якщо один з його кутів дорівнює а.
15.49 (9-10). Довжини сторін a, b, с, d опуклого чотирикутника такі,
що його площа дорівнює + сс^- Доведіть, що вершини чоти¬
рикутника лежать на одному колі.
15.50 	(9-10). На площині дано трикутники А,В,та А2В2С2 з площами
S, та S2 відповідно. Відомо, що вектори А1В1 та A^B2 пропорційні з від’ємним коефіцієнтом, те саме відомо про пари векторів
ДС, та ДС2, BjCj та В2С2 (з тим же коефіцієнтом). Знайдіть
площу трикутника Л3В3С3, де Ау Ву С3 — середини відрізків ЛД, В,В2 та С,С2.
15.51 (9-11). Довжини сторін трикутника утворюють геометричну прогресію, а висоти — арифметичну. Доведіть, що трикутник рівно- сторонній.
15.52 (10). Два кола перетинаються так, що їх спільна хорда стягує центральні кути в 30° та 60°. Яка частина круга, що обмежений меншим колом, знаходиться всередині більшого кола?
15.53 (10). У трапеції ABCD з довжинами основ AD-a та ВС = Ь проведено відрізок з кінцями на бічних сторонах, який паралельний її основам і ділить її площу навпіл. Знайдіть довжину цього відрізка.
15.54 (10). У трикутнику ABC проведені медіани AM та BN, причому
AM = /Лр ВМ = т2 і SABC
2тхт2
Знайдіть АВ.
З


Планіметрія 113
15.55 (10). На сторонах ВС, СА, АВ трикутника ABC взяті точки Лр Bv С, такі, що ВА1 : ДС = СВІ : ДЛ = ЛС, : С,В = 1:2. При перетині відрізків AAt, BBV CCj утворюється трикутник. Знайдіть відношення площі цього трикутника до площі трикутника ABC.
15.56 (10). На площині дано опуклий многокутник Р. Позначимо через Ра фігуру, що складається з точок, які знаходяться від Р на відстані а (тобто точок А, для яких всередині або на межі Р знайдеться точка В така,- що АВ < а). Площа Р{ дорівнює 5р площа Р2 дорівнює S2. Знайдіть площу Р.
15.57 (10). Відомо, що в чотирикутник можна вписати коло і навколо нього можна описати коло. Доведіть, що квадрат площі цього чотирикутника дорівнює добутку довжин його сторін.
15.58 (10-11). Дано центрально-симетричний многокутник з центром у початку координат, всі вершини в точках, координати яких є цілі числа. Доведіть, що площа цього многокутника виражається цілим числом.
15.59 (11). Діагоналі ділять трапецію на чотири трикутники. Нехай
S 	— площа трапеції, S, та S2 — площі двох трикутників, що містять основи трапеції як власні основи. Доведіть, що Vs = +yfs^.
в) 	Правильні многокутники
15.60 (8-9). У гострокутному трикутнику з однієї вершини проведено висоту, з другої — медіану, а з третьої — бісектрису. При їх перетині утворився новий трикутник. Доведіть, що він не може бути правильним.
15.61 (9). Дано правильний п’ятикутник Рр вписаний в коло, і правильний п’ятикутник Р2, описаний навколо цього кола, який дотикається до нього у вершинах Рг Проведемо через вершини Р, перпендикуляри до його сторін. Вони створять правильний п’ятикутник Р3. av а2, а3 — сторони відповідно п’ятикутників Рр Р2, Р3. Доведіть, що я* = я2 - tf-
15.62 (9-10). На сторонах правильного я-кутника зовні його побудовано квадрати. Відомо, що 2я-кутник, утворений вершинами цих


114
Задачі математичних олімпіад та методи їх розв’язування
квадратів, які не є вершинами л-кутника, правильний. При яких значеннях п це можливо?
15.63 (10). Точка О — центр паралелограма ABCD, в якому АВ < ВС. На сторонах АВ та ВС побудовані на зовнішню сторону рівносто- ронні трикутники АВЕ та BCF. Доведіть, що ЕО < FO.
15.64 (10). На сторонах довільного трикутника як на основах побудовано в зовнішню сторону рівносторонні трикутники. Доведіть, що їх центри е вершинами рівностороннього трикутника.
15.65 (11). Навколо правильного трикутника зі стороною 1 описано коло. Доведіть, що сума квадратів відстаней від довільної точки кола до вершини цього трикутника стала. Знайдіть її.
г) 	Поняття ГМТ
15.66 (7-8). На площині дано трикутник ABC. Знайдіть множину точок Р, для яких 2SMBP = 35двср.
15.67 (8-9). На площині дано два відрізки АВ і CD. Знайдіть множину всіх середин відрізків, один з кінців яких належить відрізку АВ, а другий — відрізку CD.
15.68 (8-9). Знайдіть геометричне місце точок перетину висот трикутників, вписаних у дане коло.
15.69 (9). Знайдіть множину всіх точок проекцій даного відрізка АВ на площині на всі можливі прямі, які проходять через дану точку О.
15.70 (9). На площині дано два кола різних радіусів. Знайдіть геометричне місце середин відрізків, що з’єднують точки одного кола з точками іншого.
15.71 (9-10). Дано п точок Л,, Л2, ..., Ап на площині. Знайдіть множину точок на цій площині, сума квадратів відстаней яких до точок А. — стала.
І
15.72 (10). З центра кола (О; R) проведено прямі Оа та Оь, які перетинають коло в точках А та В. Розглядають пари кіл: перше з центром на Оа, друге — з центром на Оь, такі, що дотикаються кола (O’, R) зовнішнім чином в точках Л та В відповідно і такі, що дотикаються одне до одного в середині кута АОВ. Знайдіть геометричне місце точок дотику цих кіл. (Примітка. Через (О; R) позначено коло, центр якого точка О, а радіус — R).


Планіметрія
115
15.73 (10). Дано рівносторонній трикутник ABC. Знайдіть геометричне місце точок М, що трикутники АМВ та ВМС рівнобедрені.
15.74 (10). Знайдіть геометричне місце точок О перетину діагоналей прямокутників, вписаних у даний гострокутний трикутник.
15.75 (10). На сторонах АВ та АС трикутника ABC вибираються точки
М та N відповідно таким чином, що AM = -і АВ, AN - —Ц• АС.
п п +1
Доведіть, що при всіх натуральних іг прямі MN проходять через одну і ту ж точку, та знайдіть її.
ґ) Застосування геометричних перетворень
15.76 (8). Два кола радіусом R дотикаються у точці К. На одному з них взято точку А, на іншому — точку В так, що ЛАКВ = 90°. Доведіть, що АВ - 2R.
15.77 (8). Всередині прямокутника ABCD вибрано точку М. Доведіть, що існує опуклий чотирикутник з перпендикулярними діагоналями довжини АВ і ВС, сторони якого рівні AM, ВМ, CM, DM.
15.78 (8-9). В якому місці слід побудувати міст MN через річку, що розділяє два міста А та В, щоб шлях AMNB з міста А до міста В був найкоротшим? (Береги річки вважати паралельними прямими, міст перпендикулярний до берегів).
15.79 (9). На сторонах АВ, ВС, CD, DA паралелограма ABCD вибрано точки Лр Bp Ср Dl таким чином, що Л1В1С,В1 — паралелограм. Доведіть, що центри цих двох паралелограмів співпадають.
15.80 (9-10). Коло перетинає сторони ВС, СА, АВ трикутника ABC в точках Л, і Л2, Bj і В2, С, і С2 відповідно. Доведіть, що коли перпендикуляри до сторін трикутника, проведені через точки Лр В, і Ср перетинаються в одній точці, то перпендикуляри до сторін, проведені через Л2, В2 і С2, теж перетинаються в одній точці.
15.81 (9-10). На сторонах ВС і CD квадрата ABCD відмітили точки М і К відповідно так, що ЛВАМ = ЛМАК. Доведіть, що ВМ + KD = АК.
15.82 (9-10). На відрізку АЕ по один бік від нього побудовано рівносто- ронні трикутники ЛВС і CDE. М і Р — середини відрізків AD і BE. Доведіть, що трикутник СРМ рівносторонній.


116
Задачі математичних олімпіад та методи їх розв’язування
15.83 (9-10). Два кола дотикаються в точці Р. Через точку Р проведено дві січні, які перетинають перше коло в точках Л1 і Вр а друге — в точках А2 і В2. Доведіть, що трикутники РА1В1 і РА2В2 подібні.
15.84 (9-11). Доведіть, що площа довільного опуклого чотирикутника ABCD не перевищує півсуми добутку протилежних сторін:
SASCD <-(АВ-CD + ВС ■ AD).
2
15.85 (10). На бісектрисі зовнішнього кута С трикутника ABC взято точку М*С. Доведіть, що МА + MB > СА + СВ.
15.86 (10). У кут величини а вписали коло радіусом 1. Далі вписали друге коло, що дотикається першого кола зсередини кута. Далі вписали третє коло, що дотикається другого кола зсередини кута, і так далі. Знайдіть радіус 1000-го кола.
15.87 (10). Результатом послідовних відображень деякої точки М відносно всіх сторін і вершини А трикутника ABC, виконаних в деякому порядку, є знов точка М. Доведіть, що трикутник ABC прямокутний.
15.88 (10). Точка М лежить на діаметрі АВ кола. Хорда CD проходить через М і перетинає АВ під кутом 45°. Доведіть, що сума CM2 + DM2 не залежить від вибору точки М.
15.89 (10). З вершини В паралелограма ABCD проведено його висоти ВК і ВН. Відомо, що КН=а, BD = b. Знайдіть відстань від точки В до точки перетину висот трикутника ВКН.
15.90 (10-11). Рівні кола Sj і S2 дотикаються кола S внутрішнім чин.ом в точках Л1 і А2. Довільну точку С кола S з’єднано відрізками з точками Л, і Л2. Ці відрізки перетинають Sj і S2 в точках В, і В2. Доведіть, що Л,Л2 І І В,В2.
д) 	Задачі на побудову
15.91 (8). Побудуйте трикутник за серединами двох його сторін і основою висоти, проведеної до третьої сторони.
15.92 (8-9). Дано коло, точку А на колі і точку К всередині кола. Знайдіть на колі такі точки В і С, щоб точка К була точкою перетину бісектрис трикутника ABC.
15.93 (8-11). Побудуйте трикутник ABC, якщо відомо його периметр 2р, кут А, і висоту ha, проведену із вершини А.


Планіметрія
117
15.94 (8-11). Побудуйте трикутник ABC, якщо відомі положення його вершини В, а також двох прямих h і т, на одній з яких (Л) лежить висота, проведена з вершини А, на другій (т) медіана, що проведена з вершини С.
15.95 (9). Використовуючи лише лінійку, проведіть перпендикуляр з точки М кола на діаметр АВ цього кола (М Ф А, Мї В).
15.96 (9). Впишіть у даний гострий кут трикутник найменшого периметра, одна з вершин якого збігається з даною точкою А всередині кута, а вершини В і С належать двом різним сторонам кута.
15.97 (9). На основі даного трикутника знайдіть таку точку, що пряма, яка з'єднує основи перпендикулярів, проведених з цієї точки на бічні сторони, паралельна основі.
15.98 (9-11). Побудуйте трикутник по точках перетину з описаним колом медіани, висоти і бісектриси, проведених з однієї вершини.
15.99 (10). В даний гострокутний трикутник впишіть трикутник, сторони якого при кожній з його вершин утворюють рівні кути зі сторонами даного трикутника.
15.100 (10). Точки С та D лежать на прямій Z, а точки А та В — ні. За допомогою циркуля і лінійки знайдіть на прямій І точку М таку, що /BM.D = 2/АМС.
15.101 (10). Побудуйте квадрат за чотирма точками, що містяться по одній на його сторонах.
Розв’язки, вказівки, відповіді
15.1. Вказівна. Нехай Е — центр кола Ог Доведіть, що /DEB = 2/BCD.
Звідси випливає, що коло О', симетричне О, відносно прямої BD, містить точку С.
15.2. Відповідь. 108°, 36° та 36°. Вказівка. Нехай І та О центри вписаного і описаного кіл, симетричних відносно сторони ВС трикутника ABC. Тоді ЬВОС = = ЬВІС, тому ЫВС — рівнобедрений. Звідси ДЛВС — рівнобедрений. Далі скористатись тим, що /ВОС = /ВІС і /ВОС - 360° - 2/ВАС, /ВІС = 90° + — /ВАС.
15.3. Вказівка. Доведіть, що завжди {/BDE + /.BED): {/EDC + /DEA) = = 2 : 1, і виведіть звідси, що кожен з даних в задачі співвідношень дорівнює 2.
15.4. Вказівка. Опишіть навколо трикутника ABC коло та проведіть медіану AM, бісектрису AL та висоту АН до перетину з колом в точках N, Е та D відповідно. Доведіть, що МАЕ рівнобедрений. Тоді МА = МЕ. Крім того


118
Задачі математичних олімпіад та методи їх розв’язування
МВ = МС, звідки легко вивести, що ТИ — центр нашого кола. Отже, ДЛВС — прямокутний. Відповідь, а) 30° та 60°; б) 22,5° та 67,5°.
15.5. Вказівка. Оскільки AF 11 CD та AD - CF, чотирикутник ACDF є рівнобічною трапецією. Звідки /FCD = /ADC = /DAF = /CFA = а. Аналогічно доводяться рівності /ЕВС = /FCB = /CFE = /BEF = $, /ЕВА = /.DAB = = /ADE = /BED = у. Оскільки сума кутів опуклого шестикутника дорівнює 4п, то а + Р + у = л. Тоді /CDA + /СВА = п і точка D лежить на колі, що проходить через точки А, В, С. Аналогічно доводиться, що точки Е, В, С, О лежать на одному колі і точки F, С, D, Е лежать на одному колі. Тоді всі 6 точок — А, В, С, D, Е, F — лежать на одному колі.
15.6. Відповідь. 45° або 135°. Вказівка. Нехай К, L, М — середини сторін ВС, СА, АВ відповідно, О — центр описаного кола. Трикутники ABC і KLM
подібні з коефіцієнтом —. Звідки ОМ = —НС. Тому в прямокутному трикут- 2 2
нику ОМВ ОМ = MB, /МОВ = 45°. Аналогічно /МОА = 45°, отже /АОВ = 90°.
15.7. Нехай О — точка перетину відрізків BjC2 та В2С,. У прямокутному трикутнику АВХВ В,С2 — медіана, проведена з вершини прямого кута, отже АС2 = ВХС2, /С2ВхА = /С2АВї = 30° і /ОС^ = ZZ^CjAs^O0. Аналогічно /ОВ^А = = 120°. З чотирикутника ОВ2ЛС2 знаходимо, що /В2ОС2 = 360° - (30° + 120° + + 120°) = 90°.
15.8. Відповідь. 2а2. Вказівка. Нехай МА = х, МВ = у, МС = z, де Л4 — точка описаного кола, О — центр кола. Знайдіть суму х2 + у2 + z2, тричі застосувавши теорему косинусів до трикутників ОМА, ОМВ, ОМС.
15.9. Нехай Р — середина відрізка MN. Очевидно, що кути NBM і NCM прямі. Тому коло радіусом PN з центром у точці Р проходить через точки N, В,
С, М. Тоді /MNC = /МВС = - /В, /NMB = /NCB = - /С, 2 2
/BNC = 90е -
- (/CNM + /NMB) = 90° - — (ZB + ZC) = - ZA, тобто /ВРС = 2/BNC = 2 2
= /А. А це і означає, що точка Р лежить на колі, описаному навколо трикутника ABC.
15.10. 	Відповідь, a) Jr? + г22; б) Jpf + р2. Нехай а = ВС, b - АС, с = АВ. Трикутники ACD та BCD подібні до трикутника ABC, причому коефіцієнти
b а
подібності дорівнюють - та — відповідно.
с с


Планіметрія
119
Ь CL
а) Якщо г — радіус кола, вписаного в ДЛВС, тоді zj = -г, г2 =— г. Тому
с с
д2 _і_ о2
9 9 'О Т Сі 9 9
г; +г2- = — г = г.
с~
Ь CL
б) Якщо Р — периметр трикутника ABC, то Р1=—Р,Р2=—Р; тому
с с
l2 , _2
+ Д2 = ° +Q р2 = р2 1 ‘ . с2
15.11. Вказівка. ЛАКВ = ZAMB = /.В,МА, - АВ,КА,, а = ——, оскіль-
1 ВК В{К
ки трикутники АКА{ та ВКВ} подібні (за двома кутами).
15.12. Вказівка. Нехай О — точка перетину діагоналей АС та BD трапеції ABCD, a MN — відрізок, про який йдеться у задачі (причому точка М лежить на бічній стороні АВ). Для обчислення довжини МО можна використати те,
що BABD ~ &МВО, КВОС ~ KDOA, звідси
AD
МО
BD , DO , DA
= 1 + = 1 +
ВО во ВС
ab 2ая
=> МО = -. Відповідь. г-
а + Ь а+Ь
15.13. Відповідь. Не може. Нехай ABCD — трапеція, що задовольняє умову задачі; ВС = З, AD = 15. Виберемо на AD точку Е так, щоб чотирикутник АВСЕ був паралелограмом. Тоді у трикутнику CED основа ED має довжину 15-3=12, висота, проведена до основи ED, — довжину 8. Нехай D' — точка, симетрична точці D відносно прямої ВС. Тоді у прямокутному трикутнику EDEf катети
ED = 12 і Р2У = 16, a ED' = Vl22 +162 = 20. Таким чином, АВ + CD = СЕ + CD -
- СЕ + CD' > ED' = 20 > 18 = AD + ВС, що суперечить можливості вписати у трапецію ABCD коло.
15.14. Вказівка. Довести допоміжне твердження: якщо Q — середина відрізка AD і LN паралельно ВС, а М — точка перетину АС і QN, то точка Р, яка є перетином прямих ВС і LM, — середина ВС.
15.15. Вказівка. Через середину відрізка, що лежить на /2, провести пряму, паралельну
15.16. Відповідь. —R.
9
15.17. Нехай точка М всередині чотирикутника ABCD не покрита кругами. Тоді кути АМВ, BMC, CMD, DMA менше 90°, чого не може бути.


120
Задачі математичних олімпіад та методи їх розе’язування
15.18. Нехай AD — найбільша діагональ п’ятикутника ABCDE. Тоді можна вибрати діагоналі AD, АС та BD, оскільки АС + BD > AO + DO > AD, де О — точка перетину діагоналей АС і BD.
15.19. Вказівка. Доведіть, що кола, які описані навколо трикутників ABC, АНВ, АНС, ВНС, мають один і той самий радіус R. Запишіть АН, А}Н, В{Н, СХН за допомогою R та синусів кутів а, З, у трикутника ABC (використавши теорему синусів) та підставте ці вирази в праву частину рівності, що необхідно довести.
15.20. Оскільки кути Р та N — прямі, навколо чотирикутника MPCN можна описати коло з діаметром МС. Тому PN - МС • sin ZC, отже відрізок PN матиме мінімальну довжину, коли мінімальним буде відрізок МС.
15.21. Вказівка. Нехай а > b > с — довжини сторін трикутника. Тоді, при а2 > Ь2 + с2 трикутник тупокутний, при а2 = Ь2 + с2 — прямокутний і при а2< Ь2 + с2 — гострокутний (що випливає, наприклад, з теореми косинусів).
а) Довжини сторін трикутника відповідно рівні
2S 2S З > 4
2S 5 ’
де S —
його площа і
2S
\2
2S
\2
>2 '2S
>
б) Якщо та, ть, тс — довжини медіан, проведених до сторін а, Ь, с відповід¬
но, то т~ =
г2 , „2
о + с
а'
1
<2 . 2 2 , Ь + а с .
тс = — — (для доведення
: ть =
2 . 2 а + с
4
цих рівностей слід добудувати трикутник до паралелограма і скористатися тим, що в паралелограмі сума квадратів довжин сторін дорівнює сумі квадратів довжин діагоналей). З цих рівностей (якщо довжини медіан 3, 4, 5) знахо¬
димо довжини сторін:
Відповідь, а) Тупокутний; б) гострокутний.
15.22. Вказівка. Якщо М — точка кола, Л4, і М2 — основи перпендикулярів, проведених з точки М на діаметри, то кут MtMM2 дорівнює або а, або 180° - а, оскільки його сторони перпендикулярні даним діаметрам. Далі, точки Л4, і М2 лежать на колі, діаметр якого МО (О — центр кола), тому хорда МгМ2 цього кола дорівнює MtM2 = МО ■ smZ.MlMM2 = /?sina.
15.23. Нехай Z.BDA = а, тоді ZADC = 180° - a. Використавши теорему косинусів для трикутників BDA і CDA, отримаємо: AD2 + BD2 - 2AD • BD • cos a =
лл? лд2
= АВ2 і AD2 + DC2 + 2AD DC • cos a = AC2, звідки ——+BD-2ADcosa= — BD BD


Планіметрія
121
AD2 АС2 «
+ DC + 2ADcosa = . Складемо останні дві рівності A£r
1
DC
DC
+
1
BD DC
+ BD + DC = — + — = AB • — + AC BD DC DC
- = AB-AC BD
1 1 VDC + BD ;
AC AB f
(тут було використано властивість бісектриси: ), отже AD2
1
1
BD DC
+ BD + DC = АВ • АС
1_ _1 BD + DC
AD2 = АВ ■ AC - BD • CD.
\ J
15.24. Нехай прямі AC і ВС перетинають дане коло в точках А, та В, відповідно і нехай ХАМ В = 2а. Проведемо через точки А, В, С коло, центр якого — точка М. Тоді ZACB = 180° - а, і тому ZAA,B, + ZBB,A, = ZABB, + + ZBAAj = а. Оскільки ZAOB = 180 - 2a (де О — центр даного кола), то ZAA,B = 90° - а. Тому ZB,A,A + ZAA,B + ZBB,A, = 90°. Тоді ZB,BA, = 90°, а це означає, що відрізок А,В, — діаметр.
а . a — sin — 2 2
а
15.25. Відповідь. сторони ВС.
15.26. Відповідь, г- •
Va +>Jb у/a + y/b
15.27. Відповідь. 1 або 5. Вказівка. Справедливо, що з трьох довжин проекцій відрізка на сторони правильного трикутника одна дорівнює сумі двох інших. Якщо при проектуванні відрізка на сторони правильного трикутника його довжина множиться відповідно на a, Р, у, то тоді і при проектуванні сторін цього трикутника на пряму, яка містить даний відрізок, їх довжини множаться на а, р, у. Зрозуміло, що проекція однієї зі сторін трикутника є сумою проекцій двох інших сторін, тому a = Р + у (або Р = a + у, або у = a + Р).
15.28. Вказівка. Скористайтесь такою рівністю: 2(МХ2 + МУ2) = XY2 +
+ (2МО)2, де X і У — дві точки поділу, симетричні відносно центра кола О.
15.29. Вказівка. Достатньо довести, що в довільній множині точок А,, А2, А3, .... Ап (п > 5), які не утворюють опуклий многокутник, можна вибрати точку так, щоб ті, що лишились, знову не утворювали опуклого многокутника.
15.30. Вказівка. Нехай М,, М2, М3, М4 — проекції точки М на сторони АВ, ВС, CD, DA відповідно. Тоді навколо чотирикутників АМ,ММ4, ВМ2ММ,,
Вказівка. PM = QM = —, де М — середина
Z
b4a a-Jb
CMzMMr
DM4MM3 можна описати кола’, тому XM4MlM2 + ZM4M3M2 =


122
Задачі математичних олімпіад та методи їх розв’язування
= {ZM4MXM + ЛМ2МХМ) + + ЛМ2М3М) = (ЛМ4АМ + ZM4DM) +
+(ZM2BM + ZM2CM) = 90е + 90° = 180°.
ис
15.31. Відповідь. —. Вказівна. Нехай М, N, Р, Q — основи перпендику-
\ b
лярів, проведених з точки Е на прямі АВ, ВС, CD та DA відповідно. Доведіть, що трикутники EMQ та ENP подібні.
15.32. Відповідь. BD = ^(ВС + АВ- АС).
15.33. Вказівка. Нехай А1ВХВ2СХС2А2 — шуканий шестикутник
( АХА2 і і ВС, ВХВ211 AC, CjC21 І АВ). Очевидно, що ДВВ,В2 ~ &АВС. Якщо k— коефіцієнт подібності, то ВВХ = kc; BB2 = ka; BxB2 = kb; АА{ = с - Л,В, -
а АА
- ВВХ = с - k(b + с). З іншого боку АхА2=ААх- — = а L, тоді kb =
с с
1-
k(b + с)
, тобто k =
ас
Звідси випливає, що -
ab + Ьс + ас
abc
ab + Ьс + ас
15.34. Відповідь.
15.35. Відповідь.
якого дорівнюють а і
Hs.
12
— ab. 4
Ь, М
Вказівка. Чотирикутник ADCM — ромб, діагоналі — середина основи АВ.
15.36. Відповідь.
'ь'г
\aJ
b ь
S, —S, — S. Вказівка. Нехай ABCD — дана трапе- а а
ція, ВС = a, AD - b — її основи. S, і S2 — площі трикутників ВОС і AOD відповідно (О — точка перетину діагоналей). Тоді трикутники АОВ і COD
= а
J
. 5,
мають однакову площу. Позначимо цю площу через S3. Тоді:
'а? \bJ
S3 _ CO _ a S2~ AO ~ b'
звідки
S2 =
"-Ї
<a>
> Sj,
>s,.
Тому S, = S,
S, S3 —


Планіметрія
123
15.38. 	Нехай AD - а, АВ = b — сторони чотирикутника, /.BAD = а. Нехай прямі CD та АВ перетинаються в точці Е. З прямокутного трикутника ADE
а
одержуємо
АЕ -
а
cos а
Тому BE- b.
cos а
З трикутника ВСЕ знаходимо
ВС = BE • tg
ґ к 'І ос- х a-6cosa . . b-acosa
= BE • ctg a = :. Аналогічно, CD =
— a 2
sin a
2ab-(a2 +Z>2)cosa
sin a
1
тому SABCD — — (AD ♦ DC + AB • BC) — 4
£ Sin ОС
15.39. Вказівка. Якщо ВАС шуканий трикутник, то Р — середина сторони АС.
15.40. Відповідь, ab. Вказівка. Проведіть через середину, про яку йдеться в умові, пряму паралельну до сторони, довжина якої а.
15.41. 	Проведемо MN 11 AC (N є BL). Тоді MN --LC. З іншого боку, 2
АГ АК 1 1 1
bAKL~bMKN, тому = = -. Звідки AL = — MN = — CL, тобто
MN МК 2 2 4
AL = — АС. Далі. 5ЛЛІС = — S, SAKC = — SAMC - —S. Нарешті, SAKL = — SAKC =
15.43. Вказівка. Площа чотирикутника, вершини якого є середини сторін даного чотирикутника (відомо, що це паралелограм), дорівнює половині площі даного чотирикутника.
5
15.44. Відповідь. Існує. Вказівка. Скористайтесь тим, що а = —, та
доведіть нерівність +
15.45. 	Відповідь. Шукана точка О — це точка перетину двох прямих, кожна з яких проходить через середину однієї з діагоналей чотирикутника і паралельна іншій його діагоналі. Вказівка. Нехай М, N, Р, Q — відповідно
середини сторін АВ, ВС, CD та DA. Оскільки QP = MN = — АС, одержуємо, 2
Щ° BDqOP — SMBN0 — — • Гц • QP — o • Гі2 • QP, де /г,
сума висот трикутників
2


124
Задачі математичних олімпіад та методи їх розв'язування
DQP і OQP, проведених до основи QP, h2 — сума висот трикутників BMN і OMN, проведених до основи MN. Таким чином, точки D та В однаково віддалені (на відстані h = /і, = &2) від прямої, паралельної АС та проходить через середину BD.
15.46. Вказівка. Твердження задачі випливає з рівності площ трикутників
ABN та АМС, SABN = = —Ц-5ЛВС, де k = AM : MB .
k +1
15.47. Вказівка. Доведіть спочатку, що дві діагоналі ділять чотирикутник на 4 трикутники однакової площі, тобто точка перетину діагоналей ділить їх навпіл.
15.48. Відповідь. 4rsin2a. Вказівка. Якщо b, bq\ bq2, bqz — сторони чотирикутника, то b + bq2 =bq + bq3 => q = 1, тобто всі сторони чотирикутника рівні.
15.49. Вказівка. Якщо а, 3 — кути між парами сторін а, b і с, d, то площа чотири-
11 71
кутника дорівнює S = — (ab sin-a + be sin 3) < — (ab + cd). Звідси a = 3 = —.
2 2 2
1 I 9
15.50. 	Відповідь, —(s/si ~ • Вказівка. Трикутники A.B.C. подібні (і = 1,
2, 3).
15.51. Вказівка. З формули для площі трикутника випливає, що висоти також утворюють геометричну прогресію.
15.52. Нехай d — довжина спільної хорди двох даних кіл. Тоді радіус мен¬
шого кола дорівнює d, а радіус більшого
■. Площа S, сегмента, що
2 sin 15°
відтинається цією хордою від меншого кола, дорівнює різниці площ відповідно- , „ nd! d-Ji, . .
го сектора та трикутника, тобто о, = — —. Аналогічно площа S2 сегмен¬
та, що відтинається хордою від більшого кола, дорівнює
S -- °2 -
d2
12 4sin215° 4 4sin215°
Так як 4 sin215° = 2(1 - cos 30°) = 2 - 7з,
то шукане відношення дорівнює:
S, + S2 nd2
4 + л/З 12
1 + л/З 2тс
«0,043....
1
15.53. 	Відповідь, —-—. Вказівка. Нехай AD > ВС, PQ — даний відрізок (Р є АВ, Q є СВ), позначимо його довжину через х. Проведемо прямі СМ та QK, паралельні АВ (М є PQ, К є AD). Нехай Л, і h2 — висоти трапецій


Планіметрія
125
PBCQ та APQD відповідно. Тоді за умовою + = 1, а з подібності
(х + а)/^
&CMQ ~ &QKD : *~-Ь- = І- тому + = і.
а - х Лз (х + а)\а - х)
15.54. 	Відповідь, — д/m,2 + т2- Вказівка. Площа чотирикутника ABMN до-
О
рівнює — т{т2 sin а, де а — кут між діагоналями AM та BN. З іншого боку, 2
3
4
4
3
2
3
■'ABMN
= $АВС - Snmc =:7Sabc> тому SABC = ^SABMN = Jzn,zn2 sin а. З умови ви¬
пливає, що sina = 1. Тоді медіани AM та BN перпендикулярні. Лишилось тільки застосувати теорему Піфагора до трикутника АОВ, це О — точка перетину медіан AM та BN.
15.55. Відповідь. —.
1
15.56. 	Відповідь. 2S, - S2 + 2д. Вказівка. Ра складається з Р, кількох прямокутників загальної площі а • р, де р — периметр Р, і кількох секторів, що складають круг радіуса а. Отже, Sa = S + ар + да2. З умови маємо:
Sj = S + р + д $ S, = S + 2р + 4д
2S, - S2 + 2д.
15.57. 	Вказівка. Нехай a, b, с, d — довжини відрізків, на які сторони чотирикутника розбиваються точками дотику вписаного кола, г — радіус вписаного кола (рис. а)). Прикладемо один до одного два зафарбованих трикутники, як показано на рис. б). З того, що навколо даного чотирикутника можна описати коло, випливає, що сума гострих кутів одержаного трикутника дорівнює 90°, тобто цей трикутник прямокутний. Тоді г - 4ас. Аналогічно r = 4bd, отже ас - bd. Площа чотирикутника дорівнює (а + b + с + d} • г, та лишається, використавши рівність ас = bd, довести, що (a + b + с + d)2ac =
= (а + b)(b + с)(с + d){d + а).


126
Задачі математичних олімпіад та методи їх розв’язування
рис. а) рис. б)
15.58. Вказівка. Даний многокутник складається з подвоєної суми площ трикутників, вершини яких мають цілі координати. Подвоєні площі таких трикутників завжди цілі.
15.59. Позначимо довжини основ трапеції через а та Ь, висоти відповідних
трикутників — через hu та hb. Тоді
о а + b,. , ч
•S = —т—\ha + /і6),
b h &
З 	подібності — = -L. Позначимо — = t. Отже, b = ta, h. = th . В такому разі a h„ а “
S = (t + І)2
2 bhK
Звідси й випливає шукана рівність.
15.60. 	Вказівка. Нехай в трикутнику ABC проведені медіана AM, висота ВН і бісектриса СЦ А, = AM n ВН, Вх = ВН n CL, Cx=CLr\ AM. Припусти¬
мо, що трикутник правильний. Тоді 60° = ZAXBXCX = Z.HBC + Z.LCB =
= (90° - ЛАСВ) + —ZACB = 90° - ±ААСВ, звідки ZACB = 60°. Але тоді
& L
ЛАМВ = ЛАХМВ = 180° -{ЛВАХМ + ZAXBM} = 180° - (60° + 30°) = 90°. Отже,
AM — висота і медіана, тобто ABC — рівнобедрений трикутник, а тому правильний.
15.61. 	Вказівка. Покладемо а = 18°. Легко бачити, що а, =———, cos 2а
а.
а3 = ах tga. Скориставшись тим, що cos4a = cos72° = sin 18° = sina,
cos a
дістанемо: a\ + #з = ai
2 2 2 a,2(l-sina)2 2 2 -2sina 2a,2
2a,2
cos a
1 — sin a 1 + sina 1 +cos 4a
2a,
2 cos2 2a
= O22.


Планіметрія
127
15.62. Відповідь, п = 6. Вказівка. Нехай АВ і ВС дві сторони даного правильного n-кутника, ABKL і BCMN — квадрати, побудовані на цих сторонах. Тоді трикутник BKN — правильний.
15.63. Оскільки ЕА = CD, AD = CF, XEAD = XFCD, то трикутники EAD і DCF рівні. Тому ED = FD. Розглянемо трикутники BDE і BDF. У них BD — спільна сторона, ED = FD, BE < BF і тому Z.EDB < X.FDB. Тепер розглянемо трикутники EOD та FOD. В них OD — спільна сторона, ED = FD і /ЕРО < XFDO. Тому ЕО < FO.
15.64. Нехай Ох, О2 та О3 центри рівносторонніх трикутників АВСХ, ВСАХ та АСВ{, побудованих на сторонах АВ, ВС, СА. Трикутники ОХВО2 та АВАХ
подібні, оскільки
О,В О,В 1
—— - -т-г = —f= і ZO,BO2 = ХАВАЇ = ХАВС + 60е. З подібно- АВ А{В V3
сті випливає, що О,О9=-^Д. Аналогічно 090, _АД подібності 7з 2 3 уіЗ
&О2СО3 ~ ДА,СА ). Отже, О,О2 = О2О3. Так само доводиться, що О,О2 = О,О3.
15.66. Вказівка. Скориставшисть тим, що відстані від точок А та С до прямої ВР відносяться як 3:2, доведіть, що шукана множина — пряма, що проходить через точку В.
15.67. Вказівка. Якщо точка X є [А; В] — фіксована, а точка У «бігає» по відрізку CD, то середина ТИ відрізка ХУ пробігає середню лінію трикутника XCD. Відповідь. Паралелограм з вершинами в серединах відрізків AC, AD, ВС, BD. (Якщо АВ 11 CD, то цей паралелограм вироджується у відрізок).
15.68. Відповідь. Круг без межі, концентричний даному колу такий, що має втричі більший радіус. Вказівка. Якщо кут А трикутника ABC дорівнює а, то кут між висотами, проведеними з вершин В і С дорівнює я - а. Тому точка перетину висот лежить на колі, рівному даному, причому такому, що перетинається з ним у точках В і С.
15.69. Відповідь. Шукана множина — це об’єднання двох кругів, діаметри яких ОА і ОВ, виключаючи їх спільну частину.
15.70. Відповідь. Кільце, центром якого є середина відрізка, що з’єднує центри даних кіл, а радіуси зовнішнього і внутрішнього кіл рівні, відповідно, півсумі і піврізниці радіусів даних кіл. Вказівка. Нехай R і г — радіуси даних кіл (R > г). Зафіксуємо точку А більшого кола. Середини відрізків, що з’єдну¬
ють її з точками меншого кола, складають коло радіуса центр В якого 2
збігається з серединою відрізка, що з’єднує А з центром меншого кола. Коли
R
точка А пробігає більше коло, точка В пробігає коло радіусом —, центром 2


128 Задачі математичних олімпіад та методи їх розв'язування
якого є середина відрізка, що з’єднує центри даних кіл, а побудоване вище
г
коло радіусом % замальовує вказане кільце.
15.71. Відповідь. Коло з центром в центрі ваги точок Л,, .... Ап. Вказівка. Задача розв’язується за допомогою введення системи координат.
15.72. Вказівка. Якщо Р та Q — центри кіл, що дотикаються в точці М, то
71 1
М лежить на відрізку PQ і PM = РА, QM = QB, звідки ЛАМ В = ЛАОВ =
2 	2
= const. Звідки випливає, що точка М лежить на дузі кола, що проходять через точки А та В. Далі переконуємось, що всі точки дуги, крім А та В, входять у шукану множину.
15.73. Відповідь. Коло з центром В і радіусом ВА без чотирьох точок Л, С і їм діаметрально протилежних, і ще дві точки: центр трикутника і точка, симетрична В відносно ЛС. Вказівка. Розглянути 9 випадків: 1) МА = MB = МС; 2) МА = МВ = ВС; 3) МА = МВ, ВС = МС; 4) МА = АВ, MB = МС; 5) МА = АВ, МВ = ВС; 6) МА = АВ, МС = ВС; 7) АВ = МВ = ВС; 8) АВ = MB = МС; 9) АВ = = МВ, ВС = МС.
15.74. Відповідь. Три відрізки, що з’єднують середини сторін з серединами відповідних висот. Вказівка. Нехай ВМ — медіана трикутника АВС,.-ВН — його висота, К — точка перетину ВМ і сторони прямокутника, вписаного в трикутник ABC, паралельна стороні АС і не лежить на ній. Центр О прямокутника збігається з серединою перпендикуляра KL до сторони ЛС. Тому пряма МО проходить через середину N висоти ВН.
15.75. Виберемо довільну точку О площини. Позначимо ОА = а, ОВ = Ь,
п - . 1 - - п-1- 1 -
ОС = с, ОМ = т, ON = п. Тоді п = -а + -с, т = а + —Ь. Нехай
п
п
п +1 п +1
п
п +1
1-ї
- Г
1
хї
а +
— с
, т = 1 -
+ —
п J
1
п
п)
а + — с. Якщо пряма MN п
b = ха + ус ■ Тоді п =
— — їх
проходить через точку О, то вектори т та п колінеарні, тобто 1 — + — = у, п п
звідси у -1 = (1 - %) —. Оскільки ця рівність повинна виконуватись для довіль- п
ного натурального п, то х = 1, у = 1. Тому Ь = а + с. Отже, точка О така, що АВСО — паралелограм.
15.76. 	Вказівка. Розглянути паралельний перенос на вектор О,О2, де О, і О2 — центри кіл.


Планіметрія 129
15.77. Вказівка. Нехай М' — образ точки М при паралельному переносі на
вектор ВС. Тоді чотирикутник МВМ'С — шуканий.
15.78. Нехай А' — образ точки А при паралельному переносі на вектор
MN. Тоді A'N = AM, тому довжина шляху AMNB дорівнює A'N + NB + MN. Оскільки довжина відрізка MN стала, то слід знайти точку N, для якої сума A'N + NB мінімальна. Очевидно, що A'N + NB мінімальна при умові, коли точка N лежить на відрізку А'В, тобто точка N є точкою перетину берега, ближчого до міста В, і відрізка А'В.
15.79. Точка перетину діагоналей паралелограма є центром його симетрії. Нехай О — центр симетрії паралелограма ABCD. При симетрії з центром О точки Л1 і В, переходять в деякі точки А2 і В2 (А2 є CD, В2 є AD) і Л,В, = В2Д.
Тому трикутники B2A2D і DtCtD мають відповідно паралельні сторони і В,Л2 = В,С,. Тому, В2 = Dl і А2 = С,. Звідси випливає, що О — центр паралелограма Л^С,/),.
15.80. Нехай перпендикуляри до сторін, проведені через точки Л,, Bv С, перетинаються в точці М. Позначимо центр кола через О. Перпендикуляр до сторони ВС, проведений через точку Л,, і перпендикуляр до сторони ВС, проведений через точку Л2, симетричні відносно точки О. Тому перпендикуляри до сторін, проведені через точки Л2, В2 і С2, перетинаються в точці, яка симетрична точці М відносно точки О.
15.81. Повернемо квадрат ABCD відносно точки А на 90° так, щоб точка В перейшла в точку D. Нехай при цьому повороті точка М переходить в точку М', а точка К — в точку К'. Очевидно, що Z.BMA = ZDM'A. Оскільки ЛМАК = = Z.MAB = Z.M'AD, то Z.MAD = ЛМ'АК. Тому ЛМ'АК = ZMAD = ЛВМА = = ZDM'A, тобто трикутник АКМ' рівнобедрений. Звідси АК = KM' =KD + DM' = = KD + ВМ.
15.82. Розглянемо поворот на 60° відносно точки С, що переводить точку Е в точку D. Тоді точка В переходить в точку А, тобто відрізок BE переходить у відрізок AD. Тому середина Р відрізка BE переходить в середину М відрізка AD, тобто трикутник СРМ рівносторонній.
15.83. Вказівка. Точка дотику двох кіл є центром гомотетії, яка переводить одне коло в друге. При цьому трикутник РЛ,В, переходить у трикутник РА2В2, тому ці трикутники подібні.
15.84. Нехай D' — точка, симетрична точці D відносно перпендикуляра, що проходить через середину відрізка АС. Тоді SABCD - SABCD. - SBAD. + SBCD. <
<-AB-AD' + — BC- CD' = —(AB • CD + BC ■ AD).
2 2 2
15.85. Нехай А' і В' — точки, симетричні точкам А і В відносно прямої СМ. Тоді AM + MB = А'М + МВ > А'В = А'С + СВ = ЛС + СВ.


130
Задачі математичних олімпіад та методи їх розв’язування
15.86. Відповідь.
, • а 1 - sm —
2
999
Вказівка. Гомотетія з центром у вершині
1 + sin
а
кута, яка переводить перше коло в друге, переводить друге коло в третє, третє — в четверте і т. д. Простий підрахунок показує, що коефіцієнт цієї гомоте-
. . а
1 - sin —
тії дорівнює
1.
+ sin—
2
15.87. 	Вказівка. Очевидно, що з чотирьох описаних перетворень тільки відображення відносно прямої ВС може змінити відстань від точки М до А. Оскільки точка М перейшла в себе, то відображення відносно ВС не замінювало цієї відстані, а це можливо лише тоді, коли це відображення лишило точку на місці. Отже, точка М переходить в себе при застосуванні послідовно відображень відносно АВ, АС і симетрії відносно точки А. Поскільки застосування двох вказаних відображень — це просто поворот на кут 2<р, де <р — кут між прямими АВ і АС, а симетрія — це поворот на кут п відносно точки А, то точка
7Е
М перейшла в себе при повороті на кут 2<р + ті відносно точки А. Тоді <р = —.
Лі
15.88. Вказівка. Позначимо точки, симетричні точкам С і D відносно прямої АВ, через С' і D' відповідно. Z.CMD = 90°; тому С7И2 + MD'2 = С'М2 + MD2 = = C'D2. Оскільки Z.C'CD = 45°, довжина хорди C'D стала.
15.89. Нехай Нх — точка перетину висот трикутника ВКН. Оскільки ННХ1 ВК і КНХ1 ВН, ННХ И AD і КНХ || DC, то HXHDK — паралелограм. Тому
при паралельному переносі на вектор НХН точка К переходить у точку D,
а точка В переходить у деяку точку Р. Оскільки PD 11 ВК, то BPDK — прямокутник і РК = BD = Ь. Так як ВНХ ± КН, то PH ± КН. Також очевидно, що РН = ВНХ. У прямокутному трикутнику РКН відомі гіпотенуза КР = Ь і катет
КН = а, тому ВНХ = PH = "]b~ - а2. Відповідь, y/b2 - а2.
15.90. 	Проведемо діаметр кола S, що є віссю симетрії кіл S, і S2. Нехай
точки С' і В2 симетричні відповідно точкам С і В2 відносно цього діаметра. Кола S, і S гомотетичні з центром гомотетії в точці Ах, причому в результаті цієї гомотетії пряма В,В2 переходить у пряму СС', тому ці прямі паралельні.
Також очевидно, що В2В2 | | СС'. Тому точки В,, В2 і В2 лежать на одній прямій, паралельній прямій СС'.


Планіметрія
131
15.91. Вказівка. Нехай М, N — середини сторін, Н — основа висоти. Побудуємо пряму І, що проходить через Н паралельно MN і точку А, симетричну точці Н відносно MN. Нехай В і С — точки перетину прямих AM і AN з прямою І. Тоді трикутник ABC шуканий.
15.92. Вказівка. Нехай D — точка перетину АК з колом. Доведіть, що BK = BD.
15.93. Припустимо, що трикутник ABC побудовано. На продовженні сторони СВ за точку В відкладемо відрізок ВВХ - АВ, на продовженні сторони ВС за точку С — відрізок СС, = АС. В утвореному трикутнику ЛВ,С, маємо:
В,С, =2р,
XB.AC =90° +-ZA 2
висота з вершини А дорівнює ha. Отже, за
даними, в умові задачі, елементами можна побудувати трикутник (на відрізку
2р побудувати дугу величини 2(90’ - — Z4) і провести до відрізка пряму пара- 2
лельну на відстані ha). Вершини В і С шуканого трикутника знаходимо, як точки перетину серединних перпендикулярів до сторін АВХ і ЛС, з прямою в,с,.
15.94. Вершину С знаходимо, як точку перетину прямої т з перпендикуляром, проведеним з точки В до прямої h. Вершину А будуємо так. Через точку В проводимо пряму, паралельну h до перетину з прямою т у точці D. Позначимо точку перетину прямих h і т через К. Через точку D проведемо пряму паралельну прямій ВК. Ця пряма перетинає h в шуканій точці А (зазначимо, що чотирикутник AKBD — паралелограм, KD і АВ — його діагоналі).
15.95. З точок А та В проведемо два промені, що перетинають коло в точках С і D (С * D), які лежать в одній півплощині від АВ, причому самі промені перетинаються в точці N (N = AC n BD), що лежить зовні кола. Спочатку проведемо перпендикуляр до АВ з точки N. Оскільки ВС і AD — висоти трикутника, то пряма МН перпендикулярна діаметру АВ, де Н — точка перетину висот ВС і AD. Нехай К і L — точки перетину побудованого перпендикуляра NH з колом; X — точка перетину МК з АВ, a Y — точка перетину LX з колом. Тоді MY1AB.
15.96. Вказівка. Нехай О — вершина кута, А' та Л/ — точки, симетричні точці А відносно сторін ОВ і ОС кута відповідно. Оскільки А'В = АВ, А"С = АС, периметр трикутника ABC дорівнює довжині ламаної А'ВСА". Тому периметр буде найменшим, коли точки В та С лежать на А'А”, тобто є точками перетину Л'Л" зі сторонами кута.
15.97. Вказівка. Нехай ЛВС — даний трикутник з основою АС. Проведемо прямі, перпендикулярні сторонам АВ в точці А і ВС в точці С. Нехай D — точка перетину цих прямих, а пряма BD перетинає АС в точці В. Точка Е — шукана.
15.98. Вказівка. Нехай Н, L, М — точки перетину з колом висоти, бісектриси і медіани відповідно, О — центр кола. З’єднайте точки О та L, після


132
Задачі математичних олімпіад та методи їх розв’язування
чого проведіть через Н пряму, паралельну OL; тоді вершина В шуканого трикутника — точка перетину цієї прямої з колом. З’єднайте точки В та М; нехай S — точка перетину прямих ВМ і OL. Провівши через S хорду, перпендикулярну радіусу OL, одержимо вершини А та С шуканого трикутника.
15.99. 	Нехай ABC — даний трикутник, А'В'С' — шуканий (А' є ВС, В' є СА, С' є АВ). Оскільки перпендикуляри до сторін АВ, АС, ВС, проведених через точки С', В', А', є бісектрисами кутів трикутника А'В'С', вони перетинаються .в деякій точці О, причому ЛС'ОВ' = я - ЛА. Нехай ЛС'А'В' = 2а. Тоді
я
ZC'OB' =
ЛВ'А'С =
я + 2а 2
ZA.
звідки випливає, що
а - 2"~ тобто ЛС'А'В =
Аналогічно, ЛВС'А' - ЛС, ЛС'В'А = ЛВ.
Тому кВС'А' ~ ДЛС'В' ~ ААВ'С' ~ LABC. З подібності зразу випливає, що
ВА' = -ВС = -(с - АС') = -(с --АВ') =
а
а
а
З-
а а
л
а
с~ b (h г&\ ,Ь а , с1 Ь* ,
= \Ь — СВ) = 1— • — СА = н а — ,
а а а b
а
а
а2 + с2 - Ь2
звідки ВА' = , де а = ВС, b - АС, с = АВ. За теоремою косинусів
2а
а2 + с2 - &2 = 2accosZB. Тому ВА' = ccosZB. Це означає, що АА' ± ВС. Аналогічно доводиться, що СС' і ВВ' перпендикулярні АВ тз,АС відповідно. Отже, вершини А', В', С' є основами висот трикутника ABC.
15.100. Побудова. Нехай А' — точка, симетрична точці А відносно даної прямої І. Проведемо кола з центрами А та А', що дотикаються даної прямої, та до кожного з цих кіл проведемо дотичні з точки В. Точки перетину цих дотичних з І позначимо через Mv М2, Му М4. Умови задачі можуть задовольняти лише точки УИ,, М2, Му М4 (доведіть!) і кожна з них задовольняє або не задовольняє ним залежно від розташування точок С та D.
15.101. Вказівна. Скористайтесь наступним фактом: якщо точки М, N, Р, К лежать на сторонах АВ, ВС, CD, DA квадрата ABCD та відрізок МР перпендикулярний відрізку NK, то MP = NK.


§16. Стереометрія
Теоретичні відомості
При розв’язуванні стереометричних задач часто доцільно розглянути проекції фігур на площину (або на пряму). Відзначимо також теореми, які розглядаються в шкільному (факультативному) курсі математики:
1) Плоскі кути а, р, у будь-якого тригранного кута задовольняють нерівності а<р + у, Р<а + у, у<а + р.
2) Сума плоских кутів довільного опуклого многогранного кута менша 360°.
3) Нехай три прямі не лежать в одній площині і перетинаються в точці А. Нехай Вх і В2 дві різні точки першої прямої, відмінні від А, С, і С2 — другої, В, і В2 — третьої. Тоді для відношення об’ємів і V2
тетраедрів ЛВ,С,В, і AB2C2D2 має місце рівність
Ц _ ЛВ, -ЛС, - ЛВ, Ц ~ ЛВ2 • ЛС2 • AD2'
4) 	Нехай S, і S2 площі двох граней довільного тетраедра, <р — величина двогранного кута між ними, а — довжина їх спільного ребра, b — довжина протилежного ребра, v — кут між цими ребрами. Тоді для
.....z 2S, -S2 - sin<p 1 , .
об ему тетраедра справедливі такі рівності V = —!—* = — ad sinxg-
За 6
5) 	Об’єм V многогранника, описаного навколо сфери радіуса г, дорів¬
нює V = — rS, де S — площа повної поверхні цього многогранника.
6) 	Нехай а, р, у — плоскі кути тригранного кута, Л, В, £ — його
двогранні кути, відповідно протилежні до плоских. Тоді мають місце такі рівності:
s*na - s^nP- = .—П-ї- (теорема синусів); біпЛ sin В sinC
cos а = cos р cos у + sin р sin у cos Л (теорема косинусів); cos Л = - cos В • cos £ + sin В • sin £ • cos у (теорема косинусів).


134 Задачі математичних олімпіад та методи їх розв’язування
Задачі
16.1 (10). Чотири довільні точки А, В, С, D простору з’єднані між
собою відрізками АВ, ВС, CD, DA', середини цих відрізків позначимо відповідно М, N, Р, Q. Яка утвориться фігура, якщо провести відрізки MN, NP, PQ, QM?
16.2 (10). В просторі дано дві мимобіжні прямі а та Ь. Побудуйте
пряму, що перетинає обидві дані прямі, а також:
а) проходить через точку М, що не лежить на даних прямих а і Ь;
б) паралельну до даної прямої Z.
В якому випадку задача має розв’язок?
16.3 (10). У просторі дано п> 4 точок, причому відомо, що для кожної
з 	них знайдеться площина, в якій ці чотири точки лежать. Чи правильно, що й всі п точок лежать в одній площині?
16.4 (10). Чи обов’язково рівні між собою два плоских гострих кути,
розташовані в просторі так, що їх сторони відповідно перпендикулярні?
16.5 (10). Скільки існує у просторі мимобіжних прямих, довільні дві з
яких взаємно перпендикулярні?
16.6 (10). Доведіть, що довільну трикутну піраміду можна перетнути
площиною так, щоб в перерізі був ромб.
16.7 (10). Доведіть, що сума кутів просторового неплоского чотирикут¬
ника менша 360°.
16.8 (10). Ортогональною проекцією прямого кута АОВ на площину а
є знову прямий кут. Доведіть, що або {АО), або {ВО) паралельна до площини а.
16.9 (10). Ламана, що лежить на поверхні тетраедра, містить всі його
вершини і середини ребер. Якою є мінімальна можлива кількість ланок цієї ламаної?
16.10 (10). З точки О у просторі виходить чотири промені таким чином, що кути між довільними двома променями рівні між собою. Знайдіть цей кут.
16.11 (10). Знайдіть відстань між мимобіжними діагоналями двох суміж¬
них граней куба з ребром а.


Стереометрія
135
16.12 (10). У просторі дано дві мимобіжні взаємно перпендикулярні прямі а та Ь. Знайдіть множину середин відрізків АВ даної довжини d таких, що А є а, В є Ь.
16.13 (11). У прямокутному паралелепіпеді ABCDAXBXC{DX зі сторонами АВ = 12, AD = 12, ААХ = ЗО точка М лежить на грані ABCD,
причому MA = MB = у/37. Точка N, яка лежить на протилежній грані А симетрична до точки М відносно точки перетину
діагоналей паралелепіпеда. Знайдіть довжину найкоротшого шляху, що проходить по поверхні паралелепіпеда і з’єднує точки ТИ та N.
16.14 (11). Одна трикутна піраміда міститься всередині другої. Чи може сума довжин ребер у внутрішньої піраміди бути більшою, ніж у зовнішньої?
16.15 (11). Чи може переріз л-кутної призми бути правильним (я + 2)- кутником?
16.16 (11). При якому положені в просторі сірникової коробки площа її тіні буде найбільшою? (Тінь — це ортогональна проекція на горизонтальну площину).
16.17 (11). Чи може в перерізі паралелепіпеда площиною утворитися п’ятикутник? А також, чи може п’ятикутник, що утвориться, бути правильним?
16.18 (11). а) Наведіть приклад, який показував би, що дві висоти тетраедра (або їх продовження) можуть не перетинатися.
б) У тетраедрі ABCD проведені висоти ААХ, ВВХ, ССХ, DDX. Доведіть, що коли прямі ААХ та ВВХ перетинаються, то прямі CCj та DDX також перетинаються.
16.19 (11). Яку форму має тінь куба на площину, перпендикулярну його діагоналі, від пучка променів світла, які паралельні цій діагоналі?
16.20 (11). Як необхідно розмістити у просторі правильний тетраедр, щоб його ортогональна проекція на дану площину мала найбільшу площу? Знайдіть значення цієї площі, якщо ребро тетраедра має довжину а.
16.21 (11). Чи можна довільний тригранний кут перетнути площиною так, щоб у перетині утворився правильний трикутник?


136
Задачі математичних олімпіад та методи їх розв'язування
16.22 (11). Доведіть, що в перерізі тригранного кута площиною, в якого всі плоскі кути прямі, можна дістати гострокутний трикутник.
16.23 (11). У прямому паралелепіпеді ABCDAiBlCiDl діагональ АС{ перпендикулярна до площини, яка проходить через точки Лр В, D. Доведіть, що цей паралелепіпед — куб.
16.24 (11). В тетраедрі ABCD всі три плоскі кути при вершині D — прямі. Доведіть, що cos /ЛВС = cos ZABD • cos Z.CBD.
16.25 (11). Дано куб ABCDAxBxCfl{ з основою ABCD. Нехай М є {ВС), Не [££>), причому |7ИС| = |ВС|, МфВ, \НВ\ = 21BD|. Доведіть, що кожна площина, паралельна площині (AJ3D), відтинає у даного куба і піраміди D{ABMH многокутники рівних площ.
16.26 (11). Доведіть, що коли сума плоских кутів при вершині піраміди більша 180°, то кожне бічне ребро піраміди менше півпериметра її основи.
16.27 (11). Доведіть, що шість площин, які проходять через ребра трикутної піраміди і середини протилежних їм ребер, перетинаються в одній точці.
16.28 (11). У чотирикутній піраміді PABCD бічні ребра РА, РВ, PC, PD рівні між собою. Доведіть, що сума двогранних кутів при ребрах РА і PC дорівнює сумі двогранних кутів при ребрах РВ і PD.
16.29 (11). У тетраедрі ABCD кути ABD, ADC, BDC тупі, а ребра AD, BD, CD рівні за довжиною. Доведіть, що трикутник ABC гострокутний.
16.30 (11). Прямі, проведені перпендикулярно до граней тетраедра через центри вписаних в них кіл, перетинаються в одній точці. Доведіть, що суми довжин протилежних ребер цього тетраедра рівні між собою.
16.31 (11). Доведіть, що коли одна з висот тетраедра перетинає дві інші висоти, то всі чотири висоти перетинаються в одній точці.
16.32 (11). Доведіть, що коли в тетраедрі всі грані рівновеликі, то вони рівні між собою.
16.33 (11). а) У тетраедрі проведено чотири відрізки, кожен з яких з’єднує вершину з точкою перетину медіан протилежної грані. Доведіть, що всі чотири відрізки перетинаються в одній точці і діляться в ній у відношенні 3:1, починаючи від вершини.


Стереометрія
137
б) Доведіть, що в довільному тетраедрі виконується нерівність R > Зг, де R і г — радіуси відповідно описаної та вписаної сфер.
16.34 (11). Доведіть, що довільна площина, яка проходить через середини двох мимобіжних ребер тетраедра, ділить його об’єм навпіл.
16.35 (11). Дано многогранник. Про його грані, крім однієї, відомо, що вони центрально-симетричні. Доведіть, що і остання грань центрально-симетрична.
16.36 (11). ABCD — правильний тетраедр, а точка Р лежить всередині грані ABC. Задані довжини відрізків РА, РВ, PC. Обчислити довжину відрізка PD.
16.37 (11)- Точки М, N, Р, Q — середини ребер АВ, AD, SC, CD чотирикутної піраміди SABCD (S — її вершина, ABCD — її основа), об’єм якої дорівнює V. Знайдіть об’єм трикутної піраміди MNPQ, якщо відомо, що SABD = SBCD.
16.38 (11). Площа основи піраміди дорівнює 1. Проведено площину, яка паралельна до основи піраміди і ділить її на дві частини рівного об’єму. Знайдіть площу перерізу.
16.39 (11). У просторі дано опуклий многогранник Р. Позначимо через Ра просторову фігуру, що складається з точок, які знаходяться від Р на відстані а (тобто точок А, для яких всередині або на його поверхні знайдеться точка В така, що АВ < а). Відомо, що об’єм фігури Р, дорівнює V,, об’єм фігури Р2 дорівнює У2, об’єм фігури Р3 дорівнює V3. Знайдіть об’єм многогранника Р.
16.40 (11). На площині розміщені три циліндричні башти з радіусами основ 1 см, 2 см, 3 см. Знайдіть точку площини, з якої їх ширина здаватиметься однаковою.
16.41 (11). Ви переливаєте воду з циліндричної склянки, поступово нахиляючи її. З’явилося дно. Ви зупинилися в той момент, коли відкрилась рівно половина дна. Скільки води залишилось у склянці — менше чверті чи більше?
Розв’язки, вказівки, відповіді
16.1. Відповідь. Паралелограм. Вказівка. Достатньо переконатися в тому,
що (MN) 11 (ЛС) 11 (PQ) і (MQ) 11 (BD) 11 (NP).
16.2. Вказівка, а) Через точку М та пряму b проведіть площину а. Якщо уу — точка перетину площини а і прямої а, то пряма MN є шуканою;


138
Задачі математичних олімпіад та методи їх розв'язування
б) через пряму b провести площину (З, паралельну до прямої І. Якщо К — точка перетину Р і прямої а, то пряма, яка проходить через точку К і паралельна до прямої /, є шуканою.
16.3. Відповідь. Правильно. Вказівна. Окремо розгляньте випадки, коли серед даних точок знайдуться три, що не лежать на одній прямій і коли таких трьох точок немає.
16.4. Відповідь. Ні, не обов’язково. Вказівка. Побудуйте контрприклад.
16.5. Відповідь. Три прямі. Вказівка. Для доведення необхідно навести приклад трьох прямих, які б задовольняли умову задачі, та пояснити, чому більша кількість таких прямих існувати не може.
16.6. Вказівка. Якщо перетнути трикутну піраміду довільною площиною, паралельною до двох протилежних ребер, то в перерізі дістанемо паралелограм. Якщо переміщати цю площину паралельно від одного ребра до другого, то одна пара протилежних сторін цього паралелограма буде збільшуватись рід 0 до Ь, а друга пара сторін буде зменшуватись від а до 0 (а та b — довжини обраних ребер). Отже, в деякому проміжному положенні довжини всіх сторін паралелограма стануть однаковими, тобто паралелограм перетвориться на ромб.
16.7. Вказівка. Нехай ABCD — довільний просторовий неплоский чотирикутник. Добудуйте його до тетраедра рис. 1 і скористаємось тим, що сума довільних двох плоских кутів тригранного кута більша від третього плоского кута:
/DAB + /АВС + /BCD + /CDA < (/ВАС + /DAC) +
+/АВС + (/ВСА + /DCA) + +/CDA = (/ВАС + /АВС + /ВСА) +
+(/DAC + /DCA + /CDA) = 180° + 180° = 360°.
16.8. Доведення. Проведемо площину Р, яка проходить через точку О і паралельна до а. Тоді проекцією кута АОВ на площину Р буде кут Л,ОВ,. Нам необхідно довести, що або ОАЛ збігається з ОА, або ОВ, — з ОВ. Нехай прямі OAt і ОА не збігаються, тоді доведемо, що збігаються прямі ОВ, та ОВ. За умовою (ОВ,)±(ОЛ,), крім того (ОВ,)±(ОЛ), тобто пряма ОВ, перпендикулярна проекції ОЛ, прямої ОА на площину р (за теоремою про три перпендикуляри); звідси випливає, що пряма ОВ, перпендикулярна до площини АОАГ Пряма ОВ також перпендикулярна до площини ЛОЛ,: вона перпендикулярна до прямої ОА (за умовою) та прямій ОЛ,. Отже, прямі ОВ та ОВ, збігаються як два перпендикуляри до площини ЛОЛ,, що проходять через точку О.
16.9. Відповідь. 6. Неважко навести приклад ламаної з шести ланок, що містять дані десять точок. Припустимо, що ці точки можна розмістити на ламаній з п’яти ланок. На деякій її ланці лежать дві (з шести) середини ребер тетраедра; отже, на цій ланці інших відзначених точок немає, а на суміжній з нею ланці їх також не більше двох. Таким чином, дві ці ланки проходять через три дані точки. Три ланки, що залишились, містять не більше шести інших даних точок: три кінцеві точки і три внутрішні точки.


Стереометрія
139
П
16.10. Відповідь, arccos
. Вказівка. Побудуйте на променях відрізки
однакової довжини ОА, ОВ, ОС, 0D. Тоді ABCD — правильний тетраедр, а точка О — його центр ваги (ділить висоту тетраедра у відношенні 3:1, починаючи від вершини).
16.11. Відповідь.
Вказівка. Спочатку доведіть, що площини AJ3D
та BlDlC перпендикулярні до діагоналі ЛС, куба ABCDAlBlClDl та ділять її на три рівні частини, тобто третя частина діагоналі ЛС, є спільним перпендикуляром до діагоналей Afi та Р,С двох суміжних граней AAfifi та D£>,C,C відповідно.
16.12. 	Вказівка. Нехай О — точка перетину прямої а з площиною, яка
проходить через пряму b і перпендикулярна до прямої а, тоді ОМ = — як меді- ана прямокутного трикутника АОВ з гіпотенузою АВ = d. Отже, шуканою
множиною точок буде коло перетину сфери з центром О та радіусом — і пло- 2
щини, яка паралельна до прямих а та b і знаходиться на однаковій відстані від них.
16.13. 	Відповідь, л/1658. Вказівка. На рисунках 1 та 2 подані фрагменти розгортки паралелепіпеда і два можливих варіанти для шляху з М в N. На рисунку 1 довжина шляху дорівнює 42, а на рисунку 2 довжина шляху дорівнює >/і 658. Оскільки 71658 < 42, то найменший шлях з М в N зображений на рисунку 2.
At
B,
C,
D
А
mJ
рис. 1
с
в
16.14. 	Відповідь. Може. Вказівка. Розгляньте правильну піраміду DABC з досить великим бічним ребром порівняно з ребром основи ABC, позначте точки К і L де-небудь на основі ABC й дві інші точки М і N, які лежали б близько


140
Задачі математичних олімпіад та методи їх розв'язування
вершини D. Сума довжин ребер піраміди KLMN майже в рази більша за суму довжин ребер піраміди DABC.
16.15. 	Відповідь. Якщо п — парне, то правильний (п + 2)-кутник можливий; якщо п непарне, то ні. Вказівка. Зазначимо, що у правильного (л + 2)- кутника у випадку непарного п немає пари паралельних сторін.
16.16. Відповідь. Площина AXCXD (див. рисунок) повинна бути горизонтальною.. Вказівка. Площа ортогональної проекції! паралелепіпеда ABCDAxBxCft{ на горизонтальну площину дорівнює подвійній площі проекції трикутника Л,С,В.
16.17. Відповідь. П’ятикутник утворитися може, правильний — ні.
Вказівка. У п’ятикутника, що є перерізом паралелепіпеда площиною, завжди існує принаймні одна пара паралельних між собою сторін (чому?),
тоді як у правильного п’ятикутника ніякі дві сторони між собою не паралельні.
16.18. Вказівка, а) Розгляньте, наприклад, тетраедр АХАВС, вершини якого є вершинами куба ABCDAlBlClDl. Його висоти, проведені з вершин Л, та С, — відрізки ЛЛ, та СВ. Очевидно, що прямі ЛЛ, та ВС не перетинаються.
б) Кожна з умов «висоти ЛЛ, та ВВ, перетинаються» та «висоти СС, та DDX перетинаються» еквівалентні умові «ребра АВ та CD перпендикулярні». Залишилось довести еквівалентність двох умов: «висоти ЛЛ, та ВВ, перетинаються» та «ребра АВ та CD перпендикулярні».
16.19. Відповідь. Правильний шестикутник.
Вказівка. Якщо ЛВСВЛ,В,С,В, — даний куб (ABCD — нижня основа, ЛЛ,, ВВ,, СС,, DDX — бічні ребра), а пучок променів світла паралельний до діагоналі куба ВВ,, тоді тінь є шестикутник з вершинами в середині тих ребер куба, які не прилягають до вершин В та D.
а
16.20. Відповідь. —.
2
Вказівка. Нехай ABCD правильний тетраедр з ребром а, тоді площина ортогональної проекції цього тетраедра на дану площину дорівнює подвійній площі проекції квадрата MNPQ, де М, N, Р, Q — середини ребер AD, АВ, ВС, CD відповідно.
16.21. Відповідь. Ні, не довільний. Вказівка. Розгляньте тригранний кут з плоскими кутами 100°, 100°, 50°. Припустимо, що перетином його деякою площиною є правильний трикутник ЛВС. Оскільки кути АОВ та ВОС, тупі, то АВ та ЛС — це найбільші сторони в трикутниках АОВ та ВОС відповідно (О — вершина тригранного кута). Тому сторона ЛС (вона рівна сторонам АВ та ВС) є найбільшою в трикутнику АОС, що неможливо, бо ЛАОС менший 60е.


Стереометрія
141
16.22. Нехай а, Ь, с — довжини сторін утвореного трикутника. Знайдіть
довжини х, у, z відрізків, які відтинає ця площина від тригранного кута, з системи: х2 + у2=а2, y2+z2=b2, z2 + х2 = с2. Матимемо, що
2х2 =с2 + а2 — Ь2 > 0; 2у2 = а2 +Ь2 -с2 >0; 2z2 -b2 + с2 - а2 > 0; додатність
правих частин цих рівностей рівносильна гострокутності трикутника.
16.23. Вказівка. Достатньо записати умову перпендикулярності відповідних векторів.
16.24. Вказівка. Подайте сторони трикутника ABC через BD і вказані кути.
16.25. Вказівка. Розбийте піраміду DXABMH на об’єднання пірамід MCKDX, DDXCK, DXDHK, DXABCD, DXDAH, де к = (ЛВ) П (МН) і для кожної з них знайдіть відповідну піраміду в кубі так, щоб площі перерізів відповідно збігалися.
16.26. Вказівка. Зробіть розгортку бічної поверхні даної піраміди.
16.27. Вказівка. Скоростайтеся тим, що відрізки, які з’єднують середини протилежних ребер будь-якої трикутної піраміди, перетинаються в одній точці.
16.28. Доведення. Опустимо з вершини піраміди Р висоту РО на основу. Зрозуміло, що О — центр описаного навколо чотирикутника ABCD кола. Нехай Л,, В,, С,, В, — середини сторін ЛВ, ВС, CD, DA відповідно. Тоді піраміди РОАХА і РОЛ,В, РОВХВ і РОВХС, РОСХС і POCXD, PODXD і PODXA симетричні відносно площин РОАХ, РОВХ, РОСХ, PODX. Далі розгляньте окремо випадки, коли О лежить всередині чотирикутника ABCD та зовні нього або на його межі.
16.29. Доведення. Позначте довжини ребер AD, BD, CD через одиницю. Зрозуміло, що квадрат довжини довільного з відрізків ЛВ, ЛС, ВС більший за 2 і менший за 4. Тому сума квадратів двох сторін трикутника ЛВС більша від квадрата третьої сторони, тобто трикутник гострокутний.
16.30. Доведення. Нехай О —точка перетину вказаних прямих; К, L, М, N — основи перпендикулярів, проведених з точки О відповідно на ребра ЛВ, ЛС, CD, BD тетраедра ABCD. Нехай далі В — центр кола, вписаного в трикутник ЛВС. Зрозуміло, що К, L точки дотику цього кола зі сторонами ЛВ і ЛС трикутника ЛВС (зробіть малюнок). Тому AK = AL. Аналогічно ВК = BN, CM = CL, DM = DN. Отже, ЛВ + CD = AC + BD. Аналогічно доводиться, що АВ + CD = AD + ВС.
16.31. Доведення. Нехай ha, hb, hc, hd — висоти тетраедра, що виходять з його вершин А, В, С, D. Виділимо три властивості цих висот.
1. Якщо дві висоти перетинаються, то дві інші висоти також перетинаються. Дійсно, якщо, скажемо, перетинаються ha і hb, то прямі ha, hb, АВ лежать в одній площині. Ця площина перпендикулярна до CD і, отже, CD ± ЛВ. Але тоді CD, hc, hd перпендикулярні до ЛВ; отже, вони лежать в одній площині і, тому, hc перетинається з hd.
2. Якщо одна з висот перетинає дві інші, то вона перетинає й третю. Дійсно, при проектуванні на грань ЛВС висоти ha, hb, hc переходять у висоти


142
Задачі математичних олімпіад та методи їх розв'язування
трикутника АВС, а висота hd проектується в точку. Якщо hd перетинає ha і hb, то ця точка лежить на двох висотах грані, але тоді вона лежить на третій . Отже, hd перетинає й hc.
3. 	Якщо три висоти попарно перетинаються, то вони всі переходять через одну точку. Дійсно, у протилежному випадку вони всі лежали б в одній площині, що очевидно, неможливо. Тоді наше твердження очевидне.
Якщо, скажімо, hd перетинає ha і hb, то в силу властивості 2) hd перетинає й hc, в силу властивості 1) ha, hb, hc попарно перетинаються, а в силу 3) — всі висоти проходять через одну точку.
16.32. Вказівка. Проведіть спільний перпендикуляр MN до протилежних ребер АВ і CD тетраедра ABCD, розгляньте симетрію тетраедра відносно прямої MN При цій симетрії пряма АВ перейде в себе, точка С перейде в точку С', що розташована від прямої АВ на такій же відстані, як точка С. Але на прямій CD, крім точки С, є не більше однієї точки, що знаходиться від прямої АВ на тій же відстані, що й точка С (при віддаленні від N відстань збільшується). З іншого боку, з умови випливає, що точка D знаходиться від прямої АВ на тій же відстані, що й точка С (ці відстані є висотами граней ADB та АС В зі спільною основою АВ). Отже, при даній симетрії вершина С переходить у вершину D. Аналогічно, вершина А переходить у вершину В та В переходить в А. Тоді трикутник CAD перейде в трикутник DBC, тобто ці трикутники рівні.
16.33. Доведення, а) Візьмемо довільні два з розглядуваних відрізків (наприклад, АК та BL). Обидва відрізки лежать в одній площині АВМ, де ТИ —
середина CD, і тому перетинаються. Далі, | КМ |= і | ВМ | (бо медіани трикут-
О
ника точкою
перетину діляться у відношенні 2:1), тому | AL |= — | АВ | і З
I AG І: I GK |=| АВ |: | KL |= 3 :1, G — точка перетину відрізків АК та BL. Отже,
довільний з розглядуваних відрізків проходить через точку G, що ділить відрізок АК у відношенні 3:1, тому всі вони перетинаються в одній точці і діляться в ній у відношенні 3:1, починаючи від вершини.
б) Вказівка.
1. Доведіть, що радіус сфери, яка має спільну точку з кожною з граней тетраедра, не менший радіуса вписаної сфери (при цьому рівність досягається тільки у випадку, коли сфера, яку розглядаємо, є вписаною).
2. При гомотетії з коефіцієнтом k = - і відносно точки G задачі а) описа-
О
R З ’
на сфера перейде в сферу радіуса
що має спільну точку з кожною з граней
тетраедра (а саме точку перетину медіан граней). Звідси випливає, що тобто R > Зг. Рівність досягається тільки для правильного тетраедра.
R
з'-Л


Стереометрія
143
16.34. 	Доведення. Нехай М та N середини ребер АВ і CD тетраедра ABCD. Якщо розглянути площину, що проходить через вершину тетраедра, то твердження, яке необхідно довести, стає очевидним. Якщо площина не проходить через вершину, то вона перетинає одну із сторін АС або ВС трикутника ABC (для визначеності сторону ЛС в точці К). Нехай Р — точка перетину цієї площини з ребром BD. Тетраедр ABCD розбивається площиною (MNKP) на два многогранники ADPMKN та CBPMNK.
Розіб’ємо кожен з них на дві піраміди: перший на піраміди BMKNP та BKNC, другий — на піраміди AMKNP та APND. У піраміді BMKNP та AMKNP спільна основа MKNP і рівні висоти, проведені до цієї основи, бо М — середина відрізка АВ. Залишилось довести, що об’єми тетраедрів BKNC і APND рівні. У тетраедрів ABCD і BKNC спільна висота, що проведена з вершини В, тому відношення їх об’ємів дорівнює відношенню
площ основ:
Увж SK№C |КС||СЛГ| 1 VABcd Sacd і ЛС I I CD і 2
ІКСІ
|лсг
Аналогично доводиться, що
^APND _ SpND Vabcd SbCD
1 |РД|
2 І РВ I
Залишилось довести,
що І КС І: I AC |=| PD |: | DB |, або (що те ж саме) | КС |: | KA |=| PD |: | РВ |.
Якщо площина перерізу паралельна до ребра AD, то це очевидно. Якщо ж вона перетинає ребро AD в точці L, то обидва відношення дорівнюють IDLІ : I LA І ( дійсно, проведемо через точку D пряму DE, яка паралельна KN, тоді |DL|:|M|=| А£|:|АЛ|=| АС|:|АЛ|, бо |АС|=|А£|). Аналогічно, I PD І: І РВ |=| DL І: | LA |.
16.35. Вказівка. Потрібно кожне ребро цієї грані відображати відносно центрів симетричних граней до тих пір, поки не дістанемо ребро вихідної грані.
16.36. Вказівка. Виразіть вектор PD через РА , РВ , PC , AD , BD , CD і обчисліть I AD I.
16.37. Відповідь. “37 V.
16
Розв’язування. З рівності площ трикутників ABD та BCD випливає, що |ЛО| = ІОС|, де О — точка перетину діагоналей чотирикутника ABCD. Відріз¬


144
Задачі математичних олімпіад та методи їх розв’язування
ки ОР та QN — середні лінії трикутників ASC та ASP, тому вони паралельні прямій AS. Отже пряма РО паралельна площині MQN. Звідси випливає, що тетраедри MNQP та MNQO рівновеликі (в них спільна основа MNQ, а довжини висот, опущених з вершин Р та О, рівні). Залишилось обчислити об’єм тетраедра MNQO. В основі цього тетраедра лежить &MON, утворений серед¬
німи лініями /SABD. Його площа дорівнює — Sabd =т;$авсо- Відстань від точки 4 8
Q до площини ABCD дорівнює половині висоти піраміди SABCD. Тому
Kvwoq — 2 8 ^SABCD — 16
16.38. 	Вказівка. Одна з двох частин — піраміда, яка подібна даній з кое¬
фіцієнтом подібності
. Відповідь.
k =
16.39. 	Відповідь. ЗЦ - ЗУ2 + V3 - 8я.
Вказівка. Ра складається з: 1) нашого многогранника Р; 2) об’єднання прямокутних «паралелепіпедів» з висотою а, що побудовані на гранях многогранника Р; 3) об’єднання циліндричних секторів, що розташовані біля ребер многогранника Р; 4) об’єднання кулевих секторів, що розташовані біля вершин. Об’єм частини: 1) дорівнює V (шуканий); частини 2) дорівнює Sot, де S — повна поверхня многогранника Р; частин 3) дорівнює /а2, де І — число, яке не залежить від а (знайдіть його самі); а сектори частин 4) складають
повну кулю радіуса а, тобто мають сумарний об’єм
Отже,
V = V + Sa +/ос2 + — гах3. “ З
Залишається підставити a= 1, 2, 3, розв’язати одер¬
жану систему рівнянь відносно V, S, І і взяти значення V.
16.40. 	Вказівка. Нехай /?,, Р2, Р3 — радіуси башт, R = і, де і = 1, 2, 3.
Ширина всіх трьох башт буде здаватись однаковою, якщо кути, утворені дотичними до кожного з кіл (основ башт), що проведені з шуканої точки, будуть рівними між собою. З рівності цих кутів випливає, що ZO3PQ = Z.O2PR. Тому
k.PRO2 ~ ДРфО3. Це означає, що
1Щ І - I Р031 R3
Множина точок, що задоволь¬
няє цю умову, є колом. Аналогічно, множина точок, з яких кола з центрами 01 і 03 видно під рівними кутами, також є колом (Аполонія). Точки перетину цих кіл є шуканими.


Стереометрія
145
16.41. 	Відповідь. Менше чверті. Вказівка. Нас цікавить об’єм фігури, що зображена на рисунку. Об’єм нашої фігури нескладно обчислити за допомо-
2 • .
гою інтеграла: він дорівнює —. А це становить близько 21,2% від об’єму Зл
циліндра.


§17. Комбінаторна геометрія
Теоретичні відомості
Ця назва стосується різноманітних оцінок, пов’язаних з розміщеннями, покриттями, різними комбінаціями геометричних фігур. Тут використовуються тільки загальні властивості, пов’язані з розташуванням фігур на площині або в просторі.
Виділимо серед них теорему Жордана: довільна замкнена ламана, без самоперетинів, ділить площину на дві області — внутрішню та зовнішню, причому довільний шлях із точки, яка лежить у внутрішній області, в точку, яка лежить у зовнішній області, перетинає цю ламану, а кожні дві точки довільної області можна з’єднати шляхом, який не перетинає ламаної.
Слід також пам’ятати означення опуклої множини (фігури) — це множина точок, яка разом з кожними двома своїми точками містить і увесь відрізок, який з’єднує ці точки. Опуклою оболонкою фігури називають найменшу опуклу множину, що містить цю фігуру; опукла оболонка скінченої множини точок — многокутник (у просторі — многогранник) з вершинами в деяких із даних точок.
Разом з даною фігурою варто розглянути її є-окіл: множина точок, найменша відстань від яких до точок фігури менша ніж є; зокрема дві фігури (дві точки) знаходяться на відстані не меншій 2є, якщо їх є-околи не перетинаються, і навпаки.
Задачі
17.1 (6-7). На яку найбільшу кількість частин розбивають круг 4 прямі
лінії?
17.2 (8). а) Скільки гострих кутів може мати опуклий п’ятикутник?
б) Яку найменшу кількість тупих кутів може мати опуклий п- кутник?
17.3 (9). Всередині трикутника взяли т точок, жодні 3 з яких не
лежать на одній прямій. їх з’єднали одна з одною і з вершинами трикутника відрізками, що попарно не перетинаються. При цьому трикутник розбився на маленькі трикутники. Яка кількість маленьких трикутників могла при цьому утворитися?


Комбінаторна геометрія
147
17.4 (7-9). На площині відмітили а) 6 точок; б) п точок, п > 3. Відомо,
що пряма, яка проходить через будь-які дві з цих точок, містить ще одну відмічену точку. Доведіть, що всі відмічені точки лежать на одній прямі.
17.5 (8-9). Доведіть, що п прямих загального положення розбивають
п2 + п + 2
площину на частин.
17.6 (8-9). На шаховій дошці 8x8 відмічені центри всіх клітинок. Чи
можна провести 13 прямих так, щоб будь-які дві відмічені точки були розділені прямою?
17.7 (8-9). Дано декілька відрізків на прямій. Будь-які два з них мають
спільну точку. Доведіть, що всі вони мають спільну точку.
17.8 (8-9). Серед п прямих немає паралельних, і через будь-яку точку
перетину двох з них проходить по меншій мірі ще одна пряма. Доведіть, що всі ці прямі проходять через одну точку.
17.9 (8-9). На площині дано декілька точок (не менше трьох). Відомо,
що для довільних трьох із цих точок знайдеться четверта, яка разом з ними є вершинами паралелограма. Доведіть, що точок всього чотири.
17.10 (8-9). На площині намальовано декілька кругів, які ще перетинаються. Доведіть, що існує круг, який дотикається:
а) не більше шести кругів;
б) не більше п’яти кругів.
17.11 (9-10). Прямокутник з довжинами сторін а та b (а, b — натураль¬
ні числа) розбито на ab одиничних квадратів. Скільки існує усіх можливих квадратів, сторони яких паралельні сторонам прямокутника, а вершини знаходяться у вершинах цих одиничних квадратів?
17.12 (8-9). Шість секторів круга, кожний з кутом не більшим 6°, зафарбовані. Доведіть, що їх одночасно можна повернути навколо центра круга на один і той самий кут таким чином, щоб всі вони опинилися у незафарбованій частині круга.
17.13 (9-11). Коридорами лабіринта є всі сторони і діагоналі опуклого п- кутника. Яку найменшу кількість ламп необхідно розмістити в лабіринті так, щоб повністю його освітити?


148
Задачі математичних олімпіад та методи їх розв’язування
17.14 (9-11). Чи може «вершник» обійти куб розміром 1979 х 1979 х 1979,
який розбито на одиничні кубики, відвідуючи кожний з них лише по одному разу, якщо в початковий момент він знаходиться у центральному кубику (рівновіддаленому від всіх граней). Одним ходом «вершник» може перейти в один з шести сусідніх, що мають з ним спільну грань.
17.15 (9-11). Всередині опуклого 391-кутника задано 392 точки, жодні три з яких не лежать на одній прямій. Будемо з’єднувати ці точки відрізками між собою так, щоб жодні два відрізки не перетиналися (вони можуть мати спільні кінці), до тих пір, поки це можливо. Чи можна в результаті цих з’єднань одержати 1984 відрізки? 1985 відрізків?
17.16 (9-11). На прямій знаходяться павук і муха. Максимальна швидкість павука вдвічі більша від максимальної швидкості мухи, але він нічого не знає про місцезнаходження мухи до тих пір, поки вона не опиняється в одній точці. Чи зможе павук наздогнати муху?
17.17 (8-11). Площину поділено на квадрати з довжиною сторін 1 м. Використовуючи лінії поділу, побудовано високу стіну, що поділяє площину на дві частини: зовнішню і внутрішню. Поряд із стіною з-під землі виліз кріт, який бачить лише на відстані до 1 м та вміє рахувати лише до десяти. Чи зможе кріт дізнатися, де він знаходиться — зовні стіни чи всередині?
17.18 (9-11). Трикутник ABC розбитий на трикутники, вершини яких не лежать у вершинах даного (але можуть лежати на сторонах трикутника ABC). Вершини трикутників пофарбовані в три кольори так, що на стороні АВ (в тому числі і на вершинах) немає кольору 1, на ЛС немає кольору 2, на ВС немає кольору 3. Доведіть, що знайдеться трикутник розбиття, всі вершини якого мають різні кольори («лема Шпернера»).
17.19 (10-11). У прямокутнику 3x4 лежать 6 точок. Доведіть, що є 2 з них на відстані не більшій л/5.
17.20 (10-11). Доведіть, що на папері в клітинку не можна намалювати правильного трикутника з вершинами у вузлах сітки.
17.21 (11). На колі взято п точок і проведено всі можливі хорди, що сполучають ці точки. Відомо, що жодні три з проведених хорд не перетинаються в одній точці. На скільки частин розбивається круг?


Комбінаторна геометрія
149
17.22 (9-11). На площині дано 5000 точок, причому жодні три з них не лежать на одній прямій. Довести, що можна побудувати 1000 п’ятикутників, які не перетинаються один з одним і вершини яких містяться в цих точках.
17.23 (11). Діагоналями, які не перетинаються, опуклий я-кутник поділено на трикутники так, що кожна вершина n-кутника є вершиною непарного числа трикутників. Доведіть, що п ділиться на три.
17.24 (11). Кожна з граней правильного тетраедра фарбується одним із даних чотирьох кольорів. Два фарбування вважаються однаковими, якщо одне з них можна перевести в інше поворотом тетраедра навколо будь-якої його осі. Скількома способами можна пофарбувати тетраедр? (Всі грані — різнокольорові).
17.25 (9-11). На кожній з двох паралельних прямих відмічено п точок і проведено кілька відрізків, що сполучають відмічені точки різних прямих. Яку найбільшу кількість цих відрізків можна провести так, щоб вони не перетинались всередині смуги між даними прямими?
17.26 (9-11). В опуклому 1986-кутнику проведено кілька діагоналей так, що кожна з них перетинає всередині многокутника не більше однієї діагоналі з числа проведених. Яке найбільше число діагоналей можна провести?
Розв’язки, вказівки, відповіді
17.1. Відповідь. На 11 частин. Вказівка. Знайдіть послідовно на яку найбільшу кількість частин ділить круг 1 пряма; 2 прямі; 3 прямі; 4 прямі.
17.2. Відповідь, а) 0, 1, 2, 3; б) 0 при я = З, п = 4, п - 3 при п > 4.
а) Те, що гострих кутів не більше 3, доведено в п. б). П’ятикутник може не мати гострих кутів (у правильного п’ятикутника всі кути дорівнюють 108°). Приклади п’ятикутників з одним гострим кутом, двома гострими кутами, трьома гострими кутами також легко будуються: наприклад, прикладаються один до одного рівними сторонами три рівнобедрених трикутники з кутом 20° при вершині, дістанемо п’ятикутник з трьома гострими кутами.
б) Припустимо, що в я-кутника є 4 не тупих кути. Позначимо їх вершини А, В, С, D . Розглянемо чотирикутник ABCD. Його кути не більші за відповідні кути я-кутника, тому їх сума не більша 360°. Але сума кутів чотирикутника дорівнює 360°. Уникнути протиріччя ми зможемо тільки у випадку, коли всі кути А, В, С, D — прямі і збігаються з кутами даного я-кутника, тобто я = 4.
17.3. Відповідь. 2я + 1.
Вказівка. Нехай утворилось я трикутників. Підрахуємо загальну суму їх кутів. З одного боку, вона дорівнює 180°я. З іншого боку — ці кути складають


150
Задачі математичних олімпіад та методи їх розв’язування
т повних (по 360°) кутів з вершинами у відмічених точках плюс три кути даного трикутника. Тому, 180° • п = 360° • т + 180°. Звідси п = 2т + 1.
17.4. а) Візьмемо дві точки А і В. За умовою на прямій АВ знайдеться відмічена точка С. Нехай одна із відмічених точок — точка D, яка не лежить на прямій АВ. Тоді на прямих AD, BD, CD повинно бути ще по одній відміченій точці. Ці точки не можуть збігатися між собою, бо вказані прямі перетинаються тільки в точці D. Всього дістанемо 7 точок, які є відміченими. Протиріччя.
б) Доведення аналогічне.
17.5. Вказівка. Скільки частин добавляє наступна пряма?
17.6. Відповідь. Ні. Вказівка. Це твердження дуже просто доводиться для центрів 28 граничних клітинок.
17.7. Вказівка. Всі ліві кінці відрізків лежать лівіше всіх їхніх правих кінців.
17.8. Вказівка. Серед всіх пар: точка перетину і пряма, яка через неї не проходить, виберіть ту, відстань між якими найменша (принцип «крайнього»!).
17.9. Вказівка. Розгляньте трикутник найбільшої площі (принцип «крайнього»!).
17.10. Вказівка, а) Випливає з пункту б).
б) Скористайтесь методом від супротивного та принципом крайнього: розгляньте найменший з даних кругів. Якщо припустити, що він дотикається 6-ти або більшої кількості кругів, то один з кругів дотику буде меншим за нього. Протиріччя.
, а(а - 1)(3д - а -1) , „ ..
17.11. Відповідь. аоЛ , якщо b > а. Вказівка. Ложен
6
квадрат задається своєю правою верхньою вершиною і розміром. При заданому розмірі права верхня вершина лежить в урізаному прямокутнику.
17.12. Вказівка. Нехай А — деяка фіксована точка кола, а Р(Л) її образ при повороті Р. Покажіть, що сума довжин дуг, які утворюють множину {Р(Л)} при всіх непідхожих поворотах Р, менша 2я. Для цього розгляньте спочатку повороти, що не підходять окремо для кожного сектора.
17.13. Відповідь, п - 1 ламп.
17.14. Відповідь. Не зможе. Вказівка. Достатньо пофарбувати кубики у чорний та білий кольори так, щоб сусідні кубики мали різні кольори, тобто у «шаховому» порядку.
17.15. Вказівка. Шукана кількість не залежить від способу з’єднання відрізками та розташування точок, і дорівнює 1985.
17.16. Відповідь. Зможе. Вказівка. Павук може рухатися, наприклад з максимальною швидкістю, змінюючи її напрям в моменти часу 1, 1 + 3, 1 + 3 + + З2, ... . При будь-якому русі мухи графік залежності відстані між павуком і мухою обов’язково перетне вісь часу.
17.17. Відповідь. Зможе. Вказівка. Якщо різниця між кількістю кутів у 270° та кутів у 90° дорівнює 4, то зовні стіни, а коли ця різниця дорівнює -4, .то всередині.


Комбінаторна геометрія
151
17.18. Вказівка. Запишіть біля кожного відрізка з різнокольоровими кінцями дві одиниці — одну по один бік відрізка, другу — по інший. Тоді сума всіх чисел всередині трикутника ABC непарна (у ній усі одиниці, крім тих, що стоять біля сторін трикутника ABC, розбиваються на пари, а за тими, що біля сторін, не важко прослідкувати). Отже, є трикутник з непарною кількістю оди- ничок всередині. Всі його вершини мають різні кольори.
17.19. Вказівка. В одну з п’яти частин, зображених на рисунку, попадають дві точки. Відстань між ними не більша за діаметр кожної з цих фігур. Але діаметр у цих фігур однаковий і дорівнює л/l2 + 22 = 7б.
17.20. 	Вказівка. Площа правильного трикутника зі стороною а дорівнює
>/3 , г
— а , причому а2 —
ціле число. Але площа трикутника з вершинами у вузлах
сітки, як відомо, півціле число, тобто раціональне. (Сторону однієї клітинки прийняли за 1).
17.21. Відповідь.
п(п - 3)  +
2
п(п - 1)(л - 2)(л - 3) 24
Вказівка. Сполу¬
чіть послідовно точки, взяті на колі, хордами і підрахуйте на скільки частин розбивається діагоналями утворений л-кутник. Для цього, діагоналі слід проводити послідовно. Після проведення кожної діагоналі число частин збільшується на число, на одиницю більше від числа точок перетину, що з’являються після проведення однієї діагоналі. Число всіх діагоналей л-кутника дорівнює
п +1 +
л(л - 3) .
-—. А число точок перетину діагоналей л-кутника дорівнює
С4 = л(л - 1)(л - 3)
" 24
17.22. Вказівка. Розгляньте пряму, що не паралельна до жодної прямої, яка визначається парою даних точок, і рухайте її до тих пір, поки вона не пройде через першу точку, потім другу, пізніше третю і т. д. Перша п’ятірка цих паралельних прямих визначає перший п’ятикутник, друга — другий, і т. д.
17.23. Вказівка. Пофарбуйте трикутники у два кольори (наприклад, чорний та білий) так, щоб будь-які два суміжні трикутники (які мають спільну сторону) були різних кольорів. Можливість такого пофарбування доведіть методом математичної індукції. Всі трикутники, які мають з многокутником спільну сторону, пофарбовані в один колір, наприклад, білий. Тоді, очевидно, сторони многокутника будуть білими, а діагоналі — чорно-білими. Якщо р — кількість трикутників білого кольору, a q — кількість трикутників чорного, то л = Зр - 3q = 3(р - q), тобто л ділиться на 3.


152
Задачі математичних олімпіад та методи їх розв'язування
17.24. Відповідь. 2 способи. Вказівка. Пронумеруйте кольори цифрами 1, 2, 3, 4. Одну грань тетраедра назвемо «нижньою», а інші — «бічними». Оскільки будь-яку грань можна сумістити з будь-якою іншою, повернувши тетраедр навколо відповідної осі, то можна вважати, що «нижня» грань пофарбована у колір 1. Поворотами осі, що проходить через центр «нижньої» грані, будь-яку з «бічних» граней можна зробити «передньою». Тому можна вважати, що передня грань пофарбована в колір 2. Тоді положення двох інших граней після цього визначається однозначно. Залежно від того, яку з цих граней пофарбовано кольором 3, матимемо два різних способи фарбування.
17.25. Відповідь. 2п - і. Вказівка. Скористайтесь методом математичної індукції; при доведенні кроку доведіть, що кількість відрізків збільшується на 2.
17.26. Відповідь.
3-1986-8
= 2975. Вказівка. Спробуйте розв’язати
задачу для довільного л-кутника. Застосуйте метод математичної індукції. {Від¬
повідь.
Зл - 8
де [х] — ціла частина Числа х).
>
2


§18. Геометричні нерівності, оцінки, екстремуми
Теоретичні відомості
Серед багатьох теорем, які використовуються в оцінках та доведеннях нерівностей геометричними засобами, слід відмітити найбільш поширені.
У трикутнику кожна сторона менша за суму двох інших (нерівність трикутника).
Кут трикутника менший, дорівнює або більший 90° залежно від того, менший, дорівнює або більший суми квадратів двох прилеглих до нього сторін квадрат протилежної сторони.
Довжина проекцій відрізка на площину чи пряму не більша довжини цього відрізка.
Площа проекцій многокутника на будь-яку площину не більша за площу многокутника.
Зауваження. Тут і далі йдеться про ортогональне проектування.
Задачі
18.1 (8). Доведіть, що у кожному дев’ятикутнику існує пара діагоналей,
кут між якими менший 7°.
18.2 (8-9). Як треба розмістити на площині трикутник так, щоб його
проекція на дану пряму мала найменшу довжину.
18.3 (8-10). Пряма на площині називається правильною, якщо вона
паралельна одній з осей координат або одній з бісектрис координатних кутів. Яка найбільша кількість правильних прямих може бути серед всіх прямих, що з’єднують б точок на площині? 1982 точки?
18.4 (9-10). На площині дано два відрізки АВ і CD. Доведіть, що довжи¬
на відрізка, який сполучає їх середини не більший півсуми довжин відрізків АС і BD.
18.5 (9-10). На площині розташовані правильні трикутники ЛДС, і Л2В2С2
з центрами О, та О2. Доведіть, що 31О,О21<| ЛД | +1В,В2 І +1 С,С21.


154 Задачі математичних олімпіад та методи їх розв’язування
18.6 	(9-10). Сума кубів довжин сторін трикутника дорівнює т3. Дове- /п2л/з
діть, що площа трикутника не більша .
18.7 (9-10). У колі одиничного радіуса проведено декілька хорд. Відомо,
що кожний діаметр перетинає не більше 6 хорд. Доведіть, що сума довжин всіх хорд менша 19.
18.8 (9-10). Довжини а і b двох сторін трикутника задовольняють умо¬
ву а > 6, а довжини відповідних їм висот дорівнюють ha і hb. Доведіть, що а + ha> b + hb. При якій умові досягається рівність?
18.9 (9). Найдовша сторона трикутника має довжину 5 см, найкорот-
ша — 1 см. Яку найбільшу площу може мати такий трикутник?
18.10 (9). На площині розташовані пряма і дві точки А та В, які знаходяться по один бік від цієї прямої. Вкажіть, на прямій точку М, таку, щоб сума відстаней була найменшою з усіх можливих.
18.11 (9). Шість різних прямих на площині розташовані так, що не всі паралельні і не всі проходять через одну точку. Яка найменша можлива кількість точок перетину цих прямих?
18.12 (9-10). Трапеція з основами а і b описана навколо кола радіуса R. Доведіть, що 47?2 < ab.
18.13 (9-10). Дано правильний шестикутник Л,Л2...Л6 і шестикутник ВхВг..Вр який описаний навколо нього, тобто Tlj є [В,В2],
З
А2 є [В,В3], .... А6 є [BgBj], Доведіть, що Л < -SMj Л.
18.14 (10). У трикутнику ABC медіани AD та BE взаємно перпендику¬
лярні. Доведіть, що ctgZ/1 + ctgZB > -.
З
18.15 	(10). Нехай а, Ь, с — сторони трикутника,-р — його півпери- метр, г — радіус вписаного кола.
Доведіть, ЩО (р _ а}г +(р_ ьу +{р_ с)2 £ г, ■
18.16 	(10-11). Площа опуклого чотирикутника дорівнює 1986 см2. Доведіть, що його периметр не менший ніж 4х 1986 см. Чи може периметр такого чотирикутника дорівнювати 4 х 1986 см?


Геометричні нерівності, оцінки, екстремуми
155
18.17 (10-11). Серед чотирикутників з довжинами діагоналей 2 і 4 та кутом 45° між ними знайти чотирикутник з найменшим периметром (досить вказати, в якому відношенні його діагоналі діляться точкою перетину).
18.18 (11). Знайдіть найбільшу площу трикутника, що міститься в квадраті зі стороною 1.
18.19 (11). Який з трикутників, вписаних у дане коло, має найбільший периметр?
18.20 (11). Знайдіть мінімальний об’єм тіла, одержаного при обертанні рівнобедреної трапеції, в яку вписане коло радіуса 1, навколо більшої основи.
18.21 (11). У півкруг радіуса 1 вписано прямокутник. Доведіть, що його площа не більша 1.
18.22 (11). Чи можна на поверхні правильного тетраедра з ребром 1 розташувати 4 точки так, щоб із будь-якої точки поверхні тетраедра можна було б дійти до однієї із вибраних точок, пройшовши
по його поверхні шлях не більший
£
2
?
Розв’язки, вказівки, відповіді
18.1. Вказівка. Всього в дев’ятикутнику
8-9
9 = 27 діагоналей, які утво¬
2
рюють 54 кути. При цьому, 360° < 7° • 54.
18.2. 	Відповідь. Найменша висота трикутника повинна бути паралельною
даній прямій.
18.3. 	Відповідь. 11; 3964 = 4 •
-•1982
2
, де [х] — ціла частина числа х.
18.4. 	Вказівка. Нехай М — середина АВ, N — середина CD, К — середина ВС. За властивістю середньої лінії трикутника, маємо МК = — АС,
2
KN = -BD. 2
Скористайтесь тепер нерівністю трикутника.
18.5. 	Вказівка. Подайте довжини відрізків у нерівності як довжини відповідних векторів.


156
Задачі математичних олімпіад та методи їх розв’язування
18.6. Вказівка. Подайте довжини сторін і площу трикутника через радіус описаного кола і його кути та скористайтесь нерівністю між середнім арифметичним і середнім геометричним.
18.7. Вказівка. Розгляньте менші дуги, що стягуються кожною хордою. Якщо сума довжин всіх таких дуг більша 6, то знайдеться ділянка, де перетинаються більше 6-ти дуг (з числа даних або діаметрально протилежних їм).
18.8. Вказівка. Маємо 2 • S = a&sjny < ab, де S — площа трикутника,
a і b. Тому (a + ha) - (b + hb) -
( 2S> a + —
Ґ. 2SA b + —
I a)
I b J
= (а - Ь)
> 0. Знак рівності досягається при 2S = ab (в цьому випадку
ab
V У
кут між сторонами а і b дорівнює 90°).
18.9. Відповідь.
Вказівка. Врахуйте те, що довжина третьої сторо¬
ни не перевищує 5.
18.10. Вказівка. Побудуйте точку В,, симетричну точці В відносно прямої, що задана. Тоді, точка перетину прямої ЛВ, з даною прямою і буде точка М. Для доведення скористайтесь нерівністю трикутника.
18.11. Відповідь. 5. Якщо одна з даних шести прямих І проходить тільки через одну точку перетину А, то інші 5 прямих або проходять через А (нехай їх zn,), або паралельні І (нехай таких zn2). Маємо zn, + zn2 = 5, zn, > 0, zn2 >0 і число точок перетину дорівнює 1 + zn,zn2; останнє рівне 5 або 7.
Припустимо, що кожна пряма проходить принаймні через дві точки перетину. Якщо точок перетину менше, ніж п’ять, то їх 4. Позначимо їх через Л, В, С, В, тоді наші прямі — це прямі ЛВ, ЛС, ЛВ, ВС, ВВ і СВ. Ці прямі не повинні мати точок перетину, які відмінні від Л, В, С, В, тому ЛВ 11 СВ, ЛС 11 ВВ та ЛВ 11 ВС. З першої та третьої умов випливає, що ABCD — паралелограм, але діагоналі ЛС і ВВ паралелограма не можуть бути паралельними. Ми отримали протиріччя.
18.12. Нехай ABCD — описана трапеція з основами ВС = а і AD = b. Не обмежуючи загальності, можна вважати, що а < Ь. Введемо позначення ЛВ = и, СВ = о, тоді и + v = а + Ь, оскільки ABCD — описана трапеція. Нехай К — точка перетину сторони ЛВ і прямої, що проходить через вершину С, паралельно стороні ЛВ. Застосовуючи до трикутника KCD, в якому КС = и і KD-b- а, теорему косинусів, дістанемо (b - а)2 = (а + b)2 - 2uv(i + cos Z.KCD). Звідси
знаходимо
cosZKCB = —-1,
uv
sin2 ZKCD =
4ab(uv ~ ab)
2 2 U4V
Тепер, З ОДНОГО


Геометричні нерівності, оцінки, екстремуми
157
боку SKCD = — uusin Z.KCD» з іншого боку, враховуючи, що висота LKCD , про- 2
ведена до основи KD, дорівнює 27?, маємо SKCD = (b - a)R. Враховуючи, що 4uv < (и + и)2 = {а + b)2, дістанемо (b - a)R = — uv sin Z.KCD, тобто (27?)2 =
u2v2 sin2 Z.KCD ab(4uv - 4ab) ab((a + b)2 - 4ab) , л .
— - = - < = = ab, тобто 47?z < ab, що
(b-a)2 (b-a)2 (b-a)2
і треба було довести.
18.13. 	Нехай G — точка перетину медіан AD і BE. За умовою AAGB = 90°. Тоді G лежить на півколі з діаметром АВ і центром О. Точки С, G,
О— колінеарні. Оскільки GO = ^AB, то
З АВ
CO = — АВ. Очевидно, що ctgZX + ctg ZB = ——,
2 hc
де hc — висота трикутника ABC, проведена з вершини С. Очевидно, що hc < тс = CO, де тс — медіана, яка проведена з вершини С. Тому,
, ,л А ZD АВ АВ АВ З s 6 hc mc CO 2
1ОІЛ d • D- 2 (p - a)(p - b)(p - c)
18.14. 	Вказівка. Відомо, що г =
Врахуйте і те, що
(р - а) + (р - Ь) + (р - с) = р. Позначивши р - а = х, р - b = у, р - с = z,
. . . .1 1 lx+y+z
нерівність можна звести до нерівності —=■ + —5- + -т- > , рівносильній
х у z xyz
нерівності
1-і
X у
1-і
У z
\2
>0.
1 1
kZ Ху
18.15. 	Нехай ABCD — довільний опуклий чотирикутник. Позначимо АВ = а, ВС -b, CD = с, DA = d. SABCD = S. Тоді з одного боку
S = — ad sin ZX + —bc sin ZC < і (ad + be). 2 2 2
(1)
При цьому знак рівності матиме місце лише тоді, коли ZX = ZC = 90°. З другого боку


158
Задачі математичних олімпіад та методи їх розв'язування
S = —ab sin ZB + — cd sin ZD < — (ab + cd). 2 2 2
(2)
При цьому рівність матиме місце лише тоді, коли ZB = ZD = 90°. Додавши
(1) і (2), матимемо: 2S < —(ab + be + cd + da) = —(а + c)(b + d). Звідси 2 2
S < — (а + c)(b + d). Скориставшись нерівністю між середнім геометричним
і середнім арифметичним, дістанемо S < — (а + c)(b + d) < — 4 4
а + b + с + d}
= — (а + b + с + d)2. Отже, якщо позначити периметр чотирикутника через Р,
то матимемо P>4a/S = 4-1986 (см). З наведених міркувань неважко встановити, що рівність має місце лише тоді, коли чотирикутник є квадратом (усі кути прямі і суми протилежних сторін однакові).
18.16. 	Вказівка. Розв’язок задачі випливає з теореми: серед усіх чотирикутників з даними діагоналями і даним кутом між ними мінімальний периметр має паралелограм. Доведення-. Нехай ABCD такий, що кут між
71
діагоналями АС і BD дорівнює а (0 < а < - ), |ЛС| = а, | BD 1 = Ь. Позначимо 2
В, і D, такі точки, що ВВ, = DDX = АС. Тоді BB{DDX — паралелограм зі сторонами а, b і кутом а між ними (або цей кут дорівнює я - а). Крім того, І АВ І + І ВС І + I CD І + I DA |=| ВС | + | В,С | + | DC | + | DXC |. З нерівності три¬
кутника випливає, що min( | ВС | + | В,С | + | DC | + | D,C |) при фіксованих В,
D, D,, В, досягається лише тоді, коли С лежить на перетині BD, і BXD, а це означає, що ABCD — паралелограм.
18.17. 	Відповідь. -L Вказівка. Найбільшу площу має трикутник, вершини
якого лежать у вершинах даного квадрата. Дійсно, нехай ABC — трикутник, що лежить всередині квадрата, і нехай С не є вершиною квадрата. Проведемо через С пряму, паралельну до АВ. Частина, що відтинається цією прямою від квадрата і яка не містить точок А і В, містить хоча б одну вершину С' цього квадрата (можливо, що С' лежить на цій прямій). Площа трикутника ABC' не менша за площу трикутника ABC.
18.18. 	Відповідь. Правильний. Вказівка. Якщо радіус даного кола дорівнює 1, то півпериметр дорівнює: р = sinx + sint/ + sinz = sinx + sinz/ + sin(x + y) =


Геометричні нерівності, оцінки, екстремуми
159
= 2 sin * + - cos ------ + sin(x + у), де х, у, z — кути трикутника. При фіксованому z, тобто при фіксованому х + у, р — набуває, очевидно, найбільшого значення, коли х = у. Отже, трикутник з найбільшим периметром слід шукати серед рівнобедрених трикутників. Обмежившись випадком х = у, ми маємо: р = 2 sin х + sin 2х; р'(х) = 2 cos х + 2 cos 2х. р'(х) = 0 на проміжку 0 < х < —
тс
тільки при х = —.
О
18.19. Відповідь. Vmin =
16>/2
71 (куб. ОД.).
18.20. Вказівка. Площа дорівнює 2аЬ, де а та b — сторони «половинного» прямокутника, вписаного у чверть даного круга, що менше, ніж а2 + Ь2 = г2 = 1 (нерівність Коші).
18.21. Відповідь. Можна. Вказівка. Ці точки потрібно відмітити у вершинах квадрата KLMN, де К, L,M,N — середини ребер AD, АС, СВ, BD правильного тетраедра ABCD.


§19. Вектори
Теоретичні відомості
Крім таких операцій над векторами як додавання, віднімання і множення на число доцільно використовувати скалярний добуток векто¬
v
рів: и • v =
и
cos(u;u). Якщо ж и = (х,; у), v - (х2; у2) — координати
цих векторів, то u-v = х,х2 + у{у2. Аналогічна формула має місце для
векторів, розташованих у просторі.
Для довільних п точок площини (чи простору) А,, А2, ..., Ап існує
єдина точка О (центр ваги) така, що ОД + ОД +... + ОАп = 6.
Для довільних п відрізків площини (чи простору) AjBp А2В2, ...,
АпВп існує єдина точка О (центр ваги) така, що /, • ОМ{ + /2 • ОМ2 +
+... + Іп • ОМп - б, де I. (Z = 1, 2, ..., п) — довжина відрізка А.В., а М. — його середина.
Для довільних п трикутників площини (чи простору) AjBjCp А2В2С2, ..., АпВпСп існує точка О (центр ваги) така, що Д ■OMl +S2 • ОМ2 +
+ ... + 5л 'ОМп = б, де S. (Z - 1, 2, ..., п) — площа трикутника А.В.С.,
а М. — точка перетину його медіан.
Теорема. Якщо М — точка перетину медіан трикутника ABC, то
для довільної точки Р (простору) справедлива рівність РМ = |(А4 + РВ + РС).
Задачі
19.1 	(9). Сума трьох векторів а, Ь, с дорівнює нулю. Розглянемо три кути: (a;S), $;с), (а;с). Доведіть, що хоча б два з них тупі.


Вектори 161
19.2 	(9-11). У площині трикутника АВС знайдіть усі такі точки М, щоб
виконувалась рівність МА{ + МВ{ + МС{ = б, де Л,, В,, С, — точки, які належать прямим ВС, АС, АВ відповідно, і MAl ТТ АС, МС'ХЇСВ, ЩТТвл.
19.3 	(9-11). Вектори а та b не паралельні. Довести, що вектори с = (а;а)а + (а;b)b і 5 = {a;b)a + (b;b)b також не паралельні. (Тут
т
(т; п) =
п
•cos(/n;n) —. скалярний добуток векторів /піп).
19.4 (9-11). Довести, що для того щоб три точки А, В, С були верши¬
нами прямокутного трикутника з вершиною прямого кута у точці С, необхідно і достатньо, щоб виконувалась така рівність: (АВ; АС) + (ВС; ВА) + (СА; СВ) = (ЛВ; ЛВ).
19.5 (9). Дано чотирикутник ABCD. Точки М і N — середини діагона¬
лей АС і BD відповідно. Виразіть вектор MN через вектори ЛВ і CD.
19.6 (10). Доведіть, що для довільного паралелограма ABCD має місце
рівність: 4 • ЛВ • AD = j А СІ2 - \BD\2.
19.7 (10-11). Точки Л,, Л9, ..., Л8 розбивають коло діаметром 1 на
8 конгруентних (рівних) дуг; В — довільна точка цього ж кола. Знайдіть модуль суми векторів ВЛ, + ВЛз +... + ВЛд.
19.8 (10-11). Сума некомпланарних векторів а,, ..., ап із спільним
початком у точці Мо дорівнює нуль-вектору. Доведіть, що через точку Мо не можна провести площину ті так, щоб усі вектори alt а2,..., ап лежали по один бік від площини тс.
19.9 (10). У трикутнику ЛВС проведено висоти ЛЛ,, ВВ,, СС,. Відомо,
що ЛЛ, + ВВ, + СС, = б. Доведіть, що трикутник ЛВС правильний.


162
Задачі математичних олімпіад та методи їх розе’язування
19.10 (10). Квадрати ABCD і Л^С,/), (вершини перелічені проти руху годинникової стрілки) розташовані на площині так, що ЛЛ, =2BD{. Точка Е — середина відрізка ААГ Знайдіть кути трикутника CECV
19.11 (10). Від вершин А і С опуклого чотирикутника ABCD відклали
вектори АР = CR, а від вершин В і D — вектори BQ = DT. Сталося так, що чотирикутник PQRT опуклий. Доведіть, що чотирикутники ABCD і PQRT рівновеликі.
19.12 (11). Знайдіть кути між векторами а,Ь,с в просторі, якщо відо¬
мо, що ці кути рівні між собою, а а
а + Ь + с
19.13 (11). У просторі задано чотири точки А, В, С, D. Доведіть, що
коли /АВС = /BCD = /CDA = /DAB = 90°, то ABCD — прямокутник.
19.14 (11). Доведіть, що коли сума квадратів довжин сторін деякого чотирикутника дорівнює сумі квадратів довжин його діагоналей, тоді цей чотирикутник — паралелограм.
19.15 (11). У трикутній піраміді ABCD ребра AD та ВС взаємно перпендикулярні. Доведіть, що |ЛВ|2 + |С£>|2 = |ЛС|2 + |ВВ|2.
19.16 (11). Чи можна на кожному ребрі тетраедра поставити стрілку таким чином, щоб сума шести одержаних векторів дорівнювала нулю?
19.17 (11). Точки Л, В, С, D площини такі, що для довільної точки площини скалярні добутки (МЛ, МВ) та (Л4С; MD) не дорівнюють один одному. Доведіть, що АС = DB.
19.18 (11). Нехай ABCD — тетраедр, в якому /DCB = /CBA = = /DAB = 90°, а М — основа перпендикуляра, опущеного з
точки D на площину ЛВС. Виразіть вектор DM через вектори а = ВЛ, b = DB, c = DC.


Вектори
163
19.19 (11). Об’єм тетраедра ABCD дорівнює V. Точки К, L, М, N такі,
що АК = СА, CL = ВС, DM = AD, DN = CD. Обчисліть об’єм тетраедра KLMN.
19.20 (11). Сторони опуклого чотирикутника ABCD є основами рівнобедрених попарно подібних трикутників APB, BQC, CRD, DSA, які лежать зовні чотирикутника PQRS. Відомо, що чотирикутник PQRS є прямокутником, причому |PQ| #= |Q/?|. Доведіть, що ABCD — ромб.
Розв’язки, вказівки, відповіді
19.1. Вказівка. За умовою задачі з векторів а, Ь, с можна скласти трикутник. Вказані кути є зовнішніми кутами цього трикутника. Оскільки у трикутнику хоча б два кути гострі, то відповідні їм зовнішні кути — тупі.
19.2. Вказівка. Шукана точка М є точкою перетину медіан трикутника.
19.3. Вказівка. Скористайтесь методом від супротивного.
Припустимо, що вектори ~с і паралельні, тоді матимемо рівність:
, тобто (а; а) • (Ь;Ь) - (а; Ь)2 = 0. Звідси дістанемо: Ы -B|2- (a;b) (b;b) 11 11
- Іа
• cos2 (а; 6) = 0, тобто а -b -sin2(a;6) = 0
Оскільки |а| * 0, |б| Ф 0 (це випливає з умови), то sin(a;£) = 0. Звідси
робимо висновок, що а 11 6. Прийшли до протиріччя.
19.4. 	Вказівка. Слід довести пряме і обернене твердження задачі. Необхідність. Нехай три точки А, В, Се вершинами прямокутного трикутни¬
ка, і точка С — вершина прямого кута. Тоді (АВ; АС) = ІА СҐ, (ВС; ВА) = І£С|2,
(СА; СВ) = б і за теоремою Піфагора маємо |ЛС|2 + |£С|2 = |Л£|2.
Достатність. Скориставшись властивостями скалярного добутку, запишемо задану в умові задачі рівність у такому вигляді:
(АВ; АС + СВ) + (СА; СВ) = (АВ; АВ),
(АВ;АВ) + (СА;СВ) = (АВ; АВ),
(CA;CB) = Q,
тобто СА ± СВ, що і треба було довести.


164
Задачі математичних олімпіад та методи їх розе’язування
19.5. 	Відповідь. MN = ±-(АВ + CD).
2
Вказівка. Точки А, В, С, D можуть бути розташованими на площині довіль¬
ним чином.
Однак, в усіх випадках, маємо:
AM = -ЛС = -(ЛВ + ВС), 2 2
BN = -BD = -(ВС + CD), тому MN = MA + АВ + BN = --(АВ + ВС) + 2 2 2
+АВ + --(ВС + CD) = - (АВ + CD), що і треба було довести. 2 2
19.6. 	Вказівка. Позначте AD = а, АВ = Ь, тоді
|ЛС|2 - |В£)|2 = (ЛС - BD)(AC + BD) = ((b + а) - (а - b))((b + а) + (а - Ь)) =
= 2Ь • 2а = 4 • ab, що і треба було довести.
19.7. 	Вказівка. ВА( = ВО + ОА( (і = 1, 2, ..., 8), де О — центр кола. Тому ВЛ, + ВЛз +... + ВЛд = 8 • ВО + (ОЛ, + ОЛз +... + ОЛд). Доведіть, що сума ОЛ, + ОА% + ... + ОЛд = 0.
Відповідь. ВЛ, + ВА% +... + ВЛ8 = 4.
19.8. 	Розв’язання. Припустимо, що така площина я існує. Нехай т — вектор, перпендикулярний до площини я, який, будучи відкладеним від точки УИ0, розміститься в тому ж півпросторі від площини я, що й вектори а,, а^, ..., ап.
За умовою задачі а, + а^ +... + ап = 0. Помножимо обидві частини цієї рівності скалярно на вектор Дістанемо
fa,m) + (а2,т) +... + (ап\т) = 0. (1)
Оскільки вектор розташований з векторами a.t (і = 1, 2, ..., п) по один
бік від площини я, то кожен із кутів, який утворює вектор з векторами
а,, 02, ..., ап не може бути тупим, а тому (at,m) = fa. • \т\ • cos(a,;/n) > 0, тобто всі доданки лівої частини рівності (1) невід’ємні числа. Оскільки вектори а,, 02» • ••» ап некомпланарні, то серед векторів а,, о,, ..., ап знайдеться принаймні один такий, що утворює з вектором т гострий кут, а отже, їх скаляр¬


Вектори
165
ний добуток буде додатне число і рівність (1) не виконуватиметься. Прийшли до протиріччя.
19.9. 	Розв’язання. Позначимо через D і Е проекції точок С, і В, на пряму АС. Тоді із рівності В,В = -ВВ1 = ЛЛ, + СС, для проекцій на пряму ЛС одержимо рівність б = АЕ + CD. Оскільки АЕ = AD + DE і CD = СЕ + ED, знаходимо, що AD + СЕ = б, тобто AD = EC. Звідси випливає, що |ЛВ| = |£С|.
З прямокутних трикутників ЛС,В і ЛСС, матимемо: |Л£>| = |ЛС| • cos2 /Л;
а з прямокутних трикутників знаходимо, що |£С| = |ЛС| • cos2 ZC. Оскільки
|ЛО| = |£С|, то дістанемо, що cos2 ZA = cos2 ZC. Аналогічно доводиться, що
cos2 ZA = cos2 ZB. Звідси випливає, що ZA = ZB = ZC = 60е, тобто АЛВС — правильний (якщо один із кутів тупий, наприклад ZC, то ZA = ZB = а, ZC = 180° - а, що неможливо, бо а + а + 180° - а= 180° <=> а = 0°).
19.10. Вказівка. Скористайтесь векторним методом та поворотом вектора на 90°.
19.11. Вказівка. Скористайтесь тим, що площа чотирикутника дорівнює половині добутку його діагоналей на синус кута між ними.
19.12. Вказівка. Нехай ф — шуканий кут, тоді а + b + с = а + от +
|>
соэф. Звідси випливає, що cos0 = -
З'
Відповідь, п - arccos —.
З
19.13. 	Вказівка. Розгляньте вектори а - АВ; b = ВС; с = CD; d = DA. Тоді ab = bc = cd = da = 0. Крім того, a + b + c + d = Q, тобто a + c = -(& + d).


166
Задачі математичних олімпіад та методи їх розв’язування
. —12 — — — — — — — — —— —— ——
Звідси слідує, що а + с| = {а + с)(а + с) = -(а + c)(b + d) = -ab -cb-ad- cd,
тобто а + с = б. Отже, вектори а = АВ і с = АВ лежать на паралельних прямих, тобто АВ 11 CD. Тому чотирикутник ABCD лежить в площині (натягнутій на ці прямі). Оскільки всі його кути прямі, то він — прямокутник.
19.14 Доведення. Нехай ABCD — даний чотирикутник. Позначимо ~АВ = а,
ВС = Ь, CD = c, DA = d, AC = е, ~BD-~f. З умови задачі випливає, що
а + b + с + d = 0, (і)
-2 —2 -2 -2 -2 -2
a +b+c+d=e+f. \*)
Оскільки е- a + b, ~f = b + с, то із (2) дістаємо, що а + t? + с + di =
= (а + b)2 + (b + с)2. Звідси випливає, що d* = 2b(a + c) + t>2. Замінивши а + с
на -(b + d) (з рівності (1)), дістанемо d.2 =-2bd-b\ тобто
d? + 2bd + b~ = (b + d)2 = 0. Тоді b = -d, що і означає, що ABCD — паралелограм.
19.15. Вказівна. Позначте ~АВ = b, АС = с, AD = d, тоді CD = d-c,
ВС = с — Ь. За умовою d • (b -с) = 0, тому d-b = d • с.
19.16. Вказівка. Покладіть тетраедр на горизонтальну площину і спроектуйте вектори на вертикальну пряму. Сума проекцій не дорівнюватиме б. Відповідь. Не можна.
19.17. Вказівка. Із умови задачі випливає, що (MA’,DB- АС) * (AC,AD), якою б не була точка М. Припустивши, що DB - АС Ф б, підставте в дану
(AC;AD)
нерівність МА = ~гх(РВ - АС) і ви прийдете до протиріччя.
рв-лс|"
19.18. Вказівка. Доведіть, що чотирикутник ABCD — прямокутник. Від-
І
повідь. DM = а - b + с.
19.19. Вказівка. Доведіть, що об’єми тетраедрів LKNM і LAKM рівні і вдвічі більші за об’єм тетраедра LCAD. Відповідь. 2V.
19.20. Вказівка. Скористайтесь векторним методом і доведіть спочатку, що коли PQRS — паралелограм, то ABCD також паралелограм.


§20. Оцінки і екстремальні задачі для наборів чисел і таблиць
Теоретичні відомості
На олімпіадах нерідко зустрічаються задачі на порівняння величини чисел деякого скінченного набору, розташування точок на прямій, оцінки сум, різниць та інших функціональних відношень, пов’язаних з числовими наборами чи таблицею.
Часто в таких задачах доцільно:
а) вибрати найбільше чи найменше число із набору («принцип крайнього»);
б) впорядкувати числа набору за величиною.
Задачі
20.1 (7-8). Числа 1, 2, 3, ..., 9 розбили на 3 групи по три числа в
кожній. Нехай С — найбільший з добутків всіх чисел однієї групи. Доведіть, що А > 72.
20.2 (8-9). Натуральні числа а , а2, ..., а49 такі, що їх сума дорівнює 999. Якого найбільшого значення може набувати їх найбільший спільний дільник?
20.3 (8-9). Чи можливо в клітинках квадратної таблиці пх п записати числа -1,0, 1, так, щоб суми в кожному рядку, кожному стовпцю і на двох його великих діагоналях були різними?
20.4 (9-11). Як заповнити клітинки нескінченної таблиці натуральними
числами так, щоб: а) кожне число п зустрічалось рівно п разів; б) найбільша з різниць чисел у сусідніх клітинках була найменшою? (Дві клітинки є сусідніми, якщо мають спільну сторону.)
20.5 (9). Знайдіть найменше значення многочлена р(х) = х6 + 2х4 + 2х3 +
+х2 + 2х — 1.
20.6 (9). Знайдіть найменше значення виразу 2х2 - 2ху + 5г/2 + 2х + 2г/.
20.7 	(9). Знайдіть найменше значення виразу
ab а2 + Ь2 a2 +b2+ ab
при до¬
датних а та Ь.


168
Задачі математичних олімпіад та методи їх розв'язування
20.8 (9-10). Знайдіть найменше значення виразу -yjx2 + (1 -у? + + \jy2 + (1— х)~.
20.9 (9-10). Сума п’яти невід’ємних чисел дорівнює одиниці. Яке найбільше
значення може мати сума абсолютних величин попарних різниць цих чисел?
20.10 (9). Яке з чисел більше: >/1986 + >/1984 чи 2>/і985 ?
20.11 (9-10). Яке з чисел більше: >/1986 + >/1984 чи 2^/1985 ?
20.12 (9). Яке з чисел більше:
5555555553
5555555557
чи
6666666664 р
6666666669'
19851986 +1
20.13 (9). Яке з двох чисел більше:
19851987 +1
19851984 +1^ 19851985 +1
20.14 (10-11). Знайдіть найменше натуральне число, яке можна представити як мінімум трьома різними способами у вигляді 13т + 75/г, де т і п — натуральні числа.
20.15 (10). Розкладіть число 1987 в суму натуральних чисел таким чином, щоб добуток цих чисел був найбільшим.
20.16 (10). Яке з двох чисел більше: 7^ чи 5^ ?
20.17 	(10). Яке з двох чисел більше:
20.18 	(10-11). Яке з двох чисел більше: cos(sinl) чи sin(cosl)?
20.19 	(11). Яке з двох чисел більше: а) 1,00011,0002 чи 1,0002і*0001; б) еп чи 71е?
20.20 (11). При якому натуральному п число
буде найбільшим?
20.21 	(11). Яке з двох чисел більше: lg2l 1 чи lgl2?
20.22 (11). Яке з двох чисел більше: 2^log2 х чи %^logx 2, х > 1?
20.23 (11). Розмістіть у порядку зростання числа 100100!, (100!)100 та (100100)! (Нагадаємо, що символ п\ означає добуток 1 -2,..- (п - 1) • п).


Оцінки і екстремальні задачі для наборів чисел і таблиць
169
20.24 	(11). Дійсні числа х, у та а — такі, що
х + у = а -1, ху = а2 -7а+ 14.
Для якого числа а сума х2 + у2 набуває найбільшого значення?
20.25 	(11). Дійсні невід’ємні числа х,, х2, ..., хп такі, що їх сума дорівнює 1. Знайдіть найбільше значення величини XjX2 + х2х3 + ...+
Розв’язки, вказівки, відповіді
20.1. Вказівка. Скористайтесь методом від супротивного, дістанете невірну нерівність 723 < 9!
20.2. Вказівка. Найменше з цих чисел не більше 20.
20.3. Вказівка. Всього цих сум 2л + 2 і вони не більші за л (по модулю). Далі застосуйте «принцип Діріхле».
20.4. Вказівка. Див. фрагмент розв’язку на рисунку.
20.5. Вказівка. Подайте даний многочлен у вигляді Р(х) = (х3 + х + І)2- 2. Звідси випливає, що найменше значення даного многочлена дорівнює -2 коли х3 + х + 1 =
= 0. (Цікавим є той факт, що найменше значення визначити можна, а відповідне значення знайти складно, потрібно застосувати формулу Кардано).
20.6. Вказівка. Виділенням повного квадрата зведіть даний вираз до ви-
Отже, найменше значення да¬
ного виразу дорівнює -1 і досягається при х = -
2
З’
Відповідь. -1.
а2 +Ь2
20.7. 	Вказівка. Покладіть х = — та доведіть, що х > 2. Відповідь. 2,5.
ао
20.8. 	Вказівка. Даний вираз дорівнює сумі довжин векторів а = (х; 1-у)
та Ь = (1 - х; у), яка не може бути менша за довжину вектора а + b = (1; 1). Відповідь. >І2.
20.9. 	Вказівка. Впорядкуйте дані числа. Нехай х, < х2 < ... < х5 — дані п’ять чисел. Сума десяти різниць х2 -х,,х3 - х,,...,х5 -х4 дорівнює, як показує підрахунок, 4х5 + 2х4 - 2х2 - 4х,, і зрозуміло, що 4х5 + 2х4 - Зх2 - 4х, <


170
Задачі математичних олімпіад та методи їх розв’язування
< 4(х5 + х4 + х3 + х2 + х,) = 4. Значення 4 досягається при х5 = 1, х4 = х2 = х, = = 0. Відповідь. 4.
20.10. 	Розгляньте квадрати цих чисел. Маємо (71986 + 71984j = 1986 + + 2ТЇ986 • ТЇ984 +1984 = 2 • 1985 + 2л/і 9852 -1, бо 1986 = 1985 + 1, 1984 =
= 1985 - 1. Оскільки 2-1985+ 2719852 -1 <2-1985 +2л/і9852 = 4-1985, то 7і986 + 7і984 < 271985. Відповідь. Друге число більше.
20.11. 	Вказівка. Достатньо порівняти дві різниці 7і986 - 71985 1986-1985
та
71985 - 71984. Для цього подайте їх у вигляді: — —-==
719862 + 71986-1985 +ТЇ985
1985-1984
7і9852 + 71985-1984 + 3/і9842 '
Оскільки 7і9862 +71986-1985 +
+ 7і9852 > 7і9852 + 71985-1984 + 7і9842 . бо 1986 > 1985 > 1984, .то
ТГ986 -ТЇ985 < ТЇ985 -ТЇ984, тобто ТЇ986 + ТЇ984 < 2ТІ985. Відповідь. Rp/re. число більше.
20.12. 	Вказівка. Подайте число 1111111111 через а. Тоді нам необхідно 5а — 2 6а — 2
порівняти числа - та Зазначимо, що (5а - 2)(6а + 3) >
> (5а + 2)(6а - 2) (бо а > 2), тому —- > ——-. Відповідь. Перше число.
5а + 2 6а + З
20.13. 	Відповідь. Позначте число 19851986 через а, a 19851984 через Ь. Тоді
скористайтесь рівністю:
а +1
1985а+ 1
Ь + 1
19856 + 1
1984(6-а) (1985а+ 1)(19856 + 1)
< 0. Від¬
повідь. Друге число.
20.14. Нехай k = 13zn, + 75n, = 13zn2 + 75п2 = 13zn3 + 75а3 і zn, < т2 < т3. Маємо 13(zn2 - zn,) = 75(п, - п2). Тому т2 - zn, ділиться на 75, бо 13 та 75 взаємно прості. Отже, zn3 > zn2 + 75 > zn, + 75 + 75 > 151. Таким чином, £>13-151 + 75 = 2038. Залишилося зауважити, що 2038 = 13 • 151 + 75 = = 13 • 76 + + 75 • 14 = 13 + 75 • 27. Відповідь. 2038.
20.15. У шуканому розкладі не можуть зустрічатись числа, які більші за 4, бо тоді таке число п можна замінити числами 2 та п - 2, і при цьому добуток збільшиться. Якщо в розкладі присутні четвірки, то ми можемо замінити кожну з них двома двійками, не змінюючи добутку. Одиниць також бути не може,


Оцінки і екстремальні задачі для наборів чисел і таблиць
171
бо ми додамо одиницю до будь-якого іншого числа і добуток збільшиться. Отже, в одному з шуканих наборів стоять тільки трійки та двійки. Якщо є три двійки, ми замінимо їх двома трійками, і добуток зйову збільшиться. Отже, наш набір містить не більше двох двійок, решта цифр набору — трійки. Відповідь. 661 трійка та 2 двійки (або 661 трійка і одна четвірка).
20.16. Вказівка, > 75 -16807 = 15625 = 56 > • Отже, врахо¬
вуючи монотонність функції у = при х > 0 дістанемо, що 7^ > бЛ
20.17. Оскільки 22Ю0 = 427", достатньо довести, що 2799 > З500, тобто довес-
>8°о /25б
^100 { « q ^100
1+ и
2800 2а
ти таку нерівність -— > 2. Дійсно, матимемо
З З
,243,
243
Залишилося скористатися декілька разів нерівністю (1 + а)2 > 1 + 2а, яка ви¬
конується для довільного а є R. Дістаємо
52
243
ч25
52
243
ч24
104
243
ч12
208
243
Відповідь. 22800 > З3500.
20.18. Вказівка. Оскільки sin 1 + cos 1 = >/2 sin
мо, що cos(sin 1) = sin
'п . /
Stfl 1
ч2
13
243
\100
ґ, 26 "і
>
1 +
243 J
\3
> 23 > 2.
416
243
< л/2 < —, то дістає-
> sin(cosl). Відповідь, cos(sinl).
20.19. Вказівка. Для того, щоб визначити, яке з двох чисел ар чи 3“ (а > 1, 3 > 1) більше, достатньо порівняти числа alnP та ріпа. Розглянемо
функцію /(•*) = . х> 0.. Вона монотонно зростає на проміжку (0; в) та
зс
монотонно спадає на проміжку (в; +«»). а) Оскільки е > 1,0002 > 1,0001, то діс- Іп 1,0002 _ In 1,0001 . ТОМу j ,0002і'0001 > 1,0001і 0002. б) Враховуючи,
таємо, що
1,0002 1,0001
In я In в
що я > е, дістанемо, що ^—>—, і тому ея>яв Відповідь, а) друге; я е
б) перше.
1 + k
\6 /
1 +
1 +
1 +
1 +
1 +
Zi + z?
/


172
Задачі математичних олімпіад та методи їх розв’язування
20.20. З умови задачі випливає, що
П2 (л-1)2 (1,1)" (1,1)"-'
Пг > (п 4-1)2
(ЙГ ■ (1,1)"' '
Тоді дістаємо
п -1
у
>1,1>
( і V 1 + -
7
1 п)
Звідси випливає, що
1
+ 1>
1 +
Оскільки 1,048 < лДЇ < 1,05, то 21,
> п >
Ти-ґ
9 > —!— +1 > п > 20. Від- 0,048
повідь. При п = 21.
20.21. Вказівка. Скористайтесь нерівністю (1 + а)2 > 1 + 2а, яка справедлива при всіх а > 0. Дійсно, lg2l 1 = (1 + lgl,l)2 > 1 + 21gl,l = 1 + lgl,21 = = lgl2,l > lgl2. Відповідь. lg2l 1.
20.22. Вказівка. Логарифми даних чисел за основою 2 рівні. Дійсно
log2 (2^°^ = 7log2 X = = Vlos*21о& х - log(x^). Відповідь. Чис¬
ла рівні.
20.23. Вказівка. Порівняйте кількість цифр у десятковому записі даних чисел. 1) Очевидно, що 100! < 10*° • 100^= 10’90, тобто в числі 100! не більше 190 цифр, а в числі (100!)100 не більше ніж 19000 цифр в десятковому його записі. 2) В числі 100100! = 102‘100! 2 • 100! + 1 цифр, тобто вочевидь більше, ніж у попередньому.
3)Нарешті (1OO,oo)!>(1OO99),OO'M_,OOM >(1OO99)^°O,M =Ю991ОО,о° >lO‘o20’, тобто в цьому числі принаймні 10201 цифр.
Відповідь. (100!)‘°° < Ю0,00! < (іОО100)!
20.24. Вираз
х2 + у2 =(х + у)2 - 2ху = (а-1)2 - 2(а2 - 7а +14) = -а2 + 12а - 27 (*)
як функція від а є квадратним тричленом, який визначений для тих а, для яких існують дійсні числа х та у, що задовольняють умови задачі. Ці значення х та у визначаються системою
х + у = а -1, ху = а2 -7а+ 14,
тобто х та у є коренями квадратного рівняння: t2 - {а - + (а2 - 7а +11) = 0,
дискримінант якого дорівнює -За2 + 26а - 55. Цей дискримінант невід’єм¬
ний при — < а < 5. Тобто дійсні значення % та у існують тільки для тих а, які З


Оцінки і екстремальні задачі для наборів чисел і таблиць
173
належать проміжку
11
;5
11
;5
Наше завдання полягає в тому, щоб на відрізку
знайти таке а, при якому тричлен (*) набував найбільшого значення.
Вершина параболи: b = -а2 + 12а -27 має абсцису а = б, яка розташована
правіше відрізка
Ц.5
з’5
. Найменше значення виразу (*) досягається на пра¬
вому кінці цього відрізка, тобто при а = 5. Відповідь, а = 5.
20.25. Нехай х, + % + х5 +... = а, х2 + х4 + х6 +... = Ь. Тоді а + b = 1, а також
х,х2 + х2х3 +... + xn_jX„ < (х, + х3 +...) х (х2 + х4 +...) = а • b = а(1 - а) =
(І
1
4
< —. Якщо покласти х, = х2 = х3 = х4 =... = хя = 0, 4 2
а
то х,х2 + х2х3 +... + хл_,хл = і. Відповідь.
V


§21. Послідовності
Теоретичні відомості
Послідовність {хп} називається періодичною, якщо виконуються рівності xn+t = хп (п = 1, 2, ...), де t — натуральне число, яке називають періодом. В ряді задач зустрічаються рекурентні послідовності {х) — такі, для яких %л+1 = /(%л), де f — деяка функція, або кожен член (починаючи з (k + 1)-го) визначається через k попередніх. Така, наприклад, є послідовність Фібоначчі: 1, 1, 2, 3, 5, ..., в якій кожен член дорівнює сумі двох попередніх. В оцінках послідовностей часто застосовується метод індукції, використовуються «грубі» округлення, допомагає монотонність.
Число а називають границею послідовності {%л}, якщо для будь- якого є > 0 знайдеться таке натуральне N, що при п > N виконується нерівність І хп - а | < є.
Задачі
21.1 (8-9). Відомі перший член а і останній член b скінченної геометрич¬
ної прогресії, а також сума S всіх її членів. Знайдіть суму квадратів всіх членів цієї прогресії.
21.2 (9). Доведіть, що будь-яка нескінченна арифметична прогресія,
складена з натуральних чисел, містить нескінченну геометричну прогресію.
21.3 (9). В арифметичній прогресії, складеній з натуральних чисел, є
член, що закінчується цифрою 3, але немає члена, що закінчувався б цифрою 5. Чи є в ній член, що закінчується цифрою 7?
21.4 (9-10). Геометрична прогресія містить числа 3-2>/2 та V2+1.
Чи може число 1 належати даній прогресії?
1989
21.5 (9-10). Знайдіть найменший член послідовності {а }, де ап = п + —х—
п п
(п = 1, 2, 3, ...).
21.6 (10). Скільки додатних чисел є серед перших ста членів послідов¬
ності sinl°, sin 10°, sin 100°, ...?


Послідовності
175
21.7 (10). Доведіть, що серед членів послідовності {ал}, де ап = —
(п = 1, 2, 3, ...) є безліч точних квадратів.
21.8 (10-11). Послідовність {ал} обмежена зверху. При всіх п> 1 вико¬
нуються нерівності: ап+1 > ап Доведіть, що існує 1італ.
п
21.9 	(10-11). Послідовність {ап} задана рекурентними співвідношеннями
а. = 2, а, = 1 та
а а , а
п П~1 Л+1
Знайдіть 1італ.
Л—»<»
21.10 	(10-11). Послідовність {ап} задана рекурентними співвідношення- а ,
• Доведіть, що існує lim ап.
ми а , = ап = 1 та аплЛ = а„ +
1~~2 . „ п(п + 1)
21.11 	(10). Знайдіть 1ітхл, якщо числа хп визначаються рекурентними
співвідношеннями х, = 42 та хл+, = G/2)x" для всіх п = 1, 2, 3,... .
21.12 	(10). Послідовності {ал} і {Ьп} задані рекурентним способом:
л , а„ + Ь„ , Іа? +Ь?
ах = а > 0, b{ = Ь > 0, ал+1 = —-—, 6Л+1 = для п > 1.
Доведіть, що при довільному п є N виконується нерівність
21.13(10). Дано натуральне число т. Послідовність {хл} будується в такий спосіб: х, = 1, а число хп+1 при п> 1 дорівнює сумі цифр числа тхп. Доведіть, що в послідовності {хя} обов’язково знайдуться два рівних числа.
21.14 (10). Дано послідовність із п чисел: av а2, ..., ап. За один крок вона змінюється на послідовність |й, - а|, fa -а|, ..., |а„ - а|,
де а — довільне дійсне число (числа а можуть бути різними на різних кроках). Доведіть, що через декілька кроків можна одержати послідовність, яка складається з одних нулів.


176
Задачі математичних олімпіад та методи їх розв’язування
21.15 (11). Чи можливо, щоб числа 3, 5 та 7 були членами (не обов’язково сусідніми) однієї геометричної прогресії?
. \ . .. Iі + 2" + З3 +... + пп
21.16 (11). Обчисліть границю lim
п—>оо
п
21.17 	(11). Дано монотонну додатню послідовність {Ьп}, п > 1. Доведіть,
ьп«-ьп
що lim
(1 + &„)(1 + 6Л+1)
21.18 	(11). Доведіть, що у послідовності {ап}, дєап = I sin( 1977л) |, п = 1, 1
2, 3, ..., існує член, який не перевищує
1997
21.19 (11). Обчисліть границю lim {(>/2 +1)2"}. (Тут {а} — дробова частина числа а).
21.20 (11). Числа ап та Ьп визначаються рекурентними співвідношеннями а{ = = 1 та ап+і = ап+ 3bn, bn+{ = ап+Ьп для всіх натураль-
а„
них п. Доведіть, що послідовність {х }, де хп = —, п = 1, 2, 3, ...,
п ьп
має границю та обчисліть її.
21.21 (11). Доведіть, що серед членів послідовності {ап}, де ап = 2" + л2, л = 1, 2, 3, ..., існує безліч таких, що діляться на 100.
21.22 (11). Члени послідовності {ап} визначаються за допомогою реку¬
рентних співвідношень.
та ап
при л = 1, 2, З,
.... Доведіть, що ця послідовність монотонна.
21.23 	(11). Знайдіть арифметичну прогресію < а2< а3< ... < a2n_p всі члени якої натуральні числа, і добуток всіх її членів — квадрат натурального числа.


Послідовності
177
21.1. Відповідь.
Розв’язки, вказівки, відповіді
(bS + aS - 2ab)S
Вказівка. Позначивши через q знамен-
S - а
2S- a-b
ник даної прогресії, а через п — кількість її члені, помічаємо, що
S-b
aq + aq2 + ... + aq"~x
= n-2- = q. Квадрати членів геометричної прогресії самі утво-
CL + CLQ + ... + CLQ
рюють геометричну прогресію зі знаменником’ q2 та сумою а =
_ 2 Q'n ~ 1 _ &V - а2 _ &2(S _ а)2 - <22(S - б)2 _ (6(S - а) - a(S - b))(a(S - о) + a(S - b)) _ ~а tf-l~ ?2-1 “ (S-a)2-(S-6)2 ~ ((S-a)-(S-b))((S-a) + (S-b))
_ (bS + aS- 2ab)(b - a)S _ (bS + aS- 2ab)S (2S - a- b)(b - a) 2S - a-b
21.2. Вказівка. Якщо a — деякий член арифметичної прогресії, d — її
різниця, то a(d +1) = а + ad — теж член нашої прогресії (арифметичної). Отже, разом з кожним числом наша прогресія містить це число, помножене на d+ 1. Тоді вона містить цілу геометричну прогресію зі знаменником d + 1. (При d = 0 ці міркування не проходять, але, вочевидь, факт все одно справедливий).
21.3. Відповідь. Ні. Вказівка. Нехай а,, а2, ..., ап, ... —наша прогресія іап закінчується цифрою 3. Нехай, далі, ат закінчується цифрою 7. Якщо т > п, скажімо, m = n + k, k > 0, то ал+2й закінчується цифрою 1, ая+ЗЙ закінчується цифрою 5 — протиріччя. Якщо т < п, скажімо, п = т +1, де І > 0, то ат+2/ закінчується цифрою 9, аот+3, — закінчується цифрою 5 — знову дійшли до протиріччя.
21.4. Відповідь. Так. Вказівка. Оскільки (72 + 1)(Т2 -1) = 1,
а (72 + 1)(Т2 -1)3 = 3 - 272, то відповідь на питання позитивна.
21.5. 	Вказівка. Обчисліть декілька перших членів послідовності £Zj = 1990; а2 = 499,25; а3 = 224;...; аї5 = 23,84; а16 = 23,76; аІ7 = 23,88;.... Виникає гіпотеза, що найменшим числом послідовності {oj є число а,6. Доведіть це. Для цього розглянь¬
те різницю Ьп ~ ап+і ~ап _ 1+ 1989 •
1
(л + І)2
1-1989-
2п +1 п2{п +1)2
Послі-
2п +1
довність сл +1)2 +1)2 ■ +1)2
монотонно спадає, бо є сумою
двох монотонно спадних послідовностей. Оскільки (див. обчислення, виконані


178
Задачі математичних олімпіад та методи їх розв'язування
вище) 616 > 0, то Ьп > 0 при всіх п > 16, тобто ап+х > ап при всіх п > 16. Отже, найменшим членом послідовності {а) є її 16-й член, тобто л16 = 23,769532.
21.6. Відповідь. 3. Вказівна. Оскільки 10"+І -10" = 360 • 25 • 10"-3, тому
sin(10"+1)° = sin(10")°, при п = 3. Тоді в нашій послідовності всі члени, починаючи з четвертого, однакові. Оскільки sinl°>0, sinl0°>0, sinl00°>0, a sin 1000° = sin280° < 0, то в нашій послідовності лише перші три члени — додатні числа, а всі інші — від’ємні.
21.7. Вказівка. Якщо ап — точний квадрат, то а4я2+4я = 4ая(2л +1)2 —
також є точним квадратом. Тому, av ад, л288, ... — точні квадрати. (Подумайте, чи є серед членів такої послідовності інші точні квадрати).
21.8. Вказівка. Покладіть при п > 2 Ь„ = ап + —і—. Тоді послідовність {Ь }
л-1 "
обмежена і зростає. Тому існує 1іт6я = 1ітая.
ГІ—>оо П—>«»
21.9. Вказівка. Доведіть, що для всіх натуральних п виконується рівність
21.10. 	Вказівка. Послідовність {ап} зростає і при цьому ап <2-
для
довільного п > 1 (Доведіть це за допомогою індукції).
21.11. 	Відповідь. 2. Вказівка. Послідовність {%п} монотонно зростає і обме¬
жена зверху числом 2.
21.12. Вказівка. Доведіть, що |&л+1 - лп+1| < -|6Я - ая|.
2
21.13. Вказівка. Доведіть, що послідовність {хп} — обмежена. Для цього застосуйте метод математичної індукції.
21.14. 	Вказівка. На г-му кроці візьміть число а =— (а,-'-,) + а^7°), де а}1’0 2
та — і-й та (і + 1)-й члени послідовності, одержані з даної послідовності
за (і - 1) кроків (а,(0) = а,, а(20} = а2, ...). Тоді після (л - 1) кроків дістанемо
послідовність, яка складається із однакових чисел. На л-му кроці візьміть а = алп~1).
21.15. 	Відповідь. Ні. Вказівка. Нехай 3 = aqk, 5 = aql, 7 = aqm, де & < / < /л.
т- • ь—д, З •
Тоді q = - та q =—; звідси 5 7
3
Рї
—
l5J
л
-/ cm-k
, тобто 7l~k = Зт~‘ ■ 5"”*. Одер-


Послідовності
179
жана рівність неможлива при натуральних k, І, пг, бо її ліва частина ділиться на 7, а права — ні.
21.16. 	Відповідь. 1. Вказівна. Доведіть, що має місце подвійна нерівність
, 1 + 22+ З3+... + ял п + п2 + ... + пп
1 < <
1-^г
1-
, при всіх натуральних п > 2.
£
п
п
п
Ь
21.17. 	Вказівка. Доведіть спочатку, що послідовність с_ = —— збіжна, 1 + k
тобто (ся+, - ся) -» 0 при я —»
21.18. 	Вказівка. Скористайтесь тим, що (sinl997n| = |sin(1977-6я)| < < |1977я - &я| і підберіть цілі я, k такі, щоб виконувалась нерівність:
|1977я-£тс|
1977
1977я
-71
1977&
. Це можна зробити, розглянувши
<=>
1
раціональні наближення числа тс.
21.19. Відповідь. 1. Вказівка. Доведіть, що {(72 +1)2" j = 1 - (72 - 1)2л при кожному натуральному я. Для цього скористайтесь формулою бінома Ньютона.
21.20. Відповідь, lim хп = 73. Вказівка. Припустіть спочатку, що границя існує, знайдіть її. Потім, за допомогою методу математичної індукції доведіть, що |%„+, -7з| < я = 1, 2, 3, ... .
21.21. Вказівка. Доведіть, що коли число виду 2” + я2, я є N ділиться на 100, то я — парне число. Враховуючи це, достатньо довести, що серед чисел 4т~1 + т2, т є N Існує безліч чисел, які діляться на 25.
21.22. Вказівка. Доведіть, що при всіх я > 1 знаки чисел я,1+1 - ап та ап ~ ап-\ однакові. Зауваження. Неважко дістати формулу я-го члена цієї по¬
слідовності. Якщо а
1
= arccos —, то Oq = cos а. З


180
Задачі математичних олімпіад та методи їх розв’язування
а
Тоді а1 =
1 + gp
1 + cos а 2
1 + COS
а
cos —, а? = 2
|1 + Д|
т.д., ап = cos — , п = 1, 2,... Звідси видно, що наша послідовність має границю, яка дорівнює 1.
21.23. 	Вказівка. Наприклад, л, = 1 • ((2л - 1)!), а2 = 2-((2л - 1)!), а3 = 3-((2л- 1)!) л2я_, = (2л- 1) • ((2л - 1)!).
Нехай А = (2л - 1)!. Оскільки (2л - 1) — непарне число, то добуток А • А2"'1 = (1 • Л)(2 • Л)...((2л - 1) • Л) є квадратом натурального числа Л", а співмножники Л, 2Л, ЗЛ, ..., (2л - 1)Л утворюють арифметичну прогресію.


§22. Ігри, переслідування, стратегії та алгоритми
Загальні відомості
Розв’язування задач, в яких йдеться про досягнення мети за допомогою послідовності ходів — зокрема, потрібно з’ясувати, хто з гравців перемагає в тій чи іншій грі — потрібно описати стратегії, правила вибору ходів, які забезпечують досягнення мети; у задачах про ігри (або в задачах про переслідування) при цьому потрібно довести, що стратегія забезпечує виграш при будь-яких діях партнера (в межах умови задачі).
Такі задачі умовно можна розділити на три класи:
1) задачі, в яких виграшна стратегія базується на ідеї симетрії;
2) задачі, в яких міркування ведеться з кінця, для відшукання початкових виграшних позицій;
3) задачі, в яких результат гри не залежить від дій обох гравців.
Хочеться зробити ще й таке зауваження: у таких задачах гравці
ходять по черзі, причому пропускати хід заборонено.
Задачі
22.1 (8-9). На полі Л8 шахової клітинки стоїть тура. За один хід її
можна пересунути вниз чи вліво (на довільну кількість клітинок). Програє той, кому нікуди ходити. Хто виграє при правильній грі: починаючий чи його партнер?
22.2 (8-9). Є дошка 50 х 50. Двоє по черзі закреслюють вибрану ним
клітинку, а також клітинки, які знаходяться над нею і справа від неї. Програє той, хто закреслить ліву нижню клітинку. Хто виграє при правильній грі: починаючий чи його партнер?
22.3 (8-9). На одному кінці полоси 1 х 103 стоїть чорна, а на другому — біла фішка. Двоє по черзі рухають кожний свою фішку на 1, 2, 3 або 4 клітинки у будь-якому напрямку (перескочити через фішку суперника заборонено). Програє той, хто не зможе зробити свій хід. Хто виграє при правильній грі: починаючий чи його партнер?
22.4 (8-9). Гра починається з числа 100. За один хід дозволяється зменшити число, яке дістали, на будь-який з його дільників. Про¬


182
Задачі математичних олімпіад та методи їх розв’язування
грає той, хто одержить нуль. Хто виграє при правильній грі: починаючий чи його партнер?
22.5 (8-9). У коробці лежить 300 сірників. За один хід дозволяється взяти із коробки не більше половини сірників, які там є. Програє той, хто не зможе зробити черговий хід. Хто виграє при правильній грі: починаючий чи його партнер?
22.6 (9). Є дві купи цукерок: у першій — 40, у другій — 45. За один
хід можна одну купу з’їсти, а другу розділити на дві (не обов’язково рівні). Програє той, хто не зможе зробити хід. Хто виграє при правильній грі: починаючий чи його партнер?
22.7 (9-10). Які поля виграшні, а які програшні на шаховій дошці 8x8
у такій грі: двоє ходять по черзі ферзем вліво, вниз чи по діагоналі вліво — вниз. Програє той, хто не зможе зробити хід. Хто виграє: починаючий чи його партнер?
22.8 (9-10). Гра починається з числа 1. За один хід можна помножити
число, яке дістали, на будь-яке натуральне число від 2 до 9. Виграє той, хто першим отримає число, яке більше 1000. Хто виграє при правильній грі: починаючий чи його партнер?
22.9 (9-10). На дошці написано число 2. Двоє гравців по черзі додають
до написаного числа деякий його дільник (відмінний від самого числа). Програє той, хто першим запише число: а) більше 1989; б) більше 1990. Хто виграє при правильній грі: починаючий чи його партнер?
22.10 (9-10). На дошці записано числа 63 та 55. За один хід дозволяється дописати ще одне число, що є різницею двох чисел, які вже записані. Числа на дошці не повинні повторюватися. Програє той, хто не зможе зробити хід. Хто виграє: починаючий чи його партнер?
22.11 (10). Двоє грають в шахи, виконуючи по черзі по два ходи підряд за звичайними правилами. Доведіть, що у другого гравця немає виграшної стратегії.
22.12 (10). У п коробках лежить 2п цукерок. Двоє гравців по черзі беруть по одній цукерці. Якщо останні дві цукерки лежать у різних коробках, то виграє перший, інакше — другий. Хто виграє при правильній грі: починаючий чи його партнер?
22.13 (10-11). Двоє грають у хрестики-нулики на нескінченній площині, яка розбита на клітинки. Перший за один хід може поставити


Ігри., переслідування, стратегії та алгоритми
183
два хрестики, а другий — один нулик. Доведіть, що перший зможе поставити 100 хрестиків в ряд.
22Л4 (10-11). Двоє грають у хрестики-нулики на нескінченній площині, розбитій на клітинки. Кожен хоче поставити свій знак 5 разів підряд по вертикалі чи по горизонталі. Доведіть, що другий гравець може грати так, щоб ніколи не програти.
22.15 (10-11). В ряд стоять 12 зірочок. Двоє по черзі замінюють зірочки на цифри. Якщо одержане 12-значне число ділиться на 77, то виграє другий гравець, інакше перший. Хто виграє при правильній грі: починаючий чи його партнер?
22.16 (10-11). На дошці 3 х 1988 стоять біла тура і .чорний слон. Доведіть, що тура може взяти слона. (Важається що дані фігури ходять по черзі за звичайними шаховими правилами).
22.17 (10-11). У смузі 1 х 1989 в трьох лівих клітинках стоїть по шашці. За один хід можна перемістити будь-яку шашку вправо, не перестрибуючи через інші. Програє, той, хто не зможе зробити хід. Хто виграє при правильній грі: починаючий чи його партнер?
22.18 (11). Границею лісу є пряма І. На перпендикулярі АС до прямої І в точках А та В (С є Z, АВ = ВС = а) знаходяться заєць та вовк відповідно. Обидва вони біжать зі сталими швидкостями, причому швидкість зайця вдвічі більша від швидкості вовка. Заєць буде схоплений вовком у деякій точці, якщо в цю точку вовк зможе прибігти або раніше від зайця, або одночасно з ним. Заєць вибирає на І точку D і біжить в ліс по відрізку AD. Як вибрати точку D, щоб заєць не зміг бути схоплений вовком на відрізку AD?
22.19 (11). Двоє гравців по черзі зафарбовують клітинки дошки 8x8. Перший гравець своїм ходом зафарбовує дві сусідні клітинки в чорний колір, а другий — довільну клітинку в білий колір. Спочатку всі клітинки були білими. Чи може другий гравець досягти того, що після кожного його ходу: а) хоча б одна кутова клітинка; б) хоча б дві кутових клітинки довільного квадрата розміром 5x5 були пофарбовані в чорний колір? (Клітинки називаються сусідніми, якщо вони мають спільну сторону; одна і та ж клітинка по ходу гри може перефарбовуватися декілька разів).
Розв’язки, вказівки, відповіді
22.1. 	Вказівка. Виграє другий. Кожним своїм ходом він повинен повертати туру на діагональ.


184
Задачі математичних олімпіад та методи їх розв’язування
22.2. Вказівка. Виграє перший. Першим своїм ходом він повинен закреслити квадрат 49 х 49, а потім ходити симетрично.
22.3. Вказівка. Виграє перший. Позиція буде програшною, якщо число клітинок між фішками ділиться на 5.
22.4. Вказівка. Парні числа виграшні, а непарні — програшні.
22.5. Вказівка. Виграє перший. У програшних позиціях число сірників дорівнює 2" - 1.
22.6. Вказівка. Виграє перший. Виграшні ті позиції, в яких хоча б одна з куч парна.
22.7. Вказівка. Див. рисунок. Програшні позиції відмічено штрихуванням.
22.8. Вказівка. Виграє перший. Програшні позиції — числа від 4 до 6 та від 56 до 111.
22.9. Вказівка. Виграє перший, а) Парні числа виграшні, а непарні — програшні, б) Розберіть два випадки: число 6 — виграшне; число 6 — програшне. В обох випадках число 4 — виграшне.
22.10. Вказівка. Виграє перший. Незалежно від ходів суперників у кінці будуть виписані всі числа від 1 до 63.
22.11. Вказівка. Якби у другого була б виграшна стратегія, то перший міг би зробити «хід на місці», а потім скористатися нею для себе.
22.12. Вказівка. Виграє другий. Після його ходів непорожніх коробок повинно залишатись вдвічі менше, ніж цукерок.
22.13. Вказівка. Спочатку потрібно поставити 2100 хрестиків по вертикалі. Принаймні 2" із них не будуть мати нулів на своїх горизонталях, а тому, і поряд з ними можна буде ставити чергові хрестики. Після цього залишиться 298 вільних пар хрестиків, і т. д. Продовжуючи цей процес вказаним чином, можна буде поставити в ряд 100 хрестиків.
22.14. Вказівка. Розіб’ємо площину на доміношки (див. рисунок) так, щоб будь-яка лінія з п’яти клітинок містила цілу доміношку. Тоді другий гравець повинен зайняти другу половину доміношки, в яку щойно походив перший.
22.15. Вказівка. Виграє другий. Врахуйте те, що число 1001 ділиться на 77.
22.16. 	Вказівка. Нехай даний слон стоїть на чорній клітинці даної шахової дошки. Поставимо туру на 61988 і будемо ходити на клітинки 61997, 61996, ... так, щоб слон був на лівій сусідній клітинці (яка має спільну вершину). У випадку, коли слон стоїть на білій клітинці, ми розташовуємо туру на 61, а далі попередня стратегія (тільки вже зліва направо).


Ігри, переслідування, стратегії та алгоритми
185
22.17. 	Вказівка. Виграє перший. Праву третю шашку він переміщує в самий кінець смуги, а потім, після кожного ходу другого (другою шашкою), він першу шашку ставить біля другої (зліва).
22.18. 	Вказівка. Точку D слід вибрати так, щоб CD>—j=. Введіть на V3
площині прямокутну систему координат Сху, в якій Л(0; 2а), £(0; а), і доведіть, що для того, щоб на відрізку AD заєць не міг бути схоплений вовком, необхідно і достатньо, щоб цей відрізок цілком складався тільки з таких точок М(х; у), координати (х; у) яких задовольняють нерівність
2 'ї
Z
<2 А
ц —а
>
— а
1 з J
ІЗ J
22.19. 	Вказівка, а) Скористайтесь тим, що для довільного квадрата 5x5 хоча б одна з клітинок, відмічених на рисунку — кутова. Відповідь. Зможе, б) Для досягнення цілі другий гравець мусить ходити так, щоб після кожного його ходу на дощці було не менше 32 білих клітинок. Перший гравець зможе йому перешкодити, якщо своїми першими 32 ходами пофарбує всі 64 клітинки дошки, а 33-м ходом пофарбує будь-які дві сусідні білі клітинки. Відповідь
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
Не зможе.


§23. Цікаві задачі та конструкції
Теоретичні відомості
У багатьох задачах найскладнішою частиною її розв’язку є не доведення, а побудова незвичайного прикладу, тобто побудова певної «конструкції» (чи здійснення певного процесу). До цих задач відносять і такі, де побудова та дослідження прикладу — «багатоповерхова» конструкція (при цьому часто використовують принцип індукції).
Серед таких задач є й такі, в яких потрібно доводити неможливість потрібної конструкції. Це робиться, як правило, методом від супротивного. Є й такі задачі, в яких потрібно побудувати «найкращу» конструкцію даного виду. Тут потрібно не тільки запропонувати конструкцію, а й довести, що «покращити» її не можна.
Задачі
23.1 (7-8). У клітинки квадрата 3x3 запишіть різні натуральні числа так,
щоб б добутків (по рядках і стовпчиках) були рівні між собою.
23.2 (6-8). Хлопчик переміщує фішку на шаховій дошці, причому за один хід дозволяється перемістити її в одну з сусідніх клітинок по діагоналі. Чи можна пофарбувати клітинки шахової дошки у чотири кольори так, щоб за два ходи не можна було б із будь-якої клітинки попасти в іншу, яка має такий же колір?
23.3 (7-9). Чи можна повністю покрити сімома синіми квадратними ковриками червоний коврик таких же розмірів так, щоб сині коврики не налягали один на одного і кожен синій коврик покривав якусь частину червоного?
23.4 (7-8). Є шахова дошка розміром 3 х 4. Чи можна обійти її шаховим
конем, побувавши при цьому на кожному полі по одному разу?
23.5 (7-8). Як відміряти 15 хвилин, щоб зварити яйця, за допомогою пісочних годинників, які відмірюють 7 хвилин та 11 хвилин?
23.6 (7-8). Мені вдалося, взявши по два рази цифри 1, 2, 3, 4, написати
восьмизначне число, в якого між одиницями стоїть одна цифра, між двійками дві, між трійками три, а між четвірками чотири цифри. Що це за число?


Цікаві задачі та конструкції
187
23.7 (8-9). В ряд розмістили ЗО стільців. Учень сідає на будь-який вільний стілець. Одночасно один з його сусідів (якщо він є) швидко встає і виходить. Так повторили декілька разів. Яка максимальна кількість стільців при цьому може бути зайнятою, якщо спочатку всі стільці були вільними?
23.8 (7-8). Чи можна заповнити дошку розміром б х б плитками 1 х 4?
23.9 (7-9). Потрібно розрізати квадратну дошку 5 х 5 на одиничні квад¬
ратики. Розрізи повинні бути прямолінійними, йти вздовж ліній сітки. Створені після чергового розрізу частини дозволяється перекладати так, щоб наступний розріз міг розсікти не одну, а одразу ж декілька частин. Яку найменшу кількість розрізів потрібно для цього зробити?
23.10 (6-8). У кабінет математики прийшли Василько, Петрик, Наталка та Надійна. Для консультації Петрику потрібно 8 хв, Наталці — 10 хв, Василькові — 4 хв, а Надійні — 5 хв. Вчитель може проконсультувати двох учнів одночасно. Як організувати роботу, щоб кабінет був зайнятим якомога менше часу?
23.11 (6-8). а) Є лінійка довжиною 13 см без поділок. Яку найменшу кількість поділок потрібно нанести на лінійку, щоб за допомогою неї можна було відкласти відрізки довжиною 1 см, 2 см, 3 см, ..., 13 см, приклавши лінійку лише один раз (у кожному випадку)? б) Така ж сама задача для лінійки довжиною 9 см.
23.12 (8-9). Чи можна пофарбувати клітинки дошки 5 х 5 у п’ять кольорів так, щоб у кожному рядку та в кожному стовпчику були клітинки всіх п’яти кольорів, а поля кожного кольору'можна було б обійти шаховим конем, побувавши в кожній клітинці один раз?
23.13 (9-11). 36 тонн вантажу упакували в мішки вагою не більше однієї тонни. Доведіть, що чотиритонний автомобіль за 11 поїздок зможе перевезти такий вантаж.
23.14 (10-11). Яку найменшу кількість коней можна розмістити на шаховій дошці 8x8 так, щоб всі білі клітинки знаходились під боєм хоча б одного із цих коней?
23.15 (10-11). На деяких клітинках шахової дошки стоїть по фішці. Ходом фішки називають її переміщення через фішку, яка стоїть на сусідній (по горизонталі, діагоналі чи вертикалі) клітинці, безпосередньо за якою на тій же лінії є вільна клітинка. Яку найбіль-


188
Задачі математичних олімпіад та методи їх розв’язування
шу кількість фішок може нараховувати таке їх розміщення на дошці, в якому будь-яка з фішок може зробити перший хід?
23.16 (10-11). На кожній клітинці шахової дошки сиділи по два таргани. У деякий момент кожен тарган переповз на сусідню (по горизонталі чи вертикалі) клітинку так, що таргани, які сиділи на одній клітинці, опинились на різних. Яка найбільша кількість клітинок могла звільнитись?
23.17 (10-11). Двадцять п’ять різних натуральних чисел розмістили в таблиці 5x5 так, що всі суми чисел по рядках однакові. Чи можуть бути при цьому однаковими всі добутки чисел по стовпчиках?
23.18 (10-11). В яку найбільшу кількість кольорів можна пофарбувати клітинки дошки 4x4 так, щоб в кожному квадраті 2x2 знайшлась пара клітинок одного кольору?
23.19 (10-11). Чи можна серед клітинок квадрата 1996 х 1996 відмітити деякі з них так, щоб довільні два квадрати 1000 х 1000 зі сторонами, що йдуть по лініях сітки, містилась різна кількість відмічених клітинок?
23.20 (10-11). Таблиця 5x5 заповнена числами 1, 2, 3, ..., 25, причому будь-які два послідовних числа записані в сусідніх (що мають спільну сторону) клітинках. Яка найбільша кількість простих чисел може опинитись в одному стовпці?
Розв’язки, вказівки, відповіді
23.1. 	Вказівка. Див. рисунок 1.
Зауваження. На рис. 2 наведено приклад більш загальної конструкції (а, Ь, с, d — взаємно прості числа (не рівні 1), всі необхідні добутки рівні abed). Ще симетричніша конструкція наведена на рис. З (a, b, с, d, е, f — різні взаємно прості числа).
23.2. 	Вказівка. Можна, див. рис. 4.


Цікаві задачі та конструкції
189
1
1
2
2
1
1
2
2
1
1
2
2
1
1
2
2
3
3
4
4
3
3
4
4
3
3
4
4
3
3
4
4
1
1
2
2
1
1
2
2
1
1
2
2
1
1
2
2
3
3
4
4
3
3
4
4
3
3
4
4
3
3
4
4
Рис. 4
23.3. 	Вказівка. Можна, див. рис. 5.
Рис. 5
23.4. 	Вказівка. Можна. Наприклад, так, як це зроблено на рисунку 6 (цифри вказують на послідовності ходів).
1
4
7
10
8
11
2
5
3
6
9
12
1
2
3
4
5
6
7
8
9
10
11
12
Рис. 6
Рис. 7
□
0
І
t
1
t
□
□
□
□
1
t
1
t
ЕЬ
Рис.
0-
8
-□


190
Задачі математичних олімпіад та методи їх розв'язування
Зауваження. Щоб не шукати обхід навмання (після декількох спроб це неважко зробити), можна скористатись «графом дошки». Занумеруємо клітинки дошки в деякому порядку (рис. 7). Намалюємо граф, ребра якого сполучають поля — вершини, які з’єднуються на дошці ходом коня (рис. 8). Тепер на графі легко побачити наведений на рис. 6 обхід клітинок (це стрілки).
23.5. Вказівка. Назвемо пісочний годинник, який відміряє 11 хв, годинником А, а 7 хв — годинником В. Кладемо одночасно годинники А і В. Коли мине 7 хв (годинник В), кладемо кастрюлю на вогонь. Годиннику А залишилось «йти» 4 хв, після цього його перевертаємо і через 11 хв знімаємо кастрюлю.
23.6. Відповідь. 41312432 або 23421314. Вказівка. Розглянемо дві трійки: 3***3. Помічаємо, що дві двійки не можуть стояти між цими трійками (мало місця). Не можуть вони стояти і зовні них (якщо вони стоять по різні боки від трійок, то відстань між ними дуже велика, а якщо по один бік — то надто мала). Отже, одна двійка стоїть всередині, а друга зовні. Такі ж міркування відносяться і до двох четвірок. Отже, між двома трійками стоять цифри 1, 2, 4 по одному разу. Зрозуміло, що одиниця може стояти тільки поруч з трійкою: 131**3 (або симетрично 3**131). «Зовнішня» двійка не може стояти зліва від цього числа (бо тоді між нею та «внутрішньою» двійкою буде не менше трьох цифр), а «зовнішня» четвірка не може стояти справа (тоді між нею та «внутрішньою» четвіркою не більше трьох цифр). Залишається єдиний варіант 4131**32, який і приводить до числа 41312432. Друге число дістаємо «симетрією».
23.7. Відповідь. 29 стільців. Вказівка. Очевидно, що всі ЗО стільців не можуть бути зайнятими одночасно. Покажемо, що 29 стільців зайняти можна. Спочатку займемо перший стілець. Далі діємо за таким алгоритмом: якщо вже зайняті перші k стільців (k < 29), то займемо спочатку (k + 2)-й стілець, потім— (k + 1)-й стілець, a (k + 2)-й звільнимо. Тепер вже зайняті 1-й, 2-й, ..., k-й, (k + 1)-й стільці.
1
2
3
4
1
2
2
3
4
1
2
3
3
4
1
2
3
4
4
1
2
3
4
1
1
2
3
4
1
2
2
3
4
1
2
3
Рис. 9
23.8. Відповідь. Не можна. Вказівка. Пофарбуйте дошку в чотири кольори так, як це вказано на рис. 9. Кожна плитка містить по одній клітинці кожного кольору, тобто всіх кольорів повинно бути порівну, якщо допустити, що покриття можливе. Але це не так — клітинок першого кольору дев’ять, а другого — десять. Протиріччя.
23.9. Відповідь. 6. Вказівка. Після першого розрізу в найбільшому з шматків буде не менше 15 клітинок. Після другого розрізу в найбільшому із шматків буде не менше
9 клітинок. Але шматок, який складається з дев’яти клітинок, не можна розрізати на окремі клітинки за три розрізи, бо максимальне число шматків після трьох розрізів дорівнює 23 = 8 (при кожному розрізі число шматків збільшується не більше, ніж вдвічі). Приклад, який показує, що шістьма розрізами можна обійтися, легко конструюється (зробіть це самостійно).


Цікаві задачі та конструкції
191
23.10. Відповідь. 14 хвилин. Вказівка. Потрібно враховувати, що час всієї консультації займатиме ціле число хвилин. Оскільки (8 + 10 + 4 + 5): 2 = 13,5, то консультацію не можна закінчити раніше ніж за 14 хв. Організувати роботу можна, наприклад, так: спочатку вчитель консультує Петрика та Наталку; як тільки Петрик зрозумів матеріал (час вичерпався) починається консультація На- дійки; як тільки закінчилась консультація Наталки, її місце займає Василько.
23.11. Відповідь, а) 4; б) 3. Вказівка. Трьох поділок у випадку а) недостатньо, бо разом з кінцями лінійки ми отримаємо 5 точок, і матимемо лише 5 • 4
= 10 відрізків, а нам потрібно відкладати 13 різних за довжиною відрізків.
+
0
+
0
+
0
+
0
+
0
+
0
+
0
+
0
+
0
+
0
+
0
+
0
+
Рис. 10
4 	поділки можна поставити, наприклад, в 1,2,6 і 10 см від лівого кінця лінійки. Легко перевірити, що тоді ми зможемо відкласти всі необхідні відрізки. У випадку б) можна поставити поділки в 1,4 і 7 см від лівого кінця лінійки. Доведення неможливості задовольнитися двома поділками аналогічно випадку а).
23.12. 	Відповідь. Ні, не можна. Вказівка. Скористайтесь методом від супротивного. Припустимо, що таке пофарбування можливе. Не¬
хай при такому фарбуванні центральна клітинка пофарбована в синій колір. Поставимо на дошці плюси та нулики в шаховому порядку (див. рис. 10). У крайньому лівому стовпчику повинна бути синя клітинка. Це не може бути кутова клітинка, бо з неї ходом коня можна попасти тільки в клітинки третього рядка чи стовпчика, але в цьому рядку та стовпчику вже знаходиться синя клітинка, а туди кінь одразу попасти не може.
Це не може бути середина стовпчика (центральний рядок вже зайнятий). Обидві клітинки, що залишились, помічені нуликом. Аналогічно в правому стовп¬
чику, верхньому рядку та нижньому рядку розташовано по одній синій клітинці всі вони помічені нуликом. Отже, з 5-ти синіх клітинок 4 помічені нуликами, а одна плюсом (центральна). Але тоді їх не можна обійти ходом коня, бо при таких ходах плюси та нулики чередуються. Протиріччя.
23.13. Вказівка. Будемо вантажити мішки на автомобіль до тих пір, поки їх загальна вага не перевищить 4 т. Тоді знімемо останній мішок і відкладемо його в сторону. При наступному навантаженні відкладений мішок участі не бере. Зробимо так 8 разів. Буде відкладено 8 мішків. Загальна вага перевезеного вантажу та відкладених мішків більша за 8 • 4 = 32 т. Отже, залишилось менше ніж 4 т, які можна перевезти дев’ятою поїздкою. Відкладені мішки перевеземо за дві останні поїздки, по 4 мішки за один раз (їх вага не більша 4 т).
23.14. Відповідь. 7. Вказівка. Розгляньте поля дошки, позначені знаком «х». Для того, щоб вони були під боєм, вже потрібно не менше шести коней (рис. 11), які стоять в клітинках, помічених цифрами від 1 до 6 (цифра може бути підкресленою, кожен кінь повинен бути на одному з полів з відповідним номером). Щоб всі шість коней били й поля, помічені знаком «+», п’ятий та


192
Задачі математичних олімпіад та методи їх розв'язування
шостий коні повинні бути розташованими лише в полях 5 та 6. При цьому одне з полів, помічене знаком «?», не буде під боєм (ці два поля можуть бути під боєм лише другого коня, але не одночасно). Таким чином, шести коней недостатньо. Сім коней вже вистачить. На рис. 12 показано їх розташування.
Рис. 11
Рис. 12
а
б
а
б
в
г
в
г
а.
б
а
б
в
г
в
г
Рис. 13
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
Рис. 14
23.15. 	Відповідь. 48. Вказівка. Розбийте дошку на 4 квадрати 4 х 4 і розгляньте один з них (рис. 13). Із 4-х полів, відмічених однією буквою, повинно бути вільним хоча б одне (інакше у фішки, яка стоїть в кутку, не буде першого ходу). Тому в кожному із чотирьох квадратів 4x4 повинні бути вільними щонайменше чотири клітинки. Отже, всього вільних клітинок на дошці повинно бути менше 16, а фішок — не більше 48. Приклад, коли кожна із 48 розташованих на дошці фішок має хід, наведено на рис. 14.
23.16. 	Відповідь. 24. Вказівка. Очевидно, що таргани, які сиділи на 20-х зафарбованих (на рис. 15) клітинках, переповзуть на різні клітинки. Отже, після цього будуть непорожніми не менше 40 клітинок. Таким чином, вільними можуть бути не більше 24 клітинок. Якщо всі таргани переповзуть на клітинки, зафарбовані на рис. 16, то вільними будуть 24 незафарбованих клітинки.
Рис. 15
Рис. 16


Цікаві задачі та конструкції
193
23.17. 	Відповідь. Можуть. Вказівка. Розгляньте таблицю на рис. 17. Добуток елементів кожного стовпчика дорівнює 8 • 3 • 5 • 7 = 840. Помітимо, що при множенні всіх елементів будь-якого рядка на одне і те ж число рівність добутків елементів стовпчиків не порушиться. Підберемо множники так, щоб суми елементів у рядках стали рівними. Для цього обчислимо ці суми у вихідній таблиці: S, = 21, S2 = 33, S3 = 45, S4 = 27, S5 = 39. Нехай найменше спільне кратне цих чисел дорівнює k. Помножимо всі елементи г-го рядка (г'= 1,
7
2
3
4
5
2
21
4
5
1
3
4
35
1
2
4
5
1
14
3
5
1
2
3
28
Рис. 17
2, ..., 5) на —. Тепер сума чисел у кожному рядку дорівнює k. Покажемо, що
в одержаній таблиці немає рівних чисел. Числа в кожному рядку таблиці (початкової) різні, тому після множення на одне й те ж саме число вони бути рівними не можуть. Числа з г-го та /-го рядків будуть рівними тільки при
— = —, тобто а : b = S(.: Sy. Числа із другого та п’ятого рядків не можуть Sf Sy
задовольняти таку пропорцію, бо відповідні суми містять множники 11 та 13, яких немає в жодних числах таблиці. S,:Sj=7:15, ^:S4=7:9,
S3 : S4 = 5 : 3. Легко перевірити, що у відповідних рядках немає чисел з такими відношеннями.
23.18. 	Відповідь. 11. Вказівка. На рис. 18, а) пофарбовані клітинки дошки 4 х 4 в 11 кольорів відповідно з умовою задачі. Припустимо тепер, що їх можна пофарбувати і в 12 кольорів. Оскільки в кожному з кутових квадратів 2x2 (рис. 18,6)) представлені не більше, ніж три кольори, а всього кольорів рівно 12, то жодні дві клітинки з різних кутових квадратів 2x2 не можуть бути одного кольору. Але тоді в центральному квадраті (рис. 18, в)) всі клітинки різних кольорів, що протирічить умові.


194
Задачі математичних олімпіад та методи їх розе*язування
23.19. 	Відповідь. Можна. Вказівка. Залишимо перші 999 рядків квадрата невідміченими, в 1000-ому рядку відмітимо останні 996 клітинок, а в рядках з 1001-го по 1996-й відмітимо всі клітинки. Розглянемо квадрат 1000 х 1000, що лежить в квадраті 1996 х 1996. Нехай його права нижня клітинка знаходиться в л-му рядку та в /я-му стовпчику квадрата 1996 х 1996. Тоді в цьому квадраті знаходиться рівно 1000(л - 1000) + (т- 1000) = 1000л +т - 1001000 відмічених клітинок. Для різних квадратів 1000 х 1000 (1000 < т < 1996, 1000 < п < 1996) ці числа різні, тобто збудовано потрібну конструкцію.
23.20. 	Відповідь. Чотири. Вказівка. Пофарбуємо клітинки таблиці в два кольори в шаховому порядку. Із умови задачі випливає, що всі парні числа опиняться в клітинках одного кольору, а всі непарні — в клітинках другого кольору. Оскільки у будь-якому стовпчику три клітинки одного кольору і дві другого кольору, в ньому буде або три парних і два непарних числа, або два парних і три непарних числа. Оскільки серед парних чисел лише одне просте — це число 2,
Рис. 19 то простих чисел у стовпчику буде не більше чоти¬
рьох. Приклад, коли їх рівно 4 показано на рис. 19.


§24. Функціональні рівняння
Загальні відомості
Клас функцій, які вивчаються в шкільному курсі математики, порівняно невеликий. До них відносяться, наприклад, лінійна, степенева, показникова, тригонометричні функції тощо. Інші функції дістаємо з основних за допомогою композицій та алгебраїчних дій над основними елементарними функціями.
Деяке співвідношення (рівність), з якого можна знайти невідому функцію, називають функціональним рівнянням. Розв’язати функціональне рівняння — означає знайти невідомі функції, що входять до нього. Значний внесок у вивчення таких рівнянь вніс О. Коші (1789 - 1857). Функціональне рівняння f(x + у) = f(x) + f(y) носить його ім’я.
Розв’язувати функціональні рівняння можна різними методами. Метод підстановок
Суть цього методу полягає ось в чому. Припустимо, що дане рівняння має розв’язок. Застосуємо до змінних, що входять в рівняння, деякі підстановки. Дістаємо систему рівнянь, одним із невідомих якої є шукана функція. Після розв’язування системи безпосередньою перевіркою необхідно переконатись, що знайдена функція задовольняє умови задачі. Основна складність цього методу полягає у виборі вдалих підстановок.
Метод застосування поняття групи
Суть цього методу полягає в наступному. Нехай у функціональному рівнянні
+••• + anf(gn) = Ь (*)
вирази, які стоять під знаком невідомої функції f(x) є елементами групи G, яка складається із п функцій: g,(x) = %, g2(x), gn(%), причому
коефіцієнти av а2, ..., ап та b — деякі функції. Припустимо, що рівняння (*) має розв’язок. Замінимо х-+ g2(x). В результаті послідовність
gv g2, gn перейде в послідовність g,og2, g2 og2, gn og2t яка
знову таки складається з усіх елементів групи G. Тому «невідомі» /fe,), f(g2), f(gn)> поміняються лише місцями і матимемо нове лінійне рівняння. Далі в рівнянні (*) зробимо заміни х —> g3(x), х —> g4(x), ..., х —> gn(x), після чого дістанемо систему із п лінійних рівнянь, яку слід


196
Задачі математичних олімпіад та методи їх розв’язування
розв’язати. Якщо розв’язок існує, то його слід перевірити, чи задовольняє він рівняння (*).
Метод застосування елементів математичного аналізу
При розв’язуванні рівнянь Коші розв’язки знаходяться за допомогою використання понять математичного аналізу зокрема таких, як границя послідовності та функції, неперервність, диференційовність тощо.
а) Метод граничного переходу. Суть цього методу полягає в наступному. Здійснюється підстановка, яка переводить вираз, що стоїть під знаком f в одному члені рівняння, у вираз, який стоїть під знаком f у другому його члені. Ця підстановка повторюється п разів. Дістанемо систему п лінійних рівнянь. Виключаючи послідовно невідомі, матимемо рівняння виду
f(x) = aj(bn) + сп,
де ап, Ьп, сп — члени деяких послідовностей, п — фіксоване натуральне число (ап, Ьп, сп — можуть бути і функціями від х).
Якщо існують границі при п —> °о послідовностей {а }, {^}, {сп}, причому lim bn = const, то граничним переходом, використовуючи не-
Л—>оо
перервність /(%), знаходимо вираз для f(x). Звичайно, перевірка є складовою частиною розв’язування функціонального рівняння.
Цим методом можуть бути розв’язані в класі неперервних функцій рівняння виду
f(kx + b) = mf(x) + Р(х), f(kx + b) = f(x) • ар{х\
де k > 1, І т І < 1, Р(х) — многочлен, а > 0.
б) Метод диференціювання. Він полягає в тому, що для знаходження розв’язку функціонального рівняння в класі диференційовних функцій доцільно продиференціювати обидві його частини, при умові, що похідна існує. В результаті дістанемо функціональне рівняння, яке містить ще й похідну невідомої функції. Розв’язуючи це рівняння, як функціональне відносно похідної, дістанемо, що шукана функція є однією з первісних для цієї похідної.
в) Метод Коші. Цим методом розв’язок рівняння знаходиться за допомогою спеціальних підстановок послідовно для натуральних, раціональних значень аргумента, а потім граничним переходом — для додатних дійсних х і, нарешті, розповсюджується на всі дійсні значення аргумента.
г) Метод рекурентних співвідношень. Нехай задане функціональне рівняння натурального аргумента має вигляд рекурентного співвідно¬


Функціональні рівняння
197
шення, тобто формули, яка виражає /(«) через попередні значення f(n - 1), f(n - 2) і т. д. Спочатку обчислюють значення функції від декількох перших чисел натурального ряду (при цьому використовується рекурентне співвідношення). Потім намагаються прогнозувати вид шуканої функції (гіпотеза!), після чого переконуються у справедливості здогадки за допомогою методу математичної індукції. Саме так знаходяться формули для я-го члена арифметичної та геометричної прогресій, послідовності Фібоначчі: /(1) = /(2) = 1, /(я) = f(n - 1) + /(я - 2) для всіх я = 3, 4, 5, ....
Слід ще нагадати наступне.
Через f:A—> В позначають функцію з областю визначення А та множиною значень в В. Функція g: В—> А називається оберненою до функції f (позначають: g = /"*), якщо справедливі такі тотожності g(f(x)) = х та f(g(y)) = у, для всіх х є А, у є В. Зрозуміло, що функція f.A-ъ В матиме обернену функцію тоді і лише тоді, коли для довільного елемента у є В існує елемент х є А, що задовольняє умову /(х) = у, і для будь-яких двох різних елементів хр х2 є А значення /(xt) та /(х2) також різні.
Композицією двох функцій f: А—> В та g: В С називається функція h: А —> С, яка визначається тотожністю: h(x) = g(/(x)), х є А.
Аналогічно означається композиція більшої кількості функцій.
- Задачі
24.1 (9-10). Знайдіть всі функції /: /?\{0; 1997} —> R, які задовольня¬
ють рівняння (1997 - х)/(х) - 2х/(1997 - х) = 1.
24.2 (10). Знайдіть всі функції /: R —> R, які задовольняють рівняння
/(xz/) = z/,997/(x).
24.3 (9-10). Знайдіть всі функції /: /? —» R, які задовольняють рівняння
/(х + у) + f(y - х) = (у + 2)/(х) + у (2 у - х2).
24.4 (10). Знайдіть всі функції /: R R, які задовольняють рівняння /(xz/) = sinz/ • /(х).
24.5 (9). Знайдіть всі функції /: 7? —» R, які задовольняють рівняння /(х
+ у) - f(x - у) = 4ху.
24.6 (9). Знайдіть всі функції /: R -> R, які задовольняють рівняння /(х + у) = /(х) + у.
24.7 (11). Знайдіть всі функції /: R R, які задовольняють рівняння
/(х + у) = f(x) • е».


198
Задачі математичних олімпіад та методи їх розв'язування
24.8 (9-10). Знайдіть всі функції /: /? —» R, які задовольняють рівняння
f(x + у) + f{x - у) = 2х2 + 2у2.
24.9 (10-11). Знайдіть всі функції /: R -> R, які задовольняють рівнян¬
ня /(х + у) + f(x - у) - 2/(х) • (1 + у) - 2ху(3у - х2).
24.10 (10-11). Знайдіть всі функції /: Я —> R, які задовольняють рівняння /(х + у) + /(х - у) = 2/(x)cosr/.
24.11 (11). Знайдіть всі функції f: R —> R, які задовольняють рівняння f(x)f(x + у) = (f(y) • /(х - у))2 • е*+4.
24.12 (10-11). Знайдіть всі функції f: R-+ R, які задовольняють рівняння /(х + у) +2f(x - у) = 3/(х) - у.
24.13 (10-11). Знайдіть всі функції f: R—ї R, які задовольняють рівняння /(х + у) - 2f(x - у) + f(x) - 2f(y) = у - 2.
24.14 (11). Знайдіть всі функції /: R+ R, які задовольняють рівняння
f(xy) + 2f
3/(х) - In у.
\У)
(Тут Я+ — множина всіх дійсних додатних чисел, R — множина всіх дійсних чисел).
24.15 (11). Знайдіть всі функції f: R —> R, які задовольняють рівняння 2/(х + 2у) + /(х) = /(х + у) • (2еу +е~у).
24.16 (10-11). Знайдіть всі функції /: Я\{-1; 0; 1} -> R, які задоволь¬
няють рівняння х/(х) + 2/
Гх-П х + 1
= 1.
к" ■ *У
24.17 (11). Знайдіть всі функції /: 7?\{0; а} R, які задовольняють
рівняння /(х) + /
а2 '
а — х , k У
= х, де а — стала, відмінна від 0.
24.18 (10-11). Знайдіть всі функції /: Я —> R, які задовольняють рівняння af(x -1) + bf(l - х) = сх, де а, Ь, с — задані дійсні числа.
24.19 (10-11). Знайдіть всі функції f: Я\{0; 1} R, які задовольняють < Р
рівняння f
X
1-х
+/
k х;
= X.


Функціональні рівняння
199
24.20 (11). Знайдіть всі функції /: 7?\[0; +«>) —> 7?, які задовольняють рівняння In(1 - ех) • fix) - 2х • /(1п(1 - ех)) = 1.
24.21 (10-11). Знайдіть всі функції /: 7?\{0; 1} —> R, які задовольняють
рівняння fix) + f
хп -1
+ хп, де п — непарне число.
24.22 (9-11). Знайдіть всі функції /: R -> R, які задовольняють рівняння 2/(х) + /(1 - х) = 3 - х • /(1).
24.23 (10-11). Знайдіть всі неперервні функції f: R R, які задовольняють рівняння 3/(2х +1) = /(х) + 5х.
24.24 (10-11). Знайдіть всі неперервні функції /: R —> R, які задовольняють рівняння /(х2) + /(х) = х2 + х.
24.25 (11). а) Знайдіть всі диференційовні функції /: (0; +«>) —> R, які задовольняють рівняння fixy) = /(х) • fiy).
. б) Знайдіть всі диференційовні функції /: (0; +«>) -> 7?, які задовольняють рівняння fixy) = f(x) + fiy).
24.26 (11). Знайдіть всі диференційовні функції /: 7? —» R, які задовольняють рівняння /(/(х)) = fix) + х.
24.27 (11). Знайдіть всі неперервні функції f: R —> R, які задовольняють рівняння fix + у) = fix) + fiy) + fix) • fiy).
24.28 (11). Знайдіть всі неперервні функції /: (0; +°°) —> R, які задоволь-
\ f(x)fiy)
няють рівняння /лх + У) - —гтт-
fix) + fiy)
24.29 (11). Знайдіть всі функції f: R—> R, які неперервні в точці х = 0 і задовольняють рівняння fix + у) - fix) + fiy) + ху.
24.30 (11). Знайдіть всі функції f: N —> R, які задовольняють наступні умови:
1) fil) = 3;
2) /(2) = 7;


200
Задачі математичних олімпіад та методи їх розв’язування
3) 	/(п) = 3/(я - 1) - 2f(n - 2), при всіх п є N, п > 2.
24.31 	(11). Знайдіть всі функції /: N —> R, які задовольняють рівняння f(n + 2) = f(ti) при всіх пе N.
Розв’язки, вказівки, відповіді
24.1. Відповідь. f(x) — і х є /?\{0; 1997}. Вказівка. Зробіть замі-
1 х-1997
ну х на 1997 - х, дістанете систему відносно /(х) та /(1997 - х).
24.2. Відповідь. /(х) = Хх1997, де X = const. Вказівка. Покладіть х = 1,
дістанете f(y) = £/*"7 • /(1). Позначивши /(1) = X, матимете відповідь. Зробіть перевірку.
24.3. Відповідь. f(x) = x~. Вказівка. Поклавши х = 0, дістанете
/(#) = у- + — у + а, де а = /(0). Перевірка покаже, що а = 0.
24.4. Відповідь, /(х) = 0. Вказівка. Поклавши х = 1, дістанете f(y) - a sin у, де а = /(1). Перевірка покаже, що а = 0.
24.5. Відповідь. f(x) = х2 + а. Вказівка. Поклавши х + у = и, х- у = о, матимете рівняння /(м) - /(о) = й2 - о2, яке розв’язується підстановкою v = 0.
24.6. Відповідь. f(x) = х + а, де а = const. Вказівка. Поклавши х = 0,
дістанете f(y) = у + а, де а = /(0). Перевірка показує, що а — будь-яка константа.
24.7. Відповідь. f(x) = аех, де а = const. Вказівка. Поклавши х = 0, дістанете f(y) = аеу, де а = /(0). Перевірка показує, що а — будь-яка константа.
24.8. Відповідь. f(x) = х2. Вказівка. Див. задачу 24.5.
24.9. Відповідь. f(x) = х3. Вказівка. Виконайте послідовно підстановки х = 0, у = t\ х = t - 1, у = 1; х = -1, у = t - 1. Дістанете систему рівнянь відносно f(t), f(-t) та f(t - 2). Виключаючи послідовно з неї f(-t) та /(/ - 2), дістанете, що f(t) = 2t3 + 2(a-b-l)t + 2a, де а = /(0), b = /(-1). Перевірка показує, що а = 0, b = -1.


Функціональні рівняння
201
24.10. 	Відповідь. f(x) = a cosx + 6 sinx, де а = const, b = const. Вказівка. Виконайте послідовно підстановки х = 0, у = і; х = ^ + /, Ух = ^’
у = — + t, в результаті чого дістанете систему рівнянь відносно f(t), f(—t) 2
та /(я + t). Виключаючи послідовно з неї f(-t) та /(я + і), дістанемо
f(t) = acost + bsint, де a = /(0), b = f
Перевірка показує, що знайдений
вираз є розв’язком даного рівняння при довільних фіксованих а та Ь.
24.11. 	Вказівка. Виконайте підстановки: х = 0, у = 1; х = 0, у = -і.
-24.12. Вказівка. Виконайте підстановки: х = Q, у = t‘, х = t, у = 2t\ х = t, У = “2t
24.13. Вказівка. Виконайте підстановки: х = 0, у = t", х = Z, у = 2t; х = 2/, У t, х t, у t.
24.14. Вказівка. Виконайте підстановки: х = 1, у = t; х = t, у = t2\ х = і, 1
24.15. Вказівка. Спочатку підстановкою х + у = t, у = z дане рівняння зводиться до рівняння 2f(t + z) + f(t - z) - f(f)(2ez + е~г). Це рівняння можна розв’язати такими підстановками: t = 0, z = и; t = и, z = 2м; t = и, z = -2м.
4x2 -х + 1
24.16. Відповідь. f(x) =
х -1
, де хє Я\{-1;0;1}. Вказівка. Врахуй¬
5х(х -1)
те, що вирази х,
групи G = <
х,
х + 1
х-1 1 х+1
X +1 ’ х ’ 1 - X
, які стоять під знаком невідомої функції /, є елементами
відносно операції« о » (композиції функцій). Тому,
замінивши послідовно х на
«невідомих» /(х), /
но /
та f
ху
X 1-х
Гх + Р
у-*,
, дістанемо систему відносно
, знаходимо: /(х) =
. Виключаючи з неї послідов-
4х2 -х + 1
5х(х -1)
■. Не забудьте
х -1 х + 1
1 х + 1
х-п '/ п
х + 1
та /
х -1 х + 1
. f
і А
х + 1 1 - X
зробити перевірку.


202
Задачі математичних олімпіад та методи їх розв’язування
24.17. Відповідь.
f(x) =
х3 - а2х + а3 2х(х - а)
де х є R \ {0; а}, а Ф 0. Вказівка.
Скористайтесь тим, що вирази х та
а - х
є елементами групи
G =
*;•
2 2 а ах - а
а- х х
відносно операції «о».
24.18. Відповідь. f(x) = х + С , якщо а2 * b2; f(x) не існує, якщо а -b а + b
а2 =Ь2,с* 0;
/(х) — будь-яка непарна функція, якщо а = Ь, с = 0;
/(х) — будь-яка парна функція, якщо а = -Ь, с = 0.
х3 + х2 + 2х + 1 . . ,
, де х є R \ {0; 1}. Вказівка. Розглянь-
24.19. Відповідь, [(х) =
2х(х +1)
1
х -1
те елементи групи G = {g,, g2, g3}, де g, = х, g2 = -—- , g3 = ——, X * 0, X * 1,
1
взяті по два, а саме g, • g2 = х •
1-х 1-х
1-х " х
1 х-1 1 о ,
. §2 • Sz =: = —• Зробив-
1-х X X
1 х-1 .
ши послідовно підстановки х —> та х -> , дістанете систему рівнянь:
1-х х
/(&
gj + Zfe • = x>
£з) + /(£з-£і) = 7-^- 1 - x
a)+f(gi • &) =
q. с/ \ г/ 1 \ 1x4“ 2x X
ЗВ.ДСИ /(g,.g2) = /(--)= 2x(1_t) .
He забудьте про перевірку.
тобто /(х) =
х3 + х~ + 2х +1 2х(х +1)


Функціональні рівняння
203
1
, де хє(-<»;0). Вказівка. Зробивши
24.20. Відповідь. f(x) =
1п(1 - ех)
заміну х —> 1п(1 - ех}, дістанете рівняння:
х • /(Іп(1 - ех)} - 21п(1 - ех) • f(x) = 1.
Розв’яжіть його сумісно з даним рівнянням. Не забудьте довести, що при х < 0, 1п(1 - ех) < 0, а також про перевірку.
24.21. Відповідь. f(x) = — 2
ЇЇ
+ ха + ?І
/2-х" І2хп -1 1-х" '
Вказівка. Зро-
J
хп-І 1
біть послідовно такі заміни у даному рівнянні х —> г—-—, х —> d , і роз-
V х v 1 - х"
в’яжіть одержану систему рівнянь сумісно з даним рівнянням. Не забудьте про перевірку.
6 3%
24.22. 	Відповідь. f{x) = . Вказівка. Зробіть послідовно такі заміни:
даним рівнянням. Матимете: /(0 - 7 та /(х) = Не забудьте про пере¬
х—>1 - х, х —> 1, х —> 0, і розв’яжіть одержану систему рівнянь сумісно з
З 5
вірку.
і/ \ 3 х — 1
24.23. 	Відповідь, iw ~ х~п- Вказівка. Зробивши заміну х -> діс¬
танете:
/w4/
Гх-п
5 х -1
(*)
Використовуючи цю ж заміну, із (*) послідовно дістанемо
-f
З
і/х-3^ 9Z
1 /х-ЗЇ
= — f 27
5 х-З d
9 4
х-7
Т~
5 х-7 27* 8 ’
х -1
= 97
/
Методом математичної індукції можна довести, що
f X
-2а +Р
1 і
f X
-2Я+1
+ й
2"
)
- Зл+1 1
1
2Я+1
У
5 х-2я+1 +1
)Л+1
)Я+1
1


204
Задачі математичних олімпіад та методи їх розв’язування
Додавши почленно всі ці рівняння, починаючи з (*), дістанемо:
№ = f
zx-2“*' +Р
пл+І
5 х-1. 5 х-3 3~
5 х-2л+1 +1
^л+і ^я+і
(**)
Враховуючи неперервність функції f, при будь-якому фіксованому х, мати¬
мемо Ііт/
Л—
Ґх-2Л+1
+ П
f X + 1
rx + 1
\\
2Л+1
= lim /
Л->ов
2Л+І
-1
= f
lim
Л—
2Л+1
-1
)
< *
Л
= /(-1). З умови
Гх-2Л+1+Р
ол+1
= 0.
5 1
легко знайти, що /(-!) = - — . Тоді Ііт^у/
ч J
Ліва частина (**) не залежить від л, тому існує її границя при л— Перейшовши до границі в рівності (**) при л-»оо, маємо:
/(х) = lim
5 х-1 5 х-3
— 1— ь
3 2 9 4
5 х-2л+1+1
>л+1
)Л+1
7
Права частина останніх трьох рівностей є сумою трьох нескінченно спадних геометричних прогресій:
5 5 5
• т X + тт X + ... + -7777 X + ... = X,
'Л+1
36
_5 _5 _ З 9
5 5
—І ь
6 36
5
2
зл+1
5
+ ^Г + - = І.
5 З
Тому /(х) = х - - +1, тобто /(х) = х - — . Перевірка це підтверджує.
24.24. 	Відповідь. f(x) = х. Вказівка. Позначивши g(x) = /(х) - х, матиме¬
мо:
g(x2) = -g(x).
Нехай х > 0. Виконаємо п разів заміну х —»4х. Тоді матимемо g(x) = -g(Vx),
-g(Jx) = g(l/x),
(*)
(-l)n-'^(2^) = (-l)".g(2^).


Функціональні рівняння
205
Додавши ці рівняння, матимемо: g(x) = (-1)" 'g^Jx^.
Зробивши тут заміну х-^К/~х, дістанемо g (>/%) = (-1)" • g(4,7x).
З останніх двох рівнянь дістаємо: g(x) = g(47x).
Але, враховуючи, що х > 0 та неперервність функцій у = Іпх і у = е*. мати-
мемо:
Врахувавши неперервність g(x), граничним переходом дістаємо:
g(x) = lim g (4Vx) = g (lim 47x) = g(l).
Із (*) знаходимо g(l) = 0, g(0) = 0, тобто при x > 0 g(x) = 0.
Оскільки g(x) — парна, то g(x) = 0, при всіх дійсних х. Отже, /(х) = х
едина функція, яка задовольняє умову задачі.
24.25. 	а) Відповідь. f(x) = 0, або /(х) = х“, де а = const. Вказівка. Очевид¬
но, що /(х) = 0 — тривіальний розв’язок. Нехай /(х) задовольняє рівняння і f(a) * 0 при деякому дійсному а, тоді
а
f(x)-f — \ = f(a)*O.
W
Отже, /(х) 0 при всіх х > 0.
Крім того /(х) > 0 при всіх х > 0, бо /(х) = /(•7х)/(>/х) > 0. За умовою
задачі / ’(х) = lim
Л-»0
/(х + А) - /(х) h
існує при всіх х > 0. Тому,
f '(х) = lim ■ Л-»0
/
X
ґі
і+—

xJl
- f(x) /(х) • f
-f(x)
= lim- л->о
lim
Л->0
1+A
X
_ Z(x)
•lim-
X
h\
І
f
h
x
h
1 + - x
h
x
1 +
h
h
-/(1)
-1
/(x)


206
Задачі математичних олімпіад та методи їх розв’язування
Оскільки існує f'(x), то існує lim —-»о
X
-/(1)
= /'(!) = ос,
а = const (не
залежить від х). Тому
Г(х) _ а /(х) х
/
Помітивши, що (In /(х)) =
/'(*)
/(х)’
одержуємо:
In /(х) = а • In х + Р, де р = const. При х = 1 знаходимо Р = 0. Тому, остаточно дістанемо /(х) = ха.
24.25. б) Відповідь. f(x) э 0 або /(х) = logax, де a = const. Вказівка. Скористайтесь методом розв’язування попередньої задачі 24.24.
24.26. Відповідь. /(х) = Хх, де X = -■ ■ Вказівка. Скористайтесь ме-
&
тодом розв’язування задачі 24.25 а).
24.27. Відповідь. f(x) = -1 або /(x) = (l + a)x -1, де a = const. Вказівка. Скористайтесь методом Коші. Замінюючи у послідовно на х, 2х, Зх,..., дістанемо:
/(2х) = 2/(х) + /2(х) = (/(х) +1)2 -1,
/(Зх) = 3/(х) + 3/2(х) + /3(х) = (/(х) +1)3 -1,
/(4х) =... = (/(х) +1)4 -1, і т.д.
Методом математичної індукції одержуємо:
/(лх) = (/(х) + 1)" - 1. (*)
для всіх л є N, х є R .
Далі, поклавши в (*) х = 1 і позначивши /(1) = а, дістанемо /(л) = (а + 1)" -1.
Замінивши в (*) х на —, де /л є М, пє N, одержуємо: л
/(/л) =
ґ
f
'т>
+ 1
п
ч
< )
У
-1.
Крім того, /(лг) = (а + l)m -1.
Звідси, враховуючи, що 1 + /(х) =
=
ґ
і + /
rxv
\2
> 0, маємо /
1
<2>.
/
<п>
m
= (а +1)" -1.


Функціональні рівняння 207
Отже, для додатних раціональних чисел х розв’язком даного рівняння буде
/(х) = (а + 0* -1.
Нехай тепер х — довільне додатне ірраціональне число. Відомо, що існує послідовність додатних раціональних чисел г,, г2, г3,.... г ,..., таких, що lim г = х.
Отже, враховуючи неперервність функції /, матимемо, що /(х) = lim /(г) =
г„-^х
= lim((l + аУп -1) = (1 + а)"'™-'" -1 = (1 + а)х -1 для всіх додатних ірраціональ-
П-»<»
НИХ X.
Отже, f(x) = (1 + а)х -1, х > 0, х є R .
Поклавши в умову х = 0, дістанемо f(y) = /(0) + f(y) - тобто
f(x) = -1 або 7(0) = 0.
При у = -х, х > 0 з умови знаходимо 0 = /(0) = /(х - х) = /(х) + /(-х) + +/(х) • /(-х) = (1 + а)х -1 + /(-х) + ((1 + а)х -1) • /(—х) = (1 + а)х -1 + /(-х) • (1 + а)х.
Звідси /(—х) = = (1 + а^~х ~ х > 0, тобто f(y) = (1 + a)v -1, при
у<0.
Здійснивши перевірку, побачимо, що обидві функції є розв’язками даного рівняння.
24.28. Відповідь. f(x) = —, де а = const. Вказівка. Скористайтесь мето-
х
дом Коші.
4" і)
24.29. Відповідь. f(x) = ax + , а = const. Вказівка. Попередньо
2
доведіть, що /(х) неперервна при всіх дійсних х.
24.30. Відповідь. f(n) = 2”+І -1. Вказівка. Скористайтесь методом математичної індукції.
24.31. Відповідь. f(n) = а + Ь- (-1)л, де а = const, b = const. Вказівка. Скористайтесь методом рекурентних співвідношень.


Список використаної літератури
1. Бабинская И.Л. Задачи математических олимпиад. — Москва: Наука, 1975.
2. Белоусов В.Д., Измай М.С., Солтан В.П., Чиник Б.И. Республиканские математические олимпиады. — Кишинев: Штиинца, 1986.
3. Васильев Н.Б., Гутенмахер В.Л., Раббот Ж.М., Тоом А.Л. Заочные математические олимпиады. — Москва: Наука, 1986.
4. Васильев Н.Б., Егоров А.А. Задачи Всесоюзных математических олимпиад. — Москва: Наука, 1988.
5. Вишенський В.А., Карташов Н.В., Михайловский В.І., Ядренко М.Й. Збірник задач Київських математичних олімпіад. — К.: Вища школа, 1984.
6. Гальперин Г.А., Толпыго А.К. Московские математические олимпиады. — Москва: Просвещение, 1986.
7. Лейфура В.М., Мітельман І.М., Радченко В.М., Ясінський В,А. Задачі міжнародних математичних олімпіад та методи їх розв’язування. — Львів: Євросвіт, 1999.
8. Лейфура В.М., Мітельман І.М., Радченко В.М., Ясінський В.А. Математичні олімпіади школярів України 1991-2000. — К.: Техніка, 2003.
9. Мітельман І.М. Розфарбуємо клітчасту дошку. — Львів: Каменяр, 2001.
10. Морозова Е.А., Петраков И.С., Скворцов В.А. Международные математические олимпиады. — Москва: Просвещение, 1976.
11. Прасолов В.В. Задачи по планиметрии, части 1,2. — Москва: Наука, 1986,1991.
12. Прасолов В.В., Шарыгин И.Ф. Задачи по стереометрии. — Москва: Наука, 1989.
13. Шарыгин И.Ф. Задачи по геометрии. Планиметрия. — Москва: Наука, 1986.
14. Шарыгин И.Ф. Задачи по геометрии. Стереометрия. — Москва: Наука, 1984.
15. Яковлев Г.Н., Купцов Л.П., Резниченко С.В., Гусятников П.Б. Всеросийские математические олимпиады школьников. Книга для учащихся. — Москва: Просвещение, 1992.
Зміст
1. Метод математичної індукції З
2. Цілі числа. Подільність 12
3. Цифри і системи числення 22
4. Числа раціональні та ірраціональні 25
5. Квадратний тричлен. Неперервні функції, графіки і корені рівнянь 30
6. Алгебра многочленів 38
7. Рівняння і системи рівнянь 46
8. Доведення нерівностей 66
9. Принцип Діріхле 74
10. Комбінаторика 79
11. Графи. Відображення 87
12. Парність, фарбування. Задачі на решітках 92
13. Операції та інваріанти 98
14. Перестановки, розміщення і комбінація цілих чисел та цифр. Турніри 103
15. Планіметрія 107
16. Стереометрія 133
17. Комбінаторна геометрія 146
18. Геометричні нерівності, оцінки, екстремуми 153
19. Вектори 160
20. Оцінки і екстремальні задачі для наборів чисел і таблиць 167
21. Послідовності 174
22. Ігри, переслідування, стратегії та алгоритми 181
23. Цікаві задачі та конструкції 186
24. Функціональні рівняння 195
Список використаної літератури 208